Podręcznik

4. Przykłady regulatorów rozmytych

4.6. Rozmyty regulator typu PID

Transmitancja operatorowa idealnego liniowego regulatora PID dana jest równaniem:

\( G(s)=k_p\left(1+\frac{1}{T_is}+T_{d}s\right) \)	(149)

Ponieważ w naszym przypadku:

\( G(s)=\frac{V(s)}{E(s)} \)	(150)

gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora. Po uwzględnieniu (149) i (150) otrzymujemy:

\( V(s)=k_p\left(1+\frac{1}{T_is}+T_{d }s\right)E(s) \)	(151)

Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:

\( v(t)=k_p\cdot e(t)+k_i\cdot \int_0^t e(t)dt+k_d\cdot\frac{de(t)}{dt} \)	(152)

gdzie: \( k_p \) - współczynnik wzmocnienia proporcjonalnego, \( k_i=k_p/T_i \) - współczynnik członu całkującego, \( k_d=k_p\cdot T_d \) - współczynnik członu różniczkującego.

Różniczkując obustronnie równanie (152) otrzymujemy:

\( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e+k_d\cdot \frac{d^2e(t)}{dt^2} \)	(153)

co prowadzi do wniosku, że działanie regulatora PID polega na tym że:

zmiana sygnału wyjściowego regulatora typu PID jest proporcjonalna do prędkości zmian odchyłki regulacji (akcja proporcjonalna) jak również do wartości tej odchyłki (akcja całkująca) oraz jej przyśpieszenia (akcja różniczkująca).

W systemach z czasem dyskretnym z okresem impulsowania \( \Delta t \) równanie (153) przybiera postać równania różnicowego:

\( \Delta v=K_p \cdot \Delta e + K_{i}\cdot e+K_D\cdot \Delta(\Delta e) \)	(154)

gdzie: \( K_p=k_P \); \( K_i=k_I\cdot \Delta t \); \( K_d=k_D⁄\Delta t \); \( \Delta t=cont=1 \).

Równanie (154) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PID. Reguły te można zapisać w postaci ogólnej:

\( jezeli\; (e=E)\cap(\Delta e=\Delta E)\cap(\Delta(\Delta e)=\Delta(\Delta E))\; to\; (\Delta v=\Delta V) \)	(155)

gdzie: \( E \), \( \Delta E \), \( \Delta (\Delta E) \), \(\Delta V \), - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji>, <zmiana zmiany odchyłki regulacji> i <zmiana wyjścia regulatora>.

Wyjście dyskretnego regulatora PID wyznaczymy w sposób analogiczny jak dla regulatora PI.

\( v=\sum_{i=1}^k \left\{k_{P}(e_i-e_{i-1})+k_I\cdot e_i+k_{D}\cdot (e_{i}-2e_{i-1}+e_{i-2})\right\}+v_0 \)	(156)

Projekt rozmytego regulatora typu PID.

Zgodnie z procedurą przedstawioną w podrozdziale 3.1, syntezę bazy reguł rozmytego regulatora typu PID przeprowadzimy w trzech krokach.

Krok 1 (formalny)

Załóżmy regulator typu PID o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e\), prędkość odchyłki regulacji \( \Delta e \) oraz przyśpieszenie odchyłki regulacji \(\Delta^2e \). Wyjściem regulatora będzie zmiana sygnału sterującego (nastawiającego) regulatora\(\Delta v \). Przyporządkujmy zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zmiennej lingwistycznej <przyśpieszenie odchyłki regulacji> symbol \( \Delta^2e \), zaś zmiennej lingwistycznej <zmiana wyjścia sterującego> symbol \( \Delta v \).

Załóżmy dalej, że zmiennej \( e \) przyporządkowano dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <prędkość ujemna odchyłki regulacji> i <prędkość dodatnia odchyłki regulacji>. Wartościom tym nadano także nazwy symboliczne: \( N_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej <przyśpieszenie odchyłki regulacji> \( \Delta^2e \) przyporządkowano wartości <przyśpieszenie ujemne odchyłki regulacji> i <przyśpieszenie dodatnie odchyłki regulacji>. Wartościom tym nadano nazwy symboliczne: \( N_{\Delta^2e} \) i \( P_{\Delta^2e} \). Zmiennej \( \Delta v \) przyporządkowano wartości <ujemna zmiana sterowania>, <zerowa zmiana sterowania> i <dodatnia zmiana sterowania>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \). Ogólny schemat struktury rozmytego regulatora PID przedstawiono na Rys. 39.

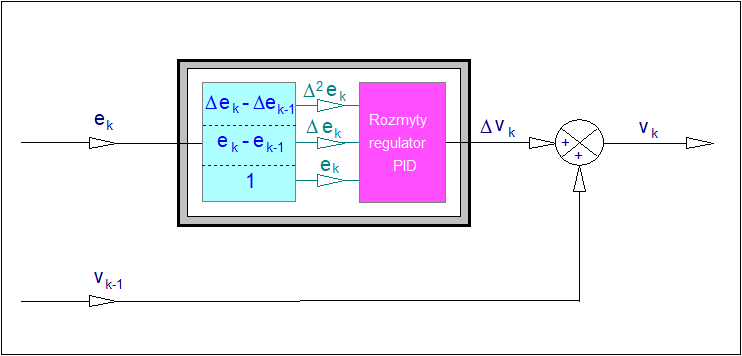
Rys. 39. Schemat ogólny struktury rozmytego regulatora typu PID.

Krok 2 (projekt zbiorów rozmytych)

Załóżmy, że kształt zbiorów rozmytych wejść i wyjścia regulatora PID będzie identyczny jak dla regulatora PI (rys. 35), jedynie z tą różnicą, że dodatkowo wprowadzimy funkcje przynależności \( \mu_N(\Delta^2e) \) i \( \mu_P(\Delta^2e) \), które będą się pokrywały z funkcjami \( \mu_N(\Delta e) \) i \( \mu_P(\Delta e) \).

Krok 3 (projekt bazy reguł)

Posiłkując się znajomością ogólnej reguły warunkowej 154 regulatora rozmytego typu PID oraz mając na uwadze zarówno kształt funkcji przynależności jak na Rys. 35 z uwagą sformułowaną w kroku nr 2 oraz dodatkowo biorąc pod uwagę ogólne wnioski z rozważań przeprowadzonych w podrozdziale 3.1, zbudujemy zupełną bazę reguł modelu regulatora rozmytego. W przypadku rozważanego regulatora typu PID mamy do czynienia z układem o trzech wejściach (i=3) i jednym wyjściu. Wejściom przyporządkowano odpowiednio: \( n_1=n_2=n_3=2 \) zbiorów rozmytych. Stąd, liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (2\cdot 2\cdot 2)=8 \). Tabelę reguł dla tego regulatora przedstawiono na Tab. 15.

Zwróćmy uwagę, że znaczna liczba reguł w tej tabeli generuje identyczne wnioski. Takie reguły, które mają różne poprzedniki lecz identyczne następniki będziemy nazywali regułami alternatywnymi. Wnioski generowane przez reguły alternatywne podlegają agregacji mnogościowej w procesie wnioskowania zgodnej ze schematem Mamdaniego.

Reguły o identycznych poprzednikach, lecz różnych następnikach są regułami sprzecznymi. Reguły takie mogą być generowane np. w systemach automatycznego wydobywania reguł z dużych zbiorów danych np. metodą Wanga-Mendela [7]. Reguły sprzeczne są ewaluowane w celu wyłonienia spośród wielu tylko jednej, którą w świetle danej metody uznaje się za najbardziej wiarygodną.

Tabela 14 zawiera reguły alternatywne. Wszystkie reguły w tej tabeli nie są sprzeczne. Reguły alternatywne w tej tabeli są bardziej konserwatywne niż agresywne. Reguły agresywne forsują silną zmienność następnika reguły przy dowolnej zmianie poprzednika. Reguły konserwatywne niekoniecznie. Zwróćmy dla przykładu uwagę na reguły nr 2 i 3. W tym przypadku silna zmiana przyśpieszenia w regule numer 3 w stosunku do reguły nr 2 nie wywołała żadnej zmiany sterowania.

Zwróćmy także uwagę na dostrzegalny w tej tabeli efekt kompensacji wpływów poprzedników na wartość następnika. Tylko jednoimienne termy zbiorów rozmytych poprzedników reguł generują współbrzmiące wyjście (por. reguły nr 1 i 8). Można potraktować tę obserwację także jako prostą regułę mnemotechniczną.

Tabela 15: Tabela sterowań rozmytych regulatora typu PD.
Reguła	\( \Delta e \)	\( e \)	\( \Delta^2e \)	\( \Delta v \)
1	\( N_{\Delta e} \)	\( N_e \)	\( N_{\Delta^2e} \)	\( N_{\Delta v} \)
2	\( N_{\Delta e} \)	\( N_e \)	\( P_{\Delta^2e} \)	\( Z_{\Delta v} \)
3	\( N_{\Delta e} \)	\( P_e \)	\( N_{\Delta^2e} \)	\( Z_{\Delta v} \)
4	\( N_{\Delta e} \)	\( P_e \)	\( P_{\Delta^2e} \)	\( Z_{\Delta v} \)
5	\( P_{\Delta e} \)	\( N_e \)	\( N_{\Delta^2e} \)	\( Z_{\Delta v} \)
6	\( P_{\Delta e} \)	\( N_e \)	\( P_{\Delta^2e} \)	\( Z_{\Delta v} \)
7	\( P_{\Delta e} \)	\( P_e \)	\( N_{\Delta^2e} \)	\( Z_{\Delta v} \)
8	\( P_{\Delta e} \)	\( P_e \)	\( P_{\Delta^2e} \)	\( P_{\Delta v} \)

Zwróćmy także uwagę, że jeśli w równaniu (154) dokonamy podstawienia \( \Delta e=0 \) i \( \Delta (\Delta e)=0 \), to regulator PID ulegnie przekształceniu do regulatora typu P. Wówczas zmiana sygnału wyjściowego będzie wprost proporcjonalna wyłącznie do zmiany odchyłki regulacji co jest charakterystyczną cechą tego typu regulatora.

\( \Delta v=K_p\cdot \Delta e \)	(157)

Technicznie przekształcenie regulatora PID do regulatora typu P polega na wyeliminowaniu z Tab. 15 kolumn \( \Delta e \) i \( \Delta^2 e \).

Podobnie regulator PID może być przekształcony do regulatora typu PI lub PD jeśli wyeliminujemy z Tab. 1 kolumnę \( \Delta^2e \). Pamiętajmy, że w tym przypadku, mimo, że tabele reguł są dla obu regulatorów identyczne, to różnią się one strukturami (por. Rys. 34 i 38).

Z powyższych rozważań wynika uwaga o dużym znaczeniu praktycznym w przypadku implementacji algorytmów regulacyjnych. Wystarcza bowiem zaimplementować jedną ogólną procedurę regulatora rozmytego. Wywołanie takiej procedury z różnymi zestawami parametrów formalnych generuje różne typy regulatorów (P, PI, PD, PID).