Podręcznik

2. Sygnały i ich charakterystyki

2.4. Operacja splotu i jej zastosowanie do opisu układów liniowych

Istotną klasą systemów w przetwarzaniu sygnałów są systemy liniowe i niezmiennicze w czasie (LTI, ang. Linear Time-Invariant). Systemy LTI to takie, które spełniają dwa podstawowe warunki:

1. liniowość, na którą składa się jednorodność i addytywność:

jeżeli sygnał wejściowy $x(t)$ systemu jest skalowany za pomocą stałego czynnika $a$ , wówczas sygnał wyjściowy $y(t)$ również jest skalowany przez ten czynnik:

$H(x(t)) = y(t)\quad\Rightarrow\quad H(a x(t)) = a\cdot y(t)$
jeżeli sygnał wejściowy systemu jest sumą sygnałów $x_1(t)$ i $x_2(t)$ , to aby ten system był addytywny, jego sygnał wyjściowy musi być sumą poszczególnych sygnałów wyjściowych:

$\begin{cases} H(x_1(t)) = y_1(t) \\ H(x_2(t)) = y_2(t) \end{cases}\quad\Rightarrow\quad H(x_1(t)+x_2(t)) = H(x_1(t)) + H(x_2(t)) = y_1(t) + y_2(t)$

2. niezmienniczość w czasie:

przesunięcie sygnału $x(t)$ o $t_0$ powoduje tylko przesunięcie wyjścia $y(t)$ o $t_0$ , bez zmiany kształtu:

$H(x(t)) = y(t)\quad\Rightarrow\quad H(x(t - t_0)) = y(t - t_0)$

Powyższe warunki składają się na zasadę superpozycji, którą można analogicznie wyprowadzić dla systemów dyskretnych.

Jeżeli system jest liniowy i niezależny od czasu, to kluczowe staje się pojęcie odpowiedzi impulsowej (ang. Impulse Response). Jest to odpowiedź systemu na pobudzenie w formie impulsu jednostkowego, nazywanego również deltą Diraca (dystrybucja delta) $\delta(t)$ :

$\delta(t) = \begin{cases} \infty, & \text{gdy } t = 0 \\ 0, & \text{gdy } t \ne 0 \end{cases}\quad \text{oraz} \quad \int_{-\infty}^{\infty} \delta(t)\,dt = 1$

Delta Diraca nie jest funkcją w klasycznym sensie, ale idealizowanym impulsem o nieskończonej amplitudzie i zerowej szerokości – używamy jej przybliżenia. Najczęściej do wizualizacji używa się wąskiego i wysokiego impulsu, np. prostokątnego (rys. 2.4) lub funkcji Gaussa (rys. 2.5).

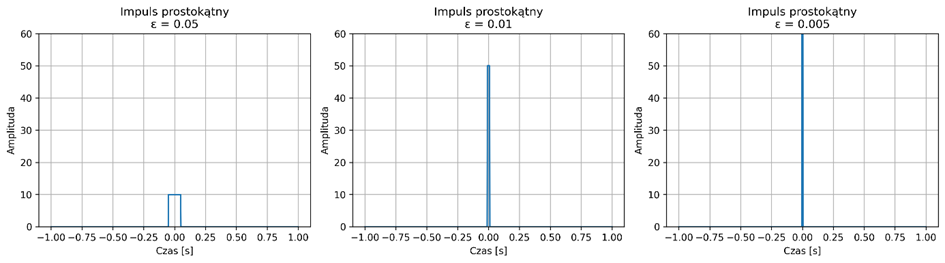
Rys. 2.4. Sekwencja przybliżeń delty Diraca przy użyciu coraz wyższych i węższych impulsów prostokątnych

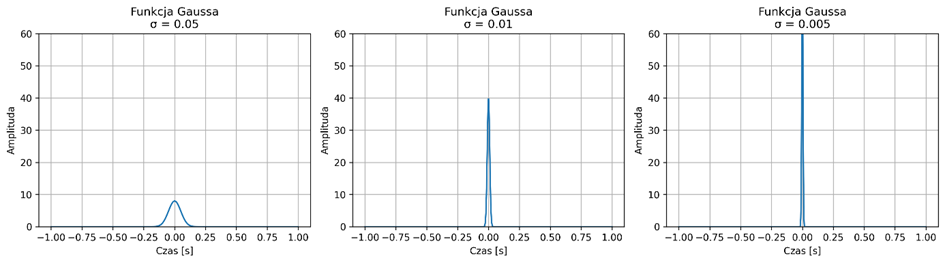
Rys. 2.5. Sekwencja przybliżeń delty Diraca przy użyciu coraz wyższych i węższych krzywych Gaussa

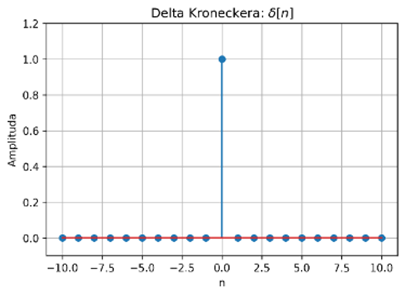
W przypadku sygnałów dyskretnych mamy do czynienia z deltą Kroneckera $\delta[n]$ :

$\delta[n] = \begin{cases} 1, & \text{gdy } n = 0 \\ 0, & \text{gdy } n \ne 0 \end{cases}$

której graficzne przedstawienie zostało pokazane na rys. 2.6. Sygnał ten jest podstawą koncepcji odpowiedzi impulsowej oraz splotu dyskretnego.

Rys. 2.6. Wykres delty Kroneckera

Odpowiedź impulsową oznaczamy $h(t)$ lub $h[n]$ , odpowiednio dla sygnałów ciągłych i dyskretnych. Jeżeli znamy odpowiedź impulsową systemu LTI, to odpowiedź systemu na pobudzenie dowolnym sygnałem możemy obliczyć jako splot tego sygnału z odpowiedzią impulsową.

Splot (ang. Convolution) jest jednym z fundamentalnych pojęć teorii sygnałów. Jest to operacja matematyczna, która oblicza odpowiedź systemu liniowego na dowolny sygnał wejściowy, nakładając odpowiedź impulsową przesuniętą w czasie.

Splot dla:

sygnałów ciągłych:

$\displaystyle y(t) = x(t)\ast h(t) = \int_{-\infty}^{\infty} x(\tau)\,h(t-\tau)\,d\tau = \int_{-\infty}^{\infty} h(\tau)\,x(t-\tau)\,d\tau$

sygnałów dyskretnych:

$y[n] = x[n]\ast h[n] = \sum_{k=-\infty}^{\infty} x[k]\,h[n-k] = \sum_{k=-\infty}^{\infty} h[k]\,x[n-k]$

gdzie $x$ jest sygnałem wejściowym, $h$ jest odpowiedzią impulsową systemu oraz $y$ jest sygnałem wyjściowym, będącym wynikiem splotu. Nakładając odpowiedź impulsową $h$ na każdą próbkę sygnału $x$ , przesuwając ją w czasie (ciągłym lub dyskretnym) i sumując wpływ wszystkich tych przesunięć, otrzymujemy wynik operacji splotu. Kluczowa jest kolejność wykonywania działań:

1. odwróć w czasie drugi z sygnałów ze względu na $\tau$ lub $k$ :

$h(\tau) \rightarrow h(-\tau)\quad\text{lub}\quad h[k] \rightarrow h[-k]$

2. przesuń go w czasie o czas $t$ lub o $n$ próbek:

$h(-\tau) \rightarrow h(t-\tau)\quad\text{lub}\quad h[-k] \rightarrow h[n-k]$

3. wymnóż pierwszy sygnał ze zmodyfikowanym drugim:

$x(\tau)\,h(t-\tau)\quad\text{lub}\quad x[k]\,h[n-k]$

4. scałkuj wynik mnożenia lub zsumuj wszystkie iloczyny próbek.

Należy zwrócić uwagę na to, że sygnał

$h$ jest odwracany w czasie, zanim będzie przesuwany i mnożony.

Znajomość pojęcia splotu pozwala na zrozumienie podstawowych właściwości impulsu Diraca:

splot z $\delta(t)$ – impuls Diraca jest elementem identycznościowym operacji splotu:

$x(t)\ast \delta(t) = x(t)$
splot z przesuniętą deltą $\delta(t - t_0)$ przesuwa sygnał w czasie o $t_0$ :

$x(t)\ast \delta(t - t_0) = x(t - t_0)$

Zatem, skoro impuls jednostkowy jest sygnałem, który podany na wejście dowolnego liniowego i niezmienniczego w czasie układu powoduje wygenerowanie odpowiedzi równej odpowiedzi impulsowej tego układu:

$\delta(t)\ast h(t) = h(t)$

to odpowiedź takiego systemu na dowolny sygnał wejściowy $x(t)$ jest jego splotem ze znaną odpowiedzią impulsową $h(t)$ :

$y(t) = x(t)\ast h(t)$

W przypadku sygnałów dyskretnych opis systemów LTI za pomocą splotu jest analogiczny:

$y[n] = x[n]\ast h[n]$

Do zilustrowania operacji splotu weźmiemy dwa proste sygnały dyskretne:

$x[n] = [1,2,3], \quad h[n] = [1,0,-1]$

Oznacza to, że:

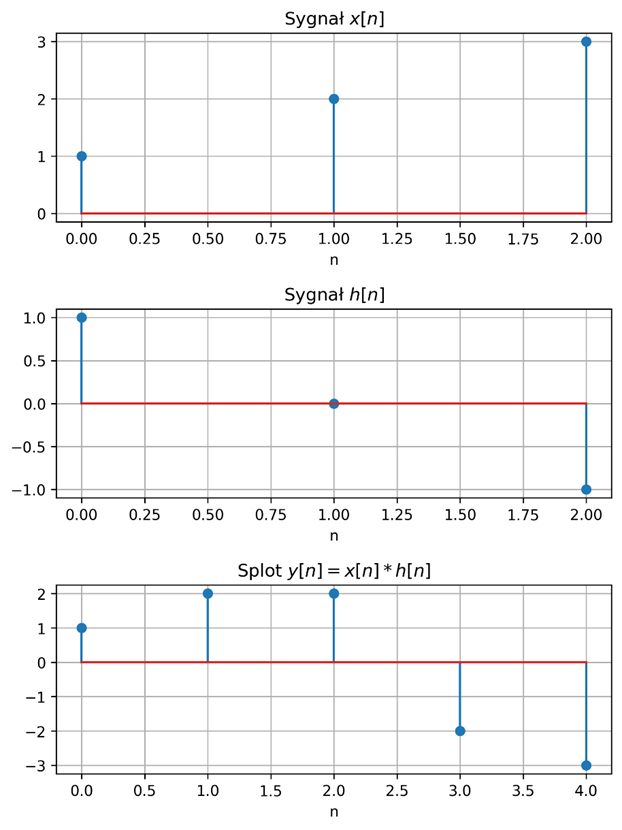
$\begin{align*} x[0] &= 1,\quad x[1] = 2,\quad x[2] = 3 \\ h[0] &= 1,\quad h[1] = 0,\quad h[2] = -1 \end{align*}$

Ponieważ $x[k]$ i $h[k]$ mają tylko 3 niezerowe próbki, splot będzie miał długość:

$N = 3 + 3 - 1 = 5$

Korzystając z definicji splotu dyskretnego:

$y[n] = x[n]\ast h[n] = \sum_{k} x[k]\cdot h[n-k]$

otrzymamy kolejne wartości sygnału $y[n]$ . Kolejne kroki zostały przedstawione w tabeli:

Poniżej przedstawiono wykresy sygnałów i ich splotu: