Podręcznik
2. Sygnały i ich charakterystyki
2.9. Charakterystyki sygnałów w języku Python
Celem poniższych ćwiczeń jest zapoznanie się z podstawowymi poleceniami w języku Python do wyznaczania wybranych charakterystyk sygnałów - parametrów energetycznych sygnałów oraz ich korelacji wzajemnej i autokorelacji.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. W trakcie realizacji ćwiczeń wykorzystywane będą następujące biblioteki:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów,
# takich jak np. prostokątny, trójkątny, piłokształtny
import scipy.integrate as integrate # numeryczne obliczanie całek
Rozwiązanie zadań wymaga znajomości podstawowych poleceń oraz funkcji dostępnych w języku Python, w tym m.in.:
np.sum # obliczanie sumy wartości próbek sygnału, np. przy wyznaczaniu energii sygnału
np.mean # wyznaczanie wartości średniej sygnału
np.abs # obliczanie wartości bezwzględnej próbek sygnału
np.max # wyznaczanie maksymalnej wartości sygnału
simpson # numeryczne całkowanie sygnału metodą Simpsona, np. do obliczania energii sygnału ciągłego
signal.correlate # obliczanie korelacji wzajemnej lub autokorelacji sygnałów
signal.correlate_lags # wyznaczanie wektora opóźnień (lagów) odpowiadających wartościom korelacji
Poniżej przedstawiono ćwiczenia zawierające przykładowe implementacje w języku Python. Autor zachęca czytelnika do uruchomienia zaprezentowanych kodów oraz do analizy charakterystyk sygnałów poprzez modyfikację wybranych parametrów sygnałów.
Obliczyć przybliżoną moc sygnału sinusoidalnego o amplitudzie \( A=2 \), częstotliwości \( f=1 \) Hz i zerowej fazie na podstawie jego próbek w przedziale czasu \([-10,10]\).
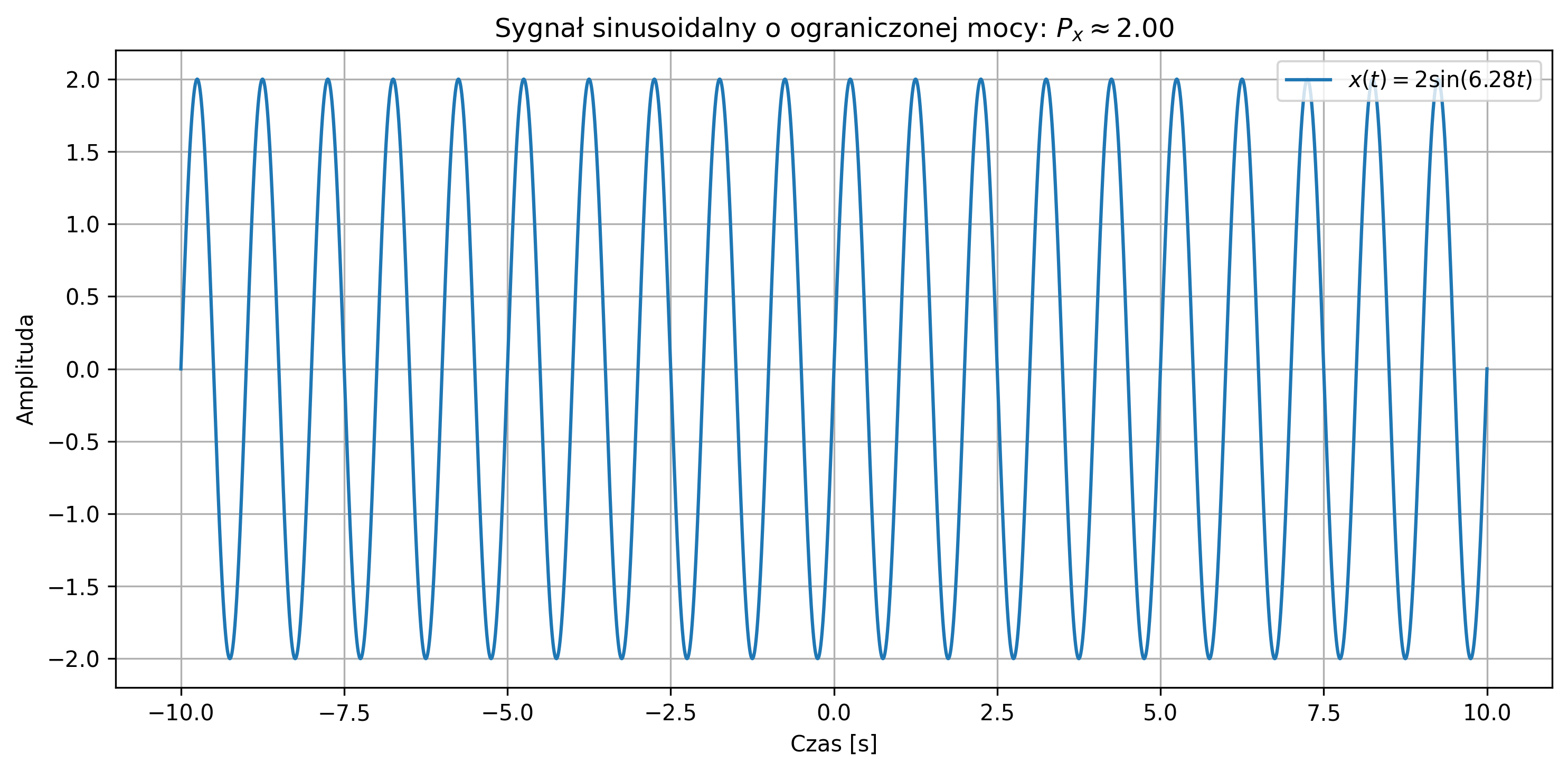
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
# Parametry sygnału
A = 2 # amplituda
f = 1 # częstotliwość [Hz]
omega = 2 * np.pi * f # pulsacja [rad/s]
# Czas obserwacji (symulacja sygnału "nieskończonego")
T_obs = 10
t = np.linspace(-T_obs, T_obs, 10000)
# Sygnał ciągły
x = A * np.sin(omega * t)
# Moc sygnału: numerycznie przybliżona całka
power = (1 / (2 * T_obs)) * simpson(x**2, t)
# Wynik
print(f"Moc sygnału: {power:.2f}")
# Wykres sygnału
plt.figure(figsize=(10, 5))
plt.plot(t, x, label=fr'$x(t) = {A}\sin({omega:.2f} t)$', color='C0')
plt.title(fr'Sygnał sinusoidalny o ograniczonej mocy: $P_x \approx {power:.2f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
Należy zaznaczyć, że do obliczania całki we wzorze na moc sygnału, musimy wykorzystać wybraną metodę numerycznego całkowania, np. metodę Simpsona. W rzeczywistości całkowanie odbywa się po skończonym przedziale – dlatego moc sygnału wynosi w przybliżeniu \(2\), a nie jak wg. teorii dokładnie \(2\) (\( A^2/2 = 4/2 = 2 \)).
Obliczyć przybliżoną energię i wartość średnią sygnału Gaussowskiego:
\( x(t) = e^{-\pi t^2}\)
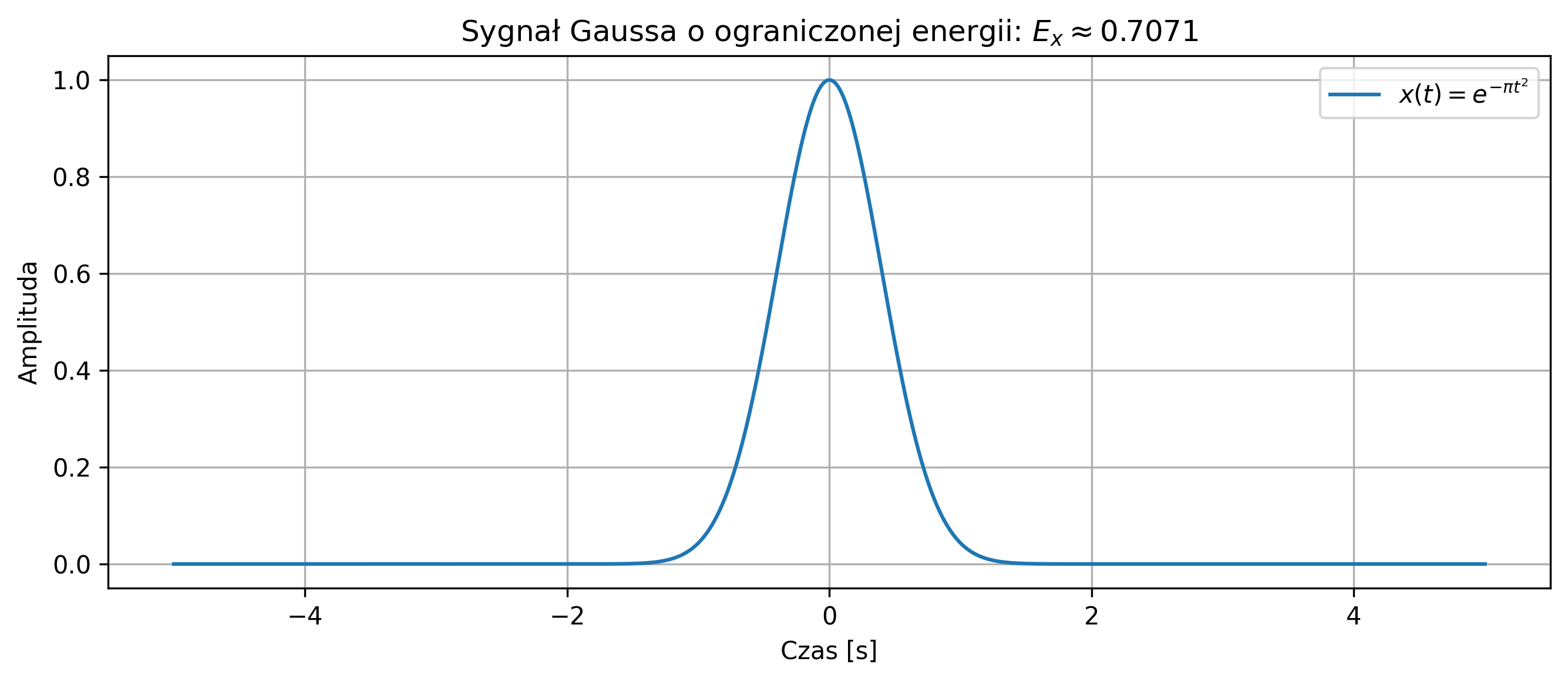
na podstawie próbek w przedziale czasu \([-5,5]\).
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
# Zakres czasu
t = np.linspace(-5, 5, 10000)
dt = t[1] - t[0]
# Sygnał Gausso
x = np.exp(-np.pi*t**2)
# Energia
energy = np.sum(np.abs(x)**2) * dt
print(f'Energia sygnału: {energy:.4f}')
# Wartość średnia
mean = np.mean(x)
print(f'Wartość średnia: {mean:.6e}')
# Wykres sygnału
plt.figure(figsize=(9, 4))
plt.plot(t, x, label=r'$x(t) = e^{-\pi t^2}$')
plt.title(fr'Sygnał Gaussa o ograniczonej energii: $E_x \approx {energy:.4f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
Sygnał Gaussa jest parzysty i symetryczny względem zera, dlatego wartość średnia sygnału dąży do zera ( \(9.999000\cdot 10^{-2}\)). Obliczona moc sygnału jest przybliżeniem teoretycznej wartości \( 1/\sqrt{2} = 0.7071067812 \).
Obliczyć przybliżoną energię i wartość średnią sygnału:
Wartość średnia sygnału wynosi w przybliżeniu \(4.989372\cdot 10^{-3}\).
\( x(t) = \mathrm{Sinc}(t)\)
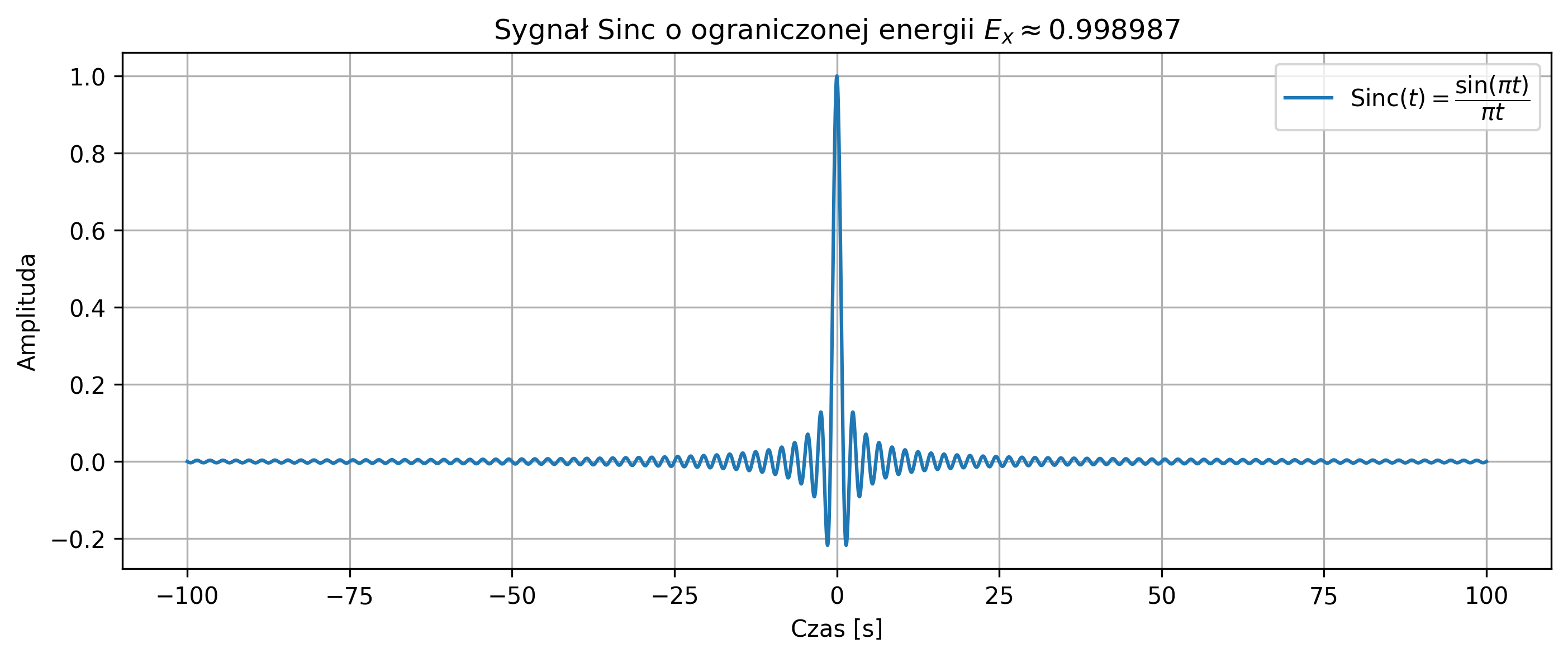
na podstawie próbek w przedziale czasu \([-100,100]\).
import numpy as np
import matplotlib.pyplot as plt
# Zakres czasu
t = np.linspace(-100, 100, 10000)
dt = t[1] - t[0]
# Sygnał Sinc
x = np.sinc(t)
# Obliczenie energii
energy = np.sum(np.abs(x)**2) * dt
print(f'Energia sygnału: {energy:.6f}')
# Wartość średnia
mean = np.mean(x)
print(rf'Wartość średnia sygnału: {mean:.6e}')
# Wykres
plt.figure(figsize=(11, 4))
plt.plot(t, x, label=r'$\mathrm{Sinc}(t) = \dfrac{\sin(\pi t)}{\pi t}$')
plt.title(fr'Sygnał Sinc o ograniczonej energii $E_x \approx {energy:.6f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.show()
Obliczyć przybliżoną moc oraz wartość średnią sygnału wykładniczego narastającego:
Rozważany sygnał jest sygnałem wykładniczym narastającym o ograniczonej mocy, lecz o nieskończonej energii. Wartość średnia sygnału wynosi w przybliżeniu \(0.9\).
\(x(t) = 1-e^{-t}\)
na podstawie jego próbek w przedziale czasu \([0,10]\).
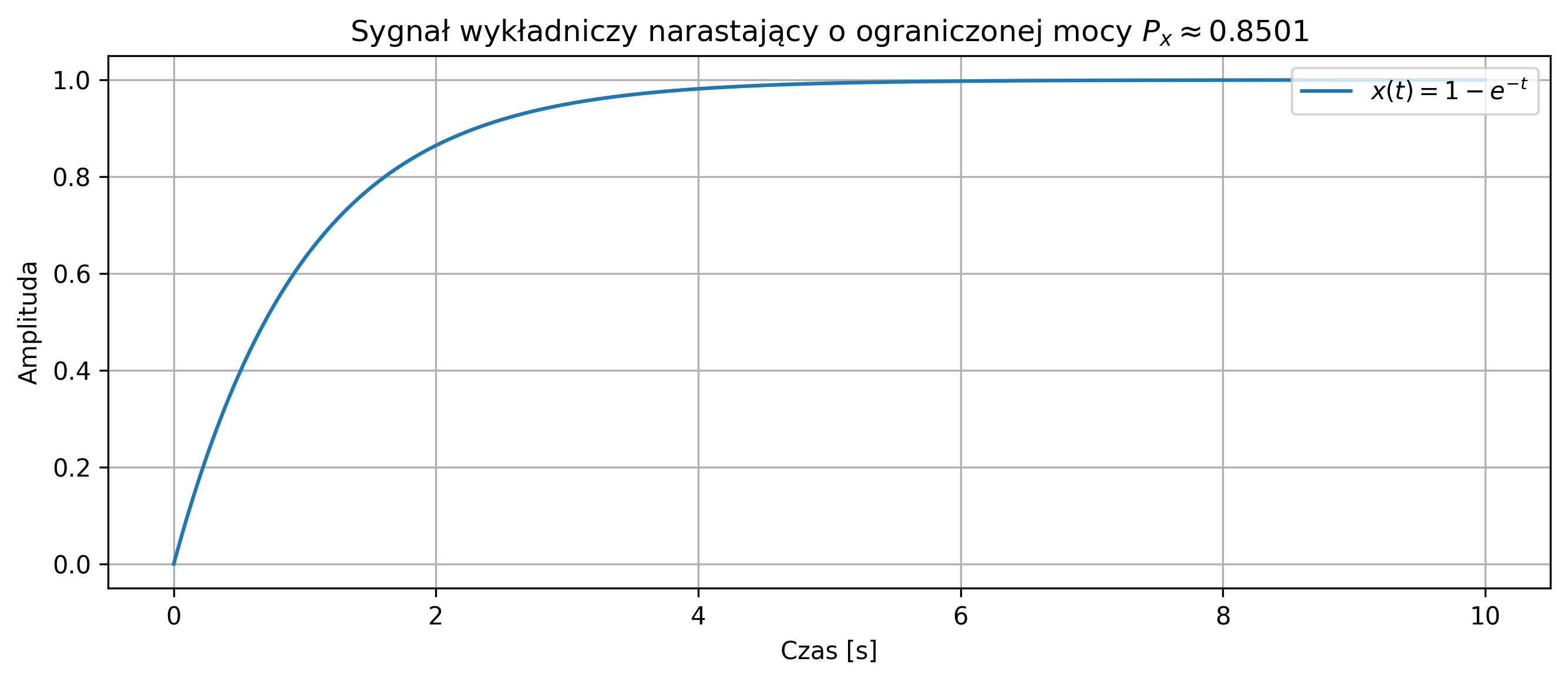
import numpy as np
import matplotlib.pyplot as plt
# Zakres czasu
t = np.linspace(0, 10, 10000)
dt = t[1] - t[0]
# Sygnał wykładniczy narastający
x = 1 - np.exp(-t)
# Moc (energia średnia na przedziale)
power = np.sum(x**2) * dt / 10
print(f'Moc sygnału: {power:.4f}')
# Wartość średnia
mean = np.mean(x)
print(f'Wartość średnia: {mean:.4f}')
# Wykres
plt.figure(figsize=(9, 4))
plt.plot(t, x, label=r'$x(t) = 1 - e^{-t}$')
plt.title('Sygnał wykładniczy narastający')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
Wyznaczyć funkcję korelacji wzajemnej sygnału \( x(t) = 2\sin(\omega t) \) o częstotliwości \( 2 \) Hz i sygnału \( y(t) \), będącego przesunięciem oryginalnego sygnału \( x(t) \) o czas \( \tau = 0.25 \) s.
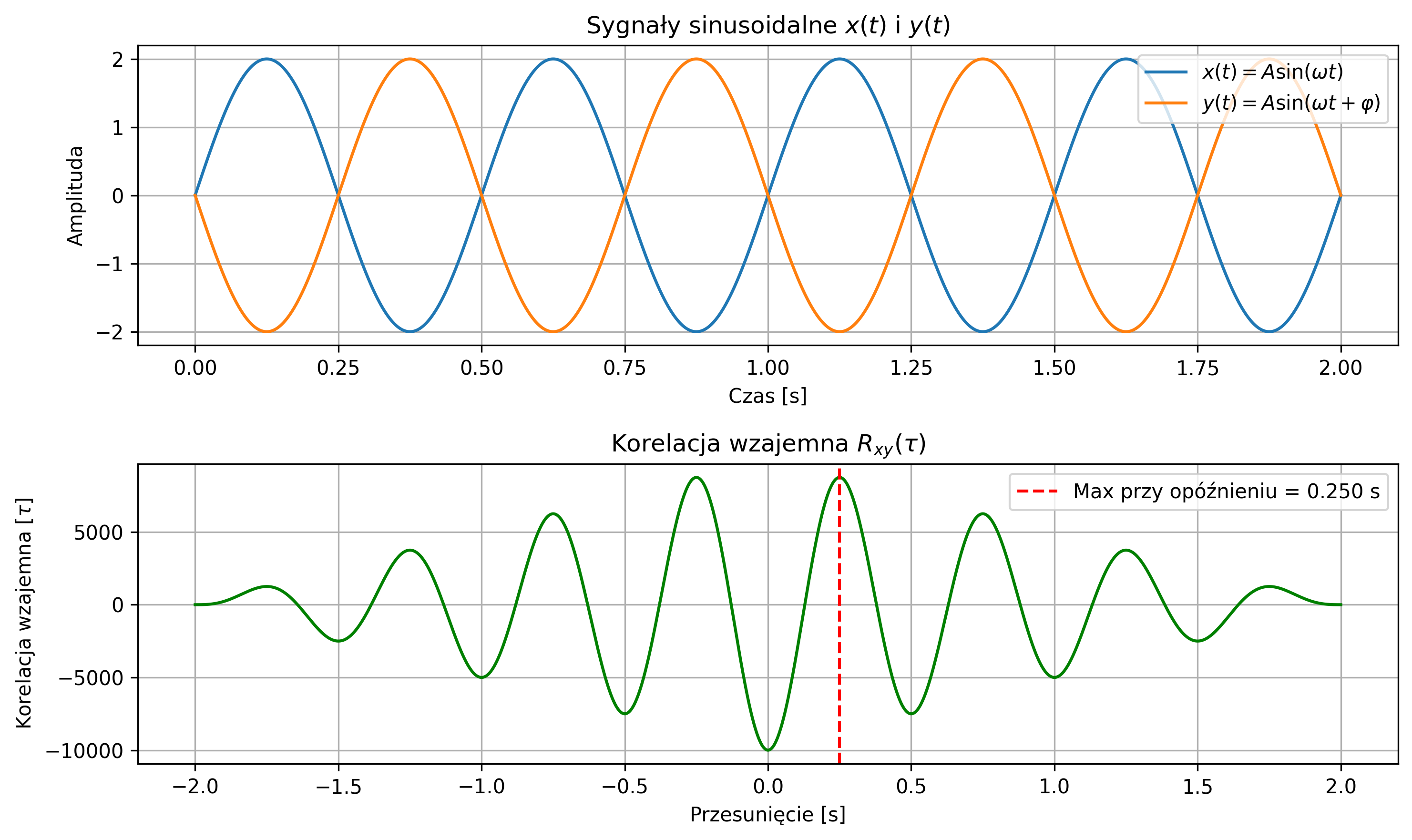
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as signal
# Parametry sygnału
A = 2 # amplituda
f = 2 # częstotliwość [Hz]
omega = 2 * np.pi * f
tau = 0.25 # opóźnienie czasowe w sekundach
varphi = -omega * tau # odpowiadające przesunięcie fazowe
# Czas
t = np.linspace(0, 2, 5000)
# Sygnały
x = A * np.sin(omega * t)
y = A * np.sin(omega * t + varphi) # przesunięcie fazowe odpowiadające opóźnieniu
# Korelacja
r_xy = correlate(y, x, mode='full')
lags = correlation_lags(len(y), len(x), mode='full')
dt = t[1] - t[0]
lags_time = lags * dt
max_lag_time = lags_time[np.argmax(r_xy)]
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
axs[0].plot(t, x, label=r'$x(t) = A \sin(\omega t)$',linestyle='-')
axs[0].plot(t, y, label=r'$y(t) = A \sin(\omega t + \varphi)$',linestyle='-')
axs[0].set_title(fr'Sygnały sinusoidalne $x(t)$ i $y(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
axs[1].plot(lags_time, r_xy, color='green')
axs[1].set_title(f'Korelacja wzajemna $R_{{xy}}(τ)$')
axs[1].axvline(max_lag_time, color='red', linestyle='--',
label = fr'Max przy opóźnieniu = {max_lag_time:.3f} s')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(fr'Korelacja wzajemna $[\tau]$')
axs[1].legend(loc='upper right')
axs[1].grid(True)
plt.tight_layout()
plt.show()
Maksymalna wartość funkcji korelacji wskazuje nam opóźnienie sygnałów względem siebie. Otrzymaliśmy spodziewany wynik.
Dla sygnału piłokształtnego o częstotliwości \(f=5\) Hz wyznaczyć opóźnienie względem siebie dwóch sygnałów: oryginalnego oraz przesuniętego o \(0.05\) s w czasie.
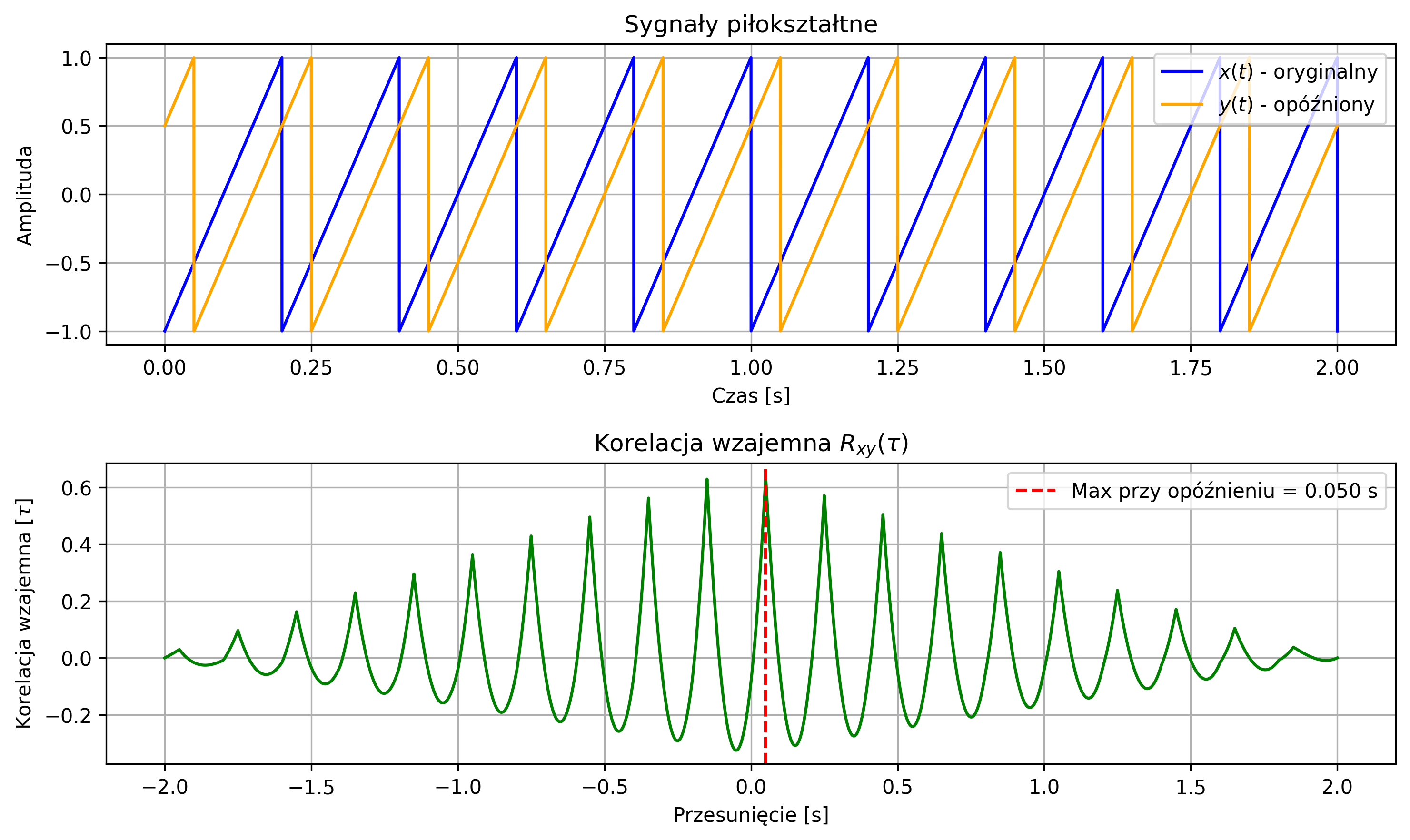
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth, correlate, correlation_lags
# Parametry ciągłego czasu
T_obs = 2 # czas obserwacji [s]
fs = 10000 # częstotliwość próbkowania [Hz]
t = np.linspace(0, T_obs, int(T_obs * fs))
dt = t[1] - t[0]
# Parametry sygnału piłokształtnego
f = 5 # Hz
x = sawtooth(2 * np.pi * f * t)
# Sygnał opóźniony
delay_sec = 0.05 # opóźnienie w sekundach
delay_samples = int(delay_sec * fs) # opóźnienie w próbkach
y = np.roll(x, delay_samples)
# Korelacja wzajemna
r_xy = correlate(y, x, mode='full') * dt
lags = correlation_lags(len(y), len(x), mode='full') * dt
# Znalezienie maksimum korelacji
max_idx = np.argmax(r_xy)
max_lag_time = lags[max_idx]
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
axs[0].plot(t, x, label=rf'$x(t)$ - oryginalny', color='blue')
axs[0].plot(t, y, label=rf'$y(t)$ - opóźniony', color='orange')
axs[0].set_title('Sygnały piłokształtne')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
axs[1].plot(lags, r_xy, color='green')
axs[1].set_title(fr'Korelacja wzajemna $R_{{xy}}(τ)$')
axs[1].axvline(max_lag_time, color='red', linestyle='--',
label=fr'Max przy opóźnieniu = {max_lag_time:.3f} s')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Korelacja wzajemna $[\tau]$')
axs[1].legend(loc='upper right')
axs[1].grid(True)
plt.tight_layout()
plt.show()
Wyznaczyć funkcję autokorelacji dla sygnału sinusoidalnego o amplitudzie \( A = 1 \), częstotliwości sygnału \( f = 5 \) Hz i zerowego przesunięcia fazowego.
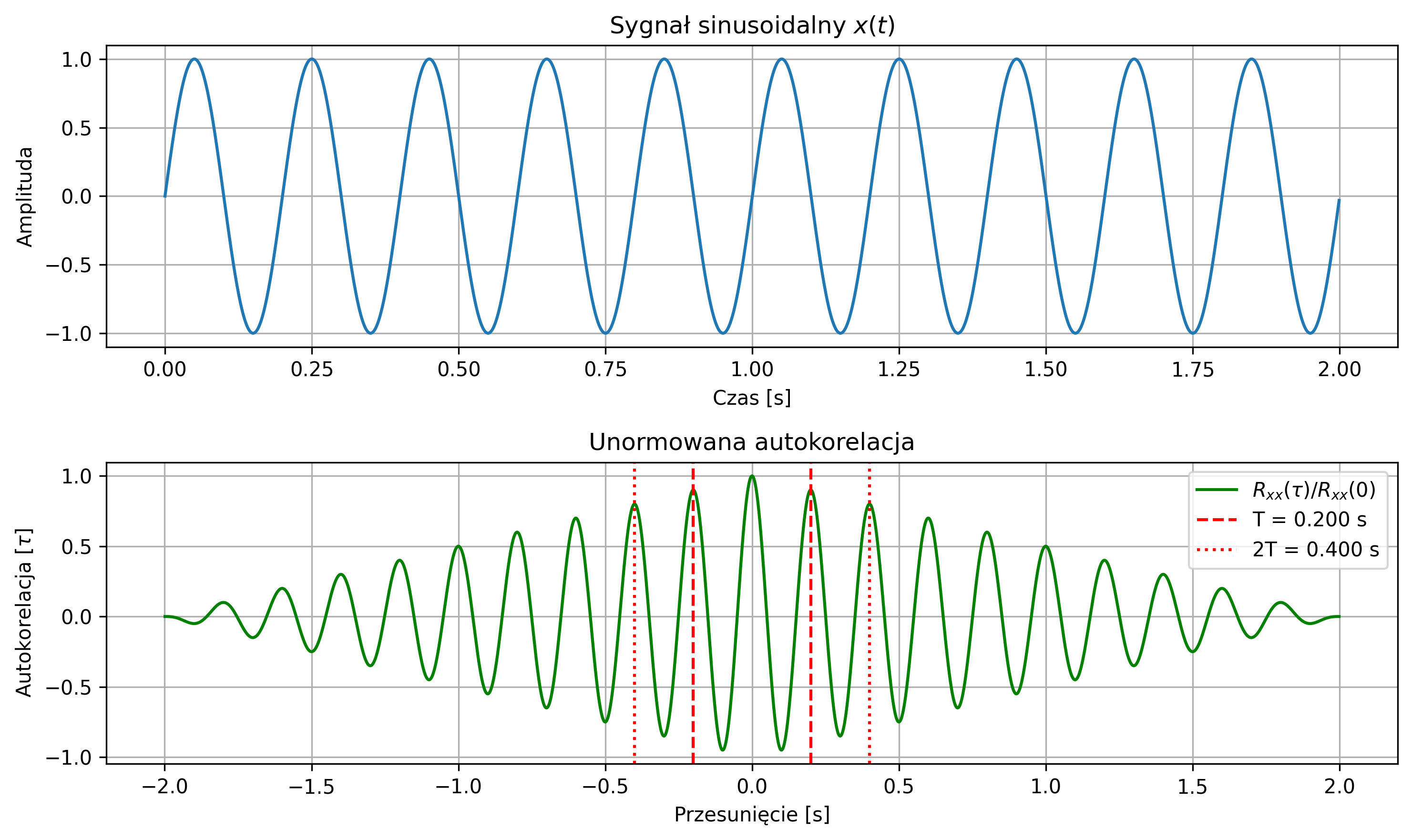
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
# Parametry
fs = 1000 # częstotliwość próbkowania [Hz]
A = 1 # amplituda sygnału
f = 5 # częstotliwość sygnału [Hz]
T = 1 / f # okres [s]
t = np.arange(0, 2, 1/fs)
x = A * np.sin(2 * np.pi * f * t)
# Autokorelacja
R_xx = correlate(x, x, mode='full')
lags = correlation_lags(len(x), len(x), mode='full') / fs
# Normalizacja (opcjonalnie)
R_xx = R_xx / np.max(R_xx)
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
# Sygnał
axs[0].plot(t, x)
axs[0].set_title(f'Sygnał sinusoidalny $x(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Autokorelacja
axs[1].plot(lags, R_xx, color='green', label=r"$R_{{xx}}(τ) / R_{{xx}}(0)$")
axs[1].axvline(T, color='r', linestyle='--', label=f'T = {T:.3f} s')
axs[1].axvline(2*T, color='r', linestyle=':', label=f'2T = {2*T:.3f} s')
axs[1].axvline(-T, color='r', linestyle='--')
axs[1].axvline(-2*T, color='r', linestyle=':')
axs[1].set_title('Unormowana autokorelacja')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].grid(True)
axs[1].legend(loc='upper right')
plt.tight_layout()
plt.show()
Unormowana funkcja autokorelacji powstaje przez podzielenie wartości funkcji autokorelacji przez energię sygnału, tak że dla zerowego przesunięcia, wartość autokorelacji przyjmuje wartość maksymalną, równą \(1\).
Wyznaczyć funkcję autokorelacji sygnału sinusoidalnego z modulowaną częstotliwością. Przyjąć amplitudę sygnału \( A=1 \), częstotliwość sygnału (częstotliwość nośna) \( f = 3.5 \) Hz, częstotliwość modulacji \( f_m = 0.5 \) Hz i głębokość modulacji \( \beta = 0.5 \).
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
from scipy.signal import find_peaks
# Parametry
fs = 1000 # częstotliwość próbkowania [Hz]
A = 1 # amplituda sygnału
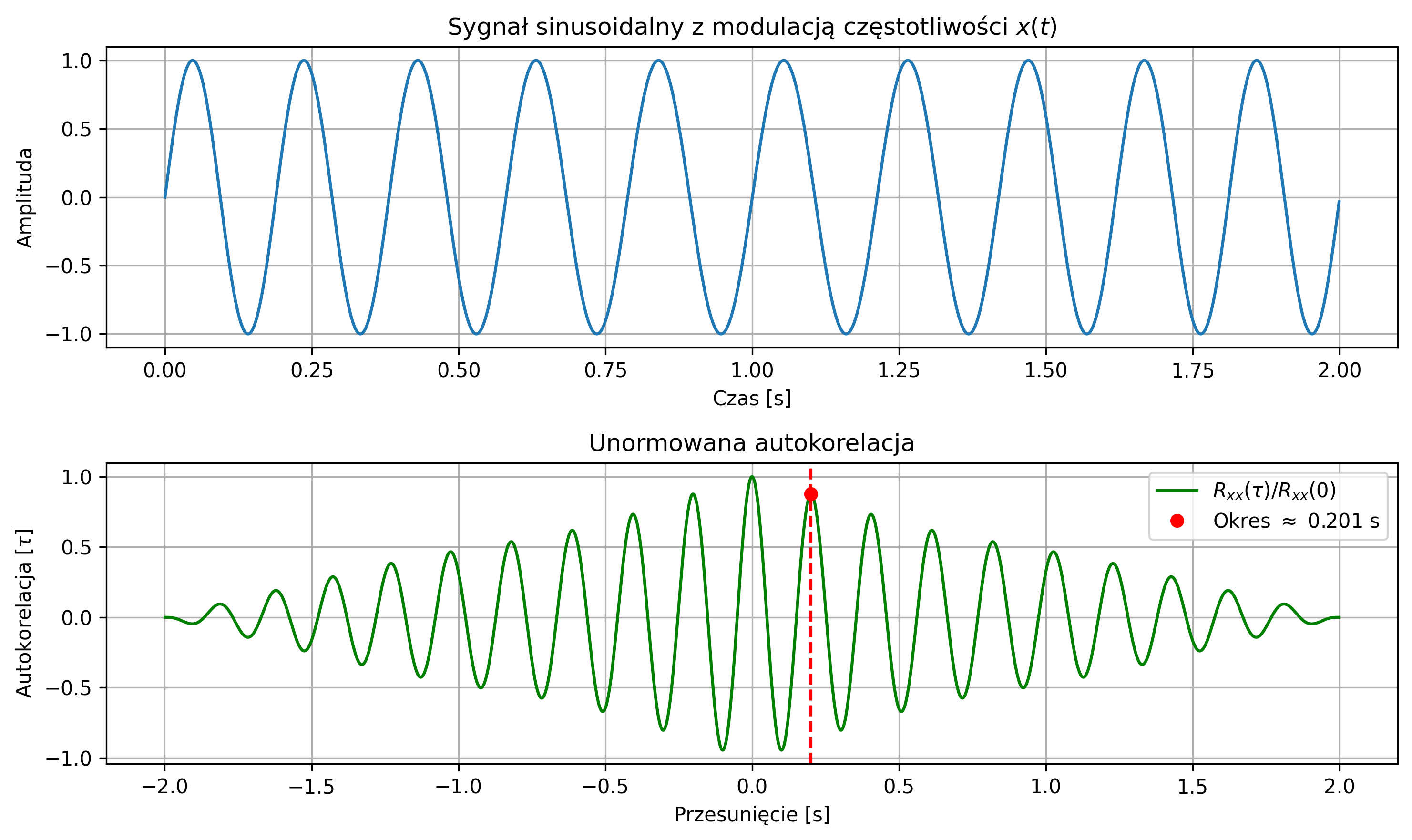
f = 3.5 # częstotliwość sygnału [Hz] (częstotliwość nośna sygnału modulowanego)
# czyli spodziewany okres wynosi w przybliżeniu 0.286 s
T = 1 / f # okres [s]
t = np.arange(0, 2, 1/fs) # czas trwania sygnału
# Sygnał pseudookresowy: sinus z modulacją częstotliwości
beta = 0.5 # większa głębokość modulacji
fm = 0.5 # czętotliwość modulacji [Hz]
x = np.sin(2 * np.pi * (f * t + beta * np.sin(2 * np.pi * fm * t)))
# Autokorelacja
R_xx = correlate(x, x, mode='full')
lags = correlation_lags(len(x), len(x), mode='full') / fs
# Normalizacja (opcjonalnie)
R_xx = R_xx / np.max(R_xx)
# Szukamy pików po stronie dodatnich opóźnień
center = len(R_xx) // 2
search_range = R_xx[center+1:] # pomijamy lag=0
lags_range = lags[center+1:]
peaks, properties = find_peaks(search_range, height=0.2, distance=int(0.05 * fs))
# wykryty pik ma mieć wartość co najmniej 0.2 - ignorujemy małe piki wynikające np. z szumu.
# minimalna odległość między pikami (w próbkach) - tu np. 0.05 * 1000 = 50 próbek,
# to chroni przed wykrywaniem zbyt blisko położonych pików.
# Szacowany okres
estimated_period = lags_range[peaks[0]] if len(peaks) > 0 else None
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=False)
# Wykres 1: sygnał
axs[0].plot(t, x)
axs[0].set_title(f'Sygnał sinusoidalny z modulacją częstotliwości $x(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel("Amplituda")
axs[0].grid(True)
# Wykres 2: autokorelacja
axs[1].plot(lags, R_xx, label=r'$R_{{xx}}(τ) / R_{{xx}}(0)$', color='green')
if estimated_period is not None:
axs[1].plot(estimated_period, R_xx[center + peaks[0]], 'ro',
label=fr'Okres $\approx$ {estimated_period:.3f} s')
axs[1].axvline(estimated_period, color='red', linestyle='--')
axs[1].set_title('Unormowana autokorelacja')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
# Informacja tekstowa
if estimated_period is not None:
print(f'Szacowana długość powtarzającego się fragmentu: {estimated_period:.3f} sekundy')
else:
print("Nie wykryto okresu")
Zauważmy, że szacowany okres jest różny od \( 1/3.5 \approx 0.286 \) s, mimo ustawienia częstotliwości sygnału na \( f = 3.5 \) Hz. Sygnał nie ma jednej częstotliwości – zmienia się ona w czasie. Autokorelacja wykrywa dominujący okres powtarzalności, który może pochodzić z modulacji (\( 1/f_m \)) albo ich kombinacji. Dlatego wykryty okres wynosi w przybliżeniu \(0.461\) s zamiast \(0.286\) s – powtarzalny fragment sygnału jest dłuższy niż oczekiwaliśmy.
Możliwymi rozwiązaniami tego problemu są:
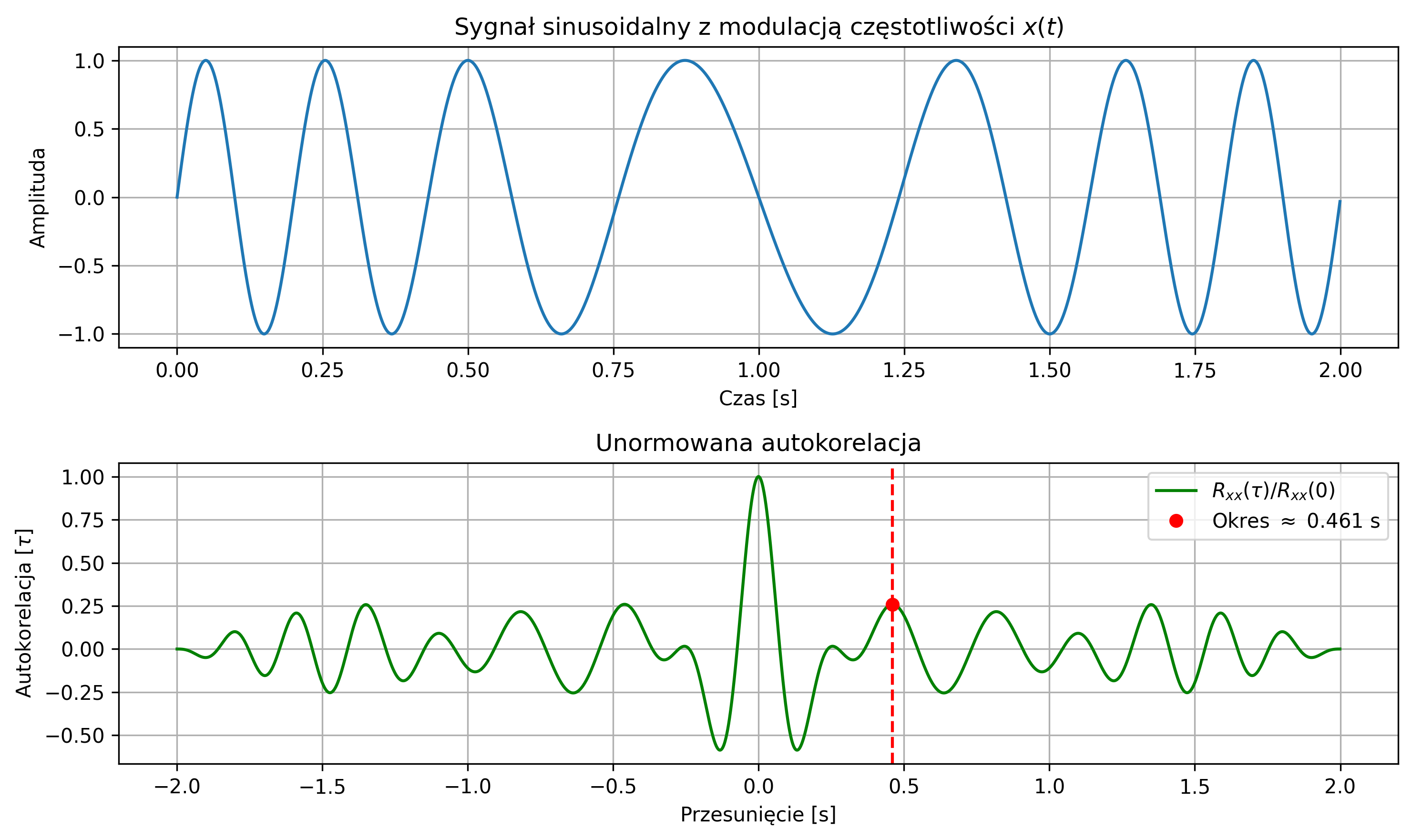
- znaczące zmniejszenie głębokości modulacji \( \beta \), by sygnał był mniej „zniekształcony”,
- zwiększenie częstotliwości nośnej,
- zamiast brania całości sygnału z modulacją, wziąć tylko krótki fragment, w którym częstotliwość się nie zmienia zbyt mocno.
Zwiększenie częstotliwości nośnej do \(5\) Hz oraz zmniejszenie głębokości modulacji \( \beta \) do poziomu \(0.1\) spowodowało wykrycie prawidłowego okresu, wynoszącego \( \approx 0.2 \).
Wyznaczyć funkcję autokorelacji zespolonego sygnału sinusoidalnego z modulacją amplitudy
\( z(t) = \bigl(1 + 0.5\cos(2\pi f_m t)\bigr)e^{j2\pi f t} \)
Przyjąć częstotliwość nośną \(50\) Hz i częstotliwość modulacji \(5\) Hz. Obliczyć moc i energię sygnału.
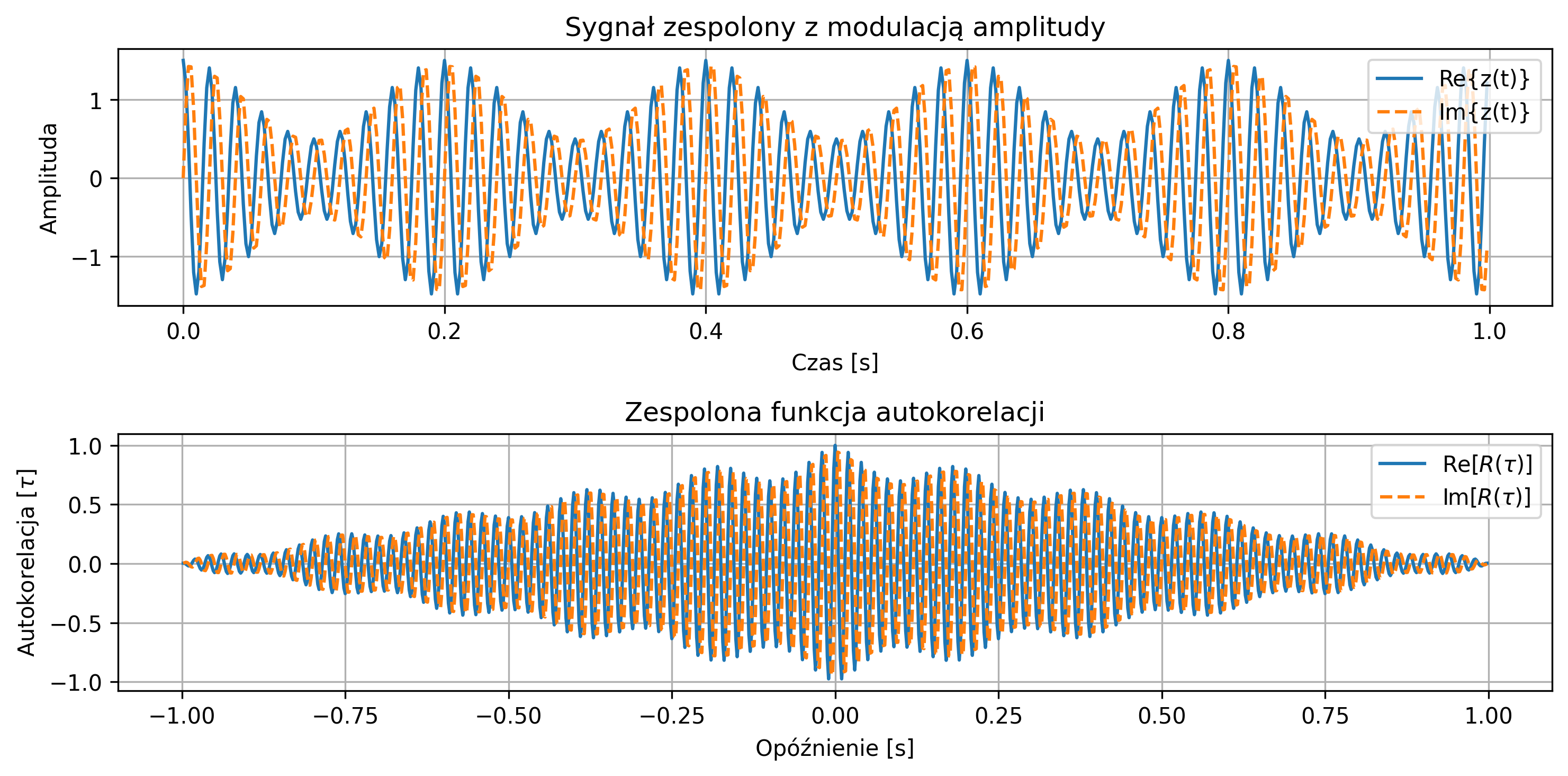
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
# Parametry czasu
fs = 500
T = 1
t = np.linspace(0, T, int(fs*T), endpoint=False)
# Parametry sygnału
f = 50 # częstotliwość nośna [Hz]
fm = 5 # częstotliwość modulacji [Hz]
# Sygnał zespolony z modulacją amplitudy
envelope = 1 + 0.5 * np.cos(2 * np.pi * fm * t) # obwiednia
z = envelope * np.exp(1j * 2 * np.pi * f * t)
# Obliczanie mocy i energii
dt = 1 / fs
power = np.mean(np.abs(z)**2)
energy = np.sum(np.abs(z)**2) * dt
# Autokorelacja
corr = correlate(z, z, mode='full') * dt
lags = correlation_lags(len(z), len(z), mode='full') / fs
corr /= np.max(np.abs(corr)) # normalizacja
# Wyniki
print(f'Moc: {power:.4f}')
print(f'Energia: {energy:.4f}')
# Wykres
fig, axs = plt.subplots(2, 1, figsize=(10, 5), sharex=False)
# Sygnał zespolony: Re i Im
axs[0].plot(t, z.real, label='Re{z(t)}')
axs[0].plot(t, z.imag, '--', label='Im{z(t)}')
axs[0].set_title('Sygnał zespolony z modulacją amplitudy')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
# Autokorelacja
axs[1].plot(lags, corr.real, label=rf'Re$[R(\tau)]$')
axs[1].plot(lags, corr.imag, '--', label=rf'Im$[R(\tau)]$')
axs[1].set_title('Zespolona funkcja autokorelacji')
axs[1].set_xlabel('Opóźnienie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
Jest to przykład zmodulowanego sygnału nośnego, gdzie obwiednia zmienia się w czasie – amplituda sygnału zmienia się sinusoidalnie. Autokorelacja ujawnia powtarzalny charakter modulacji. Energia sygnału jest skończona, gdyż całkujemy po skończonym przedziale (\(1\)s), podobne moc sygnału – obwiednia jest ograniczona i sygnał jest okresowy.