Podręcznik

4. Analiza częstotliwościowa sygnałów

4.2. Transformata Fouriera

Rozwinięcie sygnału okresowego w szereg Fouriera stanowi fundament dla ogólniejszego narzędzia – transformaty Fouriera, która umożliwia analizę również sygnałów nieokresowych poprzez przejście do dziedziny częstotliwości w sposób ciągły. Gdy sygnał jest nieokresowy, nie da się przedstawić go jako sumy sinusoid o wielokrotnościach jednej częstotliwości. Zamiast tego używa się ciągłego rozkładu po wszystkich pulsacjach \(\omega \in \mathbb{R}\):

\( X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-j\omega t} \, dt \)

To przejście można interpretować jako granicę szeregów Fouriera, gdy okres \(T \rightarrow \infty\) – dyskretne częstotliwości stają się ciągłe, a suma przechodzi w całkę. W ten sposób powstaje ciągła transformata Fouriera, opisująca ciągłe widmo częstotliwościowe.

Zespolona funkcja \(X(\omega)\) jest nazywana prostą transformatą Fouriera sygnału \(x(t)\) lub jego widmem. W celu odtworzenia sygnału z jego widma stosujemy wzór na odwrotną transformatę Fouriera:

\( x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega) e^{j\omega t} \, d\omega \)

Podobnie jak w przypadku szeregów Fouriera, dla danego sygnału \(x(t)\) transformata Fouriera opisuje, jakie składowe częstotliwościowe są obecne w sygnale. Widmo sygnału można przedstawić w postaci biegunowej:

\( X(\omega) = |X(\omega)| e^{j \,\operatorname{arg} X(\omega)} = A(\omega) e^{j \varphi(\omega)} \)

Funkcja:

\( A(\omega) = |X(\omega)| \) – widmo amplitudowe,
\( \varphi(\omega) = \operatorname{arg} X(\omega) \) – widmo fazowe.

Widmo amplitudowe pokazuje, ile i z jaką „siłą” dana częstotliwość występuje w sygnale. Widmo fazowe pokazuje przesunięcie fazowe każdej składowej częstotliwościowej w stosunku do odniesienia, co jest kluczowe przy odtwarzaniu sygnału w dziedzinie czasu. Obydwa widma są rzeczywistymi charakterystykami sygnału.

Widma amplitudowe sygnałów często przedstawia się w skali logarytmicznej – w jednostkach decybeli (dB):

\( A(\omega) = 20 \log |X(\omega)| \)

Taka prezentacja sygnału ma istotne zalety:

widmo amplitudowe często obejmuje bardzo szeroki zakres wartości – od bardzo małych do bardzo dużych; skala logarytmiczna umożliwia czytelne przedstawienie tych różnic na jednym wykresie,
skala dB upraszcza analizę układów – jest wygodna do analizy tłumienia i wzmocnienia (np. \(20\) dB oznacza dziesięciokrotny wzrost amplitudy, zaś \(-6\) dB oznacza około dwukrotne tłumienie).

Przykład pokazujący, że skala logarytmiczna odsłania „ukryte” informacje w sygnale, które są niewidoczne w skali liniowej, został przedstawiony na rys. 4.7. Na górnym wykresie widać tylko dominującą składową \(100\) Hz. Na dolnym wykresie dobrze widoczne są słabe harmoniczne – \(200\) Hz i \(300\) Hz, zauważalne są też ślady szumu w tle.

Rys. 4.7. Wykres widma amplitudowego w skali liniowej i decybelowej

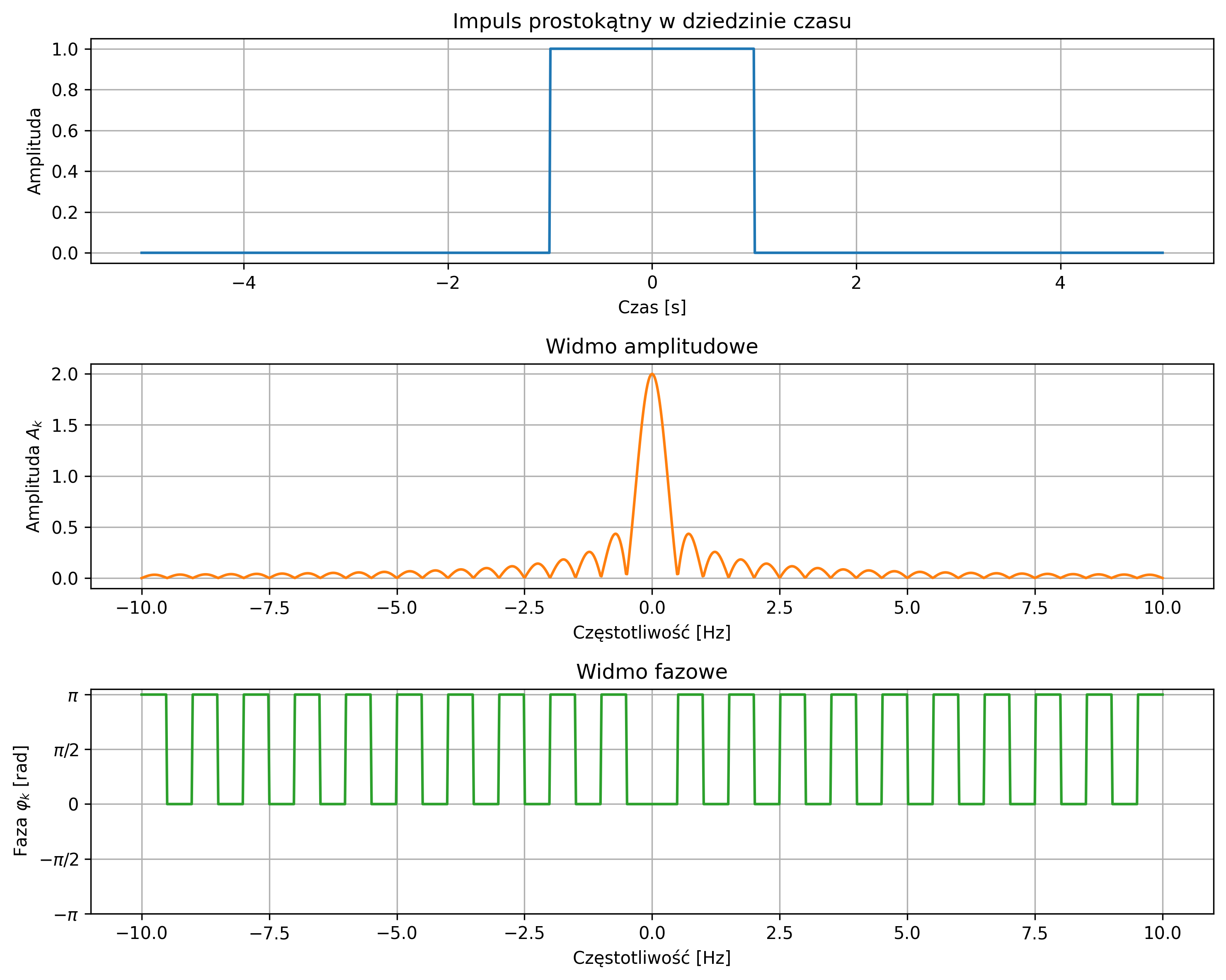
Widmo amplitudowo-fazowe dla sygnału nieokresowego – impulsu prostokątnego – zostało przedstawione na rys. 4.8. Widmo amplitudowe ma charakter ciągły i jego największa amplituda osiągana jest przy zerowej częstotliwości. Ponieważ sygnał jest wolno zmienny, na wykresie amplitudowym można zauważyć dużo niskich częstotliwości. Wykres widma fazowego pokazuje, jak są przesunięte składowe sinusoidalne. Ponieważ impuls prostokątny jest parzysty, jego faza przyjmuje wartości tylko \(0\) lub \(\pi\) (zwykłe sinusoidy i ich odbicia względem osi poziomej).

Rys. 4.8. Wykres sygnału nieokresowego i jego widma amplitudowo-fazowego

Przyjmijmy następujące oznaczenia:

\(\mathcal{F}\) – operator prostego przekształcenia Fouriera,
\(\mathcal{F}^{-1}\) – operator odwrotnego przekształcenia Fouriera.

Podstawowe własności transformaty Fouriera umożliwiają wygodne operowanie na sygnałach oraz analizę i projektowanie systemów LTI.

1. Liniowość:

\( \mathcal{F}[a x(t) + b y(t)] = a X(\omega) + b Y(\omega) \)

2. Przesunięcie w czasie:

\( \mathcal{F}[x(t - t_0)] = e^{-j\omega t_0} X(\omega) \)

3. Przesunięcie w częstotliwości (modulacja):

\( \mathcal{F}[x(t) e^{\pm j\omega_0 t}] = X(\omega \pm \omega_0) \)

4. Skalowanie w czasie i częstotliwości:

\( \mathcal{F}[x(a t)] = \dfrac{1}{|a|} X\!\left(\dfrac{\omega}{a}\right) \)

5. Mnożenie sygnałów w dziedzinie czasu:

\( \mathcal{F}[x(t) \cdot y(t)] = \dfrac{1}{2\pi}\,[X(\omega) \ast Y(\omega)] \)

6. Splot w dziedzinie czasu:

\( \mathcal{F}[x(t) \ast y(t)] = X(\omega) \cdot Y(\omega) \)

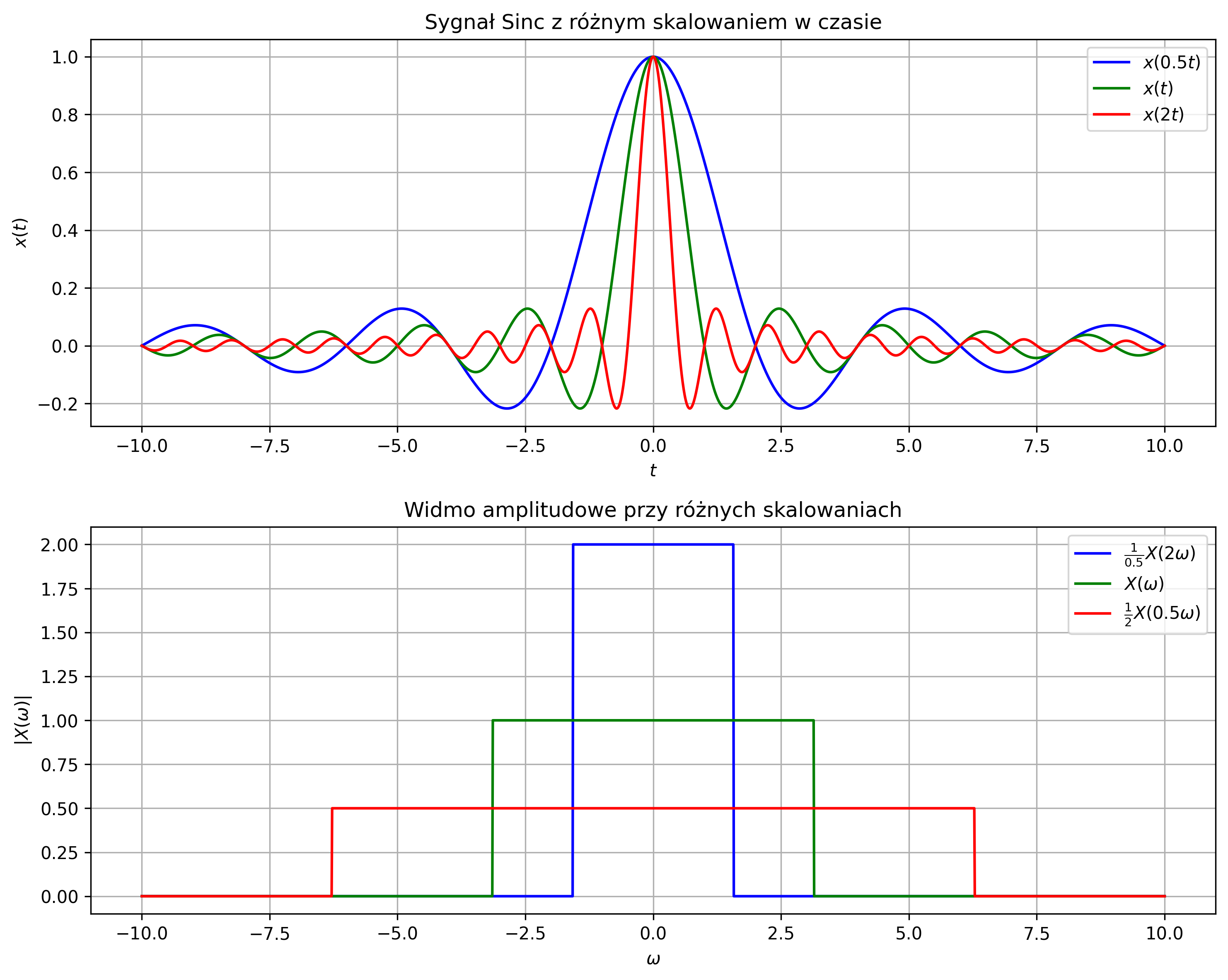
Na rys. 4.9 przedstawiono wersje sygnału \(\mathrm{Sinc}\) z różnym skalowaniem w czasie: rozciągnięty sygnał, oryginalny i ściśnięty. Odpowiadające im widma amplitudowe są odwrotnie skalowane – im bardziej sygnał rozciągnięty był w czasie, tym jego widmo stawało się węższe i wyższe.

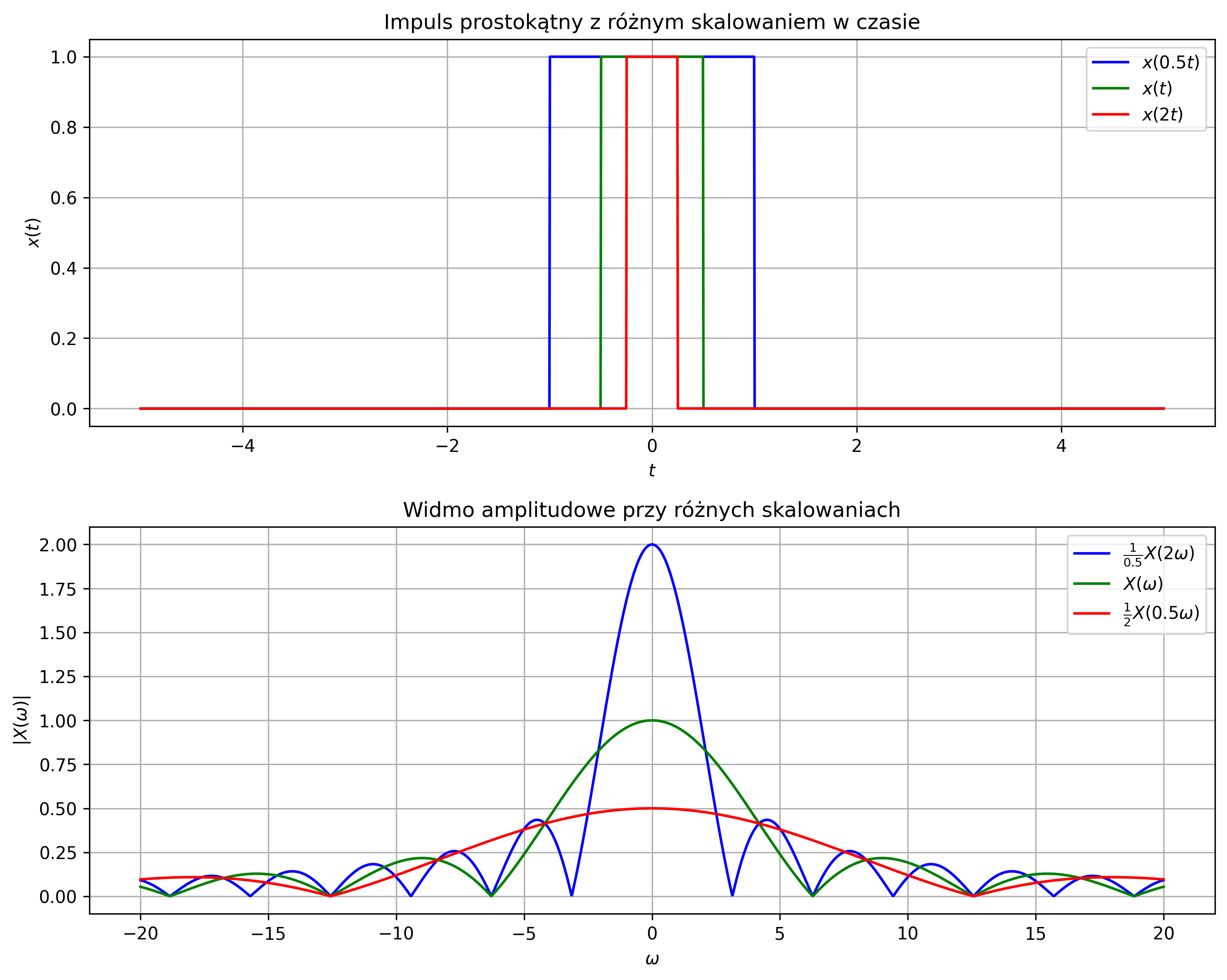
Rys. 4.9. Wykres sygnału \(\mathrm{Sinc}\) i jego widma amplitudowego w zależności od poziomu skalowania

Podobne wnioski można wyciągnąć na podstawie przebiegu impulsu prostokątnego i jego widma amplitudowego, przedstawionego na rys. 4.10. Im węższy impuls w czasie, tym szersze i niższe jest jego widmo.

Rys. 4.10. Wykres impulsu prostokątnego i jego widma amplitudowego w zależności od poziomu skalowania

Z własności transformaty Fouriera, a w szczególności z jej zachowania przy zmianie skali, wynika istotna zależność – im krócej trwa sygnał w dziedzinie czasu, tym szersze jest jego widmo w dziedzinie częstotliwości, i odwrotnie. Dlatego sygnały silnie skupione w czasie mają szerokie widmo, a sygnały o wąskim widmie muszą być rozciągnięte w czasie. Zależność tę można wyrazić ilościowo, wprowadzając odpowiednie miary „rozrzutu” sygnału:

równoważny czas trwania sygnału \(x(t)\):

\( \Delta t_x = \dfrac{1}{x(0)} \int_{-\infty}^{\infty} x(t) \, dt \)

równoważna szerokość widma \(X(\omega)\):

\( \Delta \omega_x = \dfrac{1}{X(0)} \int_{-\infty}^{\infty} X(\omega) \, d\omega \)

Iloczyn równoważnego czasu trwania sygnału i równoważnej szerokości jego widma jest ograniczony od dołu stałą wartością:

\( \Delta t_x \, \Delta \omega_x \geq \dfrac{1}{2} \)

Powyższa nierówność określana jest jako zasada nieoznaczoności w teorii sygnałów. Jeśli jedna z tych miar wzrasta, druga proporcjonalnie maleje – nie można tych miar zmniejszać jednocześnie. Równość w powyższej nierówności osiągana jest wyłącznie przez funkcję Gaussa, dlatego jest ona często wykorzystywana jako wzorzec w analizie czasowo-częstotliwościowej.

Własność splotu i mnożenia w transformat Fouriera odgrywa kluczową rolę w przetwarzaniu sygnałów za pomocą układów liniowych. Stanowi ona, że splotowi sygnałów w dziedzinie czasu odpowiada proste mnożenie ich transformat w dziedzinie częstotliwości:

\( y(t) = (x \ast h)(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) \, d\tau \quad \Rightarrow \quad Y(\omega) = X(\omega) \cdot H(\omega) \)

Dzięki temu często skomplikowaną obliczeniowo operację splotu można zastąpić łatwiejszym mnożeniem widm. Analogicznie, mnożeniu sygnałów w dziedzinie czasu odpowiada splot ich widm w dziedzinie częstotliwości:

\( y(t) = x(t) \cdot h(t) \quad \Rightarrow \quad Y(\omega) = (X \ast H)(\omega) = \int_{-\infty}^{\infty} X(\nu) H(\omega - \nu) \, d\nu \)

Jeśli sygnał \(x(t)\) o widmie \(X(\omega)\) po przejściu przez system LTI zamienia się w sygnał \(y(t)\) o widmie \(Y(\omega)\), to stosunek transformaty sygnału wyjściowego do transformaty sygnału wejściowego nazywamy transmitancją widmową:

\( G(\omega) = |G(\omega)| e^{j\varphi} \)

Wtedy, znając transmitancję widmową układu i widmo sygnału wejściowego, można łatwo wyznaczyć widmo sygnału wyjściowego:

\( Y(\omega) = G(\omega) \cdot X(\omega) \)