Podręcznik

Przykłady, w których transformata DFT dawała poprawne i przejrzyste wyniki, opierały się na starannie dobranych sygnałach wejściowych w postaci przebiegów sinusoidalnych. W takich idealnych przypadkach, częstotliwości składowych sygnału pokrywają się dokładnie z punktami na dyskretnej osi częstotliwościowej DFT, co pozwala na jednoznaczną identyfikację widmową.

W przypadku rzeczywistych sygnałów, które są próbkowane i zwykle mają złożone, nieidealne składowe częstotliwości, wyniki DFT mogą być mylące. Przyczyną tego jest między innymi niedopasowanie częstotliwości sygnału do dyskretnych częstotliwości DFT, efekt przecieku widmowego oraz ograniczona rozdzielczość częstotliwościowa. W efekcie uzyskane widmo może zawierać rozmycia, zniekształcenia i trudności w interpretacji rzeczywistych składników sygnału.

Niepoprawne próbkowanie sygnału

Dyskretną transformatę Fouriera stosuje się do sygnałów dyskretnych, o skończonej długości. Aby uzyskać poprawne wyniki, sygnał musi być odpowiednio próbkowany zgodnie z twierdzeniem Nyquista-Shannona, czyli częstotliwość próbkowania powinna być co najmniej dwukrotnie wyższa niż najwyższa częstotliwość zawarta w sygnale. Nieprzestrzeganie tej zasady prowadzi do aliasingu – zjawiska opisanego w rozdziale 3.2, w którym wyższe składowe częstotliwości „nakładają się” na niższe, co skutkuje błędną interpretacją widma. W praktyce oznacza to, że DFT nie może poprawnie rozróżnić częstotliwości.

Na rys. 4.19 pokazano przykład aliasingu w DFT – jak wyglądają widma sygnału sinusoidalnego o częstotliwości większej i mniejszej niż połowa częstotliwości próbkowania (czyli powyżej częstotliwości Nyquista). Na wykresie przedstawiono przebiegi dwóch ciągłych sygnałów sinusoidalnych o częstotliwościach \(300\) Hz i \(700\) Hz, a także próbki tych sygnałów, próbkowanych z częstotliwością \(1000\) Hz.

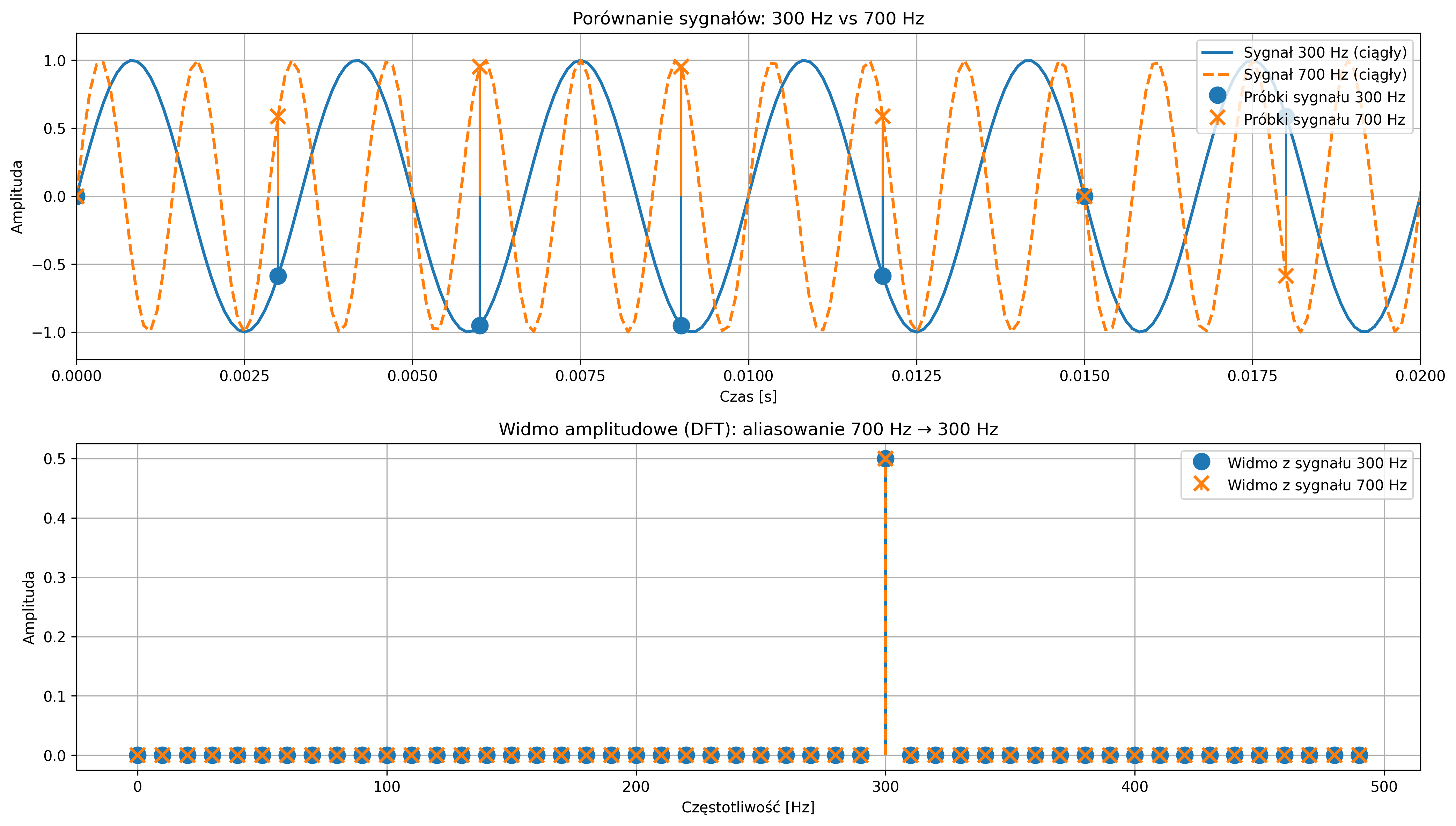
Próbki sygnału sinusoidalnego o częstotliwości \(700\) Hz nie są identyczne z próbkami sygnału \(300\) Hz – różnią się znakiem. DFT nie rozróżnia znaku częstotliwości, a więc sygnały \(300\) Hz i \(700\) Hz dają takie samo widmo amplitudowe, choć różnią się fazą. Wykresy potwierdzają, że sygnał o częstotliwości \(700\) Hz jest spróbkowany zbyt wolno. Jeśli zwiększymy częstotliwość próbkowania z \(1000\) Hz do \(2000\) Hz, to nie zaobserwujemy już aliasingu – obydwie składowe częstotliwościowe będą poprawnie zidentyfikowane (rys. 4.20).

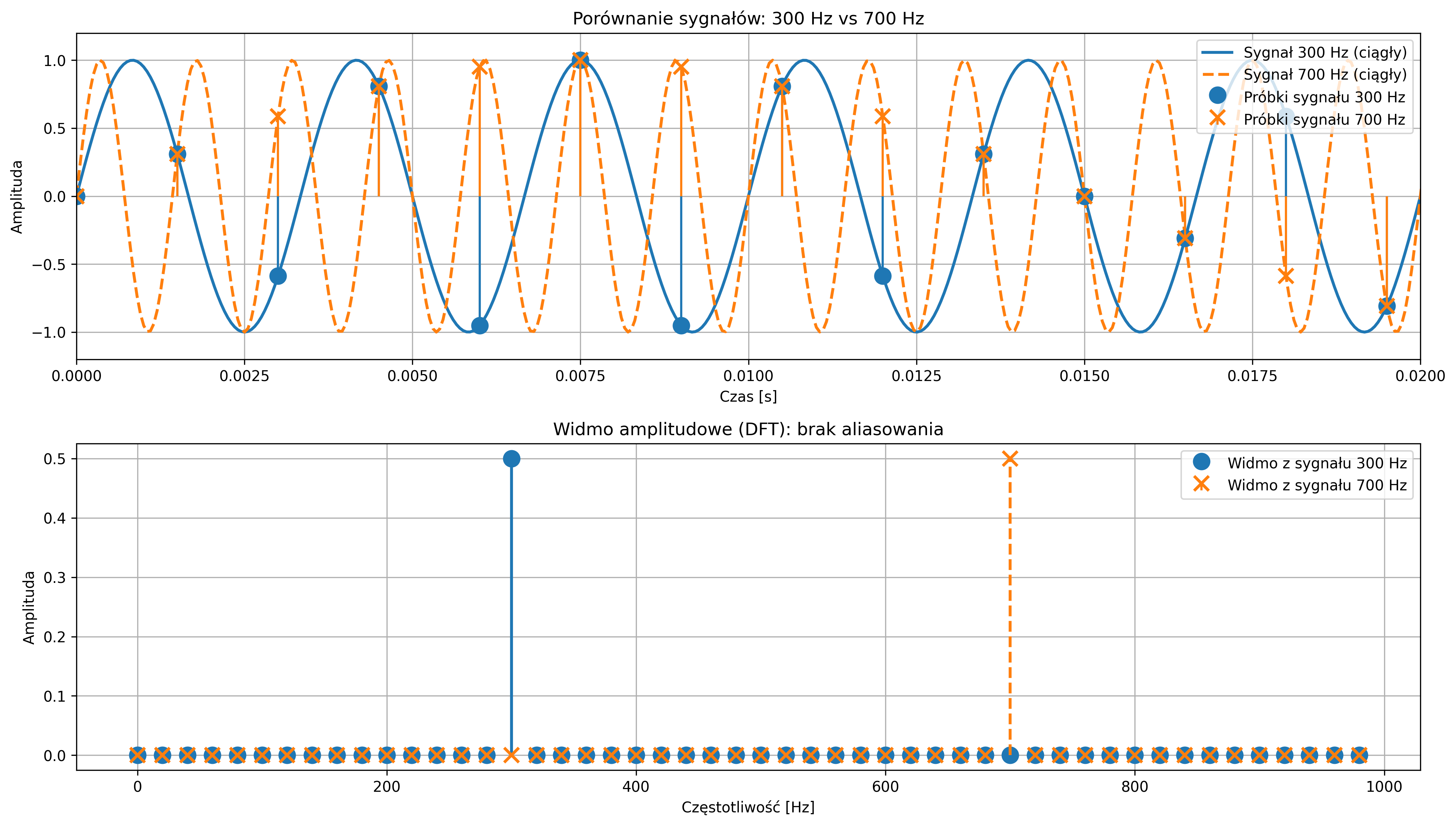
Efekt przecieku widmowego

DFT zakłada, że analizowany fragment sygnału jest okresowy, z okresem równym długości okna czasowego. Jeśli sygnał nie jest idealnie okresowy w tym oknie, w widmie pojawia się tzw. przeciek widmowy (ang. Spectral Leakage). Objawia się to rozmyciem energii sygnału na sąsiednie częstotliwości, co utrudnia dokładną identyfikację składowych widmowych. Przyczyną jest „cięcie” sygnału w czasie (zastosowanie okna prostokątnego), które w dziedzinie częstotliwości odpowiada splotowi z funkcją \(\mathrm{Sinc}\) o szerokim rozproszeniu.

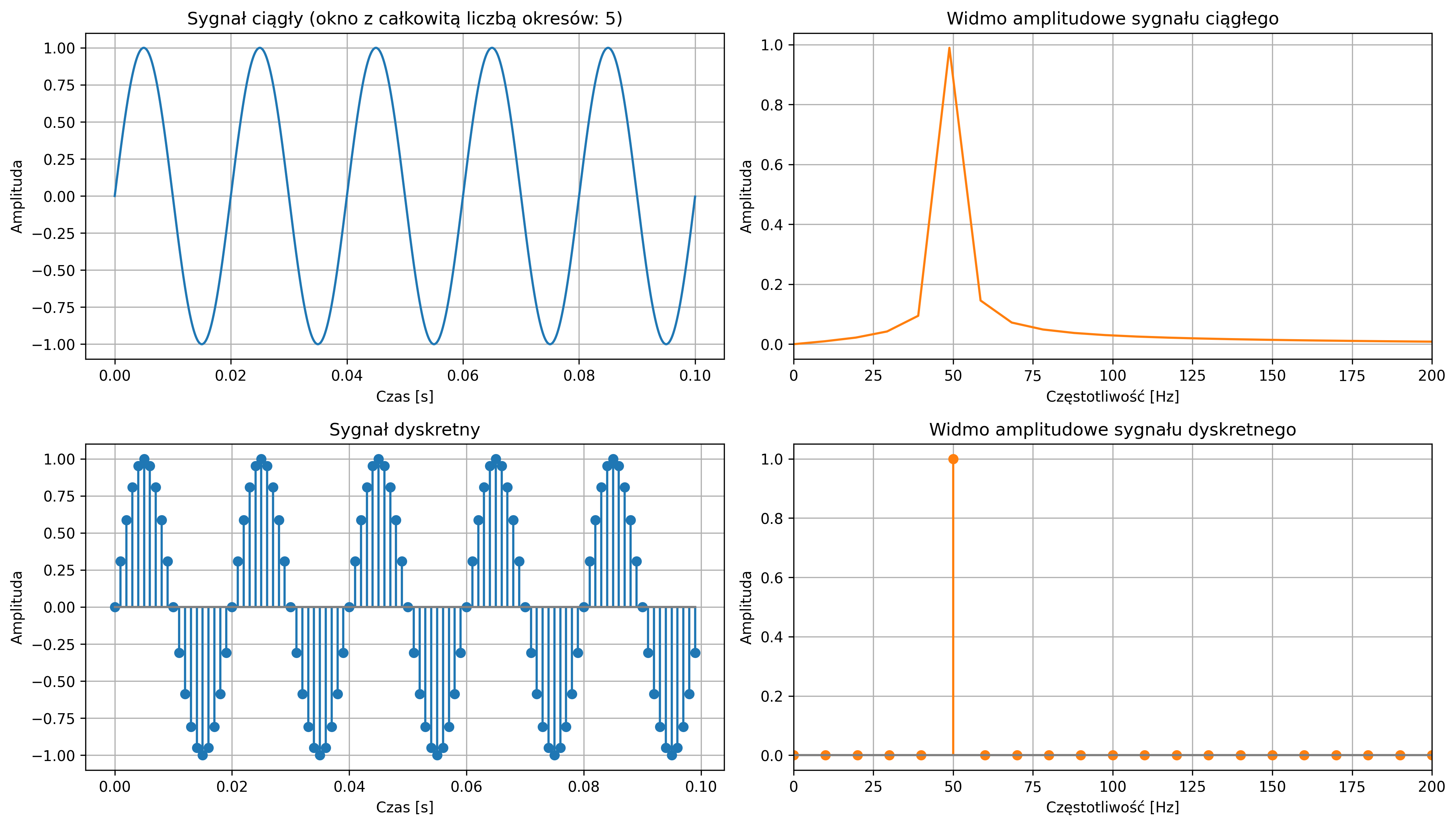
Na rys. 4.21 przedstawiono wykres sygnału sinusoidalnego o częstotliwości \(50\) Hz, który został ucięty poprzez zastosowanie funkcji okna prostokątnego. Wycięty fragment sygnału traktowany jest jako fragment reprezentujący cały, nieskończenie długi sygnał. Porównując nieskończony sygnał okresowy z sygnałem odtworzonym na podstawie wyciętego fragmentu, można zauważyć, że w wyniku zastosowania krótszego (niedopasowanego) okna analizowany sygnał nie może być już traktowany jako „czysta” sinusoida. Przeciek widmowy pojawia się, gdy granice analizowanego fragmentu (okna) „rozrywają” sygnał, czyli sygnał nie łączy się gładko na końcu okna z początkiem następnego okresu (który DFT zakłada jako kontynuację). Wtedy sygnał jest „nieciągły” na granicach okna, a nieciągłości te powodują rozmycie energii widmowej na inne częstotliwości.

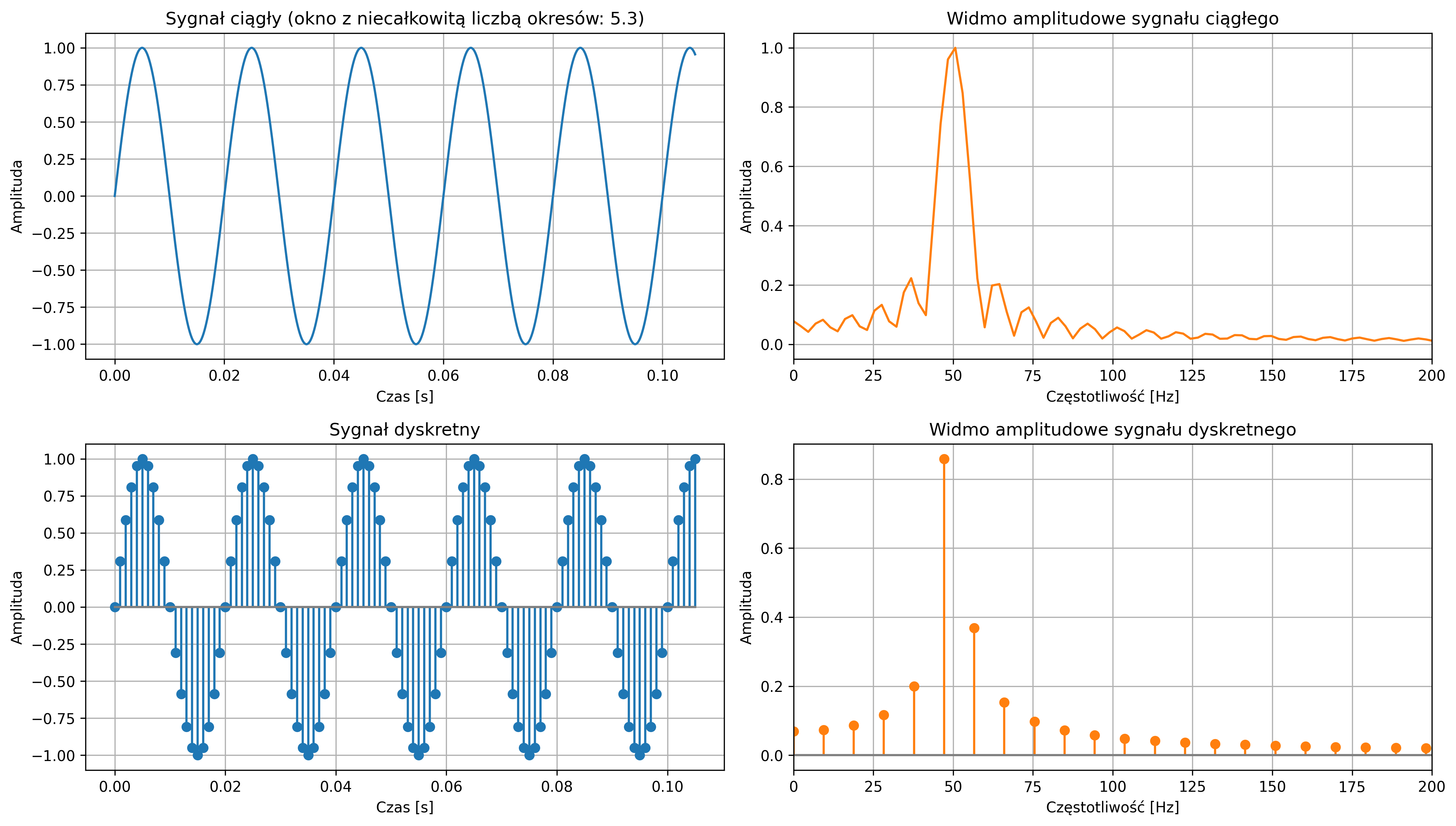
Gdy mamy dokładnie \(5\) okresów sygnału w oknie (rys. 4.22), koniec i początek sygnału idealnie się pokrywają, więc sygnał jest ciągły i okresowy z okresem długości okna – wówczas nie ma przecieku (lub jest on bardzo znikomy, ograniczony jedynie przez numeryczne niedokładności). Na wykresie amplitudowym DFT widzimy jeden prążek, który odpowiada częstotliwości wygenerowanego sygnału.

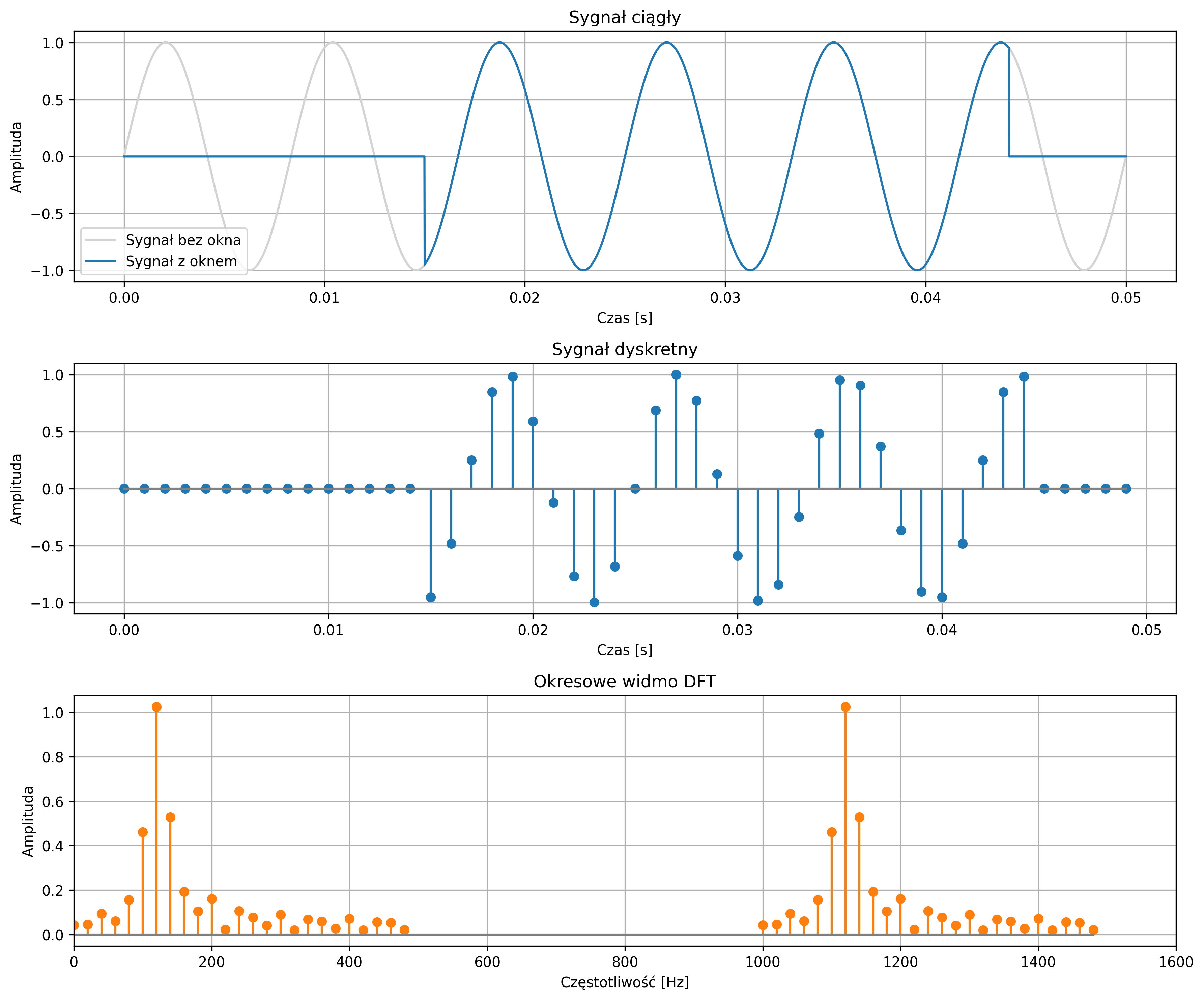
Przypomnijmy, że widmo DFT ma symetrię i zawsze jest okresowe z okresem równym częstotliwości próbkowania \( f_s = N \). Po osiągnięciu końca zakresu \(N\), widmo zaczyna się powtarzać. Dlatego, w przypadku wystąpienia przecieku, zjawisko to również będzie powtarzać się co okres \(N\) – na rys. 4.23 widmo powtarza się co \( N = f_s = 1000 \,\text{Hz} \). Dlatego, w analizie częstotliwościowej sygnału rozważamy tylko próbki w zakresie od 0 do \( \frac{N}{2} - 1 \).

W przypadku prostych sygnałów, takich jak sinusoidy, przeciek widmowy zwykle nie stanowi dużego problemu – jego efekt ogranicza się do obecności niewielkich odstępstw wokół głównego prążka widma. Jednak przy sygnałach o złożonym widmie, przecieki od wielu składowych mogą się nakładać i sumować, powodując znaczne zniekształcenia amplitudowe innych prążków.

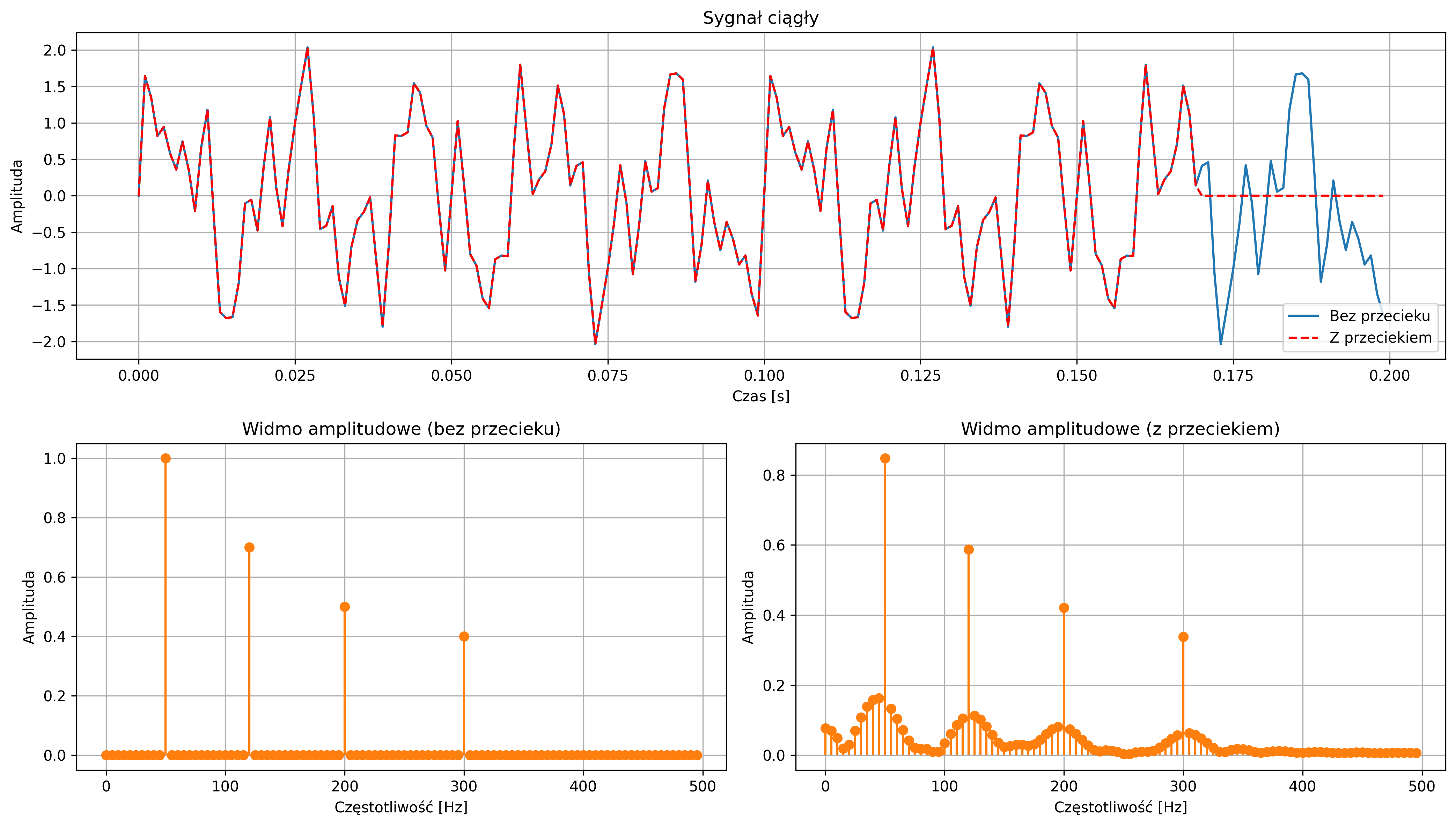
Na rys. 4.24 przedstawiono przebiegi sygnału sinusoidalnego, będącego sumą \(4\) składowych sinusoidalnych o częstotliwościach \(50\) Hz, \(120\) Hz, \(200\) Hz i \(300\) Hz. Na wykresie widmowym poprawnie wyciętego, przez okno prostokątne sygnału widać wyraźne prążki widmowe, odpowiadające składowym sygnału. Widmo sygnału uciętego w złym miejscu powoduje rozmycie prążków i zniekształcenia amplitudowe – efekt nakładających się przecieków od wielu składowych.

Maksymalny przeciek widmowy w przypadku sygnałów okresowych występuje, gdy częstotliwość analizowanego sygnału leży dokładnie w połowie odstępu pomiędzy dwiema sąsiednimi częstotliwościami widma DFT (np. \(1.5 f_s/N\)). W takiej sytuacji energia sygnału rozkłada się równomiernie na wszystkie prążki widma, a żaden z nich nie odpowiada dokładnie częstotliwości sygnału. W dziedzinie czasu sygnał nie jest wtedy okresowy w obrębie analizowanego okna, co powoduje największą możliwą nieciągłość na jego granicach, a w konsekwencji – najszersze rozmycie energii w widmie amplitudowym.

Zjawiska przecieku nie da się całkowicie uniknąć, ponieważ zawsze analizujemy skończony fragment sygnału. Istnieją jednak techniki, które pozwalają zmniejszyć skutki przecieku. W tym celu stosuje się inne funkcje okna, takie jak okna von Hanna, Hamminga, Blackmana i wiele innych. Ich wspólną cechą jest to, że wartości okna dążą do zera na jego krańcach, co łagodzi gwałtowne skoki na granicach sygnału i znacząco ogranicza przeciek widmowy.

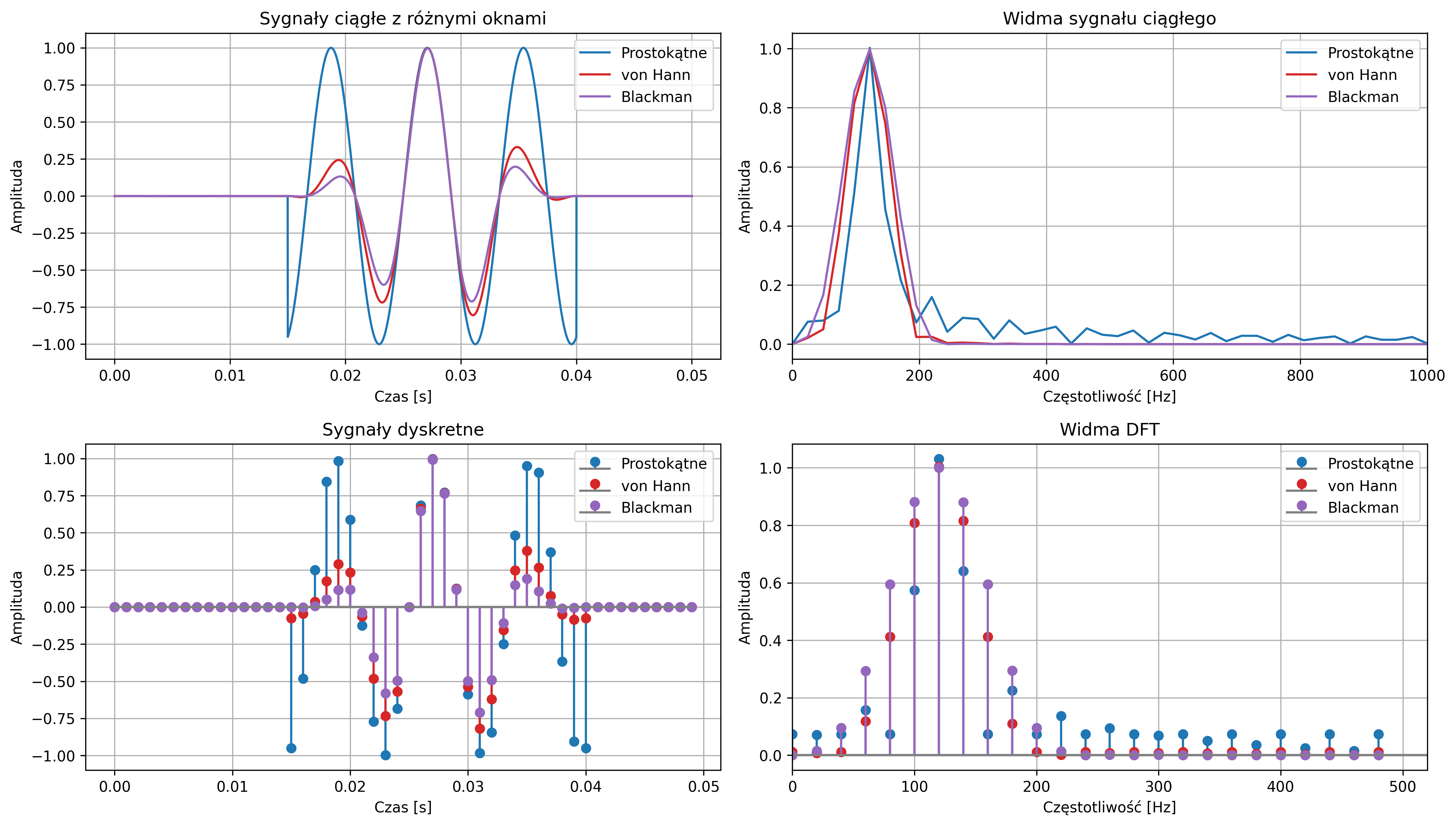
Na rys. 4.25 możemy zaobserwować, że nałożone okno von Hanna i Blackmana silniej tłumią przeciek niż okno prostokątne, ale poszerzają główny listek (prążek).

Ograniczona rozdzielczość częstotliwościowa DFT

Przypomnijmy, że w analizie sygnałów przy użyciu DFT istnieje fundamentalny kompromis między rozdzielczością czasową a częstotliwościową. Zwiększając długość analizowanego fragmentu sygnału (większe \(N\)) uzyskujemy lepszą rozdzielczość częstotliwościową, ponieważ prążki w widmie są gęściej rozmieszczone i umożliwiają dokładniejsze rozróżnienie częstotliwości. Jednak jednocześnie pogarsza się rozdzielczość czasowa – analiza dotyczy dłuższego przedziału czasowego, przez co trudniej określić, kiedy dokładnie w sygnale wystąpiły pewne zdarzenia. Odwrotnie, krótsze okna analizy pozwalają lepiej śledzić zmiany w czasie, ale ograniczają precyzję w dziedzinie częstotliwości.

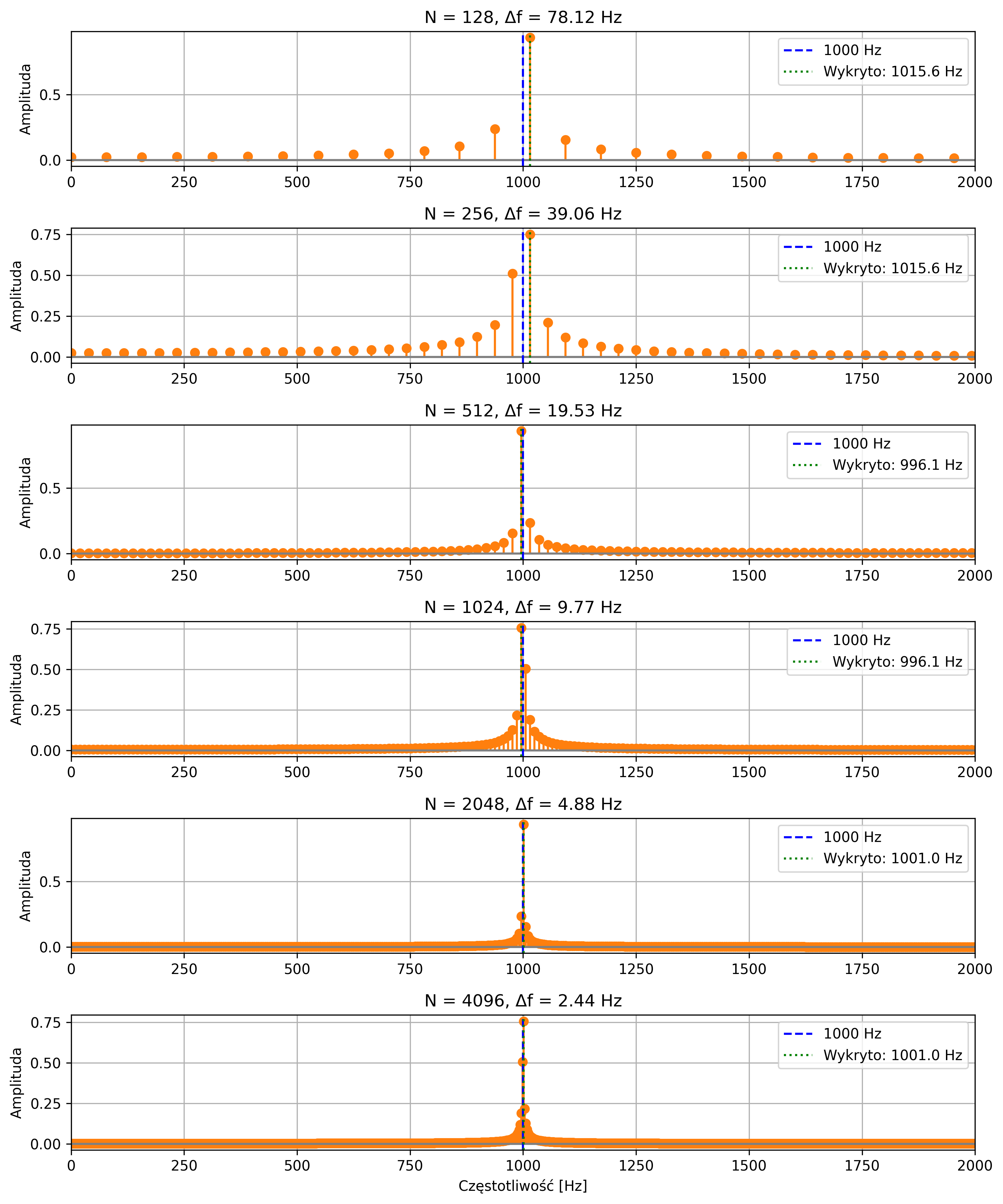
Znaczenie rozdzielczości częstotliwościowej zostało zilustrowane na rys. 4.26. Dla wygenerowanego sygnału sinusoidalnego o częstotliwości \(1000\) Hz, chcemy wykryć częstotliwość prążka widmowego z wykorzystaniem DFT o rozmiarach \(N = 128, 256, 512, 1024, 2048, 4096\).