Podręcznik

Sygnał losowy można rozumieć jako proces, w którym wartość chwilowa w danym momencie czasu nie jest z góry określona, lecz opisana w sposób probabilistyczny. Aby to formalnie ująć, każdą próbkę sygnału w chwili \( t \) traktujemy jako zmienną losową.

Zmienna losowa to wielkość, która przyjmuje wartości liczbowe w sposób losowy (stochastyczny), ale z góry określonym prawdopodobieństwem. Jeżeli zamiast jednej zmiennej losowej rozpatrujemy rodzinę zmiennych losowych uporządkowanych w czasie, otrzymujemy proces losowy \( X(t) \). Każda chwila czasu \( t=t_0 \) odpowiada wówczas innej zmiennej losowej \( X(t_0) \), a ich zbiór opisuje cały sygnał losowy. W praktyce proces losowy można traktować jako zbiór wielu możliwych realizacji przebiegu sygnału, z których każda jest jedną realizacją tego procesu. Taki opis umożliwia przejście od analizy chwilowych wartości sygnału do badania jego własności statystycznych, uśrednionych w czasie lub po realizacjach.

Klasycznym przykładem sygnałów o charakterze losowym są sygnały biomedyczne, takie jak EEG (elektroencefalograficzne) oraz EMG (elektromiograficzne). EEG rejestruje bioelektryczną aktywność mózgu przy pomocy elektrod umieszczonych na powierzchni skóry głowy. Charakteryzuje się bardzo niską amplitudą i dużą zmiennością, oraz charakterystycznymi rytmami częstotliwościowymi, związanymi z określonymi stanami pracy mózgu (np. rytmy alfa, beta, theta). Z kolei EMG odzwierciedla aktywność elektryczną mięśni szkieletowych, powstającą w wyniku sumowania potencjałów czynnościowych włókien mięśniowych. Jest to sygnał o wyższych amplitudach niż EEG, a jego przebieg zależy od rodzaju i siły skurczu mięśnia. Oba sygnały traktuje się jako procesy losowe, gdyż ich przebieg chwilowy jest trudny do przewidzenia, natomiast możliwe jest badanie ich statystycznych własności.

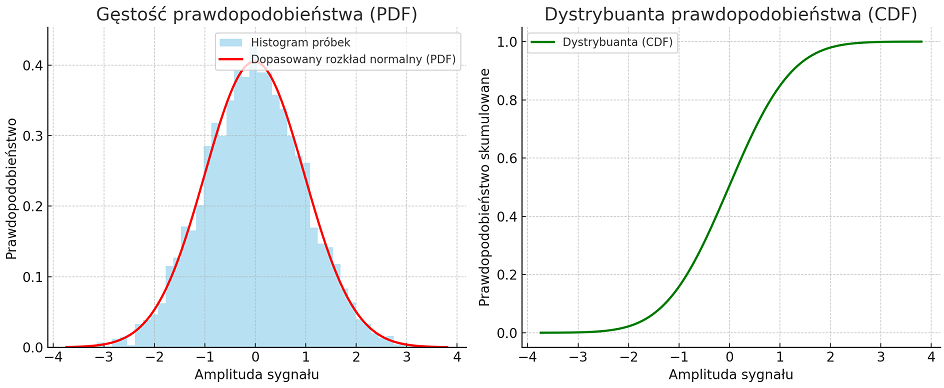
Opisem probabilistycznym zmiennej losowej \( X(t_0) \) w chwili \( t=t_0 \) jest m.in. dystrybuanta (CDF, ang. Cumulative Distribution Function), którą definiuje się jako:

czyli prawdopodobieństwo, że w chwili \( t_0 \) amplituda sygnału nie przekroczy wartości \( x \).

Dystrybuanta opisuje, jak rozkładają się wartości amplitud sygnału losowego w danym momencie czasu. Dzięki temu można np. wyznaczać progi detekcji sygnału, badać rozkład amplitud w sygnałach biomedycznych czy porównywać różne stany organizmu (np. sen vs. czuwanie w EEG) w kategoriach zmian rozkładów prawdopodobieństwa.

Dystrybuanta daje pełny opis rozkładu wartości sygnału w wersji skumulowanej – informuje o łącznym prawdopodobieństwie wystąpienia wszystkich wartości mniejszych od wartości \( x \). W praktyce, wygodniej jest analizować nie tyle wartości skumulowane, co dokładne prawdopodobieństwo pojawienia się amplitud w pobliżu danej wartości. Tę rolę spełnia funkcja gęstości prawdopodobieństwa (PDF, ang. Probability Density Function):

czyli pochodna dystrybuanty. Funkcja gęstości prawdopodobieństwa pozwala wskazać, które amplitudy sygnału występują najczęściej, a które są rzadkie, co ma kluczowe znaczenie w analizie różnych procesów losowych.