W analizie procesów losowych często nie znamy rozkładu prawdopodobieństwa ani rzeczywistych wartości ich parametrów (np. wartości oczekiwanej, wariancji). Dlatego korzystamy z estymacji, czyli wyznaczania przybliżonych wartości parametrów na podstawie próbek sygnału.
Teoretyczna wartość oczekiwana procesu w czasie ciągłym określona jest jako:
\( \mu_{X(t)} = E[X] = \int_{-\infty}^{\infty} x\,f_X(x)\,dx \)
gdzie funkcja gęstości prawdopodobieństwa \( f_{X(t)}(x) \) zależy od wartości zmiennej losowej \( x \) w danym czasie \( t \). Jest to uśrednienie po wielu możliwych realizacjach procesu. W praktyce dysponujemy jedną realizacją sygnału \( X(t) \) obserwowaną w czasie \([0, T]\). Dlatego definiujemy średnią czasową:
\( \overline{X} = \frac{1}{T} \int_{0}^{T} X(t)\,dt \)
Jeżeli proces jest stacjonarny w szerokim sensie i ergodyczny względem wartości średniej, to średnia wyznaczona na podstawie jednej realizacji w czasie jest równa średniej teoretycznej:
\( \mu_{X(t)} = \lim_{T \to \infty} \frac{1}{T} \int_{0}^{T} X(t)\,dt \)
Dla procesu losowego w czasie ciągłym, teoretyczna wariancja określona jest jako:
\( \sigma^2_{X(t)} = E\big[(X(t)-\mu_X(t))^2\big] = \int_{-\infty}^{\infty} (x-\mu_X(t))^2 f_{X(t)}(x)\,dx \)
Jeżeli proces jest stacjonarny w szerokim sensie oraz ergodyczny względem wartości średniej i autokorelacji, to wariancja wyznaczona na podstawie jednej realizacji w czasie jest równa wariancji teoretycznej:
\( \sigma_X^2 = \lim_{T \to \infty} \frac{1}{T} \int_{0}^{T} \big(X(t) - \mu_X\big)^2\,dt \)
W analizie rzeczywistych sygnałów losowych, proces w czasie ciągłym \( X(t) \) jest obserwowany jedynie w dyskretnych chwilach czasu:
\( t_n = nT,\quad n = 0,1,\ldots,N-1 \)
gdzie \( T \) oznacza okres próbkowania, a \( f_s = \frac{1}{T} \) to częstotliwość próbkowania. W wyniku próbkowania otrzymujemy proces dyskretny:
\( X[n] = X(t_n) = X(nT) \)
Jeżeli proces \( X[n] \) jest stacjonarny w szerokim sensie i ergodyczny względem wartości średniej i autokorelacji, to jego własności statystyczne można oszacować na podstawie jednej realizacji:
\( \hat{\mu}_{X[n]} = \frac{1}{N} \sum_{n=0}^{N-1} X[n] \)
\( \hat{\sigma}^2_{X[n]} = \frac{1}{N-1} \sum_{n=0}^{N-1} \big(X[n] - \hat{\mu}_{X[n]}\big)^2 \)
Wartości te stanowią estymatory wartości oczekiwanej i wariancji procesu losowego \( X[n] \). W praktyce oznacza to, że do wyznaczenia średniej procesu i rozrzutu procesu wokół średniej nie potrzeba wielu realizacji – wystarczy jedna dostatecznie długa obserwacja w czasie. Jest to warunek umożliwiający analizę widmową procesów losowych.
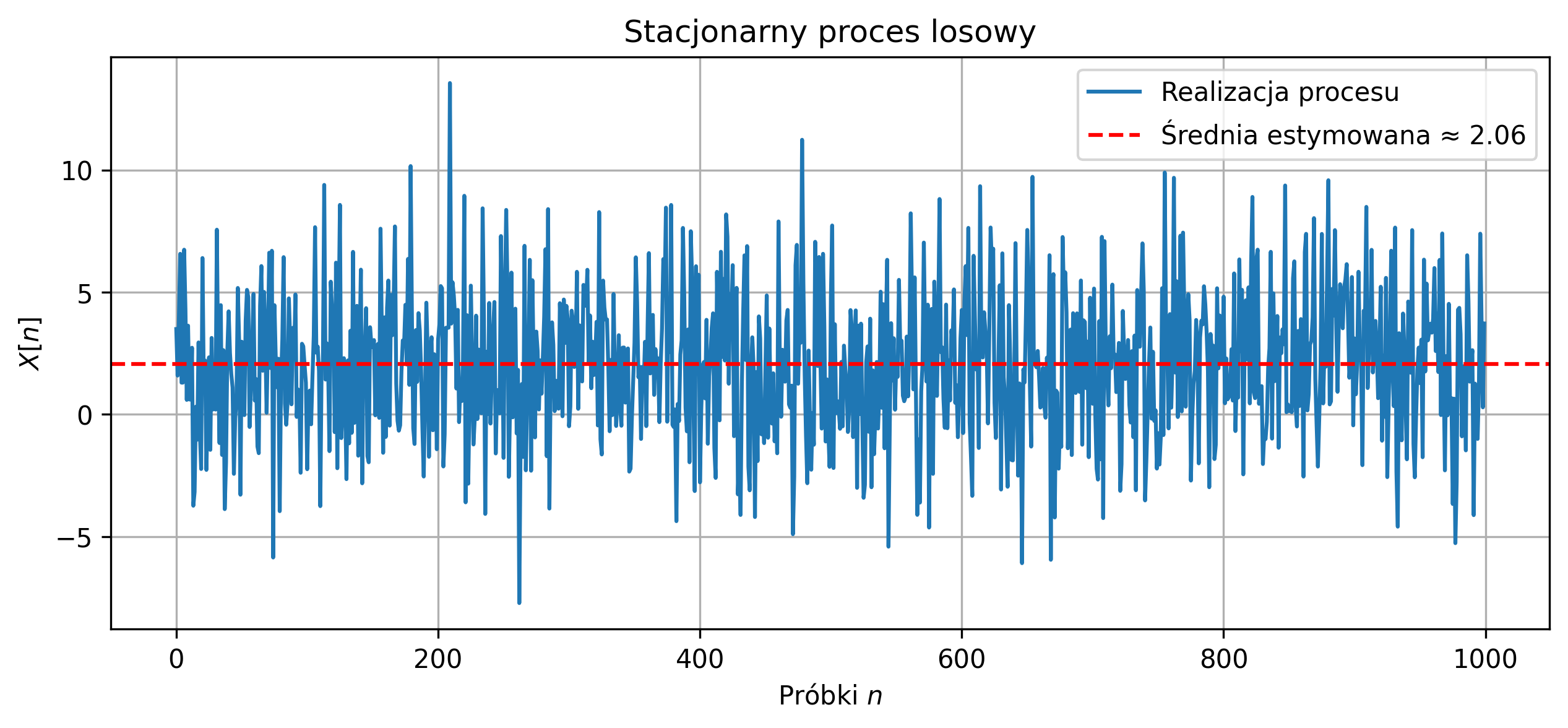
Na rysunku 5.6 przedstawiono przebieg jednej realizacji stacjonarnego procesu gaussowskiego \( N(2,3^2) \). Dla tej realizacji dokonano estymacji wartości oczekiwanej oraz wariancji procesu. Estymowana wartość oczekiwana \( \hat{\mu}_{X} \approx 2.06 \) odpowiada w przybliżeniu wartości teoretycznej \( \mu = 2 \). W przypadku estymatora wariancji \( \hat{\sigma}^2_{X} \) otrzymano wartość \(8.63\), co również jest zbliżone do wartości teoretycznej \( \sigma^2 = 9 \).
Rys. 5.6. Przebieg jednej realizacji stacjonarnego procesu gaussowskiego wraz z estymowaną wartością oczekiwaną
Nieznaczne różnice w otrzymanych wartościach estymatorów wynikają z faktu, że dysponujemy tylko jedną, skończoną realizacją procesu losowego, a estymatory są obliczane na podstawie ograniczonej liczby próbek.
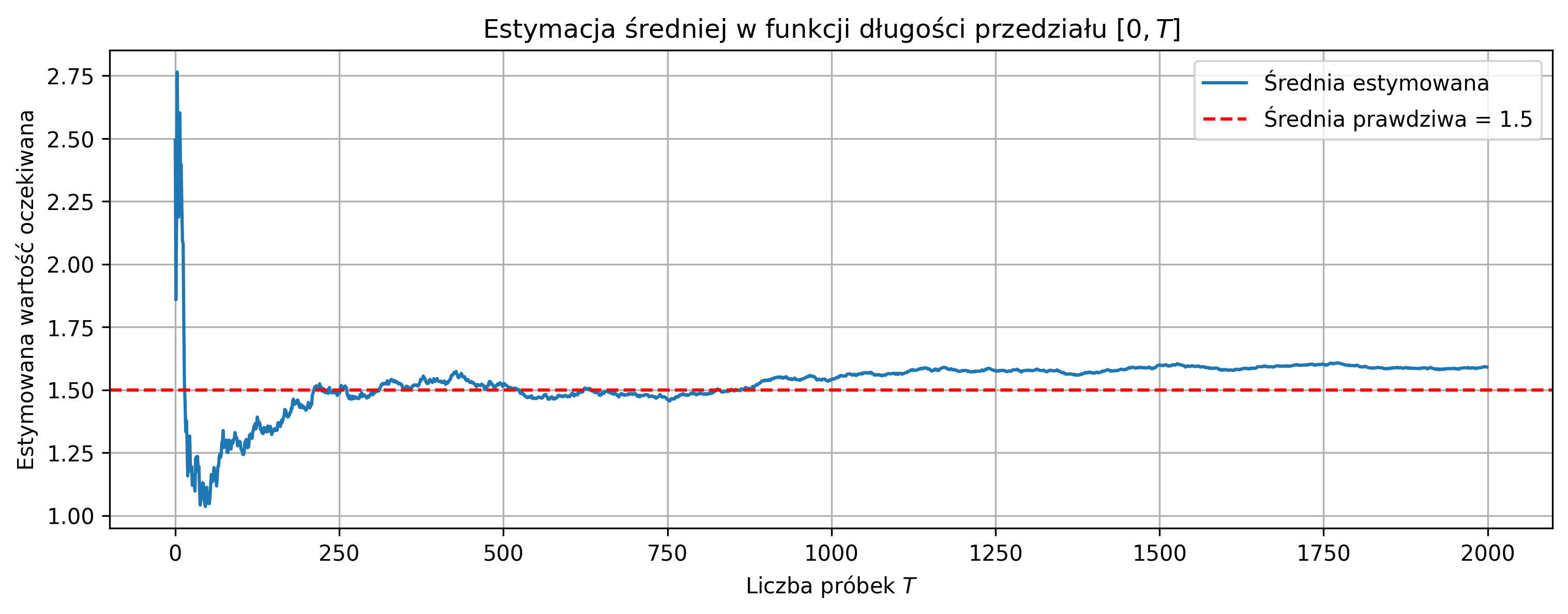
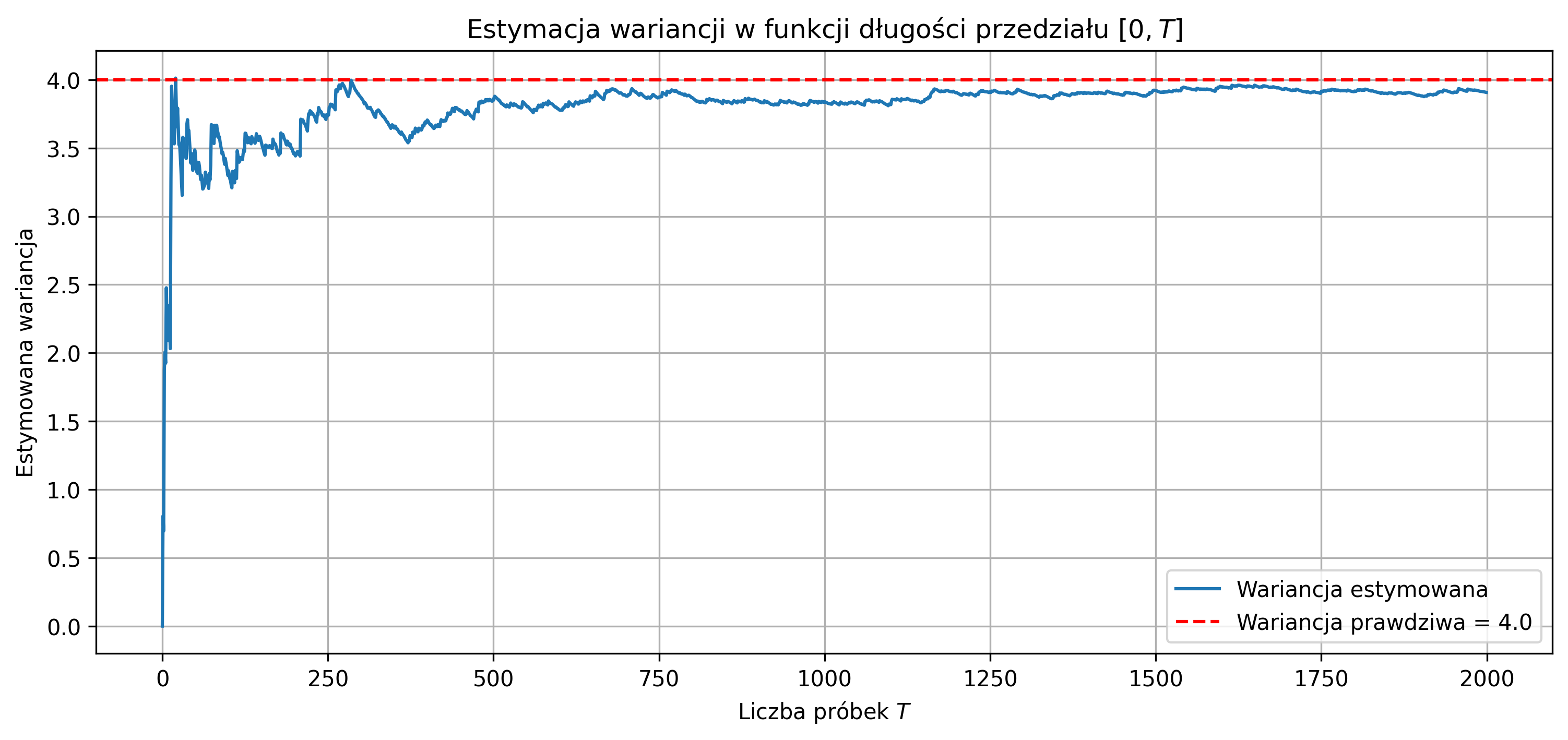
Wraz ze wzrostem liczby próbek estymatory zbliżają się do wartości teoretycznych (efekt ergodyczności procesu stacjonarnego), co zostało zilustrowane na rys. 5.7 i 5.8. Wykresy przedstawiają estymowaną wartość oczekiwaną i wariancję w funkcji długości \( T \) przedziału obserwacji sygnału dla jednej realizacji stacjonarnego procesu gaussowskiego \( N(1.5,2^2) \). Czerwona przerywana linia oznacza wartości teoretyczne – odpowiednio \( \mu = 1.5 \) i \( \sigma^2 = 4 \). Dla małych wartości \( T \) estymatory są bardziej zmienne, natomiast dla dłuższych przedziałów obserwacji sygnału estymatory zbliżają się do wartości teoretycznych.
Rys. 5.7. Estymowana wartość oczekiwana \( \hat{\mu}_X \) w funkcji długości \( T \) przedziału obserwacji sygnału
Rys. 5.8. Estymowana wariancja \( \hat{\sigma}^2_X \) w funkcji długości \( T \) przedziału obserwacji sygnału
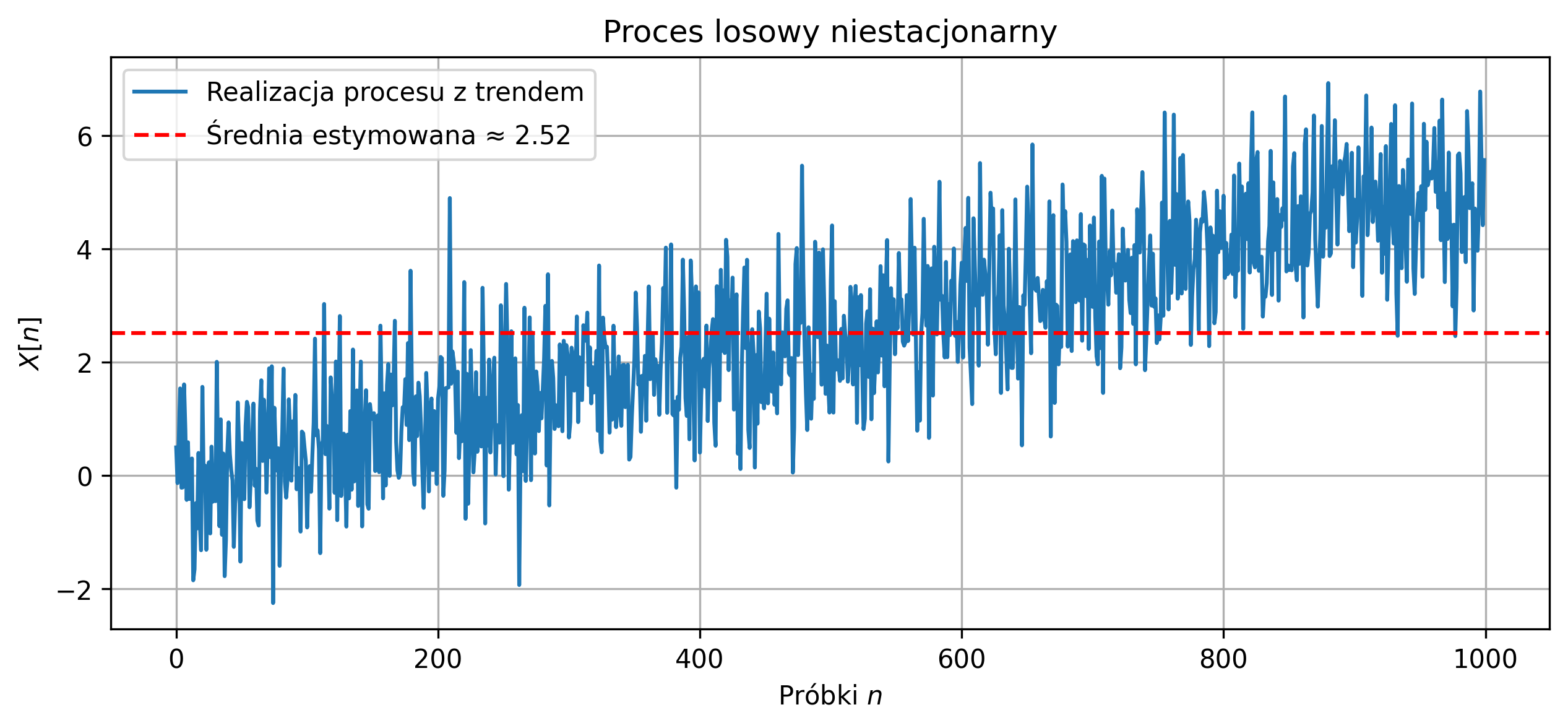
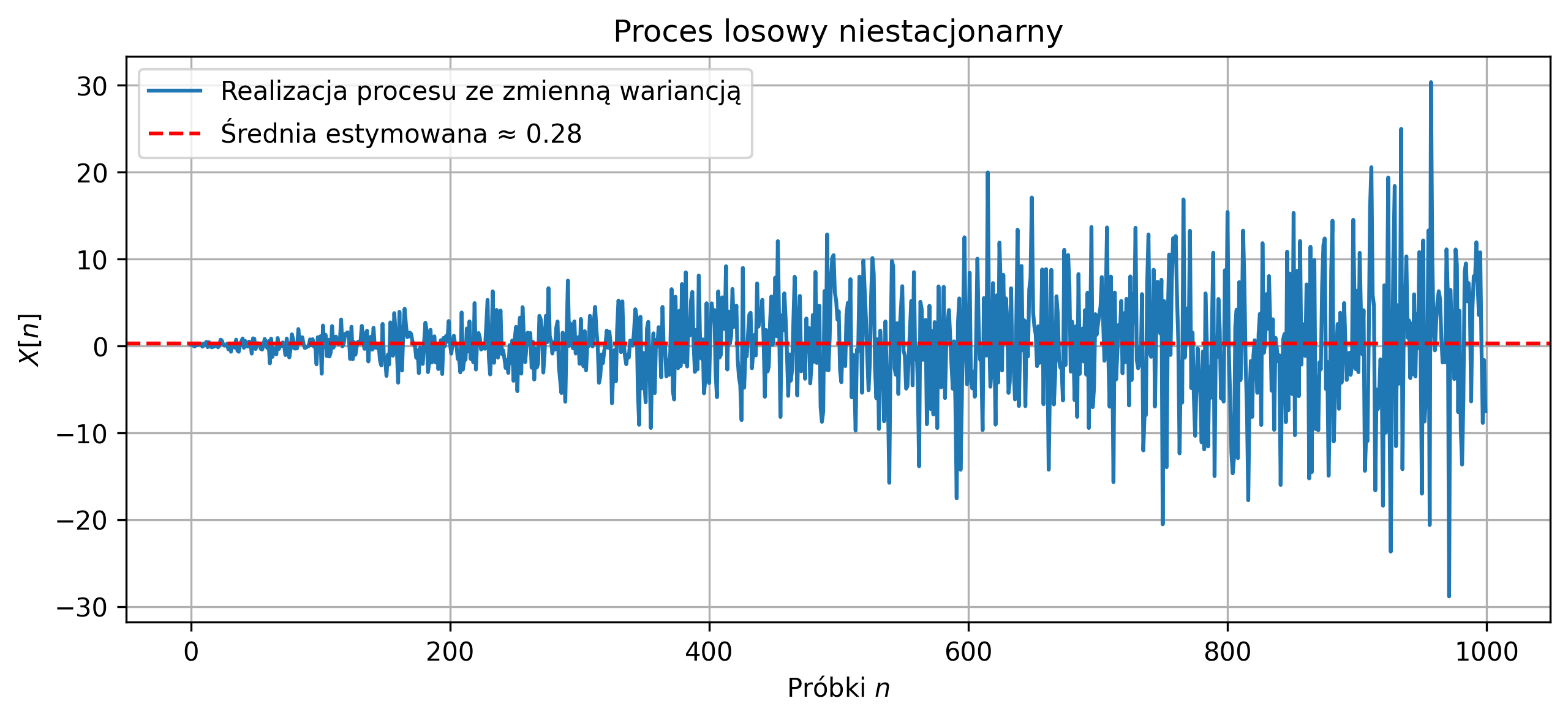
W przypadku, gdy założenia stacjonarności i ergodyczności są złamane, klasyczne estymatory wartości oczekiwanej i wariancji z jednej realizacji nie powinny być stosowane. Na rys. 5.9 i 5.10 zilustrowano proces z trendem średniej – średnia rośnie w czasie, stąd estymator z jednej realizacji nie odzwierciedla wartości typowej procesu, bo proces nie jest stacjonarny. Drugi proces ma zmienną wariancję w czasie (\( \hat{\sigma}^2_X \approx 33.28 \)), więc estymator wariancji z jednej realizacji jest zawodny. Zauważmy, że linia średniej estymowanej nie leży w „środku” sygnału przez cały czas.
Rys. 5.9. Przebieg jednej realizacji procesu losowego z rosnącym trendem liniowym
Rys. 5.10. Przebieg jednej realizacji procesu losowego o zmiennej w czasie wariancji
Z pojęciem wartości oczekiwanej związana jest teoretyczna funkcja autokorelacji, która opisuje zależność pomiędzy wartościami procesu losowego \( X(t) \) w dwóch różnych chwilach czasu \( t \) oraz \( t+\tau \). W przypadku procesu w czasie ciągłym definiuje się ją jako wartość oczekiwaną iloczynu:
\( R_X(t, t+\tau) = E\big[X(t)\,X(t+\tau)\big] \)
Dla procesu stacjonarnego w szerokim sensie funkcja ta zależy jedynie od przesunięcia \( \tau \), a nie od konkretnego momentu \( t \):
\( R_X(\tau) = E\big[X(t)\,X(t+\tau)\big] \)
Jeżeli proces jest dodatkowo ergodyczny względem autokorelacji, to funkcję tę można oszacować z jednej realizacji procesu, uśredniając iloczyny przesuniętych wartości w czasie:
\( \hat{R}_X(\tau) = \lim_{T \to \infty} \frac{1}{T} \int_{0}^{T} X(t)\,X(t+\tau)\,dt \)
Dla procesu dyskretnego \( X[n] \) funkcja autokorelacji ma postać:
\( R_X[k] = E\big[X[n]\;X[n+k]\big] \)
a jej estymator z jednej realizacji (dla \( N \) próbek) zapisuje się jako:
\( \hat{R}_X[k] = \frac{1}{N-k} \sum_{n=0}^{N-1-k} X[n]\,X[n+k],\quad k = 0,1,\ldots,N-1 \)
W praktyce, gdy wartość oczekiwana procesu nie jest znana, stosuje się estymator funkcji autokorelacji w postaci:
\( \hat{R}_X[k] = \frac{1}{N-k} \sum_{n=0}^{N-1-k} \big(X[n]-\hat{\mu}\big)\big(X[n+k]-\hat{\mu}\big) \)
gdzie \(\hat{\mu}\) jest estymowaną wartością średnią.
Wartość \( \hat{R}_X[0] \) odpowiada wariancji sygnału:
\( \hat{R}_X[0] = \hat{\sigma}^2_X \)
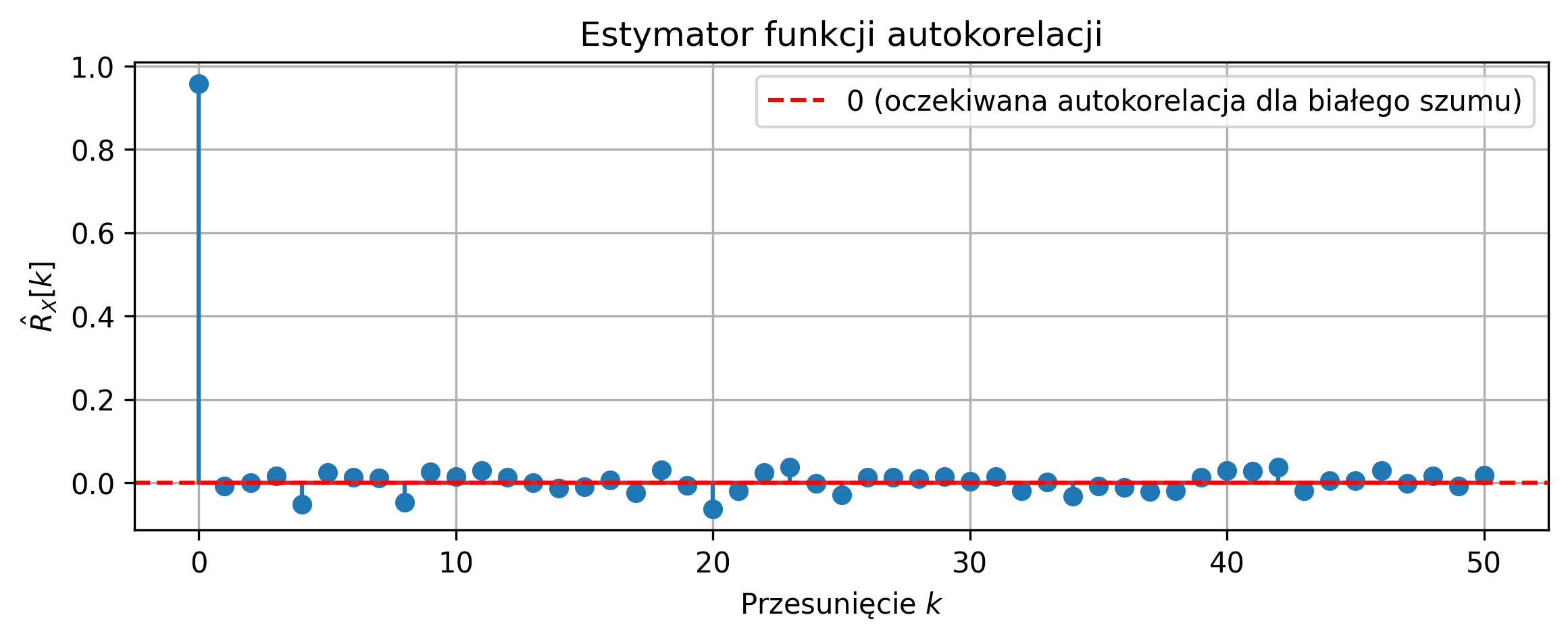
Na rys. 5.11 przedstawiono przebieg jednej realizacji stacjonarnego procesu gaussowskiego \( N(0,1) \). Dla tej realizacji dokonano estymacji funkcji autokorelacji. Dla białego szumu autokorelacja dla \( k = 0 \) jest w przybliżeniu równa wariancji \( \sigma^2 = 1 \), zaś autokorelacja dla \( k > 0 \) jest w przybliżeniu równa \(0\). Widoczny jest efekt ergodyczności – z jednej realizacji można oszacować funkcję autokorelacji procesu stacjonarnego.
Rys. 5.11. Estymator funkcji autokorelacji dla jednej realizacji białego szumu
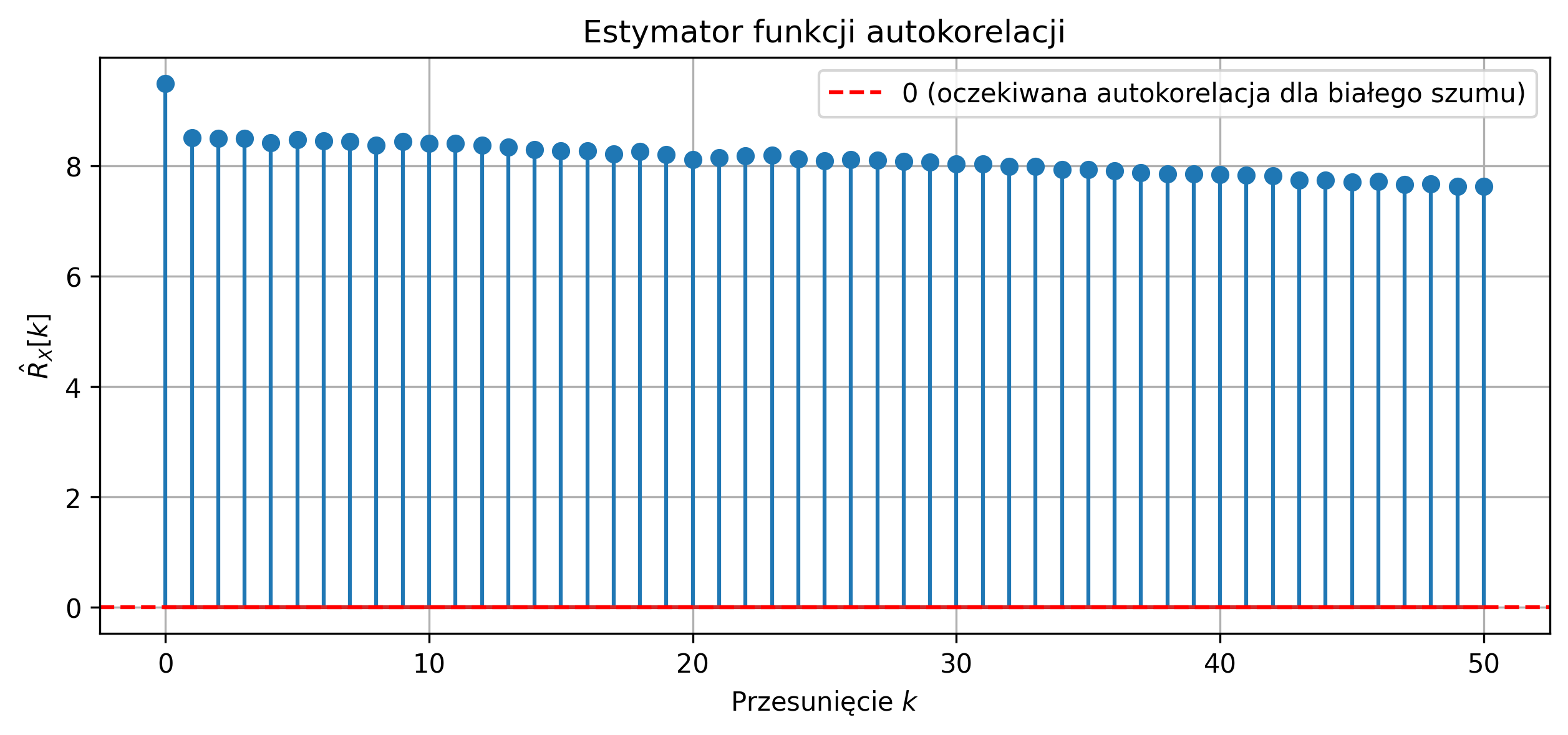
Dla niestacjonarnego lub nieergodycznego procesu estymacja autokorelacji z jednej realizacji jest zawodna (rys. 5.12). Estymator autokorelacji z jednej realizacji procesu o rosnącym trendzie daje duże dodatnie wartości dla przesunięć \( k > 0 \), co nie odpowiada teoretycznej autokorelacji procesu stacjonarnego.
Rys. 5.12. Estymator funkcji autokorelacji dla jednej realizacji niestacjonarnego procesu
Autokorelacja uwzględnia zarówno średnią, jak i zmienność sygnału, natomiast kowariancja mierzy zależności między próbkami po odjęciu wartości średniej, pokazując wyłącznie zmienną część procesu. Dla procesu losowego \( X(t) \) funkcja kowariancji określa zależność liniową między wartościami procesu w dwóch różnych chwilach \( t_1 \) i \( t_2 \):
\( C_{XX}(t_1, t_2) = E\big[(X(t_1) - \mu_X(t_1))(X(t_2) - \mu_X(t_2))\big] \)
gdzie \( \mu_X(t) = E[X(t)] \) to wartość oczekiwana procesu. Dla procesu stacjonarnego w szerokim sensie kowariancja zależy tylko od przesunięcia czasowego \( \tau = t_2 - t_1 \):
\( C_{XX}(\tau) = E\big[(X(t) - \mu_X)(X(t+\tau) - \mu_X)\big] \)
Dla dyskretnego procesu stacjonarnego i ergodycznego kowariancję można oszacować na podstawie jednej realizacji \( X[n] \):
\( \hat{C}_{XX}[k] = \frac{1}{N-k} \sum_{n=0}^{N-1-k} \big(X[n]-\bar{X}\big)\big(X[n+k]-\bar{X}\big),\quad k = 0,1,\dots,M \)
gdzie \( \bar{X} = \frac{1}{N} \sum_{n=0}^{N-1} X[n] \) to średnia z jednej realizacji, \( N \) jest liczbą próbek, a \( M \) to maksymalne przesunięcie. Dla białego szumu gaussowskiego:
\( \hat{C}_{XX}[0] \approx \sigma^2,\quad \hat{C}_{XX}[k] \approx 0 \ \text{dla}\ k > 0 \)
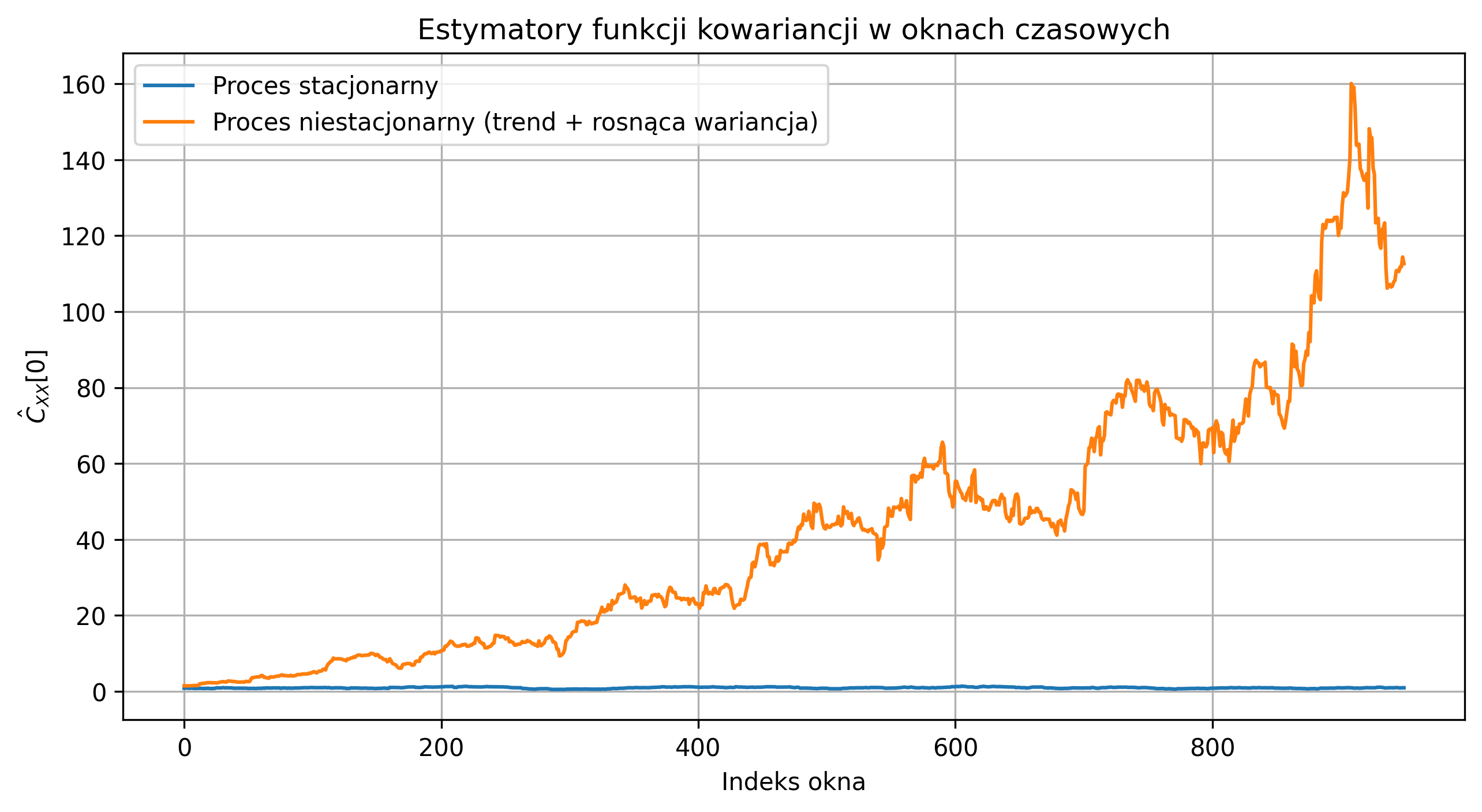
Na rys. 5.13 przedstawiono estymatory funkcji kowariancji obliczonej w przesuwanych oknach czasowych dla jednej realizacji sygnału. Oś pozioma przedstawia numer okna, czyli pozycję początkową przesuwającego się fragmentu sygnału o długości \(50\). Oś pionowa pokazuje wartość estymowanej kowariancji \( \hat{C}_{XX}[0] \) w każdym oknie.
Rys. 5.13. Estymatory funkcji kowariancji dla jednej realizacji stacjonarnego i niestacjonarnego procesu
Dla procesu stacjonarnego kowariancja oscyluje wokół stałej wartości – estymator \( \hat{C}_{XX}[k] \) jest wiarygodny i pozwala na oszacowanie funkcji autokorelacji oraz widma sygnału. Natomiast dla procesu niestacjonarnego (trend i rosnąca wariancja) widać wyraźny wzrost kowariancji w czasie, co ilustruje niestacjonarność sygnału i zawodność estymatora z jednej realizacji.
Estymacja kowariancji jest podstawą analizy widmowej sygnałów losowych, ponieważ funkcja autokorelacji jest bezpośrednio związana z gęstością widmową sygnału (poprzez transformację Fouriera), która zostanie omówiona w rozdziale 5.4.