Podręcznik

Wygenerować trzy sygnały dyskretne o długości \( N = 500 \):

• sygnał harmoniczny:
  \( x_1[n] = \cos(5 t_n), \)
• sygnał harmoniczny z szumem gaussowskim:

  \( x_2[n] = \cos(5 t_n) + 0.5\, w[n] \),  gdzie \( w[n] \sim \mathcal{N}(0,1) \),

• biały szum:
  \( x_3[n] = v[n],\; v[n] \sim N(0,1). \)

Na wspólnym wykresie czasowym przedstawić przebiegi trzech sygnałów. Na oddzielnym wykresie narysować ich znormalizowane funkcje autokorelacji. Jak zmienia się kształt funkcji autokorelacji po dodaniu szumu do sygnału harmonicznego? Dlaczego autokorelacja białego szumu ma maksimum w punkcie zerowym i szybko wygasa? Jakie cechy autokorelacji pozwalają odróżnić sygnał deterministyczny od stochastycznego?

import numpy as np
import matplotlib.pyplot as plt

# Parametry
N = 500
t = np.linspace(0, 2*np.pi, N)
np.random.seed(0)  # dla powtarzalności wyników

# Generacja sygnałów
cos_signal = np.cos(5*t)                 # czysty kosinus
noisy_signal = cos_signal + 0.5*np.random.randn(N)  # kosinus + biały szum
white_noise = np.random.randn(N)         # sam biały szum

# Funkcja znormalizowanej autokorelacji
def normalized_correlation(x, y=None):
    if y is None:
        y = x
    corr = np.correlate(x - np.mean(x), y - np.mean(y), mode='full')
    corr /= (np.std(x) * np.std(y) * len(x))
    return corr

# Obliczamy korelacje
corr_cos = normalized_correlation(cos_signal)
corr_noisy = normalized_correlation(noisy_signal)
corr_noise = normalized_correlation(white_noise)
lags = np.arange(-N+1, N)

# Wykres sygnałów
plt.figure(figsize=(12,8))

plt.subplot(2,1,1)
plt.plot(t, cos_signal, label='Kosinus')
plt.plot(t, noisy_signal, label='Kosinus + biały szum', alpha=0.7)
plt.plot(t, white_noise, label='Biały szum', alpha=0.5)
plt.title('Sygnały w czasie')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.legend()
plt.grid(True)

# Wykres autokorelacji
plt.subplot(2,1,2)
plt.plot(lags, corr_cos, label='Kosinus')
plt.plot(lags, corr_noisy, label='Kosinus + biały szum', alpha=0.7)
plt.plot(lags, corr_noise, label='Biały szum', alpha=0.5)
plt.title('Znormalizowana autokorelacja')
plt.xlabel('Opóźnienie [próbki]')
plt.ylabel('Autokorelacja')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()
   

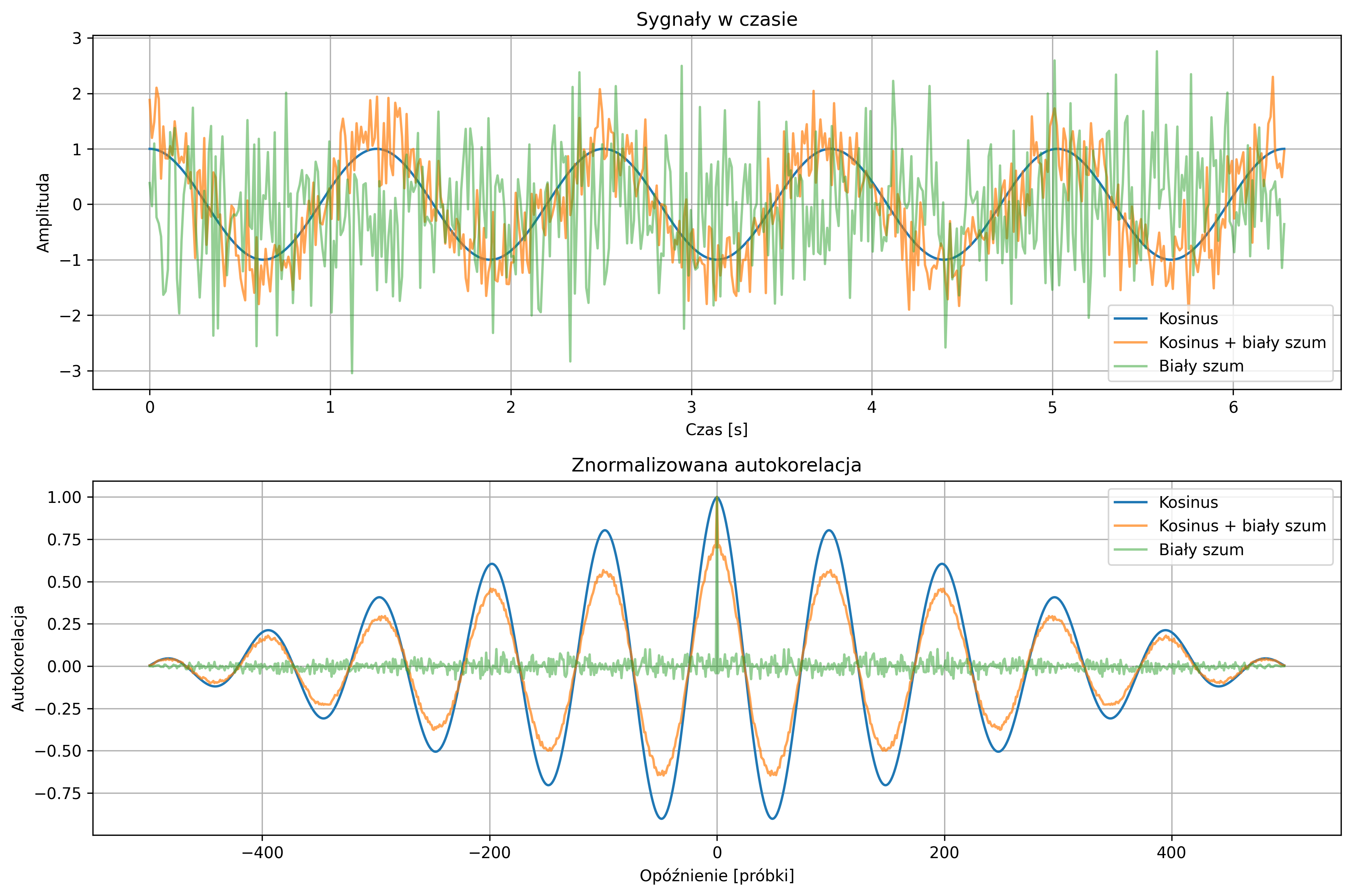
Po dodaniu białego szumu do sygnału kosinusoidalnego obserwujemy, że amplituda funkcji autokorelacji ulega zmniejszeniu, a jej przebieg staje się mniej regularny. Oznacza to, że szum wprowadza losowe zaburzenia, które zakłócają okresową strukturę sygnału deterministycznego.

Autokorelacja białego szumu osiąga maksimum przy zerowym przesunięciu, co wynika z pełnej korelacji sygnału z samym sobą w tym punkcie. Po przesunięciu w lewo lub prawo wartości autokorelacji szybko spadają do zera, ponieważ kolejne próbki szumu są statystycznie niezależne.

Sygnały deterministyczne, takie jak kosinus, mają autokorelacje regularne i często okresowe, co pozwala zauważyć ich powtarzalną strukturę w czasie. Natomiast sygnały stochastyczne, takie jak biały szum, charakteryzują się autokorelacją skoncentrowaną w zerze i bardzo szybko wygasającą poza zerowym przesunięciem, co świadczy o losowym charakterze sygnału.

Analiza autokorelacji jest skuteczną metodą do wykrywania obecności struktury deterministycznej w sygnale, do oceny wpływu zakłóceń losowych oraz pozwala odróżnić sygnały stochastyczne od deterministycznych na podstawie kształtu funkcji autokorelacji.

Wygenerować dwie realizacje sygnałów dyskretnych o długości \( N=2000 \) próbek:

• proces stacjonarny ergodyczny – biały szum gaussowski o średniej \(0\) i wariancji \(1\):

• proces niestacjonarny – biały szum gaussowski z dodanym trendem liniowym (rosnąca średnia w czasie):

Narysować przebiegi czasowe obu procesów na osobnych wykresach, tak aby można było porównać ich charakter. Narysować średnią ruchomą obu realizacji, przy użyciu okna o długości \(50\) próbek. Jakie różnice widać między procesem stacjonarnym a niestacjonarnym? Jak zachowuje się średnia ruchoma dla obu procesów? Jakie cechy procesu ergodycznego pozwalają na jego identyfikację? Dlaczego analiza średniej ruchomej jest pomocna przy wykrywaniu niestacjonarności?

import matplotlib.pyplot as plt

# Parametry

N = 2000  # liczba próbek
t = np.arange(N)

# Proces stacjonarny ergodyczny

np.random.seed(0)  # dla powtarzalności wyników
x_stationary = np.random.normal(0, 1, N)

# Proces niestacjonarny

trend = 0.002 * t  # trend liniowy (rosnąca średnia)
x_nonstationary = np.random.normal(0, 1, N) + trend

# Wykresy realizacji procesów

plt.figure(figsize=(14,6))

plt.subplot(2,1,1)
plt.plot(t, x_stationary, label='Proces stacjonarny ergodyczny', color='blue')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.title('Proces stacjonarny ergodyczny: biały szum Gaussowski')
plt.grid(True)

plt.subplot(2,1,2)
plt.plot(t, x_nonstationary, label='Proces niestacjonarny', color='darkorange')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.title('Proces niestacjonarny: biały szum z rosnącą średnią')
plt.grid(True)

plt.tight_layout()
plt.show()

# Obliczenie średnich ruchomych

window = 50  # długość okna średniej ruchomej
mean_stationary = np.convolve(x_stationary, np.ones(window)/window, mode='valid')
mean_nonstationary = np.convolve(x_nonstationary, np.ones(window)/window, mode='valid')

# Wykres porównania średnich ruchomych

plt.figure(figsize=(14,4))
plt.plot(mean_stationary, label='Średnia - proces stacjonarny', color='blue')
plt.plot(mean_nonstationary, label='Średnia - proces niestacjonarny', color='darkorange')
plt.xlabel('Czas [s]')
plt.ylabel('Średnia ruchoma')
plt.title('Porównanie średnich ruchomych procesów')
plt.legend()
plt.grid(True)
plt.show()
  

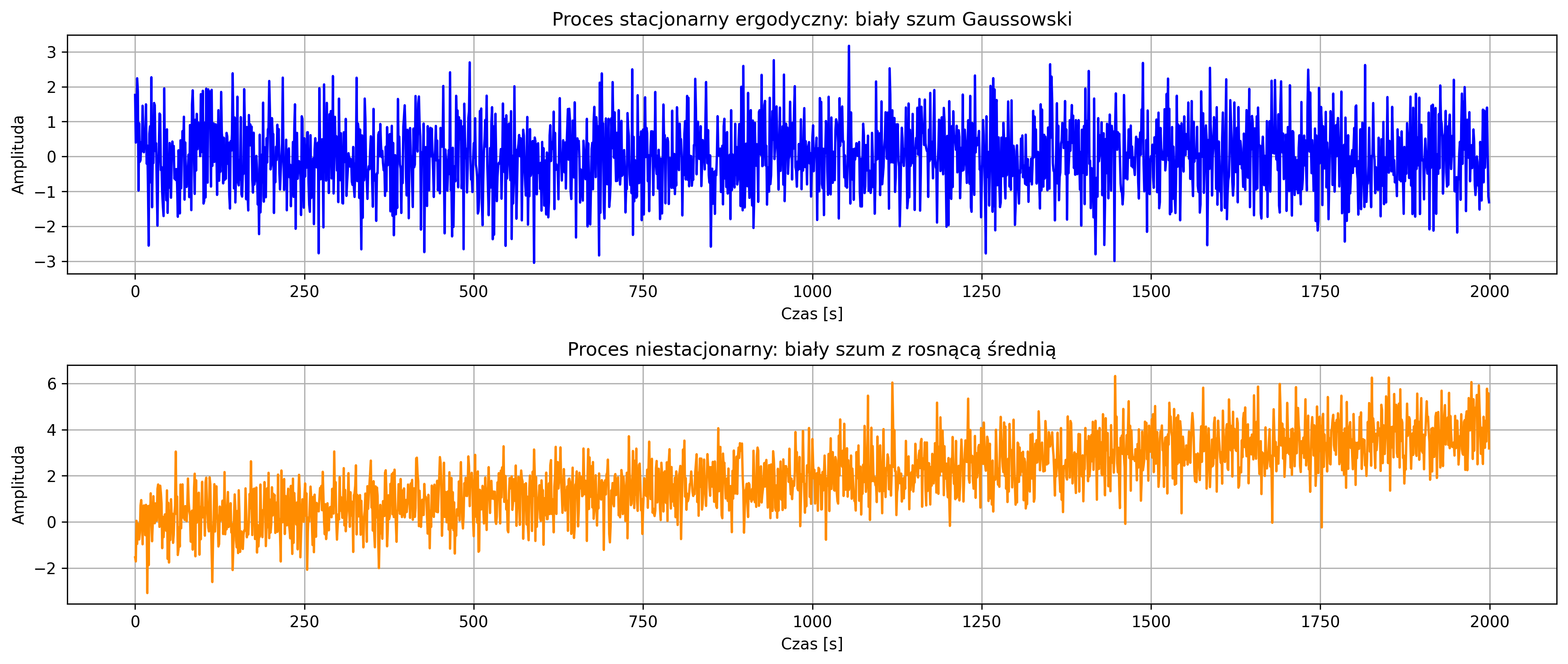
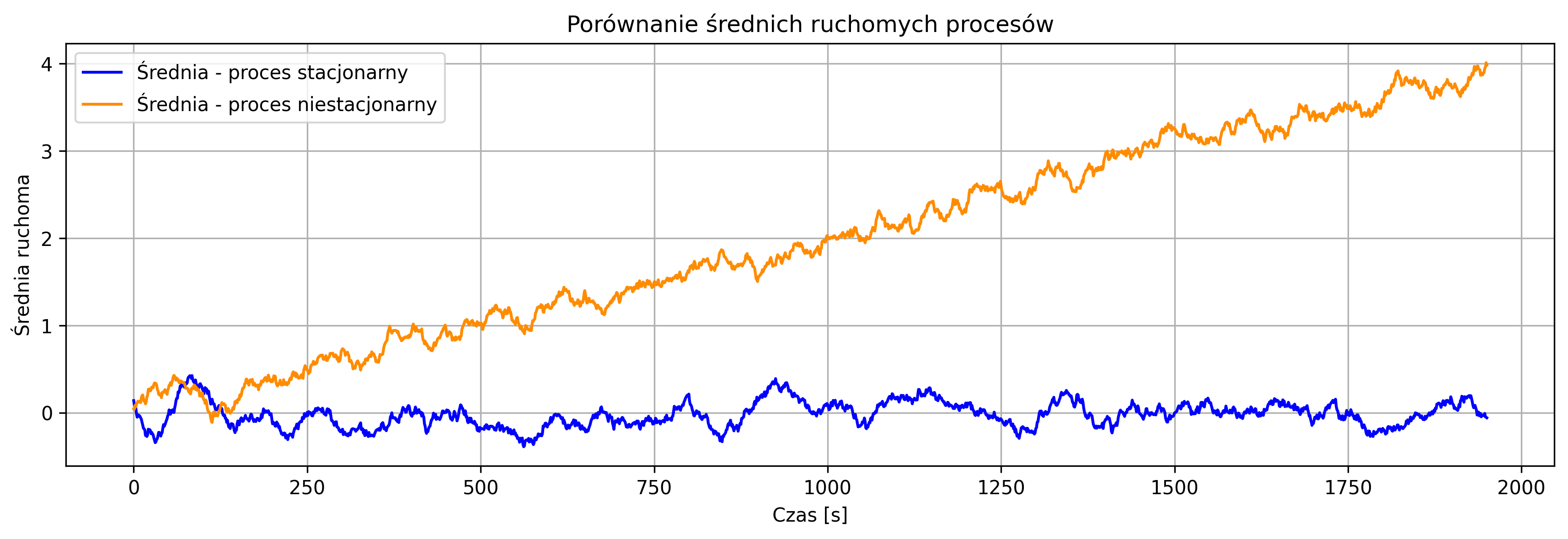
Proces stacjonarny ergodyczny charakteryzuje się losowymi zmianami wokół stałej średniej równej zero. Natomiast proces niestacjonarny wykazuje rosnącą tendencję wartości średniej w czasie, co jest widoczne jako ogólny wzrost przebiegu sygnału.

Średnia ruchoma procesu stacjonarnego oscyluje wokół stałej wartości (blisko zera) i nie wykazuje trendu. W przypadku procesu niestacjonarnego średnia ruchoma systematycznie rośnie, odzwierciedlając narastający trend sygnału.

Proces ergodyczny charakteryzuje się tym, że jego statystyki w czasie (np. średnia i wariancja) są zgodne ze statystykami ensemble, czyli można je oszacować na podstawie pojedynczej realizacji. W szczególności średnia ruchoma nie zmienia się w czasie i przebieg sygnału jest „stabilny” statystycznie.

Analiza średniej ruchomej pozwala zobaczyć zmiany trendu lub odchylenia średniej w czasie. Jeśli średnia ruchoma systematycznie rośnie lub maleje, sygnał jest niestacjonarny, natomiast jeśli oscyluje wokół stałej wartości, sygnał jest stacjonarny. Średnia ruchoma jest więc prostym narzędziem wizualnym do wykrywania niestacjonarności.

Wygeneruj realizację stacjonarnego procesu losowego (biały szum Gaussowski) o zadanej średniej \(\mu_{\text{true}}\) i wariancji \(\sigma_{\text{true}}^2\).

• Oblicz estymatory średniej \(\hat{\mu}\) i wariancji \(\hat{\sigma}^2\) dla całego przebiegu i porównaj je z wartościami prawdziwymi.
• Narysuj przebieg sygnału w dziedzinie czasu i zaznacz linią średnią estymowaną.
• Oblicz estymatory średniej i wariancji w funkcji długości przedziału \([0,n]\) dla \(n=1,2,\dots,N\).
• Narysuj wykresy estymowanej średniej i wariancji w funkcji liczby próbek wraz z liniami wartości prawdziwych \(\mu_{\text{true}}\) i \(\sigma_{\text{true}}^2\).
• Skomentuj, jak estymatory stabilizują się w miarę wzrostu liczby próbek i czy są zgodne z wartościami rzeczywistymi.

import numpy as np
import matplotlib.pyplot as plt

# Parametry procesu losowego
N_total = 2000       # liczba próbek
mu_true = 1.5        # wartość średnia procesu
sigma_true = 2.0     # odchylenie standardowe procesu
np.random.seed(42)   # dla powtarzalności

# Generacja realizacji procesu stacjonarnego (biały szum Gaussowski) 
X = np.random.normal(loc=mu_true, scale=sigma_true, size=N_total)

# Estymatory dla całego przebiegu 
mu_est = np.mean(X)
sigma2_est = np.var(X, ddof=1)
sigma_est = np.sqrt(sigma2_est)  # odchylenie standardowe

print(f'Estymowana średnia: {mu_est:.3f} (prawdziwa: {mu_true})')
print(f'Estymowana wariancja: {sigma2_est:.3f} (prawdziwa: {sigma_true**2})')

# Wykres przebiegu sygnału z estymowaną średnią i wariancją
plt.figure(figsize=(12,5))
plt.plot(X, label='Realizacja procesu')
plt.axhline(mu_est, color='r', linestyle='--', label=fr'Średnia estymowana $\approx$ {mu_est:.2f}')
plt.axhline(mu_est + sigma_est, color='g', linestyle=':', label=fr'$\pm$1 odch. std. $\approx$ {sigma_est:.2f}')
plt.axhline(mu_est - sigma_est, color='g', linestyle=':')
plt.title('Stacjonarny proces losowy')
plt.xlabel(rf'Próbki $n$')
plt.ylabel(rf'$X[n]$')
plt.legend()
plt.grid(True)
plt.show()

# Estymatory w funkcji długości podprzedziału [0, n]
mu_est_list = []
sigma2_est_list = []

for n in range(1, N_total+1):
    X_sub = X[:n]
    mu_est_list.append(np.mean(X_sub))
    if n > 1:
        sigma2_est_list.append(np.var(X_sub, ddof=1))
    else:
        sigma2_est_list.append(0.0)  # dla n=1 wariancja nie jest zdefiniowana

# Wykres stabilizacji estymowanej średniej
plt.figure(figsize=(12,4))
plt.plot(mu_est_list, label='Średnia estymowana')
plt.axhline(mu_true, color='r', linestyle='--', label=f'Średnia prawdziwa = {mu_true}')
plt.title(rf'Estymacja średniej w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana średnia')
plt.legend()
plt.grid(True)
plt.show()

# Wykres stabilizacji estymowanej wariancji
plt.figure(figsize=(12,4))
plt.plot(sigma2_est_list, label='Wariancja estymowana')
plt.axhline(sigma_true**2, color='r', linestyle='--', label=f'Wariancja prawdziwa = {sigma_true**2}')
plt.title(rf'Estymacja wariancji w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana wariancja')
plt.legend()
plt.grid(True)
plt.show()
  

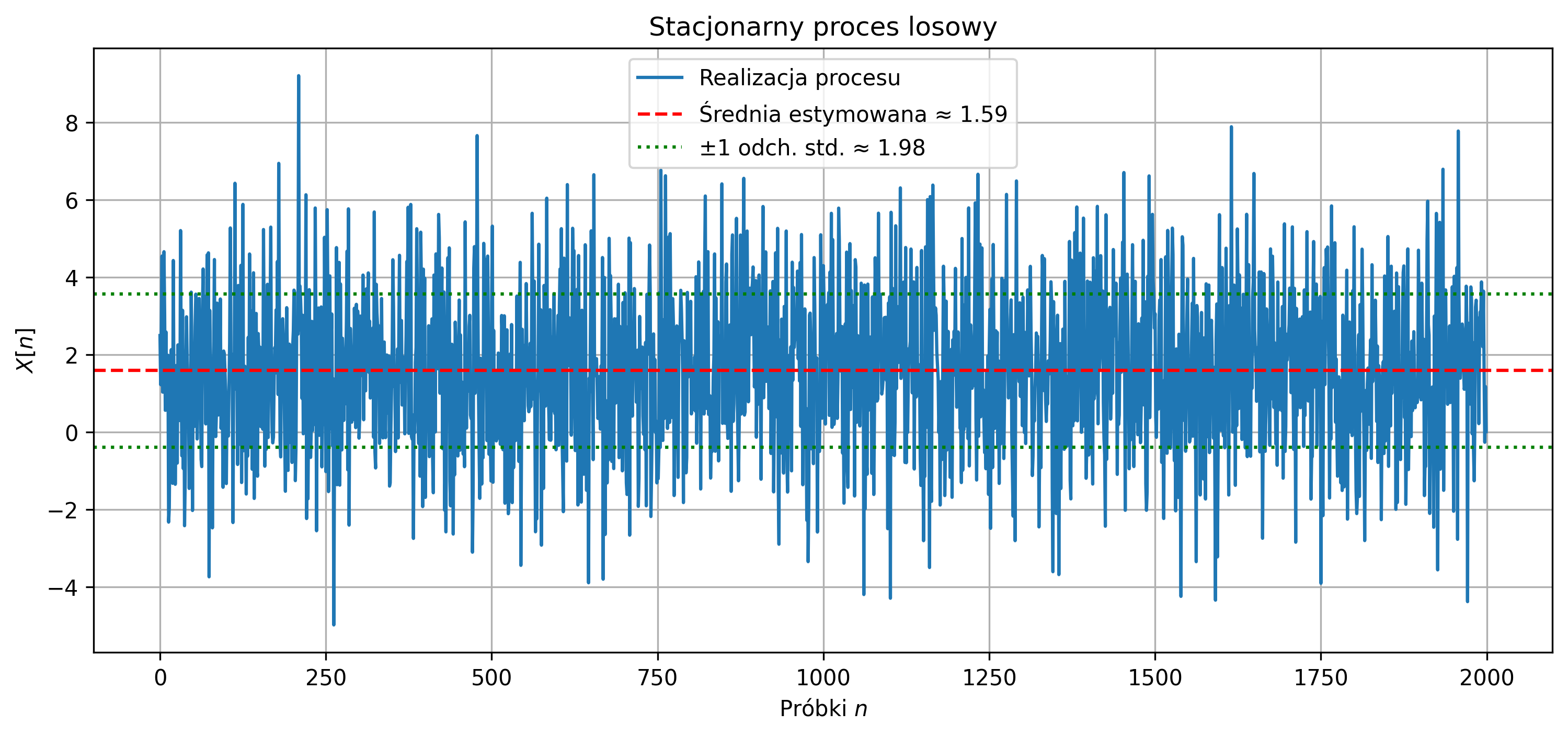
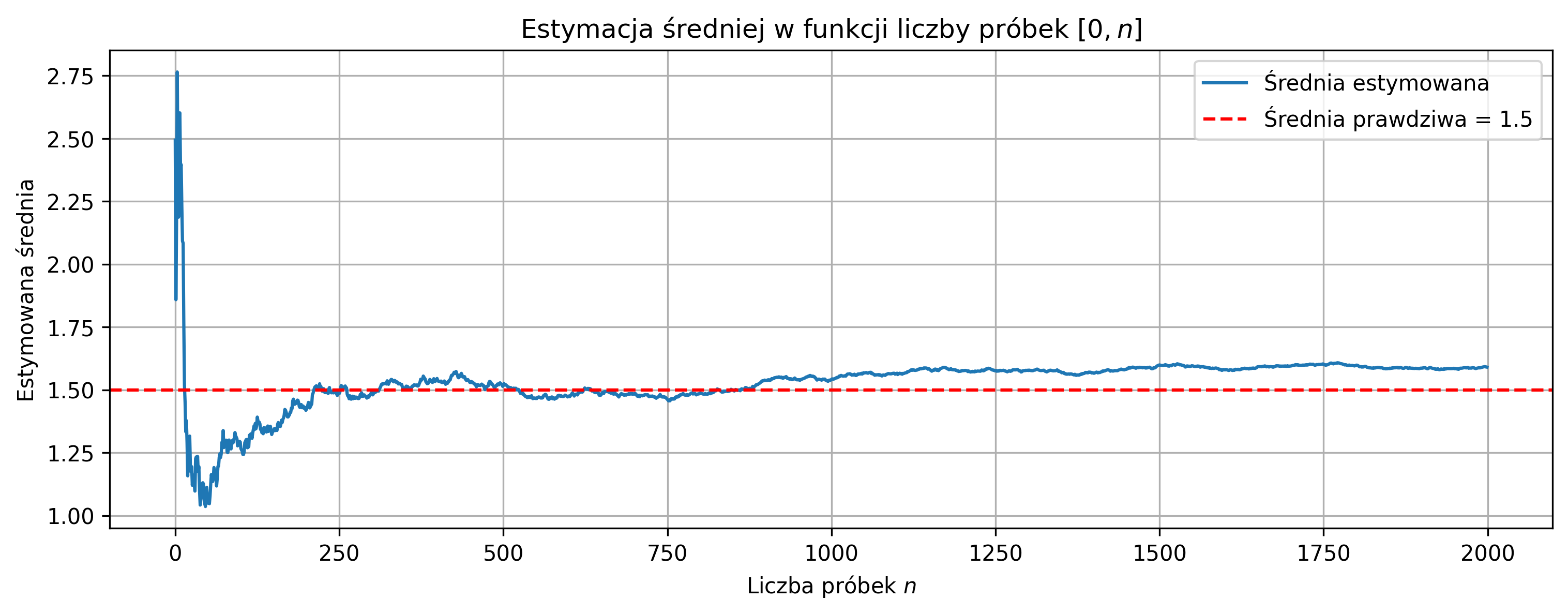
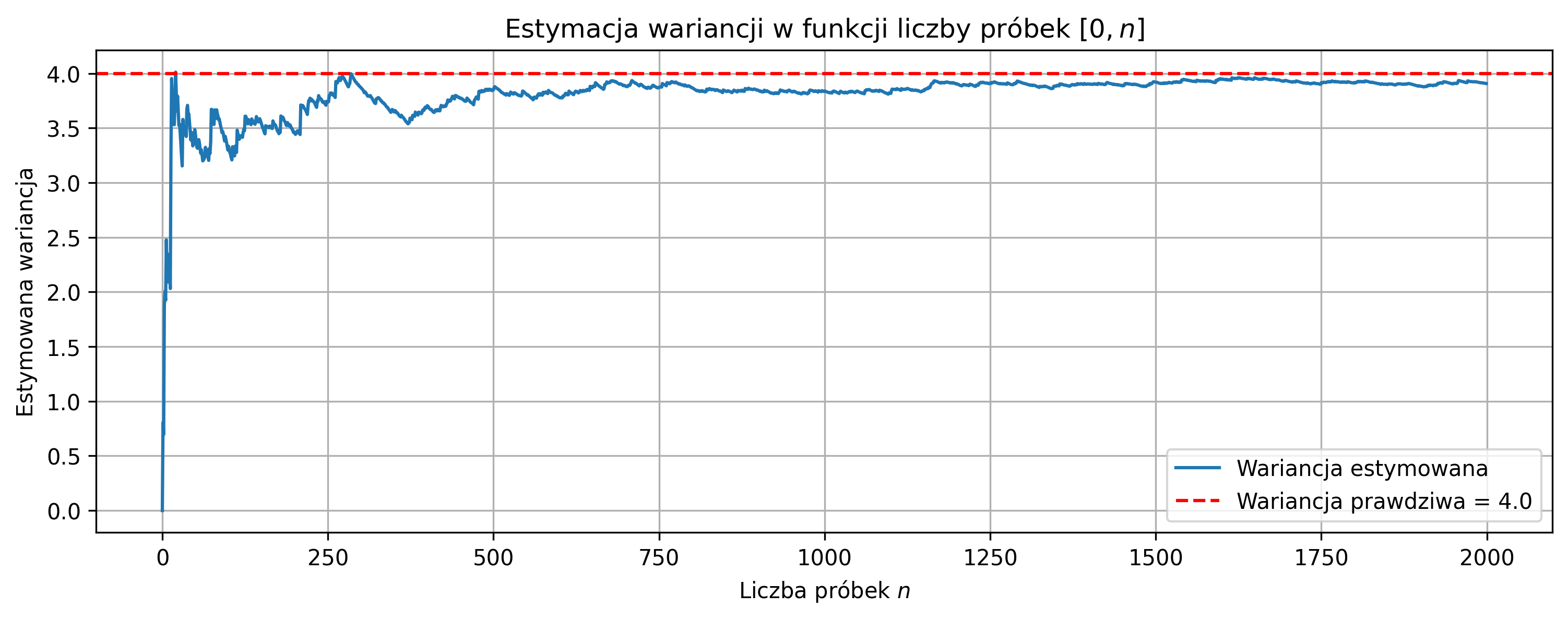
Przy małej liczbie próbek pojedyncze wartości mają duży wpływ na średnią i wariancję, dlatego estymatory są niestabilne. Wraz ze wzrostem liczby próbek średnia i wariancja próbki zbliżają się do wartości oczekiwanej i prawdziwej wariancji. Średnia i wariancja początkowo cechują się dużą zmiennością, a po przekroczeniu pewnej liczby próbek pozostają blisko wartości prawdziwych.

Estymowana średnia: \(\hat{\mu} \approx 1.49\) (prawdziwa: \(1.5\)), estymowana wariancja: \(\hat{\sigma}^2 \approx 3.92\) (prawdziwa: \(4.0\)). Estymatory dobrze przybliżają parametry procesu.

Sygnał oscyluje losowo wokół średniej, większość próbek mieści się w przedziale \(\mu \pm \sigma\), brak trendu - potwierdza to stacjonarność procesu. Większa wariancja powoduje większą zmienność i wolniejszą stabilizację estymatorów, mniejsza wariancja powoduje mniejszą zmienność i szybszą stabilizację estymatorów.

Wygeneruj realizację niestacjonarnego procesu losowego (biały szum Gaussowski) o zadanej średniej \(\mu_{\text{true}}\) i wariancji rosnącej liniowo w czasie: \[ \sigma^2[n] = \sigma_0^2 + k \cdot n, \quad n=0,1,\dots,N-1 \]

• Oblicz estymatory średniej \(\hat{\mu}\) i wariancji \(\hat{\sigma}^2\) dla całego przebiegu oraz porównaj z wartościami średniej i typowej wariancji.
• Narysuj przebieg sygnału w dziedzinie czasu.
• Oblicz estymatory średniej i wariancji w funkcji długości przedziału \([0,n]\) i narysuj wykresy ich zmian w funkcji \(n\).

import numpy as np
import matplotlib.pyplot as plt

# Parametry procesu niestacjonarnego
N_total = 2000          # liczba próbek
mu_true = 1.5           # wartość średnia procesu
sigma0 = 1.0            # początkowe odchylenie standardowe
k = 0.001               # przyrost wariancji na próbkę
np.random.seed(42)

# Generacja procesu niestacjonarnego: biały szum o rosnącej wariancji
time = np.arange(N_total)
sigma_t = sigma0 + k*time       # odchylenie standardowe w czasie
X = np.random.normal(loc=mu_true, scale=sigma_t)

# Estymatory dla całego przebiegu
mu_est = np.mean(X)
sigma2_est = np.var(X, ddof=1)

print(f'Estymowana średnia: {mu_est:.3f} (prawdziwa: {mu_true})')
print(f'Estymowana wariancja: {sigma2_est:.3f}')

# Wykres przebiegu sygnału 
plt.figure(figsize=(12,4))
plt.plot(time, X, label='Realizacja procesu')
plt.title('Niestacjonarny proces losowy (wariancja rośnie w czasie)')
plt.xlabel(rf'Próbki $n$')
plt.ylabel(rf'$X[n]$')
plt.grid(True)
plt.show()

# Estymatory w funkcji długości podprzedziału [0, n]
mu_est_list = []
sigma2_est_list = []

for n in range(1, N_total+1):
    X_sub = X[:n]
    mu_est_list.append(np.mean(X_sub))
    if n > 1:
        sigma2_est_list.append(np.var(X_sub, ddof=1))
    else:
        sigma2_est_list.append(0.0)

# Wykres estymowanej średniej
plt.figure(figsize=(12,4))
plt.plot(mu_est_list, label='Średnia estymowana')
plt.axhline(mu_true, color='r', linestyle='--', label=f'Średnia prawdziwa = {mu_true}')
plt.title(rf'Estymacja średniej w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana średnia')
plt.legend()
plt.grid(True)
plt.show()

# Wykres estymowanej wariancji
plt.figure(figsize=(12,4))
plt.plot(sigma2_est_list, label='Wariancja estymowana')
plt.title(rf'Estymacja wariancji w funkcji liczby próbek $[0,n]$ (niestacjonarny proces)')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana wariancja')
plt.legend()
plt.grid(True)
plt.show()
  

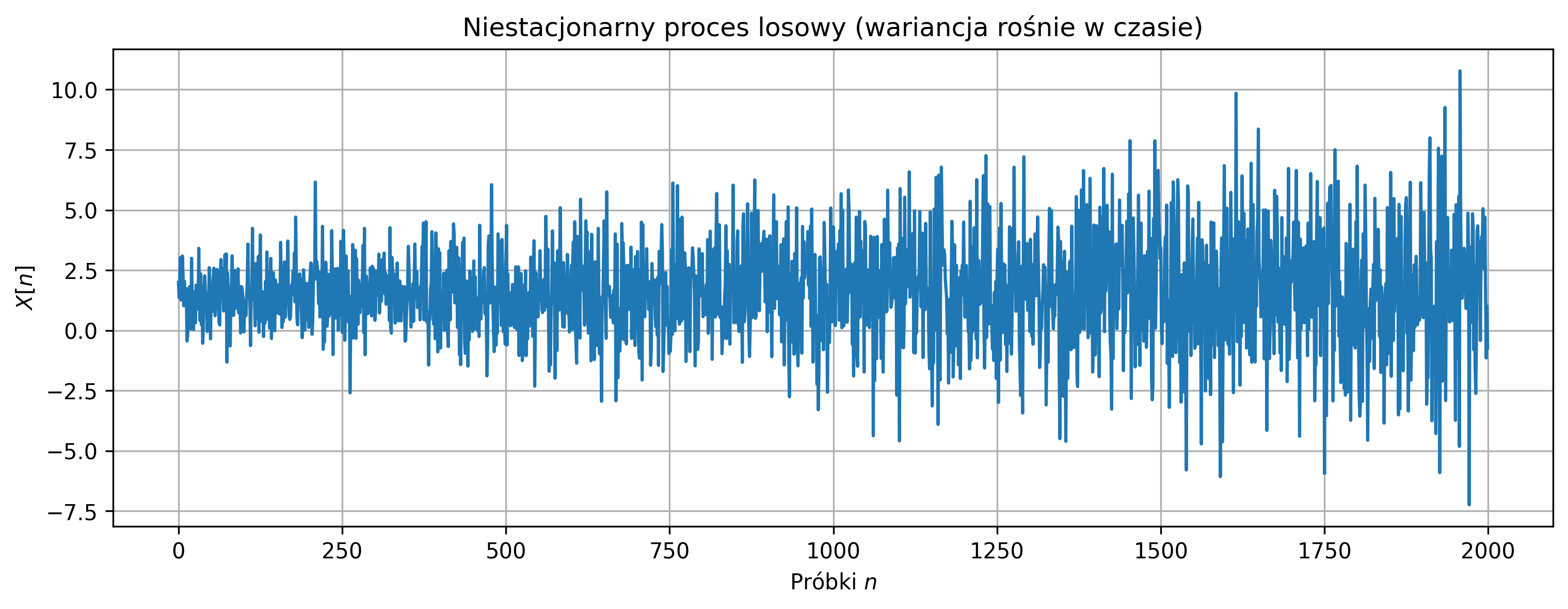
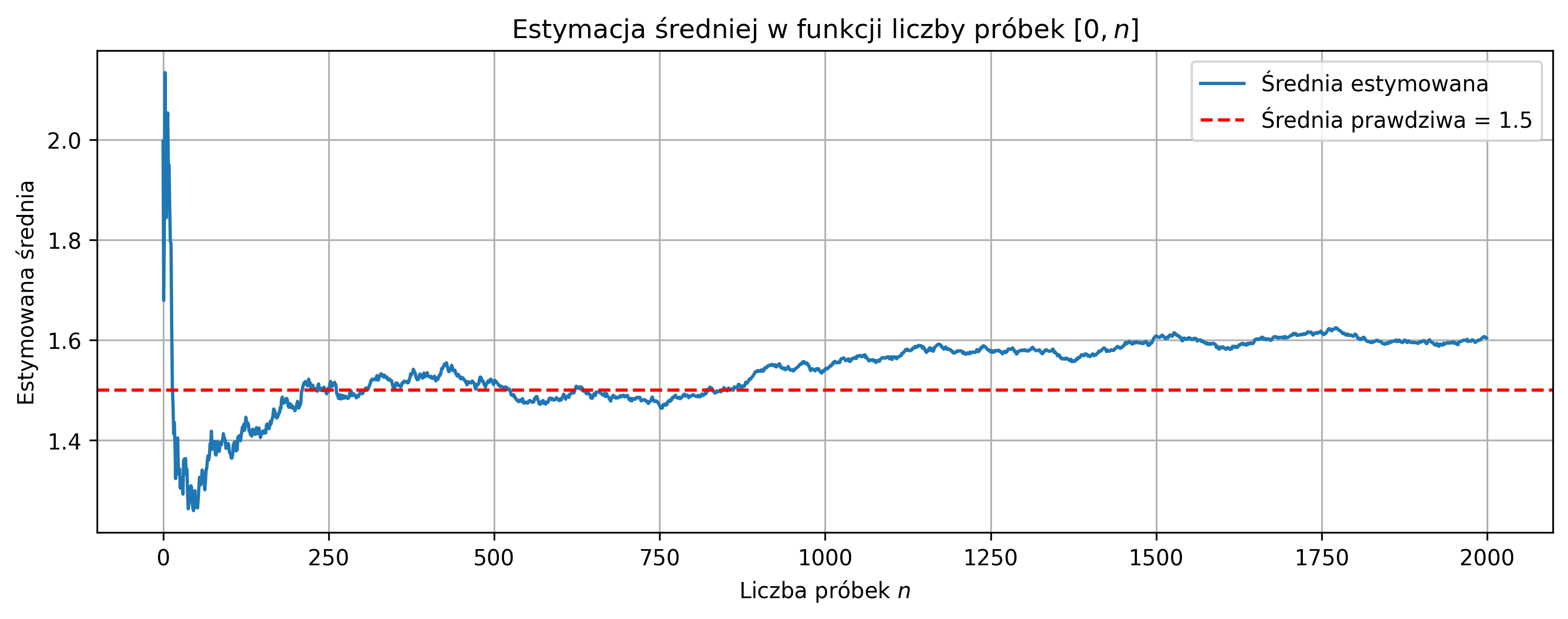
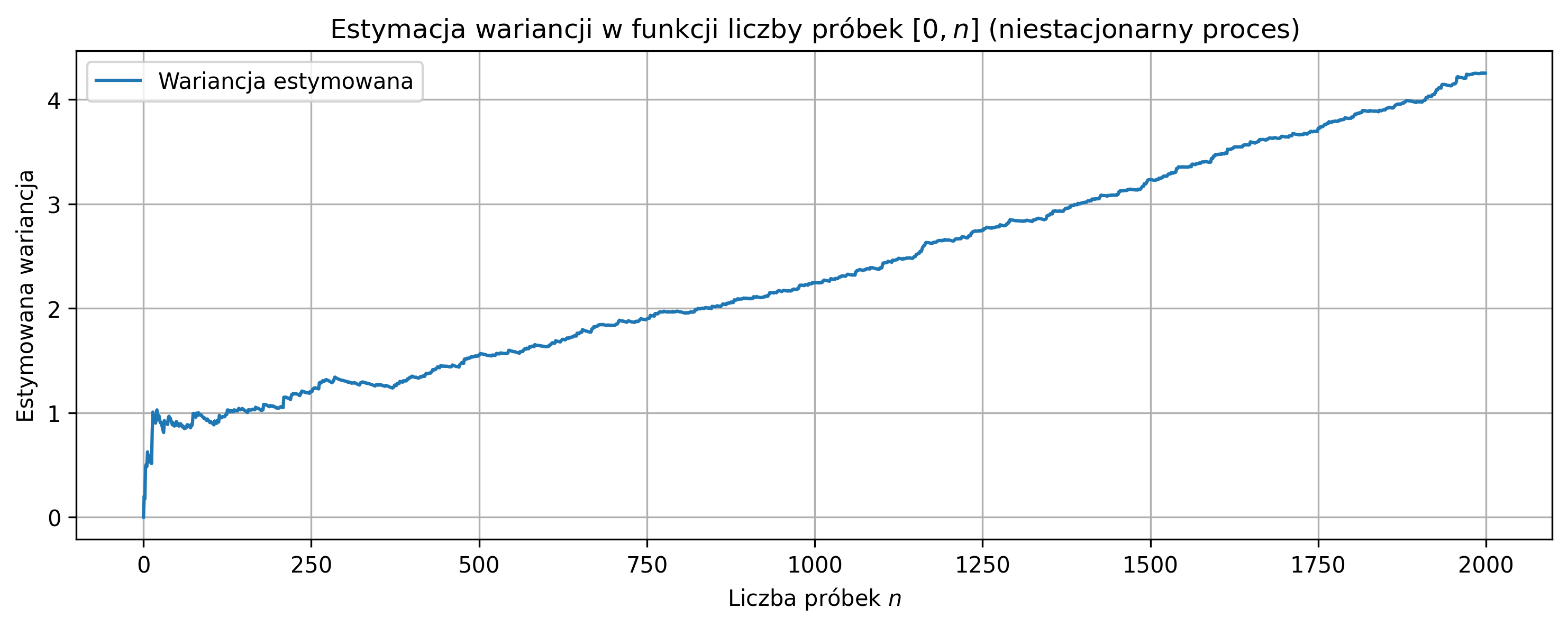
Podobnie jak w procesie stacjonarnym, mała liczba próbek powoduje duży wpływ pojedynczych wartości na średnią i wariancję, dodatkowo lokalna zmiana wariancji zwiększa niestabilność estymatorów. W przypadku niestacjonarnego procesu wariancja rośnie w czasie, więc estymator wariancji nie osiąga jednej stabilnej wartości.

Średnia estymowana stabilizuje się wokół wartości \(\mu_{\text{true}}\), natomiast wariancja rośnie wraz z liczbą próbek, odzwierciedlając niestacjonarność procesu. Estymowana średnia: \(\hat{\mu} \approx 1.50\) (blisko \(\mu_{\text{true}} = 1.5\)), estymowana wariancja: \(\hat{\sigma}^2 \approx\) średnia z całego przebiegu, ale nie odpowiada lokalnym wartościom wariancji, ponieważ proces jest niestacjonarny.

Sygnał oscyluje wokół średniej, ale amplituda próbek rośnie w czasie. Ponieważ wariancja rośnie w czasie, estymator wariancji nigdy nie stabilizuje się na jednej wartości, a średnia stabilizuje się wolniej w porównaniu do procesu stacjonarnego, jeśli początkowa wariancja jest bardzo mała.

Wygeneruj jedną realizację stacjonarnego procesu losowego - białego szumu Gaussowskiego o wartości oczekiwanej \(\mu = 0\) i odchyleniu standardowym \(\sigma = 1\). Na podstawie wygenerowanej realizacji wyznacz estymator funkcji autokorelacji \(\hat{R}_X[k]\) dla przesunięć \(k = 0,1,\dots,K\), korzystając ze wzoru: \[ \hat{R}_X[k] = \frac{1}{N-k} \sum_{n=0}^{N-k-1} \left(X[n] - \hat{\mu}\right)\left(X[n+k] - \hat{\mu}\right), \] gdzie \(\hat{\mu}\) jest estymowaną wartością średnią procesu. Narysuj wykres estymowanej funkcji autokorelacji w funkcji przesunięcia \(k\). Porównaj otrzymaną funkcję autokorelacji z teoretyczną funkcją autokorelacji białego szumu: \[ R_X[k] = \begin{cases} \sigma^2, & k = 0, \\ 0, & k \neq 0. \end{cases} \] Na podstawie wykresu oceń, czy wygenerowany proces można uznać za biały szum oraz skomentuj wpływ skończonej liczby próbek na dokładność estymacji.

import numpy as np
import matplotlib.pyplot as plt

# Parametry procesu
N = 1000            # liczba próbek
mu = 0.0            # wartość oczekiwana
sigma = 1.0         # odchylenie standardowe
max_lag = 50        # maksymalne przesunięcie
np.random.seed(42)

# Generowanie realizacji procesu losowego
# Biały szum Gaussowski N(mu, sigma^2)
X = np.random.normal(loc=mu, scale=sigma, size=N)

# Estymator funkcji autokorelacji
# \hat{R}_X[k] = 1/(N-k) * sum (X[n]-\hat{\mu})(X[n+k]-\hat{\mu})
def autocorr_estimator(x, max_lag):
    N = len(x)
    mu_hat = np.mean(x)
    R_hat = np.zeros(max_lag + 1)

    for k in range(max_lag + 1):
        R_hat[k] = np.sum(
            (x[:N-k] - mu_hat) * (x[k:] - mu_hat)
        ) / (N - k)

    return R_hat

# Estymacja autokorelacji
R_est = autocorr_estimator(X, max_lag)

# Wykres realizacji procesu
plt.figure(figsize=(10,3))
plt.plot(X)
plt.title('Realizacja białego szumu Gaussowskiego')
plt.xlabel(rf'Próbka $n$')
plt.ylabel(rf'$X[n]$')
plt.grid(True)
plt.show()

# Wykres estymowanej autokorelacji
lags = np.arange(max_lag + 1)

plt.figure(figsize=(9,3))
plt.stem(lags, R_est)
plt.axhline(0, color='r', linestyle='--',
            label=rf'Teoretyczna autokorelacja dla $k \neq 0$')
plt.title('Estymator funkcji autokorelacji')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{{R}}_{{X[k]}}$')
plt.legend()
plt.grid(True)
plt.show()
  

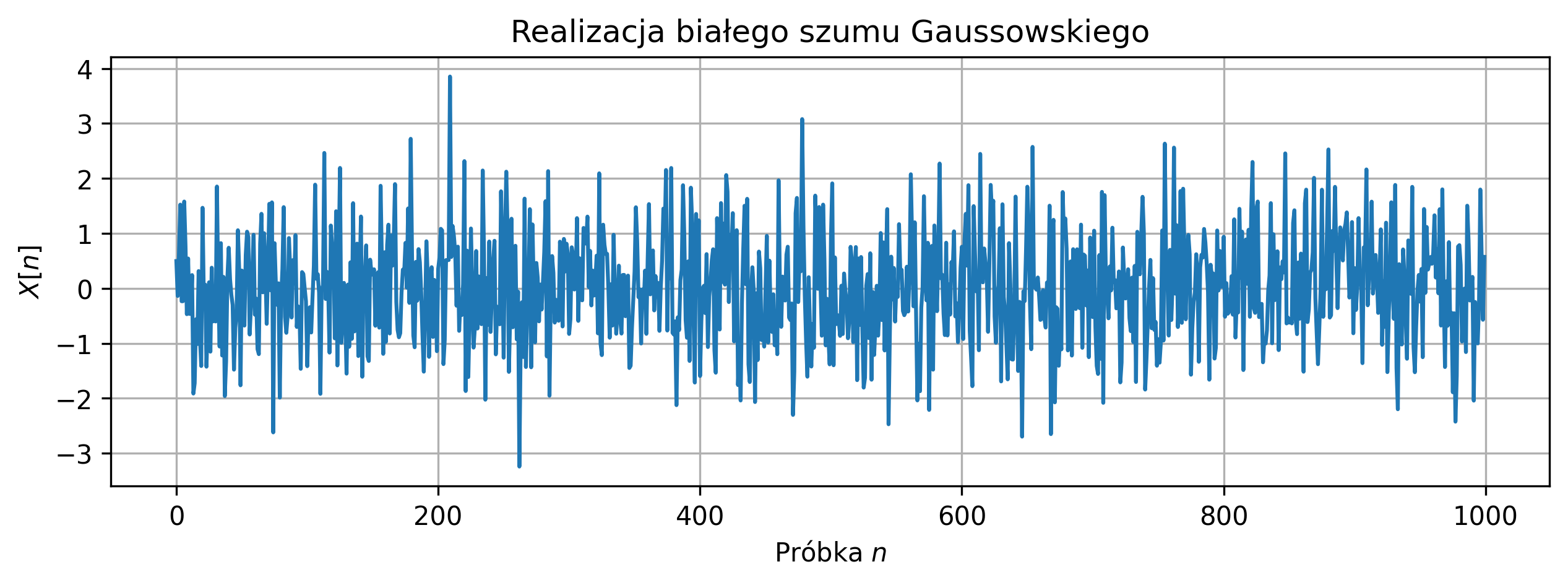
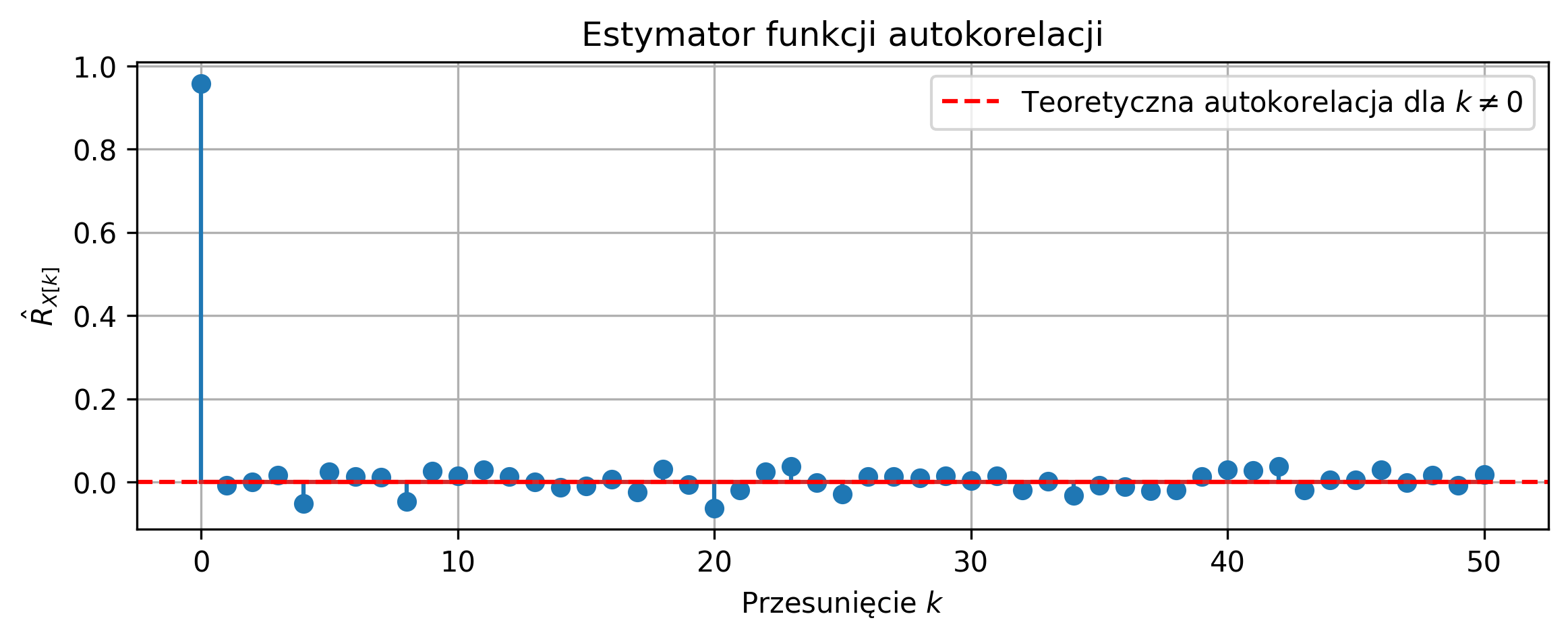
Na podstawie wykresu realizacji procesu losowego można stwierdzić, że sygnał ma charakter losowy i oscyluje wokół zera, co jest zgodne z założeniem zerowej wartości oczekiwanej białego szumu Gaussowskiego.

Estymowana funkcja autokorelacji osiąga największą wartość dla przesunięcia \(k=0\), co odpowiada wariancji procesu losowego. Dla przesunięć \(k>0\) wartości estymowanej autokorelacji są bliskie zeru, co potwierdza brak korelacji pomiędzy próbkami sygnału. Niewielkie odchylenia wartości autokorelacji od zera dla \(k>0\) wynikają ze skończonej liczby próbek i zanikają wraz ze wzrostem liczby próbek \(N\).

Otrzymane wyniki są zgodne z teoretyczną funkcją autokorelacji białego szumu, dla której \(R_X[k]=0\) dla \(k \neq 0\), co potwierdza poprawność zastosowanego estymatora.

Wygeneruj jedną realizację niestacjonarnego procesu losowego w postaci sumy trendu liniowego oraz białego szumu Gaussowskiego: \[ X[n] = a n + W[n], \] gdzie \(a\) jest współczynnikiem trendu, a \(W[n]\) jest białym szumem o zerowej wartości oczekiwanej. Wyznacz estymator funkcji autokorelacji \(\hat{R}_X[k]\) dla przesunięć \(k=0,1,\dots,K\). Narysuj wykres estymowanej funkcji autokorelacji i oceń jej kształt. Usuń trend z sygnału i wyznacz ponownie funkcję autokorelacji. Porównaj oba wykresy i wyciągnij wnioski dotyczące wpływu niestacjonarności na estymację funkcji autokorelacji.

import numpy as np
import matplotlib.pyplot as plt

# Parametry
N = 1000            # liczba próbek
a = 0.01            # współczynnik trendu liniowego
max_lag = 50        # maksymalne przesunięcie autokorelacji
np.random.seed(42)

# Generowanie procesu niestacjonarnego
# X[n] = a*n + W[n]
n = np.arange(N)
trend = a * n
noise = np.random.normal(0, 1, N)
X = trend + noise

# Estymator funkcji autokorelacji
def autocorr_estimator(x, max_lag):
    N = len(x)
    mu_hat = np.mean(x)
    R_hat = np.zeros(max_lag + 1)

    for k in range(max_lag + 1):
        R_hat[k] = np.sum(
            (x[:N-k] - mu_hat) * (x[k:] - mu_hat)
        ) / (N - k)

    return R_hat

# Autokorelacja – proces z trendem
R_trend = autocorr_estimator(X, max_lag)

# Usunięcie trendu 
X_detrended = X - trend

# Autokorelacja po usunięciu trendu
R_detrended = autocorr_estimator(X_detrended, max_lag)

# Wykres realizacji procesu
plt.figure(figsize=(12,4))
plt.plot(n, X, label='Proces niestacjonarny')
plt.plot(n, trend, 'r--', label='Trend liniowy')
plt.title('Proces niestacjonarny z trendem liniowym')
plt.xlabel(rf'Próbka $n$')
plt.ylabel(rf'$X[n]$')
plt.legend()
plt.grid(True)
plt.show()

# Autokorelacja – z trendem
lags = np.arange(max_lag + 1)

plt.figure(figsize=(10,4))
plt.stem(lags, R_trend)
plt.axhline(0, color='r', linestyle='--')
plt.title('Estymowana funkcja autokorelacji (z trendem)')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{R}_X[k]$')
plt.grid(True)
plt.show()

# Autokorelacja – po usunięciu trendu
plt.figure(figsize=(10,4))
plt.stem(lags, R_detrended)
plt.axhline(0, color='r', linestyle='--')
plt.title('Estymowana funkcja autokorelacji (po usunięciu trendu)')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{R}_X[k]$')
plt.grid(True)
plt.show()
  

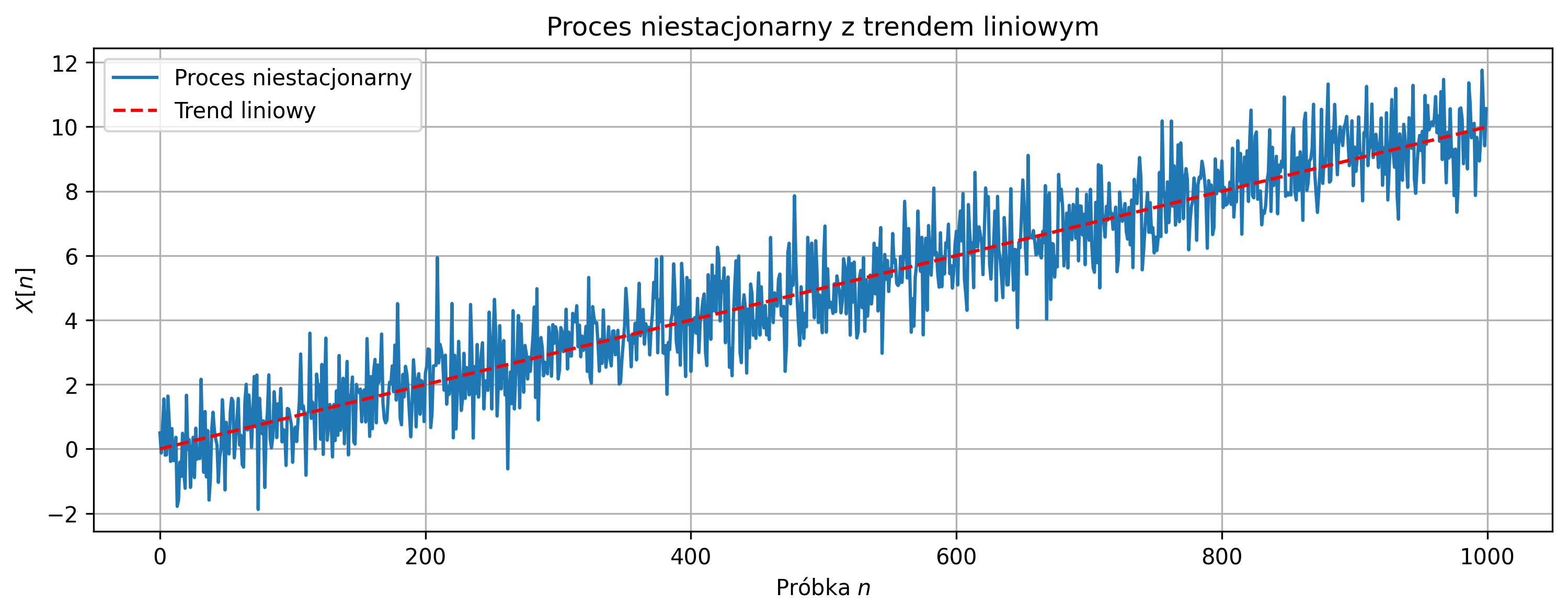
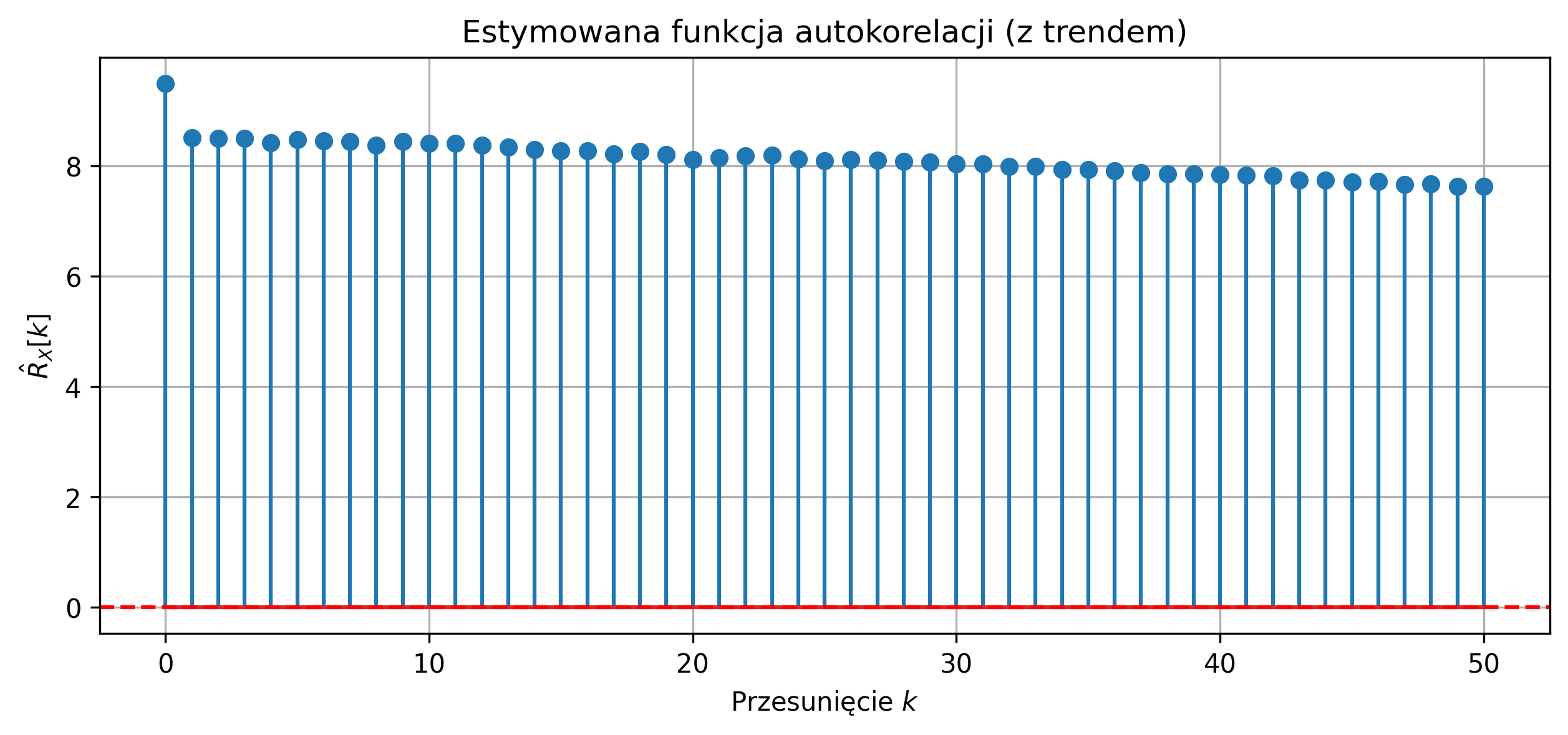
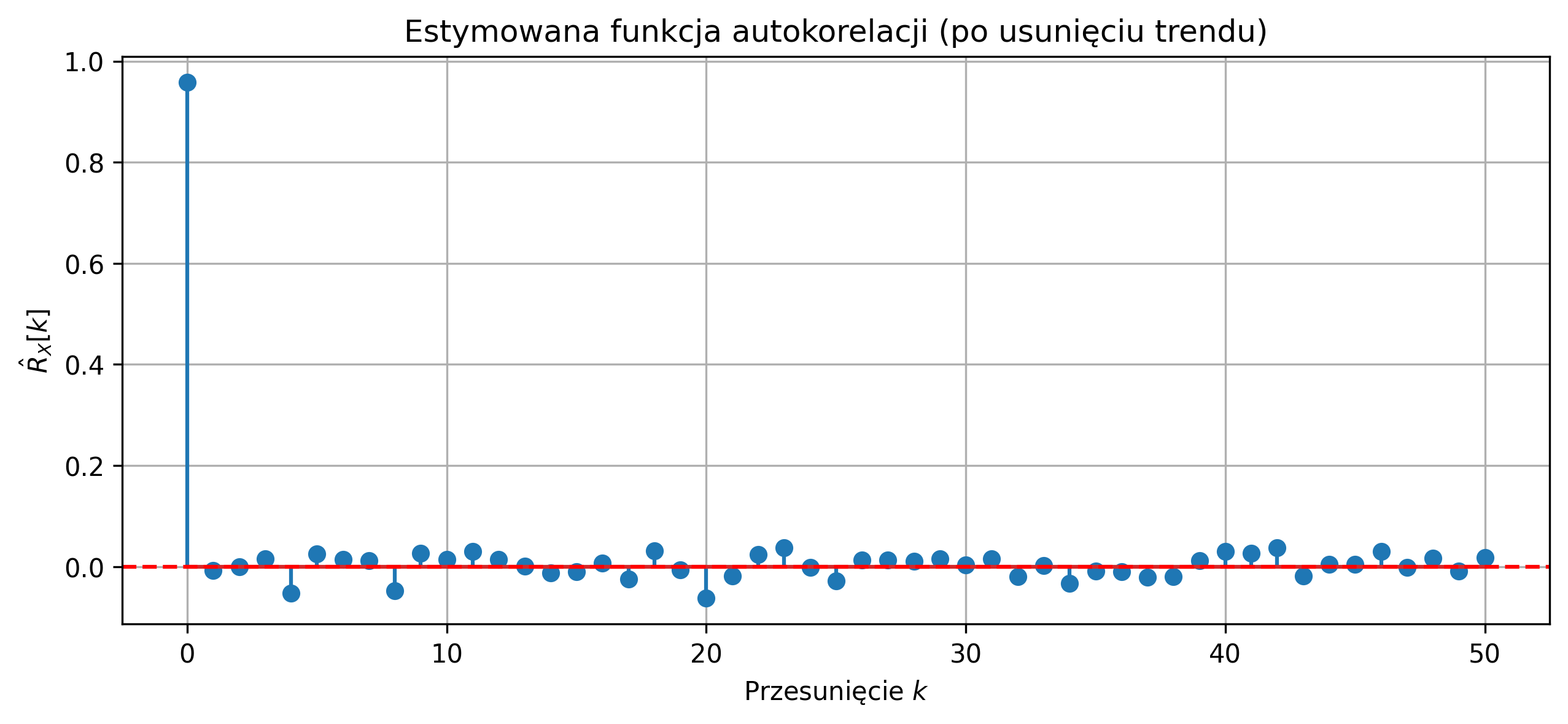
Proces z trendem liniowym jest niestacjonarny, co powoduje, że klasyczna estymacja funkcji autokorelacji nie zanika do zera dla przesunięć \(k>0\). Trend w sygnale wprowadza pozorną korelację pomiędzy próbkami, niezwiązaną z własnościami losowymi procesu. Po usunięciu trendu estymowana funkcja autokorelacji ma maksimum dla \(k=0\) i wartości bliskie zeru dla \(k>0\), co odpowiada własnościom białego szumu.

Wyniki pokazują, że przed estymacją autokorelacji proces niestacjonarny powinien zostać przekształcony do postaci stacjonarnej.

Rozważyć dyskretny proces losowy postaci \[ X[n] = w[n], \] gdzie \(w[n]\) jest białym szumem gaussowskim o zerowej wartości średniej i stałej wariancji \(\sigma_w^2\). Narysuj kilka realizacji procesu w dziedzinie czasu i porównaj ich przebiegi. Dla każdej realizacji wyznacz periodogram jako estymator widmowej gęstości mocy. Zbliżenie na niskie częstotliwości (np. \(f \approx 0\)) pozwoli ocenić, czy w procesie występuje dominująca składowa stała. Na podstawie obserwacji w dziedzinie czasu i częstotliwości oceń, czy proces jest ergodyczny i uzasadnij odpowiedź.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(2)

# Parametry
N = 2048
fs = 2000
num_realizations = 6
sigma_w = 1.0

t = np.arange(N) / fs

# Wykres realizacji w czasie
plt.figure(figsize=(12,4))
for i in range(num_realizations):
    w = np.random.normal(0, sigma_w, N)
    plt.plot(t, w, label=f'Realizacja {i+1}')
plt.title('Proces ergodyczny – realizacje w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel(r'$X[n]$')
plt.grid(True)
plt.legend()
plt.show()

# Periodogramy
freqs = np.fft.fftfreq(N, d=1/fs)
freqs = freqs[:N//2]

plt.figure(figsize=(12,4))
periodograms = []
for i in range(num_realizations):
    w = np.random.normal(0, sigma_w, N)
    Wf = np.fft.fft(w)
    PSD = (1/N) * np.abs(Wf[:N//2])**2
    periodograms.append(PSD)
    plt.semilogy(freqs, PSD, label=f'Realizacja {i+1}')

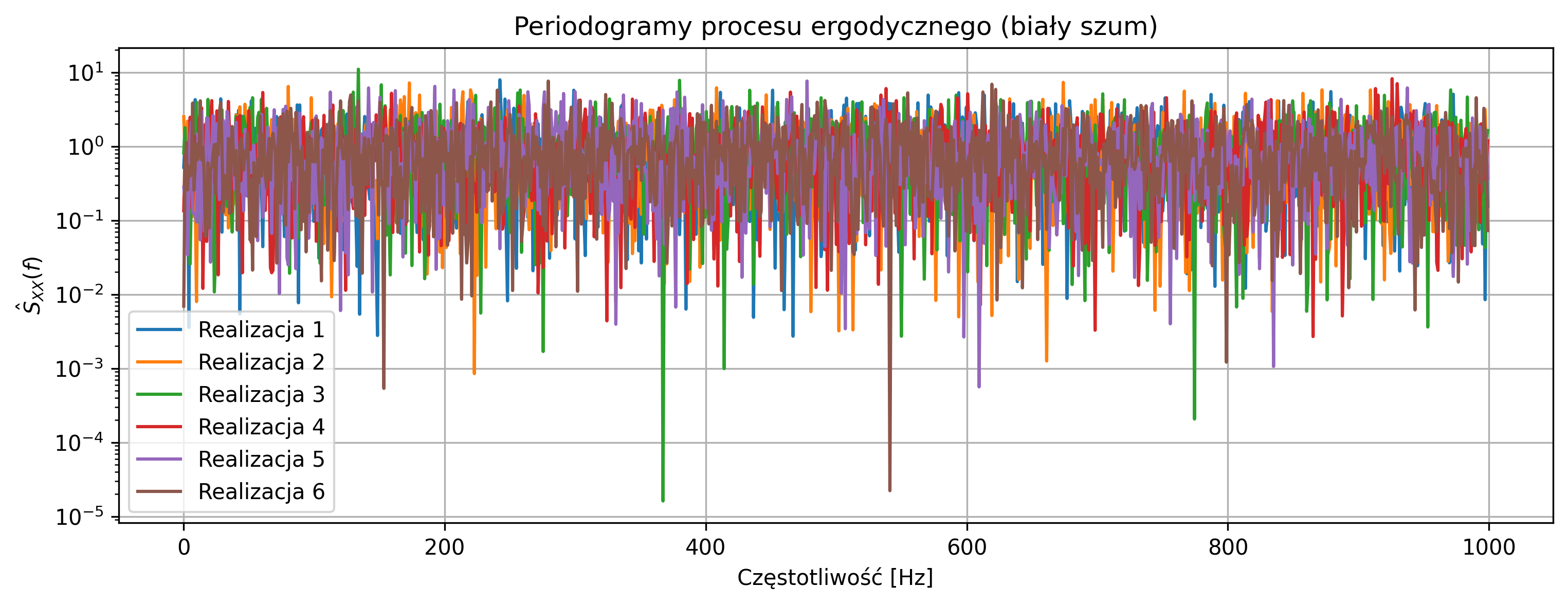
plt.title('Periodogramy procesu ergodycznego (biały szum)')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()

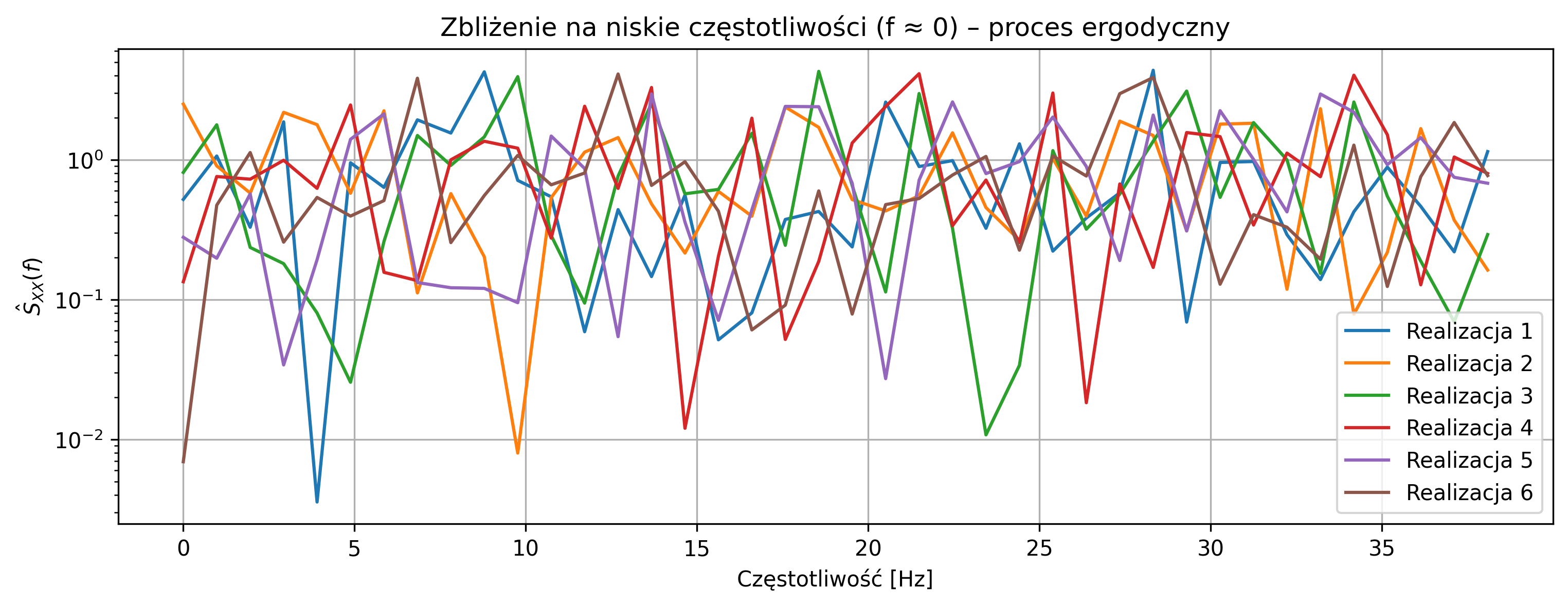
# Zbliżenie na niskie częstotliwości
plt.figure(figsize=(12,4))
for i, PSD in enumerate(periodograms):
    plt.semilogy(freqs[:40], PSD[:40], label=f'Realizacja {i+1}')

plt.title(rf'Zbliżenie na niskie częstotliwości (f $\approx$ 0) – proces ergodyczny')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
      

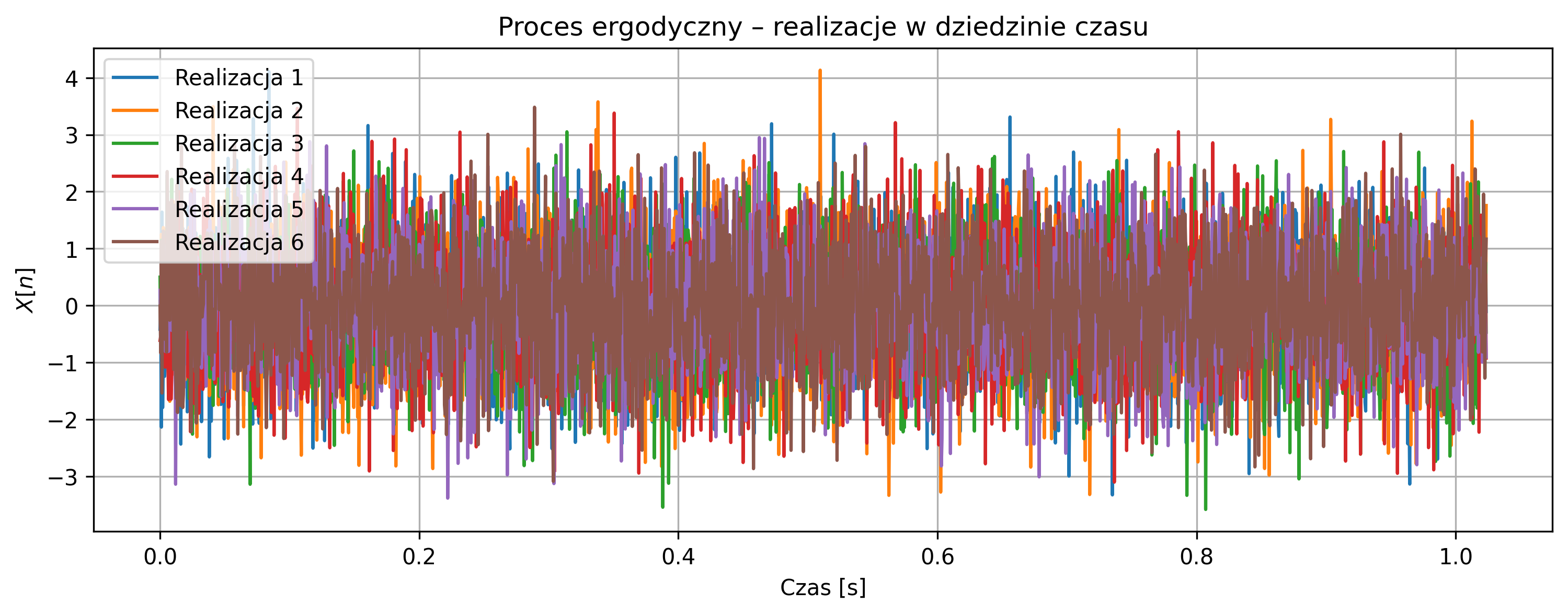
Przebiegi czasowe wszystkich realizacji są podobne i oscylują wokół zera, co wynika z braku losowej składowej stałej.

Periodogramy poszczególnych realizacji są zbliżone, a w pobliżu częstotliwości \(f \approx 0\) nie występują dominujące piki, co różni ten proces od procesu nieergodycznego.

Proces jest ergodyczny - statystyki jednej realizacji (średnia, widmo mocy) odzwierciedlają właściwości całego procesu, co potwierdza zgodność widm między realizacjami.

Wygeneruj kilka niezależnych realizacji procesu losowego w postaci: \[ X[n] = A + W[n], \] gdzie \(A\) jest losową zmienną losową o rozkładzie normalnym, stałą w czasie dla danej realizacji, natomiast \(W[n]\) jest białym szumem Gaussowskim o zerowej wartości oczekiwanej.

Narysuj wykresy kilku realizacji procesu w dziedzinie czasu i porównaj ich przebiegi. Dla każdej realizacji wyznacz periodogram jako estymator widmowej gęstości mocy sygnału. Porównaj otrzymane periodogramy oraz przeanalizuj zachowanie widma w okolicy częstotliwości \(f = 0\). Na podstawie wyników oceń, czy proces jest ergodyczny oraz uzasadnij odpowiedź na podstawie obserwacji w dziedzinie czasu i częstotliwości.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1)

# Parametry
N = 2048
fs = 2000
num_realizations = 6

sigma_A = 2.0     # wariancja losowej stałej (większa)
sigma_w = 0.05    # wariancja szumu (mniejsza)

t = np.arange(N) / fs

# Wykres realizacji w czasie
plt.figure(figsize=(12,4))

for i in range(num_realizations):
    A = np.random.normal(0, sigma_A)
    w = np.random.normal(0, sigma_w, N)
    X = A + w
    plt.plot(t, X, label=f'Realizacja {i+1}')

plt.title('Proces nieergodyczny – realizacje w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel(r'$X[n]$')
plt.grid(True)
plt.legend()
plt.show()

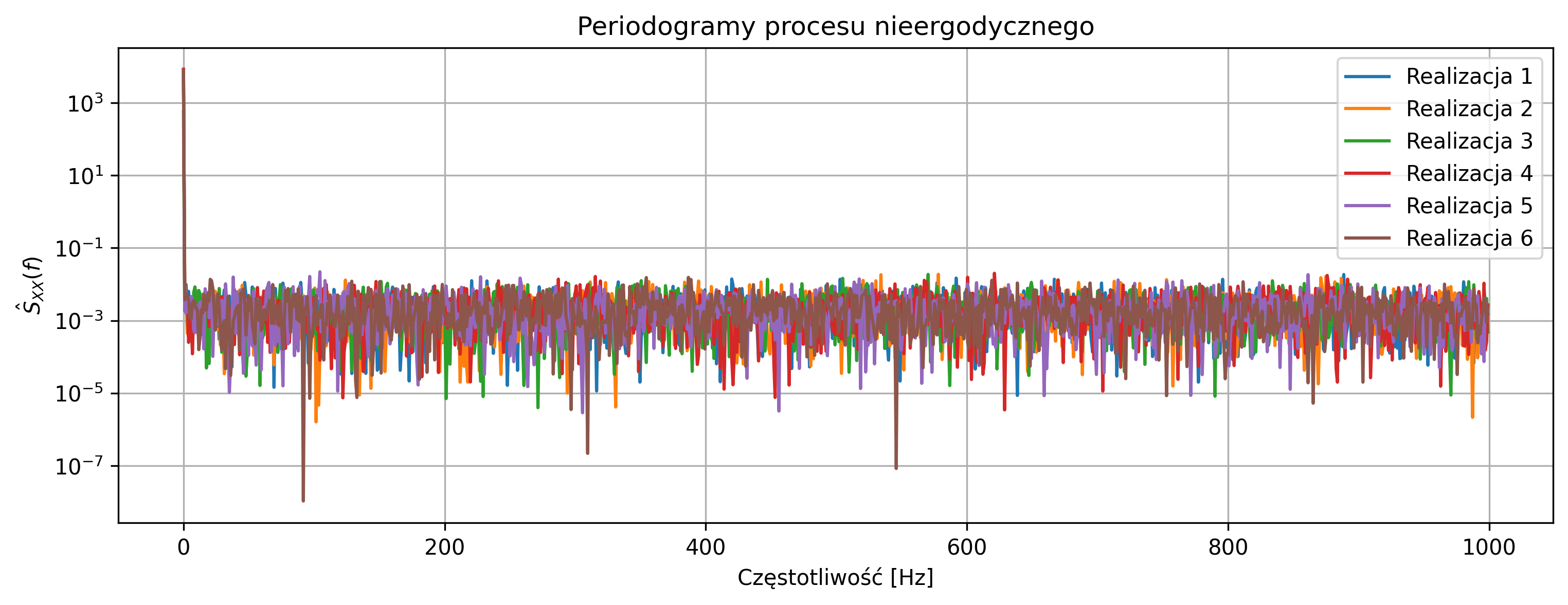
# Periodogramy
freqs = np.fft.fftfreq(N, d=1/fs)
freqs = freqs[:N//2]

plt.figure(figsize=(12,4))
periodograms = []

for i in range(num_realizations):
    A = np.random.normal(0, sigma_A)
    w = np.random.normal(0, sigma_w, N)
    X = A + w
    Xf = np.fft.fft(X)
    PSD = (1/N) * np.abs(Xf[:N//2])**2
    periodograms.append(PSD)
    plt.semilogy(freqs, PSD, label=f'Realizacja {i+1}')

plt.title('Periodogramy procesu nieergodycznego')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()

# Zbliżenie na okolice f = 0
plt.figure(figsize=(12,4))
for i, PSD in enumerate(periodograms):
    plt.semilogy(freqs[:40], PSD[:40], label=f'Realizacja {i+1}')

plt.title(rf'Zbliżenie na okolice $f=0$ (dominacja składowej stałej)')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
      

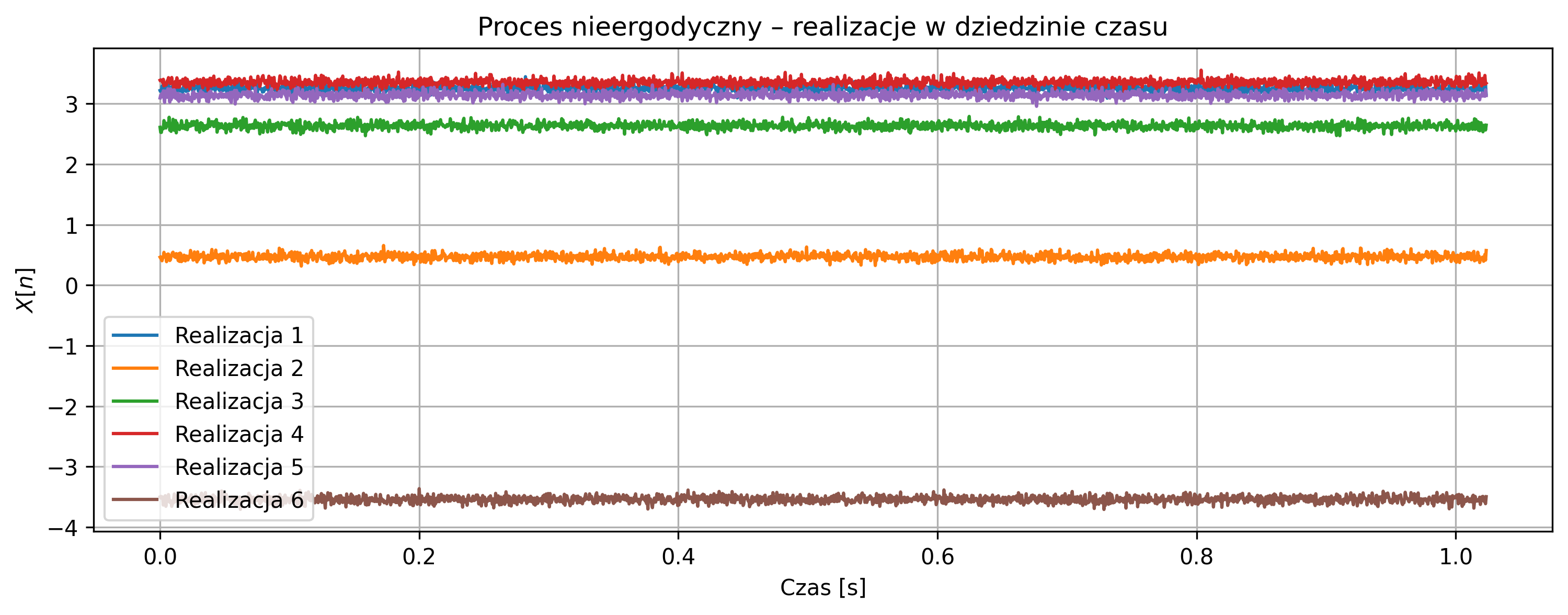
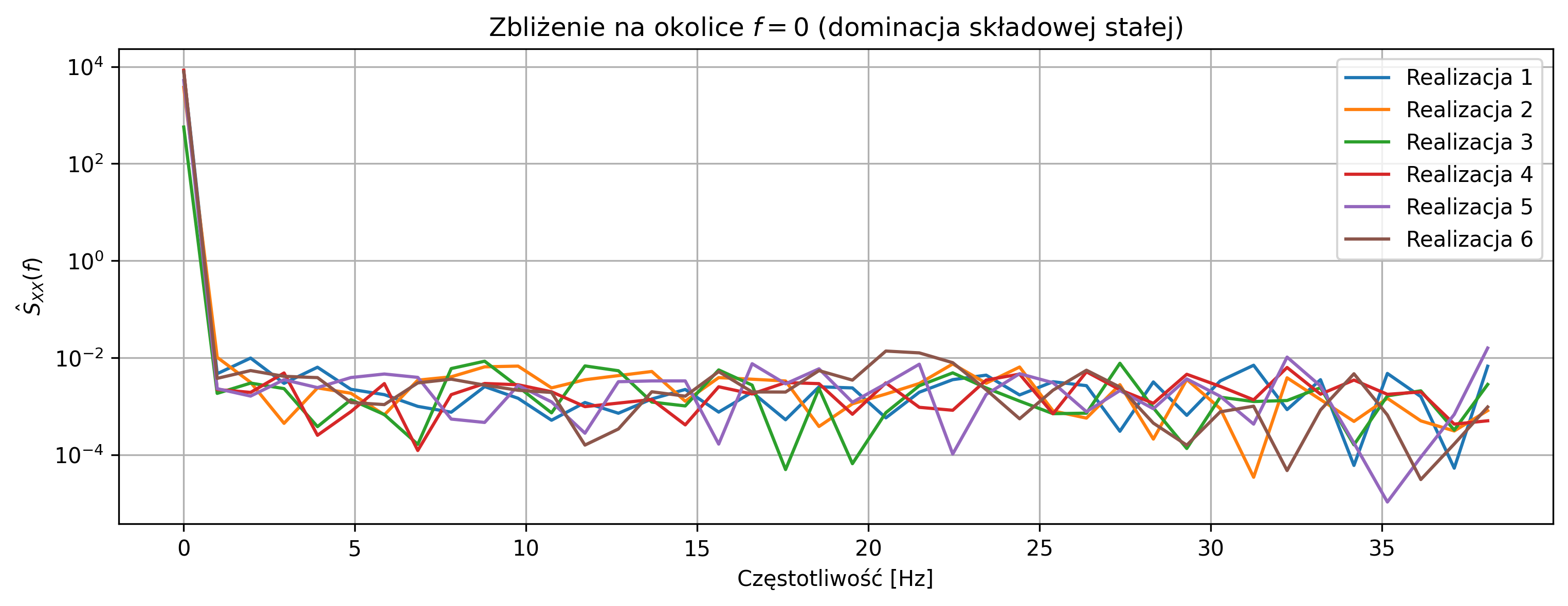
Przebiegi czasowe poszczególnych realizacji różnią się poziomem średniej, co wynika z obecności losowej składowej stałej \(A\), niezmiennej w czasie dla danej realizacji. Zwiększenie wariancji składowej stałej oraz zmniejszenie wariancji szumu powoduje, że różnice między realizacjami są wyraźniejsze zarówno w dziedzinie czasu, jak i częstotliwości.

Periodogramy różnych realizacji znacząco różnią się w okolicy częstotliwości \(f=0\), co wskazuje na losowy charakter składowej stałej i brak wspólnego widma dla wszystkich realizacji. Proces nie jest ergodyczny, ponieważ statystyki wyznaczone z jednej realizacji (np. średnia lub widmo mocy) nie są reprezentatywne dla całego zespołu realizacji.

Otrzymane wyniki potwierdzają, że proces może być stacjonarny w sensie szerokim, ale jednocześnie nie spełnia warunku ergodyczności.