Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Modelowanie obiektów nieliniowych |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 30 grudnia 2025, 17:25 |
1. Równania stanu dla obiektów nieliniowych
Przykłady modelowania podane są w kolejnych podrozdziałąch.
1.1. Przykład modelowania układu trzech zbiorników
Kwestia modelowania obiektów nieliniowych zostanie najpierw omówiona na przykładzie układu trzech zbiorników (Rys. 1.1). W układzie trzech zbiorników ciecz dopływa do pierwszego zbiornika ze ze sterowanym natężeniem \( Q_{we}(t) \) generowanym przez pompę. \( Q_{we}(t) \) pełni zatem rolę sygnału sterującego lub sygnału wejściowego. Pod wpływem różnicy ciśnień słupa cieczy, ciecz przepływa pomiędzy zbiornikiem pierwszym a zbiornikiem drugim z natężeniem \( Q_{12}(t) \) oraz pomiędzy zbiornikiem drugim a trzecim z natężeniem \( Q_{23}(t) \). Wreszcie, również pod wpływem ciśnienia generowanego przez słup cieczy, ciecz wypływa ze zbiornika trzeciego z natężeniem \( Q_{3}(t) \). Ściany zbiorników są prostopadłe do ich podstaw, a pola podstaw zbiorników w naszym przykładzie wynoszą odpowiednio \( A_1 = A \), \( A_2 = A \) oraz \( A_3 = 2A \), gdzie \( A > 0 \) jest stałą.
Rysunek 1.1 Schemat układu trzech zbiorników.
Naszym nadrzędnym celem jest regulacja poziomów cieczy w zbiornikach, które oznaczamy jako \( H_1(t) \), \( H_2(t) \) oraz \( H_3(t) \). Z tego względu zależy nam na sformułowaniu opisu zmian w czasie poziomów cieczy w zbiornikach. Jak się okaże w trakcie dalszych rozważań, dla obiektu z jednym sygnałem sterującym (w naszym przypadku \( Q_{we} \)) niemożliwa jest niezależna regulacja poziomów wody w każdym trzech zbiorników. Możemy swobodnie regulować poziom cieczy w jednym ze zbiorników, natomiast poziomy cieczy w pozostałych zbiornikach będą wynikały z własności układu. Ten poziom, który chcemy swobodnie zmieniać pełni rolę sygnału wyjściowego. Przyjmujemy, że sygnałem wyjściowym w naszym układzie jest poziom cieczy w trzecim zbiorniku \( H_3(t) \).
W niniejszym kursie skupiamy się na obiektach, które można opisać za pomocą układu równań różniczkowych zwyczajnych i właśnie taki opis sformułujemy dla układu trzech zbiorników. Proces tworzenia modelu obiektu zaczynamy od sformułowania równań fizycznych opisujących różne procesy zachodzące w obiekcie, a następnie przekształcamy te równania do dogodniejszej postaci. W przypadku układu trzech zbiorników trzon modelu stanowią równania bilansu objętości cieczy w każdym zbiorniku. Zakładamy, że ciecz jest nieściśliwa, dlatego równania bilansu objętości są równoważne z zasadą zachowania masy. Równania bilansu objętości formułujemy w postaci różniczkowej wg ogólnego schematu:
szybkość zmian objętości cieczy = natężenie dopływu cieczy - natężenie odpływu cieczy
Odpowiednie równania różniczkowe dla trzech zbiorników mają postać
\( \begin{matrix}
\dfrac{dV_1(t)}{dt} &=& Q_{we}(t) - Q_{12}(t) \qquad(1.1)\\
\dfrac{dV_2(t)}{dt} &=& Q_{12}(t) - Q_{23}(t) \qquad(1.2)\\
\dfrac{dV_3(t)}{dt} &=& Q_{23}(t) - Q_{3}(t) \qquad(1.3)
\end{matrix} \)
gdzie objętości cieczy $ V_1(t) $, $ V_2(t) $ oraz $ V_3(t) $ w zbiornikach wynoszą
\( \begin{matrix}
V_1(t) &=& A_1 H_1(t) = A\cdot H_1(t) \qquad(1.4)\\
V_2(t) &=& A_2 H_2(t) = A\cdot H_2(t) \qquad(1.5)\\
V_3(t) &=& A_3 H_3(t) = 2A\cdot H_3(t) \qquad(1.6)
\end{matrix} \)
Kolejne równania określają przepływ cieczy pomiędzy zbiornikami. Przepływ cieczy /( Q /) przez przewód lub zawór jest zwykle modelowany za pomocą równania
\( \begin{equation} Q=k\sqrt{\Delta p} \qquad(1.7) \end{equation} \)
gdzie \( \Delta p = p_a-p_b \) oznacza różnicę ciśnień na końcach \( a \) i \( b \) przewodu (lub zaworu), natomiast \( k \) jest stałą zależną od właściwości cieczy i geometrii przewodu. Przepływy \( Q_{12} \), \( Q_{23} \) oraz \( Q_{3} \) są wymuszane przez ciśnienia hydrostatyczne generowane przez słupy cieczy. Ciśnienie hydrostatyczne \( p \) jest dane wzorem
\( \begin{equation}
p = p_{atm}+\rho g H
\qquad(1.8)
\end{equation} \)
gdzie \( p_{atm} \) - ciśnienie atmosferyczne, \( \rho \) - gęstość cieczy, \( g \) - przyśpieszenie ziemskie, \( H \) wysokość słupa cieczy. Jeżeli wstawimy zależność (1.8) do równania (\1.7) to otrzymamy
\( \begin{eqnarray} Q&=&k\sqrt{\Delta p} = k\sqrt{p_a-p_b} = k\sqrt{p_{atm}+\rho g H_a-p_{atm}-\rho g H_b} \qquad(1.9)\\ &=& k\sqrt{\rho g H_a-\rho g H_b} = k\sqrt{\rho g \Delta H} = k\sqrt{\rho g} \sqrt{ \Delta H} = \alpha \sqrt{ \Delta H} \qquad(1.10) \end{eqnarray} \)
gdzie \( \alpha = k\sqrt{\rho g} \) jest stałą, a \( \Delta H = H_a-H_b \) to różnica wysokości słupów cieczy na końcach \( a \) i \( b \) przewodu. Dla uproszczenia opisu zakładamy, że wszystkie przewody przepływowe (lub zawory) są identyczne i współczynnik \( \alpha \) jest taki sam dla przepływów \( Q_{12} \), \( Q_{23} \) oraz \( Q_{3} \). Przepływy między zbiornikami są zatem dane wzorami
\( \begin{eqnarray} Q_{12}(t) &=& \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.11)\\ Q_{23}(t) &=& \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.12)\\ Q_{3}(t) &=& \alpha \sqrt{H_3(t)-0} = \alpha \sqrt{H_3(t)} \qquad(1.13) \end{eqnarray} \)
Powyższe wzory są prawidłowe pod warunkiem, że wyrażenia pod pierwiastkami są nieujemne. W przypadku, gdy znak wyrażenia pod pierwiastkiem mógłby się zmieniać należałoby zastosować wzór
\( \begin{equation} Q = sgn (\Delta H) \alpha \sqrt{| \Delta H|} \qquad(1.14) \end{equation} \)
gdzie operator \( sgn(\cdot) \) zwraca znak wyrażenia. Wykorzystanie wyrażenia \( sgn(\cdot) \) wprowadza jednak nieciągłość do opisu obiektu. Dla naszych potrzeb zakładamy, że wyrażenia pod pierwiastkami we wzorach (1.11)-(1.13) są zawsze nieujemne. Jest to uzasadnione założenie, gdyż w układach regulacji rozważamy zachowanie układu w pobliżu punktu pracy, gdzie, jak zobaczymy w kolejnej sekcji, te warunki istotnie są spełnione.
Równania (1.1) - (1.6) oraz (1.11)-(1.13) dają nam pełny opis zjawisk fizycznych zachodzących w układzie trzech zbiorników. Zauważmy, że nie uwzględniliśmy w opisie obiektu wszystkich zjawisk np.: możliwego przelania się cieczy w zbiornikach, nieszczelności prowadzących do wycieków lub przytykania się zaworów. Stopień szczegółowości opisu obiektu jest uzależniony od tego, do jakich celów jest wykorzystywany model. Jeżeli model miałby być wykorzystywany do celów diagnostyki opis ww. zjawisk byłby niezbędny. Naszym celem jest jednak przestudiowanie procesu syntezy układu regulacji i do tego celu zaprezentowany sposób opisu układu jest wystarczający.
Kolejnym krokiem przy formułowaniu modelu obiektu nieliniowego jest przekształcenie równań fizycznych do równoważnej, ale dogodniejszej postaci. W przypadku układów regulacji, jak i całej teorii sterowania równania różniczkowe są przedstawiane standardowo w postaci tzw. równań stanu. Teraz dokonamy przekształcenia równań fizycznych układu trzech zbiorników do postaci równań stanu, by następnie omówić cechy charakterystyczne tej postaci.
Wstawiając zależności (1.11)-(1.13) do równań (1.1)-(1.3) otrzymujemy
\( \begin{eqnarray} \frac{dV_1(t)}{dt} &=& Q_{we}(t) - \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.15) \\ \frac{dV_2(t)}{dt} &=& \alpha \sqrt{H_1(t)-H_2(t)} - \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.16)\\ \frac{dV_3(t)}{dt} &=& \alpha\sqrt{H_2(t)-H_3(t)} - \alpha \sqrt{H_3(t)} \qquad(1.17) \end{eqnarray} \)
Ponieważ pole podstawy zbiornika jest stałe, pochodna objętości cieczy w każdym zbiorniku spełnia warunek
\( \begin{equation} \dfrac{dV(t)}{dt} = \dfrac{d(A\cdot H(t))}{dt} = A \cdot \dfrac{dH(t)}{dt} \qquad(1.18) \end{equation} \)
Wstawiając (1.18) do wzorów (1.15)-(1.17) otrzymujemy
\( \begin{eqnarray} A\frac{d H_1(t)}{dt}&=& Q_{we}(t) - \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.19) \\ A\frac{d H_2(t)}{dt} &=& \alpha \sqrt{H_1(t)-H_2(t)} - \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.20)\\ 2A\frac{d H_3(t)}{dt} &=& \alpha\sqrt{H_2(t)-H_3(t)} - \alpha \sqrt{H_3(t)} \qquad(1.21) \end{eqnarray} \)
Podzielmy jeszcze obie strony każdego równań (1.19)-(\1.21) przez wartość odpowiedniego pola powierzchni podstawy zbiornika, aby otrzymać równania stanu dla układu trzech zbiorników
\( \begin{eqnarray} \frac{d H_1(t)}{dt} &=& \frac{1}{A}Q_{we}(t) - \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.22) \\ \frac{d H_2(t)}{dt} &=& \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \frac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.23) \\ \frac{d H_3(t)}{dt} &=& \frac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \frac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.24) \end{eqnarray} \)
Powyższe równania są równoważne równaniom fizycznym układu, jednak jest kilka cech wyróżniających równania stanu od innych równoważnych postaci. Po lewej stronie każdego z równań stanu znajduje się jedynie pochodna wysokości słupa cieczy w odpowiednim zbiorniku. Zmienne, których pochodne znajdują się po lewych stronach równań stanu nazywane są zmiennymi stanu. Dla układu trzech zbiorników zmiennymi stanu są \( H_1 \), \( H_2 \) oraz \( H_3 \). Po prawej stronie każdego z równań stanu znajduje się (być może skomplikowana i nieliniowa) funkcja. Argumentami tej funkcji mogą być jedynie trzy kategorie zmiennych
- zmienne stanu
- sygnały sterujące
- stałe
W rozważanym przykładzie zmiennymi stanu są \( H_1 \), \( H_2 \) oraz \( H_3 \), sygnałem sterującym jest \( Q_{we} \), natomiast stałymi są \( A \) oraz \( \alpha \). Z równań stanu zostały wyeliminowane inne zmienne (przepływy i objętości), pośrednio związane ww. zmiennymi.
Aby rozwiązać równania stanu czy to analitycznie, czy numerycznie, konieczne jest określenie warunków początkowych dla zmiennych stanu tzn. wielkości \( H_1(t_0) \), \( H_2(t_0) \) oraz \( H_3(t_0) \), gdzie \( t_0 \) jest wybraną chwilą początkową. Konieczna jest też znajomość wartości sygnału sterującego \( Q_{we}(t) \) na całym rozważanym horyzoncie czasu.
Równania stanu układu trzech zbiorników można rozwiązać numerycznie w środowisku MATLAB®. Na potrzeby symulacji przyjmujemy następujące wartości parametrów obiektu \( A = 0.5 \) , \( \alpha = 1 \). Na Rys. 1.2 przedstawiono przykładowe trajektorie stanów obiektu uzyskane dla stałego przepływu cieczy przez pompę \( Q_{we}(t) =0.5\) i zerowych warunków początkowych
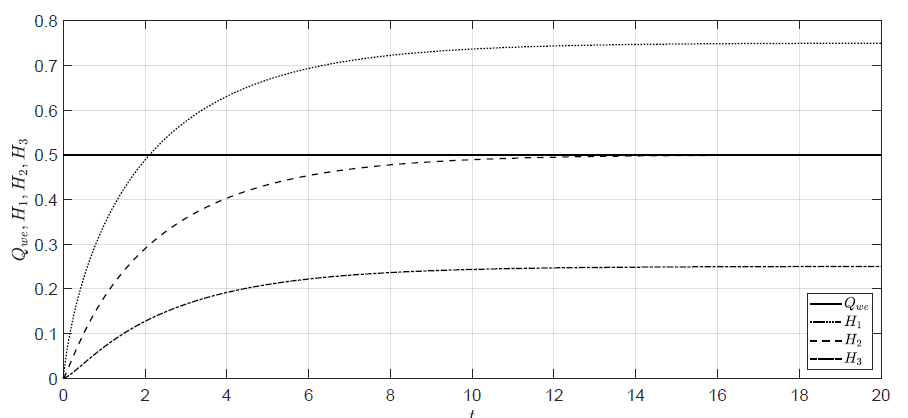
Rysunek 1.2 Trajektorie poziomów cieczy w zbiornikach dla stałego sterowania i zerowych warunków początkowych.
Przedstawione przebiegi ilustrują proces napełniania zbiorników cieczą. Początkowo puste zbiorniki napełniają się do pewnych poziomów aż do momentu, w którym w obiekcie ustali się równowaga przepływów. Po ustaleniu się równowagi przepływów, nie następują już dalsze zmiany poziomów cieczy.
Na Rys. 1.3 przedstawiono trajektorie sterowania i stanów obiektu uzyskane dla stałego przepływu cieczy przez pompę \( Q_{we}(t) =0.5\) i niezerowych warunków początkowych \( H_1(t_0) =0.8 \), \( H_2(t_0) =0.4 \), \( H_3(t_0)=0.3 \).
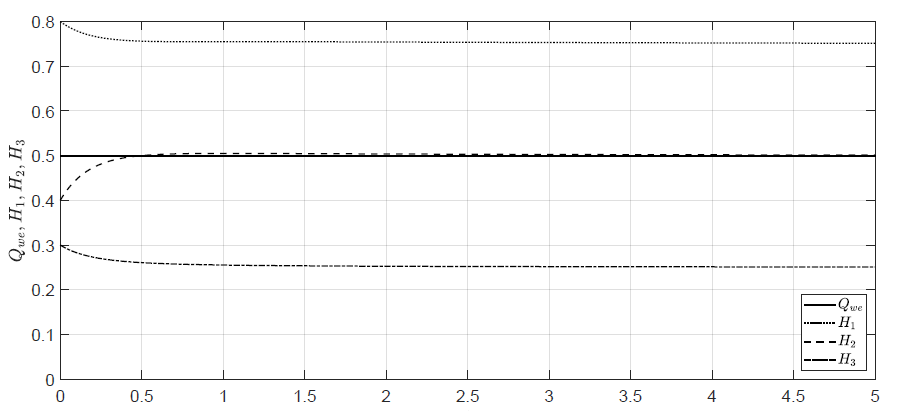
Rysunek 1.3 Trajektorie poziomów cieczy w zbiornikach dla stałego sterowania i niezerowych warunków początkowych.
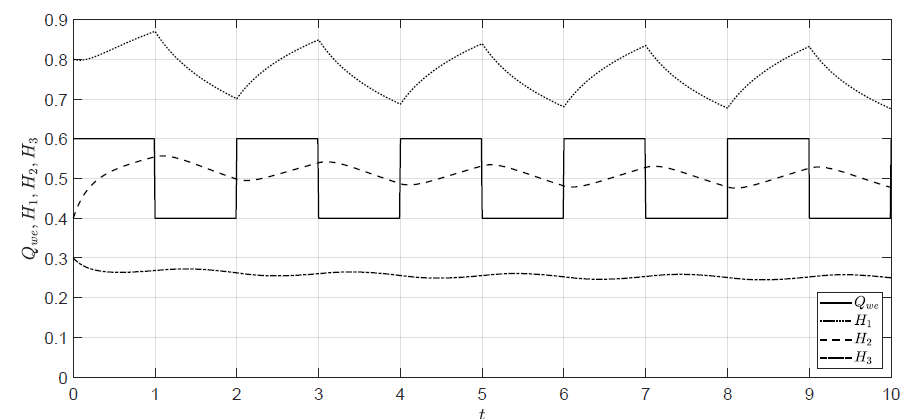
Rysunek 1.4 Trajektorie zmiennych poziomów cieczy w zbiornikach dla niezerowych warunków początkowych i sterowania w kształcie fali prostokątnej.
Poziomy cieczy w zbiornikach zmieniają się aż do chwili w której powstanie w obiekcie równowaga przepływów. Po ustaleniu się równowagi przepływów, nie następują już dalsze zmiany poziomów cieczy. Zauważmy, że poziomy cieczy ustaliły się na takich samych wartościach jak w przypadku napełniania pustych zbiorników. Ponieważ tym razem zbiorniki są w chwili początkowej napełnione do pewnych niezerowych poziomów, to czas ustalenia się równowagi przepływów jest krótszy niż w przypadku napełniania pustych zbiorników.
Na Rys. 1.4 przedstawione zostały trajektorie sterowań i stanów obiektu dla niezerowych warunków początkowych \( H_1(t_0) =0.8 \), \( H_2(t_0) =0.4 \), \( H_3(t_0)=0.3 \) i sygnału sterującego typu fala prostokątna.
Amplituda wahań \( Q_{we}(t) \) wokół wartości 0.5 wynosi 0.1. Wypełnienie fali wynosi 50\%, natomiast jej okres wynosi 2. Poziomy cieczy we wszystkich zbiornikach doznają wahań. Dla kolejnych zbiorników następuje stopniowe wygładzanie przebiegów i spadek amplitudy wahań. Symulacja numeryczna pozwala analizować zachowanie obiektu także dla innych przebiegów sygnału sterującego \( Q_{we}(t) \).
1.2. Przykład modelowania wahadła matematycznego
W niniejszej sekcji sformułujemy model odwróconego wahadła matematycznego w postaci równań stanu. Schemat wahadła został przedstawiony na Rys. 1.5.
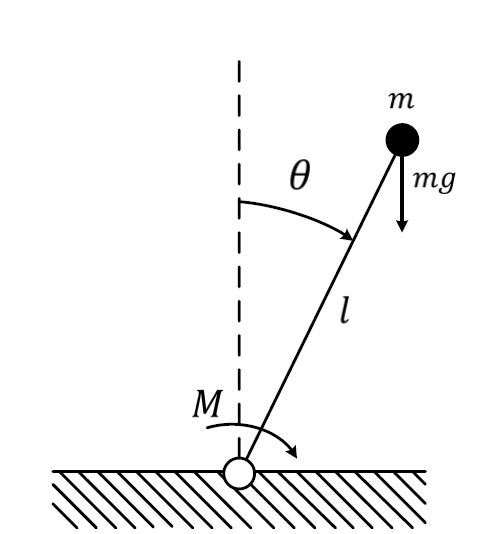
Rysunek 1.5 Schemat wahadła matematycznego.
Masa \( m \) jest osadzona na sztywnym przegubowym pręcie o długości \( l \) (pomijamy masę pręta). W przegubie podawany jest sterowany moment siły \( M \), a na masę \( m \) działa siła przyciągania ziemskiego (\( g \) - przyciąganie ziemskie). W przegubie generuje się też moment tarcia proporcjonalny do prędkości kątowej wahadła. Kąt odchylenie pręta od osi pionowej jest oznaczony jako \( \theta \). Równanie fizyczne opisujące układ to równanie Newtona dla ruchu obrotowego. Ogólna postać tego równania to
\( \begin{equation} I\epsilon(t) = \sum_{i} M_i(t) \qquad(1.25) \end{equation} \)
tzn. iloczyn momentu bezwładności ciała \( I \) i przyśpieszenia kątowego \( \epsilon \) jest równy sumie momentów sił \( M_i \) działających na ciało. Moment bezładności wahadła obliczamy przy upraszczającym założeniu o punktowości masy \( m \) i pomijalnej masie pręta. W takim przypadku mamy
\( \begin{equation} I = ml^2 \qquad(1.26) \end{equation} \)
przyśpieszenie kątowe jest równe drugiej pochodnej położenia kątowego
\( \begin{equation} \epsilon(t) = \dfrac{d^2\theta(t)}{dt^2} \qquad(1.27) \end{equation} \)
Na ciało działa moment bezwładności w przegubie \( M \), moment tarcia \( M_t \) oraz moment siły generowany przez siłę przyciągania ziemskiego \( M_g \)
\( \begin{equation} \sum_{i} M_i(t) = M(t) + M_t(t) + M_g(t) \qquad(1.28) \end{equation} \)
Moment tarcia jest proporcjonalny do prędkości kątowej \( \omega \), ze współczynnikiem proporcjonalności \( D \)
\( \begin{equation} M_t(t) = -D\omega(t) = -D\dfrac{d\theta(t)}{dt} \qquad(1.29) \end{equation} \)
Znak minus wskazuje na to, że moment tarcia działa przeciwnie do aktualnej prędkości kątowej. Moment siły od grawitacji jest równy iloczynowi siły ciążenia \( F_g=mg \), długości ramienia \( l \) na którym działa siła grawitacji oraz sinusowi kąta pomiędzy ramieniem a wektorem siły
\( \begin{equation} M_g(t) = F_g\cdot l \cdot sin\theta(t) = mglsin\theta(t) \qquad(1.30) \end{equation} \)
Wstawiając zależności (1.26)-(1.30) do równania (1.25) otrzymujemy
\( \begin{equation} ml^2 \dfrac{d^2\theta(t)}{dt^2} = mglsin\theta(t) - D \dfrac{d\theta(t)}{dt} + M(t) \qquad(1.31) \end{equation} \)
Po podzieleniu obu stron równania przez \( ml^2 \) otrzymujemy
\( \begin{equation} \dfrac{d^2\theta(t)}{dt^2} = \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \dfrac{d\theta(t)}{dt} +\dfrac{1}{ml^2} M(t) \qquad(1.32) \end{equation} \)
Równanie różniczkowe (1.32) jest równaniem drugiego rzędu. Równania stanu są równaniami pierwszego rzędu. Możemy przekształcić równanie (1.32) do dwóch równań pierwszego rzędu poprzez wprowadzenie do równań zmiennej oznaczającej prędkość kątowej
\( \begin{equation} \omega = \dfrac{d\theta(t)}{dt} \qquad(1.33) \end{equation} \)
Pierwsza pochodna prędkości kątowej jest równa drugiej pochodnej położenia kątowego
\( \begin{equation} \dfrac{d\omega(t)}{dt} = \dfrac{d^2\theta(t)}{dt^2} \qquad(1.34) \end{equation} \)
Wprowadzając powyższe zależności do (1.32) otrzymujemy równania stanu wahadła
\( \begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.35)\\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \qquad(1.36) \end{eqnarray} \)
W opisie wahadła zmiennymi stanu są \( \theta \) oraz \( \omega \), sygnałem sterującym jest moment siły \( M \), natomiast stałymi są \( g \), \( l \), \( m \) oraz \( D \). Jako sygnał wyjściowy z układu przyjmujemy położenie kątowe \( \theta \). Aby rozwiązać równania stanu, konieczne jest określenie warunków początkowych dla zmiennych stanu tzn. wielkości \( \theta(t_0) \)oraz \( \omega(t_0) \), gdzie \( t_0 \) jest wybraną chwilą początkową. Konieczna jest też znajomość wartości sygnału sterującego \( M(t) \) na całym rozważanym horyzoncie czasu.
Równania stanu dla wahadła można rozwiązać numerycznie w środowisku MATLAB®. Na potrzeby symulacji przyjmujemy następujące wartości parametrów obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Na Rys. 1.6 przedstawiono przykładowe trajektorie stanów obiektu uzyskane dla stałego momentu \( M(t) = -0.5\) i warunków początkowych \( \theta(t_0) = \dfrac{\pi}{2} \), \( \omega(t_0) = 0 \)

Rysunek 1.6 Trajektorie położenia i prędkości kątowej wahadła dla stałego sterowania.
Wahadło znajdujące się początkowo w położeniu horyzontalnym spada w dół, gdyż moment od siły ciążenia przeważa nad momentem generowanym w przegubie. Następnie, ze względu na obecność tarcia w przegubie, wahadło wykonuje oscylacje gasnące. Wreszcie wahadło stabilizuje się w położeniu, w którym moment od siły ciążenia i \( M \) wyrównują się. Po ustabilizowaniu się wahadła w pewnym położeniu kątowym, jego prędkość kątowa wynosi 0.
Na Rys. 1.7 przedstawione zostały trajektorie stanów obiektu dla warunków początkowych \( \theta(t_0) = \dfrac{\pi}{2} \), \( \omega(t_0) = 0 \) i sygnału sterującego typu fala prostokątna. Amplituda wahań \( M(t) \) wokół wartości -0.5 wynosi 0.1. Wypełnienie fali wynosi 50 %, natomiast jej okres wynosi 2. Po początkowej fazie przejściowej wahadło wykonuje oscylacje o ustalonej amplitudzie.
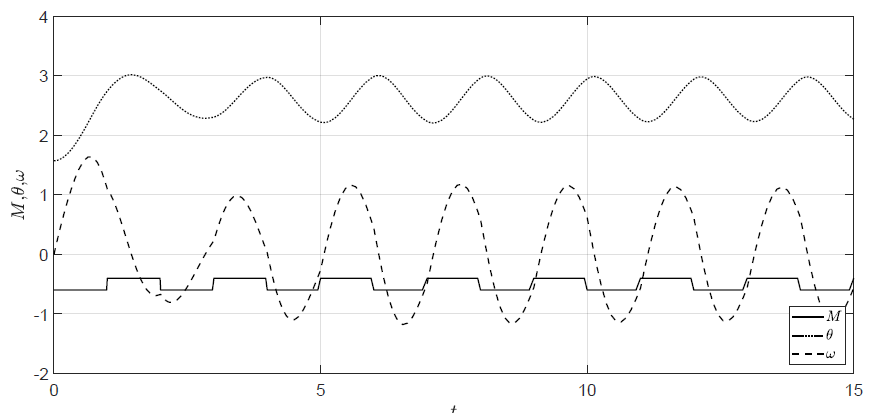
Rysunek 1.7 Trajektorie położenia i prędkości kątowej wahadła dla sterowania w kształcie fali prostokątnej.
1.3. Równania stanu w postaci ogólnej
Standardowo zmienne stanu są oznaczane jako \( x_1,x_2,\cdots,x_j,\cdots,x_n \), natomiast zmienne sterujące jako \( u_1,u_2,\cdots,u_k,\cdots,u_m \). W naszych rozważaniach odnośnie układów regulacji nie będziemy badać wpływu wartości stałych na własności modelu (tzw. {\bf analiza wrażliwościowa}), dlatego nie trzeba osobno oznaczać stałych i można je traktować jako część definicji funkcji prawych stron. Równania stanu mają w ogólnym przypadku postać
\( \begin{eqnarray} \dfrac{dx_1(t)}{dt} &=& f_1(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.37) \\ &\vdots& \\ \dfrac{dx_i(t)}{dt} &=& f_i(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.38) \\ &\vdots& \nonumber \\ \dfrac{dx_n(t)}{dt} &=& f_n(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.39) \end{eqnarray} \)
gdzie \( f_1,\cdots,f_i,\cdots,f_n \) oznaczają (w ogólnym przypadku nieliniowe) funkcje prawych stron równań stanu.
Dla skrócenia zapisu tworzy się wektory zmiennych stanu oraz zmiennych sterujących
\( \begin{equation} x(t) = \left( \begin{array}{c} x_1(t)\\ \vdots\\ x_j(t) \\ \vdots\\ x_n(t) \end{array} \right),\ u(t) = \left( \begin{array}{c} u_1(t)\\ \vdots\\ u_k(t) \\ \vdots\\ u_m(t) \end{array} \right) \qquad(1.40) \end{equation} \)
Równania stanu (1.37)-(1.39}) przyjmują wtedy postać
\( \begin{eqnarray} \dfrac{dx_1(t)}{dt} &=& f_1(x(t),u(t)) \qquad(1.41) \\ &\vdots& \nonumber \\ \dfrac{dx_i(t)}{dt} &=& f_i(x(t),u(t)) \qquad(1.42)\\ &\vdots& \nonumber \\ \dfrac{dx_n(t)}{dt} &=& f_n(x(t),u(t)) \qquad(1.43) \end{eqnarray} \)
Jeżeli wprowadzimy nowe wektory
\( \begin{equation} \dfrac{dx(t)}{dt} = \left( \begin{array}{c} \dfrac{dx_1(t)}{dt} \\ \vdots\\ \dfrac{dx_i(t)}{dt} \\ \vdots\\ \dfrac{dx_n(t)}{dt} \end{array} \right),\ f(x(t),u(t)) = \left( \begin{array}{c} f_1(x(t),u(t))\\ \vdots\\ f_i(x(t),u(t)) \\ \vdots\\ f_n(x(t),u(t)) \end{array} \right) \end{equation}\qquad(1.44) \)
to równania (1.41)-(1.43) upraszczają się do postaci
\( \begin{equation} \dfrac{dx(t)}{dt} = f(x(t),u(t)) \label{eq:ch1:rownaniaStanuWektorowo}\qquad(1.45 \end{equation}) \)
Często pomija się także podawanie czasu jako argumentu zmiennych stanu i sterowań, i równania stanu przyjmują postać
\( \begin{equation} \dfrac{dx}{dt} = f(x,u) \qquad(1.46) \end{equation} \)
Można również rozważać równania stanu, w których zmienna czasu występuje w sposób jawny
\( \begin{equation} \dfrac{dx(t)}{dt} = f(x(t),u(t),t) \qquad(1.47) \end{equation} \)
W takim przypadku w równaniach stanu oprócz zmiennych stanu, sterowań i stałych mogą pojawiać się funkcje czasu np.: \( sin(\dfrac{t}{1+t^2}) \). Obiekty w których opisie jawnie występuje zmienna \( t \) nazywamy niestacjonarnymi, natomiast obiekty w których opisie nie występuje jawnie zmienna \( t \) nazywamy stacjonarnymi. W naszych rozważaniach skupiamy się na obiektach stacjonarnych, ale analogiczne rozważania można przeprowadzić także dla układów niestacjonarnych.
Aby rozwiązać równania stanu w postaci ogólnej, konieczne jest określenie warunków początkowych dla zmiennych stanu tzn. wielkości \( x_1(t_0) \),...,\( x_j(t_0) \),...,\( x_n(t_0) \), gdzie \( t_0 \) jest wybraną chwilą początkową. Warunki początkowe można zapisać w postaci wektorowej wprowadzając oznaczenie
\( \begin{equation} x(t_0) = \left( \begin{array}{c} x_1(t_0)\\ \vdots\\ x_j(t_0) \\ \vdots\\ x_n(t_0) \end{array} \right) \qquad(1.48) \end{equation} \)
Równania stanu dla układu trzech zbiorników
\( \begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we}(t) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.49) \\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.50) \\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.51) \end{eqnarray} \)
można zapisać w ogólnej postaci wektorowej (1.45) poprzez wprowadzenie oznaczeń
\( \begin{eqnarray} x(t) &=& \left( \begin{array}{c} x_1(t)\\ x_2(t) \\ x_3(t) \end{array} \right) = \left( \begin{array}{c} H_1(t)\\ H_2(t) \\ H_3(t) \end{array} \right) \qquad(1.52)\\ x(t_0) &=& \left( \begin{array}{c} x_1(t_0)\\ x_2(t_0) \\ x_3(t_0) \end{array} \right) = \left( \begin{array}{c} H_1(t_0)\\ H_2(t_0) \\ H_3(t_0) \end{array} \right) \qquad(1.53)\\ \dfrac{dx(t)}{dt} &=& \left( \begin{array}{c} \dfrac{dx_1(t)}{dt} \\ \dfrac{dx_2(t)}{dt} \\ \dfrac{dx_3(t)}{dt} \end{array} \right) = \left( \begin{array}{c} \dfrac{dH_1(t)}{dt} \\ \dfrac{dH_2(t)}{dt} \\ \dfrac{dH_3(t)}{dt} \end{array} \right) \qquad(1.54)\\ u(t) &=& \left(u_1(t)\right) = \left(Q_{we}(t)\right)\qquad(1.55) \end{eqnarray} \)
oraz
\( \begin{eqnarray} f(x(t),u(t)) &=& \left( \begin{array}{c} f_1(x_1(t),x_2(t),x_3(t),u_1(t)) \\ f_2(x_1(t),x_2(t),x_3(t),u_1(t)) \\ f_3(x_1(t),x_2(t),x_3(t),u_1(t)) \end{array} \right) \\ &=& \left( \begin{array}{c} f_1(H_1(t),H_2(t),H_3(t),Q_{we}(t)) \\ f_2(H_1(t),H_2(t),H_3(t),Q_{we}(t)) \\ f_3(H_1(t),H_2(t),H_3(t),Q_{we}(t)) \end{array} \right) = \nonumber\\ &=&\left( \begin{array}{c} \dfrac{1}{A}Q_{we}(t) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \\ \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \\ \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \end{array} \right) \qquad(1.56) \end{eqnarray} \)
Równania stanu dla wahadła
\( \begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.57) \\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \qquad(1.58) \end{eqnarray} \)
można zapisać w postaci ogólnej (1.45) poprzez wprowadzenie oznaczeń
\( \begin{eqnarray} x(t) &=& \left( \begin{array}{c} x_1(t)\\ x_2(t) \end{array} \right) = \left( \begin{array}{c} \theta(t)\\ \omega(t) \end{array} \right) \qquad(1.59)\\ x(t_0) &=& \left( \begin{array}{c} x_1(t_0)\\ x_2(t_0) \end{array} \right) = \left( \begin{array}{c} \theta(t_0)\\ \omega(t_0) \end{array} \right) \qquad(1.60)\\ \dfrac{dx(t)}{dt} &=& \left( \begin{array}{c} \dfrac{dx_1(t)}{dt} \\ \dfrac{dx_2(t)}{dt} \end{array} \right) = \left( \begin{array}{c} \dfrac{d\theta(t)}{dt} \\ \dfrac{d\omega(t)}{dt} \end{array} \right) \qquad(1.61)\\ u(t) &=& \left(u_1(t)\right) = \left(M(t)\right)\qquad(1.62) \end{eqnarray} \)
oraz
\( \begin{eqnarray} f(x(t),u(t)) &=& \left( \begin{array}{c} f_1(x_1(t),x_2(t),u_1(t)) \\ f_2(x_1(t),x_2(t),u_1(t)) \end{array} \right) \\ &=& \left( \begin{array}{c} f_1(\theta(t),\omega(t),M(t)) \\ f_2(\theta(t),\omega(t),M(t)) \end{array} \right) \nonumber \\ &=& \left( \begin{array}{c} \omega(t) \\ \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \end{array} \right) \nonumber \end{eqnarray} \)
W przykładzie z wahadłem musieliśmy przekształcić równanie różniczkowe wyższego rzędu do układu równań różniczkowych pierwszego rzędu.
Ogólne równanie różniczkowe wyższego rzędu
\( \begin{equation} \dfrac{d^{n} x}{dt^{n}} = f(x,\dfrac{dx}{dt},\dfrac{d^2 x}{dt^2},\cdots,\dfrac{d^{n-1} x}{dt^{n-1}}) \qquad(1.64) \end{equation} \)
z warunkami początkowymi \( x(t_0), \dfrac{dx(t_0)}{dt}, \cdots, \dfrac{d^{n-1} x(t_0)}{dt^{n-1}} \) można przekształcić do układu równań pierwszego rzędu poprzez wprowadzenie nowych zmiennych
\( \begin{equation} x_1 = x, x_2 = \dfrac{dx}{dt}, \cdots, x_n = \dfrac{d^{n-1} x}{dt^{n-1}} \qquad(1.65) \end{equation} \)
Równanie (1.64) jest równoważne następującemu układowi równań
\( \begin{eqnarray} \dfrac{dx_1}{dt} &=& x_2 \qquad(1.66)\\ \dfrac{dx_2}{dt} &=& x_3\qquad(1.67) \\ &\vdots& \nonumber \\ \dfrac{dx_i}{dt} &=& x_{i+1} \qquad(1.68)\\ &\vdots& \nonumber \\ \dfrac{dx_{n-1}}{dt} &=& x_{n} \qquad(1.69)\\ \dfrac{dx_{n}}{dt} &=& f(x_1,x_2,\cdots,x_i,\cdots,x_n)\qquad(1.70) \end{eqnarray} \)
z warunkami początkowymi
\( \begin{equation} x_1(t_0) = x(t_0), x_2(t_0) = \dfrac{dx(t_0)}{dt}, \cdots, x_n(t_0) = \dfrac{d^{n-1} x(t_0)}{dt^{n-1}} \qquad(1.71) \end{equation} \)
1.4. Równania wyjść
Uzupełnieniem równań stanu są {\bf równania wyjść}. Wyjścia układu są zwykle oznaczane jako \( y_1,\cdots,y_i,\cdots,y_p \). Równania wyjść są równaniami algebraicznymi, a argumentami funkcji wyjść są zmienne stanu. Układ równań wyjść ma następującą ogólną postać
\( \begin{eqnarray} y_1(t) &=& g_1(x_1(t),\cdots,x_j(t),\cdots,x_n(t)) \qquad(1.72) \\ &\vdots& \nonumber \\ y_i(t) &=& g_i(x_1(t),\cdots,x_j(t),\cdots,x_n(t)) \qquad(1.73) \\ &\vdots& \nonumber \\ y_p(t) &=& g_p(x_1(t),\cdots,x_j(t),\cdots,x_n(t)) \qquad(1.74) \end{eqnarray} \)
Wprowadzając wektor zmiennych stanu \( x(t) = (x_1(t), \cdots, x_j(t), \cdots, x_n(t))^T \) otrzymujemy
\( \begin{eqnarray} y_1(t) &=& g_1(x(t)) \qquad(1.75) \\ &\vdots& \nonumber \\ y_i(t) &=& g_i(x(t)) \qquad(1.76) \\ &\vdots& \nonumber \\ y_p(t) &=& g_p(x(t)) \qquad(1.77) \end{eqnarray} \)
Jeżeli wprowadzimy nowe wektory
\( \begin{equation} y(t) = \left( \begin{array}{c} y_1(t)\\ \vdots\\ y_i(t) \\ \vdots\\ y_p(t) \end{array} \right),\ g(x(t)) = \left( \begin{array}{c} g_1(x(t))\\ \vdots\\ g_i(x(t)) \\ \vdots\\ g_p(x(t)) \end{array} \right)\qquad(1.78) \end{equation} \)
to równania wyjść można zapisać w postaci wektorowej
\( \begin{equation} y(t) = g(x(t)) \qquad(1.79) \end{equation} \)
Można rozważać układy w których zmienne wyjściowe zależą jawnie od sygnałów sterujących
\( \begin{equation} y(t) = g(x(t), u(t)) \end{equation}\qquad(1.80) \)
w naszych układach skupiamy się jednak na układach w których wyjścia zależą jedynie od stanów obiektu.
Równania wyjść w przykładowych obiektach są wyjątkowo proste. Dla układu trzech zbiorników mamy
\( \begin{eqnarray} y(t) &=& (y_1(t)) = (H_3(t)) \qquad(1.81)\\ y(t) &=& g(x(t)) = (g_1(x_1(t),x_2(t),x_3(t))) = (g_1(H_1(t),H_2(t),H_3(t))) = (H_3(t))\qquad(1.82) \end{eqnarray} \)
Dla wahadła mamy
\( \begin{eqnarray} y(t) &=& (y_1(t)) = (\theta(t))\qquad(1.83) \\ y(t) &=& g(x(t)) = (g_1(\theta(t),\omega(t))) = (\theta(t))\qquad(1.84) \end{eqnarray} \)
2. Charakterystyka statyczna
Charakterystyka statyczna
2.1. Przykłady wyznaczania charakterystyki statycznej
W układach regulacji interesuje nas zachowanie obiektu w pobliżu tzw. punktu równowagi obiektu. Potocznie przez punkt równowagi rozumiemy taki stan obiektu, w którym obiekt samoczynnie pozostaje (tzn. "nic się w układzie nie zmienia"). Przypomnijmy równania stanu układu trzech zbiorników
\( \begin{eqnarray} \frac{d H_1(t)}{dt} &=& \frac{1}{A}Q_{we}(t) - \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.85)\\ \frac{d H_2(t)}{dt} &=& \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \frac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.86) \\ \frac{d H_3(t)}{dt} &=& \frac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \frac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.87) \end{eqnarray} \)
W punkcie równowagi sygnały sterujące muszą mieć stałą wartość. W przeciwnym razie zmiany sygnału sterującego będą wymuszać zmiany zmiennych stanu. Oznaczmy wartość sterowania w punkcie pracy jako \( Q_{we0} \). Punktem równowagi dla układu trzech zbiorników nazwiemy taki stan w którym \( H_1(t) \), \( H_2(t) \) oraz \( H_3(t) \) pozostają stałe. Jeżeli wysokości słupów cieczy pozostają stałe, to ich pochodne w punkcie równowagi się zerują. Oznaczmy wartości zmiennych stanu w punkcie równowagi jako \( H_{10} \), \( H_{20} \) oraz \( H_{30} \). Zauważmy, że \( H_{10} \), \( H_{20} \) oraz \( H_{30} \) nie są funkcjami czasu, ale stałymi. Z równań stanu obiektu (1.85)-(1.87) i warunku zerowania się pochodnej otrzymujemy
\( \begin{eqnarray} 0 &=& \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \qquad(1.88) \\ 0 &=& \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \qquad(1.89) \\ 0 &=& \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} \qquad(1.90) \end{eqnarray} \)
Powyższe równania mają także prostą interpretację fizyczną. Punkt równowagi w układzie jest wtedy, gdy przepływy \( Q_{we} \), \( Q_{12} \), \( Q_{23} \) oraz \( Q_3 \) są sobie równe.
Układ równań algebraicznych (1.88)-(1.90) składa się z trzech równań, w których mamy cztery niewiadome \( Q_{we0} \), \( H_{10} \), \( H_{20} \) oraz \( H_{30} \). Oznacza to, że układ posiada więcej niż jeden punkt równowagi. Zbiór wszystkich możliwych punktów równowagi obiektu nazywamy charakterystyką statyczną obiektu.
Aby znaleźć równania charakterystyki statycznej przyjmujemy jedną z niewiadomych jako parametr i rozwiązujemy układ równań (1.88)-(1.90) względem pozostałych niewiadomych. Ponieważ naszym ostatecznym celem jest regulacja wielkości wyjściowej, to przyjmujemy jako parametr \( H_{30} \( i wyznaczamy wartości \( Q_{we0} \), \( H_{10} \) oraz \( H_{20} \) jako funkcje \( H_{30} \).
Równania (1.88)-(1.90) są nieliniowe, jednak ich rozwiązanie nie jest trudne. Rozpocznijmy rozwiązywanie układu równań od równania (1.90). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} = \frac{\alpha}{2A} \sqrt{H_{30}} \end{equation}\qquad(1.91) \)
Jeżeli wymnożymy obie strony równania przez \( \dfrac{2A}{\alpha} \) to otrzymamy
\( \begin{equation} \sqrt{H_{20}-H_{30}} = \sqrt{H_{30}} \end{equation}\qquad(1.92) \)
Po podniesieniu obu stron równania do kwadratu otrzymujemy
\( \begin{equation} H_{20}-H_{30} = H_{30} \end{equation}\qquad(1.93) \)
czyli
\( \begin{equation} H_{20} = 2H_{30} \qquad(1.94) \end{equation} \)
Okazuje się, że w stanie ustalonym wysokość słupa cieczy w drugim zbiorniku jest dwa razy wyższa niż wysokość wody w trzecim zbiorniku.
Przejdźmy do rozwiązania równania (1.89). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} = \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \end{equation}\qquad(1.95) \)
Jeżeli wymnożymy obie strony równania przez \( \dfrac{A}{\alpha} \) to otrzymamy
\( \begin{equation} \sqrt{H_{10}-H_{20}} = \sqrt{H_{20}-H_{30}} \end{equation}\qquad(1.96) \)
Po podniesieniu obu stron równania do kwadratu otrzymujemy
\( \begin{equation} H_{10}-H_{20} = H_{20}-H_{30} \end{equation}\qquad(1.97) \)
czyli
\( \begin{equation} H_{10} = 2H_{20}-H_{30} \end{equation}\qquad(1.98) \)
Korzystając z (1..94) mamy
\( \begin{equation} H_{10} = 2H_{20}-H_{30} = 2\cdot2H_{30}-H_{30} = 3H_{30} \qquad(1.99) \end{equation} \)
Okazuje się, że w stanie ustalonym wysokość słupa cieczy w pierwszym zbiorniku jest trzy razy wyższa niż wysokość wody w trzecim zbiorniku.
Przejdźmy do rozwiązania równania (1.88). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \dfrac{1}{A}Q_{we0} = \dfrac{\alpha}{A} \sqrt{H_{10}-H_{20}} \end{equation}\qquad(1.100) \)
Jeżeli wymnożymy obie strony równania przez \( A \) to otrzymamy
\( \begin{equation} Q_{we0} = \alpha\sqrt{H_{10}-H_{20}} \end{equation}\qquad(1.101) \)
Korzystając z (1.94) oraz (1.99) mamy
\( \begin{equation} Q_{we0} = \alpha\sqrt{H_{10}-H_{20}} = \alpha\sqrt{3H_{30}-2H_{30}} = \alpha\sqrt{H_{30}} \qquad(1.102) \end{equation} \)
Zapiszmy razem równania (1.94), (1.99) oraz (1.102)
\( \begin{eqnarray} H_{20} &=& 2H_{30} \qquad(1.103) \\ H_{10} &=& 3H_{30} \qquad(1.104)\\ Q_{we0} &=& \alpha\sqrt{H_{30}} \qquad(1.105) \end{eqnarray} \)
Definiują one charakterystykę statyczną dla układu trzech zbiorników, gdzie parametrem jest \( H_{30} \). Często pod pojęciem charakterystyki statycznej obiektu rozumie się zależność wyjść obiektu od wejść obiektu w stanie ustalonym. Z równania (1.105) mamy
\( \begin{equation} H_{30} = \dfrac{1}{\alpha^2}Q_{we0}^2 \end{equation}\qquad(1.106) \)
Na Rys. 1.8 przedstawiono wejściowo-wyjściową charakterystykę statyczną dla układu trzech zbiorników.

Rysunek 1.8 Wykres charakterystyki statycznej wejściowo-wyjściowej dla układu trzech zbiorników.
Należy jednak pamiętać, że nawet jeżeli w pewnej chwili \( t \) mamy \( Q_{we}(t) = Q_{we0} \) oraz \( H_3(t) = \dfrac{1}{\alpha^2}Q_{we0}^2 \) to obiekt nie musi znajdować się w punkcie równowagi bo możemy mieć \( H_1(t) \neq H_{10} \) lub \( H_2(t) \neq H_{20} \).
Mając równania charakterystyki statycznej możemy przeprowadzić symulację zachowania obiektu w wybranym punkcie równowagi. Przyjmujemy parametry obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt równowagi odpowiadający \( H_{30}=0.25 \). Z równań charakterystyki statycznej otrzymujemy \( H_{20}=0.75 \), \( H_{20}=0.5 \) oraz \( Q_{we0} = 0.5 \). Na Rys. 1.9 przedstawiono trajektorie stanów obiektu dla stałego sterowania \( Q_{we}(t) = Q_{we0} = 0.5 \) i warunków początkowych równych wartościom stanów w wybranym punkcie równowagi \( H_1(t_0) =H_{30}=0.75 \), \( H_2(t_0) =H_{20}=0.5 \), \( H_3(t_0)=H_{30}=0.25 \)
Rysunek 1.9 Trajektorie poziomów cieczy w zbiornikach w punkcie równowagi.
Zgodnie z oczekiwaniami w punkcie równowagi nie następują zmiany poziomów cieczy w zbiornikach. Zauważmy, że trajektorie stanu na Rys. 1.2 i 1.3 dążą dokładnie do wartości obliczonych z charakterystyki statycznej obiektu. Z kolei na Rys. 1.4 poziomy cieczy w zbiornikach wykonują oscylacje wokół wartości poziomów w punkcie równowagi.
\( \begin{eqnarray} \frac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.107) \\ \frac{d\omega(t)}{dt} &=& \frac{g}{l}sin\theta(t) - \frac{D}{ml^2} \omega(t) +\frac{1}{ml^2} M(t) \qquad(1.108) \end{eqnarray} \)
Oznaczmy wartość sterowania w punkcie pracy jako \( M_0 \). Punktem równowagi dla wahadła nazwiemy taki stan w którym \( \theta(t) \) oraz \( \omega(t) \) pozostają stałe, a ich pochodne się zerują. Oznaczmy wartości zmiennych stanu w punkcie równowagi jako \( \theta_0 \) oraz \( \omega_0 \). Z równań stanu obiektu (1.107)-(1.108) i warunku zerowania się pochodnej otrzymujemy
\( \begin{eqnarray} 0 &=& \omega_0 \qquad(1.109) \\ 0 &=& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \qquad(1.110) \end{eqnarray} \)
Powyższe równania mają następującą interpretację fizyczną. W punkcie równowagi wahadło się nie porusza, a momenty sił działające na wahadło się równoważą.
Układ równań algebraicznych (1.109)-(1.110)) składa się z dwóch równań, w których mamy trzy niewiadome \( M_0 \), \( \theta_0 \) oraz \( \omega_0 \). Przyjmujemy jako parametr wielkość wyjściową \( \theta_0 \) i wyznaczamy wartości \( M_0 \) oraz \( \omega_0 \) jako funkcje \( \theta_0 \).
Z równania (1.109))
\( \begin{equation} \omega_0 = 0 \end{equation}\qquad (1.111) \)
Z równania (1.110)
\( \begin{equation} 0 = \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \end{equation}\qquad(1.112) \)
Korzystając z (1.111)) otrzymujemy
\( \begin{equation} 0 = \dfrac{g}{l}sin\theta_0 +\dfrac{1}{ml^2} M_0 \end{equation}\qquad(1.113) \)
i stąd mamy
\( \begin{equation} \frac{1}{ml^2} M_0 = -\frac{g}{l}sin\theta_0 \end{equation}\qquad(1.114) \)
Mnożąc obie strony powyższego równania przez \( ml^2 \) otrzymujemy
\( \begin{equation} M_0 = -mglsin\theta_0 \qquad(1.115) \end{equation} \)
Zapiszmy razem równania (1.111) oraz (1.115))
\( \begin{eqnarray} \omega_0 &=& 0 \qquad(1.116)\\ M_0 &=& -mglsin\theta_0 \qquad(1.117) \end{eqnarray} \)
Definiują one charakterystykę statyczną dla wahadła. Równanie charakterystyki statycznej typu wejście-wyjście otrzymujemy z równania (1.115))
\( \begin{equation} sin\theta_0 = -\dfrac{1}{mgl}M_0 \end{equation}\qquad(1.118) \)
Z powyższego warunku mamy, że dla \( | M_0| > mgl \) układ nie ma punktów równowagi (moment siły \( M \) jest tak duży, że powoduje ciągłe obracanie się wahadła). Z kolei jeżeli \( | M_0| < mgl \) to układ ma dwa punkty równowagi
\( \begin{eqnarray} \theta_0 &=& arcsin \left(-\frac{1}{mgl}M_0\right) \qquad(1.119)\\ \theta_0 &=& \pi - arcsin \left(-\frac{1}{mgl}M_0\right)\qquad(1.120) \end{eqnarray} \)
Na Rys. 1.10 przedstawiono wejściowo-wyjściową charakterystykę statyczną dla wahadła.
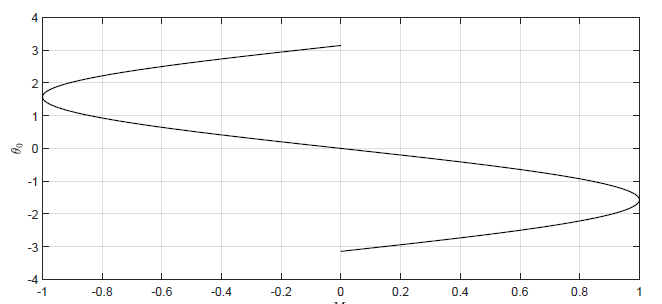
Rysunek 1.10Wykres charakterystyki statycznej wejściowo-wyjściowej dla wahadła.
Należy jednak pamiętać, że nawet jeżeli w pewnej chwili \( t \) mamy \( M(t) = M_0 \) oraz \( sin\theta_0 = \frac{1}{mgl}M_0 \) to obiekt nie musi znajdować się w punkcie równowagi bo możemy mieć \( \omega(t) \neq \omega_0 = 0 \).
Mając równania charakterystyki statycznej możemy przeprowadzić symulację zachowania obiektu w wybranym punkcie równowagi. Przyjmujemy parametry obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt równowagi odpowiadający \( \theta=\frac{5\pi}{6} \). Z równań charakterystyki statycznej otrzymujemy \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). Na Rys. 1.11 przedstawiono trajektorie stanów obiektu dla stałego sterowania \( M(t) = M_{0} = -0.5 \( i warunków początkowych równych wartościom stanów w wybranym punkcie równowagi \( \theta(t_0) =\theta_0=\frac{5\pi}{6} \), \( \omega(t_0) =\omega_0=0 \(
Rysunek 1.11 Trajektorie położenia i prędkości kątowej wahadła w punkcie równowagi.
Zgodnie z oczekiwaniami w punkcie równowagi wahadło nie zmienia swojego położenia, a jego prędkość kątowa wynosi 0. Zauważmy, że trajektorie stanu na Rys. 1.6 dążą dokładnie do wartości obliczonych z charakterystyki statycznej obiektu. Z kolei na Rys. 1.7 zmienne stanu wykonują oscylacje wokół odpowiednich wartości w punkcie równowagi.
2.2. Charakterystyka statyczna - sformułowanie ogólne
Dla równań stanu w postaci ogólnej
\( \begin{eqnarray} \frac{dx_1(t)}{dt} &=& f_1(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.121) \\ &\vdots& \nonumber \\ \frac{dx_i(t)}{dt} &=& f_i(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.122) \\ &\vdots& \nonumber \\ \frac{dx_n(t)}{dt} &=& f_n(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.123) \end{eqnarray} \)
równania charakterystyki statycznej uzyskujemy poprzez warunek zerowania pochodnych zmiennych stanu. Oznaczmy wartości stanów i sterowań w punkcie równowagi jako \( x_{10}\), \(x_{20}\), ..., \(x_{j0}\), ..., \(x_{n0} \) oraz \( u_{10}\), \(u_{20}\) ,..., \(u_{k0}\) ,..., \(u_{m0} \). Równania punktu równowagi przyjmują postać
\( \begin{eqnarray} 0 &=& f_1(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) \qquad(1.124) \\ &\vdots& \nonumber \\ 0 &=& f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) \qquad(1.125) \\ &\vdots& \nonumber \\ 0 &=& f_n(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) \qquad(1.126) \end{eqnarray} \)
Wprowadźmy wektory zmiennych stanu oraz zmiennych sterujących w punkcie równowagi
\( \begin{equation} x_0 = \left( \begin{array}{c} x_{10}\\ \vdots\\ x_{j0} \\ \vdots\\ x_{n0} \end{array} \right),\ u_0 = \left( \begin{array}{c} u_{10}\\ \vdots\\ u_{k0} \\ \vdots\\ u_{m0} \end{array} \right) \end{equation} \qquad(1.127) \)
Równania punktu równowagi (1.124)-(\1.126) przyjmują wtedy postać
\( \begin{eqnarray} 0 &=& f_1(x_0,u_0) \qquad(1.128) \\ &\vdots& \nonumber \\ 0 &=& f_i(x_0,u_0) \qquad(1.129) \\ &\vdots& \nonumber \\ 0 &=& f_n(x_0,u_0) \qquad(1.130) \end{eqnarray} \)
Jeżeli wprowadzimy oznaczenie
\( \begin{equation} f(x_0,u_0) = \left( \begin{array}{c} f_1(x_0,u_0)\\ \vdots\\ f_i(x_0,u_0) \\ \vdots\\ f_n(x_0,u_0) \end{array} \right) \end{equation} \qquad(1.131) \)
to równania punktu równowagi (1.128)-(1.130) upraszczają się do postaci
\( \begin{equation} 0 = f(x_0,u_0) \qquad(1.132) \end{equation} \)
gdzie 0 po lewej stronie równania oznacza wektor zerowy o długości \( n \). Zbiór wszystkich rozwiązań układu równań (1.132) tworzy charakterystykę statyczną obiektu.
Równania punktu równowagi dla układu trzech zbiorników
\( \begin{eqnarray} 0 &=& \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \qquad(1.133) \\ 0 &=& \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \qquad(1.134) \\ 0 &=& \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} \qquad(1.135) \end{eqnarray} \)
można zapisać w ogólnej postaci wektorowej (1.132) poprzez wprowadzenie oznaczeń
\( \begin{equation} x_0 = \left( \begin{array}{c} x_{10}\\ x_{20} \\ x_{30} \end{array} \right) = \left( \begin{array}{c} H_{10}\\ H_{20}\\ H_{30} \end{array} \right),\ u_0 = \left(u_{10}\right) = \left(Q_{we0}\right) \end{equation} \qquad(1.136) \)
oraz
\( \begin{eqnarray} f(x_0,u_0) &=& \left( \begin{array}{c} f_1(x_{10},x_{20},x_{30},u_{10}) \\ f_2(x_{10},x_{20},x_{30},u_{10}) \\ f_3(x_{10},x_{20},x_{30},u_{10}) \end{array} \right) \\ &=& \left( \begin{array}{c} f_1(H_{10},H_{20},H_{30},Q_{we0}) \\ f_2(H_{10},H_{20},H_{30},Q_{we0}) \\ f_3(H_{10},H_{20},H_{30},Q_{we0}) \end{array} \right) = \nonumber\\ &=&\left( \begin{array}{c} \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \\ \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \\ \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} \end{array} \right)\nonumber \end{eqnarray}\qquad(1.137) \)
Równania punktu równowagi dla wahadła
\( \begin{eqnarray} 0 &=& \omega_0 \qquad(1.138)\\ 0 &=& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \qquad(1.140) \end{eqnarray} \)
można zapisać w postaci ogólnej (1.132}) poprzez wprowadzenie oznaczeń
\( \begin{equation} x_0 = \left( \begin{array}{c} x_{10}\\ x_{20} \end{array} \right) = \left( \begin{array}{c} \theta_0\\ \omega_0 \end{array} \right),\ u_0 = \left(u_{10}\right) = \left(M_0\right) \end{equation} \qquad(1.140) \)
oraz
\( \begin{eqnarray} f(x_0,u_0) &=& \left( \begin{array}{c} f_1(x_{10},x_{20},u_{10}) \\ f_2(x_{10},x_{20},u_{10}) \end{array} \right) \\ &=& \left( \begin{array}{c} f_1(\theta_0,\omega_0,M_0) \\ f_2(\theta_0,\omega_0,M_0) \end{array} \right) \nonumber \\ &=& \left( \begin{array}{c} \omega_0 \\ \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \end{array} \right) \nonumber \end{eqnarray}\qquad(1.141) \)
Jeżeli chcemy wyznaczyć charakterystykę statyczną wejściowo-wyjściową, należy najpierw rozwiązać układ równań punktu równowagi (1.132), aby znaleźć zależność wektora stanu w punkcie równowagi \( x_0 \) od wektora sterowań w punkcie równowagi \( u_0 \). Układ równań może nie mieć rozwiązań, mieć jedno, kilka lub nieskończenie wiele rozwiązań, dlatego rozstrzygnięcie problemu rozwiązywalności układu równań jest niemożliwe w ogólnym przypadku. Dla układu trzech zbiorników równania punktu równowagi miały jednoznaczne rozwiązania, przynajmniej w dziedzinie w której określone są funkcje definiujące równania stanu (patrz funkcja pierwiastka). Dla wahadła równanie
\( \begin{equation} sin\theta_0 = -\frac{1}{mgl}M_0 \end{equation}\qquad(1.142) \)
może mieć jedno, dwa lub nie mieć wcale rozwiązań \( \theta_0 \), w zależności od wartości \( M_0 \).
Jeżeli jednak możliwe jest rozwiązanie układu równań (1.132) względem \( x_0 \) i uzyskanie rozwiązania postaci
\( \begin{equation} x_0 = f^u(u_0) \end{equation} \qquad(1.143) \)
to aby uzyskać charakterystyka statyczną wejściowo-wyjściową należy do równania wyjść w punkcie równowagi
\( \begin{equation} y_0 = g(x_0) \end{equation}\qquad(1.144) \)
wstawić zależność (1.143)
\( \begin{equation} y_0 = g(f^u(u_0)) = g^u(u_0) \end{equation}\qquad(1.145) \)
gdzie przyjęto następujące oznaczenia
\( \begin{equation} y_0 = \left( \begin{array}{c} y_{10}\\ \vdots \\ y_{i0}\\ \vdots \\ y_{p0} \end{array} \right),\ g(x_0) = \left( \begin{array}{c} g_1(x_{10},\cdots,x_{j0},\cdots,x_{n0}) \\ \vdots \\ g_i(x_{10},\cdots,x_{j0},\cdots,x_{n0})\\ \vdots \\ g_p(x_{10},\cdots,x_{j0},\cdots,x_{n0}) \end{array} \right) \end{equation}\qquad(1.146) \)
oraz
\( \begin{equation} f^u(u_0) = \left( \begin{array}{c} f_1^u(u_{10},\cdots,u_{k0},\cdots,u_{m0}) \\ \vdots \\ f_i^u(u_{10},\cdots,u_{k0},\cdots,u_{m0})\\ \vdots \\ f_n^u(u_{10},\cdots,u_{k0},\cdots,u_{m0}) \end{array} \right),\ g^u(u_0) = \left( \begin{array}{c} g_1^u(u_{10},\cdots,u_{k0},\cdots,u_{m0}) \\ \vdots \\ g_i^u(u_{10},\cdots,u_{k0},\cdots,u_{m0})\\ \vdots \\ g_p^u(u_{10},\cdots,u_{k0},\cdots,u_{m0}) \end{array} \right) \end{equation} \qquad(1.147) \)
Dla układu trzech zbiorników funkcja \( f^u \) ma postać
\( \begin{equation} f^u(u_0) = f^u(Q_{we0}) = \left( \begin{array}{c} f_1^u(Q_{we0}) \\ f_2^u(Q_{we0}) \\ f_3^u(Q_{we0}) \end{array} \right) = \left( \begin{array}{c} 3\frac{1}{\alpha^2}Q_{we0}^2 \\ 2\frac{1}{\alpha^2}Q_{we0}^2 \\ \frac{1}{\alpha^2}Q_{we0}^2 \end{array} \right) \end{equation} \qquad(1.148) \)
Wektor wyjść w punkcie równowagi ma postać
\( \begin{equation} y_0 = (H_{30}) \end{equation}\qquad(1.149) \)
natomiast funkcja \( g^u \) ma postać
\( \begin{equation} g^u(u_0) = g^u(Q_{we0}) = \left( g_1^u(Q_{we0}) \right) = \left( \frac{1}{\alpha^2}Q_{we0}^2 \right) \end{equation} \qquad(1.150) \)
Dla wahadła istnieją dwie gałęzie rozwiązań równania punktu równowagi. Funkcja \( f^u \) dla pierwszej gałęzi rozwiązań ma postać
\( \begin{equation} x_0 = f^u(u_0) = f^u(M_0) = \left( \begin{array}{c} f_1^u(M_0) \\ f_2^u(M_0) \end{array} \right) = \left( \begin{array}{c} arcsin \left(-\frac{1}{mgl}M_0\right) \\ 0 \end{array} \right) \end{equation} \qquad(1.151) \)
Wektor wyjść w punkcie równowagi ma postać
\( \begin{equation} y_0 = (\theta_0) \end{equation}\qquad(1.152) \)
natomiast funkcja \( g^u \) ma postać
\( \begin{equation} g^u(u_0) = g^u(M_0) = \left( g_1^u(M_0) \right) = \left( arcsin \left(- \frac{1}{mgl}M_0 \right) \right) \end{equation} \qquad(1.153) \)
Funkcja \( f^u \) dla drugiej gałęzi rozwiązań ma postać
\( \begin{equation} x_0 = f^u(u_0) = f^u(M_0) = \left( \begin{array}{c} f_1^u(M_0) \\ f_2^u(M_0) \end{array} \right) = \left( \begin{array}{c} \pi - arcsin \left(-\frac{1}{mgl}M_0\right) \\ 0 \end{array} \right) \end{equation} \qquad(1.154) \)
natomiast funkcja \( g^u \) ma postać
\( \begin{equation} g^u(u_0) = g^u(M_0) = \left( g_1^u(M_0) \right) = \left( \pi - arcsin \left( -\frac{1}{mgl}M_0 \right) \right) \end{equation} \qquad(1.155) \)
3. Linearyzacja równań modelu obiektu
3.1. Istota linearyzacji
Nieliniowe równania stanu mają ogólną postać
\( \begin{eqnarray} \frac{dx_1(t)}{dt} &=& f_1(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.156) \\ &\vdots& \nonumber \\ \frac{dx_i(t)}{dt} &=& f_i(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.157) \\ &\vdots& \nonumber \\ \frac{dx_n(t)}{dt} &=& f_n(x_1(t),\cdots,x_j(t),\cdots,x_n(t),u_1(t),\cdots,u_k(t),\cdots,u_m(t)) \qquad(1.158) \end{eqnarray} \)
Szczególnym przypadkiem równań nieliniowych są równania liniowe
\( \begin{eqnarray} \frac{dx_1(t)}{dt} &=& a_{11}x_1(t)+\cdots+a_{1j}x_j(t),\cdots+a_{1n}x_n(t) \qquad(1.159)\\ && + b_{11}u_1(t)+\cdots+b_{1k}u_k(t)+\cdots+b_{1m}u_m(t) \nonumber \\ &\vdots& \nonumber\\ \frac{dx_i(t)}{dt} &=& a_{i1}x_1(t)+\cdots+a_{ij}x_j(t),\cdots+a_{in}x_n(t) \qquad(1.160)\\ && + b_{11}u_1(t)+\cdots+b_{ik}u_k(t)+\cdots+b_{im}u_m(t) \nonumber \\ &\vdots& \nonumber \\ \frac{dx_n(t)}{dt} &=& a_{n1}x_1(t)+\cdots+a_{nj}x_j(t),\cdots+a_{nn}x_n(t) \qquad(1.161) \\ && + b_{11}u_1(t)+\cdots+b_{nk}u_k(t)+\cdots+b_{nm}u_m(t) \nonumber \end{eqnarray} \)
gdzie \( a_{11} \),..., \( a_{nn} \), \( b_{11} \),...,\( b_{nm} \) są stałymi współczynnikami.
Równania (1.159)-(1.161) można zapisać w postaci macierzowej
\( \begin{eqnarray} \left( \begin{array}{c} \frac{dx_1(t)}{dt} \\ \vdots\\ \frac{dx_i(t)}{dt} \\ \vdots\\ \frac{dx_n(t)}{dt} \end{array} \right) &=& \left( \begin{array}{ccccc} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \end{array} \right) \left( \begin{array}{c} x_1(t)\\ \vdots\\ x_j(t) \\ \vdots\\ x_n(t) \end{array} \right) \\ & & + \left( \begin{array}{ccccc} b_{11} & \cdots & b_{1k} & \cdots & b_{1m} \\ \vdots & & \vdots & & \vdots \\ b_{i1} & \cdots & b_{ik} & \cdots & b_{im} \\ \vdots & & \vdots & & \vdots \\ b_{n1} & \cdots & b_{nk} & \cdots & b_{nm} \end{array} \right) \left( \begin{array}{c} u_1(t)\\ \vdots\\ u_k(t) \\ \vdots\\ u_m(t) \end{array} \right) \nonumber \end{eqnarray}\qquad(1.162) \)
Standardowo stosuje się następujące oznaczenia macierzy
\( \begin{equation} A = \left( \begin{array}{ccccc} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \end{array} \right),\ B = \left( \begin{array}{ccccc} b_{11} & \cdots & b_{1k} & \cdots & b_{1m} \\ \vdots & & \vdots & & \vdots \\ b_{i1} & \cdots & b_{ik} & \cdots & b_{im} \\ \vdots & & \vdots & & \vdots \\ b_{n1} & \cdots & b_{nk} & \cdots & b_{nm} \end{array} \right) \end{equation} \qquad(1.163) \)
Liniowe równania stanu można wtedy zapisać w postaci wektorowej
\( \begin{equation} \dfrac{dx(t)}{dt} = Ax(t)+Bu(t) \end{equation}\qquad(1.164) \)
Uzupełnieniem liniowych równań stanu są liniowe równania wyjść
\( \begin{eqnarray} y_1(t) &=& c_{11}x_1(t)+\cdots+c_{1j}x_j(t),\cdots+c_{1n}x_n(t) \qquad(1.165) \\ &\vdots& \nonumber \\ y_i(t) &=& c_{i1}x_1(t)+\cdots+c_{ij}x_j(t),\cdots+c_{in}x_n(t) \qquad(1.166)\\ &\vdots& \nonumber \\ y_p(t) &=& c_{p1}x_1(t)+\cdots+c_{pj}x_j(t),\cdots+c_{pn}x_n(t) \qquad(1.167) \end{eqnarray} \)
gdzie \( c_{11} \),..., \( c_{pn} \) są stałymi współczynnikami.
Równania wyjść można zapisać w postaci macierzowej
\( \begin{equation} \left( \begin{array}{c} y_1(t) \\ \vdots\\ y_i(t) \\ \vdots\\ y_p(t) \end{array} \right) = \left( \begin{array}{ccccc} c_{11} & \cdots & c_{1j} & \cdots & c_{1n} \\ \vdots & & \vdots & & \vdots \\ c_{i1} & \cdots & c_{ij} & \cdots & c_{in} \\ \vdots & & \vdots & & \vdots \\ c_{p1} & \cdots & c_{pj} & \cdots & c_{pn} \end{array} \right) \left( \begin{array}{c} x_1(t)\\ \vdots\\ x_j(t) \\ \vdots\\ x_n(t) \end{array} \right) \end{equation}\qquad(1.168) \)
Standardowo stosuje się następujące oznaczenie macierzy
\( \begin{equation} C = \left( \begin{array}{ccccc} c_{11} & \cdots & c_{1j} & \cdots & c_{1n} \\ \vdots & & \vdots & & \vdots \\ c_{i1} & \cdots & c_{ij} & \cdots & c_{in} \\ \vdots & & \vdots & & \vdots \\ c_{p1} & \cdots & c_{pj} & \cdots & c_{pn} \end{array} \right) \end{equation} \qquad(1.169) \)
Równanie wyjść można wtedy zapisać w postaci wektorowej
\( \begin{equation} y(t) = Cx(t) \end{equation}\qquad(1.170) \)
Znalezienie rozwiązania nieliniowego układu równań różniczkowych jest możliwe tylko w szczególnych przypadkach. Także analiza obiektów opisanych nieliniowymi równaniami stanu nastręcza wielu trudności. Przeciwnie, liniowe układy równań różniczkowych są zasadniczo możliwe do rozwiązania z dowolną dokładnością. Również analiza własności obiektów liniowych jest dużo łatwiejsza niż obiektów nieliniowych.
Istota linearyzacji polega na przybliżeniu modelu nieliniowego poprzez model zlinearyzowany (liniowy), analizie układu zlinearyzowanego i wnioskowaniu o własnościach układu nieliniowego na podstawie własności układu zlinearyzowanego. Proces linearyzacji opiera się na na rozwinięciu w szereg Taylora nieliniowych funkcji prawych stron równań stanu i pominięciu wyrazów wyższego rzędu. Wynikają stąd pewne ograniczenia. Po pierwsze należy wybrać pewien określony punkt w pobliżu którego dokonujemy linearyzacji. Ponieważ w niniejszym podręczniku skupiamy się na regulacji stałowartościowej to punktem w którym będziemy dokonywać linearyzacji jest punkt równowagi obiektu. Jeżeli zmieniamy punkt linearyzacji to zmienia się także model zlinearyzowany. Po drugie model zlinearyzowany (podobnie jak szereg Taylora) dobrze przybliża model nieliniowy jedynie w pobliżu punktu linearyzacji. Jeżeli trajektorie stanu lub sterowań oddalą się zbytnio od punktu linearyzacji, to model zlinearyzowany przestaje przybliżać model nieliniowy z zadowalającą dokładnością. W tej sekcji szczegółowo omówimy proces linearyzacji na przykładach, a następnie przedstawimy model zlinearyzowany w postaci ogólnej.
3.2. Przykład 1 linearyzacji równań modelu obiektu
Przypomnijmy równania stanu dla układu trzech zbiorników
\( \begin{eqnarray} \frac{d H_1(t)}{dt} &=& \frac{1}{A}Q_{we}(t) - \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.171) \\ \frac{d H_2(t)}{dt} &=& \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \frac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.172)\\ \frac{d H_3(t)}{dt} &=& \frac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \frac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.173) \end{eqnarray} \)
Linearyzacja polega na rozwinięciu nieliniowych funkcji prawych stron równań stanu w szereg Taylora w punkcie równowagi z pominięciem wyrazów rzędu wyższego niż liniowy. Funkcja prawych stron z pierwszego równania stanu ma postać
\( \begin{equation} f_1(H_1,H_2,H_3,Q_{we}) = \frac{1}{A}Q_{we} - \frac{\alpha}{A} \sqrt{H_1-H_2} \end{equation}\qquad(1.174) \)
Dla skrócenia zapisu pomijamy w zapisie argument czasu \( (t) \). Pamiętamy jednak, że zmienne stanu i sterowania są funkcjami czasu.
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wokół punktu równowagi \( (H_{10},H_{20},H_{30},Q_{we0}) \) ma postać
\( \begin{eqnarray} f_1(H_1,H_2,H_3,Q_{we}) &\simeq& f_1(H_{10},H_{20},H_{30},Q_{we0}) \\ &&+ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} (H_1-H_{10}) \nonumber \\ &&+ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} (H_2-H_{20}) \nonumber \\ &&+ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} (H_3-H_{30}) \nonumber \\ &&+ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} (Q_{we}-Q_{we0}) \nonumber \end{eqnarray}\qquad(1.175) \)
gdzie np.: \( \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} \) oznacza wartość pochodnej cząstkowej funkcji \( f_1 \) względem \( H_1 \) obliczoną w punkcie równowagi \( (H_{10},H_{20},H_{30},Q_{we0}) \).
Obliczmy wartości pochodnych cząstkowych funkcji \( f_1 \) względem zmiennych stanu i sterowań w punkcie równowagi. Dla przypomnienia pochodna funkcji pierwiastek kwadratowy wynosi
\( \begin{equation} \left(\sqrt{x}\right)' = \frac{1}{2\sqrt{x}} \end{equation}\qquad(1.176) \)
Korzystając w razie potrzeby ze standardowych własności pochodnej dostajemy
\( \begin{eqnarray} \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} &=& -\frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{10}-H_{20}}} \qquad(1.177) \\ &=& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \nonumber \\ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} &=& -\frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{10}-H_{20}}} \cdot (-1) \qquad(1.178) \\ &=& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \nonumber \\ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} &=& 0 \qquad(1.179) \\ \frac{\partial f_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} &=& \frac{1}{A} \qquad(1.180) \end{eqnarray} \)
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wynosi zatem
\( \begin{eqnarray} f_1(H_1,H_2,H_3,Q_{we}) &=& \frac{1}{A}Q_{we} - \frac{\alpha}{A} \sqrt{H_1-H_2} \\ &\simeq& \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \nonumber \\ &&+ \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10}) \nonumber \\ &&+ \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_2-H_{20}) \nonumber \\ &&+ 0\cdot (H_3-H_{30}) \nonumber \\ &&+ \frac{1}{A} (Q_{we}-Q_{we0})\nonumber \end{eqnarray}\qquad(1.181) \)
Funkcja prawych stron z drugiego równania stanu ma postać
\( \begin{equation} f_2(H_1,H_2,H_3,Q_{we}) = \frac{\alpha}{A} \sqrt{H_1-H_2} - \frac{\alpha}{A} \sqrt{H_2-H_3} \end{equation}\qquad(1.182) \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wokół punktu równowagi \( (H_{10},H_{20},H_{30},Q_{we0}) \) ma postać
\( \begin{eqnarray} f_2(H_1,H_2,H_3,Q_{we}) &\simeq& f_1(H_{10},H_{20},H_{30},Q_{we0}) \\ &&+ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} (H_1-H_{10})\nonumber \\ &&+ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} (H_2-H_{20})\nonumber \\ &&+ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} (H_3-H_{30})\nonumber \\ &&+ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} (Q_{we}-Q_{we0}) \nonumber \end{eqnarray}\qquad(1.183) \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_2 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} &=& \frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{10}-H_{20}}} \qquad(1.184)\\ &=& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \nonumber \\ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} &=& \frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{10}-H_{20}}} \cdot (-1) - \frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{20}-H_{30}}} \qquad(1.185) \\ &=& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \\ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} &=& - \frac{\alpha}{A} \cdot \frac{1}{2\sqrt{H_{20}-H_{30}}} \cdot (-1) \qquad(1.186)\\ &=& \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \nonumber \\ \frac{\partial f_2(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} &=& 0 \qquad(1.187) \end{eqnarray} \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wynosi zatem
\( \begin{eqnarray} f_2(H_1,H_2,H_3,Q_{we}) &=& \frac{\alpha}{A} \sqrt{H_1-H_2} - \frac{\alpha}{A} \sqrt{H_2-H_3} \\ &\simeq& \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \nonumber\\ &&+ \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10}) \nonumber\\ &&+ \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) (H_2-H_{20}) \nonumber \\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} (H_3-H_{30})\nonumber \\ &&+ 0 \cdot (Q_{we}-Q_{we0}) \nonumber \end{eqnarray}\qquad(1.188) \)
Funkcja prawych stron z trzeciego równania stanu ma postać
\( \begin{equation} f_3(H_1,H_2,H_3,Q_{we}) = \frac{\alpha}{2A} \sqrt{H_2-H_3} - \frac{\alpha}{2A} \sqrt{H_3} \end{equation}\qquad(1.189) \)
Rozwinięcie funkcji \( f_3 \) w szereg Taylora wokół punktu równowagi \( (H_{10},H_{20},H_{30},Q_{we0}) \) ma postać
\( \begin{eqnarray} f_3(H_1,H_2,H_3,Q_{we}) &\simeq& f_3(H_{10},H_{20},H_{30},Q_{we0}) \\ &&+ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} (H_1-H_{10})\nonumber \\ &&+ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} (H_2-H_{20})\nonumber \\ &&+ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} (H_3-H_{30})\nonumber \\ &&+ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} (Q_{we}-Q_{we0})\nonumber \end{eqnarray}\qquad(190) \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_3 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} &=& 0 \qquad(1.191)\\ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} &=& \frac{\alpha}{2A} \cdot \frac{1}{2\sqrt{H_{20}-H_{30}}}\qquad(1.192) \\ &=& \frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \nonumber \\ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} &=& \frac{\alpha}{2A} \cdot \frac{1}{2\sqrt{H_{20}-H_{30}}} \cdot (-1) - \frac{\alpha}{2A} \cdot \frac{1}{2\sqrt{H_{30}}} \nonumber \\ &=& \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \qquad(1.193) \\ \frac{\partial f_3(H_{10},H_{20},H_{30},Q_{we0})}{\partial Q_{we}} &=& 0 \qquad(1.194) \end{eqnarray} \)
Rozwinięcie funkcji \( f_3 \) w szereg Taylora wynosi zatem
\( \begin{eqnarray} f_3(H_1,H_2,H_3,Q_{we}) &=& \frac{\alpha}{2A} \sqrt{H_2-H_3} - \frac{\alpha}{2A} \sqrt{H_3} \\ &\simeq& \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} \nonumber\\ &&+ 0 \cdot (H_1-H_{10}) \nonumber\\ &&+\frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} (H_2-H_{20}) \nonumber \\ &&+ \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) (H_3-H_{30}) \nonumber \\ &&+ 0 \cdot (Q_{we}-Q_{we0}) \nonumber \end{eqnarray} \qquad(1.195) \)
Obliczyliśmy rozwinięcia w szereg Taylora wszystkich funkcji prawych stron. Przepiszmy zatem jeszcze raz równania stanu, ale zamiast funkcji użyjmy przybliżeń wynikających z szeregu Taylora
\( \begin{eqnarray} \frac{dH_1}{dt} &\simeq& \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} + \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10}) \qquad(1.196) \\ &&+ \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_2-H_{20}) + 0\cdot (H_3-H_{30}) + \frac{1}{A} (Q_{we}-Q_{we0})\nonumber \\ \frac{dH_2}{dt} &\simeq& \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} + \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10})\qquad(1.197) \\ &&+ \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) (H_2-H_{20}) \nonumber \\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} (H_3-H_{30})+ 0 \cdot (Q_{we}-Q_{we0}) \nonumber \\ \frac{dH_3}{dt} &\simeq& \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} + 0 \cdot (H_1-H_{10}) \\ &&+\frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} (H_2-H_{20}) + \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) (H_3-H_{30}) \qquad(1.198)\\ &&+ 0 \cdot (Q_{we}-Q_{we0}) \nonumber \end{eqnarray} \)
Zauważmy, że na podstawie warunków na punkt równowagi następujące wyrażenia zerują się
\( \begin{eqnarray} 0 &=& f_1(H_{10},H_{20},H_{30},Q_{we0}) = \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \qquad(1.199)\\ 0 &=& f_2(H_{10},H_{20},H_{30},Q_{we0}) = \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}}\qquad(1.200)\\ 0 &=& f_3(H_{10},H_{20},H_{30},Q_{we0}) = \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}}\qquad(1.201) \end{eqnarray} \)
Wynika z tego, że możemy pominąć wyrazy stałe w rozwinięciu w szereg Taylora
\( \begin{eqnarray} \frac{dH_1}{dt} &\simeq& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10}) + \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_2-H_{20}) \\ &&+ 0\cdot (H_3-H_{30}) + \frac{1}{A} (Q_{we}-Q_{we0})\qquad(1.202) \\ \frac{dH_2}{dt} &\simeq& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} (H_1-H_{10}) \\ &&+ \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) (H_2-H_{20}) \qquad(1.203)\\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} (H_3-H_{30})+ 0 \cdot (Q_{we}-Q_{we0}) \nonumber \\ \frac{dH_3}{dt} &\simeq& 0 \cdot (H_1-H_{10}) +\frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} (H_2-H_{20}) \\ &&+ \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) (H_3-H_{30}) + 0 \cdot (Q_{we}-Q_{we0}) \qquad(1.204) \end{eqnarray} \)
Wprowadźmy następujące oznaczenia
\( \begin{eqnarray} \Delta H_1 &=& H_1-H_{10} \qquad(1.205)\\ \Delta H_2 &=& H_2-H_{20} \qquad(1.206)\\ \Delta H_3 &=& H_3-H_{20} \qquad(1.207)\\ \Delta Q_{we} &=& Q_{we}-Q_{we0} \qquad(1.208) \end{eqnarray} \)
Zmienne \( \Delta H_1 \), \( \Delta H_2 \), \( \Delta H_3 \) oraz \( \Delta Q_{we} \) określają przyrosty wartości \( H_1 \), \( H_2 \), \( H_3 \) oraz \( Q_{we} \) w stosunku do ich wartości w punkcie pracy \( H_{10} \), \( H_{20} \), \( H_{30} \) oraz \( Q_{we0} \).
Możemy teraz zapisać przybliżenia w równaniach stanu
\( \begin{eqnarray} \frac{dH_1}{dt} &\simeq& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_1 + \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_2 + 0\cdot \Delta H_3 + \frac{1}{A} \Delta Q_{we} \qquad(1.209)\\ \frac{dH_2}{dt} &\simeq& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_1 + \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \Delta H_2 \\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \Delta H_3 + 0 \cdot \Delta Q_{we} \qquad(1.210) \\ \frac{dH_3}{dt} &\simeq& 0 \cdot \Delta H_1 + \frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \Delta H_2 \\ &&+ \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) \Delta H_3 + 0 \cdot \Delta Q_{we} \qquad(1.211) \end{eqnarray} \)
Obliczmy ile wynoszą pochodne zmiennych \( \Delta H_1 \), \( \Delta H_2 \) oraz \( \Delta H_3 \).
\( \begin{eqnarray} \frac{d\Delta H_1}{dt} &=& \frac{d (H_1-H_{10})}{dt} = \frac{d H_1}{dt} - \frac{d H_{10}}{dt} = \frac{d H_1}{dt} \qquad(1.212)\\ \frac{d\Delta H_2}{dt} &=& \frac{d (H_2-H_{20})}{dt} = \frac{d H_2}{dt} - \frac{d H_{20}}{dt} = \frac{d H_2}{dt} \qquad(1.213)\\ \frac{d\Delta H_3}{dt} &=& \frac{d (H_3-H_{30})}{dt} = \frac{d H_3}{dt} - \frac{d H_{30}}{dt} = \frac{d H_3}{dt} \qquad(1.214) \end{eqnarray} \)
ponieważ \( \frac{d H_{10}}{dt} = 0 \), \( \frac{d H_{20}}{dt}=0 \) oraz \( \frac{d H_{30}}{dt}=0 \) jako pochodne funkcji stałych. Wprowadźmy zatem do przybliżeń wielkości \( \frac{d\Delta H_1}{dt} \), \( \frac{d\Delta H_2}{dt} \) oraz \( \frac{d\Delta H_3}{dt} \) zamiast \( \frac{d H_1}{dt} \), \( \frac{d H_2}{dt} \) oraz \( \frac{d H_3}{dt} \).
\( \begin{eqnarray} \frac{d\Delta H_1}{dt} &\simeq& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_1 + \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_2 + 0\cdot \Delta H_3 + \frac{1}{A} \Delta Q_{we} \qquad(1.215)\\ \frac{d\Delta H_2}{dt} &\simeq& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \Delta H_1 + \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \Delta H_2 \\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \Delta H_3 + 0 \cdot \Delta Q_{we} \qquad(1.216) \\ \frac{d\Delta H_3}{dt} &\simeq& 0 \cdot \Delta H_1 + \frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \Delta H_2 \\ &&+ \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) \Delta H_3 + 0 \cdot \Delta Q_{we} \qquad(1.217) \end{eqnarray} \)
Zauważmy, że współczynniki stojące przy \( \Delta H_1 \), \( \Delta H_2 \), \( \Delta H_3 \), oraz \( \Delta Q_{we} \) pomimo swojej skomplikowanej postaci są stałymi, ponieważ są obliczane w punkcie równowagi.
Powyższe zależności są spełnione w przybliżeniu. Aby utworzyć równania zlinearyzowane wprowadzamy nowe wielkości \( \tilde{H}_1 \), \( \tilde{H}_2 \), \( \tilde{H}_3 \) oraz \( \tilde{Q}_{we} \) oraz definiujemy równania zlinearyzowane w następujący sposób
\( \begin{eqnarray} \frac{d\tilde{H}_1}{dt} &=& \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 \qquad(1.218) \\ &&+ 0\cdot \tilde{H}_3 + \frac{1}{A} \tilde{Q}_{we} \nonumber \\ \frac{d\tilde{H}_2}{dt} &=& \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \qquad(1.219) \\ &&+ \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 + 0 \cdot \tilde{Q}_{we} \\ \frac{d\tilde{H}_3}{dt} &=& 0 \cdot \tilde{H}_1 + \frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 \\ &&+ \left( \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 + 0 \cdot \tilde{Q}_{we} \qquad(1.220) \end{eqnarray} \)
Są to równania w ścisłym sensie, gdyż zamiast znaku przybliżenia \( \simeq \) pojawia się znak równości. Przydatność linearyzacji opiera się na następującym postulacie.
Postulujemy, że jeżeli zachodzą następujące warunki
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) funkcja sterowań \( \tilde{Q}_{we}(t) \) jest dokładnie równa przyrostowi zmiennej \( Q_{we}(t) \)
\( \begin{equation} \tilde{Q}_{we}(t) = \Delta Q_{we}(t) = Q_{we}(t)-Q_{we0} \end{equation} \qquad(1.221) \)
- warunki początkowe dla zmiennych \( \tilde{H}_1 \), \( \tilde{H}_2 \), \( \tilde{H}_3 \( są dokładnie równe przyrostom zmiennych \( H_1 \), \( H_2 \) oraz \( H_3 \) w chwili początkowej
\( \begin{eqnarray} \tilde{H}_1(t_0) &=& \Delta H_1(t_0) = H_1(t_0)-H_{10} \qquad(1.222) \\ \tilde{H}_2(t_0) &=& \Delta H_2(t_0) = H_2(t_0)-H_{20} \qquad(1.223)\\ \tilde{H}_3(t_0) &=& \Delta H_3(t_0) = H_3(t_0)-H_{30} \qquad(1.224) \end{eqnarray} \)
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania nieliniowych równań stanu \( H_1(t) \), \( H_2(t) \) oraz \( H_3(t) \) pozostają w otoczeniu punktu równowagi \( (H_{10}, H_{20}, H_{30}) \) (\( C_{H_1}, C_{H_2}, C_{H_3} \) -- stałe dodatnie)
\( \begin{eqnarray} | H_1(t)-H_{10} | &=& | \Delta H_1(t) | \leq C_{H_1} \qquad(1.225) \\ | H_2(t)-H_{20} | &=& | \Delta H_2(t) | \leq C_{H_2} \qquad(1.226) \\ | H_3(t)-H_{30} | &=& | \Delta H_3(t) | \leq C_{H_3} \qquad(1.227) \end{eqnarray} \)
to rozwiązania \( \tilde{H}_1(t) \), \( \tilde{H}_2(t) \) oraz \( \tilde{H}_3(t) \) liniowych równań stanu (1.218)-(1.220) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzi przybliżony warunek
\( \begin{eqnarray} \tilde{H}_1(t) &\simeq& \Delta H_1(t) \qquad(1.228)\\ \tilde{H}_2(t) &\simeq& \Delta H_2(t) \qquad(1.229)\\ \tilde{H}_3(t) &\simeq& \Delta H_3(t) \qquad(1.230) \end{eqnarray} \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu równowagi pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{H_1}, C_{H_2}, C_{H_3} \) w równaniach (1.225})-(1.226).
Ścisły dowód tego postulatu wymaga zaawansowanego aparatu matematycznego, dlatego nie będzie zaprezentowany w tym opracowaniu. Intuicyjnie postulat ten jest jednak zrozumiały. Oczekujemy, że rozwiązania zlinearyzowanych równań stanu będą dobrze przybliżały przyrosty zmiennych stanu obiektu nieliniowego w stosunku do ich wartości w wybranym punkcie równowagi, przynajmniej w pewnym otoczeniu tego punktu. Bardzo istotna jest obserwacja, że rozwiązania zlinearyzowanych równań stanu przybliżają przyrosty zmiennych stanu obiektu nieliniowego, a nie same zmienne stanu.
Funkcja wyjść dla układu trzech zbiorników ma postać
\( \begin{equation} y_1 = g_1(H_1,H_2,H_3) = H_3 \end{equation}\qquad(1.231) \)
Linearyzacja funkcji wyjść ma postać
\( \begin{eqnarray} g_1(H_1,H_2,H_3) &\simeq& g_1(H_{10},H_{20},H_{30},Q_{we0}) \\ &&+ \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} (H_1-H_{10}) \nonumber \\ &&+ \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} (H_2-H_{20}) \nonumber \\ &&+ \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} (H_3-H_{30}) \nonumber \end{eqnarray}\qquad(1.232) \)
Wartości pochodnych cząstkowych funkcji \( g_1 \) względem zmiennych stanu i sterowań w punkcie równowagi wynoszą
\( \begin{eqnarray} \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_1} &=& 0 \qquad(1.233)\\ \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_2} &=& 0 \qquad(1.234)\\ \frac{\partial g_1(H_{10},H_{20},H_{30},Q_{we0})}{\partial H_3} &=& 1 \qquad(1.235) \end{eqnarray} \)
Rozwinięcie funkcji wyjść w szereg Taylora wynosi zatem
\( \begin{equation} y_1 \simeq y_{10} + 0 \cdot (H_1-H_{10}) + 0 \cdot (H_2-H_{20}) + 1 \cdot (H_3-H_{30}) \end{equation}\qquad(1.236) \)
gdzie \( y_{10} = g_1(H_{10},H_{20},H_{30}) \)
Jeżeli przeniesiemy \( y_{10} \) na drugą stronę przybliżenia dostajemy
\( \begin{equation} y_1- y_{10} \simeq 0 \cdot (H_1-H_{10}) + 0 \cdot (H_2-H_{20}) + 1 \cdot (H_3-H_{30}) \end{equation}\qquad(1.237) \)
Jeżeli teraz wprowadzimy do przybliżenia zmienne przyrostowe, to otrzymujemy
\( \begin{equation} \Delta y_1 \simeq 0 \cdot \Delta H_1 + 0 \cdot \Delta H_2 + 1 \cdot \Delta H_3 \end{equation}\qquad(1.238) \)
gdzie
\( \begin{equation} \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.239) \)
Aby zdefiniować zlinearyzowane równanie wyjść wprowadzamy zmienną \( \tilde{y}_1 \). Zlinearyzowane równanie wyjść ma postać
\( \begin{equation} \tilde{y}_1 = 0 \cdot \tilde{H}_1 + 0 \cdot \tilde{H}_2 + 1 \cdot \tilde{H}_3 \end{equation}\qquad(1.240) \)
Postulując takie same warunki jak w przypadku równań stanu oczekujemy, że rozwiązanie równania wyjść \( \tilde{y}_1 \) będzie dobrze przybliżać przyrost zmiennej wyjściowej \( y_1 \)
\( \begin{equation} \tilde{y}_1 \simeq \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.241) \)
Zlinearyzowane równania stanu i wyjść mogą zostać przedstawione w postaci wektorowej
\( \begin{eqnarray} \left( \begin{array}{c} \frac{d\tilde{H}_1}{dt}\\ \frac{d\tilde{H}_2}{dt} \\ \frac{d\tilde{H}_3}{dt} \end{array} \right) &=& \left( \begin{array}{ccc} \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & 0 \\ \frac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \frac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \frac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} & \frac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\ 0 & \frac{\alpha}{4A\sqrt{H_{20}-H_{30}}} & \frac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \frac{-\alpha}{4A\sqrt{H_{30}}} \end{array} \right) \left( \begin{array}{c} \tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3 \end{array} \right) \nonumber \\ &&+ \left( \begin{array}{c} \frac{1}{A} \\ 0 \\ 0 \end{array} \right) \left( \tilde{Q}_{we} \right) \end{eqnarray}\qquad(1.242) \)
\( \begin{eqnarray} \left( y_1 \right) &=& \left( \begin{array}{ccc} 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} \tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3 \end{array} \right) \end{eqnarray} \qquad(1.243) \)
3.3. Przykład 1: Porównanie przebiegów czasowych modeli
Aby przetestować zdolność modelu zlinearyzowanego do przybliżania dynamiki obiektu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt równowagi \( H_{10}=0.75 \), \( H_{20}=0.5 \) \( H_{30}=0.25 \) oraz \( Q_{we0} = 0.5 \). Aby porównać zachowanie modelu nieliniowego i zlinearyzowanego rozważamy dwa scenariusze. W pierwszym scenariuszu zakładamy, że w chwili początkowej obiekt nie znajduje się w punkcie równowagi.
Ponadto przyjmujemy, że sterowanie obiektu jest stałe i równe sterowaniu w punkcie równowagi \( Q_{we}(t) = Q_{we0}\). Ze wzoru (1.221) wynika, że sterowanie obiektu zlinearyzowanego wynosi
\( \begin{equation} \tilde{Q}_{we}(t) = Q_{we}(t)-Q_{we0} = Q_{we0}-Q_{we0}=0 \end{equation}\qquad(1.244) \)
Zmienne stanu obiektu zlinearyzowanego \( \tilde{H}_1(t) \), \( \tilde{H}_2(t) \) oraz \( \tilde{H}_3(t) \) przybliżają przyrosty zmiennych stanu obiektu nieliniowego \( \Delta H_1(t) \), \( \Delta H_2(t) \), \( \Delta H_3(t) \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
- \(\Delta H_1(t_0) = 0.2 \), \( \Delta H_2(t_0) = -0.2 \), \( \Delta H_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (1.222)-(1.224}) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0),\ \tilde{H}_2(t_0) = \Delta H_2(t_0),\ \tilde{H}_3(t_0) = \Delta H_3(t_0) \end{equation}\qquad(1.245) \)
Na Rys. 1.12 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \) obiektu nieliniowego i zmiennej \( \tilde{H}_3(t) \) obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu równowagi w chwili początkowej znajduje się obiekt, tym lepiej zmienna \( \tilde{H}_3(t) \) przybliża przebieg zmiennej \( \Delta H_3(t) \).
W drugim scenariuszu zakładamy, że w chwili początkowej obiekt znajduje się w punkcie równowagi. Taka sytuacja odpowiada zerowym warunkom początkowym
\( \begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0) = 0,\ \tilde{H}_2(t_0) = \Delta H_2(t_0) = 0,\ \tilde{H}_3(t_0) = \Delta H_3(t_0) = 0 \end{equation}\qquad(1.246) \)
Badamy teraz zachowanie układu w odpowiedzi na zmienne sterowanie \( Q_{we}(t)\). Porównajmy trajektorie obiektu nieliniowego i zlinearyzowanego dla sygnału sterującego typu fala prostokątna oscylującego wokół wartości w punkcie równowagi \( Q_{we0}=0.5 \). Wypełnienie fali wynosi 50%, natomiast jej okres wynosi 2. Amplituda wahań fali prostokątnej dla czterech testowanych przypadków wynosi odpowiednio 0.25, 0.125, 0.05, 0.025.
Sterowanie obiektu zlinearyzowanego w każdym przypadku wynosi
\( \begin{equation} \tilde{Q}_{we}(t) = Q_{we}(t)-Q_{we0} \end{equation}\qquad(1.247) \)
a) \(\Delta H_1(t_0) = 0.2 \), \( \Delta H_2(t_0) = -0.2 \), \( \Delta H_3(t_0) = 0 \)
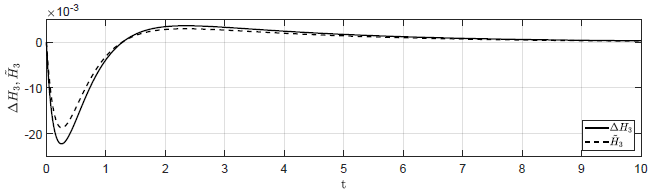
b) \(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
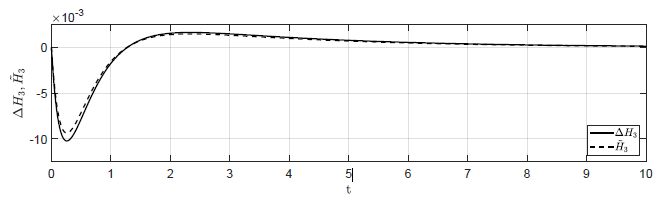
c) (\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)

d) \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
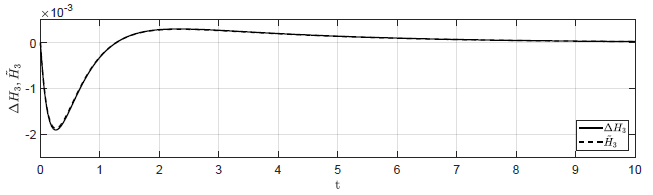
Rysunek 1.12 Porównanie trajektorii \( \Delta H_3(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{H}_3(t) \) obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
a) Amplituda fali prostokątnej 0.25
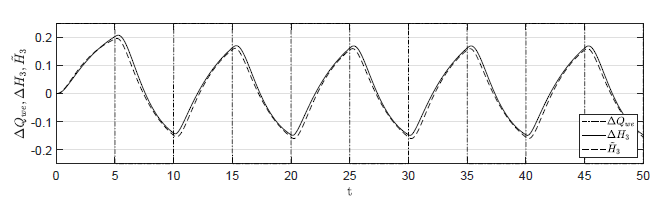
b) Amplituda fali prostokątnej 0.125

c) Amplituda fali prostokątnej 0.05
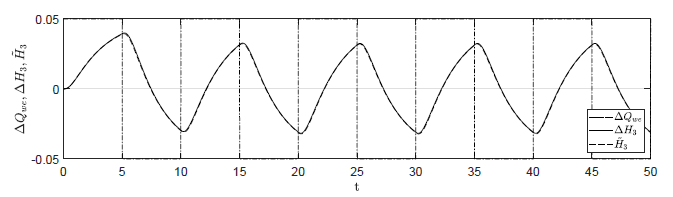
d) Amplituda fali prostokątnej 0.025

Rysunek 1.13 Porównanie trajektorii \( \Delta H_3(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{H}_3(t) \) obiektu zlinearyzowanego w odpowiedzi na sygnał sterujący typu fala prostokątna.}
Spodziewamy się, że im mniejsza będzie amplituda zmian sygnału sterującego, tym lepiej trajektorie zmiennych stanu obiektu zlinearyzowanego będą przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Na Rys. 1.13 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \( obiektu nieliniowego i zmiennej \( \tilde{H}_3(t) \) obiektu zlinearyzowanego dla sygnałów sterujących w kształcie fali prostokątnej o zmniejszającej się amplitudzie. Wyraźnie widzimy, że im mniejsza jest amplituda sygnału sterującego, tym lepiej zmienna \( \tilde{H}_3(t) \) przybliża przebieg zmiennej \( \Delta H_3(t) \).
3.4. Przykład 2 linearyzacji równań modelu obiektu
Wyprowadźmy teraz zlinearyzowane równania stanu dla wahadła. Przypomnijmy równania stanu dla wahadła
\( \begin{eqnarray} \frac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.248)\\ \frac{d\omega(t)}{dt} &=& \frac{g}{l}sin\theta(t) - \frac{D}{ml^2} \omega(t) +\frac{1}{ml^2} M(t) \qquad(1.249) \end{eqnarray} \)
Funkcja prawych stron z pierwszego równania stanu ma postać
\( \begin{equation} f_1(\theta, \omega, M) = \omega \end{equation}\qquad(1.250) \)
Dla skrócenia zapisu pomijamy w zapisie argument czasu \( (t) \).
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wokół punktu równowagi \( (\theta_0, \omega_0, M_0) \) ma postać
\( \begin{eqnarray} f_1(\theta, \omega, M) &\simeq& f_1(\theta_0, \omega_0, M_0) + \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \theta} (\theta-\theta_0) \\ &&+ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \omega} (\omega-\omega_0) + \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial M} (M-M_0) \qquad(1.251) \end{eqnarray} \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_1 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \theta} &=& 0 \qquad(1.252)\\ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \omega} &=& 1 \qquad(1.253)\\ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial M} &=& 0\qquad(1.254) \end{eqnarray} \)
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wynosi zatem
\( \begin{equation} f_1(\theta, \omega, M) \simeq \omega_0 + 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \end{equation}\qquad(1.255) \)
Funkcja prawych stron z drugiego równania stanu ma postać
\( \begin{equation} f_2(\theta, \omega, M) = \frac{g}{l}sin\theta - \frac{D}{ml^2} \omega +\frac{1}{ml^2} M \end{equation}\qquad(1.256) \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wokół punktu równowagi \( (\theta_0, \omega_0, M_0) \) ma postać
\( \begin{eqnarray} f_2(\theta, \omega, M) &\simeq& f_2(\theta_0, \omega_0, M_0) + \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \theta} (\theta-\theta_0) \\ &&+ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \omega} (\omega-\omega_0) + \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial M} (M-M_0) \qquad(1.257) \end{eqnarray} \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_2 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \theta} &=& \frac{g}{l}cos\theta_0 \qquad(1.258)\\ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \omega} &=& -\frac{D}{ml^2} \qquad(1.259)\\ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial M} &=& \frac{1}{ml^2}\qquad(1.260) \end{eqnarray} \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wynosi zatem
\( \begin{eqnarray} f_2(\theta, \omega, M) &\simeq& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 + \frac{g}{l}cos\theta_0 (\theta-\theta_0) \\ && - \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0) \nonumber \end{eqnarray}\qquad(1.261) \)
Obliczyliśmy rozwinięcia w szereg Taylora wszystkich funkcji prawych stron. Przepiszmy zatem jeszcze raz równania stanu, ale zamiast funkcji użyjmy przybliżeń wynikających z szeregu Taylora
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& \omega_0 + 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 + \frac{g}{l}cos\theta_0 (\theta-\theta_0) \qquad(1.262)\\ &&- \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0) \\qquad(1.263) \end{eqnarray} \)
Zauważmy, że na podstawie warunków na punkt równowagi następujące wyrażenia zerują się
\( \begin{eqnarray} 0 &=& f_1(\theta_0, \omega_0, M_0) = \omega_0 \qquad(1.264)\\ 0 &=& f_2(\theta_0, \omega_0, M_0)= \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0\qquad(1.265) \end{eqnarray} \)
Wynika z tego, że możemy pominąć wyrazy stałe w rozwinięciu w szereg Taylora
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \qquad(1.266)\\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 (\theta-\theta_0) - \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0)\qquad(1.267) \end{eqnarray} \)
Wprowadźmy następujące oznaczenia
\( \begin{eqnarray} \Delta \theta &=& \theta-\theta_0\qquad(1.268)\\ \Delta \omega &=& \omega-\omega_0\qquad(1.269)\\ \Delta M &=& M-M_0\qquad(1.270) \end{eqnarray} \)
Zmienne \( \Delta \theta \), \( \Delta \omega \) oraz \( \Delta M \) określają przyrosty wartości \( \theta \), \( \omega \) oraz \( M \) w stosunku do ich wartości w punkcie pracy \( \theta_0 \), \( \omega_0 \) oraz \( M_0 \). Możemy teraz zapisać przybliżenia w równaniach stanu jako
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& 0 \cdot \Delta \theta + 1 \cdot \Delta \omega + 0 \cdot \Delta M \qquad(1.271)\\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 \Delta \theta - \frac{D}{ml^2} \Delta \omega + \frac{1}{ml^2} \Delta M \qquad(1.272) \end{eqnarray} \)
Pochodne zmiennych przyrostowych \(\Delta \theta\) oraz \( \Delta \omega \) są równe pochodnym zmiennych oryginalnych
\( \begin{eqnarray} \frac{d\Delta \theta}{dt} &=& \frac{d (\theta-\theta_0)}{dt} = \frac{d \theta}{dt} - \frac{d \theta_0}{dt} = \frac{d \theta}{dt} \qquad(1.273)\\ \frac{d\Delta \omega}{dt} &=& \frac{d (\omega-\omega_0)}{dt} = \frac{d \omega}{dt} - \frac{d \omega_0}{dt} = \frac{d \omega}{dt}\qquad(1.274) \end{eqnarray} \)
Wprowadźmy zatem do przybliżeń wielkości \( \frac{d\Delta \theta}{dt} \) oraz \( \frac{d\Delta \omega}{dt} \) zamiast \( \frac{d \theta}{dt} \) oraz \( \frac{d \omega}{dt} \).
\( \begin{eqnarray} \frac{d\Delta \theta}{dt} &\simeq& 0 \cdot \Delta \theta + 1 \cdot \Delta \omega + 0 \cdot \Delta M \qquad(1.275)\\ \frac{d\Delta \omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 \Delta \theta - \frac{D}{ml^2} \Delta \omega + \frac{1}{ml^2} \Delta M \qquad(1.276) \end{eqnarray} \)
Powyższe zależności są spełnione w przybliżeniu. Aby utworzyć równania zlinearyzowane wprowadzamy nowe wielkości \( \tilde{\theta} \), \( \tilde{\omega} \), oraz \( \tilde{M} \) oraz definiujemy równania zlinearyzowane w następujący sposób
\( \begin{eqnarray} \frac{d\tilde{\theta}}{dt} &=& 0 \cdot \tilde{\theta} + 1 \cdot \tilde{\omega} + 0 \cdot \tilde{M} \qquad(1.277) \\ \frac{d\tilde{\omega}}{dt} &=& \frac{g}{l}cos\theta_0 \tilde{\theta} - \frac{D}{ml^2} \tilde{\omega} + \frac{1}{ml^2} \tilde{M} \qquad(1.278) \end{eqnarray} \)
Są to równania w ścisłym sensie, gdyż zamiast znaku przybliżenia \( \simeq \) pojawia się znak równości. Postulujemy, że jeżeli zachodzą następujące warunki
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) funkcja sterowań \( \tilde{M}(t) \) jest dokładnie równa przyrostowi zmiennej \( M(t) \)
\( \begin{equation} \tilde{M}(t) = \Delta M(t) = M(t)-M_0 \qquad(1.279) \end{equation} \)
- warunki początkowe dla zmiennych \( \tilde{\theta} \), \( \tilde{\omega} \) są dokładnie równe przyrostom zmiennych \( \theta \) oraz \( \omega \) w chwili początkowej
\( \begin{eqnarray} \tilde{\theta}(t_0) &= &\Delta \theta(t_0) = \theta(t_0) - \theta_0 \qquad(1.280) \\ \tilde{\omega}(t_0) &= &\Delta \omega(t_0) = \omega(t_0) - \omega_0 \qquad(1.281) \end{eqnarray} \)
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania nieliniowych równań stanu \( \theta(t) \) oraz \( \omega(t) \) pozostają w otoczeniu punktu równowagi \( (\theta_0, \omega_0) \) (\( C_{\theta}, C_{\omega} \) -- stałe dodatnie)
\( \begin{eqnarray} | \theta(t)-\theta_0 | &=& | \Delta \theta(t) | \leq C_{\theta} \qquad(1.282) \\ | \omega(t)-\omega_0 | &=& | \Delta \omega(t) | \leq C_{\omega} \qquad(1.282) \end{eqnarray} \)
to rozwiązania \( \tilde{\theta}(t) \) oraz \( \tilde{\omega}(t) \) liniowych równań stanu (1.277)-(1.278) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzą przybliżone warunki
\( \begin{eqnarray} \tilde{\theta}(t) &\simeq& \Delta \theta(t) \qquad(1.284)\\ \tilde{\omega}(t) &\simeq& \Delta \omega(t) \qquad(1.285) \end{eqnarray} \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu równowagi pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{\theta}, C_{\omega} \) w równaniach (1.282)-(1.283).
Funkcja wyjść dla wahadła ma postać
\( \begin{equation} y_1 = g_1(\theta,\omega) = \theta \end{equation}\qquad(1.286) \)
Linearyzacja funkcji wyjść ma postać
\( \begin{equation} g_1(\theta,\omega) \simeq g_1(\theta_0,\omega_0) + \frac{\partial g_1(\theta_0,\omega_0)}{\partial \theta} (\theta-\theta_0) + \frac{\partial g_1(\theta_0,\omega_0)}{\partial \omega} (\omega-\omega_0) \end{equation}\qquad(1.287) \)
Wartości pochodnych cząstkowych funkcji \( g_1 \) względem zmiennych stanu i sterowań w punkcie równowagi wynoszą
\( \begin{eqnarray} \frac{\partial g_1(\theta_0,\omega_0)}{\partial \theta} &=& 1 \qquad(1.288)\\ \frac{\partial g_1(\theta_0,\omega_0)}{\partial \omega} &=& 0 \qquad(1.289) \end{eqnarray} \)
Rozwinięcie funkcji wyjść w szereg Taylora wynosi zatem
\( \begin{equation} y_1 \simeq y_{10} + 1 \cdot (\theta-\theta_0)+ 0 \cdot (\omega-\omega_0) \end{equation}/qquad(1.290) \)
gdzie \( y_{10} = g_1(\theta_0,\omega_0) \).
Jeżeli przeniesiemy \( y_{10} \) na drugą stronę przybliżenia dostajemy
\( \begin{equation} y_1- y_{10} \simeq 1 \cdot (\theta-\theta_0)+ 0 \cdot (\omega-\omega_0) \end{equation}\qquad(1.291) \)
Jeżeli teraz wprowadzimy do przybliżenia zmienne przyrostowe, to otrzymujemy
\( \begin{equation} \Delta y_1 \simeq 1 \cdot \Delta \theta + 0 \cdot \Delta \omega \end{equation}\qquad(1.292) \)
gdzie
\( \begin{equation} \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.293) \)
Aby zdefiniować zlinearyzowane równanie wyjść wprowadzamy zmienną \( \tilde{y}_1 \). Zlinearyzowane równanie wyjść ma postać
\( \begin{equation} \tilde{y}_1 = 1 \cdot \tilde{\theta} + 0 \cdot \tilde{\omega} \end{equation}\qquad(1.294) \)
Postulując takie same warunki jak w przypadku równań stanu oczekujemy, że rozwiązanie równania wyjść \( \tilde{y}_1 \) będzie dobrze przybliżać przyrost zmiennej wyjściowej \( y_1 \)
\( \begin{equation} \tilde{y}_1 \simeq \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.295) \)
Zlinearyzowane równania stanu i wyjść mogą zostać przedstawione w postaci wektorowej
\( \begin{equation} \left( \begin{array}{c} \frac{d\tilde{\theta}}{dt}\\ \frac{d\tilde{\omega}}{dt} \end{array} \right) = \left( \begin{array}{cc} 0 & 1 \\ \frac{g}{l}cos\theta_0 & -\frac{D}{ml^2} \end{array} \right) \left( \begin{array}{c} \tilde{\theta}\\ \tilde{\omega} \end{array} \right) + \left( \begin{array}{c} 0 \\ \frac{1}{ml^2} \end{array} \right) \left( \tilde{M} \right) \end{equation}\qquad(1.296) \)
\( \begin{eqnarray} \left( y_1 \right) &=& \left( \begin{array}{cc} 1 & 0 \end{array} \right) \left( \begin{array}{c} \tilde{\theta}\\ \tilde{\omega} \end{array} \right) \end{eqnarray}\qquad(1.297) \)
Aby przetestować zdolność modelu zlinearyzowanego do przybliżania dynamiki obiektu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt równowagi odpowiadający \( \theta_0=\frac{5\pi}{6} \), \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). W pierwszym scenariuszu zakładamy, że w chwili początkowej obiekt nie znajduje się w punkcie równowagi.
Ponadto przyjmujemy, że sterowanie obiektu jest stałe i równe sterowaniu w punkcie równowagi \( M(t) = M_0\). Ze wzoru (1.279) wynika, że sterowanie obiektu zlinearyzowanego wynosi
\( \begin{equation} \tilde{M}(t) = M(t)-M_0 = M_0-M_0=0 \end{equation}\qquad(1.298) \)
Zmienne stanu obiektu zlinearyzowanego \( \tilde{\theta}(t) \), oraz \( \tilde{\omega}(t) \) przybliżają przyrosty zmiennych stanu obiektu nieliniowego \( \Delta \theta \), \( \Delta \omega \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
- \(\Delta \theta(t_0) = -\frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (1.280})-(1.281) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(1.299) \)
Na Rys. 1.14 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu równowagi w chwili początkowej znajduje się obiekt, tym lepiej zmienna \( \tilde{\theta}(t) \) przybliża przebieg zmiennej \( \Delta \theta(t)\).
a) \(\Delta \theta(t_0) = -\frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
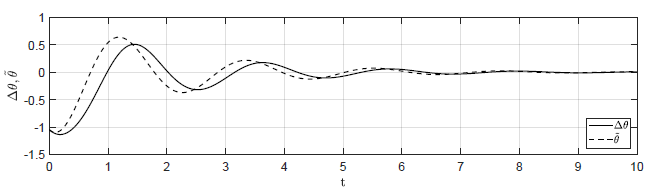
b) \(\Delta \theta(t_0) = -\frac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)

c) \(\Delta \theta(t_0) = -\frac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2\)

d) \(\Delta \theta(t_0) = -\frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
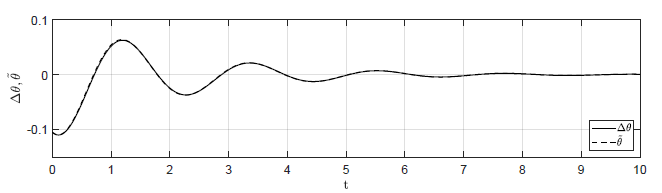
Rysunek 1.14 Porównanie trajektorii \( \Delta \theta(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{\theta}(t) \) obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Wartości sterowania \( M_{0} = -0.5 \) odpowiada także drugi punkt równowagi \( \theta_0=\frac{\pi}{6} \), \( \omega_0=0 \). Ponownie wykonujemy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
- \(\Delta \theta(t_0) = \frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
- \(\Delta \theta(t_0) = \frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
- \(\Delta \theta(t_0) = \frac{\pi}{300} \), \( \Delta \omega(t_0) = -0.01 \)
- \(\Delta \theta(t_0) = \frac{\pi}{3000} \), \( \Delta \omega(t_0) = -0.001 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Zgodnie z (1.280)-(1.281) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(1.300) \)
Na Rys. 1.15 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Tym razem zachowanie obiektu nieliniowego i zlinearyzowanego są diametralnie różne. Dla każdego zestawu warunków początkowych wahadło najpierw spada (\( \theta(t) \) rośnie), następnie wykonuje oscylacje wokół położenia kątowego \( \theta = \frac{5\pi}{6} \), by wreszcie ustabilizować się w tym położeniu. Niezależnie od tego jak blisko położenia równowagi \( \theta_0 = \frac{\pi}{6} \) znajduje się obiekt w chwili początkowej, wahadło trwale oddala się od tego położenia i stabilizuje się w innym położeniu równowagi. Trajektoria \( \tilde{\theta}(t) \) z kolei rośnie w bardzo szybkim tempie (jak funkcja \( e^t \)) i nie wykazuje żadnych drgań.
Różnica pomiędzy zachowaniem obiektu nieliniowego i zlinearyzowanego w tym przypadku wynika z niespełnienia warunków (1.282)-(1.283) na rozważanym horyzoncie czasu. Trajektorie zmiennych stanu trwale oddalają się od pierwotnego punktu równowagi niezależnie od tego jak blisko punktu równowagi znajdują się warunki początkowe.
Zauważmy jednak, że dla początkowego przedziału czasu, gdy trajektorie zmiennych stanu znajdują się jeszcze blisko punktu równowagi, trajektorie modelu zlinearyzowanego dobrze przybliżają trajektorie modelu nieliniowego. Jest to bardzo ważna cecha linearyzacji. Dopóki nie oddalamy się zbytnio od punktu równowagi, model zlinearyzowany dobrze przybliża zachowanie modelu nieliniowego. Jeżeli jednak oddalimy się zbytnio od punktu równowagi, wtedy nie możemy oczekiwać od modelu zlinearyzowanego dobrego przybliżenia dynamiki modelu nieliniowego. Oba modele mogą w takiej sytuacji dawać kompletnie odmienne rezultaty.
W drugim scenariuszu zakładamy, że w chwili początkowej obiekt znajduje się w punkcie równowagi \( \theta_0=\frac{5\pi}{6} \), \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). Taka sytuacja odpowiada zerowym warunkom początkowym
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0) = 0,\ \tilde{\omega}(t_0) = \Delta \omega(t_0) = 0 \end{equation}\qquad(1.301) \)
a) \(\Delta
\theta(t_0) = \frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
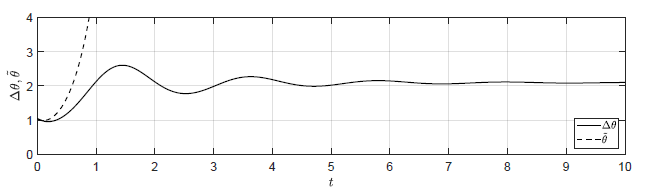
b) \(\Delta \theta(t_0) = \frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
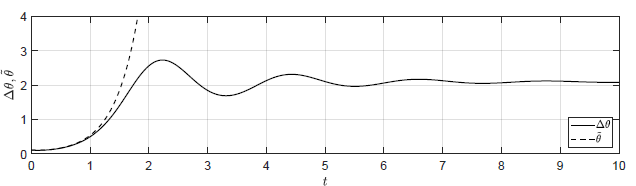
c) \(\Delta \theta(t_0) = \frac{\pi}{300} \), \( \Delta \omega(t_0) = -0.01 \)

d) \(\Delta \theta(t_0) = \frac{\pi}{3000} \), \( \Delta \omega(t_0) = -0.001 \)
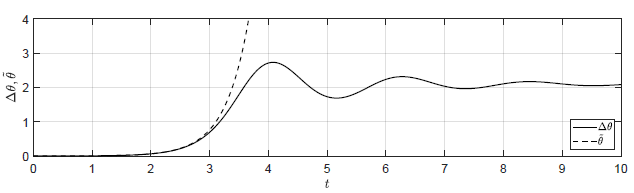
Rysunek 1.5 Porównanie trajektorii \( \Delta \theta(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{\theta}(t) \) obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
a) Amplituda fali prostokątnej 0.25
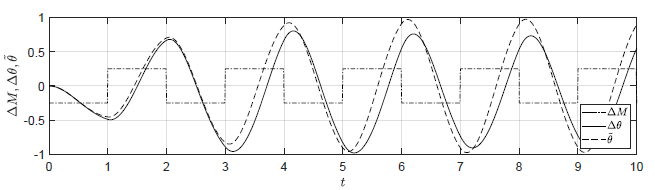
b) Amplituda fali prostokątnej 0.125

c) Amplituda fali prostokątnej 0.05
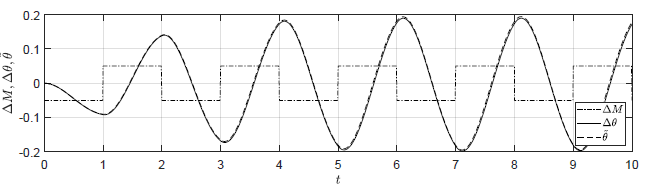
d) Amplituda fali prostokątnej 0.025
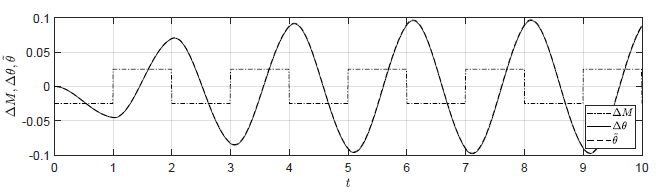
Rysunek 1.16 Porównanie trajektorii \( \Delta H_3(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{H}_3(t) \) obiektu zlinearyzowanego w odpowiedzi na sygnał sterujący typu fala prostokątna.
Badamy teraz zachowanie układu w odpowiedzi na zmienne sterowanie \( M(t)\). Porównajmy trajektorie obiektu nieliniowego i zlinearyzowanego dla sygnału sterującego typu fala prostokątna oscylującego wokół wartości w punkcie równowagi \( M_0=-0.5 \). Wypełnienie fali wynosi 50%, natomiast jej okres wynosi 2. Amplituda wahań fali prostokątnej dla czterech testowanych przypadków wynosi odpowiednio 0.25, 0.125, 0.05, 0.025.
Sterowanie obiektu zlinearyzowanego w każdym przypadku wynosi
\( \begin{equation} \tilde{M}(t) = M(t)-M_{0} \end{equation}\qquad(1.302) \)
Na Rys. 1.16 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla sygnałów sterujących w kształcie fali prostokątnej o zmniejszającej się amplitudzie. Tym razem trajektorie układu nieliniowego pozostają w pobliżu punktu równowagi na całym horyzoncie czasu. Im mniejsza jest amplituda sygnału sterującego, tym lepiej zmienna \( \tilde{\theta}(t) \) przybliża przebieg zmiennej \( \Delta \theta(t) \).
3.5. Linearyzacja równań modelu obiektu - przypadek ogólny
Rozważamy równania w postaci ogólnej
\( \begin{eqnarray} \frac{dx_1}{dt} &=& f_1(x_1,\cdots,x_j,\cdots,x_n,u_1,\cdots,u_k,\cdots,u_m) \qquad(1.303) \\ &\vdots& \nonumber \\ \frac{dx_i}{dt} &=& f_i(x_1,\cdots,x_j,\cdots,x_n,u_1,\cdots,u_k,\cdots,u_m) \qquad(1.304) \\ &\vdots& \nonumber \\ \frac{dx_n}{dt} &=& f_n(x_1,\cdots,x_j,\cdots,x_n,u_1,\cdots,u_k,\cdots,u_m) \qquad(1.305) \end{eqnarray} \)
Linearyzacja \( i \)-tej funkcji prawych stron w pobliżu punktu równowagi \( (x_0,u_0) \) ma postać
\( \begin{eqnarray} && f_i(x_1,\cdots,x_j,\cdots,x_n,u_1,\cdots,u_k,\cdots,u_m) \simeq \\ &&\qquad (1.306)f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) \nonumber \\ &&\qquad + \frac{\partial f_i(x_0,u_0)}{\partial x_1}(x_1-x_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}(x_n-x_{n0}) \nonumber \\ \nonumber \\ &&\qquad + \frac{\partial f_i(x_0,u_0)}{\partial u_1}(u_1-u_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}(u_k-u_{k0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}(u_m-u_{m0}) \nonumber \end{eqnarray} \)
gdzie dla skrócenia zapisu wprowadzamy oznaczenia
\( \begin{eqnarray} \frac{\partial f_i(x_0,u_0)}{\partial x_j} &=& \frac{\partial f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0})}{\partial x_j} \qquad(1.307)\\ \frac{\partial f_i(x_0,u_0)}{\partial u_k} &=& \frac{\partial f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0})}{\partial u_k}\qquad(1.308) \end{eqnarray} \)
Przybliżenie dla \( i \)-tego równania stanu można zapisać jako
\( \begin{eqnarray} \frac{dx_i}{dt} &\simeq& f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) \\ && + \frac{\partial f_i(x_0,u_0)}{\partial x_1}(x_1-x_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}(x_n-x_{n0}) \nonumber \\ \qquad(1.309) \\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}(u_1-u_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}(u_k-u_{k0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}(u_m-u_{m0}) \nonumber \end{eqnarray} \)
Z warunku na punkt równowagi mamy
\( \begin{equation} f_i(x_{10},\cdots,x_{j0},\cdots,x_{n0},u_{10},\cdots,u_{k0},\cdots,u_{m0}) = 0 \end{equation}\qquad(1.310) \)
i przybliżenie \( i \)-tego równania stanu może zostać zapisane jako
\( \begin{eqnarray} \frac{dx_i}{dt} &\simeq& \frac{\partial f_i(x_0,u_0)}{\partial x_1}(x_1-x_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}(x_n-x_{n0}) \nonumber \\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}(u_1-u_{10}) + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}(u_k-u_{k0}) + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}(u_m-u_{m0}) \qquad(1.311)\\ \end{eqnarray} \)
Wprowadzamy zmienne przyrostowe dla zmiennych stanu
\( \begin{equation} \Delta x_j = x_j - x_{j0},\ j = 1,\cdots,n \end{equation}\qquad(1.312) \)
oraz zmiennych sterujących
\( \begin{equation} \Delta u_k = u_k - u_{k0},\ k = 1,\cdots,m \end{equation}\qquad(1.313) \)
Przybliżenie \( i \)-tego równania stanu możemy zapisać jako
\( \begin{eqnarray} \frac{dx_i}{dt} &\simeq& \frac{\partial f_i(x_0,u_0)}{\partial x_1}\Delta x_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j} \Delta x_j + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}\Delta x_n \\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}\Delta u_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}\Delta u_k + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}\Delta u_m \nonumber \end{eqnarray}\qquad(1.314) \)
Ponieważ pochodna funkcji stałej jest równa zero to mamy \( \frac{d x_{i0}}{dt} =0 \). Pochodna zmiennej przyrostowej \(\Delta x_i\) jest zatem równa pochodnej zmiennej \(x_i\)
\( \begin{equation} \frac{d\Delta x_i}{dt} = \frac{d (x_i-x_{i0})}{dt} = \frac{d x_i}{dt} - \frac{d x_{i0}}{dt} = \frac{d x_i}{dt} \end{equation}\qquad(1.315) \)
Przybliżenie \( i \)-tego równania stanu możemy teraz zapisać jako
\( \begin{eqnarray} \frac{d\Delta x_i}{dt} &\simeq& \frac{\partial f_i(x_0,u_0)}{\partial x_1}\Delta x_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j} \Delta x_j + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}\Delta x_n \\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}\Delta u_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}\Delta u_k + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}\Delta u_m \nonumber \end{eqnarray}\qquad(1.316) \)
Powyższa zależność jest spełniona w przybliżeniu. Aby utworzyć równania zlinearyzowane wprowadzamy nowe wielkości
\( \begin{eqnarray} \tilde{x}_j,\ j =1,\cdots, n\ \tilde{u}_k,\ k =1,\cdots, m \end{eqnarray}\qquad(1.317) \)
oraz definiujemy \( i \)-te równanie zlinearyzowane w następujący sposób
\( \begin{eqnarray} \frac{d\tilde{x}_i}{dt} &=& \frac{\partial f_i(x_0,u_0)}{\partial x_1}\tilde{x}_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j} \tilde{x}_j + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}\tilde{x}_n \\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}\tilde{u}_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}\tilde{u}_k + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}\tilde{u}_m \qquad(1.318) \end{eqnarray} \)
Pełny układ równań zlinearyzowanych ma postać
\( \begin{eqnarray} \frac{d\tilde{x}_1}{dt} &=& \frac{\partial f_1(x_0,u_0)}{\partial x_1}\tilde{x}_1 + \cdots \frac{\partial f_1(x_0,u_0)}{\partial x_j} \tilde{x}_j + \cdots + \frac{\partial f_1(x_0,u_0)}{\partial x_n}\tilde{x}_n \qquad(1.319) \\ && + \frac{\partial f_1(x_0,u_0)}{\partial u_1}\tilde{u}_1 + \cdots \frac{\partial f_1(x_0,u_0)}{\partial u_k}\tilde{u}_k + \cdots + \frac{\partial f_1(x_0,u_0)}{\partial u_m}\tilde{u}_m \\ &\vdots& \nonumber\\ \frac{d\tilde{x}_i}{dt} &=& \frac{\partial f_i(x_0,u_0)}{\partial x_1}\tilde{x}_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial x_j} \tilde{x}_j + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial x_n}\tilde{x}_n \qquad(1.320)\\ && + \frac{\partial f_i(x_0,u_0)}{\partial u_1}\tilde{u}_1 + \cdots \frac{\partial f_i(x_0,u_0)}{\partial u_k}\tilde{u}_k + \cdots + \frac{\partial f_i(x_0,u_0)}{\partial u_m}\tilde{u}_m \nonumber \\ &\vdots& \nonumber \\ \frac{d\tilde{x}_n}{dt} &=& \frac{\partial f_n(x_0,u_0)}{\partial x_1}\tilde{x}_1 + \cdots \frac{\partial f_n(x_0,u_0)}{\partial x_j} \tilde{x}_j + \cdots + \frac{\partial f_n(x_0,u_0)}{\partial x_n}\tilde{x}_n \qquad(1.321)\\ && + \frac{\partial f_n(x_0,u_0)}{\partial u_1}\tilde{u}_1 + \cdots \frac{\partial f_n(x_0,u_0)}{\partial u_k}\tilde{u}_k + \cdots + \frac{\partial f_n(x_0,u_0)}{\partial u_m}\tilde{u}_m \nonumber \end{eqnarray} \)
Są to równania w ścisłym sensie, gdyż zamiast znaku przybliżenia \( \simeq \) pojawia się znak równości.
Postulujemy, że jeżeli zachodzą następujące
warunki
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) funkcje sterowań \(\tilde{u}_1(t),\cdots,\) (\tilde{u}_k(t),\cdots,\) \(\tilde{u}_m(t) \) są dokładnie równe przyrostom zmiennych \(u_1(t),\cdots,u_k(t),\cdots,\) \(u_m(t) \)
\( \begin{equation} \tilde{u}_k(t) = \Delta u_k(t) = u_k(t)-u_{k0},\ k=1,\cdots,m \end{equation}\qquad(1.322) \)
- warunki początkowe dla zmiennych \(\tilde{x}_j(t),\cdots,\tilde{x}_j(t),\cdots,\tilde{x}_n(t) \) są dokładnie równe przyrostom zmiennych \(x_1(t),\cdots,x_j(t),\cdots,x_n(t) \) w chwili początkowej
\( \begin{equation} \tilde{x}_j(t_0) = \Delta x_j(t_0),\ j=1,\cdots,n \end{equation} \qquad(1.323) \)
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania nieliniowych równań stanu \(x_1(t),\cdots,x_j(t),\cdots,x_n(t) \) pozostają w otoczeniu punktu równowagi \( (x_0, u_0) \)
\( \begin{equation} | x_j(t)-x_{j0} | = | \Delta x_j(t) | \leq C_{j} \qquad(1.324) \end{equation} \)
gdzie \( C_{j},\ j =1,\cdots,n \) są stałymi dodatnimi
to rozwiązania \(\tilde{x}_j(t),\cdots,\tilde{x}_j(t),\cdots,\tilde{x}_n(t) \) zlinearyzowanych równań stanu (1.319)-(1.321) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzą przybliżone warunki
\( \begin{eqnarray} \tilde{x}_j(t) \simeq \Delta x_j(t),\ j=1,\cdots,n \end{eqnarray}/qquad(1.325) \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu równowagi pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{j},\ j =1,\cdots,n \) w (1.324).
Podobnie rozważmy układ równań wyjść w ogólnej postaci
\( \begin{eqnarray} y_1 &=& g_1(x_1,\cdots,x_j,\cdots,x_n) \qquad(1.326) \\ &\vdots& \nonumber \\ y_i &=& g_i(x_1,\cdots,x_j,\cdots,x_n) \qquad(1.327) \\ &\vdots& \nonumber \\ y_p &=& g_p(x_1,\cdots,x_j,\cdots,x_n) \qquad(1.328) \end{eqnarray} \)
Linearyzacja \( i \)-tej funkcji prawych stron w pobliżu punktu równowagi \( (x_0,u_0) \) ma postać
\( \begin{eqnarray} && g_i(x_1,\cdots,x_j,\cdots,x_n) \simeq g_i(x_{10},\cdots,x_{j0},\cdots,x_{n0}) \nonumber \\ &&\qquad + \frac{\partial g_i(x_0)}{\partial x_1}(x_1-x_{10}) + \cdots \frac{\partial g_i(x_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \frac{\partial g_i(x_0)}{\partial x_n}(x_n-x_{n0}) \nonumber \end{eqnarray} \)
gdzie dla skrócenia zapisu wprowadzamy oznaczenie
\( \begin{equation} \dfrac{\partial g_i(x_0)}{\partial x_j} = \dfrac{\partial g_i(x_{10},\cdots,x_{j0},\cdots,x_{n0})}{\partial x_j} \end{equation}\qquad(1.329) \)
Przybliżenie dla \( i \)-tego równania wyjść można zapisać jako
\( \begin{equation} y_i \simeq y_{i0} + \frac{\partial g_i(x_0)}{\partial x_1}(x_1-x_{10}) + \cdots \frac{\partial g_i(x_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \frac{\partial g_i(x_0)}{\partial x_n}(x_n-x_{n0}) \end{equation}\qquad(1.330) \)
gdzie
\( \begin{equation} y_{i0} = g_i(x_{10},\cdots,x_{j0},\cdots,x_{n0}) \end{equation}\qquad(1.331) \)
Jeżeli przeniesiemy \( y_{i0} \) na drugą stronę przybliżenia to otrzymamy
\( \begin{equation} y_i - y_{i0} \simeq \dfrac{\partial g_i(x_0)}{\partial x_1}(x_1-x_{10}) + \cdots \dfrac{\partial g_i(x_0)}{\partial x_j}(x_j-x_{j0}) + \cdots + \dfrac{\partial g_i(x_0)}{\partial x_n}(x_n-x_{n0}) \end{equation}\qquad(1.332) \)
Wprowadźmy zmienne przyrostowe
\( \begin{equation} \Delta y_i = y_i - y_{i0},\ i = 1,\cdots,p \end{equation}\qquad(1.333) \)
Przybliżenie dla \( i \)-tego równania wyjść można teraz zapisać jako
\( \begin{equation} \Delta y_i \simeq + \dfrac{\partial g_i(x_0)}{\partial x_1}\Delta x_1 + \cdots \dfrac{\partial g_i(x_0)}{\partial x_j}\Delta x_j + \cdots + \dfrac{\partial g_i(x_0)}{\partial x_n}\Delta x_n \end{equation}\qquad(1.334) \)
Aby zdefiniować zlinearyzowane równanie wyjść wprowadzamy zmienne \( \tilde{y}_i,\ i = 1,\cdots,p \). \( i \)-te zlinearyzowane równanie wyjść ma postać
\( \begin{equation} \tilde{y}_i = \dfrac{\partial g_i(x_0)}{\partial x_1}\tilde{x}_1 + \cdots \dfrac{\partial g_i(x_0)}{\partial x_j}\tilde{x}_i + \cdots + \dfrac{\partial g_i(x_0)}{\partial x_n}\tilde{x}_n \end{equation}\qquad(1.335) \)
Układ zlinearyzowanych równań wyjść ma postać
\( \begin{eqnarray} \tilde{y}_1 &=& \dfrac{\partial g_1(x_0)}{\partial x_1}\tilde{x}_1 + \cdots \dfrac{\partial g_1(x_0)}{\partial x_j}\tilde{x}_i + \cdots + \dfrac{\partial g_1(x_0)}{\partial x_n}\tilde{x}_n \qquad(1.336)\\ &\vdots& \\ \tilde{y}_i &=& \dfrac{\partial g_i(x_0)}{\partial x_1}\tilde{x}_1 + \cdots \dfrac{\partial g_i(x_0)}{\partial x_j}\tilde{x}_i + \cdots + \dfrac{\partial g_i(x_0)}{\partial x_n}\tilde{x}_n \qquad(1.337\\ &\vdots& ) \\ \tilde{y}_n &=& \dfrac{\partial g_n(x_0)}{\partial x_1}\tilde{x}_1 + \cdots \dfrac{\partial g_n(x_0)}{\partial x_j}\tilde{x}_i + \cdots + \dfrac{\partial g_n(x_0)}{\partial x_n}\tilde{x}_n \qquad(1.338) \end{eqnarray} \)
Postulując takie same warunki jak w przypadku równań stanu oczekujemy, że rozwiązania równań wyjść \( \tilde{y}_1,\cdots,\tilde{y}_i,\cdots,\tilde{y}_p \) będą dobrze przybliżać przyrosty zmiennych wyjściowych \( y_1,\cdots,y_i,\cdots,y_p \)
\( \begin{equation} \tilde{y}_i \simeq \Delta y_i = y_i-y_{i0},\ i = 1,\cdots,p \end{equation}\qquad(1.339) \)
Zlinearyzowane równania stanu i wyjść mogą zostać przedstawione w postaci wektorowej
\( \begin{eqnarray} \left( \begin{array}{c} \dfrac{d\tilde{x}_1}{dt} \\ \vdots \\ \dfrac{d\tilde{x}_i}{dt} \\ \vdots \\ \dfrac{d\tilde{x}_n}{dt} \end{array} \right) &=& \left( \begin{array}{ccccc} \dfrac{\partial f_1(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_i(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_n(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_n(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_n(x_0,u_0)}{\partial x_n} \end{array} \right) \left( \begin{array}{c} \tilde{x}_1 \\ \vdots \\ \tilde{x}_j \\ \vdots \\ \tilde{x}_n \end{array} \right) \\ &&+ \left( \begin{array}{ccccc} \dfrac{\partial f_1(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial u_m} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_i(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial u_m} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_m(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_m(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_m(x_0,u_0)}{\partial u_m} \end{array} \right) \left( \begin{array}{c} \tilde{u}_1\\ \vdots \\ \tilde{u}_k \\ \vdots \\ \tilde{u}_m \end{array} \right) \nonumber \end{eqnarray} \qquad(1.340) \)
\( \begin{eqnarray}
\left(
\begin{array}{c}
\tilde{y}_1 \\ \vdots \\ \tilde{y}_i \\ \vdots \\ \tilde{y}_p
\end{array}
\right) &=&
\left(
\begin{array}{ccccc}
\dfrac{\partial g_1(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_1(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_1(x_0)}{\partial x_n} \\
\vdots & & \vdots & & \vdots \\
\dfrac{\partial g_i(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_i(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_i(x_0)}{\partial x_n} \\
\vdots & & \vdots & & \vdots \\
\dfrac{\partial g_n(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_n(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_n(x_0)}{\partial x_n}
\end{array}
\right)
\left(
\begin{array}{c}
\tilde{x}_1 \\ \vdots \\ \tilde{x}_j \\ \vdots \\ \tilde{x}_n
\end{array}
\right)
\end{eqnarray}
\)
Jeżeli wprowadzimy następujące oznaczenia wektorów
\( \begin{equation} \tilde{x} = \left( \begin{array}{c} \tilde{x}_1\\ \vdots\\ \tilde{x}_j \\ \vdots\\ \tilde{x}_n \end{array} \right),\ \dfrac{d\tilde{x}}{dt} = \left( \begin{array}{c} \dfrac{d\tilde{x}_1}{dt} \\ \vdots \\ \dfrac{d\tilde{x}_i}{dt} \\ \vdots \\ \dfrac{d\tilde{x}_n}{dt} \end{array} \right),\ \tilde{u} = \left( \begin{array}{c} \tilde{u}_1\\ \vdots\\ \tilde{u}_k \\ \vdots\\ \tilde{u}_m \end{array} \right),\ \tilde{y} = \left( \begin{array}{c} \tilde{y}_1\\ \vdots\\ \tilde{y}_i \\ \vdots\\ \tilde{y}_p \end{array} \right) \end{equation} \qquad(1.342) \)
oraz macierzy
\( \begin{eqnarray} \dfrac{\partial f(x_0,u_0)}{\partial x} &=& \left( \begin{array}{ccccc} \dfrac{\partial f_1(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_i(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_n(x_0,u_0)}{\partial x_1} & \cdots & \dfrac{\partial f_n(x_0,u_0)}{\partial x_j} & \cdots & \dfrac{\partial f_n(x_0,u_0)}{\partial x_n} \end{array} \right)\qquad(1.343)\\ \dfrac{\partial f(x_0,u_0)}{\partial u} &=& \left( \begin{array}{ccccc} \dfrac{\partial f_1(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_1(x_0,u_0)}{\partial u_m} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_i(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_i(x_0,u_0)}{\partial u_m} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial f_m(x_0,u_0)}{\partial u_1} & \cdots & \dfrac{\partial f_m(x_0,u_0)}{\partial u_k} & \cdots & \dfrac{\partial f_m(x_0,u_0)}{\partial u_m} \end{array} \right) \qquad(1.344)\\ \dfrac{\partial g(x_0)}{\partial x} &=& \left( \begin{array}{ccccc} \dfrac{\partial g_1(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_1(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_1(x_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial g_i(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_i(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_i(x_0)}{\partial x_n} \\ \vdots & & \vdots & & \vdots \\ \dfrac{\partial g_n(x_0)}{\partial x_1} & \cdots & \dfrac{\partial g_n(x_0)}{\partial x_j} & \cdots & \dfrac{\partial g_n(x_0)}{\partial x_n} \end{array} \right)\qquad(1.345) \end{eqnarray} \)
To zlinearyzowane równania stanu i wyjść mogą zostać zapisane w postaci zwartej
\( \begin{eqnarray} \dfrac{d\tilde{x}}{dt} &=& \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x} + \dfrac{\partial f(x_0,u_0)}{\partial u}\tilde{u} \qquad(1.346)\\ \tilde{y} &=& \dfrac{\partial g(x_0,u_0)}{\partial x}\tilde{x} \qquad(1.347) \end{eqnarray} \)
Przepiszmy jeszcze raz powyższe równania, ale tym razem z argumentem czasu
\( \begin{eqnarray} \dfrac{d\tilde{x}(t)}{dt} &=& \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x}(t) + \dfrac{\partial f(x_0,u_0)}{\partial u}\tilde{u}(t) \qquad(1.348)\\ \tilde{y}(t) &=& \dfrac{\partial g(x_0,u_0)}{\partial x}\tilde{x}(t) \qquad(1.349) \end{eqnarray} \)
Należy pamiętać, że w równaniach \( \tilde{x}(t)\), \( \tilde{u}(t) \) oraz \( \tilde{y}(t) \) są funkcjami czasu, natomiast macierze pochodnych cząstkowych \( \dfrac{\partial f(x_0,u_0)}{\partial x} \), \( \dfrac{\partial f(x_0,u_0)}{\partial u} \) oraz \( \dfrac{\partial g(x_0,u_0)}{\partial x} \) są stałe, ponieważ pochodne cząstkowe są obliczane w jednym wybranym punkcie równowagi \( (x_0,u_0) \).
Równanie równowagi dla zlinearyzowanych równań stanu ma postać
\( \begin{equation} 0 = \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x}_0 + \dfrac{\partial f(x_0,u_0)}{\partial u}\tilde{u}_0 \end{equation}\qquad(1.350) \)
Powyższy układ równań ma zawsze co najmniej jedno rozwiązanie
\( \begin{equation} \tilde{x}_0 = 0,\ \tilde{u}_0 = 0 \end{equation}\qquad(1.351) \)
Punkt równowagi układu zlinearyzowanego \( (\tilde{x}_0,\tilde{u}_0) = (0,0) \) odpowiada punktowi równowagi \( (x_0,u_0) \) układu nieliniowego. Jeżeli bowiem zachodzi
\( \begin{equation} x(t) = x_0,\ u(t) = u_0 \end{equation} \qquad(1.352) \)
to warunki początkowe dla układu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{x}(t_0) = \Delta x(t_0) = x(t_0) - x_0 = x_0 - x_0 = 0 \end{equation}\qquad(1.353) \)
a sterowania w układzie zlinearyzowanym wynoszą
\( \begin{equation} \tilde{u}(t) = \Delta u(t) = u(t) - u_0 = u_0 - u_0 = 0 \end{equation}\qquad(1.354) \)
W takim przypadku rozwiązanie układu zlinearyzowanego wynosi
\( \begin{equation} \tilde{x}(t) = 0,\ \tilde{u}(t) = 0 \end{equation}\qquad(1.355) \)
tzn. układ zlinearyzowany pozostaje w punkcie równowagi \( (\tilde{x}_0,\tilde{u}_0) = (0,0) \).