Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Układy regulacji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | niedziela, 18 stycznia 2026, 05:51 |
1. Istota regulacji
Rozważmy układ trzech zbiorników z rozdziału pierwszego i pewien punkt równowagi określony przez stały sygnał sterujący \( Q_{we0} \) oraz wartości poziomów cieczy w trzech zbiornikach \( H_{10} \), \( H_{20} \) oraz \( H_{30} \), wynikające z charakterystyki statycznej obiektu. Załóżmy też, że w pewnej chwili początkowej \( t_0 \) obiekt istotnie znajduje się w wybranym punkcie równowagi, tzn. że spełnione są warunki
\( \begin{eqnarray} H_1(t_0) &=& H_{10} \qquad(2.1)\\ H_2(t_0) &=& H_{20} \qquad(2.2)\\ H_3(t_0) &=& H_{30} \qquad(2.3) \end{eqnarray} \)
Chcielibyśmy aby obiekt pozostawał w wybranym punkcie równowagi przez cały czas. Gdyby obiekt zachowywał się dokładnie według opisu w postaci równań stanu, to dla stałego sterowania \( Q_{we}(t) = Q_{we0} \) obiekt pozostawałby w wybranym punkcie równowagi bez konieczności zewnętrznej ingerencji. Na rzeczywiste układy oddziałują jednak inne czynniki, które wytrącają obiekt z wybranego punktu równowagi. Takie czynniki nazywamy ogólnie zakłóceniami. Zakłócenia mogą być mierzalne lub niemierzalne, ale ogólnie są to sygnały, które oddziałują na obiekt, ale na które nie mamy bezpośredniego wpływu. W przypadku układu trzech zbiorników przykładami zakłóceń mogą być
- zakłócenia przepływu cieczy przez pompę
- wycieki ze zbiorników
- zużycie przewodów przepływowych lub zaworów
- zarastanie przewodów przepływowych lub zaworów
Wycieki ze zbiorników skutkują obniżeniem poziomów cieczy w zbiornikach w stosunku do poziomów cieczy w wybranym punkcie równowagi. Aby skompensować wpływ wycieków należy zwiększyć przepływ generowany przez pompę. Przytkanie przewodów przepływowych powoduje wzrost poziomu cieczy w zbiornikach. Aby skompensować ten efekt należy zmniejszyć przepływ generowany przez pompę. W podobny sposób można analizować wpływ innych zakłóceń na obiekt, jednak strategia kompensacji zakłóceń pozostaje zasadniczo taka sama. Na obniżenie poziomu cieczy w zbiornikach należy zareagować wzrostem obrotów pompy natomiast na podwyższenie poziomu cieczy w zbiornikach należy zareagować zmniejszeniem przepływu przez pompę.
Zadanie utrzymania obiektu jak najbliżej wybranego punktu równowagi \( (x_0, u_0) \) nazywamy zadaniem regulacji stałowartościowej. Wybrany punkt równowagi jest nazywany punktem pracy układu regulacji. Intuicyjnie rozumiemy, że utrzymanie obiektu dokładnie w wybranym punkcie pracy jest niemożliwe, jednak spodziewamy się, że zastosowanie kompensacji zakłóceń pozwala na utrzymanie obiektu bliżej wybranego punktu pracy, niż w przypadku gdybyśmy takiej kompensacji nie zastosowali. Możliwe jest też rozważanie innego typu zadania regulacji, w którym trajektorie układu mają podążać za wybraną trajektorią wzorcową. Takie zadanie nazywamy zadaniem regulacji nadążnej. Przykładem takiego zadania dla układu trzech zbiorników może być wymaganie, aby wysokość słupa cieczy w trzecim zbiorniku zmieniała się w sposób sinusoidalny. Synteza układu regulacji nadążnej wymaga analizowania układów niestacjonarnych. W niniejszym opracowaniu skupiamy się na zadaniu regulacji stałowartościowej, które jest nieco prostsze, a jednocześnie daje się uogólnić do zadania regulacji nadążnej.
Zasadniczym celem regulacji stałowartościowej jest kompensacja wpływu zakłóceń działających na obiekt. Realizacja procedury kompensacji zakłóceń opiera się na koncepcji sprzężenia zwrotnego. Działanie zakłóceń wpływa na zmianę zachowania obiektu, która skutkuje zmianami wartości sygnałów wyjściowych obiektu \( y(t) \) w stosunku do ich wartości w punkcie pracy \( y_0 \). Wartości wyjść w wybranym punkcie pracy nazywa się wartościami zadanymi. Wektor przyrostów wartości wyjść obiektu w stosunku do ich wartości w punkcie pracy
\( \begin{equation} \Delta y(t) = y(t)-y_0 \end{equation}\qquad(2.4) \)
nazywamy odchyłką regulacji. Odchyłka regulacji jest w literaturze często oznaczana jako \( e(t) \). Ponieważ jednak definicja odchyłki regulacji pokrywa się z definicją przyrostu zmiennej wyjściowej, to w opracowaniu konsekwentnie korzystamy z oznaczenia \( \Delta y(t) \).Na podstawie informacji o odchyłce regulacji \( \Delta y(t) \), możliwe jest skompensowanie wpływu zakłóceń poprzez z mianę wartości sygnałów sterujących obiektu \( u(t) \). Synteza układu regulacji polega na zatem na zaproponowaniu odpowiedniego algorytmu regulacji, który oblicza sygnały sterujące obiektu \( u(t) \) na podstawie informacji o odchyłce regulacji \( \Delta y(t) \) i który zapewnia kompensację wpływu zakłóceń na obiekt. System opisywany przez algorytm regulacji jest nazywany regulatorem. Wejściem regulatora jest odchyłka regulacji \( \Delta y(t) \), natomiast wyjściem regulatora są sygnały sterujące obiektu \( u(t) \). Schemat ideowy układu regulacji został przedstawiony na Rys. 2.1.
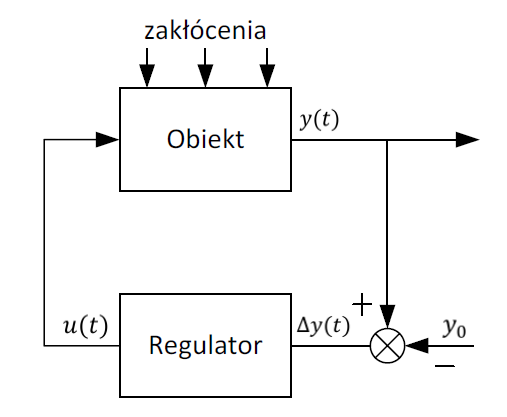
Rysunek 2.1 Schemat ideowy układu regulacji.
Idea wykorzystania sprzężenia zwrotnego do budowy układu regulacji jest stosunkowo prosta. W czasach przez erą mikroprocesorów nietrywialnym zadaniem było zaprojektowanie urządzeń realizujących sprzężenie zwrotne, które uzależnia sygnały sterujące obiektu od odchyłki regulacji. W przypadku układów hydraulicznych lub pneumatycznych należało zaprojektować zawory realizujące odpowiednie zależności. Dla układów elektrycznych należało zaprojektować układy elektroniczne z wykorzystaniem wzmacniaczy operacyjnych. W przypadku układów mechanicznych układy realizujące sprzężenie zwrotne składały się z krzywek i przekładni. Wraz z rozpowszechnieniem się mikroprocesorów i techniki cyfrowej, realizacja sprzężenia zwrotnego nie nastręcza większych trudności, jako że układy mikroprocesorowe są w stanie realizować skomplikowane obliczenia w bardzo krótkim czasie.
Wybór algorytmu regulatora nie jest jednoznaczny i dla różnych regulatorów uzyskujemy różne własności układu regulacji. Algorytmy regulacji (lub prościej regulatory) możemy podzielić na dwie zasadnicze klasy: algorytmy (regulatory) ciągłe i nieciągłe. Układy regulacji z ciągłymi i nieciągłymi regulatorami mają odmienne własności i wymagają innych narzędzi do ich analizowania. W szczególności jedynie regulatory ciągłe mogą być analizowane z wykorzystaniem techniki linearyzacji. Z tego względu w niniejszym opracowaniu skupiamy się na regulatorach ciągłych.
Najprostszym przykładem regulatora ciągłego dla układu trzech zbiorników jest następujący algorytm
\( \begin{equation} Q_{we}(t) = k_p \Delta H_3(t) + Q_{we0} = k_p(H_3(t)-H_{30}) + Q_{we0} \qquad(2.5) \end{equation} \)
gdzie \( k_p < 0 \) jest pewną stałą, natomiast odchyłka regulacji wynosi
\( \begin{equation} \Delta H_3(t) = H_3(t)-H_{30} \end{equation}\qquad(2.6) \)
Powyższy wzór można zapisać inaczej
\( \begin{equation} \Delta Q_{we}(t) = Q_{we}(t) - Q_{we0} = k_p \Delta H_3(t) \qquad(2.7) \end{equation} \)
gdzie \( \Delta Q_{we}(t) \) to korekta sygnału sterującego generowana przez regulator.
W przypadku, kiedy zmierzona wysokość słupa cieczy w trzecim zbiorniku jest równa wysokości zadanej, wartość odchyłki regulacji wynosi zero i przepływ przez pompę \( Q_{we}(t) \) jest dokładnie równy wartości przepływu w punkcie pracy \( Q_{we0} \). W przypadku, kiedy zmierzona wysokość poziomu cieczy w trzecim zbiorniku jest większa niż wysokość zadana, wartość odchyłki regulacji jest dodatnia. Po przemnożeniu tej wartości przez ujemną wartość \( k_p \) uzyskujemy ujemną korektę sterowania
\( \begin{equation} \Delta Q_{we}(t) = k_p \Delta H_3(t) = k_p(H_3(t)-H_{30}) < 0 \end{equation}\qquad(2.8) \)
Przepływ przez pompę jest mniejszy niż przepływ w punkcie pracy \( Q_{we}(t) = Q_{we0} + \Delta Q_{we}(t) < Q_{we0}\), co jest zgodne z oczekiwaniami.
W przypadku, kiedy zmierzona wysokość słupa cieczy w trzecim zbiorniku jest mniejsza niż wysokość zadana, wartość w nawiasie wzoru (2.5) jest ujemna. Po przemnożeniu tej wartości przez ujemną wartość \( k_p \) uzyskujemy dodatnią korektę sterowania
\( \begin{equation} \Delta Q_{we}(t) = k_p(H_3(t)-H_{30}) > 0 \end{equation}\qquad(2.9) \)
Przepływ przez pompę jest większy niż przepływu w punkcie pracy \( Q_{we}(t) = Q_{we0} + \Delta Q_{we}(t) > Q_{we0}\). Ze względu na to, że w zaproponowanym algorytmie regulacji korekta sterowania \( \Delta Q_{we}(t) \) jest proporcjonalna do odchyłki regulacji \( \Delta H_3(t) \), regulator ten jest nazywany regulatorem proporcjonalnym lub regulatorem P. Parametr \( k_p \) jest nazywany wzmocnieniem proporcjonalnym regulatora.
Do zagadnienia badania wpływu zakłóceń na obiekt można podejść dwojako. Z jednej strony można wprowadzić wszystkie rozważane zakłócenia do modelu obiektu, a następnie badać wpływ tych zakłóceń na obiekt. Wadą tego podejścia jest konieczność dokładnej znajomości charakteru zakłóceń i ich interakcji z obiektem, dla wszystkich rozważanych zakłóceń. W teorii sterowania bardzo płodne okazało się inne podejście. Mianowicie nie modelujemy konkretnych zakłóceń. Zamiast tego zakładamy, że pod wpływem zakłóceń obiekt zostaje wytrącony z punktu pracy \( x_0 \), tak że w chwili początkowej mamy
\( \begin{equation} x(t_0) \neq x_0 \end{equation}\qquad(2.10) \)
Następnie zakładamy, że dla chwil czasu \( t>t_0 \) działanie zakłóceń na obiekt ustaje. Interesuje nas teraz to, czy po ustaniu zakłóceń, obiekt powróci do punktu pracy, a jeżeli tak, to w jaki jest charakter tego powrotu.
Zaprezentujemy teraz symulację działania układu regulacji z regulatorem P dla trzech zbiorników. Przyjmujemy następujące wartości parametrów obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt pracy obiektu \( Q_{we0} = 0.5\), \(H_{10}=0.75 \), \( H_{20}=0.5 \), \( H_{30}=0.25 \). Regulator P jest opisany równaniem (2.5). Warunki początkowe dla obiektu wynoszą \( H_1(t_0) =0.85 \), \( H_2(t_0) =0.6 \), \( H_3(t_0)=0.35 \). Na Rys. 2.2 przedstawiono trajektorie zmiennej wyjściowej \( H_3(t) \) dla czterech wartości wzmocnienia regulatora
- \( k_p = 0 \) -- układ bez regulatora (\( Q_{we}(t) = Q_{we0}\))
- \( k_p = -1 \)
- \( k_p = -2 \)
- \( k_p = -4 \)
Dla układu bez regulatora (\( k_p = 0 \)) obiekt samoczynnie powraca do punktu pracy \( H_{30}=0.25 \). Po wprowadzeniu niezerowej wartości wzmocnienia regulatora, układ regulacji również powraca do punktu pracy, jednak dzieje się to znacznie szybciej niż dla układu bez regulatora. Aby zbliżyć się do punktu pracy na taką samą odległość co obiekt bez regulatora po czasie \( t =10 \), układ z regulatorem potrzebuje odpowiednio czasu
- \( t \simeq 3 \) dla \( k_p = -1 \)
- \( t \simeq 2 \) dla \( k_p = -2 \)
- \( t \simeq 3 \) dla \( k_p = -4 \)
Możemy też zauważyć, że charakter trajektorii \( H_3(t) \) dla coraz większych \( k_p \) zmienia się z aperiodycznego na oscylacyjny.
Na Rys. 2.3 przedstawiono trajektorie zmiennej zmiennej sterującej \( Q_{we}(t) \) dla czterech wartości wzmocnienia regulatora. Dla układu bez regulatora (\( k_p = 0 \) ) sygnał sterujący jest stały \( Q_{we}(t) = Q_{we0} \). Dla rosnących wartości \( k_p \), obserwujemy coraz większe zmiany sygnału sterującego generowanego przez regulator. Podobnie jak to było w przypadku sygnału \( H_3(t) \), dla rosnących wartości \( k_p \) charakter sygnału \( Q_{we}(t) \) zmienia się z aperiodycznego na oscylacyjny.
Zbadajmy trajektorie generowane przez układ regulacji dla jeszcze większych wartości wzmocnienia regulatora
- \( k_p = -8 \) -- układ bez regulatora (\( Q_{we}(t) = Q_{we0}\))
- \( k_p = -16 \)
- \( k_p = -24 \)
- \( k_p = -30 \)
a) \(k_p = 0 \)
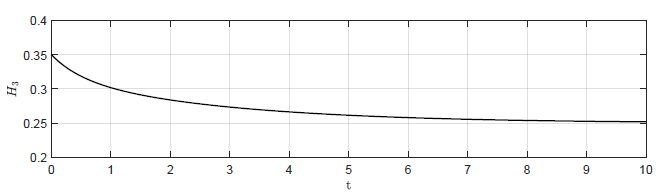
b) \(k_p = -1 \)
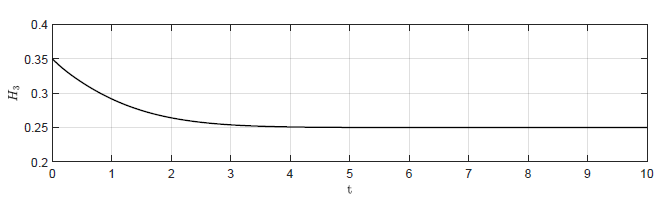
c) \(k_p = -2 \)
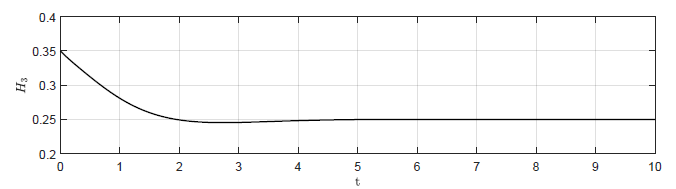
d) \(k_p = -4 \)
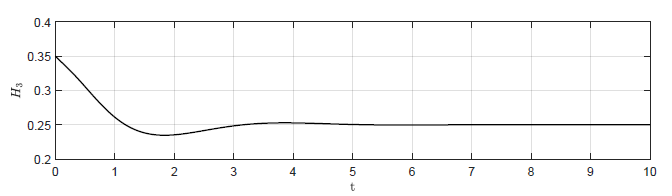
Rysunek 2.2 Trajektorie \( H_3(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
a) \(k_p = 0 \)
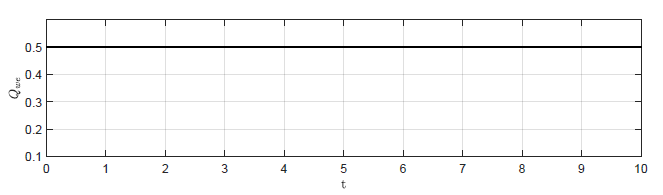
b) \(k_p = -1 \)
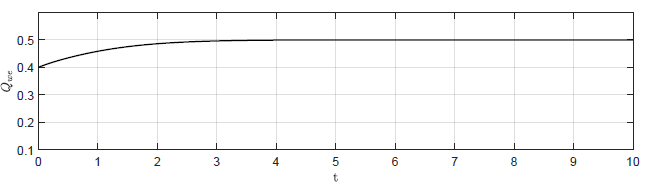
c) \(k_p = -2 \)
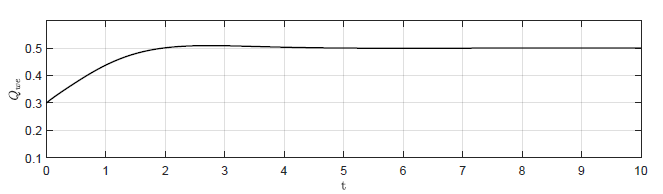
d) \(k_p = -4 \)
Rysunek 2.3 Trajektorie \( Q_{we}(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Tym razem, przyjmujemy warunki początkowe \( H_1(t_0) =0.76 \), \( H_2(t_0) =0.51 \), \( H_3(t_0)=0.26 \).
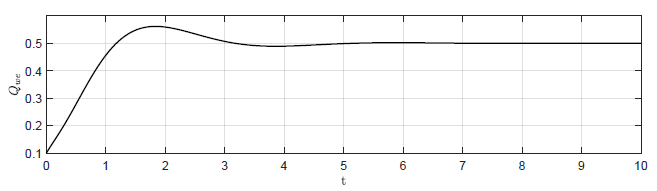
Na Rys. 2.4 przedstawiono trajektorie zmiennej wyjściowej \( H_3(t) \) dla czterech wartości wzmocnienia regulatora. Na Rys. 2.5 przedstawiono odpowiadające im trajektorie zmiennej zmiennej sterującej \( Q_{we}(t) \). Wraz ze wzrostem wartości wzmocnienia regulatora coraz silniej uwidacznia się oscylacyjny charakter odpowiedzi układu regulacji oraz sygnałów sterujących. Co ciekawe dla odpowiednio dużego \( k_p \) oscylacje w układzie regulacji nie gasną i układ nie powraca do pierwotnego punktu pracy. Dzieje się tak, pomimo tego że w układzie bez regulatora (\( k_p=0 \)) obiekt samoczynnie powraca do pierwotnego stanu pracy. Jest to bardzo istotna obserwacja. Intuicyjnie, sprzężenie zwrotne wydaje się być skutecznym narzędziem do realizacji zadania regulacji stałowartościowej. Okazuje się jednak, że istnieją istotne ograniczenia co do możliwości wykorzystania sprzężenia zwrotnego. W szczególności nieprawidłowy dobór algorytmu regulacji może doprowadzić do uzyskania efektu gorszego niż w przypadku całkowitego braku regulacji.
Regulator proporcjonalny jest szczególnym przypadkiem szerszej rodziny regulatorów proporcjonalno-całkująco-różniczkujących (PID). Wzór na algorytm regulatora PID dla układu trzech zbiorników ma postać
\( \begin{equation} \Delta Q_{we}(t) = k_p \Delta H_3(t) + k_i \int_{t_0}^{t} \Delta H_3(\tau) d \tau + k_d \frac{\Delta H_3(t)}{dt} \end{equation}\qquad(2.11) \)
Korekta sterowania jest obliczana jako suma trzech składników. Pierwszy składnik jest proporcjonalny do wartości odchyłki regulacji. Drugi składnik jest proporcjonalny do całki z odchyłki regulacji ze współczynnikiem proporcjonalności \( k_i \). Trzeci składnik jest proporcjonalny do pochodnej odchyłki regulacji ze współczynnikiem proporcjonalności \( k_d \). Przyjmując \( k_i = 0\) oraz \( k_d = 0\) otrzymujemy algorytm regulatora proporcjonalnego. Wprowadzenie dodatkowych składników ma na celu poprawę jakości regulacji w porównaniu do układu z regulatorem P. Zaletą wprowadzenia członu całkującego do algorytmu regulatora jest możliwość lepszego skompensowania wpływu zakłóceń, które nie zanikają. Odbywa się to jednak kosztem wydłużenia czasu trwania przebiegów przejściowych. W takim przypadku, aby skrócić czas dojścia układu do punktu pracy zakłóceń dodaje się człon różniczkujący. Na Rys. 2.6 przedstawiono porównanie działania regulatora P i PID. Parametry regulatorów zostały dobrane eksperymentalnie tak, aby zapewnić możliwie krótki czas dojścia układu do punktu pracy. Ponieważ badamy skuteczność regulacji w przypadku zanikających zakłóceń, nie wprowadzamy do algorytmu PID działania całkującego (\( k_i = 0 \)), które wydłuża ten czas. Dodatnie działania różniczkującego pozwala na skrócenie czasu powrotu układu do punktu pracy z \( t \simeq 3.5 \) do \( t \simeq 1.5 \). odbywa się to kosztem większych i szybszych zmian sygnały sterującego.a) \(k_p = -8 \)
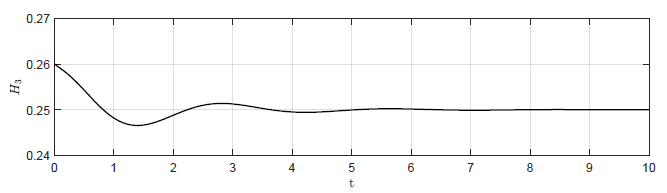
b) \(k_p = -16 \)
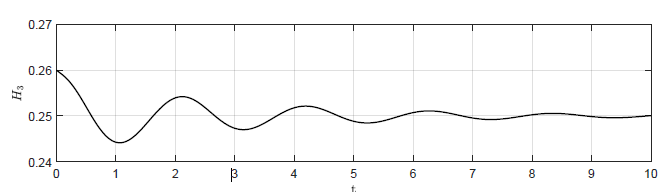
c) \(k_p = -24 \)
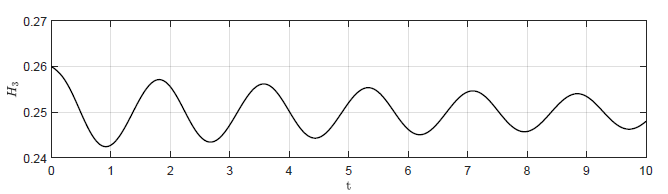
d) \(k_p = -30 \)
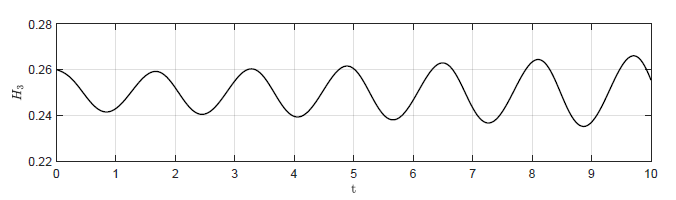
Rysunek 2.4 Trajektorie \( H_3(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
a) \(k_p = -8 \)
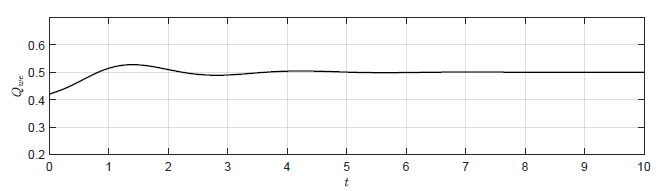
b) \(k_p = -16 \)
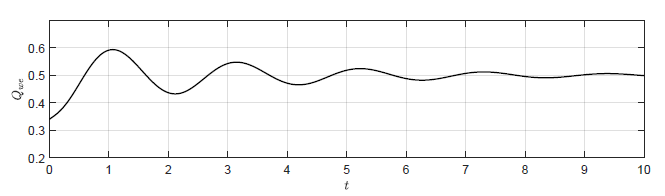
c) \(k_p = -24 \)
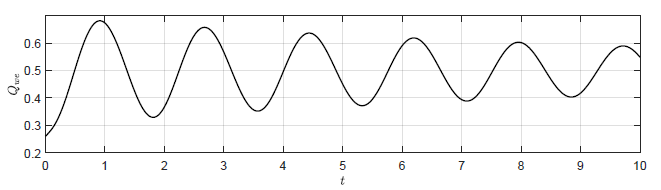
d) \(k_p = -30 \)
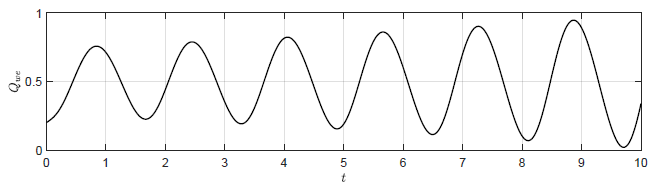
Rysunek 2. 5 Trajektorie \( Q_{we}(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
a) Trajektoria \( H_3(t) \) dla regulatora P -- \( k_p = -2.5 \)
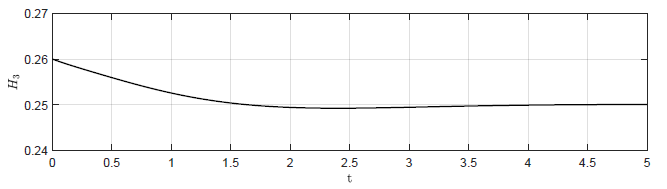
b) Trajektoria \( H_3(t) \) dla regulatora PID -- \( k_p = -12 \), \( k_i = 0 \), \( k_d = -4 \)
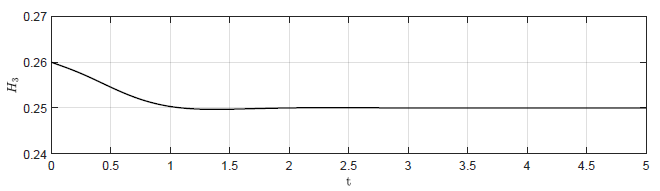
c) Trajektoria \( Q_{we}(t) \) dla regulatora P -- \( k_p = -2.5 \)
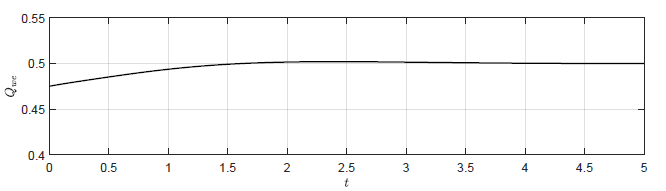
d) Trajektoria \( Q_{we}(t) \(dla regulatora PID -- \( k_p = -12 \), \( k_i = 0 \), \( k_d = -4 \)
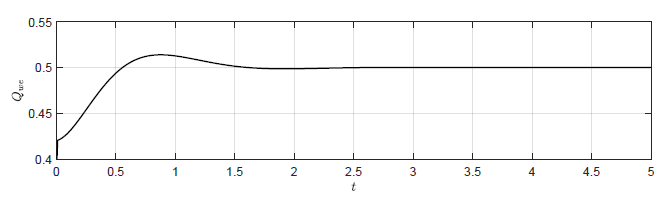
Rysunek 2.6 Porównanie działania regulatora P oraz PID.
Ponieważ całkowanie i różniczkowanie są operacjami liniowymi regulator PID można określić mianem regulatora liniowego. Możliwe jest także zaproponowanie regulatorów opisanych zależnościami nieliniowymi. Przykładem nieliniowego algorytmu regulacji może być algorytm opisany wzorem
\( \begin{equation} \Delta Q_{we}(t) = Q_{we0} \left( e^{k_{nl} \Delta H_3(t)} -1 \right) \qquad(2.12) \end{equation} \)
gdzie \( k_{nl}<0 \) jest pewną stałą. Wykres powyższej zależności dla \( Q_{we0}=0.5 \) i \( k_{nl}=-1 \) został przedstawiony na Rys. 2.7.
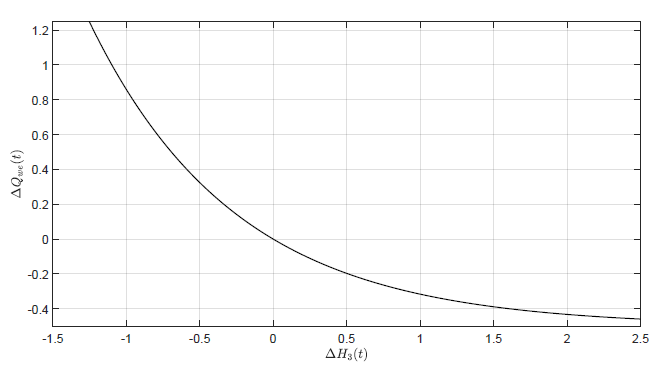
Rysunek 2.7 Charakterystyka regulatora nieliniowego.
Algorytm regulacji (2.12) ma własności podobne do regulatora proporcjonalnego. Dla zerowej odchyłki regulacji \( \Delta H_3(t) \) korekta sterowania \( \Delta Q_{we}(t) \) również wynosi zero. Dla dodatniej odchyłki regulacji korekta sterowania jest ujemna, natomiast dla ujemnej odchyłki regulacji korekta sterowania jest dodatnia. Zaletą zaproponowanego nieliniowego algorytmu regulacji jest to, że nawet dla dużych wartości \( \Delta H_3(t) \) sterowanie generowane przez regulator nigdy nie będzie ujemne. Regulator P może generować ujemny sygnał \( Q_{we}(t) \), jednak jest on nierealizowalny fizycznie, jako że w układzie trzech zbiorników pompa nie może wypompowywać cieczy z pierwszego zbiornika. W przypadku, gdy algorytm regulatora P generuje \( Q_{we}(t) < 0 \) to rzeczywisty przepływ przez pompę wynosi 0. Zaproponowany nieliniowy algorytm regulacji generuje prawidłowy sygnał sterujący w całym zakresie działania układu.
Na Rys. 2.8 przedstawiono działanie układu regulacji z regulatorem nieliniowym dla dużej wartości parametru \( k_{nl} = -30 \).
a) Trajektoria \( H_3(t) \) dla regulatora nieliniowego -- \( k_{nl} = -30 \)
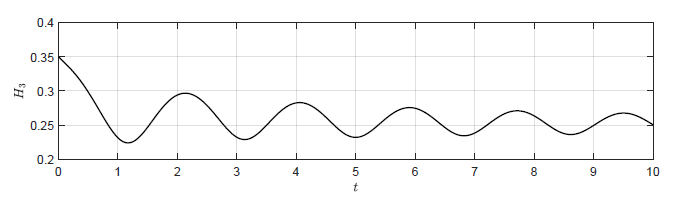
b) Trajektoria \( Q_{we}(t) \) dla regulatora nieliniowego -- \( k_{nl} = -30 \)
Rysunek 2.8 Trajektorie sygnałów w układzie regulacji z regulatorem nieliniowym.
Nawet w przypadku, gdy odchyłka regulacji przyjmuje duże wartości sterowanie generowanie przez regulator nie przyjmuje wartości mniejszych od 0.
Omówmy teraz problem regulacji stałowartościowej dla wahadła matematycznego. Naszym celem jest utrzymanie stałego położenia kątowego wahadła pomimo działających na obiekt zakłóceń. Źródłami zakłóceń w wahadle mogą być
- zakłócenia momentu generowanego przez urządzenie wykonawcze w przegubie
- stopniowe zmiany współczynnika tarcia w przegubie
- zmienne opory powietrza
- chwilowe zadziałanie na wahadło siłą zewnętrzną
W przypadku, gdy działanie zakłóceń powoduje zmniejszenie kąta wychylenia wahadła, należy zwiększyć moment w przegubie, aby umożliwić powrót wahadła do pierwotnego punktu pracy. Podobnie na zwiększenie kąta wychylenia wahadła należy zareagować zmniejszeniem momentu generowanego w przegubie.
Przeanalizujmy teraz działanie układu regulacji z regulatorem P dla wahadła matematycznego. Dla potrzeb symulacji przyjmujemy parametry modelu obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt pracy \( \theta_0=\frac{\pi}{6} \), \( \omega_0=0 \), \( M_{0} = -0.5 \). Wybrany punkt pracy jest szczególnie interesujący. Jeżeli w układzie nie ma regulatora (\( k_p = 0 \)) to po wytrąceniu wahadła ze stanu równowagi, obiekt nie powraca samoczynnie do pierwotnego punktu pracy (Rys. 1.15). Algorytm regulatora P ma dla wahadła matematycznego postać
\( \begin{equation} M(t) = k_p (\theta(t)-\theta_0) + M_0 \qquad(2.13) \end{equation} \)
Dla zapewnienia kompensacji zakłóceń wzmocnienie regulatora \( k_p \) musi być ujemne. Algorytm regulatora można zapisać także za pomocą przyrostów zmiennych
\( \begin{equation} \Delta M(t) = k_p \Delta \theta(t) \qquad(2.14) \end{equation} \)
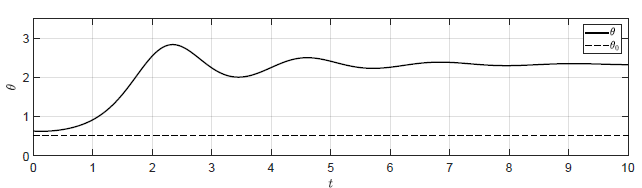
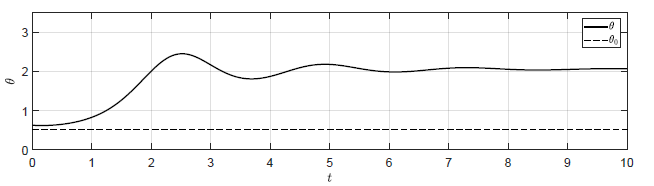
Na Rys. 2.9 przedstawiono trajektorie zmiennej \( \theta(t) \) dla układu regulacji z regulatorem P dla wzmocnień
- \( k_p = 0 \) -- układ bez regulatora (\( M(t) = M_0\))
- \( k_p = -0.125 \)
- \( k_p = -0.25 \)
- \( k_p = -0.5 \)
Przyjęto następujące warunki początkowe \( \theta(t_0) = \frac{\pi}{5} \), \( \omega(t_0) = -0.1 \). Dla wyżej wymienionych wartości wzmocnień układ regulacji nie powraca do punktu pracy. Niemniej jednak, im większe jest wzmocnienie regulatora, tym bliżej założonego punktu pracy znajduje się obiekt. Przetestujmy działanie układu regulacji dla większych wartości wzmocnienia regulatora
- \( k_p = -1 \)
- \( k_p = -2 \)
- \( k_p = -4 \)
- \( k_p = -8 \)
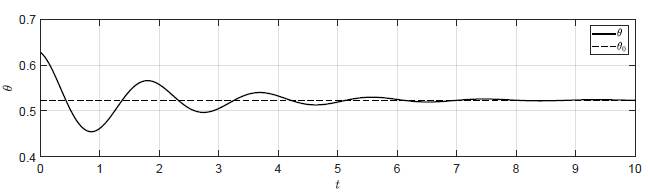
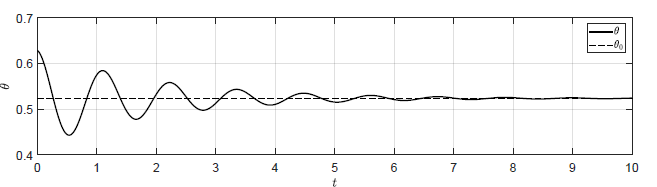
Odpowiednie wykresy zostały przedstawione na Rys. \ref{fig:ch1:wahadloTrajNLinRegP001}. Dla zaproponowanych wzmocnień układ regulacji powraca do pierwotnego punktu pracy. Im większa jest wartość wzmocnienia tym silniej zarysowuje się oscylacyjny charakter przebiegów w układzie. W przypadku wahadła matematycznego wprowadzenie regulatora może skutkować stabilizacją wahadła w założonym punkcie pracy, nawet jeżeli obiekt samoczynnie nie stabilizuje się w tym punkcie.
a) \(k_p = 0 \)
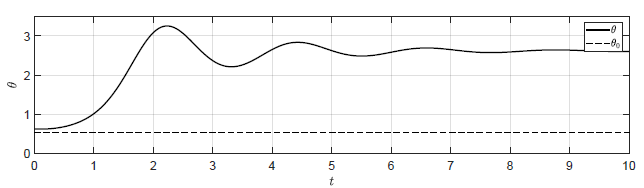
b) \(k_p = -0.125 \)
c) \(k_p = -0.25 \)
d) \(k_p = -0.5 \)
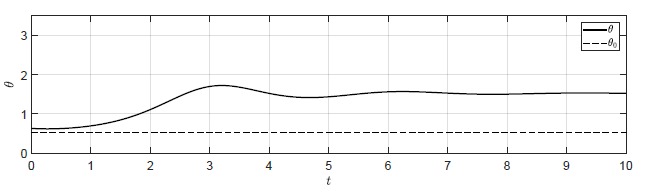
Rysunek 2.9 Trajektorie \( \theta(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
a) \(k_p = -1 \)
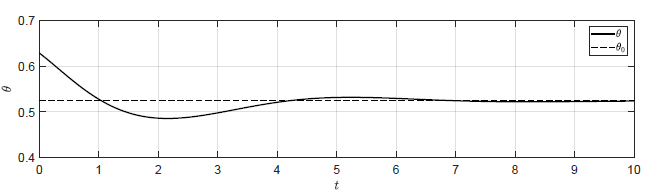
b) \(k_p = -2 \)
c) \(k_p = -4 \)
d) \(k_p = -8 \)
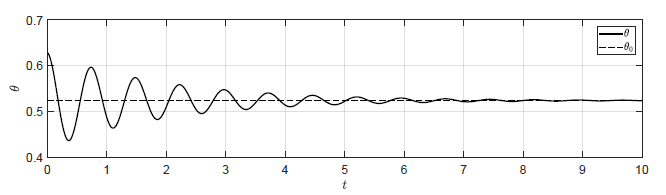
Rysunek 2.10 Trajektorie \( \theta(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Wprowadzenie sprzężenia zwrotnego do układu może skutkować stabilizacją układu w wybranym punkcie pracy bądź jego destabilizacją, poprawą lub pogorszeniem jakości regulacji. Za pomocą symulacji można przetestować działanie układu regulacji tylko dla skończonej liczby wybranych przypadków. Na podstawie badań symulacyjnych nie można zatem sformułować ogólnych wniosków odnośnie zachowania układu. Dla sformułowania ogólnych wniosków potrzebne są odpowiednie rezultaty teoretyczne. Niestety, dla nieliniowych układów regulacji nie istnieją uniwersalne warunki, które pozwoliłyby przewidzieć zachowanie każdego układu.
Z drugiej strony istnieją uniwersalne warunki, pozwalające przewidzieć zachowanie liniowych układów regulacji tzn. układów w których zarówno obiekt regulacji jak i regulator są liniowe. Wiemy ponadto, że obiekt zlinearyzowany stanowi dobre przybliżenie obiektu nieliniowego. Spodziewamy się, że także nieliniowe układy regulacji możemy przybliżać za pomocą zlinearyzowanych układów regulacji. W kolejnej sekcji omówiony zostanie problem linearyzacji układu regulacji oraz zdolności zlinearyzowanego układu regulacji do przybliżania zachowania nieliniowego układu regulacji.
2. Nieliniowe i zlinearyzowane układy regulacji - przykłady
Rozważmy układ regulacji z regulatorem P dla układu trzech zbiorników. Opis nieliniowego układu regulacji składa się z nieliniowych równań stanu obiektu
\( \begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we}(t) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(2.15) \\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(2.16) \\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(2.17) \end{eqnarray} \)
oraz równania regulatora P dla punktu pracy określonego przez \( H_{10} \), \( H_{20} \), \( H_{30} \) oraz \( Q_{we0} \)
\( \begin{equation} Q_{we}(t) = k_p(H_3(t)-H_{30}) + Q_{we0} \qquad(2.18) \end{equation} \)
Jeżeli wprowadzimy równanie regulatora P do równań stanu obiektu, to otrzymamy równania stanu układu regulacji
\( \begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}\left(k_p(H_3(t)-H_{30}) + Q_{we0} \right) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(2.19)\\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(2.20) \\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(2.21) \end{eqnarray} \)
Zauważmy, że w równaniach stanu układu regulacji formalnie nie występuje sygnał sterujący, sterowanie zależy bowiem jedynie od wyjścia układu \( H_3(t) \) i od wartości \( H_{30} \) oraz \( Q_{we0} \), które są stałymi. Opis zlinearyzowanego układu regulacji składa się ze zlinearyzowanych równań stanu obiektu
\( \begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} \tilde{Q}_{we} \qquad(2.22) \\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.23) \\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.24) \end{eqnarray} \)
oraz zlinearyzowanego równania regulatora P. Zapiszmy równanie regulatora P w postaci przyrostowej
\( \begin{equation} \Delta Q_{we}(t) = k_p \Delta H_3(t) \end{equation}\qquad(2.25) \)
Powyższe równanie jest liniowe, zatem możemy natychmiast zapisać równanie zlinearyzowanego regulatora P jako
\( \begin{equation} \tilde{Q}_{we}(t) = k_p \tilde{H}_3(t) \end{equation}\qquad(2.26) \)
Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji
\( \begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} k_p \tilde{H}_3(t) \qquad(2.27)\\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.28) \\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.29) \end{eqnarray} \)
Powyższe równania stanu moglibyśmy także uzyskać poprzez bezpośrednią linearyzację równań stanu układu regulacji (2.19)-(2.21). Podobnie jak to było w przypadku linearyzacji równań obiektu, omówionych w poprzednim module, formułujemy następujący postulat.
Postulujemy, że jeżeli zachodzą następujące warunki
• warunki początkowe dla zmiennych \( \tilde{H}_1 \), \( \tilde{H}_2 \), \( \tilde{H}_3 \) są dokładnie równe przyrostom zmiennych \( H_1 \), \( H_2 \) oraz \( H_3 \) w chwili początkowej
\( \begin{eqnarray} \tilde{H}_1(t_0) &=& \Delta H_1(t_0) = H_1(t_0)-H_{10} \qquad(2.30) \\ \tilde{H}_2(t_0) &=& \Delta H_2(t_0) = H_2(t_0)-H_{20} \qquad(2.31) \\ \tilde{H}_3(t_0) &=& \Delta H_3(t_0) = H_3(t_0)-H_{30} \qquad(2.32) \end{eqnarray} \)
• w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania \( H_1(t) \), \( H_2(t) \), \( H_3(t) \) nieliniowych równań stanu układu regulacji (2.19)-(2.21) pozostają w otoczeniu punktu pracy \( (H_{10}, H_{20}, H_{30}) \) (\( C_{H_1}, C_{H_2}, C_{H_3} \) -- stałe dodatnie)
\( \begin{eqnarray} | H_1(t)-H_{10} | &=& | \Delta H_1(t) | \leq C_{H_1} \qquad(2.33) \\ | H_2(t)-H_{20} | &=& | \Delta H_2(t) | \leq C_{H_2} \qquad(2.34)\\ | H_3(t)-H_{30} | &=& | \Delta H_3(t) | \leq C_{H_3} \qquad(2.35) \end{eqnarray} \)
to rozwiązania \( \tilde{H}_1(t) \), \( \tilde{H}_2(t) \) oraz \( \tilde{H}_3(t) \) liniowych równań stanu (2.27)-(2.29) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzi przybliżony warunek
\( \begin{eqnarray} \tilde{H}_1(t) &\simeq& \Delta H_1(t) \qquad(2.36) \\ \tilde{H}_2(t) &\simeq& \Delta H_2(t) \qquad(2.37)\\ \tilde{H}_3(t) &\simeq& \Delta H_3(t) \qquad(2.38) \end{eqnarray} \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu pracy pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{H_1}, C_{H_2}, C_{H_3} \) w równaniach (2.33)-(2.35).
Aby przetestować zdolność zlinearyzowanego modelu układu regulacji do przybliżania dynamiki układu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt pracy \( H_{10}=0.75 \), \( H_{20}=0.5 \) \( H_{30}=0.25 \) oraz \( Q_{we0} = 0.5 \). Przyjmujemy wzmocnienie regulatora \( k_p =-2 \). Zmienne stanu zlinearyzowanego układu regulacji \( \tilde{H}_1(t) \), \( \tilde{H}_2(t) \) oraz \( \tilde{H}_3(t) \) przybliżają przyrosty zmiennych stanu układu nieliniowego \( \Delta H_1(t) \), \( \Delta H_2(t) \), \( \Delta H_3(t) \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
• \(\Delta H_1(t_0) = 0.2 \), \( \Delta H_2(t_0) = -0.2 \), \( \Delta H_3(t_0) = 0 \)
• \(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
• \(\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)
• \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu układu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu układu nieliniowego. Zgodnie z (2.30)-2.32) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0),\ \tilde{H}_2(t_0) = \Delta H_2(t_0),\ \tilde{H}_3(t_0) = \Delta H_3(t_0) \end{equation}\qquad(2.39) \)
a) \(\Delta H_1(t_0) = 0.2 \), \( \Delta H_2(t_0) = -0.2 \), \( \Delta H_3(t_0) = 0 \)
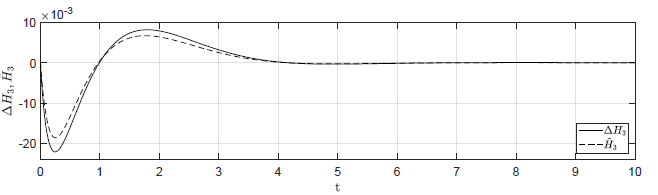
b) \(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
c) \(\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)
d) \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
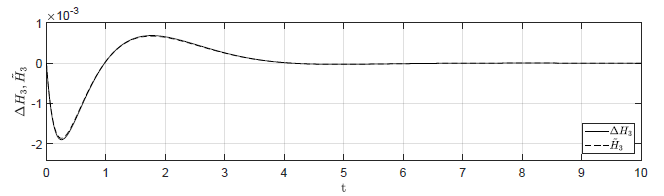
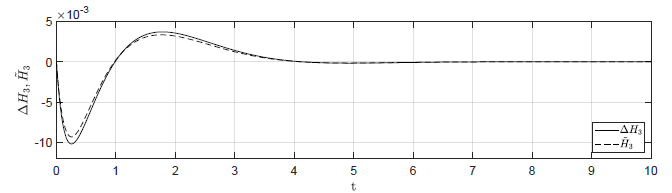
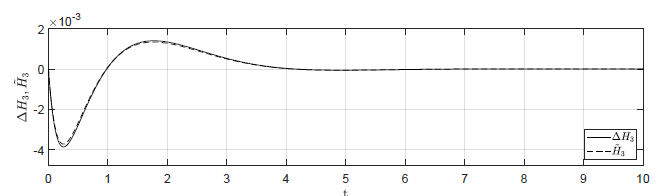
Rysunek 2.11 Porównanie trajektorii \( \Delta H_3(t) \) nieliniowego układu regulacji oraz trajektorii \( \tilde{H}_3(t) \) układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Na Rys.2.11 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \) nieliniowego układu regulacji i zmiennej \( \tilde{H}_3(t) \) układu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna \( \tilde{H}_3(t) \) przybliża przebieg zmiennej \( \Delta H_3(t) \).
W przypadku regulatora nieliniowego o algorytmie
\( \begin{equation} Q_{we}(t) = Q_{we0} \left( e^{k_{nl} (H_3(t)-H_{30})} \right) \qquad(2.40) \end{equation} \)
Równania stanu nieliniowego układu regulacji mają postać
\( \begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} Q_{we0} \left( e^{k_{nl} (H_3(t)-H_{30})} \right) \qquad(2.41)\\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.42)\\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.43) \end{eqnarray} \)
Równanie regulatora nieliniowego zapisane przy pomocy przyrostów zmiennych ma postać
\( \begin{equation} \Delta Q_{we}(t) = Q_{we0} \left( e^{k_{nl} \Delta H_3(t)} -1 \right) = r(\Delta H_3(t)) \qquad(2.44) \end{equation} \)
Musimy teraz obliczyć rozwinięcie równania regulatora w szereg Taylora
\( \begin{equation} \Delta Q_{we}(t) = r(\Delta H_3(t)) \simeq r(\Delta H_{30}) + \dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3} \Delta H_3(t) \end{equation} \qquad(2.45) \)
Wartość przyrostu \( \Delta H_{30} \) w punkcie pracy wynosi zero. Podobnie wartość funkcji regulatora w punkcie pracy \( r(\Delta H_{30}) \) wynosi zero. Pochodna cząstkowa \( \dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3} \) obliczona w punkcie pracy wynosi
\( \begin{equation} \dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3} = Q_{we0} k_{nl} e^{k_{nl} \Delta H_{30}} = Q_{we0} k_{nl} \end{equation}\qquad(2.46) \)
Rozwinięcie równania regulatora w szereg Taylora ma zatem postać
\( \begin{equation} \Delta Q_{we}(t) = Q_{we0} k_{nl} \Delta H_3(t) \end{equation} \qquad(2.47) \)
Zlinearyzowane równanie regulatora ma postać
\( \begin{equation} \tilde{Q}_{we}(t) = Q_{we0} k_{nl} \tilde{H}_3(t) \end{equation} \qquad(2.48) \)
Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji
\( \begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} Q_{we0} k_{nl} \tilde{H}_3(t) \qquad(2.49) \\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.50)\\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.51) \end{eqnarray} \)
a) \(\Delta H_1(t_0) = 0.2 \), \( \Delta H_2(t_0) = -0.2 \), \( \Delta H_3(t_0) = 0 \)
b) \(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
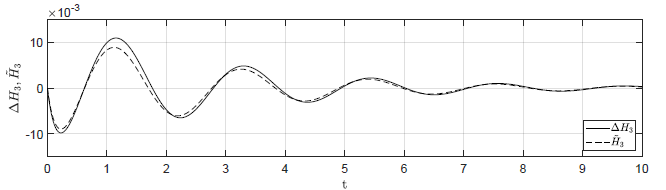
c) \(\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)
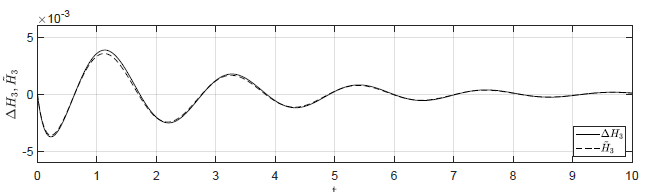
d) \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
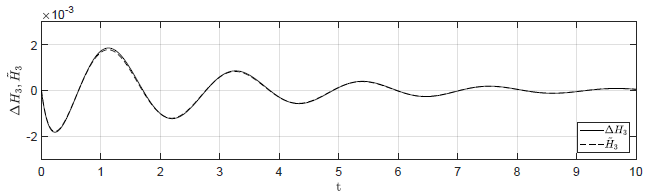
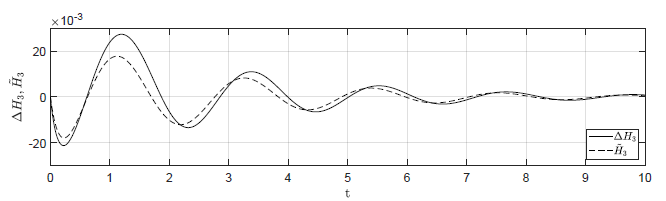
Rysunek 2.12 Porównanie trajektorii \( \Delta H_3(t) \) nieliniowego układu regulacji oraz trajektorii \( \tilde{H}_3(t) \) układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Przyjmujemy analogiczne postulaty, jak w przypadku układu regulacji z regulatorem P. Na Rys. 2.12 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \) nieliniowego układu regulacji i zmiennej \( \tilde{H}_3(t) \) układu zlinearyzowanego dla takich samych warunków początkowych jak w przypadku układu z regulatorem P. Przyjęto parametr regulatora nieliniowego \( k_{nl} = -30 \). Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna \( \tilde{H}_3(t) \) przybliża przebieg zmiennej \( \Delta H_3(t) \).
Rozważmy układ regulacji z regulatorem P dla wahadła. Opis nieliniowego układu regulacji składa się z nieliniowych równań stanu obiektu
\( \begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(2.52) \\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \qquad(2.53) \end{eqnarray} \)
oraz równania regulatora P dla punktu pracy określonego przez \( \theta_{0} \), \( \omega_{0} \) oraz \( M_{0} \)
\( \begin{equation} M(t) = k_p (\theta(t)-\theta_0) + M_0 \qquad(2.54) \end{equation} \)
Jeżeli wprowadzimy równanie regulatora P do równań stanu obiektu, to otrzymamy równania stanu układu regulacji
\( \begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(2.55) \\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} \left( k_p (\theta(t)-\theta_0) + M_0 \right) \qquad(2.56) \end{eqnarray} \)
Opis zlinearyzowanego układu regulacji składa się ze zlinearyzowanych równań stanu obiektu
\( \begin{eqnarray} \dfrac{d\tilde{\theta}}{dt} &=& \tilde{\omega} \qquad(2.57)\\ \dfrac{d\tilde{\omega}}{dt} &=& \dfrac{g}{l}cos\theta_0 \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} + \dfrac{1}{ml^2} \tilde{M} \qquad(2.58) \end{eqnarray} \)
oraz zlinearyzowanego równania regulatora P. Zapiszmy równanie regulatora P w postaci przyrostowej
\( \begin{equation} \Delta M(t) = k_p \Delta \theta(t) \end{equation}\qquad(2.59) \)
Powyższe równanie jest liniowe, zatem możemy natychmiast zapisać równanie zlinearyzowanego regulatora P jako
\( \begin{equation} \tilde{M}(t) = k_p \tilde{\theta}(t) \end{equation}\qquad(2.60) \)
Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji
\( \begin{eqnarray} \dfrac{d\tilde{\theta}}{dt} &=& \tilde{\omega} \qquad(2.61)\\ \dfrac{d\tilde{\omega}}{dt} &=& \dfrac{g}{l}cos\theta_0 \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} + \dfrac{1}{ml^2} k_p \tilde{\theta}(t) = \left( \dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2} k_p \right) \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} \qquad(2.62) \end{eqnarray} \)
Powyższe równania stanu moglibyśmy także uzyskać poprzez bezpośrednią linearyzację równań stanu nieliniowego układu regulacji. Podobnie jak to było w przypadku linearyzacji równań obiektu, omówionych w poprzednim module, formułujemy następujący postulat.
Postulujemy, że jeżeli zachodzą następujące warunki
• warunki początkowe dla zmiennych \( \tilde{\theta} \), \( \tilde{\omega} \) są dokładnie równe przyrostom zmiennych \( \theta \) oraz \( \omega \) w chwili początkowej
\( \begin{eqnarray} \tilde{\theta}(t_0) &= &\Delta \theta(t_0) = \theta(t_0) - \theta_0 \qquad(2.63) \\ \tilde{\omega}(t_0) &= &\Delta \omega(t_0) = \omega(t_0) - \omega_0\qquad(2.64) \end{eqnarray} \)
• w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania \( \theta(t) \), \( \omega(t) \) nieliniowych równań stanu układu regulacji (\ref{eq:ch2:rownanieStanuTheta001})-(\ref{eq:ch2:rownanieStanuOmega001}) pozostają w otoczeniu punktu pracy \( (\theta_0, \omega_0) \) (\( C_{\theta}, C_{\omega} \) -- stałe dodatnie)
\( \begin{eqnarray} | \theta(t)-\theta_0 | &=& | \Delta \theta(t) | \leq C_{\theta} \qquad(2.65) \\ | \omega(t)-\omega_0 | &=& | \Delta \omega(t) | \leq C_{\omega} \qquad(2.66) \end{eqnarray} \)
to rozwiązania \( \tilde{\theta}(t) \) oraz \( \tilde{\omega}(t) \) liniowych równań stanu układu regulacji 2.61)-(2.62) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzą przybliżone warunki
\( \begin{eqnarray} \tilde{\theta}(t) &\simeq& \Delta \theta(t) \qquad(2.67)\\ \tilde{\omega}(t) &\simeq& \Delta \omega(t) \qquad(2.68) \end{eqnarray} \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu pracy pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{\theta}, C_{\omega} \) w równaniach (2.65)-(2.66).
Aby przetestować zdolność zlinearyzowanego modelu układu regulacji do przybliżania dynamiki układu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt pracy odpowiadający \( \theta_0=\dfrac{\pi}{6} \), \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). Przyjmujemy wzmocnienie regulatora równe \( k_p = -1 \). Taka wartość wzmocnienia zapewnia stabilizację układu regulacji do wybranego punktu pracy. Zmienne stanu obiektu zlinearyzowanego \( \tilde{\theta}(t) \), oraz \( \tilde{\omega}(t) \) przybliżają przyrosty zmiennych stanu obiektu nieliniowego \( \Delta \theta \), \( \Delta \omega \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
• \(\Delta \theta(t_0) = \dfrac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
• \(\Delta \theta(t_0) = \dfrac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)
• \(\Delta \theta(t_0) = \dfrac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2 \)
• \(\Delta \theta(t_0) = \dfrac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
a) \(\Delta \theta(t_0) = \dfrac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
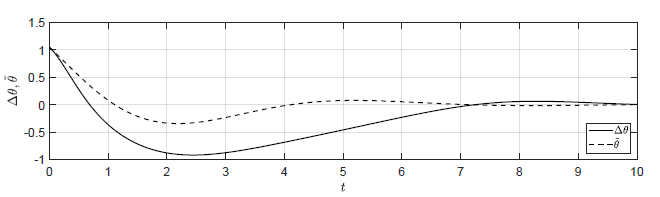
b) \(\Delta \theta(t_0) = \dfrac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)
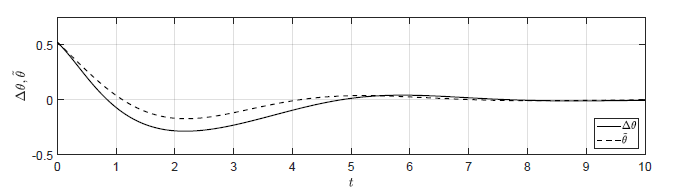
c) \(\Delta \theta(t_0) = \dfrac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2 \)
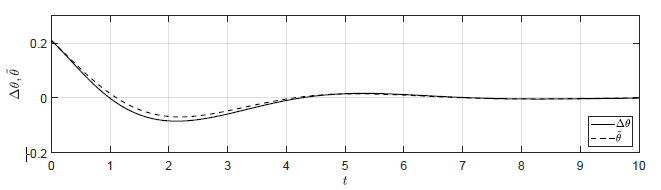
d) \(\Delta \theta(t_0) = \dfrac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
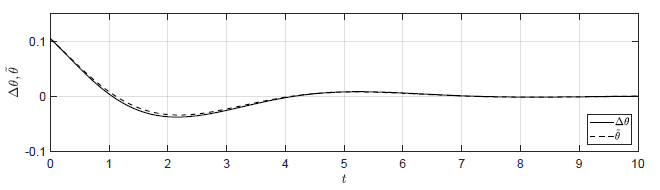
Rysunek 2.13 Porównanie trajektorii \( \Delta \theta(t) \) nieliniowego układu regulacji oraz trajektorii \( \tilde{\theta}(t) \) układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (2.63)-(2.64) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(2.69) \)
Na Rys. 2.13 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) nieliniowego układu regulacji i zmiennej \( \tilde{\theta}(t) \) układu zlinearyzowanego dla wybranych zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna \( \tilde{\theta}(t) \) przybliża przebieg zmiennej \( \Delta \theta(t)\).
3. Nieliniowe i zlinearyzowane układy regulacji - przypadek ogólny
W tej sekcji sformułujemy równania stanu dla nieliniowego i zlinearyzowanego układu regulacji w postaci ogólnej. Rozważmy obiekt opisany równaniami stanu i wyjść
\( \begin{eqnarray} \dfrac{dx(t)}{dt} &=& f(x(t),u(t)) \qquad(2.70)\\ y(t) &=& g(x(t)) \qquad(2.71) \end{eqnarray} \)
i punkt pracy określony za pomocą równań punktu równowagi
\( \begin{eqnarray} 0 &=& f(x_0,u_0) \qquad(2.72) \\ y_0 &=& g(x_0) \qquad(2.73) \end{eqnarray} \)
Załóżmy najpierw, że równanie regulatora ma postać
\( \begin{equation} u(t) = r(y(t)-y_0) + u_0 \qquad(2.74) \end{equation} \)
gdzie \( r(y(t)-y_0) \) jest pewną nieliniową funkcją odchyłki regulacji. Ten przypadek obejmuje np.: algorytm regulatora P, albo algorytm regulatora nieliniowego (2.40). Równanie regulatora można także zapisać za pomocą przyrostów
\( \begin{equation} \Delta u(t) = r(\Delta y(t)) \qquad(2.75) \end{equation} \)
Aby regulacja była możliwa, funkcja regulatora musi dawać zerową korektę sterowania dla zerowej odchyłki regulacji
\( \begin{equation} r(0) = 0 \qquad(2.76) \end{equation} \)
Jeżeli wstawimy równania (2.71) oraz (2.74) do równań stanu obiektu to otrzymujemy równania stanu dla nieliniowego układu regulacji
\( \begin{equation} \dfrac{dx(t)}{dt} = f(x(t),r(g(x(t))-y_0) + u_0) = f_r(x(t)) \qquad(2.77) \end{equation} \)
gdzie \( f_r(x(t)) \) jest nieliniową funkcją stanu dla układu regulacji. Zauważmy, że punkt pracy jest także punktem równowagi nieliniowego układu regulacji, mamy bowiem
\( \begin{eqnarray} f_r(x_0) &=& f(x_0,r(g(x_0)-y_0) + u_0) = f(x_0,r(y_0-y_0) + u_0) \qquad(2.78)\\ &=& f(x_0,r(0) + u_0) = f(x_0, u_0) = 0 \end{eqnarray} \)
Nieliniowy układ regulacji można opisać w taki sam sposób (za pomocą równań stanu) jak każdy obiekt nieliniowy. Zauważmy, że w równaniach stanu układu regulacji formalnie nie występuje sygnał sterujący. Sterowanie generowane przez regulator zależy bowiem jedynie od wyjścia układu \( y(t) \) i od wartości \( y_{0} \) oraz \( u_{0} \), które są stałymi. Obiekty, w których nie występuje sterowanie, nazywamy obiektami autonomicznymi.
Na opis zlinearyzowanego układu regulacji składają się zlinearyzowane równania obiektu
\( \begin{eqnarray} \dfrac{d\tilde{x}(t)}{dt} &=& \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x}(t) + \dfrac{\partial f(x_0,u_0)}{\partial u}\tilde{u}(t) \qquad(2.79) \\ \tilde{y}(t) &=& \dfrac{\partial g(x_0,u_0)}{\partial x}\tilde{x}(t) \qquad(2.80) \end{eqnarray} \)
oraz zlinearyzowane równanie regulatora. Rozwinięcie w szereg Taylora równania regulatora ma postać
\( \begin{equation} \Delta u(t) = r(\Delta y(t)) \simeq r(\Delta y_0) + \dfrac{\partial r(\Delta y_0)}{\partial \Delta y} \Delta y(t) \qquad(2.81) \end{equation} \)
Odchyłka regulacji w punkcie pracy wynosi 0, tzn. \( \Delta y_0 = 0 \). Mamy zatem
\( \begin{equation} \Delta u(t) \simeq \dfrac{\partial r(0)}{\partial \Delta y} \Delta y(t) \qquad(2.82) \end{equation} \)
Zlinearyzowane równanie regulatora ma postać
\( \begin{equation} \tilde{u}(t) = \dfrac{\partial r(0)}{\partial \Delta y} \tilde{y}(t) \qquad(2.83) \end{equation} \)
Jeżeli wstawimy równania (2.80) oraz (2.83) do równań stanu obiektu zlinearyzowanego otrzymamy równania stanu zlinearyzowanego układu regulacji
\( \begin{eqnarray} \dfrac{d\tilde{x}(t)}{dt} &=& \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x}(t) + \dfrac{\partial f(x_0,u_0)}{\partial u} \cdot \dfrac{\partial r(0)}{\partial \Delta y} \cdot \dfrac{\partial g(x_0,u_0)}{\partial x} \tilde{x}(t) \qquad(2.84) \\ &=& \left( \dfrac{\partial f(x_0,u_0)}{\partial x} + \dfrac{\partial f(x_0,u_0)}{\partial u} \cdot \dfrac{\partial r(0)}{\partial \Delta y} \cdot \dfrac{\partial g(x_0,u_0)}{\partial x} \right) \tilde{x}(t)\nonumber \\ &=& \dfrac{\partial f_r(x_0)}{\partial x} \tilde{x}(t) \nonumber \end{eqnarray} \)
Postulujemy, że jeżeli zachodzą następujące warunki
- warunek początkowy dla zlinearyzowanego wektora stanu \(\tilde{x}(t) \) jest równy przyrostowi wektora stanu \(x(t)\) w chwili początkowej
\( \begin{equation} \tilde{x}(t_0) = \Delta x(t_0) \end{equation}\qquad(2.85) \)
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązanie \( x(t) \) równań stanu nieliniowego układu regulacji (2.77) pozostaje w otoczeniu punktu pracy \( x_0 \)
\( \begin{equation} \| x(t)-x_0 \| = \| \Delta x(t) \| \leq C \qquad(2.86) \\ \end{equation} \)
gdzie \( C\) jest pewną stałą dodatniąto rozwiązanie \(\tilde{x}(t)\) równań stanu zlinearyzowanego układu regulacji (2.84) dobrze przybliża przyrost wektora zmiennych stanu układu nieliniowego dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzą przybliżone warunki
\( \begin{eqnarray} \tilde{x}(t) \simeq \Delta x(t) \end{eqnarray}\qquad(2.87) \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu pracy \( x_0 \) pozostaje wektor stanu \( x(t) \) tzn. im mniejsza jest stała \( C \) w (2.86).
Sytuacja jest nieco bardziej skomplikowana jeżeli rozważamy regulator PID. Aby można było zapisać algorytm regulatora PID w formalizmie równań stanu, należy odpowiednio zapisać operacje całkowania i różniczkowania w równaniu regulatora. Odpowiednie rozważania nie są skomplikowane, jednak nie będziemy ich prezentować w niniejszym opracowaniu.