Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Stabilność układów regulacji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 30 grudnia 2025, 11:30 |
1. Pojęcie stabilności
Najistotniejszym wymogiem stawianym układom regulacji jest ich stabilność. Stabilność można rozumieć jako zdolność układu regulacji do powrotu do pierwotnego punktu pracy (względnie pozostawania w jego pobliżu) po początkowym wytrąceniu układu z tego punktu. Tylko układ regulacji posiadający taką własność może skutecznie kompensować wpływ zakłóceń na obiekt. W poprzednich modułach widzieliśmy już przykłady symulacji, gdy układ regulacji przejawiał zachowanie stabilne, jak również niestabilne. W zależności od wartości wzmocnienia \( k_p \), układ regulacji z regulatorem P dla trzech zbiorników mógł zachowywać się stabilnie (Rys. 2.2) lub niestabilnie (Rys. 2.4d). Można również rozważać stabilność samego obiektu, bez dołączonego regulatora. Wyniki symulacji wskazywały, że układ trzech zbiorników bez regulatora zachowuje się stabilnie (Rys. 1.3, 1.12). W przypadku wahadła stabilność obiektu zależała od przyjętego punktu równowagi. Dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{5\pi}{6} \) obiekt przejawiał zachowanie stabilne (Rys. 1.14), podczas, gdy dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{\pi}{6} \) obiekt przejawiał zachowanie niestabilne (Rys. 1.15). Dla punktu pracy \( \theta_0 = \dfrac{\pi}{6} \) możliwe było ustabilizowanie układu regulacji, poprzez zastosowanie regulatora P o odpowiednim wzmocnieniu (Rys.2.10).
Badania symulacyjne pozwalają lepiej
zrozumieć zachowanie obiektów i układów regulacji. Nie można jednak na ich
podstawie formułować ogólnych wniosków dotyczących własności obiektów i układów
regulacji. Do tego celu konieczny jest odpowiedni aparat matematyczny, a w
szczególności precyzyjna definicja stabilności. Stabilność jest pojęciem
trudnym do zdefiniowania. Świadczy o tym fakt, że istnieje wiele
nierównoważnych definicji stabilności. Niemniej, największe znaczenie ma
definicja i cała teoria stabilności zaproponowana przez rosyjskiego matematyka
Aleksandra Lapunowa. W teorii Lapunowa rozważamy obiekty autonomiczne,
tzn. obiekty w których nie występuje w sposób jawny sterowanie. Równania stanu
obiektu autonomicznego mają postać
\( \begin{equation} \dfrac{dx(t)}{dt} = f(x(t)) \qquad(3.1) \end{equation} \)
Zauważmy, że jeżeli w obiekcie ze sterowaniem, sygnał sterujący jest stały \( u(t)=u_0 \), to możemy go również traktować jako obiekt autonomiczny, opisany równaniami stanu
\( \begin{equation} \dfrac{dx(t)}{dt} = f(x(t),u_0) = f_{u_0}(x(t)) \qquad(3.2) \end{equation} \)
gdzie stałe sterowania traktujemy jako parametry (i część definicji) równań stanu. W definicji stabilności Lapunowa mówimy o stabilności pewnego wybranego punktu równowagi obiektu, a nie stabilności całego obiektu. Takie podejście jest jak najbardziej uzasadnione, co widać na przykładzie wahadła. W zależności od wybranego punktu równowagi, obiekt wykazywał zachowanie stabilne lub niestabilne. Punkt równowagi obiektu autonomicznego \( x_0 \), spełnia równanie równowagi
\( \begin{equation} 0 = f(x_0) \qquad(3.3) \end{equation} \)
Definicja stabilności punktu równowagi obiektu autonomicznego, zaproponowana przez Lapunowa jest następująca.
\( \begin{equation} \forall_{r_{\infty}>0}\ \exists_{r_{0}>0}\ \forall_{x(t_0)}\ \left( \| x(t_0)-x_0 \| < r_0 \implies \forall_{t>t_0} \| x(t)-x_0 \| < r_\infty \right) \end{equation} \qquad(3.4) \)
Przytoczona definicja jest dość skomplikowana i dlatego zostanie teraz szczegółowo omówiona. Liczba dodatnia \( r_{\infty} \) oznacza maksymalną odległość na jaką stan obiektu \( x(t) \), może się oddalić od punktu równowagi \( x_0 \). Odległość stanu obiektu od punktu równowagi jest dana przez normę \( \| x(t)-x_0 \| \). Chcemy, aby stan obiektu \( x(t) \), dla każdej chwili późniejszej niż chwila początkowa \( t>t_0 \), znajdował się w odległości mniejszej niż \( r_\infty \) od punktu równowagi \( x_0 \). Poprzednie zdanie można zapisać za pomocą wyrażenia
\( \begin{equation} \forall_{t>t_0} \| x(t)-x_0 \| < r_\infty \qquad(3.5) \end{equation} \)
Aby osiągnąć wyżej opisany efekt wybieramy inną wartość dodatnią \( r_{0} \), która określa maksymalną odległość pomiędzy stanem początkowym obiektu \( x(t_0) \) a punktem równowagi \( x_0 \). Odległość ta jest dana wzorem \( \| x(t_0)-x_0 \| \) i ma być mniejsza niż \( r_{0} \). Poprzednie zdanie może zostać zapisane jako
\( \begin{equation} \| x(t_0)-x_0 \| < r_0 \qquad(3.6) \end{equation} \)
Dla stabilnego punktu równowagi, spodziewamy się, że jeżeli wystartujemy z dowolnie wybranego punktu początkowego (\( \forall_{x(t_0)}\ \)) który znajduje się odpowiednio blisko punktu równowagi (warunek (3.6) to dla każdej późniejszej chwili trajektoria stanu pozostanie blisko punktu równowagi (3.5). Poprzednie zdanie można zapisać jako
\( \begin{equation} \forall_{x(t_0)}\ \| x(t_0)-x_0 \| < r_0 \implies \forall_{t>t_0} \| x(t)-x_0 \| < r_\infty \qquad(3.7) \end{equation} \)
Pozostaje do rozpatrzenia następująca kwestia. Jeżeli zmniejszymy wartość \( r_\infty \), to czy uda się znaleźć jeszcze mniejsze \( r_0 \), tak że spełniony będzie warunek (3.7). Innymi słowy, czy to że stan początkowy \( x(t_0) \) będzie znajdował się jeszcze bliżej punktu równowagi (mniejsze \( r_0 \)) wystarczy, aby już zawsze \( x(t) \) pozostawał bliżej punktu równowagi niż \( r_\infty \) (dla mniejszego \( r_\infty \)). Jeżeli tak faktycznie jest to definicja Lapunowa jest spełniona i możemy powiedzieć, że punkt równowagi obiektu jest stabilny.
Reasumując, jeżeli punkt równowagi
obiektu \( x_0 \) jest stabilny, to możemy dowolnie ograniczyć maksymalną
odległość \( r_\infty \) na jaką stan \( x(t) \) oddali się od tego punktu
równowagi. Aby to osiągnąć, wystarczy aby stan początkowy \( x(t_0) \) znajdował się bliżej punktu równowagi niż \( r_0 \). Niezależnie od tego jak
małe jest \( r_\infty \), zawsze możemy dobrać jeszcze mniejsze \( r_0 \),
takie że opisany warunek jest spełniony.
Własność stabilności jest dobrze
widoczna na Rys. 1.12,
1.14,
2.11 oraz 2.13.
Im bliżej punktu równowagi znajduje się stan początkowy obiektu, tym bliżej
punktu równowagi znajduje się cała trajektoria stanu obiektu (patrz zakres osi
rzędnych na wykresach).
Zauważmy jeszcze, że definicja Lapunowa stabilności nie gwarantuje stabilności globalnej. Nie mamy gwarancji, że dla dużych \( r_{\infty} \) wartość \( r_0 \) też będzie duża. Wręcz przeciwnie, jeżeli dla pewnego \( r_{\infty} \), mamy \( r_0 \) dla którego warunek stabilności jest spełniony, to warunek stabilności jest także spełniony automatycznie dla każdego większego \( r_{\infty} \), z tym samym \( r_0 \). Nie ma jednak pewności, że wraz ze wzrostem \( r_{\infty} \), \( r_0 \) także będzie rosnąć.
Rozważmy jeszcze pojęcie niestabilności obiektu. Odpowiednia definicja niestabilności jest następująca
\( \begin{equation} \exists_{r_{\infty}>0}\ \forall_{r_{0}>0}\ \left(\exists_{x(t_0)}\ \| x(t_0)-x_0 \| < r_0 \right) \wedge \left( \exists_{t>t_0} \| x(t)-x_0 \| \geq r_\infty \right) \end{equation}\qquad(3.8) \)
Przeanalizujmy warunek niestabilności punktu równowagi. Tym razem istnieje pewna wartość graniczna \( r_{\infty} \), taka że nie można ograniczyć maksymalnej odległości \( x(t) \) od punktu równowagi poniżej \( r_{\infty} \). Niezależnie od tego jak blisko punktu równowagi byśmy startowali (\( \forall_{r_{0}>0} \)), zawsze znajdzie się pewien stan początkowy (\( \exists_{x(t_0)} \)), który
- znajduje się odpowiednio blisko punktu równowagi -- \( \| x(t_0)-x_0 \| < r_0 \)
- w pewnej chwili \( t>t_0 \) trajektoria stanu \( x(t) \) mimo wszystko oddala się od punktu równowagi na odległość co najmniej \( r_\infty \)
\( \begin{equation} \exists_{t>t_0} \| x(t)-x_0 \| \geq r_\infty \end{equation}\qquad(3.9) \)
Własność niestabilności jest dobrze widoczna na Rys. 1.15}. Niezależnie od tego, jak blisko pierwotnego punktu równowagi wahadła startujemy, ono po pewnym czasie oddali się już na stałe od tego punktu.
Zauważmy, że definicja stabilności
Lapunowa mówi jedynie o tym, że stan \( x(t) \) znajduje się zawsze w pobliżu
punktu równowagi. W definicji nie pojawia się żaden warunek, mówiący od tym że
stan \( x(t) \) powraca do pierwotnego punktu równowagi (zapewne po nieskończenie
długim czasie). Jeżeli jednak stan powraca do pierwotnego punktu równowagi to
mówimy, że punkt równowagi obiektu jest stabilny asymptotycznie
\( \begin{equation} \exists_{r_{0}>0}\ \forall_{x(t_0)}\ \left( \| x(t_0)-x_0 \| < r_0 \implies \lim_{t\rightarrow \infty} x(t) = x_0\right) \end{equation}\qquad(3.10) \)
Powyższy warunek mówi o tym, że dla wszystkich punktów początkowych (\( \forall_{x(t_0)} \)), które znajdują się bliżej punktu równowagi niż pewna ustalona wartość \( r_0 \), trajektorie stanu \( x(t) \), rozpoczynające się w tych punktach początkowych, wrócą do pierwotnego punktu równowagi (po nieskończonym czasie). Różnicę pomiędzy stabilnością asymptotyczną a stabilnością nieasymptotyczną można łatwo zobrazować na przykładzie wahadła matematycznego. Jeżeli w wahadle nie ma tarcia, to wahadło będzie wykonywać stałe oscylacje wokół stabilnego położenia równowagi. Jeżeli chcemy ograniczyć amplitudę oscylacji wahadła, wystarczy, że wystartujemy bliżej położenia kątowego równowagi \( \theta_0 \) oraz ograniczymy wartość początkowej prędkości kątowej. Jeżeli w wahadle pojawia się tarcie, to energia wahadła jest stopniowo rozpraszana. W miarę tego procesu wahadło zbliża się do pierwotnego punktu równowagi i osiąga go po (teoretycznie) nieskończonym czasie. W układach regulacji stałowartościowej standardowo żądamy, żeby wybrany punkt pracy był stabilny asymptotycznie.
Ścisła definicja matematyczna
stabilności, pozwala uporządkować intuicyjne rozumienie tego pojęcia. Niemniej
definicja sama w sobie nie pozwala w efektywny sposób stwierdzić, czy punkt
dany punkt równowagi obiektu jest stabilny. Jest tak, ponieważ w ogólnym
przypadku nie jesteśmy w stanie obliczyć rozwiązania równania stanu \( x(t) \)
w postaci jawnej. Aby umożliwić efektywne sprawdzenie stabilności punktów
równowagi obiektu, Lapunow zaproponował dwie metody.
Pierwsza metoda Lapunowa opiera
się na koncepcji funkcji Lapunowa. Funkcja Lapunowa dla obiektu
nieliniowego jest to pewna funkcja stanu obiektu oznaczana jako \( V(x(t)) \). \(
V(x(t)) \) wykazuje pewne podobieństwo do funkcji energii całkowitej układu
mechanicznego. Układ mechaniczny wraca do punktu równowagi w miarę jak
energia układu jest rozpraszana. Podobnie, jeżeli wartość funkcji Lapunowa \(
V(x(t)) \) maleje do zera to, stan układu \( x(t) \( coraz bardziej zbliża się
do punktu równowagi \( x_0 \), dla którego spełniony jest warunek \( V(x_0) = 0
\). Pierwsza metoda Lapunowa ma postać warunku wystarczającego, tzn. jeżeli
jesteśmy w stanie skonstruować funkcję Lapunowa, to możemy wnioskować o
stabilności punktu równowagi obiektu. Problemem pozostaje postać funkcji \(
V(x(t)) \). Dla pewnych szczególnych typów obiektów istnieją gotowe postacie
funkcji Lapunowa. Nie istnieje jednak uniwersalna funkcja Lapunowa, odpowiednia
dla każdego obiektu.
Dla naszych rozważań większe znaczenie
ma druga metoda Lapunowa, która opiera się na koncepcji zlinearyzowanych
równań stanu. Zlinearyzowane równania stanu dla obiektu autonomicznego
(3.1) w punkcie równowagi \( x_0 \) mają postać
\( \begin{equation} \dfrac{d\tilde{x}(t)}{dt} = \dfrac{\partial f(x_0)}{\partial x}\tilde{x}(t) \qquad(3.11) \end{equation} \)
Punkt równowagi obiektu zlinearyzowanego \( \tilde{x}_0 = 0 \) odpowiada oryginalnemu punktowi równowagi \( x_0 \). Druga metoda Lapunowa opiera się na następującym twierdzeniu
W twierdzeniu uwzględnione są przypadki
stabilności asymptotycznej i niestabilności, nie jest natomiast uwzględniony
przypadek stabilności nieasymptotycznej. Jeżeli punkt równowagi obiektu
zlinearyzowanego \( \tilde{x}_0 = 0 \) jest stabilny nieasymptotycznie, to
punkt równowagi obiektu nieliniowego \( x_0 \) może być stabilny
asymptotycznie, stabilny nieasymptotycznie lub niestabilny i kryterium nie
pozwala na rozstrzygnięcie kwestii stabilności. Nie jest to jednak duży
problem, gdyż w naszych rozważaniach zawsze będziemy żądać stabilności asymptotycznej.
Nierozwiązanym problemem pozostaje
stwierdzenie stabilności asymptotycznej lub niestabilności dla punktu
równowagi \( \tilde{x}_0 = 0 \) obiektu opisanego równaniami zlinearyzowanymi.
Jak już dyskutowaliśmy w opracowaniu, analiza obiektów liniowych jest dużo
prostsza niż analiza obiektów nieliniowych. Tak jest też w przypadku badania
stabilności. Kwestia badania stabilności obiektów liniowych zostanie
szczegółowo omówiona w następnej sekcji
2. Stabilność obiektów liniowych
Rozważamy równania stanu dla liniowego obiektu autonomicznego (bez sterowań)
\( \begin{eqnarray} \dfrac{d\tilde{x}(t)}{dt} = A\tilde{x}(t) \qquad(3.12) \end{eqnarray} \)
Obiekt ten może w szczególności być wynikiem linearyzacji równań obiektu nieliniowego. Mamy wtedy
\( \begin{equation} A= \dfrac{\partial f(x_0)}{\partial x} \end{equation}\qquad(3.13) \)
Interesuje nas punkt równowagi obiektu liniowego \( \tilde{x}_0 = 0 \). Chcemy stwierdzić, jak będzie się zachowywał obiekt liniowy, po wytrąceniu go z punktu równowagi. Oznaczmy warunek początkowy jako \( \tilde{x}(t_0) \).
Okazuje się, że rozwiązanie \( \tilde{x}(t) \) równań stanu (3.12) z warunkiem początkowym \( \tilde{x}(t_0) \) jest sumą składników postaci
- \( C_1\cdot e^{\alpha \cdot t} \)
- \( C_1\cdot t^{l}\cdot e^{\alpha\cdot t} \)
- \( C_1\cdot e^{\alpha \cdot t}\left(C_2\cdot cos(\beta\cdot t) + C_3\cdot sin(\beta\cdot t) \right) \)
- \( C_1\cdot t^{l}\cdot e^{\alpha \cdot t}\left(C_2\cdot cos(\beta\cdot t) + C_3\cdot sin(\beta\cdot t) \right) \)
gdzie \( C_1,C_2,C_3,\alpha,\beta,l \) są pewnymi stałymi. W każdym z tych składników dominującą rolę odgrywa wyrażenie \( e^{\alpha\cdot t} \). Jeżeli bowiem \( \alpha<0 \) to dla \( t\rightarrow \infty \) dany składnik będzie dążył do zera, jeżeli zaś \( \alpha>0 \) to dla \( t\rightarrow \infty \) dany składnik będzie rósł (lub malał) w sposób nieograniczony. Aby układ liniowy był stabilny asymptotycznie potrzeba zatem, aby w każdym ze składników rozwiązania równań stanu \( \tilde{x}(t) \) wykładnik funkcji eksponencjalnej był ujemny. Odwrotnie, jeżeli w przynajmniej w jednym ze składników rozwiązania równań stanu \( \tilde{x}(t) \) wykładnik funkcji eksponencjalnej jest dodatni, to rozwiązanie będzie rosło w sposób nieograniczony (tzn. układ będzie niestabilny).
O stabilności obiektu liniowego decydują zatem wykładniki funkcji eksponencjalnej w rozwiązaniu równań stanu. Okazuje się, że wartości tych wykładników zależą jedynie od macierzy \( A \), a nie zależą od warunków początkowych \( x(t_0) \). Aby znaleźć wartości tych wykładników należy znaleźć pierwiastki \( s_1,\cdots,s_j,\cdots,s_n \) następującego wielomianu nazywanego wielomianem charakterystycznym}obiektu liniowego
\( \begin{equation} W(s) = det(sI-A) = s^n+ a_{n-1}s^{n-1}+ \cdots + a_{j}s^{j} + \cdots + a_1s+a_0 \end{equation} \qquad(3.14) \)
gdzie \( a_n = 1, a_{n-1},\cdots, a_{j},\cdots, a_1, a_0 \) to współczynniki wielomianu (współczynnik przy \( s^n \) jest zawsze równy \( 1 \)), natomiast \( i \) jest macierzą jednostkową rozmiaru \( n\times n \). Nie należy mylić współczynników wielomianu charakterystycznego z współczynnikami macierzy \( A = (a_{ij}) \). To, że wyrażenie \( det(I-sA) \) jest wielomianem zmiennej \( s \), może nie być oczywiste na pierwszy rzut oka. Tak jednak jest, co będziemy mogli zobaczyć rozwiązując odpowiednie przykłady. Stopień wielomianu charakterystycznego (a zatem także liczba jego pierwiastków) jest równy liczbie zmiennych stanu \( n \). Pierwiastki wielomianu charakterystycznego są liczbami zespolonymi postaci
\( \begin{equation} s_j = \alpha_j + i\beta_j \end{equation}\qquad(3.15) \)
gdzie \( i \) to jednostka urojona. Jeżeli pierwiastek \( s_j \) jest liczbą rzeczywistą (\( \beta_j = 0 \)), to w rozwiązaniu równań liniowych pojawia się składnik \( C_1\cdot e^{\alpha_j \cdot t} \). Jeżeli pierwiastek \( s_j \) jest liczbą zespoloną i \( \beta_j \neq 0 \), to w rozwiązaniu równań liniowych pojawia się składnik \( C_1\cdot e^{\alpha_j \cdot t}\left(C_2\cdot cos(\beta_j\cdot t) + C_3\cdot sin(\beta_j\cdot t) \right) \). Jeżeli występują pierwiastki wielokrotne, to dodatkowo w tych wyrazach pojawia się czynnik \( t^{l} \), gdzie \( l+1 \) to krotność danego pierwiastka. W każdym przypadku wykładniki funkcji eksponencjalnych ze składników rozwiązania równań stanu \( \tilde{x}(t) \) są równe częściom rzeczywistym pierwiastków wielomianu charakterystycznego \( Re(s_1),\cdots,Re(s_j),\cdots,Re(s_n) \).
Reasumując, jeżeli wszystkie pierwiastki
wielomianu charakterystycznego \( s_1,\cdots,s_j,\cdots,s_n \) spełniają
warunek
\( Re(s_1) < 0,\cdots,Re(s_j) < 0,\cdots,Re(s_n) < 0 \qquad(3.16) \)
to układ liniowy jest stabilny asymptotycznie. Jeżeli jednak dla pewnego pierwiastka wielomianu charakterystycznego \( s_j \) zachodzi warunek
\( \begin{equation} Re(s_j)>0 \qquad(3.17) \end{equation} \)
to układ liniowy jest niestabilny. Przypadek \( Re(s_i)=0 \) nie jest jednoznaczny i wymaga dodatkowej analizy. Nie jest to jednak problem, gdyż w naszych rozważaniach skupiamy się na stabilności asymptotycznej.
Teraz, kiedy znamy już warunek na
stabilność asymptotyczną (oraz niestabilność) dla punktu równowagi \(
\tilde{x}_0 = 0 \) obiektu liniowego, pojawia się kolejny problem. Wyznaczanie
pierwiastków wielomianu jest możliwe tylko dla wielomianów stopnia niższego niż
5. Dla wielomianów stopnia 5 i wyższych nie istnieją ogólne wzory pozwalające
obliczać wartości pierwiastków wielomianu.
Aby poradzić sobie z tym problemem
zauważmy, że tak naprawdę nie potrzebujemy znać dokładnych wartości wszystkich
pierwiastków wielomianu. Aby stwierdzić stabilność asymptotyczną, musimy
wiedzieć czy zachodzi warunek (3.16). Okazuje się, że
istnieje kryterium pozwalające stwierdzić, czy warunek
(3.16) jest spełniony, bez konieczności obliczania
dokładnych wartości pierwiastków wielomianu. To kryterium nosi nazwę kryterium Hurwitza. Istotną rolę w kryterium Hurwitza odgrywa macierz
Hurwitza. Jest ona tworzona z pomocą współczynników wielomianu
charakterystycznego i ma następującą postać
\( \begin{equation} H = \left( \begin{array}{ccccccccc} a_{n-1} & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} & 1 & \cdots & 0 & 0 & 0 & 0 \\ a_{n-5} & a_{n-4} & a_{n-3} & a_{n-2} & \cdots & 0 & 0 & 0 & 0 \\ a_{n-7} & a_{n-6} & a_{n-5} & a_{n-4} & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & a_3 & a_4 & a_5 & a_6 \\ 0 & 0 & 0 & 0 & \cdots & a_1 & a_2 & a_3 & a_4 \\ 0 & 0 & 0 & 0 & \cdots & 0 & a_0 & a_1 & a_2 \\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & a_0 \\ \end{array} \right) \end{equation}\qquad(3.18) \)
Sposób tworzenia macierzy Hurwitza jest następujący. Macierz Hurwitza to macierz kwadratowa rozmiaru \( n\times n \). Na przekątnej macierzy Hurwitza umieszczamy kolejno współczynniki \( a_{n-1},\cdots, a_{j},\cdots, a_1, a_0 \). Następnie uzupełniamy wartości w kolejnych wierszach wg następującej reguły. Jeżeli na przekątnej mamy współczynnik \( a_j \), to na prawo od niego wypisujemy kolejno współczynniki wielomianu przy coraz wyższych potęgach \( s \): \( a_{j+1}, a_{j+2}, a_{j+3},\cdots \). Na lewo od przekątnej wypisujemy współczynniki wielomianu przy coraz niższych potęgach \( s \): \( \cdots, a_{j-3}, a_{j-2}, a_{j-1} \). Jeżeli nie mamy już współczynników do wpisania na lewo lub prawo od przekątnej, to wiersz uzupełniamy zerami.
Aby sformułować kryterium Hurwitza,
musimy jeszcze wprowadzić pojęcie minora głównego macierzy
Hurwitza. \( j \)-tym minorem głównym macierzy nazwiemy wyznacznik macierzy
powstałej z pierwszych \( j \) wierszy i pierwszych \( j \) kolumn macierzy
wyjściowej. Kolejne minory główne macierzy Hurwitza mają postać
\( \begin{equation} \left| a_{n-1} \right|,\ \left| \begin{array}{cc} a_{n-1} & 1 \\ a_{n-3} & a_{n-2} \end{array} \right|,\ \left| \begin{array}{ccc} a_{n-1} & 1 & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} \\ a_{n-5} & a_{n-4} & a_{n-3} \end{array} \right|,\ \left| \begin{array}{cccc} a_{n-1} & 1 & 0 & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} & 1 \\ a_{n-5} & a_{n-4} & a_{n-3} & a_{n-2} \\ a_{n-7} & a_{n-6} & a_{n-5} & a_{n-4} \end{array} \right| \end{equation}\qquad(3.19) \)
Ostatnie minory główne macierzy Hurwitza mają postać
\( \begin{equation} \left| \begin{array}{ccccccc} a_{n-1} & 1 & 0 & \cdots & 0 & 0 & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} & \cdots & 0 & 0 & 0 \\ a_{n-5} & a_{n-4} & a_{n-3} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_3 & a_4 & a_5 \\ 0 & 0 & 0 & \cdots & a_1 & a_2 & a_3 \\ 0 & 0 & 0 & \cdots & 0 & a_0 & a_1 \\ \end{array} \right|,\ \left| \begin{array}{cccccccc} a_{n-1} & 1 & 0 & \cdots & 0 & 0 & 0 & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} & \cdots & 0 & 0 & 0 & 0 \\ a_{n-5} & a_{n-4} & a_{n-3} & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_3 & a_4 & a_5 & a_6 \\ 0 & 0 & 0 & \cdots & a_1 & a_2 & a_3 & a_4 \\ 0 & 0 & 0 & \cdots & 0 & a_0 & a_1 & a_2 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & a_0 \\ \end{array} \right| \end{equation}\qquad(3.20) \)
Jesteśmy przygotowani na sformułowanie kryterium Hurwitza.
\( \begin{equation} W(s) = det(sI-A) = s^n+ a_{n-1}s^{n-1}+ \cdots + a_{j}s^{j} + \cdots + a_1s+a_0 \end{equation}\qquad(3.21) \)
spełnia następujące warunki
- wszystkie współczynniki wielomianu charakterystycznego są dodatnie
\( \begin{equation} a_{n-1}>0, \cdots , a_{j}>0, \cdots, a_1>0, a_0>0 \end{equation}\qquad(3.22) \)
- wszystkie minory główne macierzy Hurwitza są dodatnie
\( \begin{eqnarray} &&\left| a_{n-1} \right|>0,\ \left| \begin{array}{cc} a_{n-1} & 1 \\ a_{n-3} & a_{n-2} \end{array} \right|>0,\ \cdots, \left| \begin{array}{cccccc} a_{n-1} & 1 & \cdots & 0 & 0 & 0 \\ a_{n-3} & a_{n-2} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & a_{j+2} & a_{j+3} & a_{j+4} \\ 0 & 0 & \cdots & a_{j} & a_{j+1} & a_{j+2} \\ 0 & 0 & \cdots & a_{j-2} & a_{j-1} & a_j \\ \end{array} \right| >0 , \cdots, \nonumber \\ && det(H) = \left| \begin{array}{cccccc} a_{n-1} & 1 & \cdots & 0 & 0 & 0 \\ a_{n-3} & a_{n-2} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & a_2 & a_3 & a_4 \\ 0 & 0 & \cdots & a_0 & a_1 & a_2 \\ 0 & 0 & \cdots & 0 & 0 & a_0 \\ \end{array} \right| > 0 \end{eqnarray}\qquad(3.23) \)
to wszystkie pierwiastki wielomianu charakterystycznego \( s_1,\cdots,s_j,\cdots,s_n \) spełniają warunek
\( Re(s_1) < 0,\cdots,Re(s_j) < 0,\cdots,Re(s_n) < 0 \qquad(3.24) \)
co oznacza, że punkt równowagi obiektu liniowego \( \tilde{x}_0 = 0 \) jest stabilny asymptotycznie. Jeżeli w którymś z warunków którakolwiek ostra nierówność ma znak przeciwny, to dla pewnego pierwiastka wielomianu charakterystycznego \( s_j \) zachodzi warunek
\( \begin{equation} Re(s_j)>0 \qquad(3.25) \end{equation} \)
co oznacza, że punkt równowagi obiektu liniowego \( \tilde{x}_0 = 0 \) jest niestabilny.
Przypadki w których w kryterium Hurwitza
zamiast nierówności ostrych pojawia się równość, są potencjalnie związane ze
stabilnością nieasymptotyczną. Dla nas jednak najistotniejsze jest określenie
warunków na stabilność asymptotyczną obiektu (względnie jego
niestabilność).
3. Badanie stabilności - przykłady
Aby zbadać stabilność punktu równowagi \( x_0 \) nieliniowego obiektu autonomicznego stosujemy następujący schemat
- określamy zlinearyzowane równania stanu w punkcie równowagi \( x_0 \)
- obliczamy współczynniki wielomianu charakterystycznego
- stosujemy kryterium Hurwitza, aby sprawdzić czy spełnione są warunki (3.24) oraz (3.25)
Zastosujmy powyższy schemat do badania stabilności punktów równowagi autonomicznych, nieliniowych obiektów i układów regulacji.
Równania stanu dla układu trzech
zbiorników ze stałym sterowaniem \( Q_{we}(t) = Q_{we0} \) (obiekt
autonomiczny) mają postać
\( \begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we0} - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.26)\\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(3.27)\\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.28) \end{eqnarray} \)
Równania punktu równowagi mają postać
\(\begin{eqnarray} H_{20} &=& 2H_{30} \qquad(3.29) \\ H_{10} &=& 3H_{30} \qquad(3.30)\\ Q_{we0} &=& \alpha\sqrt{H_{30}} \qquad(3.31) \end{eqnarray}\)
Sterowanie w obiekcie zlinearyzowanym jest równe zero
\(\begin{equation} \tilde{Q}_{we} = Q_we(t) - Q_{we0} = Q_{we0} - Q_{we0} = 0 \qquad(3.32)\end{equation} \)
Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \qquad(3.33)\end{equation} \)
Z równań punktu równowagi wynika, że
\(\begin{eqnarray}H_{10}-H_{20} &=& 3H_{30}-2H_{30} = H_{30} \qquad(3.34) \\H_{20}-H_{30} &=& 2H_{30}-H_{30} = H_{30} \qquad(3.35)\end{eqnarray}\)
Wprowadźmy te zależności do zlinearyzowanych równań stanu
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{30}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{30}}} & \dfrac{-\alpha}{2A\sqrt{H_{30}}} + \dfrac{-\alpha}{2A\sqrt{H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.36)\)
Wprowadźmy następujące oznaczenie
\(\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} >0\qquad(3.37)\end{equation} \)
Zlinearyzowane równania stanu mogą zostać zapisane jako
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.38)\)
Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego
\(\begin{equation}A = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\end{equation} \qquad(3.39)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 & s & 0 \\0 & 0 & s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \\&=& det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) \nonumber\end{eqnarray}\qquad(3.40)\)
Wyznacznik macierzy rozmiaru \( 3\times 3 \) może być obliczony z następującego wzoru
\(\begin{eqnarray}det \left(\begin{array}{ccc}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right) &=& a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\&& - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{eqnarray}\qquad(3.41)\)
Mamy zatem
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + 0\cdot (-2a)(-a) \\&& - 0 \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a) \\&=& (s^2+6as+8a^2)(s+2a) - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \nonumber \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 \\&=& s^3+8as^2+14a^2s+4a^3\end{eqnarray}\qquad(3.42)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3\end{equation} \qquad(3.43)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar \( 3\times 3 \) i postać
\(\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 & a_1 & a_2 \\0 & 0 & a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 & 14a^2 & 8a \\0 & 0 & 4a^3\end{array}\right)\end{equation} \qquad(3.44)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1 \\4a^3 & 14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 & 14a^2 & 8a \\0 & 0 & 4a^3\end{array}\right|\end{equation} \qquad(3.45)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu równowagi układu trzech zbiorników
- ponieważ \( a>0 \) to wszystkie współczynniki wielomianu charakterystycznego są dodatnie
\(\begin{equation}a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3>0 \end{equation} \qquad(3.46)\)
- minory główne macierzy Hurwitza wynoszą
\(\begin{eqnarray} |8a| &=& 8a >0 \qquad(3.47)\\ \left| \begin{array}{cc} 8a & 1 \\ 4a^3 & 14a^2 \end{array} \right| &=& 8a\cdot 14a^2 - 1\cdot 4a^3 = 112a^3 - 4a^3 = 108a^3 > 0 \qquad(3.48)\\ \left| \begin{array}{ccc} 8a & 1 & 0 \\ 4a^3 & 14a^2 & 8a \\ 0 & 0 & 4a^3 \end{array} \right| &=& 8a \cdot 14a^2 \cdot 4a^3 + 1\cdot 8a \cdot 0 + 0\cdot 4a^3 \cdot 0 \\ && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0 - 1\cdot 4a^3\cdot 4a^3 \nonumber \\ &=& 448a^6 -16a^6 = 432a^6 >0 \nonumber \end{eqnarray}\qquad(3.49)\)
Mamy zatem spełniony warunek dla pierwiastków wielomianu charakterystycznego trzeciego stopnia
\(\begin{equation} Re(s_1) < 0,\ Re(s_2) < 0,\ Re(s_3) < 0 \end{equation} \qquad(3.50)\)
Punkt równowagi obiektu zlinearyzowanego \( \tilde{H}_{10} = 0 \), \( \tilde{H}_{20} = 0 \), \( \tilde{H}_{20} = 0 \) jest stabilny asymptotycznie. Z drugiej metody Lapunowa mamy zatem, że punkt równowagi obiektu nieliniowego \( H_{10} \), \( H_{20} \), \( H_{30} \) ze stałym sterowaniem \( Q_{we0} \) jest stabilny asymptotycznie. Obliczenia były prowadzone dla dowolnego punktu równowagi w układzie trzech zbiorników. Wynika z tego, że wszystkie punkty równowagi tego układu są stabilne asymptotycznie. Ten wynik jest w zgodzie z wynikami symulacji (Rys. 1.3, 1.12).
Zbadajmy teraz stabilność punktu pracy układu regulacji trzech zbiorników z regulatorem P. Równania stanu dla układu regulacji mają postać
\(\begin{eqnarray}\dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}\left(k_p(H_3(t)-H_{30}) + Q_{we0} \right) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.51) \\\dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(3.52) \\\dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.53)\end{eqnarray}\)
Rozważamy punkt pracy określony przez \( H_{10} \), \( H_{20} \), \( H_{30} \) orz \( Q_{we0} \). Zlinearyzowane równania stanu (2.22)-(2.24) dla układu regulacji zapisane w postaci macierzowej mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{k_p}{A} \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.54)\)
Podobnie jak to było w przypadku zlinearyzowanych równań stanu dla obiektu korzystamy z (3.34)-(3.35) i wprowadzamy zmienną \( a \) (3.37). Zlinearyzowane równania stanu dla układu regulacji mają teraz postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.55)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}
\right) \right) \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 & s & 0 \\0 & 0 & s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \qquad(3.56) \\&=& det \left(\begin{array}{ccc}s+2a & -2a & -\dfrac{k_p}{A} \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) r \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + \left(-\dfrac{k_p}{A}\right) (-2a)(-a) \\&& - \left(-\dfrac{k_p}{A}\right) \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a) \\&=& (s^2+6as+8a^2)(s+2a) - 2a^2\dfrac{k_p}{A} - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 - 2a^2\dfrac{k_p}{A} \\&=& s^3+8as^2+14a^2s+4a^3 - 2a^2\dfrac{k_p}{A}\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}\end{equation} \qquad(3.57)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego
\(\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 & a_1 & a_2 \\0 & 0 & a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right)\end{equation} \qquad(3.58)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right|\end{equation}\qquad(3.59) \)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu pracy układu regulacji
- dla uzyskania stabilności asymptotycznej wszystkie współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}>0\end{equation} \qquad(3.60)\)
- dla uzyskania stabilności asymptotycznej wszystkie minory główne macierzy Hurwitza muszą być dodatnie
\( \begin{eqnarray} |8a| &=& 8a >0 \qquad(3.61)\\ \left| \begin{array}{cc} 8a & 1 \\ 4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 \end{array} \right| &=& 8a\cdot 14a^2 - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \\ &=& 112a^3 - 4a^3 + 2a^2\dfrac{k_p}{A} \\ &=& 108a^3 + 2a^2\dfrac{k_p}{A} > 0 \qquad(3.62)\\ \left| \begin{array}{ccc} 8a & 1 & 0 \\ 4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\ 0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A} \end{array} \right| &=& 8a \cdot 14a^2 \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \qquad(3.63)\\ && + 1\cdot 8a \cdot 0 + 0\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot 0 \\ && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0 \\ && - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \\ &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left( 8a \cdot 14a^2 - \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \right) \\ &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right) >0 \end{eqnarray}\)
Warunki na stabilność asymptotyczną punktu pracy układu regulacji, zawierające \( k_p \), są następujące
\(\begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A}&>&0 \qquad(3.64) \\108a^3 + 2a^2\dfrac{k_p}{A} &>& 0 \qquad(3.65) \\\left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right) &>& 0 \qquad(3.66)\end{eqnarray}\)
Pozostałe warunki są spełnione ponieważ \( a>0 \). Zauważmy jeszcze, że jeżeli warunki (3.64) i (3.65) są spełnione, to automatycznie warunek (3.66) też jest spełniony. Obliczmy teraz zakres wartości \( k_p \) regulatora, dla których punkt pracy układu regulacji jest stabilny asymptotycznie. Z (3.64) mamy
\( \begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A} &>& 0\qquad\\ 4a^3 >2a^2\dfrac{k_p}{A} /\div 2a^2 \qquad\\2a>\dfrac{k_p}{A} /\cdot A \qquad\\2aA &>& k_p \qquad \\k_p & < & 2aA \qquad(3.67)\end{eqnarray} \)
Z (3.65) mamy
\(\begin{eqnarray}108a^3 + 2a^2\dfrac{k_p}{A} &>& 0\\ 2a^2\dfrac{k_p}{A} &>& -108a^3 \qquad /\div 2a^2 r\\\dfrac{k_p}{A} &>& -54a \qquad /\cdot A r\\k_p &>& -54aA \qquad(3.68)\end{eqnarray} \)
Ostatecznie, punkt pracy zlinearyzowanego, a także nieliniowego układu regulacji jest stabilny asymptotycznie, jeżeli wzmocnienie regulatora proporcjonalnego mieści się w zakresie
\(\begin{equation}-54aA < k_p < 2aA\qquad(3.69)\end{equation} \)
Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy następujące wartości parametrów obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt pracy obiektu \( Q_{we0} = 0.5\), \(H_{10}=0.75 \), \( H_{20}=0.5 \), \( H_{30}=0.25 \). Stała \( a \) wynosi
\(\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} = \dfrac{1}{4\cdot 0.5 \sqrt{0.25}} =1\end{equation} \qquad(3.70)\)
Zakres wzmocnień regulatora P, dla których punkt pracy układu regulacji pozostaje stabilny asymptotycznie (3.69) wynosi
\(\begin{equation}-27 < k_p < 1\end{equation} \qquad(3.71)\)
Przeanalizujmy uzyskany przedział \( k_p \) zapewniający stabilność asymptotyczną punktu pracy. Większa część przedziału zmienności \( k_p \) leży po stronie wartości ujemnych. Jest zgodne z intuicją, ponieważ dla \( k_p < 0 \) korekta sygnału sterującego ma kierunek, który powoduje zmniejszenie odchyłki regulacji. Ten rezultat pozostaje również w zgodzie z wynikami symulacji (Rys. 2.2-2.5). Sprawdźmy jeszcze, czy \( k_p=-27 \) wyznacza granicę stabilności układu. Na podstawie Rys. 2.5 mamy, że dla \( k_p = -24 \) oscylacje sygnału \( H_3 \) są gasnące (stabilność asymptotyczna), natomiast dla dla \( k_p = -32 \) oscylacje są narastające (niestabilność). Dla wartości granicznej \( k_p=-27 \) powinniśmy uzyskać stałe oscylacje. Odpowiedź układu regulacji na niezerowe warunki początkowe \( H_1(t_0) =0.76 \), \( H_2(t_0) =0.51 \), \( H_3(t_0)=0.26 \) dla wzmocnienia regulatora \( k_p=-27 \) została przedstawiona na Rys. 3.1. Zarówno sygnał wyjściowy \( H_{3}(t) \) jak i sygnał sterujący \(Q_{we}(t) \) charakteryzują się przebiegiem oscylacyjnym o stałej amplitudzie oscylacji. Warto zauważyć, że na granicy stabilności oscylacje sygnału sterującego i wyjściowego są przesunięte w fazie o 180 stopni.
Dla obiektu bez regulatora (\( k_p=0 \)) punkt pracy również jest stabilny asymptotycznie i jest to zgodne z wynikami symulacji (Rys. 2.2(a)). Okazuje się jednak, że także dla niewielkich wartości dodatnich \( k_p \) punkt pracy układu regulacji pozostaje stabilny asymptotycznie. Może się to wydawać niezgodne z intuicją, ponieważ dla \( k_p > 0 \) korekta sygnału sterującego ma kierunek, który powoduje zwiększanie odchyłki regulacji. Układ regulacji traci stabilność dopiero dla odpowiednio dużego dodatniego \( k_p \). Zachowanie układu regulacji dla kilku dodatnich wartości \( k_p \) została przedstawiona na Rys. 3.2.
a) Trajektoria \(H_3(t)\)
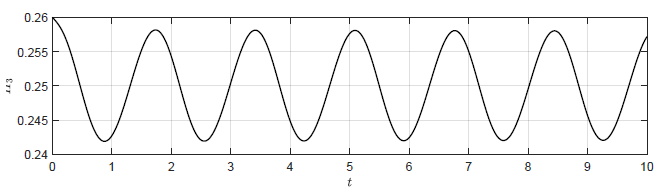
b) Trajektoria \(Q_{we}(t) \)
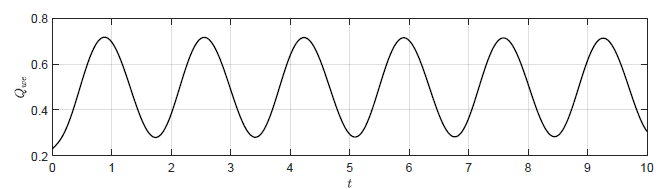
Rysunek 3.1 Trajektorie \( H_3(t) \) orz \( Q_{we} \) w układzie regulacji dla \(
k_p = -27 \).
Dodatnia wartość \( k_p \) powoduje
początkowo wydłużenie czasu regulacji w porównaniu do układu bez regulatora (\(
k_p=0 \)). Dla wartości granicznej \( k_p=1 \) wartość \( H_3(t) \) ustala się
po pewnym czasie, jednak nigdy nie powraca do wartości z punktu pracy \( H_{30}
= 0.25 \). Dla \( k_p>1 \) trajektoria \( h_3(t) \) stopniowo oddala się od
punktu pracy, co świadczy o tym, że punkt pracy układu regulacji jest
niestabilny.
Zajmijmy się teraz badaniem stabilności
punktów równowagi wahadła. Równania stanu dla wahadła ze stałym
sterowaniem \( M(t) = M_{0} \) (obiekt autonomiczny) mają postać
\(\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.72) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M_0 \qquad(3.73)\end{eqnarray}\)
Równania punktu równowagi mają postać
\(\begin{eqnarray}\omega_0 &=& 0 \qquad(3.74)\\M_0 &=& -mglsin\theta_0 \qquad(3.75)\end{eqnarray}\)
Sterowanie w obiekcie zlinearyzowanym jest równe zero
\(\begin{equation}\tilde{M} = M(t) - M_0 = M_0 - M_0 = 0\end{equation} \qquad(3.76)\)
a) \(k_p = 0 \)
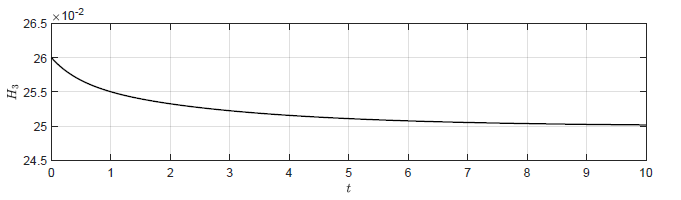
b) \(k_p = 0.5 \)
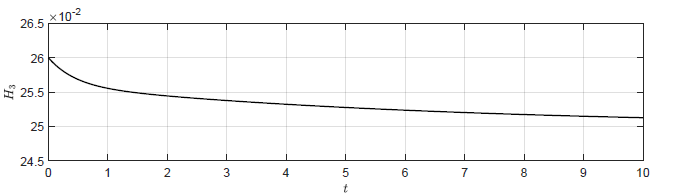
c) \(k_p = 1 \)

d) \(k_p = 1.5 \)
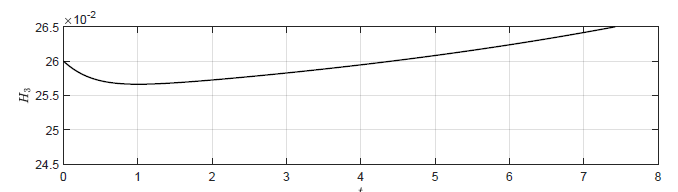
Rysunek 3.2 Trajektorie \( H_3(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) \end{equation} \qquad(3.77)\)
Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego
\(\begin{equation}A = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\end{equation}\qquad(3.78) \)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 & 1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 & s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right) \right) \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 & s+\dfrac{D}{ml^2}\end{array}\right) \qquad(3.79)\end{eqnarray}\)
Wyznacznik macierzy rozmiaru \( 2\times 2 \) może być obliczony z następującego wzoru
\(\begin{equation}det \left(\begin{array}{ccc}a_{11} & a_{12} \\a_{21} & a_{22} \end{array}\right) = a_{11}a_{22} - a_{12}a_{21} \end{equation} \qquad(3.80)\)
Mamy zatem
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 & s+\dfrac{D}{ml^2}\end{array}\right) \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 \right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0 \nonumber \end{eqnarray}\qquad(3.81)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0\end{equation} \qquad(3.82)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar \( 2\times 2 \) i postać
\(\begin{equation}H = \left(\begin{array}{cc}a_1 & a_2 \\0 & a_0\end{array}\right) = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0\end{array}\right)\end{equation} \qquad(3.83)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0\end{array}\right|\end{equation} \qquad(3.84)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu równowagi wahadła
- współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 >0 \end{equation} \qquad(3.85)\)
- minory główne macierzy Hurwitza muszą być dodatnie
\(\begin{eqnarray} \left|\dfrac{D}{ml^2}\right| &=& \dfrac{D}{ml^2} >0 \qquad(3.86)\\ \left| \begin{array}{cc} \dfrac{D}{ml^2} & 1 \\ 0 & -\dfrac{g}{l}cos\theta_0 \end{array} \right| &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0\right) - 1\cdot 0 = -\dfrac{D}{ml^2}\cdot \dfrac{g}{l}cos\theta_0 > 0 \qquad(3.87)\end{eqnarray}\)
Parametry obiektu \( m,g,l,D \) są dodatnie. O spełnieniu nierówności w kryterium Hurwitza decyduje zatem znak wyrażenia \( cos\theta_0 \). Jeżeli \( cos\theta_0 > 0\) (punkt równowagi powyżej położenia horyzontalnego wahadła), to nie wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest niestabilny. Jeżeli \( cos\theta_0 < 0\) (punkt równowagi poniżej położenia horyzontalnego wahadła), to wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest stabilny asymptotycznie. Te wnioski pozostają w zgodzie z wynikami symulacji. Dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{5\pi}{6} \) obiekt przejawiał zachowanie stabilne (Rys. 1.14), podczas, gdy dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{\pi}{6} \) obiekt przejawiał zachowanie niestabilne (Rys. 1.15).
Zbadajmy teraz stabilność punktu pracy
układu regulacji wahadła z regulatorem P. Równania stanu dla układu regulacji
mają postać
\(\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.88) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} \left( k_p (\theta(t)-\theta_0) + M_0 \right) \qquad(3.89)\end{eqnarray}\)
Rozważamy punkt pracy określony przez \( \theta_0 \), \( \omega_0 \) orz \( M_0 \). Zlinearyzowane równania stanu (2.61)-(2.62) dla układu regulacji zapisane w postaci macierzowej mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) \end{equation} \qquad(3.90)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 & 1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 & s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right) \right) \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p & s+\dfrac{D}{ml^2}\end{array}\right) \nonumber \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p \nonumber \end{eqnarray}\qquad(3.91)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{equation} \qquad(3.92)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego
\(\begin{equation}H = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right)\end{equation} \qquad(3.93)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right|\end{equation} \qquad(3.94)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu pracy układu regulacji położenia wahadła
- współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p >0 \qquad(3.95)\end{equation} \)
- minory główne macierzy Hurwitza muszą być dodatnie
\( \begin{eqnarray} \left|\dfrac{D}{ml^2}\right| &=& \dfrac{D}{ml^2} >0 \qquad(3.96)\\ \left| \begin{array}{cc} \dfrac{D}{ml^2} & 1 \\ 0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p \end{array} \right| &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) - 1\cdot 0 \\ &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) > 0 \qquad(3.97) \end{eqnarray}\)
Nierówności w kryterium Hurwitza będą spełnione jeżeli będzie spełniony warunek
\(\begin{eqnarray}-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p&>&0 \\-\dfrac{g}{l}cos\theta_0 &>&\dfrac{1}{ml^2}k_p \qquad /\cdot ml^2 \\-mglcos\theta_0 &>&k_p \\ k_p & < & -mglcos\theta_0 \end{eqnarray}\)
Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy parametry modelu obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt pracy układu regulacji \( \theta_0=\dfrac{\pi}{6} \), \( \omega_0=0 \), \( M_{0} = -0.5 \). Aby punkt pracy układu regulacji był stabilny \( k_p \) musi spełniać warunek
\(\begin{equation} k_p < -mglcos\theta_0 = -0.1\cdot 10 \cdot 1 \cdot \dfrac{\sqrt{3}}{2} = -\dfrac{\sqrt{3}}{2} \simeq -0.87\end{equation} \qquad(3.98)\)
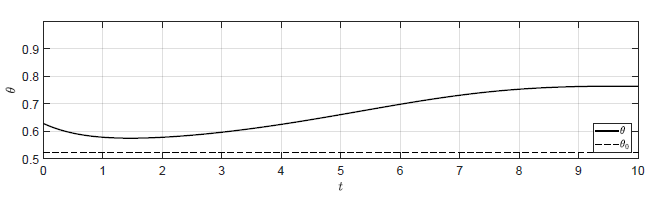
a) \(k_p = 0.75 \)

b) \(k_p = -0.8 \)
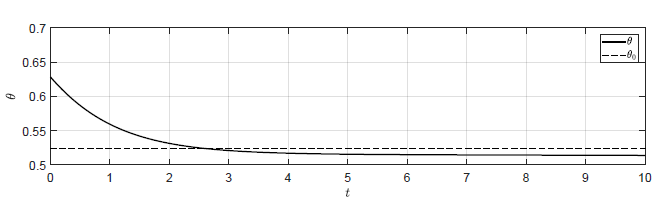
c) \(k_p = -\dfrac{\sqrt{3}}{2} \)
d) \(k_p = -0.9 \)
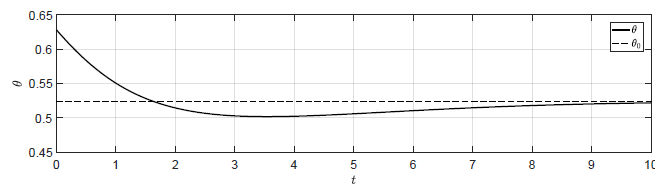
Rysunek 3.3 Trajektorie \( \theta(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Ten warunek pozostaje w zgodzie z
wynikami symulacji (Rys. 2.9 i 2.10).
Sprawdźmy jeszcze zachowanie układu dla \( k_p \) bliskich wartości granicznej.
Odpowiedź układu regulacji na warunki początkowe \( \theta(t_0) =
\dfrac{\pi}{5} \), \( \omega(t_0) = -0.1 \) dla różnych wartości \( k_p \)
została przedstawiona na Rys. 3.3. Dla \(k_p
\geq -\dfrac{\sqrt{3}}{2} \) trajektoria \( \theta(t) \) nie powraca do \(
\theta_0 \). Jednak już dla wartości \( k_p \) nieco mniejszej od wartości
granicznej trajektoria \( \theta(t) \) powraca do \( \theta_0 \).