Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Zaawansowane układy regulacji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 6 marca 2026, 02:42 |
1. Układ regulacji z regulatorem stanu
Rozważmy opis obiektu liniowego za pomocą równań stanu i wyjść
\(\begin{eqnarray}\dfrac{dx(t)}{dt} &=& Ax(t)+Bu(t) \qquad(4.1)\\y(t) &=& Cx(t) \qquad(4.2)\end{eqnarray}\)
oraz punkt pracy obiektu liniowego \( (x_0,u_0) = (0,0) \). Jeżeli obiekt ma tylko jeden sygnał sterujący oraz jedno wyjście, to algorytm regulatora P dla tego obiektu ma postać
\(\begin{equation}u(t) = k_p y(t)\end{equation}\qquad(4.3)\)\qquad(4.3)
W przypadku, gdy obiekt ma wiele sygnałów sterujących i wiele wyjść, to algorytm regulatora proporcjonalnego dla sterowania \( u_i(t),\ i=1,\cdots,m \) może zostać zapisany jako
\(\begin{equation}u_i(t) = k_{pi1} y_1(t) +\cdots + k_{pij} y_j(t)\cdots + k_{pip} y_p(t)\end{equation}\qquad(4.4)\)
Sterowanie \( u_i(t) \) jest sumą składników proporcjonalnych do wartości wyjść ze współczynnikami proporcjonalności \( k_{pi1},\cdots, k_{pip} \). Regulator stanu stanowi rozwinięcie powyższego algorytmu, z tym że zamiast wykorzystywać sygnały wyjściowe, wykorzystujemy stany obiektu. Sterowanie \( u_i(t) \) jest zatem dane wzorem
\(\begin{equation}u_i(t) = k_{i1} x_1(t) +\cdots + k_{ij} x_j(t)\cdots + k_{in} x_n(t)\end{equation}\qquad(4.5)\)
gdzie \( k_{i1},\cdots, k_{in} \) to stałe współczynniki wzmocnienia regulatora stanu. Wypiszmy równania algorytmu regulatora stanu dla wszystkich sterowań \( u_1(t),\cdots, u_m(t) \)
\(\begin{eqnarray}u_1(t) &=& k_{11} x_1(t) +\cdots + k_{1j} x_j(t)\cdots + k_{1n} x_n(t) \qquad(4.6) \\&\vdots& \\ u_i(t) &=& k_{i1} x_1(t) +\cdots + k_{ij} x_j(t)\cdots + k_{in} x_n(t) \qquad(4.7) \\&\vdots& \\ u_m(t) &=& k_{m1} x_1(t) +\cdots + k_{mj} x_j(t)\cdots + k_{mn} x_n(t) \qquad(4.8) \end{eqnarray}\)
gdzie \( k_{11} \),..., \( k_{mn} \) są stałymi współczynnikami. Równania regulatora stanu można zapisać w postaci macierzowej
\(\begin{equation}\left(\begin{array}{c}u_1(t) \\ \vdots\\ u_i(t) \\ \vdots\\ u_m(t)\end{array}\right) = \left(\begin{array}{ccccc}k_{11} & \cdots & k_{1j} & \cdots & k_{1n} \\\vdots & & \vdots & & \vdots \\k_{i1} & \cdots & k_{ij} & \cdots & k_{in} \\\vdots & & \vdots & & \vdots \\k_{m1} & \cdots & k_{mj} & \cdots & k_{mn} \end{array}\right)\left(\begin{array}{c}x_1(t)\\ \vdots\\ x_j(t) \\ \vdots\\ x_n(t)\end{array}\right) \end{equation}\qquad(4.9)\)
Standardowo stosuje się następujące oznaczenie macierzy wzmocnień regulatora
\(\begin{equation}K = \left(\begin{array}{ccccc}k_{11} & \cdots & k_{1j} & \cdots & k_{1n} \\\vdots & & \vdots & & \vdots \\k_{i1} & \cdots & k_{ij} & \cdots & k_{in} \\\vdots & & \vdots & & \vdots \\k_{m1} & \cdots & k_{mj} & \cdots & k_{mn} \end{array}\right)\end{equation}\qquad(4.10)\)
Równanie regulatora stanu można wtedy zapisać w postaci wektorowej
\(\begin{equation}u(t) = Kx(t)\end{equation}\qquad(4.11)\)
Wprowadźmy równanie regulatora stanu do równań stanu obiektu liniowego
\(\begin{equation}\dfrac{dx(t)}{dt} = Ax(t)+Bu(t) = Ax(t)+BKx(t) = (A+BK)x(t) \end{equation}\qquad(4.12)\)
Wprowadźmy oznaczenie
\(\begin{equation}A_K = A+BK\end{equation}\qquad(4.13)\)
Równanie stanu układu regulacji ma postać
\(\begin{equation}\dfrac{dx(t)}{dt} = A_K x(t) \end{equation}\qquad(4.14)\)
Układ regulacji z regulatorem stanu jest zatem układem autonomicznym. Stabilność układu regulacji z regulatorem stanu zależy od własności macierzy \( A_K = A+BK \) i jej wielomianu charakterystycznego. Ponieważ możemy dobrać wartości wzmocnień regulatora stanu w macierzy \( K \), możemy zatem wpływać na postać macierzy \( A_K \). Okazuje się, że pod pewnymi warunkami, możemy w znacznym stopniu zmieniać własności układu regulacji, poprzez odpowiedni dobór macierzy \( K \). Zagadnienie to zostanie teraz szczegółowo omówione.
Istotną rolę dla układu regulacji z regulatorem stanu odgrywa warunek sterowalności obiektu, definiowany w następujący sposób
\(\begin{equation}\dfrac{dx(t)}{dt} = Ax(t)+Bu(t) \end{equation}\qquad(4.15)\)
spełnia warunek sterowalności, jeżeli dla dowolnego stanu początkowego \( x(t_0) \), dowolnej chwili końcowej \( t_1>t_0 \) i dowolnego stanu końcowego \( x(t_1) \) istnieje sterowanie \( u(t) \), które przeprowadza układ od stanu początkowego do stanu końcowego.Jeżeli obiekt jest sterowalny, to za pomocą odpowiedniego sterowania \( u(t) \) możemy go przeprowadzić z dowolnego stanu do dowolnego innego stanu w dowolnym czasie. Istnieją odpowiednie kryteria do badania sterowalności układu, które można znaleźć w literaturze specjalistycznej. W naszych przykładach nie będziemy szczegółowo analizować kwestii sterowalności obiektu, jednak w tym miejscu konieczne było podanie odpowiedniej definicji. Wróćmy jednak do problemu regulatora stanu. Wielomian charakterystyczny dla układu regulacji z regulatorem stanu ma postać
\(\begin{equation}W_K(s) = det(sI-A_K) = det(sI-A-BK)\end{equation}\qquad(4.16)\)
Okazuje się, że jeżeli tylko obiekt liniowy jest sterowalny, to można tak dobrać macierz \( K \), żeby wielomian charakterystyczny \( w_K(s) \) miał z góry zadane pierwiastki \( s_1,\cdots,s_j,\cdots,s_n \). Pierwiastki wielomianu charakterystycznego \( w_K(s) \) mają kluczowe znaczenie dla stabilności układu regulacji, a także wpływają na innego jego własności. %Poprzez odpowiedni dobór macierzy \( K \) możemy zatem w znacznym stopniu wpływać na własności układu regulacji z regulatorem stanu.
Do omówienia pozostaje kwestia zastosowania regulatora stanu do obiektów nieliniowych. Rozważmy obiekt opisany nieliniowymi równaniami stanu
\(\begin{equation}\dfrac{dx(t)}{dt} = f(x(t),u(t)) \label{eq:ch4:eqStan}\end{equation}\qquad(4.17)\)
i punkt pracy określony za pomocą równań
\(\begin{equation}0 = f(x_0,u_0)\qquad(4.18)\end{equation}\)
Zlinearyzowane równania stanu mają postać
\(\begin{equation}\dfrac{d\tilde{x}(t)}{dt} = \dfrac{\partial f(x_0,u_0)}{\partial x}\tilde{x}(t) + d\frac{\partial f(x_0,u_0)}{\partial u}\tilde{u}(t) \qquad(4.19) \end{equation}\)
Regulator stanu dla punktu równowagi \( (\tilde{x}_0,\tilde{u}_0) = (0,0) \) zlinearyzowanego układu regulacji ma postać
\(\begin{equation}\tilde{u}(t) = K\tilde{x}(t)\end{equation}\qquad(4.20)\)
Ponieważ zmienne obiektu zlinearyzowanego przybliżają przyrosty zmiennych obiektu nieliniowego
\(\begin{eqnarray}\tilde{u}(t) &\simeq& \Delta u(t) \qquad(4.21)\\\tilde{x}(t) &\simeq& \Delta x(t)\end{eqnarray}\qquad(4.22)\)
To algorytm regulatora stanu dla obiektu nieliniowego ma postać
\(\begin{equation}\Delta u(t) = K\Delta x(t)\end{equation}\qquad(4.23)\)
lub
\(\begin{equation}u(t) = K(x(t)-x_0) + u_0\qquad(4.24)\end{equation}\)
2. Przykłady syntezy układów regulacji z regulatorem stanu
Synteza układu regulacji z regulatorem stanu dla obiektu nieliniowego składa się z następujących kroków
- linearyzacja równań stanu obiektu w wybranym punkcie pracy
- dobór macierzy \( K \) dla obiektu zlinearyzowanego
- zastosowanie regulatora stanu (4.24) z \( K \) obliczonym w poprzednim punkcie do obiektu nieliniowego
Jeżeli chodzi o punkt 2. schematu to istnieją uniwersalne wzory, pozwalające obliczyć \( K \) w przypadku ogólnym. Dla naszych prostych przykładów, będziemy jednak obliczać macierz \( K \) bezpośrednio, bez stosowania ogólnych wzorów. Przejdźmy teraz do przykładów syntezy układu regulacji z regulatorem stanu.
Równania stanu dla układu trzech zbiorników mają postać
\(\begin{eqnarray}\dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we}(t) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(4.25)\\\dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(4.26) \\\dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(4.27)\end{eqnarray}\)
Równania stanu zlinearyzowane w punkcie równowagi \( (H_{10},H_{20},H_{30},Q_{we0}) \) mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right)+\left(\begin{array}{c}\dfrac{1}{A} \\ 0 \\ 0\end{array}\right)\left( \tilde{Q}_{we} \right)\end{equation}\qquad(4.28)\)
gdzie stała \( a \) została zdefiniowana w (3.37). Macierze układu zlinearyzowanego mają postać
\(\begin{equation}A = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right),\ B = \left(\begin{array}{c}\dfrac{1}{A} \\ 0 \\ 0\end{array}\right)\end{equation}\qquad(4.29)\)
Macierz regulatora stanu ma w naszym przykładzie postać
\(\begin{equation}K = \left(\begin{array}{ccc}k_1 & k_2 & k_3\end{array}\right)\end{equation}\qquad(4.30)\)
Algorytm regulatora stanu w postaci macierzowej jest opisany równaniem
\(\begin{equation}\left( \tilde{Q}_{we} \right) = \left(\begin{array}{ccc}k_1 & k_2 & k_3\end{array}\right) \left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right)\end{equation}\qquad(4.31)\)
co jest równoważne
\(\begin{equation}\tilde{Q}_{we} = k_1 \tilde{H}_1 + k_2 \tilde{H}_2 + k_3 \tilde{H}_3\end{equation}\qquad(4.32)\)
Równania stanu dla zlinearyzowanego układu regulacji z regulatorem stanu mają zatem postać
\(\begin{eqnarray}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ d\dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) &=& \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right)+\left(\begin{array}{c}\dfrac{1}{A} \\ 0 \\ 0\end{array}\right)\left(\begin{array}{ccc}k_1 & k_2 & k_3\end{array}\right) \left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \qquad(4.33)\\&=& \left( \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) +\left(\begin{array}{c}\dfrac{1}{A} \\ 0 \\ 0\end{array}\right)\left(\begin{array}{ccc}k_1 & k_2 & k_3\end{array}\right) \right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right)\qquad(4.34)\end{eqnarray}\)
Macierz \( A_K \) układu regulacji wynosi
\(\begin{eqnarray}A_K = A+BK &=& \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) +\left(\begin{array}{c}\dfrac{1}{A} \\ 0 \\ 0\end{array}\right)\left(\begin{array}{ccc}k_1 & k_2 & k_3\end{array}\right) \qquad(4.35)\\&=& \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) +\left(\begin{array}{ccc}\dfrac{1}{A}k_1 & \dfrac{1}{A}k_2 & \dfrac{1}{A}k_3 \\ 0 & 0 & 0 \\0 & 0 & 0 \end{array}\right) \qquad(4.36)\\&=& \left(\begin{array}{ccc}-2a + \dfrac{1}{A}k_1 & 2a+\dfrac{1}{A}k_2 & \dfrac{1}{A}k_3 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \qquad(4.37)\end{eqnarray}\)
Wielomian charakterystyczny układu regulacji z regulatorem stanu wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A_K) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) - \left(\begin{array}{ccc}-2a + \dfrac{1}{A}k_1 & 2a+\dfrac{1}{A}k_2 & \dfrac{1}{A}k_3 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \qquad(4.38) \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 & s & 0 \\0 & 0 & s\end{array}\right) - \left(\begin{array}{ccc}-2a + \dfrac{1}{A}k_1 & 2a+\dfrac{1}{A}k_2 & \dfrac{1}{A}k_3 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \\&=& det \left(\begin{array}{ccc}s+ 2a - \dfrac{1}{A}k_1 & -2a-\dfrac{1}{A}k_2 & -\dfrac{1}{A}k_3 \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) \nonumber \\&=& \left(s+ 2a - \dfrac{1}{A}k_1\right)(s+4a)(s+2a) \nonumber \\&&+ \left(-2a-\dfrac{1}{A}k_2\right)(-2a)\cdot 0 + \left(-\dfrac{1}{A}k_3\right) (-2a)(-a) \nonumber \\&& - \left(-\dfrac{1}{A}k_3\right) \cdot (s+4a) \cdot 0 - \left(s+ 2a - \dfrac{1}{A}k_1 \right)(-2a)(-a) \\&&-\left(-2a-\dfrac{1}{A}k_2\right)(-2a)(s+2a) \nonumber \\&=& \left(s+ 2a \right)(s+4a)(s+2a) - \dfrac{1}{A}k_1(s+4a)(s+2a) -\dfrac{2a^2}{A}k_3 \nonumber \\&& - 2a^2\left(s+ 2a \right) + \dfrac{2a^2}{A}k_1 - 4a^2(s+2a) -\dfrac{1}{A}k_2\cdot 2a (s+2a) \nonumber \\&=& (s^2+6as+8a^2)(s+2a) - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \nonumber \\&& - (s^2+6as+8a^2)\dfrac{1}{A}k_1 -\dfrac{2a^2}{A}k_3 + \dfrac{2a^2}{A}k_1 -(2as+4a^2)\dfrac{1}{A}k_2 \nonumber\\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 - \nonumber \\&& - \dfrac{1}{A}k_1 \cdot s^2 -\left( \dfrac{6a}{A}k_1 + \dfrac{2a}{A}k_2 \right)\cdot s - \left(\dfrac{8a^2}{A}k_1 - \dfrac{2a^2}{A}k_1 + \dfrac{4a^2}{A}k_2 + \dfrac{2a^2}{A}k_3 \right) \nonumber\\&=& s^3+8as^2+14a^2s+4a^3 - \dfrac{1}{A}k_1 \cdot s^2 -\left( \dfrac{6a}{A}k_1 + \dfrac{2a}{A}k_2 \right)\cdot s \nonumber \\&& - \left(\dfrac{6a^2}{A}k_1 + \dfrac{4a^2}{A}k_2 + \dfrac{2a^2}{A}k_3 \right) \nonumber \\&=& s^3 + \left( 8a - \dfrac{1}{A}k_1 \right) s^2 + \left( 14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 \right)s \nonumber\\&& +\left( 4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 \right) \nonumber\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{eqnarray}a_3 &=& 1 \qquad(4.39)\\ a_2 &=& 8a - \dfrac{1}{A}k_1 \qquad(4.40)\\ a_1 &=& 14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 \qquad(4.41)\\a_0 &=& 4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 \qquad(4.42)\end{eqnarray}\)
Jeżeli obiekt zlinearyzowany jest sterowalny, to możemy dowolnie wybrać pierwiastki wielomianu charakterystycznego \( w_K(s) \). W naszych przykładach nie będziemy osobno sprawdzali sterowalności obiektu, a będziemy próbować wyznaczyć elementy macierzy \( K \) "z marszu", pamiętając, że jeżeli ta procedura zawiedzie, to obiekt nie jest sterowalny. Wybierzmy następujące przykładowe wartości pierwiastków wielomianu charakterystycznego \( w_K(s) \)
\(\begin{equation}s_1 = -2a,\ s_2 = -4a,\ s_3 = -6a\end{equation}\qquad(4.43)\)
Ponieważ \( a>0 \), to wybrane pierwiastki są ujemne, co zapewni stabilność asymptotyczną punktu pracy układu regulacji. Wielomian o powyższych pierwiastkach wynosi
\(\begin{eqnarray}W_K(s) &=& (s-s_1)(s-s_2)(s-s_3) = (s+2a)(s+4a)(s+6a) \qquad(4.44)\\&=& (s^2+6as+8a^2)(s+6a) = s^3+6as^2+6as^2+36a^2s+8a^2s+48a^3 \qquad(4.45)\\&=& s^3+12as^2+44a^s+48a^3\qquad(4.46)\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego dla wybranych wartości pierwiastków wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 12a,\ a_1 = 44a^2,\ a_0 = 48a^3 \end{equation}\qquad(4.47)\)
Musimy teraz dobrać wartości wzmocnień regulatora stanu \( k_1\), \( k_2\), \( k_3\), tak aby wielomian charakterystyczny dla zlinearyzowanych równań stanu układu regulacji był równy wielomianowi zadanemu, tzn. żeby odpowiednie współczynniki obu wielomianów były sobie równe. Współczynnik \( a_3 \) jest zawsze równy 1, natomiast dla pozostałych współczynników mamy
\(\begin{eqnarray}a_2 = 8a - \dfrac{1}{A}k_1 &=& 12a \qquad(4.48)\\ a_1 = 14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 &=& 44a^2 \qquad(4.49)\\a_0 = 4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 &=& 48a^3 \qquad(4.50)\end{eqnarray}\)
Z (4.48) obliczamy
\(\begin{eqnarray}8a - \dfrac{1}{A}k_1 &=& 12a \nonumber\\- \dfrac{1}{A}k_1 &=& 4a \nonumber\\k_1 &=& -4aA \qquad(4.51)\end{eqnarray}\)
Z (4.49) obliczamy
\(\begin{eqnarray}14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 &=& 44a^2 \nonumber\\ - \dfrac{2a}{A}k_2 &=& 30a^2+ \dfrac{6a}{A}k_1 \nonumber\\ - \dfrac{2a}{A}k_2 &=& 30a^2+ \dfrac{6a}{A}(-4aA) \nonumber\\ - \dfrac{2a}{A}k_2 &=& 30a^2- 24a^2 \nonumber\\ - \dfrac{2a}{A}k_2 &=& 6a^2 \nonumber\\ k_2 &=& -3aA \qquad(4.52)\end{eqnarray}\)
Z (4.50) obliczamy
\(\begin{eqnarray}4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 &=& 48a^3 \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 44a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 \nonumber\\- \dfrac{2a^2}{A}k_3 &=& 44a^3 +\dfrac{6a^2}{A}(-4aA) + \dfrac{4a^2}{A}\left(-3aA\right) \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 44a^3 -24a^3 - 12a^3 \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 8a^3 \nonumber\\ k_3 &=& -4aA \qquad(4.53)\end{eqnarray}\)
Dla wybranych pierwiastków wielomianu charakterystycznego macierz regulatora stanu ma postać
\(\begin{equation}K = \left(\begin{array}{ccc}-4aA & -3aA & -4aA\end{array}\right)\qquad(4.54)\end{equation}\)
Algorytm regulatora stanu dla obiektu nieliniowego w postaci przyrostowej ma postać
\(\begin{equation}\Delta Q_{we}(t) = k_1 \Delta {H}_1(t) + k_2 \Delta {H}_2(t) + k_3 \Delta {H}_3(t)\qquad(4.55)\end{equation}\)
Równanie regulatora stanu można zapisać jako
\(\begin{equation} Q_{we}(t) = k_1 (H_1(t)-H_{10}) + k_2 (H_2(t)-H_{20}) + k_3 (H_3(t)-H_{30}) + Q_{we0}\qquad(4.56)\end{equation}\)
Aby przetestować zdolność zlinearyzowanego układu regulacji z regulatorem stanu do przybliżania dynamiki układu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt pracy \( H_{10}=0.75 \), \( H_{20}=0.5 \) \( H_{30}=0.25 \) oraz \( Q_{we0} = 0.5 \). Dla przyjętych wartości parametrów obiektu i punktu pracy, mamy \( a=1 \). Wektor wzmocnień regulatora stanu wynosi
\(\begin{equation}K = \left(\begin{array}{ccc}-2 & -1.5 & -2\end{array}\right)\end{equation}\qquad(4.57)\)
Zmienne stanu zlinearyzowanego układu regulacji \( \tilde{H}_1(t) \), \( \tilde{H}_2(t) \) oraz \( \tilde{H}_3(t) \) przybliżają przyrosty zmiennych stanu układu nieliniowego \( \Delta H_1(t) \), \( \Delta H_2(t) \), \( \Delta H_3(t) \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe wynoszą
- \(\Delta H_1(t_0) = \tilde{H}_1(t_0)= 0.2 \), \( \Delta H_2(t_0) = \tilde{H}_2(t_0) = 0.2 \), \( \Delta H_3(t_0) = \tilde{H}_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = \tilde{H}_1(t_0)= 0.1 \), \( \Delta H_2(t_0) = \tilde{H}_2(t_0) = 0.1 \), \( \Delta H_3(t_0) = \tilde{H}_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = \tilde{H}_1(t_0)= 0.04 \), \( \Delta H_2(t_0) = \tilde{H}_2(t_0) = 0.04 \), \( \Delta H_3(t_0) = \tilde{H}_3(t_0) = 0 \)
- \(\Delta H_1(t_0) = \tilde{H}_1(t_0)= 0.02 \), \( \Delta H_2(t_0) = \tilde{H}_2(t_0) = 0.02 \), \( \Delta H_3(t_0) = \tilde{H}_3(t_0) = 0 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu układu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu układu nieliniowego.
Na Rys. 4.1 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \) nieliniowego układu regulacji z regulatorem stanu i zmiennej \( \tilde{H}_3(t) \) układu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna \( \tilde{H}_3(t) \) przybliża przebieg zmiennej \( \Delta H_3(t) \).
Przetestujmy teraz wpływ pierwiastków wielomianu charakterystycznego układu regulacji z regulatorem stanu na jakość regulacji. Przyjmujemy następujące warunki początkowe \( H_1(t_0) =0.77 \), \( H_2(t_0) =0.52 \), \( H_3(t_0)=0.25 \). Badamy zachowanie układu dla następujących wartości pierwiastków wielomianu charakterystycznego
- \( s_1 = -a,\ s_2 = -3a,\ s_3 = -5a \)
- \( s_1 = -2a,\ s_2 = -4a,\ s_3 = -6a \)
- \( s_1 = -3a,\ s_2 = -5a,\ s_3 = -7a \)
- \( s_1 = -4a,\ s_2 = -6a,\ s_3 = -8a \)
Dla kolejnych zestawów pierwiastki wielomianu charakterystycznego przyjmują coraz mniejsze ujemne wartości. Odpowiedź układu zlinearyzowanego zawiera czynniki typu \( e^{-Re(s_i)t} \). Im mniejsze jest \( Re(s_i) \), tym szybciej odpowiedź układu zlinearyzowanego będzie zbiegać do zera. Spodziewamy się zatem, że dla coraz mniejszych pierwiastków wielomianu charakterystycznego, trajektorie stanu układu nieliniowego będą coraz szybciej powracać do pierwotnego punktu pracy. Powtarzając obliczenia przedstawione w tekście możemy obliczyć wartości macierzy \( K \) dla podanych zestawów pierwiastków (\( a =1, A=0.5 \))
- \( K = \left( -aA\ \ -1.5aA\ \ 0.5aA \right) = \left( -0.5\ \ -0.75\ \ 0.25 \right) \)
- \( K = \left( -4aA\ \ -3aA\ \ -4aA \right) = \left( -2\ \ -1.5\ \ -2 \right) \)
- \( K = \left( -7aA\ \ -7.5aA\ \ -14.5aA \right) = \left( -3.5\ \ -3.75\ \ -7.25 \right) \)
- \( K = \left( -10aA\ \ -15aA\ \ -34aA \right) = \left( -5\ \ -7.5\ \ -17 \right) \)
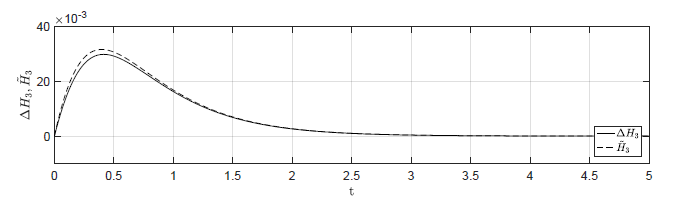
b)\(\Delta H_1(t_0) = 0.1 \), \( \Delta H_2(t_0) = -0.1 \), \( \Delta H_3(t_0) = 0 \)
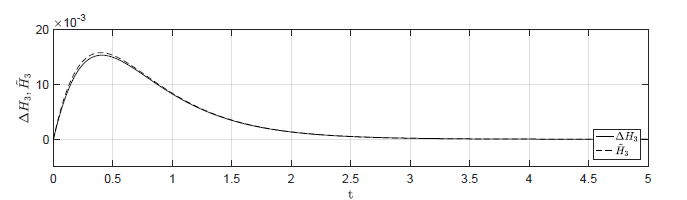
c) \(\Delta H_1(t_0) = 0.04 \), \( \Delta H_2(t_0) = -0.04 \), \( \Delta H_3(t_0) = 0 \)
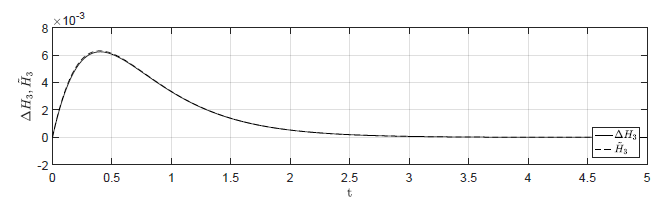
d) \(\Delta H_1(t_0) = 0.02 \), \( \Delta H_2(t_0) = -0.02 \), \( \Delta H_3(t_0) = 0 \)
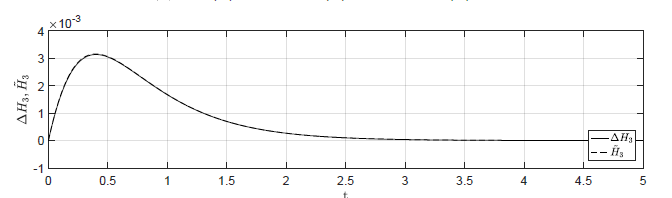
Rysunek 4.1 Porównanie trajektorii \( \Delta H_3(t) \) nieliniowego układu regulacji oraz trajektorii \( \tilde{H}_3(t) \) układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Na Rys. 4.2 przedstawiono trajektorie zmiennej wyjściowej \( H_3(t) \) dla układów regulacji z wybranymi regulatorami stanu. Istotnie, im mniejsze pierwiastki wielomianu charakterystycznego zostaną wybrane do syntezy regulatora stanu, tym szybciej trajektoria \( H_3(t) \) powraca do punktu pracy. Na Rys. 4.3 przedstawiono trajektorie zmiennej zmiennej sterującej \( Q_{we}(t) \) dla wybranych regulatorów stanu. Szybszy powrót trajektorii stanu do punktu pracy uzyskujemy za cenę większych wartości sygnału sterującego. Jest to istotne ograniczenie regulatora stanu. Przyjmując jeszcze mniejsze wartości pierwiastków wielomianu charakterystycznego, możemy teoretycznie uzyskać jeszcze krótsze czasy regulacji. Jednak w pewnym momencie sygnał sterujący generowany przez regulator przekroczy zakres sygnału sterującego możliwego do uzyskania przez urządzenie wykonawcze (w naszym przypadku maksymalny lub minimalny przepływ przez pompę). W takiej sytuacji rzeczywista jakość regulacji, będzie gorsza niż ta wynikająca z symulacji.
Porównajmy jeszcze jakość regulacji w układzie regulacji z regulatorem P i regulatorem stanu. Na Rys. 4.4 przedstawiono odpowiedzi dwóch układów regulacji na warunki początkowe \( H_1(t_0) =0.77 \), \( H_2(t_0) =0.52 \), \( H_3(t_0)=0.25 \). Wzmocnienie regulatora P wynosi \( k_p=-2.5 \), natomiast dla regulatora stanu przyjmujemy \( K =\left( -2\ \ -1.5\ \ -2 \right) \). Wykorzystując regulator stanu uzyskujemy znaczącą poprawę jakości regulacji. Ten efekt jest szczególnie widoczny dla wybranych warunków początkowych. W chwili początkowej mamy bowiem \( H_3(t_0)=H_{30}=0.25 \) i korekta sterowania \( \Delta Q_{we}(t_0) \) generowana przez regulator P w chwili początkowej wynosi 0. Korekta sterowania generowana przez regulator stanu w chwili początkowej jest niezerowa i dzięki temu układ regulacji z regulatorem stanu reaguje szybciej. Jednakże znowu, krótszy czas regulacji w układzie regulacji z regulatorem stanu osiągamy kosztem większych wartości korekty sterowania \( \Delta Q_{we}(t) \) generowanej przez regulator.
Dokonamy teraz obliczeń dla wielomianu charakterystycznego o niektórych pierwiastkach będących liczbami zespolonymi.
Wybieramy następujące wartości pierwiastków wielomianu charakterystycznego \( w_K(s) \)
\(\begin{equation}s_1 = -4a,\ s_2 = -a+2ai,\ s_3 = -a-2ai\end{equation}\qquad(4.58)\)
Jeżeli pewien pierwiastek wielomianu charakterystycznego ma niezerową część urojoną, to musimy pamiętać, że pierwiastkiem wielomianu jest także liczba zespolona sprzężona do danego pierwiastka (inaczej wielomian charakterystyczny nie będzie miał współczynników rzeczywistych). Ponieważ \( a>0 \), to wybrane pierwiastki mają części rzeczywiste ujemne, co zapewni stabilność asymptotyczną punktu pracy układu regulacji. Wielomian o powyższych pierwiastkach wynosi
\(\begin{eqnarray}W_K(s) &=& (s-s_1)(s-s_2)(s-s_3) = (s+4a)(s+a-2ai)(s+a+2ai) \qquad(4.59)\\&=& (s+4a)\left( (s+a)^2 - (2ai)^2 \right) = (s+4a)\left( (s^2+2as+a^2) + 4a^2 \right) \nonumber \\&=& (s+4a)\left( s^2+2as+5a^2 \right) = s^3 + 4as^2 +2as^2+8a^2s+5a^2s+20a^3 \nonumber\\&=& s^3 + 6as^2 +13a^2s + 20a^3 \nonumber\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego dla wybranych wartości pierwiastków wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 6a,\ a_1 = 13a^2,\ a_0 = 20a^3 \end{equation}\qquad(4.60)\)
a)\(K = \left( -aA\ \ -1.5aA\ \ 0.5aA \right)\)
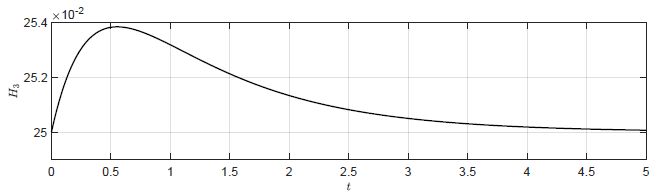
b) \(K = \left( -4aA\ \ -3aA\ \ -4aA \right)\)
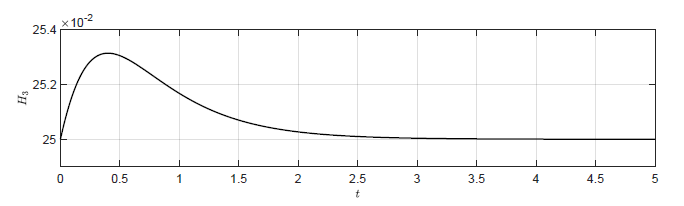
c) \(K = \left( -7aA\ \ -7.5aA\ \ -14.5aA \right) \)
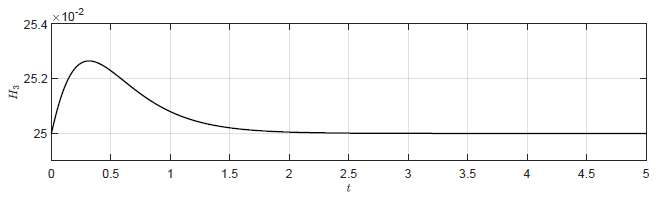
d) \(K = \left( -10aA\ \ -15aA\ \ -34aA \right) \)
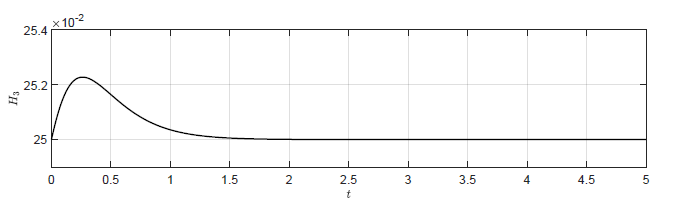
Rysunek 4.2 Trajektorie \( H_3(t) \) w układzie regulacji dla regulatorów stanu o różnych macierzach \( K \).
a) \(K = \left( -aA\ \ -1.5aA\ \ 0.5aA \right)\)
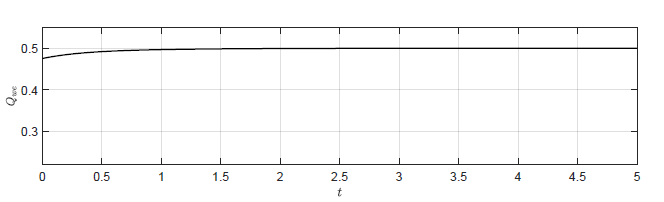
b) \(K = \left( -4aA\ \ -3aA\ \ -4aA \right)\)
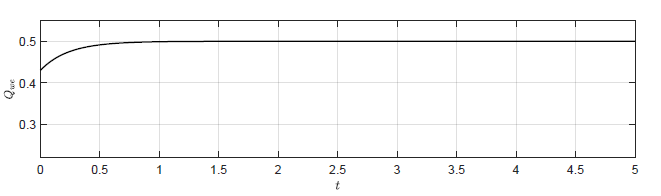
c) \(K = \left( -7aA\ \ -7.5aA\ \ -14.5aA \right) \)
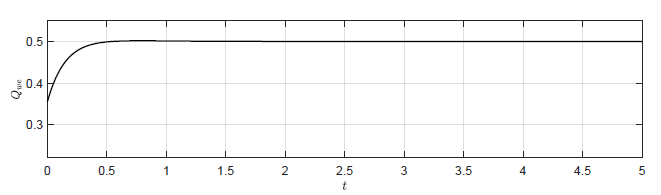
d) \(K = \left( -10aA\ \ -15aA\ \ -34aA \right) \)
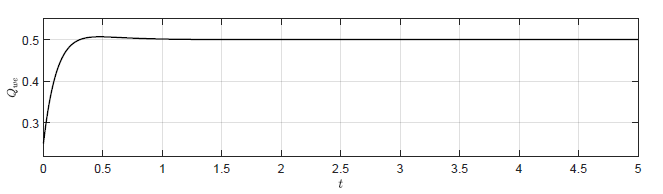
Rysunek 4.3 Trajektorie \( Q_{we}(t) \) w układzie regulacji dla regulatorów stanu o różnych macierzach \( K \).
a)Trajektoria \( H_3(t) \) -- regulator P \( k_p = -2.5 \)
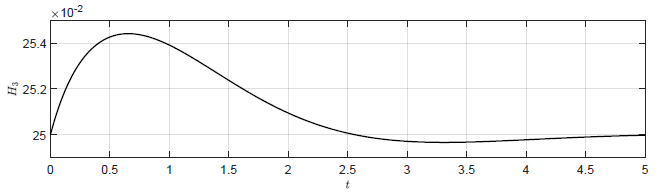
b) Trajektoria \( H_3(t) \) -- regulator stanu \( K =\left( -2\ \ -1.5\ \ -2 \right) \)
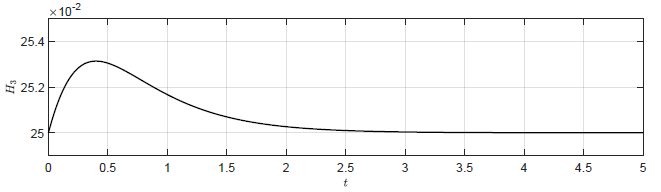
c) Trajektoria \( Q_{we}(t) \) -- regulator P \( k_p = -2.5 \)
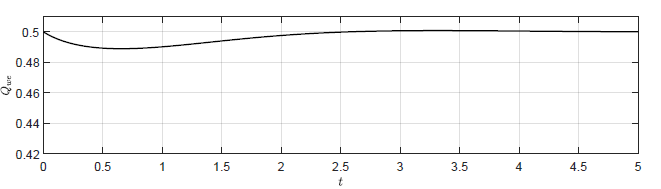
d) Trajektoria \( Q_{we}(t) \) -- regulator stanu \(K =\left( -2\ \ -1.5\ \ -2 \right) \)
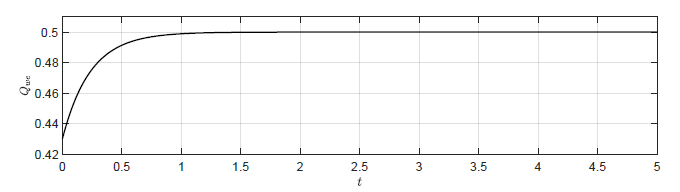
Rysunek 4.4 Porównanie działania układu regulacji z regulatorem P i regulatorem stanu.
Musimy teraz dobrać wartości wzmocnień regulatora stanu \( k_1\), \( k_2\), \( k_3\), tak aby wielomian charakterystyczny dla zlinearyzowanych równań stanu układu regulacji był równy wielomianowi zadanemu, tzn. żeby odpowiednie współczynniki obu wielomianów były sobie równe. Współczynnik \( a_3 \) jest zawsze równy 1, natomiast dla pozostałych współczynników mamy
\(\begin{eqnarray}a_2 = 8a - \dfrac{1}{A}k_1 &=& 6a \qquad(4.61)\\ a_1 = 14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 &=& 13a^2 \qquad(4.62)\\a_0 = 4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 &=& 20a^3 \qquad(4.63)\end{eqnarray}\)
Z (4.61) obliczamy
\(\begin{eqnarray}8a - \dfrac{1}{A}k_1 &=& 6a \nonumber\\- \dfrac{1}{A}k_1 &=& -2aA \nonumber\\k_1 &=& 2aA \end{eqnarray}\qquad(4.64)\)
Z (4.62) obliczamy
\(\begin{eqnarray}14a^2 - \dfrac{6a}{A}k_1 - \dfrac{2a}{A}k_2 &=& 13a^2 \nonumber\\ - \dfrac{2a}{A}k_2 &=& -a^2+ \dfrac{6a}{A}k_1 \nonumber\\ - \dfrac{2a}{A}k_2 &=& -a^2+ \dfrac{6a}{A}\cdot 2aA \nonumber\\ - \dfrac{2a}{A}k_2 &=& -a^2+ 12a^2 \nonumber\\ - \dfrac{2a}{A}k_2 &=& 11a^2 \nonumber\\ k_2 &=& -\dfrac{11}{2}aA \end{eqnarray}\qquad(4.65)\)
Z (4.63) obliczamy
\(\begin{eqnarray}4a^3 -\dfrac{6a^2}{A}k_1 - \dfrac{4a^2}{A}k_2 - \dfrac{2a^2}{A}k_3 &=& 20a^3 \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 16a^3 +\dfrac{6a^2}{A}k_1 + \dfrac{4a^2}{A}k_2 \nonumber\\- \dfrac{2a^2}{A}k_3 &=& 16a^3 +\dfrac{6a^2}{A}\cdot 2aA + \dfrac{4a^2}{A}\left( -\dfrac{11}{2}aA \right) \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 16a^3 +12a^3 - 22a^3 \nonumber\\ - \dfrac{2a^2}{A}k_3 &=& 6a^3 \nonumber\\ k_3 &=& -3aA \end{eqnarray}\qquad(4.66)\)
Dla wybranych pierwiastków wielomianu charakterystycznego macierz regulatora stanu ma postać
\(\begin{equation}K = \left(\begin{array}{ccc}2aA & -\dfrac{11}{2}aA & -3aA\end{array}\right)\end{equation}\qquad(4.67)\)
Dla parametrów obiektu i punktu pracy z poprzedniego przykładu (\( a=1 \) oraz \( A=1 \)) otrzymujemy
\(\begin{equation}K=(1,\ \ -2.75,\ \ -1.5)\end{equation}\qquad(4.68)\)
Na Rys. 4.5 przedstawiono odpowiedź układu regulacji z regulatorem stanu na warunki początkowe \( H_1(t_0) =0.77 \), \( H_2(t_0) =0.52 \), \( H_3(t_0)=0.25 \).
a) Trajektoria \( H_3(t) \)
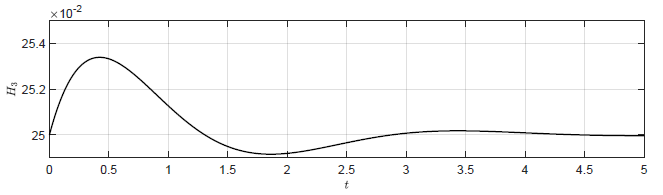
b) Trajektoria \( Q_{we}(t) \)
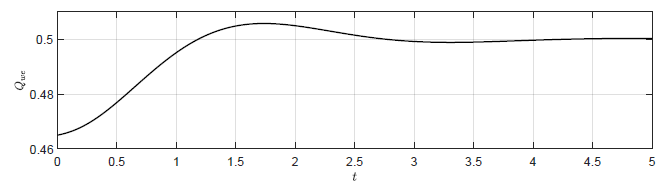
Rysunek 4.5 Oscylacyjna odpowiedź układu regulacji z regulatorem stanu dla \( K =(1,\ \ -2.75,\ \ -1.5) \).
W przeciwieństwie do przebiegów przedstawionych na Rys. 4.2 i 4.3, które mają charakter aperiodyczny, przebiegi przedstawione na Rys. 4.5 mają charakter oscylacyjny. Oscylacyjny charakter odpowiedzi układu regulacji jest związany z zespolonymi pierwiastkami wielomianu charakterystycznego. Wybierając odpowiednio pierwiastki wielomianu charakterystycznego mamy zatem także wpływ na charakter odpowiedzi układu.
Równania stanu dla wahadła mają postać
\(\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(4.69) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M_0 \qquad(4.70) \end{eqnarray}\)
Równania stanu zlinearyzowane w punkcie równowagi \( (\theta_0,\omega_0,M_0) \) mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) +\left(\begin{array}{c}0 \\ \dfrac{1}{ml^2}\end{array}\right)\left( \tilde{M} \right)\end{equation}\qquad(4.71)\)
Macierze układu zlinearyzowanego mają postać
\(\begin{equation}A = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right),\ B = \left(\begin{array}{c}0 \\ \dfrac{1}{ml^2}\end{array}\right)\end{equation}\qquad(4.72)\)
Macierz regulatora stanu ma w naszym przykładzie postać
\(\begin{equation}K = \left(\begin{array}{cc}k_1 & k_2\end{array}\right)\end{equation}\qquad(4.73)\)
Algorytm regulatora stanu w postaci macierzowej jest opisany równaniem
\(\begin{equation}\left( \tilde{M} \right) = \left(\begin{array}{cc}k_1 & k_2 \end{array}\right) \left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega} \end{array}\right)\end{equation}\qquad(4.74)\)
co jest równoważne
\(\begin{equation}\tilde{M} = k_1 \tilde{\theta} + k_2 \tilde{\omega} \end{equation}\qquad(4.75)\)
Równania stanu dla zlinearyzowanego układu regulacji z regulatorem stanu mają zatem postać
\(\begin{eqnarray}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) &=& \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) +\left(\begin{array}{c}0 \\ \dfrac{1}{ml^2}\end{array}\right)\left(\begin{array}{cc}k_1 & k_2 \end{array}\right) \left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega} \end{array}\right) \qquad(4.76)\\&=& \left( \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right) +\left(\begin{array}{c}0 \\ \dfrac{1}{ml^2}\end{array}\right)\left(\begin{array}{cc}k_1 & k_2 \end{array}\right) \right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right)\qquad(4.77)\end{eqnarray}\)
Macierz \( A_K \) układu regulacji wynosi
\(\begin{eqnarray}A_K = A+BK &=& \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)+\left(\begin{array}{c}0 \\ \dfrac{1}{ml^2}\end{array}\right)\left(\begin{array}{cc}k_1 & k_2 \end{array}\right) \qquad(4.78)\\&=& \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)+\left(\begin{array}{cc}0 & 0\\ \dfrac{1}{ml^2} k_1 & \dfrac{1}{ml^2} k_2\end{array}\right)\qquad(4.79)\\&=& \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2} k_1 & -\dfrac{D}{ml^2} + \dfrac{1}{ml^2} k_2\end{array}\right)\qquad(4.80)\end{eqnarray}\)
Wielomian charakterystyczny układu regulacji z regulatorem stanu wynosi
\(\begin{eqnarray}W_K(s) &=& det(sI-A_K) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 & 1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2} k_1 & -\dfrac{D}{ml^2} + \dfrac{1}{ml^2} k_2\end{array}\right) \right) \qquad(4.81) \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 & s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2} k_1 & -\dfrac{D}{ml^2} + \dfrac{1}{ml^2} k_2\end{array}\right) \right) \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 - \dfrac{1}{ml^2} k_1 & s+\dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2\end{array}\right) \\&=& s\left( s+\dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 - \dfrac{1}{ml^2} k_1 \right) \nonumber \\&=& s^2 + \left(\dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 \right)s -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1 \nonumber \end{eqnarray}\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{eqnarray}a_2 &=& 1 \qquad(4.82)\\ a_1 &=& \dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 \qquad(4.83) \\a_0 &=& -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1\qquad(4.84)\end{eqnarray}\)
Rozważmy dwie możliwe konfiguracje pierwiastków wielomianu charakterystycznego. W pierwszej konfiguracji pierwiastkami wielomianu charakterystycznego są dwie liczby ujemne
\(\begin{equation}s_1 = \alpha_1 < 0,\ s_2 = \alpha_2 < 0\end{equation}\qquad(4.85)\)
Wielomian charakterystyczny w tym przypadku wynosi
\(\begin{equation}W_K(s) = (s-s_1)(s-s_2) = (s-\alpha_1)(s-\alpha_2) = s^2 -(\alpha_1+ \alpha_2)s +\alpha_1\alpha_2\end{equation}\qquad(4.86)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = -(\alpha_1+ \alpha_2),\ a_0 = \alpha_1\alpha_2\end{equation}\qquad(4.87)\)
Musimy teraz dobrać wartości wzmocnień regulatora stanu \( k_1\), \( k_2\), tak aby wielomian charakterystyczny dla zlinearyzowanych równań stanu układu regulacji był równy wielomianowi zadanemu, tzn. żeby odpowiednie współczynniki obu wielomianów były sobie równe. Współczynnik \( a_2 \) jest zawsze równy 1, natomiast dla pozostałych współczynników mamy
\(\begin{eqnarray}a_1 = \dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 &=& -(\alpha_1+ \alpha_2) \qquad(4.88)\\a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1 &=& \alpha_1\alpha_2 \qquad(4.89)\end{eqnarray}\)
Z (4.88) obliczamy
\(\begin{eqnarray}\dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 &=& -(\alpha_1+ \alpha_2)\nonumber\\ - \dfrac{1}{ml^2} k_2 &=& -(\alpha_1+ \alpha_2) - \dfrac{D}{ml^2} \nonumber\\k_2 &=& ml^2 \left( \alpha_1+ \alpha_2 + \dfrac{D}{ml^2} \right) \qquad(4.90)\end{eqnarray}\)
Z (4.89) obliczamy
\(\begin{eqnarray}-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1 &=& \alpha_1\alpha_2 \nonumber\\ -\dfrac{1}{ml^2}k_1 &=& \alpha_1\alpha_2 +\dfrac{g}{l}cos\theta_0 \nonumber\\ k_1 &=& -ml^2\left( \alpha_1\alpha_2 +\dfrac{g}{l}cos\theta_0 \right) \qquad(4.91) \end{eqnarray}\)
W drugiej konfiguracji pierwiastkami wielomianu charakterystycznego są dwie liczby zespolone sprzężone
\(\begin{equation}s_1 = \alpha + \beta i,\ s_2 = \alpha - \beta i \end{equation}\qquad(4.92)\)
o ujemnych częściach rzeczywistych (\( \alpha<0 \)). Wielomian charakterystyczny w tym przypadku wynosi
\(\begin{eqnarray}W_K(s) &=& (s-\alpha - \beta i)(s-\alpha + \beta i) = (s-\alpha)^2 - (\beta i)^2 \\&=& s^2 -2\alpha s + \alpha^2 + \beta^2 \qquad(4.93)\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = -2\alpha,\ a_0 = \alpha^2 + \beta^2\end{equation}\qquad(4.94)\)
Musimy teraz dobrać wartości wzmocnień regulatora stanu \( k_1\), \( k_2\), tak aby wielomian charakterystyczny dla zlinearyzowanych równań stanu układu regulacji był równy wielomianowi zadanemu, tzn. żeby odpowiednie współczynniki obu wielomianów były sobie równe. Współczynnik \( a_2 \) jest zawsze równy 1, natomiast dla pozostałych współczynników mamy
\(\begin{eqnarray}a_1 = \dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 &=& -2\alpha \qquad(4.95)\\a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1 &=& \alpha^2 + \beta^2 \qquad(4.96)\end{eqnarray}\)
Z (4.95) obliczamy
\(\begin{eqnarray}\dfrac{D}{ml^2} - \dfrac{1}{ml^2} k_2 &=& -2\alpha \nonumber\\- \dfrac{1}{ml^2} k_2 &=& -2\alpha - \dfrac{D}{ml^2} \nonumber\\k_2 &=& ml^2 \left( 2\alpha + \dfrac{D}{ml^2} \right) \qquad(4.97)\end{eqnarray}\)
Z (4.96) obliczamy
\(\begin{eqnarray}-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_1 &=& \alpha^2 + \beta^2 \nonumber\\ -\dfrac{1}{ml^2}k_1 &=& \alpha^2 + \beta^2 +\dfrac{g}{l}cos\theta_0 \nonumber\\ k_1 &=& -ml^2\left( \alpha^2 + \beta^2 +\dfrac{g}{l}cos\theta_0 \right) \qquad(4.98() \end{eqnarray}\)
Algorytm regulatora stanu dla obiektu nieliniowego w postaci przyrostowej ma postać
\(\begin{equation}\Delta M(t) = k_1 \Delta \theta(t) + k_2 \Delta \omega(t) \end{equation}\qquad(4.99)\)
Algorytm regulatora może zostać zapisany jako
\(\begin{equation}M(t) = k_1 (\theta(t)-\theta_0) + k_2 (\omega(t)-\omega_0) +M_0 \end{equation}\qquad(4.100)\)
Obliczymy teraz wartości wzmocnień regulatora stanu dla wybranych pierwiastków wielomianu charakterystycznego i porównamy jakość regulacji w układzie regulacji z regulatorem stanu i regulatorem P. Przyjmujemy parametry modelu obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt pracy układu regulacji \( \theta_0=\dfrac{\pi}{6} \), \( \omega_0=0 \), \( M_{0} = -0.5 \). Obliczmy wartości wzmocnień regulatora stanu dla dwóch zestawów pierwiastków wielomianu charakterystycznego
- \( s_1 = -1 \), \( s_1 = -2 \)
- \( s_1 = -1+0.5i \), \( s_1 = -1-0.5i \)
W pierwszym przypadku wzmocnienia obliczamy ze wzorów (4.90) oraz (4.91)
\(\begin{equation}k_1 = -1.07,\ k_2=-0.2\end{equation}\qquad(4.101)\)
W drugim przypadku wzmocnienia obliczamy ze wzorów (4.90) oraz (4.91)
\(\begin{equation}k_1 = -0.99,\ k_2=-0.1\end{equation}\qquad(4.102)\)
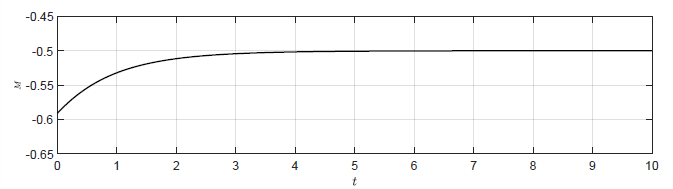
Na Rys. 4.6przedstawiono porównanie odpowiedzi układów regulacji na warunki początkowe \( \theta(t_0) = \dfrac{\pi}{5} \), \( \omega(t_0) = -0.1 \). Uwzględniono układ regulacji z regulatorem P o wzmocnieniu \( k_p=1 \) oraz układy regulacji z regulatorami stanu o obliczonych wzmocnieniach. Podobnie na Rys.4.7 przestawiono porównanie sygnałów sterujących w testowanych układach regulacji.
Dla obydwu testowanych regulatorów stanu uzyskaliśmy poprawę jakości regulacji w porównaniu do regulatora P. Co więcej, korekty sygnałów sterujących \( \Delta M(t) \) generowane przez regulatory stanu są mniejsze niż odpowiednie korekty generowane przez regulator P. Porównajmy algorytm regulatora P
\(\begin{equation}\Delta M(t) = k_p \Delta \theta(t) \end{equation}\qquad(4.103)\)
oraz algorytm regulatora stanu
\(\begin{equation}\Delta M(t) = k_1 \Delta \theta(t) + k_2 \Delta \omega(t) \end{equation}\qquad(4.104)\)
Dla wybranych regulatorów stanu wartości \( k_1 \) są bardzo bliskie wzmocnieniu regulatora proporcjonalnego \( k_p=1 \). Kluczową rolę odgrywa zatem człon korekcji pochodzący od odchyłki prędkości kątowej \( \Delta \omega(t) \) obecny w regulatorze stanu. W zależności od wartości tej odchyłki regulator stanu nieco zmniejsza korektę sterowania jeżeli wahadło zbliża się do punktu pracy, a nieco zwiększa korektę sterowania jeżeli wahadło oddala się od punktu pracy. Dzięki temu uzyskujemy bardziej zbalansowaną korektę sterowania w porównaniu do regulatora P.
a) Regulator proporcjonalny \(k_p = -1 \)
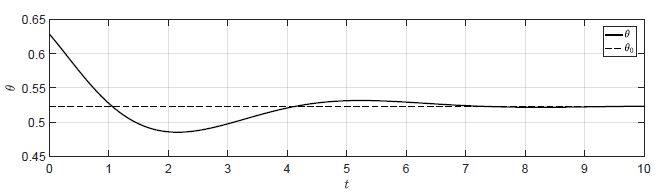
b) Regulator stanu \(K = (-1.06,\ \ -0.2) \)
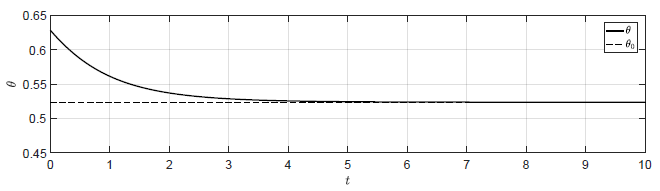
c) Regulator stanu \(K = (-0.99,\ \ -0.1) \)
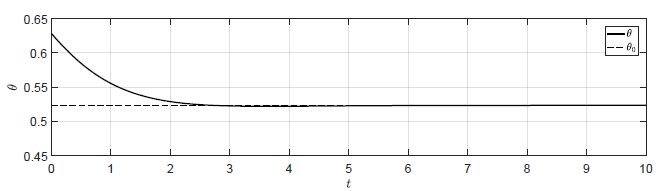
Rysunek 4.6 Porównanie działania układu regulacji wahadła z regulatorem P i regulatorem stanu.
a) Regulator proporcjonalny \(k_p = -1 \)
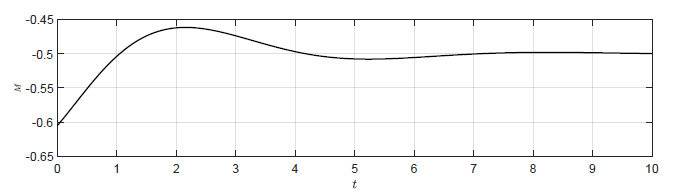
b) Regulator stanu \(K = (-1.06,\ \ -0.2) \)
c) Regulator stanu \(K = (-0.99,\ \ -0.1) \)
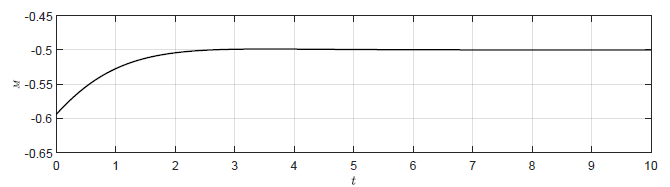
Rysunek 4.7 Porównanie sygnałów sterujących w układzie regulacji z regulatorem P i regulatorem stanu.