Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Przykłady i pojęcia podstawowe |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | niedziela, 15 lutego 2026, 19:55 |
1. Wprowadzenie
Tytuł podręcznika «Metody optymalizacji» powinien mówić sam za siebie, ale czy mówi?
Najpierw trzeba ustalić co tak naprawdę znaczy optymalizacja.
Współcześnie, najczęściej nadaje mu się znaczenie wprowadzone przez G.W. Leibniza w znamienitej pracy „Nova Methodus pro Maximis et Minimis”, 1 opublikowanej w 1684 r., której autor nazywał wartości największe lub najmniejsze jakie przybiera pewna funkcja – optymalnymi.
Wielu ludzi uważa, że w dzisiejszych czasach wszystko jest, albo co najmniej powinno być, optymalne. Człowieka tak myślącego i działającego często nazywa się homo oeconomicus. Optymalizacja więc nas otacza:
- optymalizują ludzie w życiu codziennym, np. student tak dobiera sobie program studiowania aby spełniając wymagania narzucone przez władze oraz w zgodzie z własnymi potrzebami minimalizować swoje nakłady(mierzone np. zużytym czasem) potrzebne do uzyskania dyplomu;
- optymalizują konstruktorzy – np. projektując most starają się dobrać parametry jego elementów tak, aby przy spełnieniu ograniczeń wymiarowych, sztywnościowych, wytrzymałościowych itp. sumaryczny koszt tych elementów był jak najmniejszy;
- optymalizują ludzie w organizacjach, np. zarząd korporacji podejmuje decyzje, które w aktualnej sytuacji mają przynieść maksymalny zysk;
- optymalizuje też przyroda, –ożywiona: np. mrówki wybierają najkrótsze, z dopuszczalnych, drogi powrotu z miejsc pracy/żerowania do mrowiska; –nieożywiona: np. łańcuch układa się tak, że jego energia potencjalna jest najmniejsza, a promienie światła biegną tak aby minimalizować czas podróży itd.
Podsumowując powyższe przykłady i nieco rozszerzając rozważania Leibniza, można powiedzieć, że optymalizacja polega na dążeniu do znalezienia wariantu (działania), ocenianego według ustalonego kryterium wyboru jako najlepszy spośród wariantów rozpatrywanych (porównywanych/możliwych). Szukamy wariantu ocenionego optymalnie a nie optymalnej wartości funkcji oceniającej.
Z drugiej jednak strony można zadać pytanie, czy dążenie za wszelką cenę do tego aby zrealizować wariant najlepszy z możliwych jest zawsze uzasadnione, a co ważniejsze, możliwe?
Zostawmy odpowiedź na pierwszą część pytania dla filozofów. Analiza możliwości poruszanej w jego drugiej części zostanie ograniczona do pokazania jak można w zbiorze wariantów uznanych za dopuszczalne poszukiwać wariantu, ocenianego według ustalonego kryterium wyboru jako najlepszy tj. otrzymującego najwyższą albo najniższą wartość oceny (możemy szukać rzeczy „najcenniejszej” albo „najmniej cennej”, porównujemy „cenność”). Będziemy zatem poszukiwać odpowiedzi na pytanie: jak rozwiązać zadanie optymalizacji? Przyrodzie „jest łatwiej” bo „sama z siebie” znajduje wariant optymalny, człowiek musi tego wariantu szukać. Gdy wariantów jest niewiele i przyjmiemy, że kryterium porównywania jest ustalone, to można je parami porównać i wybrać najlepszy. Ale co robić gdy wariantów jest wiele, nieskończenie wiele?
1
W tej pracy Leibniz przestawił swoją teorię rachunków (calculi) różniczkowych łącznie z używaną do dziś notacją, df(x)/dx, ułatwiającą jej zrozumienie.
Jak zawsze, w rozwiązywaniu trudnych problemów pomagają usystematyzowane i mniej lub bardziej sformalizowane rozważania – teoria – prowadzące do określenia praktycznych sposobów postępowania, w przypadku optymalizacji zwanych algorytmami, pozwalających wyznaczyć warianty najlepsze.
Tematem podręcznika jest więc – teoria optymalizacji, którą zaczął tworzyć Leibniz i algorytmy optymalizacji, których bujny rozwój zaczął się 250 lat później – w czasie II Wojny Światowej.
Jednak moim założeniem, nie jest uczynienie z Państwa specjalistów w zakresie tworzenia nowych algorytmów optymalizacji, a tylko wyjaśnienie "jak to działa" po to by potrafili Państwo świadomie z algorytmów istniejących korzystać.
Niewątpliwie najwięcej traktatów napisano o Bogu, następnie o miłości, ale jaki temat jest na trzecim miejscu? Patrioci optymalizacji twierdzą, że o optymalizacji. Sam mam ponad trzydzieści książek papierowych i ze cztery razy tyle elektronicznych poświęconych tej tematyce, a jest to tylko niewielki ułamek ich zbioru. Zatem (optymalny?) wybór tego co najistotniejsze z tej przywalającej człowieka góry informacji nie jest łatwy. W kolejnych rozdziałach tego podręcznika prezentuję swój punkt widzenia na to co ważne, a co można pominąć z nagromadzonej wiedzy związanej z metodami rozwiązywania zadania optymalizacji to jest algorytmami znajdowania takiego elementu/elementów ustalonego zbioru dla którego wybrana funkcja oceniająca przyjmuje najmniejszą/największą wartość z wartości przyjmowanych na tym zbiorze. Mam nadzieję, że spotka się on, podobnie jak jego poprzednie warianty, z pozytywnym odbiorem Czytelników.
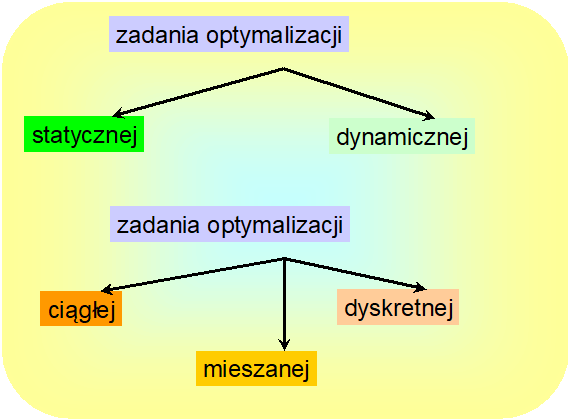
Prezentację zacznę od przykładów różnych zadań optymalizacji. Pozwolą one na formalne zdefiniowanie i klasyfikację zadań optymalizacji, w tym m. in. podział na tzw. zadania optymalizacji statycznej i dynamicznej. Dalsze rozważania będą poświęcone przedstawieniu różnych metod rozwiązywania zadań optymalizacji statycznej, tylko którą zajmiemy się w tym podręczniku.
Pierwszymi zdaniami optymalizacji statycznej dla których opracowano efektywny algorytm znajdowania rozwiązania są tzw. zadania programowania liniowego. Moduł drugi to zwięzły opis tych zadań oraz metody Simplex służącej ich rozwiązywaniu. Moduł trzeci przedstawia podstawy matematyczne niezbędne do zrozumienia tak teorii optymalizacji jak i zasad budowy i działania algorytmów optymalizacji tzw. zadań programowania nieliniowego. W module tym także opisano podstawowe iteracyjne schematy (algorytmy) optymalizacji bez ograniczeń: metodę rozsiewania punktów próbnych, metodę obszaru zaufania i metodę kierunków poprawy. Omówiono też pojęcie zbieżności algorytmu optymalizacji. Moduł czwarty to przedstawienie problemów związanych z rozwiązywaniem tzw. zadania poprawy oraz szczegółowy opis gradientowych algorytmów rozwiązywania zadań optymalizacji bez ograniczeń. Analizie matematycznej zadań z ograniczeniami jest poświęcony moduł piąty. Przedstawiono w nim, po niezbędnym przygotowaniu, podstawowe dla teorii tych zadań Twierdzenie Karusha–Kuhna–Tuckera. Ostatni, szósty moduł to prezentacja podstawowych metod znajdowania rozwiązania zadania optymalizacji z ograniczeniami: metod funkcji kary oraz rozszerzonego lagranżianu.
2. Przykłady zadań optymalizacji
Przejdziemy teraz do pierwszej grupy przykładów zadań optymalizacji. Pierwsze będzie dotyczyło tzw. optymalnego planowania produkcji, a więc zadania dla menedżera.
2.1. Zadanie optymalnego planowania produkcji
Wytwarzanie benzyn do silników spalinowych jest jednym z głównych procesów technologicznych rafinerii ropy naftowej. Przyjmijmy, że rafineria produkuje dwa rodzaje benzyny, które powstają w wyniku komponowania (zmieszania) różnych frakcji benzynowych oraz innych składników. Jeżeli z naszych rozważań wykluczymy, dla ułatwienia, procesy destylacji, rafinacji i reformingu, to uproszczony schemat przepływów związany z produkcją benzyn może być taki jak na poniższym rysunku.
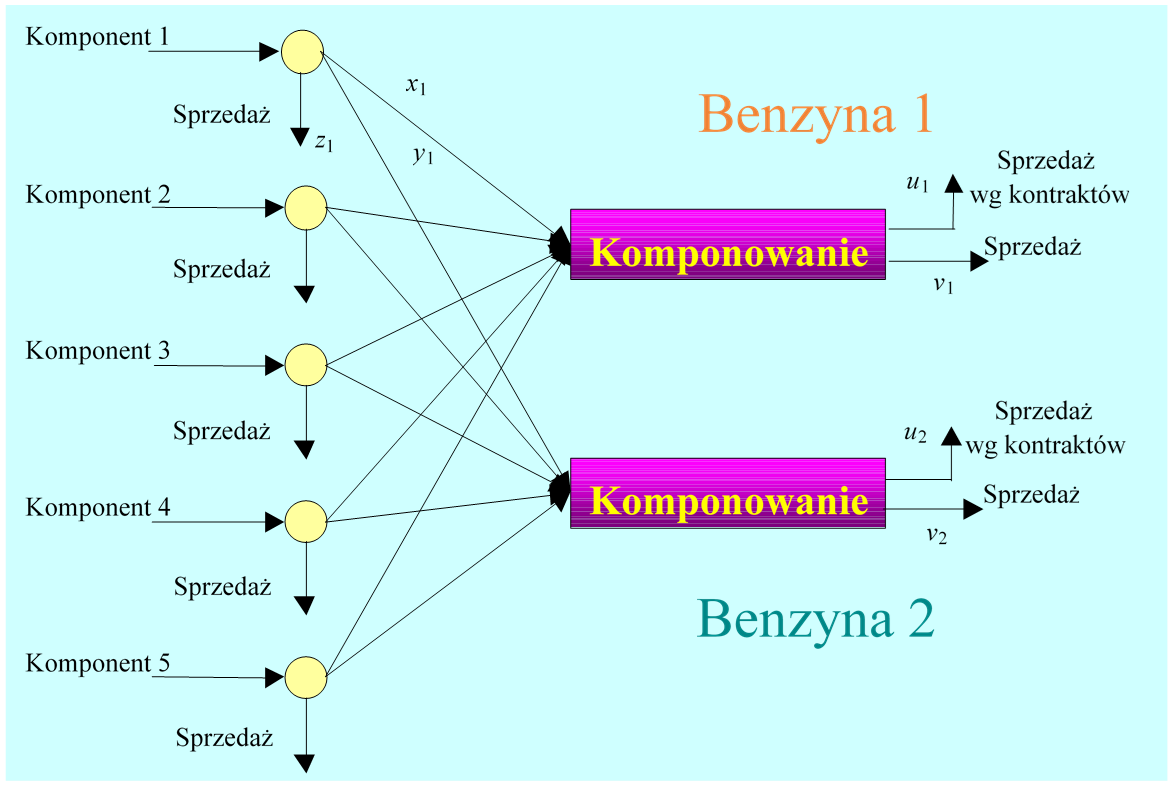
Dalej interesować nas będą tylko aspekty ekonomiczne związane z produkcją i sprzedażą benzyn w danym okresie, np. kwartale. Jeżeli znamy nakłady jednostkowe oraz jednostkowe ceny sprzedaży dla poszczególnych komponentów oraz ceny jednostkowe obu rodzajów benzyn to zadanie planowania produkcji może być sformułowane następująco:
Wybrać takie wielkości produkcji komponentów oraz produktów końcowych, które przyniosą maksymalny zysk.
gdzie: \(p_j^u\), – cena jednostki j-tej benzyny w kontrakcie, \(p_j^v \),– cena jednostki j-tej benzyny w wolnej sprzedaży, \(p_i^z\), – cena jednostki i-tego komponentu w wolnej sprzedaży, \(c_i^s \),– koszt wytworzenia jednostki komponentu i, \(c_i^b\), – koszty komponowania przeliczone na jednostkę komponentu i. Określiliśmy tym samym kryterium (funkcję oceny, wyboru) pozwalające porównywać różne zestawy rozważanych wielkości (warianty decyzji). Czy zadanie sformułowane następująco: znaleźć taki zestaw wielkości \((u_1,u_2,v_1,v_2,x_1,...,x_5,y_1,...,y_5,z_1,...,z_5)\) dla którego zysk rafinerii jest największy jest poprawne? Po chwili zastanowienia każdy odpowie – nie. Po pierwsze, wszystkie wielkości nie mogą być ujemne. Po drugie obowiązuje prawo zachowania masy i suma ilości komponentów nie może być większa niż suma ilości produktów, a przy założeniu braku strat, musi być dokładnie taka sama. W konsekwencji w poprawnym sformułowaniu zadania muszą pojawić się dodatkowe wymagania wiążące zmienne. Trzeba określić ograniczenia. Ustalenie pierwszej grupy ograniczeń jest oczywiste: \(u_j\geq0,v_j\geq0,x_i\geq0,y_i\geq0,z_i\geq0,j\in\overline{1,2,}i\in\overline{1,5}\qquad(1.2)\), są to tzw. ograniczenie znaku; do których trzeba dodać równania bilansowe \(\sum_{i}\ x_i=u_1+v_1 oraz \sum_{i}\ y_i=u_2+v_2.\) Jakie jeszcze mogą być ograniczenia? Sumaryczna ilość komponentu i-tego jaka może być dostarczona w danym okresie nie może przekroczyć zdolności produkcyjnej \( \alpha _i \) \(x_i+y_i+z_i\le\alpha_i, \qquad(1.3)\) Nierówności, określające łącznie z równaniami bilansowymi, jakość produktów kompozycji \(\sum_{i}\eta_ix_i\geq\mu_1(u_1+v_1) i \sum_{i}\eta_iy_i\geq\mu_2(u_2+v_2); \) ograniczenie na minimalną ilość benzyny sprzedawanej po cenach ustalonych w kontrakcie \( u_1 \geq U_1, \, u_2 \leq U_2. \qquad(1.4) \) Ograniczenia znaku, bilansowe, zdolności produkcyjnej, jakości oraz minimalnych ilości zawężają pole wyboru wariantów do tzw. zbioru dopuszczalnego. Poprawnie sformułowane zadanie planowania produkcji jest zatem następującym zadaniem optymalizacji (w tym przypadku maksymalizacji): znaleźć taki zestaw wielkości decyzyjnych\( (u_1,u_2,v_1,v_2,x_1,...,x_5,y_1,...,y_5,z_1,...,z_5) \); dla którego zysk rafinerii określony funkcją f jest największy, co, oznaczając \( \mathbf{x}=(u_1,u_2,v_1,v_2,x1,...,x5,y1,...,y5,z1,...,z5) , \) zapiszemy znaleźć \(\mathbf{x}^\mathbf{o}={arg\max}_{\ \mathbf{x}\in\mathbf{X}\ }f(\mathbf{x}),\)
Posumowaniem naszych rozważań będzie wyliczenie kroków, które doprowadziły nas do zbudowania (modelu) zadania optymalizacji.
- Określenie/identyfikacja wielkości, których wartości możemy wybierać, czyli zmiennych decyzyjnych. Jest ich 19, pogrupowanych w pięciu zestawach: ilości dostępnych komponentów użytych do produkcji benzyny pierwszego rodzaju \(\left(x_i\right)_{i\in\overline{1,5}}\), drugiego rodzaju i przeznaczonych na sprzedaż \(\left(z_i\right)_{i\in\overline{1,5}}\) (15 zmiennych), ilości benzyny pierwszego rodzaju sprzedawanej na podstawie kontraktów długoterminowych \(u_1\\) oraz na wolnym rynku \(v_1 \)(2 zmienne), ilości benzyny drugiego rodzaju sprzedawanej na podstawie kontraktów długoterminowych \(u_2\) oraz na wolnym rynku \(v_2\) (2 zmienne).
- Ustalenie kryterium wyboru, w tym przypadku funkcji rzeczywistej 19 zmiennych decyzyjnych. Wybrano zysk (1.1), co automatycznie, z jednej strony określiło zadanie optymalizacji jako maksymalizację, a z drugiej pociągnęło konieczność ustalenia/identyfikacji wartości dziewięciu cen (kontraktowej ceny jednostki pierwszej benzyny\(\ {\ p}_{j1}^u\) i drugiej benzyny \(p_2^u\), wolnorynkowej ceny jednostki pierwszej benzyny \(p_1^v \) i drugiej benzyny \(p_2^v\) oraz ceny jednostki każdego komponentu w wolnej sprzedaży \(p_i^z, i\in\overline{1,5}\)) i dziesięciu kosztów (\(c_i^s\) – koszt wytworzenia jednostki komponentu \(i, i\in\overline{1,5}, c_i^b\) – koszty komponowania przeliczone na jednostkę komponentu \(i, i\in\overline{1,5},\)) to jest 19 parametrów.
- Ustalenia/identyfikacji dodatkowych wymagań wiążących zmienne decyzyjne to jest ograniczeń. Ograniczenia tworzą dwie grupy:
-
ograniczenia nierównościowe; są to prawie zawsze ograniczenia znaku (1.2), ograniczenia wynikające z zasad bezpieczeństwa oraz np. tak jak w rozpatrywanym przypadku nierówności gwarantujące niezbędną jakość wyrobów, czy minimalną produkcję (1.4) zmieniając stosowne ograniczenia znaku,
- ograniczenia równościowe; najczęściej bilansowe, ale także ograniczenia wynikające z konstrukcji aparatów produkcyjnych limitujące wielkość produkcji/przetwarzania. Te ostatnie w naszym przykładzie zostały potraktowane jako ograniczenia nierównościowe, co oznacza, że modelujący zadanie optymalizacji dopuszcza niewykorzystanie wszystkich potencjalnie dostępnych zdolności produkcyjnych, nierówność (1.3).
2.2. Zadanie projektowania optymalnego regulatora PID
Przyjmijmy, że naszym zadaniem jest zaprojektowanie autopilota dla statku, tzn. takiego urządzenia, które wyręczy sternika w stałym utrzymywaniu ustalonego kursu. Nasze dalsze rozważania będziemy prowadzić przy upraszczającym założeniu, że znamy opis zależności między zmianami kąta wychylenia steru, \( \delta \), a zmianami kursu statku, \(\varphi\). Przyjmujemy, że jest to liniowe równanie różniczkowe
\(TT_{ms}\dddot{(\varphi}+(T+T_{ms})\ddot{<span>\varphi</span>}+\dot{<span>\varphi</span>}=k\delta\)
(tzw. model K. Nomoto pierwszego rzędu z maszyną sterową).
Automatycy przy projektowaniu układów sterowania zamiast „opisem różniczkowym” obiektu liniowego wolą posługiwać się równoważnym opisem transmitancyjnym przyjmując, że funkcja \(\varphi(\cdot)\) będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący \(\delta(\cdot)\)mają transformaty Laplace’a
\(s\bar{<span>\varphi</span>}(s)=\mathcal{L}(\varphi(t)), s↦\bar{\delta}(s)=L(δ(t))\).
Dokonując transformacji Laplace’a obu stron powyższego równania różniczkowego można je zapisać jako równanie algebraiczne
\(TT_{ms}s^3 \bar{</span>\varphi</span>}(s)+(T+T_{ms})s^2\bar{</span>\varphi</span>}(s)+s\bar{</span>\varphi</span>}(s)=\bar{\delta}(s),\)
a następnie w postaci transmitancyjnej
\(\bar{\varphi }=\dfrac{k}{s(Ts+1)(T_{ms}s+1)}\bar{\delta}(s)=G(s)\bar{\delta}(s)\)
\(\bar{</span>\varphi</span>}(s)=G(s)\bar{\delta}(s)\).
Strukturę sytemu sterowania wybierzemy oczywiście jako zamkniętą, ponieważ tylko taki autopilot ma szansę poradzenia sobie z różnymi zakłóceniami oddziaływującymi na statek (zniwelowania ich wpływu na kurs statku). Sterowanie (kąt wychylenia steru) będzie zatem wyznaczane w oparciu o uchyb e, tzn. różnicę miedzy zadanym, \(φ_d \), a zmierzonym, \(φ_d \),, kursem statku.
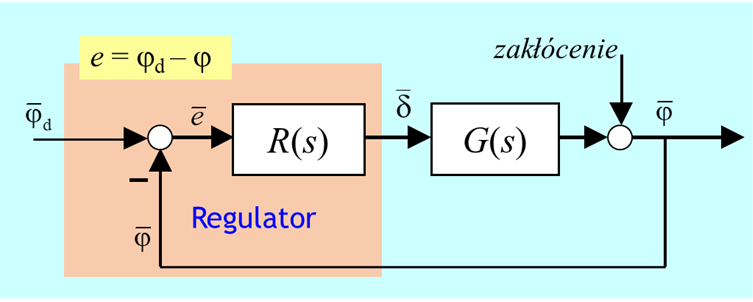
Trzeba wyznaczyć transmitancję regulatora \(\bar{\delta}(s)=R(s)\bar{</span></span></span></span></span>e}(s)\)
Wieloletnie doświadczenie, a także stosowne rozważania teoretyczne, podpowiadają w naszym przypadku wybór sposobu przetwarzania (sygnału) uchybu na sterowanie. Powinien to być tzw. algorytm regulatora PID, tj. algorytm opisywany transmitancją
\(R(s)=k_P(1+\dfrac{1}{T_Is}+T_Ds)\) (równaniem różniczkowym \(T_I\dot{\delta}=k_p(T_DT_I\ddot{e}+T_I\dot{e}+e)).\)
gdzie człon ostatni dokonuje różniczkowania uchybu (działanie D), a człon środkowy go całkuje (działanie I). „Jedynka”, łącznie z mnożnikiem \(k_P\) przetwarzają uchyb w sposób proporcjonalny (działanie P).
W transmitancji regulatora PID mamy trzy parametry – nastawy – \(k_P\), \(T_I\) oraz \(T_D\), których wartości trzeba tak wybrać aby zaprojektowany układ regulacji działał jak najlepiej.
Co znaczy przedstawione wymaganie: „działał jak najlepiej”?
Istnieje wiele odpowiedzi na to pytanie. Przedstawimy teraz krótko jedną z nich. Ponieważ znamy transmitancję statku I i transmitancję regulatora I, to możemy policzyć uchyb \(e_1(\cdot) \) w układzie regulacji dla zakłócenia będącego skokiem jednostkowym
\(\bar{e}_1(s)= \dfrac{G(s)}{1+G(s)R(s)}\dfrac{1}{s}\), \(e_1(t)=\mathcal{L}^{-1}(\bar{e}_1(s)).\)
W tej sytuacji „działał jak najlepiej” oznacza:
działał tak aby uchyb był bliski zera, tak jak tylko jest to możliwe. Jak tylko to jest możliwe, bo inżynier znający teorię regulacji wie, że np. wymaganie bezwzględnego zerowania się uchybu w każdej chwili jest nierealizowalne.
Jest oczywiste, że przebieg (kształt) uchybu zależy od nastaw regulatora:
\((\forall t \geq 0) e_1(t) = \Psi (t; k_P, T_I ,T_D )\).
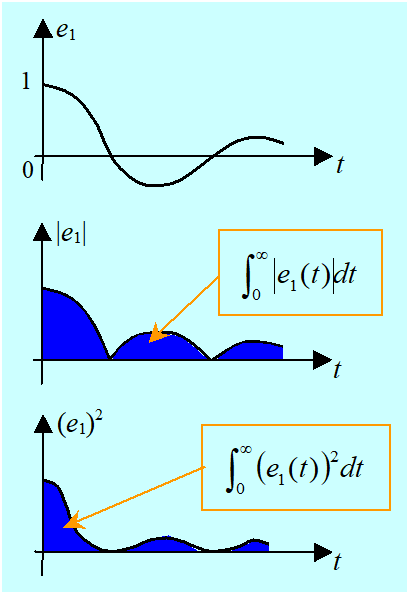
Zatem do oceny „odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu:
\((k_P,T_I,T_D)\mapsto f^1(k_P,T_I,T_D)=\int_{0}^{\infty}\left|\psi(t;k_P,T_I,T_D)\right|\ dt,\)
albo całką z kwadratu uchybu:
\((k_P,T_I,T_D)\mapsto f^2(k_P,T_I,T_D)=\int_{0}^{\infty}{\left(\psi(t;k_P,T_I,T_D)\right)^2}dt.\)
Określiliśmy więc sposób porównywania różnych zestawów nastaw: ta trójka parametrów jest lepsza, dla której kryterium (wybrana funkcja oceny) przyjmuje mniejszą wartość.
W rozważanym zadaniu optymalizacji szukamy nastaw dających jak najbliższa zeru wartość funkcji oceniającej, zatem naszym zadaniem jest, w odróżnieniu od przykładu poprzedniego, minimalizacja.
Intuicyjnie jest dość oczywiste, że całka z modułu uchybu (kryterium \(f^1\)) jest lepszą miarą jakości działania układu regulacji niż całka z kwadratu uchybu (kryterium \(f^2)\), bo małe oscylacje uchybu nie wpływają wiele na tę ostatnią.
Dlaczego więc proponowane jest kryterium drugie?
W podręcznikach automatyki można znaleźć wzory pozwalające dla znanej transmitancji obiektu wyznaczyć analityczną zależność wartości tego kryterium od nastaw regulatorów. Innymi słowy możemy stosunkowo prosto wyznaczyć wzór pozwalający obliczyć wartości funkcji \((k_P,\ T_I,T_D) \mapsto f^2(k_P,\ T_I,T_D)=\ \int_{0}^{\infty}{\left(\psi(t;k_P,T_I,T_D)\right)^2}dt\). Natomiast dla danego zestawu nastaw \(\ (k_P,\ T_I,T_D)\), wartość funkcji \(f^1(k_P,\ T_I,T_D)\) możemy w zasadzie wyznaczyć tylko drogą rozwiązywania stosownego równania różniczkowego (symulacji) i numerycznego całkowania. Co oznacza, że przy tak określonym kryterium sprawdzimy tylko wybrane „trójki parametrów” bo całkujemy numerycznie. Wybór najlepszej z nich zależy więc silnie od naszej intuicji określającej jakie trójki wybierzemy do badania.
Bez względu na to jakie kryterium porównywania/oceny wybierzemy, musimy, tak jak poprzednio, odpowiedzieć na pytanie: czy nastawy kP, TI ,TD możemy wybierać dowolnie?
Oczywiście nie. Musimy pamiętać o tym, że algorytm regulatora PID będzie realizowany przez pewien układ fizyczny, dostępny na rynku, albo zaprojektowany przez nas, w którym wartości nastaw będą mogły się zmieniać tylko w określonych granicach:
\(0 < k_P^{min}\leq \ k_P\leq \ k_P^{max},\, 0 < T_I^{min}\ \leq T_I\leq \, T_I^{max},\, 0\leq \ T_D^{min}\ \leq T_D\ \leq T_D^{max}. \qquad (1.6)\)
Nie jest wykluczone, że ze względów konstrukcyjnych wystąpią wspólne ograniczenia np.:
\(g((T_I,T_D)\leq 0 \qquad (1.7)\)
gdzie \(\mathbb{R}^2((T_I,T_D) \mapsto g((T_I,T_D)\mathbb{R}\) jest znaną funkcją.
Podsumowując, zadanie projektowania autopilota dla statku, przy założeniu, że jako regulator wybieramy regulator PID, sprowadziliśmy do następującego
zadania minimalizacji (optymalizacji):
znaleźć takie wartości nastaw kP, TI ,TD w zbiorze określonym nierównościami (1.6) i (1.7) dla których funkcja oceny (kryterialna) \(f \, (f^1 \)albo \(f^2\)) przyjmuje najmniejszą wartość na tym zbiorze,
co będziemy zapisywać:
znaleźć \((k_P^o,T_I^o,T^o_D)= \mathrm{argmin}_{(k_P,T_I,T_D) ∈ X}f(k_P,T_I,T_D)\)
gdzie
\(X = {(k_P,T_I,T_D) | 0 < k_P^{min}\ leq k_P\ leq k_P^{max},\, 0 < T_I^{min}\leq T_I\ leq T_I^{max},\, 0\ leqT_D^{min}\ leq T_D\ leq T_D^{max}, g(T_I,T_D)\leq 0 } \qquad(1.8)\)
jest zbiorem dopuszczalnym.
Zwróćmy tu uwagę na, pozornie niewielką, różnicę w określeniu (1.8) zbioru dopuszczalnego w stosunku do przekładu poprzedniego. Wśród nierówności definiujących powyższy zbiór są ostre (<) i słabe (\(\leq\)), natomiast określenie zbioru dopuszczalnego (1.5) w poprzednim przykładzie zawierało tylko nierówności słabe. W konsekwencji zbiór (1.5) jest zbiorem domkniętym, a zbiór (1.8) może nie być zbiorem domkniętym. Jak się o tym przekonamy w punkcie 1.1 modułu trzeciego może to mieć przykrą konsekwencję w postaci nieistnienia rozwiązania zadania z nie domkniętym zbiorem dopuszczalnym.
Następny, krótki przykład związany jest z teorią identyfikacji i jest w zasadzie przykładem z dziedziny matematyki stosowanej.
2.3. Zadanie optymalnej identyfikacji modelu transformacji (funkcji)
Interesuje nas określenie funkcji H opisującej zależność między dwiema wielkościami x i y. Jeżeli wartości wielkości (zmiennych) możemy mierzyć za pomocą fizycznego eksperymentu wiążącego w (uporządkowane) pary liczbowe wartości tych wielkości, znamy ciąg pomiarów \({(x_k, y_k)}\), to mamy do czynienia z tzw. zadaniem identyfikacji modelu funkcji.
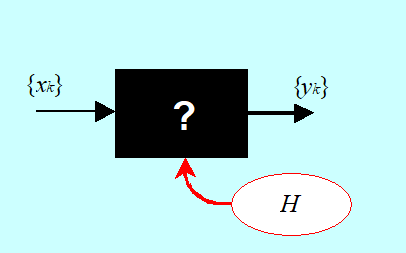
W praktyce rzadko kiedy mamy do czynienia z czarną skrzynką taką jak na rysunku. Często związek łączący zmienne znamy z dokładnością do n-wymiarowego wektora parametrów liczbowych \(\alpha = (\alpha_1,..., \alpha_n)\). Skrzynka jest „szara” i wyznaczyć trzeba konkretną wartość parametrów.
Zapiszmy teraz stosowne zadanie optymalizacji przyjmując, że mamy do czynienia z szarą skrzynką.
Przyjmujemy wiec, że znamy funkcję dwu zmiennych
\(\mathbb{R}\times\mathbb{R}^n∍(x,α)↦H(x,α)∈R\)
(\(\alpha \) jest n-wymiarowym wektorem parametrów), a także ciąg par pomiarów \({(x_k,y_k)}_{k=1}^m.\)
Jeżeli dla każdego (\(\alpha \) zdefiniujemy ciąg różnic między wielkością zmierzoną a przewidywaną przez model
\((\forall\ k\in\overline{1,m})\ r_k(\alpha)=y_k-H(x_k,\alpha),\)
to jako kryterium wyboru „najlepszego (\(\alpha \) ” powinniśmy wybrać funkcję, która te wszystkie różnice będzie minimalizować. Ponieważ dodatnie różnice są tak samo „złe” jak ujemne, to funkcja oceniająca, w najprostszym przypadku, powinna mieć jedną z dwu form
\(\alpha\mapsto\ f^1(\alpha)=\sum_{k=1}^{m}\left|r_k(\alpha)\right|\mathrm{\mathrm{\ \ }albo\ \ }\alpha\mapsto f^2(\alpha)=\sum_{k=1}^{m}\left(r_k(\alpha)\right)^2 ,\)
(proszę porównać przykład poprzedni).
Jak pamiętamy, do ostatecznego sformułowania zadania optymalizacji potrzebne jest określenie zbioru dopuszczalnego. W przypadku zadań identyfikacji czasami nie ma wyraźnych ograniczeń na wartości parametrów. Gdy takie ograniczenia występują zapiszemy je w bardzo ogólny sposób, jako wymaganie \(\alpha \in A\) , gdzie domknięty zbiór \(A \in \mathbb{R}^n \)jest znany.
Możemy więc sformułować np. następujące zadania minimalizacji (identyfikacji modelu):
- Pierwsze, wymyślone w pierwszej połowie XIX w. przez K. Gaussa: tzw. zadanie doboru parametrów modelu nieliniowego metodą najmniejszych kwadratów
znaleźć \(\alpha^o={\rm argmin}_{\alpha\in\ \mathbb{R}^n}{\sum_{k=1}^{m}\left(y_k-H(x_k,\alpha)\right)^2}.\)
- Drugie
znaleźć \(\alpha^o={\rm argmin}_{\alpha\in\ A}{\sum_{k=1}^{m}\left|y_k-H(x_k,\alpha)\right|}.\)
Zwróćmy tu uwagę na fakt, że zadanie Gaussa sformułowaliśmy jako zadanie bez ograniczeń, a zadanie drugie jako zadanie z ograniczeniami na wartości parametrów. Ponadto w praktyce, podobnie jak w przykładzie dotyczącym projektowania autopilota opisanym w punkcie 2.2, częściej parametry modelu dobiera się metodą najmniejszych kwadratów (funkcja \(f^2\)), bo to zadanie jest łatwiej rozwiązać (nawet gdy dodamy do niego ograniczenia).
Co łączy te trzy przykłady?
W obu, wykorzystując wiedzę i doświadczenie konkretnych nauk danego rodzaju sformalizowano zadanie optymalizacji, inaczej mówiąc zbudowano matematyczny model zadania optymalizacji o tej samej, typowej strukturze. Przedstawimy teraz ten abstrakcyjny model formalnie.
2.4. Ogólna postać zadania optymalizacji (dla minimalizacji)
Rozważamy n-wymiarową przestrzeń wariantów \(ℝ^n \ni x\). W przestrzeni tej zadana jest funkcja oceniająca (wyboru, celu)
\(f:\mathbb{R}^n\rightarrow\ \mathbb{R},\)
pozwalająca porównywać warianty, przy czym z dwu wariantów ten jest lepszy dla którego funkcja oceniająca przyjmuje mniejszą wartość, oraz zbiór wariantów dopuszczalnych \(D \subseteq ℝ^n,\) gdzie, dla zadania minimalizacji
\(D={x\in\mathbb{R}^n|(\forall j\in\overline{1,m})g_j(x)\le0\land(\forall k\in\overline{1,p})h_k(x)=0\land(\forall i\in\overline{1,r})\ x_i\in[x_i^-,x_i^+]}, \qquad(1.9)\)
a \(g_j:\mathbb{R}^n\rightarrow\ \mathbb{R},j\in\overline{1,m}\) to funkcje określające ograniczenia nierównościowe \(D_\leq\) , natomiast \(h_k:\mathbb{R}^n\rightarrow\mathbb{R}, k\in\overline{1,p}\) to funkcje określające ograniczenia równościowe \(D_= \). W określeniu zbioru dopuszczalnego wy-różniliśmy jeszcze, często występujące w zdaniach praktycznych, ograniczenia kostkowe \(xi \in [xi–,xi+], i\in\overline{1,r}\), oznaczymy je \(D_K\) , chociaż formalnie rzecz biorąc są to ograniczenia nierównościowe. Zauważmy, że w celu uniknięcia niebezpieczeństwa określenia zbioru pustego, ograniczeń równościowych nie może być więcej niż \(n \,(p \leq n).\) Z oczywistego powodu, ograniczeń kostkowych też nigdy nie jest więcej niż n.
Zatem zbiór wariantów dopuszczalnych (1.9) jest iloczynem trzech zbiorów
\(D=D_\le\cap D_=\cap D_K\).
Możemy teraz formalnie określić zadanie optymalizacji.
Trzeba znaleźć
że \(\forall x \in D)\,f(x^o)\leq f(x)\) .
Wiele zadań praktycznych (nie wszystkie!) można w ten sposób zapisać.
Dlaczego zapisaliśmy zadanie minimalizacji?
Wystarczy więc rozważać tylko jeden z dwu operatorów ekstremalizacji. Do systemu definicji przyjętych w matematyce, lepiej pasuje minimalizacja i w zasadzie wszystkie rozważania teoretyczne prezentowane w literaturze dotyczą minimalizacji.
Zwrócimy teraz krótko uwagę na pewne własności funkcji minimalizowanej i konsekwencje przyjętej definicji zbioru dopuszczalnego.
W zapisanym ogólnym zadaniu optymalizacji ZO trzeba
znaleźć taki wektor \(x^o\in D\), że \((\forall x \in D) f (x^o) \leq f (x)\) .
Jest to wymaganie porównania wszystkich wariantów (wektorów) x ze zbioru dopuszczalnego D i znalezienia takiego wariantu dopuszczalnego, \(x^o \in D\), którego ocena, \(f (x^o)\), w porównaniu ze ocenami wszystkich wariantów dopuszczalnych jest nie większa, \((\forall x \in D) f (x^o) \leq f (x)\). Tak określony wektor, w opracowaniach dotyczących optymalizacji nazywa się punktem minimum globalnego funkcji f na zbiorze D, bo przy jego ustalaniu porównujemy wszystkie punkty dopuszczalne.
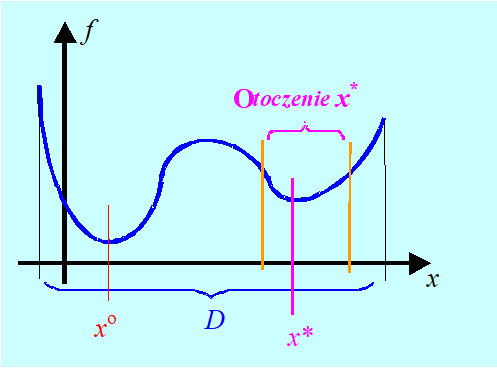
Jaka jest konsekwencja przyjęcia takiej terminologii? Popatrzmy na Rys. 1.6 przedstawiający funkcję jednej zmiennej. Obok minimum globalnego w punkcie \(x^o \)ma ona tzw. minimum lokalne w punkcie \(x^*\). Dokładna definicja jest następująca:
\((\forall x \in \textbf{O}(x*) \cap D) f (x*) \leq f (x).\)
Zauważmy, że zgodnie z tymi definicjami – punkt minimum globalnego jest najlepszym z minimów lokalnych.
W przedstawionym ogólnym zadaniu optymalizacji szukamy wariantu dopuszczalnego minimalizującego funkcję celu. Takie wymaganie nie występuje w każdym zadaniu optymalizacji. Czasami ważna jest tylko wartość optymalna funkcji oceniającej, natomiast argumenty optymalizujące – nie są interesujące. Rozważa się wtedy zadanie prostsze:
znaleźć \(f^o=\min_{x\in D}{f}(x).\)
Funkcje minimalizowane mogą być różne, a ich zachowanie zaskakujące. Wygodnym narzędziem pozwalającym zorientować się co nas może czekać w świecie minimalizacji, a także wyrabiającym intuicję są dla funkcji dwu-argumentowych wykresy poziomicowe (mapy).
Takim wykresem posłużymy się do ustalenia ile minimów lokalnych ma funkcja
\(x ↦ f (x) = 2(x_1)^2 + 4x_1(x_2)^3 – 10x_2x_1 + (x_2)^2\)
w zbiorze
\(D = {(x_1,x_2) | x_1 (x_2)^2(2.4 + x_2) \leq 3\wedge {\frac{3}{2}}x_1 + x_2 \geq 0\wedge (–3 \leq x_i \leq 3, i = 1,2)}.\)
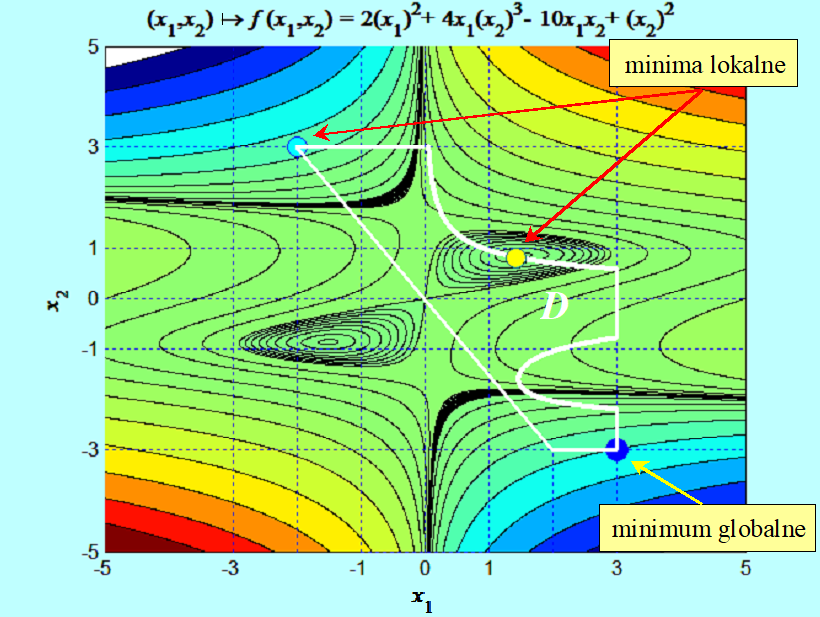
Zauważmy, że funkcja f i funkcje \(g_j \)na pierwszy rzut oka nie sprawiają wrażenia, że geometria zbiorów przez nie wyznaczonych jest tak skomplikowana. Zauważmy, że wszystkie minima lokalne (w tym przykładzie) wynikają z obecności ograniczeń, czasami mówi się, że są indukowane przez ograniczenia.
Zastanówmy się teraz przez chwilę nad strukturą zbioru dopuszczalnego (1.9). Jest on iloczynem trzech zbiorów: \(D=D_\leq \cap\ D_=\cap\ D_K.\) Naszkicujmy te zbiory.
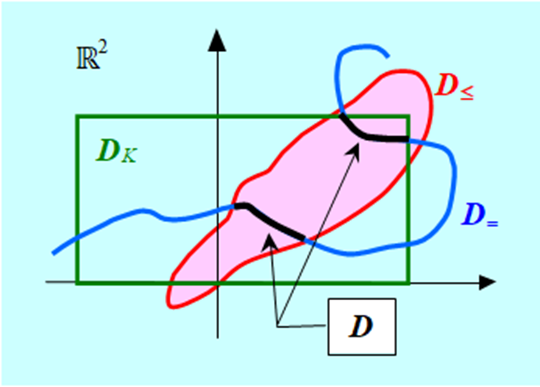
Narysowany zbiór D zaznaczony na czarno jest „mały” i na dodatek składa się z dwu rozłącznych części, które nie mają wnętrza („nie mają punktów w środku”). Widać, że najbardziej restrykcyjne są ograniczenia równościowe. Bez nich, omawiany zbiór dopuszczalny byłby spójny (składałby się z jednej części) i tak jak zbiór z rysunku poprzedniego miał niepuste wnętrze.
3. Klasyfikacje zadań optymalizacji
Każde sensowne kryterium podziału zbioru pewnych obiektów powinno być konstruowane z myślą o wartości praktycznej takiego podziału. Większość stosowanych klasyfikacji zadań optymalizacji dzieli je na zadania „łatwiejsze” i „trudniejsze”. My też pójdziemy tą drogą.
Pierwszy podział, to podział podstawowy na
- Zadania bez ograniczeń (wszystkie warianty są dopuszczalne).
- Zadania z ograniczeniami (zadania w których określono zbiór wariantów dopuszczalnych).
Rozwiązać zadanie bez ograniczeń jest prościej niż z ograniczeniami.
Drugi podział to wyróżnienie
- Zadań liniowych, w których wszystkie funkcje określające zadanie (tzn. funkcje \(f, g_j , h_k \)) są afiniczne, tzn. są, przy notacji macierzowej, funkcjami postaci
\(x\mapsto\ a^Tx+\gamma=\sum_{i=1}^{n}{a_ix_i+\gamma},\)
gdzie x jest wektorem kolumnowym, \( \alpha^T \) oznacza wektor wierszowy, a \(\gamma\) jest liczbą.
- Zadań nieliniowych, w których co najmniej jedna funkcja nie jest afiniczna.
Przy tym podziale mamy pewien kłopot terminologiczny. Dla matematyka funkcja liniowa to funkcja \(x\mapsto\ a^Tx,\) przyjmująca wartość zero w zerze. Inżynier najczęściej rozciąga tę nazwę i na funkcje afiniczne.
Funkcja \(x\mapsto f(x)=c^Tx+\gamma\) przy nieograniczonym x może przyjmować dowolnie małe albo dowolnie duże wartości. Zadanie liniowe mają więc zawsze ograniczenia.
Zadanie optymalnego planowania produkcji omawiane w punkcie 2.1 jest liniowe i nie jest to przypadek. Wiele zadań optymalizacji, które muszą rozwiązywać menedżerowie daje się zapisać jako zadania liniowe.
Rys.1.7 pokazuje, że funkcje nieliniowe mogą zachowywać się bardzo różnie. Za „najlepiej prowadzące się” funkcje nieliniowe matematycy uważają dwie klasy funkcji: klasę funkcji wypukłych i klasę funkcji gładkich. Dla porządku przypomnę ich definicje.
\((\forall0 < \alpha < 1 )(\forall x^0,x^1\in X)f(\alpha x^0+(1-\alpha)x^1)\leq\alpha f(x^0)+(1-\alpha)f(x^1).\)
Wygodniejszą z punktu analizy metod optymalizacji a równoważną definicje funkcji wypukłej podamy w punkcie 1 Modułu trzeciego.
Pewnego wyjaśnienia wymaga, jakie własności powinna mieć funkcja aby była gładka. Najsłabsze wymaganie, to wymaganie różniczkowalności. Przy czym, intuicyjnie, funkcja mająca pierwszą pochodną ciągłą jest „bardziej gładka” niż funkcja tylko różniczkowalna itd. Pokazuje to Rys. 1.9 ciągłej funkcji sklejonej
\(x\mapsto\ f(x)=\left\{\begin{matrix}\ \ \ ax^2\mathrm{\mathrm{\ \ }dla\ }x\geq0\\-ax^2\mathrm{\mathrm{\ }gdy\ przeciwnie}\\\end{matrix}\right., \, \mathrm{dla } \, a > 0.\)
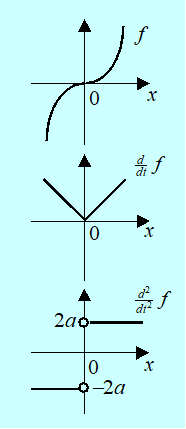
Intuicyjnie jest oczywiste, że zadnia liniowe są prostsze od nieliniowych.
Trzeci podział to
- Zadania nieróżniczkowalne gdy co najmniej jedna funkcja zadania nie jest różniczkowalna.
- Zadania gładkie klasy Cn , gdzie n jest rzędem ciągłej pochodnej funkcji występującej w zadaniu mającej ją najniższą.
Następny podział związany jest z wypukłością
- Zadania wypukłe gdy funkcja wyboru f i zbiór dopuszczalny D są wypukłe.
- Zadania niewypukłe gdy funkcja f lub zbiór D nie jest wypukły.
Odpowiedz na pytanie, kiedy zbiór dopuszczalny D określony wzorem (1.9) jest wypukły daje następujący lemat.
\((\forall j \in \overline{1,m}) g_j\) jest funkcją wypukłą i \((\forall k \in \overline{1,p}) h_k\) jest funkcją afiniczną
to zbiór dopuszczalny D określony wzorem (1.9) jest wypukły.
Zatem liniowe zadanie optymalizacji jest zadaniem wypukłum.
O zadaniach wyróżnionych przez dwie ostatnie klasyfikacje można powiedzieć, że najdogodniejsze do optymalizacji są zadania co najmniej dwukrotnie różniczkowalne w sposób ciągły i jednocześnie wypukłe.
Sformułowana w punkcie 2.4 ogólna postać zadania optymalizacji ZO jest zadaniem tzw. optymalizacji statycznej. Dlaczego statycznej? Porównywane warianty x są charakteryzowane przez wektory o skończonej liczbie współrzędnych (oznaczyliśmy ją przez n) \(x\in\ {\mathbb{R}}^n\). Nie porównujemy w nim różnych zachowań określonego obiektu w czasie, a więc różnych funkcji zmiennej, która przyjmuje wartości z pewnego przedziału liczb rzeczywistych. Takie zadania optymalizacji nazywa się zadaniami optymalizacji dynamicznej.
Jednym z najprostszych (w sformułowaniu) zadań optymalizacji dynamicznej jest tzw. zadanie wyznaczenia sterowania czaso-optymalnego.
Zadanie wyznaczenia sterowania czaso-optymalnego
Jako przykład takiego zadania rozważmy zagadnienie przesunięcia ciała (wagonika) o masie m z pewnego położenia początkowego x0 w zadane położenie końcowe xf za pomocą silnika elektrycznego.
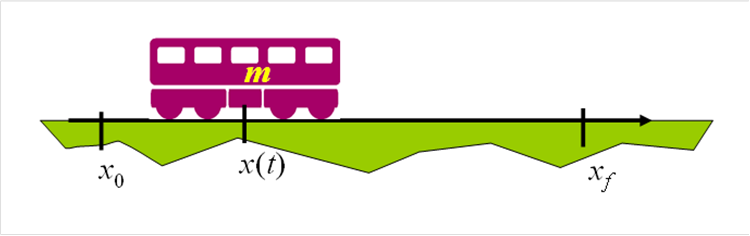
W praktyce moment rozwijany przez silnik nie może przekroczyć pewnej wartości maksymalnej Mmax , co daje pierwsze ograniczenie
\((\forall t\geq t_0)|M(t)|\leq M_{\mathrm{max}}\)
czyli nieskończoną i nieprzeliczalną liczbę ograniczeń chwilowych.
Zauważmy, że zgodnie z przyjętym określeniem w zadaniach optymalizacji statycznej liczba ograniczeń musi być przeliczalna i skończona.
Zadanie wyznaczenia sterowania czaso-optymalnego formułuje się następująco:
znaleźć takie sterowanie (zmiany w czasie momentu) \([t_0,\infty[∍t↦Mo(t)∈R\), które przeprowadzi ciało z położenia początkowego \(x_0\) do położenia końcowego \(x_f \)w jak najkrótszym czasie To i ponadto w położeniu końcowym ciało będzie w spoczynku, to znaczy
Zadanie wydaje się tak proste, że można próbować je rozwiązać kierując się tylko podstawową znajomością fizyki i zdrowym rozsądkiem.
Ponieważ przyspieszenie wagonika jest ograniczone (nie może być większe niż Mmax/m ) to przy założeniu (istotnym), że w chwili początkowej wagonik był w spoczynku:
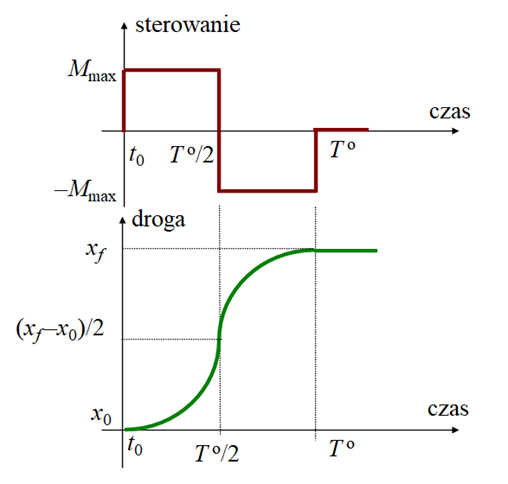
Pojawia się tu istotny problem tego typu zadań: w zbiorze jakich funkcji szukamy rozwiązań?
Z matematycznego punktu widzenia nie jest to trudne pytanie – funkcje które mogą zawierać skokowe zmiany, to tzw. funkcje przedziałami ciągłe.
Ze względu na złożoność nie będziemy analizowali dalej problemów związanych z techniczną realizacją przybliżenia sterowania optymalnego wyznaczonego w tym zadaniu.
Przykład 1.1 przedstawił podstawowe różnice między zadaniami optymalizacji statycznej i dynamicznej, w tych ostatnich
- Szukamy funkcji czasu a nie wektorów liczbowych. Nasze rozważania przenoszą się z przestrzeni \(\mathbb{R}^n\\) w dużo bardziej skomplikowane przestrzenie funkcyjne.
- Ograniczeniem jest (wektorowe) równanie różniczkowe.
- Może występować nieprzeliczalna liczba ograniczeń chwilowych.
- Często występuje wymaganie określonego zachowania rozwiązania równania różniczkowego w konkretnej chwili czasu, np. wymaganie podobne do (1.11).
Na poniższym rysunku podsumowujemy nasze dotychczasowe rozważania klasyfikacyjne.
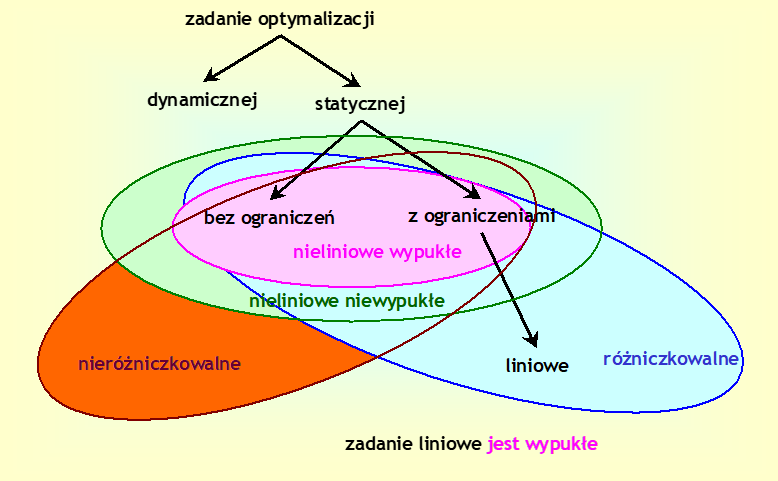
Od funkcji gj oraz hk określających zbiór dopuszczalny w definicji ogólnego zadania optymalizacji ZO nic nie wymagamy – mogą być dowolne.
Rozważmy zatem zbiór dopuszczalny określony następująco
\(D = {(x_1, x_2) | sin(\pi x_1) = 0 \wedge sin(\pi x_2) = 0}.\)
Jego obraz jest następujący.
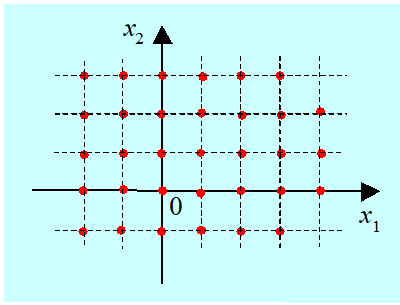
Jest to nieskończony, przeliczalny zbiór izolowanych punktów płaszczyzny, a warianty są opisywane wektorami całkowitoliczbowymi. Zbiory tego typu często nazywa się zbiorami dyskretnymi.
W związku z tym możemy jeszcze wyróżnić:
- Zadania (statycznej) optymalizacji dyskretnej (w liczbach całkowitych).
- Zadania optymalizacji (statycznej) (bez dodatkowego określenia, co oznacza, że z tym terminem związany jest zbiór dopuszczalny wektorów, których składowe mogą przyjmować dowolne wartości rzeczywiste).
Przedstawiony powyżej przykład ograniczeń definiujących zbiór całkowitoliczbowy jest przykładem teoretycznym i ma głownie na celu pokazanie bogactwa „różnorodności” jakie kryje w sobie przyjęte, pozornie proste, określenie zbioru dopuszczalnego. Teraz przedstawię przykład praktycznego zadania optymalizacji dyskretnej, zadania które musi rozwiązać kierownictwo koncernu planującego budowę nowych zakładów produkcyjnych.
Pewien koncern zamierza znacznie powiększyć udział jednego ze swoich niepodzielnych produktów (niepodzielny produkt to np. lodówka, lub lokówka, a także paleta z kubeczkami jogurtu) w rynku i w tym celu planuje wybudowanie szeregu zakładów produkcyjnych go wytwarzających. Menedżerowie koncernu chcą podjąć decyzję minimalizującą łączne koszty lokalizacji i transportu produktu. Przyjmijmy, że rozważnych jest I miejsc lokalizacji. Niech indeksem lokalizacji będzie I, zatem \(i\in\overline{1,n}\). Możliwości produkcyjne zakładu zlokalizowanego w miejscu i oznaczymy przez Si a koszt uruchomienia w nim produkcji (dla uproszczenia niezależny od wielkości produkcji) – przez \( \gamma _i\) .
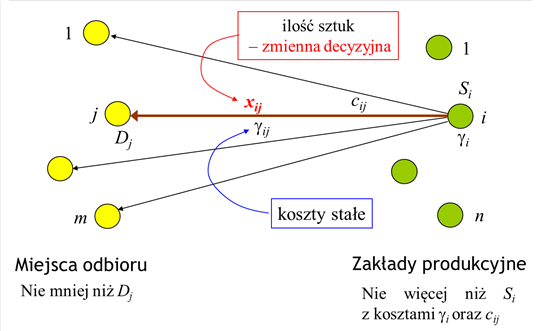
W matematycznym sformułowaniu zadania optymalizacji musimy uwzględnić jeszcze dwa fakty:
- nie jest oczywiste, że trzeba wybudować nowe fabryki we wszystkich miejscach – trzeba wybrać te miejsca, które dadzą w sumie minimalny koszt uruchomienia produkcji i transportu;
- przewożenie produktu z danego zakładu do wszystkich miejsc odbioru może być zbyt kosztowne, trzeba wybrać właściwą strukturę połączeń między dostawcami a odbiorcami.
1,\,\mathrm{gdy\,miejsce}\,i\,\mathrm{zostalo\,wybrane} \\
0,\,\mathrm{w\,przeciwnym\,przypadku} \\
\end{matrix}\right.,i\in \overline{1,n}\)
\(v_{ij}=\left\{\begin{matrix}
1,\,\mathrm{gdy\,trasa}\,i\to j\,\mathrm{jest\,wykorzystywana} \\
0,\,\mathrm{w\,przeciwnym\,przypadku} \\
\end{matrix}\right.,(i,j)\in \overline{1,n}\times \overline{1,m}\)
Oczywiste nierówności określające zbiór dopuszczalny są następujące:
- wynikające z ograniczeń możliwości produkcyjnych i-tego zakładu
- nieujemności wielkości przewozu (tylko z miejsca i do miejsca j)
Przedstawione trzy grupy nierówności nie opisują wszystkich ograniczeń, ponieważ nie są w nich uwzględnione następujące związki logiczne między xij (ilością sztuk produktu przewożonego trasą \(i \mapsto j\) )a vij (zmienną binarną określającą czy trasa \(i \mapsto j)\) jest wykorzystywana):
Związki te w obowiązujący dla sformułowania zadania optymalizacji „schemat nierówności” można włożyć następująco.
Zauważmy, że \((\forall i,j)[x_{ij}>0\Rightarrow v_{ij}=1]≡(∀i,j)[vij=0⇒xij=0]\), bo mamy ograniczenie (1.13).
Dla każdej pary \((i, j)\)oznaczamy \(L-{ij} = min{Si ,Dj }.\) Wprowadźmy ograniczenie
Zatem wprowadzenie ograniczenia (1.17) oznacza uwzględnienie wymagania logicznego (1.15).
Zauważmy teraz, że w punkcie minimalizującym \(((x_{ij}^o),(v_{ij}^o)) \) mamy
Spełnienie w punkcie minimalizującym tego warunku zwalnia nas z konieczności uwzględnienia warunku (1.16) jako równoważnego z warunkiem
\(D={((x_{ij}),(y_i),(v_{ij}))\in\mathbb{Z}^{n(2m+1)}|(\forall
i\in\overline{1,n})y_i\in{0,1}\land(\forall(i,j)\in\overline{1,n}\times\overline{1,m})v_{ij}\in{0,1}\land(1.12)\land(1.13)\land(1.14)\land(1.17)},\)
gdzie przez ℤ (die Zahlen – liczby) oznaczono zbiór liczb całkowitych tj. zbiór {...,–1,0,1,2,...}.
Dla porządku zapiszmy jeszcze zadanie, które trzeba rozwiązać.
Zadanie lokalizacji fabryk z uwzględnieniem kosztów uruchomienia produkcji i transportu
- określony powyżej zbiór dopuszczalny D przy niewłaściwym doborze parametrów Si i Dj może być pusty – jest tak gdy suma maksymalnych mocy produkcyjnych jest mniejsza od sumy minimalnych zapotrzebowań.
- sformułowane powyżej zadanie jest zadaniem tzw. liniowej optymalizacji dyskretnej.
Po wyjaśnieniach przykładu, możemy podać formalną definicję zadania optymalizacji dyskretnej.
Rozważaliśmy zadania optymalizacji, w których zmiennymi są wektory liczb rzeczywistych, jak mówimy zmienne są ciągłe oraz dyskretne zadania optymalizacji, gdzie zmienne to wektory całkowitoliczbowe (zmienne dyskretne). Mogą więc być zadania mieszane, w których część zmiennych jest ciągła, a pozostała – dyskretna.
Przedstawione dotąd rozważania pokazały, że analizując zadania optymalizacji, obok zwrócenia uwagi na stopień trudności znajdowania ich rozwiązania („łatwiejsze – trudniejsze”, czyli: bez ograniczeń – z ograniczeniami, liniowe – nieliniowe itp.) trzeba także zwrócić uwagę na ich strukturę, co prowadzi do klasyfikacji takiej jak na ostatnim rysunku tego rozdziału.
Wyposażeni w przedstawiony zestaw definicji możemy teraz precyzyjniej określić zakres tego podręcznika. Zajmować się w nim będziemy podstawowymi własnościami zadań (statycznej) optymalizacji (ciągłej) to jest zadań ZO a także poznamy algorytmy służące do rozwiązywania takich zadań.
4. Jak tworzyć algorytmy optymalizacji?
Powyżej ustaliliśmy, że zajmować się będziemy różnymi wariantami zadania statycznej minimalizacji ciągłej. Przypomnijmy jego formalne określenie, tj. postać ogólną ZO.
Dana jest n-wymiarowa przestrzeń wariantów \( ℝ^n \ni x \). W przestrzeni tej określone są
- funkcja oceniająca (wyboru, celu) \(f:\mathbb{R}^n\rightarrow\ \mathbb{R},\)
- funkcje określające ograniczenia nierównościowe \ (D \leq g_j:\mathbb{R}^n\rightarrow\mathbb{R},\,j\in\overline{1,m}, \)
- funkcje określające ograniczenia równościowe \( D= h_k:\mathbb{R}^n→\mathbb{R}, k∈¯(1,p) \), które razem z ograniczeniami kostkowymi DK określają
- zbiór wariantów dopuszczalnych
\( D = {x \in \mathbb{R} n |( \forall j \in \overline{1,m}) g_j(x) \leq 0 \wedge( \forall k \in \overline{1,p}) h_k(x) = 0 \wedge ( \forall i \in \overline{1,r}) x_i \in [x_i^–,x_i^+]}. \)
Trzeba znaleźć
\(x^o={\rm argmin}_{\ x\in D}{f}(x).\)
Jak pamiętamy, czasami rozważa się zadanie prostsze:
znaleźć \(f^o=\min_{\ x\in D}{f}(x),\)
w którym szukamy minimalnej wartości funkcji w zbiorze D.
W sformułowaniu zadania minimalizacji jest polecenie „znaleźć”. Ale, w odróżnieniu od wielu innych zadań, matematyka nie dostarcza nam wprost narzędzi pozwalających bezpośrednio to polecenie wypełnić.
Jak znaleźć (o ile istnieje) wartość zmiennej minimalizującej np. funkcję \(x\mapsto x(x-1)\)?
Najprostsza odpowiedź – narysować.
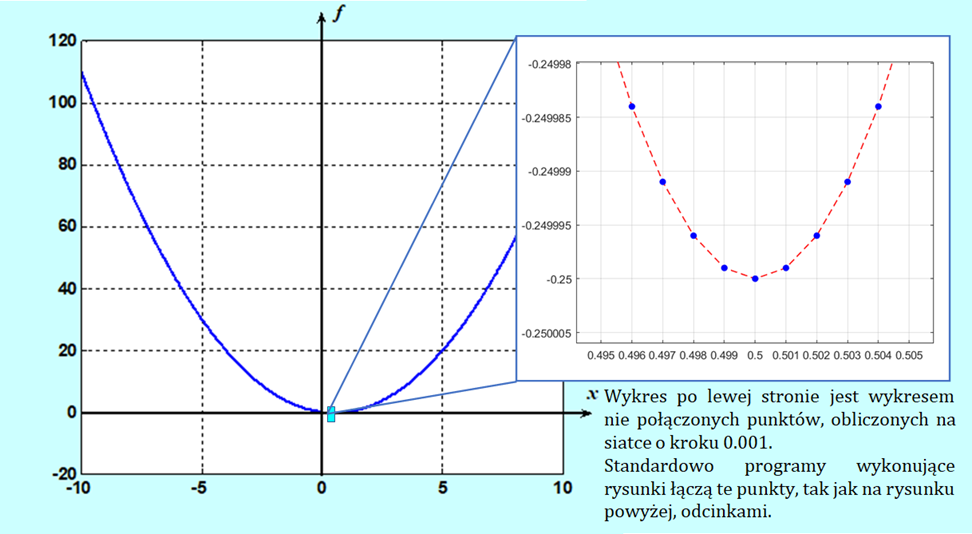
Niestety potrafimy tylko szkicować przebieg funkcji jednej zmiennej (uczyliśmy się tego w ramach badania zmienności funkcji poznając analizę matematyczną). Komputer narysuje funkcję dwu zmiennych. Lecz nawet w tych relatywnie prostych przypadkach analiza rysunku da raczej odpowiedź na pytanie: czy minimum istnieje?, a nie, gdzie dokładnie leży. Posługiwanie się metodami graficznymi (co dla rysunków komputerowych jest de facto przeglądem wartości funkcji w wybranych punktach) niesie też inne niebezpieczeństwa, o których dowiemy się w dalej.
Mamy więc jeszcze dwie drogi realizacji polecenia „znaleźć”
- droga rachunkowa,
- droga właściwie zorganizowanego poszukiwania.
Gdy chcemy pójść drogą pierwszą, tzn. gdy chcemy znaleźć rozwiązanie zadania optymalizacji drogą rachunkową musimy oryginalne sformułowanie przekształcić do postaci pozwalającej na wykonanie stosownych rachunków. Jak się o tym przekonamy (moduł trzeci i piąty) jest to najczęściej odpowiednio określony układ równań i nierówności (obecność nierówności jest kłopotliwa), którego rozwiązanie może być (warunek konieczny!) lub jest (warunek dostateczny) rozwiązaniem analizowanego zadania optymalizacji.
Gdy nie potrafimy, nie możemy, albo nie chcemy skorzystać z metody przekształcenia zadania optymalizacji, do znalezienia jego rozwiązania musimy posłużyć się mniej lub bardziej wymyślną metodą poszukiwania – wybrać algorytm wykonujący ciąg dobrze określonych operacji rachunkowych (kroków), który w momencie zatrzymania wskaże wariant będący rozwiązaniem zadania. Takich algorytmów wymyślono już tysiące. Zauważmy, że wiele z nich podobnych jest do algorytmów rozwiązywania równań i nierówności, bo przecież nie każde równanie potrafimy rozwiązać rachunkowo.
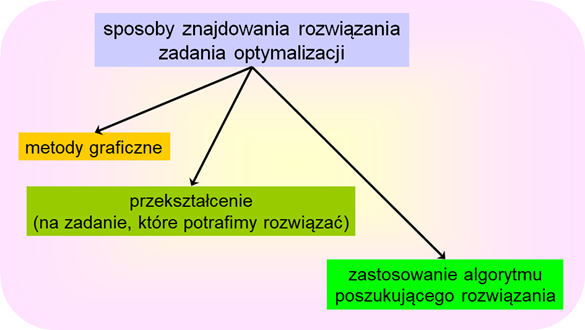
Najczęściej mamy do czynienia z ostatnim przypadkiem wspomnianym powyżej. Po prostu nie można znaleźć rozwiązania zadania optymalizacji drogą rachunkową. Zatem musimy posłużyć się wybranym algorytmem.
Z gruba rzecz biorąc każdy algorytm poszukiwania opiera się na informacji a priori oraz na stosownym przetwarzaniu informacji zdobywanej na bieżąco (w kolejnych krokach poszukiwania). Przy czym, jak się już za chwilę przekonamy, specyfika algorytmów optymalizacji polega na tym, że bieżąca informacja odnosi się tylko do aktualnego punktu (lub jego małego otoczenia), w którym „znajduje” się algorytm – bieżąca informacja jest zawsze lokalna. Informacją a priori może być każda informacja dotycząca własności i kształtu funkcji oceniającej.
Zostawiając na później rozważania teoretyczne prowadzące do określenia stosownych warunków optymalności (wspomnianych układów równań i nierówności, które musi spełniać wariant optymalny) przedstawimy teraz dyskusję prowadzącą do ustalenia podstawowych problemów jakie stoją przed twórcami algorytmów optymalizacji.
Tak się złożyło, że twórcy i badający algorytmy optymalizacji traktują zwykle w swojej codziennej pracy obiekty swoich zainteresowań jak stworzenia, co przy opisie oznacza, że ich funkcjonowanie jest przestawiane jako wynik ich rozmyślnego działania. I ja, jako współtwórca paru algorytmów optymalizacji, też przyjmę dalej taką konwencję.
Wyobraźmy więc sobie, jak może „rozumować” Algorytm (komputerowy), postawiony na schodach o stopniach różnej wysokości, którego zadaniem jest zejście do najniższego poziomu schodów.
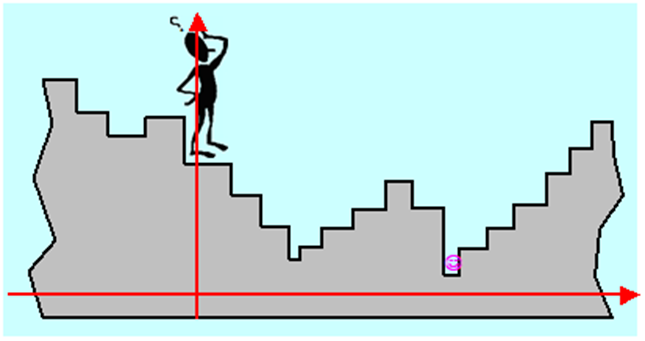
Jest rzeczą oczywistą, że Algorytm całych schodów nie widzi (ograniczenie bieżącej informacji), natomiast potrafi ocenić położenie stopnia w stosunku do ustalonego poziomu odniesienia, nazwiemy je wysokością (dla każdego wariantu potrafi obliczyć wartość funkcji celu). Wie, że stoi na jakimś stopniu i może się ruszać w jedną ze stron, przyjmijmy, że prawą i lewą. Jeżeli założymy, że jest „sprawny fizycznie” to może przeskakiwać kilka stopni na raz. Stopnie na schodach, nawet nieskończonych, można policzyć, każdy stopień to wariant, a więc zbiór wariantów jest przeliczalny.
Jeżeli liczba stopni jest skończona (zbiór dopuszczalny jest skończony, a więc ograniczony) i nie jest zbyt duża w stosunku do szybkości poruszania się po nich Algorytmu, to przy założeniu, że jest on w stanie powiązać w pary stopień i jego wysokość i zapamiętać te pary, postępowanie jest oczywiste: być na wszystkich stopniach, określić ich wysokość i wybrać ten o najniższej (przeszukać wszystkie warianty). Gdy stopni jest bardzo dużo, Algorytm może odwiedzać np. co dziesiąty (przeszukanie wybranych punktów węzłowych), albo wybierać je w sposób przypadkowy zgodnie z rozkładem równomiernym (równomierne przeszukanie przypadkowe). Takie postępowania nie gwarantują jednak znalezienia rozwiązania – Algorytm może przeskoczyć nad stopniem najniższym. Powstaje więc problem dokładności znalezionego rozwiązania, ściśle związany z ilością odwiedzonych stopni (ilością punktów próbnych) ale też i ze sposobem wybierania stopni do odwiedzenia.
Co jednak ma zrobić Algorytm gdy schodów jest nieskończenie dużo (w przypadku schodów – zbiór dopuszczalny nie jest ograniczony, w sytuacji ogólniejszej – nie jest policzalny)?
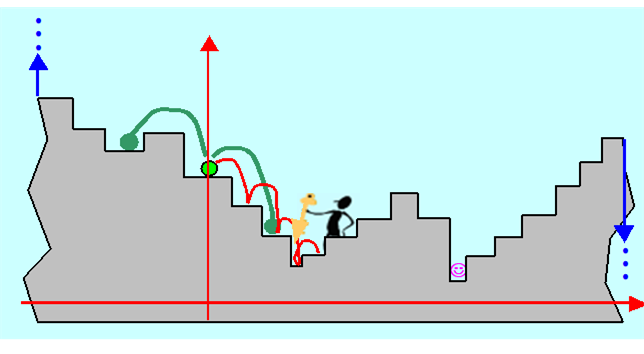
Może, startując ze stopnia, na którym stoi (jasno-zielony) wykonać krok (ustaloną liczbę kroków) w prawo, wrócić i wykonać krok w lewo. W ten sposób ustali, że lokalnie schody opadają w prawo (informacja bieżąca). Wyciągnie stąd wniosek, że należy schodzić w prawo. Gdy ma dużo czasu będzie schodził stopień po stopniu, aż zacznie się wspinać – wycofa się do poprzedniego stopnia i wie (bo przeczytał punkt 2.4), że znalazł lokalne minimum. Gdy jest leniwy to go taki rezultat zadowoli.
A jak Algorytm nie jest leniwy, to co ma robić dalej? Może trzeba zmienić zachowanie od początku, bo przecież w ten sposób znajdzie tylko lokalne minimum?
Inny problem pojawia się, gdy Algorytm nie ma dużo czasu i nie może schodzić stopień po stopniu. Wie że musi się ruszyć w prawo, ale jak długi skok ma wykonać?
Pozostawimy te pytania na razie bez odpowiedzi, a za to skomplikujmy zadanie, które ma rozwiązać nasz Algorytm. Teraz już nie „stoi” na schodach, ale na zboczu pewnego terenu:
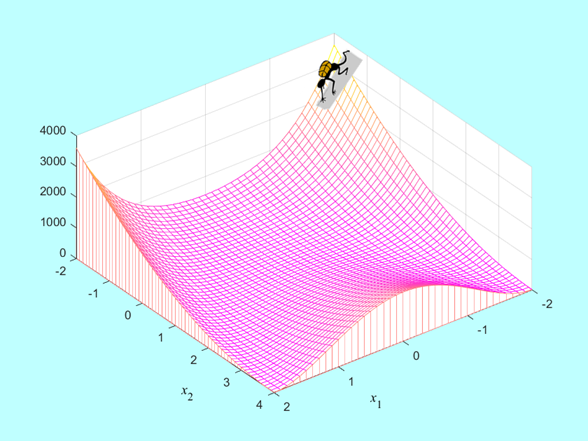
Tak jak poprzednio, Algorytm nie widzi rzeźby terenu, natomiast potrafi ocenić wysokość punktu w którym się znajduje lecz wie, że takich punktów składających się na rzeźbę nie da się policzyć.
Jak ma postępować?...
Naukowcy i praktycy pracują nad odpowiedzią na to pytanie od mniej więcej 80 lat, i dalsza część tego podręcznika jest poświęcona zwięzłemu przedstawieniu najistotniejszych, zdaniem autora, dokonań w tej dziedzinie.
Zapiszmy wnioski płynące z naszej analizy zachowania się Algorytmu optymalizacji, nieco je uogólniając.
- Ponieważ nie potrafimy przeanalizować całościowego obrazu zmienności optymalizowanej funkcji (algorytm jest ślepy) możemy się posługiwać tylko wartościami funkcji, lub innych obiektów matematycznych z nią związanych (np. funkcji pochodnej) obliczonymi w wybranych punktach.
- Określenie (wybór) tych punktów ma kluczowe znaczenie dla szybkości działania i skuteczności algorytmu.
- Trzeba określić kryterium, którego spełnienie powinno zagwarantować... I tu następny problem: jeżeli powiemy – zagwarantować znalezienie rozwiązania, to intuicja podpowiada nam, że takiego kryterium nie ma. Możemy tylko powiedzieć – zagwarantować znalezienie lokalnego optimum. Kryterium to nosi nazwę kryterium stopu.
- W sytuacji gdy zbiór dopuszczalny jest ograniczony, najprostszy algorytm, to algorytm przeszukania – deterministyczny na siatce (myślimy o siatce bo oceniane warianty z reguły są opisywane wielu zmiennymi), albo losowy (metoda Monte-Carlo). Ale algorytmy przeszukiwania są czasochłonne.
W 1997 komputer Deep Blue firmy IBM wygrał turniej z ówczesnym szachowym mistrzem świata G. Kasparowem, można zatem pomyśleć – mamy teraz superszybkie komputery dysponujące olbrzymia pamięcią i zdolnością samouczenia się, więc nie warto zajmować się wymyślnymi algorytmami optymalizacji. „Brutalna siła” prostego algorytmu przeszukania pozwoli rozwiązać, każde (nieco ostrożniej, prawie każde) zadanie optymalizacji. Dla dyskretnych zadań z nieskończoną liczbą wariantów i zadań ciągłych (więc z nieprzeliczalną liczbą wariantów) trzeba tylko ustalić dostatecznie gęstą siatkę punktów węzłowych a następnie ją przeszukać.
Stosowanie algorytmu przeszukiwania niesie jednak w sobie niebezpieczeństwo. Najprościej przeszukiwać na równomiernej siatce prostokątnej, takiej jaka posłużyła do otrzymania trójwymiarowego Rysunku 1.21. Stopień zgodności otrzymanego trójwymiarowego wykresu z rzeczywistym przebiegiem funkcji jest więc dobrą miarą trafności wyboru węzłów siatki. Intuicyjnie sądzimy, że im gęstsza siatka, tym lepiej.
Bogactwo zmienności funkcji, które można uzyskać wykonując cztery działania na funkcjach elementarnych jest jednak tak duże, że prosta intuicja nas zawodzi. Pokazuje to Rys. 1.22 przedstawiający trójwymiarowe obrazy tej samej funkcji dwu zmiennych, wykreślone na podstawie wartości obliczonych w węzłach równomiernej siatki prostokątnej o: \( 30 \times 30 = 900 \) węzłach i \(33 \times 33 = 1089\) węzłach.
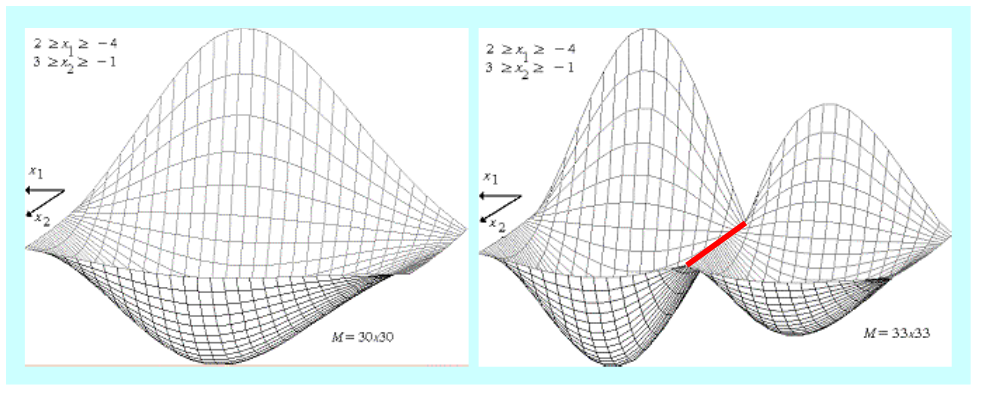
Zwiększenie liczby węzłów o 21% zmieniło całkowicie obraz funkcji:
- z funkcji o jednym minimum globalnym przeistoczyła się w funkcję o dwu minimach lokalnych i nieskończenie wielu maksimach lokalnych (cała prosta zaznaczona na czerwono), z których jedno leży tam, gdzie przedtem leżało minimum globalne!
- z drugiej strony, obliczone wartości minimalne funkcji dla rozważanych siatek nie różnią się znacznie, co intuicyjnie sugeruje, że zadanie znalezienia tylko minimalnej wartości funkcji oceniającej jest łatwiej rozwiązać.
Rysunki przedstawiają funkcję należącą do klasy
\((x_1,x_2)\mapsto-\left|w^m(x_2)\frac{1}{\alpha(x_1)}\sin{(}\beta(x_1))\right|, \qquad(1.19)\)
gdzie \(w^m\) jest wielomianem stopnia \(m\), a funkcje \( \alpha\) i \( \beta\) są funkcjami stałego znaku. Tego typu funkcje oceniające pojawiają się w pewnych zadaniach projektowych, np. związanych z przetwarzaniem sygnałów.
Nasuwa się pytanie: Jaki jest prawdziwy wygląd rozważanej funkcji?
Poniższy rysunek został wykonany na siatce o \(70 \times 70 = 4900\) węzłach i zgodnie z teorią pokazuje właściwe przybliżenie tej funkcji.
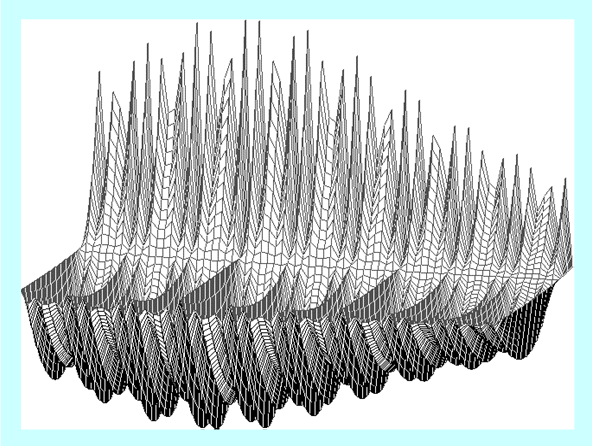
Dokładna analiza pokazała, że minimalna wartość funkcji oceniającej określona na każdej z tych trzech siatek różni się nieznacznie. Oczywiście nie można tego powiedzieć o punktach w których ta wartość jest osiągana. Jednak wyciągniecie stąd wniosku ogólnego, że zadanie w którym szukamy minimalnej wartości funkcji w zbiorze jest na pewno prostsze od „pełnego” zadania optymalizacji w którym szukamy argumentu minimalizującego badaną funkcję, jest pochopne. Tak zdarzyło się dla tej wybranej funkcji i nie wiadomo, czy to jest częsty/typowy przypadek.
Nauka jaka płynie z tego przykładu: