Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Podstawy teorii optymalizacji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 9 grudnia 2025, 21:52 |
1. Wprowadzenie do matematyki teorii optymalizacji
W tym rozdziale przedstawimy (po części przypomnimy) ciąg definicji, lematów i twierdzeń wprowadzających niezbędne pojęcia matematyczne i opisujących ich własności, a także związki między nimi.
1.1. Podstawowe pojęcia i definicje
Zaczniemy od przypomnienia pojęć rachunku różniczkowego.
\( \frac{\partial F(x)}{\partial x^T}=\begin{bmatrix} \frac{\partial F_1(x)}{\partial x_1} & \cdots &\frac{\partial F_1(x)}{\partial x_n} \\ \vdots & \cdots & \vdots \\ \frac{\partial F_q(x)}{\partial x_1} & \cdots & \frac{\partial F_q(x)}{\partial x_n} \end{bmatrix}= \begin{bmatrix} \bigtriangledown F_1(x) \\\vdots \\ \bigtriangledown F_q(x) \end{bmatrix} \)
nazywamy pochodną (macierzą Jacobiego) funkcji F w punkcie x. Wyznacznik macierzy Jacobiego \(\mathrm{det}( \frac{\partial f(x)}{\partial x^T})\) nazywa się jakobianem.
\( H(x)=\bigtriangledown ^2 f(x)=\left [ \frac{\partial^2 }{\partial x_i \partial x_j} f(x) \right ]\)
nazywamy macierzą Hessego (z niewiadomych przyczyn, wielu autorów zajmujących się optymalizacją nazywa tę macierz hesjanem, chociaż nazwy tego typu są stosowane do wyznaczników!).
Zwracamy uwagę na różnicę między różniczkowalnością funkcji wielu zmiennych w danym punkcie, a istnieniem jej gradientu w tym punkcie.
Funkcja f jest różniczkowalna w punkcie \(x. \Rightarrow \) Istnieje \(∇f(x)\).
Funkcja f jest różniczkowalna w punkcie \(x.\Leftarrow\) W otoczeniu punktu x istnieje
gradient \(∇f(x)\), ciągły w x.
Określimy teraz ważne dla teorii i algorytmów optymalizacji pojęcie pochodnej kierunkowej.
\(\lim_{\alpha \rightarrow 0^+}\frac{1}{\alpha }(f(x+\alpha d)-f(x))=D_+ f(x;d). \)
Następujący lemat pokazując związek pochodnej kierunkowej z gradientem pozwala w prosty sposób policzyć tę pierwszą dla funkcji różniczkowalnych.
Jeżeli
funkcja f jest różniczkowalna w punkcie x i określona w otoczeniu tego punktu,
to
\((∀d) D_+ f(x;d)=∇f(x)d.\)
Przedstawimy teraz lemat bardzo ważny dla konstruktorów algorytmów optymalizacji.
Jeżeli
funkcja f jest różniczkowalna w punkcie x i określona w otoczeniu tego punktu, oraz
\((∀d) D_+ f(x;d)=∇f(x)d<0,\)
to
\((∃τ ̄>0)(∀τ∈]0,τ ̄] f(x+τd)<f(x).\)
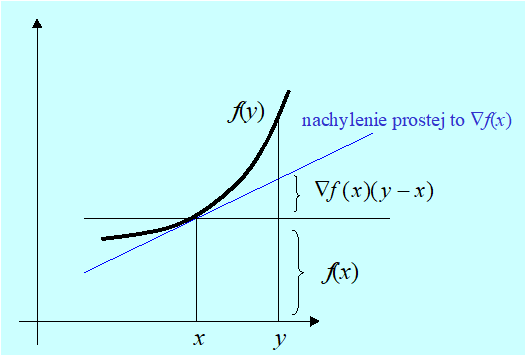
Ilustrację związków wynikających z Lematu 3.3 przedstawiamy na Rys. 3.1.
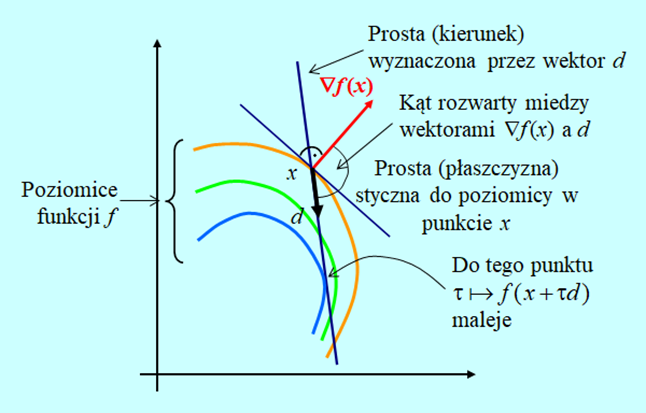
Z rozważań geometrycznych wiadomo, że iloczyn skalarny dwu wektorów jest ujemny (założenie lematu) wtedy gdy kąt miedzy nimi jest rozwarty. Tak też jest na rysunku dla wybranego wektora d.
Własność przedstawiona w Lemacie 5.3 dała dla zadań minimalizacji następującą definicję.
\(\bigtriangledown f(x)d < 0,\)
nazywamy kierunkiem poprawy (zadania minimalizacji funkcji f ).
Z Rys. 3.1 wynika, że w otoczeniu x, (inaczej mówiąc lokalnie) najlepszym kierunkiem poprawy (kierunkiem, w którym lokalnie funkcja najszybciej maleje) jest prosta wyznaczona przez wektor minus gradientu policzonego w tym punkcie, zwanego antygradientem. Pytaniem, które tu się pojawia jest: jak daleko warto poruszać się w tym kierunku? Dyskusję nad tym, wbrew pozorom, niełatwym zagadnieniem przedstawimy później – w punkcie 4.1 modułu czwartego.
W punkcie 1.3 Modułu pierwszego wspomnieliśmy o funkcjach wypukłych. Odgrywają one istotną rolę w teorii optymalizacji. Przypomnimy teraz definicje oraz podstawowe własności zbiorów i funkcji wypukłych.
Zbiór \(X⊂\mathbb{R}^n\) nazywamy wypukłym jeżeli \((∀x^a,x^b∈X) [x^a,x^b]⊆X\).
Funkcję \( f:\mathbb{R}^n→\mathbb{R}\) nazywamy wypukłą na zbiorze \(X⊆\mathbb{R}^n\) jeżeli zbiór
\(\mathrm{epi } f={(x,r)∈X×R|r≥f(x)} \)
zwany epigrafem (nadgrafem, nad-wykresem) funkcji f jest wypukły.
Zauważmy, że warunkiem koniecznym wypukłości zbioru \(\mathrm{epi } \) jest wypukłość zbioru X na którym jest określona funkcja f.
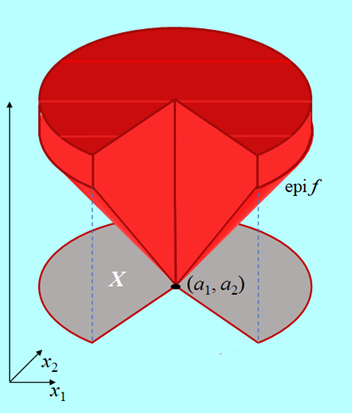
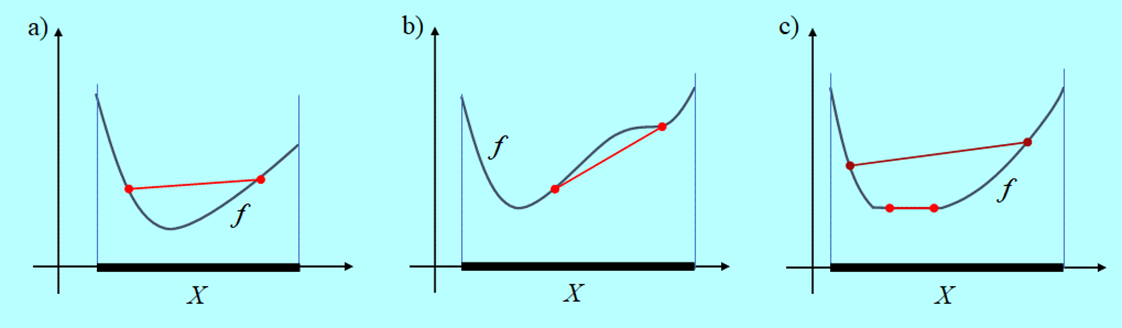
Funkcja przedstawiona na Rys. 3.2 nie jest wypukła dlatego, że zbiór X, na którym jest określona, nie jest wypukły i w konsekwencji jej epigraf nie jest zbiorem wypukłym.
Następny rysunek przedstawia inną przyczynę niewypukłości funkcji określnej na zbiorze wypukłym.
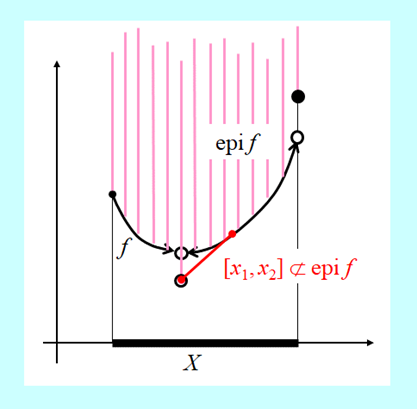
Funkcja na rysunku nie jest ciągła we wnętrzu zbioru swojego określenia X i na jego brzegu. Tylko nieciągłość wewnątrz zbioru X przeszkadza jej wypukłości.
Można udowodnić lemat następujący.
Jeżeli
funkcja f jest wypukła na zbiorze X
to
jest ciągła we wnętrzu tego zbioru.
Posługując się Definicją funkcji wypukłej można udowodnić lemat pozwalający na posługiwanie się alternatywną definicją funkcji wypukłej.
Funkcja f jest wypukła na zbiorze X wtedy i tylko wtedy gdy
- zbiór X jest wypukły i
- \((∀0<α<1) (∀x^0,x^1∈X)f(αx^0+(1-α)x^1)≤αf(x^0)+(1-α)f(x^1).\)
Następny lemat wiąże różniczkowalność i wypukłość funkcji.
Zbiór punktów nieróżniczkowalności funkcji wypukłej ma miarę zero.
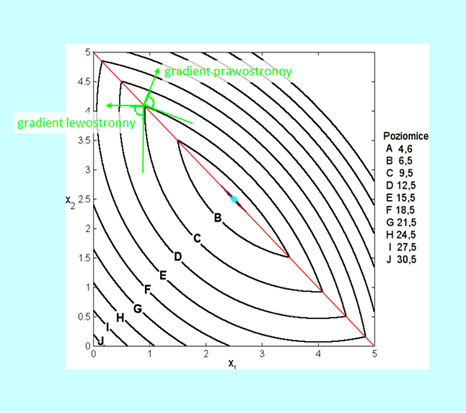
Rys. 3.4 przedstawia funkcję \(x \mapsto f(x)= \left\{\begin{matrix}((x_1-4)^2+(x_2-4)^2\, \mathrm{dla}\, x_1+x_2\leq 5, \\ (x_1-4)^2+(x_2-4)^2+10(x_1+x_2-5) \mathrm{gdy\, jest\, przeciwnie}\end{matrix}\right. \)
Prosta na płaszczyźnie ma miarę zero (naturalną miarą na płaszczyźnie jest powierzchnia, a prosta ma zerową powierzchnię). Powstaje więc pytanie: Czy zbiór miary zero, a więc mały dla matematyka, jest „duży”, czy „mały” z naszego punktu widzenia? Odpowiedź jest trudna, bo, „idąc do trzech wymiarów”, powierzchnia kuli w naturalnej mierze przestrzeni trójwymiarowej ma miarę zero, ponieważ tu naturalną miarą jest objętość, a powierzchnia ma zerową objętość, itd. Widać więc, że tam gdzie matematyka posługuję się pojęciem miary, np. w rachunku całkowym, rachunku prawdopodobieństwa, własności funkcji na zbiorze miary zero możemy pominąć. W innych sytuacjach, np. takiej z jaką się spotkamy w punkcie 6.1.4 Modułu szóstego (przedstawionej na Rys. 3.4) własności funkcji na takim zbiorze trzeba uwzględnić w analizie problemu.
Podamy teraz definicję uogólnienia funkcji kwadratowej na przypadek wielu zmiennych.
Funkcję \(x↦x^T Qx\), gdzie \(Q_{n\times n}\) jest kwadratową macierzą symetryczną nazywamy formą kwadratową.
W definicji wymagana jest symetryczność macierzy Q. Jak wiec nazwać funkcję \(x↦x^T Q ̄x\), gdzie macierz \((Q ) ̄\) nie jest symetryczna?
\(x^T \tilde{Q}x=1/2 x^T \tilde{Q}x+1/2 x^T \tilde{Q}x=1/2 x^T \tilde{Q}x+1/2 x^T (x^T \tilde{Q})^T=1/2 x^T \tilde{Q}x+1/2 x^T \tilde{Q}^T x= 1/2 x^T (\tilde{Q}+\tilde{Q}^T)x \)
a macierz 1/2(Q ̄+Q ̄^T) jest już symetryczna
Forma kwadratowa lub, w skrócie, określająca ją macierz Q jest
dodatnio półokreślona gdy \((∀x)x^T Qx≥0,\)
dodatnio określona gdy \((∀x≠0)x^T Qx>0.\)
Podamy teraz warunki wiążące wypukłość danej funkcji z określonymi własnościami jej funkcji pochodnych: gradientu i macierzy Hessego.
Niech f będzie klasy \(C^1\).
Funkcja f jest wypukła na \(X. ⇔(∀x,y∈X)f(y)≥f(x)+∇f(x)(y-x).\)
Niech f będzie klasy \(C^2\).
Funkcja f jest wypukła na \(X⊆\mathbb{R}^n.⇔(∀v)(∀x∈X) v^T ∇^2 f(x)v≥0\)
(macierz Hessego (niepoprawnie hesjan) jest dodatnio półokreślona).
Podamy teraz twierdzenie opisujące ważne dla zadań optymalizacji własności funkcji wypukłych.
Jeżeli
funkcja f jest wypukła na zbiorze \(X⊆\mathbb{R}^n\)
to
a) każdy punkt minimum lokalnego jest punktem minimum globalnego,
b) zbiór \(\mathrm{Arg\,min}_{x∈X} f(x)={x|x=\mathrm{argmin}_Xf (⋅)} \) jest zbiorem wypukłym.
Zatem dla funkcji wypukłych rozróżnianie minimum lokalnego i globalnego nie jest potrzebne
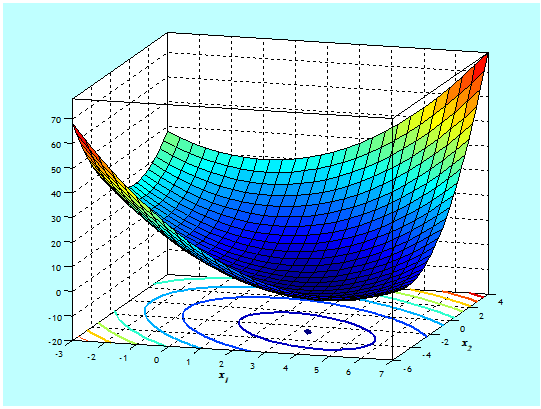
Trójwymiarowy i poziomicowy, wykresy funkcji ściśle wypukłej
\(x↦x^T \begin{bmatrix}1 & \frac{1}{2} \\\frac{1}{2}& 1 \\\end{bmatrix}x+[-4\,⋮\,\,2]x+5,\)
o minimum w \((x_1^o,x_2^o)=(10/3,-8/3)\) przedstawia Rys. 3.8.
Teraz zajmiemy się jeszcze dwiema pożytecznymi właściwościami funkcji wypukłych dotyczącymi ich pochodnej kierunkowej.
W świetle poznanych wcześniej własności, część B. twierdzenia dla wypukłych funkcji różniczkowalnych nie wnosi nowej informacji o ich zachowaniu, bo musi być spełnione: \((∀d)D_+ f(x^o,d)=∇f(x^o)d\) (Lemat 3.2) i jednoczesnie \(∇f (xo) = 0\) (podane niżej Twierdzenie 3.6). Zostało jednak przytoczone, ponieważ powyższe własności mają też funkcje nieróżniczkowalne a wiele praktycznych zadań optymalizacji nie jest gładkich, ponadto, jak się o tym przekonamy, naturalne pomysły sposobów rozwiązywania zadań optymalizacji z ograniczeniami prowadzą do zadań niegładkich.
Zanim sformułujemy warunek wystarczający istnienia rozwiązania zadania optymalizacji, dla porządku przypomnimy określenie zadania, którym się zajmujemy.
Twierdzenie 3.3 wariant twierdzenia Weierstrassa
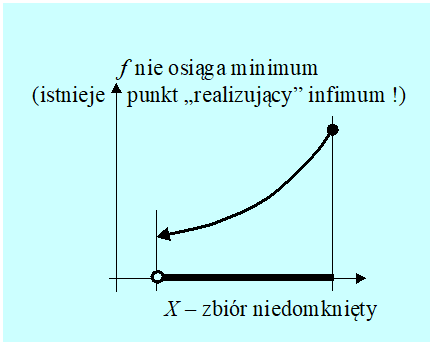
Wymagania przedstawionych wyżej warunków wystarczających można osłabić ale tylko w odniesieniu do rodzaju ciągłości funkcji, założenie o zwartości albo o domkniętości i „uciekaniu” funkcji do nieskończoności musi pozostać, por. rysunek 3.7 na którym zbiór D = X nie jest domknięty.
Dla funkcji jednej zmiennej archetypem funkcji wypukłej jest funkcja kwadratowa z dodatnim współczynnikiem. Funkcja ta oczywiście posiada minimum na dowolnym zbiorze domkniętym, także nieograniczonym. W związku z tym często sądzi się, że wypukłość gwarantuje istnienie minimum funkcji wypukłej na każdym zbiorze domkniętym. Tak jednak nie jest o czym świadczy przykład funkcji wykładniczej \(ℝ \ni x ↦ \mathrm{exp}(x) \in ℝ\), która jest ściśle wypukła i nie ma minimum w swojej, domkniętej przecież dziedzinie.
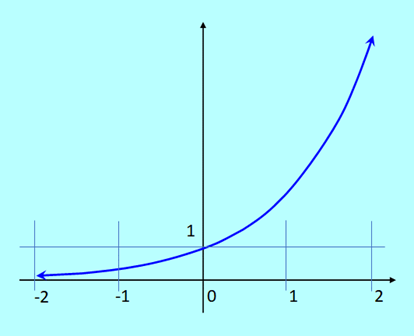
Oznacza, to że w przypadku zadań bez ograniczeń, sama wypukłość funkcji wyboru nie rozstrzyga o istnieniu rozwiązania. Inaczej mówiąc, narzędzia pozwalające rozstrzygnąć o istnieniu rozwiązania muszą się odwoływać do innych własności funkcji – muszą być bardziej skomplikowane, np. takie jak Twierdzenie 3.3B.
Przedstawimy teraz podstawowe twierdzenia pozwalające dla funkcji różniczkowalnych zastąpić zadanie optymalizacji bez ograniczeń zadaniem znalezienia rozwiązania stosownego układu równań i sprawdzenia pewnych nierówności. O takiej metodzie rozwiązywania wspominaliśmy w punkcie 1.4 Modułu pierwszego stwierdzając, że gdy chcemy znaleźć rozwiązanie zadania optymalizacji drogą rachunkową, to musimy oryginalne sformułowanie przekształcić do postaci pozwalającej na wykonanie stosownych rachunków.
Najstarsze twierdzenie pozwalające na stosowne przekształcenie zadania ZOBO, znane w swojej pierwotnej formie już P. Férmatowi około roku 1630, jest następujące.
Nazwaliśmy to twierdzenie warunkiem koniecznym optymalności I rzędu, bo są w nim wykorzystane tylko pochodne cząstkowe rzędu pierwszego funkcji minimalizowanej.
Inna nazwa tego warunku – warunek stacjonarności – nawiązuje do teorii równań różniczkowych, w której, zerowanie się pochodnej rozwiązania w jakimś przedziale, oznacza że jest ono stałe.
Jak możemy wykorzystać warunek konieczny optymalności I rzędu do znajdowania rozwiązania zadania optymalizacji bez ograniczeń? Odpowiedź zapiszemy w postaci następującej procedury.
Procedura redukcji zadania optymalizacji bez ograniczeń do układu równań
- Stosujemy warunek konieczny optymalności I rzędu do funkcji, które mają gradient w całej przestrzeni (nie możemy „czegoś przegapić”).
- Zaczynamy od pokazania, że zadanie ma rozwiązanie (możemy posłużyć się twierdzeniem Weierstrassa – twierdzenie (3.2)).
- Wyliczamy gradient otrzymując wzór określający równanie wektorowe \(∇f(x ̄ )=0. \qquad (3.1)\) (warunek stacjonarności, układ n równań skalarnych, tylu ile jest współrzędnych przestrzeni).
- Rozwiązując to równanie dostajemy zbiór rozwiązań \({x ̄}={x ̄^1,...,x ̄^j,...}.\) Interesują nas oczywiście rozwiązania (wektory) rzeczywiste.
- Elementy zbioru rozwiązań traktujemy jako „podejrzanych”, których „sprawdzamy na optymalność” tzn. wyliczamy zbiór \({f(x ̄^j)}\) wartości funkcji f, a następnie typujemy jako kandydata na rozwiązanie wektor dla którego wartość funkcji jest najmniejsza (tylko ‘kandydata na’, a nie rozwiązanie, bo twierdzenie jest warunkiem koniecznym!). Oznaczmy go \(x^P \) .
- Sprawdzamy, czy wektor xP jest punktem minimum lokalnego i gdy wiemy, że zadanie ma rozwiązanie, to możemy uznać, go za punkt minimum globalnego, \(x^P = x^o\) .
Które z przedstawionych kroków postępowania (które operacje algorytmu) są najtrudniejsze? Drugi i szósty, bo w przypadkach złożonych wymagają de facto udowodnienia pewnych lematów. Kłopotliwe bywa też szukanie wszystkich rozwiązań równania (3.1), szczególnie gdy szukamy tych rozwiązań numerycznie.
Najlepszym sposobem zwalniającym użytkownika przedstawionego algorytmu od konieczności udowadniania lematów, jest podanie ogólnego twierdzenia formułującego warunek (warunki?) wystarczające optymalności.
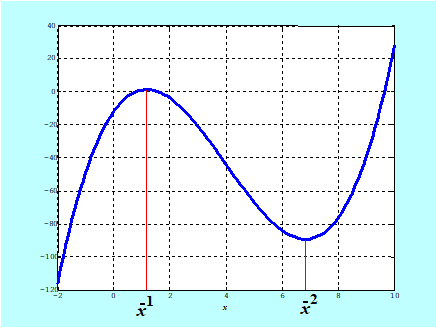
Znany przykład funkcji \(x ↦ x^3\), która w punkcie zerowania się funkcji pochodnej \(x ↦ 3x^2\) nie ma ani minimum, ani maksimum, wskazuje, że warunki wystarczające optymalności muszą być warunkami wykorzystującymi co najmniej drugie pochodne.
Pierwsze sformułowanie takich warunków pochodzi od G.W. Leibniza (Nova Methodus pro Maximis et Minimis... 1684). Podamy je w sformułowaniu współczesnym.
Twierdzenie formułuje wystarczający warunek optymalności lokalnej (w tezie jest minimum na kuli), i tak jak się spodziewaliśmy, warunek ten jest warunkiem II rzędu.
Przypomnijmy sobie Lemat 3.10 podający warunek wystarczający ścisłej wypukłości funkcji. Porównując ten lemat i twierdzenie Leibniza 3.5 widzimy, że warunek wystarczający optymalności lokalnej do warunku stacjonarności \(∇f(x ̄)=0\) dodaje warunek lokalnej ścisłej wypukłości. Wobec tego jego gwarancje też mogą być lokalne. O zachowaniu funkcji można sądzić po zachowaniu się jej pochodnych, ale informacja ta dotyczy infinitezymalnych (tak by powiedział Newton) odchyleń od punktu, w którym pochodne są liczone!
Zatem, dla funkcji dostatecznie gładkich możemy sobie poradzić z zagadnieniem punktu 6. (ostatniego) Procedury redukcji (teraz powinno być jasne, dlaczego jest tam wstawiona uwaga „gdy wiemy, że nasze zadanie ma rozwiązanie”).
Powróćmy do przykładu 3.1
Niestety, z błędami tego typu spotkałem się w poważnych, skądinąd, podręcznikach. Na szczęście tylko próbujących wykorzystać optymalizację a nie poświęconych jej teorii.
Podkreślmy też, jeszcze raz, że wszelkie rozważania oparte na własnościach funkcji pochodnych, a więc na rachunku różniczkowym mają lokalny charakter. Czy istnieją rezultaty o globalnym charakterze? Wypukłość na pewnym zbiorze ma, że tak powiem, z punktu widzenia tego zbioru, charakter całościowy – globalny. Następujące twierdzenia pokazują, że dla funkcji wypukłych można podać warunki które musi spełniać punkt rozwiązujący nasze zadanie (punkt minimum globalnego) i co więcej są to warunki konieczne i wystarczające.
Dla gładkich funkcji wypukłych konieczny warunek optymalności I rzędu jest jednocześnie warunkiem wystarczającym.
Jest to piękny rezultat teoretyczny, sprowadzający dla funkcji wypukłych Procedurę redukcji do układu równań wyłącznie do rachunków: liczenia pochodnych i rozwiązywania równań, czyli do takiego postępowania, które zastosowaliśmy w Przykładzie 3.1, niestety jak pokazał Rys. 3.10 do funkcji niewypukłej. Aby było ono poprawne trzeba (tylko) sprawdzić czy funkcja minimalizowana jest klasy \(\mathbf{C}^2\) i na początku realizacji wymagań punktu 6. policzyć macierz Hessego by posługując się Lematem 3.8 stwierdzić jej wypukłość (albo brak wypukłości). Gdy funkcja jest wypukła – istnienie rozwiązania wynika z Twierdzenia 3.5 i jednocześnie wskazany w punkcie 5. punkt (wektor) jest tym szukanym rozwiązaniem.
I jak tu się nie zgodzić z H. Minkowskim, pierwszym matematykiem, który pod koniec XIX wieku badał własności zbiorów i funkcji wypukłych i podobno stwierdził, że „wszystko co wypukłe jest piękne”.
Przedstawiona procedura rozwiązywania zadania optymalizacji bez ograniczeń przez redukcję do układu równań ma ograniczone zastosowanie.
- Po pierwsze można ją (w zasadzie) stosować tylko tam, gdzie znamy analityczny wzór określający funkcję wyboru. Jednak w wielu zadaniach praktycznych wartości tej funkcji są wyliczane za pomocą szeregu procedur numerycznych i całościowego wzoru na nią nie znamy. Często jest też tak, że nawet gdy znamy wzory, to posługiwanie się nimi jest żmudne i uciążliwe (tak jest np. w zagadnieniach optymalizacji związanych z pracą robotów) i w zasadzie robimy wszystko, by takiej pracy uniknąć. Powyżej napisaliśmy, w zasadzie, ponieważ opracowano procedury automatycznego różniczkowania (nie mylić z procedurami symbolicznego różniczkowania), które przetwarzają kod wyliczający funkcję wyboru na kod wyliczający jej pochodne. Zatem wymaganie znajomości wzoru nie jest już takie kategoryczne.
- Po drugie, trzeba równanie (3.1) rozwiązać, a analitycznie potrafimy rozwiązywać tylko równania najprostsze. Musimy więc posłużyć się numerycznymi algorytmami rozwiązywania równań. Powstaje tu pytanie, po co męczyć się nad przekształceniem, czy nie lepiej od razu zastosować numeryczny algorytm znajdowania rozwiązania zadania optymalizacji.
- I na koniec, przyczyna trzecia – wyraźnie sformułowana konieczność udowodnienia, że wyliczony punkt jest rzeczywiście rozwiązaniem, wielu odstręcza.
Zauważmy, że jednym z plusów tej metody jest to, że idealnie nadaje się do, nazwijmy to tak, sprawdzania wiadomości i zdolności rachunkowych studentów.
Jeżeli nie Procedura redukcji do układu równań, to co możemy poradzić naszemu Algorytmowi, którego jakiś czas temu zostawiliśmy samego na zboczu funkcji bananowej:
\((x1, x2) ↦ f (x1, x2) = 100(x2 – x1^2)^2 + (1 – x1)^2.\)


Odpowiedzi udzielimy w module następnym, a teraz zajmiemy się kwadratowymi przybliżeniami funkcji, które nie koniecznie są wypukłe.
1.2. Gładkie zadania optymalizacji
W
punkcie 1.3 Modułu pierwszego wyróżniliśmy gładkie (różniczkowalne) i
niegładkie zadania optymalizacji. Zajmiemy się teraz bliżej własnościami
gładkich zadań optymalizacji.
Najpierw trzeba precyzyjnie ustalić jakie zadania optymalizacji uznajemy za gładkie. Rozważania punktu poprzedniego tego rozdziału, w których posługiwaliśmy się co najwyżej drugimi pochodnymi, sugerują że dwukrotna różniczkowalność wystarczy. Mamy więc definicję.
Zadanie optymalizacji nazywamy gładkim, jeżeli wszystkie funkcje występujące w jego określeniu są klasy \(\mathbf{C}^2\).
Na razie zajmujemy się zadaniami bez ograniczeń, dlatego będziemy się interesować tylko funkcją wyboru f.
Dla funkcji f klasy \(\mathbf{C}^2\) zgodnie z twierdzeniem Taylora mamy
\((∀x ̄,x)f(x)=f(x ̄)+∇f(x ̄)(x-x ̄)+1/2(x-x ̄)^T ∇^2 f(x ̄)(x-x ̄)+ \)
+ nieskończenie mała rzędu 3,gdy \(x-x ̄→0\).
Rozpatrzmy funkcję, której mapę przestawiliśmy w punkcie 1.2.4 Modułu pierwszego, Rys.1.7.
\(=\frac{1}{2}x^T \begin{bmatrix}4 & 2\\2&-22\\\end{bmatrix}x-[-1\,⋮\,1]\begin{bmatrix}4 & 2\\2&-22\\\end{bmatrix}x+[-10\,⋮\,0]x+\)
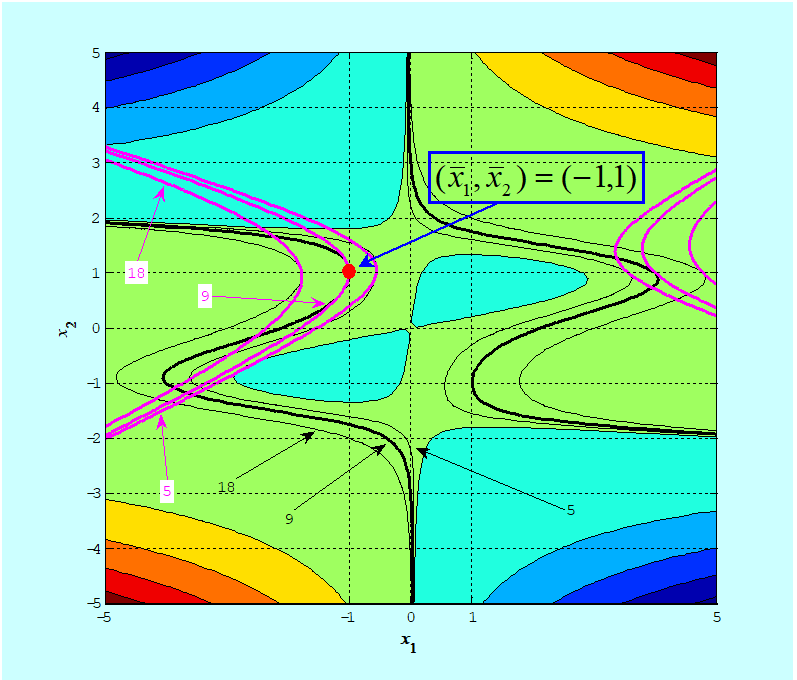

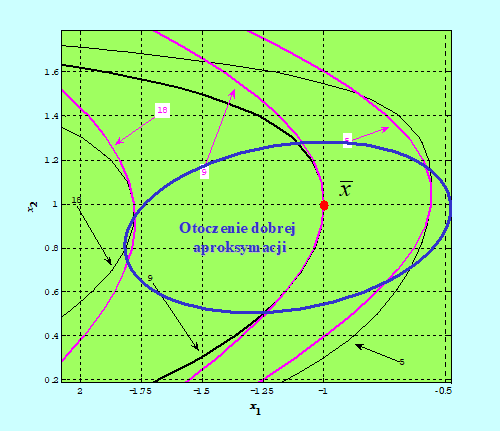

Rys. 3.13: Aproksymacja: a) trójwymiarowy wykres funkcji f ,
b) trójwymiarowy wykres funkcji aproksymującej f ̃
Podsumujmy nasze dotychczasowe rozważania.
Dla funkcji gładkich (klasy \(\mathbf{C}^2\) ) wzór
\(x↦\tilde{f} (x;x ̄)=1/2 x^T ∇^2 f(x ̄)x+c^T (x ̄)x+σ(x ̄) \qquad (3.2)\)
- nie daje dobrej aproksymacji funkcji f w całej przestrzeni (nie daje aproksymacji globalnej), natomiast
- istnieje takie otoczenie (konkretne wskazanie go jest bardzo trudne), w którym wzór ten dobrze przybliża tę funkcję – jest dobrą aproksymacją lokalną.
- pesymisty – nie korzystać ze wzoru (3.2),
- optymisty – przyjąć, że otoczenie dobrej aproksymacji to jest na tyle duże, że wykorzystanie gradientu i macierzy Hessego obliczonego w danym punkcie przy konstruowaniu algorytmu zmierzającego do punktu optymalnego nie wyprowadzi na manowce.
Tego rodzaju dylemat jest typowy dla sytuacji, w której znajduje się twórca nowych rozwiązań konstrukcyjnych – magister, a więc mistrz, inżynier – a także twórca nowych teorii naukowych. Za podejściem optymisty opowiedział się Albert Einstein, który w 1921 r. stwierdził, że „Raffiniert ist der Herrgott, aber boshaft ist er nicht”. Co w naszym przypadku przekłada się na przeświadczenie, że nieliniowe zadania optymalizacji związane z rozwiązywaniem zagadnień praktycznych, są takie, że zręczne wykorzystanie możliwości jakie daje posługiwanie się kwadratową aproksymacją (3.2) pozwoli opracować skuteczne algorytmy ich rozwiązywania. Współcześni optymiści mają sławnego poprzednika – Izaaka Newtona, który wymyślił metodę stycznych rozwiązywania równań nieliniowych opartą o jeszcze prostszą aproksymację, bo ograniczoną tylko do składnika afinicznego.
1.3. Właściwości funkcji kwadratowych
Jako optymiści musimy poznać podstawowe własności funkcji kwadratowych
x\(↦x^T Qx+c^T x+σ, \qquad (3.2)\)
o symetrycznej macierzy Q.
Zauważmy najpierw, że własności tej funkcji są zdeterminowane przez własności formy kwadratowej, czyli macierzy Q. Intuicyjnie – dodanie członu afinicznego „przesuwa” formę kwadratową nie zmieniając jej kształtu, tzn. nie zmienia jej podstawowych własności. Rysunek dla funkcji jednej zmiennej potwierdza tę intuicję.
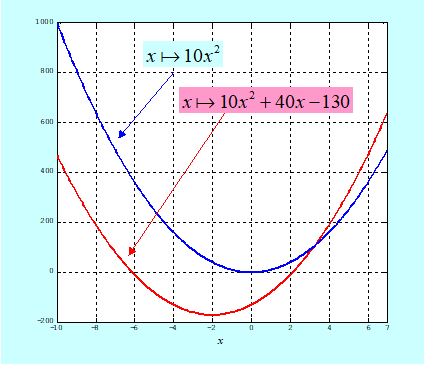

Jeżeli elementy na głównej przekątnej, \(q_{ii}\) , są niedodatnie to macierz Q nie jest dodatnio określona.
Jeżeli elementy na głównej przekątnej, \(q_{ii}\), są ujemne to macierz Q nie jest dodatnio półokreślona (a więc nie jest i dodatnio określona).
Zauważmy też, że na podstawie Lematu 3.11 o macierzy \(\begin{bmatrix}1&-2\\-2&1\\\end{bmatrix}\) możemy powiedzieć, że nie jest ujemnie półokreślona (bo macierz \(\begin{bmatrix}-1&2\\2&-1\\\end{bmatrix}\) nie jest dodatnio półokreslona), natomiast ustalenie dodatniej określoności, dodatniej połokreśloności albo nieokreśloności wymaga dalszych rachunków.
Dla macierzy \(2\times 2\) prawdziwy jest lemat
Macierz \( Q=\begin{bmatrix}q_{11}&q_{12}\\q_{12}&q_{22}\\\end{bmatrix} \) jest dodatnio określona [dodatnio półokreślona] \(\Leftrightarrow \)
Zatem macierz \(\begin{bmatrix}1&-2\\-2&1\\\end{bmatrix}\) przytoczona powyżej jest nieokreślona (nie jest ujemnie półokreślona i nie jest dodatnio półokreślona).
Różne własności kwadratowej macierzy \(Q_{n×n}\) są opisywane przez własności jej wartości własnych tj. n pierwiastków równania charakterystycznego
Zauważmy, że kwadratowa macierz Q jest odwracalna (nieosobliwa) wtedy i tylko wtedy gdy
A. Wartości własne macierzy symetrycznej są liczbami rzeczywistymi.
B. \(Q \geq 0 \Leftrightarrow (\forall i) \sigma_i (Q) \geq 0 \).
C. \(Q > 0 \Leftrightarrow (\forall i) \sigma_i (Q) > 0 \).
D. Dla dowolnej macierzy \(A_{n×n}\), macierz \(A^TA\) i macierz \(AA^T\) są dodatnio półokreślone,
a dodatnio określone gdy macierz A jest odwracalna.
Prostym wnioskiem z Lematu 3.13 jest, że macierz dodatnio (ujemnie) określona jest odwracalna (nieosobliwa).
Zauważmy też, że w świetle lematu 3.10 [3.8] funkcja kwadratowa oparta na macierzy dodatnio określonej [dodatnio półokreślonej] jest ściśle wypukła [wypukła].
Wektor \(v ^i \neq 0\) będący rozwiązaniem równania
Zilustrujemy wprowadzone pojęcia przykładem wyznaczenia wartości własnych i wektorów własnych.
Rozpatrzmy symetryczną macierz \(Q=\begin{bmatrix}2&\frac{2}{3}\\\frac{2}{3}&1\\\end{bmatrix} \).
Jej równanie charakterystyczne \(\mathrm{det}( sI-Q)=\mathrm{det}\begin{bmatrix}s-2&-\frac{2}{3}\\-\frac{2}{3}&s-1\\\end{bmatrix}=...=s^2-3s+\frac{14}{9}.\)
Jego pierwiastki (wartości własne) to: \(s_1 (Q)=\dfrac{2}{3},\, s_2 (Q)=\dfrac{7}{3}\), zatem macierz jest określona dodatnio.
Policzmy teraz wektory własne. Najpierw związany z pierwszą wartością własną\( s_1 (Q)=\dfrac{2}{3}\).
\(\begin{bmatrix}2&\dfrac{2}{3}\\\dfrac{2}{3}&1\\\end{bmatrix} \begin{bmatrix}v_1^1\\v_2^1\\\end{bmatrix}=\dfrac{2}{3} \begin{bmatrix}v_1^1\\v_2^1\\\end{bmatrix}\), czyli \(\begin{matrix}2v_1^1+\dfrac{2}{3} v_2^1=\dfrac{2}{3} v_1^1\\ \dfrac{2}{3} v_1^1+v_2^1=\dfrac{2}{3} v_2^1 \end{matrix},\) co daje \(\begin{matrix}4v_1^1+2v_2^1=0\\ 2v_1^1+v_2^1=0\end{matrix},\) skąd mamy
równanie dla pierwszego wektora własnego
\(v_2^1=-2v_1^1\).
Analogiczne rachunki dają dla drugiego wektora własnego:
\(v_2^2=1/2 v_1^1.\)
Widać zatem, że wektory własne nie są wyznaczone jednoznacznie, i nie jest to przypadek. W terminologii używanej w teorii metod optymalizacji wektory własne wyznaczają tylko kierunki (proste). Jaki jest z nich pożytek? Narysujmy wykres poziomicowy formy kwadratowej \(x↦x^T Qx\) dla macierzy Q rozważanej w przykładzie.
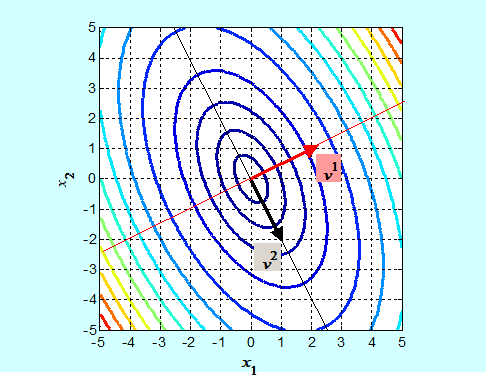
Jak widać wektory własne leżą na osiach elips, które są poziomicami rozważanej funkcji. Zauważmy, że elipsy są „rozciągnięte” w kierunku \(v^2\), a więc związanym z większą wartością własną \(s_2 (Q)=\frac{7}{3}\). Te zależności są ogólne i odnoszą się do wszystkich sytuacji z jakimi możemy się spotkać analizując funkcje kwadratowe, ale (na szczęście) stosownych wzorów nie będziemy wyprowadzać.
Przedstawimy teraz z jakimi przypadkami kształtów funkcji kwadratowej
\(x↦x^T Qx+c^T x+σ \)
możemy się spotkać.
Jest ich pięć:
- macierz Q jest dodatnio określona,
- istotnie dodatnio półokreślona (co najmniej jedna wartość własna jest zerowa),
- nie jest określona,
- jest określona ujemnie,
- jest istotnie ujemnie półokreślona.
Niestety, możemy narysować tylko funkcję dwu zmiennych (jak często mówimy, na płaszczyźnie). Przedstawmy zatem wykresy trójwymiarowe i poziomicowe dla pierwszych trzech przypadków, ponieważ funkcje określone ujemnie to „odwrócone w dół” funkcje określone dodatnio.
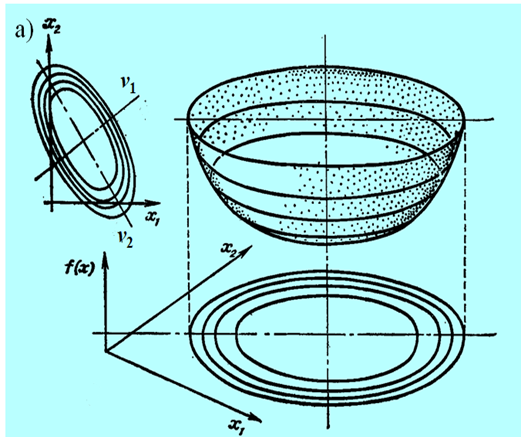
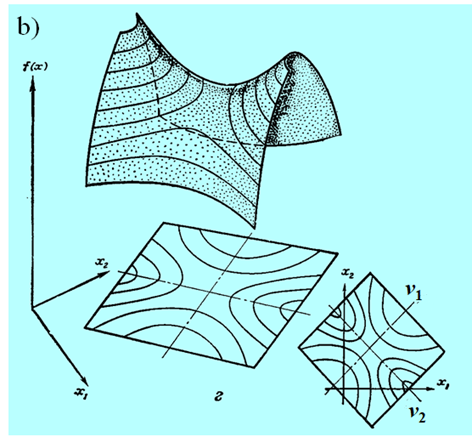
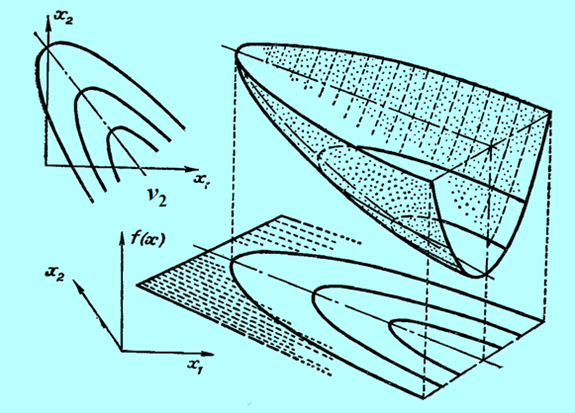
Następny rysunek nie przedstawia funkcji kwadratowej a formę kwadratową tzn. funkcję \(x↦x^T Qx\) dla tego samego przypadku, tzn. jednej wartości własnej zerowej.
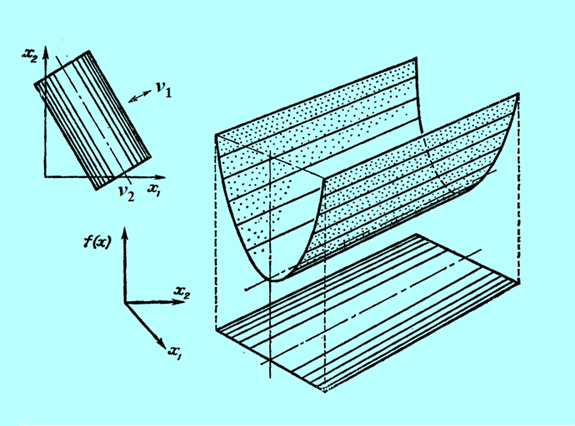
Widać, że w odróżnieniu od przypadku poprzedniego (Rys. 3.17) funkcja ta ma nieskończenie wiele minimów.
wyciągniętych w oparciu o własności funkcji jednej zmiennej na własności funkcji wielu zmiennych (nawet dwu!). Posługując się intuicją napisaliśmy parę stron wcześniej, interpretując Rys. 3.14, że „dodanie członu afinicznego ... nie zmienia podstawowych własności formy kwadratowej”. Jak widzimy, nie jest to w ogólności prawdą. Nawet gdy uznamy przypadek o zerowej wartości własnej za nietypowy, to w dokładnej analizie musimy go „wyłapać” i wyeliminować, aby uniknąć przykrych konsekwencji jakie jego wystąpienie wywołuje
Na koniec, wprowadzimy pewną jakościową charakterystykę funkcji kwadratowych. Jest dość oczywiste, że naszemu „ślepemu” Algorytmowi łatwiej jest znaleźć minimum, gdy w każdym kierunku, co najmniej lokalnie, funkcja minimalizowana zachowuje się tak samo – dla dwu zmiennych jej poziomice są zbliżone do okręgu, dla trzech – do kuli, itd. Dobrze byłoby gdyby Algorytm mógł o tym się dowiedzieć. Wiemy, że dla funkcji kwadratowych informacje o kierunkach rozciągnięcia powierzchni stałej wartości (poziomic dla funkcji dwu zmiennych) i jego wielkości niosą wektory własne (por. Rys. 3.15 i następne) ściśle związane z wartościami własnymi macierzy Q. W związku z tym można udowodnić Lemat następujący.
Jeżeli
uszeregujmy wartości własne dodatnio określonej macierzy \(Q_{n×n}\) od najmniejszej \(s_1(Q)\) do największej \(s_n(Q)\),
to
prawdziwa jest następująca nierówność: \((∀x)s_1 x^T x≤x^T Qx ≤s_n x^T x.\)
Rezultatem tej nierówności są następujące inkluzje
\((∀c){x|s_n x^T x≤c}⊆{x|x^T Qx≤c}⊆{x|s_1 x^T x≤c},\)
zwracam uwagę na odwrotną kolejność inkluzji!

Wykorzystując oczywistą interpretację powyższych inkluzji nasuwającą się na podstawie Rys. 3.19 zdefiniujemy tzw. uwarunkowanie macierzy w sposób następujący.
Dla symetrycznej macierzy Q iloraz
\(cr(Q)=\dfrac{max_i| s_i (Q)|}{min_i| s_i (Q)|}≥1\)
nazywamy jej uwarunkowaniem (condition number/ratio).
Uwarunkowanie jest tym jakościowym miernikiem własności funkcji kwadratowej którego szukamy. Powierzchnie stałej wartości funkcji kwadratowej zbudowanej na określonej dodatnio macierzy Q o uwarunkowaniu \(cr(Q)\) bliskim jedności są zbliżone do hiperkul (na płaszczyźnie – okręgów). Funkcja zmienia się w podobny sposób w każdym kierunku. Im większe jest uwarunkowanie, tym gorzej: w jednym kierunku funkcja zmienia się powoli, w prostopadłym bardzo szybko. Gdy \(cr(Q)\) jest duży, praktycznie już od kilku, to taką funkcję kwadratową nazywamy źle uwarunkowaną.
Funkcje celu, które trzeba minimalizować mogą mieć jednak różny kształt, co znakomicie utrudnia ustalenie zasad jakimi ma się kierować Algorytm, którego zadaniem jest minimalizacja.
Przyjęliśmy jednak postawę optymistyczną zakładającą, że funkcja celu f jest gładka i wzór (3.2)
\(x↦\tilde{f}(x;x ̄)=\frac{1}{2} x^T ∇^2 f(x ̄)x+c^T (x ̄)x+σ(x ̄)\)
gdzie \(x ̄↦c^T (x ̄)=-x ̄^T ∇^2 f(x ̄)+∇f(x ̄),x ̄↦σ(x ̄)=\frac{1}{2} x ̄^T ∇^2 f(x ̄ ) x ̄-∇f(x ̄ ) x ̄+f(x ̄ ) \qquad (3.3)\)
jest jej dobrą aproksymacją. Wiemy, że aproksymacja ta jest lokalna, ale bez formalnego udowadniania tego, przyjmujemy że otoczenie dobrej aproksymacji jest dostatecznie duże (optymizm), por. Rys. 3.12 i 3.13. W takiej sytuacji powyższe rozważania upoważniają do przyjęcia tezy, że jakościowe aspekty zmienności funkcji celu są, tak jak dla funkcji kwadratowych, w całości opisane jej gradientem i macierzą drugich pochodnych (macierzą Hessego).
Przedstawmy tak rozumiane uwarunkowanie dla bananowej funkcji Rosenbrocka.
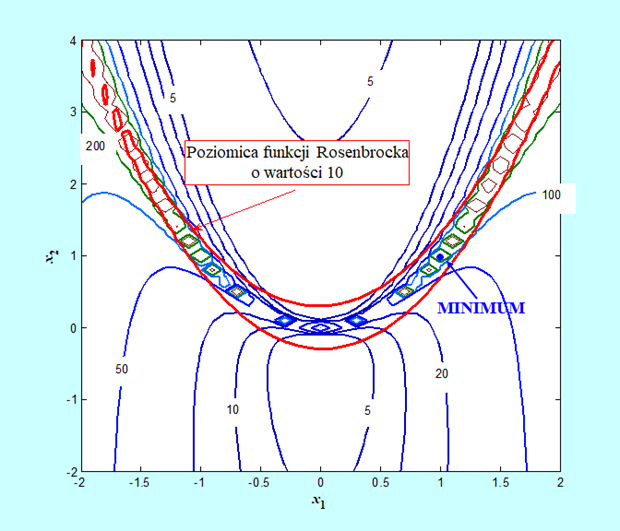
Widać, że funkcja Rosenbrocka jest dobrze dobrana jako „tor badania sprawności” dla różnych algorytmów. Tylko w centralnej części (tam gdzie nie ma minimum) jej uwarunkowanie jest mniejsze od pięciu, natomiast w okolicy minimum jest większe od 100.
Zauważmy też, że wykres (otrzymany przy pomocy MATLABa) trochę oszukuje. Linie stałego uwarunkowania nie tworzą „wysp” jak sugeruje rysunek, taki kształt wynika z przyjętego (świadomie zbyt małego) kroku siatki – 0.1 – na której wykonywany był rysunek.
2. Podstawy metod optymalizacji bez ograniczeń
Poprzednie punkty poświęciliśmy przedstawieniu podstawowych własności matematycznych obiektów składających się na zadania optymalizacji. Teraz wracamy do głównego nurtu tego podręcznika – poszukiwania odpowiedzi na pytanie jak konstruować algorytmy rozwiązujące zadania optymalizacji (algorytmy optymalizacji).
Jak już wiemy wynikająca z twierdzenia Férmaty (Twierdzenia 3.4) Procedura rozwiązywania zadania optymalizacji bez ograniczeń przez redukcję do układu równań ma ograniczone zastosowanie. Zatem: jeżeli nie procedura redukcji, to jakimi sposobami możemy konstruować algorytmy optymalizacji?
Powróćmy do naszych rozważań z punktu 1.4 Modułu pierwszego. Jak pamiętamy, Algorytm jest ślepy – nie może zobaczyć rzeźby trenu na którym się znajduje. Na schodach szedł w prawo, potem w lewo – sprawdzał swoje otoczenie. W ogólnym przypadku otoczenie ma więcej wymiarów, ale pomysł może być ten sam – sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu bieżącego, x, w którym się aktualnie znajduje. Natychmiast pojawia się pytanie – jak duże powinno być to sąsiedztwo? Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania – im mniejszy tym dokładniej).
Przyjmijmy, że zagadnienie to zostało jakoś rozwiązane i wybrano sąsiedztwo \(S(x)\) punktu \(x,\) dla ustalenia uwagi, może to być kula o promieniu \(r : \mathfrak{K}(x, r)\). „Sprawdzenie” zdefiniowanego sąsiedztwa Algorytm może robić na dwa sposoby:
- w pierwszym, przyjmuje, że nic nie wie o kształcie funkcji wyboru.
- w drugim w oparciu o wiedzę „lokalną” buduje sobie model zachowania funkcji wyboru w dużo większym obszarze.
2.1. Metody rozsiewania punktów próbnych
Przeanalizujmy sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów sąsiedztwa \(\mathbf{S}(x^{(k)})\), zaczepionego w „bieżącym” punkcie \(x^{(k)}\) Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne).
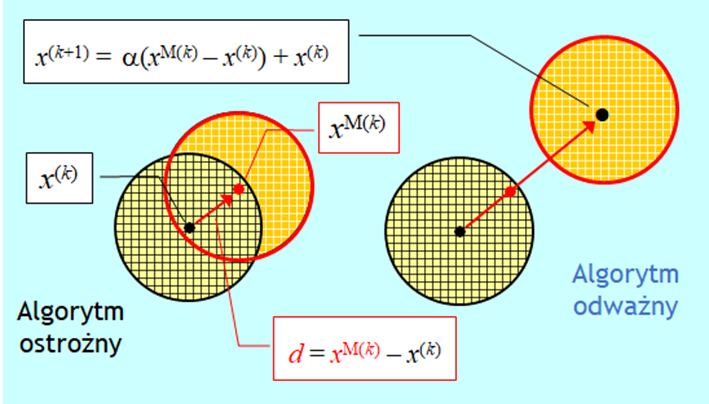
Niech punktem z próby, w którym funkcja wyboru jest najmniejsza jest punkt nazwany \(x^{M(k)}\). Algorytm teraz może być:
- ostrożny (wiem, że schody opadają w prawo, schodzę w prawo o jeden stopień) – przyjąć \(x^{M(k)}\) za „centrum” nowego sąsiedztwa \(x^{(k+1)}=x^{M(k)}\)i przeszukiwać je tak jak poprzednio;
- odważny (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) – przesunąć „centrum” sąsiedztwa poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów \(x^{M(k)} – x^{(k)}\), tzn. ustalić „centrum nowego sąsiedztwa w punkcie
\(x^{(k+1)} = \alpha (x^{M(k)} – x^{(k)}) +x^{(k)}, \, \alpha > 1 .\)
Dwa podstawowe problemy, które trzeba teraz rozwiązać, to:
- Jak wybierać \(\alpha\)? Jest to zagadnienie, w którym trzeba odpowiedzieć na trudne pytanie – jak będąc odważnym zachować rozwagę?
- Jak wybrnąć z sytuacji gdy w kolejnym kroku nie potrafimy poprawić funkcji celu – czy punkt o najmniejszej z dotychczas znalezionych wartości funkcji wyboru uznać za rozwiązanie? Jest to trudne zagadnienie ustalenia kryterium stopu.
Myślenie o sprawdzaniu sąsiedztwa jako przeszukiwaniu za pomocą równomiernie rozsiewanych punktów doprowadziło do konstrukcji wielu algorytmów probabilistycznych, których nie będziemy w ramach tego wykładu omawiać, oraz różnych algorytmów deterministycznych.
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm Neldera i Meada zwany też algorytmem pełzającego sympleksu, w którym sąsiedztwem nie jest kula ale sympleks – zbiór punktów o liczności o jeden większej niż wymiar przestrzeni poszukiwań. Nie będziemy zagłębiali się w szczegóły tego algorytmu (jak ustalić próbę początkową czyli pierwszy sympleks, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do podręcznika A. Stachurski: Wprowadzenie do optymalizacji, Oficyna Wydawnicza PW 2009, podrozdział 3.7. Przedstawimy tylko rysunek pokazujący jak takie pełzanie może wyglądać.
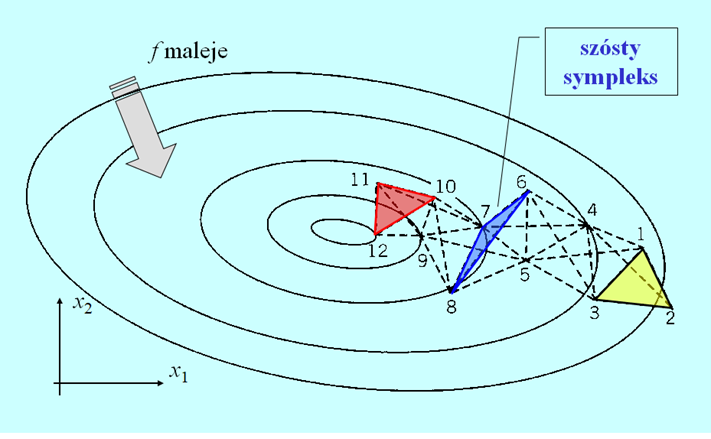
Widać, że dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo dobrze. W MATLABie jest on zaimplementowany jako funkcja fminsearch i doświadczenia wielu pokoleń studentów pokazały, że jest on narzędziem efektywnym w typowych zastosowaniach laboratoryjnych i projektowych.
2.2. Metody obszaru zaufania
Przejdźmy teraz do omówienia sposobu opartego na założeniu, że Algorytm dysponuje a priori pewną wiedzą o lokalnym zachowaniu funkcji wyboru (wiedza lokalna) i jest na tyle odważny, że chce (i potrafi) tę wiedzę „rozciągnąć” na dużo większe otoczenie. Przyjmujemy zatem, że dookoła punktu bieżącego \(x^{(k)}\) została określona kula \(\mathfrak{K}(x^{(k)}, r)\) i funkcja \(x↦f_M (x;x^{(k)})\), tzw. funkcja modelująca, będąca modelem zachowania się funkcji wyboru \(f\) w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu 3.1.2, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową (3.3)
\(x↦f_M (x;x^{(k)})=\frac{1}{2} x^T ∇^2 f(x^{(k)})x+c^T (x^{(k)})x+σ(x^{(k)})=x^T Qx+c^T x+σ.\)
W takiej sytuacji przeszukanie otoczenia punktu x(k) może oznaczać tylko jedno – szukanie punktu xM(k), minimalizującego funkcję modelującą na tzw. kuli zaufania \(\mathfrak{K}(x^{(k)}, r)\).
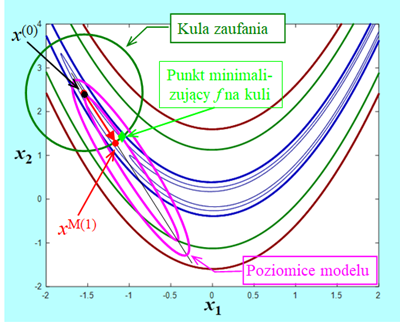
Do przedstawionego wyżej pomysłu opisującego w jaki sposób Algorytm może otrzymany punkt przetworzyć na środek nowego obszaru eksploracji trzeba dodać istotną uwagę.
- Ponieważ punkt \(x^{M(k)}\) został wygenerowany w oparciu o model, to gdy kula jest za duża. może nie być właściwy – wartość rzeczywistej funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Może to pociągnąć za sobą konieczność wielokrotnego rozwiązywania zadania minimalizującego funkcję modelującą na kuli zaczepionej w punkcie bieżącym.
\(f(x^{M(k)} \leq f(x^{(k-1)}), \qquad (3.4)\)
oznaczająca, że funkcja celu z kroku na krok maleje.
W świetle tych rozważań jest oczywiste, że algorytmy wykorzystujące podejście tego typu mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występującego w nich zadania
\(\left.\begin{matrix}\mathrm{znalezc\, liczbe\,}\alpha = \mathrm{argmin}_xf_M (x;x^{(k)})=x^T Qx+c^T x+\sigma\\\mathrm{p.o.\,} x \in \mathfrak{K}(x^{(k)},r)=\left \{((x-x^{(k)} )^T (x-x^{(k)})\leq r^2 \right \} \end{matrix}\right\}\)
co nastąpiło w połowie lat siedemdziesiątych XX w. Wtedy algorytmy tego typu były klasyfikowane jako algorytmy z ograniczonym krokiem. Koniec XX w. przyniósł ponowne zainteresowanie tym podejściem i zmianę nazwy na metody obszaru zaufania (trust region methods).
Podamy teraz podstawową strukturę algorytmu obszaru zaufania.
Podstawowy algorytm metody obszaru zaufania (ideowy)
Inicjalizacja
- Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}\).
- Ustal początkowy obszar zaufania \(T0\), np. \(T0= \mathfrak{K}(x^{(0)},r)\), podstaw \(T := T0\).
- Podstaw \(k := 0\).
- Dla punktu x wyznacz model \(f_M(\cdot ; x\)) funkcji celu w jego otoczeniu.
- Rozwiązując, np. zadanie ZKK, znajdź przybliżenie xtylda punktu \(xMk=\mathrm{argmin}_{z∈T}f_M (z;x)\).
- Sprawdź czy obszar zaufania należy zmniejszyć do \(TS(x)\) (np. równego= \(\mathfrak{K}(x^,rs)\). Jeżeli tak, podstaw \(T := TS(x)\), idź do 2. W przeciwnym przypadku podstaw \(x :=\) xtylda, idź do 4.
- Jeżeli spełnione jest kryterium (test) stopu, to \(x\) przyjmij za rozwiązanie, podstaw ilosc_iteracji := \(k\) i stop. W przeciwnym przypadku idź do 5.
- Sprawdź czy należy powiększyć obszar zaufania do \(TL(x)\) (np. równego \(\mathfrak{K}(x^,rl)\)). Jeżeli tak, podstaw \(T := TL(x)\), idź do 6. W przeciwnym przypadku idź do 6.
- Podstaw \(k := k + 1\), idź do 1.
Wyjaśnień wymaga krok 2., 3., 5. i oczywiście kryterium stopu.
Krok drugi to poszukiwanie przybliżonego rozwiązania zadania minimalizacji funkcji modelującej na obszarze zaufania, np. zadania ZKK, ponieważ wiemy, że zadanie to będzie rozwiązywane stosownie wybranym algorytmem i trzeba się liczyć z możliwością otrzymania niedokładnego rozwiązania.
Krok trzeci i piaty wymagają sprecyzowania, co jest właściwe, a co nie, przy czym ustalenie, kiedy zmniejszać obszar zaufania jest łatwiejsze (wspomnieliśmy o tym wyżej) niż ustalenie kiedy można/należy go powiększać. Wobec tego ich doprecyzowanie wymaga popartej teorią i intuicją głębszej analizy zagadnienia. Nie będziemy tego tematu dalej rozwijać.
Test stopu jest silnie związany z działaniami kroków 3. i 5., zatem nie można go poprawnie określić dla takiego ogólnego schematu. Jedną rzecz możemy jednak teraz powiedzieć – powinien zawierać warunek określający maksymalną liczbą iteracji.
Kończąc ten krótki opis metody obszaru zaufania zauważmy, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z nowymi – funkcją wyboru i ograniczeniami, ale o niezmiennej, stosunkowo prostej i typowej formie.
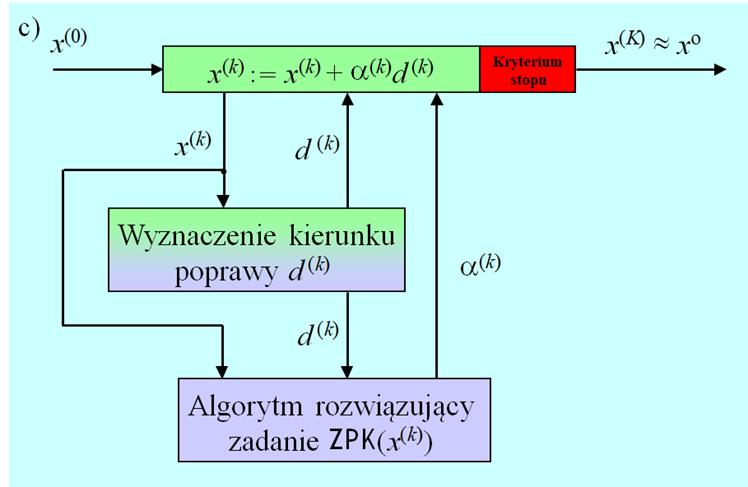
2.3. Metody kierunków poprawy
Omawialiśmy podejścia oparte na intuicyjnie oczywistym pomyśle sprawdzania wartości funkcji wyboru w sąsiedztwie punktu bieżącego. Algorytm obszaru zaufania jest odważny, bo zakłada, że kolejne sąsiedztwa będzie mógł wybierać jako „dostatecznie duże” (krok 5.), tak aby różnica \(f(x^{(k-1)})-f(x^{M(k)})\) była większa od zera (warunek (3.4)) i szybko malała (potocznie – „aby szybko zmierzać do celu”). Teraz przedstawimy idee postępowania opartego na silniejszym założeniu, że Algorytm obok umiejętności wykorzystania gradientu i macierzy Hessego do zbudowania lokalnego modelu zachowania funkcji wyboru, jest dodatkowo na tyle zmyślny, że potrafi wykorzystać tę wiedzę do wykonania kroku dającego znaczną poprawę (w naszym przypadku znaczne zmalenie) funkcji wyboru. Podejście to jest oparte na wynikach rozważań teoretycznych pozwalających na wykorzystanie związku kierunku poprawy z gradientem (Lemat 3.3 z punktu 3.1.1). Jak pamiętamy, aby kierunek d był kierunkiem poprawy dla zadania minimalizacji, dla funkcji różniczkowalnej musi zachodzić nierówność
\((∀d) D_+ f(x;d)=∇f(x)d<0. \qquad (3.5)\)
Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający najmniejszą do osiągnięcia w tym kierunku wartość funkcji celu (oczywiście mniejszą niż w punkcie bieżącym), patrz Rys. 3.1.
Co formalnie znaczy poruszać się wzdłuż kierunku? Dla danego bieżących: punktu x(k) i kierunku d(k) oznacza to pozostawanie w zbiorze
\(P(x^{(k)};d^{(k)})=\left. x \in\mathbb{R}^n |(∃α∈\mathbb{R})x=x^{(k)}+αd^{(k)} \right \}\).
Zgodnie z tym określeniem, znalezienie punktu \(x^{(k+1)}∈P(x^{(k)};d^{(k))}⊂\mathbb{R}^n\) jest równoważne ustaleniu pewnego \(α^{(k)}∈\mathbb{R}\), zatem zmieniając \(\alpha\) od zera do plus nieskończoności ruszamy się wzdłuż prostej \(P(x^{(k)}; d^{(k)})\) w kierunku malenia funkcji celu jeżeli wektor \(d^{(k)}\) spełnia warunek (3.5). Konkretną wartość \(α ̅=α^{(k)}\) – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze \(P(x^{(k)}; d^{(k)})\) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy \(\alpha^{(0)}\), gdy \(f(x^{(k)}+α^{(0)} d^{(k)})<f(x^{(k)})\) to \(\alpha^{(0)}\) uznajemy za długość kroku, gdy przeciwnie – zmniejszamy \(\alpha ^{(0)}\) do \(\alpha ^{(1)}\), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę. Idąc dalej można oprzeć wybór długości kroku na przybliżonej, a gdy się da dokładnej, minimalizacji funkcji celu f na zbiorze \(P(x^{(k)};d^{(k)})\), to znaczy rozwiązując
znaleźć liczbę \(α^((k))=\mathrm{argmin}_{α≥0}f (x^{(k)}+αd^{(k)}).\)
Formułując to zadanie minimalizacji w kierunku nie wykluczamy sytuacji, w której zadowalamy się jego rozwiązaniem przybliżonym. Ponieważ zbiór dopuszczalny \(P(x^{(k)}; d^{(k)})\) jest określony jednym ograniczeniem równościowym to zadanie ZPK. jest zadaniem minimalizacji funkcji jednej zmiennej \(\alpha (x^{(k)}\) i \(d^{(k)}\) są ustalone!).

Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie jednak istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu istotnie lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu.
Taki sposób rozumowania doprowadził do wniosku, że algorytm znajdowania rozwiązania optymalizacji może być zorganizowany w następujący sposób.
- Najpierw w oparciu na informacji o lokalnym zachowaniu funkcji w danym punkcie np. zawartej w jej pochodnych wyznacza się kierunek poprawy.
- Na tym kierunku (na, bo kierunek (prostą) traktujemy tu jako zbiór), poszukując poprawy wybiera się, jak na schodach, punkt (stopień) dający akceptowalną poprawę wartości funkcji celu. Może to być wektor dający najniższą wartości funkcji celu – punkt minimalizujący w kierunku. W tym punkcie wyznacza się nowy kierunek poprawy i proces poszukiwania nowego, lepszego punktu powtarza się.
W tym miejscu naszych rozważań warto, podobnie jak w przypadku poprzedniej metody, podkreślić, że podejście wykorzystujące kierunki poprawy zamienia zadanie znalezienia minimum funkcji wielu zmiennych na ciąg naprzemiennego wyznaczania kierunku poprawy i poszukiwaniu punktu dającego poprawę to jest zadania operującego na funkcji jednej zmiennej.
Bardziej formalnie można przedstawioną powyżej procedurę minimalizacji opartą na generowaniu kierunków poprawy opisać następująco.
Podstawowy algorytm kierunków poprawy (ideowy)
Inicjalizacja
- Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}\)
- Podstaw \(k := 0\).
Kroki algorytmu
- Dla punktu x wyznacz kierunek poprawy d.
- Ustal długość kroku w kierunku poprawy \\alpha\).
- Wylicz następny punkt podstawiając \(xnew∶=x+αd.\)
- Jeżeli spełnione jest kryterium (test) stopu, to xnew przyjmij za rozwiązanie, podstaw \(\mathrm{ilosc\,iteracji} := k\) i stop. W przeciwnym przypadku idź do 5.
- Podstaw \(k := k + 1\), podstaw \(x := xnew\), idź do 1.
Powyższy schemat ogólny nie precyzuje jak ustala się kierunek poprawy (krok 1.) i długość kroku (krok 2.), tu najczęściej będzie to zadanie ZPK, oraz nie określa testu stopu. Podobnie jak dla podstawowego algorytmu obszaru zaufania sprecyzowanie działań tych kroków jest związane ze sobą i określa konkretną postać algorytmu. Więcej szczegółów przedstawimy w punkcie 4.2 Modułu czwartego.
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający „optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. W badaniu wspomnianej wyżej „optymalności” pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o wybraną miarę „małości” gradientu.
Wspólną cechą przedstawionych metod jest ich iteracyjność – polegają one na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę funkcji celu.
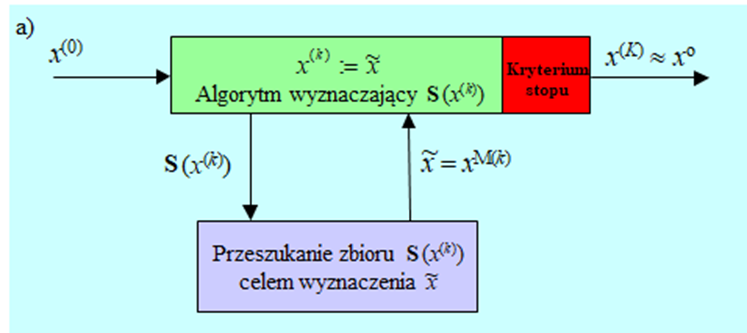
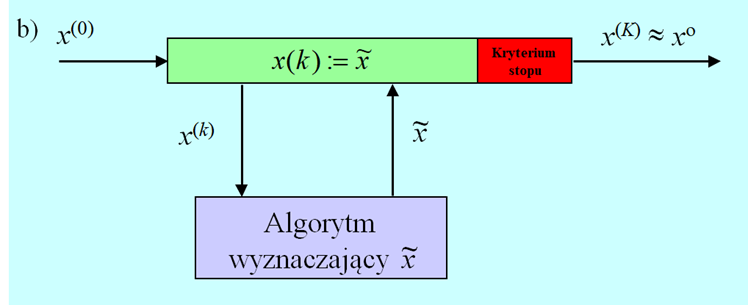
- W metodzie rozsiewania punktów próbnych zbiór do przeszukania może być generowany na różne, w tym losowe, sposoby, a przeszukanie to znalezienie w zbiorze skończonym punktu dającego najmniejszą wartość funkcji celu.
- W obu kolejnych metodach zbiór podlegającego przeszukaniu jest generowany sposób specyficzny dla metody a znalezienie „następnego” punktu bieżącego polega na:
- Dla metody obszaru zaufania – znalezieniu rozwiązania zadania wielowymiarowej minimalizacji przy ograniczeniach, funkcji modelującej, najczęściej kwadratowej.
- Dla metody kierunków poprawy – poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej.
Na schematach algorytmów przedstawionych na Rys. 2.25 wyraźnie jest zaznaczona pętla główna – zewnętrzna i algorytmy wewnętrzne, które najczęściej też są iteracyjne. Zwróćmy uwagę, że na jedną iterację zewnętrzną może wypadać wiele iteracji wewnętrznych. Tak więc miarą pracochłonności (kosztu, jak się zwykło mówić) algorytmu może być tylko iloczyn liczb tych dwu rodzajów iteracji.
W wyniku działania algorytmów dostajemy ciąg punktów \({x^{(k)} }_{k=0}^∞\), który powinien być zbieżny do rozwiązania. Dla konkretnej realizacji algorytmu tę zbieżność trzeba pokazać, co często jest trudnym zadaniem matematycznym, bo narzędzia, które wypracowała matematyka są słabo przystosowane do badania takich zagadnień.
2.4. Zbieżność metod
Algorytm generuje ciąg punktów, zatem z matematycznego punktu widzenia zbieżność algorytmu to zbieżność ciągu. Z praktycznego punktu widzenia nie jest to dobre utożsamianie, bo zbieżność matematyczna to istnienie skończonej granicy przy dążeniu liczby iteracji k do nieskończoności. Dla wielkich zadań programowania liniowego (paręset tysięcy zmiennych i ograniczeń) na rozwiązania dawane przez metodę Simpleks trzeba „długą chwilę” poczekać. Wiemy jednak, że algorytm Simplex ma tzw. zbieżność skończoną – stanie gdy znalazł rozwiązanie albo stwierdzi, ze rozwiązanie nie istnieje, możemy więc spokojnie czekać.
Zatem, od końca lat pięćdziesiątych XX w. teorii optymalizacji posługujemy się pojęciem skończonej zbieżności
Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Jednak z biegiem czasu, gdy wzrosło doświadczenie ludzi zajmujących się algorytmami optymalizacji zaczęto zauważać wadę tego pojęcia. I tak jak jego tryumf związany był z metodą Simplex tak samo jego wada została zauważona wtedy, gdy pojawiły się algorytmy skutecznie z nim konkurujące – metody punktu wewnętrznego. Metody te nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej (szybciej wpław niż dookoła po brzegu, patrz Rys. 2.5) a zamawiający wyniki nie lubią za długo czekać. Poza tym zaczęły powstawać systemy wspomagania decyzji (np. w sytuacjach nadzwyczajnych takich jak powódź czy systemy wojskowe), które powinny pracować w czasie rzeczywistym i czekanie godzinę na wynik obliczeń czynie je bezużytecznym. Zmieniło to sposób myślenia o rezultatach algorytmów optymalizacji. Już nie poszukiwanie wariantu najlepszego stało się ich celem ale wariantu ocenianego jako satysfakcjonujący, co w najprostszym przypadku oznacza dostatecznie lepszego, w określonym sensie, od wariantu początkowego. Dla nas prowadzi to do wniosku ogólnego – z praktycznego punktu widzenia użytkownika/projektanta algorytmu optymalizacji, w sytuacji w której algorytm generuje ciąg o zbieżności nieskończonej szybko zmierzający do niewielkiego otoczenia wariantu (rozwiązania) optymalnego, algorytm o zbieżności skończonej z bardzo dużym K można uznać za gorszy. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod znajdowania rozwiązania zadania programowania liniowego wykorzystujących punkty wewnętrzne.
Tu istotna uwaga. Jak pamiętamy punkt stacjonarny x ̂ może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być rożne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje poniższy rysunek funkcji
\((x_1,x_2)↦f(x_1,x_2)=x_1^3+x_2^3\).
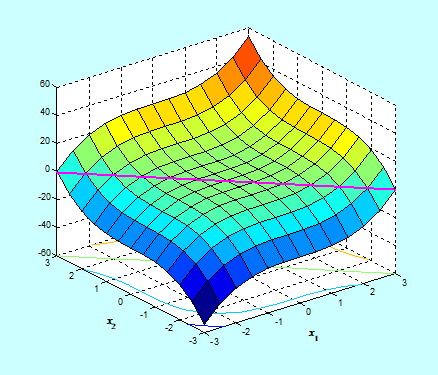

W przypadku tej funkcji punkt stacjonarny to x ̂=(0,0), a ten punkt nie jest, nawet lokalnym, ekstremum. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony na Rys. 2.26, są bardzo rzadkie.
Czasami twórcom algorytmów udaje się udowodnić własność jeszcze słabszą.
Akceptacja takiej zbieżności po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym optymistyczno/satysfakconujacym podejściu do analizy sytuacji.
W teorii optymalizacji wprowadza się jeszcze dwa rodzaje zbieżności.
⁕ Algorytm jest zbieżny globalnie, gdy jest zbieżny przy starcie z dowolnego punktu początkowego.
Wspomnieliśmy wyżej, że zbieżność może być szybsza lub wolniejsza. Wprowadzono następujące klasy szybkości zbieżności (orders of covergence).
Ciąg \(\left \{ x^{(k)} \right.\left. \right \}_{k=0}^{\infty }\) otrzymany w kolejnych krokach algorytmu zbieżny do \(x^o\) jest:
- zbieżny liniowo, gdy
\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }v\in ]0,1[\)
(w „głębokim przybliżeniu” ‖x^((k+1))-x^o ‖=ν‖x^((k))-x^o ‖),
- superliniowo tj. szybciej niż liniowo, gdy
\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }0\),
- kwadratowo, gdy
\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }v\geq 0\),
Nazwy klas zbieżności związane są z szybkością zbiegania do zera typowych ciągów:
- dla zbieżności liniowej – postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. o wzorze
\(h^{(k)}=2^{-k},\,k∈\overline {1,∞}; \,Ν(k)= \dfrac{2^{-(k+1)}}{2^{-k}} =\dfrac{1}{2}⟶\dfrac{1}{2}>0,\)
- dla zbieżności superliniowej – np. ciągu o wzorze \(h^{(k)}=k^{-k},k∈\overline {1,∞};\, Ν(k)=\dfrac{k^{-(k+1)}}{k^k} =\dfrac{1}{k}→0,\)
- dla zbieżności kwadratowej – np. ciągu o wzorze \(h^{(k)}=2^{-2^k },\,k∈\overline {1,∞};\), \(Ν(k)=(\dfrac{2^{-2^{k+1} }} {((2^{-2^k } )^2 )}=\dfrac{2^{-2}}{2^{-2^k }} →0).\)
Szybkość zbieżności ilustruje poniższy rysunek, na którym przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów.
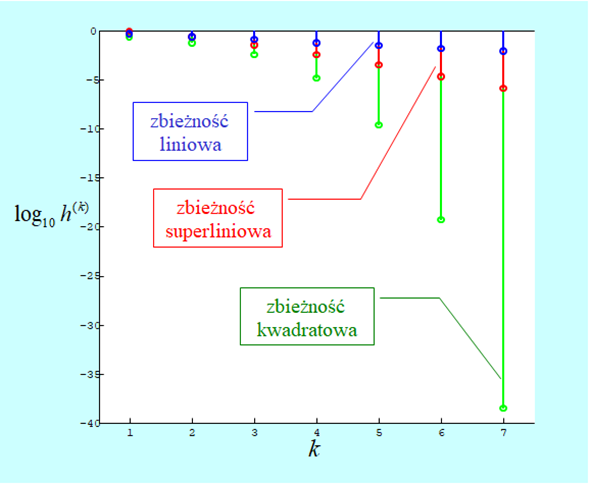
Widać, że zbieżność liniowa jest najwolniejsza, a kwadratowa najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych: szybkość liniowa jest do zaakceptowania, gdy granica jest dostatecznie mała (praktycznie nie większa niż ¼), zbieżność superliniowa jest w zupełności zadawalająca a kwadratowa jest w zasadzie pojęciem teoretycznym.
2.5. Podsumowanie
Podsumujmy nasze dotychczasowe rozważania.
Zajmujemy się rozwiązywaniem zadania optymalizacji bez ograniczeń ZO:
znaleźć \(x^o=\mathrm{argmin}_{ x∈R^n }f (x).\)
Rozważania teoretyczne i „optymistyczne” podejście do trudności z jakimi się spotykamy („Bóg jest w swoich działaniach misterny a nie złośliwy”), pozwoliły na do sformułowania czterech ogólnych schematów postępowania:
- Przez redukcję do układu równań (patrz punkt 3.1.1).
- Przez rozsiewanie (w tym losowe) skończonej liczby punktów próbnych, a następnie wybieranie najlepszego.
- Przez generowanie obszarów zaufania, a następnie ich przeszukiwanie.
- Przez generowanie kierunków poprawy i poruszanie się w tych kierunkach.
Pierwszy sposób został omówiony dokładnie w punkcie 3.1.1 i została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania trzech następnych schematów iteracyjnych jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). Dla metody rozsiewania, szukanie to określenie w zbiorze skończonym punktu dającego najmniejszą wartość funkcji celu. Zwięzły opis postępowania tego typu został przedstawiony w punkcie 3.2.1. W metodzie obszarów zaufania (punkt 3.2.2) szukanie polega na rozwiązywaniu zadanie poprawy ZKK, które jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy (punkt 3.2.3) jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej – zadanie minimalizacji w kierunku ZPK. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Takie dopracowanie zostanie przedstawione, dość szczegółowo w odniesieniu do metody kierunków poprawy.
Jeżeli to podsumowanie ma podawać ogólną klasyfikacją możliwych schematów postępowania przy rozwiązywaniu zadań optymalizacji, to trzeba dodać jeszcze schemat piąty:
- Postępowanie oparte o różne inne pomysły i ciekawe analogie, tak fizyczne, jak i biologiczne (pamiętamy ze wstępu, że Natura optymalizuje „sama z siebie”).
Ze względu na ograniczony zakres tego podręcznika analiza tego podejścia została pominięta.