Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Metody rozwiązywania zadania optymalizacji bez ograniczeń |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 16 stycznia 2026, 07:36 |
1. Metody rozwiązywania zadania poprawy
Istotnym elementem przedstawionego w poprzednim rozdziale podstawowego algorytmu kierunków poprawy jest zadanie poprawy w kierunku. Wprowadźmy dokładne określenie.
Określenie sposobu znalezienia rozwiązania zadania poprawy w kierunku, to przypominając rozważania punktu 1.4 Modułu pierwszego, pomoc dla Algorytmu, który stoi na schodach i nie bardzo wie jak szybko znaleźć dostatecznie nisko położony stopień, Dla zadania minimalizacji w kierunku to pomoc w jak najszybszym dotarciu na najniższy stopień. W obu przypadkach naturalne postępowanie to metoda prób i błędów (najpierw w prawo, gdy niżej to dalej w prawo, gdy teraz wyżej to w lewo,...), ale nie bardzo wiadomo jak daleko się ruszać (skakać) w kolejnym kroku.
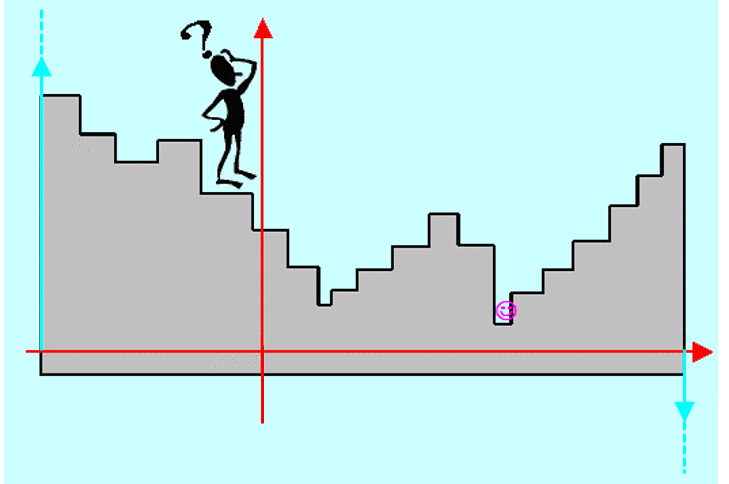
Posługując się rysunkami poziomicowymi przedstawmy podstawowe problemy z jakimi możemy się spotkać. Zwróćmy uwagę na fakt, że rozważania będą ogólne, ponieważ jest dość oczywiste, że napisanie wzoru dla funkcji dwu zmiennych o poziomicach naszkicowanych na rysunkach to tylko kwestia chęci i czasu.
Przyjmijmy, że kierunki poprawy to kierunki antygradientu i algorytm doszedł do punktu \(x^{(k)}\), w którym wyznaczył kierunek poprawy \(d^{(k)}\)– Rys. 4.2.
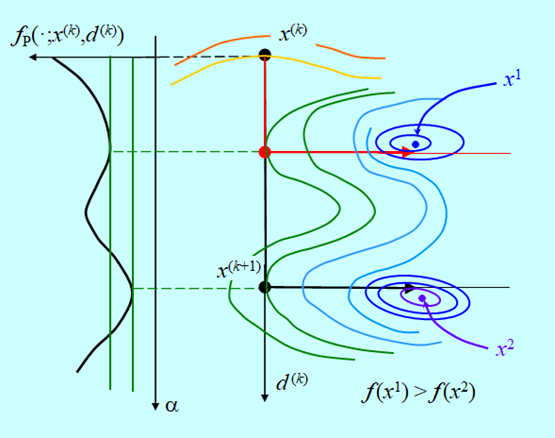
Rysunek powyższy pokazuje sytuację, w której dokładna minimalizacja w kierunku „przeskoczy” lokalne minimum funkcji \(f_P (⋅;x^{(k)},d^{(k)})\) i da punkt \(x^{(k+1)}\). Kierunek poprawy „wystawiony” w tym punkcie zaprowadzi do minimum globalnego funkcji f. Gdyby skończyć poszukiwanie minimum w kierunku we wcześniej napotkanym minimum lokalnym funkcji \(f_P\), to kierunek poprawy zaprowadzi do minimum lokalnego funkcji f.
Dokładna minimalizacja w kierunku pozwala znaleźć rozwiązanie zadania minimalizacji. Ale przecież nietrudno jest nieco zmodyfikować sytuację. Co się stanie gdy mamy sytuację taką jak na Rys. 4.3?
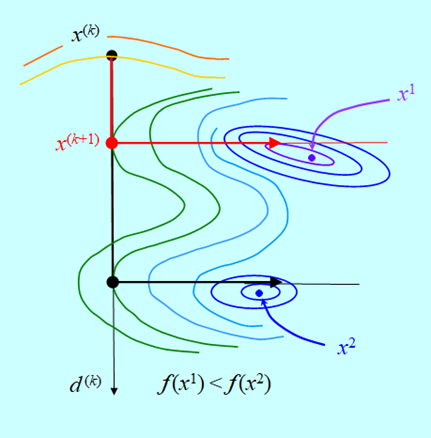
Teraz, „zatrzymanie” minimalizacji w kierunku w punkcie minimum lokalnego funkcji \(f_P\) daje dobry rezultat, a dokładna minimalizacja tej funkcji „wpycha” algorytm w obszar przyciągania minimum lokalnego funkcji f.
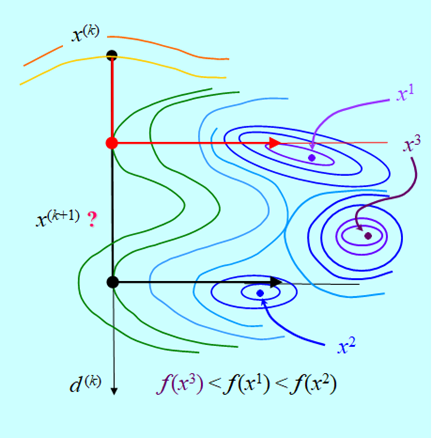
Ten rysunek pokazuje niestety, że algorytm kierunków poprawy przy dokładnej i nie dokładnej minimalizacji w kierunku może „wpaść” w obszar przyciągania któregoś z minimów lokalnych i w konsekwencji nigdy nie znaleźć rozwiązania zadania minimalizacji.
Jakie wnioski należy wyciągnąć z tej analizy.
- Bez dodatkowych założeń o funkcji minimalizowanej albo dodatkowych zabezpieczeń, algorytm kierunków poprawy może znaleźć tylko minimum lokalne.
Wybrać wspomniane wyżej dodatkowe założenia jest prosto, np. funkcja f powinna być wypukła. Oczywiście muszą one zawężać klasę funkcji dla których algorytm kierunków poprawy na pewno znajdzie rozwiązanie zadania minimalizacji.
W zasadzie nie udało się wymyślić praktycznych zabezpieczeń gwarantujących znalezienie minimum globalnego. Teoretyczne dowody zbieżności dla wszystkich algorytmów kierunków poprawy mówią o zbieżności do minimum lokalnego, lub nawet słabiej, do punktu stacjonarnego gradientu.
- Dokładna minimalizacja w kierunku nie zawsze jest potrzebna, a czasem (Rys. 4.4) jest wręcz szkodliwa. Ważne jest aby poprawić funkcję celu w dostateczny sposób, tzn. aby różnica \(f(x^{(k)}) – f (x^{(k)} + \alpha ^{(k)}d^{(k)}) \) była dodatnia i nie za mała (formalne określa ją współczynnik ? wprowadzony w definicji zadania ZPK).
Wybór długości kroku można więc próbować oprzeć o jak najprostsze sposoby postępowania. Intuicyjnie jest jednak oczywiste, że poprawa (zmalenie, bo minimalizujemy) funkcji celu powinna być w jakimś relatywnym sensie znaczna.
Zagadnieniem określenia warunków jakie musi spełniać poprawa aby wystarczyło to do zbieżności algorytmów zaczęto się zajmować na początku lat sześćdziesiątych XX w. Mniej więcej w ich połowie udowodniono dla gładkich funkcji celu twierdzenia pokazujące, że dla szerokiej klasy sposobów generowania kierunków poprawy można zapewnić zbieżność algorytmów do punktu stacjonarnego gradientu bez konieczności dokładnej minimalizacji w kierunku (rozwiązywania zadania ZK), pod warunkiem, że algorytm wyznaczania \(\alpha {(k)}\) zapewnia uniknięcie zbyt długich kroków. Wszystkie metody, które będą przedstawione w punkcie następnym są metodami tej klasy.
Przedstawimy teraz warunek, który jest najczęściej stosowany. Jest to tak zwana reguła L. Armijo .
Występujący w powyższej nierówności wektor \(d^{(k)}\) jest kierunkiem poprawy w punkcie \(x^{(k)}\), zatem zgodnie z definicją \(∇f(x^{(k)})d^{(k)}<0\). Ponieważ \( \alpha^{(k)}\) i \(\eta\) są większe od zera, to
\(ηα^{(k)} ∇f(x^{(k)})d^{(k)}<0.\)
Wobec tego, przy założeniu że funkcja f ma minimum, z Lematu 3.3 wynika, że
\((∃\alpha ^M>0)(∀\alpha \in ]0,\alpha ^M [ ) f (x^{(k)} + \alpha d^ {(k)}) – f (x{(k)} < 0.\)
Powyższa nierówność pozwala na przedstawienie oczywistej graficznej interpretacji reguły Armijo.
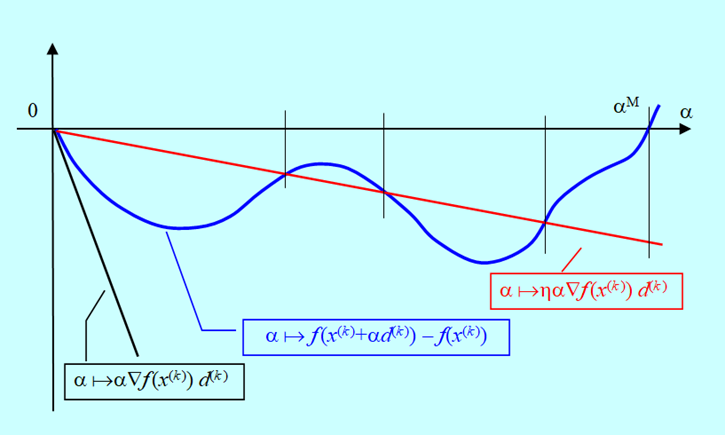
W oparciu o tę regułę można podać następujący, prosty algorytm wyznaczania długości kroku w kierunku, przy założeniu, że potrafimy obliczyć gradient.
Algorytm wyznaczania długości kroku w kierunku oparty na regule Armijo (backtracking line search)
Inicjalizacja
Wybierz początkową długość kroku \(s > 0\).
Wybierz parametry algorytmu \(\eta\) i \(\beta\) (doświadczenie podpowiada \(\eta \in [10–5,0.1] oraz \beta \in [0.1,0.5])\)
Podstaw i := 0.
Kroki algorytmu
- Sprawdź nierówność \(f(x^{(k)}+β^i sd^{(k)})-f(x^{(k)})≤ηβ^i s∇f(x^{(k)})d^{(k)}\). (\(β^i\) to \(β\) do potęgi i). Jeżeli spełniona, podstaw \(α^{(k)}:=β^i s\) i stop. Jeśli nie przejdź do 2.
- Podstaw \( i := i + 1\), przejdź do 1.
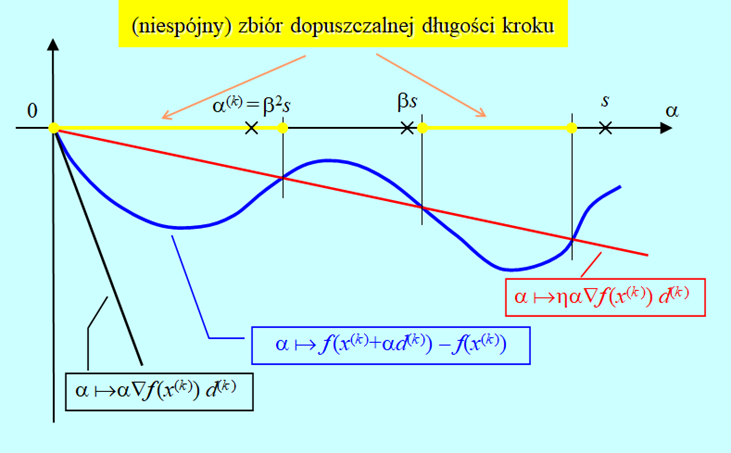
Rys. 4.6 pokazuje, że algorytm wyznaczy \(\alpha^{(k)}\) w skończonej ilości kroków (dowód formalny opuszczamy), oraz że wielkość otrzymanego zmalenia funkcji celu zależy w sposób istotny od początkowej długości kroku s.
Algorytm oparty na regule Armijo wyznacza długość kroku w kilku iteracjach. Jest to istotna zaleta w sytuacji, gdy obliczenia wartości funkcji celu są, jak się to często mówi, kosztowne, tzn. zajmują dużo czasu.
Jednak w niektórych przypadkach pożądana jest dobra aproksymacja minimum w kierunku. Algorytmem, który daje taką dobrą aproksymację jest tzw. algorytm złotego podziału, który dla tzw. funkcji unimodalnych pozwala zlokalizować minimum z dowolną dokładnością.
Algorytm złotego podziału
Inicjalizacja
Wybierz początkową długość kroku \(m > 0\).
Wybierz dokładność lokalizacji minimum \(\varepsilon > 0\).
Kroki algorytmu
- Oblicz \(f(x^{(k)}+md^{(k)})\).
- Jeżeli \(f(x^{(k)}+md^{(k)})≥f(x^{(k)})\) podstaw \(a_0 := 0, b_0 := m\) i idź do 5. Jeśli nie, podstaw \(j := 0\) i\(\alpha_j := 0\), a następnie przejdź do 3.
- Podstaw \(\alpha_j +1 := \alpha_j + m\) i oblicz \(f(x^{(k)}+α_{j+1} d^{(k)}).\)
- Jeżeli \(f(x^{(k)}+α_{j+}) d^{(k)})≥f(x^{(k)}+α_j d^{(k)})\) podstaw \(a_0:= \alpha_{j –1}, b_0 := \alpha_{j +1}\) i idź do 5. Jeśli nie, podstaw \(j := j +1\) i idź do 3.
- Podstaw \(i := 0\).
- Podstaw \(l_i := b_i – a_i\).
- Jeżeli \(l_i \leq \varepsilon\) idź do 10. Jeżeli nie, idź do 8.
- Podstaw \(v_i:=a_i+\dfrac{1}{2}(3-√5)l_i\) oraz \(w_i:=a_i+\dfrac{1}{2}(√5-1)l_i.\) Oblicz \(f(x^{(k)}+v_i d^{(k)})\) oraz \(f(x^{(k)}+w_i d^{(k)})\).
- Jeżeli \(f(x^{(k)}+v_i d^{(k)}) < f(x^{(k)}+w_i d^{(k)})\)., podstaw \(a_{i+1}:= a_i, b_{i+1} := w_i\) , podstaw \(i := i+1\) i idź do 6. Jeśli nie, podstaw \(a_{i+1}:= v_i, b_{i+1} := b_i\) , podstaw \(i := i+1\) i idź do 6.
- Przyjmij za rozwiązanie \(\alpha^{(k)} := \dfrac{1}{2}(a_i +b_i)\) i stop.
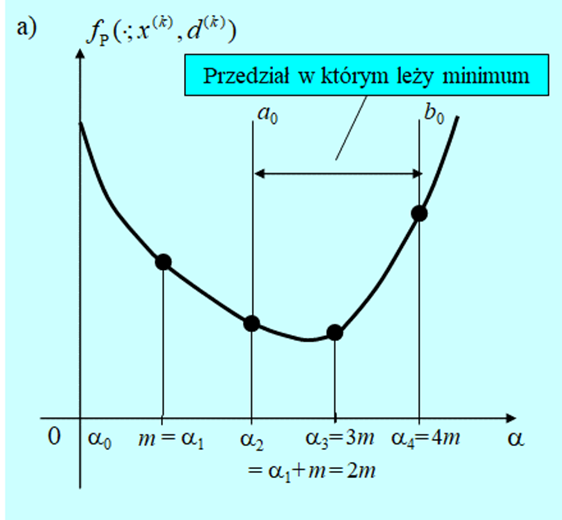
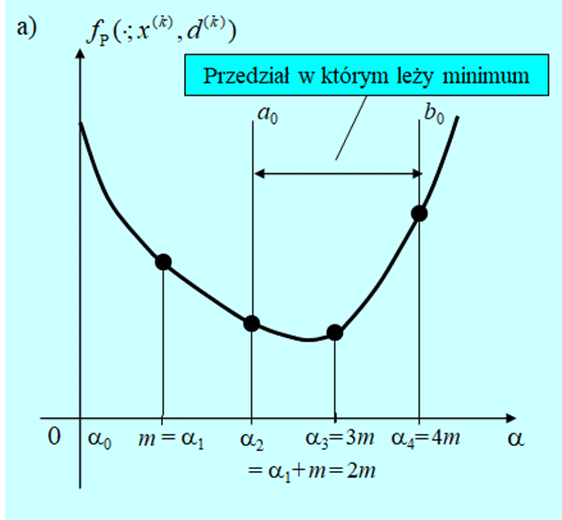
Pierwsze cztery kroki przedstawionego algorytmu to lokalizacja przedziału w którym powinien znajdować się punkt minimalizujący. Jeżeli funkcja \(f_P (⋅;x^{(k)},d^{(k)})\) jest unimodalna dla każdego \(\alpha >0\), to taki przedział na pewno zostanie znaleziony. Natomiast gdy funkcja minimalizowana nie jest unimodalna to w ten sposób zostanie zlokalizowane jej minimum lokalne.
Następne kroki to symetryczna redukcja przedziału \([a_0, b_0]\) do przedziału o długości mniejszej niż zadana dokładność \(\varepsilon\), i wybór jako rozwiązania średniej arytmetycznej z wartości końców tego przedziału (stosujemy tu heurystyczną regułę postępowania: jak nie wiemy gdzie punkt leży, to przyjmujemy, że w środku przedziału).
Nazwa metody wzięła się stąd, że konstruując ten algorytm dla zachowania symetrii posłużono się znanymi już starożytnym zasadami złotego podziału odcinka, które dały niewymierne mnożniki użyte w kroku 8. Zauważmy, że jedną z własności ciągu przedziałów generowanych przez ten algorytm jest stałość stosunku długości podprzedziału usuwanego do aktualnej długości przedziału poszukiwań. Ponieważ nie wiemy, który przedział będzie usunięty, to przy naszych oznaczeniach jest to warunek
\(\dfrac{v_k-a_k}{b_k-a_k }=\dfrac{b_k-w_k}{b_k-a_k }=const=\dfrac{1}{2}(3-√5).\)
Doświadczenia zebrane w ciągu ponad półwiecza stosowania algorytmu złotego podziału potwierdziły jego przydatność jako metody rozwiązywania zadania minimalizacji w kierunku. Jest to więc wspaniała, w zasadzie heurystyczna, odpowiedź na pytanie męczące nasz Algorytm stojący na schodach na Rys. 4.1.
Innym algorytmem, który jest stosowany w sytuacji gdy uważamy, że trzeba posłużyć się algorytmem dokładniejszym niż algorytm oparty na regule Armijo jest procedura wykorzystująca (kwadratowy) wielomian interpolacyjny Lagrange’a opisana np. w podręczniku A. Stachurski: Wprowadzenie do optymalizacji, Oficyna Wydawnicza PW 2009, podrozdział 3.6.
Intuicyjnie oczywistym założeniem potrzebnym do poprawnego działania algorytmu złotego podziału (podobnie jak i algorytmu interpolacji kwadratowej), jest wymaganie unimodalności funkcji minimalizowanej w kierunku \(f_P (⋅;x^{(k)},d^{(k)})\). Ponieważ przeważnie nie wiemy, czy funkcje, z którymi mamy do czynienia spełniają ten warunek, praktyczne implementacje algorytmów tego typu są wyposażane, tak jak przedstawiony algorytm złotego podziału, w fazę pierwszą która ma doprowadzić (cały czas jesteśmy optymistami) do określenia przedziału unimodalności funkcji \(f_ P\).
Podsumujmy rozważania tego krótkiego rozdziału.
- Bez dodatkowych założeń o funkcji minimalizowanej albo dodatkowych zabezpieczeń algorytm kierunków poprawy może znaleźć tylko minimum lokalne.
- Zadanie poprawy rozwiązywane w każdym kroku metody kierunków poprawy nie musi być zadaniem minimalizacji. Ważne jest aby poprawić funkcję celu, tzn. aby różnica
- Jeżeli rezygnujemy z minimalizacji w kierunku (rozwiązywane zadanie poprawy nie jest zadaniem minimalizacji w kierunku), to algorytm wyznaczania długości kroku musi dawać krok spełniający pewne warunki, np. regułę Armijo.
2. Gradientowe algorytmy rozwiązywania zadań optymalizacji bez ograniczeń
W punkcie 3.2 Modułu trzeciego przedstawiłem, między innymi, dwa podstawowe algorytmy znajdowania rozwiązania zadania optymalizacji: algorytm obszaru zaufania i algorytm kierunków poprawy. Podane tam sformułowania algorytmów są ogólnymi schematami postępowania i kroki istotne dla ich działania nie zostały dokładnie opisane. Jak pamiętamy, opis algorytmów obszaru zaufania nie będzie dalej rozwijany w tym podręczniku i dlatego w rozdziale poprzednim nie poruszaliśmy zagadnień związanych z rozwiązywaniem zadania minimalizacji funkcji modelującej na obszarze zaufania, zadania ZKK, a skupiliśmy się tylko na opisie metod rozwiązywania zadania poprawy dla algorytmu kierunków poprawy, zadania ZPK. Zatem pierwszy element szczegółowego opisu algorytmu kierunków poprawy został już przedstawiony. Do pełnego ich określenia pozostaje nam jeszcze ustalenie metody wyznaczanie kierunku poprawy oraz dyskusja nad kryterium stopu. Tym zagadnieniom poświęcony będzie ten punkt.
2.1. Algorytm gradientu prostego
Przypomnijmy zadanie, którym będziemy się dalej zajmować.
Zadanie optymalizacji bez ograniczeń (ZOBO):
znaleźć \(x^o=\mathrm{argmin}_{x∈\mathbb{R}^n }f (x)\)
Zgodnie z przyjętym optymistycznym podejściem omawianym w rozdziale piątym zakładamy, że w ZOBO
- funkcja wyboru \(f\) jest gładka,
- potrafimy wyliczyć jej gradient \(\bigtriangledown f\),
- gdy potrzebna – wyznaczyć macierz Hessego \(\bigtriangledown ^2 f \).
Definicja kierunku poprawy d „wystawionego” w punkcie bieżącym \(x{(k)},\) wymaga aby „ruch wzdłuż niego” dał zmalenie funkcji wyboru, co przy naszych założeniach zgodnie z Lematem 3.3, oznacza, że d jest kierunkiem poprawy gdy \(∇f(x^{(k)})d<0.\)
Wobec tego narzucającym się kierunkiem poprawy jest kierunek antygradientu \(d=-∇^T f(x^{(k)})\) (oczywiście w sytuacji gdy jest niezerowy) ponieważ
\((∀x^{(k)}) ∇f(x^{(k)})(-∇^T f(x^{(k)}))=-‖∇f(x^{(k)})‖^2 < 0.\)
Przy takim wyborze kierunku poprawy możemy podstawowy algorytm kierunków poprawy ukonkretnić do algorytmu realnego.
Algorytm gradientu (prostego) (Algorytm największego spadku, Algorytm Cauchy’ego)
Inicjalizacja
Ustal dokładność algorytmu \(\varepsilon > 0\).
Wybierz punkt początkowy \(x^{(0)}\), podstaw \( x := x^{(0)}\),.
Podstaw \(k := 0.\)
Kroki algorytmu
- Oblicz \(∇f(x)\), podstaw \(grad := ∇f(x)\).
- Jako kierunek poprawy wybierz kierunek antygradientu podstawiając \(d:=-(grad)^T\).
- Wyznacz długość kroku \(\alpha^{(k)}\) w kierunku antygradientu (kierunku poprawy) d, podstaw \(α:=α^{(k)}\).
- Wylicz następny punkt podstawiając \(xnew:=x+α*d\).
- Podstaw \(k := k + 1\). Oblicz \(∇f(xnew)\), oraz \(||∇f (xnew)||\), podstaw \(grad := ∇f(xnew)\), podstaw \(norm := ||∇f(xnew)||\). Jeżeli \(norm < \varepsilon\), to \(xnew\) przyjmij za rozwiązanie, podstaw \(ilosc_iteracji := k\) i stop. W przeciwnym przypadku podstaw \(x := xnew\) i idź do 2
Nie sprecyzowaliśmy jak w kroku 2. algorytmu ustalić długość kroku w kierunku antygradientu. Trzeba zrobić to tak aby można było pokazać, że generowany przez algorytm ciąg punktów \( \left\{ x^{(k)}\left. \right \}\right. _{k=0}^∞\) jest w określonym sensie zbieżny. Rozwiązanie tego zagadnienia daje następujące twierdzenie.
Jeżeli
funkcja f jest różniczkowalna oraz ograniczona od dołu a jej gradient \(∇f\) spełnia warunek Lipschitza na \(\mathbb{R}^n\), to znaczy \((∃L∈\mathbb{R})(∀x,y∈\mathbb{R}^n) ‖(∇f(x)-∇f(y))‖≤L‖x-y‖\),
to
nieskończony ciąg \(\left\{ x^{(k)}\left. \right \}\right. _{k=0}^∞\) generowany przez algorytm gradientu prostego, w którym długość kroku w kierunku antygradientu \(\alpha^{(k)}\). jest ustalona:
– przez rozwiązanie zadania minimalizacji w kierunku:
zbiega do punktu stacjonarnego gradientu, tzn. \(\left\| \bigtriangledown f(x^{(k)})\right\|_{ \overrightarrow{k \to \infty }}0\).
Zatem przy stosunkowo słabych założeniach mamy relatywnie słabą zbieżność algorytmu największego spadku – zbieżność nieskończoną do punktu stacjonarnego gradientu.
Przy odpowiednio mocniejszych założeniach o funkcji wyboru można pokazać, że algorytm ten zbiega liniowo do punktu minimalizującego.
Wiemy już, że teoretycznie, algorytm gradientu prostego może znaleźć rozwiązanie zadania minimalizacji. Zbadajmy jego zachowanie rozwiązując proste zadanie minimalizacji.
Rezultaty działania algorytmów optymalizacji można przedstawiać na dwa sposoby: za pomocą tabelek, lub rysunków. Jeżeli funkcja celu ma więcej niż trzy argumenty, to wymyślenie dobrego rysunku ilustrującego zachowanie się algorytmu może być trudne i pozostają tylko tabelki. Natomiast dla funkcji dwu-argumentowych stosowne rysunki pokazujące kolejne kroki (trajektorię) algorytmu na płaszczyźnie na tle wykresu poziomicowego funkcji minimalizowanej niosą w sobie najpełniejszą, intuicyjnie zrozumiałą informację o zachowaniu się algorytmu. Trzeba tylko dobrze dobrać funkcję celu – dostatecznie trudną dla algorytmów lecz o stosunkowo łatwych do narysowania poziomicach.
Rysunek prezentowany w tym przykładzie przedstawia poszczególne punkty znalezione przez algorytm największego spadku z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który miał znaleźć rozwiązanie zadania minimalizacji funkcji dwu zmiennych

I nie jest to przypadek. Zatrzymanie algorytmu relatywnie daleko od punktu minimalizującego wynika z właściwości funkcji, która w sporym otoczeniu minimum zmienia się niewiele (wartość poziomicy w punkcie \(x^{(3)}\) wynosi 0.09!). Takie zachowanie funkcji ścisłe wypukłych nie jest rzadkością – po prostu, wiele funkcji ściśle wypukłych w zbyt dużym otoczeniu swojego minimum, z praktycznego punktu widzenia, traci swoją ścisłą wypukłość stając się funkcjami „prawie stałymi”, w naszym przypadku o wartości niewiele różnej od zera. W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu.
Jeżeli zatem zależy nam na dokładnym wyznaczeniu punktu minimalizującego funkcję celu, której zachowania w okolicy minimum nie znamy (a tak jest przecież najczęściej), to musimy w kryterium stopu wybrać bardzo wysoką dokładność, tzn. bardzo małe \(\varepsilon\), rzędu 10–4 lub mniejsze. Ceną jaką możemy za takie wymaganie zapłacić może być bardzo wiele kroków algorytmu, a więc długi czas obliczeń.
Jaki rysunek dostajemy dla zwiększonej dokładności?
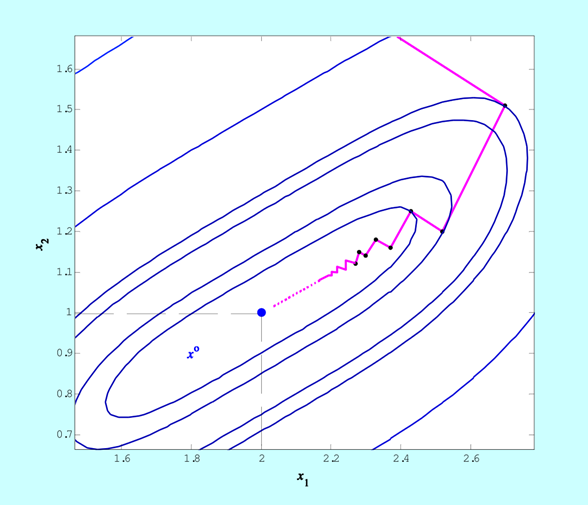
Przedstawione w przykładzie zachowanie – zygzakowanie – omawianego algorytmu, szczególnie wyraźne gdy napotka na długą i powoli opadającą „dolinę”, oznacza bardzo powolne zbliżanie się do rozwiązania i stanowi podstawową wadę algorytmu największego spadku. Kłopoty w takiej sytuacji są powiększane jeszcze tym, że składowe gradientu są coraz mniejszymi liczbami, a więc ich wyznaczenie jest obarczone coraz większym błędem względnym, co oznacza, że ruch w kierunku punktu minimalizującego jest nie tylko powolny ale i coraz bardziej niepewny.
Funkcja rozpatrywana powyżej była mniej złośliwa niż bananowa funkcja Rosenbrocka, której poziomice rysowaliśmy w poprzednich modułach. Jak poradzi sobie algorytm gradientu prostego ze znalezieniem minimum funkcji o której wiemy, że spełnia nasze optymistyczne założenia tylko w niewielkich otoczeniach punktu bieżącego?
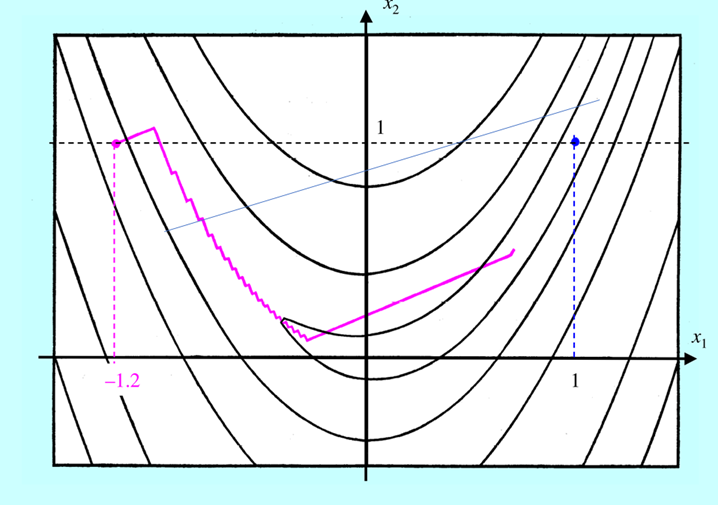
Jak widać nie najlepiej. Algorytm szybko zaczął „zygzakować”, potem odważnie „wyskoczył” z doliny prowadzącej do minimum, lecz po powrocie na jej dno zaczął zmierzać do celu tak drobnymi zygzakami, że przez pozostałe 960 iteracji posunął się bardzo niewiele. „Odwaga” była tu jednak przypadkowa. Od mniej więcej szóstej iteracji algorytm generuje kierunek poprawy (zaznaczony linią) na którym funkcja minimalizowana w kierunku f P ma dwa minima lokalne: „bliższe”, położone koło punktu startowego i „dalsze’, położone z drugiej strony góry które jest globalne. Do trzydziestej szóstej iteracji, zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum (przypomnijmy sobie rysunek 4.2) i dopiero w trzydziestej ósmej – „przeskoczyła” to lokalne minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania”.
Obie omawiane funkcje spełniają założenia, nawet tych silniejszych twierdzeń o zbieżności. Przedstawione przykłady pokazują więc, że zbieżność teoretyczna to jedno, a
czyli zdolność do znalezienia rozwiązania w rozsądnej liczbie iteracji (rozsądnym czasie).
Badanie zbieżności teoretycznej jest bardzo ważne przy konstruowaniu algorytmów. Trzeba przecież sprawdzić czy algorytm, który wymyśliliśmy ma w ogóle szansę na „dobiegnięcie” do rozwiązania. Teoria pozwala odrzucić pomysły bez sensu. Niestety bardzo rzadko rozważania teoretyczne pozwalają wyeliminować od razu pomysły, które w praktycznej realizacji są nieudane. Wynika to z faktu, że narzędzia (system pojęć składających się na modele analizy matematycznej) nie są dostosowane do potrzeb analizy zachowania algorytmów czyli tzw. analizy numerycznej.
Rożne próby zastosowania metody największego spadku pokazały już dawno, że metoda ta w rozsądnym czasie może dać rozwiązanie tylko dla najprostszych, dobrze uwarunkowanych w całej przestrzeni zadań. Zatem, gdy chcemy mieć skuteczniejsze narzędzia musimy albo metodę gradientu zmodyfikować, albo (w ramach metod kierunków poprawy) wymyślić zupełnie inne podejście.
Z wielu pomysłów, które pojawiły się w ostatnich sześćdziesięciu paru latach próbę praktycznej przydatności przetrwały w zasadzie tylko dwa algorytmy. Zanim je przedstawimy, przez chwilę zastanowimy się, dlaczego algorytm gradientu prostego działa tak źle.
Posłużenie się regułami zapisanymi w dowolnym algorytmie przeznaczonym do znalezienia rozwiązania zadania optymalizacji (algorytmie optymalizacji) daje ciąg punktów zaczynający się od punktu startowego (z numerem 0), którego wyznaczanie można opisać następującym wzorem
\(x^{(k+1)}=\mathfrak{A} (x^{(k)},...),\, x^{(0)}\,\, \mathrm{ dane .} \qquad (4.1)\)
W operatorze \(\mathfrak{A} \) nie wpisaliśmy wszystkich argumentów, ponieważ sposób generacji nowego punktu musi zależeć od punktu bieżącego i może zależeć od punktów poprzednich, od historii. Innymi słowy algorytm może być bez pamięci i z pamięcią. Wypisując wzór, tej drugiej możliwości nie chcieliśmy wykluczyć, a także nie chcieliśmy określić tzw. głębokości pamięci, to znaczy określić ile kroków wstecz jeszcze uwzględniamy. Dla matematyka wzór (4.1) to równanie różnicowe, „bliski krewny” równań różniczkowych zwyczajnych rozważanych w pierwszym wykładzie. Badanie zbieżności algorytmów optymalizacji, to nic innego jak badanie asymptotycznych własności rozwiązań (szczególnych) takich równań różnicowych.
Jeżeli w ten sposób analizować zachowanie algorytmu gradientu prostego, to mamy
\(x^{(k+1)}=x^{(k)}-α^{(k)} ∇^T f(x^{(k)})=\mathfrak{A} (x^{(k)})\),
i łatwo jest zauważyć, że główną przyczyną zygzakowania jest brak pamięci – nowy kierunek w żaden sposób nie jest związany z poprzednim, a intuicyjnie jest oczywiste, że wprowadzenie takiego związku uspokoiłoby zbyt nerwowe ruchy algorytmu. Nie może jednak „przedawkować ze środkiem uspokajającym”, bo i tak, jak widzieliśmy, po pewnym czasie zygzaki stają się zygzaczkami i algorytm prawie że stoi w miejscu. Można jednak zapisać dwa warianty modyfikacji mogące dać poprawę zachowania:
- prostszy, polegający na dodaniu „poprawki” zależnej od „historii”:
\(x^{(k+1)}=x^{(k)}-α^{(k)} (∇^T f(x^{(k)})+p(x^{(k)},x^{(k-1)},...))=\mathfrak{A} (x^{(k)},x^{(k-1)},...)\),
- i mniej oczywisty – przeskalowujący gradient, też w zależności od „historii”:
\(x^{(k+1)}=x^{(k)}-α^{(k)} \mathfrak{D}(x^{(k)},x^{(k-1)},...)∇^T f(x^{(k)})=\mathfrak{A} (x^{(k)},x^{(k-1)},...)\).
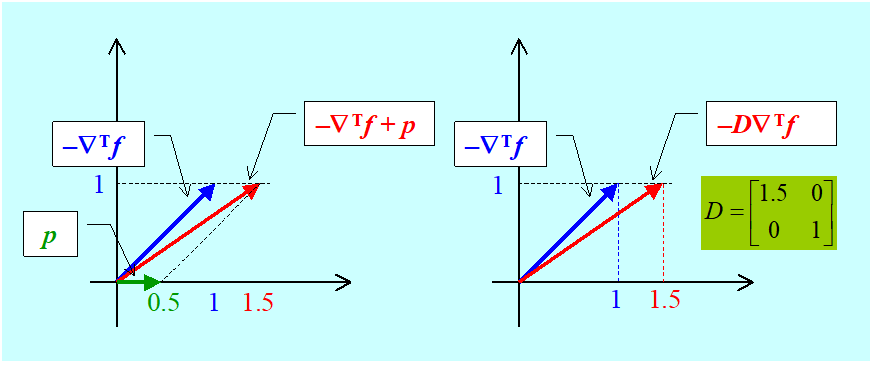
Jak zatem określać poprawkę addytywną \(p(\cdot )\) albo, w najprostszym przypadku, kwadratową macierz transformacji \(D(\cdot ) = \mathfrak{D}(\cdot )\) ?
Odpowiemy na to pytanie w dwu kolejnych punktach.
2.2. Algorytm gradientu sprzężonego
Zajmiemy się najpierw przypadkiem pierwszym – poprawką addytywną.
Przyjmijmy na moment, że chcemy minimalizować metodą gradientu prostego funkcję kwadratową o dodatnio określonej macierzy Q:
\(x↦f(x)=x^T Qx+c^T x+σ\).
Rysunek zrobimy dla funkcji dwu zmiennych.

Algorytm wystartował z punktu \(x^{(0)}\) i w kierunku antygradientu \(d^{(0)}=-∇^T f(x^{(0)})\) dokładnie minimalizując w kierunku znalazł punkt \(x^{(1)}=x^{(0)}-α^{(0)} ∇^T f(x^{(0)})\). Następny krok zaprowadzi go do punktu \(x^{(2)}\) leżącego na prostej wyznaczonej przez antygradient \(-∇^T f(x^{(1)})=d^{(1)}\), i tak dalej. Zauważmy, że tak wyznaczane kolejne kierunki poprawy (antygradienty) są do siebie prostopadłe
\(∇f(x^{(k)})∇^T f(x^{(k+1)})=0,\, k=0,1,\qquad (4.2)\)
nie tylko dla funkcji kwadratowych, ale dla dowolnych funkcji różniczkowalnych, ponieważ kolejne punkty \(x^{(k+1)}=x^{(k)}-α^{(k)} ∇^T f(x^{(k)})\) są punktami minimalizującymi funkcję
\(α↦f_P (α;x^{(k)},-∇^T f(x^{(k)}))=f(x^{(k)}-α∇^T f(x^{(k)}))\),
co oznacza, że spełniony jest warunek (różniczkowanie funkcji złożonej)
\(0=\dfrac{d}{dα} f(x^{(k)}-α^{(k)} ∇^T f(x^{(k)}))=∇f(x^{(k)}-α^{(k)} ∇^T f(x^{(k)}))(-∇^T f(x^{(k)})) =-∇f(x^{(k+1)})∇^T f(x^{(k)})\).
Rysunek pokazuje, że w punkcie \(x^{(1)}\) istnieje kierunek lepszy od antygradientu, oznaczmy go q, mający tą własność, że dokładna minimalizacja na tym kierunku doprowadzi do rozwiązania \(x^o\). Wyznaczyć ten kierunek jest łatwo. Przy naszych założeniach rozwiązanie zadania optymalizacji musi spełniać równanie (Twierdzenie 3.6):
\(0=∇^T f(x^o)=2Qx^o+c\), co daje \(x^o=-\dfrac{1}{2}Q^{(-1)} c\).
Zatem \(q=x^o-x^{(1)}=-\dfrac{1}{2}Q^{(-1) }c-x^{(1)}\). Jak na razie, te obliczenia nic ciekawego nie dają, ale policzmy czemu równa się iloczyn \(d ^{(0)}Qq = –\bigtriangledown f (x^{(0)} )Qq\). Najpierw zauważmy, że
\(∇^T f(x^{(1)})=2Qx^{(1)}+c\) i jak pamiętamy \(∇f(x^{(0)})∇^T f(x^{(1)})=0\).
Teraz możemy policzyć wartość interesującego nas iloczynu
\(-∇f(x^{(0)})Qq=-∇f(x^{(0)})Q(-\dfrac{1}{2}Q^(-1) c-x^{(1)})=∇f(x^{(0)})(1/2 c+Qx^{(1)})=\)
\(=∇f(x^{(0)})(\dfrac{1}{2} ∇^T f(x^{(1)}))=0\).
czyli
\(-∇f(x^{(0)})Qq=0.\qquad (4.3)\)
Wprowadźmy następujące definicje:
Niezerowe, wektory \(d_i\) oraz \(d_j\) takie, że istnieje dodatnio określona macierz \(Q\), dla której
\(r\) elementowy zbiór niezerowych wektorów \(d_1,...,d_r\) przestrzeni n-wymiarowej, \(r∈\overline{2,n}\), nazywamy układem \(r\) wektorów wzajemnie sprzężonych względem dodatnio określonej macierzy Q (układem Q-sprzężonym) jeżeli
Prawdzie jest następujące stwierdzenie
Układ r wektorów Q-sprzężonych jest liniowo niezależny
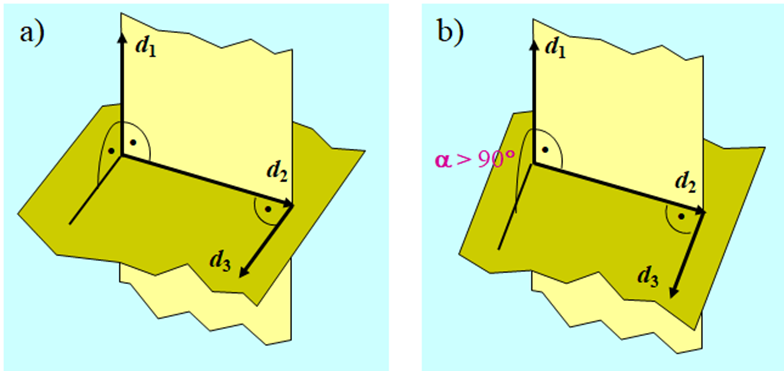
Najprostszym przykładem dwu wektorów sprzężonych są wektory prostopadłe, które są sprzężone względem macierzy jednostkowej. Trzy wektory w przestrzeni trójwymiarowej są sprzężone względem macierzy jednostkowej jeżeli każdy z nich jest prostopadły do płaszczyzny wyznaczonej przez dwa pozostałe. Zatem już w przestrzeni trójwymiarowej sprzężenie względem macierzy jednostkowej to inna własność niż prostopadłość.
Wzór (4.3): \(-∇f(x^{(0)})Qq=0\), pokazuje, że wektor antygradientu obliczony w punkcie początkowym \(-∇^T f(x^{(0)})\) i wektor \(q\) ustalający kierunek na którym leży punkt minimalizujący są sprzężone względem macierzy \(Q\) określającej minimalizowaną funkcję kwadratową.
Wektor \(q\) jest dany wzorem \(q=-\dfrac{}{2} Q^{-1} c-x^{(1)}\), zatem aby go obliczyć trzeba odwrócić macierz \(Q\).
Zastanowimy się teraz nad odpowiedzią na pytanie: czy można go wyznaczyć bez odwracania macierzy?
Przyjmiemy zatem, że
\(q=-∇^T f(x^{(1)})-β∇^T f(x^{(0)}), \qquad (4.4)\)
gdzie współczynnik \(\beta\) trzeba wyznaczyć. Do jego wyliczenia posłużmy się warunkiem Q-sprzężoności wektorów \(-∇^T f(x^{(0)})\) i \(q\) czyli równaniem \(-∇f(x^{(0)})Qq=0\). Zauważmy najpierw, że
\(x^{(1)}=x^{(0)}-α^{(0)} ∇^T f(x^{(0)})\), czyli \(-∇f(x^{(0)})=\dfrac{1}{α^{(0)} }(x^{(1)}-x^{(0)} )^T\),
a także
\(∇f(x^{(1)})-∇f(x^{(0)})=2(x^{(1)} )^T Q+c^T-2(x^{(0)} )^T Q-c^T=2(x^{(1)}-x^{(0)} )^T Q\).
Mamy zatem
\(0=-∇f(x^{(0)} )Qq=-∇f(x^{(0)} )Q(∇^T f(x^{(1)} )+β∇^T f(x^{(0)} ))=\)
\( =\dfrac{1}{2α^ {(0)} }(∇f(x^ {(1)})-∇f(x^ {(0)}))(∇^T f(x^ {(1)})+β∇^T f(x^ {(0)}))\)
co daje
\(∇f(x^ {(1)})∇^T f(x^ {(1)})+ \underset{=0}{\underbrace{β∇f(x^ {(1)})∇^T f(x^ {(0)})}}-\underset{=0}{\underbrace{∇f(x^ {(1)})∇^T f(x^ {(0)})}}-β∇f(x^ {(0)})∇^T f(x^ {(0)})=0,\)
Czyli
\(β =\dfrac{∇f(x^{(1)} ) ∇^T f(x^{(1)} )}{∇f(x^{(0)} ) ∇^T f(x^{(0)} ) }. \qquad(4.5)\)
Wzory (4.4) i (4.5) pozwalają więc wyznaczyć dla zadania optymalizacji o kwadratowej funkcji celu z macierzą Q, posługując się tylko gradientami, kierunek sprzężony względem Q z początkowym kierunkiem antygradientu.
Dla dwuwymiarowego przykładu tak określony kierunek „zaprowadzi” do rozwiązania (jest wektorem q). Jednak w przypadku wielowymiarowym tak być nie musi, bo wektorów sprzężonych do antygradientu jest nieskończenie wiele (jak wiemy, już w przestrzeni trójwymiarowej, jest nieskończenie wiele wektorów prostopadłych do danego wektora – leżą one na płaszczyźnie prostopadłej do tego wektora) a tylko jeden „prowadzi” do punktu minimalizującego. Nie znaleziono metody pozwalającej od razu wybrać ten właściwy wektor, udowodniono natomiast twierdzenie następujące.
Dla danej funkcji kwadratowej \(x↦f(x)=x^T Qx+c^T x+σ\) o dodatnio określonej macierzy \(Q_{n×n}\) (a więc kwadratowej funkcji ścisłe wypukłej) i dowolnego punktu początkowego \(x^ {(0)}\) określamy ciąg n punktów \(\left \{ x^ {(k)} \right \}_{k=1}^n\) następująco:
\(β^ {(k)} =\dfrac{∇f(x^ {(k)})∇^T f(x^ {(k)})}{∇f(x^ {(k-1)})∇^T f(x^ {(k-1)})}, \,k=1,2,...,n-1. \qquad(4.8)\)
b) \( ∇f(x^{(n)})=0\), co przy poczynionych założeniach, że funkcja f jest kwadratowa i macierz Q jest dodatnio określona, oznacza (Twierdzenie 3.6) że \(x^{(n)}=\mathrm{argmin}_x\left\{f(x)=x^TQx+c^Tx+\sigma \right \}. \).
Teza b) powyższego twierdzenia stwierdza więc, że za pomocą opisanego algorytmu można znaleźć rozwiązanie zadania minimalizacji funkcji kwadratowej w co najwyżej n krokach, inaczej mówiąc – dla funkcji kwadratowej algorytm ma skończoną zbieżność (pod warunkiem, że minimalizacja w kierunku jest dokładna, wzór (4.6)). Napisaliśmy „w co najwyżej...”, ponieważ teza a) twierdzenia mówi o tym, że kolejne kierunki są sprzężone z pierwszym – wektorem antygradientu, zatem zgodnie z naszymi wcześniejszymi rozważaniami kierunek prowadzący do minimum może zostać wyznaczony szybciej niż dopiero w n-tym kroku. Zauważmy też, że wzór (4.8) określający współczynnik ustalający „wkład” poprzedniego kierunku do nowego kierunku poprawy jest uogólnieniem wyprowadzonego poprzednio wzoru (4.5).
W twierdzeniu 4.2 został sformułowany algorytm o skończonej zbieżności pozwalający znaleźć rozwiązanie zadania minimalizacji ściśle wypukłej funkcji kwadratowej. Około 1963 R. Fletcher i C.M. Reeves zastosowali ten algorytm do minimalizacji funkcji wypukłej. Byli niepoprawnymi optymistami, bo z dowodu twierdzenia wynika, że skończona zbieżność algorytmu jest konsekwencją tego, że kolejne kierunki powiększają zbiór wektorów Q-sprzężonych, a przecież dla nie kwadratowej funkcji wypukłej nie można mówić o kierunkach sprzężonych względem macierzy Q, bo nie ma macierzy Q! Co więcej ta „kolejna sprzężoność” może nie być zachowana nawet dla funkcji kwadratowej gdy minimalizacja w kierunku nie jest dokładna. Ale udało się – algorytm zachowywał się nadspodziewanie dobrze, potrafił na przykład bez zygzakowania, w rozsądnej liczbie kroków przy interpolacyjnej metodzie minimalizacji w kierunku znaleźć rozwiązanie dla bananowej funkcji Rosenbrocka. W artykule opublikowanym w 1964 r. Fletcher i Reeves nazwali swój algorytm Conjugate Gradient Method – metoda gradientu sprzężonego, i tak zostało, pomimo tego że kierunki generowane przez ich algorytm, choć oparte o gradient (patrz wzór (4.7)) dla funkcji nie kwadratowych nie są sprzężone. Intensywne badania metody gradientu sprzężonego prowadzone w drugiej połowie lat sześćdziesiątych doprowadziły do opublikowania w 1969 r. następującego algorytmu, w którym współczynnik \(\beta^{(k)}\) jest wyliczany według innej zależności, zwanej wzorem Poljaka, Polaka, Ribière’a
\(β^ {(k)}=\dfrac{∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))}{∇f(x^ {(k-1)})∇^T f(x^ {(k-1)})}. \)
Algorytm gradientu sprzężonego (wersja Poljaka, Polaka, Ribière’a z odnową)
Inicjalizacja
Ustal dokładność algorytmu \(\varepsilon > 0.\)
Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}\).
Podstaw \(k := 0\).
Kroki algorytmu
- (Odnowa) Oblicz \(∇f(x)\), podstaw \(grad := ∇f(x)\), jako kierunek poprawy wybierz kierunek antygradientu podstawiając \(d:=-(grad)^T\). Podstaw \(l := 0\), idź do 4.
- Podstaw \(β:=\dfrac{gradnew*((gradnew)^T-(grad)^T)}{grad*(grad)^T }\), (stosujemy wzór Poljaka, Polaka, Ribière’a (4.9)). Jako kandydata na kierunek poprawy wybierz wektor \(dnew\), podstawiając \(dnew:=-(gradnew)^T+β*d \) (wzór (4.7)).
- Jeżeli \(gradnew*dnew<0\) (\(dnew\) jest kierunkiem poprawy), podstaw \(x := xnew, d := dnew\) oraz \(grad:=gradnew \)i przejdź do 4. W przeciwnym przypadku podstaw \(x := xnew\) i przejdź do 1 (dokonaj odnowy).
- Wyznacz długość kroku \(\alpha^{(k)}\) w kierunku poprawy \(d,\) podstaw\( α:=α^ {(k)}\).
- Wylicz następny punkt podstawiając \(xnew:=x+α*d\).
- Oblicz \(∇f (xnew)\), oraz \(||∇f (xnew)||\), podstaw \(gradnew := ∇f (xnew)\), podstaw \(norm := ||∇f (xnew)||\).
- Jeżeli \(norm < \varepsilon\), to \(xnew\) przyjmij za rozwiązanie, podstaw \(ilosc_iteracji := k + 1\) i stop.
- W przeciwnym przypadku idź do 7.
- Podstaw \(k := k + 1,\) podstaw \(l := l + 1.\) Jeżeli \(l < n\), gdzie\( n\) jest wymiarem przestrzeni poszukiwań, to idź do 2. W przeciwnym przypadku podstaw \(x := xnew\) i idź do 1 (odnowa po \(n\) krokach od ostatniej odnowy).
Przeanalizujmy istotne aspekty działania przedstawionego wyżej algorytmu gradientu sprzężonego.
Jeżeli w kroku 4 algorytmu wykonamy dokładną minimalizację w kierunku, to kierunki wyznaczone w kroku 2 będą kierunkami poprawy, co poniżej pokażemy.
Jak pamiętamy, przy naszych założeniach, kierunek \(d^{(k)}\) jest kierunkiem poprawy gdy \(∇f(x^ {(k)})d^ {(k)}<0\). Policzmy zatem ten iloczyn
\(∇f(x^ {(k)})d^ {(k)}=∇f(x^ {(k)})(-∇^T f(x^ {(k)})+β^ {(k)} d^ {(k-1)})=-‖∇f(x^ {(k)})‖^2+β^ {(k)} ∇f(x^ {(k)})d^ {(k-1)}. (4.10)\)
Pokażemy, że \(∇f(x^ {(k)})d^ {(k-1)}=0\). Przy dokładnej minimalizacji w kierunku, dla punktu \(x(k)\) zachodzą równości
\(x^ {(k)}=x^ {(k-1)}+α^ {(k-1)} d^ {(k-1)}\)
\(α^ {(k-1)}=\mathrm{argmin}_{α≥0}f (x^ {(k-1)}-αd^ {(k-1)}),\)
co oznacza, że spełniony jest warunek
\(0=\dfrac{d}{dα} f(x^{(k-1) }-α^{(k-1) } d^{(k-1) }))=∇f(x^{(k-1) }-α^{(k-1) )}d^{(k-1)})(-d^{(k-1)})=-∇f(x^{(k)})d^{(k-1) }.\)
Zatem z równości (4.10) wynika, że \(∇f(x^ {(k)})d^ {(k)}<0.\)
Oznacza to, że przy dokładnej minimalizacji w kierunku krok 3, sprawdzający czy kierunki wyznaczone w kroku 2 są kierunkami poprawy, nie jest potrzebny.
Wiemy jednak, że każda praktyczna realizacja minimalizacji w kierunku jest obarczona pewnym błędem. Zatem konstruując algorytm, który ma naprawdę służyć do rozwiązywania zadań optymalizacji musimy pamiętać o stosownych zabezpieczeniach pozwalających pokonać trudności związane z różnego rodzaju niedokładnościami obliczeniowymi. Warunek kroku 3 sprawdza czy wyliczony kierunek jest kierunkiem poprawy. Jeżeli nie jest, dokonuje się tak zwanej odnowy – jako kierunek poszukiwań wybierany jest antygradient, który (gdy nie jest zerowy) jest zawsze kierunkiem poprawy. Jeżeli jednak zbyt często będziemy zmuszeni stosować odnowę, to działanie algorytmu będzie niewiele różnić się od działania algorytmu największego spadku – w szczególności wystąpi „zygzakowanie”. Dlatego przy implementacjach metody gradientu sprzężonego do znajdowania długości kroku w kierunku najczęściej wybiera się jedną z metod dających dobrą aproksymację minimum w kierunku.
- Analizując zachowanie algorytmu największego spadku (gradientu prostego) upatrywaliśmy przyczyn jego złego zachowania – zygzakowania – w braku pamięci. Wzór (4.7) określający nowy kierunek poprawy jest realizacją pierwszego z zaproponowanych podejść mających temu zaradzić – dodaniu poprawki zależnej od historii, ponieważ wiąże nowy kierunek poprawy z poprzednim kierunkiem poprawy, a także poprzez współczynnik (k) wyliczany wg wzoru (4.9) z gradientem obliczonym w kroku poprzednim. Ponieważ w kroku 4 nie możemy zapewnić dokładnej minimalizacji w kierunku, to okazało się, że kierunki wyznaczone w ten sposób mogą „prowadzić na manowce” – w tę stronę gdzie funkcja celu maleje powoli. Wobec tego aby zabezpieczyć się przed taką sytuacją, lub ją przerwać („oczyścić” pamięć) gdy już wystąpiła, przyjęto że odnowa następuje gdy od poprzedniej „upłynęło” n kroków. Wybór długości okresu, po którym następuje odnowa jako równego ilości zmiennych jest w zasadzie wyborem heurystycznym i odnosi się do zadań o dużej wymiarowości (kilkanaście zmiennych). Dla zadań o kilku zmiennych zręczniej jest dokonywać odnowy co 3n lub co 2n kroków, ponieważ z odnową co n kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku.
- Zauważmy, że przy dokładnej minimalizacji w kierunku wzory Fletchera – Reevesa (4.8) i Poljaka – Polaka – Ribière’a (4.9) dają tą samą wartość współczynnika \(\beta ^{(k)}\), ponieważ wtedy
\(∇f(x^ {(k)})∇^T f(x^ {(k-1)})=0, k=1,2,... \)(patrz wzór (4.2)),
a więc odjemnik w liczniku wzoru (4.9) jest równy zeru:
\(∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))=∇f(x^ {(k)})∇^T f(x^ {(k)})-∇f(x^ {(k)})∇^T f(x^ {(k-1)}))=∇f(x^ {(k)})∇^T f(x^ {(k)})\).
Dlaczego wybraliśmy wersję Poljaka – Polaka – Ribière’a (Rosjanina B.T. Poljaka, Amerykanina E. Polaka i Francuza G. Ribière) (4.9) a nie Fletchera – Reevesa (4.8)?
Ponieważ testy różnych wersji wzoru określającego wpływ poprzedniego kierunku poprawy na kierunek bieżący (zaproponowano ich więcej niż tylko przedstawione dwa wyrażenia) pokazały, że algorytm posługujący się wzorem Poljaka – Polaka – Ribière’a częściej znajduje rozwiązanie w mniejszej liczbie iteracji aniżeli algorytm ze wzorem Fletchera – Reevesa. Ponadto częściej potrafi znaleźć rozwiązanie w sensownej liczbie iteracji przy obniżonej dokładności minimalizacji w kierunku – jest więc bardziej odporny błędy wyznaczania kolejnych punktów. Formalnego wyjaśnienia tego faktu nie ma.
M.J.D. Powell przedstawił następującą hipotezę. Ponieważ minimalizowana funkcja nie jest kwadratowa i minimalizacja w kierunku nie jest dokładna, to przy minimalizacji wielu funkcji celu mamy do czynienia z sytuacją, w której kolejne kroki są coraz krótsze – \(x^{(k)}\) leży coraz bliżej \(x^{(k–1)}\), algorytm rusza się coraz wolniej, jak się często mówi – grzęźnie. Bliskość kolejnych punktów oznacza, że gradienty w nich wyliczane są prawie takie same: \(∇f(x^ {(k)})≈∇f(x^ {(k-1)})\).Dla formuły Fletchera – Reevesa (4.8) mamy więc \(β^ {(k)}≈1.\) Natomiast dla formuły Poljaka – Polaka – Ribière’a (4.9) dostajemy \(β^ {(k)}≈0\), co daje \(d^ {(k)}≈-∇^T f(x^ {(k)})\) Algorytm ma zdolność do samo-odnowy w sytuacji ugrzęźnięcia. Takiej własności dla implementacji algorytmu ze wzorem Fletchera – Reevesa nie zaobserwowano.
Ponieważ odnowa – ruch w kierunku antygradientu – następuje wtedy gdy wyznaczony według wzoru (4.7) kierunek przestaje być kierunkiem poprawy, a także gdy od ostatniej odnowy „upłynęło” n kroków, to w nieskończonym ciągu \(\left\{x^ {(k)}\right\}\) generowanym przez algorytm zawiera się nieskończony podciąg \(\left\{ x^{(j)}\right \}_{j \in J}\) punktów wyznaczonych na kierunkach określonych przez stosowne antygradienty \(–∇f (x^{(j–1)})\). Zatem twierdzenie określające warunki dające zbieżność algorytmu gradientu sprzężonego jest podobne do twierdzenia dla algorytmu gradientu prostego.
Jeżeli
funkcja f jest różniczkowalna oraz ograniczona od dołu a jej gradient \(∇f\) spełnia warunek Lipschitza na \( \mathrm{R}^n\),
to
nieskończony ciąg \(\left\{x^ {(k)}\right\}_{k=0}^∞\) generowany przez algorytm gradientu sprzężonego, w którym długość kroku w kierunku antygradientu \(\alpha^{(k)}\). jest ustalona:
– przez rozwiązanie zadania minimalizacji w kierunku:
jest taki, że dla związanego z nim ciągu normy gradientu \({||∇f(x^ {(k)})||}_{k=0}^∞ \)prawdziwa jest równość
\(\lim_{ k\to \infty (k)} ‖∇f(x^{(k)})‖\).
Przy odpowiednio mocniejszych założeniach o funkcji wyboru oraz wymaganiu dokładnej minimalizacji w kierunku, można pokazać, że algorytm ten zbiega superliniowo do punktu minimalizującego.
Powiedzieliśmy, że algorytm gradientu sprzężonego jest lepszy od algorytmu największego spadku. Aby nie być gołosłownym musimy teraz to pokazać.
Wyniki testów muszą być porównywalne, rozważmy więc tą samą funkcję dwu zmiennych co w Przykładzie 8.2:
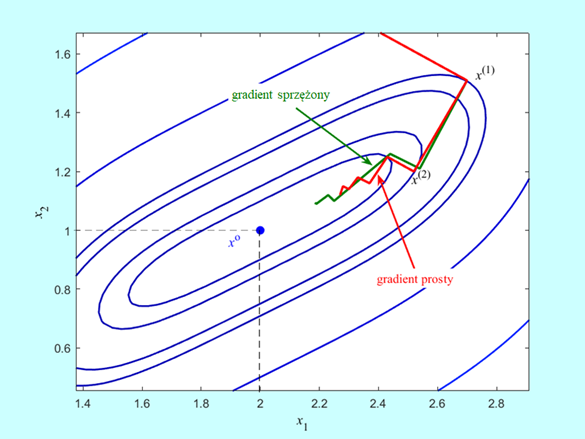
Algorytm wykonał siedem kroków i zatrzymał się w punkcie \(x^{(7)} = (2.185,1.094)\) w którym \(‖∇f(2.185,1.094)‖=0.02\), wartość funkcji celu \(f (2.185,1.094) = 0.0012\), a odległość proponowanego rozwiązania od punktu optymalnego jest równa \(‖x^{(7)}-x^o ‖=0.208\) (w Przykładzie 4.1 była równa 0.3).
Krok pierwszy z \(x^ {(0)}=(0,3)\) do \(x^ {(1)}=(2.70,1.51)\) był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ \(x^{(6)} = = (2.190,1.090)\) a \(x^{(7)} = (2.185,1.094)\). Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty \(x^{(2)}\) wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty \(x^{(3)}\), które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie \(x^{(3)}\) wyliczonym przez algorytm najszybszego spadku jest równy \([-0.18⋮-0.28]\), a kierunek poprawy wyznaczony w swoim punkcie \(x^({3)}\) przez algorytm gradientu sprzężonego jest równy \([-0.30⋮-0.25]\). Ta różnica spowodowała, że algorytm gradientu sprężonego wyznaczył jako punkt \(x^{(4)}\) punkt o współrzędnych \((2.25,1.10)\), co dało wartość funkcji celu \(f (2.25,1.10) = 0.0064\), a algorytm gradientu prostego – punkt o współrzędnych \((2.37,1.16)\) z wartością funkcji celu \(f (2.37,1.16) = 0.02\). W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt \(x^{(5)} = (2.23,1.12)\) dający wartość funkcji celu \(f (2.23,1.12) = 0.003\) i wartość normy gradientu \(‖∇f(2.23,1.12)‖=0.05\), a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt \((2.27,1.12)\) w którym \(f (2.27,1.12) = 0.0062\), oraz \(‖∇f(2.27,1.12)‖=0.09)\).
Algorytm gradientu sprzężonego (z za częstą odnową) zatrzymał się w punkcie oddalonym od rozwiązania o nieco ponad 0.02 z wartością funkcji celu większą od optymalnej o 0.0012 (algorytm prostego gradientu osiągnął, odległość – 0.09 i wartość większa od minimalnej o 0.0062). Okazał się wiec lepszy od współzawodnika, ale też nie bardzo poradził sobie z praktyczną utratą ścisłej wypukłości przez funkcję celu.
A jak algorytm gradientu sprzężonego poradził sobie ze znalezieniem minimum funkcji Rosenbrocka ?
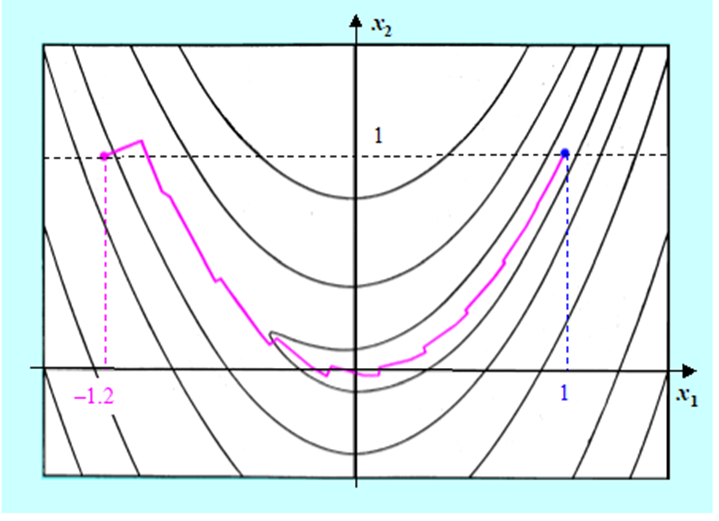
Rysunek pokazuje kolejne kroki algorytmu gradientu sprzężonego bez odnowy (bo funkcja Rosenbrocka jest dwuwymiarowa) i z minimalizacją w kierunku wykorzystującą wielomian interpolacyjny. Widać, że Algorytm wykonał 24 iteracje poruszając się po dnie doliny bez zygzakowania (8 iteracji), dobrze przebył zakręt (8 iteracji) a następnie dość szybko „pomaszerował” w kierunku punktu minimalizującego (8 iteracji). Zastosowana modyfikacja gradientu w tym teście się sprawdziła. Widać jednak, że dla twórców algorytmów trudniej jest nauczyć Algorytm jak ma sobie poradzić z „rozpłaszczeniem się rzeźby terenu” niż z zaproponowaniem efektywnej metody poruszania się „w krętych wąskich dolinach”.
Jak już powiedzieliśmy algorytm gradientu sprzężonego jest realizacją pierwszego z zaproponowanych podejść wzbogacenia algorytmu gradientu prostego w pamięć – dodaniu poprawki zależnej od historii. Zastanówmy się teraz nieco głębiej nad tym jak ta zależność od historii wygląda.
Przepiszmy wzór z piątego kroku określający kolejne punkty generowane przez algorytm gradientu sprzężonego (zapominając o potencjalnej odnowie wynikającej z nie wygenerowania kierunku poprawy rozpoczynanej w trzecim kroku algorytmu), a także wyrażenia określające jego poszczególne składniki (przyjmujemy, że \(n \geq 3)\)
\(x^{(k+1)}=x^ {(k)}+α^ {(k)} (-∇^T f(x^ {(k)})+β^ {(k)} d^ {(k-1)}), \,k=1,...,n-1, (\star)\)
\(β^ {(k)} =\dfrac{∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))}{∇f(x^ {(k-1)})∇^T f(x^ {(k-1)})}. \qquad (4.9)\)
\(d^ {(0)}=-∇^T f(x^ {(0)})\)
\(d^ {(k-1)}=-∇^T f(x^{(k-1) })+β^{(k-1) }d^{(k-2)},\, k=2,...,n-1\)
Widać, że algorytm ma dwa rodzaje pamięci zawarte w składniku \(β^ {(k)} d^ {(k-1)}\) wzoru \(\star). \)
- Pierwszą, potrzebną do obliczenia bieżącej wartości współczynnika skalującego
\(β^ {(k)}=\mathfrak{B} (∇f(x^ {(k)}),∇f(x^ {(k-1)})).\)
Jej stan \(β\) nie zależy od wartości tego współczynnika w kroku poprzednim, a z wielkości wyznaczonych uprzednio wykorzystuje tylko gradient. Taką pamięć można nazwać krótkookresową, bo nie ma w niej efektu kumulacji informacji zawartej w stanach poprzednich współczynnika skalującego.
- Drugą – określoną przez sposób obliczania kierunków poprawy
\(d^ {(k-1)}=\mathfrak{C} (∇f(x^ {(k-1)}),β^ {(k-1)}),d^{(k-2)}).\)
Po pierwsze, jej stan d jest w naturalny sposób opóźniony o takt (kierunek poprawy w takcie k możemy obliczyć tylko na podstawie kierunku wyznaczonego w takcie poprzednim). Bieżący stan tej pamięci zależy od jej stanu poprzedniego, co wobec tego że wzór \((\star)\) jest sumą oznacza, że w kolejnym wektorze kierunku poprawy jest w swoisty sposób „podsumowywana” cała dotychczasowa historia działania algorytmu. Jest to więc pamięć długookresowa. Kumulacja niedokładności obliczeniowych w tej pamięci może powodować, wspomniane wyżej „prowadzenie na manowce”. Odnowa, to oczyszczenie pamięci długookresowej ze złej informacji i wprowadzenie do niej kierunku, o którym wiemy, że na pewno jest kierunkiem poprawy.
2.3. 3 Algorytmy quasi-newtonowskie
Omówiliśmy realizację pierwszego z zaproponowanych podejść wzbogacenia algorytmu gradientu prostego w pamięć, a polegającego na dodaniu poprawki zależnej od historii. Teraz przyszedł czas na zapoznanie się z drugim podejściem, w którym przeskalowujemy gradient za pomocą macierzy transformacji, w stosowny sposób „zależnej od historii”. Przy tym podejściu krok wykonujemy w kierunku
\(d^ {(k)}=-\mathfrak{D} (x^ {(k)},x^((k-1)),...)∇^T f(x^ {(k)})\).
Jak więc dobrze określić zależność macierzy transformacji od bieżącej i przeszłej informacji?
W punkcie piątym Procedury redukcji zadania optymalizacji bez ograniczeń przedstawionej w punkcie 3.1.1 Modułu trzeciego napisałem:
„Elementy zbioru rozwiązań równania
\(∇f(x ̄)=0.\)
traktujemy jako „podejrzanych”, których „sprawdzamy na optymalność” tzn. wyliczamy zbiór \({f(x ̄^j)}\) wartości funkcji f , a następnie typujemy jako kandydata na rozwiązanie wektor dla którego wartość funkcji jest najmniejsza (tylko kandydata na, a nie rozwiązanie, bo Twierdzenie 3.4 jest warunkiem koniecznym!).”
Podane twierdzenia o zbieżności algorytmów gradientu prostego i sprzężonego (Twierdzenia 4.1 i 4.1GS) mówią, że algorytmy te de facto rozwiązują to równanie, co jest jeszcze podkreślone przez użyte w nich kryterium stopu: \(||∇f(x^ {(k)})||<ε.\) Wobec tego do poszukiwania rozwiązania zadania optymalizacji możemy zastosować zaproponowaną w 1669 roku przez I. Newtona metodę stycznych (w dziele De Analysi per Aequationes Numeri Terminorum Infinitas, w XVII w. nawet Anglicy pisali traktaty naukowe po łacinie). Zapiszmy ją dla naszego zadania polegającego na szukaniu rozwiązania równania
\( F(x)=0,\) gdzie
\(\mathbb{R}^n∍x↦F(x)=∇^T f(x)∈\mathbb{R}^n.\)
Algorytm zaproponowany przez Newtona jest następujący:
wybierz punkt początkowy \(x^{(0)}\), kolejne przybliżenia obliczaj według wzoru
\(x^ {(k+1)}=x^ {(k)}-[\dfrac{∂}{∂x^T} F(x^ {(k)})]^{-1} F(x^ {(k)}). \qquad (4.11)\)
Przy naszym określeniu funkcji F, pochodna występująca we wzorze (4.11) to macierz Hessego funkcji f. Wobec tego wzór ten można zapisać następująco
\(x^ {(k+1)}=x^ {(k)}-[∇^2 f(x^ {(k)})]^{-1} ∇^T f(x^ {(k)}). \qquad (4.12)\)
Mamy więc wzór określający macierz transformacji, nie jest on jednak zależny od „historii” a tylko od macierzy Hessego – „czynnika określającego krzywiznę funkcji celu” – policzonej w bieżącym punkcie.
Stosowanie wzoru (4.12) do znajdowania rozwiązania zadania optymalizacji jest niepraktyczne z dwu powodów.
- Po pierwsze trzeba w nim odwracać macierz, a wiemy że jest to operacja trudna gdy chcemy ją dokładnie wykonać numerycznie.
- Po drugie algorytm Newtona zbiega szybko, bo kwadratowo, do rozwiązania, ale tylko wtedy gdy funkcja f jest taka, że jej macierz Hessego jest w kolejnych punktach odwracalna a algorytm wystartuje w stosownym otoczeniu rozwiązania (zbieżność jest lokalna bo transformacja kierunku wyznaczonego przez gradient jest zależna tyko od informacji bieżącej, a więc lokalnej).
Wobec tego podjęto szereg prób modyfikacji algorytmu Newtona mających na celu zachowanie kwadratowej zbieżności przy wyeliminowaniu konieczności odwracania macierzy i zapewnieniu zbieżności globalnej.
Przedstawimy teraz podstawowe elementy rozważań, które doprowadziły w drugiej połowie lat sześćdziesiątych XX w. do przedstawienia takich sposobów określania macierzy transformacji, które dały skuteczne algorytmy rozwiązywania zadań optymalizacji.
Rozważania przedstawione w punkcie 3.1.2 pokazały, że dla funkcji klasy \(\mathbf{C}^2\) (gładkich) wzór
\(x↦\tilde{f} (x;x^ {(k)})=f(x^ {(k)})+∇f(x^ {(k)})(x-x^ {(k)})+\dfrac{1}{2}(x-x^ {(k)} )^T ∇^2 f(x^ {(k)})(x-x^ {(k)})\)
określa aproksymację \(\tilde{f}\) funkcji f w otoczeniu punktu bieżącego \(x^{(k)}\). Jeżeli przyjąć za „lokalną” zmienną niezależną przyrost zmiennej po której minimalizujemy w stosunku do punktu bieżącego \(p^ {(k)}=x-x^ {(k)},\) to wzór określający zmiany funkcji aproksymującej \(\tilde{f}\) w otoczeniu punktu \(x^ {(k)}\) w stosunku do jej wartości w tym punkcie \(\tilde{f }(x^ {(k)};x^ {(k)})=f(x^ {(k)})\) jest następujący
\(p^{(k)}\mapsto f_a(p^{(k)};x^{(k)})=\tilde{f}(p^{(k)}+x^{(k)};x^{(k)})-f(x^{(k)})=∇f(x^{(k)})p^{(k)}+\dfrac{1}{2}(p^{(k)})^T∇^2f(x^{(k)})p^{(k)}. \qquad (4.13)\)
Przy naszym podejściu optymisty przyjmujemy, że otoczenie, w którym to przybliżenie daje właściwą informację o zmianach funkcji celu jest duże, co oznacza, że zakładamy, że wektor \(p ̄^ {(k)} \) minimalizujący funkcję (4.13) jest w tym otoczeniu dobrym przybliżeniem kierunku w którym funkcja celu f „najwięcej” zmaleje (pod warunkiem, że macierz Hessego jest dodatnio określona). Funkcja \(f_a\) jest dwukrotnie różniczkowalna więc równanie jakie ten wektor musi spełniać jest następujące \(∇_{p^ {(k)} } f_a (p ̄^ {(k)};x^ {(k)})=0\) czyli
\(∇^2 f(x^ {(k)})p ̄^ {(k)}=-∇^T f(x^ {(k)}). \)
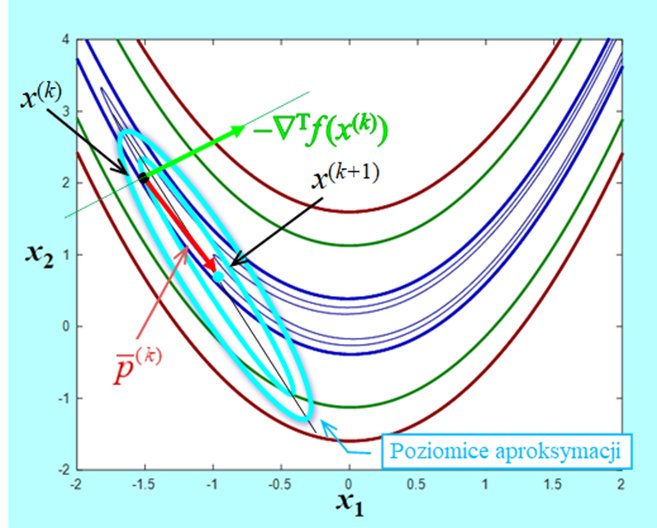
Zatem przy założeniu, że \(∇^2 f(x^ {(k)})>0 \) mamy
\(∇f(x^ {(k)})p ̄^ {(k)}=(p ̄^ {(k)} )^T ∇^T f(x^ {(k)})=-(p ̄^ {(k)} )^T ∇^2 f(x^ {(k)})p ̄^ {(k)} < 0, \qquad (4.15)\)
co oznacza, że \(p ̄^ {(k)}\) jest kierunkiem poprawy i nasze rozumowanie jest poprawne.
Porównując wzory (4.12) i (4.14) łatwo zauważyć, że
\(x^ {(k)}+p ̄^ {(k)}=x^ {(k)}-[∇^2 f(x^ {(k)})]^{-1} ∇^T f(x^ {(k)})=x^ {(k+1)} \qquad(4.16)\)
pod warunkiem, że odwrotność macierzy Hessego istnieje, a jak pamiętamy jest tak wtedy gdy np. macierz ta jest dodatnio określona. Oznacza to, że zastosowanie metody stycznych Newtona do rozwiązywania zadania optymalizacji to nic innego jak przyjęcie, że bieżące przybliżenie kwadratowe (4.13) dobrze opisuje zachowanie funkcji minimalizowanej w otoczeniu każdego punktu bieżącego. Zatem z bieżącego punktu należy przejść do punktu w którym funkcja aproksymująca osiąga minimum. W pobliżu lokalnego minimum funkcji celu na pewno takie postępowanie doprowadzi do tego minimum, ale w dużej odległości od niego tak być nie musi, stąd wspomniana wada metody Newtona – gwarantowana zbieżność tylko wtedy gdy algorytm wystartuje w stosownym otoczeniu rozwiązania.
Algorytm Newtona (4.12) jest więc konsekwencją przyjęcia za bieżące przybliżenia funkcji minimalizowanej przybliżenia kwadratowego dla przyrostów \(f_a (⋅;x^ {(k)})\) (wzór 4.13) opartego na macierzy drugich pochodnych funkcji celu obliczanej w bieżących punktach, co dało warunek (4.14) jaki musi spełniać wektor \(p ̄^ {(k)}\)a w konsekwencji pozwoliło wyprowadzić wzór (4.16).
Szukając sposobów poprawienia algorytmu Newtona twórcy algorytmów optymalizacji w „swoim optymizmie starali się pójść dalej” i zaczęli szukać warunków jakie powinna spełniać funkcja kwadratowa aproksymująca funkcję celu w otoczeniu punktu bieżącego tak aby mogła być podstawą do wyznaczenia lepszego niż newtonowski kierunku poprawy. Po pierwsze, powinna być oparta na dodatnio określonej (a więc odwracalnej) macierzy \(D(k)\) zależnej co najmniej od punktu bieżącego \(x^ {(k)}.\) Rozważmy taką funkcję, np. o postaci:
\(p^ {(k)}↦f_d (p^ {(k)};x^ {(k)})=∇f(x^ {(k)})p^ {(k)}+\dfrac{1}{2}(p^ {(k)} )^T (D^ {(k)} )^{-1} p^ {(k)}, (4.17)\)
gdzie, tak jak poprzednio, \(p^ {(k)}=x-x^ {(k)}\), jest przyrostem zmiennej po której minimalizujemy w stosunku do punktu bieżącego. Minimum funkcji (4.17) jest dane wektorem spełniającym warunek
\((D^ {(k)} )^{-1} p ̂^ {(k)}=-∇^T f(x^ {(k)}),\) czyli \(p ̂^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)}). \qquad (4.18)\)
Rozumując jak poprzednio, wzór (4.15), można pokazać, że tak wyznaczony kierunek \(p ̂^ {(k)}\) jest kierunkiem poprawy dla funkcji f.
Zauważmy teraz, że dla dowolnych punktów \(x^ {(k+1)}\) i \(x^ {(k)}\) mamy następujący wzór na zmianę gradientu funkcji celu f
\( ∇^T f(x^ {(k)})-∇^T f(x^ {(k+1)})=∇^2 f(x^ {(k+1)})(x^ {(k)}-x^ {(k+1)})+\)
+ nieskończenie mała rzędu 2, gdy \(x^{(k)} – x^{(k+1)} \to 0.\)
Oznacza to, że dla dostatecznie małej różnicy \(x^{(k)} – x^{(k+1)}\) dostaniemy
\(∇^2 f(x^ {(k+1)})(x^ {(k+1)}-x^ {(k)})≈∇^T f(x^ {(k+1)})-∇^T f(x^ {(k)}).\)
Intuicyjnie przyjęto, że macierz \(D^{(k)}\) określająca funkcję (4.17) powinna spełniać powyższy warunek dokładnie tzn. (uwzględniając zależność \(∇_p^2 f_d (p;x^ {(k+1)})=(D^ {(k+1)} )^{-1}) \)powinna być spełniona równość
\(D^ {(k+1)} (∇^T f(x^ {(k+1)})-∇^T f(x^ {(k)}))=x^ {(k+1)}-x^ {(k)}. \qquad (4.19)\)
Wymaganie zapisane równością (4.19) nosi nazwę warunku quasi-newtonowskiego.
Jeżeli teraz przyjmiemy, że wzór określający macierz \(D^{(k+1)}\) powinien mieć pamięć długookresową, tzn. być zależny od \(D^{(k)}\), to do warunku quasi-newtonowskiego możemy dodać wymaganie
\(D^{(k+1)}=D^{(k)}+V^{(k)} \qquad (4.20)\),
gdzie poprawka \(V^{(k)}\)zależna co najmniej od punktu bieżącego \( x^{(k)}\) powinna dawać dodatnio określoną macierz \(D^ {(k+1)}\) gdy macierz \(D^ {(k+1)}\) jest też okreslona dodatnio)
Analiza równania (4.19) i wymagania (4.20) pokazała, że poprawka \(V^{(k)}\) nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw. rodzina poprawek Broydena. Określmy najpierw wektory przyrostów w stosunku do punktu bieżącego:
argumentu funkcji celu \(p^ {(k)}=x^ {(k+1)}-x^ {(k)}\)
gradientu funkcji celu \(g^ {(k)}=∇^T f(x^ {(k+1)})-∇^T f(x^ {(k)}).\)
Dla ustalonej liczby \(φ∈[0,1] \) rodzina poprawek Broydena jest określona dla \(k = 0,1,2,...\) wzorami
\(V_φ^{(k)}=\dfrac{p^{(k)}(p^{(k)})^T}{(p^{(k)})^T g^{(k)}}-\dfrac{D^{(k)}g^{(k)}(g^{(k)})^T D^((k) )}{(g^{(k)})^T D^{(k)}g^{(k)}}+φτ^{(k)}w^{(k)}(w^{(k)})^T\)
\( w^ {(k)}=\dfrac{p^ {(k)}}{(p^ {(k)} )^T g^ {(k)} }-\dfrac{D^ {(k)} g^ {(k)}}{τ^ {(k)} }, τ^ {(k)}=(g^ {(k)} )^T D^ {(k)} g^ {(k)}, \qquad (4.21)\),
gdzie \(D^{(0)}>0.\)
Wzory już od samego patrzenia przyprawiają o gęsią skórkę, ale pomyślcie Państwo o tych co je wyprowadzali. Musieli przecież sprawdzać warunki (4.19) i (4.20)!
Wymagana w warunku (4.20) dodatnia określoność każdej macierzy\( D^{(k)}\) gwarantująca, że kierunki \(d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})\) będą kierunkami poprawy została „zaszyta” we wzorach (4.21) przy założeniu, że punkt następny \(x^ {(k+1)}\), potrzebny do obliczenia przyrostów \(p^ {(k)}\) i \( g^ {(k)}\), został wyznaczony w wyniku dokładnej minimalizacji w kierunku \(d^ {(k)}\), tzn. przy przyjęciu, że ciąg punktów \({x^ {(k)}}\) jest generowany przez algorytm
\(\left.\begin{matrix} x^{(0)}\, \mathrm{dane,} \,D^{(0)}>0\, \mathrm{dana}, \, d^{(k)}=-D^{(k)} ∇^T f(x^{(k)} )\\ α^{(k)}=\mathrm{argmin}_{α ≥0}f (x^{(k)}+αd^{(k)}) \\ x^{(k+1)}=x^{(k)}+α^{(k)}d^{(k)},\\ D^{(k+1)}=D^{(k)}+V_φ^{(k)}\,\,\, k=0,1,2,…\end{matrix}\right\}\qquad (4.22)\)
Jeżeli punkt \(x^{(k+1)}\) obliczony w oparciu o kierunek \(d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})\) zapewnia tylko poprawę funkcji celu w stosunku do wartości w punkcie \(x^{(k)}\) (nie stosujemy dokładnej minimalizacji w kierunku), to w praktycznej realizacji algorytmu trzeba zastosować stosowne zabezpieczenie gwarantujące, że kolejny kierunek \(d^{(k+1)}\) będzie kierunkiem poprawy.
Poprawka \(V_0^{(k)}\) wyliczona wg wzoru (4.21), w którym położono \(φ= 0\) nosi nazwę poprawki Davidona – Fletchera – Powella (poprawki DFP), a poprawka \(V_1^{(k)}\)wyliczona dla \(φ = 1\), to poprawka Broydena – Fletchera – Goldfarba – Shanno (poprawka BFGS), od nazwisk autorów, którzy je wprowadzili – pierwszą na początku lat sześćdziesiątych XX w., a drugą w 1970 roku.
W 1972 r. L.C.W. Dixon pokazał, że z teoretycznego punktu widzenia wszystkie poprawki rodziny Broydena są równoważne – przy dokładnej minimalizacji w kierunku kolejne punkty \(x(^{(k)}\) obliczone według wzorów (4.22) są przy użyciu dowolnej z nich takie same. Pokazano także twierdzenie analogiczne do twierdzenia (4.2) o skończonej zbieżność algorytmu kierunków Q-sprzężonych przy stosowaniu do minimalizacji funkcji kwadratowej. ustanawiające skończoną zbieżność algorytmu (4.22) w analogicznym przypadku.
Jak pamiętamy wymaganie jakie musi spełniać macierz transformacji \(D^{(n)}\) zapisane równością (4.19) nosi nazwę warunku quasi-newtonowskiego. Stąd wynikła powszechnie używana nazwa algorytmów w których nowy kierunek poprawy \(d^{(n)}\) jest określany za pomocą tej macierzy: \(d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})\) – są to algorytmy quasi-newtonowskie.
Twierdzenie 4.2QN wskazuje na związek miedzy algorytmami quasi-newtonowskimi i algorytmami gradientu sprzężonego. Można też wskazać i różnice.
Jeżeli pozbawimy wzór określający macierz transformacji pamięci długookresowej przyjmując w nim \(D^{(k-1)}=I\), to wzór określający kolejną macierz transformacji dla poprawki BFGS będzie następujący
\(D_I^ {(k)}=I+\dfrac{p^{(k-1)}(p^{(k-1)})^T}{(p^{(k-1)})^T g^{(k-1)}}(1-\dfrac{(g^{(k-1)})^T g^({(k-1)}}{(p^{(k-1)})^T g^{(k-1)}})-\dfrac{g^{(k-1)}(p^{(k-1)})^T+p^{(k-1)}(g^{(k-1)})^T}{(p^{(k-1)})^T g^{(k-1)}}\).
Jeżeli teraz dokonamy dokładnej minimalizacji na kierunku \(x^ {(k)}-αD_I^ {(k)} ∇^T f(x^ {(k)})\) otrzymując punkt \(x^ {(k+1)},\) to drogą prostych rachunków można pokazać, że
\(d^ {(k+1)}=-D_I^ {(k+1)} ∇^T f(x^ {(k+1)})=-∇^T f(x^ {(k+1)})+β^ {(k+1)} d^ {(k)},\)
gdzie współczynnik \(β^ {(k+1)}\) określony jest wzorem (4.8) lub równoważnym w tym przypadku wzorem (4.9). Oznacza to, że tzw. algorytm BFGS bez pamięci jest równoważny algorytmowi gradientu sprzężonego. Ponieważ pokazaliśmy, że w algorytmie gradientu sprzężonego pamięć długookresowa występuje, to stwierdzenie powyższe można interpretować jako stwierdzenie faktu, że w pełnym algorytmie quasi-newtonowskim poprawny wpływ poprzednich kierunków poprawy na kierunek bieżący jest większy aniżeli w metodzie gradientu sprzężonego, co uzasadnia empirycznie stwierdzoną przewagę (w większości przypadków szybciej zbiegały) tych pierwszych.
Zebrane w ciągu ponad półwiecza doświadczenia pokazały, że najlepszym algorytmem ogólnego przeznaczenia tj. pierwszym algorytmem jakiego należy użyć gdy zadanie optymalizacji nie ma specjalnych własności (struktury), jest quasi-newtonowski algorytm BFGS. Wypisany wyżej wzór dla algorytmu BFGS bez pamięci jest już wystarczająco skomplikowany, dlatego starano się znaleźć prostszą formułę wzoru pełnego niż zaproponowana oryginalnie. W 1980 roku J. Nocedal podał wzory następujące:
\(\begin{matrix} η^ {(k)}=\dfrac{1}{(p^ {(k)} )^T g^ {(k)} },\, W^ {(k)}=I-η^ {(k)} g^ {(k)} (p^ {(k)} )^T\\D^ {(k+1)}=(W^ {(k)} )^T D^ {(k)} W^ {(k)}+η^ {(k)} p^ {(k)} (p^ {(k)} )^T, D^{(0)}>0).\end{matrix} \qquad(4.23) \)
Praktyczna realizacja quasi-newtonowskiego algorytmu BFGS może być następująca.
Algorytm quasi-newtonowski (wersja BFGS z odnową i skalowaniem macierzy początkowej)
Ustal dokładność algorytmu \( \varepsilon > 0.\)
Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}.\)
- podstaw \(p := xnew – x \) oraz \(g := (gradnew)T – (grad)T\)
- podstaw \(D:=\dfrac{p^T g}{g^T g}I\) (skalujemy początkową macierz transformacji), idź do 10.
(stosujemy wzór Broydena – Fletchera – Goldfarba – Shanno w wersji Nocedala (4.23)). Jako kandydata na kierunek poprawy wybierz wektor d, podstawiając \(d:=-Dnew*(gradnew)^T.\)
6. Jeżeli \(gradnew*d < 0 \)(d jest kierunkiem poprawy), podstaw \(x := xnew , grad:=gradnew\) oraz \(D := Dnew\) i przejdź do 7. W przeciwnym przypadku podstaw \(x := xnew \)i przejdź do 1 (dokonaj odnowy).
7. Wyznacz długość kroku \(α^{(k)}\) w kierunku poprawy d, podstaw
\(α:=α^ {(k)}\).
8. Wylicz następny punkt podstawiając \(xnew:=x+α*d.\)
9. Oblicz \(∇f (xnew)\), podstaw \(gradnew :=∇f (xnew)\).
10. Oblicz \(||∇f (xnew)||\), podstaw \(norm := ||∇f (xnew)||.\)
Jeżeli \(norm < \varepsilon\), to \(xnew\) przyjmij za rozwiązanie, podstaw
\(ilosc_iteracji := k +1 \) i stop .W przeciwnym przypadku idź do
11.
11. Jeżeli \(l = 0\), to podstaw \(k := k + 1,\) podstaw \(l := l + 1
\)i idź do 5. W przeciwnym przypadku idź do 12.
12. Podstaw \(k := k + 1\). Podstaw \(l := l + 1\). Jeżeli \(l < 2n + 1,\) gdzie n jest wymiarem przestrzeni poszukiwań, to idź do 4. W przeciwnym przypadku podstaw \(x := xnew\) i idź do 1 (odnowa po \(2n + 1 \)krokach od ostatniej odnowy).
Omówmy krótko różnice miedzy przedstawionym powyżej algorytmem a jego teoretycznym prototypem danym wzorami (4.22).
- Nie zakładamy dokładnej minimalizacji w kierunku. Musimy zatem liczyć się z tym, że kolejny kierunek \(d ^{(k+1)}\) może nie być kierunkiem poprawy. Dlatego wprowadzono krok szósty wywołujący odnowę gdy trzeba „sprowadzić algorytm ze złej drogi”. Ponadto, podobnie jak dla algorytmu gradientu sprzężonego, wprowadzono odnowę, tym razem co \(2n + 1\) kroków. Liczba ta wzięła się z wieloletnich doświadczeń i uwzględnia fakt, że algorytm BFGS stosuje się często do znajdowania rozwiązania zadań o niewielkiej wymiarowości.
- Wzór (4.21), a za nim zastosowany w algorytmie wzór (4.23), nie określa jak wybierać macierz początkową \(D^{(0)}\). Jedyne wymaganie to jej dodatnia określoność. Najprostszy pomysł to wybranie jako początkowej – macierzy jednostkowej. Praktyka jednak pokazała, że istotne przyspieszenie zbieżności początkowych iteracji można uzyskać skalując w sposób dobrany do własności zadania tę macierz. Przedstawiono stosowne nieco skomplikowane rozważania pozwalające określić dla pewnych klas zadań wzory ustalające wartość współczynnika skalującego. Z drugiej strony swój korzystny wpływ na szybkość zbieżności algorytmu dla wielu różnych zadań, tzn. swoją uniwersalność, potwierdził współczynnik określony prostym wzorem
\(γ=\dfrac{(x^{(1)}-x^{(0)})^T (∇^T f(x^{(1)})-∇^T f(x^{(0)}))}{(∇f(x^{(1)})-∇f(x^{(0)}))(∇^T f(x^{(1)})-∇^T f(x^{(0)}))}\).
- Algorytm BFGS, jak wszystkie algorytmy quasi-newtonowskie, jest algorytmem, który opiera się na założeniu, że funkcja kwadratowa dobrze aproksymuje zachowanie funkcji minimalizowanej w dostatecznie dużym otoczeniu punktu bieżącego. Badania teoretyczne pokazały, że do udowodnienia zbieżności np. sama wypukłość funkcji celu nie wystarczy. Ponieważ, po pierwsze – nikomu nie chce się sprawdzać tych warunków (najczęściej jest to co najmniej trudne) i po drugie – praktyka pokazała, że algorytmy quasi-newtonowskie potrafią znaleźć rozwiązanie i dla zadań nie spełniających tych założeń, pod warunkiem, że wystartują z dobrego punktu początkowego, to w praktycznych wariantach tych algorytmów stosuje się co z góry ustaloną liczbę (w naszym przypadku \(2n + 1)\) kroków odnowę. Jak pamiętamy gwarantuje to przy słabych założeniach: różniczkowalności funkcji celu i lipschitzowości jej gradientu, że dolna granica ciągu, którego elementami są normy gradientu liczone w kolejnych punktach wyliczanych przez algorytm, jest równa zeru, nawet bez konieczności dokonywania dokładnej minimalizacji w kierunku. Podobnie jak dla algorytmów gradientu sprzężonego przy mocniejszych założeniach pokazano, że algorytmy quasi-newtonowskie zbiegają superliniowo do punktu minimalizującego.
Przedstawimy teraz krótkie porównanie zachowania quasi-newtonowskiego algorytmu BFGS bez odnowy z algorytmem gradientu sprzężonego w wersji PPR minimalizujących bananową funkcję Rosenbrocka. W obu algorytmach minimalizacja w kierunku wykorzystywała wielomian interpolacyjny.
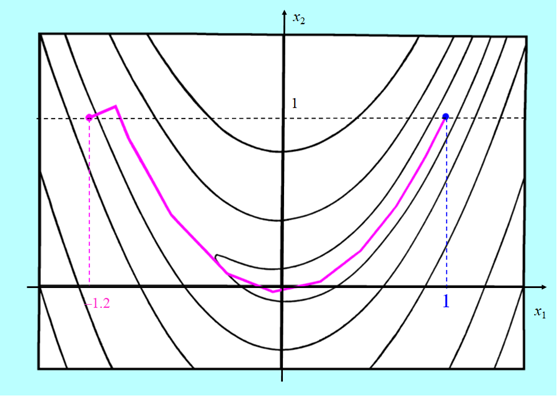
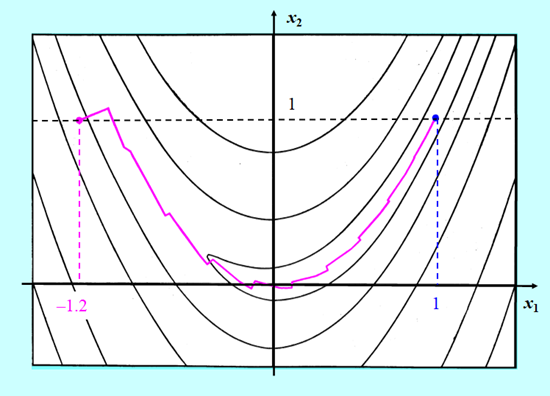
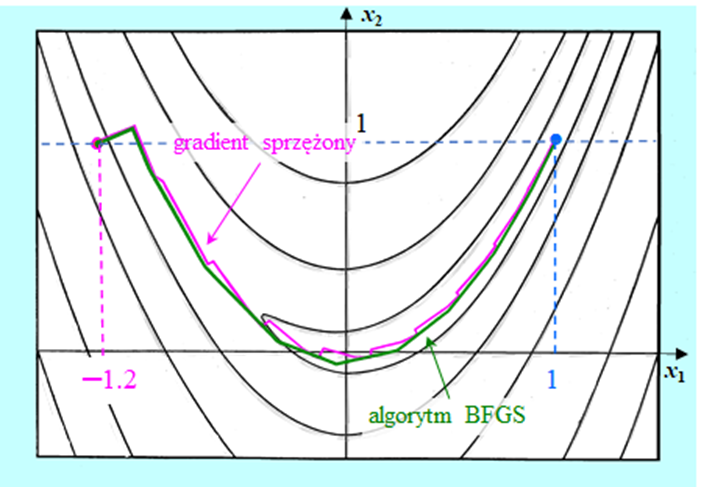
Algorytm gradientu sprzężonego zużył 24 iteracje na dotarcie do rozwiązania, a quasi-newtonowskiemu algorytmowi BFGS wystarczyło tylko 11 iteracji.
Przedstawione rysunki pokazują wyższość algorytmu BFGS. Nie jest to przypadek. Szerokie badania porównawcze prowadzone od początku lat osiemdziesiątych XX w. wykazały, że algorytm ten, jak już wspomniano, jest pierwszym algorytmem jakim należy się posłużyć gdy zadanie optymalizacji nie ma specjalnych własności (struktury) – jest najefektywniejszym algorytmem ogólnego przeznaczenia dla zadań o niezbyt dużej wymiarowości.
2.4. Uwagi dotyczące implementacji algorytmów gradientu sprzężonego i quasi-newtonowskiego
Poruszymy teraz trzy najważniejsze problemy implementacyjne gradientowych algorytmów optymalizacji:
Pierwszy jest związany z wykonaniem podstawowego polecenia z początku każdego algorytmu punktu 4.2: „oblicz \(∇f (x)\)”. Od tego jak dokładnie wyliczymy gradient bardzo istotnie zależy jakość otrzymanej propozycji rozwiązania zadania minimalizacji.
Dwa pozostałe zasygnalizowano na początku punktu 3.2.1: jak ustalić kryterium stopu i jak będąc odważnym zachować rozwagę.
Jeżeli znamy wzór określający funkcję f możemy wyznaczyć wzór określający gradient, chociaż dla bardziej złożonych funkcji może być to kłopotliwe. Wyznaczony wzór trzeba wstawić w odpowiednie miejsce algorytmu. Gdy dysponujemy odpowiednim oprogramowaniem, komputer może nas zwolnić z niewdzięcznej pracy i wyznaczyć stosowny wzór na gradient drogą różniczkowania symbolicznego. Przy rozwiązywaniu zadań praktycznych często mamy do czynienia z sytuacją, w której funkcja f jest obliczana przez dany z zewnątrz program. Jeżeli ten program do wyznaczenia wartości funkcji dla danego argumentu wykorzystuje cztery działania arytmetyczne i funkcje elementarne , to na podstawie jego kodu drogą automatycznego różniczkowania można otrzymać program obliczający wartość gradientu funkcji. Przystępne wprowadzenie do zagadnień związanych z automatycznym różniczkowaniem Czytelnik znajdzie w rozdziale 7.2 monografii J. Nocedal S.J. Wright: Numerical Optimization, 2nd ed. Springer 1999.
Co robić w sytuacji gdy nie mamy programu automatycznego różniczkowania przetwarzającego kod języka, którym posłużono się do napisania programu wyliczającego wartości funkcji celu? Zostaje nam estymacja gradientu. Estymacja gradientu funkcji celu f w punkcie bieżącym \(x^ {(k)}\) polega na obliczeniu wartości tej funkcji w pewnej liczbie punktów próbnych \(y^{(j)},j∈\overline{1,J}\) leżących w otoczeniu punktu bieżącego. Poszczególne elementy estymaty gradientu funkcji f wyznaczane są na podstawie różnic jej wartości w tych punktach. Stosowane metody estymacji różnią się liczbą i sposobem ustalenia punktów próbnych. Jedna z najprostszych metod, to metoda różnic centralnych, w której przyjmuje się następujące przybliżenie
\(\dfrac{∂}{(∂x_i )}f(x^ {(k)})≈\dfrac{f(x^ {(k)}+Δx_i e^i)-f(x^ {(k)}-Δx_i e^i)}{2Δx_i }, \,i=1,...,n\)
gdzie wektory \(e^1,…,e^n\) są naturalną bazą przestrzeni \(\mathbb{R}^n\), a \(Δx_i \)– przyrostami kolejnych współrzędnych. Jak widać w tej metodzie estymatę gradientu obliczamy na podstawie wartości funkcji w dwu punktach próbnych. Zauważmy, że stosowny wybór wielkości przyrostów \(Δx_i\)może być trudny dla funkcji wolno zmieniających się, ponieważ małym przyrostom mogą odpowiadać zmiany funkcji celu porównywalne lub mniejsze od dokładności reprezentacji liczb w komputerze, co może doprowadzić do przedwczesnego uznania, że dana współrzędna gradientu jest zerowa. W konsekwencji obliczona norma gradientu zostanie uznana za dostatecznie małą i, zgodnie z zastosowanym kryterium stopu, algorytm przedwcześnie zatrzyma się. W związku z tym twórcy komercyjnych pakietów rozwiązywania zadań optymalizacji wyposażają swoje produktu w specjalne algorytmy wyznaczania wielkości przyrostów.
W przedstawionych wersjach algorytmów jako kryterium stopu wybrano „zerowanie” się normy gradientu, co w praktyce oznacza wybór dokładności \(\varepsilon\)równej co najmniej 10–4 i zatrzymanie działania algorytmu gdy
\(||∇f(x^ {(k)})|| <ε.\)
Oznacza to, że najczęściej stosowane algorytmy gradientowe rozwiązują zadanie optymalizacji bez ograniczeń stosując metodę redukcji do układu równań
\(∇f(x)=0, \qquad (3.1)\)
opisaną ogólnie w punkcie 3.1.1., z dodatkowymi warunkami ograniczającymi, aby nie doszło do znalezienia punktów siodłowych albo wielowymiarowych powierzchni przegięcia takich jak na Rys. 3.26. Ze złożoności tego problemu nieliniowego z którymi spotkaliśmy się w punkcie 3.1.1. i powrócimy do nich przy bardziej skompli-kowanych warunkach w punkcie 5.2. Modułu piątego wynika, że jak napisali J.E Dennis i R.B. Schnabel na początku swej klasycznej monografii Numerical Methods for Unconstrained Optimization and nonlinear Equations z 1983 r.
„Jest mało prawdopodobne, że kiedykolwiek powstanie taki algorytm, który będzie mógł rozwiązać problemy związane z istnieniem i jednoznacznością rozwiązania zadań rozpatrywanych w tej książce. Wydaje się, że udzielenie odpowiedzi na te pytania wykracza poza możliwości, jakich można oczekiwać od algorytmów. (…) W związku z tym, odpowiedź każdego algorytm zastosowanego do problemu nieliniowego może być tylko dwojaka: «Przybliżonym rozwiązaniem problemu jest _____» albo «W wyznaczonym czasie / Po wyznaczonej ilości iteracji nie znaleziono przybliżonego rozwiązania problemu».”
Pozostałe proponowane w rożnym czasie kryteria:
- małości relatywnego przyrostu kroku: \(\dfrac{||x^ {(k+1)}-x^ {(k)} ||}{||x^ {(k)} ||}<ε\) albo
- braku dostatecznego postępu w ciągu N krokóww przestrzeni argumentów: \(||x^ {(k+N)}-x^ {(k)} ||<ε\), albo
w przestrzeni wartości: \(|f(x^ {(k+N)})-f(x^ {(k)})|<ε,\)
stosowane są rzadko, ponieważ praktyka pokazała, że często zawodzą powodując zatrzymanie algorytmu daleko od rozwiązania. Omawiając wybór kryterium stopu trzeba także przypomnieć wymaganie, na które zwracaliśmy już uwagę, tj. wymaganie mówiące, że praktyczna implementacja każdego algorytmu powinna zawierać zabezpieczenie przed wynikającą z nałożenia się różnych niedokładności, możliwością jego „zapętlenia się”, w postaci warunku przerwania obliczeń po wykonaniu maksymalnej liczby iteracji.
W przedstawionych metodach gradientowych odpowiedzi na pytanie „jak będąc odważnym zachować rozwagę?” udzielono odpowiedzi poprzez wykorzystanie narzędzia odnowy pamięci, która buduje rozwagę lecz z biegiem czasu może hamować śmiałe działania.
W obu metodach zastosowano „sztywny program odnowy”, co n kroków w metodzie gradientu sprzężonego, i co \(2n + 1 \) kroków w przedstawionej metodzie quasi-newtonowskiej przy czym n to liczność zmiennych zadania. Obie liczby wyniknęły z doświadczenia i przy rozwiązywaniu konkretnego zadania optymalizacji mogą być zmienione. Dlaczego pierwsza liczba jest mniejsza? Patrząc na rys. 4.16 widzimy, że algorytm BFGS jest lepszy od algorytmu gradientu sprzężonego. Dlatego dla niewielkich (do mniej więcej 10 zmiennych) zadań optymalizacji zaleca się jego stosowanie. Dla zadań dużych – kilkadziesiąt i więcej zmiennych stosowanie algorytmu quasi-newtonowskiego może być kłopotliwe, ponieważ trzeba pamiętać macierz transformacji D. Wobec tego do rozwiązywania dużych zadań częściej stosuje się metodę gradientu sprzężonego. Widać więc, że n dla zadania dużego może być dużo większe niż \(2n + 1 \) dla zadania małego i nie ma niebezpieczeństwa, że działanie algorytmu gradientu sprzężonego stanie się podobne do działania nieefektywnego algorytmu największego spadku.