Podręcznik Grafika komputerowa i wizualizacja
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Część 1. Wstęp, podstawowe operacje grafiki komputerowej |
| Książka: | Podręcznik Grafika komputerowa i wizualizacja |
| Wydrukowane przez użytkownika: | Gość |
| Data: | czwartek, 5 marca 2026, 03:54 |
Spis treści
- Rozdział 1. WPROWADZENIE
- Rozdział 2. PODSTAWOWE OPERACJE RASTROWE
- Rozdział 3. ELEMENTY GEOMETRII OBLICZENIOWEJ
- 3.1. Przykłady problemów niezwiązanych bezpośrednio z grafiką komputerową
- 3.2. Historia geometrii obliczeniowej
- 3.3. Funkcja alfa
- 3.4. Zorientowanie punktów na płaszczyźnie
- 3.5. Sprawdzenie przynależności punktu do wielokąta
- 3.6. Otoczka wypukła (wypukła skorupka)
- 3.7. Podział wielokąta na trójkąty
- 3.8. Wyznaczenie przecięć w zbiorze odcinków na płaszczyźnie. Metoda zamiatania
- Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
- 4.1. Współrzędne jednorodne znormalizowane
- 4.2. Przekształcenia 2D
- 4.3. Przekształcenia 3D
- 4.4. Składanie przekształceń. Przekształcenie odwrotne
- 4.5. Przekształcenia izometryczne
- 4.6. Przykład obrotu punktu wokół dowolnej prostej
- 4.7. Problem dokładności obliczeń w przekształceniach geometrycznych
- 4.8. Kwaterniony
Rozdział 1. WPROWADZENIE
Rozdział pierwszy jest wprowadzeniem w tematykę przedmiotu. Grafika komputerowa została tutaj przedstawiona jako jedna z dziedzin informatyki zajmująca się obrazem. W rozdziale tym zaprezentowano historię grafiki oraz jej najważniejsze zastosowania w różnych dziedzinach niezwiązanych bezpośrednio z informatyką, a także rolę jaką grafika pełni w interakcji człowieka z komputerem. Czytelnik znajdzie tutaj także informacje dotyczące grafiki rastrowej i wektorowej, różnic w technologicznym podejściu do wyświetlania obrazu i konsekwencji z tego wynikających.
1.1. Wstęp
Podręcznik ten pozwoli zapoznać się z podstawowymi zagadnieniami grafiki komputerowej. Przedstawi najważniejsze metody i algorytmy stosowane w grafice. Natomiast realizacja zadania projektowego będzie próbą praktycznego wykorzystania zdobytej wiedzy
Autor przyjął, że czytelnik posiada wiedzę dotyczącą
- Podstaw algorytmów i struktur danych.
- Podstaw geometrii.
- Podstaw algebry liniowej.
- Umiejętności programowania.
Bardzo często podczas tworzenia obrazów graficznych, szczególnie obiektów trójwymiarowych, pożądana jest tak zwana wyobraźnia przestrzenna, co formalnie jest nazywane zdolnościami przestrzennymi (kategorie wg. M.Linn i A.Petersen - 1985) i jest kategoryzowane w następujący sposób:
- Wyobraźnia przestrzenna (zrozumienie powiązań przestrzennych pomiędzy obiektami).
- Umiejętność realizacji obrotu brył w wyobraźni (oraz konsekwencji wykonania innych prostych operacji afinicznych np. translacji).
- Spostrzeganie przestrzenne (umiejętność lokalizacji określonych kierunków i płaszczyzn w złożonym układzie – np. lokalizacja pionu i poziomu.
Tematyka podręcznika
Podręcznik został podzielony na cztery części (moduły) obejmujące 15 rozdziałów. W rozdziałach tych opisane są następujące zagadnienia:
- Wprowadzenie, zastosowania grafiki komputerowej, grafika rastrowa i wektorowa, sprzęt dla potrzeb grafiki, interfejs użytkownika.
- Podstawowe operacje rastrowe wraz z elementarnymi zadaniami geometrii obliczeniowej.
- Przekształcenia geometryczne, operacje macierzowe we współrzędnych jednorodnych.
- Reprezentacja przestrzeni trójwymiarowej na płaszczyźnie – rzutowanie, kamera i wirtualne studio.
- Modelowanie obiektów w grafice komputerowej.
- Modelowanie krzywych i powierzchni.
- Modelowanie obiektów naturalnych. Modelowanie fraktalne.
- Eliminacja elementów zasłoniętych, algorytmy rozstrzygania widoczności.
- Światło, oko i widzenie, modele barw w grafice komputerowej.
- Modelowanie oświetlenia, modele odbicia (przenikania) światła.
- Oświetlenie globalne, metoda śledzenia promieni, metoda energetyczna.
- Dążenie do realizmu - tekstura.
- Elementy animacji.
Tematyka wykładu obejmuje algorytmy i techniki potrzebne do realizacji określonych zadań graficznych oraz do uzyskania pewnych efektów widocznych na obrazie. Zadań graficznych, które być może znamy z doświadczeń w obsłudze różnych programów. Czytelnik nie uzyska jednak informacji o gotowych pakietach graficznych lub różnicach między nimi ani, tym bardziej, nie dowie się jak się nimi posługiwać. Będzie mógł za to poznać algorytmy, jakie były potrzebne, żeby taki pakiet mógł powstać.
Literatura podstawowa
Istnieje bardzo wiele książek dotyczących grafiki komputerowej dostępnych w księgarniach lub bibliotekach. Na końcu każdego rozdziału jest wymieniona literatura związana z zagadnieniami omawianymi w tym rozdziale. Spośród wielu pozycji literatury, można wymienić kilka o charakterze podstawowym (autor nazwał to zestawem minimum).
Hughes J.F., van Dam A., McGuire M., Sklar D.F., Foley J.D., Feiner S.K., Akeley K.: Computer Graphics, Principles and Practice, third ed., Addison-Wesley Publ. Co. 2013.
Jest to jeden z najlepszych podręczników akademickich dotyczących grafiki komputerowej. Jego jedyną wadą jest fakt, że powstał ponad dziesięć lat temu.
Marschner St., Shirley P. i inni: Fundamentals of Computer Graphics, fifth ed., Taylor and Francis (CRC Press), 2021.
Współczesny podręcznik akademicki., niestety niektóre zagadnienia są w książce autorów: Hughes, van Dam i inni znacznie szerzej opisane.
Hearn D., Baker P.M., Carithers W.: Computer Graphics with Open GL, 4th. ed. Pearson 2010 (wznowienie 2013).
Wielokrotnie wznawiany i uzupełniany podręcznik akademicki.
Trzy zaproponowane pozycje wzajemnie się uzupełniają stanowiąc zestaw minimum, który powinien być znany każdemu, kto chciałby w zakresie podstawowym zajmować się grafiką komputerową. Osoby zainteresowane poszczególnymi tematami na pewno sięgną do pozostałych pozycji. Z drugiej strony, każda z wymienionych wyżej pozycji stanowi dobry podręcznik akademicki obejmujący wszystkie podstawowe zagadnienia standardowego wykłady grafiki komputerowej.
Zestaw minimum warto uzupełnić o dwie starsze pozycje polskich autorów.:
Zabrodzki J. (red.): Grafika Komputerowa, metody i narzędzia, WNT 1994.
Nie jest to typowy podręcznik akademicki – nie obejmuje wszystkich zagadnień tematu. Ale za to zagadnienia, które się tam znalazły są omówione bardzo szeroko.
Jankowski M.: Elementy grafiki komputerowej, WNT 1990 (wydanie 2006 praktycznie niezmienione).
Książka najstarsza z prezentowanych tutaj. jednak napisana w bardzo przejrzysty sposób i przedstawiająca również algorytmy rzadko opisywane w podstawowych podręcznikach do grafiki.
Ze względu na powszechną dostępność, do zestawu literatury podstawowej można byłoby dodać książkę:
Foley J.D., van Dam A., Feiner St.K., Hughes J.F., Phillips R.L.: Wprowadzenie do grafiki komputerowej, WNT 1995 (wydanie 2. z 2001 roku).
Należy jednak pamiętać, że jest to tłumaczenie skróconej wersji podręcznika tych autorów. Książka zaproponowana w zestawie minimum zawiera dużo więcej informacji i jest nowsza.
1.2. Grafika komputerowa i dziedziny pokrewne
Grafika komputerowa jest dziedziną zajmującą się generowaniem obrazów metodami cyfrowymi. Jest jednym z trzech działów informatyki zajmujących się obrazem. Dwa pozostałe to przetwarzanie obrazów i rozpoznawanie obrazów.
Ponieważ wszystkie trzy dziedziny zajmują się obrazami, wiele zagadnień i problemów jest rozwiązywanych podobnymi lub tymi samymi metodami. Jednak generalny podział jest widoczny, gdy wyróżni się dane wejściowe i wyjściowe.
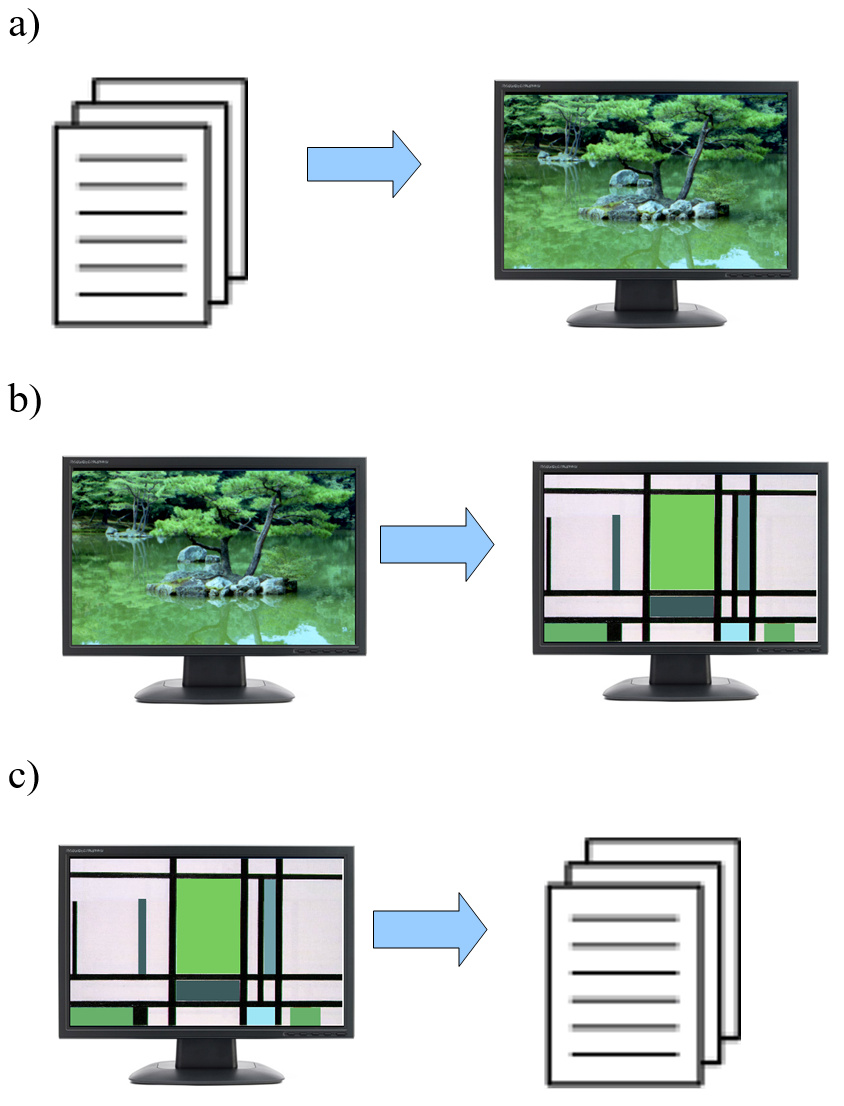
Rys.1.1. Trzy pokrewne dziedziny informatyki
zajmujące się obrazem.
Grafika komputerowa. Dane wejściowe : opis ( w postaci programu lub zbioru danych – w szczególnych przypadkach mogą to być inne obrazy np. tekstury, które będą podlegały przetwarzaniu). Dane wyjściowe : obraz. Typowym przykładem jest generacja efektów specjalnych dla współczesnej kinematografii.
Przetwarzanie obrazów. Dane wejściowe : obraz. Dane wyjściowe : obraz. Jako dane wejściowe należałoby także potraktować opis sposobu obróbki. Typowym przykładem jest obróbka zdjęć cyfrowych w celu uzyskania określonego efektu, np. wydobycie standardowo niewidocznych szczegółów w cieniach.
Rozpoznawanie obrazów. Dane wejściowe : obraz. Dane wyjściowe : opis. Postać uzyskanego wyjściowego opisu jest bardzo silnie zależna od celu, w jakim dane zadanie było wykonane. Typowym przykładem jest analiza obrazu tęczówki oka w celu przeprowadzenia identyfikacji osoby.
Można zadać pytanie dlaczego grafika komputerowa jest tak ważna i wykorzystywana w wielu różnych dziedzinach.
- Większość informacji dociera do człowieka za pośrednictwem wzroku.
- Łatwiej przekazać duże ilości informacji w postaci prezentacji graficznej.
- Możliwość kreowania dowolnych scen, nawet zupełnie nierzeczywistych.
- Twórcy reklam i filmów dostają narzędzia dające, praktycznie, nieograniczone możliwości.
- W wielu dziedzinach można obejrzeć wreszcie to, co dotychczas było niemożliwe do zobaczenia.
Warto zwrócić uwagę na jeszcze jeden aspekt. Relację uzyskanych efektów do poniesionych kosztów. Łatwiej i taniej jest zrealizować wirtualną dekorację dla dowolnej sceny filmowej niż zbudować ją z rzeczywistych materiałów (lub nawet ich „filmowych” imitacji). Dzisiejsze możliwości grafiki komputerowej pozwalają dopracować szczegóły z, praktycznie, dowolną; zadaną dokładnością.
Nie zawsze jednak jakość efektu końcowego przewyższa efekty uzyskane metodami tradycyjnymi. Znane są np. znakomite dekoracje antyczne do produkcji filmowych z lat 60 i 70 jak również niechlubne wyjątki stosowania współczesnej grafiki komputerowej do realizacji antycznych dekoracji z mizernym skutkiem.
1.3. Historia grafiki komputerowej
Pierwsze próby użycia grafiki komputerowej miały charakter militarny ze względu na bardzo wysokie koszty sprzętu. W latach pięćdziesiątych XX wieku powstały pierwsze monitory graficzne. Od tego momentu w laboratoriach wojskowych rozpoczęto badania.
Bracia John i James Whitney pod koniec lat pięćdziesiątych wygenerowali obrazy abstrakcyjne wykorzystując ekran komputera (w ramach eksperymentu „visual feedback loops”).
Ivan Sutherland był w latach sześćdziesiątych XX wieku doktorantem MIT. W 1962 roku skonstruował pierwszą stację graficzną – kompletny system składający się monitora, klawiatury, urządzenia wskazującego (pióra świetlnego) i oprogramowania obsługi interaktywnej. Co prawda zaproponowana przez niego nazwa (sketchpad) nie przyjęła się, ale do dzisiaj praktycznie wszystkie stacje graficzne są budowane według jego pomysłu. Również użytkownicy komputerów osobistych maję, na co dzień, do czynienia z tym samym schematem interfejsu.
Parę lat później w 1969 roku I. Sutherland razem z Davidem Evansem założyli pierwszą firmę zajmującą się zastosowaniami grafiki komputerowej. Firma produkowała stacje graficzne oraz wyposażenie i oprogramowanie dla systemów symulacji (w szczególności dla symulatorów lotu).
W latach sześćdziesiątych i siedemdziesiątych ubiegłego stulecia na Uniwersytecie w Utah pracował pierwszy zespół naukowy zajmujący się grafiką komputerową. Powstało tam wiele podstawowych algorytmów stosowanych do dzisiaj. Pracowali tam między innymi: Ivan Sutherland, James Blinn, Edwin Catmull i wiele innych osób, których nazwiska są kojarzone jednoznacznie z określonymi algorytmami, i które to nazwiska są wymieniane w każdym podręczniku do grafiki komputerowej..
W 1969 roku powstała grupa SIGGRAPH. ( Special Interest Group on GRAPHics ) w ramach organizacji ACM. Była pierwszą grupą tematyczną poświęconą grafice komputerowej w ramach organizacji skupiającej profesjonalistów związanych z informatyką (ACM – Association for Computing Machinery). Obecna pełna nazwa grupy: Special Interest Group on Graphics and Interactive Techniques.
Pierwsze laboratorium graficzne założył Edwin Catmull w 1974 roku w New York Institute of Technology. Razem z Edem Emshwillerem pracowali nad zastosowaniami grafiki komputerowej w kinematografii. Laboratorium rozwijało metody animacji komputerowej.
W 1980 roku Turner Whitted opublikował artykuł opisujący metodę tworzenia obrazów, o których po raz pierwszy można było powiedzieć, że są „realistyczne”. Tak powstała metoda śledzenia promieni (ang. ray tracing). Za okres powstania metody śledzenia uznaje się początek lat osiemdziesiątych chociaż pierwsze uwagi na ten temat można odnaleźć w pracach wcześniejszych.
Badania prowadzone przez B.Mandelbrota i rozwój technik fraktalnych, a później zastosowanie ich do grafiki komputerowej pozwoliło zmienić podejście do modelowania powierzchni naturalnych (np. krajobrazu górskiego czy chmur).
W 1984 roku ukazała się praca C.Gorala, K.Torrance’a, D.Greenberga i B.Battaile’a proponująca metodę energetyczną (ang. radiosity) jako nowe podejście do wizualizacji. Następne lata przyniosły szybki rozwój tej techniki. Ponieważ metoda energetyczna rozwiązywała skutecznie problemy, z jakimi borykali się twórcy metody śledzenia promieni, więc niektórzy oczekiwali rychłego końca ray tracingu. Tak się oczywiście nie stało i już w latach 90 powstały próby łączenia obu technik.
Mapowanie fotonowe (ang. photon mapping) jest najnowszym etapem rozwoju metody śledzenia promieni. Opisane w książce H.Jensena z 2001 roku, chociaż tak naprawdę pierwsze próby stosowania tej techniki znalazły odbicie w artykułach w połowie lat 90.
W roku 1982 powstał Tron. Był to pierwszy film, w którym zastosowano grafikę komputerową. Co prawda dzisiejsi odbiorcy nie potrafią już tego docenić, ale w 1982 roku film ten wzbudził sensację. Rzecz dzieje się w wirtualnym świecie we wnętrzu komputera gdzie trafili bohaterowie – programiści. Scenografia, kostiumy – tak naprawdę wszystko oprócz twarzy i dłoni (!) zostało wykreowane przy pomocy komputera. Dziennikarze przewidywali, że następnym (i to w niedługim czasie) krokiem będzie zastąpienie aktorów przez postacie wykreowane przez komputer. Na szczęście te prognozy się nie sprawdziły i nadal możemy podziwiać grę (rzeczywistych) aktorów. Jednak od tego czasu grafika komputerowa stała się jednym z podstawowych narzędzi wykorzystywanych w kinematografii.
Efekty specjalne (pierwsze komputerowe) w filmie Star Trek tworzył dział animacji firmy Lucasfilm. Z działu tego powstała później firma Pixar, znana z wielu znakomitych filmów animowanych – tworzonych oczywiście z wykorzystaniem technik komputerowych. Toy Story – wyprodukowany przez wytwórnię Pixar w 1995 roku – był pierwszym filmem zrealizowanym w całości za pomocą grafiki komputerowej. Akcja filmu rozgrywa się w świecie zabawek, co pozwoliło zaakceptować pewną umowność szczegółów. Dzisiaj zdecydowaną większość efektów specjalnych na potrzeby kinematografii uzyskuje się dzięki grafice komputerowej. Często o wiele łatwiej wykreować wymyślną scenografię, nie tylko w filmach science fiction z wykorzystaniem komputerów niż budować ją w rzeczywistości. Oglądając piękne filmowe krajobrazy czy zachody słońca często nie zdajemy sobie sprawy, że jest to wytwór wyobraźni reżysera i scenografa, a „zbudowany” przez zespół programistów z wykorzystaniem grafiki komputerowej.
XXI wiek przyniósł bardzo szybki rozwój sprzętu, a tym samym widoczny wzrost mocy obliczeniowej komputerów. Współczesne smartfony dysponują pamięcią i mocą obliczeniową procesorów porównywalną do specjalizowanych stacji graficznych z lat osiemdziesiątych ubiegłego wieku. Natomiast współczesne komputery wykorzystywane przez programistów wytwórni filmowych pozwoliły w pełni wykorzystać wiele algorytmów graficznych, które przedtem miały czasem wartość akademicką i publikacyjną. Ale fakt, że te algorytmy powstały (i co najważniejsze, są dalej rozwijane) w połączeniu z współczesnym sprzętem, pozwolił uzyskać takie efekty specjalne jakie oglądaliśmy np. w filmach Avatar (2009), czy Diuna (2021 – część pierwsza, 2024 – część druga). Współczesna grafika komputerowa pozwoliła spełnić marzenia pierwszych twórców kinematograficznych efektów specjalnych – na ekranie zobaczyliśmy aktorów, którzy niestety już nie mogli wystąpić. W filmie Blade Runner 2049 (2017) „zagrała” Sean Young, chociaż postać grana przez nią w 1982 roku nie zestarzała się mimo upływu 35 lat i aktorka nie byłaby w stanie zagrać postaci mimo najlepszych prób charakteryzacji. W reklamie czekolady Galaxy (2013) „wystąpiła” Audrey Hepburn. Przypomnijmy, że wielka aktorka odeszła w 1993 roku.
Na świecie organizowanych jest rocznie kilkaset konferencji poświęconych grafice komputerowej. Równie duża jest liczba czasopism drukujących artykuły z tej dziedziny. Dwie najpoważniejsze konferencje organizowane są przez wspomniane towarzystwo SIGGRAPH (konferencje od 1974 roku) oraz przez EUROGRAPHICS – towarzystwo europejskie (konferencje od 1980 roku). Warto zajrzeć na stronę SIGGRAPH (www.siggraph.org). Można tam znaleźć nie tylko wiele dobrych przykładów grafiki komputerowej, ale przede wszystkim bardzo bogatą bibliografię z tej dziedziny.
Computer Graphics to najstarsze czasopismo graficzne, jest wydawane przez ACM od 1967 roku. Drukowało także sprawozdania z konferencji SIGGRAPH. Do 2001 roku jeden numer czasopisma zawierał wszystkie referaty konferencyjne. Od 2002 roku referatów i sprawozdań z konferencji SIGGRAPH należy szukać w, wydawanym od 1982 roku, ACM Transaction on Graphics. Jest to nie tylko najlepsze czasopismo dotyczące grafiki komputerowej, ale także jedno z najlepszych czasopism informatycznych na świecie. Spośród wielu czasopism poświęconych grafice komputerowej należy przynajmniej wymienić dwa: IEEE Computer Graphics & Applications wydawane od 1980 oraz Machine Graphics & Vision wydawane w Polsce przez Instytut Podstaw Informatyki PAN.
Grafika komputerowa jako przedmiot akademicki pojawiła się w końcu lat 70 XX wieku. Na początku lat 80 wykłady z grafiki komputerowej na Uniwersytecie Warszawskim prowadził dr M. Jankowski, a na Politechnice Warszawskiej mgr G. Prochowski (od połowy lat 80 wykład prowadził prof. J. Zabrodzki). Były to, najprawdopodobniej, pierwsze wykłady tego typu w Polsce.
1.4. Zastosowania grafiki komputerowej
Z grafiką komputerową spotykamy się dzisiaj prawie na każdym kroku. I najczęściej nie zdajemy sobie z tego sprawy, a przecież coraz większa grupa urządzeń elektronicznych, z których korzystamy jest obsługiwana za pośrednictwem interfejsu graficznego. Być może łatwiej byłoby dzisiaj pokazać dziedzinę, która nie korzysta z grafiki komputerowej. Zaprezentowana lista zastosowań jest pewną próbą klasyfikacji. Próbą, gdyż trzeba mieć świadomość przenikania dziedzin, ich wzajemnych powiązań i ciągłego rozwoju.
- Graficzny interfejs użytkownika (GUI)
- Zastosowania prezentacyjne, wizualizacja informacji. Zastosowania biurowe
- Wspomaganie prac inżynierskich (CAD/CAM)
- Symulacja i wirtualna rzeczywistość
- Poligrafia i skład drukarski (systemy DTP)
- Kartografia i systemy informacji przestrzennej (GIS)
- Medycyna
- Przemysł rozrywkowy
Graficzny interfejs użytkownika
Dzisiaj, graficzna komunikacja z komputerem (GUI – Graphical User Interface) praktycznie wyparł interfejs tekstowy nie tylko w sprzęcie powszechnego użytku, ale także w sprzęcie specjalistycznym. Jest to pierwsze, najpowszechniejsze zastosowanie grafiki, znane chyba każdemu użytkownikowi komputerów (rys. 1.2). Okienkowy system interfejsu stał się na tyle powszechny, że dla przeciętnego użytkownika komputer bez okienek byłby bezużytecznym przedmiotem. Nawet administratorzy systemowi coraz częściej dostają do dyspozycji narzędzia okienkowe i nie wszystkie operacje muszą wykonywać z linii poleceń.
Rys.1.2. Okienka Linuksa.
Prace nad graficznym interfejsem zostały zapoczątkowane w połowie lat 60 w firmie Xerox Parc. Na rozwój interfejsu graficznego miała bardzo silny wpływ praca Ivana Sutherlanda w MIT i jego sketchpad – pierwsza stacja graficzna skonstruowana w 1962 roku.
W 1964 roku na Uniwersytecie Stanforda użyto po raz pierwszy urządzenia wskazującego, które później nazwano myszą. Był to nieporęczny klocek drewniany z przyciskiem. (rys. 1.3.a).

Rys.1.3. a) Pierwsza mysz
komputerowa. b) Komputer Alto Xerox Parc.
W 1973 roku firma Xerox Parc zbudowała pierwszy
komputer z graficznym interfejsem : Alto Xerox Parc (rys.1.3.b). Komputer był wyposażony w graficzny wyświetlacz, mysz z 3 przyciskami,
był podłączony do sieci Ethernet. Graficzny interfejs obejmował niezależne pola
wyboru („okienka”), menu, przyciski wyboru różnego typu oraz ikony w postaci
odpowiednich symboli.
Warto pamiętać, że pierwsze okienka o funkcjonalności zbliżonej do dzisiejszych wcale nie zostały zaprojektowane przez firmę Microsoft.
W 1983 roku powstał komputer Lisa firmy Apple z funkcjonalnym zestawem okien o różnych przeznaczeniach (rys.1.4). System ten był krokiem milowym w rozwoju komunikacji człowieka z komputerem i jest uznawany za pierwszy interfejs okienkowy.
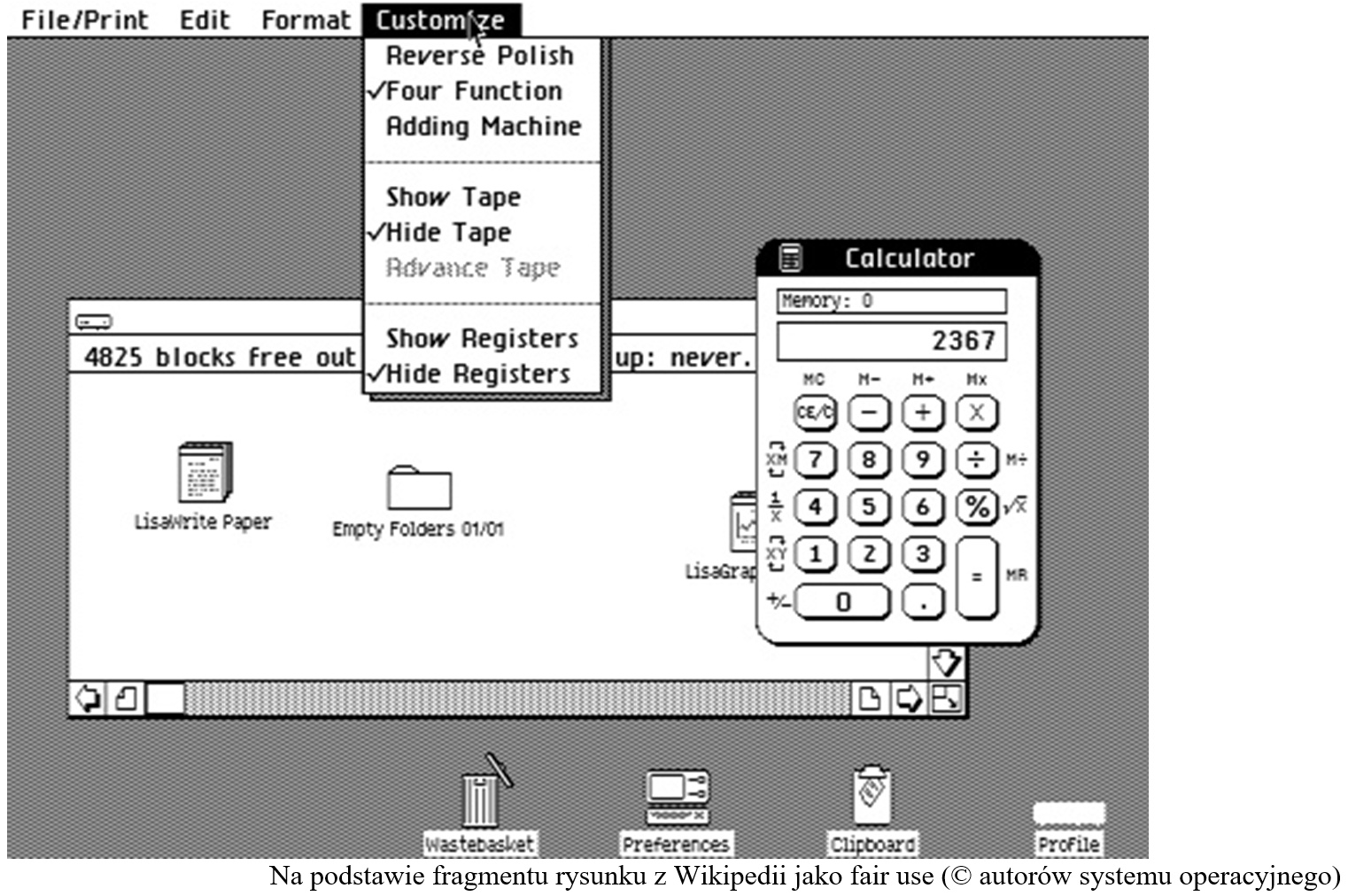
Rys.1.4. Okienka graficzne komputera Lisa z 1983 roku.
W roku 1984 pojawiły się, między innymi:
- Komputer Macintosh firmy Apple z w pełni skalowalnymi i nakładającymi się na siebie oknami graficznymi.
- System okienkowy X Window System opracowany w MIT, początkowo działający na maszynach VAX, później rozpowszechniony jako całkowicie przenośny system okien dla różnych platform sprzętowych.
Dopiero w 1985 roku firma Microsoft zaproponowała swoje pierwsze Windowsy, których okna graficzne nie mogły się nakładać, ani zajmować dowolnego położenia.
Warto także wspomnieć o interfejsach Open Look i OSF/Motif będącymi warstwą obsługi X Windows, gdyż zdobyły one ważną pozycję w systemach UNIXowych.
Dzisiaj spośród różnych dostępnych systemów okien graficznych warto wymienić między innymi KDE, GNOM, Mac OS oraz systemy 3D takie jak np. Compiz, BumpTop.
Strona http://www.guidebookgallery.org/ ; jest poświęcona interfejsowi. Można tam między innymi zobaczyć jak wyglądały ekrany interfejsu różnych systemów.
Grafika prezentacyjna
Równolegle z interfejsem rozwijała się wizualizacja danych ułatwiająca interpretację danych liczbowych czy różnego typu zjawisk. Wyspecjalizowane programy matematyczne i edukacyjne pozwalają obecnie rysować dowolne wykresy, krzywe czy powierzchnie. Ta grupa zastosowań obejmuje prezentację danych w postaci różnego typu wykresów i innych obrazów ułatwiających przekazanie określonych informacji.
Z jednej strony są to wykresy przedstawiające wielkości fizyczne, matematyczne, ekonomiczne lub techniczne, których prezentacja graficzna ułatwia zrozumienie zjawiska, przekazanie informacji lub podjęcie decyzji.
Z drugiej strony są to obrazy zależności i powiązań między określonymi treściami. Wykorzystanie graficznych symboli służy wspomaganiu prezentacji we wszystkich, praktycznie, dziedzinach (rys. 1.5). Ułatwia to przekazanie i zrozumienie określonych treści. Podobne formy prezentacji można dzisiaj spotkać np. na szkoleniu dla pracowników firm ubezpieczeniowych, jak i na seminarium poświęconym problemom ekologii. W wielu programach symbole zostały bardzo rozbudowane. Znacznie ułatwia to tworzenie prezentacji. Czasem jednak patrząc na przykład na liczbę symboli różnych strzałek dostępnych w programach prezentacyjnych można się zastanawiać czy na pewno forma służy prezentacji treści informacji a nie odwrotnie.

Rys.1.5. Wykres słupkowy
prezentujący zbiór danych.
b) Przykłady zestawu symboli obiektów i powiązań
między nimi.
Jest to dziedzina, która ułatwia pracę inżynierom różnych specjalności. Wykorzystanie grafiki w projektowaniu pozwala zajrzeć do wnętrza projektowanych urządzeń i narysować ich dowolne przekroje (rys.1.6). Pierwsze dostępne programy wspomagające pracę architektów i urbanistów pochodzą z lat 70. XX wieku. Z dzisiejszej perspektywy miały prymitywny interfejs, ale pozwalały „zobaczyć” jak będzie wyglądał projektowany budynek – a wygląd jest w tym przypadku bardzo ważny.

Rys.1.6. Projekt rozrusznika.
Rysunek opracowany przez M.Świderskiego
w Zakładzie Maszyn Elektrycznych
Politechniki Warszawskiej.
Wyróżnia się kilka systemów wspomagających:
- Projektowanie wspomagane komputerowo (Computer Aided Design - CAD)
- Komputerowe wspomaganie kreślenia i projektowania (Computer Aided Drafting and Design - CADD)
- Komputerowe wspomaganie procesu wytwarzania (Computer Aided Manufacturing - CAM)
- Komputerowo zintegrowana produkcja (Computer Integrates Manufacturing - CIM)
- Komputerowe wspomaganie działalności inżynierskiej (Computer Aided Engineering - CAE)
Komputer ”uczestniczy” w produkcji przedmiotu na każdym etapie jego powstawania. Poczynając od pomysłu (wizji projektanta), poprzez modelowanie kształtu, wybór odpowiedniej technologii wytwarzania, opracowanie dokumentacji i uwzględnienie właściwości materiałowych, aż do sterowania obrabiarką numeryczną. Najistotniejsze jest to, że wszystkie etapy są ze sobą ściśle powiązane. Wprowadzenie poprawek i uzupełnień nie stanowi żadnego problemu. Pozwala to znacznie uprościć proces zarówno projektowy jak i wytwarzania. Stosowana jest również tzw. inżynieria odwrotna. Na podstawie istniejącego, rzeczywistego obiektu jest opracowywana pełna dokumentacja projektowa i technologiczna, która może posłużyć do dalszej obróbki. Na przykład zrobienia wiernej kopii.
Grafika komputerowa stała się nieocenionym
narzędziem w pracowniach urbanistów i architektów. Także architektów krajobrazu
i projektantów wnętrz. Dzisiaj projektując np. kuchnię swojego mieszkania można
skorzystać z prostego oprogramowania, które pozwoli „zobaczyć” jak będzie ona
wyglądała. Współczesne programy tego typu mają ogromne możliwości i dają
obrazy, które można porównać do zdjęć (rys.1.7, rys.1.8).

Rys.1.7. Budynek
Metropolitan, pl.Piłsudskiego w Warszawie. Wizualizacja projektu zanim
rozpoczęto
prace budowlane. Rendering zamieszczony dzięki uprzejmości firmy
HINES.

Rys.1.8. Budynek Metropolitan, pl.Piłsudskiego w Warszawie. Zdjęcia rzeczywistego obiektu.
Specyficznym zastosowaniem, które pojawiło się w ostatnich latach, łączącym architekturę i sztukę z techniką świetlną jest wizualizacja oświetlenia budynków dla opracowania ich iluminacji (rys.1.9). Pozwala to często wydobyć nie dostrzegane kształty i podkreślić piękno obiektu. Grafika komputerowa daje możliwość sprawdzenia projektu oraz wyboru różnych wariantów oświetlenia. Co w warunkach rzeczywistych bez instalacji sprzętu byłoby praktycznie niemożliwe.

Rys.1.9. Projekty iluminacji. a) Wizualizacja iluminacji
gmachu Collegium Novum UJ w Krakowie.
b) Wizualizacja iluminacji Muzeum de Waag w Holandii.
Rysunki zamieszczone dzięki
uprzejmości W.Żagana.
Jest to zestaw czynności związanych z przygotowaniem publikacji zrealizowany za pomocą systemów komputerowych zamiast tradycyjnymi metodami poligraficznymi (typograficznymi). Czynności te obejmują obróbkę tekstu i obrazów, łączenie ich w zamierzoną formę publikacji, a także prace związane z dostosowaniem barw do wykorzystywanych urządzeń drukujących. Podstawowy zakres takiego działania wykonują dzisiaj edytory tekstu komputerów osobistych. Wszyscy korzystamy z udogodnień przy pisaniu tekstów, jakie daje współczesny program edytorski. Nie wyobrażamy sobie dzisiaj pracy bez takich narzędzi.

Symulacje i wirtualna rzeczywistość
Wizualizacja i symulacja różnych zjawisk ułatwia pracę nie tylko fizykom, chemikom i biologom, dzisiaj korzystają z tego praktycznie wszystkie grupy zawodowe. Ze względów finansowych, bardzo dużą grupę zastosowań stanowią symulatory wykorzystywane w szkoleniu personelu obsługującego drogi i skomplikowany sprzęt: samoloty, statki czy dowolne pojazdy wojskowe. Grafika komputerowa pozwala stworzyć iluzję rzeczywistości, a to daje możliwość symulowania realnych warunków i problemów. Dzięki temu szkolenie jest tańsze niż w rzeczywistych warunkach. Nie ma niebezpiecznych konsekwencji potencjalnych błędów. A jednocześnie można zasymulować wszystkie, nawet bardzo rzadko występujące w rzeczywistości, przypadki..
Symulacja urządzeń jest znana od dawna. Pierwsze symulatory lotu posługiwały się techniką filmowa. Niedoskonałość takiego rozwiązania polegała przede wszystkim na braku możliwości reakcji systemu na niestandardową sytuację – problemem było pozyskiwanie materiału filmowego. Drugim etapem rozwoju (lata sześćdziesiąte) była technika wykorzystująca makietę terenu i poruszającą się nad nią kamerę. Trzeci etap to symulatory wykorzystujące grafikę komputerową (lata siedemdziesiąte XX wieku). Współczesne symulatory lotu dają pełnię wrażeń obsługi rzeczywistego samolotu.
Dzięki odpowiednio sterowanym podnośnikom hydraulicznym jest możliwość zasymulowania również zmian położenia, wstrząsów i przeciążeń. Dodając do tego inne wrażenia odczuwane przez pilota (np. hałas) oraz pełne wyposażenie kabiny można uzyskać wrażenie rzeczywistego lotu. Oczywiście kluczowym zagadnieniem jest zapewnienie wrażeń wzrokowych. Jest to bardzo trudne zadanie stojące przed grafiką komputerowa, wymaga bowiem przygotowania skomplikowanych realistycznych wizualizacji w czasie rzeczywistym.
Symulatory lotu zapewniają możliwość prowadzenia szkolenia pilotów w sposób bezpieczny i tani. I jednocześnie dają możliwość przeprowadzenia ćwiczeń dowolnie wybranych zdarzeń w dowolnych warunkach – co nie byłoby osiągalne w warunkach rzeczywistych.
Symulatory stosowane są dzisiaj wszędzie tam gdzie wymagane jest szkolenie obsługi drogiego i cennego sprzętu oraz gdzie stawiane są wysokie wymagania związane z bezpieczeństwem. Poza symulatorami lotu jest to przede wszystkim sprzęt wojskowy, ale nie tylko. Znane są np. konstrukcje symulatorów wózków widłowych.
Obok symulatorów profesjonalnych (symulatory loty, trenażery wojskowe, symulatory innych obiektów) warto wspomnieć o symulatorach opracowanych w celach rozrywkowych np. do gier komputerowych.
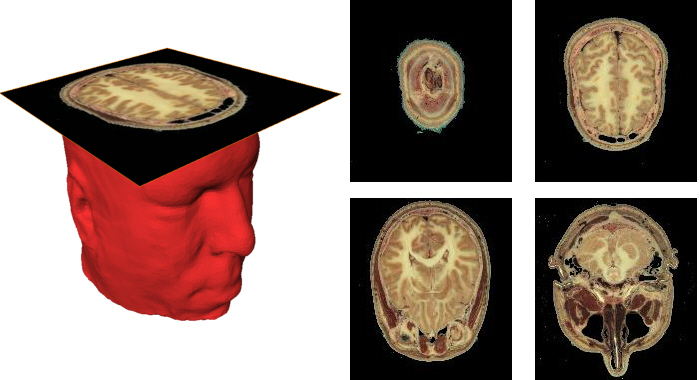
Zastosowania grafiki w medycynieZastosowania grafiki w medycynie (rys.1.11) pozwalają postawić diagnozę łatwiej, szybciej i z mniejszym ryzykiem błędu. Bez tomografii komputerowej czy rezonansu magnetycznego współczesna medycyna nie byłaby w stanie postawić często właściwej diagnozy. Ale wszystkie narzędzi diagnostyki obrazowej, także USG czy RTG w gabinecie stomatologicznym dostarczają wyników w postaci cyfrowej – w postaci obrazu na monitorze zamiast tradycyjnej kliszy fotograficznej. Tych narzędzi nie byłoby bez przetwarzania obrazów i grafiki komputerowej.
Zastosowania w przemyśle rozrywkowym
Shrek oraz inni bohaterowie filmów animowanych, reklamy, czy efekty specjalne stanowią przykłady bardzo rozległej grupy zastosowań w przemyśle rozrywkowym. Przemyśle wymagającym olbrzymich nakładów finansowych, realizującym wieloletnie projekty, wymagającym specjalistycznych laboratoriów i sprzętu. „Toy Story” z 1995 roku – pierwszy film animowany zrealizowany w całości za pomocą grafiki komputerowej, wykorzystywał sieć 117 komputerów, a prace nad filmem trwały aż 4,5 roku. Ale efekty są czasem rzeczywiście zaskakujące. Postać Golluma we „Władcy Pierścienia” jest zrealizowana na tyle perfekcyjnie, że nie można zauważyć, w których ujęciach mamy do czynienia z aktorem, a w których z grafiką komputerową. Mimo rozwoju sprzętu komputerowego i ogromnemu wzrostowi mocy obliczeniowej nadal wykreowanie dobrych efektów zajmuje bardzo dużo czasu. W filmie Blade Runner 2049 (z 2017 roku) konieczne było odtworzenie postaci granej 35 lat wcześniej przez Sean Young. Powstała sekwencja trwająca tylko 2 minuty. Komputerowe wykreowanie postaci i przygotowanie tej sekwencji zajęło twórcom filmu cały rok ! Ale praca opłaciła się. Widzowie oglądając film nie mają wątpliwości – Sean Young „zagrała” w nim. filmu Osobną grupę zastosowań w przemyśle rozrywkowym stanowią gry komputerowe. Od czasu powstania gry „Doom” w 1993 roku – pierwszej gry typu „z perspektywy bohatera” („First Person Perspective”) – gdzie widzimy świat oczami bohatera gry, producenci prześcigają się we wprowadzaniu coraz to nowszych i doskonalszych realistycznych efektów.
1.5. Sprzęt wykorzystywany w grafice komputerowej
Bardzo dużą rolę odgrywa sprzęt, jaki jest wykorzystywany w grafice komputerowej. Często decyduje on o jakości obrazu i jego odbiorze. W latach 50. i 60. XX wieku na wykorzystanie grafiki mogło sobie pozwolić tylko wojsko i organizacje rządowe w bogatych krajach. Dzisiaj wprawdzie każdy właściciel PC-ta jest jednocześnie posiadaczem podstawowego zestawu graficznego, ale nadal jakość sprzętu odbija się na jakości obrazu – wiedzą o tym szczególnie fani najnowszych gier komputerowych pracujący na starych kartach graficznych.
Sprzęt prezentujący obrazy można podzielić na dwie grupy:
- Sprzęt wyświetlający (monitory CRT, wyświetlacze TFT/LCD, urządzenia stereoskopowe).
- Sprzęt pozwalający tworzyć trwałą kopię (drukarki, plotery, a także urządzenia nagrywające VHS, CD, DVD).
Osobną grupę urządzeń graficznych stanowią:
- Urządzenia wskazujące (mysz, trackball, tablet, ekran dotykowy, manipulatory),
- Urządzenia służące wprowadzaniu danych obrazowych (skanery 2D i 3D, cyfrowe aparaty fotograficzne i kamery),
- Urządzenia sterujące prezentacją (lub wspomagające ją) (procesory graficzne, karty graficzne),
- Nie można zapomnieć o klawiaturze, która wprawdzie nie jest urządzeniem graficznym, ale służy do wprowadzania informacji – związanych z grafiką również.
Warto zwrócić szczególną uwagę na sprzęt wyświetlający, jego jakość decyduje przede wszystkim o odbiorze informacji obrazowej. Jeszcze do niedawna powszechne były monitory (i telewizory) tradycyjne – CRT. Dzisiaj w większości przypadków zostały one zastąpione przez wyświetlacze ciekłokrystaliczne (LCD) lub plazmowe. Warto pamiętać o różnicach między tymi urządzeniami. Są ona nadal widoczne pomimo szalonego rozwoju technologii.
Typowe cechy monitora LCD.
Zalety:
- Waga i rozmiary (monitory LCD są stosunkowo lekkie i płaskie).
- Mały pobór energii.
- Brak zniekształceń geometrycznych.
- Brak lub pomijalne migotanie obrazu (zależnie od sposobu podświetlania ekranu).
Wady:
Mały kontrast.
- Ograniczony kat obserwacji (dla większych związane jest to ze znacznymi zniekształceniami barwy i/lub jasności).
- Mała szybkość odpowiedzi (reakcji).
- Tylko jedna natywna rozdzielczość ekranu, możliwość wyświetlania obrazu o innej rozdzielczości związana z utratą jakości.
- Ograniczony zakres reprezentacji barwy (zdefiniowany określonym i ograniczonym zestawem bitów).
- Możliwość pojawiania się „martwych pikseli” (także w urządzeniach nowych).
Oczywiście przytoczone tutaj wady i zalety urządzeń wyświetlających podlegają zmianom związanym z rozwojem technologii. Monitory CRT praktycznie odeszły do historii (poza specjalistycznymi zastosowaniami). Należy przypuszczać że szybki rozwój technologii pozwoli zminimalizować wady współczesnych urządzeń wyświetlających lub o części z nich w ogóle zapomnieć. Jednocześnie ciągle poprawiane parametry będą podkreślały ich zalety.
Bardzo duży wpływ na rozpowszechnienie grafiki komputerowej i jej zastosowań miał rozwój kart graficznych i procesorów graficznych. Jeszcze w latach 90 XX wieku rola karty graficznej w popularnych komputerach typu PC ograniczała się do wyświetlania informacji na ekranie lub ewentualnie realizacji najprostszych operacji. Zaawansowana grafika była realizowana na specjalnych stacjach graficznych, gdzie specjalizowane procesory graficzne wykonywały z dużą szybkością nie tylko większość zadań grafiki dwuwymiarowej (rysowanie prymitywów, obcinanie itp.) ale także złożone zadania trójwymiarowe jak np. wspomaganie eliminacji elementów zasłoniętych. Czasami były to całe komputery o specjalnie dobranej architekturze na potrzeby zastosowań w programowaniu animacji lub wspomaganiu projektowania (CAD). Szybki rozwój technologii elektronicznej pozwolił konstruować specjalizowane procesory graficzne (GPU) wspomagające sprzętowo realizację typowych zadań grafiki komputerowej. Współczesne karty graficzne wyposażone są w wielordzeniowe procesory, które nie tylko znacznie przyspieszają realizację zadań graficznych ale mogą być wykorzystywane do innych celów.
1.6. Grafika rastrowa i wektorowa
W klasycznym monitorze CRT obraz na ekranie powstaje dzięki strumieniowi elektronów (w monitorze kolorowym dzięki trzem strumieniom – każdy związany z jedną składową barwy), który padając na luminofor ekranu „zapala” plamkę (piksel). Zmieniając kierunek strumienia i jego energię można wpłynąć na położenie i jasność plamki (piksela). W monitorze LCD podając odpowiedni zestaw bitów dla określonego piksela uzyskuje się zadaną barwę.
Wyróżnia się dwa tryby pracy urządzeń prezentujących obraz:
- Tryb wektorowy (grafika wektorowa), gdy możliwe jest sterowanie położeniem oraz jasnością (barwą) plamki. Takie sterowanie pozwala utworzyć na ekranie np. odcinek o dowolnie położonych końcach (rys.1.12a). Konsekwencją takiego sposobu sterowania są następujące właściwości: brak zniekształceń wnoszonych przez samo urządzenie (linie ukośne są zawsze gładkie) tym samy odbiór rysunku jest niezależny od urządzenia, sekwencyjna struktura danych obrazowych, zajętość pamięci zależna od kształtu rysunku, możliwość dowolnego skalowania rysunku, możliwość operowania kreską ale trudności w operowaniu plamą. Przykładem tak pracującego urządzenia jest ploter lub oscyloskop.
- Tryb rastrowy (grafika rastrowa), gdy możliwe położenia plamki są z góry ustalone i nie można na nie wpłynąć, natomiast można sterować jasnością (barwą) plamki (rys.1.12b). Podstawowe właściwości takiego trybu to: zniekształcenia powodowane rastrem (ukośny odcinek jest schodkowy), kształt rysunku nie wpływa na zajętość pamięci, brak możliwości dowolnego skalowania (bez utraty jakości), odbiór rysunku zależny od urządzenia, możliwość operowania kreską i plamą (z dokładnością do rastra). Przykładem może być telewizor lub monitor typu LCD.
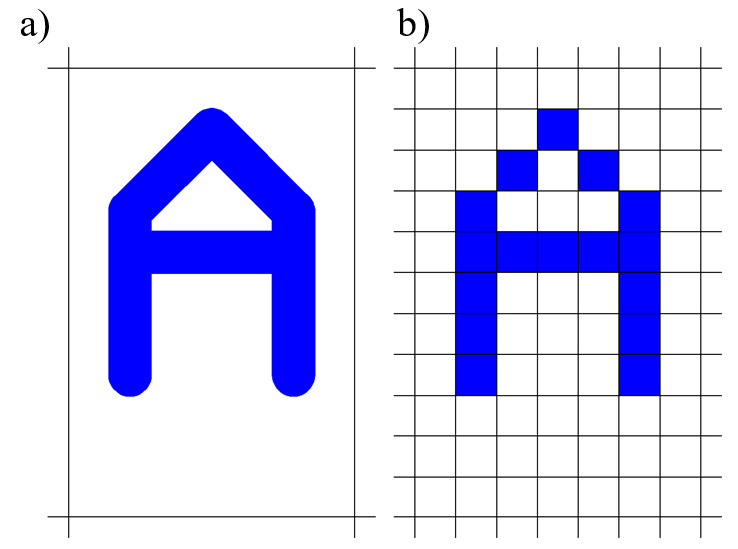
Rys. 1.12. Litera A narysowana w dwóch trybach pracy. a) W trybie wektorowym. b) W trybie rastrowym.
Praktycznie wszystkie urządzenia wyświetlające pracują dzisiaj w trybie rastrowym. Monitory wektorowe dostępne były od połowy lat sześćdziesiątych. W latach osiemdziesiątych zostały praktycznie całkowicie wyparte przez monitory rastrowe. Również zdecydowana większość urządzeń drukujących i rysujących na różnych materiałach działa w trybie rastrowym. Pisaki XY (plotery), w których naturalnym sposobem sterowania jest sterowanie wektorowe przestały być popularne w takiej postaci - ze względów technologicznych, wykonywane są jako urządzenia rastrowe o bardzo dużej rozdzielczości.. Wydawać by się więc mogło, że o trybie wektorowym będzie się w grafice komputerowej mówić tylko w aspekcie historycznym. Jednak zalety trybu wektorowego (przede wszystkim skalowalność) sprawiły, że przetrwał on i jest nadal stosowany. Występuje on w warstwie programowej i interfejsu użytkownika. Dzięki temu można zdefiniować a następnie przechować rysunek, który nie będzie tracił jakości podczas np. obracania i skalowania. Natomiast po przeliczeniu go do konkretnej rozdzielczości, będzie mógł być wyświetlony na rastrowym monitorze lub wydrukowany na rastrowej drukarce.
Oprogramowanie graficzne pozwala użytkownikowi tworzyć obrazy w trybie wektorowym, ale jest on wyświetlany na rastrowym monitorze. Z drugiej strony nawet jeśli ploter przyjmuje rozkazy sterowania wektorowego, to zastosowanie odpowiedniego sterowania może powodować, że pisak będzie poruszał się po niewidocznym dla oka rastrze. Zamiana trybu wektorowego na rastrowy nosi nazwę rasteryzacji.
Tworzenie obrazu na urządzeniu rastrowym związane jest z dwoma problemami, które wymagają rozwiązania. Pierwszym jest zapewnienie wysokiej jakości obrazu pomimo skończonego rozmiaru rastra. Drugim jest umożliwienie narysowania zestawu podstawowych figur (prymitywów) takich jak np. odcinek lub łuk okręgu na mapie rastra. Za pomocą prymitywów można potem utworzyć dowolny rysunek.
Raster i skończone rozmiary piksela powodują, że rysunek zostaje zniekształcony. Wszystkie ukośne linie przybierają „schodkowy” kształt (przykład odcinka na rys.1.13a). Dla złożonych obrazów może to utrudniać interpretację rysunku – przykładem może być szachownica widziana pod kątem (rys. 1.13b). Naturalnym rozwiązaniem tego problemu wydaje się, po prostu, zmniejszenie rozmiarów piksela, czyli zwiększenie rozdzielczości rastra. Niestety nie jest to takie proste. Na przeszkodzie stają właściwości oka ludzkiego, które stara się powiększyć różnicę jasności sąsiadujących ze sobą pól. Dzięki temu możemy czytać gazetę o zmierzchu, ale powoduje to również, że idealny obraz mogą zakłócić nam nawet najdrobniejsze rysy. Zwiększenie rozdzielczości rastra, w pewnym zakresie, niewiele więc daje. Oczywiście jest pewna granica rozdzielczości kątowej, powyżej której można „oszukać” oko. W fotografii cyfrowej i poligrafii przyjmuje się, że taką granicą jest 300dpi (dots per inch – punktów na cal) dla zdjęć i publikacji oglądanych „na wyciągnięcie ręki”, czyli z odległości 40 – 60 cm. Taka rozdzielczość zapewnia, że oko nie zauważy rastrowego charakteru rysunku. Oznacza to np., że aby zapewnić dobrą jakość zdjęcia 10x15 cm (4x6 cali), to powinno ono mieć rozdzielczość1200x1800 pikseli. Dwa razy większe zdjęcie – dwa razy większa rozdzielczość. Oczywiście np. plakaty reklamowe oglądamy z zupełnie innej odległości, stąd aby zapewnić odpowiednią rozdzielczość kątową potrzebna jest inna rozdzielczość obrazu.
Nie zawsze odpowiednia rozdzielczość jest możliwa do osiągnięcia. Aby w takiej sytuacji poprawić odbiór rastrowego obrazka wykorzystuje się tzw. antyaliasing – metodę poprawy wyglądu bazującą na teorii sygnałów. Tak naprawdę problem wynika z próbkowania z określoną rozdzielczością. Oprócz schodkowych odcinków może się więc pojawić problem znikania (i czasowego pojawiania się) obiektów na tyle małych, że mogą zmieścić się pomiędzy próbkami. Błędy próbkowania zamienia się na błędy zaszumienia – na które oko ludzkie jest mniej wrażliwe. Stosując odpowiednie filtrowanie dokonuje się „rozmycia”, dotychczas kontrastowej, barwy sąsiednich pikseli (rys.1.14a). Oko ludzkie dokona pewnego rodzaju uśrednienia, co prawda operacja taka nie doda szczegółów, ale problem schodków przestaje przeszkadzać. Nawet widok szachownicy (rys.1.14b) sprawia wtedy wrażenie poprawnego. Warunkiem koniecznym uzyskania tego efektu jest duża liczba barw lub stopni szarości dla każdego piksela. Biorąc pod uwagę możliwość rozróżniania barw przez oko ludzkie przyjmuje się, że aby pokazać pełną paletę barw potrzeba 24 bity na piksel (po 8 bitów na każdą składową RGB). Standardem dla kart graficznych stało się przechowywanie informacji w postaci 32 bitów na piksel.
W takich rozwiązaniach dodatkowe bity mogą być wykorzystane do opisu innych właściwości np. przezroczystości. Czasami stajemy przed dylematem czy, z dwojga złego, lepiej wybrać tryb pracy o mniejszej rozdzielczości np. 800x600, ale z pełną skalą barw (24 bity na piksel), czy wyższej rozdzielczości np. 1200x1024 ale z ograniczoną skalą na przykłąd tylko 8 bitów na piksel. Biorąc pod uwagę właściwości oka ludzkiego i możliwości programów graficznych, rozstrzygnięcie będzie oczywiste. Poza wyjątkowymi i szczególnymi przypadkami, pierwszy wariant pozwoli uzyskać lepszy i przyjemniejszy w odbiorze obraz.
Więcej na ten temat można przeczytać w książkach[2, 5]. Podstawowe problemy związane z percepcją barwy, właściwościami i budową oka ludzkiego będą omawiane w rozdziale 10. tego podręcznika.
1.7. Interakcja człowiek - komputer
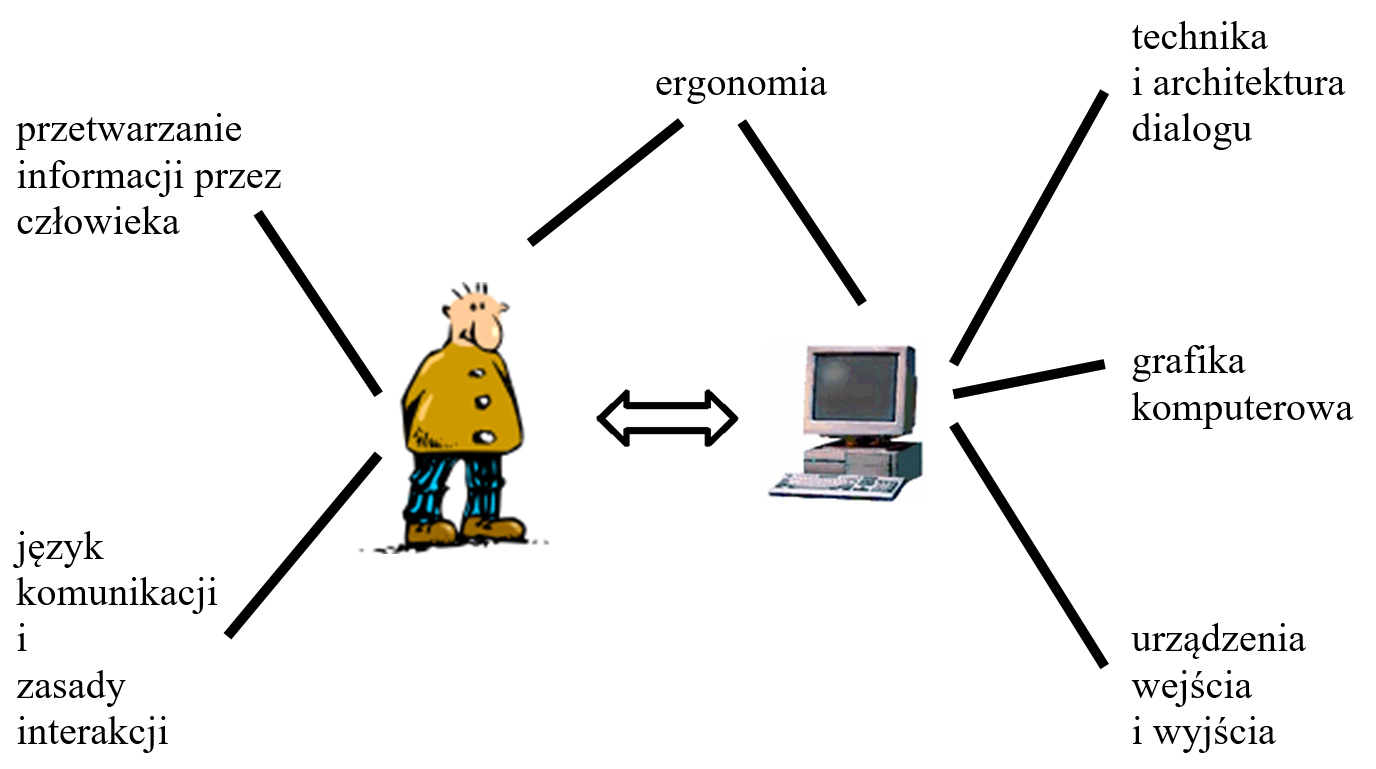
Problem budowy optymalnego interfejsu komplikuje fakt, że na odbiór informacji (także tych w dialogu z komputerem) ma wpływ wiele czynników związanych bezpośrednio z użytkownikiem. Najczęściej dzieli się je na cechy indywidualne i społeczne.

Więcej informacji na temat interakcji człowiek komputer czytelnik może znaleźć w książkach [1, 4].
1.8. Standardy w grafice kokmputerowej
Potrzeba standaryzacji operacji i możliwości przenoszenia oprogramowania pojawiła się wraz z upowszechnieniem się sprzętu wykorzystywanego do grafiki w latach siedemdziesiątych. Pierwszy standard (3D Core Graphics System - 1977) został opracowany przez ACM SIGGRAPH. Przez wiele lat, praktycznie do lat dziewięćdziesiątych powszechnie stosowanym standardem w rozwiązaniach przemysłowych był GKS (Graphical Kernel System – 1985, rozszerzony do GKS 3D w 1988). Wynikało to z prostej konstrukcji operacji 2D i typowego stosowania grafiki 2D we wspomaganiu prac inżynierskich. Bardziej rozbudowane możliwości zaoferował PHIGS (Programmer’s Hierarchical Interactive Graphics System – 1988), dając do dyspozycji hierarchiczne struktury prymitywów. Standard ten był rozszerzany o możliwości tworzenia grafiki realistycznej do postaci PHIGS+ oraz PHIGS PLUS. Dodatkową zaletą tych systemów jest efektywne wykorzystanie wspomagania sprzętowego. Obecnie wydaje się, że najpowszechniejszym standardem jest OpenGL opracowany w 1993 przez Silikon Graphics (SGI) – firmę przodująca w rozwiązaniach dla potrzeb grafiki realistycznej. Obecnie standard ten rozwija Khronos Group.
Na bazie OpenGL, w 2016 roku Khronos Group zaproponował nowe rozwiązanie – Vulkan. Jest to API, które o wiele bardziej wspiera rozwiązania sprzętowe (kontrolę pamięci i wielowątkowość) zapewniając obiektowość danych.
Niezależnie popularność zyskał Direct3D zaproponowany w 1985 przez firmę Microsoft dla potrzeb obsługi gier komputerowych. Jako DirectX jest najpowszechniej akceptowanym standardem w środowisku kart graficznych.
Warto wspomnieć także o VRML (Virtual Realisty Modelling Language - 1994) ułatwiającym korzystanie z grafiki 3D w Internecie. Standard ten w zasadzie przestał być używany, jednak był podstawą do wprowadzenia kilku nowszych rozwiązań. Wydaje się że dzisiaj (w 2024 roku) powszechniejsze są standardy takie jak glTF, czy X3D (Extensible 3D) jako standard ISO/IEC.
Formaty graficzne można podzielić na dwie grupy:
- Związane z grafiką rastrową (nieskalowalne),
- Związane z grafiką wektorową (skalowalne).
Do pierwszej grupy (rastrowej) miedzy innymi można zaliczyć:
- BMP (i DIB) – zapis w postaci mapy bitowej bezstratnej o różnej dostępnej palecie barw: 1,4,8,24 bity na piksel.
- GIF – zapis z indeksacją barwy – paleta ograniczona do 256 pozycji, bezstratna kompresja LZW, możliwość zapisu kilku obrazów w pliku – GIF animowany.
- PCX – format stosowany w programach Paint/Paintbrush, istnieje kilka wersji zapisu, paleta 1,4,8,24 bity na piksel.
- TIFF – zapis bezstratny, paleta 1,4,8,24 bity na piksel, stosowane różne metody kompresji najczęściej LZW. Format pierwotnie przeznaczony dla poligrafii.
- TGA – (Targa) mapa bitowa z opcjonalną kompresją RLE, paleta 8,16,24,32 bity na piksel, dodatkowo TGA ma możliwość zapisania informacji o przezroczystości (tzw. kanał Alfa).
- JPG (JPEG) zapis z pełną paleta barw ale stratną kompresją DCT. Zaletą jest bardzo wydajna kompresja. Najnowsza wersja JPEG 2000 o znacznie podwyższonej jakości stratnej kompresji.
- PNG – unowocześniona wersja formatu GIF, wydajniejsza kompresja bezstratna, pełna paleta barw, obsługa kanału Alfa. Dodatkową zaletą jest brak ograniczeń licencyjnych.
Do drugiej grupy (wektorowej) można między innymi zaliczyć:
- WMP – zapis stosowany w MS Windows.
- EPS, PS – Postscript – język opisu strony opracowany przez firmę Adobe.
- HPGL – język sterowania ploterami firmy HP.
- DXF – przemysłowy standard stosowany przez firmę Autodesk w swoich aplikacjach (AutoCAD).
- SVG – standard opracowany w oparciu o XML na potrzeby WWW.
Więcej informacji na temat standardów graficznych oraz budowy i przechowywania plików graficznych można znaleźć w książkach [3, 6].
Rozdział 2. PODSTAWOWE OPERACJE RASTROWE
W rozdziale drugim
przedstawiono podstawowe problemy związane z rastrowym sposobem wyświetlania
informacji. Omówione zostały tutaj podstawowe algorytmy rastrowe takie jak
rysowanie odcinka i łuku okręgu, wypełnianie obszaru i zadania obcinania. Są to wszystko operacje, które są ściśle związane z technologią wyświetlania informacji, z których nie zdajemy sobie sprawy korzystając z komputera, a które muszą być efektywnie zrealizowane.
Rysowanie obrazu na monitorze lub urządzeniu drukującym wymaga wypełnienia wybranego obszaru pikseli określonymi barwami w taki sposób, aby powstał zamierzony rysunek. Korzystając z edytora graficznego wybieramy pewne obiekty podstawowe – tak zwane prymitywy (np. odcinek) i żądamy narysowania ich w określonym miejscu. Nie zastanawiamy się w tym momencie nad tym, że żądanie to, z pozoru bardzo proste, wymaga rozwiązanie wielu problemów geometrycznych oraz opracowania skutecznych i szybkich algorytmów. I to bez względu na to czy będzie to realizowane przez odpowiednią bibliotekę czy tez sprzętowo przez kartę graficzną. Rysowanie figury na mapie rastra (rys.2.1) wymaga dokonania wyboru pikseli, które mają tworzyć rysunek. Zadanie nie jest trywialne biorąc pod uwagę fakt, że musi to być jednoznacznie interpretowane, powtarzalne i szybkie.
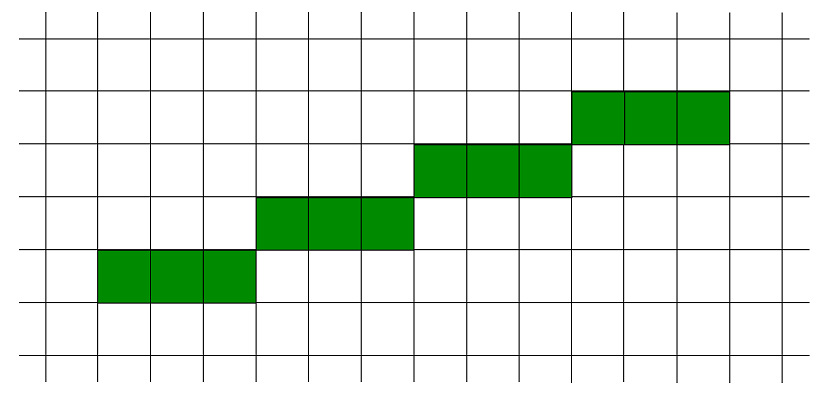
Rys.2.1. Odcinek na rastrze pikseli
2.1. Rysowanie odcinka i łuku okręgu
Jednym z podstawowych problemów tego typu jest zadanie narysowania odcinka na mapie pikseli. Analizując rysunek odcinka na mapie pikseli (rys.2.1) można zaproponować prosty sposób postępowania: należy rysować od lewej do prawej zwiększając za każdym razem o 1 współrzędną x , czasem zwiększając y , kiedy wynika to z położenia punktu odcinka. Jednocześnie w tym problemie można wykorzystać symetrie osiowe w kartezjańskim układzie współrzędnych. Zmiana nachylenia odcinka – powyżej 45 wymagałaby zmiany postępowania (rysować od dołu do góry zwiększając y o 1 , przy czym w zależności od położenia punktu powiększając x o 1). Ale przecież jest to tylko zamiana współrzędnych. Algorytm postępowania pozostaje bez zmian. Analizując w ten sposób odcinki o dowolnych nachyleniach (dowolne współrzędne początku i końca odcinka) można zauważyć, że wystarczy zaproponować skuteczny algorytm rysowania dla odcinków, których nachylenie mieści się w przedziale od 0o do 45o. Pozostałe przypadki można uzyskać stosując ten sam algorytm dla zamienionych współrzędnych lub zmieniając znak przed odpowiednią współrzędną.
Najprostszym rozwiązaniem zadania
wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem  . Następnie wyznaczenie wartości
. Następnie wyznaczenie wartości  dla całkowitych
wartości
dla całkowitych
wartości  odpowiadających
kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne
odpowiadających
kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne  do wartości
całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek
tzn.
do wartości
całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek
tzn.  , gdzie
, gdzie  jest operacją
zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma
podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania,
zaokrąglania).
jest operacją
zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma
podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania,
zaokrąglania).
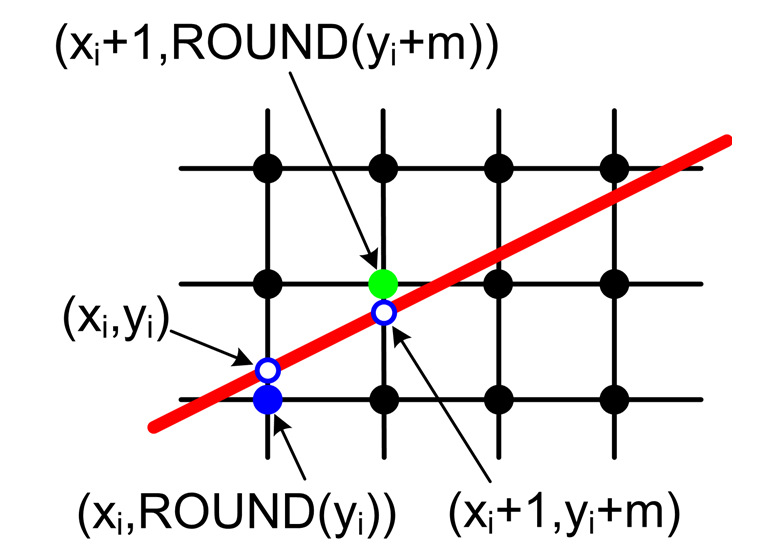
Rys.2.2. Rysowanie odcinka, algorytm wykorzystujący
operacje zmiennopozycyjne.
Piksele na tym rysunku zostały zaznaczone jako węzły
siatki kolejnych wartości współrzędnych.
Najprostsza procedura rysowania odcinka Line dla x2>x1, y2>y1, 0<m<1 .:
procedure Line (x1, x2, y2, y2,)
begin
dx := x2-x1; dy := y2-y1
m := dy/dx; y := y1;
for xINTEGER:=x1 to x2 do
begin
set_pixel(xINTEGER, ROUND( y ));
y=y+m;
end;
end;
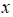 wzrasta w każdym kroku
o 1, tzn.
wzrasta w każdym kroku
o 1, tzn.  . Bez zmniejszania
ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka
od 0 do 1. Dla innych wartości można bowiem odpowiednio zamienić zmienne. Wzrost
. Bez zmniejszania
ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka
od 0 do 1. Dla innych wartości można bowiem odpowiednio zamienić zmienne. Wzrost  w takim przypadku
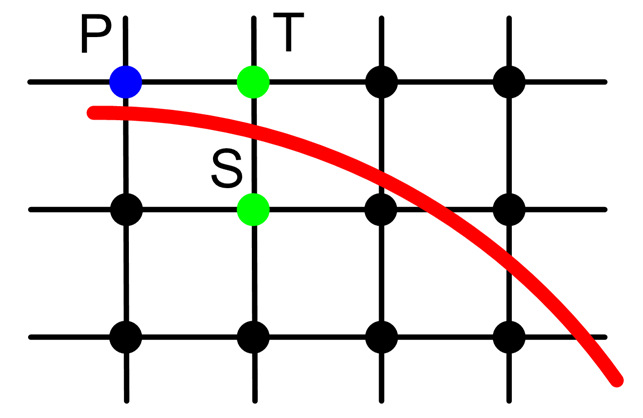
zależy od wyboru piksela, który jest bliżej teoretycznej prostej (S lub T na rysunku 2.3). O wyborze decyduje zmienna kontrolna d , która jest uaktualniana w każdym kroku.
w takim przypadku
zależy od wyboru piksela, który jest bliżej teoretycznej prostej (S lub T na rysunku 2.3). O wyborze decyduje zmienna kontrolna d , która jest uaktualniana w każdym kroku.
Jeśli di < 0 (piksel S ) to  .
.
Jeśli di >= 0 (piksel T ) to 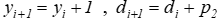 .
.
Przy czym wartość początkowa  oraz
oraz  , gdzie dx , dy są różnicami
współrzędnych między końcem a początkiem odcinka.
, gdzie dx , dy są różnicami
współrzędnych między końcem a początkiem odcinka.
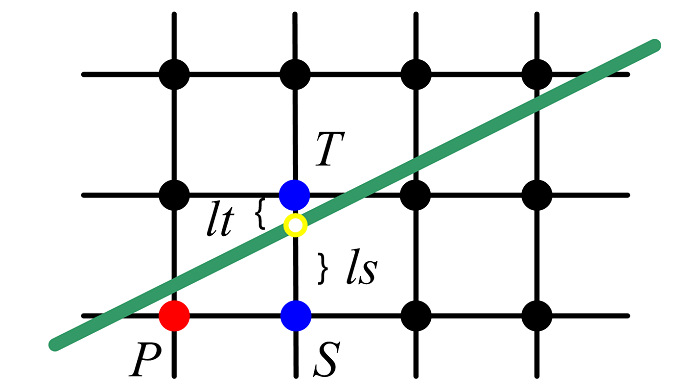
Rys.2.3. Wybór punktów w algorytmie Bresenhama rysowania
odcinka.
Z bieżącego piksela P wybieramy piksel następny spośród
pikseli T i S.
Przecięcia linii pionowych i poziomych czarnej kraty
oznaczają środki pikseli.
Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak:
procedure Bresline (x1,x2, y2,y2,)
begin
dx := x2-x1; dy := y2-y1
p1 := 2*dy-dx; p2 := 2*(dy-dx);
x := x1; y := y1;
xend := x2;
set_pixel(x,y);
while (x<xend) do begin
x := x+1;
if (d<0) d := d+p1;
else begin
d := d+p2;
y := y+1;
end;
set_pixel(x,y);
end;
end;
Algorytm taki, wykorzystujący tylko operacje całkowite jest również użyteczny w rozwiązaniach sprzętowych. Takie, podobne i bardziej skomplikowane zadania we współczesnych kartach graficznych realizowane są sprzętowo.
Omawiany w rozdziale 1. problem próbkowania jest już widoczny w przypadku najprostszego zadania. Korzystanie z rastra w przypadku rysowania odcinka może prowadzić do następujących problemów.:
Pierwszym
jest problem „schodków” (rys.2.4). Poprawę wyświetlania można uzyskać przez
odpowiednią modyfikację barw pikseli sąsiednich.
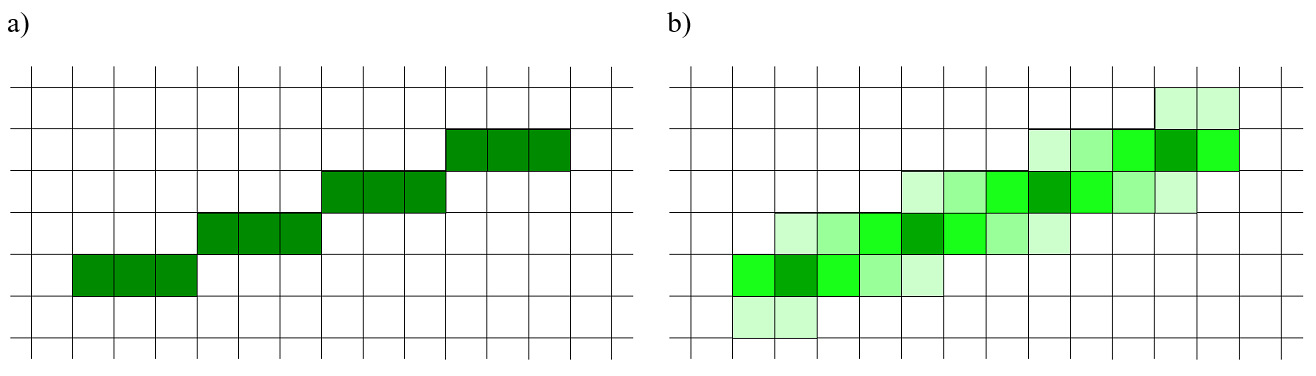
Rys.2.4. a) Proste
rysowanie odcinka na rastrze (algorytm naiwny).
b)
Rysowanie odcinka + algorytm antyaliasingu (jasność/luminancja proporcjonalna
do powierzchni „zakrywanej” przez teoretyczny odcinek).
Drugim problemem jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych.
Trzecim,
chyba najmniej spodziewanym problemem jest postrzegana zmiana jasności (i/lub
szerokości odcinka) związana z położeniem i nachyleniem odcinka. Oba odcinki na
rysunku 2.5 składają się z 7 punktów. Tylko że odcinek po przekątnej rastra
jest ![]() razy dłuższy od
odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra
i powstaje podobnie do problemu „schodków” odcinka.
razy dłuższy od
odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra
i powstaje podobnie do problemu „schodków” odcinka.
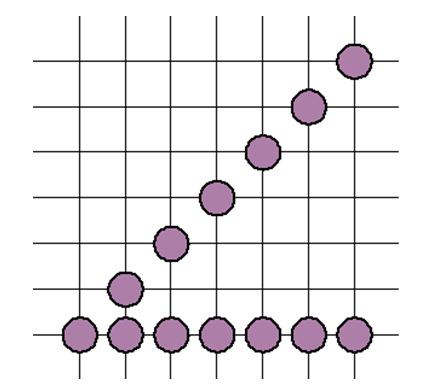
Rys.2.5. Odcinki o różnej długości zbudowane na mapie pikseli z 7 punktów.
Rys.2.6. Rysowanie łuku okręgu na mapie pikseli.
Przy okazji rysowania okręgu warto zwrócić uwagę na parametr charakteryzujący proporcje boków rastra pikseli w pionie i w poziomie, czyli aspekt. Jeśli proporcje rozdzielczości dla kart graficznych 1024x768 wynoszą 4:3, natomiast dla rozdzielczości 1280x1024 wynoszą 5:4, to jeśli chcemy wyświetlić takie obrazy na tym samym monitorze, to proporcje trzeba przeliczyć uwzględniając aspekt. Inaczej narysowany okrąg albo w jednym albo w drugim przypadku będzie miał kształt elipsy.
2.2. Wypełnianie obszaru
Wypełnianie obszaru jest drugim po rysowaniu odcinka
lub łuku, najczęściej występującym problemem związanym z prymitywami. Zadanie
dla szczególnych przypadków (np. dla prostokąta) jest zadaniem trywialnym.
Natomiast w ogólnym przypadku algorytm powinien pracować poprawnie dla
dowolnego wielokąta (także wklęsłego), również dla wielokątów z „dziurami”.

Rys.2.7. Wypełnianie obszaru. Równoważność problemów a)
wypełniania i b) zmiany barwy obszaru.
Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne (rys.2.7). W wypełnianiu obszaru brzegiem są piksele o barwie linii ograniczającej obszar, w zmianie barwy brzegiem są piksele o barwie tła. Algorytm rozwiązujący jedno zadanie może posłużyć do rozwiązania drugiego.
Niech na mapie pikseli dana będzie krzywa zamknięta, zdefiniowana w postaci zbioru sąsiadujących ze sobą pikseli o danej barwie. Zadaniem jest wypełnienie tego obszaru, czyli zmiana barwy wewnętrznych pikseli na zadaną barwę wypełnienia. Znane są dwa klasyczne sposoby rozwiązania tego zadania.
- Wypełnianie przez spójność (nazywane czasem wypełnianiem przez sianie).
- Wypełnianie przez kontrolę parzystości.
Warto zwrócić tutaj uwagę na problem sąsiedztwa
i konieczność dostosowania do niego kształtu brzegu. Można wyróżnić dwa
przypadki. Gdy ruchy po mapie pikseli mogą odbywać się analogicznie do ruchów
wieży po szachownicy – wtedy piksel ma 4 sąsiadów – siatka jest czterospójna
(rys.2.8a). Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to kierunkom
ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna
(rys.2.8b). Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli
brzegu dla obu przypadków aby stanowił on figurę zamkniętą z punktu widzenia
możliwości ruchu.
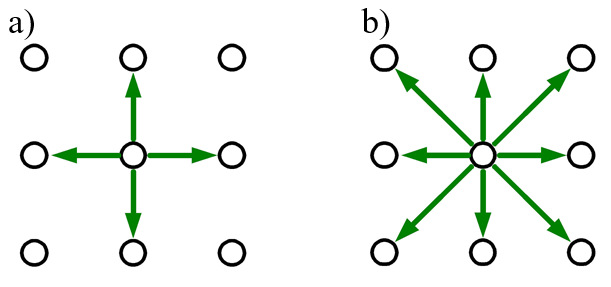
Rys.2.8. Możliwości poruszania się po mapie pikseli. a) siatka czterospójna, b) siatka ośmiospójna.
Algorytm wypełniania przez spójność dla siatki czterospójnej (rys.2.9) wygląda następująco (przyjęto: c_b – barwa brzegu, c_f – barwa wypełnienia).:procedure wypełnij1(x,y)
begin
set_pixel(x,y,c_f);
if (barwa(x-1,y) inna niż c_b i inna niż c_f) wypełnij1(x-1,y);
if (barwa(x+1,y) inna niż c_b i inna niż c_f) wypełnij1(x+1,y);
if (barwa(x,y-1) inna niż c_b i inna niż c_f) wypełnij1(x,y-1);
if (barwa(x,y+1) inna niż c_b i inna niż c_f) wypełnij1(x,y+1);
end;
Czytelnik może zaproponować korektę algorytmu obejmującą siatkę ośmiospójną.
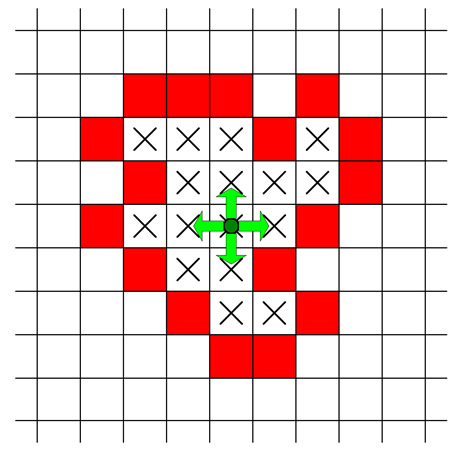
Rys.2.9. Punkt startowy („ziarno”) oraz kierunki wypełniania w pierwszym kroku wypełniania przez spójność.
Przedstawiona postać algorytmu wypełniania przez spójność jest algorytmem rekurencyjnym. Daje to łatwość opisu ale związane jest także problemami realizacyjnymi. Z tego powodu znane są wersje niniejszego algorytmu w postaci nierekurencyjnej.

Rys.2.10.
Wypełnianie przez kontrolę parzystości.
Odcinki pomiędzy nieparzystym a
parzystym punktem przecięcia z figurą są w jej wnętrzu.
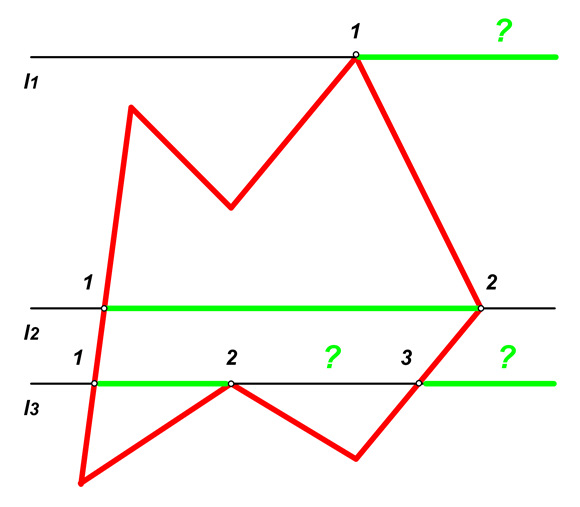
Rys.2.11. Problemy brzegowe wypełniania przez kontrolę parzystości.
Na rysunku 2.11 prosta l2 przecina wielokąt w wierzchołku (punkt 2) ale jest to przecięcie zwykłe – pozostałe końce przecinanych boków są po przeciwległych stronach prostej l2. Prosta l3 również przecina wielokąt w wierzchołku (punkt 2) ale jest to ekstremum lokalne – pozostałe końce boków są po tej samej stronie prostej l3.
W szczególnych przypadkach mogą pojawić się obszary nie dające się wypełnić w sposób spójny – problem „drzazgi” (rys. 2.12). Jedynym sposobem rozwiązania tego problemu jest nadpróbkowanie. Należy spróbkować i wypełnić drzazgę z większą rozdzielczością, a następnie uśrednić barwę/luminancję wracając do rozdzielczości rastra.

Rys.2.12.
Problem drzazgi. Taki obszar jest trudny do wypełnienia zarówno algorytmem
wypełniania przez spójność jak i przez kontrolę parzystości.
W książkach [1, 2] można znaleźć szczegółowe opisy oraz pseudokody dla rozwiązania różnych problemów rysowania prymitywów w technice rastrowej.
2.3. Algorytmy obcinania
Większość rysowanych obiektów jest definiowana w
rzeczywistym układzie kartezjańskim. Przedstawienie takiego obiektu na ekranie
monitora (lub z wykorzystaniem innego urządzenia) wymaga określenia fragmentu,
który jest obrazowany. Jeśli tylko część prymitywu jest zobrazowana, to oprócz
algorytmu rysowania prymitywu jest potrzebny algorytm obcinania go do
widocznego fragmentu.
Obcinanie jest to operacja rastrowa pozwalająca wydzielić fragment figury, który mieści się w prostokątnym oknie (rys.2.13).

Rys.2.13. Zadanie obcinania. Przerywane odcinki powinny zostać usunięte.
Algorytm Cohena-Sutherlanda (1974) służy do obcinania
odcinków do prostokątnego okna. Oznacza to, że należy wybrać odcinki (lub ich
fragmenty) do obcięcia na podstawie położenia ich końców.
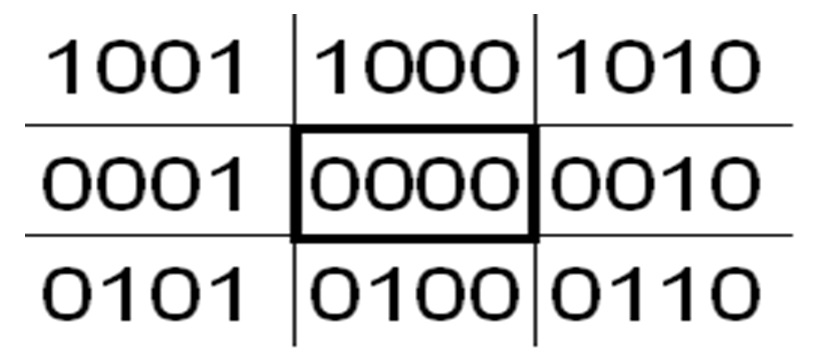
Rys.2.14.
Podział płaszczyzny na obszary w algorytmie Cohena i Sutherlanda.
Kolejne
bity od lewej: ograniczenie górne, dolne, prawe, lewe.
Płaszczyzna została podzielona na 9 obszarów . Prostokąt centralny odpowiada obszarowi okna. Jednocześnie krawędzie okna wyznaczają cztery proste: prawą, lewą, górna i dolną. Każdemu obszarowi został przypisany czterobitowy kod. Kolejne bity kodu określają poziome i pionowe pasy. Operacja AND przeprowadzona na kodach końców odcinka pozwala odrzucić te odcinki, które na pewno są poza oknem. Spośród pozostałych odcinków należy wybrać te, które rzeczywiście mają wspólne punkty z oknem oraz przyciąć do jego rozmiaru. Operacja AND pozwala w tym przypadku wybrać prostą obcinającą.
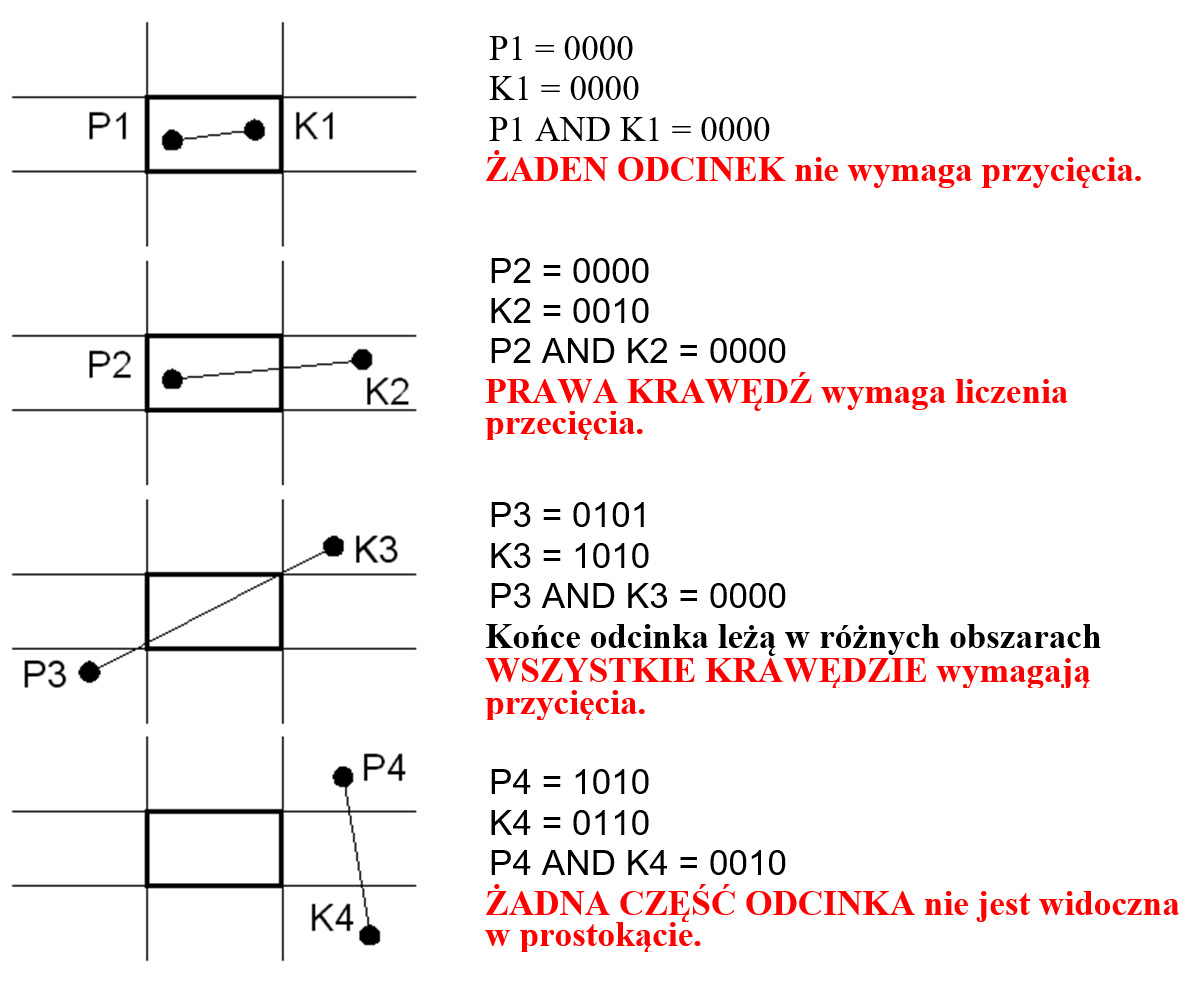
Rys.2.15. Rozważane przypadki w algorytmie obcinania Cohena i Sutherlanda.
- Jeśli wynik operacji AND jest różny od zera – należy odrzucić odcinek jako nie mający na pewno punktów wspólnych z oknem.
- Jeśli wynik operacji AND jest zerowy – odcinek może przecinać okno.
- W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna.
-
Natomiast jeśli kody końców są niezerowe to określają
one którymi prostymi należy przyciąć odcinek. Odcinek
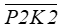 należy przyciąć prostą
prawą (K2=0010). Odcinek
należy przyciąć prostą
prawą (K2=0010). Odcinek 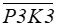 prostymi lewą i dolną
(P3=0101) oraz prawą i górną (K3=1010).
prostymi lewą i dolną
(P3=0101) oraz prawą i górną (K3=1010).
Algorytm Cohena-Sutherlanda bardzo efektywnie klasyfikuje odcinki i jednocześnie jest bardzo prosty w implementacji. Powoduje to, że jest chyba najczęściej stosowanym algorytmem przycinania odcinków do prostokątnego okna. Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania.

Rys.2.16. Wykorzystanie zorientowania do przyspieszenia obcinania. Algorytm Cyrusa-Becka.
Jeśli opiszemy prostą parametrycznie, to wzrost
parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają
odpowiednio parametrom t=0 i t=tk dla k>0. Wektor ![]() określa zwrot prostej.
Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego
(skierowanego na zewnątrz) do boku wielokąta. Jeśli
określa zwrot prostej.
Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego
(skierowanego na zewnątrz) do boku wielokąta. Jeśli![]() to parametr tk określa punkt Pk., który może być „maksymalnym” punktem przecięcia z wielokątem
(np. punkt dla t=t2 na rysunku 2.16).
to parametr tk określa punkt Pk., który może być „maksymalnym” punktem przecięcia z wielokątem
(np. punkt dla t=t2 na rysunku 2.16).
Jeśli ![]() to parametr tk określa punkt Pk., który może być „minimalnym” punktem przecięcia z wielokątem
(np. punkt dla t=t1 na rysunku 2.16).
to parametr tk określa punkt Pk., który może być „minimalnym” punktem przecięcia z wielokątem
(np. punkt dla t=t1 na rysunku 2.16).
Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony przez Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych.
Zestawiając wybrane algorytmy przycinania można zwrócić uwagę na cechy je wyróżniające.:
- Cohen-Sutherland
- Skomplikowane powtarzanie przycinania
- Najefektywniejsze wykorzystanie gdy możliwa prosta akceptacja/odrzucenie dla wielu odcinków
- Efektywny dla implementacji sprzętowej
-
Cyrus-Beck
- Upraszcza wyznaczanie przecięcia parametrycznego
- Jednokrotne obliczenia punktu przycięcia
- Algorytm nie jest oparty na prostej akceptacji/odrzuceniu
- Najlepsze efekty gdy wiele odcinków musi być przyciętych
-
Liang-Barsky
- Optymalizacja algorytmu Cyrus-Beck
W przypadku obcinania wielokąta, zastosowanie algorytmu obcinania odcinków przynosi tylko połowiczny sukces. Wielokąt tworzy bowiem zbiór uporządkowanych wierzchołków. Każdy wierzchołek jest początkiem pewnego boku i jednocześnie jest końcem poprzedniego boku w danym uporządkowaniu. Potraktowanie boków wielokąta jako zbioru odcinków i przycięcie ich powoduje, że tracimy informacje o ich połączeniach.
Przykładem algorytmu rozwiązującego ten problem jest algorytm Sutherlanda-Hodgmana obcinania wielokąta.
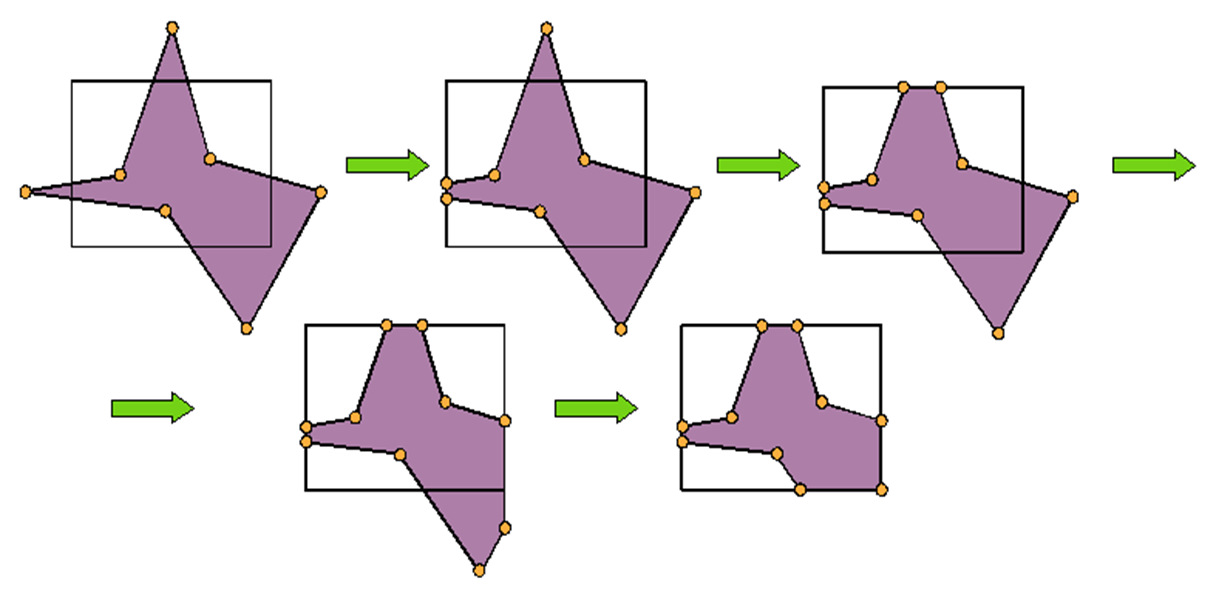
Rys.2.17.
Algorytm Sutherlanda-Hodgmana. Obcinanie wielokąta do prostokątnego okna
z
zachowaniem ciągłości listy wierzchołków wielokąta.
Niech kolejne wierzchołki wielokąta tworzą listę cykliczną. Obcinanie odbywa się kolejno dla prostych zawierających boki okna w ustalonym porządku – np. tak jak na rysunku 2.17 zgodnie z ruchem wskazówek zegara poczynając od krawędzi lewej. W każdym kroku algorytmu rozpatrywany jest jeden wierzchołek leżący poza oknem przycinania. Wierzchołek taki jest usuwany z listy ale w jego miejsce wstawiane są wierzchołki „odpowiadające mu” na brzegu okna. Oczywiście należy wziąć pod uwagę również i takie przypadki, w których dodany wierzchołek będzie leżał na prostej zawierającej bok okna ale będzie to wierzchołek, który zostanie również usunięty np. w następnym kroku. Z drugiej strony możliwy jest także przypadek, kiedy kolejne wierzchołki wielokąta leżą na zewnątrz okna i wtedy kilka z nich może zostać zastąpionych jednym punktem na brzegu okna.
Wszystkie stacje graficzne realizują operacje na prymitywach w sposób sprzętowy. Współczesne karty graficzne dla sprzętu klasy PC mogą realizować operacje związane z prymitywami w sposób sprzętowy. Praktycznie wszystkie powszechnie używane kompilatory proponują zestaw gotowych procedur graficznych. Również korzystając z bibliotek graficznych takich jak np. OpenGL mamy do dyspozycji gotowe i zoptymalizowane procedury. Często jednak w realizacji specyficznych zadań zachodzi potrzeba niestandardowej zmiany postępowania – ingerencji we wnętrze procedury – na co ani rozwiązania sprzętowe ani biblioteczne nie pozwalają. Wiedza o specyfice operacji rastrowych i technice działania na prymitywach jest wtedy niezbędna.
Rozdział 3. ELEMENTY GEOMETRII OBLICZENIOWEJ
Rozdział trzeci zawiera podstawowe informacje dotyczące geometrii obliczeniowej
– narzędzi niezbędnych do rozwiązywania problemów geometrycznych. Zostały
omówione takie zagadnienia jak badanie zorientowania punktów na płaszczyźnie i sprawdzenie
przynależności punktu do wielokąta. Prezentowane rozwiązania pokazują także
sposób podejścia do problemów geometrycznych w grafice komputerowej.
Złożone operacje na prymitywach, zaawansowane algorytmy graficzne wymagają często rozwiązania problemów, które są na tyle złożone, że stanowią odrębne zadania algorytmiczne. Takie problemy jak np. sprawdzenie przynależności punktu do wielokąta (lub dowolnego obszaru), podział dowolnego wielokąta na trójkąty, wyznaczenie wypukłej otoczki (wypukłej skorupki), wyznaczenie przecięć w zbiorze odcinków są domeną dziedziny zwanej geometrią obliczeniową (ang. computational geometry). Jest to stosunkowo nowa dziedzina informatyki. Z jednej strony jest często traktowana jako narzędzie niezbędne do realizacji algorytmów w grafice komputerowej, z drugiej pozwoliła również wprowadzić do grafiki nowe struktury danych lub je usystematyzować. Wiele zagadnień stanowi samodzielne problemy geometrii obliczeniowej, a jednocześnie rozwiązania problemów tego typu są niezbędne w różnych zastosowaniach, niekoniecznie związanych z grafiką komputerową.
3.1. Przykłady problemów niezwiązanych bezpośrednio z grafiką komputerową
Istnieje bardzo wiele problemów, z którymi spotykamy się w codziennym życiu nie zdając sobie sprawy z tego, że są to typowe problemy geometrii obliczeniowej. Co więcej, problemy te są znane od setek lat, a ich rozwiązanie spędzało sen z powiek wielu matematykom. Niektóre z tych zadań są na tyle trudne, że prace nad ich rozwiązaniem trwają dalej. Dla innych udowodniono, że nie istnieją proste i efektywne rozwiązania. Jest również grupa zadań, dla których opracowano skuteczne i efektywne algorytmy postępowania, co pozwoliło przyspieszyć prace nad rozwiązaniami stosowanymi potem powszechnie w naszym życiu. Telefonia komórkowa jest jednym z przykładów powszechnie wykorzystywanej techniki, która nie mogłaby być stosowana bez odpowiedniego rozwiązania problemów geometrii obliczeniowej.
Problem ochrony galerii (problem muzealny)
Wyobraźmy sobie galerię obrazów zajmującą wiele połączonych ze sobą sal (rys. 3.1). Każdy obraz jest cenny, każdy wymaga uwagi personelu, który musi zadbać o to, aby nikt nie uszkodził ani nie ukradł zbiorów galerii. Powstaje pytanie: ile co najmniej osób musi pilnować zbiorów galerii. Oczywiście zamiast strażników można wykorzystać odpowiednie czujniki lub kamery. .Przyjmuje się, że jeden punktowy czujnik (kamera lub osoba) może „obserwować” (a tym samym chronić) przestrzeń wokół siebie spełniając następujące założenie:
- jest nieruchomy,
- obserwuje w kącie pełnym (2p) przestrzeń wokół siebie,
- może obserwować obiekty z dowolnego dystansu (odległość nie jest istotna),
- nie widzi przez ściany (ściany są nieprzezroczyste).

Rys.3.1. Problem ochrony galerii.Rysunek pochodzi z
wikipedii (CC BY).
Tak sformułowany problem nosi w literaturze nazwę art gallery problem. Istnieje twierdzenie V.Chvátala (tzw. twierdzenie o galerii sztuki lub twierdzenie o wartownikach), że jeśli sale galerii są ograniczone n ścianami to minimalna liczba strażników wynosi floor(n/3). Gdzie floor(x) oznacza największą liczbę całkowitą mniejszą lub równą x. Twierdzenie to zostało udowodnione w1975 roku.
Niech danych będzie n węzłów na płaszczyźnie. Należy podzielić płaszczyznę na n wielokątów wypukłych (rys. 3.2) w taki sposób, aby spełnione były następujące warunki:
- w każdym wielokącie znajduje się dokładnie jeden węzeł,
- odległość dowolnego punktu wielokąta od węzła danego wielokąta jest mniejsza nić odległość od innego węzła.
Tak sformułowane zadanie rozpatrywał w 1644 roku René Descartes, a później J.Dirichlet w 1850 roku. Nazwa problemu pochodzi od nazwiska Gieorgija Woronoja, który w 1907 roku uogólnił zadanie do problemu wielowymiarowego.

Rys.3.2. Diagram Voronoi. Rysunek pochodzi z wikipedii (CC BY).
Diagram Voronoi można wyznaczyć ze złożonością O(nlogn). Pierwszy tego typu algorytm wykorzystujący metodę dziel i korzystaj zaproponowali M.I.Shamos i D.Hoey w 1975 roku. Wyznaczenie diagramu Voronoi jest jednym z najbardziej znanych zadań geometrii obliczeniowej. Istnieje bardzo bogata literatura problemu. Zadanie to (czasami pod różnymi nazwami) można spotkać w wielu dziedzinach niezwiązanych bezpośrednio z informatyką i geometrią. Ciekawymi przykładami są zastosowania w biologii i naukach przyrodniczych. W książce A.Okabego, B.Bootsa i K.Sugihary Spatial Tessellations: Concepts and Applications of Voronoi Diagrams z 1992 roku podano nie tylko ciekawe właściwości diagramu i różne rozwiązania zadania ale także wiele aspektów aplikacyjnych z różnych dziedzin.
Warto zwrócić uwagę na fakt, że telefonia komórkowa wymaga rozwiązania analogicznego problemu. Stacje bazowe dzielą przestrzeń na obszary, w których odległość do stacji jest najmniejsza. I w takim obszarze, z tą a nie z żadną inną stacją łączy się nasza komórka. Jeśli zmienimy położenie i znajdziemy się w innym obszarze, to wtedy nasza komórka połączy się z inną stacją bazową.
3.2. Historia geometrii obliczeniowej
Geometria obliczeniowa jest stosunkowo młodą dziedziną informatyki. Jednak wiele problemów ma bardzo długą historię. Warto to sobie uświadomić spoglądając na rozwój geometrii obliczeniowej
- 1644 Diagram Voronoi był rozpatrywany przez Kartezjusza (René Descartes). Nie potrafił on podać algorytmu podziału (wyznaczenia diagramu) ale jest to najprawdopodobniej pierwsze udokumentowane i sformalizowane zagadnienie współczesnej geometrii obliczeniowej.
- 1759 Euler & Vandermonde rozpatrują problem komiwojażera (TSP) w przestrzeni euklidesowej. Nie podali oni rozwiązania problemu jednak im zawdzięczamy pierwszą sformalizowaną definicję tego problemu. Komiwojażer ma odwiedzić różne miasta (każde dokładnie raz) i powrócić do miejsca startu. Znane są odległości między miastami. Zadaniem jest wyznaczenie najkrótszej trasę przejazdu. Problem komiwojażera jest jednym z problemów teorii grafów, natomiast w geometrii obliczeniowej jest rozpatrywany przy okazji drzew rozpinających.
- 1800 William Hamilton definiuje problem komiwojażera (TSP) w postaci ogólnej jako cykl hamiltonowski w grafie.
- 1972 Ronald Graham publikuje rozwiązanie problemu wypukłej otoczki.
- 1978 Michael I. Shamos pisze pracę doktorską, która obejmuje zestaw najważniejszych problemów geometrii obliczeniowej. Podaje formalne definicje oraz rozwiązania i ich warunki realizacji. Datę tę można uznać za początek współczesnej geometrii obliczeniowej.
- 1985 Nakładem wydawnictwa Springer-Verlag ukazuje się pierwszy podręcznik do geometrii obliczeniowej.: Preparata F.P., Shamos M.I.. Computational Geometry. An Introduction.
Oczywiście należy pamiętać, że problemy geometrii obliczeniowej są rozpatrywane w informatyce w ramach teorii algorytmów. Ksiązki i wykłady poświęcone algorytmom i strukturom danych zawsze obejmowały również zadania geometryczne. Warto na to zwrócić uwagę czytając np. dzieło D.E.Knutha Sztuka programowania. Jako niezależny wykład geometria obliczeniowa pojawiła się na studiach informatycznych w latach 80 XX wieku. Pierwszym w Polsce (i chyba jednym z pierwszych w Europie) był wykład prowadzony na Uniwersytecie Warszawskim w połowie lat 80 przez dra J. Jaromczyka. Dr Jaromczyk jest od wielu lat profesorem w University of Kentucky (https://www.engr.uky.edu/directory/jaromczyk-jerzy). Warto zwróci uwagę, na fakt, że 75% zespołu zajmującego się teorią algorytmów na University of Kentucky stanowią obecnie (w 2024 roku) Polacy (https://www.engr.uky.edu/research-areas/theory-algorithms).
3.3. Funkcja alfa
Często spotykanym problemem jest konieczność uporządkowania punktów w układzie biegunowym. Wyznaczenie kąta na podstawie współrzędnych kartezjańskich nie jest trudne, ale wymagałoby użycia funkcji trygonometrycznych, co znacznie spowalniałoby rozwiązanie zadania. Funkcja alfa (rys.3.3) daje możliwość porównania kątów bez wyznaczania ich wartości. Należy jednak pamiętać, że wartość funkcji alfa nie jest liniowo związana z wartością kąta i próba szacowania kąta na tej podstawie byłaby poważnym błędem.

Rys.3.3. Funkcja alfa(P) określona niezależnie w każdej ćwiartce układu współrzędnych
dla 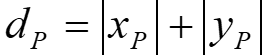 . Zamiast porównywać kąty i sprawdzać
czy aP1 < aP2
. Zamiast porównywać kąty i sprawdzać
czy aP1 < aP2
wystarczy sprawdzić
czy alfa(P1) < alfa(P2) .
3.4. Zorientowanie punktów na płaszczyźnie
Drugim bardzo prostym zagadnieniem, które często
występuje w zagadnieniach graficznych jest określenie zorientowania trójki
punktów na płaszczyźnie (rys.3.4). Dane są trzy punkty na płaszczyźnie, należy
określić ich zorientowanie. Oczywiście należy pamiętać o przypadkach
szczególnych, stąd rozpatruje się punkty różne i niewspółliniowe. Zadanie to ma
oczywiście eleganckie rozwiązanie w postaci wektorowej. Wystarczy wyznaczyć dwa
wektory rozpięte na badanych trzech punktach, a następnie obliczyć ich iloczyn
wektorowy. Analiza zwrotu wektora wynikowego pozwala określić poszukiwane
zorientowanie.
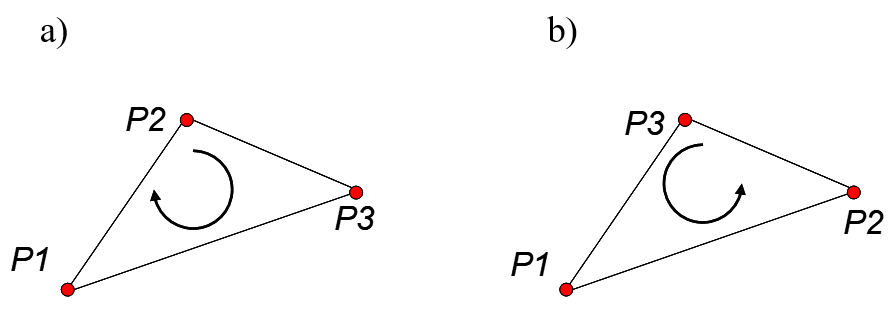
Rys.3.4. Zorientowanie punktów a) zgodnie z ruchem wskazówek zegara, b) przeciwne do ruchu wskazówek zegara.
Zastosowanie macierzy współrzędnych (przez analogię do macierzy określającej iloczyn wektorowy) upraszcza obliczenia.
Niech dane będą trzy niewspółliniowe punkty P1[x1,y1], P2[x2,y2], P3[x3,y3]. Zadaniem jest określenie zorientowania (rys.3.4).
Można wyznaczyć macierz M :

Analiza wyznacznika tej macierzy pozwala w prosty sposób rozwiązać zadanie.
- Jeśli det M > 0 mówimy o dodatnim zorientowaniu (lewoskrętnym lub przeciwnym do ruchu wskazówek zegara (CCW – counter-clockwise).
- Jeśli det M < 0 mówimy o ujemnym zorientowaniu (prawoskrętnym lub zgodnym z ruchem wskazówek zegara (CW – clockwise).
3.5. Sprawdzenie przynależności punktu do wielokąta
Dość często spotykanym zadaniem geometrycznym
jest sprawdzenie położenia badanego punktu względem określonych obiektów. Może
to obejmować badanie przynależności do określonego obszaru lub lokalizację
położenia na mapie. Najprostszym zadaniem tego typu jest określenie czy badany
punkt znajduje się wewnątrz lub na zewnątrz danego wielokąta.
Badanie przynależności punktu do wielokąta wypukłego
Zagadnienie sprawdzenia przynależności punktu do wnętrza wielokąta ma bardzo proste rozwiązanie dla wielokąta wypukłego. Jeśli wziąć pod uwagę prostą wyznaczoną przez dwa kolejne wierzchołki wielokąta, to prosta ta dzieli płaszczyznę na dwie półpłaszczyzny, z których tylko jedna zawiera wielokąt (rys.3.5). Podstawiając więc współrzędne badanego punktu do równania prostej można na podstawie znaku równania stwierdzić po której stronie prostej punkt się znajduje. A zatem punkt P1 na rysunku będzie po tej samej stronie prostej wyznaczonej przez V1 V2 co np. wierzchołek V4. Natomiast punkty P2 i V4 będą po przeciwnych stronach tej prostej.

Rys.3.5.
Przynależność punktu do wielokąta wypukłego określona na podstawie prostej
wyznaczonej przez kolejne dwa wierzchołki.
Algorytm sprawdzania przynależności punktu do wnętrza wielokąta wypukłego jest następujący.
ALGORYTM PRZYNALEŻNOŚCI 1
Obejdź wielokąt zgodnie z porządkiem kolejnych jego wierzchołków ;
W każdym kroku wyznacz prostą przechodzącą przez bieżący i następny wierzchołek ;
Sprawdź czy badany punkt jest po tej samej stronie prostej co jeden z wierzchołków wielokąta; jeśli w którymkolwiek kroku badany punkt nie spełnia tego warunku, przerwij sprawdzanie – punkt jest na zewnątrz ;
Jeśli po obejściu całego wielokąta okaże się, że punkt był zawsze (!) po tej samej stronie co reszta wielokąta to punkt jest wewnątrz ;
Opisany algorytm należy, w zależności od potrzeb, uzupełnić o analizę samego wielokąta – przynależność lub nie do odpowiednich odcinków brzegu, co jest zabiegiem prostym technicznie i nie stanowi problemu.
Algorytm ten jest łatwy w implementacji i szybki. Jednak jego podstawową wadą jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych proste wyznaczone przez kolejne wierzchołki mogą przecinać wielokąt. A w takiej sytuacji założenie, że tylko jedna półpłaszczyzna będzie zawierała elementy wielokąta nie jest prawdziwe.
Dla wielokątów dowolnych problem można rozwiązać algorytmem kontroli parzystości lub algorytmem analizy sumy kątów zorientowanych.
Warto przy tym zwrócić uwagę, że rozpatrywane są tylko wielokąty zwykłe, to znaczy takie, których krawędzie nie mają punktów wspólnych poza wierzchołkami.
Przez analogię do wypełniania wielokąta przez kontrolę parzystości na rastrze pikseli można zaproponować algorytm sprawdzania przynależności punktu do wielokąta.
ALGORYTM PRZYNALEŻNOŚCI 2
Z badanego punktu poprowadź półprostą (w dowolnym kierunku – z punktu widzenia kierunków układu współrzędnych wygodna będzie np. półprosta pozioma) ;
Półprosta ta może przeciąć wielokąt, sprawdź liczbę przecięć:
- jeśli liczba przecięć z bokami
wielokąta jest nieparzysta to punkt leży wewnątrz wielokąta (np.
punkt P1 na rysunku 3.6);
-
jeśli liczba przecięć jest parzysta,
to punkt jest na zewnątrz (np. punkt P2 na rysunku 3.6) ;
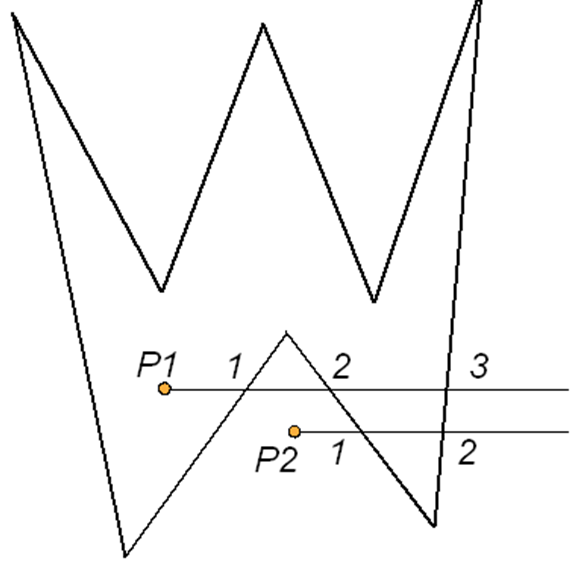
Rys.3.6. Sprawdzenie przynależność punktu do wielokąta wypukłego na podstawie kontroli parzystości przecięć.
Algorytm jest bardzo prosty, jednak pamiętając o
problemach ze szczególnymi przypadkami w algorytmie wypełniania przez kontrolę
parzystości, należy przypuszczać, że podobne sytuacje wystąpią i tutaj.
Oczywiście rozwiązanie jest również analogiczne . Do algorytmu należy dodać dwa
warunki.
- Jeśli punkt przecięcia jest ekstremum lokalnym, to liczymy go podwójnie.
- Jeśli półprosta zawiera cały bok wielokąta, to traktujemy to jako jeden pseudowierzchołek.
Drugim rozwiązaniem problemu sprawdzenia przynależności punktu do wielokąta jest analiza kątów zorientowanych (rys.3.7).

Rys.3.7.
Sprawdzenie przynależność punktu do wielokąta wypukłego
na podstawie sumy kątów zorientowanych. a) suma kątów = 0o , b) suma kątów = 360o.
Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli suma = 360o to punkt jest wewnątrz wielokąta. Jeśli suma = 0o to na zewnątrz.
Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni, że w implementacji nie ma błędu, to warunki można postawić jako: suma > 180o i suma < 180o.
3.6. Otoczka wypukła (wypukła skorupka)
Niech S będzie zbiorem n punktów na płaszczyźnie (rys.3.8). Problem otoczki wypukłej (Convex Hull - CH(S)) polega na wyznaczeniu wielokąta który:
- zawiera wszystkie punkty S (tzn. punkty są wewnątrz wielokąta lub na jego brzegu),
- jest wypukły,
- jest najmniejszy z możliwych.
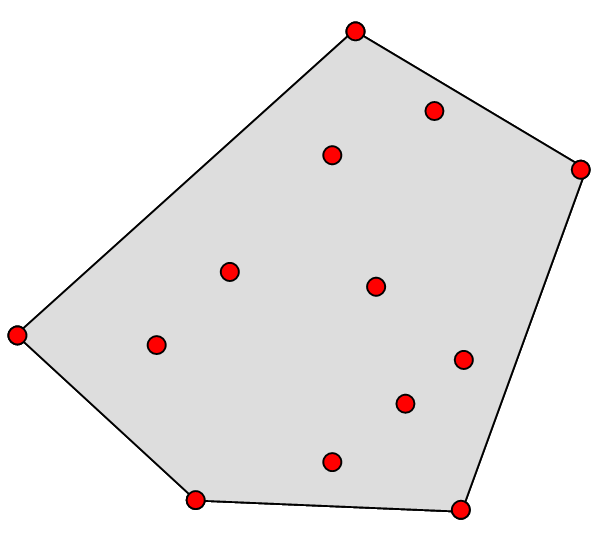
Rys.3.8. Otoczka wypukła
Analizując problem (CH(S)) można zauważyć że:
SPOSTRZEŻENIE_1
Jeśli punkty tworzące (CH(S)) nazwiemy punktami skrajnymi, to można zadanie wyznaczenia (CH(S)) podzielić na dwa etapy.
- W pierwszym należy wyznaczyć zbiór punktów skrajnych.
- W drugim należy posortować zbiór punktów skrajnych pod względem rosnącego kąta w biegunowym układzie współrzędnych, którego początek znajduje się wewnątrz (CH(S)).
SPOSTRZEŻENIE_2
Aby wskazać punkt, który znajduje się wewnątrz zbioru punktów, wystarczy wyznaczyć współrzędne jako średnie arytmetyczne ze współrzędnych punktów tego zbioru.
SPOSTRZEŻENIE_3
Aby wskazać jeden (dowolny) punkt skrajny wystarczy wybrać punkt o ekstremalnej (maksymalnej lub minimalnej) współrzędnej, jeśli jest takich punktów kilka, to spośród nich wybrać ten, którego druga współrzędna jest ekstremalna.
SPOSTRZEŻENIE_4
Punkt skrajny nie należy do wnętrza żadnego trójkąta, którego wierzchołkami są punkty ze zbioru.
SPOSTRZEŻENIE_5
Aby posortować zbiór punktów skrajnych wystarczy wskazać punkt wewnątrz (CH(S)), umieścić w nim początek biegunowego układu współrzędnych. Biorąc pod uwagę współrzędne punktów skrajnych w układzie biegunowym posortować te punkty pod względem rosnącego kąta.
Wykorzystując powyższe spostrzeżenia można zaproponować najprostszy algorytm wyznaczenia (CH(S)):
ALGORYTM CH_1
for every trójka punktów P1,P2,P3 z S do
for every punkt q z S do
if q leży wewnątrz trójkąta (P1,P2,P3) then usunąć q z S ;
Algorytm ten jest bardzo
prosty i łatwy w realizacji. Można byłoby nawet powiedzieć, że jest dość
elegancki. Ma jednak jedną, dyskwalifikującą go wadę: wysoką złożoność
obliczeniowa. Jeśli zbiór S liczy n punktów, to liczba
wszystkich trójkątów o wierzchołkach ze zbioru S jest rzędu n3
(dokładnie ![]() ). A zatem liczba operacji rozpoczętych w kroku 1. jest rzędu
n3.
W kroku 2. dla każdego trójkąta brany
jest pod uwagę każdy punkt ze zbioru, czyli liczba operacji rośnie n
razy. A zatem asymptotyczna złożoność obliczeniowa algorytmu CH_1 wynosi O(n4).
). A zatem liczba operacji rozpoczętych w kroku 1. jest rzędu
n3.
W kroku 2. dla każdego trójkąta brany
jest pod uwagę każdy punkt ze zbioru, czyli liczba operacji rośnie n
razy. A zatem asymptotyczna złożoność obliczeniowa algorytmu CH_1 wynosi O(n4).
Spośród wielu znanych algorytmów – efektywnie rozwiązujących problem wypukłej otoczki warto przytoczyć dwa: algorytm Grahama i algorytm Jarvisa.
Algorytm Grahama wyznaczania wypukłej otoczki

Rys.3.9. Wypukła
otoczka wyznaczana algorytmem Grahama. Stan po
przejrzeniu
7 kolejnych punktów (łącznie ze startowym). Dwa spośród nich
zostały już wyeliminowane.
Czytelnik może przeanalizować następne dwa kroki
przeglądania:
położenie kolejnego punktu powoduje, że nie
tylko ostatni ale i przedostatni punkt
dołączony do tymczasowej
wypukłej skorupki zostanie wyeliminowany.
ALGORYTM CH_2 (Grahama)
umieść początek układu biegunowego wewnątrz CH(S) ;
posortuj punkty S względem kąta i odległości (leksykograficznie) (dla punktów o tym samym kącie o kolejności decyduje odległość);
wskaż punkt startowy VSTART , który na pewno należy do CH(S) (zgodnie ze SPOSTRZEŻENIEM 3. wybieramy punkt najniżej i na lewo) ;
startując od VSTART „przejrzyj” punkty zgodnie z ich posortowaną kolejnością:
jeśli przyjmiemy, że w tym kroku tworząc wypukłą otoczkę obejdziemy zbiór punktów przeciwnie do ruchu wskazówek zegara (CCW), to gdyby trzy kolejne punkty tworzyły CH(S), to będą one miały zorientowanie CCW. Jeśli tak nie będzie, to na pewno środkowy punkt nie należy do CH(S); a zatem:
operując na stosie reprezentującym CH weź pod uwagę zorientowanie ostatnich 2 punktów stosu i punktu bieżącego
jeśli zorientowanie jest CCW dodaj bieżący do stosu ;
jeśli nie CCW, to zdejmij ostatni punkt ze stosu ;
Można zastanowić się nad złożonością obliczeniową algorytmu Grahama przyjmując, że w zbiorze S jest n punktów. O złożoności całego algorytmu będą decydowały kroki 2. i 4. algorytmu. Złożoność sortowania (operacja 2.) nie podlega dyskusji i wynosi O(nlogn). Wątpliwości mogłaby budzić operacja 4. Wydawać by się mogło, że jest to wielokrotne cofanie i przeglądanie punktów – branie czasem wielokrotnie tego samego jako bieżącego. Proszę jednak zwrócić uwagę na fakt, że każde takie cofanie w punkcie 4. jest związane z eliminacją dokładnie jednego punktu ze stosu. A to oznacza, że takich „wielokrotnych” cofań mogłoby być co najwyżej n. A zatem krok 4. algorytmu ma złożoność liniową ! Oznacza to, że złożoność całego algorytmu CH_2 (Grahama) wynosi O(nlogn).
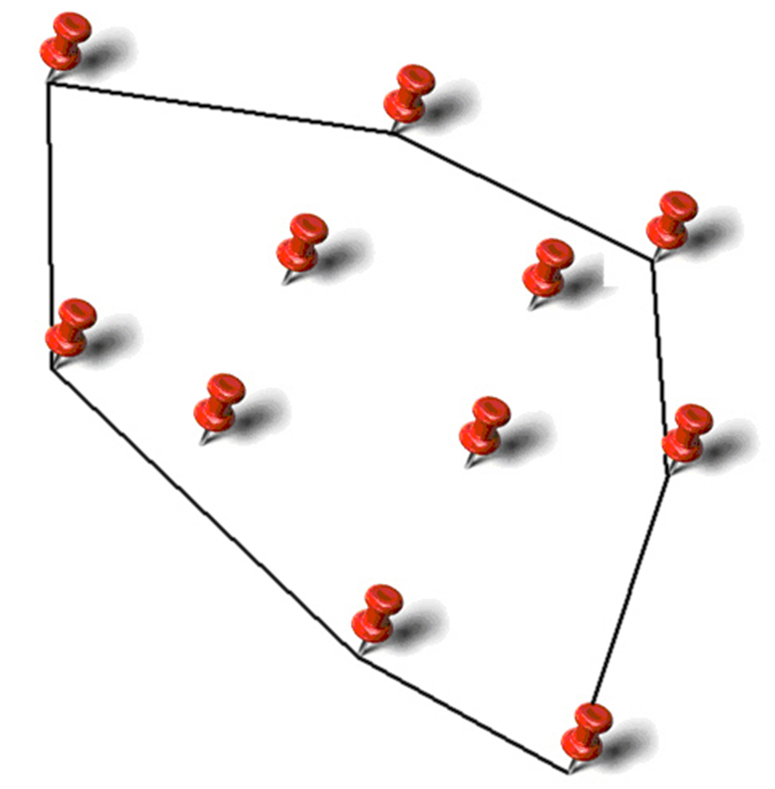
Rys.3.10. Jak
wyznaczyć wypukłą otoczkę mając do dyspozycji tablicę, młotek,
gwoździe i sznurek.
Algorytm Jarvisa
jest czasem nazywany „algorytmem owijania prezentu”.
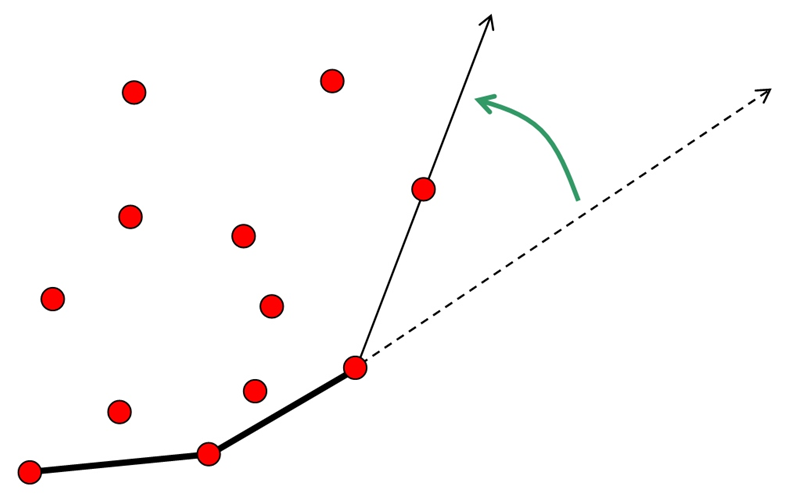
Rys.3.11. Dołączanie kolejnego punktu do wypukłej otoczki w algorytmie Jarvisa
ALGORYTM CH_3 (marsz Jarvisa)
wyznacz punkt startowy należący do CH(S) (- położony najniżej i najbardziej na lewo) ; punkt startowy staje się punktem bieżącym algorytmu; dodaj go do wypukłej otoczki; zdefiniuj półprostą dotychczasową jako półprostą wychodzącą z punktu startowego poziomo w prawo ;
w punkcie bieżącym umieść początek układu biegunowego ; „owiń prostą” biorąc pod uwagę kąty do kolejnych punktów zbioru w tym celu wybierz punkt, który definiuje półprostą tworzącą najmniejszy kąt z dotychczasową półprostą ; punkt ten staje się punktem bieżącym; dodaj go do wypukłej otoczki ; zdefiniowana przez ten punkt półprosta staje się półprostą dotychczasową ;
powtórz krok 2. dla kolejnego punktu aż do dotarcia do punktu startowego;
Niech w zbiorze S jest n punktów. O złożoności całego algorytmu będzie decydowała liczba powtórzeń kroku 2. oraz złożoność operacji w tym kroku. Wybór punktu związanego z najmniejszym kątem nie wymaga sortowania, ale wymaga sprawdzenia kątów wszystkich punktów. Zatem jednorazowe wykonanie kroku 2. algorytmu wymaga wykonania n operacji. Z drugiej strony krok ten będzie powtarzany tyle razy ile wynosi liczba punktów wypukłej otoczki. Jeśli przyjmiemy, że jest to k , to złożoność całego algorytmu wyniesie O(nk) .
Jest to ciekawy przypadek algorytmu, którego złożoność zależy od wprowadzonych danych (położenia punktów). Gdyby k i n były porównywalne (w skrajnym przypadku równe czyli wszystkie punkty zbioru tworzą CH(S)), to algorytm miałby złożoność bliską kwadratowej i byłby gorszy pod tym względem od algorytmu Grahama. Jeśli jednak k<<n (co w praktyce często się zdarza) to algorytm Jarvisa byłby bardzo efektywny.
Więcej na temat wypukłej otoczki i algorytmów z nią związanych (np. łączenia dwóch otoczek) można znaleźć w książkach [2,4,9]. Problem ten rozpatruje się także w trzech wymiarach. Algorytmy wyznaczania wypukłej skorupki w 3D są opisane między innymi w [3, 5, 8].
3.7. Podział wielokąta na trójkąty

Rys.3.12. Podział
na trójkąty: a) wielokąta wypukłego b)
wielokąta typu gwiazda.
Wielokąt typu
gwiazda jest wielokątem, dla którego można pokazać taki punkt wewnątrz,
którego
połączenie odcinkiem z dowolnym wierzchołkiem jest całkowicie zawarte
w wielokącie.
Innym przypadkiem wielokąta dla którego można wskazać dość prosty i efektywny algorytm podziału na trójkąty jest wielokąt monotoniczny.

Rys.3.13. Dla
wielokąta monotonicznego można wskazać taką prostą,
że rzutowanie wierzchołków
na tę prostą zachowuje ich kolejność (w dwóch łańcuchach).
Innym przypadkiem wielokąta dla którego można wskazać dość prosty i efektywny algorytm podziału na trójkąty jest wielokąt monotoniczny.
Niech dany będzie
wielokąt zwykły o n węzłach P1...Pn,Pn+1 = P1 .
Wielokąt nazywamy monotonicznym, jeżeli istnieje prosta l taka, że rzuty
prostokątne wierzchołków Pi
na l
są uporządkowane w dwóch grupach w takiej samej kolejności jak punkty Pi (rys.3.13).

Rys.3.14. Podział
na trójkąty wielokąta monotonicznego zgodnie z zaproponowanym algorytmem.
Czytelnik może prześledzić kolejne kroki łączenia wierzchołków.
ALGORYTM PODZIAŁU WIELOKĄTA MONOTONICZNEGO
1. utwórz jedną posortowaną listę wierzchołków (rys.3.14) ;
2. P1 na stos ; P2, na stos ; niech R1, R2 ... Ri oznacza aktualną zawartość stosu
3. for (j=3,4,... n) do
4. if (Pj sąsiaduje z R1, ale nie z Ri) then
połącz: PjR2, PjR3 ... PjRi ;
wyzeruj stos ;
Ri na stos ; Pj na stos ;
else
5. if (Pj sąsiaduje z Ri ale nie z R1) then
begin
LOOP: if (i=1 lub wewnętrzny kąt Ri >=180o) then
Pj na stos ;
else
begin
połącz PjRi-1 ;
zdejmij Ri ze stosu ;
i=i-1 ;
go to LOOP ;
end
end
else
6. if (Pj sąsiaduje z R1 i Pj sąsiaduje z Ri) then
połącz PjR2, PjR3 ... PjRi-1 ;
Przedstawiony algorytm triangulacji wielokąta monotonicznego jest algorytmem przeglądania wierzchołków zgodnie z ich kolejnością wynikającą z monotoniczności. Jednocześnie branie pod uwagę kolejnego wierzchołka jest związane z połączeniem go z innym wierzchołkiem tak, aby „odciąć” trójkąt. Ze względu na wzajemne położenie wierzchołków możliwe są trzy różne (i wykluczające się !) konfiguracje. Kroki 4., 5. i 6. algorytmu opisują postępowanie w odpowiednich przypadkach. Czytelnik może przeanalizować geometrię rozpatrywanych konfiguracji wierzchołków. W książce M.Jankowskiego [6] można znaleźć szczegóły przedstawionego algorytmu.
Warto zwrócić uwagę na problem złożoności obliczeniowej triangulacji wielokąta monotonicznego. Monotoniczność zapewnia odpowiednie posortowanie wierzchołków. A zatem krok 1. algorytmu nie wymaga sortowania. W związku z tym asymptotyczna złożoność obliczeniowa całego algorytmu wynosi O(n).
Przedstawiony algorytm triangulacji nie zapewnia możliwości podziału na trójkąty dowolnego wielokąta. Istnieje jednak twierdzenie, które mówi, że dowolny wielokąt można rozciąć na sumę wielokątów monotonicznych.
Rozpatrzmy wielokąt wklęsły, który nie jest monotoniczny. Jeśli przetniemy go prostymi równoległymi przechodzącymi przez wszystkie wierzchołki (rys.3.15), to można przeprowadzić analizę, które wierzchołki „psują” monotoniczność. Rozpatrzmy pasy (warstwy) pomiędzy sąsiednimi prostymi tnącymi. Jeśli prosta brzegowa pasa przechodzi przez wierzchołek wielokąta, to mogą zaistnieć dwa przypadki. Albo krawędź wielokąta wychodząca z tego wierzchołka przecina pas (P1 na rys.3.15), albo nie (P2 na rys.3.15). W tym drugim przypadku mamy do czynienia z ekstremum lokalnym, które „psuje” monotoniczność. W takiej sytuacji należy połączyć ten wierzchołek z dowolnym wierzchołkiem po drugiej stronie pasa. Połączenia mogą być dowolne i wielokrotne, ale istotne jest aby każdy wierzchołek „psujący” monotoniczność w danym pasie był przynajmniej raz połączony z wierzchołkiem z przeciwległego brzegu (prostej) pasa. Każde, tak wykreowane połączenie rozcina wielokąt.
ALGORYTM PODZIAŁU NA WIELOKĄTY MONOTONICZNE
1. posortuj wierzchołki wielokąta pod względem współrzędnej y ;
2. przetnij wielokąt prostymi równoległymi do osi OX przechodzącymi przez
wszystkie wierzchołki ;
3. for each pas Wi do
4. for each wierzchołek Pj na brzegu pasa Wi do
5. if Pj psujący monotoniczność then
połącz Pj z dowolnym wierzchołkiem na drugim brzegu
pasa Wi. Połączenie to rozcina wielokąt.

Rys.3.15.
Rozcięcie wielokąta na wielokąty monotoniczne. Po połączeniu
punktów „psujących”
z wierzchołkami po drugiej stronie pasa
(zielone odcinki) powstają trzy wielokąty monotoniczne.
Posortowanie wierzchołków w 1. kroku algorytmu ułatwia późniejsze wyszukiwanie odpowiednich wierzchołków i jednocześnie powoduje, że rozcięte w wyniku działania algorytmu wielokąty monotoniczne mają również posortowane wierzchołki. Oczywiście asymptotyczna złożoność obliczeniowa algorytmu podziału na wielokąty monotoniczne wynosi O(nlogn) .
Biorąc pod uwagę przedstawione algorytmy podziału, można zaproponować rozwiązanie dwuetapowe zadania triangulacji wielokąta dowolnego:
ALGORYTM TRIANGULACJI WIELOKĄTA
1. podziel wielokąt na wielokąty monotoniczne ;
2. podziel na trójkąty wielokąty monotoniczne ;
3.8. Wyznaczenie przecięć w zbiorze odcinków na płaszczyźnie. Metoda zamiatania
Niech dany będzie zbiór odcinków l1, l2 ... ln na płaszczyźnie. Zadanie polega na wyznaczeniu wszystkich przecięć w tym zbiorze. Oczywiście można zaproponować bardzo prosty algorytm, który analizując wszystkie pary (metodą „każdy z każdym”) wyznaczy przecięcia ze złożonością O(n2) . Jednak takie postępowanie nie jest opłacalne, gdyż najczęściej liczba przecięć w takim zbiorze jest dużo mniejsza niż n2.
Zadanie to można rozwiązać stosując tzw. metodę zamiatania. Metoda ta polega na przeglądaniu elementów na płaszczyźnie zgodnie ze wzrostem współrzędnej x („od lewej do prawej”). Do przeglądania wykorzystujemy prostą pionową („miotłę”), która przesuwa się napotykając kolejne elementy. W dowolnym momencie postępowania elementy na płaszczyźnie można podzielić na trzy rozłączne podzbiory (rys.3.16):
- przetworzone : to elementy, które są po lewej stronie miotły,
- aktywne : to elementy, które miotła przecina,
- oczekujące : elementy po prawej stronie miotły.
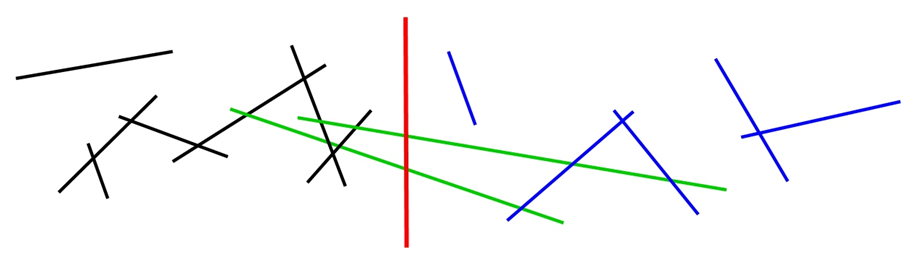
Rys.3.16. „Miotła”
(czerwona) przesuwana w zbiorze odcinków.
Trzy podzbiory
odcinków: przetworzone (czarne), aktywne (zielone),
oczekujące (niebieskie).
- Każde dwa odcinki mają co najwyżej jeden punkt wspólny.
- Żaden odcinek nie jest pionowy.
- Żadna dwa punkty końcowe odcinków nie mają tej samej współrzędnej x.
Założenia te umożliwiają prawidłowe sortowanie zgodnie ze wzrostem współrzędnej x i realizację algorytmu nie wprowadzając zbędnych ograniczeń.
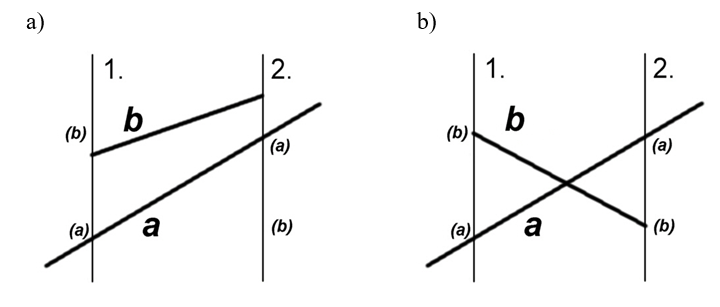
Rys.3.17. Przecięcia
„miotły” z odcinkami:
a) odcinki a i b nie przecinają się: w 1. i w 2.
położeniu „miotła” przecina najpierw a potem b ,
b) odcinki a
i b
przecinają się: w 1. położeniu „miotła” przecina a, potem b, w 2. najpierw b, potem
a .
Warto zauważyć, że jeśli rozpatrujemy „miotłę” czyli prostą pionową, która przecina odcinki na płaszczyźnie, to wyszukanie przecinających się odcinków może być wynikiem prostej analizy wzajemnego położenia odcinków i „miotły” (rys.3.17). Rozpatrzmy dwa kolejne położenia „miotły”. Jeśli odcinki a i b nie przecinają się (rys.3.17a), to kolejność (związana ze wzrostem współrzędnej y) przecięć „miotły” z odcinkami jest w obu położeniach taka sama. Natomiast jeśli odcinki a i b przecinają się (rys.3.17b), to kolejność przecięć „miotły” z odcinkami jest różna. A zatem aby sprawdzić czy dwa odcinki przecinają się wystarczy sprawdzić jaka jest kolejność przecięć „miotły” z odcinkami w odpowiednich położeniach. Takie sprawdzenie jest szybsze niż analityczne wyznaczenie przecięcia odcinków (lub stwierdzenie, że nie może ono mieć miejsca).
ALGORYTM WYSZUKIWANIA PRZECIĘĆ
1. utwórz x-strukturę-L biorąc pod uwagę mniejszą współrzędną x końców odcinka;
2. utwórz x-strukturę-P biorąc pod uwagę większą współrzędną x końców odcinka;
3. przesuwaj „miotłę” po xi biorąc pod uwagę i x-strukturę-L i x-strukturę-P ;
4. if xi należy do x-struktury-L then
dodaj do listy aktywnej odcinek, którego koniec określa xi ;
5. if xi należy do x-struktury-P then
begin
sprawdź, przez analizę przecięć z „miotłą”, czy odcinek, którego
koniec określa xi przecina któryś z odcinków listy aktywnej,
jeśli tak to wyznacz odpowiednie przecięcie ;
usuń z listy aktywnej odcinek, którego koniec określa xi ;
end
Zaprezentowany algorytm wyszukiwania przecięć wykorzystuje efektywnie właściwości stosowania metody zamiatania. Korzystanie z x-struktur i przesuwania „miotły” pozwala ograniczyć sprawdzanie przecięć tylko do grupy odcinków należących do listy aktywnej. Jednocześnie zastosowanie analizy przecięć odcinków z „miotłą” pozwala stwierdzić przecięcie odcinków bez jego wyznaczania. Przedstawiona postać algorytmu jest bardzo ogólna. Nie zawiera między innymi szczegółów operacji na strukturach danych. Złożoność obliczeniowa algorytmu zależy od jego implementacji i sposobu obsługi struktur danych – w analizie przecięć z „miotłą” można wykorzystać odpowiednią y-strukturę odcinków listy aktywnej. Efektywny algorytm wyszukiwania przecięć metodą zamiatania zaproponowali J.L.Bentley i T.A.Ottmann w 1979 roku. Jego asymptotyczna złożoność obliczeniowa wynosi O((s+n)logn) , gdzie s jest liczbą przecięć odcinków. Warto zwrócić uwagę, że gdyby s=n2 (złośliwy przypadek gdy każdy odcinek w zbiorze przecina wszystkie pozostałe) to wyznaczenie przecięć tym algorytmem byłoby znacznie mniej efektywne niż zastosowanie algorytmu naiwnego (analiza każdy z każdym). Jednak w praktyce taki przypadek występuje bardzo rzadko. Najlepszym znanym algorytmem wyszukiwania przecięć odcinków na płaszczyźnie jest algorytm zaproponowany przez I.J.Balabana w 1995 roku. Jego asymptotyczna złożoność obliczeniowa wynosi O(s+nlogn) i jest to algorytm optymalny, gdyż taka złożoność jest dolnym ograniczeniem dla problemu wyszukania wszystkich przecięć odcinków. Natomiast ciekawą właściwością algorytmu I.J.Balabana jest możliwość wyszukiwania przecięć również dla krzywych na płaszczyźnie.
Wybrane zagadnienia geometrii obliczeniowej można znaleźć w książce M.Jankowskiego [6], oraz w książkach dotyczących algorytmów i struktur danych [1]. Zainteresowanych tematem odsyłam do książek: M.Berg M. de, Kreveld, M. van, Overmars, O. Schwarzkopf [2] oraz F.P.Preparata i M.I.Shamos [9], które są podstawowymi podręcznikami z tej dziedziny. Dobór i organizacja struktury danych jest ważnym i trudnym problemem w geometrii obliczeniowej; jest także trudnym problemem w grafice komputerowej. Problemowi temu poświęcona jest książka E.Langetepe’a i G.Zachmanna [7]. Książka [10] jest opisem bardzo praktycznych narzędzi geometrycznych (często dość podstawowych) wykorzystywanych w rozwiązywaniu zaawansowanych problemów. Książka [4] zawiera ciekawe rozważania, przede wszystkim, teoretyczne związane ze złożonością obliczeniową różnych wariantów stosowanych algorytmów. Podobne analizy można znaleźć w książce [5], jednak tutaj mamy do czynienia z o wiele bardziej praktycznym podejściem do tematu. Książka ta jest dzisiaj (2024 rok) najprawdopodobniej najobszerniejszym przewodnikiem po narzędziach i algorytmach geometrii obliczeniowej, obejmującym także rzadko spotykane problemy. Warto zwrócić uwagę na fakt, że jest to zbiór kilkudziesięciu obszernych prac (niezależnych artykułów) napisanych przez różnych autorów (zajmuje to ponad 1900 stron). Całość tworzy dość jednorodny podręcznik dzięki trzem redaktorom całości (Goodman J.E. O'Rourke J., Csaba D.T.). Na stronie https://www.csun.edu/~ctoth/Handbook/HDCG3.html jest dostępny pełny tekst (pdf) wstępnej wersji tego podręcznika.
Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
Rozdział czwarty jest poświęcony podstawowym przekształceniom geometrycznym stosowanym w grafice komputerowej. Zostały zaprezentowane współrzędne jednorodne znormalizowane jako sposób opisu położenia, umożliwiający efektywne stosowanie rachunku macierzowego do realizacji przekształceń. W rozdziale tym zaprezentowano przykłady najważniejszych przekształceń afinicznych dwu- i trójwymiarowych podając macierze, które je opisują. Zostały omówione także takie zagadnienia jak składanie przekształceń i przekształcenie odwrotne oraz konsekwencje i błędy stosowania pewnych zestawień operacji. Omówiony przykład obrotu punktu wokół dowolnej prostej w przestrzeni pokazuje możliwość zastosowania tradycyjnego; macierzowego opisu przekształceń. W rozdziale omówiono podstawowe właściwości kwaternionów i ich wykorzystanie w grafice komputerowej.
4.1. Współrzędne jednorodne znormalizowane
Współczesna grafika komputerowa operując na milionach elementów (punktów, trójkątów) wymaga opisu operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Zastosowanie opisu macierzowego pozwala spełnić te założenia. Wymaga to jednak zmiany tradycyjnego opisu położenia na opis we współrzędnych jednorodnych.
Można zastanowić się nad tym, dlaczego stosowana są współrzędne jednorodne, czy nie można analogicznych operacji opisać po prostu we współrzędnych punktu.
Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). Można zaproponować macierz 2x2, która, opisuje obrót punktu wokół początku układu współrzędnych. Analogiczny opis można zaproponować dla operacji skalowania.
Niech ![]() opisuje położenie punktu na płaszczyźnie.
opisuje położenie punktu na płaszczyźnie.
Niech macierz 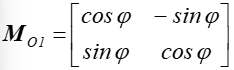 opisuje obrót punktu
wokół początku układu współrzędnych (rys 4.1 a).
opisuje obrót punktu
wokół początku układu współrzędnych (rys 4.1 a).
![]() czyli
czyli  i jest to zgodne z oczekiwaniami.
i jest to zgodne z oczekiwaniami.
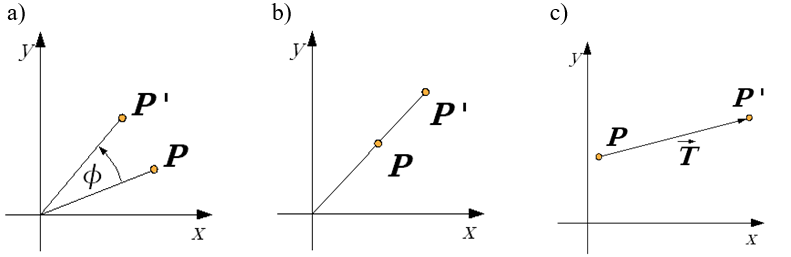
Rys.4.1.
a) Obrót punktu na płaszczyźnie wokół początku układu współrzędnych.
b)
Skalowanie względem początku układu współrzędnych. c)
Przesunięcie o wektor.
Analogicznie można opisać operację skalowania.
Macierz ![]() opisuje skalowanie
względem początku układu współrzędnych (rys 4.1 b).
opisuje skalowanie
względem początku układu współrzędnych (rys 4.1 b).
![]() czyli
czyli 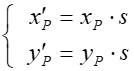
Ale czy można tak opisać translację (przesunięcie) – rysunek 4.1c) ???
Niech ![]() . Niech wektor
. Niech wektor ![]() opisuje translację
punktu na płaszczyźnie.
opisuje translację
punktu na płaszczyźnie.
Czy można znaleźć takie ![]() , aby
, aby 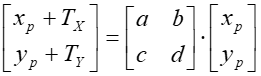 dla
dla ![]() i
i ![]() .
.
Widać że nie jest to możliwe dla współrzędnych
dowolnego punktu. Punkt ![]() byłby punktem stałym
takiego przekształcenia.
byłby punktem stałym
takiego przekształcenia.
Niech xp, yp, zp,
opisują położenie punktu w 3D kartezjańskim układzie współrzędnych. W grafice
komputerowej do opisu położenia oraz opisu operacji (transformacji
geometrycznych), którym punkty będą podlegały, jest używany układ współrzędnych jednorodnych
znormalizowanych. Dzięki temu wszystkie stosowane transformacje
geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia
macierzowego. Jeśli współrzędne xp,
yp, zp opisują położenie punktu to odpowiada temu wektor ![]() we współrzędnych
jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten
miałby postać
we współrzędnych
jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten
miałby postać ![]() dla
dla ![]() , ale takich reprezentacji mogłoby być nieskończenie wiele.
Problem takiej niejednoznaczności rozwiązuje operacja normalizacji:
, ale takich reprezentacji mogłoby być nieskończenie wiele.
Problem takiej niejednoznaczności rozwiązuje operacja normalizacji: 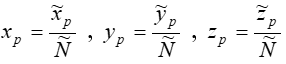 .
.
Wszystkie opisy położenia w niniejszym podręczniku będą się odnosić do współrzędnych jednorodnych znormalizowanych.
Niech zatem położenie punktu o współrzędnych (xp, yp, zp) reprezentuje wektor P :
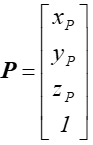
Jeśli
macierz ![]() opisuje pewną
transformację geometryczną to operację tę można opisać następująco:
opisuje pewną
transformację geometryczną to operację tę można opisać następująco:
![]()
czyli:
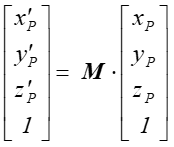
gdzie ![]() opisuje położenie punktu po przekształceniu. Oczywiście jeśli
wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
opisuje położenie punktu po przekształceniu. Oczywiście jeśli
wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Zastosowanie
w tym przypadku współrzędnych jednorodnych można sobie wyobrazić jako
umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie
współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu
(tzn. dla ![]() ). Wtedy analogiczne opisanie operacji translacji na
płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt
stały – początek układu współrzędnych jest poza płaszczyzną, na której jest
wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej
samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych,
czyli pracować na płaszczyźnie
). Wtedy analogiczne opisanie operacji translacji na
płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt
stały – początek układu współrzędnych jest poza płaszczyzną, na której jest
wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej
samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych,
czyli pracować na płaszczyźnie ![]() . Analogicznie dla przekształceń trójwymiarowych można
wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu
współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on
początku układu współrzędnych.
. Analogicznie dla przekształceń trójwymiarowych można
wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu
współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on
początku układu współrzędnych.
W grafice komputerowej operacje na płaszczyźnie opisuje macierz 3x3 w układzie 3D, natomiast operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D. Oczywiście w układach znormalizowanych.
Można
powiedzieć, że macierz ![]() definiuje liniowe
funkcje określające każdą ze współrzędnych punktu tzn.:
definiuje liniowe
funkcje określające każdą ze współrzędnych punktu tzn.:

Wykorzystując rachunek macierzowy przekształcenia punktu można opisać również za pomocą prawostronnego mnożenia macierzy. Wtedy, dla przyjętych wyżej danych operacja wyglądałaby tak.
![]()
Jak widać tę samą operację można zapisać jako mnożenie lewostronne lub prawostronne przez macierz przekształcenia.
Tak naprawdę trudno byłoby wskazać uzasadnienie dla wyboru jednej lub drugiej formy zapisu. W książkach dotyczących grafiki komputerowej w ostatnich latach częściej stosowany jest zapis lewostronnego mnożenia, chociaż są autorzy, którzy nadal konsekwentnie trzymają się mnożenia prawostronnego. Natomiast sposób używania zależy od przyzwyczajeń i upodobań użytkownika. Jedno jest jednak bardzo istotne – konsekwencja. Nie można mieszać postaci opisu.4.2. Przekształcenia 2D
Niech położenie punktu o współrzędnych (xp, yp) na płaszczyźnie reprezentuje wektor P :

Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco:
![]()
czyli:
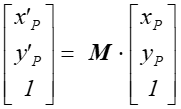
gdzie P’ opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Translacja.

Rys.4.2. Translacja o wektor na płaszczyźnie.
Jak opisać translację na płaszczyźnie?
Operację tę opisuje macierz
translacji 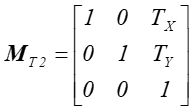 .
.
Między współrzędnymi zachodzi następujący związek:
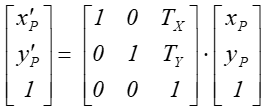
i jest to równoważne opisowi translacji o wektor w postaci układu równań:
 .
.
Symetrie osiowe.
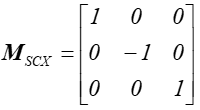

Rys.4.3 Symetria osiowa względem osi 0X.

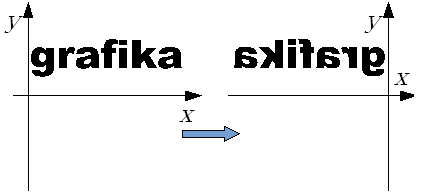
Rys.4.4 Symetria osiowa względem osi 0Y.
Symetria środkowa.
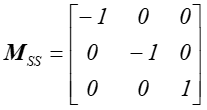
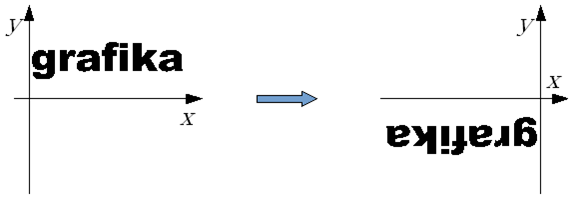
Rys.4.5
Symetria środkowa względem punktu [0,0] .
Obrót wokół początku układu współrzędnych.
 f
f 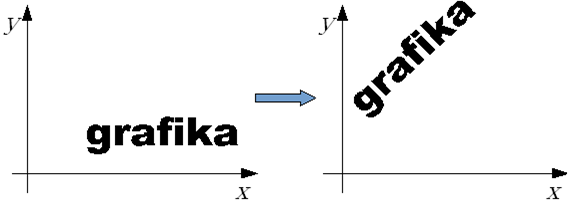
Rys.4.6 Obrót wokół początku układu współrzędnych o zadany kąt.
Skalowanie.

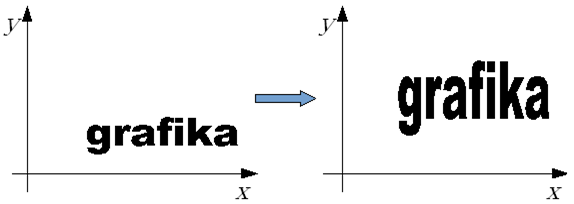
Rys.4.7
Symetria środkowa względem punktu [0,0] .
Skalowanie jest przykładem przekształcenia nieizometrycznego, to znaczy niezachowujacego odległości punktów.
Pochylenie.


Rys.4.8 Pochylenie:
zmiana współrzędnej y .


Rys.4.9 Pochylenie: zmiana współrzędnej x .
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne.
4.3. Przekształcenia 3D
Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych (rys.4.10). Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym.
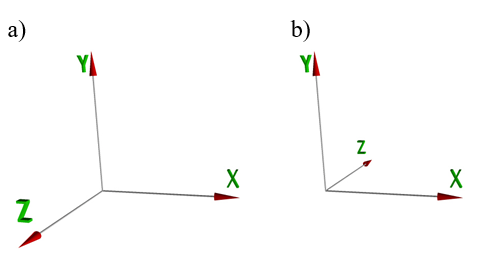
Rys.4.10. Trójwymiarowy
układ współrzędnych. a) układ prawoskrętny, b) układ lewoskrętny.
Popatrzmy na układ z punktu (0,0,-d)
dla d > 0 .
Jeśli oś OX obrócimy o 90o zgodnie
z ruchem wskazówek zegara
i pokryje się ona wtedy z osią OY, to
układ jest prawoskrętny.
Operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Macierz 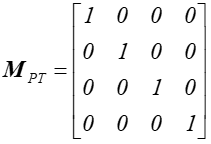
jest macierzą przekształcenia tożsamościowego tzn. takiego, że P' = P . Zmieniając znaki przed współczynnikami (jedynkami) tej macierzy można uzyskać macierze symetrii środkowej względem początku układu współrzędnych, symetrii osiowych względem osi układu współrzędnych i symetrii płaszczyznowych względem płaszczyzn wyznaczonych przez osie układu.
Symetrie osiowe.
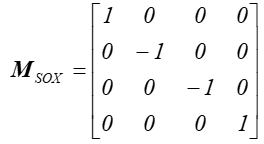

Rys.4.11 Symetria osiowa względem osi OX.
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami.
Symetrie płaszczyznowe.
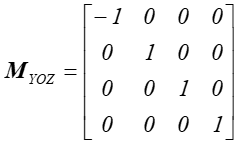

Rys.4.12 Symetria płaszczyznowa względem YOZ.
Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. Warto natomiast zwrócić uwagę na symetrię względem XOY gdyż z punktu widzenia układu współrzędnych przekształcenie to zmienia skrętność układu (rys.4.13).
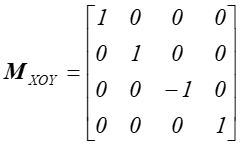
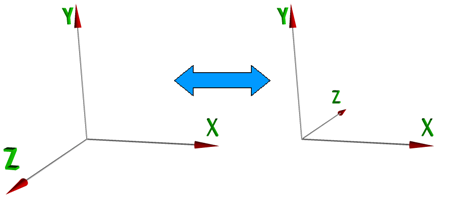
Rys.4.13
Symetria płaszczyznowa względem XOY.
Zmiana skrętności układu współrzędnych.
Symetria środkowa.
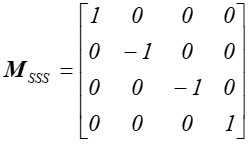
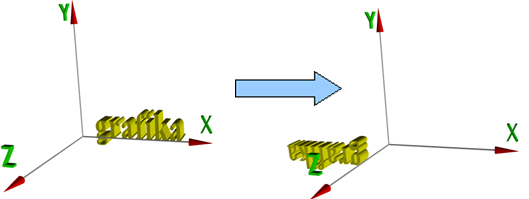
Rys.4.14 Symetria środkowa.
Przesunięcie (translacja).


Rys.4.15 Przesunięcie o wektor T[Tx,Ty,Tz] .
Obroty wokół osi układu współrzędnych.
W układzie współrzędnych kartezjańskich trójwymiarowych zdefiniowanie obrotów wokół osi układu wymaga przyjęcia reguł uznawania obrotów za dodatnie. Najczęściej przyjmuje się konwencję, według której dodatnie obroty są zdefiniowane zgodnie z rysunkiem 4.16.

Rys.4.16. Definicja dodatnich obrotów w prawoskrętnym układzie współrzędnych.
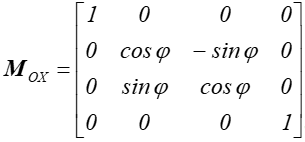

Rys.4.17 Obrót
o kąt ![]() wokół osi 0X. Obiekt na
rysunku został obrócony o kat - 45o.
wokół osi 0X. Obiekt na
rysunku został obrócony o kat - 45o.


Rys.4.18 Obrót
o kąt ![]() wokół osi 0Y. Obiekt na
rysunku został obrócony o kat 45o.
wokół osi 0Y. Obiekt na
rysunku został obrócony o kat 45o.


Rys.4.19 Obrót
o kąt ![]() wokół osi 0X. Obiekt na rysunku
został obrócony o kat 45o.
wokół osi 0X. Obiekt na rysunku
został obrócony o kat 45o.
Skalowanie.

Rys.4.20 Skalowanie obiektu .
gdzie ![]() , są współczynnikami skali w odpowiednich osiach.
, są współczynnikami skali w odpowiednich osiach.
Skalowanie jest przykładem przekształcenia nieizometrycznego (niezachowującego odległości punktów).
Warto
zwrócić uwagę na fakt, że jeśli ![]() to skalowanie można
opisać macierzą:
to skalowanie można
opisać macierzą:
 wtedy
wtedy 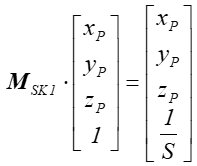
Ale wynik tej operacji nie jest znormalizowany. Zgodnie z przyjętymi wcześniej zasadami posługiwania się współrzędnymi jednorodnymi taka operacja jest w tym przypadku niezbędna.
Zatem  co odpowiada skalowaniu ze współczynnikiem S.
co odpowiada skalowaniu ze współczynnikiem S.
Pochylenie 3D.


Rys.4.21 Przykład pochylenia przy zachowaniu kształtu przekroju w płaszczyźnie równoległej do XOY.
Pochylenie jest przykładem przekształcenia nieizometrycznego. Analogicznie można zaproponować przekształcenia i macierze je opisujące dla pochylenia w dwóch pozostałych płaszczyznach.
4.4. Składanie przekształceń. Przekształcenie odwrotne
Niech dane będą przekształcenia wykonywane kolejno M1 i M2 ,
czyli P' = M1 · P i P'' = M2 · P' .
Podstawiając wynik pierwszej operacji do drugiego równania : P'' = M2 · M1 · P .
Mnożenie macierzy jest operacją łączną więc :
P'' = M21 · P gdzie M21 = M2 · M
Jeśli zatem MC opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych
M1 , M2 , M3 , . . . MN ( w takiej kolejności) to :
MC = MN · . . . · M3 · M2 · M1
Oczywiście mnożenie macierzy jest operacją łączną ale nie jest operacją przemienną – złożenie najpierw translacji a potem obrotu jest innym przekształceniem niż złożenie najpierw obrotu a potem translacji.
Często pojawiającym się problemem w próbach implementacji przekształceń geometrycznych w grafice jest problem punktu odniesienia operacji.
Skalowanie jest operacją zmieniającą proporcje
wymiarów względem początku układu współrzędnych. Punkt [0,0,0] jest punktem stałym tego przekształcenia. Wyobraźmy sobie
dwukrotne powiększenie pewnego obiektu (np. powiększenie domu jak na rysunku 4.22).
Powiększenie dwukrotne oznacza nie tylko, że zwiększą się wymiary obiektu.
Oznacza również, że każdy punkt obiektu zwiększy dwukrotnie odległość od
początku układu współrzędnych. A przecież obiekt jest „osadzony” w pewnych
realiach sceny – np. wejście do domu jest w określonym miejscu. Prosta
realizacja skalowania prowadzi do pewnych konfliktów. Aby tego uniknąć należy
wybrać punkt obiektu, który powinien zachować współrzędne – punkt odniesienia.
A następnie zrealizować skalowanie względem tego punktu odniesienia. Efekt takiej (złożonej) operacji będzie uwzględniał
uwarunkowania punktu odniesienia (rys. 4.23).
W przypadku skalowania złożenia operacji wygląda następująco:
- Przesunięcie obiektu, aby punkt odniesienia znalazł się w początku układu współrzędnych.
- Skalowanie obiektu.
- Przesunięcie odwrotne do operacji 1.
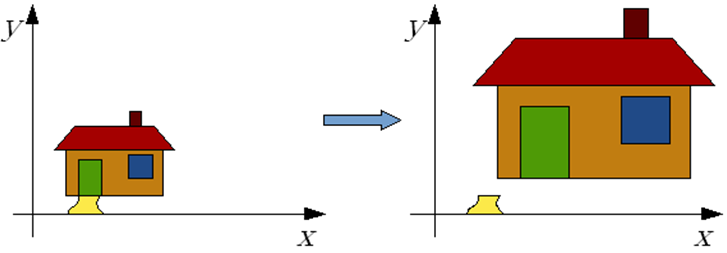
Rys.4.22. Skalowanie bez uwzględnienia punktu odniesienia.
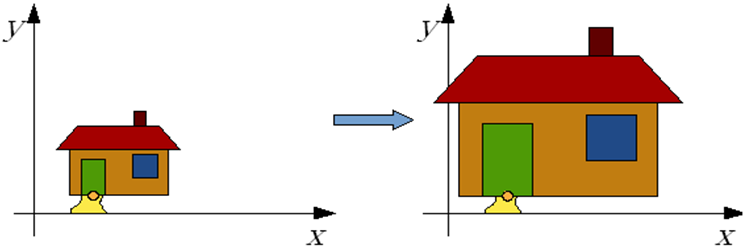
Rys.4.23. Skalowanie uwzględniające punkt odniesienia.
Jeśli macierz M opisuje pewną transformację geometryczną, przekształcenie współrzędnych jest opisane równaniem
P' = M · P
i jeśli istnieje przekształcenie odwrotne opisane macierzą M -1 to
P = M -1 · P'
Oczywiście nie zawsze konieczne jest wyznaczanie macierzy odwrotnej, np. dla translacji o dany wektor przekształceniem odwrotnym będzie translacja o wektor przeciwny, dla obrotu o zadany kąt obrót wokół tej samej osi o kąt przeciwny itp.
Ponieważ symetrie, translacja, obroty i skalowanie opisane odpowiednimi macierzami są operacjami odwracalnymi, to w bardzo prosty sposób można pokazać, że dowolna operacja będąca złożeniem dowolnego zestawu tych operacji, jest też operacją odwracalną.
Jeśli zatem MC opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych
MC = MN · . . . ·M3 · M2 · M1
i jeśli każde z nich jest odwracalne to :
MC-1 = M1-1 · M2-1 · M3-1 · . . . · MN-1
4.5. Przekształcenia izometryczne
Niech X , Y będą przestrzeniami metrycznymi z metrykami dX, dY (odpowiednio).
Niech ƒ: X → Y będzie przekształceniem.
ƒ jest przekształceniem izometrycznym (izometrią) gdy dY((f(p1),f(p2)) = dX(p1,p2)
Jeśli będziemy rozpatrywać przestrzeń Euklidesową oraz przekształcenia geometryczne w tej przestrzeni, to izometria będzie takim przekształceniem, które zachowuje odległości punktów.
Bezpośrednio z definicji wynika również, że składanie izometrii jest także izometrią. Można wykazać, że w przestrzeni Euklidesowej symetrie, translacje i obroty są izometriami.
W rozdziale tym przedstawione są różne (podstawowe) przekształcenia geometryczne opisane za pomocą rachunku macierzowego. Niech M będzie macierzą rozpatrywanego przekształcenia geometrycznego. Warto zadać sobie pytanie:
Jak sprawdzić czy przekształcenie to jest izometrią ???
Pobieżna analiza zagadnienia może prowadzić do (częstego) błędu, że wystarczy obliczyć wyznacznik macierzy M i sprawdzić czy det(M) = 1 (lub -1) . Jeśli sprawdzenie przyniesie pozytywny wynik to macierz M opisuje przekształcenie izometryczne. Niestety rozumowanie takie NIE JEST POPRAWNE.
Rozpatrzmy bowiem trzy przykładowe przekształcenia i macierze je opisujące:
skalowanie translacja pochylenie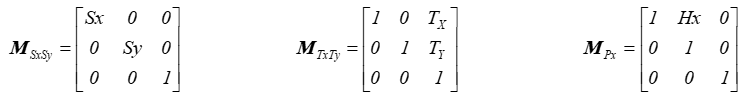
Jak łatwo obliczyć det(MSxSy) = Sx .Sy , det(MTxTy) = 1 , det(MPx) = 1 . Oczywiście skalowanie nie zawsze jest przekształceniem izometrycznym (chyba że skala=1) i analiza problemu na podstawie wyznacznika dałaby poprawny wynik. Ale z pozostałych dwóch przekształceń tylko translacja jest izometrią. W przypadku pochylenia wynik jest BŁĘDNY.
Jedyną możliwością sprawdzenia czy przekształcenie jest izometrią jest porównanie odpowiednich odległości.
Prawdziwe jest natomiast twierdzenie:
Jeśli przekształcenie opisane macierzą M jest izometrią to det(M) = 1 (lub -1) .
W praktyce stosując znane przekształcenia wykorzystujemy najczęściej twierdzenie, że składanie przekształceń izometrycznych jest izometrią. Stosując nieznaną macierz (macierz przekształcenia o nieznanych właściwościach) niestety pozostaje sprawdzić właściwości tego przekształcenia przez porównanie odległości odpowiednich punktów.
4.6. Przykład obrotu punktu wokół dowolnej prostej
Dana jest prosta 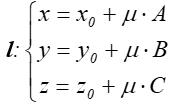
Na prostej tej
znajdują się dwa punkty T1 [x0,y0,z0] i T2 [x0+A,y0+B,z0+C],
wektor ![]() określa zorientowanie
prostej.
określa zorientowanie
prostej.
Zadanie: obrócić dowolny punkt P wokół prostej l o kąt![]() . (rys.4.24).
. (rys.4.24).
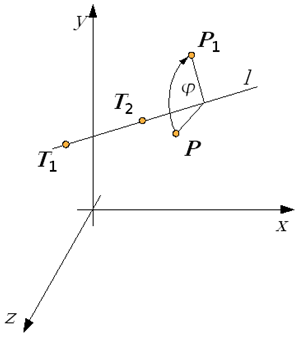
Rys.4.24. Zadanie: obrócić punkt wokół dowolnej prostej.
Zestaw podstawowych operacji obejmował obroty,
ale tylko wokół osi układu współrzędnych. Obrót wokół dowolnej osi musi być
zatem zrealizowany jako złożenie operacji. Można przyjąć założenie, że
generalnie celem operacji wstępnych jest takie przekształcenie przestrzeni, aby
zadana oś obrotu (prosta l na rysunku) pokryła się z wybraną
osią układu współrzędnych. Przy czym przyjęty zwrot osi obrotu powinien być
zgodny ze zwrotem osi okładu. Takie warunki pozwolą obrót o kąt ![]() wokół
zadanej osi zrealizować bezpośrednio jako obrót o kąt
wokół
zadanej osi zrealizować bezpośrednio jako obrót o kąt ![]() wokół osi układu.
wokół osi układu.
Zadanie można rozwiązać na wiele sposobów. Przyjęto następujący zestaw operacji:
- Przesunięcie, aby punkt T1 znalazł się w początku układu współrzędnych.
- Obrót wokół osi OX.
- Obrót wokół osi OY. Obroty (etap 2. i 3. ) zapewniają, że zadana oś obrotu (prosta l) pokryje się (z uwzględnieniem zwrotów) z osią OX układu współrzędnych.
- Realizacja zadanego
obrotu o kąt
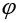 wokół
osi OX.
wokół
osi OX. - Obrót będący operacją odwrotną do operacji 3.
- Obrót będący operacją odwrotną do operacji 2.
- Przesunięcie odwrotne do przesunięcia 1.
Etap 1. Translacja o wektor [-x0, -yo, -zo]
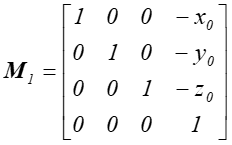
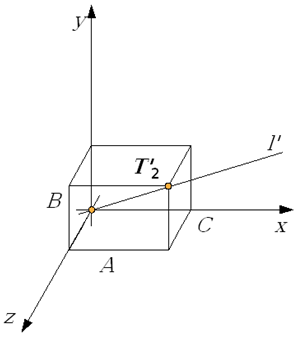
Rys.4.25 wynik pierwszej operacji – przesunięcia. Zadana oś obrotu zawiera teraz przekątną prostopadłościanu o bokach A, B, C. Ułatwi to definicje kątów obrotu.
Etap
2. Obrót wokół oso OX i kąt ϕX taki,
że: ![]()
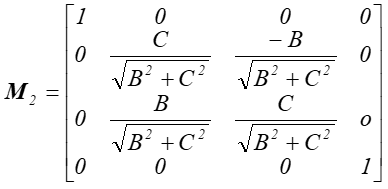
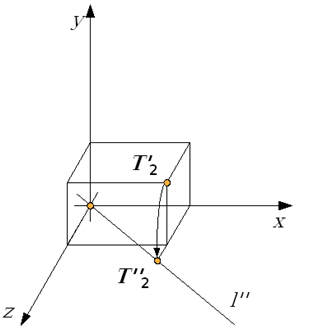
Rys.4.26 Po zrealizowaniu obrotu wokół OX prosta l znalazła się na płaszczyźnie XOZ.
Etap 3. Obrót wokół osi 0Y o kąt kąt ϕY taki że: 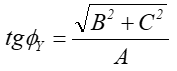
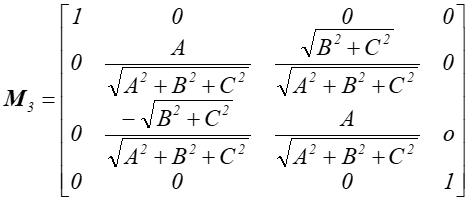
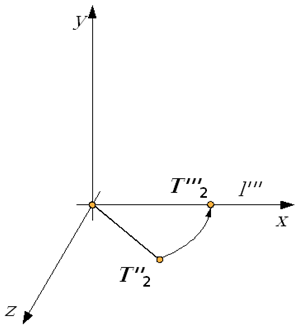
Rys.4.27 Po zrealizowaniu obrotu wokół OY prosta l pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi.
Etap 4. Obrót wokół osi OX o kąt ![]()
g 

Rys.4.28 Teraz
można wreszcie wykonać obrót o kąt ![]() wokół
prostej l co, dzięki odpowiednim operacjom wstępnym,
odpowiada obrotowi o kąt
wokół
prostej l co, dzięki odpowiednim operacjom wstępnym,
odpowiada obrotowi o kąt ![]() wokół osi OX układu współrzędnych.
wokół osi OX układu współrzędnych.
Następnymi etapami (5., 6., 7) będą operacje przeciwne do operacji 1., 2., 3. realizowane w odwrotnej kolejności.
Macierz przekształcenia całkowitego jest iloczynem macierzy opisujących przekształcenia odpowiadające kolejnym przedstawionym etapom.
A zatem macierz przekształcenia całkowitego jest opisana następującą zależnością:
MC = M1-1 · M2-1 · M3-1 · M4 · M3 · M2 · M1
4.7. Problem dokładności obliczeń w przekształceniach geometrycznych
Problem dokładności obliczeń przy wykorzystaniu komputerów jest znany od kiedy istnieją komputery. Wiadomo, że liczby w komputerze są reprezentowane przez skończony ciąg cyfr. W przypadku liczb całkowitych stosowana jest reprezentacja stałopozycyjna i i jeśli rozpatrzymy arytmetykę binarną, to liczbie takiej odpowiada rozwinięcie dwójkowe o określonej długości słowa. Liczby rzeczywiste reprezentowane są zmiennopozycyjnie w postaci cechy i mantysy. Stosowanie określonej długości słowa do reprezentacji mantysy powoduje powstanie dokładności danej arytmetyki. Oznacza to, że reprezentacja liczb rzeczywistych obarczona jest zawsze pewnym błędem wynikającym z tej arytmetyki. Przeprowadzanie operacji graficznych wymaga często wielokrotnych obliczeń. Błędy reprezentacji (dokładność arytmetyki) mogą w widoczny sposób wpływać na efekt (graficzny !) obliczeń. Stosowane algorytmy powinny być tak realizowane, aby, o ile jest to możliwe, minimalizować te błędy.

Rys.4.29. Rysunek zegara.
Rozpatrzmy przykład zegara, dla którego należy wyznaczyć położenie wskazówek – rysunek 4.29. Zadanie można sformułować w następujący sposób. Jeśli wskazówka minutowa co minutę obraca się o kąt da , to należy wyznaczyć kąty ai kolejnych położeń tej wskazówki.
Najprostszym rozwiązaniem jest algorytm iteracyjny powiększający w każdym kroku bieżący kąt położenia o zadany przyrost. Niestety takie rozwiązanie prowadzi do powstania widocznych na tarczy zegara błędów już po kilkudziesięciu godzinach.
Algorytm naiwny.
i = 0;
a0 = 0;
while ()
{
i = i+1;
ai = ai-1+da;
}

Rys. 4.30. Zegar wskazujący „dokładnie” godzinę drugą po kilkudziesięciu godzinach pracy.
Jeśli przeanalizujemy ten najprostszy algorytm, to okaże się, że wraz z powiększaniem wartości kąta dodajemy błędy. Każda operacja arytmetyczna wykonywana przez komputer jest obarczona błędem wynikającym z reprezentacji liczb w postaci skończonej liczby bitów.
Jeśli repr (x) oznacza reprezentację liczby x , natomiast e błąd reprezentacji to:
repr (x) = x .(1+e ) gdzie |e | < d , d Î (10 -16,10 -7)
repr (x+y) = (x+y ).(1+e )
Jeśli wykonywane są operacje w sposób iteracyjny i jednocześnie bieżąca wartość pewnej wielkości jest obarczona błędem z poprzedniej wartości tej samej wielkości, to błąd całej operacji nie jest tylko problemem bieżącym, ale odzwierciedla całą dotychczasową historię obliczeń. A więc błąd się nakłada wraz z postępowaniem obliczeń. Po wielu powtórzeniach może osiągnąć znaczącą wartość. Kumulowanie się błędu w algorytmie naiwnym dla kolejnych iteracji można przedstawić jako:
i=1 : repr (a1 ) = (0+da ) .(1+e1 )
i=2 : repr (a2 ) = ((0+da ) .(1+e1 ) +da ) .(1+e2 )
i=3 : repr (a3 ) = (((0+da ) .(1+e1 ) +da ) .(1+e2 ) +da ) .(1+e3 )
. . .
Zadanie z zegarem może zostać rozwiązane tak,. aby nie doprowadzić do narastania błędu.
Algorytm poprawiony.
i = 0;
a0 = 0;
da = 2*p/60;
while ()
{
i = i+1;
ai = i*da;
}
Realizując algorytmy graficzne należy zawsze zwracać uwagę na dokładność obliczeń numerycznych. Aby błąd zaokrągleń nie wpłynął na efekt obliczeń i nie zniweczył naszej pracy, psując efekt końcowy.
4.8. Kwaterniony
Kwaterniony (quaternions) są czterowymiarowym rozwinięciem liczb zespolonych, to znaczy można je traktować jako rozszerzenie do liczby o trzech składowych urojonych. q=s+ix+jy+kz (rys. 4.31). Kwaterniony zostały zaproponowane przez Williama Hamiltona w 1843 roku. Jako ciekawostkę warto dodać, że kwaterniony powstały jako kolejna próba rozszerzenia liczb zespolonych. Początkowo Hamilton próbował rozszerzenia z dwóch na trzy wymiary jednak okazał się, że jest to niemożliwe. Dopiero rozwinięcie czterowymiarowe okazało się dobrym rozwiązaniem. Hamilton wpadł na swój genialny pomysł przechodząc przez most w Dublinie. Przypomina o tym tablica (rys. 4.32).
Kwaternion może też być zapisany w postaci wektorowej jako:
![]()
gdzie ![]() .
.

Rys.4.31 Właściwości jednostek urojonych kwaterniona.

Fragment rysunku z Wikipedii (Autorstwa Cone83 - Praca własna, CC)
Rys.4.32 Tablica na moście w Dublinie upamiętniająca genialny pomysł Sir W.R Hamiltona.
Właściwości jednostek urojonych kwaterniona.
Dla dowolnego kwaterniona ![]() istnieje kwaternion przeciwny (sprzężony) o
postaci
istnieje kwaternion przeciwny (sprzężony) o
postaci ![]() .
.
Czyli ![]() .
.
Kwaternion przeciwny bywa
także oznaczany jako ![]() .
.
Można określić normę w postaci:
![]() .
.
Dla dowolnych kwaternionów p i q oraz liczby rzeczywistej a
![]() oraz
oraz ![]()
Kwaternion jednostkowy (jego norma jest równa 1)
![]()
Dla każdego kwaterniona ![]() różnego od zera istnieje kwaternion odwrotny
różnego od zera istnieje kwaternion odwrotny
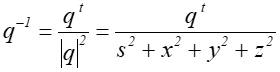
więc
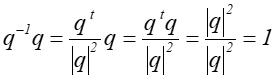 .
.
Zdefiniowane są też operacje dodawania i mnożenia kwaternionów.
Niech ![]() oraz
oraz ![]()
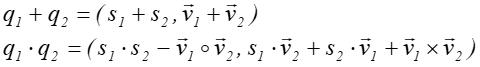
Dodawanie kwaternionów jest operacją łączną i przemienną.
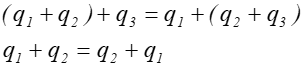
Mnożenie kwaternionów jest operacją łączną i nie jest operacją przemienną.

Kwaterniony są stosowane w teorii liczb i algebrze. Są bardzo użytecznym narzędziem do opisu zorientowania i obrotów. Stąd zastosowania w mechanice, robotyce i grafice komputerowej.
W grafice komputerowej kwaterniony są wykorzystywane w związku z jedną operacją w przestrzeni trójwymiarowej: z obrotem punktu wokół dowolnie zdefiniowanej osi.
Aby skorzystać z tej możliwości należy zdefiniować reprezentację punktu w postaci kwaternionu.
Dany jest punkt ![]() ,
odpowiada mu kwaternion
,
odpowiada mu kwaternion ![]() gdzie
gdzie ![]()
Niech jednostkowy
wektor ![]() reprezentuje oś obrotu w przestrzeni.
reprezentuje oś obrotu w przestrzeni.
Biorąc pod uwagę kwaternion jednostkowy postaci
![]()
związany
z tym wektorem jednostkowym, można wyznaczyć kwaternion ![]() o postaci.
o postaci.
![]()
Kwaternion ten reprezentuje punkt będący obrazem w
obrocie wokół osi wyznaczonej przez wektor ![]() o kąt
o kąt ![]() .
.
Aby dokonać obrotu punktu ![]() o kąt
o kąt ![]() wokół osi określonej przez wektor
wokół osi określonej przez wektor ![]() należy:
należy:
- wyznaczyć
kwaternion
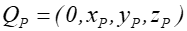 ,
, -
wyznaczyć kwaternion
 oraz
oraz  ,
, -
wyznaczyć kwaternion
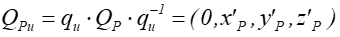 ,
, -
na podstawie
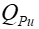 wyznaczyć
wyznaczyć 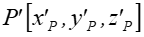 .
.
Porównując to rozwiązanie z zadaniem opisanym wcześniej widać prostotę operacji obrotu wykonywanej z wykorzystaniem kwaternionów.
Większość obrotów realizowanych w grach komputerowych jest wykonywana w taki sposób.
Więcej informacji na temat kwaternionów wraz z przykładami można znaleźć w pracach [2,4].
Problem obrotu w przestrzeni wokół dowolnie zdefiniowanej osi można rozwiązać korzystając z twierdzenia Eulera (rys.4.33).
Każdy obrót w przestrzeni może być opisany za pomocą trzech kątów w odpowiednim układzie współrzędnych.

Rys.4.33. Kąty Eulera definiujące dowolny obrót w
przestrzeni
Naturalną implementacją twierdzenia Eulera jest złożenie trzech macierzy
![]()
Takie podejście byłoby bardzo wygodne, gdyby nie problem niejednoznaczności, tzw. problem blokady przegubowej (gimbal lock). W trakcie realizacji tak zdefiniowanego obrotu może się bowiem zdarzyć, że dwie osie obrotu znajdą się na jednej prostej. Wtedy obrót wokół jednej osi wpływa na obrót wokół drugiej. Nazwa problemu pochodzi od mechanizmu przegubowego stosowanego np. do obsługi żyroskopu lub kompasu (rys.4.34), gdzie problem ten uniemożliwia jednoznaczne sterowanie urządzeniem.
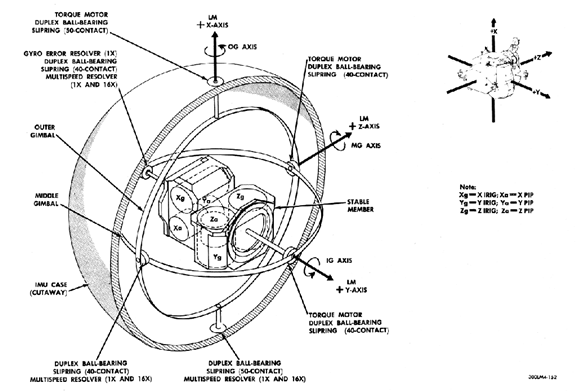
Rys.4.34. Przykład mechanizmu przegubowego do sterowania żyroskopem modułu księżycowego NASA. Rysunek pochodzi z Wikimedii (Public Domain) na podstawie https://www.nasa.gov/wp-content/uploads/static/history/alsj/lm10handbookvol1.pdf
Oczywiście stosując twierdzenie Eulera o trzech kątach w grafice komputerowej do opisania obrotów w zadanej sytuacji, można byłoby przewidzieć problem blokady przegubowej i zmienić warunki (np. kolejność operacji) aby nie dopuścić do niejednoznaczności. Niestety nie zawsze jest to wygodne, a często nie jest to możliwe, szczególnie w sytuacji interpolacji obrotu np. dla potrzeb animacji.
Realizacja obrotu z wykorzystaniem kwaternionów jest pozbawione tej wady. W tym przypadku definiowany jest od razu obrót wokół dowolnego wektora bez rozkładania na kolejne obroty składowe.
Podsumowując rozważania o kwaternionach warto porównać realizację obrotu za pomocą złożenia macierzy i operacji na kwaternionach. Tradycyjne składanie macierzy opisuje obrót w postaci sekwencji trzech, kolejno po sobie następujących operacji. Jest to podejście intuicyjne i łatwe w interpretacji. I niestety są to jedyne zalety. Składanie takie jest skomplikowane obliczeniowo. A przede wszystkim sekwencyjna realizacja obrotów może prowadzi do niejednoznaczności (gimbal lock). Tej podstawowej wady jest pozbawiona realizacja za pomocą kwaternionów, gdyż daje ona możliwość definicji obrotu bez rozbijania na składowe. Realizacja ta jest jednocześnie prostsza obliczeniowo. Jedyną wadą realizacji obrotów z wykorzystaniem kwaternionów jest złożona i trudna interpretacja operacji.
Więcej informacji na temat zastosowania kwaternionów i problemów związanych z obrotami można znaleźć w pracach [2,5,7].