Podręcznik Grafika komputerowa i wizualizacja
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Część 2. Kreowanie wirtualnego świata |
| Książka: | Podręcznik Grafika komputerowa i wizualizacja |
| Wydrukowane przez użytkownika: | Gość |
| Data: | sobota, 14 marca 2026, 00:45 |
Opis
Spis treści
- Rozdział 5. RZUTOWANIE I WIRTUALNA KAMERA
- Rozdział 6. MODELOWANIE OBIEKTÓW
- Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI
- Rozdział 8. MODELOWANIE OBIEKTÓW NATURALNYCH. MODELOWANIE FRAKTALNE I WOLUMETRYCZNE
- Rozdział 9. ELIMINACJA ELEMENTÓW ZASŁONIĘTYCH
- 9.1. Wprowadzenie
- 9.2. Bryła wypukła i zorientowanie ściany, klasy algorytmów
- 9.3. Bryła dowolna, zbiór brył
- 9.4. Algorytm malarski
- 9.5. Algorytm skaningowy
- 9.6. Algorytm podziału binarnego
- 9.7. Algorytm bufora głębokości
- 9.8. Algorytm rysowania wykresu funkcji z=f(x,y)
- 9.9. Złożoność obliczeniowa algorytmów rozstrzygania widoczności
Rozdział 5. RZUTOWANIE I WIRTUALNA KAMERA
Rozdział piąty stanowi wprowadzenie w tematykę rzutowania. Zostały przedstawione stosowane rodzaje rzutowania i ich podstawowe właściwości. Zaprezentowano zastosowanie rachunku macierzowego do opisu rzutowania. Omówione zostały takie zagadnienia jak ostrosłup widzenia (z jego parametrami) i wirtualna kamera. W rozdziale przedstawiono także zagadnienie przekształcenia perspektywicznego jako specyficznego połączenia rzutowania z innymi operacjami grafiki komputerowej.
5.1. Rodzaje rzutowania i ich podstawowe właściwości
Rzutowanie jest operacją pozwalającą przedstawić trójwymiarowy świat (trójwymiarowe obiekty) na dwuwymiarowej powierzchni. Obraz powstaje na powierzchni rzutni dzięki promieniom rzutującym (prostym rzutującym). Obrazem rzutowanego punktu przestrzeni jest punkt będący przecięciem rzutni i promienia rzutującego, przechodzącego przez rzutowany punkt.
Powszechna definicja rzutu jako przekształcenia na płaszczyznę jest pewnym uproszczeniem gdyż rozpatruje się też np. rzuty na powierzchnię walca lub na wycinek sfery. Jednak rzeczywiście z rzutowaniem na płaszczyznę mamy najczęściej do czynienia (grafika komputerowa, fotografia).
Na kształt rzutu danego obiektu mają wpływ: położenie rzutni i kierunki promieni rzutujących. Wyróżnia się dwa podstawowe i najczęściej stosowane przypadki rzutowania na płaszczyznę:
- Rzutowanie równoległe, gdy promienie rzutujące są prostymi równoległymi. Dodatkowo mówimy o rzutowaniu równoległym prostokątnym, jeśli rzutnia jest prostopadła do kierunku rzutowania oraz o rzutowaniu równoległym ukośnym w każdym innym przypadku.
- Rzutowanie perspektywiczne (czasem nazywane środkowym lub centralnym), gdy promienie rzutujące tworzą pęk prostych. Oczywiście, mówienie w tym przypadku o prostopadłości (lub nie) rzutni nie ma sensu, gdyż zawsze w rzutowaniu perspektywicznym dokładnie jeden promień może być prostopadły do płaszczyzny rzutni, a wszystkie pozostałe tworzą z nią kąty mniejsze od kąta prostego.
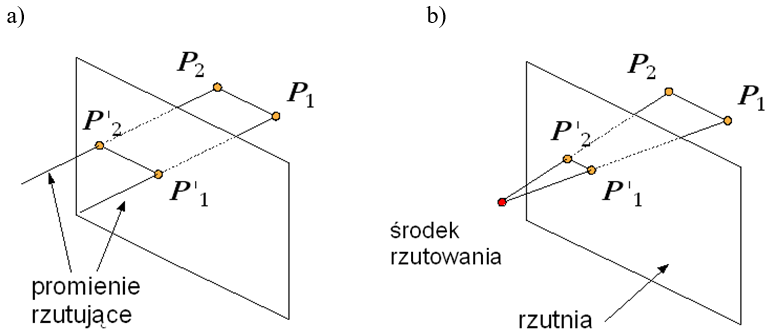
Rys.5.1 Powstawanie rzutu a) równoległego, b) perspektywicznego.
Z rzutowaniem równoległym mamy najczęściej do czynienia w różnego typu zastosowaniach technicznych np. rzuty prostokątne na 3 lub 6 płaszczyzn – tradycyjny rysunek techniczny. Rzutowanie równoległe nie pozwala przedstawić obiektu zgodnie z naszym wyobrażeniem – zgodnie z widzeniem człowieka. Pozwala natomiast zdefiniować i wyznaczyć wymiary przedmiotu. Rzutowanie równoległe zachowuje równoległość prostych oraz proporcje długości odcinków równoległych.
Rzutowanie perspektywiczne pozwala uzyskać obraz zbliżony do postrzeganego przez człowieka. Trzeba jednak pamiętać o tym, że obraz na siatkówce oka powstaje w wyniku rzutu środkowego na wycinek sfery (w przybliżeniu). Zatem wszystkie promienie rzutujące będą w tym przypadku prostopadle padały na rzutnię.
O rzutowaniu równoległym mówimy, że jest prostokątne wtedy, gdy promienie rzutujące są prostopadłe do płaszczyzny rzutni. W przeciwnym przypadku rzutowanie równoległe jest ukośne.
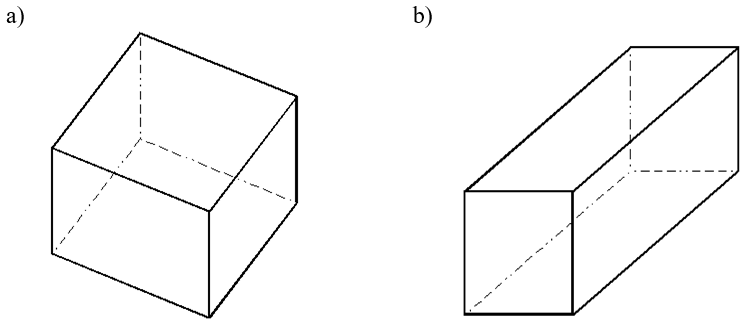
Rzutowanie prostokątne jest powszechnie stosowane w mechanice. Podstawową zaletą takiego rozwiązania jest fakt, że wymiary rysunku odpowiadają wymiarom obiektu to znaczy długość odcinka równoległego do płaszczyzny rzutni jest równa długości rzutu tego odcinka. Aby na podstawie rzutu można było określić wymiary przedmiotu stosuje się zestaw trzech rzutów danego przedmiotu na rzutnie, które są wzajemnie prostopadłe. Ze względu na konieczność jednoznacznego przedstawienia widoków obiektu czasami (w przypadku bardzo złożonych elementów) stosuje się sześć rzutów. Tzn. są to rzuty na trzy płaszczyzny wzajemnie prostopadłe, ale dla każdej z nich wykonuje się po dwa rzuty dla wzajemnie przeciwnych kierunków.
Rys.5.2. Rzuty równoległe sześcianu:
a) rzut
prostokątny (żadna z krawędzi sześcianu nie jest równoległa do rzutni), b) rzut
ukośny.
Można wykazać, że rzutowanie ukośne pozwala praktycznie dowolnie zmieniać proporcje wymiarów obiektu (rys. 5.2). To znaczy jeśli rozpatrzymy wzajemnie prostopadłe odcinki o takiej samej długości to można uzyskać dowolne proporcje ich rzutów dobierając odpowiednio kierunek rzutowania i położenie płaszczyzny rzutni. Z tego względu, w praktycznych zastosowaniach rzutowania równoległego ukośnego w mechanice najczęściej definiuje się rzut przez podanie zmian proporcji odległości wzdłuż każdej z osi układu współrzędnych, a nie przez podanie położenia rzutni i promieni rzutujących. Na przykład perspektywa kawalerska, perspektywa gabinetowa i perspektywa wojskowa są rodzajami rzutowania równoległego ukośnego zdefiniowanymi na tej zasadzie.
Uzyskanie dowolnej zmiany proporcji wymiarów oznacza, że możliwe jest uzyskanie rzutu sześcianu jak na rysunku 5.2.b). Jest to całkowicie poprawny rzut równoległy ukośny sześcianu. Tylko że całkowicie niezgodny z naszym sposobem widzenia.
W każdym rzucie perspektywicznym istnieje przynajmniej jedna rodzina prostych równoległych i nie równoległych do rzutni, taka, że rzuty tych prostych przecinają się w jednym punkcie zwanym punktem zbiegu. W zależności od położenia rzutni względem obiektu mówimy o rzutowaniu perspektywicznym jednozbiegowym, dwuzbiegowym lub trójzbiegowym (rys.5.3.).
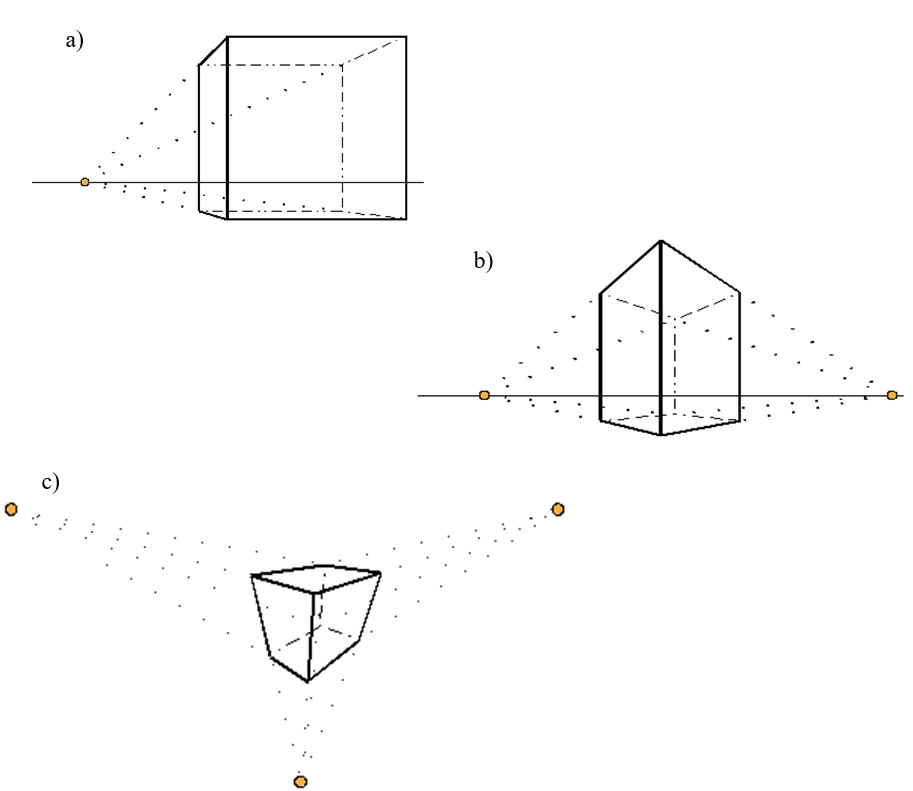
Rys.5.3. Rzuty
perspektywiczne sześcianu: a) perspektywa jednozbiegowa,
b) perspektywa dwuzbiegowa,
c) perspektywa trójzbiegowa.
Skrót perspektywiczny jest efektem wizualnym polegającym na tym, że wielkość rzutu perspektywicznego jest odwrotnie proporcjonalna do odległości obiektu od środka rzutowania. Z tego względu nie ma praktycznie możliwości uzyskania informacji o wymiarach obiektu na podstawie jego rzutu perspektywicznego.
Z drugiej strony efekty wizualne uzyskane w rzutowaniu perspektywicznym są zbliżone do wrażeń wzrokowych oraz do efektów fotograficznych. Warto jednak pamiętać, że o ile w fotografii mamy rzeczywiście do czynienia z rzutem na płaszczyznę, to obraz w oku powstaje w wyniku rzutowania na wycinek sfery.
5.2. Układy współrzędnych związane z rzutowaniem
Naturalnym i najczęściej stosowanym układem współrzędnych związanym z rzutowaniem i obserwatorem jest lewoskrętny kartezjański układ współrzędnych. Kierunki osi 0X i 0Y są zgodne ze współrzędnymi definiującymi położenie na płaszczyźnie rzutni natomiast współrzędna Z określa odległość od obserwatora.
Ponieważ położenie przedmiotów wyimaginowanego świata jest opisywane w układzie prawoskrętnym, to zachodzi konieczność nie tylko związania położenia obserwatora i kierunku rzutowania z układem świata, ale także zapewnienia zmiany skrętności układu. Trzeba o tym pamiętać definiując macierze opisujące odpowiednie operacje. Mówimy o układzie współrzędnych obiektu (sceny lub świata) i przestrzeni obiektu oraz układzie obserwatora (lub rzutu) i przestrzeni obserwatora. Takie rozdzielenie funkcjonalne znacznie ułatwia manipulację i definiowanie odpowiednich parametrów. Położenie punktów rzutu opisuje układ rzutni. Natomiast dodatkowo wyróżnia się układ urządzenia (fizyczny) związany bezpośrednio z urządzeniem wyświetlającym (drukującym) obraz.
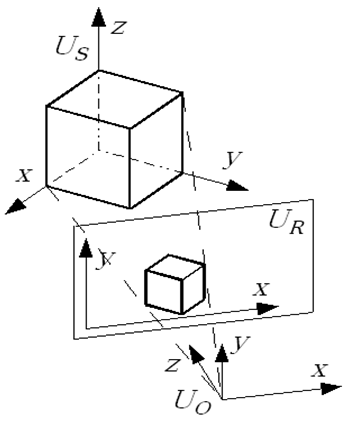
Rys.5.4. Układy współrzędnych związane z rzutowaniem:
UO – układ obserwatora, US
– układ sceny, UR – układ rzutni.
Rzutowanie jest realizowane w układzie obserwatora (lewoskrętnym). Przekształcenia i definiowanie obiektów w układzie sceny (prawoskrętnym). Jeśli przekształcenie punktu z jednego układu do drugiego opiszemy odpowiednią macierzą takiego przekształcenia, to funkcjonowanie obu układów współrzędnych ułatwi realizację tworzenie obrazu.
5.3. Opis macierzowy rzutowania
Rzutowanie może być opisane macierzowo, analogicznie do opisu operacji geometrycznych zaprezentowanych wcześniej.
Rozpatrzmy rzutowanie
perspektywiczne w przestrzeni obserwatora. Współrzędne opisują położenie w
lewoskrętnym układzie współrzędnych obserwatora 0XYZ. Niech obserwator (środek
rzutowania) znajduje się w początku układu współrzędnych, a rzut jest dokonywany
na płaszczyznę z = d dla d>0 (rys.5.5). Rzutem
punktu P o współrzędnych (xp,yp,zp) będzie punkt P' o współrzędnych (x'p,y'p,z'p) , który zgodnie z definicją rzutu perspektywicznego będzie
należał do płaszczyzny rzutni i jednocześnie do prostej przechodzącej przez
środek rzutowania i punkt P .
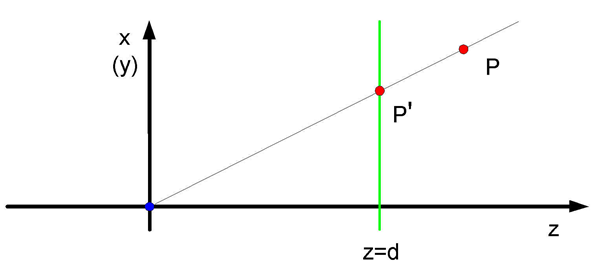
Rys.5.5. Rzut perspektywiczny. Rzutnia o
równaniu z = d ,
środek rzutowania (niebieski punkt) o współrzędnych (0,0,0)
, d>0 .
Uwzględniając proste zależności geometryczne można pokazać, że macierz opisująca tak zdefiniowane rzutowanie perspektywiczne ma postać:
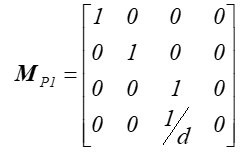
Warto zwrócić uwagę na to, że macierz ta definiuje operację wymagającą normalizacji, bowiem zależność między współrzędnymi punktu i jego rzutu ma postać:
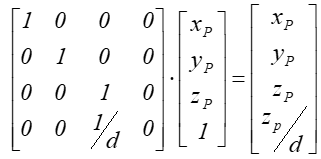 po normalizacji
po normalizacji 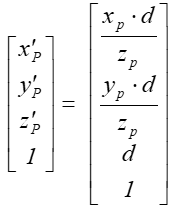
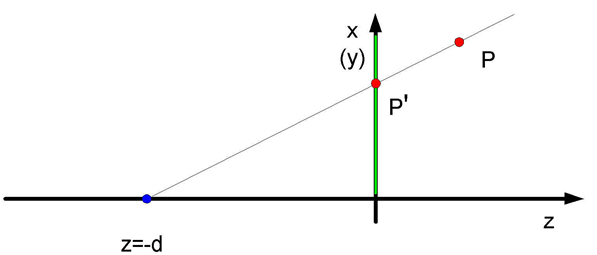
Rys.5.6. Rzut
perspektywiczny (wersja druga). Rzutnia o równaniu z = 0 ,
środek rzutowania (niebieski
punkt) o współrzędnych (0,0,-d) , d>0 .
Rzutowanie perspektywiczne można również prosto zdefiniować w nieco inny sposób (rys. 5.6.). Niech w analogicznym układzie współrzędnych obserwator (środek rzutowania) znajduje się w punkcie (0,0,-d) dla d>0 , a płaszczyzna rzutni ma równanie z = 0 (rys.5.6). Macierz rzutowania będzie wtedy miała postać:
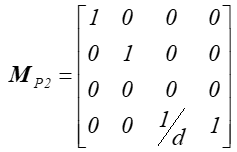
Zaś zależność między współrzędnymi punktu i jego rzutu ma teraz postać.:
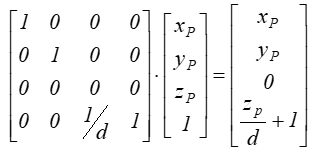 po normalizacji
po normalizacji 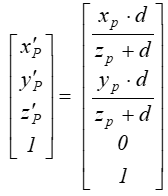
Oba warianty definicji rzutowania perspektywicznego mogą być stosowane zamiennie zależnie od sytuacji.
Jeżeli w drugim
przypadku przyjmiemy, że d →![]() to promienie rzutujące
zamiast pęku prostych utworzą proste równoległe i uzyskamy rzutowanie
równoległe prostokątne (rys.5.7).
to promienie rzutujące
zamiast pęku prostych utworzą proste równoległe i uzyskamy rzutowanie
równoległe prostokątne (rys.5.7).
Rys.5.7. Rzut równoległy. Rzutnia o równaniu z = 0 .
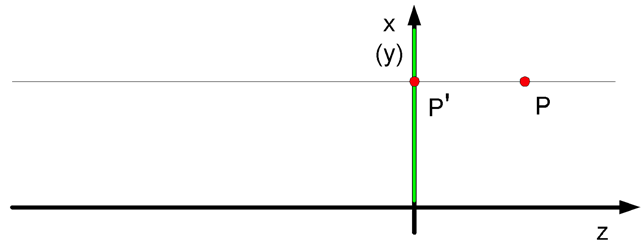
O rzutowaniu równoległym można powiedzieć, że jest szczególnym przypadkiem rzutowania perspektywicznego, gdy środek rzutowania znajduje się w nieskończoności. Macierz opisująca ten przypadek będzie miała postać:
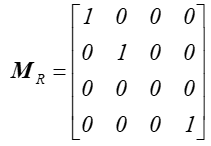
a zależność między współrzędnymi:
g 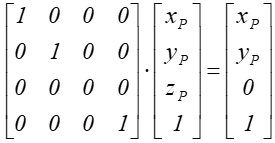 czyli
czyli 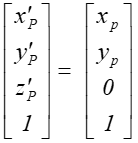
Operacja ta nie wymaga normalizacji.
5.4. Ostrosłup widzenia, wirtualna kamera
W dotychczasowych rozważaniach o rzutowaniu nie zwróciliśmy w ogóle uwagi na to, które obiekty (lub ich fragmenty) – które punkty przestrzeni zostaną zrzutowane. A przecież każdy użytkownik aparatu fotograficznego wie, że tylko wybrany przez niego fragment przestrzeni zostanie utrwalony na zdjęciu. To znaczy, że operacje matematyczne wynikające z rzutowania powinny zostać zrealizowane tylko w odniesieniu do określonego zbioru punktów (określonych obiektów). Jeżeli przyjmiemy, że dokonujemy rzutowania perspektywicznego na płaszczyznę i interesuje nas prostokąt obrazu jako część rzutni, to środek rzutowania i prostokąt obrazu wyznaczą pewien fragment przestrzeni, który może zostać „utrwalony”. Jeżeli do tego dodamy dwie płaszczyzny równoległe do rzutni, które ograniczą wybrany fragment z przodu i z tyłu (rys.5.8.), to powstanie figura będąca ostrosłupem ściętym o podstawie prostokątnej nazywana ostrosłupem widzenia lub piramidą widzenia. Zatem po zdefiniowaniu położenia obserwatora (środka rzutowania), rzutni i ostrosłupa widzenia, należy wydzielić te obiekty i punkty przestrzeni, które będą rzutowane. Powstaje problem obcinania w przestrzeni trójwymiarowej. Algorytmy Cohena-Sutherlanda i Cyrusa-Becka można rozszerzyć o możliwość obcinania trójwymiarowego.
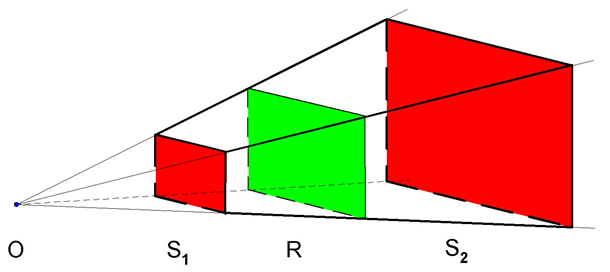
Rys.5.8. Ostrosłup widzenia. R – rzutnia, O – środek
rzutowania,
S1 – przednia płaszczyzna obcinająca, S2 –
tylna płaszczyzna obcinająca.
Dla rzutowania równoległego odpowiednia bryła widzenia zdefiniowana analogicznymi parametrami będzie prostopadłościanem.
Rzutnia 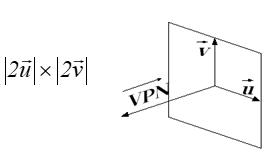
Rys. 5.9. Opis parametrów rzutu.
Realizacja rzutowania perspektywicznego wymaga
definicji parametrów tak, aby jednoznacznie określić bryłę widzenia – rys.5.9.
Najczęściej używa się do definicji trójki wektorów ![]() . Wektor
. Wektor![]() definiuje oś widzenia
(kierunek patrzenia prostopadły do płaszczyzny rzutni). Jednocześnie długość
tego wektora określa wysokość ostrosłupa widzenia. Stosowane są dwa podejścia
do określenia zwrotu tego wektora. Przyjęty wariant na rysunku powoduje, że
kierunek patrzenia wzdłuż osi optycznej jest przeciwny do wektora
definiuje oś widzenia
(kierunek patrzenia prostopadły do płaszczyzny rzutni). Jednocześnie długość
tego wektora określa wysokość ostrosłupa widzenia. Stosowane są dwa podejścia
do określenia zwrotu tego wektora. Przyjęty wariant na rysunku powoduje, że
kierunek patrzenia wzdłuż osi optycznej jest przeciwny do wektora ![]() . Wektory
. Wektory ![]() definiują płaszczyznę
rzutni, a także prostokąt rzutni gdzie będzie powstawał obraz (poprzez długości
tych wektorów). Jednocześnie kierunki wektorów określają obrót rzutni wokół osi
optycznej. Zestaw wektorów
definiują płaszczyznę
rzutni, a także prostokąt rzutni gdzie będzie powstawał obraz (poprzez długości
tych wektorów). Jednocześnie kierunki wektorów określają obrót rzutni wokół osi
optycznej. Zestaw wektorów ![]() definiuje
jednoznacznie ostrosłup prawidłowy o podstawie prostokąta. Daje to możliwość
określenia kąta patrzenia w rzutowaniu perspektywicznym. Komplet parametrów
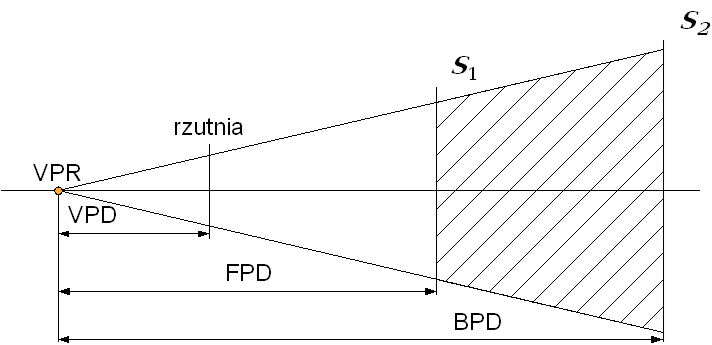
rzutowania wymaga definicji: środka rzutowania (punkt VPR) oraz trzech
odległości wzdłuż osi optycznej względem środka rzutowania. Pierwszą jest
odległość do płaszczyzny rzutni (VPD). Dwie pozostałe (FPD i BPD) definiują
położenie dwóch płaszczyzn (przedniej S1 i tylnej S2),
które określają ostrosłup ścięty - wyznaczają fragment przestrzeni, która
będzie rzutowana.
definiuje
jednoznacznie ostrosłup prawidłowy o podstawie prostokąta. Daje to możliwość
określenia kąta patrzenia w rzutowaniu perspektywicznym. Komplet parametrów
rzutowania wymaga definicji: środka rzutowania (punkt VPR) oraz trzech
odległości wzdłuż osi optycznej względem środka rzutowania. Pierwszą jest
odległość do płaszczyzny rzutni (VPD). Dwie pozostałe (FPD i BPD) definiują
położenie dwóch płaszczyzn (przedniej S1 i tylnej S2),
które określają ostrosłup ścięty - wyznaczają fragment przestrzeni, która
będzie rzutowana.
Patrząc na rzutowanie poprzez analogię do aparatu fotograficznego warto zwrócić uwagę na parametry decydujące o obrazie, który powstanie. Fotograf, wybierając temat do zdjęcia, określa położenie aparatu i kierunek fotografowania. Określa także ogniskową obiektywu (funkcja zoom) czyli kąt „widzenia” aparatu – rys.5.10. Warto przy tym pamiętać, że zdjęcie wykonane obiektywem szerokokątnym z bliskiej odległości jest inne niż obiektywem wąskokątnym (teleobiektywem) z dużej odległości, pomimo pozornego podobieństwa wybranych fragmentów (rys.5.10). Zmiana położenie obserwatora (translacja) powoduje zmiany wzajemnych relacji między punktami obiektu i obserwatorem. Natomiast zmiana ogniskowej obiektywu – kata widzenia (zoom) nie zmienia położenia obserwatora a tym samym nie zmienia wzajemnych relacji między punktami obiektu i obserwatorem. Dobranie właściwego ostrosłupa widzenia jest szczególnie istotne w grach komputerowych i zastosowaniach filmowych grafiki komputerowej.

Rys.5.10. Zdjęcia Gmachu Głównego Politechniki wykonane z
różnych miejsc, przy różnych
ostrosłupach widzenia zdefiniowanych za pomocą
ogniskowej obiektywu.
Przekładając parametry ruchu aparatu (fotografa) na parametry rzutowania definiujemy wirtualną kamerę. Jaki jest minimalny zestaw operacji, zapewniający pełną swobodę manipulacji taką kamerą?
- Translacja kamery w układzie współrzędnych świata, odpowiadająca przesuwaniu aparatu w dowolnym kierunku (przemieszczanie się fotografa).
- Obroty wokół osi własnego układu współrzędnych kamery, pozwalające symulować skierowanie aparatu w dowolnie wybranym kierunku.
- Zmiany kątów ostrosłupa widzenia np. poprzez definicję odległości rzutni o zadanym prostokącie obrazu od środka rzutowania (obserwatora). Odpowiada to zmianie ogniskowej (kąta „widzenia”) obiektywu.
Związanie definicji kształtu ostrosłupa widzenia i obrotów z własnym układem współrzędnych wirtualnej kamery zapewnia wygodę manipulacji oraz zgodność symulacji z rzeczywistością.
Jeśli opisywane dotychczas parametry rzutowania odniesiemy do powstawania obrazu w fotografii, to praktycznie jedynym parametrem aparatu fotograficznego, o którym nie było dotychczas mowy, jest ostrość. Parametr ten nie daje się w prosty sposób przenieść na opis rzutowania. Ostrość zdjęcia jest wynikiem zależności między właściwościami optycznymi obiektywu, a odległością obiektu od obiektywu. Rzutowanie natomiast odwzorowuje wszystkie obiekty w sposób ostry. Niestety, nie jest to zaletą wirtualnej kamery, jeśli obraz ma być zgodny z naszym widzeniem, gdyż akomodacja oka powoduje powstanie widocznych sfer ostrości. Szczególnie jest to niekorzystne w sytuacji wykorzystywania grafiki komputerowej w kinematografii, gdzie nieostrość danego obiektu może być zamierzonym efektem reżysera.
Rzeczywisty obiektyw aparatu daje ostry obraz punktu w dokładnie określonym miejscu – na płaszczyźnie powstawania obrazu. Zarówno bliżej jak i dalej obrazem punktu jest plamka rozproszenia (rozmyte koło) – stąd nieostry obraz. Analizę zjawiska przeprowadził E. Lommel w końcu XIX wieku. Zaproponował on pewne uproszczenia, stosowane w opisie ostrości do dzisiaj.:
- Plamka rozproszenia ma średnicę wprost proporcjonalną do odległości między płaszczyzną, na której powstała, a płaszczyzną ostrego obrazu.
- Wewnątrz plamki rozproszenia jasność jest w przybliżeniu odwrotnie proporcjonalna do odległości od środka plamki. W przybliżeniu, gdyż w środku plamki jasność ma pewną skończoną wartość, natomiast na brzegu plami (w skończonej odległości równej promieniowi plamki) maleje do zera.
- Zmiana ostrości nie powoduje zmian jasności całego obrazu, tylko zmianę rozkładu jasności.
Pierwsze próby symulacji głębi ostrości na potrzeby grafiki komputerowej zostały podjęte przez M.Potmesila i I.Charkravarty’ego w 1981 roku [3]. Najczęściej stosowanym rozwiązaniem jest dzisiaj sztuczne rozmycie symulujące nieostrość w wybranych fragmentach obrazu. Dokonuje się tego albo stosując bufor akumulacji albo odpowiednie filtrowanie. Więcej na ten temat zainteresowani mogą przeczytać w pracy P.Rokity [4]
5.5. Przekształcenie perspektywiczne
Zaproponowane macierze rzutowania, zarówno
perspektywicznego jak równoległego mają jedną zerową kolumnę lub wiersz.
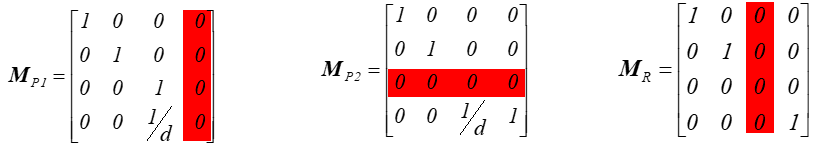
Oznacza to że nie jest możliwe wyznaczenie macierzy odwrotnej. Wszystkie te macierze są nieodwracalne. Rzutowanie jest operacją nieodwracalną. W rzutowaniu obrazem każdego punktu leżącego na prostej (promieniu) rzutującej jest jeden (i ten sam) punkt na rzutni. Czyli nie jest możliwe odtworzenie trzeciego wymiaru tylko i wyłącznie na podstawie rzutu obiektu.
Często do następnych operacji (na przykład do eliminacji elementów zasłoniętych) niezbędna jest informacja o trzecim wymiarze (odległości od obserwatora - głębokości). Rozwiązanie tego problemu przynosi operacja nazywana przekształceniem perspektywicznym (a nie rzutowaniem). Jest to operacja, która pozwala wyznaczyć rzut perspektywiczny i jednocześni daje informację o odległości.
Jeśli rozpatrzymy znormalizowaną bryłę widzenia perspektywicznego – ostrosłup ścięty, to promienie rzutujące tworzą pęk prostych w wierzchołku tego ostrosłupa. Można dokonać przekształcenia, które przekształci ostrosłup ścięty na prostopadłościan (rys.5.11). Wtedy pęk prostych (promieni rzutujących) stanie się zbiorem prostych równoległych. A to oznacza, że po takim zniekształceniu przestrzeni wszystkie punkty leżące na prostej rzutującej będą miały jednakowe współrzędne odpowiadające współrzędnym rzutu.
Operacja ta wymaga normalizacji współrzędnych. Współrzędne punktów ostrosłupa ściętego muszą spełniać następujące warunki:
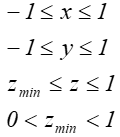
Macierz przekształcenia perspektywicznego ma postać:
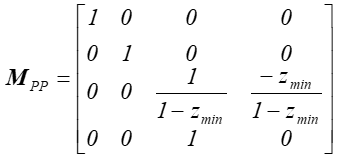
Zaś zależność między
współrzędnymi punktu i jego rzutu ma teraz postać.:
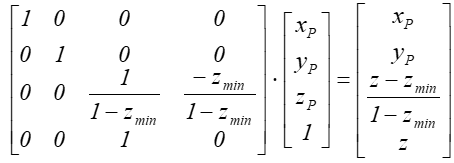 po normalizacji
po normalizacji 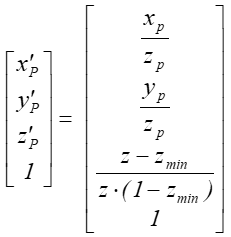
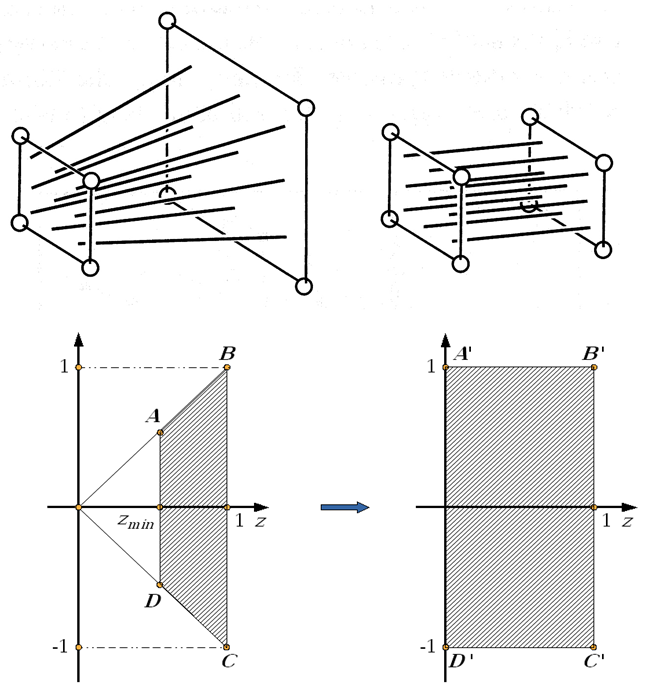
Rys. 5.11. Przekształcenie perspektywiczne. Na podstawie [6].
Macierz przekształcenia perspektywicznego wymaga normalizacji operacji. Wynik na rysunku jest podany z uwzględnieniem normalizacji.
Jak widać współrzędne xP i yP obrazu punktu odpowiadają współrzędnym rzutu perspektywicznego przy założeniu, że środek rzutowania jest w początku układu współrzędnych. Jednocześnie współrzędna z obrazu daje informację o położeniu względem osi OZ. Warto zwrócić uwagę na fakt, że przekształcenie wartości głębokości jest operacją nieliniową, ale zachowującą porządek na prostej, co w zupełności wystarcza do oceny głębokości.
5.6. Wirtualne studio
Umieszczenie w wyimaginowanym świecie wirtualnej kamery, która daje możliwość manipulacji zgodnie ze znanymi realiami pozwala łączyć obrazy rzeczywiste z wirtualnymi. Przykładem takiego „graficznego świata” jest wirtualne studio, coraz częściej wykorzystywane przez stacje telewizyjne. Zamiast budować dekoracje do nowego programu, tworzy się je za pomocą grafiki komputerowej.
Program powstaje w ten
sposób, że niezależnie prowadzi się dwie rejestracje. Rejestrację prezenterów
(lub innych osób występujących) rzeczywistą kamerą oraz „rejestrację”
wirtualnej dekoracji wirtualną kamerą. Obie kamery mają odpowiednio zgodne
parametry funkcjonalne oraz w pełni zsynchronizowane ruchy. Oba obrazy składa
się następnie techniką blue boxu, tworząc to, co potem oglądamy na ekranie.
Oczywiście możliwe są dowolne warianty łączenia elementów rzeczywistych i
wirtualnych łącznie z dowolnym zasłanianiem jednych przez drugie (rys.5.12,
rys.5.13).
Technika wirtualnej kamery
pozwala zaoszczędzić nie tylko pieniądze, czas i materiały przy tworzeniu
dekoracji, pozwala też „zaoszczędzić” powierzchnię studia telewizyjnego, gdzie
odbywa się realizacja programu. Oglądając program wierzymy w masywne dekoracje
rozstawione na olbrzymiej przestrzeni (rys.5.14), a w rzeczywistości prezenter
może siedzieć w ciasnym wnętrzu. Zainteresowanych tematem wirtualnego studia
zachęcam do przeczytania pracy [7].

Rys.5.12. Prezenter i wirtualna dekoracja. Warto zwróci uwagę na cień. Rzeczywisty prezenter rzuca cień na wirtualną dekorację ! Fotografia dzięki uprzejmości Orad Hi-Tec Systems Poland.

Rys.5.13. Wirtualna kuchnia. Oprócz prezenterek również
niektóre meble i sprzęt kuchenny są rzeczywiste.
Fotografia dzięki uprzejmości Orad Hi-Tec Systems Poland.

Rys.5.14. Wirtualne studio. Fotografia dzięki uprzejmości Orad Hi-Tec Systems Poland.
Rozdział 6. MODELOWANIE OBIEKTÓW
6.1. Wprowadzenie
Zastosowania CAD/CAM, zastosowania symulacyjne często wymagają definicji obiektów trójwymiarowych, które odzwierciedlałyby pewne wybrane cechy fizyczne. We wspomaganiu projektowania ważne staje się na przykład rozgraniczenie na powierzchnie wewnętrzne i zewnętrzne, położenie środka ciężkości czy objętość obiektu. Oprogramowanie wykorzystywane w tego typu zastosowaniach powinno dawać możliwość edycji (wprowadzenia i późniejszego poprawiania) kształtu obiektu i możliwość efektywnego przechowywania opisu obiektu. Zwykle wymagane jest także współdziałanie modułu edycji z programami specjalistycznymi w zakresie wyznaczania parametrów fizycznych. Oczywiście modelowanie i edycja powinno być efektywne to znaczy dawać możliwość łatwego definiowania opisu skomplikowanych elementów. Potrzeba opisu spełniającego takie warunki – reprezentacji obiektu – doprowadziła do powstania kilku różnych metod reprezentacji wymagających niezależnego omówienia.
Dążenie do realizmu – do tego aby obraz grafiki komputerowej jak najbardziej przypominał widok obiektu rzeczywistego pociąga za sobą co raz większą dbałość o szczegóły. Z punktu widzenia odbiorcy obrazu, detale i ich właściwości mają bardzo istotny; wręcz decydujący wpływ na postrzeganie obrazu. Rzeczywiste kształty są najczęściej bardzo skomplikowane. Można zaproponować bardzo prostą zależność:
Im
więcej szczegółów odpowiadających rzeczywistości,
tym
bardziej realistyczny obraz.
Ale dbanie o szczegóły wiąże się, niestety, z kilkoma poważnymi problemami::
- wymaga to bardziej skomplikowanego modelowania obiektów,
- wymaga dłuższego czasu modelowania i kreowania obrazu,
- zajmuje więcej pamięci.
W kontekście modelowania dążenie do realizmu oznacza bardziej skomplikowany system opisu i definicji obiektów, powierzchni i ich właściwości. Oczekiwanym rozwiązaniem byłaby możliwość uzyskania większej liczby szczegółów „na życzenie”.
6.2. Właściwości bryły, problem domknięcia
W zasadzie można byłoby stwierdzić, że oczekiwane właściwości końcowe projektu i wyobraźnia projektantów powinna być jedynymi ograniczeniami narzuconymi na proces wspomagania projektowania. W takim razie przez obiekt graficzny należałoby rozumieć cokolwiek, co da się narysować przy pomocy komputera. Wydaje się jednak, że celem nie jest jedynie swoboda projektowania, ale efekt końcowy, jakim jest realizacja fizyczna danego obiektu. I z tego powodu bardzo często wprowadza się pewne ograniczenia reprezentacji. Ograniczenia, które nie ograniczając wyobraźni projektanta powinny, wbrew pozorom, ułatwić mu pracę.
Najczęściej rozpatrywany zestaw cech jakie będą oczekiwane od brył, które są rozpatrywane przez systemy modelowania geometrycznego:
- Podzbiór przestrzeni R3.
- Sztywna.
- Jednorodna topologicznie.
- Skończona.
- Ograniczona.
- Domknięta.
- Opis dający możliwość realizacji efektywnych operacji.
Zaproponowany zestaw właściwości bryły jest pewnym kompromisem między swobodą projektowania a zastosowaniami praktycznymi, kompromisem, który daje przy tym możliwość efektywnego wspomagania projektowania. Przykładem jak należy rozumieć ten kompromis jest jednorodność topologiczna. Z jednej strony nie ma w zasadzie żadnych przeciwwskazań w grafice komputerowej aby tworzyć obiekty niejednorodne (np. krzesło w postaci trójwymiarowego sześciennego siedziska połączonego z dwuwymiarowym prostokątnym oparciem). Ale jednocześnie ujednolicenie opisu może uprościć podejście do różnie definiowanych elementów. Natomiast jeśli popatrzymy na problem od strony praktycznej; technologicznie realizacyjnej, to okaże się, że problem w zasadzie nie istnieje ponieważ żyjemy wśród obiektów trójwymiarowych jednorodnych topologicznie i praktyczne wykonanie prostokątnego oparcie dla rozpatrywanego krzesła i tak będzie wymagało określenia trzeciego wymiaru – jego grubości. Jeśli już nawet dla spełnienia wizji projektanta jest niezbędne istnienie niejednorodności topologicznej to prościej jest założyć, że w ramach jednej bryły zachowujemy jednorodność i w ostateczności dopuszczamy zestawienie różnych brył w ramach jednego procesu. Chociaż i tak w efekcie końcowym na etapie technologii zostanie to ujednolicone. Podobnie problem występuje ze sztywnością bryły. Sztywność nie musi oznaczać niezmienności kształtu, ale raczej niezmienność struktury lub budowy obiektu. Pręt stalowy może podlegać pewnym drobnym zmianom kształtu (ugięcie, skręcenie) bez zmiany struktury czy budowy. Dopiero przyłożenie większej siły powoduje np. jego zgięcie czy złamanie. W tym kontekście gumka do ścierania może być, w pewnych sytuacjach, traktowana jako bryła sztywna.
Elementem opisu właściwości bryły, na który warto zwrócić uwagę jest domknięcie
bryły. To co widzimy obserwując dowolny przedmiot jest efektem odbicia światła
od powierzchni tego przedmiotu. Jeśli zostanie on przekrojony to zobaczymy
powierzchnię przekroju – to znaczy będzie to nowy brzeg powstały przecięcia. Powierzchnia
brzegu obiektu jest więc bardzo istotna w procesie rysowania – wizualizacji
obiektu.
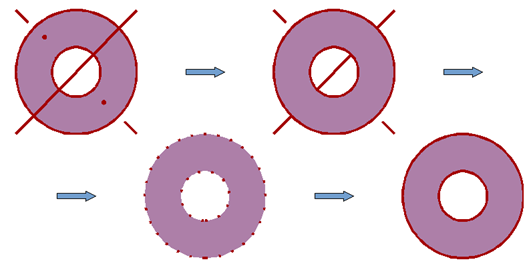
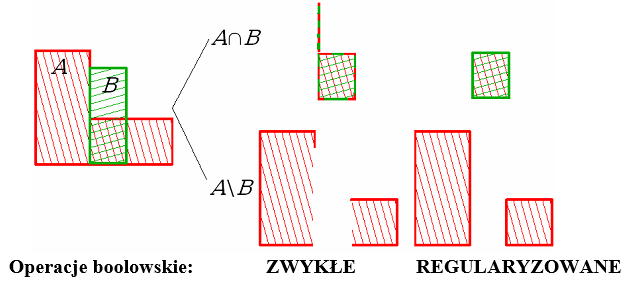
Rys.6.1. Domknięcie – regularyzacja zbioru.
Proces rozwiązania problemu domknięcia bryły nazywany jest regularyzacją zbioru (rys. 6.1). Jeśli rozpatrzymy dowolny obiekt jako pewien zbiór punktów to można wyróżnić punkty wewnętrzne tworzące zbiór otwarty, punkty brzegowe (punkty, których odległość zarówno od obiektu jak i jego uzupełnienia jest równa zeru) oraz zbiór domknięty, zawierający wszystkie jego punkty wewnętrzne i wszystkie brzegowe. Rysunek pokazuje regularyzację zbioru. Kolejne etapy to: domknięcie poprzez przejęcie do wnętrza ewentualnych punktów zdefiniowanych jako brzeg (np. w wyniku jakiejś operacji na zbiorach), a które w rzeczywistości znajdują się we wnętrzu. Otwarcie zbioru pozwalające wyeliminować punkty brzegowe niepołączone z wnętrzem. Ponowne domknięcie dające regularyzację zbioru.
Można zastanowić się jak efektywnie opisać bryłę? Jakie jej cechy wykorzystać?
- Wykorzystać kształt (zewnętrzny) ? – opis powierzchni (zbiór powierzchni definiujących kształt)
- Wykorzystać podzbiór przestrzeni ? – opis przestrzenny (brzeg plus wnętrze - zbiór punktów)
Biorąc pod uwagę te dwa, różne podejścia do opisu bryły, wyróżnia się cztery podstawowe metody reprezentacji obiektów najczęściej stosowane w grafice komputerowej:
- Konstruktywna
geometria brył (CSG)
- definicja zbioru punktów w przestrzeni z wykorzystaniem operacji typu boolowskiego.
- Reprezentacja
brzegowa (Boundary-Representation)
- definicja powierzchni brzegowej.
-
Reprezentacja
z przesunięciem (Sweep)
- niebezpośrednia definicja zbioru punktów.
-
Podział
przestrzeni
- bezpośrednie wskazanie zbioru punktów.
6.3. Konstruktywna geometria brył
Konstruktywna geometria brył (ang. constructive solid geometry – CSG) jest metodą reprezentacji obiektów polegająca na definicji obiektu jako wyniku regularyzowanych operacji boolowskich (rys. 6.2). Obiekt jest zapisywany (pamiętany) jako drzewo o odpowiedniej budowie ( z określonymi operacjami w węzłach i prymitywami w liściach.
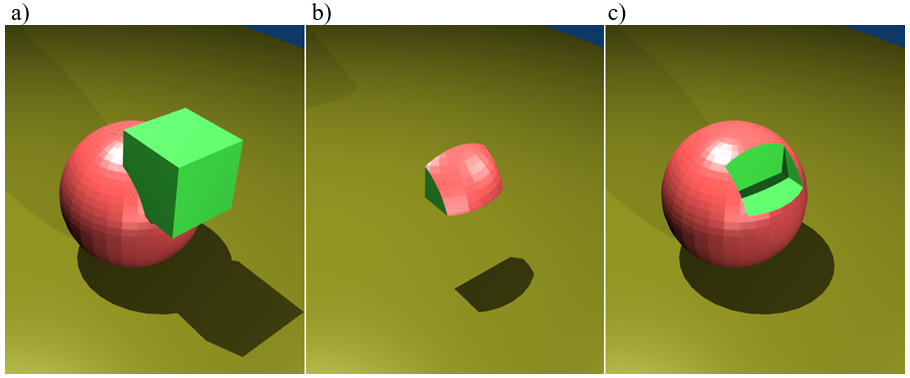
Rys.6.2. a) Suma obiektów, b) iloczyn (część wspólna), c) różnica.
Aby zdefiniować obiekt trzeba podać, z jakich elementów go zbudować (z jakich prymitywów jest on skonstruowany) oraz podać w jaki sposób prymitywy te konstruują obiekt (podać drzewo operacji koniecznych do uzyskania obiektu) – rys.6.3. Najczęściej stosowane operacje to suma, iloczyn (przecięcie), różnica zbiorów.
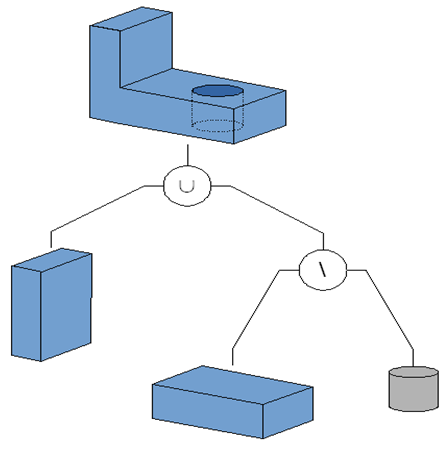
Rys.6.3. Drzewo konstrukcji prostego elementu mechanicznego. Rysunki na podstawie [1].
Zbiór prymitywów:
- Zestaw „klocków” dobranych dla danej sceny, obiektu.
- Prymitywy mogą być definiowane w sposób bardzo ogólny. Np. jako dowolna półprzestrzeń — zbiór punktów (xP, yP, zP) takich że f (xP, yP, zP) < 0, przy czym f jest funkcją ciągłą.
Zestaw prymitywów należy rozumieć bardzo szeroko. Z jednej strony jest to zestaw „klocków” potrzebny do definicji danego zestawu elementów na scenie. Z drugiej strony zestaw ten powinien być na tyle szeroki aby nie stwarzać problemów przy definicji dowolnych elementów sceny w ramach pewnej klasy. Można na przykład założyć że scena będzie zawierała tylko elementy wielościenne. Wtedy naturalnym byłoby zestawienie zbioru prymitywów w postaci wzorców każdego rozpatrywanego typu wielościanu.
Można się zastanowić, czy wygodniejszym nie byłoby użycie tylko jednego prymitywu – półprzestrzeni. W takiej sytuacji za pomocą różnych ustawień półprzestrzeni i operacji boolowskich (regularyzowanych) można byłoby skonstruować dowolny wielościan bez żadnych ograniczeń i co ważne, zawsze w taki sam sposób. Jednak w takiej sytuacji należałoby pamiętać o tym, że w przeciwieństwie do operacji na klockach będących bryłami, operacje przeprowadzane na półprzestrzeniach mogą w ogóle nie dawać bryły. I regularyzacja operacji w takiej sytuacji nie pomoże. Wybór prymitywów jest sprawą bardzo ważną . Powinien być dokonany w zależności od typu obiektów jakie pojawiają się na scenie oraz możliwości systemu modelowania i celów dla jakich został on zbudowany..
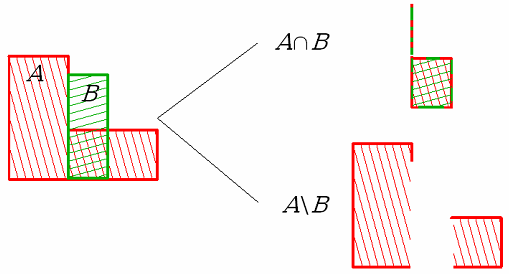
Rys.6.5. Rozwiązanie problemu brzegu (niejednorodności topologicznej) za pomocą regularyzacji operacji.
Konstruktywna geometria brył jest techniką, w której poważnym problemem jest definicja brzegu i wyznaczenie go po wykonaniu operacji boolowskich. Z punktu widzenia obserwatora brzeg jest tym, co świadczy o kształcie obiektu. Patrząc na obiekt widzimy brzeg obiektu (powierzchnię zewnętrzną) i jego właściwości. I na tej podstawie wyrabiamy sobie opinię o obiekcie. W tym kontekście rysowanie brzegu obiektu nie może być związane z jakimikolwiek niejednoznacznościami (rys.6.4). Konsekwentne stosowania operacji regularyzowanych może rozwiązać tego typu problemy (rys.6.5).. Jeśli wykonamy iloczyn lub różnicę brył A i B, to mogą pojawić się obszary dla których nie będzie zdefiniowany brzeg, ale również obszary dla których brzeg będzie określony niejednoznacznie. Zastosowanie regularyzacji zbioru (regularyzowanych operatorów boolowskich) zapewnia poprawność konstrukcji.
Podstawowe właściwości konstruktywnej geometrii brył można scharakteryzować w sposób następujący.
- Zalety
- Bezpośrednia reprezentacja (punkty) w oparciu o operacje boolowskie.
- Reprezentacja zwięzła i efektywna.
- Szczególnie użyteczna w zastosowaniach śledzenia promieni (ray-tracing).
-
Wady
- Aproksymacja obiektu 3D (zależnie od opisu CSG).
- Wizualizacja (czasem) utrudniona (wymaga opisu właściwości powierzchni brzegowej).
- Problem regularyzacji (nietrywialny).
6.4. Reprezentacja brzegowa
Reprezentacja
brzegowa (ang. b-rep – boundary representation) opisuje obiekt za pośrednictwem
opisu jego brzegu – powierzchni ograniczającej obiekt (rys.6.6). Możemy tu mieć do czynienia z modelem wielościennym (ang. polygonal representation) lub
powierzchniowym, w którym kształt brzegu obiektu jest opisany parametrycznie.
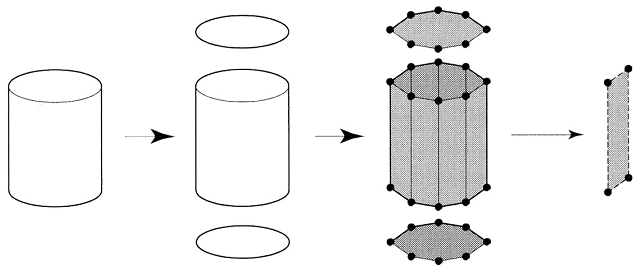
Rys.6.6. Bryła modelowana jako zbiór powierzchni
formujących jej brzeg.
Bryła => Powierzchnie
=> Wielokąty =>
Węzły (Krawędzie).
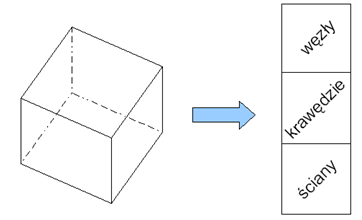
Rys.6.7. Bryła reprezentowana przez jej powierzchnię
brzegową.
Dla wielościanu struktura danych pozwala zapamiętać listy (lub
tablice) węzłów, krawędzi i ścian.
Dla modelu wielościennego istotnym problemem jest organizacja struktury danych zapamiętującej obiekt. Realizowane jest to w postaci list lub tablic ścian, krawędzi i wierzchołków. Pamiętanie powiązań między elementami obiektów prowadzi do struktur redundantnych. Wiąże się to oczywiście ze wzrostem kosztu pamięciowego. Czasami celowo wprowadzane są struktury redundantne w celu przyspieszenia wyszukania elementów. Takimi strukturami są na przykład DCEL (double connected edg list) i struktura krawędziowa Baumgarta. Są to struktury, w których deskryptory krawędzi zawierają wskazania na sąsiednie krawędzie, węzły i ściany (rys.6.8).

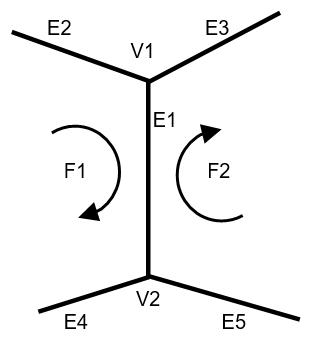
Rys.6.8. „Skrzydlata gałąź” Baumgarta (zaproponowana w 1972).
Zastosowanie tego typu struktur danych ułatwia wyszukiwanie określonych ciągów elementów. Np. korzystając ze skrzydlatej gałęzi Baumgarta można szybko wyznaczyć pętlę krawędzi dla ściany, albo pętlę krawędzi dla wierzchołka.
Model wielościenny może być reprezentowany dowolną siatką wielokątów. Rodzaj siatki zależy od budowy obiektu i sposobu jego definiowania. Przypisanie położenia poszczególnym punktom i powiązań tworzących siatkę może być realizowane ręcznie przez konstruktora. Może wynikać z matematycznego opisu obiektu – można wykorzystać charakterystyczne przekroje obiektu, albo linie stałego parametru. Może to być zrealizowane automatycznie na podstawie pomiarów położenia i kształtu obiektu rzeczywistego lub jego modelu. Często wykorzystywane są siatki trójkątów, gdyż przy dowolnym rozmieszczeniu węzłów siatka taka gwarantuje, że każde jej oczko zawsze będzie figurą płaską – wielokątem.
Problemem na który często jest zwracana uwaga jest trudna weryfikacja poprawności struktury B-rep
- Poprawność topologiczna:
- Problemy struktury – połączenia między elementami (np. wierzchołkami) muszą być zgodne z budową i pozostałymi elementami obiektu.
- Problem orientacji – sąsiadujące elementy muszą dawać zgodność orientacji.
-
Poprawność geometryczna:
- Położenia muszą odpowiadać oczekiwaniom budowy obiektu.
- Wyznaczone położenie i orientacja muszą być zgodne z topologią.
Wyróżnia się wielościan zwykły (prosta bryła Eulera) dla którego :
- ściany ograniczone zamkniętą łamaną krawędzi,
- każda krawędź łączy dokładnie dwie ściany,
- każda krawędź łączy dokładnie dwa wierzchołki,
- każdy wierzchołek łączy co najmniej 3 krawędzie,
- nie występują otwory w ścianach ani tunele w bryle,
- dowolne dwa punkty bryły można połączyć łamaną zawartą w bryle.
Reguła Eulera
w-k+s=2
gdzie:
w — liczba wierzchołków,
k — liczba krawędzi
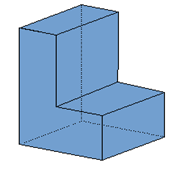
w=12. k=18, s=8
Uogólniona reguła Eulera
w-k+s=2 . (c-t)+d
gdzie:
c — liczba rozłącznych elementów składowych,t — liczba tuneli (w bryle),
d — liczba dziur (w ścianach)
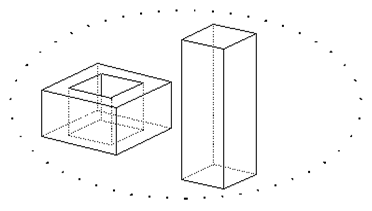
w=24, k=36, s=16, c=2, t=1, d=2
Rys.6.9.Reguła Eulera i uogólniona reguła Eulera.
Dla każdego wielościanu zwykłego spełniona jest reguła Eulera. Rozszerzoną klasę obiektów - rozmaitości dwuwymiarowych obowiązuje uogólniona (rozszerzona) reguła Eulera (rys.6.9).
Należy jednak pamiętać że spełnienie tych warunków jest warunkiem koniecznym ale niewystarczającym przynależności do odpowiedniej klasy. Na przykład sześcian, do którego krawędzi doczepiono prostokąt nie jest już wielościanem zwykłym ale regułę Eulera (podstawową) spełnia.
141788 wielokątów 35305 wielokątów 8993 wielokąty
Rys.6.10. Problem aproksymacji kształtu przy modelu
wielościennym.
Rysunek pochodzi z Viewpoint Digital’s catalogue.
Reprezentacja brzegowa jest bardzo efektywna dla obiektów (brył)
wielościennych. Dla innych wymagana jest aproksymacja kształtu (np. dla
obiektów typu kula czy obiekty obrotowe. Jeśli chcemy oddać kształt obiektu w
sposób satysfakcjonujący, to wymagana jest duża liczba wielokątów (rys.6.10). Przy
źle zaprojektowanej reprezentacji właściwości modelu wielościennego (i
aproksymacji kształtu) mogą prowadzić do utraty cech wizualnych obiektu.
Reprezentacja
brzegowa jest często łączona w systemach modelowania z konstruktywną geometrią
brył.
Podsumowując, właściwości reprezentacji brzegowej można scharakteryzować w następujący sposób
- Zalety
- Prosta (intuicyjna) definicja obiektu (Formalna definicja powierzchni obiektu).
- Prosta i efektywna (szybka) wizualizacja (są zdefiniowane ściany i ich właściwości).
- Możliwe operacje boolowskie (ale nie są proste !)
-
Wady
- Aproksymacja obiektu 3D (w zależności od możliwości opisu powierzchni brzegowej).
- Problem poprawności reprezentacji.
- Problemy numeryczne wpływające na skomplikowanie reprezentacji i wizualizację.
- Reprezentacja mało zwięzła.
6.5. Reprezentacja z przesunięciem
Reprezentacja z przesunięciem (ang. sweep) nazywane czasem zagarnianiem lub zakreślaniem przestrzeni buduje obiekt przez przemieszczenie przekroju wzdłuż pewnej trajektorii. Obiekt tworzą wszystkie punkty znajdujące się na drodze przekroju. Najprostsze do takiej definicji są obiekty podobne do przedstawionego na rysunku 6.11. Ale również kula torus czy spirale są proste do takiego definiowania. Dla bardziej skomplikowanych kształtów można zaproponować możliwość zmiany kształtu w funkcji trajektorii oraz podział na fragmenty /sekcje (zagarnianie wielosekcyjne). Reprezentacja z przesunięciem stanowi niebezpośrednią definicję obiektu (w pewnym sensie także jego powierzchni). Bryła może być traktowana jako zbiór punktów – reprezentacja przestrzenna. Jednak konstrukcja obiektu jest realizowana przez pośrednią definicję: jak powstaje brzeg obiektu (jakie punkty przestrzeni będą tworzyły obiekt). Warto zwrócić uwagę na fakt, że takie podejście ma ograniczony zakres stosowania, brak jest formalnej teorii opisu, a także brak jest zasad określania/sprawdzania poprawności i schematu regularyzacji. Problemy te powodują, że reprezentacja z przesunięciem nie stanowi samodzielnego sposobu opisu. Najczęściej jest łączona z reprezentacją powierzchniową i służy do definicji położenia węzłów siatki wielokątów. Ewentualnie (rzadziej) jest łączona z konstruktywną geometrią brył.
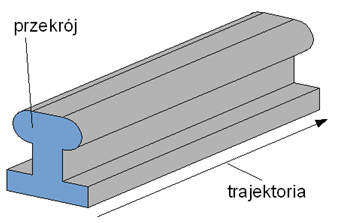
Rys.6.11. Przekrój i trajektoria definiują obiekt.
Jak w prosty sposób zdefiniować szynę kolejową?
Podstawowe właściwości reprezentacji z przesunięciem można przedstawić jako:
- Zalety
- Naturalny i prosty sposób opisu obiektu.
- Intuicyjna definicja.
-
Wady
- Skomplikowana wizualizacja (brak definicji powierzchni bocznej obiektu !).
- Definicja pośrednia.
- Praktycznie funkcjonuje jako interfejs użytkownika (w środowisku aplikacji opis przekształcony w reprezentację CSG lub B-rep).
- Problem z opisem geometrii oraz opisem manipulacji obiektem.
6.6. Podział przestrzeni
Podział przestrzeni jest sposobem opisu polegającym na rozkładzie obiektu na elementy składowe, prostsze.
Woksel (voxel) jest najmniejszym elementem przestrzeni 3D (analogicznym do piksela na płaszczyźnie). Wokselowi można przypisać właściwości obiektu/powierzchni:
- położenie (zajętość przestrzeni),
- barwa,
- właściwości refleksyjne (odbicie, przenikanie światła),
- inne (temperatura, właściwości mechaniczne).
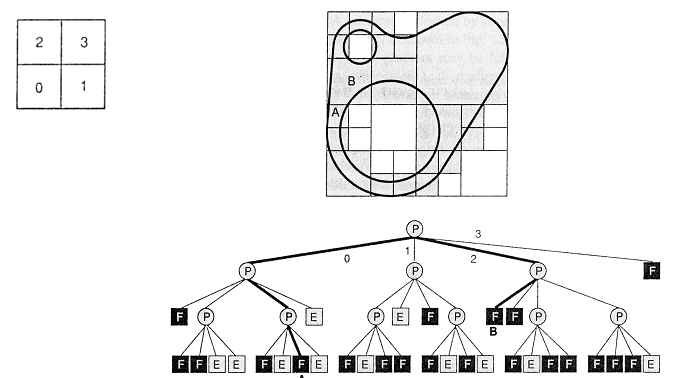
Rys.6.12. Wskazanie
przynależności fragmentów przestrzeni do obiektu
na
płaszczyźnie za pomocą hierarchii 2D : każdy element w
drzewie może być:
F = full (należy
całkowicie), P = partially full
(należy częściowo),
E = empty (nie należy). Rysunki na podstawie
[1].
Można zdefiniować obiekt wskazując, które woksele on zajmuje: reprezentacja przez wskazanie (enumerated representation). Taka reprezentacja jest dekompozycją na komórki, które tworzą regularną siatkę w przestrzeni. Podstawową cechą reprezentacji tego typu jest aproksymacja kształtu z zadaną rozdzielczością. Struktura danych opisująca tak dekomponowaną bryłę będzie listą zajętych komórek.
Podobny efekt można uzyskać strukturą hierarchiczną – drzewem ósemkowym (rys.6.13) wskazując w przestrzeni kolejne prostopadłościenne elementy będące wielokrotnością woksela. W tym przypadku jednak struktura danych (drzewo ósemkowe) da efektywniejszy sposób zapisu (mniejszy koszt pamięciowy). Natomiast aproksymacja kształtu z zadaną rozdzielczością wokselową będzie identyczna. Porównanie różnych podziałów dla tego samego obiektu 2D przedstawiono na rysunku 6.14.
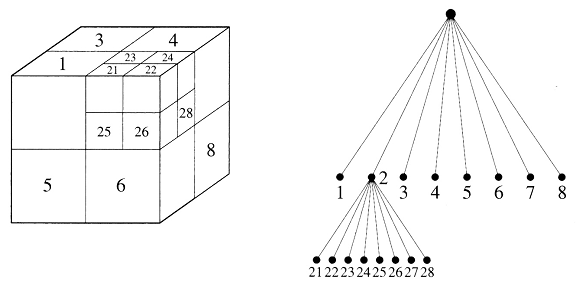
Rys.6.13. Przestrzenne drzewo przynależności: Hierarchia 3D.
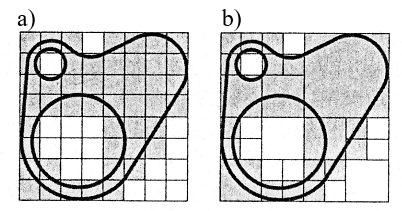
Rys.6.14. Realizacja dwóch różnych podziałów przestrzeni
dla tego samego obiektu 2D:
a) podział równomierny (reprezentacja
przez wskazanie,
b) hierarchia 2D – drzewo czwórkowe. Rysunki na podstawie [1].
Alternatywą dla drzewa ósemkowego mogłoby być drzewo podziału binarnego (ang. BSP tree – binary space partitioning tree), w którym na każdym etapie podziału można wskazać którą półprzestrzeń reprezentuje dany fragment obiektu. Drzewa tego typu nie są jednak stosowane jako samodzielne systemy modelowania. Są natomiast wykorzystywane w algorytmach eliminacji elementów zasłoniętych.
Przechowywanie informacji o budowie obiektu w reprezentacji typu podział przestrzeni prowadzi do problemów zajętości pamięci. Dla podziału N x N x N uzyskujemy złożoność pamięciowa O(N3). Podział 1000x1000x1000 prowadzi do zapamiętania informacji o 1 miliardzie wokseli, a dla każdego może być potrzebna informacja o jego właściwościach.
Warto zwrócić uwagę na aproksymację kształtu obiektu, która zawsze ma miejsce w reprezentacjach realizowanych podziałem przestrzeni (w reprezentacjach wokselowych). Oczywiście błędy aproksymacji maleją ze zmniejszaniem rozmiarów wokseli ale pociąga to za sobą wzrost liczby elementów (lub zwiększanie głębokości drzewa podziału), a tym samym wzrost zajętości pamięci.
Podział przestrzeni daje możliwość stosunkowo prostej realizacji operacji boolowskich. W przypadku reprezentacji przez wskazanie (enumerated representation) należy porównać położenie i zrealizować operację boolowską na poziomie Voxel – Voxel. W przypadku hierarchii (drzewa ósemkowego) należy porównać położenie i zrealizować operację na poziomie region – region. Warto podkreślić, że podczas realizacji operacji boolowskich dla podziału przestrzeni nie występuje problem regularyzacji.
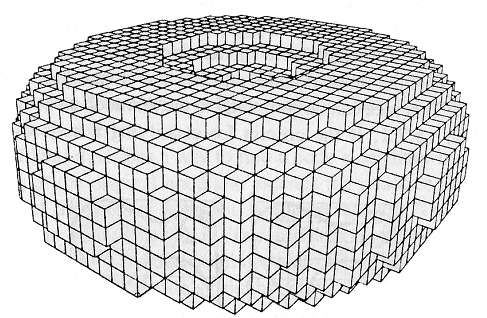
Rys.6.15. Torus reprezentowany przez podział przestrzeni.
Rysunek na podstawie artykułu A.Christensena SIGGRAPH 80.
Podstawowe właściwości podziału przestrzeni można scharakteryzować w następujący sposób.
- Zalety
- Jednoznaczne określenie regionu przestrzeni.
- Prosta struktura.
- Naturalna możliwość wprowadzania informacji.
- Praktycznie taka sama złożoność reprezentacji dla dowolnych obiektów.
- Możliwa realizacja operacji boolowskich.
-
Wady
- Problem aproksymacji kształtu powierzchni (!).
- Dość duże wymagania pamięciowe.
- Problem z opisem geometrii kształtu - i manipulacji tym opisem.
- Problemy z wizualizacją (brak bezpośredniej definicji właściwości wizualnych powierzchni !)
6.7. Porównanie reprezentacji
Podsumowując zaprezentowane sposoby reprezentacji obiektów można porównać ich podstawowe właściwości.
Dokładność.
Jeśli na scenie znajdują się obiekty wielościenne to reprezentacje wielościenne mogą dać dokładny opis obiektu. W pozostałych przypadkach tylko reprezentacja powierzchniowa z opisem kształtu za pomocą powierzchni Béziera, B-sklejanych, lub funkcji wymiernych może dać dobre przybliżenie kształtu. Z reguły mamy do czynienia z pewną aproksymacją zależną od wielu czynników np. od rozdzielczości siatki wokseli.
Dziedzina (zakres stosowania).
Podział przestrzeni może być stosowany do dowolnych obiektów, przy czym zawsze będzie istniał problem aproksymacji zależny od siatki wokselowej. Pozostałe metody reprezentacji mogą być stosowane do określonej klasy obiektów. Na przykład w konstruktywnej geometrii brył klasa reprezentowanych obiektów bardzo silnie zależy od zastosowanego zestawu prymitywów.
Jednoznaczność/unikatowość.
W zasadzie tylko podział przestrzeni za pomocą drzewa ósemkowego i reprezentacja wokselowa zapewniają unikatowośc reprezentacji w tym sensie, że istnieje tylko jeden zestaw wokseli reprezentujący dany obiekt. W pozostałych systemach modelowania istnieje wiele możliwości opisu tego samego obiektu. Szczególnym przypadkiem jest konstruktywna geometria brył gdzie dany obiekt można uzyskać nie tylko korzystając z różnych drzew, ale także z różnych zestawów prymitywów.
Poprawność.
Podział przestrzeni jest zawsze poprawny – zawsze uzyskamy poprawny fragment przestrzeni. Pytanie oczywiście czy jest to ten fragment o który chodziło konstruktorowi. W pozostałych przypadkach wymagane jest sprawdzenie czy wynik definiowania/operacji jest poprawnym obiektem w danej klasie. Najtrudniejsze do sprawdzenia są opisy reprezentacji powierzchniowej.
Efektywność.
Najprostsze w reprezentacji są metody wokselowe, gdyż pozwalają na szybkie manipulowanie takimi obiektami. Również konstruktywna geometria brył daje prosty nieprzetworzony (wymagający przetworzenia w trakcie np. rysowania) mechanizm, pozwalający dodatkowo na szybką modyfikacje obiektów.
6.8. Hierarchia w modelowaniu obiektów
Wiele obiektów wykazuje naturalne cechy budowy hierarchicznej (rys.6.16). Modelowanie takich obiektów z wykorzystaniem odpowiedniej hierarchi może ułatwić pracę nie tylko na etapie ich opisu i konstrukcji, ale na dalszych etapach obróbki danych np. w animacji.
Wykorzystanie hierarchii:
- Interakcja: można manipulować całą grupą prymitywów, niezależnie od metody konstrukcji.
- Efektywne wykorzystanie pamięci: definicja powtarzających się elementów może być reprezentowana/pamiętana jednokrotnie.
- Wspólne właściwości wizualne: można grupować dowolne atrybuty dla obiektów, barwy, przezroczystości, widoczności itp.
- Możliwość grupowania transformacji: grupy prymitywów mogą podlegać wspólnym transformacjom (np. obrót całej ręki robota).
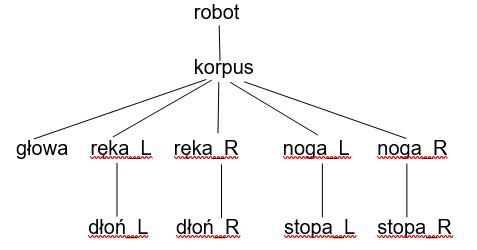
Warto również zwrócić uwagę na korzyści jakie niebezpośrednio może przynosić stosowanie hierarchicznej budowy obiektów. Ułatwia to konstrukcję złożonych, skomplikowanych obiektów w modularnej postaci poprzez przenoszenie pewnych cech z poziomu na poziom. Pozwala przenosić właściwości elementów przez całą strukturę obiektu. Takie wykorzystanie hierarchii prawie zawsze prowadzi do efektywniejszego gospodarowania pamięcią.
Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI
Rozdział siódmy jest poświęcony problemom modelowania krzywych i powierzchni. Problemom opisu kształtu za pomocą odpowiednich równań parametrycznych. Omówione zostały najczęściej stosowane metody reprezentacji krzywych i powierzchni: krzywe Béziera w postaci zwykłej i wymiernej, krzywe B-sklejane w postaci zwykłej i wymiernej oraz odpowiadające tym reprezentacjom opisy powierzchni.
7.1. Wprowadzenie
Komputerowe wspomaganie projektowania jest dziedziną stosunkowo nową, ale szeroko wykorzystywaną przez różnych specjalistów. Różnorakie zastosowania wymagają definicji – opisu reprezentacji różnych obiektów. Z jednej strony typowe obiekty mechaniczne czy architektoniczne, z drugiej efekty specjalne filmów science fiction, gdzie jedynym ograniczeniem jest wyobraźnia twórców. Z drugiej strony systemy wspomagania projektowania dają dodatkowe możliwości wykonywania wielu obliczeń związanych bezpośrednio z dziedziną zastosowania – obliczeń konstrukcyjnych czy wytrzymałościowych. Oczywiście grafika komputerowa daje możliwość zobaczenia projektu – możliwość wizualizacji wyobrażeń projektanta. Niezbędne staje się narzędzie do modelowania kształtu – obiektu, powierzchni. Warto zwrócić uwagę na fakt, że użytkownicy takich systemów reprezentują różne poziomy przygotowania informatycznego. System modelowania powinien być więc prosty i efektywny, powinien dawać możliwość definicji kształtu za pomocą minimalnej liczby parametrów, a modyfikacja kształtu powinna dotyczyć wybranego fragmentu, a nie całości krzywej czy powierzchni.
W latach sześćdziesiątych XX wieku w fabryce Renault rozpoczął pracę pierwszy system modelowania geometrycznego na użytek komputerowego wspomagania projektowania. Twórcą tego systemu był P. Bézier – będący jedną z najważniejszych postaci w tej dziedzinie. Dzisiaj każda fabryka samochodów projektuje kształty karoserii wykorzystując modelowanie geometryczne.
Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia.
7.2. Interpolacja
Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie
zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą
– najprościej wielomianową.
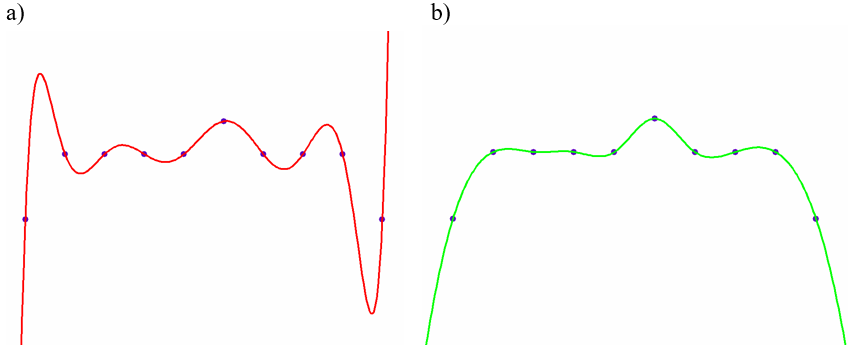
Rys.7.1. Próba modelowania kształtu z wykorzystaniem
interpolacji.
a) Krzywą wielomianową stopnia 9. b) Krzywymi sklejanymi stopnia 3.
Jeżeli dany jest ciąg parami różnych liczb t0, t1, t2, …tn – węzłów interpolacyjnych i odpowiadających im punktów P0, P1, P2,…Pn. To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:
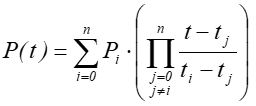
Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek 7.1 a). Dodatkowo każdy fragment krzywej zależy od położenia wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola kształtu krzywej pomiędzy węzłami jest trudna.
Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne.
7.3. Parametryzacja krzywych i powierzchni
Wiele krzywych
jest opisanych równaniem uwikłanym postaci ![]() . Taka reprezentacja nie daje możliwości kontroli konkretnego
fragmentu krzywej.
. Taka reprezentacja nie daje możliwości kontroli konkretnego
fragmentu krzywej.
Wygodnym sposobem opisu krzywych i powierzchni jest opis parametryczny.
Parametryczna
reprezentacja krzywych: ![]() .
.
Powierzchni: ![]() .
.
Za pomocą doboru wartości parametru można zdefiniować dowolny fragment krzywej,
a kierunek wzrostu parametru jednoznacznie określa np. kierunki stycznych
połączonych fragmentów.
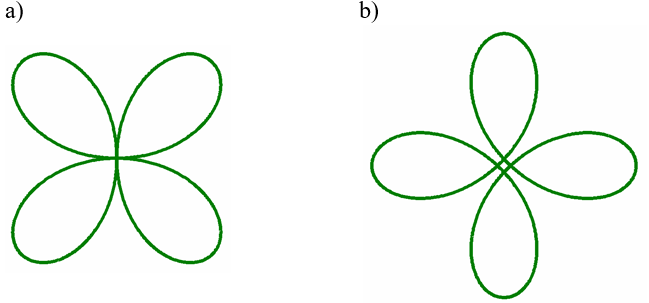
Rys.7.2. Czterolistna koniczyna. Różne reprezentacje parametryczne krzywej .
Przykładowa czterolistna koniczyna jest narysowana na rysunku 7.2 a w postaci rozety czterolistnej o reprezentacji parametrycznej:
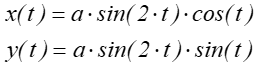 dla
dla 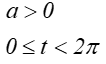
Na rysunku 7.2 b w postaci hipotrochoidy:
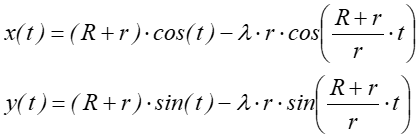 dla
dla 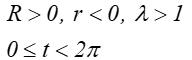
Często stosowany jest opis kształtu powierzchni obiektów wykorzystujący równanie drugiego stopnia. Powierzchnie drugiego stopnia to elipsoida, walec (cylinder), stożek, paraboloida eliptyczna, paraboloida hiperboliczna, hiperboloida jednopowłokowa, hiperbolida dwupowłokowa. Ich równanie uwikłane ma postać:
![]()
gdzie Q jest macierzą współczynników postaci 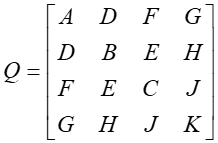
oraz 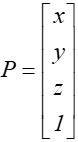
Przy czym dla każdej powierzchni drugiego stopnia jest znana reprezentacja
parametryczna. Przykładowa hiperboloida jednopowłokowa, zaprezentowana na
rysunku: 7.3, o równaniu uwikłanym postaci 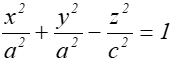 , została
przedstawiona parametrycznie jako:
, została
przedstawiona parametrycznie jako:
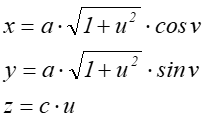 dla
dla ![]()
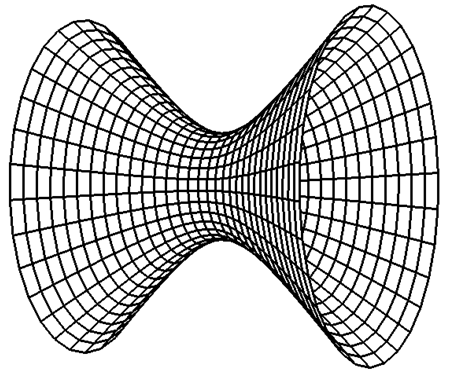
Rys.7.3. Hiperbola jednopowłokowa.
Zalety stosowania powierzchni drugiego stopnia:
- Możliwość łatwego wyznaczenia wektora normalnego
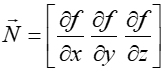 .
. - Możliwość szybkiego wyznaczenia przecięcia powierzchni z prostą – efektywność stosowania w algorytmach związanych z metodą śledzenia promieni.
- Możliwość szybkiego wyznaczenia z na podstawie x i y – przydatne w algorytmach eliminacji elementów zasłoniętych.
- Powierzchnia drugiego stopnia jest praktycznie użyteczna w wielu aplikacjach technicznych (wystarczająco skomplikowane kształty).
7.4. Krzywe Béziera
Krzywe Béziera są zdefiniowane w bazie wielomianów Bernsteina. Ich właściwości mają decydujący wpływ na właściwości krzywych.
Wielomiany Bernsteina są zdefiniowane w następujący sposób:
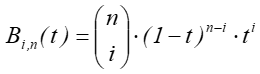 dla
dla ![]()
Podstawowe właściwości:
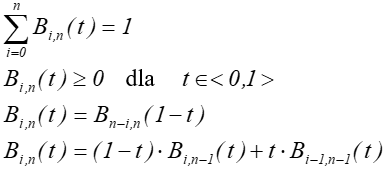

Rys. 7.4. Wykresy wielomianów Bernsteina 2, 3, 4 i 5 stopnia.
Ostatnia właściwość (zależność rekurencyjna) prowadzi do algorytmu wyznaczania punktów na krzywej bazującej na wielomianach Bernsteina.
Najczęściej mamy do czynienia z wielomianami stopnia 3. W tym przypadku:
![]()
Krzywą Béziera
opisuje następujące równanie parametryczne:
![]() punkty Beziera
punkty Beziera ![]()
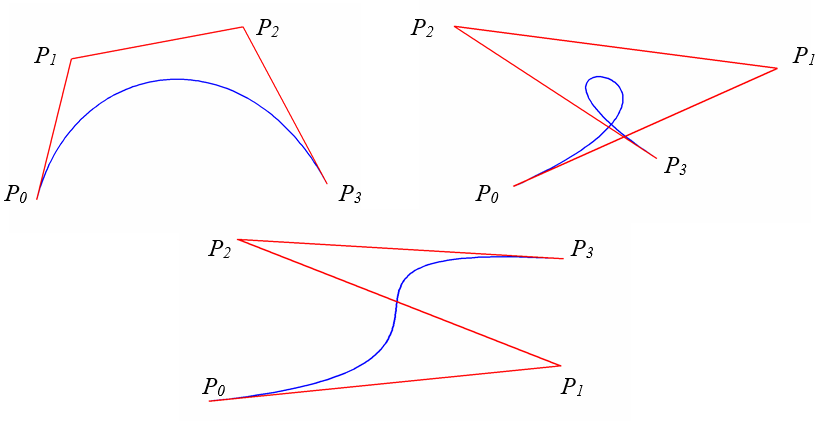
Rys. 7.5. Przykłady krzywych Béziera
Krzywa Béziera zawdzięcza swą nazwę Pierre’owi Bézierowi, warto jednak pamiętać, że rozwiązanie to miało dwóch niezależnych twórców. Drugim był P. de Casteljau. Jego nazwiskiem został opatrzony podstawowy algorytm wyznaczania punktu krzywej.
Krzywa Béziera stopnia n jest definiowana przez n+1 punktów P0, P1, P2,…Pn w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. Użytkownicy komputerów spotykają się z nimi na co dzień w postaci fontów, których kształt jest najczęściej projektowany właśnie z wykorzystaniem krzywych Béziera stopnia 3.
Właściwości krzywych Béziera
- Końcowe wierzchołki łamanej P0 i Pn są jednocześnie końcowymi punktami krzywej.
-
Odcinki łamanej
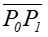 i
i 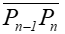 są styczne do krzywej.
są styczne do krzywej.
Krzywa Béziera zawiera się całkowicie w wielościanie wypukłym (wypukłej skorupce), którego wierzchołkami są wierzchołki łamanej.
Zmiana numeracji wierzchołków łamanej (od n do 0 zamiast od 0 do n) nie spowoduje zmiany kształtu krzywej.
Krzywa Béziera interpoluje dwa końcowe punkty kontrolne i aproksymuje pozostałe. Oznacza to, że dla krzywej stopnia 3 , jeśli ustalone są punkty końcowe (a tak jest najczęściej), to dwa pozostałe punkty decydują o kształcie.
Wady krzywych Béziera
- Brak możliwości reprezentacji krzywych stożkowych.
- Zmiana reprezentacji krzywej po rzutowaniu perspektywicznym.
Korzystając z właściwości rekurencyjnej wielomianów Bernsteina można wyznaczyć punkty krzywej Béziera algorytmem de Casteljau
Algorytm de Casteljau (rys. 7.6)
Wyznaczanie punktu leżącego na krzywej Béziera na podstawie ciągu punktów kontrolnych P0, P1, P2,…Pn
for i:= 0 to n do Pi,0 = Pi;
for j:=1 to n do
for i:=j to n do
Pi,j
:= (1-t).Pi-1,j-1
+ t.Pi,j-1;

Rys. 7.6. Algorytm de Casteljau. Wyznaczanie punktu leżącego na krzywej Béziera
Jeśli zadaniem jest wyznaczenie dużej liczby punktów leżących na krzywej Béziera to tańszym obliczeniowo rozwiązaniem będzie przejście w wielomianach Bernsteina do postaci naturalnej wielomianu i obliczanie jego wartości algorytmem Hornera.
Łączenie krzywych BézieraŁączenie segmentów krzywej wymaga zwrócenia uwagi na problem ciągłości. Można wyróżnić różne rodzaje ciągłości łączenia segmentów oraz kryteria z tym związane:
Ciągłość geometryczna: definiowana na podstawie właściwości kierunku (tylko !) wektora stycznego :
G0: początek jednego segmentu końcem drugiego,
G1: zgodne kierunki wektorów stycznych.
Ciągłość parametryczna: definiowana na podstawie ciągłości pochodnej odpowiedniego rzędu. (Cn – pochodna rzędu n). W praktyce najczęściej:
C0: początek jednego segmentu końcem drugiego,
C1: („prędkość”) zgodne kierunki wektorów stycznych,
C2: („przyspieszenie”) zgodność kierunków i długości wektorów stycznych.
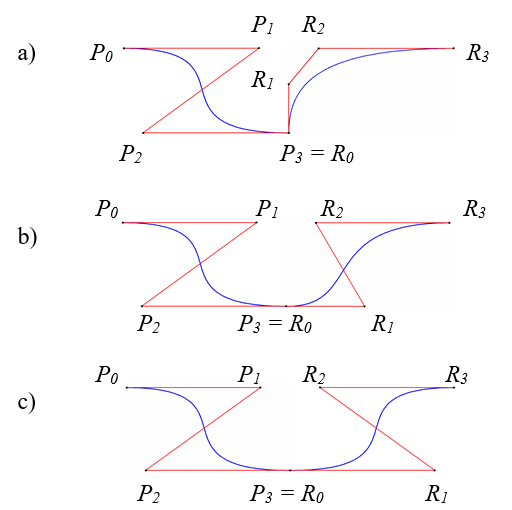
Rys.7.7.
Łączenie krzywych Béziera: a) bez zachowania ciągłości, b) z zachowaniem
ciągłości
geometrycznej, c) z zachowaniem ciągłości parametrycznej.
W praktyce rzadko kiedy używa się krzywych Béziera wysokiego stopnia. Ponieważ każdy punkt krzywej Béziera zależy od wszystkich punktów kontrolnych, więc w takiej sytuacji trudno byłoby kontrolować kształt krzywej. O wiele prościej jest złożyć całą krzywą z fragmentów, każdy niskiego stopnia.
Rozpatrzmy dwa segmenty krzywych (rys.7.7) P0 , P1 , P2 , P3 i R0 , R1 , R2 , R3 , połączone w punkcie P3 = R0 .
Jeżeli punkty P2 , P3 = R0 , R1 są współliniowe mówimy o ciągłości geometrycznej G1 krzywej (rysunek 7.7 b).
Jeżeli punkty P2 , P3 = R0
, R1 są współliniowe i sąsiednie odcinki łamanej są równej
długości
odległość ( P2 , P3) = odległość (R0 , R1)
to mówimy o ciągłości parametrycznej C1 krzywej (rysunek 7.7 c).
Wymierna Krzywa Beziera opisana jest w sposób następujący:
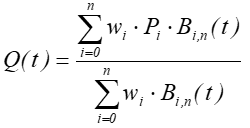 dla
dla gdzie Pi punkty Beziera natomiast wi wagi tych punktów. Wartość wagi wpływa na kształt krzywej niezależnie od położenia punktu kontrolnego.
Krzywe wymierne Béziera opisane są w przestrzeni jednorodnej. Oznacza to, że analogicznie do przekształceń geometrycznych opisanych macierzowo w przestrzeni jednorodnej, krzywe płaskie będą opisane w R3, natomiast krzywe trójwymiarowe będą opisane w przestrzeni R4.
Krzywa taka ma następujące cechy:
- Dana krzywa może mieć nieskończenie wiele reprezentacji we współrzędnych jednorodnych. Pomnożenie wszystkich wag przez tę samą stałą różną od zera nie zmienia krzywej.
- Krzywa wymierna jest uogólnieniem krzywej wielomianowej. Dla równej wartości wszystkich wag otrzymujemy krzywą wielomianową Béziera.
- Jeśli wszystkie wagi są tego samego znaku (wszystkie dodatnie lub wszystkie ujemne), to punkty krzywej leżą w wypukłej otoczce zbioru punktów kontrolnych.
- Jeśli w0 ≠ 0 to P(0)=P0 oraz jeśli wn ≠ 0 to P(1)=Pn .
- Konstrukcja krzywej wymiernej jest niezmiennicza afinicznie. Krzywa wyznaczona na podstawie ciągu punktów kontrolnych jest taka sama jak krzywa wyznaczona na podstawie ciągu punktów kontrolnych poddanych przekształceniom afinicznym.
- Zmieniając odpowiednio wagi można uzyskać wszystkie krzywe stożkowe. Ta cecha była nieosiągalna w przypadku krzywych wielomianowych Béziera.
Analogicznie do zwykłej krzywej Béziera, dla krzywej wymiernej istnieje wymierny algorytm de Casteljau wyznaczania punktu na krzywej. Opis algorytmu można znaleźć w książce P.Kiciaka [5].
Dla trzech niewspółliniowych punktów P0 , P1 , P2 jeśli w0=w2=1 , to waga w1 określa rodzaj krzywej stożkowej :
w1 =1 - łuk paraboli (krzywa wielomianowa)
0<w1 <1 - krótszy łuk elipsy (lub okręgu)
w1 =0 - odcinek
-1 <w1 <0 - dłuższy łuk elipsy (lub okręgu)
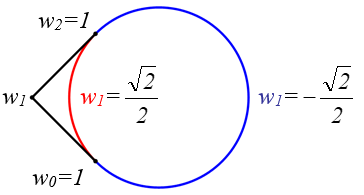
Rys. 7.8. Okrąg reprezentowany w postaci dwóch krzywych wymiernych Béziera.
7.5. Krzywe B-sklejane
Krzywa
B-sklejana jest definiowana jako kombinacja liniowa funkcji sklejanych ![]() o współczynnikach
odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są
przedziałami stopnia m, co nie jest
związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to
rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście
przedziałami w tym przypadku) od liczby punktów kontrolnych.
o współczynnikach
odpowiadających punktom kontrolnym (punktom de Boora). Funkcje sklejane są
przedziałami stopnia m, co nie jest
związane z liczbą punktów tak jak w przypadku krzywych Béziera. Oznacza to
rzeczywiście uniezależnienie stopnia wielomianu opisującego krzywą (oczywiście
przedziałami w tym przypadku) od liczby punktów kontrolnych.
Krzywa B-sklejana opisana jest jako:
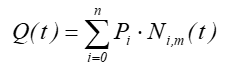
punkty kontrolne Pi nazywane są punktami de Boora.
Funkcje sklejane ![]() określa się
rekurencyjnie:
określa się
rekurencyjnie:
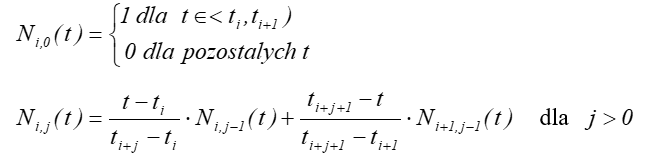
Funkcje
sklejane ![]() są przedziałami
wielomianami i mają następujące właściwości:
są przedziałami
wielomianami i mają następujące właściwości:
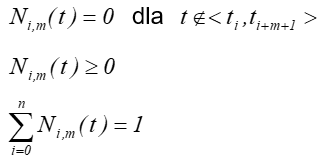
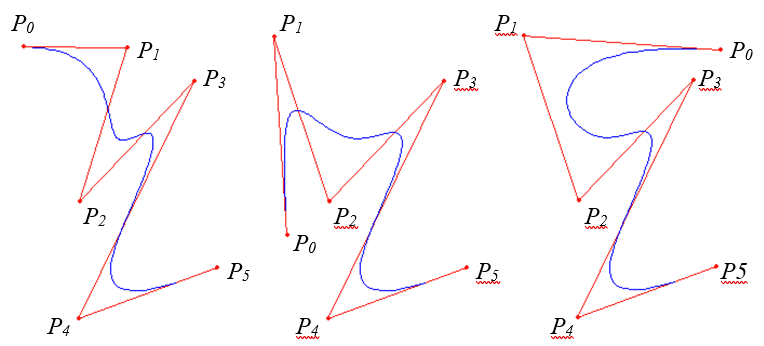
Rys.7.9. Przykłady
krzywych B-sklejanych. Zmiana położenia
punktów kontrolnych P0 i P1 powoduje
lokalne (tylko !) zmiany kształtu krzywej. Nie wpływa to na
kształt pozostałej części krzywej.
Zakłada się, że węzły ti są uporządkowane niemalejąco tzn. ti ≤ ti+1 co oznacza, że mogą istnieć równe węzły (wielokrotne). Przyjmuje się wtedy, że 0/0=0. Takie założenia generalnie definiują krzywą dla węzłów które nie musza być równoodległe. Jednocześnie możliwość dodania (wstawienie) węzła pomiędzy dwa już istniejące, lub zwielokrotnienia węzła daje dodatkowe możliwości wpływania na kształt krzywej. Czasami jednak rozpatruje się krzywe o węzłach równoodległych.
Istnieje algorytm de Boora i Coxa wyznaczania punktów krzywej B-sklejanej (analogiczny do algorytmu de Casteljau dla krzywej Béziera) [3]. Jeśli wyznaczanych jest wiele punktów krzywej to tańszym rozwiązaniem będzie obliczenie współczynników postaci naturalnej wielomianu w kolejnych podprzedziałach i skorzystanie z algorytmu Hornera.
Właściwości krzywych B-sklejanych
Pierwsza właściwość – zerowanie funkcji sklejanej poza przedziałem ![]() jest bardzo istotna
dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów (rys.7.9).
Rozpatrzmy podprzedział
jest bardzo istotna
dla modelowania kształtu. Oznacza bowiem lokalność wpływu parametrów (rys.7.9).
Rozpatrzmy podprzedział ![]() dla
dla ![]() niezerowe są tylko funkcje
niezerowe są tylko funkcje ![]() o indeksach i=j-m, j-m+1, j-m+2, j . W takim przedziale wartość Q(t) , a tym samym kształt krzywej,
zależy tylko od punktów kontrolnych Pj-m
, Pj-m+1 , Pj-m+2 , … Pj . Z drugiej strony
punkt kontrolny Pi wpływa
jedynie na fragment krzywej odpowiadający
o indeksach i=j-m, j-m+1, j-m+2, j . W takim przedziale wartość Q(t) , a tym samym kształt krzywej,
zależy tylko od punktów kontrolnych Pj-m
, Pj-m+1 , Pj-m+2 , … Pj . Z drugiej strony
punkt kontrolny Pi wpływa
jedynie na fragment krzywej odpowiadający ![]() .
.
Indeks j zmienia się od 0 do m , natomiast i od 0
do n . Cały zakres takiej krzywej
definiują więc węzły: ![]() . Ale danych jest n+1 punktów kontrolnych (de Boora).
Punkty P0 , P1, P2 , … Pm definiują krzywą dla
. Ale danych jest n+1 punktów kontrolnych (de Boora).
Punkty P0 , P1, P2 , … Pm definiują krzywą dla ![]() , natomiast punkty Pn-m, Pn-m+1, Pn-m+2,…Pn definiują krzywą dla
, natomiast punkty Pn-m, Pn-m+1, Pn-m+2,…Pn definiują krzywą dla ![]() . Węzły
. Węzły ![]() oraz
oraz ![]() nazywane są węzłami
brzegowymi. Jeśli krzywa jest otwarta, to znaczy
nazywane są węzłami
brzegowymi. Jeśli krzywa jest otwarta, to znaczy ![]() , i
, i ![]() oraz
oraz ![]() to krzywa przechodzi
przez końcowe punkty kontrolne, czyli
to krzywa przechodzi
przez końcowe punkty kontrolne, czyli ![]() .
.
Podobnie jak było w przypadku krzywych Béziera, styczne do krzywej w punktach końcowych mają kierunek końcowych odcinków łamanej kontrolnej. Dla krzywej zamkniętej przyjmuje się, że punkty de Boora i węzły kontrolne są cykliczne (Pn=P0).
Jest spełniony warunek wypukłej skorupki (krzywa zawiera się całkowicie w wypukłej skorupce zbudowanej na punktach kontrolnych), ale tylko w sąsiedztwie punktów !
Wymierne krzywe B-sklejane (NURBS)Wymierne krzywe B-sklejane (ang. Non-Uniform Rational B-Splines) to rozwiązanie, które łączy zalety krzywych Béziera i krzywych B-sklejanych. Krzywe te opisane są w sposób następujący:
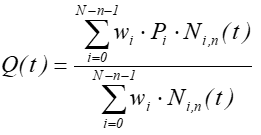
Punkty Pi (de Boora ) są punktami kontrolnymi, wi są wagami tych punktów.
- Krzywe wymierne dają możliwość wykreślenia dowolnej krzywej stożkowej.
- Konstrukcja wykorzystująca funkcje sklejane pozwala opisywać krzywą wielomianami, których stopień jest niezależny od liczby punktów kontrolnych.
- Wpływ punktu kontrolnego na kształt krzywej istnieje tylko w zakresie lokalnym.
- Dodatkowo wagi każdego punktu kontrolnego pozwalają na precyzyjne zmiany kształtu krzywej (też lokalnie).
- Krzywe wymierne są niezmiennicze względem przekształceń obrotu, skalowania i przesunięcia oraz przekształcenia perspektywicznego punktów kontrolnych.
7.6. Modelowanie powierzchni
Powierzchnię określa się jako produkt iloczynu tensorowego. Rodzaj powierzchni i jej właściwości będą zależały od tego jaka baza funkcji zostanie wykorzystania.
Jeśli jako funkcje bazowe przyjmiemy wielomiany Bernsteina, to otrzymamy powierzchnie Béziera.
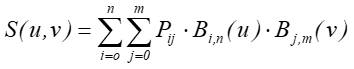
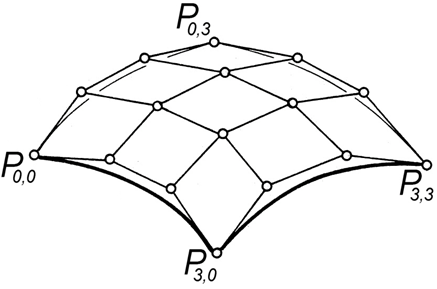
Rys.7.10. Siatka punktów kontrolnych opisująca powierzchnię Beziera. Rysunek na podstawie [1].
Jeśli jako funkcje bazowe przyjmiemy funkcje sklejane, to otrzymamy powierzchnie B-sklejane.
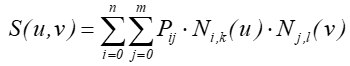
Właściwości powierzchni są analogiczne do właściwości krzywych konstruowanych z wykorzystaniem tych samych funkcji bazowych. Z drugiej strony przyjmując stałość jednego parametru (u lub v) otrzymujemy krzywą (rodzinę krzywych dla różnych wartości parametru
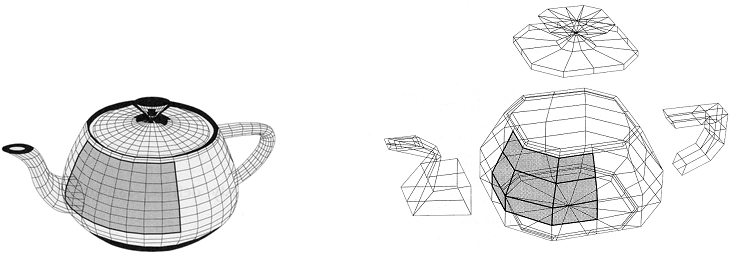
Rys.7.11. Czajnik z Utah i siatka punktów kontrolnych.
Obiekt jest modelowany jako zbiór 32 płatów Béziera.
Kształt przykładowego
ciemniejszego fragmentu (płata) jest kontrolowany
przez zaznaczony fragment siatki węzłów. Na
podstawie [7].
Podczas modelowania powierzchni warto zwrócić uwagę na zalety możliwości lokalnej kontroli kształtu. Zarówno przy wykorzystaniu powierzchni B-sklejanych (gdzie lokalna kontrola jest jedną z podstawowych cech reprezentacji), jak i przy składaniu powierzchni całego obiektu z płatów (np. Beziera jak na rys.7.11).
a
7.7. Przykłady innych sposobów modelowania krzywych i powierzchni
Przedstawione tutaj sposoby modelowania kształtu krzywej i powierzchni należą do najbardziej uniwersalnych i najczęściej stosowanych.. Istnieje jednak wiele innych reprezentacji.
Wykorzystując bazę wielomianów Hermite’a otrzymamy krzywe i powierzchnie Hermite’a.
Płaty Coonsa są definiowane za pomocą czterech krzywych brzegowych mających wspólne punkty narożne oraz interpolacji między nimi.
Powierzchnie Gordona są uogólnieniem płatów Coonsa,. definiują powierzchnię za pomocą dwóch wzajemnie przecinających się rodzin krzywych.
Stosowane jest również modelowanie kształtu powierzchni w oparciu o fragmenty trójkątne. Zarówno w postaci powierzchni Béziera jak i B-sklejanej.
7.8. Modelowanie przez deformację
Modelowanie kształtu może być procesem wieloetapowym. Obiekt uzyskany wcześniej można poddać dodatkowym deformacjom (uzyskując pożądany efekt (rys.7.10). Deformacje mogą być nieliniowe, niezależne od reprezentacji obiektu i niezależne od dotychczasowego modelowania kształtu.
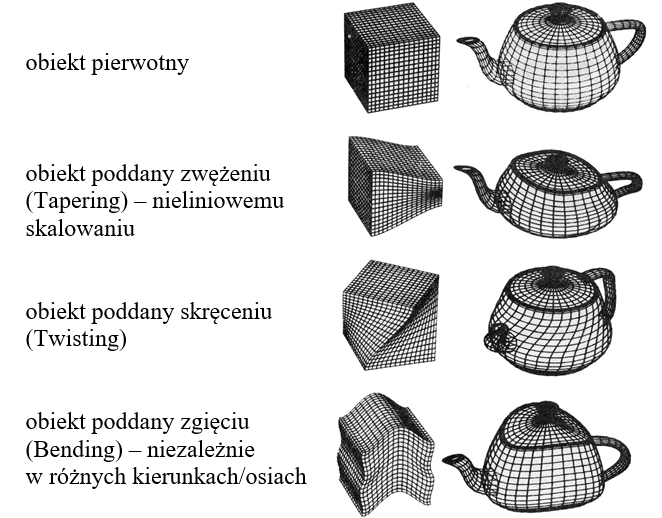
Rys.7.12. Modelowanie przez deformacje. Na podstawie [8].
Rozdział 8. MODELOWANIE OBIEKTÓW NATURALNYCH. MODELOWANIE FRAKTALNE I WOLUMETRYCZNE
Rozdział ósmy zawiera informacje dotyczące modelowania obiektów, których opis analityczny jest trudny lub niemożliwy. Omówione zostały takie techniki jak modelowanie fraktalne, wykorzystanie gramatyk oraz modelowanie wolumetryczne.
8.1. Wprowadzenie
Rośliny, chmury, mgła czy inne obiekty naturalne występują bardzo często w reklamach, filmach animowanych lub w postaci różnych efektów specjalnych generowanych na potrzeby kinematografii. Z jednej strony obiekty te są bardzo dobrze znane odbiorcom – człowiek ma z nimi na co dzień do czynienia. Stwarza to potrzebę osiągnięcia na tyle wiernego wyglądu aby nie wzbudzało to wątpliwości u oglądającego. Z drugiej strony praktycznie żadnego z tych obiektów nie da się opisać ani prostym równaniem matematycznym, ani zamodelować złożoną techniką projektowania kształtu powierzchni tak jak się to robi w przypadku np. karoserii samochodu. Trudno byłoby również modelować mgłę czy rośliny stosując modelowanie brzegowe wielościenne czy budując odpowiednie drzewa CSG. Obiekty naturalne wymagają zupełnie innego podejścia. Najczęściej stosuje się modelowanie fraktalne i wolumetryczne oraz wiele złożonych metod wykorzystujących różne techniki graficzne. Z drugiej strony warto pamiętać, że techniki fraktalne, najczęściej kojarzone z modelowaniem obiektów naturalnych, są stosowane także w przetwarzaniu obrazów w kompresji fraktalnej.
8.2. Samopodobieństwo

Rys.8.1. Przykłady
samopodobieństwa: a) paprotka, b) Różyczka brokułu (brassica oleracea)
tworząca fraktal
- zdjęcie Jona Sullivana udostępnione w Wikimedii jako public domain,
c)
fraktal – zbiór Mandelbrota.
Wiele obiektów naturalnych (rośliny, formy skalne, linia brzegowa, zbocza gór itp.) a także sztucznych (np. polimery) ma cechę samopodobieństwa. Obrazy tych obiektów są podobne bez względu na skalę w jakiej, są oglądane.
Często klasyfikuje się to pojęcie
- Samopodobieństwo dokładne – mówimy o nim wtedy, kiedy występuje wierna kopia powiększonego lub pomniejszonego fragmentu. Taką cechę mają fraktale IFS.
- Quasi-samopodobieństwo – gdy występuje przybliżona kopia powiększonego lub pomniejszonego fragmentu. Charakterystyczne dla wielu fraktali definiowanych pewną zależnością rekurencyjną definiującą położenie punktów w przestrzeni.
- Samopodobieństwo statystyczne – tę cechę mają fraktale losowe.
Rysunek 8.1.c pokazuje
jeden z najbardziej znanych fraktali -
tak zwany zbiór Mandelbrota. Zbiór ten powstaje przez interpretację barwami
właściwości ciągu liczb zespolonych postaci ![]() .
.
8.3. Modelowanie fraktalne
Definicja fraktala zaproponowana przez Mandelbrota:
Fraktal to obiekt geometryczny, który:
- Ma cechę samopodobieństwa.
- Jest definiowany rekurencyjnie.
- Ma strukturę trudną do opisania (najczęściej) w ramach geometrii euklidesowej np. wzorem analitycznym.
- Ma (najczęściej) wymiar niebędący liczbą całkowitą.
Twórcą geometrii fraktalnej i samego pojęcia fraktal jest B.Mandelbrot - francuski matematyk polskiego pochodzenia. Przykładem najprostszym iteracyjnie generowanego fraktala jest tak zwana Śnieżynka Kocha zaproponowana przez H. von Kocha w 1904 roku. W każdym kroku iteracji każdy odcinek jest dzielony na trzy części (segmenty) po czym w miejsce jednego segmentu (środkowego) są wstawiane dwa segmenty tworząc z podstawą trójkąt równoboczny. Przy liczbie iteracji dążącej do nieskończoności otrzymuje się figurę, której każdy fragment jest zbudowany dokładnie na tej samej zasadzie (samopodobieństwo) i jednocześnie tak uzyskana krzywa ma nieskończoną długość oraz nie ma stycznej w żadnym punkcie.
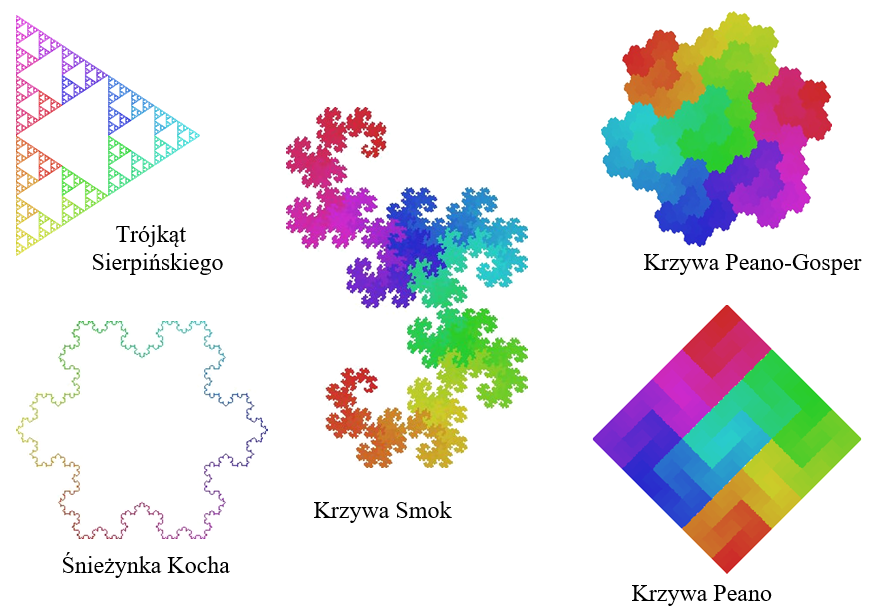
Rys.8.2. Przykłady fraktali definiowanych na płaszczyźnie. Rysunki M.Paterczyka © publikowane za zgodą Autora.
Rys.8.3. Przykłady fraktali definiowanych w przestrzeni
3D.
Rysunki: Solkoll udostępnione w Wikimedii jako public domain.
Problemem pozostaje wymiar takiej krzywej. Dla fraktali określa się wymiar Hausdorffa. F.Hausdorff – matematyk niemiecki zaproponował pojęcie wymiaru jako miarę wzrostu liczby kul (lub kół na płaszczyźnie) o promieniu e potrzebnych do pokrycia danego zbioru przy e dążącym do zera. Wymiar Hausdorffa nigdy nie jest mniejszy niż wymiar topologiczny danego zbioru. Dla fraktali jest liczbą ułamkową. Śnieżynka Kocha (rys.8.2) ma wymiar d=ln4/ln3=1,2618…
Układ funkcji iterowanych
Metryka Hausdorffa określa odległości między zbiorami.
Jeśli rozpatrzymy dwa zbiory A i B, to odległością d(a,B) punktu a ze zbioru A od zbioru B jest najmniejsza odległość spośród odległości tego punktu od wszystkich punktów zbioru B. Odległością d(A,B) zbioru A od zbioru B jest to największa odległość spośród odległości punktu zbioru A od zbioru B.
Metryka Hausdorffa h(A,B) jest określona wyrażeniem: h(A,B)=max(d(A,B), d(B,A))
Atraktory rozpatrywane są w przestrzeni metrycznej zupełnej, w której obowiązuje metryka Hausdorffa.
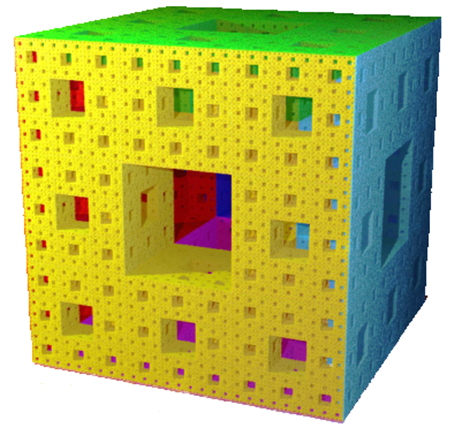
Rys.8.4. Kostka Mengera – przykład atraktora IFS.
Rysunek: Solkoll udostępniony w Wikimedii jako public domain
Bardzo trudno byłoby klasycznymi metodami modelowania (np. CSG lub reprezentacja powierzchniowa) wygenerować obrazy roślin – gałęzi, liści itp. Elementy roślin zachowują samopodobieństwo i podlegają pewnym regułom związanym z rozwojem - wzrostem rośliny. A.Lindenmayer zaproponował w 1969 roku sposób opisu wzrostu oparty na prostych regułach gramatycznych. Taki sposób opisu został nazwany L-systemem lub L-układem. System ten był później rozwijany, między innymi przez A.R.Smitha i P.Prusinkiewicza.
L-systemy służą, przede wszystkim, do opisu wzrostu roślin, kreowania elementów roślinnych, „drzewopodobnych”, korzeni, liści itp. Jest to metoda oparta o aksjomat (pewien ciąg wyjściowy; początkowy) oraz regułę produkcji, która opisuje sposób postępowania w każdej iteracji. Paprotka Barnsleya jest chyba najbardziej znanym przykładem wykorzystania gramatyk do modelowania roślin.

Rys.8.5. Paprotka Barnsleya.
Kolejne kroki budowy obiektu definiowane są zgodnie z zestawem operacji elementarnych. Podstawowy zestaw wprowadzony przez P. Prusinkiewicza wraz z przykładem notacji rozszerzonej przedstawiono w Tabeli 8.1. Na tej samej zasadzie można opisać grafikę żółwia rozkładając ruch pióra na proste reguły sterowania.

(*)Paterczyk M.,
Sawicki D.: Grammar systems for 3d
objects modeling,
Monograph „Computer
Applications in Electrical Engineering”, Politechnika Poznańska 2008, ss.24-31.
W opisie reguł produkcji można także wykorzystać takie atrybuty jak długość i szerokość odcinka czy barwę. Pozwala to dość swobodnie definiować reguły wzrostu.
Warto zwrócić uwagą na fakt, że również fraktale takie jak śnieżynka Kocha czy dywan Sierpińskiego można wygenerować za pomocą L-systemu.
Na przykład dla śnieżynki Kocha z rysunku 8.6 (dla pojedynczego boku startowego trójkąta !)
reguła produkcji: F -> F-F++F-F
gdzie F oznacza ruch do przodu z rysowaniem, - oznacza obrót w lewo o zadany kąt α , + oznacza obrót w prawo o zadany kąt a. Dla śnieżynki Kocha a wynosi 60 stopni.
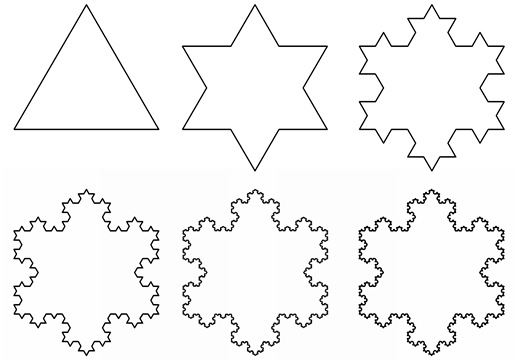
Rys.8.6. Śnieżynka Kocha. Kolejne iteracje.
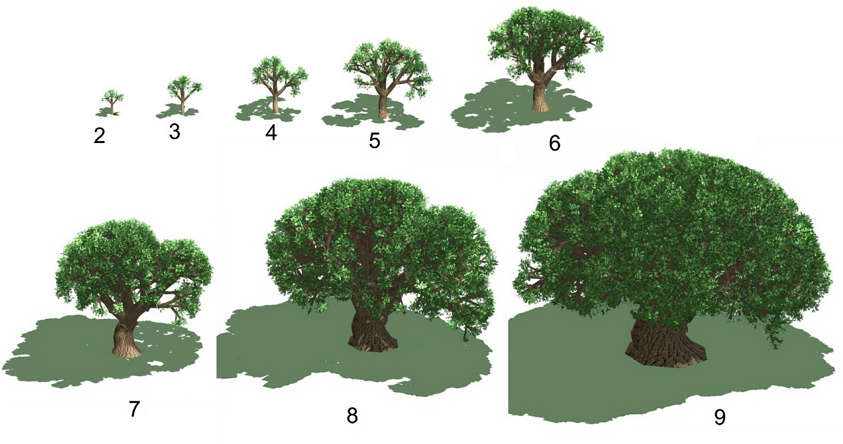
Rys.8.7. Kolejne etapy wzrostu dębu. Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.
Powstanie L-Systemów związane było z badaniami nad rozwojem organizmów. Tak budowane fraktale znakomicie nadają się do symulacji wzrostu roślin. Rysunek 8.7. pokazuje przykład modelowania wzrostu drzewa: kolejne iteracje odpowiadające kolejnym etapom wzrostu. Warto zwrócić uwagę na fakt, że taki sposób modelowania nie daje możliwości symulacji ciągłego wzrostu (przyrostu) roślin – wzrost jest ściśle związany z kolejnymi iteracjami. A to daje możliwość pokazania określonych stanów rozwoju.
L-system można niezależnie uzupełnić o dodatkowe zasady „obowiązujące” roślinę w trakcie wzrostu. Pozwala to symulować naturalne zjawiska takie jak tropizm (naturalne kierowanie się rośliny w kierunku słońca) i geotropizm (reakcja wzrostowa roślin na siłę ciężkości) – rysunek 8.8.b.
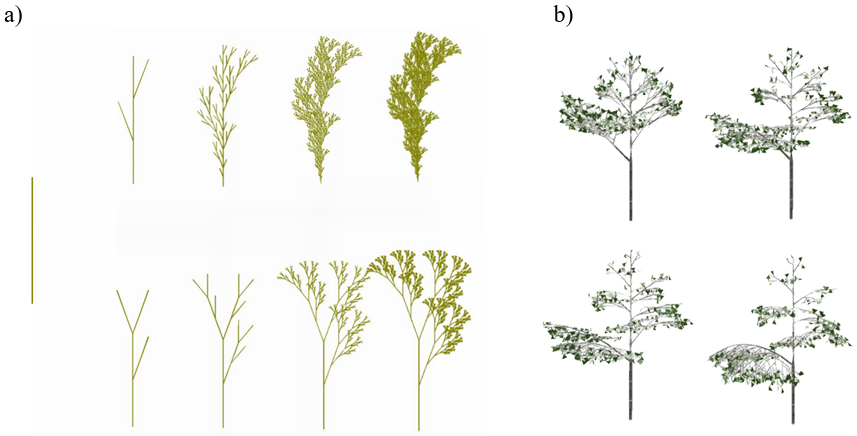
Rys.8.8. Przykład modelowania z wykorzystaniem gramatyk.
a)
Modelowanie gałązki żywotnika – ten sam aksjomat ale różne reguły produkcji.
b)
Wpływ geotropizmu na wzrost i wygląd roślin.
Rysunki Agnieszka Ziemianek ©
rysunki za publikowane za zgodą Autorki.
Pierwotne języki równoległych gramatyk grafowych zostały przez Lindenmayera rozszerzone o dodanie nawiasów (różnych, co daje możliwość rozróżnienia operacji) pozwalających na zagnieżdżanie operacji z wykorzystaniem stosu. L-System odpowiada formalnie gramatyce bezkontekstowej w hierarchii Chomsky’ego. Podstawowa różnica między L-Systemem a gramatyką Chomsky’ego: w L-Systemie produkcja jest stosowana „równolegle” (np. jednocześnie zamienia wszystkie odpowiednie odcinki na krótsze), a nie sekwencyjnie.
8.4. "The Fractal Geometry of Nature"
Fraktale
stosuje się w grafice komputerowej przede wszystkim do modelowania kształtu
obiektów naturalnych wykazujących samopodobieństwo. Pozwalają kreować
nieregularne kształty roślin, (rzeźby) terenu, muszli, śniegu, efektów
atmosferycznych, itd., itp. Tytuł tego rozdziału został zaczerpnięty z książki
B.Mandelbrota [2]. Łączenie różnych metod modelowania z modelowaniem fraktalnym
daje możliwość uzyskania obiektów o kształtach zbliżonych lub bardzo podobnych
do obiektów naturalnych. Trudno jest jednak mówić o regułach takiego
modelowania czy projektowania obiektów, gdyż ze względu na różnorodność
kształtów występujących w naturze zasady modelowania są dobierane indywidualnie
do danego przypadku. Przykładem może być modelowanie krajobrazu. Fourier,
Fussel i Carpenter zaproponowali zastosowanie iteracyjnego podziału do
generowania fraktalnej góry. Jeśli podstawę góry będziemy dzielić
systematycznie na pół, to po odpowiedniej liczbie iteracji uzyskamy punkty o
zadanej dokładności. Wysokość dla każdego punktu podziału określa się na
podstawie wysokości punktów poprzedniego kroku iteracji oraz pewnej funkcji
zaburzenia, można też użyć parametrów terenu (mapy). W zależności od przyjętej
funkcji zaburzenia można w ten sposób otrzymać odpowiedni charakter zmian
wysokości (łagodne pagórki lub ostre szczyty).

Rys.8.9. „Wyspa Mandelbrota” przykład zastosowania technik
fraktalnych do modelowania
obiektów o wyglądzie zbliżonym do naturalnych.
Rysunek opracowany przez Prokofiev
i udostępniony w Wikimedii na licencji Creative Commons.
Można zaproponować prosty schemat generacji
rzeźby terenu (rys.8.10):
- Zdefiniować siatkę.
- W każdym węźle określić wysokość używając parametrów terenu (mapy) oraz/lub wartości losowych.
- Wygenerować nowe węzły – pośrednie (zagęścić siatkę) oraz określić ich wysokość (też mapa i/lub losowo).
- Sterując zakresem używanych wartości losowych określić kształt terenu (mniej lub bardziej płaski/pofałdowany).
Rys.8.10. Kolejne etapy modelowania rzeźby terenu.
Z WIkimedii jako Public Domain.

Rys.8.11. Góry fraktalne. Rysunek wygenerowany programem
Terragen
i udostępniony w Wikimedii na licencji Creative Commons.
Klasyczne modelowanie roślin z wykorzystaniem L-Systemu daje możliwość zachowania w pełni samopodobieństwa modelowanego obiektu. Jest to związane z powtarzalnością iteracji i pełną symetrią generowanych kształtów. Jest to oczywiście podstawową zaletą tego mechanizmu. Jednak w sytuacji obiektów naturalnych takie zachowanie nie zawsze jest pożądane. Bogactwo kształtów obiektów naturalnych zawsze wykracza poza przyjęty i dowolnie zaawansowany schemat, poza pełną symetrię i poza całkowitą powtarzalność iteracji. Kształty roślin zachowują samopodobieństwo, jednak w rzeczywistości zależą od bardzo wielu czynników (także losowych) i nigdy nie są w stu procentach powtarzalne. W pełni symetryczne rośliny wyglądają po prostu zupełnie nienaturalnie (rys.8.12.a). Mechanizm iteracyjnego modelowania kształtu obiektów naturalnych wymaga „naturalnego” zaburzenia symetrii. Dobrym rozwiązaniem jest dodanie elementu losowego w trakcie generowania obiektu w ramach L-Systemu (rys.8.12.b).
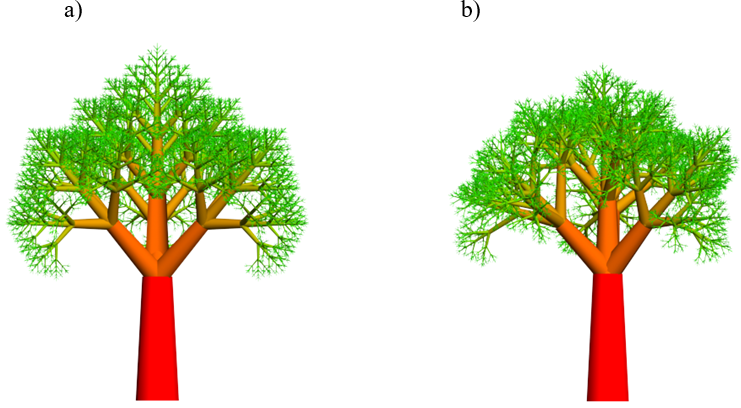
Rys.8.12. a) Nienaturalna symetria tradycyjnej generacji,
b) to samo drzewo po dodaniu wyboru losowego parametrów.
Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.

Rys.8.13. Obrazy liści i kory zastosowane do modelowania
dębu.
Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.
8.5. Modelowanie wolumetryczne
Modelowanie wolumetryczne jest próbą rozwiązania problemu modelowania i wizualizacji zjawisk, które nie dają się opisać w prosty sposób klasycznymi metodami, a które to zjawiska związane są z objętościowym rozproszeniem światła. Efekt taki powstaje zazwyczaj na skutek istnienia pewnego dodatkowego czynnika zmieniającego warunki rozchodzenia się światła. Przykładem może być mgła, chmury lub wydobywający się gaz.
Podobne efekty mogą powstawać przy przechodzeniu światła przez niejednorodne ośrodki półprzezroczyste np. powierzchnię morza.
Wykorzystując modelowanie wolumetryczne modeluje się przekroje na potrzeby prześwietleń w medycynie. Są to wizualizacje trójwymiarowego pola skalarnego. Dane uzyskane ze skanowania obiektów w tomografii komputerowej (Computer Tomography - CT), rezonansie magnetycznym (Magnetic Resistance Imaging - MRI), tomografii pozytronowej (Positron Emission Tomography - PET). Najczęściej jest to związane z wizualizacją trójwymiarowej funkcji pochłaniania promieniowania. Funkcja ta określona jest dla każdego punktu przestrzeni pokazując właściwości badanej tkanki. W symulacjach naukowych również często stosuje się wizualizacje pola trójwymiarowego wykorzystując dane z modeli matematycznych lub informacje uzyskane z przeprowadzonych eksperymentów.

Rys.8.14.
Przykład modelowania wolumetrycznego. Nocne szachy i nocne szachy z mgiełką.
Rysunki Łukasz Stelmach ©, POV-Ray.
Rysunki publikowane za zgodą Autora.
Wizualizacja zjawisk naturalnych jako pola skalarnego może obejmować naturalne zjawiska atmosferyczne takie jak np. mgła, deszcz, chmury. Zjawiska gazowe takie jak np. turbulencje powietrza, para, płomień.
Najczęściej w grafice komputerowej stosuje się następujące metody:
- Metody uproszczone. Wizualizacja za pomocą tekstur (dwuwymiarowych rzadziej trójwymiarowych). Wizualizacja za pomocą półprzepuszczalnych płaszczyzn (jednej lub kilku) z nałożonymi obrazami zjawiska. Metody te dają dobre efekty i są efektywnie obliczeniowo, ale związane są tylko z określonym kierunkiem patrzenia. Metody takie stosuje się do uproszczonego modelowania mgły i chmur oraz podobnych zjawisk (np. w grach komputerowych).
- Metoda próbek w przestrzeni (particle tracing) polegająca na umieszczeniu (zazwyczaj półprzezroczystych) elementów (kul, walców, sześcianów) w przestrzeni, mających rozpraszać światło – lub generalnie zmieniać warunki jego rozchodzenia się. Metodami takimi wizualizuje się chmury, mgłę i podobne zjawiska.
- Metoda analizy objętościowej. (volume rendering) polegająca na przypisaniu właściwości rozpraszających określonym punktom w przestrzeni. Jest to realizowane najczęściej w postaci wokselowej – każdy weksel ma określone parametry związane z przechodzeniem światła. Podczas śledzenia promieni wyznaczane są woksele na drodze promienia i ich parametry wpływają na barwę promienia. Analogicznie jest analizowane tak zwane światło wolumetryczne (volume light). Metody te stosuje się przede wszystkim w medycynie. Czasami stosuje się je do modelowania mgły lub chmur. Światło wolumetryczne pozwala symulować reflektory świecące we mgle, kurz unoszący się w powietrzu i rozpraszający światło w delikatny sposób, zadymione pomieszczenia.
- Metody uproszczonego opisu fizycznego zjawiska. Opis szumu trójwymiarowego i turbulencji, wykorzystanie szumu Perlina. Takie metody najczęściej stosuje się do wizualizacji płomienia, dymu, chmur, tworzenia efektu ognia i wybuchu. Metody te są często realizowane w postaci złożonej tekstury trójwymiarowej.
Aby uprościć zadanie modelowania wolumetrycznego stosuje się podział przestrzeni na komórki elementarne. Najczęściej wymaga się od komórek, aby były one wypukłe, minimalne (elementarne) na tyle, na ile pozwalają zobrazować oczekiwane szczegóły, niezależne w ramach podziału przestrzeni.
W zależności od celu wizualizacji, obiektu (pola skalarnego) oraz przyjętego uproszczenia można stosować różne rodzaje komórek:
- Sześcienne (woksele odpowiadające podziałowi równomiernemu w układzie współrzędnych).
- Regularne (prostopadłościenne).
- Regularne o zmiennych rozmiarach.
- „Strukturalne” (proste wielościany).
- „Niestrukturalne” (skomplikowane wielościany, piramidy).
- Hybrydowe (kombinacje powyższych).
Dobrym przykładem modelowania wolumetrycznego wykorzystującego najprostszy podział przestrzeni jest modelowanie chmur (rys.8.15). W zależności od kształtu chmury jej gęstości i barwy, wybierane są odpowiednie komórki przestrzeni, w których „znajduje się” chmura. Następnie przeprowadzane jest wygładzanie sąsiednich komórek w przestrzeni. Ostatni etap to wizualizacja z uwzględnieniem lokalnych zmian barwy komórek oraz przezroczystości. Przedstawiony sposób jest rzeczywiście jednym z najprostszych metod rysowania chmur, jednak dającym dość dobre rezultaty. Istnieje wiele innych metod uwzględniających także właściwości fizyczne takie jak pochłanianie czy załamanie światła. Odpowiednie opisy można znaleźć w literaturze.
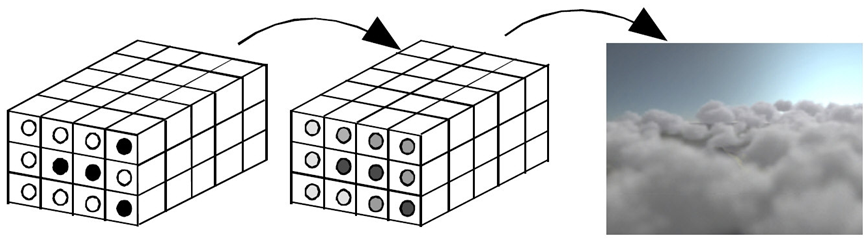
Rys.8.15. Przykład
wolumetrycznego modelowania chmur.
Rysunki na podstawie: Dobashi Y.: A Simple, Efficient Method for
Realistic Animation of Clouds, SIGGRAPH’00.
Przykładem podejścia „warstwowego” w modelowaniu wolumetrycznym może być
modelowanie płomienia (rys.8.16). Prezentowana metoda wykorzystuje dodatkowe
techniki dając bardzo efektywne rozwiązanie. Płomień jest w tej metodzie
modelowany następującymi etapami:
- Przestrzeń obejmującą płomień jest dzielona na warstwy.
- W każdej warstwie generowana jest tekstura na podstawie bardzo prostego modelu zmian temperatury (i barwy).
- Tekstura jest zaburzana funkcją turbulencji.

Rys.8.16. Przykład warstwowego modelowania płomienia. Na podstawie [5].
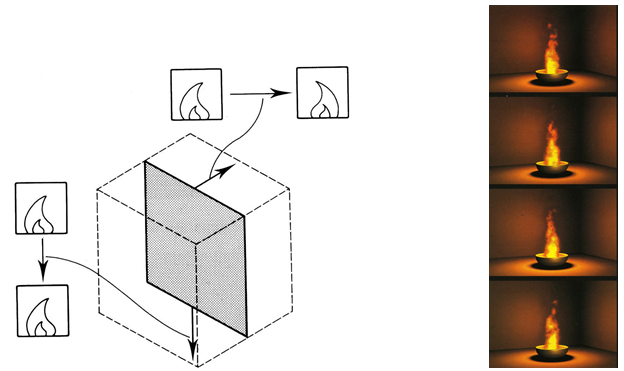
Rys.8.17. Modelowanie kolejnych klatek animacji płomienia. Na podstawie [5].
Modelowanie wolumetryczne wykorzystuje wiele różnych metod, czasami dość zaskakująco łączonych ze sobą. Często stosowane są techniki teksturowania oraz funkcje wprowadzające lokalne zaburzenia lub szum. Warto zwrócić uwagę na funkcję szumu opracowaną przez K.Perlina w 1985 roku (uzupełnioną w 2002). Funkcja ta jest gładką interpolacją wektora gradientu między węzłami siatki. Jest ona prosta w implementacji i daje zaskakująco dobre efekty. Z tego powodu szum Perlina jest często dodawany do tekstur różnych powierzchni, aby podkreślić drobne niejednorodności rzeczywistych obiektów i nadać im naturalny wygląd.
Rozdział 9. ELIMINACJA ELEMENTÓW ZASŁONIĘTYCH
W Rozdziale dziewiątym zostały omówione problemy związane z zagadnieniem eliminacji elementów zasłoniętych (rozstrzygania widoczności). We wprowadzeniu przedstawiono podstawowe problemy: zorientowanie ścian, klasy algorytmów i możliwości wykorzystania zasad spójności. Omówione zostały najważniejsze algorytmu ogólnego przeznaczenia takie jak algorytm skaningowy, malarski, podziału binarnego, bufora głębokości. Jako przykład algorytmu do określonych zastosowań przedstawiono algorytm rysowania wykresu funkcji z=f(x,y). Czytelnik znajdzie tutaj także informacje dotyczące problemu złożoności obliczeniowej algorytmów rozstrzygania widoczności.
9.1. Wprowadzenie
Zadanie eliminacji elementów zasłoniętych (zwany także zadaniem rozstrzygania widoczności lub zadaniem wyznaczania powierzchni widocznych) polega na określeniu, które fragmenty obiektów sceny mogą być widoczne przez wirtualną kamerę (przez obserwatora). Problem wydaje się nam banalny, ale aby w wirtualnym świecie zaszło naturalne dla naszego widzenia zasłanianie jednych obiektów przez drugie, to trzeba to opisać odpowiednim algorytmem.
Jest to przykład zadania, dla którego nie jest znane jedno, uniwersalne
rozwiązanie.
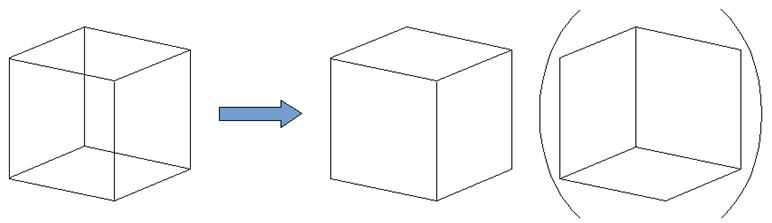
Rys.9.1. Zadanie rozstrzygania widoczności.
Generalnie rzecz biorąc, zadanie to można traktować jako szeroko rozumiany problem sortowania. Z punkt widzenia obserwatora obiekty leżące dalej są zasłonięte przez obiekty leżące bliżej. Niestety to proste stwierdzenie nie przekłada się na równie prosty algorytm. Już samo określenie „jeden obiekt leżący dalej od drugiego” może prowadzić do niejednoznaczności, gdyż trudno przypisać jedną miarę odległości obiektowi zajmującemu pewien obszar w przestrzeni. Jak więc porównać położenia tych obiektów, a tym bardziej wyciągnąć wnioski o ich wzajemnym zasłanianiu. W skrajnym przypadku można wyobrazić sobie sytuację, że dwa obiekty zasłaniają się w taki sposób, że każdy jest częściowo zasłonięty przez drugi z nich. Do tego relacja częściowego zasłaniania nie jest relacją przechodnią. A zatem wyciągnięcie właściwego wniosku dotyczącego zasłaniania na podstawie wzajemnego położenia obiektów jest zadaniem trudnym.
Znanych jest bardzo wiele różnych algorytmów rozstrzygania widoczności. W latach siedemdziesiątych i osiemdziesiątych XX wieku powstało ich rzeczywiście dużo. Warto wspomnieć przynajmniej o kilku z nich.
9.2. Bryła wypukła i zorientowanie ściany, klasy algorytmów
Rozpatrzmy przypadek wielościanu wypukłego. Jest to jeden z przykładów problemu eliminacji elementów zasłoniętych, dla którego można pokazać kilka efektywnych i jednocześnie prostych algorytmów. Można zauważyć, że jeżeli na scenie jest dowolny wielościan wypukły (ale tylko jeden !), to wnioskowanie o widoczności jego elementów jest dość proste. Traktując taką scenę jako zbiór wielokątów (z których każdy jest oczywiście ścianą wielościanu), można ten zbiór podzielić na trzy grupy:
- Wielokąty widoczne przez obserwatora (wielokąty przednie).
- Wielokąty niewidoczne – zasłonięte (wielokąty tylne).
- Wielokąty, których rzut jest odcinkiem.
Wielokąty ostatniej grupy są pomijalne, odpowiednie odcinki zostaną i tak narysowane jeśli pojawią się wielokąty widoczne.
W pierwszej i drugiej grupie występują wielokąty, które w całości podlegają określonym zasadom widoczności i przynależności do grupy. Nie może zachodzić przypadek, że tylko część wielokąta jest widoczna (a druga część zasłonięta). A zatem rozwiązanie zadania wyboru elementów widocznych w przypadku wielościanu wypukłego sprowadza się do określenia zbioru wielokątów należących do pierwszej grupy. I one powinny być (w całości) narysowane.
Można pokazać kilka różnych sposobów rozwiązanie tak zdefiniowanego
zdania.
Rozwiązanie A
(pierwszy sposób) polega na analizie położenia obiektów w przestrzeni. Definiowane są określone
wektory a następnie jest wyznaczany iloczyn skalarny tych wektorów (rys.9.2).
Niech ![]() . Znak tego iloczynu
określa przynależność do określonej grupy: jeśli
. Znak tego iloczynu
określa przynależność do określonej grupy: jeśli ![]() to ściana S1 jest widoczna z punktu P0
. (ściana S1 jest przednia). Zwróćmy
uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie.
Położenie obserwatora w przestrzeni w zupełności wystarczy.
to ściana S1 jest widoczna z punktu P0
. (ściana S1 jest przednia). Zwróćmy
uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie.
Położenie obserwatora w przestrzeni w zupełności wystarczy.
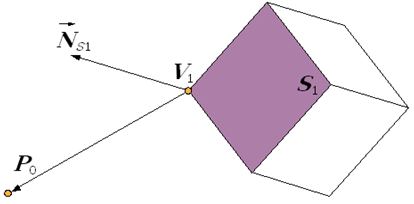
Rys.9.2. Wektory, na podstawie których badane jest zorientowanie ściany
(a w konsekwencji jej
zorientowanie).
Rozwiązanie B korzysta z informacji zarówno pochodzących z przestrzeni obiektu (sceny), jak i z informacji jakie dostarcza rzut. – Porównywane jest zorientowanie ściany obiektu (w przestrzeni obiektu) i zorientowanie rzutu ściany (w przestrzeni rzutu). Najpierw należy przypisać zorientowanie każdej ścianie, a następnie sprawdzić, czy zorientowanie rzutu ściany jest takie samo. Jeśli oba zorientowania są jednakowe, to ściana jest widoczna (przednia).
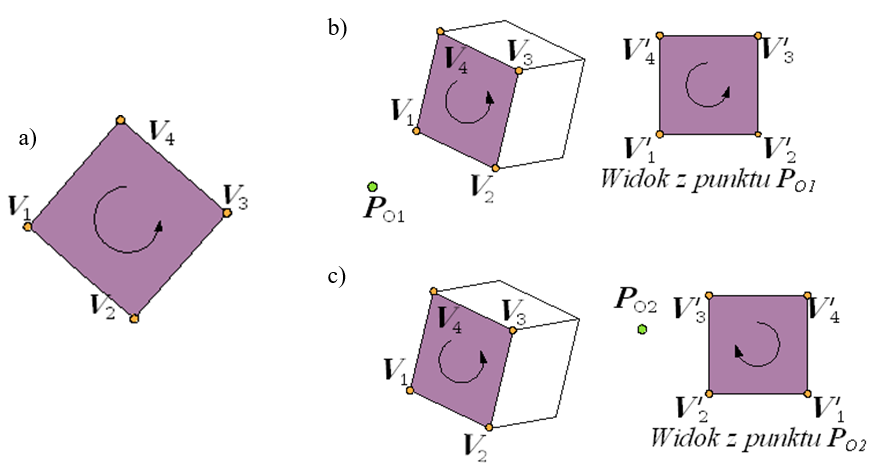
Rys.9.3. a)
Zorientowanie przypisane ścianie.
b) Porównanie
zorientowania ściany i zorientowania jej rzutu z punktu widzenia P01 .
c) Porównanie
zorientowania ściany i zorientowania jej rzutu z punktu widzenia P02 .
Zadanie określenia widoczności elementów wielościanu wypukłego można więc rozwiązać na dwa sposoby korzystając z rozwiązań A i B sprawdzających zorientowanie poszczególnych ścian.
Sposób A. Określić zorientowanie każdej ściany korzystając z rozwiązania A. Jeżeli ściana jest „przednia”, to jest widoczna.
Sposób B. Określić zgodność zorientowania każdej ściany korzystając z rozwiązania B. Jeśli orientacja ściany i jej rzutu są zgodne to ściana jest „przednia” i jest widoczna.
Analizę widoczności w przypadku wielościanu wypukłego, można przeprowadzić
opierając się tylko na informacji z przestrzeni rzutu – sposób C. W tym celu należy podzielić wierzchołki rzutu na dwa typy
– rysunek 9.4. Pierwszy typ (węzły: ![]() ) charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie
są widoczne. O pozostałych krawędziach i ich widoczności nie można nic
powiedzieć. Drugi typ (węzły:
) charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie
są widoczne. O pozostałych krawędziach i ich widoczności nie można nic
powiedzieć. Drugi typ (węzły:![]() ) charakteryzuje się tym , że co prawda nie można stwierdzić
czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam
atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i
wszystkie jego krawędzie są widoczne.
) charakteryzuje się tym , że co prawda nie można stwierdzić
czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam
atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i
wszystkie jego krawędzie są widoczne.
Korzystając z klasyfikacji węzłów można zaproponować sposób C wyznaczania widoczności elementów wielościanu wypukłego. Określając widoczność jednego węzła drugiego typu można przenieść ten sam atrybut widoczności do sąsiednich węzłów, przechodząc od jednego węzła do drugiego. W ten sposób powstają dwa komplementarne obrazy. W takim postępowaniu nie jest potrzebna informacja z przestrzeni obiektu. Wystarczy tylko informacja dotycząca rzutu.
Klasy algorytmów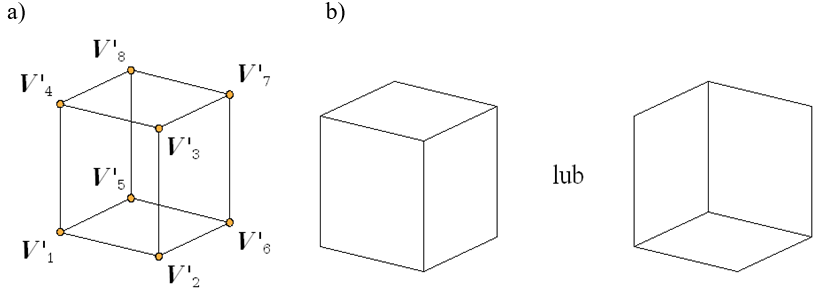
Rys.9.4. Na podstawie klasyfikacji węzłów (a) można
wyeliminować
węzły (i krawędzie) niewidoczne doprowadzając do rysunku b).
Najczęściej wyróżnia się trzy klasy algorytmów rozstrzygania widoczności
- Pracujące w przestrzeni obserwatora (np. sposób A).
- Pracujące w przestrzeni rzutu (np. sposób C).
- Wykorzystujące informacje z obu przestrzeni (np. sposób B).
Trzy sposoby rozwiązania problemu widoczności pokazują trzy sposoby wykorzystania informacji, pochodzących albo z przestrzeni obiektu (sceny), albo przestrzeni rzutu, albo obu. Oczywiście o ile w przypadku wielościanu wypukłego ten podział jest bardzo ostry i jednoznaczny, o tyle w przypadku dowolnego innego algorytmu podział będzie zdecydowanie mniej ostry i będzie oznaczał, że dany algorytm w większym stopniu wykorzystuje informację z jednej lub drugiej przestrzeni. Taki podział algorytmów można przeprowadzić dla dowolnych brył, nie tylko wypukłych.
Z drugiej strony często mówi się o precyzji obrazowej lub obiektowej danego algorytmu. Oznacza to, że algorytmy pracujące z precyzją obrazowa wykonują obliczenia z dokładnością urządzenia wyświetlającego (wynikającą z wyświetlania pojedynczego piksela). Algorytmy pracujące z precyzją obiektowa wykonują obliczenia z dokładnością związaną z definicją obiektów, a nie pikseli.
Aby określić złożoność algorytmów określania widoczności należy zdefiniować miarę złożoności sceny (obiektu). Najczęściej przyjmuje się, liczbę ścian jako taką miarę.
Złożoność trzech wariantów algorytmów eliminacji elementów zasłoniętych dla wielościanu wypukłego (sposoby A, B, C) jest liniowa. Jest to szczególny przypadek wśród algorytmów określania widoczności.
9.3. Bryła dowolna, zbiór brył
W przypadku bryły dowolnej (a więc także wklęsłej) lub zestawu dowolnych brył, podział ścian na przednie i tylne nie wystarczy, gdyż taka analiza nie uwzględnia wzajemnego zasłaniania ścian (rys.9.5), jakie może wystąpić między obiektami lub ścianami tego samego obiektu. Problem taki występuje także dla zestawu brył wypukłych, tylko dla jednej bryły wypukłej można pokazać prostszy algorytm.
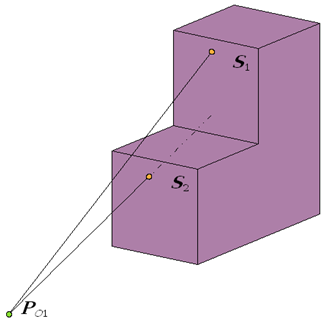
Rys.9.5. Co prawda obie ściany S1 i S2 są przednie,
ale to nie jest warunkiem wystarczającym
aby były widoczne gdyż jedna ściana
zasłania drugą.
Naturalnym podejściem jest analiza wzajemnego położenia ścian, ale w takim przypadku trzeba przeanalizować wszystkie pary ścian (analiza „każdy z każdym”). Prowadzi to oczywiście do kwadratowej złożoności obliczeniowej algorytmu. Najprostszym mechanizmem przyspieszającym takie postępowanie jest test MINMAX czyli „opakowanie” wielokątów prostopadłościanami definiującymi minimum i maksimum po każdej współrzędnej dla danego wielokąta. Porównując wzajemne położenie prostopadłościanów opakowujących (co jest prostsze gdyż jest porównaniem minimów i maksimów współrzędnych) można wyeliminować wiele przypadków, gdy wielościany nie mogą się zasłaniać. Oczywiście takie postępowanie nie zmienia asymptotycznej złożoności obliczeniowej. Test MINMAX jest często stosowany do różnych algorytmów eliminacji elementów zasłoniętych.
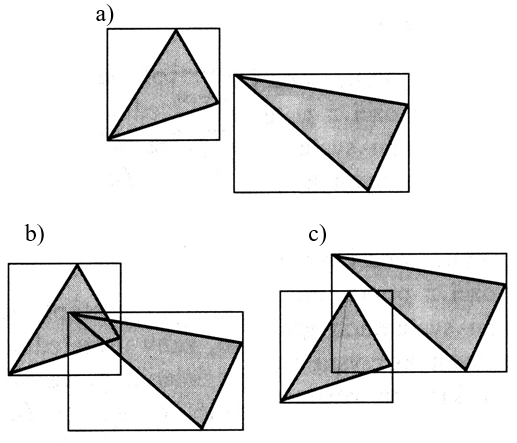
Rys.9.6.
Test MINMAX – porównanie otoczenia: a) jeśli otoczenia prostokątne są rozłączne,
to
elementy nie mogą mieć punktów wspólnych i zasłaniać się,
jeśli
otoczenia nie są rozłączne, elementy mogą się zasłaniać (b) lub nie (c).
Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej.
Zasady spójności
Sutherland, Sproull i Schumacker zwrócili uwagę na pewną cechę analizy występującą w algorytmach określania widoczności. Jest nią spójność – pewne podobieństwo cech pozwalające wnioskować o zasłanianiu lub widoczności. Wyróżnia się:
- Spójność sceny
- Spójność obiektów (jako całości)
- Spójność elementów obiektów (ściany, krawędzie)
-
Spójność rzutu
- Spójność linii (powierzchni)
- Spójność głębokości
- Spójność ramek
Jeśli na przykład rozpatrzymy scenę zawierającą wielościany, to o widoczności wierzchołków możemy np. wnioskować na podstawie widoczności ściany.: Jeśli ściana jest widoczna to również jej węzły są widoczne, Tego typu wnioski powinny być ostrożnie formułowane, gdyż nie wszystkie sytuacje są oczywiste (np. wniosek, że odcinek łączący widoczne węzły jest widoczny, nie zawsze jest prawdziwy.
9.4. Algorytm malarski
Algorytm malarski (algorytm sortowania ścian) należy do grupy algorytmów z listą priorytetów. Algorytmy te wykorzystują informacje zarówno z przestrzeni obiektu jak i z przestrzeni rzutu (łączą operacje z precyzją obiektową i operacje z precyzją obrazową). Algorytm malarski zaproponowany przez Newella, Newella i Sancha w 1972 roku. Jest jednym z najprostszych opisowo i jednocześnie efektywnym. Polega on na posortowaniu elementarnych fragmentów sceny (wielokątów) zależnie od odległości od obserwatora: od najdalszego do najbliższego. Fragmenty są następnie rysowane w tej kolejności. Zakłada się przy tym, że rysunek powstaje analogicznie do malowania obrazu olejnego (stąd nazwa algorytmu) – rysunek 9.7. Tzn. fragment później namalowany zasłania (zamalowuje) wszystko, co było dotychczas namalowane w tym miejscu. Oczywiście tę cechę ma każde urządzenie wyświetlające (monitor, wyświetlacz LCD), ale stosowanie tego algorytmu bezpośrednio na drukarce byłoby niemożliwe.

Rys.9.7. Powstawanie kolejnych
planów na obrazie – idea algorytmu malarskiego eliminacji elementów zasłoniętych.
ALGORYTM_MALARSKI
Posortuj wielokąty w kolejności wynikającej z głębokości (odległości od obserwatora).
Rozstrzygnij wszystkie niejednoznaczności.
Rysuj w kolejności od najdalszego.
Złożoność obliczeniowa takiego algirytmu O(nlogn), gdzie n to liczba wielokątów.
Posortowanie wielokątów jest zadaniem trudnym i może prowadzić do niejednoznaczności. Jeżeli rozpatrzymy dwa wielokąty dowolnie ustawione w przestrzeni, to podstawowym problemem jest ustalenie który z nich jest dalej od obserwatora. To znaczy,. który z nich będzie zasłonięty przez drugi wielokąt z punktu widzenia obserwatora. Żeby to określić stosuje się różne kryteria porównywania położenia. Najprostsze rozwiązanie polega na porównaniu współrzędnych z wielokątów. Jeżeli maksymalna współrzędna z jednego wielokąta jest mniejsza niż minimalna współrzędna z drugiego to pierwszy jest bliżej obserwatora. Oczywiście taki przypadek zachodzi rzadko, najczęściej zakresy współrzędnych wielokątów zazębiają się nie dając możliwości prawidłowego posortowania ich na podstawie takiego kryterium. Lepszym kryterium jest porównanie położenia środków ciężkości wielokątów – bliżej obserwatora znajduje się ten, którego środek ciężkości znajduje się bliżej. Niestety i to kryterium w pewnych sytuacjach zawodzi (czytelnik zechce przeanalizować położenia wielokątów kiedy sortowanie na podstawie położenia środków ciężkości dawałoby niepoprawne rysunki). O wiele lepszym kryterium (chociaż bardziej skomplikowanym obliczeniowo) jest analiza położenia jednego wielokąta względem płaszczyzny wyznaczonej przez drugi wielokąt .Jeżeli pierwszy z nich jest po tej samej stronie płaszczyzny co obserwator, to jest rzeczywiście bliżej obserwatora i nie może być zasłonięty przez drugi wielokąt.
Uwzględniając powyższe rozważania można zaproponować skuteczny algorytm analizy dla algorytmu malarskiego. Dla wielokątów Q i P które mogą się zasłaniać, przeprowadzić zestaw testów. Pierwsze spełnienie testu wyklucza zasłanianie, więc zakończyć testowanie:
TESTY_DLA_ALGORYTMU_MALARSKIEGO
Sprawdzić
zasłanianie między wielokątami Q i P:
pierwsza
odpowiedź pozytywna wyklucza zasłanianie i kończy test.
Czy są otoczenia prostokątne Q i P, które wykluczają zasłanianie ?
Czy rzuty Q i P wykluczają zasłanianie ?
Czy P jest w całości po przeciwnej stronie niż obserwator względem płaszczyzny wyznaczonej przez Q ? Przyjmując, że Q zasłania P !
Czy Q jest w całości po tej samej stronie co obserwator względem płaszczyzny wyznaczonej przez P ? Przyjmując, że Q zasłania P !
(!) Jeśli żaden z testów 1-4 nie dał pozytywnej odpowiedzi, zamienić wielokąty rolami, przyjmując że P zasłania Q, i powtórzyć kroki 3. i 4.
(!!) Jeśli również test 5. nie przyniósł rozwiązania, podzielić jeden z wielokątów i przeprowadzić testowanie od początku.
Jednak nawet kryterium wykorzystujące analizę położenia względem płaszczyzny nie radzi sobie w szczególnych przypadkach. Należą do nich: zasłanianie cykliczne i przecinanie się wielokątów (rys.9.8). Pierwszy z nich stanowi tak naprawdę problem w wielu algorytmach rozstrzygania widoczności. Co prawda w praktyce występuje niezmiernie rzadko, ale dobrze skonstruowany algorytm powinien również w takim przypadku pracować poprawnie. (Przykładem występowania zasłaniania cyklicznego może być przysłona obiektywu fotograficznego, której kolejne elementy zachodzą na siebie.) Oba problemy mogą zostać rozwiązanie przez przecięcie jednego z wielokątów na dwie części i potraktowanie każdej z tych części jako niezależnego wielokąta w przeprowadzanej analizie położenia.
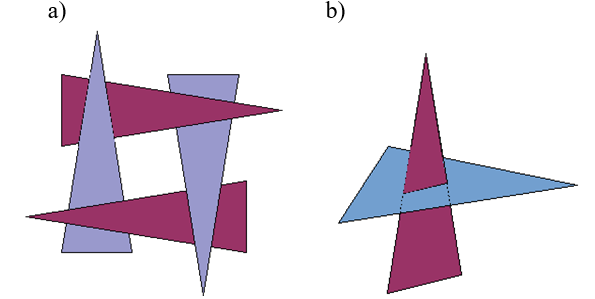
Rys.9.8. Problemy algorytmu
malarskiego:
a) zasłanianie cykliczne, b) przecinanie się wielokątów.
Podstawowe właściwości algorytmu malarskiego można scharakteryzować w sposób następujący:
- Zalety
- Prosta i zwarta konstrukcja algorytmu.
- Dość prosty algorytm sortowania.
-
Wady
- Skomplikowane kryteria sortowania aby uzyskać poprawny wynik.
- Proste sortowanie nie zawsze daje poprawne wyniki (czasem jest to w ogóle niemożliwe ! )
- Ze względu na skomplikowane kryteria i przypadki sortowanie może zajmować dużo czasu.
- Konstrukcja algorytmu powoduje wielokrotne wypełnianie tego samego piksela (problemy ze sprzętem )
9.5. Algorytm skaningowy
Algorytm skaningowy (przeglądania liniami poziomymi) jest przykładem algorytmu
pracującego w przestrzeni rzutu (działającego z precyzją obrazową). Zasada
pracy tego algorytmu oparta jest na założeniu, że w każdym kroku postępowania
przeglądana jest jedna linia pozioma obrazu. Można wskazać dwa źródła takiego
postępowania. Z jednej strony można bezpośrednio powiązać algorytm z
urządzeniem wyświetlającym funkcjonującym na podobnej zasadzie. Przykładem może
być monitor, na którym obraz jest powstaje przez generację kolejnych poziomych
linii. Z drugiej strony jest to związane z algorytmem wypełniania wielokąta
poziomymi liniami. Modyfikując taki algorytm wypełniania można zapewnić
dodatkowo eliminację elementów zasłoniętych. Pierwsze artykuły opisujące
algorytm tego typu ukazały się w 1967 roku. Autorzy algorytmu skaningowego to
Wylie, Romney, Evans, Erdahl.
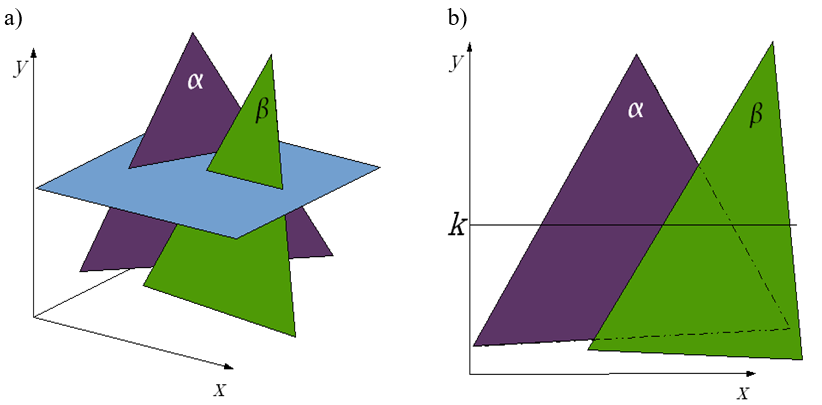
Rys.9.9. Płaszczyzna przecinająca i odpowiadająca jej k-ta linia przeglądanie.
Kolejne linie poziome obrazu można rozpatrywać jako przecięcie ekranu i pewnej płaszczyzny prostopadłej do ekranu – rysunek 9.9. Taka płaszczyzna przetnie wszystkie obiekty sceny. Każda linia obrazu może być rozpatrywana niezależnie. Problem rozstrzygania widoczności można zatem uprościć do niezależnej analizy każdej linii, przechodząc z analizy położenia wielokątów w przestrzeni trójwymiarowej do analizy położenia odcinków na płaszczyźnie.
ALGORYTM_SKANINGOWY
Posortuj wielokąty pod względem wzrostu max(y) ich rzutów.
Przeglądaj kolejne linie obrazu traktując każdą z nich niezależnie.
W ramach jednej linii określ dla kolejnych punktów przynależność do odpowiednich wielokątów.
W sytuacjach wątpliwych wybierz element najbliższy obserwatorowi.
Złożoność algorytmu skaningowego O(nlogn), gdzie n — liczba wielokątów
Najczęściej zakłada się, że wielokąty sceny, które podlegają analizie nie
przecinają się – chociaż możliwa jest analiza algorytmem skaningowym również i
takich przypadków. Dla danej linii analizuje się tablicę krawędzi
(przynależności do wielokąta). Tablica ta określa dla danego piksela do rzutu
jakich wielokątów ten piksel należy. Najprościej taką tablicę uzyskać traktując
linię przeglądania jako prosta przecinana przez krawędzie kolejnych rzutów
wielokątów. Podobnie jak w algorytmie wypełniania istnieje problem krawędzi
poziomych. Często zakłada się, że bez zmniejszania ogólności można przyjąć, że
taki przypadek nie będzie zachodził. Prościej jednak przeanalizować ten
przypadek podobnie jak w wypełnianiu wielokąta liniami poziomymi. Mianowicie
przyjąć że odcinek poziomy nie tworzy przecięć z linią przeglądająca ale w
całości należy do przecinanego wielokąta (rzutu). Natomiast końce odcinka
definiują początek i koniec tej
przynależności.
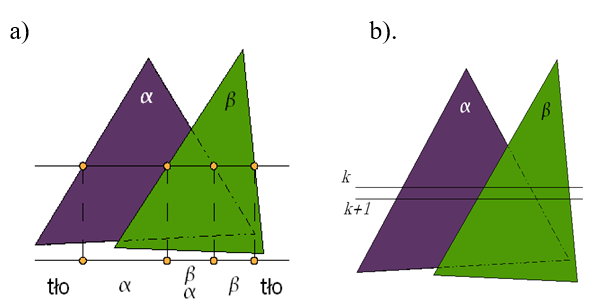
Rys.9.10. a) Analiza kolejnych
odcinków linii przeglądania. Każdemu odcinkowi
jest przypisywany element w przestrzeni, który może wpływać na widoczność tego odcinka.
b)
Podobieństwo sąsiednich linii.
Analiza widoczności polega na analizie kolejnych odcinków między punktami przecięć w tablicy krawędzi (rys.9.10). Punkty takiego pojedynczego odcinka należą do pewnego zbioru rzutów wielokątów.
Jeśli ten zbiór jest pusty, to odcinek ten (tzn. odpowiadające mu piksele urządzenia wyświetlającego) należy wypełnić barwą tła.
Jeśli zbiór jest jednoelementowy, to znaczy, że piksele tego odcinka należą dokładnie do jednego rzutu wielokąta. A to oznacza że nie zachodzi żadne zasłanianie i piksele odpowiadające temu odcinkowi należy wypełnić barwą rzutu danego wielokąta.
Jeśli zbiór rzutów jest dwu lub więcej elementowy, to do wypełniania należy użyć barwy tego wielokąta, który jest najbliżej obserwatora. Oczywiście w tym przypadku wybór elementu najbliższego jest bardzo prosty, gdyż rozpatrujemy przecięcia wielokątów i płaszczyzny tnącej, czyli zbiór odcinków na płaszczyźnie.
Algorytm skaningowy był wielokrotnie usprawniany poprzez dodanie mechanizmów przyspieszających jego działanie. Najciekawszą modyfikacją jest uproszczona analiza sąsiednich linii. Można zauważyć, że najczęściej dla sąsiednich linii schemat przynależności kolejnych pikseli do odpowiednich rzutów nie zmienia się – rysunek 9.10.b. Oznacza to, że można raz zrobić pełną analizę widoczności, a następnie korzystać z niej przy kolejnych liniach przeglądających, dopóki schemat przynależności w tablicy krawędzi się nie zmieni.
Złożoność algorytmu jest taka jak sortowania i wynika z pierwszej fazy algorytmu. Modyfikacje usprawniające (takie jak na przykład uproszczona analiza sąsiednich linii) nie wpływają na złożoność asymptotyczną, ale mogą w określonych sytuacjach przyspieszyć działanie algorytmu.
Algorytm skaningowy rozwiązuje również problem zasłaniania cyklicznego. Ponieważ w pojedynczym kroku analizujemy jedną linię obrazową czyli jedno przecięcie płaszczyzną tnącą, to zasłanianie cykliczne nie stanowi problemu, gdyż na tej płaszczyźnie nie może zachodzić zasłanianie cykliczne odcinków – rysunek 9.11.
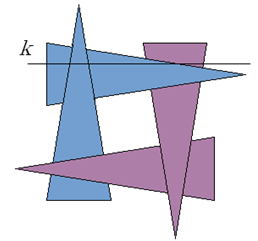
Rys.9.11. Algorytm skaningowy pracuje poprawnie także jeśli zachodzi zasłanianie cykliczne.
Podstawowe właściwości algorytmu skaningowego można scharakteryzować w następujący sposób:
- Zalety
- Wykorzystuje zalety spójności aby przyspieszyć działanie.
- Nie wymaga dodatkowej pamięci (poza bieżącą obróbką danych).
- Jest niewrażliwy na typowe „pułapki” (zasłanianie cykliczne, przenikanie).
-
Wady
- Dość złożony algorytm (geometrycznie).
- Wymaga analizy położenia wszystkich wielokątów (ich rzutów) przed rysowaniem.
- Użyteczny w połączeniu ze sprzętem pracującym w trybie przeglądania linii (skaningowym).
9.6. Algorytm podziału binarnego
Pomysł wykorzystania zorientowania ścian pochodzący z 1969 roku (Schumacker) został zastosowany w latach 1980-1983 do budowy algorytmu rozstrzygania widoczności zwanego algorytmem drzewa binarnego podziału przestrzeni (ang. BSP tree). Autorami algorytmu są Fuchs, Kedem, Taylor.
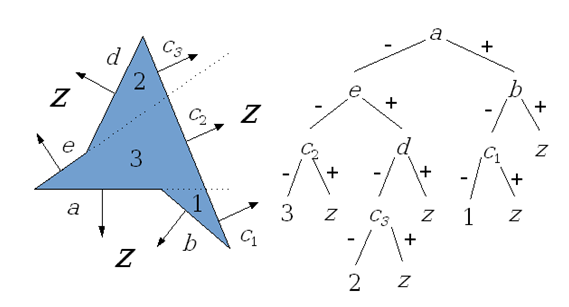
Rys.9.12. Podział przestrzeni płaszczyznami a,b,c,d,e oraz
odpowiadające temu podziałowi
drzewo binarne. Strzałki oznaczają
zorientowanie dodatnie (+), z – oznacza obszar zewnętrzny.
Rozpatrzmy przypadek jak na rysunku 9.12. Każdej płaszczyźnie można przypisać zorientowanie (zaznaczone strzałkami, zwrot zgodny ze strzałkami w drzewie został zaznaczony + , zwrot przeciwny został oznaczony - ). Kolejność analizy (budowy drzewa podziału) – to znaczy wybór kolejnych płaszczyzn jest dowolny. Może to oczywiście wpłynąć na kształt drzewa, wpływa także na konieczność podziału ścian wielościanu. Na przykład ściana c na rysunku została podzielona na fragmenty c1, c2 i c3 co wynika z wcześniejszego podziału przestrzeni. Algorytm podziału binarnego w takiej postaci może zostać także wykorzystany do sprawdzenia czy dany punkt należy do wnętrza wielościanu.
ALGORYTM_PODZIAŁU_BINARNEGO
1. zbuduj drzewo BSP tak, aby każdy obiekt (przynajmniej) znalazł się w odrębnej komórce.
2. przeglądaj drzewo w kolejności INORDER z uwzględnieniem zorientowania.
procedure przeglądaj_BSP (drzewo)
begin
if drzewo jest niepuste then
if obserwator „z przodu” (+) korzenia drzewa then
begin
przeglądaj_BSP (tylne (-) poddrzewo);
narysuj obiekt z korzenia drzewa;
przeglądaj_BSP (przednie (+) poddrzewo);
end;
else // tu obserwator „z tyłu” (-) korzenia drzewa
begin
przeglądaj_BSP (przednie (+) poddrzewo);
narysuj obiekt z korzenia drzewa;
przeglądaj_BSP (tylne (-) poddrzewo);
end;
end;
W warunkach rzeczywistej analizy sceny przy wyborze płaszczyzn podziału warto posługiwać się płaszczyznami związanymi bezpośrednio z obiektami (zawierającymi na przykład ściany). Przykład przekroju sceny i odpowiadające mu drzewo podziału prezentuje rysunek. Zakładamy dla uproszczenia, że w każdym obszarze (ponumerowanym) znajduje się jeden obiekt. Stosując algorytm binarnego podziału należy wyznaczyć kolejność rysowania, w taki sposób, aby z punktu widzenia obserwatora rysować obiekty od najdalszych do najbliższych (najpierw zasłaniane potem zasłaniające). Drzewo uwzględnia wszystkie ściany i pozwala wskazać kolejność zasłaniania po przejściu zaproponowanym algorytmem drzewa.
Oczywiście drzewo nie uwzględnia położenia obserwatora, natomiast położenie to wpływa na drogę przejścia przez drzewo. Rysunek 9.13 pokazuje różne kolejności rysowania obiektów dla dwóch różnych położeń obserwatora.
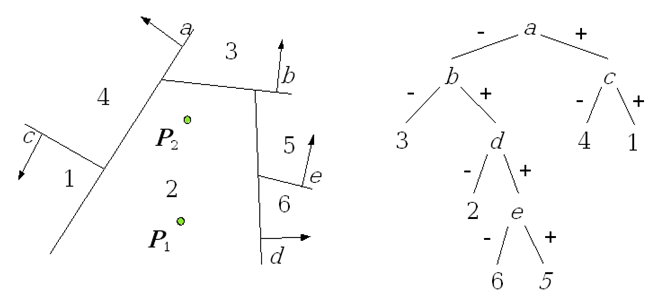
Rys.9.13. Podział przestrzeni i odpowiadające mu drzewo
BSP.
Kolejność rysowania obiektów zależna od położenia obserwatora.
Obserwator w P1
kolejność rysowania: 4,1,3,5,6,2.
Obserwator w P2
kolejność rysowania: 1,4,3,6,5,2.
Ciekawym przypadkiem jest sytuacja, gdy obserwator znajduje się wewnątrz obszaru. Wtedy drzewo binarnego podziału pokazuje właściwą kolejność bez względu na kierunek patrzenia obserwatora !
Algorytm drzewa binarnego podziału przestrzeni był bardzo długo traktowany jako niezwykle elegancka ciekawostka, ze względu na skomplikowanie tworzenia drzewa podziału. Dopiero silny rozwój gier komputerowych w latach 90 dwudziestego wieku spowodował, że algorytm ten przeżywa swój renesans. Zauważono bowiem, że warto na użytek gier rozdzielić etap tworzenia drzewa od etapu przeglądania. Jeśli przyjmiemy, że w każdym elemencie podziału znajduje się jeden obiekt sceny, to samo przeglądanie algorytmem INORDER ma złożoność liniową ze względu na liczbę obiektów i to niezależnie od zbalansowania drzewa.
Drzewo zostaje zatem utworzone przez twórców gry w momencie generowania „mapy” gry. Natomiast przeglądane jest w momencie realizacji (wirtualnego poruszania się gracza/bohatera po świecie gry). Co więcej, sprawę można dodatkowo uprościć dzieląc mapę na obszary, w których jest ustalona kolejność rysowania obiektów, a następnie zapisać gotowe schematy kolejności dla poszczególnych obszarów. W tym przypadku podczas realizacji gry nawet przeglądanie drzewa nie jest potrzebne.
Warto dodać, że w latach 1992-1995 (prace Tellera, Luebkego, Georgesa) powstała metoda wyboru potencjalnych elementów widocznych (ang.PVS – Potentially Visible Set) pozwalająca określić przybliżony zakres widoczności obiektów. Metoda ta jest często łączona z generacją drzewa BSP.
Podstawowe właściwości algorytmu podziału binarnego można scharakteryzować w następujący sposób:
- Zalety:
- Prosty i elegancki. Niepotrzebna informacja o głębokości.
- Tylko zapis do bufora rysunku (framebuffer), niepotrzebne porównywanie bieżącego położenia (jak w Z_buforze), ani sortowania (jak w malarskim).
- Można podzielić na preprocesing (budowanie drzewa) i przeglądanie drzewa (rysowanie) !!!
- Bardzo szybkie rysowanie – złożoność O(n) , efektywne wykorzystanie w grach komputerowych.
-
Wady:
- Duża złożoność preprocesingu ogranicza zastosowanie do scen statycznych.
- Konstrukcja drzewa: O(nlogn) podziału i sortowania.
- Podział powiększa liczbę wielokątów: O(n2) .
9.7. Algorytm bufora głębokości
Algorytm bufora głębokości (Z-bufora) został zaproponowany przez Catmulla w 1974 roku. Jest jednym z najprostszych w implementacji algorytmów rozstrzygania widoczności. Zakłada istnienie bufora o rozmiarze całego wyświetlanego obszaru (ekranu) – występuje w tym przypadku odpowiedniość pozycji piksela ekranu i odpowiadającej mu pozycji w buforze. Dla każdego piksela w buforze zapamiętywana jest odpowiadająca mu głębokość czyli współrzędna zP.
Na początku pracy algorytmu bufor Z jest wypełniany maksymalną wartością
współrzędnej z, jaka może wystąpić w analizowanym obszarze. Jednocześnie
wszystkie piksele obrazu przyjmują barwę tła. Następnie rysowane są wielokąty
(w dowolnej kolejności) – to znaczy wypełniane są ich rzuty odpowiednią barwą.
Podczas wypełniania zwykła procedura wypełniająca jest poszerzona o sprawdzenie
głębokości odpowiadającej danemu pikselowi. Piksel jest wypełniony tylko wtedy,
kiedy jego z jest mniejsze niż wartość zapisana w buforze – rysunek 9.14.
Mechanizm ten powoduje, że podczas wypełniania kolejnych wielokątów szukany jest piksel, którego współrzędna z jest najmniejsza – to znaczy szukany jest punkt leżący najbliżej obserwatora – czyli punkt rzeczywiście widoczny.
Algorytm eliminacji elementów zasłoniętych z wykorzystaniem bufora głębokości można zapisać następująco:
ALGORYTM_BUFORA_GŁEBOKOŚCI
1. zdefiniuj bufor Z, który dla każdego piksela (xP,yP) ekranu zapamiętuje głębokość zP ;
2. rysuj kolejne wielokąty poprzez wypełnianie ich rzutów pikselami
o odpowiedniej barwie;
w przypadku każdego piksela weź pod uwagę wartość z bufora :
3. jeżeli nowa wartość z > zP to nie wypełniaj piksela.
w przeciwnym przypadku wypełnij piksel i uaktualnij zP ;
Obliczenie głębokości danego punktu wielokąta może zostać przeprowadzone jako interpolacja bilingowa, zgodnie z rysunkiem 9.15.
Rys. 9.15. Obliczanie głębokości punktu (współrzędnej z)
w algorytmie bufora głębokości.
Algorytm bufora głębokości rozstrzyga widoczność dla dowolnych scen wielościennych, jest niewrażliwy na zasłanianie cykliczne ani przecinanie obiektów. Nie wymaga żadnych dodatkowych struktur danych ani operacji wstępnych. Nie jest potrzebne żadne wstępne sortowanie wielokątów, ani żadne porównywanie obiekt-obiekt czy ściana-ściana! Dodatkowo, biorąc pod uwagę fakt, że wielokąty są obiektami płaskimi można wyznaczyć proste zależności przyrostowe wiążąc kolejne zmiany współrzędnych z wypełnianiem wielokąta liniami. Powoduje to, że dodatkowy czas potrzebny na rozszerzenie algorytmu wypełniania o rozstrzyganie widoczności jest niewielki. Przyjmuje się, że jest to algorytm o złożoności liniowej ze względu na liczbę wielokątów, ale dla ich dużej liczby czas rozstrzygania widoczności staje się w przybliżeniu praktycznie niezależny od liczby wielokątów w danej bryle widzenia.
Algorytm ma tylko jedną wadę – potrzebuje pamięci o rozmiarze obrazu, pozwalającej zapisać odległość dla każdego piksela. Jeszcze do niedawna (koniec dwudziestego wieku) był to warunek trudny do spełnienia. Realizacja algorytmu wymagała dodatkowo wykonania podziału obrazu na fragmenty, które mogły być razem z odpowiadającym mu buforem zmieszczone do pamięci. Dzisiaj nie stanowi to żadnego problemu.
Prostota algorytmu sprzyja również implementacji sprzętowej. Stacje graficzne i większość dobrych kart graficznych ma dzisiaj możliwość sprzętowej realizacji bufora głębokości.
Podstawowe właściwości algorytmu bufora głębokości można scharakteryzować w następujący sposób:
- Zalety
- Bardzo prosty !!! Pracuje w każdych warunkach !!!
-
Łatwy do implementacji sprzętowej.
Algorytm Z-Buffer jest bardzo często realizowany przez sprzęt kart graficznych !!! - Pozwala przetwarzać wielokąty w dowolnej kolejności. Złożoność O(n), gdzie n — liczba wielokątów.
-
Nie jest potrzebne żadne wstępne sortowanie wielokątów,
ani żadne porównywanie obiekt-obiekt
czy ściana-ściana !!! - Rozwiązuje zasłanianie cykliczne, przenikanie obiektów i inne problemy geometryczne.
- Może być efektywnie wykorzystany także w cieniowaniu.
-
Wady
- Wymaga dużej ilości pamięci
- Wymaga szybkiej pamięci (typowa pętla to odczyt, modyfikacja, zapis).
- Trudno uwzględnić (równie efektywnie) antyaliasing.
- Trudna realizacja przezroczystości.
9.8. Algorytm rysowania wykresu funkcji z=f(x,y)
Zadanie rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest jednym z częściej realizowanych zadań grafiki prezentacyjnej. Dodatkowo można zauważyć, że jest to dobry sposób uproszczonego rysowania rzeźby terenu.
Powierzchnia
będąca wykresem funkcji z=f(x,y)
należy do szczególnej klasy obiektów trójwymiarowych, dla której można pokazać
uproszczony algorytm rozstrzygania widoczności.
Rys.9.14. Wykres funkcji 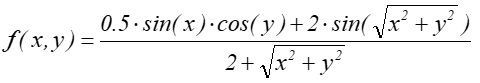
Można przyjąć, że dziedziną D funkcji dla rozpatrywanego fragmentu powierzchni jest prostokątem określonym przez zakresy zmiennych [xmin,xmax] X [ymin,ymax]. Jeśli dziedzinę D podzielimy równomierną siatką za pomocą linii równoległych odpowiednio do osi x i osi y, to punkt [xi,yj] będzie węzłem takiej siatki (dla 1 ≤ i ≤ NX oraz 1 ≤ j ≤ NY, gdzie NX, NY określają liczbę linii siatki dla każdej współrzędnej). Punkt [zij,xi,yj] dla zij=f(xi,yj) jest węzłem siatki rozpiętej na powierzchni będącej wykresem punkcji. Taki przykład najczęściej występuje w zastosowaniach praktycznych, gdzie wartości węzłowe pochodzą na przykład z pomiarów lub symulacji. Przybliżoną powierzchnię rysujemy łącząc węzły odcinkami.
Watkins w 1974 roku zaproponował algorytm maskowania pozwalający rysować
kolejne krzywe (łamane) siatki rozpiętej na powierzchni będącej wykresem
funkcji – rys.9.15. Można zauważyć, że dotychczas narysowany fragment
(pierwszym takim fragmentem jest obszar powierzchni pomiędzy pierwszymi dwoma
krzywymi/łamanymi) może zasłaniać wszystkie później rysowane elementy
powierzchni. A zatem do realizacji algorytmu wystarczy zdefiniować bufor górny
(ograniczenie górne YOG we
współrzędnych rzutu) i bufor dolny (ograniczenie dolne YOD we współrzędnych rzutu), a następnie w każdym kroku
sprawdzać położenie rysowanego fragmentu (odcinka) względem buforów. Jeśli
element jest powyżej ograniczenia górnego lub poniżej dolnego to jest rysowany,
w przeciwnym przypadku (między ograniczeniami) to nie jest rysowany (rys.9.15).
Oczywiście każdy narysowany element powiększa (rozszerza w danym kierunku) odpowiednie
ograniczenie.
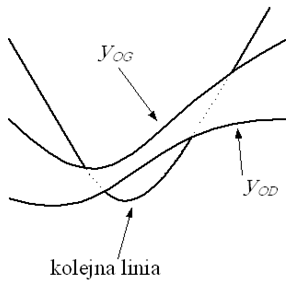
Rys.9.15. Idea algorytmu maskowania Watkinsa. Fragmenty
rysowanej linii
między ograniczeniem dolnym (linia określona dla yOD) a górnym (dla yOG) są zasłonięte.
Standardowe podejście w algorytmie maskowania Watkinsa wymaga podczas rysowania analizy położenia odcinka względem łamanej (górnego ograniczenia lub dolnego). Tego typu zadanie jest klasycznym zadaniem geometrii obliczeniowej i nie należy do najprostszych – wymagałoby dodatkowego, znaczącego czasu realizacji. Można zmodyfikować problem tak, aby nie było to w ogóle konieczne.
W tym celu rozpatrzmy tę samą sytuację ale na mapie pikseli. Ograniczenia górne i dolne w tym przypadku odpowiadają zestawowi pikseli, które w kolejnych kolumnach określają minimalną i maksymalną wysokość. Rysując każdy nowy piksel wystarczy sprawdzić jego położenie względem tego minimum lub maksimum. A to jest operacją bardzo prosta. Jeśli nowy piksel jest powyżej maksimum (lub poniżej minimum) to jest rysowany, jeśli pomiędzy minimum i maksimum to rysowany nie jest. Oczywiście rysowany piksel przesuwa odpowiednie maksimum (lub minimum).
Zaproponowany
mechanizm maskowania dla mapy pikseli może zostać połączony z algorytmem
Bresenhama rysowania odcinka. Tak zmodyfikowany algorytm będzie rysował odcinki
z uwzględnieniem rozstrzygania widoczności dla siatki rozpiętej na powierzchni
będącej wykresem funkcji dwóch zmiennych – rys.9.16. Można pokazać że
modyfikacja algorytmu Bresenhama wymaga dodania jednej instrukcji porównania i
jednej instrukcji podstawienia. Nie zmienia to więc znacząco czasu realizacji samego
rysowania odcinków.
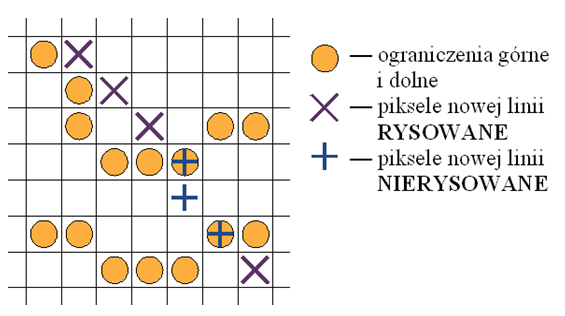
Rys.9.16. Podczas rysowania
pikseli na mapie pikseli (np. algorytmem Bresenhama)
każdy piksel nowej linii
jest sprawdzany. Jest rysowany tylko wtedy,
gdy znajduje się poza ograniczeniem
dolnym i górnym.
Piksele pomiędzy ograniczeniami dolnym i górnym nie są
rysowane.
Złożoność liniowa algorytmu wykorzystującego metodę maskowania Watkinsa wynosi O(n), gdzie n — liczba krawędzi wykresu (lub węzłów).
Dodatkowo należy zwrócić uwagę na kolejność wyboru do rysowania odcinków siatki. Jeśli byłyby one rysowane w naturalnej kolejności związanej z rodzinami linii dla stałego x, i dla stałego y, to mogłyby wystąpić problemy z wzajemnym zasłanianiem. Dobrym rozwiązaniem jest kolejność typu ZIG-ZAG (tzn. odcinki na przemian z każdej rodziny) lub kolejność zaproponowana na rysunku 9.17 a).
Warto dodatkowo zwrócić uwagę na fakt, że taka wersja algorytmu poprawnie pracuje tylko dla rzutu równoległego wykresu funkcji. Analiza rysowania na mapie pikseli z uwzględnieniem minimum i maksimum kolumny pokazuje, że dla odcinków rysowanych w rzucie perspektywicznym wystąpią błędy.
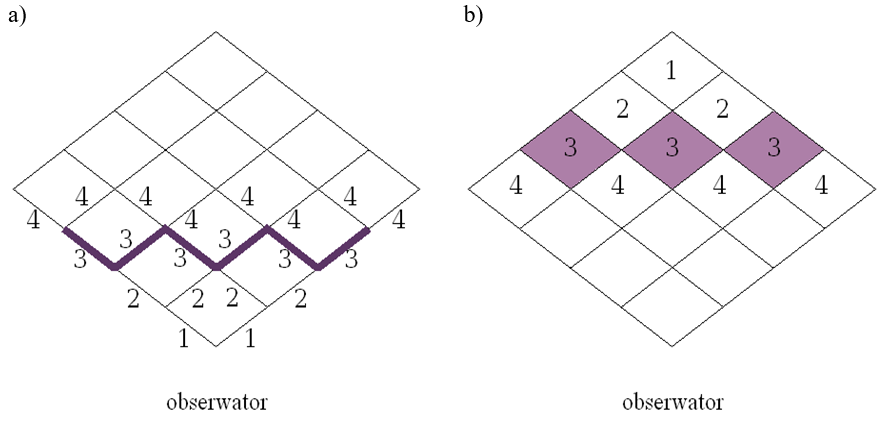
Rys.9.17. a) Kolejność ZIG-ZAG rysowania odcinków
stosowana
w rysowaniu wykresu funkcji metodą maskowania Watkinsa.
b) Kolejność rysowania (wypełniania) czworokątów
przy zastosowaniu algorytmu malarskiego do rysowania wykresu
funkcji.
Inną możliwością rysowania powierzchni wykresu funkcji jest zastosowanie algorytmu malarskiego. Oczywiście wykres funkcji pozwala zrezygnować z sortowania koniecznego w algorytmie malarskim. W tym przypadku wystarczy uwzględnić kolejność wynikającą z odległości „oczek” siatki dziedziny funkcji od obserwatora. Rysunek 9.17 b) pokazuje kolejność rysowania oczek siatki w takim przypadku. Oczka o tym samym numerze mogą być rysowane w dowolnej kolejności – nie zmienia to rysunku gdyż nie mogą się one wzajemnie zasłaniać.
Zastosowanie algorytmu malarskiego ma dodatkową zaletę: algorytm ten poprawnie rysuje powierzchnię będącą wykresem funkcji także dla rzutu perspektywicznego.
Algorytm rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest przykładem algorytmu rozstrzygania widoczności dla szczególnej klasy obiektów trójwymiarowych. Drugim przykładem tego typu zadania jest algorytm rysowania figur obrotowych. Szczegóły tego algorytmu czytelnik może znaleźć w książce M.Jankowskiego Elementy grafiki komputerowej [3].
9.9. Złożoność obliczeniowa algorytmów rozstrzygania widoczności
Wnioski jakie płyną z tych analiz:
- Dla algorytmów w przestrzeni obiektu decydujące jest zastosowane sortowanie geometryczne. Dla typowych („niezłośliwych”) scen, można uzyskać złożoność postaci O(nlogn), gdzie n — liczba wielokątów.
- Dla algorytmów pracujących w przestrzeni rzutu można uzyskać złożoność O(n), gdzie n — liczba wielokątów.
Analizy te pokazują, że nawet najtrudniejsze przypadki mogą zostać rozwiązane ze złożonością kwadratową. Z drugiej strony można się zastanawiać nad minimalną liczbą operacji, niezbędnych do rozwiązania problemu zasłaniania. W większości przypadków wyrafinowane algorytmy wyznaczają elementy zasłonięte ze złożonością O(nlogn), gdzie n jest miarą złożoności sceny (liczbą wielokątów lub krawędzi). Oczywiście dla algorytmów pracujących w przestrzeni rzutu (z precyzją obrazową) nie jest możliwe uzyskanie złożoności lepszej niż liniowa.
Można pokazać, że dla wybranych scen minimalna złożoność algorytmów pracujących w przestrzeni obiektu musi być rzędu kwadratowego. Wynika to z budowy sceny. Wyrafinowane algorytmy mogą w tym przypadku dać rozwiązanie gorsze niż kwadratowe. Przykłady takich „złośliwych” scen pokazuje rysunek 9.18. W obu przypadkach liczba różnych fragmentów wymagających analizy zasłaniania jest rzędu n2, jeśli n jest np. liczbą obiektów. Zatem algorytm eliminacji elementów zasłoniętych pracujący w przestrzeni obiektu nie może mieć niższej złożoności.
Rys.9.18. Przykłady sceny
„złośliwej”.
a) Mata „plecionka” – obiekty nie są płaskie.
b) Mata w wersji
prostszej – obiekty są płaskie.