Podręcznik Grafika komputerowa i wizualizacja
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Część 3. Światło, barwa i problemy renderowania |
| Książka: | Podręcznik Grafika komputerowa i wizualizacja |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 20 lutego 2026, 12:39 |
Opis
Spis treści
- Rozdział 10. ŚWIATŁO I BARWA W GRAFICE KOMPUTEROWEJ
- Rozdział 11. MODELOWANIE OŚWIETLENIA
- Rozdział 12. OŚWIETLENIE GLOBALNE: METODA ŚLEDZENIA PROMIENI
- 12.1. Wprowadzenie
- 12.2. Idea metody śledzenia promieni
- 12.3. Śledzenie klasyczne (Whitteda)
- 12.4. Rzeczywiste (niepunktowe) źródło światła
- 12.5. Całkowanie Monte Carlo
- 12.6. Śledzenie stochastyczne
- 12.7. Mapowanie fotonowe
- 12.8. MLT
- 12.9 Rosyjska ruletka
- 12.10. Problem cienia
- 12.11. Metoda śledzenia promieni a CSG
- 12.12. Metody przyspieszające śledzenie promieni
- Rozdział 13. OŚWIETLENIE GLOBALNE: METODA BILANSU ENERGETYCZNEGO
Rozdział 10. ŚWIATŁO I BARWA W GRAFICE KOMPUTEROWEJ
Rozdział dziesiąty poświęcony jest problemom percepcji widzenia i wykorzystania barwy w grafice komputerowej. Przedstawiono podstawowe pojęcia związane ze światłem i barwą. Omówiono budowę oka i właściwości wzroku oraz zagadnienie postrzegania barw. Przedstawiono teorię trójpobudzenia Younga-Helmholtza oraz prawa Grassmana, Webera Fechnera, Bezolda – Bruckego oraz zjawisko hamowania obocznego. Przedstawione zostały także podstawowe model barwL model CIE XYZ, CIE Lab, RGB, CMY (CMYK), HSV i HLS. Czytelnik znajdzie również informacje dotyczące problemu reprodukcji barw, zakresu barw urządzenia i korekcji Gamma.
10.1. Wprowadzenie, pojęcia podstawowe
Światło — promieniowanie elektromagnetyczne rejestrowane przez oko. Zakres promieniowania odpowiadający przedziałowi widma od ok. 380nm (fiolet) do ok. 700nm (czerwień).
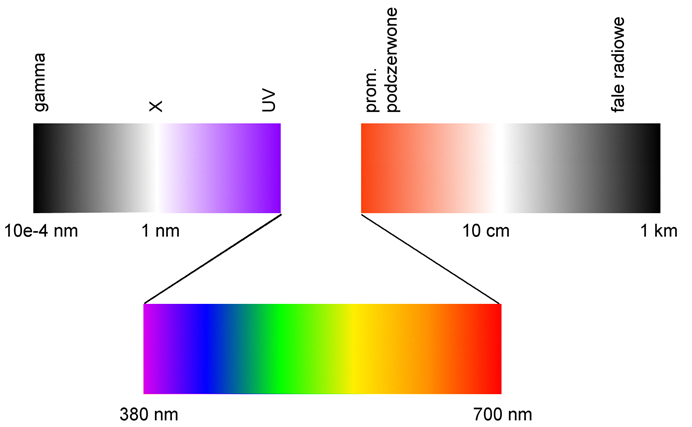
Rys.10.1. Promieniowanie widzialne jest częścią promieniowania elektromagnetycznego.
Barwa to wrażenie wzrokowe wywołane w mózgu przez padające na receptory oka promieniowanie.
Atrybuty barwy
- Odcień barwy (ton, walor) to wrażenie związane z konkretną długością fali,
- Nasycenie to „mieszanie” (0 – 100%) barwy czystej z barwą białą,
- Jasność (luminancja) to wrażenie związane z wielkością strumienia świetlnego (umowna skala 0 – 1).
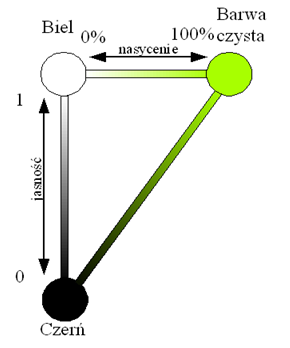
Rys.10.2. Atrybuty barwy.
Aby uniknąć problemów z nazewnictwem, w dyscyplinach takich jak kolorymetria, technika świetlna i grafika komputerowa zaproponowano używanie pojęcia barwa na określenie wrażeń wzrokowych. Powszechnie używane określenie kolor jest kalką językową i prowadziłoby do nieporozumień ( np. w przypadku barw achromatycznych).
Biel, czerń oraz wszystkie barwy występujące między nimi nazywane są barwami achromatycznymi. Są one w pełni nienasycone. Wszystkie pozostałe (o nasyceniu większym od zera) to barwy chromatyczne.
Mieszanie barw
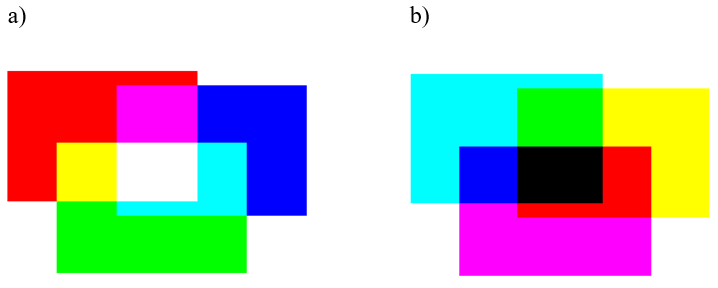
Rys.8.3. Mieszanie barw: a) addytywne, .b) subtraktywne.
Mieszanie
addytywne jest mieszaniem świateł. Mieszaniem promieniowania.
Oznacza to, że
jeśli do oka padają dwa rodzaje promieniowania o różnych odcieniach, to wrażenie
sumaryczne jest wypadkową obu. Przykładem takiego mieszania jest oświetlenie
sceny teatralnej reflektorami z różnymi filtrami.
Wypadkowa mieszania addytywnego dąży do bieli.
Z drugiej strony barwa biała (np. światła słonecznego) zawiera wszystkie składowe barwne. I jest efektem addytywnego mieszania tych wszystkich składowych.
Mieszanie subtraktywne jest mieszaniem farb. Farba jest substancją pochłaniającą składowe promieniowania o określonej długości fali. Np. farba niebieska pochłania wszystkie składowe oprócz niebieskiej. A więc jeśli oświetlimy niebieską powierzchnię światłem białym to odbije ona tylko promieniowanie niebieskie i taką barwę postrzegamy.
Wypadkowa mieszania subtraktywnego dąży do czerni. (Znany z przedszkola eksperyment: co powstanie ze zmieszania wszystkich farb z palety?)
Barwy dopełniające to dwie takie barwy, których mieszanie addytywne daje biel, a subtraktywne czerń.
Terminologia
Kolorymetria jest dyscypliną zajmującą się barwami: definiowaniem i opisywaniem barw oraz ich właściwościami. Istnieją różnice terminologiczne między określeniami potocznymi i określeniami definiowanymi w kolorymetrii.
Percepcja, określenia potoczne Kolorymetria
kolor, odcień barwy dominująca długość fali
nasycenie czystość pobudzenia
jasność
(obiekty odbijające) luminancja
jaskrawość
(obiekty świecące) luminancja
10.2. Budowa oka i właściwości wzroku
Oko jest narządem zmysłu pozwalającym na postrzeganie otoczenia. Gałka oczna ma kształt zbliżony do kuli o średnicy od ok. 16 mm (dzieci) do ok. 24 mm (osoby dorosłe). Wypełniona jest przezroczystą, galaretowatą substancją (zwaną ciałem szklistym) utrzymującą kształt oka. Gałka oczna pokryta jest twardówką – wytrzymałą i nieprzezroczystą (białą) błoną. Jej przednia, widoczna część, zwana rogówka, jest przezroczysta i stanowi naturalna ochronę oka. Twardówka jest wyścielona od wewnątrz naczyniówką – warstwą naczyń krwionośnych. Oko jako przyrząd optyczny pozwala na odbiór wrażeń dzięki dwóm elementom : soczewce skupiającej i warstwie receptorów, na której powstaje odwrócony, rzeczywisty i pomniejszony obraz. Soczewka ma możliwość zmiany krzywizny, dzięki czemu długość ogniskowej może się zmieniać w granicach od ok. 23 mm do ok. 19 mm. Zmianę kształtu soczewki powodują mięśnie rzęskowe. W stanie spoczynku soczewka zapewnia ostre widzenie obiektów znajdujących się w dużej odległości (w nieskończoności). Skurcz mięśni rzęskowych powoduje rozciągnięcie soczewki i zmniejszenie jej krzywizny. Dzięki temu możliwe jest ostre widzenie obiektów znajdujących się bliżej. Proces dostosowywania się oka do odległości w celu zapewnienia ostrego widzenia nazywa się akomodacją oka. Soczewka przysłonięta jest tęczówką działającą jak przysłona aparatu fotograficznego. Otwór w tęczówce – źrenica zapewnia możliwość regulacji ilości światła wpadającego do oka. Mięśnie tęczówki (okrężne zmniejszające źrenicę i promieniowe rozszerzające ją) tworzą niepowtarzalny wzór wykorzystywany przez biometrię oka. Obraz powstaje na siatkówce, na której znajdują się receptory połączone nerwem wzrokowym z mózgiem.
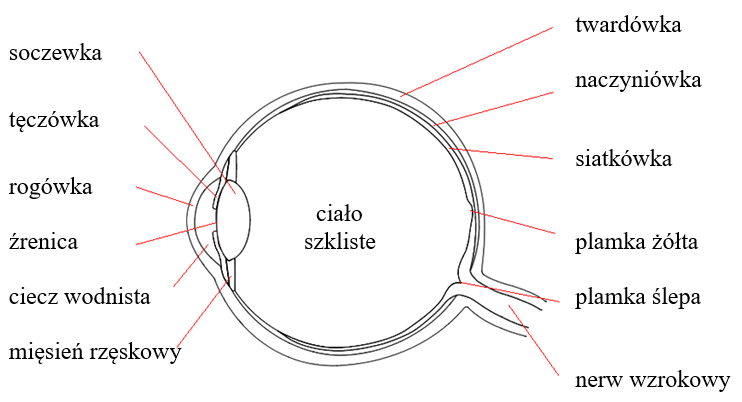
Rys.10.4. Budowa oka.
Warto dodać, że para oczu daje człowiekowi możliwość oceny odległości. Jeśli patrzymy na zbliżający się obiekt, to osie optyczne obu gałek przecinają się pod coraz większym kątem. Analiza tego kąta przez mózg pozwala wnioskować o odległości do obiektu. Z drugiej strony jednak, analiza odległości i położenia w przestrzeni jest dokonywana na podstawie postrzeganych wzajemnych relacji (np. wzajemnego zasłaniania) między przedmiotami, akomodacji oraz zdobytego doświadczenia. Na tej podstawie osoby, które utraciły jedno oko również potrafią ocenić odległości.
Zdobyte doświadczenie jest również wyjaśnieniem problemu postrzegania świata „do góry nogami”. Soczewka oka odwraca obraz i dopiero mózg interpretuje obraz właściwie. Nie jest to umiejętność wrodzona ale nabyta. Dziecko do ok. pół roku nabiera doświadczeń ruchowych i najprawdopodobniej dopiero wtedy następuje odwrócona interpretacja.
Siatkówka – pole na którym powstaje obraz. Percepcja obrazu następuje za pomocą dwóch rodzajów receptorów:
Czopków — widzenie dzienne, fotopowe
Pręcików — widzenie nocne, skotopowe
Czopki i pręciki zostały odkryte przez Maxa Schultza w 1866 roku.
Siatkówka jest wielowarstwową tkanką nerwową zawierającą ponad 120 mln receptorów. Fotony trafiając do receptorów wywołują reakcje elektrochemiczne tworząc impulsy nerwowe przenoszone do mózgu.
Na siatkówce jest ok. 120 mln pręcików i ok. 6 mln czopków. Receptory te są rozłożone nierównomiernie na siatkówce w okolicach plamki żółtej (zwanej też dołkiem centralnym), przy czym pręciki znajdują się na całej siatkówce poza plamką żółtą, natomiast czopki głównie w plamce żółtej. Połączenie nerwu wzrokowego z siatkówka tworzy tzw. plamkę ślepą na, której nie ma żadnych receptorów. Plamka żółta pokrywa kąt ok. 1 stopnia pola widzenia. Gęstość czopków jest tam największa – rozmieszczone są one tak, że odległość między ich środkami jest równa ich średnicy (ok. 0,002 mm). Poza tym polem gęstość receptorów gwałtownie spada. Pręciki, mimo że na całej siatkówce, to także rozmieszczone są nierównomiernie. Ich największe skupienie występuje w odległości kątowej ok. 15 stopni od plamki żółtej (dlatego o widzeniu nocnym mówimy, że jest widzeniem peryferyjnym).
Gęstość rozmieszczenia receptorów jest związana z rozdzielczością widzenia, czyli minimalną odległością między punktami, które są postrzegane w postaci dwóch niezależnych punktów a nie jednej plamy. Doświadczalnie stwierdzono, że maksymalna rozdzielczość oka ludzkiego wynosi ok. 1 minuty kątowej. Rozdzielczość tę nazywa się minimum separabile.
Podstawowe różnice między receptorami decydują o sposobie postrzegania świata przez człowieka.
Czopki pozwalają na rejestracją wrażeń barwnych i rozróżnianie odcieni barwnych. Do pobudzenia wymagają dużej ilości światła - odpowiadają za widzenie dzienne, nazywane fotopowym.
Pręciki pozwalają na rejestrację tylko odcieni szarości, do pobudzenia wystarczy im wielokrotnie mniej światła – odpowiadają za widzenie nocne. W nocy widzimy bez barw („w nocy wszystkie koty są czarne”), główne kształty i kontury.
Warto zwrócić uwagę na połączenia receptorów z mózgiem. Liczba połączeń nerwowych siatkówki w nerwie wzrokowym wynosi ok. 1 mln (wobec ok. 126 mln receptorów). A zatem nie ma odpowiedniości 1 receptor – 1 połączenie. Już na etapie przetwarzania na siatkówce obraz poddawany jest „kompresji”. Połączenia nerwowe doprowadzone są do tzw. jednostek receptorowych – pól, które grupują receptory. Jednostki plamki żółtej obejmują po jednym receptorze (czopku), natomiast poza nią grupują od kilkudziesięciu do kilkuset receptorów. W ramach plamki żółtej każdy receptor (czopek) jest więc indywidualnie połączony z nerwem wzrokowym. Szacuje się że te kilka procent powierzchni siatkówki tworzy ok. 50 % połączeń. Reszta obejmuje pozostały obszar siatkówki.
Czopki i pręciki maja również różne zależności pobudzenia od długości fali. Kształt zależności w obu przypadkach jest praktycznie identyczny – jest to krzywa dzwonowa obejmująca prawie cały obszar promieniowania widzialnego. Ale maksima tych krzywych są przesunięte. Dla widzenia dziennego (fotopowego) jest to ok. 555 nm, dla widzenia nocnego (skotopowego) ok. 515 nm. Efektem tego jest wrażenie, że powierzchnie niebieskozielone postrzegamy w nocy jako jaśniejsze niż w dzień, natomiast żółtoczerwone jako ciemniejsze (efekt Purkiniego).
Stan pośredni między widzeniem skotopowym a fotopowym (o świcie i o zmierzchu) nazywamy widzeniem mezopowym.
10.3. Postrzeganie barw
Teorie postrzegania barw
W 1802 roku T.Young zaproponował istnienie trzech niezależnych receptorów, każdy odpowiedzialny za inną składową barwną. H.Helmholtz rozwinął i sformalizował tę teorię w 1850 roku. Teoria trójpobudzeniowa postrzegania barw Younga – Helmholtza zakłada, że wrażenia barwne są odbierane w oku przez trzy rodzaje niezależnych receptorów, każdy związany z inną długością fali. Wrażenie barwne jest wynikiem mieszania barw składowych. Teoria ta została częściowo potwierdzona w latach sześćdziesiątych XX wieku. Warto zwrócić uwagę na fakt, że koncepcja T.Younga powstała wcześniej niż odkryto czopki i pręciki w siatkówce oka (M.Schultz: w 1866 roku.)
W 1892 roku E.Hering: zaproponował zupełnie inną teorię postrzegania barw: teorię przeciwstawieństw. Teoria postrzegania barw Heringa zakłada, że do mózgu trafia informacja nie o pojedynczych składowych, ale o różnicach barw (biały-czarny, czerwony-zielony, niebieski-żółty). Zaproponowane pary tworzone są przez barwy, które bardzo rzadko występują jednocześnie. Trudno wskazać obiekt, który jest jednocześnie i biały i czarny. Natomiast może on być szary czyli jego barwa będzie określona właśnie przez relacje (proporcje) między bielą a czernią.
Dzisiejsza fizjologia pokazuje współdziałanie obu, pozornie wykluczających się teorii. Zwoje nerwowe siatkówki łączą czopki wrażliwe na różne barwy. Do mózgu trafia zarówno informacja o poszczególnych składowych (z pojedynczych czoków określonej barwy), jak i różnicach (proporcjach) między nimi.
Percepcja barw
Można wyróżnić trzy procesy niezbędne do tego aby dostrzec barwy:
- Emisja światła (proces fizyczny).
- Pobudzenie receptora siatkówki (proces fizjologiczny).
- Wytworzenia wrażenia wzrokowego (proces psychofizyczny).
Postrzeganie
barwy silnie zależy od czynników towarzyszących bezpośrednio powstawaniu
strumienia świetlnego padającego do oka. Dobrym przykładem jest wpływ tła
(otoczenia) na jakim znajduje się postrzegana barwa. Zjawisko to nazywane jest
najczęściej problemem sąsiedztwa barw (rys.10.5). Pomimo identyczności
pobudzenia receptorów siatkówki przez barwę danej plamy, jej otoczenie /
sąsiedztwo wpływa na wytworzenie określonych wrażeń.
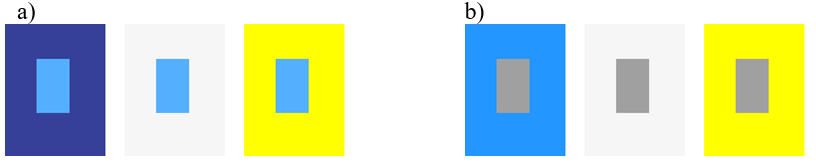
Rys.10.5. Problemy sąsiedztwa
barw. a) Prostokąt niebieski wydaje się
ciemniejszy lub jaśniejszy w zależności od tła na jakim
się znajduje.
b) Prostokąt szary „uzyskuje” barwę w zależności od tła na
jakim się znajduje.
Podobnie na odbiór wpływa oświetlenie i wielkość rysunku. Zmiana składowych światła oświetlającego plamę barwną wpływa na zestaw składowych odbitych od tej plamy. Receptory są pobudzone składowymi zależnymi od odbicia. Przy zmianach wielkości rysunku może dochodzić do niezamierzonego mieszania barw sąsiednich pól, czego wynikiem będzie wytworzenie zupełnie nowego wrażenia.
Warto dodać do tego problemy wynikające z naszych przyzwyczajeń i doświadczeń. Czytając gazetę na plaży o zachodzie słońca nie zdajemy sobie sprawy z faktu, że powinniśmy widzieć czarne litery na czerwonym tle. Wynika to bowiem z barwy zachodzącego słońca i odbicia światła o takiej barwie od białej kartki. Widzimy jednak czarne litery na białej kartce bo tak nam podpowiada doświadczenie i zdobyta wiedza. Jak zaskakująco silny jest wpływ wiedzy i doświadczeń; na ile nasz mózg może wpłynąć na odbiór barw można przekonać się oglądając eksperymenty przeprowadzone w Lottolab Studio (http://www.lottolab.org/index.asp).
Percepcja barw jest procesem subiektywnym. Oznacza to, że każdy postrzega barwy w inny sposób. Możliwe są również minimalne różnice między lewym a prawym okiem. Do tego trzeba dodać różnice interpretacyjne zależne od doświadczeń i kultury. Znane są różnice łączenia barw z emocjami uwarunkowane kulturowo (np. postrzegania bieli i czerni) oraz przypisywania barwom określonych znaczeń.
Prawa Grassmana
Zasada trójchromatyczności (1. Prawo Grassmana)
Każdą dowolną
barwę można przedstawić za pomocą trzech składowych – barw podstawowych
(takich, że żadna z nich nie jest wypadkową dwóch pozostałych – są niezależne
kolorymetrycznie).
Zasada ciągłości (2. Prawo Grassmana)
Jeśli mamy do
czynienia z mieszaniną dwóch barw, to ciągła zmiana jednej składowej powoduje
ciągłą zmianę mieszaniny.
Zasada addytywności (3. Prawo Grassmana)
Barwa
mieszaniny nie zależy od jej składu widmowego tylko od barw składników.
Prawo Webera Fechnera
Prawo odkryte w 1849 roku przez E.Webera, wyrażone matematycznie przez G.Fechnera w 1860 roku.
Jeśli rozpatrzymy wrażenie wywołane przez dany bodziec, to aby wywołać zauważalny przyrost wrażenia , przyrost bodźca musi być proporcjonalny do aktualnego poziomu bodźca. Oznacza to, że poziom wrażenia wzrasta wprost proporcjonalnie do logarytmu z poziomu bodźca. Prawo to zostało potwierdzone dla wrażeń słuchowych i wzrokowych.
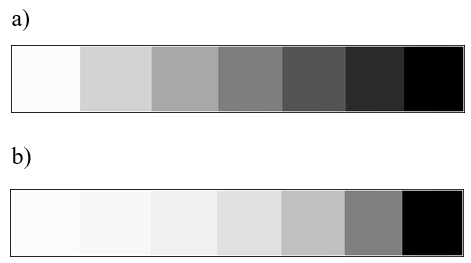
Rys.10.6. Prawo
Webera-Fechnera. a) Poziom barwy czarnej wzrasta
liniowo – wrażenie
logarytmiczne (wrażenie zbyt szybko narastającej czerni).
b) Poziom barwy
czarnej wzrasta wykładniczo – wrażenie liniowe.
Prawo Bezolda - Bruckego
Zachodzi pytanie czy atrybuty barwy (odcień barwy, nasycenia i jasność) są niezależne.
Badania wykazały, że zachodzi percepcyjny związek między atrybutami barwy. Zmiana jednego z nich pociąga za sobą zmiany pozostałych..
Zmniejszenie
luminancji wiąże się wrażeniem zmniejszenia składowych żółtej i błękitnej.
Zmniejszenie
nasycenia wiąże się z wrażeniem
zwiększenia składowych żółtej i błękitnej.
Warto pamiętać o tym nawet podczas najprostszej obróbki obrazów (np. zdjęć cyfrowych). Zmiana jasności albo kontrastu może spowodować nienaturalny wygląd (postrzegalną zmianę barw) przedmiotów na zdjęciu.
Zjawisko hamowania obocznego
Receptory siatkówki wpływają wzajemnie na proces percepcji barwy. Jest to widoczne na granicy pól o różnej luminancji. Receptory odbierające barwę jaśniejszą są pobudzane przez sąsiednie receptory odbierające barwę ciemniejszą. W odwrotnej sytuacji receptory odbierające barwę ciemniejszą są blokowane. Działanie takie powoduje wrażenie zwiększenia kontrastu na granicy luminancji - rys. 10.7.
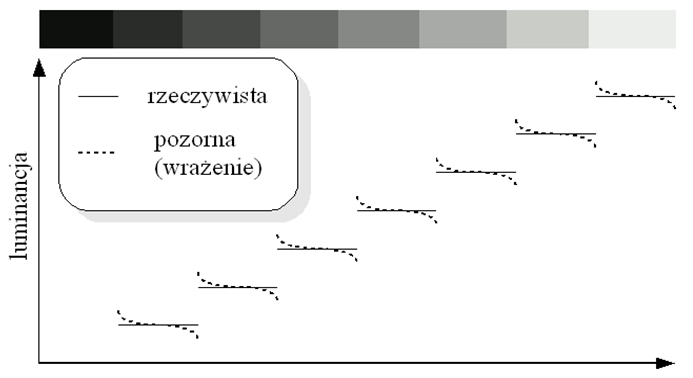
Rys.10.7. Zjawisko hamowania obocznego. Zmiana luminancji: rzeczywista i postrzegana.
Mechanizm ten jest bardzo użyteczny dla człowieka. Potrafimy dzięki temu dostrzec szczegóły przy słabym oświetleniu (np. czytać o zmierzchu). Ale zły dobór barw np. przy realizacji ciągłej zmiany między dwiema określonymi barwami zostanie natychmiast wychwycony przez oko. Powstają wtedy tzw. pasma Macha.
Metameryzm
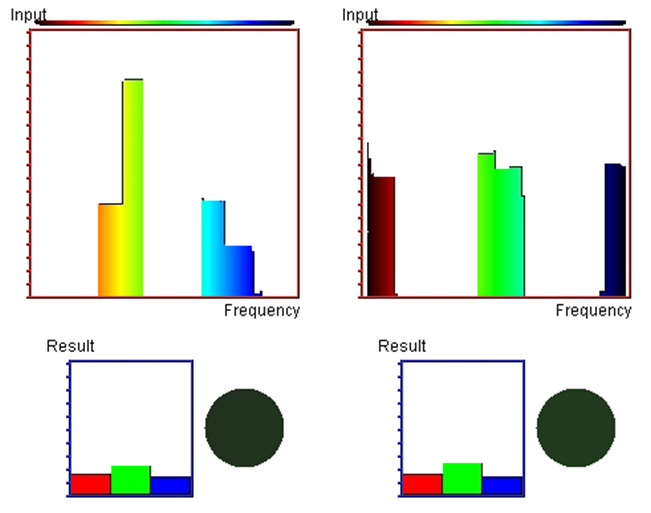
Rys.10.8. Zjawisko metameryzmu.
Okrągłe pola mają tak samo postrzegane barwy. Co więcej
ich składowe RGB są identyczne.
Ale powstały one z całkowicie różnych
składowych widmowych.
Metameryzm — zjawisko polegające na tym, że ta sama barwa może być inaczej postrzegana w różnych warunkach.
Percepcja barwy nie zależy od jej składowych widmowych. Oko nie jest miernikiem składowych widmowych barwy.
Z metameryzmem możemy mieć do czynienia w różnych sytuacjach. Z jednej strony może być tak, że np. gazeta została wydrukowana dwoma rodzajami czarnej barwy i w warunkach drukarni różnice nie były w ogóle widoczne. Zauważyli je dopiero czytelnicy w innych warunkach oświetleniowych.
Z drugiej strony istnieją zestawy barw, które wyglądają identycznie pomimo otrzymywania ich z różnych składowych. Przykładem może być barwa czerwona którą otrzymywano z drogich składników, ze względów finansowych zastąpiono innymi – tańszymi. Mimo różnego rozkładu widmowego wrażenie jest identyczne.
Metameryzm stanowi bardzo poważny problem w poligrafii.
10.4. Modele barw
System barw Munsella
System wzorców barwy opisanych za pomocą 3 składowych : odcienia, nasycenia i jasności.
Odcień barwy oznaczony H (od ang. Hue) tworzy okrąg. Został on podzielony na 10 głównych segmentów, a te z kolei na 10 segmentów pośrednich. System oznaczeń literowo-cyfrowych pozwala odnaleźć właściwy segment. Opisuje on położenie na zasadzie odległości kątowej od początku segmentu liczonej zgodnie z ruchem wskazówek zegara. W ten sposób zdefiniowano 100 różnych odcieni barw.
Wartość (jasność) oznaczone V (od ang. Value) zestawiono w 10 poziomach przy czym oba poziomy skrajne są teoretyczne (nie są realizowalne praktycznie)..
Nasycenia oznaczone C (od ang. Chroma) jest przedstawione w postaci odległości od osi V barw w pełni nienasyconych.
Atlasy barw Munsella zawierają 100 tablic dla różnych odcieni. Na każdej tablicy znajduje się 9 poziomów wartości i od 1 do 28 poziomów nasycenia.
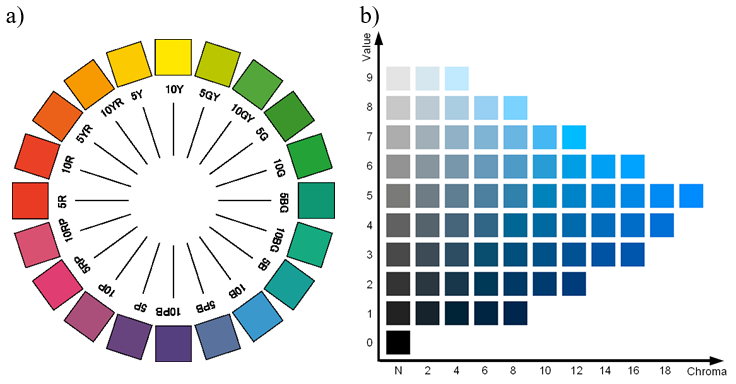
Rys.10.9. System barw Munsella.
a) Koło barw Munsella. b) Przykładowa strona barw dla Hue=10B.
Brak możliwości jednoznacznego opisu przestrzeni barw w taki sposób, aby było to użyteczne we wszystkich praktycznych zastosowaniach sprawia, że istnieje wiele różnych modeli barw. Niektóre opracowane specjalnie dla konkretnych zastosowań (np. określonych systemów telewizji).
Teoria trójpobudzenia RGB
Wychodząc z założenia możliwości uzyskania dowolnej barwy w wyniku mieszania barw podstawowych można zaproponować model oparty o barwy czerwoną, zieloną i niebieska. W latach trzydziestych XX wieku doświadczalnie wybrano wartości składowych trójchromatycznych. O doborze określonych barw decydowała między innymi praktyczna możliwość uzyskania barwy o określonej długości fali poprzez wydzielenie prążków ze światła łuku rtęciowego. Okazało się, że aby pokryć pełny zakres barw widmowych składowa czerwona musiałaby przyjmować w pewnym zakresie wartość ujemną – rysunek 10.10. Taki warunek nie ma interpretacji fizycznej – nie jest możliwa zatem realizacja praktyczna takiego mieszania.
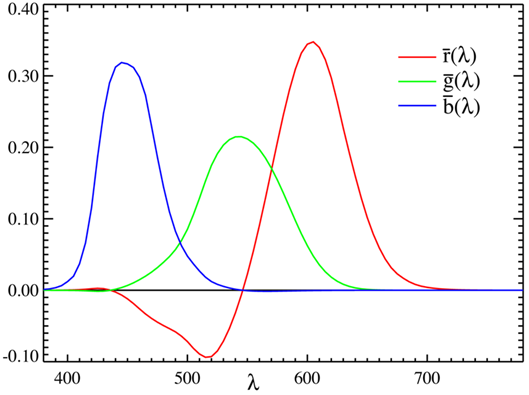
Rys.10.10. Widmowe składowe trójchromatyczne w układzie RGB.
Teoria trójpobudzenia XYZ

Rys.10.11. Widmowe składowe trójchromatyczne w układzie XYZ.
W 1931 roku Międzynarodowa Komisja Oświetleniowa (CIE – Commission
Internationale de l’Eclairage) zaproponowała zestaw trzech składowych
trójchromatycznych, których mieszanie może pokryć pełny zakres barw widmowych i
jednocześnie wartość każdej ze składowych jest zawsze większa od zera. Składowe
oznaczono jako ![]() .
.
Definiują one barwy
X Y Z w postaci:
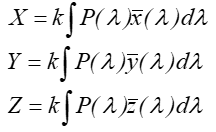
gdzie ![]() jest rozkładem energetycznym strumienia świetlnego, k jest współczynnikiem dobieranym tak
aby maksymalna wartość Y wyniosła 100.
jest rozkładem energetycznym strumienia świetlnego, k jest współczynnikiem dobieranym tak
aby maksymalna wartość Y wyniosła 100.
Barwa Y
została tak zdefiniowana, aby krzywa składowej ![]() odpowiadała dokładnie
krzywej czułości oka na światło o stałej luminancji. W ten sposób składowa
odpowiadała dokładnie
krzywej czułości oka na światło o stałej luminancji. W ten sposób składowa ![]() odpowiada informacji o
strumieniu światła, natomiast pozostałe dwie składowe odpowiadają wyłącznie za
informacje o barwie.
odpowiada informacji o
strumieniu światła, natomiast pozostałe dwie składowe odpowiadają wyłącznie za
informacje o barwie.
Barwy
podstawowe, które zostały wybrane do tego modelu są barwami teoretycznymi – ich
poziom nie jest realizowalny fizycznie. Dodatkowo trzeba zwrócić uwagę na fakt,
że składowa ![]() ma dwa maksima –
rysunek 10.11.
ma dwa maksima –
rysunek 10.11.
Model CIE XYZ
Przyjmując normalizację składowych w postaci:
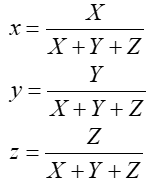
otrzymujemy x+y+z=1 . Jest to równanie płaszczyzny w przestrzeni barw. Płaszczyznę te przedstawia się najczęściej w postaci rzutu na płaszczyznę xy. Tak powstaje wykres chromatyczności układu CIE XYZ – rysunek 10.12.
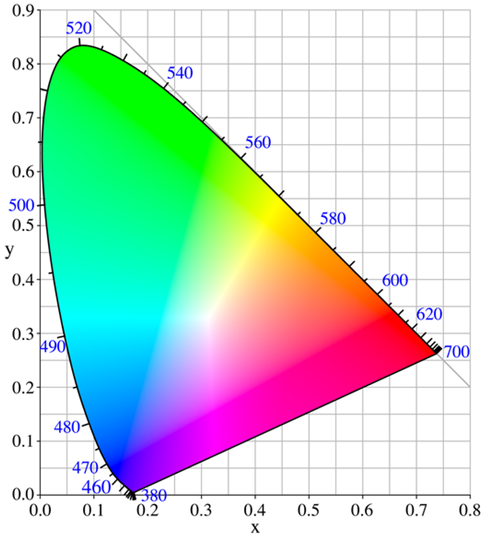
Rys.10.12. Wykres chromatyczności CIE.
Na obwodzie wykresu znajdują się barwy nasycone odpowiadające określonym długościom fali.
Przestrzeń barw CIE XYZ jest przestrzenią liniowa. Oznacza to, że w przestrzeni tej obowiązuje prawo dodawania wektorów i mnożenia wektora przez skalar. Dzięki temu można wyznaczać w prosty sposób barwy wynikowe np. mieszania barw.
Barwa biała jest barwą w pełni nienasyconą. Jednak każdy z doświadczenia wie, że biel bieli nierówna. Potocznie mówimy o bieli z odcieniem (niebieskiego, różowego itd.). Biel światła słonecznego jest inna w godzinach porannych a inna w południe.
Z punktu widzenia budowy modelu CIE XYZ uzasadnionym punktem bieli jest punkt o jednakowych współrzędnych tzn.
![]()
Barwa o takich współrzędnych nosi nazwę bieli równoenergetycznej i została zaznaczona na wykresie jako punkt CE (często oznaczany również E) – rysunek 10.13 a).
W przypadku światła słonecznego mówi się o jego przybliżeniu w postaci standardowego światła białego odpowiadającego światłu dziennemu dla skorelowanej temperatury barwowej 674 K. Jest to tzw. iluminat C (biel C) o współrzędnych x=0,310 , y=0,316 , z=0,374 .
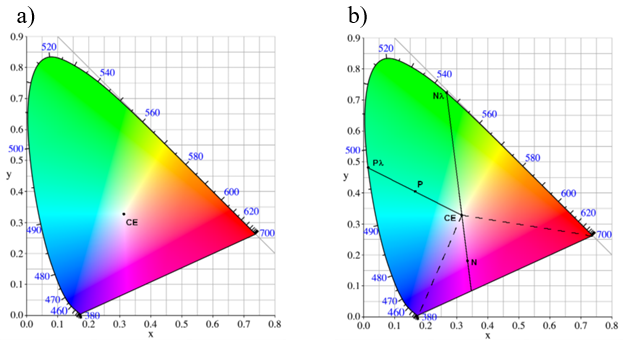
Rys.10.13. a) CE – biel równoenergrtyczna. b) Barwy
dominujące.
Osoby zajmujące się fotografią tradycyjną wiedzą, że sprzedawane materiały fotograficzne (dla tradycyjnej - analogowej fotografii) dostosowane są do dwóch różnych parametrów bieli. Albo do światła o temperaturze 6500 K (światła naturalnego; dziennego), albo do światła o temperaturze 3200 K (sztucznego ; żarowego). Wykonanie zdjęcia na pierwszym materiale przy świetle sztucznym daje efekt „zażółcenia”, na drugim materiale w świetle słonecznym efekt „zaniebieszczenia”. Współczesne aparaty cyfrowe dają możliwość korekcji tego problemu dzięki programom balansu bieli.
Jeśli punkt CE odpowiada bieli (barwie w pełni nienasyconej) a punkt na obrzeżu „podkowy” wykresu chromatyczności barwie czystej (w pełni nasyconej) to połączenie tych punktów odcinkiem wyznacza zmiany nasycenia barwy (rys.10.13 b). W takim razie dla dowolnej barwy np. dla punktu P na wykresie można wyznaczyć odpowiadającą jej barwę czystą czyli barwę dominującą (punkt Pλ na rys.10.13 b). Powstaje problem z punktami takimi jak N na wykresie. Dla dolnej części podkowy nie istnieje możliwość przypisania długości fali. W przypadku barwy zaznaczonej punktem N mówi się, że jej barwą dominującą jest dopełnienie barwy Nλ. W trójkącie, zaznaczonym na rysunku 10.13 b) linią przerywaną, znajdują się barwy niespektralne: purpury i magenty.
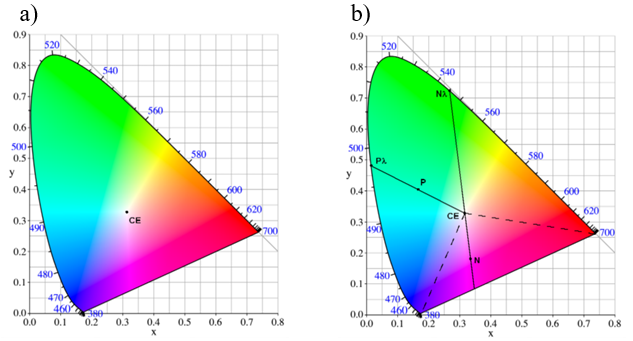
Rys.10.13. a) CE – biel równoenergetyczna. b) Barwy dominujące.
Warto dodać, że wykres chromatyczności w postaci rzutu płaszczyzny x+y+z=1 na płaszczyznę xy nie uwzględnia zmiany luminancji. A to oznacza, że nie są reprezentowane barwy, których wrażenie wzrokowe zależy od luminancji. Na przykład nie występuje na tym przekroju barwa brązowa. Barwa ta występuje na innym przekroju bryły CIE XYZ.
Barwę brązową na urządzeniach korzystających ze standardowego wykresu chromatyczności CIE XYZ uzyskuje się mieszając barwę pomarańczową z czernią (czyli zmniejszając jej luminancję).
Wykres chromatyczności CIE pozwala w prosty sposób wyznaczyć barwy dopełniające : punkty D1 i D2 na rysunku 10.14 a).
Wykres chromatyczności CIE daje także możliwość wyznaczenia barwy mieszaniny. Jeśli mieszamy barwy P1 i P2 to barwa wynikowa P3 znajduje się na odcinku łączącym te punkty – rysunek 10.14 b). Długości odcinków P1P3 i P2P3 zależą od proporcji ilości użytych barw.
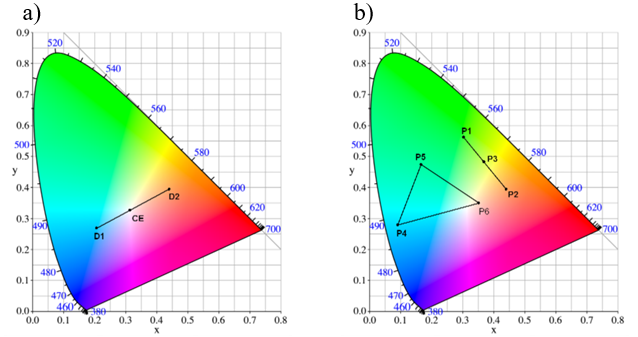
Rys.10.14. a) D1 i D2 - Barwy dopełniające. b) P3 – wynik mieszania barw P1 i P2.
Analogicznie można mieszać trzy barwy np. P4, P5 i P6 – barwa wynikowa mieszaniny leży w trójkącie (rys.10.14 b). Mieszając trzy składowe nie da się uzyskać barwy spoza trójkąta składowych! A to oznacza że nie ma możliwości pokrycia całego wykresu chromatyczności za pomocą mieszaniny trzech składowych.
Model CIE Lab
Model CIE XYZ ma jedną wadę: nie jest percepcyjnie jednorodny. Oznacza to, że operacje wektorowe na wykresie chromatyczności nie są zgodne z odczuwaniem przez człowieka: np. zmiana dwóch barw o taki sam wektor nie musi być postrzegana tak samo. Ponieważ problem percepcji jest bardzo ważny w dziedzinach związanych z poligrafią, komisja CIE opracowała w 1976 roku modele CIE LUV i CIE Lab (czasami oznaczany jako CIELa*b*). Są to modele niezależne od sprzętu. dające możliwość uzyskania jednorodności percepcyjnej. Opierają się one na teorii barw przeciwstawnych wykorzystywanej do opisu widzenia człowieka. Zgodnie z tą teorią człowiek koduje barwy jako trzy sygnały: jasność, stosunek czerwień/zieleń, stosunek błękit/żółć. Oznacza to że nie może być postrzegana barwa jednocześnie czerwona i zielona (analogicznie jednocześnie niebieska i żółta). Wyznaczenie luminancji (przeliczenie z układu CIE XYZ) jest realizowane za pomocą pierwiastka trzeciego stopnia. Komisja CIE wybrała taką zależność jako najbardziej odpowiadającą postrzeganiu zmian jasności przez człowieka.
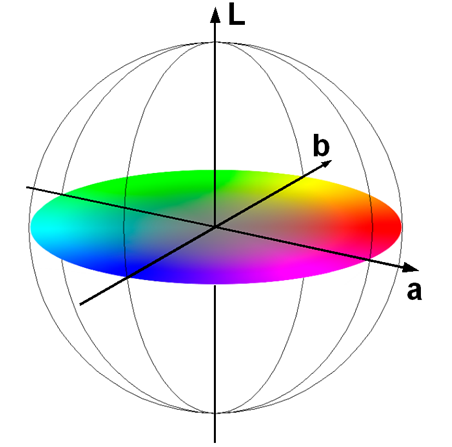
Rys.10.15. Model CIE Lab. L – luminancja, a – stosunek czerwień/zieleń, b – stosunek błękit/żółć.
Model RGB
Model bezpośrednio wywodzący się z teorii trójpobudzenia. Przestrzeń barw reprezentuje sześcian wyznaczony przez trzy barwy podstawowe: czerwoną, zieloną i niebieską. Warto pamiętać, że nie ma możliwości pokrycia całego pola barw wykresu chromatyczności CIE za pomocą mieszania dowolnych trzech składowych. Równocześnie barwa biała (R=1, G=1, B=1) nie odpowiada żadnej bieli CIE uzasadnionej fizycznie.
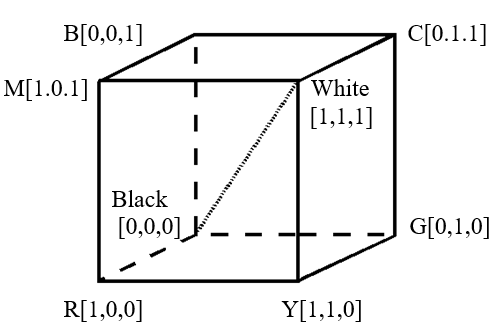
Rys.10.16. Model barw RGB
Model RGB nie jest jednorodny percepcyjnie. Zmiany barw nie są odczuwane proporcjonalnie do zmian wartości.
Model RGB jest modelem dyskretnym. NB bitów pozwala zakodować 2NB różnych barw. Powszechnie stosuje się 24 bity (po 8 dla każdej składowej) do zapisu barwy. oznacza to 16,7 mln barw. Z drugiej strony człowiek jest w stanie rozróżniać dla każdej składowej od 100 do 200 różnych barw. Dawałoby to w sumie możliwość rozpoznawania ok. 8 mln barw. W zależności od badań przyjmuje się, że liczba ta nie przekracza 10 mln. Wydawać by się więc mogło, że liczba 16mln dla zapisu barw w systemie RGB za pomoca 24 bitów jest całkowicie wystarczająca. Tak jednak nie jest ze względu na nieliniowość procesu percepcji.
Dodatkowo występuje problem ciągłości zmiany barw. Jeśli jedna składowa wykorzystuje do zapisu NS bitów, co pozwala zakodować 2NS różnych barw, to w dyskretnym sześcianie barw MS x MS x MS między dowolnymi barwami istnieje łączące je ścieżka, mająca maksymalnie 3.MS-2 poziomów. Taka (maksymalna) wartość występuje tylko między przekątnymi sześcianu, w każdym innym przypadku poziomów pośrednich będzie o wiele mniej. Oznacza to, że ciągłe przejście między barwami o różnych odcieniach będzie zrealizowane na stosunkowo małej liczbie poziomów. Dla modelu wykorzystującego 8 bitowe kodowanie może to oznaczać przejście między barwami z liczbą barw pośrednich dużo mniejszą niż 100 – co będzie zauważalne przez człowieka.
Modele CMY i CMYK
Model CMY subtraktywnego mieszania barw jest oparty o barwy C (Cyan – zielononiebieska), M (Magenta – purpurowa), Y (Yellow – żółta). Model ten został opracowany dla potrzeb poligrafii i wszystkich urządzeń wykorzystujących subtraktywne mieszanie barw.
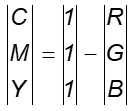
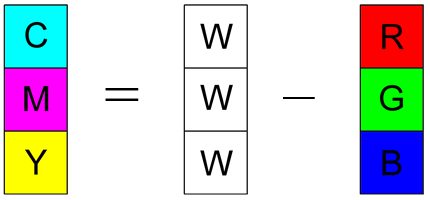
Rys.10.17. Model barw CMY
CMY jest modelem analogicznym do RGB pod względem właściwości.
Ze względu na technologiczne problemy uzyskania barwy czarnej mieszaniny (teoretyczna możliwość przy odpowiednich proporcjach farb) zaproponowano dodanie barwnika czarnego (K). Wtedy można usunąć składową szarą G: G=min(C,M,Y) zmieniając wartości barw:
M = M - G
Y = Y - G
K = k * G
gdzie k jest współczynnikiem dobieranym doświadczalnie dla danego urządzenia.
Modele HSV i HLS
Modele HSV i HLS to modele intuicyjne oparte na niezależności wielkości związanych z odczuciami w percepcji barwy. A zatem : odcień barwy widmowej , nasycenie, jasność lub wartość – rysunek 10.18. Modele te nie są opisane przestrzenią liniowa (tak jak CIE XYZ). Nie jest więc możliwe dodawanie wektorów w tych modelach.
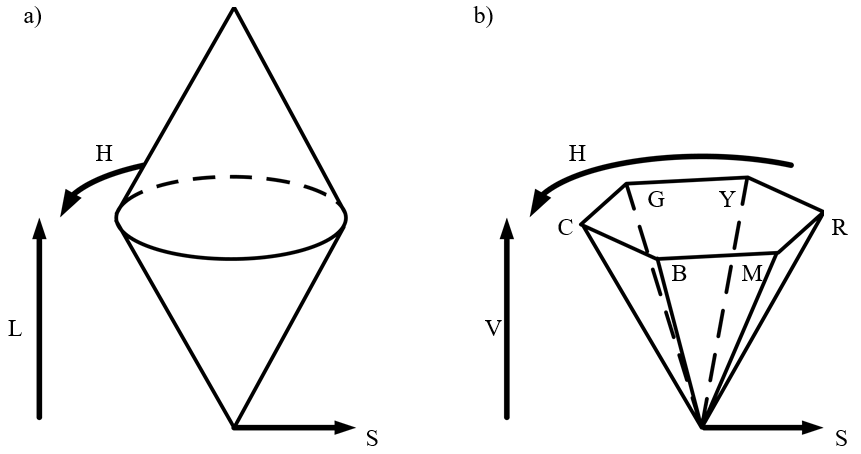
Rys.10.18. a) Model barwy HLS. b) Model HSV.
10.5. Problemy reprodukcji barw
Gamut – zakres barw urządzenia
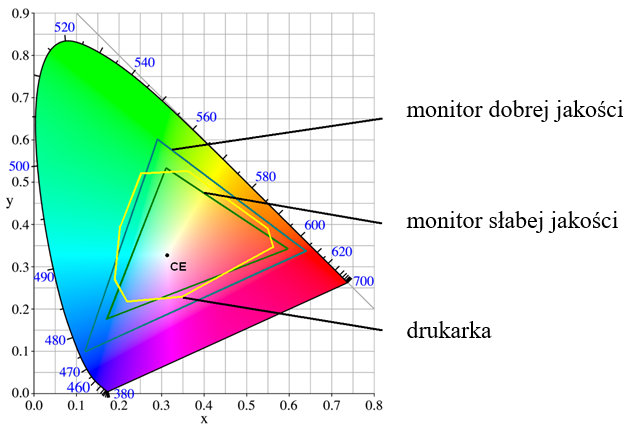
Rys.10.19. Przykładowe zakresy barw trzech urządzeń.
Istnieje możliwość przeliczenia barwy z jednej reprezentacji na drugą. Między modelami RGB, CMY (CMYK), HSV (HLS) można przeliczyć barwy bezstratnie. Tzn teoretycznie istnieje odpowiedniość barwy w każdym z tych modeli. W praktyce jednak każde urządzenie pozwala na reprodukcję pewnego zakresu barw wynikającego ze stosowanej technologii – rysunek 10.19. W ten sposób teoretyczne przeliczenie jest mapowane na praktyczne możliwości techniczne. Zakres barw urządzenia nazywa się gamutem. Oczywiście ponieważ mieszanie RGB pokrywa tylko część barw wykresu chromatyczności i jednocześnie gamut urządzenia wprowadza dodatkowe ograniczenia, to nigdy nie mamy możliwości zobaczenia na dowolnym urządzeniu zakresu barw dostępnego w przyrodzie. Trzeba natomiast podkreślić, że różnice w jakości między np. obrazem wyświetlanym przez monitor, a tym samym obrazem wydrukowanym na drukarce nie wynikają, jak niektórzy sądzą z przejścia z RGB na CMYK, ale z możliwości technologicznych tych urządzeń. Praktycznie zawsze zakres barw dobrego monitora będzie szerszy niż zakres dobrej drukarki. Podobnie jak slajd fotografii tradycyjnej jest zawsze lepszy niż odbitka na papierze.
Problemy zgodności w reprodukcji barw
Aby maksymalnie dopasować możliwości różnych urządzeń stosuje się profile barw. Stosując odpowiednie przyrządy pomiarowe (spektrofotometry) można zmierzyć zakres barw (gamut) danego urządzenia reprodukującego np. monitora czy drukarki. A następnie sprawdzić jak uzyskane wyniki odpowiadają standardowym wartościom w odpowiednim modelu (RGB lub CMY). Pozwala to zaproponować przeliczenie rzeczywistych wartości z jednego urządzenia na wartości z drugiego w taki sposób, aby reprodukowane barwy maksymalnie sobie odpowiadały. Organizacja ICC (International Color Consortium) zaproponowała przemysłowy standard profili ICC stosowany zarówno w urządzeniach poligraficznych jak i sprzęcie powszechnego użytku. Należy jednak zwrócić uwagę na możliwości realizacyjne. Stosowane modele RGB i CMY są modelami dyskretnymi. Jeśli zatem będziemy próbowali dopasować gamut RGB karty graficznej do gamutu RGB monitora, to może się okazać, że rozbieżności w reprodukcji barw dadzą po wprowadzeniu odpowiednich profili ograniczenie dyskretnej przestrzeni barw. Aby temu zaradzić producenci profesjonalnych monitorów stosują szerszą przestrzeń RGB (np. 10 bitów dla każdej składowej).
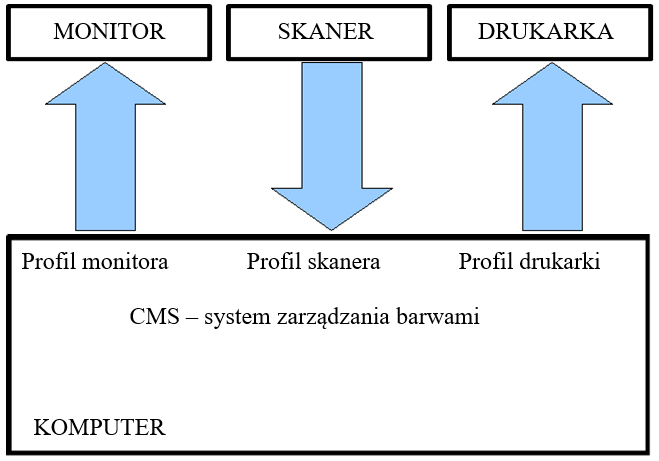
Rys.10.20. Profilowanie urządzeń dołączonych do komputera.
Proces profilowania barw jest jednym z etapów kalibracji urządzenia. Np. dla monitora kalibracja będzie także obejmowała korekcje zniekształceń geometrycznych. Warto pamiętać, że parametry urządzeń podlegają zmienności w czasie i aby utrzymać standard jakości urządzenia powinny być regularnie kalibrowane.
Korekcja Gamma
Jednym z etapów kalibrowania monitora jest korekcja gamma. Proces powstawania barwy na ekranie jest procesem nieliniowym. Jeśli rozważymy napięcie sterujące ekranu monitora U i natężenie światła I świecącego luminoforu to:
I = c · Uγ
gdzie c jest pewną stałą natomiast γ charakteryzuje nieliniowość sterowania monitora.
Dla stosowanych monitorów γ zawiera się w przedziale od ok. 1,5 do ok. 2,5. Często wartość tego parametru jest związana z określonym producentem lub klasą sprzętu. Np. γ dla monitorów komputerów Macintosh jest niższa (1,8) niż monitorów sprzętu PC (2,2). Wyświetlacze (ekrany) telewizyjne mają zazwyczaj stałą γ na poziomie 2,35. Oczywiście współczesne monitory LED wyświetlają barwy na innej zasadzie niż monitory kineskopowe. Odpowiednia nieliniowość charakterystyki wyświetlania barwy jako odpowiedzi na określony zakres podanego napięcia wejściowego jest uzyskiwana dzięki tablicy pośredniej (LUT – Look Up Table). Jednak wartości parametru natomiast γ zostały utrzymane. Dobre monitory pozwalają wybrać wartość w ramach ustawień dostępnych użytkownikowi. Dodatkowym parametrem charakteryzującym jakość wyświetlanego obrazu jest liczba bitów przetwarzanych w tablicy LUT. W najtańszych rozwiązaniach wykorzystywanych jest 8 bitów co daje możliwość uzyskania tylko 256 poziomów wyświetlania dla pojedynczej barwy. Znacznie lepszym rozwiązaniem (ale i droższym) jest wykorzystywanie 10 lub 14 bitów w tablicy LUT. Takie wyświetlanie barw daje możliwość uzyskania gładkich (i niezauważalnych dla oka) przejść między odcieniami.
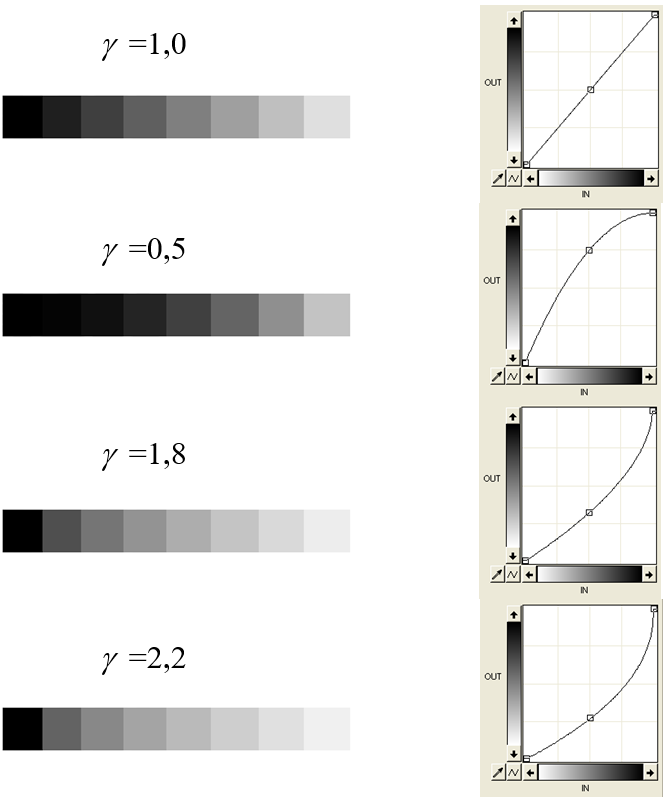
Rys.10.21. Odwzorowanie skali szarości dla różnych wartości parametru γ.
10.6. Zniekształcenia spowodowane rastrem
Raster i skończone rozmiary piksela
powodują, że rysunek zostaje zniekształcony. Wszystkie ukośne linie przybierają
„schodkowy” kształt (przykład odcinka na rysunku). Dla złożonych obrazów może
to utrudniać interpretację rysunku – przykładem może być szachownica widziana
pod kątem. Naturalnym rozwiązaniem tego problemu wydaje się, po prostu,
zmniejszenie rozmiarów piksela, czyli zwiększenie rozdzielczości rastra.
Niestety nie jest to takie proste. Na przeszkodzie stają właściwości oka
ludzkiego, które stara się powiększyć różnicę jasności sąsiadujących ze sobą
pól. Dzięki temu możemy czytać gazetę o zmierzchu, ale powoduje to również, że
idealny obraz mogą zakłócić nam nawet najdrobniejsze rysy. Zwiększenie
rozdzielczości rastra, w pewnym zakresie, niewiele więc daje. Oczywiście jest
pewna granica rozdzielczości kątowej, powyżej której można „oszukać” oko. W
fotografii cyfrowej i poligrafii przyjmuje się, że taką granicą jest 300dpi
(dots per inch – punktów na cal) dla zdjęć i publikacji oglądanych „na wyciągnięcie
ręki”, czyli z odległości 40 – 60
cm. Taka rozdzielczość zapewnia, że oko nie zauważy
rastrowego charakteru rysunku. Oznacza to np., że aby zapewnić dobrą jakość
zdjęcia 10x15 cm (4x6 cali), to powinno ono mieć rozdzielczość1200x1800
pikseli. Dwa razy większe zdjęcie – dwa razy większa rozdzielczość. Oczywiście
np. plakaty reklamowe oglądamy z zupełnie innej odległości, stąd aby zapewnić
odpowiednią rozdzielczość kątową potrzebna jest inna rozdzielczość obrazu.
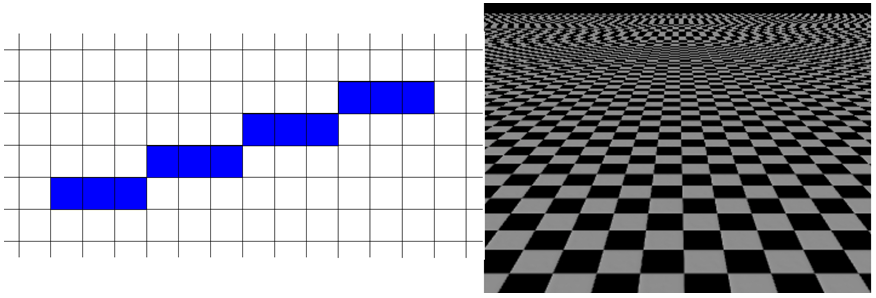
Rys.10.22. Przykład zniekształceń spowodowanych
rastrem.

Rys.10.23. Zastosowanie antyaliasingu do poprawy
wyglądu rysunku w technice rastrowej.
Nie zawsze odpowiednia rozdzielczość jest możliwa do osiągnięcia. Aby w takiej sytuacji poprawić odbiór rastrowego obrazka wykorzystuje się tzw. antyaliasing – metodę poprawy wyglądu bazującą na teorii sygnałów (rys.10.22 i 10.23). Tak naprawdę problem wynika z próbkowania z określoną rozdzielczością. Oprócz schodkowych odcinków może się więc pojawić problem znikania (i czasowego pojawiania się) obiektów na tyle małych, że mogą zmieścić się pomiędzy próbkami. Błędy próbkowania zamienia się na błędy zaszumienia – na które oko ludzkie jest mniej wrażliwe. Stosując odpowiednie filtrowanie dokonuje się „rozmycia”, dotychczas kontrastowej, barwy sąsiednich pikseli (odcinek na rysunkach 10.22 i 10.23). Oko ludzkie dokona pewnego rodzaju uśrednienia, co prawda operacja taka nie doda szczegółów, ale problem schodków przestaje przeszkadzać. Nawet widok szachownicy sprawia wtedy wrażenie poprawnego. Warunkiem koniecznym uzyskania tego efektu jest duża liczba barw lub stopni szarości dla każdego piksela.
Biorąc pod uwagę możliwość rozróżniania barw przez oko ludzkie przyjmuje się, że aby pokazać pełną paletę barw potrzeba 24 bity na piksel (po 8 bitów na każdą składową RGB). Standardem dla kart graficznych stało się przechowywanie informacji w postaci 32 bitów na piksel. W takich rozwiązaniach dodatkowe bity mogą być wykorzystane do opisu innych właściwości np. przezroczystości. Czasami stajemy przed dylematem czy, z dwojga złego, lepiej wybrać tryb pracy o mniejszej rozdzielczości np. 800x600, ale z pełną skalą barw (24 bity na piksel), czy wyższą rozdzielczość np. 1200x1024 ale tylko 8 bitów na piksel. Biorąc pod uwagę właściwości oka ludzkiego i możliwości programów graficznych, rozstrzygnięcie będzie oczywiste. Poza wyjątkowymi i szczególnymi przypadkami, pierwszy wariant pozwoli uzyskać lepszy i przyjemniejszy w odbiorze obraz.
10.7 Obrazy o zwiększonym zakresie tonalnym
Człowiek potrafi poprawnie rozpoznawać szczegóły przedmiotów oświetlonych blaskiem księżyca, a także czytać na plaży przy bardzo silnym oświetleniu południowym słońcem.
Można próbować analizować możliwości oka porównując wartości luminancji lub zakresy tonalne wybranych obiektów.
- Wartości
luminancji wybranych obiektów
- Tarcza słoneczna 1600000000 cd/m2
- Błękit nieboskłonu 5000 cd/m2
- Jasne pola ekranu monitora komputerowego 200 cd/m2
- Powierzchnia oświetlonej kartki 100 cd/m2
- Gwiazdy na nocnym niebie 0,001 cd/m2
-
Zakres tonalny (jako stosunek luminancji partii jasnych
i ciemnych obrazu)
- Oglądany, rzeczywisty krajobraz 100000:1
- Typowy monitor komputerowy 1000:1
- Druk barwny; poligrafia 500:1 (256:1)
- Barwa zapisana przy użyciu 8 bitów 256:1
Zestawienie luminancji wybranych obiektów pokazuje, że zakres tonalny (rozumiany jako stosunek luminancji pól jasnych do ciemnych) naturalnych obiektów i ich zestawień może być bardzo duży.
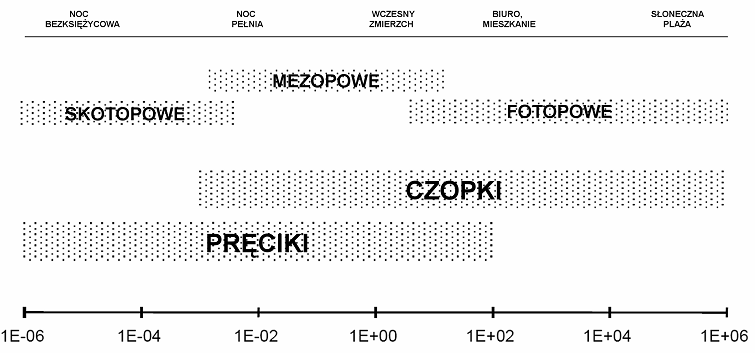
Rys.10.24. Zakres „poprawnej
pracy” receptorów siatkówki oka,
zakres widzenia skotopowego, mezopowego i fotopowego.
Opisując w tym rozdziale model RGB zwrócono uwagę na liczbę barw rozróżnianych przez człowieka – człowiek jest w stanie rozróżniać dla każdej składowej maksymalnie od 100 do 200 różnych barw. Jednak takie rozważania nie uwzględniają zdolności adaptacyjnych oka do różnych warunków oświetleniowych. Zdolności te są związane z dwoma mechanizmami. Pierwszym jest praca mięśni tęczówki zmniejszających źrenicę. Pozwala to wielokrotnie zmniejszyć ilość światła docierającego do siatkówki oka. Drugim mechanizmem jest praca fotoreceptorów w zakresie widzenia fotopowego i skotopowego (rys.10.24). Przyjmuje się, że oko pozwala poprawnie rejestrować szczegóły w zakresie tonalnym ok. 10000:1. Jednocześnie zakres pracy naszego zmysłu wzroku odpowiada natężeniu oświetlenia od 0,2 luksa (odpowiada to powierzchni Ziemi przy pełni Księżyca) do 100000 luksów (powierzchnia Ziemi oświetlona światłem słonecznym). Oczywiście oglądając krajobraz z różnie oświetlonymi obiektami nigdy nie odbieramy obrazu jako całości – kierując wzrok na określony obiekt oko dostosowuje się do jego luminancji. Dopiero z tak zebranych informacji o fragmentach budujemy obraz całości pola widzenia. Dzięki temu dostrzegamy szczegóły obrazu niemożliwe do zarejestrowania aparatem fotograficznym i wydrukowania na papierze, niemożliwe także do pokazania na monitorze. Pod tym względem oko okazuje się o wiele lepszym instrumentem do rejestracji wrażeń barwnych niż film fotograficzny czy matryce cyfrowe
Można oczywiście mówić o różnicach indywidualnych oraz dowolnych przypadkach nieakceptowania słabego lub silnego oświetlenia. Jedno jest natomiast pewne. Żadne urządzenie; żadna współczesna technologia nie pozwala na uzyskanie zakresu pracy zbliżonego do zakresu pracy oka. Jednym z najbardziej spektakularnych przykładów jest analiza możliwości rejestracji obrazów z wykorzystaniem zarówno tradycyjnej (analogowej) jak i współczesnej (cyfrowej) fotografii. Problem zakresu tonalnego (rys.10.25) jest znany praktycznie od początków fotografii. Okazuje się, że obserwując dany obiekt poprawnie postrzegamy jasne i ciemne pola. Natomiast robiąc zdjęcie mamy często po prostu do wyboru albo dobrze naświetlone pola jasne (wtedy cienie są nieoświetlone i nie widać w nich szczegółów), albo dobrze naświetlone pola ciemne (wtedy prześwietlone pola jasne są praktycznie niewidoczne). Pogodzenie tych warunków jest najczęściej niemożliwe.

Rys.10.25. Jak na zdjęciu oddać rzeczywisty zakres tonalny ?
Dobrym rozwiązaniem problemu zakresu tonalnego jest skorzystanie z techniki generowania obrazów o zwiększonym zakresie tonalnym – HDRI (High Dynamic Range Imaging).
Można wyróżnić kilka metody pozyskiwania lub generowania obrazów HDRI:
- Metody grafiki komputerowej wykorzystujące zależności fizyczne oraz przestrzeń barw i standardy zapisu, pozwalające na rejestracje zwiększonego zakresu tonalnego.
- Fotografia cyfrowa : metody wielokrotnej rejestracji obrazu o różnym stopniu naświetlenia.
- Wykorzystanie sprzętu specjalistycznego pozwalającego na rejestrację w nieco szerszym zakresie niż sprzęt powszechnego użytku.
Obrazy o zwiększonym zakresie tonalnym (HDRI) są próbą oddania rzeczywistego zakresu tonalnego. Oczywiście należy wziąć pod uwagę możliwości urządzenia pozyskującego i prezentującego obraz. Pojawiają się w ostatnich latach specjalistyczne urządzenia wykorzystujące przestrzenie barw o zwiększonym zakresie tonalnym. Przykładem są kamery HDR stosowane w systemach zabezpieczenia i monitoringu. Pozwalają one pokazać jednocześnie szczegóły w miejscach oświetlonych i zacienionych, co dotychczas wymagało stosowania kilku urządzeń. Podobnie pojawiają się urządzenia wyświetlające HDR. Jednak cena tego typu urządzeń nie pozwala przypuszczać, że będą one w najbliższym czasie powszechnie wykorzystywanie. Z drugiej strony nie ma dzisiaj żadnego projektu drukowania obrazu HDR.
A zatem nawet jeśli uzyskamy obraz o zwiększonej skali tonalnej, to będzie on pokazywany na typowym urządzeniu, na przykład na typowym monitorze o bardzo ograniczonym zakresie tonalnym. Aby poprawić odbiór obrazu w takiej sytuacji dokonuje się rzutowania przestrzeni barw o zwiększonym zakresie tonalnym na przestrzeń o ograniczonym zakresie. Metody realizujące to zadanie są stratne i nieliniowe. Wykorzystuje się analizę właściwości odbiciowych powierzchni obiektów znajdujących się na obrazie oraz analizę właściwości percepcyjnych człowieka. Pozwala to zapewnić odpowiednie lokalne zmiany luminancji (szczegóły zarówno w światłach jak i w cieniach) mimo niedoskonałości technologicznych sprzętu.
Do zapisu zdjęć w aparatach cyfrowych jest także wykorzystywany sposób kodowania RAW. Sposób ten wykorzystuje właściwości matrycy danego aparatu bez żadnej dodatkowej obróbki obrazu. Powiązanie z właściwościami i konstrukcją matrycy powoduje, że zapis ten jest niestandardowy i zależny od producenta aparatu. Najczęściej zapis ten wykorzystuje od 12 do 16 bitów dla składowej barwnej. Zapis RAW nie jest uznawany za kodowanie obrazu o zwiększonym zakresie tonalnym. Niemniej jednak fotografia zapisana jako RAW zawiera więcej informacji o barwie niż w standardowym zapisie 24-bitowym i może być „wywołana” do kilku, różnie naświetlonych obrazów. Daje to możliwość znacznej poprawy jakości zdjęcia.

Rys.10.26. Wnętrze Stanford
Memorial Chuch. Obraz HDRI został wygenerowany na podstawie
16 różnie
naświetlonych zdjęć. Jeden z najbardziej znanych przykładów
i jednocześnie
jeden z pierwszych obrazów HDRI. Obrazy ze strony www.debevec.org ©
Ciekawym przykładem możliwości uzyskania obrazów o podwyższonym zakresie tonalnym jest zastosowanie techniki wielokrotnej rejestracji ze zmianą stopnia naświetlania. Zestaw zdjęć pokrywa cały zakres tonalny (fragmentami na różnych zdjęciach). Docelowy obraz jest generowany programem składającym poszczególne zdjęcia z uwzględnieniem ich różnic tonalnych (rys.10.26).
Więcej informacji na temat obrazów HDRI można znaleźć w książce [5].
Rozdział 11. MODELOWANIE OŚWIETLENIA
W rozdziale jedenastym zostały omówione problemy reakcji światła z materią – odbicie i załamanie (przenikanie) światła. Przedstawiono podstawowe problemy tego zagadnienia oraz sposób opisu odbicia w grafice komputerowej z wykorzystaniem funkcji współczynnika odbicia dwukierunkowego (funkcji BRDF). W roozdziale omówiono najważniejsze modele oświetlenia: model Phonga, Cooka-Torrance’a, Warda, Orena-Nayara, Ashikhmina-Shirleya, model He. Zostały także porównane ich podstawowe właściwości. Przedstawiony został problem cieniowania (interpolacji) - trzy sposoby realizacji: cieniowanie płaskie, Gourauda, Phonga.
11.1. Wprowadzenie
Reakcja światła z materią
Kolejnym problemem wymagającym rozwiązania, jeśli chcemy osiągnąć realizm rysunku, jest problem oświetlenia. Każda powierzchnia reaguje w jej właściwy sposób na padające na nią światło. Barwy, faktury i inne właściwości przedmiotów postrzegamy dzięki temu, że przedmioty te są oświetlone i odbijają światło w naszym kierunku. Symulacja tych zjawisk pozwala oddać realny wygląd elementów wirtualnej sceny.
Można wyróżnić dwa niezależne przypadki: odbicie światła i przenikanie światła (dla materiałów przezroczystych). Oczywiście może zachodzić jeszcze pochłanianie, ale z punktu widzenia obserwatora jest to najmniej interesujący przypadek. Dla przypadku odbicia mówimy o odbiciu kierunkowym (lustrzanym) lub rozproszonym (dyfuzyjnym). W pierwszym przypadku padający promień odbija się pod kątem równym kątowi padania. W drugim przypadku odbicie może być widoczne pod dowolnym kątem. Analogiczna sytuacja może zajść dla przenikania światła.
Właściwości reakcji na padające światło zależą od:
- Właściwości materiałowych – metale tylko odbijają światło, dla dielektryków zachodzi i odbijanie i przenikanie. Struktura dielektryka może wpływać na rozpraszanie przenikającego światła. Może zachodzić rozpraszanie w dowolnym punkcie przedmiotu, przez który przenika światło..
- Właściwości powierzchni (obróbka, wykończenie) wpływają na rozproszenie zarówno odbijanego jak i przenikającego światła (promieni załamanych). Obróbka materiału może wpłynąć także na właściwości odbicia (przenikania) kierunkowego oraz właściwości kierunkowe zjawiska (anizotropia).

Rys.11.1. Odbicie światła od powierzchni materiału: a) .Odbicie kierunkowe
idealne.
b) Odbicie kierunkowe rzeczywiste. c) Odbicie powrotne. d) Odbicie
rozproszone.
e) Odbicie sumaryczne (wynikowe) rzeczywiste.
Odbicie rzeczywiste od powierzchni materiału jest zjawiskiem złożonym. Nawet dla najlepszych zwierciadeł promień odbity jest widoczny w pewnym niewielkim (niezerowym) kącie wokół kierunku odbicia idealnego (teoretycznego). W najprostszym przypadku wyróżnia się odbicie kierunkowe i rozproszone. Dla rzeczywistych powierzchni zawsze zachodzą oba przypadki i jednocześnie odbicie kierunkowe nie występuje w postaci idealnej. Dodatkowo może występować składowa odbicia powrotnego (współdrożnego) w kierunku, z jakiego padało światło. Można więc przyjąć rzeczywiste odbicie jako wypadkową 4 składowych (rys.11.1): rozproszonej, kierunkowej idealnej, kierunkowej rzeczywistej (ang. glossy – odbicia połysku), powrotnej. Analogiczne przypadki można wyróżnić rozpatrując załamanie promieni.
Rozkład kątów i wektorów związanych z odbiciem pokazano na rysunku 11.2.

Rys.11.2. Rozkład wektorów związanych z opisem
odbicia światła ![]() - wektor normalny do powierzchni w punkcie odbicia światła,
- wektor normalny do powierzchni w punkcie odbicia światła, ![]() - wektory skierowane odpowiednio do obserwatora i do źródła
światła,
- wektory skierowane odpowiednio do obserwatora i do źródła
światła, ![]() - wektor idealnego
odbicia,
- wektor idealnego
odbicia, ![]() - wektor wyznaczający
dwusieczną kąta między
- wektor wyznaczający
dwusieczną kąta między ![]() .
.
Anizotropia odbicia światła
Anizotropia jest zjawiskiem polegającym na zależności właściwości fizycznych od charakterystycznych kierunków materiału. Pojęcie anizotropii optycznej jest najczęściej kojarzone z przechodzeniem światła przez kryształy i zjawiskiem dwójłomności. Spowodowane to jest zależnością współczynnika załamania światła od kierunku rozchodzenia się fali względem głównego przekroju kryształu. Wyróżnia się anizotropię naturalną (wykazuje ją większość kryształów) i anizotropię wymuszoną, spowodowaną takimi czynnikami zewnętrznymi jak działanie pól elektrycznych (zjawisko Kerra) i magnetycznych (zjawisko Cottona-Moutona) lub odkształcenia mechaniczne (ściskanie lub rozciąganie w zadanym kierunku). Z anizotropią mamy także do czynienia w przypadku odbicia promieniowania od powierzchni materiału. Wiele powierzchni, zarówno naturalnych, jak i uzyskanych w wyniku technologicznej obróbki odbija światło w sposób anizotropowy, zależny od kierunku jego padania – w sposób zależny od usytuowania powierzchni względem źródła światła.
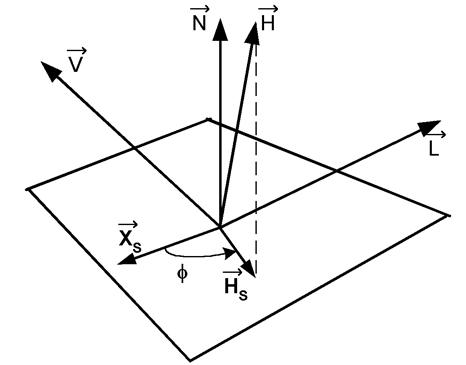
Rys.11.3. Anizotropia odbicia – rozkład wektorów. ![]() - wektory jak na rysunku 11.2.
- wektory jak na rysunku 11.2.
![]() - wektor określający
charakterystyczny kierunek na powierzchni,
- wektor określający
charakterystyczny kierunek na powierzchni,
![]() - rzut prostokątny
wektora
- rzut prostokątny
wektora ![]() na płaszczyznę styczną
do powierzchni w punkcie
odbicia światła.
na płaszczyznę styczną
do powierzchni w punkcie
odbicia światła.
Dobrym przykładem powierzchni wykazującej naturalne właściwości anizotropowe jest powierzchnia drewna. Odbija ona światło zależnie od kąta między kierunkiem padania a kierunkiem słojów przekroju. Powierzchnia metalu poddana obróbce mechanicznej (np. polerowaniu) będzie odbijała światło zależnie od kąta między padającym promieniem, a kierunkiem obróbki.
11.1.3 Model odbicia Phonga
Najstarszy, z praktycznie wykorzystywanych w grafice komputerowej modeli odbicia, zaproponował Bui Tuong Phong w 1975 roku Model Phonga jest modelem eksperymentalnym, nieuzasadnionym fizycznie i niespełniającym zasady zachowania energii. Mimo to jest, chyba, najczęściej stosowanym modelem odbicia w grafice komputerowej, gdyż pozwala szybko uzyskać rysunki o wystarczająco realistycznych barwach. W literaturze są opisywane metody poprawy modelu Phonga, aby spełniał on zasadę zachowania energii.
Równanie oświetlenia ma w tym modelu postać:
![]()
gdzie I jest wynikowym
natężeniem światła w punkcie analizowanego obiektu, Ia jest natężeniem
światła otoczenia (tła), Ip jest natężeniem
światła punktowego, ka , kd , ks - są współczynnikami odbicia tła, rozproszonego
i kierunkowego, fatt jest współczynnikiem
tłumienia źródła zależnym od odległości, ![]() określa gładkość
powierzchni – im wartość tego parametru jest większa, tym powierzchnia bardziej zbliża
się do lustra idealnego.
określa gładkość
powierzchni – im wartość tego parametru jest większa, tym powierzchnia bardziej zbliża
się do lustra idealnego.
Pierwszy składnik wzoru opisuje światło otoczenia (tła). Zakłada się, że jest ono rozproszone i bezkierunkowe oraz, że na skutek wielokrotnych odbić pada jednakowo pod wszystkimi kierunkami na rozpatrywane powierzchnie. Oczywiście również Ia jest jednakowe dla wszystkich obiektów.
Drugi składnik opisuje odbicie rozproszone tak zwane lambertowskie. Powierzchnie matowe; rozpraszające światło jednakowo we wszystkich kierunkach opisane są prawem Lamberta, zgodnie z którym światłość promieniowania odbitego jest proporcjonalne do kosinusa kata padania. Oczywiście rzeczywiste powierzchnie rozpraszające zachowują się zgodnie z tym prawem tylko w pewnym zakresie kąta. Niemniej jednak taki opis odbicia rozproszonego jest najczęściej stosowany w modelach odbicia.
Trzeci składnik opisuje odbicie kierunkowe (zwierciadlane). Maksimum natężenia promieniowania światłą odbitego występuje dla zerowego kąta α natomiast potęga n we wzorze charakteryzuje właściwości odbiciowe danego materiału.
Warto jeszcze zwrócić uwagę na współczynnik tłumienia źródła światła. Wiemy z fizyki, że strumień światła pochodzący z punktowego źródła światła maleje z kwadratem odległości jaką przebywa. Zastosowanie tej reguły w modelu odbicia Phonga nie daje, niestety, w praktyce dobrych rezultatów. Dla dużych odległości od źródła zmiany są zbyt mało zauważalne, z kolei dla małych odległości zmiany występują zbyt szybko. Okazało się, że w praktyce dobre rezultaty można uzyskać dla współczynnika postaci fatt=1/(c+r) gdzie c jest pewną stałą.
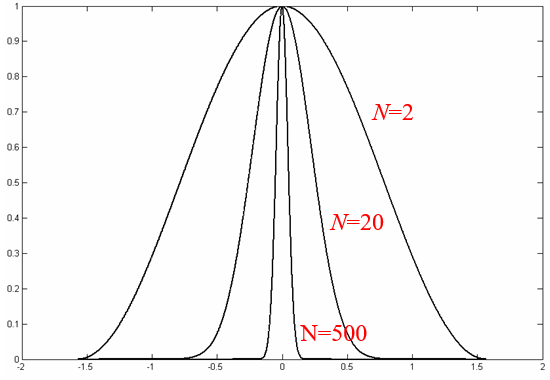
Rys.11.4.Wykres funkcji f(α) = cosN(α) dla N=2, N=20 i N=500.
Funkcja f(α) = cosN(α) opisuje odbicie kierunkowe (zwierciadlane) przy czy N charakteryzuje dany materiał (właściwości odbiciowe powierzchni). Warto zwrócić uwagę na właściwości tej funkcji. Idealne odbicie kierunkowe to takie, w którym odbicie występuje tylko dla zerowego kąta a (to znaczy poza tym kątem natężenie światła odbitego jest zerowe). Funkcja f(α) = cosN(α) opisuje taki przypadek dla N dążącego do nieskończoności. Zatem im większa wartość N tym bardziej powierzchnia zbliża się do powierzchni lustrzanej. Tym lepsze właściwości kierunkowe charakteryzują odbicie od tej powierzchni. W praktyce już dla N rzędu kilkuset mamy do czynienia z bardzo dobrym lustrem.
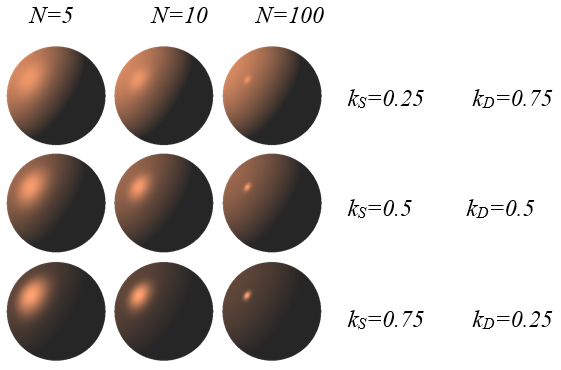
Rys.11.5. Kule o różnych właściwościach odbiciowych oświetlone źródłem punktowym.
Na rysunku 11.5 widać wpływ parametrów modelu odbicia Phonga na obraz odbicia światła na symulowanej powierzchni. Górny rząd charakteryzuje się przewagą odbicia rozproszonego, dolny – kierunkowego. Jednocześnie kolumny charakteryzują odbicie kierunkowe od lewej o złych parametrach odbicia kierunkowego (N=5) do prawej zbliżającej się do właściwości lustrzanych.
11.2. Podstawowe wielkości fotometryczne
Strumień świetlny Φ (całoprzestrzenny) danego źródła światła opisuje ilość energii przenoszonej przez fale świetlne w jednostce czasu. Strumień jest podstawową wielkością fotometryczną – odpowiednikiem mocy. Jednostką strumienia jest lumen [lm]
Strumień świetlny charakteryzuje przede wszystkim źródło światła, chociaż mówimy również o strumieniu odbitym.
Światłość I punktowego źródła światła (lub elementu powierzchni źródła niepunktowego), w danym kierunku jest ilorazem elementarnego strumienia świetlnego dΦ i kąta bryłowego dω , w którym ten strumień został wyemitowany. Jednostka światłości to kandela [cd] .
![]()
Światłość jest gęstością kątową strumienia świetlnego. Jednostką światłości jest kandela – należąca do siedmiu podstawowych jednostek miar.
Luminancja L elementarnego obszaru dS , w danym kierunku obserwacji jest ilorazem światłości I oraz pola powierzchni dS' będącej rzutem obszaru dS , na płaszczyznę prostopadłą do kierunku obserwacji.
Luminancja jest najbliższa pojęciowo odczuciu intensywności światła spośród wielkości fotometrycznych. Odpowiada pojęciom jaskrawości (dla obiektów emitujących światło) i jasności (dla obiektów odbijających). Warto pamiętać, że odczucia jaskrawości lub jasności są wrażeniami bardzo subiektywnymi. Dodatkowo silnie zależą różnych czynników zewnętrznych np. od jasności tła na jakim jest obserwowany obiekt oraz od stanu adaptacji wzroku.
Luminancja nie zależy od odległości od obiektu. Jeśli rozpatrzymy źródło światła i wszystkie parametry geometryczne są stałe, to luminancja źródła jest proporcjonalna do energii emitowanej przez źródło.
Natężenie oświetlenia (napromieniowanie) E jest ilorazem strumienia świetlnego dΦ oraz pola powierzchni dS oświetlonej tym strumieniem.
![]()
Prawo Lamberta: Światłość elementu powierzchni ciała doskonale czarnego jest proporcjonalna do pozornej powierzchni tego elementu widzianego z danego kierunku.
![]()
gdzie ![]() jest kątem między danym kierunkiem a normalną do powierzchni.
jest kątem między danym kierunkiem a normalną do powierzchni.
Prawo Lamberta odnosi się także do odbicia światła od idealnie rozpraszającej powierzchni (powierzchni lambertowskiej). Powierzchnie rzeczywiste odbijają światło zgodnie z prawem Lamberta tylko w pewnym kącie. Dobrym przykładem materiału, którego powierzchnia odbija w przybliżeniu zgodnie z prawem Lamberta jest kreda.
11.3. Funkcja rozkładu współczynnika odbicia dwukierunkowego (BRDF)
Funkcję rozkładu współczynnika odbicia dwukierunkowego (funkcję BRDF) ![]() definiuje się jako iloraz luminancji obserwowanej z kierunku
definiuje się jako iloraz luminancji obserwowanej z kierunku ![]() , do natężenia napromieniowania światła padającego z kierunku
, do natężenia napromieniowania światła padającego z kierunku ![]() .
.
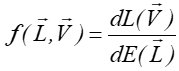
Funkcja BRDF jest wielkością wyrażoną w 1/sr .
Aby funkcja BRDF opisywała zjawisko zgodnie z zasadami fizyki powinna spełniać dwa warunki:
- Zasada wzajemności Helmholtza, Funkcja BRDF
powinna być symetryczna, oznacza to, że zamiana obserwatora i źródła światła
nie spowodowałaby zmiany opisu zjawiska,. to znaczy
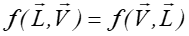 .
. - Drugim warunkiem jest zasada zachowania energii, zgodnie z którą suma całkowitej energii wypromieniowanej na skutek odbicia światła od powierzchni jest nie większa niż energia światła padającego.
Rzeczywiste odbicie jako wypadkową 4 składowych (rozdział 11.1): rozproszonej, kierunkowej idealnej, kierunkowej rzeczywistej (glossy – odbicia połysku), powrotnej. Analogiczne przypadki można wyróżnić rozpatrując załamanie promieni.
Całkowita funkcja BRDF będzie więc wyrażona równaniem:
gdzie ![]() reprezentuje odbicie
rozproszone,
reprezentuje odbicie
rozproszone, ![]() reprezentuje odbicie
kierunkowe, rozkładane czasami na dwa składniki:
reprezentuje odbicie
kierunkowe, rozkładane czasami na dwa składniki: ![]() - odbicie kierunkowe teoretyczne
(idealne) i
- odbicie kierunkowe teoretyczne
(idealne) i ![]() - składowa rzeczywista
odbicia kierunkowego (odbicie kierunkowo-rozproszone),
- składowa rzeczywista
odbicia kierunkowego (odbicie kierunkowo-rozproszone), ![]() - reprezentuje odbicie
powrotne. Większość modeli odbicia przyjmuje, że odbicie rozproszone jest
odbiciem lambertowskim (zgodnym z prawem Lamberta). Modele te podają więc opisy
odbicia kierunkowo-rozproszonego (kierunkowego rzeczywistego) w postaci
składowej
- reprezentuje odbicie
powrotne. Większość modeli odbicia przyjmuje, że odbicie rozproszone jest
odbiciem lambertowskim (zgodnym z prawem Lamberta). Modele te podają więc opisy
odbicia kierunkowo-rozproszonego (kierunkowego rzeczywistego) w postaci
składowej ![]() . Odbicie powrotne jest pomijane.
. Odbicie powrotne jest pomijane.
11.4. Modele odbicia światła
Wybrane modele odbicia światła
- Phonga (1975 r.),
- Cooka-Torrance'a (1981 r.),
- He-Torrance'a-Silliona-Greenberga (1991 r.),
- Warda (1992 r.),
- Orena-Nayara (1994 r.),
- Ashikhmina-Shirleya (2000 r.).
W literaturze można wskazać wiele prac porównujących, przede wszystkim pod względem obliczeniowym, różne podejścia do opisu zjawiska odbicia. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teoretycznego, ale są dobrą aproksymacją rzeczywistych zjawisk. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. Obie jednak grupy są pewnym przybliżeniem rzeczywistości. Natomiast ze względów praktycznych nie zawsze jest celowe korzystanie z funkcji BRDF powstałych na podstawie pomiarów rzeczywistej powierzchni, gdyż jest to bardzo kosztowne obliczeniowo. Nawet w takich przypadkach stosuje się pewne aproksymacje . Warto więc zastanowić się nad wyborem odpowiedniej funkcji BRDF. Szczególnie jest to istotne w sytuacji prowadzenia obliczeń z wykorzystaniem gotowych pakietów numerycznych gdzie wybór dostępnych parametrów może być ograniczony.
Model Cooka-Torrance’a (1981 r.)
Zaproponowany przez Cooka i Torrance’a w 1981 roku na podstawie wcześniejszych prac Torrance’a i Sparrowa dotyczących fizycznego opisu gładkości (chropowatości) powierzchni oraz rozważań Blinna. Model Cooka-Torrance’a jest modelem uzasadnionym fizycznie, spełniającym zasadę wzajemności i zasadę zachowania energii, chociaż znane są w literaturze rozważania wskazujące na pewne problemy, które mogą się pojawić dla kątów padania promienia bliskich kątowi prostemu.
Funkcja BRDF opisująca odbicie kierunkowo-rozproszone w tym modelu jest dana zależnością:
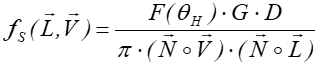
gdzie ![]() jest
współczynnikiem odbicia Fresnela opisującym zależność odbicia światła od kąta
padania i od długości fali.
jest
współczynnikiem odbicia Fresnela opisującym zależność odbicia światła od kąta
padania i od długości fali.
G opisuje tłumienie geometryczne. W modelu Cooka-Torrance’a założono, że powierzchnia materiału jest wielościanem złożonym z mikroelementów (mikroluster). Ich rozmiary i rozkład położeń decydują o chropowatości lub gładkości powierzchni. Przyjęto, że powierzchnia pokryta jest wgłębieniami typu V – to znaczy są to wgłębienia o kształcie ostrosłupa.
Tłumienie geometryczne jest wzajemnym zasłanianiem mikroelementów powierzchni i jest opisane następującą zależnością.
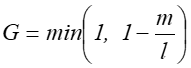
Biorąc pod uwagę rozkład wektorów i fakt, że analogiczne zasłanianie zachodzi przy zamianie źródła z obserwatorem (symetria) otrzymuje się:
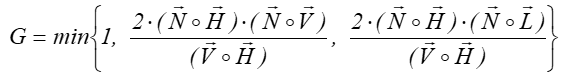
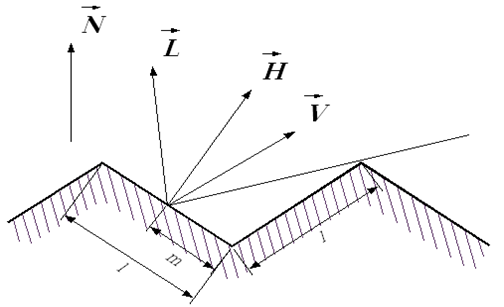
Rys.11.6. Tłumienie geometryczne – rozkład wektorów.
D jest funkcją rozkładu mikroelementów tworzących powierzchnię . Cook i Torrance zaproponowali użycie funkcji rozkładu Beckmanna jako najbardziej odpowiadającej wielościennemu charakterowi powierzchni dla różnych materiałów:
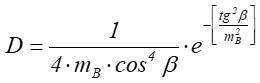
![]() opisuje właściwości
powierzchni, im mniejsza wartość tym powierzchnia gładsza (odbicie bliższe
idealnemu kierunkowemu).
opisuje właściwości
powierzchni, im mniejsza wartość tym powierzchnia gładsza (odbicie bliższe
idealnemu kierunkowemu).
Znane jest również uproszczenie modelu Cooka-Torance’a - model Schlicka, zaproponowany w 1994 roku. Autor starał się dokonać uproszczenia z zachowaniem fizycznego charakteru modelu pierwotnego. Starał się jednocześnie znacznie podnieść atrakcyjność obliczeniową. W modelu Cooka-Torrance’a w równaniu zastąpione zostały wielkości G i D (funkcja rozkładu Beckmanna) prostszymi funkcjami wymiernymi.
Współczynnik Fresnela
Współczynnik Fresnela opisuje zależność odbicia światła od kąta padania i długości fali. Określa stosunek energii światła odbitego do energii światła padającego. Współczynnik ten jest wykorzystywany przez wszystkie modele odbicia opierające się na zależnościach fizycznych. Warto pamiętać, że kształt zależności kątowych tego współczynnika zależy od długości fali oraz polaryzacji światła.
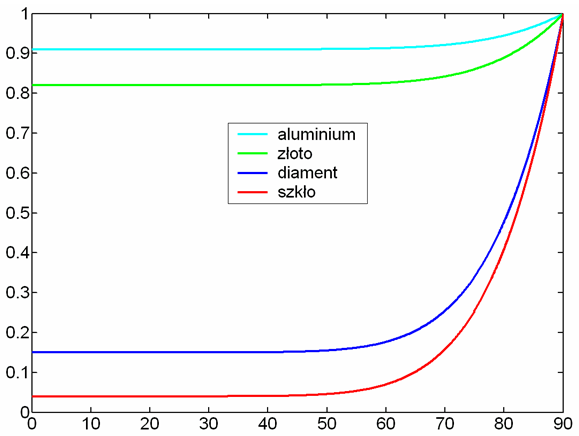
Rys.11.7. Przykłady współczynnika
Fresnela ![]() dla różnych
materiałów.
dla różnych
materiałów.
Prezentowane wykresy pokazują wartości średnie światła
niespolaryzowanego.
Schlick zaproponował dobrą aproksymację tej funkcji (według autora aproksymacji błąd jest mniejszy niż 1%). Opisuje ją wielomianowa funkcja kąta i wartość współczynnika F0 dla zerowego kąta oraz określonej długości fali. Wartości F0 są podawane przez tablice materiałowe.
![]()
Funkcja rozkładu mikropowierzchni
O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). Funkcja tego typu jest również wykorzystywana przez większość modeli odbicia. D jest najczęściej funkcją kąta β lub kąta a (jak np. w przypadku modelu Phonga) – rysunek 11.2. Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność:
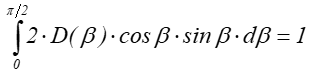
Autorzy funkcji dystrybucji nie zawsze dbali o spełnienie tego warunku. Czasem dopiero niezależne prace późniejsze doprowadzały do spełnienia zasady zachowania energii – tak było np. w przypadku modelu odbicia Phonga.
Istnieje wiele różnych funkcji dystrybucji – funkcji o podobnym charakterze – rys.11.8. Blinn w 1977 roku zasugerował możliwość zastąpienia jednej funkcji drugą. Czasami jest to opłacalne obliczeniowo, jednak może powodować powstanie drobnych różnic w rozkładzie światła symulowanego odbicia. Różnice te mogą być widoczne na rysunku.
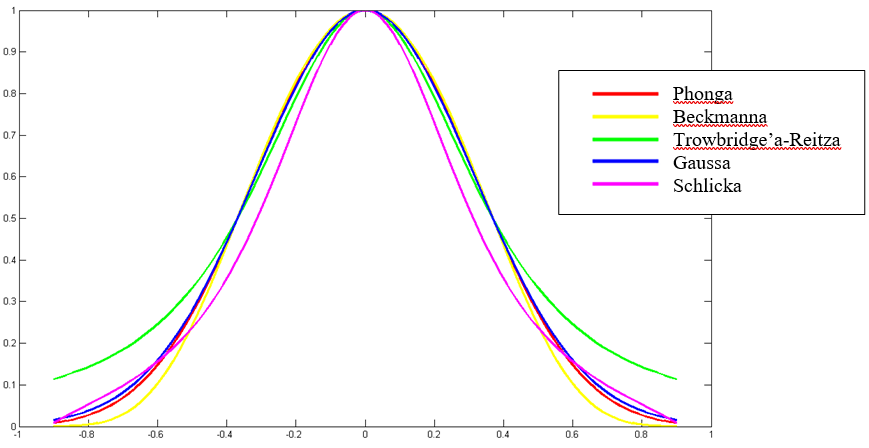
Rys.11.8 Wykresy znormalizowanych funkcji rozkładu mikropowierzchni.
Na rysunku 11.8 są pokazane różne
funkcje rozkładu mikropowierzchni w postaci znormalizowanej (oznaczone jako![]() ) tzn. takie, że
) tzn. takie, że ![]() . Normalizacja pozwala
porównać właściwości różnych funkcji. Dla
większości funkcji dystrybucji (wszystkich tutaj rozpatrywanych) jej maksimum
występuje dla β = 0 .
. Normalizacja pozwala
porównać właściwości różnych funkcji. Dla
większości funkcji dystrybucji (wszystkich tutaj rozpatrywanych) jej maksimum
występuje dla β = 0 .
W pracy [9] przedstawiono różne funkcje rozkładu mokropowierzchni. Można przeczytać o ich właściwościach oraz możliwościach zastąpienia jednej funkcji drugą oraz konsekwencjach wizualnych takiego zastąpienia.
Model Warda (1992 r.)
Model Warda zaproponowany w 1992 roku uwzględnia anizotropię odbicia światła. Jest to jeden z pierwszych tego typu modeli i jednocześnie jest on nadal często używany – jest często dostępny w gotowych pakietach oprogramowania.
Model Warda niestety nie uwzględnia współczynnika Fresnela, co nie daje możliwości opisania w pełni właściwości materiałowych i uwzględnienia zależności kątowych. Jest to szczególnie widoczne dla dużych kątów padania światła. Składowa kierunkowa (kierunkowo-rozproszona) jest wyrażona w tym modelu wzorem:
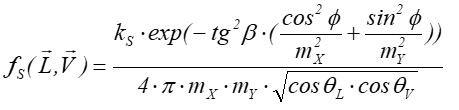
ks - jest współczynnikiem materiałowym, mx oraz my opisują gładkość niezależnie wzdłuż kierunków prostopadłych powierzchni
Model Orena-Nayara (1994 r.)
Oren i Nayar zwrócili uwagę na rozkład postrzeganej luminancji na rzeczywistych powierzchniach rozpraszających. Zastosowanie modelu odbicia Lambertowskiego (opisu idealnego odbicia rozproszonego), tak jak w większości modeli oświetlenia, powoduje. że efekt często całkowicie odbiega od rzeczywistego. Jest to spowodowane przede wszystkim rzeczywistym odbiciem rozproszonym, które odbiega od modelu Lambertowskiego. Rzeczywiste obiekty (np. porcelana nieszkliwiona) odbijają w taki sposób, że dla dużych kątów padania światła luminancja odbicia jest większa niż w modelu Lambertowskim.
W modelu Orena-Nayara funkcja opisująca odbicie rozproszone (dyfuzyjne) ma postać:
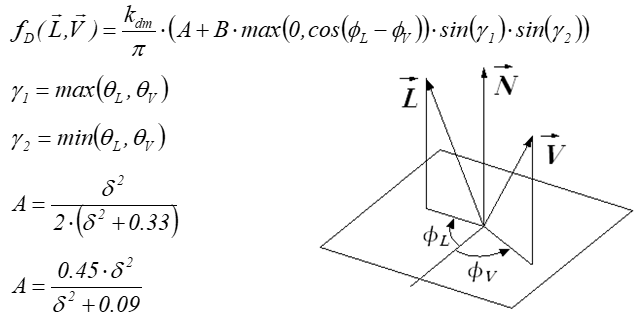
kdm jest współczynnikiem odbicia rozproszonego, d jest stałą materiałową.
Oren i Nayar opracowali model, w którym przybliżyli powierzchnię obiektu powierzchnią wielościenną. Założyli, że obiekt pokryty jest wgłębieniami typu V podobnie jak w modelu Cooka-Torrance’a. Przy czy w modelu Orena-Nayara mikropowierzchnie nie są lustrzane ale rozpraszają w sposób lambertowski. To znaczy dla każdej pojedynczej mikropowierzchni jest stosowany Lambertowski model odbicia.
Dla takiego modelu powierzchni zastosowali rozkład Gaussa kierunku wektora normalnego do powierzchni wielościennej. W efekcie uzyskali model uwzględniający wzajemne zasłanianie powierzchni wielościennej typu V ale przy lambertowskim odbiciu od mikropowierzchni. Ponieważ uzyskany opis był zbyt skomplikowany do zastosowań praktycznych, zaproponowali aproksymację prostymi równaniami.
Model Ashikhmina-Shirleya (2000r.)
Model Ashikhmina-Shirleya jest współczesnym modelem odbicia. Jest on niejako rozszerzeniem modelu Phonga, ale spełnia on wszystkie podstawowe wymagania (zasada wzajemności, zasada zachowania energii, uwzględnia współczynnik Fresnela odbicia światła). Odbicie kierunkowe w tym modelu opisuje równanie:
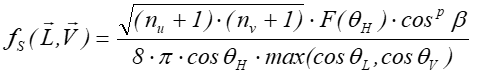
przy czym ![]() , gdzie współczynniki nu oraz nv opisują gładkości
niezależnie wzdłuż odpowiednich prostopadłych kierunków powierzchni – im
większa wartość tym powierzchnia gładsza.
, gdzie współczynniki nu oraz nv opisują gładkości
niezależnie wzdłuż odpowiednich prostopadłych kierunków powierzchni – im
większa wartość tym powierzchnia gładsza.
Model został sformułowany w taki sposób, że może być wykorzystywany w dowolnych obliczeniach graficznych – także we wszystkich wariantach metody śledzenia promieni. Pozwala także uwzględnić anizotropię odbicia pokazaną na rys. 11.9.

Rys.11.9. Rysunki kul
o powierzchniach charakteryzujących się anizotropią odbicia,
wartości współczynników we współrzędnych
sferycznych ![]() .
.
W modelu Ashikhmina-Shirleya opisano także odbicie rozproszone. Przy czym opisano je w sposób bliższy zmianom rzeczywistym niż uwzględnia teoretyczny opis Lamberta.
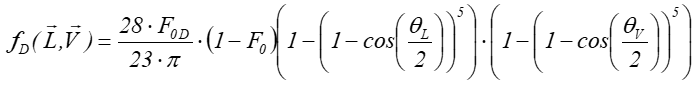
F0 — współczynnik Fresnela dla zerowego kąta,
F0D — współczynnik Fresnela dla zerowego kąta dla odbicia dyfuzyjnego.
Jednocześnie trzeba podkreślić, że jest to inne podejście do opisu odbicia rozproszonego niż w modelu Orena-Nayara. W modelu Ashikhmina-Shirleya wykorzystano opis oparty na pomyśle Schlicka aproksymacji wielomianowej.
Model Ashikhmina-Shirleya ma dodatkowo jeszcze jedną zaletę: jest modelem atrakcyjnym obliczeniowo.
Model He-Torrance’a-Silliona-Greenberga (1991 r.)
Model He-Torrance’a-Silliona-Greenberga został opracowany jako rozszerzenie modelu Cooka-Torrance’a.
Jest to najpełniejszy ze znanych modeli odbicia, uwzględnia praktycznie wszystkie znane zjawiska fizyczne z tym związane (polaryzację, dyfrakcję, interferencję). Ma tylko jedną wadę: jest całkowicie niepraktyczny, czas obliczeń może być kilkaset (100 – 300) razy dłuższy w stosunku do innych opisywanych tutaj modeli. Dodatkowo, ze względu na sposób prowadzenia obliczeń nie może być wykorzystywany w algorytmach typu Monte-Carlo. Złożoność modelu uniemożliwia również jego prostą prezentację.
Porównanie właściwości
Na rysunku 11.10 przedstawiono zmianę kształtu funkcji odbicia w zależności od kąta padania światła dla przykładowych wartości parametrów. Aby możliwe było porównanie różnych modeli odbicia przeprowadzono przeliczenie parametrów między modelami w taki sposób, aby uzyskać zgodność dla kątów odpowiadających połowie wartości funkcji. – Takie postępowanie opisał Blinn w 1977 roku dla funkcji rozkładu mikropowierzchni. Jednocześnie dokonano normalizacji funkcji dla zerowego kąta padania światła. Dzięki temu możliwe staje się zastąpienie jednej funkcji drugą. Możliwe jest także porównanie kształtów – właściwości poszczególnych funkcji.
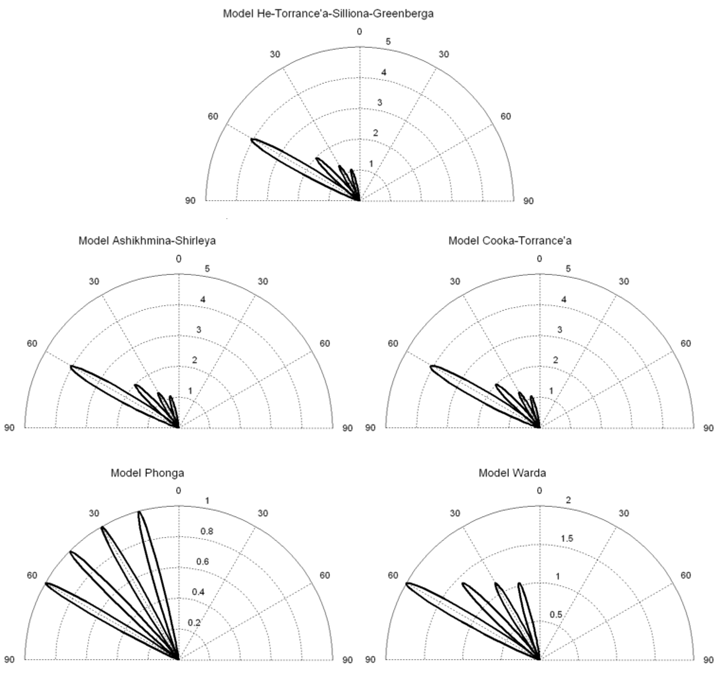
Rys.11.10. Wykresy znormalizowanej funkcji BRDF różnych modeli dla kątów padania światła : 15o, 30o, 45o, 60o
Jak widać modele Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga i Warda wykazują zbliżone kształty funkcji BRDF dla różnych kątów padania światła. Przy czym zależności Warda dają inne proporcje zależności kątowych. Model ten nie uwzględnia współczynnika Fresnela. Stąd wartości maksymalne w opisie Warda odbiegają od wartości w modelach Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga.
Jako punkt odniesienia przyjmuje się model He-Torrance’a-Silliona-Greenberga. Badania doświadczalne pokazały, że najlepiej opisuje on zachowanie rzeczywistych powierzchni. Niemniej jednak, ze względu na złożoność obliczeniową i jednocześnie bardzo zbliżone właściwości (rys.11.10) modele Cooka-Torrance’a oraz Ashikhmina-Shirleya są atrakcyjniejsze. Warto pamiętać jednocześnie, że model He-Torrance’a-Silliona-Greenberga nie może być stosowany w odmianach metody śledzenia promieni, gdzie wymagana jest funkcja gęstości prawdopodobieństwa.
Model Phonga nie pasuje do pozostałych, gdyż w ogóle nie uwzględniono w nim ani kąta padania, ani współczynnika Fresnela.
11.5 Odbicie a przenikanie i załamanie światła. BRDF, BTDF, BSSRDF, BSDF
W rozdziale 11.4 zostały zaprezentowane wybrane przykłady funkcji BRDF, związane z wybranymi modelami opisu odbicia światła od powierzchni materiału. Ale odbicie światła jest tylko jednym ze zjawisk jakie zachodzi gdy światło pada na powierzchnię materiału. Z drugiej strony analiza drogi promienia po napotkaniu powierzchni przedmiotu pokazuje drogę promienia odbitego i załamanego (jeśli takie zjawisko zachodzi). Jeśli rozpatrzymy te zjawiska jako teoretyczne – idealnie kierunkowe, to wyznaczenie odpowiedniego wektora dla odbicia lub załamania nie jest zadaniem trudnym. Zgodnie z prawem odbicia: kąt padania jest równy kątowi odbicia i jednocześnie oba wektory (określające kierunek padania światła i odbicia) oraz wektor normalny są w jednej płaszczyźnie. Analogiczna analiza dla zjawiska załamania światła prowadzi do równie prostego wyznaczenia odpowiednich wektorów. Również i w tym przypadku wektory określające kierunek padania światła i załamania oraz wektor normalny są w jednej płaszczyźnie. Jedyną różnicą przy wyznaczeniu kąta załamania światła jest konieczność uwzględnienia współczynnika załamania zgodnie z prawem załamania światła (Snella-Descartes’a). Do opisu załamania rzeczywistego tak jak przy odbiciu rzeczywistym stosuje się analogiczne modele obliczeniowe.
Z formalnego punktu widzenia w grafice komputerowej wyróżnia się kilka niezależnych opisów zjawisk jakie zachodzą kiedy promień światła pada na powierzchnię materiału:
- BRDF (Bidirectional Reflectance Distribution Function) – funkcja służąca do opisu odbicia światła od powierzchni materiału.
- BTDF (Bidirectional Transmittance Distribution Function) – funkcja służąca do opisu załamanie światła. Funkcja ta jest skonstruowana identycznie jak BRDF tzn jest to iloraz luminancji światła załamanego (przechodzącego przez materiał) i natężenia napromieniowania światła padającego na powierzchnię materiału.
- BSSRDF (Bidirectional Surface Scattering Reflectance Distribution Function) – rozszerzona funkcja BRDF. Jest to iloraz luminancji światła odbitego od powierzchni materiału i natężenia napromieniowania światła padającego. Ale w tym przypadku światło odbite obejmuje także światło, które odbiło się od wewnętrznych struktur/warstw materiału.
- BSDF (Bidirectional Scattering Distribution Function) – rozszerzona funkcja obejmująca odbicie i załamanie. Tzn. najczęściej BSDF = BRDF + BTDF.
11.6. Inne metody opisu odbicia
Modele analityczne zaprezentowane dotychczas są bardzo wygodne do zastosowań praktycznych, jednak często nie dają możliwości opisu skomplikowanej - rzeczywistej powierzchni odbijającej. Stosuje się kilka sposobów bardziej złożonych.
Modele warstwowe
Modele wielowarstwowe (np. model Hanrahana i Kreugera z 1993 roku). Wiele obiektów odbija światło wielowarstwowo. Z jednej strony materiały dielektryczne odbijają w sposób rozproszony dzięki tak zwanemu odbiciu objętościowemu. Światło wnika w materiał i po wielokrotnych odbiciach od cząstek materiału, część tego światła wychodzi na zewnątrz, tworząc składową rozproszoną odbicia. Z drugiej strony często mamy do czynienia z materiałami zbudowanymi z warstw o różnej przenikalności światła (i innych właściwościach odbiciowych). Dobrym przykładem jest skóra, której naturalna barwa jest bardzo trudna do uzyskania bez modeli wielowarstwowych. Osobną grupę materiałów o właściwościach trudnych do opisu i symulacji są materiały pokryte różnymi warstwami zmieniającymi właściwości odbiciowe. Szczególne przypadki pokrycia powierzchni farbami (np. lakiery bezbarwne, farby do drewna, pokrycia karoserii samochodów lakierami typu metalik), patyna w naturalny sposób pokrywająca powierzchnię metali wymagają zastosowania modeli wielowarstwowych odbicia światła.
Więcej informacji na ten temat czytelnik może znaleźć w książce [1].
Modele tablicowane
Zamiast próbować modelować skomplikowaną strukturę i właściwości powierzchni można zmierzyć właściwości odbiciowe i na tej podstawie zbudować tablicę współczynników dla różnych kątów – tablicowaną funkcję BRDF. Oczywiście problem polega na tym, że żeby model pomiarowy był użyteczny to pomiary muszą być dokonane z rozdzielczością wymaganą w obliczeniach związanych z danym obrazem i obiektem. Z drugiej strony wybrana próbka musi być reprezentatywna dla danego materiału. Strona internetowa [4] zawiera tablicowane dane dla wybranych materiałów.
Harmoniczne sferyczne
Jeżeli funkcję BRDF potraktować jako funkcję kątów w układzie sferycznym, to naturalnym sposobem opisu, będzie aproksymacja w postaci harmonicznych sferycznych (warto zajrzeć np.. do prac Westina z 1992 roku). Dzięki temu można rozłożyć opis odbicia na zestaw składowych, które mogą być używane z określoną dokładnością. Jeśli nie są potrzebne szczegóły powierzchni to można użyć prostszego zestawu opisu funkcji BRDF – bez składowych wyższych harmonicznych.
Stosowane są również inne formy opisu aproksymacji: z wykorzystaniem wielomianów Zernike lub metodami falkowymi.
11.7. Interpolacja odbicia - cieniowanie
Wyznaczenie barwy związanej z modelem oświetlenia dla każdego punktu/piksela jest zadaniem kosztownym. Można zatem rozpatrywać interpolację, która pozwoli wypełnić barwą wielokąty w sposób uproszczony. Stosuje się trzy warianty takiego wypełnienia – trzy warianty interpolacji (cieniowania).
- Cieniowanie płaskie (cieniowanie stałą wartością), gdy cały wielokąt jest wypełniony taką samą barwa.
- Cieniowanie Gouroud.
- Cieniowanie Phonga.
Cieniowanie płaskie jest zgodne z rzeczywistością, gdy obserwator lub źródło światła znajduje się w nieskończoności. Może być także stosowane, gdy wielokąt reprezentuje rzeczywiście powierzchnię modelowaną – mamy wtedy do czynienia z rzeczywistą powierzchnią wielościenną.
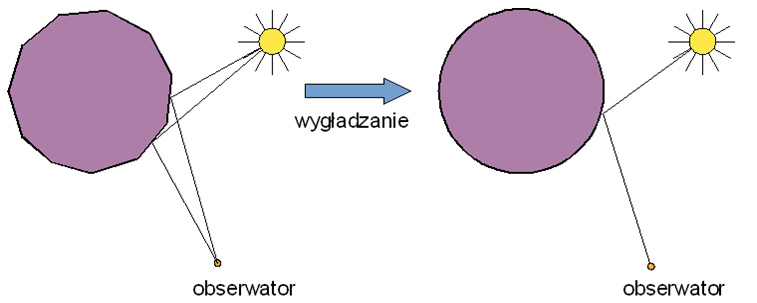
Rys.11.11. Wygładzanie
wielościennego obiektu. W praktyce nie ma możliwości zmiany
kształtu
powierzchni obiektu. Nie ma zatem możliwości wygładzenia kształtu.
Można jednak
ten sam efekt uzyskać zmieniając rozkład barw
na powierzchni.
Jeżeli jednak złożony kształt powierzchni obiektu jest przybliżony wielościanem, to można za pomocą cieniowania wygładzić (pozornie – rysunek 11.11) obiekt niwelując wielościenny charakter.
Cieniowanie Gouraud
Cieniowanie Gouraud pozwala wypełnić wielokąty przez liniową interpolację barwy, jest procesem dwuetapowym:
W pierwszym etapie jest wyznaczana (hipotetyczna) barwa w wierzchołkach wielościanu. W tym celu wyznaczamy hipotetyczny wektor normalny jako średnią arytmetyczną wektorów normalnych wszystkich ścian, do których ten wierzchołek należy. Następnie na podstawie wektora normalnego wyznaczamy barwę wierzchołka korzystając z wybranego modelu odbicia światła.
W drugim etapie dokonywana jest liniowa interpolacja barwy zgodnie z zaprezentowanymi wzorami na rysunku 11.12.

Rys.11.12. Cieniowanie Gouraud. Poszukujemy barwy w punkcie E.
11.6.2 Cieniowanie Phonga
Cieniowanie Phonga polega na analogicznej interpolacji jak w cieniowaniu Gouraud, tylko że interpolowana jest nie barwa ale wektor normalny.
W pierwszym etapie wyznaczamy wektor normalny w wierzchołkach w ten sam sposób jak w cieniowaniu Gouraud.
W drugim etapie wyznaczamy interpolowany wektor normalny dla każdego piksela (to znaczy dla punktu powierzchni odpowiadającego pikselowi) – rysunek 11.13. Następnie wyznaczamy barwę piksela, na podstawie interpolowanego wektora normalnego korzystając z wybranego modelu odbicia światła.
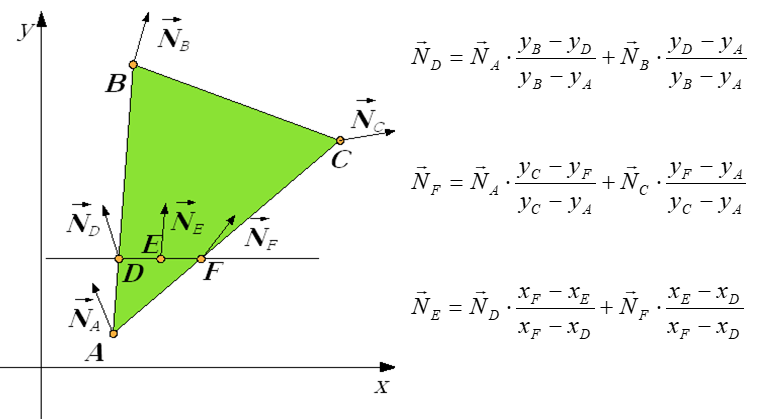
Rys.11.13.
Cieniowanie Phonga. Poszukujemy wektora normalnego w punkcie E.
Na jego podstawie
wyznaczana jest barwa w punkcie E.
Cieniowanie – porównanie interpolacji
Porównując cieniowanie Gouraud i Phonga (rys.11.14) można wskazać właściwości każdego z nich.
- Obie metody zapewniają ciągłą zmianę barwy eliminując skokowe zmiany cieniowania płaskiego.
- Cieniowanie Gouraud nie daje możliwości powstania lokalnego ekstremum (np. rozbłysku światła) w ramach jednego elementu płaskiego. Powoduje to uśrednienie jasności na powierzchni obiektu. Cieniowanie Phonga nie ma tej wady. Interpolacja wektora oddaje poprawnie lokalne ekstrema również w ramach pojedynczego elementu płaskiego.
- Cieniowanie Gouraud dopuszcza, niestety, powstawanie pasm Macha. Wady tej jest praktycznie pozbawione cieniowanie Phonga.
- Wadą cieniowania Phonga jest fakt, że jest ono ponad dwukrotnie droższe obliczeniowo od cieniowania Gouraud.
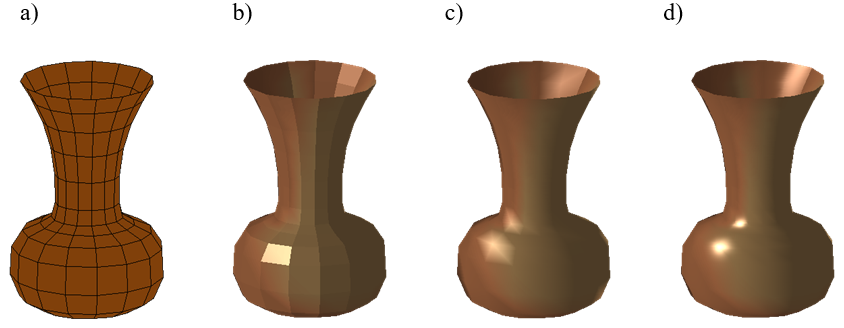
Rys.11.14. a) Model nieoświetlony, b) Cieniowanie płaskie, c) Cieniowanie Gouraud, d) Cieniowanie Phonga.
Problemy cieniowania
Obie przedstawione tutaj metody przybliżają rzeczywisty rozkład barw. W specyficznych sytuacjach powoduje to, powstawanie błędów. Obie metody są wrażliwe na orientację cieniowanego obiektu. Jeśli obiekt ma różne barwy w wierzchołkach i zostanie obrócony, to interpolacja da różne efekty w zależności od położenia obiektu.
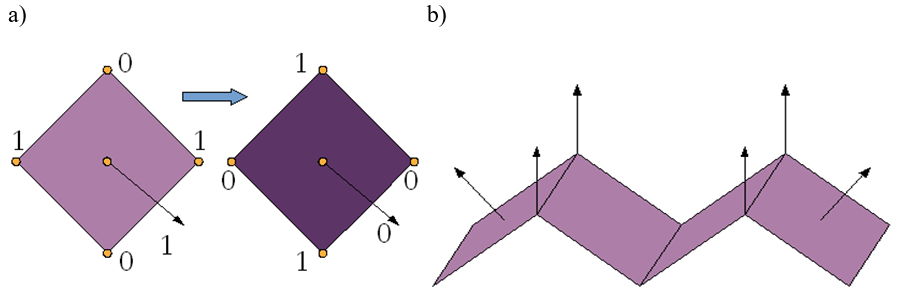
Rys.11.15. Powstawanie błędów cieniowania. a) Obrót obiektu. b) Problem z interpolowanymi wektorami normalnymi.
Rozpatrzmy kwadrat, który ma różne barwy wierzchołków (rysunek 11.15 a). Niech wartości luminancji dla kolejnych wierzchołków wyniosą odpowiednio 0, 1, 0, 1. Jeśli dla takiego kwadratu luminancja środka kwadratu będzie liczona z zastosowaniem interpolacji liniowej, to uzyskana wartość będzie zależała od położenia wierzchołków kwadratu względem kierunku interpolacji. Obrócenie kwadratu zmienia efekt interpolacji – rysunek 11.15 a).
W obu metodach liczy się hipotetyczne wektory normalne w wierzchołku
wielościanu na podstawie średniej arytmetycznej wektorów normalnych
sąsiadujących ścian. Może to spowodować powstanie błędnie skierowanych wektorów
interpolowanych. Na rysunku 11.15 b) wektory interpolowane
wewnętrznych ścian będą inaczej skierowane niż rzeczywiste wektory normalne.
Dodatkowo powstaje nieoczekiwany wpływ ścian sąsiednich. Ruch jednaj ściany
zewnętrznej spowoduje zmianę hipotetycznego wektora normalnego w wierzchołku
(przez wpływ na średnią), a w konsekwencji tego zmianę wektora interpolowanego
ściany wewnętrznej.
Rozdział 12. OŚWIETLENIE GLOBALNE: METODA ŚLEDZENIA PROMIENI
Rozdział dwunasty jest poświęcony zagadnieniu oświetlenia globalnego.
Przedstawiono ogólne równanie renderingu Kajiya oraz wynikające z niego dwa sposoby rozwiązania
zadania oświetlenia globalnego – metodę śledzenia promieni i metodę bilansu
energetycznego. W Rozdziale tym opisano metodę śledzenia promieni. Uwzględniono różne rodzaje
stosowanych rozwiązań oraz algorytmy przyspieszające śledzenie.
12.1. Wprowadzenie
Ogólne równanie renderingu
Modelowanie lokalnego odbicia (lub przenikania) światła nosi czasem nazwę problemu oświetlenia lokalnego. Uwzględnia bowiem tylko lokalne właściwości powierzchni. Problem oświetlenia globalnego jest natomiast opisem zależności związanych z rozchodzeniem się światła, ale uwzględniającym wzajemne oddziaływanie między powierzchniami – np. wielokrotne odbicie światła między różnymi przedmiotami. Zależności te opisują proces docierania światła do dowolnego miejsca sceny. Oczywiście bierzemy pod uwagę opis rozchodzenia się światła na scenie z uwzględnieniem wszystkich zjawisk (odbicia, przenikania, powstawania cienia itd.).
Próby rozwiązania tego problemu na poziomie modelu odbicia lokalnego sprowadzały się do uwzględnienia średniej wartości oświetlenia we wszystkich punktach sceny – oświetlenia tła. Taka składowa jest uwzględniona w modelu Phonga. Jest to oczywiście bardzo dużym uproszczeniem rzeczywistości.
W grafice komputerowej stosowane są dwie ogólne metody rozwiązania problemu oświetlenia globalnego:
- Metoda śledzenia promieni (ang. ray tracing).
- Metoda bilansu energetycznego (ang. radiosity).
Ogólne równanie renderingu Kajiya – opis transportu światła na scenie.
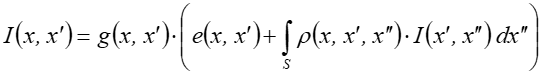
gdzie
I(x , x') - intensywność promieniowania światła elementu x’ w kierunku elementu x ,
g(x , x') - funkcja
widoczności ![]()
r – odległość między x a x' ,
e(x , x') - emisja własna x’ w kierunku x,
ρ(x , x' , x") - współczynnik określający ile światła dotrze z x" do x po odbiciu od x' (odpowiada to funkcji BRDF).
Transport światła odbywa się na scenie na drodze wielokrotnych odbić od poszczególnych fragmentów powierzchni. Ogólne równanie renderingu opisuje zależność między oświetleniem wzajemnym elementarnych fragmentów powierzchni. Rozpatrując dwa fragmenty x i x’ określamy transport od x’ do x . Równanie uwzględnia przy tym zarówno emisję własną fragmentu x’ jak i odbicie przez x’ . Takie sformułowanie daje możliwość zbudowania zależności rekurencyjnej między wszystkimi fragmentami sceny. Z drugiej strony jeśli podzielić całą scenę na fragmenty elementarne, to uwzględnienie równania renderingu wymaga analizy „każdy z każdym” tych fragmentów. Prowadzi to oczywiście do złożoności kwadratowej problemu oświetlenia globalnego.
Równanie wizualizacji zaproponowane przez Kajiya z 1986 roku pozwala prześledzić rekurencyjnie drogę promieni i wyznaczyć intensywności oświetlenia określonych powierzchni. Uwzględnienie wielkości świetlnych doprowadziło do powstania luminancyjnego równania wizualizacji opisywanego przez Cohena w 1993. Pozwala prowadzić obliczenia w grafice komputerowej z uwzględnieniem zasad fizyki. Po uwzględnieniu wielkości świetlnych luminancyjne równanie wizualizacji wyznacza rozkład luminancji.
Typy odbić wzajemnych
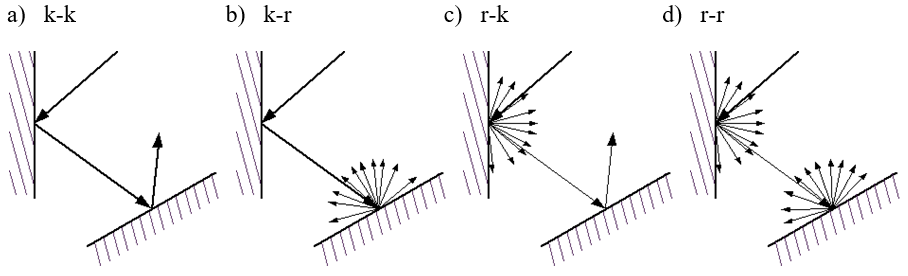
Rys.12.1.
Typy odbić wzajemnych: a) kierunkowe – kierunkowe, b) kierunkowo – rozproszone,
c) rozproszono – kierunkowe, d) rozproszono – rozproszone.
Dobrą klasyfikacją zachowania się algorytmów oświetlenia globalnego jest klasyfikacja pokazująca w jaki sposób są implementowane wzajemne odbicia między dwiema powierzchniami. Biorąc pod uwagę dwa rodzaje odbicia: rozproszone i kierunkowe, możemy mieć do czynienia z czterema możliwościami odbić wzajemnych.
Kierunkowe-kierunkowe – jest to implementowane przez klasyczną metodę śledzenia promieni (Whitteda). I praktycznie metoda klasyczna śledzenia nie pozwala na opis innych odbić wzajemnych.
Rozproszone-rozproszone – jest to implementowane przez klasyczną metodę energetyczną. Podobnie jak śledzenie, klasyczna metoda energetyczna nie pozwalana na implementację innych wariantów odbić.
Rozproszone-kierunkowe (także kierunkowe-rozproszone) – może być implementowane w nowszych rozwiązaniach metody śledzenia.
12.2. Idea metody śledzenia promieni
Traktując model kamery jako mechanizm realizacji rzutowania perspektywicznego, można zauważyć, że barwa danego piksela ekranu powstaje dzięki światłu docierającemu do niego z kierunku wynikającego z rzutowania. Można zatem prześledzić „drogę światła”, które dociera do piksela i na tej podstawie wyznaczyć barwę.
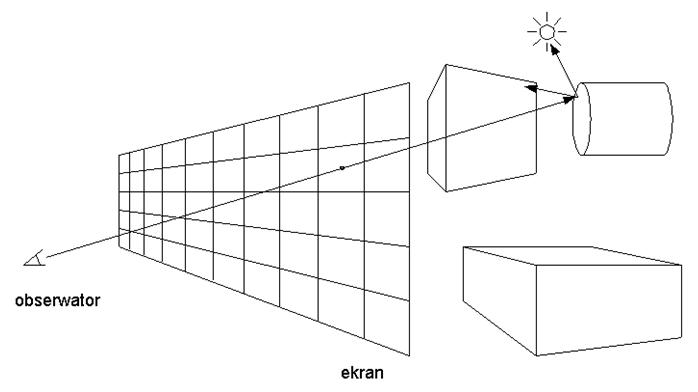
Rys.12.2.
Metoda śledzenia promieni – analizowana jest droga promienia między
obserwatorem
a obiektami sceny i źródłami światła.
Metoda śledzenia
promieni
polega na analizie przebiegu promieni między obserwatorem a źródłem światła.
Drogę promieni opisuje drzewo przecięć, którego węzły reprezentują zjawiska
jakie zachodzą między promieniem a powierzchniami obiektów. Korzeń drzewa
odpowiada promieniowi docierającemu do obserwatora zaś liście — źródłom
światła. Zjawiska odbicia, przenikania i pochłaniania opisane są odpowiednimi
modelami matematycznymi. Wyznaczenie barwy danego piksela polega na analizie
odpowiedniego drzewa.
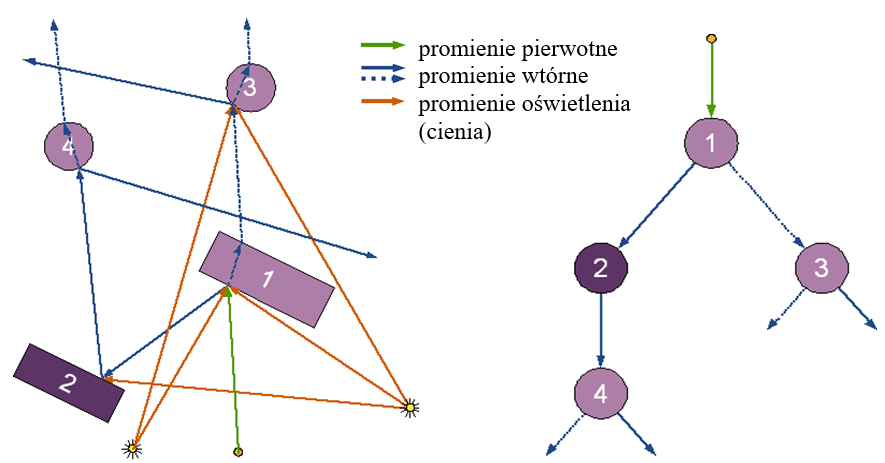
Rys.12.3 Powstawanie drzewa przecięć w metodzie śledzenia promieni.
W najprostszym rozwiązaniu analizę „drogi światła” prowadzi się od obserwatora (kamery – środka rzutowania) do obiektów na scenie. To znaczy w kierunku przeciwnym do rzeczywistego rozchodzenia się światła. Stąd czasami metodę nazywa się metodą (śledzenia) promienia odwrotnego.
Każde napotkanie obiektu przez promień (promień pierwotny) wymaga analizy. Zawsze jest wyznaczany promień odbity o kierunku zależnym od powierzchni obiektu. Jeśli obiekt jest przezroczysty, to wyznaczany jest promień załamany (promień przechodzący przez obiekt) o kierunku zależnym od właściwości materiałowych obiektu. Oba promienie: odbity i załamany nazywane są promieniami wtórnymi. Zawsze są również wyznaczane tak zwane promienie cienia (czasami nazywane promieniami oświetlenia) w kierunku każdego źródła światła. Promienie cienia pozwalają wyznaczyć oświetlenie danego elementu obiektu przez źródła światła, oczywiście jeśli na drodze promienia cienia do źródła światła jest inny obiekt nieprzezroczysty (źródło jest zasłonięte) to oświetlenie nie jest liczone. Promienie wtórne mogą wskazać następne przecięcia z obiektami, stając się wtedy promieniami pierwotnymi kolejnej analizy. Tak stworzone drzewo promieni jest obliczane metodą zstępującą, Barwa każdego węzła jest liczona jako funkcja barwy potomków. Gałąź w takim drzewie kończy się, gdy promienie wtórne (odbite i załamane) nie przecinają się z kolejnymi obiektami.
Może też być stosowane inne zakończenie procesu budowy i/lub analizy drzewa: gdy osiągnięto określony/zadany poziom rekurencji, albo po prostu gdy zabrakło pamięci na następne poziomy.
Analiza śledzenia promieni wymaga wiedzy o:
- Położeniu obserwatora (punktu widzenia, kamery) i parametrach rzutowania.
- Konstrukcji (geometrii) sceny.
-
Obiektach.
- Położenie.
- Kształt i geometria.
- Właściwości optyczne powierzchni (odbicie/przenikanie światła).
-
Źródłach światła.
- Położenie.
- Kształt i geometria.
- Właściwości emisyjne.
Istnieje kilka różnych wersji realizacji tego algorytmu:
- Śledzenie klasyczne (Whitteda), polegające na analizie pojedynczego promienia poczynając od obserwatora - odwrotnie niż rzeczywiste rozchodzenie się światła,
- Śledzenie stochastyczne, kiedy promienie wysyłane są na zasadzie próbkowania pewnego obszaru, również odbicie (załamanie) światła jest modelowane na zasadzie funkcji prawdopodobieństwa, która określa w którym kierunku odbije się (załamie) promień.
- Śledzenie dwukierunkowe, kiedy analiza jest przeprowadzana w obu kierunkach: poczynając od obserwatora i poczynając od źródła światła.
- Mapowanie fotonowe (Jensena) jest śledzeniem dwukierunkowym rozszerzonym o tworzenie pośrednich źródeł światła na powierzchniach rozpraszających.
Rozwój możliwości metody śledzenia promieni polega na dodawaniu coraz bardziej skomplikowanych przypadków, które mogą się pojawić na drodze promienia pomiędzy źródłem a obserwatorem. Najprościej jest opisać przebieg odbicia kierunkowego (lustrzanego), najtrudniej wielokrotne odbicie rozproszone i pośrednie oddziaływania typu składowej kierunkowej padającej na powierzchnię rozpraszającą.
12.3. Śledzenie klasyczne (Whitteda)
Pierwszą pracę na temat śledzenia promieni w grafice komputerowej opublikował Apple w 1968 roku. Opisał on ray casting – metodę określania widoczności (i barwy) na podstawie śledzenia promienia od obserwatora do pierwszego przecięcia z obiektem. Do powstania metody przyczynił się również Kay (1970). Za autora metody śledzenia promieni w wersji klasycznej uznaje się Whitteda (artykuł z 1980 roku), ze względu na znaczące rozszerzenia jakie wprowadził do powstającej metody. Opisany proces budowy i analizy drzewa promieni w rozdziale 12.2 odpowiada opisowi Whitteda.

Rys.12.4.
Jeden z pierwszych rysunków zrealizowanych metodą śledzenia.
Fragment rysunku z artykułu Whitteda © z 1980 roku.
Pierwsze rysunki wygenerowane przez Whitteda (rys.12.4) wzbudziły podziw. Pokazywały w perfekcyjny sposób odbicie i załamanie światła przez sferyczne metalowe i szklane obiekty. Takie efekty były nieosiągalne innymi metodami. Warto zauważyć, że opisany sposób analizy drzewa promieni odpowiada, tak naprawdę, tylko kierunkowemu rozchodzeniu się światła. Oznacza to, że dobre efekty takiej analizy uzyskać można dla obiektów, które charakteryzują się właśnie kierunkowym charakterem odbicia i przenikania. Propozycja Whitteda nie rozwiązuje w pełni równania renderingu.
Można mówić o wielu wadach klasycznego śledzenia promieni:
- Analizowane są tylko promienie związane z idealnym – kierunkowym odbiciem lub załamaniem światła.
- Uwzględnia się tylko punktowe źródła światła.
- Barwa piksela jest wyznaczana na podstawie jednego promienia co może prowadzić do zniekształceń związanych z próbkowaniem (tzw. zniekształceń intermodulacyjnych).
Podstawowym problemem obliczeniowym śledzenia klasycznego (i tak naprawdę każdej późniejszej modyfikacji metody, a więc także wariantów stochastycznych śledzenia) jest szybkie wyznaczenie przecięcia promienia z obiektem. Stąd powstało wiele algorytmów przyspieszających metodę śledzenia promieni, które zajmują się szybkim wyszukiwaniem przecięć promienia z obiektami sceny.
12.4. Rzeczywiste (niepunktowe) źródło światła
Problem z opisem rzeczywistych obiektów za pomocą klasycznego śledzenia Whitteda zaczyna się pojawiać gdy, weźmiemy pod uwagę rzeczywiste źródło światła (o skończonych – niepomijalnych rozmiarach). Analiza oświetlenia na drodze jednego promienia przestaje odpowiadać rzeczywistości. Ani osiągnięcie obrazu miękkiego półcienia, ani wyznaczenie oświetlenia pochodzącego od powierzchniowego źródła jest całkowicie niemożliwe.
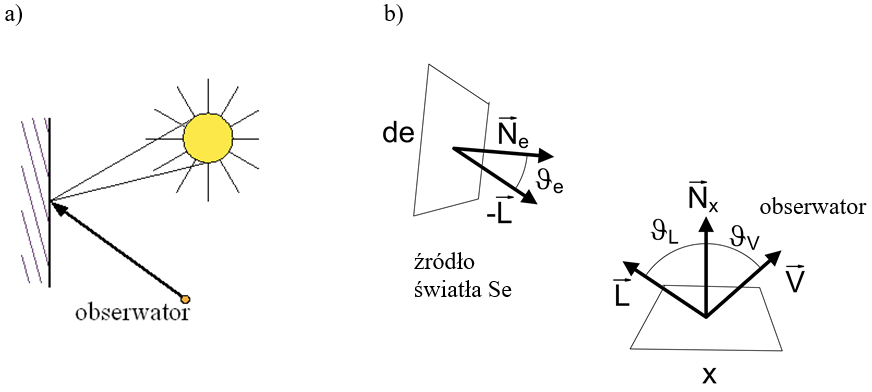
Rys.12.5. Problem
powierzchniowego źródła światła. a) Na skutek
nieidealnie kierunkowego odbicia
od powierzchni na obraz odbicia postrzegany
przez obserwatora ma wpływ cała powierzchnia źródła.
b) Aby uwzględnić to
w opisie należy całkować luminancję po powierzchni źródła uwzględniając
właściwości odbiciowe (BRDF) powierzchni x.
Rozpatrując
fragment powierzchni oświetlony bezpośrednio przez źródło powierzchniowe (rys.12.5)
i biorąc pod uwagę równanie wizualizacji Kajiya, można wykazać, że luminancja ![]() postrzegana na powierzchni x z kierunku wektora
postrzegana na powierzchni x z kierunku wektora ![]() (przez obserwatora) będzie
opisana następującym równaniem.
(przez obserwatora) będzie
opisana następującym równaniem.
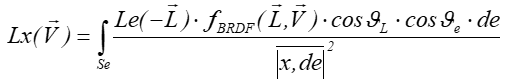
Poprawny wynik może dać tylko analiza uwzględniająca całkowanie po powierzchni źródła światła.
Przykładem dobrej aproksymacji zastępującej całkowanie sumą przy wykorzystaniu klasycznej metody śledzenia jest model Verbecka-Greenberga z 1984 roku. W modelu tym założono, że źródło powierzchniowe jest przybliżone zbiorem źródeł punktowych rozłożonych na powierzchni źródła. Każde źródło punktowe emituje strumień elementarny. Strumień źródła powierzchniowego jest odpowiednią (uwzględniającą kierunki) sumą strumieni elementarnych.
12.5. Całkowanie Monte Carlo
Rozwiązanie analityczne równania renderingu praktycznie nie ma sensu. Autorzy publikacji dotyczących tego tematu czasami sugerują możliwość rozwiązania analitycznego dla wybranego; wydzielonego i wyizolowanego problemu obejmującego na przykład pojedyncze elementy odbijające i jedno źródło światła o prostym opisie geometrycznym. Dla bardziej skomplikowanych scen trudności pojawiają się już na etapie opisu wzajemnego zasłaniania i kształtu jednego elementu widzianego z powierzchni drugiego.
Dobrym rozwiązanie w takiej sytuacji – rozwiązaniem uniwersalnym jest zastosowanie całkowania Monte Carlo. Na przykład dla problemu pojedynczego powierzchniowego źródła światła można wygenerować zbiór promieni biegnących w kierunku odwrotnym od obserwatora do powierzchni i dalej odbijających się zgodnie z pewnym prawdopodobieństwem zależnym od właściwości odbiciowych powierzchni. Promienie odbite trafią (lub nie) w określony punkt powierzchni źródła, z którym to punktem będzie związana określona luminancja i barwa. Jeśli na podstawie analizy zachowania się takich promieni wyznaczymy wartość luminancji postrzeganej przez obserwatora to zadanie jest rozwiązane. Taką właśnie możliwość daje w tym przypadku całkowanie Monte Carlo.
W najprostszym przypadku jednowymiarowym, jeśli chcemy obliczyć całkę
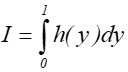
to możemy skorzystać z N liczb losowych o rozkładzie równomiernym x1, x2, ,,,xN , stanowiących pewną realizację zmiennej losowej X. Wtedy
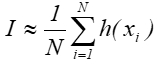
Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale S i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny.
Jak wyznaczyć
całkę 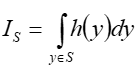 ?
?
Niech ![]() gdzie
gdzie ![]() jest gęstością
prawdopodobieństwa
jest gęstością
prawdopodobieństwa 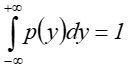 .
.
Należy
wygenerować N próbek xi zgodnie z ![]() .
.
Wartość oczekiwana wyniesie:
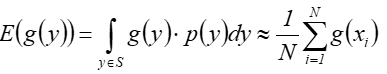
więc
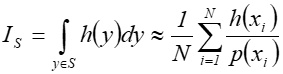
Warto zwrócić
uwagę na zależności dotyczące błędu estymacji całki metodą Monte Carlo. Można
pokazać, że wariancja estymacji jest proporcjonalna do ![]() natomiast odchylenie
standardowe do
natomiast odchylenie
standardowe do ![]() . W związku z tym,
jeśli chcemy zmniejszyć błąd o połowę to N
musi wzrosnąć czterokrotnie.
. W związku z tym,
jeśli chcemy zmniejszyć błąd o połowę to N
musi wzrosnąć czterokrotnie.
Generowanie próbek
Zastosowanie całkowania Monte Carlo wymaga wygenerowania próbek o określonym rozkładzie i w zdefiniowanym obszarze. Niestety programy biblioteczne najczęściej pozwalają uzyskać ciąg próbek pseudolosowych o rozkładzie równomiernym w obszarze prostokątnym jednostkowym.
Jak
wygenerować N próbek xi zgodnie z![]() , gdzie
, gdzie![]() jest gęstością
prawdopodobieństwa.
jest gęstością
prawdopodobieństwa. 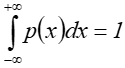 .
.
Generowanie wartości losowych zgodnie z zadanym rozkładem gęstości prawdopodobieństwa może być zrealizowane jedną ze znanych metod. Najczęściej stosuje się metodę funkcji odwrotnej do dystrybuanty lub metodę eliminacji próbek niepasujących.
Metoda funkcji odwrotnej do dystrybuanty
Metoda ta wymaga analitycznego wyznaczenia dystrybuanty D(x) na podstawie funkcji gęstości prawdopodobieństwa, a następnie wyznaczenia funkcji odwrotnej. Uzyskana funkcja przelicza próbki o rozkładzie równomiernym na próbki o zadanym rozkładzie.
Niech 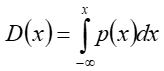
- Wygenerować N
próbek
 o rozkładzie
równomiernym, takich że
o rozkładzie
równomiernym, takich że 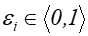 .
. -
Wyznaczyć
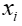 takie że
takie że 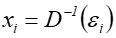 .
.
![]() są poszukiwanymi
próbkami.
są poszukiwanymi
próbkami.
Metoda ta jest bardzo efektywna, ale nie zawsze możliwe jest wyznaczenie odpowiedniej funkcji odwrotnej.
Dobrym przykładem wykorzystania metody funkcji odwrotnej do dystrybuanty jest wygenerowanie próbek o rozkładzie równomiernym w kole o zadanym promieniu R.
Wydawać by się mogło, że najprostszym rozwiązaniem takiego zadania będzie wygenerowanie próbek w prostokącie jednostkowym a następnie przeliczenie ich współrzędnych do współrzędnych biegunowych. Takie rozwiązanie nie daje rozkładu równomiernego w kole.
Można to natomiast osiągnąć stosując metodę funkcji odwrotnej do dystrybuanty.
Niech dane
będą próbki ![]() o rozkładzie
równomiernym, takie że
o rozkładzie
równomiernym, takie że ![]() .
.
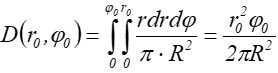
stąd próbki w układzie biegunowym:
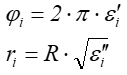
Podane wzory pokazują przeliczenie współrzędnych z układu prostokątnego (gdzie są wygenerowane próbki pseudolosowe o rozkładzie równomiernym w prostokącie jednostkowym) na układ biegunowy koła. Takie przeliczenie zapewnia równomierność rozkładu próbek w kole.
Metoda eliminacji próbek (niepasujących)
- Określić najmniejszy obszar prostokątny obejmujący zadany obszar.
- Wygenerować próbki o rozkładzie równomiernym w prostokącie.
- Odrzucić próbki niepasujące – (te, które należą do prostokąta ale nie należą do zadanego obszaru).
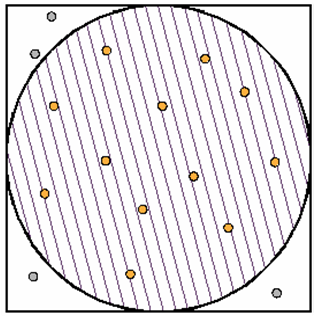
Rys.12.6. Zastosowanie metody usuwania próbek niepasujących do generowania próbek wewnątrz koła.
Metoda ta wymaga zdefiniowania prostokąta obejmującego zadany obszar i wygenerowania próbek o rozkładzie równomiernym. Oczywiście część z nich będzie poza zadanym obszarem – należy je odrzucić. Metoda ta może być praktycznie zawsze zastosowana – nie ma żadnych ograniczeń ani problemów analitycznych. Nie jest ona jednak efektywna, gdyż wymaga generowania dużej liczby próbek, które nie są potem wykorzystywane.
Na rysunek 12.6 pokazano zastosowanie tej metody do generowania próbek w kole, część próbek leżących poza obszarem koła zostaje odrzucona.
12.6. Śledzenie stochastyczne
Śledzenie stochastyczne (ang. distributed ray tracing) jest odmianą metody śledzenia promieni, stanowiącą rozwiązanie podstawowych wad śledzenia klasycznego Whitteda. Śledzenie stochastyczne zaproponowali Cook, Porter i Carpenter w 1984 roku. Istnieje wiele odmian i rozwiązań zaawansowanych wykorzystujących próbkowanie w metodzie śledzenia: path tracing zaproponowany przez Kajiya w 1986 r., śledzenie dwukierunkowe zaproponowali Lafortune i Willems oraz Veach i Guibas w 1994r. transport typu Metropolis - Veach i Guibas w 1997r.
W śledzeniu stochastycznym generowanych jest wiele promieni (9, 16 lub nawet więcej) na piksel. Każdy z promieni może „pójść własną drogą” – to znaczy dla każdego będzie analizowane inne drzewo przecięć. Barwa piksela jest uśrednieniem tych promieni. Odbicie (załamanie) promienia trafiającego w powierzchnię obiektu zależy od funkcji BRDF traktowanej jako gęstość prawdopodobieństwa. Oznacza to, że kolejne promienie padające na daną powierzchnię (nawet pod tym samym kątem) mogą odbić się pod różnymi kątami. Jednak dla odpowiednio dużej liczby promieni rozkład ich odbić będzie odpowiadał gęstości prawdopodobieństwa, a tym samym będzie odpowiadał właściwościom odbiciowym powierzchni opisanym przez funkcję BRDF.
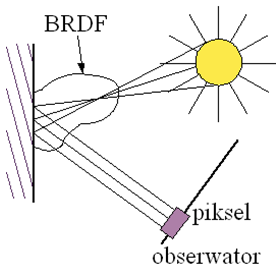
Rys.12.7. Idea postępowania w śledzeniu stochastycznym.
Postępowanie:
- Wygenerować zestaw promieni dla danego piksela.
- Traktując BRDF jako gęstość prawdopodobieństwa wyznaczyć promienie odbite.
- Uśrednić barwę dla piksela.
Wygenerowanie promieni przechodzących przez piksel w sposób zdeterminowany w regularnej siatce powoduje powstanie takich samych zniekształceń intermodulacyjnych jak w klasycznym śledzeniu (efekt schodkowy, mory na obszarach pokrytych teksturą). Aby temu zaradzić można generować próbki losowo na obszarze piksela. Jednak w tym przypadku pojawia się bardzo silny szum nakładający się na wyznaczone barwy. Najlepszym rozwiązaniem byłoby wygenerowanie próbek w taki sposób, aby utrzymać między nimi pewną minimalną odległość. Spowodowałoby to znaczną redukcję amplitudy szumu. Niestety takie rozwiązanie jest zbyt kosztowne obliczeniowo. Dobrym kompromisem (i najczęściej stosowanym) jest generowanie próbek na regularnej siatce, ale z dodatkiem przypadkowych przesunięć (ang. jittering sampling lub stratified sampling). Jest to proste obliczeniowo i jednocześnie jeśli przesunięcia są nieskorelowane, to występuje znacząca redukcja szumu przy minimalnych zniekształceniach intermodulacyjnych.
Zastosowanie próbkowania stochastycznego pozwala traktować wyznaczenie barwy piksela jako całkowanie po obszarze piksela. Dzięki temu możliwe jest uzyskanie miękkich cieni i rozmycia odbicia światła, możliwe jest uwzględnienie odbić nieidealnych kierunkowo i rozproszonych.
Próbkowanie piksela nie jest jedyną możliwością zastosowania śledzenia stochastycznego. Próbkowanie „w innym wymiarze” (całkowanie w innym obszarze) pozwala uzyskać dodatkowe efekty, niemożliwe do osiągnięcia w śledzeniu klasycznym :
- Rozmycie ruchu (rozproszenie w czasie).
- Głębia ostrości (rozproszenie promieni na powierzchni obiektywu).
- Powierzchnia chropowata/pofałdowana: rozmycie odbicia lub przenikania kierunkowego (lustrzanego) (rozproszenie odpowiednio do odbicia/przenikania i pofałdowanej powierzchni).
- Miękkie cienie (rozmycie cienia): rozproszenie promieni na powierzchni źródła i obiekty zasłaniającego je.
Wadą próbkowania stochastycznego jest pojawiający się szum, który można redukować przez zwiększenie liczby promieni, co z kolei, niestety, pociąga za sobą zwiększenie czasu realizacji.
Warto pamiętać, że dzisiaj przyjęło się, że jeśli występuje nazwa „metoda śledzenia promieni” bez dodatkowych określeń to jest to rozumiane właśnie jako śledzenie stochastyczne, a nie klasyczne Whitteda.
12.7. Mapowanie fotonowe
Mapowanie fotonowe jest najnowszym rozszerzeniem metody śledzenia promieni. Twórcą jego jest Jansen (książka dotycząca mapowania fotonowego z 2001 roku). Pierwsze artykuły dotyczące tego pomysłu ukazały się w połowie lat dziewięćdziesiątych XX wieku.
Mapowanie fotonowe jest przykładem śledzenia dwukierunkowego i jest procesem dwuetapowym.
- Etap1. Rozsyłanie fotonów. Na powierzchni źródła generowane są fotony, które są rozsyłane zgodnie z kierunkiem rozchodzenia się światła. Symuluje to emisję światła przez powierzchnię źródła. Ruch wyemitowanych fotonów odbywa się zgodnie z zasadami optyki geometrycznej. Zjawiska odbicia i przenikania (załamania) są opisane za pomocą odpowiednich modeli matematycznych (BRDF ). Każdy foton pokonuje pewną drogę napotykając na niej kolejne powierzchnie. Na każdej z nich, przy każdym odbiciu lub załamaniu, foton może pozostawić część swojego strumienia. W ten sposób z tych „pozostałości” powstaje mapa fotonowa. Struktura danych tej mapy obejmuje nie tylko wartość pozostawionego w danym punkcie strumienia, ale także parametry geometryczne – współrzędne punktu i kierunek padania fotonu.
- Etap2. Zbieranie fotonów. Aby stworzyć obraz, przez każdy piksel ekranu jest prowadzony promień zgodnie ze zdefiniowanym sposobem patrzenia przez obserwatora (zgodnie z odpowiednim rzutowaniem). Droga tego promienia jest następnie analizowana tak jak w klasycznym śledzeniu promieni. Luminancja danego piksela jest wyznaczana tak jak w śledzeniu stochastycznym, ale całkowaniu Monte Carlo podlegają zgromadzone na danej powierzchni fotony.
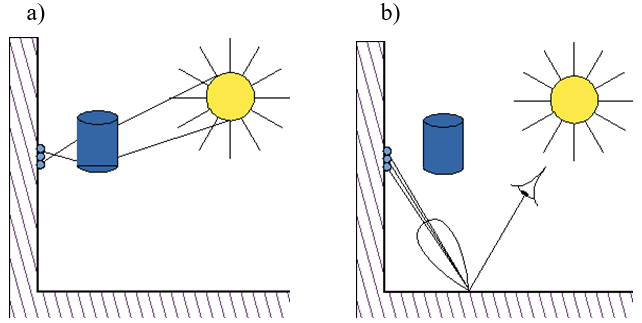
Rys.12.8. Mapowanie
fotonowe: a) Etap rozsyłania i „osiadania” fotonów na powierzchni rozpraszającej.
b) Etap
zbierania fotonów.
Mapowanie fotonowe zostało opracowane jako mechanizm uzupełniający śledzenie promieni w celu symulacji zjawisk takich jak np., skupienie światła (caustic). Pozwala także uwzględnić nieidealne właściwości odbijające zarówno powierzchni rozpraszających jak i lustrzanych.
Na rysunku 12.9 pokazano przykłady obrazów wygenerowanych z wykorzystaniem mapowania fotonowego. Dzięki zastosowaniu tej techniki w metodzie śledzenia promieni możliwe stało się uzyskanie takich efektów jak rozproszenie światła z jednoczesnym mieszaniem barw za szklanką z płynem na rysunku 12.9 a), oraz skupienia światła (caustic) na rysunku 12.9 b) i 12.9 c).
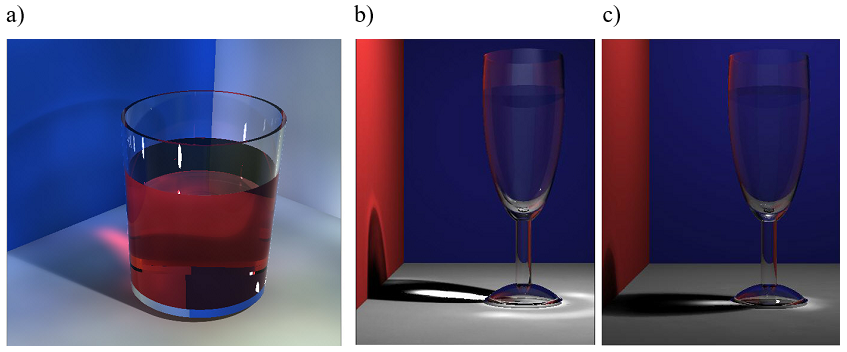
Rys.12.9.
Mapowanie fotonowe. a) „Kompot wiśniowy” – rozproszenie światła na skutek
przejścia
przez szklankę z płynem. b) i c) Skupienie światła załamanego przez
szkło
dla różnych położeń źródła światła. Implementacja mapowania fotonowego
oraz opracowanie rysunków Michał Jelicz © , za zgodą autora.
12.8. MLT
Metropolis Light Transport (MLT) jest jedną z
najciekawszych metod rozwiązania problemu oświetlenia globalnego. MLT pojawiło się
grafice komputerowej w 1997 roku w artykule E.Veach i L.Guibas [11]. Autorzy zaadaptowali
metodę próbkowania zaproponowaną wcześniej przez Metropolis (i innych) [12] do
efektywnego próbkowania w statystycznym rozwiązywaniu problemów fizycznych. Podstawową
zaletą stosowania MLT w śledzeniu promieni jest możliwość adaptacyjnego próbkowania
ścieżek promieni światła i niezależnego rozpatrywania lokalnych „porcji”
światła, w oparciu o bardzo prosty mechanizm. Najczęściej stosowanym
mechanizmem wyboru próbek jest uzależnienie go, po prostu od wartości funkcji
opisującej lokalne zmiany luminancji. Dzięki temu łatwiejsze stało się
analizowanie przypadków, gdzie właśnie lokalne zmiany są najsilniejsze jak np.
zjawiska kaustyczne. Metoda MLT zrewolucjonizowała rozwiązanie problemu
oświetlenia globalnego, dając możliwość efektywniejszego (a tym samym
szybszego) uzyskania zadowalających obrazów (rys.12.10). Metoda MLT była wielokrotnie
uzupełniana i doskonalona. M.Pauly (i inni) w artykule [13] zaproponowali
zastosowanie metody do scen zawierających mgłę i dym. Wiele prac dotyczy próby
poprawy zbieżności i właściwości statystycznych MLT [14, 15]. Praktyczne uwagi
dotyczące współczesnych zastosowań MLT można znaleźć także w [6].

Rys.12.10. a) Obraz
wygenerowany z wykorzystaniem dwukierunkowego śledzenia ścieżek
i
nadpróbkowania 40 próbek na piksel. b) Obraz wygenerowany z zastosowaniem MLT,
250 mutacji na piksel. Czas realizacji w obu przypadkach taki sam.
Prezentowane rysunki
są fragmentami rysunków pochodzących z pracy [11].
Fair use – dozwolony użytek w celach edukacyjnych.
Niech dana będzie funkcja f(x) nieujemna w rozpatrywanym przedziale. Jeśli chcemy spróbkować funkcję f(x) algorytmem Metropolis, to algorytm ten uzależnia generowanie próbek od wartości funkcji f(x). Takie podejście jest bardzo wygodne, nie wymaga odwracania funkcji, odpowiednich normalizacji czy wyznaczania całki. Wystarczy tylko wartość funkcji. Jest to szczególnie wygodne w sytuacjach gdy inne metody próbkowania stwarzają problemy.
Proces generowania próbek jest rozpoczynany od
wygenerowania startowej, losowej próbki x0.
Każda następna jest generowana na podstawie próbki poprzedniej za pomocą
funkcji mutacji xi+1=M(xi).
Funkcja ta zmienia wartość próbki, w najprostszym przypadku może to być
generowanie nowej wartości losowej, niezależnie od próbki poprzedniej. Do
generowania próbek wykorzystywane są jeszcze dwie funkcje. Pierwszą jest
funkcja przejścia P(xi,xi+1)
określająca prawdopodobieństwo przejścia ze stanu xi do xi+1
z wykorzystaniem mutacji M(x). Drugą
jest funkcja akceptacji ![]() określająca prawdopodobieństwo akceptacji
zrealizowanej mutacji. Jeśli punkcja przejścia jest symetryczna tzn. P(xi,xi+1) = P(xi+1,xi) to
określająca prawdopodobieństwo akceptacji
zrealizowanej mutacji. Jeśli punkcja przejścia jest symetryczna tzn. P(xi,xi+1) = P(xi+1,xi) to ![]() .
Generowanie próbek opisuje Algorytm Metropolis.
.
Generowanie próbek opisuje Algorytm Metropolis.
ALGORYTM Metropolis
x0=RAND() , i=0
powtarzaj następujący zestaw
operacji aż i osiągnie wartość N
begin
wyznacz nową próbkę xi+1=M(xi)
określ poziom akceptacji a = A(xi, xi+1)
jeśli (RAND()<a) to i=i+1 oraz zapamiętaj xi
end
określ poziom akceptacji a = A(xi, xi+1)
jeśli (RAND()<a) to i=i+1 oraz zapamiętaj xi
Algorytm generuje N próbek zgodnie z rozkładem określanym pośrednio przez funkcję akceptacji. Nieujemną funkcją f(x) wykorzystywaną w MLT jest funkcja luminancji ścieżki. Oznacza to, że przy najprostszej mutacji (nowa wartość losowa) próbki są generowane w taki sposób, że promienie są kierowane w obszary lokalnie jaśniejsze. Takie podejście pozwala wydobyć szczegóły w jasnych miejscach obrazów. W ten sposób, niejako, faworyzowane są te ścieżki, które prowadzą do źródeł światła, a pomijane te, które nie wnoszą lokalnych zmian lub są po prostu ciemne. Takie podejście jest w dużym stopniu zgodne z naszą percepcją – w zróżnicowanym tonalnie obrazie łatwiej zauważyć szczegóły, czy zmiany barwy, w jasnych obszarach niż w obszarach ciemnych
Warto także zwrócić uwagę na wady próbkowania Metropolis w śledzeniu promieni. Jest to próbkowanie zależne od stanu (rozkładu barw) pikseli obrazu. Nie jest metodą uniwersalną, która przyspieszy zawsze obliczenia. Jeśli scena jest równomiernie oświetlona lub decydujące w oświetleniu jest bezpośrednie źródło światła, to tradycyjne śledzenie ścieżek da szybciej lepsze rozwiązanie. MLT sprawdzi się jednak zawsze tam gdzie występują widoczne lokalne zmiany oświetlenia i przeważa oświetlenie pośrednie (po wielokrotnych odbiciach).
12.9 Rosyjska ruletka
Światło dociera do obserwatora po nieskończonej liczbie odbić pośrednich. Stosując całkowanie stochastyczne w realizacji śledzenia promienni wykorzystuje się skończoną liczbę promieni, skończona liczbę poziomów rekurencji, czy skończoną długość ścieżki promienia w śledzeniu ścieżek. Wybór liczby tego typu elementów jest zadaniem trudnym. Problemem jest podjęcie decyzji kiedy przerwać operacje rekurencyjne albo jakiej długości powinna być ścieżka promienia. Zawsze można przecież przeprowadzić jeszcze jedną iterację, pytanie tylko, czy uzyskane dzięki temu efekty warte będą nakładu włożonej dodatkowo pracy. Najczęściej stosowanym mechanizmem pozwalającym podjąć decyzję o odpowiednim przerwaniu obliczeń jest tzw. rosyjska ruletka.
Niech dane będzie wyrażenie X którego wartość jest wyznaczana w sposób rekurencyjny. Aby podjąć decyzję czy przerwać obliczenia wystarczyłoby sprawdzić, czy X mieści się w pewnym przedziale tzn. jeśli X<TX. Jednak takie podejście powoduje, że jeśli to postępowanie będzie wielokrotnie powtarzane (np. dla wielu pikseli) to określenie wartości granicznej przedziału wpływałoby w sposób systematyczny na uzyskiwane wartości. Zastosowanie rosyjskiej ruletki pozwala uniknąć tego problemu.
ALGORYTM Rosyjskiej Ruletki
if X<TX then
begin
s = RAND[0,1]
if
s < P then przerwij obliczenia
else X = X/(1-P)
end
if s < P then przerwij obliczenia
else X = X/(1-P)
przy czym RAND[0,1] generuje wartość losową o równomiernym rozkładzie z przedziału [0,1]. P jest przyjętym prawdopodobieństwem przerwania obliczeń. Zwiększając wartość P można zdecydować o szybszym przerwaniu obliczeń ale należy się liczyć z tym że wartość X będzie odbiegała od oczekiwanej. Zmniejszenie wartości P powoduje zwiększenie prawdopodobieństwa osiągnięcia dokładniejszej wartości X , zmniejsza wariancję. Ale konsekwencją zmniejszenia wartości P jest również wydłużenie czasu obliczeń.
Takie podejście nie zmienia wartości oczekiwanej, ![]() .
.
Rosyjska ruletka jest nieobciążoną metodą zakończenia obliczeń statystycznych na pewnym poziomie rekurencji. Taki mechanizm może być w analogiczny sposób stosowany w wyznaczaniu wartości całki czy określaniu długości ścieżki w śledzeniu ścieżek.
Zastosowanie mechanizmu rosyjskiej ruletki w grafice komputerowej zostało zaproponowane przez J.Arvo i D.Kirka w 1990 roku [16]. Więcej na ten temat można również znaleźć w podręcznikach [2,6].
12.10. Problem cienia
Cień jest bardzo ważny na scenie, podkreśla relacje przestrzenne. Pośrednio wskazuje położenie źródeł światła. Zwiększa wrażenie realności sceny. Kształt powierzchni zacienionej („geometria cienia”), jest trudny do przewidzenia i określenia bez dokładnej analizy. Można rozważać pewne właściwości cienia. Bardzo rzadko mamy do czynienia z ostrą krawędzią brzegu powierzchni zacienionej, częściej występuje łagodna zmiana oświetlenia. Powierzchniowe źródło światła powoduje powstanie umbry i penumbry. Umbra jest obszarem całkowicie zasłoniętym, gdzie światło nie dociera. Penumbra jest częściowo oświetlonym obszarem, dociera tam część strumienia ze źródła światła. Powstawanie cienia zależne jest od rodzaju źródła światła.
Pomysł podstawowy rozwiązania problemu cienia to : określenie obszar, który może być „widoczny” z punktu widzenia źródła światła. Obszar niewidoczny ze źródła jest w cieniu. Punkt P jest w cieniu wtedy i tylko w tedy, gdy P jest zasłonięty z punktu widzenia źródła światła. Można stosować algorytmy eliminacji elementów zasłoniętych, w których przeprowadza się analizę nie z punktu widzenia obserwatora, ale z punktu widzenia źródła światła. Algorytmy najczęściej rozpatrywane w takim podejściu:
- Z-bufor cienia, dwuetapowy z-bufor (mapa cieni).
- Podejście objętościowe (3D mapa cieni).
- Algorytm Weiler-Atherton (docelowo opracowany właśnie do analizy cieni !).
Analiza rozkładu oświetlenia sceny realizowana metodą śledzenia promieni daje także informacje o rozkładzie cieni. Trzeba jednak pamiętać, że ich wygląd będzie bardzo silnie zależał od sposobu uwzględniania powierzchniowych źródeł światła.
12.11. Metoda śledzenia promieni a CSG
Warto zauważyć, że omawiana wcześniej metoda modelowania – konstrukcyjna geometria brył może być bezpośrednio połączona z metodą śledzenia promieni. Jeśli zachodzi pewien mechanizm operacji wolumetrycznej modelowania, na przykład określenie części wspólnej (iloczynu) obiektów A i B, to operacja ta również odnosi się do prostej będącej analizowanym promieniem w metodzie śledzenia – rys.12.11. Przy czym odniesienie tego do promienia oznacza operację na odcinkach o końcach wyznaczonych przecięciem promienia z powierzchnią obiektów. Wyznaczenie operacji boolowskich odcinków na prostej jest zadaniem bardzo prostym. W takim razie nie jest w ogóle potrzebne niezależne wyznaczanie powierzchni będących rezultatem operacji boolowskich. Można to zrobić podczas rysowania obrazu. Wystarczy, że analizując przecięcia dla każdego promienia zostanie uwzględniony mechanizm modelowania obiektu metodą konstrukcyjnej geometrii brył i wyznaczone odpowiednie punkty przecięć.
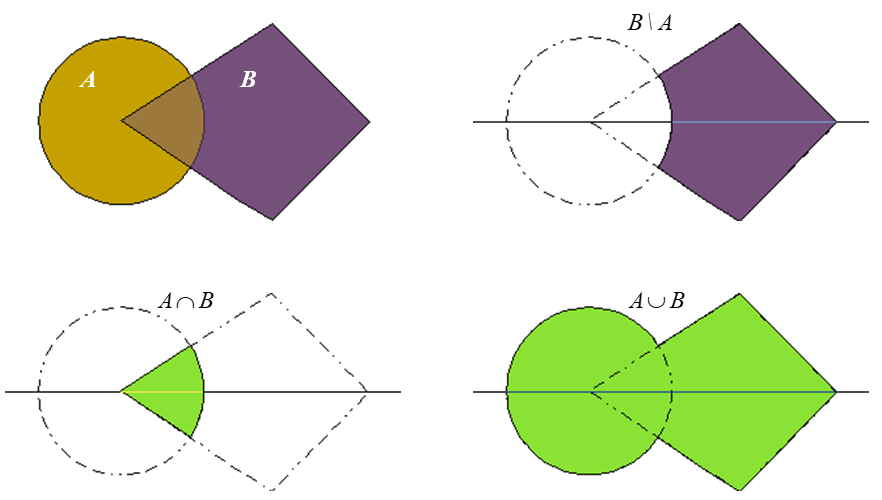
Rys.12.11. Operacje booolowskie realizowane z wykorzystaniem śledzenia promieni.
12.12. Metody przyspieszające śledzenie promieni
Barwa każdego piksela obrazu jest wyznaczana w podobny sposób przez analizę odpowiedniego drzewa przecięć. Liczba operacji z tym związanych rzutuje na czas obliczeń całości. Z drugiej strony można wskazać operacje, które pojawiają się najczęściej – są to z reguły operacje związane z szukaniem przecięcia promienia z powierzchnią obiektu. Stąd algorytmy przyspieszające metodę śledzenia próbują zredukować koszty obliczeń albo przez przyspieszenie wyznaczania przecięć, albo przez zmniejszenie nakładu pracy związanej z analizą drzewa.
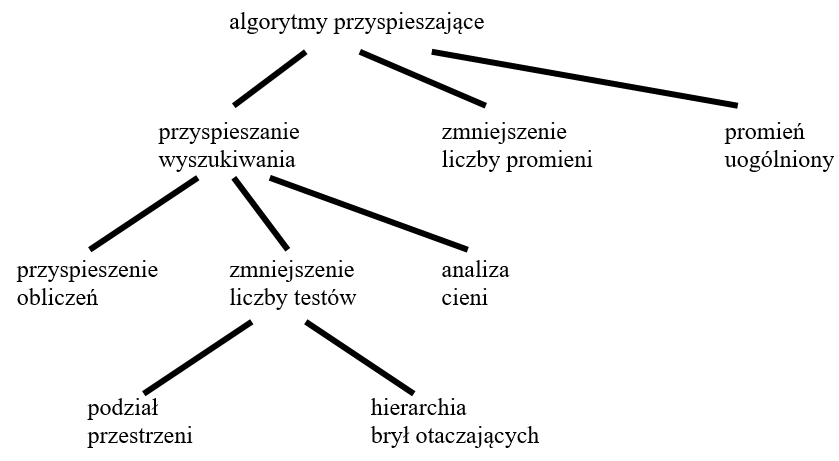
Rys.12.12. Wybrane algorytmy przyspieszania.
Zmniejszenie kosztów obliczeń przecięć promieni z powierzchniami
Metody te koncentrują się z jednej strony na operacjach numerycznych, a z drugiej na technice wyboru promieni do analizy. Stąd najczęściej wymienia się następujące grupy metod:
- Efektywne algorytmy wyznaczania przecięć.
- Właściwie dobrana parametryzacja.
- Jeśli jest to możliwe zamiana rozwiązań numerycznych na algebraiczne.
Stosowane operacje matematyczne i uproszczenia opisu mają na celu wyłącznie zmniejszenie powtarzanych obliczeń. Odbywa się to przez wyznaczenie wartości pewnych wyrażeń (wybierane są takie wyrażenia, których wartości są niezależne od równania promienia) w preprocesingu przed analizą biegu promienia. Wyniki tych obliczeń są później wykorzystywane w trakcie śledzenia promieni. Dzięki temu unika się wielokrotnego powtarzania tych samych operacji matematycznych. Oczywiście możliwość optymalizacji tą drogą wymaga dość żmudnej analizy równań powierzchni, a efektywność przyspieszenia bardzo ściśle zależy od opisu powierzchni. Nie prowadzi to natomiast do przybliżenia ani zmiany wartości obliczeń końcowych.
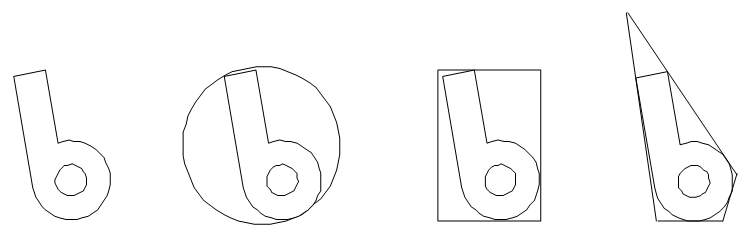
Rys.12.13. Przykłady różnych
brył otaczających. Kula daje możliwość
szybszego
wyznaczenia przecięcia ale gorzej przylega do obiektu.
Wielościan może ciasno przylegać do obiektu ale trudniej wyznaczyć przecięcie z
promieniem.
Zmniejszenie liczby testów
Stwierdzenie czy promień przecina dany obiekt jest zadaniem trudnym. Zastosowanie odpowiedniej techniki wyboru promieni, które mają szansę na przecięcie, pozwala wyeliminować zbędne przypadki, dla których nie trzeba przeprowadzać długiej i kosztownej, pełnej analizy biegu promienia.
Techniki wyboru promieni (techniki zmierzające do zmniejszenia liczby testów) można podzielić na dwie grupy: zastosowanie brył otaczających i podział przestrzeni.
Hierarchia brył otaczających
- Bryła otaczająca powinna:
- Dobrze („ciasno”) przylegać do obiektu.
- Dać możliwość szybkiego wyznaczania przecięć z promieniem.
- Najczęściej stosowane bryły otaczające to: kula, warstwa równoległa, prostopadłościan.
Zanim rozpocznie się wyznaczanie przecięcia promienia z powierzchnią obiektu, można wykorzystując hierarchię brył otaczających spróbować wyznaczyć przecięcie z bryłą otaczającą obiekt. Jeśli promień nie przecina takiej bryły, to analiza przecięcia z obiektem nie jest konieczna. Oczywiście aby w takiej sytuacji można było mówić o przyspieszeniu obliczeń powinny być spełnione dwa warunki. Bryła powinna „ściśle” (ciasno) otaczać obiekt oraz wyznaczenie przecięcia promienia z bryłą powinno być wielokrotnie prostsze (i szybsze) niż przecięcia z obiektem. Często te warunki są sprzeczne. Najczęściej stosuje się kule, wielościany lub „pasy” równoległych płaszczyzn jako bryły otaczające. Kula jest obiektem, dla której najszybciej można stwierdzić, czy jest przecięta prostą czy nie. Wystarczy znaleźć odległość prostej od środka kuli i porównać z promieniem. Jest to szybsze niż sprawdzanie przecięcia prostej z prostopadłościanem. Wadą kuli jako obiektu otaczającego jest najczęściej niezbyt ciasne obejmowanie obiektu. Warto zwrócić uwagę na przecięcia z obiektami typu AABB (ang. Axis-Aligned Bounding Box - prostopadłościan o krawędziach wyznaczonych przez proste równoległe do osi układu współrzędnych) i OBB (ang. Oriented Bounding Box - prostopadłościan dowolnie zorientowany) Aby zwiększyć efektywność działania metody można skonstruować hierarchię brył otaczających.
Podział przestrzeni
- Podział równomierny.
-
Podziała nierównomierny
- drzewo ósemkowe,
- drzewo binarne.
Niejako odwrotne podejście do problemu w stosunku do hierarchii brył otaczających stanowi podział przestrzeni. W tym przypadku całą przestrzeń sceny dzieli się na prostopadłościenne sektory. Następnie zamiast otaczać obiekt przyporządkowuje się mu odpowiedni sektor (sektory), w którym obiekt się znajduje. Dzięki temu analizując drogę promienia przez kolejne fragmenty przestrzeni można sprawnie wybrać obiekty, które w nich się znajdują. Stosuje się podział równomierny lub nierównomierny. W tym drugim przypadku jest podział hierarchiczny: drzewo ósemkowe lub binarne.
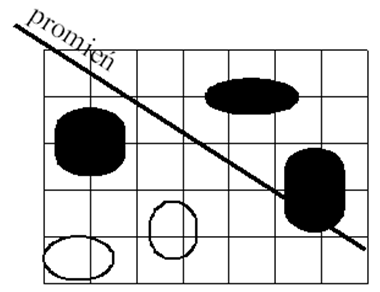
Rys.12.14. Równomierny podział przestrzeni.
Zmniejszenie liczby promieni
Wyróżnia się dwa przypadki. Zmniejszenie liczby promieni pierwotnych i/lub zmniejszenie liczby promieni wtórnych.
W pierwszym przypadku zakłada się, że barwy sąsiednich pikseli są zbliżone. Można więc przeprowadzić dokładne obliczenia dla mniejszej rozdzielczości rastra niż w rzeczywistości (np. dla co czwartego piksela), natomiast pozostałe piksele wyznaczyć dokonując interpolacji. Oczywiście warto zastosować mechanizm adaptacyjny. Przyjąć maksymalną różnicę wartości, która dopuszcza interpolację – przekroczenie jej spowoduje wyznaczenie wartości piksela po przeprowadzeniu dokładnych obliczeń, a nie w wyniku interpolacji.
W drugim przypadku dla każdego piksela zmniejsza się głębokość drzewa kolejnych przecięć lub odbić, dzięki czemu nie są brane pod uwagę kolejne promienie.
Pominięcie niektórych pikseli lub zmniejszenie rozdzielczości rastra oznacza po prostu zmniejszenie dokładności wyznaczenia rozkładu oświetlenia. Podobny problem powstanie w przypadku nadpróbkowania. Jeśli jest ono stosowane, to liczba próbek na piksel wynika z założonej dokładności obliczeń i rezygnacja nawet adaptacyjna z pewnej liczby próbek pogarsza tę dokładność. Przy wykorzystaniu metody adaptacyjnej redukcji promieni pierwotnych w typowych zastosowaniach metody śledzenia często oprócz wspomnianego warunku wartości progowej uwzględnia się kilka innych wymaganych do skorzystania z interpolacji.:
- Warunek wspólnego drzewa odbić: dopuszcza się interpolację, jeśli promienie, które mają służyć do wyznaczenia podstawy do interpolacji, mają to samo (lub podobne) drzewo przecięć.
- Warunek wspólnego obiektu: dopuszcza się interpolację, jeśli promienie pierwotne trafiają w ten sam obiekt.
- Warunek cienia/oświetlenia: dopuszcza się interpolację, gdy oba piksele mające być podstawą interpolacji, są albo oświetlone, albo w cieniu.
Metoda jest bardzo atrakcyjna obliczeniowo, jednak może pogarszać jakość końcową. Dobór właściwie zastosowanych kryteriów korzystania z interpolacji powinien zapewnić kompromis dający niewidoczne spadki jakości przy zauważalnej redukcji czasu obliczeń.
Zmniejszenie kosztów wyznaczania cieni
Metody te można podzielić na podgrupy:
- Przyspieszenie znalezienia obiektów
zasłaniających źródła światła. Wyróżnia
się
- adaptacyjne zmniejszenie głębokości drzewa promieni wtórnych po wykryciu obiektu nieprzezroczystego,
- metody statystyczne oparte na analizie gęstości obszarów.
- Zmniejszenie liczby promieni potrzebnych do analizy kształtu cienia.
Metody analizy
gęstości zakładają, że jeśli promień trafi, na drodze do źródła światła, w
obszar w którym znajduje się odpowiednio duża liczba obiektów („gęstość”
powyżej pewnego progu), to zostanie on zatrzymany i do tego źródła nie dotrze.
Można tak przyjąć z dużym prawdopodobieństwem, bez analizy przecięć z
konkretnymi obiektami z tego obszaru. Takie postępowanie czasami prowadzi do
błędów, które wprawdzie nie przeszkadzają w odbiorze filmów czy reklam, ale
mogą zafałszować obraz rozkładu oświetlenia. Problemu tego nie stwarzają metody
zmniejszające głębokość drzewa promieni wtórnych po znalezieniu obiektu
zasłaniającego źródło światła. Przy analizie oświetlenia złożonych elementów,
przy dużej liczbie obiektów i jednocześnie dużej liczbie źródeł światła
powstaną strefy cienia dające możliwość redukcji obliczeń tą metodą.
Przetwarzanie równoległe
Proces obliczeniowy dla pojedynczego piksela jest praktycznie niezależny od obliczeń związanych z sąsiednimi pikselami. Teoretycznie więc, każdy piksel mógłby być liczony przez niezależny komputer, a potem z gotowych pikseli można byłoby złożyć obraz. W praktyce bardzo rzadko zdarza się możliwość dysponowania tak dużą liczbą jednostek obliczeniowych. Można więc, podzielić obraz na dowolne fragmenty i rozdzielić je pomiędzy jednostki obliczeniowe maszyny równoległej.
Podczas produkcji filmów wykorzystuje się możliwość niezależnego, równoległego wyznaczania całych obrazów, np. kolejnych klatek filmu lub możliwość innego rozłożenia filmu na obrazu lub fragmenty do równoległej obróbki. Wymaga to oczywiście udziału wielu komputerów lub specjalizowanego sprzętu wieloprocesorowego
Promienie uogólnione
Analizowana
jest wiązka promieni w postaci stożka lub walca.
Technika ta jest stosunkowo rzadko wykorzystywana. Chociaż analiza wiązek
promieni może być zgodna z oczekiwaniem wyznaczenia kierunków, z jakich cały
obiekt jest oświetlony przez dane źródło. A zatem teoretycznie byłoby to
pomocne np. gdy na scenie znajduje się wiele przedmiotów i oświetlone są one
kilkoma źródłami światła. Jednak teoretyczne korzyści metody wiążą się niestety
z wieloma problemami pojawiającymi się w praktycznych zastosowaniach.
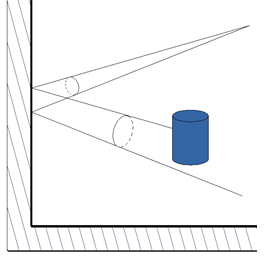
Rys.12.15. Przecięcie promienia uogólnionego z obiektem.
Rozdział 13. OŚWIETLENIE GLOBALNE: METODA BILANSU ENERGETYCZNEGO
Rozdział trzynasty jest drugą częścią materiału poświęconego zagadnieniu oświetlenia globalnego.
Przedstawiono drugą metodę rozwiązania tego zagadnienia - metodę
bilansu energetycznego. Czytelnik znajdzie opis właściwości oraz podstawowych zagadnień jakie muszę być rozwiązane w tej metodzie: informacje dotyczące współczynnika
sprzężenia i metod jego wyznaczania oraz sposobów rozwiązania równania bilansu. Zostały pokazane najważniejsze różnice między metodą śledzenia promieni a metodą energetyczną. W rozdziale tym przedstawiono także podstawowe zagadnienia grafiki nie fotorealistycznej (Non-Photorealistic Rendering – NPR).
13.1. Wprowadzenie
Transport światła odbywa się na scenie na drodze wielokrotnych odbić od poszczególnych fragmentów powierzchni. Równanie wizualizacji zaproponowane przez Kajiya w 1986 roku opisuje zależności między oświetleniem wzajemnym elementarnych fragmentów powierzchni. Pozwala to prześledzić rekurencyjnie drogę promieni. Można jednak to równanie wykorzystać inaczej: podzielić całą scenę na fragmenty elementarne oraz określić ich wzajemne relacje związane z transportem światła (w wyniku odbijania i/lub załamania). Takie podejście pozwala analizować rozchodzenie się światła na scenie, jednak jest to inna analiza niż w przypadku śledzenia promieni. Śledzenie promieni było ściśle związane z określonymi kierunkami tzn. przebiegało w taki sposób, aby uwzględnić położenie obserwatora i jego sposób obserwacji sceny (odpowiednie warunki rzutowania). Natomiast analiza oparta na wzajemnych relacjach między fragmentami elementarnymi nie uwzględnia w ogóle obserwatora. Pozwala jedynie wyznaczyć rozkład światła w wyniku wzajemnego oddziaływania. Takie uwzględnienie równania renderingu wymaga analizy „każdy z każdym” fragmentów elementarnych. Prowadzi to oczywiście do złożoności kwadratowej problemu oświetlenia globalnego.
Metoda bilansu energetycznego (ang. radiosity), rozwinęła się na bazie metody elementu skończonego (MES) oraz na doświadczeniach jej wykorzystywania w technice cieplnej do opisu emisji i odbicia promieniowania cieplnego. Metoda ta jest często nazywana po prostu metodą energetyczna.
Metoda bilansu energetycznego pojawiła się w literaturze dotyczącej grafiki komputerowej w latach 1984-1985. Wśród autorów należy wymienić Gorala, Cohena, Greenberga, Nishitę i Nakamaego.
13.2. Idea metody bilansu energetycznego
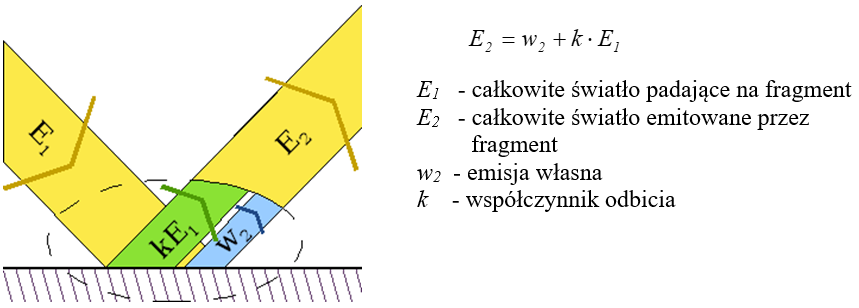
Rys.13.1. Metoda bilansu energetycznego. Założenie zachowania energii w zamkniętym środowisku.
Przyjmuje się następujące założenia:
- Elementarne fragmenty mają skończone rozmiary i są płaskie.
- Wszystkie fragmenty elementarne podlegają tym samym regułom emisji, odbicia, przenikania lub absorpcji promieniowania.
- Pojedynczy fragment odbija światło w sposób równomiernie rozproszony (zachodzi idealne; Lambertowskie odbicie rozproszone).
- Emisja i właściwości odbiciowe są stałe w ramach całego fragmentu elementarnego.
- Pomiędzy dowolną parą elementarnych fragmentów zachodzą zjawiska związane z transportem światła.
Postępowanie w metodzie energetycznej:
- Wszystkie powierzchnie zostają podzielone na dyskretne, płaskie fragmenty, o skończonych rozmiarach, z których każdy emituje i odbija światło równomiernie we wszystkich kierunkach.
-
Proces dwuetapowy
- Wyznaczyć rozkład oświetlenia na całej scenie (niezależnie od obserwatora).
- Uwzględniając obserwatora zdefiniować rzutowanie i wygenerować obraz metodą uproszczonego śledzenia promieni (ang. ray casting) .
Metoda energetyczna umożliwia przeprowadzenie przede wszystkim analizy zjawisk rozproszonych. O wiele trudniejszym do opisu jest odbicie kierunkowo-rozproszone. Natomiast założenie odbicia rozproszonego przez elementarne fragmenty praktycznie wyklucza analizę odbić kierunkowych na scenie.
Cechą charakterystyczną metody energetycznej jest fakt, że w opisach transportu nie występuje obserwator (co tak naprawdę jest zgodne z rzeczywistością – światło rozchodzi się bez względu na to czy obserwator będzie brał w tym udział czy nie). Obserwator zostaje uwzględniony dopiero w fazie wizualizacji. Oznacza to, że do przeprowadzenia generacji obrazu metodą bilansu energetycznego i tak na końcu trzeba uruchomić metodę śledzenia promieni w najprostszej postaci (ray casting).
Równanie bilansu energetycznego
Dla i-tego fragmentu sceny
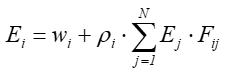
gdzie:
wi – emisja własna (natężenie oświetlenia) fragmentu i ,
ri – współczynnik odbicia fragmentu i ,
Fij – współczynnik sprzężenia optycznego pomiędzy fragmentami i oraz j .
A zatem uwzględniając zależności między wszystkimi fragmentami sceny powstaje układ N równań liniowych, których rozwiązanie pozwala wyznaczyć natężenia oświetlenia dla każdego fragmentu.
W tak przedstawionym układzie równań suma współczynników (Form Factors) wzdłuż wierszy nie przekracza 1 - powstaje macierz z dominującą przekątną. Prosta iteracja typu Gauss-Seidel daje gwarancję szybkiej zbieżności w poszukiwaniu rozwiązania.
Każda powierzchnia elementarna odbija i emituje światło równomiernie we wszystkich kierunkach. Równanie bilansu energetycznego jest więc równaniem bezkierunkowym. Współczynniki odbicia danego fragmentu również są wielkościami bezkierunkowymi i określają tylko odpowiednie proporcje. Współczynnik sprzężenia optycznego uwzględnia kształty i relatywne orientacje powierzchni. Dodatkowo należy uwzględnić długości fali. emitowanej w ramach emisji własnej powierzchni oraz fakt, że współczynnik odbicia może być również zależny od długości fali.
W praktyce najczęściej prowadzi się obliczenia dla poszczególnych składowych R,G,B.
13.3. Współczynnik sprzężenia
Współczynnik sprzężenia można
wyznaczyć na podstawie cząstkowych współczynników dla powierzchni
elementarnych:
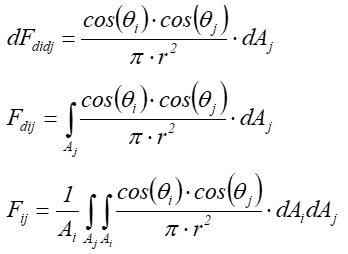
Współczynnik sprzężenia optycznego jest większy od zera jeśli powierzchnie „widzą się”, lub jest zerem gdy powierzchnie „nie widzą się”.
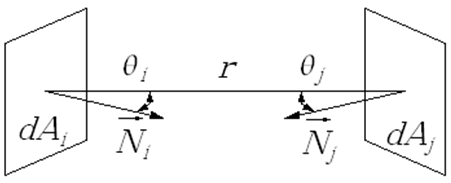
Rys.13.2. Wyznaczanie współczynnika sprzężenia optycznego.
Dla dowolnych powierzchni Ai oraz Aj
![]()
czyli
![]()
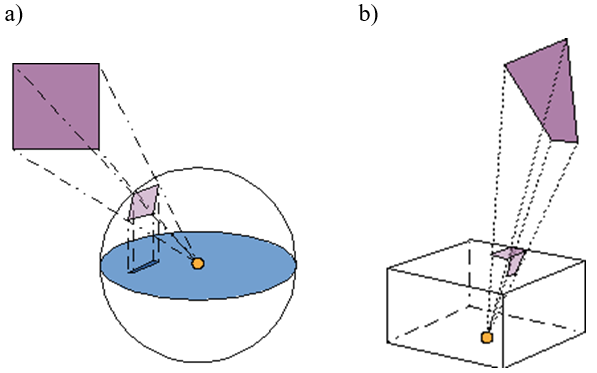
Rys.13.3.
Wyznaczanie współczynnika sprzężenia optycznego. a) Rzut na półsferę – metoda
Nusselta.
b) Rzut na półsześcian – metoda Cohena i Greenberga.
Współczynnik sprzężenia nie jest zależny od obserwatora, jest zależny natomiast od właściwości powierzchni obiektów i ich wzajemnego ustawienia. Powinien być wyznaczony dla każdej pary powierzchni przed przystąpieniem do rozwiązywania układu równań bilansu energetycznego.
Zależności geometryczne współczynnika sprzężenia można
opisać rzutując jeden z płatów na drugi.
Pośrednio jako:
Rzut obrazu ze sfery na powierzchnię drugiego płata.
W praktyce współczynnik sprzężenia bardzo rzadko jest liczony analitycznie.
Nusselt zauważył, że jeśli element i zostanie otoczony półsferą i dokonamy rzutu elementu j na tę półsferę, to z punktu widzenia oddziaływania w postaci współczynnika sprzężenia, obiekt j oraz jego rzut są równoważne. To znaczy, że obiekty mające taki sam rzut na półsferę maja takie same współczynniki sprzężenia.
Jeśli półsfera byłaby otoczona półsześcianem, to rzut na półsześcian tego samego obiektu byłby równoważny jego rzutowi na półsferę. Metodę opartą na tym spostrzeżeniu zaproponowali Cohen i Greenberg w 1985 roku.
W praktyce rzut na półsześcian okazał się najefektywniejszy obliczeniowo. Półsześcian dzieli się na powierzchnie elementarne (prostokątne „piksele”) i wyznacza współczynnik sprzężenia na podstawie rzutu obiektu na mapę pikseli półsześcianu.
13.4. Rozwiązanie równania bilansu energetycznego
Po opisaniu równaniem bilansu zależności między wszystkimi parami powierzchni elementarnych sceny uzyskuje się układ równań. Wszystkie równania są równaniami liniowymi identycznej postaci. Ze względu na dużą ich liczbę (setki tysięcy, miliony) rozwiązywanie w sposób tradycyjny nie ma sensu.
Układ równań bilansu energetycznego jest rozwiązywany w postaci iteracyjnej. Pierwsze przybliżenie zakłada istnienie niezerowych wartości oświetlenia tylko tych elementów, które wykazują emisję własną (powierzchnie opisujące źródła światła). Na tej podstawie wyznacza się pierwsze przybliżenie wartości oświetlenia, na jego podstawie kolejne itd.
Czyli dla
pierwszej iteracji oświetlenie ![]() można wyznaczyć jako:
można wyznaczyć jako:
![]()
W każdej
następnej iteracji liczona jest poprawka, tzn. oświetlenie ![]() w k+1 iteracji jest liczone na
podstawie oświetlenia
w k+1 iteracji jest liczone na
podstawie oświetlenia ![]() z iteracji k .
z iteracji k .
![]()
Iteracje należy powtarzać aż do osiągnięcia oczekiwanej zmiany barw.
Cohen i Greenberg zaproponowali w 1985 roku stosowanie metody Gaussa-Seidela do iteracyjnego rozwiązywania układu równań bilansu energetycznego, aby szybciej osiągnąć zadany poziom rozwiązania.
13.5. Siatka podziału na fragmenty
W metodzie energetycznej cała scena (wszystkie obiekty) musi zostać podzielona na fragmenty elementarne. Stosuje się podział równomierny lub adaptacyjny. W ten sposób uzyskuje się siatkę fragmentów pokrywającą całą scenę. Stosuje się różne rodzaje siatek, najprostszymi i najczęściej najefektywniejszymi są siatki trójkątne lub czworokątne.
- Siatka równomierna.
Istotnym problemem jest dobór rozmiaru siatki.- Jeśli jest zbyt rzadka – pojawiają się widoczne różnice barw nieodpowiadające rzeczywistym zmianom barw.
- Jeśli jest zbyt gęsta – czas realizacji jest zbyt długi.
-
Siatka adaptacyjna.
Podział na mniejsze elementy jeżeli występują duże lokalne zmiany luminancji lub barwy.
Ponieważ jakość uzyskanego obrazu zależy bardzo silnie od liczby powierzchni elementarnych (i tym samym od ich wielkości), to najlepiej byłoby prowadzić obliczenia dla możliwie dużej liczby powierzchni. Jednak ze względu na kwadratową złożoność obliczeniową takiego zadania trudno uzyskać dobre efekty w rozsądnym czasie. Cohen w 1986 roku zaproponował metodę adaptacyjną podziału powierzchni zależną od gradientu oświetlenia. Proces obliczeniowy rozpoczyna się od zadanego (najczęściej przez użytkownika) poziomu podziału. Następnie prowadzi się obliczenia iteracyjne uwzględniając podział powierzchni w obszarach o dużym gradiencie oświetlenia. Tak realizowany algorytm zapewnia możliwość uzyskania oczekiwanej dokładności (osiągnięcia założonych różnic między podziałami) bez potrzeby prowadzenia obliczeń z dużą dokładnością na całej scenie.
Symulacje
oświetlenia pokoju przedstawione na rysunku 13.4. zostały zrealizowane metodą
bilansu energetycznego. Przyjęto różne warianty podziału sceny na fragmenty
elementarne. Górny rząd jest to podział równomierny. Dolny rząd podział
adaptacyjny. Lewa kolumna – podział na większe elementy. Prawa kolumna – podział
na mniejsze elementy. Widać różnice w wyznaczeniu barw dla różnych schematów
podziału. Podział gęsty równomierny, co prawda prosty realizacyjnie, ale nie
zapewnia możliwości uzyskania szczegółów chociaż jak widać dla wielu
powierzchni podział ten jest już zbyt gęsty (nie uzyskuje się różnic w stosunku
do rysunku z podziałem bardzo rzadkim). Szczegóły
pojawiają się dopiero przy podziale adaptacyjnym.

Rys.13.4.
Symulacja oświetlenia pokoju wykonana metodą bilansu energetycznego
dla różnych siatek
podziału powierzchni. Górny rząd podział równomierny,
dolny – adaptacyjny. Z
lewej siatka rzadka, z prawej gęsta.
Opracowanie rysunków
Krzysztof Wandachowicz ©, publikowane za zgodą autora.
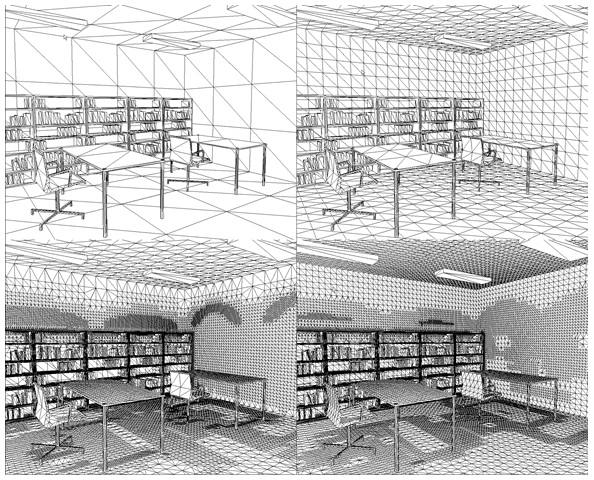
Rys.13.5.
Siatki podziału dla symulacji z rysunku 13.4.
Opracowanie rysunków
Krzysztof Wandachowicz ©, publikowane za zgodą autora.
Warto zwrócić uwagę na odbiór całego obrazu. Brak realności jest cechą, którą można przypisać rysunkowi 13.4 a). Ale nie dlatego że jest ewidentny brak szczegółów oświetlenia na ścianach, ale dlatego, że brak szczegółów cienia przy nogach stołów sprawia, że mamy wrażenie jakby meble wisiały w powietrzu. W wielu sytuacjach generowania realistycznych obrazów w grafice warto zwrócić uwagę na szczegóły, które decydują o odbiorze rysunku. I bardzo często są to drobiazgi niezwiązane bezpośrednio z najtrudniejszymi i najbardziej pracochłonnymi zadaniami.
13.6. Śledzenie promieni a metoda energetyczne - porównanie metod
Porównując metody realizacji oświetlenia globalnego można zauważyć pewne cechy charakterystyczne:
- Radiosity:
- Praca w przestrzeni obiektu (bez obserwatora !)
- Tylko odbicia rozproszone (kierunkowe zbyt drogie obliczeniowo)
- Niezależne od obserwatora i kamery (rzutowania).
-
Klasyczny (zaawansowany) RT:
- Praca w przestrzeni rzutu (z obserwatorem)
- Tylko odbicia kierunkowe (kierunkowe w ramach ścieżki).
- Zależne od obserwatora i kamery (rzutowania).
Paul Heckbert w swoim artykule na konferencji SIGGRAPH’ 90 zaproponował notację opisu transportu światła (przechodzenia pomiędzy kolejnymi odbiciami).
- Końcami pojedynczej ścieżki lub elementami pośrednimi
mogą być:
- L : źródło światła (light source)
- E : obserwator/kamera (the eye)
- S : odbicie kierunkowe (specular reflection)
- D: odbicie rozproszone (diffuse reflection)
- G: odbicie połysku (semi-diffuse (glossy) reflection)
-
Używa się wyrażeń regularnych:
- (K)+ : jeden lub więcej zdarzeń/elementów K
- (K)* : zero lub więcej K
- (K)? : zero lub jeden K (czasem notacja: K0..1)
- (K | M) : K lub M
W tym kontekście metoda energetyczna realizuje ścieżkę L(D)*E. W praktyce oznacza to znakomite odbicia rozproszone i całkowite ignorowanie odbicia kierunkowego. Śledzenie promieni w wersji klasycznej opisuje ścieżkę L(S)*E. Natomiast dodanie nowych technik śledzenia rozszerza jego możliwości praktycznie do L(S|D)*E. Często mówi się o śledzeniu, że pozwala opisać znakomite odbicia kierunkowe i aproksymowane odbicia rozproszone. Oznacza to, że praktycznie dowolne zależności odbiciowe mogą być realizowane metodą śledzenia promieni. Oczywiście otwartą sprawą pozostaje efektywność takiej realizacji. Jednak faktem pozostaje rozwój metody śledzenia i jej możliwości adaptacyjne.
Natomiast mimo wieloletniego rozwoju metoda energetyczna nie zyskała nowych technik zmieniających możliwości realizacyjne. Pozostała metodą hermetyczną ograniczoną do jednego rodzaju transportu światła.
Z drugiej strony natomiast w obu przypadkach, zarówno w przypadku śledzenia promieni jak i metody energetycznej nastąpił bardzo silny rozwój algorytmów związanych z realizacją zadania. Algorytmów, które decydują o czasie realizacji i które pozwoliły znacznie skrócić potrzebne obliczenia. Jednocześnie w ostatnich latach (początek XXI wieku) można zaobserwować bardzo szybki rozwój sprzętu komputerowego, w szczególności kart graficznych wykorzystujących specjalizowane, wielordzeniowe procesory. Połączenie wyrafinowanych algorytmów i zaawansowanego sprzętu daje możliwość realizacji wybranych zadań oświetlenia globalnego w czasie rzeczywistym, co jeszcze niedawno wydawało się całkowicie nierealne.
13.7. Metody hybrydowe
Fakt, że metoda śledzenia promieni i metoda energetyczna inaczej analizują odbijanie (i załamanie) światła przez powierzchnie można traktować jako wzajemne uzupełnianie się. Stąd naturalne wydawałoby się łączenie metod na zasadzie łączenia wyników obliczeń: odbicie rozproszone pochodzące z metody energetycznej natomiast odbicie kierunkowe z metody śledzenia. Oczywiście takie połączenie jest bardzo trudne do realizacji. Stosowane są implementacje hybrydowe, w których obliczenia prowadzone są w sposób niejako równoległy obydwoma metodami. Najpierw uzyskiwane są wyniki częściowe np. metodą energetyczną. Następnie w zależności od przyjętej strategii można rysunek poprawić uzupełniając o szczegóły związane z odbiciem kierunkowym stosując metodę śledzenia promieni i wykorzystując częściowo policzone rozkłady oświetlenia.
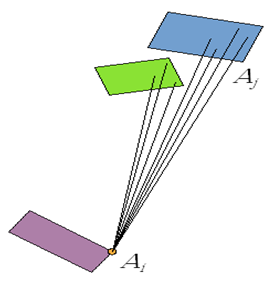
Rys.13.6. Próbkowanie
fragmentów elementarnych z wykorzystaniem śledzenia
promieni
w celu wyznaczenia współczynnika sprzężenia.
Bardzo użyteczne jest zastosowanie jednej metody w wybranym problemie realizowanym drugą metodą. Dobrym przykładem jest wyznaczenie współczynnika sprzężenia z wykorzystaniem śledzenia promieni. Śledzenie pozwala obliczyć całkę metodą Monte Carlo dla określonego punktu powierzchni – rysunek 13.6.
13.8. Grafika nierealistyczna
Metody i algorytmy prezentowane w tym i poprzednich rozdziałach były opracowywane w celu jak najwierniejszego oddania fizycznych właściwości opisujących rozchodzenie się światła. Taki cel przyświecał opracowywaniu kolejnych modeli odbicia światła, algorytmów opisu oświetlenia globalnego. Porównania metody śledzenia promieni i metody energetycznej uwzględniają, przede wszystkim, ich wierność oddania barw w stosunku do widoku rzeczywistych obiektów. Do tego wierność geometrii zapewniona regułom odpowiedniego rzutowania. Porównujemy te efekty do wrażeń związanych z obserwacją rzeczywistości – wrażeń wzrokowych. A także do wrażeń związanych z odbiorem fotografii – niedoskonałej przecież. Warto jednak pamiętać, że grafika realistyczna to tylko jeden z nurtów rozwoju grafiki komputerowej. Co prawda rzeczywiście liczne zastosowania sprawiają, że grafika realistyczna jest chyba najważniejszą i najszybciej rozwijającą się częścią grafiki. Jednak nie zawsze potrzebne są obrazy realistyczne. Często ważniejsze są obrazy symboliczne, uproszczone i schematyczne. Oprogramowanie pozwalające kreować takie obrazy jest stosowane do ilustracji książek, prezentacji czy instrukcji obsługi. W ten sposób rozwinęła się technika zwana grafiką (lub renderingiem) nierealistycznym (Non-Photorealistic Rendering – NPR). Formalnie można próbować podzielić NPR na różne obszary zastosowań:
- Wizualizacje danych, a więc wykresy 2D i 3D w różnych formach. Tego typu rysunki mogą być generowane np. programami obliczeniowymi i arkuszami kalkulacyjnymi.
- Rysunki dokumentujące rozwiązania techniczne na potrzeby określonej technologii lub np. pokazujące działanie urządzeń. Proste symulacje wybranych funkcji urządzeń lub nawet zdarzeń rzeczywistych. Także instrukcje obsługi.
- Rysunki ilustracyjne na potrzeby reklamy lub wykorzystania w dowolnych mediach. Ilustracje w książkach i czasopismach. Czasami wyróżnia się w tej kategorii ilustracje do książek dla dzieci, gdyż zwraca się szczególną uwagę na ich jakość.
- Elementy systemów komunikacji człowiek – komputer. Od pojedynczych ikon do całej „zabudowy” graficznej okien. Tworzeniu tych rysunków towarzyszy specyficzne podejście: realistyczność nie tylko nie jest konieczna ale wręcz unikana. Najważniejsza jest jednoznaczność interpretacji pozwalająca przyspieszyć komunikację.
- Animacja pseudo tradycyjna. Kiedy twórcy celowo posługują się określonym poziomem umowności lub symboliki. Współczesne filmy animowane często nawiązują stylem do produktów największych twórców animacji z początków kina. Oczywiście wykorzystując grafikę komputerową a nie tradycyjne malowanie na celuloidzie.
- Sztuka. Twórca posługując się grafiką komputerową może uzyskać efekty jakie daje określona technika. Obrazy (także w postaci odpowiednich rzutów świata trójwymiarowego) zgodnie z wyobrażeniami dowolnego stylu ilustracyjnego (malarstwo, szkic, rysunek ołówkiem, akwaforta, litografia, itp. itd.). Znane są przykłady programów umożliwiających przetworzenie np. zdjęcia na obraz wykonany określoną techniką (np. olej lub akwarela) lub też na obraz namalowany w określonym stylu (np. impresjonizm).

Rys.13.7. Przykłady
grafiki nierealistycznej (Non-Photorealistic Rendering – NPR)
wszystkie rysunki są udostępniane w domenie publicznej wikimedia i wikipedia
na licencji Creative Commons
Z drugiej strony można zastanawiać się nad rozwojem różnych technik grafiki komputerowej. Grafika typu NPR wymusiła określone metody renderowania. Wydaje się że najciekawszymi przykładami są dwie techniki cieniowania, niestosowane w renderowaniu realistycznym:
Cieniowanie kwantyzowane (cel shading lub toon shading) [7]. W cieniowaniu tym wykorzystywany jest standardowy model obiektu 3D dla którego wyznacza się barwy elementów (docelowo poszczególnych pikseli rysunku) zgodnie z przyjętym modelem odbicia światła. Jednak w końcowej fazie definiowania barwy stosuje się bardzo mały zbiór różnych dostępnych barw. Barwy zostają skwantyzowane. Daje to efekt bardzo podobny do uproszczonego ręcznego rysowania obiektów 3D. Nazwa cel shading pochodzi od arkuszy celuloidu stosowanych do przygotowywania obrazów w tradycyjnej animacji. Arkusze takie potocznie nazywane były cel.
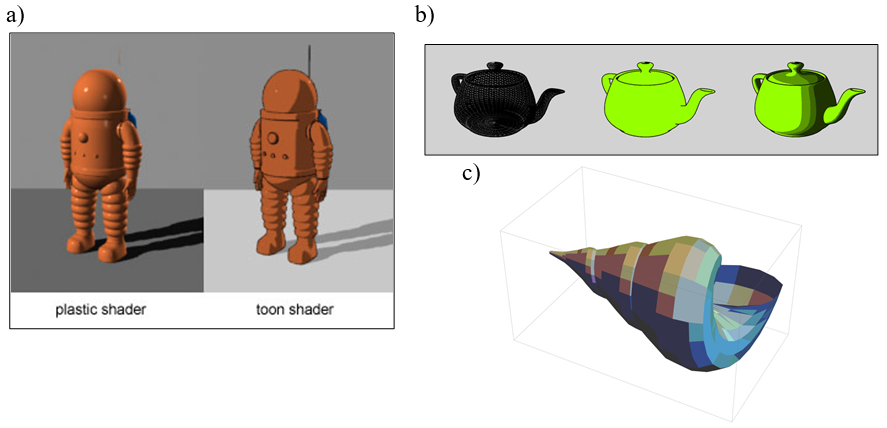
Rys.13.8. a) Porównanie grafiki
realistycznej (powierzchnia plastikowa)
i cieniowania kwantyzowanego (cel shading),
b) Przykład cieniowania kwantyzowanego, c)
przykład cieniowania Goocha.
wszystkie rysunki są udostępniane w domenie publicznej wikimedia i wikipedia
na licencji Creative Commons.
Książki [5,6] są w całości poświęcone technice Non-Photorealistic Rendering. Dobry przegląd technik i narzędzi programistycznych stosowanych w NPR można znaleźć w artykule [9]. Jest to również publikacja, w której autorzy na wielu przykładach pokazali rozwój NPR jako działu grafiki komputerowej od początku tej techniki (lata sześćdziesiąte ubiegłego stulecia) do czasów współczesnych.