Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 1. Wprowadzenie |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | środa, 31 grudnia 2025, 20:20 |
Opis
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
1. Wskaźniki, tablice i listy dynamiczne
W trakcie nauki programowania na początku przedstawiane są typu zmiennych jakiego typu mogą być zmienne w języku C++. Teraz poruszymy zagadnienia związane z zapisem zmiennych w pamięci oraz przedstawimy typy ze względu na miejsce zapisu oraz ich zasięg w aplikacji. W języku C++ zmienne są przechowywane w różnych segmentach pamięci, w zależności od ich typu, czasu życia i sposobu alokacji. Ogólnie, pamięć procesu można podzielić na kilka segmentów:- Stos (ang. stack) - przechowuje zmienne lokalne (automatyczne, bez static), wskaźniki oraz informacje o wywołaniach funkcji (stos wywołań).
- Sterta (ang. heap) - przechowuje zmienne dynamiczne alokowane przez operator
new. - Segment danych statycznych (ang. data segment) - podzielony jest na dwie części:
- Zainicjalizowane zmienne statyczne (ang. Initialized Data Segment) - przechowuje zmienne globalne i statyczne, które są zainicjalizowane przed uruchomieniem aplikacji.
- Niezainicjalizowane dane statyczne (ang. Block Started by Symbol - BSS) - przechowuje zmienne globalne i statyczne, które nie zostały jawnie zainicjalizowane.
- Segment kodu (ang. Text Segment) - przechowuje kod wykonywalny programu (instrukcje maszynowe).
Sterta rośnie w górę, a pamięć jest przydzielana i zwalniana dynamicznie. Jeżeli sterta zostanie w pełni zapełniona, próba alokacji pamięci może spowodować błąd (brak dostępnej pamięci). Stos natomiast rośnie w dół, zmniejszając adresy pamięci. Przy każdym wywołaniu na stosie zapisywane są lokalne zmienne i adres powrotu. Przepełnienie stosu może wystąpić w przypadku głębokiej rekurencji lub alokacji dużych zmiennych lokalnych.
Znajomość tego schematu pamięci jest kluczowa przy programowaniu w C++, zwłaszcza jeśli chodzi o zarządzanie dynamiczną pamięcią, optymalizację programu oraz unikanie błędów, takich jak wycieki pamięci lub przepełnienie stosu.W języku C++ istnieje możliwość podziału zmiennych uwzględniając różne kryteria klasyfikacji, takie jak np. zasięg, czas życia lub sposób alokacji pamięci.
Ze względu na zasięg możemy podzielić zmienne na:
- Zmienne globalne - są one deklarowane poza funkcjami lub klasami. Są widoczne w całym pliku źródłowym i mogą być widoczne w innych plikach, jeżeli nie są zadeklarowane jako static.
- Zmienne lokalne - są deklarowane wewnątrz funkcji, bloków kodu lub metod. Dostępne są jedynie w zakresie danego bloku lub funkcji w której zostały zadeklarowane.
- Zmienne statyczne globalne - są deklarowane poza funkcjami z użyciem słowa kluczowego static. Inicjalizowane są na początku programu i istnieją przez cały czas jego działania, ale mają ograniczony zasięg do pliku, w którym zostały zadeklarowane.
- Zmienne statyczne lokalne - są deklarowane wewnątrz funkcji lub metod z użyciem słowa kluczowego static. Widoczne są tylko w funkcji, w której były zadeklarowane ale ich czas życia jest taki sam jak czas trwania programu. Ich wartość nie jest resetowana przy kolejnych wywołaniach funkcji.
- Zmienne automatyczne - są deklarowane wewnątrz funkcji lub bloku (bez słowa kluczowego static). Alokowane są na stosie i zwalniane automatycznie po zakończeniu działania bloku/funkcji.
- Zmienne statyczne - pamięć na tego typu zmienne przydzielana jest na początku działania programu oraz zwalniana po jego zakończeniu. Mogą być zadeklarowane jako globalne (statyczna globalna) lub lokalnie w funkcji, gdzie zachowują wartość między wywołaniami funkcji.
- Zmienne dynamiczne - tworzone są w trakcie działania programu przez dynamiczną alokacje pamięci (na stercie) np. za pomocą operatora
new. Ich czas życia zależy od tego, kiedy są jawnie zwlaniane przez programistę np. za pomocą operatordelete.
Możemy także podzielić zmienne ze względu na miejsce alokacji pamięci:
- Zmienne na stosie (ang. stack) - dotyczy zmiennych automatycznych. Pamięć jest przydzielana automatycznie gdy zmienna jest deklarowana i zwalniana gdy zmienna wychodzi z zakresu.
- Zmienne na stercie (ang. heap) - dotyczy zmiennych dynamicznych alokowanych za pomocą operatora
new. Pamięć musi zostać zwolniona przez programistę. - Zmienne w sekcji danych statycznych (ang. static data segment) - dotyczy zmiennych globalnych oraz statycznych. Pamięć jest przydzielana na poczatku programu i zwlaniana po jego zakończeniu.
W wiekszości zastosowań praktycznych istnieje potrzeba deklarowania zmiennych w trakcie działania aplikacji tzn. zmiennych dynamicznych.
Po co więc stosujemy zmienne dynamiczne:
- umożliwiają tworzenie bardzo dużych tablic,
- umożliwiają tworzenie struktur dynamicznych o nie znanej z góry wielkości (listy dynamiczne, drzewa),
- można je w każdej chwili podczas działania programu usunąć z pamięci i na zwolnionym miejscu utworzyć nową zmienną dynamiczną - w tym samym lub innym programie. Ułatwiają więc równoległą pracę wielu programów w systemie operacyjnym.
Do zmiennych dynamicznych mamy dostęp przez ich adres, nazwany wskaźnikiem. Adres w C++ to lokalizacja (numer) w pamięci, gdzie przechowywana jest określona wartość lub obiekt. Każda zmienna w programie ma swój adres, który wskazuje, gdzie w pamięci została przechowana.
1.1. Wskaźnik
Każda komórka pamięci ma swój unikalny adres, który jest liczbą całkowitą (zwykle w systemie szesnastkowym, np. 0x7FFEEB1A2C). Adres jest używany przez procesor do lokalizowania i manipulowania danymi.
- Jednostka pamięci: Najczęściej jest to jeden bajt, który jest najmniejszym adresowalnym blokiem pamięci.
- Adres bazowy: Pierwszy bajt każdej zmiennej (lub bloku pamięci) ma swój adres bazowy.
- Słowo pamięci: W zależności od architektury (np. 32-bit, 64-bit), procesor może przetwarzać dane w jednostkach większych niż bajt.
Do danych w pamięci możemy odwoływać się nie tylko przez zwykłe nazwy, ale również przez adresy (wskaźniki) do nich.
Wskaźnik wskazujący jakąś daną w pamięci ilustruje się zwykle następująco:
Zmienna wsk wskazuje na miejsce w pamięci gdzie znajduje się zadeklarowana zmienna. Nazwy wskaźników podobnie jak nazwy zmiennych mogą być dowolne (bez znaków specjalnych).
typ_zmiennej wskazywanej *nazwa_wskaźnika;
Jeżeli chcemy utworzyć zmienną dynamiczna oraz zapamiętać adres do tej zmiennej w pamięci możemy to zrobić w następujący sposób:
int* wsk = new int;
new int tworzy zmienną dynamiczną w pamięci. Adres zmiennej jest zapisywany we wskaźniku wsk. Możliwe jest wyświetlenie adresu zmiennej. Po wykonaniu następujacego kodu:
cout << wsk;
*).
*wsk = 20;
cout << *wsk; // Wyświetlona zostanie wartość 20
delete.
delete wsk;
int* wsk = new int;
*wsk = 10;
delete wsk;
cout << *wsk; // Błąd
NULL.
int* wsk = NULL; // Wskaźnik pusty
NULL np. po usunięciu zmiennej wskazywanej.
delete nie jest automatycznie zerowany wskaźnik. Wskazuje dalej w to samo pamięci.
int *wsk1, *wsk2, *wsk3; // tak deklarujemy kilka wskaźników int *wsk1, wsk2, wsk3; // a tu wskaźnikiem jest tylko wsk1, zaś wsk2 i wsk3 to zwykłe zmienne typu int
1.2. Tablice dynamiczne
Na kursie Programowania dowiedzieliście się w jaki sposób zadeklarować tablicę. Były to jednak tablice statyczne, których rozmiar musiał być określony na etapie kompilacji aplikacji. Możliwa więc była deklaracja tablicy w następujący sposób:
const int n=10;
int tab[n];
int n;
cin >> n;
int tab[n]; // TAK NIE WOLNO !!! taki zapis oznacza tablicę statyczną
n jest ustalane dopiero podczas działania programu (ang. runtime).
Tablice statyczne w C++ są przechowywane w strefie stosu (stack) i ich rozmiar musi być stały, ponieważ kompilator musi wiedzieć z góry, ile miejsca zarezerwować. Rozmiar zmiennej n jest ustalany dopiero w trakcie działania programu (np. na podstawie wejścia użytkownika), dlatego kompilator nie może tego obsłużyć.Dlaczego ten zapis działa w GCC lub Clang jako rozszerzenie? W niektórych kompilatorach, takich jak GCC i Clang, podany zapis może działać dzięki obsłudze Variable Length Arrays (VLA), które są nieformalnym rozszerzeniem języka. Jednak:
- Nie jest to zgodne ze standardem C++,
- Kod nie jest przenośny – kod może nie działać na innych kompilatorach (np. MSVC),
- Należy tego unikać, ponieważ korzystanie z VLA może prowadzić do nieprzewidywalnego zachowania.
int n;
cout << "Podaj rozmiar tablicy" << endl;
cin >> n;
int* tab = new int[n];
for (int i=0;i<n;i++){
cin >> tab[i]; // Wczytywanie danych do tablicy dynamicznej o rozmiarze n
}
delete []tab;
[].zmienna_wskaźnikowa = new nazwa_typu_elementów[rozmiar];
Tablicę jednowymiarową usuwamy zaś z pamięci za pomocą operatora delete wywoływanego następująco:
delete [] zmienna_wskaźnikowa;
[] po słowie kluczowym delete. Dzięki temu usunięte zostaną wszystkie elementy tablicy dynamicznej. Wywołanie operatora bez nawiasów spowoduje usunięcie jedynie pierwszego elementu tablicy. We wskaźniku w przypadku tablicy przechowywany jest adres pierwszego elementu tablicy.Tablica jest przechowywana w sposób ciągły. Każdy kolejny element znajduje się zaraz za poprzednim. Tablica
int tab[5] zawiera 5 elementów. Typ int zajmuje 4 bajty (zależy od architektury, ale na większości współczesnych systemów jest to prawdziwe). Adres początkowy tablicy to 0x1000. tab[0] ma adres 0x1000, a wartość 10. tab[1] ma adres 0x1004 (0x1000 + 1 * 4), a wartość 20.Jeśli
int* ptr = tab;, to:ptrwskazuje na0x1000(adrestab[0]),ptr + 1wskazuje na0x1004(adrestab[1]).
Dodanie wartości 1 do adresu T oznacza powiększenie adresu o rozmiar elementu pamiętanego w tablicy, czyli wyznaczenie adresu elementu następnego w tablicy - wiemy przecież, że są one poukładane za sobą w spójnym obszarze pamięci.
Mozliwe jest także deklarowanie tablic dynamicznych z większą liczbą wymiarów. Poniżej przedsatwiono kod aplikacji, który umożliwia deklarację tablicy dwuwymiarowej dynamicznej.
int w,k;
cout << "Podaj rozmiar tablicy w i k" << endl;
cin >> w >> k;
// Deklaracja tablicy dwuwymiarowej w x k
int** tab = new int*[w];
for (int i=0;i<w;i++){
tab[i]=new int[k]
}
// Odwołanie do elementów tablicy - wczytywanie danych
for (int i=0;i<w;i++){
for (int i=0;i<k;i++){
cin >> tab[i][j];
}
}
// Usuwanie tablicy w x k
for (int i=0;i<w;i++){
delete []tab[i];
}
delete []tab;
int** tab). Następnie, dla każdego wiersza (pierwszy wymiar), alokujemy pamięć na poszczególne elementy (drugi wymiar). Odwołanie do poszczególnych elementów tablicy możemy zademonstrować na rysunku.Oczywiście możliwe jest także odwołanie do poszczególnych elementów za pomoca indeksów. Aby zwolnić pamięć, musimy wykonać
delete[] dla każdego wiersza (alokowanego za pomocą new int[k]), a potem usunąć samą tablicę wskaźników (delete[] tab). Dotychczasowa wiedza to jedynie podstawy operowania wskaźnikami. Wskaźniki oraz bezpośredni dostęp do pamięci w języku C++ oferują ogromne możliwości i znajdują szerokie zastosowanie. Przedstawiliśmy ich użycie na przykładzie tablic, lecz ponieważ nasz materiał nie obejmuje pełnego kursu C++, temat ten pozostawiamy na tym etapie. W kolejnym rozdziale poruszymy zagadnienia związane z jedną z podstawowych struktur danych jakim jest lista jednokierunkowa.1.3. Listy dynamiczne
W poprzednich częściach podręcznika wyjaśniliśmy pojęcie wskaźnika oraz w jaki sposób wykorzystać zmienne dynamiczne do deklaracji tablic dynamicznych, czyli podstawowych struktur danych dynamicznych. Stosowanie dynamicznych tablic umożliwia dostosowanie ich rozmiaru do potrzeb w trakcie działania aplikacji. Możemy deklarować tablice o rozmiarze podanym przez użytkownika. Co zrobić jednak w przypadku, gdy w trakcie działania aplikacji istnieje potrzeba zwiększenia rozmiaru zadeklarowanej już tablicy dynamicznej? W języku C++ tablica dynamiczna, której rozmiar został ustalony podczas alokacji pamięci, nie może być bezpośrednio powiększona. Jednak możliwe jest osiągnięcie efektu zwiększenia jej rozmiaru poprzez utworzenie nowej tablicy o większym rozmiarze, skopiowanie istniejących elementów, a następnie zwolnienie pamięci zajmowanej przez starą tablicę. Możemy przedstawić opisaną sytuację na prostym przykładzie.Możemy zaobserwować, że nie mamy możliwości zwiększenia rozmiaru zadeklarowanej tablicy dynamicznej. Należy zadeklarować tablice o jeden większą niż poprzednio zadeklarowana oraz przepisać do niej wszystkie elementy. Oczywiście im więcej jest elementów w tablicy, tym więcej czasu będzie potrzebne na wykonanie takiej operacji. Istnieje więc potrzeba deklarowania struktur danych, które umożliwią swobodne zwiększanie rozmiaru przechowywanych elementów i jednocześnie nie powodując zwiększenia narzutu czasowego na wykonanie takiej operacji. W tym celu powstały listy dynamiczne. W porównaniu do tablic dynamicznych, listy dynamiczne pozwalają na łatwe dodawanie i usuwanie elementów w dowolnym miejscu, bez konieczności kopiowania pozostałych danych. Istnieje wiele różnych implementacji list dynamicznych m.in.:
- Lista dynamiczna jednokierunkowa (ang. Single Linked List).
- Lista dynamiczna dwukierunkowa (ang. Double Linked List).
- Lista dynamiczna cykliczna (ang. Circular Linked List).
2. Listy jednokierunkowe
Po lekturze poprzedniego rozdziału powinniście mieć już solidną wiedzę na temat wskaźników oraz zrozumienie przyczyn, dla których w niektórych sytuacjach bardziej efektywne i elastyczne okazuje się stosowanie list zamiast tradycyjnych tablic dynamicznych. Tablice, choć proste w użyciu, mają swoje ograniczenia przede wszystkim wymagają wcześniejszego określenia rozmiaru lub kosztownej operacji realokacji pamięci przy zmianie ich wielkości. Wskaźniki natomiast dają możliwość dynamicznego zarządzania pamięcią oraz tworzenia bardziej złożonych i elastycznych struktur danych.
W kolejnych rozdziałach przyjrzymy się dokładnie, jak można wykorzystać te możliwości poprzez implementację list jednokierunkowych. Listy jednokierunkowe są jednymi z podstawowych i jednocześnie bardzo użytecznych struktur danych, które stanowią fundament dla wielu bardziej zaawansowanych rozwiązań w informatyce. Ich budowa opiera się na sekwencji elementów (zwanych węzłami), z których każdy przechowuje dane oraz wskaźnik do kolejnego elementu w liście.
Poznanie zasad działania i implementacji list jednokierunkowych pozwoli Wam lepiej zrozumieć sposób zarządzania dynamiczną pamięcią, mechanizmy iteracji po strukturach o zmiennym rozmiarze oraz przygotuje grunt pod dalsze eksplorowanie innych typów list, takich jak listy dwukierunkowe czy listy cykliczne. Co więcej, umiejętność samodzielnego tworzenia i modyfikowania takich struktur jest niezwykle cenna w praktyce programistycznej — niezależnie od wybranego języka czy dziedziny zastosowania.
2.1. Podstawowe informacje o listach jednokierunkowych
Lista jednokierunkowa to wzajemnie połączone ze sobą liniowo elementy. Każdy element posiada jakieś dane oraz adres kolejnego elementu na liście.Dzięki temu lista może dynamicznie zmieniać swój rozmiar tzn. elementy mogą być dowolnie dodawane lub usuwane bez konieczności przesuwania pozostałych elementów, jak ma to miejsce w tablicy.Przechowywanie listy jednokierunkowej w pamięci odbywa się poprzez dynamiczną alokację. Węzły są tworzone w obszarze pamięci zwanym stertą (ang. heap), który służy do przechowywania obiektów o dynamicznie określonym czasie życia. W przeciwieństwie do tablicy, w której elementy są przechowywane w kolejnych komórkach pamięci, węzły listy mogą być rozmieszczone w dowolnych, niepowiązanych ze sobą adresach pamięci. To właśnie wskaźniki przechowywane w każdym węźle zapewniają powiązanie między nimi i pozwalają na odtworzenie logicznego porządku listy.
Każdy węzeł składa się z dwóch części: pola przechowującego dane użytkownika (na przykład liczby lub tekst) oraz pola przechowującego wskaźnik do kolejnego węzła. Wskaźnik ten jest adresem pamięci, pod którym znajduje się następny element listy. Ostatni węzeł w liście ma ustawiony wskaźnik na wartość pustą (NULL), co sygnalizuje koniec listy.
Na rysunku poniżej pokazano prezentację graficzną jednego elementu listy.
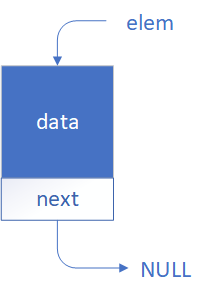
struct Element{
int data;
Element* next;
};
new.
Element* elem = new Element;
(*elem).data = 42; // przykładowa wartość
(*elem).next = NULL; // na razie brak następnego elementu
elem->data = 42; // przykładowa wartość
elem->next = NULL; // na razie brak następnego elementu
#include <iostream>
struct Element {
int data;
Element* next;
};
int main() {
// Utworzenie pierwszego elementu
Element* elem = new Element;
elem->data = 42;
elem->next = nullptr;
// Wyświetlenie wartości
std::cout << "Element data: " << elem->data << std::endl;
// Zwolnienie pamięci
delete elem;
return 0;
}
Adres ma taką samą wartość jak przed usunięciem obiektu.
Element* e1 = new Element;
Element* e2 = new Element;
Element* e3 = new Element;
e1->next = e2;
e2->next = e3
e3->next = NULL;
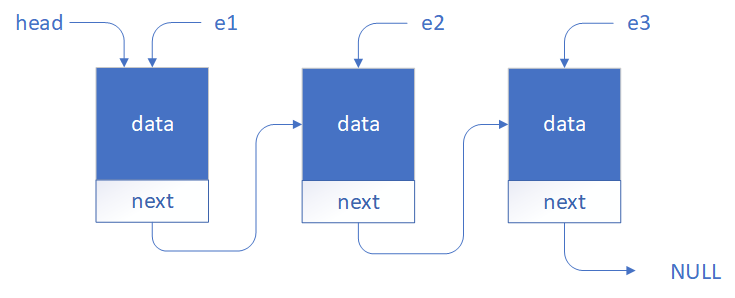
Widzimy na rysunku, że pojawił się dodatkowy wskaźnik
head. Jest to adres pierwszego elementu na liście. Posiadając adres pierwszego elementu na liście możemy uzyskać dostęp do dowolnego elementu na liście.
cout << head->data; // Wyświetla wartość w pierwszym elemencie listy
cout << head->next->data; // Wyświetla wartość w drugim elemencie listy
cout << head->next->next->data; // Wyświetla wartość w trzecim elemencie listy
head = NULL;
cout << head->data; // Jeżeli head=NULL to otrzymamy błąd dostępu do pamięci
Symulacja listy jednokierunkowej
struct Element { int data; Element* next; }; Element* current = head; while (current != nullptr) { std::cout << current << " " << current->data << " " << current->next << std::endl; current = current->next; }
#include <iostream>
using namespace std;
// Definicja elementu listy
struct Element {
int data;
Element* next;
};
// Funkcja dodająca element na koniec listy
void append(Element*& head, int value) {
Element* newElement = new Element;
newElement->data = value;
newElement->next = nullptr;
if (head == nullptr) {
head = newElement;
} else {
Element* current = head;
while (current->next != nullptr) {
current = current->next;
}
current->next = newElement;
}
}
// Funkcja drukująca listę
void printList(Element* head) {
Element* current = head;
while (current != nullptr) {
cout << "Adres: " << current << "wartość: " << current->data << " Adres następnego: " << current->next << endl;
current = current->next;
}
}
int main() {
Element* head = nullptr;
cout << "Podaj liczby do listy (0 konczy wprowadzanie):" << endl;
int value;
do {
cout << "Podaj liczbe: ";
cin >> value;
if (value != 0) {
append(head, value);
}
} while (value != 0);
cout << "\nUtworzona lista:" << endl;
printList(head);
// Zwolnienie pamięci
Element* current = head;
while (current != nullptr) {
Element* toDelete = current;
current = current->next;
delete toDelete;
}
return 0;
}
Element* current = head;
while (current != nullptr) {
\\ Tutaj mamy dostęp do kolejnych elementów znajdujących się na liście
current = current->next; \\ Przejście do kolejnego elementu na liście
}
2.2. Przykładowe operacje na listach jednokierunkowych
Dopisywanie elementu na koniec listy
Korzystając z zasad pokazanych w poprzednim rozdziale napiszemy funkcję, która do listy o strukturze Tos dopisuje na jej końcu dodatkowy element.
void dopiszNaKoncu (Tos *&glowa, string ktos) {
// funkcja dopisuje osobę o imieniu ktos na końcu listy
// zaczynającej się pod adresem glowa
// glowa może się zmienić w trakcie działania funkcji, dlatego jest przy niej &
Tos *nowy, *akt; // wskażniki pomocnicze
// tworzymy nowy, dodatkowy rekord,
// wpisujemy do niego imie ktos i adres NULL,
// bo to ma być rekord końcowy:
nowy=new Tos;
nowy->imie=ktos;
nowy->nast=NULL;
// jeśli lista była pusta, to teraz będzie składała się
// tylko z tego nowego rekordu:
if (glowa==NULL)
glowa=nowy;
else { // a jeśli nie była pusta, to:
akt=glowa; // wracamy na początek listy
while (akt->nast!=NULL) // wolno napisać taki warunek, bo lista nie jest pusta
akt = akt->nast; // dojeżdżamy do elementu, który w polu nast ma NULL
// teraz akt jest adresem ostatniego elementu listy
// możemy do niego dołączyć nowy, końcowy element:
akt->nast=nowy;
}
}
Wstawianie i usuwanie elementów
Przyszła teraz pora na pokazanie, jak do istniejącej listy wstawiamy dodatkowe elementy i jak je z niej usuwamy. W zasadzie czynność wstawienia elementu sprowadza się do dwu kroków: po pierwsze musimy wstawiany element utworzyć w pamięci (za pomocą operatora new), a następnie zmodyfikować istniejące powiązania w liście. Podobnie z usuwaniem elementów. Tym razem musimy jedynie odwrócić kolejność działań, czyli najpierw zmienić powiązania, a potem element usunąć przy pomocy operatora delete. Poniżej znajduje się prosta symulacja umożliwiająca wstawianie 4 elementu do listy oraz usuwanie wskazanego elementu z listy.
Symulacja listy jednokierunkowej: Wstawianie oraz Usuwanie
Wstawianie
Element* current = head; int i = 1; while (i < 4 - 1) { current = current->next; i++; } Element* newElement = new Element; newElement->next = current->next; current->next = newElement;
Usuwanie
Element* current = head; int i = 1; while (i < pos - 1) { current = current->next; i++; } Element* temp = current->next; current->next = temp->next; delete temp;
void dopiszNaKoncu (Tos *&glowa, string ktos) {
Tos* do_usunięcia = head;
head = head->next;
delete do_usuniecia;
void dopiszNaKoncu (Tos *&glowa, string ktos) {
Tos* nowy_element = new Tos;
nowy_element->next; = head;
head = nowy_element;
3. Stosy i kolejki jako elementarne struktury danych
Kolejka (ang. queue)jest bardzo prostą i intuicyjną strukturą, która odpowiada wielu sytuacjom z życia codziennego. Wyobraźcie sobie np. kolejkę do okienka w urzędzie, kolejkę do kasy w sklepie czy też kolejkę pasażerów wchodzących do autobusu. Zasada jest zawsze taka sama: osoby (elementy) dołączają na końcu kolejki, a obsługa odbywa się od początku.
Pod względem technicznym kolejka to struktura dynamiczna lub statyczna, która udostępnia dwa podstawowe operatory:- enqueue (dodanie elementu do kolejki, zwykle na końcu),
- dequeue (usunięcie elementu z kolejki, czyli wyjęcie pierwszego elementu).
Czasami udostępnia się też operator peek (podgląd pierwszego elementu bez usuwania go), dzięki czemu można sprawdzić, jaki element będzie obsłużony jako następny.
Struktura FIFO znajduje zastosowanie w bardzo wielu algorytmach i systemach informatycznych. Przykładowo:
- kolejki zadań w systemach operacyjnych,
- buforowanie danych w transmisji sieciowej,
- implementacja algorytmu przeszukiwania grafu (ang. BFS — Breadth-First Search),
- obsługa zdarzeń w grach komputerowych lub w interfejsach użytkownika.
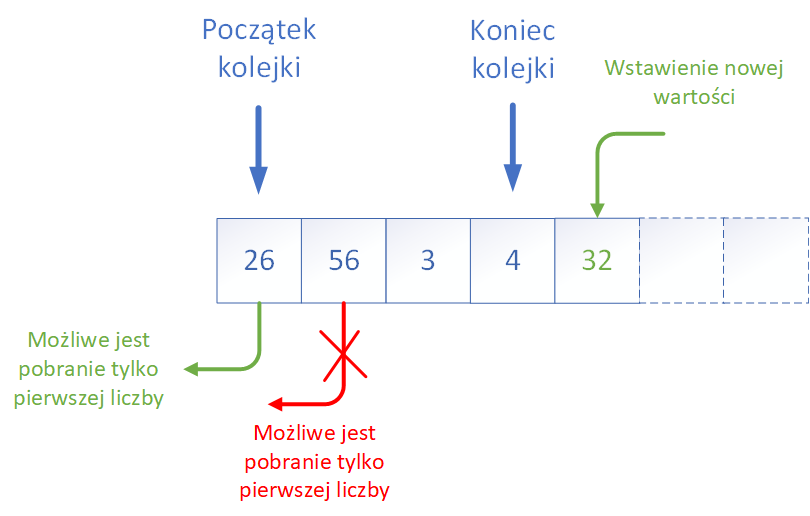
- jako tablicę z dwoma indeksami (początku i końca),
- jako listę jednokierunkową, gdzie nowe elementy dodawane są na końcu, a usuwane z początku,
- z wykorzystaniem gotowych struktur dostępnych w językach wysokiego poziomu (np. queue w C++, Queue w Javie czy collections.deque w Pythonie).
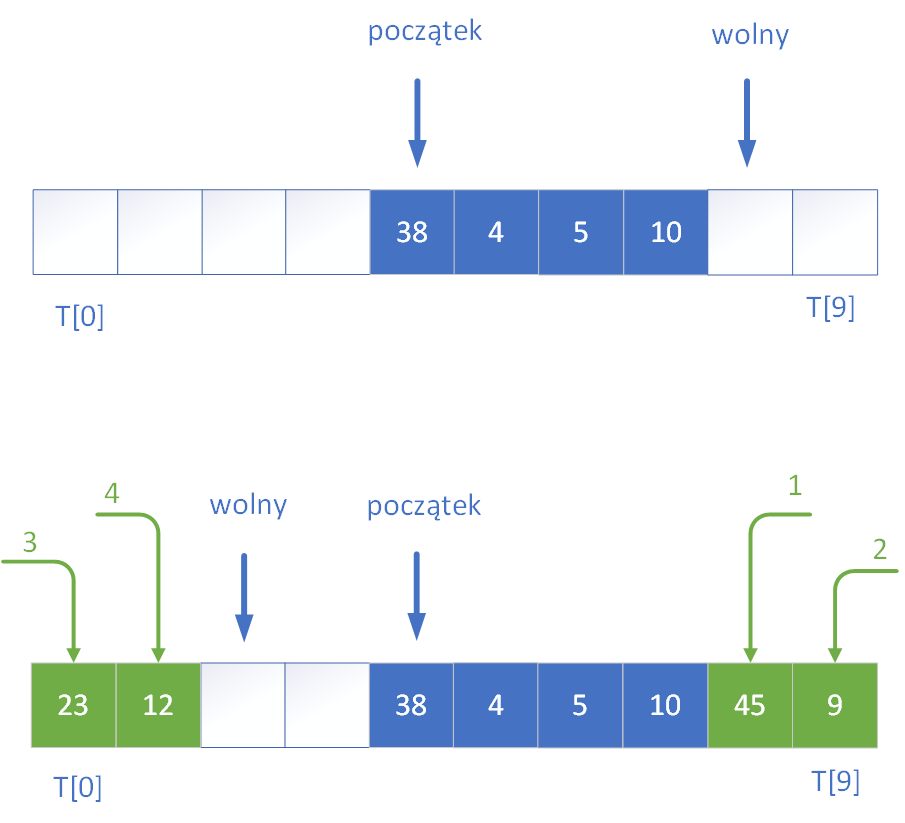
Kolejny przykład rysunkowy demonstruje w jaki sposób pobrać elementy z kolejki. W przykładzie pobierane są dwie wartości z kolejki.
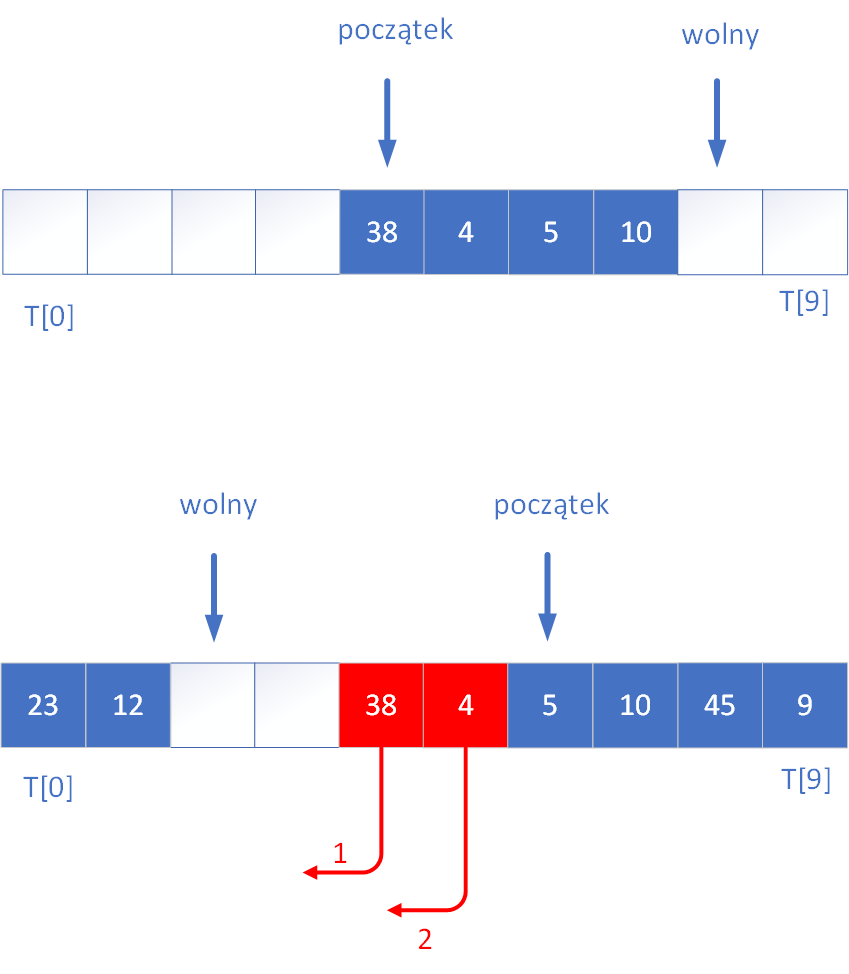
Zauważcie tylko przyglądając się rysunkowi, że w pełniącej rolę bufora cyklicznego tablicy, która ma miejsce na n elementów, zawsze jedno miejsce pozostaje nie wykorzystane, dzięki czemu możemy odróżnić stan, kiedy kolejka jest pusta (indeksy poczatek i wolny są sobie równe) od stanu jej zapełnienia (poczatek=wolny+1).
Struktura kolejki jest wykorzystywana w wielu algorytmach komputerowych, a jednym z najważniejszych zastosowań jest kolejkowanie procesów oczekujących na wykonanie na procesorze komputera.
Stos (ang. stack) jest jedną z najważniejszych struktur danych używanych w algorytmach komputerowych. Podstawowe cechy można zawrzeć w stwierdzeniu "ostatni wchodzi - pierwszy wychodzi", czyli w skrócie LIFO (Last In – First Out).
Obsługa stosu polega na tym, że dostęp do danych możliwy jest wyłącznie z jednej strony – od góry stosu. Można to porównać do układania kart do gry jedna na drugiej. Nowe karty zawsze kładziemy na wierzchu, a jeśli chcemy sięgnąć po kartę znajdującą się niżej, musimy najpierw zdjąć wszystkie leżące nad nią. Aby dotrzeć do pierwszej z położonych kart, konieczne jest usunięcie kolejnych – aż odsłonimy tę, której szukamy. Oznacza to, że elementy są zdejmowane w odwrotnej kolejności niż zostały dodane.
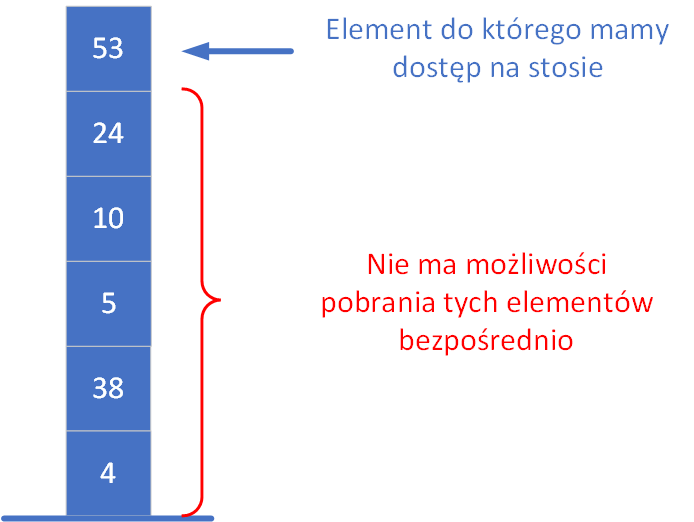
Przy implementacji stosu zazwyczaj definiuje się dwie podstawowe operacje, które umożliwiają jego obsługę. Najczęściej nazywa się je:
- push(x) – dodaje element x na szczyt stosu. To tak, jakby położyć nową kartę na samą górę stosu. Operacja ta zwiększa rozmiar stosu o jeden i sprawia, że nowo dodany element staje się pierwszym do usunięcia.
- pop() – usuwa element znajdujący się aktualnie na szczycie stosu i zwykle go zwraca. Jeśli stos jest pusty, próba wykonania tej operacji może zakończyć się błędem (w zależności od implementacji), ponieważ nie ma elementu do usunięcia.
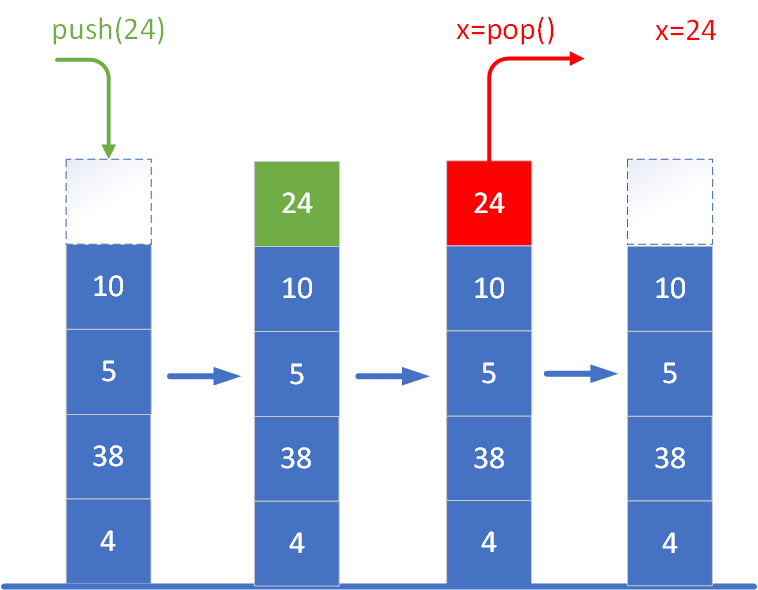
W praktycznych implementacjach stosu (np. w językach programowania takich jak Python, Java, C++) często dodaje się również dodatkowe metody pomocnicze, takie jak:
- peek() lub top() – pozwala podejrzeć element znajdujący się na szczycie stosu bez jego usuwania,
- isEmpty() – sprawdza, czy stos jest pusty,
- size() – zwraca liczbę elementów znajdujących się aktualnie na stosie.
Stos jest taką strukturą danych, która skutecznie pomaga zwiększyć efektywność niektórych algorytmów. Pokażemy to na przykładzie obliczeń związanych z Odwrotną Notacją Polską (ONP). Odwrotna Notacja Polska (ONP), nazywana również notacją postfiksową, to sposób zapisu wyrażeń arytmetycznych, w którym operatory występują po operandach, a nie pomiędzy nimi – jak ma to miejsce w tradycyjnym zapisie infiksowym. Przykładowo, wyrażenie „2 + 3” w ONP przyjmuje postać „2 3 +”. Choć taki zapis może początkowo wydawać się mniej intuicyjny, niesie ze sobą liczne korzyści, szczególnie w kontekście przetwarzania wyrażeń przez komputer. Jedną z najważniejszych cech ONP jest to, że nie wymaga ona stosowania nawiasów. Kolejność wykonywania operacji wynika wprost z kolejności, w jakiej występują operatory i operandy. Dzięki temu unika się niejednoznaczności i konieczności stosowania dodatkowych zasad pierwszeństwa działań. W wyrażeniach ONP zawsze operujemy na dwóch ostatnich liczbach umieszczonych wcześniej w ciągu.
Wyrażenia zapisane w ONP są wyjątkowo łatwe do przetwarzania algorytmicznego, zwłaszcza przy użyciu stosu. Podczas obliczeń elementy (liczby) są kolejno umieszczane na stosie. Kiedy napotkamy operator, zdejmujemy ze stosu dwa ostatnie elementy, wykonujemy odpowiednią operację i wynik odkładamy z powrotem na stos. Proces ten powtarza się aż do momentu przetworzenia całego wyrażenia, a końcowy wynik znajduje się na szczycie stosu jako jedyny pozostały element.
Słowny opis algorytmu przetwarzania jednego znaku pobranego z wejścia można w skrócie przedstawić tak:
- jeżeli znak odczytany z wejścia jest cyfrą, dodaj go do łańcucha wyjściowego
- jeżeli odczytany znak jest operatorem, to:
- jeśli na szczycie stosu znajduje się operator o wyższym lub równym priorytecie względem priorytetu operatora odczytanego z wejścia, zdejmij ten "silniejszy" operator ze stosu i dodaj do kolejki wyjściowej - powtarzaj to aż do momentu, gdy na (nowym) szczycie stosu znajdzie się operator o niższym priorytecie, wtedy:
- odłóż odczytany z wejścia operator na stos – tak samo postąp, gdy stos będzie pusty (od razu bądź też po zdjęciu ze stosu innych operatorów)
- jeżeli odczytany znak jest lewym nawiasem, to odłóż go na stos, natomiast
- jeżeli oczytany znak jest prawym nawiasem, to zdejmuj po kolei operatory ze stosu i przekazuj na wyjście aż do momentu, gdy na szczycie stosu znajdzie się lewy nawias – wtedy zdejmij ten nawias ze stosu.
Poniżej przedstawiono tabelę priorytetów dla czterech podstawowych operandów arytmetycznych.

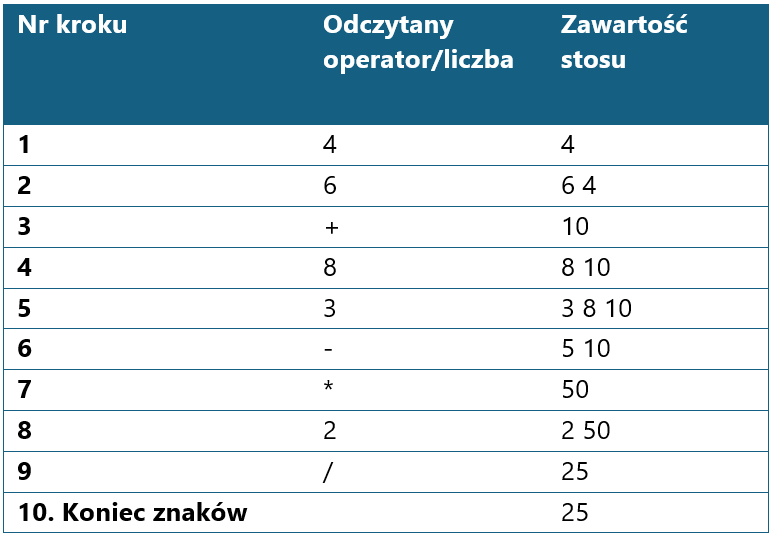
Najlepiej zademonstrować działanie algorytmu na prostym przykładzie. Jako ciąg wejściowy wprowadzamy wyrażenie: (4+6)*(8-3)/2.
Symulacja konwersji na ONP
Wyrażenie: (4 + 6) * (8 - 3) / 2
Dla każdego tokena w wyrażeniu: jeśli to liczba → dodaj do wyjścia jeśli to '(' → połóż na stos jeśli to ')' → zdejmuj ze stosu do '(' jeśli to operator → zdejmuj silniejsze operatory ze stosu, potem połóż Po zakończeniu → zdejmij wszystko ze stosu
Stos operatorów:
Wyjście (ONP):
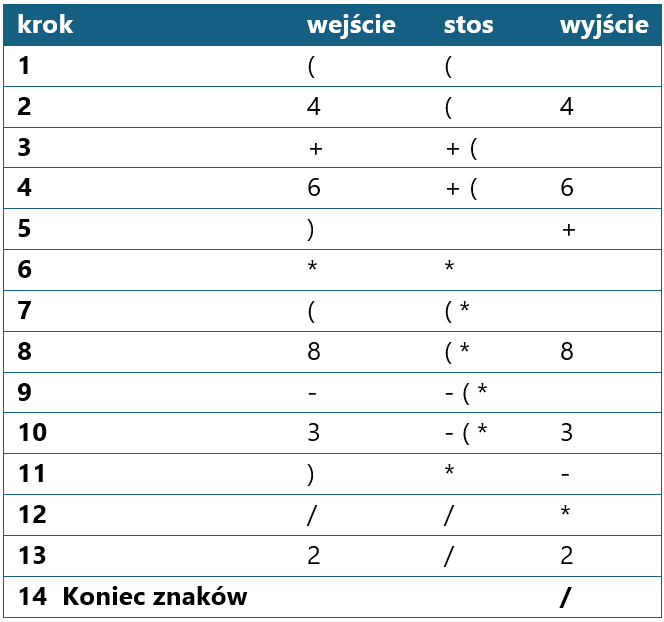
Ciąg znaków wyjściowych: 4 6 + 8 3 - * 2 /
Wiemy już, jak przetworzyć zapis w notacji konwencjonalnej do postaci ONP. Za chwilę dowiemy się, jak za pomocą stosu - tym razem liczbowego - w szybki sposób obliczać wartość wyrażenia przedstawionego właśnie w zapisie postfiksowym.
Okazuje się, że taki algorytm może być naprawdę prosty w zapisie, a przy tym efektywny. Tym razem jest nam potrzebny ciąg wejściowy będący zapisem wyrażenia w notacji ONP oraz stos pozwalający na przechowywanie liczb. Wynik wyrażenia jest zdejmowany ze stosu na samym końcu.
Kroki algorytmu są następujące:
- jeżeli znak odczytany z wejścia jest cyfrą, to pobieraj kolejne znaki budując z nich liczbę, aż natrafisz na znak nie będący cyfrą - wtedy otrzymaną liczbę odłóż na stos
- jeżeli znak jest operatorem, to
- zdejmij ze stosu dwie liczby (pierwszą zdjętą niech będzie x, drugą y)
- oblicz wartość wyrażenia y operator x
- odłóż obliczoną wartość na stos
- gdy już skończą się znaki w ciągu wejściowym, zdejmij ze stosu końcowy wynik.
Symulacja obliczania wartości ONP
Wyrażenie ONP: 4 6 + 8 3 - * 2 /
Dla każdego tokena w wyrażeniu: jeśli to liczba → odłóż na stos jeśli to operator: zdejmij x i y ze stosu oblicz y operator x i odłóż wynik na stos Na końcu zdejmij wynik ze stosu
Stos liczbowy:
Aktualny token:
4. Rekurencja
Rekurencja to technika programistyczna i koncepcja matematyczna, w której funkcja wywołuje samą siebie w celu rozwiązania mniejszej części tego samego problemu. Jest to bardzo potężne narzędzie, które pozwala w elegancki sposób rozwiązywać złożone zadania poprzez ich sprowadzanie do prostszych przypadków. W kodzie możemy zaprezentować rekurencję w następujący sposób:
void funkcja_rekrencyjna(){
...
funkcja_rekrencyjna();
...
}
int silnia(int n) {
if (n == 0 || n == 1) {
return 1; // silnia z 0 i 1 to 1
} else {
return n * silnia(n - 1); // rekurencyjne wywołanie
}
}
int silnia(int n) {
int wynik = 1;
for (int i = 2; i <= n; ++i) {
wynik *= i;
}
return wynik;
}
Z kolei iteracja opiera się na konstrukcjach pętli, takich jak for czy while, i działa w sposób bardziej techniczny. Zajmuje mniej pamięci, ponieważ nie wymaga dodatkowego miejsca na stosie wywołań funkcji, co ma znaczenie przy dużych wartościach n. Dzięki temu iteracyjne podejście jest zwykle wydajniejsze i bezpieczniejsze w środowiskach o ograniczonych zasobach.
Główne zalety rekurencji wynikają z jej elegancji, przejrzystości i bezpośredniego odwzorowania logicznej struktury wielu problemów. Poniżej przedstawiam kluczowe korzyści płynące z jej stosowania.
Przede wszystkim rekurencja pozwala na bardzo zwięzłe i czytelne wyrażenie algorytmów, które mają charakter powtarzalny lub dzielą problem na mniejsze podproblemy. Problemy takie jak silnia, ciąg Fibonacciego, przeszukiwanie struktur drzewiastych (np. drzewa binarnego), rozwiązywanie zadań typu "dziel i zwyciężaj" (np. sortowanie szybkiego podziału – quicksort) dają się naturalnie wyrazić właśnie rekurencyjnie.
Drugą zaletą rekurencji jest to, że wiele złożonych struktur danych (takich jak drzewa, grafy, listy zagnieżdżone) można przetwarzać w sposób bardzo intuicyjny – odwiedzając je w głąb (DFS – depth-first search) bez konieczności ręcznego stosowania struktur pomocniczych, takich jak stos czy kolejka.
Rekurencja bywa też niezastąpiona w algorytmach, które wymagają eksploracji wielu wariantów rozwiązania, np. w problemach kombinatorycznych, algorytmach typu backtracking (jak rozwiązywanie sudoku, znajdowanie ścieżek w labiryncie) czy generowaniu permutacji i podzbiorów.
5. Złożoność obliczeniowa
Zagadnienia złożoności obliczeniowej algorytmów stanowią fundament matematycznej analizy efektywności aplikacji komputerowych. Stanowią one istotny punkt wyjścia w nauce algorytmiki. Umożliwiają ocenę jakości danego rozwiązania niezależnie od konkretnego sprzętu, języka programowania czy implementacji. Głównym celem wyznaczania złożoności obliczeniowej jest efektywność działania algorytmu rozumiana jako ilość zasobów niezbędnych do jego wykonania, w szczególności czasu oraz pamięci. Wprowadzenie tych pojęć pozwala sformułować precyzyjne miary porównawcze dla różnych metod rozwiązania tego samego problemu.
Z matematycznego punktu widzenia, złożoność czasowa i pamięciowa algorytmu jest wyrażana jako funkcja zmiennej naturalnej n, która opisuje rozmiar danych wejściowych. Interesuje nas przy tym przede wszystkim asymptotyczne zachowanie tej funkcji, czyli jak rośnie liczba operacji lub potrzebna pamięć, gdy . Do zapisu tego wzrostu stosuje się tzw. notację dużego O – oznaczaną jako , gdzie jest funkcją ograniczającą wzrost złożoności od góry. Przykładowo, jeśli algorytm wykonuje maksymalnie 3 operacji, to jego złożoność asymptotyczna to , ponieważ składnik kwadratowy dominuje dla dużych wartości .
W praktyce często porównujemy algorytmy poprzez analizę ich złożoności w różnych przypadkach: najgorszym, średnim i najlepszym. Taka analiza pozwala przewidywać zachowanie algorytmu nie tylko w idealnych, ale i w rzeczywistych warunkach. Na przykład wyszukiwanie liniowe ma złożoność w najgorszym przypadku, ale wyszukiwanie binarne – już tylko , co wprowadza jakościową różnicę przy dużych zbiorach danych.
W algorytmice nie chodzi jednak wyłącznie o zminimalizowanie złożoności. Równie istotna jest czytelność, poprawność i łatwość implementacji algorytmu. Czasem prostszy, choć teoretycznie wolniejszy algorytm, może okazać się lepszym wyborem, szczególnie w sytuacjach, gdy dane wejściowe mają niewielki rozmiar lub gdy istotna jest szybkość implementacji rozwiązania. Ważne jest także, by algorytm spełniał warunek stopu, czyli kończył działanie dla danych poprawnych w skończonym czasie – co formalnie oznacza, że musi on być funkcją totalną.
Wprowadzenie pojęcia złożoności pozwala zidentyfikować i poprawić nieefektywne fragmenty algorytmów. Na przykład, odczytanie głównej przekątnej macierzy można wykonać w czasie , używając jednej pętli. Jednak początkujący mogą nieświadomie zastosować algorytm złożony z dwóch pętli z warunkiem , co prowadzi do złożoności – mimo że problem da się rozwiązać znacznie szybciej. W tym miejscu ujawnia się praktyczna wartość analizy złożoności: pozwala ona uniknąć niewidocznych gołym okiem nieefektywności.
Ostatecznie, złożoność obliczeniowa to narzędzie matematyczne, które służy nie tylko do porównywania algorytmów, lecz również do ich projektowania i optymalizacji. Dzięki niej jesteśmy w stanie zrozumieć granice obliczalności problemów, klasyfikować zadania według trudności (np. klasy P, NP, NP-zupełne) oraz podejmować świadome decyzje projektowe. Choć złożoność pamięciowa jest dziś mniej krytyczna z racji dużej dostępności RAM, nadal pozostaje istotna np. w systemach wbudowanych lub przy pracy na wielkich zbiorach danych. Jednak to złożoność czasowa pozostaje najczęściej analizowanym i najważniejszym aspektem efektywności algorytmicznej.
Notacja dużego O (czyli tzw. big-O notation) to kluczowe narzędzie matematyczne służące do opisu zachowania algorytmu przy dużych danych wejściowych. Zamiast analizować dokładną liczbę operacji, jakie wykonuje program, interesuje nas ogólny trend wzrostu tej liczby w zależności od rozmiaru wejścia. Umożliwia to ocenę i porównanie efektywności algorytmów niezależnie od konkretnej maszyny czy języka programowania.
Formalnie, mówimy, że funkcja ma złożoność , jeśli istnieją stałe oraz , takie że dla wszystkich zachodzi nierówność:
Oznacza to, że dla dużych n, funkcja jest ograniczona z góry przez pewną wielokrotność funkcji . Intuicyjnie: nie rośnie szybciej niż , pomnożone przez jakąś stałą. Taka definicja opisuje asymptotyczny kres górny, czyli zachowanie algorytmu „na dłuższą metę” – ignorując drobne różnice dla małych wartości , a skupiając się na tym, jak zachowuje się on, gdy rozmiar danych rośnie do nieskończoności.
Na przykład, jeśli algorytm wykonuje operacji, to mówi się, że ma on złożoność . Pomijamy tutaj współczynniki stałe (takie jak 3 czy 5), ponieważ interesuje nas jedynie kształt wzrostu funkcji. Z tego względu funkcje takie jak i również uznaje się za rzędu O( n2 ), mimo że ich wartości dla konkretnych n mogą być różne.
Często spotykane klasy funkcji używanych w notacji dużego O to:
-
– stała złożoność (niezależna od rozmiaru wejścia),
-
– logarytmiczna (np. przeszukiwanie binarne),
-
– liniowa (np. przeglądanie tablicy),
-
– liniowo-logarytmiczna (np. szybkie algorytmy sortowania),
-
, – złożoności wielomianowe (np. sortowanie bąbelkowe, algorytmy dynamiczne),
-
, – złożoności wykładnicze i silniowe (dla problemów trudnych obliczeniowo, np. w teorii grafów, NP-trudne zadania).
Z wykresu funkcji takich jak , , n, , widać, jak drastycznie różni się ich tempo wzrostu. Funkcja – charakterystyczna dla szybkich algorytmów sortowania – leży pomiędzy funkcją liniową a kwadratową, ale rośnie znacznie wolniej niż ta druga. Tymczasem wznosi się tak stromo, że dla nawet umiarkowanie dużych danych staje się praktycznie nieużyteczna.
W praktyce, kiedy szukamy najlepszego algorytmu, dążymy do tego, by jego złożoność była jak najmniejsza – np. zamiast algorytmu , warto znaleźć taki, który działa w , a idealnie – w , jeśli to możliwe. Złożoność w notacji dużego O pozwala więc nie tylko na efektywne porównywanie algorytmów, ale także stanowi fundament teorii obliczalności i klasyfikacji problemów pod kątem ich trudności obliczeniowej.
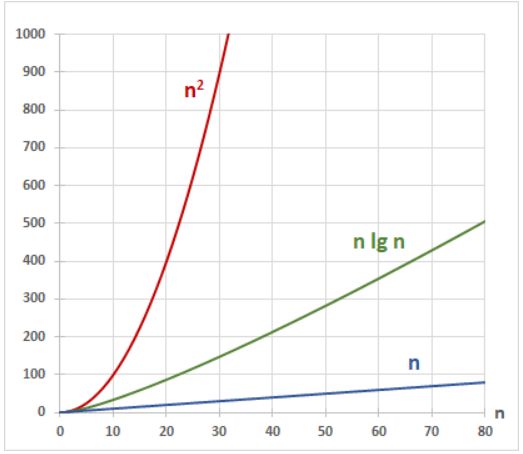
Na wykresie pokazano złożoność obliczeniową w zależności od liczby danych.
6. Przegląd metod konstruowania algorytmów
Obecnie informatyka opiera się na efektywnym rozwiązywaniu problemów. Sercem tego procesu są oczywiście algorytmy. W celu utworzenia skutecznego algorytmu, projektanci sięgają po zestaw sprawdzonych metod konstrukcyjnych. Do najważniejszych z nich należą:
- metody typu „dziel i zwyciężaj”,
- algorytmy bazujące na programowaniu dynamicznym,
- algorytmy zachłanne,
- algorytmy z powrotami,
- metody heurystyczne,
- algorytmy probabilistyczne,
- algorytmy iteracyjne (np. gradientowe),
- algorytmy przeszukiwania.
Metody typu „dziel i zwyciężaj"
Metoda „dziel i zwyciężaj” polega na podziale problemu na mniejsze, prostsze podproblemy, które są następnie rozwiązywane niezależnie, a ich wyniki łączone w rozwiązanie problemu głównego. To podejście często wykorzystuje się w algorytmach sortowania, takich jak sortowanie szybkie czy sortowanie przez scalanie. Technika ta opiera się na rekurencji i umożliwia uzyskanie znacznej poprawy wydajności w porównaniu do metod naiwnych.
Oto przykłady zastosowania podejścia dziel i zwyciężaj:
-
Sortowanie przez scalanie (ang. Merge Sort) – dzieli tablicę na dwie połowy, sortuje je rekurencyjnie, a następnie scala w jedną posortowaną tablicę.
-
Sortowanie szybkie (ang. Quick Sort) – wybiera element główny (pivot), dzieli tablicę na elementy mniejsze i większe od pivota, a następnie sortuje każdą część osobno.
-
Mnożenie dużych liczb (algorytm Karatsuby) – rozkłada liczby na mniejsze części, mnoży je i łączy wynik przy mniejszej liczbie mnożeń niż klasyczny algorytm.
-
Przeszukiwanie binarne – dzieli uporządkowaną listę na pół i przeszukuje tylko tę część, w której może znajdować się szukany element.
-
Algorytm znajdowania największego wspólnego dzielnika (NWD) – rekurencyjnie dzieli problem na mniejsze, korzystając z własności dzielników.
-
Znajdowanie maksimum i minimum w tablicy – dzieli tablicę na części, znajduje lokalne maksimum i minimum, a następnie wybiera globalne.
-
Algorytmy do przetwarzania obrazów (np. kompresja JPEG) – dzielą obraz na mniejsze bloki i przetwarzają każdy blok niezależnie.
-
Szybkie przekształcenie Fouriera (FFT) – dzieli problem przekształcenia sygnału na mniejsze podproblemy, przekształca je i łączy wynik.
-
Zliczanie inwersji w tablicy – łączy sortowanie przez scalanie z liczeniem par elementów w złej kolejności.
-
Algorytmy do znajdowania najbliższej pary punktów na płaszczyźnie – dzielą zbiór punktów i łączą wyniki przy pomocy sprytnej analizy geometrycznej.
Algorytmy bazujące na programowaniu dynamicznym
Programowanie dynamiczne to technika, która sprawdza się w problemach z nakładającymi się podproblemami i optymalną strukturą. W odróżnieniu od „dziel i zwyciężaj”, gdzie podproblemy są niezależne, tutaj ich rozwiązania są przechowywane i wykorzystywane wielokrotnie, co zapobiega redundantnym obliczeniom. Programowanie dynamiczne stosuje się na przykład w problemie plecakowym, w obliczaniu wartości ciągów czy w analizie sekwencji biologicznych. Metoda ta pozwala znacząco skrócić czas działania algorytmu, choć często kosztem zwiększonego zużycia pamięci.
Do tej pory nic nie mówiliśmy o typowych zastosowaniach programowania dynamicznego. Otóż wzorcowymi przykładami wykorzystania PD są zadania polegające na:
- Rozwiązaniu problemu „plecakowego”,
- Znalezieniu najkrótszych ścieżek między parami węzłów grafu – algorytm Floyda-Warshalla,
- Obliczeniu wyrazów ciągu Fibonacciego lub kolejnych wartości symbolu Newtona.
Algorytmy zachłanne
Algorytmy zachłanne działają według prostej zasady: wybieraj na każdym kroku najlepszą lokalnie opcję, mając nadzieję, że doprowadzi to do najlepszego globalnego rozwiązania. Choć nie zawsze dają one wynik optymalny, to w wielu przypadkach, takich jak znajdowanie minimalnego drzewa rozpinającego czy wyznaczanie najkrótszej ścieżki w grafie, okazują się skuteczne i bardzo szybkie. Kluczem do ich stosowania jest możliwość wykazania, że lokalne decyzje prowadzą do optymalnego globalnego wyniku, co nie zawsze jest możliwe.
Przykładami zastosowania podejścia zachłannego są takie algorytmy, jak m.in.:
- algorytm Dijkstry – służący do znajdowania najkrótszych ścieżek w grafach,
- metoda Kruskala – używana do wyznaczania minimalnego drzewa rozpinającego,
- konstrukcja drzewa kodowego Huffmana służącego do kompresji danych,
- algorytmy szeregowania zadań.
Algorytmy z powrotami
Technika z powrotami, znana także jako backtracking, wykorzystywana jest w problemach, gdzie konieczne jest przeszukiwanie dużych przestrzeni rozwiązań. Polega ona na budowaniu rozwiązania krok po kroku i wycofywaniu się z błędnych ścieżek, gdy okaże się, że nie prowadzą do celu. Tę metodę stosuje się często w zagadkach logicznych, takich jak sudoku, układanie hetmanów na szachownicy czy generowanie kombinacji i permutacji. Choć jej czas działania może być wykładniczy, jest niezwykle uniwersalna i stosunkowo prosta do zaimplementowania.
Istnieje wiele różnych zagadnień, do rozwiązania których stosuje się algorytmy z powrotami, m.in.:
- problem „plecakowy” (optymalnego wyboru),
- grupa problemów dotyczących gier (w szachach, warcabach), np.:
- problem rozmieszczenia n-królowych na szachownicy (znany najczęściej w wersji z 8 hetmanami (królowymi) ),
- problem znalezienia drogi konika szachowego (odwiedzenie każdego pola szachownicy dokładnie raz) – Knight’s Tour.
- problemy „grafowe”, np.:
- problem kolorowania grafu (należy w taki sposób użyć m kolorów, by każde dwa sąsiednie węzły były różnego koloru.
Metody heurystyczne
Metody heurystyczne to podejście stosowane w sytuacjach, gdzie rozwiązanie optymalne jest trudne lub niemożliwe do znalezienia w rozsądnym czasie. Heurystyki nie gwarantują najlepszego możliwego wyniku, ale dostarczają rozwiązań wystarczająco dobrych w praktyce. Stosuje się je w problemach NP-trudnych, takich jak komiwojażer czy optymalizacja tras. Do metod heurystycznych należą między innymi algorytmy genetyczne, symulowane wyżarzanie czy lokalne przeszukiwanie. Ich zaletą jest elastyczność i możliwość adaptacji do wielu różnych dziedzin.
Metodami heurystycznymi posługujemy się najczęściej w problemach, gdy brakuje nam pewnych danych, dzięki którym bylibyśmy w stanie znaleźć rozwiązanie przy użyciu klasycznych algorytmów.
Przykładami takich problemów są chociażby:
- prognozowanie pogody,
- wykrywanie wirusów i robaków internetowych.
Algorytmy probabilistyczne
Algorytmy probabilistyczne to klasa algorytmów, które wykorzystują element losowości w swoim działaniu. Mogą podejmować decyzje w sposób losowy lub korzystać z losowych danych pomocniczych. Ich wynik lub czas działania nie zawsze jest taki sam przy każdym uruchomieniu, nawet dla tych samych danych wejściowych.Przykłady zastosowań:
- Testy pierwszości liczb (Miller–Rabin, Fermata) ,
- Algorytmy w kryptografii (np. generowanie kluczy, testy losowości),
- Symulacje fizyczne i finansowe (metody Monte Carlo),
- Grafika komputerowa (np. rozpraszanie światła, wygładzanie krawędzi),
- Algorytmy na grafach (np. randomizowane wyszukiwanie cykli),
- Optymalizacja (np. symulowane wyżarzanie – wykorzystuje probabilistyczne przejścia).
Algorytmy iteracyjne
Algorytmy iteracyjne (np. gradientowe) stanowią klasę metod, które rozwiązują problemy poprzez sukcesywne przybliżanie rozwiązania. W przeciwieństwie do innej klasy algorytmów nie dzielą problemu na mniejsze podproblemy, tylko rozpoczynają od pewnego stanu początkowego, a następnie modyfikują go krok po kroku, aż osiągną wynik spełniający określone kryterium zbieżności lub dokładności. Charakterystyczne dla tego podejścia jest użycie pętli, w których każda iteracja przybliża rozwiązanie coraz bardziej do wartości optymalnej. Algorytmy tego typu są powszechnie stosowane w optymalizacji matematycznej, analizie numerycznej i uczeniu maszynowym, gdzie często nie da się wyznaczyć dokładnego wyniku analitycznie. Dobrym przykładem jest metoda spadku gradientowego (ang. gradient descent), która znajduje minimum funkcji poprzez poruszanie się w kierunku przeciwnym do gradientu. Algorytmy iteracyjne mogą działać zarówno na liczbach rzeczywistych, jak i dyskretnych strukturach danych, a ich główną zaletą jest możliwość szybkiego uzyskania przybliżonego rozwiązania nawet dla bardzo dużych i złożonych problemów. W praktyce często łączy się je z innymi technikami, takimi jak heurystyki czy metody probabilistyczne, w celu zwiększenia skuteczności i stabilności.Algorytmy przeszukiwania
Algorytmy przeszukiwania (ang. search-based algorithms) to grupa algorytmów, które rozwiązują problemy poprzez systematyczne eksplorowanie przestrzeni możliwych rozwiązań. Zamiast budować wynik wprost, analizują możliwe stany lub konfiguracje problemu i wybierają ścieżki prowadzące do rozwiązania na podstawie określonej strategii przeszukiwania. Przestrzeń rozwiązań może być reprezentowana jako drzewo lub graf, w którym węzły odpowiadają stanom, a krawędzie – możliwym przejściom między nimi. Algorytmy te są szczególnie istotne w sztucznej inteligencji, teorii gier, grafach oraz planowaniu działań i tras. Podstawowe techniki przeszukiwania to przeszukiwanie wszerz (ang. BFS – Breadth-First Search) i przeszukiwanie w głąb (ang. DFS – Depth-First Search). Algorytmy te różnią się kolejnością eksplorowania węzłów i mają odmienne właściwości dotyczące kompletności, optymalności i zużycia pamięci. W bardziej zaawansowanych zastosowaniach wykorzystuje się przeszukiwanie z heurystyką, takie jak algorytm A*, który łączy rzeczywisty koszt przebytej drogi z oszacowaniem odległości do celu, co pozwala znacząco przyspieszyć proces rozwiązywania. Inne znane metody to przeszukiwanie iteracyjno-głębokie, przeszukiwanie z kosztem jednolitym czy przeszukiwanie bidirectionalne. Algorytmy przeszukiwania mogą być zarówno deterministyczne, jak i probabilistyczne, zależnie od rodzaju problemu i użytych technik pomocniczych. W przypadku dużych lub nieskończonych przestrzeni stanów, stosuje się ograniczenia głębokości, przeszukiwanie heurystyczne lub losowe eksplorowanie węzłów. Choć nie zawsze prowadzą do rozwiązania optymalnego, często pozwalają znaleźć zadowalające odpowiedzi w akceptowalnym czasie. Ich siłą jest uniwersalność – mogą być stosowane do szerokiego zakresu problemów: od rozwiązywania łamigłówek, przez sterowanie robotami, aż po analizę struktur danych i sieci komputerowych.7. Problem skoczka szachowego
Problem skoczka szachowego (ang. Knight's Tour Problem) to klasyczny problem kombinatoryczny z teorii grafów i algorytmiki, który polega na znalezieniu takiej sekwencji ruchów skoczka szachowego, aby odwiedził on każde pole szachownicy dokładnie raz. Skoczek porusza się zgodnie z regułami gry w szachy – wykonuje ruch w kształcie litery „L”, czyli dwa pola w jednym kierunku (poziomo lub pionowo), a następnie jedno pole prostopadle. Celem jest zaplanowanie takiej trasy, która obejmuje wszystkie pola na szachownicy bez powtórzeń, czyli tzw. pełnej trasy.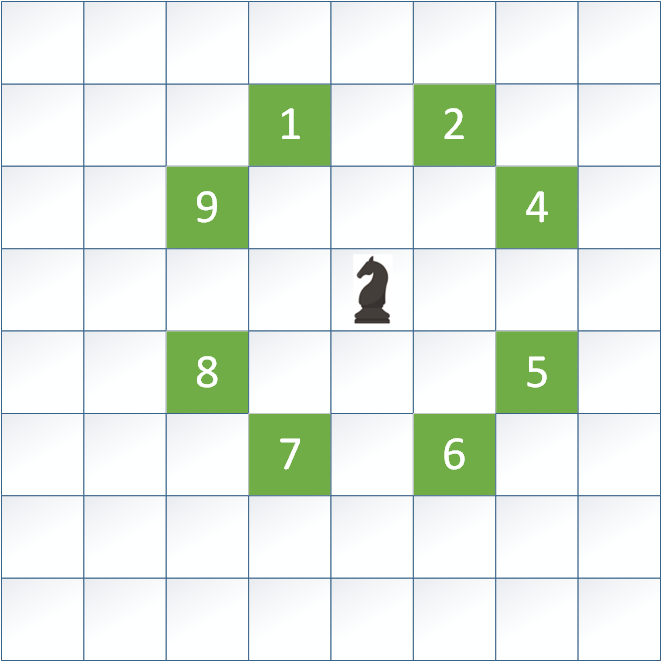
Problemem poruszania się konika po szachownicy zajmowało się w przeciągu ostatnich dwustu lat bardzo wielu wybitnych matematyków i naukowców. Dzisiaj wiemy na przykład, że w przypadku szachownicy o rozmiarze m x n, gdzie min(m,n) >= 5, zawsze istnieje ścieżka skoczka przechodząca przez wszystkie pola dokładnie raz. Dla naszego przypadku 8 istnieje pewność, że możliwe jest znalezienie rozwiązania.
Poniżej przedstawiono kod umożliwiający rozwiązanie problemu skoczka przy pomocy algorytmu z powrotami (ang. backtracking).
#include <iostream>
#include <iomanip>
const int N = 8; // rozmiar szachownicy
// Możliwe ruchy skoczka (x, y)
int dx[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int dy[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Funkcja do weryfikacji czy ruch jest możliwy
bool isSafe(int x, int y, int board[N][N]) {
return (x >= 0 && x < N &&
y >= 0 && y < N &&
board[x][y] == -1);
}
// Funkcja do rekurencyjnego rozwiązania problemu skoczka
bool solveKnightTour(int x, int y, int moveCount, int board[N][N]) {
if (moveCount == N * N) return true;
for (int i = 0; i < 8; i++) {
int nextX = x + dx[i];
int nextY = y + dy[i];
if (isSafe(nextX, nextY, board)) {
board[nextX][nextY] = moveCount;
if (solveKnightTour(nextX, nextY, moveCount + 1, board))
return true;
else
board[nextX][nextY] = -1;
}
}
return false;
}
// Funkcja uruchamiająca algorytm
void startKnightTour() {
int board[N][N];
// Inicjalizacja planszy
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
board[i][j] = -1;
int startX = 0, startY = 0; // punkt startowy
board[startX][startY] = 0; // pierwszy ruch
if (solveKnightTour(startX, startY, 1, board)) {
// Wyświetlenie rozwiązania
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
std::cout << std::setw(2) << board[i][j] << " ";
std::cout << std::endl;
}
} else {
std::cout << "Brak rozwiązania." << std::endl;
}
}
int main() {
startKnightTour();
return 0;
}
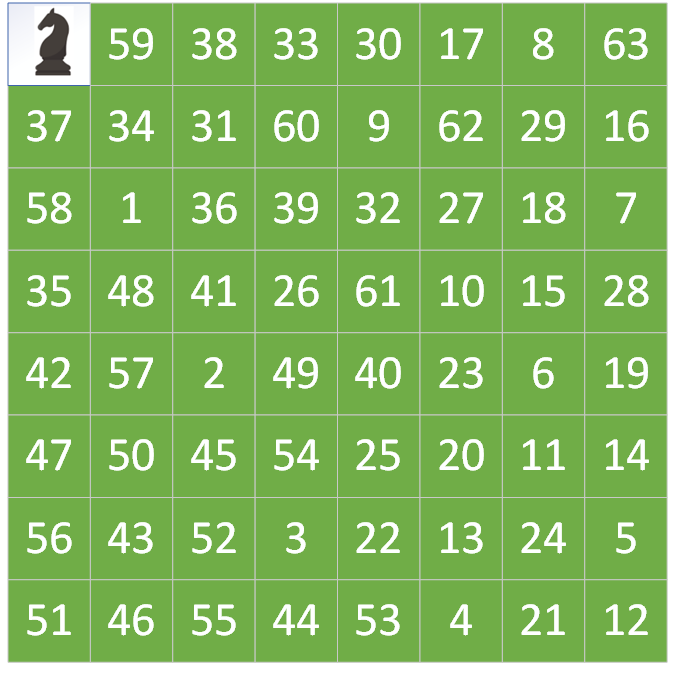
Można zaobserwować analizując poszczególne ruchy, że każde pole zostało odwiedzone tylko raz oraz że zostały odwiedzone wszystkie pola na szachownicy.
Poniżej macie symulator za pomocą którego możecie symulować działanie algorytmu z powrotami dla dowolnego punktu startowego oraz wielkości planszy <5;8>. Po każdym uruchomieniu za pomocą Start należy użyć Stop, aby było możliwe ponowne uruchomienie symulatora.
Symulacja problemu skoczka szachowego
8. Problem plecakowy
Problem plecakowy (ang. knapsack problem) jest przykładem zagadnienia optymalizacyjnego, które może być rozwiązywanie za pomocą wielu technik algorytmicznych (oczywiście z różną efektywnością). Niemniej jednak jest to doskonałe „modelowe” zadanie, dzięki któremu jesteśmy w stanie w przybliżony sposób zaprezentować sposoby działania kilku grup algorytmów. O trudności tego problemu niech świadczy fakt, że nie istnieje (przynajmniej nie został jeszcze odkryty) algorytm rozwiązujący dyskretny problem plecakowy, którego pesymistyczna złożoność obliczeniowa byłaby lepsza niż wykładnicza O(2n). Nie powinno nas to dziwić, gdyż problem plecakowy jest głównym przykładem algorytmu tzw. NP-trudnego – szczególnie zainteresowanych tematyką klasyfikacji problemów odsyłamy do naukowej literatury.
Główna zasada tego problemu brzmi: mamy pewien zbiór mniej lub bardziej cennych przedmiotów scharakteryzowanych za pomocą dwóch parametrów:
Oprócz tych obiektów mamy pewien zbiorczy obiekt, zwyczajowo nazywany plecakiem, który z kolei posiada jeden parametr – całkowitą pojemność W (a ściślej rzecz biorąc powinna być to wytrzymałość na obciążenie). Zadanie jakie stoi przed osobą, która dokonuje załadunku przedmiotów do plecaka (zamiast turysty wyruszającego na długą wyprawę w opisach tego zadania często spotykany jest np. złodziej w muzeum sztuki), jest następujące:
- Należy dokonać takiego wyboru przedmiotów do plecaka, by ich sumaryczna wartość była możliwie maksymalna, zachowując przy tym ograniczenia dotyczące pojemności W plecaka.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Funkcja rozwiązująca problem plecakowy 0-1
int knapsack(const vector<int>& val, const vector<int>& wt, int W) {
int n = val.size();
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
// Budowanie tabeli dp
for (int i = 1; i <= n; i++) {
for (int w = 0; w <= W; w++) {
if (wt[i - 1] <= w) {
dp[i][w] = max(
dp[i - 1][w], // nie bierzemy przedmiotu
dp[i - 1][w - wt[i - 1]] + val[i - 1] // bierzemy przedmiot
);
} else {
dp[i][w] = dp[i - 1][w]; // nie zmieści się więc nie bierzemy
}
}
}
return dp[n][W]; // maksymalna wartość możliwa do uzyskania
}
int main() {
vector<int> val = {60, 100, 120};
vector<int> wt = {10, 20, 30};
int W = 50;
cout << "Maksymalna wartość, którą można zmieścić w plecaku: "
<< knapsack(val, wt, W) << endl;
return 0;
}