Podręcznik

1. Elementarne algorytmy sortowania

Pierwszą grupą algorytmów, którą omówimy w tym rozdziale, są tzw. metody sortowania elementarnego. Są to proste, intuicyjne algorytmy sortujące, które choć nie należą do najbardziej wydajnych, odgrywają istotną rolę w nauce podstaw algorytmiki. Charakteryzują się łatwą implementacją i przejrzystą logiką działania, dzięki czemu często stanowią punkt wyjścia do zrozumienia bardziej zaawansowanych metod sortowania. Do sortowania elementarnego zalicza się:

• sortowanie przez wybieranie (ang. SelectionSort), 
• sortowanie przez wstawianie (ang. InsertionSort),
• sortowanie bąbelkowe (ang. BubbleSort).

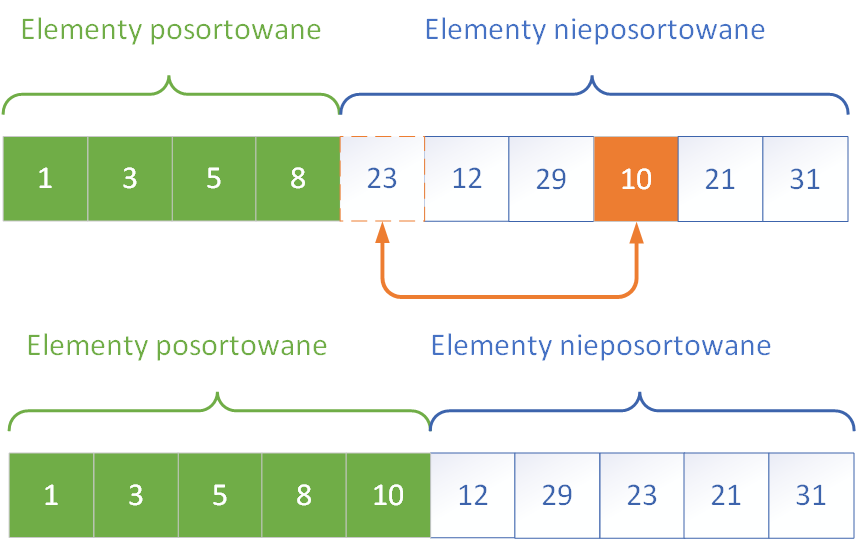
Sortowanie przez wybieranie (ang. SelectionSort)

Sortowanie przez wybieranie, znane również jako SelectionSort, polega na wyszukiwaniu najmniejszego elementu z nieposortowanej części tablicy i zamianie go z pierwszym elementem tej części. Proces ten jest powtarzany dla kolejnych pozycji aż do momentu, gdy cała tablica zostanie uporządkowana. Choć liczba porównań pozostaje stała niezależnie od rozkładu danych, metoda ta nie wymaga dodatkowej pamięci i może być efektywna dla bardzo małych zbiorów danych.

Sortowanie przez wstawianie (ang. InsertionSort)

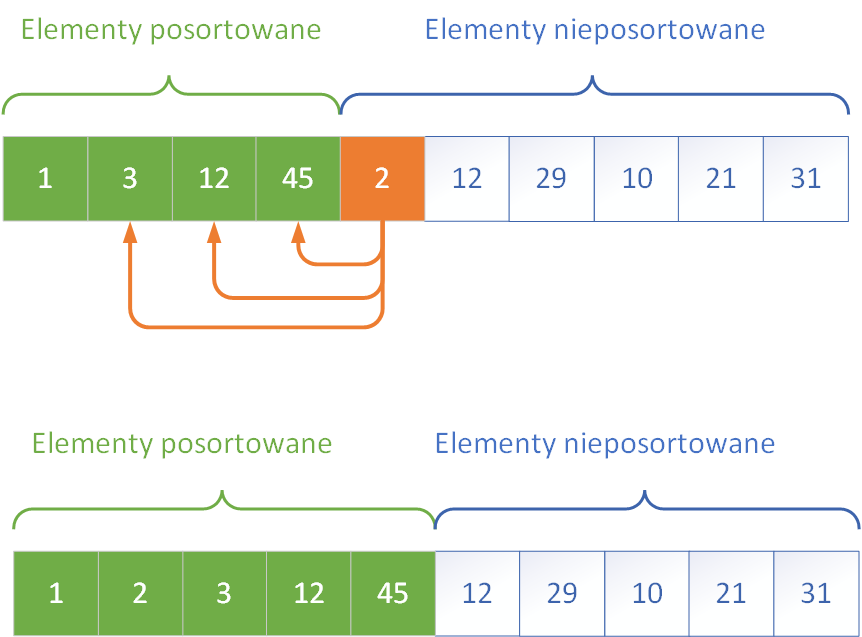
Sortowanie przez wstawianie, czyli InsertionSort, działa w sposób przypominający układanie kart w ręku podczas gry. Każdy kolejny element tablicy jest porównywany z elementami już posortowanymi i wstawiany w odpowiednie miejsce, przesuwając większe elementy w prawo. Metoda ta dobrze sprawdza się w przypadku prawie posortowanych danych, ponieważ w takim przypadku liczba przesunięć jest minimalna.

Sortowanie bąbelkowe (ang. BubbleSort)

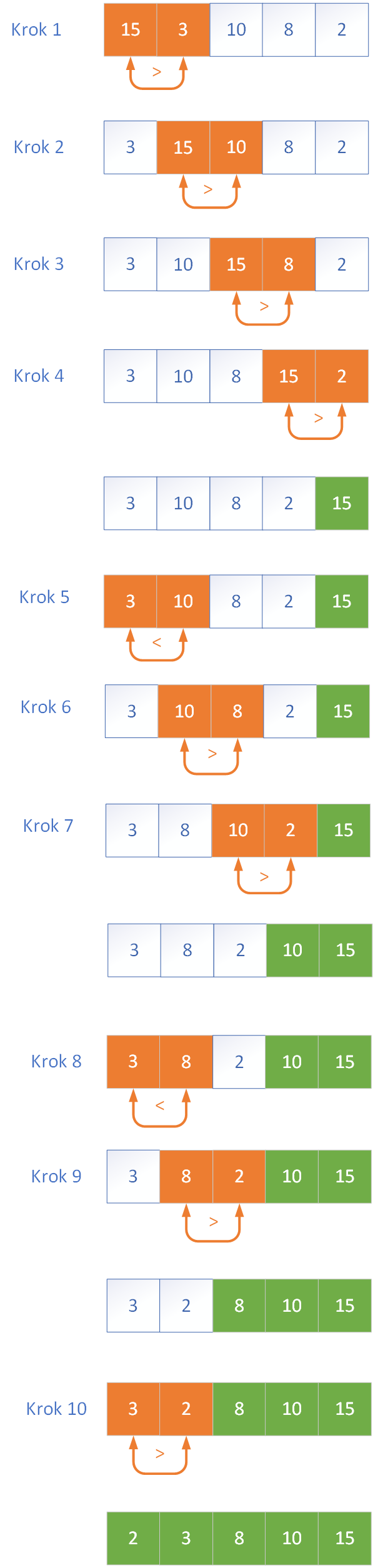
Trzecią klasyczną metodą sortowania elementarnego jest sortowanie bąbelkowe, znane jako BubbleSort. Działa ono na zasadzie porównywania sąsiadujących ze sobą elementów i zamieniania ich miejscami, jeśli znajdują się w złej kolejności. W wyniku kolejnych przebiegów największe elementy „wypływają” na koniec tablicy, stąd nazwa bąbelkowe. Choć jest to najwolniejszy z opisywanych algorytmów, jego koncepcja jest bardzo łatwa do zrozumienia i często wykorzystywana w celach edukacyjnych.

2. Sortowanie szybkie

Sortowanie szybkie, znane powszechnie pod nazwą QuickSort, to jeden z najwydajniejszych i najczęściej stosowanych algorytmów sortujących w praktyce. Został opracowany w 1960 roku przez brytyjskiego informatyka Tony'ego Hoare’a i od tego czasu zdobył ogromną popularność ze względu na swoją szybkość oraz elegancką, rekurencyjną strukturę. Mimo że w najgorszym przypadku jego złożoność czasowa wynosi O(n²), to w większości rzeczywistych zastosowań działa z wydajnością O(n log n), co czyni go bardzo skutecznym wyborem. Podstawową ideą sortowania szybkiego jest technika „dziel i zwyciężaj”. Działanie algorytmu możemy podzielić na następujące etapy:

• Etap dziel - algorytm wybiera specjalny element zwany pivotem (osią podziału), a następnie przekształca tablicę w taki sposób, że wszystkie elementy mniejsze od pivota trafiają na lewo od niego, a większe – na prawo. Dzięki temu pivot znajduje się na swojej właściwej, końcowej pozycji w tablicy, nawet jeśli pozostałe elementy nie są jeszcze uporządkowane.
• Etap zwyciężaj - po podziale na dwie podtablice – lewą i prawą względem pivota – każda z nich jest sortowana niezależnie. Etap ten przebiega rekurencyjnie: algorytm stosuje dokładnie ten sam schemat (czyli „dziel i zwyciężaj”) dla obu części aż do momentu, gdy tablice zawierają po jednym lub żadnym elemencie, co oznacza, że są już z natury posortowane.
• Etap połącz - w algorytmie QuickSort ma charakter niejawny. W przeciwieństwie do innych algorytmów opartych na tej samej strategii, takich jak sortowanie przez scalanie, QuickSort nie wymaga dodatkowego etapu łączenia. Dzięki temu, że wszystkie zamiany elementów dokonywane są bezpośrednio w tablicy T, po zakończeniu wszystkich rekurencyjnych wywołań otrzymujemy posortowaną wersję tej samej tablicy. Nie zachodzi potrzeba kopiowania danych czy tworzenia pomocniczych struktur – posortowany wynik jest po prostu efektem końcowym operacji wykonanych w miejscu.

W pierwszej kolejności pokażemy wybór środkowego elementu tablicy jako elementu rozdzielającego oraz podział na partycje

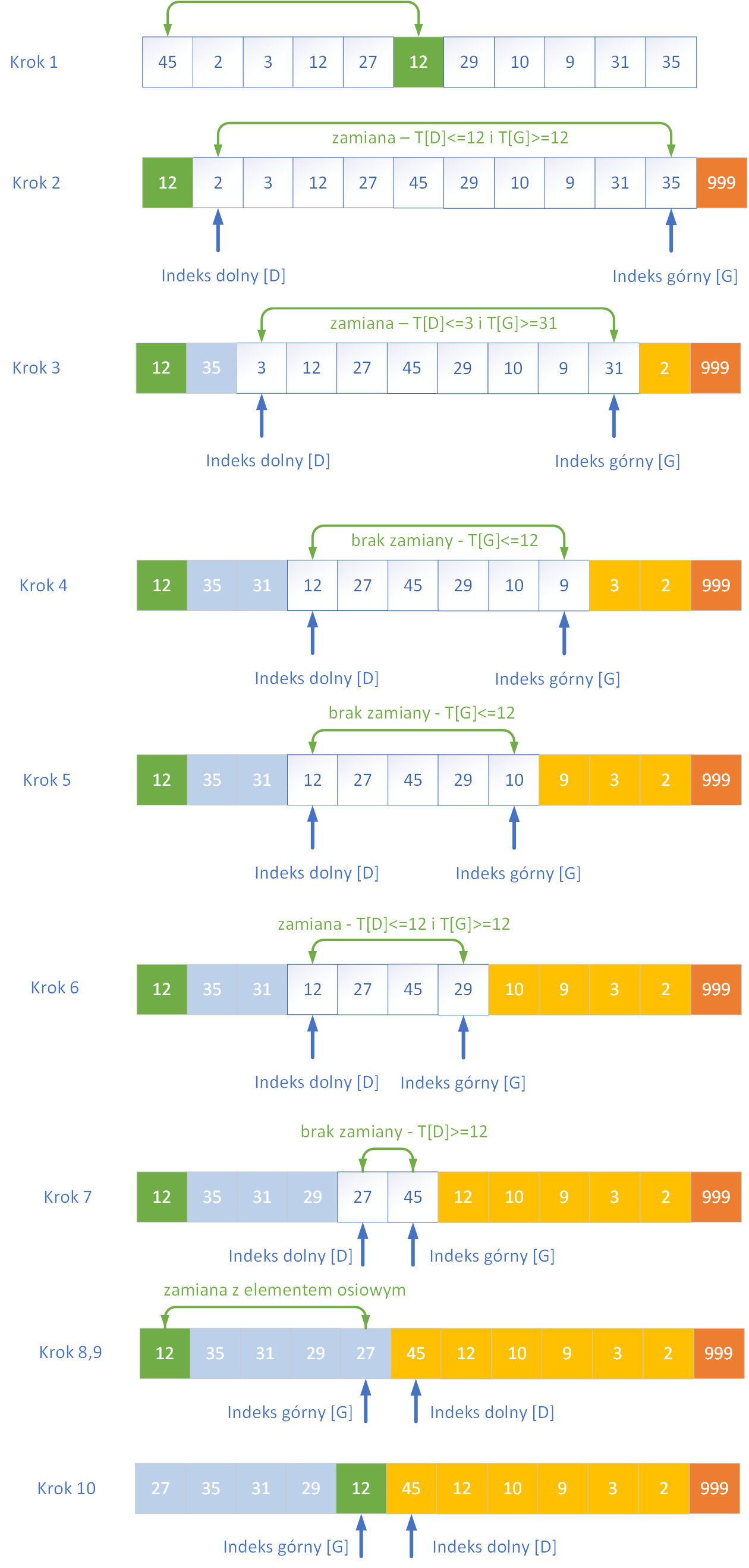
Działanie podziału przebiega według następującego schematu:

1. Wybierz element środkowy tablicy i zamień go z pierwszym elementem – stanie się on elementem osiowym (pivotem). 
2. Ustaw wskaźnik dolny na pozycji T[1], a wskaźnik górny na pozycji T[n–1].
3. W ostatniej komórce T[n] umieść wartownika – bardzo dużą wartość większą od wszystkich pozostałych elementów tablicy. 
4. Rozpocznij przesuwanie wskaźników: 
   • dolny[D] przesuwa się w prawo, górny[G] – w lewo. 
   • wskaźnik dolny[D] zatrzymuje się, gdy napotka element większy lub równy pivotowi. 
   • wskaźnik górny[G] zatrzymuje się, gdy natrafi na element mniejszy lub równy pivotowi. 
   • jeśli wskaźniki się nie minęły, zamień miejscami elementy wskazywane przez dolny i górny wskaźnik. 
5. Powtarzaj kroki do momentu, aż wskaźniki się miną (czyli dolny > górny). Gdy wskaźniki się miną, zamień element osiowy (T[0]) z elementem wskazywanym przez wskaźnik górny (T[G]). Element osiowy znajduje się teraz we właściwym miejscu, a tablica jest podzielona na dwie części gotowe do dalszego sortowania.

Po zakończeniu podziału tablicy względem elementu osiowego (pivotu), algorytm kontynuuje działanie w dwóch niezależnych częściach. QuickSort wywoływany jest rekurencyjnie dla lewej oraz prawej podtablicy powstałych po podziale. W każdej z nich ponownie wybierany jest nowy pivot i przeprowadzany jest lokalny podział. Proces ten powtarza się aż do momentu, gdy każda podtablica będzie zawierać co najwyżej jeden element – wówczas dalsze sortowanie nie jest już potrzebne. W ten sposób cała tablica zostaje posortowana, bez potrzeby dodatkowego scalania fragmentów. Poniżej przedsatwiono przykładowy kod realzujący sortowanie szybkie.

#include <iostream>
#include <vector>
using namespace std;

// Funkcja pomocnicza do zamiany elementów
void swap(int& a, int& b) {
    int temp = a;
    a = b;
    b = temp;
}

// Funkcja dzieląca tablicę – wybór pivota i podział
int partition(vector<int>& T, int left, int right) {
    int pivot = T[right]; // wybór elementu osiowego (pivot)
    int i = left - 1;

    for (int j = left; j < right; j++) {
        if (T[j] < pivot) {
            i++;
            swap(T[i], T[j]);
        }
    }

    swap(T[i + 1], T[right]); // pivot na właściwym miejscu
    return i + 1;
}

// Rekurencyjna funkcja sortująca
void quickSort(vector<int>& T, int left, int right) {
    if (left < right) {
        int pivotIndex = partition(T, left, right); // podział tablicy na partycje

        // Rekurencyjne wywołania sortujące lewą i prawą część
        quickSort(T, left, pivotIndex - 1);
        quickSort(T, pivotIndex + 1, right);
    }
}

// Pomocnicza funkcja do wypisania tablicy
void printArray(const vector<int>& T) {
    for (int x : T) {
        cout << x << " ";
    }
    cout << endl;
}

// Przykład użycia
int main() {
    vector<int> T = { 9, 3, 7, 1, 5, 8, 2, 6, 4 };

    cout << "Przed sortowaniem: ";
    printArray(T);

    quickSort(T, 0, T.size() - 1);

    cout << "Po sortowaniu: ";
    printArray(T);

    return 0;
}

3. Sortowanie przez scalanie

Sortowanie przez scalanie (ang. MergeSort) to klasyczny algorytm oparty na metodzie „dziel i zwyciężaj”. Charakteryzuje się bardzo dobrą złożonością czasową O(n log n) niezależnie od charakteru danych wejściowych, dzięki czemu znajduje zastosowanie w sytuacjach, gdzie wymagana jest przewidywalność wydajności. Sortowanie przez scalanie działa stabilnie i nieprzerwanie oraz odgrywa ważną rolę w implementacjach systemowych oraz bibliotek standardowych wielu języków programowania. Algorytm ten opiera się na dzieleniu tablicy na coraz mniejsze części, aż do momentu, gdy każda z nich zawiera tylko jeden element. Taka jednoelementowa tablica jest już posortowana, więc może być poddana scaleniu z inną. Scalanie dwóch posortowanych tablic polega na porównywaniu ich elementów i dokładaniu ich w odpowiedniej kolejności do nowej tablicy wynikowej. Ten etap gwarantuje, że z dwóch uporządkowanych części powstaje nowa, również uporządkowana całość. Poniżej na rysunku przedstawiono działanie algorytmu przez scalanie.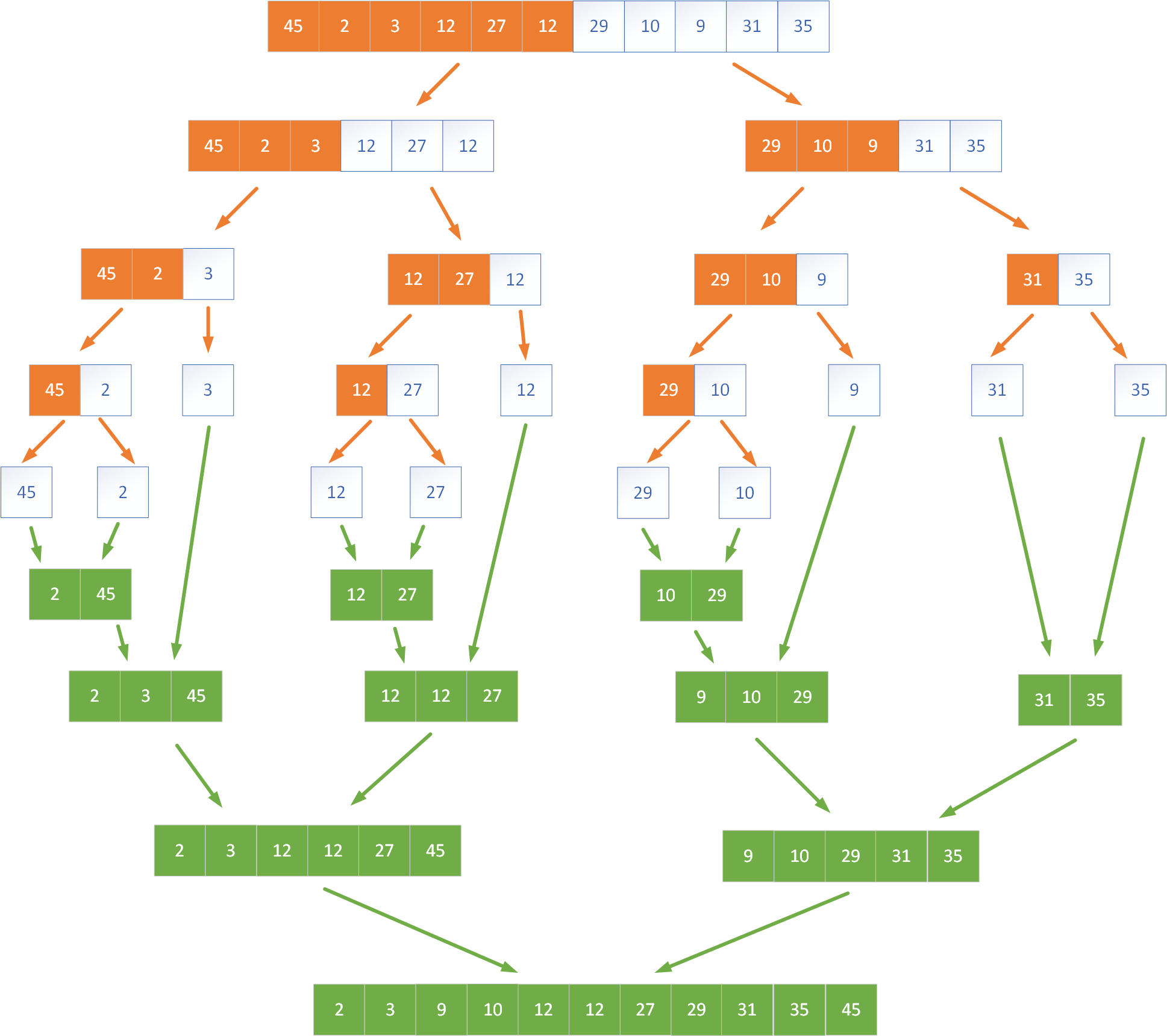


Scalenie podtablic odbywa się poprzez użycie funkcji, która w implementacjach najczęściej nosi nazwę Merge. Jej zadaniem jest przenoszenie danych z dwóch posortowanych podtablic do tablicy w taki sposób, aby otrzymać ciąg danych posortowanych. Metoda Merge tworzy pomocnice tablice, do których przepisywane są dwie podtablice, które należy scalić. Do źródłowej tablicy T przepisywane są z powrotem elementy tablic L i P – za każdym razem porównujemy ze sobą 2 najmniejsze elementy L i P, które jeszcze nie zostały przepisane do T. Wybieramy mniejszego z nich, którego należy umieścić w „dużej” tablicy, a następnie procedurę porównywania i przekazywania elementów prowadzimy do momentu „wyczerpania się” tablic L oraz P. Aby zmusić algorytm do wykorzystania wszystkich elementów ze wspomnianych tablic, używamy wartowników o dużej wartości w ostatnich komórkach tablic – dzięki temu, gdy z jednej z tablic zostaną już przepisane wszystkie elementy, nastąpi potem przepisanie reszty pozostałych elementów w drugiej tablicy do tablicy T. Poniżej przedstawiono schemat działania metody Merge w algorytmie.

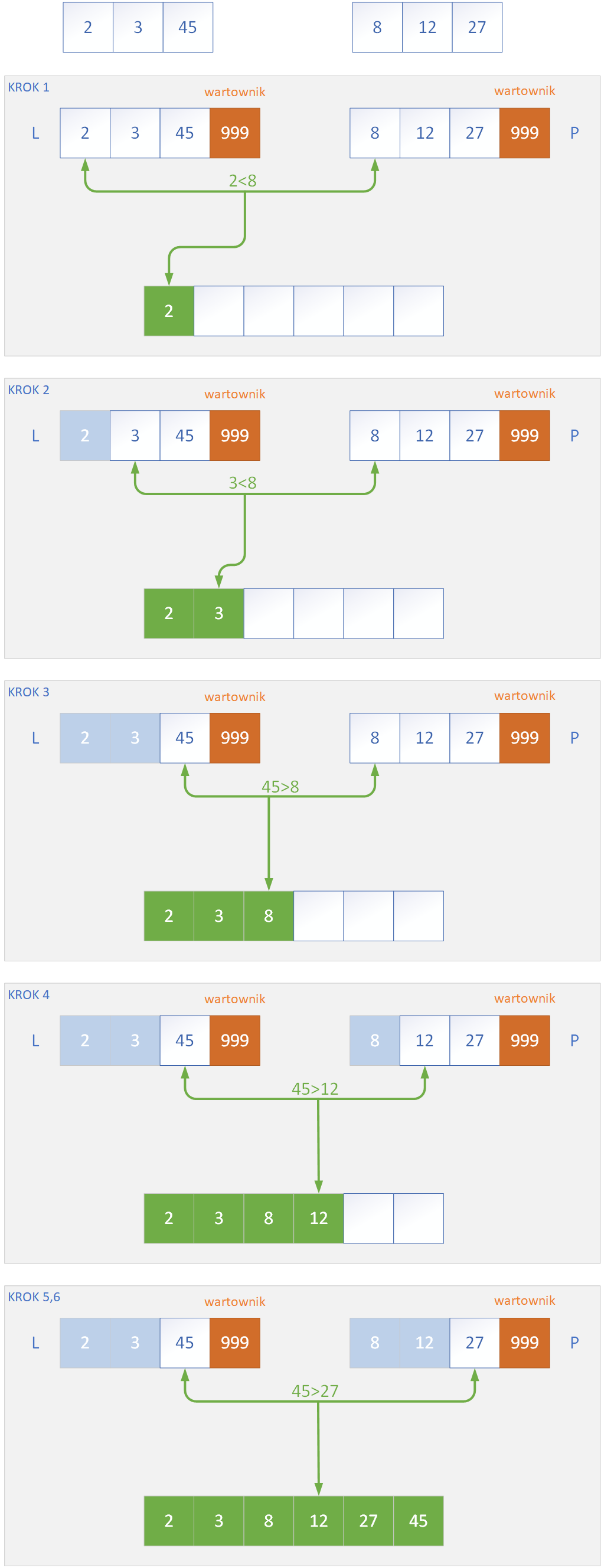
 Poniżej przedsatwiono kod w C++ do realizacji algorytmu sortowania przez scalanie.

#include <iostream>
#include <vector>
using namespace std;

void merge(vector<int>& T, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
    vector<int> L(n1), R(n2);

    for (int i = 0; i < n1; i++)
        L[i] = T[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = T[mid + 1 + j];

    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            T[k] = L[i];
            i++;
        } else {
            T[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        T[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        T[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(vector<int>& T, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(T, left, mid);
        mergeSort(T, mid + 1, right);
        merge(T, left, mid, right);
    }
}

void printArray(const vector<int>& T) {
    for (int x : T)
        cout << x << " ";
    cout << endl;
}

int main() {
    vector<int> T = { 38, 27, 43, 3, 9, 82, 10 };

    cout << "Przed sortowaniem: ";
    printArray(T);

    mergeSort(T, 0, T.size() - 1);

    cout << "Po sortowaniu: ";
    printArray(T);

    return 0;
}

4. Sortowanie kubełkowe

Sortowanie kubełkowe (ang. Bucket Sort) to algorytm sortujący, który opiera się na założeniu, że dane wejściowe są równomiernie rozłożone na pewnym przedziale wartości. Zamiast porównywać elementy między sobą, jak w klasycznych metodach sortowania, algorytm ten dzieli dane na grupy zwane kubełkami (ang. buckets), a następnie sortuje każdy kubełek osobno i łączy ich zawartość w jeden uporządkowany ciąg. Działanie algorytmu rozpoczyna się od podzielenia przestrzeni możliwych wartości na określoną liczbę przedziałów. Każdy z tych przedziałów reprezentuje osobny kubełek, do którego trafiają elementy spełniające odpowiedni warunek – na przykład wartości mieszczące się w danym zakresie. Po przydzieleniu wszystkich elementów do odpowiednich kubełków, każdy z nich jest sortowany osobno, zwykle za pomocą prostych metod, takich jak sortowanie przez wstawianie. Na koniec zawartość kubełków jest scalana w jedną uporządkowaną tablicę. Algorytm ten najlepiej sprawdza się w przypadku danych rzeczywistych (np. liczb zmiennoprzecinkowych z przedziału [0, 1)), których rozkład jest stosunkowo równomierny. W idealnych warunkach, gdy dane rozkładają się równomiernie, sortowanie kubełkowe może osiągnąć złożoność czasową O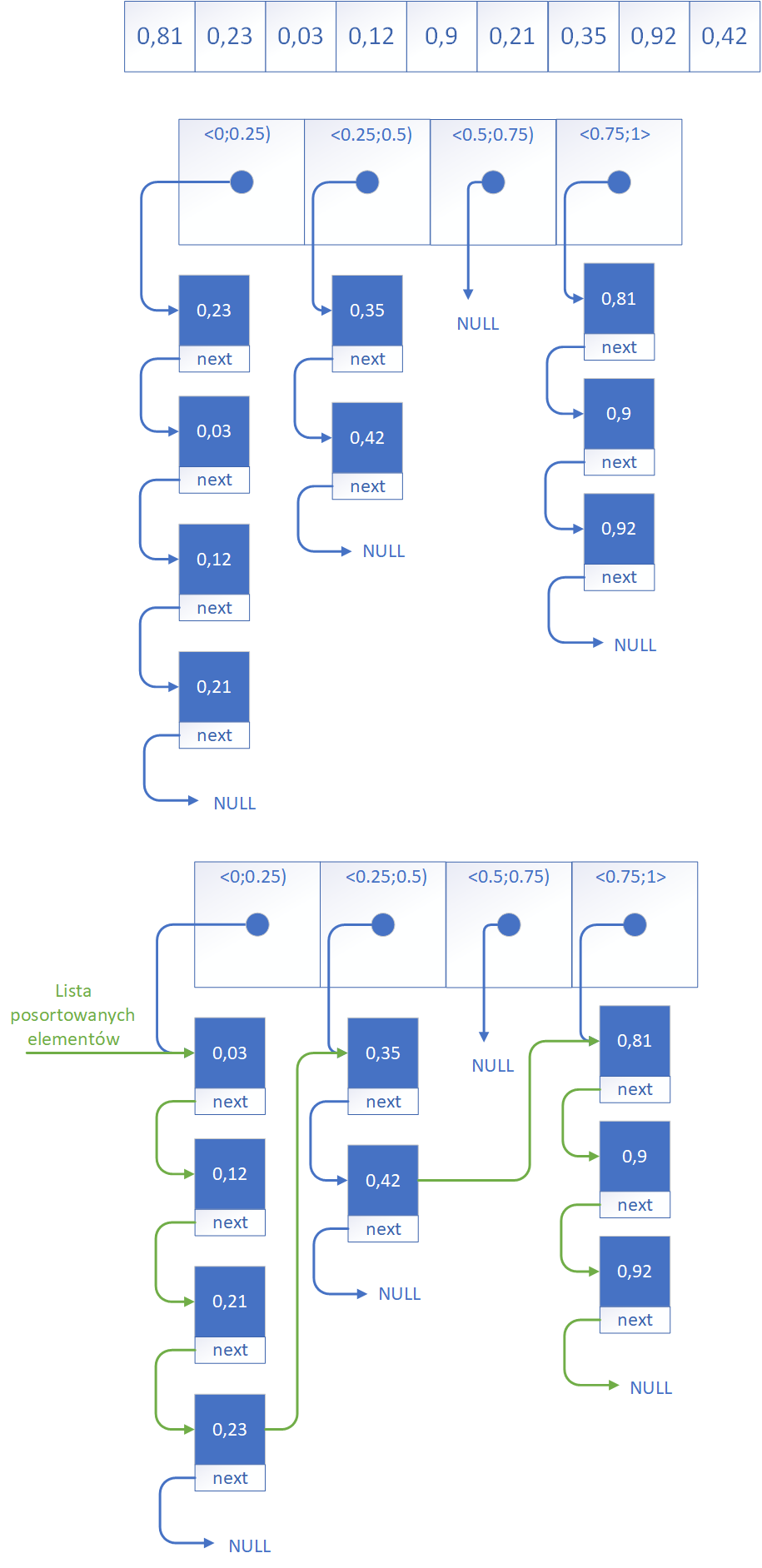. Jednak w mniej korzystnych przypadkach – na przykład gdy wszystkie dane trafią do jednego kubełka – wydajność może spaść nawet do O(n²), jeśli wewnątrz kubełków użyjemy sortowania elementarnego.
Poniżej na rysunku zostanie przedstawiony przykład działania sortowania kubełkowego dla tablicy liczb rzeczywistych z przedziału <0;1>. Zdecydowano się podzielić zakres na następujące podprzedziały oznaczające kubełki: <0;0.25), <0.25;0.5), <0.5;0.75), <0.75;1>.

Działanie algorytmu możemy prześledzić na przykładzie rysunkowym. Składa się z następujących etapów:

• Podział przedziału liczbowego na m równych części (kubełków) - na samym początku algorytm określa zakres wartości, w którym mieszczą się wszystkie dane wejściowe. Jest to wymagane aby nie pominąć żadnej wartości. Zakres jest następnie dzielony na m równych podprzedziałów. Każdy z tych podprzedziałów stanowi osobny kubełek (ang. bucket), do którego trafią elementy należące do danego fragmentu zakresu. Wybór liczby kubełków oraz sposobu podziału zależy od charakteru danych i ma wpływ na efektywność sortowania.
• Przenoszenie elementów do odpowiednich kubełków - następnie każdy element ze zbioru danych jest analizowany pod względem swojej wartości i umieszczany w odpowiednim kubełku. W podprzedziale, do którego należy. Na przykład liczba 0,34 trafi do kubełka obejmującego przedział <0.25; 0.5). Proces ten przypomina klasyfikowanie elementów według ich przybliżonego położenia w uporządkowanej tablicy. Każdy kubełek zawiera wskaźnik na początek listy w której znajdują się wartości do niego należące.
• Sortowanie elementów wewnątrz każdego kubełka - po dokonaniu podziału danych do kubełków, każdy z nich może zawierać kilka elementów, które należy jeszcze uporządkować. Wewnątrz każdego kubełka stosuje się zazwyczaj prosty i szybki algorytm sortujący, taki jak sortowanie przez wstawianie (ang. Insertion Sort), ponieważ liczba elementów w pojedynczym kubełku jest zwykle niewielka. Ten krok zapewnia, że każdy kubełek będzie lokalnie posortowany.
• Scalanie zawartości kubełków w jedną strukturę wynikową - ostatni krok polega na połączeniu wszystkich posortowanych kubełków w jednej strukturze wynikowej. Kubełki są scalane w kolejności odpowiadającej ich zakresom, czyli od najmniejszego do największego. Dzięki temu, że każdy kubełek zawiera elementy z określonego fragmentu całego zakresu, a jego zawartość została wcześniej uporządkowana, scalona tablica jest już w pełni posortowana. Nie ma potrzeby wykonywania dodatkowego sortowania po złączeniu zawartości kubełków. Należy połączyć wszystkie listy w jedną posortowaną listę wartości.

5. Sterty i sortowanie kopcowe

Sterta (ang. heap) to specjalna struktura danych w postaci drzewa binarnego, która spełnia warunek porządku kopca. Oznacza to, że w kopcu maksymalnym (ang. max-heap) każdy rodzic ma wartość większą lub równą swoim dzieciom, natomiast w kopcu minimalnym (ang. min-heap) każdy rodzic ma wartość mniejszą lub równą swoim dzieciom. Dzięki tej właściwości sterta pozwala w bardzo krótkim czasie zidentyfikować element o największym lub najmniejszym priorytecie, co czyni ją idealną podstawą do implementacji kolejki priorytetowej. 

Jednym z podstawowych typów struktur danych są właśnie kolejki priorytetowe, które przechowują elementy zbioru, na którym zdefiniowana jest relacja porządku. Każdemu elementowi przypisuje się klucz (priorytet), według którego ustalana jest kolejność operacji. W przeciwieństwie do zwykłej kolejki, gdzie elementy są usuwane w kolejności ich wstawienia (FIFO), w kolejce priorytetowej elementy są zdejmowane na podstawie wartości klucza. Wyróżniamy dwa główne typy takich kolejek: kolejki typu max, gdzie usuwany jest element o największym priorytecie, oraz kolejki typu min, w których priorytet ma wartość najmniejsza.

Kolejka priorytetowa musi być zaimplementowana w taki sposób, aby można było wykonywać na niej niżej wymienione operacje:

• Insert(S, x) – wstawienie elementu x do kolejki S
• FindMax(S) – poszukiwanie w kolejce S elementu o największym kluczu; funkcja zwraca ten element jako wynik
• DelMax(S) – usunięcie z kolejki S elementu o największym kluczu; funkcja zwraca ten element jako wynik

Choć kolejkę priorytetową można zaimplementować w oparciu o listę lub tablicę, to jednak takie rozwiązania są nieefektywne, zwłaszcza przy dużych zbiorach danych. Zdecydowanie lepszą alternatywą jest wykorzystanie struktury sterty, która pozwala na wykonywanie operacji w czasie logarytmicznym względem liczby elementów. Sterta jest najczęściej implementowana w formie tablicy, w której dla każdego elementu o indeksie i jego lewy potomek znajduje się na pozycji 2i + 1, a prawy potomek na pozycji 2i + 2. Dzięki temu możliwa jest efektywna nawigacja po strukturze bez potrzeby tworzenia jawnych węzłów drzewa. Ta reprezentacja umożliwia również przekształcenie dowolnej tablicy w stertę w czasie liniowym. W literaturze anglojęzycznej częściej wykorzystuje się pojęcie kopiec (ang. Heap). Są to pojęcia tożsame i można nazw używać zamiennie. Na rysunku poniżej przedstawiono przykładowy kopiec wraz z deklaracją w postaci tablicy jednowymiarowej.


Jeżeli na danym poziomie wszystkie miejsca są zapełnione oznacza to że drzewo jest pełne na danym poziomie. Jedynie ostatni poziom może nie być wypełniony do końca. Widzimy też, że kopiec jest często implementowany jako tablica jednowymiarowa, w której elementy drzewa binarnego zapisywane są kolejno w taki sposób, by zachować zależności rodzic–dziecko. Dzięki temu możliwe jest odwzorowanie struktury drzewa bez użycia wskaźników, a dostęp do poszczególnych węzłów oraz ich potomków może być realizowany za pomocą prostych obliczeń indeksów. Mianowicie, jeśli interesujący nas węzeł znajduje się w tablicy pod indeksem i, to:

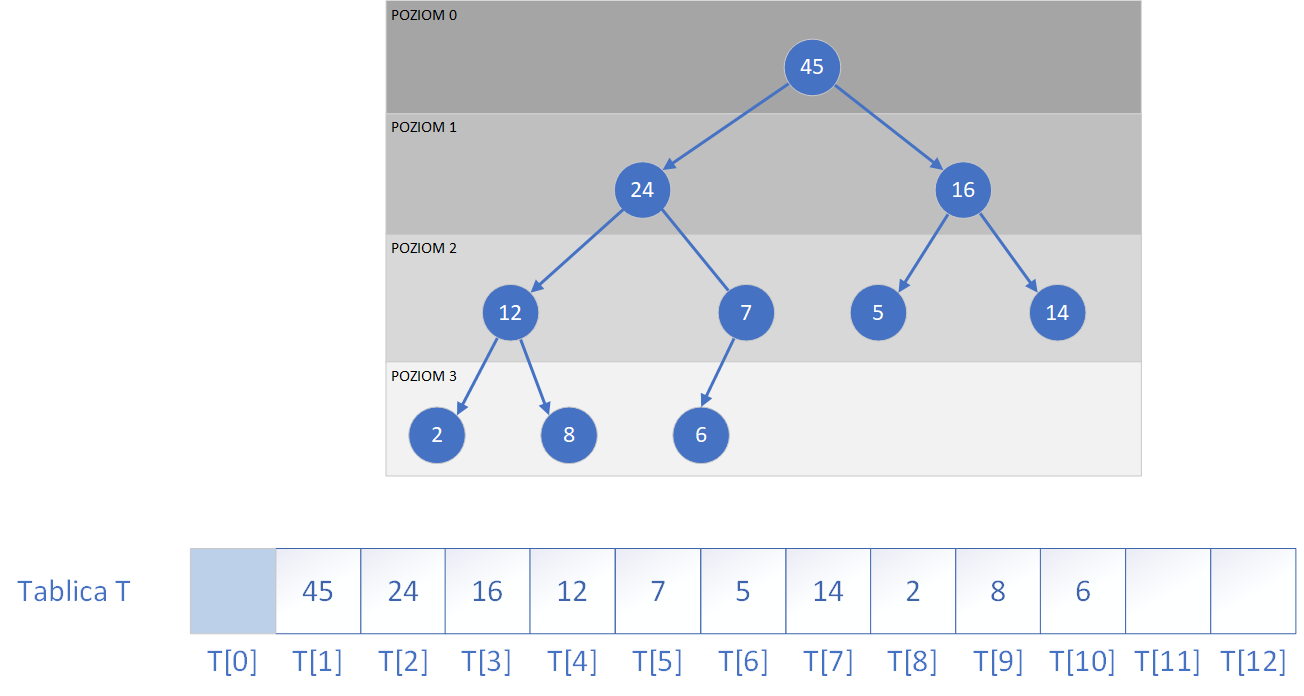
•  indeks jego ojca (rodzica) to ⌊i / 2⌋, czyli część całkowita z połowy wartości i (dla i > 1), 
•  indeks lewego potomka wynosi 2 * i, 
•  indeks prawego potomka wynosi 2 * i + 1.

Dzięki tej właściwości, poruszanie się po strukturze drzewa zaimplementowanej jako tablica jest bardzo szybkie i nie wymaga stosowania złożonych struktur danych. W praktyce indeksowanie zaczyna się najczęściej od i = 1 (pomijając komórkę 0) w celu uproszczenia obliczeń, choć w niektórych implementacjach używa się również indeksowania od 0, z odpowiednio przesuniętymi wzorami.
Dzięki wykorzystaniu tej definicji możemy skonstruować algorytm, który będzie sortował wartości w tablicy. Wiemy, że zawsze w korzeniu drzewa kopca będzie przechowywana największa wartość. Jeżeli będziemy pobierać za każdym razem korzeń drzewa i umieszczać w tablicy posortowanych liczb to otrzymamy algorytm sortowania przez kopcowanie. Oczywiście brakuje nam jeszcze wiedzy w jaki sposób po pobraniu wartości korzenia drzewa przywrócić ponownie jego własności. Jednym z mechanizmów utrzymujących strukturę sterty jest metoda przywracania własności kopca (ang. heapify). Jej zadaniem jest upewnienie się, że poddrzewo o korzeniu na danym indeksie i spełnia warunek kopca. W przypadku kopca maksymalnego oznacza to, że element znajdujący się na pozycji i powinien być nie mniejszy niż jego dzieci. Jeżeli warunek ten nie jest spełniony, to element i należy zamienić z większym z jego dwóch synów, co powoduje tzw. „spłynięcie w dół” (ang. sift down) danego elementu w hierarchii drzewa. Po takiej zamianie konieczne jest sprawdzenie poprawności struktury dla nowego położenia tego elementu, czyli rekursywne wywołanie funkcji dla odpowiedniego poddrzewa.

// Funkcja przywracająca własność kopca dla poddrzewa o korzeniu i
void heapify(vector<int>& T, int n, int i) {
    int largest = i;            // Zakładamy, że korzeń jest największy
    int left = 2 * i + 1;       // Indeks lewego dziecka
    int right = 2 * i + 2;      // Indeks prawego dziecka

    // Jeśli lewe dziecko jest większe niż korzeń
    if (left < n && T[left] > T[largest])
        largest = left;

    // Jeśli prawe dziecko jest większe niż największy dotąd
    if (right < n && T[right] > T[largest])
        largest = right;

    // Jeśli największy nie jest korzeniem, zamień i kontynuuj
    if (largest != i) {
        swap(T[i], T[largest]);
        heapify(T, n, largest);  // Rekurencyjnie przywracaj własność kopca
    }
}

Widzimy, że w przykładowej implementacji rekurencyjnie wywoływana jest funkcja przywracania własności kopca. Proces ten jest powtarzany aż do momentu, gdy żadne dalsze zamiany nie będą potrzebne i kopiec odzyska swoją właściwość.

// Pobiera największy element z kopca (korzeń) i przywraca strukturę
int extractMax(vector<int>& heap, int& size) {
    if (size <= 0) throw out_of_range("Sterta jest pusta.");

    int maxElement = heap[0];  // największy element (korzeń)

    heap[0] = heap[size - 1];  // przenosimy ostatni element na początek
    size--;                    // zmniejszamy rozmiar kopca

    heapify(heap, size, 0);    // przywracamy własność kopca od korzenia

    return maxElement;
}

Poniżej przedstawiono przykład rysunkowy pobierania wartości maksymalnej z drzewa, a więc jego korzenia.

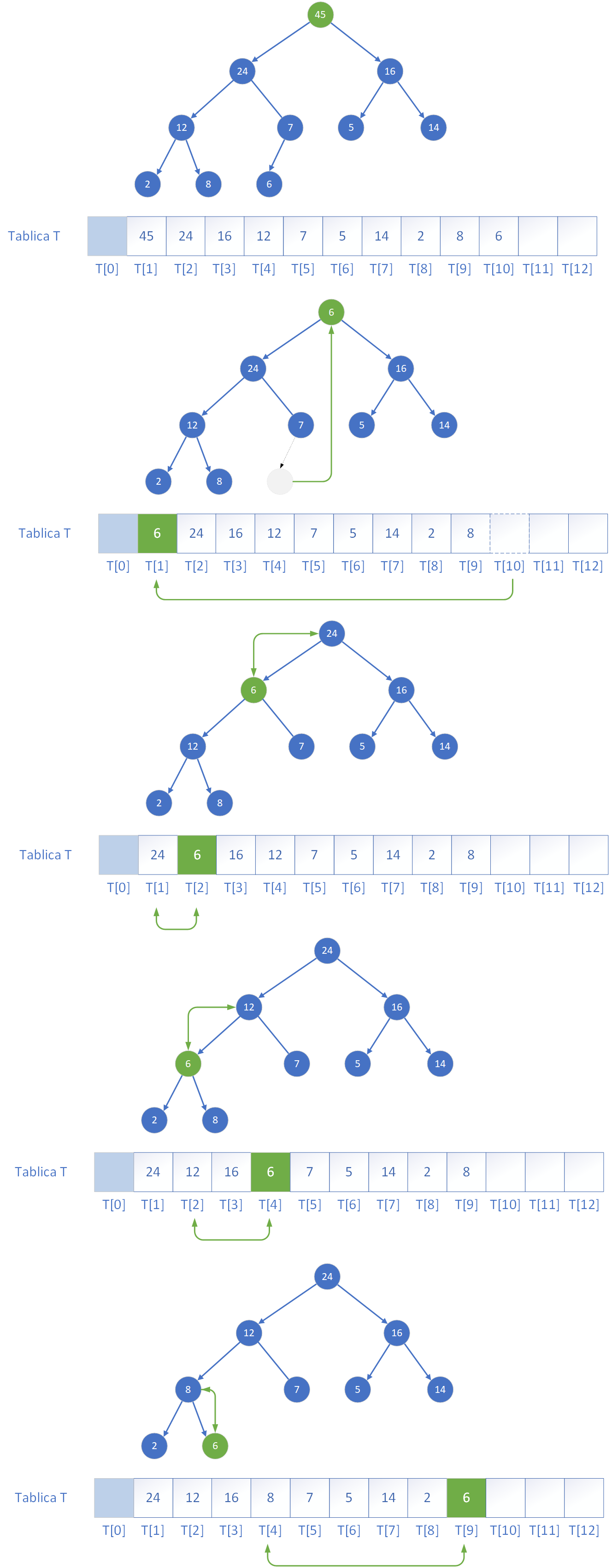
Kolejną metodą przydatną do operowania na kopcu jest dodawanie do niego elementów. Dodawanie nowego elementu do kolejki priorytetowej opartej na kopcu maksymalnym polega na wstawieniu go jako nowego liścia na najniższym, najbardziej prawym wolnym miejscu w drzewie (czyli na końcu tablicy reprezentującej stertę). Jednak po takim dodaniu własność kopca może być naruszona, jeśli nowy element ma większy klucz niż jego ojciec. W takiej sytuacji należy przywrócić poprawną strukturę kopca poprzez tzw. „wynurzanie się” elementu – czyli przesuwanie go w górę drzewa przez zamiany z jego rodzicem aż do momentu, gdy znajdzie się w odpowiednim miejscu (lub zostanie korzeniem). Ten proces można przeprowadzić na dwa sposoby:

void insert(vector<int>& heap, int& size, int value) {
    size++;
    int i = size - 1;
    heap[i] = value;

    while (i > 0 && heap[i] > heap[(i - 1) / 2]) {
        swap(heap[i], heap[(i - 1) / 2]);
        i = (i - 1) / 2;
    }
}

W innej wersji nie zamieniamy elementów tylko przesuwamy ojców w dół. Gdy znajdziemy odpowiednie miejsce, wpisujemy nowy element w ostatnim kroku. W praktyce ta metoda może być szybsza, ponieważ zmniejsza liczbę operacji kopiowania danych.

void insert(vector<int>& heap, int& size, int value) {
    size++;
    int i = size - 1;

    // Znalezienie miejsca na nowy element przez przesuwanie ojców w dół
    while (i > 0 && value > heap[(i - 1) / 2]) {
        heap[i] = heap[(i - 1) / 2];
        i = (i - 1) / 2;
    }
    heap[i] = value;
}

Poniżej przedstawiono przykład rysunkowy pokazujący wstawienie nowej wartości do kopca oraz przywróceniu jego własności.

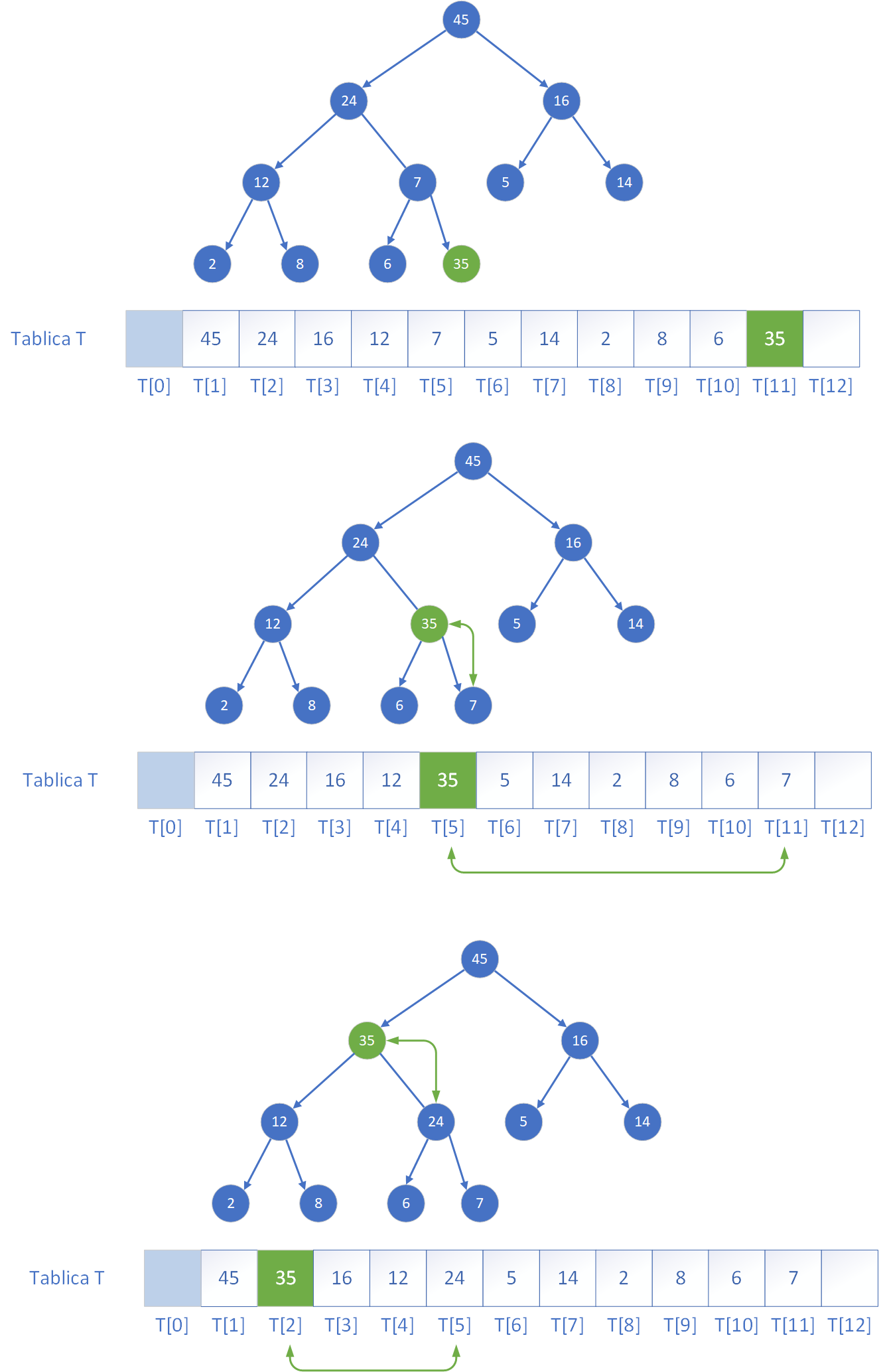
Skoro poznaliśmy już procedurę przywracania własności kopca, możemy przejść do pytania, w jaki sposób zbudować stertę z danych znajdujących się w tablicy, o których nic nie wiemy – to znaczy danych, które nie są w żaden sposób uporządkowane i nie spełniają warunku kopca. Co istotne, elementy tablicy tworzą logicznie strukturę drzewa binarnego, lecz bardzo rzadko jest ona od razu stertą. Aby utworzyć poprawną strukturę kopca, należy zadbać o to, by każde z poddrzew tej struktury spełniało własność kopca – a więc by każdy węzeł był większy (w przypadku kopca maksymalnego) od swoich dzieci. Pomysł polega na zastosowaniu metody przywrocWlasnoscKopca (heapify) dla każdego węzła wewnętrznego, zaczynając od najniższego poziomu drzewa, aż po korzeń. Ponieważ liście są już jednoelementowymi drzewami, które z definicji są kopcami, nie wymagają przetwarzania. Dlatego wystarczy rozpocząć od ostatniego węzła, który posiada dzieci, czyli od indeksu ⌊n/2⌋ − 1 (gdzie n to liczba elementów w tablicy), i wykonywać heapify w kolejnych krokach dla wszystkich poprzedzających go indeksów, aż do 0. W ten sposób, przekształcając najpierw najmniejsze poddrzewa, a następnie coraz większe, aż do całego drzewa, otrzymujemy strukturę spełniającą warunek kopca. Poniżej zamieszczony jest kod C++ do budowy kopca z tablicy zawierające liczby w dowolnej kolejności.

// Buduje kopiec maksymalny z nieuporządkowanej tablicy
void buildMaxHeap(vector<int>& T) {
    int n = T.size();

    // Wywołujemy heapify od ostatniego rodzica do korzenia
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(T, n, i);
    }
}

Po zdefiniowaniu podstawowych operacji na kopcu możemy przejść do sortowania przez kopcowanie. Sortowanie kopcowe to algorytm sortowania oparty na strukturze kopca, który działa w dwóch głównych fazach. W pierwszej fazie, z danych wejściowych zapisanych w tablicy T, budowany jest kopiec maksymalny. Oznacza to, że największy element zbioru trafia na początek tablicy, czyli do korzenia kopca. W drugiej fazie rozpoczyna się właściwe sortowanie. Największy element, znajdujący się w korzeniu, zostaje zamieniony miejscami z ostatnim elementem kopca (czyli z węzłem o największym indeksie). W ten sposób największy element „odpada” z kopca i trafia na ostateczne miejsce w tablicy wynikowej. Następnie rozmiar kopca zostaje logicznie zmniejszony o 1, a na pozostałej części tablicy ponownie przywracana jest własność kopca. Proces ten – polegający na pobieraniu największego elementu z kopca i umieszczaniu go na końcu – jest wykonywany iteracyjnie aż do momentu, gdy w kopcu pozostaną tylko dwa elementy. Wówczas wystarczy ostatnia zamiana miejsc między nimi, aby cała tablica była już w pełni posortowana w porządku rosnącym. Algorytm ten nie wymaga dodatkowej pamięci, działa w miejscu, a jego złożoność czasowa wynosi O(n log n) niezależnie od danych wejściowych.

6. Przeszukiwanie liniowe i binarne

W różnych zastosowaniach informatycznych pojawia się konieczność wyszukania określonego elementu w zbiorze danych. Jest to problem, który występuje bardzo często oraz istnieje bardzo różnych metod poszukiwania danego elementu w zbiorze danych. W zależności od tego, czy dane są uporządkowane, oraz od oczekiwanej wydajności, można zastosować różne metody przeszukiwania. Dwiema najbardziej podstawowymi i jednocześnie powszechnie używanymi metodami są przeszukiwanie liniowe i przeszukiwanie binarne.

Przeszukiwanie liniowe (sekwencyjne) jest jedną z najprostszych metod znajdowania elementu w danym zbiorze. Polega ono na przeglądaniu elementów jeden po drugim, od początku do końca tablicy, aż do momentu odnalezienia poszukiwanej wartości lub zakończenia całego przeglądu. Metoda ta nie wymaga żadnego wcześniejszego uporządkowania danych i może być stosowana do dowolnych zbiorów – zarówno uporządkowanych, jak i nieuporządkowanych. Jego wadą jest jednak niska wydajność w przypadku dużych zbiorów, ponieważ w najgorszym przypadku konieczne jest sprawdzenie każdego elementu. Złożoność czasowa tej metody wynosi O. Algorytm ten możemy zrealizować przy pomocy bardzo prostego kodu aplikacji: 

#include <iostream>
#include <vector>
using namespace std;

int linearSearch(const vector<int>& T, int value) {
    for (int i = 0; i < T.size(); ++i) {
        if (T[i] == value) return i; // Zwracamy indeks znalezionego elementu
    }
    return -1; // Element nie został znaleziony
}

Znacznie szybszą metodą, ale działającą wyłącznie na zbiorach uporządkowanych, jest przeszukiwanie binarne. Nie przeszukuje ona danych sekwencyjnie lecz, wykorzystując fakt uporządkowania tablicy, dzieli ją na pół w każdym kroku. Na początku porównuje szukany element ze środkowym elementem tablicy. Jeśli jest mniejszy to poszukiwania kontynuowane są w lewej połowie, jeśli większy to w prawej. Proces ten jest powtarzany rekurencyjnie lub iteracyjnie, aż do odnalezienia szukanego elementu lub zawężenia obszaru poszukiwań do pustego przedziału. Przeszukiwanie binarne jest bardzo wydajne – jego złożoność czasowa wynosi O(log n) – ale, co istotne, wymaga wcześniejszego posortowania danych, co w pewnych sytuacjach może stanowić dodatkowy koszt. Poniżej przedstawiono przykładowy kod wyszukiwania binarnego:

#include <iostream>
#include <vector>
using namespace std;

int binarySearch(const vector<int>& T, int value) {
    int left = 0;
    int right = T.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (T[mid] == value) return mid;        // Zwracamy indeks
        else if (T[mid] < value) left = mid + 1;
        else right = mid - 1;
    }

    return -1; // Element nie został znaleziony
}

Dodatkowe informacje

Inną ciekawą metodą wyszukiwania elementów w zbiorze jest wykorzystanie algorytmów haszujących. Algorytmy haszujące (ang. hashing algorithms) to grupa technik umożliwiających szybkie odnajdywanie danych w zbiorach poprzez bezpośrednie obliczanie ich lokalizacji za pomocą funkcji haszującej. Zamiast przeszukiwać zbiór element po elemencie (jak w przeszukiwaniu liniowym) lub dzielić go na części (jak w przeszukiwaniu binarnym), algorytmy haszujące wyznaczają indeks tablicy, w którym dany element powinien się znajdować, a następnie sprawdzają tylko to miejsce. Podstawą działania tego typu algorytmów jest funkcja haszująca to specjalna funkcja matematyczna, która dla danego klucza (np. liczby, tekstu, obiektu) wylicza wartość całkowitą z określonego zakresu, odpowiadającą pozycji w tablicy. Jeśli dwa różne klucze dają ten sam wynik (co nazywa się kolizją), system musi je odpowiednio obsłużyć, np. przez zastosowanie listy jednokierunkowej w danym indeksie (tzw. łańcuchowanie) lub przez przeszukiwanie kolejnych komórek (ang. open addressing). Hashowanie jest bardzo efektywne w typowych zastosowaniach czas dostępu do elementu jest stały, czyli O(1). Dla porównania, przeszukiwanie binarne wymaga danych posortowanych i wykonuje O(log n) porównań.

7. Przeszukiwanie tekstów

Przeszukiwanie tekstów stanowi jedno z fundamentalnych zagadnień algorytmicznych. Występuje bardzo często w różnych zastosowaniach informatycznych. Polega ono na odnalezieniu wystąpień określonego wzorca (ciągu znaków) w dłuższym tekście. Problem ten występuje w wielu zastosowaniach np. w edytorach tekstu, czy wyszukiwarkach internetowych. Często stawiamy sobie pytanie: czy zadany ciąg znaków (wzorzec) występuje w tekście, a jeśli tak to gdzie? Najprostszym podejściem do tego problemu jest metoda naiwna, w której przesuwamy wzorzec znak po znaku przez tekst i porównujemy go z odpowiadającym fragmentem tekstu. Poniżej przedstawiono kod aplikacji realizujący taki naiwny algorytm wyszukiwania wzorców. Tego typu podejście często nazywane jest szukanie metodą Brute Force (czyli naiwną).

int szukajBRF(const string& tekst, const string& wzorzec) {
    int n = tekst.length();
    int m = wzorzec.length();

    for (int i = 0; i <= n - m; ++i) {
        int j = 0;
        while (j < m && tekst[i + j] == wzorzec[j]) {
            j++;
        }
        if (j == m) return i; // znaleziono wzorzec w pozycji i
    }

    return -1; // nie znaleziono
}

Jak możecie się domyślić tego typu podejście jest mało efektywne w przypadku długich tekstów oraz wzorców. Złożoność czasowa tego algorytmu w najgorszym przypadku wynosi O(n·m), gdzie n to długość tekstu, a m – długość wzorca.

Z tego powodu zostały opracowane inne bardziej efektywne metody wyszukiwania wzorców w tekście np. algorytm Knutha-Morrisa-Pratta (KMP). Dzięki wcześniejszemu przetworzeniu wzorca pozwala uniknąć niepotrzebnych porównań. Wzorzec jest analizowany i na podstawie jego struktury tworzona jest tzw. tablica prefiksowa, dzięki której możliwe jest pomijanie niektórych znaków tekstu bez ponownego przeszukiwania. Algorytm KMP działa w czasie O(n + m).

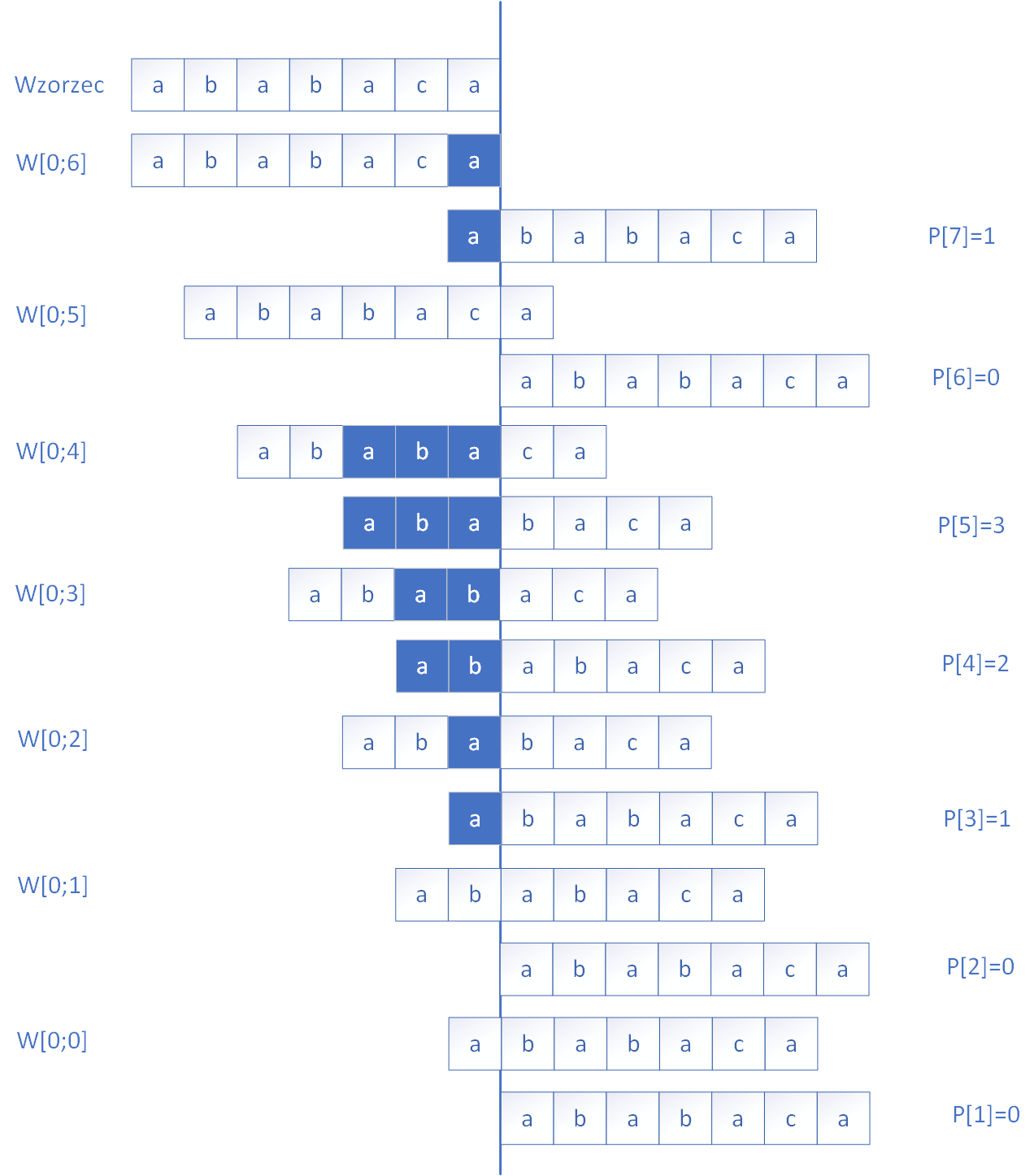
Podstawą algorytmu jest tzw. tablica P, która dla każdej pozycji i wzorca w[0..i] zawiera informację o długości najdłuższego prefiksu wzorca, który jest jednocześnie sufiksem tego fragmentu. Tablica ta pozwala algorytmowi "wiedzieć", ile początkowych liter wzorca można zachować po niezgodności, bez potrzeby rozpoczynania porównywania od początku. Budowa tej tablicy polega na porównywaniu kolejnych liter wzorca z jego początkiem i, jeśli występują dopasowania, zapisywaniu ich długości. W przypadku niezgodności algorytm cofa się w tablicy P, szukając krótszego dopasowania. Poniżej na rysunku zademonstrowano sposób wyznaczenia tablicy P dla przykładowego wzorca.

Po zbudowaniu tablicy prefiksowej P algorytm przystępuje do właściwego przeszukiwania tekstu. Wskaźnik i porusza się po tekście, a wskaźnik j – po wzorcu. Jeśli t[i] == w[j], porównywanie postępuje. W przypadku niezgodności KMP nie wraca w tekście, lecz sprawdza tablicę prefiksową i przesuwa wskaźnik j we wzorcu do pozycji podanej przez P[j−1], co pozwala natychmiast wznowić porównywanie od miejsca, gdzie znów istnieje potencjalna zgodność. Poniżej na przykładzie rysunkowym przedstawiono działanie algorytmu KMP dla przykładowego tekstu:

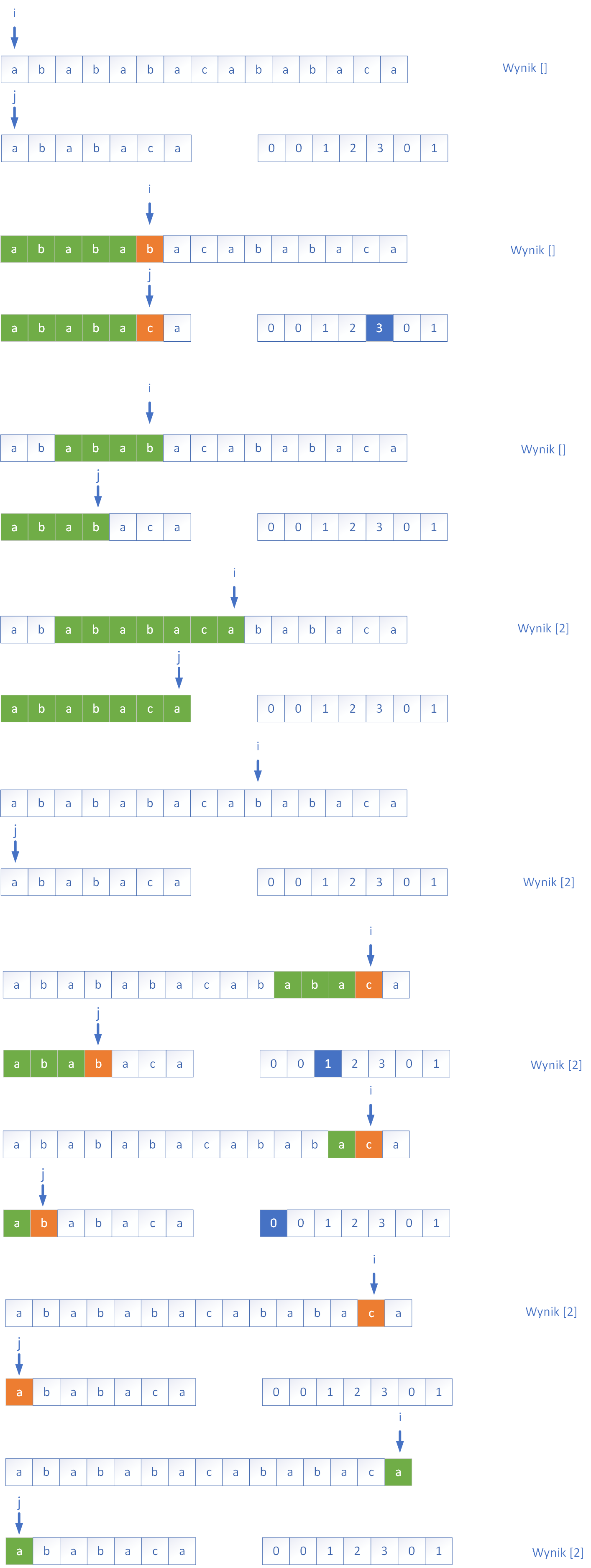
W przykładzie znaleziono tylko jedno miejsce o indeksie 2 w którym powtarza się szukany wzorzec.