Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 3. Drzewa |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | środa, 14 stycznia 2026, 22:24 |
Opis
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
1. Drzewa binarnego wyszukiwania (BST)
Bardzo ważną oraz często wykorzystywaną strukturą danych jest drzewo binarne. Jest to struktura hierarchiczna, w której każdy węzeł może mieć co najwyżej dwóch potomków. Zazwyczaj określa się ich jako lewy i prawy syn. Węzeł, który nie posiada żadnego potomka, nazywany jest liściem drzewa, natomiast węzeł bez poprzednika to korzeń drzewa. Drzewa binarne są powszechnie stosowane w wielu dziedzinach, m.in. w algorytmach sortowania, wyszukiwania, kompresji danych (np. drzewa Huffmana) czy w systemach plików. Dzięki hierarchicznej budowie pozwalają na efektywną organizację i przeszukiwanie danych.Drzewa binarne mogą być:
- pełne – jeśli każdy węzeł ma 0 lub 2 dzieci,
- zupełne – jeśli wszystkie poziomy są zapełnione, oprócz ewentualnie ostatniego, który jest wypełniany od lewej,
- zrównoważone – gdy różnica wysokości lewego i prawego poddrzewa dla każdego węzła nie przekracza określonego limitu.
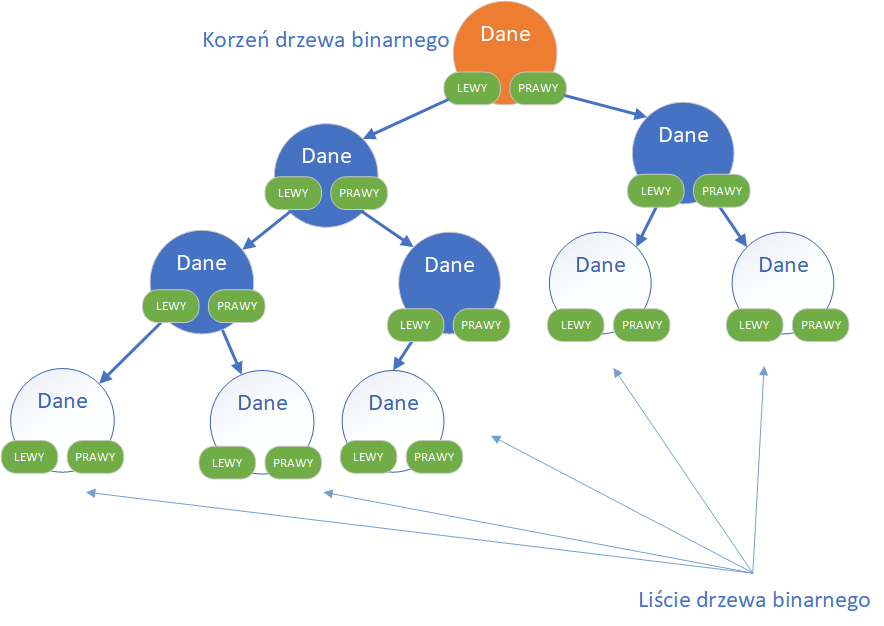
Każdy węzeł zawiera pole do przechowywania informacji oraz dwa wskaźniki. Jak widzimy, wskaźniki w węźle zostały nazwane mianem lewego oraz prawego – na ogół stosuje się właśnie takie nazewnictwo, w którym węzeł może mieć lewego oraz prawego syna. Ale węzeł w drzewie binarnym nie musi mieć obu synów – może nie mieć żadnego, może mieć również tylko jednego (lewego lub prawego).
Drzewa binarne są fundamentem wielu bardziej złożonych struktur np. drzewa binarnego przeszukiwania (ang. Binary Search Tree - BST). Drzewo binarnego wyszukiwania to specjalny typ drzewa binarnego, który wprowadza konkretną regułę porządkowania danych. Główną zaletą BST jest możliwość szybkiego wyszukiwania, wstawiania i usuwania elementów. W idealnym przypadku w czasie logarytmicznym.
Dla każdego węzła drzewa:
W tabeli poniżej przedstawiono złożoność obliczeniową poszczególnych operacji wykonywanych w drzewie BST.- wszystkie wartości w lewym poddrzewie są mniejsze niż wartość w tym węźle,
- wszystkie wartości w prawym poddrzewie są większe.
- każdy węzeł posiadał unikatową wartość danej - to bardzo ważne: elementy drzewa BST nie mogą się powtarzać!
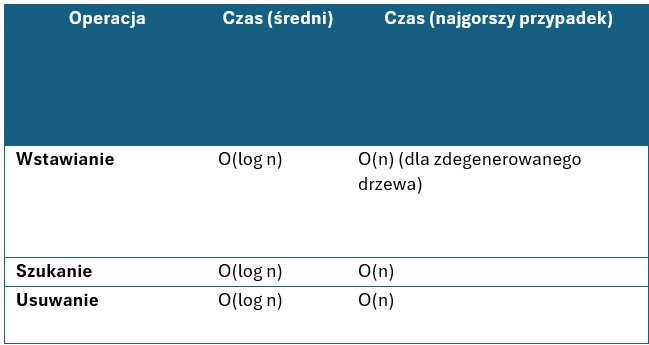
Na drzewie BST mozemy wykonywać podstawowe operacje takie jak: dodawanie węzła, usuwanie węzła oraz wyszukiwanie węzłą o podanej wartości. W kolejnych podrozdziałach przedsatwiono te podstawowe operacje.
1.1. Metody poruszania się po drzewie BST
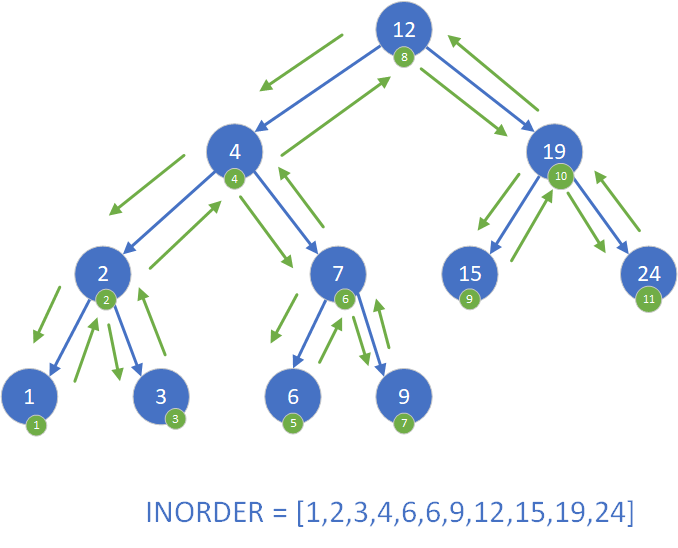
Wyróżniamy trzy podstawowe sposoby poruszania się po BST (w tzw. przechodzeniu w głąb, ang. depth-first traversal):- w kolejności inorder: najpierw lewe poddrzewo, potem węzeł, a następnie prawe poddrzewo,
- w kolejności preorder: najpierw węzeł, potem lewe poddrzewo, a następnie prawe poddrzewo,
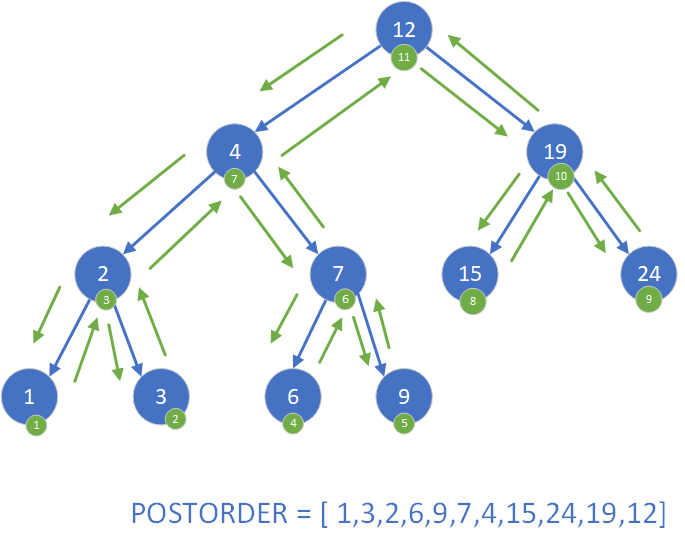
- w kolejności postorder: najpierw lewe poddrzewo, potem prawe poddrzewo, a na samy końcu węzeł.
struct Node {
int key;
Node* left;
Node* right;
};
void inorder(Node* root) {
if (root != nullptr) {
inorder(root->left);
cout << root->key << " ";
inorder(root->right);
}
}
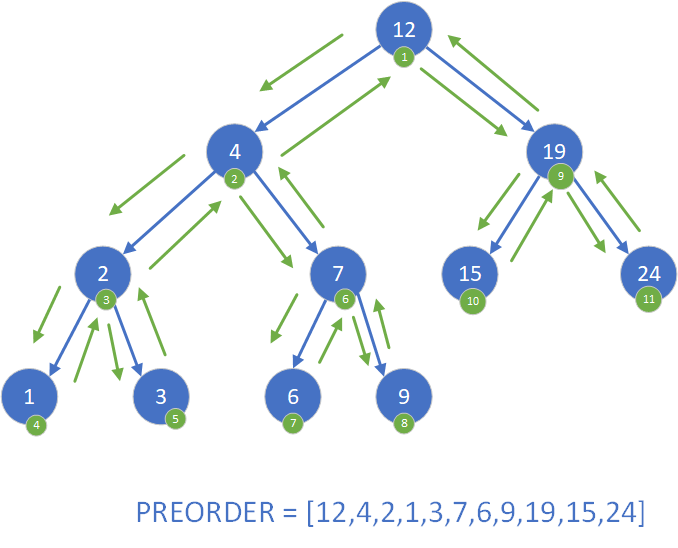
Inną metodą jest preorder, gdzie najpierw przetwarzany jest bieżący węzeł, następnie przechodzi się do lewego poddrzewa, a na końcu do prawego. Taki sposób przechodzenia sprawdza się dobrze przy zapisywaniu struktury drzewa do pliku lub przy klonowaniu drzewa, ponieważ zachowuje hierarchię węzłów. Poniżej przedstawiono kod aplikacji realizujący przejście preorder po drzewie BST.
void preorder(Node* root) {
if (root != nullptr) {
cout << root->key << " ";
preorder(root->left);
preorder(root->right);
}
}
 Postorder to metoda, w której najpierw przetwarzane są oba poddrzewa najpierw lewe, potem prawe, a dopiero na końcu sam węzeł. Jest szczególnie przydatna wtedy, gdy musimy usunąć całe drzewo, ponieważ pozwala najpierw pozbyć się potomków, zanim usuniemy ich rodziców. Poniżej przedstawiono kod funkcji do przechodzenia po drzewie w kolejności postorder.
Postorder to metoda, w której najpierw przetwarzane są oba poddrzewa najpierw lewe, potem prawe, a dopiero na końcu sam węzeł. Jest szczególnie przydatna wtedy, gdy musimy usunąć całe drzewo, ponieważ pozwala najpierw pozbyć się potomków, zanim usuniemy ich rodziców. Poniżej przedstawiono kod funkcji do przechodzenia po drzewie w kolejności postorder.
void postorder(Node* root) {
if (root != nullptr) {
postorder(root->left);
postorder(root->right);
cout << root->key << " ";
}
}
1.2. Wyszukiwanie w drzewie BST
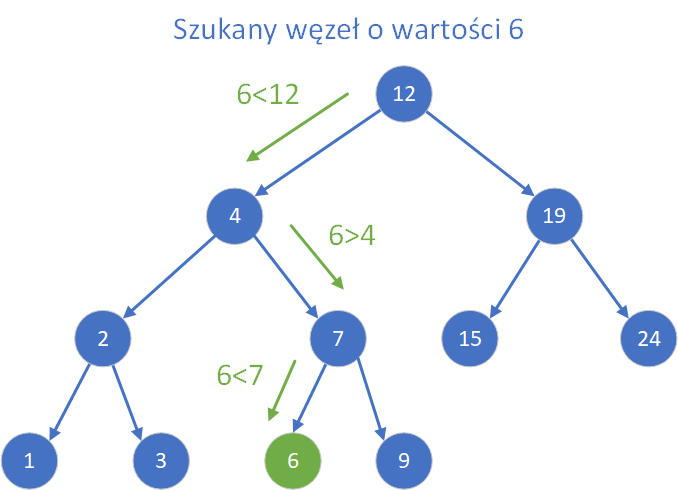
Jednym z głównych powodów implementacji drzew binarnego wyszukiwania (BST) jest jego zdolność do szybkiego oraz efektywnego wyszukiwania danych. Dzięki unikalnej strukturze drzewa BST, która opiera się na zasadzie porządkowania elementów wszystkie wartości w lewym poddrzewie są mniejsze, a w prawym większe niż wartość węzła. Dzięki temu możliwe jest szybkie odnalezienie poszukiwanego elementu poprzez kolejne porównania, podobnie jak w wyszukiwaniu binarnym.Proces wyszukiwania rozpoczyna się od korzenia drzewa. Jeśli wartość, której szukamy jest równa wartości w korzeniu, operacja kończy się sukcesem. W przeciwnym razie, jeśli szukana wartość jest mniejsza, algorytm przechodzi do lewego poddrzewa, natomiast jeśli większa to do prawego. Proces ten jest powtarzany rekurencyjnie lub iteracyjnie aż do momentu znalezienia wartości albo dotarcia do pustego wskaźnika (braku potomka), co oznacza, że dana wartość nie istnieje w drzewie. Poniżej na rysunku pokazano wyszukiwanie węzła o wybranej wartości na drzewie BST.
Poniżej przedstawiono kod aplikacji do wyszukiwania węzłów o podanej wartości w drzewie BST.
Node* searchRecursive(Node* root, int target) {
if (root == nullptr || root->key == target)
return root;
if (target < root->key)
return searchRecursive(root->left, target);
else
return searchRecursive(root->right, target);
}
1.3. Usuwanie drzewa BST i wybranych węzłów
Usuwanie elementów z drzewa binarnego wyszukiwania jest bardziej złożone niż ich dodawanie czy wyszukiwanie, ponieważ należy zadbać o to, aby struktura drzewa nadal spełniała warunki BST po usunięciu węzła. Zatem usuwanie drzewa rozpoczynamy od „likwidowania” liści, a kończymy na usunięciu liścia, który jest zarazem korzeniem drzewa. W celu utrzymania struktury drzewa, tuż przed usunięciem konkretnego liścia następuje ustawienie wskaźnika jego ojca (wskazującego do tej pory na ten liść) na wartość NULL. Proces ten przypomina klasyczne przechodzenie drzewa w porządku post-order, czyli: najpierw lewe poddrzewo, potem prawe, a na końcu bieżący węzeł. Dla każdego węzła rekurencyjnie wywołujemy procedurę usuwania jego dzieci, a dopiero po tym usuwamy sam węzeł. Tuż przed fizycznym usunięciem danego liścia należy ustawić wskaźnik ojca na NULL, co jest istotne dla utrzymania spójności struktury.
void deleteTree(Node* &root) {
if (root == nullptr) return;
// Rekurencyjnie usuwamy lewe i prawe poddrzewo
deleteTree(root->left);
deleteTree(root->right);
// Usuwamy bieżący węzeł
cout << "Usuwam węzeł: " << root->key << endl;
delete root;
root = NULL; // Ustawiamy wskaźnik na NULL, by „odłączyć” od ojca
}
- Przypadek 1: Węzeł o zadanym kluczu nie istnieje - w tym przypadku funkcja przeszukująca drzewo nie odnajduje węzła o danym kluczu, więc nie zostaje wykonane żadne usunięcie. Drzewo pozostaje bez zmian.
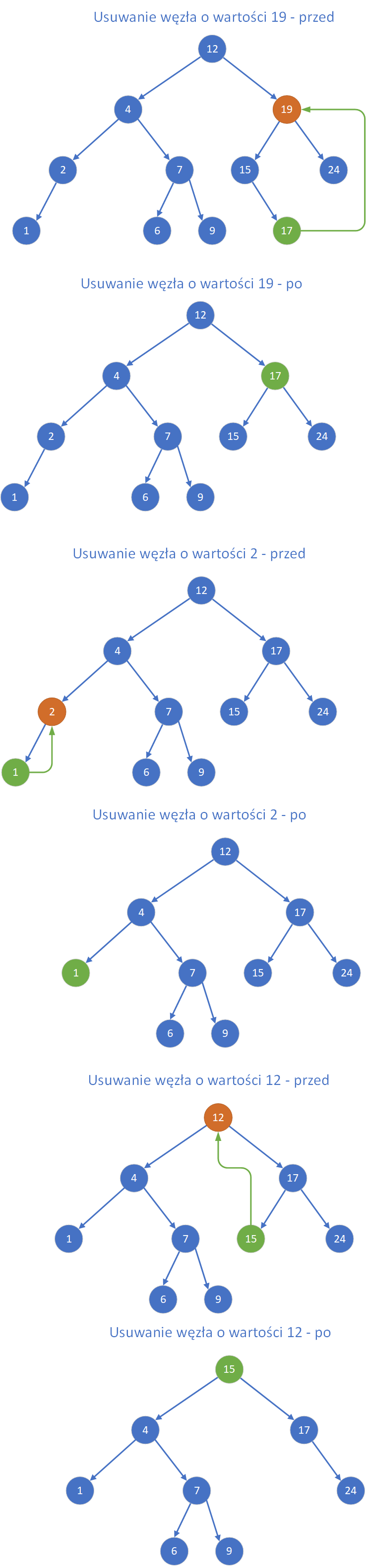
- Przypadek 2: Węzeł ma co najwyżej jednego syna - jeśli usuwany węzeł nie posiada żadnych dzieci (jest liściem), można go bezpiecznie usunąć i przypisać NULL do wskaźnika jego ojca, który go wskazywał. Jeżeli węzeł ma tylko jedno dziecko, to usuwany węzeł można zastąpić wskaźnikiem do jego jedynego dziecka drzewo pozostaje poprawne, a usunięty węzeł znika z pamięci.
- Przypadek 3: Węzeł ma dwóch synów - to najtrudniejsza sytuacja, ponieważ węzeł nie może zostać po prostu usunięty bez naruszenia struktury drzewa. Dlatego stosujemy jedno z dwóch klasycznych rozwiązań:
- zastąpienie usuwanego węzła przez jego bezpośredniego następnika (successora), czyli najmniejszy element w jego prawym poddrzewie (najbardziej lewy węzeł z prawego poddrzewa).
- zastąpienie przez poprzednika (predecessora), czyli największy element w jego lewym poddrzewie (najbardziej prawy węzeł z lewego poddrzewa).
2. Drzewa AVL
Drzewo AVL to jedna z najstarszych i najbardziej klasycznych struktur danych typu drzewo binarnego wyszukiwania (BST). Jego główną cechą jest samoczynne utrzymywanie zrównoważonej wysokości. Zostało zaproponowane przez dwóch radzieckich matematyków: G.M. Adelsona-Welskiego i E.M. Landisa w 1962 roku. Nazwa AVL pochodzi od pierwszych liter ich nazwisk.
Widzimy, że w zależności od kolejności wstawiania węzłów do drzewa możemy uzyskać inną wysokość drzewa, a więc liczbę poziomów od korzenia do liści.
Dla każdego węzła drzewa AVL definiujemy tzw. balance factor, czyli różnicę wysokości jego lewego i prawego poddrzewa:
\( balanceFactor \left( węzeł \right) = wysokosc \left( lewe poddrzewo \right)−wysokosc \left(prawe poddrzewo\right) \)
- –1 – prawe poddrzewo jest wyższe o 1,
- 0 – oba poddrzewa mają tę samą wysokość,
- +1 – lewe poddrzewo jest wyższe o 1.
Jeśli wynik wychodzi spoza przedziału <–1;1 >, to znaczy, że drzewo w tym miejscu jest niezrównoważone, i trzeba wykonać odpowiednią rotację. Poniżej przedstawiono kod funkcji do wyznaczania wskaźnika niewyważenia.
int height(Node* node) {
if (node == nullptr) return 0;
return node->height;
}
int getBalance(Node* node) {
if (node == nullptr) return 0;
return height(node->left) - height(node->right);
}
2.1. Rotacja i wskaźnik wyważenia
Drzewa AVL są równoważone w taki sposób, by różnica wysokości lewego i prawego poddrzewa dowolnego wynosiła nie więcej niż 1.Jeśli po wstawieniu (lub usunięciu) węzła, równowaga drzewa zostaje naruszona, to należy je przebudować lokalnie, wykonując odpowiednie rotacje. Istnieją cztery typy rotacji:
- Rotacja jednokrotna w prawo – przypadek lewo-lewo (LL),
- Rotacja jednokrotna w lewo – przypadek prawo-prawo (RR),
- Rotacja lewo-prawo (LR) – najpierw w lewo, potem w prawo,
- Rotacja prawo-lewo (RL) – najpierw w prawo, potem w lewo.
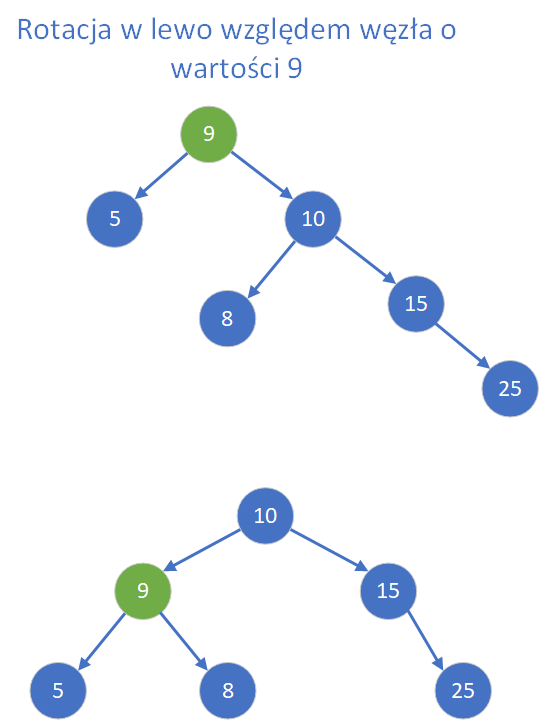
Lewa rotacja względem węzła polega na tym, że prawy syn tego węzła (nie może być on równy NULL) wchodzi na jego miejsce, przesuwając ojca w lewo: węzeł-ojciec staje się teraz lewym synem swojego dotychczasowego syna.
Prawa rotacja względem węzła polega na tym, że lewy syn tego węzła (nie może być on równy NULL) wchodzi na jego miejsce, przesuwając ojca w prawo: węzeł-ojciec staje się teraz prawym synem swojego dotychczasowego syna.
Prawa rotacja względem węzła polega na tym, że lewy syn tego węzła (nie może być on równy NULL) wchodzi na jego miejsce, przesuwając ojca w prawo: węzeł-ojciec staje się teraz prawym synem swojego dotychczasowego syna.
#include <iostream>
using namespace std;
// Struktura węzła drzewa AVL
struct Node {
int key;
Node* left;
Node* right;
int height;
Node(int k) : key(k), left(nullptr), right(nullptr), height(1) {}
};
// Funkcja pomocnicza: wysokość węzła
int height(Node* node) {
return node ? node->height : 0;
}
// Maksimum z dwóch wartości
int max(int a, int b) {
return (a > b) ? a : b;
}
// Obliczanie wskaźnika równowagi węzła
int getBalance(Node* node) {
if (node == nullptr) return 0;
return height(node->left) - height(node->right);
}
// Rotacja w lewo
Node* rotateLeft(Node* x) {
Node* y = x->right;
Node* T2 = y->left;
// Rotacja
y->left = x;
x->right = T2;
// Aktualizacja wysokości
x->height = 1 + max(height(x->left), height(x->right));
y->height = 1 + max(height(y->left), height(y->right));
return y;
}
// Rotacja w prawo
Node* rotateRight(Node* y) {
Node* x = y->left;
Node* T2 = x->right;
// Rotacja
x->right = y;
y->left = T2;
// Aktualizacja wysokości
y->height = 1 + max(height(y->left), height(y->right));
x->height = 1 + max(height(x->left), height(x->right));
return x;
}
2.2. Operacje na drzewach AVL
Operacje na drzewach AVL są podobne do tych w klasycznym drzewie BST (binarnego drzewa wyszukiwania), ale z dodatkowym warunkiem: po każdej operacji drzewo musi pozostać zrównoważone. AVL gwarantuje, że różnica wysokości lewego i prawego poddrzewa dla każdego węzła nie przekroczy 1, co zapewnia logarytmiczną złożoność operacji.Operacja wstawiania wartości do drzewa AVL
Pierwszym krokiem algorytmu jest klasyczne przeszukiwanie drzewa BST w celu znalezienia odpowiedniego miejsca dla nowego węzła. W trakcie wykonywania operacji porównywana jest wartość nowego wierzchołka z wartościami już istniejącymi. Schodzi się w dół drzewa aż do miejsca w którym można bez naruszenia zasad BST wstawić nowy element. Proces ten nie różni się niczym od zwykłego wstawiania węzła do drzewa binarnego.
Po umieszczeniu nowego wierzchołka w odpowiednim miejscu, algorytm nie kończy działania, lecz zaczyna wracać w górę drzewa po tej samej ścieżce, którą schodził, aktualizując po drodze tzw. współczynniki wyważenia węzłów (oznaczane zwykle jako ww lub balance factor). Ten współczynnik odzwierciedla różnicę wysokości między lewym a prawym poddrzewem danego węzła i może przyjmować wartości od –1 do 1 w przypadku drzewa AVL, bez naruszenia jego struktury. Mamy wtedy kilka możliwości:
- współczynnik wyważenia jakiegoś węzła przyjmie wartość 0, oznacza to, że jego poddrzewa pozostały zrównoważone i ich wysokość się nie zmieniła. W takiej sytuacji nie ma potrzeby dalszego działania i algorytm kończy się, ponieważ nie doszło do naruszenia równowagi.
- współczynnik wyważenia staje się równy 1 lub –1, to wskazuje, że jedno z poddrzew stało się wyższe o jeden poziom, ale nadal całość spełnia warunki drzewa AVL. W takim przypadku kontynuujemy śledzenie ścieżki w górę do korzenia, ponieważ równowaga mogła zostać zachwiana wyżej w drzewie.
- współczynnik osiąga wartość 2 lub –2, oznacza to, że dane poddrzewo straciło wyważenie – różnica wysokości między jego lewym i prawym poddrzewem przekroczyła dopuszczalny próg. Wówczas należy zastosować odpowiednią rotację w celu przywrócenia równowagi. W zależności od kierunku wzrostu drzewa (czy nadmiar występuje po lewej, czy po prawej stronie, oraz w którym kierunku został dodany nowy wierzchołek), wykonuje się rotację pojedynczą (lewo-lewo lub prawo-prawo) albo podwójną (lewo-prawo lub prawo-lewo).
Operacja wstawiania wartości do drzewa AVL
Analogicznie do operacji wstawiania, również operacja usuwania wierzchołka z drzewa AVL składa się z kilku logicznych kroków, których celem jest zachowanie zarówno poprawnej struktury drzewa BST, jak i zrównoważenia AVL. Różnica polega na tym, że w usuwaniu wprowadzana jest potencjalna redukcja wysokości drzewa, co również może prowadzić do naruszenia równowagi.
Pierwszym krokiem algorytmu jest klasyczne przeszukiwanie drzewa BST w celu znalezienia wierzchołka, który ma zostać usunięty. Przechodząc przez kolejne węzły, porównywana jest wartość klucza docelowego z bieżącym węzłem i odpowiednio schodzi się w dół do lewego lub prawego poddrzewa, aż zostanie znaleziony wierzchołek o poszukiwanej wartości. Ta część procesu nie różni się niczym od usuwania elementu w zwykłym drzewie BST.
Gdy zostanie odnaleziony węzeł do usunięcia, algorytm rozpoznaje jeden z trzech przypadków:
- węzeł nie ma dzieci - zostaje po prostu usunięty.
- węzeł ma jedno dziecko - dziecko zastępuje węzeł w jego miejscu.
- węzeł ma dwóch potomków, węzeł zostaje zastąpiony przez następnika (najmniejszy węzeł w prawym poddrzewie) lub poprzednika (największy węzeł w lewym poddrzewie), a jego oryginalna pozycja zostaje fizycznie usunięta w sposób analogiczny do poprzednich przypadków.
- współczynnik wyważenia jakiegoś węzła przyjmie wartość 0, oznacza to, że jego poddrzewa pozostały zrównoważone i ich wysokość się nie zmieniła. W takiej sytuacji nie ma potrzeby dalszego działania i algorytm kończy się, ponieważ nie doszło do naruszenia równowagi.
- współczynnik wyważenia staje się równy 1 lub –1, to wskazuje, że jedno z poddrzew stało się wyższe o jeden poziom, ale nadal całość spełnia warunki drzewa AVL. W takim przypadku kontynuujemy śledzenie ścieżki w górę do korzenia, ponieważ równowaga mogła zostać zachwiana wyżej w drzewie.
- współczynnik osiąga wartość 2 lub –2, oznacza to, że dane poddrzewo straciło wyważenie – różnica wysokości między jego lewym i prawym poddrzewem przekroczyła dopuszczalny próg. Wówczas należy zastosować odpowiednią rotację w celu przywrócenia równowagi. W zależności od kierunku wzrostu drzewa (czy nadmiar występuje po lewej, czy po prawej stronie, oraz w którym kierunku został dodany nowy wierzchołek), wykonuje się rotację pojedynczą (lewo-lewo lub prawo-prawo) albo podwójną (lewo-prawo lub prawo-lewo).
3. Drzewa czerwono-czarne
Drzewa czerwono-czarne (ang. Red-Black Tree - RBT) to rodzaj zrównoważonych binarnych drzew wyszukiwania (BST), w których stosuje się mechanizmy kolorowania węzłów oraz odpowiednie operacje rotacji w celu utrzymania równowagi struktury. Drzewa RBT zostały stworzone kilkanaście lat później niż drzewa AVL, w latach 1972-78 i od tej pory były coraz coraz powszechniej używane w wielu prężnie rozwijających się dziedzinach informatyki (m.in. w algorytmach geometrii obliczeniowej i gier komputerowych). Każdy węzeł drzewa RBT zawiera dodatkową informację - kolor, który może być albo czerwony, albo czarny. Ten dodatkowy bit informacji w węźle pozwala na wykonywanie operacji równoważenia drzewa, pełni więc tę samą rolę jak wskaźnik wyważenia w drzewie AVL.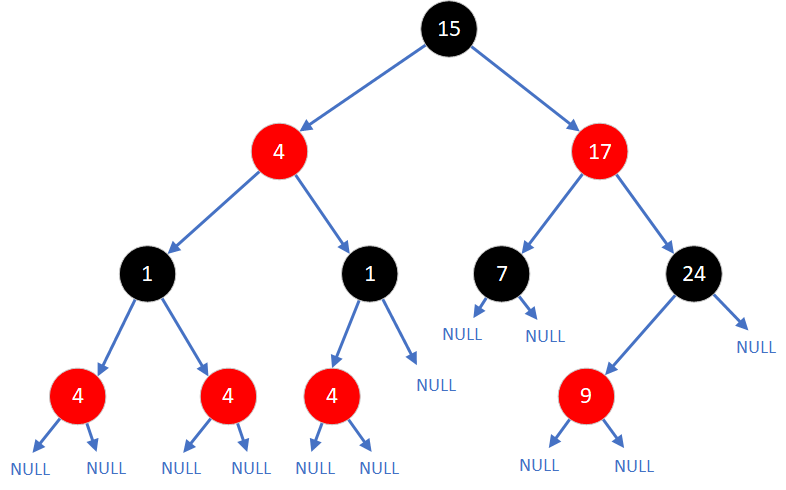
Warto dodać, że na ogół nie rysuje się liści drzewa RBT, gdyż wiadomo, że wszystkie liście są czarne i nie wnoszą żadnych istotnych informacji.
3.1. Rodzaje i własności
Głównym celem stosowania drzew czerwono-czarnych jest zapewnienie, że wysokość drzewa pozostaje logarytmiczna względem liczby węzłów, co gwarantuje wydajność operacji takich jak wstawianie, usuwanie i wyszukiwanie na poziomie O(log n).
Aby drzewo binarne można było uznać za czerwono-czarne, musi ono spełniać ściśle określone warunki strukturalne i kolorystyczne:
Poprzez ustalenie warunków na następstwo kolorów na ścieżkach, gwarantowane jest, że każda ścieżka jest co najwyżej dwukrotnie dłuższa niż dowolna inna ścieżka prowadząca z tego samego wierzchołka. Wynika to z faktu, że najkrótsza możliwa ścieżka zawiera kolejno same węzły czarne, a najdłuższa - czerwone i czarne na przemian. A ponieważ wiemy, że na każdej ścieżce musi być tyle samo węzłów czarnych, to czerwonych może być co najwyżej drugie tyle. Klasyfikuje to drzewa RBT do grupy w przybliżeniu zrównoważonych.- Każdy węzeł drzewa ma przypisany kolor: czerwony lub czarny.
- Korzeń drzewa jest zawsze czarny.
- Wszystkie liście drzewa (czyli węzły typu NULL) są traktowane jako czarne.
- Jeśli dany węzeł jest czerwony, to oboje jego synowie muszą być czarni. W ten sposób unika się występowania dwóch czerwonych węzłów bezpośrednio po sobie na ścieżce.
- Każda ścieżka od dowolnego wierzchołka do jego liścia zawiera dokładnie tyle samo czarnych węzłów, co określa się mianem czarnej głębokości (ang. black height) danego węzła.
Oryginalna koncepcja drzew czerwono-czarnych doczekała się ważnej modyfikacji przez samego autora, profesora Roberta Sedgewicka z Princeton University. Po 30 latach (!) od swojego pierwotnego pomysłu, w 2008 roku, opracował on zmianę w algorytmie tworzenia drzew, który zakłada pełną jednoznaczność przedstawienia drzewa czerwono-czarnego. Drzewa takie noszą nazwę Left-Leaning Red Black Trees - LLRBT). W klasycznym drzewie czerwono-czarnym czerwone krawędzie (czyli połączenia rodzic–dziecko, w których jedno z tych węzłów jest czerwone) mogą występować zarówno po lewej, jak i prawej stronie. W praktyce jednak taka elastyczność komplikuje implementację, zwłaszcza podczas wstawiania i usuwania elementów, ponieważ trzeba obsługiwać więcej przypadków rotacji i kolorowań.
Drzewa LLRBT (czyli drzewa czerwono-czarne pochylone w lewo) wprowadzają uproszczenie:
Wszystkie czerwone krawędzie muszą prowadzić do lewego dziecka.
3.2. Wstawianie i usuwanie węzłów
Operacje wstawiania oraz usuwania węzłów w drzewach czerwono-czarnych mają na celu nie tylko utrzymanie poprawnej struktury binarnego drzewa wyszukiwania, ale również zachowanie jego zrównoważenia zgodnie z regułami kolorowania. W klasycznych typach drzew czerwono-czarnych procedury te bywają dość złożone. Wymagają uwzględnienia wielu przypadków oraz wariantów rotacji oraz kolorowania. Modyfikacja w postaci drzew LLRBT upraszczają ten proces, ponieważ narzucają dodatkowe ograniczenie tzn. wszystkie czerwone krawędzie muszą być „pochylone w lewo”, czyli czerwony węzeł nie może być prawym dzieckiem. Dzięki temu algorytm wstawiania w LLRBT można podzielić na jasne, powtarzalne etapy i obsługiwać go za pomocą prostego, rekurencyjnego podejścia.Możemy wyróżnić następujące etapy wstawienia do drzewa LLRBT:
- Dodanie nowego węzła jako czerwonego liścia - nowy węzeł zawsze wstawiany jest jako czerwony oraz dzięki temu nie narusza to czarnej głębokości ścieżek. Jego kolor może zostać łatwo dostosowany w trakcie przywracania struktury.
- Zamiana kolorów tzw. rozdzielenie 4 węzła - jeśli nowy węzeł został dodany jako dziecko węzła, który ma już dwóch czerwonych synów, to znaczy, że lokalnie utworzył się węzeł 4-elementowy (według analogii z drzewami 2-3-4). Aby przywrócić strukturę drzewa 2-3, następuje zamiana kolorów: ojciec staje się czerwony, a obaj jego synowie – czarni.
- Lewa rotacja tzn. eliminacja czerwonego prawego syna - jeśli po dodaniu nowego węzła powstała sytuacja, w której węzeł ma czerwonego prawego syna, należy wykonać rotację w lewo, by zachować zasadę „pochylania w lewo”.
- Prawa rotacja tzn. eliminacja dwóch czerwonych pod rząd - jeśli po lewej stronie występują dwa czerwone węzły z rzędu (ojciec i lewy syn), wykonuje się rotację w prawo. Dzięki temu eliminujemy sytuację, w której czerwony węzeł ma czerwonego lewego potomka, co narusza zasady LLRBT.
- jeśli obaj synowie są czerwoni – zmienia kolory.
- jeśli prawy syn jest czerwony, a lewy nie – rotuje w lewo.
- jeśli lewy syn i jego lewy syn są czerwoni – rotuje w prawo.