Podręcznik

1. Wprowadzenie do grafów

Graf to jedna z podstawowych i najbardziej uniwersalnych struktur danych w informatyce i matematyce dyskretnej. Jest to zbiór wierzchołków (nazywanych również punktami lub nodami), pomiędzy którymi istnieją połączenia – zwane krawędziami. Grafy służą do modelowania relacji między obiektami, co sprawia, że mają szerokie zastosowanie w wielu dziedzinach, takich jak informatyka, logistyka, sieci komputerowe, biologia, ekonomia czy teoria baz danych.

Zazwyczaj graf przedstawia się za pomocą symboli G = (V, E), gdzie V jest to zbiór wierzchołków grafu, zwanych również węzłami (ang. vertex), natomiast E to zbiór krawędzi grafu (ang. edge).

Grafy dzielimy zasadniczo na dwa rodzaje – grafy skierowane oraz nieskierowane. 

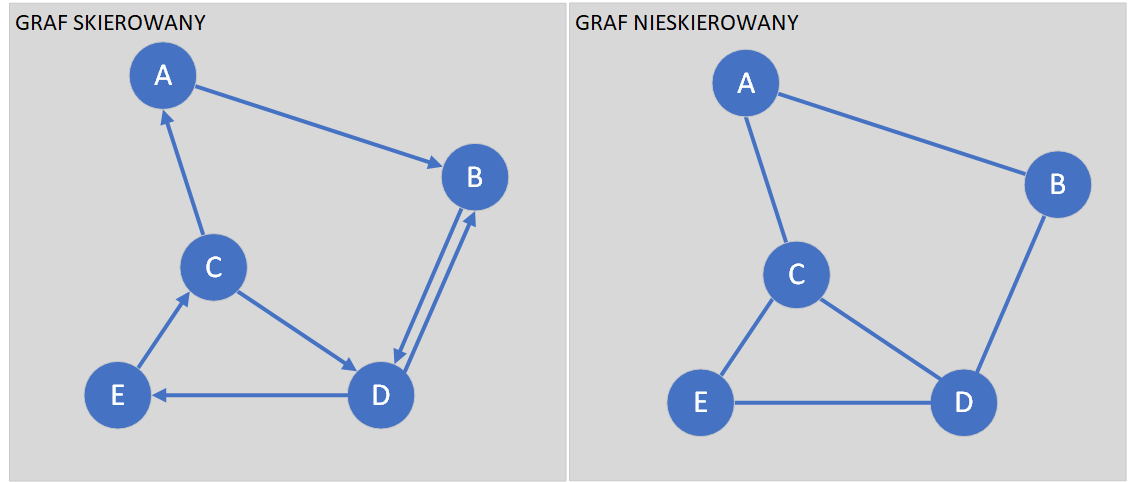
Najczęściej w pamięci grafy przechowywane są za pomocą:

• list sąsiedztwa,
• macierzy sąsiedztwa.

Lista sąsiedztwa są strukturą danych, w której dla każdego wierzchołka przechowywana jest lista wierzchołków, z którymi ma on bezpośrednie połączenia (czyli sąsiadów). Reprezentacja ta stanowi bardzo efektywna pamięciowo w przypadku grafów rzadkich, czyli takich, gdzie liczba krawędzi jest znacznie mniejsza niż maksymalna możliwa liczba połączeń. Dla każdego wierzchołka tworzy się osobną listę (lub tablicę dynamiczną), w której umieszczane są wszystkie sąsiednie wierzchołki. Ta reprezentacja pozwala na szybki dostęp do listy sąsiadów danego węzła, a dodawanie krawędzi odbywa się w czasie stałym. Możliwe są dwie wersje list sąsiedztwa:  lista węzłów, do których prowadzą krawędzie wychodzące z danego wierzchołka oraz lista węzłów, z których prowadzą krawędzie przychodzące do danego wierzchołka.

Dla grafu nieskierowanego przedstawionego na rysunku powyżej lista sąsiedztwa będzie wyglądała następująco:

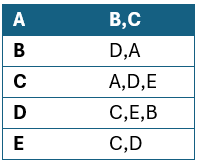
W przypadku grafu skierowanego istotne jest czy w zapisie uwzględniamy węzły skierowane od danego wierzchołka, czy odwrotnie. W przypadku grafu skierowanego nie ma to znaczenia.

Macierz sąsiedztwa natomiast to kwadratowa tablica dwuwymiarowa o rozmiarze $nxn$, gdzie 𝑛 to liczba wierzchołków w grafie. Wartość na pozycji ( 𝑖 , 𝑗 ) w tej tablicy wskazuje, czy istnieje krawędź pomiędzy wierzchołkiem 𝑖  a 𝑗 . W grafach ważonych ta wartość może odpowiadać wagom krawędzi. Macierz sąsiedztwa umożliwia bardzo szybkie sprawdzenie istnienia połączenia między dowolnymi dwoma wierzchołkami wystarczy jedno odwołanie do elementu tablicy. Jednak jej główną wadą jest duże zużycie pamięci, zwłaszcza w przypadku grafów rzadkich, ponieważ wymaga przechowywania $n^2$ wartości, niezależnie od rzeczywistej liczby krawędzi.

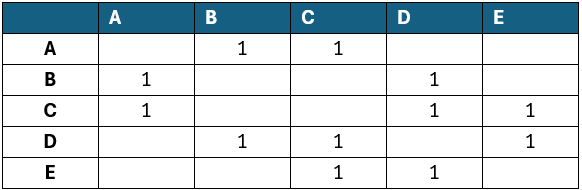
Podsumowując, reprezentacja grafu jako lista sąsiedztwa jest bardziej oszczędna pamięciowo i lepiej sprawdza się w grafach rzadkich, natomiast macierz sąsiedztwa oferuje szybszy dostęp do informacji o krawędziach, co może być korzystne w gęstych grafach lub w algorytmach często sprawdzających istnienie połączeń między wierzchołkami. Wybór reprezentacji powinien więc zależeć od charakterystyki konkretnego problemu i rodzaju wykonywanych operacji.

Przeszukiwanie grafów w głąb

Przeszukiwanie w głąb (ang. Depth-First SearchDFS) polega na eksploracji grafu „najdalej jak się da” tzn. zanim wróci się i zacznie badać inne możliwe ścieżki. Zazwyczaj jest realizowane rekurencyjnie lub przy użyciu stosu. Algorytm DFS odwiedza sąsiadów wierzchołka, następnie sąsiadów tych sąsiadów, i tak dalej, aż dotrze do punktu, w którym nie można już pójść głębiej – wtedy algorytm się cofa i kontynuuje badanie pozostałych gałęzi. Przeszukiwanie w głąb doskonale sprawdza się w przypadkach, gdy zależy nam na pełnym zbadaniu struktur rozgałęzionych, takich jak drzewa, i jest fundamentem np. algorytmu Tarjana do znajdowania punktów artykulacji czy mostów w grafie.

lgorytm przeszukiwania w głąb może być stosowany zarówno dla grafów nieskierowanych, jak i dla grafów skierowanych. Działa również poprawnie dla obu rodzajów grafów w przypadku innego podziału – dla grafów spójnych i niespójnych. Teraz jest więc już najwyższy czas na wprowadzenie ich definicji.

Graf nazywamy spójnym, gdy między dwoma jego dowolnymi wierzchołkami istnieje łącząca je ścieżka (czyli z dowolnego miejsca w grafie można dotrzeć do każdego innego). Jeśli graf nie posiada takiej cechy, to jest on grafem niespójnym.

W przypadku grafu spójnego procedura odwiedzDFS będzie wywołana tylko jeden raz wewnątrz procedury DFS (gdyż „za jednym zamachem” zostaną odwiedzone wszystkie wierzchołki grafu – z definicji są one osiągalne z węzła początkowego). Natomiast dla grafu niespójnego procedura ta będzie uruchamiana kilkakrotnie. W przypadku grafów skierowanych spójność grafów można podzielić na dwie grupy: słabą spójność oraz silną spójność.

Graf skierowany jest słabo spójny, jeśli odpowiadający mu graf nieskierowany (czyli po odrzuceniu kierunków krawędzi) jest spójny. Natomiast graf jest silnie spójny, gdy dla dowolnej pary węzłów u i v można znaleźć ścieżkę prowadząca zarówno z u do v, jak i z v do u.

Przeszukiwanie grafów wszerz

Przeszukiwanie grafu wszerz (ang. Breadth-First Search - BFS) – to druga podstawowa technika odwiedzania wierzchołków grafu. W przeciwieństwie do DFS, która „schodzi” najgłębiej jak się da w grafie, zanim się cofnie, BFS przeszukuje graf „poziomami”, czyli najpierw odwiedza wszystkich sąsiadów danego wierzchołka, a dopiero potem przechodzi do ich sąsiadów. Do realizacji algorytmu BFS potrzebna jest reprezentacja grafu (najczęściej lista sąsiedztwa) oraz struktura kolejki, w której przechowywane są wierzchołki oczekujące na odwiedzenie. Wierzchołki odwiedzone są zaznaczane w pomocniczej tablicy odwiedzony, dzięki czemu nie trafiają ponownie do kolejki. Algorytm rozpoczyna się od zainicjowania stanu wszystkich wierzchołków jako nieodwiedzonych. Następnie do kolejki wrzucany jest wierzchołek startowy, oznaczany jako odwiedzony. Algorytm w pętli wyciąga kolejne wierzchołki z kolejki, przetwarza je (np. wypisuje), a wszystkich ich nieodwiedzonych sąsiadów dodaje na koniec kolejki i oznacza jako odwiedzonych. Proces trwa do momentu, aż kolejka stanie się pusta, co oznacza, że odwiedzono wszystkie wierzchołki dostępne z punktu startowego. BFS pozwala bardzo efektywnie wyznaczać najkrótszą ścieżkę w grafach nieskierowanych i nieskrajnie ważonych (tzn. gdy wagi wszystkich krawędzi są równe). Ponadto jest używany w wielu klasycznych algorytmach grafowych, m.in. w rozpoznawaniu składowych spójnych, wykrywaniu cykli czy znajdowaniu minimalnych ścieżek.

BFS jest zwykle implementowany iteracyjnie i ma złożoność czasową O(V + E), gdzie V to liczba wierzchołków, a E – liczba krawędzi. To czyni go bardzo wydajnym narzędziem w analizie struktur grafowych, szczególnie wtedy, gdy zależy nam na eksploracji szerokości drzewa odwiedzin.

2. Algorytm Floyda-Warshalla

Algorytm Floyda-Warshalla to klasyczna metoda znajdowania najkrótszych ścieżek między wszystkimi parami wierzchołków w grafie. Działa zarówno dla grafów skierowanych, jak i nieskierowanych, pod warunkiem że nie zawierają ujemnych cykli. W przeciwieństwie do algorytmu Dijkstry, który oblicza odległości z jednego źródła, algorytm Floyda-Warshalla działa na całościowym podejściu macierzowym. Rozwiązanie problemu jest również zapisywane w postaci tablicy dwuwymiarowej D o wymiarach n x n gdzie n jest liczbą wierzchołków grafu. W rezultacie wykonania algorytmu w każdej komórce D[i,j] znajduje się wartość odpowiadająca kosztowi najkrótszej ścieżki prowadzącej z wierzchołka i do wierzchołka j, co widać poniżej.

Oprócz samego kosztu najkrótszej drogi prowadzącej między dwoma wierzchołkami, równie cenna jest informacja o przebiegu takiej ścieżki (czyli przez jakie pośrednie wierzchołki przechodzi ta droga). W tym celu równolegle do wyznaczania kosztów ścieżek w tablicy D, wyznaczane są indeksy poprzedników (węzłów poprzedzających inne węzły) znajdujących się na najkrótszych ścieżkach prowadzących do konkretnych węzłów. Jest to zapisywane, i w trakcie działania algorytmu sukcesywnie aktualizowana jest tablica zawierająca indeksy poprzedników (również o rozmiarze n x n), która oznaczymy jako P i szczegółowo omówimy później na przykładzie.

Wartościową zaletą algorytmu Floyda-Warshalla jest fakt, że może być on stosowany dla grafów o ujemnych wagach (w przeciwieństwie do algorytmu Dijkstry wyznaczającego najkrótsze ścieżki z jednego węzła źródłowego – dowiecie się o nim w następnym podrozdziale). Omawiany algorytm jest przykładem metody stosującej zasady programowania dynamicznego. Niebawem w skrócony sposób wyjaśnimy, dlaczego tak właśnie jest.

Na razie spróbujemy Wam przedstawić w sposób możliwie prosty i zwięzły sposób główną ideę algorytmu. Należy przyjąć, że zgodnie z macierzą sąsiedztwa węzły grafu są oznaczone indeksami od 1 do n. Początkowo elementy tablicy D są równe odpowiadającym im elementom macierzy sąsiedztwa T (wystarczy proste przepisanie wartości). Należy pamiętać, że macierz sąsiedztwa T jest konstruowana w taki sposób, że:

• T[i,j] jest równa wadze krawędzi łączącej węzły i, j, jeśli w grafie jest taka krawędź
• T[i, j] = 0, jeśli i=j
• T[i,j]= +Inf, jeżeli nie istnieje krawędź łącząca wierzchołki i, j

A zatem we wstępnej fazie algorytmu najkrótsze ścieżki między dowolną parą węzłów posiadają koszt równy wadze krawędzi łączącej te dwa wierzchołki (jeśli takowa istnieje - najkrótsza ścieżka nie może zawierać w tym momencie żadnych węzłów pośrednich). W kolejnych krokach algorytm rozpatruje kolejno węzły oznaczone indeksem 1,2,....,k,....,n. Najpierw sprawdzane jest (dla każdej pary węzłów i, j), czy ścieżka z i do j prowadząca przez pośredni węzeł o indeksie 1 jest krótsza niż aktualnie znana najkrótsza droga między wierzchołkami i oraz j (bez żadnych węzłów pośrednich). Jeśli tak właśnie jest, to długość najkrótszej ścieżki jest aktualizowana (wiedzie ona teraz przez węzeł 1). W kolejnym kroku algorytm sprawdza, czy włączenie węzła 2 do najkrótszej ścieżki z i do j nie poprawi wartości jej długości. Wówczas wartość D[i,j] będzie zawierać długość najkrótszej ścieżki prowadzącej bezpośrednio z węzła i do j lub też zawierającej co najwyżej węzły 1 oraz 2 jako wierzchołki pośrednie. W ogólności, po k-tym kroku, zostaną obliczone najkrótsze ścieżki między parami wierzchołków, zawierające węzły pośrednie ze zbioru wierzchołków o indeksach (1,..,k). Tym samym po zakończeniu działania algorytmu w tablicy D będą wyliczone koszty najkrótszych ścieżek, które mogą przebiegać przez wszystkie węzły grafu G – w tym momencie otrzymywane jest ostateczne rozwiązanie problemu znalezienia najkrótszych ścieżek miedzy parami wierzchołków grafu.

Procedurę możemy przedstawić za pomocą następującego pseudokodu:

skopiuj wartości macierzy sąsiedztwa T do tablicy D
	inicjalizuj tablicę P zerami

	for (każdy węzeł k grafu spośród węzłów (1,..,n) )
		for (każdy węzeł i grafu spośród węzłów (1,..,n) )
			for (każdy węzeł j grafu spośród węzłów (1,..,n) )
				if (D[i,k]+D[k,j] < D[i,j])	{
					D[i,j] = D[i,k] + D[k,j] 	//najkrótsza ścieżka prowadzi teraz przez węzeł k
					P[i,j] = k
				}

Poniżej przedstawiony jest przykład graficzny działania algorytmu Floyda-Warshalla.



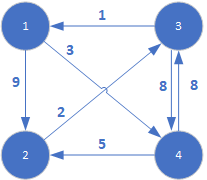
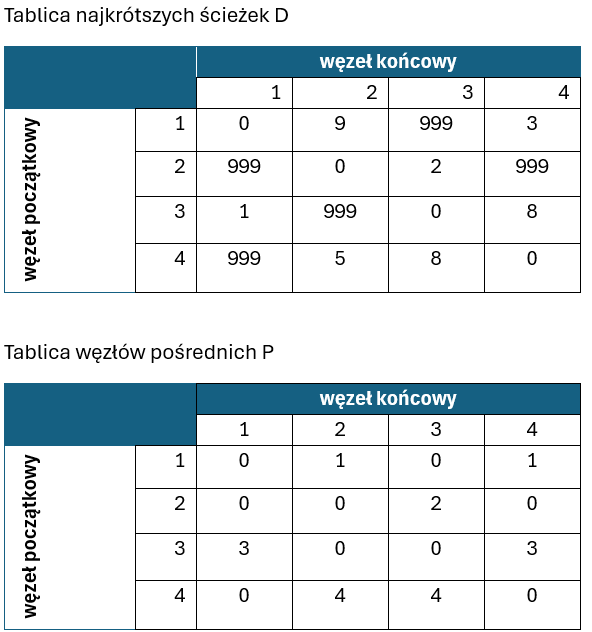
Wartość 999 w komórkach tablicy D jest odpowiednikiem +Inf, natomiast wartość 0 w tablicy P oznacza, że na ścieżce między wierzchołkiem początkowym a końcowym nie ma ani jednego wierzchołka pośredniego (0 jest praktycznym zapisem wartości NULL). 

Rozpoczynamy właściwy, pierwszy krok nadrzędnej pętli. Sprawdzamy, czy wstawienie wierzchołka k=1 poprawi wartości najkrótszych ścieżek między wierzchołkami grafu:

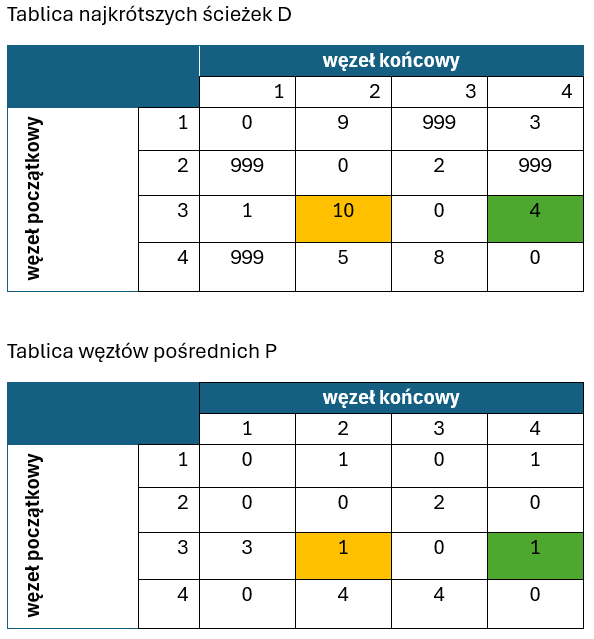
Okazuje się, że zastosowanie węzła 1 jako wierzchołka pośredniego poprawia długość najkrótszej ścieżki między węzłami 3->2 oraz 3->4. Zmiany wartości najkrótszych ścieżek zaznaczono pomalowaniem odpowiednich komórek tablicy T. W związku z dodaniem nowego węzła pośredniego do ścieżek, w odpowiednie miejsca w tablicy P wstawiana jest wartość indeksu węzła 1.

Przechodzimy do drugiego kroku iteracji. W tym momencie próbujemy poprawić najkrótsze ścieżki przy użyciu węzła o indeksie k=2:

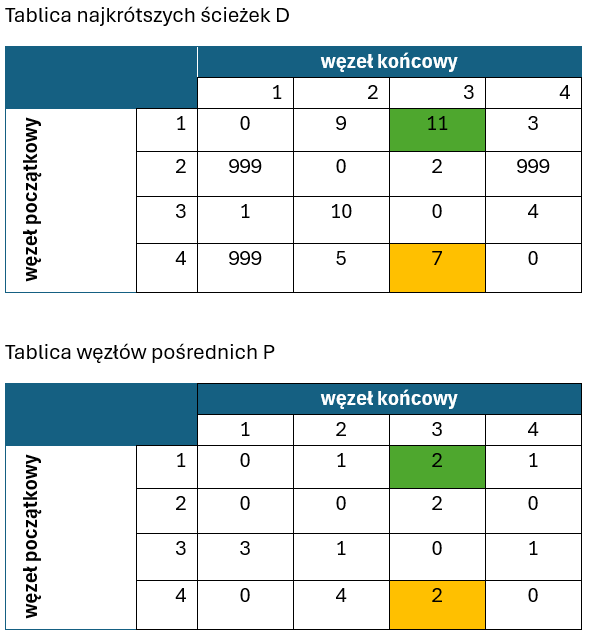
W tym kroku algorytm poprawia dwie ścieżki poprzez umieszczenie w nich węzła 2. Mianowicie dotyczy to:

• drogi 1->3, gdyż T[1,2]+T[2,3] = 9 +2 = 11 i jest mniejsze niż T[1,3]= 999 (oczywiście mamy na myśli dotychczasową wartość T[1,3], która właśnie jest modyfikowana)
• drogi 4->3, gdyż T[4,2]+T[2,3] = 5 + 2 = 7 i jest mniejsze niż T[4,3] = 8

Tak jak w poprzedniej iteracji, zmienione wartości najkrótszych ścieżek, a w tablicy P wstawiono dla uaktualnionych ścieżek indeks nowo umieszczonego węzła pośredniego.

Przejdźmy do iteracji o numerze k=3:

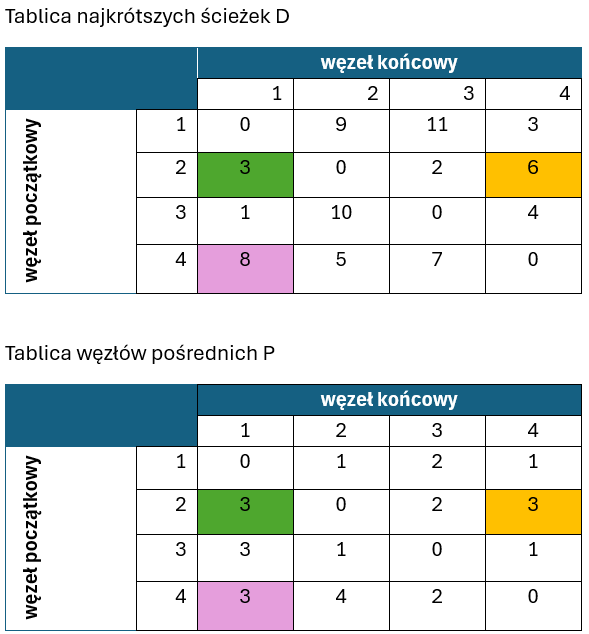
Tym razem aż trzy ścieżki wymagały poprawienia. Są nimi:

• ścieżka 2->1, gdyż T[2,3]+T[3,1] = 2 +1 = 3 i jest mniejsze niż T[2,1]= 999
• ścieżka 2->4, gdyż T[2,3]+T[3,4] = 2 +4 = 6 i jest mniejsze niż T[2,4]= 999
• ścieżka 4->1, gdyż T[4,3]+T[3,1] = 7 +1 = 8 i jest mniejsze niż T[4,1]= 999

W tablicy P w odpowiednich miejscach wstawiamy indeks węzła 3.

Pozostał nam już tylko ostatni, czwarty krok iteracji:

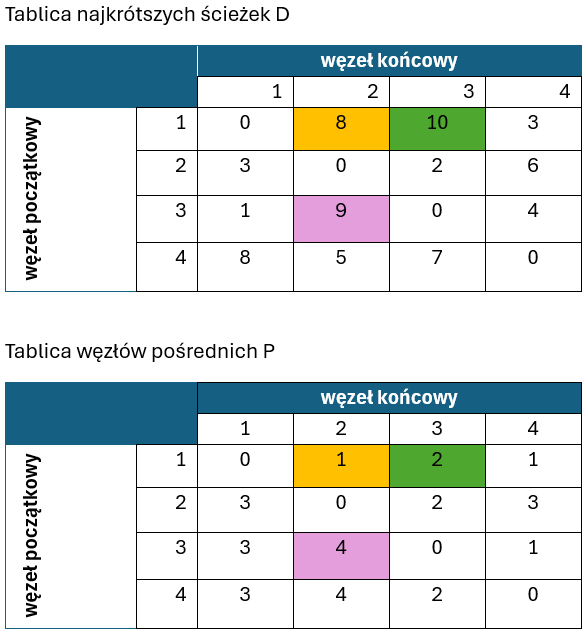
Jak się okazało, ponownie trzy drogi wymagały uaktualnienia – w tym przypadku za pomocą węzła o indeksie 4. Odnosi się to do ścieżek:

• 1->2, gdyż T[1,4]+T[4,2] = 3 +5 = 8 i jest mniejsze niż T[1,2]= 9
• 1->3, gdyż T[1,4]+T[4,3] = 3 +7 = 10 i jest mniejsze niż T[1,3]= 11
• 3->2, gdyż T[3,4]+T[4,2] = 4 +5 = 9 i jest mniejsze niż T[3,2]= 10

Ponieważ sprawdziliśmy już wszystkie cztery węzły w roli wierzchołków pośrednich należących do najkrótszych ścieżek, algorytm Floyda-Warshalla kończy w tym miejscu swój proces. Wszystkie najkrótsze ścieżki między każdą parą węzłów grafu zostały wyznaczone.

Możemy również na podstawie tablicy P odtworzyć przebieg najkrótszej ścieżki: przykładowo chcemy wiedzieć, którędy biegnie najkrótsza droga z węzła 1 do węzła 3. W tym celu celu odczytujemy P[1,3] = 4, następnie sprawdzamy P[1,4] = 1 (czyli ścieżka ta jest pojedynczą krawędzią) oraz P[4,3]= 2. Następnie odczytujemy wartość P[4,2] = 4 oraz P[2,3] = 2, a zatem doszliśmy już do elementarnych części tej ścieżki. Przebiega ona w sposób następujący: 1->4->2->3.

3. Algorytm Dijkstry

Algorytm Dijkstry to jeden z najbardziej znanych i najczęściej używanych algorytmów grafowych. Służy do znajdowania najkrótszych ścieżek od jednego wierzchołka (źródła) do wszystkich innych wierzchołków w grafie o nieujemnych wagach krawędzi. Został opracowany przez holenderskiego informatyka Edsgera Dijkstrę w 1956 roku. Jest podstawą wielu zastosowań, m.in. w systemach GPS, analizie sieci, komunikacji i teorii tras. 

Metoda Dijkstry polega na wprowadzeniu podziału zbioru wierzchołków grafu na trzy zbiory:

• zbiór Q, w którym znajdują się wierzchołki, do których „dotarł” już algorytm, ale nie możemy jeszcze określić, czy znaleziono do nich najkrótszą ścieżkę ze źródła
• zbiór S, w którym znajdują się wierzchołki (węzły) grafu o już ustalonej najkrótszej ścieżce ze źródła, dalej nie będą już rozpatrywane w algorytmie
• pozostałe węzły, czyli zbiór V- Q – S, gdzie V jest zbiorem wszystkich wierzchołków grafu G = (V, E)

Warto nadmienić, że częściej spotykana wersja algorytmu Dijkstry zakłada, że do zbioru Q trafiają „od razu” wszystkie węzły grafu G, a następnie są po kolei pobierane pojedynczo węzły, które trafiają do zbioru S.

Idea omawianego algorytmu jest następująca. Rozpoczynamy od dodania węzła źródłowego r do zbioru Q. Następnie rozpoczynamy cykliczne wykonywanie ciągu operacji, na który składa się:

• wybranie ze zbioru Q wierzchołka o znanej najmniejszej odległości od źródła (nazwijmy go Vi)
• dodanie powyższego węzła do zbioru S
• przejrzenie wszystkich sąsiednich węzłów wierzchołka Vi, które nie należą do zbioru S – następnie jest sprawdzane, czy droga ze źródła do sąsiada (oznaczmy ten węzeł jako Vj) prowadząca przez węzeł Vi jest krótsza niż najkrótsza ścieżka znana do tej pory, jeśli tak jest, to następuje uaktualnienie najkrótszej ścieżki oraz dodanie tego węzła do zbioru Q

Jeżeli w pewnym momencie okaże się, że zbiór Q jest pusty, to należy zakończyć działanie algorytmu – najkrótsze ścieżki do wszystkich węzłów osiągalnych ze źródła zostały już wyznaczone.

Czynność sprawdzania, czy ścieżka przechodząca przez Vi i prowadząca do Vj jest krótsza od dotychczas znanej najkrótszej ścieżki do Vj, jest nazywana relaksacją krawędzi (Vi, Vj). W przypadku gdy powyższy warunek jest spełniony, długość najkrótszej ścieżki oraz ostatni węzeł poprzedzający Vj na tej ścieżce muszą zostać zapamiętane.

Relaksacja krawędzi jest jedynym miejscem w algorytmie, w którym długości najkrótszych ścieżek oraz określenie poprzedników węzłów są zmienianie. Podobnie i inne algorytmy wyznaczające najkrótsze ścieżki w grafie z jednym źródłem korzystają z metody relaksacji krawędzi – np. znany algorytm Bellmana-Forda.

Procedurę możemy przedstawić za pomocą pseudokodu:

  S – zbiór pusty
	Q – zbiór pusty
	for (każdy węzeł i grafu G(V, E) ) {

		D[i] = nieskończoność 	//tablica D przechowująca wartości aktualnie najkrótszej 
					//ścieżki od źródła do węzła vi

		P[i] = 0	//tablica P przechowująca indeks węzła, który jest 
				//poprzednikiem węzła i na najkrótszej ścieżce od źródła 
				//do i
	}
	dodaj źródło (węzeł) r do zbioru Q
	D[r] = 0
 
	while (zbiór Q nie jest pusty) {
		wybierz ze zbioru Q wierzchołek o indeksie i, dla którego wartość D[i] będzie najmniejsza
		dodaj wierzchołek i do zbioru S

		for (każdy wierzchołek j sąsiadujący z wierzchołkiem i, który nie należy do S)
			if  (D[i] +w[i,j] < D[j]) {	//oznacza to, że znaleziono krótszą ścieżkę 
							//do i przez węzeł j niż znaleziona do tej 
							//pory, należy 
							//ją zaktualizować i określić 
							//nowego poprzednika
				D[j] = D[i] +w[i,j]
				P[j] = i
				dodaj węzeł j do zbioru Q
			}
	}

Poniżej przedstawiono przykład rysunkowy algorytmu Dijkstry dla przykładowego grafu nieskierowanego:

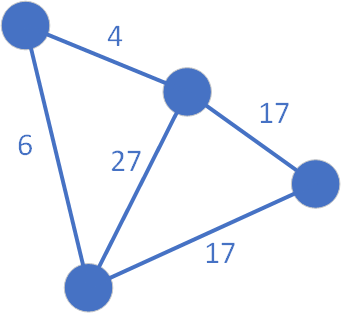
Następnie ustalamy jeden z wierzchołków jako węzeł źródłowy (ten z wartością 0 w środku):


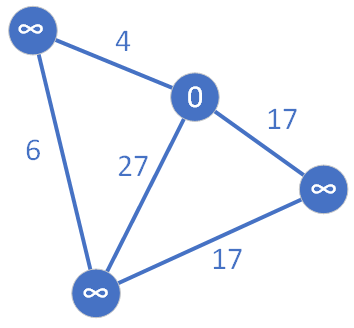
Zgodnie z algorytmem węzeł startowy trafia do zbioru Q i ponieważ jest on jedynym wierzchołkiem w tym zbiorze, wybieramy go i przenosimy do zbioru S. Następnie przeglądamy wszystkich jego trzech sąsiadów, dla których zostają wyznaczone aktualnie znane najkrótsze ścieżki. Węzły te przyjmują kolor zielony. Natomiast węzeł źródłowy został pomalowany na kolor żółty.

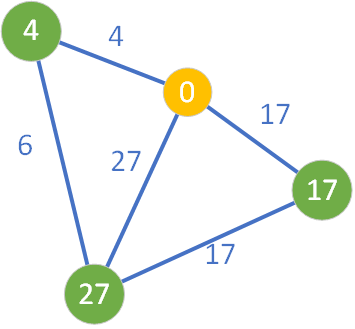
W tym momencie w zbiorze Q znajdują się 3 węzły. Wybieramy ten węzeł, który ma najmniejszą wartość wpisaną w kółko obrazujące dany wierzchołek. Algorytm wybiera zatem węzeł o wartości D=4 (znajdujący się skrajnie po lewej stroni) – krok ten jest zobrazowany pomalowaniem węzła na kolor jasnofioletowym:

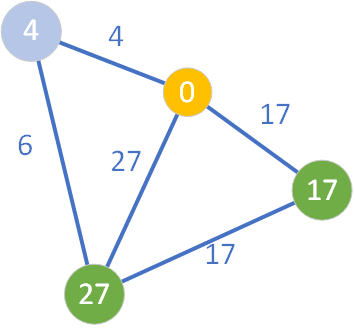
Następnie należy przejrzeć wszystkie sąsiednie węzły wierzchołka jasnofioletowego, które nie należą do zbioru S (a zatem nie są koloru żółtego). Okazuje się, że jest jeden taki węzeł – o wartości D=27. Przeglądanie sąsiada i sprawdzenie, czy można dokonać relaksacji, „odnotowywane” jest pomalowaniem go na kolor fioletowy:

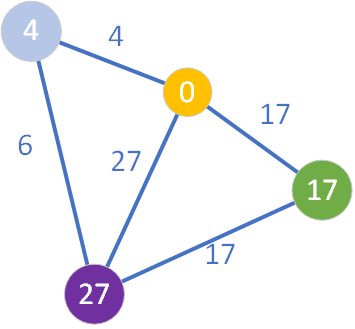
Jak widzimy, ścieżka prowadząca przez węzeł „4” do węzła o etykiecie „27” jest krótsza niż znana do tej pory. Zachodzi więc relaksacja krawędzi łączącej te dwa wierzchołki i uaktualnienie (zmniejszenie) wartości D.

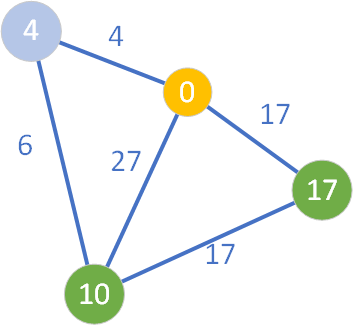
Ponieważ wszyscy sąsiedzi zostali już sprawdzeni, wierzchołek o wartości D=4 staje się węzłem żółtym. W kolejnym kroku pętli algorytmu wybieramy węzeł o etykiecie „10” (ponieważ 10<17).

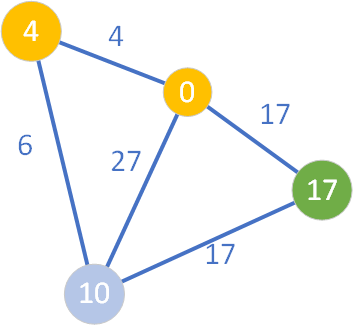
Aktualny węzeł jasnofioletowy posiada tylko jednego sąsiada w kolorze innym niż żółty (jest nim węzeł o wartości D=17). Ponieważ ścieżka ze źródła do węzła „17” prowadząca przez węzeł „10” nie jest krótsza niż najkrótsza ścieżka znana do tej pory (gdyż 10+17=27 nie jest mniejsze niż 17), więc nie następuje relaksacja i uaktualnienie wartości D dla wierzchołka o etykiecie „17”. Węzeł „10” jest przenoszony do zbioru S, a następnie zostaje wybrany spośród zbioru Q węzeł o etykiecie „17”.

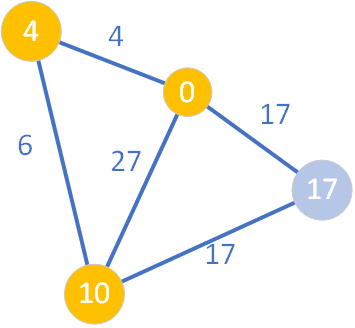
Ponieważ wszyscy jego sąsiedzi mają znalezione (ustalone) najkrótsze ścieżki ze źródła, nie dokonujemy relaksacji żadnej z krawędzi. Węzeł o wartości D=17 również trafia do zbioru S – najkrótsza ścieżka prowadząca do niego ze źródła ma wartość (koszt) równy 17.

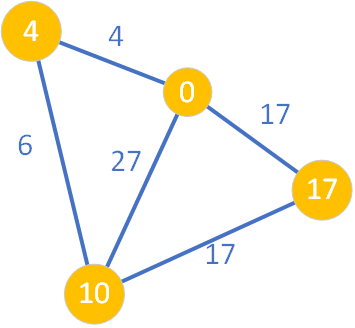
Jak łatwo zauważyć, nie ma już węzłów w kolorze zielonym – zbiór Q stał się pusty. Tym samym wszystkie najkrótsze ścieżki ze źródła do pozostałych wierzchołków grafu zostały wyznaczone. Potwierdza do graficznie schemat grafu, gdyż wszystkie węzły są w kolorze żółtym.

4. Algorytm A-star

Algorytm A* to zaawansowana metoda znajdowania najkrótszej ścieżki pomiędzy dwoma punktami w grafie, szczególnie popularna w grach komputerowych, systemach nawigacyjnych i robotyce. Jest to algorytm informowany (heurystyczny), łączący zalety algorytmu Dijkstry i przeszukiwania best-first.

Podstawą działania algorytmu A* jest funkcja oceny f(v) = g(v) + h(v), gdzie g(v) to koszt przebycia ścieżki od punktu początkowego do węzła v, a h(v) to heurystyczna ocena kosztu dotarcia z v do punktu końcowego. Heurystyka h(v) musi być oszacowaniem nie większym niż rzeczywisty koszt, by zapewnić poprawność działania algorytmu. 

W najprostszych implementacjach najczęściej używa się następujących funkcji heurystycznych:

• standardowa odległość euklidesowa  (dla uproszczenia obliczeń zakłada się zwykle, że jeśli bok kwadratu=10, to jego przekątna ma długość równą 14) – taka funkcja zapewnia niedoszacowanie wartości odległości od celu (nie ma drogi krótszej, niż odcinek łączący dwa punkty) i tym samym znalezienie optymalnego rozwiązania.
• typu Manhattan (odległość dwóch węzłów to suma ich odległości w pionie i w poziomie – „poruszamy się po ulicach”) - nie ma ona własności niedoszacowania, ale kosztem pewności wyniku przyspiesza znacznie obliczenia.

Etapy działania algorytmu A*:

1. Inicjalizacja - tworzymy dwie główne struktury danych:
   • kolejkę otwartą (ang. open set) – zawiera węzły do odwiedzenia, uporządkowane według wartości f(v).
   • kolejkę zamkniętą (ang. closed set) – zawiera węzły już odwiedzone
   Wstawiamy wierzchołek początkowy do kolejki otwartej. Ustawiamy g(start) = 0 i f(start) = h(start).
2. Przeglądanie kolejnych wierzchołków - Dopóki kolejka otwarta nie jest pusta:
   • wybieramy wierzchołek v z najniższą wartością f(v) (czyli najbardziej obiecujący)
   • jeśli v to cel – zakończ algorytm i odtwórz ścieżkę
   • w przeciwnym razie: przenieś v do kolejki zamkniętej
3. Aktualizacja sąsiadów - dla każdego sąsiada n węzła v:
   • jeśli n jest w zamkniętej liście – pomiń
   • oblicz koszt dotarcia do n przez v: tentative_g = g( v ) + koszt(v, n)
   • jeśli n nie jest w kolejce otwartej lub tentative_g < g( n ):
     • zaktualizuj g( n ) i oblicz f( n ) = g( n ) + h( n )
     • ustaw v jako rodzica n (potrzebne do odtworzenia ścieżki)
     • jeśli n nie jest w kolejce otwartej – dodaj go
4. Zakończenie algorytmu - jeżeli kolejka otwarta stanie się pusta, a cel nie został znaleziony to nie istnieje ścieżka między punktami.

5. Minimalne drzewa rozpinające (MST)

Minimalne drzewo rozpinające (ang. Minimum Spanning Tree - MST) jest to takie drzewo rozpinające, które w przypadku grafu ważonego posiada najmniejszą z możliwych całkowitą sumę wag wszystkich krawędzi. Ponieważ każda krawędź łączy dokładnie dwa wierzchołki i poszukujemy drzewa rozpinającego, to do połączenia ze sobą n wierzchołków wystarczy nam dokładnie n-1 krawędzi. Dotyczy to grafu spójnego, w przeciwnym razie wystarczy mniej krawędzi, ale nie utworzymy wówczas jednego drzewa rozpinającego – potrzebnych będzie ich kilka.

Najbardziej znanymi algorytmami znajdowania minimalnego drzewa rozpinającego są powszechnie używane: algorytm Prima oraz algorytm Kruskala.

Algorytm Kruskala to klasyczny i bardzo efektywny sposób wyznaczania minimalnego drzewa rozpinającego (MST) w grafie nieskierowanym i ważonym. Główna idea algorytmu opiera się na metodzie zachłannej w każdym kroku wybierana jest krawędź o najmniejszej wadze, która nie tworzy cyklu w aktualnie budowanym drzewie.

Etapy działania algorytmu Kruskala:

1. Posortuj wszystkie krawędzie grafu według ich wag - na początku algorytm tworzy uporządkowaną listę wszystkich krawędzi od tej o najmniejszej wadze do tej o największej. 
2. Inicjalizacja zbiorów rozłącznych - dla każdego wierzchołka tworzony jest osobny zbiór. Zbiory te będą później łączone co odpowiada łączeniu komponentów grafu. 
3. Przechodzenie po posortowanych krawędziach - dla każdej krawędzi sprawdzamy, czy łączy ona dwa różne zbiory (czyli czy nie tworzy cyklu). Jeśli tak to dodajemy ją do wyniku i łączymy odpowiadające jej zbiory. 
4. Kryterium końca algorytmu - proces powtarza się, aż zostanie dodanych V - 1 krawędzi (gdzie V to liczba wierzchołków grafu). Wtedy otrzymujemy minimalne drzewo rozpinające.

Poniżej zamieszony jest przykład działania algorytmu Kruskala dla grafu:

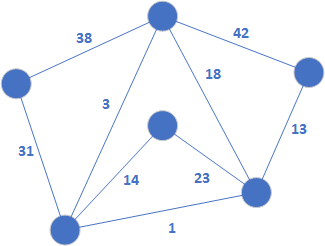
W pierwszym kroku należy posortować krawędzie grafu w porządku niemalejącym. Kolejność ta będzie przedstawiała się następująco:
1, 3, 13, 14, 18, 23, 31, 38, 42.

Każdy wierzchołek jest początkowo odrębnym drzewem. Algorytm ma za zadanie sprawdzać w kolejności sortowania poszczególne krawędzie. I tak:

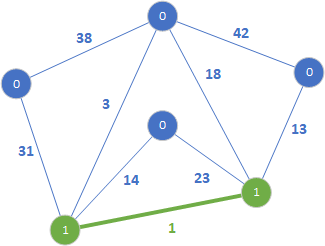
Krawędź o wadze 1 połączyła dwa rozłączne drzewa w jedno (zielona krawędź oraz oznaczenie 1). Następnie sprawdzamy krawędź o wadze 3.

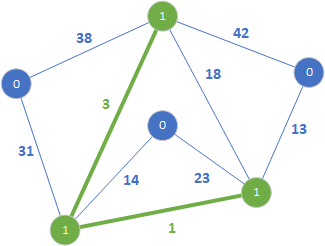
Końce tej krawędzi należą do różnych drzew, więc dodajemy ją do lasu rozpinającego. W kolejnym kroku sprawdzamy krawędź 13:

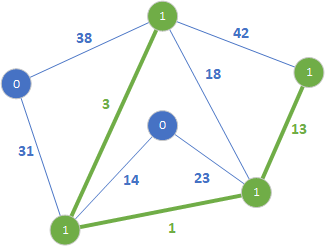
Końce tej krawędzi należą do różnych drzew, więc dodajemy ją do lasu rozpinającego. W kolejnym kroku sprawdzamy krawędź 14:

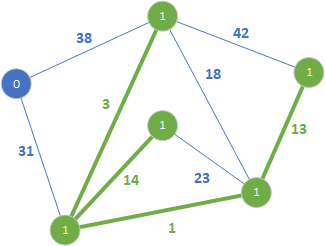
Podobnie jak poprzednio rozszerzony został las rozpinający o wartości 1. Kolejną krawędzią jest 18.

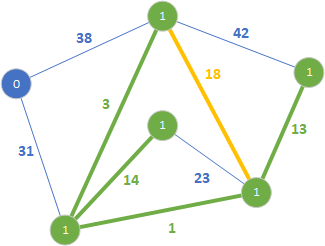
Nie dodajemy krawędzi ponieważ tworzy cykl. Przechodzimy do kolejnej krawędzi o wartości 23.

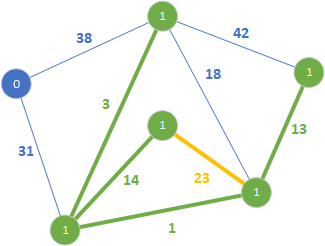
Podobnie jak poprzednio nie dodajemy krawędzi 23, bo tworzy cykl. Przechodzimy do kolejnej krawędzi o wadze 31.

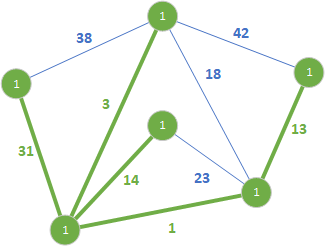
Rozszerzamy las rozpinający o wartość krawędzi 31. Kolejne krawędzie 38 i 42 nie są dodawane bo tworzą cykl. Na tym kończy się działanie algorytmu. Powyższy rysunek potwierdza, że zostało utworzone minimalne drzewo rozpinające – wszystkie wierzchołki grafu zostały włączone do jednego wspólnego drzewa i żaden węzeł nie pozostał odosobniony.

Całkowita suma wszystkich wag krawędzi należących do MST jest równa 62 i jest to minimalna wartość dla tego grafu.