Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Zastosowania Algorytmów Inteligencji Masowej |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | środa, 14 stycznia 2026, 22:24 |
Spis treści
- 1. Optymalizacja
- 2. Zadanie minimalizacji
- 2.1. Wprowadzenie do problemu minimalizacji
- 2.2. Przestrzeń ciągła i dyskretna - czyli gdzie szuka algorytm
- 2.3. Klasyczne metody przeszukiwania – od pełnego przeglądu po losowe strzały
- 2.4. Algorytmy gradientowe - matematyczna droga w dół ...
- 2.5. Uwzględnianie ograniczeń w optymalizacji – kiedy nie wszystko wolno
- 3. Algorytmy genetyczne
- 4. Particle Swarm Optimization
1. Optymalizacja
Po co nam optymalizacja?
Wyobraźmy sobie codzienne sytuacje: chcemy dojechać do pracy jak najszybciej, wybrać najtańszy lot na wakacje czy zaprojektować konstrukcję mostu, który wytrzyma największe obciążenia przy jak najniższym koszcie. We wszystkich tych przypadkach chodzi o to samo: znaleźć najlepsze możliwe rozwiązanie, zgodne z przyjętym kryterium.
Tym właśnie zajmuje się optymalizacja. Matematycznie rzecz ujmując, optymalizacja to poszukiwanie minimum lub maksimum funkcji celu przy zadanych ograniczeniach. Funkcja celu to matematyczny opis tego, co chcemy zmaksymalizować (np. zysk) lub zminimalizować (np. koszt). Zmiennymi decyzyjnymi są parametry, które możemy kontrolować, a ograniczenia to zbiór warunków, które rozwiązanie musi spełniać, by było dopuszczalne.
Optymalizacja pojawia się wszędzie tam, gdzie trzeba podejmować decyzje. Trzeba jednak pamiętać, że nie każda decyzja intuicyjnie najlepsza jest naprawdę optymalna w sensie matematycznym — różnica ta staje się istotna w zastosowaniach inżynierskich czy ekonomicznych, gdzie nieoptymalny wybór może skutkować realnymi stratami.
Trudności w optymalizacji
Pierwszą trudnością w wielu problemach optymalizacyjnych jest rozmiar przestrzeni poszukiwań. Gdy liczba zmiennych jest duża, liczba możliwych rozwiązań rośnie wykładniczo, a pełne przeszukiwanie staje się praktycznie niemożliwe. Przykładowo, przy 100 zmiennych binarnych mamy do rozważenia wariantów. Nawet najpotężniejsze komputery nie są w stanie przetworzyć takiej ilości danych w sensownym czasie.
Drugi problem to natura samej funkcji celu. W praktyce funkcje te są często nieliniowe, nieciągłe, a czasem nawet stochastyczne. Może się okazać, że drobna zmiana parametrów powoduje duży i nieprzewidywalny skok wartości funkcji celu. Taka „dzika” topologia przestrzeni rozwiązań utrudnia klasyczne metody optymalizacji bazujące na pochodnych i gradientach.
Trzecią barierą są ograniczenia — formalne lub ukryte. Wiele rzeczywistych problemów zawiera trudne do opisania warunki dopuszczalności: fizyczne, techniczne, prawne, czy związane z bezpieczeństwem. Dodanie ich do modelu optymalizacyjnego komplikuje analizę i znacząco zmniejsza liczbę dopuszczalnych rozwiązań, często do bardzo nieregularnych obszarów.
Ostatni, ale nie mniej ważny problem to lokalne ekstrema. W przypadku funkcji nieliniowych algorytmy mogą „utknąć” w minimum lokalnym — rozwiązaniu, które wygląda na dobre, ale nie jest najlepsze globalnie. Problem ten jest szczególnie dotkliwy w optymalizacji dyskretnej i złożonych problemach inżynierskich, gdzie nie widać łatwej drogi ucieczki z takiego minimum bez globalnej wiedzy o przestrzeni rozwiązań
Przykłady zastosowania optymalizacji
Poniżej przedstawiamy kilka klasycznych przykładów pokazanych na slajdach prezentacji AE1 2020.
Optymalizacja konstrukcji
Transport 1000 m³ chemikaliów ma się odbywać w szczelnych, prostopadłościennych pojemnikach. Każdy pojemnik ma ściany boczne nazywane odpowiednio A i B, oraz dno i górę. Każdy pojemnik można zbudować przy zachowaniu konkretnych warunków:
- materiał na górę kosztuje 65 PLN za metr kwadratowy
- materiał na boki A kosztuje 35 PLN za metr kwadratowy
- materiał na boki B oraz dno jest dostępny za darmo (pochodzi z odpadów), natomiast jest ograniczenie w jego ilości - możemy wykorzystać nie więcej niż 10 metrów kwadratowych na pojemnik
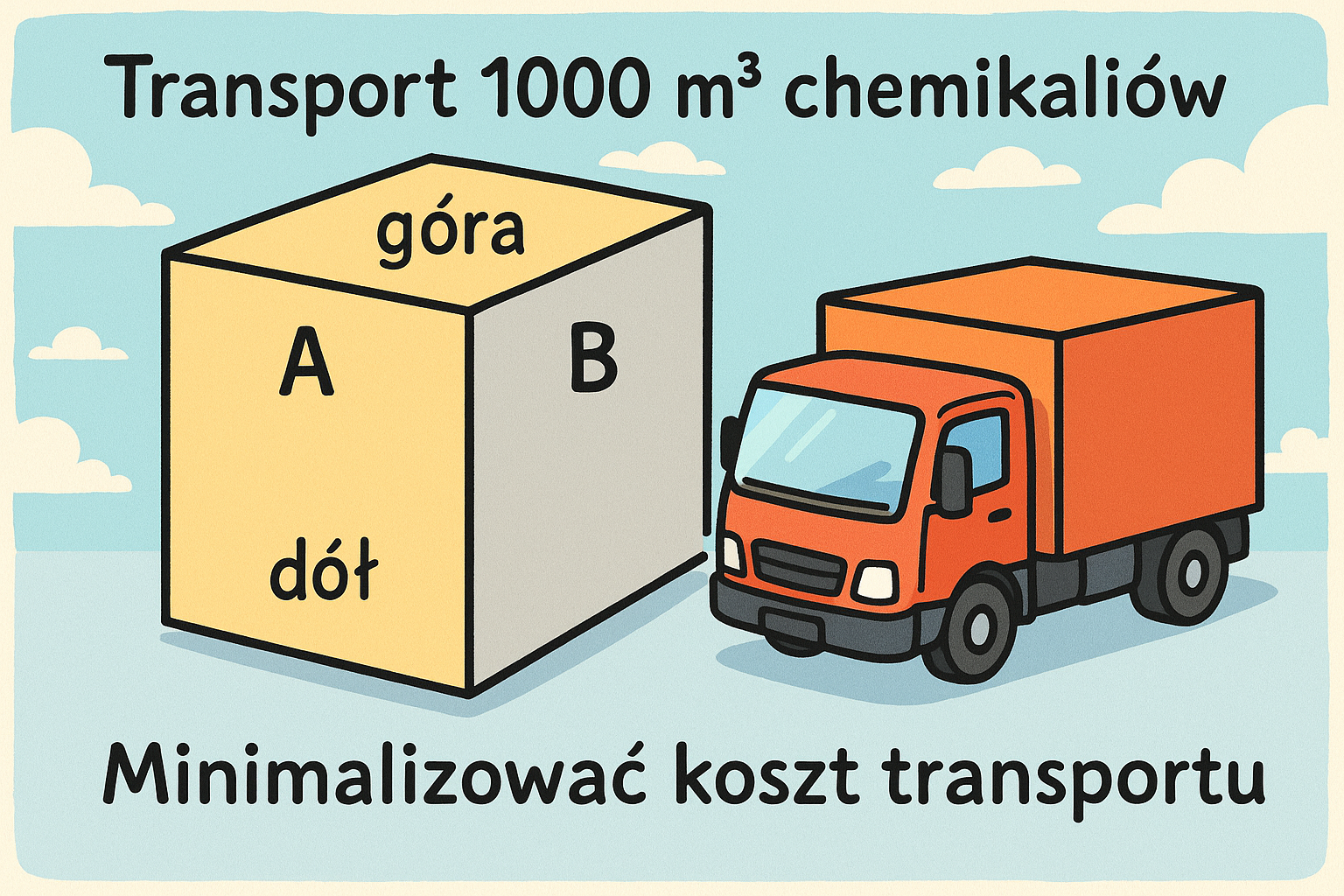
Transport pojemnika kosztuje 4 PLN, niezależnie od jego wielkości. Celem jest minimalizacja kosztu transportu. To klasyczny przykład zadania liniowego z ograniczeniami — zmienne decyzyjne to wymiary pojemników, a funkcja celu może zależeć np. od kosztów materiałów i liczby pojemników.
\(
k_j(x_1, x_2, x_3) = km_A \cdot 2(x_2 \cdot x_3) + km_{góra} \cdot (x_1 \cdot x_2) + k_{transport} \)
gdzie:
\(\begin{align*}
x_3 &\text{ — wysokość pojemnika,} \\
x_1 &\text{ — szerokość pojemnika,} \\
x_2 &\text{ — głębokość pojemnika,} \\
k_{transport}&\text{ — koszt transportu pojedynczego pojemnika}
\end{align*}\)
Znając wymiary pojemnika możemy też obliczyć ile ich potrzebujemy:
\( z= \frac{V_{całkowita}}{x_1*x_2*x_3} \)
No i finalnie dochodzimy do wzoru na koszt całkowity
\( f(x_1,x_2,x_3)=z*k_j = \frac{V_{całkowita}}{x_1*x_2*x_3} * (km_A \cdot 2(x_2 \cdot x_3) + km_{góra} \cdot (x_1 \cdot x_2) + k_{transport} ) \)
Optymalizacja portfela inwestycyjnego
Optymalizacja portfela inwestycyjnego to jeden z klasycznych przykładów zastosowania metod optymalizacyjnych w finansach. Wyobraźmy sobie inwestora, który dysponuje pewnym kapitałem i chce go ulokować w różnych aktywach: np. akcjach dużych stabilnych spółek (tzw. blue chips), sektorze paliwowym, nieruchomościach oraz obligacjach. Każde z tych aktywów cechuje się określoną historyczną stopą zwrotu oraz zmiennością (czyli ryzykiem). Celem inwestora jest znalezienie takiego podziału środków, który zapewni możliwie wysoki zysk przy jednocześnie możliwie niskim ryzyku.
Zmiennymi decyzyjnymi w tym przypadku są procentowe udziały kapitału przeznaczone na każdą z czterech kategorii inwestycji, oznaczmy je odpowiednio jako x₁, x₂, x₃, x₄. Suma tych udziałów musi być równa 1 (czyli 100%), co stanowi podstawowe ograniczenie zadania. Dodatkowo mogą występować ograniczenia dolne i górne, np. minimalny udział w obligacjach albo maksymalny udział w akcjach wysokiego ryzyka.
| Typ inwestycji | Roczna stopa zwrotu | ||||||
|---|---|---|---|---|---|---|---|
| Rok | 1 | 2 | 3 | 4 | 5 | 6 | średnia |
| Blue Chip | 18,24 | 12,12 | 15,23 | 5,26 | 2,62 | 10,42 | 10,65 |
| Paliwa | 12,24 | 19,16 | 35,07 | 23,46 | -10,62 | -7,43 | 11,98 |
| Nieruchomości | 8,23 | 8,96 | 8,35 | 9,16 | 8,05 | 7,29 | 8,34 |
| Obligacje | 8,12 | 8,95 | 8,26 | 8,34 | 9,01 | 9,12 | 8,63 |
Funkcja celu w tym problemie ma charakter dwuwymiarowy. Z jednej strony chcemy zmaksymalizować średnią wartość zysku (czyli kombinację średnich stóp zwrotu poszczególnych aktywów ważonych przez x₁ do x₄), a z drugiej strony zminimalizować ryzyko, które najczęściej mierzy się poprzez wariancję lub odchylenie standardowe wartości portfela.
\( V_{j j}=\frac{1}{n} \sum_{k=1}^n\left(r_{j k}-\mu_j\right)^2 \)
Wariancja całego portfela nie zależy tylko od wariancji poszczególnych aktywów, ale również od ich kowariancji — czyli tego, jak bardzo dane aktywa „poruszają się razem”. Dlatego do zadania wprowadza się macierz kowariancji pomiędzy wszystkimi parami inwestycji. Każda komórka tej macierzy pokazuje wariancję wzajemną:
\( V_{i j}=\frac{1}{n} \sum_{k=1}^n\left(r_{i k}-\mu_i\right)\left(r_{j k}-\mu_j\right) \)
Teraz możemy już zapisać ryzyko:
\(
\text{Ryzyko} = \mathbf{x}^T \mathbf{V} \mathbf{x}
\)
Potem powinniśmy jeszcze uwzględnić ograniczenia (zmienne decyzyjne muszą sumować się do jedynki - musimy podzielić całe środki, i jednocześnie nie przekroczyć budżetu). Drugim ograniczeniem będzie zysk - chcemy mieć średni zysk co najmniej 10%:
\( 10.65*x_1+11.98*x_2+8,34*x_3+8,64*x_4 \geq10 \)
Ostatecznie zadaniem można zapisać jako
\( min {x^TVx} \)
Z ograniczeniami podanymi wyżej, przy dodatkowym założeniu, że żadna ze zmiennych decyzyjnych nie może być mniejsza od zera.
Formalnie zapisane, zadanie optymalizacji portfela przyjmuje postać problemu kwadratowego z ograniczeniami. Funkcja celu jest funkcją kwadratową (ze względu na macierz kowariancji), a ograniczenia mają postać równań liniowych (suma udziałów równa 1) oraz ewentualnie nierówności (udziały nieujemne, minimalne progi). Dodatkowy warunek na minimalny oczekiwany zysk — np. inwestor deklaruje, że chce mieć co najmniej 10% średniego zwrotu - też jest ograniczeniem liniowym.
Tego rodzaju problemy są idealnym kandydatem dla zastosowania algorytmów ewolucyjnych, zwłaszcza gdy w grę wchodzą nieliniowe zależności, dyskretne zmienne (np. minimalny próg inwestycyjny), nietypowe ograniczenia lub wiele konkurencyjnych celów naraz (np. zysk, ryzyko, płynność). Algorytmy genetyczne pozwalają łatwo modelować takie złożone sytuacje i znaleźć zbiór kompromisowych rozwiązań — tzw. front Pareto — dający inwestorowi wachlarz dobrze zbilansowanych opcji inwestycyjnych.
Alokacja zasobów (środek owadobójczy)
Wyobraźmy sobie plantację w kształcie kwadratu, na której zlokalizowano 12 aktywnych gniazd os. Każde z nich stanowi zagrożenie dla ludzi i upraw, dlatego konieczne jest ich unieszkodliwienie. Do dyspozycji mamy trzy pojemniki ze środkiem owadobójczym, które należy rozmieszczać na tej przestrzeni w taki sposób, by skutecznie zneutralizować jak największą liczbę gniazd.
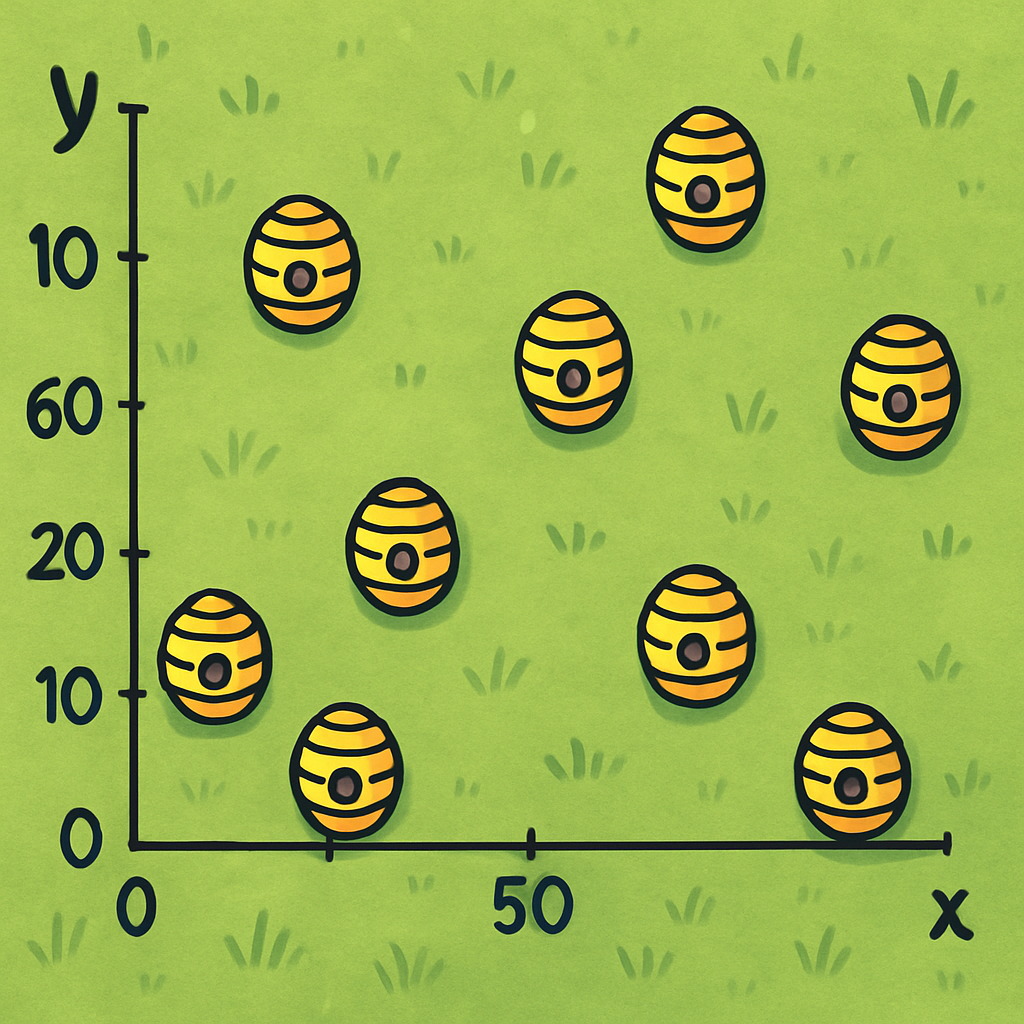
Zmiennymi decyzyjnymi w tym problemie są współrzędne położenia każdego z trzech pojemników, co oznacza, że mamy do czynienia z problemem optymalizacji w przestrzeni sześciowymiarowej: (x₁, y₁, x₂, y₂, x₃, y₃). Każdy punkt w tej przestrzeni określa możliwe ustawienie pojemników na polu. Ograniczenia wynikają z fizycznych granic plantacji (np. wszystkie współrzędne muszą mieścić się w zakresie od 0 do 100 metrów, jeśli pole ma 100 m długości) oraz z odległości minimalnych między pojemnikami (np. ze względów bezpieczeństwa nie mogą znajdować się zbyt blisko siebie).
Funkcja celu opisuje skuteczność działania rozmieszczenia. Załóżmy, że każdy pojemnik działa w sposób radialny — jego skuteczność maleje z odległością od centrum działania. Możemy przyjąć model, w którym środek owadobójczy działa z pełną skutecznością w promieniu np. 10 m, a dalej jego efektywność spada np. wykładniczo. Dla każdego gniazda obliczamy wtedy skumulowany wpływ wszystkich pojemników i określamy, czy dawka przekracza próg skuteczności. Jeśli tak — gniazdo uznaje się za unieszkodliwione.
W ten sposób funkcja celu przyjmuje postać nieliniową i niegładką: jest to liczba gniazd os, które udało się zneutralizować przy danym ustawieniu pojemników. Funkcja ta może mieć wiele lokalnych maksimów (np. ustawienia pojemników skupiające się na części pola) i dlatego stanowi poważne wyzwanie dla klasycznych metod optymalizacji bazujących na pochodnych.
Dodatkową trudnością jest to, że zmienne są ciągłe, a przestrzeń rozwiązań nie jest prostą siatką — ma nieregularny kształt. Oznacza to, że metody optymalizacji wymagają inteligentnych strategii przeszukiwania, które potrafią unikać minimum lokalnych i są odporne na brak ciągłości lub nieregularność funkcji celu. Algorytmy genetyczne doskonale się w tym sprawdzają — operując populacją rozwiązań i stosując operatory krzyżowania i mutacji, mogą eksplorować różnorodne konfiguracje rozmieszczenia pojemników i z czasem wyłaniać te najbardziej skuteczne.
To przykład zadania nieliniowego z ograniczeniami, gdzie przestrzeń poszukiwań jest ciągła, ale funkcja celu — nieliniowa i trudna do zapisania analitycznie.
Optymalizacja produkcji
Przykład optymalizacji produkcji dotyczy zakładu przemysłowego, który wytwarza dwa rodzaje produktów przy użyciu dwóch różnych procesów technologicznych i dwóch rodzajów surowców: A i B. Zakład musi zaspokoić określone zapotrzebowanie rynkowe (np. 30 jednostek produktu X i 20 jednostek produktu Y), a jednocześnie działa w warunkach ograniczeń zasobów (np. dostępność 60 jednostek surowca A i 90 jednostek surowca B).
Zmiennymi decyzyjnymi są liczby cykli produkcyjnych w procesach I i II, oznaczane jako x₁ i x₂. Każdy cykl zużywa określoną ilość surowców A i B oraz dostarcza określoną liczbę produktów X i Y. Znając macierz współczynników technologicznych (ile surowca zużywa dany proces, ile produktu wytwarza), można sformułować model matematyczny całego systemu produkcyjnego.
Celem jest maksymalizacja zysku — różnicy między przychodem ze sprzedaży produktów a kosztem zużycia surowców. Zakłada się, że produkty X i Y mają znane ceny jednostkowe, a surowce A i B — znane koszty jednostkowe. Funkcja celu to więc wyrażenie liniowe zależne od zmiennych x₁ i x₂. Ograniczenia obejmują:
-
dostępność surowców: łączne zużycie A i B w obu procesach nie może przekroczyć ich dostępnych zasobów,
-
minimalne zamówienia: produkcja X i Y musi pokrywać popyt,
-
nieujemność zmiennych: liczba cykli produkcyjnych nie może być ujemna.
Formalnie jest to typowe zadanie programowania liniowego z ograniczeniami liniowymi. Rozwiązanie można znaleźć metodami klasycznymi (np. Simplex), ale w sytuacjach bardziej złożonych — np. gdy:
-
liczba produktów lub procesów wzrasta,
-
pojawiają się nieliniowe koszty (np. rabaty przy dużych zamówieniach),
-
występują zależności logiczne lub dyskretne zmienne (np. ograniczona liczba maszyn, minimalna seria produkcyjna), warto sięgnąć po algorytmy metaheurystyczne.
Algorytmy genetyczne dobrze radzą sobie w takich warunkach. Dzięki pracy na populacji rozwiązań i mechanizmowi selekcji, krzyżowania oraz mutacji są w stanie znajdować rozwiązania nie tylko poprawne, ale często zaskakująco dobre — zwłaszcza w przestrzeniach rozwiązań, w których metody klasyczne zawodzą lub wymagają znacznego uproszczenia modelu.
Celem jest maksymalizacja zysku. Zmiennymi są liczby cykli produkcyjnych dla obu typów procesów. Ograniczenia obejmują zużycie surowców i wymagania produkcyjne. To typowe zadanie liniowe z ograniczeniami.
Sterowanie napędem prądu stałego (DC)
Sterowanie napędem prądu stałego to klasyczny problem z zakresu automatyki, w którym celem jest tak dobrać parametry regulatora, aby układ reagował szybko, bez przeregulowań i z jak najmniejszym błędem ustalonym. Tu rozpatrujemy przypadek optymalizacji odpowiedzi skokowej układu napędowego z regulatorem typu PID (proporcjonalno-całkująco-różniczkującego).
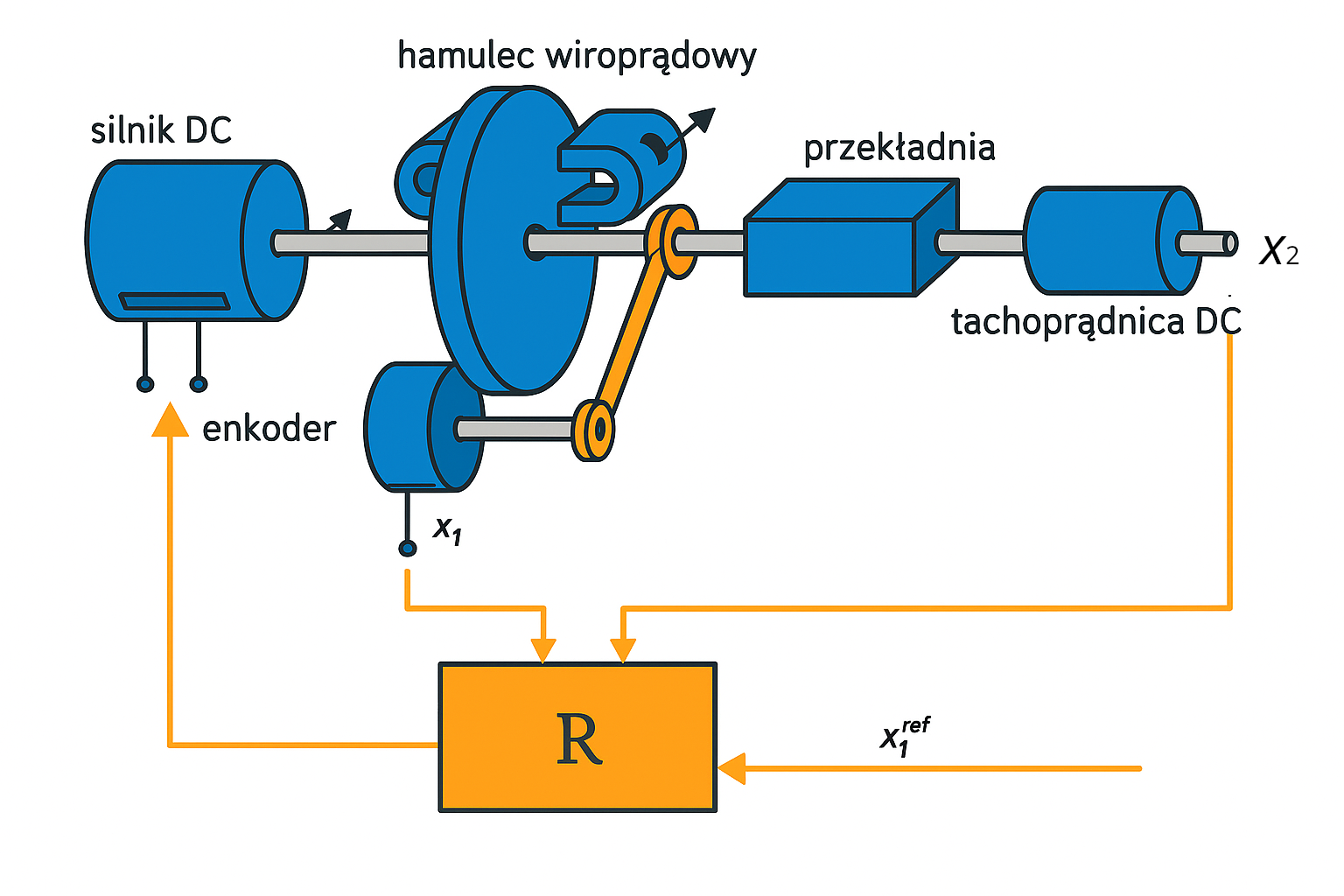
Zmiennymi decyzyjnymi w tym zadaniu są trzy współczynniki regulatora PID: Kₚ (wzmocnienie proporcjonalne), Tᵢ (czas całkowania) i Td (czas różniczkowania). To właśnie od ich wartości zależy jakość odpowiedzi układu: czas osiągania wartości zadanej, poziom przeregulowania oraz tłumienie oscylacji.
Aby ocenić jakość działania danego zestawu parametrów, definiujemy funkcję celu, która wyraża kompromis między różnymi wskaźnikami jakości regulacji. Najczęściej stosuje się kombinację:
- całkowego wskaźnika błędu (IAE, ISE lub ITAE),
- czasu regulacji (czas potrzebny do osiągnięcia zadanego poziomu z tolerancją),
- oraz maksymalnego przeregulowania.
W zależności od wag przypisanych poszczególnym składnikom funkcji celu, możemy preferować szybsze dojście do zadanej wartości kosztem większego przeregulowania, lub odwrotnie — stabilność kosztem szybkości.
Symulacja odpowiedzi skokowej dla każdego zestawu parametrów odbywa się numerycznie, najczęściej z użyciem pakietów typu MATLAB/Simulink lub podobnych narzędzi. Funkcja celu ma charakter nieliniowy i czarno-skrzynkowy, co oznacza, że nie jest znana w postaci analitycznej, a jej wartość można jedynie wyznaczyć przez symulację.
To czyni zadanie trudnym dla klasycznych metod optymalizacji gradientowej, ale bardzo dobrze przystosowanym do podejść ewolucyjnych. Algorytmy genetyczne pozwalają swobodnie eksplorować przestrzeń parametrów PID, a ich operatory krzyżowania i mutacji pomagają unikać utkwienia w minimach lokalnych. Dodatkowo, jeśli użyjemy podejścia wielokryterialnego, możemy uzyskać front Pareto przedstawiający kompromisy między czasem regulacji a przeregulowaniem.
Problem sterowania napędem DC ilustruje, jak teoria optymalizacji przekłada się na bardzo praktyczne, inżynierskie zastosowania — od przemysłu po robotykę mobilną i mechatronikę.
Dobór czynników do modelu predykcyjnego cen energii
W dziedzinie analizy szeregów czasowych jednym z ambitniejszych problemów jest przewidywanie przyszłych cen energii na podstawie danych historycznych. Zakładamy, że dysponujemy rozbudowanym zestawem zmiennych wejściowych: historyczne ceny energii, poziomy produkcji energii (np. z wiatru, fotowoltaiki, gazu), wskaźniki inflacyjne, indeksy giełdowe (np. WIG, S&P500), kursy walut (np. EUR/PLN), notowania surowców (ropa, gaz, węgiel), a także dane pogodowe (temperatura, siła wiatru, nasłonecznienie).
Zadanie polega na znalezieniu najlepszego modelu predykcyjnego (np. regresji liniowej, sieci neuronowej, drzewa decyzyjnego), który na podstawie wybranych zmiennych wejściowych pozwoli możliwie najdokładniej przewidzieć cenę energii w przyszłym kroku czasowym. Istotą problemu jest jednak dobór optymalnego podzbioru czynników wejściowych — nie chcemy używać ich wszystkich, ponieważ:
część może nie wnosić informacji (szum),
część może być redundantna,
większy model oznacza większą złożoność i trudność interpretacji.
Zmiennymi decyzyjnymi są tutaj kombinacje czynników wejściowych — problem ma charakter kombinatoryczny, ponieważ dla potencjalnych zmiennych istnieje możliwych podzbiorów. Dla 20 zmiennych to już ponad milion kombinacji. Dodatkowo, możemy rozważać także wybór typu modelu, hiperparametrów, lagów czasowych — co czyni problem jeszcze bardziej złożonym.
Funkcja celu mierzy jakość predykcji — może to być np. średni błąd bezwzględny (MAE), średni błąd kwadratowy (MSE) lub inna miara dopasowania, obliczana na podstawie danych walidacyjnych. Ponieważ funkcja celu nie ma analitycznego wyrazu i zależy od wyników trenowania modelu, mamy do czynienia z czarną skrzynką, którą można ocenić tylko przez symulację lub eksperyment.
Algorytmy genetyczne są doskonale przystosowane do tego typu problemów. Przestrzeń przeszukiwań to zbiory binarne (czy dany czynnik uwzględniamy), a operatory krzyżowania i mutacji pozwalają dynamicznie eksplorować nowe kombinacje. Warianty permutacyjne i wielokryterialne algorytmów pozwalają uwzględniać równocześnie jakość predykcji i prostotę modelu (np. liczbę zmiennych). Dzięki temu można uzyskać front Pareto modeli — od prostych i umiarkowanie skutecznych, po złożone o bardzo wysokiej trafności.
Ten przykład pokazuje, że optymalizacja nie ogranicza się tylko do „fizycznych” problemów inżynierskich, ale odgrywa coraz większą rolę w eksploracji danych, sztucznej inteligencji i nowoczesnej energetyce.
2. Zadanie minimalizacji
W niniejszym rozdziale zajmiemy się bardziej klasycznym podejściem do optymalizacji. Skupimy się przy tym na problemie minimalizacji - co nie powinno być żadnym ograniczeniem ... w praktyce prawie każdy problem polegający na maksymalizacji (np. zysku) można przekształcić w problem minimalizacji, po prostu odwracając znak funkcji celu. No właśnie - a co to jest wspomniana funkcja celu?2.1. Wprowadzenie do problemu minimalizacji
Zanim zaczniemy szukać rozwiązań, warto wiedzieć, czego w ogóle szukamy. W optymalizacji chodzi o znajdowanie najlepszych możliwych rozwiązań dla danego problemu. A w przypadku minimalizacji – po prostu takich, które dają najmniejszą możliwą wartość jakiejś funkcji. To właśnie tę funkcję nazywamy funkcją celu.
Brzmi ogólnie? To dobrze – bo tak naprawdę minimalizować można praktycznie wszystko: czas produkcji, koszt transportu, ryzyko inwestycji, liczbę strat podczas rozładunku, ilość odpadów, czy nawet… liczbę popełnionych błędów przy projektowaniu mostu.
Funkcja celu – czyli co właściwie minimalizujemy?
Funkcja celu to matematyczny sposób na opisanie tego, co chcemy zoptymalizować. Zazwyczaj oznacza się ją jako \(f(x)\), gdzie \(x\) to zestaw tzw. zmiennych decyzyjnych – czyli tego, na co mamy wpływ.
Przykład? Proszę bardzo – wróćmy do zadania z poprzedniego rozdziału, w którym projektowaliśmy prostopadłościenne zbiorniki do transportu chemikaliów. Celem było zminimalizowanie kosztów transportu, a zmiennymi decyzyjnymi były wymiary pojemników (np. wysokość, szerokość i długość). Funkcja celu mogła więc wyglądać np. tak:
\( f(x_1,x_2,x_3)=z*k_j = \frac{V_{całkowita}}{x_1*x_2*x_3} * (km_A \cdot 2(x_2 \cdot x_3) + km_{góra} \cdot (x_1 \cdot x_2) + k_{transport} ) \)
Szukaliśmy takiego zestawu wymiarów, który pozwala przewieźć zadaną objętość przy jak najmniejszym koszcie.
Ograniczenia – bo nie wszystko nam wolno
W rzeczywistości nie da się „po prostu” minimalizować. Zawsze są jakieś ograniczenia. To one wyznaczają granice naszej wolności w doborze zmiennych decyzyjnych. Ograniczenia pilnują, żeby proponowane rozwiązanie miało sens praktyczny, fizyczny, techniczny, ekonomiczny albo formalny.
Ograniczenia możemy podzielić na kilka rodzajów:
-
Twarde (formalne) – muszą być spełnione zawsze. Ich naruszenie oznacza, że rozwiązanie nie ma prawa istnieć. Np.:
-
\(x \geq 0\): długości, czasy, liczby jednostek nie mogą być ujemne,
-
\(\sum x_i = 1\): suma udziałów w portfelu inwestycyjnym musi wynosić 100%,
-
\(T_r \leq 10,\text{s}\): czas regulacji musi być mniejszy niż 10 sekund.
-
-
Miękkie (preferencyjne) – nie są obowiązkowe, ale zalecane. Zwykle wprowadza się je jako dodatkowe funkcje kary. Np.:
-
"unikaj użycia aluminium, jeśli nie jest konieczne",
-
"preferuj rozwiązania o mniejszej liczbie elementów ruchomych".
-
-
Geometryczne / fizyczne – wynikają z fizyki lub geometrii zadania:
-
pojemnik musi się zmieścić w kontenerze,
-
odległość między pojemnikami nie może być mniejsza niż 1 m,
-
długość pręta musi być większa niż 0, ale mniejsza niż 2,5 m.
-
-
Logiczne – np. zakaz inwestowania w firmy z określonego sektora, ograniczenia zgodne z regulaminem czy normą prawną.
W języku matematyki ograniczenia zapisujemy najczęściej jako:
-
nierówności: \(g(x) \leq 0\),
-
równości: \(h(x) = 0\).
W przykładzie portfela inwestycyjnego (z rozdziału 1) ograniczenia wyglądały tak:
-
\(\sum_{i=1}^4 x_i = 1\) – całość kapitału musi być zainwestowana,
-
\(x_i \geq 0\) – nie można inwestować ujemnych pieniędzy,
-
\(\sum_{i=1}^4 x_i \mu_i \geq 0.1\) – oczekiwany zysk powyżej 10%.
W przykładzie sterowania napędem, ograniczenia dotyczyły:
-
zakresów parametrów regulatora PID (np. \(K_r \in [0.1, 2.5]\)),
-
dopuszczalnych wartości odchyłki regulacji (\(e_\infty \leq 0.05\) mm),
-
fizycznych ograniczeń wynikających z modelu siłownika.
A w zadaniu rozmieszczenia pojemników z insektycydem mieliśmy np.:
-
pozycje pojemników musiały mieścić się na polu uprawnym,
-
minimalna odległość między nimi musiała gwarantować efektywne działanie,
-
niektóre rejony mogły być wykluczone ze względów bezpieczeństwa.
Dobre zdefiniowanie ograniczeń to często połowa sukcesu – od nich zależy, czy algorytm będzie przeszukiwał rozsądny obszar przestrzeni, czy błądził w miejscach kompletnie nieużytecznych.
Przestrzeń poszukiwań i rozwiązań dopuszczalnych
Zmiennych decyzyjnych zwykle jest kilka lub kilkanaście. Ich wszystkie możliwe kombinacje tworzą tzw. przestrzeń poszukiwań – czyli wszystkie teoretycznie dostępne rozwiązania.
Ale tylko część z nich spełnia wszystkie ograniczenia – i to właśnie ta część nazywa się przestrzenią rozwiązań dopuszczalnych. Przykładowo: możemy mieć 10 miliardów potencjalnych rozwiązań, ale tylko 5 milionów z nich spełnia warunki techniczne, prawne albo biznesowe.
Z punktu widzenia algorytmu optymalizacyjnego najważniejsze pytanie brzmi:
Przykłady z życia – optymalizacja jako chleb powszedni
Spróbujmy wrócić do przykładów z poprzedniego rozdziału:
-
Portfel inwestycyjny – minimalizujemy ryzyko inwestycji (wariancję zysków), ale przy założeniu, że średni zysk musi wynosić co najmniej 10%. Zmiennymi decyzyjnymi są udziały różnych aktywów. Ograniczenia? Łączna suma udziałów = 100%, żaden nie może być ujemny, zysk powyżej 10%.
-
Rozmieszczenie pojemników z insektycydem na polu – minimalizujemy liczbę przeżywających os (czyli maksymalizujemy skuteczność środka). Zmiennymi są współrzędne pojemników, a ograniczenia wynikają z rozmiarów pola, działania środka, bezpiecznych odległości.
-
Sterowanie napędem – minimalizujemy czas reakcji albo przeregulowanie, dbając o to, żeby układ był stabilny. Ograniczenia: dopuszczalne zakresy parametrów regulatora, wymogi na odpowiedź skokową, granice fizyczne układu.
Wszystkie te zadania są przykładami problemów minimalizacji, które pojawiają się w prawdziwej inżynierii, ekonomii i logistyce. A skoro już wiemy, że są – czas dowiedzieć się, jak się za nie zabrać.
2.2. Przestrzeń ciągła i dyskretna - czyli gdzie szuka algorytm
Zanim zaczniemy wybierać konkretne algorytmy optymalizacji, musimy się zastanowić: jak wygląda przestrzeń, w której będziemy szukać rozwiązań? To jedno z najważniejszych pytań, jakie należy sobie zadać w kontekście minimalizacji.
Przestrzeń poszukiwań – nie tylko zbiór liczb
W poprzednim rozdziale wprowadziliśmy pojęcie przestrzeni poszukiwań – zbioru wszystkich możliwych konfiguracji zmiennych decyzyjnych. Teraz dodajmy coś istotnego: ten zbiór może mieć bardzo różną strukturę.
Najczęściej spotykamy dwie sytuacje:
-
zmienne decyzyjne mogą przyjmować wartości ciągłe – np. długość pręta w metrach: 1.37 m, 2.03 m, 0.88 m, itd.
-
lub wartości dyskretne – np. wybór trasy w problemie komiwojażera, rozmieszczenie urządzeń na siatce, przypisanie pracowników do zadań.
Niektóre problemy można też przedstawić jako mieszane – część zmiennych jest ciągła, a część dyskretna. Takie przypadki są typowe np. w inżynierii procesowej.
Przestrzeń ciągła – gładka, ale nie zawsze łatwa
Przestrzeń ciągła to taka, w której zmienne mogą przyjmować dowolne wartości z pewnego przedziału. Matematycznie mówimy wtedy, że \(x \in \mathbb{R}^n\).
Zaletą przestrzeni ciągłej jest to, że możemy używać narzędzi analizy matematycznej – np. obliczać pochodne, badać gradienty, korzystać z metod iteracyjnych typu Newtona czy spadku gradientu. Tyle że jest pewien haczyk: takie metody zakładają gładkość funkcji celu (czyli że nie ma skoków, ostrych minimów ani zerwań ciągłości).
Problemy:
-
minimum może być lokalne, a nie globalne,
-
funkcja może być „płaska” – przez co gradient nic nie mówi,
-
ograniczenia mogą tworzyć bardzo wąskie lub nieregularne obszary.
Przestrzeń dyskretna – przeliczalna, ale ogromna
Z kolei przestrzeń dyskretna to taka, w której zmienne mogą przyjmować jedynie określone, policzalne wartości – np. liczby całkowite, ciągi permutacji, konfiguracje binarne.
Przykład:
-
Problem komiwojażera: przestrzeń to zbiór wszystkich permutacji miast (czyli $n!$ możliwości).
-
Alokacja pracowników do zmian: przestrzeń to zbiór możliwych macierzy przydziału z warunkami logicznymi.
Zaletą przestrzeni dyskretnej jest to, że nie potrzebujemy pochodnych, a każdy punkt jest „jednostką”, którą da się jednoznacznie opisać. Ale przestrzenie dyskretne rosną wykładniczo – tzn. liczba możliwych rozwiązań może szybko przekroczyć zdolność obliczeniową nawet dużych komputerów.
Problemy:
-
przeszukiwanie wyczerpujące staje się niemożliwe,
-
często nie ma pojęcia "bliskich" rozwiązań – trudno stosować pojęcie lokalnego minimum,
-
konieczne są sprytne strategie eksploracji (np. losowe skoki, heurystyki).
Różnice w optyce algorytmów
Wybór algorytmu powinien być dostosowany do rodzaju przestrzeni, bo algorytmy myślą (a raczej "liczą") w zupełnie inny sposób zależnie od tego, czy mają do czynienia z przestrzenią ciągłą czy dyskretną.
W przestrzeni ciągłej algorytmy często opierają się na lokalnej analizie funkcji celu:
szukają kierunku największego spadku (gradient),
opierają się na pochodnych, macierzy Hessego lub metodach quasi-Newtona,
iteracyjnie poprawiają rozwiązanie w stronę minimum,
zakładają pewną gładkość i regularność przestrzeni.
Typowe algorytmy:
metoda największego spadku,
metoda Newtona i quasi-Newtona (BFGS),
algorytmy ewolucyjne z kodowaniem rzeczywistoliczbowym.
W przestrzeni dyskretnej wszystko wygląda inaczej:
nie mamy pojęcia o "nachyleniu", bo między punktami nie istnieje pojęcie pochodnej,
bliskość rozwiązań nie zawsze przekłada się na podobieństwo funkcji celu,
konieczne są inne strategie eksploracji: permutacje, losowanie, heurystyki lokalne.
Typowe podejścia:
algorytmy zachłanne i lokalne przeszukiwanie (hill climbing),
algorytmy metaheurystyczne: symulowane wyżarzanie, algorytmy genetyczne,
strategie oparte na populacjach i losowym próbkowaniu.
Przykład porównawczy
Załóżmy, że projektujemy most i chcemy:
-
w przestrzeni ciągłej: dobrać grubości, długości i przekroje belek,
-
w przestrzeni dyskretnej: wybrać z katalogu gotowe komponenty (typu prefabrykaty).
Pierwszy problem daje więcej swobody, ale może prowadzić do rozwiązań nierealnych. Drugi wymaga kompromisów, ale łatwiej go uwzględnić w kosztorysie i harmonogramie.
2.3. Klasyczne metody przeszukiwania – od pełnego przeglądu po losowe strzały
Zanim rzucimy się w wir algorytmów ewolucyjnych, warto poznać kilka klasycznych podejść do przeszukiwania przestrzeni rozwiązań. Choć czasem uznawane za przestarzałe, wciąż stanowią punkt odniesienia dla każdej bardziej zaawansowanej metody. W tym podrozdziale skupimy się na przestrzeni dyskretnej – czyli takiej, gdzie liczba możliwych rozwiązań jest skończona (choć może być bardzo duża).
Przeszukiwanie pełne (brute force)
Najbardziej oczywista metoda: sprawdź wszystkie możliwe rozwiązania i wybierz najlepsze. Działa idealnie... pod warunkiem, że masz do przeszukania małą przestrzeń. Niestety, w praktyce:
- liczba możliwych rozwiązań rośnie wykładniczo z liczbą zmiennych,
- przy nawet kilku zmiennych dyskretnych zakres możliwości może sięgać miliardów,
- szybko przekraczamy możliwości obliczeniowe dostępnego sprzętu.
Przykład: jeśli mamy 10 zmiennych całkowitych przyjmujących po 10 wartości, to mamy \(10^{10} = 10,000,000,000\) rozwiązań.
Zalety:
- gwarantuje znalezienie najlepszego rozwiązania (jeśli istnieje),
- działa niezależnie od natury funkcji celu,
- bardzo prosta implementacja.
Wady:
- totalnie niepraktyczne dla większych problemów,
- nie wykorzystuje żadnej wiedzy o strukturze przestrzeni.
Przeszukiwanie losowe
Zamiast sprawdzać wszystko – losujemy. Algorytm losowy wybiera kolejne rozwiązania zupełnie przypadkowo z przestrzeni dyskretnej i ocenia ich jakość. Jeśli uda się znaleźć dobre – super. Jeśli nie – próbujemy dalej.
Jak to wygląda w praktyce:
- losujemy rozwiązanie \(x\),
- obliczamy wartość funkcji celu \(f(x)\),
- zapamiętujemy najlepszy wynik dotąd,
- powtarzamy przez ustaloną liczbę iteracji.
Zalety:
- prostota implementacji – dosłownie kilka linijek kodu,
- możliwość działania równoległego (każdy proces może losować osobno),
- działa w każdej przestrzeni dyskretnej (nie wymaga żadnych założeń).
Wady:
- zupełna przypadkowość – możemy długo błądzić zanim trafimy coś sensownego,
- nie wykorzystuje wiedzy z poprzednich prób – "ślepe strzelanie",
- nie gwarantuje znalezienia rozwiązania lepszego od startowego.
Mimo wad, algorytmy losowe bywają zaskakująco skuteczne w przestrzeniach, gdzie lokalne strategie często wpadają w minima lokalne – np. przy wielu zaporowych ograniczeniach.
Przeszukiwanie losowe z pamięcią
Wariant bardziej zaawansowany: próbujemy wykorzystać doświadczenia z poprzednich losowań. Czyli: pamiętamy coś o przeszłości i nie działamy całkiem na oślep. Oto dwie popularne techniki:
Symulowane wyżarzanie (simulated annealing)
Metoda inspirowana procesami fizycznymi – konkretnie wyżarzaniem metali. Algorytm:
- zaczyna od losowego rozwiązania,
- losowo modyfikuje je (tworzy sąsiada),
- jeśli sąsiad jest lepszy – przyjmuje go,
- jeśli jest gorszy – może go przyjąć z pewnym prawdopodobieństwem \(p = e^{-\Delta f / T}\),
- temperatura \(T\) maleje w czasie – co zmniejsza prawdopodobieństwo akceptowania gorszych rozwiązań.
To podejście pozwala wyjść z minimum lokalnego, ale z czasem staje się coraz bardziej zachowawcze – koncentruje się na najlepszych rozwiązaniach.
Algorytm tabu (tabu search)
Tutaj z kolei prowadzimy rodzaj "czarnej listy" – pamiętamy, gdzie już byliśmy i unikamy powtórek. Algorytm:
- przechodzi od rozwiązania do jego najlepszego sąsiada,
- jeśli sąsiad był niedawno odwiedzony – jest oznaczany jako tabu (czyli zakazany),
- lista tabu działa jak bufor cykliczny (np. ostatnie 100 odwiedzin),
- pozwala to uniknąć cyklicznego krążenia wokół tego samego minimum.
Algorytmy z pamięcią są inteligentniejszą odmianą przeszukiwania losowego – uczą się w czasie, nie pozwalają wracać do kiepskich punktów, próbują eksplorować nowe rejony przestrzeni.
Dyskretyzowane problemy ciągłe
W tym rozdziale skupiliśmy się na problemach dyskretnych, ale czy nie da się tego zastosować dla czasu ciągłego? Pewnie się da ... przecież komputery w naturalny sposób nie są w stanie pamiętać liczb rzeczywistych, ale rozwiązują problemy z nimi związane. Można więc działać tak jak typowy system cyfrowy - zastosować podejście zwane dyskretyzacją przestrzeni ciągłej.
Jak to działa:
- dzielimy przestrzeń ciągłą na siatkę (np. co 0.1 jednostki),
- traktujemy punkty siatki jako osobne, dyskretne rozwiązania,
- stosujemy klasyczne metody dyskretne (np. losowe przeszukiwanie, tabu search).
Zalety:
- umożliwia stosowanie metod dyskretnych tam, gdzie oryginalnie są zmienne ciągłe,
- pozwala testować algorytmy bez potrzeby obliczania pochodnych.
Wady:
- precyzja zależy od gęstości siatki – im dokładniej, tym więcej punktów do przeszukania,
- może prowadzić do pomijania istotnych cech funkcji celu (np. minimów między węzłami siatki).
2.4. Algorytmy gradientowe - matematyczna droga w dół ...
W przypadku optymalizacji w przestrzeni ciągłej, jedną z najstarszych i najbardziej klasycznych grup metod są algorytmy gradientowe. Ich zasada działania opiera się na założeniu, że funkcja celu jest gładka – czyli ciągła i różniczkowalna.
Intuicja: jak zejść po schodach w ciemności
Wyobraź sobie, że stoisz na środku zbocza i chcesz zejść na sam dół. Nie widzisz całej doliny – widzisz tylko to, co masz bezpośrednio wokół siebie. Możesz dotknąć ziemi wokół i ocenić, gdzie jest najstromiej w dół – i właśnie w tę stronę zrobisz krok. To właśnie jest gradient: wektor wskazujący kierunek najszybszego spadku wartości funkcji.
Gradient i krok
Jeśli funkcja celu to \(f(x)\), a \(x \in \mathbb{R}^n\), to gradient to:
\( \nabla f(x) = \left[ \frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right] \)
Podstawowa iteracyjna formuła wygląda następująco:
\( x_{k+1} = x_k - \alpha \nabla f(x_k) \)
- \(x_k\) to punkt aktualny,
- \(\alpha\) to współczynnik uczenia (długość kroku),
- \( \nabla f(x_k)\) to gradient w punkcie \(x_k\).
Metoda największego spadku
To najprostszy algorytm gradientowy. Za każdym razem idziemy w kierunku przeciwnym do gradientu – czyli w stronę, gdzie funkcja maleje najszybciej. W praktyce ważne jest dobranie odpowiedniej wartości \(\alpha\), bo:
- zbyt duży krok może przeskoczyć minimum,
- zbyt mały krok prowadzi do powolnej zbieżności.
Metoda Newtona i quasi-Newtona
Metoda Newtona wykorzystuje nie tylko gradient, ale też drugą pochodną – tzw. hesjan (macierz drugich pochodnych cząstkowych):
\[ H(x) = \left[ \frac{\partial^2 f}{\partial x_i \partial x_j} \right] \]
Formuła iteracyjna:
\[ x_{k+1} = x_k - H^{-1}(x_k) \nabla f(x_k) \]
Dlaczego druga pochodna daje nam przewagę? Bo zawiera informację o krzywiźnie funkcji celu. Gradient mówi tylko, w którą stronę funkcja maleje – ale nie mówi, jak szybko. Hesjan dostarcza wiedzy o tym, jak zakrzywiona jest funkcja w danym punkcie. Dzięki temu można:
- lepiej dobrać długość kroku (adaptacyjnie, zamiast na sztywno),
- szybciej zbliżyć się do minimum – zwłaszcza w pobliżu punktu optymalnego,
- unikać efektu "zygzakowania" w przypadku funkcji o bardzo różnych krzywiznach w różnych kierunkach.
Warunki stopu
W algorytmach gradientowych zatrzymujemy się, gdy:
- \(\| \nabla f(x_k) \| < \epsilon\) – gradient jest prawie zerowy,
- \(\| x_{k+1} - x_k \| < \delta\) – zmiana rozwiązania jest minimalna,
- osiągnięto maksymalną liczbę iteracji.
Ograniczenia i trudności
- Minimum lokalne – mogą "utknąć" w lokalnym minimum, nie docierając do globalnego,
- Brak gładkości – jeśli funkcja celu nie jest różniczkowalna, nie możemy użyć pochodnych,
- Siodła i płaskowyże – gradient może nie prowadzić w dobrą stronę.
Przykłady zastosowań
- Optymalizacja kształtów elementów mechanicznych,
- Minimalizacja strat w sieciach neuronowych (np. SGD w ML),
- Wyznaczanie parametrów modeli analitycznych,
- Problemy portfela inwestycyjnego, gdzie funkcja ryzyka i zwrotu ma formę analityczną.
W kolejnym rozdziale zobaczymy, jak w algorytmach klasycznych i gradientowych można wprowadzać ograniczenia – zarówno twarde (jawne) jak i miękkie (np. kary za przekroczenie dopuszczalnego zakresu).
2.5. Uwzględnianie ograniczeń w optymalizacji – kiedy nie wszystko wolno
Uwzględnianie ograniczeń w optymalizacji – kiedy nie wszystko wolno
W większości realistycznych problemów optymalizacyjnych nie możemy swobodnie dobierać zmiennych – jesteśmy ograniczeni przez warunki fizyczne, ekonomiczne, prawne czy techniczne. W tym rozdziale przyjrzymy się, jak klasyczne algorytmy radzą sobie z ograniczeniami. Omówimy metody jawne i niejawne, twarde i miękkie, dokładne i przybliżone.
Rodzaje ograniczeń
Zacznijmy od klasyfikacji. Ograniczenia w problemie optymalizacji można zapisać jako:
- Ograniczenia równościowe: \(h_i(x) = 0\)
- Ograniczenia nierównościowe: \(g_j(x) \leq 0\)
Mogą one dotyczyć jednej zmiennej lub całego ich zestawu, np. \(x_i \in [a_i, b_i]\).
Z punktu widzenia praktyki dzieli się je na:
- twarde (hard) – muszą być spełnione bez wyjątku,
- miękkie (soft) – można je naruszyć, ale z konsekwencjami (np. kara w funkcji celu).
Dodatkowo, wyróżniamy:
- ograniczenia jawne – znane i zapisane bezpośrednio,
- ograniczenia niejawne – wynikające z ukrytej logiki zadania lub symulacji.
Przypomnijmy sobie zadanie z rozdziału 2.1, gdzie projektowaliśmy prostopadłościenne zbiorniki na chemikalia. Naszą funkcją celu był koszt transportu, a zmiennymi decyzyjnymi były wymiary pojemników.
W tym przypadku ograniczenia obejmowało:
- \(x_1, x_2, x_3 > 0\) – bo pojemniki muszą mieć dodatnie rozmiary,
- ( \(2*x_1*x_3+x_1*x_2 \leq 10 \) - bo nie można zużyć za dużo materiału z recyklingu na jedno pudełko,
Metoda eliminacji – tylko to, co dopuszczalne
Najprostsza strategia to nie wpuszczać do przestrzeni przeszukiwania żadnego punktu, który nie spełnia ograniczeń. To tzw. metoda eliminacji (feasibility filter).
Jak to działa?
- Generujemy kandydatów (np. losowo lub iteracyjnie),
- Sprawdzamy, czy spełniają wszystkie ograniczenia,
- Jeśli nie – odrzucamy i szukamy dalej.
Zalety:
- prostota,
- 100% pewności, że rozwiązania są dopuszczalne.
Wady:
- może być ekstremalnie nieefektywna, jeśli dopuszczalna przestrzeń jest wąska,
- problematyczna w przestrzeniach ciągłych o trudnych ograniczeniach geometrycznych.
Metoda ta jest powszechna w prostych algorytmach przeszukiwania losowego.
Kara - niedobrze jak opuścisz obszar poszukiwań
Inna popularna strategia to włączenie ograniczeń do funkcji celu w postaci dodatkowej kary (penalty function). To pozwala naruszać ograniczenia, ale z kosztami.
Nowa funkcja celu ma postać:
\(f'(x) = f(x) + P(x)\)
gdzie \( P(x) \) to funkcja kary, np.:
\(P(x) = \sum_{i} r_i \cdot \max(0, g_i(x))^2 + \sum_{j} s_j \cdot h_j(x)^2\)
Parametry \(r_i\) i /(s_j\) to współczynniki kar. Ich dobór jest krytyczny – zbyt małe kary powodują lekceważenie ograniczeń, zbyt duże całkowicie blokują eksplorację.
Zalety:
- łatwa do zastosowania w istniejących algorytmach,
- działa także z funkcjami niegładkimi.
Wady:
- trudność w doborze wag kary,
- ryzyko, że dobre rozwiązania dopuszczalne będą pominięte, jeśli punkt niedopuszczalny ma niską wartość oryginalnej funkcji celu.
Metoda barier – podejście od wewnątrz
Alternatywą dla kar jest metoda barier, szczególnie w przestrzeni ciągłej. Zamiast pozwalać wejść do strefy niedozwolonej, bariera zapobiega zbliżaniu się do granicy dopuszczalności.
Typowa postać funkcji barierowej:
\[ f'(x) = f(x) + \mu \cdot \sum_j \frac{1}{-g_j(x)} \]
Bariera działa tylko dla punktów wewnątrz dopuszczalnego obszaru – im bliżej granicy, tym kara większa. to współczynnik kontrolujący siłę działania bariery.
Zalety:
- zachowujemy się "bezpiecznie", nie przekraczając granic,
- sprzyja optymalizacji wewnątrz trudnych wielowymiarowych obszarów.
Wady:
- nie działa dla równości,
- wymaga funkcji różniczkowalnej i pochodnych,
- może prowadzić do utknięcia daleko od minimum globalnego.
Metody rzutowania – powrót na ścieżkę
Jeśli w kolejnych krokach algorytmu zdarza się, że punkt wyjdzie poza dopuszczalną przestrzeń, możemy go ręcznie przywrócić do niej – poprzez tzw. rzutowanie.
Mamy ograniczenie \( x \in [0,1] \). Jeśli nowy punkt \( x_k = 1.3 \), to zamiast odrzucić, robimy ustawiamy \( x_k = 1.0 \).
Rzutowanie działa na granicy dopuszczalności i zachowuje sens matematyczny przeszukiwania.
Zalety:
- prosta implementacja,
- pozwala używać standardowych algorytmów nawet w obecności ograniczeń.
Wady:
- może prowadzić do "ślizgania się" po granicy,
- nie uwzględnia geometrii problemu.
Naprawianie (repair) – sprytna korekta
Zamiast odrzucać lub karać – można próbować naprawiać niedopuszczalne rozwiązania. Np. jeśli suma udziałów w portfelu przekracza 100%, można je przeskalować. Jeśli punkt leży poza granicą, można przesunąć go najkrótszą drogą do wnętrza.
Zalety:
- elastyczne i skuteczne w praktyce,
- pozwala korzystać z silnych heurystyk bez komplikowania algorytmu.
Wady:
- często wymaga znajomości problemu i specjalnych procedur,
- może zaburzać rozkład rozwiązań (np. w metodach losowych).
Metody hybrydowe i adaptacyjne
W rzeczywistości często stosuje się kombinacje powyższych metod:
- kara + rzutowanie,
- bariera + naprawianie,
- kara adaptacyjna – która zmienia siłę działania w czasie (np. rośnie w miarę trwania optymalizacji).
Szczególnie algorytmy ewolucyjne często korzystają z adaptacyjnych funkcji kary, które uwzględniają np. liczbę spełnionych ograniczeń w danej populacji.
Uwagi praktyczne
Dobór odpowiedniej strategii postępowania z ograniczeniami w optymalizacji zależy od wielu czynników. Przede wszystkim trzeba wziąć pod uwagę naturę problemu: czy mamy do czynienia z przestrzenią ciągłą, gdzie możemy wykorzystać pochodne i gładkość funkcji celu, czy z przestrzenią dyskretną, gdzie takie założenia nie obowiązują. Problemy ciągłe z ograniczeniami równościowymi wymagają często stosowania metod analitycznych lub przybliżających – na przykład przez przekształcenie równości w funkcje kary kwadratowe. W przypadku ograniczeń nierównościowych dobrze sprawdzają się metody barierowe lub adaptacyjne kary. Z kolei w przestrzeniach dyskretnych bardziej praktyczne okazują się metody naprawcze lub prosta eliminacja rozwiązań niedopuszczalnych.
Ważną rolę odgrywa także geometria przestrzeni rozwiązań – w niektórych problemach dopuszczalny obszar jest nieregularny, pełen dziur i nieciągłości. W takich przypadkach warto rozważyć metody rzutowania lub adaptacyjne przekształcanie przestrzeni przeszukiwania. W praktyce inżynierskiej, zwłaszcza w dziedzinach takich jak projektowanie mechaniczne, inżynieria materiałowa czy chemiczna, dobrze działa połączenie strategii optymalizacji z wiedzą ekspercką. Na przykład zamiast jedynie penalizować naruszenie granic geometrycznych, można wprowadzić sprytne algorytmy naprawcze, które przekształcają rozwiązania w realne i wykonalne, zgodnie z zasadami fizyki czy standardami technicznymi.
Warto też zauważyć, że sposób traktowania ograniczeń może wpływać nie tylko na skuteczność optymalizacji, ale również na jakość znalezionych rozwiązań – zwłaszcza w problemach, gdzie między ograniczeniami a funkcją celu istnieje subtelna zależność. Dlatego wybór metody powinien być dokonywany świadomie, w oparciu o analizę problemu, a nie przez przyzwyczajenie czy wygodę implementacyjną. (np. optymalizacja konstrukcji) warto wspomagać się informacjami z domeny.
3. Algorytmy genetyczne
W tym rozdziale przejdziemy już do klasycznych algorytmów genetycznych
3.1. Historia
Badania nad genetyką
Choć same zasady dziedziczności były obserwowane i opisywane znacznie wcześniej – wystarczy wspomnieć prace Grzegorza Mendla z połowy XIX wieku dotyczące krzyżówek grochu – to prawdziwa eksplozja wiedzy na temat genów i mechanizmów dziedziczenia rozpoczęła się dopiero w XX wieku. W 1910 roku po raz pierwszy wprowadzono pojęcie genu, jako najmniejszej, abstrakcyjnej jednostki dziedziczenia, odpowiedzialnej za pojawianie się określonych cech u organizmów. Początkowo nie było wiadomo, z czego ten gen się składa ani jak dokładnie działa – rozumiano go bardziej jako koncepcję niż konkretną strukturę biologiczną.
Tymczasem jeszcze wcześniej, bo w 1869 roku, niemiecki chemik Johann Friedrich Miescher, badając skład chemiczny jąder komórkowych, wyizolował substancję, którą nazwał „nukleiną”. Dziś wiemy, że była to forma DNA. Nie potrafiono jeszcze wtedy przypisać jej roli nośnika informacji genetycznej – dopiero z czasem okazało się, że to właśnie ten „niepozorny kwas” zapisuje wszystko, co dotyczy budowy i działania organizmów.
Punktem zwrotnym dla współczesnej genetyki był rok 1953. Wtedy to James Watson i Francis Crick – bazując m.in. na danych rentgenowskich Rosalind Franklin – opisali strukturę DNA jako podwójną helisę zbudowaną z czterech typów nukleotydów: adeniny (A), tyminy (T), guaniny (G) i cytozyny (C). Dzięki ustaleniu reguł łączenia się tych cząsteczek (A z T, G z C) zrozumiano, jak możliwe jest kopiowanie i przechowywanie informacji genetycznej.
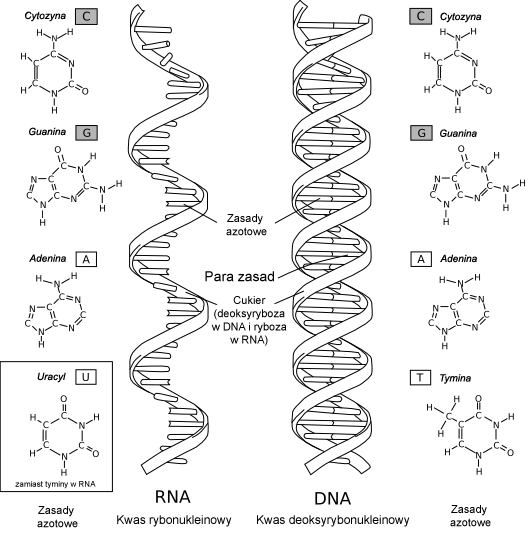
Źródło - wikipedia
Z czasem poznano kolejne etapy „przepływu” informacji w organizmach żywych:
- Replikacja – czyli tworzenie kopii DNA, co umożliwia przekazywanie informacji do komórek potomnych, a więc i dziedziczenie cech.
- Transkrypcja – przepisanie fragmentu DNA na RNA, czyli swoistą roboczą kopię zawierającą instrukcję.
- Translacja – przetworzenie RNA w łańcuch aminokwasów, z których powstają białka, a więc budulec i „narzędzia” komórek.
W skrócie – DNA to nie tylko „kod”, ale raczej cały system zapisu, kompilacji i wykonania. Oczywiście, w genach zaszyte są też inne mechanizmy – jak mutacje (czyli losowe zmiany w zapisie) oraz mechanizmy naprawcze. Wszystko to razem stworzyło bazę wiedzy, która pozwoliła nie tylko lepiej zrozumieć życie, ale też zainspirować informatyków do tworzenia nowych metod optymalizacji – takich jak właśnie algorytmy genetyczne.
Teoria ewolucji
Gdy spojrzymy wstecz na historię biologii, zobaczymy, że jedną z najbardziej rewolucyjnych idei była teoria ewolucji przez dobór naturalny, zaproponowana przez Karola Darwina w połowie XIX wieku. W swoim dziele „O powstawaniu gatunków” Darwin zaproponował odważną myśl: że wszystkie organizmy żywe pochodzą od wspólnego przodka, a zmiany w ich cechach są wynikiem długotrwałego, stopniowego procesu selekcji.

Ewolucja – jak zauważył Darwin – działa trochę jak bardzo powolny, naturalny „algorytm”: losowe zmiany (mutacje) pojawiają się w populacji, a środowisko „ocenia”, które cechy są korzystne, a które nie. Organizmy o korzystniejszych cechach mają większą szansę na przeżycie i rozmnożenie się – czyli przekazanie tych cech dalej. To właśnie nazywamy doborem naturalnym. Główne filary teorii ewolucji to:
- Organizmy są śmiertelne – nie każdy przeżyje, więc istnieje presja selekcyjna.
- Rozmnażają się – ale ich potomstwo nie jest identyczne (istnieje zmienność).
- Cechy są dziedziczone – czyli potomstwo dziedziczy część cech od rodziców.
- Środowisko jest ograniczone – nie wystarczy zasobów dla wszystkich, więc trwa rywalizacja.
Warto podkreślić, że dobór naturalny działa niezależnie od jakiejkolwiek inteligencji czy celu – to czysty mechanizm statystyczny. Ale jego efekty – przystosowania, strategie przetrwania, niezwykłe złożone formy życia – są tak zaskakujące, że aż proszą się o porównania z projektowaniem.
Teoria ewolucji doczekała się wielu potwierdzeń – od badań nad muszką owocową, przez zapis kopalny, aż po symulacje komputerowe. I właśnie to ostatnie stało się punktem wyjścia dla informatyków i inżynierów: skoro natura potrafi znaleźć dobre (czasem zaskakująco dobre!) rozwiązania, to może warto od niej pożyczyć kilka sztuczek?
Syntetyczna teoria ewolucji
Na styku dwóch wielkich teorii – genetyki i darwinowskiej ewolucji – narodziło się podejście znane jako syntetyczna teoria ewolucji. To właśnie ono stanowi bezpośrednią inspirację dla algorytmów genetycznych, które stosujemy dziś w optymalizacji.
Syntetyczna teoria mówi: ewolucja to nie tylko „przetrwają najlepiej dostosowani”, ale cały złożony system oparty na:
- mutacjach – czyli losowych, często niewielkich zmianach w genotypie, które mogą prowadzić do nowych cech,
- rekombinacji – wymieszaniu materiału genetycznego dwóch organizmów (czyli krzyżowaniu),
- selekcji – w tym dobór naturalny, ale też np. seksualny, sztuczny, stabilizujący, itd.,
- dziedziczeniu – czyli transmisji informacji do potomstwa.
To wszystko razem tworzy „algorytm” przyrody, który jest zdolny – bez nadzoru, bez projektanta – tworzyć rozwiązania trudnych problemów przetrwania. Brzmi znajomo?
Takie właśnie podejście zostało zaadaptowane do tworzenia algorytmów genetycznych. Informatycy zrobili to, co najlepiej potrafią: formalizowali obserwacje, zdefiniowali pojęcia (osobnik, populacja, gen, funkcja celu), i zaczęli symulować ten proces. Algorytmy genetyczne tworzą sztuczne populacje rozwiązań, poddają je działaniu krzyżowania, mutacji, selekcji – i patrzą, co z tego wyjdzie.
Z czasem pojawiły się całe rodziny algorytmów ewolucyjnych (np. strategie ewolucyjne, programowanie ewolucyjne, algorytmy rojowe). Ale to właśnie genetyka – z jej strukturą DNA, z jej ideą genotypu i fenotypu – była tą najpierwszą, najbardziej inspirującą bazą.
Dzięki syntetycznej teorii ewolucji mamy dziś nie tylko lepsze zrozumienie przyrody, ale też potężne narzędzia optymalizacyjne, które z powodzeniem stosujemy w inżynierii, robotyce, finansach, a nawet sztuce.
3.2. Klasyczny algorytm genetyczny
Zgodnie z definicją podaną przez Goldberga (1995), algorytmy genetyczne stanowią klasę algorytmów poszukujących, które opierają swoje działanie na inspiracji mechanizmami znanymi z biologii: dziedzicznością oraz doborem naturalnym. Ich funkcjonowanie odzwierciedla sposób, w jaki ewolucja kształtuje populacje organizmów w naturze.
W ramach tego podejścia, algorytm operuje na całej populacji potencjalnych rozwiązań danego problemu – a nie tylko na pojedynczym rozwiązaniu, jak ma to miejsce w klasycznych metodach optymalizacji. Każdy osobnik w tej populacji stanowi konkretną propozycję rozwiązania. Osobniki funkcjonują w środowisku - które umożliwia ocenianie i porównywanie osobników, i jest zależne od funkcji celu. Każdy osobnik ma przyporządkowaną wartość liczbową, nazywaną stopniem przystosowania lub po prostu przystosowaniem. Przystosowanie określa bezpośrednio jakość danego osobnika, i zazwyczaj jest ona wyliczana na na podstawie funkcji celu, odpowiadającej konkretnemu zadaniu optymalizacyjnemu.
W naturze przetrwanie i możliwość rozmnażania się zależy od tego, jak dobrze organizm radzi sobie w danym środowisku. Im lepiej jest przystosowany, tym większe ma szanse na przekazanie swoich genów potomstwu. AG próbują wykorzystać tę ideę do rozwiązywania problemów optymalizacyjnych. Szukają rozwiązań, które w danym kontekście mają największe "szanse przetrwania" – czyli są najlepsze w sensie przyjętej funkcji celu.
Zamiast operować tylko na jednym kandydacie rozwiązania (jak robi to wiele klasycznych metod), AG pracują na całej populacji. Każdy osobnik tej populacji to konkretne rozwiązanie problemu – lepsze lub gorsze. W każdej iteracji (czyli pokoleniu) populacja ewoluuje: osobniki są selekcjonowane, krzyżowane, poddawane mutacjom. Dzięki temu, z pokolenia na pokolenie, jakość populacji (czyli jakość rozwiązań) zwykle się poprawia.
Genotyp i fenotyp – czym się różnią?
W AG każdy osobnik opisuje potencjalne rozwiązanie zadania, ale żeby algorytm mógł nad tym pracować, musi jakoś je zapisać. Dlatego stosuje się dwa poziomy reprezentacji:
-
Genotyp to zakodowana forma rozwiązania. Można o nim myśleć jak o "DNA" osobnika. Zwykle jest to wektor (lista) liczb, np.:
g = [g1, g2, ..., gng]W zależności od problemu, te liczby mogą być bitami (0 lub 1), wartościami rzeczywistymi, permutacjami elementów itd. Algorytm operuje właśnie na genotypie – krzyżuje go, mutuje itd. Sama forma genotypu jest zrozumiała dla AG, natomiast może być nieczytelna dla rozwiązującego. Jest to punkt w przestrzeni kodów - a nie konkretny zestaw parametrów stanowiących rozwiązanie problemu.
-
Fenotyp to rozkodowane (czyli przekształcone) rozwiązanie, które można bezpośrednio ocenić. To forma, którą rozumie funkcja celu – np. zestaw parametrów wejściowych do jakiegoś modelu lub układu. Fenotyp wynika z genotypu poprzez proces dekodowania (który może być prosty lub złożony, zależnie od zastosowania).
Przykład: jeśli mamy zadanie doboru parametrów regulatora PID, to:
- genotyp może zawierać binarne lub rzeczywiste zakodowanie wartości Kr, Ti, Td;
- fenotyp to konkretne wartości tych parametrów użyte do symulacji układu i obliczenia błędu regulacji.
Zatem genotyp to sposób przechowywania i operowania rozwiązaniami w AG, a fenotyp to to, co naprawdę reprezentują – ich realna "forma" z punktu widzenia zadania optymalizacyjnego.
Inne istotne pojęcia, które "odziedziczyliśmy" z nauk biologicznych:
- Populacja – zbiór osobników w danym pokoleniu. Jest to główny obiekt przetwarzania w AG – algorytm nie działa na jednym rozwiązaniu, lecz na całej grupie.
- Osobnik – pojedynczy element populacji. Reprezentuje jedno konkretne rozwiązanie problemu.
- Chromosom – struktura danych opisująca genotyp osobnika. Można go traktować jako kompletną reprezentację rozwiązania w postaci zakodowanej.
- Gen – najmniejszy element składowy chromosomu. Odpowiada jednej zmiennej problemu lub jednej cechy rozwiązania.
- Genotyp – cały zbiór genów osobnika, zakodowany w chromosomie. To właśnie na nim operują krzyżowanie i mutacja.
- Allel – wartość konkretnego genu. Czyli: gen to miejsce w chromosomie, allel to to, co tam siedzi. Np. jeśli gen odpowiada za kolor, to allel to „czerwony”, „zielony” itp.
- Locus – pozycja genu w chromosomie. Umożliwia jednoznaczną identyfikację, gdzie dany gen się znajduje.
Wszystkie te pojęcia wspólnie tworzą podstawowy język, w którym opisujemy działanie algorytmów genetycznych. W praktyce – dobre zrozumienie tych terminów pomaga w projektowaniu skutecznych algorytmów.
3.3. Schemat działania
Schemat działania algorytmu genetycznego
Działanie klasycznego algorytmu genetycznego przebiega w pętli, w której każda iteracja odpowiada kolejnemu pokoleniu osobników. Schemat zamieszczony poniżej prezentuje pętlę, w której nastepują po sobie kolejno: reprodukcja, operacje genetyczne, ocena i sukcesja. Czasami reprodukcje i sukcesje określa się łącznym mianem selekcji. Reprodukcja w połączeniu z operacjami genetycznymi modeluje rozmnażanie, podczas którego materiał genetyczny rodziców przekazywany jest potomkom.
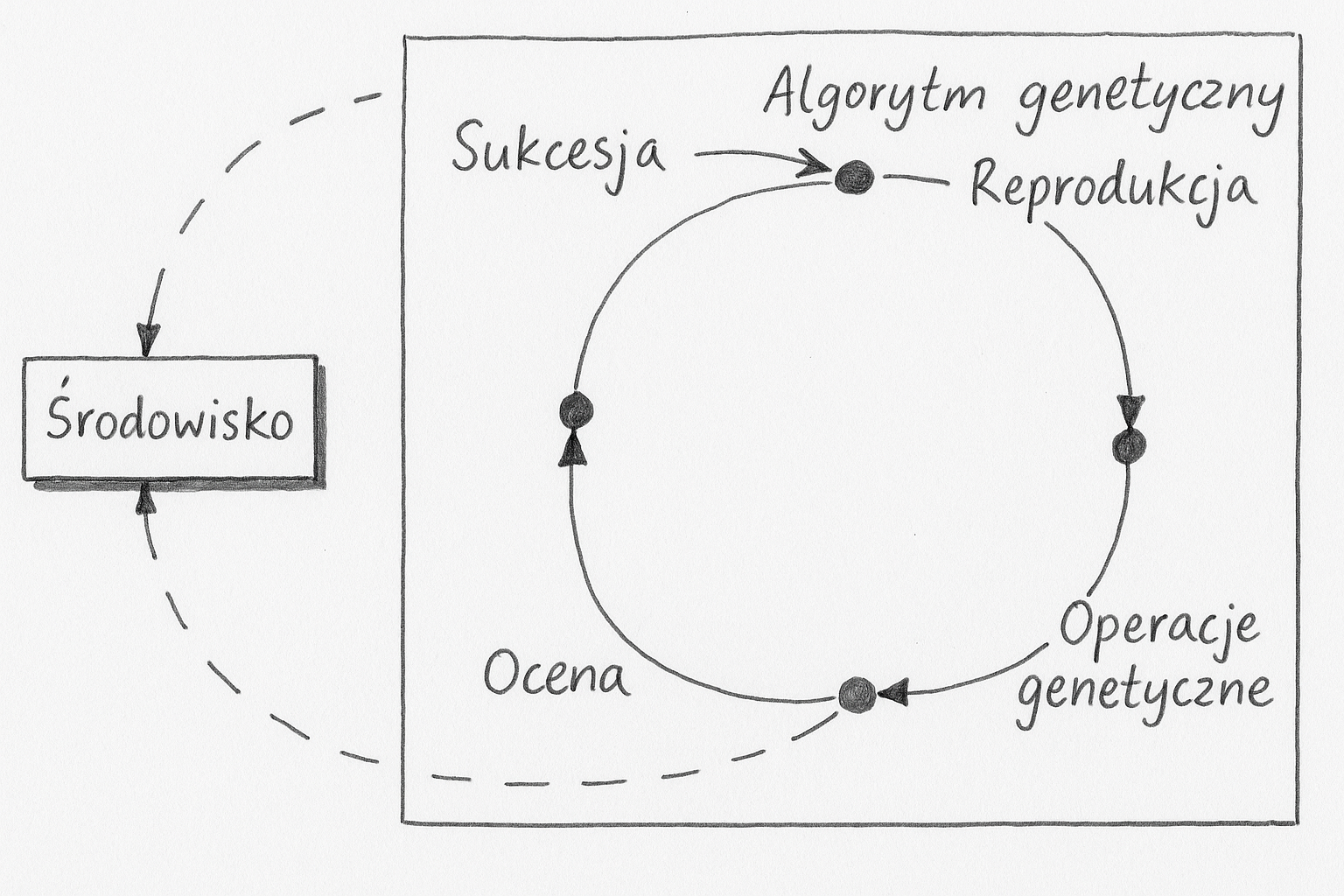
Najprostszy algorytm genetyczny operuje na dwóch populacjach: bazowej oraz potomnej. Dodatkowo wykorzystywane jest również pojęcie populacji tymczasowej. W każdej populacji zawarta jest jednakowa liczba osobników.
Typowy schemat działania algorytmu genetycznego rozpisany bardziej dokładnie wygląda następująco:
Inicjalizacja populacji
- Tworzymy początkową populację osobników. Zazwyczaj są one generowane losowo. Populacja powinna być zróżnicowana, aby dobrze pokryć przestrzeń poszukiwań.
- Dekodowanie genotypów do fenotypów
- Każdy osobnik jest dekodowany z formy genotypowej (czyli zapisanej w chromosomie) do fenotypu, czyli rzeczywistego rozwiązania problemu.
- Ocena przystosowania
- Na podstawie fenotypu obliczana jest wartość funkcji celu, która pełni rolę miary przystosowania osobnika. Lepsze rozwiązania mają wyższą wartość przystosowania (lub niższą – w zależności od problemu).
- Selekcja
- Wybieramy osobniki do rozrodu. Lepsze osobniki mają większą szansę na wybór, co odzwierciedla mechanizm doboru naturalnego. Najczęściej używane metody to selekcja ruletkowa, rankingowa oraz turniejowa.
- Krzyżowanie (rekombinacja)
- Łączymy pary wybranych osobników, tworząc nowe osobniki-potomków. Krzyżowanie pozwala mieszać cechy rodziców i eksplorować nowe fragmenty przestrzeni rozwiązań.
- Mutacja
- W genomie potomków losowo modyfikujemy niektóre geny. To wprowadza dodatkową zmienność i pozwala uniknąć zbyt szybkiego zbiegania do lokalnego optimum.
- Tworzenie nowej populacji (sukcesja)
- Nowa generacja może całkowicie zastąpić poprzednią, albo współistnieć z nią przez kilka pokoleń. Istnieją różne strategie: np. elitaryzm (najlepsi osobnicy są automatycznie przenoszeni dalej), sukcesja częściowa itd.
- Ocena nowego pokolenia
- Osobniki z nowej populacji, którzy jeszcze nie zostali ocenieni, są dekodowani do fenotypu, i poddawani ocenie.
- Sprawdzenie warunku zakończenia
- Algorytm kończy działanie, gdy spełniony jest określony warunek: osiągnięto maksymalną liczbę pokoleń, rozwiązania nie poprawiają się od kilku iteracji, lub osiągnięto wystarczające przystosowanie. Jeśli nie - wracamy do kroku 4.
Ten schemat jest podstawą działania większości wariantów algorytmów genetycznych. W bardziej zaawansowanych wersjach mogą pojawić się dodatkowe elementy, jak presja selekcyjna, adaptacja parametrów, koewolucja czy wielokrotne populacje działające równolegle. Jednak fundament pozostaje taki sam – inspirowany działaniem ewolucji w naturze.
3.4. Kodowanie
Kodowanie genomu w algorytmach genetycznych
Kodowanie genomu to sposób reprezentacji potencjalnych rozwiązań problemu optymalizacyjnego w postaci chromosomów – czyli łańcuchów danych, na których operują algorytmy genetyczne. Wybór odpowiedniego rodzaju kodowania ma kluczowe znaczenie dla efektywności działania algorytmu, ponieważ wpływa na to, jak łatwo można zastosować operatory genetyczne (krzyżowanie, mutację) oraz jak dobrze przestrzeń poszukiwań jest odwzorowywana.
Klasyfikacja metod kodowania
Najczęściej stosowane techniki kodowania genotypu dzielą się na:
Kodowanie klasyczne (wektorowe)
W tym podejściu genotyp reprezentowany jest jako wektor wartości – może być to wektor binarny, liczbowy, całkowity itp. Każdy gen odpowiada za jedną cechę rozwiązania. To najczęściej stosowane podejście, zwłaszcza w problemach optymalizacji ciągłej lub dyskretnej.
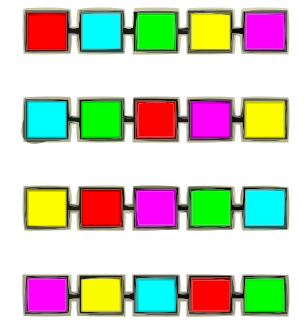
Kodowanie permutacyjne
Tutaj chromosom zawiera permutację elementów – typowe zastosowanie to problemy kombinatoryczne, takie jak problem komiwojażera (TSP), harmonogramowanie zadań, kolejki produkcyjne itp. Operatory krzyżowania muszą być specjalnie przystosowane, by nie generowały nieprawidłowych permutacji.
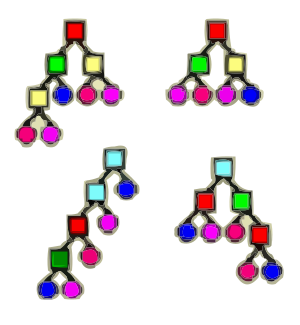
Kodowanie drzewiaste
Stosowane głównie w programowaniu genetycznym. Genotyp ma strukturę drzewa – węzły to funkcje lub operatory, a liście to argumenty lub dane wejściowe. Struktura ta umożliwia reprezentację złożonych wyrażeń matematycznych, reguł lub algorytmów. Przykład: \( (x + y) * z \).
Kodowanie grafowe
Zamiast drzew czy wektorów, genotypem może być graf – używane np. w ewolucyjnej optymalizacji sieci (np. topologie połączeń neuronów w neuroewolucji). Pozwala to na reprezentowanie bardziej ogólnych struktur i zależności.
Kodowanie listy instrukcji (linearne kodowanie genów)
Popularne w ewolucyjnych algorytmach programujących. Genotyp zawiera liniową sekwencję poleceń lub instrukcji, podobnych do kodu asemblera. Taka reprezentacja ułatwia mutacje i krzyżowanie na poziomie składni.
Kodowanie symboliczne
Używane w problemach, gdzie rozwiązania mają strukturę symboliczną – np. ewolucja formuł logicznych, automaty, reguły IF-THEN. Genotyp zawiera symbole ze skończonego alfabetu, np. {A, B, C, ¬, ∧, ∨}.
Reprezentacja pojedynczych genów
Poza strukturą całego genotypu, istotne jest to, w jaki sposób kodowane są pojedyncze geny. Najczęściej stosuje się dwa podejścia: reprezentację binarną (w tym kod Graya) oraz reprezentację rzeczywistoliczbową.
Kodowanie binarne
W tym przypadku każda zmienna kodowana jest jako ciąg bitów. Długość ciągu określa precyzję odwzorowania. Na przykład, wartość z przedziału \([a, b]$\) reprezentujemy za pomocą \( n \) bitów, co pozwala wyróżnić \( 2^n \) wartości dyskretnych. Zamiana bitów na wartość rzeczywistą wymaga przeskalowania:
\[
x = a + \frac{b - a}{2^n - 1} \cdot \text{wartość binarna}
\]
Zaletą tego podejścia jest prostota operacji krzyżowania i mutacji. Wadą – ograniczona rozdzielczość i nieliniowość odwzorowania, szczególnie w problemach ciągłych.
Kodowanie Graya
Kod Graya to wariant kodowania binarnego, w którym dwie kolejne wartości różnią się tylko jednym bitem. Redukuje to problem „skokowych” zmian wartości przy małych mutacjach. Przydatny zwłaszcza tam, gdzie zmiana jednego bitu nie powinna prowadzić do dużej zmiany w wartości odwzorowanej.
Kodowanie rzeczywistoliczbowe
Zamiast bitów, gen przyjmuje bezpośrednio wartość rzeczywistą z określonego przedziału. Przykład: gen \( x_i \in [0, 10] \) może mieć wartość 7.35. Operatory genetyczne muszą być dostosowane do przestrzeni ciągłej – mutacja może np. polegać na dodaniu losowego zakłócenia \( \sim N(0, \sigma) \), a krzyżowanie – na liniowej kombinacji rodziców.
Zaletą tego podejścia jest jego naturalność i brak potrzeby dekodowania. Dobrze sprawdza się w optymalizacji ciągłej. Wadą jest większe ryzyko wyjścia poza dopuszczalne zakresy oraz konieczność dostosowania operatorów.
Podsumowanie
Dobór odpowiedniego kodowania zależy od rodzaju rozważanego problemu:
- dla problemów ciągłych preferowane jest kodowanie rzeczywiste,
- dla problemów kombinatorycznych – kodowanie permutacyjne,
- dla problemów strukturalnych – kodowanie drzewiaste, grafowe lub instrukcyjne.

Dodatkowo należy pamiętać, że rodzaj kodowania wpływa na konstrukcję operatorów genetycznych oraz na efektywność przeszukiwania przestrzeni rozwiązań. W praktyce często konieczne jest eksperymentalne dobranie najbardziej efektywnej reprezentacji.
3.5. Inicjacja
Czym są operatory inicjalizacji?
Operatory inicjalizacji to procedury odpowiedzialne za wygenerowanie pierwszej populacji w algorytmie genetycznym. To, jak zostaną rozłożone początkowe punkty w przestrzeni rozwiązań, może mieć ogromne znaczenie dla skuteczności dalszego poszukiwania. Celem inicjalizacji jest zapewnienie odpowiedniej różnorodności genetycznej, by uniknąć przedwczesnej zbieżności populacji.
Typowe metody inicjalizacji
W literaturze i praktyce algorytmów genetycznych spotyka się kilka głównych podejść:
Inicjacja równomierna (jednorodna)
Inicjalizacja równomierna (jednorodna) to najprostszy i najczęściej stosowany sposób generowania początkowej populacji w algorytmach genetycznych. Polega na tym, że każda zmienna decyzyjna (gen) losowana jest niezależnie z rozkładu jednostajnego w zadanym przedziale dopuszczalnych wartości. Dzięki temu cała przestrzeń poszukiwań jest wstępnie przeszukiwana z równym prawdopodobieństwem, co zapewnia dobrą eksplorację już od pierwszej generacji.
Wzór opisujący losowanie jednego genu \(g_i\) z rozkładu jednostajnego wygląda następująco:
\[g_i = a_i + (b_i - a_i) \cdot U(0,1)\]
- \(a_i\) i \(b_i\) to odpowiednio dolna i górna granica przedziału dla genu \(g_i\),
- \(U(0,1)\) to liczba losowa z rozkładu jednostajnego w przedziale \(<0,1>\).
Zaletą inicjalizacji równomiernej jest jej prostota i niskie wymagania obliczeniowe. Nie wymaga żadnych dodatkowych parametrów (jak np. średnia i odchylenie standardowe w rozkładzie normalnym), ani wstępnej wiedzy o funkcji celu. Jest idealna do zadań, gdzie brakuje jakiejkolwiek wiedzy wstępnej o położeniu optymalnych rozwiązań.
Wadą tej metody może być jednak zbyt rzadkie pokrycie przestrzeni w wysokich wymiarach — przy dużej liczbie zmiennych liczba możliwych kombinacji rośnie wykładniczo, przez co nawet duże populacje mogą „nie trafić” w istotne obszary.
Rozkład normalny (Gaussa)
Rozkład normalny (Gaussa) to klasyczny rozkład symetryczny, którego kształt opisywany jest przez funkcję dzwonową. Jego parametrami są średnia , wokół której skupiają się wartości, oraz odchylenie standardowe , określające szerokość rozrzutu. Rozkład ten jest szeroko stosowany w algorytmach genetycznych do lokalnej inicjalizacji populacji, szczególnie gdy znane jest przybliżone położenie optimum.
Funkcja gęstości prawdopodobieństwa rozkładu normalnego zapisana w postaci matematycznej wygląda następująco:
Rozkład normalny (Gaussa) to klasyczny rozkład symetryczny, którego kształt opisywany jest przez funkcję dzwonową. Jego parametrami są średnia , wokół której skupiają się wartości, oraz odchylenie standardowe , określające szerokość rozrzutu. Rozkład ten jest szeroko stosowany w algorytmach genetycznych do lokalnej inicjalizacji populacji, szczególnie gdy znane jest przybliżone położenie optimum.
Funkcja gęstości prawdopodobieństwa rozkładu normalnego zapisana w postaci matematycznej wygląda następująco:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right) \]
Rozkład normalny pozwala w naturalny sposób regulować intensywność eksploracji poprzez manipulowanie – im większe odchylenie, tym większy zasięg losowanych wartości. Jest często stosowany jako alternatywa dla rozkładu jednostajnego, gdy zależy nam na zbliżeniu się do konkretnych obszarów przestrzeni decyzyjnej.
Kiedy używać rozkładu normalnego do inicjalizacji?
Rozkład normalny (Gaussa) jest szczególnie użyteczny w sytuacjach, gdy chcemy skoncentrować generowane punkty w pobliżu znanego lub przypuszczalnego optimum. Jest to korzystne np. w zadaniach, gdzie:
- przestrzeń poszukiwań jest bardzo duża, a eksploracja całej przestrzeni byłaby nieefektywna,
- dysponujemy wcześniejszą wiedzą o typowym zakresie dobrych rozwiązań,
- potrzebujemy szybko zbliżyć się do dobrego punktu początkowego,
- wymagane jest utrzymanie populacji w ograniczonym zasięgu wokół konkretnego rozwiązania,
- zależy nam na dokładnej eksploracji lokalnej okolicy (eksploatacja zamiast eksploracji).
Stosując rozkład normalny, możemy łatwo regulować „rozrzut” poprzez parametr odchylenia standardowego σ – co czyni ten rozkład bardzo praktycznym narzędziem do lokalnego poszukiwania rozwiązań.
Inne operatory inicjalizacji spotykane w literaturze
Oprócz standardowych metod, w literaturze opisywane są również bardziej zaawansowane operatory inicjalizacji, które zwiększają jakość pokrycia przestrzeni poszukiwań. Przykładem jest Latin Hypercube Sampling (LHS), który zapewnia, że próbki są równomiernie rozmieszczone wzdłuż każdego wymiaru. Dzięki temu unika się sytuacji, w której populacja początkowa przypadkowo pomija duże obszary przestrzeni rozwiązań. LHS znajduje zastosowanie głównie w zadaniach o dużej liczbie zmiennych ciągłych, gdzie losowanie niezależnych wartości z rozkładu jednostajnego mogłoby prowadzić do nadmiernego skupienia próbek.
Rozkład Cauchy’ego zasługuje na osobne omówienie ze względu na jego unikalne właściwości. W przeciwieństwie do rozkładu normalnego, Cauchy charakteryzuje się tzw. grubymi ogonami – co oznacza, że wartości znacznie oddalone od średniej mają wyraźnie większe prawdopodobieństwo wystąpienia. Dzięki temu inicjalizacja z wykorzystaniem rozkładu Cauchy’ego może skutecznie wspierać eksplorację przestrzeni poszukiwań, zwłaszcza w problemach, gdzie dobre rozwiązania mogą występować daleko od środka przestrzeni decyzyjnej. Jest to zatem doskonała opcja w przypadkach, gdy zależy nam na agresywnym przeszukiwaniu całej przestrzeni, a nie tylko jej wycinka.
Drugą rodziną podejść są tzw. sekwencje niskiej dyskrepancji, takie jak Sobola, Haltona czy Faure’a. Są to quasi-losowe ciągi, które rozmieszczają punkty bardziej równomiernie niż czysto losowe próbkowanie. Dzięki temu zapewniają systematyczne i powtarzalne pokrycie przestrzeni, co czyni je przydatnymi np. w testowaniu algorytmów lub optymalizacji deterministycznej. Ich zaletą jest pełna kontrola nad rozkładem punktów oraz możliwość odwzorowania przestrzeni nawet w wysokich wymiarach.
Ciekawą propozycją jest również inicjalizacja warstwowa (layered), która łączy różne podejścia w jednej populacji. Na przykład, część populacji może być losowana z rozkładu jednostajnego dla szerokiej eksploracji, a inna część z rozkładu normalnego wokół znanych dobrych punktów – dla precyzyjnej eksploatacji. Takie połączenie działań eksploracyjnych i eksploatacyjnych już na etapie inicjalizacji pozwala algorytmowi rozpocząć poszukiwania z bardziej zrównoważonym rozkładem potencjalnych rozwiązań.
Nadinicjalizacja
Pojęcie nadinicjalizacji oznacza sytuację, w której generuje się znacznie więcej osobników niż wynosi docelowa liczność populacji – a następnie wybiera z nich najlepsze bądź najbardziej zróżnicowane. Pomaga to w uzyskaniu lepszej jakości początkowej populacji, ale wiąże się z większym kosztem obliczeniowym.
Można też rozumieć „nadinicjalizację” jako próbę kompensacji ubogiej struktury inicjalnej populacji przez sztuczne zwiększenie jej rozrzutu – np. przez silną mutację na etapie inicjalizacji lub przez celowe zwiększenie zakresów poszukiwań.
Podsumowanie
Wybór operatora inicjalizacji nie jest błahy:
- dla eksploracji warto korzystać z rozkładu równomiernego, Cauchy’ego lub LHS,
- dla eksploatacji – z rozkładów skoncentrowanych (np. normalnego, beta, wykładniczego),
- inicjalizacja hybrydowa (np. kilka punktów heurystycznych + losowanie) daje często najlepsze efekty.
Dobrze zaprojektowana inicjalizacja może zdecydować, czy algorytm w ogóle znajdzie sensowne rozwiązania.
3.6. Selekcja
Operatory selekcji w algorytmach genetycznych
Selekcja to kluczowy etap algorytmu genetycznego, w którym wybierane są osobniki do reprodukcji – czyli do krzyżowania i/lub mutacji. Celem selekcji jest premiowanie lepiej przystosowanych jednostek, a zarazem zachowanie pewnej różnorodności genetycznej w populacji. Istnieje wiele technik selekcji, z których każda ma inne właściwości pod względem presji selekcyjnej i zbieżności.
Selekcja ruletkowa (proporcjonalna)
Selekcja ruletkowa (ang. "roulette wheel selection") jest jedną z najprostszych i najbardziej intuicyjnych metod. Każdemu osobnikowi przypisywany jest wycinek koła proporcjonalny do jego wartości funkcji przystosowania (fitness). Im lepszy osobnik, tym większe ma szanse na wybór. Wyobrażamy to sobie jak koło fortuny, w którym sektory odpowiadają poszczególnym osobnikom – im większy sektor, tym większe prawdopodobieństwo trafienia.
Z matematycznego punktu widzenia, prawdopodobieństwo selekcji osobnika wyraża się jako:
\[P(i) = \frac{f_i}{\sum_{j=1}^{N} f_j}\]
gdzie:
- \(f_i\) to wartość funkcji przystosowania osobnika \(i\),
- \(N\) to liczba osobników w populacji.
Selekcja ruletkowa jest szybka i prosta, ale ma kilka wad. Przede wszystkim, jeśli w populacji znajduje się jeden bardzo dobrze przystosowany osobnik, to dominuje on selekcję – co może prowadzić do przedwczesnej zbieżności. Z drugiej strony, gdy wartości funkcji przystosowania są zbliżone, presja selekcyjna spada, a algorytm „drepcze w miejscu”.
Selekcja rankingowa
W selekcji rankingowej osobniki są najpierw sortowane według przystosowania (od najlepszego do najgorszego), a następnie każdemu przypisywana jest wartość selekcyjna zależna od jego pozycji (rangi), a nie od bezwzględnej wartości funkcji celu. Dzięki temu unika się problemów związanych z dużymi różnicami w wartościach funkcji przystosowania.
Presję selekcyjną można regulować poprzez funkcję przekształcającą rangę na prawdopodobieństwo – np. liniowo, wykładniczo lub z wykorzystaniem rozkładów losowych. Rankingowa metoda zapewnia bardziej kontrolowaną presję selekcyjną i pozwala uniknąć dominacji pojedynczych osobników, ale kosztem większej złożoności obliczeniowej (sortowanie).
Selekcja turniejowa
W selekcji turniejowej tworzy się losowo grupy (turnieje) złożone z osobników (zwykle lub ). W każdej grupie wygrywa najlepszy osobnik, który trafia do puli reprodukcyjnej. Metoda ta jest prosta do zaimplementowania i nie wymaga znajomości wartości funkcji przystosowania całej populacji.
Presję selekcyjną reguluje się wielkością turnieju – większe oznacza silniejszą presję. Przykładowo, turniej zachowuje sporo losowości, natomiast może szybko prowadzić do utraty różnorodności. Istnieją też warianty turnieju probabilistycznego, w którym zwycięzca wybierany jest z prawdopodobieństwem zależnym od jego jakości.
Porównanie technik
- Ruletka – szybka, ale wrażliwa na rozkład przystosowań; może prowadzić do dominacji jednego osobnika.
- Ranking – stabilna i odporna na ekstremalne wartości funkcji celu; presja zależna od rangi.
- Turniej – bardzo elastyczny, szybki i łatwy do równoleglenia; dobrze sprawdza się w praktyce.
Dobór operatora selekcji ma istotny wpływ na zachowanie algorytmu – jego zbieżność, eksplorację i eksploatację przestrzeni. W praktyce często testuje się różne metody dla konkretnego problemu, by dobrać najbardziej efektywną konfigurację.
Ciekawostka: Uruchamiając poniższy program możecie zobaczyć / testować jak działają omówione operatory selekcji:
import numpy as np
import matplotlib.pyplot as plt
# Generowanie populacji i przypisanie funkcji przystosowania
np.random.seed(42)
population_size = 20
fitness = np.sort(np.random.rand(population_size))[::-1] # Posortowane od najlepszego
# Selekcja ruletkowa
def roulette_selection(fitness, num_selected):
probabilities = fitness / fitness.sum()
return np.random.choice(len(fitness), size=num_selected, p=probabilities)
# Selekcja rankingowa (liniowa)
def ranking_selection(fitness, num_selected):
ranks = np.argsort(np.argsort(-fitness)) # 0 - najlepszy
rank_weights = (len(fitness) - ranks)
probabilities = rank_weights / rank_weights.sum()
return np.random.choice(len(fitness), size=num_selected, p=probabilities)
# Selekcja turniejowa
def tournament_selection(fitness, num_selected, tournament_size=3):
selected = []
for _ in range(num_selected):
participants = np.random.choice(len(fitness), tournament_size, replace=False)
winner = participants[np.argmax(fitness[participants])]
selected.append(winner)
return np.array(selected)
# Zastosowanie selekcji
num_selected = 1000
roulette_counts = np.bincount(roulette_selection(fitness, num_selected), minlength=population_size)
ranking_counts = np.bincount(ranking_selection(fitness, num_selected), minlength=population_size)
tournament_counts = np.bincount(tournament_selection(fitness, num_selected), minlength=population_size)
# Wizualizacja
plt.figure(figsize=(12, 6))
plt.plot(roulette_counts, label='Ruletkowa', marker='o')
plt.plot(ranking_counts, label='Rankingowa', marker='s')
plt.plot(tournament_counts, label='Turniejowa (k=3)', marker='^')
plt.title("Porównanie technik selekcji w algorytmie genetycznym")
plt.xlabel("Indeks osobnika (0 = najlepszy)")
plt.ylabel("Liczba wybrań w selekcji (z 1000 prób)")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
3.7. Krzyżowanie
Krzyżowanie (ang. crossover) to kluczowy operator genetyczny odpowiedzialny za wymianę informacji pomiędzy osobnikami w populacji. Jego celem jest tworzenie nowych rozwiązań poprzez kombinację cech rodziców. Skuteczny operator krzyżowania powinien z jednej strony umożliwiać eksploatację dobrych rozwiązań, a z drugiej zachować wystarczającą różnorodność w populacji.
W zależności od rodzaju kodowania genotypu, stosuje się różne techniki krzyżowania. Poniżej przedstawiamy najważniejsze z nich.
Krzyżowanie dla kodowania binarnego (klasycznego)
Jednopunktowe (single-point crossover)
Losowany jest jeden punkt podziału chromosomu. Dzieci dziedziczą część genów od jednego rodzica przed punktem, a drugą część od drugiego rodzica.
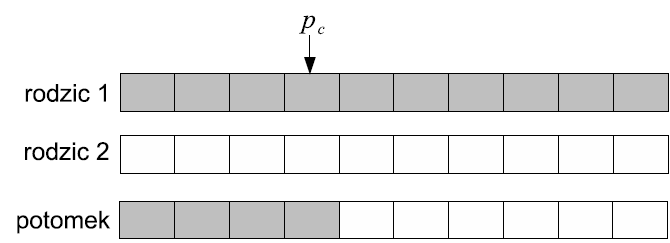
Dwupunktowe (two-point crossover)
Losowane są dwa punkty podziału. Fragment między nimi jest zamieniany pomiędzy rodzicami. Pozwala to na bardziej zróżnicowaną rekombinację.
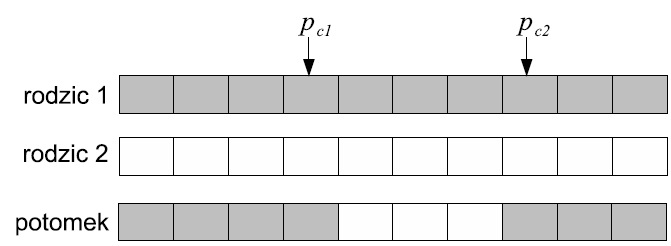
Jednorodne (uniform crossover)
Dla każdego genu losowo (z prawdopodobieństwem np. 0.5) wybierany jest jeden z rodziców. Zapewnia to największe wymieszanie cech.
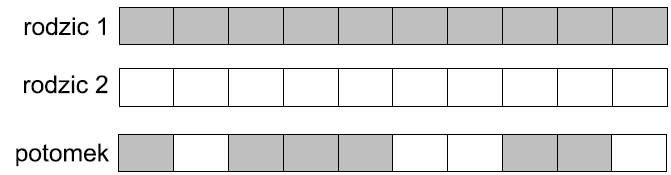
Zalety tych metod to prostota, niska złożoność i szerokie zastosowanie w kodowaniu binarnym. Wadą może być generowanie dziwnych struktur rozwiązań – operacje są niezależne od semantyki problemu.
Krzyżowanie dla kodowania rzeczywistego
Krzyżowanie arytmetyczne
Potomkowie wyznaczani są jako liniowa kombinacja rodziców:
\[ \text{Potomek} = \alpha \cdot \text{Rodzic}_1 + (1 - \alpha) \cdot \text{Rodzic}_2\]
gdzie \( \alpha \in [0,1] \) to losowy współczynnik.
Krzyżowanie blendowane (BLX-\(\alpha\))}
Nowe geny losowane są z przedziału szerszego niż zakres między genami rodziców. Umożliwia eksplorację nowych wartości:
\[x = U[\text{min} - d \cdot \alpha,\ \text{max} + d \cdot \alpha]\]
gdzie \( d = |x_1 - x_2| \).
Krzyżowanie z zakłóceniem (SBX)
Imituje rozkład krzyżowania binarnego, ale w przestrzeni ciągłej, operując bezpośrednio na liczbach rzeczywistych. Simulated Binary Crossover (SBX) jest zaprojektowany tak, aby zachowywać podobne statystyczne właściwości jak klasyczne krzyżowanie dwupunktowe, ale działa w przestrzeni rzeczywistej, co czyni go użytecznym w optymalizacji ciągłej. Główna idea polega na losowym generowaniu wartości potomnych wokół wartości rodziców z kontrolowaną zmiennością, regulowaną parametrem rozkładu (ang. distribution index).
SBX jest szczególnie popularny w strategiach ewolucyjnych i algorytmach różnicowych. Dzięki parametrowi rozkładu można kontrolować zakres eksploracji: niska wartość parametru sprzyja dużym odchyleniom (eksploracja), natomiast wyższe wartości skutkują generowaniem potomków bardzo bliskich rodzicom (eksploatacja). To czyni SBX elastycznym narzędziem, dobrze dostosowanym do różnych etapów procesu optymalizacji.
Krzyżowanie dla kodowania permutacyjnego
W przypadku permutacji, celem jest zachowanie unikalności elementów – klasyczne krzyżowanie nie może być stosowane. Zamiast tego stosujemy:
Krzyżowanie cykliczne (CX)
Krzyżowanie cykliczne (CX) polega na identyfikowaniu pozycyjnych cykli pomiędzy dwoma rodzicami. Dla każdego osobnika wyznacza się cykl elementów, które w tych samych pozycjach znajdują się u obojga rodziców, zachowując ich wzajemne relacje. Potomkowie dziedziczą cyklicznie pozycje z jednego rodzica, a pozostałe wypełniają elementami z drugiego, z zachowaniem unikalności.
Metoda ta dobrze zachowuje strukturę pozycyjną oryginalnych rozwiązań i jest odporna na utratę informacji porządkowej. W porównaniu do innych operatorów dla permutacji, CX generuje poowy niż np. PMX czy OX, co czyni go dobrym wyborem tam, gdzie istotne jest zachowanie względnych pozycji w permutacjach.
Krzyżowanie PMX
Krzyżowanie PMX (Partially Mapped Crossover) polega na losowym wybraniu fragmentu permutacji z jednego z rodziców i bezpośrednim przepisaniu go do potomka. Następnie dla pozostałych pozycji stosowane jest odwzorowanie elementów z drugiego rodzica na podstawie zależności utworzonych przez wspólny fragment. Dzięki temu zachowana zostaje zgodność z permutacyjną strukturą – każdy element występuje tylko raz.
PMX dobrze radzi sobie z zachowaniem względnych pozycji i unikalności elementów, co czyni go popularnym w problemach typu TSP i alokacyjnych. Metoda ta jest bardziej „lokalna” niż krzyżowanie cykliczne – silniej zachowuje lokalne fragmenty jednego z rodziców, przez co umożliwia zarówno eksploatację, jak i pewien stopień eksploracji przestrzeni rozwiązań.
Order Crossover (OX)
Krzyżowanie OX (Order Crossover) to technika, która zachowuje porządek występowania elementów oraz ich względną kolejność. Proces polega na losowym wybraniu fragmentu permutacji z jednego rodzica i bezpośrednim przepisaniu go do potomka. Następnie, uzupełnia się pozostałe miejsca w chromosomie, przechodząc kolejno przez elementy drugiego rodzica, pomijając te już zapisane, zachowując ich oryginalną kolejność.
Metoda ta jest niezwykle skuteczna w zachowywaniu informacji o sąsiedztwie elementów – co jest istotne np. w problemach trasowania czy harmonogramowania. Pozwala na przenoszenie całych sekwencji z rodziców do potomków, co może wspomóc zachowanie lokalnych struktur rozwiązania, które wykazują dobrą jakość.
OX, w porównaniu do innych operatorów dla permutacji, takich jak PMX czy CX, lepiej nadaje się do problemów, gdzie kolejność elementów ma większe znaczenie niż ich konkretne pozycje. Jest także stosunkowo łatwy do zaimplementowania, co czyni go jednym z najpopularniejszych operatorów krzyżowania w problemach kombinatorycznych.
Krzyżowanie dla kodowania drzewiastego
Krzyżowanie poddrzew
Krzyżowanie poddrzew (subtree crossover) to najczęściej stosowany operator w programowaniu genetycznym. Działa poprzez losowe wybranie węzła w drzewie każdego z rodziców, a następnie zamianę odpowiadających im poddrzew. Operacja ta pozwala na generowanie potomków, którzy łączą elementy strukturalne obu rodziców, zachowując przy tym składniową poprawność wyrażeń.
Zaletą tego podejścia jest jego naturalność w kontekście drzewiastych reprezentacji – poddrzewa mogą reprezentować całe podfunkcje, wyrażenia lub bloki instrukcji. Dzięki temu krzyżowanie może wprowadzać znaczące zmiany w funkcjonalności osobników, co sprzyja eksploracji przestrzeni rozwiązań. Jednocześnie zachowuje spójność semantyczną potomków, co jest kluczowe dla unikania błędnych lub niekompilowalnych struktur.
Aby zapobiec nadmiernemu wzrostowi rozmiarów drzew (tzw. "bloat"), często stosuje się ograniczenia na maksymalną głębokość drzewa potomka lub kontroluje się prawdopodobieństwo wyboru węzłów w zależności od ich poziomu. Taka regulacja pozwala zachować równowagę między eksploracją a stabilnością populacji, ograniczając tworzenie zbyt dużych, trudnych do zinterpretowania struktur.
Krzyżowanie jedno- i wielopunktowe
Zamiast zamiany całych poddrzew, możliwa jest zamiana pojedynczych gałęzi lub zestawów gałęzi, zgodnie z zadanymi regułami syntaktycznymi. Taki sposób krzyżowania pozwala na bardziej precyzyjne operowanie strukturą drzewa – można np. wymieniać tylko konkretne operatory matematyczne, fragmenty wyrażeń lub konkretne funkcje warunkowe. Podejście to umożliwia drobniejsze i bardziej kontrolowane modyfikacje, co może być korzystne w końcowych etapach ewolucji, gdy poszukiwane są optymalne drobne zmiany.
Wersje jedno- i wielopunktowe krzyżowania na poziomie drzewa mogą także uwzględniać kontekst syntaktyczny, np. tylko zamianę węzłów o tej samej arności (liczbie argumentów) albo tej samej kategorii (np. operatorów logicznych). Zapewnia to zachowanie poprawności semantycznej i składniowej potomków oraz pozwala utrzymać strukturę kodu w granicach oczekiwanej złożoności. Dobrze zaprojektowane krzyżowanie na poziomie gałęzi może skutkować bardziej stabilną i przewidywalną ewolucją programu.
Te operatory pozwalają generować złożone struktury, np. funkcje matematyczne, ale wymagają kontroli poprawności składniowej potomków.
Inne techniki krzyżowania
Krzyżowanie heurystyczne
Tworzy potomek przesunięty w kierunku lepszego z rodziców:
\[
x = x_1 + r \cdot (x_1 - x_2)
\]
gdzie $\(x_1 \) jest lepszy od \( x_2 \), a \( r \) – losowa liczba.
Krzyżowanie topologiczne
Krzyżowanie topologiczne znajduje zastosowanie przede wszystkim w algorytmach, które operują na strukturach grafowych, takich jak ewolucja architektury sieci neuronowych (neuroewolucja) czy optymalizacja połączeń logicznych. W takich przypadkach genotypem nie jest prosty ciąg bitów czy liczb, lecz graf reprezentujący połączenia pomiędzy węzłami (neurony, funkcje, jednostki przetwarzające). Krzyżowanie polega na łączeniu części struktury dwóch rodziców w sposób, który tworzy nową sensowną topologię – np. przez zachowanie wspólnych połączeń oraz wstawienie unikalnych fragmentów z każdego z rodziców.
Dla sieci neuronowych najczęściej krzyżowane są zarówno struktury połączeń (czyli które węzły są ze sobą połączone), jak i wagi tych połączeń. Przykładem jest algorytm NEAT (NeuroEvolution of Augmenting Topologies), który identyfikuje odpowiadające sobie węzły i połączenia poprzez mechanizm numerowania genów, a następnie tworzy potomka z części wspólnych oraz zmutowanych nowych połączeń. Dzięki temu możliwe jest ewolucyjne rozwijanie złożonych sieci, które zachowują funkcjonalność poprzedników.
Zaletą krzyżowania topologicznego jest możliwość tworzenia coraz bardziej zaawansowanych i nieliniowych architektur, jednak jego projektowanie wymaga dużej ostrożności. Istotne jest zachowanie poprawności strukturalnej (np. unikanie cykli w sieciach jednokierunkowych) oraz funkcjonalności potomków. Operatory te bywają złożone, ale stanowią fundament dla nowoczesnych metod neuroewolucyjnych i programowania strukturalnego.
Podsumowanie
Wybór operatora krzyżowania zależy bezpośrednio od typu kodowania i charakteru problemu. Odpowiedni operator powinien:
- zachowywać poprawność semantyczną rozwiązań,
- sprzyjać eksploracji i eksploatacji,
- być dopasowany do struktury genotypu.
W praktyce operator krzyżowania bywa kluczowym czynnikiem wpływającym na skuteczność algorytmu genetycznego. Dobór operatora często wymaga eksperymentalnej walidacji i dostosowania do konkretnego zadania.
3.8. Mutacja
Mutacja to podstawowy operator różnicowania genetycznego w algorytmach ewolucyjnych. Jej głównym zadaniem jest wprowadzanie losowych zmian w strukturze genotypu, co pozwala na eksplorację nowych rejonów przestrzeni rozwiązań. Mutacja uzupełnia działanie operatora krzyżowania – podczas gdy krzyżowanie miesza informacje już istniejące w populacji, mutacja wprowadza nowy materiał genetyczny.
Dobór odpowiedniej techniki mutacji zależy od typu kodowania rozwiązania – inne metody stosuje się dla chromosomów binarnych, inne dla rzeczywistych, permutacyjnych czy drzewiastych.
Mutacja w kodowaniu binarnym
Najprostszą i najczęściej stosowaną metodą jest tzw. mutacja bitowa (bit flip mutation). Polega na odwróceniu wartości bitu z 0 na 1 lub odwrotnie z pewnym prawdopodobieństwem $p_m$. Dla każdego bitu w chromosomie generowany jest losowy wynik, który decyduje o tym, czy dany bit zostanie odwrócony.
Z matematycznego punktu widzenia, dla chromosomu \(g = (g_1, g_2, ..., g_n)\), po mutacji:
\[
g_i' = \begin{cases}
1 - g_i & \text{z prawdopodobieństwem } p_m \\
g_i & \text{w przeciwnym razie}
\end{cases}
\]
Parametr \(p_m\) (np. 0.01 lub 1/n) określa siłę mutacji. Zbyt wysoka wartość może prowadzić do losowej eksploracji (efekt "szumu"), zbyt niska – do stagnacji populacji.
Mutacja w kodowaniu rzeczywistoliczbowym
W tej klasie problemów mutacja polega na dodaniu niewielkiego zaburzenia do wartości genu. Najczęściej stosuje się mutację gaussowską (normalną), gdzie do każdego genu dodawana jest wartość losowa z rozkładu normalnego:
\[
g_i' = g_i + N(0, \sigma^2)
\]
gdzie \(\sigma\) to parametr określający intensywność mutacji.
Wadą mutacji gaussowskiej może być ryzyko wyjścia poza dopuszczalny przedział. Aby tego uniknąć, wartości są zwykle przycinane lub odbijane od granic. Alternatywnie można stosować mutację Cauchy'ego (o grubych ogonach), która częściej generuje większe zmiany – sprzyja eksploracji globalnej.
Inną metodą jest tzw. unbounded mutation, gdzie nowe wartości są losowane z całego przedziału zmienności, np.:
\[
g_i' = U(a_i, b_i)
\]
Mutacja permutacyjna
W problemach, gdzie rozwiązania są reprezentowane jako permutacje (np. TSP), standardowe metody mutacji nie mają zastosowania. Zamiast tego stosuje się modyfikacje struktur permutacyjnych:
- Swap mutation – losowo wybierane są dwa indeksy i ich wartości są zamieniane: \[ g = (..., g_i, ..., g_j, ...) \Rightarrow (..., g_j, ..., g_i, ...) \]
- Insertion mutation – jeden element jest usuwany i wstawiany w innym miejscu w permutacji.
- Inversion mutation – losowy fragment permutacji jest odwracany.
Mutacja w strukturach drzewiastych
W programowaniu genetycznym mutacja najczęściej dotyczy struktury drzewa – np. podmiany pojedynczego węzła, zastąpienia poddrzewa nowym lub modyfikacji terminali.
- Subtree mutation – losowy węzeł drzewa zostaje zastąpiony losowo wygenerowanym poddrzewem.
- Point mutation – zmiana wartości operatora lub terminala w wybranym węźle.
Inne techniki mutacji
- Mutacja ograniczona (boundary mutation) – gen może przyjąć wartość jednego z krańców dopuszczalnego zakresu.
- Non-uniform mutation – siła mutacji zmniejsza się w miarę upływu czasu, np.:\[ g_i' = g_i + \Delta(t, b_i - g_i) \]
gdzie- \(\Delta(t, d)\) to funkcja malejąca wraz z czasem (np. logarytmiczna),
- \(t\) – numer pokolenia.
- Adaptive mutation – parametr mutacji (np. \(\sigma\)) zmienia się w trakcie działania algorytmu w odpowiedzi na tempo poprawy rozwiązania.
Podsumowanie
Mutacja pełni niezwykle ważną rolę w utrzymywaniu różnorodności populacji. W zależności od typu kodowania, należy dobierać odpowiednie operatory:
- binarne – odwracanie bitów,
- rzeczywiste – zakłócenia losowe (np. gaussowskie),
- permutacyjne – przekształcenia pozycji,
- drzewiaste – manipulacje strukturą drzewa.
Dobór intensywności mutacji i jej rodzaju wpływa na zdolność algorytmu do eksploracji i unikania zbieżności do lokalnych minimów. W praktyce często stosuje się również mechanizmy adaptacyjne, które dynamicznie dostosowują siłę mutacji w trakcie działania algorytmu.
3.9. Warunek końca
Warunki zakończenia są istotnym elementem sterującym działaniem algorytmu genetycznego. To one decydują, kiedy proces ewolucyjny zostaje zatrzymany, a najlepsze znalezione rozwiązanie uznane za wynik końcowy. Ich odpowiedni dobór wpływa zarówno na jakość rozwiązań, jak i na czas działania algorytmu.
W praktyce stosuje się kilka klas warunków zakończenia, często wykorzystywanych równolegle.
Zakończenie po ustalonej liczbie pokoleń
Najczęstszy i najprostszy sposób zatrzymania działania algorytmu. Proces ewolucyjny kończy się po osiągnięciu ustalonej liczby iteracji (pokoleń).
\[ \text{Stop, jeśli } t \geq T_{max} \]
gdzie \(t\) to aktualny numer pokolenia, a \(T_{max}\) – maksymalna liczba pokoleń.
Zaletą tej metody jest jej przewidywalność i łatwość implementacji. Wadą – brak związku z faktyczną jakością rozwiązań. Może prowadzić do zakończenia przedwcześnie lub kontynuowania obliczeń mimo osiągnięcia optimum.
Zakończenie po czasie działania
Algorytm zatrzymuje się po upływie określonego czasu rzeczywistego. Stosowane w systemach o ograniczonych zasobach obliczeniowych lub tam, gdzie wymagane są wyniki w czasie rzeczywistym.
\[\text{Stop, jeśli } \text{czas} \geq T_{czasowy}\]
Ten sposób pozwala dostosować pracę algorytmu do ograniczeń środowiska (np. wbudowane systemy, przetwarzanie online). Jednak, podobnie jak poprzedni, nie uwzględnia postępu jakościowego.
Zakończenie przy braku poprawy
Algorytm zatrzymuje się, gdy przez kolejne \(N\) pokoleń nie następuje istotna poprawa najlepszego osobnika:
\[ \text{Stop, jeśli } \max(F_{best}^{(t - N)} \dots F_{best}^{(t)}) - F_{best}^{(t)} \leq \epsilon \]
gdzie \(F_{best}^{(t)}\) to wartość funkcji celu najlepszego osobnika w pokoleniu \(t\), a \(\epsilon\) to zadana tolerancja.
Metoda ta jest bardziej adaptacyjna – pozwala zakończyć działanie algorytmu, gdy dalsze przeszukiwanie nie przynosi postępu. Często używana w połączeniu z limitem pokoleń.
Zakończenie po osiągnięciu wartości celu
Jeśli algorytm znajdzie rozwiązanie o jakości przekraczającej z góry określony próg, zatrzymuje się natychmiast:
\[ \text{Stop, jeśli } F_{best}^{(t)} \geq F_{target} \]
To podejście jest szczególnie przydatne w sytuacjach, gdy znamy wartość globalnego optimum lub poziom, który uznajemy za wystarczający.
Zakończenie na podstawie różnorodności populacji
Zanik różnorodności (np. ujednolicenie genotypów) może wskazywać, że algorytm osiągnął stagnację. Wówczas możemy zakończyć jego działanie:
\[ \text{Stop, jeśli } \text{diversity}(P_t) \leq \delta \]
gdzie \(\text{diversity}(P_t)\) mierzy zróżnicowanie populacji \(P_t\).
Miara różnorodności może opierać się na odległości Hammingowej, wariancji genów, entropii lub innych statystykach. To podejście pozwala wykryć, że populacja „utknęła” w jednym optimum lokalnym.
Złożone i adaptacyjne warunki zakończenia
W praktyce często łączy się kilka kryteriów – np. maksymalna liczba pokoleń ORAZ brak poprawy przez $N$ pokoleń. Stosuje się także warunki adaptacyjne, gdzie próg tolerancji czy oczekiwany postęp zmieniają się w czasie działania algorytmu.
Możliwe jest także zastosowanie monitorowania pochodnych, prędkości zbieżności lub metryk pochodzących z uczenia maszynowego do przewidywania zatrzymania.
Podsumowanie
Warunki zakończenia to jeden z kluczowych parametrów kontrolnych algorytmu genetycznego. Wpływają na jego efektywność, koszt obliczeniowy i jakość wyniku końcowego. Ich dobór powinien uwzględniać:
- charakterystykę problemu,
- wymagania czasowe lub sprzętowe,
- oczekiwany poziom dokładności,
- strategię eksploracji i eksploatacji.
Stosowanie złożonych i wielokryterialnych warunków zakończenia może znacząco poprawić skuteczność i elastyczność algorytmu.
3.10. Prosty przykład AG
W przypadku algorytmów genetycznych - to co Wam pokażę to rozwiązanie problemu dyskretnego - problemu komiwojażera. Zaczniemy od definicji problemu:
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
num_points = 50
points_coordinate = np.random.rand(num_points, 2)
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
'''Funkcja celu. Parametrem wejściowym jest trasa, zwracana jest jej długość
'''
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
W następnym kroku uruchamiany jest algorytm genetyczny. My stosujemy wersję dedykowaną do optymalizacji permutyzacyjnej - kiedy genom jest zakodowany w formie listy.
- func - funkcja celu
- n_dim - liczba wymiarów funkcji celu
- size_pop - wielkość populacji
- max_iter - liczba iteracji
- prob_mut - prawdopodobieństwo mutacji
from sko.GA import GA_TSP
ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=50, max_iter=1000, prob_mut=1)
best_points, best_distance = ga_tsp.run()Pozostaje nam narysowanie wyników
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()
3.11. Implementacje
Na koniec mamy dla Was przegląd dostępnych darmowych bibliotek do obliczeń genetycznych w językach Python i C++. To zestawienie może posłużyć jako pomocna mapa drogowa dla każdego, kto chce zastosować algorytmy genetyczne w praktyce – od prostych problemów inżynierskich po zaawansowaną optymalizację wielokryterialną.Python
Python to jedno z najbardziej popularnych środowisk do eksperymentów z algorytmami genetycznymi – głównie dzięki swojej prostocie, ogromnej liczbie gotowych bibliotek oraz wsparciu społeczności. Oto najbardziej godne uwagi biblioteki:
- DEAP (Distributed Evolutionary Algorithms in Python) Jest to zdecydowanie najbardziej kompletna biblioteka do algorytmów ewolucyjnych w Pythonie. Obsługuje GA, ES, PSO, NSGA-II i wiele innych technik. Umożliwia szybkie prototypowanie dzięki modularnej architekturze i integracji z `numpy`. Strona projektu: https://github.com/DEAP/deap Plusy: wsparcie dla wielokryterialności (np. fronty Pareto), elityzm, analiza wyników, wsparcie dla rozproszenia obliczeń. Minusy: wysoki próg wejścia.
- SKO (Scikit-Optimize) To biblioteka oparta na `scikit-learn`, zaprojektowana do optymalizacji funkcji czarnej skrzynki, w tym również za pomocą metod ewolucyjnych. SKO umożliwia stosowanie algorytmu ewolucyjnego (GA) jako strategii przeszukiwania, alternatywnej wobec metod bayesowskich. Strona projektu: https://scikit-optimize.github.io/ Plusy: łatwa integracja z pipeline’ami `scikit-learn`, możliwość użycia GA do strojenia hiperparametrów modeli ML, prosta składnia. Minusy: ograniczone możliwości dostosowania operatorów genetycznych w porównaniu do bibliotek takich jak DEAP.
- PyGAD Lekka biblioteka GA, idealna do szybkich testów i edukacji. Wspiera różne typy mutacji, selekcji i krzyżowania, również dla danych typu ciągłego i dyskretnego. Strona projektu: https://pygad.readthedocs.io/ Plusy: świetna dokumentacja, prostota integracji z sieciami neuronowymi (np. Keras). Minusy: nie obsługuje bezpośrednio optymalizacji wielokryterialnej.
- Evol Kompaktowa i deklaratywna biblioteka, inspirowana programowaniem funkcyjnym. Strona projektu: https://github.com/godatadriven/evol Plusy: bardzo czytelna składnia, łatwość pisania własnych operatorów. Minusy: mniejsze możliwości przy złożonych problemach.
- Inspyred Dość elastyczna biblioteka, zawierająca także implementacje strategii ewolucyjnych i innych metaheurystyk. Strona projektu: https://github.com/aarongarrett/inspyred Plusy: dobre narzędzia diagnostyczne. Minusy: nie jest już aktywnie rozwijana, co może być problematyczne w dłuższej perspektywie.
C++
C++ to język chętnie wykorzystywany w zastosowaniach przemysłowych, gdzie liczy się wydajność. Znalezienie dobrych, aktywnie rozwijanych bibliotek open-source jest trudniejsze niż w Pythonie, ale oto najciekawsze z nich:
- EO (Evolving Objects) Biblioteka w pełni poświęcona obliczeniom ewolucyjnym – wspiera algorytmy genetyczne, strategie ewolucyjne, roje cząstek, programowanie genetyczne i wiele więcej. Strona projektu: https://github.com/eodev/eo Plusy: bardzo dobra architektura, aktywne wsparcie dla optymalizacji wielokryterialnej (np. NSGA-II). Minusy: wymaga dobrej znajomości C++ i nie jest już bardzo aktywnie rozwijana.
- Paradiseo Właściwie rozszerzenie EO – stanowi framework do optymalizacji metaheurystycznej, zawiera m.in. biblioteki do hybrydowych algorytmów, optymalizacji wielokryterialnej (Paradiseo-MO) oraz rozproszonej. Strona projektu: https://paradiseo.github.io/ Plusy: modularność, wysoka wydajność. Minusy: bardzo techniczne i wymaga głębszego wejścia w kod.
- GALib Jedna z najstarszych bibliotek (MIT), która wciąż jest wykorzystywana w edukacji i niektórych zastosowaniach przemysłowych. Strona projektu: http://lancet.mit.edu/ga/ Plusy: prostota, dobra dokumentacja. Minusy: przestarzała składnia, brak wsparcia dla nowoczesnych rozwiązań typu NSGA-II.
4. Particle Swarm Optimization
Wstęp historyczny i przyrodniczo-matematyczne inspiracje dla PSO
W historii nauki wiele wielkich pomysłów brało swój początek nie z głębokich analiz równań różniczkowych, ale z... obserwacji. Obserwacji życia, przyrody, zachowań społecznych. Tak właśnie było z algorytmem PSO – zrodził się nie w sali wykładowej matematyki stosowanej, ale w głowie psychologa i inżyniera, którzy próbowali opisać coś, co każdy z nas kiedyś widział: płynny, zsynchronizowany lot stada ptaków lub falującą niczym jeden organizm ławicę ryb.
Na początku lat 90. XX wieku James Kennedy (psycholog społeczny) i Russell Eberhart (inżynier) analizowali zachowania społeczne ptaków i ryb. Zamiast skupiać się na biologicznym realizmie, postanowili wyciągnąć z obserwacji kilka prostych zasad i przełożyć je na język obliczeń. Tak w 1995 roku narodził się PSO – Particle Swarm Optimization. Zamiast pytać „jaka jest trajektoria idealnego lotu?”, Kennedy i Eberhart zapytali: „czy możemy zasymulować te zbiorowe zachowania, by rozwiązywać problemy optymalizacyjne?”. To, co opracowali w odpowiedzi właśnie poznajecie.

Czy zastanawialiście się kiedyś dlaczego np. ptaki lecąc w wielkich stadach utrzymują spójność, zmieniają razem jako stado kierunek, czy też nie zderzają się? W sumie dzieje się tak dzięki 3 regułom:
- separacja - nie lubię być byt blisko. Jak jestem za blisko - oddalam się.
- Wyrównanie kierunku - widzę swoich sąsiadów, i idę tam gdzie oni - w sensie średniego kierunku ich ruchu.
- Wyrównanie położenia - widzę sąsiadów - staram się być pośrodku między tymi najbliższymi
Te reguły wystarczą już do opisania ruchu stada ptaków. Jeśli tylko każda jednostka będzie się ich trzymać - całe stado jest w stanie zachowywać zwartą, optymalną formację i zmieniać (nawet gwałtownie) kierunek w którym się porusza.
Zbiory bez lidera: inteligencja rozproszona
Podstawowa koncepcja PSO zakłada, że rozwiązania problemu (cząstki) poruszają się w przestrzeni poszukiwań, kierując się trzema impulsami:
- Własną pamięcią – cząstka pamięta, gdzie wcześniej było dobrze.
- Obserwacją sąsiadów – cząstka wie, jak poszło innym.
- Tendencją do zmiany – ruch odbywa się z pewną inercją.
To nie są złożone algorytmy decyzyjne. To trzy wektory sił, działających jednocześnie. I właśnie ich połączenie daje efekt podobny do tego, co widzimy w naturze: adaptacyjne, grupowe, ale i rozproszone zachowanie.
Cząstki nie potrzebują centralnego koordynatora. Nie ma tu lidera ani „dyspozytora ruchu”. Całość działa na zasadzie prostych reguł lokalnych. Brzmi znajomo? Tak – to dokładnie ta sama idea, która stoi za automatem komórkowym.
Automaty komórkowe – matematyczne odbicie przyrody
Zanim jeszcze wymyślono PSO, matematycy i informatycy teoretyczni pracowali nad tzw. automatami komórkowymi (ang. cellular automata). Jeden z najsłynniejszych przykładów to „Gra w życie” Johna Conwaya. W tym modelu, każdy punkt na siatce (komórka) decyduje o swoim stanie na podstawie stanu swoich sąsiadów – i to wszystko. A jednak, z tych prostych zasad wyłaniają się niezwykle złożone zachowania.
Warto tu zwrócić uwagę na analogię: w PSO też mamy „siatkę” – tym razem nie przestrzenną, lecz abstrakcyjną przestrzeń możliwych rozwiązań problemu. Cząstki nie są przypisane do stałych komórek, ale poruszają się, dynamicznie aktualizując swoją pozycję. A ich ruch jest wynikiem prostych lokalnych reguł, działających w czasie.
Zarówno PSO, jak i automaty komórkowe korzystają z:
- lokalnej informacji zamiast globalnej wiedzy o systemie,
- prostej logiki lokalnych decyzji,
- nieliniowych i często nieprzewidywalnych efektów grupowych.
W obu przypadkach to, co się liczy, to interakcja – nie pojedynczy byt, ale jego relacja z sąsiedztwem.
Biologia, matematyka i emergencja
W biologii, zachowania zbiorowe to klasyczny przypadek tzw. zjawisk emergentnych – takich, które nie wynikają wprost z właściwości pojedynczych elementów, ale pojawiają się dopiero na poziomie całego układu. Przykłady?
- Mrówki, które potrafią budować z siebie mosty.
- Termity, które bez planu architektonicznego tworzą złożone kolonie.
- Pszczoły, które kolektywnie podejmują decyzje o miejscu nowego gniazda.
W PSO też występuje emergencja. Żadna cząstka nie zna najlepszego rozwiązania. Ale razem, przez dzielenie się informacją, dążą do coraz lepszych obszarów przestrzeni rozwiązań. Efekt? Często zaskakująco dobre przybliżenia globalnego optimum.
To wszystko ma swój matematyczny wymiar. Ruch każdej cząstki w PSO można modelować jako losową dynamikę różnicową z komponentą socjalną. A cały system jako złożony układ dynamiczny z lokalnymi interakcjami i pamięcią.
Dlaczego to działa?
Bo łączy w sobie:
- Eksplorację – cząstki są rozproszone po całej przestrzeni.
- Eksploatację – z czasem skupiają się wokół obiecujących rejonów.
- Pamięć i adaptację – każda cząstka wie, gdzie jej było dobrze.
- Współdzielenie wiedzy – najlepsze rozwiązania są przekazywane innym.
Takie podejście, będące mieszanką biologii, matematyki i heurystyki, okazało się wyjątkowo skuteczne – szczególnie tam, gdzie gradienty są nieznane, funkcje są nieciągłe, a przestrzeń rozwiązań ogromna.
4.1. Jak to działa
Na podstawie pracy Abrahama, Das i Roya (2007) można zidentyfikować kilka fundamentalnych powodów, dla których algorytmy rojowe – w szczególności PSO (Particle Swarm Optimization) – są skuteczne w rozwiązywaniu problemów optymalizacyjnych, zarówno w przestrzeniach dyskretnych, jak i ciągłych. Ich efektywność wynika z kombinacji prostoty lokalnych reguł, mechanizmów komunikacji oraz emergencji zachowań grupowych.
Proste zasady, złożone efekty
Jednym z najważniejszych argumentów przytoczonych przez Abrahama i współautorów jest to, że złożone wzorce mogą wyłaniać się z prostych zachowań jednostek. W PSO każda cząstka kieruje się tylko kilkoma regułami: porusza się po przestrzeni rozwiązań pod wpływem własnego najlepszego doświadczenia oraz najlepszej znalezionej dotąd pozycji w swoim otoczeniu. To wystarczy, by cała populacja, nawet w bardzo złożonym krajobrazie funkcji celu, stopniowo zbiegała się do optymalnych (lub bliskich optymalnym) regionów.
Wymiana informacji i adaptacja
Drugi kluczowy element skuteczności PSO to zdolność komunikacji i adaptacji. Cząstki nie działają niezależnie – dzielą się informacją. W zależności od zastosowanej topologii (np. sąsiedztwa globalnego lub lokalnego), każda cząstka może korzystać z doświadczenia innych. To „uczenie się od innych” sprawia, że zamiast losowego błądzenia, mamy do czynienia z kierunkowym przeszukiwaniem, przy jednoczesnym zachowaniu różnorodności.
Brak potrzeby informacji gradientowej
W klasycznych algorytmach optymalizacyjnych, jak np. metoda gradientu, potrzebna jest znajomość pochodnych funkcji celu. PSO, podobnie jak inne algorytmy ewolucyjne, działa wyłącznie na podstawie wartości funkcji celu, bez potrzeby jej analitycznego opisu. To sprawia, że PSO jest odporny na nieliniowości, nieciągłości i szum – a zatem doskonale sprawdza się tam, gdzie tradycyjne metody zawodzą.
Eksploracja vs. eksploatacja
Według Abrahama, Das i Roya algorytmy rojowe osiągają skuteczność dzięki naturalnemu balansowi między eksploracją (badaniem nowych obszarów przestrzeni) a eksploatacją (lokalnym udoskonalaniem znanych rozwiązań). Początkowo cząstki przemieszczają się bardziej chaotycznie, dzięki czemu mogą „zajrzeć” do wielu regionów. Z czasem jednak, gdy znajdą obiecujące obszary, ich ruch staje się bardziej skupiony i następuje zbieżność.
Elastyczność i skalowalność
PSO działa dobrze niezależnie od wymiarowości przestrzeni problemu i może być z łatwością dostosowany do różnych zastosowań. Autorzy podkreślają, że dzięki temu algorytmy rojowe są elastyczne, łatwe do implementacji i wydajne obliczeniowo – szczególnie w środowiskach, gdzie wiele jednostek może działać równolegle.
Przejdźmy zatem do formalnej definicji algorytmu PSO, zaczynając od założeń:
Założenia algorytmu PSO – co wie każda cząstka?
W algorytmie PSO (Particle Swarm Optimization) modelujemy rozwiązania problemu jako cząstki poruszające się w przestrzeni przeszukiwań. Każda z tych cząstek (zwanych też osobnikami) posiada zestaw cech, który pozwala jej podejmować decyzje na podstawie lokalnych i sąsiedzkich informacji.
Wiedza i pamięć cząstki
Każda cząstka w roju:
- zna swoje aktualne położenie w przestrzeni (np. współrzędne),
- potrafi ocenić jakość swojego położenia, czyli zna wartość funkcji celu w swoim punkcie,
- porusza się z określoną prędkością i w zadanym kierunku,
- zapamiętuje najlepsze położenie, jakie kiedykolwiek odwiedziła (tzw. pozycję własnego optimum),
- zna wartość funkcji celu w tym najlepszym punkcie.
Interakcje społeczne
Cząstka nie działa w izolacji:
- wie, kim są jej sąsiedzi – czyli z kim „wymienia się” informacją,
- zna najlepsze pozycje osiągnięte przez sąsiadów,
- zna też wartość funkcji celu w tych pozycjach.
Efekt emergentny
Ten zestaw prostych właściwości daje niesamowicie efektywne zachowanie: cząstki potrafią samodzielnie, bez centralnego sterowania, gromadzić się wokół optymalnych punktów przestrzeni.
Dzięki połączeniu pamięci własnej i „inteligencji zbiorowej” algorytm PSO jest w stanie skutecznie eksplorować przestrzeń rozwiązań, a jednocześnie zbiegać do punktów optymalnych.
Realizacja
Jeśli już mamy założenia, pora ubrać je w algorytm. Zakładamy więc, że każda cząstka lata w n-wymiarowej przestrzeni:\[ x_i=[x_{i1}, x_{i2}, \ldots, x_{in}]^T
x_{i}^{k+1}=x_i^k+v_i^k \]
Pytanie skąd mamy wziąć prędkość?

Na to odpowiadają nam wcześniejsze założenia. A więc:
Każda cząstka porusza się z pewną inercją - nie chce zmieniać kierunku:
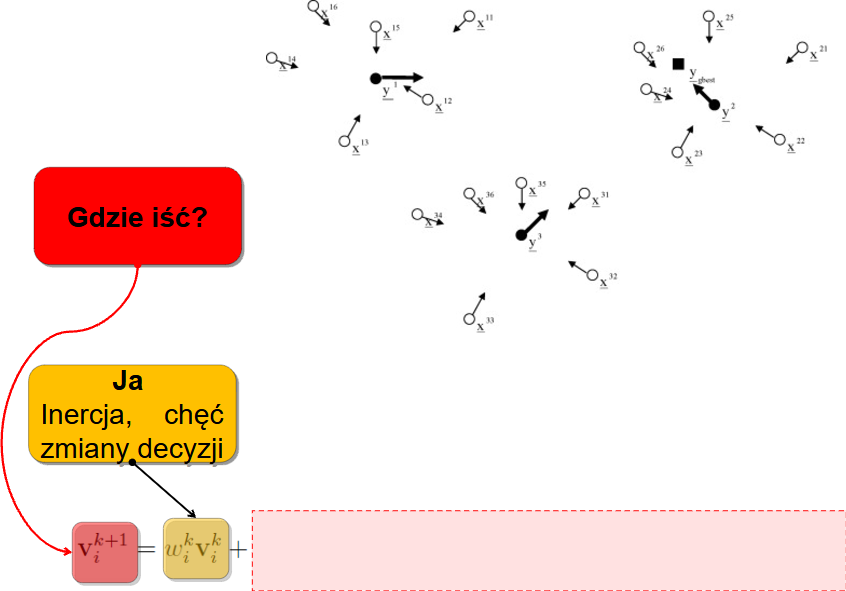
Każdy dąży też do miejsca gdzie mu było do tej pory najlepiej - więc mamy składową, która kieruje nas w miejsce najlepiej ocenione w historii konkretnej cząstki:
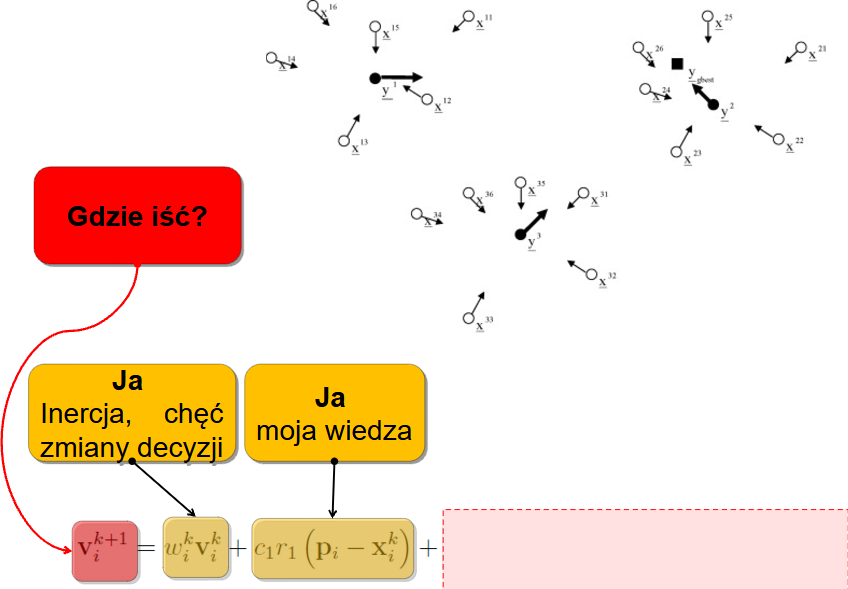
Założenie jednak mówiło, że nie tylko moja wiedza jest istotna - także mam dzielić się informacjami z innymi. Mogę więc podglądać sąsiadów:
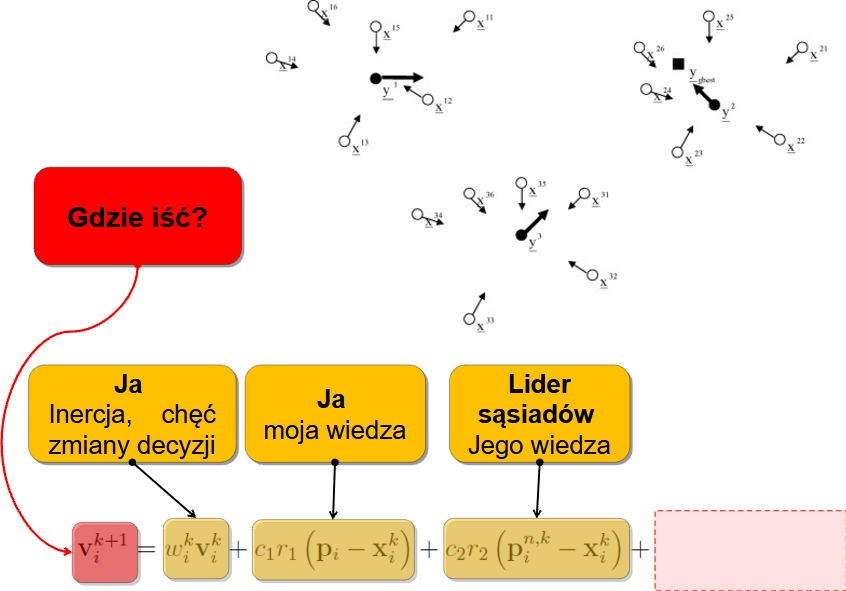
No i - last but not least - mogę patrzeć na ideały, czyli podążać w kierunku definiowanym przez najlepszą cząstkę w całym roju:
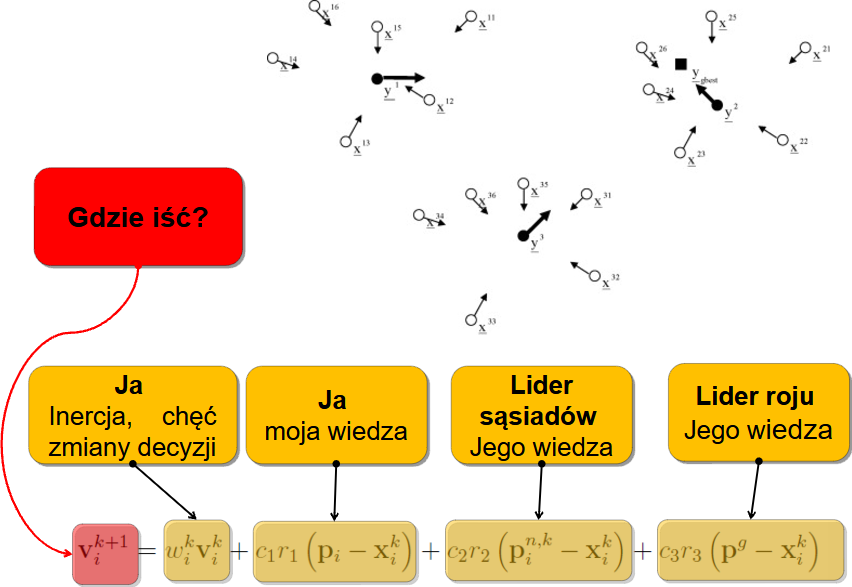
I to już całe wyrażenie które kieruje ruchem każdej cząstki. Finalnie więc mamy wyrażenie:
\[
v_i^{k+1}=w_i^k v_i^k + c_1 r_1(p_i-x_i^k)+c_2r_2(p_i^{n,k}-x_i^k)+c_3r_3(p^{g}-x_i^k)
\]
gdzie:
- \( v_i^k \) – prędkość cząstki i w chwili k,
- \( x_i^k \) - aktualna pozycja cząstki i.
- \( p_i \) - najlepsza dotąd pozycja cząstki i
- \( p_i^{n,k} \) - najlepsza pozycja w sąsiedztwie cząstki
- \( p^g \) - najlepsza w ogóle pozycja w roju,
- \( w \) - współczynnik inercji
- \( c_1,c_2, c_3 \) - współczynniki socjalne (przyciąganie do własnego, lokalnego i globalnego optimum)
- \( r_1,r_2, r_3 \) - wartości losowe generowane niezależnie dla każdego wymiaru i każdej cząstki
4.2. Sąsiedzi
Jednym z kluczowych pojęć w algorytmie PSO jest sąsiedztwo (ang. neighborhood). O ile w algorytmach genetycznych osobniki współpracują przez mechanizmy doboru, krzyżowania i mutacji, to w PSO wymiana informacji opiera się na obserwacji – każda cząstka aktualizuje swoje zachowanie na podstawie wyników innych cząstek, które zna. Ale których konkretnie? Tu właśnie wkracza pojęcie sąsiedztwa.
Dlaczego sąsiedztwo jest ważne?
W klasycznej wersji PSO każda cząstka ma dostęp do najlepszego rozwiązania ze wszystkich cząstek w populacji. To podejście nazywane jest topologią globalną. Choć skuteczne, niesie ono pewne ryzyko: bardzo szybka zbieżność może prowadzić do utknięcia w minimum lokalnym. Dlatego wprowadzono alternatywy, w których cząstka zna tylko pewien wycinek populacji – czyli swoje sąsiedztwo.
Odpowiednie zdefiniowanie sąsiedztwa pozwala osiągnąć kompromis między:
- eksploracją (szukanie nowych rozwiązań),
- eksploatacją (dopieszczanie już znanych dobrych wyników).
Innymi słowy: sąsiedztwo to mechanizm, który równoważy rozbieganie się roju i jego skupianie się wokół obiecujących punktów.
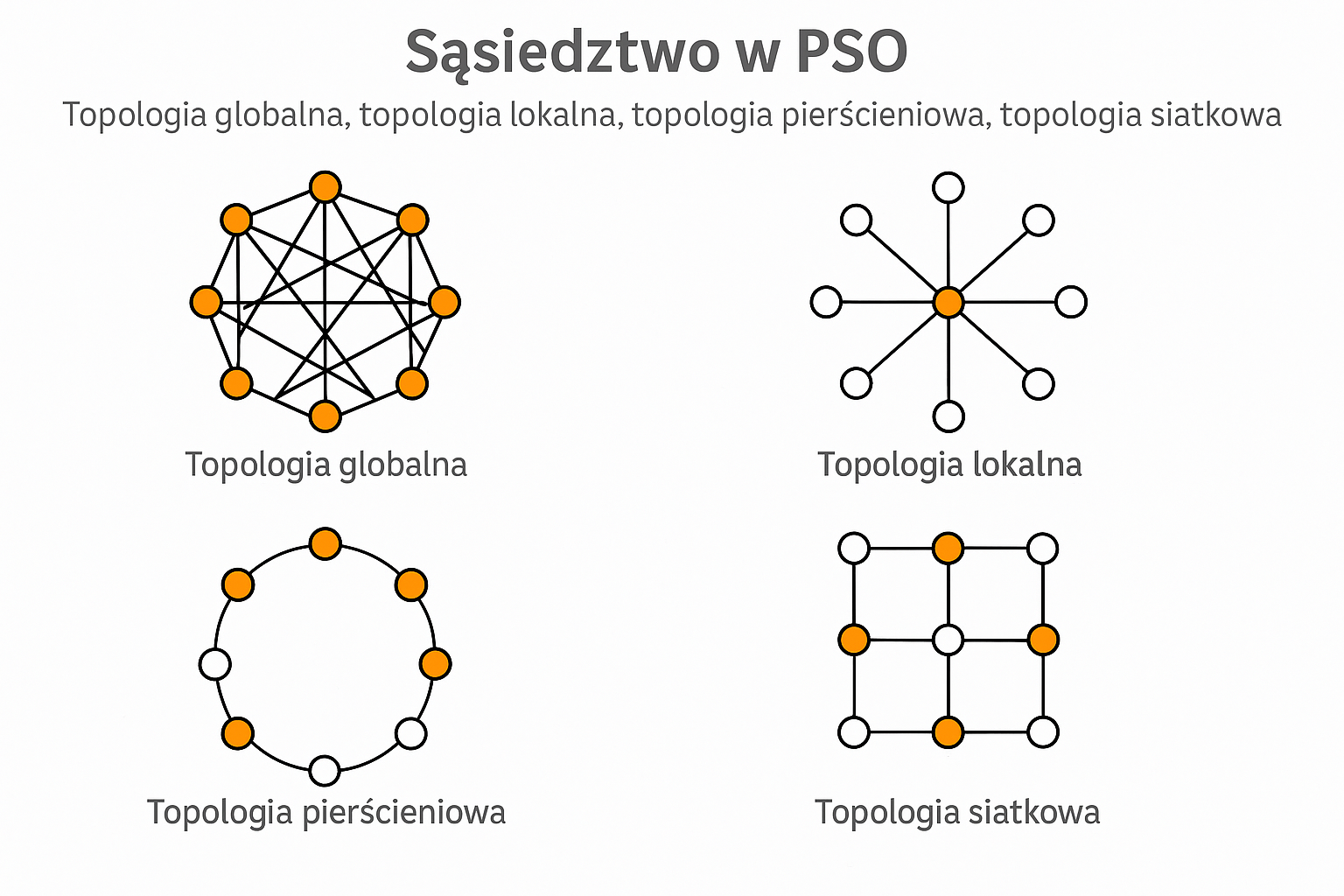
Rodzaje topologii sąsiedztwa
W praktyce najczęściej stosuje się trzy główne rodzaje topologii:
Topologia globalna (gBest)
Najprostszy wariant: każda cząstka zna najlepsze rozwiązanie znalezione przez dowolną cząstkę w populacji. Oznacza to, że każda z nich ma ten sam „punkt odniesienia społecznego”.
Zalety:
- bardzo szybka zbieżność (mała liczba iteracji do znalezienia rozwiązania),
- skuteczna, gdy krajobraz funkcji celu nie jest zbyt zdradliwy (np. niewiele ekstremów lokalnych).
Wady:
- ryzyko przedwczesnej zbieżności – gdy cząstki „za szybko” skupią się wokół lokalnego optimum, ignorując resztę przestrzeni.
Topologia lokalna (lBest)
Tutaj każda cząstka zna tylko cząstki ze swojego lokalnego sąsiedztwa. To może być np. grupa kilku sąsiadów z lewej i prawej strony (na przykład w sensie indeksów na liście populacji), lub osobniki znajdujące się najbliżej w przestrzeni.
Zalety:
- większa różnorodność ruchów w populacji – różne cząstki podążają za różnymi liderami,
- mniejsze ryzyko utknięcia w minimum lokalnym,
- dobra równowaga między eksploracją a eksploatacją.
Wady:
- wolniejsza zbieżność (więcej iteracji potrzebnych do osiągnięcia rozwiązania),
- większy koszt obliczeniowy, jeśli sąsiedztwo jest dynamicznie aktualizowane w przestrzeni (np. na podstawie odległości).
Topologia pierścieniowa
To szczególny przypadek topologii lokalnej. Zakładamy, że cząstki są ustawione w pierścień, a każda cząstka zna tylko kilku sąsiadów po lewej i prawej stronie. Przykład: jeśli liczność populacji to , a liczba sąsiadów to 2, to cząstka zna cząstki i .
Zalety:
- bardzo stabilna zbieżność,
- dobre zachowanie w problemach wielowymiarowych.
Inne, mniej klasyczne topologie
Choć powyższe trzy typy dominują w praktyce, w literaturze spotyka się też inne:
Topologia siatkowa (2D grid)
Cząstki są rozłożone w siatce (np. 10×10), a każda zna tylko najbliższych sąsiadów (góra, dół, lewo, prawo). Działa podobnie jak pierścień, ale w dwóch wymiarach.
Topologia dynamiczna
Sąsiedztwo cząstki może się zmieniać w czasie – np. zależnie od aktualnej odległości od innych cząstek, wyników funkcji celu, czy losowych fluktuacji. Takie podejście może symulować zjawiska naturalne, jak np. tymczasowe grupowanie się ławic ryb w obliczu drapieżnika.
Topologie hybrydowe
W rzeczywistych zastosowaniach czasem łączy się różne podejścia: np. globalne sąsiedztwo w pierwszych iteracjach, a lokalne w późniejszych. Takie strategie zwiększają szanse na skuteczne odnalezienie optimum globalnego.
Sąsiedztwo jako parametr algorytmu
Topologia sąsiedztwa można traktować jako hiperparametr – coś, co nie jest optymalizowane przez sam PSO, ale co można dobrać eksperymentalnie (lub przez metody metaoptymalizacyjne, np. algorytmy genetyczne lub grid search). Dobór sąsiedztwa może mieć ogromny wpływ na wydajność algorytmu, zwłaszcza w problemach wielomodalnych lub wysokowymiarowych.
W algorytmie PSO pojęcie sąsiedztwa pełni rolę kanału wymiany informacji. Cząstki nie potrzebują znać całej populacji – wystarczy, że obserwują lokalne otoczenie. To właśnie różnorodność możliwych topologii daje PSO elastyczność w dopasowywaniu się do różnych typów problemów: od gładkich funkcji z jednym optimum, po chaotyczne krajobrazy z wieloma pułapkami lokalnymi.
Dobór odpowiedniej topologii to jak wybór strategii przeszukiwania: czy lepiej iść za tłumem, czy trzymać się własnej ścieżki i lokalnych znajomych? Odpowiedź zależy od tego, jak wygląda przestrzeń problemu – a tu nie ma jednej recepty. Ale dobrze rozumiane sąsiedztwo to klucz do sukcesu w algorytmach rojowych.
4.3. Schemat dzialania
Algorytm PSO opiera się na populacji cząstek poruszających się w przestrzeni rozwiązań, gdzie każda z nich aktualizuje swoją pozycję na podstawie własnego doświadczenia oraz obserwacji sąsiadów. Poszukiwanie rozwiązania odbywa się iteracyjnie, a cały proces można przedstawić jako cykl aktualizacji prędkości i położenia, z wykorzystaniem informacji lokalnej i społecznej.
Etapy działania algorytmu
-
Inicjalizacja populacji
- Pozycje i prędkości cząstek są losowo inicjalizowane.
- Dla każdej cząstki oblicza się wartość funkcji celu.
- Zapamiętywane są najlepsze pozycje własne (personal best) oraz najlepsze pozycje w sąsiedztwie (np. globalne lub lokalne optimum).
-
Pętla optymalizacyjna (iteracje)
-
Dla każdej cząstki:
- Aktualizowana jest prędkość na podstawie trzech komponentów: inercji, dążenia do własnego najlepszego punktu i dążenia do najlepszego punktu społecznego.
- Obliczana jest nowa pozycja.
- Obliczana jest wartość funkcji celu w nowej pozycji.
- Jeżeli nowa pozycja jest lepsza niż dotychczasowy personal best – zostaje zaktualizowana.
- Jeśli lepsza jest również od najlepszej pozycji w sąsiedztwie – sąsiedztwo jest informowane.
Warunek zakończenia
- Algorytm kończy działanie po osiągnięciu maksymalnej liczby iteracji lub po spełnieniu kryterium dokładności (np. brak poprawy przez N kroków).
-
Pseudokod algorytmu PSO
Wejście:
- funkcja celu f(x),
- liczba cząstek N,
- liczba iteracji T,
- współczynniki: ω, c1, c2
1. Dla każdej cząstki i = 1 do N wykonaj:
- losowo zainicjalizuj pozycję xi
- losowo zainicjalizuj prędkość vi
- ustaw pi ← xi // najlepsza pozycja własna
- oblicz f(pi)
2. Wyznacz g ← najlepsze pi w całej populacji lub w sąsiedztwie
3. Dla t = 1 do T wykonuj:
Dla każdej cząstki i = 1 do N:
- wylosuj r1, r2 ∈ U(0, 1)
- zaktualizuj prędkość:
vi ← ω * vi + c1 * r1 * (pi - xi) + c2 * r2 * (g - xi)
- zaktualizuj pozycję:
xi ← xi + vi
- oblicz f(xi)
- jeśli f(xi) < f(pi) to:
pi ← xi
- jeśli f(xi) < f(g) to:
g ← xi
4. Zwróć: g jako przybliżone optimum
Ograniczenia prędkości i ich wpływ na działanie algorytmu
W praktyce działania algorytmu PSO często wprowadza się ograniczenia na maksymalną dopuszczalną prędkość cząstek (oznaczaną jako v_max). Prędkość cząstki decyduje o tym, jak duży krok wykonuje ona w przestrzeni poszukiwań – a zbyt duże kroki mogą powodować niekontrolowane skoki i pomijanie wartościowych obszarów.
Wprowadzenie ograniczenia v_max powoduje, że prędkość cząstki jest każdorazowo przycinana według wzoru:
if |v_i| > v_max then v_i ← sign(v_i) * v_max
Efekty zastosowania ograniczenia:
- Stabilizacja algorytmu – cząstki poruszają się w sposób bardziej kontrolowany i nie „uciekają” z obszaru poszukiwań.
- Większa precyzja – małe kroki pozwalają dokładniej zbadać obszary w pobliżu lokalnych minimów.
-
Zwiększone ryzyko utknięcia – zbyt niskie
v_maxmoże sprawić, że cząstki ugrzęzną w minimum lokalnym i nie będą w stanie się z niego wydostać.
Dobór v_max to kompromis między eksploracją (duże kroki, większe v_max) a eksploatacją (małe kroki, mniejsze v_max). Zazwyczaj wartości v_max są skalowane względem rozmiaru przestrzeni poszukiwań, np. jako 10–20% długości danego wymiaru.
4.4. Przykład PSO
Będziemy korzystali z biblioteki PSO zawartej jako część biblioteki SciKit. Nie jest to jedyna implementacja PSO którą mamy dostępną - ale jest stabilna, powszechnie używana, i ciągle uzupełniana.
By można było z niej korzystać - należy ją najpierw zainstalować. Robimy to, korzystając z menager-a pakietów pythona (jeśi ćwiczenie wykonujecie poza Colab - to te polecenia muszą zostać wykonane w terminalu, ewentualnie możecie zainstalować bibliotekę korzystając z opcji środowiska programistycznego)
!pip install scikit-optPo zainstalowaniu bibliotek należy zaimportować potrzebne biblioteki (sko - to SciKit Optimization).
import matplotlib.pyplot as plt
import numpy as np
from sko.PSO import PSO
Pierwszym krokiem optymalizacji jest definicja funkcji celu. W przykładzie wykorzystamy prostą, trójwymiarową funkcję kwadratową
def demo_func(x):
x1, x2, x3 = x
return x1;**2+(x2-0.05)**2+ x3 ** 2
W drugim kroku uruchamiamy algorytm optymalizacyjny.
Parametry przekazywane do PSO:
- func - funkcja celu
- n_dim - liczba wymiarów funkcji celu
- size_pop - wielkość roju
- max_iter - liczba iteracji
- lb - dolne ograniczenie zmienności parametrów
- ub - górne ograniczenie zmienności parametrów
- w - inercja cząstki
- c1 - waga dążenia do najlepszej dotychczasowej pozycji (moja wiedza)
- c2 - waga dążenia do pozycji lidera roju (wiedza najlepszego)
- constraint_ueq - ograniczenia nierównościowe
pso = PSO(func=demo_func, n_dim=3, pop=40, max_iter=300, lb=[-100, -100, -100], ub=[100, 100, 100], w=0.8, c1=0.5, c2=0.5)
pso.run()
print('Znaleziony wektor parametrów ', pso.gbest_x, 'wartość funkcji', pso.gbest_y
W trzecim kroku - rysujemy jak zmieniała się wartość funkcji celu w trakcie obliczeń
import matplotlib.pyplot as plt
plt.plot(pso.gbest_y_hist)
plt.show()
Komplet parametrów
Teraz przygotujemy animację która pokaże jak cząstki zachowywały się w trakcie obliczeń. Wykorzystana zostanie znów standardowa wersja PSO zaimplementowana w SCIKIT.
Wykorzystamy do tego celu dwuwymiarową funkcję celu, i dodamy do niej ograniczenie przeszukiwania do okręgu:
import numpy as np
from sko.PSO import PSO
def demo_func_2(x):
x1, x2 = x
return 2 * x1 ** 2 - 1.05 * x1 ** 4 + (x1 ** 6) / 6 + x1 * x2 + x2 ** 2
# return -20 * np.exp(-0.2 * np.sqrt(0.5 * (x1 ** 2 + x2 ** 2))) - np.exp(
# 0.5 * (np.cos(2 * np.pi * x1) + np.cos(2 * np.pi * x2))) + 20 + np.e
constraint_ueq = (
lambda x: (x[0] - 1) ** 2 + (x[1] - 0) ** 2 - 0.5 ** 2,
)
Narysujmy naszą funkcję celu z ograniczeniami
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
fig, ax = plt.subplots(1, 1)
ax.set_title('title', loc='center')
line = ax.plot([], [], 'b.')
X_grid, Y_grid = np.meshgrid(np.linspace(-2.0, 2.0, 40), np.linspace(-2.0, 2.0, 40))
Z_grid = demo_func_2((X_grid, Y_grid))
ax.contour(X_grid, Y_grid, Z_grid, 30)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
t = np.linspace(0, 2 * np.pi, 40)
ax.plot(2 * np.cos(t) + 1, 2 * np.sin(t), color='r')
plt.ion()
p = plt.show()
Wykonamy obliczenia - poszukajcie tutaj innych parametrów optymalizacji
max_iter = 50
pso = PSO(func=demo_func_2, n_dim=2, pop=40, max_iter=max_iter, lb=[-2, -2], ub=[2, 2])
#, constraint_ueq=constraint_ueq)
pso.record_mode = True
pso.run()
print('Znaleziony wektor parametrów ', pso.gbest_x, 'Wartość funkcji', pso.gbest_y)
W ostatnim kroku przygotujemy animację - jak wyglądały zmiany w roju w trakcie obliczeń
record_value = pso.record_value
X_list, V_list = record_value['X'], record_value['V']
def update_scatter(frame):
i, j = frame // 10, frame % 10
ax.set_title('iter = ' + str(i))
X_tmp = X_list[i] + V_list[i] * j / 10.0
plt.setp(line, 'xdata', X_tmp[:, 0], 'ydata', X_tmp[:, 1])
return line
ani = FuncAnimation(fig, update_scatter, blit=True, interval=25, frames=max_iter * 10)
plt.show()
ani.save('pso.gif', writer='pillow')
4.5. Implementacje
Python
PySwarms
PySwarms to rozbudowana biblioteka badawcza, skierowana do użytkowników, którzy potrzebują elastyczności i narzędzi wspomagających badania nad PSO:
- Zawiera gotowe klasy optymalizatorów PSO (np. globalne, lokalne), funkcje testowe oraz wizualizację przebiegu optymalizacji.
- Umożliwia łatwe dostosowanie takich parametrów jak wielkość roju, współczynniki przyciągania, czy ograniczenie prędkości.
- Dodatkowo oferuje wsparcie do strojenia hiperparametrów i analizowanie wydajności (linia kosztów, ruchy cząstek itp.) .
To rozwiązanie idealne do badań, eksperymentów dydaktycznych – pozwala szybko wdrożyć algorytm i zobaczyć wyniki działania wizualnie.
Enhanced Particle Swarm Optimization
Enhanced PSO to klasyczna, dobrze udokumentowana implementacja PSO z dodatkowymi wariantami adaptacyjnymi:
- Implementuje m.in. adaptacyjne zmiany wag inercji i współczynników przyciągania oraz kontrolę maksymalnej prędkości cząstek.
- Kod jest przejrzysty, oparty o NumPy, wzbogacony o przykłady działania i wizualizacje.
- Świetny wybór dla tych, którym zależy na zrozumieniu, jak przebiegające w czasie zmiany parametrów wpływają na efektywność PSO .
Dzięki temu łatwo porównać klasyczne PSO z adaptacyjną wersją w tym samym środowisku.
scikit-opt
To rozbudowana biblioteka do optymalizacji heurystycznej, która integruje różne algorytmy, w tym PSO, w stylu zgodnym z konwencją scikit-learn. Implementacja PSO w scikit-opt charakteryzuje się prostym interfejsem, możliwością pracy z ograniczeniami oraz dobrą integracją z typowymi zadaniami optymalizacji nieliniowej.
Zaletą tej biblioteki jest także duża elastyczność i przejrzystość kodu, który może być łatwo modyfikowany przez użytkownika. Można szybko eksperymentować z różnymi ustawieniami i zintegrować algorytm z klasycznym pipeline uczenia maszynowego. Idealna opcja dla tych, którzy pracują już z narzędziami scikit-learn i szukają zgodnego stylu kodowania.
C++
pso-cpp
pso-cpp to biblioteka napisania ze szczególnym naciskiem na wygodę:
- Pojedynczy header, korzysta z bibliotek Eigen3 do operacji na wektorach i macierzach.
- Wystarczy załączyć plik wraz z Eigen – brak skomplikowanych zależności.
- Prosty, czytelny interfejs: wystarczy przekazać funktor celu, skonfigurować parametry i uruchomić optymalizację .
To doskonałe rozwiązanie do szybkiej integracji PSO w aplikacjach C++, zarówno wymagających, jak i edukacyjnych.
ErfanFathi/pso
PSO w wersji ErfanFahti to implementacja w C++ z wizualizacją na żywo z użyciem OpenCV. Oprócz samego algorytmu PSO pozwala zwizualizować ruch cząstek (np. przeszukanie obrazu do znalezienia celu). Umożliwia ustawienie różnych parametrów (c1, c2 etc.), a dzięki interfejsowi OpenCV można łatwo obserwować efekty zmian. W zasadzie to świetne narzędzie dydaktyczne – by „naocznie” zobaczyć działanie PSO w 2D. Trochę gorzej w tym wypadku wygląda aktualność samej biblioteki - projekt nie jest już od jakiegoś czasu aktualizowany. Niemniej to niezłe narzędzie dla osób uczących się metod metaheurystycznych i potrzebujących wizualnego sprzężenia zwrotnego.