Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Zastosowania Logiki Rozmytej |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | środa, 14 stycznia 2026, 19:21 |
Opis
Wstęp do logiki rozmytej
Spis treści
- 1. Wprowadzenie do teorii zbiorów rozmytych
- 2. Elementy teorii zbiorów rozmytych
- 3. Modelowanie rozmyte
- 3.1. Przykład modelowania analitycznego i rozmytego
- 3.2. Model analityczny
- 3.3. Model rozmyty
- 3.4. Uogólniony schemat wnioskowania rozmytego
- 3.5. Rozmywanie
- 3.6. Maszyna wnioskująca
- 3.7. Wnioskowanie oparte na pojedynczej regule
- 3.8. Wnioskowanie oparte na zbiorze reguł
- 3.9. Wyostrzanie zbiorów rozmytych
- 3.10. Metoda środka ciężkości
- 3.11. Metoda środka sum
- 3.12. Metoda środka największego obszaru (COLA)
- 3.13. Metoda wysokości (HM)
- 3.14. Metoda wysokości (FOM)
- 3.15. Metoda wysokości (LOM)
- 3.16. Metoda wysokości (MOM)
- 4. Przykłady regulatorów rozmytych
- 5. Implikacja Takagi-Sugeno
- 6. Przykłady zastosowań logiki rozmytej
1. Wprowadzenie do teorii zbiorów rozmytych
Teoria zbiorów rozmytych jest pewną alternatywną teorią mnogości umożliwiającą formalne ujęcie niepewności i nieścisłości pewnych pojęć i zależności. Logika rozmyta operująca na zbiorach rozmytych znajduje zastosowania teoretyczne i praktyczne w technice, biologii jak również w naukach ekonomicznych i społecznych. Po części spowodowane jest to faktem, że przedmiotem zainteresowania wszystkich tych dziedzin stają są coraz częściej obiekty o złożonej strukturze wewnętrznej i skomplikowanymi relacjami pomiędzy ich elementami.
Logika jest w istocie pewnym systemem rachunku zdań, która na podstawie predefiniowanych aksjomatów i przesłanek, pozwala na określenie stopnia ich prawdziwości.
Definicja powyższa ma charakter ogólny w tym sensie, że jest właściwa zarówno logice wielowartościowej (w tym binarnej) jak również logice rozmytej. Stopień prawdziwości zdań może być bowiem wyrażany zarówno w postaci wartości wielkości logicznych {prawda, fałsz}, jak również w postaci wartości dyskretnych \( \left\{-1, 0, +1\right\} \), ciągłych należących do przedziału \( [0..1] \) lub przedziałami ciągłych.
Logikę rozmytą rozumieć należy w kategoriach rozszerzenia klasycznej logiki wielowartościowej. Za bazę logiki rozmytej przyjmuje się standardową logikę nieskończenie wartościową Łukasiewicza zwaną \( Ł_{k-1} \), w której wartości prawdy są liczbami rzeczywistymi z przedziału \( [0,1] \).
1.1. Co to są zbiory rozmyte?
Jednym z fundamentów matematyki jest bez wątpienia teoria mnogości, a jej podstawowym elementem jest pojęcie zbioru. Nie wdając się w zbyt formalne rozważania, przeliczalny zbiór Z możemy określić w postaci enumeratywnej np. jako podzbiór złożony z n elementów \( x_i\in X \).
| \( Z = \left\{x_1, x_2, x_3, x_4, ... x_n\right\} \) | (1) |
|---|
Jeśli \( X=\left\{N\right\} \), gdzie N jest zbiorem liczb naturalnych, to np.: zbiór liczb naturalnych wyrażających: całkowite oceny postępów w nauce można w notacji (1) zapisać w postaci:
| \( Z = \left\{1, 2, 3, 4, 5, 6\right\} \) | (2) |
|---|
Z oczywistych powodów powyższy zapis jest użyteczny tylko wówczas gdy liczba \( n \) elementów zbioru Z jest niewielka. Ten sam zbiór Z można określić również w postaci:
| \( Z = \left\{x\in X: W(x)\right\} \) | (3) |
|---|
gdzie: \( W(x) \) jest pewną właściwością elementów zbioru \( Z \). Właściwość \( W(x) \) pozwala na przyporządkowanie do zbioru \( Z \) tych elementów zbioru \( X=\left\{x\right\} \), które spełniają warunek \( W(x) \).
Jeśli \( X=\left\{N\right\} \) jest zbiorem liczb naturalnych, to zbiór liczb naturalnych wyrażających np. zbiór całkowitych i pozytywnych ocen postępów w szkole średniej można zapisać w postaci:
| \( Z = \left\{x\in N: 2 \leqslant x \leqslant 6\right\} \) | (4) |
|---|
Jeśli \( X=\left\{R\right\} \) jest zbiorem liczb rzeczywistych, to zbiór dodatnich liczb rzeczywistych można zapisać w postaci (4) lub w postaci:
| \( Z = \left\{x\in R: x > 0\right\} \) | (5) |
|---|
Innym sposobem notacji zbioru \( Z \) jest zdefiniowanie jego funkcji charakterystycznej. Funkcją charakterystyczną zbioru \( Z \) jest taka funkcja \( \phi(x) \), która każdemu elementowi zbioru \( Z \) przypisuje wartość 1 lub 0 zależnie od tego czy element ten należy (\( \phi(x)=1 \)), czy też nie należy (\( \phi(x)=0 \)) do tego zbioru.
| \( \phi(x) : X \rightarrow\ \left\{0,1\right\} \) | (6) |
|---|
taka, że:
| \( \phi(x) = \left\{ \begin{array}{c} 0\;\ dla\;\ x\notin Z\\ 1 \;\ dla\;\ x\in Z\\ \end{array}\right. \) | (7) |
|---|
Stąd równoważną formą notacji zbioru \( Z \) z funkcją charakterystyczną jest zbiór par:
| \( Z = \left\{\left(\phi(x),x\right)\right\} \) | (8) |
|---|
Jeśli \( X=\left\{N\right\} \), gdzie \( N \) jest zbiorem liczb naturalnych, to zbiór liczb naturalnych wyrażających całkowite pozytywne oceny postępów w nauce w szkole średniej można zapisać w postaci (4) lub postaci par:
| \( Z = \left\{(0,0), (0,1), (1,2), (1,3), (1,4), (1,5), (1,6) (0,7),\, ...\,\right\} \) | (9) |
|---|
Jak więc widzimy dwuwartościowa funkcja charakterystyczna pozwala na wskazanie, które z elementów zbioru \( X \) należą, a które nie należą do zbioru \( Z \).
Zważmy dalej, że definicje (1), (3) i (7) są definicjami ściśle określonymi. W praktyce używa się jednak pewnych sformułowań i pojęć określonych w sposób nieścisły np: "wysokie ciśnienie", "średni wzrost", "niska inflacja", "niewielka odchyłka regulacji" itp. I tu pojawia się pytanie, czy tak nieprecyzyjne sformułowania można w jakikolwiek sposób wyrazić w sposób sformalizowany? Jeśli założymy, że tak to jak łatwo zauważyć natychmiast pojawiają się następne trudności, bowiem pod pojęciem "duża masa" będziemy rozumieli prawdopodobnie zupełnie coś innego w odniesieniu do przysłowiowej myszy i słonia. W naturalny sposób pojęcie "duża masa" wyraża w jakiś sposób zrelatywizowaną informację odwołując się do relacji pomiędzy pewną właściwością obiektu (masą), a pomiędzy pewną właściwością uznaną za normatywną (wzorcową lub odniesienia), przy czym zarówno jedna jak i druga nie muszą być zawsze zdefiniowane precyzyjnie. Ocena zatem co jest "duże", a co "małe" jest oceną z jednej strony zrelatywizowaną, z drugiej zaś oceną subiektywną w tym sensie, że zależy nie tylko od przyjętej normy relacji, ale również pewnej formy wnioskowania przyjętego w trakcie dokonywania oceny.
Np.: czy "wysoki wzrost mężczyzny" to: 180cm, czy 190cm, a może 200cm. Widać wyraźnie, że zaliczenie mężczyzny o wzroście 180cm do grupy mężczyzn o wysokim wzroście niekoniecznie musi być jednoznaczne przez wszystkich oceniających, a jeśli już, to jest uwarunkowane miejscem i czasem oceny. Oczywiście można tutaj wprowadzić ścisłą granicę uznając, że każdy z mężczyzn o wzroście powyżej 180cm jest wysokim mężczyzną, a każdy, którego wzrost jest poniżej 180cm jest już mężczyzną o niskim wzroście. Cóż wtedy powiedzą mężczyźni o wzroście 179cm, którzy będą mogli poczuć się urażeni.
Na Olimpiadzie Zimowej w 2002 r. w Salt Lake City w konkursie drużynowym skoków narciarskich złoty medal zdobyła drużyna niemiecka. Zwycięstwo osiągnęła zdobywając 740,1 punktów to znaczy zaledwie o 0,1 punktu więcej niż druga w kolejności drużyna fińska. W przeliczeniu na metry daje to wynik różniący się o 5 cm. Pomiary w konkursach skoku wykonywane są z rozdzielczością 0,5m. Czy drużyna fińska może poczuć się rozczarowana takim rozstrzygnięciem jury? Wydaje się że tak, ponieważ właściwsze byłoby rozstrzygnięcie ex aequo. Pojawia się w związku z tym pytanie, czy w związku z tym dyskretna ocena jest uzasadniona we wszystkich przypadkach?
W 1965 roku Zadeh [1] wprowadził pojęcie zbioru rozmytego. Analogicznie do (8) zbiór rozmyty \( A \) został określony w pewnej przestrzeni \( X \) zwanej dalej przestrzenią rozważań. Zbiór rozmyty \( A \) można przedstawić w postaci zbioru par:
| \( A = \left\{\left(\mu_A(x),x\right)\right\} \) | (10) |
|---|
gdzie:
| \( A = \mu_A(x):X\rightarrow \left[0,1\right] \) | (11) |
|---|
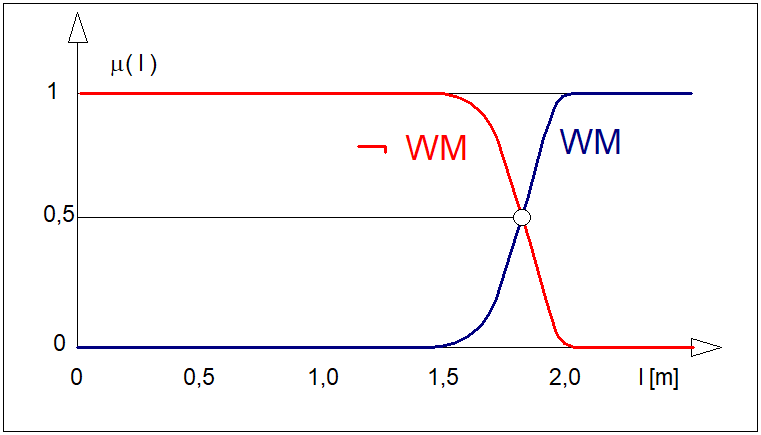
jest funkcją przynależności, która każdemu elementowi przestrzeni \( X \) przyporządkowuje stopień przynależności \( \mu_A(x) \) do danego zbioru rozmytego \( A \) począwszy od całkowitej nieprzynależności (\( \mu_A(x)=0 \)), przez przynależność częściową (\( 0<\mu_A(x)<1 \)), aż do przynależności całkowitej (\( \mu_A(x)=1 \)). W odróżnieniu od funkcji charakterystycznej, w której mamy do czynienia albo z "całkowitą nieprzynależnością" albo z "całkowitą przynależnością", występuje tutaj przypadek przynależności częściowej. Dla ilustracji załóżmy, że funkcja przynależności zbioru rozmytego \( WM \) ("wysoki mężczyzna") ma postać jak na rysunku poniżej.
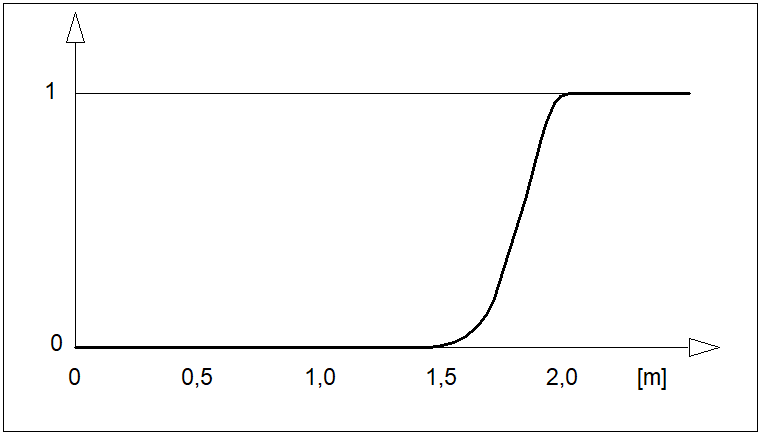
Przebieg funkcji przynależności z rysunku powyżej można interpretować następująco: mężczyznę o wzroście poniżej 150 cm na pewno nie można zaliczyć do grupy mężczyzn wysokich. Do grupy wysokich, z całą pewnością zaliczymy tych mężczyzn, których wzrost przekracza 200 cm. Mężczyzna o wzroście 180 cm jest w znacznym stopniu mężczyzną wysokim, a stopień przynależności tego mężczyzny do grupy wysokich mężczyzn może być odczytany bezpośrednio z przebiegu funkcji przynależności. Zwróćmy dalej uwagę, że funkcja przynależności ma w tym przypadku charakter czysto subiektywny. Jej przebieg zależy nie tylko od miejsca, czasu i osoby definiującej tę funkcję. Zwróćmy także uwagę, że dyskretna funkcja przynależności jest przypadkiem zdegenerowanymi i szczególnym funkcji ciągłej, a zatem definicję zbioru o postaci (10) należy uznać za bardziej ogólną od definicji (8).
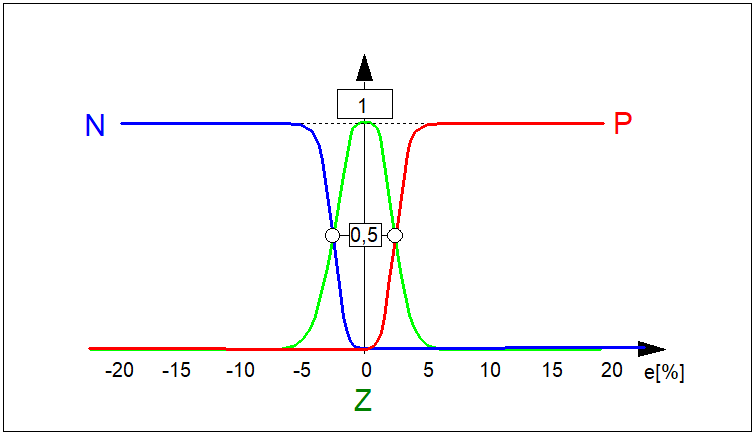
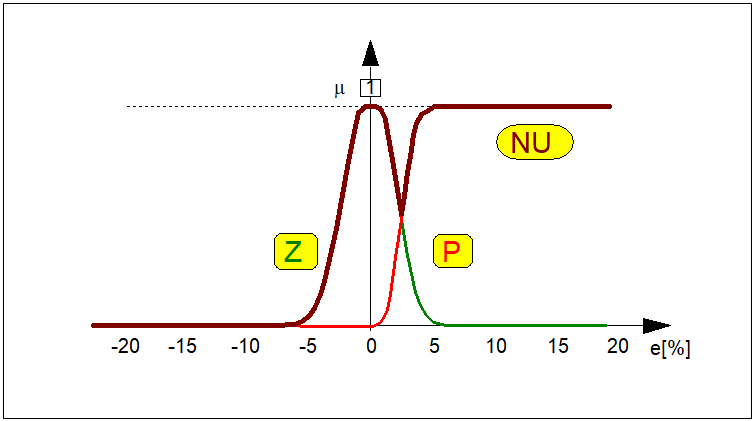
Rys. 5. Przykład przebiegu ciągłych funkcji przynależności:
\( \mu_N(e) \) zbioru rozmytego \( N \) ("ujemna odchyłka regulacji"),
\( \mu_Z(e) \) zbioru rozmytego \( Z \) ("zerowa odchyłka regulacji"),
\( \mu_P(e) \) zbioru rozmytego \( N \) ("dodatnia odchyłka regulacji").
Przebieg tych funkcji jest istotny w zastosowaniach logiki rozmytej w automatyzacji procesów technicznych.
Z podanych przykładów wynika, że funkcja przynależności może mieć postać zarówno funkcji ciągłej, nieciągłej lub przedziałami ciągłej.
1.2. Geneza zbiorów rozmytych
Teoria zbiorów rozmytych wyrosła na gruncie rozwoju teorii sterowania i logik wielowartościowych. W teorii sterowania i teorii systemów do połowy lat 60 XX wieku występowała tendencja do ścisłego i sformalizowanego opisu obiektów sterowania w postaci równań wynikających z praw fizyki, mechaniki, elektrodynamiki, termodynamiki, itp. Taki "mechanistyczne" opis zjawisk i procesów dawał pewną elegancję matematyczną i możliwość zastosowania wielu zaawansowanych metod matematycznych np.: teorii optymalizacji. Wyniki praktyczne stosowania tego typu opisów były w miarę zadawalające w zadaniach typu technicznego (układy sterowania), natomiast raczej negatywne w tych systemach, których istotnym elementem był człowiek.
Z drugiej zaś strony, w zadaniach, w których zawodziły metody ścisłe, człowiek, o którym mówiono, że nie jest w stanie ściśle myśleć i przetwarzać ogromnych ilości informacji, dawał sobie radę (np.: gra w szachy). Te fakty doprowadziły Zadeha [1] do sformułowania następującej zasady:
"Ogólnie rzecz biorąc, złożoność i precyzja są ze sobą w relacji odwrotnej w tym sensie, że jeśli złożoność rozpatrywanego problemu wzrasta, to zmniejsza się możliwość jego precyzyjnej analizy".
Zasada ta koresponduje w jakimś sensie ze słynną znaną z fizyki zasadą nieoznaczoności Heisenberga. A zatem wszelkie próby wprowadzenia nadmiernej precyzji do opisu i modelowania zwłaszcza systemów złożonych zarówno technicznych, ekonomicznych, biologicznych czy społecznych nie konieczne ze względu na występujące niepewności deskryptorów i relacji opisujących te systemy.
Dosyć zaskakujące jest stwierdzenie, że człowiek daje sobie radę w takich sytuacjach, w których próby zastosowania formalizmu matematycznego kończą się niepowodzeniem. Ma to miejsce np. wtedy gdy z różnych powodów nie można zbudować lub zidentyfikować modelu matematycznego systemu.
Rozważmy przypadek zadania sterowania rowerem autonomicznym. Z punktu widzenia technicznego rozwiązanie tego zadania nie jest trywialne. Wymaga zaangażowania potężnej wiedzy, pomiarów, sterowań identyfikacji w locie, wykonania szeregu eksperymentów, itd. Tymczasem człowiek rozwiązuje to zadanie sterowania bezproblemowo.
Powody tego stanu rzeczy leżą w umiejętności przybliżonego wnioskowania umysłu ludzkiego. Zadeh uważał, że rozumowanie ścisłe jest rozumowaniem "narzuconym" niejako człowiekowi przez rozwój metod i teorii matematycznych, natomiast z gruntu właściwym człowiekowi jest rozumowanie w kategoriach przybliżonych.
Teoria logiki rozmytej jest teorią próbującą wyjaśnić lub zaimplementować pewien uproszczony model ludzkiego rozumowania. W istocie, uwikłana w formalizm matematyczny stara się stworzyć model rozumowania przybliżonego przy użyciu narzędzi ścisłych. Ta pozorna sprzeczność może być wyjaśniona tylko wówczas gdy stosowany formalizm jest akceptowalny.
Istotną zaletą logiki rozmytej jest to, że już po krótkim okresie swego rozwoju znalazła rozległe zastosowania praktyczne w tym zwłaszcza w zastosowaniach w układach regulacji automatycznej.
2. Elementy teorii zbiorów rozmytych
Logika rozmyta jest rodzajem rachunku zdań, w którym występują więcej niż dwie wartości logiczne. Jest więc jedną z logik wielowartościowych. Szczególnymi wartościami logicznymi w przypadku logiki rozmytej są właśnie zbiory rozmyte. Ten rozdział wprowadzi nas w obszar podstawowych definicji i działań matematycznych ze zbiorami rozmytymi, w tym zwłaszcza z tymi, które są niezbędne dla zrozumienia dalszej części wykładu.
2.1. Zbiór rozmyty
Zbiór rozmyty, jak to już wspomnieliśmy wcześniej, służy do formalnego zdefiniowania pojęć nieostrych, nieprecyzyjnych czy wieloznacznych np. "mała odchyłka regulacji", "szeroka strefa histerezy", "duże przeregulowanie", "stan bliski granicy stabilności".
Rzecz jasna są to pojęcia relatywne. Weźmy dla przykładu pojęcie "duża liczba". Inną liczbę będziemy uważali za dużą, jeśli ograniczymy się do przedziału \( [0,10] \), a inną w przypadku gdy ograniczymy się np.: do przedziału \( [0,100] \). W pierwszym przypadku liczbę 9 będziemy traktowali jako dużą, w drugim przypadku tę samą liczbę będziemy traktowali jako małą. Tak więc pojęcie zbioru rozmytego wymaga określenia przestrzeni rozważań, będącej nierozmytym zbiorem elementów, w obrębie której się poruszamy. Może to być przedział liczbowy np.: \( [1..5] \), zbiór imion np.: \( \left\{Jan, Maciej, Maria\right\} \), zbiór cech np.: \( \left\{niski, średni, wysoki\right\} \), itp. Przestrzeń rozważań będziemy oznaczali dużymi literami łacińskimi np. \( X=\left\{x\right\} \) lub w przypadku skończeniewymiarowym \( X=\left\{x_1, x_2, x_3, x_4, ... x_n\right\} \).
Zbiorem rozmytym \( F \) w pewnej przestrzeni rozważań \( X=\left\{x\right\} \), co zapisujemy jako \( F\subseteq X \) nazywamy zbiór par:
| \( F=\left\{\left(\mu_F(x),x\right)\right\};\;\forall x\in X \) | (12) |
|---|
gdzie: \( \mu_F(x): X\to[0, 1] \) jest funkcją przynależności zbioru rozmytego \( F \), która każdemu elementowi \( x\in X \) przypisuje jego stopień przynależności do zbioru rozmytego \( F \); \( mu_F(x)\in [0, 1] \).
Porównując definicję (12) z (7) i (8) można interpretować funkcję przynależności jako uogólnioną funkcję charakterystyczną.
Dla uproszczenia dalszych rozważań parę \( \left\{\mu_F(x), x\right\} \) oznaczać będziemy \( \mu_F(x)/x \), a zbiór rozmyty o nieskończenie wielkiej liczbie elementów symbolem \( X=\left\{x\right\} \):
| \( \sum_{x\in X} \mu_F(x)/x \) | (13) |
|---|
Dla przestrzeni o skończonej liczbie elementów \( X = \left\{x_1, x_2, x_3, x_4, ... x_n\right\} \) :
| \( \sum_{i=1}^n \mu_F(x_i)/x_i= \mu_F(x_1)/x_{1}+\mu_F(x_2)/x_{2}+\dots+ \mu_F(x_n)/x_{n} \) | (14) |
|---|
gdzie symbole: \( \sum \) i \( + \) są symbolami sumy mnogościowej. Zapisy (13) i (14) oznaczają, że zbiór rozmyty jest sumą mnogościową elementów \( x_i \). W zapisie zbioru rozmytego pomijane są te pary, dla których \( mu_F(x)=0 \).
Pojęcie duża liczba.
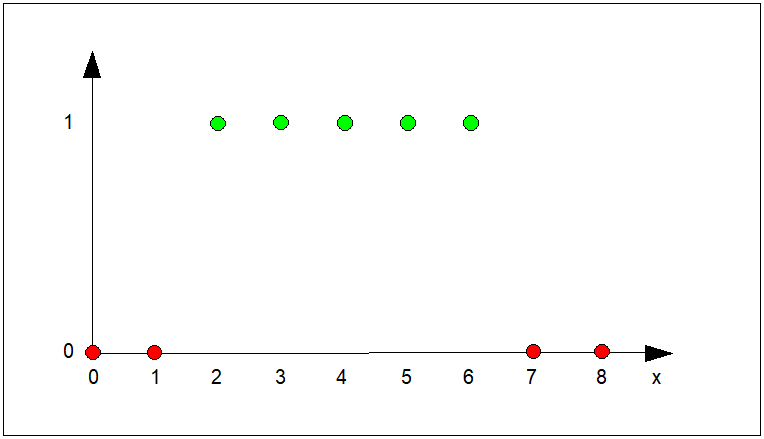
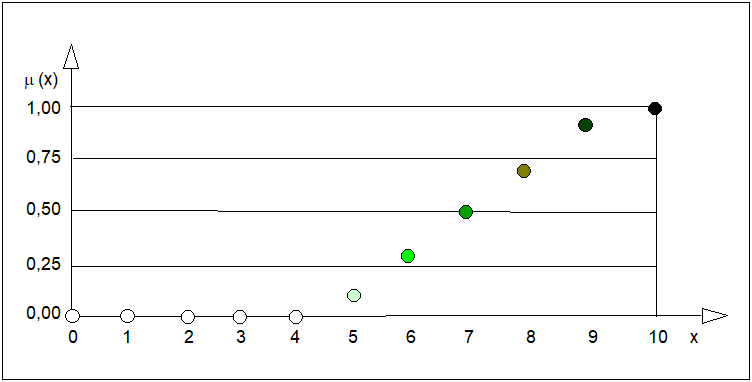
Załóżmy przestrzeń rozważań \( X \) o skończonej liczbie elementów \( X=\left\{0, 1, 2, ..., 10\right\} \). Niech "duża liczba" określona w tej przestrzeni będzie miała postać następującego zbioru rozmytego o nazwie \( DL \):
| \( DL = 0,1/5 + 0,3/6 + 0,5/7 + 0,7/8 + 0,9/9 + 1,0/10 \) | (15) |
|---|
Interpretację graficzną tego zbioru przedstawia rysunek poniżej.
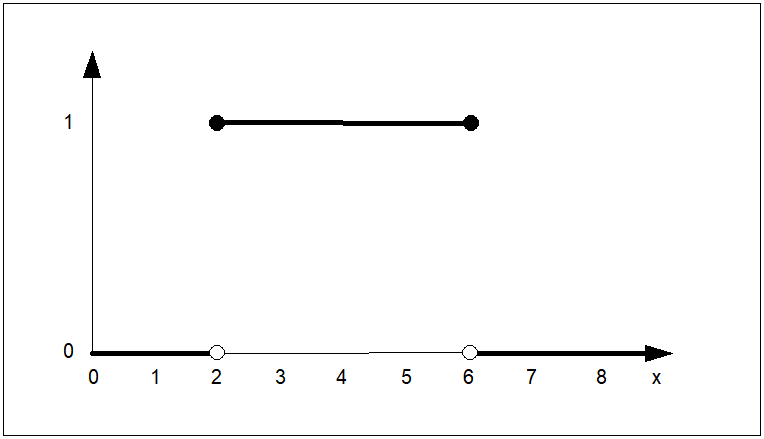
Pojęcie "duża liczba" można również przedstawić w przestrzeni o nieskończenie wielkiej liczbie elementów \( X =[0, 10] \). Wówczas funkcję \( mu_{DL}(x) \) wygodniej jest przedstawić w postaci analitycznej lub graficznej jak np. na rysunku poniżej.
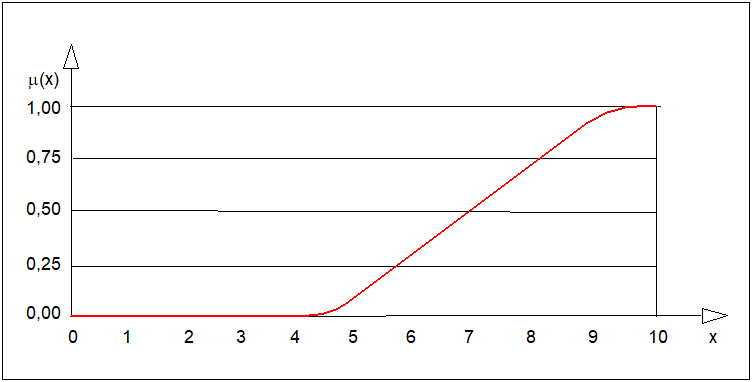
Na gruncie klasycznej teorii zbiorów nierozmytych liczba \( x \) w powyższym przykładzie mogłaby: albo należeć albo nie należeć do zbioru "duża liczba". To dwuwartościowe rozstrzygnięcie nie jest wygodne w przypadku, gdy o liczbie trudno powiedzieć czy jest liczbą dużą czy też nie (np.: liczba 5 w przykładzie). W przypadku zbiorów rozmytych o liczbie 5 można powiedzieć, że w stopniu równym 0,1 jest liczbą dużą. Funkcja przynależności pozwala zatem na rozmytą kwantyfikację elementów zbioru rozmytego. Z tego powodu dość często, choć nieprecyzyjnie, będziemy utożsamiać pojęcie zbioru rozmytego z jego funkcją przynależności.
Warto na chwilę zatrzymać się nad zbiorem wartości funkcji przynależności \( mu_{F}(x) \). Zbiór tych wartości należy do przedziału liczbowego \( [0, 1] \). Przedział ten przyjęto głównie dla prostoty. Tę samą rolę, tzn. wprowadzenie pewnego uporządkowania mógłby równie dobrze spełnić dowolny zbiór całkowicie uporządkowany.
Zbiór rozmyty \( F\subseteq X \) jest pusty, co zapisujemy \( F = 0 \) wtedy i tylko wtedy gdy \( mu_F(x) = 0 \) dla każdego \( x\in X \).
| \( F = \textbf{0}\Leftrightarrow\ \mu_F(x)=0 \; ;\;\forall x\in X \) | (16) |
|---|
Zbiór rozmyty \( F\subseteq X \) azwiemy zbiorem jednostkowym, co zapisujemy \( F = 1 \) wtedy i tylko wtedy gdy \( mu_F(x) = 1 \) dla każdego \( x\in X \).
| \( F = \textbf{1}\Leftrightarrow\ \mu_F(x)=1 \; ;\;\forall x\in X \) | (17) |
|---|
Z definicji (17) wynika, że każdy zbiór nierozmyty może być traktowany jako szczególny przypadek zbioru rozmytego z jednostkową funkcją przynależności. Oznacza to dalej, że działania na zbiorach rozmytych mają charakter uogólniający i mogą być, drogą podstawień typu: \( \mu_F(x) = 1 \) sprowadzone do działań na zbiorach nierozmytych.
Zbiór wszystkich elementów zbioru rozmytego, którym przyporządkowano niezerową wartość funkcji przynależności nazywać będziemy dalej nośnikiem lub suportem zbioru rozmytego.
Nośnikiem (suportem) zbioru rozmytego \( F \) jest zbiór nierozmyty elementów \( x \in X \), spełniających warunek:
| \( support(F)=\left\{x\in X : \mu_F(x)>0\right\} \) | (18) |
|---|
Jak łatwo zauważyć, suport zbioru pustego jest pusty, a suport zbioru jedynkowego zawiera wszystkie elementy zbioru \( X \).
Wartość funkcji przynależności zgodnie z definicją przyjmuje wartości z przedziału \( [0, 1] \). Nie oznacza to jednak, że wartość maksimum każdej funkcji przynależności jest zawsze równe \( 1 \). W teorii zbiorów rozmytych wprowadzono pojęcie wysokości zbioru rozmytego. Wysokość zbioru rozmytego jest liczbowo równa wartości maksimum globalnego funkcji przynależności.
Wysokością zbioru rozmytego \( F\subseteq X \) jest wartość maksymalna funkcji przynależności tego zbioru dla każdego \( x \in X \).
| \( h(F)=\bigcup_{x\in X}\mu_F(x) \; ;\;\forall x\in X \) | (19) |
|---|
Oczywiście jeśli \( \mu_F(x) \in [0,1] \Leftarrow h(F) \in [0,1] \).
Jak łatwo zauważyć, wysokość zbioru pustego \( F = 0 \) jest równa 0, zaś wysokość zbioru jednostkowego \( F = 1 \) jest równa 1.
Wysokość zbioru.
Załóżmy przestrzeń rozważań \( X \) o skończonej liczbie elementów \( X= \left\{0, 1, 2, ..., 10\right\} \). Określmy zbiór rozmyty \( F \) w tej przestrzeni w postaci:
| \( F= 0,1/1 + 0,3/3 + 0,5/5 + 0,4/7 + 0,2/9 \) | (20) |
|---|
Wysokością tego zbioru jest wartość \( h(F)=0,5 \).
Wysokość zbioru.
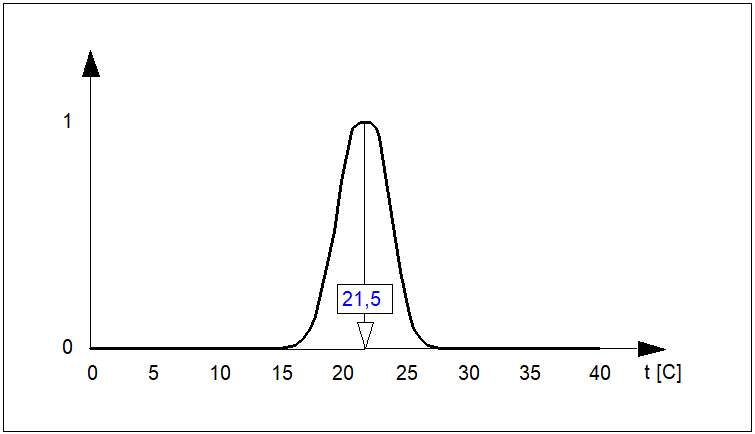
Załóżmy ciągłą przestrzeń rozważań \( X=[0, 100] \). Określmy zbiór rozmyty \( F \) w tej przestrzeni, którego funkcja przynależności opisuje kształt funkcji przynależności zbioru rozmytego "komfortowa temperatura" przedstawionego na rys. 4:
| \( \mu_F(x)=e^{-\left(\frac{x-21,5}{1,5}\right)^2} \) | (21) |
|---|
Wysokością tego zbioru jest wartość \( h(F)=1,0 \).
2.2. Operacje na zbiorach rozmytych
Zbiorem subnormalnym lub podnormalnym będziemy określali każdy niepusty zbiór rozmyty \( F\subseteq X \), którego wysokość \( h(F) \) jest mniejsza od 1.
Niepusty subnormalny zbiór rozmyty może być przekształcony do postaci zbioru znormalizowanego przez zastosowanie odpowiedniego przekształcenia (operacji normalizacji).
Unormowaniem lub normalizacją subnormalnego zbioru rozmytego \( F\subseteq X \) nazywać będziemy operację przekształcenia go w zbiór rozmyty \( F^N\subseteq X \) o wysokości \( h(FN)=1 \). Funkcję przynależności tego zbioru wyznaczymy przez operację skalowania zgodnie z (21):
| \( \mu_{F^N(x)}=\frac{\mu_F(x)}{h(F)} \; ;\;\forall x\in X \; ;\;h(F)\ne 0 \) | (22) |
|---|
Normalizacja zbioru rozmytego.
Załóżmy przestrzeń rozważań \( X \) o skończonej liczbie elementów \( X= \left\{0, 1, 2, ..., 10\right\} \). Określmy zbiór rozmyty \( F \) w tej przestrzeni jak w przykładzie 6:
| \( F = 0,1/1 + 0,3/3 + 0,5/5 + 0,4/7 + 0,2/9 \) | (23) |
|---|
Wysokością tego zbioru jest wartość \( h(F)=0,5 \). Zbiór \( F \) jest więc zbiorem subnormalnym. Unormowany zbiór rozmyty \( F^N \) będzie miał następującą postać:
| \( F^N = 0,2/1 + 0,6/3 + 1,0/5 + 0,8/7 + 0,4/9 \) | (24) |
|---|
Normalizacja zbioru jest w istocie operacją mnożenia zbioru rozmytego przez skalar \( \beta \) o wartości:
| \( \beta= h(F) ^{-1}\; ;\;\forall x\in X \) | (25) |
|---|
Iloczyn zbioru rozmytego \( F\subseteq X \) i nieujemnej liczby rzeczywistej \( \beta \), co oznaczać będziemy jako \( \beta F \), definiujemy w postaci:
| \( \mu_{F\beta}(x)= \beta \cdot \mu_F(x) \) | (26) |
|---|
gdzie: \( \forall x\in X \); \( \beta \in \left\{0, R^{+}\right\} \); \( \mu_{F}(x) \in [0, 1] \).
Z Def. 8 wynika, że: \( 0\leqslant \mu_{\beta F}(x) \leqslant 1 \forall x\in X \) oraz właściwość przemienności względem operacji mnożenia:
| \( \beta \cdot\mu_F(x)= \mu_F(x)\cdot\beta \) | (27) |
|---|
Jeśli \( \beta \ne 1 \) i \( h(F) = 1 \) to operacja zdefiniowana powyżej może być określana mianem denormalizacji zbioru normalnego.
Iloczyn zbioru rozmytego i liczby rzeczywistej
Niech \( X \in [0, 10] \); \( \beta =0,2 \); zaś:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (28) |
|---|
stąd:
| \( \beta \cdot F = 0,02/1 + 0,04/2 + 0,06/3 + 0,08/4 + 0,06/5 + 0,04/6 \) | (29) |
|---|
W analogiczny sposób do (27) zdefiniujemy teraz iloczyn arytmetyczny dwóch zbiorów rozmytych.
Iloczynem dwóch zbiorów rozmytych \( F,G \subseteq X \), jest taki zbiór rozmyty \( FG \), którego funkcja przynależności jest iloczynem funkcji przynależności obu tych zbiorów:
| \( \mu_{FG}(x) = \mu_{F}(x)\times \mu_{G}(x)\; ;\;\forall x\in X \) | (30) |
|---|
gdzie: \( \forall x\in X \); \( \beta \in \left\{0, R^{+}\right\} \); \( \mu_{F}(x) \in [0, 1] \).
Z Def. 9 wynika, że dla normalnych zbiorów \( F,G \subseteq X \) i \( \forall x\in X \) zachodzi:
| \( 0\leqslant \mu_{FG}(x)\leqslant 1 \) | (31) |
|---|
oraz
| \( F \times G = G \times F \) | (32) |
|---|
Iloczyn zbiorów rozmytych:
Niech \( X \in [0,10] \) zaś:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (33) |
|---|
| \( G = 0,10/2 + 0,50/3 + 0,70/4 + 1,00/5 + 1,00/6 \) | (34) |
|---|
stąd:
| \( FG = 0,02/2 + 0,15/3 + 0,28/4 + 0,30/5 + 0,20/6 \) | (35) |
|---|
Jeśli \( F \equiv G \) to Def. 9 określa drugą potęgę zbioru \( F \). Ogólnie:
Potęgę k-tą zbioru rozmytego \( F\subseteq X \) oznaczać będziemy jako \( F^k \) i definiujemy jako zbiór rozmyty o funkcji przynależności \mu_{F^k}:
| \( \mu_F^k(x) = \left(\mu_F(x)\right)^k \; ;\;\forall x\in X \; ;\;\ k>0 \) | (36) |
|---|
Potęga zbioru rozmytego:
Niech \( X \in [0,10] \), \( k=2 \) oraz:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (37) |
|---|
stąd:
| \( F^k = 0,01/1+ 0,04/2 + 0,09/3 + 0,16/4 + 0,09/5 + 0,04/6 \) | (38) |
|---|
Jak już wiemy, parametrem charakterystycznym zbioru rozmytego jest jego wysokość \( h(F) \). Zbiór rozmyty może być scharakteryzowany także przez jego moc (liczbę kardynalną) lub moc kwadratową.
Moc nierozmytą (liczbę kardynalną lub krótko mocą) zbioru rozmytego \( F\subseteq X \) rozpiętego na skończonej przestrzeni \( X \) o przeliczalnej liczbie elementów \( n \) definiujemy jako sumę arytmetyczną postaci:
| \( \left\vert F\right\vert=\sum_{i=1}^n \mu_F(x_{i}) \; ;\;\forall x\in X \) | (39) |
|---|
Jeśli \( \mu_{F}(x)\in [0, 1] \) to jak łatwo zauważyć:
| \( 0\leqslant\left\vert F\right\vert\leqslant n \) | (41) |
|---|
Moc zbioru rozmytego:
Niech \( X \in [0,10] \) oraz:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (42) |
|---|
stąd:
| \( |F| = 0,10 + 0,20 + 0,30 + 0,40 + 0,30 + 0,20 = 1,50 \) | (43) |
|---|
Moc nierozmytą kwadratową (kwadratową liczbę kardynalną) zbioru rozmytego \( F\subseteq X \) rozpiętego na skończonej przestrzeni \( X \) o przeliczalnej liczbie elementów \( n \) definiujemy jako sumę arytmetyczną postaci:
| \( \left\vert F\right\vert^2=\sum_{i=1}^n \left(\mu_F(x_{i})\right)^2 \; ;\;\forall x\in X \) | (44) |
|---|
Jeśli \( \mu_{F}(x)\in [0,1] \) to jak łatwo zauważyć:
| \( 0\leqslant\left\vert F\right\vert^2\leqslant n \) | (45) |
|---|
| \( \left\vert F\right\vert^2\leqslant \left\vert F\right\vert \) | (46) |
|---|
Moc kwadratowa zbioru rozmytego:
Niech \( X \in [0,10] \) oraz zbiór \( F \) będzie identyczny jak w przykładzie 12:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (47) |
|---|
stąd:
| \( |F|^2= 0,01 + 0,04 + 0,09 + 0,16 + 0,09 + 0,04 = 0,43 \) | (48) |
|---|
Dopełnienie bezwzględne zbioru rozmytego \( F\subseteq X \) w przestrzeni rozważań \( X=\left\{x\right\} \) oznaczać będziemy jako \( \neg F \) i definiować jako:
| \( \mu_{\neg F}(x)= 1-\mu_F(x)\; ;\;\forall x\in X; \mu_F(x)\in[0,1] \) | (49) |
|---|
Dopełnienie zbioru rozmytego:
Niech \( X \in [0,10] \) oraz \( F \) będzie identyczne jak w przykładzie 12:
| \( F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6 \) | (47) |
|---|
stąd:
| \( \neg F= 0,90/1 + 0,80/2 + 0,70/3 + 0,60/4 + 0,70/5 + 0,80/6 \) | (48) |
|---|
Jak łatwo zauważyć, funkcja przynależności zbioru rozmytego i jej dopełnienie są zwierciadlanymi odbiciami względem prostej \( \mu (x)=0,5 \)(por. Rys. 8). Ponadto można zauważyć, że:
| \( {\neg \textbf 0=\textbf 1} \) | (52) |
|---|
| \( {\neg \textbf 1=\textbf 0} \) | (53) |
|---|
Sumę mnogościową zbiorów rozmytych \( F,G\subseteq X \), oznaczać będziemy jako \( F+G \) lub \(F\cup G \). Funkcję przynależności tego zbioru definiujemy jako obwiednię maksymalnych wartości funkcji przynależności obu zbiorów:
| \( \mu_{F\cup G}(x) = \mu_{F}(x)\cup\ \mu_{G}(x)\; ;\;\forall x\in X \) | (49) |
|---|
gdzie symbol \( \cup \) oznacza operację maksimum.
Z (54) wynika, że:
| \( \textbf 0 \cup \textbf 0=\textbf 0 \) | (55) |
|---|
| \( \textbf 0 \cup \textbf 1=\textbf 1 \) | (56) |
|---|
| \( \textbf 1 \cup \textbf 0=\textbf 1 \) | (57) |
|---|
| \( \textbf 1 \cup \textbf 1=\textbf 1 \) | (58) |
|---|
| \( F\cup F= F \) | (59) |
|---|
| \( F \cup \textbf 0 = F \) | (60) |
|---|
| \( F \cup \textbf 1 = \textbf 1 \) | (61) |
|---|
| \( \neg F \cup \neg F = \neg F \) | (62) |
|---|
Właściwości (55...62) są co do ogólnej formy zapisu zgodne z analogicznymi zapisami logiki boolowskiej. Jak łatwo wywieść, suma mnogościowa charakteryzuje się właściwościami przemienności (63) i łączności (64).
| \( F\cup G = G\cup F \) | (63) |
|---|
| \( \left(F\cup G\right) \cup H= F\cup \left(G \cup H\right) \) | (64) |
|---|
Suma mnogościowa zbiorów rozmytych:
Niech \( X \in [0,10] \) oraz \( F \) będzie identyczne jak w przykładzie 12:
| \( \quad\quad F \quad\quad=0,1/1 + 0,2/2 + 0,3/3 + 0,4/4 + 0,3/5 + 0,2/6 \) | (65) |
|---|
oraz:
| \( \quad\quad G\quad\quad =0,2/1 + 0,8/2\quad\quad\quad\;\,\, +1,0/4 + 0,1/5 + 0,2/6 \) | (66) |
|---|
stąd:
| \( \quad\quad F\cup G\, = 0,2/1 + 0,8/2 + 0,3/3 + 1,0/4 + 0,3/5 + 0,2/6 \) | (67) |
|---|
Przecięcie mnogościowe zbiorów rozmytych \( F,G\subseteq X \) oznaczać będziemy jako \( F\cap G \). Funkcję przynależności tego zbioru definiujemy jako obwiednię minimalnych wartości funkcji przynależności obu zbiorów:
| \( \mu_{F\cap G}(x) = \mu_{F}(x)\cap\ \mu_{G}(x)\; ;\;\forall x\in X \) | (68) |
|---|
Z (68) wynika, że:
| \( \textbf 0 \cap \textbf 0=\textbf 0 \) | (69) |
|---|
| \( \textbf 0 \cap \textbf 1=\textbf 0 \) | (70) |
|---|
| \( \textbf 1 \cap \textbf 0=\textbf 0 \) | (71) |
|---|
| \( \textbf 1 \cap \textbf 1=\textbf 1 \) | (72) |
|---|
| \( F\cap F= F \) | (73) |
|---|
| \( F \cap \textbf 0 = \textbf 0 \) | (74) |
|---|
| \( F \cap \textbf 1 = \textbf 1 \) | (75) |
|---|
| \( \neg F \cap \neg F = \neg F \) | (76) |
|---|
Zapisy (69..76) są co do ogólnej formy zgodne z analogicznymi zapisami algebry boolowskiej. Jak łatwo wywieść przecięcie mnogościowe, podobnie jak suma mnogościowa, charakteryzuje się właściwościami przemienności (77) i łączności (78).
| \( F\cap G = G\cap F \) | (77) |
|---|
| \( \left(F\cap G\right) \cap H= F\cap \left(G \cap H\right) \) | (78) |
|---|
Przecięcie mnogościowe zbiorów rozmytych:
Niech \( X \in [0,10] \) oraz \( F \) i \( G \) będą identyczne jak w przykładzie 15:
| \( \quad\quad F \quad\quad=0,1/1 + 0,2/2 + 0,3/3 + 0,4/4 + 0,3/5 + 0,2/6 \) | (79) |
|---|
oraz:
| \( \quad\quad G\quad\quad =0,2/1 + 0,8/2\quad\quad\quad\;\,\, +1,0/4 + 0,1/5 + 0,2/6 \) | (80) |
|---|
stąd:
| \( \quad\quad F\cap G\, = 0,1/1 + 0,2/2 + 0,0/3 + 0,4/4 + 0,1/5 + 0,2/6 \) | (81) |
|---|
Na definicji 14 oparta jest definicja implikacji znanej w literaturze z dziedziny sterowania rozmytego implikacją Mamdaniego. Implikacja Mamdaniego jest relacją wzajemną zbiorów rozmytych. Została ona zdefiniowana według zasady minimum. Oznacza to, że każdy element każdego zbioru jest w relacji z każdym elementem innego zbioru. Według rozmytej implikacji Mamdaniego każdej takiej relacji przypisywana jest wartość równa minimalnej wartości funkcji przynależności spośród elementów, dla których jest wyznaczana.
Relacja rozmyta \( Rc \) zbiorów rozmytych \( F\subseteq X \), \( G\subseteq Y \) w ujęciu Mamdaniego, jest zdefiniowana jako hiperpowierzchnia rozpięta nad iloczynem kartezjańskim suportów zbiorów będących w relacji z punktami wsparcia o wartościach wyznaczonymi zgodnie z definicją przecięcia wartości funkcji przynależności.
| \( \mu_{R_{c}}(x,y) = \mu_{F}(x)\cap\ \mu_{G}(y)\; ;\;\forall x\in X\; ;\;\forall y\in Y \) | (82) |
|---|
Implikacja Mamdaniego:
Niech \( X,Y\in [0, 10] \) oraz \( F \) i \( G \) będą następujące:
| \( F = 0,1/1 + 0,2/2 + 0,3/3 \) | (83) |
|---|
oraz:
| \( G= \quad\quad\quad\;\;\:0,2/4 + 0,8/5 \) | (84) |
|---|
Suportami obu zbiorów są odpowiednio:
\( Support(F) =\left\{1, 2, 3\right\} \)
\( Support(G) =\left\{4, 5\right\} \)
Iloczyn kartezjański suportów \( F \times G =\left\{1,4 1,5 2,4 2,5, 3,4 3,5\right\} \)
stąd:
| \( R_{c} (F,G)=0,1/1,4+0,1/1,5+0,2/2,4+0,2/2,5+0,2/3,4+0,3/3,5 \) | (85) |
|---|
Relację \( R_c(F,G) \) można dla przejrzystości przedstawić w postaci tabelarycznej
| \( R_C(F,G) \) | \( F \) | ||
|---|---|---|---|
| G | 1 | 2 | 3 |
| 4 | 0,1 | 0,2 | 0,2 |
| 5 | 0,1 | 0,2 | 0,3 |
lub w postaci reguł typu jeżeli to, np:
| \( \begin{array}{c} \textbf{jezeli}\; (x=1 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,1)\; \textbf{inaczej}\\ \textbf{jezeli}\; (x=1 \cap y=5)\; \textbf{to}\; (Rc (F,G) = 0,1)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=2 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=2 \cap y=5)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=3 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=3 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,3)\;.\quad\quad\quad \end{array} \) | (86) |
|---|
Jak można zauważyć z (86) implikacja jest w istocie metodą wnioskowania bazującą na zbiorze reguł warunkowych. Wniosek wynikający z każdej reguły jest uwarunkowany wartością przesłanki. Zatem, aby mógł być wywiedziony wniosek, konieczne jest wyznaczenie wartości tej przesłanki. W przypadku relacji rozmytej w ujęciu Mamdaniego zarówno przesłanka jak i wniosek mają charakter rozmyty.
3. Modelowanie rozmyte
Modelowanie to próba opisu rzeczywistości i zachodzących w niej procesów. Precyzja modelu polega na tym jak bardzo wiernie opisuje on tę rzeczywistość. Ponieważ rzeczywistość jest bardzo złożona, to i jej precyzyjne modele zapewne też takie być muszą. Powstaje jednak pytanie czy dążenie do uzyskania modeli precyzyjnych jest zawsze konieczne, możliwe i celowe? Zadeh, odpowiadając na to pytanie sformułował pewną ogólną kontradykcję, którego interpretacja może być następująca ”ze wzrostem złożoności systemu maleje możliwość jego precyzyjnego opisu i tym bardziej nie ma sensu tworzenia jego precyzyjnego modelu”. Skoro modele mogą być nieprecyzyjne, to pojawia się pytanie, czy możliwe jest tworzenie takich modeli z wykorzystaniem logiki rozmytej działającej przecież na wielkościach nieprecyzyjnych? Ten rozdział jest właśnie poświęcony udzieleniu odpowiedzi na tak zadane pytanie.
3.1. Przykład modelowania analitycznego i rozmytego
W tym rozdziale zostaną przedstawione dwa podejścia do modelowania (opisu) właściwości pewnego prostego obiektu fizycznego. Pierwsze podejście (klasyczne) bazuje na modelowaniu z zastosowaniem praw fizyki, drugie rozmyte, polega na zastosowaniu wniosków wynikających z obserwacji i wiedzy o zachowaniu obiektu (wiedzy heurystycznej). Przykład wskazuje na możliwości zastosowania opisu rozmytego obiektów zarówno tam, gdzie wiedza ścisła jest dostępna jak również tam gdzie jest trudna do uzyskania, natomiast znane przewidywalne są zachowania obiektu.
Wyprowadźmy prawa sterowania dla obiektu w postaci procesu regulacji wysokości słupa cieczy w zbiorniku (Rys. 11).
3.2. Model analityczny
Podejście klasyczne polega na wyznaczeniu modelu matematycznego obiektu i doborze układu regulacji z uwzględnieniem zdefiniowanych kryteriów jakości.
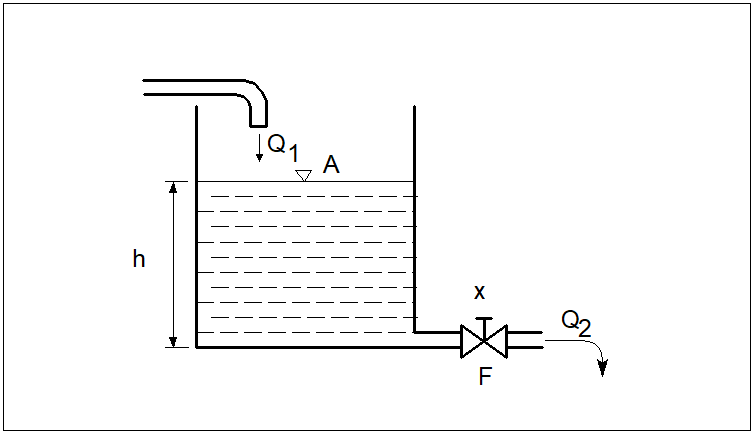
Oznaczenia: \( A \) - powierzchnia zbiornika, \( h \) - wysokość słupa cieczy, \( Q_1 \) - strumień objętościowy cieczy dopływającej, \( Q_2 \) - strumień objętościowy cieczy wypływającej, \( x \) - stopień otwarcia zaworu dławiącego wypływ, \( F \) - powierzchnia przepływowa zaworu.
Załóżmy, że wielkością wejściową jest stopień otwarcia \( x \) zaworu dławiącego wypływ ze zbiornika, zaś wielkością wyjściową jest wysokość słupa cieczy \( h \). W podejściu klasycznym, przy zastosowaniu opisu liniowego, poszukiwana jest transmitancja operatorowej obiektu \( G(s) \) w postaci:
| \( G(s)= \frac{H(s)}{X(s)} \) | (87) |
|---|
gdzie:
\( H(s) \) - transformata Laplace'a sygnału wyjściowego
\( X(s) \) - transformata Laplace'a sygnału wejściowego
Załóżmy dalej, dla uproszczenia, że \( Q_1 = const \).
Zmiana wysokości słupa cieczy \( \delta h \) wynika z różnicy strumieni objętościowych: cieczy wpływającej \( Q_1 \) i wypływającej \( Q_2 \):
| \( A\Delta h =\Delta t (Q_1 - Q_2) \) | (88) |
|---|
Strumień objętościowy \( Q_2 \) można wyrazić w postaci:
| \( Q_2 =\alpha \cdot x \cdot \sqrt {2gh} \) | (89) |
|---|
gdzie:
\( \alpha \)- współczynnik przepływu
\( g \) - przyśpieszenie ziemskie
Po linearyzacji, nieliniowej względem \( h \), zależności (89) w otoczeniu punktu \( h_o \), \( x_o \) otrzymujemy:
| \( \Delta Q_2 =\left\vert{\frac{\partial Q_2}{\partial x}}\right\vert _{x=x_o}\Delta x+\left\vert{\frac{\partial Q_2}{\partial h}}\right\vert _{h=h_o}\Delta h \) | (90) |
|---|
a zatem:
| \( \Delta Q_2 =\alpha \cdot \sqrt {2gh_{0}}\cdot \Delta x +x_{0}\cdot\alpha \cdot\sqrt {\frac{g}{2h_0}}\cdot\Delta h \) | (91) |
|---|
podstawiając:
| \( k_1 =\alpha \cdot \sqrt {2gh_{0}}\;\;\;\; ; \quad k_2=x_{0}\cdot\alpha \cdot\sqrt {\frac{g}{2h_0}} \) | (92) |
|---|
otrzymujemy zlinearyzowaną postać na \( \Delta Q_2 \):
| \( \Delta Q_2 =k_{1}\cdot \Delta x +k_{2}\cdot\Delta h \) | (93) |
|---|
Przedstawiając równanie (88) w formie równania różnicowego otrzymujemy:
| \( A\Delta(\Delta h) =\Delta t (\Delta Q_1 - \Delta Q_2) \) | (94) |
|---|
a ponieważ \( Q_1 = const \) oraz po uwzględnieniu (93) otrzymujemy:
| \( A\Delta(\Delta h) =-\Delta t\cdot k_{1}\cdot\Delta x -\Delta t\cdot k_{2}\cdot\Delta h \) | (95) |
|---|
Stąd w granicy dla \( t\rightarrow 0 \)
| \( A\Delta h =- k_{1}\cdot\Delta x - k_{2}\cdot\Delta h \) | (96) |
|---|
Oznaczając: \( H(s) = L\left\{\Delta h\right\} \) oraz \( X(s) = L\left\{x\right\} \) otrzymujemy ostatecznie:
| \( G(s)= \frac{H(s)}{X(s)}=-\frac{k}{Ts+1} \) | (97) |
|---|
gdzie: \( T = A / k_2 \); \( k= k_1 / k_2 \)
Jak łatwo zauważyć transmitancja operatorowa (97) ma postać właściwą elementowi inercyjnemu rzędu pierwszego. Znak minus poprzedzający transmitancję należy interpretować w ten sposób, że wzrost stopnia otwarcia zaworu \( x \) na wypływie powoduje spadek, a nie wzrost wielkości wyjściowej jaką jest wysokość słupa cieczy \( h \).
Transmitancja (97) jest bardzo wygodna do prowadzenia analizy właściwości dynamicznych obiektu, doboru układu regulacji, badania stabilności, itp. Wartości współczynników \( k_1 \) i \( k_2 \) są jednak zależne od wyboru punktu pracy. Wartości te mogą być traktowane jako wartości stałe tylko w niewielkim otoczeniu punktu pracy \( (x_o , h_o ) \).
W praktyce uzyskanie modeli analitycznych obiektów sterowania nie jest proste. Wynika to głównie ze złożoności procesów zachodzących w rzeczywistych obiektach, niemożliwości zastosowania opisu liniowego, braku dostatecznej wiedzy co do wartości parametrów opisujących proces, konieczności przeprowadzenia kosztownej identyfikacji parametrów modelu, itp. W takich sytuacjach należy rozważyć opis jakościowy procesu możliwy do uzyskania na podstawie wiedzy heurystycznej, wiedzy uzyskanej z eksperymentu myślowego lub wiedzy eksperckiej.
3.3. Model rozmyty
Spróbujemy teraz opisać właściwości obiektu przedstawionego na Rys. 11 w postaci zbioru reguł warunkowych. Załóżmy, że wejście x będzie przyjmowało tylko trzy wartości reprezentowane przez zbiory rozmyte: pozycja nominalna \( N_x \), pozycja zwiększenia wypływu \( W_x \) i pozycja zmniejszenia wypływu \( M_x \). Podobnie załóżmy, że wyjście h będzie przyjmowało wartości reprezentowane przez trzy zbiory rozmyte: poziom nominalny \( N \), poziom za wysoki \( W \) i poziom za mały \( M \).
Abstrahując od kształtu i położenia funkcji przynależności tych zbiorów możliwe jest sformułowanie trzech następujących reguł opisujących wpływ stopnia otwarcia zaworu na poziom cieczy w zbiorniku:
| \( \begin{array}{c} jezeli\; (x=M_x)\; to\; (h= W)\; inaczej\\ jezeli\; (x=N_x)\; to\; (h= N)\; inaczej \\ jezeli\; (x=W_x)\; to\; (h= M)\;.\quad\quad\quad \end{array} \) | (98) |
|---|
Reguły te tworzą tzw. bazę reguł wykorzystywaną w procesie wnioskowania rozmytego. Baza reguł może być przedstawiona w przejrzystej postaci tabelarycznej. Mówimy wówczas o tabeli reguł.
| \( x \) | \( h \) |
|---|---|
| \( M_x \) | \( W \) |
| \( N_x \) | \( N \) |
| \( W_x \) | \( M \) |
Gdybyśmy chcieli wykorzystać te reguły do zadania sterowania wysokości słupa cieczy w zbiorniku, to wówczas po zamknięciu układu regulacji i założeniu ujemnego sprzężenia zwrotnego prawo sterowania można zapisać w postaci analogicznej do przedstawionej w Tab. 2 z tą różnicą, że wejściem w tym przypadku jest odchyłka regulacji \( e = h_o - h \) ; gdzie \( ho \) - wartość zadana, natomiast wyjściem stopień otwarcia zaworu \( x \). Jeśli odchyłka regulacji \( e \) będzie przyjmowała tylko trzy wartości rozmyte: \( N \), \( Z \),\( P \) (jak na Rys. 5) to prawo sterowania może być przedstawione w postaci trzech prostych reguł:
| \( \begin{array}{c} jezeli\; (e=N)\; to\; (x= W_{x})\; inaczej\\ jezeli\; (e=Z)\; to\; (x= N_{x})\; inaczej \\ jezeli\; (e=P)\; to\; (x= M_x)\;.\quad\quad\quad \end{array} \) | (99) |
|---|
Prawo to może być również przedstawione w postaci tabeli reguł zwanej tabelą sterowań rozmytych.
| \( e \) | \( x \) |
|---|---|
| \( N \) | \( W_x \) |
| \( Z \) | \( N_x \) |
| \( P \) | \( M_x \) |
Powyższy przykład wskazuje na relatywnie prosty i szybki sposób uzyskania regułowego modelu rozmytego obiektu. Jest to niewątpliwie ogromna zaleta tego typu podejścia. Dyskusyjną kwestią pozostaje oczywiście jakość tego modelu i jego przydatność w procesie sterowania. Na te pytania spróbujemy odpowiedzieć w następnych rozdziałach.
3.4. Uogólniony schemat wnioskowania rozmytego
Proces wnioskowania rozmytego może być przedstawiony w trzech alternatywnych formach: albo w postaci relacji (implikacji) rozmytej albo w postaci zdań warunkowych albo w postaci tabeli sterowań rozmytych.
Jak już wspomniano wcześniej, implikacja może być interpretowana jako metoda wnioskowania bazującą na zbiorze alternatywnych reguł warunkowych. Stąd nasuwa się wniosek, że proces wnioskowania rozmytego można wyrazić w postaci zbioru alternatywnych reguł warunkowych.
Każda reguła warunkowa definiuje warunek, który wymaga spełnienia aby wniosek wypływający z reguły był prawdziwy. Notacja reguły warunkowej składa się z dwóch słów kluczowych, przesłanki i wniosku.
\( \textbf{jeżeli} \langle przesłanka \rangle \textbf{to} \langle wniosek \rangle \)
Przesłanka reguły bywa także nazywaną poprzednikiem reguły lub premisą, a wniosek bywa nazywany konkluzją reguły.
W odróżnieniu od reguły klasycznej (ostrej), reguła rozmyta na podstawie rozmytej przesłanki określa nie tyle prawdziwość lub nieprawdziwość wniosku lecz stopień jego spełnienia. Stopień spełnienia wniosku zdefiniowany jest w zakresie liczbowym \( [0..1] \). Stopień ten można interpretować w taki sposób, że jeśli przyjmuje on wartość zerową to wniosek wynikający z tej reguły nie jest spełniony, jeśli przyjmuje wartość równą jeden, to jest spełniony w stopniu najwyższym, jeśli przyjmuje wartość pośrednią pomiędzy zerem i jedynką to jest spełniony częściowo.
Należy wspomnieć, że zależnie od definicji implikacji rozmytej, wniosek może ale nie musi mieć postaci rozmytej. Implikacja Mamdaniego na podstawie rozmytych przesłanek przyporządkuje stopień spełnienia rozmytych wniosków. Z kolei implikacja Takagi-Sugeno na podstawie rozmytych przesłanek przyporządkuje stopień spełnienia wniosku ostryego.
W szczególności implikacja rozmyta może być wykorzystana do sterowania np. w ten sposób, że rozmytej odchyłce sterowania przyporządkowuje rozmyty sygnał nastawiający regulatora. Bezpośrednie zastosowanie implikacji rozmytej do konstrukcji regulatorów jest o tyle trudne, że w praktyce zarówno wejścia regulatora jak i jego wyjścia mają raczej charakter ostry, a nie rozmyty. Stwierdzenie to można uogólnić, ponieważ dotyczy nie tylko sterowania lecz także zdecydowanej większości zastosowań metod logiki rozmytej w praktyce.
Praktyczne wykorzystanie rachunku zbiorów rozmytych wymaga zatem zastosowania dwóch dodatkowych przekształceń:
- przekształcenia wejść ostrych do postaci rozmytej,
- przekształcenia rozmytego wyjścia regulatora do postaci ostrej.
Pierwsze przekształcenie nosi nazwę operacji rozmywania lub fuzyfikacji. Drugie przekształcenie nosi nazwę operacji wyostrzania lub defuzyfikacji.
Operację przekształcenia wejść rozmytych w wyjścia rozmyte nazywać będziemy dalej operacją wnioskowania lub inferencji rozmytej. Realizacja operacji związanych z rozmywaniem wejść i wyostrzaniem wyjść jest kosztowna czasowo. Czas realizacji tych operacji, w tym zwłaszcza operacji wyostrzania nie jest bez znaczenia w zastosowaniach krytycznych czasowo.
Na rysunku poniżej przedstawiono ogólny schemat wnioskowania rozmytego stosowany w zastosowaniach praktycznych.
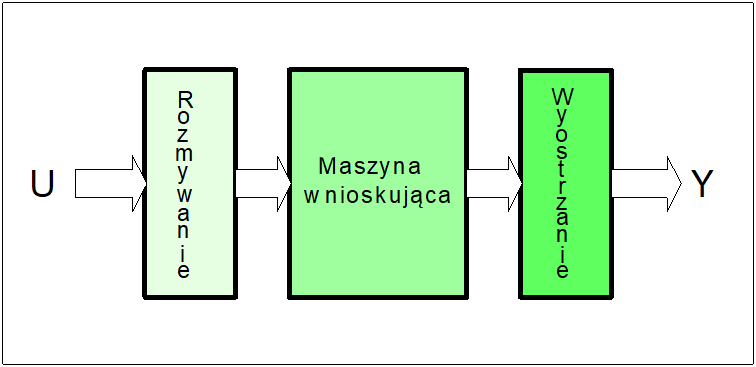
W nielicznych przypadkach praktycznych operacja wyostrzania wniosków rozmytych nie jest stosowana. Dotyczy to np. zastosowania logiki rozmytej w diagnostyce procesów do realizacji zadania lokalizacji uszkodzeń. W tym przypadku wyjściem procesu wnioskowania są rozmyte stopnie wystąpienia poszczególnych uszkodzeń. Stopnie te wyznaczane są na podstawie reguł, których przesłankami są wartości rozmyte sygnałów diagnostycznych właściwych każdemu uszkodzeniu. Agregacja wszystkich wniosków (stopni) w procesie wyostrzania, w tym przypadku nie ma większego sensu.
3.5. Rozmywanie
Rozmywaniem będziemy określali operację przekształcenia wielkości ostrej do postaci rozmytej.
| \( u\Rightarrow u^F \) | (100) |
|---|
gdzie: \( u \) – wielkość ostra, \( u^F \) – wielkości rozmyta.
W praktyce operacja rozmywania realizowalna jest w stosunkowo prosty sposób. Algorytm rozmywania jest następujący:
- Krok 1 (formalny)
Przyporządkować każdej wielkości ostrej nazwę lingwistyczną. - Krok 2 (projekt zbiorów rozmytych)
Przyporządkować każdej wielkości ostrej wartości w postaci znormalizowanych zbiorów rozmytych. Przyporządkować unikalne etykiety lingwistyczne do każdego zbioru rozmytego. - Krok 3 (wyznaczenie wartości rozmytej)
Na podstawie znajomości wartości wielkości ostrej oraz znajomości zbiorów rozmytych przyporządkowanych tej wielkości (Krok 2) wyznaczyć wartości funkcji przynależności dla wszystkich tych zbiorów odpowiadających wartości rozmywanej wielkości ostrej.
Jak łatwo zauważyć, jeśli zmiennej ostrej przyporządkujemy n zbiorów rozmytych, to w wyniku operacji rozmywania każdej wartości tej wielkości ostrej przyporządkowana jest n wartości funkcji przynależności. Zgodnie z definicją rozmywania, wszystkie wartości wszystkich funkcji przynależności należą do przedziału domkniętego obustronnie \( [0, 1] \).
Rozmywanie
Niech wielkością ostrą będzie sygnał odchyłki regulacji \( e\in \left\{E\right\} \) będący różnicą pomiędzy wartością zadaną i wartością mierzoną.
- Krok 1 (formalny)
Odchyłce \( e \) nadamy etykietę < odchyłka regulacji > i będziemy dalej traktować ją jako zmienną lingwistyczną. - Krok 2 (projekt zbiorów rozmytych)
Zmiennej lingwistycznej < odchyłka regulacji > przyporządkujmy trzy wartości: < ujemna odchyłka regulacji >, < zerowa odchyłka regulacji > i < dodatnia odchyłka regulacji >. Każda z wartości zmiennej lingwistycznej < odchyłka regulacji > jest zbiorem rozmytym o określonej funkcji przynależności lecz zdefiniowanej tej samej przestrzeni rozważań. Przestrzenią rozważań jest w tym przypadku zbiór wartości odchyłek regulacji. Dla uproszczenia zapisu wartościom zmiennej lingwistycznej < odchyłka regulacji > przyporządkujmy odpowiednio symbole \( N \), \( Z \) i \( P \). -
Krok 3 (wyznaczenie wartości rozmytej)
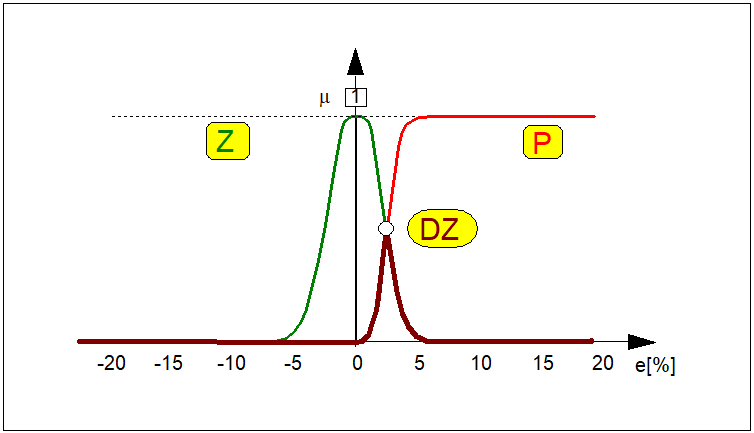
Załóżmy, że wartość odchyłki regulacji w pewnej chwili czasowej wynosi \( e=3,0% \) (por. Rys. 13). Odchyłce tej odpowiadają wartości funkcji przynależności \( \left\{0,00, 0,33, 0,78 \right\} odpowiednio zbiorów \( N \), \( Z \) i \( P \). Zatem operację rozmywania możemy w tym przypadku przedstawić w postaci:\( e(0,03)\Rightarrow \left\{0,00 , 0,33 , 0,78\right\} \) (101) Podobnie można wyznaczyć odpowiednie trójki dla każdej wartości \( e\in \left\{E\right\} \). Operację rozmywania można przedstawić w postaci blokowej jak na Rys. 14.
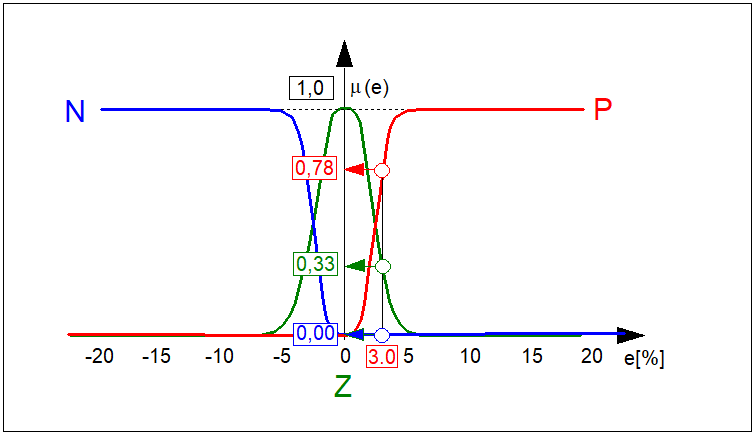
- \( \mu_N(e) \) zbioru rozmytego \( N \) (< ujemna odchyłka regulacji >),
- \( \mu_Z(e) \) zbioru rozmytego \( Z \) (< zerowa odchyłka regulacji >),
- \( \mu_P(e) \) zbioru rozmytego \( P \) (< dodatnia odchyłka regulacji >).
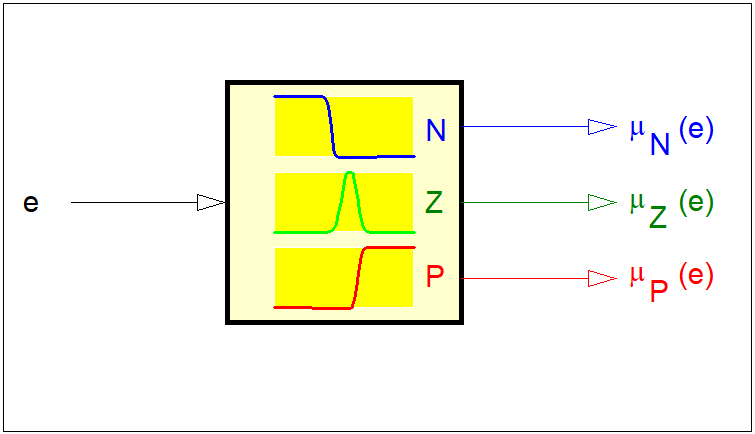
3.6. Maszyna wnioskująca
W wyniku operacji rozmywania każdej wartości ostrej przyporządkowany zostaje zbiór ostrych wartości funkcji przynależności wszystkich zbiorów rozmytych przyporządkowanych rozmywanej wielkości ostrej.
Wartości rozmyte (zbiory rozmyte) nazywane są termami lub etykietami lingwistycznymi. Dla przykładu etykieta < zerowa odchyłka regulacji > jest wartością rozmytą zmiennej lingwistycznej < odchyłka regulacji >. Podobnie etykieta < niski poziom cieczy w zbiorniku > jest wartością rozmytą zmiennej lingwistycznej < poziom cieczy w zbiorniku > czy etykieta < zbyt szybkie narastanie ciśnienia pary > jest wartością zmiennej < narastanie ciśnienia pary >. W istocie etykieta zmiennej lingwistycznej może określać pewną jej cechę (atrybut), zaś wartości funkcji przynależności przypisanej etykiecie - intensywność tej cechy.
Maszyna wnioskująca realizuje proces wnioskowania z zastosowaniem reguł właściwych danej logice. Rozmyta maszyna wnioskująca prowadzi proces wyznaczania wniosków rozmytych na podstawie:
- przesłanek (wejść) rozmytych,
- reguł wnioskowania,
- logiki (sposobu) ewaluacji przesłanek.
W przypadku wnioskowania rozmytego zarówno przesłanki jak i wnioski mają charakter rozmyty. Wejściami maszyny wnioskującej w tym przypadku są przesłanki rozmyte, a wyjściami wnioski rozmyte. Mapowanie wejść na wyjścia w maszynie wnioskującej przebiega zgodnie z regułami i logiką przetwarzania przesłanek. Zestaw reguł tworzy tzw. bazę reguł. Jeśli znane są wszystkie relacje pomiędzy wszystkimi przesłankami i wszystkimi wnioskami to baza reguł nazywana jest bazą zupełną.
Liczba reguł bazy zupełnej zależna jest od:
- liczby wejść ostrych,
- liczby zbiorów rozmytych przyporządkowanych każdemu wejściu ostremu.
Uwagi:
- Liczba reguł bazy zupełnej zależy wyłącznie od liczności wejść rozmytych.
- Liczba wyjść rozmytych bazy zupełnej nie przekracza liczby reguł.
Dla układu rozmytego o \( n \) wejściach ostrych, z których każde zostało rozmyte na \( k_i \) zbiorów rozmytych liczba reguł bazy zupełnej wynosi:
| \( r=\prod_{i=1}^n k_i \) | (102) |
|---|
Liczba reguł bazy zupełnej
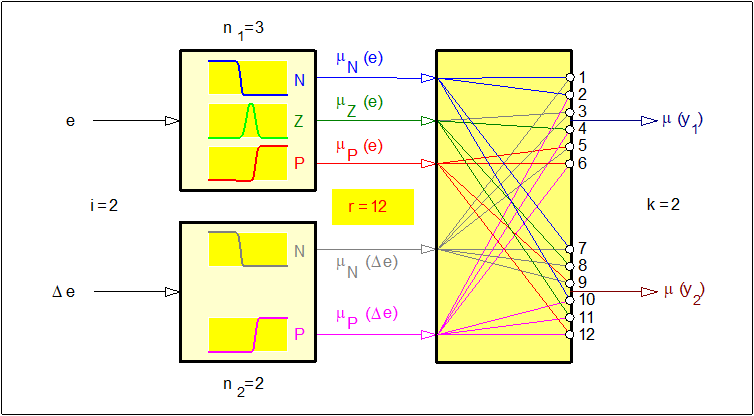
Załóżmy (Rys. 15), że mamy do czynienia z układem rozmytym o dwóch wejściach ostrych. Do każdego wejścia ostrego zostało przyporządkowane odpowiednio: \( k_1=3 \) i \( k_2=2 \) zbiorów rozmytych. Liczba reguł bazy zupełnej zgodnie ze wzorem (102) liczy:
\( r=k_1\times k_2=3\times 2=6 \)
Liczba reguł bazy zupełnej jest istotna z punktu widzenia zastosowań praktycznych. Im większa jest liczba tych reguł, tym proces wnioskowania jest bardziej złożony i kosztowny obliczeniowo. Dla przykładu w przypadku układu rozmytego o trzech wejściach ostrych i w którym każdemu z wejść przyporządkowano tylko po 5 zbiorów rozmytych powoduje, że liczba reguł bazy zupełnej zgodnie z formułą (102) rośnie do 125. Tak znaczna liczba reguł stanowi istotny czynnik wydłużający realizację operacji rozmywania, wnioskowania i wyostrzania. Liczba reguł w jakimś sensie może być wskaźnikiem pomocnym do oceny mocy obliczeniowych koniecznych do realizacji regulatora rozmytego. Jest to szczególnie ważne w układach czasu rzeczywistego w sterowaniu procesów krytycznych czasowo np. w układach sterowania antypoślizgowego ASR. W przypadkach sterowania procesów krytycznych czasowo stosowane jest również wnioskowanie z niezupełną bazą reguł. Wbrew pozorom, takie wnioskowanie jest możliwe mimo, że brak niektórych reguł może być interpretowany jako częściowy brak wiedzy koniecznej do przekształcenia wejść w wyjścia. Brak tej wiedzy może być kompensowany do pewnego stopnia ze względu na nadmiarowość informacyjną zawartą w zdefiniowanych regułach. Ta obserwacja ma także duże znaczenie praktyczne, ze względu na charakterystyczną dla wnioskowania rozmytego odporność na błędy w regułach.
Wnioskowanie realizowane przez maszynę wnioskującą może być:
- wnioskowaniem opartym na pojedynczej regule lub
- wnioskowaniem opartym na zbiorze (złożeniu) reguł.
3.7. Wnioskowanie oparte na pojedynczej regule
We wnioskowaniu opartym na pojedynczej regule, do oceny stopnia spełnienia wniosku wykorzystuje się zwyczajowo implikację Mamdaniego. Stopień spełnienia wniosku nazywany jest również stopniem aktywacji reguły lub poziomem jej zapłonu. Jak wynika z (82) reguła jest zapisem relacji rozmytej pomiędzy poprzednikiem reguły a jej następnikiem. Rozważmy przykład pojedynczej reguły:
| \( jeżeli\; (x=N_x)\cap(y=N_y)\; to\; (x= N_{z}) \) | (103) |
|---|
W tej regule wyrażenia \( (x=N_x) \) i \( (y=N_y) \) poprzedzające słowo kluczowe to są poprzednikami reguły, zaś wyrażenie \( (z =N_z) \) następujące po słowie to jest następnikiem reguły. Symbole \( x \), \( y \), \( z \) są nazwami zmiennych lingwistycznych, a symbole \( N_x \) ,\( N_y \),\( N_z \) są etykietami funkcji przynależności zbiorów rozmytych będących wartościami odpowiednio zmiennych \( x \), \( y \) i \( z \).
W procesie rozmywania wejść każda przesłanka przyjmuje wartość ze znormalizowanego zakresu \([0,1]\).
Załóżmy, że w chwili \( t_o \) wartości funkcji przynależności \( N_x \) i \( N_y \) są odpowiednio równe \( \mu_{N_x}=0,4 \) i \( \mu_{N_y}=0,7 \). Postać szczególna reguły (103) na wówczas postać:
| \( jezeli\; (\mu_{N_x}=0,4)\cap(\mu_{N_y}=0,7)\; to\; (\mu_{N_z}=?) \) | (104) |
|---|
Powstaje pytanie jaką wartość \( \mu_{N_z} \) implikuje przesłanka złożona z dwóch przesłanek prostych:
| \( (\mu_{N_x}=0,4)\cap(\mu_{N_y}=0,7) \) | (105) |
|---|
W istocie jest to pytanie, w jaki sposób z przesłanki złożonej wyprowadzić prawidłowy wniosek, a zatem pytanie o istotę i mechanizm wnioskowania. Jest oczywiste, że odpowiedź na to pytanie ma fundamentalne znaczenie w logice rozmytej.
Wartości funkcji przynależności określają stopień przynależności do zbioru rozmytego. Rozważmy poprzednik reguły (105). Znane są co prawda wartości funkcji przynależności obu przesłanek, natomiast nieznany jest stopień przynależności całego poprzednika. Znajomość tego stopnia jest istotna ponieważ określa stopień spełnienia wniosku wynikającego z tej reguły.
Zwróćmy uwagę, że trudno byłoby przyjąć w naszym przykładzie, że stopień ten wynosi 0,7 ze względu na fakt, że stopień spełnienia drugiej przesłanki wynosi zaledwie 0,4. Stosując racjonalne i ostrożne rozumowanie należy uznać, że stopień spełnienia przesłanki złożonej tej reguły może być co najwyżej równy 0,4 tzn. równy mniejszej z wartości przesłanek prostych. Skoro tak, to należy przyjąć, że w takim samym stopniu spełniony jest następnik reguły. Ponieważ minimalna wartość funkcji przynależności przesłanki prostej wynosi 0,4, to w tym przypadku, mówimy, że reguła odpaliła lub wypaliła na poziomie \( \tau =0,4\). Z formalnego punktu widzenia rozumowanie to dobrze opisuje implikacja Mamdaniego (82).
Należy uznać, że poziom zapłonu reguły wyznacza nieprzekraczalny poziom wartości funkcji przynależności następnika (wniosku). Zatem w naszym przykładzie także wartość \( \mu_{N_z} \) nie powinna w chwili \( t_o \) przekraczać wartości 0,4. Stąd wynika, że poziom zapłonu reguły ogranicza funkcję przynależności następnika odcinając ją na poziomie zapłonu reguły. Operację tę zilustrowano na rysunku poniżej
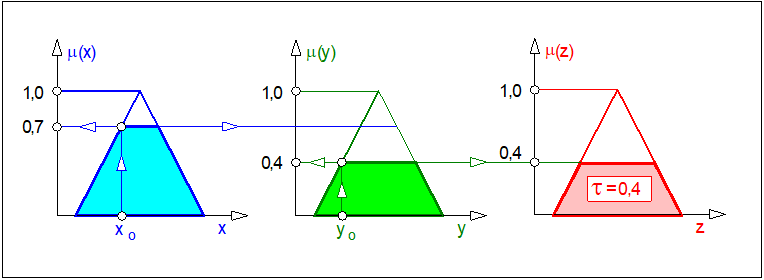
Odcięcie zbioru rozmytego następnika może być traktowane jako wyznaczenie wagi reguły.
Wnioskowanie oparte na pojedynczej regule stosowane jest powszechnie w zastosowaniach praktycznych z uwagi na efektywność obliczeniową i niewielkie wymagania na wielkość zasobów pamięciowych.
W literaturze dotyczącej sterowania rozmytego występuje także tak zwane wnioskowanie skalowane. Polega ono wyznaczeniu stopnia spełnienia przesłanek \( \beta \) tak jak w implikacji Mamdaniego i przeskalowaniu liniowym zbioru następnika wyznaczonym stopniem \( \beta \). Schemat wnioskowania skalowanego dla pojedynczej reguły podano na rys. 17
| \( \mu^s(z)=\bigcup_{j=1}^{n}min\left(\mu_j(x_j)\cdot \mu(z)\right)\quad;\quad\forall x_j\in X_j \) | (106) |
|---|
gdzie:
- \( \mu_j(x_j) \) - funkcja przynależności j-tego zbioru rozmytego przesłanki złożonej,
- \( \mu (z) \) - funkcja przynależności zbioru rozmytego następnika,
- \( \mu^s(z) \) - funkcja przynależności przeskalowanego zbioru rozmytego następnika.
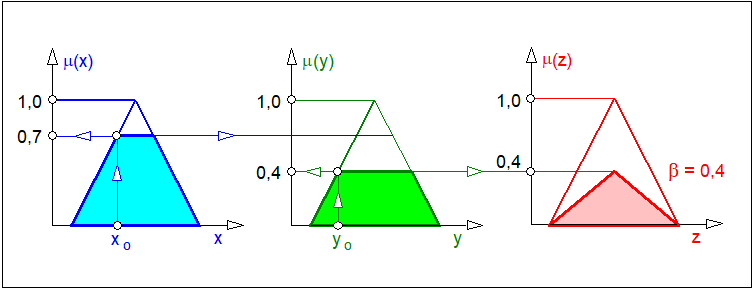
3.8. Wnioskowanie oparte na zbiorze reguł
Powyżej rozpatrywaliśmy wnioskowanie oparte na pojedynczej regule. W praktycznych zadaniach mamy do czynienia zwykle nie z pojedynczą regułą, ale zbiorem reguł. Zastosowanie wnioskowania opartego na pojedynczej regule dla każdej reguły z tego zbioru generuje zbiór wniosków cząstkowych. Pojawia się pytanie w jaki sposób można wyprowadzić wniosek końcowy w takim przypadku?
Rozumowanie może być następujące: Jeśli uznamy, że wnioski cząstkowe wyprowadzone na podstawie ostrożnej ewaluacji pojedynczych reguł są racjonalne, to racjonalna jest też suma mnogościowa tych wniosków. Jeśli zatem wnioski cząstkowe tworzone były zgodnie z zasadą minimum to wnioskowanie oparte na zbiorze reguł może być traktowane jako operacja sumy mnogościowej wniosków z pojedynczych reguł. Formalnie ten sposób wnioskowania możemy zapisać w postaci:
| \( \mu(y)=\bigcup_{i=1}^{n}\mu_i(y)\cap \tau_i \) | (107) |
|---|
gdzie: \( \mu (y) \) – funkcja przynależności zagregowanego wniosku ze zbioru reguł,
\( \mu_i(y)\cap \tau_i \) – obcięta funkcja przynależności wniosku z i-tej reguły.
Wnioskowanie oparte na zbiorze reguł
Załóżmy, że mechanizm wnioskowania opartego na zbiorze reguł wykorzystamy do wyznaczenia wyjścia rozmytego regulatora typu P z jednym wejściem i jednym wyjściem. Wielkością wejściową regulatora jest odchyłka regulacji \( e \), wielkością wyjściową regulatora jest wartość nastawiająca (sterująca) \( y \). Załóżmy dalej, że dokonano rozmycia wejścia \( e \) i wyjścia \( y \) w taki sposób, że zmiennej lingwistycznej < odchyłka regulacji > przyporządkowano trzy wartości < ujemna >, < zerowa >, < dodatnia > i podobnie zmiennej lingwistycznej < sterowanie > przyporządkowano wartości < zmniejsz >, < bez zmian >, < zwiększ >. Etykietom < ujemna >, < zerowa >, < dodatnia > przyporządkowano dla uproszczenia odpowiednio symbole \( N_e \),\( Z_e \), \( P_e \). Podobnie etykietom < zmniejsz >, < bez zmian >, < zwiększ > przyporządkowano symbole \( N_y \),\( Z_y \), \( P_y \). Założono kształt funkcji przynależności jak na Rys. 18. Opierając się na wiedzy heurystycznej skonstruowano tabelę sterowań rozmytych jak poniżej.
| Reguła | \( e \) | \( y \) |
|---|---|---|
| 1 | \( N_e \) | \( N_y \) |
| 2 | \( Z_e \) | \( Z_y \) |
| 3 | \( P_e \) | \( P_y \) |
Schemat sposobu wyznaczenia wniosku ze zbioru reguł opisujących rozmyty regulator typu P przedstawiono na rysunku poniżej. Jak łatwo zauważyć zagregowany wniosek ma charakter rozmyty. Z punktu widzenia praktycznego, poza nielicznymi wyjątkami, wniosek taki nie jest przydatny. Konieczne jest zatem przekształcenie wniosku rozmytego do postaci ostrej akceptowalnej w świecie realnym. Należy zwrócić uwagę na stratność takiego przekształcenia wynikająca z faktu przekształcenia obiektu dwuwymiarowego do obiektu zerowymiarowego tj. numerycznej wartości ostrej.
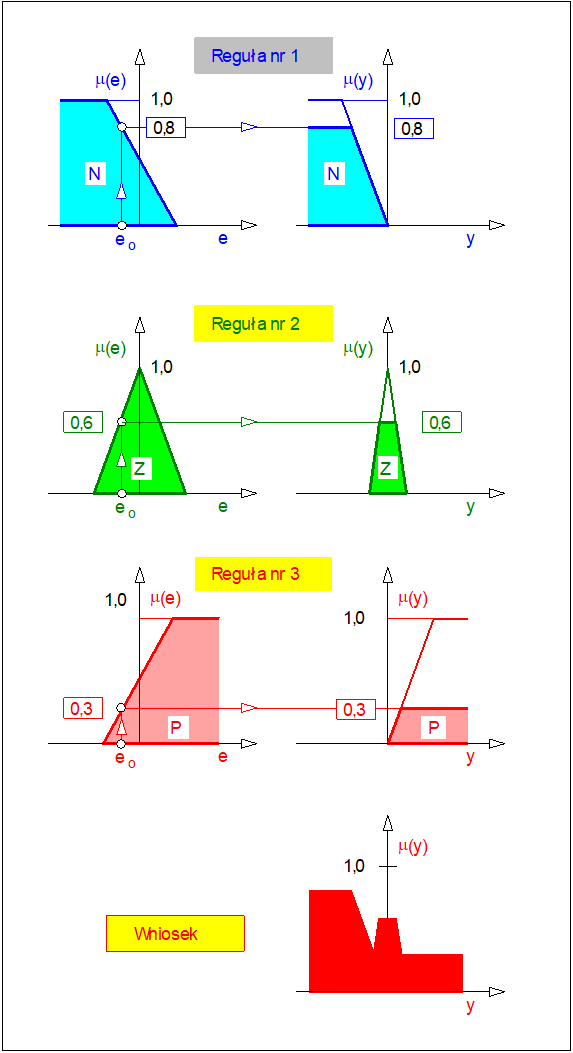
3.9. Wyostrzanie zbiorów rozmytych
Wnioskowanie oparte na zbiorze reguł prowadzi do uzyskania wniosku rozmytego (por. Rys. 18). W praktyce wniosek w takiej postaci jest mało użyteczny. Oczekuje się bowiem sformułowania wniosku w formie ostrej. Dla przykładu, w rzeczywistym regulatorze interesująca jest ostra wartość sygnału sterującego regulatora, a nie funkcja przynależności rozmytego sygnału sterującego. Z tego powodu potrzebne jest zastosowanie metody transformacji umożliwiającej przekształcenie zbioru rozmytego do postaci wartości ostrej. W istocie chodzi o operację odwrotną do operacji rozmywania (100).
Wyostrzeniem zbioru rozmytego będziemy określali operację transformacji dwuwymiarowego zbioru rozmytego do zerowymiarowej wartości ostrej.
| \( D:\mu(x)\Rightarrow y \quad;\quad\forall x\in X \) | (108) |
|---|
Z powyższej definicji nie wynika w sposób bezpośredni w jaki sposób ma być dokonane przekształcenie. Definicja ta również nie zakłada konieczności dokonania wcześniejszej normalizacji zbioru podlegającego wyostrzaniu.
Sformułowano wiele metod wyostrzania. Metody te zakwalifikować można do dwóch zasadniczych grup:
- metod obszarowych (COG, COS, COLA),
- metod wysokościowych (HM, LOM, FOM, MOM).
3.10. Metoda środka ciężkości
Metoda środka ciężkości (COG) zwaną czasami metodą środka obszaru (COA) jest najbardziej popularną metodą wyostrzania. Istota tej metody polega na następującym rozumowaniu.
Funkcja przynależności zagregowanego wniosku rozmytego zakreśla pewien obszar na dwuwymiarowej półpłaszczyźnie wyznaczonej przez osie przestrzeni rozważań wyjścia ostrego i funkcji przynależności (por. Rys. 18). Obszar ten jest ograniczony od góry funkcją przynależności wniosku rozmytego, a od dołu przestrzenią rozważań ostrego wyniku wniosku. Redukcja dwuwymiarowego wniosku rozmytego do wniosku zerowymiarowego wymaga zatem ekstrakcji z tego obszaru podstawowej cechy reprezentowanej przez ten wniosek. Racjonalnym rozwiązaniem jest próba wyważenia wniosku rozmytego. Powstaje jednak pytanie, w jaki sposób można wyważyć wniosek i na czym on polega
Zgodnie z Def. 17, zadanie wyostrzania sprowadza się do rzutowania na oś przestrzeni rozważań wyjścia pewnego punktu charakterystycznego reprezentującego wniosek. W przypadku metody środka ciężkości zaproponowano, aby tym punktem był środek ciężkości obszaru wniosku rozmytego, a reprezentacją ostrą wniosku rozmytego była odcięta tego punktu. W ogólnym przypadku sprowadza się to do wyznaczenia ostrej wartości wniosku \( y^* \) z formuły:
| \( y^*=\frac{\int_{y_{min}}^{y_{max}}y\cdot\mu (y)dy}{\int_{y_{min}}^{y_{max}}\mu (y)dy} \) | (109) |
|---|
W przypadku, gdy funkcja przynależności wyjścia ma kształt linii poligonowej o \( m \) odcinkach i \( (m+1) \) węzłach (jak np. na Rys. 19) i znane są wszystkie współrzędne węzłów tej linii \( [y_k,\mu_k] \), to środek ciężkości obszaru pod tą linią może być wyznaczony z formuły:
| \( y^*=\frac{\sum_{k=0}^{m-1}(y_{k+1}-y_k)\left[ (2y_{k+1}+y_k)\mu_{k+1} + (2y_{k}+y_{k+1})\mu_{k} \right]}{3\sum_{k=0}^{m-1}(y_{k+1}-y_k) (\mu_{k+1}+\mu_k) } \) | (110) |
|---|
Wyostrzanie zbioru rozmytego
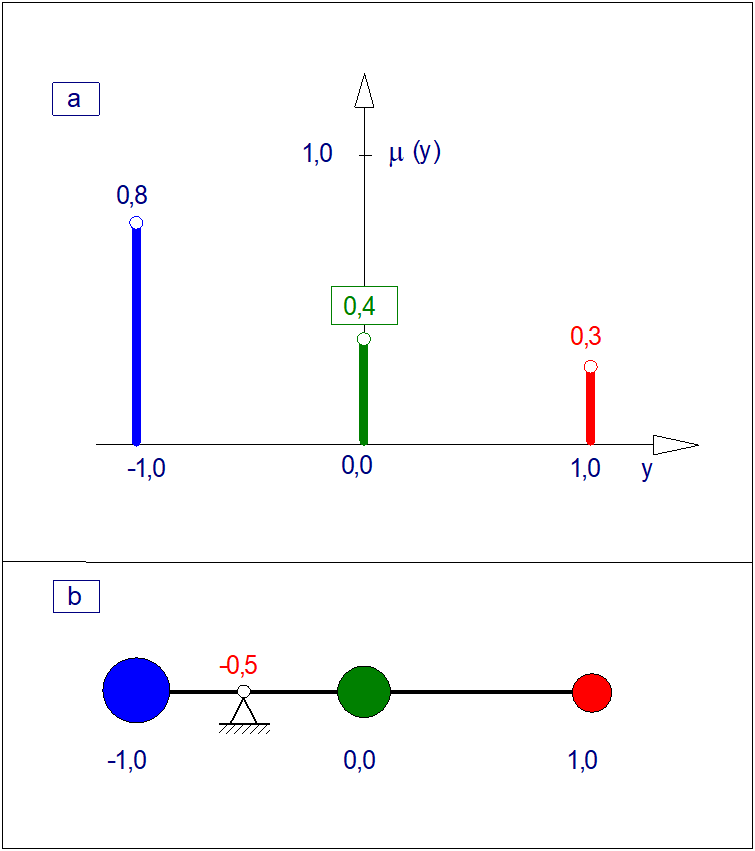
Załóżmy, że funkcje przynależności wszystkich rozmytych wniosków cząstkowych mają postać singletonów czyli zbiorów jednoelementowych jak pokazano na Rys. 20. Ta szczególna postać zbioru rozmytego jest niezwykle ważna z praktycznego punktu widzenia. Pozwala ona bowiem na wyostrzanie wniosku metodą środka ciężkości przy minimalnym nakładzie mocy obliczeniowych.
Ponieważ powierzchnia obszaru pod singletonem jest równa zeru, to bezpośrednie zastosowanie formuły (109) jest niemożliwe. W tym przypadku o wadze każdego wniosku cząstkowego decyduje wysokość i lokalizacja poszczególnych singletonów. W tym przypadku wyznaczenie odciętej punktu ciężkości można sprowadzić do zadania zastępczego polegającego na poszukiwaniu punktu podparcia nieważkiej dźwigni obciążonej masami o wartościach liczbowych równych wysokościom (stopniom aktywacji) singletonów (co zilustrowano na Rys. 20 b). W tym przypadku ważoną wartość ostrą wniosku można wyznaczyć ze zależności:
| \( y^*=\frac{\sum_{i=0}^{n-1}y_i\cdot \mu_i}{\sum_{k=0}^{n-1}\mu_i } \) | (111) |
|---|
Z formuły (111) możemy wywnioskować, że ważoną wartość ostrą określa stosunek sumy pierwszych momentów wysokości singletonów do mocy zbioru rozmytego \( y \).
Niech: \( n=3 \); \( \mu_1 (-1)=0,8 \); \( \mu_2 (0)=0,4 \); \( \mu_3 (1)=0,3 \). Stąd:
| \( y^*=\frac{(-1)\cdot 0,8+(0)\cdot 0,4+(+1)\cdot 0,3}{0,8+0,4+0,3}=-\frac{0,5}{1,5}=-\frac{1}{3} \) | (112) |
|---|

- Funkcja przynależności zbioru wniosku rozmytego w postaci trzech singletonów.
- Metoda wyostrzania tego zbioru metodą środka ciężkości.
3.11. Metoda środka sum
Metoda środka sum (COS) jest metodą pokrewną do metody środka ciężkości. W metodzie COG wyznaczenie wartości ostrej (poza przypadkami szczególnymi) wymaga poniesienia dość intensywnych nakładów mocy obliczeniowych (por. wzór 109). Znacznie prostsze implementacyjnie rozwiązanie problemu wyostrzania uzyskać można stosując metodę wyznaczania środka ciężkości znając współrzędne wszystkich środków ciężkości wszystkich wniosków cząstkowych wynikających ze wszystkich reguł. Jak dowiemy się o tym później, ten sposób jest stosowany do wyostrzania wniosków w aproksymatorze Takagi-Sugeno.
Na dobrą sprawę, także taki sposób został zastosowany w przykładzie 22 w celu wyznaczenia środka ciężkości dla szczególnej (singletonowej) postaci funkcji przynależności wniosku. Powstaje jednak pytanie czy w przypadku ogólnym wynik wyostrzania metodą środka sum jest równoważny wynikowi uzyskiwanemu metodą środka obszaru? Odpowiedź na to pytanie jest negatywna. A skoro tak jest, to pojawia się następne pytanie czy wynik wyostrzania zależy nie tylko od wyostrzanej funkcji przynależności, ale także od użytej metody wyostrzania? Odpowiedź w tym przypadku jest niepokojąco pozytywna. W tym miejscu u czytelnika powstaje zapewne wątpliwość jaki ma sens wprowadzanie innych metod wyostrzania i czy mają one jakieś znaczenie praktyczne? Otóż odpowiedź na to pytanie jest dość prosta. Wszystkie metody wyostrzania przedstawione dalej w tym skrypcie zostały zaprojektowane tylko w jednym celu, a mianowicie po to aby zmniejszyć koszt obliczeniowy w stosunku do metody COG. Niestety odbyło się to kosztem zwiększenia niepewności wyznaczenia wniosku ostrego. Problem ten będzie szerzej skomentowany na zakończenie tego podrozdziału.
W metodzie środka sum milcząco zakłada się, że uzyskanie dobrego efektu zmniejszenia mocy obliczeniowej można uzyskać w przypadku, gdy funkcje przynależności wniosków cząstkowych mają postać prostych figur geometrycznych. Założenie takie nie jest bezpodstawne, bowiem w praktyce dość powszechnie stosowane są proste funkcje przynależności o kształcie trójkątnym (typ \( \Delta \)) lub trapezowym (typ \( \Pi \)), dla których wyznaczenie środka ciężkości obszaru jest trywialne.
Ponadto warto zauważyć, że wnioski z reguł cząstkowych mają bardzo często kształt trapezowy i to niezależnie od tego, czy funkcje przynależności wniosków cząstkowych projektowane są w postaci trójkątów, czy trapezów. Jest to widoczne między innymi na Rys. 18. Funkcje trapezowe wniosków cząstkowych powstają w wyniku efektu „przycinania” pierwotnych funkcji przynależności tych wniosków na poziomie zapłonu reguły. W tym przypadku efekt „przycięcia” przekształca trójkąty w trapezy i trapezy w trapezy.
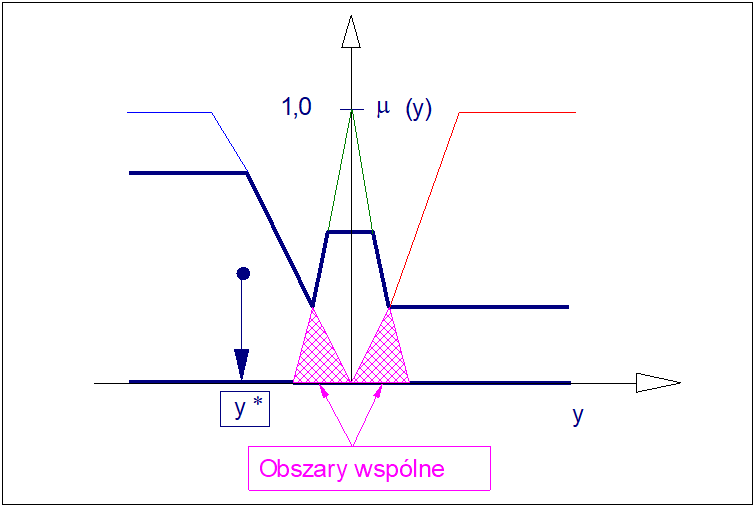
Rozbieżność wyników wyostrzania uzyskiwanych metoda COG i COS można wyjaśnić następująco. W metodzie COG obszary wspólne wszystkich wniosków cząstkowych (dla których istnieją przecięcia niezerowe) podlegają agregacji metodą sumy mnogościowej. Zatem w tej metodzie są uwzględniane tylko raz do wyznaczenia wartości ostrej \( y^* \). W przypadku metody COS obszary wspólne wniosków cząstkowych są uwzględniane tyle razy ile razy występują niezerowe przecięcia tych wniosków. Jeśli zatem wnioski cząstkowe mają wyłącznie przecięcia puste (jak np. w przypadku funkcji przynależności zbiorów singletonowych (por. Rys. 20) to metody wyostrzania COG i COS generują identyczne wyniki. Ze względu na prostotę, algorytm wyostrzania metodą COS jest dość powszechnie stosowany w praktyce. W ogólnym przypadku wartość ostrą z \( n \) wniosków cząstkowych wyznaczyć można znając współrzędne środków ciężkości tych wniosków:
| \( y^*=\frac{\sum_{i=0}^{n}y_i^*\cdot \mu_i^*}{\sum_{i=0}^{n}\mu_i^* } \) | (113) |
|---|
gdzie: \( [y_i^*,\mu_i^*] \) - współrzędne wniosku ostrego i-tej reguły cząstkowej.
Łatwo zauważyć podobieństwo postaci wzorów (112) i (113). Można je wyjaśnić w ten sposób, że metoda środka sum w istocie dokonuje transformacji funkcji przynależności wniosków z reguł cząstkowych do postaci singletonowej.
Ilustrację problemu wielokrotnego uwzględniania obszarów o przecięciu niezerowym w wyznaczeniu wniosku ostrego ze zbioru reguł rozmytych metodą środka ciężkości sum (COS) przedstawiono na rysunku poniżej.
3.12. Metoda środka największego obszaru (COLA)
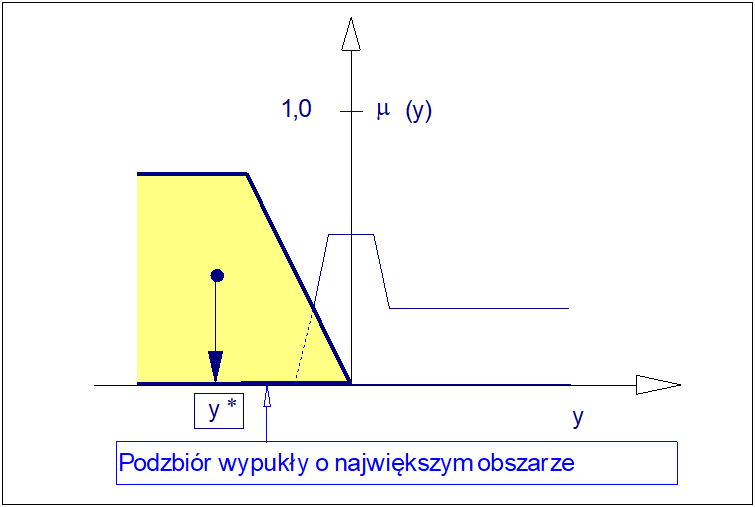
Metoda środka największego obszaru (COLA) jest metodą stosowaną wyłącznie dla zbiorów rozmytych niewypukłych tzn. złożonych co najmniej z dwóch podzbiorów wypukłych. Spośród podzbiorów wypukłych wybierany jest tylko podzbiór o największym obszarze. Pozostałe podzbiory nie są dalej brane pod uwagę. W tym miejscu nasuwa się refleksja, że w metodzie COLS decydujący wpływ na wartość ostrą wniosku ma wyłącznie jedna reguła ze zbioru reguł, o dominującym znaczeniu dla określonych wartości przesłanek.
Następnie wyznaczana jest odcięta środka ciężkości wybranego podzbioru metodą COG. Metoda ta jest szczególnie użyteczna, gdy niewypukły zbiór rozmyty zawiera jeden podzbiór dominujący. Zysk obliczeniowy polega w tym przypadku na eliminacji kłopotliwych w wyznaczaniu momentów sił ciężkości małoistotnych podzbiorów. W istocie algorytm COLA jest odmianą zdegenerowaną algorytmu COG.
3.13. Metoda wysokości (HM)
Jeśli przyjąć założenie, że wysokość zbioru rozmytego jest w jakimś stopniu przybliżoną miarą jego obszaru, to wyobrażalne jest wykonanie operacji wyostrzania zmodyfikowanymi metodami COG lub COS w taki sposób, że przybliżone położenie odciętej środka ciężkości obszaru będzie wyznaczone przez substytucję obszarów przez wysokości zbiorów rozmytych wniosków cząstkowych. Redukcja wymiarowości pozwala na znaczne uproszczenie sposobu wyznaczania wartości ostrej, a tym samym istotnie zmniejsza zapotrzebowanie na moce obliczeniowe.
Do realizacji metody HM potrzebna jest jedynie znajomość współrzędnych wysokości zbiorów rozmytych wniosków cząstkowych. W ten sposób z procesu wyostrzania wyeliminowano kłopotliwe rachunkowo operacje związane z wyznaczaniem zerowych i pierwszych momentów funkcji przynależności wniosków jak w metodach obszarowych COG, COS i COLA.
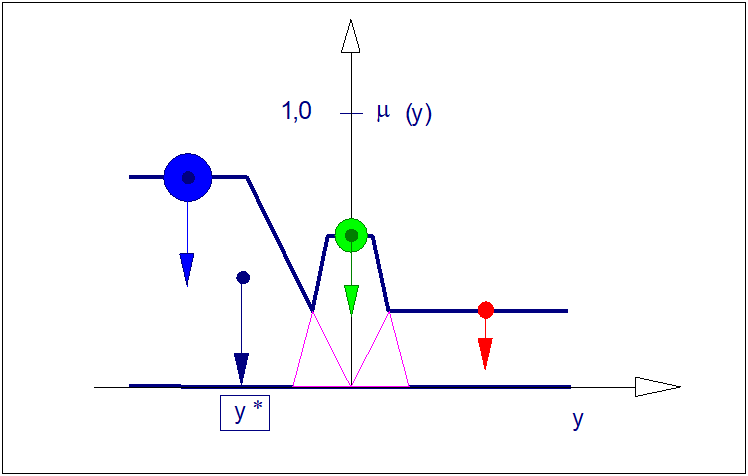
W przypadku, gdy odcięta wysokości zbioru nie jest jednoznaczna (np. dla zbiorów typu \( \Pi \) o trapezowej funkcji przynależności) to w metodzie HM wyznacza się ją jako średnią arytmetyczną jej odciętych prawo- i lewobrzeżnych. Metoda HM sprowadza zatem problem wyostrzania do realizacji metody COG z funkcjami singletonowymi. Możliwe jest zatem w tym przypadku zastosowanie wzoru (111) z zastrzeżeniem, że w miejsce \( \mu_i \) podstawimy uśrednioną wysokość wniosku rozmytego z i-tej reguły \( h_i \), zaś w miejsce \( y_i \) zostanie podstawiona odcięta uśrednionej wartości tej wysokości. Stąd:
| \( y^*=\frac{\sum_{i=1}^{n}h_i\cdot \mu_i}{\sum_{i=1}^{n}h_i } \) | (114) |
|---|
Ilustrację sposobu wyostrzania (defuzyfikacji) metoda HM przedstawiono na rysunku poniżej.
3.14. Metoda wysokości (FOM)
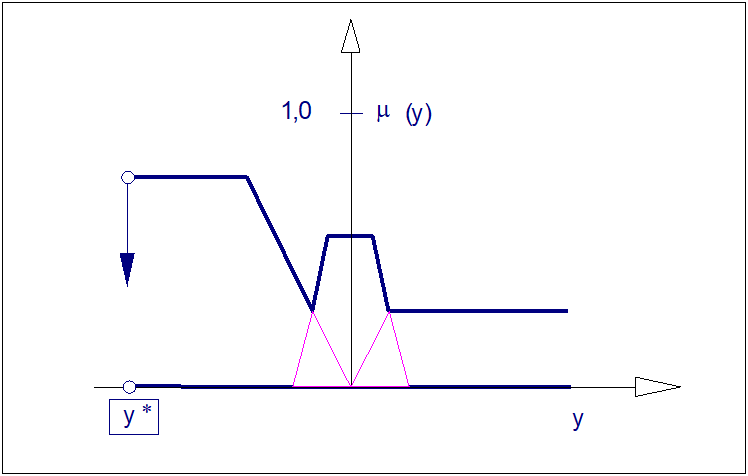
Metoda wysokości FOM zwana metodą "pierwszy z największych" jest metodą bardzo szybkiego wyostrzania. Metoda ta znajduje zastosowania wszędzie tam, gdzie istotna jest nie tyle precyzja wyostrzenia, co czas jego realizacji. Metoda FOM polega na uznaniu za wartość ostrą lewostronnej odciętej wysokości zbioru o maksymalnej wysokości. Zatem:
| \( y^*=inf\left\{y\in Y:\mu_Y(y)=sup(\;\mu_Y (y)) \right\} \) | (115) |
|---|
Z wzoru (115) wynika, że w metodzie FOM, jak zresztą także we wszystkich pozostałych metodach wysokościowych nieistotny jest kształt funkcji przynależności. Zaskakujące jest także to, że w tej metodzie nieistotna jest także wartość wysokości zbioru. W metodzie FOM ważna jest tylko lokalizacja najmniejszej lewostronnej odciętej zbioru o największej wysokości. Ilustrację operacji wyostrzania metodą FOM pokazano na rysunku poniżej.
3.15. Metoda wysokości (LOM)
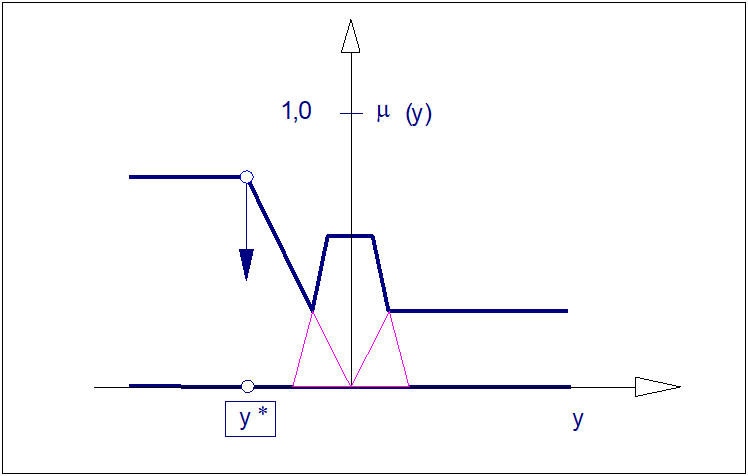
Metoda wysokości LOM zwana metodą "ostatni z największych" jest metodą bardzo szybkiego wyostrzania. Metoda ta jest metodą pokrewną względem metody FOM. Polega ona na uznaniu za wartość ostrą prawostronnej odciętej wysokości zbioru o maksymalnej wysokości. Zatem:
| \( y^*=sup\left\{y\in Y:\mu_Y(y)=sup(\;\mu_Y (y)) \right\} \) | (116) |
|---|
W metodzie tej, jak i w pozostałych metodach wysokościowych nieistotny jest kształt funkcji przynależności lecz największa odcięta prawostronna wysokości największego zbioru rozmytego. Ilustrację operacji wyostrzania metodą LOM pokazano na Rys. 25.
Zwróćmy uwagę, że zarówno w metodzie FOM jak i LOM o wartości wyjścia ostrego decyduje najwyższy rozmyty wniosek cząstkowy, a więc de facto reguła dominująca, która go generuje. Należy uznać, że w obu metodach zastosowano mechanizm selekcji decydującej reguły, podobnie jak to miało miejsce w przypadku obszarowej metody COLA.
3.16. Metoda wysokości (MOM)
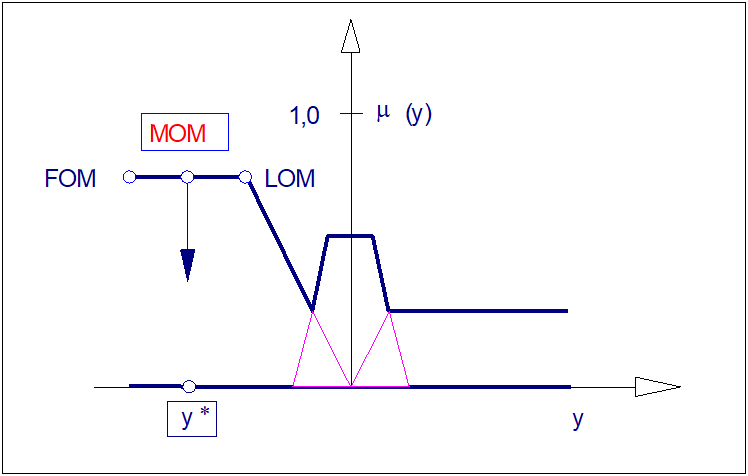
Metoda wysokości MOM zwana metodą "środkowy z największych" jest metodą szybkiego wyostrzania łączącą cechy metod: FOM i LOM. Metoda polega na uznaniu za wartość ostrą średniej arytmetycznej prawo- i lewostronnych odciętych wysokości zbioru wniosku cząstkowego o maksymalnej wysokości. Wartość ostrą metodą MOM wyznaczamy jako:
| \( y^*=\frac{inf \left\{sup\ \mu_Y(y)\right\}+sup \left\{sup\ \mu_Y(y)\right\}}{2} \) | (117) |
|---|
lub prościej jako:
| \( y^*=\frac{y^*_{FOM}+y^*_{LOM}}{2} \) | (118) |
|---|
Metoda MOM jest kompromisową metodą wysokościową. Dość oczywiste jest preferowanie jej w praktyce, ze względu na fakt powszechnego występowania obciętych wniosków rozmytych. W rezultacie zastosowania metody FOM uzyskiwana jest mniejsza zmienność wartości ostrych wniosków w stosunku do metod LOM czy FOM. Ma to znaczenie zwłaszcza w przypadkach gdy defuzyfikacji podlegają sygnały sterowania generowane przez regulatory rozmyte. Ograniczona zmienność wyjścia regulatora przekłada się na mniejszy wysiłek elementu wykonawczego, a tym samym sprzyja wydłużeniu jego trwałości.
W metodzie FOM, podobnie jak w pozostałych metodach wysokościowych, nieistotny jest kształt funkcji przynależności lecz lokalizacja lewo- i prawostronnych odciętych zbioru rozmytego o najwyższej wysokości. Ilustrację operacji wyostrzania metodą LOM pokazano na rysunku poniżej.
Wyostrzanie zbioru rozmytego
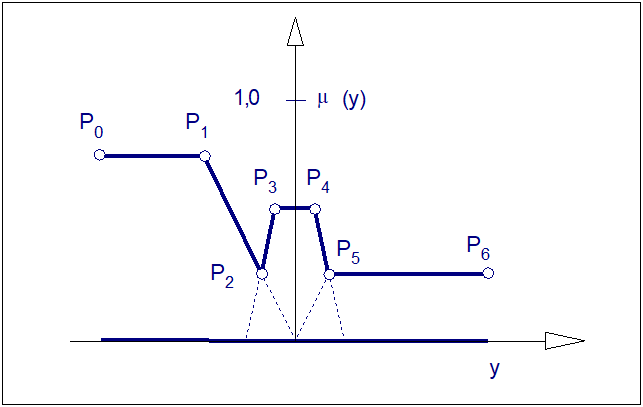
Wyostrzyć zbiór rozmyty przedstawiony na Rys. 27 metodami obszarowymi i wysokościowymi.
Z rysunku odczytujemy współrzędne punktów charakterystycznych funkcji przynależności zbioru.
|
\( P_0[-1.00,0.80] \) \( P_1[-0.50,0.80] \) \( P_3[-0.15,0.50] \) \( P_5[0.25,0.25] \) |
\( P_2[-0.25,0.25] \) \( P_4[0.15,0.50] \) \( P_6[1.00,0.25] \) |
|
|
Metoda COG Metoda COS Metoda COLA Metoda HM Metoda FOM Metoda LOM Metoda MOM |
\( y^*=-0.322 \) \( y^*=-0.284 \) \( y^*=-0.722 \) \( y^*=-0.286 \) \( y^*=-1.000 \) \( y^*=-0.500 \) \( y^*=-0.750 \) |
(ze wzoru 110) (ze wzoru 113, Rys. 21) (ze wzoru 110, Rys. 22) (ze wzoru 114, Rys. 23) (ze wzoru 115, Rys. 24) (ze wzoru 116, Rys. 25) (ze wzoru 118, Rys. 26) |
Z przykładu wynika, że dla tego samego zbioru rozmytego uzyskano znaczną rozbieżność wartości wyjścia ostrego. W zasadzie wspólną cechą wszystkich uzyskanych wyników jest to, że wszystkie one są ujemne i nie większe niż 0,284. Przykład ilustruje stwierdzenie o niejednoznaczności transformacji zbioru rozmytego do wartości ostrej. Zależność wyniku tej transformacji od zastosowanej metody wnioskowania jest ewidentna.
W związku z tym pojawia się pytanie którą z metod wyostrzania należy uznać za metodę referencyjną. Z racjonalnego punktu widzenia taką metodą jest metoda COG. Często stosowana jest również metoda COS jako substytut metody COG. Metoda MOM stosowana jest zwłaszcza w układach regulacji procesów o dużej dynamice dysponujących bardzo ograniczonymi mocami obliczeniowymi.
4. Przykłady regulatorów rozmytych
Niewątpliwie najbardziej spektakularnym osiągnięciem teorii zbiorów rozmytych w teorii sterowania było wprowadzenie i zastosowanie regulatorów rozmytych. Regulatory rozmyte znajdują obecnie liczne zastosowania przemysłowe i komercyjne. Stosowane są powszechnie do sterowania procesów silnie nieliniowych.
W tym rozdziale omówimy podejścia do konstrukcją wybranych rozmytych algorytmów regulacyjnych. Dla skoncentrowania uwagi w dalszym ciągu będziemy zajmować się regulatorami przeznaczonymi do zastosowań w jednoobwodowych układach regulacji z ujemnym sprzężeniem zwrotnym. Schemat blokowy takiego układu przedstawiono na rysunku poniżej.
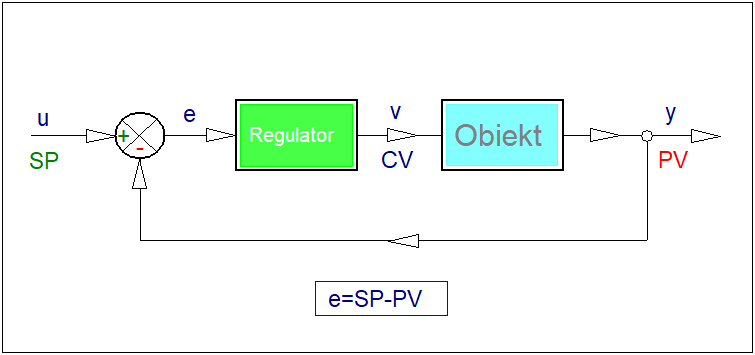
W układzie sterowania automatycznego odchyłka regulacji jest miarą różnicy pomiędzy wartością zadaną (pożądaną), a wartością mierzoną (rzeczywistą) na wyjściu obiektu regulacji. Do konstrukcji algorytmów regulacji rozmytej istotne jest oczywiste, aczkolwiek ważne spostrzeżenie, że ujemna wartość odchyłki regulacji oznacza, że wartość mierzona ma wartość zbyt wysoką i odwrotnie: dodatnia wartość odchyłki regulacji wskazuje, że wartość mierzona jest zbyt mała. W przypadku odchyłki ujemnej regulator powinien kształtować w taki sposób sterowanie CV, aby sprowadzić odchyłkę regulacji do wartości zerowej lub przynajmniej bliskich zeru. W najprostszym przypadku jeśli odchyłka regulacji jest ujemna, to regulator powinien skompensować ją przez zmniejszenie sygnału sterowania CV, jeśli odchyłka jest zerowa, to regulator nie powinien zmieniać sygnału sterującego, jeśli odchyłka jest dodatnia to powinien zwiększyć sterowanie. Łatwo zwrócić uwagę, że w ten sposób dokonaliśmy lingwistycznego opisu pewnego, dobrze znanego regulatora o działaniu bezinercyjnym. Szczególnym przypadkiem takiego regulatora jest regulator typu P.
Syntezę regulatorów rozmytych będziemy realizowali zgodnie z przedstawioną w podrozdziale 3.1 metodyką projektowania modeli rozmytych. Metodykę projektowania regulatorów rozmytych można scharakteryzować w postaci sześciu zasadniczych kroków:
Krok 1 (formalny)
Każdej zmiennej ostrej (zarówno wejściowej jak i wyjściowej) przyporządkować nazwę lingwistyczną.
Krok 2 (projekt zbiorów rozmytych)
Każdej zmiennej lingwistycznej przyporządkować wartości w postaci znormalizowanych zbiorów rozmytych.
Krok 3 (projekt bazy reguł)
Na podstawie wiedzy matematycznej, heurystycznej, eksperckiej, doświadczalnej, sformułować relacje rozmyte wiążące wejścia i wyjścia.
Krok 4 (wyznaczenie wartości rozmytej wejść)
Na podstawie znajomości wartości wejść ostrych oraz znajomości zbiorów rozmytych wejść (krok 2) wyznaczyć zbiór wartości funkcji przynależności każdej zmiennej lingwistycznej odpowiadający wartościom ostrym wejść.
Krok 5 (wyznaczenie wartości rozmytej wyjść)
Na podstawie znajomości wartości rozmytych wejść (krok4) oraz relacji (krok 3) wyznaczyć zbiór wartości funkcji przynależności każdej zmiennej lingwistycznej wyjścia.
Krok 6 (wyznaczenie wartości wyjść ostrych)
Na podstawie znajomości wartości wyjść rozmytych stosując odpowiednią metodę wyostrzania wyznaczyć wartości ostre wyjścia.
Pozostaje sprawą dyskusyjną, czy zastosowanie tak złożonej procedury do realizacji prostego liniowego regulatora typu P ma jakikolwiek sens praktyczny?
Znacznie prościej regulator taki realizowany jest metodami właściwymi podejściom ostrym. Jakkolwiek odpowiedź na to pytanie w przypadku realizacji nieliniowego rozmytego regulatora bezinercyjnego typu P nie jest już tak jednoznaczna.
4.1. Rozmyty regulator typu P
Do syntezy rozmytego regulatora typu P zastosujmy przedstawiony wyżej algorytm złożony z sześciu kroków.
Krok 1 (formalny)
Rozważmy regulator typu P o strukturze SISO. Wejściem regulatora jest sygnał odchyłki regulacji \( e \), a jego wyjściem jest sygnał sterujący (nastawiający) \( v \). Oba sygnały są wielkościami ostrymi, których wartości należą do znormalizowanych przedziałów \( [-1, 1] \).
Następnie przyporządkujmy odchyłce regulacji \( e \) nazwę lingwistyczną <odchyłka regulacji>, oraz sygnałowi sterującemu v nazwę lingwistyczną <sygnał sterujący>. W celu skrócenia notacji, w dalszym ciągu będziemy stosowali nazwy alternatywne e i v odpowiednio dla <odchyłki regulacji> i <sygnału sterującego>.
Następnie zmiennej <odchyłka regulacji> przyporządkujemy dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano alternatywne nazwy: \( N_e \) i \( P_e \). W podobny sposób zmiennej <sygnał sterujący> przyporządkujemy dwie wartości <zmniejsz sterowanie> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio krótsze alternatywne nazwy symboliczne \( N_s \) i \( P_s \). Wartości \( N_e \) , \( P_e \) , \( N_s \) i \( P_s \) są już zbiorami rozmytymi, których funkcje przynależności zostaną zdefiniowane w następnym kroku.
Krok 2 (projekt zbiorów rozmytych)
Projekt zbiorów rozmytych \( N_e \) , \( P_e \) , \( N_s \) i \( P_s \) przedstawiony został w formie graficznej na Rys. 29. Wszystkie funkcje przynależności wszystkich zbiorów zdefiniowano w znormalizowanej i ograniczonej obustronnie przestrzeni rozważań \( [-1,1] \). Zbiory rozmyte reprezentujące wartości rozmytego sygnału wejściowego zaprojektowano w postaci dwóch symetrycznych funkcji trójkątnych. Natomiast wyjście rozmyte zaprojektowano w postaci zbiorów singletonowych. Dzięki temu, (jak wiemy z rozdziału 3) możliwe jest znakomite uproszczenie procesu wyostrzania. W ogólności funkcje przynależności wartości wejść i wyjść mogą mieć dowolne kształty. Z punktu widzenia formalnego ważne jest jedynie to aby zbiory te były zbiorami znormalizowanymi.
Krok 3 (projekt bazy reguł)
Na podstawie analizy przeprowadzonej w komentarzu do Rys. 28, bazę reguł w postaci tabeli sterowań rozmytych regulatora bezinercyjnego o działaniu P przedstawiono w Tabeli 5.
| Reguła | \( e \) | \( y \) |
|---|---|---|
| 1 | \( N_e \) | \( N_s \) |
| 2 | \( P_e \) | \( P_s \) |
Kroki 4, 5, 6 (wyznaczenie wartości rozmytej wejść, wartości rozmytej wyjść i wartości wyjść ostrych)
Na podstawie znajomości wartości wejść ostrych, znajomości zbiorów rozmytych wejść (krok 2) oraz znajomości tabeli reguł (krok 3) wyznaczamy wyjścia ostre stosując metodę środka ciężkości obszaru (COG). Metoda ta, ze względu na dobór charakterystycznych funkcji przynależności wyjścia rozmytego (singletony), jest w naszym przypadku równoważna metodom COS i HM. W Tabeli 6 przedstawiono przebieg procesu wnioskowania rozmytego dla wartości odchyłki regulacji w zakresie jej zmienności w granicach [-1,1].
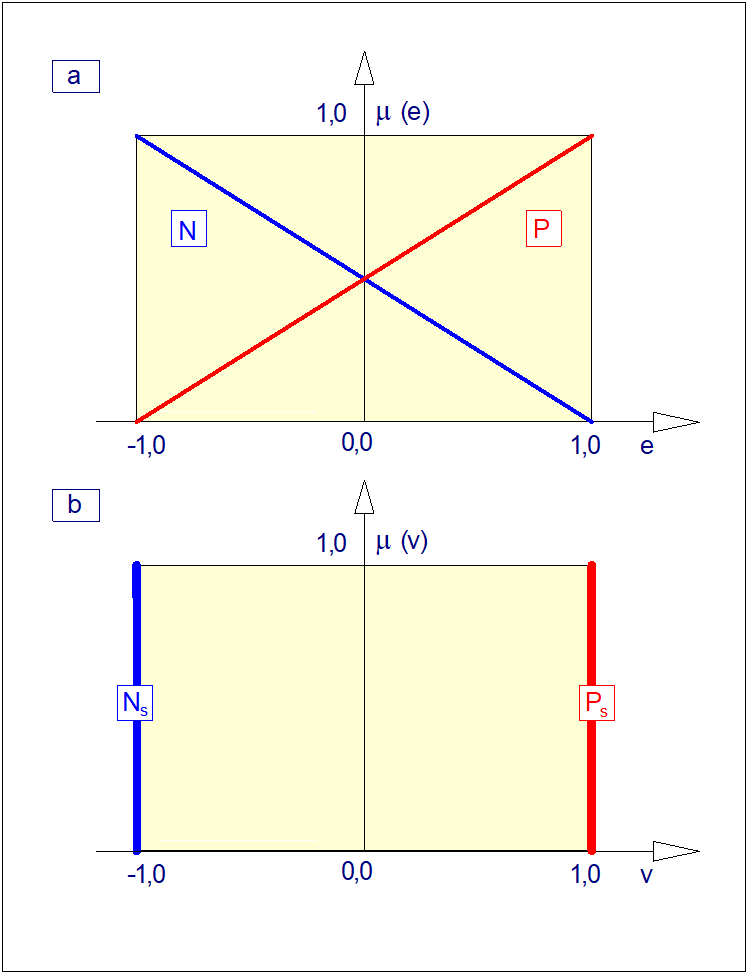
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
| \( e \) | \( \mu_N(e) \) | \( \mu_P(e) \) | \( \mu_{N_s}(v) \) | \( \mu_{P_s}(v) \) | \( v \) |
|---|---|---|---|---|---|
| -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,75 | 0,88 | 0,13 | 0,88 | 0,13 | -0,75 |
| -0,50 | 0,74 | 0,25 | 0,75 | 0,25 | -0,50 |
| -0,25 | 0,63 | 0,38 | 0,63 | 0,38 | -0,25 |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 |
| 0,25 | 0,38 | 0,63 | 0,38 | 0,63 | 0,25 |
| 0,50 | 0,25 | 0,75 | 0,25 | 0,75 | 0,50 |
| 0,75 | 0,13 | 0,88 | 0,13 | 0,88 | 0,75 |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 1,00 |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | ||
Zależność \( v = f(e) \) nazywać będziemy funkcją lub charakterystyką sterowania. Dla przypadku wielowymiarowego gdy \( v = f(e) \) zdefiniujemy pojęcia tzw. powierzchni i przestrzeni sterowania.
Powierzchnią sterowania będziemy określali hiperpowierzchnię rozpiętą w przestrzeni (n+1) wymiarowej odwzorowującej przekształcenie n-wymiarowego wejścia w wyjście jednowymiarowe.
| \( v = f(\mathbf{e})\quad;\quad \forall e_i \in E_i\quad ;\quad \forall v\in V \) | (119) |
|---|
Przestrzenią sterowania będziemy określali hiperprzestrzeń rozpiętą w przestrzeni (n+m)-wymiarowej odwzorowującej operację przekształcenia n-wymiarowego wejścia w m-wymiarowe wyjście.
| \( \mathbf{v} = f(\mathbf{e})\quad;\quad \forall e_i \in E_i\quad ;\quad \forall v_i\in V_k \) | (120) |
|---|
Ponieważ dla rozważanego przypadku regulatora P (n=m=1), to przestrzeń sterowania jest dwuwymiarowa (Rys. 30).
Jak łatwo zauważyć, funkcja sterowania regulatora skonstruowanego do tej pory jest funkcją liniową. A więc regulator posiada stałe wzmocnienie, którego wartość jest równa pochodnej funkcji sterowania względem sygnału wejściowego. Z Rys. 30 wynika, że wzmocnienie tego regulatora jest równe 1. Pojawia się pytanie czy w ogóle, a jeśli tak to w jaki sposób można kształtować wzmocnienie tego regulatora? Tę kwestię wyjaśnimy poniżej.
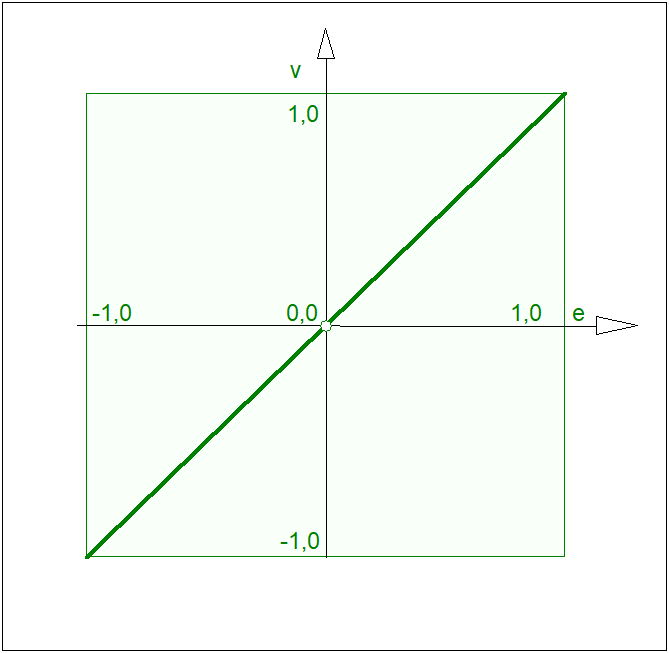
Jak łatwo zauważyć, w naszym przykładzie wartość wyjścia v wyznaczana jest z:
| \( v = \mu_{Ps}(v)-\mu_{Ns}(v)\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (121) |
|---|
gdzie: \( E \) i \( V \) ą odpowiednio przestrzeniami rozważań sygnału wejściowego i wyjściowego regulatora.
Ponieważ z reguł wnioskowania wynika, że:
| \( \mu_{Ps}(v)=\mu_{Pe}(e)\quad i\quad \mu_{Ns}(v)=\mu_{Ne}(e) \) | (122) |
|---|
to ostatecznie:
| \( v = \mu_{Pe}(e)-\mu_{Ne}(e)\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (123) |
|---|
Funkcje przynależności wartości \( P_e \) i \( N_e \) można zapisać w postaci funkcji liniowych będącymi kombinacjami liniowymi parametrów stałych: \( k_P \) , \( C_P \) , \( k_N \), \( C_N \):
| \( \mu_{Pe}(e)=k_{Pe}\cdot e + C_{Pe} \quad;\quad \mu_{Ne}(e)=k_{Ne}\cdot e+C_{Ne} \) | (124) |
|---|
stąd:
| \( v=(k_{Pe}-k_{Ne})\cdot e + (C_{Pe}-C_{Ne})\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (125) |
|---|
Z (125) wynika, że wzmocnienie regulatora można wyznaczyć z różnicy nachyleń funkcji przynależności <odchyłki regulacji>:
| \( k=(k_{P}-k_{N}) \) | (126) |
|---|
Podobnie, przesunięcie funkcji sterowania w kierunku osi sygnału wyjściowego v można wyznaczyć z różnicy przesunięć w tym kierunku obu funkcji przynależności <odchyłki regulacji>:
| \( C=(C_{P}-C_{N}) \) | (127) |
|---|
Ostatecznie otrzymujemy prawo sterowania w postaci funkcji liniowej:
| \( v=k\cdot e+C \) | (128) |
|---|
Zatem zmiana wzmocnienia regulatora rozmytego typu P sprowadza się do zadania kształtowaniu wartości współczynników nachylenia funkcji przynależności wejścia.
W naszym przykładzie \( k_{P_e} =0,5 \), \( k_{N_e} =-0,5 \), \( C_{P_e} =0,5 \), \( C_{N_e}=0,5 \) stąd zgodnie z wzorami (126) i (127) \( k =1 \); \( C =0 \).
Zaprojektować liniowy regulator rozmyty typu P o współczynniku wzmocnienia równym \( k_P=2 \).
Z zależności (126) otrzymujemy:
| \( k_p=k_{Pe}-k_{Ne}=2 \) | (129) |
|---|
Ponieważ równanie (125) jest równaniem z dwoma niewiadomymi to w celu jego rozwiązania przyjmiemy, że współczynniki kierunkowe obu funkcji przynależności zmiennej \ltodchyłka regulacji\gt będą identyczne co do wartości lecz będą miały znaki przeciwne, tzn. \( k_{Pe}=-k_{Ne}=k_e \). Po podstawieniu, z (129) wyznaczamy wartość \( k_e=1 \).
Dodatkowo założymy, aby funkcja sterowania przechodziła przez punkt o współrzędnych \( [0, 0] \) co zgodnie z (125) implikuje równość \( C_{Pe}=C_{Ne} \). Z (126) wynika, że wzmocnienie jest niezależne od doboru wartości stałych \( C_{Pe} \) i \( C_{Ne} \). W związku z tym przykładzie przyjmiemy arbitralnie \( C_{Pe}=C_{Ne}=0,5 \).
Na Rys. 35 przedstawiono wykres wartości funkcji przynależności sygnałów odchyłki regulacji i nastawiającego oraz funkcję sterowania. Natomiast w Tabeli 7 przedstawiono przebieg procesu wnioskowania.
| \( e \) | \( \mu_N(e) \) | \( \mu_P(e) \) | \( \mu_{N_s}(v) \) | \( \mu_{P_s}(v) \) | \( v \) |
|---|---|---|---|---|---|
| -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,75 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,50 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,25 | 0,75 | 0,25 | 0,75 | 0,25 | -0,50 |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 |
| 0,25 | 0,25 | 0,75 | 0,25 | 0,75 | 0,50 |
| 0,50 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| 0,75 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | ||
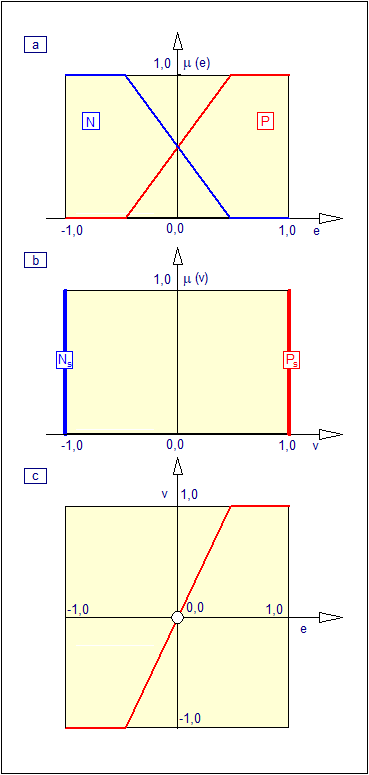
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
c) Funkcja sterowania
4.2. Rozmyty regulator dwustawny
W poprzednim rozdziale stwierdziliśmy, że dla rozpatrywanego w nim przypadku, wzmocnienie regulatora rozmytego typu P jest wprost proporcjonalne do różnicy pochodnych liniowych funkcji przynależności wartości wejścia. Zwiększenie nachylenia tych funkcji skutkuje wzrostem wzmocnienia. Jeśli pochodne osiągną wartości teoretycznie nieskończenie wielkie, to wzmocnienie regulatora osiągnie także osiągnie taką wartość. W takim przypadku uzyskujemy przełączającą funkcję sterowania właściwą regulatorom dwustawnym (Rys. 32).
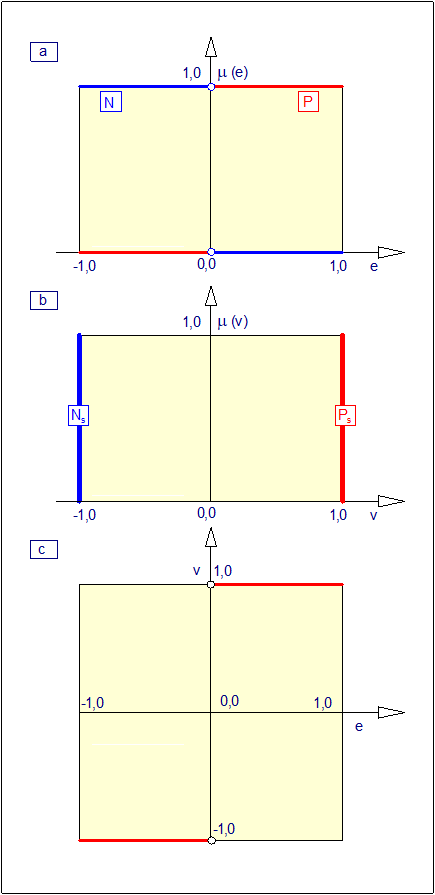
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
c) Funkcja sterowania
4.3. Rozmyty regulator trójpołożeniowy
Jeśli zwiększymy liczbę wartości rozmytych: wejścia i wyjścia do trzech i rozszerzymy tabelę reguł regulatora P, to analogicznie jak dla regulatora dwustawnego możemy uzyskać regulator trójpołożeniowy (trójstawny). W Tab. 8 przedstawiono tabelę sterowań dla takiego regulatora, a przykład jego projektu na Rys. 33.
| Reguła | \( e \) | \( y \) |
|---|---|---|
| 1 | \( N \) | \( N_s \) |
| 2 | \( Z \) | \( Z_s \) |
| 3 | \( P \) | \( P_s \) |
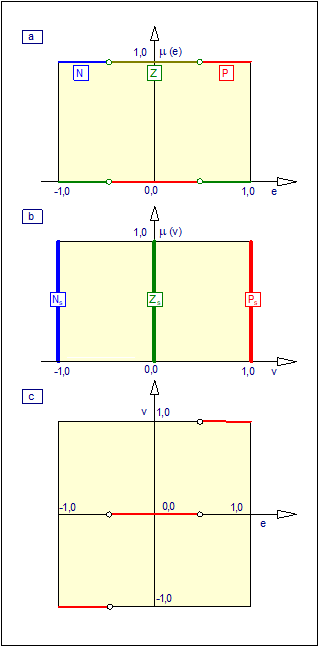
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
c) Funkcja sterowania
4.4. Rozmyty regulator typu PI
Transmitancja operatorowa liniowego regulatora PI dana jest równaniem:
| \( G(s)=k_p\left(1+\frac{1}{T_is}\right) \) | (130) |
|---|
gdzie: \( k_p \) – współczynnik wzmocnienia proporcjonalnego, \( T_i \) – stała czasowa całkowania.
Ponieważ w naszym przypadku:
| \( G(s)=\frac{V(s)}{E(s)} \) | (131) |
|---|
gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora. Po uwzględnieniu (130) i (131) otrzymujemy:
| \( V(s)=k_p\left(1+\frac{1}{T_is}\right)E(s) \) | (132) |
|---|
Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:
| \( v(t)=k_p\cdot e(t)+k_i\cdot \int_0^t e(t)dt \) | (133) |
|---|
gdzie: \( k_i=k_p/T_i \) - współczynnik członu całkującego.
Różniczkując obustronnie równanie (133) otrzymujemy:
| \( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e \) | (134) |
|---|
co prowadzi do wniosku, że cechą charakterystyczną regulatora PI jest to, że:
zmiana sygnału wyjściowego liniowego regulatora typu PI jest proporcjonalna zarówno do prędkości zmian odchyłki regulacji (akcja proporcjonalna) jak również do wartości samej odchyłki (akcja całkująca).
W systemach z czasem dyskretnym z okresem impulsowania ∆t równanie (134) przybiera postać następującego równania różnicowego:
| \( \Delta v=K_P \cdot \Delta e + K_I\cdot e \) | (135) |
|---|
gdzie: \(K_P=k_P \); \(K_I=k_I\Delta t \) ; \(\Delta t=const=1 \).
Równanie (135) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PI. Reguły te można zapisać w postaci ogólnej:
| \( jezeli\; (e=E)\cap(\Delta e=\Delta E)\; to\; (\Delta v= \Delta V) \) | (136) |
|---|
gdzie: \( E \), \( \Delta E \), \( \Delta V \) - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji> i <zmiana wyjścia regulatora>.
Wyjście dyskretnego regulatora PI (Rys. 34) w chwili k-tej jest sumą jego wyjścia \( v_{k-1} \) w chwili poprzedniej (k-1) i zmiany jego wyjścia \( \Delta v_{k-1} \) (korekty) dokonanej w chwili k- tej. Stąd:
| \( v_k= v_{k-1}+\Delta v_k \) | (137) |
|---|
Stąd:
| \( v=\sum_{i=1}^k\Delta v_i+v_0 \) | (138) |
|---|
gdzie: \( v_o \) – wartość początkowa (offset) wyjścia.
Podstawiając (135) do (138) otrzymujemy ostatecznie rekurencyjny wzór na wyjście rozmytego regulatora PI:
| \( v=\sum_{i=1}^k \left\{k_{P}(e_i-e_{i-1})+k_I\cdot e_i\right\}+v_0 \) | (139) |
|---|
Rozwiązanie: Zgodnie z procedurą syntezy układów rozmytych przedstawioną w podrozdziale 3.1, projekt rozmytego regulatora typu PI przeprowadzimy w sześciu krokach.
Krok 1 (formalny)
Załóżmy regulator typu PI o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e \) oraz prędkość tej odchyłki \( \Delta e \). W realizacjach praktycznych prędkości odchyłki regulacji w dyskretnej chwili k wyznaczymy z różnicy wartości odchyłki \( e \) w chwili k-tej i w chwili poprzedniej tj. \( e_{k-1} \).
| \( \Delta e_k=k_e \cdot (e_{k}-e_{k-1}) \) | (140) |
|---|
gdzie: \( k_e=1⁄{\Delta t}=const \); \( \Delta t \) - okres impulsowania.
Wyjściem regulatora jest zmiana sygnału nastawiającego \( \Delta v_k \). Przyporządkujmy zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zaś zmiennej lingwistycznej <zmiana sygnału wyjściowego> symbol \( \Delta v \). Załóżmy dalej, że zmiennej \( e \) przyporządkujemy dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna wartość prędkości odchyłki regulacji> i <dodatnia wartość prędkości odchyłki regulacjigt. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej lingwistycznej \( v \) przyporządkowano wartości <zmniejsz sterowanie>, <pozostaw sterowanie bez zmian> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \).
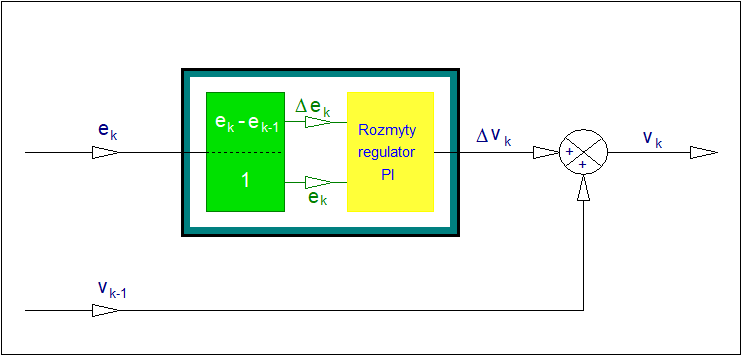
Projekt zbiorów rozmytych wejścia i wyjścia przedstawimy graficznie na Rys. 35. W tym przypadku wyjście rozmyte zaprojektowano w postaci singletonów, co jak już wspomniano wcześniej znakomicie upraszcza i przyśpiesza proces wyostrzania.
Krok 3 (projekt bazy reguł)
Posiłkując się znajomością ogólnej reguły warunkowej (136) regulatora rozmytego typu PI; mając na uwadze kształt funkcji przynależności jak na Rys. 35, zbudujemy zupełną bazę reguł modelu regulatora. W tym przypadku mamy do czynienia z układem rozmytym o dwóch wejściach (i=2) i jednym wyjściu (k=1). Obu wejściom przyporządkowano odpowiednio: \( n_1=2 \) i \( n_2=2 \) zbiorów rozmytych. Stąd liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (2\cdot 2)=4 \).
| Reguła | \( \Delta e \) | \( e \) | \( \Delta y \) |
|---|---|---|---|
| 1 | \( N_{\Delta e} \) | \( N_e \) | \( N_{\Delta v} \) |
| 2 | \( N_{\Delta e} \) | \( P_e \) | \( Z_{\Delta v} \) |
| 3 | \( P_{\Delta e} \) | \( N_e \) | \( Z_{\Delta v} \) |
| 2 | \( P_{\Delta e} \) | \( P_e \) | \( P_{\Delta v} \) |
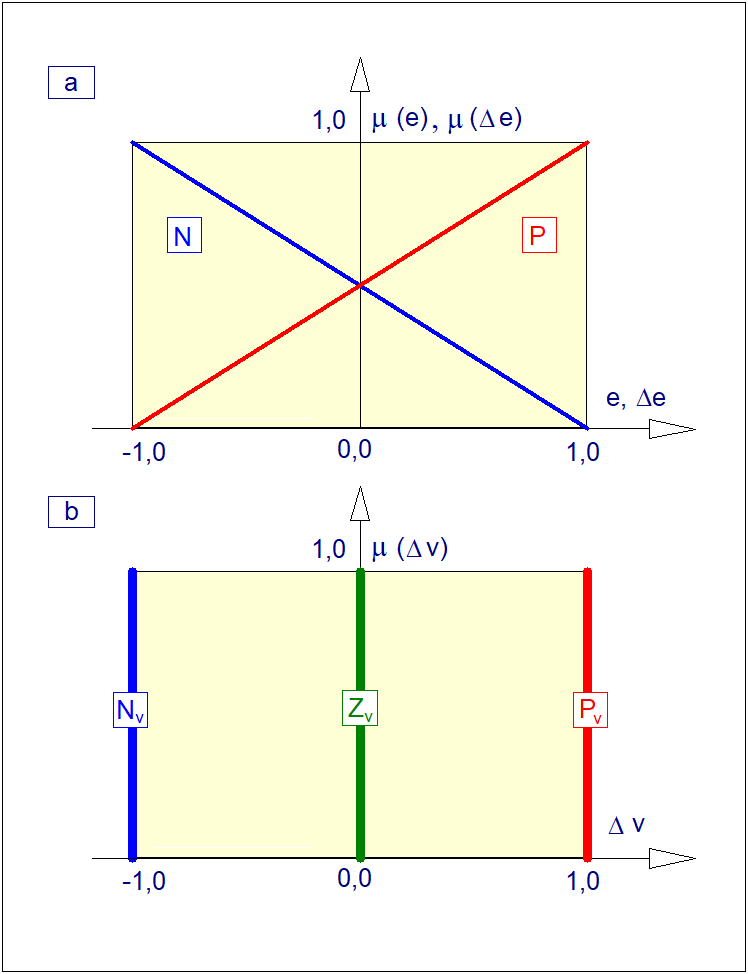
a) Funkcje przynależności wejścia \( e \) i \( \Delta e \)
b) Funkcje przynależności wyjścia \(\Delta v \)
Krok 4, 5, 6 (wyznaczenie wartości rozmytej wejść, wyznaczenie wartości rozmytej wyjścia, wyznaczenie wartości wyjścia ostrego)
Na podstawie znajomości wartości wejść ostrych, znajomości zbiorów rozmytych wejść (krok 2) oraz znajomości tabeli reguł (krok 3) wyznaczymy wyjścia ostre regulatora PI stosując implikację Mamdaniego (82), agregację wniosków rozmytych zgodnych z formułą sumy mnogościowej (106) oraz wyostrzanie metodę środka ciężkości COG (111). Ze względu na singletonowy kształt funkcji przynależności przyporządkowanych do wyjścia regulatora, wynik wyostrzania metodą COG jest w tym przypadku równoważny wynikom uzyskiwanym metodami COS i HM. W tabeli 10 przedstawiono przebieg procesu wnioskowania, a na Rys. (36 przedstawiono powierzchnię sterowania regulatora. Powierzchnia sterowania, która ma kształt płaszczyzny jest charakterystyczna dla liniowych regulatorów PI. Konstrukcja nieliniowego regulatora PI możliwa jest np. przez zmianę kształtu i położenia funkcji przynależności wejścia.
| Reguła | 1 | 2 | 3 | 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \( \Delta e \) | \( e \) | \( \mu_N(\Delta e) \) | \( \mu_P(\Delta e) \) | \( \mu_N(e) \) | \( \mu_P(\Delta e) \) | \( \mu_N(\Delta v) \) | \( \mu_Z(\Delta v) \) | \( \mu_Z(\Delta v) \) | \( \mu_P(\Delta v) \) | \( \Delta v \) |
| -1,00 | -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 | -1,00 |
| -0,50 | 0,75 | 0,25 | 1,00 | 0,00 | 0,75 | 0,00 | 0,25 | 0,00 | -1,00 | |
| 0,00 | 0,50 | 0,50 | 1,00 | 0,00 | 0,50 | 0,00 | 0,50 | 0,00 | -0,50 | |
| 0,50 | 0,25 | 0,75 | 1,00 | 0,00 | 0,25 | 0,00 | 0,75 | 0,00 | -0,25 | |
| 1,00 | 0,00 | 1,00 | 1,00 | 0,00 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | |
| -1,00 | -0,50 | 1,00 | 0,00 | 0,75 | 0,25 | 0,75 | 0,25 | 0,00 | 0,00 | -0,75 |
| -0,50 | 0,75 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,25 | -0,40 | |
| 0,00 | 0,50 | 0,50 | 0,75 | 0,25 | 0,50 | 0,25 | 0,50 | 0,25 | -0,20 | |
| 0,50 | 0,25 | 0,75 | 0,75 | 0,25 | 0,25 | 0,25 | 0,75 | 0,25 | 0,00 | |
| 1,00 | 0,00 | 1,00 | 0,75 | 0,25 | 0,00 | 0,00 | 0,75 | 0,25 | 0,25 | |
| -1,00 | 0,00 | 1,00 | 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 | 0,00 | -0,50 |
| -0,50 | 0,75 | 0,25 | 0,50 | 0,50 | 0,50 | 0,50 | 0,25 | 0,25 | -0,20 | |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 | |
| 0,50 | 0,25 | 0,75 | 0,50 | 0,50 | 0,25 | 0,20 | 0,50 | 0,50 | 0,20 | |
| 1,00 | 0,00 | 1,00 | 0,50 | 0,50 | 0,00 | 0,00 | 0,50 | 0,50 | 0,50 | |
| -1,00 | 0,50 | 1,00 | 0,00 | 0,25 | 0,75 | 0,05 | 0,75 | 0,00 | 0,00 | -0,25 |
| -0,50 | 0,75 | 0,25 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,00 | |
| 0,00 | 0,50 | 0,50 | 0,25 | 0,75 | 0,25 | 0,50 | 0,25 | 0,50 | 0,20 | |
| 0,50 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,25 | 0,75 | 0,75 | |
| 1,00 | 0,00 | 1,00 | 0,25 | 0,75 | 0,00 | 0,00 | 0,25 | 0,75 | 0,75 | |
| -1,00 | 1,00 | 1,00 | 0,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 |
| -0,50 | 0,75 | 0,25 | 0,00 | 1,00 | 0,00 | 0,75 | 0,00 | 0,25 | 0,25 | |
| 0,00 | 0,50 | 0,50 | 0,00 | 1,00 | 0,00 | 0,50 | 0,00 | 0,50 | 0,50 | |
| 0,50 | 0,25 | 0,75 | 0,00 | 1,00 | 0,00 | 0,25 | 0,00 | 0,75 | 0,75 | |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 | 1,00 | 1,00 | |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | |||||||
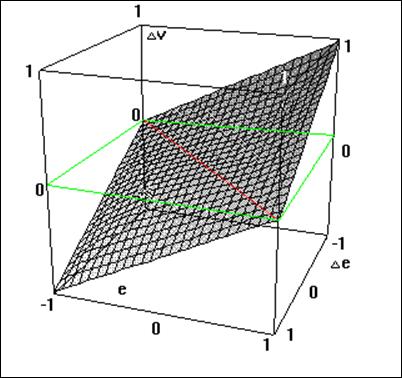
Redukcja regulatora rozmytego typu PI do regulatora P
Zaprojektujemy tabelę reguł rozmytego regulatora typu PI o trzech wartościach zmiennej \( e \), trzech wartościach zmiennej \( \Delta e \) i trzech wartościach zmiennej \( \Delta v \) jak na Rys. 37. Odchyłce regulacji \( e \) przyporządkujemy trzy wartości <odchyłka ujemna>, <odchyłka zerowa> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \), \( Z_e \) i \( P_e \). W podobny sposób zmiennej <zmiana odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna zmiana odchyłki regulacji>, <brak zmiany odchyłki regulacji> i <dodatnia zmiana odchyłki regulacji>. Wartościom tym nadano także nazwy symboliczne: \( N_{\Delta e} \), \( Z_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej \( \Delta v \) przyporządkowano wartości <zmniejsz sterowanie> , <sterowanie bez zmian> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \).
Rozwiązanie: Na podstawie ogólnej reguły warunkowej (136) dla regulatora rozmytego typu PI, mając na uwadze kształt funkcji przynależności jak na Rys. 37, oraz wnioski z rozważań przeprowadzonych w tym rozdziale, zbudujemy bazę zupełną regulatora. W tym przypadku mamy do czynienia z układem o dwóch wejściach (i=2). Obu wejściom przyporządkowano odpowiednio: \( n_1=3 \) i \( n_2=3 \) zbiorów rozmytych. Stąd liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (3\cdot 3)=9 \). Tabelę sterowań tego regulatora przedstawiono w Tabeli 11.
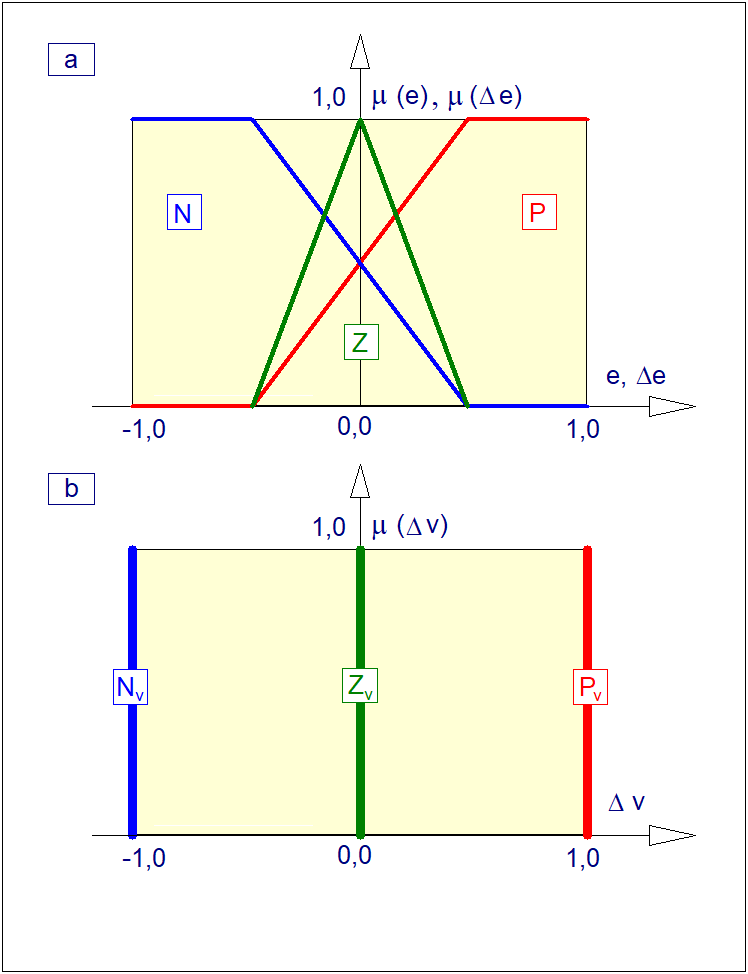
a) Funkcje przynależności wejść \( e \) i \( \Delta e \)
b) Funkcje przynależności wyjścia \( \Delta v \)
| Regulator rozmyty typu PI |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | \( N_{\Delta v} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) |
| \( Z_{\Delta e} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | |
| \( P_{\Delta e} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | \( P_{\Delta v} \) | |
Zwróćmy uwagę, że jeśli w równaniu (133) dokonamy podstawienia \( e=0 \), to regulator PI ulegnie redukcji do regulatora typu P. Wówczas zmiana sygnału wyjściowego będzie wprost proporcjonalna do zmiany odchyłki regulacji.
| \( \Delta v=K_p \cdot \Delta e \) | (141) |
|---|
A zatem \( {\Delta v}/{\Delta e}=const \) i \( \lim_{t \to \infty } \frac{\Delta v}{\Delta e}=v/e \) co jest charakterystyczną cechą regulatora o działaniu proporcjonalnym.
Technicznie redukcja regulatora PI do regulatora typu P polega na wyeliminowaniu z tabeli sterowań 11, dwóch kolumn, dotyczą wartości niezerowych rozmytych odchyłek regulacji. Postać zredukowanej tabeli sterowań dla regulatora typu P przedstawiono w Tabeli 12.
| Regulator rozmyty typu PI |
\( e \) | |||
|---|---|---|---|---|
| - | \( Z_e \) | - | ||
| \( \Delta e \) | \( N_{\Delta e} \) | - | \( N_{\Delta v} \) | - |
| \( Z_{\Delta e} \) | - | \( Z_{\Delta v} \) | - | |
| \( P_{\Delta e} \) | - | \( P_{\Delta v} \) | - | |
Zwróćmy także uwagę, że przekształcenie klasycznego regulatora PI do regulatora typu P może być dokonane przez podstawienie \( k_i=k_p/T_i =0 \) we wzorze (134). Technicznie można tego dokonać albo przez maksymalizację stałej czasowej całkowania \( T_i \), albo przez wyeliminowanie akcji całkującej z wzoru (134). Pierwszy sposób realizowany był w regulatorach analogowych starszych typów, zaś drugi jest obecnie stosowany powszechnie we współczesnych regulatorach implementowanych w technice cyfrowej.
4.5. Rozmyty regulator typu PD
Transmitancja operatorowa idealnego liniowego regulatora PD dana jest równaniem:
| \( G(s)=k_p\left(1+T_{d}s\right) \) | (142) |
|---|
Ponieważ
| \( G(s)=\frac{V(s)}{E(s)} \) | (143) |
|---|
gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora.
Po uwzględnieniu (142) i (143) otrzymujemy:
| \( V(s)=k_p\left(1+T_{d }s\right)E(s) \) | (144) |
|---|
Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:
| \( v(t)=k_p\cdot e(t)+k_d\cdot\frac{de(t)}{dt} \) | (145) |
|---|
gdzie: \( k_d=k_p\cdot T_d \) - współczynnik członu różniczkującego.
Jak wynika ze wzoru (145), cechą charakterystyczną regulatora PD jest to, że: jego sygnał wyjściowy jest proporcjonalny zarówno do odchyłki regulacji (akcja proporcjonalna) jak i jej prędkości (akcja różniczkująca).
W systemach z czasem dyskretnym z okresem impulsowania \( \Delta t \) równanie (145) przybiera postać następującego równania różnicowego:
| \( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e \) | (146) |
|---|
gdzie: \( K_p=k_p \); \( K_d=k_d/\Delta t \); \( \Delta t=const \).
Równanie (146) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PD. Reguły te można zapisać w postaci ogólnej:
| \( v=K_P \cdot e + K_D\cdot \Delta e \) | (147) |
|---|
gdzie: \( E \), \( \Delta E \), \( V \) - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji> i <wyjście regulatora>.
Projekt rozmytego regulatora typu PD.
Rozwiązanie: Zgodnie z procedurą przedstawioną w tym rozdziale syntezę bazy reguł rozmytego regulatora typu PD przeprowadzimy w trzech krokach.
Krok 1 (formalny)
Załóżmy regulator typu PD o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e \) i prędkość tej odchyłki \( \Delta e \). Prędkość odchyłki \( \Delta e \) w dyskretnej chwili k wyznaczymy z różnicy wartości odchyłki \( e \) w chwili k-tej i w chwili ją poprzedzającej tj. \( e_{k-1} \). Wyjściem regulatora jest sygnał sterujący (nastawiający) regulatora \( v \). Przyporządkujmy odchyłce regulacji zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zaś zmiennej lingwistycznej <wyjście regulatora>" symbol \( v \). Załóżmy dalej, że zmiennej \( e \) przyporządkujemy trzy wartości <odchyłka ujemna>, <odchyłka zerowa> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \) , \( Z_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna prędkość odchyłki regulacji>, <zerowa prędkość odchyłki regulacji> i <dodatnia prędkość odchyłki regulacji>. Wartościom tym nadano nazwy symboliczne: \( N_{\Delta e} \), \( Z_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej \( v \) przyporządkowano wartości <ujemne wyjście regulatora>, <zerowe wyjście regulatora> i <dodatnie wyjście regulatora>. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_v \), \( Z_v \) i \( P_v \).
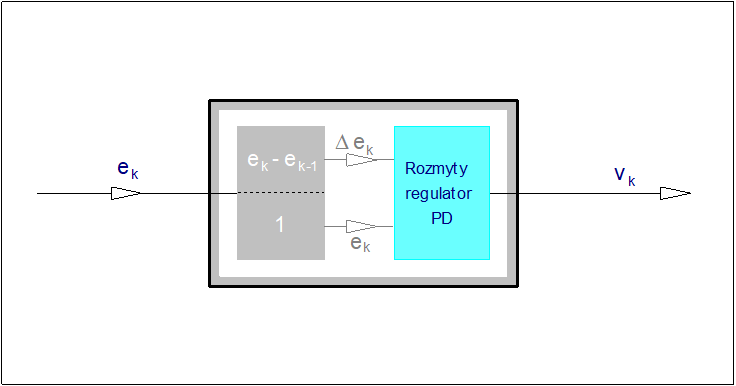
Założymy, że kształty zbiorów rozmytych wejść i wyjścia regulatora będą identyczne jak dla regulatora PI (Rys. 35), jedynie z tą jedynie różnicą, że w miejsce symbolu \( \Delta v \) na tym rysunku zostanie podstawiony symbol \( v \).
Krok 3 (projekt bazy reguł)
Posiłkując się znajomością ogólnej reguły warunkowej (147) regulatora rozmytego typu PD oraz mając na uwadze kształt funkcji przynależności jak na Rys. 35, zbudujemy zupełną bazę reguł modelu regulatora rozmytego. W przypadku rozważanego regulatora typu PD mamy do czynienia z układem o dwóch wejściach (i=2) i jednym wyjściu. Obu wejściom przyporządkowano odpowiednio: \( n_1=3 \) i \( n_2=3 \) zbiorów rozmytych. Stąd, liczba reguł bazy zupełnej zgodnie ze wzorem (102).
wynosi: \( r=1\cdot (3\cdot 3)=9 \). Tabelę reguł dla tego regulatora przedstawiono w Tab. 13.| Regulator rozmyty typu PD |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | \( N_{\Delta v} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) |
| \( Z_{\Delta e} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | |
| \( P_{\Delta e} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | \( P_{\Delta v} \) | |
Dość zaskakujące jest to, że jest ona identyczna jak dla regulatora typu PI.
Nasuwa to praktyczny wniosek, że proces wnioskowania i wyniki tego procesu będą identyczne jak w przypadku regulatora PI (Tab. 10). Dotyczy to oczywiście także identycznej powierzchni sterowania przedstawionej na Rys. 36. Wniosek ten ma duże znaczenie praktyczne. W przypadku implementacji różnych algorytmów sterowania wystarcza bowiem zaimplementować jedną ogólną procedurę regulatora rozmytego. Wywołanie takiej procedury z różnymi zestawami parametrów formalnych generuje różne typy regulatorów (P, PI, PD).
Z podobieństwa tabel sterowania regulatorów PI i PD można próbować wyprowadzić wniosek o uniwersalności reguł sterowania, co niewątpliwie ma duże znaczenie praktyczne. Tak jest w istocie. W praktyce dostępne są uniwersalne (tzw. szablonowe) bazy reguł, które można implementować do modelowania całej klasy pokrewnych układów rozmytych. Stosowane są one często jako bazy wyjściowe w procesie iteracyjnym polegającym na strojeniu reguł bazy, liczby, kształtu i położenia funkcji przynależności. Zagadnienie strojenia układów rozmytych wychodzi jednak poza zakres tego skryptu.
Powstaje w związku z tym pytanie, na czym polega różnica pomiędzy implementacją regulatorów typu PI i PD. Otóż różnica polega nie tyle na różnicy w metodzie prowadzeniu procesu wnioskowania rozmytego, co na różnicy struktur obu regulatorów, co zilustrowano na Rys. 34 i Rys. 38.
Zwróćmy także uwagę, że jeśli w równaniu (145) dokonamy podstawienia \( \Delta e=0 \), to regulator PD ulegnie przekształceniu do regulatora typu P. Wówczas sygnał wyjściowy będzie wprost proporcjonalny wyłącznie do odchyłki regulacji co jest charakterystyczną cechą regulatora o działaniu proporcjonalnym.
| \( jezeli\; (e=E)\cap(\Delta e=\Delta E)\; to\; (v=V) \) | (148) |
|---|
Technicznie redukcja regulatora PD do regulatora typu P polega na wyeliminowaniu z Tab. 13 wierszy dotyczą wartości niezerowych rozmytych prędkości odchyłek regulacji. Postać zredukowanej tabeli sterowań dla regulatora typu P przedstawiono w Tab. 14.
| Regulator rozmyty typu PD |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | |||
| \( Z_{\Delta e} \) | \( N_{v} \) | \( Z_{v} \) | \( P_{v} \) | |
| \( P_{\Delta e} \) | ||||
Zwróćmy także uwagę, że przekształcenie klasycznego regulatora PI do regulatora typu P może być dokonane przez podstawienie \( k_d=k_p\cdot T_d=0 \) we wzorze (145). Technicznie można tego dokonać albo przez przyrównanie stałej czasowej różniczkowania \( T_d \) do zera albo przez wyeliminowanie akcji różniczkującej z wzoru (145). Pierwszy sposób realizowany był w regulatorach analogowych starszych typów, zaś drugi jest obecnie stosowany powszechnie we współczesnych regulatorach implementowanych w technice cyfrowej.
4.6. Rozmyty regulator typu PID
Transmitancja operatorowa idealnego liniowego regulatora PID dana jest równaniem:
| \( G(s)=k_p\left(1+\frac{1}{T_is}+T_{d}s\right) \) | (149) |
|---|
Ponieważ w naszym przypadku:
| \( G(s)=\frac{V(s)}{E(s)} \) | (150) |
|---|
gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora. Po uwzględnieniu (149) i (150) otrzymujemy:
| \( V(s)=k_p\left(1+\frac{1}{T_is}+T_{d }s\right)E(s) \) | (151) |
|---|
Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:
| \( v(t)=k_p\cdot e(t)+k_i\cdot \int_0^t e(t)dt+k_d\cdot\frac{de(t)}{dt} \) | (152) |
|---|
gdzie: \( k_p \) - współczynnik wzmocnienia proporcjonalnego, \( k_i=k_p/T_i \) - współczynnik członu całkującego, \( k_d=k_p\cdot T_d \) - współczynnik członu różniczkującego.
Różniczkując obustronnie równanie (152) otrzymujemy:
| \( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e+k_d\cdot \frac{d^2e(t)}{dt^2} \) | (153) |
|---|
co prowadzi do wniosku, że działanie regulatora PID polega na tym że:
zmiana sygnału wyjściowego regulatora typu PID jest proporcjonalna do prędkości zmian odchyłki regulacji (akcja proporcjonalna) jak również do wartości tej odchyłki (akcja całkująca) oraz jej przyśpieszenia (akcja różniczkująca).
W systemach z czasem dyskretnym z okresem impulsowania \( \Delta t \) równanie (153) przybiera postać równania różnicowego:
| \( \Delta v=K_p \cdot \Delta e + K_{i}\cdot e+K_D\cdot \Delta(\Delta e) \) | (154) |
|---|
gdzie: \( K_p=k_P \); \( K_i=k_I\cdot \Delta t \); \( K_d=k_D⁄\Delta t \); \( \Delta t=cont=1 \).
Równanie (154) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PID. Reguły te można zapisać w postaci ogólnej:
| \( jezeli\; (e=E)\cap(\Delta e=\Delta E)\cap(\Delta(\Delta e)=\Delta(\Delta E))\; to\; (\Delta v=\Delta V) \) | (155) |
|---|
gdzie: \( E \), \( \Delta E \), \( \Delta (\Delta E) \), \(\Delta V \), - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji>, <zmiana zmiany odchyłki regulacji> i <zmiana wyjścia regulatora>.
Wyjście dyskretnego regulatora PID wyznaczymy w sposób analogiczny jak dla regulatora PI.
| \( v=\sum_{i=1}^k \left\{k_{P}(e_i-e_{i-1})+k_I\cdot e_i+k_{D}\cdot (e_{i}-2e_{i-1}+e_{i-2})\right\}+v_0 \) | (156) |
|---|
Projekt rozmytego regulatora typu PID.
Zgodnie z procedurą przedstawioną w podrozdziale 3.1, syntezę bazy reguł rozmytego regulatora typu PID przeprowadzimy w trzech krokach.
Krok 1 (formalny)
Załóżmy regulator typu PID o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e\), prędkość odchyłki regulacji \( \Delta e \) oraz przyśpieszenie odchyłki regulacji \(\Delta^2e \). Wyjściem regulatora będzie zmiana sygnału sterującego (nastawiającego) regulatora\(\Delta v \). Przyporządkujmy zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zmiennej lingwistycznej <przyśpieszenie odchyłki regulacji> symbol \( \Delta^2e \), zaś zmiennej lingwistycznej <zmiana wyjścia sterującego> symbol \( \Delta v \).
Załóżmy dalej, że zmiennej \( e \) przyporządkowano dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <prędkość ujemna odchyłki regulacji> i <prędkość dodatnia odchyłki regulacji>. Wartościom tym nadano także nazwy symboliczne: \( N_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej <przyśpieszenie odchyłki regulacji> \( \Delta^2e \) przyporządkowano wartości <przyśpieszenie ujemne odchyłki regulacji> i <przyśpieszenie dodatnie odchyłki regulacji>. Wartościom tym nadano nazwy symboliczne: \( N_{\Delta^2e} \) i \( P_{\Delta^2e} \). Zmiennej \( \Delta v \) przyporządkowano wartości <ujemna zmiana sterowania>, <zerowa zmiana sterowania> i <dodatnia zmiana sterowania>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \). Ogólny schemat struktury rozmytego regulatora PID przedstawiono na Rys. 39.
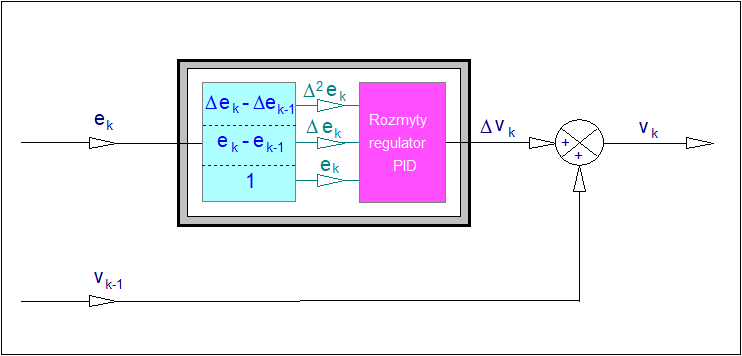
Krok 2 (projekt zbiorów rozmytych)
Załóżmy, że kształt zbiorów rozmytych wejść i wyjścia regulatora PID będzie identyczny jak dla regulatora PI (rys. 35), jedynie z tą różnicą, że dodatkowo wprowadzimy funkcje przynależności \( \mu_N(\Delta^2e) \) i \( \mu_P(\Delta^2e) \), które będą się pokrywały z funkcjami \( \mu_N(\Delta e) \) i \( \mu_P(\Delta e) \).
Krok 3 (projekt bazy reguł)
Posiłkując się znajomością ogólnej reguły warunkowej 154 regulatora rozmytego typu PID oraz mając na uwadze zarówno kształt funkcji przynależności jak na Rys. 35 z uwagą sformułowaną w kroku nr 2 oraz dodatkowo biorąc pod uwagę ogólne wnioski z rozważań przeprowadzonych w podrozdziale 3.1, zbudujemy zupełną bazę reguł modelu regulatora rozmytego. W przypadku rozważanego regulatora typu PID mamy do czynienia z układem o trzech wejściach (i=3) i jednym wyjściu. Wejściom przyporządkowano odpowiednio: \( n_1=n_2=n_3=2 \) zbiorów rozmytych. Stąd, liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (2\cdot 2\cdot 2)=8 \). Tabelę reguł dla tego regulatora przedstawiono na Tab. 15.
Zwróćmy uwagę, że znaczna liczba reguł w tej tabeli generuje identyczne wnioski. Takie reguły, które mają różne poprzedniki lecz identyczne następniki będziemy nazywali regułami alternatywnymi. Wnioski generowane przez reguły alternatywne podlegają agregacji mnogościowej w procesie wnioskowania zgodnej ze schematem Mamdaniego.
Reguły o identycznych poprzednikach, lecz różnych następnikach są regułami sprzecznymi. Reguły takie mogą być generowane np. w systemach automatycznego wydobywania reguł z dużych zbiorów danych np. metodą Wanga-Mendela [7]. Reguły sprzeczne są ewaluowane w celu wyłonienia spośród wielu tylko jednej, którą w świetle danej metody uznaje się za najbardziej wiarygodną.
Tabela 14 zawiera reguły alternatywne. Wszystkie reguły w tej tabeli nie są sprzeczne. Reguły alternatywne w tej tabeli są bardziej konserwatywne niż agresywne. Reguły agresywne forsują silną zmienność następnika reguły przy dowolnej zmianie poprzednika. Reguły konserwatywne niekoniecznie. Zwróćmy dla przykładu uwagę na reguły nr 2 i 3. W tym przypadku silna zmiana przyśpieszenia w regule numer 3 w stosunku do reguły nr 2 nie wywołała żadnej zmiany sterowania.
Zwróćmy także uwagę na dostrzegalny w tej tabeli efekt kompensacji wpływów poprzedników na wartość następnika. Tylko jednoimienne termy zbiorów rozmytych poprzedników reguł generują współbrzmiące wyjście (por. reguły nr 1 i 8). Można potraktować tę obserwację także jako prostą regułę mnemotechniczną.
| Reguła | \( \Delta e \) | \( e \) | \( \Delta^2e \) | \( \Delta v \) |
|---|---|---|---|---|
| 1 | \( N_{\Delta e} \) | \( N_e \) | \( N_{\Delta^2e} \) | \( N_{\Delta v} \) |
| 2 | \( N_{\Delta e} \) | \( N_e \) | \( P_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 3 | \( N_{\Delta e} \) | \( P_e \) | \( N_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 4 | \( N_{\Delta e} \) | \( P_e \) | \( P_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 5 | \( P_{\Delta e} \) | \( N_e \) | \( N_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 6 | \( P_{\Delta e} \) | \( N_e \) | \( P_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 7 | \( P_{\Delta e} \) | \( P_e \) | \( N_{\Delta^2e} \) | \( Z_{\Delta v} \) |
| 8 | \( P_{\Delta e} \) | \( P_e \) | \( P_{\Delta^2e} \) | \( P_{\Delta v} \) |
Zwróćmy także uwagę, że jeśli w równaniu (154) dokonamy podstawienia \( \Delta e=0 \) i \( \Delta (\Delta e)=0 \), to regulator PID ulegnie przekształceniu do regulatora typu P. Wówczas zmiana sygnału wyjściowego będzie wprost proporcjonalna wyłącznie do zmiany odchyłki regulacji co jest charakterystyczną cechą tego typu regulatora.
| \( \Delta v=K_p\cdot \Delta e \) | (157) |
|---|
Technicznie przekształcenie regulatora PID do regulatora typu P polega na wyeliminowaniu z Tab. 15 kolumn \( \Delta e \) i \( \Delta^2 e \).
Podobnie regulator PID może być przekształcony do regulatora typu PI lub PD jeśli wyeliminujemy z Tab. 1 kolumnę \( \Delta^2e \). Pamiętajmy, że w tym przypadku, mimo, że tabele reguł są dla obu regulatorów identyczne, to różnią się one strukturami (por. Rys. 34 i 38).
Z powyższych rozważań wynika uwaga o dużym znaczeniu praktycznym w przypadku implementacji algorytmów regulacyjnych. Wystarcza bowiem zaimplementować jedną ogólną procedurę regulatora rozmytego. Wywołanie takiej procedury z różnymi zestawami parametrów formalnych generuje różne typy regulatorów (P, PI, PD, PID).
5. Implikacja Takagi-Sugeno
Takagi i Sugeno [9] zaproponowali schemat wielowymiarowego rozumowania rozmytego bazując na zbiorze specyficznych implikacji rozmytych, które, jak to pokażemy później, przy pewnych założeniach dodatkowych mogą być uważane za szczególne przypadki zmodyfikowanej implikacji Mamdaniego. Implikacja zaproponowana przez Takagi i Sugeno (T-S) ma następująca postać ogólną:
| \( R: If\quad f(x_1 \:is\: A_1,\;\dots,x_n \:is\: A_n)\quad then\quad y=g(x_1,\dots,x_n) \) | (158) |
|---|
gdzie: \( y \) – zmienna wyjściowa, której wartość podlega wnioskowaniu, \( x_1 \),…, \( x_n \) – zmienne ostre poprzednika i następnika implikacji, \( A_1 \),…, \( A_n \) – zbiory rozmyte o liniowych funkcjach przynależności reprezentujące podprzestrzenie rozważań, zmiennych \( x_1 \),…, \( x_n \)( , \( f \) - funkcja logiczna określająca związek następnika i poprzednika implikacji, \( g: \mathbb{R}^k\to \mathbb{R} \) – funkcja, która określa wartość zmiennej wyjściowej \( y \).
Jak łatwo zauważyć implikacja T-S przypisuje stopień spełnienia funkcji ostrej wejść ostrych na podstawie oceny rozmytej poprzednika reguły. Czy nie jest to więc implikacja będąca szczególnym przypadkiem implikacji Mamdaniego? W tym celu musimy odpowiedzieć na pytanie czy następnik tej implikacji spełnia warunki konieczne funkcji rozmytej. Otóż w ogólnym przypadku można ostrą i zależną od wejść wartość wyjścia potraktować jako dynamiczny rozmyty zbiór singletonowy, ale tylko wtedy, gdy jego wysokość zawierać się będzie w przedziale domkniętym \( [0,1] \). Takiego warunku jednak Takagi i Sugeno nie postawili. W sensie formalnym implikacja T-S nie może być więc uznana za szczególny przypadek implikacji Mamdaniego.
Gdybyśmy jednak zrelaksowali warunek na wysokość zbiorów rozmytych wyłącznie do poprzedników implikacji, to implikacja T-S mogłaby być uznana za specyficzną, zmodyfikowaną implikację Mamdaniego.
Wnioskowanie rozmyte z implikacją T-S realizowane jest w oparciu zarówno na pojedynczej jak i na w zbiorze reguł \( R^{(n)} \)
5.1. Wnioskowanie bazujące na pojedynczej regule
Wnioskowanie T-S bazujące na pojedynczej regule polega na przyporządkowaniu stopnia spełnienia wyjścia ostrego identycznie jak w przypadku implikacji Mamdaniego (82), a więc w istocie na wyznaczeniu relacji rozmytej. Wniosek ma więc charakter rozmyty.
Wnioskowanie z jedną regułą typu Takagi-Sugeno
Zadanie: Wyznaczyć wniosek z reguły Takagi-Sugeno w postaci:
| \( R: If\quad (e\:\:is\:\: N_e)\cap(\Delta e\:\:is\:\: N_{\Delta e} )\quad then\quad (\Delta v=0,5e-\Delta e+0,1) \) | (159) |
|---|
dla: \( e_0=0,8 \); \( \Delta e_0=0,2 \); \( \mu_N(e_0)=0,7 \); \( \mu_{N\Delta e}(\Delta e_0)=0,9 \).
Rozwiązanie: Zgodnie z zasadami wnioskowania, stopień spełnienia następnika reguły wynosi:
| \( \tau = min (0,7,\;0,9) =0,7 \) | (160) |
|---|
Z relacji (159) dla \( e_0=0,8 \); \( \Delta e_0=0,2 \) uzyskujemy:
\( \Delta v=0,5\cdot 0,8-1\cdot 0,2+0,1=0,3 \)
Zatem wniosek z reguły może być interpretowany jako singletonowy zbiorem rozmyty \( \{0,3/0,7\} \).
Interpretować ten wniosek należy w ten sposób, że dla wejść regulatora równych odpowiednio: \( e_0=0,8 \); \( \Delta e_0=0,2 \) , jego wyjście jest równe \( 0,3 \) w stopniu \( 0,7 \).
Wnioskowanie oparte na pojedynczej regule można traktować jako transformację wejść ostrych w singletonowy rozmyty zbiór wyjściowy. Dla wszystkich możliwych kombinacji wejść, wyjściem reguły jest hiperpowierzchni zbiorów rozmytych rozpiętej w przestrzeni rozważań wejść.
W przykładzie 28 wyjściem reguły jest singletonowy zbiór rozmyty definiujący punkt hiperpowierzchni wyjść rozpiętej nad dwuwymiarową przestrzenią rozważań wejść \( e\times \Delta e \).
5.2. Wnioskowanie bazujące na zbiorze reguł
Takagi i Sugeno zaproponowali niezwykle prosty schemat wyostrzania rozmytych wniosków cząstkowych generowanych przez wszystkie reguły zbioru reguł. Motywacją do propozycji takiego sposobu było następujące rozumowanie, które obaj autorzy wyłożyli w [9]. W zadaniach modelowania bazujących na danych istotne są dwa elementy. Jednym z nich jest narzędzie matematyczne prowadzące do definicji tego modelu, a drugim jest metoda identyfikacji parametrów tego modelu. Zdaniem Takagi i Sugeno narzędzie matematyczne powinno być proste i mieć charakter generalizujący.
Zwróćmy uwagę, że jeśli wnioski rozmyte wyprowadzone na podstawie wnioskowania bazujących pojedynczych reguł uznamy za racjonalne to wniosek oparty na zbiorze reguł, a więc na zbiorze wniosków cząstkowych może być wyznaczony w prostu sposób jako arytmetyczna suma ważona tych wniosków:
| \( y^*=\frac{\sum_{i=1}^{n}y_i\cdot \mu_i}{\sum_{i=1}^{n}y_i } \) | (161) |
|---|
Właśnie ten sposób wyostrzania wniosków ze zbioru reguł został przyjęty przez Takagi i Sugeno. Zwróćmy także uwagę, że jest to sposób identyczny jak w przypadku wyostrzania w metodzie wnioskowania Mamdaniego metodą COG, COS i COLA dla przypadku gdy wyjścia reguł mają kształt singletonów.
W przypadku szczególnym wnioskowania opartego wyłącznie na jednej regule wzór (161) przybiera postać:
| \( y^*=y \) | (162) |
|---|
W związku z tym, po wyostrzeniu wniosku z reguły (159) w przykładzie 28 otrzymujemy ostatecznie: \( \Delta v^*=0,3 \).
Ogólny algorytm wnioskowania Takag-Sugeno sprowadzić można do trzech zasadniczych kroków:
- Krok 1: Wyznaczenie stopnia spełnienia (wag) przesłanek każdej reguły
- Krok 2: Wyznaczenie wyjścia ostrego każdej reguły
- Krok 3: Wyznaczenie wyjścia ostrego ze zbioru reguł
Wnioskowanie S-T oparte na zbiorze reguł
Zadanie: Wyznaczyć wyjście aproksymatora S-T danego w postaci zbioru czterech następujących reguł:
| \( \begin{array}{c} R^{(1)}:if\; (e\:\:is\:\:N_e)\;\cap\; (\Delta e\:\:is\:\:N_{\Delta e})\; then\; (\Delta v=0,5e-0,5\Delta e+0,5)\; \\ R^{(2)}:if\; (e\:\:is\:\:N_e)\;\cap\; (\Delta e\:\:is\:\:P_{\Delta e})\; then\; (\Delta v=0,5e+0,5\Delta e+0,1)\;\\ R^{(3)}:if\; (e\:\:is\:\:P_e)\;\cap\; (\Delta e\:\:is\:\:N_{\Delta e})\; then\; (\Delta v=1,5e-2,5\Delta e+1,3)\\ R^{(4)}:if\; (e\:\:is\:\:P_e)\;\cap\; (\Delta e\:\:is\:\:P_{\Delta e})\;\; then\; (\Delta v=2,5e-4,0\Delta e-1,0)\; \end{array} \) | (163) |
|---|
dla wejść w chwili czasowej \( t_0 : e_0=0,8; \Delta e_0=0,2 \), którym po rozmyciu przyporządkowano wartości funkcji przynależności:
\( \mu_N(e_0)=0,7; \mu_{N\Delta e}(\Delta e_0)=0,9; \mu_P(e_0)=0,4; \mu_{P\Delta e}(\Delta e_0)=0,6 \).
Rozwiązanie:
Krok 1. Zgodnie z zasadą ewaluacji przesłanek jak w implikacji Mamdaniego, wyznaczymy stopnie przynależności wszystkich poprzedników reguł według zasady minimum:
| \( \begin{array}{c} \mu^{(1)}_{\Delta v}(e_0, \Delta e_0)=min(0,7,\;0,9)=0,7\\ \mu^{(2)}_{\Delta v}(e_0, \Delta e_0)=min(0,7,\;0,6)=0,6\\ \mu^{(3)}_{\Delta v}(e_0, \Delta e_0)=min(0,4,\;0,9)=0,4\\ \mu^{(4)}_{\Delta v}(e_0, \Delta e_0)=min(0,4,\;0,6)=0,4\\ \end{array} \) | (164) |
|---|
Krok 2. Ze zbioru reguł (163) wyznaczmy wyjścia ostre \( \Delta v_0 \) z każdej reguły:
| \( \begin{array}{c} \Delta v^{(1)}(e_0, \Delta e_0) =0,5\cdot 0,8-0,5\cdot 0,2+0,5=0,8\\ \Delta v^{(1)}(e_0, \Delta e_0) =0,5\cdot 0,8+0,5\cdot 0,2+0,1=0,6\\ \Delta v^{(1)}(e_0, \Delta e_0) =1,5\cdot 0,8-2,5\cdot 0,2+1,3=2,0\\ \Delta v^{(1)}(e_0, \Delta e_0) =2,5\cdot 0,8-4,0\cdot 0,2+1,0=2,2\\ \end{array} \) | (165) |
|---|
Krok 3. Ze wzoru (161) wyznaczmy wyjścia ostre ze zbioru reguł:
\( \Delta v^*(e_0,\Delta e_0)=\frac{0,7\times 0,8+0,6\times 0,6+0,4\times 2,0+0,4\times 2,2}{0,7+0,6+0,4+0,4}=1,238 \).
Do istotnych zalet implikacji rozmytej i sposobu wnioskowania zaproponowanego przez Takagi i Sugeno należy zaliczyć przejrzysty sposób wnioskowania i niewątpliwie prostą i szybką w implementacji procedurę wyostrzania. Między innymi z tego powodu regulator Sugeno-Tanga znalazł liczne zastosowania praktyczne zwłaszcza do zadań modelowania (aproksymacji). Z tego powodu wnioskowanie T-S bywa nazywane wnioskowaniem aproksymującym a sam mechanizm wnioskowania nazywany jest aproksymatorem Takagi-Sugeno.
6. Przykłady zastosowań logiki rozmytej
Niewątpliwie najbardziej spektakularnym osiągnięciem teorii zbiorów rozmytych w teorii sterowania było wprowadzenie i zastosowanie praktyczne regulatorów rozmytych. Regulatory rozmyte znajdują obecnie liczne zastosowania zwłaszcza w sterowaniu procesów silnie nieliniowych.
Przykładem jednego z takich urządzeń jest regulator EFTRONIK FM produkcji MERA-PNEFAL S.A.
6.1. Regulator mikroprocesorowy EFTRONIK XF typ U496
Źródło: Dokumentacja techniczno-ruchowa DTR-U496-01, wydanie I, Zakład Systemów Automatyki MERA-PNEFAL S.A., 1997, s. 96.
Czterokanałowy regulator mikroprocesorowy EFTRONIK XF typ U496 produkcji Zakładu Systemów Automatyki MERA-PNEFAL S.A.
Podstawową zaletą regulatora EFTRONIK XF jest możliwość zastosowania liniowych algorytmów regulatorów PID do sterowania procesów nieliniowych. W przypadku procesów nieliniowych, przy znacznych zmianach wartości zadanej SP lub znacznej amplitudzie zakłóceń, regulatory realizujące konwencjonalne algorytmy PID mogą być nieskuteczne w tym sensie, że nie zapewniają uzyskania założonych kryteriów jakości regulacji lub wręcz prowadzą do utraty stabilności.
Jeśli właściwości dynamiczne lub/i parametry regulownego procesu zależą od wartości zadanej, to dla każdej jej wartości (punktu pracy) i niewielkiego otoczenia tego punktu można dobrać lokalny liniowy regulator PID zapewniający spełnienie wymaganych kryteriów jakości regulacji. Można też pokusić się o projekt regulatora PID o parametrach będącymi ciągłymi bądź nieciągłymi funkcjami wartości zadanej. W praktyce można w tym celu posłużyć się zbiorem kilku lub kilkunastu zestawów nastaw (\( k_p \), \( T_i \),\( T_d \)) regulatorów lokalnych zaprojektowanych dla różnych punktów pracy.
Taką właściwość posiada regulator EFTRONIK XF. Umożliwia on zapis i zapamiętanie łącznie do 10 zestawów lokalnych nastaw PID w każdym z jego czterech kanałów regulacyjnych.
Przykładową charakterystykę nieliniowego obiektu regulacji, w którym współczynnik wzmocnienia obiektu \( k_{ob} \) jest funkcją punktu pracy przedstawiono na Rys. 41. Na tym rysunku przedstawiono również sposób określania wartości punktów węzłowych \( SP_i \), dla których wyznaczane są zestawy parametrów lokalnych regulatorów PID.
Sposób ten jest następujący. Najpierw zakres zmian wartości zadanej \( SP \) dzielony jest na obszarów (partycji) wyznaczonych dyskretnymi punktami \( SP_i \). Wartości \( SP_i \) dobierane są w taki sposób, aby różnicom wartości zadanych \( SP_i-SP_{i-1} \) odpowiadały w przybliżeniu takie same zmiany współczynnika wzmocnienia obiektu \( k_{ob} \). Jak można zauważyć, ten sposób wyznaczania punktów \( SP_i \) pozwala w istocie na dokonanie liniowej aproksymacji odcinkowej funkcji \( k_{ob}=f(SP) \).
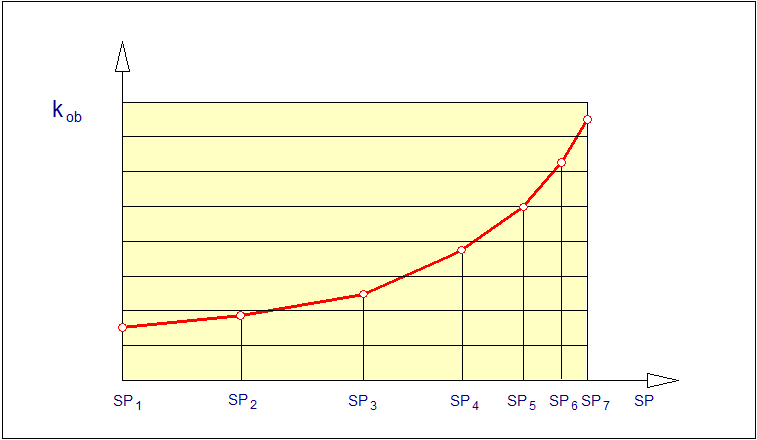
Przypuśćmy, że dla małych odchyleń wielkości regulowanej od wartości \( SP_1 \) uzyskano doświadczalnie zbiór nastaw \( (k_p^{(1)},T_i^{(1)},T_d^{(1)}) \) lokalnego regulatora \( PID^{(1)} \). Podobnie, dla wartości zadanej \( SP_2 \) uzyskano zbiór nastaw \( (k_p^{(2)},T_i^{(2)},T_d^{(2)}) \), itd. Przy zachowaniu odpowiedniej procedury postępowania uzyskane zestawy nastaw mogą być zapisane do pamięci regulatora w postaci odpowiednich tablic.
W przypadku realizacji sterowania rozmytego, w każdym kroku sterowania, a więc dla każdej chwilowej wartości wielkości regulowanej PV następuje wyznaczenie chwilowych nastaw regulatora PID. W tym celu tworzone są w regulatorze w sposób automatyczny zbiory rozmyte o trójkątnych funkcjach przynależności (jak na rys. 42). Liczba zbiorów rozmytych jest równa liczbie zestawów parametrów regulatorów lokalnych wprowadzonych do pamięci kanału regulacyjnego regulatora. Funkcje przynależności tych zbiorów są tak skonstruowane, że każdej wartości regulowanej (mierzonej) \( PV_i \) odpowiadają co najwyżej dwa punkty przecięcia \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \) jak pokazano na Rys. 42.
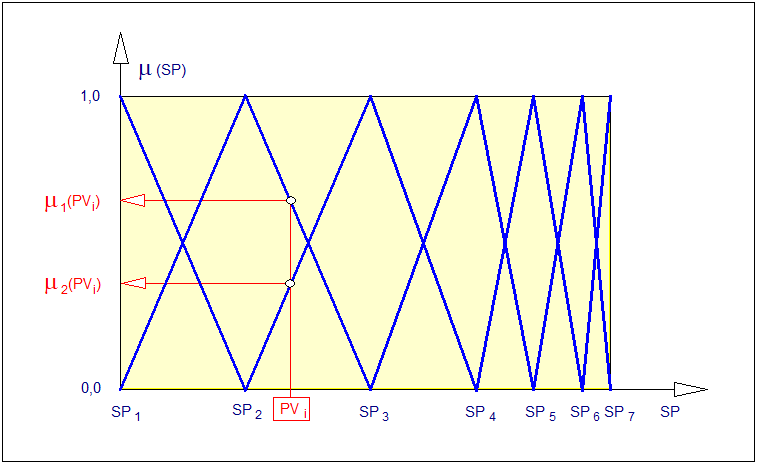
Jeśli zatem wartość sygnału wyjściowego obiektu w i-tej chwili czasowej jest równa \( PV_i \) (tzn. dynamiczny punkt pracy jest równy \( PV_i \)) to odpowiadają mu wartości funkcji przynależności \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \), przy założeniu, że przestrzenie rozważań dla \( SP \) i \( PV \) są tożsame. Z Rys. 42 wynika, że:
| \( \mu_1(PV_i)=\frac{(SP_3-PV_i)}{(SP_3-SP_2)} \) | (166) |
|---|
| \( \mu_2(PV_i)=1-\mu_1(PV_i) \) | (167) |
|---|
Stąd wyznaczane są wartości \( k_p(PV_i) \), \( T_i(PV_i) \) i \( T_d(PV_i) \) z zależności:
| \( k_p(PV_i)=\mu_1(PV_i)\cdot k_{p2}+\mu_2(PV_i)\cdot k_{p3} \) | (168) |
|---|
| \( T_i(PV_i)=\left(\mu_1(PV_i)\cdot k_{p2}\cdot T_{i2} +\mu_2(PV_i)\cdot k_{p3}\cdot T_{i3}\right)/kp_2(PV_i) \) | (169) |
|---|
| \( T_d(PV_i)=0,25\cdot T_i(PV_i)\cdot W_{PID} \) | (170) |
|---|
gdzie: \( k_{p2} \), \( k_{p3} \) - współczynniki wzmocnienia w punktach pracy \( SP_2 \) i \( SP_3 \),
\( T_{i2} \), \( T_{i3} \) - czasy zdwojenia (całkowania)w punktach pracy \( SP_2 \) i \( SP_3 \),
\( PV_i \) - rzeczywisty punkt pracy obiektu regulacji,
\( W_{PID} \) - współczynnik przyjmujący wartość 1 dla regulatora PID i wartość 0 dla regulatora PI.
Spróbujemy wykazać, że ten prosty algorytm rozmytego doboru parametrów regulatora PID jest równoważny wnioskowaniu Takagi-Sugeno. Dla skoncentrowania uwagi przypatrzmy się zależności (166).
Ponieważ \( \mu_1(PV_i) \) (patrz Rys. 42) jest dopełnieniem \( \mu_2(PV_i) \) to ich suma arytmetyczna zgodnie z (49) jest równa 1. Zatem wyrażenie (166) można traktować jako średnią ważoną wartości \( k_{p2} \) i \( k_{p3} \). Współczynnikami wagowymi są tutaj wartości funkcji przynależności \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \). Możemy zatem sądzić, że zależność (166) może być jedną z postaci rozwinięcia wzoru (156). Skoro tak, to dokonamy rekonstrukcji zbioru reguł regulatora pozwalających na wyznaczenie współczynnika wzmocnienia \( k_p \) w postaci:
| \( \begin{array}{c} R^{(1)}:if\; (PV\:\:is\:\:SP_1)\; then\; k_{p}=k_{p1}\\ R^{(2)}:if\; (PV\:\:is\:\:SP_2)\; then\; k_{p}=k_{p2}\\ \dots\dots\\ R^{(n)}:if\; (PV\:\:is\:\:SP_n)\; then\; k_{p}=k_{pn} \end{array} \) | (171) |
|---|
W podobny sposób wyznaczane są: stała czasowa całkowania \( T_i \) oraz stała czasowa różniczkowania \( T_d \).
Zatem regulator EFTRONIK XF należy traktować jako regulator PID, w którym dobór jego parametrów jest zależny od wartości regulowanej i jest realizowany automatycznie z wykorzystaniem wnioskowania aproksymatora rozmytego Sugeno-Takagi.
6.2. Układ regulacji poziomu stali w kokili odlewniczej
Źródło: Kiupel N., Frank P. PI Fuzzy D, International Workshop on Fuzzy Technologies in Automation and Intelligent Systems, Fuzzy Duisburg '94, s. 272..384, Uniwersytet w Duisburgu, 1994.
W procesie ciągłego odlewania stali do regulacji poziomu stali w kokili odlewniczej stosowany jest układ konwencjonalnego regulatora PI. W stanach ustalonych odchyłka regulacji poziomu stali (±1,5 mm) jest wystarczająco mała dla zapewnienia odpowiednio wysokiej jakości produkowanej blachy stalowej. Stosunkowo rzadko zdarzają się jednak istotne zakłócenia procesu polegające na gwałtownym zwiększeniu poziomu stali w kokili. Główną przyczyną tak istotnych zakłóceń jest zjawisko okresowego i gwałtownego odrywania się osadów z powierzchni grzyba zaworu w układzie zasilania kokili (Rys. 43). Zakłócenia te są o tyle groźne, że nie mogą być dostatecznie szybko i skutecznie skompensowane w klasycznym układzie regulacji z regulatorem PI.
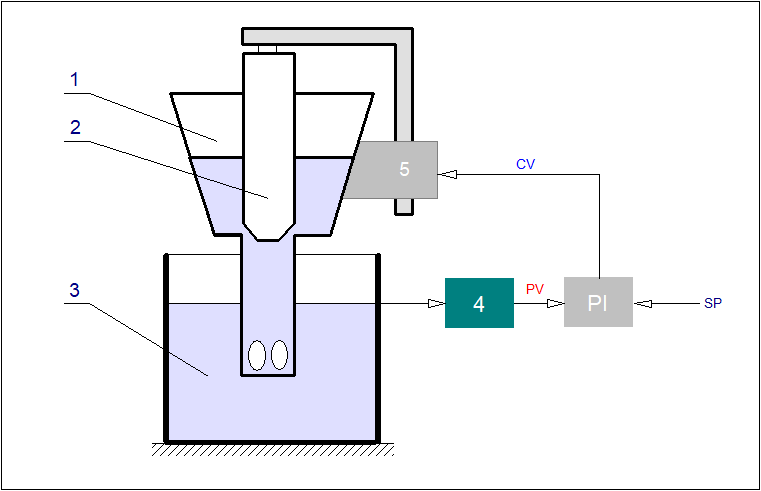
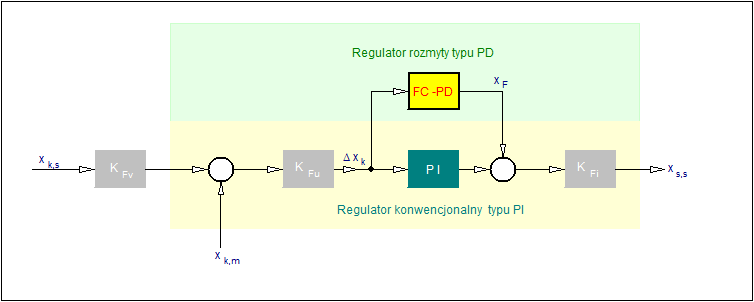
W pierwszym podejściu próbowano skonstruować rozmyty regulator nieliniowy o algorytmie zbliżonym do PI zastępujący regulator klasyczny. Regulator rozmyty przy zwiększonej niewrażliwości zakłóceniowej wykazywał większe odchyłki w stanach ustalonych i odwrotnie. Satysfakcjonującego rozwiązania tzn. małej odchyłki regulacji w stanach ustalonych i wysokiej odporności zakłóceniowej niestety nie dało się uzyskać. W związku z tym przyjęto koncepcję hybrydowego rozmytego regulatora PID złożonego z konwencjonalnego regulatora typu PI i rozmytej akcji różniczkującej (Rys. 44). W regulatorze tym akcja różniczkująca FC-PD jest dołączana do regulatora PI, tylko wówczas, gdy poziom odchyłki regulacji poziomu stali przekroczy pewną wartość progową (\( \pm 4 mm \)) (Rys. 45).
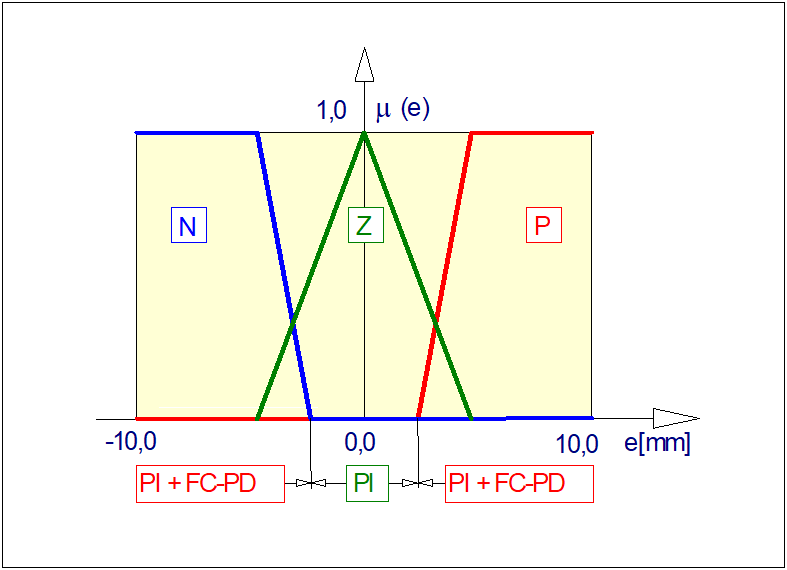
Zastosowano tu ciekawą technikę płynnego kształtowania właściwości dynamicznych regulatora (jego struktury) w zależności od wartości odchyłki regulacji. Dla odmiany w rozdziale 6.1 przedstawiono technikę rozmytego strojenia parametrów regulatora o stałej strukturze.
Na Rys. 46 przedstawiono funkcje przynależności wejścia i wyjścia części różniczkującej zastosowanego regulatora, a w Tab. 16 bazę reguł tego regulatora.
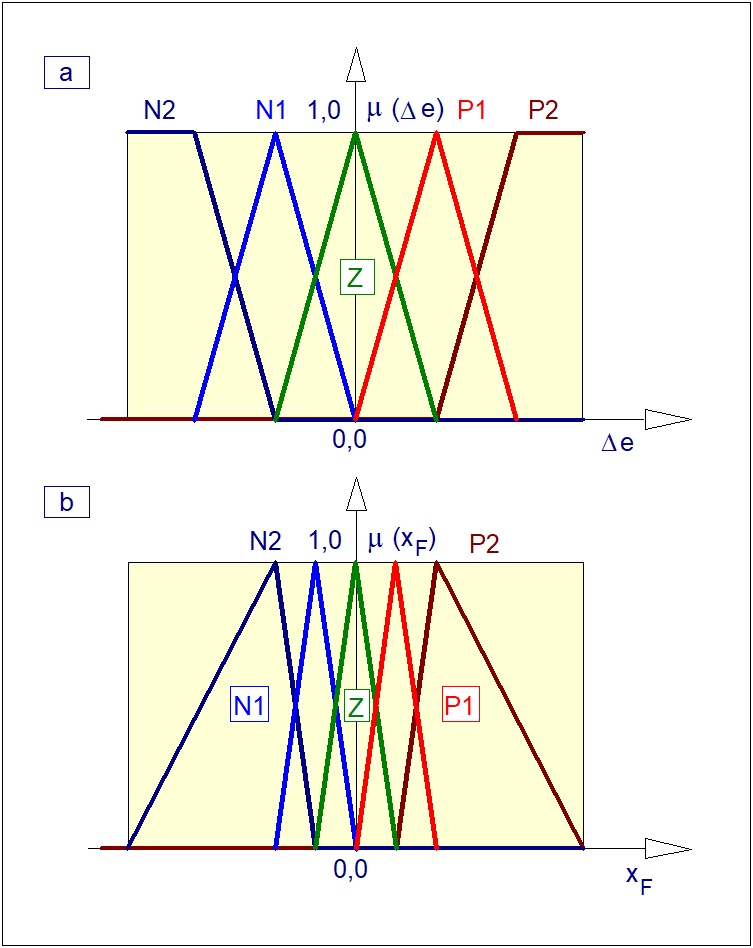
a) Funkcje przynależności wejścia \( \Delta e \)
b) Funkcje przynależności wyjścia \( x_F \) .
| Regulator rozmyty typu PI-FC-D |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N2_{\Delta e} \) | \( N2_F \) | \( Z_F \) | \( Z_F \) |
| \( N1_{\Delta e} \) | \( N2_F \) | \( Z_F \) | \( Z_F \) | |
| \( Z_{\Delta e} \) | \( N2_F \) | \( Z_F \) | \( P1_F \) | |
| \( P1_{\Delta e} \) | \( N1_F \) | \( Z_F \) | \( P1_F \) | |
| \( P2_{\Delta e} \) | \( Z_F \) | \( Z_F \) | \( P1_F \) | |
Z bazy reguł wynika, że w przypadku zerowej odchyłki regulacji wyjście regulatora rozmytego przyjmuje wartość zerową niezależnie od pochodnej odchyłki regulacji. Dotyczy to oczywiście przypadku gdy odchyłka regulacji nie przekracza wartości ±4mm. Jeśli natomiast odchyłka jest dostatecznie ujemna i ujemna jest pochodna tej odchyłki to sterowanie xF wywołuje przemieszczenie grzyba zaworu w dół w celu ograniczenia dopływu stali do kokili i zapobieżenia nadmiernemu wzrostowi poziomu stali. Ze względu na nieliniową charakterystykę sterowania grzyba, funkcje przynależności (Rys. 46) są asymetryczne. Wyniki badań symulacyjnych wskazały, że zastosowanie regulatora rozmytego w tym przypadku pozwoliło na zmniejszenie maksymalnej odchyłki regulacji w odpowiedzi na wymuszenie skokowe nawet o 50%.
Niewątpliwą zaletą tego rozwiązania jest to, że proponuje ono rozwiązanie rgulatora, który w istotny sposób poprawia odporność istniejącego układu regulacyjnego na zakłócenia. Taki, ewolucyjny sposób wdrożenia regulatorów rozmytych jest, jak się wydaje, akceptowalny w praktyce przemysłowej.
6.3. Układ przeciwdziałania blokadzie kół firmy Nisssan
Źródło: Dewitz H., Kasper C, Lieven K.: Entwicklungen und Applikationen von Hardware-Lösungen mit integrierter Fuzzy-Logik. Studie der Fuzzy-Initiative NRW, Düsseldorf, 1993, s. 62.
W przypadku silnego i gwałtownego hamowania pojazdu pojawia się niebezpieczeństwo blokady kół napędowych i utraty sterowności pojazdu. Zadaniem układu ABS jest przeciwdziałanie zjawisku blokowaniu się kół, a przez to zmniejszenie niebezpieczeństwa wpadnięcia pojazdu w poślizg. Z tego powodu często, aczkolwiek mylnie o systemie ABS mówimy jako o systemie antypoślizgowym. Zadanie sterowania jest krytyczne czasowo. Polega ono na automatycznym sterowaniu ciśnienia w układzie hamulcowym w taki sposób, aby nie dopuścić do wystąpienia zjawiska blokady. Ze względu na różne warunki trakcyjne układ ABS musi oddziaływać niezależnie na każde z kół pojazdu. Zwykle spotykane jest rozwiązanie, w którym dla każdego koła pojazdu instalowany jest niezależny układ ABS.
Współczynnik tarcia \( \mu \) koła pojazdu o podłoże w głównym stopniu jest funkcją poślizgu koła \( \lambda \) wyznaczanej z zależności:
| \( \lambda =\frac{v_p-v_k}{v_p}\quad ;\quad v_p\neq0 \) | (172) |
|---|
gdzie: \( v_p \) - prędkość chwilowa pojazdu,
\( v_k \) - prędkość obwodowa koła pojazdu.
Jeśli dla \( v_p>0 \) współczynnik \( \lambda \) jest równy zeru to oznacza, że poślizg nie występuje, a więc prędkość pojazdu jest równa prędkości obwodowej kół. Przypadek taki oczywiście ma znaczenie wyłącznie teoretyczne. Jeśli współczynnik \( \lambda \) jest równy jeden, to oznacza, że koło jest zablokowane, a pojazd porusza się. Przypadek ten niestety nie należy do przypadków wyjątkowych. W stanie pełnego zablokowania kół pojazd traci sterowność, co może doprowadzić do przykrych konsekwencji. W wyniku długotrwałych badań doświadczalnych wyznaczono optymalną wartość współczynnika \( \lambda_{opt}=0,2 \) zapewniającą najkrótszą drogę hamowania pojazdu, bez utraty jego sterowności. Zadanie sterowania układu ABS sformułować można zatem następująco:
Zadaniem układu ABS jest utrzymywanie w czasie hamowania wartości poślizgu kół pojazdu na poziomie optymalnym (\( \lambda_{opt}=0,2 \)).
Wiele rozwiązań systemów ABS bazuje na wyznaczeniu wartości ciśnienia sterującego układem hamulcowym z odpowiednich dwuwymiarowych tabel, w których przechowywano zdyskretyzowane wartości ciśnienia sterowania w zależności od przyśpieszenia kątowego i poślizgu \( \lambda \) kół pojazdu. Efektem ubocznym tego rozwiązania były skokowe zmiany ciśnienia sterującego w układzie hamulcowym ze względu na naturalne ograniczenia w wymiarach stosowanych tablic. Zastosowanie logiki rozmytej pozwoliło na uzyskanie ciągłości sygnału sterującego bez konieczności zwiększania objętości tablic. Ogólny schemat zrealizowanego sprzętowo układu sterowania ABS przedstawiono na Rys. 48. Układ posiada pięć wielkości wejściowych (prędkość pojazdu \( v_p \), przyśpieszenie pojazdu \( dv_p/dt \), prędkość kół pojazdu \( v_k \), przyśpieszenie kół pojazdu \( dv_k/dt \) oraz współczynnik poślizgu kół pojazdu \( \lambda \).
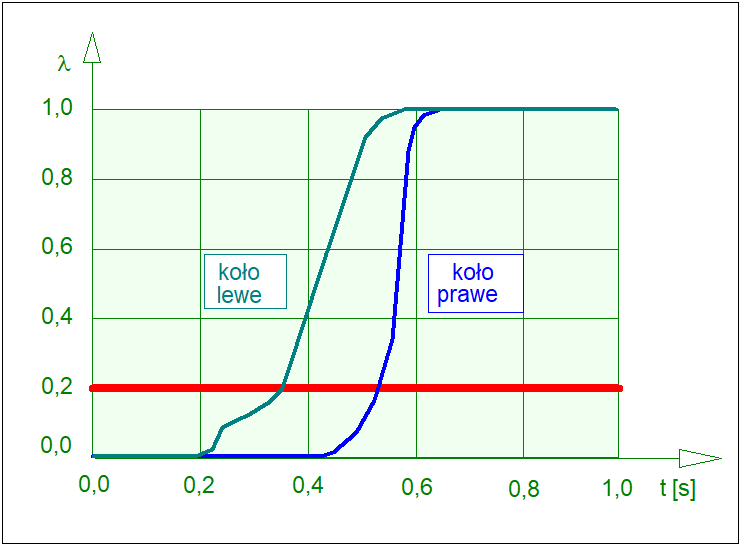
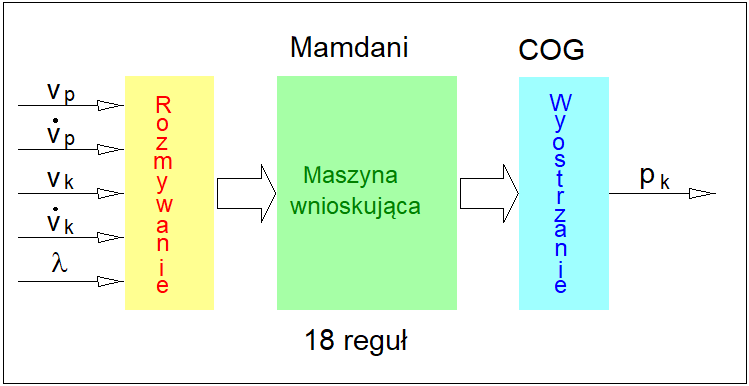
Wyjściem układu jest ciśnienie sterujące układu hamulcowego pk. Postać funkcji przynależności zarówno wejść jak i wyjść chroniona jest tajemnicą firmową. W układzie zastosowano maszynę wnioskującą opartą na wnioskowaniu z zestawu 18 reguł zgodnie ze schematem Mamdaniego.
Na podstawie tak małej liczby reguł w stosunku do liczby wejść należy się domyślać, że zastosowano niezupełna bazę reguł. Wyostrzanie wniosku rozmytego dokonywane jest metodą środka ciężkości obszaru (COG). Maksymalny okres impulsowania tego typu regulatora nie może przekraczać wartości 5 ms. Z tego powodu algorytm sterowania został realizowany sprzętowo.
Dzięki zastosowaniu logiki rozmytej poprawiono warunki eksploatacji układu hamulcowego i wyeliminowano nieprzyjemne dla użytkownika pojazdu pulsowanie pedału hamulca w czasie hamowania.
6.4. Układ antypoślizgowy ASR
Źródło: Hiller M., Schmitz T., Schuster C.: Design of a Fuzzy Traction Control System Using Spatial Vehicle Dynamics Simulation, International Workshop on Fuzzy Technologies in Automation and Intelligent Systems, Fuzzy Duisburg '94, s. 117..126, Uniwersytet w Duisburgu, 1994.
Nadmierne przyśpieszenie pojazdu w warunkach nierównomiernych właściwości ciernych powierzchni jezdni prowadzić może do utraty sterowalności pojazdu ze względu na powstanie niekontrolowanych składowych sił tarcia w kierunku jazdy. Pojazdy o napędzie na przednie koła tracą sterowność, natomiast pojazdy o napędzie na tylne koła zachowują się w sposób nieprzewidywalny.
Systemy ASR są systemami sterowania automatycznego pozwalającymi na ograniczenie współczynnika poślizgu kół do poziomu zapewniającego osiągnięcie właściwych parametrów trakcyjnych pojazdu.
Ograniczenie współczynnika poślizgu wiąże się z aktywnym oddziaływaniem na charakterystyki trakcyjne pojazdu. Istnieją w zasadzie dwa sposoby sterowania właściwościami trakcyjnymi pojazdu. Z jednej strony możliwe jest zmniejszenie momentu obrotowego silnika przez dławienie dopływu mieszanki paliwowo-powietrznej i odpowiednie oddziaływanie na układ zapłonu silnika, z drugiej zaś strony moment napędowy każdego z kół może być ograniczony np. przez odpowiednio kontrolowane hamowanie kół. Obydwie metody w różnym stopniu stosowane są we współczesnych układach ASR. W zakresie niewielkich prędkości pojazdu nadmierne dławienie dopływu mieszanki paliwowej do silnika jest niemożliwe ze względu na potencjalną możliwość zadławienia silnika, w zakresie zaś większych prędkości stosowanie metody ograniczania momentu napędowego przez hamowanie prowadziłoby do zbyt dużego zużycia okładzin hamulcowych i opon kół bieżnych.
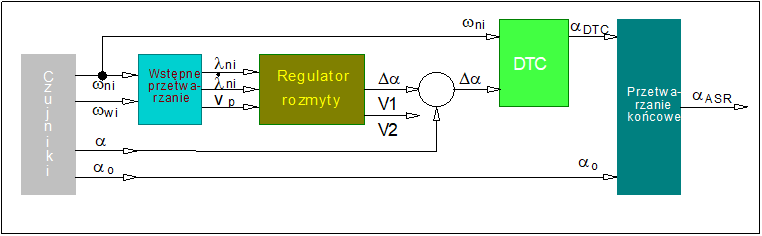
Na podstawie pomiaru prędkości obrotowej kół napędowych i kół ciągnionych (wolnych) (\( \omega_{ni} \), \( \omega_{wi} \)) w układzie wstępnego przetwarzania danych (Rys. 49) następuje wyznaczenie współczynników poślizgów \( \lambda_{ni} \) kół napędowych, \( \lambda_{wi} \) kół wolnych oraz średniej prędkości obwodowej kół wolnych \( v_p \).
| \( v_p =0,5\cdot r_r\left(\omega_{w1}+\omega_{w2} \right) \) | (173) |
|---|
gdzie: \( r_r \) - promień dynamiczny koła, \( \omega_{w1}, \omega_{w2} \) – prędkości kątowe pierwszego i drugiego koła wolnego.
Współczynnik poślizgu \( \lambda_{ni} \) każdego z kół napędowych (i=1, 2) wynosi:
| \( \lambda_{ni} =1-\frac{\omega_{wi}}{\omega_{ni}}\quad ;\quad v_p\neq0 \) | (174) |
|---|
Pochodną współczynnika poślizgu względem czasu można przybliżyć stosunkiem przyrostu współczynnika poślizgu do czasu, w którym on występuje:
| \( \frac{d\lambda_{ni}}{dt}\approx\frac{\lambda_{ni}(t)-\lambda_{ni}(t-\Delta t)}{\Delta t} \) | (175) |
|---|
gdzie: \( \Delta t \) - okres impulsowania regulatora.
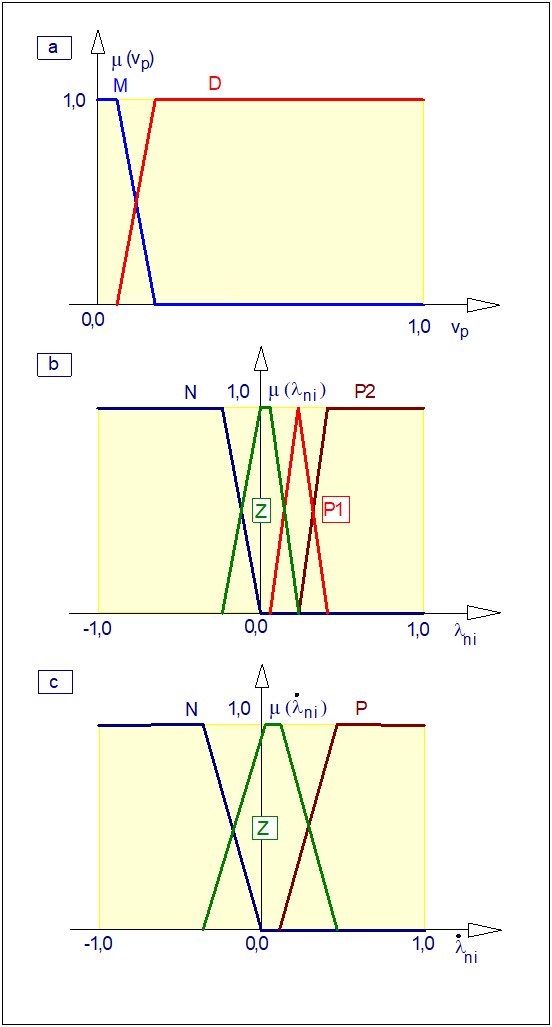
Wielkości \( v_p \), \( \lambda_{ni} \) i \( \frac{d\lambda_{ni}}{dt} \) są wejściami regulatora rozmytego. Na Rys. 50. przedstawiono funkcje przynależności tych wejść. Prędkości średniej pojazdu przyporządkowano dwie wartości: <mała> i <duża>, współczynnikowi poślizgu *ni przyporządkowano cztery wartości: <ujemny>, <zerowy>, <niewielki dodatni> i <duży dodatni>, prędkości współczynnika poślizgu \( \frac{d\lambda_{ni}}{dt} \) przyporządkowano trzy wartości: <ujemny>, <zerowy> i <dodatni>.
Wyjściami regulatora rozmytego są: sygnał zmiany położenia kątowego przepustnicy \( \Delta \alpha \) oraz wartości sterowań rozdzielaczy elektrohydraulicznych o działaniu proporcjonalnym w układach hamulcowych kół napędzających \( V1 \) i wolnych \( V2 \). Na Rys. 51. przedstawiono funkcje przynależności wyjść regulatora rozmytego. Zmianie kąta przepustnicy \( \Delta \alpha \) przyporządkowano pięć wartości: <ujemny duży>, <ujemny mały>, <bez zmian>, <dodatni mały> i <dodatni duży> sygnałom sterującym \( V1 \) i \( V2 \) przyporządkowano po trzy wartości: <zmniejsz sterowanie>, <sterowanie bez zmian> i <zwiększ sterowanie>.
| Regulator rozmyty układ ASR |
\( \lambda_{ni} \) | ||||
|---|---|---|---|---|---|
| \( P2 \) | \( P1 \) | \( Z \) | \( N \) | ||
| \( \Delta \lambda_{ni} \) | \( P \) | \( P \) | \( P \) | \( Z \) | \( N \) |
| \( Z \) | \( P \) | \( P \) | \( N \) | \( N \) | |
| \( N \) | \( P \) | \( Z \) | \( N \) | \( N \) | |
| Regulator rozmyty układ ASR |
\( \lambda_{ni} \) | ||||
|---|---|---|---|---|---|
| \( P2 \) | \( P1 \) | \( Z \) | \( N \) | ||
| \( \Delta \lambda_{ni} \) | \( P \) | \( N2 \) | \( N2 \) | \( Z \) | \( Z \) |
| \( Z \) | \( N2 \) | \( N1 \) | \( P2 \) | \( N1 \) | |
| \( N \) | \( N1 \) | \( Z \) | \( P1 \) | \( N2 \) | |
W maszynie wnioskującej zastosowano schemat wnioskowania Mamdaniego. Oprócz regulatora rozmytego system sterowania trakcyjnego zawiera układ DTC oraz układ końcowego przetwarzania danych. Układ DTC zabezpiecza przepustnicę przed całkowitym zamknięciem, tak aby nie dopuścić do zatrzymania silnika. Końcowy układ przetwarzania danych spełnia rolę komparatora porównującego położenie kątowe przepustnicy (sygnał wyjściowy z regulatora rozmytego ASR) z sygnałem tempomatu w celu ewentualnej korekcji położenia kątowego przepustnicy.
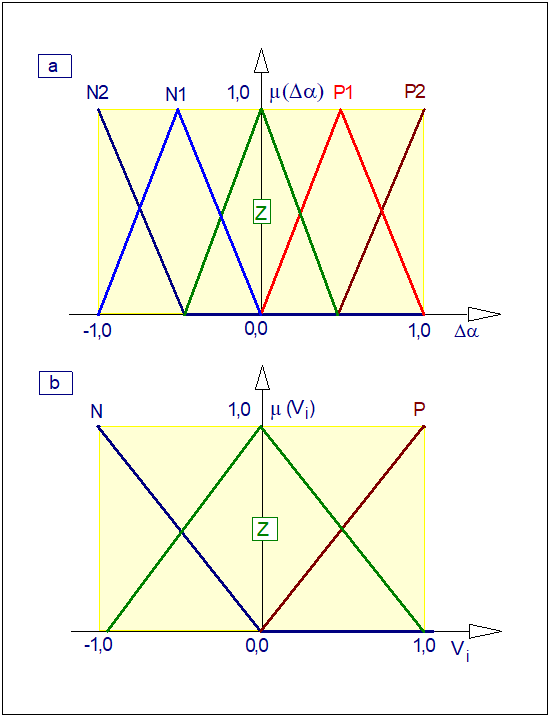
Wyniki symulacji pracy układu dla samochodu Mercedes-Benz W140 przedstawiono na Rys. 52.
Przykład ten wskazuje na walory aplikacyjne regulatorów rozmytych zwłaszcza w warunkach gdy nie jest znany model analityczny obiektu regulacji. Przykład wskazuje również, że do syntezy układów regulacji może być użyta z powodzeniem jakościowa wiedza heurystyczna.