Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Zastosowania Sieci Neuronowych |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | środa, 14 stycznia 2026, 22:03 |
1. Wprowadzenie
Sieci neuronowe są obecnie dynamicznie rozwijającą się dziedziną uczenia maszynowego. Obserwujemy intensywny rozwój modeli językowych (jak czat GPT) oraz modeli do generacji obrazów. Wiele algorytmów wykorzystujących sieci możemy napotkać w codziennym życiu. Do przykładowych zastosowań należą [Chollet, 2022]:
klasyfikacja obrazów (rozpoznawanie jaki obiekt jest na zdjęciu),
detekcja obiektów na obrazach (np. detekcja twarzy na obrazie z kamery),
dopasowanie treści i reklam na portalach społecznościowych do użytkownika,
tłumaczenie maszynowe i korekta tekstu,
systemy odpowiadające na pytania w języku naturalnym,
pojazdy autonomiczne,
cyfrowi asystenci (np. Amazon Alexa),
zamiana mowy na tekst i tekstu na mowę,
programy grające w gry (np. szachy).
Sieci neuronowe znajdują również zastosowania w automatyce i robotyce. Do przykładowych zastosowań należą:
Budowa modeli odwzorowujących wartości zmiennych procesowych (np. model temperatury pary za przegrzewaczem na podstawie temperatury przed przegrzewaczem i wartości sygnału sterującego zaworem). Modele takie mogą być wykorzystywane jako sensory wirtualne, w celu zastąpienia drogich urządzeń pomiarowych, w sterowaniu predykcyjnym lub w diagnostyce przemysłowej, gdzie wyjście modelu porównujemy z mierzonym sygnałem i istotna różnica może być symptomem wystąpienia uszkodzenia [Rostek et al., 2015] [Sztyber-Betley et al., 2023].
Detekcja anomalii. Modele detekcji anomalii mogą być budowane dla pomiarów w dziedzinie czasu (np. temperatura), częstotliwości (np. wibroakustyczna diagnostyka łożysk) oraz dla wizyjnych systemów kontroli jakości [Kocon et al., 2024].
Systemy wizyjne w robotyce - pozwalają robotom na rozpoznawanie i lokalizację obiektów na podstawie obrazu z kamery [Koguciuk et al., 2019] [Gromada et al., 2022].
Interfejsy człowiek-maszyna w robotyce. Tu zastosowania znajdują systemy wizyjne rozpoznawania twarzy i emocji oraz rozwiązania do przetwarzania języka naturalnego, syntezy i rozpoznawania mowy.
Inteligentne rolnictwo - systemy wizyjne do rozpoznawania i lokalizacji roślin mogą być wykorzystywane w robotach do automatycznego zbioru owoców lub usuwania chwastów [Chechliński et al., 2019]. Systemy wizyjne pozwalają również na rozpoznawanie i klasyfikację chorób roślin.
Optymalizacja. Modele predykcyjne (np. cen energii elektrycznej [Kuliński and Sztyber-Betley, 2024]) pozwalają racjonalne planowanie produkcji i gospodarowanie zasobami.
Celem modułu jest przybliżenie zasady działania i algorytmów uczenia sieci neuronowych. Omówimy również bibliotekę Keras (https://keras.io/), pozwalającą na proste i szybkie budowanie złożonych modeli. W części dotyczącej sieci konwolucyjnych przybliżone zostanie działanie systemów wizyjnych wykorzystujących sieci neuronowe. W części projektowej skoncentrujemy się na modelach zmiennych ciągłych, wykorzystywanych w diagnostyce i sterowaniu.
Literatura
|
[Chollet, 2022]
|
Chollet, F. (2022). Deep Learning with Python, Second Edition. Manning. |
|
[Rostek et al., 2015]
|
Rostek, K., Łukasz Morytko, and Jankowska, A. (2015). Early detection and prediction of leaks in fluidized-bed boilers using artificial neural networks. Energy, 89:914--923. [ | DOI | http ] |
|
[Sztyber-Betley et al., 2023]
|
Sztyber-Betley, A., Syfert, M., Kościelny, J. M., and Górecka, Z. (2023). Controller cyber-attack detection and isolation. Sensors, 23(5). [ | DOI | http ] |
|
[Kocon et al., 2024]
|
Kocon, M., Malesa, M., and Rapcewicz, J. (2024). Ultra-lightweight fast anomaly detectors for industrial applications. Sensors, 24(1). [ | DOI | http ] |
|
[Koguciuk et al., 2019]
|
Koguciuk, D., Chechliński, L., and El-Gaaly, T. (2019). 3d object recognition with ensemble learning---a study of point cloud-based deep learning models. In Bebis, G., Boyle, R., Parvin, B., Koracin, D., Ushizima, D., Chai, S., Sueda, S., Lin, X., Lu, A., Thalmann, D., Wang, C., and Xu, P., editors, Advances in Visual Computing, pages 100--114, Cham. Springer International Publishing. |
|
[Gromada et al., 2022]
|
Gromada, K., Siemiątkowska, B., Stecz, W., Płochocki, K., and Woźniak, K. (2022). Real-time object detection and classification by uav equipped with sar. Sensors, 22(5). [ | DOI | http ] |
|
[Chechliński et al., 2019]
|
Chechliński, L., Siemiątkowska, B., and Majewski, M. (2019). A system for weeds and crops identification—reaching over 10 fps on raspberry pi with the usage of mobilenets, densenet and custom modifications. Sensors, 19(17):3787. |
|
[Kuliński and Sztyber-Betley, 2024
|
Kuliński, W. and Sztyber-Betley, A. (2024). Day ahead electricity price forecasting with neural networks - one or multiple outputs? |
2. Uczenie maszynowe
Sieci neuronowe są jednym z algorytmów uczenia maszynowego. Celem tego rozdziału nie jest wyczerpujące wprowadzenie do tematyki, a jedynie przedstawianie podstawowych pojęć, które będą niezbędne dla dalszego zgłębiania sieci neuronowych. Czytelnikowi zainteresowanemu pogłębieniem wiedzy z zakresu uczenia maszynowego polecamy [Geron, 2019] [James et al., 2023].
W problemach uczenia maszynowego możemy wyróżnić:
-
Zadanie - na przykład rozpoznanie czy na zdjęciu znajduje się pies czy kot.
-
Model - pewien zbiór funkcji (np. funkcje liniowe, sieci neuronowe), o dostrajanych parametrach.
-
Funkcję kosztu - liczbową miarę, określającą, jak dobrze model radzi sobie z postawionym zadaniem. Im lepiej model sobie radzi, tym mniejsza wartość funkcji kosztu.
-
Dane - na przykład zestaw oznaczonych zdjęć psów i kotów.
Algorytmy uczenia maszynowego dobierają parametry modelu (np. współczynniki modelu liniowego) minimalizując funkcję kosztu na podstawie wykorzystywanych danych uczących. Dla sieci neuronowych parametry to wagi połączeń między neuronami (rozdział 3). Jest to zmiana paradygmatu w stosunku do klasycznego programowania, ponieważ tu nie precyzujemy konkretnej funkcji realizowanej przez model, a oczekujemy, że model dostroi się do określonego zadania na podstawie danych w procesie uczenia.
Wśród zadań uczenia możemy wyróżnić:
-
Uczenie nadzorowane - algorytm dostaje zbiór danych i oraz prawidłową, oczekiwaną odpowiedź dla każdego przykładu (na przykład zestaw oznaczonych zdjęć psów i kotów). Prawidłową, oczekiwaną odpowiedź, dla danego przykładu, będziemy nazywać etykietą.
-
Uczenie nienadzorowane - algorytm dostaje zbiór danych bez informacji o prawidłowej odpowiedzi. Celem algorytmu jest odkrycie zależności i powiązań w danych. Przykładem jest segmentacja grupy klientów.
-
Uczenie ze wzmocnieniem - algorytm jest agentem, który otrzymuje obserwacje ze środowiska, może wykonywać akcje i dostaje nagrody za swoje działanie. Forma ta jest często wykorzystywana w grach (np. algorytm do gry w szachy).
W tym module będziemy się koncentrować na zadaniach uczenia nadzorowanego. W uczeniu nadzorowanym możemy wyróżnić dwie podstawowe grupy problemów:
-
Regresja - model wyznacza liczbę bądź liczby rzeczywiste. Przykładem jest predykcja cen energii.
-
Klasyfikacja - zadaniem modelu jest przyporządkowaniem przykładu do jednej z dyskretnych klas. Przykładem jest rozpoznawanie, czy na zdjęciu jest pies czy kot.
Literatura
|
[Geron, 2019]
|
Geron, A. (2019). Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. O'Reilly Media, Inc., 2nd edition. |
|
[James et al., 2023]
|
James, G., Witten, D., Hastie, T., Tibshirani, R., and Taylor, J. (2023). An Introduction to Statistical Learning with Applications in Python. Springer Texts in Statistics. Springer, Cham. [ | DOI | http ] |
2.1. Niedouczenie i przeuczenie
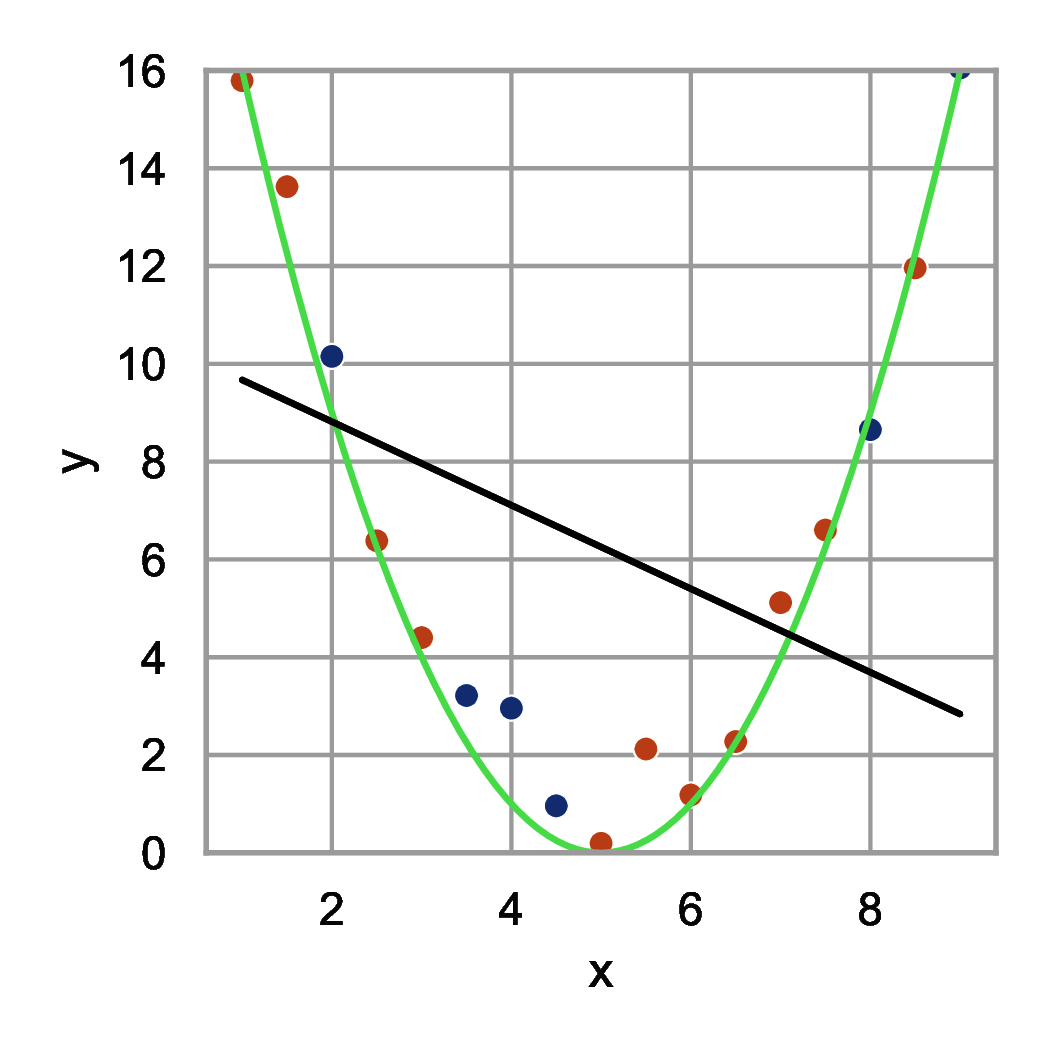
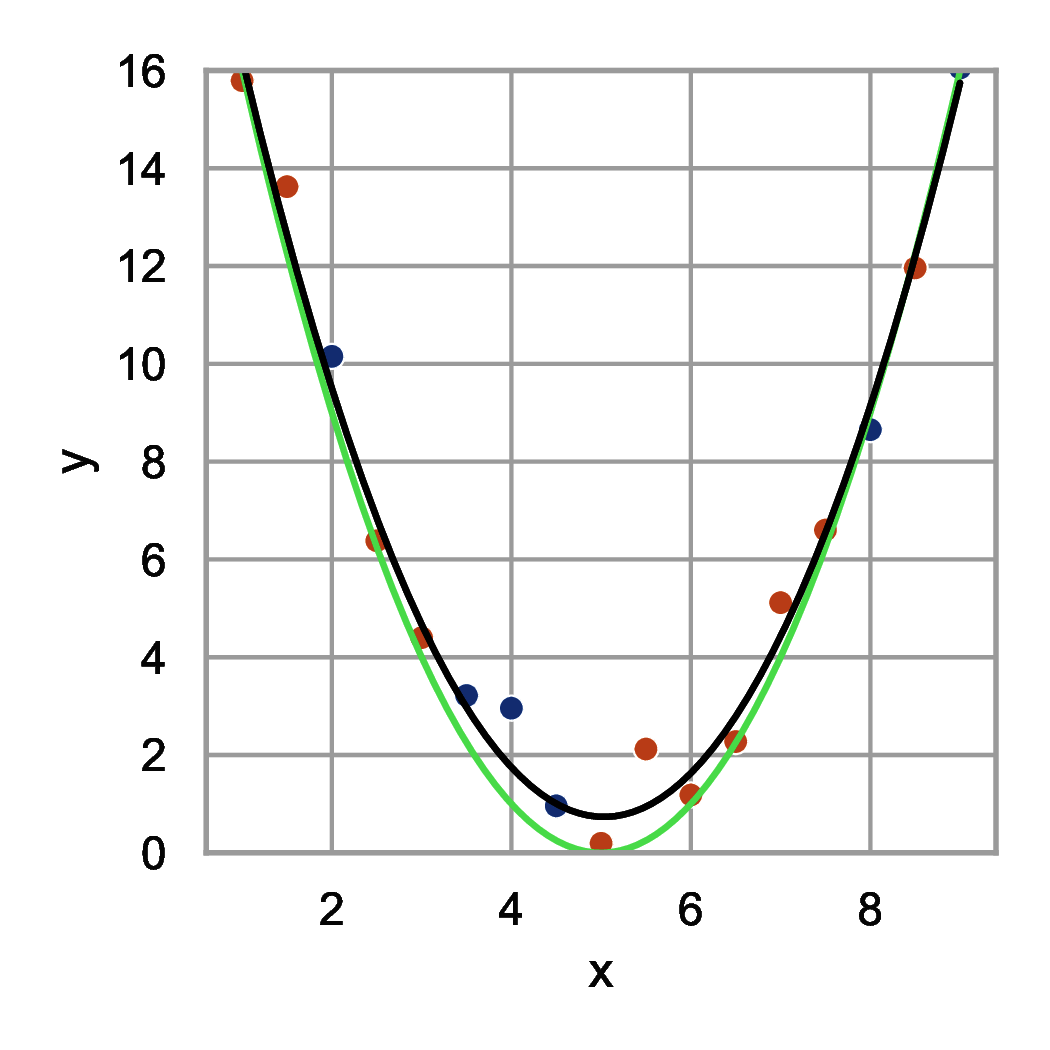
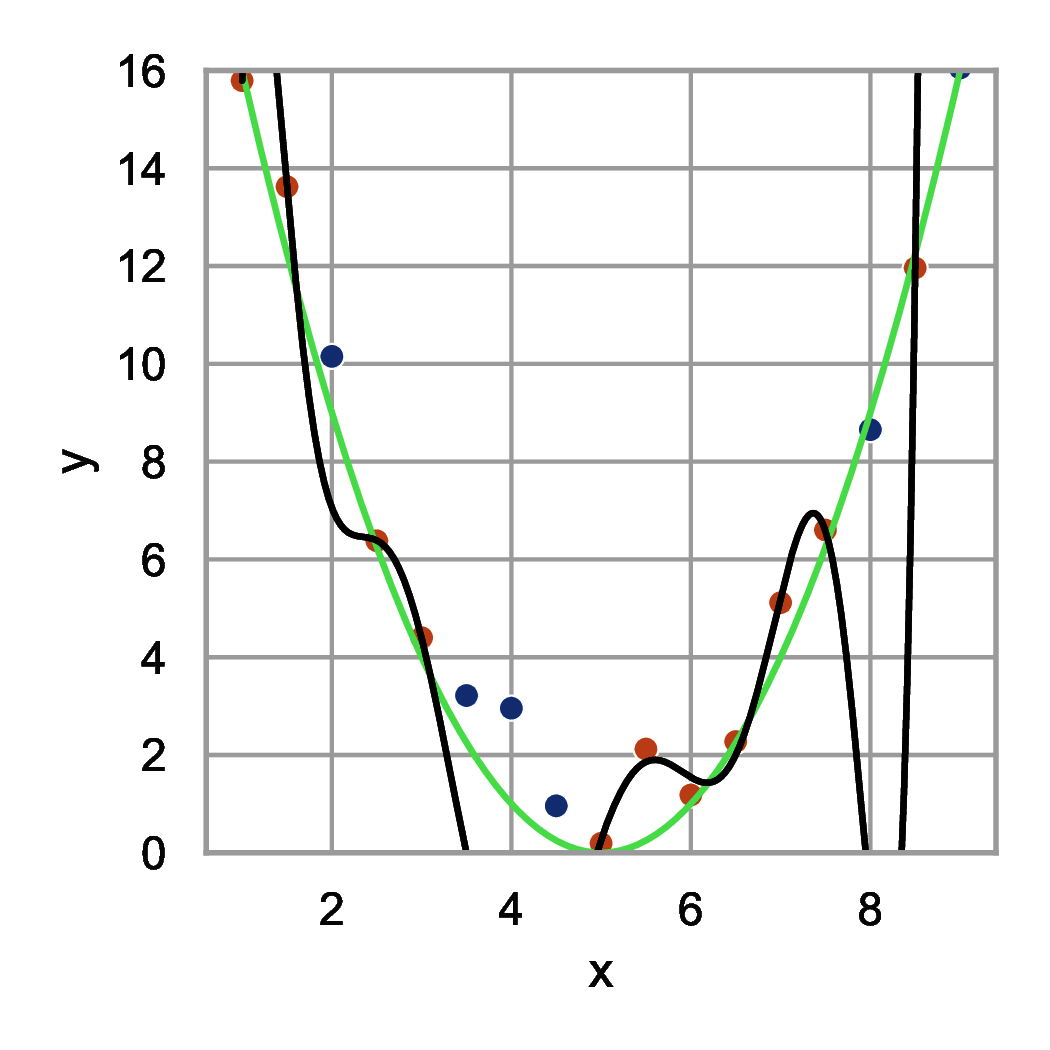
Przyjrzyjmy się wykresom przedstawionym na rysunku 1. Punkty na wykresie (kropki czerwone i niebieskie) zostały wygenerowane na podstawie wzoru \( y(x) = (x-5)^2 \) z dodatkiem szumu. Następnie dopasowano do kropek czerwonych funkcje opisane wielomianami różnych stopni. Podzbiór danych, na podstawie którego dopasowujemy współczynniki modelu (tu współczynniki wielomianu) nazywamy zbiorem uczącym. Podzbiór, na podstawie którego będziemy oceniać, które podejście do modelowania jest najlepsze nazywamy zbiorem walidacyjnym. W naszym przykładzie zbiór walidacyjny stanowią kropki niebieskie i służą one do doboru stopnia wielomianu.
Na rysunku 1(a) widzimy dopasowanie funkcji liniowej (wielomian pierwszego stopnia). Model ten źle odwzorowuje zarówno dane ze zbioru uczącego jak i zbioru walidacyjnego. Mamy do czynienia z modelem zbyt prostym, który nie jest w stanie odwzorować rzeczywistej funkcji generującej dane.
Na rysunku 1(b) widzimy dopasowanie funkcji kwadratowej (wielomianu drugiego stopnia). Model ten dobrze odwzorowuje charakter danych ze zbioru uczącego i walidacyjnego. W tym przypadku wiemy również, że dobraliśmy właściwy stopień wielomianu - taki sam jak użyty do generacji danych. Jednak w praktycznych problemach uczenia zazwyczaj takiej informacji nie mamy i musimy wnioskować na podstawie wielkości błędów dla odpowiednich zbiorów danych.
Na rysunku 1(c) widzimy dopasowanie wielomianu dziewiątego stopnia. Funkcja ta jest bardzo dobrze dopasowana do kropek czerwonych (niemalże przechodzi przez każdy punkt) i bardzo źle do kropek niebieskich. Mamy do czynienia z przeuczeniem modelu. Nasz model dopasował się do szumu i nauczył prawie idealnie przykładów ze zbioru uczącego. Jest to zjawisko bardzo niekorzystne, ponieważ model nie będzie sobie radził dla punktów, które nie zostały wykorzystane w procesie uczenia.
Podsumowując, w uczeniu maszynowym wykorzystujemy następujące zbiory:
-
Zbiór uczący - jest to zbiór wykorzystywany do doboru parametrów modelu. W przykładzie parametrami modelu były współczynniki wielomianu. Dla sieci neuronowych parametry stanowią wagi neuronów.
-
Zbiór walidacyjny - służy do doboru hiper-parametrów modelu. Hiper-parametry to parametry opisujące klasę funkcji przeszukiwanych w procesie uczenia. W przykładzie hiper-parametrem był stopień wielomianu. Dla sieci neuronowych przykładowym hiper-parametrem jest liczba warstw.
-
Zbiór testowy - nie jest wykorzystywany do strojenia parametrów i hiper-parametrów. Służy do wiarygodnej oceny gotowego modelu na nowych danych.
2.2. Algorytmy gradientowe
Algorytmy gradientowe są istotną klasą algorytmów optymalizacji wykorzystywaną szeroko w uczeniu sieci neuronowych. Celem optymalizacji jest dobór parametrów modelu, tak, aby zminimalizować funkcję kosztu. Funkcja kosztu opisuje błąd popełniany przez model dla przykładów ze zbioru uczącego i chcemy ją zmniejszać. Konkretne wzory na funkcje kosztu w różnych zastosowaniach omówimy w rozdziale 3.4.
W podstawowej wersji algorytm minimalizacji metodą spadku działa następująco. Wariant ten nazywamy metodą gradientu prostego:
-
ustaw wartość początkową \( w \) na \( w_0 \)
-
dopóki nie warunek stopu \[ w \gets w - \alpha \frac{\partial J}{\partial w} \]
-
idź do 2.
Poprzez \( w \) oznaczamy parametry naszego modelu (np. wagi sieci neuronowej). Może to być pojedyncza liczba, ale najczęściej jest to wektor lub macierz wielu liczb. Algorytm rozpoczynamy od przypisania wartości początkowej \( w_0 \). Następnie wyznaczamy gradient funkcji kosztu \( J \) po parametrach \( \frac{\partial J}{\partial w} \) i modyfikujemy wartości \( w \) według wzoru \( w \gets w - \alpha \frac{\partial J}{\partial w} \). \( \alpha \) nazywamy współczynnikiem uczenia. Jest to niewielka liczba dodatnia określająca wielkość kroków wykonywanych przez algorytm. Zapętlamy ten krok aż do osiągnięcia warunku stopu.
Warunkiem stopu może być:
-
Wykonanie określonej liczby iteracji lub przekroczenie czasu obliczeń. Warunek ten odnosi się do wykorzystania zasobów obliczeniowych.
-
Osiągnięcie wystarczająco małej wartości funkcji kosztu \( J \). Warunek ten odnosi się do uzyskania zakładanej jakości modelu. Zamiast funkcji kosztu można wykorzystać inną metrykę. Dla uniknięcia zjawiska przeuczenia, zalecane jest wykonywanie sprawdzenia na zbiorze walidacyjnym.
-
Brak poprawy funkcji kosztu w kolejnych iteracjach. Warunek ten odnosi się do braku perspektyw na dalszą poprawę rozwiązania. Dla uniknięcia zjawiska przeuczenia, zalecane jest wykonywanie sprawdzenia na zbiorze walidacyjnym.
-
Osiągnięcie odpowiednio małej wartości modułu gradientu \( \frac{\partial J}{\partial w} \). Małe wartości modułu gradientu oznaczają małe kroki algorytmu. Warunek ten odnosi się do braku perspektyw na dalszą poprawę rozwiązania.
Rozważmy zestaw przykładów dla wypukłej funkcji kosztu i jednowymiarowego \( w \) przedstawiony na rysunku 2. Funkcja ta ma jedno globalne minimum dla wartości \( w^* = 5 \) i \( J(5) = 1 \).
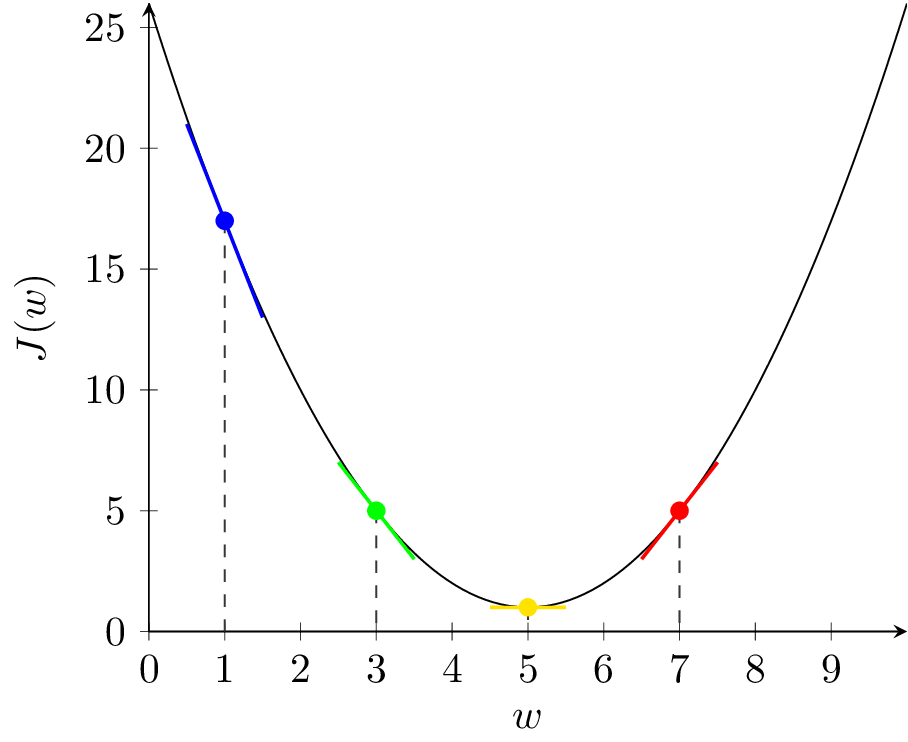
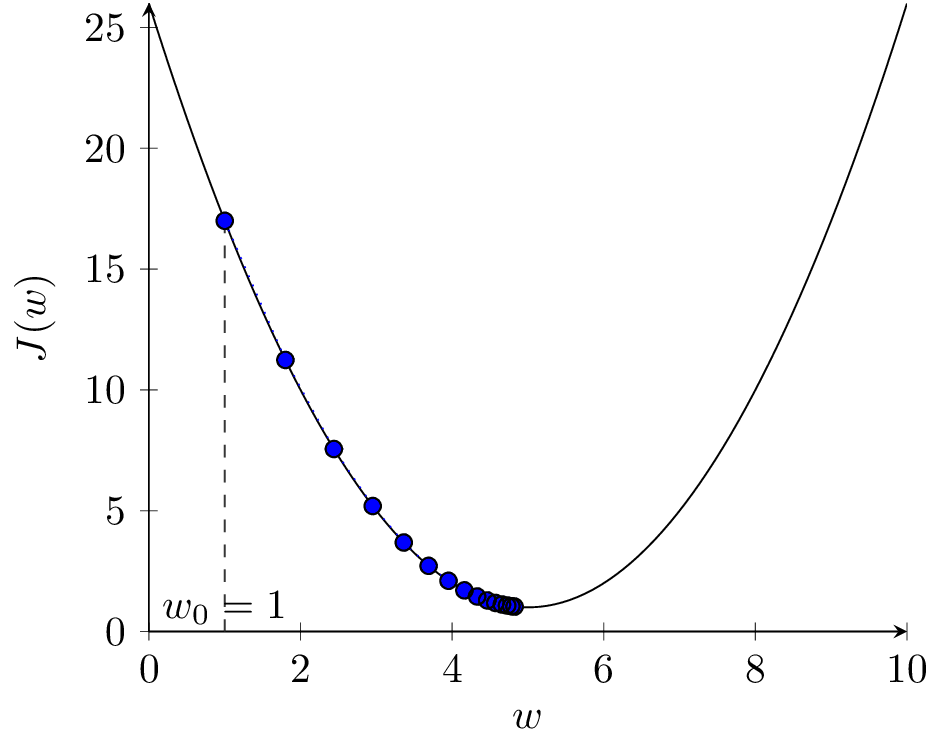
Pochodna \( \frac{\partial J}{\partial w} \) jest współczynnikiem kierunkowym prostej stycznej do wykresu funkcji \( J(w) \). Na rysunku 2(a), w punkcie niebieskim pochodna \( \frac{\partial J}{\partial w} \) ma wartość ujemną. Zatem \( - \alpha \frac{\partial J}{\partial w} \) ma wartość dodatnią i kolejnym kroku zwiększymy wartość \( w \) (przesuniemy się w prawo). Jest to działanie prawidłowe, ponieważ znajdujemy się w punkcie \( w = 1 \) i zwiększanie przybliża nas do optymalnej wartości \( w^* = 5 \). Analogicznie wygląda sytuacja dla punktu zielonego, tylko nachylenie stycznej (pochodna) jest mniejsze, więc algorytm wykona mniejszy krok (mniej zwiększy wartość \( w \)). Odwrotnie, dla punktu czerwonego, pochodna jest dodatnia, więc \( - \alpha \frac{\partial J}{\partial w} \) ma wartość ujemną i w kolejnym kroku zmniejszymy wartość \( w \). Również jest to działanie prawidłowe. Punkt żółty znajduje się w optimum i pochodna wynosi zero. Jeśli trafimy w ten punkt, algorytm się zatrzyma.
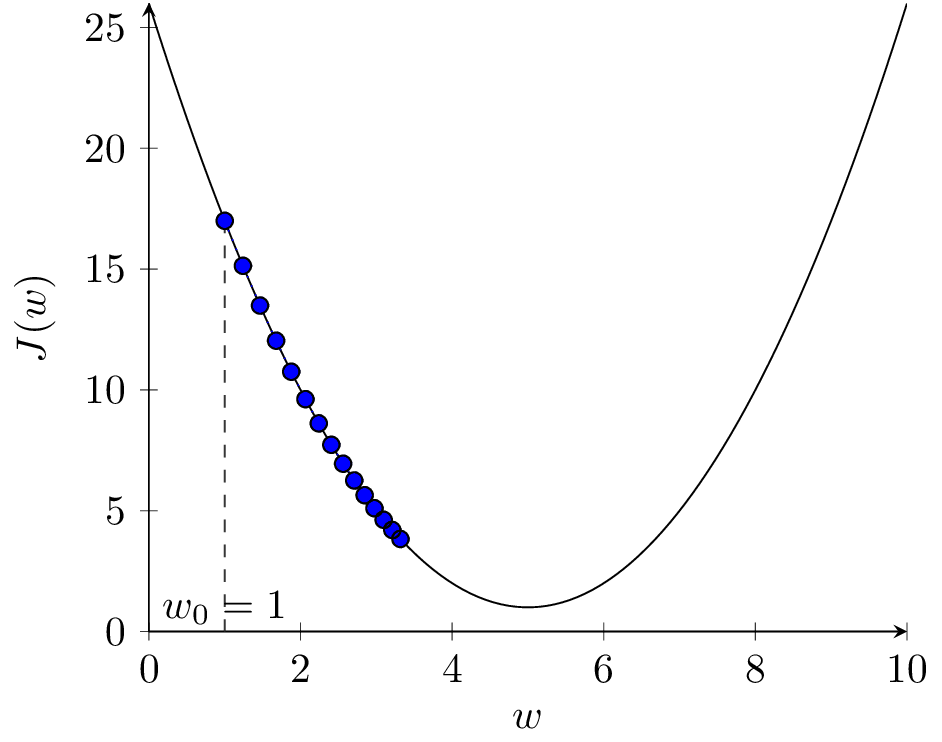
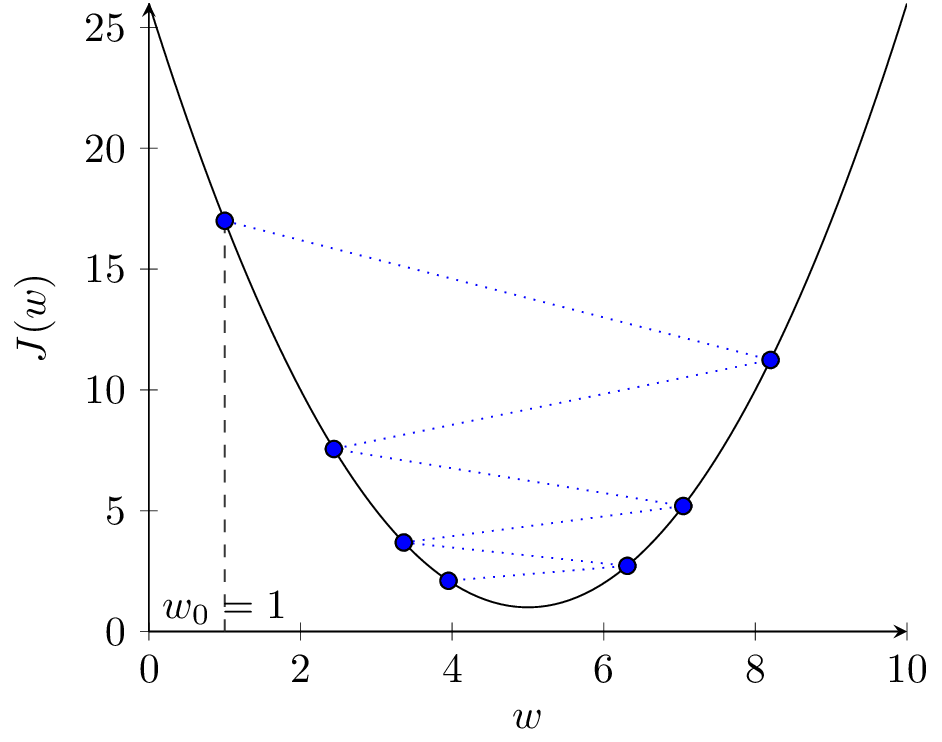
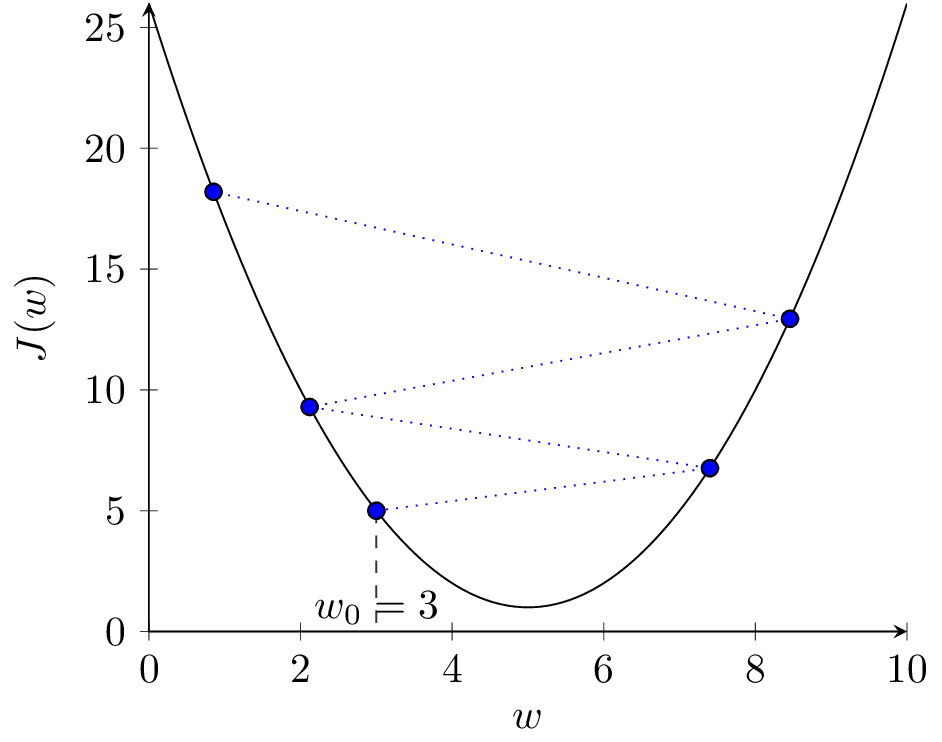
Na rysunku 2(b) przedstawione zostały kolejne kroki algorytmu dla \( \alpha = 0.1 \). Widzimy, że po 15 iteracjach algorytm znajduje się bardzo blisko optimum. Dla mniejszej wartości \( \alpha = 0.03 \) (rys. 2(c)) algorytm porusza się dobrym kierunku, ale wolniej. Dla większej wartości \( \alpha = 0.9 \) (rys. 2(d)) algorytm zaczyna przeskakiwać z jednej strony minimum na drugą, funkcja kosztu się zmniejsza, ale algorytm staje się mniej stabilny. Dalsze zwiększanie \( \alpha \) do wartości 1.1 prowadzi do sytuacji jak na rysunku 2(e). Kroki algorytmu są za duże, funkcja kosztu zwiększa wartość w kolejnych krokach, algorytm jest rozbieżny.
Wartość współczynnika uczenia \( \alpha \) jest jednym z hiper-parametrów w uczeniu sieci neuronowych i ma istotne znaczenie dla działania algorytmu.
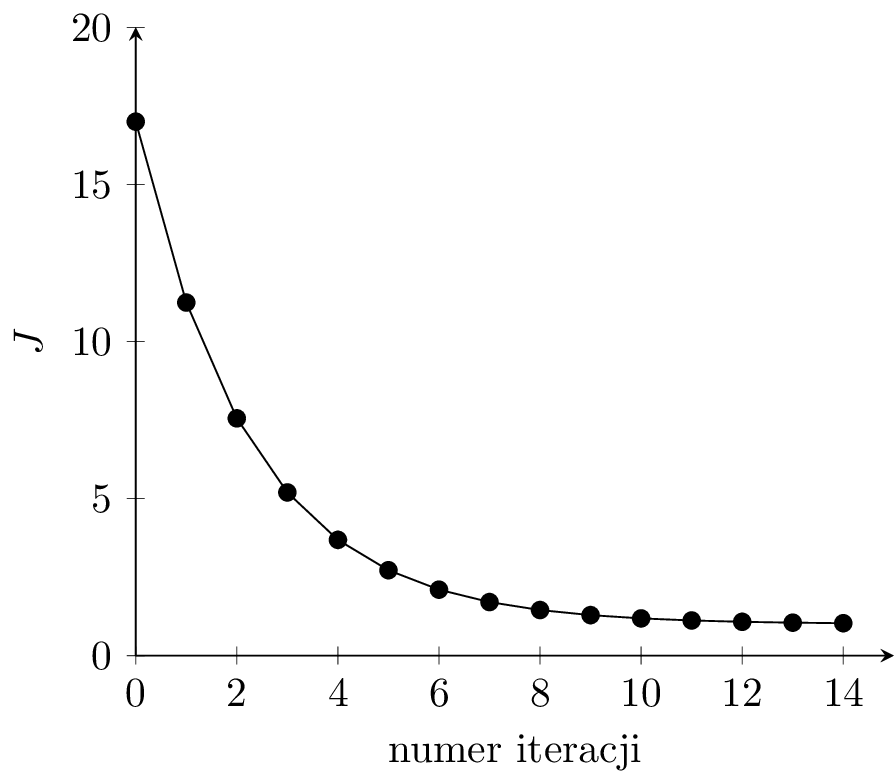
Na rysunku 2(f) widzimy wykres wartości funkcji kosztu w kolejnych iteracjach dla \( \alpha = 0.1 \). Dla prawidłowo przebiegającego procesu uczenia funkcja kosztu powinna spadać w kolejnych iteracjach uczenia dla zbioru uczącego. Jeśli model zacznie się przeuczać, to koszt dla zbioru walidacyjnego w pewnym momencie może zacząć rosnąć. Jest to znak, że powinniśmy przerwać uczenie.
3. Perceptron wielowarstwowy
W tym rozdziale omówimy podstawową architekturę sieci neuronowej - perceptron wielowarstwowy (ang. MLP - Multi Layer Perceptron). Poznamy również podstawowe koncepcje przydatne również w bardziej złożonych sieciach. Schemat perceptoronu został przedstawiony na rysunku 3. Neurony (okręgi na rysunku) ułożone są w warstwy. Warstwa wejściowa odpowiada za wejście modelu, warstwa wyjściowa za wyjście, a warstwy pośrednie nazywamy warstwami ukrytymi. Sieć powinna posiadać przynajmniej jedną warstwę ukrytą. Często posiada ich więcej, a sieci głębokie [Goodfellow et al., 2016] zawierają dużo (nawet kilkaset) warstw ukrytych. W perceptronie wszystkie neurony warstwy poprzedniej są połączone z wszystkimi neuronami warstwy kolejnej.
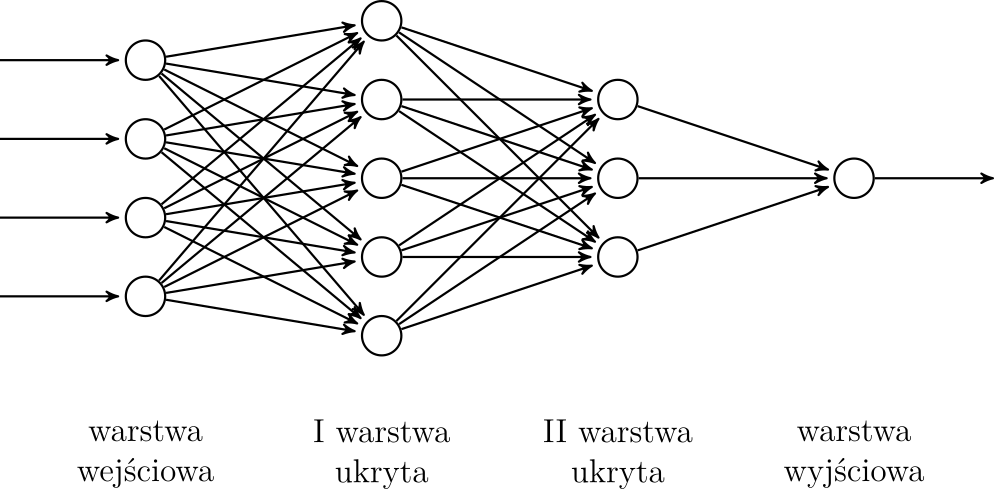
Literatura
|
[Goodfellow et al., 2016]
|
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press. http://www.deeplearningbook.org. |
3.1. Neuron
Przyjrzyjmy się teraz jak działa pojedynczy neuron (rysunek 4).
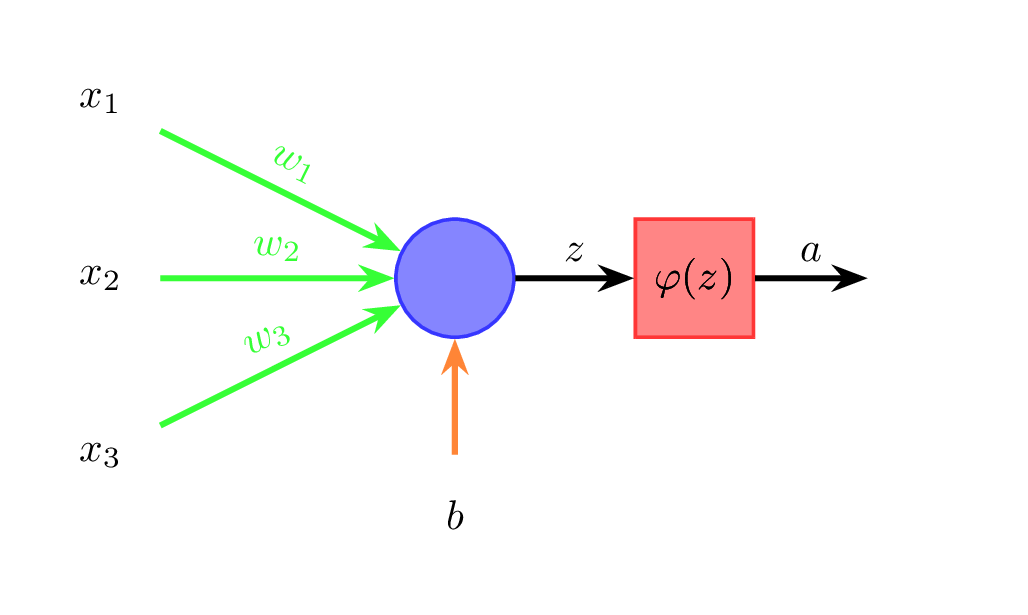
Dane wejściowe (na rysunku \( x_1 \), \( x_2 \), \( x_3 \)) mnożone są przez odpowiednie wagi (\( w_1 \), \( w_2 \), \( w_3 \)) i sumowane. Do sumy dodawany jest jeszcze wyraz wolny \( b \) (ang. bias) (wzór 1):
\[ z = w_1 x_1 + \ldots + w_n x_n + b \]Do otrzymanej sumy \( z \) stosowana jest funkcja aktywacji \( \varphi \) (wzór 2):
\[ a = \varphi(z) \]Wyjście neuronu oznaczamy poprzez \( a \). W perceptronie wielowarstwowym wyjścia neuronów warstwy poprzedniej stają się wejściami neuronów warstwy kolejnej. Każda strzałka pomiędzy neuronami na rysunku 3 ma przypisaną wagę, a każdy neuron ma przypisany wyraz wolny.
Analogie biologiczne
Działanie perceptornu ma pewne podobieństwa do neuronów biologicznych. Biologiczny neuron jest układem o wielu wejściach (dendryty) i jednym wyjściu (akson). Sygnały przekazywane przez dendryty są wzmacniane lub osłabiane przez synapsy. Gdy suma ważonych sygnałów przekracza wartość progową następuje tzw. zapłon neuronu, który objawia się wygenerowaniem serii impulsów, przekazywanych przez akson do innych neuronów. Najcenniejszą cechą biologicznej sieci neuronowej jest zdolność do uczenia się, tzn. modyfikowania działania na podstawie kolejnych doświadczeń. Uczenie neuronów biologicznych polega między innymi na modyfikacji siły połączeń synaptycznych. W sztucznej sieci neuronowej odpowiada to modyfikacji wag.
3.2. Wyznaczanie wyjścia sieci
Schemat perceptronu wielowarstwowego został przedstawiony na rysunku 3. Pojedynczy neuron działa według wzorów (1) i (2). Dla konkretnego przykładu z danych uczących jego wartości cech (\( x \)) stanowią warstwę wejściową i podawane są na wejścia pierwszej warstwy ukrytej sieci. Dla każdego z neuronów tej warstwy wykonujemy obliczenia według wzorów (1) i (2). Aktywacje neuronów pierwszej warstwy ukrytej podawane są jako wejścia neuronów drugiej warstwy ukrytej (o ile istnieje). Proces ten jest kontynuowany aż do dotarcia do warstwy wyjściowej. Wartość wyjścia sieci będziemy oznaczać przez \( \hat{y} \) w odróżnieniu od prawdziwej etykiety \( y \). Wyznaczenie wyjścia sieci nazywamy krokiem w przód (ang. forward).
3.3. Funkcje aktywacji
Jednym z wyborów przy projektowaniu struktury sieci neuronowej jest wybór funkcji aktywacji \( \varphi \) (równanie (2)). Funkcja aktywacji jest zazwyczaj taka sama dla wszystkich neuronów danej warstwy, ale może być różna dla różnych warstw. Funkcja aktywacji warstwy wyjściowej powinna być dostosowana do modelowanego problemu (np. czy chcemy mieć na wyjściu liczbę z zakresu \( < 0, 1> \) czy dowolną wartość).
Parametry sieci neuronowej (\( w \) i \( b \), równanie (1) uczymy stosując algorytmy gradientowe (zobacz rozdział 2.2). Do wyznaczenia pochodnej funkcji kosztu konieczne jest również wyznaczenie pochodnych funkcji aktywacji, zatem funkcje te powinny być różniczkowalne prawie wszędzie. Algorytmy gradientowe dobrze działają gdy pochodne nie mają bardzo małych (rys. 2(b) - wtedy algorytm robi małe, powolne kroki) ani bardzo dużych wartości (rys. 2(e) - wtedy algorytm może się zdestabilizować).

Dostępnych funkcji aktywacji jest bardzo wiele i wciąż powstają nowe. Omówimy teraz kilka najpopularniejszych rozwiązań (rysunek 5).
Sigmoidalna (rys. 5a) funkcja aktywacji dana jest wzorem (wzór 3):
\[ \sigma(z) = \frac{1}{1 + \exp(-z)} \]a jej pochodna wzorem (wzór 4):
\[ \sigma'(z) = \frac{1}{1 + \exp(-z)}\left(1 - \frac{1}{1 + \exp(-z)}\right) = \sigma(z)(1 - \sigma(z)) \]Jest ona zazwyczaj stosowana w warstwie wyjściowej w problemach klasyfikacji binarnej, czyli takich, gdzie rozważamy tylko dwie klasy oznaczane jako 0 i 1. Na wyjściu funkcji sigmoidalnej otrzymujemy liczby z zakresu (0, 1). Możemy to interpretować jako prawdopodobieństwo/pewność, że dane wejściowe powinny być zaklasyfikowane do klasy 1. Pochodna funkcji sigmoidalnej ma wartości bliskie zeru dla szerokiego zakresu wartości \(z\), co może spowodować wolne działanie algorytmów gradientowych. W praktyce jest to funkcja rzadko stosowana w warstwach ukrytych, gdyż prawie zawsze lepiej jest ją zastąpić tangensem hipepbolicznym.
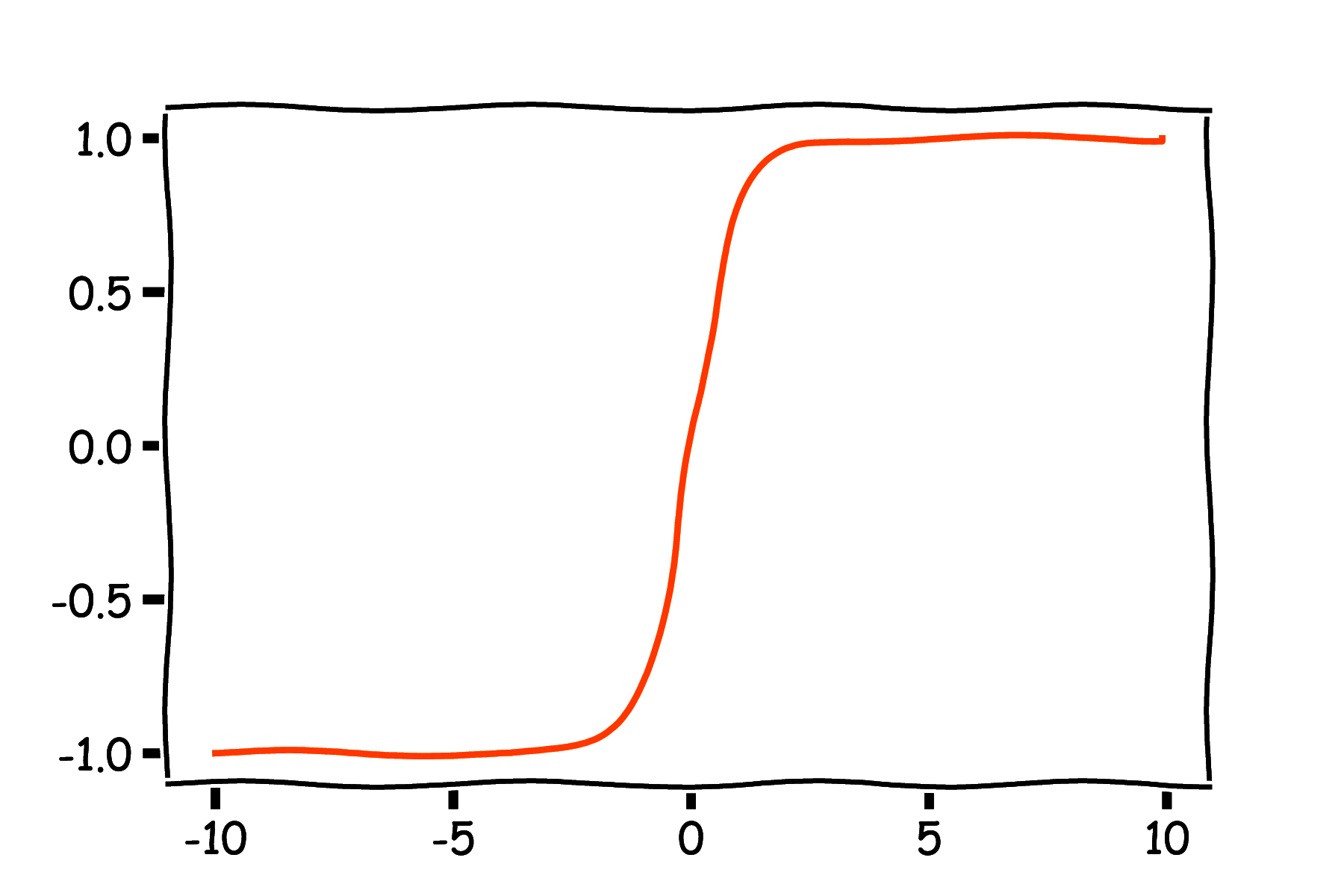
Tangens hiperboliczny (rys. 5b) dany jest wzorem (wzór 5):
\[ \varphi(z) = \tanh(z) = \frac{\exp(z) - \exp(-z)}{\exp(z) + \exp(-z)} \]a jego pochodna wzorem (wzór 6):
\[ \varphi'(z) = (1 - \tanh(z)^2) \]Przewagę tej funkcji nad funkcją sigmoidalną zapewnia symetria zakresu wartości względem zera, co może wpływać korzystnie na numeryczne działanie algorytmów, jednak pochodna również ma wartości bliskie zeru dla szerokiego zakresu wartości \(z\).
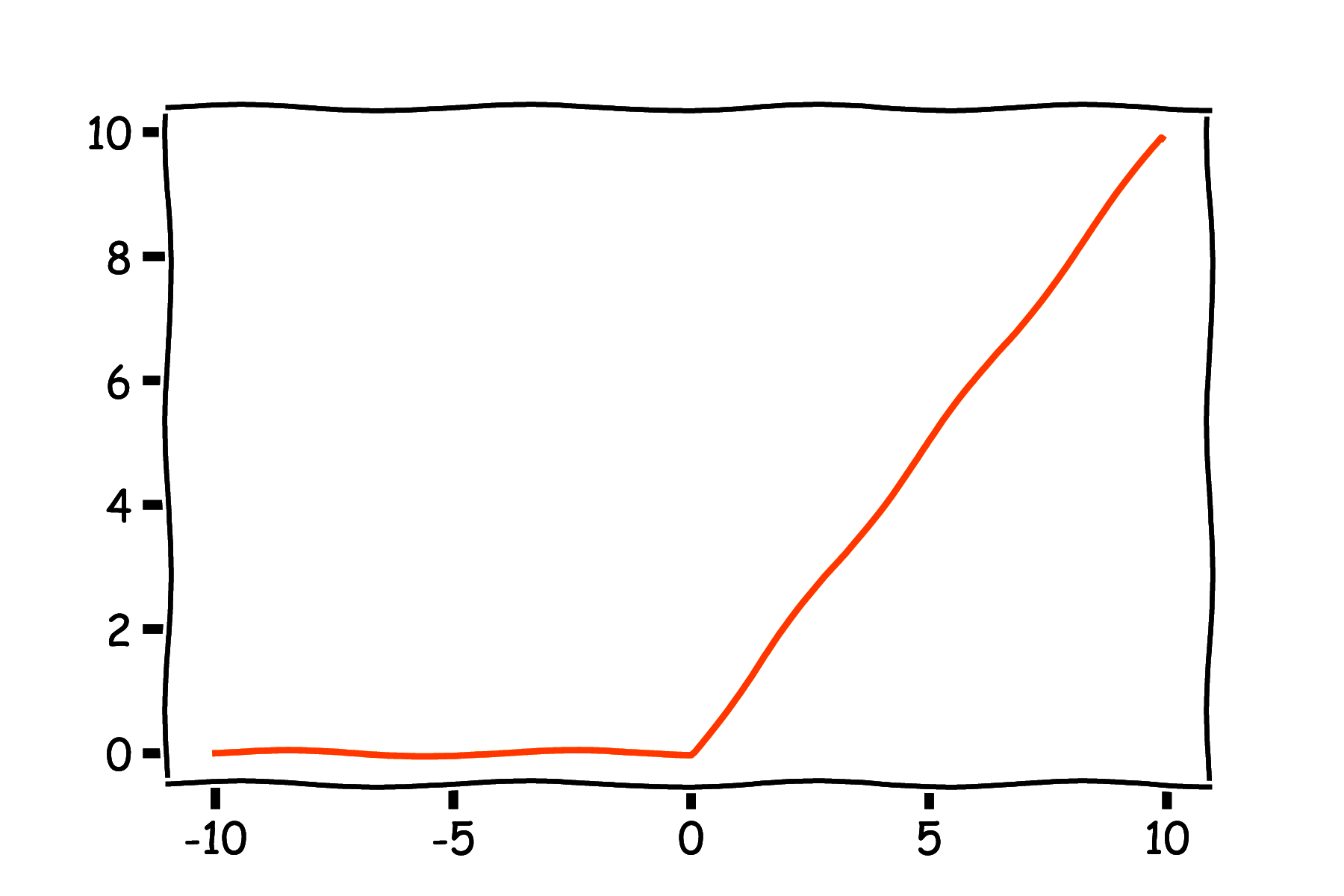
Nowszą i ogromnie popularną w praktyce funkcją aktywacji jest ReLU (rys. 5c) (ang. Rectified Linear Unit), dany wzorem (wzór 7):
\[ \varphi(z) = \max(0, z) \]Pochodna ReLU dana jest wzorem (wzór 8):
\[ \varphi'(z) = \begin{cases} 0 & \text{if } z < 0 \\ 1 & \text{if } z > 0 \\ ? & \text{if } z = 0 \\ \end{cases} \]Możemy zaobserwować, że w punkcie \(z=0\) pochodna jest nieciągła. W praktyce w obliczeniach numerycznych prawie nigdy nie trafiamy idealnie w 0 i można dla tego punktu przyjąć dowolną wartość (0 lub 1). Dla ReLU występuje zjawisko tzw. martwych neuronów - jeśli jakiś neuron często wpada w obszar \(z<0\), to pochodna dla wag tego neuronu zawsze jest 0 i przestaje on aktualizować swoje wagi w procesie uczenia i brać czynny udział w wyznaczaniu wyjścia sieci.
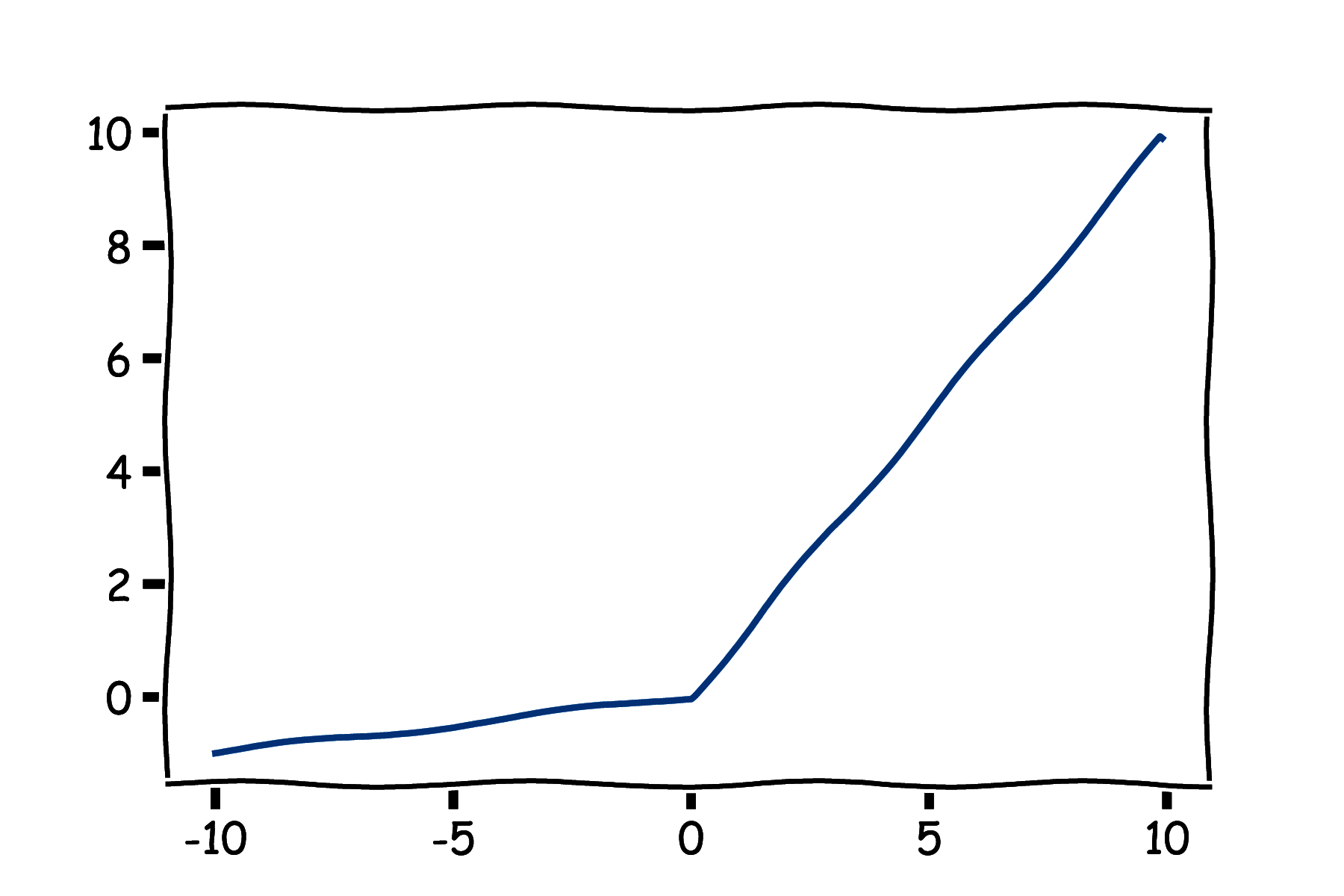
Z tego powodu stworzono funkcję Leaky ReLU (rys. 5d), daną wzorem (wzór 9):
\[ \varphi(z) = \max(0.01z, z) \]z pochodną daną wzorem (wzór 10):
\[ \varphi'(z) = \begin{cases} 0.01 & \text{if } z < 0 \\ 1 & \text{if } z > 0 \\ ? & \text{if } z = 0 \\ \end{cases} \]W ten sposób dla \( z < 0 \) pochodna ma małą, ale niezerową wartość co eliminuje zjawisko martwych neuronów. Zamiast 0.01 można zastosować również inną małą liczbę.
Stosuje się również liniową funkcję aktywacji (wzór 11):
\[ \varphi(z) = z \]o pochodnej (wzór 12):
\[ \varphi'(z) = 1 \]Oznacza to brak funkcji aktywacji. Liniowa funkcja aktywacji może być stosowana jako warstwa wyjściowa w problemach regresji, kiedy nie chcemy ograniczać zakresu wyjścia sieci. Nie ma sensu stosowanie liniowej funkcji aktywacji w warstwach ukrytych. Ponieważ złożenie dwóch warstw ukrytych z liniową funkcją aktywacji daje dalej odwzorowanie liniowe to efekt byłby taki sam jak zastosowanie jednej warstwy. Dopiero nieliniowe aktywacje w warstwach ukrytych pozwalają sieciom uczyć się ciekawych zależności.
Funkcja aktywacji softmax stosowana jest jako warstwa wyjściowa w problemach klasyfikacji, kiedy występują więcej niż dwie klasy. Dla \( M \) klas stosujemy \( M \) neuronów w warstwie wyjściowej. Przed zastosowaniem aktywacji mamy \( M \) wartości: \( z_1, z_2, \ldots, z_M \) i dla każdego \( z_i \) stosujemy przekształcenie (wzór 13):
\[ \sigma(z_i) = \frac{\exp(z_i)}{\sum_{i=1}^M \exp(z_i)} \]W ten sposób otrzymujemy \( M \) liczb o wartościach z zakresu (0, 1) i sumujących się do zera. Możemy to interpretować jako rozkład prawdopodobieństwa na klasach.
3.4. Funkcje kosztu
Do zastosowania algorytmów uczenia gradientowego (rozdział 2.2) wymagane jest wyznaczenie wartości funkcji kosztu \(J\) oraz jej pochodnych po parametrach sieci. W tym rozdziale zostaną omówione podstawowe funkcje kosztu.
W problemach regresji najczęściej stosujemy błąd średniokwadratowy (ang. MSE - Mean Squared Error) (wzór 14):
\[ \frac{1}{m} \sum_{j=1}^m (y_j - \hat{y}_j)^2 \]gdzie \( m \) jest liczbą przykładów, \( y_j \) prawidłową etykietą dla \( j \)-tego przykładu, a \( \hat{y}_j \) wyjściem sieci dla \( j \)-tego przykładu. Błąd średniokwadratowy polega na wyznaczeniu różnicy między prawidłową wartością a wyjściem sieci, podniesieniu do kwadratu i uśrednieniu dla wszystkich przykładów.
W problemach klasyfikacji binarnej (klasyfikacji dla dwóch klas) stosujemy binarną entropię krzyżową (ang. BCE - binary cross-entrophy) (wzór 15):
\[ -\frac{1}{m} \sum_{j=1}^m \left( y_j \log(\hat{y}_j) + (1 - y_j)\log(1-\hat{y}_j)\right) \]Funkcja ta na pierwszy rzut oka wydaje się trudna do zrozumienia. Spróbujmy zbudować sobie intuicje odnośnie jej działania. Dla pojedynczego przykładu (pomijamy sumowanie po \( m \)) rozważmy funkcję kosztu daną wzorem (wzór 16):
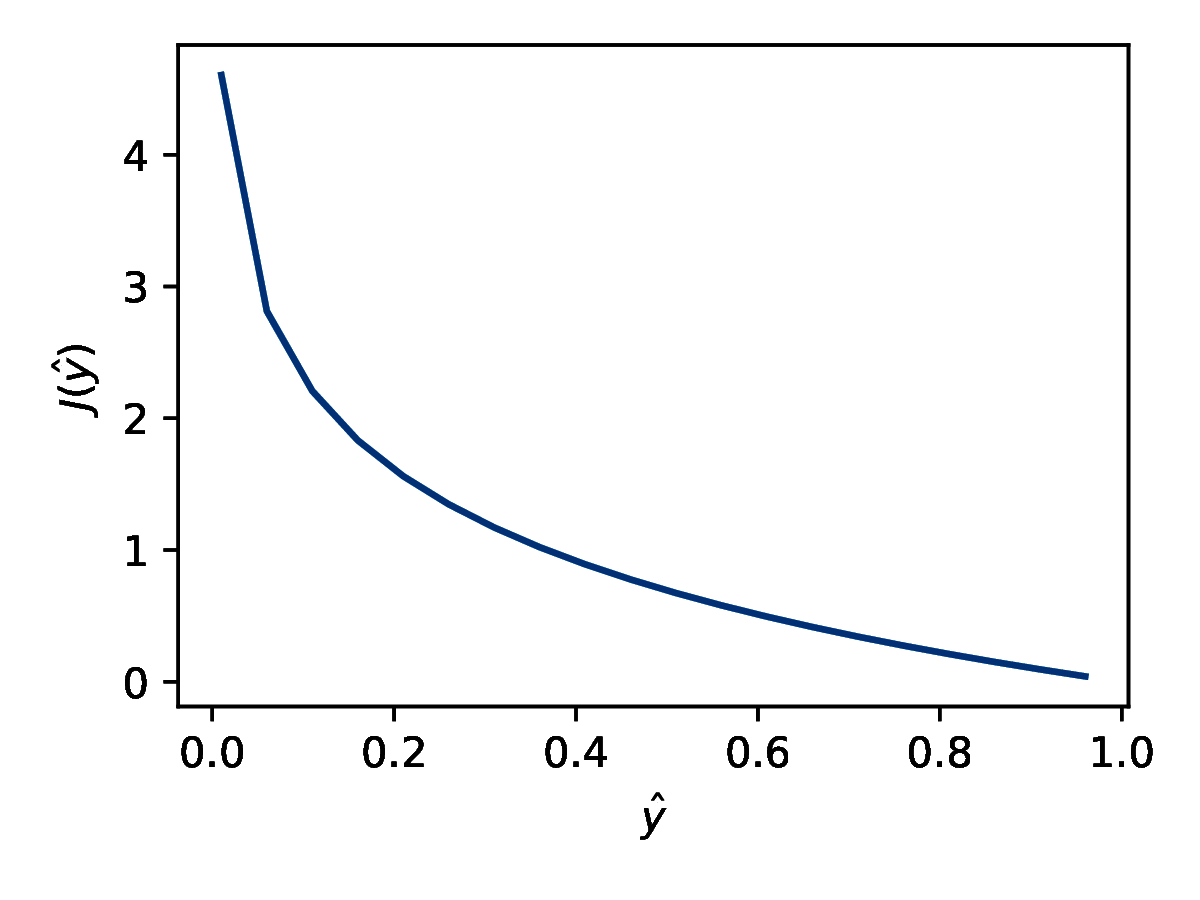
\[ \text{koszt}(\hat{y}^{(j)}, y^{(j)})= \begin{cases} -\log(\hat{y}^{(j)}) & \text{dla } y^{(j)}=1 \\ -\log(1 - \hat{y}^{(j)}) & \text{dla } y^{(j)}=0 \\ \end{cases} \]Dla problemów klasyfikacji binarnej w warstwie wyjściowej stosujemy sigmoidalną funkcję aktywacji i wyjście sieci ma wartości z zakresu (0, 1). Dla \( y = 0 \) rozważamy funkcję kosztu przedstawioną na wykresie 6a. Jeśli wyjście sieci \( \hat{y} \) ma wartość 0 to koszt jest zerowy. Im bliżej \( \hat{y} \) jest wartości 1 tym większa wartość funkcji kosztu, czyli dla predykcji nieprawidłowej klasy z dużą pewnością model dostaje silną negatywną informację zwrotną.
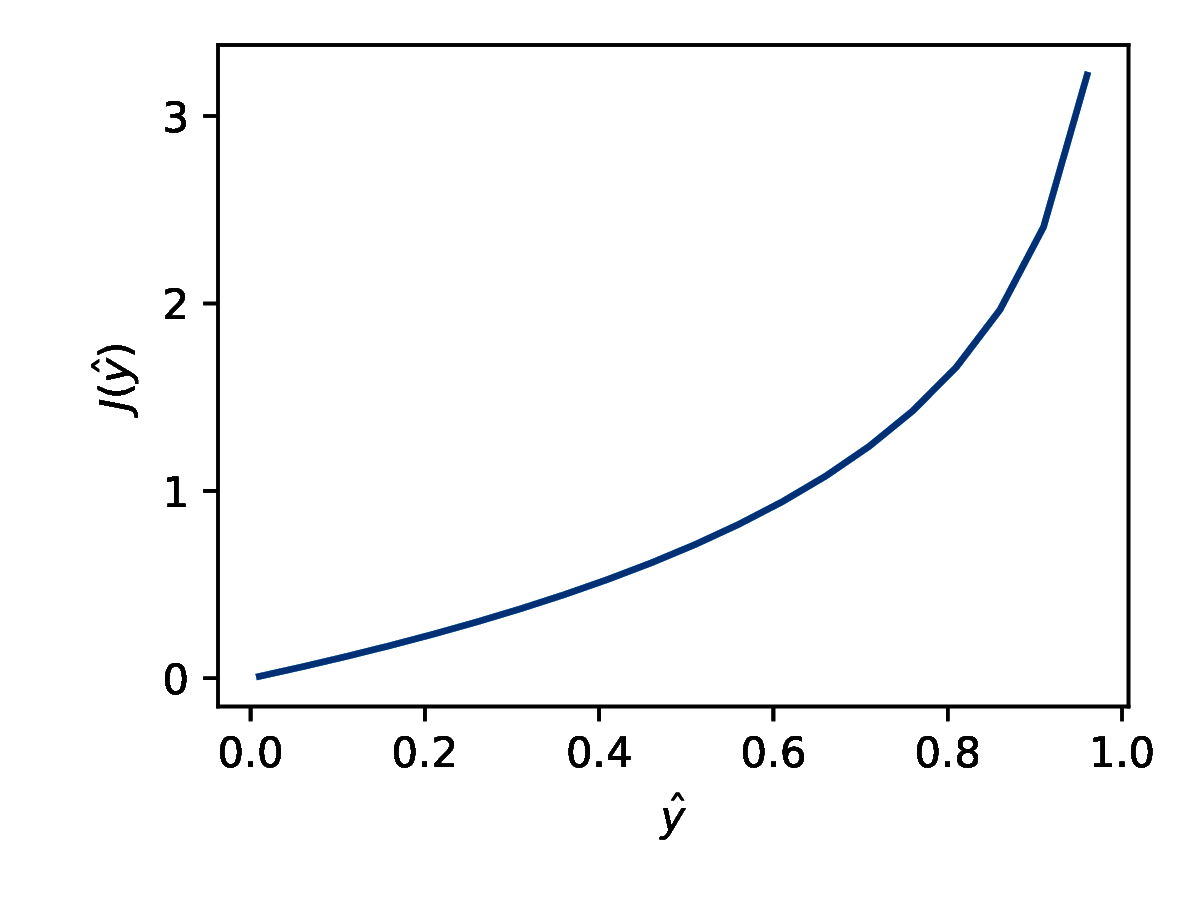
Odwrotnie dla \( y = 1 \) stosujemy funkcję kosztu przedstawioną na rysunku 6b. Jeśli \( \hat{y} = 1 \) to koszt jest zerowy. Im bliżej \( \hat{y} \) jest zera, tym większy koszt. Jeżeli przyjrzymy się uważnie wzorowi (15), dostrzeżemy, że jest to inna forma zapisu (16) (i dodatkowo uwzględnienie wielu przykładów).
Dla wielu klas stosujemy entropię krzyżową wieloklasową (ang. categorical cross-entrophy) (wzór 17):
\[ -\frac{1}{m} \sum_{j=0}^m \sum_{c=1}^M y_{jc}\log(\hat{y}_{jc}) \]gdzie \( M \) oznacza liczbę klas, a \( c \) jest indeksem klasy. Interpretacja jest taka sama jak dla binarnej entropii krzyżowej, ale tu uwzględniamy w wyliczeniu tylko wyjście sieci odpowiadające prawidłowej klasie.
3.5. Algorytm wstecznej propagacji błędów
W procesie uczenia sieci chcemy aktualizować wartości wag i wyrazów wolnych na podstawie danych uczących. Wagi sieci będziemy oznaczać \( w_{kl}^{[i]} \), a wyrazy wolne \( b_{k}^{[i]} \), gdzie \( i \) jest indeksem warstwy, \( k \) numerem neuronu w danej warstwie, a \( l \) indeksem wagi neuronu.
Algorytm uczenia odbywa się w dwóch krokach:
-
W przód (ang. forward) - wyznaczenie wyjścia sieci i wartości funkcji kosztu J. Wyjście sieci wyznaczamy przeliczając aktywacje warstw - od pierwszej do ostatniej.
-
Wstecz (ang. backward) - wyznaczenie wszystkich pochodnych wag i wyrazów wolnych. Pochodne w warstwie [i] można wyznaczyć na podstawie pochodnych w warstwie [i+1]. Zatem obliczenia prowadzimy od ostatniej warstwy do pierwszej. Z tego wględu mówimy o algorytmie wstecznej propagacji błędów.
Obecnie dostępnych jest wiele narzędzi, które krok wstecz wykonują w sposób automatyczny, takich jak TensorFlow (https://www.tensorflow.org), PyTorch (https://pytorch.org/) lub JAX (https://github.com/google/jax). W tym module przedstawimy przykłady kodu z wykorzystaniem TensorFlow z interfejsem Keras.
Algorytm uczenia sieci przebiega w następujących krokach:
-
Przypisz wagom losowe wartości początkowe
-
Wyznacz wyjście sieci \( \hat{y} \)
-
Wyznacz wartość funkcji kosztu \( J \)
-
\[ dW = \frac{\partial J}{\partial W} \qquad db = \frac{\partial J}{\partial b} \] \[ W = W - \alpha dW \] \[ b = b - \alpha db \]
-
dopóki nie warunek stopu idź do 2
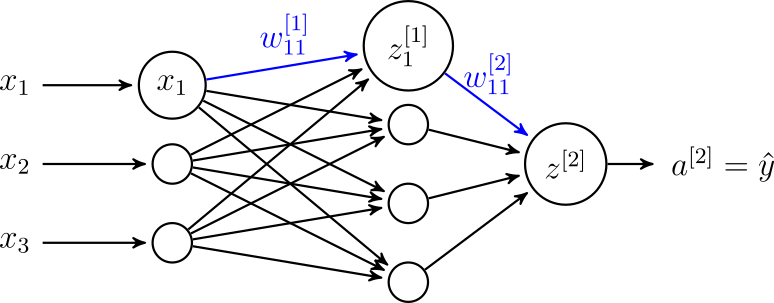
Rozważmy sieć przedstawioną na rysunku 7. Chcemy wyznaczyć \( \frac{\partial J}{\partial w_{11}^{[1]}} \) (a po drodze \( \frac{\partial J}{\partial w_{11}^{[2]}} \)). Dla uproszczenia przyjmijmy, że wyznaczamy wyjście sieci \( \hat{y} \) na podstawie jednego przykładu uczącego.
Przyjmijmy, że sieć realizuje zadanie klasyfikacji binarnej. Zatem odpowiednią funkcją kosztu jest binarna entropia krzyżowa (równanie 15) (wzór 18):
\[ J = -(y\log(\hat{y})+(1-y)\log(1-\hat{y})) \]Pochodna funkcji kosztu po wyjściu sieci \( \frac{\partial J}{\partial \hat{y}} \) wynosi (wzór 19):
\[ \frac{\partial J}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}} \]Wyjście sieci \( \hat{y} \) odpowiada aktywacji neuronu ostatniej warstwy. Dla klasyfikacji binarnej stosujemy sigmoidalną funkcję aktywacji.
\[ \hat{y} = a^{[2]} = \frac{1}{1 + \exp(-z^{[2]})} \]gdzie \( a^{[2]} \) jest aktywacją neuronu w warstwie drugiej, a \( z^{[2]} \) wyjściem neuronu warstwy drugiej przed zastosowaniem funkcji aktywacji.
Pochodne wyznaczamy idąc wstecz, zatem w kolejnym kroku chcemy wyznaczyć \( \frac{\partial J}{\partial z^{[2]}} \), korzystając przy tym ze wzoru na pochodną funkcji złożonej (wzór 20):
\[ \frac{\partial J}{\partial z^{[2]}} = \frac{dJ}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z^{[2]}} \]Wartość \( \frac{\partial J}{\partial \hat{y}} \) już wyliczyliśmy. Korzystając ze wzoru na pochodną funkcji sigmoidalnej (równanie 4) otrzymujemy (wzór 21):
\[ \frac{\partial \hat{y}}{\partial z^{[2]}} = \hat{y}(1 - \hat{y}) \]Wstawiając (21) i (19) do (20) powyższe do wzoru otrzymujemy (wzór 22):
\[ \frac{\partial J}{\partial z^{[2]}} = \hat{y} - y \]Następnie wyznaczamy \( \frac{\partial J}{\partial w_{11}^{[2]}} \) (wzór 23):
\[ \frac{\partial J}{\partial w_{11}^{[2]}} = \frac{dJ}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial w_{11}^{[2]}} \]W tym celu potrzebujemy wyliczyć \( \frac{\partial z^{[2]}}{\partial w_{11}^{[2]}} \). Pamiętamy (z równania 1), że (wzór 24):
\[ z^{[2]} = a_1^{[1]} w_{11}^{[2]} + \ldots + a_4^{[1]} w_{14}^{[2]} + b_1^{[2]} \]Zatem (wzory 25 i 26):
\[ \frac{\partial z^{[2]}}{\partial w_{11}^{[2]}} = a_1^{[1]} \] \[ \frac{\partial J}{\partial w_{11}^{[2]}} = \frac{dJ}{\partial z^{[2]}} a_1^{[1]} \]Wyznaczmy również pochodną dla wyrazu wolnego \( b_1^{[2]} \) (wzór 27):
\[ \frac{\partial J}{\partial b_1^{[2]}} = \frac{dJ}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial b_1^{[2]}} = \frac{dJ}{\partial z^{[2]}} \]Idąc dalej wgłąb wyliczamy \( \frac{dJ}{\partial z_1^{[1]}} \) (wzór 28):
\[ \frac{dJ}{\partial z_1^{[1]}} = \frac{dJ}{\partial a^{[1]}} \varphi'(z_1^{[1]}) \]gdzie \( \varphi'(z_1^{[1]}) \) jest pochodną funkcji aktywacji w warstwie pierwszej po \( z_1^{[1]} \). W tej warstwie możemy zastosować różne funkcje aktywacji i konkretna postać wzoru będzie zależała od wybranej funkcji. Wykorzystując wcześniejsze wzory dostajemy (wzór 29):
\[ \frac{dJ}{\partial a^{[1]}} = \frac{dJ}{\partial z^{[2]}} w_{11}^{[2]} \]Zauważmy, że (wzór 30):
\[ z_1^{[1]} = w_{11}^{[1]} x_1 + \ldots + w_{13}^{[1]} x_3 + b_1^{[1]} \]Ostatecznie dostajemy (wzór 31):
\[ \frac{\partial J}{\partial w_{11}^{[1]}} = \frac{\partial J}{\partial z_1^{[1]}} \frac{\partial z_1^{[1]}}{\partial w_{11}^{[1]}} =\frac{dJ}{\partial z_1^{[1]}} x_1 \]oraz (wzór 32)
\[ \frac{\partial J}{\partial b_{1}^{[1]}} = \frac{\partial J}{\partial z_1^{[1]}} \frac{\partial z_1^{[1]}}{\partial b_{1}^{[1]}} = \frac{dJ}{\partial z_1^{[1]}} \]Na podstawie wyznaczonych pochodnych możemy wykonać krok algorytmu gradientowego.
Mini-batche
Być może zauważyliście pewną niekonsekwencję pojawiającą się w dotychczasowych rozważaniach. W przykładzie obliczeniowym wyznaczaliśmy pochodne dla jednego przykładu, a w innych miejscach wspominany był cały zbiór uczący. Ogólnie algorytmy gradientowe stosujemy w trzech wariantach:
-
Standardowa metoda spadku gradientu (ang. gradient descent) - w każdym kroku wyliczamy pochodne dla całego zbioru uczącego. Pozwala to na dokładne wyliczenie kierunku spadku funkcji kosztu dla całego zbioru, ale jest kosztowne obliczeniowo. W przypadku większych zbiorów danych (np. przetwarzanie obrazu) może być niewykonalne ze względu na niemożliwość jednoczesnego załadowania całego zbioru do pamięci RAM.
-
Stochastyczna metoda spadku gradientu (ang. stochastic gradient descent) - w każdym kroku przetwarzamy tylko jeden przykład ze zbioru uczącego. Czas obliczeń w pojedynczym kroku się skraca, ale dostajemy jedynie oszacowanie gradientu dla całego zbioru. Taka metoda nie pozwala również na wykorzystanie zoptymalizowanych funkcji przetwarzających całe macierze.
-
Przetwarzanie w mini-batchach (ang. batch gradient descent lub mini-batch gradient descent) - stanowi kompromis pomiędzy powyższymi metodami i jest najczęściej stosowane w praktyce. Dane uczące są przetwarzane w paczkach (ang. batch). Pozwala to na wydajne wykorzystanie możliwości sprzętu obliczeniowego.
Przejście przez cały zbiór danych uczących nazywamy epoką (ang. epoch).
Rozszerzenia metody gradientu prostego
Funkcje kosztu dla realnych problemów uczenia sieci neuronowych mają wiele lokalnych minimów i nie są wypukłe. Pewne wyzwanie stanowi również dobranie odpowiedniej wartości współczynnika uczenia α. Mogą występować takie problemy jak oscylacje, zanikające (płaska funkcja kosztu) lub wybuchające (stroma funkcja kosztu) gradienty.
Powstały modyfikacje metody gradientu prostego pozwalające na przyśpieszenie procesu uczenia. Do najbardziej popularnych algorytmów należą momentum [Qian, 1999], rmsprop [Hinton et al., ] i Adam [Kingma and Ba, 2014].
Literatura
|
[Qian, 1999]
|
Qian, N. (1999). On the momentum term in gradient descent learning algorithms. Neural Networks, 12(1):145 -- 151. [ | DOI | http ] |
|
[Kingma and Ba, 2014]
|
Kingma, D. P. and Ba, J. (2014). Adam: A method for stochastic optimization. CoRR, abs/1412.6980. [ | arXiv | http ] |
|
[Hinton et al.,] ]
|
Hinton, G., Srivastava, N., and Swersky, K. Overview of mini-batch gradient descent. Neural Networks for Machine Learning, http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf. |
3.6. Uwagi praktyczne
Algorytmy gradientowe startują z pewnego losowego punktu, jednak punkt startowy może mieć wpływ na wynik działania algorytmu.
Nie powinniśmy ustawiać wszystkich wartości początkowych wag na zero, ponieważ wtedy w sieci powstanie symetria: aktywacje wszystkich neuronów na początku są takie same, wszystkie gradienty są takie same i wagi już zawsze będą takie same. W celu przełamania symetrii wagi sieci inicjalizuje się małymi wartościami losowymi. Wyrazy wolne można zainicjalizować zerami.
Parametrami sieci nazywamy wagi \(w\) i wyrazy wolne \(b\), które dobierane są w procesie uczenia, za pomocą algorytmów gradientowych, na zbiorze uczącym.
Inne ustawienia nazywamy hiper-parametrami, należą do nich, między innymi:
liczba warstw,
liczba neuronów w warstwach,
liczba iteracji algorytmu gradientowego,
funkcje aktywacji,
wartość współczynnika uczenia.
Hiper-parametry dobieramy najczęściej eksperymentalnie na podstawie wartości funkcji straty lub innej metryki wyznaczanej dla zbioru walidacyjnego.
W praktycznych zastosowaniach należy mieć na uwadze następujące zagadnienia:
Sieci nie mają właściwości ekstrapolacyjnych. Oznacza to, że jeśli na wejście sieci podamy dane spoza zakresu wykorzystywanego w procesie uczenia (np. w danych uczących pewna cecha miała wartości z zakresu (0, 10) a teraz obserwujemy wartość 20) możemy dostać dowolnie bezsensowny wynik.
Dane uczące powinny być reprezentatywne dla całego zakresu zmienności wejść. Oznacza to, że przy modelowaniu procesów przemysłowych powinniśmy zgromadzić dane z różnych punków pracy.
Do budowy sieci o wielu parametrach potrzebujemy dużo danych. Wyjątek stanowi tu powtórne wykorzystanie sieci przeznaczonej do rozwiązywania podobnego problemu (transfer learning, rozdział 5.5).
Modelowane zjawiska (np. proces przemysłowy) zmieniają się w czasie - model będzie tracił dokładność. Dla zachowania dokładności konieczne jest ciągłe lub okresowe douczenie modelu. Nie jest to zagadnienie trywialne, ze względu na skłonność modeli do zapominania poprzednio zgromadzonej wiedzy.
3.7. Metody regularyzacji
Metody regularyzacji służą do ograniczania zjawiska przeuczenia modelu.
Regularyzacja L2
Do najstarszych metod regularyzacji należą metody ograniczania wartości parametrów modeli. Przy dopasowywaniu funkcji wielomianowych zjawisko przeuczenia charakteryzuje się tym, że współczynniki dopasowanego wielomianu mają bardzo duże wartości bezwzględne (sytuacja taka wygląda jak na rysunku 3d). Podobne zjawisko możemy zaobserwować w sieciach neuronowych i dotyczy ono dużych wartości bezwzględnych wag oraz wyrazów wolnych. W celu zastosowania regularyzacji L2 [Hoerl and Kennard, 1970] modyfikujemy funkcję kosztu w następujący sposób:
\[ J(w) = \text{błąd jak dotychczas} + \lambda \sum_{i=1}^n w_i^2 \]Duże wartości wag są karane proporcjonalnie do kwadratu ich wartości. Do członu odpowiadającego z regularyzację dodajemy wagę \( \lambda \) (liczba dodatnia). Im większa wartość \( \lambda \) tym silniejsza regularyzacja.
Gradient dla zmodyfikowanej funkcji kosztu jest następujący:
\[ \frac{\partial J}{\partial w_i} = \text{gradient jak dotychczas} + 2 \lambda w_i \]co oznacza, że wagi dodatnie są zmniejszane, a ujemne zwiększane. Siła zmniejszania/zwiększania jest proporcjonalna do wartości bezwzględnej wagi. Regularyzacja L2 silnie oddziałuje na wagi o dużych wartościach bezwzględnych.
Regularyzacja L1
Regularyzacja L1 [Tibshirani, 1996] działa bardzo podobnie do L2, ale kara nakładana jest na wartości bezwzględne wag. Otrzymujemy zmodyfikowaną funkcję kosztu:
\[ J(w) = \text{błąd jak dotychczas} + \lambda \sum_{i=1}^n |w_i| \]oraz gradient:
\[ \frac{\partial J}{\partial w_i} = \text{gradient jak dotychczas} + \lambda \operatorname{sign}(w_i) \]Należy zwrócić uwagę, że gradient zależy tylko od znaku danej wagi, co oznacza, że L1 oddziałuje tak samo silnie na małe i duże wagi. Interesującym efektem zastosowania L1 jest uzyskanie wartości części wag równych dokładnie 0.
Dropout
Dropout [Srivastava et al., 2014] (w przeciwieństwie do L1 i L2) jest metodą dedykowaną do sieci neuronowych. Rozważmy sieć przedstawioną na rysunku 8. Jest to sieć MLP, połączenia między warstwami zostały pominięte dla czytelności. Dropout polega na pominięciu w sposób losowy jakiejś części neuronów z danej warstwy w danym kroku algorytmu. Pominięte neurony zostały zaznaczone szarym kolorem i linią przerywaną na rysunku 8. Pominięcie oznacza, że wyjścia tych neuronów w danej iteracji są zerowane (wyjścia pozostałych neuronów warstwy są przeskalowywane), a algorytm gradientowy nie modyfikuje ich wag. W kolejnym kroku algorytmu neurony do pominięcia są losowane ponownie. Parametrem warstwy dropout jest prawdopodobieństwo pominięcia neuronów.
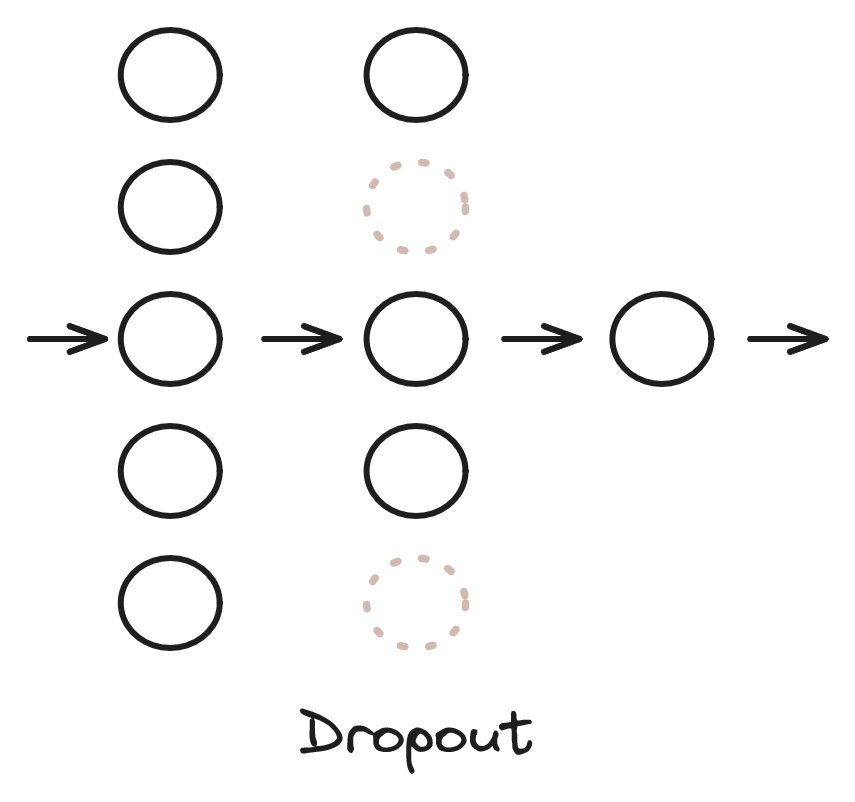
W nauczonym modelu wykorzystujemy już wszystkie neurony. Celem tej metody jest zabezpieczenie się przed nadmierną specjalizacją neuronów. Dropout można również interpretować jako jednoczesne uczenie wielu modeli (w każdej iteracji uczymy sieć o trochę innej strukturze).
Batch normalization
Jeżeli dane wejściowe modelu zmienią swój rozkład w stosunku do danych uczących, to działanie modelu zazwyczaj znacząco się pogorszy. Metoda batch normalization [Ioffe and Szegedy, 2015] próbuje normalizować dane wewnątrz paczek danych (batchy) w celu zapewnienia podobnego rozkładu danych wejściowych do kolejnych warstw.
Batch normalization działa w następujący sposób (wzory 33-36):
\[ \mu = \frac{1}{B} \sum_{b=1}^B x_b \]\[ \sigma^2 = \frac{1}{B} \sum_{b=1}^B (x_b - \mu)^2 \]
\[ \hat{x}_b = \frac{x_b - \mu}{\sqrt{\sigma^2 + \epsilon}} \]
\[ y_b = \gamma \hat{x}_b + \beta \]
gdzie \( x_b \) jest wektorem danych wejściowych do warstwy batch normalization, \( B \) rozmiarem batcha (liczbą przykładów), \( \mu \) średnią liczoną w wymiarze batcha, a \( \sigma^2 \) odchyleniem standardowym. Następnie wyznaczane są znormalizowane wartości \( \hat{x}_b \) (\( \epsilon \) - mała liczba dodatnia, służy zapewnieniu stabilności numerycznej - nie chcemy dzielić przez 0), a potem wartości \( \hat{x}_b \) są przeskalowywane liniowo. Współczynniki \( \gamma \) i \( \beta \) należą do uczonych współczynników modelu. W ten sposób algorytm może dostosować dogodny zakres danych wejściowych dla kolejnej warstwy. \( y_b \) jest wyjściem warstwy normalizacji.
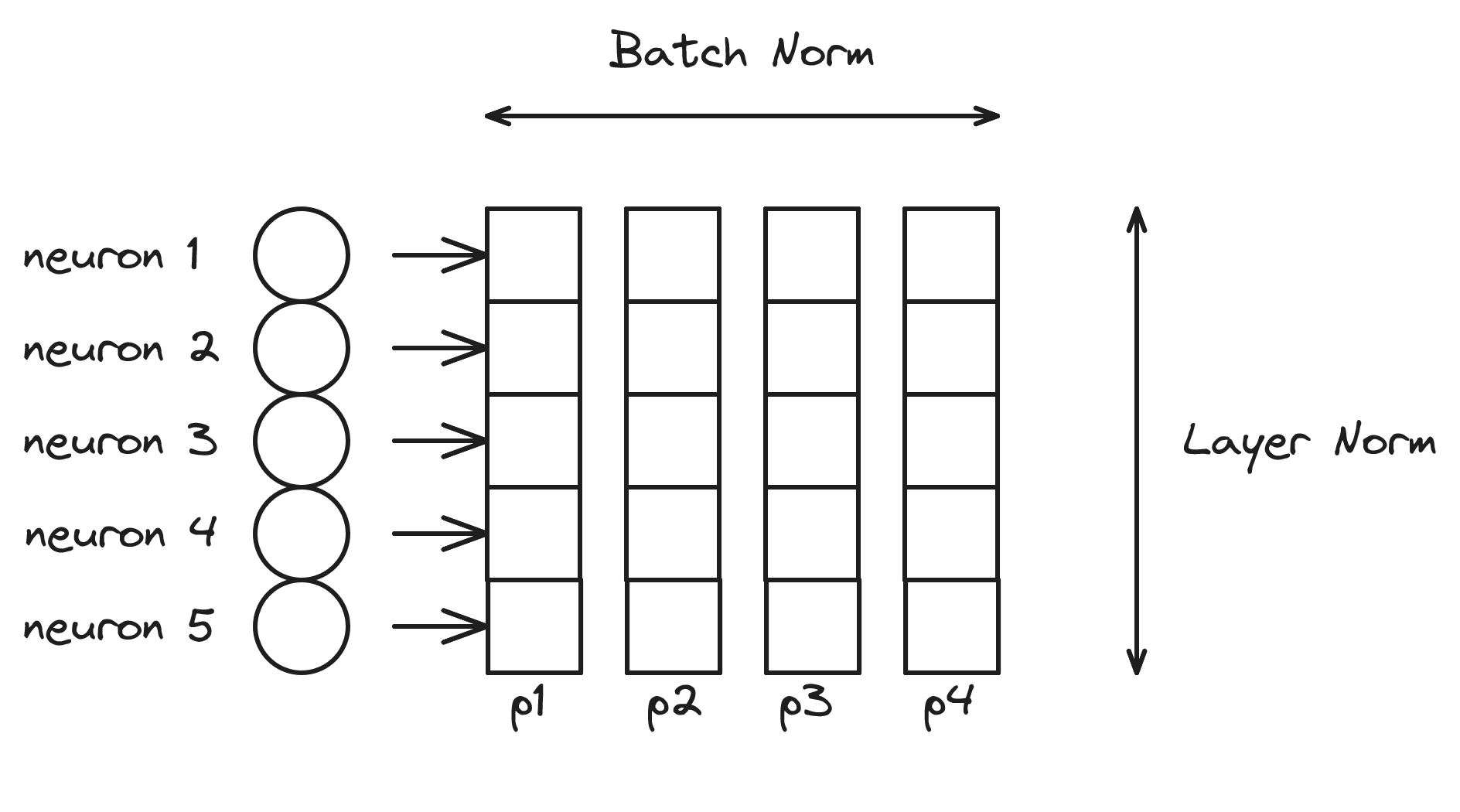
Rozważmy warstwę sieci przedstawioną na rysunku 9. Warstwa ta ma 5 neuronów. Przetwarzamy batch o rozmiarze 4, złożony z przykładów \( p1 \) - \( p4 \). Warstwa batch normalization normalizuje wartości w wymiarze batcha - średnia i odchylenie standardowe są liczone dla przykładów \( p1 \) - \( p4 \). Przetwarzanie odbywa się dla każdej cechy (wyjść poszczególnych neuronów) niezależnie.
Spotykana jest również inna wersja normalizacji layer norm [Ba et al., 2016], która normalizuje wartości w wymiarze neuronów, czyli średnia i odchylenie standardowe wyznaczane są dla neuronów od 1 do 5. Zazwyczaj batch normalization spotykamy w przetwarzaniu obrazów (sieci konwolucyjne), a layer norm w przetwarzaniu tekstu (sieci rekurencyjne, transformery), ale nie ma przeszkód, aby metody te stosować do innych problemów i struktur sieci.
Literatura
|
[Srivastava et al., 2014]
|
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929--1958. [ | .html ] |
|
[Ioffe and Szegedy, 2015]
|
Ioffe, S. and Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. [ | arXiv ] |
|
[Ba et al., 2016]
|
Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer normalization. [ | arXiv ] |
|
[Hoerl and Kennard, 1970]
|
Hoerl, A. E. and Kennard, R. W. (1970). Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 12(1):55--67. |
|
[Tibshirani, 1996]
|
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1):267--288. [ | http ] |
4. Sieci konwolucyjne
W klasycznych sieciach typu perceptron wielowarstwowy przetwarzanie obrazów jest trudne. Przykładowy okrazek przedstawiony na rysunku 10 ma szerokość i wysokość 768 pikseli. Zatem cały obraz to \( 768 * 768 * 3 = 1769472 \) wartości (3 ze względu na 3 kanały RGB), co daje bardzo dużo cech przykładu uczącego i przekłada się na ogromną liczbę parametrów sieci. Zazwyczaj zmniejsza się rozdzielczość przetwarzanych obrazów, ale wciąż jest to dużo danych. Kolejnym problemem w strukturze MLP jest brak możliwości odzwierciedlenia przestrzennych zależności pomiędzy pikselami.

Sieci konwolucyjne są dedykowane do przetwarzania obrazów. Najpowszechniejszym zastosowaniem jest przetwarzanie standardowych zdjęć. W takim przypadku plik obrazu ma trzy kanały RGB (R - czerwony, G - zielony, B - niebieski). Przetwarzamy jednak również obrazy w skali szarości (1 kanał), obrazy medyczne np. RTG, obrazy z dodanym kanałem D - głębokości (szeroko stosowane w robotyce), pomiary z kamer termowizyjnych lub zdjęcia satelitarne (gdzie najczęściej mamy dostępne więcej kanałów oprócz pasma widzialnego).
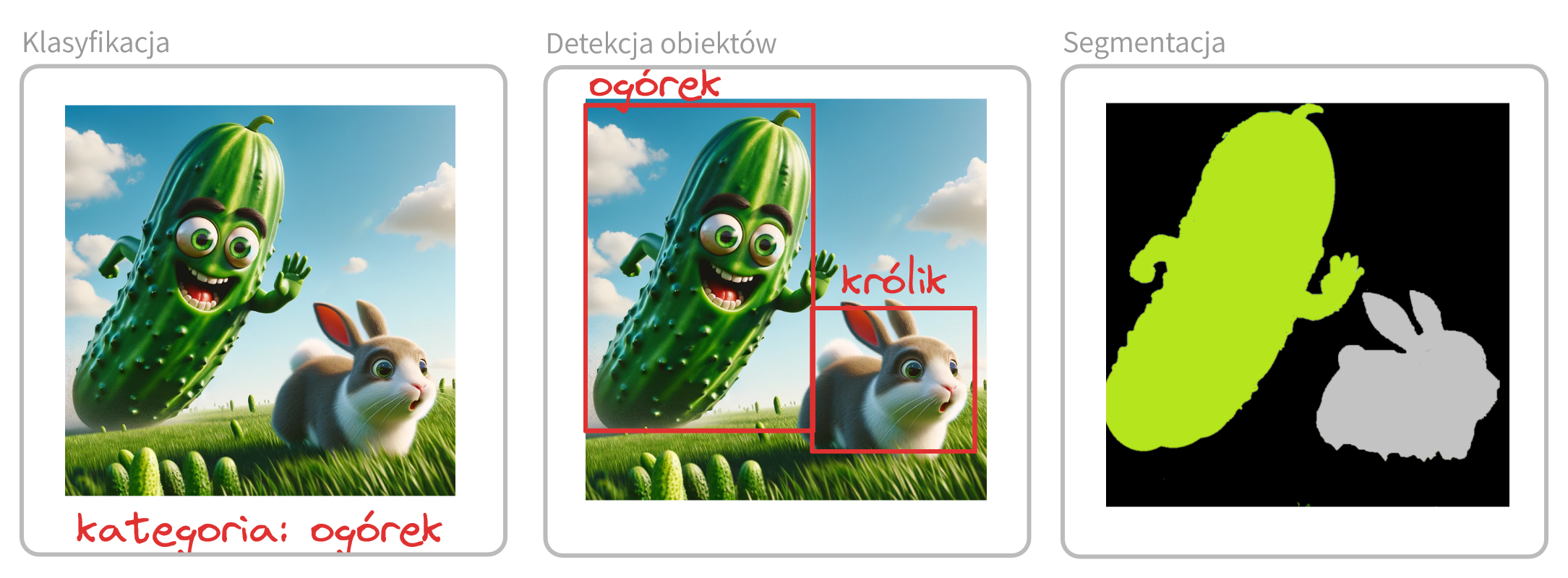
Do najpopularniejszych zadań w przetwarzaniu obrazów należą (rysunek 11):
klasyfikacja - określenie do jakiej dyskretnej kategorii należy przypisać zawartość obrazu (np. kot czy pies);
detekcja obiektów - zadanie znalezienia ramek ograniczających dla określonych klas obiektów. Zadanie to łączy klasyfikację z wyznaczaniem położenia obiektów. Najczęściej stosowane są prostokątne ramki ograniczające.
segmentacja obrazu - oznaczanie pikseli reprezentujących konkretną klasę lub klasy np. oznaczanie pól uprawnych na zdjęciach satelitarnych. Oznaczenia w tym przypadku są realizowane na poziomie pojedynczych pikseli i nie muszą mieć określonych kształtów.
4.1. Operacja konwolucji (splotu)
W sieciach konwolucyjnych podstawową rolę pełni operacja splotu (ang. convolution). Przykład operacji splotu został przedstawiony na rysunku 12. Filtr nakładany jest na przetwarzany obraz, a następnie wartości wag filtra i pikseli obrazu są przemnażane. Wyniki poszczególnych mnożeń dodajemy. Zatem dla położenia filtra jak na rysunku 12 otrzymujemy: \( 1 * (−1) + 2 * 0 + 2 * 1 + 1 * (−1) + 2 * 0 + 2 * 1 + 1 * (−1) + 2 * 0 + 3 * 1 = 4 \). Uzyskaną wartość wstawiamy w odpowiadające miejsce nowego obrazu.
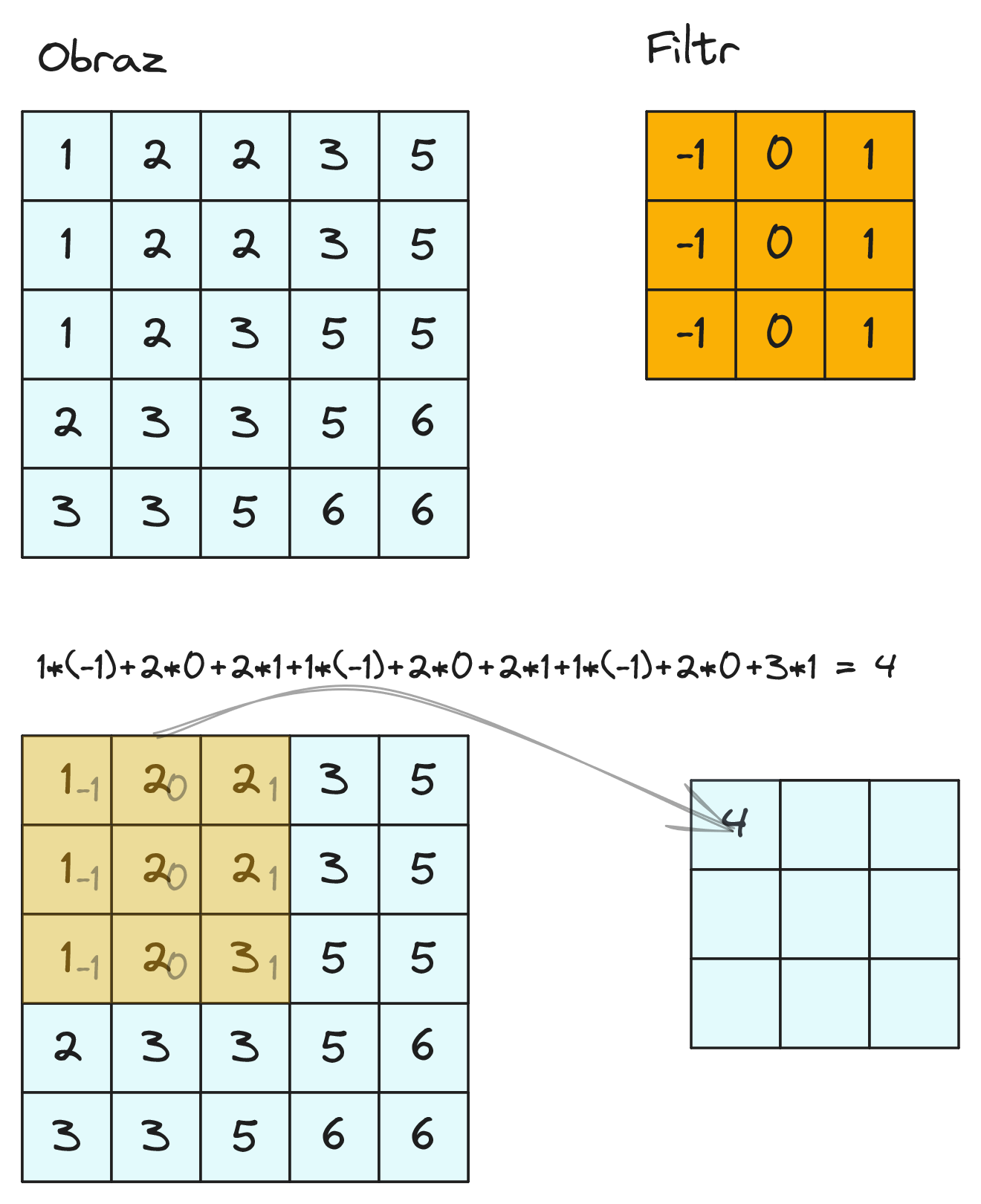
Operacja filtracji/splotu/konwolucji jest szeroko stosowana w klasycznym przetwarzaniu obrazu. Przykład zastosowania filtrów krawędziowych został przedstawiony na rysunku 13. Filtr górny wykrywa krawędzie poziome a dolny pionowe.
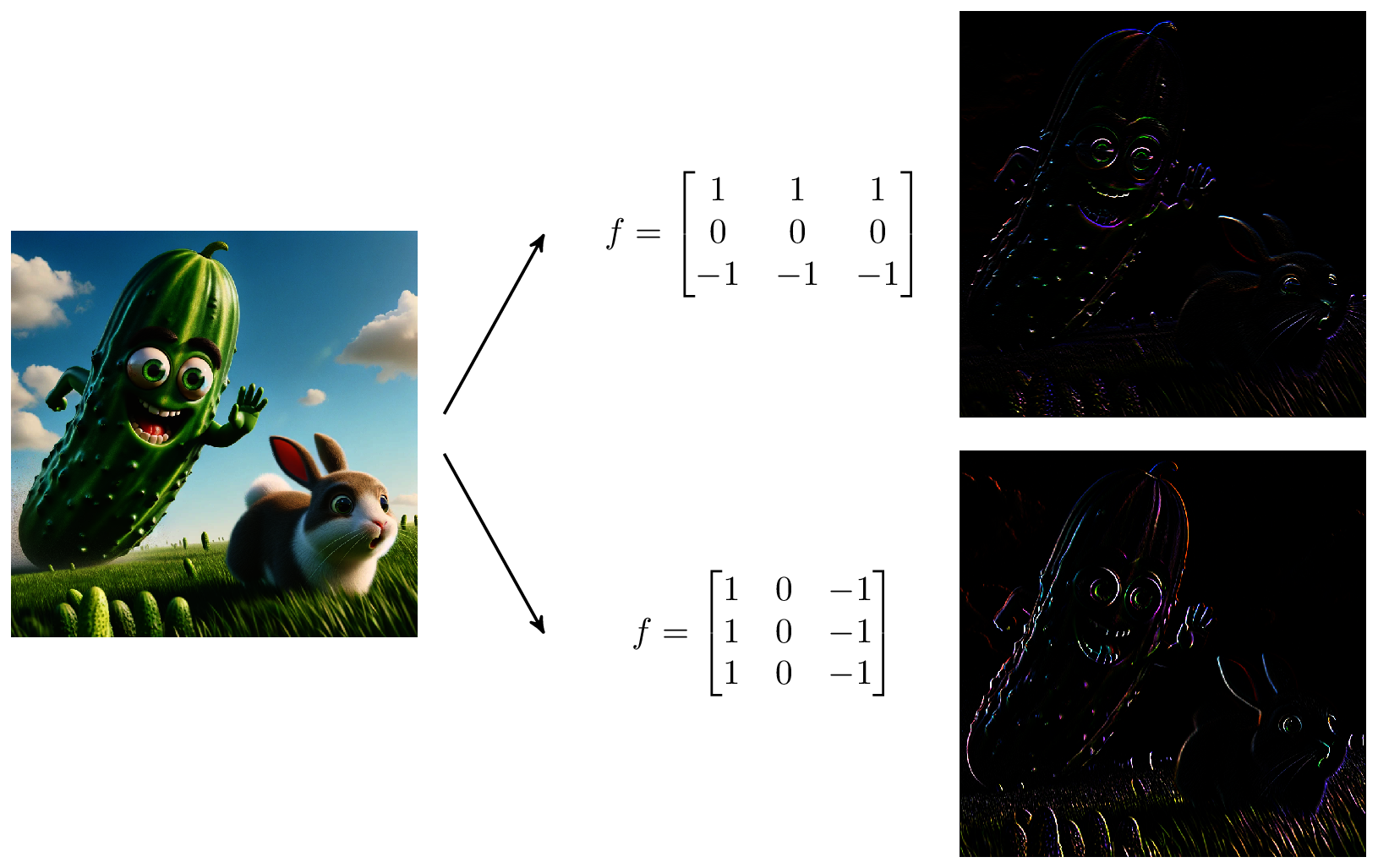
Przykład detekcji krawędzi pionowej dla mikro obrazu został przedstawiony na rysunku 14. Widzimy, że w obrazie wyjściowym duże wartości pikseli odpowiadają lokalizacji krawędzi na obrazie wejściowym.
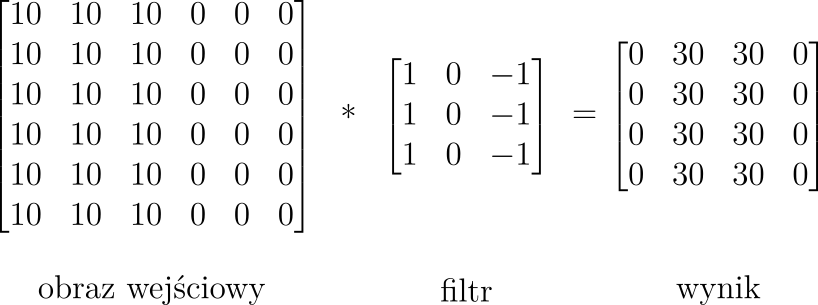
W klasycznym przetwarzaniu obrazu stosujemy filtry zaprojektowane przez ludzi, takie jak filtry krawędziowe pokazane na rysunkach 13 i 14. W sieciach konwolucyjnych stosujemy w każdej warstwie zbiór filtrów o uczonych wagach. Zatem wagi filtrów w pewnym sensie będziemy traktować analogicznie jak wagi połączeń w perceptronie wielowarstwowym. Są one dostrajane za pomocą algorytmów gradientowych na podstawie zbioru uczącego.
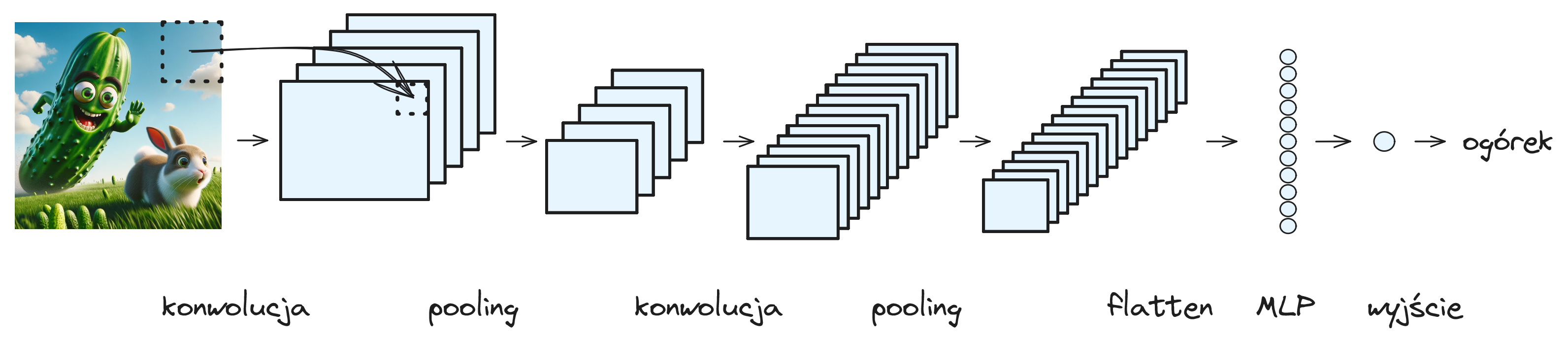
4.2. Architektura sieci konwolucyjnej
Na rysunku 15 przedstawiona została architektura całej sieci konwolucyjnej. Przedstawiona przykładowa sieć realizuje klasyfikację binarną - czy na obrazie znajduje się ogórek czy nie. Końcowe warstwy sieci (neuron wyjściowy i warstwa gęsto połączona przed nim) odpowiadają temu co znamy z perceptronu wielowarstwowego. Działanie warstw konwolucyjnych zostanie objaśnione w dalszych częściach tego rozdziału. Możemy zaobserwować, że warstwy konwolucyjne przetwarzają objętość 3D: szerokość x wysokość x liczba kanałów. Liczba kanałów obrazu wejściowego wynosi 3 w przypadku standardowych kolorowych obrazów. Liczba kanałów w kolejnych warstwach sieci zazwyczaj zwiększa się, a szerokość i wysokość przetwarzanego obrazu maleją. Kolejne kanały wyjścia warstwy konwolucyjnej odpowiadają różnym filtrom i reprezentują różne cechy obrazu. W pierwszej warstwie mogę to być bardzo proste cechy jak występowanie krawędzi pionowych. W kolejnych warstwach filtry wykrywają coraz bardziej złożone cechy.
Zaletą sieci konwolucyjnych w przetwarzaniu obrazów jest zachowanie korelacji przestrzennej - obraz przetwarzany jest w postaci macierzy pikseli. Filtr (i jego wagi) stosowany jest w takiej samej postaci do wielu miejsc na obrazie, co radykalnie zmniejsza liczbę parametrów sieci w zastosowaniach dla większych obrazów. Dodatkowo zapewnia to detekcję cech i obiektów niezależnie od ich położenia.
4.3. Stride
Przyglądaliśmy się do tej pory jak działa filtr w konkretnym miejscu obrazu (rysunek 12). Przeanalizujmy teraz jak filtr przemieszczany jest na obrazie. Wartość o jaką przesuwany jest filtr w kolejnych krokach nazywamy stride. Na rysunku 16 widzimy jak tworzony jest obraz wyjściowy dla stride równego 1x1 lub 2x2. Widzimy, że w obu przypadkach obraz wyjściowy jest mniejszy niż wejściowy oraz wielkość przesunięcia ma wpływ na rozmiar obrazu wyjściowego. Domyślnie najczęściej stosujemy stride 1x1.
Możemy również zaobserwować (rysunek 16, stride 1x1), że piksel w lewym górnym rogu obrazu bierze udział tylko w jednej operacji konwolucji, a tym samym wpływa tylko na jeden piksel obrazu wyjściowego (ten czerwony). Ogólnie piksele w środkowej części obrazu mają większy wpływ niż piksele na krawędziach obrazu.
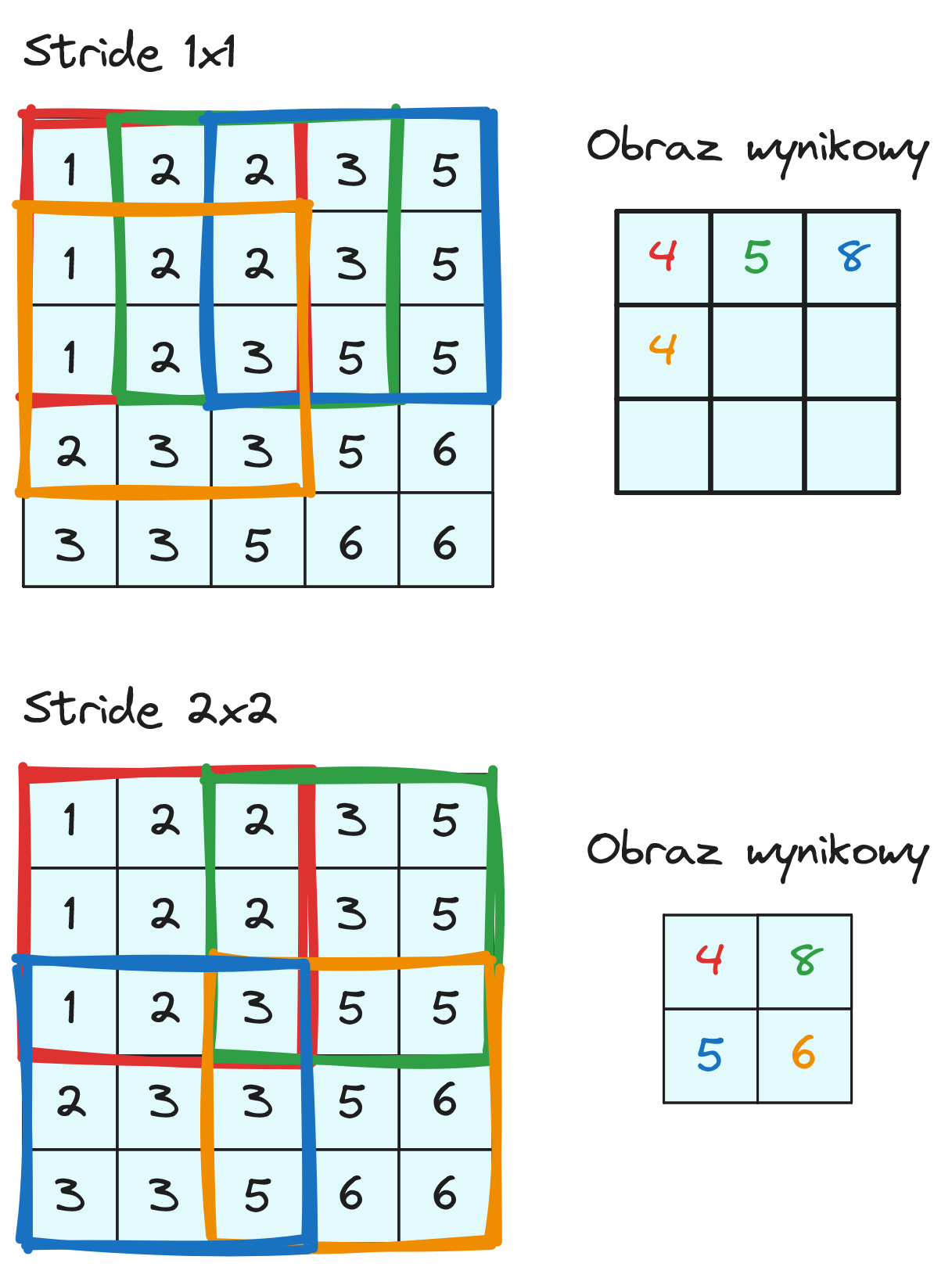
Na rysunku 17 widzimy jak zmienia się rozmiar obrazu wyjściowego dla stride 1x1. Dla obrazu o szerokośći i wysokości \( n \) i rozmiarze filtra \( f \) dostajemy na wyjściu obraz o rozmiarze \((n-f+1)\times(n-f+1)\).
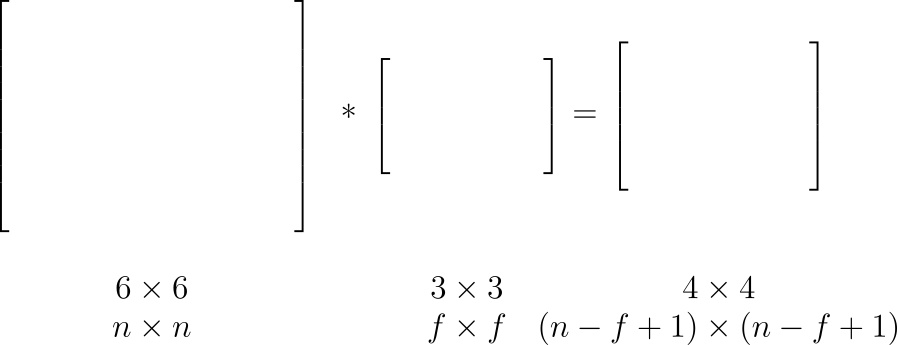
4.4. Padding
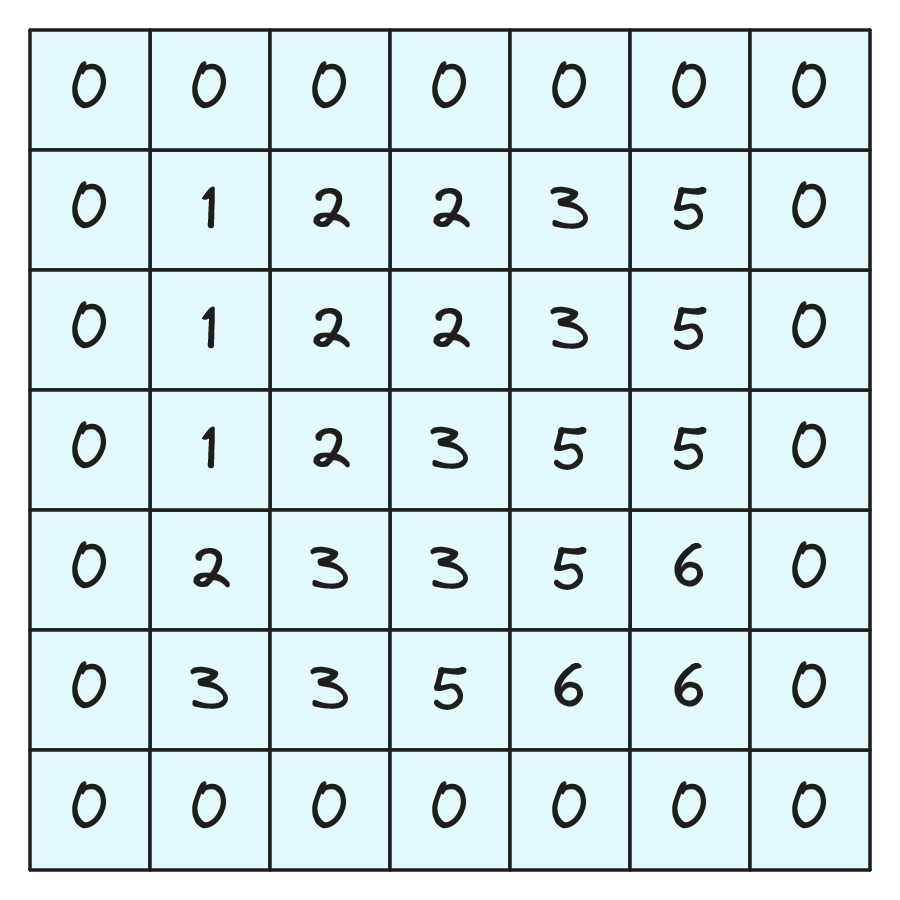
Jeżeli nie chcemy, aby obraz po filtracji się zmniejszał oraz żeby wszystkie piksele obrazu wejściowego miały taki sam wpływ na wynik możemy zastosować padding. Padding to uzupełnianie obrazu wejściowego ramką złożoną z zer (rys. 18).
Możemy stosować dowolną szerokość ramki zer, ale najczęściej stosuje się dwa warianty paddingu:
padding valid - bez uzupełniania obrazu ramką zer,
padding same - taki rozmiar ramki, żeby obraz wyjściowy miał taki sam rozmiar jak wejściowy.
Na rozmiar obrazu wyjściowego ma również wpływ rozmiar stosowanego filtru \( f \). Najczęściej spotykamy filtry o rozmiarach: \( 3 \times 3 \), \( 5 \times 5 \) i \( 7 \times 7 \). Stosujemy prawie wyłącznie filtry o rozmiarach nieparzystych. Jest to konwencja z klasycznego przetwarzania obrazu, ale jest ona dogodna ponieważ w każdym filtrze istnieje element środkowy. Dodatkowo, dla filtra o rozmiarze parzystym, musielibyśmy stosować niesymetryczny padding same (inny rozmiar ramki z prawej i lewej).
4.5. Przetwarzanie dla wielu kanałów
Do tej pory nasze rozważania prowadziliśmy w 2D. Teraz jest czas, aby dodać do tego trzeci wymiar. Wiemy, że obrazy wejściowe najczęściej mają trzy kanały RGB, a wraz z przechodzeniem wgłąb sieci liczba kanałów rośnie (rys. 15). Operacja splotu dla wielu kanałów została przedstawiona na rysunku 19. Tak naprawdę, kiedy mówimy o filtrze 3 × 3 to mamy do czynienia z filtrem 3 × 3 × liczba kanałów obrazu wejściowego. Daje to sieci większe możliwości: w celu znalezienia krawędzi pionowych dla wszystkich kanałów powtarzamy dla każdego kanału ten sam filtr krawędziowy; w celu detekcji obszarów czerwonych możemy ustawić wartości 1 dla filtra dla kanału R i zera dla pozostałych kanałów. Wagi filtrów są oczywiście uczone, celem przykładów jest zobrazowanie możliwości modelu. W dalszych warstwach sieci, gdzie występują bardziej złożone cechy, wymiar głębokości filtra pozwala na łączenie wyników z różnych kanałów.

Do obrazu wynikowego dodawany jest wyraz wolny (jedna wartość dla całego obrazu). Następnie do wartości pikseli stosowana jest funkcja aktywacji element po elemencie. Do wyboru mamy taki sam zestaw funkcji aktywacji jak w perceptronie wielowarstwowym. Operacje te zostały przedstawione na rysunku 20.
Wynik splotu obrazu i pojedynczego filtra jest obrazem 2D (o jednym kanale). W warstwach sieci konwolucyjnej stosujemy wiele filtrów (zazwyczaj od kilku do kilkuset). Wynik kolejnych filtrów są dodawane jako kolejne kanały obrazu wyjściowego (rys. 21). Zatem wyjściem warstwy konwolucyjnej jest obraz 3D o głębokości równej liczbie filtrów w poprzedzającej warstwie.

4.6. Pooling
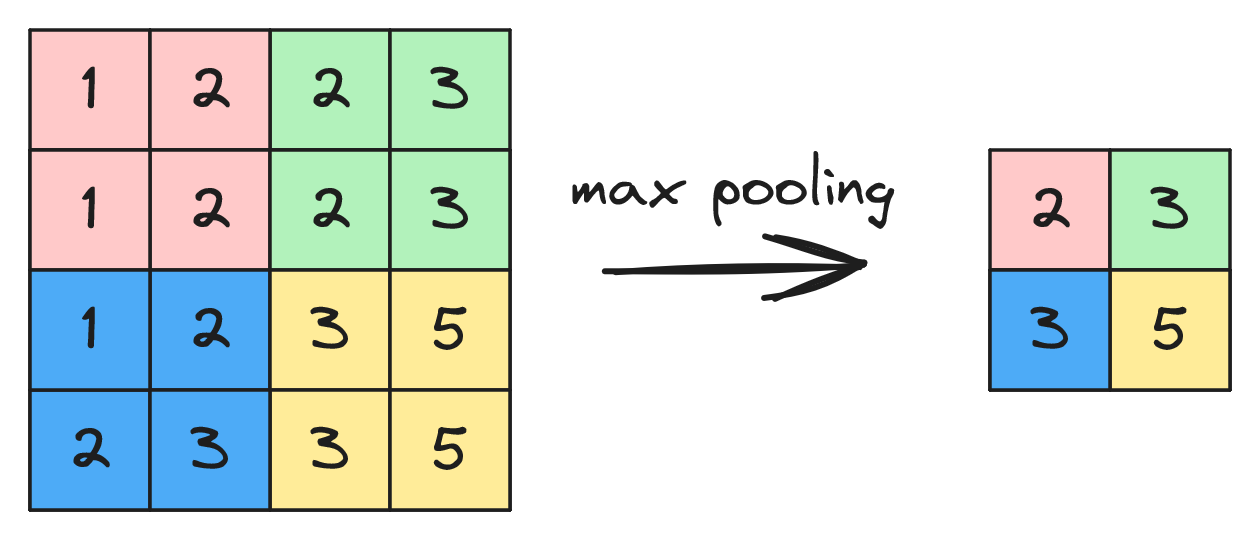
Oprócz operacji konwolucji w sieciach konwolucyjnych istotną rolę odgrywa operacja poolingu. Została ona przedstawiona na rysunku 22. Widzimy tu max pooling w oknie 2x2, czyli z każdego obszaru 2x2 (oznaczone kolorami) wybieramy wartość największą i wstawiamy ją w obraz wynikowy. Jeżeli stosujemy przesunięcie okna (stride) 2x2 to po tej operacji uzyskujemy dwukrotne zmniejszenie szerokości i wysokości obrazu. Pooling stosowany jest do każdego kanału obrazu oddzielnie.
Stosowane są dwa podstawowe rodzaje poolingu:
max pooling - wybieranie wartości największej,
mean (average) pooling - wybieranie wartości średniej w oknie.
Bardziej popularny jest max pooling - pozwala przekazać dalej informację jak bardzo dana cecha wystąpiła w danym oknie. Mean pooling można stosować w ostatniej warstwie sieci w celu przejścia z przetwarzania danych 3D na 1D. Przykładowo, w ostatniej warstwie sieci konwolucyjnej otrzymujemy obraz 7x7x1000, a następnie stosujemy mean pooling w oknie 7x7, co daje obraz 1x1x1000, czyli w praktyce dane jednowymiarowe, które dalej możemy przetwarzać za pomocą warstw gęsto połączonych.
Operacja poolingu pozwala na uogólnienie operacji z poprzednich kroków, redukcję wymiaru i złożoności obrazu, redukcję szumów oraz bardziej odporną detekcję cech. Zwróćmy uwagę, że po zastosowaniu poolingu, filtry warstw kolejnych pracują na danych z większego obszaru obrazu wejściowego (filtry mogą wykrywać coraz większe obiekty). Warstwa poolingu nie ma uczonych parametrów. Należy ustawić rozmiar okna oraz jego przesunięcie. Domyślnie przesunięcie jest równe rozmiarowi okna - w ten sposób okna nie nakładają się.
4.7. Warstwa wypłaszczająca (flatten)
Po przetwarzaniu przez warstwy konwolucyjne należy dodać warstwę lub kilka warstw wyjściowych dostosowanych do problemu rozwiązywanego przez sieć. Najczęściej stosujemy warstwy gęsto połączone. W tym celu potrzebujemy zmienić kształt przetwarzanych danych z 3D na 1D. Służy do tego warstwa wypłaszczająca (ang. flatten). Warstwa ta nie ma żadnych parametrów, po prostu zmienia kształt przetwarzanego tensora. Przykład działania warstwy flatten wraz z warstwą wyjściową został przedstawiony na rysunku 23.

4.8. Typowe architektury sieci konwolucyjnych
Przyjrzyjmy się jeszcze raz pełnej architekturze sieci konwolucyjnej (rys. 15). Zazwyczaj:
-
stosujemy na przemian warstwy konwolucyjne i poolingu (pooling może być raz na kilka wartw konwolucyjnych),
-
potem warstwa flatten,
-
a następnie warstwy gęsto połączone i wyjściowa.
Często korzystne jest również dodanie warstw służących regularyzacji w celu zapobiegania przeuczeniu (rozdział 3.7). Sieci konwolucyjne rozwijają się dynamicznie i często dobrym pomysłem jest wykorzystanie architektury z literatury. Do najpopularniejszych należą (oraz ich kolejne wersje): LeNet-5 [Lecun et al., 1998], AlexNet [Krizhevsky et al., 2012], VGG [Simonyan and Zisserman, 2015], ResNet [He et al., 2015] oraz Inception [Szegedy et al., 2014]. Często dostępne są również wagi dla popularnych architektur uczonych na dużych bazach obrazów. Pozwala to szybko i skutecznie budować własne aplikacje przetwarzania obrazów. Więcej na ten temat w rozdziale 5.5.
Literatura
|
[Krizhevsky et al., 2012]
|
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Pereira, F., Burges, C. J. C., Bottou, L., and Weinberger, K. Q., editors, Advances in Neural Information Processing Systems 25, pages 1097--1105. Curran Associates, Inc. [ | .pdf ] |
|
[Lecun et al., 1998]
|
Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. In Proceedings of the IEEE, pages 2278--2324. |
|
[Simonyan and Zisserman, 2015]
|
Simonyan, K. and Zisserman, A. (2015). Very deep convolutional networks for large-scale image recognition. [ | arXiv ] |
|
[He et al., 2015]
|
He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep residual learning for image recognition. [ | arXiv ] |
|
[Szegedy et al., 2014]
|
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., and Rabinovich, A. (2014). Going deeper with convolutions. [ | arXiv ] |
5. Inne struktury sieci
W tym rozdziale zostaną krótko przedstawione inne struktury sieci. Rozdział ten nie jest wyczerpujący i wciąż pojawiają się nowe obiecujące rozwiązania (jak Mamba z roku 2023 [Gu and Dao, 2023]).
Literatura
|
[Gu and Dao, 2023]
|
Gu, A. and Dao, T. (2023). Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752. |
5.1. Modelowanie dynamiki w perceptronie wielowarstwowym
Na początku wróćmy do struktury perceptronu wielowarstwowego i zastanówmy się jak można ją wykorzystać do modelowania dynamiki. Sygnały pomiarowe w automatyce (np. ciśnienia, temperatury) i robotyce (np. położenia, prędkości) odwzorowują zmienne dynamiczne, czyli takie, że ich wartości zależą od aktualnych wejść oraz pewnej funkcji stanu obiektu. W podstawowym ujęciu perceptron realizuje odwzorowanie statyczne, czyli uwzględnia sygnały wejściowe, ale nie uwzględnia stanu.
Najprostsze podejście do modelowania dynamiki zostało przedstawione na rysunku 24. W celu modelowania dynamiki wprowadzamy na wejścia opóźnione próbki sygnałów (można również podać opóźniony sygnał wyjściowy). Na rysunku \( k \) oznacza aktualną chwilę czasu, a \( p \) horyzont predykcji (chcemy przewidywać wartość \( y \) na \( p \) kroków w przód.
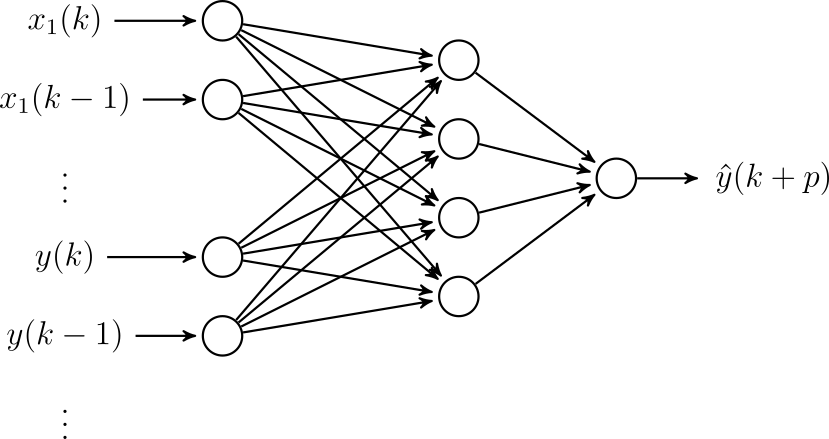
Wśród innych metod modelowania dynamiki z wykorzystaniem sieci neuronowych możemy wymienić:
sieci globalnie rekurencyjne (ze sprzężeniem z wyjścia na wejście),
splot 1D (jak filtracja sygnału w dziedzinie czasu),
sieci o neuronach rekurencyjnych (rozdział 5.4),
oraz sieci z mechanizmem atencji jak transformery.
Jednak podejście z perceptronem wielowarstwowym jest koncepcyjnie i realizacyjnie najprostsze, a modele te mogą mieć mało parametrów i szybko się uczyć, więc jest to podejście, które polecam przynajmniej jako pierwszą próbę.
5.2. Sieci RBF
Sieci RBF (ang. radial basis function) to sieć, w której jako funkcje aktywacji stosujemy radialne funkcje bazowe [Broomhead and Lowe, 1988]. Radialna funkcja bazowa to funkcja, której wartość zależy tylko od odległości od określonego punktu.
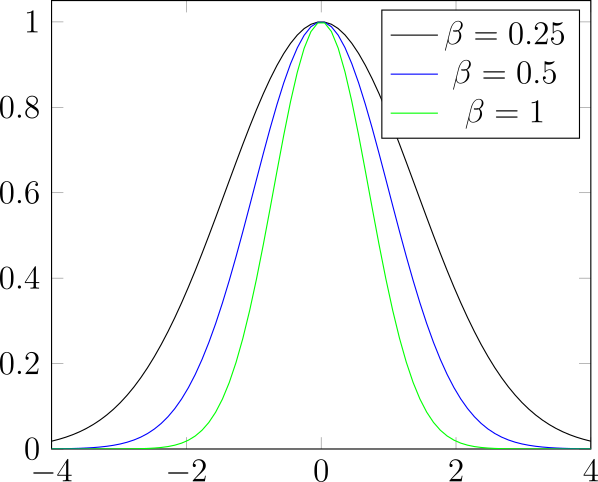
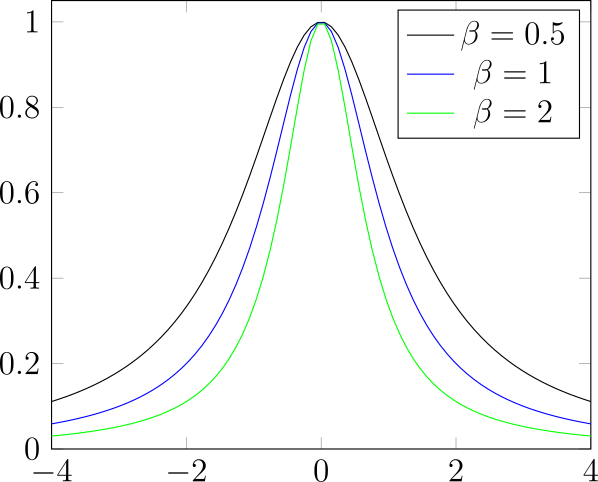
Przykłady radialnych funkcji bazowych zostały przedstawione na rysunku 25. Neurony o radialnych funkcjach aktywacji możemy interpretować jako sprawdzające jak blisko dane wejściowe są określonego punktu.
Sieci RBF możemy wykorzystywać w zadaniach regresji (aproksymacji funkcji) oraz klasyfikacji.
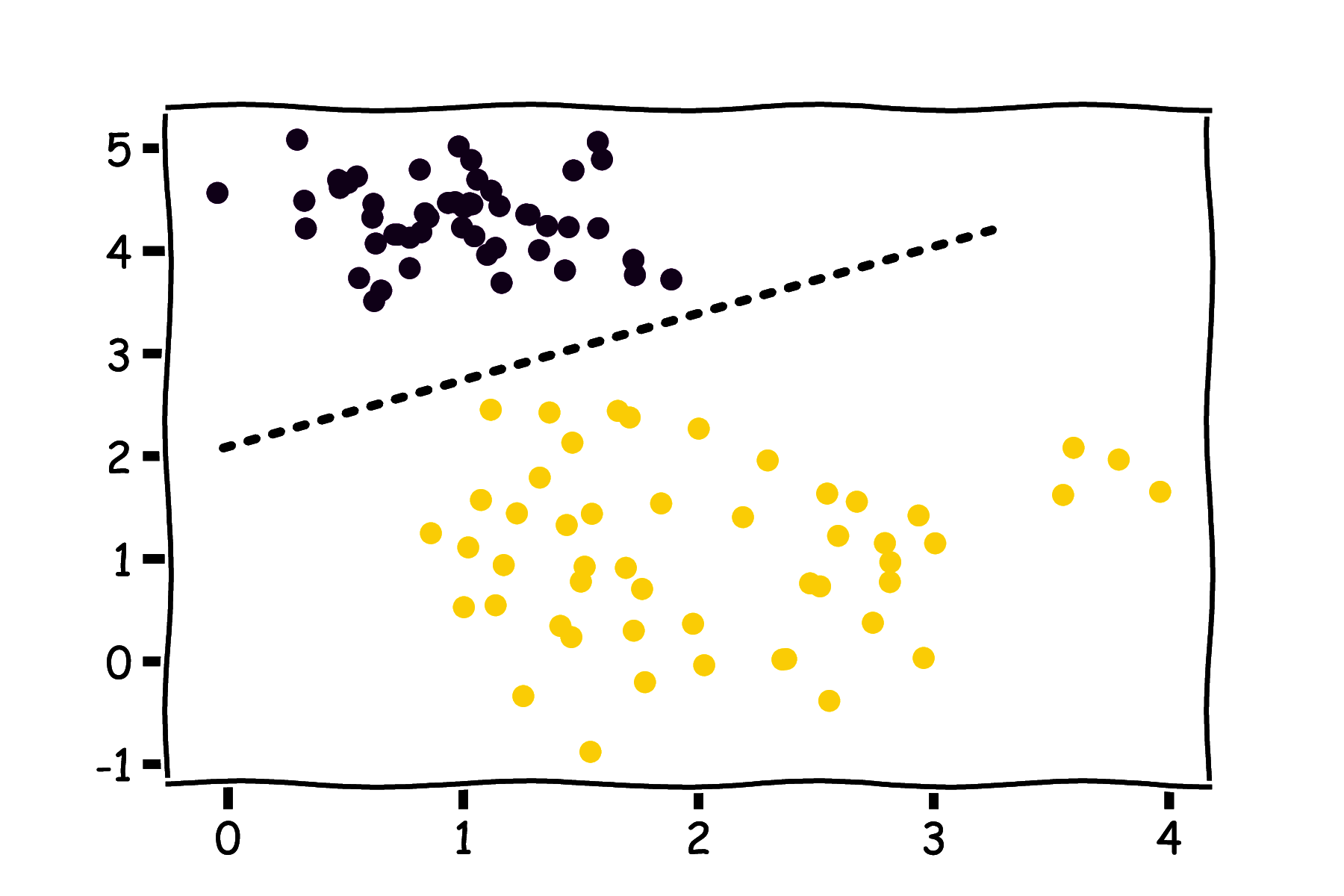
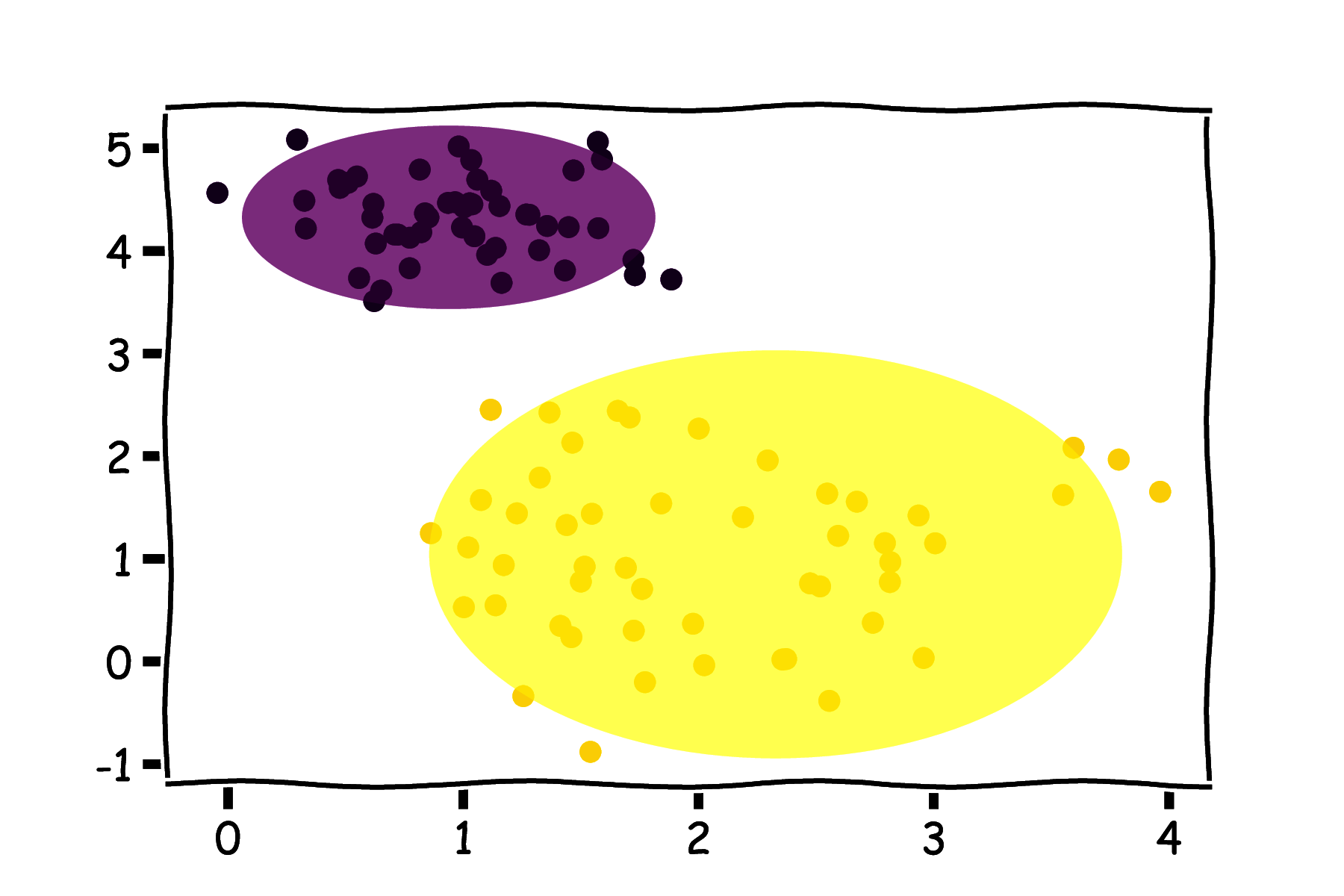
Możemy zauważyć, że w neuronach RBF mamy do czynienia z pewną zmianą paradygmatu w stosunku do perceptronu. Perceptron realizuje liniowy podział przestrzeni danych wejściowych (rysunek 26a), natomiast neuron RBF wybiera pewien podzbiór przestrzeni danych wejściowych ograniczony odległością do konkretnego punktu (rysunek 26b).
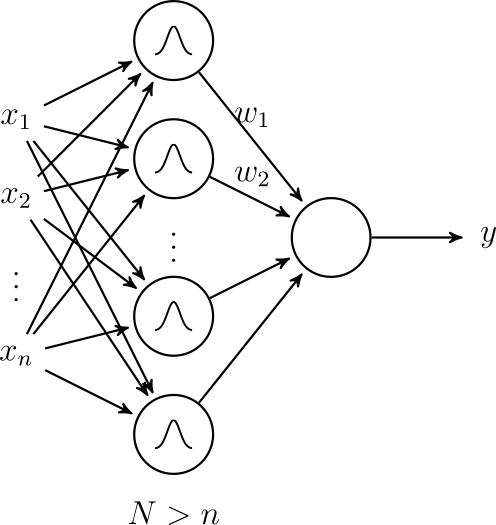
Struktura całej sieci RBF została przedstawiona na rysunku 27. Zawiera ona tylko jedną warstwę ukrytą z neuronami o radialnych aktywacjach. Odpowiada to przekształceniu przestrzeni zmiennych wejściowych w inną przestrzeń (o większej liczbie wymiarów), z nadzieją, że w nowej przestrzeni uda się zrealizować dopasowanie liniowe. Jest to popularne podejście w uczeniu maszynowym (tzw. kernel trick).
Warstwa wyjściowa sieci realizuje dopasowanie liniowe (wzór 37):
\[ y = \sum_{i=1}^N w_i \rho(\|x-c_i\|) \]gdzie \( c_i \) to punkt centralny dla neuronu \( i \).
Uczenie sieci RBF składa się z dwóch kroków. W pierwszym, w sposób nienadzorowany, dobierane są środki ci. Mogą być one wybrane losowo spośród punktów z danych uczących lub z wykorzystaniem algorytmów grupowania (np. k-średnich). Następnie wagi wi są uczone w sposób nadzorowany. Można tu wykorzystać dobrze już nam znane algorytmy gradientowe lub inne metody dopasowywania współczynników funkcji liniowej.
Sieci RBF zostały zaproponowane przed rozwojem uczenia głębokiego i najczęściej nie znajdziemy ich wprost w pakietach do uczenia głębokiego jak Keras. Jednak własna implementacja nie stanowi większego problemu ze względu na prostotę rozwiązania.
Literatura
|
[Broomhead and Lowe, 1988]
|
Broomhead, D. and Lowe, D. (1988). Multivariable functional interpolation and adaptive networks. Complex Syst., 2. |
5.3. Autoenkodery
Kolejną interesującą architekturą są autoenkodery. Przykład autoenkodera został przedstawiony na rysunku 28. Na wejściu mamy dane o n cechach. Pierwsza część sieci - enkoder - przekształca te dane w reprezentację o mniejszym wymiarze k. Druga część - dekoder - próbuje odtworzyć z powrotem dane wejściowe.
Jako funkcji kosztu możemy użyć błędu średniokwadratowego:
\[ \frac{1}{m} \sum_{i=1}^m (x_i - \hat{x}_i)^2 \]gdzie \( \hat{x}_i \) oznaczają wartości cech danych zrekonstruowanych (wyjście sieci). W tym podejściu wykorzystujemy algorytmy uczenia nadzorowanego, ale nie potrzebujemy żadnych etykiet. Prawidłowym wzorem są dane wejściowe (na wyjściu chcemy odtworzyć możliwie dokładnie wejście).
W warstwie sieci po enkoderze uzyskujemy reprezentację danych wejściowych o mniejszym wymiarze \( k < n \), reprezentacja ta powinna odwzorowywać kluczowe cechy danych wejściowych. Nauczonego autoenkodera można używać jako całej sieci (np. odszumianie) lub jako samego enkodera w celu uzyskania reprezentacji o zmniejszonym wymiarze.
Do zastosowań autoenkoderów należą:
redukcja wymiarowości,
wizualizacja,
wyszukiwanie podobieństw (np. między dokumentami tekstowymi),
odszumianie,
kompresja,
kolorowanie obrazów (autoenkodery konwolucyjne),
detekcja anomalii.
5.4. Modelowanie sekwencji
W rozdziale 5.1 wspomnieliśmy o modelowaniu układów dynamicznych z wykorzystaniem perceptronu wielowarstwowego. Istnieje również wiele innych podejść do modelowania danych w postaci sekwencji. Do przykładowych zastosowań należą przetwarzanie tekstu i mowy.
Sieci o neuronach rekurencyjnych
Jednym z możliwych podejść do modelowania sekwencji jest wykorzystanie sieci o neuronach rekurencyjnych. Najprostszą wersję takiej sieci nazywamy RNN (ang. Recurrent Neural Network).
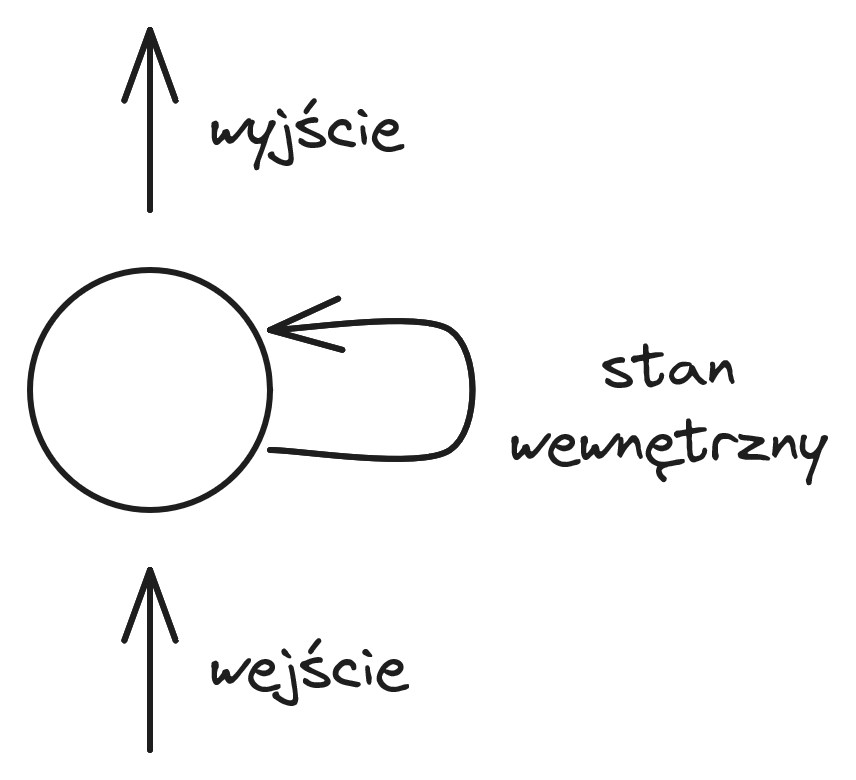
Neuron rekurencyjny został przedstawiony na rysunku 29. Dodatkową cechą takiego neuronu jest posiadanie stanu wewnętrznego, który jest aktualizowany na podstawie wejść i wpływa na wyjście neuronu. Przy stosowaniu algorytmu propagacji wstecznej dla sieci RNN musimy sieć "rozwinąć" dla wszystkich elementów sekwencji. Gradienty z kolejnych kroków są przemnażane, co może prowadzić do zjawiska wybuchających lub zanikających gradientów. W praktyce sieci te słabo się sprawdzają w przypadku dłuższych sekwencji i skuteczniej jest stosować modyfikacje neuronów rekurencyjnych, takie jak LSTM (ang. Long Short-Term Memory) lub GRU (ang. Gated Recurrent Unit).
Transformery
Obecne duże modele językowe (LLM - Large Language Model) są oparte o architekturę typu transformer, która wykorzystuje mechanizm atencji. Mechanizm atencji został zaproponowany w artykule [Vaswani et al., 2023]. Modele te przewidują najbardziej prawdopodobne słowo na podstawie początku tekstu (i tak w kółko dla generacji dłuższych wypowiedzi).
Literatura
|
[Vaswani et al., 2023]
|
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. (2023). Attention is all you need. [ | arXiv ] |
5.5. Uczenie transferowe
W tym podrozdziale omówimy uczenie transferowe (ang. transfer learning), które nie stanowi nowej architektury sieci, ale jest niezwykle skuteczną sztuczką pozwalającą na uzyskanie dobrych wyników przy małej liczbie danych uczących. Jest to podejście szczególnie skuteczne i łatwe w przetwarzaniu obrazów. Przykład takiego podejścia został przedstawiony na rysunku 30.
W uczeniu transferowym wykorzystujemy sieć, która była uczona na dużym zbiorze danych do podobnego zadania. Przykładowo chcemy wykrywać źle zakręcone butelki na linii produkcyjnej, a korzystamy z sieci trenowanej do klasyfikacji zdjęć do wielu kategorii. Postępujemy w następujący sposób:
ściągamy gotową sieć uczoną na dużym zbiorze danych,
pozbywamy się ostatniej warstwy,
uczymy tylko nową ostatnią warstwę
lub kilka warstw (jeśli mamy trochę więcej danych).