Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 1. Podstawy sieci neuronowych |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 30 grudnia 2025, 15:18 |
Spis treści
- 1. Modele neuronów
- 2. Sieć perceptronu wielowarstwowego MLP
- 2.1. Wprowadzenie
- 2.2. Struktura sieci wielowarstwowej MLP
- 2.3. Proces uczenia sieci metodami gradientowymi optymalizacji
- 2.4. Generacja gradientu z użyciem grafów przepływu sygnałów
- 2.5. Metody wyznaczania kierunku minimalizacji
- 2.6. Dobór współczynnika uczenia
- 2.7. Metody heurystyczne uczenia sieci
- 2.8. Inicjalizacja wartości początkowych wag sieci
- 2.9. Program MLP do uczenia sieci wielowarstwowej
- 2.10. Zadania i problemy
- 2.11. Słownik
- 3. Zdolności generalizacyjne sieci neuronowych
- 3.1. Wprowadzenie pojęcia zdolności generalizacyjnych sieci
- 3.2. Miara VCdim i jej związek z generalizacją
- 3.3. Przegląd metod zwiększania zdolności generalizacyjnych sieci
- 3.4. Wstępny dobór architektury sieci
- 3.5. Poprawa zdolności generalizacyjnych poprzez regularyzację
- 3.6. Selekcja cech diagnostycznych
- 3.7. Zwiększanie zdolności generalizacyjnych poprzez użycie zespołu wielu sieci
- 3.8. Przykład metody zwiększania zdolności generalizacyjnych sieci
- 3.9. Zadania i problemy
- 3.10. Słownik
- 4. Literatura
1. Modele neuronów
Wprowadzenie
Sztuczne sieci neuronowe powstały na bazie wiedzy o działaniu systemu nerwowego istot żywych i stanowią próbę wykorzystania zjawisk zachodzących w systemach nerwowych przy poszukiwaniu nowych rozwiązań technologicznych tworząc interdyscyplinarną dziedzinę badań powiązaną z biocybernetyką, elektroniką, metodami optymalizacyjnymi, statystyką, automatyką, a nawet medycyną [18,24,32].
Komórka nerwowa, zwana w skrócie neuronem, stanowi podstawowy element systemu nerwowego. Poznanie mechanizmów działania poszczególnych neuronów i ich współdziałania jest szczególnie istotne dla zrozumienia procesów pozyskiwania, przesyłania i przetwarzania informacji zachodzących w sieciach neuronowych. Informacje te posłużyły zbudowaniu modelu sztucznego neuronu, który stanowi podstawę struktury sieci neuronowej – układu neuronów połączonych ze sobą w określony sposób.
1.1. Model McCullocha-Pittsa
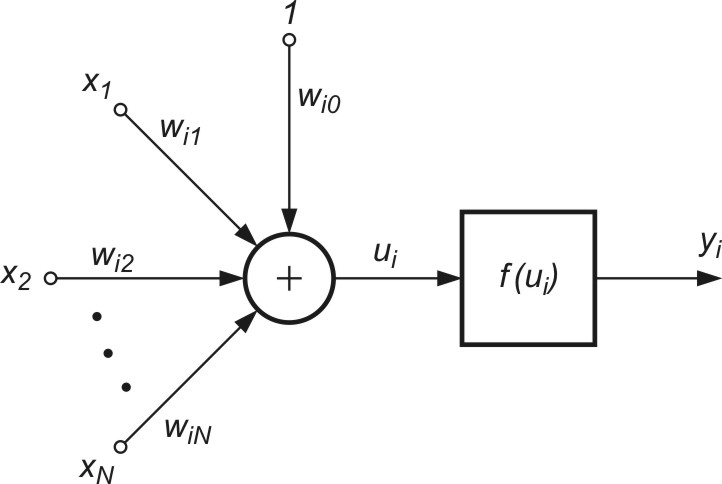
Na podstawie działania rzeczywistej komórki nerwowej stworzono wiele modeli matematycznych, w których uwzględnione zostały w większym lub mniejszym stopniu własności rzeczywistej komórki nerwowej. Pierwszym takim rozwiązaniem był model McCullocha-Pittsa, generujący wynik \( y_i = f ( \sum_{j=1}^N w_{ij} x_{j} + w_{i0} ) \). Na wynik składa się sumator wagowy sygnałów wejściowych oraz blok nieliniowy, realizujący funkcję aktywacji \( f(u_i) \) neuronu, w którym argumentem jest sygnał sumacyjny \( u_i = \sum_{j=1}^N w_{ij} x_{j} + w_{i0} \). Funkcja \( f(u_i) \) jest w modelu McCullocha opisana jest wzorem [24,46]
| \( f(u)= \begin{cases} { \begin{matrix} 1 \textrm{ dla } u>0 \\ 0 \textrm{ dla } u \leq 0 \end{matrix} } \end{cases} \) |
(1.1) |
Współczynniki \( w_{ij} \) występujące we wzorze (1.1) reprezentują wagi połączeń synaptycznych. Wartość dodatnia wagi oznacza synapsę pobudzającą, ujemna - hamującą, natomiast zerowa świadczy o braku połączenia między neuronem i-tym i j-tym.
Strategie uczenia
W adaptacji wartości wag neuronów stosuje się różne strategie [24,46]:
-
uczenie z nauczycielem, zwane również uczeniem pod nadzorem. (ang. supervised learning)
-
uczenie bez nauczyciela (ang. unsupervised learning)
-
uczenie ze wzmocnieniem (ang. reinforcement learning)
W trybie uczenia z nauczycielem przyjmuje się, że oprócz sygnałów wejściowych tworzących wektor x znane są również pożądane sygnały wyjściowe neuronu \( d_i \) tworzące wektor \( \textbf{d} \) (ang. destination), a dobór wag musi być przeprowadzony w taki sposób, aby aktualny sygnał wyjściowy neuronu \( y_i \) był najbliższy wartości zadanej \( d_i \). Istotnym elementem procesu jest tu znajomość zadanej wartości sygnału wyjściowego neuronu.
W strategii uczenia bez nauczyciela dobór wag odbywa się na innych zasadach i wiąże się z wykorzystaniem bądź to konkurencji neuronów między sobą (strategia Winner Takes All - WTA lub Winner Takes Most – WTM), bądź korelacji sygnałów uczących (uogólnione metody hebbowskie). Tego typu rozwiązania stosuje się w zadaniach grupowania danych (na przykład w sieciach Kohonena) bądź w różnego rodzaju transformacjach liniowych bądź nieliniowych (transformacje PCA, LDA, ICA, BSS, itp.).
Strategia uczenia ze wzmocnieniem wykorzystuje interakcje agenta ze środowiskiem, ukierunkowaną na zmaksymalizowanie zwracanej nagrody. Wzmacnianie polega na odpowiedniej polityce zbierania danych o środowisku, wytrenowaniu sieci na podstawie tych danych i powtarzaniu procesu dla uzyskania najlepszych wyników (typowe zastosowania to różnego rodzaju gry). W każdej iteracji agent otrzymuje informację o aktualnym stanie procesu i nagrody, na podstawie której wybiera następną akcję, której celem jest zwiększenie skumulowanej nagrody.
1.2. Model sigmoidalny neuronu
Struktura modelu sigmoidalnego neuronu przedstawiona na rys. 1.1) jest podobna do modelu McCullocha-Pittsa, z tą różnicą, że funkcja aktywacji jest ciągła i przyjmuje postać funkcji sigmoidalnej unipolarnej \( f_u(u) \) lub bipolarnej \( f_b(u) \) [46]. Funkcje te zapisuje się zwykle w postaci
| \( f(u) = \frac{1}{1+exp(-bu)} \) | (1.2a) |
| \( f_b(u)=tgh(bu) \) |
(1.2b) |
gdzie ![]() jest sygnałem sumacyjnym i-tego neuronu, zmienne \( x_i \) (i=1, 2, …, N) stanowią składowe wektora x a \( x_0 \) oznacza sygnał polaryzacji równy zwykle 1 (przy braku polaryzacji równy zeru). Wagi wij stanowią wartości połączeń synaptycznych reprezentowane zwykle poprzez wektor \( \textbf{w}_i = [ w_{i0}, w_{i1}, \ldots, w_{iN}]^T \).
jest sygnałem sumacyjnym i-tego neuronu, zmienne \( x_i \) (i=1, 2, …, N) stanowią składowe wektora x a \( x_0 \) oznacza sygnał polaryzacji równy zwykle 1 (przy braku polaryzacji równy zeru). Wagi wij stanowią wartości połączeń synaptycznych reprezentowane zwykle poprzez wektor \( \textbf{w}_i = [ w_{i0}, w_{i1}, \ldots, w_{iN}]^T \).
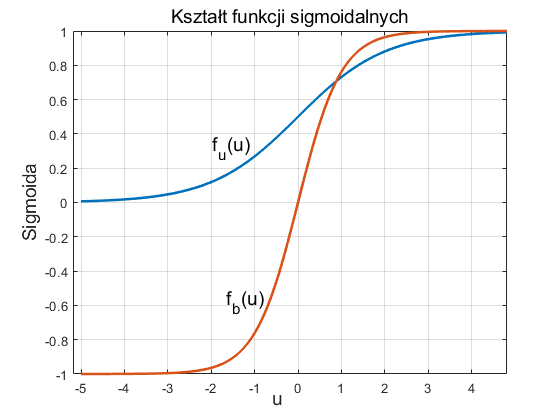
Na rys. 1.2a i 1.2b przedstawiono przebiegi funkcji odpowiednio sigmoidalnej unipolarnej i bipolarnej względem zmiennej \( u \). Przez wprowadzenie bardzo dużej wartości współczynnika \( b \) skalującego sygnał sumacyjny \( u \) funkcja sigmoidalna może odwzorować funkcję skokową, identyczną z funkcją aktywacji perceptronu McCulocha-Pitsa.
Ważną cechą funkcji sigmoidalnej jest jej różniczkowalność. W przypadku funkcji unipolarnej jej pochodna wyraża się wzorem
| \( \frac{df_u(u)}{du}=b f_u(u)(1-f_u(u)) \) |
(1.3) |
natomiast funkcji bipolarnej
| \( \frac{df_b(u)}{du} = b ( 1-f_b^2(u)) \) |
(1.4) |
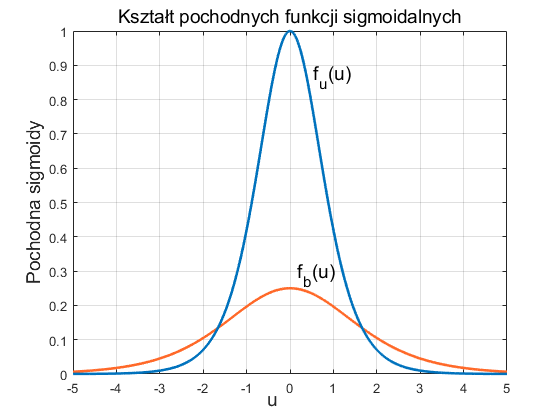
Zauważmy, że dla funkcji sigmoidalnych wartość pochodnej jest całkowicie określona przez wartość samej funkcji. W obu przypadkach wykres zmian pochodnej względem zmiennej u ma kształt krzywej dzwonowej, z maksimum odpowiadającym wartości u=0, jak to przedstawiono na rys. 1.3.
Uczenie neuronu sigmoidalnego odbywa się zwykle w trybie z nauczycielem, przez minimalizację funkcji celu, zwaną również kosztem uczenia, która w przypadku jednej pary uczącej (x, d) definiowana jest dla i-tego neuronu w postaci
| \( E = \frac{1}{2} ( y_i - d_i)^2 \) | (1.5) |
przy czym aktualny sygnał wyjściowy neuronu określony jest w postaci
| \( y_i=f(u_i)=f ( \sum_{j=0}^{N} w_{ij}x_j ) \) | (1.6) |
Funkcja \( f(u_i) \) jest funkcją sigmoidalną, a \( d_i \) wartością zadaną na wyjściu i-tego neuronu. W przypadku zbioru par uczących funkcja celu jest sumą składników dla każdej pary uczącej.
Założenie ciągłej funkcji aktywacji umożliwia zastosowanie w uczeniu metody gradientowej. Najprostszym rozwiązaniem jest zastosowanie metody największego spadku, zgodnie z którą aktualizacja wektora wagowego w odbywa się iteracyjnie z kroku na krok w kierunku ujemnego gradientu funkcji celu
| \( \textbf{w} (k+1)=\textbf{w}(k)-\eta \frac{\partial E}{\partial \textbf{w}} \) | (1.7) |
Dla j-tej wagi i-tego neuronu wzór powyższy przyjmie postać
| \( w_{ij} (k+1)=w_{ij}(k)-\eta \frac{\partial E}{\partial w_{ij}} \) | (1.8) |
Dla przyjętej definicji funkcji celu E łatwo pokazać, że
| \( \frac{\partial E}{\partial w_{ij}} = x_j ( y_i -d_i ) \frac{df(u_i)}{du_i} \) | (1.9) |
Wzór (1.9) w połączeniu z wyrażeniem określającym pochodną funkcji aktywacji definiują algorytm uczenia neuronu sigmoidalnego. Na skuteczność uczenia ma duży wpływ dobór wartości współczynnika uczenia η. W stosowanych rozwiązaniach praktycznych przyjmuje się go bądź to jako wielkość stałą, bądź zmienianą w trakcie uczenia w sposób adaptacyjny. Należy podkreślić, że metoda gradientowa zastosowana w uczeniu neuronu gwarantuje osiągnięcie jedynie minimum lokalnego odpowiadającego wstępnej inicjalizacji wag.
W przypadku funkcji celu wielomodalnej (o wielu minimach lokalnych) znalezione minimum lokalne może być odległe od globalnego. Wyjście ze strefy przyciągania określonego minimum lokalnego nie jest możliwe przy zastosowaniu prostego algorytmu największego spadku. Pewną pomocą może być zastosowanie uczenia z tak zwanym momentem rozpędowym. W metodzie tej proces aktualizacji wag uwzględnia nie tylko informację o gradiencie funkcji, ale również aktualny trend zmian wag. Matematycznie ten sposób uczenia można opisać za pomocą następującego wzoru określającego przyrost wartości wag [24,46]
| \( \Delta w_{ij} (k+1) = - \eta \frac{\partial E}{\partial w_{ij}} + \alpha \Delta w_{ij} (k) \) |
(1.10) |
w którym pierwszy składnik odpowiada zwykłej metodzie największego spadku, natomiast składnik drugi, zwany składnikiem momentu rozpędowego uwzględnia ostatnią zmianę wag i jest niezależny od aktualnej wartości gradientu. Współczynnik momentu α jest zwykle przyjmowany z zakresu [0, 1] Należy zauważyć, że im większa jest wartość tego współczynnika, tym składnik wynikający z momentu ma większy wpływ na dobór wag. Jego wpływ wzrasta w sposób istotny w pobliżu minimum lokalnego, gdzie wartość gradientu jest bliska zeru. W tym przypadku możliwe są zmiany wag, prowadzące do wzrostu wartości funkcji celu, a więc pokonania bariery ograniczającej minimum lokalne. Ilustracja takiego przypadku przedstawiona jest na rys. 1.4, w zastosowaniu do sieci aproksymującej (spełniającej rolę układu aproksymującego dane wejściowe).
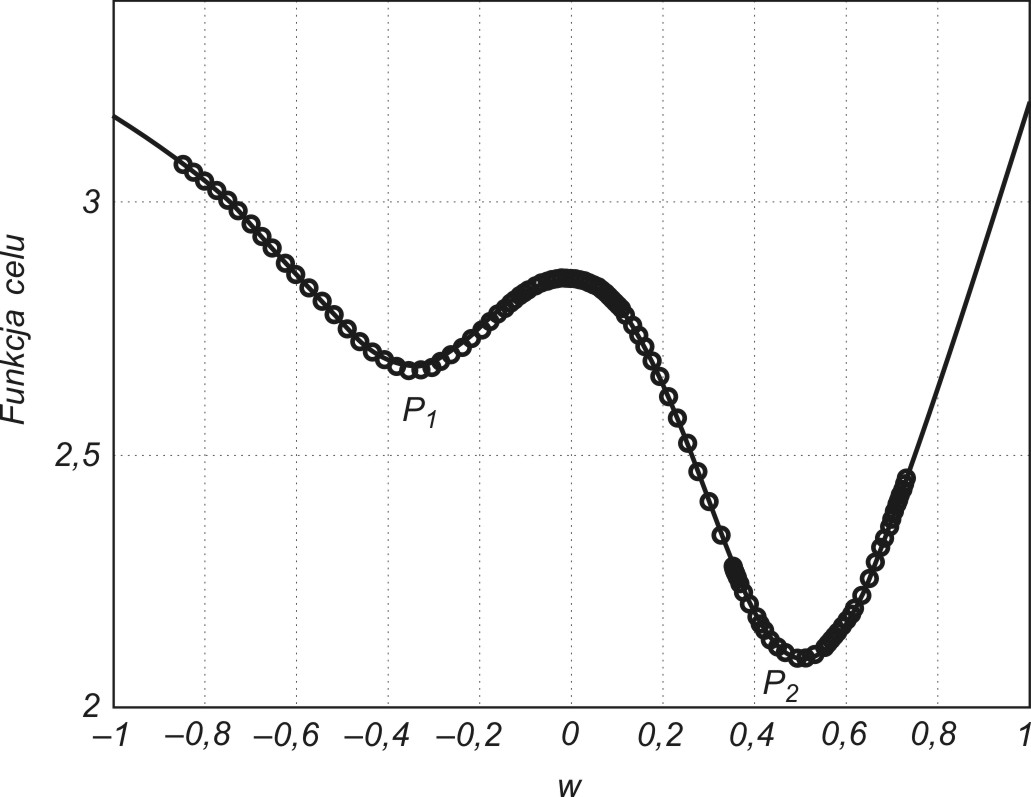
Punkty zaznaczone na wykresie oznaczają wartości funkcji celu uzyskiwane w kolejnych krokach uczących. Minimum lokalne P1 zostało opuszczone w wyniku działania momentu. Umożliwiło to znalezienie nowego minimum w punkcie P2 o mniejszej wartości funkcji celu, a więc korzystniejszego ze względu na dopasowanie wartości yi do wartości zadanej di. Należy podkreślić, że czynnik momentu nie może całkowicie zdominować procesu uczenia, gdyż prowadziłoby to do braku stabilizacji algorytmu. Zwykle kontroluje się wartość błędu (yi-di) w procesie uczenia, dopuszczając do jego wzrostu jedynie w ograniczonym zakresie, np. o 5%. W takim przypadku, jeśli wzrost błędu w kolejnym kroku jest mniejszy niż 5% krok jest akceptowany i w efekcie następuje uaktualnienie wartości wag. Jeśli natomiast wartość błędu przekracza założoną wartość 5% zmiany są ignorowane. Przy jednoczesnym założeniu \( \Delta w_{ij} (k) = 0 \) we wzorze (1.10) składnik gradientowy odzyskuje dominację nad składnikiem momentu zmuszając algorytm do działania zgodnego z klasycznym algorytmem największego spadku.
1.3. Funkcja ReLU aktywacji neuronu
Model sigmoidalny wykorzystuje sigmoidę jako funkcję aktywacji neuronu. Jest to funkcja gładka, zachowując ciągłość również dla pierwszej pochodnej (element ważny w procesie optymalizacji). Cechą charakterystyczną tego modelu jest jego aktywny charakter tylko w ograniczonym zakresie wartości i wystąpienie stanu nasycenia poza tym zakresem. Daje to efekt stagnacji w procesie uczenia, spowalniając dojście do rozwiązania, zwłaszcza przy bardzo dużej liczbie optymalizowanych parametrów (sieci głębokie).
Dogłębne badania problemu wykazały, że ciągłość pochodnej w procesie optymalizacji nie jest warunkiem koniecznym. Dużo lepsze wyniki uzyskuje się stosując znacznie uproszczoną, odcinkami liniową postać funkcji aktywacji, eliminując stan nasycenia. Powszechnie stosowaną formą w sieciach głębokich jest funkcja ReLU (ang. Rectified Linear Unit), którą można zapisać w postaci [78]
| \( y(x) = \begin{cases} { \begin{matrix} x \textrm{ dla } x>0 \\ 0 \textrm{ dla } x \leq 0 \end{matrix} } \end{cases} \) |
(1.11) |
Jest to postać liniowa dla dodatnich wartości argumentu i zero dla wartości ujemnych. Pochodna tej funkcji jest równa 1 w zakresie dodatnim i zero dla wartości ujemnych argumentu. Współcześnie występuje wiele różnych modyfikacji tej funkcji. Więcej na ich temat będzie w rozdziale dotyczącym sieci głębokich.
1.4. Model radialny neuronu
Innym rozwiązaniem stosowanym w sieciach neuronowych jest neuron o radialnej funkcji bazowej (aktywacji). Jest to zwykle funkcja typu gaussowskiego, która dla wielkości skalarnych może być opisana wzorem [24]
| \( \varphi (x) = \exp \left( - \frac{(x-c)^2}{\sigma^2 } \right) \) |
(1.12) |
Wartość funkcji różna od zera występuje jedynie dla zmiennych \( x \) w pobliżu centrum \( c \). Wartość parametru \( \sigma \) decyduje o szerokości tej funkcji. Przy założeniu, że każdy neuron radialny poddany jest działaniu \( N \) sygnałów wejściowych tworzących wektor \( \mathbf{x} \) wartość sygnału wyjściowego \( y(\mathbf{x}) \) tego neuronu można wyrazić wzorem
| \( \varphi (\textbf {x}) = \exp \| - \frac{(\textbf{x}-\textbf{c})^2}{\sigma^2 } \| \) |
(1.13) |
w którym \( \mathbf{x} \) jest \( N \)-wymiarowym wektorem wejściowym, podobnie jak wektor centrów \( \mathbf{c} \). Jeżeli weźmiemy pod uwagę, że \( \Vert \textbf{x}-\textbf{c} \Vert ^2 =(x_1-c_1)^2 + (x_2-c_2)^2 + ... + (x_N-c_N)^2 \) wówczas strukturę szczegółową modelu neuronu radialnego można przedstawić w postaci pokazanej na rys. 1.5.
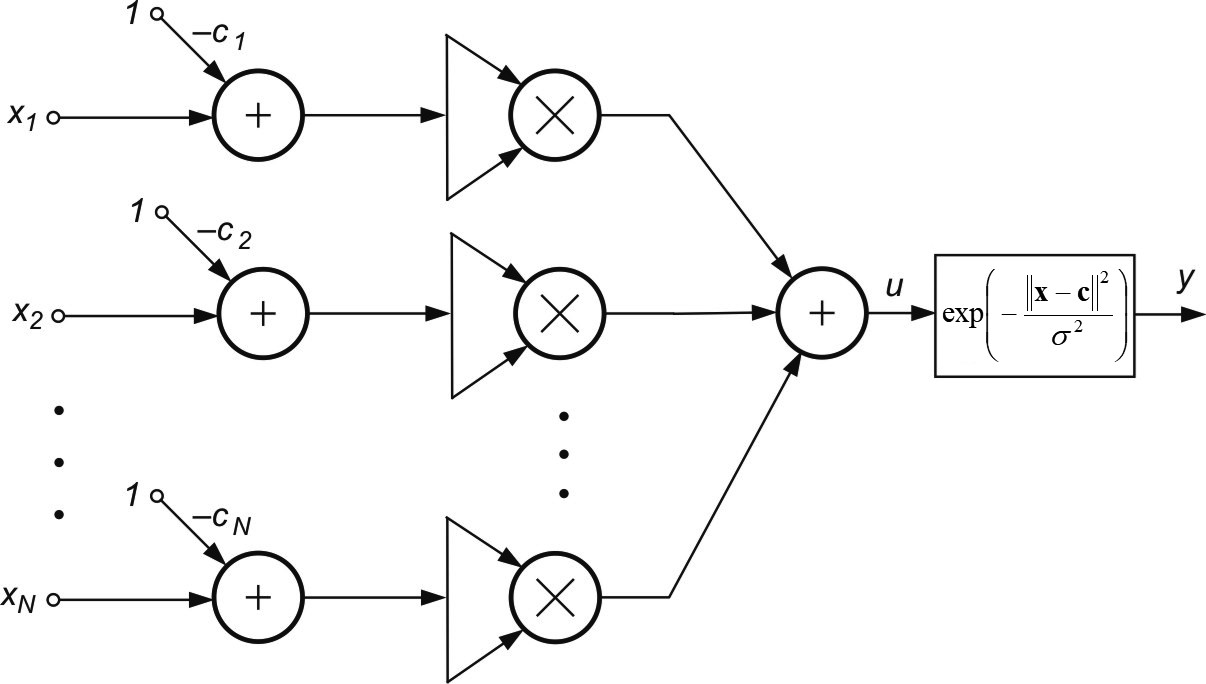
Pomimo pozornego podobieństwa ogólnej postaci neuronu sigmoidalnego i radialnego ich szczegółowe realizacje różnią się znacznie między sobą. Nieliniowość w neuronie radialnym dotyczy wartości sygnału obliczanego nie według zależności liniowej, jak dzieje się to w neuronie sigmoidalnym, ale według zależności nieliniowej (norma euklidesowa wektora).
Uczenie neuronu radialnego polega na doborze wektora centrum i szerokości funkcji radialnej \( \sigma \). Ze względu na lokalny charakter funkcji Gaussa (niezerowa wartość funkcji jedynie w pobliżu centrum) możliwe są tu znaczne uproszczenia, poprzez zastosowanie algorytmu samoorganizacji, adaptującego optymalne położenia centrów dla poszczególnych zmiennych jako środek odpowiedniej grupy danych uczących reprezentowanych przez wektory wejściowe \( \mathbf{x} \).
Najprostszy algorytm samoorganizacji polega na prezentacji wektorów uczących \( \mathbf{x} \) i obliczeniu ich odległości od centrów \( \mathbf{c}_i \) neuronów (na początku wagi centrów są dobierane losowo). Każdy wektor \( \mathbf{x}_i \) jest przypisywany do wektora \( \mathbf{c}_i \) najbliższego mu. Zbiór wektorów \( \mathbf{x} \) przypisanych do jednego centrum tworzy klaster, dla którego oblicza się nowe centrum będące średnią ze wszystkich wektorów \( \mathbf{x} \) przypisanych do niego
| \( \textbf{c}_i = \sum_{j=1}^{N_i} \textbf{x}_j \) |
(1.14) |
Uaktualnianie wartości wszystkich centrów odbywa się równolegle. Proces prezentacji zbioru wektorów \( \mathbf{x} \) oraz uaktualniania wartości centrów powtarzany jest wielokrotnie aż do ustalenia się wartości centrów.
Współczynnik \( \sigma \) jest dobierany w taki sposób, aby wartości funkcji radialnych sąsiednich neuronów pokrywały się częściowo ze sobą (dla zapewnienia gładkiego odwzorowania). Często przyjmuje się wartość stałą dla wszystkich neuronów (dla danych znormalizowanych typowa wartość to \( \sigma \cong 1 \)).
1.5. Model neuronów samoorganizujących się poprzez współzawodnictwo
Specjalny typ stanowią neurony samoorganizujące się poprzez konkurencję. W klasycznym ujęciu mają one stopień wejściowy w postaci standardowego sumatora wagowego o wagach \( w_{ij} \)(rys. 1.6), dla którego sygnał wyjściowy \(i\)-tego sumatora opisany jest relacją| \( u_i = \sum_{j=1}^N w_{ij} x_j = \mathbf{w}_i^T \mathbf{x} = \mathbf{x}^T \mathbf{w}_i \) |
(1.15) |
w której x jest znormalizowanym \( N \)-wymiarowym wektorem wejściowym a \( \mathbf{w}_i \) wektorem wagowym \( i \)-tego neuronu.
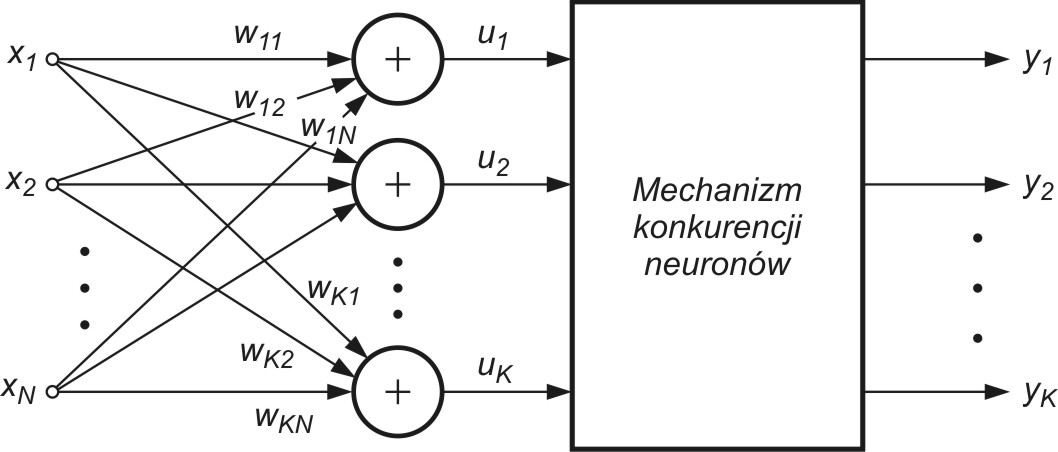
Grupa neuronów współzawodniczących ze sobą pobudzana jest tymi samymi sygnałami wejściowymi \( \mathbf{x}_j \). W zależności od aktualnych wartości sygnałów sumacyjnych \( \mathbf{u}_i \) poszczególnych neuronów za zwycięzcę uważa się neuron, którego wartość \( \mathbf{u}_i \) jest największa. Neuron zwycięzca przyjmuje na swoim wyjściu stan \( 1 \), a pozostałe (przegrywające) stan zero. Ze względu na normalizację sygnałów wejściowych neuronem zwycięskim jest zawsze ten, który znajduje się najbliżej aktualnego wektora wejściowego \( \mathbf{x} \), a więc o najmniejszej wartości normy \( d(\mathbf{x},\mathbf{w_i}) = \Vert \mathbf{x} - \mathbf{w}_i \Vert \). W praktyce zamiast obliczać sumy wagowe poszczególnych neuronów w procesie wyłaniania zwycięzcy oblicza się miary odległościowe i na tej podstawie wyłania zwycięzcę [46]. Najprostsza adaptacja wag neuronów jest typu WTA (ang. Winner Takes All) i nie wymaga nauczyciela. Na wstępie przyjmuje się losowe, znormalizowane wartości wag poszczególnych neuronów. Po podaniu wektora wejściowego \( \mathbf{x} \) wyłaniany jest zwycięzca. Neuron zwyciężający w konkurencji przyjmuje stan 1, a pozostałe 0. Aktualizacja wag odbywa się według wzoru Grosberga zapisanego w formie skalarnej dla \( j \)-tej wagi wektora \( i \)-tego
| \( w_{ij} (k+1) = w_{ij} (k) + \eta [ x_j - w_{ij}(k) ] \) |
(1.16) |
lub wektorowej
| \( \mathbf{w}_{i} (k+1) = \mathbf{w}_{i} (k) + \eta [ \mathbf{x} - \mathbf{w}_{i}(k) ] \) |
(1.17) |
Zauważmy, że w formule WTA jedynie neurony zwycięskie o sygnale wyjściowym \( y_i = 1 \) uaktualniają swoje wagi. Neurony przegrywające konkurencję nie zmieniają swoich wag. W efekcie takiej organizacji algorytmu uczącego wektory wagowe neuronów podążają za wektorami uczącymi \( \mathbf{x} \), przyjmując w efekcie uśrednione wartości wektorów wejściowych, dla których dany neuron był zwycięzcą. W praktyce stosuje się również strategię WTM (Winner Takes Most), w której neurony przegrywające konkurencję uczestniczą również w adaptacji swoich wag, ale przy współczynniku adaptacji \( \eta \) uzależnionym od odległości tych neuronów od wektora wejściowego \( \mathbf{x} \).
W wyniku zwycięstwa neuronu następuje douczenie jego wag, przybliżające je do odpowiednich składowych danego wektora \( \mathbf{x} \). Przy podaniu na wejście sieci wielu wektorów zbliżonych do siebie, zwyciężać będzie ciągle ten sam neuron, w wyniku czego jego wagi odpowiadać będą uśrednionym wartościom wektorów wejściowych, dla których dany neuron był zwycięzcą. Neurony przegrywające nie zmieniają swoich wag. Dopiero zwycięstwo przy następnej prezentacji wektora wejściowego umożliwi im dokonanie aktualizacji wag i rozpoczęcie procesu douczania przy kolejnych zwycięstwach. W efekcie takiego współzawodnictwa następuje automatyczne grupowanie danych. Neurony dopasowują swoje wagi w ten sposób, że przy prezentacji grup wektorów wejściowych zbliżonych do siebie zwycięża zawsze ten sam neuron. Neuron ten reprezentować będzie swoimi wagami wszystkie wektory \( \mathbf{x} \) znajdujące się w jego strefie dominacji. W efekcie powstaje samoczynny podział danych na klastry reprezentowane przez neuron zwycięzcę. Układy tego typu są stosowane najczęściej do grupowania danych jak również do klasyfikacji wektorów.
1.6. Model neuronu Hebba
Donald O. Hebb, badając działanie komórek nerwowych [24] zauważył, że powiązanie wagowe dwóch komórek jest wzmacniane, jeśli obie komórki są jednocześnie pobudzone (stają się aktywne). Jeśli \( j \)-ta komórka o sygnale wyjściowym \( y_j \) powiązana jest z \( i \)-tą o sygnale wyjściowym \( y_i\) przez wagę \( w_{ij} \), wówczas na stan powiązań tych komórek wpływają wartości ich sygnałów \( y_j \) oraz \( y_i \).
D. Hebb zaproponował regułę matematyczną, w której uwzględniony został wynik tej obserwacji. Zgodnie z regułą Hebba, zmiana wagi \( w_{ij}\) neuronu odbywa się proporcjonalnie do iloczynu jego sygnału wejściowego oraz wyjściowego [46]
| \( w_{ij} (k+1) = w_{ij} (k) + \eta y_i y_j \) |
(1.18) |
przy współczynniku \(\eta\) reprezentującym wartość stałej uczenia. Reguła Hebba może być stosowana do różnego typu struktur sieci neuronowych i różnych funkcji aktywacji zastosowanych w modelu neuronu.
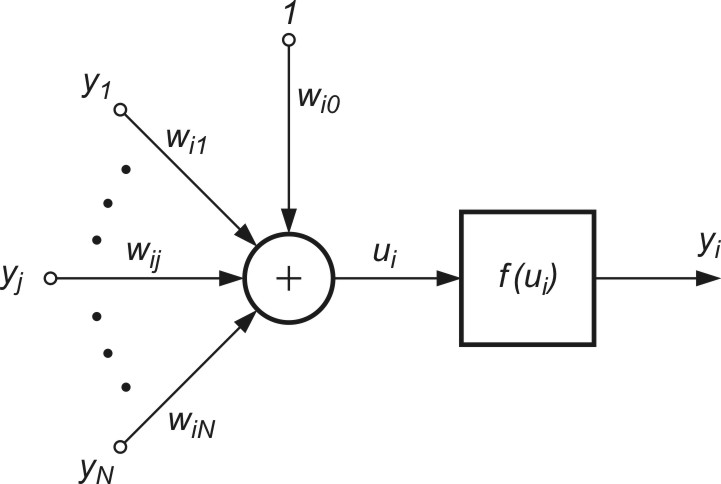
Ogólny model neuronu Hebba, przedstawiony na rys. 1.7, odpowiada standardowej postaci modelu. Waga \( w_{ij} \) włączona jest między sygnałem wejściowym \( y_j \) a węzłem sumacyjnym \( i \)-tego neuronu o sygnale wyjściowym \( y_i \).
Uczenie neuronu z zastosowaniem reguły Hebba może się odbywać w trybie bez nauczyciela lub z nauczycielem. W pierwszym przypadku w regule Hebba używa się aktualnej wartości \( y_i \) sygnału wyjściowego neuronu (wzór (1.18)). W uczeniu z nauczycielem wartość sygnału wyjściowego \( y_i \) zastępuje się wartością zadaną \( d_i \) dla tego neuronu. Regułę Hebba można wówczas zapisać w postaci
| \( w_{ij} (k+1) = w_{ij} (k) + \eta d_i y_j \) |
(1.19) |
Reguła Hebba charakteryzuje się tym, że w jej wyniku wagi mogą przybierać wartości dowolnie duże i nie podlegają stabilizacji, gdyż w każdym cyklu uczącym następuje proces sumowania aktualnych przyrostów wartości wag.
Jedną z metod poprawy stabilności procesu uczenia według reguły Hebba jest przyjęcie przy aktualizacji wag nie ostatniej wartości \( w_{ij} \) ale wartości zmniejszonej o tak zwany współczynnik zapominania \( \gamma \) Wówczas regułę Hebba można zapisać w postaci
| \( w_{ij} (k+1) = (1-\gamma) w_{ij} (k) + \eta y_i y_j \) |
(1.20) |
Współczynnik zapominania \(\gamma\) zawiera się zwykle w przedziale (0, 1) i stanowi najczęściej niewielki procent stałej uczenia \(\eta\). Przyjęcie dużej wartości \(\gamma\) powoduje, że neuron zapomina większość tego, co zdołał nauczyć się w przeszłości. Uczenie Hebba zaliczane jest do uczenia typu korelacyjnego, gdyż w swojej istocie uwzględnia korelacje zachodzące między sygnałami neuronów sieci.
Stabilizacja reguły Hebba przez wprowadzenie współczynnika zapominania zawodzi w przypadku neuronu liniowego. Dla neuronu liniowego Hebba jego sygnał wyjściowy opisany jest zależnością linową \(y_i=\mathbf{w}_i^T \mathbf{x}=\mathbf{x}^T \mathbf{w}_i\), w której \( \mathbf{w}_i\) jest wektorem wagowym neuronu \(i\)-tego a \( \mathbf{x}\) wektorem sygnałów wejściowych tego neuronu. Zostało udowodnione, że w takim przypadku wartości wag \( \mathbf{x}\) procesie uczenia nigdy nie stabilizują się, a proces uczenia się nie kończy. Stabilizacja wag (połączona z jednoczesną normalizacją) jest możliwa przez wprowadzenie modyfikacji reguły Hebba. Zgodnie z modyfikacją zaproponowana przez E. Oję [46] aktualizacja wag \( w_{ij} \) wektora \( \mathbf{w}_i\) przebiega według wzoru
| \( w_{ij} (k+1) = w_{ij} (k) + \eta ( x_j - w_{ij} y_i ) \) |
(1.21) |
Reguła ta przypomina propagację wsteczną, gdyż sygnał \(x_j\) jest modyfikowany przez sygnał wsteczny, pochodzący od sygnału wyjściowego \(y_i\) neuronu. Przy jednym neuronie reguła Oji jest regułą lokalną, gdyż w procesie modyfikacji sygnału \(x_j\) bierze udział tylko waga, którą aktualnie adaptujemy.
1.7. Zadania i problemy
1. Narysować przebiegi funkcji sigmoidalnej unipolarnej \( f(u)= \frac{1}{1+ \exp ( - \beta u )} \) oraz bipolarnej \( f_b(u) = \text{tgh} (\beta u) \) w funkcji zmiennej u dla różnych wartości współczynnika \( \beta \) od 0.1 do 10.
2. Inną postacią funkcji sigmoidalnej jest \( f(u) = \frac{u}{\sqrt{1+u^2}} \). Wykreślić jej przebieg w funkcji zmiennej u. Udowodnić, że pochodna tej funkcji jest równa \( \frac{df(u)}{du} = \frac{f^3(u)}{u^3} \). Wykreślić przebieg pochodnej jako funkcję zmiennej u.
3. Neuron otrzymuje pobudzenie w postaci sygnałów wejściowych tworzących wektor \(\mathbf{<span>x}=[10 \; -10 \; 2 \; -2]^T\)
. Wektor wag wejściowych jest równy \(\mathbf{<span>x}=[0.4 \; 0.3\; -1\; 0.8]^T\). Określić odpowiedź tego neuronu przy założeniu, że-
neuron jest liniowy
-
neuron jest reprezentowany przez model McCullocha-Pittsa
-
neuron jest sigmoidalny bipolarny \( f_b(u) = \text{tgh}(u) \).
4. Porównać kształt funkcji radialnej gaussowskiej przy różnych wartościach parametru \( \sigma \). Wykreślić te funkcje na wspólnym wykresie. Narysować wykres zmian zależności sumy trzech funkcji gaussowskich o centrach przesuniętych w taki sposób, że suporty każdej z nich częściowo pokrywają się ze sobą, przy różnych wartościach \( \sigma \) jako funkcje zmiennej wejściowej \(x\).
5. Neuron RBF o gaussowskiej funkcji aktywacji z centrum \(\mathbf{<span>c}=[1 \; 0.5 \; 0.2 ]^T \) i wartością \( \sigma = 0.5\) otrzymał pobudzenie sygnałami \(x\) tworzącymi wektor trójwymiarowy \(\mathbf{x}=[0.8 \; 0.2 \; 0.1]^T \). Określić sygnał wyjściowy neuronu dla każdego z tych pobudzeń.
6. Dwa neurony o wagach: \(\mathbf{w}_1=[ 0.1 \; -0.2 \; 0.5 ]^T \), \(\mathbf{w}_2= [ -0.5 \; 0.5 \; 0.8]^T\) trenowane są poprzez współzawodnictwo w trybie WTA. Określić ich wagi po pierwszej iteracji przy istnieniu następujących wektorów uczących: \(\mathbf{x}=[ 0.1 \; 0.1 \; 0.6 ]^T \), \(\mathbf{x}= [ 0.2 \; -0.3 \; 0,7 ]^T \), \(\mathbf{x}= [ 0 \; -0.31 \; 0.9 ]^T \), \(\mathbf{x} = [ -0.4 \; 0.4 \; 0.9]^T \), \(\mathbf{x}= [-0.3 \; 0.6 \; 0.7]^T\), \(\mathbf{x}= [ 0.1 \; 0 \; 0.5]^T \), \(\mathbf{x}= [ -0.2 \; 0.6 \; 0.9]^T \), \(\mathbf{x}= [ -0.6 \; 0.3 \; 0.7]^T \) przy założeniu \(\eta=0.2\).
7. Dwa neurony o wagach \(\mathbf{w}_1=[ 0.2 \; 0.3 \; 0.8 ]^T \), \(\mathbf{w}_2= [ -1 \; 0.5 \; 0.5]^T \) pobudzono tymi samymi sygnałami \(x\) tworzącymi wektor \(\mathbf{x}= [ 0.1 \; 0.4 \; 0.6]^T \). Określić zwycięzcę posługując się miarą odległościową oraz iloczynem skalarnym wektorów.
1.8. Słownik
Słownik opanowanych pojęć
- Model neuronu – matematyczny opis przetwarzania sygnałów wzorujących się na procesach neuronowych w organizmach żywych.
- Model McCullocha-Pittsa – model neuronu stosujący skokową funkcję aktywacji.
- Model sigmoidalny – model neuronu stosujący sigmoidalną funkcję aktywacji
- Model radialny – model neuronu stosujący jako aktywację funkcję gaussowską.
- Model Hebba – model neuronu w którym zmiana wagi neuronu odbywa się proporcjonalnie do iloczynu jego sygnału wejściowego oraz wyjściowego.
- ReLU – funkcja aktywacji odcinkowo-liniowa opisana wzorem y(x)=x dla x>0 i zero w przeciwnym przypadku.
- Uczenie z nauczycielem – proces adaptacji parametrów sieci wykorzystujący parę danych (x,d), gdzie x reprezentuje sygnały wejściowe, a d wartość zadaną na wyjściu.
- Uczenie bez nauczyciela – proces adaptacji parametrów sieci przy znajomości jedynie danych wejściowych x (bez wartości zadanej na wyjściu).
- Uczenie ze wzmocnieniem – sposób adaptacji parametrów sieci wykorzystujący interakcje agenta ze środowiskiem, ukierunkowaną na zmaksymalizowanie zwracanej nagrody.
- Sztuczne sieci neuronowe – układ połączeń neuronów między sobą wzorujący się na sposobie przetwarzania danych w organizmach żywych.
- Moment rozpędowy – poprawka w uczeniu metodą największego spadku uwzględniająca ostatnią zmianę parametrów.
- Uczenie ze współzawodnictwem – metoda adaptacji parametrów neuronów współzawodniczących ze sobą pod względem odległości do aktualnego wektora wejściowego x.
- Reguła uczenia Oji – poprawiona przez Oję reguła Hebba w której sygnał wejściowy jest modyfikowany przez sygnał wsteczny, pochodzący od sygnału wyjściowego neuronu.
2. Sieć perceptronu wielowarstwowego MLP
Neurony połączone między sobą tworzą strukturę, zwykle w układzie warstwowym, która jest nazywana sztuczną siecią neuronową, w skrócie siecią neuronową. W zależności od sposobu połączenia neuronów mogą to być sieci jednokierunkowe lub rekurencyjne (ze sprzężeniem zwrotnym). Spośród wielu istniejących rodzajów sieci neuronowych dużym zainteresowaniem cieszy się w dalszym ciągu sieć jednokierunkowa, wielowarstwowa o neuronach typu sigmoidalnego, zwana w skrócie MLP (ang. MultiLayer Perceptron - MLP).
2.1. Wprowadzenie
Metody uczenia sieci jednokierunkowej, wielowarstwowej o neuronach typu sigmoidalnego są proste i łatwe w implementacji praktycznej, zwykle z nauczycielem, a podstawą uczenia jest zbiór stowarzyszonych par uczących (x, d) , w których x jest wektorem wejściowym, a d odpowiadającym mu, zadanym wektorem wyjściowym sieci. Sieć nazywana jest heteroasocjacyjną, jeśli wektory x oraz d są różne. W przypadku gdy x=d , sieć nosi nazwę autoasocjacyjnej. Funkcja aktywacji neuronu stosowana w sieciach MLP jest typu sigmoidalnego. W wykładzie tym przedstawione zostaną podstawowe zależności odnoszące się do sieci wielowarstwowych sigmoidalnych. Omówione zostaną najważniejsze aspekty metod gradientowych uczenia tych sieci, w tym algorytm propagacji wstecznej generacji, metody poszukiwania kierunku minimalizacji oraz współczynnika uczenia.
2.2. Struktura sieci wielowarstwowej MLP
Sieć wielowarstwową MLP tworzą neurony ułożone w warstwach połączonych kolejno między sobą, przy czym oprócz warstwy wejściowej i wyjściowej istnieje co najmniej jedna warstwa ukryta.
| a) | 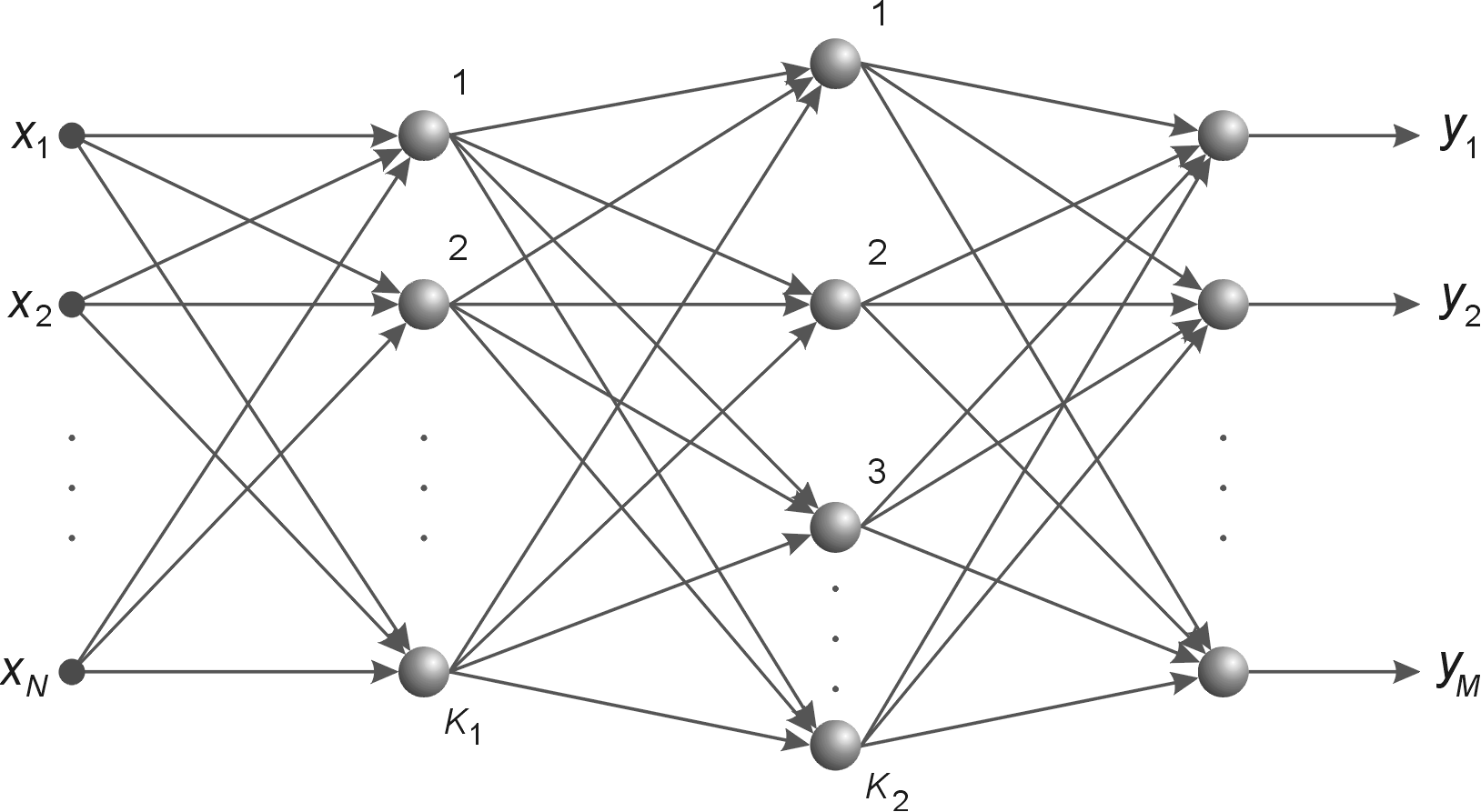 |
| b) | 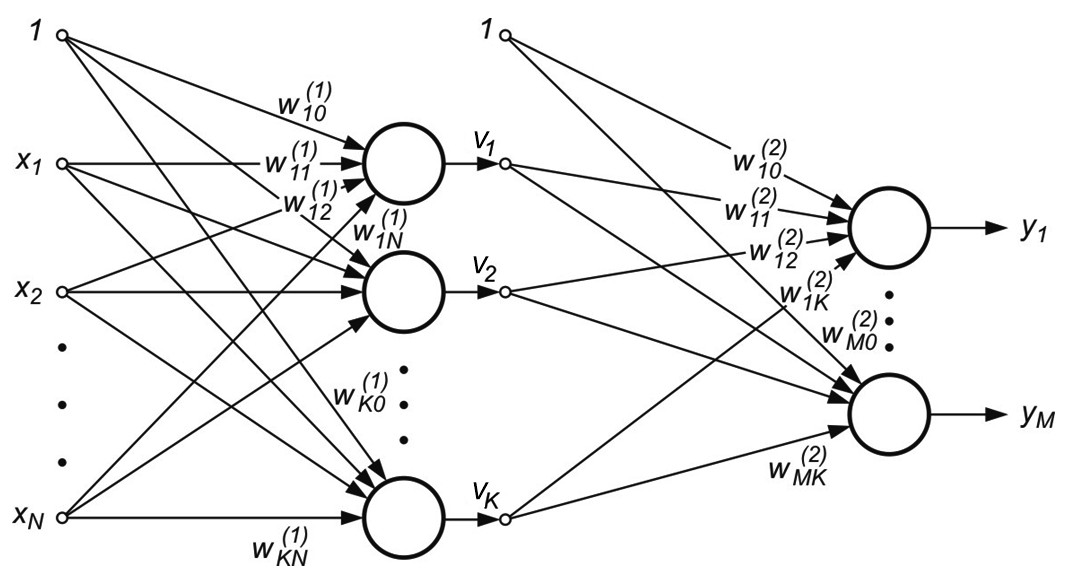 |
Rys. 2.1 a) Ogólny schemat sieci neuronowej sigmoidalnej o dwu warstwach ukrytych, b) sieć o jednej warstwie ukrytej z oznaczeniem połączeń wagowych i polaryzacją
Na rys. 2.1b przedstawiono sieć o jednej warstwie ukrytej [46]. Połączenia międzyneuronowe występują jedynie między sąsiednimi warstwami (w kierunku od wejścia do wyjścia). Stosowane będą oznaczenia sygnałów i wag zgodnie z rysunkiem. Wagi neuronów warstwy ukrytej otrzymają wskaźnik górny (1), natomiast warstwy wyjściowej wskaźnik (2). Sygnały wyjściowe neuronów warstwy ukrytej oznaczone są symbolem \( v_j (j=1, 2, \ldots, K) \), a warstwy wyjściowej symbol \( y_j (j=1, 2, \ldots, M) \). Zakłada się, że funkcja aktywacji neuronów jest dana w postaci sigmoidalnej unipolarnej bądź bipolarnej. Dla uproszczenia oznaczeń przyjęte będzie rozszerzone oznaczenie wektora wejściowego \( \textbf{x} \) sieci w postaci \( \textbf{x}=[x_0, x_1, x_2, \ldots, x_N]^T \), w którym \( x_0=1 \) oznacza sygnał jednostkowy polaryzacji. Z wektorem \( \textbf{x} \) są związane dwa wektory wyjściowe sieci: wektor aktualny \( \textbf{y}=[y_1, y_2, \ldots, y_M]^T \) oraz wektor zadany \( \textbf{d}=[d_1, d_2, \ldots, d_M]^T \).
Celem uczenia jest określenie wartości wag \( w_{ij}^{(1)} \) oraz \( w_{ij}^{(2)} \) wszystkich warstw sieci w taki sposób, aby przy zadanym wektorze wejściowym \( \textbf{x} \) uzyskać na wyjściu wartości sygnałów wektora \( \textbf{y} \) odpowiadające z dostateczną dokładnością wartościom zadanym reprezentowanym przez wektor \( \textbf{d} \). Traktując jednostkowy sygnał polaryzujący jako jedną ze składowych wektora wejściowego \( \textbf{x} \), wagi polaryzacji można włączyć do wektora wag poszczególnych neuronów obu warstw. Przy takim oznaczeniu sygnał wyjściowy \( i \)-tego neuronu warstwy ukrytej daje się opisać wzorem
| \( v_i=f\left(\sum_{j=0}^N w_{i j}^{(1)} x_j\right) \) | (2.1) |
w której wskaźnik \( j=0 \) odpowiada sygnałowi oraz wagom polaryzacji. W przypadku warstwy wyjściowej \( k\)-ty neuron wytwarza sygnał wyjściowy opisany następująco
| \( y_k=f\left(\sum_{i=0}^K w_{k i}^{(2)} v_i\right)=f\left(\sum_{i=0}^K w_{k i}^{(2)} f\left(\sum_{j=0}^N w_{i j}^{(1)} x_j\right)\right) \) | (2.2) |
Powyższy wzór reprezentuje formułę tak zwanego uniwersalnego aproksymatora, gdyż definiuje jawną postać funkcji aproksymującej, realizowanej przez sieć. Jak wynika z zależności (2.2), na wartość sygnału wyjściowego mają wpływ wagi obu warstw, których właściwy dobór pozwala dopasować wartości funkcji aproksymującej do wielkości zadanych (\( \textbf{x} \), \( \textbf{d} ) \).
2.3. Proces uczenia sieci metodami gradientowymi optymalizacji
Podstawę uczenia sieci MLP stanowi minimalizacja wartości funkcji celu (błędu), definiowanej klasycznie jako suma kwadratów różnic między aktualnymi wartościami sygnałów wyjściowych sieci a wartościami zadanymi. W przypadku pojedynczej próbki uczącej \( (\mathbf{x},d) \) i zastosowaniu normy euklidesowej funkcję celu definiuje się w postaci
| \( E=\frac{1}{2} \sum_{i=1}^M\left(y_i(\mathbf{x})-d_i\right)^2 \) | (2.3) |
W przypadku wielu par uczących (\( (\textbf{x}_k, \textbf{d}(\textbf{x}_k)) \) dla \( k=(1, 2, \ldots, p) \) funkcję celu stanowi suma błędów po wszystkich parach uczących
| \( E=\frac{1}{2} \sum_{k=1}^p\left\|y\left(\mathbf{x}_k\right)-\mathbf{d}\left(\mathbf{x}_k\right)\right\|^2=\frac{1}{2} \sum_{k=1}^p \sum_{i=1}^M\left(y_i\left(\mathbf{x}_k\right)-d_i\left(\mathbf{x}_k\right)\right)^2 \) | (2.4) |
W uproszczeniu można założyć, że celem uczenia sieci jest określenie wartości wag neuronów wszystkich warstw sieci w taki sposób, aby przy zadanym wektorze wejściowym \( \mathbf{x} \) uzyskać na wyjściu sieci wartości sygnałów wyjściowych \(y_i(\mathbf{x}) \), odpowiadające z dostateczną dokładnością wartościom zadanym \( d_i(\textbf{x}) \) dla \( i=1, 2, \ldots, M \). Obliczanie wartości funkcji celu i związane z nim uaktualnianie wartości wag w procesie uczenia może odbywać się po każdorazowej prezentacji każdej próbki uczącej (uczenie typu on-line) lub jednorazowo, po prezentacji wszystkich próbek tworzących cykl uczący (uczenie wsadowe typu off-line). Niezależnie od sposobu uczenia wartość błędu tworzącą funkcję celu należy obliczać po każdorazowej prezentacji pary uczącej. Uczenie sieci przy zastosowaniu algorytmu propagacji wstecznej składa się z kilku faz.
W fazie pierwszej następuje pobudzenie sieci poprzez sygnały wejściowe tworzące wektor \( \textbf{x} \) i obliczenie wartości sygnałów poszczególnych neuronów w sieci. Dla danego wektora \( \textbf{x} \) obliczane są wartości sygnałów \( v_i \) neuronów warstwy ukrytej, a następnie wartości \( y_i \) odpowiadające neuronom warstwy wyjściowej. Wykorzystuje się przy tym zależności (2.1) i (2.2). Po obliczeniu wartości sygnałów wyjściowych \( y_i \) możliwe staje się określenie aktualnej wartości funkcji celu \( E \) danej wzorem (2.3) lub (2.4).
W drugiej fazie algorytmu następuje minimalizacja wartości tej funkcji. Przy założeniu ciągłości funkcji celu najskuteczniejszymi metodami uczenia są gradientowe algorytmy optymalizacyjne, w których adaptacja wektora wag (uczenie) odbywa się zgodnie ze wzorem
| \( \textbf{w}(k+1)=\textbf{w}(k)+\eta\textbf{p}(k) \) | (2.5) |
w którym \( \eta \) jest współczynnikiem uczenia, a \( \textbf{p}(k) \) wektorem kierunkowym minimalizacji w przestrzeni wielowymiarowej utworzonej przez wektor wszystkich wag sieci \( \textbf{w} \). Adaptacja wag odbywa się iteracyjnie z kroku na krok zmieniając wartości elementów wektora \( \textbf{w} \) wzdłuż kierunku \( \textbf{p}(k) \). Kierunek ten jest bezpośrednio związany z wektorem gradientu \( \textbf{g}=\frac{\partial E}{\partial \textbf{w}} \), który powinien być wyznaczany w każdej iteracji. Jedynie w przypadku wag warstwy wyjściowej zadanie to jest określone w prosty sposób poprzez różniczkowanie funkcji prostej określonej wzorem (2.2). Warstwy pozostałe wymagają zastosowania specjalnej strategii postępowania, która w dziedzinie sieci neuronowych nosi nazwę algorytmu propagacji wstecznej (ang. backpropagation) utożsamianym często z procedurą uczenia sieci neuronowej [46].
W ogólności algorytm gradientowy uczenia sieci MLP wymaga wykonania następujących etapów obliczeniowych.
-
Analiza sieci neuronowej o zwykłym kierunku przepływu sygnałów przy pobudzeniu sieci poprzez sygnały wejściowe równe elementom aktualnego wektora \( \textbf{x} \). W wyniku analizy otrzymuje się wartości sygnałów wyjściowych neuronów warstw ukrytych oraz warstwy wyjściowej, a także odpowiednie pochodne funkcji aktywacji w poszczególnych warstwach.
-
Utworzenie sieci propagacji wstecznej przez odwrócenie kierunków przepływu sygnałów, zastąpienie funkcji aktywacji przez ich pochodne o wartości obliczonej w punkcie pracy elementu oryginalnego sieci, a także przyłożenie na byłym wyjściu sieci (obecnie wejściu) wymuszenia w postaci odpowiedniej różnicy między wartością aktualną i zadaną. Dla tak utworzonej sieci propagacji wstecznej należy obliczyć wartości odpowiednich sygnałów w poszczególnych punktach tej sieci.
-
Na podstawie wyników analizy sieci oryginalnej i sieci o propagacji wstecznej określa się wektor gradientu \( \textbf{g} \) a następnie na jego podstawie kierunek minimalizacji \( \textbf{p}(k) \) oraz współczynnik uczenia \( \eta \).
-
Adaptacja wag (uczenie sieci) w \( k \)-tym cyklu uczącym odbywa się według wzoru (2.5) na podstawie wyników uzyskanych w punkcie 3.
-
Opisany w punktach 1, 2, 3, 4 proces należy powtórzyć wielokrotnie dla wszystkich wzorców uczących, kontynuując go do chwili spełnienia warunku zatrzymania algorytmu. Działanie algorytmu kończy się w momencie, w którym norma gradientu spadnie poniżej pewnej z góry określonej wartości tolerancji, określającej dokładność procesu uczenia.
Podstawowym elementem w tym algorytmie uczenia jest wyznaczenie wektora gradientu funkcji celu, stanowiącego podstawę wyznaczania kierunku minimalizacji. W sieciach MLP wektor ten jest określany przy zastosowaniu algorytmu propagacji wstecznej. Algorytm ten zilustrujemy przy użyciu grafów przepływowych.
2.4. Generacja gradientu z użyciem grafów przepływu sygnałów
Algorytm propagacji wstecznej stanowi podstawowy etap w uczeniu gradientowym, gdyż pozwala w prosty sposób określić gradient minimalizowanej funkcji celu. Jest on uważany za jeden ze skuteczniejszych sposobów generacji pochodnej funkcji celu dla sieci wielowarstwowej. W metodzie tej dla uniknięcia bezpośredniego różniczkowania złożonej funkcji celu stosuje się graficzną reprezentację systemu za pomocą grafów przepływowych. Przykład symbolicznej reprezentacji sieci MLP o \( N \) wejściach i \( M \) neuronach wyjściowych za pomocą grafu przepływowego przedstawiono na rys. 2.2a. W grafie tym wyróżniona została gałąź liniowa o wadze \( w_{ij} \) łącząca węzeł o sygnale \( v_j \) z węzłem o sygnale \( v_i \) oraz gałąź nieliniowa \( f(v_l) \) określająca sygnał \( v_k=f(v_l) \), w której \( f(v_l) \) w sieci MLP jest funkcją sigmoidalną.
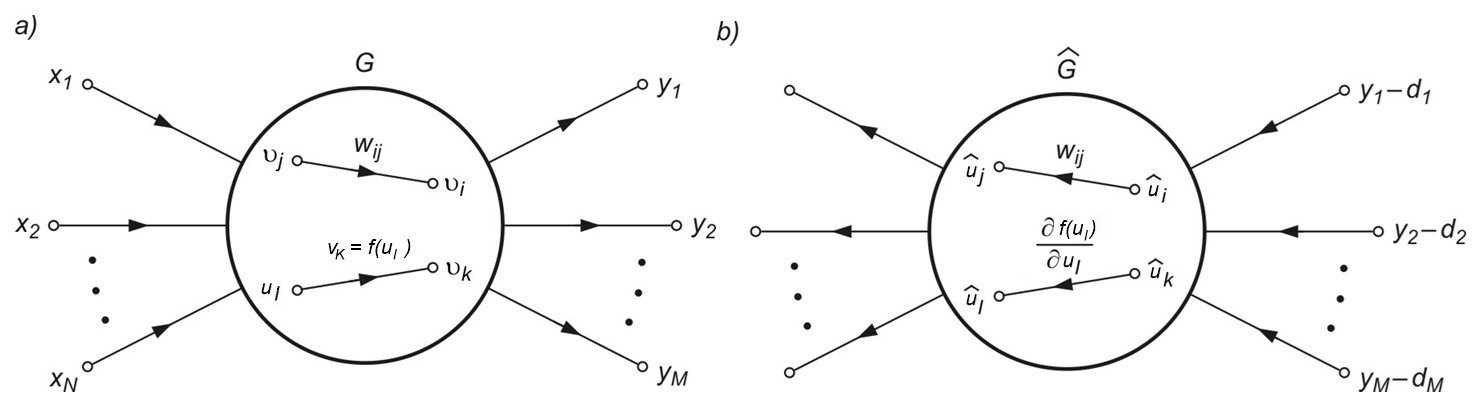
W generacji gradientu metodą grafów wykorzystuje się zależności odnoszące się do wrażliwości systemu badanego metodą układów dołączonych. Z teorii systemów wiadomo [46], że wrażliwość układu rozumiana jako pochodna dowolnego sygnału w tym układzie względem wartości wag może być określona na podstawie znajomości sygnałów w grafie zwykłym (oznaczonym przez \( G \)) oraz grafie dołączonym (zwanym również grafem sprzężonym) oznaczonym przez \( \hat{G} \). Graf \( \hat{G} \) jest zdefiniowany jak oryginalny graf \( G \) , w którym kierunki wszystkich gałęzi zostały odwrócone. Opis liniowej gałęzi grafu \( G \) i odpowiadającej jej gałęzi grafu dołączonego \( \hat{G} \) jest identyczny. W przypadku gałęzi nieliniowej \( f(u_l) \), gdzie \( u_l \) jest zmienną wejściową, odpowiadająca jej gałąź grafu \( \hat{G} \) staje się gałęzią zlinearyzowaną, o wzmocnieniu równym \( \frac{\partial f(u_l)}{u_l} \)obliczonym dla aktualnego punktu pracy nieliniowego grafu \( G \). Graf dołączony reprezentuje więc system zlinearyzowany. Przykład grafu dołączonego \( \hat{G} \) do grafu oryginalnego sieci MLP z rys. 2.2a przedstawiono na rys. 2.2b. Dla obliczenia gradientu funkcji celu konieczne jest jeszcze odpowiednie pobudzenie grafu dołączonego.
Jak zostało pokazane, dla określenia gradientu należy sieć dołączoną (graf \( \hat{G} \)) zasilić na zaciskach wyjściowych sieci oryginalnej (obecnie wejściowych) sygnałami wymuszającymi w postaci różnic między wartościami aktualnymi sygnałów wyjściowych \( y_i \) a ich wartościami pożądanymi \( d_i \), jak to pokazano na rys. 2.3 b. Przy takim sposobie tworzenia grafu dołączonego każdy składnik wektora gradientu będzie określony na podstawie odpowiednich sygnałów grafu G oraz grafu dołączonego \( \hat{G} \). W odniesieniu do wagi \( w_{ij} \) odpowiedni składnik gradientu będzie opisany wzorem
| \( \frac{\partial E}{\partial w_{ij}} =v_j \hat{v_i} \) | (2.6) |
w którym sygnał \( v_j \) odnosi się do grafu \( G \) systemu oryginalnego a \( \hat{v_i} \) do grafu \( \hat{G} \) systemu dołączonego. Należy podkreślić, że podane zależności odnoszą się do dowolnych systemów (liniowych, nieliniowych, rekurencyjnych itp.). Metodę wyznaczania gradientu zilustrujemy przykładem grafu sieci MLP o 2 wejściach, 2 neuronach ukrytych i dwu neuronach wyjściowych przedstawionym na rys. 2.3a [46].
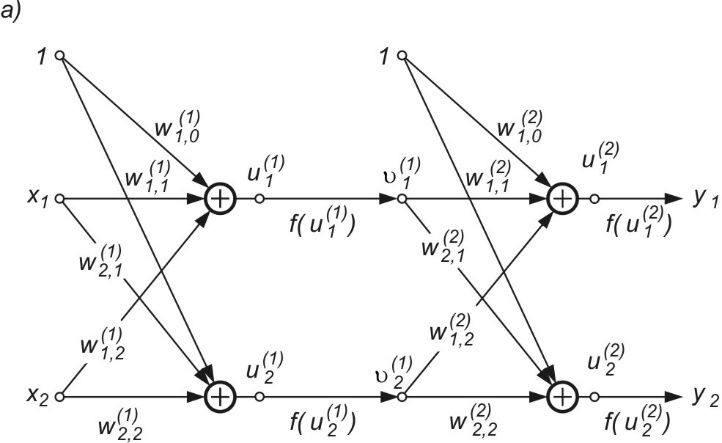
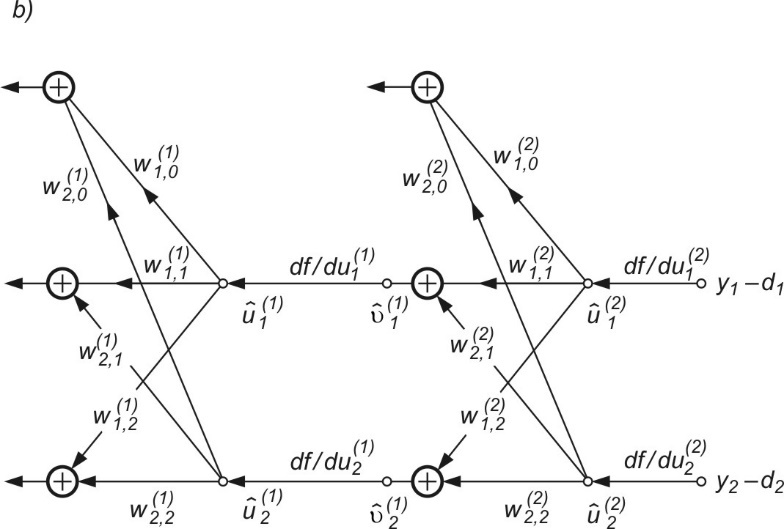
W celu wyznaczenia wszystkich składników gradientu względem wag poszczególnych warstw sieci wykorzystany zostanie graf dołączony \( \hat{G} \) przedstawiony na rys. 2.3b. Pobudzenie grafu dołączonego stanowią różnice między wartościami aktualnymi sygnałów wyjściowych \( y_i \) a wartościami zadanymi \( d_i \) dla \( i=1,2 \). Nieliniowe gałęzie \( f(u) \) grafu \( G \) zastąpione zostały w grafie dołączonym \( \hat{G} \) pochodnymi \( \frac{\partial f}{\partial u} \), obliczonymi odpowiednio w odpowiednich punktach pracy dla każdej warstwy oddzielnie. Zauważmy, że jeśli funkcja aktywacji neuronów ma postać sigmoidalną unipolarną \( f(u)=\frac{1}{1+\exp (-u)} \), wtedy \(\frac{\partial f}{\partial u}=f(u)(1-f(u))\) jest określona bezpośrednio na podstawie znajomości wartości funkcji sigmoidalnej w punkcie pracy \( u \) i nie wymaga żadnych dodatkowych obliczeń wartości funkcji. Wykorzystując wzór (2.6) można teraz określić poszczególne składowe wektora gradientu \( \mathbf{g}=\frac{\partial E}{\partial \mathbf{w}} \) dla dowolnej wagi, zarówno w warstwie ukrytej jak i wyjściowej. Przykładowo
| \( \frac {\partial E} {\partial w_{12}^{(1)}} =x_2 \hat{u}_1^{(1)} \) |
| \( \frac{\partial E}{\partial w_{20}^{(1)}} = \hat{u}_2^{(1)} \) |
| \( \frac{\partial E}{\partial w_{11}^{(2)}} =v_1^{(1)} \hat{u}_1^{(2)} \) |
| \( \frac{\partial E}{\partial w_{21}^{(2)}} =v_1^{(1)} \hat{u}_2^{(2)} \) |
Jak wynika z tych sformułowań, ogólna postać wzoru określającego odpowiedni składnik gradientu jest (przy zachowaniu odpowiednich oznaczeń sygnałów) identyczna, niezależnie od tego, w której warstwie neuronów znajduje się odpowiednia waga. Jest to reguła bardzo prosta w zastosowaniach, wymagająca przy określeniu składowej gradientu znajomości tylko dwóch sygnałów: sygnału węzła, z którego waga startuje w grafie zwykłym oraz sygnału węzła, będącego punktem startowym wagi w grafie dołączonym. Pod tym względem stanowi ona regułę lokalną.
2.5. Metody wyznaczania kierunku minimalizacji
Kierunek minimalizacji \( \textbf{p} \) w procesie optymalizacji wyznacza taki wektor kierunkowy w przestrzeni wielowymiarowej, w którym następuje zmniejszanie się wartości funkcji celu w następnym kroku. Metody wyznaczania takiego kierunku opierają się na rozwinięciu w szereg Taylora funkcji celu \( E \) w najbliższym sąsiedztwie (wzdłuż kierunku \( \textbf{p} \)) znanego, aktualnego punktu rozwiązania określonego wektorem \( \textbf{w} \) [14,18,45]
| \( E(\mathbf{w}+\mathbf{p})=E(\mathbf{w})+\mathbf{g}^T \mathbf{p}+\frac{1}{2} \mathbf{p}^T \mathbf{H} \mathbf{p}+\ldots \) | (2.7) |
W rozwinięciu tym \( \textbf{w} \) oznacza \( n \)-wymiarowy wektor wszystkich wag sieci, \( \textbf{p} \) – wektor kierunku poszukiwań, \( \textbf{g} \) – wektor gradientu a \( \textbf{H} \) - macierz drugich pochodnych funkcji celu (hesjan) wyznaczane w aktualnym punkcie pracy \( \textbf{w} \)
| \( \mathbf{H}=\left[\begin{array}{cccc} \frac{\partial^2 E}{\partial w_1^2} & \frac{\partial^2 E}{\partial w_1 \partial w_2} & \ldots & \frac{\partial^2 E}{\partial w_1 \partial w_n} \\ \frac{\partial^2 E}{\partial w_2 \partial w_1} & \frac{\partial^2 E}{\partial w_2^2} & \ldots & \frac{\partial^2 E}{\partial w_2 \partial w_n} \\ \ldots & \ldots & \ldots & \ldots \\ \frac{\partial^2 E}{\partial w_n \partial w_1} & \frac{\partial^2 E}{\partial w_n \partial w_2} & \ldots & \frac{\partial^2 E}{\partial w_n^2} \end{array}\right] \) |
W praktyce wykorzystuje się co najwyżej trzy pierwsze składniki wzoru (2.7) pomijając pozostałe. Zależność (2.7) jest wówczas kwadratowym przybliżeniem funkcji \( E( \textbf{w} ) \) w najbliższym sąsiedztwie znanego punktu rozwiązania \( \textbf{w} \). Dla uproszczenia zapisu wartości zmiennych uzyskane w \( k \)-tym cyklu oznaczane będą symbolem ze wskaźnikiem dolnym \( k \). Punkt rozwiązania \( \textbf{w} = \textbf{w}_k \) jest punktem odpowiadającym minimum wartości funkcji celu \( E \), jeśli pierwsza pochodna funkcji celu (gradient) jest równy zeru, a macierz hesjanu \( \textbf{H} \) jest dodatnio określona (warunki Kuhna-Tuckera [14]). Przy spełnieniu tych warunków funkcja w dowolnym punkcie należącym do sąsiedztwa \( \textbf{w} \) ma wartość większą niż w samym punkcie \( \textbf{w} \), a zatem punkt rozwiązania aktualnego \( \textbf{w} \) jest rozwiązaniem odpowiadającym minimalnej wartości funkcji celu.
Na \( k \)-tym etapie poszukiwania punktu minimalnego wartości funkcji celu kierunek poszukiwań \( \textbf{p} = \textbf{p}_k \) oraz krok \( \eta \) powinny być dobrane w taki sposób, aby dla nowego rozwiązania
| \( \textbf{w}_{k+1} = \textbf{w}_{k} + \eta \textbf{p}_{k} \) | (2.8) |
była spełniona zależność \( E (\textbf{w}_{k+1}) < E (\textbf{w}_{k}) \). Poszukiwania minimum funkcji celu trwają dopóty, dopóki norma gradientu nie spadnie poniżej założonej, dopuszczalnej wartości błędu bądź też nie będzie przekroczony określony czas obliczeń (liczba iteracji). Ogólny algorytm adaptacji wag sieci przedstawić można w następującej postaci (zakłada się, że dana jest wartość początkowa wektora optymalizowanego \( \textbf{w}_{k} = \textbf{w}_{0} \).
-
Test na zbieżność i optymalność aktualnego rozwiązania \( \textbf{w}_{k} \). Jeżeli aktualny punkt \( \textbf{w}_{k} \) spełnia warunki zatrzymania procesu ze względu na gradient - koniec obliczeń. W przeciwnym razie przejście do punktu 2.
-
Wyznaczenie wektora kierunku minimalizacji \( \textbf{p}_{k} \) w punkcie rozwiązania \( \textbf{w}_{k} \).
-
Wyznaczenie takiego kroku \( \eta \) na kierunku \( \textbf{p}_{k} \), że spełniony jest warunek \( E(\textbf{w}_{k} +\eta \textbf{p}_k) < E (\textbf{w}_{k}) \).
-
Określenie nowego punktu rozwiązania \( \textbf{w}_{k+1} = \textbf{w}_{k} + \eta \textbf{p}_{k} \) oraz odpowiadającej mu wartości \( E (\textbf{w}_{k+1}) < E (\textbf{w}_{k}) \) i powrót do punktu 1.
2.5.1 Algorytm największego spadku
Przy ograniczeniu się w rozwinięciu Taylora (2.7) do liniowego przybliżenia funkcji celu w najbliższym sąsiedztwie aktualnego rozwiązania \( \textbf{w} \) otrzymuje się algorytm największego spadku. Aby była spełniona zależność \( E (\textbf{w}_{k+1}) < E (\textbf{w}_{k}) \) , wystarczy dobrać \( \textbf{g}_k^T \textbf{p}_k < 0 \).
Przyjęcie wektora kierunkowego w postaci [18]
| \( \textbf{p} = - \textbf{g} \) | (2.9) |
spełnia wymagany warunek zmniejszenia wartości funkcji celu. Adaptacja wag przebiega wówczas według wzoru
| \( \mathbf{w}_{k+1}=\mathbf{w}_k-\eta \mathbf{g}_k \) | (2.10) |
określającego metodę największego spadku. Ograniczenie się w rozwinięciu Taylora do składnika pierwszego rzędu powoduje niewykorzystanie informacji o krzywiźnie funkcji zawartej w hesjanie. To sprawia, że metoda jest wolno zbieżna (zbieżność liniowa: oznacza ona, iż przy spełnieniu założeń metody, odległości pomiędzy kolejnymi przybliżeniami \( \mathbf{x}_k \), a rzeczywistym minimum \( \mathbf{x}^{*} \) funkcji maleją liniowo, czyli \( \left\|\mathbf{x}^*-\mathbf{x}_{k+1}\right\| \leq c\left\|\mathbf{x}^*-\mathbf{x}_k\right\| \)). Wada ta oraz brak postępów minimalizacji w okolicy punktu optymalnego, gdzie gradient przyjmuje bardzo małe wartości, spowodowały, że metoda ta jest mało efektywna. Niemniej jednak, ze względu na jej prostotę, małe wymagania co do wielkości pamięci i małą złożoność obliczeniową stanowiła ona przez lata i nadal pozostaje podstawową metodą stosowaną w uczeniu sieci wielowarstwowych.
Poprawy efektywności poszukuje się przez modyfikację (zwykle heurystyczną) wzoru określającego kierunek. Dobre wyniki przynosi zwykle zastosowanie uczenia z momentem rozpędowym (w skrócie uczenie z momentem) W przypadku zastosowania tej techniki zmiana wektora wag sieci \( \Delta\mathbf{w} \) w \( k \)-tej iteracji uwzględnia nie tylko gradient, ale również zmianę wartości wag z poprzedniej \( (k-1) \) iteracji. Adaptacja wag przebiega wówczas według wzoru [43,46]
| |
(2.11) |
w którym \( \alpha \) jest współczynnikiem momentu, przyjmowanym zwykle w przedziale wartości [0, 1].
Składnik \( \eta \mathbf{g}_k \)tego wyrażenia odpowiada zwykłej metodzie uczenia największego spadku, natomiast drugi \( \alpha\left(\mathbf{w}_k-\mathbf{w}_{k-1}\right) \)uwzględnia ostatnią zmianę wag i jest niezależny od aktualnej wartości gradientu. Im większa jest wartość współczynnika \( \alpha \), tym składnik wynikający z momentu rozpędowego ma większy wpływ na adaptację wag. Jego wpływ wzrasta w sposób istotny na płaskich odcinkach funkcji celu oraz w pobliżu minimum lokalnego, gdzie wartość gradientu jest bliska zeru. Na płaskich odcinkach funkcji celu przyrost wag \( \Delta \mathbf{w} \), przy stałej wartości współczynnika uczenia \( \eta \) jest w przybliżeniu równy, co oznacza, że \( \Delta \mathbf{w}_k=-\eta \mathbf{g}_k+\alpha \Delta \mathbf{w}_k \). Wynika stąd, że efektywny przyrost wartości wag określa teraz relacja
| \( \Delta \mathbf{w}_k=-\frac{\eta}{1-\alpha} \mathbf{g}_k \) | (2.12) |
Przy wartości współczynnika \( \alpha=0,9 \) oznacza to 10-krotny wzrost efektywnej wartości współczynnika uczenia, a więc również 10-krotne przyśpieszenie procesu uczenia (na płaskich odcinkach funkcji celu). W pobliżu minimum lokalnego składnik momentu jako nie związany z wartością gradientu może spowodować zmianę wag, prowadzącą do wzrostu wartości funkcji celu i opuszczenie strefy ,,przyciągania" tego minimum. Przy małej wartości gradientu czynnik momentu może stać się dominujący we wzorze (2.11) i spowodować przyrost wag odpowiadający wzrostowi wartości funkcji celu i umożliwić opuszczenie bieżącego minimum lokalnego.
Czynnik momentu nie może przy tym całkowicie zdominować procesu uczenia, gdyż prowadziłoby to do niestabilności algorytmu. Zwykle kontroluje się wartość funkcji celu \( E \) w procesie uczenia, dopuszczając do jej wzrostu jedynie w ograniczonym zakresie, np. 4%. W takim przypadku, jeśli w kolejnych iteracjach \( k \) oraz \( k+1 \) spełniona jest relacja \( E(k+1) < 1,04E(k) \), krok jest akceptowany i następuje uaktualnienie wartości wag; jeżeli natomiast \( E(k+1) > 1,04E(k) \), zmiany są ignorowane i przyjmuje się \( \left(\mathbf{w}_k-\mathbf{w}_{k-1}\right)=\mathbf{0} \). W takim przypadku składnik gradientowy odzyskuje dominację nad składnikiem momentu i proces przebiega zgodnie z kierunkiem minimalizacji wyznaczonym przez wektor gradientu. Należy podkreślić, że dobór wartości współczynnika momentu jest zagadnieniem niełatwym i wymaga wielu eksperymentów, mających na celu dopasowanie jego wartości do specyfiki rozwiązywanego problemu.
2.5.2 Algorytm zmiennej metryki
Metoda zmiennej metryki wywodzi się z metody optymalizacyjnej Newtona, wykorzystującej kwadratowe przybliżenie funkcji celu w sąsiedztwie znanego rozwiązania \( \mathbf{w}_k \). Ograniczając się we wzorze (2.7) do trzech pierwszych składników, minimum funkcji celu \( E \) wyznacza się przyrównując do zera pochodną \( E(\textbf{w}+\textbf{p}) \) względem wektora \( \textbf{p} \), czyli \( \frac{\partial E(\mathbf{w}+p)}{\partial \mathbf{p}}=\mathbf{0} \). Po wykonaniu tej operacji mamy
| \( \textbf{g}+\textbf{Hp}=\textbf{0} \) | (2.13) |
Ze wzoru tego otrzymuje się wyrażenie określające kierunek newtonowski wyznaczający minimum funkcji celu w \( k \)-tej iteracji [45]
| \( \mathbf{p}_k=-\mathbf{H}_k^{-1} \mathbf{g}_k \) | (2.14) |
Wzór (2.14) wyznacza w sposób jednoznaczny taki kierunek \( \mathbf{p}_k \), który zapewnia minimum funkcji celu w danym kroku i stanowi istotę newtonowskiego algorytmu optymalizacji, jest zależnością czysto teoretyczną, gdyż wymaga zapewnienia dodatniej określoności hesjanu w każdym kroku, co w przypadku ogólnym jest niemożliwe do spełnienia.
Z tego powodu w praktycznych implementacjach algorytmu rezygnuje się z dokładnego wyznaczania hesjanu \( \mathbf{H} \), a w zamian stosuje się jego przybliżenie \( \mathbf{G} \) spełniające warunek dodatniej określoności. Jedną z najpopularniejszych metod jest przy tym metoda zmiennej metryki, posiadająca wiele odmian. W metodzie tej, w każdym kroku modyfikuje się hesjan (lub jego odwrotność) z kroku poprzedniego o pewną poprawkę. Oznaczmy przez \( \mathbf{s}_{\mathrm{k}}=\mathbf{w}_{\mathrm{k}}-\mathbf{w}_{\mathrm{k}-1} \) oraz \( \mathbf{r}_{\mathrm{k}}=\mathbf{g}_{\mathrm{k}}-\mathbf{g}_{\mathrm{k}-1} \), odpowiednio przyrosty wektora \( \mathbf{w} \) oraz gradientu \( \mathbf{g} \) w dwu kolejnych iteracjach, a przez \( \mathbf{V} \) - macierz odwrotną przybliżonego hesjanu \( \mathbf{V} = \mathbf{G}^{-1} \), to zgodnie z najefektywniejszą formułą Broydena-Fletchera-Goldfarba-Shanno (BFGS) proces uaktualniania macierzy \( \mathbf{V} \) opisuje się zależnością rekurencyjną [14]
| \( \mathbf{V}_k=\mathbf{V}_{k-1}+\left(1+\frac{\mathbf{r}_k^T \mathbf{V}_{k-1} \mathbf{r}_k}{\mathbf{s}_k^T \mathbf{r}_k}\right) \frac{\mathbf{s}_k \mathbf{s}_k^T}{\mathbf{s}_k^T \mathbf{r}_k}-\frac{\mathbf{s}_k \mathbf{r}_k^T \mathbf{V}_{k-1} \mathbf{r}_k \mathbf{s}_k^T}{\mathbf{s}_k^T \mathbf{r}_k} \) |
(2.15) |
Jako wartość startową przyjmuje się zwykle \( \mathbf{V}_{0}=\mathbf{1} \), co oznacza, że pierwsza iteracja przeprowadzana jest zgodnie z algorytmem największego spadku. Zostało wykazane [14], że przy wartości startowej \( \mathbf{V}_{0}=\mathbf{1} \) i zastosowaniu procedury minimalizacji kierunkowej w każdym kroku optymalizacyjnym można zawsze zapewnić dodatnią określoność aproksymowanej macierzy hesjanu.
Metoda zmiennej metryki charakteryzuje się szybszą zbieżnością (zbieżność superliniowa) niż metoda największego spadku (zbieżność liniowa). Poza tym fakt, że hesjan w każdym kroku spełnia warunek dodatniej określoności, daje pewność, że spełnienie warunku \( \mathbf{g}=\mathbf{0} \) odpowiada rozwiązaniu problemu minimalizacji. Metoda ta należy obecnie do grupy najlepszych technik optymalizacji funkcji wielu zmiennych. Jej wadą jest znaczna złożoność obliczeniowa (konieczność wyznaczenia w każdym cyklu \( n^2 \) elementów hesjanu), a także duże wymagania w odniesieniu do pamięci przy przechowywaniu macierzy hesjanu, co w przypadku funkcji z dużą liczbą zmiennych może być pewnym problemem.
Najważniejszym ograniczeniem jest jednak pogarszanie się uwarunkowania problemu przy znacznym wzroście liczby wag. Wzrastający wymiar hesjanu pociąga za sobą rosnącą wartość współczynnika uwarunkowania \( \text{cond}(\mathbf{H}) \) i pogarszającą się dokładność obliczeń. Z tego względu stosuje się ją do niezbyt dużych sieci. W przypadku komputerów PC jej skuteczne działanie zostało sprawdzone dla sieci o liczbie wag rzędu kilkuset (poniżej tysiąca).
2.5.3 Algorytm Levenberga-Marquardta
Inną implementacją newtonowskiej strategii optymalizacji jest metoda Levenberga-Marquardta. W metodzie tej dokładną wartość hesjanu \( \mathbf{H} \) we wzorze (2.14) zastępuje się wartością również aproksymowaną \( \mathbf{G} \), ale określaną na podstawie informacji zawartej w gradiencie z uwzględnieniem czynnika regularyzacji. Dla wprowadzenia metody przyjęta będzie definicja funkcji celu w postaci odpowiadającej istnieniu jednego wzorca uczącego, co przy \( M \) wyjściach sieci odpowiada
| \( E=\frac{1}{2} \sum_{i=1}^M\left(y_i(\mathbf{x})-d_i\right)=\sum_{i=1}^M e_i[(\mathbf{x})]^2 \) |
(2.16) |
gdzie \( e_i(\mathbf{x})=\left(y_i(\mathbf{x})-d_i\right) \) oznacza błąd na \( i \)-tym wyjściu sieci przy prezentacji wektora \( \mathbf{x} \). Przy wprowadzeniu oznaczeń (\( \mathbf{J} \) – macierz Jacobiego)
| \( \mathbf{e}(\mathbf{x})=\left[\begin{array}{c}
e_1(\mathbf{x}) \\
e_2(\mathbf{x}) \\
\ldots \\
e_M(\mathbf{x})
\end{array}\right] \) |
\( \mathbf{J}=\left[\begin{array}{cccc} \frac{\partial e_1}{\partial w_1} & \frac{\partial e_1}{\partial w_2} & \ldots & \frac{\partial e_1}{\partial w_n} \\ \frac{\partial e_2}{\partial w_1} & \frac{\partial e_2}{\partial w_2} & \ldots & \frac{\partial e_2}{\partial w_n} \\ \cdots & \cdots & \ldots & \ldots \\ \frac{\partial e_M}{\partial w_1} & \frac{\partial e_M}{\partial w_2} & \ldots & \frac{\partial e_M}{\partial w_n} \end{array}\right] \) |
wektor gradientu \( \mathbf{g} \) i aproksymowana macierz hesjanu \( \mathbf{G} \) odpowiadające funkcji celu (2.16) określane są w postaci [14,46]
| \( \mathbf{g}=\mathbf{J}^T \mathbf{e}(\mathbf{x}) \) |
(2.17) |
| \( \mathbf{G}=\mathbf{J}^T \mathbf{J}+v \mathbf{1} \) |
(2.18) |
W równaniu tym współczynnik \( v \) zwany parametrem regularyzacyjnym Levenberga-Marquardta jest wielkością skalarną, dążącą do zera w trakcie procesu optymalizacyjnego. Na starcie procesu uczenia, gdy aktualna wartość wektora wagowego \( \mathbf{w}_k \) jest daleka od rozwiązania (duże wartości składowych wektora błędu \( \mathbf{e} \)), przyjmuje się wartość parametru \( v \) bardzo dużą w porównaniu z największą wartością własną macierzy \( \mathbf{J}^T \mathbf{J} \). W takim przypadku hesjan jest reprezentowany przede wszystkim przez czynnik regularyzacyjny \( v \mathbf{1} \) a poszukiwanie kierunku odbywa się podobnie jak w metodzie największego spadku \( \mathbf{p}_k=-\mathbf{g}_k / v \). W miarę zmniejszania się residuum błędu i zbliżania do rozwiązania, parametr \( v \) ulega redukcji i pierwszy składnik sumy we wzorze (2.18) określającym hesjan odgrywa coraz większą rolę.
O skuteczności działania algorytmu decyduje odpowiedni dobór wartości \( v\). W praktyce wartość ta podlega ciągłej adaptacji przy zastosowaniu metody Levenberga-Marquardta [43]. Przy aktualnym rozwiązaniu bliskim optymalnemu hesjan jest dostatecznie wiernie reprezentowany przez składnik \( \mathbf{J}^T \mathbf{J} \) wzoru aproksymacyjnego (2.18). W takim przypadku czynnik regularyzacji \( v \mathbf{1} \) może być pominięty (\( v=0 \)) i proces określania hesjanu opiera się bezpośrednio na aproksymacji pierwszego rzędu, a kierunek wyznaczony jest wzorem \( \mathbf{p}_k=-\left[\mathbf{J}_k^T \mathbf{J}_k\right]^{-1} \mathbf{g}_k \). Algorytm Levenberga-Marquardta przechodzi wówczas w klasyczny algorytm Gaussa-Newtona [14], charakteryzujący się kwadratową zbieżnością do rozwiązania optymalnego. W praktyce algorytm Levenberga-Marquardta ma zbieżność super liniową i obok metody zmiennej metryki jest uważany za najlepszy algorytm uczący sieci MLP przy założeniu sieci o niezbyt dużej liczbie adaptowanych wag.
2.5.4 Algorytm gradientów sprzężonych
Metody newtonowskie bardzo dobrze sprawdzają się w zadaniach uczenia sieci MLP przy liczbie wag nie przekraczających kilkuset. Przy zbyt dużej liczbie zmiennych optymalizowanych pojawia się problem złego uwarunkowania macierzy \( \mathbf{H} \). W takim przypadku lepsze wyniki uczenia uzyskuje się zwykle stosując metodę gradientów sprzężonych [14]. W metodzie tej podczas wyznaczania kierunku minimalizacji rezygnuje się z bezpośredniej informacji o hesjanie. W zamian za to kierunek poszukiwań \( \mathbf{p} \) jest konstruowany w taki sposób, aby był ortogonalny oraz sprzężony ze wszystkimi poprzednimi kierunkami poszukiwań. W \( k \)-tej iteracji warunek ten jest spełniony przy doborze kierunku \( \mathbf{p} \) według wzoru
| \( \mathbf{p}_k=-\mathbf{g}_k+\beta \mathbf{p}_{k-1} \) |
(2.19) |
Ze wzoru (2.19) wynika, że nowy kierunek minimalizacji zależy tylko od wartości gradientu w aktualnym punkcie rozwiązania oraz od poprzedniego kierunku poszukiwań \( \mathbf{p}_{k-1} \), pomnożonego przez współczynnik sprzężenia \( \beta \). Współczynnik sprzężenia odgrywa bardzo ważną rolę, kumulując w sobie informacje o poprzednich kierunkach poszukiwań i zapewniając ich ortogonalność względem kierunku aktualnego. Spośród wielu sposobów wyznaczania wartości tego współczynnika ograniczymy się do reguły Polaka-Ribiery [46]
| \( \beta=\frac{\mathbf{g}_k^T\left(\mathbf{g}_k-\mathbf{g}_{k-1}\right)}{\mathbf{g}_{k-1}^T \mathbf{g}_{k-1}} \) |
(2.20) |
Ze względu na kumulację błędów zaokrąglenia podczas kolejnych cykli obliczeniowych metoda gradientów sprzężonych w praktyce zatraca własność ortogonalności między wektorami kierunków minimalizacji. Dlatego też po wykonaniu \( m \) iteracji (\( m \) przyjmuje się jako funkcję liczby zmiennych \( n \) podlegających optymalizacji) przeprowadza się jej restart, zakładając w pierwszym kroku po restarcie kierunek minimalizacji zgodnie z algorytmem największego spadku w aktualnie osiągniętym punkcie rozwiązania.
W praktyce obliczeniowej metoda gradientów sprzężonych wykazuje zbieżność super liniową, choć o mniejszej wartości wykładnika zbieżności niż metoda zmiennej metryki. Z tego powodu jest mniej skuteczna niż metody pseudo newtonowskie (zmiennej metryki i Levenberga-Marquardta), ale zdecydowanie szybsza niż metoda największego spadku. Stosuje się ją powszechnie jako skuteczny algorytm optymalizacji przy bardzo dużej liczbie zmiennych, sięgających nawet kilku tysięcy. Dzięki małym wymaganiom co do pamięci i niewielkiej złożoności obliczeniowej metoda ta pozwala na efektywne rozwiązanie stosunkowo dużych problemów optymalizacyjnych.
1.
2.6. Dobór współczynnika uczenia
2.6 Dobór współczynnika uczenia
Po wyznaczeniu kierunku poszukiwań p konieczne jest jeszcze określenie wartości współczynnika uczenia η aby można było jednoznacznie wyznaczyć nowy punkt rozwiązania \( \textbf{w}_{k+1} = \textbf{w}_{k} + \eta \textbf{p}_{k} \), spełniający warunek \( E(\textbf{w}_{k+1} ) < E (\textbf{w}_{k}) \). Pożądany jest taki dobór \( \eta \) aby nowy punkt rozwiązania \( w_{k+1} \) leżał możliwie blisko minimum funkcji celu na kierunku \( \textbf{p}_k \). Właściwy dobór współczynnika \( \eta \) ma ogromny wpływ na zbieżność algorytmu optymalizacyjnego. Im wartość \( \eta \) bardziej odbiega od wartości, przy której funkcja celu osiąga minimum na danym kierunku \( \textbf{p}_k \), tym większa liczba iteracji jest potrzebna do wyznaczenia optymalnego rozwiązania. Przyjęcie zbyt małej wartości \( \eta \) powoduje niewykorzystanie możliwości zminimalizowania wartości funkcji celu w danym kroku i konieczność jego powtórzenia w następnym. Zbyt duży krok powoduje ,,przeskoczenie" minimum funkcji i podobny efekt jak poprzednio. Istnieje wiele sposobów doboru wartości \( \eta \).
Najprostszy z nich (obecnie stosunkowo rzadko stosowany, głównie w uczeniu on-line) polega na przyjęciu stałej wartości \( \eta \) w całym procesie optymalizacyjnym. Stosuje się go praktycznie tylko w połączeniu z metodą największego spadku. Jest to sposób mało efektywny, gdyż nie uzależnia wartości współczynnika uczenia od aktualnego wektora gradientu, a więc i kierunku \( \textbf{p} \) w danej iteracji. Dobór wartości \( \eta \) odbywa się zwykle oddzielnie dla każdej warstwy sieci przy wykorzystaniu różnych zależności empirycznych. Jednym z rozwiązań jest przyjęcie oszacowania minimalnej wartości tego współczynnika dla każdej warstwy w postaci
| \( \eta \leq \min ( \frac{1}{n_i}) \) | (2.21) |
gdzie \( n_i \) oznacza liczbę wejść \( i \)-tego neuronu w warstwie.
Inną bardziej skuteczną metodą doboru wartości współczynnika uczenia jest założenie ciągłej adaptacji, dopasowującej się do aktualnych zmian wartości funkcji celu w procesie uczenia. W metodzie tej na podstawie porównania wartości funkcji celu w \( i \)-tej iteracji z jej poprzednią wartością, określa się strategię zmian wartości współczynnika uczenia. W celu przyspieszenia procesu uczenia w metodzie powinno się dążyć do ciągłego zwiększania wartości \( \eta \), jednocześnie sprawdzając, czy wartość funkcji błędu nie rośnie w porównaniu z błędem obliczanym przy starej wartości \( \eta \). Dopuszcza się przy tym nieznaczny wzrost wartości tego błędu w stosunku do wartości z poprzedniej iteracji. Jeżeli przez \( E(i-1) \) oraz \( E(i) \) oznaczymy wartość funkcji celu odpowiednio w \( (i-1) \) oraz w \( i \)-tej iteracji, a przez \( \eta_{i-1}, \eta_{i} \) współczynniki uczenia w odpowiednich iteracjach, to w przypadku, gdy \( E(i) > k_w E(i-1) \) (\( k_w \) - dopuszczalny współczynnik wzrostu błędu) powinno nastąpić zmniejszenie wartości \( \eta \), zgodnie z zależnością [43]
| \( \eta_{i+1}=\alpha_d\eta_i \) | (2.22) |
gdzie \( \alpha_d \) jest współczynnikiem zmniejszania wartości \( \eta \). W przeciwnym razie, gdy \( E(i) < k_{w} E(i-1) \) przyjmuje się
| \( \eta_{i+1}=\alpha_i\eta_i \) | (2.23) |
gdzie αi jest współczynnikiem zwiększającym wartość \( \eta \). Mimo pewnego zwiększenia nakładu obliczeniowego (potrzebnego do wyznaczenia dodatkowej wartości \( \eta \)) możliwe jest istotne przyspieszenie procesu uczenia. Charakterystyczna jest przy tym postać zmian wartości tego współczynnika w czasie uczenia. Zwykle na starcie (przy bardzo małej wartości startowej \( \eta \)) dominuje proces jego zwiększania, po czym po osiągnięciu pewnego stanu quasi-ustalonego jego wartość zmienia się, cyklicznie, narastając i zmniejszając się w następujących po sobie cyklach. Należy jednak podkreślić, że metoda adaptacyjna doboru \( \eta \) jest bardzo uzależniona od aktualnej postaci funkcji celu i wartości współczynników \( k_w, \alpha_d, \alpha_i \). Wartości optymalne przy jednej postaci funkcji mogą być dalekie od optymalnych przy zmianie postaci tej funkcji. Stąd w praktycznej realizacji tej metody należy uwzględnić mechanizmy kontroli i sterowania wartościami współczynników, dobierając je odpowiednio do specyfiki zadania.
Najefektywniejszy, choć zarazem najbardziej złożony, sposób doboru współczynnika uczenia polega na minimalizacji funkcji celu na wyznaczonym wcześniej kierunku \( \textbf{p} \). Należy tak dobrać skalarną wartość \( \eta \), aby nowe rozwiązanie odpowiadało minimum funkcji celu na tym kierunku \( \textbf{p} \). Zauważmy, że przy znanym kierunku \( \textbf{p} \) jest to zadanie znalezienia minimum funkcji jednej zmiennej (\( \eta \)). Wśród najpopularniejszych metod wyznaczania minimum kierunkowego można wyróżnić metody bez gradientowe i gradientowe. W metodach bez gradientowych korzysta się jedynie z informacji o wartościach funkcji celu i wyznacza jej minimum w wyniku kolejnych podziałów założonego na wstępie zakresu wektora \( \textbf{w} \). Przykładem takich metod są: metoda bisekcji, złotego podziału odcinka, metoda Fibonacciego czy lokalna aproksymacja funkcji celu przy użyciu wielomianu drugiego stopnia [14]. Jedną z najbardziej popularnych metod gradientowych jest aproksymacja funkcji celu przy użyciu wielomianu drugiego lub trzeciego stopnia. Do wyznaczenia jego współczynników wykorzystuje się zarówno informację o wartości aktualnej funkcji celu w dwu sąsiednich punktach jak i jej pochodnej (gradientu). Szczegóły dotyczące tych algorytmów można znaleźć w podręcznikach dotyczących optymalizacji.
2.7. Metody heurystyczne uczenia sieci
Oprócz algorytmów uczących implementujących wypróbowane metody optymalizacji nieliniowej funkcji celu, takie jak metoda zmiennej metryki, metoda Levenberga-Marquardta czy metoda gradientów sprzężonych, opracowano pewną liczbę algorytmów typu heurystycznego, stanowiących modyfikację metody największego spadku bądź metody gradientów sprzężonych. Modyfikacje takie, opierające się na algorytmach powszechnie znanych, wprowadzają do nich pewne poprawki, przyspieszające (zdaniem autorów) działanie algorytmu. Nie mają one najczęściej ścisłego uzasadnienia teoretycznego, zwłaszcza przy doborze wartości parametrów sterujących działaniem poprawki, ale uwzględnione są w nich doświadczenia różnych autorów z zakresu prac nad sieciami neuronowymi. Do najbardziej znanych algorytmów heurystycznych należą Quickprop S. Fahlmana oraz RPROP R. Riedmillera i H. Brauna, zaimplementowany w programie SNNS oraz w Matlabie. Tutaj ograniczymy się do przedstawienia jedynie algorytmu RPROP (skrót od angielskiej nazwy Resilient backPROPagation) [54]
W algorytmie tym przy zmianie wag uwzględnia się jedynie znak składowej gradientu, ignorując jej wartość. W efekcie w każdej iteracji algorytmu uczącego określa się zmianę wektora wagowego według prostego wzoru
| \( \Delta w_{i j}(k)=-\eta_{i j}(k) \operatorname{sgn}\left(\frac{\partial E}{\partial w_{i j}}\right) \) | (2.24) |
Współczynnik uczenia dobierany jest indywidualnie dla każdej wagi \( \textbf{w}_{ij} \) na podstawie zmian wartości gradientu
| \( f(u)= \begin{cases} { \begin{matrix} \min \left(a \eta_{i j}(k-1), \eta_{\max }\right) && \textrm{ dla } g_{i j}(k) g_{i j}(k-1)>0 \\ \max \left(b \eta_{i j}(k-1), \eta_{\min }\right) && \textrm{ dla } g_{i j}(k) g_{i j}(k-1) < 0 \\ \eta_{i j}(k-1) && \textrm{ dla } g_{i j}(k) g_{i j}(k-1)=0 \end{matrix} } \end{cases} \) | (2.25) |
W równaniu tym \( \textbf{g}_{ij}(k)=\frac{\partial E}{\partial \textbf{w}_{ij}} \) oznacza wartość składową gradientu funkcji celu w \( k \)-tej iteracji, \( a \) i \( b \) są współczynnikami liczbowymi (\( a=1.2 \), \( b=0.5 \)), natomiast \( \eta_{\min} \) i \( \eta_{\max} \) oznaczają odpowiednio minimalną i maksymalną wartość współczynnika uczenia, równą w algorytmie RPROP odpowiednio 10-6 oraz 50. Funkcja sgn oznacza znak argumentu (+1 lub -1). Zgodnie ze strategią doboru wag zakłada się ciągły wzrost współczynnika uczenia, jeśli w dwu kolejnych krokach znak gradientu jest taki sam, natomiast jego redukcję, gdy ten znak jest różny. Algorytm RPROP, ignorujący informację o wartości gradientu, pozwala na znaczne przyspieszenie procesu uczenia w tych obszarach, w których nachylenie funkcji celu jest niewielkie.
2.8. Inicjalizacja wartości początkowych wag sieci
Uczenie sieci neuronowych, nawet przy zastosowaniu najefektywniejszych algorytmów uczących, jest procesem trudnym i nie zawsze prowadzącym do właściwych wyników. Problemem są nieliniowości wprowadzane przez funkcje aktywacji, będące głównym powodem wytworzenia szeregu minimów lokalnych, w których może zatrzymać się proces uczenia. Wprawdzie zastosowanie odpowiedniej strategii postępowania (np. symulowane wyżarzanie, metoda multistaru, algorytmy genetyczne [11,15,44]) mogłoby zmniejszyć prawdopodobieństwo zatrzymania procesu w minimum lokalnym, ale konsekwencją tego jest duży nakład pracy i znaczne wydłużenie czasu uczenia. Ponadto zastosowanie tych metod wymaga dużego doświadczenia w trudnych zagadnieniach optymalizacji globalnej, zwłaszcza przy właściwym doborze parametrów procesu.
Na wyniki uczenia ogromny wpływ ma dobór wstępnych wartości wag sieci. Pożądany byłby start z wartości wag zbliżonych do optymalnych. Unika się w ten sposób nie tylko zatrzymania się w niewłaściwym minimum lokalnym, ale jednocześnie znacznie przyspiesza proces uczenia. Niestety, w ogólnym przypadku nie istnieją metody doboru wag, zapewniające optymalny punkt startowy niezależnie od rodzaju zadania. Stąd w większości zastosowań używa się nadal głównie losowego doboru wag, przyjmując ich rozkład równomierny w określonym przedziale liczbowym. Zły dobór zakresu wartości losowych wag może prowadzić do zjawiska przedwczesnego nasycenia neuronów, w wyniku którego mimo upływu czasu błąd średniokwadratowy pozostaje prawie stały w procesie uczenia. Jest on zwykle wynikiem zbyt dużych wartości startowych wag. Przy określonych sygnałach uczących, w węzłach sumacyjnych neuronów generowane są sygnały ui o wartościach odpowiadających głębokiemu nasyceniu funkcji sigmoidalnej aktywacji, przy czym polaryzacja nasycenia jest odwrotna do pożądanej (sygnał wyjściowy neuronu \( +1 \) przy pożądanej wartości \( -1 \) i odwrotnie). W punkcie nasycenia sygnał zwrotny generowany w metodzie propagacji wstecznej, jako proporcjonalny do pochodnej funkcji aktywacji, jest bliski zeru i zmiany wartości wag wyprowadzające neuron ze stanu nasycenia są bardzo powolne. Proces uczenia utyka na długo w punkcie siodłowym. Należy zauważyć, że tylko część neuronów może być w stanie nasycenia, pozostałe znajdują się w zakresie liniowym i dla nich sygnał zwrotny uczący przyjmie normalną postać. Oznacza to, że wagi związane z tymi neuronami zmieniają się w sposób normalny i w ich przypadku proces uczenia prowadzi do szybkiej redukcji błędu. W efekcie neuron pozostający w nasyceniu nie bierze udziału w odwzorowaniu danych, zmniejszając w ten sposób efektywną liczbę neuronów sieci. W wyniku tego następuje znaczne spowolnienie procesu uczenia, powodujące, że stan nasycenia pewnych neuronów może trwać prawie nieprzerwanie aż do wyczerpania limitu iteracji.
Inicjalizacja losowa, jako jedyna uniwersalna metoda przypisania wartości wstępnych wagom sieci, musi zatem zapewnić na wstępie taki punkt pracy neuronów, który jest daleki od nasycenia. Osiąga się to przez ograniczenie zakresu wartości krańcowych w losowaniu. Oszacowanie dolne i górne zakresu tego przedziału, proponowane przez różnych badaczy na podstawie wielu przeprowadzonych eksperymentów numerycznych, różnią się w szczegółach rozwiązania, ale prawie wszystkie znajdują się w przedziale [0, 1].
Jedną z najbardziej popularnych sposobów inicjalizacji wag jest metoda Nguyen’a i Widrow’a [43]. Optymalny zakres wartości losowych elementów wektora wagowego neuronów warstw ukrytych powinien według nich być równy \( \pm \sqrt[n_{in}]{N_h} \), gdzie \( N_h \) oznacza liczbę neuronów ukrytych w warstwie, a \( n_{in} \) liczbę wejść danego neuronu. Wartości wstępne wag neuronów wyjściowych powinny być losowe w zakresie [-0,5 0,5]. Tego typu strategia inicjalizacji wag została między innymi zastosowana w algorytmach uczących zaimplementowanych w programie MATLAB [43].
2.9. Program MLP do uczenia sieci wielowarstwowej
W wykładzie tym przedstawimy program MLP uczenia i użytkowania w trybie testującym sieci MLP. Program ten w postaci interfejsu graficznego został stworzony na bazie oprogramowania neuronowego toolboxu „Neural Network” Matlaba. Przedstawimy szczegóły dotyczące tego interfejsu, podstawowe opcje wykorzystania programu oraz wyniki testu na aproksymacji danych wielowymiarowych.
2.9.1 Opis programu
Wykorzystując toolbox "Neural Network" i inne funkcje wbudowane w programie Matlab zaimplementowano wszystkie wymienione w wykładzie trzecim algorytmy uczące w postaci pakietu programów pod nazwą MLP (plik uruchomieniowy mlp.m). Uruchomienie programu następuje w oknie komend Matlaba po napisaniu nazwy mlp programu. Pojawi się wówczas menu główne przedstawione na rys. 5.1 [46].
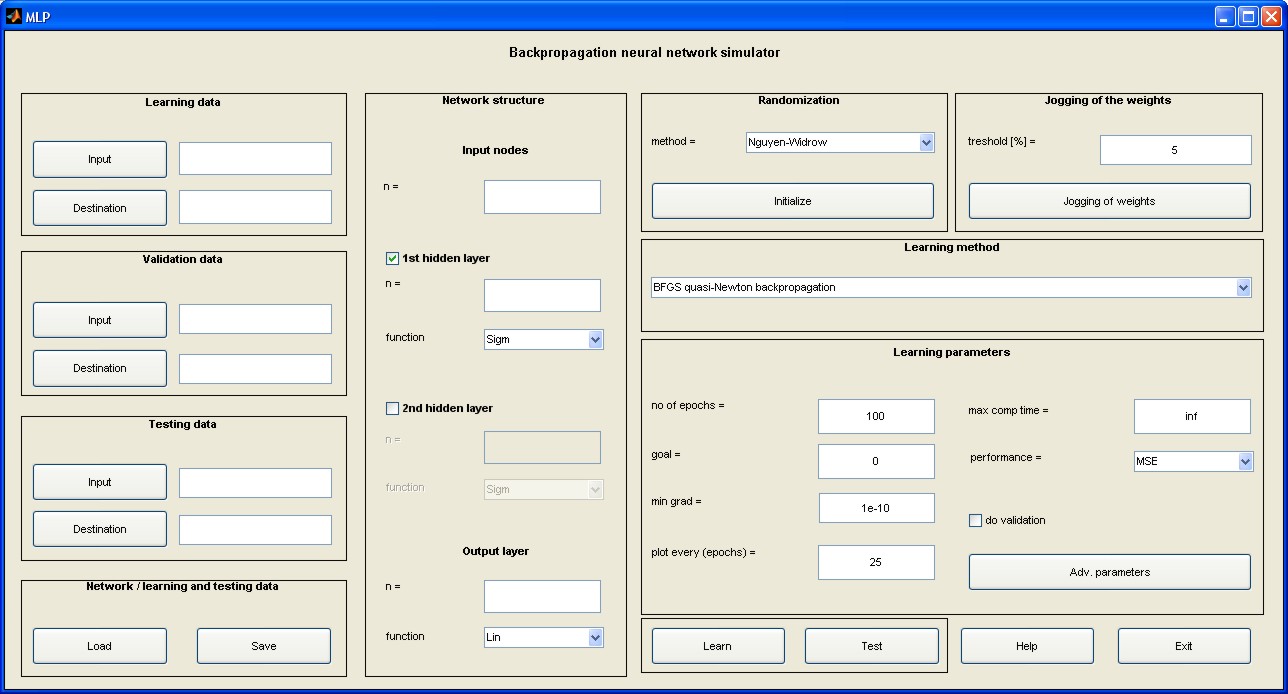
W lewej części menu znajdują się: pole do zadawania danych uczących (pole Learning data), weryfikujących (pole Validation data) oraz testujących, nie uczestniczących w uczeniu (pole Testing data). Przycisk Input służy do wczytania nazwy pliku z rozszerzeniem .mat zawierającego zbiór wektorów \( \textbf{x} \) zorganizowany w formie macierzy (liczba wierszy odpowiada liczbie tych wektorów, a liczba kolumn jest równa wymiarowi wektora \( \textbf{x} \)). Przycisk Destination pozwala na podanie nazwy pliku, również z rozszerzeniem .mat, zawierającego zbiór wektorów zadanych \( \textbf{d} \) stowarzyszonych z wektorami wejściowymi \( \textbf{x} \). Można również zapamiętać całą sesję uczącą (przycisk Save) lub załadować jej zawartość wcześniej zapamiętaną (przycisk Load). Po naciśnięciu przycisku Load pojawia się okno dialogowe menu wyboru struktury sieci i danych przedstawione na rys. 2.5 (xu – macierz zawierająca zbiór wektorów uczących \( \textbf{x}_u \), xt – macierz zawierająca zbiór wektorów testujących \( \textbf{x}_t \), du - macierz zawierająca zbiór zadanych (znanych) wektorów uczących \( \textbf{d}_u \) na wyjściu sieci stowarzyszonych z wektorami \( \textbf{x}_u \), dt - macierz zawierająca zbiór zadanych wektorów testujących \( \textbf{d}_t \) na wyjściu sieci stowarzyszonych z wektorami \( \textbf{x}_t \).
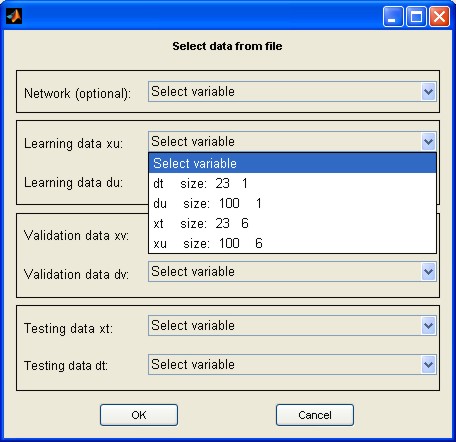
Wybierając nazwę wcześniej zapisanej struktury sieci można podać plik zawierający kompletne dane sieci MLP zapisane w poprzedniej sesji uczącej. Można również wybrać opcję wczytywania danych uczących, weryfikujących i testujących zapisanych w jednym wspólnym pliku, z wyróżnionymi nazwami odpowiednich zmiennych.
Definiowanie struktury sieciowej odbywa się w polu środkowym menu (pole Network structure). Należy wybrać liczbę warstw ukrytych (dostępne są dwie) oraz liczbę neuronów w każdej warstwie, jak również rodzaj funkcji aktywacji neuronów. Dostępne są następujące funkcje: liniowa (Lin), sigmoidalna jednopolarna (Sigm) oraz sigmoidalna bipolarna (Bip). Liczba węzłów wejściowych oraz neuronów wyjściowych są automatycznie wyznaczane na podstawie wymiaru wektorów \( \textbf{x} \) oraz \( \textbf{d} \) i użytkownik nie może ich zmienić.
Przed rozpoczęciem uczenia należy dokonać inicjalizacji wag sieci (pole Randomization) naciskając przycisk Initialize. W programie zaimplementowano specjalną metodę randomizacji Ngyen-Widrowa [43]. Przy utknięciu procesu uczenia w minimum lokalnym można dokonać losowej zmiany wag przez naciśnięcie przycisku Jogging of weights w polu Jogging of weights i kontynuacji uczenia z nowego punktu startowego wag. Przedtem należy ustawić zakres randomizacji (threshold).
Przed uruchomieniem procesu uczenia należy jeszcze ustawić wartości parametrów procesu w polu Learning parameters, w tym liczby cykli uczących (no of epochs), wartości oczekiwanej optymalnej wartości funkcji celu (goal), minimalnej wartości gradientu (min grad) kończącej proces uczenia, maksymalnego czasu uczenia (max comp time), a także sposobu definiowania funkcji celu (performance). Dostępne są następujące miary funkcji celu: MSE - wartość średnia sumy kwadratów błędów (Mean Squared Error) - zalecana, SSE - suma kwadratów błędów (Sum Squared Error), MAE - wartość średnia błędów absolutnych (Mean Absolute Error).
W trakcie uczenia program automatycznie wykreśla wartości aktualne funkcji celu z krokiem wybranym w polu plot every (epochs). Przy wielokrotnej kontynuacji procesu uczenia tworzony jest dodatkowy zbiorczy wykres postępów minimalizacji funkcji celu. Jeżeli w procesie uczenia przewiduje się weryfikację działania sieci na danych weryfikujących, należy uaktywnić przycisk do validation. Przy takim wyborze jednocześnie z krzywą uczenia wykreślany jest aktualny błąd dla danych weryfikujących.
Uruchomienie procesu uczenia sieci odbywa się przez naciśnięcie przycisku Learn, a sprawdzenie działania sieci na danych testujących poprzez naciśnięcie przycisku Test. Po zakończeniu procesu uczenia program automatycznie przeprowadza symulację działania na danych uczących odtwarzając sygnały wyjściowe w postaci zbioru wektorów \( \textbf{y} \) odpowiadających wymuszeniom zawartym w zbiorze wektorów \( \textbf{x} \) użytych w uczeniu. Aktualne odpowiedzi sieci zarówno na danych uczących jak i testujących przypisane są zmiennej \( y \) i są dostępne na bieżąco w polu roboczym Matlaba.
2.9.2 Przykład aproksymacji funkcji za pomocą sieci MLP
Problemem testowym jest jednoczesna aproksymacja czterech funkcji przedstawionych na rys. 2.6. Są to funkcje: prostokątna, trójkątna, sinusoidalna oraz wartość absolutna funkcji sinc.
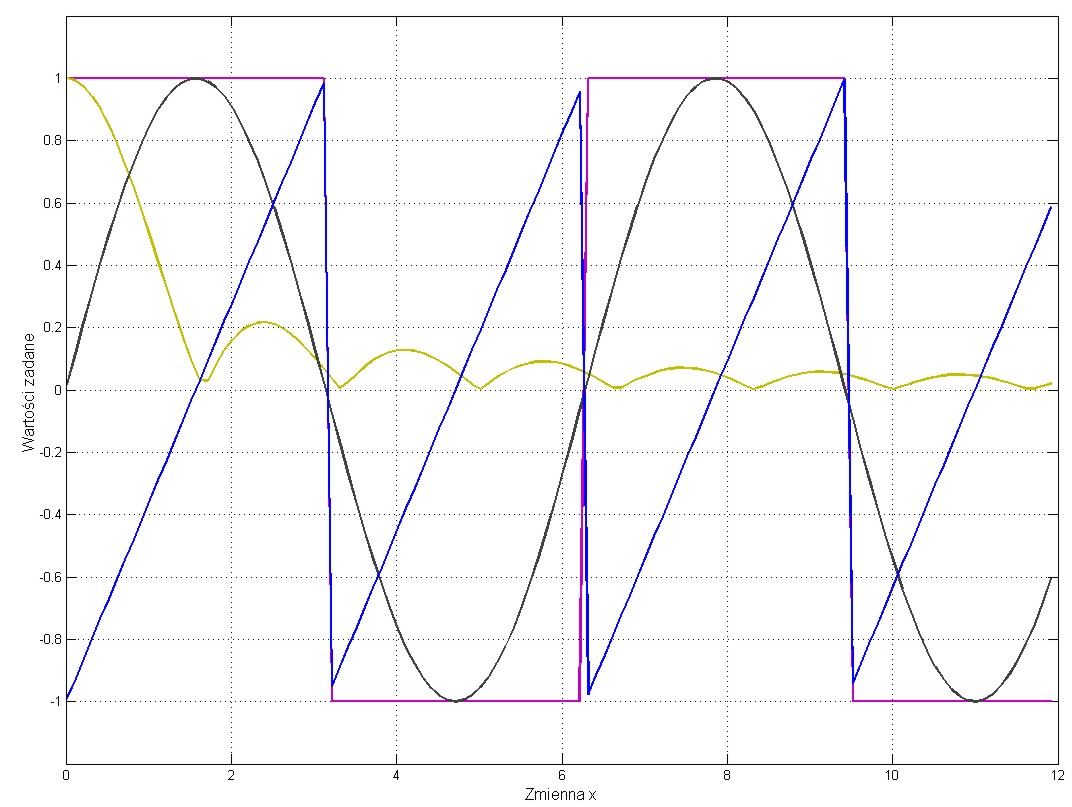
Pierwszym etapem rozwiązania jest generacja danych uczących i testujących (różnych od uczących). Dane testujące wygenerowano dla tych funkcji tablicując ich wartości w punktach \( x \) różnych od tych użytych dla celów uczenia.
Wstępne eksperymenty numeryczne pokazały, że dobre wyniki generalizacji sieci uzyskuje się już przy \( n_h = 20 \) neuronach ukrytych, co oznacza że strukturę sieci można zapisać w postaci 1-20-4. Dane wejściowe stanowią kolejne punkty czasu użytego w generacji danych uczących a wartości zadane wektora czterowymiarowego \( \textbf{d} \) na wyjściu sieci odpowiadają wartościom czterech funkcji poddanych modelowaniu dla zadanych na wejściu punktów czasowych.
Na rys. 2.7 przedstawiono krzywe uczenia sieci aproksymującej przy zastosowaniu różnych algorytmów uczących.
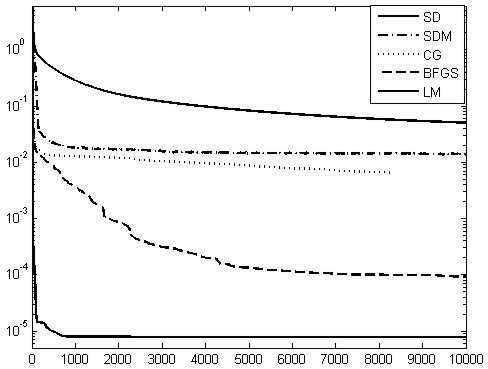
Nie ulega wątpliwości, że najlepszy jest algorytm Levenberga-Marquardta (LM) zarówno pod względem czasu uczenia jak i uzyskanej wartości funkcji celu, a najgorszy algorytm największego spadku (SD). Dla porównania złożoności procesu uczenia przy zastosowaniu różnych algorytmów uczących zaprojektowano dodatkowo sieć przewymiarowaną zawierającą aż \( n_h = 140 \) neuronów ukrytych. Liczba wag sieci optymalnej 1-20-4 jest równa 124, natomiast sieci przewymiarowanej 1-140-4 aż 845.
W tabeli 2.1 przedstawiono (dla porównania skuteczności metod uczenia) liczbę cykli uczących, operacji zmienno-przecinkowych oraz czasy uczenia przy wartości pożądanej funkcji celu równej goal=1e-4 dla obu przyjętych w eksperymencie liczbach neuronów ukrytych 20 oraz 140 (wyniki dotyczą starej wersji Matlaba, w obecnej wersji Matlaba liczba operacji zmiennoprzecinkowych jest niedostępna, a czasy uczenia i liczba cykli uczących zdecydowanie krótsze.
Tabela 2.1 Zestawienie wyników uczenia sieci aproksymującej przy różnej liczbie neuronów ukrytych i różnych metod uczenia
|
Metoda uczenia |
Liczba cykli uczących |
Liczba operacji zmiennoprzecinkowych |
Czas uczenia |
|||
|
\( n_h = 20 \) |
\( n_h = 140 \) |
\( n_h = 20 \) |
\( n_h = 140 \) |
\( n_h = 20 \) |
\( n_h = 140 \) |
|
|
SD |
84785 |
202982 |
1.7e10 |
5.7e10 |
22min 21sek |
51min 28sek |
|
SDM |
10205 |
27822 |
5.2e10 |
6.4e10 |
104sek |
342sek |
|
CG |
226 |
301 |
3.9e8 |
5.4e8 |
20.79sek |
35.5sek |
|
BFGS |
97 |
2094 |
5.9e9 |
5.1e10 |
51.51sek |
342sek |
|
LM |
5 |
43 |
7.9e8 |
7.4e9 |
5.86sek |
67.3sek |
Tym razem wynik oceny jakości algorytmu uczącego w sposób zdecydowany zależy od wielkości sieci. Dla sieci małej najskuteczniejszy pod każdym względem jest znów algorytm Levenberga-Marquardta. W przypadku sieci dużej (845 wag) zdecydowaną przewagę uzyskuje algorytm gradientów sprzężonych (CG) zarówno pod względem czasu uczenia jak i liczby operacji zmienno-przecinkowych.
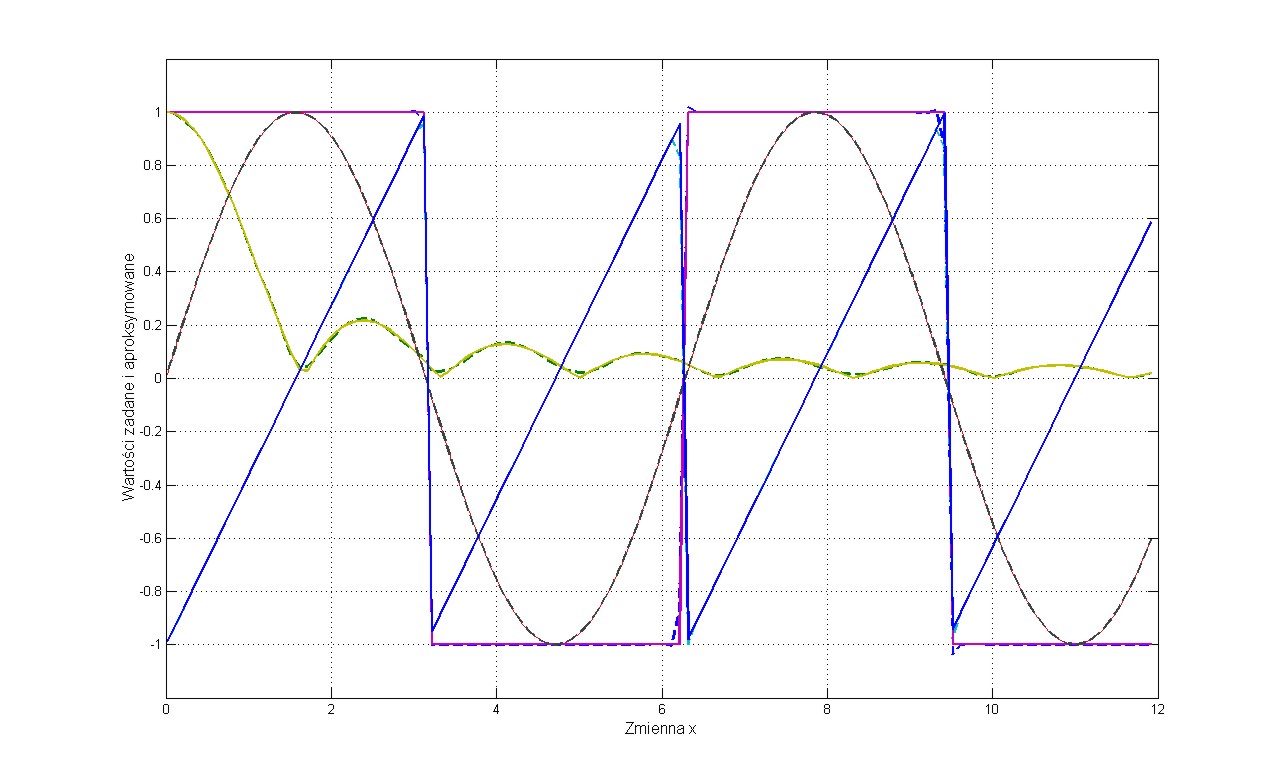
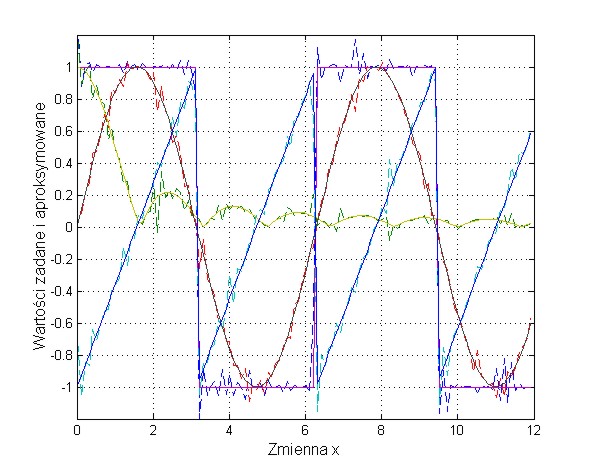
Interesujący jest efekt przewymiarowania sieci neuronowej z punktu widzenia zdolności generalizacyjnych. Zbyt duża sieć neuronowa powoduje utratę tych zdolności w trybie testującym na danych nie uczestniczących w uczeniu. Efekt ten jest przedstawiony na rys. 2.8 (rys. 2.8a - 20 neuronów ukrytych, rys. 2.8b - 140 neuronów ukrytych). Przy 140 neuronach ukrytych krzywe zrekonstruowane przez sieć neuronową charakteryzują się dużymi odkształceniami od przebiegu pożądanego.
Na podstawie wielu przeprowadzonych badań symulacyjnych z użyciem różnorodnych problemów testowych można stwierdzić, że najmniej efektywny jest prosty algorytm największego spadku, szczególnie w przypadku wyboru stałego kroku uczącego. Strategia wyboru metody poszukiwania kierunku minimalizacji \( \textbf{p} \) jest kluczowa dla efektywności algorytmu. Generalnie na podstawie wielu różnych badań testowych można stwierdzić, że algorytmy newtonowskie, w tym metoda zmiennej metryki i Levenberga-Marquardta przewyższają zwykle pod względem efektywności zarówno metodę największego spadku jak i metodę gradientów sprzężonych, ale ta zdecydowana przewaga zanika przy znacznym zwiększeniu rozmiarów sieci. Już przy kilkuset wagach metoda gradientów sprzężonych może górować nad pozostałymi. Metoda największego spadku z momentem rozpędowym jest znacznym udoskonaleniem zwykłej metody największego spadku, choć w badanych przypadkach nieco odbiega od metod newtonowskich. Tym niemniej charakteryzuje się ona dobrą generalizacją, ze względu na możliwość wydostania się z minimum lokalnego dzięki mechanizmowi rozpędu.
2.9.3 Przykład kompresji obrazów przy użyciu sieci MLP
Sieć MLP jest modelem uniwersalnym aproksymatora globalnego. Ma zastosowanie zarówno w zadaniach klasyfikacji (sygnał wyjściowego neuronu sigmoidalnego jest binaryzowany do wartości 1 lub 0 oznaczając przynależność do klasy lub jej brak) jak i regresji (zwykle neurony wyjściowe liniowe). W tym punkcie przedstawimy zastosowanie sieci MLP w problemie kompresji stratnej obrazów (sieć typu regresyjnego). Można przy tym posłużyć się jedną z opcji wyboru w specjalnym programie, którego graficzny interfejs przedstawiony jest na rys. 2.9.
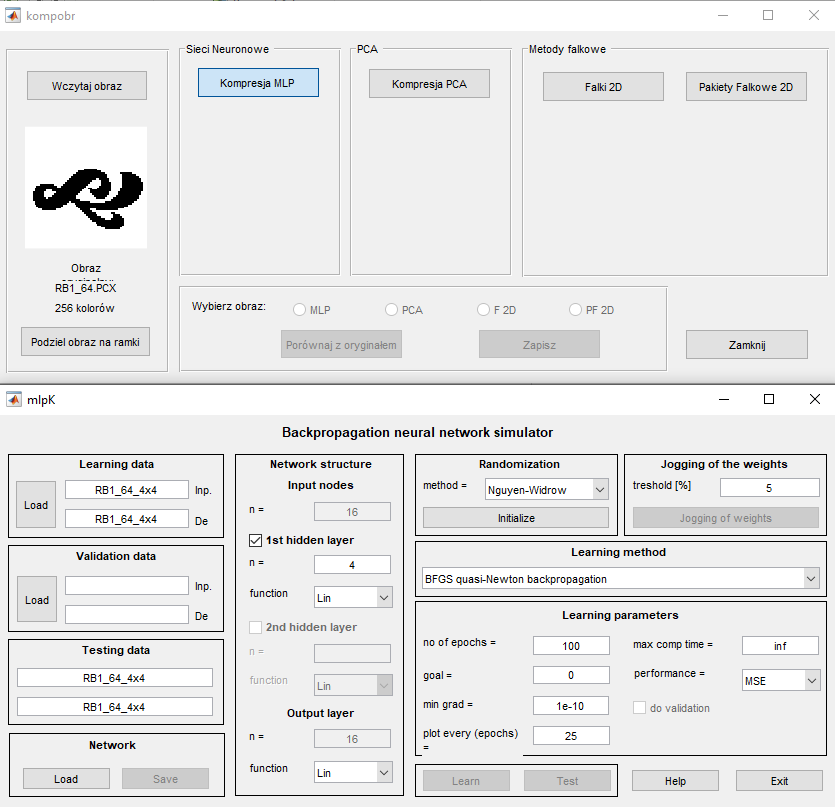
W pierwszym eksperymencie kompresji poddano obraz czarno-biały (obraz oryginalny na rys. 2.10) o wymiarach 64x64 podzielony na ramki o wymiarach 4x4 uzyskując 256 ramek uzytych a w uczeniu. Po zastosowaniu kompresji ze współczynnikiem równym 4 (16 sygnałów wejściowych, 4 neurony ukryte sieci) obraz został zrekonstruowany. Wyniki rekonstrukcji po kompresji i obraz błędnych pikseli (różnica między oryginałem i obrazem odtworzonym) są przedstawione na rys. 2.10. Średni błąd względny odtworzenia jest równy 2.19%.

W drugim eksperymencie kompresji poddano obraz „BOAT” o wymiarze 512x512, podzielony na ramki 8x8 (wymiar ramki 64) uzyskując w sumie 4096 ramek. Przy 8 neuronach ukrytych sieci współczynnik kompresji jest równy 8.

Na rys. 2.11 przedstawiono wyniki graficzne kompresji i rekonstrukcji przedstawiające obraz oryginalny, obraz odtworzony po kompresji (rysunek środkowy) oraz obraz różnicowy (z prawej strony). Tym razem średni błąd odtworzenia jest równy 5.47%.
2.10. Zadania i problemy
1. Dany jest zbiór trzech wektorów trójwymiarowych
\( \mathbf{x}_1=\left[\begin{array}{c} 1 \\ 3 \\ \sqrt{2} \end{array}\right] \), \( \quad \mathbf{x}_2=\left[\begin{array}{c} 2 \\ -2 \\ \sqrt{8} \end{array}\right] \), \( \quad \mathbf{x}_3=\left[\begin{array}{c} 3 \\ -1 \\ \sqrt{6} \end{array}\right] \).Określić kąt między poszczególnymi parami wektorów. Jak daleko jest do spełnienia warunku ortogonalności dla każdego przypadku?
2. Funkcja błędu dla sieci neuronowej określona jest wzorem \( E=0.2-\mathbf{g}^{\top} \mathbf{w}+0.5 \mathbf{w}^{\top} \mathbf{H} \mathbf{w} \), gdzie
\( \mathbf{g}=\left[\begin{array}{l}
0.8 \\
0.3
\end{array}\right] \), \( \quad \mathbf{H}=\left[\begin{array}{cc}
1 & 0,8 \\
0,8 & 1
\end{array}\right] \).
- Określić wartość optymalną wektora \( \mathbf{w} \) przy której funkcja celu osiągnie swoje minimum.
- Zastosować metodę największego spadku przy \( \eta = 0.3 \) oraz \( \eta = 1 \) dla wyznaczenia tego minimum.
3. Wygenerować zestaw danych jednowymiarowych typu losowego o rozkładzie gaussowskim należących do dwu klas:
Klasa 1: \( \sigma_{1}=1 \), \( c_{1}=-10 \)
Klasa 2: \( \sigma_{2}=1 \), \( c_{2}=10 \)
Zaprojektować klasyfikator MLP separujący te dane. Zilustrować wynik separacji na tle danych. Czy istnieje tylko jedno rozwiązanie teoretyczne? Skomentować wynik.
4. Narysować schemat sieci MLP o 2 wejściach, 3 sigmoidalnych neuronach ukrytych i jednym neuronie wyjściowym (również sigmoidalnym) oraz sieć dołączoną do niej dla generacji gradientu. Napisać wzory na składowe gradientu względem wag sieci.
5. Wagi klasyfikatora liniowego 2-wejściowego (rys. 2.12) są znane i równe \( w_{0}=-1 \), \( w_{1}=1.5 \), \( w_{2}=2 \). Na klasyfikator podano 4 wektory \( \mathbf{x} \)
| \( \mathbf{x}_1=\left[\begin{array}{l} 1 \\ 1 \end{array}\right] \) | \( \mathbf{x}_2=\left[\begin{array}{l} 1 \\ -2 \end{array}\right] \) | \( \mathbf{x}_3=\left[\begin{array}{l} -1 \\ -2 \end{array}\right] \) | \( \mathbf{x}_4=\left[\begin{array}{l} 3 \\ -1 \end{array}\right] \) |
Określić przynależność tych wektorów do klasy 1 (u>0) lub klasy 2 (u<0). Zilustrować ich przynależność do klas na płaszczyźnie (x1, x2). Na podstawie tego rozkładu zaproponować inne wagi klasyfikatora, również rozwiązujące problem separacji obu klas.
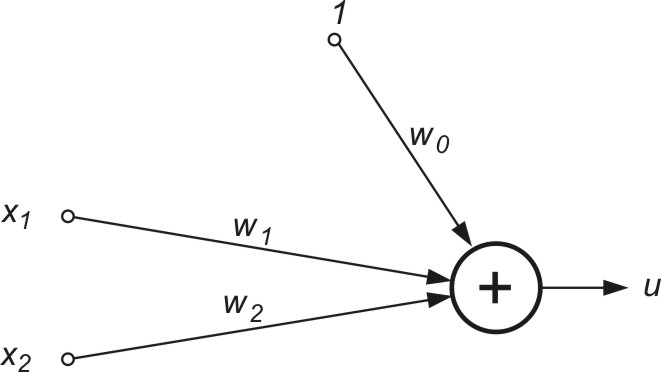
6. Określić przynależność 3 wektorów wejściowych x do jednej z 2 klas przy użyciu sieci MLP o strukturze jak na rys. 2.13.
Przyjąć bipolarną funkcję aktywacji neuronów ukrytych oraz wyjściowych oraz następujące wartości wag: w10=-1, w11=1, w12=1, w20=1, w21=2, w22=4, w0=-1, w1=1, w2=1.
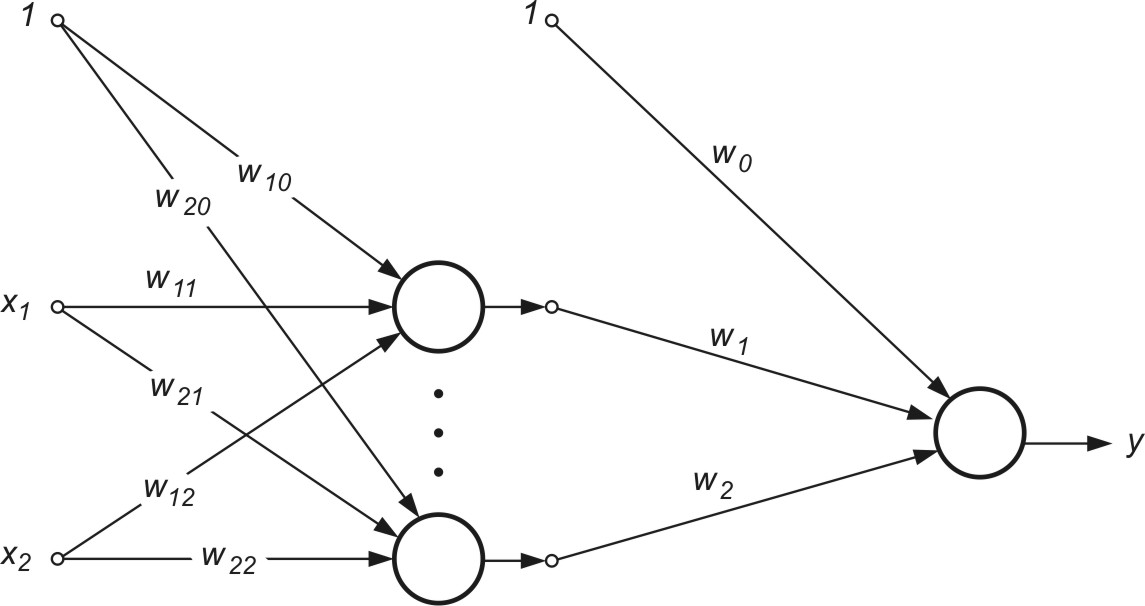
7. Sieć neuronowa jednowyjściowa realizuje następującą funkcję aproksymacyjną
\(
y(x)=f\left(w_1 f\left(w_{11} x_1+w_{12} x_2\right)+w_2 f\left(w_{21} x_1+w_{22} x_2\right)\right)
\)
w której \( f() \) reprezentuje funkcję sigmoidalną unipolarną.
Zakładając wartości startowe wag sieci: \( w_1=-0.2; w_2=0.1; w_{11}=-0.3; w_{12}=0.5; w_{21}=1; w_{22}=-0.7 \) określić gradient i hesjan funkcji celu dla jednej pary uczącej równej \( (\mathbf{w}, d) \), gdzie \( \mathbf{x}=[1 \; 2]^T \), \( d=0.5 \).
8. Dla danych z poprzedniego zadania wyznaczyć kierunek minimalizacji odpowiadający metodzie największego spadku oraz klasycznej metodzie Newtona (wzór 2.14). Sprawdzić czy zastosowanie metody newtonowskiej prowadzi w danych warunkach do minimum funkcji celu.
2.11. Słownik
Słownik opanowanych pojęć
Wykład 2
Sieć neuronowa MLP – sieć wielowarstwowa bez sprzężenia zwrotnego (jednokierunkowa) stosująca sigmoidalną funkcję aktywacji.
Sieć autoasocjacyjna – sieć trenowana z nauczycielem, w którym wektor zadany na wyjściu jest tożsamy z wektorem wejściowym.
Sieć heteroasocjacyjna – sieć trenowana z nauczycielem, w którym wektor zadany na wyjściu jest różny od wektora wejściowego.
Polaryzacja neuronu – dodatkowy (poza wektorem sygnałów wejściowych) sygnał jednostkowy neuronu.
Funkcja celu – funkcja definiująca minimalizowany błąd sieci na danych uczących (zwana również funkcją kosztu lub błędu).
Uczenie on-line – sposób uczenia sieci, w którym adaptacja parametrów odbywa się natychmiast po zaprezentowaniu pojedynczej danej uczącej.
Uczenie off-line – sposób uczenia sieci, w którym adaptacja parametrów odbywa się dopiero po zaprezentowaniu całego zbioru danych uczących.
Algorytm propagacji wstecznej – sposób generacji gradientu poprzez analizę przepływu sygnałów w sieci oryginalnej i sieci o odwróconym kierunku przepływu sygnałów, zasilanej sygnałem błędu na wyjściu.
Graf sieci – sposób przedstawienia struktury sieci neuronowej przy zastosowaniu symboliki grafu przepływu sygnałów.
Graf dołączony sieci – graf sieci odpowiadający przeciwnemu kierunkowi przepływu sygnałów.
Wektor kierunkowy minimalizacji – wektor wyznaczający kierunek minimalizacji wartości funkcji celu w przestrzeni parametrów.
Gradient – wektor reprezentujący pochodną funkcji celu względem wszystkich parametrów sieci.
Hesjan – macierz drugich pochodnych funkcji celu względem wszystkich parametrów.
Współczynnik uczenia – wielkość określająca krok w kierunku wyznaczonym przez wektor kierunkowy minimalizacji.
Metoda największego spadku – algorytm uczący sieci w którym wektor kierunkowy minimalizacji jest równy ujemnemu gradientowi.
Metoda największego spadku z momentem rozpędowym – metoda największego spadku zmodyfikowana o poprawkę uwzględniającą ostatnią zmianę parametrów.
Algorytm BFGS – algorytm pseudo-newtonowski zmiennej metryki aproksymujący hesjan na podstawie ostatnich zmian wartości adaptowanych parametrów sieci i gradientu.
Algorytm Levenberga-Marquardta – algorytm pseudo-newtonowski stanowiący modyfikację metody Gaussa-Newtona, polegający na wprowadzeniu poprawki gwarantującej dodatnią określoność hesjanu.
Algorytm gradientów sprzężonych – metoda wyznaczania wektora kierunkowego minimalizacji, w której to kierunek poszukiwań jest ortogonalny oraz sprzężony ze wszystkimi poprzednimi kierunkami.
Algorytm RPROP – metoda heurystyczna uczenia sieci, w której przy zmianie parametrów uwzględnia się jedynie znak składowej gradientu, ignorując jej wartość.
Macierz dodatnio określona - macierz której wszystkie wartości własne są dodatnie.
Macierz nieujemnie określona - macierz której wszystkie wartości własne są dodatnie lub zerowe.
Macierz ujemnie określona - macierz której wszystkie wartości własne są ujemne.
Inicjalizacja parametrów – nadanie wartości startowych parametrom sieci (zwykle losowe z określonego zakresu).
Program MLP.m – program uczenia i testowania sieci w Matlabie zaimplementowany w formie GUI.
3. Zdolności generalizacyjne sieci neuronowych
Praktyczne wykorzystanie sieci MLP do efektywnego rozwiązania rzeczywistych zadań występujących w technice i biznesie wymaga zapoznania się z wieloma problemami tworzenia i doboru optymalnych struktur sieci neuronowych, gwarantujących najwyższą jakość rozwiązania. Szczególnie istotne są problemy zdolności generalizacyjnych sieci, gdyż na nich opiera się możliwość ich wykorzystania. W wykładzie tym omówimy pojęcie generalizacji sieci oraz sposoby projektowania struktur oraz przeprowadzenia uczenia sieci MLP gwarantujące osiągnięcie optymalnych zdolności generalizacyjnych przez sieć neuronową.
3.1. Wprowadzenie pojęcia zdolności generalizacyjnych sieci
Pod pojęciem generalizacji rozumieć będziemy umiejętność generowania właściwej odpowiedzi sieci przy określonym pobudzeniu nie biorącym udziału w procesie uczenia. Zauważmy, że jakkolwiek dobór wag w procesie uczenia odbywa się na zbiorze uczącym, główne działanie sieci to tryb odtwarzania, w którym po zamrożeniu wartości wytrenowanych wag, podaje się na wejście sieci jedynie sygnały wejściowe \( \mathbf{x} \) nie wchodzące w skład zbioru uczącego, dla których w danej chwili nieznane są właściwe odpowiedzi, jak to miało miejsce w trybie uczenia.
Należy zdać sobie sprawę, że głównym celem uczenia sieci jest taka adaptacja wag, aby na podstawie zbioru próbek uczących charakterystycznych dla danego procesu sieć była w stanie nauczyć się cech charakterystycznych danego procesu (mechanizmu tworzenia danych we-wy procesu), a nie dostosować się jedynie do wartości zadanych próbek uczących. Sieć wytrenowana na określonym zbiorze wzorców uczących przenosi więc swoją wiedzę na zbiory tzw. testujące (walidacyjne), które nie uczestniczyły w uczeniu. Aby uzyskać dobrą generalizację, proces uczenia musi spełniać pewne podstawowe warunki.
-
Dane uczące powinny być reprezentatywne dla modelowanego procesu i odzwierciedlać jego główne cechy statystyczne. Sieć powinna dopasować swoje wagi w taki sposób, aby móc dobrze odtwarzać te cechy a nie dopasowywać się do indywidualnych wartości zadanych.
-
Aby to uzyskać liczba danych uczących powinna być zatem znacznie większa od liczby dobieranych parametrów (wag) sieci. Umożliwi to dopasowanie wartości wag do statystyki reprezentowanej przez dane uczące, uniemożliwiając adaptację wag do dokładnych wartości konkretnych par wektorów uczących.
-
Struktura sieci powinna być z kolei o możliwie najmniejszej liczbie wag (zwiększy to relację liczby danych uczących do liczby wag), umożliwiającej jednak uzyskanie akceptowalnego poziomu błędu odwzorowania na zbiorze danych uczących.
-
Proces uczenia powinien być prowadzony przy zastosowaniu efektywnego algorytmu uczącego i nie powinien ciągnąć się w nieskończoność, ale zakończony w momencie uzyskania minimum błędu na zbiorze sprawdzającym (zbiór walidacyjny różny od uczącego).
Teoria generalizacji sieci neuronowych bazuje bezpośrednio na zależnościach statystycznych. Błąd średni \( E \) odtworzenia danych na zbiorze danych \( (\mathbf{x}, \mathbf{d}) \), dla którego znane są wartości zadane (wektor \( \mathbf{d} \)) może być zinterpretowany jako wartość oczekiwana różnicy między wartością aktualną funkcji \( y_i(\mathbf{x}) \) dla poszczególnych wyjść sieci a odpowiadającą im wartością zadaną \( d_i \). Może być on rozdzielony na część odpowiadającą obciążeniu \( B_i \) (ang. bias) oraz wariancji \( V_i \), przy czym \( E_i^2=B_i^2+V_i \) [24]. Obciążenie \( B_i \) wyraża niezdolność sieci do dokładnej aproksymacji funkcji zadanej \( d_i(\mathbf{x}) \) i może być uważane za błąd aproksymacji (w praktyce utożsamiany jest z błędem uczenia).
Składnik \( V_i \) jest wariancją funkcji aproksymującej mierzoną na zbiorze danych \( (x_i, d_i) \). Wyraża sobą nieadekwatność informacji zawartej w zbiorze danych uczących w stosunku do rzeczywistej funkcji \( d_i \) i może być uważana za błąd estymacji. W praktyce za miarę wariancji przyjmuje się błąd sieci na danych testujących. Przy określonej wartości błędu średniokwadratowego małe obciążenie musi być okupione zwiększoną wariancją. Jedynie przy nieskończonej liczbie danych uczących można mieć nadzieję na minimalizację błędu średniokwadratowego prowadzącą do jednoczesnej minimalizacji zarówno obciążenia jak i wariancji.
3.2. Miara VCdim i jej związek z generalizacją
Problem optymalnego uczenia sieci polega na wyselekcjonowaniu struktury sieci i doboru jej parametrów w taki sposób, aby aproksymować wartości zadane \( \mathbf{d}(\mathbf{x}_k) \) dla \( k=1,2,\ldots,p \) z minimalnym błędem, i optymalnością definiowaną w sensie statystycznym. W teorii optymalnego uczenia kluczową rolę odgrywa pojęcie miary Vapnika-Chervonenkisa (VCdim), zdefiniowane dla sieci realizującej funkcję klasyfikatora.
Miara VCdim została zdefiniowana dla sieci klasyfikacyjnej jako liczebność \( n \) największego zbioru danych wzorców, dla których system może zrealizować wszystkie możliwe \( 2^n \) dychotomii tego zbioru (podział zbioru na dwie części za pomocą linii prostej). VCdim jest miarą pojemności lub zdolności sieci do realizacji funkcji klasyfikacyjnej wzorców. Miara VCdim odgrywa istotną rolę przy określaniu minimalnej liczby danych uczących \( p \), gdyż dla uzyskania dobrej generalizacji powinien być spełniony warunek \( p \gg VCdim \).
Zostało dowiedzione, że dla sieci jednowarstwowej o jednym neuronie wyjściowym i \( N \) wejściach miara \(VCdim \) jest równa \( N+1 \), czyli równa liczbie połączeń wagowych z uwzględnieniem polaryzacji. Dla sieci jednowyjściowej (jeden neuron wyjściowy) zawierającej jedną warstwę ukrytą i skokowej funkcji aktywacji neuronów miara \(VCdim \) jest równa także \( N+1 \). Dla sieci o dowolnej liczbie warstw ukrytych i skokowej funkcji aktywacji miara \(VCdim \) jest proporcjonalna do \( n_w \lg (n_w) \), gdzie \( n_w \) jest całkowitą liczbą wag sieci. Zastosowanie sigmoidalnej funkcji aktywacji zwiększa tę miarę do wartości proporcjonalnej do \( n_w^2 \). Dla porównania, w sieci liniowej o liczbie wag \( n_w \) miara \(VCdim \) jest proporcjonalna do liczby wag. Jak z powyższego widać niezależnie od zastosowanej funkcji aktywacji neuronów w sieci MLP miara \(VCdim \) jest zawsze skończona i uzależniona od liczby wag.
Jeżeli przez \( P_u \) oznaczymy prawdopodobieństwo wystąpienia błędu na zbiorze danych uczących (względny błąd klasyfikacji dla danych uczących) a przez \( P_t \) - prawdopodobieństwo wystąpienia błędnej klasyfikacji w przyszłym użytkowaniu sieci na danych nie uczestniczących w uczeniu (testowanie) to istotnym problemem jest oszacowanie spodziewanego błędu na tych danych, zwłaszcza jego górnej granicy. Zostało udowodnione, że prawdopodobieństwo wystąpienia błędu testowania większego o wartość \( \varepsilon \) od błędu uczenia dla sieci MLP jest określone wzorem [24,68]
| \( P\left\{\sup _{\mathbf{w}}\left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right\} \leq\left(\frac{2 e p}{h}\right)^h e^{-\varepsilon^2 p} \) | (3.1) |
w którym \( P \) oznacza prawdopodobieństwo, \( P_t \) i \( P_u \) – prawdopodobieństwo popełnienia błędu klasyfikacyjnego (przez sieć o wagach określonych wektorem \( \mathbf{w} \) na danych odpowiednio testujących i uczących, \( p \) - liczbę danych uczących, \( e \) - podstawę logarytmu naturalnego a \( h \) - aktualne oszacowanie miary \( VCdim \). Funkcja wykładnicza \( e^{-\varepsilon^2 p} \) ![]() wskazuje, że wraz ze wzrostem liczby danych uczących prawdopodobieństwo wystąpienia błędu klasyfikacji ma niższą wartość ograniczenia górnego. Przy skończonej wartości \( h \) i liczbie wzorców uczących dążącej do nieskończoności prawdopodobieństwo popełnienia tego błędu dąży do zera. Jeśli przez \( \alpha \) oznaczymy prawdopodobieństwo wystąpienia zdarzenia \( \alpha=P\left(\sup \left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right) \) wtedy z prawdopodobieństwem \( 1 - \alpha \) można stwierdzić, że \( P_t \le P_u + \varepsilon \). Na podstawie tych zależności otrzymuje się
wskazuje, że wraz ze wzrostem liczby danych uczących prawdopodobieństwo wystąpienia błędu klasyfikacji ma niższą wartość ograniczenia górnego. Przy skończonej wartości \( h \) i liczbie wzorców uczących dążącej do nieskończoności prawdopodobieństwo popełnienia tego błędu dąży do zera. Jeśli przez \( \alpha \) oznaczymy prawdopodobieństwo wystąpienia zdarzenia \( \alpha=P\left(\sup \left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right) \) wtedy z prawdopodobieństwem \( 1 - \alpha \) można stwierdzić, że \( P_t \le P_u + \varepsilon \). Na podstawie tych zależności otrzymuje się
| \( \alpha=\left(\frac{2 e p}{h}\right)^h \exp \left(-p \varepsilon^2\right) \) | (3.2) |
Wprowadźmy oznaczenie \( \varepsilon_0(p, h, \alpha) \)
| \( \varepsilon_0(p, h, \alpha)=\sqrt{\frac{h}{p}\left[\lg \left(\frac{2 p}{h}\right)+1\right]-\frac{1}{p} \lg (\alpha)} \) | (3.3) |
Wartość \( \varepsilon_0(p, h, \alpha) \) określa przedział ufności odpowiadający prawdopodobieństwu \( \alpha \) na zbiorze danych uczących przy \( p \) danych i aktualnej mierze \( VCdim=h \). Oszacowanie \( P_t \le P_u + \varepsilon \) odpowiada najgorszemu przypadkowi. Przy małej wymaganej w praktyce wartości \( P_t \) oszacowanie powyższe można znacznie uściślić. W takim przypadku z prawdopodobieństwem \( (1-\alpha) \) można stwierdzić, że [24]
| \( P_t \leq P_u+\varepsilon_1\left(p, h, \alpha, P_u\right) \) | (3.4) |
gdzie
| \( \varepsilon_1\left(p, h, \alpha, P_u\right)=2 \varepsilon_0^2(p, h, \alpha)\left(1+\sqrt{1+\frac{P_u}{\varepsilon^2(p, h, \alpha)}}\right) \) | (3.5) |
W tym przypadku przedział ufności zależy również od błędu uczenia \( P_u \). Przy pomijalnej wartości błędu uczenia \( P_u \) wartość \( \varepsilon_1 \) upraszcza się do wyrażenia
| \( \varepsilon_1(p, h, \alpha)=4 \varepsilon_0^2(p, h, \alpha) \) | (3.6) |
w której przedział ufności \( \varepsilon_0 \) określony jest zależnością (3.3) i jest funkcją jedynie parametrów \( p, h, \alpha \). W świetle teorii generalizacji można stwierdzić, że z prawdopodobieństwem \( (1-\alpha) \) przy liczbie danych uczących \( p>h \) (\( h \) – aktualna wartość miary \( VCdim\) ) błąd generalizacji będzie mniejszy niż wartość gwarantowana \( P_g \) określona wzorem
\( P_g=P_u+\varepsilon_1\left(p, h, \alpha, P_u\right) \),
w którym wartość \( \varepsilon_1 \) jest w ogólności zdefiniowana zależnością (3.5), lub przy bardzo małej wartości błędu uczenia \( P_u \) wzorem (3.6).
Na rys. 3.1 przedstawiono typowe zależności błędu uczenia, gwarantowanego ograniczenia górnego błędu generalizacji oraz przedziału ufności w funkcji miary VCdim.
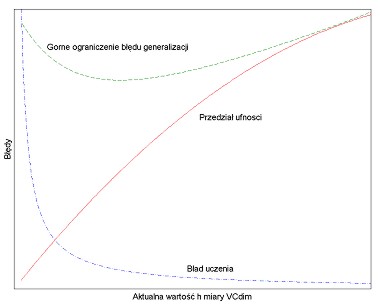
Dla wartości \( h \) mniejszej niż wartość optymalna \( h_{opt} \) pojemność sieci jest zbyt mała dla prawidłowego odwzorowania szczegółów danych uczących i stąd górne ograniczenie błędu generalizacji jest na wysokim poziomie. Dla \( h > h_{opt} \) jest ona z kolei zbyt duża i dlatego błąd generalizacji również rośnie. Osiągnięcie punktu optymalnego (minimum błędu generalizacji) wymaga zwykle trenowania wielu sieci i wybrania tej, która zapewnia otrzymanie minimum gwarantowanego błędu.
Z wartością miary \( VCdim \) oraz zadanym poziomem ufności \( \varepsilon \) odpowiadającym prawdopodobieństwu \( \alpha \) związana jest reguła doboru liczby wzorców uczących wystarczających do uzyskania żądanej dokładności. Zgodnie z pracą [68] liczba próbek uczących powinna spełniać warunek
| \( p \geq \frac{A}{\varepsilon}[h \lg (1 / \varepsilon)+\lg (1 / \alpha)] \) | (3.7) |
gdzie \( A \) jest bliżej nieokreśloną stałą. Z zależności powyższej widać, że liczba próbek uczących powinna być wielokrotnością miary \( VCdim \) (określonej w tym wzorze symbolem \( h \)) i powinna wzrastać wraz ze zmniejszaniem się przedziału ufności. Według opinii Vapnika w klasycznym uczeniu sieci neuronowych dobrą generalizację obserwuje się, jeśli liczba danych uczących jest co najmniej 20 razy większa niż miara \( \mathbf{VCdim} \). Z drugiej strony należy zaznaczyć, że w wielu przypadkach można uzyskać dobre zdolności generalizacyjne sieci MLP przy dalece niewystarczającej liczbie danych uczących [68]. Świadczy to o skomplikowanym mechanizmie generalizacji i naszej niewystarczającej wiedzy teoretycznej w tym zakresie. Stąd wyprowadzone wcześniej oszacowania należy traktować jako ogólną wskazówkę postępowania przy budowie struktury sieci, zmuszającą do maksymalnej redukcji jej stopnia złożoności, przy zapewnieniu akceptowalnego poziomu błędu uczenia.
3.3. Przegląd metod zwiększania zdolności generalizacyjnych sieci
Rozważania teoretyczne przedstawione w poprzednim punkcie pokazały ścisły związek zdolności generalizacyjnych sieci MLP z liczbą wag wyrażoną poprzez miarę \( VCdim \). Dla uzyskania dobrej generalizacji sieci należy minimalizować liczbę wag do pewnej granicy określonej wymaganiami dotyczącymi błędu uczenia.
W praktyce minimalizację struktury sieci przeprowadza się w pierwszym etapie projektowania przez wielokrotne powtarzanie procesu uczenia na różnych strukturach i wybranie tej, która przy zadowalającym poziomie błędu uczenia pozwala uzyskać najmniejszy błąd odtwarzania danych nie uczestniczących w uczeniu. W następnych etapach projektowania sieci optymalnej poprawę generalizacji można uzyskać przez obcinanie wag najmniej znaczących, czyli wag o najmniejszej wartości bezwzględnej bądź wag o najmniejszym wpływie na wartość funkcji błędu, (niekoniecznie najmniejszych).
Redukcję wag i neuronów osiągnąć można różnymi metodami, z których najbardziej skuteczne opierają się na wykorzystaniu metod wrażliwościowych pierwszego lub drugiego rzędu (np. OBD, OBS) bądź też zastosowaniu w uczeniu metod funkcji kary, karzących za nadmierną liczbę połączeń wagowych. Ten kierunek działania polega na dodaniu do konwencjonalnej definicji funkcji celu składników proporcjonalnych do liczby i wartości wag sieci. W procesie optymalizacji funkcji celu minimalizacji podlegają wówczas również wartości wag sieci. Po zakończeniu procesu uczenia wagi najmniejsze są obcinane i w ten sposób złożoność sieci również ulega redukcji.
Techniką która umożliwia polepszenie zdolności generalizacyjnych sieci jest również wtrącanie szumu do próbek uczących, upodobniające warunki uczenia do warunków przyszłego użytkowania. Istotą tego podejścia jest założenie, że podobne sygnały wejściowe powinny generować podobne odpowiedzi (zasada ciągłości), nawet wtedy, gdy nie wchodziły w skład wektorów uczących. Zbiór uczący wzbogaca się o dane, będące "zaszumioną" wersją sygnałów oryginalnych (przy tych samych wartościach zadanych) i trenuje sieć na rozszerzonym zbiorze danych. Zostało udowodnione, że taki sposób uczenia odpowiada w efekcie minimalizacji funkcji celu zmodyfikowanej o czynnik modelujący wrażliwość względną sieci, odpowiadającą zmianom wartości odpowiedzi neuronów wyjściowych spowodowanych zmianami wartości zmiennych wejściowych (zmiana upodobniająca warunki uczenia do warunków testowania na danych nie biorących udziału w uczeniu sieci).
Zwiększenie efektywności działania sieci uzyskać można poprzez stosowanie wielu sieci neuronowych na raz, tzw. zespół sieci. Technika ta może być zastosowana w każdym trybie działania sieci, w tym w trybie aproksymacji (regresji) jak i w trybie klasyfikacyjnym. Istotą metody jest zastosowanie wielu sieci rozwiązujących na raz ten sam problem. Końcowy wynik może być ustalony na wiele sposobów: głosowanie w przypadku klasyfikacji bądź różnego rodzaju uśrednianie w przypadku aproksymacji. Warunkiem poprawnego działania zespołu jest zastosowanie jednostek o niezależnym działaniu. Można to osiągnąć stosując między innymi różne rozwiązania klasyfikatorów, zróżnicowane zbiory uczące bądź zastosowanie różnych metod przekształcenia danych pomiarowych na cechy diagnostyczne procesu.
Innym problemem jest wpływ sposobu i czasu uczenia na zdolności generalizacyjne sieci. Jak zostało zaobserwowane na przykładzie wielu eksperymentów numerycznych wraz z upływem czasu błąd uczenia maleje i błąd testowania również (przy ustalonej liczbie próbek uczących p oraz wartości miary VCdim). Taka sytuacja trwa zwykle do pewnego momentu uczenia, poczynając od którego błąd testowania pozostaje stały bądź zaczyna rosnąć, pomimo, że błąd uczenia nadal nieznacznie maleje [68].
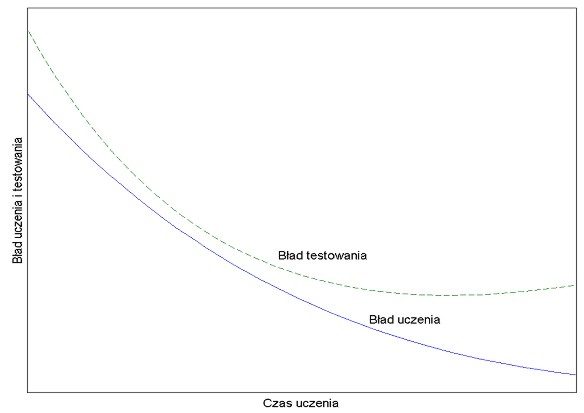
Typowy przebieg obu błędów przedstawiono na rys. 3.2, na którym błąd uczenia zaznaczony jest linią ciągłą, a błąd generalizacji (testowania) linią przerywaną. Z wykresu na rysunku wynika jednoznacznie, że zbyt długie uczenie może doprowadzić do tak zwanego ,,przeuczenia" sieci, a więc do zbyt drobiazgowego dopasowania wag do nieistotnych szczegółów danych uczących. Taka sytuacja ma miejsce w przypadku sieci o nadmiarowej w stosunku do potrzeb liczbie wag i jest tym bardziej widoczna, im większa nadmiarowość wag występuje w sieci. Wagi ,,niepotrzebne" dopasowują się do wszelkich nieregularności danych uczących, traktując je jako cechę główną. W procesie testowania sieci na danych testujących, w którym brakuje tych nieregularności, powstają w efekcie dodatkowe błędy odtwarzania. W celu uniknięcia przeuczenia wydziela się ze zbioru uczącego część danych weryfikujących (zbiór V na rys. 3.3), które służą w procesie uczenia okresowemu sprawdzaniu aktualnie nabytych zdolności generalizacyjnych. Uczenie przerywa się, gdy błąd generalizacji na tym zbiorze osiągnie wartość minimalną (zaczyna wzrastać). Zalecane proporcje danych uczących do weryfikujących to 4:1.
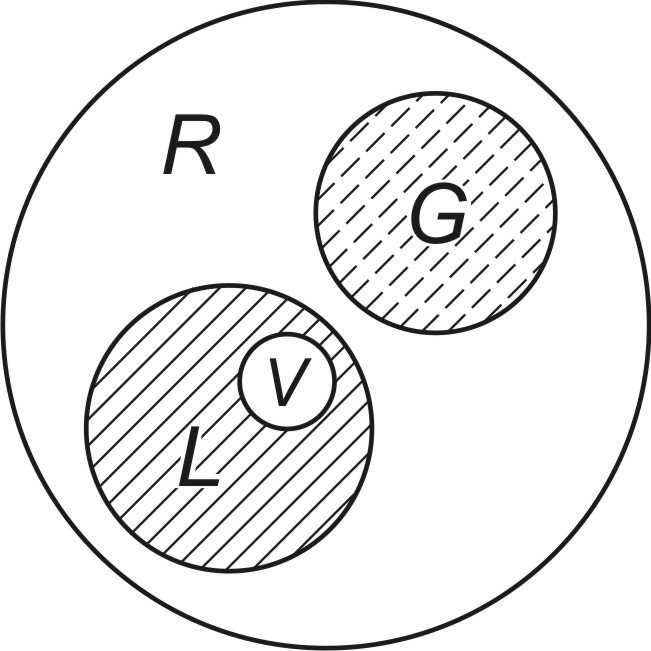
Z uwagi na błąd generalizacji ważny jest stosunek liczby próbek uczących do liczby wag sieci. Mała liczba próbek uczących przy ustalonej liczbie wag oznacza dobre dopasowanie sieci do próbek uczących, ale złą generalizację, gdyż w procesie uczenia nastąpił nadmiar parametrów dobieranych (wag) względem dopasowywanych do siebie wartości zadanych i aktualnych sygnałów wyjściowych sieci. Parametry te zostały zbyt precyzyjnie, a przy tym wobec nadmiarowości wag w sposób niekontrolowany poza punktami dopasowania, dobrane do konkretnych danych, a nie do zadania, które miało być reprezentowane przez te dane uczące. Zadanie aproksymacji zostało niejako sprowadzone do zadania bliższego interpolacji. W efekcie, wszelkiego rodzaju nieregularności danych uczących spowodowane przez przypadkowe zmiany i szumy pomiarowe mogą być odtworzone jako cecha podstawowa procesu. Funkcja, odwzorowana w zadanych punktach uczących jest dobrze odtwarzana tylko dla nich. Minimalne nawet odejście od tych punktów powoduje znaczny wzrost błędu, co przejawia się jako błąd generalizacji.
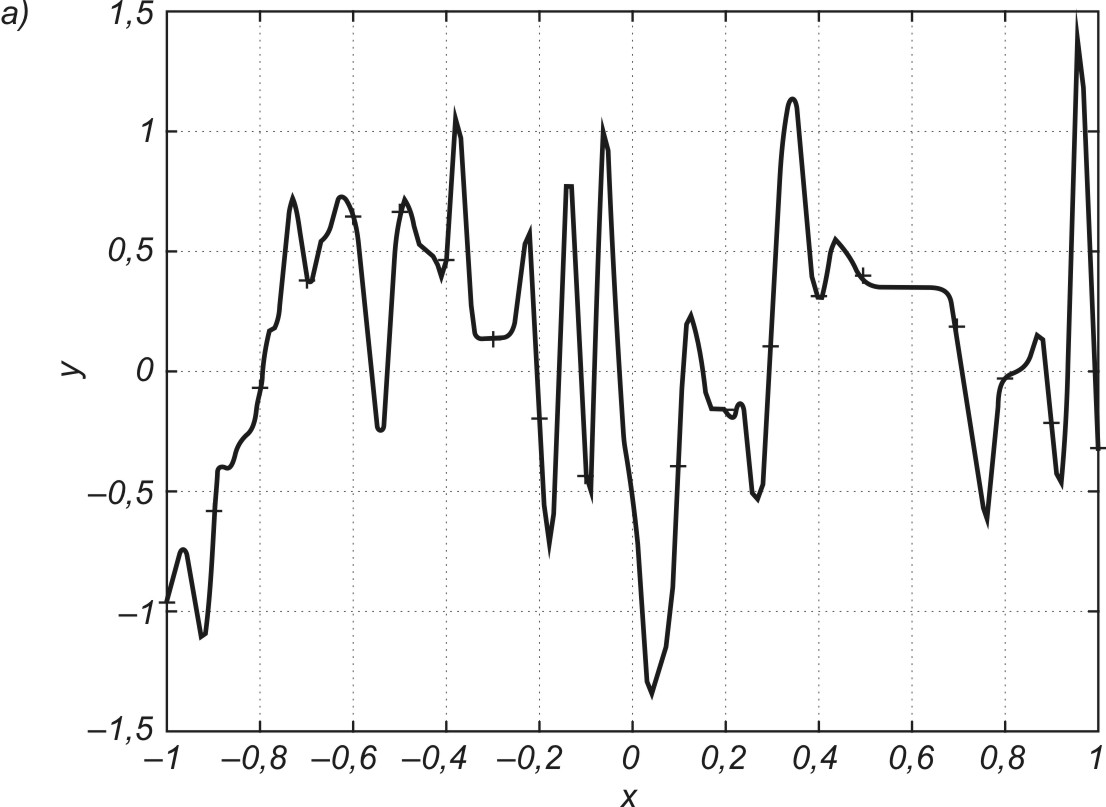
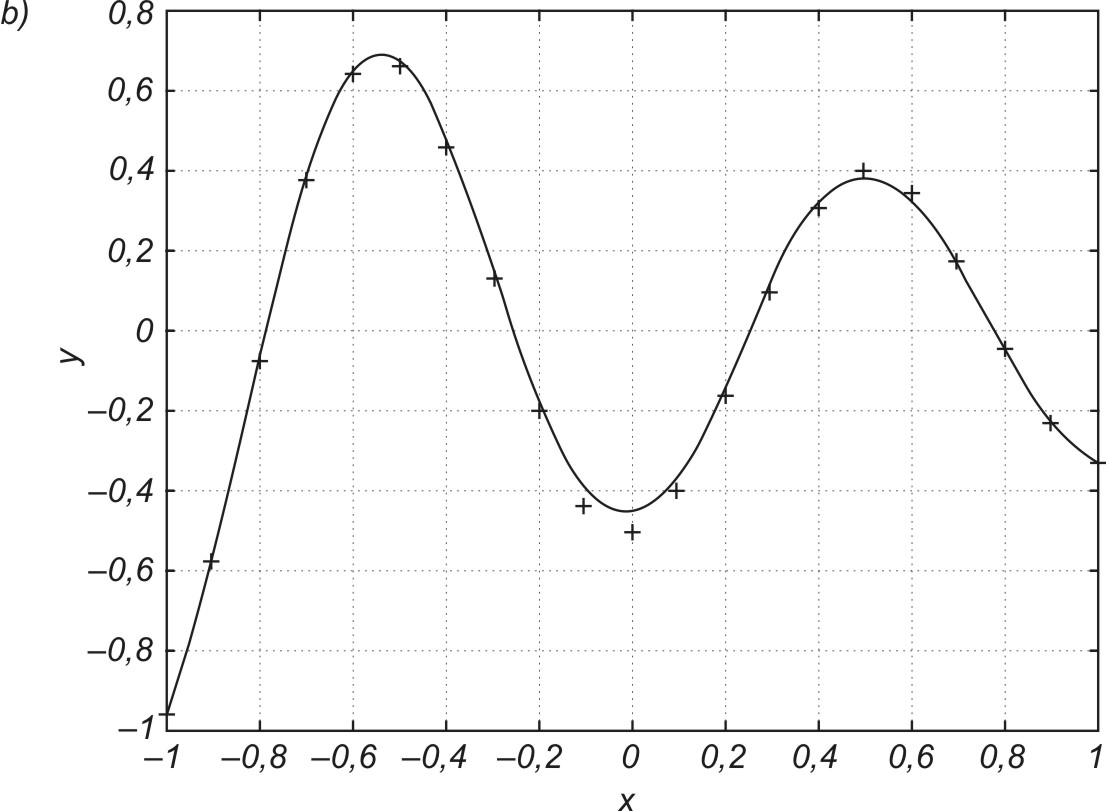
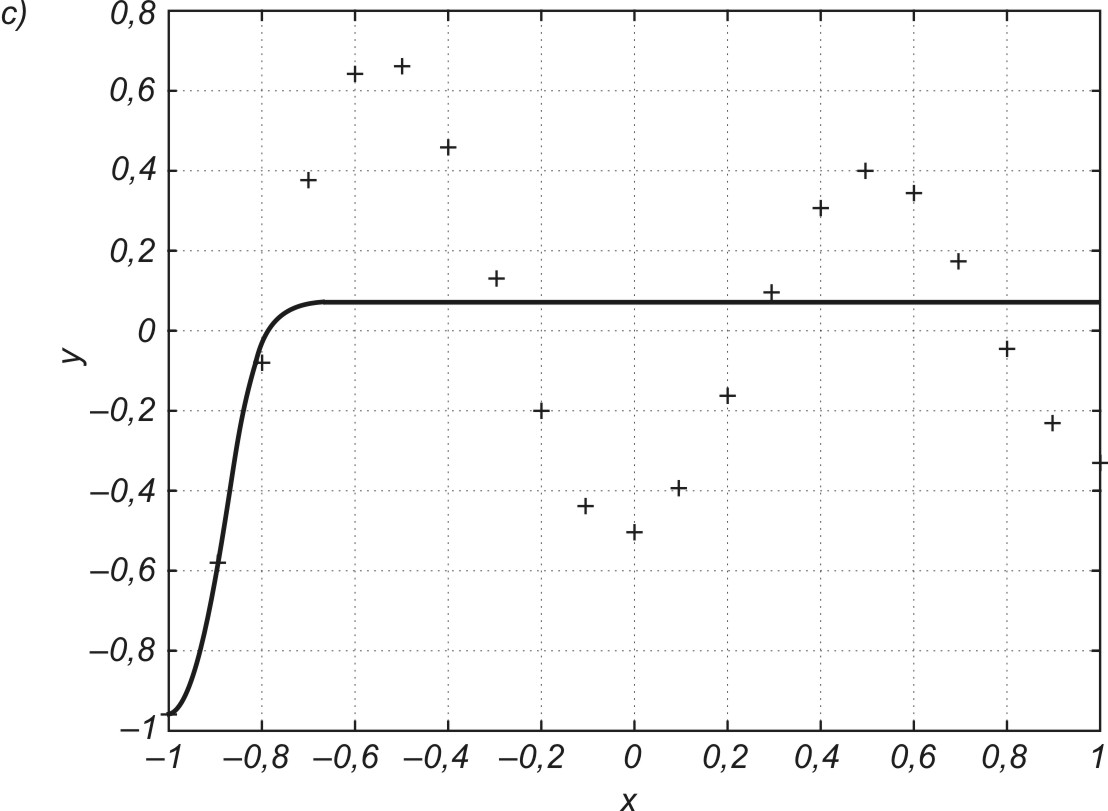
Na rys. 3.4a przedstawiono graficzną ilustrację efektu przewymiarowania sieci, często kojarzone z tak zwanym przeuczeniem sieci występującym przy zbyt dużej liczbie neuronów i połączeń wagowych. Sieć aproksymująca zawierająca 80 neuronów w warstwie ukrytej (241 wag) dopasowała swoje odpowiedzi do 21 zadanych punktów sinusoidy poddanej aproksymacji, na zasadzie interpolacji, dając zerowy błąd uczenia. Minimalizacja błędu uczenia na zbyt małej (w stosunku do liczby wag) liczbie danych uczących spowodowała dowolność wartości wielu połączeń wagowych, która przy zmianie punktów testujących względem uczących jest przyczyną znacznego odchylenia aktualnej wartości y od spodziewanej wartości d. Zmniejszenie liczby neuronów ukrytych do 5 (odpowiada temu 16 wag sieci), przy nie zmienionej liczbie próbek uczących, pozwoliło uzyskać zarówno mały błąd uczenia, jak i dobrą zdolność generalizacji (rys. 3.4b). Dalsze zmniejszanie liczby neuronów ukrytych może spowodować niezdolność sieci do akceptowalnej dokładności odwzorowania danych uczących (zbyt duży błąd uczenia). Przypadek taki zilustrowano na rys. 3.4c, gdzie użyto tylko jednego neuronu ukrytego (liczba połączeń wagowych równa 4). Sieć nie była zdolna dokonać poprawnego odwzorowania danych uczących, gdyż liczba stopni swobody (4 wagi) takiej sieci jest za mała w stosunku do wymagań odwzorowania 21 punktów zadanych. W takim przypadku nie można oczywiście uzyskać dobrych zdolności generalizacyjnych, gdyż zależą one w sposób oczywisty od poziomu błędu uczenia.
Istotnym problemem jest obiektywna ocena rozwiązania. Powszechnie stosowana metoda jest walidacja krzyżowa (ang. cross validation) służącej do oceny jakości działania sieci neuronowej. Technika ta polega na podziale dostępnego zbioru danych na M podzbiorów, z których (M-1) jest używanych do uczenia a pozostały podzbiór do testowania. Uczenie sieci przeprowadza się wielokrotnie stosując wszystkie możliwe kombinacje podzbiorów do tworzenia zbioru uczącego i pozostawiając zawsze jeden podzbiór do testowania. W ten sposób wszystkie dostępne dane uczestniczą w procesie walidacji (testowania na danych nie uczestniczących w uczeniu). Ocena jakości działania sieci wynika z uśrednionych (po wszystkich próbach) wyników testowania.
Szczególną postacią tej formy jest technika ,,leave one out" w której każdy podzbiór jest jednoelementowy. Przy p parach danych oznacza to uczenie sieci na (p-1) wzorcach i testowanie ograniczone do jednego wzorca. Uczenie przeprowadza się p razy zamieniając za każdym razem jedną próbkę testującą. Jakość rozwiązania ocenia się na podstawie uśrednionych wyników wszystkich prób. Jest to technika polecana w przypadku małej liczby dostępnych danych.
Powszechnie stosowaną metodą jest również wielokrotne powtórzenie uczenia/testowania na losowo dobranych zbiorach uczącym i testującym (typowy podział to 0.7 danych do uczenia i 0.3 danych do testowania. W każdej powtórce procesu inny jest zestaw testujący. Przy wielokrotnym powtórzeniu procesu (np. 100 razy) uzyskuje się wartość średnią odwzorowującą obiektywną informację o jakości działania sieci.
3.4. Wstępny dobór architektury sieci
Przy rozwiązywaniu jakiegokolwiek zadania z wykorzystaniem sieci neuronowej należy przede wszystkim zaprojektować wstępną strukturę sieci, dopasowaną do danego zadania. Oznacza to wybór liczby warstw sieci i neuronów w każdej warstwie oraz powiązań między warstwami. Dobór liczby wejść sieci jest uwarunkowany wymiarem wektora wejściowego \( \mathbf{x} \). Podobnie jest w warstwie wyjściowej, w której liczba neuronów równa się wymiarowi wektora zadanego \( \mathbf{d} \). Istotnym problemem pozostaje jedynie dobór warstw ukrytych i liczby neuronów w każdej warstwie, który pozwoli na dopasowanie odpowiedzi sieci do wartości zadanych na etapie uczenia oraz zapewni dobre zdolności generalizacyjne sieci.
Wskazówki teoretyczne rozwiązania problemu dopasowania do danych uczących (w sensie warunku wystarczającego) zostały podane przez matematyków zajmujących się aproksymacją funkcji wielu zmiennych. Warto tu zauważyć, że sieć neuronowa pełni rolę uniwersalnego aproksymatora danych uczących [24]. W trakcie uczenia dobierane są współczynniki tej funkcji (wartości wag poszczególnych neuronów). Na etapie odtwarzania, przy ustalonych wartościach wag, następuje zwykłe obliczenie wartości funkcji aproksymującej przy danym wektorze wejściowym \( \mathbf{x} \).
Określenie minimalnej liczby warstw ukrytych sieci opiera się na własnościach funkcji aproksymujących. Kołmogorow udowodnił, że dla funkcji ciągłej transformującej \( N \)-wymiarowy zbiór danych wejściowych \( \mathbf{x} \) w \( M \)-wymiarowy wektor wielkości zadanych \( \mathbf{d} \) na wyjściu wystarczy zwykle użycie sieci o jednej warstwie ukrytej. Przy \( N \) neuronach wejściowych warstwa ukryta powinna wówczas zawierać \( 2N+1 \) neuronów sigmoidalnych [24]. Brakuje procedury pozwalającej efektywnie zaimplementować taką sieć do aktualnego zadania.
W przypadku ogólnym funkcji odwzorowania jedna warstwa ukryta może nie wystarczać i wtedy konieczne jest użycie drugiej warstwy neuronów sigmoidalnych. Oznacza to, że niezależnie od rodzaju aproksymowanej funkcji wielowejściowej maksymalna liczba warstw ukrytych wystarczających do aproksymacji zadanego odwzorowania nie przekracza dwu. Wynik uzyskany dzięki zastosowaniu teorii Kołmogorowa jest rezultatem czysto teoretycznym, określającym maksymalną liczbę warstw i neuronów w warstwach, wystarczających do aproksymacji zadanego odwzorowania. Twierdzenie nie precyzuje ani rodzaju funkcji nieliniowych, ani sposobu i metody uczenia sieci w celu zrealizowania takiego odwzorowania. Stanowi jednak ważny element w dochodzeniu do optymalnej architektury sieci neuronowej.
W praktycznych rozwiązaniach sieci MLP zarówno liczba warstw, jak i neuronów w warstwie ukrytej może być różna od zaproponowanej w teorii Kołmogorowa i zależeć zarówno od liczby wejść jak i wyjść sieci. W przypadku sieci o jednej warstwie dobrą praktyką jest przyjęcie wstępnej liczby neuronów ukrytych proporcjonalnej do średniej geometrycznej liczby wejść i wyjść sieci, to znaczy \( n_h \approx \sqrt{N M} \). Liczba ta może podlegać odpowiednim zmianom w procesie kształtowania optymalnej struktury sieci.
3.5. Poprawa zdolności generalizacyjnych poprzez regularyzację
Decyzja co do wyboru ostatecznej postaci sieci może być podjęta dopiero po pełnym nauczeniu wielu struktur (redukcja błędu do poziomu uznanego za satysfakcjonujący) i wybraniu tej, która gwarantuje najlepsze działanie na danych testujących nie biorących udziału w uczeniu. Dodatkowym krokiem prowadzącym do poprawy zdolności generalizacyjnych może być regularyzacja sieci polegająca na obcinaniu wag lub redukcji liczby neuronów ukrytych. Zwykłe, bezpośrednie metody obcięcia wagi w trakcie uczenia, polegające na okresowym przypisaniu jej wartości zerowej i podjęciu decyzji o jej ponownym włączeniu w proces uczenia na podstawie obserwowanych zmian wartości funkcji celu (jeśli przyrost wartości funkcji celu po obcięciu wagi jest zbyt duży - należy włączyć wagę ponownie) są nie do przyjęcia w praktyce, ze względu na dużą złożoność obliczeniową takiego procesu.
Większość stosowanych obecnie algorytmów redukcji sieci dokonuje obcięcia wag po zakończeniu podstawowego etapu uczenia. Obcinanie wag w trakcie uczenia jest niewskazane, gdyż mała wrażliwość sieci na daną wagę może wynikać z chwilowej wartości tej wagi lub być spowodowana złym punktem startowym (np. utknięcie neuronu w głębokim nasyceniu).
3.5.1 Metody funkcji kary
Podstawowa technika redukcji sieci to obcięcie wag o najmniejszej wartości absolutnej. Mała wartość wagi oznacza słaby wpływ danego połączenia synaptycznego na wartość sygnałów wyjściowych sieci. Dla uzyskania efektywności redukcji wag należy tak zorganizować proces uczenia, aby wymusić samoczynne zmniejszanie się wartości wag prowadzące do ich obcięcia po zakończeniu procesu uczenia, gdy ich wartość spadnie poniżej pewnego progu. W metodach tych modyfikuje się zwykle definicję funkcji celu wprowadzając dodatkowy czynnik związany z wartościami wag. Najprostszą modyfikacją tej funkcji jest dodanie do niej składnika kary za duże wartości wag
| \( E=E_0+\gamma \sum_{i, j} w_{i j}^2 \) | (3.8) |
We wzorze tym \( E_0 \) oznacza standardową definicję funkcji celu przyjętą na przykład w postaci normy euklidesowej wektora błędu, a \( \gamma \) jest współczynnikiem kary za osiągnięcie dużych wartości wag. Proces uczenia można wówczas rozdzielić w każdym cyklu na 2 etapy: minimalizacja wartości funkcji E0 standardową metodą optymalizacji i następnie korekcji wartości wag, wynikającej z czynnika modyfikującego. Jeśli przez \( w_{i j}^0 \) oznaczy się wartość wagi \( w_{i j} \) po etapie pierwszym, to na etapie korekcji w danej iteracji waga ta zostanie zmodyfikowana według metody gradientowej największego spadku, zgodnie ze wzorem
| \( w_{i j}=w_{i j}^0(1-\eta \gamma) \) | (3.9) |
gdzie \( \eta \) oznacza stałą uczenia. Tak zdefiniowana funkcja kary wymusza zmniejszenie wszystkich wartości wag, nawet wtedy, gdy ze względu na specyfikę problemu pewne wagi powinny przyjmować duże wartości. Poziom wartości, przy którym eliminuje się daną wagę, musi być tu starannie dobrany na podstawie wielu eksperymentów, wskazujących, przy jakim progu obcięcia proces uczenia sieci jest najmniej zakłócony.
Lepsze efekty, niepowodujące obniżenia poziomu wartości wszystkich wag, uzyskać można modyfikując definicję funkcji celu do postaci
| \( E=E_0+\frac{1}{2} \gamma \sum_{i, j} \frac{w_{i j}^2}{1+\sum_k w_{i k}^2} \) | (3.10) |
Minimalizacja tej funkcji powoduje nie tylko redukcję powiązań międzyneuronowych, ale może prowadzić również do eliminacji tych neuronów, dla których \( \sum_{k} w_{i k}^2 \) jest bliska zeru. Przy małych wartościach wag \( w_{i k} \) prowadzących do \( i \)-tego neuronu w kolejnych iteracjach następuje dalsze zmniejszenie ich wartości, co prowadzi do redukcji sygnału wyjściowego tego neuronu i w efekcie (przy wartości bliskiej zeru) eliminację danego neuronu z sieci. Przy dużych wartościach wag prowadzących do i-tego neuronu, część korekcyjna ma wartość pomijalnie małą i w bardzo niewielkim stopniu wpływa na redukcję wag. W wyniku usunięcia wielu połączeń wagowych neuronu może zdarzyć się całkowita jego eliminacja .
3.5.2 Metody wrażliwościowe redukcji
Najbardziej efektywna metoda redukcji polega na badaniu wrażliwości funkcji celu na usunięcie wagi lub neuronu dla wytrenowanej sieci. Wagi o najmniejszej wrażliwości, mające najmniej widoczny wpływ na wartość funkcji celu, są usuwane, a proces uczenia kontynuowany na tak zredukowanej sieci. Takie podejście pozwala usunąć nawet wagi o większych wartościach, mających mały wpływ na zmianę funkcji celu.
Podejście to jest uzasadnione rozwinięciem Taylora funkcji celu. Zgodnie z tym rozwinięciem, zmianę wartości funkcji celu spowodowaną perturbacją wag można wyrazić wzorem
| \( \Delta E=\sum_{i=1}^n g_i \Delta w_i+\frac{1}{2} \sum_{i=1}^n h_{i i}\left[\Delta w_{i i}\right]^2+\frac{1}{2} \sum_{i \neq j}^n h_{i j}\left[\Delta w_i \Delta w_j\right]+\ldots \) | (3.11) |
w którym \( \Delta w_i \) oznacza perturbację wagi \(i\)-tej, \( g_i\) jest \(i\)-tym składnikiem wektora gradientu względem tej wagi, a \( h_{ij}\) - elementem hesjanu \( h_{i j}=\frac{\partial^2 E}{\partial w_i \partial w_j} \). Obcięcie wag (regularyzacja sieci) następuje dopiero po zakończeniu procesu uczenia, gdy wszystkie neurony osiągną swoje wartości ustalone. To wyklucza zastosowanie gradientu jako wskaźnika wrażliwości, gdyż minimum funkcji celu charakteryzuje się gradientem równym zero. Pozostaje zatem wybór drugich pochodnych funkcji celu (elementów hesjanu) jako wskaźnika ważności danej wagi.
Jednym z rozwiązań jest metoda OBD (ang. Optimal Brain Damage) zaproponowana przez LeCunna. Wobec dodatniej określoności hesjanu, macierz \( \mathbf{H} \) jest diagonalnie dominująca. W metodzie OBD uwzględniane są jedynie składniki diagonalne \( h_{ij}\) z pominięciem wszystkich pozostałych. Miarą ważności \(i\)-tej wagi w OBD jest współczynnik \(S_i\) zdefiniowany w postaci
| \( S_i=\frac{1}{2} h_{i i} w_i^2 \) | (3.12) |
Wagi o najmniejszej wartości współczynnika \(S_i\) mogą ulec obcięciu bez istotnego zaburzenia działania sieci. Procedurę OBD redukcji sieci można przedstawić w następującej postaci:
-
Pełne wytrenowanie wstępnie wyselekcjonowanej struktury sieci przy użyciu dowolnej metody uczenia.
-
Określenie elementów diagonalnych hesjanu \( h_{ii}\) odpowiadających każdej wadze i obliczenie wartości odpowiedniego współczynnika asymetrii \(S_i \) określającego znaczenie danego połączenia synaptycznego dla działania sieci.
-
Posortowanie wag według przypisanych im wartości współczynników \(S_i \) i obcięcie tych, których wartości są najmniejsze.
-
Powtórne douczenie zredukowanej sieci i powrót do punktu pierwszego aż do pozbycia się wszystkich wag o znacząco małym wpływie na wartość funkcji celu.
Metoda OBD jest uważana za jedną z najlepszych metod redukcji sieci spośród metod wrażliwościowych. Przy jej zastosowaniu uzyskuje się dobre własności generalizacji sieci.
Rozwinięciem procedury OBD jest tak zwana metoda OBS (ang. Optimal Brain Surgeon). Punktem wyjścia w tej metodzie, podobnie jak w OBD, jest rozwinięcie (3.11) funkcji celu w szereg Taylora i pominięcie składowych pierwszego rzędu. W metodzie tej (w odróżnieniu od OBD) uwzględnia się wszystkie składowe hesjanu, a współczynnik ważności wagi definiuje się w postaci
| \( S_i=\frac{1}{2} \frac{w_i^2}{\left[\mathbf{H}^{-1}\right]_{i i}} \) | (3.13) |
w której \( \left[\mathbf{H}^{-1}\right]_{i i} \) oznacza \( i\)-ty diagonalny element macierzy odwrotnej hesjanu. Obcięciu ulega waga o najmniejszej wartości \(S_i \). Dodatkowym rezultatem tego podejścia jest prosty wzór korekcyjny wszystkich pozostałych wag, sprowadzający z powrotem stan sieci do minimum funkcji celu mimo obcięcia wagi (be potrzeby powtórnego douczania zredukowanej sieci). Korekta pozostałych (nie obciętych) wag tworzących wektor \( \mathbf{w} \) zachodzi według wzoru
| \( \Delta \mathbf{w}=\frac{w_i}{\left[\mathbf{H}^{-1}\right]_{i i}} \mathbf{H}^{-1} \mathbf{e}_i \) | (3.14) |
w którym \(\mathbf{e}_i \) oznacza wektor jednostkowy z jedynką na \( i\)-tej pozycji i zerami na pozostałych. Korekta wag jest przeprowadzana po każdorazowym obcięciu wagi i zastępuje powtórne douczenie sieci, które jest wymagane w metodzie OBD. Należy podkreślić, że jakkolwiek w metodzie OBS nie wymaga się powtórnego douczania zredukowanej sieci to jej złożoność obliczeniowa jest znacznie większa niż w metodzie OBD ze względu na konieczność określania wszystkich elementów hesjanu i obliczania macierzy odwrotnej \( \mathbf{H}^{-1} \) .
3.6. Selekcja cech diagnostycznych
Ważnym elementem poprawy generalizacji sieci jest minimalizacja liczby parametrów (wag) podlegających adaptacji, Jak zostało pokazane w punkcie poprzednim realizuje się to poprzez obcinanie wag połączeń między-neuronowych. Podobny efekt można osiągnąć poprzez zastosowanie na wejściu sieci ograniczonej liczby sygnałów (cech diagnostycznych) generowanych ze zbioru sygnałów pomiarowych. Zwykle przetwarzanie sygnałów pomiarowych w deskryptory numeryczne procesu odbywa się w sposób automatyczny na podstawie algorytmów opracowanych przez użytkownika. W wyniku takiej procedury liczba deskryptorów jest nadmiarowa i powinna podlegać redukcji poprzez właściwą selekcję, zmniejszając w ten sposób wymiar wektora wejściowego dla sieci i redukując liczbę połączeń neuronowych. Selekcja deskryptorów powinna wytworzyć zbiór cech diagnostycznych podawanych na wejście sieci dobrze charakteryzujących modelowany proces i reprezentować tylko te deskryptory które są najlepiej skorelowane z decyzją ostateczną podejmowaną przez model sieci. Dozwolone jest stosowanie różnych metod przetwarzania, które pozwolą reprezentować modelowany proces w sposób umożliwiający podjęcie jednoznacznej decyzji.
W praktyce stosowane są różne metody selekcji, prowadzące, w zależności od rodzaju procesu, do lepszych lub gorszych wyników działania sieci neuronowej [49]. W ogólności wyróżnić można metody dostosowane do oceny pojedynczej cechy odseparowanej od zbioru pozostałych, bądź ocena jakości danej cechy działającej w otoczeniu innych. Stosowane są różnorodne podejścia do selekcji, między innymi [49]: metoda dyskryminacyjna Fishera, metoda korelacji cechy z klasą, zastosowanie liniowej sieci SVM do walidacji cech, liniowa regresja krokowa, zastosowanie algorytmu genetycznego, zastosowanie lasu drzew decyzyjnych, testy statystyczne chi2, Kołmogorowa-Smirnowa czy Wilcoxona-Manna-Whitneya, algorytm Relieff, analiza najbliższych sąsiadów (NCA) czy metoda maksymalnego znaczenia i jednocześnie minimalnej redundancji (MRMR). W wyniku zastosowania takich metod ze zbioru deskryptorów wyłaniany jest ich ograniczony zbiór (cechy diagnostyczne są utożsamiane z wyselekcjonowanymi deskryptorami).
Innym podejściem do redukcji wymiaru wektora wejściowego jest zastosowanie transformacji liniowej przetwarzającej oryginalny zbiór deskryptorów w wektor o ograniczonym wymiarze, będący sumą wagową deskryptorów oryginalnych. Taka technika jest stosowana między innymi w transformacji według składników głównych (PCA) lub dyskryminacyjnej analizie Fishera (LDA).
Niezależnie od zastosowanego podejścia do selekcji cech w wyniku ich zastosowania wyłaniany jest zredukowany zbiór tworzący cechy diagnostyczne procesu. W ten sposób zmniejszany jest wymiar wektora wejściowego sieci \( (N) \) pociągający za sobą zmniejszoną liczbę połączeń wagowych sieci (efekt regularyzacji sieci).
3.7. Zwiększanie zdolności generalizacyjnych poprzez użycie zespołu wielu sieci
W wielu zastosowaniach możliwe jest zwiększenie zdolności generalizacyjnych systemu poprzez równoległe zastosowanie wielu sieci na raz [49]. Jest to tak zwany zespół sieci neuronowych. Istnieje wiele metod rozwiązania zarówno uczenia poszczególnych sieci wchodzących w skład zespołu jak i integracji ich wyników działania. Przy ograniczonej liczbie danych istotne staje się przygotowanie danych uczących dla każdej sieci, prowadzących do możliwie niezależnych wyników dla każdej z nich.
Jednym z podejść jest zastosowanie tak zwanej techniki bagging (skrót od angielskojęzycznej nazwy Bootstrap AGGregatING). Przy zastosowaniu wielu sieci neuronowych dane uczące dla każdej z nich tworzy podzbiór \( p \) próbek wybieranych losowo z pełnego dostępnego zbioru danych. W ten sposób każda sieć jest trenowana na znacznie zróżnicowanym zbiorze danych, prowadząc w efekcie do różnych wyników testowania przy prezentacji na wejściu określonego wektora \( \mathbf{x} \).
Ostateczny wynik działania w trybie aproksymacji jest zwykle ustalany jako średnia lub średnia ważona z sygnałów wyjściowych poszczególnych sieci. Stosowane są również bardziej rozbudowane formy ustalania odpowiedzi bazujące na technice PCA lub ślepej separacji sygnałów [8]. W przypadku zadania klasyfikacyjnego stosuje się głosowanie klasyfikatorów, przy czym może być to zwykłe głosowanie większościowe (ang. majority voting) lub głosowanie większościowe ważone (ang. weighted majority voting) [65].
W przypadku głosowania większościowego ważonego wskazanie każdego klasyfikatora brane jest z odpowiednią wagą. Wagi te mogą być dobierane na wiele różnych sposobów [49]. Jednym z nich jest uwzględnienie dokładności lub precyzji poszczególnych klasyfikatorów na dostępnych danych uczących. Sprawniejszemu klasyfikatorowi przypisuje się większą wagę i w ten sposób wpływa on bardziej na wynik ostateczny klasyfikacji.
3.8. Przykład metody zwiększania zdolności generalizacyjnych sieci
Jako przykład możliwości zwiększenia zdolności generalizacyjnych sieci rozważymy problem rozpoznania zmian czerniakowych skóry od innych zmian skórnych. Przykłady obrazów ilustrujących oba rodzaje zmian przedstawiono na rys. 3.5 [35].
|
Zmiany inne (nie czerniakowe) |
Czerniak |
|
|
|
|
|
|
Obrazy podlegające rozpoznaniu tworzą 2 klasy: czerniak i nie czerniak). Zostały one poddane różnego rodzaju opisom tworzącym zbiór deskryptorów numerycznych obrazu (deskryptory statystyczne bazujące na teorii Kołmogorowa-Smirnowa, deskryptory perkolacyjne, teksturalne, fraktalne itp.). W sumie wygenerowano zbiór 81 deskryptorów. Jako klasyfikator zastosowano sieć SVM. Przy podaniu pełnego zbioru deskryptorów na sieć uzyskano dokładność rozpoznania obu klas równą 85.47%. Redukcja liczby deskryptorów poprzez zastosowanie selekcji cech pozwoliła zdecydowanie zwiększyć tę dokładność, przy czym różne metody selekcji prowadziły do różniących się wyników. Najlepszą okazała się metoda dyskryminacyjna Fishera, zgodnie z która każdej cesze przy rozpoznaniu 2 klas (A i B) przypisuje się wagę \( S_{AB}(f) \) określoną wzorem
| \( S_{A B}(f)=\frac{\left|c_A(f)-c_B(f)\right|}{\sigma_A(f)+\sigma_B(f)} \) | (3.15) |
Parametry \( c_A \) i \( c_B \) są wartościami średnimi cechy \( f \) dla klasy \( A \) i \( B \), natomiast \( \sigma_A \) i \( \sigma_B \) reprezentują odchylenia standardowe cechy w obu klasach. Im większa wartość wagi \( S_{AB}(f) \) tym ważniejsza jest dana cecha w rozpoznaniu obu klas. W przypadku rozpoznania czerniaka uzyskano wykres zmian wartości tej wagi dla poszczególnych deskryptorów jak na rys. 3.6.
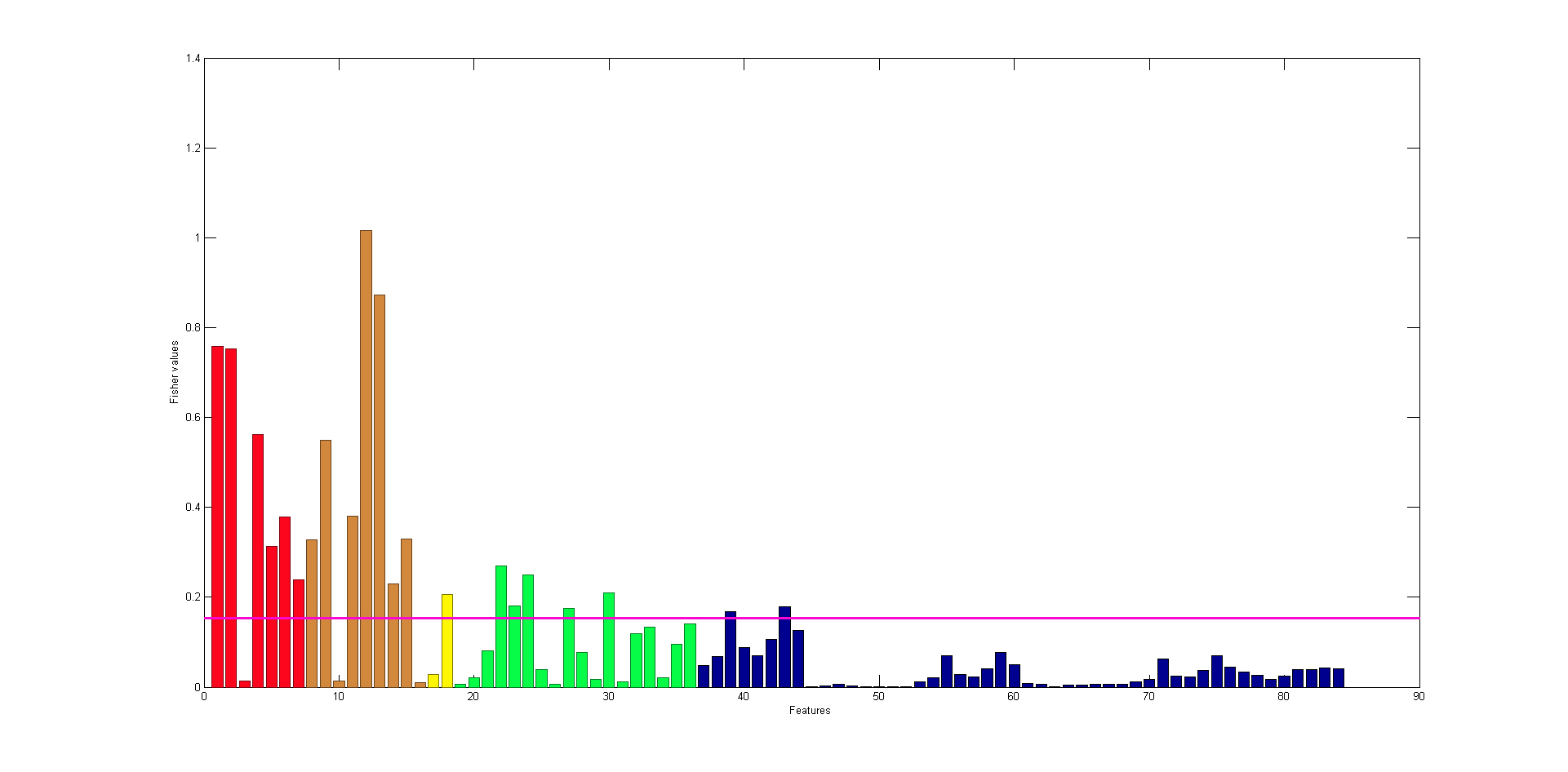
Ustanawiając próg ważności (pozioma linia różowa) można łatwo wyselekcjonować te cechy, które są powyżej tej linii jako cechy diagnostyczne procesu. W tym przypadku z 81 deskryptorów selekcjonuje się tylko zbiór 21 deskryptorów traktowanych jako cechy diagnostyczne (atrybuty wejściowe dla klasyfikatora). Przy zastosowaniu tego zbioru uzyskano podwyższoną dokładność rozpoznania obu klas równą 93.76% (wzrost dokładności o 8.27 punktów procentowych).
3.9. Zadania i problemy
1. Zaprojektować sieć MLP modelującą krzywą magnesowania pierwotnego żelaza.
2. Zespół trzech klasyfikatorów został wytrenowany na tych samych danych uczących do rozpoznania 2 klas danych. W wyniku testowania zespołu na pięciu wektorach \( \mathbf{x} \) uzyskano następujące wskazania klas klasyfikatorów dla poszczególnych danych \( \mathbf{x}_i \):
Klasyfikator 1: 1( \( \mathbf{x}_1 \)), 2( \( \mathbf{x}_2 \)), 2( \( \mathbf{x}_3 \)), 1( \( \mathbf{x}_4 \)), 2( \( \mathbf{x}_5 \))
Klasyfikator 2: 2( \( \mathbf{x}_1 \)), 1( \( \mathbf{x}_2 \)), 2( \( \mathbf{x}_3 \)), 2( \( \mathbf{x}_4 \)), 2( \( \mathbf{x}_5 \))
Klasyfikator 3: 1( \( \mathbf{x}_1 \)), 2( \( \mathbf{x}_2 \)), 1( \( \mathbf{x}_3 \)), 1( \( \mathbf{x}_4 \)), 2( \( \mathbf{x}_5 \))
Podać ostateczne przypisania wektorów \( \mathbf{x}_i \) (\(i = 1, 2, 3, 4, 5\)) do klas stosując zasadę głosowania większościowego (majority voting).
3. Zaproponować wzory na współczynniki wagowe zespołu 3 klasyfikatorów neuronowych 2-klasowych działających na zasadzie większości ważonej. Przyjąć, że współczynniki te są zależne od znanej z góry dokładności klasyfikacji poszczególnych klasyfikatorów na \( p \) danych uczących.
4. Sieć neuronowa o 6 wagach \( w_1 = 10; w_2=5; w_3=2; w_4=1; w_5=0,5; w_6=0,1 \) została wytrenowana przy użyciu algorytmu uczącego 2-go rzędu dla którego macierz hesjanu określona jest wzorem
\( \mathbf{H}=\left[\begin{array}{rrrrrr}
1 & 0,1 & -0,2 & 0,4 & 0,1 & 0,1 \\
0,1 & 2 & 0,5 & -0,3 & -0,4 & 0,2 \\
-0,2 & 0,5 & 5 & 0,2 & 1,5 & -0,8 \\
0,4 & -0,3 & 0,2 & 4 & 1,5 & -1,2 \\
0,1 & -0,4 & 1,5 & 1,5 & 10 & 3,2 \\
0,1 & 0,2 & -0,8 & -1,2 & 3,2 & 8
\end{array}\right] \)
Wyznaczyć wartości współczynnika ważności \( S_i \) metodą OBD i OBS (przy obliczeniach macierzowych można wykorzystać program Matlab). Porównać wyniki obu metod i numery wag, podlegające obcięciu.
5. Wyjaśnić pojęcia: przeuczenie sieci, technika "cross validation" oraz leave-one-out.
6. Korzystając z programu MLP.m (patrz opis programu w wykładzie 2) sprawdzić zdolność generalizacji dwu sieci neuronowych MLP o jednym wejściu, jednym wyjściu i dwu różnych liczbach neuronów ukrytych (\( K=10 \) oraz \( K=150 \)) realizujących aproksymację funkcji sinusoidalnej w jednym okresie przy wykorzystaniu 10 par danych uczących \( x, d \) odpowiadających temu okresowi. Dane testujące wygenerować w tym samym okresie poprzez przesunięcie zmiennej \( x \) w stosunku do danych uczących. Narysować wykresy funkcji aproksymowanej przez obie sieci na tle wartości zadanych.
3.10. Słownik
Słownik opanowanych pojęć
Wykład 3
Zdolność generalizacji sieci - umiejętność generowania właściwej odpowiedzi sieci przy określonym pobudzeniu nie biorącym udziału w procesie uczenia.
Obciążenie – wielkość wyrażająca niezdolność sieci do dokładnej aproksymacji funkcji zadanej uważana za błąd aproksymacji (w praktyce utożsamiana jest z błędem uczenia, tzw. bias).
Wariancja – wielkość wyrażająca nieadekwatność informacji zawartej w zbiorze danych uczących w stosunku do rzeczywistej funkcji zadanej na wyjściu i uważana za błąd estymacji (w praktyce za miarę wariancji przyjmuje się błąd sieci na danych testujących).
VCdim – miara Vapnika-Czerwonenkisa związana ze złożonością sieci określająca zdolność do realizacji funkcji klasyfikacyjnej wzorców.
Błąd uczenia – sumaryczny błąd sieci na danych uczących.
Błąd walidacji – sumaryczny błąd sieci na danych walidacyjnych wyselekcjonowanych ze zbioru uczącego.
Błąd testowania – sumaryczny błąd sieci na danych testujących nie biorących udziału w uczeniu sieci.
Regularyzacja sieci – proces modyfikujący strukturę sieci i definicję funkcji celu ukierunkowany na polepszenie zdolności generalizacyjnych sieci.
Zespół sieci – zbiór równolegle działających sieci realizujących to samo zadanie i generujący ostateczny wynik poprzez fuzję (integrację) decyzji poszczególnych składników zespołu.
Przeuczenie sieci – stan w którym ze względu na zbyt rozbudowaną strukturę sieciową błąd testowania rośnie wraz z przedłużającym się procesem uczenia (błąd uczenia w dalszym ciągu malejący).
Niedouczenie sieci – stan sieci o zbyt małej licznie parametrów, nieadekwatny do złożoności zadania, charakteryzujący się zbyt dużym błędem zarówno uczenia jak i testowania/walidacji.
Walidacja krzyżowa – metoda uczenia i testowania służąca do obiektywnej oceny jakości działania sieci neuronowej.
Technika ,,leave one out" - technika walidacji krzyżowej, w której uczenie przeprowadza się zamieniając za każdym razem tylko jedną próbkę uczącą z testującą.
Regularyzacja metodą funkcji kary – sposób modyfikacji minimalizowanej funkcji celu poprzez dodanie składników uzależnionych od wartości parametrów sieci. Wagi o najmniejszej wartości absolutnej podlegają obcięciu.
Regularyzacja wrażliwościowa - sposób poprawy generalizacji poprzez obcięcie wag najmniej wpływających na wartość funkcji celu.
Selekcja cech – ocena jakości cechy w rozwiązaniu problemu klasyfikacji lub regresji, połączona z wyborem określonej liczby cech najlepszych.
Deskryptory numeryczne – matematyczne wielkości opisujące określone cechy procesu. Po selekcji deskryptory stają się cechami diagnostycznymi procesu.
Transformacja PCA – liniowa transformacja wektorowa (ang. Principal Component Analysis) używana do redukcji wymiaru danych według składników głównych.
Transformacja LDA – transformacja Fishera (ang. Linear Discriminant Analysis) do redukcji wymiaru danych z uwzględnieniem przynależności klasowej.
Bagging – technika losowego wyboru danych z pełnego dostępnego zbioru, używana w tworzeniu zespołu.
Głosowanie większościowe – technika ustalania zwycięzcy w zespole klasyfikatorów.
Metoda dyskryminacyjna Fishera – metoda selekcji cech diagnostycznych w klasyfikatorze dwuklasowym z uwzględnieniem wartości średnich i wariancji danych obu klas.
4. Literatura
1. Bengio Y., LeCun Y., Hinton G., Deep Learning, Nature, 2015, vol. 521, pp. 436–444.
2. Brownlee J., Deep Learning for Natural Language Processing. Develop Deep Learning Models for your Natural Language Problems, Ebook, 2018.
3. Breiman L., Random forests, Machine Learning, 2001, vol. 45, No 11, pp. 5–32.
4. Banerjee S., Linear algebra and matrix analysis for statistics, 2012, London.
5. Brudzewski K., Osowski S., Markiewicz T., Ulaczyk J., Classification of gasoline with supplement of bio-products by means of an electronic nose and SVM neural network, Sensors and Actuators - Chemical, 2006, vol. 113, No 1, pp. 135-141.
6. Chen S., Cowan C.F., Grant P.M., Orthogonal least squares learning algorithm for radial basis function networks, IEEE Trans. Neural Networks, 1991, vol. 2, pp. 302–309.
7. Christensen R., Johnson W. O., Branscum A. J., Hanson T. E., Bayesian ideas and data analysis: an introduction for scientists and statisticians, 2010, Chapman & Hall/CRC Science
8. Cichocki A., Amari S. I., Adaptive blind signal and image processing, 2003, Wiley, New York.
9. Crammer K. , Singer Y., On the learnability and design of output codes for multiclass problems. Computational Learning Theory, 2000, pp. 35-46.
10. Duda, R.O., Hart, P.E., Stork, P., Pattern classification and scene analysis, 2003, Wiley, New York.
11. Fogel, L.J., Intelligence through simulated evolution : forty years of evolutionary programming, 1999, Wiley, New York.
12. Fukushima K.: Neocognitron - a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 1980, vol.. 36, No 4, pp. 193–202, doi:10.1007/bf00344251.
13. Genc H., Cataltepe Z., Pearson T., A new PCA/ICA based feature selection method, IEEE 15th In Signal Processing and Communications Applications, 2007, pp. 1-4.
14. Gill P., Murray W., Wright M., Practical optimization, 1981, Academic Press, London.
15. Goldberg D., Algorytmy genetyczne i ich zastosowania, 2003, WNT Warszawa.
16. Golub G., Van Loan C., Matrix computations, 1996, John Hopkins University Press, Baltimore.
17. Gao H., Liu Z., Van der Maaten L., Weinberger K., Densely connected convolutional networks, CVPR, vol. 1, no. 2, p. 3. 2017.
18. Goodfellow I., Bengio Y., Courville A.: Deep learning 2016, MIT Press, Massachusetts (tłumaczenie polskie: Deep Learning. Współczesne systemy uczące się, Helion, Gliwice, 2018).
19. Goodfellow I., Pouget-Abadie J., Mirza M, Xu M., Warde-Farley B., Ozair D., Courville A. Bengio Y., Generative Adversarial Nets (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680.
20. Greff K., Srivastava R. K., Koutník J., Steunebrink B. R., Schmidhuber J., LSTM: A search space odyssey, IEEE Transactions on Neural Networks and Learning Systems, vol. 28, No 10, pp. 2222-2232, 2017.
21. Gunn S., Support vector machines for classification and regression, ISIS Technical report, 1998, University of Southampton.
22. Guyon I., Elisseeff A., An introduction to variable and feature selection, J. Mach. Learn. Res., 2003, vol. 3, pp. 1157-1182.
23. Guyon, I., Weston, J., Barnhill, S., Vapnik, V., Gene selection for cancer classification using Support Vector Machines, Machine Learning, 2002, vol. 46, pp. 389-422.
24. Haykin S., Neural networks, a comprehensive foundation, Macmillan College Publishing Company, 2000, New York.
25. He K., Zhang X, Ren S, Sun J., Deep Residual Learning for Image Recognition, 2015, http://arxiv.org/abs/1512.03385.
26. Hinton G. E., Salakhutdinov R. R., Reducing the dimensionality of data with neural networks, Science, 313:504-507, 2006.
27. Howard A., Zhu M., Chen B., Kalenichenko D., MobileNets: Efficient convolutional neural networks for mobile vision applications, arXiv: 1704.04861v1 [cs.CV], 2017.
28. Hsu, C.W., Lin, C.J., A comparison methods for multi class support vector machines, IEEE Trans. Neural Networks, 2002, vol. 13, pp. 415-425.
29. Huang G., Liu Z., van der Maaten L., Weinberger K., Densely connected convolutional networks, arXiv: 1606.06993v5 [cs.CV] 2018.
30. Iandola F, Han S., Moskevicz M., Ashraf K., Dally W., Keutzer K, Squeezenet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size, Conference ICLR, 20017. pp. 1-13.
31. Joachims T., Making large scale SVM learning practical, (in ”Advances in kernel methods - support vector learning”, B. Scholkopf, C. Burges, A. Smola eds). MIT Press, Cambridge, 1998, pp. 41-56.
32. Kecman V., Support vector machines, neural networks and fuzzy logic models, 2001, Cambridge, MA: MIT Press.
33. Kingma P, Welling M., An introduction to variational autoencoders, Foundations and Trends in Machine Learning, 12:307-392, 2019.
34. Krizhevsky A., Sutskever I., Hinton G., Image net classification with deep convolutional neural networks, Advances in Neural Information Processing Systems, vol. 25, pp. 1-9, 2012.
35. Kruk M., Świderski B., Osowski S., Kurek J., Słowińska M., Walecka I., Melanoma recognition using extended set of descriptors and classifiers, Eurasip Journal on Image and Video Processing, 2015, vol. 43, pp. 1-10, DOI 10.1186/s13640-015-0099-9
36. Kuncheva L., Combining pattern classifiers: methods and algorithms, 2015, Wiley, New York.
37. LeCun Y., Bengio Y., Convolutional networks for images, speech, and time-series. 1995, in Arbib M. A. (editor), The Handbook of Brain Theory and Neural Networks. MIT Press, Massachusetts.
38. Lecture CS231n: 2017, Stanford Vision Lab, Stanford University.
39. Lee K.C., Han I., Kwon Y., Hybrid Neural Network models for bankruptcy prediction, Decision Support Systems, 18 (1996) 63-72.
40. Leś T., Osowski S., Kruk M., Automatic recognition of industrial tools using artificial intelligence approach, Expert Systems with Applications, 2013, vol. 40, pp. 4777-4784.
41. Lin C. J., Chang, C. C., LIBSVM: a library for support vector machines. http://www. csie. ntu. edu. tw/cjlin/libsvm
42. Markiewicz T., Sieci neuronowe SVM w zastosowaniu do klasyfikacji obrazów komórek szpiku kostnego, rozprawa doktorska Politechniki Warszawskiej, 2006.
43. Matlab user manual MathWorks, 2021, Natick, USA.
44. Michalewicz Z., Algorytmy genetyczne + struktury danych = programy ewolucyjne, WNT, Warszawa 1996.
45. Osowski S., Cichocki A., Siwek K., Matlab w zastosowaniu do obliczeń obwodowych i przetwarzania sygnałów, 2006, Oficyna Wydawnicza PW.
46. Osowski S., Sieci neuronowe do przetwarzania informacji, 2020, Oficyna Wydawnicza PW.
47. Osowski S., Szmurło R., Siwek K., Ciechulski T., Neural approaches to short-time load forecasting in power systems – a comparative study, Energies, 2022, 15, pp. 3265.
48. Osowski S., Siwek K., R. Szupiluk, Ensemble neural network approach for accurate load forecasting in the power system, Applied Mathematics and Computer Science, 2009, vol.19, No.2, pp. 303-315.
49. Osowski S., Metody i narzędzia eksploracji danych , Wydawnictwo BTC, Warszawa, 2013
50. Patterson J., Gibson A., Deep Learning: A Practitioner's Approach (tłumaczenie polskie : Deep learning. Praktyczne wprowadzenie), Helion, Gliwice, 2018.
51. Platt L., Fast training of SVM using sequential optimization (in Scholkopf, B., Burges, B., Smola, A., Eds. Advances in kernel methods – support vector learning. Cambridge: MIT Press), 1998, 185-208.
52. Redmon J., Divval S., Girshick R., Farhafi A., You Only Look Once: unified. Real time object detection, axXiv: 1506.02640v5 [cs.CV], 2016
53. Ren S., He K., Girshick R., Sun J., Faster R-CNN: toward real time object detection with region proposal networks, IEEE trans. PAMI, vol. 39, pp. 1137-1149, 2017
54. Riedmiller M., Braun H.: RPROP – a fast adaptive learning algorithm. Technical Report, University Karlsruhe, Karlsruhe 1992.
55. Ridgeway G., Generalized Boosted Models: A guide to the gbm package. 2007
56. Ronneberger O., Fischer P., Brox T.: U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015, arXiv:1505.04597.
57. Sammon J. W., A nonlinear mapping for data structure analysis, IEEE Trans. on Computers, 1969, vol. 18, pp. 401-409.
58. Schmidhuber J., Deep learning in neural networks: An overview, Neural Networks, vol. 61, pp. 85-117, 2015.
59. Schölkopf B., Smola A., Learning with kernels, 2002, MIT Press, Cambridge MA.
60. Schurmann J., Pattern classification, a unified view of statistical and neural approaches, 1996, Wiley, New York.
61. Sandler, M., Howard, A., Zhu, M., Zhmoginov, A. and Chen, L.C. "MobileNetV2: Inverted Residuals and Linear Bottlenecks." In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 4510-4520). IEEE.
62. Swiderski B., Kurek J., Osowski S., Multistage classification by using logistic regression and neural networks for assessment of financial condition of company, Decision Support Systems, 2012, vol. 52, No 2, pp. 539-547
63. Szegedy C, Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., Going deeper with convolutions, arXiv: 1409.4842v1, 2014.
64. Szegedy C, Ioffe S., Vanhoucke V. Inveption-v4, Inception-ResNet and the impact of residual connections on learning, arXiv:1602.07261v2, 2016.
65. Tan P.N., Steinbach M., Kumar V., Introduction to data mining, 2006, Pearson Education Inc., Boston.
66. Tan M. Le Q., EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, arXiv:1905.11946 [cs.LG], 2020
67. Van der Maaten L., Hinton G., Visualising data using t-SNE, Journal of Machine Learning Research, 2008, vol. 9, pp. 2579-2602.
68. Vapnik V., Statistical learning theory, 1998, Wiley, New York.
69. Wagner T., Texture analysis (w Jahne, B., Haussecker, H., Geisser, P., Eds. Handbook of computer vision and application. Boston: Academic Press), 1999, ss. 275-309.
70. Zeiler M. D., Fergus R.: Visualizing and Understanding Convolutional Networks. 2013, pp. 1-11, https://arxiv.org/abs/1311.2901.
71. Zhang X., Zhou X., Lin M., Sun J., ShuffleNet: an extremely efficient convolutional neural network for mobile devices, arXiv: 1707.01083v2 [cs.CV], 2017.
72. Zheng G., Liu S., Zeming F. W., Sun L. J., YOLOX: Exceeding YOLO Series in 2021, arXiv:2107.08430v2 [cs.CV]
73. https://www.analyticsvidhya.com/blog/2021/09/adaboost-algorithm-a-complete-guide-for-beginners/
74. http://www.bsp.brain.riken.jp/ICALAB, ICALAB Toolboxes. A. Cichocki, S. Amari, K. Siwek, T. Tanaka et al.
75. https://github.com/BVLC/caffe/tree/master/models/bvlc_googlenet.
76. https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
77. https://www.jeremyjordan.me/variational-autoencoders/
78. Osowski S., Szmurło R., Matematyczne modele uczenia maszynowego w językach matlab i Python, OWPW, 2023, Warszawa.