Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 3. Sieci samoorganizacji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 30 grudnia 2025, 07:46 |
Spis treści
- 1. Sieci samoorganizujące poprzez współzawodnictwo
- 1.1. Podstawy matematyczne działania sieci
- 1.2. Algorytmy uczące sieci samoorganizujących się przez współzawodnictwo
- 1.3. Odwzorowanie Sammona
- 1.4. Program Kohon
- 1.5. Porównanie algorytmów samoorganizacji
- 1.6. Sieć odwzorowań jedno- i dwuwymiarowych
- 1.7. Przykłady zastosowań sieci samoorganizujących w kompresji danych
- 1.8. Zadania i problemy
- 1.9. Słownik
- 2. Transformacja i sieci neuronowe PCA
- 3. Ślepa separacja sygnałów
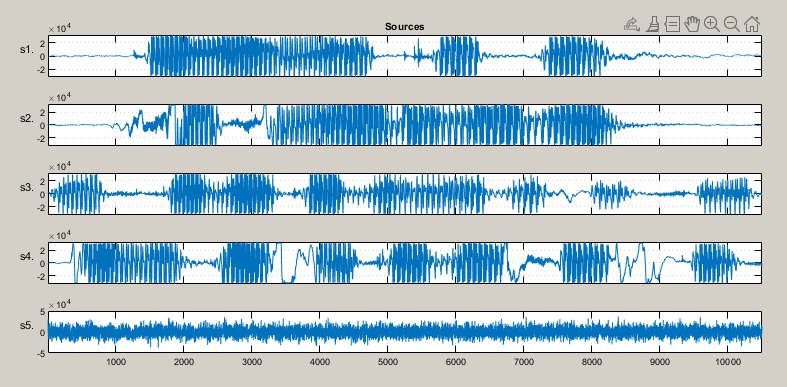
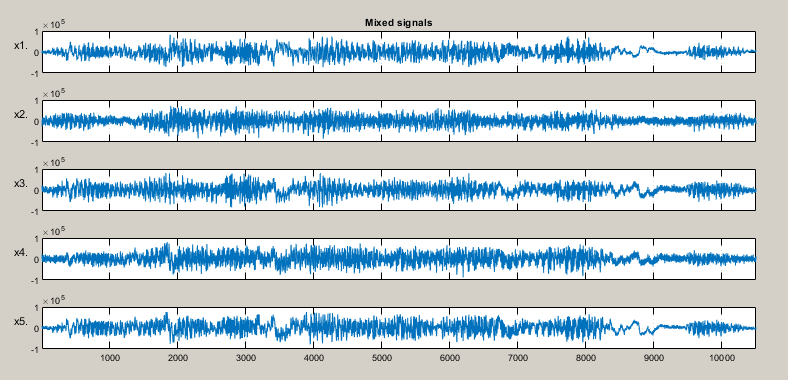
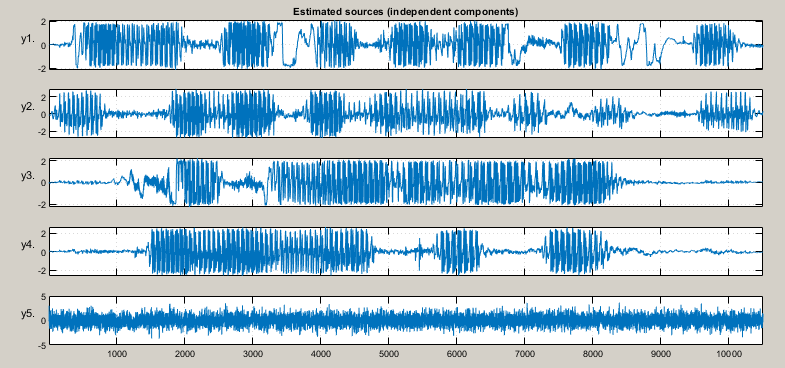
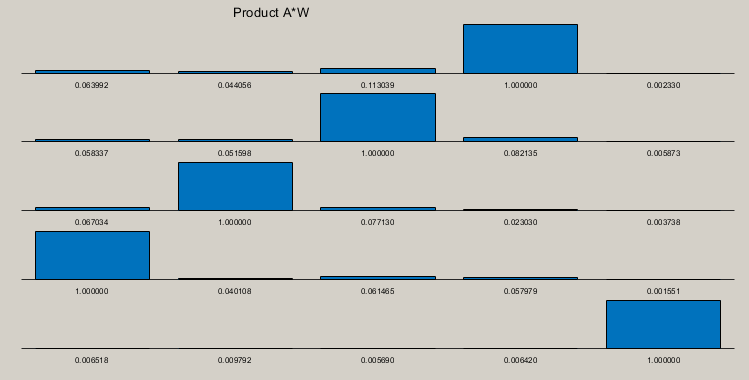
- 3.1. Wprowadzenie
- 3.2. Niezależność statystyczna sygnałów
- 3.3. Struktura rekurencyjna sieci separującej
- 3.4. Algorytmy uczące sieci rekurencyjnej
- 3.5. Sieć jednokierunkowa do separacji sygnałów
- 3.6. Toolbox ICALAB
- 3.7. Przykład zastosowania ICALAB do separacji sygnałów mowy
- 3.8. Zadania i problemy
- 3.9. Słownik
- 4. Literatura
1. Sieci samoorganizujące poprzez współzawodnictwo
Podstawę samoorganizacji sieci neuronowych stanowi zaobserwowana prawidłowość, że globalne uporządkowanie sieci jest możliwe przez działania samoorganizujące prowadzone lokalnie w różnych punktach sieci, niezależnie od siebie. W wyniku przyłożonych sygnałów wejściowych następuje w różnym stopniu aktywacja neuronów, dostosowująca się poprzez zmiany wartości wag synaptycznych do zmian wzorców uczących. W procesie uczenia istnieje tendencja do wzrostu wartości wag, dzięki której tworzy się rodzaj dodatniego sprzężenia zwrotnego: większe sygnały pobudzające, większe wartości wag, większa aktywność neuronów. Następuje przy tym naturalne zróżnicowanie wśród grup neuronów. Pewne neurony lub grupy neuronów współpracujące ze sobą uaktywniają się w odpowiedzi na pobudzenie w postaci określonych wzorców, przewyższając inne swoją aktywnością. Można tu mówić zarówno o współpracy między neuronami tej samej grupy, jak i o konkurencji występującej wewnątrz grupy i między grupami. Spośród mechanizmów samoorganizacji można wyróżnić dwie podstawowe klasy: mechanizm samoorganizacji oparty na regule korelacyjnej Hebba oraz mechanizm współzawodnictwa między neuronami opierający się na ogólnie pojętej regule współzawodnictwa Kohonena.
Wykład ten poświęcony będzie sieciom samoorganizującym się poprzez współzawodnictwo, zwanym powszechnie sieciami Kohonena. Przedstawimy podstawowe zależności, algorytmy uczące tych sieci oraz ich implementację komputerową w postaci programu Kohon i jego zastosowanie w różnych zadaniach grupowania danych.
1.1. Podstawy matematyczne działania sieci
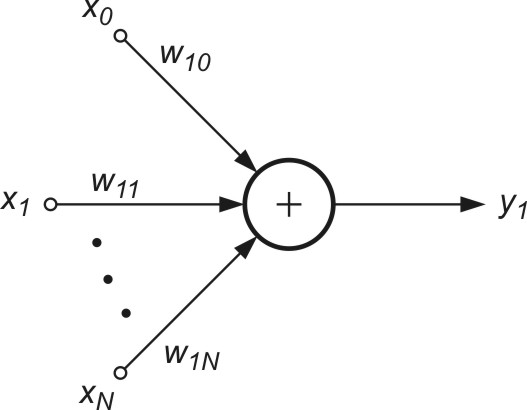
Sieci samoorganizujące, dla których podstawą uczenia jest konkurencja między neuronami stanowią zwykle sieci jednowarstwowe, w których każdy neuron połączony jest ze wszystkimi składowymi \( N \)-wymiarowego wektora wejściowego \( \mathbf{x} \), jak to przedstawiono schematycznie dla \( N = 2 \) na rys. 7.1 [46].
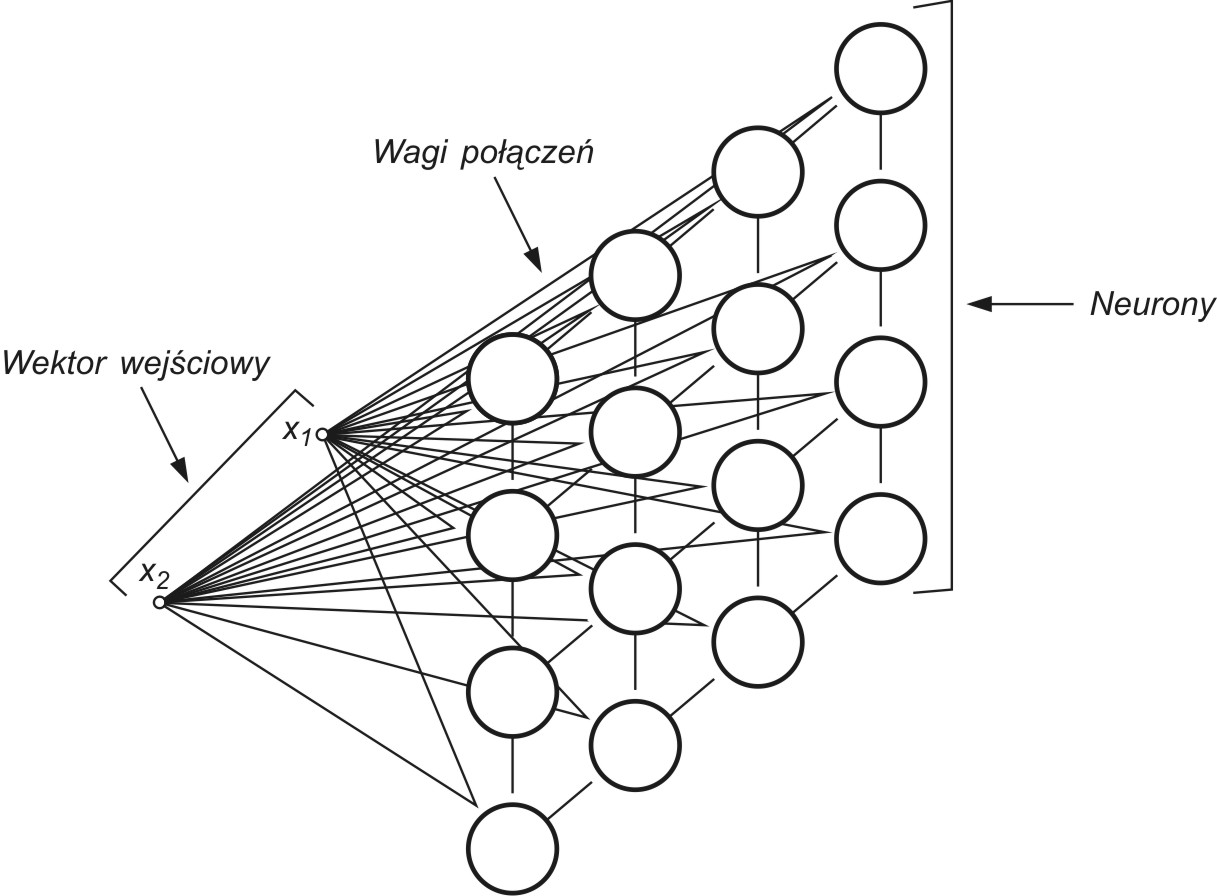
Wagi połączeń synaptycznych połączeń\( i \)-tego neuronu tworzą wektor \( \mathbf{w}_i=[w_{i1}, w_{i2}, …, w_{iN}]^T \). Przy założeniu normalizacji wektorów wejściowych po pobudzeniu sieci wektorem \( \mathbf{x} \) zwycięża we współzawodnictwie neuron, którego wagi najmniej różnią się od odpowiednich składowych tego wektora. Zwycięzca, neuron \( w \)-ty, spełnia relację
| \( d\left(\mathbf{x}, \mathbf{w}_w\right)=\min _{1 \leq i \leq n} d\left(\mathbf{x}, \mathbf{w}_i\right) \) | (7.1) |
gdzie \( d \left(\mathbf{x}, \mathbf{w}_i \right) \) oznacza odległość w sensie wybranej metryki między wektorem x i wektorem wi, a n jest liczbą neuronów. W uczeniu (adaptacji wag) stosuje się bądź strategię typu Winner Takes All (WTA) lub Winner Takes Most (WTM).
W strategii WTM wokół neuronu zwycięzcy przyjmuje się topologiczne sąsiedztwo Sw(k) o określonym promieniu malejącym w czasie. Neuron zwycięzca i wszystkie neurony położone w obszarze sąsiedztwa podlegają adaptacji, zmieniając swoje wektory wag w kierunku wektora x, zgodnie z regułą Kohonena [46].
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta_i(k)\left(\mathbf{x}-\mathbf{w}_i(k)\right) \) | (7.2) |
w której ![]() jest współczynnikiem uczenia i-tego neuronu z sąsiedztwa Sw(k) w k-tej chwili. W regule Kohonena wartość
jest współczynnikiem uczenia i-tego neuronu z sąsiedztwa Sw(k) w k-tej chwili. W regule Kohonena wartość ![]() może być taka sama lub różna dla wszystkich neuronów z sąsiedztwa. Wagi neuronów spoza sąsiedztwa Sw(k) nie podlegają zmianom. Rozmiar sąsiedztwa oraz wartości współczynników uczenia poszczególnych neuronów są funkcjami malejącymi w czasie. Zostało wykazane, że przy takim sposobie uczenia funkcja gęstości rozkładu wektorów wi poszczególnych neuronów jest zbliżona do zdyskretyzowanego rozkładu gęstości wektorów wymuszeń. Po przyłożeniu dwóch różnych wektorów x, np. x1 i x2, uaktywnią się dwa neurony sieci, każdy reprezentujący wagi najbliższe współrzędnym wektorów odpowiednio x1 i x2. Wagi te oznaczone w postaci wektorowej w1 i w2 mogą być zilustrowane w przestrzeni jako dwa punkty. Zbliżenie do siebie wektorów x1 i x2 powoduje podobne zmiany położeń wektorów w1 i w2. W granicy w1=w2 wtedy i tylko wtedy, gdy x1 i x2 są sobie równe lub zbliżone do siebie. Sieć spełniająca te warunki nazywa się mapą topograficzną (mapą Kohonena).
może być taka sama lub różna dla wszystkich neuronów z sąsiedztwa. Wagi neuronów spoza sąsiedztwa Sw(k) nie podlegają zmianom. Rozmiar sąsiedztwa oraz wartości współczynników uczenia poszczególnych neuronów są funkcjami malejącymi w czasie. Zostało wykazane, że przy takim sposobie uczenia funkcja gęstości rozkładu wektorów wi poszczególnych neuronów jest zbliżona do zdyskretyzowanego rozkładu gęstości wektorów wymuszeń. Po przyłożeniu dwóch różnych wektorów x, np. x1 i x2, uaktywnią się dwa neurony sieci, każdy reprezentujący wagi najbliższe współrzędnym wektorów odpowiednio x1 i x2. Wagi te oznaczone w postaci wektorowej w1 i w2 mogą być zilustrowane w przestrzeni jako dwa punkty. Zbliżenie do siebie wektorów x1 i x2 powoduje podobne zmiany położeń wektorów w1 i w2. W granicy w1=w2 wtedy i tylko wtedy, gdy x1 i x2 są sobie równe lub zbliżone do siebie. Sieć spełniająca te warunki nazywa się mapą topograficzną (mapą Kohonena).
Inny sposób uczenia sieci reprezentuje strategia WTA. Zmiana wag zachodzi tu również według zależności (7.2), ale adaptacja dotyczy jedynie neuronu zwycięzcy. Neurony przegrywające konkurencję nie zmieniają swoich wag.
7.1.1 Miary odległości między wektorami
Proces samoorganizacji wymaga na każdym etapie wyłonienia zwycięzcy, czyli neuronu, którego wektor wagowy różni się najmniej od przyłożonego na wejściu sieci wektora x. Istotnym problemem staje się w tej sytuacji wybór metryki, w jakiej mierzona będzie odległość między wektorem x i wektorem wi. Najczęściej używanymi miarami odległości są [10,16]:
-
miara euklidesowa
| \( d_{i j}=\left\|\mathbf{x}_i-\mathbf{x}_j\right\|_2=\sqrt{\left(\mathbf{x}_i-\mathbf{x}_j\right)^T\left(\mathbf{x}_i-\mathbf{x}_j\right)}=\sqrt{\sum_{k=1}^N\left(x_{i k}-x_{j k}\right)} \) | (7.3a) |
-
miara Mahalanobisa
| \( d_{i j}=\sqrt{\left(\mathbf{x}_i-\mathbf{x}_j\right)^T \mathbf{S}^{-1}\left(\mathbf{x}_i-\mathbf{x}_j\right)} \) | (7.3b) |
gdzie S oznacza macierz kowariancji obu wektorów. W tej definicji wielkości nieskorelowane mają większy wpływ na końcowy wynik niż te, które są mocno lub średnio skorelowane.
-
iloczyn skalarny
| \( d\left(\mathbf{x}, \mathbf{w}_i\right)=1-\mathbf{x} \bullet \mathbf{w}_i=1-\|\mathbf{x}\|\left\|\mathbf{w}_i\right\| \cos \left(\mathbf{x}, \mathbf{w}_i\right) \) | (7.4) |
-
miara według normy \( L_1 \) (Manhattan)
| \( d\left(\mathbf{x}, \mathbf{w}_i\right)=\sum_{j=1}^N\left|x_j-w_{i j}\right| \) | (7.5) |
-
miara według normy \( L_ \infty \) (Czebyszewa)
| \( d\left(\mathbf{x}, \mathbf{w}_i\right)=\max _j\left|x_j-w_{i j}\right| \) | (7.6) |
-
miara Minkowskiego \( L_m \)
| \( d\left(\mathbf{x}, \mathbf{w}_i\right)=\sqrt[m]{\sum_{j=1}^N\left|x_j-w_{i j}\right|^m} \) | (7.7) |
Przy użyciu miary euklidesowej podział przestrzeni na regiony dominacji neuronów jest równoważny mozaice Voronoia, w której przestrzeń wokół punktów centralnych stanowi strefę dominacji danego neuronu. Zastosowanie innej miary przy samoorganizacji kształtuje podział stref wpływów poszczególnych neuronów nieco inaczej. Szczególnie zastosowanie iloczynu skalarnego bez normalizacji wektorów może prowadzić do niespójnego podziału przestrzeni, przy którym występuje kilka neuronów w jednym regionie, a w innym nie ma żadnego.
Wykazano, że proces samoorganizacji prowadzi zawsze do spójnego podziału przestrzeni danych, jeśli wektory \( \mathbf{x} \) podlegają normalizacji. Przy znormalizowanych wektorach uczących \( \mathbf{x} \), wektory wag, nadążając za nimi, stają się automatycznie znormalizowane (norma wektora równa 1). Jednakże normalizacja wektora wagowego powoduje, że jeśli \( \| \mathbf{x}_i\|=const \), wtedy dla wszystkich neuronów iloczyn \( \| \mathbf{w}_i\| \| \mathbf{x}_i\| \) jest także stały przy określonej wartości \( \mathbf{x} \). O zwycięstwie neuronu decyduje więc wartość kąta między wektorami \( \mathbf{x} \) i \( \mathbf{w}_i \) zgodnie z zależnością \( \cos(\mathbf{x}, \mathbf{w}_i ) \).
Badania eksperymentalne potwierdziły potrzebę stosowania normalizacji wektorów przy małych wymiarach przestrzeni, np. \(N=2\), \(N=3\), natomiast nie jest już tak istotna dla przestrzeni o bardzo dużych wymiarach. Normalizacja wektorów może być dokonana w dwojaki sposób [45]:
-
redefinicja składowych wektora według wzoru
| \( x_i \leftarrow \frac{x_i}{\sqrt{\sum_{j=1}^N x_j^2}} \) | (7.8) |
-
zwiększenie wymiaru przestrzeni o jeden, przy takim wyborze dodatkowej składowej \((N+1)\)-szej wektora \( \mathbf{x} \), że
| \( \sum_{j=1}^{N+1} x_j^2=1 \) | (7.9) |
Przy wyborze tego sposobu normalizacji zachodzi zwykle konieczność wcześniejszego przeskalowania składowych wektora \( \mathbf{x} \) w przestrzeni \( R^N \) w taki sposób, aby możliwe było spełnienie równości (7.9). Przy zwiększaniu wymiaru wektora wejściowego efekt normalizacji staje się coraz mniej widoczny i przy dużych wymiarach sieci, \( N > 100 \), normalizacja nie odgrywa większej roli w procesie samoorganizacji.
7.1.3 Problem neuronów martwych
Przy losowej inicjalizacji wag sieci i ograniczeniu wielkości sąsiedztwa neuronów podlegających adaptacji może się zdarzyć, że część neuronów znajdzie się w strefie, w której nie ma danych lub ich liczba jest znikoma. Neurony takie mają niewielkie szanse na zwycięstwo i adaptację swoich wad, pozostając martwymi. W ten sposób dane wejściowe reprezentowane będą przez mniejszą liczbę neuronów (część neuronów martwa), a błąd reprezentacji danych, zwany również błędem kwantyzacji
| \( \varepsilon=\frac{1}{p} \sqrt{\sum_{i=1}^p\left(\mathbf{x}_i-\mathbf{w}\left(\mathbf{x}_i\right)\right)^2} \) | (7.10) |
(\ \mathbf{w}(\mathbf{x}_i) \) oznacza wektor wagowy neuronu zwycięzcy dla wektora wejściowego \( \mathbf{x}_i \), natomiast \(p\) jest liczbą danych) staje się większy. Istotnym problemem jest zatem uaktywnienie wszystkich neuronów sieci.
Można to osiągnąć, jeśli w algorytmie uczącym będzie uwzględniona liczba zwycięstw poszczególnych neuronów, a proces uczenia zostanie zorganizowany w taki sposób, aby dać szansę zwycięstwa neuronom mniej aktywnym. Sugestia takiej organizacji uczenia bierze się z obserwacji zachowania neuronów biologicznych, gdzie neuron wygrywający tuż po zwycięstwie pauzuje przez określony czas „odpoczywając” przed następnym współzawodnictwem [46]. Taki sposób uwzględniania aktywności neuronów nazywany jest mechanizmem zmęczenia. Oryginalna nazwa conscience mechanism jest w języku polskim określana również mianem mechanizmu świadomości.
Istnieje wiele mechanizmów uwzględniających aktywność neuronów w procesie uczenia. Jednym ze sposobów uaktywnienia wszystkich neuronów jest uwzględnienie liczby zwycięstw neuronu przy obliczaniu efektywnej odległości wag od wzorca uczącego \( \mathbf{x} \), modyfikując ją proporcjonalnie do liczby zwycięstw danego neuronu w przeszłości (na początku wszystkim przypisuje się liczbę zwycięstw równą 1). Jeśli oznaczy się liczbę zwycięstw \(i\)-tego neuronu przez \( N_i \), modyfikację taką można przyjąć w postaci
| \( d\left(\mathbf{x}, \mathbf{w}_w\right) \leftarrow N_i d\left(\mathbf{x}, \mathbf{w}_w\right) \) | (7.11) |
Neurony aktywne o dużej wartości \( N_i \) są karane sztucznym zawyżeniem tej odległości. Należy zaznaczyć, że modyfikację odległości stosuje się jedynie przy wyłanianiu zwycięzcy. W momencie uaktualniania wagi bierze się pod uwagę odległość rzeczywistą. Modyfikacja odległości ma za zadanie uaktywnić wszystkie neurony przez wprowadzenie ich w obszar o dużej liczbie danych. Po wykonaniu zadania (zwykle po dwóch lub trzech cyklach uczących) wyłącza się ją, pozwalając na niezakłóconą konkurencję neuronów [46].
1.2. Algorytmy uczące sieci samoorganizujących się przez współzawodnictwo
Celem uczenia sieci samoorganizujących się poprzez współzawodnictwo jest takie uporządkowanie neuronów (dobór wartości ich wag), które zminimalizuje wartość oczekiwaną zniekształcenia (błędu kwantyzacji), określaną jako błąd popełniany przy aproksymacji wektora wejściowego \(\mathbf{x}\) wartościami wag neuronu zwyciężającego w konkurencji. Przy \(p\) wektorach wejściowych \( \mathbf{x} \) i zastosowaniu normy euklidesowej błąd kwantyzacji może być wyrażony w postaci zależności (7.10). Zadanie to zwane jest również kwantyzacją wektorową (ang. Vector Quantization - VQ). Numery neuronów zwyciężających przy kolejnych prezentacjach wektorów x tworzą tak zwaną książkę kodową.
W klasycznym rozwiązaniu kodowania stosuje sią algorytm K-uśrednień (ang. K-means) określany również jako uogólniony algorytm Lloyda [65]. W przypadku sieci neuronowych odpowiednikiem algorytmu Lloyda jest algorytm WTA (ang. Winner Takes All). W algorytmie tym po prezentacji wektora \( \mathbf{x} \) określana jest jego odległość od wektorów wagowych wszystkich neuronów. Zwycięzcą staje się neuron o najmniejszej odległości. Zwycięzca (\(w\)-ty neuron) ma przywilej adaptacji swoich wag w kierunku wektora \( \mathbf{x} \) według reguły [46]
| \( \mathbf{w}_w(k+1)=\mathbf{w}_w(k)+\eta_i(k)\left(\mathbf{x}-\mathbf{w}_w(k)\right) \) | (7.12) |
Pozostałe neurony nie podlegają adaptacji, czyli
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k) \) | (7.13) |
Algorytm umożliwia uwzględnienie zmęczenia neuronów poprzez uwzględnienie liczby zwycięstw neuronu i faworyzowanie jednostek o najmniejszej aktywności, dla wyrównania ich szans na zwycięstwo. Modyfikację taką, jak zaznaczono uprzednio, stosuje się głównie w początkowych fazach algorytmu, wyłączając ją po uaktywnieniu wszystkich neuronów. Ostatni sposób uczenia jest zaimplementowany w programie Kohon w postaci opcji CWTA. CWTA pochodzi od angielskiej nazwy algorytmu Conscience Winner Takes All i jest jednym z najlepszych i najszybciej działających algorytmów samoorganizacji.
Oprócz algorytmów WTA, w których tylko jeden neuron może podlegać adaptacji w każdej iteracji, w uczeniu sieci samoorganizujących stosuje się powszechnie algorytmy typu WTM (ang. Winner Takes Most), w których oprócz zwycięzcy uaktualniają swoje wagi również neurony z jego sąsiedztwa, przy czym im dalsza jest odległość neuronu od zwycięzcy, tym mniejsza jest zwykle zmiana wartości wag tego neuronu. Proces adaptacji wektora wagowego może być opisany uogólnioną zależnością [46] z funkcją sąsiedztwa \( G(i, \mathbf{x} ) \) \(i\)-tego neuronu względem wektora wejściowego \( \mathbf{x} \)
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta_i(k) G(i, \mathbf{x})\left(\mathbf{x}-\mathbf{w}_i(k)\right) \) | (7.14) |
dla wszystkich neuronów \(i\) należących do sąsiedztwa zwycięzcy \(w\). We wzorze tym oddzielono współczynnik uczenia \( \eta \) każdego neuronu od jego odległości względem neuronu zwycięzcy lub od prezentowanego wektora x, mającej wpływ na funkcję sąsiedztwa \(G(i, \mathbf{x})\). Definiując tę funkcję w postaci
| \( G(i, \mathbf{x})=\left\{\begin{array}{llc} 1 & \text { dla } & i=1 \\ 0 & \text { dla } & i \neq w \end{array}\right. \) | (7.15) |
gdzie w oznacza numer zwycięzcy, otrzymuje się klasyczny algorytm WTA. Istnieje wiele różnych odmian algorytmów WTM, różniących się przede wszystkim postacią funkcji \( G(i, \mathbf{x}) \). Przedstawimy tu dwa rozwiązania: algorytm gazu neuronowego oraz algorytm klasyczny Kohonena dostosowany do tworzenia mapy.
7.2.2 Algorytm gazu neuronowego
Znaczącą poprawę samoorganizacji sieci w sensie mniejszego błędu kwantyzacji można uzyskać, stosując metodę zwaną przez autorów algorytmem gazu neuronowego ze względu na podobieństwo dynamiki zmian położenia neuronów do ruchu cząsteczek gazu.
W algorytmie tym wszystkie neurony podlegają sortowaniu w każdej iteracji w zależności od ich odległości ich wektorów wagowych względem wektora x. Neurony są ustawiane w kolejności odpowiadającej narastającej odległości \( d_0 \), gdzie \( d_m=\left\|\mathbf{x}-\mathbf{w}_m\right\| \) oznacza odległość neuronu zajmującego w wyniku sortowania \(m\)-tą pozycję w szeregu za neuronem zwycięzcą, któremu przyporządkowano odległość \( d_0 \). Wartość funkcji sąsiedztwa dla \(i\)-tego neuronu jest określona zależnością [46]
| \( G(i, \mathbf{x})=\exp \left(-\frac{m(i)}{\lambda}\right) \) | (7.16) |
w której zmienna \(m(i)\) oznacza kolejność uzyskaną w wyniku sortowania \( (m(i) = 0,1,\ldots, n-1) \), gdzie 0 oznacza neuron zwycięzcę, a \( \lambda \) jest parametrem (analogicznie do promienia sąsiedztwa w algorytmie Kohonena), malejącym w czasie. Przy \( \lambda=0 \) tylko neuron zwycięzca podlega adaptacji i algorytm WTM przekształca się w zwykły algorytm WTA, natomiast przy \( \lambda > 0 \) adaptacji podlegają wagi wielu neuronów w stopniu uzależnionym od wartości funkcji \(G(i, \mathbf{x})\).
Algorytm gazu neuronowego przypomina strategię zbiorów rozmytych, w której każdemu neuronowi przypisuje się wartość funkcji przynależności do sąsiedztwa, określoną zależnością (7.18). W celu uzyskania dobrych rezultatów samoorganizacji proces uczenia powinien rozpoczynać się z dużą wartością \( \lambda \), po czym powinna ona maleć wraz z upływem czasu do wartości minimalnej (najczęściej zerowej). Zmiana \( \lambda(k) \) może być liniowa bądź wykładnicza. Współczynnik uczenia i-tego neuronu \( \lambda(k) \) może również zmieniać się bądź liniowo bądź wykładniczo. W praktyce lepsze wyniki organizacji uzyskuje się zwykle przy liniowej zmienności \( \lambda(k) \).
Algorytm gazu neuronowego, obok CWTA uwzględniającego aktywność neuronów jest w praktyce najskuteczniejszym narzędziem samoorganizacji neuronów w sieci ze współzawodnictwem. Dobierając odpowiednio parametry sterujące procesem można uzyskać bardzo dobrą organizację sieci przy szybkości działania znacznie przewyższającej klasyczny algorytm Kohonena. Tym nie mniej należy zauważyć, że algorytm ten nie ma zastosowania przy tworzeniu mapy Kohonena, gdyż nie przenosi adaptacji wag na neurony położone w obszarze bliskiego sąsiedztwa (nie zachowuje spójności obszaru aktywności neuronów przy adaptacji).
7.2.3 Algorytmy uczące mapy Kohonena
Algorytm Kohonena należy do najstarszych metod uczenia WTM generujących mapę i w chwili obecnej istnieje wiele jego odmian. W klasycznym algorytmie Kohonena dostosowanym do tworzenia mapy inicjalizuje się sieć, przyporządkowując neuronom określone miejsce w przestrzeni i stowarzyszając je (łącząc) z sąsiadami. Stowarzyszenie to może być interpretowane na siatce prostokątnej (sąsiedztwo prostokątne) lub heksagonalnej (sąsiedztwo heksagonalne). Interpretacja obu rodzajów sąsiedztwa przedstawiona jest na rys. 7.2. Kontury wewnętrzne o kształcie prostokąta lub sześciokąta odpowiadają granicom sąsiedztwa o promieniu odpowiednio zerowym (jedynie zwycięzca – brak sąsiadów), pierwszym, drugim lub trzecim.
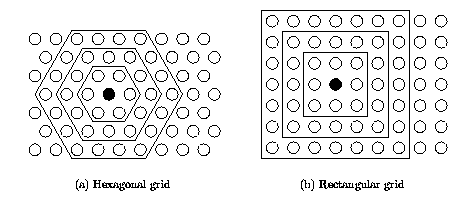
W momencie wyłonienia zwycięzcy uaktualnieniu podlegają nie tylko jego wagi, ale również wagi jego sąsiadów, pozostających w najbliższym sąsiedztwie. W ten sposób adaptacji podlega cała grupa neuronów wokół zwycięzcy zbliżając swoje wagi do prezentowanego wektora x, jak to pokazano w sposób graficzny na rys. 7.3.
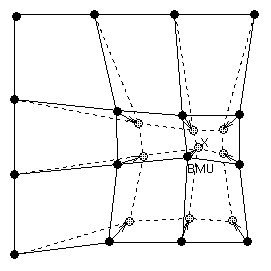
Funkcja sąsiedztwa \(G(i, \mathbf{x})\) w mapie Kohonena może zmieniać się w sposób skokowy (sąsiedztwo prostokątne) lub ciągły. W pierwszym sposobie zwanym przez Kohonena funkcją „bubble” jest ona definiowana w postaci
| \( G(i, \mathbf{x})=\left\{\begin{array}{ccc} 1 & \text { dla } & d(i, w) < \lambda \\ 0 & \text { dla } & \text { reszty } \end{array}\right. \) | (7.17) |
We wzorze tym \(d(i,w)\) może oznaczać bądź odległość euklidesową między wektorami wag zwycięzcy (neuron \(w\)-ty) oraz neuronu \(i\)-tego, bądź odległość mierzoną w liczbie neuronów. Współczynnik \( \lambda \) jest promieniem sąsiedztwa o wartości malejącej, poczynając od zadanej na wstępie wartości maksymalnej aż do zera, przy czym wielkość ta zmienia się w sposób skokowy, wyłączając z sąsiedztwa w kolejnych iteracjach neurony znajdujące się na krańcach obszaru sąsiedztwa. Zauważmy, że tak zdefiniowana funkcja sąsiedztwa \(G(i, \mathbf{x})\) przyjmuje identyczne wartości dla wszystkich neuronów znajdujących się aktualnie w obszarze sąsiedztwa podlegającym adaptacji.
Drugim powszechnie stosowanym typem funkcji sąsiedztwa w mapach Kohonena jest sąsiedztwo typu gaussowskiego, w którym funkcja \(G(i, \mathbf{x})\) określona jest wzorem [46]
| \( G(i, \mathbf{x})=\exp \left(-\frac{d^2(i, w)}{2 \lambda^2}\right) \) | (7.18) |
O stopniu adaptacji neuronów z sąsiedztwa zwycięzcy decyduje nie tylko odległość euklidesowa \(d(i,w)\) neuronu \(i\)-tego od zwycięzcy (neuronu w-tego), ale również promień sąsiedztwa \( \lambda \). W odróżnieniu od sąsiedztwa typu prostokątnego, gdzie każdy neuron należący do sąsiedztwa zwycięzcy podlegał adaptacji w jednakowym stopniu, przy sąsiedztwie typu gaussowskiego stopień adaptacji jest zróżnicowany i zależy od wartości funkcji Gaussa. Dla zwycięzcy obowiązuje \( G(w, w) = 1 \), dla pozostałych neuronów \( 0 < G(i, w) < 1 \). Sąsiedztwo gaussowskie prowadzi zwykle do lepszych rezultatów uczenia i lepszej organizacji sieci niż sąsiedztwo prostokątne.
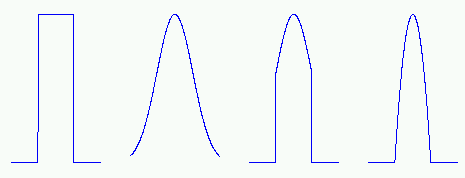
Istotny wpływ na uczenie sieci Kohonena wywiera dobór wartości współczynnika uczenia \( \eta \) w poszczególnych iteracjach. W ogólności wartość ta powinna maleć w miarę czasu uczenia. Na rys. 7.4 przedstawiono typowe sposoby zmian tego współczynnika.
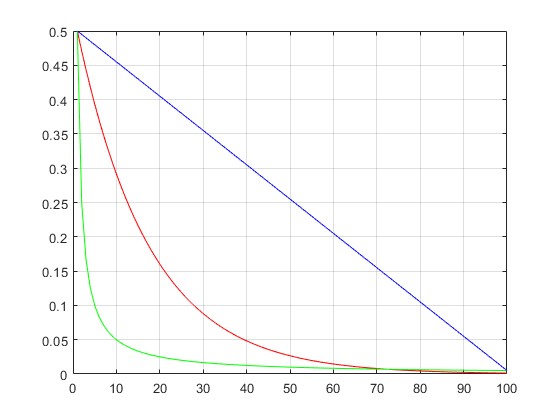
W praktyce najlepsze wyniki samoorganizacji uzyskuje się przy zastosowaniu liniowej formy zmienności współczynnika uczenia.
W mapie Kohonena definiuje się z góry siatkę dwuwymiarową która będzie odzwierciedlała rzut położenia danych wielowymiarowych na płaszczyźnie. Należy z góry określić liczbę neuronów rozmieszczonych w osi poziomej i pionowej. Ogólna liczba neuronów w sieci będzie wówczas równa ich iloczynowi. Neurony te zajmują odpowiednie miejsce w przestrzeni dwuwymiarowej, zachowując powiązanie ze swoimi sąsiadami w procesie uczenia. W efekcie po zakończenia uczenia na etapie testowania zwycięstwo określonego neuronu jest przenoszone na pozycję tego neuronu w siatce dwuwymiarowej (mapie) odzwierciedlając w ten sposób jego rzut na mapę topograficzną. Mapa Kohonena stanowi więc sposób przedstawienia rozkładu danych wielowymiarowych na płaszczyźnie.
Rozkład ten może być przedstawiony na kilka sposobów. Rys. 7.5 przedstawia trzy najczęściej stosowane kształty: mapa płaska, cylindryczna oraz toroidalna. W mapie cylindrycznej dane na dwu przeciwległych krańcach zbliżone są do siebie. W mapie toroidalnej zbliżenie dotyczy dwu przeciwległych krańców w osi x i y.

Dane które w przestrzeni wielowymiarowej są odległe od siebie zajmują również odległe pozycje na mapie. Dane bliskie sobie w przestrzeni wielowymiarowej są również bliskie na mapie.
7.2.4 Przykład mapy Kohonena w analizie obciążeń elektroenergetycznych
Na rys. 7.6 przedstawiono mapę Kohonena o wymiarze 7×7 dla danych dotyczących obciążeń elektroenergetycznych w Polskim Systemie Elektroenergetycznym (PSE). Uwzględniono 12 rodzajów obciążeń odpowiadających 12 miesiącom roku (Jan – styczeń, Feb – luty, Mar – marzec, Apr – kwiecień, May – May, June – czerwiec, July – lipiec, Aug – sierpień, Sep – wrzesień, Oct – październik, Nov – listopad oraz Dec - grudzień). Dane rzeczywiste obciążeń dotyczą wektorów 24-wymiarowych (obciążenia 24 godzin doby). Dzięki mapie Kohonena zostały one zrzutowane na płaszczyznę reprezentując mapę obciążeń odpowiadających poszczególnym miesiącom roku [46].
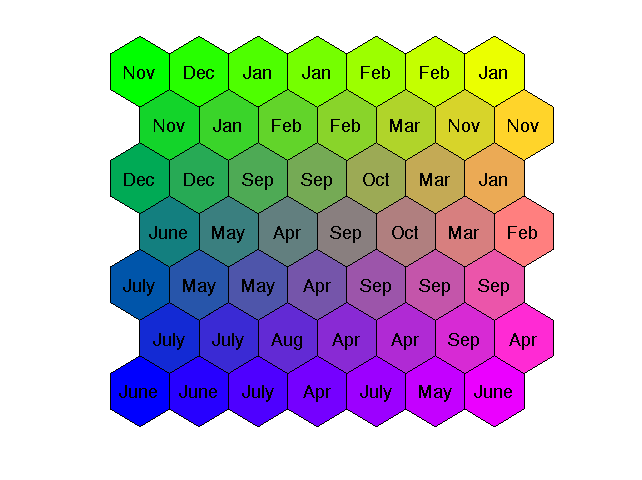
Zauważmy, że dane dotyczące miesięcy letnich i zimowych są odległe od siebie, podczas gdy te związane z wiosną i jesienią są podobne i położone na mapie w bliskim sąsiedztwie. Podobnie można zrzutować obciążenia 24-godzinne na mapę odzwierciedlającą podział na dni tygodnia ( Mon – poniedziałki, Tue – wtorki, Wed – środy, Thu – czwartki, Fri – piątki, Sat – soboty, Sun – niedziele), jak to przedstawiono na rys. 7.7.
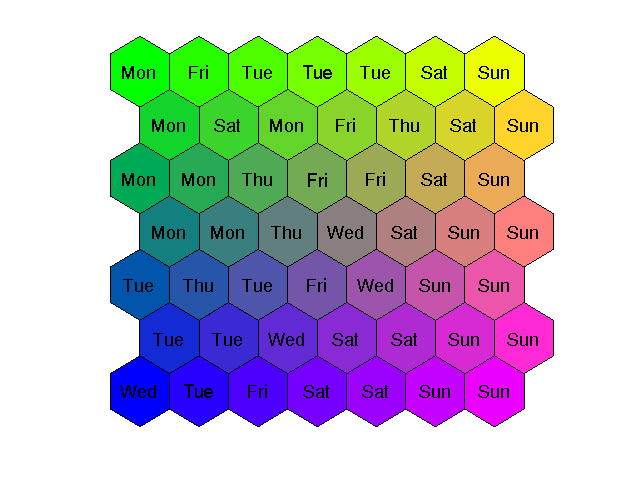
Wyraźnie widoczne są skupienia neuronów reprezentujących dni robocze (od poniedziałku do piątku) oraz oddzielnie świąteczne (Sun). Pomiędzy nimi znajdują się soboty (Sat).
Interesująca jest również mapa profili obciążenia reprezentowana przez wagi neuronów zwycięzców dla poszczególnych rejonów (rys. 7.8). Można zauważyć znaczne podobieństwo miedzy najbliższymi sąsiadami, zarówno w pionie jak i poziomie. Ponadto jest ewidentne, że wagi neuronów odległych od siebie na mapie (np. neurony górne i dolne lub neurony z prawej i lewej strony w tym samym wierszu mapy) są znacznie różniące się.

1.3. Odwzorowanie Sammona
Rozkład danych wielowymiarowych uzyskanych w sieci samoorganizującej może być przedstawiony na płaszczyźnie lub w przestrzeni trójwymiarowej przy zastosowaniu rzutowań innych niż mapa Kohonena. Jednym ze znanych jest nieliniowe odwzorowanie Sammona [57]. Odwzorowanie to pozwala na rzutowanie danych z dowolnej przestrzeni N-wymiarowej w przestrzeń M-wymiarową (np. M=2 lub M=3) zachowując podstawowe cechy rozkładu danych z oryginalnej przestrzeni wielowymiarowej.
Niech będzie danych n wektorów N-wymiarowych xi (i=1, 2, …n). Odpowiednio do nich definiuje się n wektorów w przestrzeni M-wymiarowej oznaczonych przez yi. Odległości między poszczególnymi wektorami w przestrzeni N-wymiarowej oznaczane będą przez \( d_{i j}^*=d\left(\mathbf{x}_i, \mathbf{x}_j\right) \) a w przestrzeni M-wymiarowej przez \( d_{i j}=d\left(\mathbf{y}_i, \mathbf{y}_j\right) \). W określeniu odległości między wektorami można zastosować dowolną metrykę, w szczególności euklidesową. Zadanie odwzorowania nieliniowego Sammona polega na takim doborze wektorów y, aby zminimalizować funkcję błędu E zdefiniowaną wzorem [57]
| \( \min E=\frac{1}{c} \sum_{i < j}^n \frac{\left(d_{i j}^*-d_{i j}\right)^2}{d_{i j}^*} \) | (7.19) |
gdzie
| \( c=\sum_{i < j}^n d_{i j}^* \) | (7.20) |
| \( d_{i j}=\sqrt{\sum_{k=1}^M\left(y_{i k}-y_{j k}\right)^2} \) | (7.21) |
W zależnościach tych yij oznacza j-tą składową wektora yi. W minimalizacji funkcji błędu (7.19) Sammon zastosował uproszczoną metodę optymalizacyjną Newtona, która pozwala wyrazić rozwiązanie z kroku na krok w sposób rekurencyjny w postaci
| \( y_{i j}(k+1)=y_{i j}(k)-\eta \Delta_{i j}(k) \) | (7.22) |
| \( \Delta_{i j}(k)=\frac{\partial E / \partial y_{i j}}{\left|\partial^2 E / \partial y_{i j}^2\right|} \) | (7.23) |
Wzór wyrażający poprawkę ![]() reprezentuje iloraz odpowiedniej składowej gradientu przez diagonalny składnik hesjanu, określony w k-tej iteracji. Współczynnik \( \eta \) jest odpowiednikiem stałej uczenia i przyjmowany jest z zakresu [0,3, 0,4]. Przy definicji funkcji błędu w postaci (7.19) odpowiednie składowe gradientu i hesjanu opisane są wzorami [57]
reprezentuje iloraz odpowiedniej składowej gradientu przez diagonalny składnik hesjanu, określony w k-tej iteracji. Współczynnik \( \eta \) jest odpowiednikiem stałej uczenia i przyjmowany jest z zakresu [0,3, 0,4]. Przy definicji funkcji błędu w postaci (7.19) odpowiednie składowe gradientu i hesjanu opisane są wzorami [57]
| \( \frac{\partial E}{\partial y_{i j}}=-\frac{2}{C} \sum_{\substack{p=1 \\ p \neq i}}^n\left[\frac{d_{i p}^*-d_{i p}}{d_{i p} d_{i p}^*}\right]\left(y_{i j}-y_{p j}\right) \) | (7.24) |
| \( \frac{\partial^2 E}{\partial y_{i j}^2}=-\frac{2}{c} \sum_{\substack{p=1 \\ p \neq i}}^n \frac{1}{d_{i p} d_{i p}^*}\left[\left(d_{i p}^*-d_{i p}\right)-\frac{\left(y_{i j}^*-y_{p j}\right)^2}{d_{i p}}\left(1+\frac{d_{i p}^*-d_{i p}}{d_{i p}}\right)\right] \) | (7.25) |
W wyniku wielu iteracji składowe wektorów yi przyjmują wartości ostateczne minimalizujące wartość zdefiniowanej na wstępie funkcji błędu.
Na rys. 7.9 przedstawiono rzutowanie Sammona dla tych samych danych dotyczących obciążeń elektroenergetycznych w Polskim Systemie Elektroenergetycznym (PSE) przedstawionych na mapie Kohonena. Uwzględniono rodzaje obciążeń odpowiadających czterem porom roku (kolor zielony – wiosna, czerwony – lato, magenta – jesień oraz niebieski – zima). Dane rzeczywiste obciążeń dotyczą wektorów 24-wymiarowych (obciążenia 24 godzin doby).
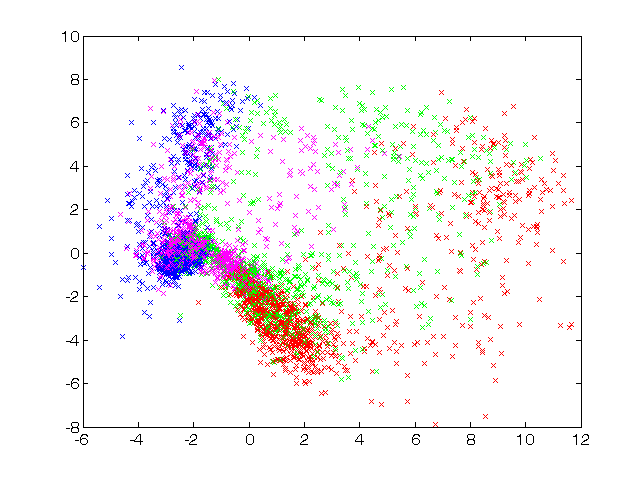
Zauważmy, że również przy tym rzutowaniu dane dotyczące lata i zimy są odległe od siebie, podczas gdy te związane z wiosną i jesienią są bliskie sobie i położone na mapie w bliskim sąsiedztwie. Ponadto charakterystyczne jest, że dane dotyczące zimy są stosunkowo mało rozproszone w stosunku do innych pór roku, natomiast dane wiosenne charakteryzują się rozproszeniem największym (duże różnice między najwyższą i najniższą temperatura powodują duże zróżnicowanie w poborze energii elektrycznej).
1.4. Program Kohon
Pakiet programów KOHON, napisany w języku Matlab wywoływany jest poleceniem kohon [46]. Umożliwia zarówno uczenie jak i testowanie sieci Kohonena. Może służyć do rozwiązywania różnorodnych problemów praktycznych. Oprócz programów uczących i testujących, pakiet zawiera szereg programów niezbędnych do wygenerowania danych uczących, konwersji obrazów graficznych i plików dźwiękowych na dane numeryczne, jak również programy do graficznego odzwierciedlenia danych uczących, mapy oraz wyników uczenia. Obsługa tego programu jest intuicyjnie prosta.
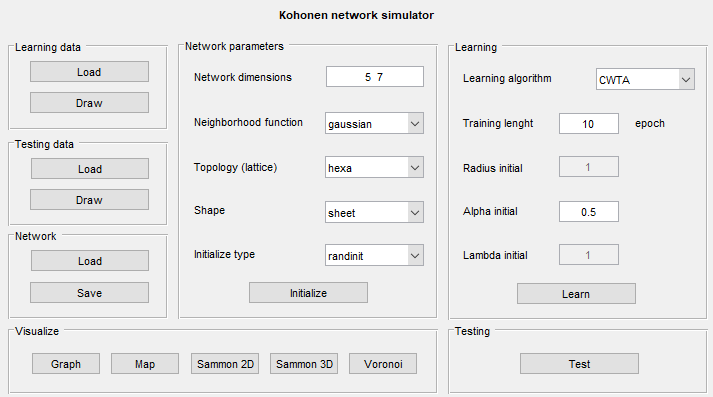
Na rys. 7.10. przedstawiono wygląd okna menu głównego programu. Pola Learning data, Testing data oraz Network z lewej strony menu służą do zadawania odpowiednio danych uczących, testujących oraz zapamiętywania i wczytywania zapamiętanej sieci Kohonena. Format danych powinien zawierać w pierwszej linii wymiar wektora x. Następne linie zawierają kolejne wektory x stanowiące zasadniczą treść danych.
Środkowa cześć menu (Network parameters) zawiera podstawowe informacje dotyczące definicji struktury sieci i sposobu tworzenia mapy odwzorowań. Są to:
-
Network dimension – określa ilość neuronów umieszczonych w osi poziomej i pionowej. Należy podać dwie liczby, np. 5 7, z których pierwsza określa rozmiar mapy w osi x (równy 5) a druga w osi y (rozmiar 7). Liczba neuronów jest równa wówczas iloczynowi obu liczb (w przykładzie n=35).
-
Neighborhood function – określa rodzaj zastosowanej funkcji sąsiedztwa. Dostępne są następujące typy: bubble –prostokątne, gaussian – gaussowskie, cutgaussian – zmodyfikowane gaussowskie z obciętą i podwyższoną podstawą oraz ep=max(0, 1-x2).
-
Topology – rodzaj siatki określającej topologię sąsiedztwa. Dostępna jest siatka prostokątna (rect) oraz heksagonalna (hexa).
-
Shape – określa sposób rysowania mapy Kohonena. Możliwe są 3 typy przedstawień mapy: sheet (struktura płaska mapy), cylinder (struktura cylindryczna) i toroid (struktura toroidalna).
-
Initialization type - sposób inicjalizacji wartości wag początkowych sieci. Są możliwe dwie metody: randinit (przypisanie losowych wartości wag) oraz lininit – przypisanie wag według specjalnej procedury korzystającej z zależności liniowych odpowiadających danym uczącym.
-
Initialize – przycisk do faktycznej inicjalizacji wag sieci według wybranej wcześniej procedury inicjalizacji.
Z prawej strony menu występują parametry definiujące sposób uczenia sieci (pole Learning). Na pole to składa się:
-
Wybór algorytmu uczenia (Learning algorithm) w ramach którego można wybrać spośród następujących metod uczenia: WTA (metoda Winner Takes All), CWTA (metoda WTA z mechanizmem zmęczenia), WTM batch (algorytm Kohonena aktualizujący wagi po prezentacji wszystkich danych z pliku uczącego), WTM seq (algorytm Kohonena aktualizujący wagi sieci w sposób on-line) oraz Neural gas (algorytm gazu neuronowego).
-
Training length – ustala liczbę cykli (epok) uczących
-
Radius initial – podaje początkową wielkość sąsiedztwa (w liczbie neuronów) przy zastosowaniu algorytmu Kohonena)
-
Alpha initial – początkowa wartość stałej uczenia \( \alpha \)
Po ustawieniu tych wielkości należy przycisnąć przycisk Learn, uruchamiający proces uczenia. Testowanie wytrenowanej sieci odbywa się na danych testujących po przyciśnięciu przycisku Test w polu Testing. Program umożliwia różny sposób wizualizacji wyników. Dostępne są następujące opcje (po wybraniu odpowiedniego przycisku):
-
Graph – ilustracja położeń danych 2D na tle danych uczących.
-
Map – przedstawienie położenia danych wielowymiarowych jako mapy Kohonena. Aby to uzyskać należy przeprowadzić uczenie sieci przy użyciu algorytmu Kohonena (możliwe jest krótkie douczenie przy zastosowaniu innych algorytmów).
-
Sammon 2D i Sammon 3D – ilustracja położenia danych uczących odpowiednio w przestrzeni 2-wymiarowej (2D) lub trójwymiarowej (3D) przy zastosowaniu algorytmu Sammona.
-
Voronoi – ilustracja położenia danych 2D i neuronów jak mozaiki Voronia.
W skład pakietu Kohon wchodzą również programy konwertujące dane obrazów graficznych zapisane w formacie PCX (pcxkoh.exe) na format plików pakietu Kohon i koh2pcx.exe dokonujące konwersji w drugą stronę. Program koherror.bat umożliwia natomiast obliczenie błędu PSNR (w dB) wyrażającego różnicę pomiędzy obrazem oryginalnym, a odtworzonym.
1.5. Porównanie algorytmów samoorganizacji
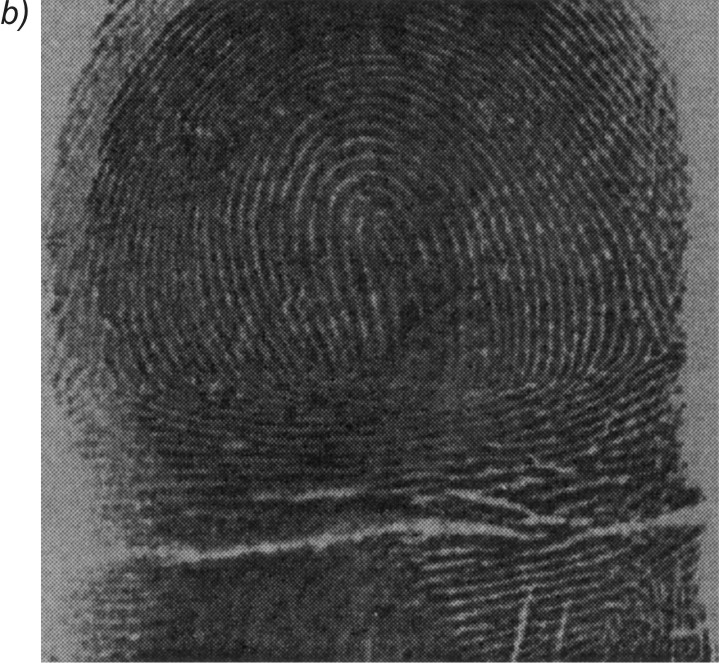
Porównania przedstawionych wcześniej algorytmów dokonano na przykładzie odwzorowania danych uczących dwuwymiarowych tworzących złożony kształt, przedstawiony na rys. 7.12.
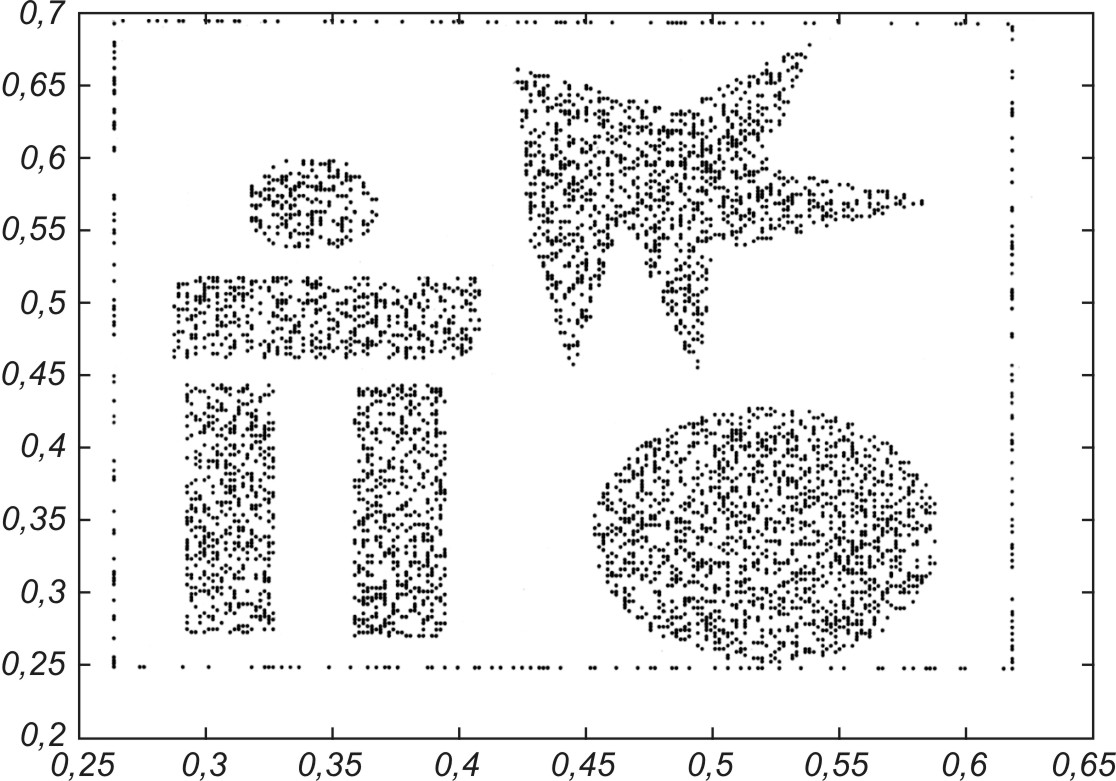
Do odwzorowania użyto 200 neuronów. Dobre odwzorowanie danych przez sieć neuronową wymaga, aby neurony plasowały się w rejonach o dużym zagęszczeniu danych, a nie tam, gdzie jest ich brak. Na rys. 7.13 podano uzyskany wynik samoorganizacji 200 neuronów przy zastosowaniu trzech omówionych w tym rozdziale algorytmów: CWTA (rys. 7.13a), gazu neuronowego (rys. 7.13b) oraz algorytmu Kohonena (rys. 7.13c).
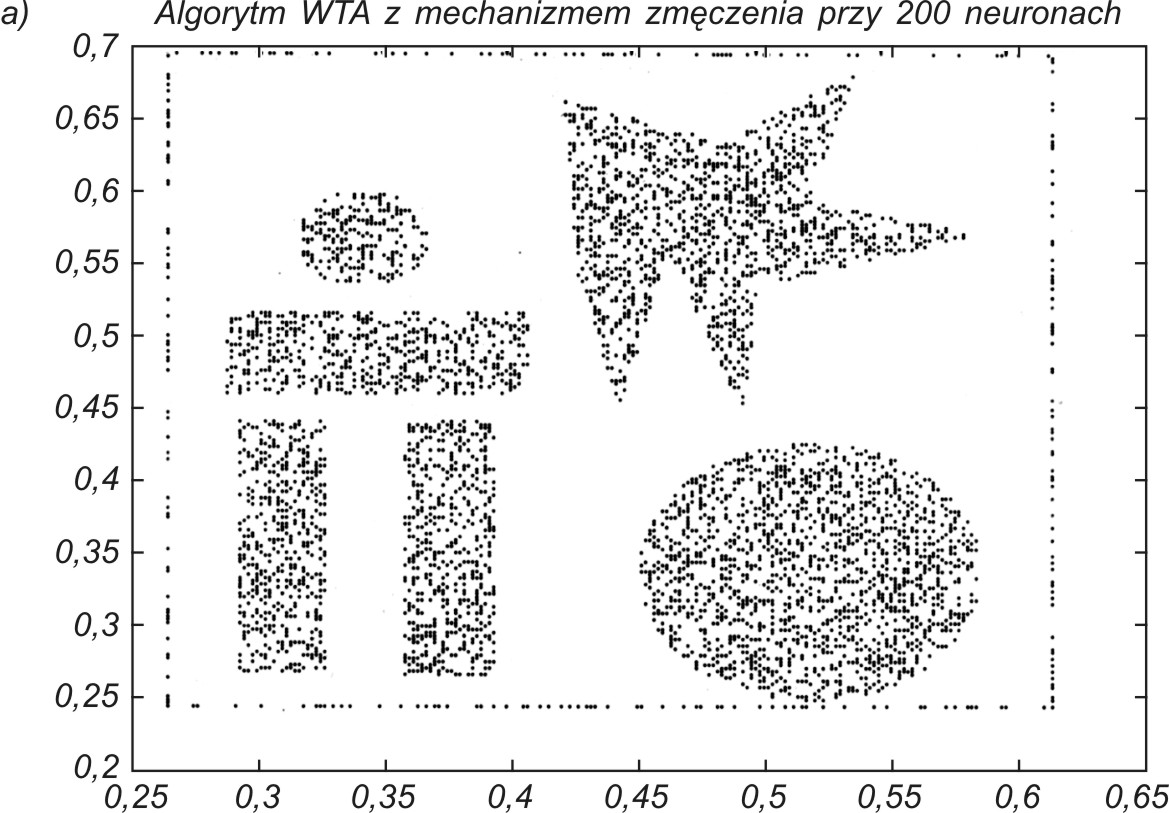
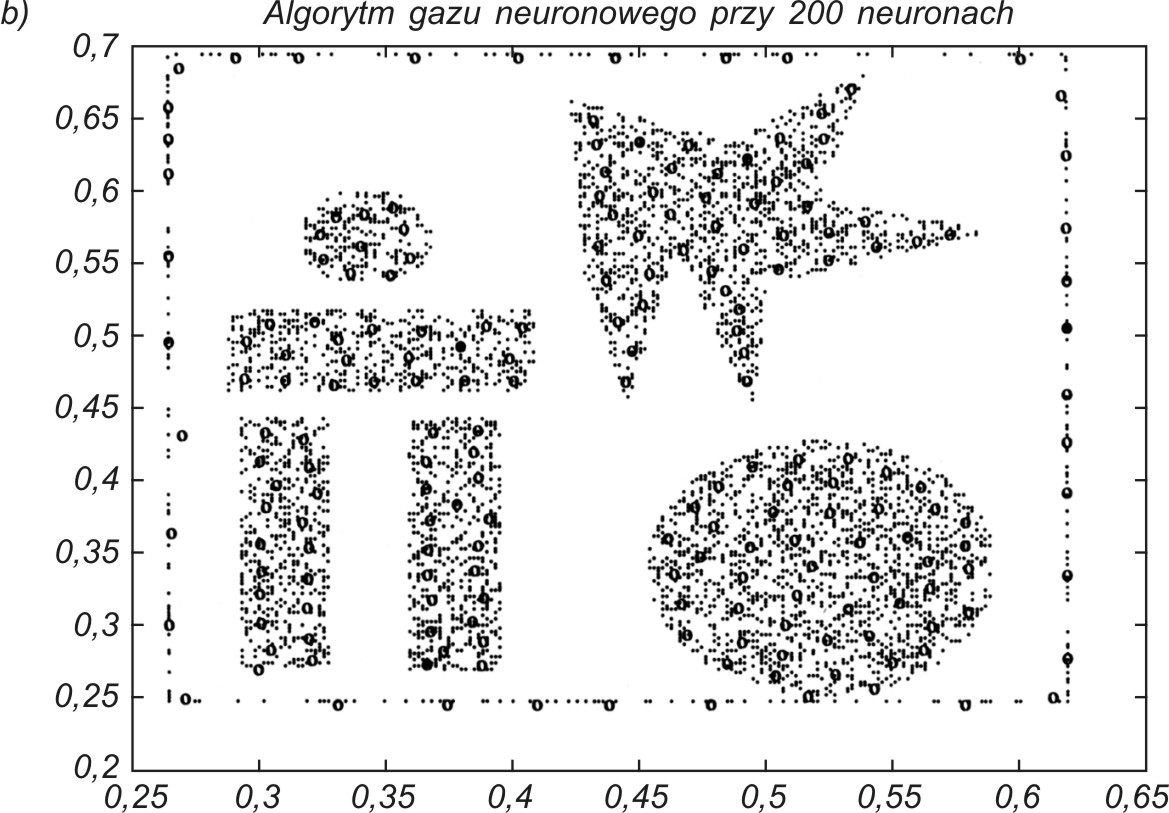
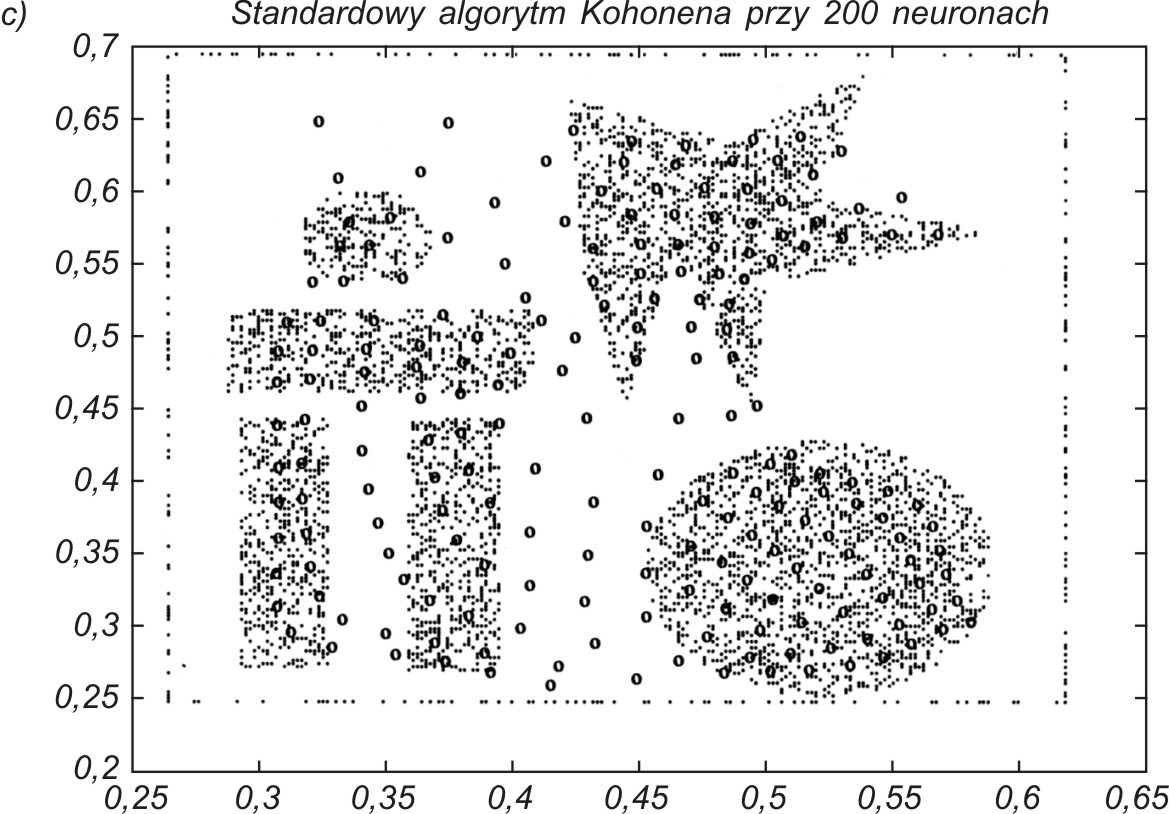
Najlepsze wyniki organizacji otrzymuje się za pomocą algorytmu CWTA oraz gazu neuronowego, przy czym ten ostatni ze względu na sortowanie jest zdecydowanie wolniejszy od CWTA. Oryginalny algorytm Kohonena okazał się najmniej efektywny, nie pozwalając na dobre odwzorowanie danych (pewna liczba neuronów jest uplasowana w obszarze pozbawionym danych).
Dobre porównanie ilościowe wyników samoorganizacji otrzymuje się, zestawiając uzyskane błędy kwantyzacji ε (wzór (7.9)) dla każdego przypadku. Przy 200 neuronach uzyskano: ε= 0,007139 - dla CWTA, ε = 0,007050 - dla gazu neuronowego oraz ε= 0,010763 - dla algorytmu Kohonena. Wyniki liczbowe potwierdzają wzrokową ocenę odwzorowania danych, że algorytmy CWTA i gazu neuronowego dają podobne (najlepsze) wyniki, a algorytm Kohonena jest najmniej efektywny.
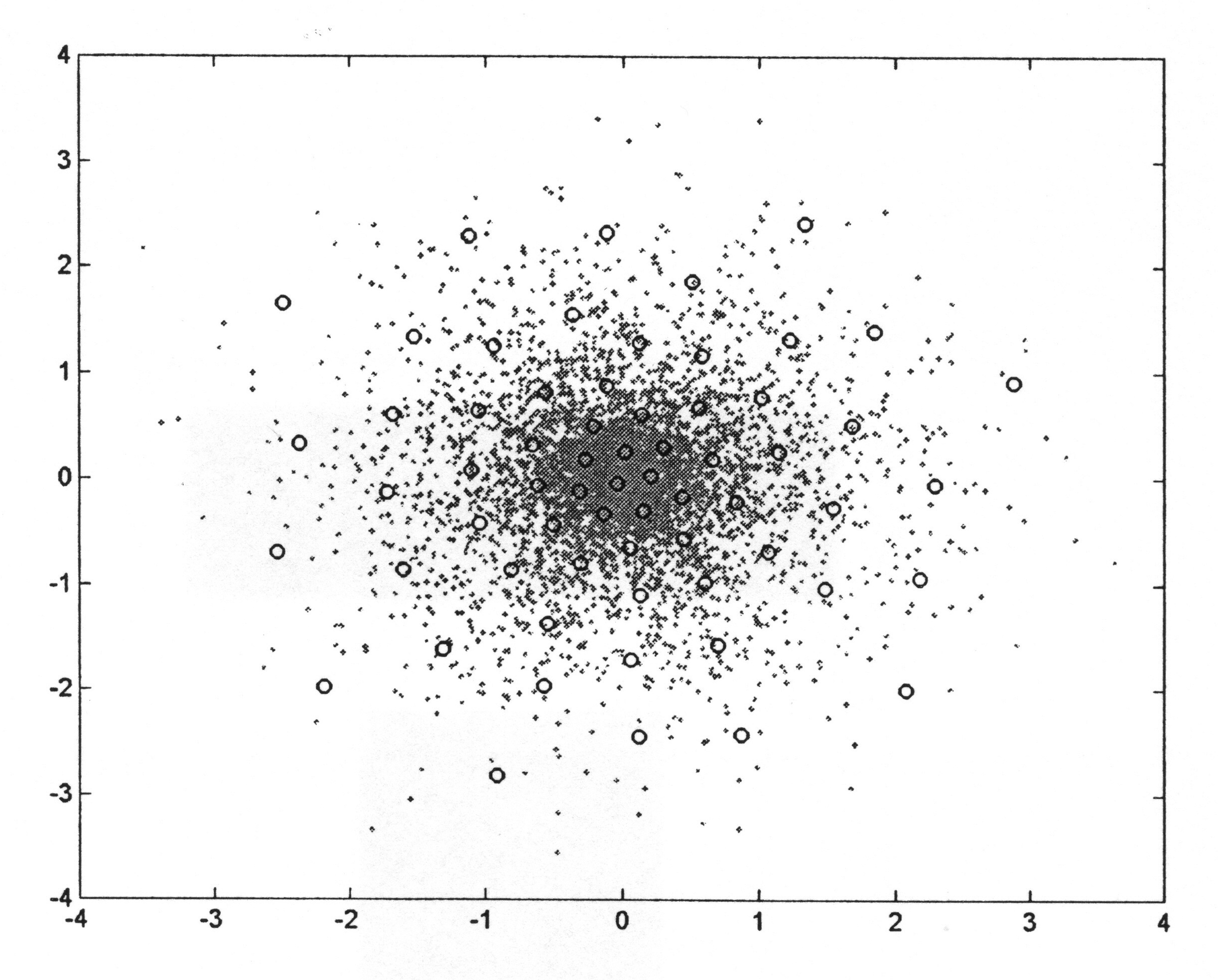
Na rys. 7.14 przedstawiono wynik odwzorowania danych o rozkładzie nierównomiernym przy zagęszczeniu danych w środku obszaru. Uzyskany rozkład neuronów bardzo dobrze odzwierciedla rozkład punktów danych, tworząc gęstsze skupiska w rejonach środkowych, gdzie jest największe zagęszczenie danych.
1.6. Sieć odwzorowań jedno- i dwuwymiarowych
Przy ocenie jakości sieci neuronowej samoorganizującej ważną rolę odgrywa odwzorowanie danych jedno- i dwuwymiarowych, ze względu na czytelny i przejrzysty sposób interpretacji wyników na płaszczyźnie \(x, y \). Biorąc pod uwagę, że wagi neuronów są odpowiednikiem współrzędnych punktów centralnych klastrów, na jakie dzielony jest zbiór danych, można każdemu wektorowi wagowemu przypisać odpowiedni punkt na płaszczyźnie. Łącząc te punkty z najbliższymi sąsiadami otrzymuje się regularną siatkę, odwzorowującą topograficzny rozkład danych (siatka prostokątna lub heksagonalna). Przy równomiernym rozkładzie wektorów uczących \( x \) na płaszczyźnie spodziewane odwzorowanie wagowe poszczególnych neuronów przedstawione na płaszczyźnie powinno być równomierne. Jeśli rozkład danych jest nierównomierny, zagęszczenie wystąpi tam, gdzie prawdopodobieństwo wystąpienia wektorów uczących jest większe (patrz rys. 7.14).
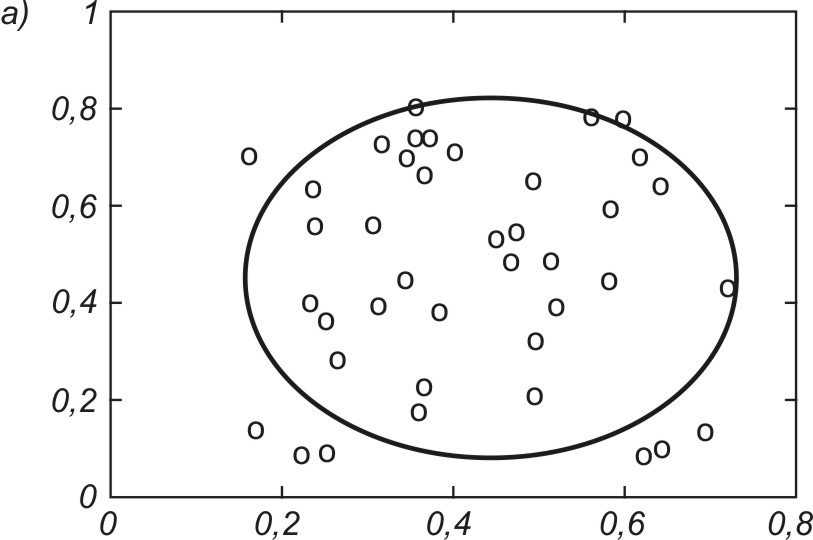
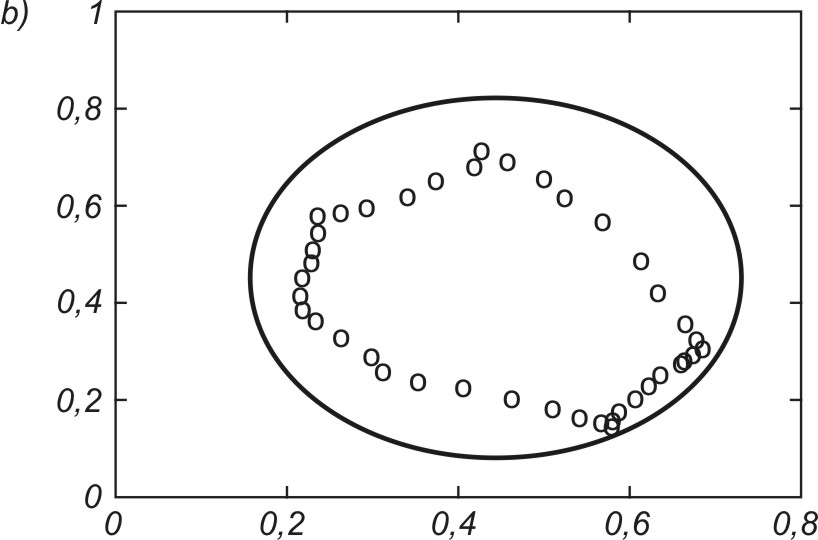
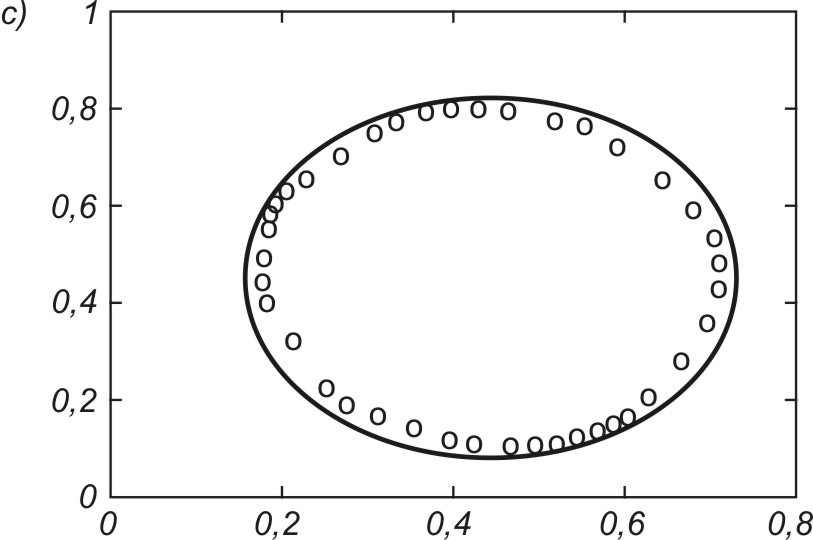
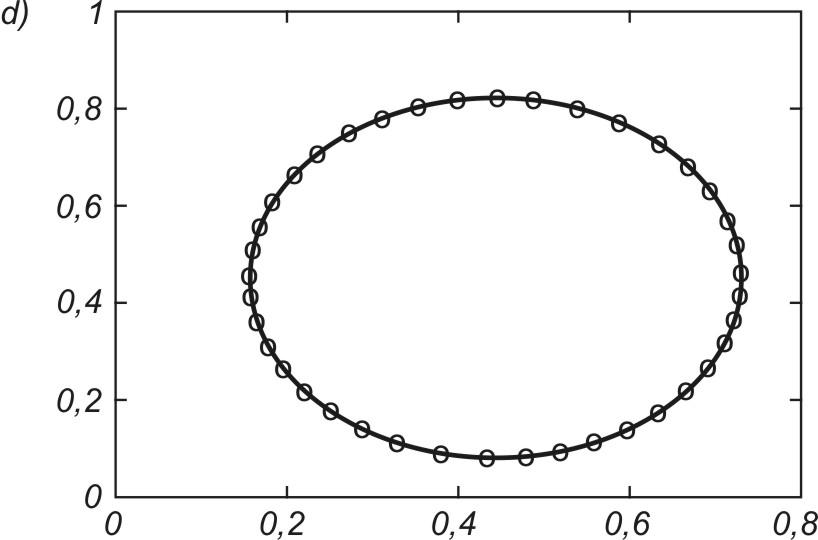
Dobrym testem algorytmów uczących sieci jest odwzorowanie kształtu danych jednowymiarowych za pomocą sieci samoorganizującej. Przykładowo na rys. 7.15 zilustrowano proces samoorganizacji 40 neuronów odwzorowujących układ danych tworzących kształt eliptyczny (pozycje neuronów zaznaczone kółkami). Rys. 7.15a przedstawia stan wyjściowy wag neuronów (rozkład losowy), rys. 7.15b – stan po dwóch cyklach uczących, rys. 7.15c – stan po pięciu cyklach uczących, a rys. 7.15d – stan końcowy (po dziesięciu cyklach) na tle danych uczących tworzących kształt eliptyczny. Uczenie było przeprowadzone przy użyciu programu Kohon i algorytmu gazu neuronowego.
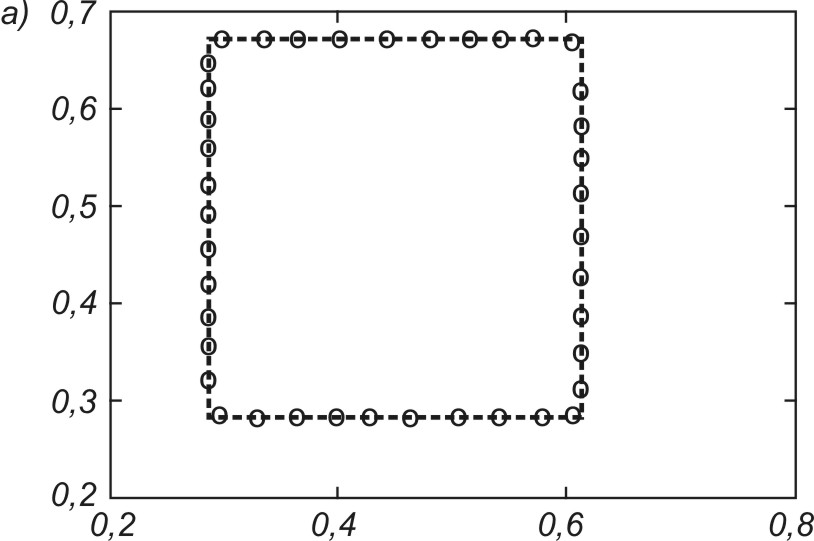
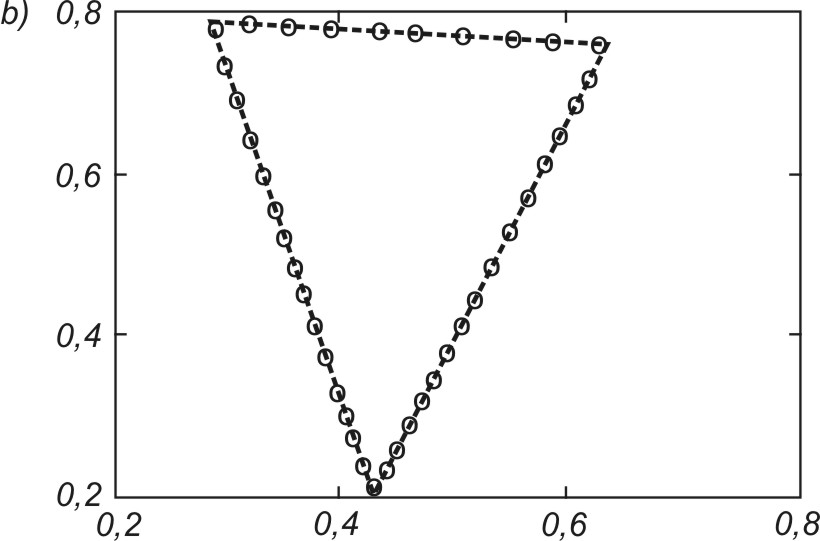
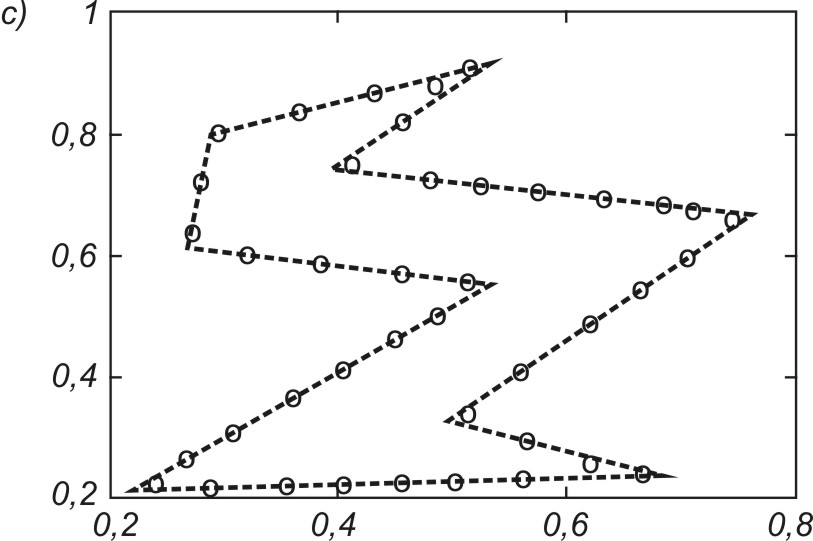
Na rys. 7.16 podano wyniki końcowe uporządkowania neuronów przy odwzorowaniu różnego rodzaju kształtów utworzonych przez dane na płaszczyźnie (x,y). W każdym przypadku wagi neuronów plasują się w strefach występowania danych w taki sposób, aby zminimalizować błąd kwantyzacji. Należy nadmienić, że podstawowa zaleta sieci samoorganizujących się jest widoczna w całej pełni dopiero przy danych wielowymiarowych, gdzie zawodzi zdolność człowieka do wyobrażenia sobie ich rozkładu przestrzennego.
Mechanizmy samoorganizacji wbudowane w algorytmy uczące takich sieci działają niezależnie od wymiarowości problemu. Istotną funkcją pełnioną przez sieć jest tutaj kwantowanie wektorowe, polegające na tym, że ogromna liczba danych tworzących klaster jest odwzorowana przez wektor wagowy jednego neuronu reprezentującego każdy punkt w przestrzeni. Rozkład przestrzenny neuronów pozwala więc określić rozkład skupień danych w przestrzeni wielowymiarowej oraz zasadnicze cechy statystyczne rozkładu danych, przydatne z punktu widzenia użytkownika (centra grup, rozproszenie mierzone wariancją danych w grupie, odległości między centrami różnych grup, itp.)
1.7. Przykłady zastosowań sieci samoorganizujących w kompresji danych
Podstawową cechą sieci samoorganizujących się jest kompresja danych, polegająca na tym, że duże grupy danych tworzących klaster reprezentowane są przez pojedynczy wektor wagowy neuronu zwycięzcy. Przy p danych podzielonych na P klastrów i reprezentacji każdego klastra przez jeden z n neuronów uzyskuje się znaczne zmniejszenie ilości informacji, zwane kompresją. Jest to kompresja typu stratnego, której towarzyszy pewien błąd kwantowania określony zależnością (7.10).
Przykładem wykorzystania kompresyjnych własności sieci Kohonena jest kompresja stratna obrazów, mająca za zadanie zmniejszenie ilości informacji reprezentującej dany obraz, przy zachowaniu błędu odwzorowania na określonym poziomie (zapewnienie odpowiednio dużej wartości współczynnika PSNR mierzącego stosunek sygnału do szumu). Zakłada się, że obraz o wymiarach \( N_x \times N_y \) pikseli podzielony jest na równomierne ramki zawierające \( n_x \times n_y \) pikseli. Piksele każdej ramki stanowią składowe wektorów wejściowych \( \mathbf{x} \). Każdy zawiera \( n_x n_y \) składników, reprezentujących stopień szarości poszczególnych pikseli w ramce. Przyporządkowanie pikselom wektora może się odbywać przez złączenie poszczególnych wierszy ramki w jeden ciąg bądź przez zastosowanie przyporządkowania typu zygzakowego, stosowanego między innymi w standardzie JPEG.
Sieć samoorganizująca zawiera n neuronów, każdy połączony wagami synaptycznymi ze wszystkimi składnikami wektora wejściowego \( \mathbf{x} \). Uczenie sieci przy zastosowaniu jednego z algorytmów samoorganizacji polega na takim doborze wag poszczególnych neuronów, aby zminimalizować błąd kwantyzycji (7.10). W wyniku procesu uczenia następuje taka organizacja sieci, przy której wektorowi \( \mathbf{x} \) każdej ramki odpowiada wektor wagowy neuronu zwycięzcy minimalizujący błąd kwantyzacji. Przy podobnym ukształtowaniu składników wektora \( \mathbf{x} \) różnych ramek zwyciężać będzie ten sam neuron albo grupa neuronów o podobnych wektorach wagowych. Podczas kolejnej prezentacji ramek ustala się numery neuronu zwycięzcy dla poszczególnych ramek np. 1, 1, 3, 80 itd. Numery neuronów zwycięzców tworzą książkę kodową, a wagi tych neuronów reprezentują uśrednioną wartość odpowiadającą poszczególnym składowym wektora \( \mathbf{x} \) (stopień szarości pikseli tworzących ramkę). Wektory te będą przy odtwarzaniu obrazu reprezentować poszczególne ramki. Biorąc pod uwagę, że liczba neuronów \( n \) jest zwykle dużo mniejsza od liczby ramek \( N_r \), otrzymuje się zmniejszenie ilości informacji przypisanej danemu obrazowi (kompresja).
Przy określaniu stopnia kompresji należy uwzględnić również określoną liczbę bitów użytych do zakodowania numerów neuronów zwycięzców dla poszczególnych ramek. Ostatecznie współczynnik kompresji obrazu definiuje się w postaci [46].
| \( K_r=\frac{N_r n_x n_y T}{N_r \lg _2 n+n n_x n_y t} \) | (1.1) |
gdzie \( n_x \) i \( n_y \) oznaczają wymiary ramki w osiach \(x , y, N_r \) - liczbę ramek, \( n \) - liczbę neuronów, a \( T \) i \( t \) - liczbę bitów przyjętych w reprezentacji odpowiednio stopnia szarości pikseli i wartości wag. Jakość obrazu odtworzonego charakteryzuje się najczęściej przy użyciu miary PSNR, określonej wzorem
| \( PSNR=10 \log \left(\frac{255^2}{MSE}\right) \) |
(1.1) |
gdzie \(MSE\) oznacza wartość błędu średniokwadratowego obrazu odtworzonego względem obrazu oryginalnego. Zastosowanie sieci samoorganizującej do kompresji umożliwia uzyskanie współczynnika kompresji obrazów rzędu nawet 16 przy współczynniku \(PSNR\) około 25-28 dB.
Na rys. 7.17a przedstawiono wyniki uczenia sieci Kohonena dla obrazu Barbara o wymiarach \( 512 \times 512 \) pikseli, podzielonego na ramki 16-elementowe (podobrazy o wymiarach \( 4 \times 4 \)) [43]. Sieć Kohonena zawierała 512 neuronów. Przy 8-bitowej reprezentacji danych uzyskano stopień kompresji równy: \( K_r = 9.9 \). Na rys. 7.17b pokazano obraz odtworzony na podstawie wag neuronów zwyciężających przy prezentacji kolejnych ramek. Współczynnik \( PSNR \) dla obrazu odtworzonego wynosił 26,2dB. Różnice w jakości obrazu oryginalnego (rys. 7.17a) i odtworzonego (rys. 7.17b) są stosunkowo małe. Widoczne jest to na rys. 7.17c, oddającym obraz błędu, który jest różnicą między obrazem oryginalnym a odtworzonym po kompresji.



Ważną zaletą sieci neuronowych, z całą wyrazistością uwidaczniającą się przy kompresji obrazów, jest zdolność generalizacji, a więc możliwość skompresowania (przyporządkowania poszczególnym ramkom nowego obrazu numerów neuronów zwycięzców wytrenowanej wcześniej sieci) i zdekompresowania (przypisania odpowiednich wektorów wagowych zwycięzców poszczególnym ramkom). Jakość odtworzonego obrazu, który nie podlegał wcześniej procesowi uczenia, nie odbiega daleko od jakości obrazu poddanego uczeniu, pod warunkiem, że stopnie zróżnicowania obu obrazów są podobne.
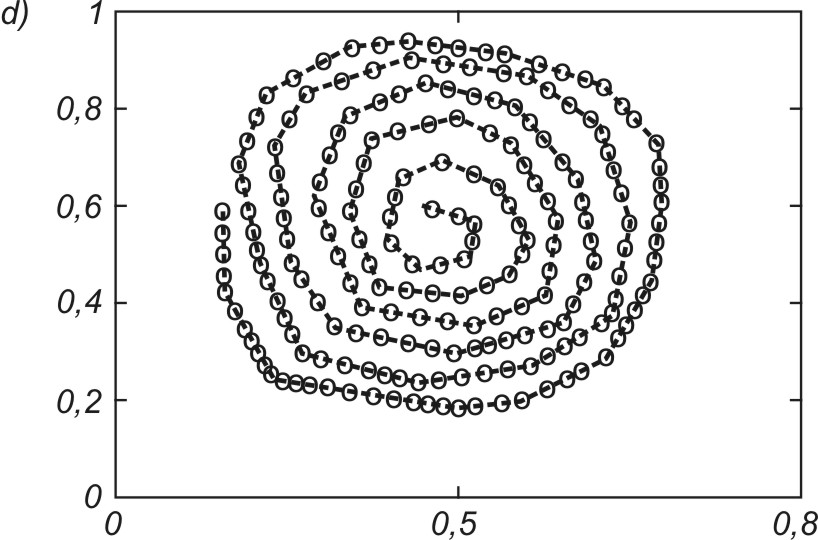
Na rys. 7.18 przedstawiono przykładowy obraz linii papilarnych, poddany procesowi kompresji i dekompresji za pomocą sieci Kohonena, wytrenowanej przy zastosowaniu obrazu z rys. 7.17 [43]. Rysunek 9.18a jest obrazem oryginalnym, rys. 7.18b - obrazem zrekonstruowanym po kompresji, a rys. 7.18c obrazem różnicowym ilustrującym błąd kompresji. Stopień zniekształcenia obrazu odtworzonego jest porównywalny z obrazem poddanym uczeniu, a współczynnik zniekształcenia \( PSNR = 26,4 dB\).


1.8. Zadania i problemy
1. Określić i porównać ze sobą odległości między dwoma wektorami
\( \mathbf{x}_1 =\begin{bmatrix} 0,2 \\ 0,6 \\ -0,5 \\ 0.4 \\ 0.9 \\ 0.7 \end{bmatrix},\; \mathbf{x}_2 =\begin{bmatrix} -0,2 \\ 0,1 \\ 0,6 \\ -0.3 \\ 0.4 \\ -0.2 \end{bmatrix}.\; \)
stosując różne normy: euklidesową, \( L_1, L_\infty, L_M \) oraz w postaci iloczynu skalarnego.
2. Dwa neurony o wagach \( \mathbf{w}_1 = [ 0.8 \; 0.9 \; 0.3] \), \(\mathbf{w}_2=[-0.1 \; 0.7 \; 0.5] \) otrzymały pobudzenia \( \mathbf{x}_1 = [0.5 \; 0.7 \; 0]\) , \(\mathbf{x}_2 = [0.1 \; 0.7 \; 0.4], \mathbf{x}_3 =[0.2 \; 0.5 \; 0.3] \). Wyłonić zwycięzców dla każdego pobudzenia.
3. Trzy neurony o wagach \( \mathbf{w}_1 =[0.3 \; 0.8 \; 0.9] \), \( \mathbf{w}_2 =[-0.2 \; 0.5 \; 0.1]\), \( \mathbf{w}_3 =[-0.7 \; -0.4 \; 0.6]\) otrzymały pobudzenie w postaci wektora \( \mathbf{x} =[0.2 \; 0.6 \; 0.5] \). Określić kolejność neuronów konkurujących ze sobą w algorytmie gazu neuronowego. Wyznaczyć wartość funkcji sąsiedztwa w metodzie gazu neuronowego przy założeniu \( \lambda = 0.5 \).
4. Dokonać normalizacji wektorów \( \mathbf{x} \) danych w postaci \( \mathbf{x}_1 = [1 \; 3 \; 8]\), \( \mathbf{x}_2 = [5 \;9 \; 20]\) stosując rozszerzenie wektora i bez rozszerzania.
5. Korzystając z programu KOHON dokonać odwzorowania liniowego (jeden z wymiarów w osi \( x \) lub \( y \) równy \( 1 \)) danych jednowymiarowych tworzących różne kształty (spirala, koło, wielobok) stosując odwzorowanie Kohonena z uwzględnieniem dwu sąsiadów.
6. Korzystając z programu KOHON określić położenia wektorów wag neuronów mapy Kohonena odwzorowujących różne rozkłady danych na płaszczyźnie: rozkład równomierny w założonym kształcie maski, rozkład gaussowski, maski nieregularne. Zastosować odwzorowanie Kohonena z uwzględnieniem czterech sąsiadów.
7. Korzystając z programu KOHON określić położenia wektorów wag neuronów mapy Kohonena odwzorowujących rozkład danych na płaszczyźnie przy zadanym kształcie maski (koło, prostokąt trójkąt). Zastosować odwzorowanie jednowymiarowe Kohonena z uwzględnieniem tylko dwu sąsiadów (jeden z wymiarów \(n_x \) lub \( n_y \) równy \( 1\)).
1.9. Słownik
Wykład 7
Sieci Kohonena – sieci samoorganizujące poprzez współzawodnictwo i służące do grupowania danych wielowymiarowych w klastry reprezentowane przez centra.
WTA – strategia uczenia sieci samoorganizujących się przez konkurencję, gdzie tylko neuron zwycięzca adaptuje swoje wagi.
CWTA – zmodyfikowana strategia wyłaniania zwycięzcy w uczeniu WTA sieci samoorganizujących przez konkurencję, gdzie tylko neuron zwycięzca adaptuje swoje wagi.
WTM – strategia uczenia sieci samoorganizujących się przez konkurencję, gdzie neuron zwycięzca i jego najbliższe otoczenie adaptują swoje wagi.
Mapa Kohonena – sposób graficznego przedstawienia rozkładu danych wielowymiarowych w przestrzeni dwu-wymiarowej.
Normalizacja wektorów – przeskalowanie wektorów do określonego zakresu zmian wartości ich elementów.
Neuron martwy – neuron, który nigdy nie zwyciężył w konkurencji.
Kwantyzacja wektorowa – zastąpienie wartości wektorów w klastrze danych przez centrum danego klastra.
Błąd kwantyzacji – sumaryczny błąd popełniany przy reprezentacji danych tworzących klaster przez centrum tego klastra.
Algorytm gazu neuronowego – jedna z implementacji strategii WTM w uczeniu sieci samoorganizujących poprzez konkurencję.
Odwzorowanie Sammona – nieliniowe rzutowanie danych z dowolnej przestrzeni N-wymiarowej w przestrzeń M-wymiarową
Program Kohon – graficzny interfejs użytkownika w Matlabie do eksperymentów z siecią Kohonena.
PSNR – miara jakości obrazu zrekonstruowanego w stosunku do obrazu oryginalnego.
2. Transformacja i sieci neuronowe PCA
Ważnym typem sieci samoorganizujących są sieci, dla których w procesie uczenia wykorzystuje się współzależności między sygnałami. Sieci takie należą do klasy sieci korelacyjnych, zwanych również hebbowskimi. W trakcie uczenia wykrywają one istotne cechy powiązań korelacyjnych między sygnałami, ucząc się ich i dostosowując do nich wartości swoich wag synaptycznych. W tym rozdziale zostaną omówione aspekty samoorganizacji przy zastosowaniu transformacji PCA (ang. Principal Component Analysis). Transformacja ta jest z natury liniowa (neurony liniowe, powiązania międzyneuronowe liniowe) pozwalając na redukcję wymiarowości wektora wejściowego przy zachowaniu maksimum informacji w nim zawartej.
2.1. Transformacja PCA
Analiza składników głównych PCA jest metodą statystyczną określającą przekształcenie liniowe \( \mathbf{y} = \mathbf{Wx} \) transformujące opis stacjonarnego procesu stochastycznego dany w postaci zbioru N-wymiarowych wektorów \( \mathbf{x} \) w zbiór wektorów \( \mathbf{y} \) o zredukowanej wymiarowości \( K \le N \) [13,46]. Przekształcenie to odbywa się za pośrednictwem macierzy \( \mathbf{W} \) o wymiarach \( K \times N \) w taki sposób, że przestrzeń wyjściowa o zredukowanym wymiarze zachowuje najważniejsze informacje dotyczące procesu. Innymi słowy, transformacja PCA zamienia dużą ilość informacji zawartej we wzajemnie skorelowanych danych wejściowych w zbiór statystycznie niezależnych składników, według ich ważności. Stanowi zatem formę kompresji stratnej, znanej w teorii komunikacji jako transformacja Karhunena--Loeve.
Dla zachowania maksimum informacji oryginalnej w zbiorze wektorów \( \mathbf{y} \) o zredukowanym wymiarze macierz transformacji \( \mathbf{W} \) powinna być dobrana w taki sposób, aby zmaksymalizować wartość wyznacznika \( J \) [49]
| \( \max _{\mathbf{w}} J=\left|\mathbf{W}^T \mathbf{R}_{xx} \mathbf{W}\right| \) | (8.1) |
W wyrażeniu tym \( \mathbf{R}_{\mathbf{xx}} \) oznacza macierz kowariancji wektorów \( \mathbf{x} \) (przy zerowych wartościach średnich zbioru \( x \) macierz kowariancji jest równa macierzy korelacji). W praktyce centrowanie wektorów nie jest konieczne i można posługiwać się macierzą korelacji, niezależnie od zerowania się wartości średnich. Rozwiązanie powyższego problemu optymalizacyjnego uzyskuje się na podstawie rozkładu macierzy kowariancji zbioru wektorów \( \mathbf{x} \) według wartości własnych.
Przyjmijmy, że \( \mathbf{x} = [x_1, x_2, \ldots, x_N]^T \) oznacza wektor losowy o zerowej wartości średniej, a \( \mathbf{R}_{\mathbf{xx}} = E[\mathbf{xx}]^T \) oznacza wartość oczekiwaną (średnią) macierzy autokorelacji (autokowariancji) po wszystkich wektorach \( \mathbf{x} \). Macierz tę, przy skończonej liczbie \( p \) wektorów \( \mathbf{x} \), można estymować przy pomocy zależności
| \( \mathbf{R}_{\mathbf{xx}}=\frac{1}{p} \sum_{k=1}^p \mathbf{x}^k \mathbf{x}_k^T=\frac{1}{p} \mathbf{X} \mathbf{X}^T \) | (8.2) |
gdzie macierz danych \( \mathbf{X} \) tworzą kolejne wektory uczące \( \mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_p]^T \). Oznaczmy przez \( \lambda_i \) wartości własne macierzy autokorelacji \(\mathbf{R_{xx}} \), a przez \( \mathbf{w}_i \) ortogonalne wektory wartości własnych, skojarzone z nimi, przy czym \( \mathbf{w} = [w_{i1}, w_{i2}, , \ldots, w_{iN}]^T \). Wartości własne oraz wektory własne macierzy \( \mathbf{R_{xx}} \) powiązane są zależnością
| \( \mathbf{R}_{x x} \mathbf{w}_i=\lambda_i \mathbf{w}_i \) | (8.3) |
dla \( i=1, 2, …, N \). Wartości własne symetrycznej, nieujemnie określonej macierzy korelacji \(\mathbf{R_{xx}} \) są rzeczywiste i nieujemne. Uporządkujmy je w kolejności malejącej poczynając od wartości największej \( \lambda_1 > \lambda_2 > \ldots \lambda_N \ge 0 \). W identycznej kolejności ustawimy wektory własne \( \mathbf{w}_i \) skojarzone z odpowiednimi wartościami własnymi \( \lambda_i \). Przy ograniczeniu się do \( K \) największych wartości własnych macierz \( \mathbf{W} \) przekształcenia PCA definiuje się w postaci
| \( \mathbf{W}=\left[\mathbf{w}_1, \mathbf{w}_2, \cdots, \mathbf{w}_K\right]^T \) | (8.4) |
Macierz ta określa transformację PCA jako przekształcenie liniowe
| \( \mathbf{y}=\mathbf{Wx} \) | (8.5) |
Wektor y =[y1, y2,…, yK]T stanowi wektor składników głównych PCA, mających największy wpływ na rekonstrukcję oryginalnego wektora danych x =[x1, x2,…, xN]T. Transformacja PCA jest więc ściśle związana z rozkładem macierzy korelacji według wartości własnych. Uwzględnia zatem jedynie powiązania liniowe między wektorami danych.
Oznaczmy przez \( \mathbf{L} \) macierz diagonalną utworzoną z wartości własnych \( \lambda_i \) uwzględnionych w odwzorowaniu, to jest \( \mathbf{L} = diag\{ {\lambda_1, \lambda_2, \ldots, \lambda_K}\} \). Przy takich oznaczeniach macierz korelacji można przedstawić w postaci zdekomponowanej
| \( \mathbf{R}_{\mathbf{xx}} \cong \mathbf{W}^T \mathbf{L W} \) | (8.6) |
gdzie znak przybliżenia wynika z uwzględnienia skończonej liczby (mniejszej niż wymiar macierzy korelacji) składników głównych. Przy \( K=N \) zależność (8.6) będzie spełniona ze znakiem równości. Uwzględniając symetrię macierzy korelacji zależność tę można jednocześnie przedstawić w postaci
| \( \mathbf{R}_{\mathbf{xx}} \cong \sum_{i=1}^K \lambda_i \mathbf{w}_i \mathbf{w}_i^T \) | (8.7) |
Z punktu widzenia statystycznego transformacja PCA określa zbiór \( K \) wektorów ortogonalnych (kolejne wiersze macierzy \( \mathbf{W} \)), mających największy wkład w wariancję danych wejściowych. Pierwszy składnik główny odpowiadający wektorowi \( \mathbf{x} \) jest równy iloczynowi skalarnemu wektora własnego \( \mathbf{w}_1 \) i wektora wejściowego \( \mathbf{x} \)
| \( y_1=\mathbf{w}_1^T \mathbf{x} \) | (8.8) |
Wektor własny \( \mathbf{w}_1 \) określa zatem kierunek w przestrzeni wielowymiarowej w którym występuje największa wariancja (zmienność wartości) danych wejściowych zawartych w wektorach \( \mathbf{x} \). Wariancja ta jest równa wartości własnej \( \lambda_1 \)
| \( \lambda_1=\operatorname{var}\left(y_1\right)=\operatorname{var}\left(\mathbf{w}_1^T \mathbf{x}\right) \) | (8.9) |
Celem transformacji PCA jest określenie kierunków \( \mathbf{w}_1, \mathbf{w}_2, \ldots, \mathbf{w}_K \) (zwanych kierunkami głównymi) w taki sposób, aby zmaksymalizować wielkość iloczynu skalarnego \( \mathbf{E} (\mathbf{w}_i^T\mathbf{x}) \) dla kolejnych wartości \( i=1, 2, …, K \) przy spełnieniu warunku ortogonalności kolejnych wektorów \( \mathbf{w} \) ze sobą, to jest \( \mathbf{w}_i^T \mathbf{w}_j = 0\) oraz \( \mathbf{w}_i^T \mathbf{w}_i = 1\) .
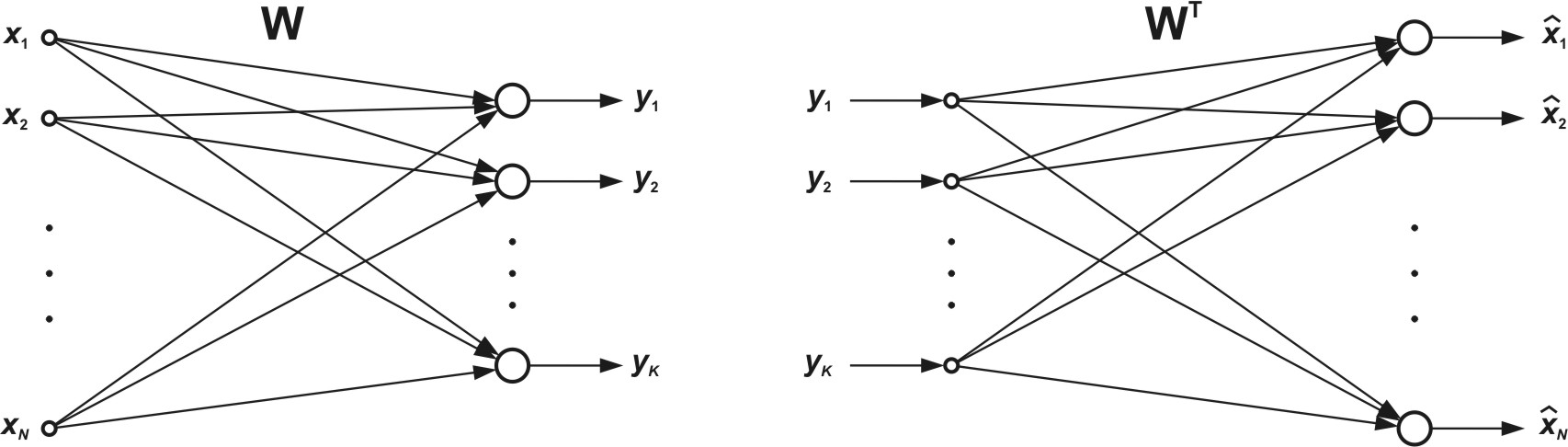
Rekonstrukcja wektora \( \mathbf{x} \) na podstawie znajomości wektora składników głównych \( \mathbf{y} \) oraz macierzy ortogonalnej \( \mathbf{W} \) przekształcenia PCA odbywa się zgodnie z zależnością [46]
| \( \hat{\mathbf{x}}=\mathbf{W}^T \mathbf{y} \) | (8.10) |
Macierz \( \mathbf{W} \) dekompozycji PCA i macierz rekonstrukcji (\( \mathbf{W}^T \)) stanowią wzajemne transpozycje. PCA minimalizuje wartość oczekiwaną błędu rekonstrukcji danych, przy czym błąd ten określony jest wzorem ogólnym
| \( \varepsilon_r = E[ \| \mathbf{x}-\hat{\mathbf{x}} \| ]^2 \) | (8.11) |
Przy ograniczeniu się do \( K \) największych wartości własnych (\(K\) składników głównych), błąd ten jest proporcjonalny do sumy odrzuconych wartości własnych \( \sum_{i=K+1}^N \lambda_i \).
Ze wzoru tego wynika, że minimalizacja błędu rekonstrukcji danych przy uwzględnieniu \(K\) składników jest równoważna maksymalizacji wariancji rzutowania \( \varepsilon_v \) na etapie rozkładu PCA
| \( \max \varepsilon_v=\sum_{i=1}^K \lambda_i \) | (8.12) |
Zarówno \( \varepsilon_r \), jak i \( \varepsilon_v \) są nieujemne, gdyż wszystkie wartości własne macierzy korelacji, jako macierzy symetrycznej i nieujemnie określonej, są dodatnie bądź zerowe. Wnosimy stąd, że reprezentacja wektora danych \( \mathbf{x} \) przez największe składniki główne \( y_1, y_2, \ldots, y_K \) tworzące wektor \( \mathbf{y} \) jest równoważna zachowaniu informacji o największej porcji energii zawartej w zbiorze danych.
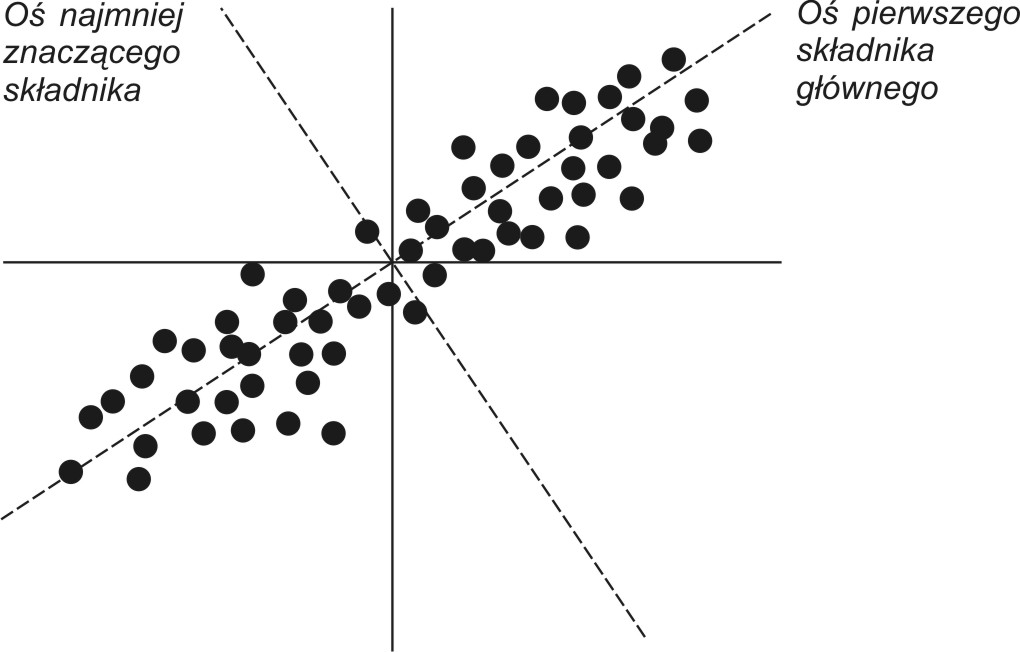
Pierwszy (największy) składnik główny powiązany z \( \lambda_1 \) przez swój wektor własny \( \mathbf{w}_1 \) określa kierunek w przestrzeni wielowymiarowej, w którym wariancja danych jest maksymalna. Ostatni najmniejszy składnik główny (ang. Minor Principal Component) wskazuje kierunek, w którym wariancja jest najmniejsza. Na rys. 8.1 przedstawiono interpretację geometryczną najbardziej znaczącego i najmniej znaczącego składnika głównego transformacji PCA dla danych 2-wymiarowych. Pierwszy składnik główny odpowiada kierunkowi największej zmienności mierzonej poprzez wariancję (energię) sygnałów. Dokonując reprezentacji danych tylko za pomocą jednego składnika głównego oraz skojarzonego z nim wektora własnego i wybierając jako reprezentanta największy ze składników głównych (\(y_1\)), popełnia się najmniejszy błąd rekonstrukcji, maksymalizując jednocześnie wariancję transformacji. Najmniej znaczący składnik główny ma najmniejszy wpływ na dokładność odtworzenia danych. Stąd kompresja danych (zmniejszenie ilości informacji z najmniejszą stratą dla rekonstrukcji) wymaga reprezentowania tych danych przez zbiór największych składników głównych. Pominięcie składników najmniejszych ma najmniej znaczący wpływ na dokładność rekonstrukcji danych.
Transformacja PCA jest ściśle związana z korelacją zachodzącą między wieloma zmiennymi w zbiorze danych. Jeśli te zmienne są skorelowane ze sobą, to znajomość jedynie części z nich wystarczy do określenia pozostałych. Stąd taki zbiór danych może być reprezentowany przez mniejszą liczbę zmiennych. W przypadku gdy nie występuje korelacja między zmiennymi tworzącymi wektor x, predykcja części z nich na podstawie pozostałych jest niemożliwa.
8.1.2 Przykład zastosowania PCA w ekonomii
Jako przykład ilustrujący właściwości rozkładu danych na składniki główne rozpatrzone będą dane GUS-u dotyczące wielkości związanych z miesięcznymi wartościami odpowiadającymi wskaźnikowi cen i usług konsumpcyjnych (wcu), stopie bezrobocia (sb), wartości produkcji sprzedanej w przemyśle (wps) oraz średniej płacy miesięcznej (spm) w Polsce. Przykład ten wykorzystuje dane statystyczne GUS z 10.5 lat (126 wartości).
Wektory pomiarowe x tworzą w tym przypadku cztery składowe, kolejno: wcu, sb, wps oraz spm. Stosując definicję macierzy korelacji (wzór 10.2) w wyniku obliczeń otrzymano macierz korelacji Rxx w postaci
\( \mathbf{R}_{\mathbf{xx}}=10^6\left[\begin{array}{llll}
0.0108 & 0.0017 & 0.0175 & 0.2564 \\
0.0017 & 0.0003 & 0.0027 & 0.0390 \\
0.0175 & 0.0027 & 0.0286 & 0.4226 \\
0.2564 & 0.0390 & 0.4226 & 6.2953
\end{array}\right] \)
Dokonując dekompozycji tej macierzy według wartości własnych uzyskuje się następujące wartości własne (w kolejności malejącej):
\( \lambda_1 = 6334324.26 \)
\( \lambda_2 = 590.69 \)
\( \lambda_3 = 24.10 \)
\( \lambda_4 = 7.48 \)
oraz skojarzone z nimi wektory własne
\( \mathbf{w}_1=\left[\begin{array}{r} 0.0406 \\ 0.0062 \\ 0.0669 \\ 0.9969 \end{array}\right] \), \( \mathbf{w}_2=\left[\begin{array}{r} -0.7609 \\ -0.1859 \\ -0.6173 \\ 0.0736 \end{array}\right] \), \( \mathbf{w}_3=\left[\begin{array}{r} -0.6464 \\ 0.2778 \\ 0.7102 \\ -0.0231 \end{array}\right] \), \( \mathbf{w}_4=\left[\begin{array}{r} -0.0402 \\ -0.9424 \\ 0.3316 \\ -0.0148 \end{array}\right] \)
Na tej podstawie określa się pełną macierz transformacji PCA, zawierającą wszystkie wektory własne ułożone według największego znaczenia (w zależności od wielkości wartości własnych \( \lambda_i \)): \(\mathbf{W}=\left[\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3, \mathbf{w}_4\right]^T\) w postaci
\( \mathbf{W}=\left[\begin{array}{rrrr}0.0406 & 0.0062 & 0.0669 & 0.9969 \\ -0.7609 & -0.1859 & -0.6173 & 0.0736 \\ -0.6464 & 0.2778 & 0.7102 & -0.0231 \\ -0.0402 & -0.9424 & 0.3316 & -0.0148\end{array}\right] \)
oraz macierz diagonalną \(\mathbf{L}\) złożoną z wartości własnych macierzy \(\mathbf{R_{xx}} \) ułożonych według malejących wielkości \( \mathbf{L} = diag \{6334324.26, 590.69, 24.10, 7.48 \} \). Największa wartość własna \( \lambda_1 = 6334324.26\) skojarzona jest z pierwszym składnikiem głównym odpowiadającym wektorowi własnemu \( \mathbf{w}_1 \), stanowiącemu pierwszy wiersz macierzy \(\mathbf{W} \). Składnik ten przy wektorze wejściowym \(\mathbf{x} \) złożonym z czterech elementów (\(wcu, sb., wps, spm\)) opisany jest relacją \( y_1 = \mathbf{w}_1^T\mathbf{x}\), która w tym przypadku przybiera konkretną postać: \( y_1 = 0,0406*wcu + 0,0062*sb + 0,0.0669*wps + 0.9969*spm \). Jak widać największy wpływ na składnik główny \( y_1\) ma zmienna \( spm \). Każda z wartości własnych \( \lambda_i \) odpowiada wariancji jaką reprezentuje dany składnik główny. Względny wkład poszczególnych składników głównych w łączną wariancję danych (energię) można określić wzorem:
\(r_i=\frac{\lambda_i}{\sum_{j=1}^4 \lambda_j}\)
Wartości te są następujące: \( r_1 = 0.9999, r_2 = 9,32E-5, r_3 = 3.8E-6, r_4=1.18E-6\). Jak wynika z rozkładu tych wartości, największy składnik główny ma \( 99,99\%\) udziału w łącznej wariancji danych. Przy odtwarzaniu wszystkich składników (\(wcu, sb, wps, spm\)) na podstawie wektora \( \mathbf{y} \) można ograniczyć się jedynie do jego największej składowej \( y_1 \), pomijając pozostałe jako nie wnoszące istotnego wkładu informacyjnego. Oznacza to 3-krotną redukcję ilości przetworzonej informacji. Po odtworzeniu w ten sposób danych uzyskano odtworzony zbiór danych, ze średnim błędem względnym równym \( 0.97\% \) (zdefiniowanym jako stosunek normy euklidesowej macierzy błędu do normy euklidesowej danych przyjętych w postaci macierzy \(4 \times 126\)).
2.2. Neuronowe metody wyznaczania rozkładu PCA
Klasyczna transformacja PCA wymaga wyznaczenia na podstawie danego zbioru wektorów \(\mathbf{x}\) najpierw macierzy korelacji \(\mathbf{R_{xx}}\), a następnie rozkładu tej macierzy według wartości własnych. Jest to prosta i łatwa w zastosowaniu metoda (ciąg dekompozycji QR), jeśli problem jest dobrze uwarunkowany (współczynnik uwarunkowania \( cond (\mathbf{R_{xx}}) \) przyjmuje małe wartości). Wystarczy w tym celu zastosować funkcję eig.m w Matlabie. Przy bardzo dużych wymiarach wektorów x (powyżej kilku tysięcy) problem obliczeniowy wyznaczenia wartości własnych macierzy \(\mathbf{R_{xx}}\) staje się zwykle źle uwarunkowany i trudny do przeprowadzenia. W takich przypadkach konkurencyjne może być zastosowanie metod neuronowych adaptacji pozwalających na wyznaczenie macierzy przekształcenia \(\mathbf{W}\) bez tworzenia macierzy korelacyjnej, a jedynie poprzez bezpośrednie przetwarzanie wektorów wejściowych \(\mathbf{x}\). Przetwarzanie sygnałów może być wówczas przedstawione w typowo sieciowy sposób jako liniowa sieć PCA zawierająca jedną warstwę.
8.2.1 Estymacja pierwszego składnika głównego
Wyznaczenie wektorów własnych \(\mathbf{w_{i}}\) może przebiegać przy zastosowaniu metod adaptacyjnych, typowych dla sieci neuronowych. Są one oparte na uogólnionej regule Hebba i pozwalają na bezpośrednie przetworzenie wektorów wejściowych \(\mathbf{x}\), bez potrzeby jawnego definiowania macierzy \(\mathbf{R_{xx}}\). Metody te są niezastąpione w przypadkach akwizycji danych w trybie on-line, w którym utworzenie jawnej postaci macierzy korelacji byłoby niemożliwe. Powstały różne odmiany algorytmów, a w każdym z nich wykorzystuje się korelację zachodzącą między wektorami reprezentującymi dane wejściowe.
Bezpośrednie zastosowanie uogólnionej reguły Hebba dotyczy wyznaczenia jednego (największego) składnika głównego. Algorytm ten odpowiada zastosowaniu sieci liniowej jednowarstwowej o jednym neuronie wyjściowym przedstawionej na rys. 8.2.
Sygnał wyjściowy takiej sieci określony jest wzorem
| \( y_1=\mathbf{w}_1^T \mathbf{x}=\sum_{j=0}^N w_{1 j} x_j \) | (8.13) |
Dobór wag wektora \(\mathbf{w_{1}}\) odbywa się według uogólnionej (znormalizowanej) reguły Hebba, zwanej regułą Oji, którą zapisać można w formie skalarnej [24,46]
| \( w_{1 j}(k+1)=w_{1 j}(k)+\eta y_1(k)[ x_j(k)-w_{1 j}(k) y_1(k)] \) | (8.14) |
| \( \mathbf{w}_1(k+1)=\mathbf{w}_1(k)+\eta y_1(k) [ \mathbf{x}(k)-\mathbf{w}_1(k) y_1(k) ] \) | (8.15)) |
We wzorach tych \( \eta \) oznacza współczynnik uczenia malejący w czasie. W procesie uczenia sieci powtarza się wielokrotnie te same wzorce uczące, aż do ustabilizowania się wag sieci. Pierwszy składnik obu wzorów odpowiada zwykłej regule Hebba, a drugi zapewnia samo-normalizację wektorów wagowych, to jest \( \| \mathbf{w}_1\|^2=1 \). Dobór wartości \( \eta \) ma istotny wpływ na zbieżność algorytmu. Dobre rezultaty uzyskuje się, przyjmując wartości \( \eta(k) \) malejące wraz z upływem czasu uczenia.
Jakkolwiek metoda Oji pozwala wyznaczyć jedynie pierwszy składnik główny może być ona w prosty sposób przystosowana do wyznaczenia pozostałych składników. Przy uwzględnieniu wielu składników i wektorów własnych można sukcesywnie redukować wpływ wyselekcjonowanego składnika pierwszego odkrywając w ten sposób następny, traktowany w przekształconym wektorze \(\mathbf{x}\) jako pierwszy składnik główny, dla którego można powtórzyć poprzednia procedurę. Przyjmując oznaczenie \(i\)-tego wektora własnego w postaci \(\mathbf{w_{i1}} = [w_{i1}, w_{i2}, \ldots, w_{iN}]^T\) można zauważyć, że składowe wektora \(\mathbf{x}\) można wyrazić w postaci
| \( x_i=w_{i 1} x_1+\sum_{j=2}^K w_{i j} y_j \) | (8.16) |
dla \(i=1, 2, \ldots, N\). Składnik pierwszy tego wzoru po wyznaczeniu pierwszego składnika głównego jest już znany i może zostać wyeliminowany poprzez utworzenie nowego wektora \(\mathbf{x}^\prime\) o elementach zdefiniowanych następująco
| \( x_i^{\prime}=x_i-w_{i 1} x_1 \) | (8.17) |
Dla nowego wektora \( x_i^{\prime} \) największą wartością własną jest teraz \( \lambda_2 \), gdyż wpływ \( \lambda_1 \) został wyeliminowany dzięki działaniu wyrażonemu wzorem (8.17). Procedura wyznaczenia tej wartości jest identyczna do omówionej wcześniej. Powtarzając te operacje \(N\) razy można wyznaczyć wszystkie wektory własne stowarzyszone z kolejnymi wartościami własnymi.
8.2.2 Algorytm estymacji wielu składników głównych jednocześnie
Wyznaczanie wielu kolejnych składników PCA wymaga zastosowania wielu neuronów w warstwie wyjściowej sieci. Sieć neuronowa zawiera zatem tyle neuronów, ile składników głównych rozkładu ma być uwzględnionych. Są one ułożone w jednej warstwie - stąd sieć PCA jest siecią jednowarstwową o liniowych funkcjach aktywacji neuronów (rys. 8.3).
Istnieje wiele algorytmów uczenia takiej sieci. Tutaj ograniczymy się do reguły Sangera [24,46], będącej regułą lokalną, nie wymagającą w procesie uczenia rozwiązania układu równań. Przy \(K\) neuronach liniowych w warstwie sygnały wyjściowe \(y_i\) w kolejnych iteracjach \(k\) określane są według wzoru
| \( y_i(k)=\mathbf{w}_i^T(k) \mathbf{x}(k)=\sum_{j=1}^N w_{i j} x_j \) | (8.18) |
Adaptacja wag sieci w kolejnych iteracjach wykorzystuje aktualnie znane (zaadaptowane) wartości wag i przebiega według następującego wzoru
| \( w_{i j}(k+1)=w_{i j}(k)+\eta y_i(k)\left[x_j(k)-\sum_{h=1}^i y_h(k) w_{h j}(k)\right] \) | (8.19) |
dla \(j=1, 2, …, N \) oraz \(i=1, 2, …, K\). Przyjmując oznaczenie
| \( x_j^{\prime}(k)=x_j(k)-\sum_{h=1}^{i-1} w_{h j}(k) y_h(k) \) | (8.20) |
| \( w_{i j}(k+1)=w_{i j}(k)+\eta y_i(k)\left[x_j^{\prime}(k)-y_i(k) w_{i j}(k)\right] \) | (8.21) |
Jest oczywiste, że nawet przy istnieniu \(K\) neuronów w warstwie wyjściowej reguła uczenia pozostaje nadal lokalną, pod warunkiem zmodyfikowania wartości sygnału wejściowego \( x_j^\prime \). Zauważmy, że modyfikacja tego sygnału odbywa się przy wykorzystaniu wcześniej zaadaptowanych już wartości wag, a więc nie wymaga rozwiązania układu równań. Zależności skalarne (8.20) i (8.21) można zapisać w prostszej formie wektorowej wygodniejszej w działaniach
| \( \mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\sum_{h=1}^{i-1} y_h(k) \mathbf{w}_h(k) \) | (8.22) |
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta y_i(k)\left[\mathbf{x}^{\prime}(k)-y_i(k) \mathbf{w}_i(k)\right] \) | (8.23) |
dla \(i=1, 2,…, K\). Zauważmy, że dla neuronu pierwszego (pierwszy składnik główny PCA) mamy \(\mathbf{x}^{\prime}(k)=\mathbf{x}(k)\). Dla neuronu drugiego otrzymuje się \(\mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\mathbf{w}_1(k) y_1(k)\) - wzór uzależniony od znanych już wag neuronu pierwszego. Podobnie dla trzeciego neuronu \(\mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\mathbf{w}_1(k) y_1(k)-\mathbf{w}_2(k) y_2(k)\) i wszystkich pozostałych, modyfikacja wektora \(\mathbf{x} \) wyrażona jest przez wielkości wag wcześniej określone, w efekcie czego proces uczenia przebiega identycznie jak w przypadku algorytmu Oji, z samo-normalizującymi się wektorami \(\mathbf{x} \), czyli \(\left\|\mathbf{w}_i\right\|=1\).
Obecnie istnieje wiele różnych algorytmów neuronowych, pozwalających adaptacyjnie określić parametry transformacji PCA. Do najważniejszych, oprócz algorytmu Sangera, zalicza się algorytm Foldiaka, Rubnera oraz APEX (ang. Adaptive Principal component EXtraction). Szczegóły rozwiązań znaleźć można w opracowaniu książkowym Diamantarosa i Kunga.
2.3. Zastosowania transformacji PCA
Główne zastosowania transformacji PCA związane są z kompresją danych, która jest nieodłącznym składnikiem każdego przekształcenia PCA. Własność ta może być bezpośrednio wykorzystana do kompresji stratnej informacji – mówimy wtedy o kompresji sygnałów (dane jednowymiarowe) bądź obrazów (dane 2-D). Niezastąpionym zastosowaniem PCA jest ilustracja rozkładu danych wielowymiarowych na płaszczyźnie (układ 2-współrzędnych w postaci 2 najważniejszych składników głównych) lub w przestrzeni 3-D (układ 3-współrzędnych w postaci 3 najważniejszych składników głównych). Ponadto transformacja PCA reprezentująca \(N\)-wymiarowy wektor \(\mathbf{x}\) przez \(K\)-wymiarowy (\(K<N\)) wektor \(\mathbf{y}\) składników głównych pozwala traktować wektor \(\mathbf{y}\) jako wektor cech diagnostycznych procesu reprezentowanego przez zbiór wektorów \(\mathbf{x}\).
8.3.1 PCA w zastosowaniu do kompresji stratnej danych
Kompresja danych z zastosowaniem PCA polega na przekształceniu \(N\)-elementowego wektora wejściowego \(\mathbf{x}\) w wektor \(\mathbf{y}\) o zmniejszonym wymiarze \(K\) (\(K<N\)). Redukcja wymiaru wektora \(\mathbf{x}\) poprzez PCA zapewnia optymalność przekształcenia poprzez zachowanie w wektorze zredukowanym największej możliwie dawki informacji oryginalnej (przy założonej wartości \(K\)).
Na rys. 8.4 przedstawiono sieć PCA do kompresji (rys. 8.4a) oraz do rekonstrukcji (dekompresji) danych (rys. 8.4b). W sieci kompresyjnej wektor oryginalny \(\mathbf{x}\) jest transformowany w wektor \(\mathbf{y}\) o zredukowanym wymiarze \(K\), przy czym \(\mathbf{y} = \mathbf{Wx}\). Wektor \(\mathbf{y}\) może podlegać bądź to transmisji na odległość bądź zapisaniu na dysku. W każdym przypadku możliwe jest odtworzenie wektora oryginalnego na podstawie jego zredukowanej formy \(\mathbf{y}\), korzystając z sieci rekonstrukcyjnej z rys. 8.4b, wykonującej operację odwrotną \(\mathbf{\hat{y}} = \mathbf{W^Tx}\). Biorąc pod uwagę pewną utratę informacji spowodowaną obcięciem wymiaru wektora odtworzenie to jest z pewnym przybliżeniem \( \hat{\mathbf{x}} \simeq \mathbf{x} \).
O współczynniku kompresji decyduje liczba składników głównych \(K\) uwzględnionych w przekształceniu PCA. Przy dużej liczbie wektorów \(\mathbf{x}\) podlegających przekształceniu można pominąć liczbę bitów do kodowania wag sieci i współczynnik kompresji wyrazić wzorem przybliżonym
| \(K_r \cong \frac{N}{K}\) | (8.24) |
Im wyższy współczynnik kompresji tym większa oszczędność pamięci, ale gorsza jakość odtworzonego obrazu (większa porcja informacji utracona bezpowrotnie w wyniku redukcji wymiaru wektora oryginalnego).




Na rys. 8.5 przedstawiono obraz oryginalny (rys. 8.5a) oraz trzy obrazy zrekonstruowane na podstawie odpowiednio 1, 3 i 5 składników głównych PCA (rys. 8.5 b,c,d). Obraz poddany kompresji miał wymiar \(512 \times 512 \) pikseli i został podzielony na ramki o wymiarach \(8 \times 8 \) (wymiar wektora \(\mathbf{x}\) równy \(64\)). Jakość odtworzonego obrazu jest ściśle uzależniona od liczby \(K\) składników głównych uwzględnionych w odtwarzaniu. Im więcej jest tych składników, tym lepsza jakość obrazu, ale mniejszy współczynnik kompresji. Przy największym współczynniku kompresji (jeden składnik główny) wyraźnie widoczne są poszczególne ramki w obrazie. Obraz odtworzony na podstawie pięciu składników głównych nie różni się wzrokowo od obrazu oryginalnego. Współczynniki PSNR otrzymane dla poszczególnych obrazów są odpowiednio równe: 18,80 dB, 25,43 dB oraz 27,58 dB, przy czym \(\mathbf{</span><span style="font-size: 0.9375rem; text-align: left;">PSNR}\) określany jest wzorem
| \( PSNR=10 \log \left(\frac{255^2}{MSE}\right) \) | (8.25) |
gdzie \(MSE\) oznacza wartość błędu średniokwadratowego odtworzonego obrazu względem obrazu oryginalnego.
8.3.2 Przykład zastosowania PCA do ilustracji rozkładu danych wielowymiarowych
Oryginalne zastosowanie znalazło PCA w ilustracji graficznej rozkładu danych wielowymiarowych poprzez zrzutowanie ich w przestrzeń 2-D lub 3-D. Wybierając \(K=2\) rzutujemy każdy \(N\)-wymiarowy wektor \(\mathbf{x}\) w przestrzeń dwuwymiarową. W ten sposób każdy wektor \(\mathbf{x}\) jest reprezentowany przez wektor \(\mathbf{y} = [y_1 y_2]\), którego położenie może być bez problemu zilustrowane na płaszczyźnie, której oś poziomą stanowi teraz składnik główny \( y_1 \), a oś pionową składnik główny \( y_2 \). Wektory \(\mathbf{x}\) „podobne” do siebie zajmą wówczas bliskie sobie położenia na płaszczyźnie, a wektory „dalekie” – położenia odległe.
Ta unikalna własność znajduje szerokie zastosowania w problemach klasyfikacyjnych, gdzie służy do badania jednorodności rozkładów danych w ramach poszczególnych klas oraz do określania średnich odległości między klasowych
Przykład takiego zastosowania pokażemy w przestrzeni 2-wymiarowej ilustrującej graficznie położenie poszczególnych województw Polski (na płaszczyźnie reprezentowanej przez 2 najważniejsze składniki główne). Wyniki dotyczą przykładowych danych GUS z jednego roku. Rzutowanie dotyczyło 13-wymiarowych elementów informacji GUS dla każdego województwa. Informacje dotyczą następujących elementów:
-
Procent ludności mieszkających w miastach
-
Odsetek zgonu niemowląt
-
Przyrost naturalny ludności
-
Stopa bezrobocia
-
Wynagrodzenie miesięczne brutto
-
Zasoby mieszkaniowe przypadające na 10000 ludności
-
Liczba osób hospitalizowanych w roku przypadających na 10000 ludności
-
Liczba ciągników rolniczych przypadająca na 100 ha gruntów
-
Produkcja sprzedana przemysłu przypadająca na głowę ludności
-
Produkcja sprzedana budownictwa przypadająca na głowę ludności
-
Liczba kilometrów dróg przypadających na 10km2 w przeliczeniu na głowę ludnosci
-
Wartość PKB per capita
-
Liczba firm zarejestrowanych w bazie REGON przypadająca na głowę ludności
Dla uproszczenia opisów przyjęto numeryczne oznaczenia poszczególnych województw w kolejności jak niżej:
-
Dolnośląskie
-
Kujawsko-pomorskie
-
Lubelskie
-
Lubuskie
-
Łódzkie
-
Małopolskie
-
Mazowieckie
-
Opolskie
-
Podkarpackie
-
Podlaskie
-
Pomorskie
-
Śląskie
-
Świętokrzyskie
-
Warmińsko-mazurskie
-
Wielkopolskie
-
Zachodniopomorskie
Tabela 8.1 przedstawia dane oryginalne dotyczące tych zagadnień. Wektor x dla każdego województwa tworzy wybranych 13 elementów informacji dotyczącej ekonomii, dostępności edukacji i opieki medycznej. Użyto następujących skrótów:
Tabela 8.1 Dane liczbowe GUS dotyczące 13 elementów informacji województw w Polsce. Wiersze reprezentują województwa (od 1 do 16), kolumny elementy uwzględnionej informacji (od 1 do 13)
|
Województwo |
Kolejne 13 elementów informacji |
||||||||||||
|
1 |
70,6 |
6,9 |
-0,8 |
11,8 |
2861 |
357 |
1860 |
6,5 |
72588 |
7161 |
91,2 |
26620 |
308,3 |
|
2 |
61,1 |
6,1 |
0,7 |
15,2 |
2443 |
328 |
1638 |
8,5 |
36918 |
3573 |
78,9 |
22474 |
188,5 |
|
3 |
46,6 |
6,1 |
-0,7 |
13 |
2486 |
328 |
1874 |
11,9 |
23230 |
2851 |
72,7 |
17591 |
151,5 |
|
4 |
63,9 |
6 |
1,3 |
14,2 |
2430 |
337 |
1615 |
4,2 |
17481 |
1370 |
57,8 |
23241 |
106,5 |
|
5 |
64,4 |
4,8 |
-3,2 |
11,5 |
2471 |
374 |
2035 |
12,2 |
40644 |
5209 |
92,2 |
23666 |
240,9 |
|
6 |
49,4 |
6,4 |
1,4 |
8,8 |
2666 |
318 |
1611 |
17,9 |
53890 |
8241 |
145 |
21989 |
293,8 |
|
7 |
64,7 |
4,9 |
0,4 |
9,2 |
3671 |
371 |
1759 |
10,5 |
176121 |
37752 |
84,5 |
40817 |
627,3 |
|
8 |
52,5 |
4,4 |
-1,1 |
12 |
2607 |
325 |
1579 |
7,8 |
19312 |
1857 |
88,9 |
21347 |
94,9 |
|
9 |
40,6 |
6 |
1,5 |
14,4 |
2373 |
291 |
1747 |
16 |
28228 |
3140 |
79,2 |
17789 |
142,1 |
|
10 |
59,5 |
5 |
-0,5 |
10,7 |
2525 |
340 |
1901 |
9 |
14011 |
2836 |
54,6 |
19075 |
88,7 |
|
11 |
66,7 |
6,4 |
2,7 |
10,9 |
2883 |
334 |
1553 |
6,3 |
49272 |
5810 |
63,2 |
25308 |
232,8 |
|
12 |
78,4 |
6,7 |
-0,8 |
9,3 |
2933 |
363 |
1820 |
12,2 |
151323 |
12174 |
164 |
27792 |
427,4 |
|
13 |
45,4 |
5 |
-1,4 |
15,1 |
2467 |
327 |
1903 |
14,3 |
19516 |
2386 |
104 |
19274 |
106,9 |
|
14 |
60 |
5,4 |
1,9 |
19 |
2398 |
328 |
1808 |
5 |
19709 |
2514 |
50,6 |
19709 |
113,1 |
|
15 |
56,6 |
6,7 |
2,1 |
8 |
2611 |
314 |
1869 |
8,8 |
89537 |
12655 |
85,1 |
27553 |
352,2 |
|
16 |
68,9 |
7,4 |
0,8 |
16,6 |
2616 |
346 |
1789 |
3,4 |
23234 |
3044 |
55,8 |
23924 |
210,8 |
Na rys. 8.6 przedstawiono ilustrację dwuwymiarową położenia względnego 16 województw Polski na podstawie danych statystycznych dotyczących rozwoju ekonomicznego, stanu edukacyjnego i opieki medycznej.
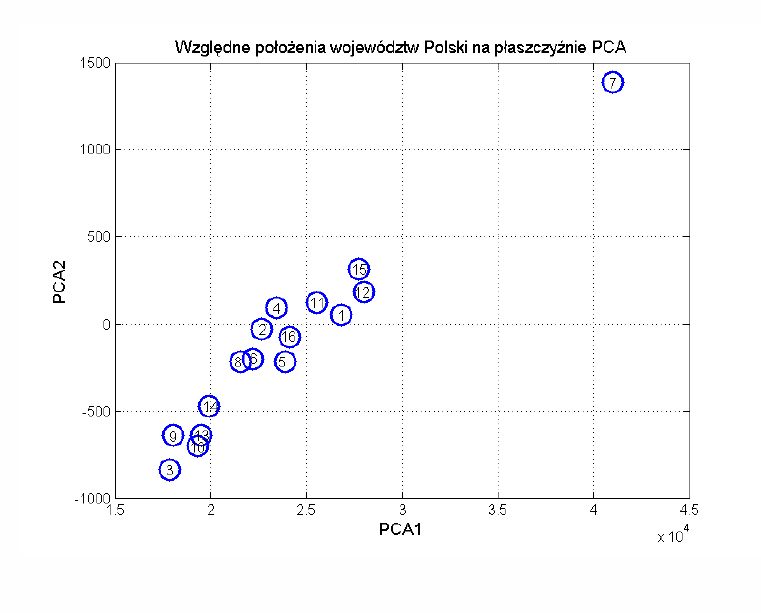
Bliskie położenie na płaszczyźnie oznacza podobieństwo cech charakteryzujących te województwa. Większe odległości miedzy poszczególnymi punktami oznaczają większe różnice w rozwoju tych województw (pod względem uwzględnionych 13 wskaźników ekonomicznych i społecznych). Najbardziej odstającym województwem, wyróżniającym się w grupie analizowanych jednostek okazało się województwo Mazowieckie. Najbardziej odległe od niego są województwa: Lubelskie, Podkarpackie, Podlaskie, Świętokrzyskie i Warmińsko-mazurskie. Najbliższe województwu Mazowieckiemu okazało się województwo Wielkopolskie i Śląskie. Zauważmy, że w tej analizie nie uwzględnia się wartości składników głównych, a jedynie względne odległości między położeniami na płaszczyźnie utworzonej przez dwa najważniejsze składniki główne. Należy dodatkowo zaznaczyć, że powyższy rozkład został uzyskany przy uwzględnieniu jedynie wybranych 13 parametrów, spośród wielu dostępnych w publikacjach GUS i dotyczy danych jednego roku.
2.4. Zadania i problemy
1. Korzystając z oprogramowania Matlaba określić macierz korelacji \( \mathbf{R}_{\mathbf{xx}} \) dla ciągu 20 wektorów 4-wymiarowych \( \mathbf{x} \) utworzonych dla 20 kolejnych chwil czasowych w przedziale czasu \( 0 < t < 2 \). Wektor ten opisują zależności
\( \mathbf{x}=\left[\begin{array}{llll}\sin (3 t) & \exp (-0.1 * t) & \sin (3 * t) * \cos (0.5 * t) & \sin (3 * t-\cos (t))\end{array}\right]^T \)
Wyznaczyć wartości i wektory własne tej macierzy.
2. Dany jest ciąg 20 wektorów losowych o wymiarze 10 i rozkładzie a) równomiernym, b) gaussowskim. Określić wartości własne i stowarzyszone z nimi wektory własne dla odpowiadających im macierzy korelacji \( \mathbf{R}_{\mathbf{xx}} \). Porównać odpowiadające sobie wartości własne i ich rozkład w obu przypadkach przedstawiając je na wspólnym wykresie.
3. Dany jest zbiór wektorów \(\mathbf{x} \) o postaci
\( \mathbf{x}_1=\left[\begin{array}{r}1 \\ 2 \\ 0\end{array}\right], \; \mathbf{x}_2=\left[\begin{array}{r}0,8 \\ 1,8 \\ 0,5\end{array}\right], \; \mathbf{x}_3=\left[\begin{array}{r}1,3 \\ 2,5 \\ -0,5\end{array}\right], \; \mathbf{x}_4=\left[\begin{array}{r}0 \\ 1 \\ 2\end{array}\right], \; \mathbf{x}_5=\left[\begin{array}{r}0,5 \\ 1,5 \\ 3\end{array}\right], \; \mathbf{x}_6=\left[\begin{array}{r}0,8 \\ 2 \\ 4\end{array}\right] \)
Określić macierz korelacji tych wektorów. Wyznaczyć wartości i wektory własne. Określić macierz PCA odwzorowującą te wektory w przestrzeń 2D. Zrekonstruować macierz korelacji na podstawie 2 najważniejszych składników głównych. Zrzutować wektory xi w przestrzeń 2D. Narysować położenia tych rzutów w przestrzeni 2D.
4. Sygnał pomiarowy x tworzą funkcje czasu: \( \sin(\omega_1 t) \), \( \cos(\omega_2 t) \), \( \exp(-\alpha t ) \cdot \sin(\omega_3 t) \), \( \operatorname{sinc}(\omega_4 t) \) oraz dwie składowe szumowe o rozkładzie równomiernym i gaussowskim. Utworzyć zbiór 20 takich wektorów dla 20 różnych chwil czasowych. Każdy wektor x ma więc wymiar 6. Określić wartości własne macierzy korelacji tego zbioru wektorów. Dokonać przekształcenia PCA odpowiadającego 4 największym wartościom własnym macierzy korelacji. Odtworzyć te wektory i wykreślić je (zależność czasowa) na tle wartości oryginalnych.
5. Dla powyższego zbioru 20 wektorów zilustrować ich położenie na płaszczyźnie utworzonej przez dwa składniki główne: \( y_1 \) oraz \( y_2 \) (\(K=2\)).
6. Dana jest transmitancja operatorowa drugiego rzędu \(H(s)=\frac{b_0}{s^2+a_1 s+a_0}\). Założyć określone wartości współczynników \( a_i\), \( b_i\) dla \( i = 0, 1\) (na przykład \( a_0 = 1\), \( a_1 = 0,7\), \( b_0 = 1\). Wykreślić charakterystykę amplitudową i fazową układu dla 10 wybranych pulsacji (np. wartości zmieniające się od \( \omega=0.1 \) do \( \omega=2 \)). Utworzyć 20-wymiarowy wektor \( \mathbf{x} \) zawierający wartość modułu \(\left|H\left(j \omega_i\right)\right|\) fazy \( arg(H(j\omega_1)) \) dla przyjętych wartości częstotliwości (każdy punkt częstotliwości odpowiada dwu wartościom: amplitudy i fazy). Utworzyć ciąg takich wektorów dla wartości współczynników \( a_0\), \( a_1\), \( b_0\), \( b_1\) zmieniających się od zera do wartości nominalnej (w każdym przypadku zmiana wartości jednego współczynnika). Dokonać przekształcenia PCA dla takiego zbioru wektorów. Narysować wykres zmian położeń tych wektorów na płaszczyźnie utworzonej przez dwa pierwsze składniki główne: \( y_1\) i \( y_2\).
7. Przedstawić na płaszczyźnie utworzonej przez dwa najważniejsze składniki główne rozkład danych odpowiadających rozwojowi ekonomicznemu województwa wielkopolskiego i podlaskiego w latach 2004-2008 według danych zgromadzonych w pliku pca_zad5.mat.
2.5. Słownik
Słownik opanowanych pojęć
Wykład 8
PCA – transformacja liniowa stosowana do redukcji wymiaru danych (bazuje na transformacji Karhunena-Loewe).
Macierz kowariancji – macierz stanowiąca uogólnienie pojęcia wariancji na przypadek wielowymiarowy
Wartości własne – pierwiastki \( \lambda \) równania \( det(\lambda \mathbf{1} - \mathbf{R}_{\mathbf{xx}} ) = 0 \), gdzie \( \mathbf{R}_{\mathbf{xx}} \) jest macierzą kowariancji.
Wektory własne – wektory \(\mathbf{w}_i \) stowarzyszone z wartościami własnymi i macierzą \( \mathbf{R}_{\mathbf{xx}} \) poprzez relację \( \mathbf{R}_{\mathbf{xx}} \mathbf{w}_i = \lambda_i \mathbf{w}_i \).
Składniki główne – elementy wektora wyjściowego \( \mathbf{y} \) po transformacji PCA, \( \mathbf{y} = \mathbf{Wx} \).
Reguła Oji – uogólnienie reguły Hebba w implementacji on-line transformacji PCA.
Kompresja stratna danych – reprezentacja przybliżona danych poprzez zredukowaną (w stosunku do oryginału) liczbę elementów.
3. Ślepa separacja sygnałów
Sieci do ślepej separacji sygnałów [8] są sieciami liniowymi samoorganizującymi się przy wykorzystaniu uogólnionej reguły Hebba. Należą do klasy sieci korelacyjnych. Ich koncepcja w odniesieniu do składników niezależnych (ang. Independent Component Analysis – ICA) została opracowana w połowie lat osiemdziesiątych przez profesorów J. Heraulta i C. Juttena. Dzisiaj ta koncepcja została znacznie rozszerzona i obejmuje również rozkład sygnałów na składniki gładkie, rzadkie, ortogonalne itp. stanowiąc dział badawczy zwany BSS (ang. Blind Signal Separation) [8]. Pierwotna struktura sieci ICA miała postać rekurencyjną. W chwili obecnej znacznie częściej używana jest postać jednokierunkowa. Co więcej rezygnuje się zwykle z jawnej definicji struktury sieciowej ograniczając się do algorytmu separacji.
Tym nie mniej algorytmom separacji sygnałów, niezależnie od sposobu ich graficznej prezentacji można przypisać adaptacyjną strukturę liniową, dokonującą przetwarzania sygnałów w czasie rzeczywistym (on-line). Funkcje nieliniowe stosowane w algorytmie uczącym pełnią bardzo ważną rolę w adaptacji wag, nie wpływając na samą strukturę połączeń wagowych.
W wykładzie przedstawimy algorytmy ślepej separacji poczynając od oryginalnego rozwiązania Heraulta-Juttena prezentując aspekty zarówno obliczeniowe jak i strukturalne towarzyszących im sieci. Zaprezentujemy programy ślepej separacji umożliwiające dekompozycję sygnałów na składniki bazowe statystycznie niezależne.
3.1. Wprowadzenie
Oryginalne rozwiązanie Heraulta-Juttena dotyczyło problemu separacji sygnałów \( s_j (t) \) zmiennych w czasie na podstawie informacji zawartej w ich liniowej superpozycji. Przyjmiemy za ich twórcami, że danych jest n niezależnych (nieznanych) sygnałów \( s_j (t) \) oraz macierz mieszająca \( \mathbf{A} \) (również nieznana) o wymiarze \( n \times n \). Dla pomiarów dostępne są jedynie sygnały \( x_i (t) \) będące liniową superpozycją \( s_j (t) \) przy czym [8]
| \(x_i(t)=\sum_{j=1}^n a_{i j} s_j\) | (9.1) |
dla \( i = 1, 2, \ldots, n \). Główna trudność polega na tym, że zarówno \( a_{ij} (t) \) jak i \( s_j (t) \) nie są znane. Przy założeniu statystycznej niezależności sygnałów J. Herault i C. Jutten zaproponowali rozwiązanie problemu z wykorzystaniem sieci neuronowej [8].
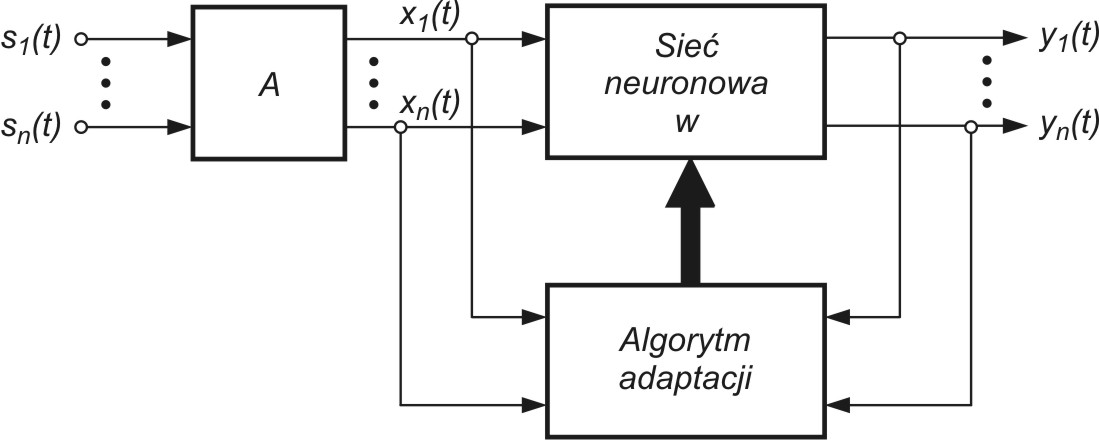
Schemat ogólny włączenia tej sieci w system pomiarowy przedstawiono na rys. 9.1. Istotnym założeniem w ich rozwiązaniu jest statystyczna niezależność sygnałów źródłowych.
3.2. Niezależność statystyczna sygnałów
Niezależność statystyczna sygnałów losowych jest pojęciem ogólniejszym niż dekorelacja. Pojęcie korelacji dotyczy jedynie pojęcia liniowej zależności występującej między sygnałami, natomiast niezależność statystyczna dowolnej zależności, w tym nieliniowej, istniejącej między sygnałami. W ogólnym przypadku dwie zmienne losowe \(y_i\) oraz \(y_j\) są statystycznie niezależne, jeśli informacja o jednej zmiennej nie wnosi żadnej wiedzy o zachowaniu drugiej zmiennej. Z matematycznego punktu widzenia niezależność statystyczna oznacza, że dwuwymiarowa łączna gęstość prawdopodobieństwa \(p\left(y_i, y_j\right)\) jest równa iloczynowi jednowymiarowych funkcji gęstości zmiennej \(y_i\) oraz \(y_j\)
| \(p\left(y_i, y_j\right)=p\left(y_i\right) p\left(y_j\right)\) | (9.2) |
Dla sygnałów statystycznie niezależnych uogólniona macierz kowariancji funkcji \( f(y_i) \) oraz \( f(y_j) \) (obie funkcje muszą być nieparzyste) tworzy nieosobliwą macierz diagonalną, mającą postać
| \( \mathrm{E}\left[\mathbf{f}(\mathbf{y}) \mathbf{g}^T(\mathbf{y})\right]-\mathrm{E}[\mathbf{f}(\mathbf{y})] \cdot \mathrm{E}\left[\mathbf{g}^T(\mathbf{y})\right]=\left|\begin{array}{ccc}\mathrm{E}\left[f\left(y_1\right) g\left(y_1\right)\right]-E\left[f\left(y_1\right)\right] \cdot E\left[g\left(y_1\right)\right] & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \mathrm{E}\left[f\left(y_n\right) g\left(y_n\right)\right]-E\left[f\left(y_n\right)\right] \cdot E\left[g\left(y_n\right)\right]\end{array}\right| \) | (9.3) |
W równaniu tym symbol E oznacza wartość oczekiwaną. Z warunku niezależności statystycznej wynika, że wszystkie uogólnione kowariancje wzajemne są zerowe, a zatem \( \mathrm{E}\left[\mathbf{f}(\mathbf{y}) \mathbf{g}^T(\mathbf{y})\right]-\mathrm{E}[\mathbf{f}(\mathbf{y})] \cdot \mathrm{E}\left[\mathbf{g}^T(\mathbf{y})\right]=0 \), natomiast kowariancje własne są niezerowe \( \mathrm{E}\left[\mathbf{f}(\mathbf{y}) \mathbf{g}^T(\mathbf{y})\right]-\mathrm{E}[\mathbf{f}(\mathbf{y})] \cdot \mathrm{E}\left[\mathbf{g}^T(\mathbf{y})\right] \neq 0 \). Warunek statystycznej niezależności sygnałów jest utożsamiony z zerowaniem się kumulantów wzajemnych wyższego rzędu [8].
3.3. Struktura rekurencyjna sieci separującej
W rozwiązaniu problemu separacji sygnałów statystycznie niezależnych J. Herault i C. Jutten zaproponowali sieć neuronową liniową ze sprzężeniem zwrotnym, przedstawioną na rys. 9.2.
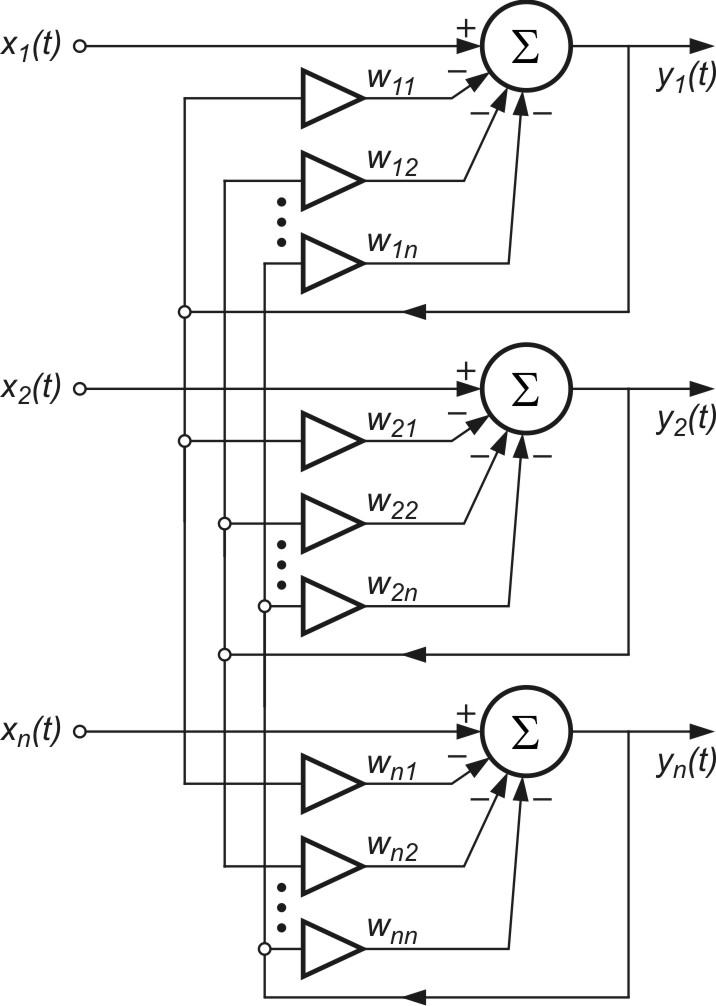
Sieć zawiera \( n\) liniowych neuronów, powiązanych ze sobą przez wzajemne sprzężenia zwrotne. Wagi synaptyczne \( w_{ij} \) w rozwiązaniu oryginalnym Heraulta i Juttena są różne od zera tylko przy sprzężeniach wzajemnych (zasada ta została odrzucona przez prof. Cichockiego pozwalając na lepsze działanie systemu). Każdy neuron w sieci generuje sygnał wyjściowy
| \(y_i(t)=x_i(t)-\sum_{j=1}^n w_{i j} y_j(t)\) | (9.4) |
Przy oznaczeniu przez \( \mathbf{A} \) macierzy mieszającej, przez \( \mathbf{W} \) macierzy wagowej (obie kwadratowe o tych samych wymiarach)
| \(\mathbf{W}=\left[\begin{array}{llll}w_{11} & w_{12} & \cdots & w_{1 n} \\ w_{21} & w_{22} & \cdots & w_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ w_{n 1} & w_{n 2} & \cdots & w_{n n}\end{array}\right]\) | (9.5) |
a przez \( \mathbf{x}(t) \), \( \mathbf{s}(t) \) oraz \( \mathbf{y}(t) \) wektorów odpowiednio obserwowanych sygnałów \( x_i(t) \) przetworzonych według zależności (9.1), wektora sygnałów źródłowych \( s_i(t) \) oraz wektora sygnałów wyjściowych \( y_i(t) \) sieci, gdzie
| \(\mathbf{x}(t)=\left[\begin{array}{c}x_1(t) \\ x_2(t) \\ \cdots \\ x_n(t)\end{array}\right]\), \(\mathbf{s}(t)=\left[\begin{array}{c}s_1(t) \\ s_2(t) \\ \cdots \\ s_n(t)\end{array}\right]\), \(\mathbf{y}(t)=\left[\begin{array}{c}y_1(t) \\ y_2(t) \\ \ldots \\ y_n(t)\end{array}\right]\) | (9.6) |
działanie sieci z rys. 9.2 można opisać równaniem macierzowym
| \(\mathbf{y}(t)=\mathbf{x}(t)-\mathbf{W y}(t)\) | (9.7) |
Przy nieznanej macierzy mieszającej \(\mathbf{A} \) i wektorze \( \mathbf{s}(t) \) oraz założeniu statystycznej niezależności składników wektora \( \mathbf{s}(t) \), zadanie sieci sprowadza się do takiego określenia wektora rozwiązania \( \mathbf{y}(t) \), które umożliwi odtworzenie sygnałów pierwotnych \( s_i(t) \) tworzących wektor \( \mathbf{s}(t) \). Z równania (9.7) wynika, że rozwiązanie takie musi spełniać warunek
| \( \mathbf{y}(t)=(\mathbf{1}+\mathbf{W})^{-1} \mathbf{x}(t) \) | (9.8) |
Wektor \( \mathbf{y}(t) \) będzie odtwarzał wektor poszukiwanych sygnałów źródłowych \( \mathbf{s}(t) \). Odtworzenie to jest możliwe z dokładnością do pewnej, bliżej nieokreślonej skali \( d_i \), czyli \( \mathbf{y}(t) = \mathbf{Ds}(t)\) gdzie \( \mathbf{D} \) jest macierzą diagonalną, \(\mathbf{D}=\operatorname{diag}\left\{d_1, d_2, \ldots, d_n\right\}\), przy praktycznie dowolnej kolejności występowania poszczególnych składników \( \mathbf{y}(t) \) w wektorze \( \mathbf{y}(t) \) (przy nieznanej postaci składników wektora sygnałów źródłowych nie ma to praktycznie żadnego znaczenia). Stąd podstawowym celem jest rekonstrukcja „kształtu” sygnałów źródłowych. Innymi słowy, poszukiwanym systemem separującym jest taka macierz \( \mathbf{W} \), że zachodzi relacja
| \(\mathbf{y}(t)=\mathbf{W A s}(t)=\mathbf{P D s}(t)\) | (9.9) |
Można przyjąć, że macierz estymowana \(\hat{\mathbf{A}}=\mathbf{W}^{+}\) jest w rzeczywistości określona jako \(\hat{\mathbf{A}}=\mathbf{A P D}\) oraz \(\mathbf{W A} \hat{\mathbf{A}}=\mathbf{W} \mathbf{W}^{+}=\mathbf{1}_n\), gdzie \( \mathbf{P} \) jest macierzą permutacji odpowiedzialnej za przestawienie kolejności składników wynikowych \( y_i \), \( \mathbf{D} \) – macierz diagonalna skalująca wartości sygnałów wynikowych, \( \mathbf{W}^{+} \) jest macierzą pseudo-odwrotną do macierzy \( \mathbf{W} \).
Rozwiązanie określające wektor \(\mathbf{y}(t) \) spełniający warunek (9.8) jest możliwe do osiągnięcia przy dowolnej liczbie \(n\) sygnałów. Przy większej niż dwa liczbie źródeł i nieznanych z góry wartościach współczynników \( a_{ij} \) macierzy mieszającej można osiągnąć separację sygnałów, stosując jedynie metody algorytmiczne adaptacyjnego doboru wag sieci neuronowej.
3.4. Algorytmy uczące sieci rekurencyjnej
Rozwiązanie problemu separacji sygnałów przy zastosowaniu sieci rekurencyjnej zostało zaproponowane przez J. Heraulta i C. Juttena i ulepszone przez Cichockiego [8] sprowadza się do rozwiązania układu równań różniczkowych, opisujących zmiany wag sieci neuronowej dla każdej chwili czasowej \(t\).
Zgodnie z modyfikacja Cichockiego wprowadza się sprzężenie zwrotne własne neuronu z wagą \(w_{i i} \neq 0\). Sprzężenie to powoduje samo-normalizację sygnałów wyjściowych, sprowadzając je wszystkie do takiego samego poziomu liczbowego (wartości znormalizowanej) i ułatwiając w ten sposób proces separacji. Wówczas zależności adaptacyjne wag opisane są wzorami (przy założeniu, że \(y_i(t)\) nie zawierają składowej stałej)
| \( \frac{d w_{i j}}{d t}=\eta(t) f\left(y_i(t)\right)g\left(y_j(t)\right) \) | (9.10) |
dla wag łączących różne neurony \( i \neq j\), oraz
| \( \frac{d w_{i i}}{d t}=\eta(t)\left[f\left(y_i(t)\right)g\left(y_i(t)\right)-1\right] \) | (9.11) |
dla kolejnych wag sprzężenia własnego (wagi diagonalne macierzy \(\mathbf{W}\)). Obie zależności można zapisać w postaci macierzowej wspólnej dla obu rodzajów wag
| \(\frac{d \mathbf{W}}{d t}=\eta(t)\left[\mathbf{f}(\mathbf{y}(t)) \mathbf{g}^T(\mathbf{y}(t))-\mathbf{1}\right]\) | (9.12) |
w której \(\mathbf{W}\) oznacza macierz wag sieci o wymiarze \( n \times n \), a \( \mathbf{f}(\mathbf{y}) \) i \( \mathbf{g}(\mathbf{y}) \) oznaczają wektory sygnałowe, \(\mathbf{f}(\mathbf{y})=\left[f\left(y_1(t)\right), f\left(y_2(t)\right), \ldots, f\left(y_n(t)\right)\right]^T\), \(\mathbf{g}(\mathbf{y})=\left[g\left(y_1(t)\right), g\left(y_2(t)\right), \ldots, g\left(y_n(t)\right)\right]^T\).
W praktyce stosuje się różne rodzaje funkcji \(f(x)\) i \(g(x)\), najczęściej przyjmując jedną z nich typu wypukłego, a drugą typu wklęsłego. Przykładowy wybór funkcji to \(f(x)=x^3\), \(f(x)=x^5\). W przypadku funkcji \(g(x)\) dobre rezultaty uzyskuje się przy \(g(x)=tanh(x)\), \(g(x)=arctg(x)\), \(g(x)=x\), \(g(x)=sgn(x)\), itp. Jak zostało udowodnione w pracy [8] obie funkcje \(f(x)\) oraz \(g(x)\) odpowiadają momentom statystycznym wyższych rzędów, które przy założeniu statystycznej niezależności sygnałów automatycznie zapewniają wartość średnią \( \overline{f\left(y_i(t)\right) g\left(y_i(t)\right)} \) równą zeru, co jest warunkiem zbieżności algorytmu uczącego. Wybór współczynnika uczenia \( \eta(t) \) odgrywa istotną rolę w procesie adaptacji. W przypadku sygnałów stacjonarnych na początku uczenia jest to wartość stała, a następnie maleje do wartości minimalnej w miarę upływu czasu.
Z rozwiązania układu równań różniczkowych opisanych zależnością (9.12) otrzymuje się aktualne wartości wag, służące do określenia sygnałów wyjściowych opisanych wektorem \(\mathbf{y}(t)\), przy czym przy \(\mathbf{y}(t)=(\mathbf{1}+\mathbf{W})^{-1} \mathbf{x}(t)\).
Głównym źródłem zwiększonej efektywności algorytmu jest samo-normalizacja (do wartości jednostkowej) sygnałów wyjściowych \(y_i(t)\). Mianowicie w stanie ustalonym \(\frac{d \mathbf{W}}{d t}=\mathbf{0}\), skąd wynika, że \( \overline{f\left(y_i(t)\right) g\left(y_i(t)\right)} = 1 \), co oznacza, że niezależnie od aktualnego poziomu sygnałów \(s_i(t)\) następuje automatyczne skalowanie wszystkich sygnałów w sieci do poziomu jednostkowego. Badania symulacyjne sieci o zmodyfikowanym algorytmie uczenia wykazały, że możliwa jest separacja sygnałów o amplitudach różniących się nawet w stosunku \( 1 : 10^9 \).
Program został przetestowany przy separacji wielu różnorodnych sygnałów, wykazując się bardzo dobrą skutecznością.
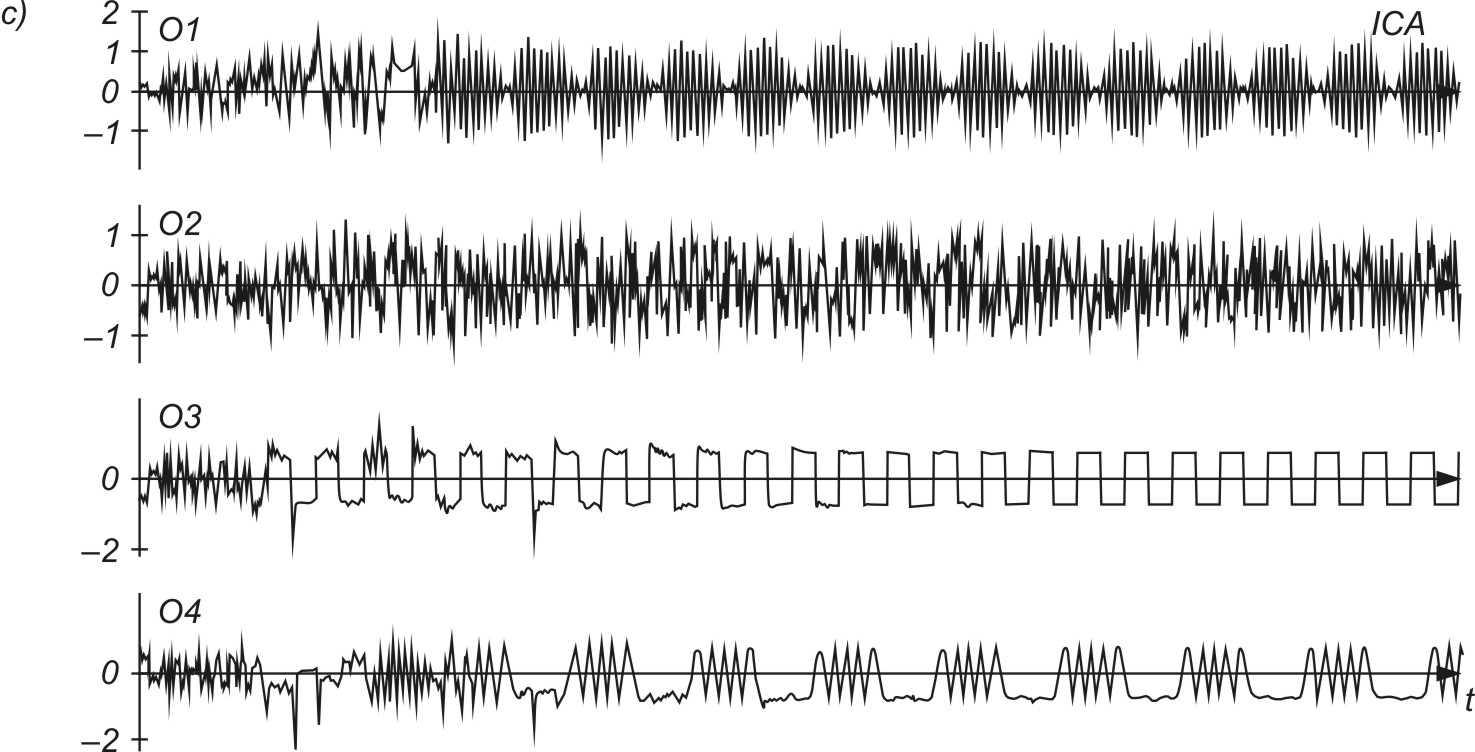
Na rys. 9.3 przedstawiono ilustracje procesu separacji czterech sygnałów si(t) o znacznie różniących się amplitudach
\(\begin{aligned} & s_1(t)=0,001 \sin (300 t+6 \cos (60 t)) \\ & s_2(t)=\operatorname{rand}(0,00001, t) \\ & s_3(t)=0,001 \operatorname{sgn}(\cos (155 t)) \\ & s_4(t)=0,00001 \sin (1200 t) \sin (50 t)\end{aligned}\)
Rys. 9.3a przedstawia (u góry) sygnały oryginalne \(s_i(t)\), rys. 9.3b - sygnały zmieszane \(x_i(t)\), a rys. 9.3c (na dole) - sygnały estymowane przez sieć neuronową w procesie separacji (sygnały niezależne będące repliką sygnałów oryginalnych). Sygnałami wejściowymi sieci neuronowej są sygnały zmieszane (trzy środkowe wykresy czasowe na rys. 9.3b). Ze względu na ogromną różnicę amplitud sygnałów oryginalnych w sygnałach zmieszanych podawanych na sieć widoczne są jedynie największe sygnały szumu, natomiast sygnały o małej amplitudzie są niezauważalne.
Proces separacji przeprowadzony został przy zastosowaniu funkcji nieliniowych \(f(x) = x^3\) i \(f(x) = tgh(10x)\) oraz współczynniku uczenia \( \eta(t) \) zmienianym adaptacyjnie przy wartości startowej równej 2000. Taki dobór parametrów pozwolił na separację wszystkich sygnałów, niezależnie od poziomu amplitud (trzy dolne wykresy czasowe na rys. 9.3c). Odseparowane przez sieć sygnały charakteryzowały się jednakowym poziomem amplitud, uzyskanym dzięki wprowadzeniu sprzężenia własnego neuronów. Ich kolejność występowania jest inna niż kolejność sygnałów oryginalnych.
3.5. Sieć jednokierunkowa do separacji sygnałów
Wadą sieci rekurencyjnej jest potrzeba zapewnienia bezwzględnej stabilności przy separacji sygnałów, szczególnie wtedy, gdy macierz mieszająca \( \mathbf{A} \) jest bardzo źle uwarunkowana, a sygnały źródłowe różnią się znacznie pod względem amplitud. Należy ponadto zauważyć, że w sieci rekurencyjnej w każdym kroku występuje konieczność inwersji macierzy wagowej (wzór 9.8), co wydatnie zwiększa złożoność obliczeniową algorytmu. Zastosowanie sieci jednokierunkowej bez sprzężeń zwrotnych pozwala wyeliminować te problemy. Większość współczesnych rozwiązań ślepej separacji unika tych problemów stosując przekształcenie liniowe
| \( \mathbf{y} = \mathbf{Wx} \) | (9.13) |
odpowiadające sieci liniowej o jednym kierunku przepływu sygnałów. Macierz \( \mathbf{W} \) występująca w tej zależności jest macierzą pełną (nie występują założenia co do wartości zerowych pewnych wag). Sieć jednokierunkowa odpowiadające tej zależności pełni identyczną funkcję jak sieć sprzężeniem zwrotnym. Przyjmując, że wektor wyjściowy \( \mathbf{y} \) w obu rodzajach sieci jest równy sobie, można zapisać
| \( \mathbf{W} \mathbf{x}(t)=\left(\mathbf{1}+\mathbf{W}_r\right)^{-1} \mathbf{x}(t) \) | (9.14) |
W równaniu tym \( \mathbf{W}_r \) oznacza macierz wag sieci rekurencyjnej, a \( \mathbf{W} \) macierz sieci jednokierunkowej. Oznacza to, że obie sieci będą sobie równoważne, jeśli
| \( \mathbf{W}=\left(\mathbf{1}+\mathbf{W}_r\right)^{-1} \) | (9.15) |
W praktyce odchodzi się od równań różniczkowych na rzecz równania różnicowego, jako powszechnie stosowanej metody rozwiązania równań różniczkowych. Powstało wiele odmian algorytmów uczących implementujących relacje (9.13), charakteryzujących się szczególnie dobrymi własnościami separacji przy złym uwarunkowaniu macierzy mieszającej \( \mathbf{A} \) lub przy dużym zróżnicowaniu amplitud sygnałów źródłowych si(t). Można je w ogólności zaliczyć do algorytmów bazujących na statystykach drugiego rzędu (ang. Second Order Statistics - SOS) oraz na statystykach wyższych rzędów (ang. Higher Order statistics - HOS) [8]. Większość z tych algorytmów rozwinęła się na bazie teorii statystycznego przetwarzania sygnałów i nie wykorzystuje bezpośrednio zależności odnoszących się do sieci neuronowych.
Jednym z najprostszych algorytmów klasy SOS jest AMUSE (ang. Algorithm for Multiple Unknown Source Extraction). Algorytm ten bazuje na diagonalizacji macierzy kowariancji (9.3). Wykorzystuje dwie podstawowe operacje: wybielanie (ang. prewhitening) oraz diagonalizację macierzy kowariancji dla jednego opóźnienia czasowego. Można go traktować jako dwukrotne zastosowanie metody składników głównych PCA [8].
-
W pierwszym kroku estymowana jest macierz kowariancji oryginalnych wektorów \( \mathbf{x} \) bez opóźnień
| \( \mathbf{R}_{x x}(0)=\mathrm{E}\left[\mathbf{x}(k) \mathbf{x}^T(k)\right] \) | (9.16) |
-
Następnie obliczana jej dekompozycja macierzy kowariancji według wartości własnych (ang. Eigen Value Decomposition - EVD),
| \( \mathbf{R}_{x x}(0)=\mathbf{V} \mathbf{L} \mathbf{V}^T \) | (9.17) |
w której \( \mathbf{V} \) jest macierzą ortogonalną, a \( \mathbf{L} \) macierzą diagonalną.
-
Następnie obliczana jest macierz \( \mathbf{Q} \) liniowej transformacji wybielającej
| \( \mathbf{Q}=\left[\mathbf{R}_\mathbf{xx}(0)\right]^{-1 / 2}=\left(\mathbf{V L}^{-1 / 2}\right) \mathbf{V}^T \) | (9.18) |
Wektor sygnałów obserwowanych \( \mathbf{x}(k) \) w wyniku wybielenia jest transformowany w wektor sygnałów wybielonych \( \mathbf{z}(k) \)
| \(\mathbf{z}(k)=\mathbf{Q} \mathbf{x}(k)\) | (9.19) |
-
Dla sygnałów wybielonych (zdekorelowanych) \( \mathbf{z}(k) \) obliczana jest nowa macierz kowariancji, tym razem z opóźnieniem czasowym równym jeden, z jednoczesną dekompozycją SVD
| \( \mathbf{R}_\mathbf{zz}(1)=\mathrm{E}\left[\mathbf{z}(k) \mathbf{z}^T(k-1)\right]=\mathbf{U S} \mathbf{V}^T \) | (9.20) |
gdzie \( \mathbf{S} \) jest macierzą diagonalną wartości osobliwych macierzy \( \mathbf{R}_\mathbf{zz}(1) \) a macierze \( \mathbf{U} \), \( \mathbf{V} \) są ortogonalne.
-
Macierz separującą \( \mathbf{W} \) stanowiącą inwersję macierzy mieszającej \( \mathbf{A} \) (\( \mathbf{W} = \mathbf{A}^{-1} \)) określa wówczas wzór
| \( \mathbf{W} = \mathbf{U}^{T}\mathbf{Q} \) | (9.21) |
Nieznana macierz mieszająca \( \mathbf{A} \) może więc być estymowana w postaci odwrotnej do \( \mathbf{W} \), czyli (\( \mathbf{A} = \mathbf{Q}^{T}\mathbf{U} \)). Algorytm AMUSE jest zwykle dość wrażliwy na szum zakłócający pomiary. Dla zwiększenia jego odporności można w drugim kroku zamiast macierzy kowariancji dla jednego opóźnienia czasowego użyć liniowej kombinację wielu macierzy kowariancji dla różnych opóźnień czasowych. Można zastosować równoczesną diagonalizację kilkunastu lub nawet kilkudziesięciu macierzy kowariancji. W takim przypadku macierz kowariancji \( \mathbf{R}_{zz}\) jest wartością oczekiwaną (średnią) z macierzy kowariancji obliczonych dla wielu (\(K\)) realizacji.
| \(\mathbf{R}_\mathbf{zz}(p)={E}\left[\mathbf{z}(k) \mathbf{z}^T(k-p)\right]=\mathbf{U S} \mathbf{V}^T\) | (9.27) |
dla \(p=1,2,…,K\). Taki sposób postępowania został zaimplementowany miedzy innymi w algorytmie SOBI (ang. Second Order Blind Identification).
W przypadku algorytmów bazujących na statystykach wyższych rzędów wykorzystuje się niezależność statystyczną sygnałów (ICA). We współczesnych rozwiązaniach algorytmów uczących macierz \( \mathbf{W} \) otrzymuje się z iteracji na iterację w postaci dyskretnej
| \(\mathbf{W}(k+1)=\mathbf{W}(k)+\Delta \mathbf{W}(k)\) | (9.28) |
unikając w ten sposób potrzeby rozwiązania układu równań różniczkowych. Istnieje wiele różnych rozwiązań ślepej separacji należących do rodziny ICA. Spośród nich można wymienić [8]:
-
algorytm Cichockiego-Amari-Younga
| \( \Delta \mathbf{W}(k)=\eta(t) [ \mathbf{L}-\mathbf{f}(\mathbf{y}(k)) \mathbf{g}^T(\mathbf{y}(k)) ] \mathbf{W}^{-1} \) | (9.29) |
gdzie \( \mathbf{L} \) jest macierzą diagonalną o elementach \( \lambda_{ii} \geq 0 \) (najczęściej \( \lambda_{ii} = 1 \)).
-
algorytm opierający się na gradiencie naturalnym prof. Amari
| \( \left.\Delta \mathbf{W}(k)=\eta(t) [ \mathbf{L}-\mathbf{f}(\mathbf{y}(k)) \mathbf{g}^T(\mathbf{y}(k))\right] \mathbf{W} \) | (9.30) |
Macierz \( \mathbf{L} \) dobiera się podobnie jak w algorytmie Cichockiego-Amari-Younga.
-
algorytm Cardossa
| \( \Delta \mathbf{W}(k)=\eta(t)\left[\mathbf{1}-\mathbf{y}(k) \mathbf{y}^T(k)-\alpha \mathbf{f}(\mathbf{y}(k)) \mathbf{g}^T(\mathbf{y}(k))+\beta \mathbf{g}(\mathbf{y}(k)) \mathbf{f}^T(\mathbf{y}(k))\right] \mathbf{W} \) | (9.31) |
gdzie \(\alpha\) i \( \beta\) są współczynnikami liczbowymi z zakresu \( [0, 1]\).
Podobnie jak w sieciach rekurencyjnych, współczynnik uczenia \(\eta(k)\) stanowi funkcję malejącą w czasie do zera. Zwykle jest to funkcja wykładnicza postaci \(\eta(t)=A e^{-\alpha k / \tau}\), o wartości amplitudy \( A\) i stałej czasowej \( \tau\) dobieranej indywidualnie dla poszczególnych przypadków.
3.6. Toolbox ICALAB
W chwili obecnej dostępny jest zbiór programów Matlaba do ślepej separacji sygnałów, tworzący oddzielny specjalizowany toolbox, zwany ICALAB [74]. Został opracowany koncepcyjnie przez zespół pracowników RIKEN pod kierownictwem prof. A. Cichockiego i S. I. Amari. Pakiet programów ICALAB umożliwia separację sygnałów zmieszanych przy wykorzystaniu różnych kryteriów, takich jak niezależność statystyczna sygnałów, dekorelacja, predykcja liniowa, gładkość sygnałów, rzadkość macierzy. Szczegóły dotyczące tego programu wykraczają poza zakres podręcznika. Można je znaleźć bądź w książce [8] bądź w pomocy (help) do programu ICALAB. W procesie separacji sygnałów zastosowano trzy podstawowe grupy operacji [8]:
-
wstępne przetwarzanie sygnałów (preprocessing),
-
właściwą ślepą separację sygnałów (ICA/BSS)
-
końcowe przetwarzanie sygnałów (postprocessing)
jak to przedstawiono na rys. 9.4, przy czym preprocessing oraz postprocessing są opcjonalne.
Preprocessing umożliwia wstępną filtrację sygnałów, redukcję danych przy użyciu metody składników głównych PCA, dekompozycję sygnałów szerokopasmowych na wiele sygnałów wąskopasmowych itd. Blok ICA/BSS odpowiada za właściwą separację sygnałów, czyli dekompozycję sygnałów na prostsze składniki (np. składniki niezależne, zdekorelowane, gładkie, itp.).
Właściwa ślepa separacja sygnałów (ICA/BSS, SCA, NMF) odbywa się przy zastosowaniu różnych algorytmów separacji wybieranych przez użytkownika spośród wielu zainstalowanych w programie
Postprocessing umożliwia eliminację niepożądanych składników oraz szumów poprzez tak zwaną deflację. Deflacja polega na odtworzeniu sygnałów oryginalnych xi(t) na podstawie sygnałów odseparowanych yi(t) przy wyzerowaniu wybranych przez użytkownika sygnałów odseparowanych.
Program pozwala też badać wpływ poszczególnych składników i sygnałów źródłowych na sygnały obserwowane oraz ich rozkład, lokalizację i wizualizację. Został również uogólniony na ślepą separację obrazów. Pakiet ICALAB może być użyteczny w takich zastosowaniach jak: estymacja nieznanych sygnałów źródłowych oraz określenie ich liczby, redukcja szumów i eliminacja niepożądanych interferencji, redukcja modelu i eliminacja redundancji, dekompozycja złożonych sygnałów na składniki prostsze lub łatwiej interpretowalne fizycznie.
3.7. Przykład zastosowania ICALAB do separacji sygnałów mowy
Przykład zastosowania programu ICALAB dotyczy separacji wypowiedzi czterech wyrażeń: Politechnika Warszawska, Wojskowa Akademia Techniczna, Sieci neuronowe oraz Ala ma kota. Sygnały te zostały uzupełnione przez sygnał losowy. Wszystkie 5 sygnałów zostały zmieszane przy pomocy macierzy losowej A. W następnym etapie tak zmieszane wektory podlegały ślepej separacji przy użyciu jednego z wybranych algorytmów typu SOS (AMUSE) [74]. Na rys. 9.5 przedstawiono wyniki wygenerowane przez program przedstawiające: sygnały oryginalne przed zmieszaniem, sygnały po zmieszaniu, sygnały odtworzone oraz macierz przedstawiającą iloczyn A*W (przy idealnej separacji powinna to być postać macierzowa o wartości 1 na jednej z 5 pozycji w każdym kanale odtworzonym). Wynik działania jest zbliżony do idealnego (przesłuchy z innych kanałów są minimalne, co odzwierciedlone jest na niediagonalnych pozycjach macierzy \(\mathbf{AW}\) w postaci bardzo małych wartości, największa wartość niediagonalna to 0.1130). Odtworzenie słuchowe sygnałów wynikowych potwierdza bardzo dobre działanie systemu separacji.
|
a) |
|
b) |
|
c) |
|
d) |
3.8. Zadania i problemy
1. Wykorzystując funkcję xcorr Matlaba wyznaczyć funkcje autokorelacji i korelacji wzajemnej dwu losowych wektorów 100 elementowych o rozkładzie gaussowskim (wartości znormalizowane). Narysować przebieg tej funkcji dla różnych opóźnień.
2. Wykorzystując funkcję xcorr Matlaba wyznaczyć funkcje autokorelacji i korelacji wzajemnej dwu wektorów 100 elementowych z których jeden składa się z elementów funkcji sinusoidalnej \( x_1(t)=\sin(2t) \) a drugi funkcji wykładniczej \( x_2(t)=\exp(-0.1t) \). Narysować przebieg tej funkcji dla różnych opóźnień.
3. Wykorzystując program ICALAB dokonać separacji dwu sygnałów: prostokątnego (np. \( A_1 \cdot \textrm{sign}( \sin( \omega_1 t)) \) oraz sinusoidalnego (np. \( A_2 \cdot \sin( \omega_2 t) \) dla wybranych wartości \(\omega_1\) oraz \(\omega_2\) i zróżnicowanych wartości \(A_1\) i \(A_2\), np. \(A_1 = 1\), \(A_2 = 100\) oraz \(A_1 = 1\), \(A_2 = 10^8\).
4. Sprawdzić działanie sieci separującej (program ICALAB) dla 5 sygnałów wygenerowanych w sposób dowolny. Rozważyć przypadek sygnałów zależnych i niezależnych oraz sygnałów będących superpozycją sygnału deterministycznego i szumu losowego.
5. Pokazać związek występujący między macierzą wag \( \mathbf{W} \) sieci separującej rekurencyjnej i jednokierunkowej.
6. Korzystając z funkcji audiorecorder Matlaba dokonać nagrania 3 różnych wypowiedzi tworząc 3 wektory o tej samej długości. Utworzyć z nich macierz X dodając czwarty sygnał szumu losowego (funkcja randn Matlaba) o dużej wariancji (amplituda szumu wielokrotnie większa od amplitudy sygnałów mowy). Wykorzystując program ICALAB sygnały te poddać zmieszaniu przy założeniu różnej macierzy mieszającej \( \mathbf{A} \), a następnie separacji. Odtworzyć dźwiękowo sygnały zmieszane oraz sygnały odseparowane używając funkcji soundsc.
7. Sprawdzić i porównać działanie różnych algorytmów ślepej separacji sygnałów zaimplementowanych w programie ICALAB wykorzystując sygnały wbudowane w bazie danych tego pakietu.
3.9. Słownik
Słownik opanowanych pojęć
Wykład 9
ICA – ślepa separacja sygnałów niezależnych (ang. Independent Component Analysis).
BSS – uogólnienie ICA na inne rodzaje dekompozycji sygnałów (BSS - ang. Blind Signal Separation) .
Niezależność statystyczna sygnałów – własność sygnałów oznaczająca, że dwuwymiarowa łączna gęstość prawdopodobieństwa \(p(y_i,y_j)\) jest równa iloczynowi jednowymiarowych funkcji gęstości zmiennej \( y_i\) oraz \(y_j\).
SOS – statystyki drugiego rzędu (ang. Second Order Statistics).
HOS – statystyki wyższych rzędów (ang. Higher Order Statistics).
EVD – dekompozycja macierzy według wartości własnych (ang. Eigen Value Decomposition).
AMUSE – jeden z algorytmów dekompozycji BSS wykorzystujący SOS.
Toolbox ICALAB – program komputerowy z interfejsem graficznym w Matlabie do ślepej separacji sygnałów.
Preprocessing – wstępne przetwarzanie sygnałów.
Postprocessing – końcowe przetwarzanie sygnałów po właściwej operacji.
4. Literatura
1. Bengio Y., LeCun Y., Hinton G., Deep Learning, Nature, 2015, vol. 521, pp. 436–444.
2. Brownlee J., Deep Learning for Natural Language Processing. Develop Deep Learning Models for your Natural Language Problems, Ebook, 2018.
3. Breiman L., Random forests, Machine Learning, 2001, vol. 45, No 11, pp. 5–32.
4. Banerjee S., Linear algebra and matrix analysis for statistics, 2012, London.
5. Brudzewski K., Osowski S., Markiewicz T., Ulaczyk J., Classification of gasoline with supplement of bio-products by means of an electronic nose and SVM neural network, Sensors and Actuators - Chemical, 2006, vol. 113, No 1, pp. 135-141.
6. Chen S., Cowan C.F., Grant P.M., Orthogonal least squares learning algorithm for radial basis function networks, IEEE Trans. Neural Networks, 1991, vol. 2, pp. 302–309.
7. Christensen R., Johnson W. O., Branscum A. J., Hanson T. E., Bayesian ideas and data analysis: an introduction for scientists and statisticians, 2010, Chapman & Hall/CRC Science
8. Cichocki A., Amari S. I., Adaptive blind signal and image processing, 2003, Wiley, New York.
9. Crammer K. , Singer Y., On the learnability and design of output codes for multiclass problems. Computational Learning Theory, 2000, pp. 35-46.
10. Duda, R.O., Hart, P.E., Stork, P., Pattern classification and scene analysis, 2003, Wiley, New York.
11. Fogel, L.J., Intelligence through simulated evolution : forty years of evolutionary programming, 1999, Wiley, New York.
12. Fukushima K.: Neocognitron - a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 1980, vol.. 36, No 4, pp. 193–202, doi:10.1007/bf00344251.
13. Genc H., Cataltepe Z., Pearson T., A new PCA/ICA based feature selection method, IEEE 15th In Signal Processing and Communications Applications, 2007, pp. 1-4.
14. Gill P., Murray W., Wright M., Practical optimization, 1981, Academic Press, London.
15. Goldberg D., Algorytmy genetyczne i ich zastosowania, 2003, WNT Warszawa.
16. Golub G., Van Loan C., Matrix computations, 1996, John Hopkins University Press, Baltimore.
17. Gao H., Liu Z., Van der Maaten L., Weinberger K., Densely connected convolutional networks, CVPR, vol. 1, no. 2, p. 3. 2017.
18. Goodfellow I., Bengio Y., Courville A.: Deep learning 2016, MIT Press, Massachusetts (tłumaczenie polskie: Deep Learning. Współczesne systemy uczące się, Helion, Gliwice, 2018).
19. Goodfellow I., Pouget-Abadie J., Mirza M, Xu M., Warde-Farley B., Ozair D., Courville A. Bengio Y., Generative Adversarial Nets (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680.
20. Greff K., Srivastava R. K., Koutník J., Steunebrink B. R., Schmidhuber J., LSTM: A search space odyssey, IEEE Transactions on Neural Networks and Learning Systems, vol. 28, No 10, pp. 2222-2232, 2017.
21. Gunn S., Support vector machines for classification and regression, ISIS Technical report, 1998, University of Southampton.
22. Guyon I., Elisseeff A., An introduction to variable and feature selection, J. Mach. Learn. Res., 2003, vol. 3, pp. 1157-1182.
23. Guyon, I., Weston, J., Barnhill, S., Vapnik, V., Gene selection for cancer classification using Support Vector Machines, Machine Learning, 2002, vol. 46, pp. 389-422.
24. Haykin S., Neural networks, a comprehensive foundation, Macmillan College Publishing Company, 2000, New York.
25. He K., Zhang X, Ren S, Sun J., Deep Residual Learning for Image Recognition, 2015, http://arxiv.org/abs/1512.03385.
26. Hinton G. E., Salakhutdinov R. R., Reducing the dimensionality of data with neural networks, Science, 313:504-507, 2006.
27. Howard A., Zhu M., Chen B., Kalenichenko D., MobileNets: Efficient convolutional neural networks for mobile vision applications, arXiv: 1704.04861v1 [cs.CV], 2017.
28. Hsu, C.W., Lin, C.J., A comparison methods for multi class support vector machines, IEEE Trans. Neural Networks, 2002, vol. 13, pp. 415-425.
29. Huang G., Liu Z., van der Maaten L., Weinberger K., Densely connected convolutional networks, arXiv: 1606.06993v5 [cs.CV] 2018.
30. Iandola F, Han S., Moskevicz M., Ashraf K., Dally W., Keutzer K, Squeezenet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size, Conference ICLR, 20017. pp. 1-13.
31. Joachims T., Making large scale SVM learning practical, (in ”Advances in kernel methods - support vector learning”, B. Scholkopf, C. Burges, A. Smola eds). MIT Press, Cambridge, 1998, pp. 41-56.
32. Kecman V., Support vector machines, neural networks and fuzzy logic models, 2001, Cambridge, MA: MIT Press.
33. Kingma P, Welling M., An introduction to variational autoencoders, Foundations and Trends in Machine Learning, 12:307-392, 2019.
34. Krizhevsky A., Sutskever I., Hinton G., Image net classification with deep convolutional neural networks, Advances in Neural Information Processing Systems, vol. 25, pp. 1-9, 2012.
35. Kruk M., Świderski B., Osowski S., Kurek J., Słowińska M., Walecka I., Melanoma recognition using extended set of descriptors and classifiers, Eurasip Journal on Image and Video Processing, 2015, vol. 43, pp. 1-10, DOI 10.1186/s13640-015-0099-9
36. Kuncheva L., Combining pattern classifiers: methods and algorithms, 2015, Wiley, New York.
37. LeCun Y., Bengio Y., Convolutional networks for images, speech, and time-series. 1995, in Arbib M. A. (editor), The Handbook of Brain Theory and Neural Networks. MIT Press, Massachusetts.
38. Lecture CS231n: 2017, Stanford Vision Lab, Stanford University.
39. Lee K.C., Han I., Kwon Y., Hybrid Neural Network models for bankruptcy prediction, Decision Support Systems, 18 (1996) 63-72.
40. Leś T., Osowski S., Kruk M., Automatic recognition of industrial tools using artificial intelligence approach, Expert Systems with Applications, 2013, vol. 40, pp. 4777-4784.
41. Lin C. J., Chang, C. C., LIBSVM: a library for support vector machines. http://www. csie. ntu. edu. tw/cjlin/libsvm
42. Markiewicz T., Sieci neuronowe SVM w zastosowaniu do klasyfikacji obrazów komórek szpiku kostnego, rozprawa doktorska Politechniki Warszawskiej, 2006.
43. Matlab user manual MathWorks, 2021, Natick, USA.
44. Michalewicz Z., Algorytmy genetyczne + struktury danych = programy ewolucyjne, WNT, Warszawa 1996.
45. Osowski S., Cichocki A., Siwek K., Matlab w zastosowaniu do obliczeń obwodowych i przetwarzania sygnałów, 2006, Oficyna Wydawnicza PW.
46. Osowski S., Sieci neuronowe do przetwarzania informacji, 2020, Oficyna Wydawnicza PW.
47. Osowski S., Szmurło R., Siwek K., Ciechulski T., Neural approaches to short-time load forecasting in power systems – a comparative study, Energies, 2022, 15, pp. 3265.
48. Osowski S., Siwek K., R. Szupiluk, Ensemble neural network approach for accurate load forecasting in the power system, Applied Mathematics and Computer Science, 2009, vol.19, No.2, pp. 303-315.
49. Osowski S., Metody i narzędzia eksploracji danych , Wydawnictwo BTC, Warszawa, 2013
50. Patterson J., Gibson A., Deep Learning: A Practitioner's Approach (tłumaczenie polskie : Deep learning. Praktyczne wprowadzenie), Helion, Gliwice, 2018.
51. Platt L., Fast training of SVM using sequential optimization (in Scholkopf, B., Burges, B., Smola, A., Eds. Advances in kernel methods – support vector learning. Cambridge: MIT Press), 1998, 185-208.
52. Redmon J., Divval S., Girshick R., Farhafi A., You Only Look Once: unified. Real time object detection, axXiv: 1506.02640v5 [cs.CV], 2016
53. Ren S., He K., Girshick R., Sun J., Faster R-CNN: toward real time object detection with region proposal networks, IEEE trans. PAMI, vol. 39, pp. 1137-1149, 2017
54. Riedmiller M., Braun H.: RPROP – a fast adaptive learning algorithm. Technical Report, University Karlsruhe, Karlsruhe 1992.
55. Ridgeway G., Generalized Boosted Models: A guide to the gbm package. 2007
56. Ronneberger O., Fischer P., Brox T.: U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015, arXiv:1505.04597.
57. Sammon J. W., A nonlinear mapping for data structure analysis, IEEE Trans. on Computers, 1969, vol. 18, pp. 401-409.
58. Schmidhuber J., Deep learning in neural networks: An overview, Neural Networks, vol. 61, pp. 85-117, 2015.
59. Schölkopf B., Smola A., Learning with kernels, 2002, MIT Press, Cambridge MA.
60. Schurmann J., Pattern classification, a unified view of statistical and neural approaches, 1996, Wiley, New York.
61. Sandler, M., Howard, A., Zhu, M., Zhmoginov, A. and Chen, L.C. "MobileNetV2: Inverted Residuals and Linear Bottlenecks." In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 4510-4520). IEEE.
62. Swiderski B., Kurek J., Osowski S., Multistage classification by using logistic regression and neural networks for assessment of financial condition of company, Decision Support Systems, 2012, vol. 52, No 2, pp. 539-547
63. Szegedy C, Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., Going deeper with convolutions, arXiv: 1409.4842v1, 2014.
64. Szegedy C, Ioffe S., Vanhoucke V. Inveption-v4, Inception-ResNet and the impact of residual connections on learning, arXiv:1602.07261v2, 2016.
65. Tan P.N., Steinbach M., Kumar V., Introduction to data mining, 2006, Pearson Education Inc., Boston.
66. Tan M. Le Q., EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, arXiv:1905.11946 [cs.LG], 2020
67. Van der Maaten L., Hinton G., Visualising data using t-SNE, Journal of Machine Learning Research, 2008, vol. 9, pp. 2579-2602.
68. Vapnik V., Statistical learning theory, 1998, Wiley, New York.
69. Wagner T., Texture analysis (w Jahne, B., Haussecker, H., Geisser, P., Eds. Handbook of computer vision and application. Boston: Academic Press), 1999, ss. 275-309.
70. Zeiler M. D., Fergus R.: Visualizing and Understanding Convolutional Networks. 2013, pp. 1-11, https://arxiv.org/abs/1311.2901.
71. Zhang X., Zhou X., Lin M., Sun J., ShuffleNet: an extremely efficient convolutional neural network for mobile devices, arXiv: 1707.01083v2 [cs.CV], 2017.
72. Zheng G., Liu S., Zeming F. W., Sun L. J., YOLOX: Exceeding YOLO Series in 2021, arXiv:2107.08430v2 [cs.CV]
73. https://www.analyticsvidhya.com/blog/2021/09/adaboost-algorithm-a-complete-guide-for-beginners/
74. http://www.bsp.brain.riken.jp/ICALAB, ICALAB Toolboxes. A. Cichocki, S. Amari, K. Siwek, T. Tanaka et al.
75. https://github.com/BVLC/caffe/tree/master/models/bvlc_googlenet.
76. https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
77. https://www.jeremyjordan.me/variational-autoencoders/
78. Osowski S., Szmurło R., Matematyczne modele uczenia maszynowego w językach matlab i Python, OWPW, 2023, Warszawa.