Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 4. Przykłady zastosowań sieci neuronowych |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 16 stycznia 2026, 08:41 |
Spis treści
- 1. Zespoły klasyfikatorów
- 2. Metody oceny jakości rozwiązań
- 3. Przykłady zastosowań sieci neuronowych w zadaniach biznesowych
- 3.1. Wprowadzenie
- 3.2. Prognozowanie wskaźnika inflacji
- 3.3. Prognozowanie sygnałów kupna i sprzedaży spółek na giełdzie
- 3.4. Klasyfikacja przedsiębiorstwa pod względem zdolności kredytowych na podstawie wskaźników finansowych
- 3.5. Klasyfikacja przedsiębiorstw pod względem podatności na bankructwo
- 3.6. Zadania i problemy
- 3.7. Słownik
- 4. Prognozowanie obciążeń 24-godzinnych w systemie elektroenergetycznym z użyciem zespołu sieci neuronowych
- 5. Literatura
1. Zespoły klasyfikatorów
Dla polepszenia jakości działania systemu klasyfikacyjnego stosuje się wiele klasyfikatorów działających równolegle i rozwiązujących ten sam problem. Wyniki ich działania podlegają integracji (fuzji) dla wypracowania ostatecznego wyniki na danych podlegających testowaniu.
1.1. Struktura zespołu i metody integracji
Najbardziej oczywisty i najprostszy wybór werdyktu końcowego zespołu klasyfikatorów to zastosowanie głosowania większościowego (ang. majority voting). Każdy wzorzec charakteryzowany przez odpowiedni zestaw cech podawany jest na wszystkie klasyfikatory i podlega niezależnej klasyfikacji, będąc przypisany do odpowiedniej klasy. Następnie zliczana jest liczba przypisań tego wektora do każdej klasy. Zwycięża klasa, która uzyska największą liczbę wskazań. Jedną z odmian tego trybu jest przyjęcie założenia, że zwycięzca musi uzyskać minimum 50% plus jeden głos. W przeciwnym przypadku przyjmuje się brak rozstrzygnięcia.
Jeśli przyjąć identyczne prawdopodobieństwo \( \rho \) prawidłowego wskazania klasy przez wszystkie niezależnie działające klasyfikatory i założyć ich nieparzystą liczbę \( M \) to zostało udowodnione, że w głosowaniu większościowym statystyczna dokładność zespołu może być wyrażona wzorem [36]
| \( Acc=\sum_{m=[M / 2]+1}^M\left(\begin{array}{c} M \\ m \end{array}\right) p^m(1-p)^{M-m} \) | (11.1) |
W tabeli 11.1 przedstawiono wartości dokładności wskazań zespołu przy założeniu różnych wartości prawdopodobieństwa p (identycznego dla każdego klasyfikatora) dla liczby klasyfikatorów tworzących zespół, równej odpowiednio 3, 5, 7 oraz 9. Przyjmuje się pełną niezależność działania klasyfikatorów.
Tabela 11.1 Wartości dokładności Acc wskazania klasy przez zespół M niezależnych, jednakowej jakości klasyfikatorów
|
|
M=3 |
M=5 |
M=7 |
M=9 |
|
p=0.6 |
0.648 |
0.683 |
0.710 |
0.733 |
|
p=0.7 |
0.784 |
0.837 |
0.874 |
0.901 |
|
p=0.8 |
0.896 |
0.942 |
0.967 |
0.980 |
|
p=0.9 |
0.972 |
0.991 |
0.997 |
0.999 |
Zostało udowodnione teoretycznie, że jeśli wartość \( p > 0,5 \) to przy liczbie członków zespołu dążącej do nieskończoności dokładność wskazania klasy przez zespół dąży do 100%. Jeśli natomiast \( p < 0,5 \) to zwiększanie liczby członków zespołu zmniejsza dokładność. Przy \( M \rightarrow \infty \) dokładność zespołu zmaleje do zera. Dla \( p = 0,5 \) zastosowanie zespołu nie zmienia dokładności rozpoznania klasy.
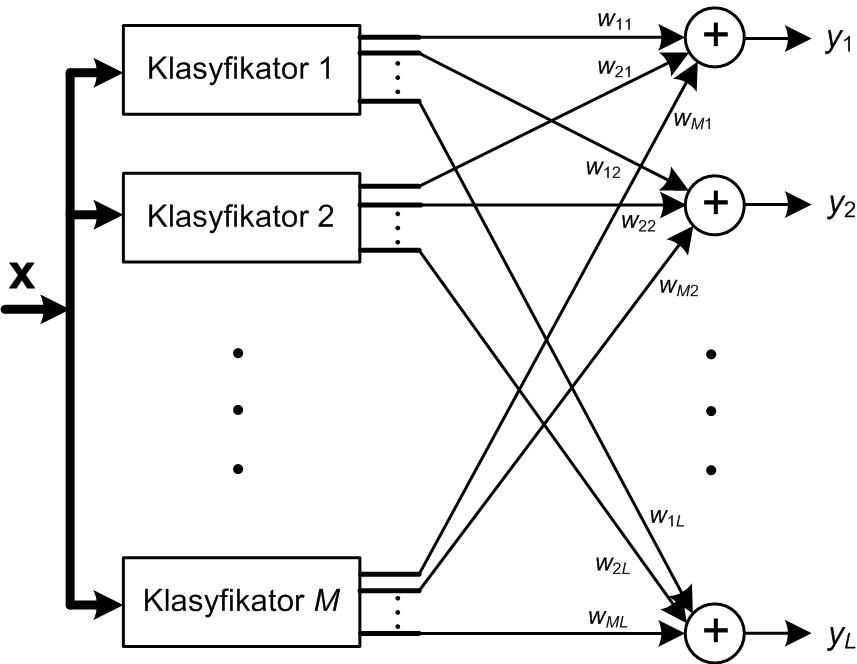
W praktyce rzadko można uzyskać identyczną dokładność wszystkich klasyfikatorów. Eksperymenty numeryczne pokazały, że w takim przypadku głosowanie większościowe nie zawsze gwarantuje uzyskanie wyniku zespołu lepszego niż najlepszy wynik indywidualny. W przypadku nierównej jakości poszczególnych klasyfikatorów można stosować głosowanie większościowe ważone. W tym rozwiązaniu siła głosu klasyfikatora indywidualnego zależy od jego dokładności rozpoznania poszczególnych klas, zmierzoną dla danych uczących (zakłada się, że dane uczące są reprezentatywne dla rozwiązywanego problemu klasyfikacji). Przy M klasyfikatorach tworzących zespół określa się wielkość yi(x) proporcjonalną do prawdopodobieństwa przynależności wektora x do i-tej klasy według wzoru [49]
| \( y_i(x)=\sum_{k=1}^M w_{k i} z_{k i}(x) \) | (11.2) |
w którym wki jest wagą z jaką k-ty klasyfikator jest uwzględniany przy rozpoznaniu i-tej klasy, natomiast zki jest sygnałem wyjściowym k-tego klasyfikatora odpowiedzialnym za rozpoznanie i-tej klasy (sygnał i-tego wyjścia klasyfikatora). Sygnał ten przyjmuje wartość 1 przy rozpoznaniu przez klasyfikator danej klasy bądź zero w przeciwnym przypadku.
Wartości wag wki mogą być wyznaczane w różny sposób, uwzględniający jakość poszczególnych członków zespołu. Do typowych rozwiązań należy
| \( w_{k i}=\frac{\eta_{k i}^m}{\sum_{j=1}^M \eta_{k i}^m} \) | (11.3) |
gdzie \( \eta_{k i}^m \) oznacza wskaźnik jakości (np. dokładność, czułość, precyzję) k-tego klasyfikatora przy rozpoznaniu i-tej klasy, m – wykładnik różnicujący wpływ poszczególnych jednostek zespołu na wynik działania zespołu (np. m= 1, 2, 3). Inny wzór wykorzystuje w integracji zespołu funkcje logarytmiczną [36]
| \( w_{k i}=\lg \left(\frac{\eta_{k i}}{1-\eta_{k i}}\right) \) | (11.4) |
Integracja zespołu klasyfikatorów (lub regresorów) jest również możliwa przy zastosowaniu dodatkowej sieci neuronowej, na wejścia której podawane są sygnały decyzyjne wszystkich członków zespołu. Sieć integrująca trenowana jest na danych (X, d), gdzie macierz wejściowa X jest utworzona z decyzji poszczególnych klasyfikatorów a wektor d reprezentuje przynależność klasową (bądź wartość zadaną w problemie regresji) poszczególnych obserwacji.
Zupełnie innym podejściem do integracji zespołu jest zastosowanie naiwnej reguły Bayesa [7]. Oznaczmy przez P(Dj) prawdopodobieństwo, że j-ty klasyfikator przypisuje wektor wejściowy x do odpowiedniej klasy i załóżmy niezależność działania klasyfikatorów.
Prawdopodobieństwo wskazania klasy \(d_i\)przez zespół \(M\) klasyfikatorów jest wówczas równe
| \( P\left(d_i \mid \mathbf{D}\right)=\frac{P\left(d_i\right) P\left(\mathbf{D} \mid d_i\right)}{P(\mathbf{D})}=\frac{P\left(d_i\right) \prod_{k=1}^M\left(D_k \mid d_i\right)}{P(\mathbf{D})} \) | (11.5) |
Ponieważ mianownik powyższej zależności nie zależy od klasy dk prawdopodobieństwo wskazania k-tej klasy przez zespół przy wystąpieniu na wejściu zespołu wektora wejściowego x jest proporcjonalne do wyrażenia z licznika powyższej zależności (założenie naiwnego klasyfikatora Bayesa). Oznaczmy ten współczynnik proporcjonalności przez µk(x). Wówczas
| \( \mu_i(\mathbf{x}) \approx P\left(d_i\right) \prod_{k=1}^M P\left(D_k \mid d_i\right) \) | (11.6) |
Prawdopodobieństwa występujące w tym wyrażeniu określa się na podstawie macierzy R rozkładu empirycznego klas (macierz pomyłek). Dla każdego klasyfikatora buduje się taką macierz na podstawie jego wyników klasyfikacji dla danych uczących. Przy M klasach jest to macierz M×M. Niech Nk oznacza całkowitą liczbę obserwacji (wektorów x zbioru uczącego ) należących do klasy k. Wówczas prawdopodobieństwo 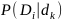 może być estymowane w postaci [49]
może być estymowane w postaci [49]
| \( P\left(D_k \mid d_i\right)=\prod_{k=1}^M\left(\frac{1}{N_i} R_{i D_k}\right) \) | (11.7) |
gdzie \( R_{i D_k} \) oznacza element macierzy R odpowiadający k-temu wierszowi i Di-tej kolumnie na którą wskazał i-ty klasyfikator. Przyjmijmy równe prawdopodobieństwo wystąpienia k-tej klasy wśród całej populacji n danych w postaci ułamka
| \( P\left(d_i\right)=\frac{N_i}{n} \) | (11.8) |
Wówczas współczynnik proporcjonalności dla wyznaczenia prawdopodobieństwo wskazania i-tej klasy przez zespół może być estymowany w postaci
| \( \mu_i(x) \approx \frac{1}{N_i^{M-1}} \prod_{k=1}^M R_{i D_k} \) | (11.9) |
Powyższą procedurę zastosowania metody naiwnej Bayes’a do integracji zespołu klasyfikatorów zilustrujemy na przykładzie hipotetycznego zespołu zawierającego dwa klasyfikatory do rozpoznania 3 klas. Liczba obserwacji uczących jest równa n=30 (każda klasa reprezentowana przez 10 obserwacji). Przyjmijmy, że macierze rozkładu klas dla obu klasyfikatorów są dane w postaci
| \( \mathbf{R}(1)=\left[\begin{array}{lll} 6 & 2 & 2 \\ 2 & 5 & 3 \\ 1 & 3 & 6 \end{array}\right], \;\;\; \mathbf{R}(2)=\left[\begin{array}{lll} 2 & 4 & 4 \\ 2 & 5 & 3 \\ 4 & 0 & 6 \end{array}\right] \) |
Każdy wiersz macierzy odpowiada danym należącym do jednej klasy. Kolumna j-ta macierzy wskazuje, ile przypadków zostało przez dany klasyfikator rozpoznanych jako klasa j-ta. Elementy diagonalne odpowiadają danym rozpoznanym właściwie. Element Rij pokazuje ile razy obserwacja należąca do klasy i-tej została rozpoznana jako klasa j-ta. Dane z obu macierzy wskazują, że N1=10, N2=10, N3=10.
Załóżmy, że testowany wektor x został przypisany przez klasyfikator pierwszy do klasy drugiej, D1(x)=d2, a klasyfikator drugi D2(x)=d1 wskazał klasę pierwszą jako zwycięzcę. Rozpoznanie ostateczne klasy przez zespół klasyfikatorów będzie zależało od wartości µi dla i=1, 2, 3
| \( \begin{aligned} & \mu_1(\mathbf{x}) \approx \frac{1}{10} \times 2 \times 2=0.4 \\ & \mu_2(\mathbf{x}) \approx \frac{1}{10} \times 5 \times 2=1 \\ & \mu_3(\mathbf{x}) \approx \frac{1}{10} \times 3 \times 4=1.2 \end{aligned} \) | (11.10) |
Największą wartość osiągnął współczynnik µ3, stąd decyzją zespołu będzie wskazanie klasy trzeciej jako zwycięskiej dla tej obserwacji x. Zauważmy, że zwyciężyła klasa która nie uzyskała żadnego wskazania klasyfikatorów. To rozwiązanie integracji różni się znacząco od poprzedniej metody, w której zwycięzca był wyłaniany jedynie spośród klas, na którą wskazał co najmniej jeden klasyfikator.
1.2. Warunki właściwego działania zespołu
Uwzględnienie w zespole wielu rozwiązań na raz i ich integracja w jeden końcowy wynik ma sens tylko wtedy, gdy poszczególne rozwiązania są niezależne od siebie a ich wskaźniki jakości są do siebie zbliżone. Łączenie ich ze sobą stwarza wówczas szansę skompensowania pewnych błędów i poprawy dokładności klasyfikatora bądź regresora. Należy jednak podkreślić, że poszczególne rozwiązania nie mogą znacząco różnić się co do jakości, gdyż to najsłabsze może pogorszyć działanie całego zespołu [36].
Niezależność działania pojedynczych rozwiązań można uzyskać na wiele sposobów. Jednym z nich jest zastosowanie rozwiązania bazującego na innej zasadzie działania poszczególnych elementów zespołu. Na przykład zastosowanie klasyfikatora MLP, RBF, SVM daje dobrą przesłankę niezależności, gdyż każdy z nich opiera swój werdykt na innej zasadzie: MLP jest aproksymatorem globalnym, RBF lokalnym, natomiast SVM stosuje odmienne podejście do uczenia. W ramach każdego rozwiązania można również stosować struktury układu zróżnicowane pod względem złożoności (np. liczby neuronów ukrytych).
Innym rozwiązaniem problemu niezależności jest zastosowanie w uczeniu każdego członka zespołu różniących się zbiorów uczących. Takie podejście powoduje, że parametry poszczególnych układów dobrane w procesie uczenia będą inne, a więc ich działanie w trybie odtworzeniowym również odmienne. Problemem może być ograniczony zasób danych przeznaczonych do uczenia. Można go złagodzić przez zastosowanie procedury losowania danych, w której każdy układ stosuje określony procent całego zbioru danych zmieniany każdorazowo w procesie uczenia (np. procedura zwana bagging).
Innym rozwiązaniem jest stosowanie zróżnicowanego sposobu generacji cech diagnostycznych stanowiących informację wejściową dla każdego indywidualnego członka zespołu [22,49,60]. Cechy te generowane są na podstawie tych samych danych pomiarowych. W takiej sytuacji każde z indywidualnych rozwiązań systemu ma dostęp do pełnej informacji pomiarowej, ale inaczej przetworzonej.
1.3. Techniki tworzenia silnych rozwiązań na bazie słabych predyktorów
Interesującą techniką poprawy zdolności generalizacyjnych w uczeniu maszynowym jest tworzenie silnych predyktorów (klasyfikatorów bądź układów regresyjnych o podwyższonej dokładności) poprzez zastosowanie zespołów zbudowanych na bazie słabych rozwiązań predyktorów (mało dokładnych), na przykład lasu drzew decyzyjnych, nieoptymalnie dobranych struktur sieci neuronowych RBF lub MLP, itp. Klasyczne techniki tworzenia zespołu poprzez zastosowanie wielu równoległych rozwiązań indywidualnych predyktorów tego samego typu, ale trenowanych na losowo wybranych danych uczących (tzw. bagging), stosowane na przykład w lesie losowym drzew decyzyjnych [3] nie zawsze prowadzą do optymalnego wyniku pod względem generalizacji. Pojawiło się wiele ulepszonych rozwiązań tego typu zespołów. Do najbardziej znanych należą systemy wzmacniana (tzw. boosting), które wpływają na działanie zespołu już na etapie ich tworzenia, ingerując silnie w algorytm uczący. W tym punkcie przedstawione zostaną dwie techniki tworzenia takiego zespołu słabych predyktorów: wzmacnianie adaptacyjne (tzw. adaptive boosting) zwane w skrócie AdaBoost, oraz wzmacnianie gradientowe, zwane w skrócie gradient boosting.
11.3.1 AdaBoost
W technice AdaBoost każdy nowo dodawany członek zespołu (np. nowe drzewo decyzyjne czy klasyfikator MLP) jest trenowany na losowo wybranym zestawie danych uczących, przy czym każda próbka ucząca podlegająca losowaniu ma przypisaną wagę, której wartość jest uzależniona od aktualnego statystycznego błędu dla danej obserwacji przez aktualny stan zespołu [73]. Na starcie wszystkie obserwacje uczące mają identyczne wartości przypisanych wag, stąd prawdopodobieństwo ich wylosowania do zbioru uczącego danego członka zespołu jest identyczne. W wyniku ewaluacji danych przez aktualnie wytrenowany zespół następuje zwiększenie wagi dla obserwacji trudnych w testowaniu oraz zmniejszenie wagi dla danych, które dobrze wypadły na etapie ewaluacji. W efekcie obserwacje o większej wartości wagi mają zwiększone prawdopodobieństwo wylosowania do zbioru uczącego następnego członka zespołu (np. dodawanego drzewa decyzyjnego). Nowy członek zespołu w procesie uczenia specjalizuje się więc w rozpoznaniu przypadków trudniejszych. Każdy następny dodawany członek zespołu poddawany jest trenowaniu na zbiorze uczącym zawierającym coraz trudniejsze przypadki danych, źle rozpoznawane przez istniejących członków zespołu. Wynik działania tak powstałego zespołu jest sumą wagową wskazań poszczególnych członków, przy czym waga jest związana z wartością wagi przypisaną poszczególnym obserwacjom, dobraną wcześniej w procesie dodawania nowych członków zespołu. Jest to zasadnicza różnica w stosunku do klasycznej metody zwykłego głosowania większościowego, stosowanego w technice bagging [73].
Załóżmy, że dany jest zbiór par danych uczących klasyfikatora (xi, di) dla i=1, 2, …, p, gdzie xi jest wektorem wejściowym a di oznacza klasę kodowana na przykład w postaci binarnej (1, -1). Załóżmy, że zespół składa się z M słabych klasyfikatorów generujących wynik yi przynależności klasowej 1 lub -1 dla każdego wektora wejściowego xi. W wyniku (m-1) cykli tworzenia nowego członka powstanie zespół, którego werdykt przy pobudzeniu wektorem xi będzie sumą wagową wskazań wszystkich członków [73]
| \( F_{m-1}\left(\mathbf{x}_i\right)=\alpha_1 y_1\left(\mathbf{x}_i\right)+\alpha_2 y_2\left(\mathbf{x}_i\right)+\cdots+\alpha_{m-1} y_{m-1}\left(\mathbf{x}_i\right) \) | (11.11) |
Po dodaniu \( m \)-tego słabego predyktora wynik działania zespołu można przedstawić w postaci
| \( F_m\left(\mathbf{x}_i\right)=F_{m-1}\left(\mathbf{x}_i\right)+\alpha_m y_m\left(\mathbf{x}_i\right) \) | (11.12) |
Zadanie polega na doborze takiej wartości wagi \( \alpha_m \) oraz wyniku \( y_m\left(\mathbf{x}_i\right) \) sklasyfikowania wektora \( \mathbf{x}_i \) przez \( m \)-ty klasyfikator aby polepszyć działanie całego zespołu. Funkcję błędu (ang. loss function) definiuje się w postaci wykładniczej dla wszystkich wektorów \( \mathbf{x}_i \) biorących udział w procesie uczenia
| \( E=\sum_{i=1}^p e^{-d_i F_m\left(\mathbf{x}_i\right)}=\sum_{i=1}^p e^{-d_i F_{m-1}\left(\mathbf{x}_i\right)} e^{-d_i \alpha_m y_m\left(\mathbf{x}_i\right)} \) | (11.13) |
Wprowadźmy oznaczenia wagowe w powyższym wzorze
-
w pierwszym cyklu tworzenia zespołu \( w_i^{(1)} \)
-
w \( m \)-tym (\( m > 1\) cyklu \( w_i^{(m)}=e^{-d_i F_{m-1}\left(\mathbf{x}_i\right)} \)
Wówczas wyrażenie na funkcję błędu przyjmie postać
| \( E=\sum_{i=1}^p w_i^{(m)} e^{-d_i \alpha_m y_m\left(\mathbf{x}_i\right)} \) | (11.14) |
Rozdzielając to wyrażenie na dwa składniki:
-
jeden prawidłowo sklasyfikowany dla którego \( d_i y_m\left(\mathbf{x}_i\right)=1 \)
-
drugi sklasyfikowany z błędem dla którego \( d_i y_m\left(\mathbf{x}_i\right)=-1 \)
otrzymuje się wyrażenie na funkcję błędu w postaci
| \( E=\sum_{d_i=y\left(x_i\right)} w_i^{(m)} e^{-\alpha_m}+\sum_{d_i \neq y\left(x_i\right)} w_i^{(m)} e^{\alpha_m}=\sum_{i=1}^p w_i^{(m)} e^{-\alpha_m}+\sum_{d_i \neq y\left(x_i\right)} w_i^{(m)}\left(e^{\alpha_m}-e^{-\alpha_m}\right) \) | (11.15) |
Analiza powyższego wzoru wskazuje, że wartość błędu \(E\) zależy jedynie od czynnika \( \sum_{y\left(x_i\right) \neq d_i} w_i^{(m)} e^{\alpha_m} \), gdzie \( w_i^{(m)}=e^{-d_i F_{m-1}\left(\mathbf{x}_i\right)} \) . Minimalizacja błędu wymaga aby pochodna funkcji błędu względem \( \alpha_m \) była równa zeru, co oznacza
| \( \frac{d E}{d \alpha_m}=\frac{d\left(\sum_{y\left(x_i\right)=d_i} w_i^{(m)} e^{-\alpha_m}+\sum_{y\left(x_i\right) \neq d_i} w_i^{(m)} e^{\alpha_m}\right)}{d \alpha_m}=0 \) |
(11.16) |
Rozwiązanie powyższej zależności określa optymalną wartość \( \alpha_m \) w postaci
| \( \alpha_m=\frac{1}{2} \ln \left(\frac{\sum_{y\left(x_i\right)=d_i} w_i^{(m)}}{\sum_{y\left(x_i\right) \neq d_i} w_i^{(m)}}\right) \) | (11.17) |
Oznaczając względny błąd \( m \)-tego klasyfikatora jako \( \varepsilon_m \), przy czym
| \( \boldsymbol{\varepsilon}_m=\left(\frac{\sum_{y\left(x_i\right) \neq d_i} w_i^{(m)}}{\sum_{i=1}^p w_i^{(m)}}\right) \) | (11.18) |
wzór na wartość wagi \( \alpha_m \) przyjmie ostateczną postać
| \( \alpha_m=\frac{1}{2} \ln \left(\frac{1-\varepsilon_m}{\varepsilon_m}\right) \) | (11.19) |
Wartość ta będzie użyta w \( m \)-tym kroku przy dodaniu następnego klasyfikatora do zespołu. Wynik klasyfikacji tak rozszerzonego zespołu dla wektora wejściowego \( \mathbf{x}_i \) określa wówczas wzór
| \( F_m\left(\mathbf{x}_i\right)=\alpha_1 y_1\left(\mathbf{x}_i\right)+\alpha_2 y_2\left(\mathbf{x}_i\right)+\ldots+\alpha_m y_m\left(\mathbf{x}_i\right) \) | (11.20) |
gdzie \( y_i \) \( (i=1,2, \ldots, m) \) oznacza wskazanie klasy przez kolejnych członków zespołu, a współczynnik \( \alpha_m \) wagę z jaka to wskazanie jest brane pod uwagę.
Technika zwana gradient boosting stosuje inne rozwiązanie tworzenia i trenowania zespołu słabych predyktorów [2,55]. W odróżnieniu od metody AdaBoost stosującej wagi przypisane obserwacjom w zależności od skali trudności w ich rozpoznaniu technika gradient boosting koncentruje się na gradiencie funkcji strat \( E(d_i, y_i) \) przy czym funkcja strat może być rozumiana tradycyjnie jako różnica między wartościami aktualnymi i pożądanymi albo koncentrować się jedynie na określeniu jakości modelu, definiowanej dowolnie przez użytkownika. Kolejni członkowie są dodawani wybierając kierunek ujemnego gradientu funkcji strat, nie zmieniając przy tym parametrów dotychczasowych członków zespołu.
Podobnie jak w metodzie AdaBoost dany jest zbiór par danych uczących klasyfikatora \( (\mathbf{x}_i, d_i) \) dla \( (i=1,2, \ldots, p) \), gdzie \( \mathbf{x}_i \) jest wektorem wejściowym a \( d_i \) oznacza klasę kodowana na przykład w postaci binarnej \( (1, -1) \). Załóżmy, że zespół składa się z \( M \) słabych klasyfikatorów generujących wynik \( y_i \) przynależności klasowej \(1 \) lub \(-1\) dla każdego wektora wejściowego \( \mathbf{x}_i\). Celem jest stworzenie zespołu, którego działanie na zbiorze uczącym minimalizuje wartość średnią błędu. Wynik działania zespołu \(M\) predyktorów przy pobudzeniu wektorem \( \mathbf{x}_i \) będzie składał się z sumy wagowej wskazań poszczególnych jego członków
| \( F(\mathbf{x})=\sum_{i=1}^M \alpha_i y_i(\mathbf{x})+\mathrm{const} \) | (11.21) |
Dodanie \( m \)-tego członka zespołu powinno zmienić wynik działania w kierunku minimalizacji wartości funkcji strat. Działanie zespołu złożonego teraz z \( m \) członków można zapisać w postaci
| \( F_m(\mathbf{x})=F_{m-1}(\mathbf{x})+\underset{y_m}{\arg \min }\left(\sum_{i=1}^p E\left(d_i, F_{m-1}\left(\mathbf{x}_i\right)\right)+y_m\left(\mathbf{x}_i\right)\right) \) | (11.22) |
Rozwiązanie zastosowane w metodzie gradient boosting wykorzystuje metodę optymalizacyjną największego spadku, przy czym równanie (11.21) zastępuje się liniową aproksymacją uwzględniającą jedynie czynnik gradientowy (metoda największego spadku)
| \( F_m(\mathbf{x})=F_{m-1}(\mathbf{x})-\eta \sum_{i=1}^p \nabla_{F_{m-1}} E\left(d_i, F_{m-1}\left(\mathbf{x}_i\right)\right) \) | (11.23) |
gdzie \( \eta \) jest wielkością kroku w kierunku malejącej wartości gradientu funkcji strat \( \nabla_{F_{m-1}} E\left(d_i, F_{m-1}\left(\mathbf{x}_i\right)\right) \). Wartość \( \eta \) może podlegać optymalizacji w taki sposób, aby uzyskać minimum funkcji strat \( E\) w każdym cyklu dodawania członka zespołu.
| \( \eta_{o p t}=\underset{\eta}{\arg \min } \sum_{i=1}^p E\left[d_i, F_{m-1}\left(\mathbf{x}_i\right)-\eta \nabla_{F_{m-1}} E\left(d_i, F_{m-1}\left(\mathbf{x}_i\right)\right)\right] \) | (11.24) |
Po dodaniu \(m\)-tego członka wynik działania zespołu przy pobudzeniu wektorem \( \mathbf{x} \) określa zmodyfikowany model
| \( F_m(\mathbf{x})=F_{m-1}(\mathbf{x})+\eta y_m(\mathbf{x}) \) | (11.25) |
Technika gradient boosting jest najczęściej stosowana przy użyciu drzew decyzyjnych jako słabych predyktorów. Badania tego algorytmu pokazały, że najlepsze rezultaty uzyskuje się przy zastosowaniu liczby poziomów decyzyjnych od 4 do 8. W praktyce stosuje się dodatkowo inne metody regularyzacji.
Jednym z nich jest ograniczenie liczby drzew biorących udział w zespole. Wprawdzie zwiększenie ich liczby redukuje zwykle błąd uczenia, ale może prowadzić do „przeuczenia” pogarszając zdolność generalizacji (działanie modelu na danych nie uczestniczących w procesie uczenia). Zwykle obserwuje się zwiększoną efektywność działania zespołu jedynie do określonego poziomu populacji. Po uzyskaniu etapu stagnacji należy zaprzestać dodawania nowych członków.
Inna metoda regularyzacji wprowadza zmniejszenie wartości kroku \( \eta \) w procesie adaptacyjnym, zastępując wzór (11.25) określający działanie zespołu jego zmodyfikowaną wersją
| \( F_m(\mathbf{x})=F_{m-1}(\mathbf{x})+v \eta y_m(\mathbf{x}) \) | (11.26) |
w której współczynnik \( v \) jest ułamkiem. Typowa wartość to \( v=0.1\). Tym nie mniej należy zwrócić uwagę, że oznacza to zmniejszenie realnej wartości kroku uczenia, wydłużające cały proces adaptacji systemu.
Jeszcze innym podejściem jest zastosowanie w uczeniu kolejnych członków zespołu zredukowanej liczby obserwacji losowo wybieranych ze zbioru uczącego (tzw. dropout ratio). Przyspiesza to proces uczenia nie pogarszając zdolności generalizacyjnych (typowa regularyzacja typu niejawnego).
Jako czynnik regularyzacyjny stosuje się również wprowadzenie minimalnej liczby obserwacji dopuszczalnej w węzłach decyzyjnych zanim podział zbioru będzie możliwy. Stosuje się również karanie za zbyt dużą liczbę węzłów decyzyjnych oraz liści w drzewach. Istotnym parametrem działającym jako regularyzacja jest wprowadzenie ograniczenie czasu uczenia poprzez obserwacje postępu w kolejnych cyklach dodawania członków zespołu. Proces podlega zakończeniu, jeśli dodanie kolejnych członków nie poprawia działania zespołu powyżej założonego progu względnego. Zastosowanie wielu metod regularyzacyjnych na raz polepsza zdolności generalizacji zespołu pozwalając przy użyciu słabych predyktorów uzyskać bardzo dobre wyniki klasyfikacji całego zespołu.
W tworzeniu zespołu klasyfikatorów można łączyć ze sobą różnego rodzaju systemy: neuronowe, sieci głębokie CNN, drzewa decyzyjne czy klasyfikatory bayesowskie. W szczególności pojedyncze jednostki zespołu mogą zawierać wewnątrz inne podzespoły, na przykład zastosowanie lasu drzew decyzyjnych (typowy zespół klasyfikatorów) w zespole z pojedynczą siecią MLP, RBF czy SVM. Każde rozwiązanie prowadzące do polepszenia wyników klasyfikacji jest akceptowalne.
1.4. Przykład zastosowania zespołu klasyfikatorów w rozpoznaniu twarzy
Jako przykład zastosowania zespołu klasyfikatorów pokażemy jego działanie przy rozpoznaniu obrazów twarzy. Jako narzędzie klasyfikacyjne zastosowane zostaną sieci głębokie CNN powiązane w zespole. Istnieje aktualnie kilkanaście dostępnych w Matlabie sieci pre-trenowanych, miedzy innymi alexnet, shufflenet, darknet53, efficientnetb0, squeezenet, googlenet; inceptionv3, mobilenetv2, resnet50, xception, inceptionresnetv2, nasnetmobile, densenet201. Zespół sieci można tworzyć na wiele sposobów. Jednym z nich jest przyjęcie jednego rodzaju sieci i wielokrotne powtórzenie procesu z losowymi wartościami startowymi i zmieniona strukturą końcową. Inny sposób to zastosowanie wielu różnych rozwiązań na raz w zespole. Badanie obu rozwiązań zostanie zaimplementowane w rozpoznaniu obrazów twarzy tworzących 68 klas. Każda klasa była reprezentowana przez 20 przykładowych próbek. Różnice między członkami tych samych klas są duże, co pokazano dla 3 klas na rys. 11.2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Przykładowa implementacja programu w Matlabie:
% Program w Matlabie do rozpoznania obrazów twarzy przy użyciu zespołu pre-trenowanych sieci CNN
addpath 'pliki'
addpath 'pliki2'
addpath 'pliki3'
wyn=[]; wynVal=[];
Pred_y=[]; Pred_yVal=[]; time=[];
%% %Load Data
imds = imageDatastore( 'c:\chmura\ALEX_obrazy_all',...
'IncludeSubfolders',true,...
'ReadFcn', @customreader, ...
'LabelSource','foldernames');
[imdsTrain,imdsValidation] = splitEachLabel(imds,0.7,'randomized');
kk=10;
for i=1:kk
i
tic
% if i==1
net = alexnet;
% elseif i==2
% net = shufflenet;
% elseif i==3
% net = darknet53;
% elseif i==4
% net=efficientnetb0;
% elseif i==5
% net = squeezenet;
% elseif i==6
% net = googlenet;
% elseif i==7
% net = inceptionv3;
% elseif i==8
% net = mobilenetv2;
% elseif i==9
% net = resnet50;
% elseif i==10
% net = xception;
% elseif i==11
% net = inceptionresnetv2;
% elseif i==12
% net = nasnetmobile;
% elseif i==13
% net = densenet201;
% else
% end
analyzeNetwork(net)
net.Layers(1)
inputSize = net.Layers(1).InputSize;
lgraph = layerGraph(net);
[learnableLayer,classLayer] = findLayersToReplace(lgraph);
[learnableLayer,classLayer]
numClasses = numel(categories(imdsTrain.Labels));
if isa(learnableLayer,'nnet.cnn.layer.FullyConnectedLayer')
newLearnableLayer = fullyConnectedLayer(numClasses, ...
'Name','new_fc', ...
'WeightLearnRateFactor',10, ...
'BiasLearnRateFactor',10);
elseif isa(learnableLayer,'nnet.cnn.layer.Convolution2DLayer')
newLearnableLayer = convolution2dLayer(1,numClasses, ...
'Name','new_conv', ...
'WeightLearnRateFactor',10, ...
'BiasLearnRateFactor',10);
end
lgraph = replaceLayer(lgraph,learnableLayer.Name,newLearnableLayer);
newClassLayer = classificationLayer('Name','new_classoutput');
lgraph = replaceLayer(lgraph,classLayer.Name,newClassLayer);
figure('Units','normalized','Position',[0.3 0.3 0.4 0.4]);
plot(lgraph)
ylim([0,10])
layers = lgraph.Layers;
connections = lgraph.Connections;
layers(1:10) = freezeWeights(layers(1:10));
lgraph = createLgraphUsingConnections(layers,connections);
%TRAIN
pixelRange = [-30 30];
scaleRange = [0.9 1.1];
imageAugmenter = imageDataAugmenter( ...
'RandXReflection',true, ...
'RandXTranslation',pixelRange, ...
'RandYTranslation',pixelRange, ...
'RandXScale',scaleRange, ...
'RandYScale',scaleRange);
augimdsTrain = augmentedImageDatastore(inputSize(1:2),imdsTrain, ...
'DataAugmentation',imageAugmenter);
augimdsValidation = augmentedImageDatastore(inputSize(1:2),imdsValidation);
miniBatchSize = 10;
valFrequency = floor(numel(augimdsTrain.Files)/miniBatchSize);
options = trainingOptions('sgdm', ...
'MiniBatchSize',miniBatchSize, ...
'MaxEpochs',5, ...
'ExecutionEnvironment','gpu',...
'InitialLearnRate',3e-4, ...
'Shuffle','every-epoch', ...
'ValidationData',augimdsValidation, ...
'ValidationFrequency',valFrequency, ...
'Verbose',false, ...
'Plots','training-progress');
net = trainNetwork(augimdsTrain,lgraph,options);
[YPred,probs] = classify(net,augimdsValidation);
accuracy = mean(YPred == imdsValidation.Labels)
%i=i+1
toc
%STATYSTYKA
Pred_y=[double(YPred) double(imdsValidation.Labels)];
dtest=double(imdsValidation.Labels);
wyn=[wyn accuracy]
time=[time toc]
end
nclass=numClasses
%ZESPÓŁ
dy=[dtest Pred_y]
nclass=numClasses
clear dz
[lw,lk]=size(dy);
for i=1:lw
for j=1:nclass
d=0;
for k=2:lk
if (j==double(dy(i,k)))
d=d+1;
else
end
end
dz(i,j)=d;
% klasa=dy(:,1)
end
end
dz;
[q,cl_max]=max(dz');
zgod_class=length(find(double(dy(:,1))==cl_max'));
dokl_zesp=zgod_class/lw*100
median_zesp=median(wyn)
max_zesp=max(wyn)
mean_zesp=mean(wyn)
odch_zesp=std(wyn)
[C,order] = confusionmat(double(dtest),double(cl_max));
Confusion=C
for i=1:nclass,
sen(i)=C(i,i)/sum(C(i,:));
end
for i=1:nclass,
prec(i)=C(i,i)/sum(C(:,i));
end
lc1t=sum(dtest==1);
lc2t=sum(dtest==2);
%ROC
for i=1:length(dtest)
ydz(i)=dz(i,1)/(dz(i,1)+dz(i,2));
end
for i=1:lc1t
dtestroc(i)=1;
end
for i=lc1t+1:length(dtest)
dtestroc(i)=0;
end
wyn
sen
prec
F1_zesp=2*prec.*sen./(prec+sen)
time
Program stosuje aktualnie 10 członków zespołu (kk=10), generując wyniki poszczególnych członków oraz wyniki zespołu zintegrowanego poprzez głosowanie większościowe. W efekcie obliczone są takie miary jakości, jak dokładność, precyzja, czułość i miara F1 rozpoznania poszczególnych klas. Wyniki rozpoznania klas przedstawione zostaną dla 2 rozwiązań. Pierwszy zespół został zbudowany na bazie ALEXNET, wywołanym 10 razy z losowymi wartościami parametrów startowych. W drugim przypadku zespół złożony by z 10 różnych struktur sieci (w kolejności zadeklarowanej w liniach programu w Matlabie).
Tabela 11.2 przedstawia wartości średnie dokładności rozpoznania wszystkich klas przez klasyfikator ALEXNET w kolejnych próbach działania na tych samych danych testujących oraz przy zastosowaniu 10 różnych struktur sieciowych (kolejność jak w programie)
Tabela 11.2 Średnia dokładność rozpoznania 68 klas przez 2 zespoły: zespół zbudowany na bazie ALEXNET
i zespół złożony z 10 różnych struktur sieciowych CNN
|
Klasyfikator |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Mean ±std |
Zespół |
|
Zespół ATEXNET |
85.0 |
78.7 |
77.7 |
88.5 |
83.5 |
82.11 |
86.3 |
80.1 |
86.5 |
85.8 |
83.4±3.64 |
94.12 |
|
Zespół 10 różnych sieci |
85.3 |
87.0 |
99.0 |
62.7 |
60.3 |
75.5 |
75.6 |
87.2 |
91.2 |
54.4 |
77.87±14.7 |
81.37 |
Zastosowanie integracji wyników poszczególnych klasyfikatorów metodą głosowania większościowego zdecydowanie poprawiło końcową dokładność rozpoznania, która dla zespołu zbudowanego na bazie ALEXNET jest równa 94.12% (wzrost dokładności względem wartości średniej klasyfikatorów o 12.8%). W drugim przypadku ten przyrost był znacznie mniejszy ( z wartości 77.87 do 81.37%). Tym razem znacznie lepsze wyniki uzyskano w zespole zbudowanym na bazie jednego rodzaju sieci. Gorszy wynik zespołu zbudowanego z różnych sieci był spowodowany niewydolnością aż 3 rodzajów rozwiązań (sieć 4, 5 i 10) dla których dokładność rozpoznania była bardzo niska i zdecydowanie odbiegała od średniej pozostałych rozwiązań. Eliminacja tych słabszych sieci z zespołu pozwala uzyskać znacznie lepsze wyniki, przewyższające wyniki zespołu zbudowanego na bazie jednej sieci.
Należy przy tym zauważyć, że głosowanie większościowe (jakkolwiek najprostsze) nie zapewnia w każdym przypadku lepszych wyników zespołu niż najlepszy klasyfikator indywidualny ze względu na duże różnice dokładności poszczególnych rozwiązań (jest to widoczne w drugim przypadku eksperymentów).
Na rys. 12.3 przedstawiono wartości czułości i precyzji klasowej uzyskanej dla poszczególnych klas przez zespół klasyfikatorów. Wartość średnia precyzji klasowej jest równa 95.22%, natomiast czułości rozpoznania klas przez zespół równa 94.12%. Oba wyniki można uznać za bardzo dobre biorąc pod uwagę liczbę rozpoznawanych klas (68) jak i duże różnice w reprezentacji próbek należących do tej samej klasy.
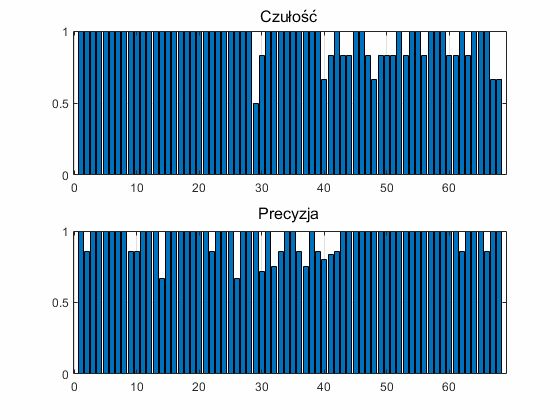
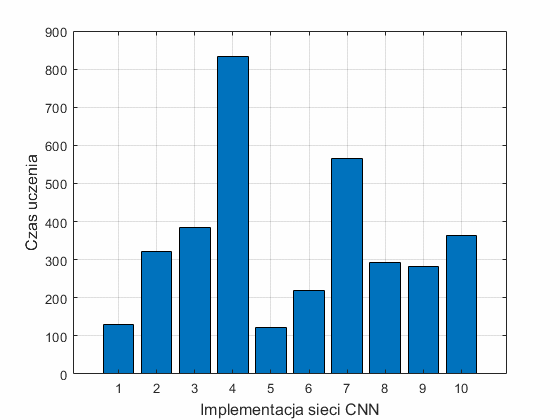
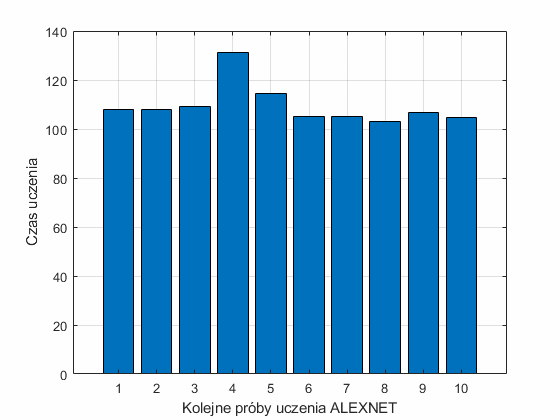
Interesujące są również czasy działania poszczególnych implementacji sieci CNN. Na rys. 12.4 przedstawiono 2 wykresy ilustrujące czasy potrzebne na treningi poszczególnych rozwiązań sieci. Rys. 12.4a przedstawia czasy uczenia różnych implementacji sieci CNN, natomiast rys. 12.4b czas uczenia tej samej sieci ALEXNET w 10 kolejnych próbach.
Najdłuższy czas uczenia odpowiadał sieci czwartej (efficientnetb0) oraz sieci siódmej (inceptionv3). Najmniej wymagająca pod względem czasowym okazała się sieć piąta (squeezenet) oraz pierwsza (ALEXNET). Niewielkie różnice w czasach uczenia zaobserwować można przy powtarzanych próbach uczenia sieci ALEXNET. Średni czas w tych próbach był równy 109.5 sekund, przy odchyleniu standardowym 8.2 sekund.
|
a) |
b) |
1.5. Zadania i problemy
11.5 Zadania i problemy
1. Trzy klasyfikatory zastosowane do rozpoznania 2 klas dały wyniki uczenia w postaci macierzy rozbieżności klasowej \( \mathbf{R1} \), \(\mathbf{R2}\) i \( \mathbf{R3}\) o postaci
\( \mathbf{R1} =\left[\begin{array}{cc} 15 & 5 \\ 8 & 10 \end{array}\right], \mathbf{R2} =\left[\begin{array}{cc} 8 & 12 \\ 15 & 3 \end{array}\right], \mathbf{R3}=\left[\begin{array}{cc} 19 & 1 \\ 9 & 9 \end{array}\right] \)
Przy testowaniu wektorem testowym \(\mathbf{x}_{t1} \) poszczególne klasyfikatory wskazał następujące klasy:
-
Klasyfiktor 1 - -> klasa 2, klasyfikator 2 -> klasa 1, klasyfikator 3 -> klasa 1
Przy testowaniu wektorem testowym xt2 poszczególne klasyfikatory wskazał następujące klasy:
-
Klasyfiktor 1 - -> klasa 1, klasyfikator 2 -> klasa 2, klasyfikator 3 -> klasa 2
Jaki będzie wynik przynależności klasowej zespołu dla obu wektorów przy integracji większościowej oraz większościowej ważonej stosującej wzór (11.10b)
\( w_{k i}=\lg \left(\frac{\eta_{k i}}{1-\eta_{k i}}\right) \)
2. Zastosować naiwną regułę Bayes’a do integracji zespołu zawierającego dwa klasyfikatory do rozpoznania 3 klas. Liczba obserwacji uczących jest równa n=30. Macierze rozkładu klas dla obu klasyfikatorów są dane w postaci
\( \mathbf{R} 1=\left[\begin{array}{ccc} 5 & 3 & 0 \\ 1 & 6 & 2 \\ 2 & 1 & 10 \end{array}\right], \mathbf{R} 2=\left[\begin{array}{lll} 4 & 1 & 3 \\ 0 & 6 & 3 \\ 3 & 4 & 6 \end{array}\right] \)
Załóżmy, że testowany wektor \(\mathbf{x}_{t} \) został przypisany przez klasyfikator pierwszy do klasy drugiej, a klasyfikator drugi wskazał klasę pierwszą jako zwycięzcę.
3. Sprawdzić działanie pojedynczych sieci głębokich przy rozpoznaniu obrazów twarzy zawartych w bazie MUCT. Wykorzystać postać programu w Matlabie dla sieci przetrenowanych. Porównać czasy uczenia sieci.
4. Sprawdzić działanie zespołu różnych sieci głębokich przy rozpoznaniu obrazów twarzy zawartych w bazie MUCT. Wykorzystać postać programu w Matlabie dla sieci przetrenowanych. Porównać wyniki dla różnej liczby użytych członków zespołu.
5. Sprawdzić działanie zespołu sieci głębokich utworzonych na bazie jednej struktury sieciowej przy rozpoznaniu obrazów twarzy zawartych w bazie MUCT. Wykorzystać postać programu w Matlabie dla sieci przetrenowanych. Porównać wyniki dla różnej liczby użytych członków zespołu.
1.6. Słownik
Słownik opanowanych pojęć
Wykład 11
Zespół – zbiór indywidualnych rozwiązań zintegrowanych dla wytworzenia jednego wspólnego werdyktu końcowego (dotyczy klasyfikatorów lub systemów regresyjnych).
Integracja zespołu – sposób wytworzenia końcowego werdyktu zespołu (fuzja wyników członków zespołu).
Głosowanie większościowe – sposób wyłonienia zwycięzcy w systemie klasyfikacyjnym poprzez bezpośrednie zliczanie głosów na określoną klasę.
Głosowanie większościowe ważone – sposób wyłonienia zwycięzcy w systemie klasyfikacyjnym poprzez zliczanie głosów na określoną klasę z uwzględnieniem wagi każdego klasyfikatora.
Naiwna reguła Bayesa – metoda wyłonienia klasy na podstawie analizy prawdopodobieństwa a priori i aposteriori (stosowana między innymi w integracji zespołu).
Bagging – technika stosowana w uczeniu członków zespołu trenowanych na losowo wybranych danych uczących.
Boosting – technika wzmacniania stosowana w uczeniu członków zespołu trenowanych na wybranych danych uczących uwzględniająca błędy popełniane na każdej próbce uczącej.
AdaBoost – technika uczenia ze wzmacnianiem, w której każdy nowo dodawany członek zespołu jest trenowany na losowo wybranym zestawie danych uczących, przy czym każda próbka ucząca ma przypisaną wagę, której wartość jest uzależniona od aktualnego statystycznego błędu dla danej obserwacji.
Gradient boosting – technika tworzenia zespołu koncentrująca się na gradiencie funkcji strat.
2. Metody oceny jakości rozwiązań
Model odwzorowujący badany proces dokonuje estymacji odpowiedzi tego procesu na podstawie danych wejściowych. Dokładność tej odpowiedzi, czyli jej zgodność z wartością spodziewaną, może być różna w zależności od jakości zbudowanego modelu. Dla oceny modelu stosuje się różne miary, które pozwalają na ocenę jego jakości. W zależności od rodzaju zadania regresji (regresja czy klasyfikacja) stosuje się różne rodzaje tych miar.
2.1. Miary jakości regresji
W zadaniu regresji odpowiedź modelu określa wartość jego odpowiedzi na wymuszenie w postaci atrybutów wejściowych i jest wyrażona w postaci rzeczywisto-liczbowej. Dokładność modelu stanowi podstawowe kryterium, na podstawie którego jest oceniana jego przydatność.
Dla twórcy algorytmu prognozowania dokładność regresji określa, na ile dany model predykcyjny odtwarza poprawnie dane, które są już znane konstruktorowi. Dla użytkownika systemu prognostycznego istotne jest, na ile wiarygodna jest prognoza i czy spełni ona w przyszłości założone kryteria dokładnościowe. Miary dokładności regresji, obliczane są niejako po fakcie, to znaczy najpierw wyliczana jest prognoza, a później dokonywana jej ocena w oparciu o napływające dane rzeczywiste (dokładne). Stąd należą one do miar klasy ex post.
Załóżmy, że dla każdego rekordu danych dostępne są estymowane odpowiedzi modelu oznaczone przez \( y_i \) oraz znane wartości dokładne oznaczone symbolem \( d_i \) dla \( i = 1, 2, \ldots, n \), gdzie \( n \) oznacza liczbę rekordów. Chwilowy błąd estymacji jest różnicą między wartością estymowaną a wartością dokładną
| \( e_i=d_i-y_i \) | (12.1) |
Miara jakości modelu jest związana zwykle ze statystyką błędu estymacji. Wyróżnia się różne definicje błędów statystycznych. Do najbardziej popularnych należą [49]:
-
błąd średni absolutny (ang. Mean Absolute Error - \( \operatorname{MAE} \))
| \( \operatorname{MAE} =\frac{1}{n}\left(\sum_{i=1}^n\left|d_i-y_i\right|\right) \) | (12.2) |
-
względny błąd średni absolutny (ang. Mean Absolute Percentage Error - \( \operatorname{ MAPE }\))
| \( \operatorname{ MAPE }=\frac{1}{n}\left(\sum_{i=1}^n \frac{\left|d_i-y_i\right|}{\left|d_i\right|}\right) \cdot 100 \% \) | (12.3) |
Błąd MAPE jest najbardziej reprezentatywnym rodzajem oceny jakości regresji, niezależnym od wartości absolutnych ciągu poddanego regresji, stąd najczęściej stosowanym w praktyce. W przypadku, gdy część wartości zadanych \( d_i = 0 \) miara powyższa staje się równa nieskończoności, przez co staje się bezużyteczna. W takim przypadku przyjmuje się miarę uproszczoną w postaci wyrażonej poprzez normy wektorowe
| \( \operatorname{MAPE} \simeq \frac{\|d-y\|}{\|d\|} \cdot 100 \% \) | (12.4) |
gdzie \( \mathbf{d} \), \( \mathbf{y} \)oznaczają formę wektorową zbioru wartości, odpowiednio zadanych i estymowanych.
-
błąd średniokwadratowy (ang. Root Mean Squared Error - \( \operatorname{RMSE}\))
| \( \operatorname{RMSE}=\sqrt{\frac{1}{n} \sum_{i=1}^n\left|d_i-y_i\right|^2} \) | (12.5) |
-
błąd maksymalny (ang. Maximum Error - \( \operatorname{MAXE} \))
| \( \operatorname{MAXE} =\max _i\left|d_i-y_i\right| \) | (12.6) |
-
błąd maksymalny procentowy (ang. Maximum Percentage Error - \( \operatorname{MAXPE}\))
| \( \operatorname{MAXPE} =\max _i \frac{\left|d_i-y_i\right|}{\left|d_i\right|} \) | (12.7) |
W wielu zastosowaniach ważną rolę odgrywa miara korelacyjna między wartościami estymowanymi i rzeczywistymi zdefiniowana w postaci współczynnika korelacji
-
miara korelacyjna
| \( R=\frac{R_{y d}}{\operatorname{std}(y) \operatorname{std}(d)} \) | (12.8) |
We wzorze tym \( R_{yd} \) oznacza kowariancję między obu ciągami wartości, a \( \operatorname{std}\) jest oznaczeniem odchylenia standardowego. Im większa wartość miary korelacji tym lepsza jest jakość predyktora.
Niezależnie od zastosowanej miary jakości regresji ważnym czynnikiem oceny zastosowanego algorytmu jest porównanie osiągniętych wyników z wynikami predyktora naiwnego. Za najprostszy predyktor naiwny uznaje się ekstrapolator zerowego rzędu, przyjmujący jako prognozę wartość znaną dokładnie (element wektora \( \mathbf{d} \)) z poprzedniego kroku, czyli \( y_i = d_{i-1} \). Ograniczając się do miary \( \operatorname{MAPE} \) błąd naiwnej prognozy będzie wyrażony wzorem
| \( \operatorname{MAPE}_{n p}=\frac{1}{n-1}\left(\sum_{i=2}^n \frac{\left|d_i-d_{i-1}\right|}{\left|d_i\right|}\right) \cdot 100 \% \) | (12.9) |
Różnica między błędem metody naiwnej \( \operatorname{MAPE}_{n p} \) i błędem \( \operatorname{MAPE} \) odpowiadającym badanej (z definicji bardziej złożonej) metodzie
| \( \Delta=\operatorname{MAPE}_{np}-\operatorname{MAPE} \) | (12.10) |
stanowi miarę pozwalająca ocenić i porównać skuteczność zastosowanej metody regresji. Inną miarą oceniającą jakość testowanej metody regresji względem metody naiwnej jest współczynnik Theila [49], porównujący względną wartość błędu średniego badanej metody z odpowiadająca mu wartością błędu prognozy naiwnej. Jest on zdefiniowany wzorem
| \( U=\sqrt{\frac{\sum_{i=1}^{n-1}\left(\frac{y_i-d_i}{d_i}\right)^2}{\sum_{i=1}^{n-1}\left(\frac{d_{i+1}-d_i}{d_i}\right)^2}} \) | (12.11) |
Współczynnik ten jest równy zeru tylko wtedy, gdy zastosowana prognoza jest idealna, czyli gdy \( y_i = d_i \). W przypadku niezgodności regresji i wartości rzeczywistych wartość tego współczynnika staje się równa \( 1 \) tylko wtedy, gdy różnice między wynikami zastosowanej metody regresji i metody naiwnej są równe zeru. Oznacza to, że obie metody stanowią równie dobre podejścia do prognozowania. Jeśli \( U < 1 \) wówczas metoda badana jest lepsza niż podejście naiwne. W przeciwnym przypadku metoda naiwna jest lepsza i nie ma potrzeby stosowania bardziej złożonej metody regresji.
2.2. Metody oceny jakości rozwiązań w zadaniach klasyfikacji
W przypadku klasyfikacji miary jakości klasyfikatora są zdefiniowane na podstawie zgodności estymowanej etykiety klasy z etykietą rzeczywistą (prawdziwą). Najbardziej reprezentatywnym sposobem prezentacji wyników jest tutaj zastosowanie macierzy pomyłek, zwanej również macierzą niezgodności klasowej lub macierzą pomyłek (ang. confusion matrix), w której elementy wierszy reprezentują liczbę wzorców należących do kolejnych klas, a elementy kolumn – liczbę wzorców rozpoznanych przez klasyfikator jako dana klasa [65]. Przykład takiej macierzy dla trzech klas przedstawiono w tabeli 12.1. Elementy diagonalne macierzy reprezentują liczbę poprawnie rozpoznanych wzorców. Każdy element pozadiagonalny macierzy reprezentuje błędne rozpoznanie. Element ij-ty macierzy określa liczbę przypadków klasy i-tej rozpoznanych jako klasa j-ta. Klasa pierwsza jest reprezentowana przez pierwszy wiersz, klasa druga przez drugi a klasa trzecia przez wiersz trzeci.
Tabela 12.1 Przykład prezentacji wyników klasyfikacji wzorców 3 klas w postaci macierzy rozkładu klas
|
|
Klasa 1 |
Klasa 2 |
Klasa 3 |
|
Klasa 1 |
95 |
3 |
12 |
|
Klasa 2 |
8 |
20 |
2 |
|
Klasa 3 |
6 |
0 |
80 |
Przykładowo spośród 110 przypadków klasy pierwszej 95 zostało rozpoznanych poprawnie, 3 rozpoznanych błędnie jako klasa druga a 12 jako klasa trzecia.
12.2.1 Miary jakości klasyfikatora
Na podstawie wyników klasyfikacji przedstawionych w macierzy rozkładu klas można stworzyć wiele różnych wskaźników jakości klasyfikatora. Najbardziej ogólnym wskaźnikiem jest średni błąd względny w którym odnosi się liczbę klasyfikacji błędnych do liczby wszystkich przypadków poddanych badaniu. Błąd ten można zdefiniować na dwa sposoby: błąd średni dla całego zbioru bez uwzględnienia liczebności klas oraz z ich uwzględnieniem. Oznaczając elementy macierzy rozkładu klas przez aij, oba rodzaje błędów można zdefiniować w następujący sposób.
-
Błąd średni bez uwzględnienia liczebności klas
| \( \varepsilon_{w 1}=\frac{\sum_{i \neq j} a_{i j}}{\sum_{i, j} a_{i j}} \) | (12.12) |
-
Błąd średni ważony z uwzględnieniem liczebności klas
| \( \varepsilon_{w 2}=\frac{1}{K} \sum_{i=1}^K \frac{\sum_{j=1, j \neq i}^K a_{i j}}{K_i} \) | (12.13) |
We wzorach tych K oznacza liczbę klas, a \(K_i\) liczbę elementów \(i\)-tej klasy. W przypadku równej liczebności wszystkich klas oba wskaźniki przyjmują identyczne wartości. Przy nierównych populacjach klas wskaźnik drugi jest bardziej wymagający. Przykładowo dla danych z tabeli 12.1 \(\varepsilon_{w1}=31/226=0.137\), podczas gdy \(\varepsilon_{w2}=(15/110+10/30+6/86)/3=0.180\).
Wskaźniki zdefiniowane powyżej nie odzwierciedlają problemów występujących w przypadku dużego niezrównoważenia klas. Przykładowo, jeśli w zbiorze danych 99% danych należy do klasy pierwszej a tylko 1% do klasy drugiej (rzadkiej), wówczas przy pełnym rozpoznaniu klasy pierwszej i zerowej skuteczności rozpoznania klasy rzadkiej średni błąd rozpoznania \( \varepsilon_{w1}=1\% \), co jest rezultatem zwykle satysfakcjonującym z ogólnego punktu widzenia ale zupełnie nie odzwierciedlającym problemu (1% klasy rzadkiej może reprezentować właśnie te przypadki, które chcemy wykryć w populacji przypadków normalnych, np. chorobę nowotworową w grupie badanych pacjentów). Problem oceny klasyfikatora stosowanego do przypadków rzadkich wymaga innego podejścia do definicji miar jakości, gdyż przypomina szukanie igły w stogu siana.
Rozpatrzmy przypadek klasyfikacji danych należących do dwu klas. Klasę rzadką oznaczymy symbolem + a większościową symbolem –. W takim przypadku macierz rozkładu klasowego może być przedstawiona w postaci jak w tabeli 12.2 [49,65].
Tabela 12.2 Oznaczenia stosowane w macierzy rozkładu klas (+ oznacza klasę rzadką, natomiast – klasę większościową, reprezentującą pozostałe przypadki)
|
|
Klasa + |
Klasa – |
|
Klasa + |
a++ (TP) |
a+– (FN) |
|
Klasa – |
a–+ (FP) |
a– – (TN) |
Element a++ macierzy oznacza liczbę prawdziwie rozpoznanych przypadków rzadkich (ang. True Positive – TP), element a+– oznacza liczbę przypadków rzadkich rozpoznanych jako większościowe (ang. False Negative – FN), element a–+ oznacza liczbę przypadków większościowych rozpoznanych jako rzadkie (ang. False Positive – FP), a element a– – oznacza liczbę prawdziwie rozpoznanych przypadków większościowych (ang. True Negative – TN). Na bazie tych oznaczeń definiuje się szereg wskaźników jakości szerzej naświetlających problem klasyfikacji w przypadku klas rzadkich [45]. Pierwszym z nich jest czułość oznaczana zwykle symbolem TPR (ang. True Positive Rate), definiowana jako stosunek liczby poprawnie rozpoznanych przypadków rzadkich do liczby wszystkich przypadków rzadkich
| \( TPR = \frac{TP}{TP+FN} \) |
(12.14) |
Drugim ważnym parametrem jest specyficzność oznaczana symbolem TNR (ang. True Negative Rate), definiowana jako stosunek liczby poprawnie rozpoznanych przypadków większościowych do liczby wszystkich przypadków większościowych
| \( TNR = \frac{TN}{TN+FP} \) | (12.15) |
Inną miarą jest wskaźnik rozpoznań fałszywie pozytywnych oznaczany symbolem FPR (ang. False Positive Rate) zdefiniowany jako stosunek liczby przypadków większościowych sklasyfikowanych jako rzadkie do liczby wszystkich przypadków większościowych
| \( FPR = \frac{FP}{TN+FP} \) | (12.16) |
Miara ta jest znana również jako wskaźnik fałszywych alarmów FA (ang. False Alarm), określający względny udział błędnych kwalifikacji przypadków większościowych jako rzadkie (np. uznanie pacjenta zdrowego za chorego). Wskaźnik ten jest ściśle powiązany ze specyficznością TNR
| \( FA=FPR=\frac{FP}{FP+TN}=1-TNR \) | (12.17) |
Analogicznie definiuje się wskaźnik rozpoznań fałszywie negatywnych (szczególnie niebezpiecznych) oznaczany symbolem FNR (ang. False Negative Rate). Jest on zdefiniowany jako stosunek liczby przypadków rzadkich sklasyfikowanych jako większościowe do liczby wszystkich przypadków rzadkich
| \( FNR = \frac{FN}{TP+FN} \) | (12.18) |
Dwa dodatkowe wskaźniki definiują wartości prognostyczne metody. Dodatnia wartość prognostyczna PPV reprezentująca precyzję rozpoznawania przypadków rzadkich (ang. Positive Predictivity Value) określa jaka część przypadków zdiagnozowanych jako rzadkie (TP) jest rzeczywiście rzadka (percepcja rozpoznawania klasy rzadkiej)
| \( PPV = \frac{TP}{TP+FP} \) | (12.19) |
Ujemna wartość prognostyczna NPV (ang. Negative Predictivity Value) określa jaka część przypadków zdiagnozowanych jako większościowa (TN) jest rzeczywiście większościowa (percepcja rozpoznawania klasy większościowej)
| \( NPV = \frac{TN}{TN+FN} \) | (12.20) |
Ważną praktycznie miarą jakości systemu klasyfikacyjnego jest precyzja klasowa klasyfikatora. Jest ona definiowana jako stosunek prawdziwej liczby rozpoznanych przypadków danej klasy do wszystkich przypadków rozpoznanych przez klasyfikator jako dana klasa. Miara ta dotyczy każdej klasy, w tym większościowej i rzadkiej, oznaczonych jako PPV i NPV
Inną miarą uniwersalną systemu klasyfikacyjnego jest F1. Definiowana jest dla każdej klasy oddzielnie na podstawie precyzji oraz czułości klasowej. Oznaczając precyzję rozpoznania klasy k-tej przez \(\operatorname{Prec}(k)\) i czułość rozpoznania klasy przez \(\operatorname{Sens}(k) \) miara \( \operatorname{F1}(k) \) jest zdefiniowana w postaci
| \( \operatorname{F1}(k)=\frac{\operatorname{Prec}(k) * \operatorname{Sens}(k)}{0.5(\operatorname{Prec}(k)+\operatorname{Sens}(k))} \) | 12.21 |
Średnia dokładność prognozy ACC (ang. ACCuracy) określająca procent dobrze sklasyfikowanych przypadków może być zdefiniowana wzorem
| \( AC=\frac{TP+TN}{TP+TN+FP+FN} \) | (12.22) |
Oznacza ona liczbę prawidłowo sklasyfikowanych przypadków (rzadkich i większościowych) odniesioną do liczby wszystkich przypadków poddanych klasyfikacji. Miara ta jest ściśle związana ze średnim błędem względnym \(\varepsilon_{w1}\) zdefiniowanym wcześniej (zależność 12.12)
| \( \varepsilon_{w 1}=1-ACC=\frac{FP+FN}{TP+TN+FP+FN} \) | (12.23) |
Przedstawione powyżej miary jakości charakteryzują klasyfikator z różnych punktów widzenia. Maksymalizacja jednego wskaźnika jest często sprzężona z pogorszeniem innego.
W przypadku większej liczby klas przyjmuje się porównanie wybranej klasy z pozostałymi traktowanymi jako grupa wspólna (klasa zbiorowa). W ten sposób problem oceny sprowadza się do zadania 2-klasowego.
12.2.2 Charakterystyka ROC
Ważnym elementem oceny klasyfikatora jest porównanie jego działania z klasyfikatorem losowym [49,65]. Porównanie takie umożliwia reprezentacja graficzna wyników w postaci charakterystyki ROC (ang. Receiver Operating Characteristics). Krzywa ROC przedstawia relację między miarą TPR (oś pionowa y) a miarą FPR (oś pozioma x). Każdy punkt krzywej odpowiada innemu doborowi parametrów modelu klasyfikatora. Dwa typy możliwych przebiegów krzywej ROC dla klasyfikatorów K1 oraz K2 w porównaniu z klasyfikatorem losowym Kr (klasyfikacja poprzez losowanie) przedstawione są na rys. 12.1.
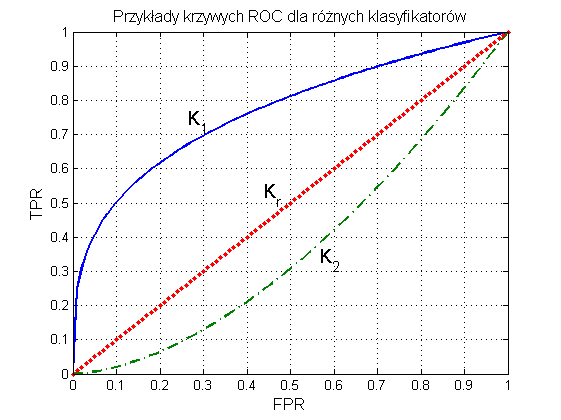
W krzywej ROC można wyróżnić kilka istotnych punktów [65].
-
(TPR=0, FPR=0) – klasyfikator kwalifikuje każdy przykład jako klasę większościową
-
(TPR=1, FPR=1) – klasyfikator kwalifikuje każdy przykład jako klasę rzadką
-
(TPR=1, FPR=0) – model idealny, rozpoznający bezbłędnie wszystkie przypadki
-
punkty (TPR, FPR) położone na prostej diagonalnej oznaczają klasyfikację całkowicie losową.
Dobry klasyfikator powinien mieć krzywą ROC położoną tak blisko jak to możliwe lewego górnego punktu o współrzędnych (0, 1). Miara jakości klasyfikatora może być oceniana na podstawie pola powierzchni SROC pod krzywą ROC. Pole powierzchni SROC=1 oznacza klasyfikator idealny. Wartość pola SROC=0.5 oznacza klasyfikację losową (rozwiązanie klasyfikatora bezsensowne). Im SROC jest bliższe jedności, tym lepsza jest ocena takiego rozwiązania modelu klasyfikacyjnego. Miara nosi popularną nazwę AUC (Area Under Curve).
Aby utworzyć krzywą ROC należy dysponować sygnałem wyjściowym klasyfikatora w postaci ciągłej (przed binaryzacją). Może to być aktualna wartość prawdopodobieństwa w klasyfikatorze Bayes’a, bezpośrednia wartość funkcji sigmoidalnej w klasyfikatorze MLP, wartość sumy wagowej neuronu wyjściowego sieci RBF czy wartość ciągła y(x) wytworzona w klasyfikatorze SVM. Procedurę tworzenia krzywej ROC można przedstawić w następujących punktach.
-
Ustaw wyniki klasyfikacji (rekordy danych testowych) w kolejności rosnącej (od najmniejszego do największego) sygnału wyjściowego klasyfikatora.
-
Wyselekcjonuj rekord o najmniejszej wartości sygnału. Sklasyfikuj wybrany rekord i wszystkie powyżej niego jako klasę rzadką (oznaczenie +). To oznacza w rzeczywistości przyjęcie, że wszystkie rekordy danych należą do klasy rzadkiej.
-
Przesuń się o jeden rekord w górę i sklasyfikuj wybrany rekord oraz wszystkie powyżej niego jako klasę rzadką, natomiast wszystkie poniżej niego jako klasę większościową (oznaczenie –). Dla każdego przypadku określ miary jakości w postaci wskaźników TP, FP, TN, FN, a następnie TPR oraz FPR.
-
Powtórz krok 3 dla wszystkich kolejnych rekordów, określając wartości wymienionych wyżej miar jakości.
-
Wykreśl otrzymaną zależność TPR=f(FPR), stanowiąca krzywą ROC.
-
Wyznacz pole powierzchni AUC pod krzywą ROC.
Charakterystyka ROC pozwala w prosty sposób porównać rozwiązania różnych rozwiązań systemu klasyfikacyjnego 2 klas. Istotna jest przy tym wartość pola pod krzywą ROC, tzw. AUC. Jest ona zawsze z przedziału [ 0, 1]. Im wyższa wartość AUC, tym lepsze jest rozwiązanie.
Procedurę wyznaczania krzywej ROC zilustrujemy przykładem dla wyników dwu różnych klasyfikatorów.
W pierwszym przypadku wyniki działania modelu na danych testujących przedstawiono w tabeli 12.3, w której wiersz pierwszy oznacza prawdziwą przynależność do klasy, a wiersz drugi sygnał wyjściowy klasyfikatora (przed poddaniem działaniu funkcji dyskryminującej klas).
Tabela 12.3 Wyniki testowania klasyfikatora pierwszego
|
Klasa |
+ |
– |
– |
+ |
– |
+ |
– |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.4 |
0.6 |
0.8 |
0.9 |
1.0 |
Stosując procedurę tworzenia charakterystyki ROC otrzymuje się wyniki przedstawione w tabeli 12.4.
Tabela 12.4 Ilustracja kolejnych etapów tworzenia charakterystyki ROC dla klasyfikatora pierwszego
|
Klasa |
+ |
– |
– |
+ |
– |
+ |
– |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.4 |
0.6 |
0.8 |
0.9 |
1.0 |
|
TP |
4 |
3 |
3 |
3 |
2 |
2 |
1 |
1 |
|
FP |
4 |
4 |
3 |
2 |
2 |
1 |
1 |
0 |
|
TN |
0 |
0 |
1 |
2 |
2 |
3 |
3 |
4 |
|
FN |
0 |
1 |
1 |
1 |
2 |
2 |
3 |
3 |
|
TPR |
1 |
3/4 |
3/4 |
3/4 |
2/4 |
2/4 |
1/4 |
1/4 |
|
FPR |
1 |
1 |
3/4 |
2/4 |
2/4 |
1/4 |
1/4 |
0 |
Na rys. 12.2 przedstawiono graficzną postać charakterystyki ROC. Pole powierzchni pod krzywą AUC=SROC wynosi 0.56. Jakość klasyfikatora jest więc jedynie nieznacznie lepsza od klasyfikatora losowego dla którego to pole wynosi 0.5. Jest to również uwidocznione na rysunku, gdzie prosta przerywana oznacza ROC dla klasyfikatora losowego.
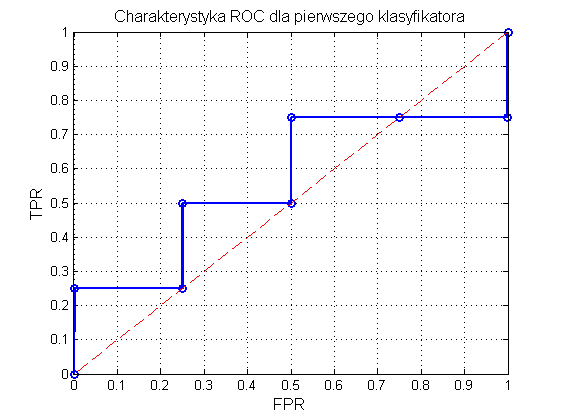
Rys. 12.2 Charakterystyka ROC klasyfikatora z przykładu pierwszego
Dla porównania w tabeli 12.5 przedstawiono wyniki klasyfikacji innego klasyfikatora oraz obliczenia dotyczące miar jakości służące do wyznaczenia krzywej ROC.
Tabela 12.5 Ilustracja kolejnych etapów tworzenia charakterystyki ROC dla klasyfikatora drugiego
|
Klasa |
– |
– |
– |
+ |
– |
+ |
+ |
+ |
|
Sygnał wyjściowy |
0.1 |
0.3 |
0.4 |
0.5 |
0.7 |
0.8 |
0.9 |
1.0 |
|
TP |
4 |
4 |
4 |
4 |
3 |
3 |
2 |
1 |
|
FP |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
|
TN |
0 |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
|
FN |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
|
TPR |
1 |
1 |
1 |
1 |
3/4 |
3/4 |
2/4 |
1/4 |
|
FPR |
1 |
3/4 |
2/4 |
1/4 |
1/4 |
0 |
0 |
0 |
Na rys. 12.3 przedstawiono graficzną postać charakterystyki ROC odpowiadającej wynikom zawartym w tabeli 12.4. Pole powierzchni pod krzywą AUC=SROC wynosi tym razem 0.94, a więc jest bliskie jedności. Jakość klasyfikatora jest zdecydowanie lepsza od klasyfikatora losowego.
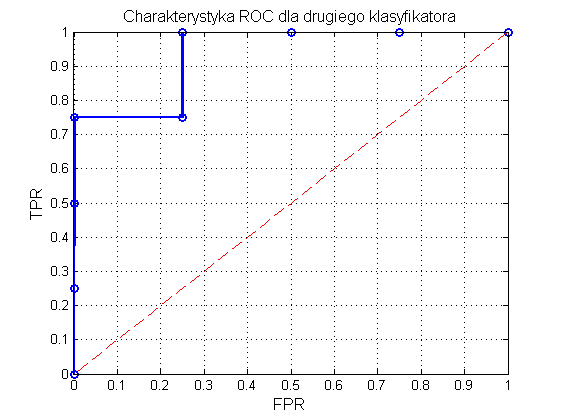
Program Matlab zawiera gotowe funkcje do wykreślania charakterystyki ROC i obliczania wartości AUC. Przykład takiego programu dla danych zawartych w tabeli podany jest poniżej.
Tabela 12.6 Dane do utworzenia krzywej ROC i obliczenia wartości AUC
|
Klasa |
– |
– |
+ |
– |
+ |
+ |
+ |
+ |
– |
+ |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.35 |
0.45 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
y=[0.1 0.2 0.3 0.35 0.45 0.5 0.6 0.7 0.8 0.9 1]
d=[0 0 1 0 1 1 1 1 0 1 1]
[tpr,fpr,th]=roc(d,y);
figure(1), plot(fpr,tpr)
grid, xlabel('FPR'),ylabel('TPR'), title ('ROC')
[X,Y,T,AUC] = perfcurve(d,y,1)
figure(2), plotroc(d,y), grid
W wyniku uzyskuje się AUC=0.7857.
2.3. Metody poprawy jakości klasyfikatora
Dla uzyskania poprawy jakości rozwiązania klasyfikatora rozpoznającego dwie klasy o niezrównoważonej liczebności można stosować różne metody. Do najbardziej znanych należy zróżnicowanie kosztu błędnych klasyfikacji odpowiadających różnym rodzajom błędu, metody równoważenia klas, specjalne metody kodowania klas, czy stosowanie zespołu klasyfikatorów omówione w rozdziale poprzednim.
12.3.1 Metoda różnicowania kosztu błędnej klasyfikacji
Dla uzyskania lepszych miar jakości przy rozpoznawaniu elementów klasy rzadkiej można zastosować w uczeniu funkcję kary uwzględniającą koszt złego rozpoznania elementów tej klasy [58]. Niech \(K_{ij}\) oznacza koszt związany z błędnym rozpoznaniem przez model klasyfikatora klasy \(i\)-tej jako klasa \(j\)-ta. Jednocześnie można nagradzać klasyfikator za poprawną klasyfikację poprzez przyjęcie wartości ujemnej wagi dla kosztu \(K_{ij}\). Przy oznaczeniu klasy rzadkiej symbolem \(+\) a klasy większościowej symbolem \(–\) i uwzględnieniu przyjętych oznaczeń jak w tabeli 12.2 całkowity koszt klasyfikacji przy użyciu modelu M można wyrazić wzorem [65]
| \( K_c(M)=TP \times K_{TP}+FP \times K_{FP}+FN \times K_{FN}+TN \times K_{TN} \) | (12.24) |
Zauważmy, że przyjęcie standardowych wartości \(K_{TP}=K_{TN}=0\) oraz \(K_{FP}=K_{FN}=1\) oznacza klasyczne podejście do oceny jakości (równa kara za oba rodzaje błędów i brak nagrody za poprawną klasyfikację), gdyż
| \( K_c(M)=(TP+TN) \times 0+(FN+FP) \times 1=FN+FP \) | (12.25) |
Funkcja kary jest w tym przypadku równa liczbie błędnych klasyfikacji. Dla zilustrowania wpływu doboru wartości wag elementów kosztu na ocenę modelu klasyfikatora przyjmijmy wartości tych wag jak niżej:
\(K_{TP}=0\)
\(K_{FP}=1\)
\(K_{FN}=100\)
\(K_{TN}=0\)
W przyjętej definicji funkcji kary zakwalifikowanie błędne klasy rzadkiej do większościowej jest karane 100-krotnie bardziej niż przypadek fałszywego alarmu (zakwalifikowanie rekordu należącego do klasy większościowej jako rekordu klasy rzadkiej).
Rozważmy dla porównania dwa przypadki wyników odpowiadające dwu modelom klasyfikatora \(M_1\) oraz \(M_2\) jak przedstawiono w tabelach 12.7 oraz 12.8.
Tabela 12.7 Wyniki klasyfikacji przy użyciu modelu \(M_1\)
|
Model M1 |
Klasa + |
Klasa – |
|
Klasa + |
200 (TP) |
60 (FN) |
|
Klasa – |
50 (FP) |
300 (TN) |
Tabela 12.8 Wyniki klasyfikacji przy użyciu modelu \(M_2\)
|
Model M2 |
Klasa + |
Klasa – |
|
Klasa + |
180 (TP) |
80 (FN) |
|
Klasa – |
5 (FP) |
345 (TN) |
W przypadku klasycznej definicji kosztów klasyfikacji (oba rodzaje błędów traktowane z jednakową wagą równą 1) otrzymuje się
\( K_c\left(\mathrm{M}_1\right)=200 \times 0+60 \times 1+50 \times 1+300 \times 0=110 \)
\( K_c\left(\mathrm{M}_2\right)=180 \times 0+80 \times 1+5 \times 1+345 \times 0=85 \)
Lepszym klasyfikatorem jest tutaj model \(M_2\), gdyż jego funkcja kosztu jest mniejsza.
Koszty całkowite w przypadku przyjętego różnicowania wag błędnych klasyfikacji wynoszą
\( K_c\left(\mathrm{M}_1\right)=200 \times 0+100 \times 60+50 \times 1+300 \times 0=6050 \)
\( K_c\left(\mathrm{M}_2\right)=180 \times 0+80 \times 100+5 \times 1+345 \times 0=8005 \)
Tym razem lepszym klasyfikatorem okazał się model \(M_1\), gdyż wartość kosztu klasyfikacji z nim skojarzona jest mniejsza.
Zmodyfikowana metoda obliczania kosztu błędnej klasyfikacji może posłużyć odpowiedniemu zaprojektowaniu klasyfikatora. Jako funkcję celu w uczeniu definiować można nie liczbę wszystkich błędnych klasyfikacji traktowanych jednakowo (podejście klasyczne), ale z odpowiednimi mnożnikami za poszczególne rodzaje błędów które zmuszą klasyfikator do odpowiedniego ukształtowania granic przynależności do obu klas. W wyniku takiego podejścia próg przynależności do obu klas ulega takiemu przesunięciu, aby kosztem zwiększenia liczby fałszywych alarmów zmniejszyć liczbę błędnego rozpoznania elementów klasy rzadkiej.
12.3.2 Metody równoważenia klas
Inną metodą pozwalającą na polepszenie jakości klasyfikacji w przypadku dwu klas niezrównoważonych jest próba poprawy stopnia zrównoważenia poprzez zastosowanie odpowiedniego próbkowania [24,49,65]. W wyniku takiego podejścia względna reprezentacja klasy rzadkiej powinna zostać wzbogacona w stosunku do klasy większościowej. W praktycznym rozwiązaniu tego problemu stosuje się zarówno zmniejszanie liczebności klasy większościowej użytej w uczeniu jak i zwiększanie liczby reprezentantów klasy rzadkiej.
Najprostszym rozwiązaniem jest zredukowanie liczby danych uczących klasy większościowej do poziomu reprezentowanego przez klasę rzadką. Powstaje wówczas problem doboru próbek uwzględnionych w uczeniu. Jednym z rozwiązań jest stworzenie wielu klasyfikatorów, z których każdy trenowany jest na pełnym zbiorze próbek rzadkich i wybranym podzbiorze (innym dla każdego klasyfikatora) próbek większościowych. Na przykład, jeśli klasa rzadka jest reprezentowana przez 100 próbek uczących, a większościowa przez 1000, można wytrenować 10 klasyfikatorów, każdy na innym podzbiorze klasy większościowej. W następnym etapie tworzy się zespół klasyfikatorów a wynik końcowy może być otrzymany na zasadzie głosowania większościowego (ang. majority voting).
Innym rozwiązaniem, które nadaje się do zastosowań w pewnych przypadkach (np. dane wejściowe dwuwymiarowe, dane wielowymiarowe zrzutowane na płaszczyznę bądź w przestrzeń trójwymiarową) jest wizualizacja rozkładu danych obu klas. Bez utraty zdolności generalizacyjnych można odrzucić te próbki większościowe, które położone są daleko od przewidywanej granicy obu klas. W zbiorze uczącym pozostawia się jedynie reprezentatywną liczbę próbek, porównywalną z populacją klasy próbek rzadkich.
W przypadku podejścia drugiego celem jest zwiększenie liczby reprezentantów klasy rzadkiej do poziomu populacji klasy większościowej. Odbywa się to poprzez sztuczne dodawanie do zbioru uczącego dodatkowych próbek klasy rzadkiej na zasadzie interpolacji między oryginalnymi punktami danych. Współrzędne dodawanych punktów tworzy się na zasadzie uśredniania współrzędnych kilku najbliższych sąsiadów należących do tej samej klasy. Innym rozwiązaniem jest dodawanie szumu losowego do współrzędnych istniejących punktów klasy rzadkiej i tworzenie w ten sposób nowych danych klasy rzadkiej. Tego typu podejście wyrównuje liczebność obu klas, ale nie wzbogaca informacji o modelowanym procesie. Zapobiega jedynie obcięciu pojedynczych próbek rzadkich umieszczonych w otoczeniu próbek klasy większościowej.
Najczęściej łączy się oba podejścia, redukując zarówno liczebność klasy większościowej jak i wzbogacając reprezentację klasy rzadkiej. Takie podejście do problemu równoważenia klas jest najbardziej zalecane w praktyce, gdyż w stosunkowo najmniejszym stopniu zaburza oryginalny rozkład danych obu klas.
12.3.3 Problemy klasyfikacji wieloklasowej
Niektóre metody klasyfikacyjne, na przykład SVM są w oryginale zaprojektowane do klasyfikacji binarnej i są w stanie rozróżnić jedynie 2 klasy. Rozróżnianie wielu klas wymaga stosowania specjalnych technik stosujących kombinację klasyfikatorów binarnych. Do najbardziej znanych podejść należy metoda jeden przeciw jednemu i jeden przeciw pozostałym [59,68].
W pierwszej metodzie przy M klasach tworzy się M(M-1)/2 klasyfikatorów binarnych odpowiedzialnych za rozpoznanie kombinacji 2 klas kolejno parowanych ze sobą. Przy podaniu na wejście wszystkich klasyfikatorów wektora testowego x ostatecznym zwycięzcą jest ta klasa, która zostanie wskazana przez większość głosujących.
W metodzie jeden przeciw reszcie przy M klasach konstruuje się M klasyfikatorów, z których każdy trenowany jest do rozróżnienia między pojedynczą klasą a klasą zbiorczą złożoną z pozostałych. Przy podaniu na wejście takiego klasyfikatora wektora testowego x zwycięska klasa (pojedyncza lub wszystkie klasy zbiorowe tworzące resztę) jest nagradzana głosem. Klasa która otrzyma najwięcej głosów jest uważana za zwycięzcę.
Zdecydowana większość rozwiązań klasyfikatorów umożliwia rozróżnienie wielu klas jednocześnie w jednym układzie klasyfikacyjnym. Wymaga to zdefiniowania wektora etykiet klas (wektor \(\mathbf{d}\)). Najczęściej stosowanym rozwiązaniem jest wówczas zwykłe kodowanie zero-jedynkowe. Etykieta klasy do której należy wektor \(\mathbf{x}\) jest kodowana poprzez wartość 1, a pozostałe klasy przez zero. Wzorzec testowany \(\mathbf{x}\) należy do klasy, na którą wskazuje jedynka, przy czym wartość 1 przypisuje się neuronowi o największej wartości sygnału wyjściowego. Pozostałe neurony przyjmują zerową wartość sygnału wyjściowego. Przy takim rozwiązaniu liczba neuronów wyjściowych klasyfikatora jest równa liczbie klas.
Przykładowo przy zwykłym (pojedynczym) kodowaniu zero-jedynkowym czterech klas można je przyporządkować przy użyciu kodu przedstawionego w tabeli 12.9
Tabela 12.9 Przykład zwykłego kodowania zero-jedynkowego binarnego czterech klas
|
Klasa |
Kod klasy |
|
Klasa 1 |
1000 |
|
Klasa 2 |
0100 |
|
Klasa 3 |
0010 |
|
Klasa 4 |
0001 |
Należy zauważyć, że na etapie odtwarzania może powstać problem interpretacji binarnej wyniku rzeczywisto-liczbowego generowanego zwykle przez klasyfikator. Najczęściej wyjściu klasyfikatora o największym sygnale przypisuje się wartość 1 a pozostałym wyjściom zero. Problemem może być podobna wartość dwu lub więcej sygnałów lub ich bardzo mały (zbliżony do zera) poziom wartości. W takich przypadkach wiarygodność wyniku klasyfikacji opartej na jednej wartości jedynkowej jest stosunkowo mała.
Innym rodzajem kodowania zero-jedynkowego jest tak zwane kodowanie rozproszone, w którym liczba jedynek użyta w kodowaniu klasy może być dowolna. Oznacza to, że liczba neuronów wyjściowych w takim klasyfikatorze może być różna od liczby klas. Po określeniu sygnałów wyjściowych \(y_i\) poszczególnych neuronów i zaokrągleniu ich wartości do zera (gdy \(y < 0.5 \)) lub jedynki (gdy \(y > 0.5 \)) porównuje się wektor wyjściowy \(\mathbf{y}\) z wektorami kodowymi klas obliczając odległość Hamminga (odległość ta jest sumą różnic między poszczególnymi składowymi obu wektorów binarnych). Wzorzec przypisuje się do klasy dla której ta odległość jest najmniejsza. Przykład takiego kodowania dla czterech klas przy użyciu 5 neuronów wyjściowych przedstawiono w tabeli 12.10.
Tabela 12.10 Przykład kodowania zero-jedynkowego rozproszonego czterech klas
|
Klasa |
Kod klasy |
|
Klasa 1 |
00000 |
|
Klasa 2 |
00111 |
|
Klasa 3 |
11001 |
|
Klasa 4 |
11110 |
Zaletą kodowania rozproszonego jest mniejsza wrażliwość układu na wszelkiego rodzaju niedokładności klasyfikatora spowodowane szumem, zwłaszcza w przypadku, gdy sygnały wyjściowe neuronów są bliskie sobie i przypisanie jedynki największemu z nich może rodzić pewne wątpliwości.
2.4. Obiektywna ocena zdolności generalizacyjnych systemu
12.4 Obiektywna ocena zdolności generalizacyjnych systemu
Rozwiązując w sposób maszynowy problem klasyfikacji lub regresji należy podzielić dostępny zbiór danych na podzbiór uczący, na którym dobierane są optymalne wartości parametrów układu oraz podzbiór testujący (weryfikujący) nie uczestniczący w uczeniu a służący sprawdzaniu zdolności generalizacyjnych wytrenowanego układu. Z punktu widzenia użytkownika najważniejsze są wyniki testowania (weryfikacji), gdyż one ilustrują przyszłe zachowanie się systemu na danych rzeczywistych uzyskanych on-line w badanym procesie.
Zwykle zbiór dostępnych danych dzieli się w proporcji zbliżonej do 2:1 lub 3:1, w której większa część służy do uczenia a pozostała do testowania systemu. Podział danych jest najczęściej losowy (np. przy użyciu funkcji randperm Matlaba). Wiąże się z tym problem losowości uzyskanych wyników testowania. Jednokrotny test może nie być reprezentatywny dla zwykłego działania systemu i przyjęcie jego wyników jako obiektywnych nie jest uzasadnione.
Zalecane jest wielokrotne powtórzenie procesu uczenia i testowania przy innym zestawie danych uczących i testujących. Wynik takiego testu jest średnią z wyników poszczególnych prób. W praktycznej implementacji tego podejścia są stosowane różne metody. Jedną z najczęściej stosowanych jest k-krotna walidacja krzyżowa (ang. k-cross validation) [46,65]. Dostępny zbiór danych dzieli się na k części (często k jest równe 10), spośród których (k-1) jest użyte w uczeniu a jedna część pozostawiona do testowania. Próby uczenia i testowania przeprowadza się k razy zmieniając za każdym razem podzbiór testujący. Wynik ostateczny testu jest średnią ze wszystkich k eksperymentów.
Tego typu podejście jest trudne do przeprowadzenia przy bardzo małej liczbie danych, gdyż powoduje nadmierne zubożenie danych uczących. W takim przypadku polecaną metodą jest zastosowanie strategii leave-one-out, w której zbiór testujący zawiera tylko jedną daną, pozostałe służą uczeniu. Proces uczenia i testowania powtarza się tyle razy ile jest danych, za każdym razem zmieniając daną testującą.
Innym możliwą odmianą strategii walidacji krzyżowej jest losowanie wielokrotne danych uczących i testujących z pełnego zbioru. Każda próba uczenia i testowania poprzedzona jest losowaniem zbioru uczącego i testującego ze zbioru pełnego. Proporcje danych uczących i testujących mogą być przy tym dowolne, ustalane przez projektanta systemu, najczęściej w proporcji 2:1. Wynik końcowej oceny jest średnią ze wszystkich prób. W tym rozwiązaniu część danych testujących powtarza się wprawdzie z próby na próbę, ale przy dużej liczbie przeprowadzonych prób nie ma to istotnego znaczenia w obiektywnej ocenie rozwiązania.
2.5. Zadania i problemy
1. Zaproponować schemat kodowania zero-jedynkowego rozproszonego do rozpoznaniania 5 klas.
2. Porównać miary jakości 2 modeli: M1 i M2 przy standardowej definicji funkcji kosztu oraz funkcji różnicującej przypadki FN i FP. Przyjąć przy tym współczynniki KFP=1 i KFN=200. Macierze rozkładu klas są jak poniżej.
|
Model M1 |
Klasa + |
Klasa – |
|
Klasa + |
500 (TP) |
50 (FN) |
|
Klasa – |
50 (FP) |
1000 (TN) |
|
Model M2 |
Klasa + |
Klasa – |
|
Klasa + |
525 (TP) |
25 (FN) |
|
Klasa – |
250 (FP) |
800 (TN) |
3. Narysować krzywą ROC dla klasyfikatora o wynikach
|
Klasa |
+ |
– |
+ |
+ |
- |
– |
+ |
+ |
- |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.8 |
0.9 |
0.95 |
1.0 |
Określić wartość AUC.
4.Macierz rozkładu klas jest dana w postaci
\( \mathbf{R}=\left[\begin{array}{cccc}
100 & 8 & 10 & 2 \\
3 & 150 & 0 & 7 \\
30 & 50 & 200 & 20 \\
7 & 3 & 90 & 500
\end{array}\right] \)
Określić następujące miary jakości: dokładność, precyzje klasowe oraz czułości rozpoznania poszczególnych klas.
5. Wyniki regresji uzyskane przez sieć neuronową ( y ) oraz wartości rzeczywiste procesu ( d ) podane są w tablicy poniżej
|
d |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
y |
0.87 |
2.3 |
3.2 |
3.9 |
5.1 |
6.5 |
7.5 |
7.8 |
8.5 |
10.1 |
11.6 |
12.7 |
12.9 |
14.8 |
13.9 |
Narysować rozkład obu wartości na wspólnym wykresie oraz rozkład błędów. Wyznaczyć wartości miar jakości: MAPE, RMSE oraz miarę korelacyjną.
2.6. Słownik
Słownik opanowanych pojęć
Chwilowy błąd estymacji – różnica między wartością estymowaną a wartością dokładną mierzonej wielkości.
Miara jakości rozwiązania – przyjęty sposób oceny jakości wyników działania systemu w stosunku do wartości rzeczywistych.
MAE – błąd średni absolutny (ang. Mean Absolute Error).
MAPE – średni błąd względny absolutny (ang. Mean Absolute Percentage Error).
RMSE – średni błąd kwadratowy (ang. Root Mean Squared Error).
MAXE – maksymalny błąd bezwzględny (ang. Maximum Error )
MAXPE –względny (procentowy) błąd maksymalny (ang. Maximum Percentage Error - MAXPE)
Miara korelacyjna – miara uwzględniająca korelację wyników wyjściowych z wartościami rzeczywistymi.
Współczynnik Theila – współczynnik porównujący względną wartość błędu średniego badanej metody z odpowiadającą mu wartością błędu prognozy naiwnej.
Macierz niezgodności klasowej – macierz prezentująca wyniki rozpoznania klas na tle wartości prawdziwych (macierz pomyłek).
Klasa rzadka – klasa reprezentowana przez małą liczbę obserwacji.
Klasa większościowa – klasa reprezentowana przez dominującą liczbę obserwacji.
TP – (ang. True Positive) oznacza przypadki prawdziwie pozytywne w rozpoznaniu pożądanej (rzadkiej) klasy (traktowanej jako pozytywna).
TN – (ang. True Negative) oznacza przypadki prawdziwie negatywne w rozpoznaniu klasy przeciwnej (traktowanej jako negatywna) .
FP – (ang. False Positive) oznacza przypadki prawdziwie negatywne rozpoznane jako klasa rzadka.
FN – (ang. False Negative) oznacza przypadki prawdziwie pozytywne (rzadkie) rozpoznane jako klasa większościowa.
TPR – (ang. True Positive Rate) oznacza stosunek liczby poprawnie rozpoznanych przypadków rzadkich do liczby wszystkich przypadków rzadkich – wielkość traktowana jako czułość klasowa.
TNR – (ang. True Negative Rate) oznacza stosunek liczby poprawnie rozpoznanych przypadków większościowych do liczby wszystkich przypadków większościowych – wielkość zwana również specyficznością.
FPR – (ang. False Positive Rate) zdefiniowany jako stosunek liczby przypadków większościowych sklasyfikowanych jako rzadkie do liczby wszystkich przypadków większościowych.
FNR – (ang. False Negative Rate) zdefiniowany jako stosunek liczby przypadków rzadkich sklasyfikowanych jako większościowe do liczby wszystkich przypadków rzadkich.
Precyzja klasowa – stosunek prawdziwej liczby rozpoznanych przypadków danej klasy do wszystkich przypadków rozpoznanych przez klasyfikator jako dana klasa.
ACC – (ang. ACCuracy) dokładność klasyfikatora określająca procent dobrze sklasyfikowanych przypadków przynależności klasowej.
F1 – miara jakości klasyfikatora uwzględniająca jednocześnie precyzję i czułość rozpoznania danej klasy (określana dla każdej klasy oddzielnie).
ROC – (ang. Receiver Operating Characteristics) charakterystyka przedstawiająca graficznie relację między miarą TPR (oś pionowa) a miarą FPR (oś pozioma).
AUC – (ang. Area Under Curve) – wielkość pola pod krzywą ROC.
Kodowanie rozproszone – sposób kodowania klas na wyjściu sieci w którym liczba jedynek użyta w kodowaniu klasy może być dowolna.
K-krotna walidacja krzyżowa – (ang. k-cross validation) technika wielokrotnej oceny jakości systemu w której dostępny zbiór danych dzieli się na k części (często k jest równe 10), spośród których (k-1) jest użyte w uczeniu a jedna część pozostawiona do testowania.
Leave-one-out – technika k-krotnej walidacji krzyżowej, w której zbiór testujący zawiera tylko jedną daną, pozostałe służą uczeniu.
3. Przykłady zastosowań sieci neuronowych w zadaniach biznesowych
W tym rozdziale pokazane zostaną wybrane zastosowania sieci neuronowych w zadaniach biznesowych. Będą to głównie zadania należące do kategorii klasyfikacji i regresji.
3.1. Wprowadzenie
Zadania rozwiązywane w biznesie należą zwykle do trudnych, odpowiedzialnych finansowo i wymagających najwyższej precyzji. Niezależnie od szczególnej tematyki tych problemów można je zwykle zakwalifikować zarówno do zadań klasyfikacji, aproksymacji jak i predykcji.
Spośród problemów biznesowych należących do zadań klasyfikacyjnych można wymienić między innymi takie jak selekcja firm, których akcje będą zwyżkować, a których tracić na wartości, ocena zdolności kredytowej poszczególnych klientów, ocena niebezpieczeństwa bankructwa firmy, zakwalifikowanie określonych państw do odpowiedniej klasy wiarygodności kredytowej. Typowymi zadaniami predykcji jest przewidywanie wartości akcji poszczególnych firm na giełdzie, przewidywanie poziomu wskaźników giełdowych w poszczególnych dniach (WIG, WIG20), przewidywanie trendu rozwoju gospodarki danego kraju, przewidywanie kursu walut i wiele innych.
Każde z tych zadań ma swoją własną specyfikę. Nawet w ramach tego samego typu zadania należy uwzględnić szczególne uwarunkowania z nim związane. Na przykład przy ocenie zdolności spłaty kredytu przez kredytobiorcę ważne jest czy jest to kredytobiorca w postaci państwa, konkretnej firmy prowadzącej działalność gospodarczą czy osoby prywatnej. W przypadku pożyczek rządowych przy ocenie pożyczkobiorcy ocenia się jego wskaźniki makroekonomiczne, podczas gdy w przypadku firmy jej ogólną wartość, rodzaj produkcji, strategię rozwoju czy zdolności menedżerskie kadry zarządzającej.
Również dane użyte w uczeniu sieci neuronowych będą różnić się zasadniczo dla każdego rodzaju kredytobiorcy. Dla firmy podstawą będą roczne sprawozdania finansowe wskazujące na jej zdolności kredytobiorcze. W przypadku klientów indywidualnych tego typu dane nie występują. W zamian można użyć informacji dotyczącej ich stanu posiadania, zaangażowania finansowego w aktualne inwestycje czy historii ich dotychczasowych kredytów.
Inaczej szacuje się również ryzyko udzielenia kredytu dla różnego rodzaju podmiotów gospodarczych. Można tu wyróżnić kilka rodzajów takich podmiotów: rząd i przedsiębiorstwa sektora publicznego, sektor bankowy, przedsiębiorstwa gospodarcze i klienci indywidualni. Najmniejsze ryzyko odpowiada zwykle pożyczkom rządowym i sektora publicznego, podczas gdy klienci indywidualni są najtrudniejsi we właściwej ocenie tego ryzyka.
Dane używane w rozwiązywaniu problemów biznesowych można podzielić na trzy główne kategorie:
-
Dane ilościowe – są one związane z miarami ilościowymi, możliwymi do bezpośredniego zmierzenia bądź predykcji. Dotyczyć one mogą teraźniejszości, przeszłości lub przewidywań dotyczących przyszłości. Przykładami są roczne wyniki finansowane, stan konta bankowego, bilanse transakcji kredytowych w określonym czasie itp.
-
Dane typu jakościowego – są to dane bezpośrednio niemierzalne dotyczące oceny działalności danego przedsiębiorstwa, w tym ocena kadry zarządzającej i jej umiejętności, ocena sektora gospodarki w którym dane przedsiębiorstwo działa, ocena strategii biznesowej stosowanej dotychczas. Ważna jest również ocena stanu zaplecza technicznego i informatycznego danego przedsiębiorstwa, dająca świadectwo o stanie jego nowoczesności.
-
Dane zewnętrzne – są to informacje uzyskane z instytucji zewnętrznych nie związanych bezpośrednio z danym przedsiębiorstwem, np. dane z urzędu statystycznego, agencji ratingowych, prasy fachowej itp.
Dla uzyskania optymalnych rezultatów każde z zadań biznesowych wymaga odpowiedzi na kilka podstawowych pytań:
-
Jak zdefiniować wielkości wyjściowe aby uzyskać najwyższą efektywność (dokładność) działania sieci neuronowej?
-
Jakie wielkości wejściowe sieci (cechy diagnostyczne) mają największy wpływ na zmienne wyjściowe podlegające estymacji?
-
Jak dokonać selekcji optymalnego zestawu tych cech gwarantującego najlepsze wyniki działania sieci?
-
Jak dobrać rodzaj zastosowanej w rozwiązaniu sieci neuronowej i jak zdefiniować optymalną strukturę takiej sieci?
Każde z tych pytań ma kluczowe znaczenie dla uzyskania jak najlepszych wyników w biznesie. Przykładowo, jeśli zadaniem sieci jest predykcja aktualnego wskaźnika WIG na podstawie obserwowanego trendu z dnia na dzień musimy zdać sobie sprawę ze skali trudności. Przy założeniu, że przeciętny poziom tego wskaźnika zmienia się od 6000 do 6500, przeciętna zmiana tygodniowa w granicach około 50 punktów, odpowiada zmianie względnej równej około 0,8%. Oczywiście aktualne zmiany te mogą być w niektórych tygodniach znacznie większe lub mniejsze. Załóżmy, że akceptowalna dokładność predykcji to około 0,1%, czyli około 6 punktów. Uzyskanie takiej dokładności przy predykcji pełnej wartości tego wskaźnika jest praktycznie niemożliwe ze względu na duże obserwowane wahania dzienne.
Sytuacja zmieni się, jeśli zamiast całkowitej wartości wskaźnika będziemy dokonywać predykcji zmiany jego wartości. W takiej sytuacji dokładność predykcji równa 6 punktów przy założonym zakresie tygodniowych zmian równym 50 punktów odpowiada wymaganej dokładności względnej równej 12%, a więc całkowicie realistycznej w praktyce. Stąd projektując sieć należy nastawić się raczej na predykcję zmian a nie całkowitej wartości prognozowanego poziomu wskaźnika.
Przy prognozowaniu zmian dziennych wskaźnika można wyróżnić znów dwa podejścia do rozwiązania. Pierwsze – to predykcja wartości absolutnych zmian wskaźnika, druga – to predykcja jego zmian względnych odnoszonych do wartości średniej tych zmian z określonego okresu, np. ostatniego tygodnia. W zależności od rodzaju danych jedna lub druga metoda prowadzić będzie do lepszych (dokładniejszych) lub gorszych wyników predykcji. Zwykle jedyną drogą rozstrzygnięcia tego problemu jest przeprowadzenie symulacji obu rodzajów rozwiązań i wybranie tego, który jest dokładniejszy.
3.2. Prognozowanie wskaźnika inflacji
Inflacja jest zjawiskiem monetarnym wywołanym szybszym przyrostem ilości pieniądza niż produkcji. W efekcie obserwuje się na rynku długotrwały wzrost średniego poziomu cen dóbr i usług konsumpcyjnych i nie konsumpcyjnych wchodzących do tak zwanego koszyka dóbr. Lista tych dóbr i usług jest każdorazowo określona przez Główny Urząd Statystyczny i ewentualnie nowelizowana odpowiednio do preferencji konsumentów.
13.2.1 Wprowadzenie
Miernikiem inflacji stosowanym praktyce jest indeks cen towarów i usług konsumpcyjnych, definiowany jako stosunek kosztów określonych dóbr konsumpcyjnych wchodzących w skład koszyka do kosztów tych samych dóbr w okresie przyjętym za bazowy.
Inflacja jest faktem obiektywnym i poprzez swój związek z wartością pieniądza i stopami procentowymi musi być brana pod uwagę przy podejmowaniu decyzji związanych z inwestowaniem i zarządzaniem finansami. Istnieje więc potrzeba prognozowania indeksu cen, ponieważ oczekiwania inflacyjne wpływają na wiele decyzji biznesowych podejmowanych w skali zarówno mikro- jak i makroekonomicznej.
Na inflację wpływa aktualny popyt na określone towary na rynku jak również sfera produkcji oraz organizacja współczesnego społeczeństwa. Jednym z najistotniejszych elementów który musi być określony w modelu prognozy jest zdefiniowanie cech diagnostycznych, które będą wpływały w sposób bezpośredni na wynik prognozy. W niniejszych badaniach uwzględnione będą następujące wielkości odniesione do kolejnych miesięcy:
-
wskaźnik cen i usług konsumpcyjnych (\( {wcu} \))
-
średnia płaca miesięczna (\( {spm} \))
-
stopa bezrobocia (\( {sb} \))
-
wartość produkcji sprzedanej w przemyśle (\( {wps} \))
W prognozie na dany miesiąc brać będziemy pod uwagę powyższe wielkości odniesione do określonej liczby miesięcy z przeszłości.
13.2.2 Model neuronowy predykcji
Podstawowym elementem, który musi być rozwiązany w pierwszej kolejności jest wybór i ewentualna selekcja cech diagnostycznych, które będą uwzględniane w modelu. Cztery wymienione wyżej czynniki brane pod uwagę w modelu mogą dotyczyć wiele miesięcy wstecz, pozwalając w ten sposób na uwzględnienie dynamiki ich zmian na wartość prognozowanego wskaźnika cen i usług. Ponadto jako cechy diagnostyczne mogą być traktowane same wielkości bądź ich miesięczne przyrosty. W naszym modelu neuronowym prognozy wzięto pod uwagę każdy z 4 wymienionych wyżej czynników biorąc pod uwagę ich wielkości rzeczywiste. Dla zapewnienia porównywalności wpływu każdej wielkości wszystkie zmienne związane z prognozą podlegały normalizacji według wzoru
| \(x_n=\frac{x_{rz}-x_{\min }}{x_{\max }-x_{\min }}\) | (13.1) |
We wzorze tym \(x_{rz}\) oznacza wielkość rzeczywistą, \(x_{n}\) – wartość znormalizowaną, \(x_{min}\) – wartość minimalną a \(x_{max}\) – wartość maksymalną zmiennej \(x\).
Przy wyborze ilości miesięcy branych wstecz dla uwzględnienia trendu zmian dla każdej z 4 cech prognostycznych zdecydowano się uwzględniać ich wartości z trzech poprzedzających miesięcy. Stąd przy prognozowaniu współczynnika cen i usług na miesiąc \(m\)-ty wektor wejściowy \(\mathbf{x}\) w prognozie miał postać:
\( \mathbf{x}=[{wcu}(m-1), \ldots, {wcu}(m-3), {spm}(m-1), \ldots, {spm}(m-3), {sb}(m-1), \ldots, {sb}(m-3), {wps}(m-1), \ldots, {wps}(m-3)] \)
Jest to wektor 12-elementowy. Prognoza dotyczyć będzie wskaźnika cen towarów i usług konsumpcyjnych w odniesieniu do tego samego miesiąca sprzed roku. W eksperymentach numerycznych wykorzystano dostępną aktualnie bazę danych GUS z lat od stycznia 1999 do czerwca 2006. Zawiera ona dane dotyczące 126 miesięcy. Na rys. 13.1 przedstawiono graficznie wartości wskaźników dotyczące tych miesięcy.
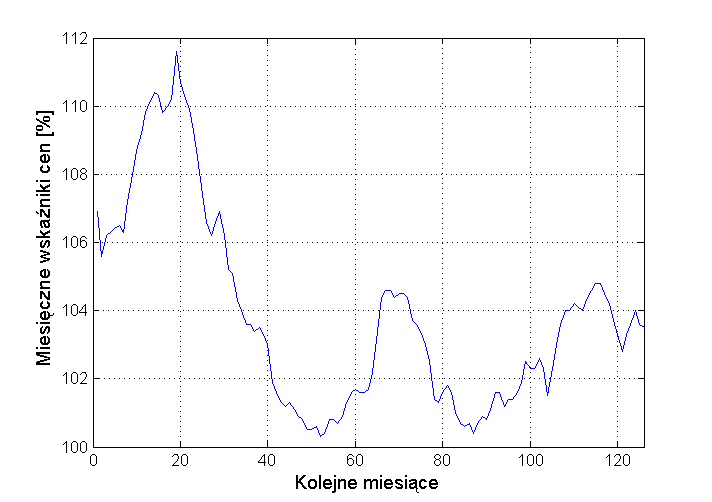
Połowa z tych danych (63) została użyta w uczeniu a druga połowa pozostawiona do testowania wytrenowanej sieci. Dane użyte w uczeniu i testowaniu podlegały wyborowi losowemu (funkcja randperm Matlab) a wszystkie obliczenia powtarzane 10-krotnie z obliczeniem wartości średnich błędów.
13.2.3 Wyniki badań eksperymentalnych prognozy
Badania zdolności prognostycznych sieci neuronowych w problemie predykcji wskaźnika cen towarów i usług przeprowadzono dla dwu rodzajów sieci neuronowych: sieć perceptronowa (MLP) oraz SVM. W przypadku sieci MLP zastosowana struktura miała postać: 12-5-1 (liczba neuronów ukrytych została dobrana w wyniku eksperymentów wstępnych). Sieć SVM do regresji posiadała identyczną liczbę wejść (12) i jedno wyjście. Liczba funkcji jądra jest natomiast dobierana automatycznie przez program uczący na podstawie danych uczących i wartości hiperparametrów. W uczeniu zastosowano stałą regularyzacji \(C=1000\), współczynnik tolerancji \( \varepsilon=0,02 \) i jądro gaussowskie o stałej \( \gamma=0,008 \)
Prognozowane wartości wskaźnika \( {wcu} \) zostały porównane z odpowiednimi wartościami rzeczywistymi wziętymi z bazy danych GUS. Jako miary jakości zastosowano trzy podstawowe rodzaje błędów (\(n\) oznacza liczbę miesięcy uczestniczących w teście, \( {wcu}(m) \) – rzeczywistą wartość wskaźnika \( {wcu} \) w miesiącu \(m\), \( \widehat{wcu} \) - wartość przewidywaną przez program):
-
Średni względny błąd procentowy (MAPE)
| \( \text { MAPE }=\frac{1}{n} \sum_{m=1}^n \frac{|wcu(m)-\widehat{wcu}(m)|}{\left|wcu(m)\right|} \cdot 100 \% \) | (13.2) |
-
Maksymalny błąd względny procentowy (MAXPE)
| \( MAXPE=\max \frac{|w c u(m)-\widehat{wcu}(m)|}{\left|wcu(m)\right|} \cdot 100 \% \) | (13.3) |
-
Średniokwadratowy błąd procentowy (RMSE)
| \( RMSE=\sqrt{\frac{1}{n} \sum_{m=1}^n\left(\frac{wcu(m)-\widehat{wcu}(m)}{ (wcu(m)} \right)^2} \cdot 100 \% \) | (13.4) |
W tabeli 13.1 zestawiono uzyskane wartości błędów prognozy dla danych testujących (63 miesiące) nie uczestniczących w uczeniu.
Tabela 13.1 Zestawienie błędów prognozy dla danych testujących nie uczestniczących w uczeniu sieci neuronowych
|
|
MAPE |
RMSE |
MAXPE |
|
SVM |
0.31% |
1.47 |
2.45% |
|
MLP |
0.58% |
1.97 |
3.85% |
Uzyskane wartości błędów świadczą o bardzo dobrym działaniu predykcyjnym sieci neuronowych. Zarówno błędy średnie jak i maksymalne pozostają na małym (akceptowalnym w praktyce) poziomie. Na rys. 13.2 przedstawiono na wspólnym wykresie wartości wskaźnika inflacji wcu prognozowane przez sieć SVM oraz wielkości rzeczywiste (wykres górny). Na wykresie dolnym zobrazowano zmiany miesięczne błędów predykcji wyrażone w procentach.
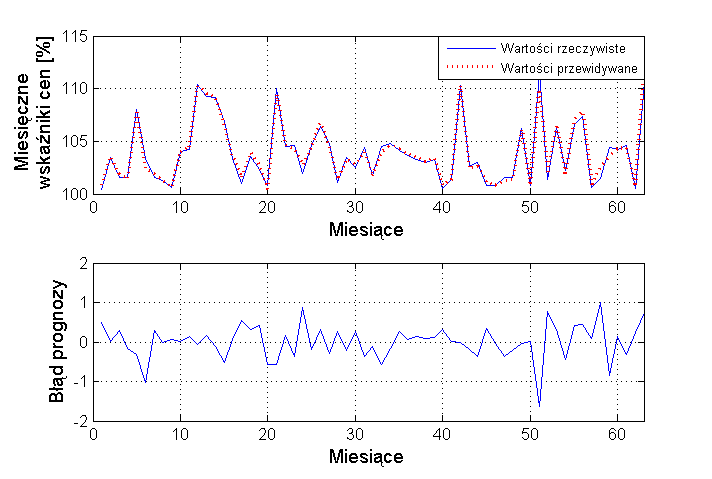
Widoczna jest bardzo dobra zgodność wielkości prognozowanych i rzeczywistych. Błąd prognozy pozostaje na bardzo małym (zbliżonym do zera) poziomie.
3.3. Prognozowanie sygnałów kupna i sprzedaży spółek na giełdzie
Celem zastosowania sieci neuronowej w tej aplikacji jest określenie prawdopodobnej zmiany kursów akcji na giełdzie na podstawie danych dostarczonych na wejście sieci. Analiza zmian kursu akcji w określonym horyzoncie czasowym umożliwi inwestorowi podjęcie decyzji dotyczącej kupna lub sprzedaży tych akcji na giełdzie. Na rys. 13.3 przedstawiono przykładowy wykres zmian kursu spółki giełdowej PKOBP w kolejnych 120 dniach roku (krzywa ciągła) oraz kursu uśrednionego po 3 dniach. Rysunek dolny przedstawia wykres zmian współczynników kierunkowych \(a1\) zmian wartości uśrednionych akcji wyznaczonych na podstawie 7-elementowej próby.
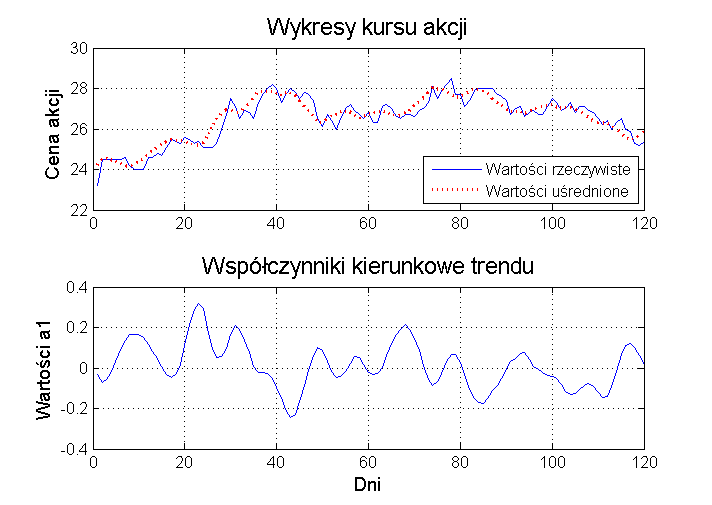
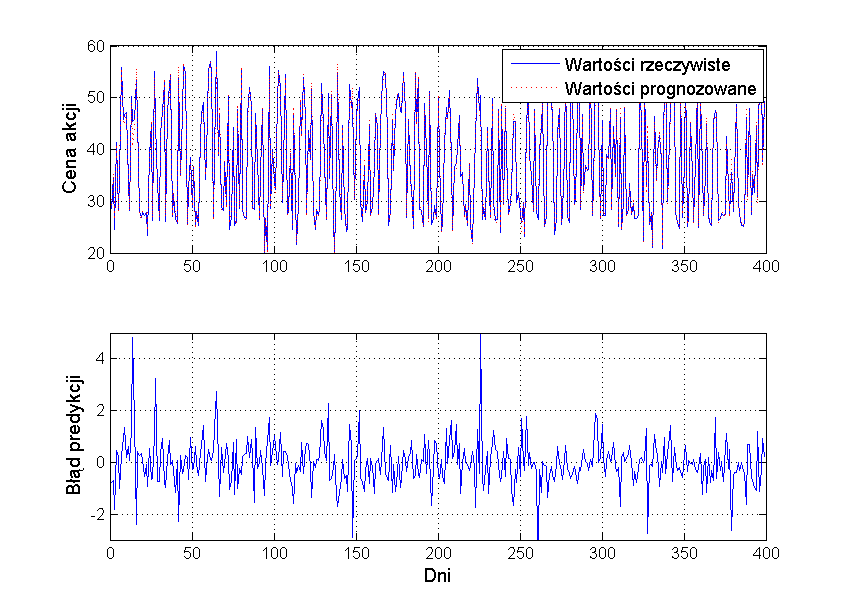
Sygnały transakcji (kupna lub sprzedaży akcji) znajdują się w punktach przecięcia krzywej nachylenia kursu z osią czasu. Sygnał sprzedaży akcji jest generowany w momencie przecięcia osi czasu z malejącą krzywą nachylenia kursu, natomiast sygnał sprzedaży z krzywą rosnącą. W analizowanym okresie widocznych jest 15 następujących po sobie sygnałów kupna i sprzedaży. Porównując ceny kupna i sprzedaży w kolejnych punktach można wyznaczyć zysk na transakcji.
Najistotniejszym czynnikiem decydującym o jakości działania predyktora jest wybór zmiennych wejściowych dla sieci. Najprostszym, choć jednocześnie najmniej dokładnym rozwiązaniem jest predykcja na podstawie jedynie kursów akcji spółki w określonym horyzoncie czasowym (np. 30 dni). Większą dokładność można uzyskać biorąc pod uwagę szerszy zbiór parametrów dotyczących giełdy i otoczenia giełdowego, w tym
-
kursy akcji w minionych sesjach giełdowych
-
wolumen obrotów akcjami danej spółki,
-
wartość obrotu wszystkimi akcjami na giełdzie,
-
wartość i zmiana wartości indeksu WIG,
-
aktualne zmiany indeksów giełdowych na giełdzie amerykańskiej i wybranych giełdach azjatyckich.
Dla zapewnienia porównywalności poszczególnych zmiennych wejściowych dane te powinny podlegać pewnej standaryzacji i normalizacji. W związku z powyższym zamiast bezpośrednich kursów akcji na wejście sieci neuronowej podaje się zwykle stopy zwrotu kt zamiast bezpośredniej wartości kursu akcji definiowane wzorem
| \( k_t=\ln \left(\frac{K_t}{K_{t-1}}\right) \) | (13.5) |
W równaniu tym \( K_t \) oznacza kurs akcji dla \(t\)-tej sesji giełdowej wyrażony w złotych. W przypadku wolumenu obrotów akcjami danej spółki bierze się zwykle pod uwagę logarytm naturalny z tego wolumenu, czyli
| \(v_t=\ln \left(V_t\right)\) | (13.6) |
gdzie \( V_t \) oznacza wolumen obrotów akcjami spółki w trakcie trwania sesji \(t\)-tej, wyrażony w złotych.
W przypadku indeksu WIG bierze się pod uwagę logarytm z jego wartości lub stopę zmian tego indeksu w dwu kolejnych sesjach
| \(w_t=\ln \left(\frac{W I G_t}{W I G_{t-1}}\right)\) | (13.7) |
W przypadku całkowitych obrotów zanotowanych w trakcie sesji giełdowych preferuje się logarytm wartości względnej definiowany w postaci
| \(O_t=\ln \left(\frac{3 O_t}{O_{t-1}+O_{t-2}+O_{t-3}}\right)\) | (13.8) |
W wyrażeniu tym \( O_t \) oznacza całkowite obroty giełdy w trakcie trwania \(t\)-tej sesji wyrażone w złotych.
Wielkość wyjściowa podlegająca predykcji może być ustalana w różny sposób. Najbardziej oczywistym jest bezpośrednie przewidywanie stopy zwrotu, czyli przyjęcie sygnału wyjściowego sieci neuronowej równego przewidywanej na następną sesję wartości stopu wzrostu, czyli
| \(y_t=\ln \left(\frac{K_{t+1}}{K_t}\right)\) | (13.9) |
Przy znanej wartości wyjściowej \( K_t \) wartość \( y_t \) pozwala natychmiast określić spodziewaną stopę wzrostu akcji na następnej sesji.
3.4. Klasyfikacja przedsiębiorstwa pod względem zdolności kredytowych na podstawie wskaźników finansowych
13.4 Klasyfikacja przedsiębiorstwa pod względem zdolności kredytowych na podstawie wskaźników finansowych
Badanie zdolności kredytowej przedsiębiorstw ubiegających się o kredyt należy najczęściej do zadań klasyfikacji dychotomicznej (przyznanie kredytu przez bank bądź nie). Do podjęcia właściwej decyzji konieczny jest zestaw danych wejściowych dla sieci stanowiących potencjalne cechy diagnostyczne. Najczęściej jako zmienne diagnostyczne stosowane są wskaźniki finansowe wyznaczane na podstawie sprawozdań finansowych przedsiębiorstwa dla roku poprzedzającego złożenie wniosku i dla okresu bieżącego danego roku. Można zdefiniować wiele takich wskaźników bądź służących do zdefiniowania takich współczynników. Należą do nich między innymi
-
Rentowność aktywów (ROA)
-
Rentowność kapitału własnego (ROE)
-
Rentowność sprzedaży
-
Rentowność brutto
-
Rentowność netto
-
Płynność bieżąca
-
Krótkoterminowa płynność finansowa
-
Długoterminowa płynność finansowa
-
Rotacja należności (wyrażona w dniach)
-
Rotacja zapasów (wyrażona w dniach)
-
Produktywność aktywów
-
Poziom kosztów
-
Okres płacenia zobowiązań (wyrażony w dniach)
-
Rotacja majątku trwałego
-
Rotacja majątku obrotowego
-
Ryzyko aktywów
-
Ogólne zadłużenie
-
Pokrycie majątku trwałego kapitałem stałym
-
Dług
-
Zadłużenie kapitału własnego
-
Pokrycie obsługi długu
-
Pokrycie odsetek
-
Zadłużenie środków trwałych
-
Stopa zadłużenia
Wybór cech diagnostycznych definiowanych dla roku poprzedzającego złożenie wniosku i okresu bieżącego może dotyczyć zbioru zawierającego w sumie kilkadziesiąt zmiennych, które stanowią składowe wektora wejściowego x podawanego na klasyfikator. Dodatkowo mogą być brane są jeszcze pod uwagę zmienne szacowane przez inspektorów kredytowych dotyczące cech jakościowych przedsiębiorstwa. Dotyczą one między innymi możliwości zbytu, perspektyw rozwojowych firmy, kwalifikacji kierownictwa firmy itp. W przypadku klasyfikacji dychotomicznej klasyfikator posiada jedno wyjście, którego wartość decyduje o przydzieleniu bądź nie kredytu (wartość sygnału wyjściowego większa od progu – przydzielenie kredytu, mniejsza od przyjętego progu – odmowa).
W wielu wypadkach zamiast klasyfikacji dychotomicznej (przydzielić bądź nie przydzielać kredytu) stosuje się przydzielenie klienta do określonej grupy ryzyka, co z kolei może stanowić przesłankę do przydzielenia bądź nie kredytu na odpowiednio zmienionych warunkach. Przyjmuje się zwykle 4 grupy (choć możliwa jest dowolna liczb takich grup, odpowiednio zdefiniowanych):
-
Klient mało wiarygodny nie kwalifikujący się do udzielenia kredytu,
-
Klient wysokiego ryzyka,
-
Klient przeciętnego ryzyka,
-
Klient wiarygodny.
W tym przypadku klasyfikator musi klasyfikować aktualne dane wejściowe do jednej z 4 zdefiniowanych klas. W przypadku klasyfikatora MLP lub RBF będzie to sieć z odpowiednią liczbą wyjść. Przy zastosowaniu SVM należy wykształcić odpowiednią liczbę klasyfikatorów dwuklasowych, zgodnie z metodyka opisaną w wykładzie 8.
W uczeniu sieci klasyfikującej należy użyć odpowiednio dużej bazy danych, obejmującej wiele przykładów dla każdej klasy. Im więcej danych uczących, tym większa szansa uzyskania lepszych (bardziej wiarygodnych) wyników na etapie odtwarzania
Jako przykład zastosowania przedstawimy wyniki uzyskane w pracy [62] przy ocenie zdolności kredytowych przedsiębiorstw amerykańskich. Dostępne dane z bazy Standard and Poor’s Compustat dotyczyły 265 przypadków i pochodziły z 36 banków komercyjnych z lat 1991 – 2000. W klasyfikacji zdolności kredytowej przyjęto 5 klas przedsiębiorstw ubiegających się o kredyt: AA, A, BBB, BB oraz B (klasa AA – najwyższa zdolność kredytowa, klasa B - najniższa). Tabela 13.2 przedstawia rozkład dostępnych danych w poszczególnych klasach.
Tabela 13.2 Rozkład danych dotyczących zdolności kredytowej przedsiębiorstw
|
Klasa |
AA |
A |
BBB |
BB |
B |
Razem |
|
Liczba danych |
20 |
181 |
56 |
7 |
1 |
265 |
Jak widać rozkład danych w poszczególnych klasach jest nierównomierny. Najwięcej jest przypadków przynależności do klasy A, najmniej (bo tylko 1) do klasy najsłabszej (B). Przy stosunkowo małej liczbie dostępnych danych kluczową sprawą jest redukcja liczby cech diagnostycznych do najmniejszego zbioru cech najbardziej dyskryminujących klasy między sobą. Spośród kilkudziesięciu możliwych do wygenerowania cech należy wybrać kilka (co najwyżej kilkanaście) najbardziej reprezentatywnych, gwarantujących najlepsze działanie na danych nie uczestniczących w uczeniu. W selekcji cech diagnostycznych można zastosować wiele różnych metod wartościowania tych cech. W pracy [62] zastosowano test statystyczny ANOVA określający dla każdej cechy wartość poziomu jej istotności p-value przy dyskryminacji klas. Mała wartość poziomu istotności dla danej cechy pozwala odrzucić hipotezę zerową, że cecha ta jest nieistotna przy rozróżnianiu klas (cecha taka pozostaje w zbiorze danych wejściowych dla klasyfikatora). Odrzucane są cechy dla których wartość poziomu istotności jest powyżej pewnego (z góry ustalonego progu). W pracy [62] za wartość taką uznano p=0.30. W wyniku analizy ANOVA wyselekcjonowano wąską grupę kilkunastu cech diagnostycznych mających największy wpływ na wynik klasyfikacji. Należą do nich:
-
całkowity majątek firmy – x1
-
całkowite zadłużenie – x2
-
stosunek zadłużenia długoterminowego do całkowitego kapitału inwestycyjnego firmy – x3
-
stopa zadłużenia – x4
-
współczynnik TIE (Time Interest Earning) – x5 (definiowany jako stosunek zysku firmy przed opodatkowaniem i zapłatą rat kredytu (EBIT) do zobowiązań wynikających z zaciągniętych kredytów)
-
stopa zysku operacyjnego – x6 (definiowana jako stosunek dochodu do sprzedaży netto)
-
stosunek kapitału udziałowego powiększonego o pożyczki długoterminowe do dochodu stałego – x7
-
współczynnik ROTA (Return on Total Assets) – x8 (definiowany jako stosunek wartości EBIT do aktywów netto)
-
współczynnik rentowności kapitału własnego ROE – x9 (definiowany jako stosunek wpływów netto po opodatkowaniu do kapitału udziałowego)
-
stosunek przychodów operacyjnych do kapitału zainwestowanego – x10
-
stosunek wpływów netto do kapitału zainwestowanego (received) – x11
-
stopa zysku netto – x12
-
zysk z jednej akcji – x13
-
marża z zysku brutto – x14
-
stosunek wpływów netto przed opodatkowaniem do wartości sprzedaży – x15
Na podstawie tych wielkości zdefiniować można różne składy wektorów wejściowych dla klasyfikatorów neuronowych. Tradycyjnie w prognozie dokonywanej przez ekspertów amerykańskich za najważniejsze uznaje się cechy: x1, x2, x3, x4, x6. Wektor cech wejściowych x=[ x1, x2, x3, x4, x6] będzie traktowany jako model I. Innym wyborem poddanym analizie w pracy [62] było przyjęcie wskaźników wyselekcjonowanych przez metodę ANOVA. W takim przypadku wektor cech diagnostycznych x zawierał wszystkie wyselekcjonowane cechy x=[x1, x2, …, x15]. Model odpowiadający mu będzie oznaczony jako II.
Mała liczba danych uczestniczących w badaniach zmusza do zastosowania specjalnych technik oceny wyników uczenia i testowania. W pracy [62] zastosowano 2 metody: 10-krotna walidacja krzyżowa oraz metoda „leave-one-out”. W pierwszym podejściu 90% danych branych losowo uczestniczyło w uczeniu klasyfikatora, a pozostałe 10% w jego testowaniu (walidacji). Próby uczenia i testowania powtarzano 10-krotnie za każdym razem zmieniając kolejno skład danych testujących. Jako wynik ostateczny przyjęto średnią ze wszystkich prób testowania. W metodzie „leave-one-out” w uczeniu uczestniczy (p-1) danych uczących (p – liczba danych) a nauczona sieć testowana jest na pozostałej danej (1 dana). Proces uczenia i testowania powtarza się p-krotnie zmieniając za każdym razem daną testującą. Na wynik ostateczny uczenia składają się wyniki testowania z p prób. Autorzy pracy przeprowadzili eksperymenty z dwoma rodzajami klasyfikatora neuronowego: siecią SVM oraz MLP. W tabeli 13.03 przedstawiono uzyskane wyniki w postaci średniej dokładności klasyfikacji (w porównaniu z wynikami eksperta ludzkiego)
Tabela 13.3
|
|
Cross-validation |
Leave-one-out |
||
|
SVM |
MLP |
SVM |
MLP |
|
|
Model I (5 cech) |
78.87% |
80.00% |
80.38% |
80.75% |
|
Model II (15 cech) |
80.00% |
79.25% |
80.00% |
75.68% |
Z przedstawionych wyników widać, że oba klasyfikatory pozwoliły uzyskać porównywalną dokładność klasyfikacji (zwłaszcza przy zastosowaniu uproszczonego modelu I). W przypadku modelu bardziej rozbudowanego lepsze wyniki pozwoliła uzyskać sieć SVM (przy dużym wektorze wejściowym sieć ta jest mniej czuła na małą liczbę danych uczących niż MLP).
Należy podkreślić, że wybór optymalnych cech diagnostycznych nie jest całkowicie jednoznaczny. Jest on w dużej mierze zależny od zastosowanej techniki selekcji cech. Należy ponadto zwrócić uwagę na fakt, że zbiór cech diagnostycznych branych pod uwagę jest w dużej mierze uzależniony od rodzaju działalności firm ubiegających się o kredyt jak również od dostępności danych.
3.5. Klasyfikacja przedsiębiorstw pod względem podatności na bankructwo
Sieci neuronowe mogą pełnić użyteczną rolę w ocenie podatności przedsiębiorstwa na bankructwo. W zastosowaniu tym wykorzystuje się ich funkcję klasyfikatora porównującego aktualne dane wejściowe z wektorem wzorcowym ukształtowanym w procesie uczenia na danych dotyczących przedsiębiorstw zdrowych i bankrutujących. W zależności od relacji do wektora wzorcowego wektor wejściowy danych aktualnych jest zaliczany albo do odpowiedniej klasy przedsiębiorstw zdrowych (wartość d=1) albo bankrutujących (d=0). Za bankrutującą firmę uznaje się taką dla której jest ogłoszona upadłość, firmę kończącą działalność biznesową z powodu trudności rynkowych, firmę która od kilku lat regularnie przynosi straty i jest pod kontrolą ustawową.
Najważniejszymi elementami decydującymi o skuteczności działania takiego klasyfikatora są cechy diagnostyczne, na podstawie których klasyfikator będzie podejmował decyzję. Potencjalne cechy tworzy się na podstawie danych finansowych przedsiębiorstwa. Do najważniejszych należą:
-
Wskaźniki wzrostu, na przykład majątku całkowitego, majątku trwałego, sprzedaży, dochodu, dochodu netto, całkowitych należności z tytułu spłat długu
-
Rentowność przedsiębiorstwa wyrażana poprzez stosunek różnego rodzaju dochodów do innych danych finansowych, na przykład dochodu ze sprzedaży do majątku całkowitego, dochodu netto do majątku całkowitego, dochodu ze sprzedaży do kapitału firmy, dochodu oraz dochodu netto ze sprzedaży do wartości akcji firmy na giełdzie czy do kapitału akcyjnego, dochodu oraz dochodu netto do wartości sprzedaży, zysku do wartości sprzedaży, wydatków finansowych do wartości sprzedaży czy dywidendy do kapitału akcyjnego.
-
Stabilność wyrażana przez takie wskaźniki jak stosunek kapitału akcyjnego do całkowitego majątku firmy, wskaźnik zobowiązań bieżących, stałych i krótkoterminowych, wskaźnik zadłużenia, wskaźnik płatności bieżących i stałych, całkowite płatności i zadłużenie firmy, stosunek rezerw do wartości majątku i aktualna zmiana tego wskaźnika, aktualne odsetki od zaciągniętego długu, wskaźnik pokrycia tych odsetek.
-
Przepływy pieniężne, w tym przepływ kapitału do majątku udziałowców, koszty pokrycia długów i obligacji, koszty poniesione dla zwiększenia majątku firmy czy na zwiększenie sprzedaży.
-
Aktywność wyrażająca się fluktuacją majątku całkowitego, majątku udziałowców, majątku stałego, rezerw, zmian wartości rezerw.
-
Wiarygodność firmy wyrażana przez takie wskaźniki jak stosunek płatności do należności i jego zmiana, stosunek płatności do aktualnych zobowiązań i jego zmiana, zmiana stosunku należności do bieżącego majątku firmy.
W pracy [39] rozważono 57 wskaźników ekonomicznych bazujących na wymienionych wyżej danych finansowych badając ich znaczenie w przewidywaniu bankructwa 126 firm koreańskich na przestrzeni 12 lat. Jednym z ważniejszych czynników decydujących o skuteczności predykcji jest ocena wartości diagnostycznej poszczególnych wskaźników ekonomicznych. Z kilku rozważanych metod selekcji cech diagnostycznych najlepszą efektywnością wykazała się miara dyskryminacyjna Fishera oraz drzewo decyzyjne stosujące miarę entropijną [3,18].
Przy zastosowaniu miary Fishera wyselekcjonowano 17 najważniejszych wskaźników, należących do wszystkich wymienionych grup. Jako klasyfikator została zastosowana sieć MLP o jednej warstwie ukrytej zawierającej 17 neuronów sigmoidalnych. Uzyskano dokładność predykcji równą 80%.
Przy zastosowaniu drzewa decyzyjnego liczba wyselekcjonowanych cech diagnostycznych była równa 9, a zastosowana sieć neuronowa MLP uznana za optymalną miała 9 neuronów ukrytych. Przy zastosowaniu tego rozwiązania uzyskano dokładność predykcji bankructwa firm sięgającą 82,5%.
3.6. Zadania i problemy
-
Korzystając z danych GUS narysować wykres zmian wskaźnika cen i usług konsumpcyjnych (wcu) dla kilku ostatnich lat przy odniesieniu się do miesiąca poprzedniego. Obliczyć wartość średnią i odchylenie standardowe krzywej zmian.
-
Korzystając z danych GUS narysować wykres zmian średniej płacy miesięcznej (spm) w kraju dla kilku ostatnich lat przy odniesieniu się do miesiąca poprzedniego. Obliczyć wartość średnią i odchylenie standardowe krzywej zmian spm. Określić współczynnik korelacji zmian wcu oraz spm. Narysować rozkład danych (wcu, spm) na płaszczyźnie zdefiniowanej przez te 2 zmienne.
-
Sprawdzić działanie sieci predykcyjnej SVM i MLP dla przewidywania zmian spm na podstawie jedynie zmian wartości tej zmiennej w przeszłości (biorąc pod uwagę np. kilka ostatnich miesięcy jako zmienne wejściowe dla sieci). Skomentować wyniki predykcji pod względem dokładności w stosunku do wartości rzeczywistych..
-
Rozwiązać zadanie poprzednie przy użyciu zespołu predyktorów (sieć MLP, SVM, RBF, Elmana) stosując integrację przy użyciu dodatkowej sieci neuronowej, np. SVM lub MLP. Porównać dokładność rozwiązań indywidualnych oraz zespołu.
3.7. Słownik
Przykłady zastosowań sieci neuronowych w zadaniach biznesowych
Słownik opanowanych pojęć
Wykład 13
Dane biznesowe – wielkości związane z biznesem należące do trzech podstawowych grup: dane typu ilościowego, jakościowego oraz informacje pozyskiwane z instytucji zewnętrznych.
Inflacja – zjawisko monetarne wywołane szybszym przyrostem ilości pieniądza niż produkcji.
Stopa zwrotu akcji - wielkość definiowana w postaci \(y_t=\ln \left(\frac{K_{t+1}}{K_t}\right)\), gdzie \(K_t\) oznacza wartość akcji na \(t\)-tej sesji giełdowej.
WIG – Warszawski indeks giełdowy typu dochodowego, obejmujący akcje spółek notowanych na rynku podstawowym giełdy warszawskiej.
Zdolność kredytowa – zdolność kredytobiorcy, czyli podmiotu ubiegającego się o kredyt, do spłaty kwoty kredytu, rozumianego jako kapitał wraz z odsetkami w umownych terminach płatności.
Standard & Poor’s (S&P) – agencja ratingowa publikująca analizy i raporty dotyczące spółek akcyjnych, emitowanych przez nie obligacji, a także przeprowadzająca ratingi różnych podmiotów gospodarczych (spółki akcyjne, miasta, państwa) przyznając im oceny ratingowe w skali od „AAA” do „D”.
Bankructwo – procedura wszczynana w razie niewypłacalności dłużnika, polegająca głównie na wspólnym dochodzeniu roszczeń przez wszystkich jego wierzycieli (zwana również upadłością lub plajtą).
Rentowność przedsiębiorstwa – wskaźnik liczbowy wyrażany poprzez stosunek różnego rodzaju dochodów do innych danych finansowych.
Wiarygodność firmy – wielkość wyrażana przez takie wskaźniki jak stosunek płatności do należności i jego zmiana, stosunek płatności do aktualnych zobowiązań i jego zmiana, zmiana stosunku należności do bieżącego majątku firmy itp.
4. Prognozowanie obciążeń 24-godzinnych w systemie elektroenergetycznym z użyciem zespołu sieci neuronowych
Wykład ten poświęcony będzie zastosowaniu sztucznych sieci neuronowych w prognozowaniu obciążeń 24-godinnych z wyprzedzeniem dobowym w Polskim Systemie Elektroenergetycznym. Problem dotyczy predykcji szeregu czasowego o 24 składnikach, każdy odpowiadający jednej godzinie doby. W rozwiązaniu problemu zastosujemy wiele sieci neuronowych na raz. Prognozy 24-godzinne wyprodukowane przez każdą siec neuronową na podstawie tej samej informacji wejściowej podlegać będą integracji tworząc zespół predyktorów. Pokażemy kilka różnych podejść do integracji, między innymi uśrednianie ważone, zastosowanie ślepej separacji sygnałów generowanych przez każdą sieć czy zastosowanie oddzielnej sieci neuronowej. Wyniki eksperymentów numerycznych przedstawione w tym wykładzie potwierdzają wysokość sprawność działania takiego systemu eksperckiego.
4.1. Wprowadzenie
Metody prognozowania zapotrzebowania 24-godzinnego na energię elektryczną stanowią ważny czynnik poprawy efektywności gospodarowania energią, gdyż umożliwiają precyzyjne planowanie w tej dziedzinie gospodarki. Z tego powodu tematyka ta jest rozwijana na świecie od wielu lat. Stosować można różne metody prognozowania, poczynając od metod liniowych, takich jak algorytmy autoregresyjne (ARX, ARMAX, ARIMA), poprzez różnego rodzaju dekompozycje (Fouriera, SVD, PCA, falkowa), klasyczne metody optymalizacyjne, w tym optymalizacji globalnej (algorytmy genetyczne, ewolucyjne, symulowanego wyżarzania) aż po najczęściej dziś stosowane sztuczne sieci neuronowe [11,24,32,47,48,].
Zwykle próbuje się różnych metod wybierając spośród nich tę, która zapewnia najlepsze działanie systemu prognostycznego na danych weryfikujących, nie biorących udziału w uczeniu. Należy podkreślić, że prognozowanie obciążeń 24-godzinnych należy do zadań trudnych, gdyż obserwuje się dużą zmienność w przebiegu godzinnym obciążeń. Na rys. 14.1 przedstawiono typowy wykres obciążeń godzinnych występujący w Polskim Systemie Elektroenergetycznym (PSE) w jednym roku (8670 godzin).
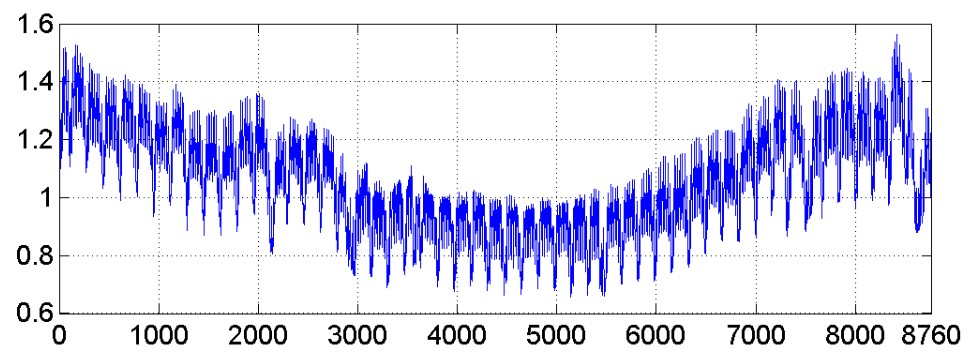
Widoczne jest wyraźne zróżnicowanie obciążeń odpowiadającym różnym godzinom, typom dnia, jak również porze roku. Miesiące zimowe (początek i koniec wykresu) charakteryzują się znacznie większym zapotrzebowaniem na energię, podczas gdy w miesiącach letnich zapotrzebowanie to spada. Widać to wyraźnie na przykładowych danych jednorocznych pokazanych dla małego systemu elektroenergetycznego w tabeli 14.1.
Tabela 14.1 Typowe wartości średniej i odchylenia standardowego odpowiadające różnym porom roku (wartości w MW dla małego systemu elektroenergetycznego
|
Pora roku |
Wartość średnia |
STD |
STD/ Wartość średnia |
|
Zima |
405.2926 |
74.4464 |
0.1836 |
|
Wiosna |
308.8839 |
79.8236 |
0.2584 |
|
Lato |
207.6937 |
65.2883 |
0.3143 |
|
Jesień |
383.2715 |
92.3161 |
0.2409 |
Obciążenie średnie zimą jest najwyższe, przy stosunkowo małej wartości odchylenia standardowego. Obserwując obciążenia poszczególnych dni tygodnia można również zauważyć istotne różnice dla poszczególnych dni, co uwidoczniono w postaci statystyki w tabeli 14.2. Wyraźnie widoczne jest zmniejszenie zapotrzebowania na energię elektryczna w dni świąteczne i weekendy, w stosunku do dni roboczych.
Tabela 14.2 Typowe wartości statystyki odpowiadające różnym dniom tygodnia (wartości w MW dla małego systemu elektroenergetycznego)
|
Dzień |
Wartość średnia |
STD |
Skośność |
Kurtoza |
||||
|
Poniedziałek |
351.8200 |
71.5773 |
0.0990 |
1.7778 |
||||
|
Wtorek |
363.2043 |
70.9437 |
0.0325 |
1.8698 |
||||
|
Środa |
362.4143 |
73.3263 |
-0.0778 |
2.1365 |
||||
|
Czwartek |
361.5417 |
77.7123 |
-0.2110 |
2.2284 |
||||
|
Piątek |
361.4712 |
72.0333 |
0.0829 |
1.7781 |
||||
|
Sobota |
311.5938 |
66.7496 |
0.1659 |
1.7059 |
||||
|
Niedziela |
270.4487 |
65.0778 |
0.2587 |
1.7625 |
||||
Skala powtarzalności predykcji dla poszczególnych dni tygodnia jest odzwierciedlona poprzez stosunek wartości standardowego odchylenia względem wartości średnich (powyżej 20%). Przy takiej skali zmienności obciążeń prognoza naiwna przenosząca wzorzec obciążenia godzinnego doby z jednego tygodnia na drugi generowałaby zbyt duże błędy. Sytuację tę dobrze ilustrują również zależności korelacyjne między poszczególnymi dniami tygodnia. W tabeli 14.3 przedstawiono typowe wartości współczynnika korelacji dla danych małego systemu elektroenergetycznego i jednego roku.
Tabela 14.3 Typowe wartości współczynnika korelacji między poszczególnymi dniami tygodnia
|
|
Sobota |
Niedziela |
Poniedziałek |
Wtorek |
Środa |
czwartek |
Piątek |
|
Sobota |
1 |
0.9290 |
0.8807 |
0.8815 |
0.8828 |
0.8975 |
0.9063 |
|
Niedziela |
0.9290 |
1 |
0.8123 |
0.8148 |
0.8207 |
0.8306 |
0.8360 |
|
Poniedziałek |
0.8807 |
0.8123 |
1 |
0.9747 |
0.9451 |
0.9344 |
0.9451 |
|
Wtorek |
0.8815 |
0.8148 |
0.9747 |
1 |
0.9578 |
0.9398 |
0.9502 |
|
Środa |
0.8828 |
0.8207 |
0.9451 |
0.9578 |
1 |
0.9545 |
0.9545 |
|
czwartek |
0.8975 |
0.8306 |
0.9344 |
0.9398 |
0.9545 |
1 |
0.9871 |
|
Piątek |
0.9063 |
0.8360 |
0.9451 |
0.9502 |
0.9545 |
0.9871 |
1 |
Dni weekendowe są słabiej skorelowane z dniami roboczymi, natomiast dużo lepiej skorelowane są ze sobą. Podobnie dobra korelacja występuje między samymi dniami roboczymi (wartości powyżej 0.93)
W tym wykładzie przedstawimy specjalne podejście do prognozowania, bazujące na zastosowaniu wielu układów prognostycznych na raz. Każdy system prognozy działa na tych samych danych wejściowych. Wyniki działania każdego z nich mogą być integrowane w jednym wspólnym zespole sieci. Takie rozwiązanie pozwala wykorzystać dobre cechy każdego predyktora, pozwalając w ten sposób na uzyskanie precyzyjniejszej prognozy. Pokażemy kilka podejść do integracji wyników działania wielu predyktorów. Wyniki badań teoretycznych zostaną przetestowane na danych rzeczywistych dotyczących Polskiego Systemu Elektroenergetycznego (PSE).
4.2. Sieci neuronowe użyte w predykcji szeregu czasowego
Ważnym elementem najnowszego podejścia do prognozowania jest jednoczesne użycie wielu sieci neuronowych, wykonujących to samo zadanie przy użyciu identycznego zbioru danych pomiarowych, z którego losuje się zbiór uczący dla każdego członka zespołu [36]. Przy użyciu niezależnych predyktorów działających w oparciu o różne zasady działania i zastosowania różniących się zbiorów uczących można spodziewać się niezależnych od siebie wyników predykcji. Oznacza to, że błędy predykcji popełnione przez poszczególne układy predykcyjne będą miały różne rozkłady. Stąd uwzględnienie wszystkich wyników na raz w jednym wspólnym układzie integrującym stwarza realną szansę na kompensację pewnych błędów i w efekcie polepszenie dokładności działania całego systemu predykcyjnego.
Wybór poszczególnych predyktorów powinien uwzględniać jak największe zróżnicowane sposobu działania każdego z nich, aby wyniki predykcji były jak najbardziej niezależne od siebie. Stosować można różne rodzaje predyktorów, w tym sieć perceptronu wielowarstwowego (MLP), sieć radialną RBF, sieć Support Vector Machine (SVM), sieci rekurencyjne oraz sieć Kohonena. Pierwsze trzy predyktory należą do sieci trenowanych z nauczycielem wykorzystując w swym działaniu własność uniwersalnego aproksymatora. Sieć Kohonena jest siecią samoorganizującą i działa poprzez grupowanie danych w przestrzeni wielowymiarowej. Spośród pierwszych trzech rodzajów sieci MLP wykorzystuje sigmoidalną funkcję aktywacji neuronów, realizując aproksymację globalną. Sieć SVM o jądrze gaussowskim jest typową siecią o działaniu lokalnym, natomiast sieci rekurencyjne Elmana lub LSTM są z natury sieciami typu rekurencyjnego o całkowicie odmiennym sposobie przetwarzania danych.
Powyższe rozwiązania należą do klasycznych układów płytkich (o małej liczbie parametrów). W ostatnich latach do grona rozwiązań dołączyły sieci głębokie, takie jak sieć rekurencyjna LSTM, liczne rozwiązania sieci konwolucyjnych CNN czy autoenkoder. Powstał w ten sposób szeroki wachlarz wyboru indywidualnych predyktorów, zwiększając prawdopodobieństwo niezależności wyników predykcji każdego z nich (podstawowy warunek poprawnego działania zespołu).
14.2.1 Model predykcji przy użyciu sieci jednokierunkowej z nauczycielem
Zastosowanie modeli płytkich wymaga oddzielnego etapu przygotowania atrybutów wejściowych dla sieci predykcyjnej (cech diagnostycznych procesu) na podstawie danych pomiarowych. Jest to bardzo ważny element rozwiązania decydujący o właściwym działaniu systemu. Ten etap rozwiązania może stosować bądź rozwiązanie eksperckie (wybór cech na podstawie wiedzy eksperta ludzkiego) bądź maszynowe, na przykład z zastosowaniem transformacji PCA lub autoenkodera.
Przyjmijmy, że predykcja dotyczyć będzie obciążenia \( \hat{P}(d,h) \) w dniu \(d\) i godzinie \(h\). Proponowany model nieliniowy uzależnia prognozę od typu dnia (zmienna t), pory roku, (zmienna s), wybranej liczby rzeczywistych obciążeń z dni i godzin poprzednich \( \hat{P}(d-i,h-j) \) oraz od samych parametrów sieci neuronowej reprezentowanych przez wektor \(\mathbf{w}\). Ogólna postać modelu może być wyrażona wzorem [46]
| \(\hat{P}(d, h)=f[\mathbf{w}, t, s, P(d, h-1), \ldots, P(d, h-H), P(d-1, h, \ldots, P(d-D, h-H)]\) | (14.1) |
W równaniu tym \(H\) i \(D\) reprezentują odpowiednio liczbę godzin i dni wstecz branych pod uwagę w modelu (wielkości uzależnione od wiedzy eksperta). Typ dnia koduje się zwykle binarnie w postaci zero-jedynkowej. Pora roku w naszym klimacie może być zakodowana w postaci 2 bitów (każda kombinacja 0 i 1 oznacza jedną porę roku), \( \hat{P}(d,h) \) reprezentuje wynik prognozy, natomiast \( P(d-i,h-j) \) wartości rzeczywistych obciążeń z przeszłości. Wszystkie dane muszą być znormalizowane. Zwykle wystarczy każdą kolumnę danych (cechę prognostyczną) podzielić przez największą wartość z tej kolumny. W ten sposób wszystkie kolumny będą reprezentować dane zawarte w przedziale [0, 1]. Jeśli prognoza dotyczy małego obszaru (np. rejonu energetycznego) w modelu tym można dodać jeszcze zmienną temperaturową, pod warunkiem, że tego typu dane są dostępne.
W przyjętym tu modelu matematycznym celowo została pominięta temperatura, gdyż proponowany model prognozy dotyczy globalnych wielkości obciążenia w skali kraju. Przy dużej zmienności temperatury, zwłaszcza zimą, trudno byłoby ustalić jaką temperaturę należy przyjąć w obliczeniach. Można ją łatwo dołączyć do parametrów branych pod uwagę w prognozie dotyczącej małego obszaru kraju, np. małego rejonu energetycznego. Model matematyczny prognozy zostanie wówczas wzbogacony o dodatkową zmienną przy podobnym podejściu do samej prognozy.
Szczególna struktura zastosowanego predyktora zależy od aktualnie wybranej sieci. W przypadku MLP stosującej funkcję sigmoidalną neuronów wystarczy zwykle użycie co najwyżej dwu warstw ukrytych (najczęściej jedna warstwa ukryta wystarcza) [46]. Liczba wejść sieci zależy od zastosowanego modelu predykcji, natomiast liczba wyjść jest równa liczbie prognozowanych obciążeń godzinowych (w przypadku prognozy na 24 godziny naprzód jest to liczba 24).
W przypadku zastosowania sieci RBF jako predyktora stosowana jest tylko jedna warstwa ukryta o gaussowskiej funkcji aktywacji [24], przy czym liczba neuronów ukrytych, ze względu na lokalny charakter funkcji aktywacji, jest dużo większa niż w przypadku sieci MLP. Struktura wejścia i wyjścia takiej sieci jest identyczna jak w sieci MLP.
W przypadku sieci rekurencyjnej Elmana [46] stosuje się jedną warstwę ukrytą o sigmoidalnej funkcji aktywacji posiadającej sprzężenie zwrotne z wejściem sieci, co oznacza odpowiednie zwiększenie wymiaru wejściowego sieci. Liczba zewnętrznych wejść i wyjść sieci jest identyczna jak w MLP. Uczenie obu rodzajów sieci odbywa się poprzez minimalizację różnic między wartościami historycznymi (znanymi) obciążeń a ich predykcją przy pomocy algorytmów gradientowych, na podstawie bazy danych uczących dotyczących obciążeń z przeszłości. Najczęściej używanym algorytmem jest algorytm Levenberga-Marquardta (przy małej liczbie wag) lub gradientów sprzężonych (przy bardzo dużej liczbie wag).
Sieć SVM jest specyficzną strukturą sieciową o jednym neuronie wyjściowym [59]. Z tego powodu należy zastosować w rozwiązaniu 24 takie sieci zasilane tymi samymi sygnałami wejściowymi, każda specjalizująca się w prognozie na określoną godzinę doby. Najczęściej stosowaną funkcją jądra jest funkcja gaussowska [59]. Uczenie sieci SVM prowadzone na zbiorze danych uczących identycznych jak dla MLP jest wyjątkowo efektywne ze względu na sformułowanie problemu uczenia jako zadania programowania kwadratowego. Jest ono wielokrotnie szybsze niż w przypadku sieci MLP i Elmana.
W ogólności proces prognozowania obciążenia przy zastosowaniu sieci neuronowej trenowanej z nauczycielem składa się z następujących etapów:
-
wybór danych uczących i składników wektorów wejściowych na podstawie których będzie dokonywana prognoza
-
dobór rodzaju i architektury sieci neuronowej odpowiedzialnej za predykcję
-
trening sieci neuronowej przy zastosowaniu wybranego algorytmu uczącego
-
weryfikacja działania sieci na zbiorze danych weryfikujących i przeprowadzenie ewentualnie dalszego douczenia sieci
-
użycie sieci jako predyktora obciążenia godzinnego w fazie odtworzeniowej (właściwy etap użytkowania)
-
ewentualna adaptacja sieci po upływie pewnego okresu, na przykład roku.
14.2.2 Model predykcji przy użyciu sieci Kohonena
W przypadku zastosowania w prognozowaniu sieci Kohonena wykorzystuje się jej zdolność grupowania danych w przestrzeni wielowymiarowej [46]. Dla uniknięcia problemu zróżnicowania poziomu obciążeń w różnych latach należy przeprowadzić specjalną normalizację danych, transformującą obciążenia godzinowe rzeczywiste \( P(d,h) \) w tak zwane profile obciążeń godzinowych \( p(d,h) \) definiowane wzorem
| \( p(d, h)=\frac{P(d, h)-P_m(d)}{\sigma(d)} \) | (14.2) |
Pm(d) oznacza wartość średnią obciążenia dnia \( d \), natomiast \( \sigma(d) \) jest odchyleniem standardowym obciążeń godzinowych tego dnia. Zbiór 24 profili godzinowych tworzy wektor profilu obciążenia dla dnia \( d \),
| \( \hat{\mathbf{p}}(d)=[\hat{p}(d, 1), \hat{p}(d, 2), \ldots, \hat{p}(d, 24)]^T \) | (14.3) |
definiowany dla każdego dnia roku. Sieć Kohonena jest trenowana w taki sposób, aby ograniczona liczba neuronów centralnych reprezentowała wektory profilowe z najmniejszym błędem kwantyzacji. W uczeniu wykorzystuje się algorytm Kohonena lub gazu neuronowego [46]. W wyniku tego każdy wektor profilowy z bazy danych jest przypisany do jednego wybranego neuronu zwycięzcy. Jest to neuron zwycięzca o wagach najlepiej dopasowanych do uśrednionych wag wektorów profilowych tworzących dany klaster. Reprezentuje on określoną klasę. Charakterystyczne jest, że sąsiednie wektory mają zbliżone charakterystyki profilowe. Na rys. 14.2 przedstawiono wektory profilowe 49 neuronów wytrenowanych na danych PSE z kilku ostatnich lat. Widoczne są bliskie sobie zgrupowania danych o podobnych wektorach profilowych. Potwierdza to znany w energetyce fakt podobnych profili obciążenia dla dni roboczych i zbliżone do siebie profile dla dni świątecznych.

Podobieństwo wag neuronów położonych blisko siebie jest zrozumiałe biorąc pod uwagę mechanizm sąsiedztwa w algorytmach samoorganizacji. Oznacza to, że ten sam dzień roku w różnych latach, przy drobnych różnicach w obciążeniach godzinnych, może pobudzać różne neurony położone blisko siebie i tworzące rodzaj klastrów, grupujących podobne sobie klasy.
Nanosząc wagi neuronów zwycięzców na płaszczyznę \((x, y)\) i przypisując każdemu z nich odpowiednie rodzaje dni, dla których zwyciężały, można zauważyć wspólne rejony obszaru charakterystyczne dla obciążeń świątecznych i osobno dla dni roboczych
Znajomość tablicy rozkładów zwycięstw poszczególnych neuronów sieci pozwala stosunkowo prosto przewidzieć profile obciążenia godzinnego dla dowolnego dnia roku z dowolnym wyprzedzeniem czasowym (znacznie ogólniejsza metoda predykcji w porównaniu z sieciami trenowanymi z nauczycielem). Przy predykcji profili tworzy się tablicę przynależności każdego dnia roku do obszaru dominacji określonego neuronu, z zaznaczeniem liczby zwycięstw neuronu dla wszystkich dni z przeszłości. Przykładowa tablica dotycząca wtorków w lipcu na przestrzeni ostatnich 5 lat przedstawiona jest poniżej (w symulacji użyto 100 neuronów, uporządkowanych w tablicy 10×10).
Tabela 14.4 BRAK PODPISU
|
Miesiąc |
Dzień tygodnia |
Neuron zwycięzca |
Liczba zwycięstw |
|
Maj |
środa |
56 |
6 |
|
Maj |
środa |
54 |
7 |
|
Maj |
środa |
57 |
5 |
|
Maj |
środa |
65 |
4 |
|
Maj |
środa |
47 |
3 |
Dla wyznaczenia przewidywanego profilu obciążenia aktualnego dnia (np. środa) w danym miesiącu (np. maju) przyjmuje się uśrednione wartości wag neuronów zwycięzców do których przynależał w przeszłości dany typ dnia. Jeśli liczbę zwycięstw i-tego neuronu odpowiadającą \(d\)-temu dniu oznaczymy w postaci \( k_{di} \), a odpowiednie wektory wagowe klasy przez \(\mathbf{w}_i\), to przewidywany wektor profilowy dnia \(d\)-tego estymuje się według wzoru [46]
| \(\hat{\mathbf{p}}(d)=\frac{\sum_{i=1}^n k_{d i} \mathbf{w}_i}{\sum_{i=1}^n k_{d i}}\) | (14.4) |
w którym \( k_{di} = 0\), jeśli określony neuron nigdy nie zwyciężył w danej klasyfikacji. Przykładowo dla danych przedstawionych w tabeli 14.1 wektor profilowy dla wszystkich śród w maju będzie określony wzorem
| \(\mathbf{p}(\) środa, maj \()=\frac{1}{25}\left(6 \mathbf{w}_{56}+7 \mathbf{w}_{54}+5 \mathbf{w}_{57}+4 \mathbf{w}_{65}+3 \mathbf{w}_{47}\right)\) | (14.5) |
Po określeniu wektora profilowego rzeczywiste obciążenie odpowiadające poszczególnym godzinom danego dnia oblicza się na podstawie wzoru (14.2), który tutaj przepiszemy w postaci
| \(\hat{P}(d, h)=\hat{\sigma}(d) \hat{p}(d, h)+\hat{P}_m(d)\) | (14.6) |
We wzorze tym wielkości prognozowane oznaczone są symbolem \( \hat{} \). Wynika z niego, że dla uzyskania pełnej prognozy należy dodatkowo dokonać predykcji wartości średniej i odchylenia standardowego dla każdego dnia, dla którego tworzona jest prognoza. Predykcja taka może być wykonana poprzez zastosowanie analizy statystycznej wartości średnich i wariancji z przeszłości bądź przy zastosowaniu specjalnej sieci perceptronowej wytrenowanej tylko do tego celu (oddzielna sieć jednowyjściowa dla predykcji wartości średniej i oddzielana dla wariancji).
Predykcja wartości średniej i odchylenia standardowego dla konkretnego dnia przy zastosowaniu sieci MLP odbywa się w identyczny sposób jak prognoza obciążenia 24-godzinnego, z tym, że tym razem sieć ma jeden neuron wyjściowy, którego sygnał oznacza bądź wartość średnią bądź odchylenie standardowe (w zależności od prognozowanej zmiennej) prognozowane na następny dzień [46]. Wielkości wejściowe dla takich sieci są analogiczne jak dla obciążeń 24-godzinnych, z tym, że zmienne historyczne dotyczą wielkości prognozowanych (wartości średniej bądź odchylenia standardowego).
14.2.3 Prognozowanie z zastosowaniem sieci LSTM
Sieć LSTM wykorzystuje w predykcji informacje o powiązaniu sygnałów podlegających prognozie z wartościami z najbliższej przeszłości [47]. Na tej podstawie dokonywana jest prognoza. Biorąc pod uwagę ciągłość zmian szeregu czasowego reprezentującego wielkości obciążeń godzinnych sieć taka jest z natury działania dobrze przystosowana do zadania predykcji. Wielkości wejściowe sieci zawierają składowe 24-wymiarowego znanego wzorca obciążeń x(d-1) z dnia poprzedzającego predykcję. W przypadku znanych danych temperaturowych możliwe jest zwiększenie tego wymiaru poprzez dołączenie ich do wektora wejściowego.
Na etapie uczenia wektor wejściowy jest skojarzony z wektorem x(d) zadanym na wyjściu dla dnia podlegającego predykcji, tworząc parę uczącą \( (\mathbf{x}(d-1), \mathbf{x}(d)) \) używaną w procesie uczenia sieci. Hiperparametry sieci (liczba komórek LSTM, wybór algorytmu uczącego, liczba cykli uczących, próg gradientu kończący uczenie, wartości wstępne współczynnika uczenia, itp.) są ustalane przez użytkownika przy zastosowaniu wstępnego uczenia na danych spoza zbioru uczącego.
Po wytrenowaniu sieci i zamrożeniu wartości parametrów sieć poddaje się testowaniu na danych nie uczestniczących w uczeniu. W procesie tworzenia wektora wyjściowego \(\mathbf{y}(d)\) dla dnia \(d\) na wejście sieci podawany jest wektor znanych wartości z dnia poprzedniego \( \mathbf{x}(d-1) \) i na tej podstawie przy znanych parametrach sieci tworzona jest aktualna prognoza.
Analizując rozkłady obciążeń rocznych można łatwo zauważyć znaczące różnice w nietypowych okresach roku, na przykład w okresie Bożego Narodzenia i Nowego Roku. Dla takiego okresu należy stworzyć oddzielny model, generujący prognozę wyłącznie dla tego okresu. Problemem w tym przypadku jest bardzo mała populacja danych, które mogą być użyte w uczeniu (od tego zależy zdolność generalizacji modelu). Przykłady zastosowania sieci LSTM oraz zespołu zbudowanego z tych sieci można znaleźć w pracach [47].
4.3. Integracja zespołu predyktorów
Każdy z zastosowanych predyktorów neuronowych wykonuje identyczne zadanie predykcji szeregu liczbowego odpowiadającego przewidywanym obciążeniom 24 godzin dnia następnego przy wykorzystaniu tej samej bazy danych obciążeń z przeszłości. Wyjściem każdego z nich jest 24-elementowy wektor x przewidywanych obciążeń. Na ich podstawie integrator (rys. 14.3) ma za zadanie wytworzyć ostateczną postać tego 24-godzinnego wzorca obciążeń na dzień następny, najlepiej odzwierciedlającego przyszłe zapotrzebowanie na moc [47].
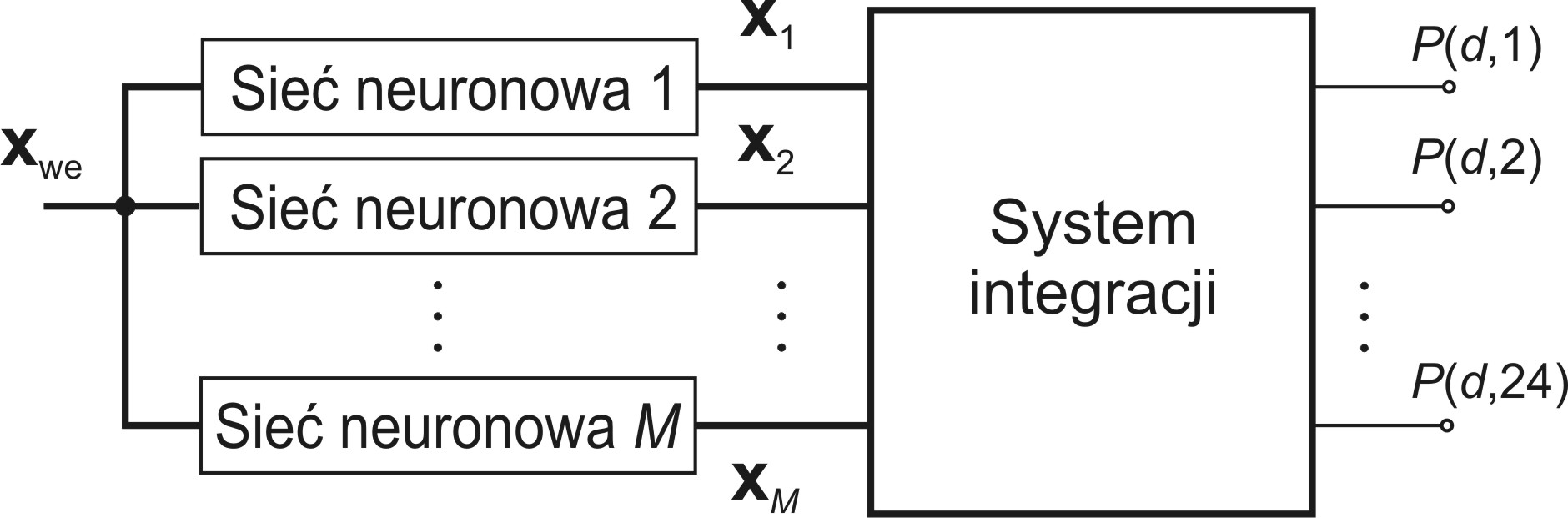
W pracy przedstawimy różne elementy przetwarzania danych w integracji, w tym uśrednianie ważone, ślepą separację sygnałów, zastosowanie dodatkowej sieci neuronowej jako integratora, czy integrację dynamiczną.
14.3.1 Integracja poprzez uśrednianie ważone
Integracja poprzez uśrednianie polega na przyjęciu prognozy końcowej jako średniej z wyników wszystkich predyktorów tworzących zespół. Zwykłe uśrednianie prowadzi do poprawy wyników, jeśli wszystkie modele indywidualne mają porównywaną dokładność, co jest w praktyce zjawiskiem rzadkim. W efekcie wynik zespołu może być gorszy niż najlepszy wynik indywidualny.
W przypadku nierównej jakości poszczególnych klasyfikatorów dużo lepsze wyniki uzyskuje się poprzez uśrednianie ważone dla każdej godziny podlegającej predykcji. W tym rozwiązaniu przy \(M\) predyktorach tworzących zespół określa się wielkość wyjściową zespołu \(y_i(\mathbf{x})\) dla \(i\)-tej godziny jako średnia ważoną wyników predyktorów indywidualnych dla tej godziny
| \( y_i\left(\mathbf{x}_{w e}\right)=\sum_{k=1}^M w_{k i} x_{k i} \) | (14.7) |
w którym \(w_{ki}\) jest wagą z jaką \(k\)-ty klasyfikator jest uwzględniany przy predykcji obciążenia dla \(i\)-tej godziny, natomiast \(x_{ki}\) jest wartością predykcji \(k\)-tego predyktora dla \(i\)-tej godziny (sygnał \(i\)-tego wyjścia predyktora).
Wartości wag \(w_{ki}\) mogą być wyznaczane w różny sposób, uwzględniający jakość poszczególnych członków zespołu. Do typowych rozwiązań należy
| \( w_{k i}=\frac{\eta_{k i}^m}{\sum_{j=1}^M \eta_{k i}^m} \) | (14.8) |
gdzie \( \eta_{k i}^m \) oznacza wskaźnik jakości (np. dokładność w sensie MAPE, MAE, RMSE) \(k\)-tego predyktora przy prognozie obciążenia dla \(i\)-tej godziny na danych uczących, \(m\) – wykładnik różnicujący wpływ poszczególnych jednostek zespołu na wynik działania zespołu (np. \(m = 1, 2, \ldots \)). Można zastosować również w integracji zespołu wzór wykorzystujący funkcję logarytmiczną [36]
| \( w_{k i}=\lg \left(\frac{\eta_{k i}}{1-\eta_{k i}}\right) \) | (14.9) |
14.3.2 Integracja przy zastosowaniu BSS
W integracji zespołu wykorzystującej metodę ślepej separacji sygnałów (BSS) [8] wszystkie 24-elementowe wektory \( \mathbf{x}_i \) prognozowane przez członków zespołu dla kolejnych \(q\) dni użytych w uczeniu (wytworzone przez poszczególne sieci neuronowe) tworzą dane uczące opisane macierzą \( \mathbf{X} \subset \mathbf{R}^{M \times p} \), w której \(p=24q\) natomiast \(M\) jest liczbą predyktorów. Sygnały opisane tą macierzą podlegają ślepej separacji mającej na celu określenie \(M\) składników niezależnych. Operację BSS opisuje zależność liniowa [48]
| \( \mathbf{Y}=\mathbf{W X} \) | (14.10) |
w której \(\mathbf{W}\) jest macierzą kwadratową o wymiarze \(M\), \( \mathbf{W} \subset \mathbf{R}^{M \times M} \). Każdy wiersz macierzy \(\mathbf{Y}\) reprezentuje składniki niezależne rozkładu macierzy \(\mathbf{X}\). Część z tych składników zawiera istotną informację dotyczącą rozkładu obciążeń, natomiast pozostała część może reprezentować nieregularności występujące w rozkładach dziennych obciążeń (na przykład wynik gwałtownych zaburzeń pogodowych, nieoczekiwanych wydarzeń wpływających na pobór mocy itp.), które są traktowane jako szum pomiarowy. Eliminacja składników szumowych „odkrywa” istotne elementy informacji i umożliwia odtworzenie wektora prognozowanych obciążeń pozbawionego wpływu tych nieregularności. Rekonstrukcja macierzy \(\mathbf{X}\) (tzw. deflacja) na podstawie jedynie istotnych składników odbywa się według wzoru
| \( \hat{\mathbf{X}}=\mathbf{W}^{-1} \hat{\mathbf{Y}} \) | (14.11) |
W równaniu tym \( \hat{\mathbf{X}} \) oznacza zrekonstruowaną macierz \( \mathbf{X} \) a \( \hat{\mathbf{Y}} \) - macierz \( \mathbf{Y} \) zmodyfikowaną w ten sposób, że wiersze odpowiadające składnikom szumowym zostały zastąpione przez zera. Problemem jest wybór tych składników „szumowych” (podlegających eliminacji). W praktyce przy wystąpieniu wątpliwości można stworzyć wiele rekonstrukcji sygnałów pomijając różne składniki traktowane jako szumowe, wybierając ostatecznie to rozwiązanie, które zapewnia najlepsze wyniki na danych uczących. W wyniku takiej rekonstrukcji odtworzone zostają wszystkie \(M\) kanały predykcji. Ostateczna integracja przeprowadzona na przykład metodą uśredniania ważonego dotyczyć będzie tych zrekonstruowanych prognoz. Ogólny schemat postępowania w tej metodzie zilustrowano na rys. 14.4. Klucze reprezentują włączenie bądź wyłączenie danego składnika niezależnego z procesu rekonstrukcji.
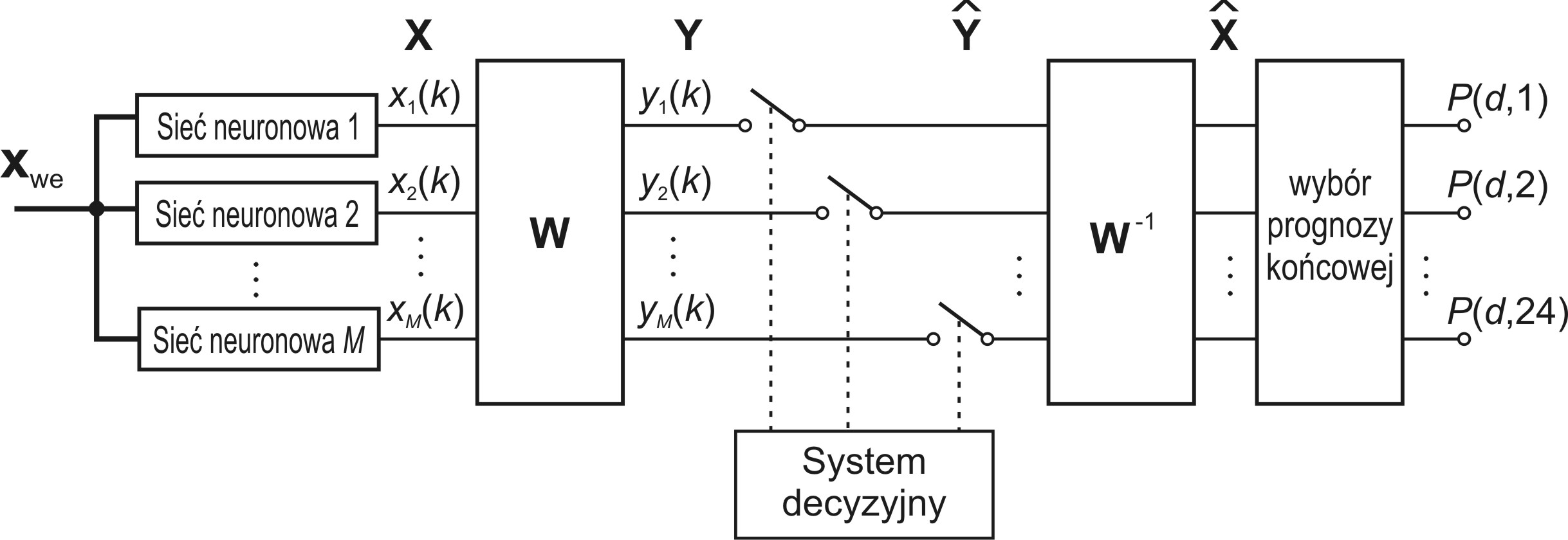
Problemem w tej metodzie pozostaje oczywiście rozpoznanie, które składniki niezależne należy traktować jako nieistotne. Niekiedy z obserwacji przebiegu czasowego składników niezależnych można z dużą dozą prawdopodobieństwa rozpoznać powtarzalne wzorce odpowiadające składnikom istotnym rozkładu. Najlepszym sposobem potwierdzenia tego jest określenie macierzy autokorelacji odpowiadającej każdemu z tych składników. Szum jest zwykle nieskorelowany (bądź słabo skorelowany), co przejawia się poziomem współczynnika korelacji bliskim zeru dla opóźnień różnych od zera.
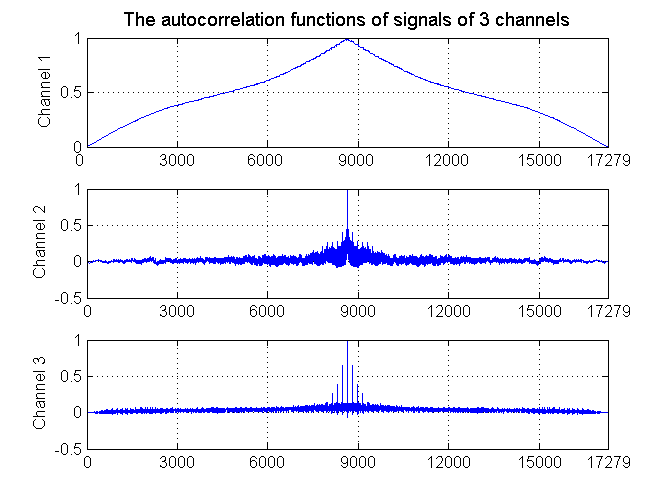
Sytuację taką przy trzech składnikach niezależnych dla kolejnych opóźnień odpowiadających 8600 godzinom (dla PSE) w roku przedstawiono na rys. 14.5. Składnik pierwszy reprezentuje najważniejszy sygnał użyteczny. Składnik drugi odpowiada typowemu szumowi natomiast w składniku trzecim poza szumem można również wyodrębnić również niewielką zawartość istotnej informacji.
14.3.3 Integracja przy użyciu sieci neuronowej
Innym sposobem integracji wyników wielu predyktorów jest zastosowanie jako integratora dodatkowej sieci neuronowej. W metodzie tej wektory 24-elementowe wygenerowane przez poszczególne predyktory łączone są w jeden wektor wejściowy \( \mathbf{z}=\left[\begin{array}{llll} \mathbf{x}_1^T, & \mathbf{x}_2^T, & \ldots, & \mathbf{x}_M^T \end{array}\right]^T \). Przy M predyktorach wymiar takiego wektora jest równy 24M. Pierwszym krokiem tej procedury musi być redukcja wymiaru takiego wektora. Jest ona dokonywana poprzez dekompozycję PCA [46], stanowiącą transformację liniową \(\mathbf{y}=\mathbf{Az}\), w której macierz \( \mathbf{A} \subset R^{K \times 24 M} \) jest tworzona na podstawie najważniejszych wektorów własnych macierzy autokowariancji odpowiadającej wektorom z. W wyniku tej dekompozycji wektor y zawiera jedynie wybraną przez użytkownika liczbę \(K\) składników głównych, które stanowić będą sygnały wejściowe dla sieci neuronowej stanowiącej integrator. Może nim być dowolna sieć neuronowa z nauczycielem (np. MLP lub SVM). Schemat integracji przy wykorzystaniu tej metody przedstawiony jest na rys. 14.6 [48].
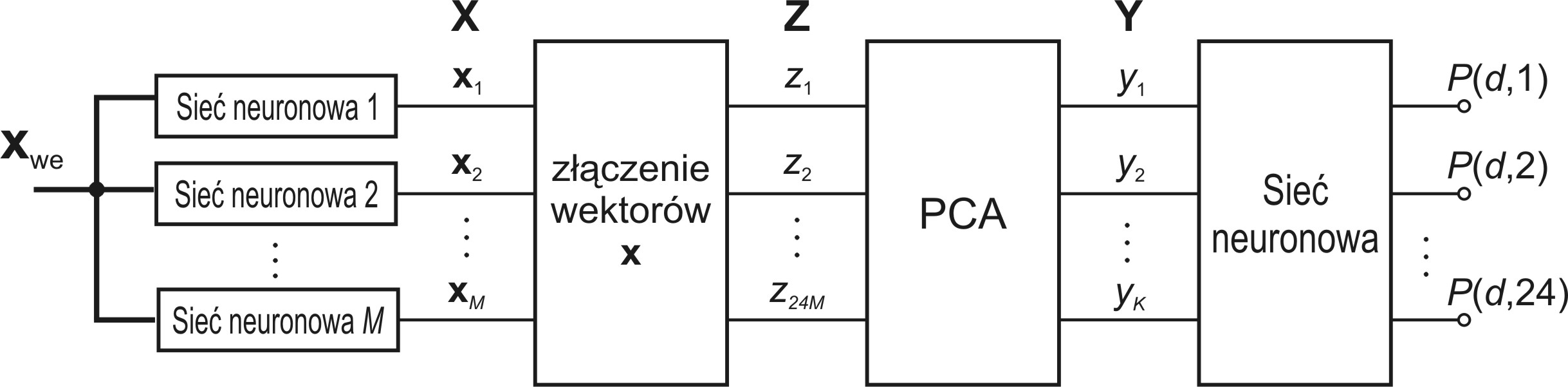
W wyniku badań stwierdzono, że zarówno sieć MLP jak i SVM dobrze sprawdzają się w roli integratora ze względu na efektywny algorytm uczący i dobrą skuteczność tego typu sieci, znacznie przewyższającą pozostałe rozwiązania.
14.3.4 Integracja dynamiczna zespołu
Integracja dynamiczna zespołu zakłada zasadniczo inną filozofię działania [47]. W zespole składającym się z \(M\) predyktorów wybiera się ten, który najlepiej sprawdził się na uczących danych wejściowych \(\mathbf{x}_l\) najbliższych danym testującym \(\mathbf{x}_t\) i on generuje ostateczną prognozę zespołu. Bliskość wektorów określa się przy pomocy wybranej przez użytkownika metryki, na przykład L1, czy L2, obliczając normę różnicy wektorów, najczęściej L1
| \( d\left(\mathbf{x}_t, \mathbf{x}_l\right)=\left\|\mathbf{x}_t-\mathbf{x}_l\right\|_1 \) | (14.12) |
Predyktor który zapewniał najmniejszą wartość błędu prognozy w procesie uczenia dla tego wektora \(\mathbf{x}_l\) jest wybierany z grona \(M\) indywidualnych rozwiązań do wykonania ostatecznej prognozy przy wektorze testowym \(\mathbf{x}_t\). W efekcie takiego rozwiązania dla każdego wektora testowego \(\mathbf{x}_t\) wybór ostatecznego predyktora może być różny. W przypadku wyników uczenia dla wektora \(\mathbf{x}_l\) które są bliskie sobie dla kilku rodzajów predyktorów można zastosować większą liczbę predyktorów i połączyć ich wyniki na wektorze \(\mathbf{x}_t\) metodą uśredniania.
4.4. Przykładowe wyniki eksperymentów numerycznych
W tym punkcie przedstawimy wybrane wyniki eksperymentów przeprowadzone dla danych pochodzących z bazy Polskich Sieci Elektroenergetycznych z trzech lat (ponad 26280 godzin). Pierwsze dwa lata zostały użyte w uczeniu wszystkich sieci, natomiast dane z roku trzeciego posłużyły jedynie testowaniu poszczególnych rozwiązań. W rozwiązaniu zastosowano cztery rodzaje rozwiązań: MLP, Elmana, SVM do regresji oraz sieć Kohonena.
W pierwszym etapie badań konieczne jest zaprojektowanie oraz wytrenowanie indywidualnych predyktorów neuronowych. W przypadku sieci sigmoidalnej MLP w wyniku wielu eksperymentów za optymalną uznano strukturę 23-20-19-24 wytrenowaną przy użyciu algorytmu gradientów sprzężonych. Sygnałami wejściowymi dla tej sieci były znormalizowane wartości obciążeń z ostatnich 4 godzin dnia aktualnego oraz 5 godzin (godzina aktualna plus 4 godziny wstecz) z 3 dni poprzedzających prognozę (w sumie 19 składników). Typ dnia zakodowano w postaci 2 bitów (11 – dni robocze, 10 – soboty, 01 – piątki, 00 – święta) podobnie jak porę roku (00 – wiosna, 01 - lato, 10 – jesień, 11 – zima). Każdy neuron wyjściowy reprezentował prognozowane obciążenie o określonej godzinie doby. Ze względu na rozbudowaną strukturę sieci w uczeniu zastosowano metodę gradientów sprzężonych.
Sieć Elmana miała identyczną warstwę wejściową i wyjściową jak MLP. Liczba neuronów ukrytych została ustalona na 8, stąd struktura tej sieci może być zapisana w postaci 23-8-24. W uczeniu tej sieci wykorzystano algorytm Levenberga-Marquardta.
Sygnały wejściowe dla sieci SVM były identyczne jak dla sieci MLP (23 węzły wejściowe). Ze względu na specyfikę sieci SVM należało zastosować równolegle 24 sieci, każda wytrenowana do predykcji obciążenia na określoną godzinę doby. W uczeniu zastosowano zmodyfikowany algorytm programowania sekwencyjnego [51], zaimplementowany na platformie Matlaba [43]. Liczba funkcji jądra (odpowiednik liczby neuronów ukrytych) była każdorazowo dobierana automatycznie przez algorytm uczący przy poziomie wartości tolerancji ε=0.01.
W przypadku zastosowania sieci Kohonena zastosowano 100 neuronów trenowanych za pośrednictwem algorytmu gazu neuronowego na zbiorze uczącym utworzonym z profili zgodnie ze wzorem (14.2). Po wytrenowaniu i zamrożeniu wag nastąpiła analiza sieci, przypisująca zwycięzcę każdemu profilowi wektorowemu dnia. Wyniki testowania były zapisywane w bazie danych. Na etapie rzeczywistego prognozowania wektora profilowego obciążenia na dzień następny odczytuje się z tej bazy zwycięzców odpowiadających temu typowi dnia (np. czwartki miesiąca lipca) i na tej podstawie estymuje się wektor profilowy według wzoru (14.4). Wartości średnie obciążenia prognozowanego dnia i odchylenia standardowe otrzymano z sieci MLP wytrenowanej do tego celu. W przypadku predykcji wartości średnich zastosowano sieć MLP o strukturze 10-6-1 a w przypadku odchylenia standardowego 14-8-1.
Wyniki prognozy dla poszczególnych godzin były porównywane z wartościami rzeczywistymi dotyczącymi danych historycznych. Przy oznaczeniu przez \( P(h) \) i \( \hat{P}(h) \) obciążenia odpowiednio rzeczywistego i estymowanego w godzinie h zdefiniowano następujące rodzaje błędów [65].
-
Średni względny błąd procentowy (MAPE)
| \( MAPE=\frac{1}{n} \sum_{h=1}^n \frac{|P(h)-\hat{P}(h)|}{|P(h)|} \cdot 100 \% \) | (14.13) |
-
Błąd średni predykcji (MSE)
| \( MSE=\frac{1}{n} \sum_{h=1}^n[P(h)-\hat{P}(h)]^2 \) | (14.14) |
-
Znormalizowany błąd średni predykcji (NMSE)
| \( NMSE=\frac{MSE}{[mean(P)]^2} \) | (14.15) |
gdzie \( mean(P) \) jest wartością średnią rzeczywistych obciążeń godzinnych podlegających predykcji.
-
Maksymalny błąd średni procentowy (MAXPE)
| \( MAXPE=\max \left\{\frac{|P(h)-\hat{P}(h)|}{P(h)} \cdot 100 \%\right\} \) | (14.16) |
Powyższe błędy są określane zarówno dla danych uczących jak I weryfikujących (testujących) nie uczestniczących w procesie uczenia. W dalszej części pracy ograniczymy się wyłącznie do błędów testowania na danych nie uczestniczących w uczeniu. Tabela 14.5 przedstawia wartości zdefiniowanych wyżej rodzajów błędów prognozy dla 365 dni roku nie uczestniczącego w uczeniu dla czterech rodzajów sieci zastosowanych jako predyktory (MP – sieć perceptronowa, SVM – sieć SVM, Elman – sieć Elmana, SO – sieć Kohonena).
Tabela 14.5. Błędy predykcji obciążeń w PSE dla danych z jednego roku nie uczestniczących w uczeniu dla 4 indywidualnych predyktorów neuronowych
|
Zastosowany predyktor |
MAPE [%] |
MAXPE |
MSE |
NMSE |
|
MLP |
2.07 |
16.92 |
1.75e5 |
6.82e-4 |
|
SVM |
2.24 |
28.32 |
2.94e5 |
1.17e-3 |
|
Elman |
2.26 |
24.95 |
3.14e5 |
1.22e-3 |
|
SO |
2.37 |
18.10 |
2.40e5 |
9.35e-4 |
Wyniki wskazują na sieć MLP jako najlepszy predyktor. Dotyczy to wszystkich kategorii błędów. Następnie wyniki indywidualnych predyktorów zostały zintegrowane przy użyciu 2 różnych metod integracji: BSS oraz sieci neuronowej. Wyniki integracji w postaci zestawienia poszczególnych rodzajów błędów są przedstawione w tabeli 14.6. W przypadku integracji neuronowej zbadano zastosowanie dwu rodzajów sieci: SVM oraz MLP. W przypadku zastosowania BSS do odtworzenia prognozy końcowej zastosowano jedynie 2 składniki niezależne wyselekcjonowane metoda prób i błędów z 4 występujących w rozkładzie.
Tabela 14.6. Błędy predykcji obciążeń w PSE dla zespołu predyktorów neuronowych dla danych z roku nie uczestniczących w uczeniu
|
. Metoda integracji |
MAPE |
MAXPE |
MSE |
NMSE |
|
BSS |
1.71 |
16.21 |
1.22e+5 |
0.47e-3 |
|
SVM |
1.35 |
10.74 |
9.50e+4 |
3.70e-4 |
|
MLP |
1.48 |
14.29 |
1.04e+5 |
4.07e-4 |
Uzyskane wyniki wskazują na bardzo wysoką sprawność zespołu predyktorów w stosunku do pojedynczej sieci. Porównując poszczególne rodzaje błędów uzyskane przy użyciu najlepszej metody integracji (integracja neuronowa pry użyciu SVM) w stosunku do najlepszej sieci indywidualnej (MLP) uzyskano redukcję błędu MAPE o 28%, MSE o 46% i MAXPE o 36%. Na rys. 14.7 przedstawiono wykresy przewidywanych i rzeczywistych obciążeń godzinnych dla 1100 godzin w roku na danych nie uczestniczących w uczeniu (linia ciągła – dane rzeczywiste, linia przerywana – wielkości prognozowane). Widać bardzo dobra zgodność prognozy z wartościami rzeczywistymi.
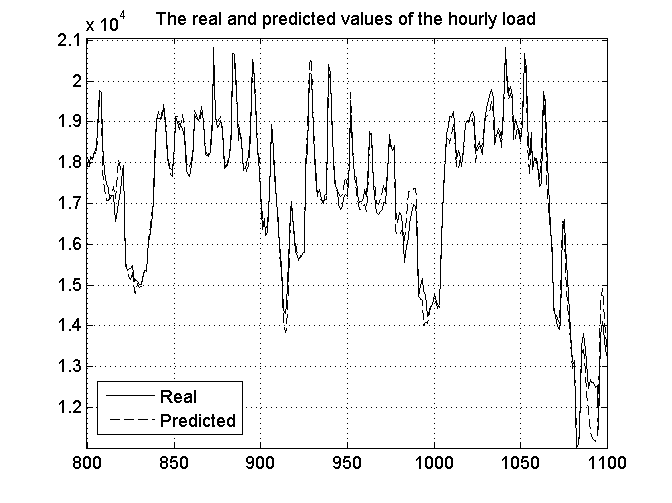
Rys. 14.8 przedstawia rozkład błędów prognozy dla 4300 godzin poddanych prognozie (dane te nie uczestniczyły w uczeniu sieci). Dotyczą one historii obciążeń PSE z dwu różnych lat (2006 i 2007). Charakterystyczny jest zbliżony do siebie poziom błędów prognozy dla poszczególnych godzin. Tylko w niewielkiej ilości godzin błąd ten odstaje od wartości średnich.
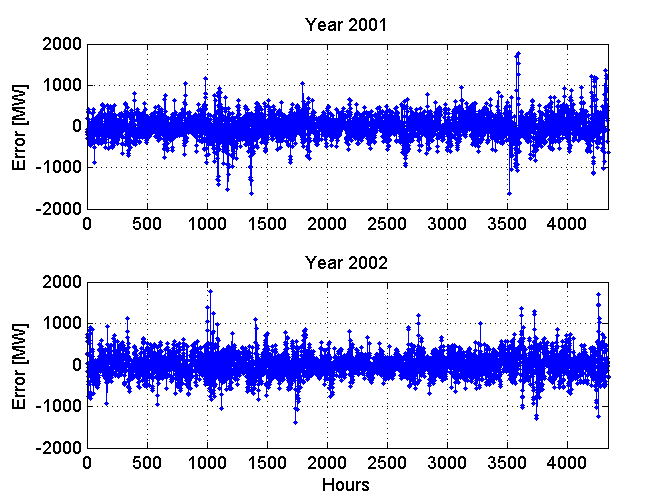
Wyniki badań symulacyjnych na danych rzeczywistych z PSE pokazały, że obie metody integracji (BSS lub sieć neuronowa) dobrze sprawują się w praktyce, choć nieco lepsze wyniki uzyskano przy użyciu nieliniowego integratora neuronowego w postaci sieci SVM. Przy zastosowaniu tej techniki uzyskano redukcję błędu MAPE o prawie 30%, błędu MSE o prawie 50% i maksymalnego błędu procentowego MAXPE o ponad 35%. Nie oznacza to jednak wcale, że przy innych zadaniach prognostycznych integracja neuronowa zawsze będzie lepsza niż przy zastosowaniu BSS.
4.5. Zadania i problemy
-
Określić rozkład statystyczny danych obciążeń 24-godzinnych w PSE (plik PSE.mat) w postaci wartości średnich i odchyleń standardowych dziennych oraz tygodniowych. Narysować te wielkości używając funkcji bar Matlaba.
-
Określić średnie wartości obciążeń oraz ich odchylenia standardowe odpowiadające 12 miesiącom roku oraz poszczególnym 4 porom roku. Narysować te wielkości używając funkcji bar Matlaba i porównać ich rozkład.
-
Wykorzystując program MLP dokonać predykcji wartości średnich obciążeń dziennych. Jako zmienne wejściowe dla sieci przyjąć ich wartości z dni poprzednich oraz typ dnia (roboczy, nieroboczy) i porę roku. Wyniki przedstawić w formie rozkładu błędów dziennych predykcji oraz błędu skumulowanego MAPE.
-
Wykorzystując program Kohon wygenerować mapę obciążeń 24-godzinnych dla jednego wybranego roku z bazy danych PSE.mat. Przyjąć podział danych na 4 pory roku.
-
Wykorzystując program Kohon wygenerować mapę obciążeń 24-godzinnych dla jednego wybranego roku z bazy danych PSE.mat. Przyjąć podział danych na 2 rodzaje dni: robocze (R) i świąteczne (S).
-
Wykorzystując programy MLP, SVM i RBF dokonać predykcji wartości średnich obciążeń dziennych. Jako zmienne wejściowe dla sieci przyjąć ich wartości z dni poprzednich oraz typ dnia (roboczy, nieroboczy) i porę roku. Następnie dokonać integracji zespołu tych 3 predyktorów wykorzystując jako integrator sieć MLP orz SVM. Wyniki przedstawić w formie rozkładu błędów dziennych predykcji oraz błędu skumulowanego MAPE dla wszystkich pojedynczych predyktorów oraz zespołu.
4.6. Słownik
Słownik opanowanych pojęć
Wykład 14
PSE – Polski System Elektroenergetyczny
Mały system elektroenergetyczny – ograniczony pod względem obszaru rejon działania PSE na terenie kraju.
Model predykcji – system sztucznej inteligencji oparty na rozwiązaniach neuronowych lub innych używany do przewidywania wartości szeregów czasowych na podstawie znanych wielkości z przeszłości.
Profil obciążeń – wycentrowany wektor obciążeń 24-godzinnych z uwzględnieniem wartości średniej i odchylenia standardowego.
Sieci neuronowe predykcyjne – rodzaje rozwiązań predykcji opartych na sieciach neuronowych (MLP, RBF, SVM, LSTM).
Zespół predyktorów – zbiór równolegle działających rozwiązań predykcyjnych zintegrowanych w jeden system prognozy.
Integracja zespołu predyktorów – metoda wypracowania wspólnego wyniku predykcji na podstawie wyników indywidualnych członków (najczęściej fuzja wyników poprzez uśrednianie zwykłe lub ważone).
Integracja dynamiczna zespołu – metoda wybierająca do końcowej predykcji lub klasyfikacji tego z M predyktorów który najlepiej sprawdził się na uczących danych wejściowych xl najbliższych danym testującym xt. Wybrany członek zespołu generuje ostateczną prognozę zespołu.
5. Literatura
1. Bengio Y., LeCun Y., Hinton G., Deep Learning, Nature, 2015, vol. 521, pp. 436–444.
2. Brownlee J., Deep Learning for Natural Language Processing. Develop Deep Learning Models for your Natural Language Problems, Ebook, 2018.
3. Breiman L., Random forests, Machine Learning, 2001, vol. 45, No 11, pp. 5–32.
4. Banerjee S., Linear algebra and matrix analysis for statistics, 2012, London.
5. Brudzewski K., Osowski S., Markiewicz T., Ulaczyk J., Classification of gasoline with supplement of bio-products by means of an electronic nose and SVM neural network, Sensors and Actuators - Chemical, 2006, vol. 113, No 1, pp. 135-141.
6. Chen S., Cowan C.F., Grant P.M., Orthogonal least squares learning algorithm for radial basis function networks, IEEE Trans. Neural Networks, 1991, vol. 2, pp. 302–309.
7. Christensen R., Johnson W. O., Branscum A. J., Hanson T. E., Bayesian ideas and data analysis: an introduction for scientists and statisticians, 2010, Chapman & Hall/CRC Science
8. Cichocki A., Amari S. I., Adaptive blind signal and image processing, 2003, Wiley, New York.
9. Crammer K. , Singer Y., On the learnability and design of output codes for multiclass problems. Computational Learning Theory, 2000, pp. 35-46.
10. Duda, R.O., Hart, P.E., Stork, P., Pattern classification and scene analysis, 2003, Wiley, New York.
11. Fogel, L.J., Intelligence through simulated evolution : forty years of evolutionary programming, 1999, Wiley, New York.
12. Fukushima K.: Neocognitron - a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 1980, vol.. 36, No 4, pp. 193–202, doi:10.1007/bf00344251.
13. Genc H., Cataltepe Z., Pearson T., A new PCA/ICA based feature selection method, IEEE 15th In Signal Processing and Communications Applications, 2007, pp. 1-4.
14. Gill P., Murray W., Wright M., Practical optimization, 1981, Academic Press, London.
15. Goldberg D., Algorytmy genetyczne i ich zastosowania, 2003, WNT Warszawa.
16. Golub G., Van Loan C., Matrix computations, 1996, John Hopkins University Press, Baltimore.
17. Gao H., Liu Z., Van der Maaten L., Weinberger K., Densely connected convolutional networks, CVPR, vol. 1, no. 2, p. 3. 2017.
18. Goodfellow I., Bengio Y., Courville A.: Deep learning 2016, MIT Press, Massachusetts (tłumaczenie polskie: Deep Learning. Współczesne systemy uczące się, Helion, Gliwice, 2018).
19. Goodfellow I., Pouget-Abadie J., Mirza M, Xu M., Warde-Farley B., Ozair D., Courville A. Bengio Y., Generative Adversarial Nets (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680.
20. Greff K., Srivastava R. K., Koutník J., Steunebrink B. R., Schmidhuber J., LSTM: A search space odyssey, IEEE Transactions on Neural Networks and Learning Systems, vol. 28, No 10, pp. 2222-2232, 2017.
21. Gunn S., Support vector machines for classification and regression, ISIS Technical report, 1998, University of Southampton.
22. Guyon I., Elisseeff A., An introduction to variable and feature selection, J. Mach. Learn. Res., 2003, vol. 3, pp. 1157-1182.
23. Guyon, I., Weston, J., Barnhill, S., Vapnik, V., Gene selection for cancer classification using Support Vector Machines, Machine Learning, 2002, vol. 46, pp. 389-422.
24. Haykin S., Neural networks, a comprehensive foundation, Macmillan College Publishing Company, 2000, New York.
25. He K., Zhang X, Ren S, Sun J., Deep Residual Learning for Image Recognition, 2015, http://arxiv.org/abs/1512.03385.
26. Hinton G. E., Salakhutdinov R. R., Reducing the dimensionality of data with neural networks, Science, 313:504-507, 2006.
27. Howard A., Zhu M., Chen B., Kalenichenko D., MobileNets: Efficient convolutional neural networks for mobile vision applications, arXiv: 1704.04861v1 [cs.CV], 2017.
28. Hsu, C.W., Lin, C.J., A comparison methods for multi class support vector machines, IEEE Trans. Neural Networks, 2002, vol. 13, pp. 415-425.
29. Huang G., Liu Z., van der Maaten L., Weinberger K., Densely connected convolutional networks, arXiv: 1606.06993v5 [cs.CV] 2018.
30. Iandola F, Han S., Moskevicz M., Ashraf K., Dally W., Keutzer K, Squeezenet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size, Conference ICLR, 20017. pp. 1-13.
31. Joachims T., Making large scale SVM learning practical, (in ”Advances in kernel methods - support vector learning”, B. Scholkopf, C. Burges, A. Smola eds). MIT Press, Cambridge, 1998, pp. 41-56.
32. Kecman V., Support vector machines, neural networks and fuzzy logic models, 2001, Cambridge, MA: MIT Press.
33. Kingma P, Welling M., An introduction to variational autoencoders, Foundations and Trends in Machine Learning, 12:307-392, 2019.
34. Krizhevsky A., Sutskever I., Hinton G., Image net classification with deep convolutional neural networks, Advances in Neural Information Processing Systems, vol. 25, pp. 1-9, 2012.
35. Kruk M., Świderski B., Osowski S., Kurek J., Słowińska M., Walecka I., Melanoma recognition using extended set of descriptors and classifiers, Eurasip Journal on Image and Video Processing, 2015, vol. 43, pp. 1-10, DOI 10.1186/s13640-015-0099-9
36. Kuncheva L., Combining pattern classifiers: methods and algorithms, 2015, Wiley, New York.
37. LeCun Y., Bengio Y., Convolutional networks for images, speech, and time-series. 1995, in Arbib M. A. (editor), The Handbook of Brain Theory and Neural Networks. MIT Press, Massachusetts.
38. Lecture CS231n: 2017, Stanford Vision Lab, Stanford University.
39. Lee K.C., Han I., Kwon Y., Hybrid Neural Network models for bankruptcy prediction, Decision Support Systems, 18 (1996) 63-72.
40. Leś T., Osowski S., Kruk M., Automatic recognition of industrial tools using artificial intelligence approach, Expert Systems with Applications, 2013, vol. 40, pp. 4777-4784.
41. Lin C. J., Chang, C. C., LIBSVM: a library for support vector machines. http://www. csie. ntu. edu. tw/cjlin/libsvm
42. Markiewicz T., Sieci neuronowe SVM w zastosowaniu do klasyfikacji obrazów komórek szpiku kostnego, rozprawa doktorska Politechniki Warszawskiej, 2006.
43. Matlab user manual MathWorks, 2021, Natick, USA.
44. Michalewicz Z., Algorytmy genetyczne + struktury danych = programy ewolucyjne, WNT, Warszawa 1996.
45. Osowski S., Cichocki A., Siwek K., Matlab w zastosowaniu do obliczeń obwodowych i przetwarzania sygnałów, 2006, Oficyna Wydawnicza PW.
46. Osowski S., Sieci neuronowe do przetwarzania informacji, 2020, Oficyna Wydawnicza PW.
47. Osowski S., Szmurło R., Siwek K., Ciechulski T., Neural approaches to short-time load forecasting in power systems – a comparative study, Energies, 2022, 15, pp. 3265.
48. Osowski S., Siwek K., R. Szupiluk, Ensemble neural network approach for accurate load forecasting in the power system, Applied Mathematics and Computer Science, 2009, vol.19, No.2, pp. 303-315.
49. Osowski S., Metody i narzędzia eksploracji danych , Wydawnictwo BTC, Warszawa, 2013
50. Patterson J., Gibson A., Deep Learning: A Practitioner's Approach (tłumaczenie polskie : Deep learning. Praktyczne wprowadzenie), Helion, Gliwice, 2018.
51. Platt L., Fast training of SVM using sequential optimization (in Scholkopf, B., Burges, B., Smola, A., Eds. Advances in kernel methods – support vector learning. Cambridge: MIT Press), 1998, 185-208.
52. Redmon J., Divval S., Girshick R., Farhafi A., You Only Look Once: unified. Real time object detection, axXiv: 1506.02640v5 [cs.CV], 2016
53. Ren S., He K., Girshick R., Sun J., Faster R-CNN: toward real time object detection with region proposal networks, IEEE trans. PAMI, vol. 39, pp. 1137-1149, 2017
54. Riedmiller M., Braun H.: RPROP – a fast adaptive learning algorithm. Technical Report, University Karlsruhe, Karlsruhe 1992.
55. Ridgeway G., Generalized Boosted Models: A guide to the gbm package. 2007
56. Ronneberger O., Fischer P., Brox T.: U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015, arXiv:1505.04597.
57. Sammon J. W., A nonlinear mapping for data structure analysis, IEEE Trans. on Computers, 1969, vol. 18, pp. 401-409.
58. Schmidhuber J., Deep learning in neural networks: An overview, Neural Networks, vol. 61, pp. 85-117, 2015.
59. Schölkopf B., Smola A., Learning with kernels, 2002, MIT Press, Cambridge MA.
60. Schurmann J., Pattern classification, a unified view of statistical and neural approaches, 1996, Wiley, New York.
61. Sandler, M., Howard, A., Zhu, M., Zhmoginov, A. and Chen, L.C. "MobileNetV2: Inverted Residuals and Linear Bottlenecks." In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 4510-4520). IEEE.
62. Swiderski B., Kurek J., Osowski S., Multistage classification by using logistic regression and neural networks for assessment of financial condition of company, Decision Support Systems, 2012, vol. 52, No 2, pp. 539-547
63. Szegedy C, Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., Going deeper with convolutions, arXiv: 1409.4842v1, 2014.
64. Szegedy C, Ioffe S., Vanhoucke V. Inveption-v4, Inception-ResNet and the impact of residual connections on learning, arXiv:1602.07261v2, 2016.
65. Tan P.N., Steinbach M., Kumar V., Introduction to data mining, 2006, Pearson Education Inc., Boston.
66. Tan M. Le Q., EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, arXiv:1905.11946 [cs.LG], 2020
67. Van der Maaten L., Hinton G., Visualising data using t-SNE, Journal of Machine Learning Research, 2008, vol. 9, pp. 2579-2602.
68. Vapnik V., Statistical learning theory, 1998, Wiley, New York.
69. Wagner T., Texture analysis (w Jahne, B., Haussecker, H., Geisser, P., Eds. Handbook of computer vision and application. Boston: Academic Press), 1999, ss. 275-309.
70. Zeiler M. D., Fergus R.: Visualizing and Understanding Convolutional Networks. 2013, pp. 1-11, https://arxiv.org/abs/1311.2901.
71. Zhang X., Zhou X., Lin M., Sun J., ShuffleNet: an extremely efficient convolutional neural network for mobile devices, arXiv: 1707.01083v2 [cs.CV], 2017.
72. Zheng G., Liu S., Zeming F. W., Sun L. J., YOLOX: Exceeding YOLO Series in 2021, arXiv:2107.08430v2 [cs.CV]
73. https://www.analyticsvidhya.com/blog/2021/09/adaboost-algorithm-a-complete-guide-for-beginners/
74. http://www.bsp.brain.riken.jp/ICALAB, ICALAB Toolboxes. A. Cichocki, S. Amari, K. Siwek, T. Tanaka et al.
75. https://github.com/BVLC/caffe/tree/master/models/bvlc_googlenet.
76. https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
77. https://www.jeremyjordan.me/variational-autoencoders/
78. Osowski S., Szmurło R., Matematyczne modele uczenia maszynowego w językach matlab i Python, OWPW, 2023, Warszawa.