Podręcznik

Strona:	SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych
Kurs:	2. Programowanie dynamiczne
Książka:	Podręcznik

Wydrukowane przez użytkownika:	Gość
Data:	sobota, 12 lipca 2025, 18:44

Opis

Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.

Wykłady W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu

Spis treści

1. Programowanie dynamiczne
- 1.1. Formalizacja elementów PD
- 1.2. Przykładowe zadanie

1. Programowanie dynamiczne

Programowanie dynamiczne (PD) to metoda wyznaczania rozwiązania problemów optymalizacji dyskretnej dla zadań o specjalnej, dynamicznej, wieloetapowej/sekwencyjnej strukturze.

Bazą PD jest sformułowanie problemu w postaci równania Bellmana. Równanie to jest nazywane też funkcją optymalizacji Bellmana/ programowania dynamicznego. Równanie Bellmana rozwiązuje problem optymalizacji, jeżeli jest on dekomponowalny. Wtedy, rekurencyjnie przeprowadza się wielokrotne rozwiązywanie (dowolną metodą) równania Bellmana.

Nie ma ogólnej metody, procedury wyznaczenia równania Bellmana. Jednak sformułowanie zadania jako programowania dynamicznego jest dość naturalne, gdy wymagane jest wyznaczenie sekwencji decyzji.

Rozważmy prosty przykład, który posłuży nam do wprowadzenia najważniejszych koncepcji podejścia opartego na programowaniu dynamicznym do rozwiązywania problemów wieloetapowych. Poniższy rysunek przedstawia plan ulic łączących dwa punkty, A i L, powiedzmy parkingi w domu i w centrum miasta. Krawędzie odpowiadają ulicom, a węzły skrzyżowaniom.
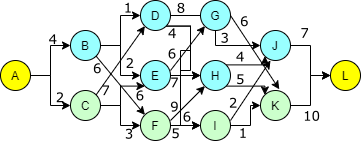
węzły A-L połączone krawędziami z opisanymi parametrami czasów

węzły A-L połączone krawędziami z opisanymi parametrami czasów

Znany jest czas przejazdu konkretną ulicą, zapisany na rysunku. Do tego znany jest też czas oczekiwania na każdym ze skrzyżowań: B - 5, C - 8, D - 3, E - 3, F - 6, G - 4, H - 2, I - 6, J - 5, K - 3. Naszym zadaniem jest wyznaczenie najkrótszej drogi przejazdu z A do L.
Naiwne podejście mogłoby polegać na wygenerowaniu wszystkich możliwych ścieżek i wybraniu najkrótszej z nich. PD pozwala na zmniejszenie liczby obliczeń, budując optymalne rozwiązanie w sposób systematyczny, sekwencyjnie dokładając kolejne elementy rozwiązania.
Zauważmy, że przejazd z A do L wymaga pokonania 5 ulic, dla każdego układu parametrów czasowych. Można więc powiedzieć, że podróż składa się z 5 etapów, gdzie ostatni etap to osiągnięcie zamierzonego celu. W każdym z wcześniejszych etapów należy podjąć decyzję o wyborze konkretnej ulicy, która doprowadzi nas do kolejnego etapu. Decyzja ta nie zależy od dotychczasowej, przebytej drogi.
Załóżmy, że analizujemy sieć przejazdu wstecz, czyli od ostatniego etapu. Znajdując się w czwartym etapie możemy być na skrzyżowaniu J lub K, przy czym nie mamy wpływu na sposób dostania się do L, bo prowadzi tam tylko jedna ulica. Wiemy natomiast ile czasu zajmie nam dotarcie do L jeżeli znajdziemy się na jednym z tych skrzyżowań: 12 minut jeśli droga biegnie przez J, albo 13 minut jeśli droga biegnie przez K.
Podobną analizę przeprowadzamy teraz w trzecim etapie, dla skrzyżowań G, H, I. Tym razem, znajdując się na konkretnym skrzyżowaniu musimy podjąć decyzję, którą drogę wybrać, aby przejść do następnego etapu, czyli znaleźć się na skrzyżowaniu J lub K. Przy wyborze kierujemy się nie tylko czasem potrzebnym na pokonanie konkretnej ulicy, ale też czasem potrzebnym na dotarcie do celu ze skrzyżowania do którego ta ulica prowadzi. Czyli np. dla skrzyżowania G jasne jest, że lepiej jest wybrać drogę prowadzącą do J, co da w sumie 15 minut do osiągnięcia celu, zamiast drogi do K, co wymagałoby 19 minut na osiągnięcie celu. Gdy doliczymy czas oczekiwania na skrzyżowaniu G to możemy stwierdzić, że droga biegnąca przez to skrzyżowanie będzie wymagać 19( = 15 + 4) minut na dojazd do L. Analogicznie, dla skrzyżowań H oraz I otrzymujemy optymalny czas dojazdu do celu równy: 18 dla H, oraz 20 dla I.
Powtarzamy obliczenia dla kolejnych etapów, aż znajdziemy się w punkcie wyjścia A, czyli niejako etapie zerowym. Można sprawdzić, że najkrótsza trasa wynosi 37 minut.

Przedstawiona w przykładzie procedura przebiegała sekwencyjnie, w każdym etapie obliczyliśmy optymalne częściowe rozwiązanie, wynikające ze znalezienia się w konkretnym stanie, czyli na konkretnym skrzyżowaniu. Koncepcje te sformalizujemy w następnym podrozdziale.

1.1. Formalizacja elementów PD

Programowanie dynamiczne wymaga wyróżnienia etapów (ang. stages), w których są podejmowane decyzje (akcje, ang. actions) specyficzne dla konkretnych stanów (ang. states) procesu decyzyjnego. Przejścia (ang. transitions) z jednego stanu do drugiego, wiążą się z kosztem i są efektem podjętej decyzji, lub losowego zdarzenia (deterministyczne vs. stochastyczne PD).

Własność Markowa. Stan (czyli wartość) zmiennych decyzyjnych

$x$ w danym etapie

$t$ zależy tylko od stanu oraz akcji

$u$ z poprzedniego etapu

$t-1$ , zgodnie z funkcją przejścia

$g(\cdot)$ :

$x_{t+1} = g(x_t, u_t),\;\; \forall t = 1\ldots T-1$

Proces decyzyjny spełniający tę własność jest procesem Markowa, który można przedstawić tak jak na poniższym schemacie.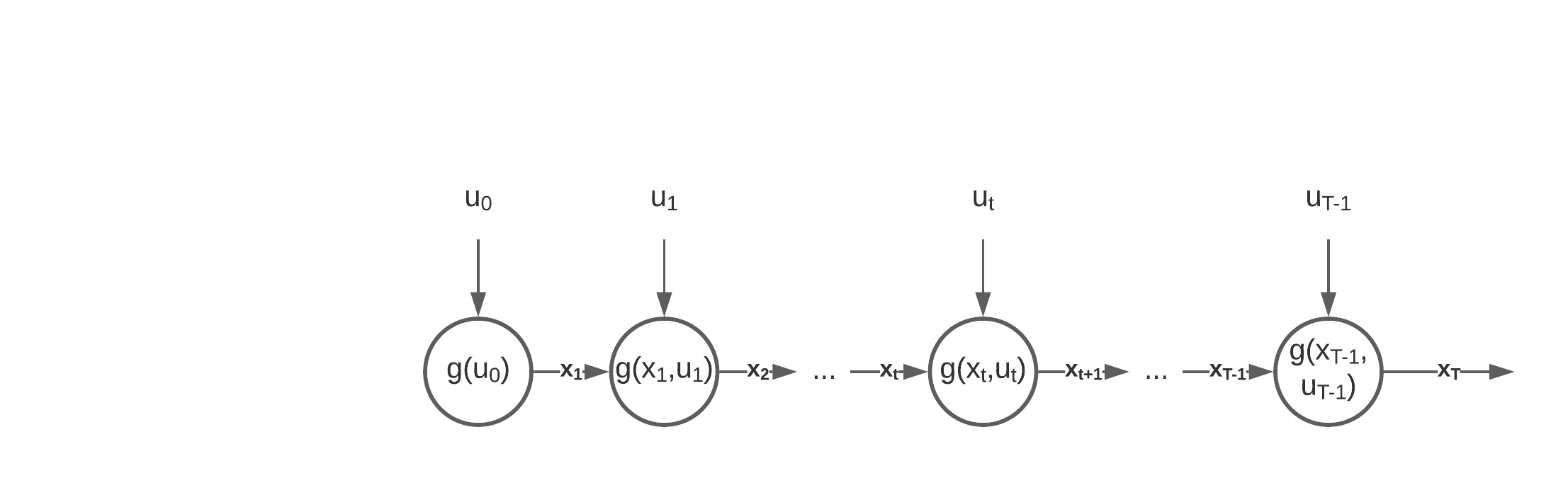 schemat procesu markowa

Zauważmy, że w końcowym etapie T nie podejmujemy decyzji.

Własność Markowa musi być spełniona aby można było zastosować PD. Drugim warunkiem jest możliwość dekompozycji funkcji celu na stany i etapy.

Separowalność funkcji celu. Funkcja celu jest separowalna jeśli można ją zdekomponować na mniejsze funkcje, operujące na zmiennych i parametrach odnoszących się do konkretnych etapów:

$f(u_0, x_1, u_1, x_2\ldots, u_{T-1}, x_T) = H(f_1(x_1,u_0), f_{t+1}(x_{t+1},u_t),\ldots,f_T(x_T,u_{T-1}))$
Najczesciej oznacza to addytywnosc komponentów f. celu. Inna mozliwosc to np. mnożenie, etc..

Podsumowując, dla problemów spełniających powyższe własności definiujemy następujące elementy PD:

Etapy,
Stany – wartości, które mogą przyjmować zmienne decyzyjne w każdym z etapów,
Przejścia z jednego stanu do kolejnego, które są efektem podjętej decyzji,
Funkcja Bellmana (value function), która określa w konkretnym etapie najlepszą wartość funkcji celu, osiągalną z konkretnego stanu.

Funkcja Bellmana. Dla addytywnie separowalnej funkcji celu:

$\min_{x,u} f(u_0, x_1, u_1, x_2\ldots, u_{T-1}, x_T) = \min_{u_0}f_1(x_1,u_0)+ \min_{u_t} f_{t+1}(x_{t+1},u_t),\ldots, \min_{u_{T-1}} f_T(x_T,u_{T-1})$
Optymalne rozwiązanie wyznaczymy szukając decyzji, która oprócz lokalnej funkcji celu uwzględnia wartość w kolejnym etapie.

dla każdego $x_T$ (stan końcowy) przyjmujemy $V_T(x_T)=f(x_T)$ (terminal value function)
do stanu końcowego doprowadza nas decyzja $u_{T-1}$ podjęta w stanie $x_{T-1}$
dla optymalnej decyzji $u_{T-1}$ dojścia ze stanu $x_{T-1}$ do $x_{T}$ wyznaczymy wartość:
$V_{T-1}(x_{T-1})=\min_{u_{T-1}}\left\{ V_T(x_T) + f_{T}(x_{T},u_{T-1})\right\}$
z równania stanu wiemy, że $x_{t+1} = g(x_t, u_t)$ , czyli:
$V_{T-1}(x_{T-1})=\min_{u_{T-1}}\left\{V_T(g(x_{T-1},u_{T-1})) + f_{T}((g(x_{T-1},u_{T-1}),u_{T-1})\right\}$
w ogólnej postaci, rekurencyjne równanie Bellmana zapisujemy jako:
$V_t(x_t) = \min_{u_t} \left\{ V_{t+1}(g(x_t,u_t))+f_{t+1}(g(x_t, u_t),u_t)\right\}$

1.2. Przykładowe zadanie

Rozwiążemy problem inwestycyjny, definiując poszczególne elementy PD.

Załóżmy, że inwestor dysponuje budżetem 10 mln zł. Ma do wyboru 8 różnych możliwości, każda z nich charakteryzuje się różną stopą zwrotu, podaną w tabeli. Aby ograniczyć ryzyko nadmiernej koncentracji kapitału inwestor nie chce wydać więcej niż 4 mln zł na pojedynczą opcję. Przyjmuje się, że można zainwestować tylko wielokrotności 1 mln zł. Pozostała, niezainwestowana gotówka daje zwrot w wysokości 5 tys. zł za każdy milion.
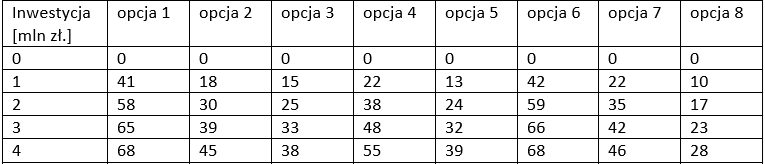
wartości zwrotu dla każdej opcji inwestycyjnej, przy danym poziomie inwestycji

wartości zwrotu dla każdej opcji inwestycyjnej, przy danym poziomie inwestycji

Dla powyższego zadania, które jest odmianą problemu plecakowego definiujemy:

etapy $t$ : opcje inwestycyjne,
stany $x_t$ : zainwestowana gotówka przed rozważeniem opcji $t$ ,
sterowanie $u_t$ : ile zainwestować gotówki w opcję $t$ ,
funkcja przejścia: $x_{t+1}=x_t+u_t$ ,
wartość końcowa w tym zadaniu nie jest zerowa, określa ją zwrot z pozostałej, niezainwestowanej gotówki: $V_T(x_T)=(10-x_T)\cdot 0.5$ ,
funkcja Bellmana odnosi się w tym przypadku tylko do zysku z decyzji: $V_t(x_t)=\max_{u_t}\{f(u_t)+V_{t+1}(x_t+u_t)\}$ .

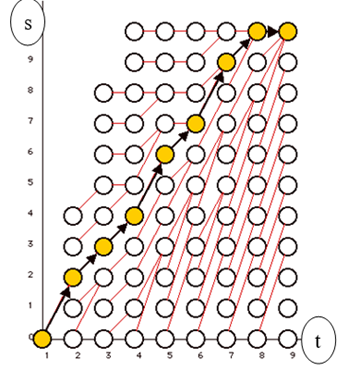
Problem ten można przedstawić w postaci grafu PD, tak jak na poniższej ilustracji, gdzie zaznaczono też optymalne rozwiązanie.

Zadanie w postaci grafu PD

Klasyczne zadanie odpowiednie do rozwiązywania metodą PD to tzw. problem połowu ryb.
Połów (catching fishes). Określ wielkość połowu ryb w każdym roku w przeciągu 10 lat, wiedząc, że obecnie (rok 1) w jeziorze jest 10000 ryb, a ich tempo rocznego przyrostu wynosi 20% (ilości ryb w jeziorze na początku każdego roku). Ryby są sprzedawane w cenie 5$ za sztukę.
Niech (\x\) oznacza liczbę złowionych ryb. Koszt połowu dany jest funkcją:

$0.4x + 100$ , gdy

$x \leq 5000;$

$0.3x + 5000$ , gdy

$5000\leq x \leq 10000;$

$0.2x + 10000$ , gdy

$x > 10000;$
Przyszłe zyski podlegają dyskontu zgodnie ze współczynnikiem 0.8/rok.
Rozwiązane można znaleźć w Miranda, Mario J., and Paul L. Fackler. Applied Computational Economics and Finance, MIT Press, 2002.