Podręcznik

Strona:	SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych
Kurs:	4. Programowanie w ograniczeniach, heurystyki
Książka:	Podręcznik

Wydrukowane przez użytkownika:	Gość
Data:	niedziela, 26 października 2025, 10:28

Opis

Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.

Wykłady W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu

1. Programowanie w ograniczeniach

Programowanie w ograniczeniach (Constraint Programming) jest jedną z ogólnych metod rozwiązywania problemów, w których występują zmienne dyskretne. Choć może być wykorzystywane do optymalizacji rozwiązań, to w pierwotnym sformułowaniu bazuje na poszkiwaniu rozwiązania dopuszczalnego dla zadanego zbioru ograniczeń oraz zmiennych wraz z ich domenami (brak funkcji celu).

Problem spełnienia ograniczeń (Constraint satisfaction problem, CSP) jest opisywany przez trójkę

$(X,D,C)$ , gdzie

$X=\{x_1, \ldots, x_n\}$ jest zbiorem zmiennych problemu,
$D=\{D_1, \ldots, D_n\}$ jest zbiorem dziedzin zmiennych,
$C=\{C_1, \ldots, C_m\}$ jest zbiorem ograniczeń.

Ograniczenie

$C_i$ jest definiowane przez zbiór możliwych wartości

$R_i$ podzbioru

$k$ zmiennych

$X_i =\{x_{i_1}, \ldots, x_{i_k}\}$ , a więc

$R_i \subseteq D_{i_1} \times \ldots \times D_{i_k}$ , jakie zmienne

$X_i$ mogą jednocześnie przyjąć.

Domeną zmiennej decyzyjnej

$x$ jest zbiór wartości, które zmienna może przyjąć. Przykładowo, jeżeli

$x$ jest zmienną binarną jej domeną jest zbiór

$\{0,1\}$ . W wyniku działania algorytmów domeny mogą być zawężane. Przykładowo, załóżmy następujące ograniczenie

$16x_1 + 8x_2 + 5x_3 \geq 20$
gdzie

$x_1, x_2, x_3$ są zmiennymi binarnymi. Początkowa domena zmiennej

$x_1$ jest

$\{0,1\}$ . Jedna jak łatwo zauważyć, w przypadku

$x_1=0$ nie jest możliwe spełnienie ograniczenia, a zatem domena dla

$x_1$ może zostać zawężona do zbioru jednoelementowego

$\{1\}$ .

W trakcie rozwiązywania problemu do zmiennych przypisywane są wartości z ich domen. Przypisanie może być częściowe lub całkowite. Przypisanie

$A=(X_A,V_A)$ przypisuje podzbiorowi zmiennych

$X_A\subseteq X$ wartości

$\{v_{A_1}, \ldots, v_{A_n}\} \in \{ D_{A_1}, \ldots, D_{A_n}\}$ . Rozwiązaniem problemu CSP jest kompletne przypisanie

$A$ takie, że zbiór wartości

$V_A$ należy do każdego zbioru

$R_i$ (czyli spełnia wszystkie ograniczenia).

Problem optymalizacji w ograniczeniach (Constraint optimization problem, COP) jest problemem spełnienia ograniczeń wraz z przypisaną funkcją celu. Rozwiązanie optymalne to rozwiązanie skojarzonego problemu CSP, które minimalizuje (maksymalizuję) funkcję celu.
Jednak COP może być używane nie tylko w kontekście poszukiwania rozwiązania najlepszego. Inne możliwe scenariusze to poszukiwanie rozwiązania dopuszczalnego (np. dla problemów, w których znalezienie dopuszczalności jest już zadaniem trudnym), udowodnienie optymalności zadanego rozwiązania lub udowodnienie sprzeczności problemu.

1.1. Backtracking i propagacja

Programowanie w ograniczeniach bazuję na dwóch głównych koncepcjach:

propagacji oraz
backtrakingu.

Backtracking ekploruje częściowe przypisania do momentu znalezienia kompletnego przypisania. Polega on na inkrementacyjnym budowaniu przypisań częściowych spełniających ograniczenia, zwanych dalej kandydatami na rozwiązanie, oraz odrzucaniu dotychchasowych przypisań częściowych, jeżeli tylko można wydedukować, że nie jest możliwe osiągnięcie rozwiązania (całkowitego przypisania spełniającego wszystkie ograniczenia) przez dalsze budowanie bieżącego kandydata na rozwiązanie. W takiej sytuacji następuje powrót do poprzedniego kandydata i podjęcie próby utworzenia z niego innego rozwiązania. Wnioskowanie o możliwości dalszego budowania rozwiązania jest oparte o propagację, która polega na eliminacji wartości z domen zmiennych, które nie mogą być przyjęte ze względu na ograniczenia przy bieżącym stanie kandydata. Rozważmy przykład problemu czterech hetmanów, których należy rozstawić na planszy o wymiarach 4x4, tak, aby w żadnym wierszu, kolumnie oraz przękątnych był doładnie jeden hetman.

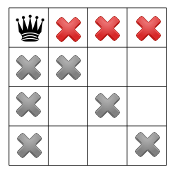
Załóżmy, że w pierwszym kroku algorytm ustawia hetmana w pierwszym wolnym miejscu, na przyład lewym górnym rogu. Następnie, na skutek propagacji, z domen pozostałych zmiennych reprezentujących ustawienie pozostałych hetmanów usuwane są pozycje w pierwszej kolumnie, pierwszym wierszu i jednej diagonali. Teraz algorytm może wybrać miejsce dla drugiego hetmana, ale domena zmiennej reprezentujące to miejsce jest już zawężona.

Załóżmy, że algorytm wybiera kolejne wolne miejsce, na przykład tak, jak ma to miejsce na poniższym rysunku:

co powoduje, że nie jest możliwe wstawienie czwartego hetmana, gdyż po wstawieniu trzeciego hetmana, domena dla zmiennej reprezentującej ustawienie czwartego hetmana stała się pusta.
Algorytm dokonuje teraz backtrakingu i wraca do sytuacji po pierwszym kroku, ale teraz już wie, że wstawienie drugiego hetmana w trzecim wierszu prowadzi do niedopuszczalności. Dlatego algorytm próbuje wstawić drugiego hetmana w czwartym wierszu.

Powyższy przykład dla problemu hetmanów jest przykładem algorytmu przeszukiwania wyczerpującego. Przeszukiwane są wszystkie możliwe przypisania w sposób niejawny, tzn. niektóre przypisania mogą zostać odrzucone bez osiągnięcia przypisania całkowitego. Z przeszukiwaniem związane jest drzewo przeszukiwań. Zazwyczaj przyjmuje się strategię przeszukiwania w głąb drzewa, co pozwala na szybsze osiągnięcie przypisania całowitego.

1.2. Algorytmy spójności

Alternatywą do algorytmu przeszkiwania są tzw. algorytmy spójności (consistency algorithms). Zbiór ograniczeń jest spójny, jeżeli każde częściowe przypisanie do zmiennych, które nie narusza ograniczeń jest dopuszczalne, a w szczególności może zostać rozszerzone do dopuszczalnego całkowitego przypisania. Należy zwrócić uwagę, że spójność nie jest tożsama ze zbiorem rozwiązań dopuszczalnych. Spójność wyklucza wszelki częściowe przypisania przez ograniczenia. Dla spójnych ograniczeń nie jest konieczne przeszukiwanie zbioru rozwiązań z backtrakingiem, gdyż każde dopuszczalne częściowe przypisanie doprowadzi do dopuszczalnego całkowitego przypisania.
Jeżeli pewne ograniczenie nie jest spójne, tzn. istnieją pewne wartości zmiennych występujących w tym ograniczeniu, takie, że spełniają to ograniczenie, ale cały problem nie ma rozwiązania, to można takie wartości usunąć z domen tych zmiennych, czyniąc ograniczenie spójnym. Jest to realizowane przez algorytm Generlized Arc Consistency (GAC). Algorytm GAC rozważa kolejno ograniczenia i w przypadku niespójności ograniczenia dokonuje redukcji domeny zmiennych do wartości zapewniających spójność. Może to powodować konieczność ponownego rozważnie ograniczeń, które już wczesniej zostały uzznane za spójne.
Zamiast formalizować szczegóły algorytm, prześledźmy jego przykładowe działania dla poniższego problemu dla trzech zmiennych $x_1, x_2, x_3$ , z których każda może przyjąć wartości ze zbioru $\{1, 2, 3\}$ , przy poniższych ograniczeniach:
$x_1 > x_2$
$x_2 > x_3$
Oznaczmy przez $dom_x$ domenę zmiennej $x$ . Aby doprowadzić do spójności pierwsze ograniczenie należy ograniczyć domenę $x_1$ do $dom_{x_1}=\{2,3\}$ oraz domenę zmiennej $x_2$ do $dom_{x_2}=\{1,2\}$ . Następnie, drugie ograniczenie powoduje redukcję domeny $dom_{x_3}=\{1,2\}$ oraz $dom_{x_2}=\{2\}$ . Ponieważ $x_2$ może teraz przyjąć tylko wartość 2, to powoduje redukcję $dom_{x_3}=\{1\}$ i konieczność weryfikacji spójności ograniczenia pierwszego, co w efekcie prowadzi do $dom_{x_1}=\{3\}$ . W ten sposób uzyskaliśmy jednoznaczne rozwiązanie $(x_1, x_2,x_3)= (3,2,1)$ , choć oczywiście w ogólnym przypadku domeny zmiennych po zastosowaniu GAC nie muszą być jednoelementowe.

1.3. Podział domen i eliminacja zmiennych

Podział domen (branching)
Aby efektywniej prowadzić przeszukiwanie rozwiązań stosuje się metodę podziału zmiennych (ich domen) w sposób podobny do metody podziału i oszacowań dla zadań programowania całowitoliczbowego. Wiąże się z tym problem wyboru zmiennej do podziału oraz problem wyboru sposobu podziału. Dla zmiennej binarnej naturalny jest podział na dwa podproblemy, każdy dla jednej wartości jaką zmienna może przyjąć. Jeżeli domena zmiennej zawiera więcej niż dwa elementy można stosować różne strategie, ale typowo przyjmuje się podział na rozłączne podzbiory, np. dla każdej możliwej wartości z domeny zmiennej lub na podzbiory $\{1,2\}$ i $\{3\}$ dla zmiennej z rozważanego powyżej przykładu. Taki podział może być prowadzony rekurencyjnie w głąb, aż do uzyskania sytuacji, w której podproblem można rozwiązać.

Eliminacja zmiennych
Podejście komplementarne do redukcji domen zmiennych jest redukcja zmiennych. Usunięcie zmiennej pociąga za sobą konieczność dodania nowych ograniczeń zdefiniowanych dla pozostałych zmiennych, które odpowiadają za wpły w zmiennej na pozostałe zmienne. Ograniczenia te zastępują dotychczasowe ograniczenia odnoszące się do eliminowanej zmiennej. Postępowanie jest powtarzanie rekurencyjnie, najlepiej aż do redukcji problemu do pojedynczej zmiennej. Rozważmy przykład wprowadzony powyżej, ale przyjmując, że każda zmienna może przyjmować wartości ze zbioru $\{1,2,3,4\}$ . Zauważmy, że możliwa jest eliminacja zmiennej $x_2$ , przymując, że pozostałe zmienne mogą przyjąć wartości $(x_1,x_3)\in\{(3,2), (4,2), (4,3)\}$ . W ten sposób rozmiar problemu wyjściowego został istotnie zredukowany.

1.4. Rodzaje ograniczeń

Rodzaje ograniczeń
Można zauważyć, że rozważając różne problemy pewne rodzaje ograniczeń występują częściej. Dlatego często wyróżnia się specjalne typy ograniczeń, szczególnie jeżeli dla nich można dostarczyć specjalne, bardzie efektywne, metody obsługi, w szczególności redukcji domen i eliminacji zmiennych. Przytoczymy teraz często występujące ograniczenia:

ograniczenia logiczne np. wynikanie, np. jeżeli x=1 => y=0
alldifferent (x,y,z) (w skrócie alldiff) - każda zmienna musi przyjąć inną wartość
circuit(succ) - wartości w succ muszą tworzyć cykla Hamiltona, czyli sekwencja 1, succ[1], succ[succ[1]], ... tworzy pętlę 1,...,n
distribute(car, value, base) - liczba wystąpień value[i] w base musi wynieść card[i]
pack - upakowuje elementy w pojemniki o ograniczonych pojemnościach
lexicographic - wymusa leksykograficzny porządek pomiędzy podzbiorami zmiennych decyzyjnych
ograniczenia dotyczące sekwencji, np. before, prev, first/last, noOverlap

Przykład modelowania
Jako przykład rozważym problem komiwojażera. Niech

$c_{ij}$ będzie odległością pomiędzy miastami

$i$ oraz

$j$ . Zadanie polega na znalezieniu najkrótszej drogi, która odwiedza wszystkie miasta dkoładnie jeden raz. Jedno ze standardowych sformułowań programowania całkowitoliczbowego przyjmuje następującą postać:

$\min \sum_{ij} c_{ij}x_{ij}$
przy ograniczeniach

$\sum_ix_{ij}=1 \quad \forall j$

$\sum_jx_{ij}=1 \quad \forall i$

$\sum_{i\in V}\sum_{j\in W}x_{ij} \geq 1, \quad \forall V,W\subset\{1,\ldots,n\}, V\cap W=\emptyset$

$x_{ij} \in \{0,1\}$
gdzie,

$x_{ij}$ przyjmuje wartość 1, jeżeli miasto

$j$ jest odwiedzane bezpośrednio po mieście

$i$ .
Trzecie ograniczenie odpowiada za eliminację podcykli.
Przykładowe sformułowanie problemu jako zadnia programowania w ograniczeniach może być następujące:

$\min \sum_k c_{y_k,y_{k+1}}$
przy ograniczeniach

$alldiff(y_1, \ldots, y_n)$

$y_k \in \{1,\ldots, n\}$
gdzie

$y_k$ przyjmuje wartość równą numerowi miasta odwiedzanego w

$k$ -tej kolejności. Pierwsze ograniczenie

$alldiff$ oznacza, iż każda zmienna musi przyjąć inną wartość.

1.5. Programowanie w ograniczeniach vs programowanie matematyczne

Poniższa tabela charateryzuje programowanie w ograniczeniach na tle programowania matematycznego.

Programowanie w ograniczeniach vs programowanie matematyczne
Programowanie matematyczne	Programowanie w ograniczeniach
Obliczenia numeryczne	Przetwarzanie w logice
Relaksacja	Inferencja (propagacja ograniczeń)
M. in. metoda podziału	Metoda podziału
Ograniczenia liniowe	Wysokopoziomowe modelowania
Niezależność od modelu	Przetwarzanie bazujące na ograniczeniach

W programowaniu matematycznym ograniczenia opisują problem, ale w ogólnej sytuacji, nie określają jak problem można rozwiązać. W programowaniu w ogrniczeniach, każdego ograniczenie uruchamia procedurę, która odcina rozwiązania niedopuszczalne. Rozwiązywanie problemu w programowaniu matematycznym to przede wszystkim przekształcenia algebraiczne, podczas gdy w programowaniu w ograniczeniach znaczącą rolę odgrywa dedukcja logiczna dotycząca dopuszczalności i zawężania domen zmiennych. Jednym z podstawowych narzędzie w programowaniu matematycznym, w szczególności ze zmiennymy całkowitoliczbowymi, jest relaksacja ograniczeń i rozwiązanie tak otrzymanego zadania. Dla programowania w ograniczeniach podstawowym narzędziem jest wnioskowanie, inferencja w oparciu o ograniczenia przy zadanym cząstkowym rozwiązaniu. Oba podejścia często wykorzystują metodę podziału domeny zmiennych, przy czym dla programowania matematycznego jest to rozwiązanie opcjonalne (istnieją inne metody), a dla programowania w ograniczeniach jest to podejście centralne.
Programowanie matematyczne często wymaga liniowości ograniczeń (programowanie liniowe), co powoduje, że może być niezbędne zastosowanie pewnych zabiegów związanych z modelowaniem, w szczególności wymagających wprowadzenia dodatkowych zmiennych lub ograniczeń. Ograniczenia w programowaniu w ograniczeniach mogą mieć dość dowolny charakter i w szczególności przedstawiać zależności logiczne, które w programowaniu liniowym mogą wymagać specjalnego modelowania.
Nie można powiedzieć, że któreś z obydwu podejść jest lepsze w ogólnym przypadku. Programowanie w ograniczeniach bywa często bardziej efektywne w zadaniach harmonogramowania, szczególnie, gdy relaksacja okazuje się słabym narzędziem. Język modelowania w przypadku programowania w ograniczeniach jest bardziej elastyczny i ekspresyjny, dzięki czemu modele często są mniejsze, bardzie zwarte i jednocześnie czytelniejsze i bardziej podatne na zmiany. Z drugiej strony programowanie w ograniczeniach ma trudności ze zmiennymi ciągłymi, choć prowadzi do znalezienia rozwiązań dopuszczalnych to może być nie wystarczające do znalezienia rozwiązań optymalnych. Wymaga również dobrej propagacji ograniczeń, tzn. propagacji, która będzie efektywnie zawężać domeny zmiennych, co nie zawsze ma miejsce. Właściwości obu metod skłaniają do pomysłu integracji programowania matematycznego i programowania w ograniczeniach, np. w postaci rozszerzenia metody podziału i oszacowań o propagacje ograniczeń lub wykorzystania propagacji ograniczeń do generowania silniejszych cięć w metodzie płaszczyzn tnących.

2. Heurystyki

Heurystyczne metody optymalizacji to klasa technik mających na celu znalezienie rozwiązań zbliżonych do optymalnych w złożonych problemach optymalizacyjnych, w rozsądnym czasie. W przeciwieństwie do metod dokładnych, które gwarantują znalezienie optymalnego rozwiązania, ale mogą wymagać ogromnych zasobów obliczeniowych (szczególnie dla problemów o dużej skali), heurystyki koncentrują się na efektywnym poszukiwaniu dobrych jakościowo rozwiązań, bez konieczności przeszukiwania całej przestrzeni możliwości.

Heurystyki są szczególnie użyteczne w przypadku problemów klasy NP-trudnych, gdzie dokładne rozwiązanie wymagałoby czasu obliczeniowego rosnącego wykładniczo wraz ze wzrostem rozmiaru problemu. Do takich problemów należą znane zagadnienia, jak problem komiwojażera (TSP), problem plecakowy, problem trasowania pojazdów (VRP) i wiele innych, spotykanych w logistyce, badaniach operacyjnych, sztucznej inteligencji oraz inżynierii.

Kluczowe cechy metod heurystycznych obejmują:

Prostota: Często są łatwe w implementacji i nie wymagają głębokiej znajomości matematycznych właściwości problemu.
Szybkość: Heurystyki zazwyczaj znajdują rozwiązania w krótkim czasie, co sprawia, że są idealne do zastosowań w czasie rzeczywistym lub w sytuacjach, gdzie decyzje muszą być podejmowane szybko.
Elastyczność: Mogą być stosowane do szerokiego zakresu problemów bez potrzeby specjalistycznego dostosowania.

Chociaż heurystyki nie gwarantują znalezienia globalnie optymalnego rozwiązania, koncentrują się na znajdowaniu "wystarczająco dobrych" rozwiązań w efektywny sposób.

W kolejnych częściach przyjrzymy się szczegółowo kluczowym technikom heurystycznej optymalizacji, omówimy ich zasady, zastosowania oraz potencjalne ograniczenia. Wśród tych metod znajdą się m.in. heurystyki zachłanne, symulowane wyżarzanie, przeszukiwanie zmiennego sąsiedztwa oraz algorytmy ewolucyjne.

2.1. Algorytmy zachłanne

Algorytmy zachłanne (ang. greedy algorithms) to klasa prostych, ale bardzo skutecznych algorytmów wykorzystywanych do rozwiązywania problemów optymalizacyjnych, zwłaszcza w przypadkach, gdy konieczne jest szybkie znalezienie przyzwoitego rozwiązania. Algorytmy te charakteryzują się tym, że w każdej iteracji podejmują decyzje, wybierając lokalnie najlepsze rozwiązanie, bez oglądania się na konsekwencje przyszłych wyborów.

Zasada działania

Algorytm zachłanny działa na podstawie następującej strategii:

W danym momencie algorytm wybiera ten krok, który wydaje się najbardziej obiecujący – jest to tzw. lokalnie optymalny wybór.
Decyzje podejmowane są sekwencyjnie, a każde kolejne rozwiązanie opiera się na wcześniej podjętych decyzjach.
Algorytm nie wraca do poprzednich wyborów, co oznacza, że raz podjęta decyzja jest ostateczna.

Algorytmy zachłanne często nie gwarantują znalezienia globalnie optymalnego rozwiązania, ale w wielu przypadkach mogą dać zadowalające wyniki w krótkim czasie.

Przykłady problemów i zastosowań

1. Problem plecakowy (Knapsack Problem)

W klasycznym problemie plecakowym mamy zbiór przedmiotów o określonej wadze i wartości, a celem jest wybranie podzbioru tych przedmiotów, aby maksymalizować wartość, nie przekraczając maksymalnej pojemności plecaka.

W wersji zachłannej algorytm wybiera przedmioty w kolejności malejącej wartości w stosunku do wagi (czyli w zależności od tego, które przedmioty mają największy stosunek wartości do wagi). Taka strategia może nie zawsze prowadzić do optymalnego rozwiązania, ale daje szybki i prosty sposób na uzyskanie dobrego wyniku.

2. Problem komiwojażera (Traveling Salesman Problem, TSP)

W problemie komiwojażera celem jest znalezienie najkrótszej trasy, która odwiedzi wszystkie miasta i wróci do punktu początkowego. W heurystyce zachłannej można zastosować strategię, w której algorytm w każdej iteracji wybiera najbliższe nieodwiedzone miasto.

Chociaż taka metoda może prowadzić do zadowalających rozwiązań w prostych przypadkach, w praktyce często prowadzi do tras znacznie dłuższych od optymalnych, zwłaszcza w przypadku bardziej złożonych problemów.

3. Problem pokrycia zbioru (Set Cover Problem)

W tym problemie mamy zbiór elementów oraz kolekcję podzbiorów, a celem jest wybranie jak najmniejszej liczby podzbiorów, które razem pokryją cały zbiór. Heurystyka zachłanna może działać w taki sposób, że w każdej iteracji wybiera podzbiór, który pokrywa największą liczbę niepokrytych jeszcze elementów. Takie podejście nie gwarantuje optymalnego wyniku, ale jest stosowane w praktyce, ponieważ jest proste i efektywne.

Zalety algorytmów zachłannych

Szybkość i prostota: Algorytmy zachłanne są łatwe do zrozumienia i implementacji, a także działają szybko, co czyni je atrakcyjnymi w sytuacjach, gdzie czas jest kluczowy.
Efektywność: Heurystyki zachłanne często znajdują rozwiązania wystarczająco dobre, nawet jeśli nie są one optymalne. Są szczególnie użyteczne w przypadkach, gdy dokładne rozwiązanie problemu byłoby zbyt kosztowne obliczeniowo.
Brak potrzeby pamięci o wcześniejszych decyzjach: Algorytmy zachłanne nie wymagają pamięci o poprzednich stanach, co czyni je mniej zasobochłonnymi w porównaniu do innych metod.

Wady

Brak gwarancji optymalności: Największym ograniczeniem heurystyk zachłannych jest brak gwarancji, że znajdą rozwiązanie optymalne. W rzeczywistości, ponieważ algorytm podejmuje decyzje na podstawie lokalnych informacji, może łatwo „utknąć” w suboptymalnym rozwiązaniu. W takich przypadkach inne podejścia heurystyczne, jak np. algorytmy metaheurystyczne (np. wyżarzanie symulowane, algorytmy ewolucyjne), mogą okazać się bardziej skuteczne.
Zależność od struktury problemu: Algorytmy zachłanne dobrze działają tylko w niektórych klasach problemów. W problemach, gdzie lokalne decyzje mogą prowadzić do złych globalnych wyników, heurystyki zachłanne nie są skuteczne.

2.2. Symulowane wyżarzanie

Symulowane wyżarzanie (ang. simulated annealing, SA) to probabilistyczna technika inspirowana procesem wyżarzania w metalurgii, w którym materiał jest podgrzewany do wysokiej temperatury, a następnie powoli chłodzony, aby uzyskać stabilną strukturę krystaliczną przy minimalnej energii. Ten proces fizyczny jest analogiczny do poszukiwania globalnego minimum w problemie optymalizacji.

Podstawy teoretyczne

Główną ideą stojącą za SA jest umożliwienie okazjonalnym ruchom pod górę (pogarszającym funkcję celu) wyjścia poza lokalne minima, przy czym akceptacja takich ruchów jest kontrolowana przez parametr temperatury, który stopniowo maleje w czasie.

Funkcja energii i przestrzeń stanów

Funkcja energii: W terminologii optymalizacyjnej energia odpowiada funkcji celu $f(x)$ , którą staramy się zminimalizować.
Przestrzeń stanów: Zbiór wszystkich możliwych rozwiązań tworzy przestrzeń stanów, w której każdy stan $x$ reprezentuje rozwiązanie dopuszczalne

Kryterium Metropolisa

W każdej iteracji nowe rozwiązanie $x'$ jest generowane z bieżącego rozwiązania $x$ . Zmiana energii (wartość funkcji celu) jest obliczana jako:

$\Delta E = f(x') - f(x)$

Prawdopodobieństwo akceptacji $P$ nowego stanu $x′$ jest dane przez kryterium Metropolisa:

$P = \begin{cases} 1, & \text{if } \Delta E \leq 0 \\ \exp\left(-\frac{\Delta E}{T}\right), & \text{if } \Delta E > 0 \end{cases}$

Gdzie $T$ jest aktualną temperaturą a $\text{exp}$

Algorytm

Inicjalizacja:
- Wybierz rozwiązanie początkowe $x_0$
- Ustaw początkową temperaturę $T_0$
Pojedyncza iteracja:
- Generowanie sąsiedztwa: Generuj nowe proponowane rozwiązanie z sąsiedztwa $N(x)$ aktualnego rozwiązania $x$ .
- Wyliczenie zmiany energii: Policz $\Delta E = f(x') - f(x)$
- Decyzja o akceptacji: Akceptuj $x'$ jako nowe rozwiązanie aktualne z prawdopodobieństwem $P$ określonym przez kryterium Metropolisa.
- Schemat schładzania: Modyfikuj temperaturę $T$ $T_{k+1} = \alpha T_$ , where $\alpha \in (0,1)$ .
Zakończenie:
- Zatrzymaj algorytm, po osiągnięciu kryterium stopu, np. $T$ .

Schematy schładzania

Schemat chłodzenia decyduje o tym, w jaki sposób temperatura ma spadać w czasie i jest kluczowy dla wydajności algorytmu.

Geometryczny:
$T_{k+1} = \alpha T_k$
gdzie $\alpha$ jest stałym współczynnikiem mniejszym od 1.
Liniowy:
$T_{k+1} = T_k - \beta$
gdzie $\beta$ jest dodatnią stałą.
Logarytmiczny:
$T_k = \frac{T_0}{\ln(k + c)}$
gdzie $c$ jest stałą a $k$ .

Struktura sąsiedztwa

The choice of neighbourhood structure $N(x)$ [LaTeX: N(x)] defines how new candidate solutions are generated.

Wybór struktury sąsiedztwa $N (x)$ definiuje sposób generowania nowych rozwiązań. Np . w problemach takich jak Problem Komiwojażera (TSP) sąsiedztwa można generować za pomocą operacji takich jak zamiana dwóch miast, odwrócenie sekwencji miast (2-opt) lub przesunięcie miasta na nową pozycję.

Zbieżność metody

W pewnych warunkach i przy odpowiednim harmonogramie chłodzenia można udowodnić, że symulowane wyżarzanie zbiega się do globalnego optimum z prawdopodobieństwem 1.

Rozważania praktyczne

Temperatura początkowa $T_0$ : Powinna być wystarczająco wysoka, aby umożliwić eksplorację przestrzeni stanów.
Temperatura końcowa $T_{\text{final}}$ : Określa, kiedy algorytm się zatrzyma; często jest ustawiana blisko zera.
Liczba iteracji w każdej temperaturze: może być stała lub dynamiczna; więcej iteracji pozwala na lepszą eksplorację na każdym poziomie temperatury.
zybkość schładzania $\alph$ : Wpływa na szybkość spadku temperatury; wartość bliska 1 spowalnia chłodzenie i pozwala na dokładniejszą eksplorację..

Zalety i ograniczenia SA

Zalety:

Unikanie lokalnych optimów: Akceptując gorsze rozwiązania, SA może uniknąć lokalnego minimum.
Prostota i elastyczność: łatwość implementacji i adaptacji do nowych problemów.
Solidne podstawy teoretyczne: bazuje na solidnych prawach mechaniki statystycznej.

Ograniczenia:

Powolna zbieżność: właszcza przy powolnym harmonogramie chłodzenia, SA może być czasochłonne.
Wrażliwość na parametry: Wydajność zależy w dużej mierze od wyboru początkowej temperatury, harmonogramu chłodzenia i liczby iteracji.
Brak gwarancji optymalności w praktyce: Podczas gdy teoretycznie zbieżność jest gwarantowana w pewnych warunkach, praktyczne implementacje mogą nie osiągnąć globalnego optimum z powodu ograniczeń czasowych

2.3. Przeszukiwanie zmiennego sąsiedztwa

Przeszukiwanie Zróżnicowanego Sąsiedztwa (ang. Variable Neighborhood Search, VNS) to metaheurystyczna metoda optymalizacji, która opiera się na idei dynamicznego zmieniania sąsiedztwa w celu unikania pułapek związanych z lokalnymi minimami. VNS zostało zaproponowane przez Mihaia Mladenovicia i Pierre'a Hansena w latach 90., i od tego czasu znalazło szerokie zastosowanie w rozwiązywaniu różnych problemów optymalizacyjnych, w tym zarówno problemów dyskretnych, jak i ciągłych.

Cechą charakterystyczną algorytmu VNS jest jego zdolność do ucieczki z lokalnych minimów poprzez systematyczne i kontrolowane zwiększanie zakresu poszukiwań w różnych obszarach przestrzeni rozwiązań. Kluczowym elementem tego podejścia jest koncepcja wielokrotnego przeszukiwania różnych sąsiedztw, co pozwala na bardziej globalne spojrzenie na problem optymalizacyjny.

Zasada działania algorytmu VNS

Algorytm VNS działa na podstawie sekwencyjnego przeszukiwania różnych sąsiedztw (grup rozwiązań) wokół bieżącego rozwiązania. Proces ten można podzielić na kilka kluczowych kroków:

Definiowanie sąsiedztwa:
- Algorytm rozpoczyna się od wyboru początkowego rozwiązania oraz zdefiniowania różnych struktur sąsiedztwa. Sąsiedztwo to zbiór rozwiązań, które można uzyskać poprzez wprowadzenie niewielkich zmian w bieżącym rozwiązaniu. W zależności od problemu, sąsiedztwo może być definiowane na różne sposoby, np. poprzez zamianę elementów, permutacje lub inne transformacje.
Poszukiwanie lokalne (Local Search):
- W pierwszym kroku algorytm przeprowadza dokładne poszukiwanie w bieżącym sąsiedztwie, próbując znaleźć lokalne minimum. Poszukiwanie lokalne polega na przeszukiwaniu sąsiadujących rozwiązań i akceptowaniu tych, które poprawiają funkcję celu.
Zwiększanie sąsiedztwa:
- Jeśli przeszukiwanie lokalne doprowadzi do lokalnego minimum, algorytm rozszerza rozmiar sąsiedztwa, zwiększając zakres poszukiwań. Zwiększenie sąsiedztwa oznacza, że algorytm zaczyna eksplorować bardziej odległe rozwiązania w nadziei na znalezienie lepszych globalnych minimów. Zbiór sąsiedztwa aktualnego rozwiązania $x$ oznacza się przez $N(k(x)$ , gdzie $k$ oznacza rozmiar sąsiedztwa, tzn. im większa wartość $k$ tym potencjalnie większy obszar wokół aktualnego rozwiązania brany jest pod uwagę.
Wstrząsanie (Shaking):
- Jednym z kluczowych kroków algorytmu VNS jest tzw. "wstrząsanie" rozwiązania. W momencie, gdy algorytm nie znajduje lepszych rozwiązań w danym sąsiedztwie, wprowadza losowe zmiany w bieżącym rozwiązaniu, aby przesunąć się do nowego obszaru przestrzeni poszukiwań. Dzięki temu unika zablokowania się w lokalnym minimum.
Zakończenie:
- Proces zwiększania sąsiedztwa oraz wstrząsania powtarza się aż do spełnienia określonych warunków zakończenia, np. po osiągnięciu maksymalnej liczby iteracji lub braku poprawy przez określoną liczbę kroków.

Kroki algorytmu VNS

Inicjalizacja: Wybierz początkowe rozwiązanie $x_0$ oraz ustal różne struktury sąsiedztwa $N_k$ dla $k = 1, 2, \dots, k_{\max}$
Powtarzaj:
- Wstrząsanie: Losowo wybierz rozwiązanie $x^{'}$ z sąsiedztwa $N_k(x)$ .
- Poszukiwanie lokalne: Wykonaj poszukiwanie lokalne zaczynając od $x^{'}$ , aby znaleźć lokalne minimum $x^{''}$ .
- Akceptacja: Jeśli $x''$ jest lepsze od $x$ , ustaw $x = x^{''}$ , a $k = 1$ ; w przeciwnym razie, zwiększ $k$ . Gdy $k$ osiągnie $k_{\text{max}}$ , wróć do $k=1$ .
- Powtarzaj aż do spełnienia warunków zakończenia.

Zalety VNS

Unikanie lokalnych minimów: Dzięki mechanizmowi zmiany sąsiedztwa oraz wstrząsania, VNS jest w stanie unikać utknięcia w lokalnych minimach, co jest częstym problemem w tradycyjnych metodach przeszukiwania lokalnego.
Prostota i elastyczność: Algorytm VNS jest stosunkowo prosty do zrozumienia i implementacji. Można go łatwo dostosować do różnych typów problemów, poprzez modyfikację definicji sąsiedztwa oraz mechanizmów wstrząsania.
Szerokie zastosowanie: VNS znalazł zastosowanie w wielu dziedzinach, od logistyki i transportu, przez optymalizację trasowania pojazdów, aż po problemy planowania i harmonogramowania.

Ograniczenia VNS

Podobnie jak w symulowanym wyżarzaniu metoda nie gwarantuje zbieżności i jest zależna od parametrów algorytmu. Dodatkowo, często definiowanie sąsiedztwa oraz algorytmów przeszukiwania lokalnego wymaga dostosowania do konkretnych właściwości rozpatrywanego problemu.

Zastosowania

Algorytm VNS jest szeroko stosowany w problemach dyskretnych i kombinatorycznych. Przykłady zastosowań: problem komiwojażera (TSP), harmonogramowanie zadań, problem trasowania pojazdów (VRP).

2.4. Algorytmy ewolucyjne

Algorytmy ewolucyjne (EA) to klasa metaheurystycznych technik optymalizacji inspirowanych zasadami ewolucji biologicznej. Są one wykorzystywane do znajdowania przybliżonych rozwiązań złożonych problemów optymalizacji, szczególnie w przypadku problemów optymalizacji dyskretnej, w których przestrzeń rozwiązań jest nieciągła i często duża. Algorytmy ewolucyjne są szczególnie skuteczne w optymalizacji dyskretnej ze względu na ich zdolność do eksploracji i wykorzystywania różnych regionów przestrzeni rozwiązań. Wykorzystują mechanizmy analogiczne do doboru naturalnego, mutacji i krzyżowania, aby iteracyjnie ulepszać rozwiązania.

Podstawowe elementy algorytmów ewolucyjnych

Populacja: Zbiór rozwiązań kandydackich problemu optymalizacji. Każde rozwiązanie w populacji jest oceniane na podstawie funkcji dopasowania, która mierzy jego jakość.
Selekcja: Proces wybierania najlepiej działających rozwiązań z bieżącej populacji, które mają pełnić rolę rodziców dla następnego pokolenia. Często opiera się to na wartościach dopasowania, przy czym lepsze rozwiązania mają większą szansę na wybranie.
Krzyżowanie (rekombinacja): Operator genetyczny używany do łączenia części dwóch rozwiązań rodzicielskich w celu stworzenia potomstwa. Chodzi o odziedziczenie dobrych cech od obojga rodziców w celu wytworzenia potencjalnie lepszych rozwiązań.
Mutacja: Operator genetyczny wprowadzający małe losowe zmiany do rozwiązania. Pomaga to utrzymać różnorodność genetyczną w populacji i umożliwia algorytmowi eksplorację nowych obszarów przestrzeni rozwiązań.
Zastępowanie: Proces tworzenia nowej populacji poprzez zastąpienie części lub całości starej populacji nowymi rozwiązaniami. Można to zrobić, stosując różne strategie, takie jak zastąpienie całej populacji lub tylko jej części.
Zakończenie: Kryteria zakończenia algorytmu. Może to być maksymalna liczba pokoleń, kryterium zbieżności, w którym rozwiązania nie ulegają już znaczącej poprawie, lub znalezienie zadowalającego rozwiązania.

Przykłady algorytmów ewolucyjnych

Algorytmy genetyczne(GAs):
- .
Strategie ewolucyjne (ES):
Strategie ewolucyjne koncentrują się na optymalizacji parametrów o wartościach rzeczywistych, ale można je dostosować do problemów optymalizacji dyskretnej. ES można stosować w problemach, w których rozwiązania są kodowane jako liczby rzeczywiste, ale mają charakter dyskretny, takich jak optymalizacja parametrów sieci neuronowych w uczeniu maszynowym. Jednakże obsługa rozwiązań dyskretnych wymaga dodatkowych technik kodowania i ostrożnego postępowania z operacjami mutacji i rekombinacji.

Reprezentacja rozwiązań w algorytmach ewolucyjnych

W algorytmach ewolucyjnych (EA) reprezentacja rozwiązań jest krytycznym aspektem, ponieważ bezpośrednio wpływa na sposób ewolucji rozwiązań za pomocą operatorów genetycznych, takich jak krzyżowanie, mutacja i selekcja. Prawidłowa reprezentacja zapewnia, że algorytm może skutecznie eksplorować przestrzeń rozwiązań i skutecznie stosować operatory genetyczne w celu ulepszania rozwiązań. Reprezentacja rozwiązań w algorytmach ewolucyjnych różni się w zależności od rodzaju rozwiązywanego problemu. Przykłady reprezentacji.

Reprezentacja binarna

Reprezentacja binarna koduje rozwiązania jako ciągi cyfr binarnych (0 i 1). Jest to jedna z najprostszych i najczęściej używanych reprezentacji w algorytmach ewolucyjnych. W przypadku problemu, w którym rozwiązanie obejmuje wybranie elementów z zestawu (jak problem plecakowy), ciąg binarny może reprezentować, czy każdy element jest uwzględniony (1), czy wykluczony (0). Jeśli są 4 przedmioty, rozwiązanie może być reprezentowane w ten sposób:

[1, 0, 1, 0]

Oznacza to, że pierwszy i trzeci element znajdują się w plecaku, natomiast drugi i czwarty nie.

Krzyżowanie i mutacja w reprezentacji binarnej:

Krzyżowanie: Powszechnie stosuje się krzyżowanie jednopunktowe i dwupunktowe. Na przykład krzyżowanie jednopunktowe może zamieniać segmenty ciągów binarnych pomiędzy sobą.
Mutacja: Powszechnie stosowana jest mutacja bitowa, w której każdy bit w ciągu ma szansę (z określonym prawdopodobieństwem) na zmianę (0 na 1 lub 1 na 0).

Przykład krzyżowania:

Wyobraźmy sobie dwa rozwiązania binarne:

Rodzic 1: [1, 0, 0, 1]
Rodzic 2: [0, 1, 1, 0]

Krzyżowanie jednopunktowe może wyglądać następująco:

Punkt krzyżowania: 2

Potomstwo 1: [1, 0, 1, 0]

Potomstwo 2: [0, 1, 0, 1]

Reprezentacja permutacyjna

Reprezentacja permutacyjna jest używana w problemach, gdzie rozwiązania są permutacjami zbioru elementów. Jest to popularna reprezentacja w problemach kombinatorycznych, takich jak problem komiwojażera (TSP).

Przykład: W TSP rozwiązanie może być reprezentowane jako permutacja miast. Dla 5 miast oznaczonych A, B, C, D i E, możliwa permutacja to:

Rozwiązanie = [B, D, A, E, C]

To oznacza, że trasa zaczyna się w mieście B, następnie przechodzi do D, A, E, a kończy w C.

Krzyżowanie i mutacja w reprezentacji permutacyjnej:

Krzyżowanie: Krzyżowanie porządkowe (OX) i krzyżowanie częściowo mapowane (PMX) są dostosowane do permutacji bez duplikowania elementów (jak np. w problemie komiwojażera, gdzie nie chcemy, żeby miasta się powtarzały, nawet po wykonaniu krzyżowania).
Mutacja: Mutacja wymiany (wymiana dwóch elementów) i mutacja inwersji (odwrócenie kolejności segmentu) są powszechnie stosowane.

Przykład krzyżowania:

Rodzic 1: [A, B, C, D, E]
Rodzic 2: [C, A, B, E, D]

Krzyżowanie porządkowe może wyglądać tak:

Obszar krzyżowania: 2 do 4

Potomstwo 1: [A, B, C, E, D]

Potomstwo 2: [C, A, D, B, E]

Reprezentacja Wartości Rzeczywistych

Reprezentacja wartości rzeczywistych używa zmiennych ciągłych do kodowania rozwiązań. Jest to powszechne w problemach optymalizacji, gdzie przestrzeń rozwiązań jest ciągła, jak w optymalizacji parametrów w uczeniu maszynowym.

Dla problemu optymalizacji funkcji rozwiązanie może być reprezentowane jako wektor liczb rzeczywistych

Rozwiązanie = [1.5, -2.3, 0.7]

Ten wektor reprezentuje wartości zmiennych, które są optymalizowane w celu minimalizacji lub maksymalizacji funkcji celu.

Krzyżowanie i Mutacja:

Krzyżowanie: Krzyżowanie arytmetyczne, gdzie wartości potomków są interpolowane między wartościami rodziców. Np.jeśli punkt krzyżowania został wybrany jako a=0.6, to potomek 1 (x1') jest wyliczany jako x1'=a*x1 + (1-a)*x2, a potomek 2 (x2') jest wyliczany jako x2' = (1-a)*x1 + a*x2.
Mutacja: Często jest stosowana tzw. mutacja gaussowska, która dodaje losową wartość z rozkładu normalnego do wybranej zmiennej.

Przykład:

Rodzic 1: [1.5, -2.3, 0.7]
Rodzic 2: [2.0, -1.5, 1.2]

Krzyżowanie artymetyczne:

Punkt Krzyżowania: a=0.6,
Potomstwo 1: [1.7, -1.98, 0.9]
Potomstwo 2: [1.8, -1.82, 1.0]