Podręcznik

Wprowadzenie

Wiele zagadnień związanych z badaniami operacyjnymi jest formułowanych w sposób ścisły lub przybliżony przy pomocy modeli programowania liniowego. Opracowanie algorytmu sympleks pozwoliło na stosunkowo łatwe wyznaczanie rozwiązań optymalnych takich zadań. Pomimo, że w najgorszym przypadku złożoność obliczeniowa tego algorytmu rośnie wykładniczo, to jednak przeciętnie zadania są rozwiązywane bardzo efektywnie.

Istnieje jednak grupa problemów, które choć formalnie zaliczają się do zadań programowania liniowego, to jednak rozwiązanie ich klasycznymi metodami jest nieopłacalne, głównie ze względu na wielkość zajmowanej pamięci, ale także ze względu na czas obliczeń. Cechą charakterystyczną tych zadań jest występowanie bardzo dużej liczby zmiennych, przy stosunkowo niewielkiej liczbie ograniczeń. W niektórych przypadkach liczba zmiennych może być nieskończona lub trudna do wyznaczenia. Oczywiste jest, że przechowywanie w pamięci całej macierzy ograniczeń takiego zadania oraz wykonywanie przekształceń na wszystkich jej elementach jest niemożliwe, a w najlepszym razie nieefektywne.

Rozwiązaniem jest zastosowanie metody generacji kolumn. Jest ona oparta na skorygowanej metodzie sympleks, w której przechowuje się tylko aktualną macierz bazową. Różnica między obydwiema metodami polega na tym, że w metodzie generacji kolumn nowe kolumny wprowadzane do bazy w każdej iteracji nie są bezpośrednio wyszukiwane w macierzy ograniczeń, lecz są wyznaczane w oddzielnym zadaniu optymalizacji.

Skorygowana metoda prymalna sympleks

Rozważmy następujące zadanie programowania liniowego:

Zmaksymalizować

Przy ograniczeniach

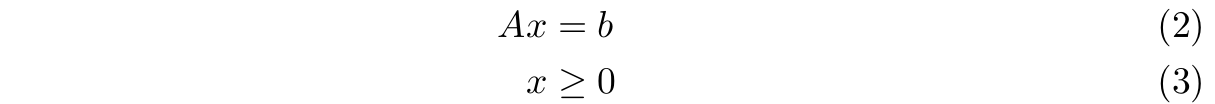
Załóżmy, że kolumny macierzy $A$ zostały przedstawione w taki sposób, że $A = (B, N )$, gdzie $B$ jest macierzą bazową o wymiarach $m$ × $m$ (det $B \ne 0$), $N$ jest macierzą utworzoną z pozostałych kolumn macierzy $A$. Niech ponadto $x = (x_B , x_N )$, gdzie $x_B$ jest wektorem zmiennych bazowych odpowiadających kolumnom macierzy $B$, natomiast $x_N$ jest wektorem zmiennych niebazowych odpowiadających kolumnom macierzy $N$ . Warunek $Ax = b$ możemy teraz zapisać następująco:

Ponieważ $B$ jest macierzą nieosobliwą, zatem istnieje macierz odwrotna $B^{−1}$ . Możemy więc wyrazić $x_B$ w zależności od $x_N$ :

Rozwiązanie bazowe $x_B = B^{-1} b$ otrzymujemy, gdy zmienne niebazowe $x_N$ są na swoich dolnych ograniczeniach, czyli $x_N = 0$. Twierdzenie mówiące, że jeśli zadanie programowania liniowego ma rozwiązanie optymalne, to ma również rozwiązanie bazowe optymalne, pozwala nam, przy poszukiwaniu rozwiązania optymalnego, ograniczyć się tylko do przeszukiwania rozwiązań bazowych dopuszczalnych.

W algorytmie skorygowanej metody prymalnej sympleks, wychodząc od dowolnego dopuszczalnego rozwiązania bazowego, znajdujemy kolejno inne dopuszczalne rozwiązania bazowe polepszające wartość fukcji celu $x_0$ . Przejście pomiędzy dwoma kolejnymi dopuszczalnymi rozwiązaniami bazowymi odbywa się poprzez wprowadzenie do bazy jednej ze zmiennych niebazowych.

Załóżmy, że mamy wyjściowe rozwiązanie bazowe określone wzorem (5). Chcemy teraz znaleźć inne dopuszczalne rozwiązanie bazowe dające większą wartość funkcji celu $x_0$ . Niech $c = (cB , cN )$, wtedy

wykorzystując równanie (5) eliminujemy $x_B$ i otrzymujemy

Po podstawieniu $x_N = 0$ w powyższym równaniu otrzymujemy wartość rozwiązania bazowego równą  $x_0 = c_B B^{−1} b$. Zapiszmy równania (5) i (7) w następujący sposób

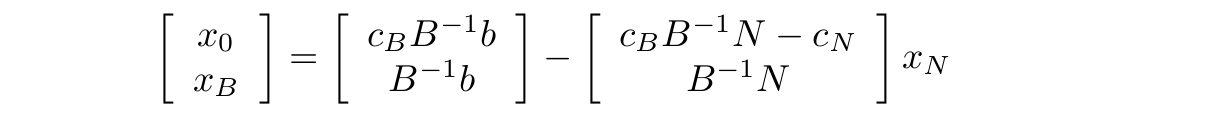
Oznaczmy przez $x_B_0$ wartość funkcji celu $x_0$ , a przez $x_{B_{1}}, ..., x_{B_{m}}$ elementy wektora xB . Niech N będzie zbiorem indeksów kolumn macierzy N , a ponadto

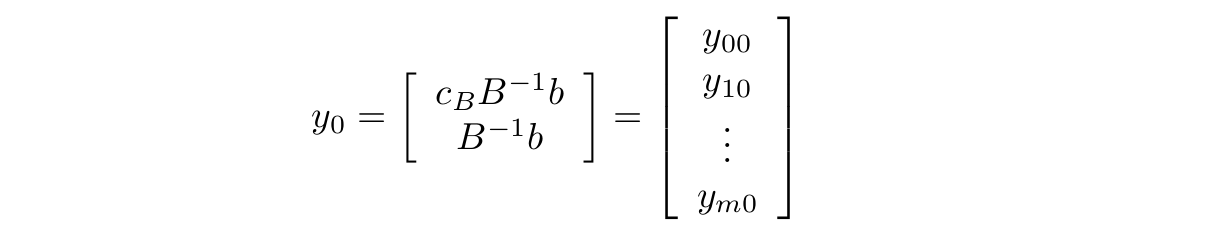
oraz

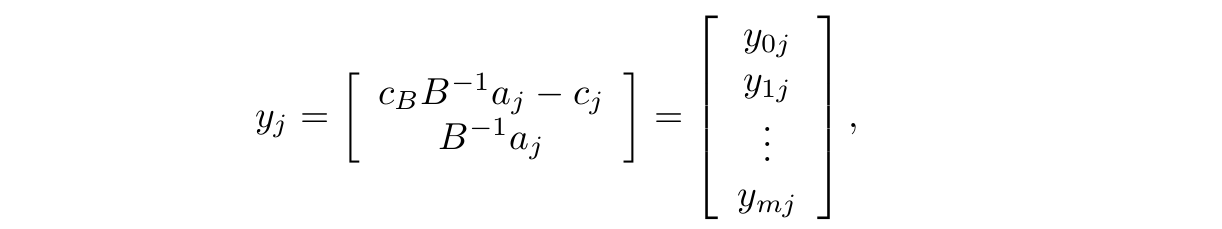
gdzie $a_j , j \in N$ , jest kolumną macierzy $N$ . Możemy teraz równania (5) i (7) zapisać następująco:

Zadaniem naszym jest wybór takiej zmiennej niebazowej, aby, po wprowadzeniu jej do bazy, nowe rozwiązanie było lepsze od poprzedniego. Załóżmy, że do bazy chcemy wprowadzić jedną ze zmiennych niebazowych $x_k (k \in N )$. Spróbujmy więc stopniowo zwiększać wartość zmiennej $x_k$ , która do tej pory była na swym dolnym ograniczeniu. Z równania (8) widzimy, że wartość funkcji celu $x_{B_{0}}$ będzie się zwiększała tylko wtedy, gdy $y_{0k}$ będzie mniejsze od zera. Oznacza to, że zmienną wprowadzaną do bazy możemy wybrać tylko spośród tych zmiennych niebazowych $x_j$ , dla których parametry $y_{0j}$ nazywane cenami zredukowanymi są ujemne ($y_{0j} = c_B B^{−1} a_j − c_j < 0)$. Zauważmy, że zwiększaniu się zmiennej $x_k$ towarzyszy także zmiana wartości zmiennych bazowych $x_{B_{i}} (i = 1, . . . , m)$. Ponieważ wartość żadnej z nich nie może być ujemna, to, jeśli któryś ze współczynników $y_{ik}$ w równaniach (8) jest dodatni, wtedy określa on maksymalną wartość, którą może przyjąć zmienna $x_k$ bez naruszenia ograniczenia $x_{B_{i}} > 0$:

Ponieważ ograniczenie to musi być spełnione dla wszystkich zmiennych bazowych $x_{B_{i}}$ , to

Po osiągnięciu przez wybraną zmienną niebazową $x_k$ wartości $x_k$ max jedna lub kilka zmiennych bazowych znajdzie się na swym dolnym ograniczeniu; spośród nich wybieramy zmienną, która zostanie usunięta z bazy.

Zmienną niebazową wprowadzaną do bazy może być dowolna zmienna $x_k (k \in N )$, dla której $y_{0k} < 0$. Na ogół jednak, w celu polepszenia szybkości zbieżności, wybiera się taką zmienną $x_k$ dla której

Algorytm skorygowanej metody prymalnej sympleks

W algorytmie skorygowanej metody prymalnej sympleks nie operuje się tzw. macierzą sympleksową, lecz macierzą bazową oraz całą macierzą ograniczeń. W każdej iteracji przegląda się wszystkie kolumny aj odpowiadające zmiennym niebazowym. Poszczególne kroki algorytmu przedstawiają się następująco:

Należy pamiętać o tym, że, tak jak w zwykłej metodzie sympleksowej, wyłącznie zmienne bazowe mogą przyjmować wartości niezerowe i, wraz z odpowiadającymi im kolumnami, stanowią pełne rozwiązanie zadania (1)–(3).

Wykrywanie nieograniczoności

Wyznaczanie początkowego dopuszczalnego rozwiązania bazowego

Rozpoczęcie obliczeń metodą sympleksową jest uwarunkowane znajomością początkowego dopuszczalnego rozwiązania bazowego. Jeśli początkowe dopuszczalne rozwiązanie bazowe nie jest łatwo dostępne, wtedy trzeba je wygenerować rozwiązując skorygowaną prymalną metodą sympleksową następujące zadanie pomocnicze:

Zmaksymalizować

przy ograniczeniach

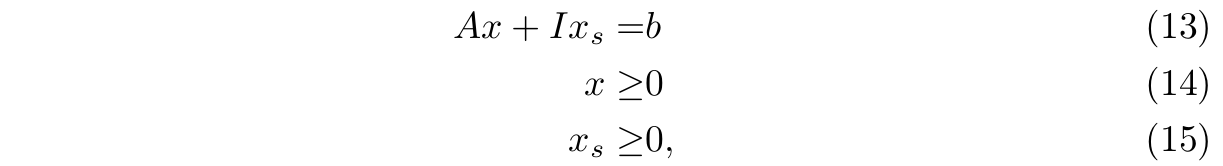
gdzie $b \ge 0$, a $x_s$ jest m-wymiarowym wektorem tzw. zmiennych sztucznych.

Dla zadania tego można z łatwością określić początkowe dopuszczalne rozwiązanie bazowe ${x \brack x_s} = { 0 \brack b }$. Po zakończeniu rozwiązywania tego zadania mogą wystąpić następujące przypadki:

1. 1) min ŵ = w < 0 – zbiór rozwiązań dopuszczalnych zadania wyjściowego jest pusty (zadanie wyjściowe jest sprzeczne).
2. 2) ŵ = 0 i wśród zmiennych bazowych nie występują zmienne sztuczne – wyznaczono początkowe dopuszczalne rozwiązanie bazowe.
3. 3) ŵ = 0 i wśród zmiennych bazowych występują zmienne sztuczne. Możliwe są wówczas dwa warianty:
   • a) Zmienna bazowa $x_{B_{i}}$ jest zmienną sztuczną oraz $y_{ij} = 0$ dla każdego $j \in N$ – w zadaniu wyjściowym występuje redundancja.
   • b) Zmienna bazowa $x_{B_{i}}$ jest zmienną sztuczną oraz istnieje $j \in N$ takie, że $y_{ij} \ne 0$ – należy zastąpić zmienną $x_{B_{i}}$ zmienną $x_j$ , a otrzymane początkowe dopuszczalne rozwiązanie bazowe jest zdegenerowane (istnieją zmienne bazowe równe 0).

Metoda generacji kolumn

W skorygowanej metodzie prymalnej sympleks posługujemy się w sposób jawny całą macierzą ograniczeń – z góry znamy liczbę kolumn oraz jej zawartość. Możemy jednak łatwo dojść do wniosku, że znajomość całej macierzy ograniczeń nie jest konieczna. W każdym kroku wstawiamy do macierzy bazowej nową kolumnę odpowiadającą zmiennej niebazowej, nie jest jednak istotne czy nowa kolumna została wybrana z podanej ‘explicite’ macierzy ograniczeń, czy też została wyliczona w jakiś inny sposób. Najważniejsze jest aby odpowiadająca tej kolumnie cena zredukowana $y_{0j}$ była jak najmniejsza, a jeśli jest przy tym ujemna, to wprowadzenie nowej kolumny spowoduje poprawienie poprzedniego rozwiązania. Zadanie wyznaczenia nowej kolumny możemy więc w sposób ogólny zapisać następująco:

gdzie $a_j$ jest szukanym wektorem zmiennych minimalizującym cenę zredukowaną $y_{0j}$ , który jako nowa kolumna zostanie wprowadzony do macierzy bazowej (indeks $j$ ma tylko znaczenie symboliczne), $\pi = c_B B^{ −1}$ – wektor cen dualnych, $c_j$ – cena w funkcji celu odpowiadająca znalezionej kolumnie.

Zauważmy, że jeśli w wyniku rozwiązania tego zadania otrzymamy kolumnę, która już znajduje się w bazie, to wartość ceny zredukowanej odpowiadającej tej kolumnie będzie wynosiła 0, czyli nastąpi zakończenie algorytmu.

Metoda generacji kolumn działa analogicznie do skorygowanej metody prymalnej sympleks z tą tylko różnicą, że nowe kolumny wstawiane w każdym kroku do macierzy bazowej są wyznaczane w oddzielnym zadaniu optymalizacji. Takie podejście pozwala na rozwiązywanie zadań z macierzą ograniczeń o potencjalnie nieskończonej liczbie kolumn. Nie jest bowiem konieczne pamiętanie całej tej macierzy; do znalezienia kolejnego dopuszczalnego rozwiązania bazowego wystarczy znajomość aktualnej macierzy bazowej.

Na poniższym rysunku przedstawiono schemat działania metody generacji kolumn. Możemy wyróżnić zadanie nadrzędne, będące głównym zadaniem optymalizacji oraz zadanie podrzędne. W każdej iteracji do zadania podrzędnego przekazywany jest wektor cen dualnych $\pi$, który służy do obliczenia nowej kolumny $a_j$. Kolumna ta jest następnie zwracana do zadania nadrzędnego.

Zadanie podrzędne

W zadaniu podrzędnym wyznaczane są kolumny z macierzy ograniczeń o najmniejszych wartościach ceny zredukowanej $y_{0j}$ . Aby zadanie to miało sens, na kolumnę $a_j$ muszą zostać nałożone pewne ograniczenia. Na przykład można ograniczyć zakres wartości jakie mogą przyjmować poszczególne elementy kolumny $a_j$ : $d \le [a_j ]_{i=1,...,m} \le e$. Ograniczenia nałożone na rozwiązanie zadania podrzędnego zawężają zbiór kolumn, które mogą być wstawione do macierzy bazowej zadania nadrzędnego, czyli – zbiór wszystkich rozwiązań dopuszczalnych zadania podrzędnego określa wszystkie możliwe kolumny występujące w macierzy ograniczeń zadania nadrzędnego. Jeżeli na przykład do ograniczenia $d \le [a_j]_{i} \le e$ dodamy warunek całkowitoliczbowości, wtedy macierz ograniczeń zadania nadrzędnego będzie składała się ze skończonej liczby kolumn, w których każdy element musi należeć do przedziału [d, e] i być liczbą całkowitą. Bardziej złożone ograniczenia nakładane na kolumny wyznaczane w zadaniu podrzędnym zostały przedstawione w przykładach w dalszej części tej pracy.

W metodzie generacji kolumn, poza wyznaczeniem w kolejnej iteracji nowej kolumny wstawianej do macierzy bazowej, konieczne jest określenie wartości ceny cj w funkcji celu odpowiadającej tej kolumnie. Cena ta na ogół nie jest podana w sposób jawny, lecz zależy od wyznaczanego wektora $a_j$ : $c_j = f (a_j )$. Skutkiem tego może być poważne zwiększenie złożoności funkcji celu zadania podrzędnego

Chcemy rozwiązać następujące zadanie programowania liniowego całkowitoliczbowego (ZPLC):

$\max_{x\in X} x_0=c^Tx$

$X= \{ x: Ax \leq b, x \geq 0, \texttt{całkowitoliczbowe} \}$

gdzie $A, b$ są całkowitoliczbowe.

Ograniczenia zadania modelują zależności wynikające bezpośrednio z treści zadania lub pośrednio, np. modelujące wymagane zależności logiczne lub inne powiązania między zmiennymi nie wyrażone bezpośrednio w zadaniu. Ja przykład może służyć wyznaczenie maksymalnej wartości z zmiennych, co zazwyczaj modeluje się dodatkową zmienną ograniczającą od góry zmienne stanowiące argument funkcji maksimum. Często problem można zamodelować w różny sposób, np. różnie ujmując ograniczenia, a nawet przyjmując różne definicje zmiennych decyzyjnych. Możemy więc mieć różne modele matematycznego dla danego problemu. Pytanie, które czy są modele "lepsze" lub "gorsze" z punktu widzenia zasobów potrzebnych do rozwiązania problemu.

Rozważmy optymalizację produkcji wyrobów A i B z surowca AB. Do wytworzenia produktów A lub B wymagana jest maszyna, która jest dostępna przez 5h oraz wymagani są specjaliści, którzy są dostępni w wymiarze 21 rbh. Dodatkowo nie można zaplanować większej produkcji wyrobu B niż A. Załóżmy dane liczbowe, dla których model jest następujący:

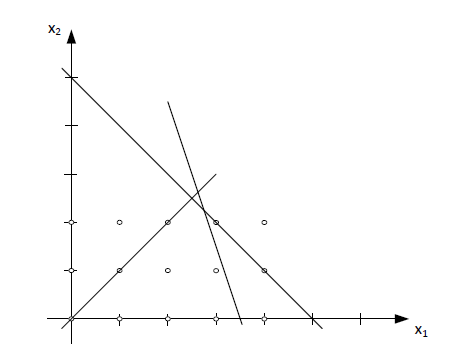
$\left[ \begin{array}{cc} 1 & 1 \\ -1 & 1 \\ 6 & 2 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 5 \\ 0 \\ 21 \\ \end{array} \right]$
$x_1, x_2 \geq 0, \texttt{całkowitoliczbowe}$

Zbiór rozwiązań dopuszczalnych jest następujący $X=\{(0,0), (1,0), (2,0), (3,0), (1,1), (2,1), (3,1), (2,2)\}$ i na rysunku wygląda w następujący sposób:


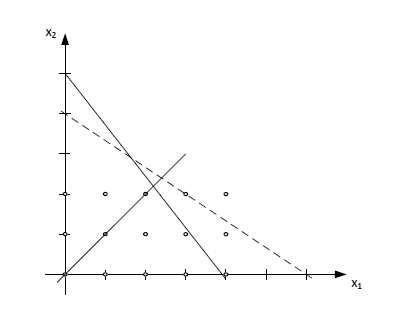
Ale zbiór $X$ można opisywać na wiele sposobów, np.:
$\left[ \begin{array}{cc} 1 & \frac{3}{2} \\ -1 & 1 \\ \frac{26}{5} & 4 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 6 \\ 0 \\ 20 \\ \end{array} \right]$
Wówczas zbiór rozwiązań dopuszczalnych wygląda jak na poniższym rysunku



Który z opisów jest lepszy? Czy lepiej oznacza więcej czy mniej ograniczeń? Czy to ma znaczenie?

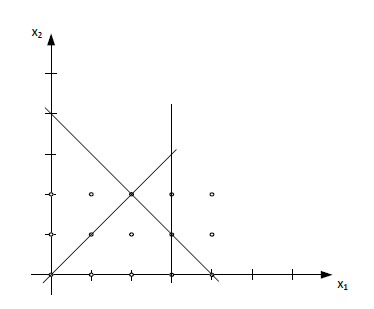
Najlepszy modele problemu jest opis zwarty, a więc taki, że wzystkie punkty zbioru dopuszczlnego $X$ stają się wierzchołami wielościanu. Wówczas można pominąć warunek całkowitoliczbowości w modelu i rozwiązać problem liniowy ze zmiennymi ciągłymi, który jak wiemy jest znacznie prostszy obliczeniowo.

Kontynuując poprzedni przykład rozważmy następujący model:
$\left[ \begin{array}{cc} 1 & 1 \\ -1 & 1 \\ 6 & 0 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 4 \\ 0 \\ 18 \\ \end{array} \right]$
$x_1, x_2 \geq 0,  \texttt{całkowitoliczbowe}$

Ten najbardziej zwarty opis na rysunku wygląda następująco:

Zbiór $conv(X)$ jest wielościanem, którego wszystkie punkty ekstremalne (wierzchołkowe) należą do $X$.

Punkty ekstremalne tworzą minimalny podzbiór $X_d \subseteq X$ punktów dominujących zbioru $X$ takich, że $conv(X_d)=conv(X)$.

Punkty $x\in X \setminus X_d$ są punktami zdominowanymi (są kombinacją liniową punktów dominujących).

Dla dowolnego zbioru dyskretnego $X$ zadanie optymalizacji $\max\{c^Tx: x \in X\}$ można zastąpić zadaniem programowanie liniowego $\max\{c^Tx: x \in conv(X)\}$. Niestety, idealny opis otoczki wypukłej zbioru dyskretnego $X$ może wymagać wprowadzenia wykładniczej liczby ograniczeń.

W szczególnych przypadkach zadań dyskretnych liczba nierówności jest ograniczona wielomianowo. Takie zadania należą do klasy P i są rozwiązywane w czasie wielomianowym. Na przykład zadania w sieciach przepływowych (własność totalnej unimodularności macierzy $A$)

Dla każdego zbioru $X=P \cap \mathbb{Z}^n$, przy czym $P=\{x\in \mathbb{R}^n_+, Ax \leq b\}$ jest opisem wielościennym tego zbioru, zachodzi $X \subseteq conv(X) \subseteq P$.

Opis $P_1$ jest \emph{silniejszym} (bardziej zwartym) od opisu $P_2$, jeżeli $P_1 \subset P_2$.

Dla każdego zbioru $X=P \cap \mathbb{Z}^n$, przy czym $P=\{x\in \mathbb{R}^n_+, Ax \leq b\}$ jest opisem wielościennym tego zbioru, zachodzi $X \subseteq conv(X) \subseteq P$.

Opis $P_1$ jest \emph{silniejszym} (bardziej zwartym) od opisu $P_2$, jeżeli $P_1 \subset P_2$.

Jako przykład rozważmy zadanie lokalizacji. Niech $v_j$ oznacza zmienną binarną wskazującą wybór $j$-tej lokalizacji, a $x_{ij}$ porcję zapotrzebowania $i$-tego klienta obsługiwaną z $j$-tej lokalizacji, przy czym $m$ jest liczbą klientów, a $n$ liczbą lokalizacji. Rozważmy dwa sofrmułowania problemu.

Sformułowanie 1
$\sum_{j=1}^n x_{ij} = 1 \qquad i=1, \ldots, m \\ \sum_{i=1}^m x_{ij} \leq mv_j \qquad j=1, \ldots, n \\ x_{ij} \geq 0, v_j \in\{0,1\} \qquad \forall i,j$
Sformułowanie 2
$\sum_{j=1}^n x_{ij} = 1 \qquad i=1, \ldots, m \\ x_{ij} \leq v_j \qquad \forall i,j \\ x_{ij} \geq 0, v_j \in\{0,1\} \qquad \forall i,j$
Rozważym przykład dla dwóch lokalizacji i dwóch klientów.
Sformułowanie 1
$x_{1,1} + x_{1,2} = 1 \\ x_{2,1} + x_{2,2} = 1 \\ x_{1,1} + x_{2,1} \leq 2v_1 \\ x_{1,2} + x_{2,2} \leq 2v_2$
Zobaczmy przestrzeń rozwiązań dopuszczalnych np. dla $x_{1,1}=1$, $x_{2,1}=0$ to $v_1 \in \langle 0,5;1 \rangle$:


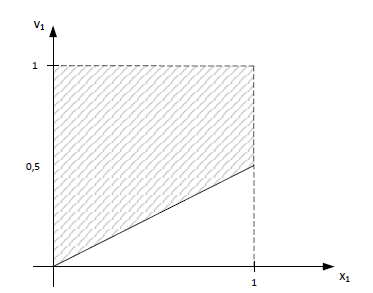
Sformułowanie 2
$x_{1,1} + x_{1,2} = 1 \\ x_{2,1} + x_{2,2} = 1 \\ x_{1,1} \leq v_1 \\ x_{2,1} \leq v_1 \\ x_{1,2} \leq v_2 \\ x_{2,2} \leq v_2$
Teraz dla $x_{1,1}=1$ to $v_1=1$ wygląda w następujący sposób:

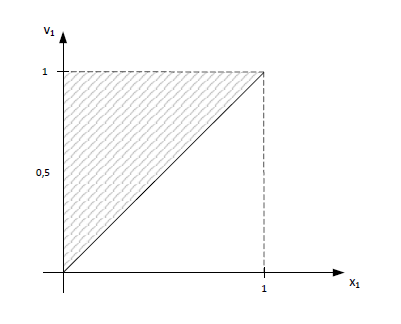
Rysunki wskazują, że sformułowanie 2 jest silniejsze (przynajmniej w rozważanym obszarze).

W ogólnym przypadku trudno jest uzyskać najbardziej zwarty opis $X$, bo liczb ograniczeń rośnie wykładniczo lub szybciej, ale można przybliżać uwypuklenie zbioru $X$ w pewnym otoczeniu punktu optymalnego.

Idea metody płaszczyzn tnących polega na stopniowym zawężaniu opis wielościennego $P$ w wyniku dodawania ograniczeń do już istniejących $Ax\leq b$ nowych o postaci $Dx \leq d$, tak aby:

• dodatkowe ograniczenia odcinały pewne rozwiązania $x \in P$ nie należące do $conv(X)$
• poszukiwane rozwiązanie ZPLC stawało się punktem wierzchołkowym opis wielościennego $P^*=\{x: Ax \leq b, Dx \leq d, x \geq 0 \}$
• funkcja celu ZPL osiągała maksimum na $P$ w punkcie wierzchołkowym całkowitoliczbowym

Dodatkowe ograniczenia nie powinny odcinać rozwiązań dopuszczalnych oryginalnego problemu. Tego typu ograniczenia nazwywamy nierównościami zgodnymi.

Np. zgodne są pierwotne ograniczenia problemu lub ograniczenia opisujące $conv(X)$.

Różne pakiety optymalizacyjne umożliwiają zastosowanie różnych cięć. Przykładowo IBM ILOG Cplex zawiera m.in. następujące cięcia:

• Clique Cuts (co najwyżej jedna zmienna binarna równa 1)
• Cover Cuts (dla ograniczeń plecakowych)
• Disjunctive Cuts (cięcia zgodne dla jednego podproblemu drzewa podziału i niezgodne dla drugiego)
• Flow Cover Cuts (wielkość przepływu uzależniona od zmiennej binarnej, podobne do plecaka)
• Flow Path Cuts
• Gomory Fractional Cuts
• Generalized Upper Bound (GUB) Cover Cuts
• Implied Bound Cuts
• Mixed Integer Rounding (MIR) Cuts
• Zero Half Cuts

Warto,wiedzieć jakie cięcia są wykorzystywane, aby świadomie sterować procesem. W szczególności zazwyczaj można odczytać liczbę dodanych cięć lub dla każdego typu cięcia można ustawiać parametry takie jak częstość danego rodzaju cięć, zakaz cięć, strategia (np. umiarkowana lub agresywana) stosowania cięć danego rodzaju.

Cięcia Cover cuts

Rozważamy ograniczenie typu ($x_j$ -- zmienna binarna)

$\sum_{j=1}^n a_jx_j \leq b$

Zbiór $C \subseteq N =\{1, \ldots, n\}$ jest pokryciem jeżeli

$\sum_{j\in C} a_j > b$

Pokrycie jest minimalne jeżeli $C \setminus \{j\}$ nie jest pokryciem dla dowolnego $j \in C$.

Zauważmy, że cięcie 

$\sum_{j\in C} x_j \leq |C|-1$

jest zgodne. Pytanie, czy można wygenerować lepsze cięcia? Rozważmy następujący przykład.

Ogólnie, cover cut można poszerzyć

$\sum_{j\in E(C)} x_j \leq |C|-1$

gdzie

$E(C)=C \cup \{j: \forall i \in C, a_j \geq a_i \}$

Cięcia Chvatala-Gomory'ego

Niech $a=[a]+\{a\}$ przy czym $[a]$ jest największą liczbą całkowitą nie większa od $a$, zaś $\{a\}$ odpowiednią liczbą ułamkową.

Niech $u \in \mathbb{R}^m_+$. Wówczas nierówność skalarna

$\sum_{j=1}^n ua_jx_j \leq ub_j$

jest zgodna z $P$, gdyż $u\geq 0$ oraz $\sum_{j=1}^n a_jx_j \leq b_j$.

Nierówność

$\sum_{j=1}^n [ua_j]x_j \leq ub_j$

jest zgodna z $P$, gdyż $x\geq 0$.

Nierówność

$\sum_{j=1}^n [ua_j]x_j \leq [ub_j]$

jest zgodna z $P$, gdyż $x$ jest całkowite i $\sum_{j=1}^n [ua_j]x_j$ jest całkowite

Chvatal pokazał, że w ten sposób można generować dowolne cięcia.

W poszukiwanym rozwiązaniu optymalnym muszą być spełnione następujące warunki optymalności dla zadania ZPL z dodanymi cięciami $\max\{c^Tx: Ax \leq b, Dx \leq d, x \geq 0\}$

1. prymalna dopuszczalność ($y_{i0}\geq 0, i=1, \ldots, m$)
2. całkowitoliczbowość ($y_{i0}$ całkowite)
3. dualna dopuszczalność ($y_{0j}\geq 0, j \in N$)

Możliwe są trzy podejścia, w których dwa z powyższych warunków są zawsze spełnione, natomiast trzeci ulega relaksacji. Trzy podstawowe algorytmy metod płaszczyzn tnących są  następujące 

1. algorytm form całkowitych (spełnione warunki 1 i 3)
2. metoda prymalna całkowitoliczbowa (spełnione warunki 1 i 2)
3. metoda dualna całkowitoliczbowa (spełnione warunki 2 i 3)

Ogólny schemat algorytmu form całowitych jest następujący

1. Krok $t=0$, $P^t=P$
2. Rozwiąż ZPL
   $\max\{c^Tx: x \in P^t \}$
   Niech $x^t$ będzie rozwiązaniem na $P^t$
   1. Jeżeli spełnione są wszystkie warunki optymalności to STOP
   2. Skonstruuj płaszczyznę tnącą odcinającą $x^t$ rozwiązując problem separowalności $x^t$ od $conv(X)$.
   3. $t=t+1$, idź do 2 poziom wyżej

Jest to ogólny schemat, który pozostawia otwarte pytanie w jaki sposób generować nowe cięcia.

Metoda płaszczyzn odcinających jest często stosowana razem z metodą podziału i oszacowań tworząc jeden z najsilniejszych algorytmów optymalizacji liniowej dyskretnej. Taka kombinacja nazywana jest metodą podziału i odcięć (Branch & Cut) i ma następujący schemat:

1. Inicjacja listy problemów $L=P^0$
2. Niech $x^{*}=null$ i $v^{*}=-\infty$
3. Dopóki $L$ niepusty
   1. Wybierz i usuń problem z $L$
   2. Rozwiąż relaksację ciągłą
   3. Idź do 3 jeżeli zadanie sprzeczne. W p.p. oznaczmy rozwiązanie przez $x$ i funkcję celu przez $v$.
   4. Jeżeli $v\leq v^{*}$, idź do 3.
   5. Jeżeli  $x$ całkowitoliczbowe, to $v^{*}\leftarrow v,x^{*}\leftarrow x$ i idź do 3.
   6. W razie potrzeby, znajdź płaszczyzny odcinające $x$. Jeżeli istnieją to dodaje od relaksacji LP i idź do 3.2.
   7. Podziel problem na nowe problemy i dodaj je do $L$. Idź do 3.
4. Zwróć $x^{*}$