Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 3. Modelowanie celów i preferencji |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | poniedziałek, 29 grudnia 2025, 23:01 |
Opis
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
Wykłady
W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu
1. Modelowanie celów i preferencji
Optymalizacja wielokryterialna i wspomaganie decyzji.1.1. Optymalizacja wielokryterialna
Zadanie optymalizacji wielokryterialnej (wielokryterialne zadanie programowania matematycznego) może być sformułowane następująco:\(\max\{(f_1({\bf x}), f_2({\bf x}), \ldots, f_m({\bf x})) : {\bf x} \in Q\}\),
gdzie
- \({\bf f} = (f_1, f_2, \ldots, f_m)\) jest funkcją (wektorową) przekształcającą przestrzeń decyzji \(X = R^n\) w przestrzeń ocen \(Y = R^m\);
- poszczególne współrzędne \(f_i\) reprezentują skalarne funkcje oceny;
- \(I = \{1, 2, \ldots, m\}\) jest zbiorem indeksów ocen;
- \(Q \subset X\) oznacza zbiór dopuszczalny (zbiór decyzji dopuszczalnych);
- \({\bf x} \in X\) oznacza wektor zmiennych decyzyjnych.
Zakładamy, że wybór decyzji (rozwiązania) bierze pod uwagę tylko wektory ocen i decyzje o jednakowych wektorach ocen są jednakowo dobre. Tym samym problem wyznaczenia najlepszej decyzji możemy ograniczyć do zagadnienia wyboru najlepszego wektora ocen w zbiorze ocen osiągalnych (osiągalnych wektorów ocen)
\(A = \{{\bf y} : {\bf y} = {\bf f}({\bf x}), {\bf x} \in Q\}\)
podczas gdy odpowiednia decyzja prowadząca do wybranego wektora ocen może być zidentyfikowana w końcowej fazie analizy problemu. Prowadzi to do modelu wielokryterialnego w przestrzeni ocen
\(\max\{ {\bf y} = (y_1, \ldots, y_m) : {\bf y} \in A\}\),
gdzie oceny są bezpośrednio określone jako pojedyncze zmienne.
Rozpatrzmy dwukryterialne zadanie programowania liniowego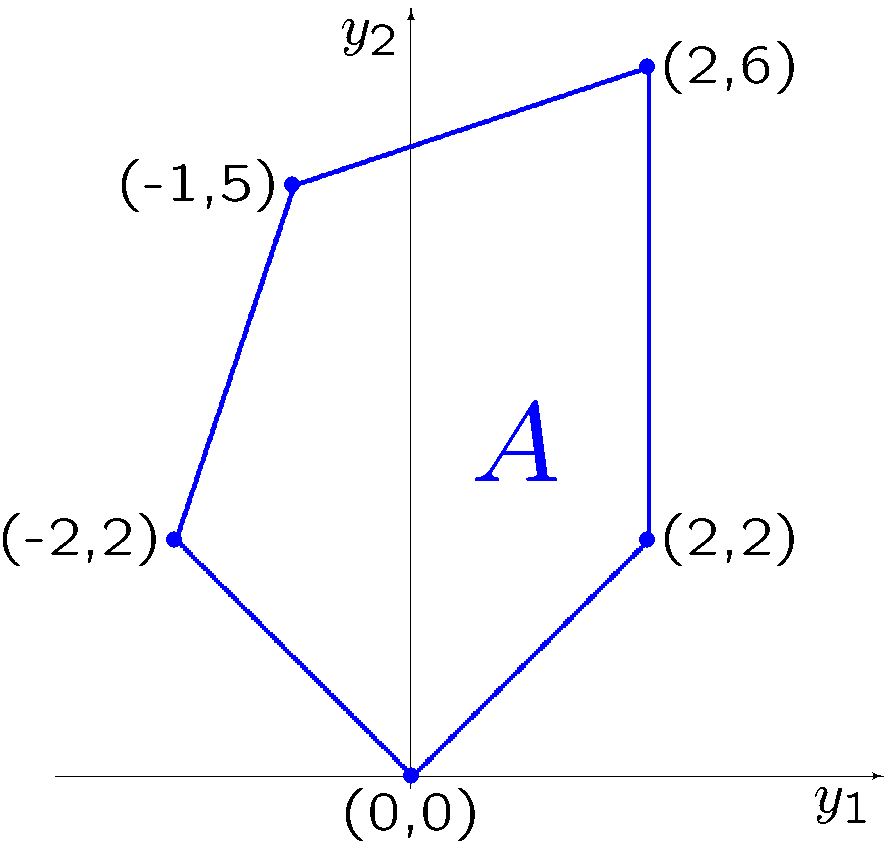
W odróżnieniu od modeli optymalizacji jednokryterialnej model decyzyjny optymalizacji wielokryterialnej nie precyzuje ściśle jednej koncepcji najlepszego (optymalnego) rozwiązania. Zapis maksymalizacji w modelu wielokryterialnym oznacza jedynie, że dla każdej pojedynczej oceny preferowana jest większa wartość.
Tym samym, rozważane preferencje są reprezentowane przez racjonalne relacje preferencji, spełniające warunki zwrotności, przechodniości i ścisłej monotoniczności.\(\begin{array}{rl}
\max & (x_2 - x_1, x_1 + x_2)\\
\mbox{p.w.} & -x_1 + x_2 \le 2\\
\max & (x_2 - x_1, x_1 + x_2)\\
\mbox{p.w.} & -x_1 + x_2 \le 2\\
& 2x_1 + x_2 \le 8\\
& 2x_1 - x_2 \ge 4\\
& x_1, x_2 \ge 0.\\
\end{array}\)
\end{array}\)
W przestrzeni decyzji zbiór dopuszczalny jest pięciokątem o
wierzchołkach (0,0), (0,2), (2,4), (3,2) i (2,0). Kierunki maksymalizacji dla pojedynczych ocen są określone odpowiednimi warstwicami (por. poniższy rysunek).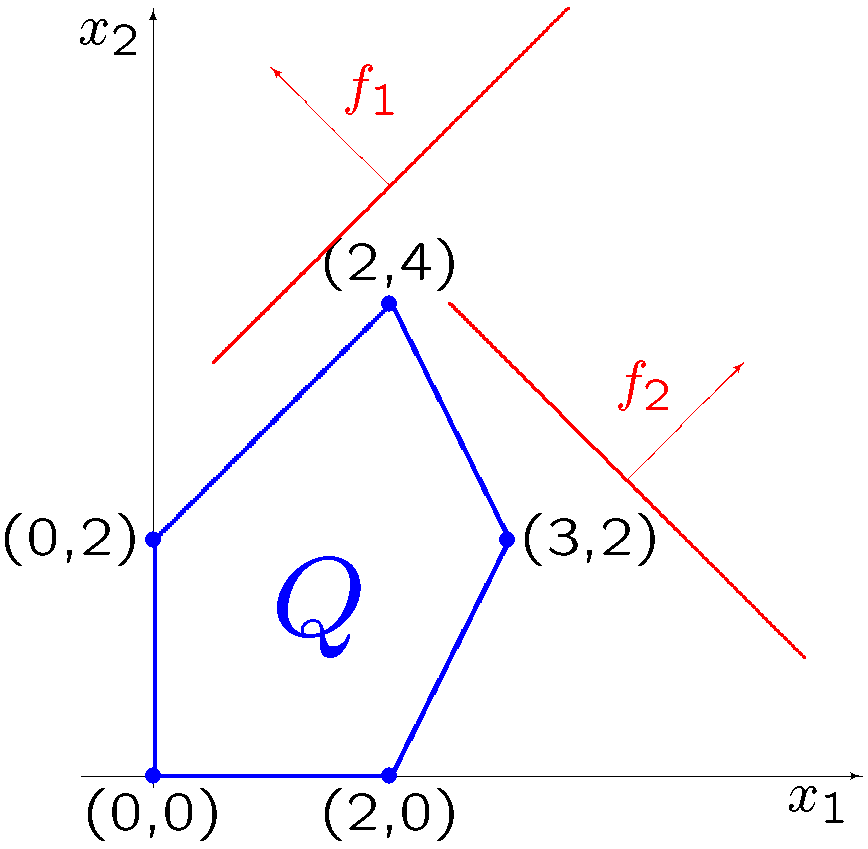

Dwukryterialne zadanie programowania liniowego w przestrzeni decyzji
Ponieważ funkcje wyrażające oceny są liniowe, a zbiór dopuszczalny jest uwypukleniem swoich pięciu wierzchołków, to obraz zbioru dopuszczalnego w przestrzeni ocen jest uwypukleniem obrazu wierzchołków. Tym samym, zbiór ocen osiągalnych \(A\) przyjmuje postać pięciokąta
przedstawionego na poniższym rysunku, gdzie wierzchołek (0,0) jest obrazem punktu (0,0), wierzchołek (-2,2) jest obrazem punktu (0,2), wierzchołek (2,6) jest obrazem punktu (2,4), wierzchołek (-1,5) jest obrazem punktu (3,2), wierzchołek (2,2) jest obrazem punktu (2,0).
Dwukryterialne zadanie programowania liniowego w przestrzeni ocen
Kierunki maksymalizacji poszczególnych ocen pokrywają się z osiami układu współrzędnych.Nawet nie znając relacji preferencji (wiedząc jedynie, że jest to racjonalna relacja preferencji), możemy stwierdzić, że pewne wektory ocen nie mogą być maksymalne w sensie danej relacji. Wynika to z faktu, że pewne wektory ocen są gorsze od innych dla wszystkich racjonalnych relacji preferencji. Można to sformalizować za pomocą relacji racjonalnej dominacji. Ponieważ model racjonalnych relacji preferencji jest najogólniejszym modelem preferencji, relacje racjonalnej dominacji nazywa się po prostu relacją dominacji.
Relacja dominacji. Mówimy, że wektor ocen \(\bf y^\prime\) (racjonalnie) dominuje \(\bf y^{\prime\prime}\), lub \(\bf y^{\prime\prime}\) jest (racjonalnie) dominowany przez \(\bf y^\prime\) wtedy i tylko wtedy, gdy \(\bf y^\prime \succ \bf y^{\prime\prime}\) dla wszystkich racjonalnych relacji preferencji.
Relacja dominacji zazwyczaj nie spełnia warunku spójności i dlatego może istnieć wiele wektorów ocen maksymalnych w sensie relacji racjonalnej dominacji, z których żaden nie jest największy. To znaczy, na ogół nie istnieje wektor ocen dominujący wszystkie pozostałe. Zatem relacja dominacji nie pozwala na jednoznaczne określenie najlepszego wektora ocen. Umożliwia ona jedynie wyróżnienie zbioru niezdominowanych wektorów ocen w odróżnieniu od zdominowanych wektorów ocen. Zdominowane wektory ocen odpowiadają oczywiście decyzjom nieoptymalnym, ponieważ są one gorsze od innych osiągalnych wektorów ocen w sensie każdej racjonalnej relacji preferencji. Jeżeli wektor ocen \(\bf y^{\prime\prime}\) jest dominowany przez \(\bf y^\prime\), to może on być wyeliminowany z
poszukiwań, ponieważ wszyscy racjonalni decydenci preferują \(\bf y^\prime\) w stosunku do \(\bf y^{\prime\prime}\). Wystarczy zatem ograniczyć poszukiwania właściwego wyboru do niezdominowanych wektorów ocen.
Osiągalny wektor ocen \({\bf y} \in A\) nazywamy (racjonalnie) niezdominowanym
wtedy i tylko wtedy, gdy nie istnieje \({\bf y^\prime} \in A\) taki, że \(\bf y\) jest dominowany przez \(\bf y^\prime\).
Pojęcie niezdominowanych wektorów ocen dotyczy elementów przestrzeni ocen \(Y\). W wielokryterialnym problemie decyzyjnym interesują nas raczej odpowiednie wektory dopuszczalne w przestrzeni decyzji \(X\).
Rozwiązania efektywne. Wektor dopuszczalny \({\bf x} \in Q\) nazywamy rozwiązaniem efektywnym (Pareto-optymalnym, sprawnym) zadania optymalizacji wielokryterialnej wtedy i tylko wtedy, gdy odpowiadający mu wektor ocen \({\bf y} = {\bf f}({\bf x})\) jest wektorem niezdominowanym.
Pojedyncze rozwiązania efektywne zadania optymalizacji wielokryterialnej można wyznaczać poszukując w zbiorze ocen osiągalnych \(A\) wektorów największych w sensie pewnej spójnej racjonalnej relacji preferencji. W szczególności, można w tym celu rozwiązywać jednokryterialne skalaryzacje zadania.1.2. Programowanie celowe
W wielokryterialnych problemach decyzyjnych relacja preferencji nie jest znana a priori i dlatego ostatecznego wyboru rozwiązania może dokonać jedynie decydent. Ze względu na liczność zbioru rozwiązań efektywnych, nawet w przypadku wyznaczenia metodami obliczeniowymi całego zbioru rozwiązań efektywnych decydent nie może dokonać wyboru rozwiązania bez pomocy odpowiedniego interaktywnego systemu informatycznego. System taki, nazywany tu systemem wspomagania decyzji, umożliwia sterowany przegląd zbioru rozwiązań efektywnych. Na podstawie podawanych przez decydenta wartości pewnych parametrów sterujących system przedstawia różne rozwiązania efektywne do analizy. Tym samym, parametry sterujące określają pewną parametryzację zbioru rozwiązań efektywnych. Zauważmy, że taka parametryczna analiza zbioru rozwiązań efektywnych pozwala uniknąć konieczności bezpośredniego wyznaczania całego zbioru rozwiązań efektywnych. Zamiast tego system wspomagania decyzji zawierający odpowiedni moduł optymalizacyjny może każdorazowo wyznaczać jedno rozwiązanie efektywne odpowiadające bieżącym wartościom parametrów sterujących.Parametry sterujące powinny spełniać postulat intuicyjności i sterowalności. To znaczy, parametry powinny reprezentować łatwo rozumiane przez decydenta wielkości rzeczywiste charakteryzujące jego preferencje i umożliwiające sterowanie procesem wyboru rozwiązania. Panuje dość powszechne przekonanie, że postulat ten spełniają wagi kompensacyjne używane w skalaryzacji ważonej sumy. Istotnie, w przypadku problemu dwukryterialnego, określenie dodatnich wag \(w_1\) i \(w_2\) dla skalaryzacji ważonej sumy określa tzw. współczynnik wymiany (substytucji) (ang. trade-off) jednostek jednej oceny na drugą. Skalaryzacja ważonej sumy może być wtedy wyrażona jako
\(s({\bf y}) = w_1y_1 + w_2y_2 = w_1(y_1+t_{21}y_2)\),
gdzie \(t_{21} = w_2/w_1\) jest współczynnikiem wymiany jednostek \(y_2\) na jednostki \(y_1\). Określa on preferencje wskazując, że pogorszenie o jednostkę wartości \(y_2\) może być zrekompensowane przez poprawę o \(t_{21}\) jednostek wartości \(y_1\). Niestety interpretacja ta zawodzi w przypadku większej
liczby ocen. Przy większej liczbie ocen wagi kompensacyjne nadal określają współczynniki wymiany dla poszczególnych par ocen, ale nie zapewniają intuicyjnego opisu preferencji względem większych grup ocen. W konsekwencji brak jest intuicyjnści w sterowaniu wagami dla interaktywnego poszukiwania rozwiązania.
Dobrymi parametrami sterującymi reprezentującymi łatwo rozumiane przez decydenta wielkości rzeczywiste są wartości ocen. Wartości ocen traktowane jako pożądane wyniki prosto charakteryzują preferencje decydenta i umożliwiają sterowanie procesem wyboru rozwiązania. Takie parametry sterujące są zgodne z wprowadzonym przez Simona na podstawie badań socjologicznych tzw. zadowalającym modelem procesu decyzyjnego (ang. satisficing model, gdzie satisficing jest słowem sztucznie utworzonym do określenia modelu).
W zadowalającym (satysfakcyjnym) modelu procesu decyzyjnego przyjmuje się, że decydent rozwiązując problem decyzyjny określa poziomy aspiracji jako pożądane wartości poszczególnych ocen. Jeżeli wartości ocen nie osiągają poziomów aspiracji, to decydent stara się znaleźć lepsze rozwiązanie. Jeżeli jednak wartości pewnych ocen osiągnęły odpowiednie poziomy aspiracji, to decydent nie interesuje się ich dalszą poprawą, koncentrując uwagę jedynie na poprawie wartości tych ocen, które nie osiągnęły swoich poziomów aspiracji.
Model zadowalający jest zwykle formalizowany w terminach relacji preferencji jako założenie, że wektor aspiracji jest maksymalny w sensie relacji preferencji, czyli żaden wektor ocen nie jest ściśle preferowany w stosunku do wektora poziomów aspiracji \(\bf a\). Łatwo zauważyć, że warunek ten jest w ogólnym przypadku sprzeczny z warunkiem ścisłej monotoniczności relacji preferencji stanowiącym podstawę koncepcji racjonalności preferencji. Dlatego model preferencji odpowiadający zadowalającemu modelowi procesu decyzyjnego jest nazywany racjonalnością ograniczoną. Dokładniej, jest on sprzeczny jeżeli istnieje osiągalny wektor ocen \(\bf y\) o wszystkich współrzędnych co najmniej równych odpowiednim poziomom aspiracji, a przynajmniej jednej większej. Taki wektor \(\bf y\) jest ściśle preferowany w stosunku do wektora \(\bf a\) przy dowolnej racjonalnej relacji preferencji, co kłóci się z przyjętą interpretacją wektora poziomów aspiracji. Interpretacja modelu zadowalającego w postaci założenia maksymalności wektora aspiracji jest podstawą technik programowania celowego, gdzie poziomy aspiracji są traktowane jako definicje celów przynależności i funkcje osiągnięcia wyrażające odpowiednie odległości są minimalizowane. Podstawowe techniki programowania celowego spełniają zasadę niezdominowania, tylko wtedy gdy wektor poziomów aspiracji spełnia warunek, że żadna ocena nie może przekroczyć swojego poziomu aspiracji.
1.3. Techniki optymalizacji wielokryterialnej
Rozwiązanie efektywne zadania optymalizacji wielokryterialnej\(\max\{(f_1({\bf x}), f_2({\bf x}), \ldots, f_m({\bf x})) : {\bf x} \in Q\}\)
stanowi uogólnienie pojęcia rozwiązania optymalnego i w przypadku optymalizacji jednokryterialnej \((m = 1)\) te dwa pojęcia są tożsame. Tym niemniej, istnieje istotna różnica pomiędzy tymi dwoma pojęciami jako koncepcjami rozwiązań odpowiednich zadań. W optymalizacji jednokryterialnej wszystkie rozwiązania optymalne dają ten sam wynik. Naturalną formalizacją zadania optymalizacji jednokryterialnej jest więc problem wyznaczenia dowolnego rozwiązania optymalnego. W optymalizacji wielokryterialnej różne rozwiązania efektywne generują różne i wzajemnie nieporównywalne wektory ocen. Jedyną formalną specyfikacją matematycznego zadania optymalizacji wielokryterialnej może być wyznaczenie wszystkich rozwiązań efektywnych. Jest to zazwyczaj zdanie skomplikowane i poza przypadkiem problemu dwukryterialnego w niewielkim stopniu przybliżające do rozwiązania odpowiedniego problemu decyzyjnego. Niewątpliwie poszukiwania rozwiązania problemu decyzyjnego powinny być ograniczone do zbioru rozwiązań efektywnych zadania optymalizacji wielokryterialnej i dlatego istotne są techniki generowania takich rozwiązań.
Pojedyncze rozwiązania efektywne zadania optymalizacji wielokryterialnej można wyznaczać poszukująć w zbiorze ocen osiągalnych \(A\) wektorów największych w sensie pewnej spójnej racjonalnej relacji preferencji. W szczególności, można w tym celu rozwiązywać jednokryterialne skalaryzacje zadania.
Skalaryzacją zadania optymalizacji wielokryterialnej nazywamy zadanie optymalizacji jednokryterialnej
\(\max\{s(f_1({\bf x}), f_2({\bf x}), \ldots, f_m({\bf x})) : {\bf x} \in Q\}\)
z funkcją skalaryzującą \(s : R^m \rightarrow R\).
1.4. Metody punktu odniesienia
Zauważmy, że model zadowalający pomija możliwość osiągnięcia poziomów aspiracji przez wszystkie oceny. Faktycznie, w typowym procesie decyzyjnym realizowanym przez decydenta poziomy aspiracji są na ogół stawiane w postaci wielkości nieosiągalnych, a przynajmniej nieosiągalnych jednocześnie. Tym samym, osiągnięcie wszystkich poziomów aspiracji jest sytuacją nierealną. Inaczej rzecz się ma w przypadku systemu wspomagania decyzji i optymalizacji parametrycznej skalaryzacji. Tutaj, model decyzyjny może być wykorzystywany początkowo do rozpoznawania problemu i poziomy aspiracji mogą być wielokrotnie określane próbnie w postaci różnych wielkości. Mogą to być wartości osiągalne, a jednocześnie optymalizacja skalaryzacji umożliwia łatwe wynaczanie rozwiązań najlepszych. Dlatego istotne jest uściślenie modelu decyzyjnego o przypadek osiągalnych poziomów aspiracji. Prowadzi to do tzw. quasi-zadowalającego modelu procesu decyzyjnego wprowadzonego przez Wierzbickiego.W quasi-zadowalającym (quasi-satysfakcyjnym) modelu procesu decyzyjnego przyjmuje się, że decydent rozwiązując problem decyzyjny określa poziomy aspiracji jako pożądane wartości poszczególnych ocen. Jeżeli wartości ocen nie osiągają poziomów aspiracji, to decydent stara się znaleźć lepsze rozwiązanie. Jeżeli wartości pewnych ocen osiągnęły odpowiednie poziomy aspiracji, to decydent koncentruje uwagę na poprawie wartości tych ocen, które nie osiągnęły swoich poziomów aspiracji. Jeżeli wszystkie oceny osiągną założone poziomy aspiracji, to decydent jest zainteresowany dalszą poprawą ocen, o ile jest to możliwe.
Istnieje możliwość konstrukcji parametrycznych skalaryzacji wykorzystujących poziomy aspiracji jako główne parametry sterujące w procesie analizy interaktywnej, a jednocześnie spełniających zasadę niezdominowania rozwiązań. Techniki parametrycznej skalaryzacji spełniające postulaty:
- zasadę niezdominowania rozwiązań,
- zupełnej parametryzacji zbioru niezdominowanego,
- efektywności obliczeniowej,
- intuicyjności i sterowalności parametrów sterujących
Metody punktu odniesienia (MPO) łączą prostotę i otwartość sterowania procesem analizy interaktywnej ze ścisłym przestrzeganiem zasady niezdominowania generowanych rozwiązań i zupełnej parametryzacji zbioru niezdominowanego. Używają one poziomów aspiracji jako głównych parametrów sterujących, ale interpretują je zgodnie z zasadami modelu quasi-zadowalającego. Dokładniej, model preferencji reprezentowany przez skalaryzacje używane w metodach punktu odniesienia spełnia następujące dwa postulaty:
P1. Relacja preferencji jest racjonalną relacją preferencji, czyli przestrzegana jest zasada niezdominowania.
P2. Rozwiązanie ze wszystkimi indywidualnymi ocenami \(y_i\) równymi odpowiadającym im poziomom aspiracji jest preferowane w stosunku do rozwiązania z przynajmniej jedną indywidualną oceną gorszą (mniejszą) od odpowiedniego poziomu aspiracji.
Klasyczna metoda punktu odniesienia polega na maksymalizacji funkcji skalaryzującej
\(s({\bf y}) = \min_{i=1,\ldots,m} s_i(a_i,y_i) + \varepsilon \sum_{i=1}^{m} s_i(a_i,y_i)\)
z indywidualnymi funkcjami osiągnięcia postaci
\(s_i (a_i,y_i) = \left\{ \begin{array}{rl} \beta \lambda_i ( y_i - a_i ),\quad \mbox{jeśli} \quad y_i \ge a_i \\ \lambda_i ( y_i - a_i ),\quad \mbox{jeśli} \quad y_i < a_i
\end{array} \right.,\)
gdzie \(\lambda_i\) są dodatnimi mnożnikami skalującymi, a \(\beta\) jest małym parametrem dodatnim \(0 < \beta < 1\).
\end{array} \right.,\)
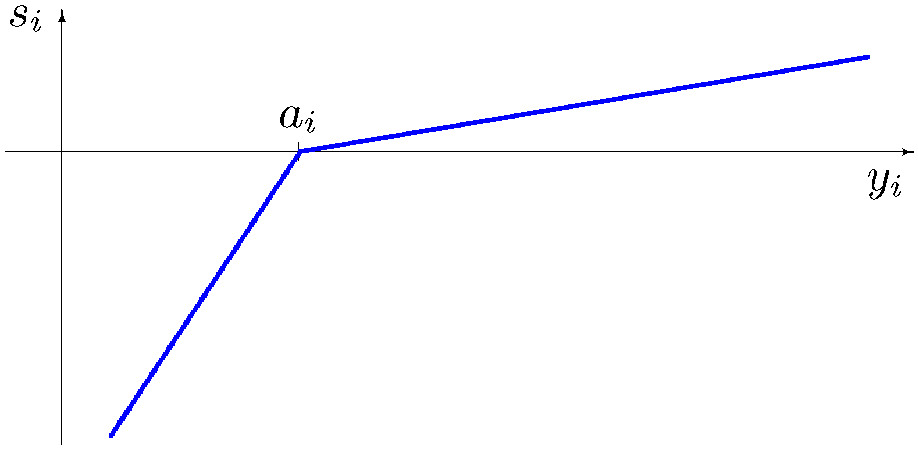
Indywidualna funkcja osiągnięcia klasycznej wersji MPO
Zauważmy, że indywidualne funkcje osiągnięcia przesuwają początek układu współrzędnych w przestrzeni ocen do wektora poziomów aspiracji. Tym samym, przypisują miarę osiągnięcia 0 wartości oceny równej poziomowi aspiracji, ujemne miary osiągnięcia wartościom oceny poniżej poziomu aspiracji i dodatnie miary wartościom oceny przekraczającym poziom aspiracji. Następnie wszystkie oceny są przeskalowane za pomocą mnożników \(\lambda_i\) dla znormalizowania ich zakresów zmienności. Dalej, wartości dodatnie wyrażające znormalizowane nadmiary wartości
ocen ponad poziomy aspiracji są pomniejszane przez czynnik \(\beta\). Najczęściej przyjmuje się \(\beta\) rzędu \(10^{-3}\). W konsekwencji przyrost wartości oceny ponad poziomem aspiracji powoduje znacznie mniejszy przyrost wartości funkcji osiągnięcia niż w przypadku nieosiągania poziomu aspiracji.
Maksymalizacja funkcji skalaryzującej na zbiorze ocen osiągalnych \(A\) wyznacza niezdominowany wektor ocen \({\bf y}\) i generujące go rozwiązanie efektywne \({\bf x}\). Wyznaczone rozwiązanie efektywne zależy od wartości dwóch grup parametrów: poziomów aspiracji \(a_i\) i czynników skalujących \(\lambda_i\). Czynniki skalujące określają kierunek przechodzącej przez punkt odniesienia \({\bf a}\) prostej równych indywidualnych osiągnięć, wzdłóż której dokonuje się maksymalizacja regularyzowanej skalaryzacji maksyminowej.
Metoda punktu odniesienia nie traktuje wektora aspiracji jako bezwględnego celu a jedynie jako punkt odniesienia. Dlatego nawet w przypadku osiągalnego wektora aspiracji MPO wyznacza niezdominowany wektor ocen.