Podręcznik

1. Elementy teorii gier

Wprowadzenie

Pojęcie gry jest szeroko znane, występuje m.in. w popkulturze, literaturze, sporcie, polityce. Chyba każdy zna grę planszową w szachy, drużynową grę w piłkę nożną, czy grę wideo "Wiedźmin". W początkowych latach XXI w. rekordy popularności odnosił serial "Gra o tron", oparta o sagę o tym samym tytule autorstwa Georga R. R. Martina.
Jednak zastanówmy się nad tym, jak można zdefiniować grę w sensie teorii gier. Otóż sytuacja w której mamy do czynienia z taką grą, w której uczestniczy (gra) wielu, co najmniej dwóch, graczy, z których każdy ma do wyboru pewną liczbę możliwych strategii, które określają w jaki sposób rozegra daną grę.
Gracz jest to niekoniecznie człowiek, można traktować go jako firmę, państwo, grupę społeczną, w końcu program komputerowy.

Zakłada się, że gracze działają racjonalnie, to jest podejmują takie decyzje, aby maksymalizować swoją użyteczność.

Istotne jest to, że strategie, a szerzej decyzje, podejmowane przez każdego z graczy wpływają na wynik gry.

Istnieje wiele definicji teorii gier, przytoczę jedną z nich, za dr. Adamem Woźniakiem, z książki "Decyzje w warunkach współzawodnictwa":

Teoria gier to niewłaściwa nazwa dla wieloosobowej teorii podejmowania decyzji badającej procesy decyzyje w sytuacji, gdzie co najmniej dwu powiązanych ze sobą graczy podejmuje decyzje, przy czym powiązani są w taki sposób, że rezultaty decyzji jednego gracza zależą od decyzji co najmniej jednego z pozostałych, czyli znajdują się w sytuacji współzawodnictwa.

Gracz w sytuacji gry może:

współzawodniczyć z innymi graczami (np. o wspólne zasoby);
współpracować z innymi (np. aby wspólnie wykonać pewne zadanie);
tworzyć bądź dołączać do koalicji aby:

wykonywać wspólne działania i osiągać dzięki temu większe zyski (w porównaniu z innymi koalicjami),
konkurować z innymi graczami lub koalicjami.

Te zagadnienia będą rozwijane w kolejnych rozdziałach.

1.1. Niekooperatywna teoria gier - wprowadzenie

Aby wprowadzić w tematykę niekooperatywnej teorii gier, podać podstawowe definicje i pojęcia posłużę się przykładową grą śmieciową.

Załóżmy, że istnieje dwoje graczy: Pan Wiersz i Pani Kolumna. Obydwoje są właścicielami sąsiadujących ze sobą działek letniskowych. Obydwoje nie posiadają podpisanej umowy o wywóz śmieci, koszt podpisania takiej umowy to 2000 PLN/rok. Obecnie, mają możliwość składowania śmieci na tyłach swoich działek. Jednak, miejsce składowania śmieci na jednej działce, znajduje się bezpośrednio domku sąsiada. W takiej sytuacji Pan Wiersz, decydując się wyrzucać swoje śmieci na tyłach swojej działki, powoduje brzydki zapach u Pani Kolumny. Podobnie Pani Kolumna, wyrzucając śmieci na tyłach swojej działki, powoduje, że u Pana Wiersza śmierdzi.

Obydwoje gracze mają do dyspozycji dwie możliwe decyzje: podpisać umowę o wywóz śmieci lub wysypywać je na tyłach swojej działki. Zapiszmy to formalnie:

$D^W = \{ \textrm{wywożenie śmieci} (d^W), \textrm{składowanie śmieci na tyłach działki} (g^W) \} \ni c^W$

$D^K = \{ \textrm{wywożenie śmieci} (d^K), \textrm{składowanie śmieci na tyłach działki} (g^K) \} \ni c^K$

$D^W$ i $D^K$ są zbiorami decyzji odpowiednio Pana Wiersza i Pani Kolumny. $d^W, g^W, d^K, g^K$ są poszczególnymi decyzjami. $c^W$ i $c^K$ są konkretnymi podjętymi decyzjami.

Wynik gry można opisać za pomocą funkcji rezultatów $q_X$ . Argumentem tej funkcji są decyzje graczy, zaś wynikiem są jej rezultaty dla graczy. W wypadku naszej gry: $q_X(c^W,c^K)=(x^W,x^K)$ . Zbiorem rezultatów dla Pana Wiersza jest $X^W$ , zaś zbiorem rezultatów dla Pani Kolumny jest $X^K$ . Te zbiory nie muszą być sobie równe, jednak w przypadku naszej gry są sobie równe:
$X^W = X^K = \{ \textrm{nie śmierdzi za darmo, nie śmierdzi i kosztuje, śmierdzi za darmo, śmierdzi i kosztuje} \}$

Do prezentacji wypłat można wykorzystać tzw. macierz wypłat. Jest to wygodna forma, ale możliwa do wykorzystania dla mniejszych gier.

Macierz wypłat dla gry śmieciowej
$q_X$	$d^K$	$g^K$
$d^W$	nie śmierdzi i kosztuje, nie śmierdzi i kosztuje	śmierdzi i kosztuje, nie śmierdzi za darmo
$g^W$	nie śmierdzi za darmo, śmierdzi i kosztuje	śmierdzi za darmo, śmierdzi za darmo

Macierz wypłat zwyczajowo zapisuje się w taki sposób, że decyzje pierwszego gracza (w tym wypadku Pana Wiersza) zapisujemy w kolejnych wierszach macierzy, natomiast decyzje drugiego gracza (w tym wypadku Pani Kolumny) zapisujemy w kolejnych kolumnach macierzy. W każdej komórce macierzy zapisujemy wartości dla pierwszego gracza, a następnie (po przecinku) dla drugiego gracza.

Taka macierz uzupełniona opisowymi bądź symbolicznymi zbiorami wyników tworzy tzw. osnowę gry.

Aby z osnowy uzyskać grę, należy uzupełnić ją o indywidualne preferencje graczy odnośnie rezultatów.

Przykładowe preferencje dla Pani Kolumny:
nie śmierdzi za darmo

$\succ$ nie śmierdzi i kosztuje

$\succ$ śmierdzi za darmo

$\succ$ śmierdzi i kosztuje

Gra uzupełniona o preferencje odnośnie rezultatów może być analizowana. Rezultaty gry można także przedstawić za pomocą liczb, tzw. indykatorów preferencji lub inaczej funkcji wartościujących.

Taka funkcja wartościująca dla każdego gracza ma postać $w_O: X \mapsto \mathbb{R}$ - jej argumentem jest rezultat gry, zaś wynikiem liczba rzeczywista.

Przykładowe funkcje wartościujące dla Pana Wiersza:

i dla Pani Kolumny:

Na podstawie powyższego przykładu można zauważyć, że funkcje wartościujące mogą być różne, co więcej preferencje graczy odnośnie rezultatów gry także mogą się różnić.

Preferencje Pana Wiersza (wynikające z poprzedniego przykładu):

$\textrm{nie śmierdzi za darmo} \succ \textrm{śmierdzi za darmo} \succ \textrm{nie śmierdzi i kosztuje} \succ \textrm{śmierdzi i kosztuje}$ .
Preferencje Pani Kolumny (wynikające z poprzedniego przykładu):

$\textrm{nie śmierdzi za darmo} \succ \textrm{nie śmierdzi i kosztuje} \succ \textrm{śmierdzi za darmo} \succ \textrm{śmierdzi i kosztuje}$ .

Ostatecznie można zapisać macierz gry z funkcjami wartościującymi:

Macierz wypłat z funkcjami wartościującymi dla gry śmieciowej
$q_X$	$d^K$	$g^K$
$d^W$	-2000, -2000	-2500,0
$g^W$	0,-3000	-500, -2500

Dla gry opisanej poniżej zapisz: graczy, zbiory ich decyzji, zbiory rezultatów, osnowę gry, macierz gry oraz macierz gry z funkcjami wartościującymi.
Wyobraźmy sobie Pana Wiersza i Panią Kolumnę, którym zależy na tym aby się spotkać, ale są zbyt nieśmiali żeby się umówić. Obydwoje wiedzą też, że lubią chodzić do dwóch klubów: ,Atabaska’ i ,Bajlando’, ale nie wiedzą do którego aktualnie pójdzie druga osoba. Kiedy spotkają się w jednym z klubów, obydwoje będą bardzo zadowoleni (wypłata dla obydwojga +10). W ,Atabasce’ będzie relacja z meczu (wypłata dla P. Wiersza +3 jeśli tam będzie), natomiast w ,Bajlando’ na pewno będą przyjaciółki P. Kolumny (wypłata dla P. Kolumny +4 jeśli tam będzie, dla P. Wiersza -2 jeśli tam będzie).

1.2. Niekooperatywna teoria gier - gry o sumie zerowej

W tym rozdziale zajmiemy się gramai o sumie zerowej. Jak można zdefiniować taką grę? Otóż dla gier dwuosobowych można posłużyć się następującą defnicją:

W grze dwuosobowej o sumie zerowej wygrana gracza pierwszego oznacza stratę gracza drugiego.

Dla gier wieloosobowych, definicja jest następująca:

Gra jest grą o sumie zerowej, gdy dla każdej kombinacji decyzji graczy, suma wypłat dla wszystkich graczy wynosi zero.

Przykładowe gry o sumie zerowej to gra w rzut monetą, gra w "papier-kamień-nożyce".

Gra w "papier-kamień-nożyce"
$q_X$	$p^K$	$n^K$	$k^K$
$p^W$	0,0	-1,1	1,-1
$n^W$	1,-1	0,0	-1,1
$k^W$	-1,1	1,-1	0,0

Postać ogólna dwuosobowej gry o sumie zerowej przedstawia się następująco:

Postać ogólna gry o sumie zerowej
$q_X$	$d_1^K$	$d_2^K$
$d_1^W$	$x_1,-x_1$	$x_2,-x_2$
$d_2^K$	$x_3,-x_3$	$x_4,-x_4$

Taka postać wynika wprost z defnicji - wygrana Pana Wiersza (

$x_n)$ odpowiada stracie Pani Kolumny (

$-x_n)$ .

Dlatego też, dla tych gier (dwuosobowych) wygodnie jest opisywać jest w podstaci skróconej, w której przedstawiamy jedynie wypłaty Pana Wiersza (pierwszego z graczy):

Postać ogólna gry o sumie zerowej
$q_X$	$d_1^K$	$d_2^K$
$d_1^W$	$x_1$	$x_2$
$d_2^K$	$x_3$	$x_4$

Problem "rozwiązywania" gier o sumie zerowej rozwiązał John von Neumann w 1928 r. Sformułował on algorytm podejmowania decyzji tzw. strategię minimaks, która maksymalizuje zyski gracza i minimalizuje straty przeciwnika. Algorytm ten został stworzony dla gier dwuosobowych o sumie zerowej i kompletnej informacji.

Założenie o kompletnej infomacji oznacza, że gracze mają pełną informację o możliwych wynikach gry, czyli znają funkcje wypłat swoją i pozostałych graczy, znają także zbiory możliwych decyzji wszyskich graczy.

Minimaks jest to największa wartość, którą określony gracz (z którego punktu widzenia analizujemy grę, zazwyczaj jest to Pan Wiersz) może uzyskać nie wiedząc, którą decyzję wybiorą przeciwnicy.

W grach dwuosobowych można wyznaczyć także maksimin (analizując grę z punktu widzenia przeciwnika Pana Wiersza).

Należy pamiętać, że maksimin jest ujemną wypłatą dla Pani Kolumny.

Przykład - graficzne obliczanie wartości minimaks
$q_X$	$d_1^K$	$d_1^K$	min. wiersza
$d_1^W$	1	4	1	maksimin
$d_2^W$	0	2	0
maks. kolumny	1	4
	minimaks

Aby obliczyć wartość minimaks, można posłużyć się macierzą wypłat. Obliczamy wartość maksymalną w każdej kolumnie, a następnie wybieramy najmniejszą z tych wartości (w przykładzie jest to wartość 1, odpowiadająca decyzji $d_1^K$ ). Analogicznie, obliczemy wartość minimalną w każdym wierszu i wybieramy największą z tych wartości (w przykładzie jest to wartość 1, odpowiadająca decyzji $d_1^W$ ).

Wynik gry nazywamy punktem siodłowym jeśli jego wartość jest:

mniejsza lub równa każdej wartości w jego wierszu

większa lub równa każdej wartości w jego kolumnie

W naszym przykładzie punkt siodłowy istnieje i jego wartość wynosi 1. Decyzje które prowadzą do jego wyboru to

$d_1^W$ i

$d_1^K$ .

Wykres 3D obrazujący ideę punktu siodłowego. Oś X to decyzje Pana Wiersza, oś Y to decyzje Pani Kolumny.

Wykres 3D obrazujący ideę punktu siodłowego. Oś X to wybory Pana Wiersza, oś Y Pani Kolumny.

Jeżeli gra ma punkt siodłowy wówczas obydwoje graczy powinni wybrać decyzje, które prowadzą do jego wyboru.

Punkt siodłowy nie zawsze istnieje. Taka sytuacja zachodzi wówczas, gdy wartości minimaks i maksimin się różnią.

Przykład - brak punktu siodłowego
$q_X$	$d_1^K$	$d_1^K$	min. wiersza
$d_1^W$	4	2	2	maksimin
$d_2^W$	0	3	0
maks. kolumny	4	3
		minimaks

Istnieje także możliwość, że jest wiele takich punktów.

Wiele punktów siodłowych
$q_X$	$d_1^k$	$d_2^k$	$d_3^k$	min. wiersza
$d_1^W$	6	0	-1	-1
$d_2^W$	3	1	1	1	maksimin
$d_3^W$	4	1	1	1	maksimin
maks. kolumny	6	1	1
		minimaks	minimaks

Zdefiniujmy pojęcie strategii czystej.

Strategia, w której gracz podejmuje jedną, konkretną decyzję i jej nie zmienia nazywamy strategią czystą.

Przykład
$q_X$	$d_1^K$	$d_1^K$	min. wiersza
$d_1^W$	1	4	1	maksimin
$d_2^W$	0	2	0
maks. kolumny	1	4
	minimaks

Przykładem strategii czystej dla Pana Wiersza jest $d_1^W$ , zaś dla Pani Kolumny strategią czystą to $d_1^K$ . W przypadku istnienia dokładnie jednego punktu siodłowego, obydwoje graczy posiada strategie czyste, które odpowiadają punktowi siodłowemu. Stosując strategię czystą, gracz powoduje maksymalizację swoich zysków (minimalizację strat).

Jednak, gdy nie istnieje dokładnie jeden punkt siodłowy, gracze mogą stosować strategię mieszaną.

Strategia mieszana określa rozkład prawdopodobieństwa nad zbiorem decyzji, z jakim dokonuje on wyboru.

Przykład - strategia mieszana
$q_X$	$d_1^K$	$d_1^K$	min. wiersza
$d_1^W$	4	2	2	maksimin
$d_2^W$	0	3	0
maks. kolumny	4	3
		minimaks

Jak jednak wyznaczyć taki rozkład prawdopodobieństwa? Zastanówmy się najpierw jaki wynik przyniosłoby stosowanie przez Panią Kolumnę decyzji w oparciu o rzut monetą - czyli wybieranie decyzji $d_1^K$ z prawdopodobieństwem 1/2 i $d_2^K$ z prawdopodobieństwem 1/2.

Wówczas, wybór $d_1^W$ przez Pan Wiersza powodowałby oczekiwaną wypłatę dla niego równą: $1/2 \cdot 4 + 1/2 \cdot 2 = 3$ .

Zaś wybór $d^2_W$ dawałby Panu Wierszowi wypłatę równą $1/2 \cdot 0 + 1/2 \cdot 3 = 3/2$ .

Z tych prostych kalkulacji wynika, że Pan Wiersz, wiedząc że Pani Kolumna stosuje strategię mieszaną: $d_1^K$ z prawd. = 1/2, i $d_2^K$ z prawd. = 1/2, zawsze wybierze $d_1^W$ .

Wprowadźmy kryterium wartości oczekiwanej. Jeśli gracz W wie, że jego przeciwnik (gracz K) gra określoną strategią mieszaną i gracz K będzie ją stosował niezależnie od tego, jaką strategią gra gracz W, wówczas gracz W powinien stosować strategię dającą największą wartość oczekiwaną wypłaty.

Wobec kryterium wartości oczekiwanej, zastanówmy się, czy istnieje taka strategia mieszana dla Pani Kolumny, że Pan Wiersz nie będzie mógł wykorzystać tego, że ją zna przeciwko Pani Kolumnie.

Załóżmy, że Pani Kolumna wybiera

$d_1^K$ z prawdopodobieństwem

$p$ , zaś

$d_2^K$ z prawdopodobieństwem

$1-p$ .

Jeśli Pan Wiersz wybierze $d_1^W$ , wówczas jego oczekiwana wypłata będzie równa: $4 \cdot p + 2 \cdot (1-p) = 2 \cdot p + 2$

Jeśli Pan Wiersz wybierze $d_w^W$ , wówczas jego oczekiwana wypłata będzie równa: $0 \cdot p + 3 \cdot (1-p) = -3 \cdot p + 3$

Aby Pan Wiersz nie mógł wykorzystać wiedzy o znajomości strategii Pani Kolumny, należy znaleźć takie

$p$ , aby jego wybór niczego nie zmienił, czyli:

$2 \cdot p + 2 = -3 \cdot p + 3 \Rightarrow p =1/5$
Sprawdźmy wypłaty dla Pana Wiersza dla

$p=1/5$ :

Pan Wiersz wybiera $d_1^W$ , jego oczekiwana wypłata: $4 \cdot 1/5 + 2 \cdot 4/5 = 12/5$

Pan Wiersz wybiera $d_2^W$ , jego oczekiwana wypłata: $0 \cdot 1/5 + 3 \cdot 4/5 = 12/5$

W takiej sytuacji Pan Wiersz, niezależnie od decyzji otrzyma oczekiwaną wypłatę

$12/5$ .

W analogiczny sposób można wyznaczyć strategię mieszaną dla Pana Wiersza, zakładając, że wybiera decyzję $d_1^W$ z prawdopodobieństwem $q$ i $d_2^W$ z prawdopodobieństwem $1-q$ . Wówczas:

jeśli Pani Kolumna zagra $d_1^K$ otrzyma oczekiwaną wypłatę: $-4 \cdot q + 0 \cdot (1-q) = -4 \cdot q$
jeśli Pani Kolumna zagra $d_2^K$ otrzyma oczekiwaną wypłatę: $-2 \cdot q - 3 \cdot (1-q) = -3 + q$

Pani Kolumna nie wykorzysta znajomości strategii Pana Wiersza gdy: $-4 \cdot q = -3 + q \Rightarrow q = 3/5$ .

Sprawdź, jakie będą oczekiwane wypłaty dla Pana Wiersza dla

$q = 3/5$ .

Na koniec kilka wniosków i twierdzeń.

Strategia czysta jest szczególnym przypadkiem strategii mieszanej.

Twierdzeniem o minimaksie (John von Neumann, 1928).
Każda gra

$n \times m$ (n wyborach Pana Wiersza i m wyborach Pani Kolumny) o sumie zerowej ma rozwiązanie w strategiach mieszanych (lub czystych).

Podczas gdy znalezienie strategii mieszanej dla gry $2 \times 2$ jest proste, to znalezienie jej dla gier $n \times m$ jest bardziej skomplikowane. Jednak literatura podaje na to kilka sposobów:

redukcja gry poprzez wykreślanie rozwiązań zdominowanych (por. rozdział 7.3)
rozwiązanie algebraiczne układu równań (por. Straffin P. "Teoria Gier, 2001, rozdział 3)
rozwiązanie zadania metodą graficzną (por. Straffin P. "Teoria Gier, 2001, rozdział 3)
Rozwiązanie zadania programowania liniowego (por. Raghavan, T. E. S. "Zero-sum two-person games." Handbook of game theory with economic applications 2 (1994): 735-768)

1.3. Niekooperacyjna teoria gier - gry przeciwko naturze

Gra przeciwko naturze to taka gra, w której jednego z graczy nazywamy Naturą. Zakłada się, że pozostali gracze nie wiedzą nic o macierzy wypłat Natury, strategiach jakie Natura wybierze, ani o rozkładach prawdopodobieństwa wyboru poszczególnych strategii Natury.

Dobry przykład do analizy gier przeciwko naturze został opracowany przez Williama Davenporta na podstawie analizy antropologicznej jamajskich rybaków (W. Davenport "Jamaican fishing: A game theory analysis", 1960).

W tym przykładzie rozważana jest sytuacja jamajskich rybaków, którzy mają do wybory trzy strategie:

[W] rozstawić kosze do połowu ryb na łowiskach wewnętrznych
[Z] rozstawić kosze do połowu ryb na łowiskach zewnętrznych
[P] rozstawić kosze do połowu ryb pośrednio: na łowiskach wewnętrznych i zewnętrznych

Natomiast Natura na dwie strategie:

[A] prądy wodne są aktywne
[N] prądy wodne są nieaktywne

W trakcie wielu lat połowów, rybacy oszacowali wartości wypłat dla tak zdefiniowanej gry:

Macierz wypłat dla rybaków
	A	N
W	17,3	11,5
Z	-4,4	20,6
P	5,2	17,0

W jaki sposób rybacy powinni podjąć decyzję odnośnie strategii? Przeanalizujmy cztery kryteria znane z literatury:

kryterium wartości oczekiwanej (Laplace'a)
kryterium maksyminowe (Waldegrave'a)
kryterium Savage'a (L.J. Savage)
kryterium Hurwicza (L. Hurwicz)

Kryterium Laplace'a zakłada, że obliczamy wartość oczekiwaną dla każdej decyzji gracza, przy założonym rozkładzie decyzji Natury. Jeśli nie mamy żadnych wiadomości / obserwacji na temat strategii Natury, należy założyć rozkład proporcjonalny.

Kryterium Laplace'a (zakładany rozkład 50/50)
	A	N	Wartość oczekiwana
W	17,3	11,5	*14,4 := 0,5 17,3 + 0,5 * 11,5**
Z	-4,4	20,6	8,1 := 0,5 * (-4,4) + 0,5 * 20,6
P	5,2	17,0	11,1 := 0,5 * 5,2 + 0,5 * 17

Największa wartość oczekiwana (14,4) jest przy decyzji rybaka W (rozstaw kosze na łowiskach Wewnętrznych). Zmiana rozkładu prawdopodobieństwa na inny, wynikający przykładowo z obserwacji Natury, może jednak zmienić decyzję rybaków.

Oblicz wartość kryterium Laplace'a i wynikające z tego decyzję dla rybaków dla rozkładu prawdopodobieństwa 10/90.

Kryterium maksyminowe zakłada, że ostrożny rybak będzie podejmował decyzję kierując się zasadą najlepszego rezultatu gwarantowanego. Innymi słowy, rybak stosujący kryterium maksyminowe podejmie decyzję, która przy najgorszej (dla niego) decyzji Natury, da najlepszy rezultat.

Kryterium maksyminowe
	A	N	Wartość oczekiwana
W	17,3	11,5	11,5 := min(17,3; 11,5)
Z	-4,4	20,6	-4,4 := min(-4,4; 20,6)
P	5,2	17,0	5,2 := min(5,2; 17,0)

Najlepszy rezultat gwarantowany, zakładając najgorszą decyzję (dla rybaka) Natury, to 11,5. Rybak powinien podjąć decyzję o rozstawieniu koszy do połowu ryb na łowiskach wewnętrznych.

Kryterium Savage'a opiera się na minimalizacji żalu. Rybak po realizacji decyzji może pomyśleć: "Zdecydowałem się rozstawić kosze na obydwu łowiskach: wewnętrznych i zewnętrznych (decyzja P), liczyłem, że prądy będą nieaktywne (decyzja Natury N) i zarobię 17. Natomiast okazało się, że prądy były aktywne (Natura wybrała decyzję A) i zarobiłem tylko 5,2!". Metoda Savage'a polega na zbudowaniu macierzy strat i zminimalizowaniu maksymalnej straty jakiej rybak może doświadczyć. Budowanie macierzy strat polega na tym, że każda komórka tej macierzy otrzymuje wartość będącą różnicą pomiędzy maksymalną wartością z kolumny z macierzy wypłat a wartością z komórki z macierzy wypłat.

Kryterium Savage'a -- macierz strat
	A	N	strata
W	0	9,1	max(0; 9,1) := 9,1
Z	21,7	0	max(21,7;0) := 21,7
P	12,1	3,6	max(12,1;3,6) := 12,1

Kryteria Savage'a i Waldegrave'a są krytykowane za zbytnią ostrożność. Kryterium zaporponowane przez Leonida Hurwicza łączy najgorszą i najlepszą opcję, wprowadzając tzw. wskaźnik optymizmu-pesymizmu, lub wskaźnik ostrożności $\theta \in [0;1]$ .

Przykładowo, dla współczynnika ostrożności $\theta = 0,95$ , czyli dla bardzo ostrożnego rybaka wybór będzie polegał na rozstawieniu koszy na łowiskach wewnętrznych.

Kryterium Hurwicza $\theta =0,95$
	A	N	kryterium Hurwicza
W	17,3	11,5	*11,79 := 0,95 min(17,3;11,5) + 0,05max(17,3;11,5)*
Z	-4,4	20,6	-3,15 := 0,95 * min(-4,4;20,6) + 0,05*max(-4,4;20,6)
P	5,2	17,0	5,79 := 0,95 * min(5,2;17) + 0,05*max(5,2;17)

Zadanie: wyznacz decyzję dla rybaka "ryzykanta", którego wskaźnik ostrożności wynosi

$\theta = 0,05$

1.4. Niekooperacyjna teoria gier - gry o sumie niezerowej

Gra o sumie zerowej to taka gra, w której wygrana jednego gracza nie musi oznaczać straty drugiego.

Najbardziej znaną i najbardziej zbadaną grą o sumie zerowej jest gra w dylemat więźnia.

Dwóch podejrzanych zostało zatrzymanych przez policję. Policja, nie mając wystarczających dowodów do postawienia zarzutów, rozdziela więźniów i przedstawia każdemu z nich tę samą ofertę: jeśli będzie zeznawać przeciwko drugiemu, a drugi będzie milczeć, to zeznający wyjdzie na wolność, a milczący dostanie dziesięcioletni wyrok. Jeśli obaj będą milczeć, obaj odsiedzą 6 miesięcy za inne przewinienia. Jeśli obaj będą zeznawać, obaj dostaną pięcioletnie wyroki. Każdy z nich musi podjąć decyzję niezależnie i żaden nie dowie się, czy drugi milczy czy zeznaje, aż do momentu wydania wyroku. Jak powinni postąpić? (za Wikipedia: https://pl.wikipedia.org/wiki/Dylemat_więźnia).

Dla gry w dylemat więźnia, macierz wypłat przedstawia się następująco:


$q_x$	K milczy	K zeznaje
W milczy	-0,5; -0,5	-10; 0
W zeznaje	0;-10	-5; -5

Zastanówmy się, która decyzja dla Pani Kolumny i dla Pana Wiersza będzie najlepsza, najbardziej korzystna. Pierwszym pojęciem, które wprowadzimy będzie dominacja strategii.

Strategia S dominuje strategię T, jeżeli każdy wynik dawany przy użyciu S jest niegorszy od wyniku dawanego przy użyciu T, a przynajmniej jeden wyniki dawany przy użyciu S jest lepszy od wyniku dawanego przy użyciu T.

Kolejnym pojęciem będzie strategia dominująca:

Strategia dominująca jest to strategie, która jest zawsze nie gorsza od pozostałych strategii, niezależnie od wyboru strategii przez przeciwnika.

Jeśli w grze, dla jednego z graczy występuje strategia dominująca, wówczas racjonalny gracz powinien zawsze wybierać tę właśnie strategię.

Sprawdź, czy w danej grze dylemat więźnia znajduje się strategia dominująca.

Strategię nazywamy strategią zdominowaną, jeśli daje gorsze wyniki od innych strategii, dla wszystkich wyborów przeciwnika.

Z punktu widzenia racjonalnego gracza, nie ma sensu rozpatrywać strategii zdominowanych.

Na podstawie powyższych definicji, możemy zaproponować jeden ze sposobów wyznaczania rozwiązań gier o sumie niezerowej. Polega on na wyznaczeniu strategii zdominowanych dla każdego z graczy i rozgrywanie gry za ich pomocą. Niestety, takie strategie rzadko występują w rzeczywistych grach.

Kolejną definicją jest optymalność wyniku gry w sensie Pareto.

Wynik gry jest optymalny w sensie Pareto (lub krócej parerooptymalny) jeśli gra nie ma innego wyniku niegorszego dla obydwu graczy i dającego jednemu graczowi wyższą wypłatę.

Warto przedstawić także definicję nieoptymalności wyniku gry w sensie Pareto.

Wynik gry jest nieoptymalny w sensie Pareto (paretonieefektywny) jeśli gra ma inny wynik, niegorszy dla obydwu graczy i dający przynajmniej jednemu graczowi wyższą wypłatę.

Z powyższych definicji możemy zdefiniować kryterium Pareto: tylko wynik optymalny w sensie Pareto może być akceptowalny jako rozwiązanie gry. Kryterium Pareto stanowi podstawową zasadę racjonalności grupowej.

Sprawdźmy, czy rozwiązania gry w dylemat więźnia są optymalne w sensie Pareto. Naszkicujmy wszystkie rozwiązania tej gry w dwuwymiarowej przestrzeni wypłat:

Wyniki gry w dylemat więźnia przedstawiony w dwuwymiarowej przestrzeni wypłat

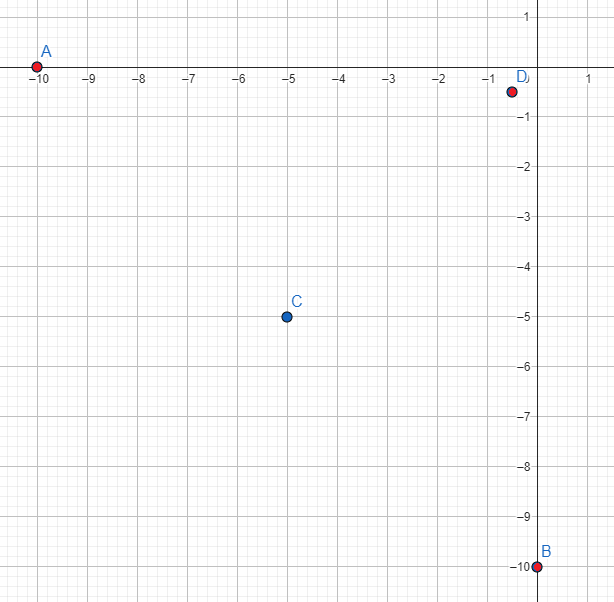
Wyniki gry, które są oznaczone czerwonym kolorem ( $(W_m, K_m), (W_m, K_z), (W_z, K_m)$ ), są optymalne w sensie Pareto. Dalej, spełniają kryterium racjonalności grupowej. Spełnienie tego kryterium przez rozwiązanie gry powoduje, że gracz nie może zyskać więcej, bez spowodowania straty dla drugiego gracza.

Poznaliśmy pojęcie strategii dominującej i możliwość (rzadką) na poszukiwanie rozwiązania gry. Poznaliśmy kryterium Pareto, które wskazuje racjonalne grupowo rozwiązania. Jednak poszukiwanie "dobrych" rozwiązań gry może zostać przeprowadzone przy użyciu tzw. koncepcji rozwiązania (ang. solution concept). Tworzy pewne założenia co do rozwiązania gry i formalnie tłumaczy ono jak zostanie rozegrana gra. Większość koncepcji rozwiązania jest oparta o koncepcje równowagowe.

Najbardziej znana koncepcja rozwiązania została zaproponowana przez Johna Nasha w 1951 r. Zakłada ona, że w grze znajdującej się w równowadze żaden z graczy nie ma zachęt jednostronnie odstępować o strategii równowagii. Równowaga Nasha (w strategiach czystych) jest to taki profil strategii czystych $a^*\in A$ , że dla każdego $i \in N$ i dla każdej strategii czystej $a_i$ gracza i-tego spełnia:

$u_i(a^*) = u_i(a_1^*, ..., a_i^*, ..., a_n^*) \geq u_i(a_1^*, ..., a_i, ..., a_n^*)$

Nash udowonił, że każda skończona gra ma przynajmniej jeden punkt równowagi Nasha (niekoniecznie w strategiach czystych). Jednak w tym podręczniku nie będziemy zajmować się strategiami mieszanymi.

Jednostronne odstępstwo oznacza tyle, że jeden z graczy zmienia decyzję, podczas gry pozostali gracze pozostają przy obecnych.

Przeanalizujmy teraz grę w dylemat więźnia i pokażmy jedną z metod wyznaczania punktów równowagowych Nasha.


$q_x$	K milczy		K zeznaje
W milczy	-0,5; -0,5	$\rightarrow$	-10; 0
	$\downarrow$		$\downarrow$
W zeznaje	0;-10	$\rightarrow$	-5; -5

Rozpocznijmy naszą analizę do punktu

$W_m, K_m$ . Czy Pan Wiersz ma zachęty do jednostronnej zmiany swojej decyzji W obecnej sytuacji jego wypłata wynosi -0.5, przy zmianie decyzji na

$W_z$ otrzymały on większą wypłatę równą 0. Wobec tego Pan Wiersz ma jednostonną zachętę na zmianę decyzji. Jest to oznaczane strzałką. Obecnie znajdujemy się w punkcie

$W_z, K_m$ , przeanalizujmy czy Pani Kolumnie opłaca się jednostronnie zmienić strategię. Obecnie jej wypłata jest równa -10, zaś przy zmianie jej strategii na

$K_z$ jej wypłata rośnie do -5. Zatem Pani Kolumna ma zachętę do jednostronnej zmiany decyzji, co znowu oznaczone jest strzałką. Teraz jesteśmy w punkcie

$W_z, K_z$ , sprawdźmy teraz, czy Panu Wierszowi opłaci się jednostronnie zmienić swoją decyzję na

$W_m$ . Jego obecena wypłata to -5, po zmianie decyzji wynosi ona -10. Wobec tego, Panu Wierszowi (ani Pani Kolumnie) nie opłaca się jednostronnie zmienić swojej decyzji, co oznacza, że punkt

$W_z, K_z$ jest punktem równowagi Nasha.

Sprawdź drugą "ścieżkę" wnioskowania: od punktu

$W_m, K_m$ analizuj czy Pani Kolumna ma zachęty do jednostronnej zmiany decyzji, aż do punktu równowagi Nasha.

Strona:	SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych
Kurs:	4. Elementy teorii gier
Książka:	Podręcznik

Wydrukowane przez użytkownika:	Gość
Data:	wtorek, 8 kwietnia 2025, 13:24