Podręcznik

Strona:	SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych
Kurs:	1. Podstawy modelowania matematycznego
Książka:	Podręcznik

Wydrukowane przez użytkownika:	Gość
Data:	wtorek, 7 stycznia 2025, 03:20

Opis

Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.

Wykłady W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu

1. Podstawy programowania matematycznego

Modelowanie matematyczne to pojemne pojęcie, które obejmuje zarówno szerokie pole narzędzi matematycznych, jak również duży wachlarz zastosowań. W tak ogólnym ujęciu nie sposób objąć tematyki w jednym, a zapewne nawet i w kilku kursach. W niniejszym kursie zawężamy pojęcie modelowania matematycznego do zagadnień związanych z podejmowaniem decyzji, a i to w zakresie głównie dotyczącym modeli liniowych ze zmiennymi ciągłymi i dyskretnymi. Kurs ma za zadanie przybliżyć tematykę z horyzontalnego punktu widzenia, tzn. ma zbudować w miarę szerokie podstawy wiedzy, ale nie koniecznie wnikać głęboko w szczegóły każdego z poruszanych obszarów. Ponad to, skupia on się na modelowaniu, a w mniejszym stopniu, lub wręcz pomija, aspekty algorytmiczne. Osoby zainteresowane algorytmiką odsyłamy do komplementarnego kursu „Metody optymalizacji dyskretnej”.

1.1. Wprowadzenie

Modelowanie matematyczne łączy świat matematyki z resztą świata. Budujemy modele matematyczne, aby odzwierciedlić pewną rzeczywistość, którą chcemy analizować. Z różnych powodów może to być atrakcyjne, a czasem wręcz jedyne możliwe, podejście do zagadnienia. Takim powodem mogą być konsekwencję zastosowania modeli matematycznych, czyli w rozważanym tutaj zakresie, konsekwencje podejmowanych decyzji. Przykładowo, buduje się modele matematyczne dotyczące optymalizacji rozkładu jazdy pociągów. Bez modelu matematycznego można próbować w praktyce pewne rozkłady i patrzeć jakie to przynosi ze sobą skutki, ale wówczas trzeba ponieść koszty prób decyzji dalekich od optymalnych. Co więcej, praca z obiektem rzeczywistym, na „żywym organizmie”, zamiast modelu matematycznego mogłaby nieść ryzyko wystąpienia kolizji pociągów. Budowanie harmonogramu jazdy pociągów w ramach modelu matematycznego pozwala na eliminację kolizji oraz optymalizację ustalony celów, np. kosztowych. Dopiero decyzje zweryfikowane w ramach symulacji z wykorzystaniem modeli matematycznych mogą przejść do etapu wdrożenia, eliminując w ten sposób wspomniane ryzyka.

Model matematyczny możemy przedstawić jako funkcję $F(x)$ , która przetwarza pewne wejście w wyjście, tak jak jest to zobrazowane na poniższym rysunku.

Punktem wyjścia jest pytanie, na które chcemy poznać odpowiedź. Pytanie to jest reformułowane do język matematyki, np. dokonujemy pewnego zakodowania problemu w postaci zmiennych, funkcji, grafów, itd. Następnie używamy narzędzi matematyki do znalezienia odpowiedzi. Ponieważ używamy języka matematyki to odpowiedź będzie również w nim wyrażona. Dlatego ostatnim krokiem jest translacja otrzymanego rozwiązania do pierwotnej domeny problemu.

Predykcja, identyfikacja i racjonalizacja

Jakie pytania możemy sobie zadawać względem modelu? Jeżeli mamy znany model matematyczny oraz znane są jego wejścia, zaś chcemy poznać wyjścia, tak jak pokazano to na poniższym rysunku

to mamy do czynienia z predykcją wyjścia na podstawie wejścia z użyciem modelu. Na przykład może to być predykcja generacji prądu elektrycznego dla zadanych prognoz pogodowych oraz modelu elektrowni wiatrowej.

Jeżeli zaś znane jest wejście oraz wyjście, to pytanie skupia się na tym jak powinien wyglądać model, który oddaje relację wyjścia od wejście.

Takie zadanie nazywamy zadaniem identyfikacji, gdyż chcemy zidentyfikować model najlepiej odpowiadający relacji pomiędzy wyjściem a wejściem.

Możliwa jest też sytuacja, w której znany jest model oraz wyjście, zaś nie znamy wejścia:

Wyjście należy rozumieć jako pożądane wyjścia, a wówczas pytanie dotyczy tego jako powinniśmy przyłożyć wejścia, aby uzyskać pożądaną sytuację na wyjściu. Wyjście może być zdefiniowane w sposób bezwzględny, ale w szczególności możemy oczekiwać wyjścia jak największego lub jak najmniejszego. Przykładowo, jeżeli na wyjściu są koszty, to możemy szukać takiego wejścia, które będzie minimalizować owe koszty. Omawiane podejście polega na racjonalizacji decyzji na wejściu, tak aby osiągnąć pożądane (racjonalne) wyjście. Dlatego mówimy, że mamy to do czynienia z zadaniem racjonalizacji.

Zauważmy, że o ile predykcja jest często kojarzona z domeną uczenia maszynowego, identyfikacja zaś często jest domeną teorii sterowania (oczywiście oba obszar nie są ograniczone tylko do tych dziedzin). Gdzie zaś w naukach lokuje się zazwyczaj racjonalizacja? Otóż, w dziedzinie Badań operacyjnych (BO).

Badania operacyjne (Operations research, OR) to interdyscyplinarna dziedzina, która zajmuje się wykorzystaniem metod ilościowych do poszukiwania jak najlepszych decyzji. Decyzje często są związane z pieniędzmi, wydatkami, kosztami, stąd znacząca rola ekonomii w badaniach operacyjnych. Ale decyzje są związane z ludźmi, ludzie je podejmują i finalnie dotyczą ludzi. Dlatego nie bez znaczenia dla badań operacyjnych jest np. psychologia czy socjologia. Jednak podstawowym narzędziem są modele matematyczne oraz algorytmika – czyli matematyka i informatyka. Namacalnym produktem łączącym poszczególne elementy są informatyczne systemy wspomagania decyzji. Wreszcie, badania operacyjne znajdują zastosowania w bardzo wielu dziedzinach i muszą uwzględnia i wykorzystywać również wiedzę dziedzinową. Ta możliwość zastosowania ogólnych metod badań operacyjnych w tak wielu odległych od siebie praktycznych obszarach jest czasem subiektywnie oceniania jako cenny walor dziedziny. Badania operacyjne można więc sprowadzić do następującej nieformalnej definicji: dyscyplina wykorzystująca modele i narzędzia matematyki i informatyki z uwzględnieniem aspektów ekonomii i psychologii podejmowanych decyzji, ukierunkowania na wytwarzanie narzędzi informatycznych wspomagających decydentów w podejmowaniu decyzji. Mimo interdyscyplinarnego charakteru, badania operacyjne ze względu na kluczowe aspekty algorytmiki i zagadnienia złożoności obliczeniowej są zazwyczaj umiejscawiana w dyscyplinie informatyki.

Na koniec tego podrozdziału chcielibyśmy zwrócić uwagę na definicję badań operacyjnych wg MIT, według której jest to dyscyplina dotycząca zastosowań zaawansowanych analitycznych metod, takich jak optymalizacja, statystyka, uczenie maszynowe, probabilistyka, do podejmowania lepszych decyzji, które mają pozytywny wpływ na społeczność i świat. Ważnym elementem tej definicji jest aplikowalność/stosowalność – badania operacyjne mają rozwiązywać rzeczywiste problem. Równie ważnym jest pewna społeczna odpowiedzialność za którą idzie poczucie kreowania lepszego świata, co np. odzwierciedla się w wielu działaniach na rzecz ubóstwa (optymalizacja dystrybucji dóbr), sprawiedliwości, czy ochrony środowiska.

1.2. Badania operacyjne vs sztuczna inteligencja

Przez wiele lat środowisko badań operacyjnych rozwijało się w pewnej separacji od środowiska sztucznej inteligencji, co przejawiało się oddzielnymi konferencjami, czasopismami, czy zespołami naukowymi. Należy jednak wspomnieć, że obszar taki jak np. systemy ekspertowe w ramach tzw. starej dobrej sztucznej inteligencji, był postrzegany przez środowisko badań operacyjnych jako obszar przynależny do BO. Dziedziny te więc czerpały od siebie nawzajem (uczenie to przecież nic innego jak optymalizacja decyzji!) pozostając w pewnej separacji, co skutkuje dziś pewnym dysonansem pojęciowym. W niniejszym podrozdziale zaproponujemy choć częściowe zmniejszenie owego dysonansu.

Można postawić hipotezę zgodnie z którą badania operacyjne są częścią dziedziny sztucznej inteligencji. Dziedzina ta zajmuje się konstrukcją systemów przejawiających inteligentne zachowania. Inteligentne planowania, podejmowanie decyzji w oparciu o modele ilościowe leży w naturze badań operacyjnych, a zatem mogłyby być traktowane jako część sztucznej inteligencji.

Z drugiej strony można powiedzieć, że dziedzina sztuczna inteligencja jest częścią badań operacyjnych. Badania operacyjne to dziedzina zajmująca się zastosowaniem matematyki i informatyki do tworzenia lepszych decyzji, a przecież temu finalnie służą metody sztucznej inteligencji. Być może zatem, należałoby przyjąć, że badania operacyjne są komplementarne do sztucznej inteligencji. W wielu sytuacjach wykorzystuje się narzędzia sztucznej inteligencji do predykcji danych, które następnie są danymi wejściowymi dla modeli badań operacyjnych. Z drugiej strony metody optymalizacji rozwijane w obszarze badań operacyjnych są jednym z podstawowych komponentów w wielu narzędziach sztucznej inteligencji.

Ze względu na brak formalnych definicji dziedzin, a nawet brak jednomyślności w zakresie nieformalnych definicji, nie jest obecnie możliwe rozstrzygnięcie dylematu. Jednak, jednym z interesujących podejść porządkujących oba świat jest interpretacja przyjęta na poniższym rysunku

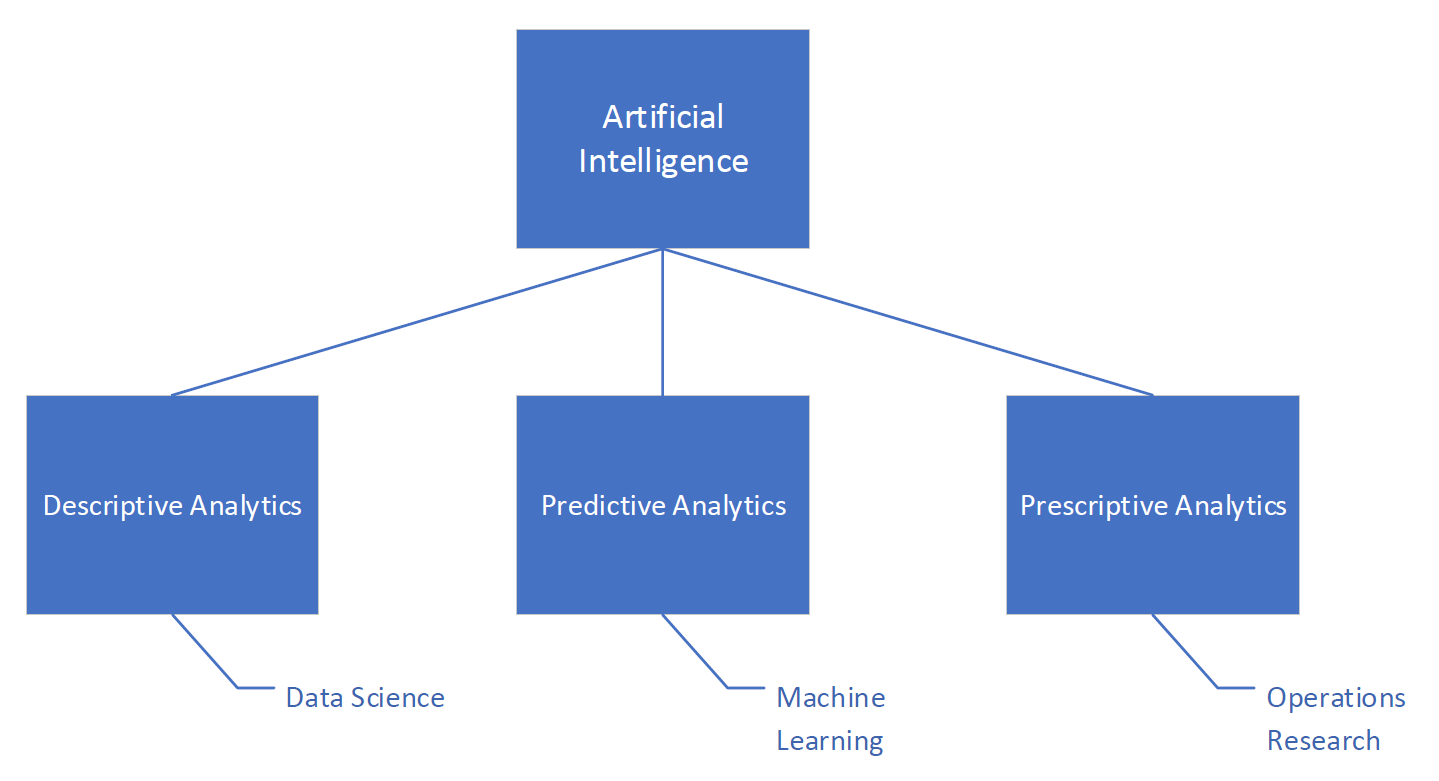
Ogólnie rozumianą sztuczną inteligencję można podzielić na trzy obszary. Pierwszy obszar dotyczy analityki deskryptywnej, gdzie dominują rolę odgrywa Data Science. Obszar drugi, analityka predykcyjna, to domena uczenia maszynowego. Zaś badania operacyjne dominują w obszarze analityki preskryptywnej, inaczej „nakazowej”. W tym obszarze wyznacza się sugestie (nakaz, zalecenie) jakie kroki i decyzje należy podjąć, aby uzyskać postawione cele. Należy zauważyć, że podział nie jest ostry i niektóre sytuacje mogą prowadzić do rozwiązań pośrednich.

Nieco inne ujęcie zagadnienia, przedstawia poniższy rysunek:

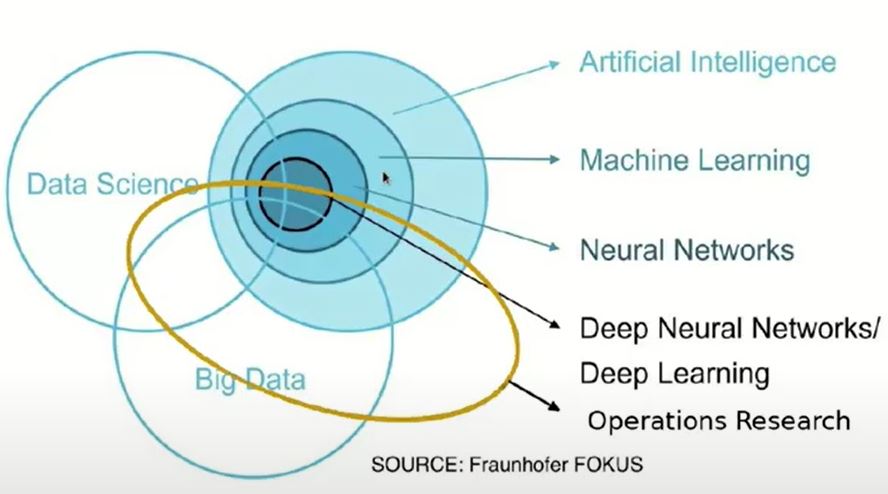
Jak widać badania operacyjne są tu zlokalizowane na wskroś poszczególnych obszarów sztucznej inteligencji, Bid Data i Data Science.

Na koniec chcieliśmy zauważyć, że jednym z najbardziej obiecujących bieżących trendów w badaniach operacyjnych jest ich ścisłe połączenie z metodami sztucznej inteligencji, szczególnie uczenia maszynowego. Prowadzi to do koncepcji hybrydyzacji badan operacyjnych i uczenia maszynowego, która może przybierać różne formy. W jednym z podejść metody uczenia maszynowego i badań operacyjnych mogą są widziane dla siebie nawzajem jako czarne skrzynki. Przykładowo, metody uczenia maszynowego znajdują pewne rozwiązania wstępne, które następnie są optymalizowane metodami badań operacyjnych. Uczenie maszynowe może być również wykorzystanie do poprawy algorytmów badań operacyjnych, np. do wyboru właściwych heurystyk w danym kontekście. Również metody badań operacyjnych mogą być wykorzystane do poprawy metod uczenia maszynowego, np. dzięki zaawansowanym algorytm optymalizacji.

1.3. Metodyka badań operacyjnych

Metodyka badań operacyjnych składa się z kilku kroków przedstawionych na poniższym rysunku:

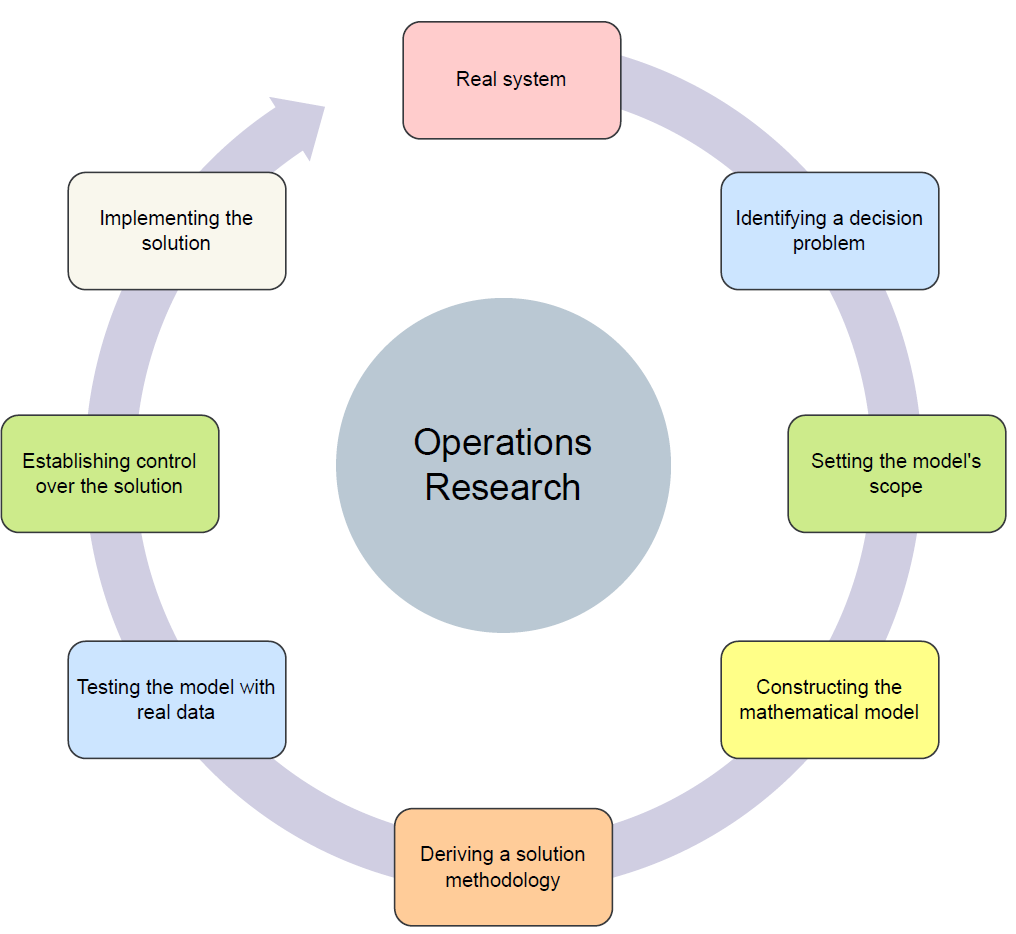
Na początku następuje identyfikacja problemu, która często wymaga udziału ekspertów dziedzinowych, potencjalnych użytkowników i może być pewną analogią do procesu gromadzenia wymagań w inżynierii oprogramowania. Następnie ustalany jest zakres modelu, w szczególności co będzie uwzględnione, a co będzie wykluczone oraz jakie są założenia. Kolejny krok to budowa modelu matematycznego. Istotne jest rozróżnienie sformułowania matematycznego problemu od określenia metody rozwiązania, która jest dopiero w olejnym kroku. Mając model i algorytmy, kolejny rok polega na weryfikacji rozwiązania z danymi rzeczywistymi. W przypadku potwierdzenia zasadności rozwiązania jest ono wdrażane do procesów biznesowych, a następnie w pełni implementowane. W ten sposób cykl metodyki zamyka się rzeczywistym systemem, który można obserwować i oceniać sposób jego funkcjonowania. Oczywiście jest to ogólny schemat i w rzeczywistości często mogą pojawić się nawroty lub pewne przeskoki. Tym niemniej metodyka stanowi pewien wyznacznik dla sposobu postępowania.

1.4. Wypukłość w optymalizacji

Wprowadzimy teraz serię podstawowych pojęć, w szczególności związanych z wypukłością, która jest niezmiernie ważna w problemach optymalizacji.

Problem decyzyjny – jest to problem, który odpowiada tak/nie na postawione pytanie, np. mając dwie liczby

$x$ i

$y$ , czy

$x$ jest dzielnikiem

$y$ ?

Problem funkcyjny – problem, w którym odpowiedź może być bardziej złożona i przyjmuje wartość pewnej funkcji, np. mając dwie liczby

$x$ i

$y$ , jaki jest wynik dzielenia

$y$ przez

$x$ ?

Problem optymalizacyjny – problem polegający na wyszukaniu najlepszej odpowiedzi, np. mając dwie liczby

$x$ i

$y$ , wyznaczyć największy wspólny dzielnik.

Złożoność obliczeniową problemów definiujemy w ramach klas złożoności.

Klasa P – problemy rozwiązywalne w czasie wielomianowym (na maszynie Turinga)
Klasa NP – problemy weryfikowalne w czasie wielomianowym na maszynie Turing, a rozwiązywalne w czasie wielomianowym na niedeterministycznej maszynie Turinga (maszynie z wyrocznią)
Klasa NP-zupełnych – problemy z NP., takie, że dowolny problem z NP może być zredukowany do problemu w klasie NP-zupełnej w czasie wielomianowym.
NP-trudny – problem co najmniej tak trudny jak każdy problem z klasy NP (ale potencjalnie jeszcze trudniejszy)

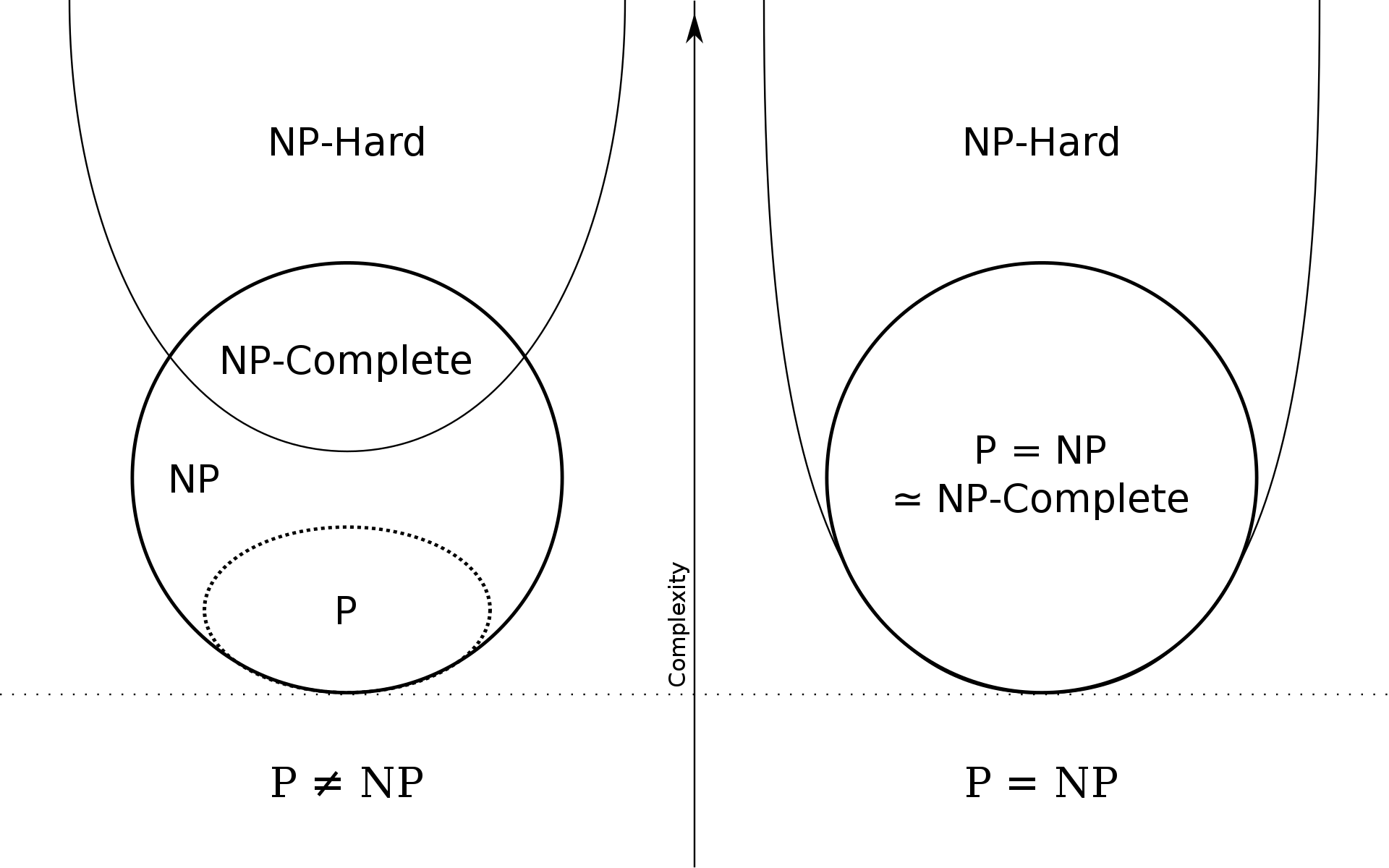
źródło: wikipedia

Optymalizacja (programowanie matematyczne)

$\min_x f(x)$
p.o.

$x \in \mathcal{F}$

Skrót “p.o” należy czytać „przy ograniczeniach”. W modelu $x \in \mathbb{R}^n$ to zmienne decyzyjne. Zmienne $x$ mogą być ciągłe lub dyskretne. $\mathcal{F} \subset \mathbb{R}^n$ to zbiór rozwiązań dopuszczalnych. Jego opis może przyjmować postać zbioru funkcji liniowych lub zbiór funkcji wypukłych. W niektórych sytuacjach może nie być podany jawnie, a np. być dostępny przez algorytm/symulacje. Funkcja celu to $f:\mathcal{F} \mapsto \mathbb{R}$ .

Tak ogólnie postawiony problem może być trudny do rozwiązania, a czasem nawet znalezienia rozwiązania dopuszczalnego jest kłopotliwe. Dlatego szczególnie interesuje nas znajomość przynależności danego problemu/modelu do klasy problemów, które mogą być efektywnie rozwiązywane. Do problemów łatwych należy zaliczyć np. zadania programowania liniowego (ze zmiennymi ciągłymi) oraz modele sieci przepływowych. Są to przykłady problemów wypukłych (lub możliwych do uwypuklenia). Generalnie optymalizacja wypukła jest zadaniem, które można efektywnie rozwiązać. Stąd ważkość zagadnienia wypukłości, którą dalej poruszamy.

Zbiór wypukły – jeżeli dla dwóch dowolnych punktów zawartych w zbiorze, odcinek łączący te punkty również zawiera się w zbiorze.

Przyładowy zbiór wypukły:

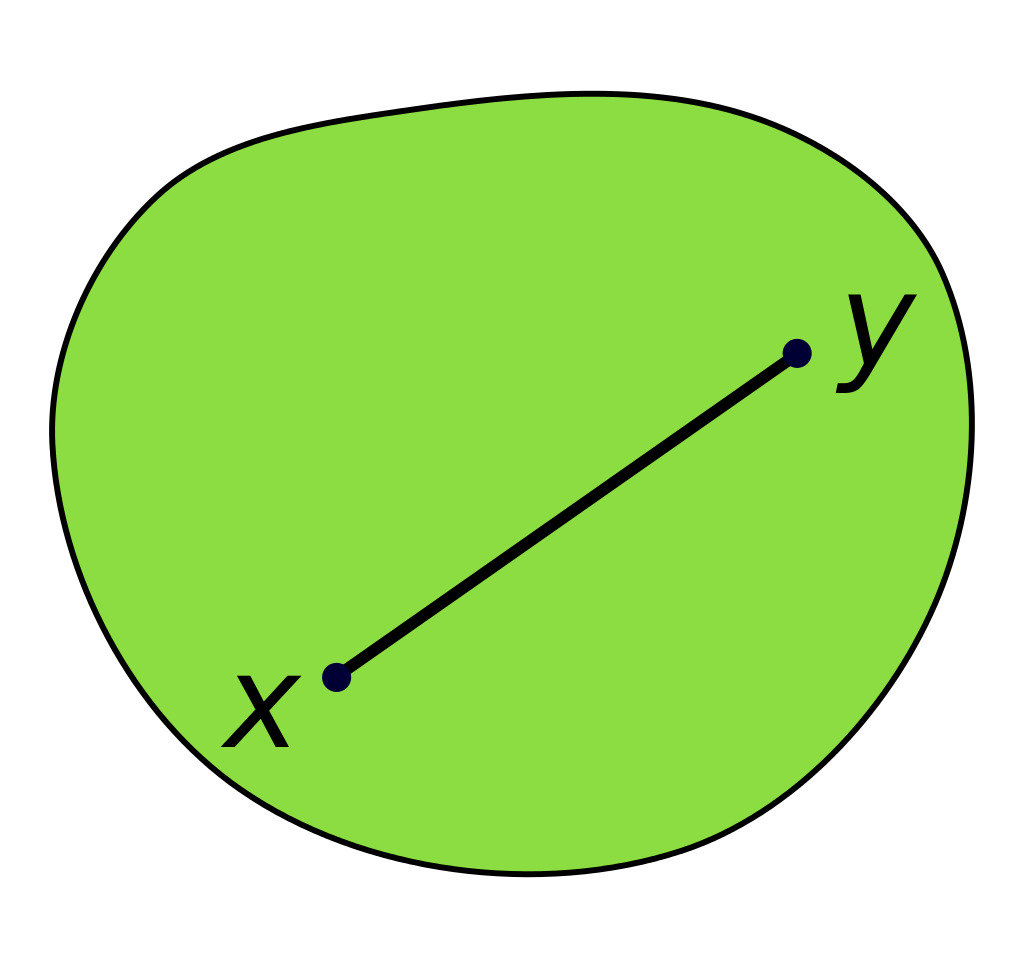
Oraz przykład zbioru niewypukłego:

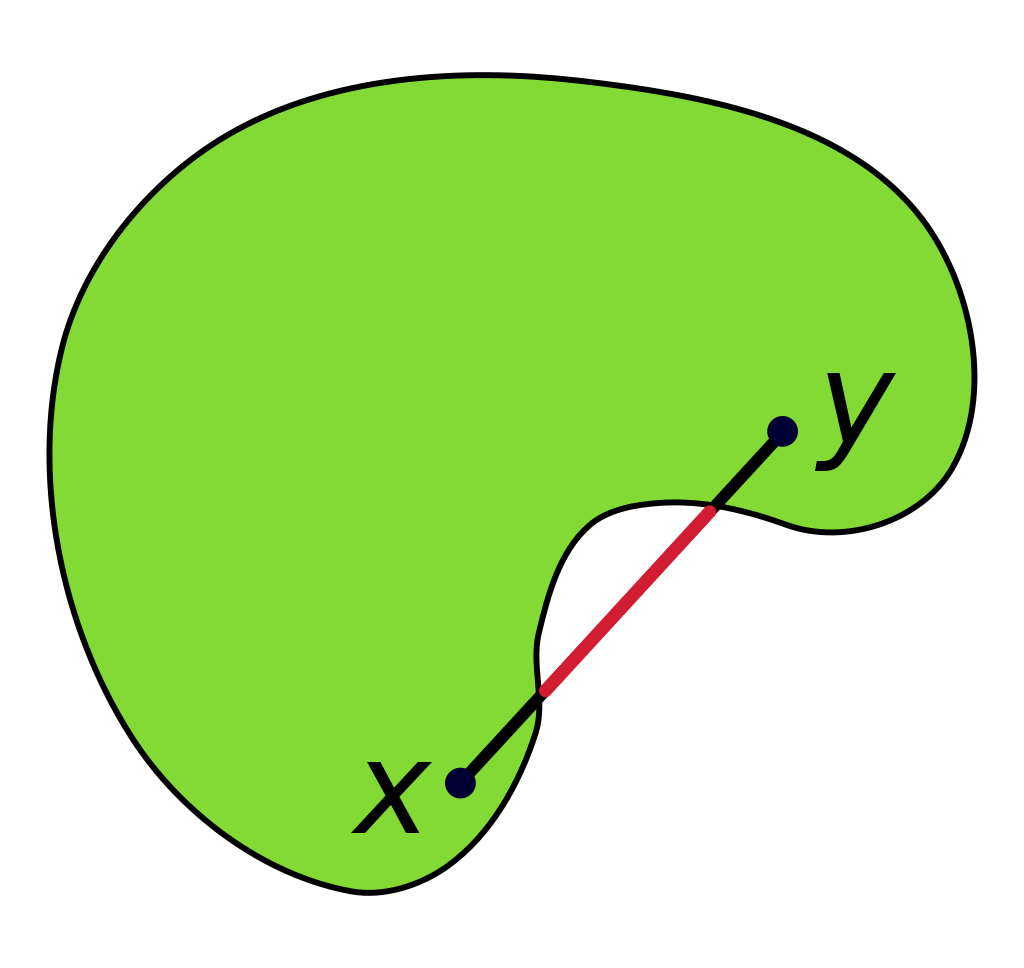
Przykłady innych zbiorów wypukłych:

Odcinek

Prosta

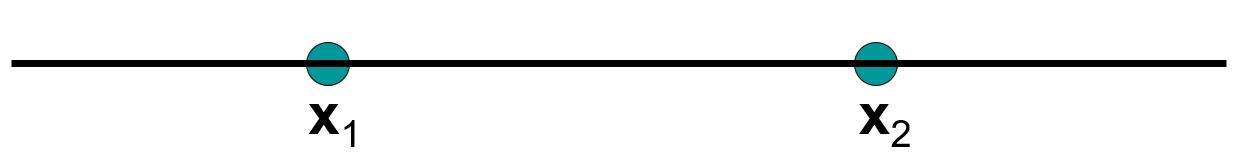
Hiperpłaszczyzna

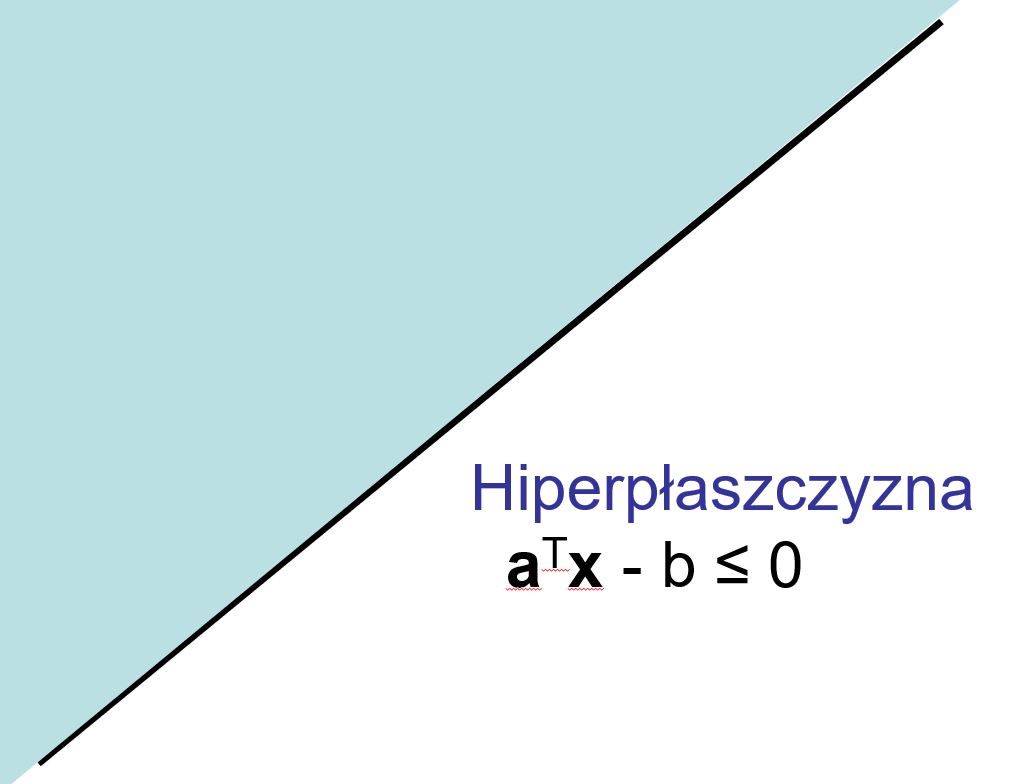
Stożek

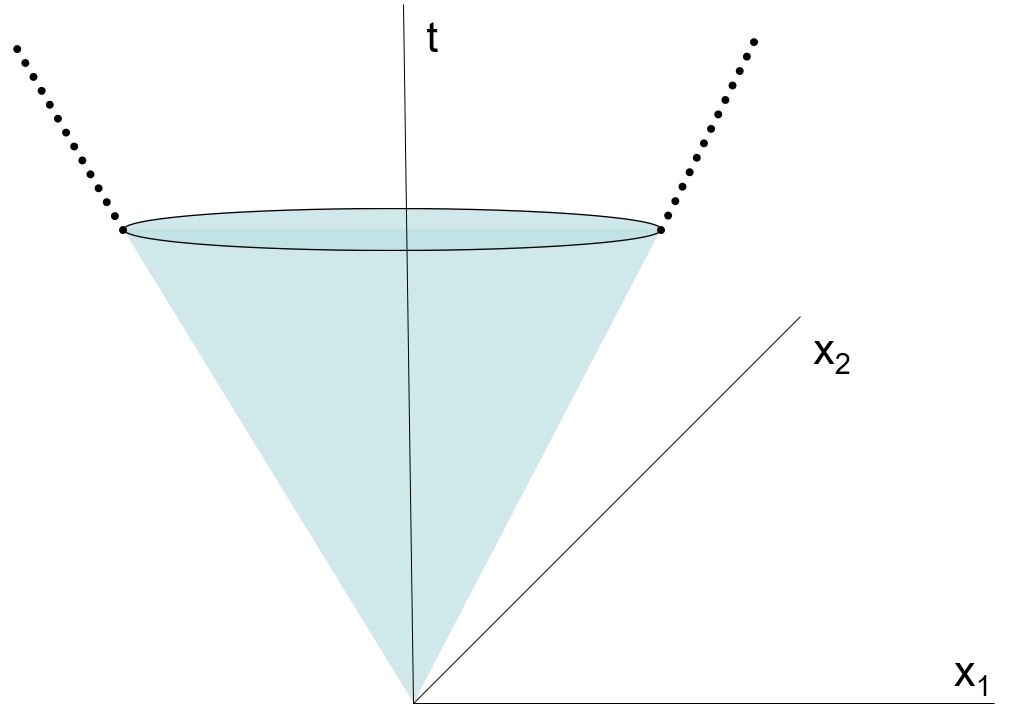
Niektóre operacja na zbiorach mogą zachowywać wypukłość. Przykładowe operacje zachowujące wypukłość:

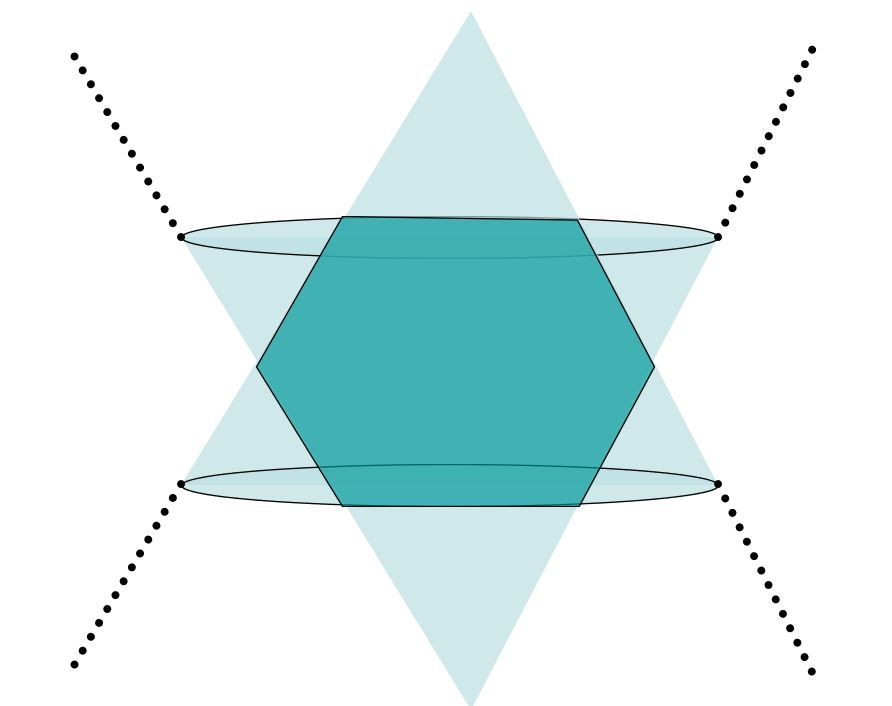
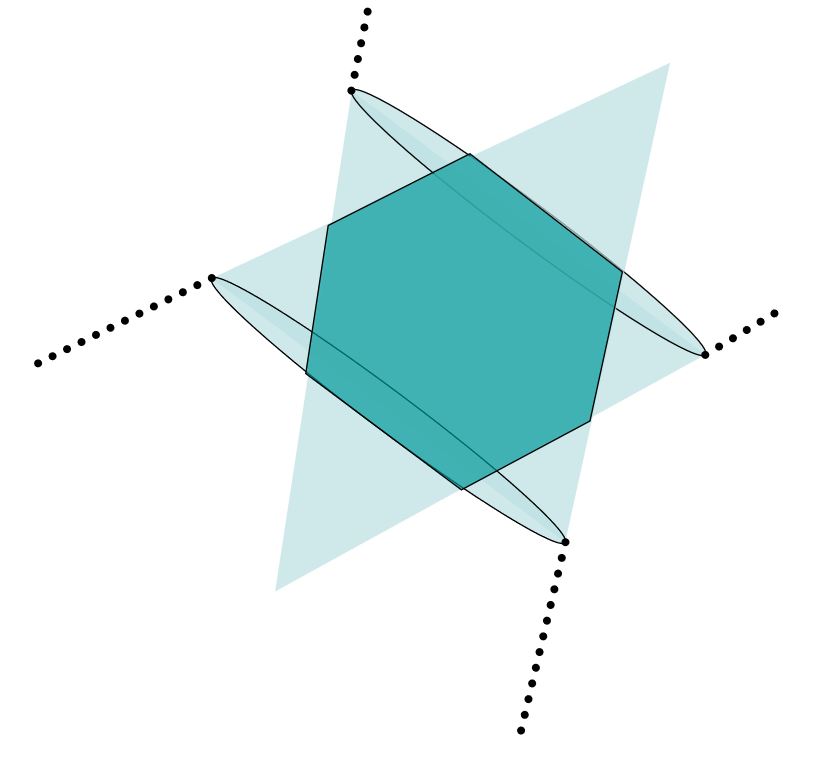
Przecięcie zbiorów

Przekształcenie afiniczne $x \longmapsto Ax + b$

Otoczka wypukła zbioru

$X$ to najmniejszy zbiór wypukły zawierający

$X$ .

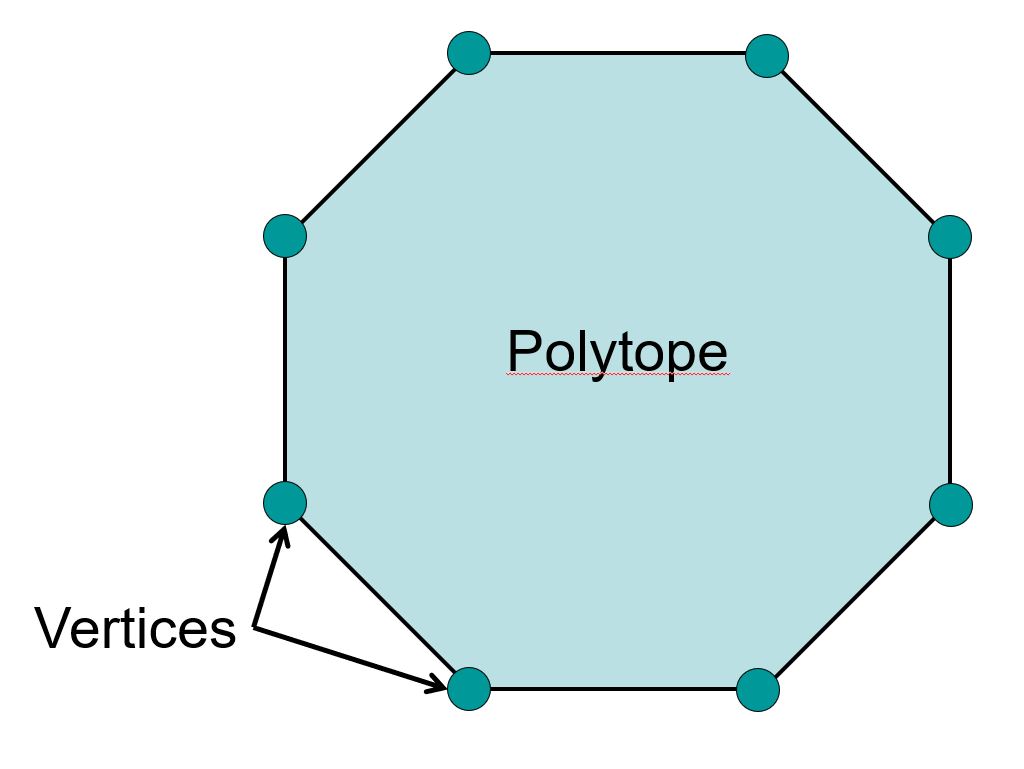
$\texttt{conv } X = \bigcap\{M: X\subset M \wedge M \texttt{ jest wypukły}\}$

Otoczka wypukła jest szczególnie ważna w przypadku zbiorów dyskretnych

Funkcja $g: X \longrightarrow \mathbb{R}$ określona na zbiorze wypukłym $X$ jest wypukła, jeżeli dla każdego $0 \leq t \leq 1$ i $x_1, x_2 \in X$ spełniona jest nierówność

$g(tx_1+(1-t)x_2) \leq tg(x_1)+(1-t)g(x_2)$ , co obrazuje poniższy obrazek

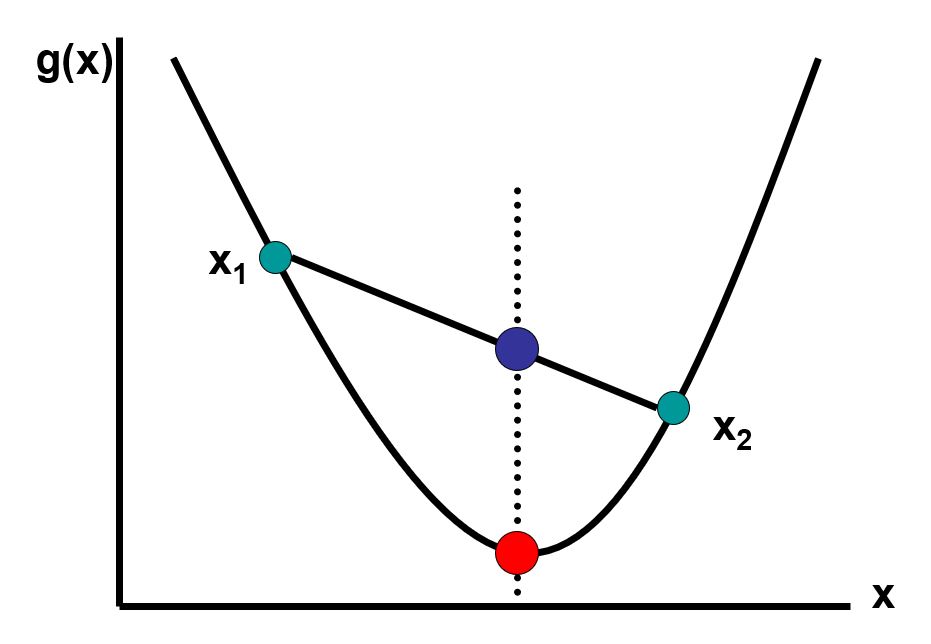
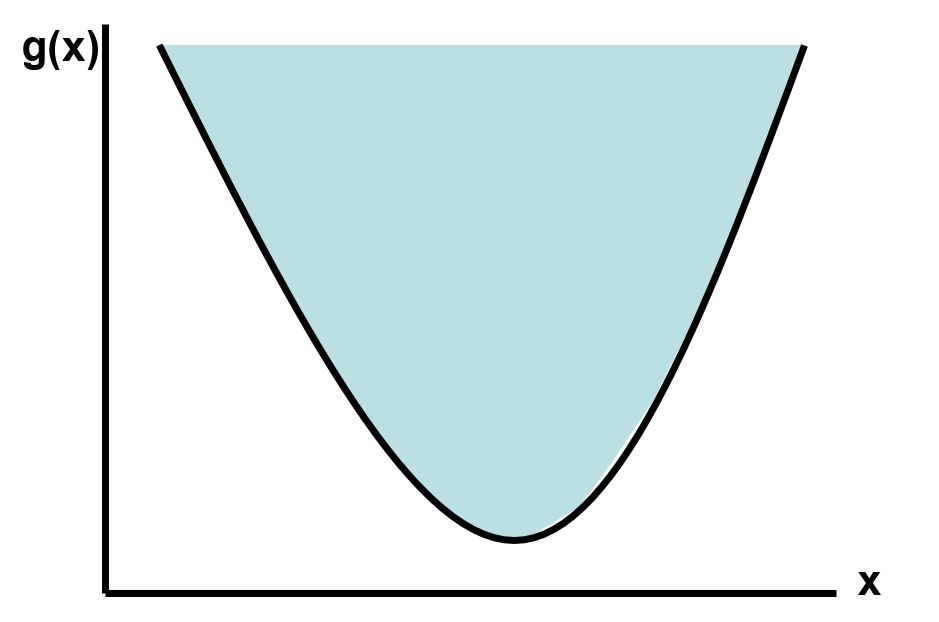
Funkcja jest wypukła, jeżeli jej nadgrafik jest zbiorem wypukłym:

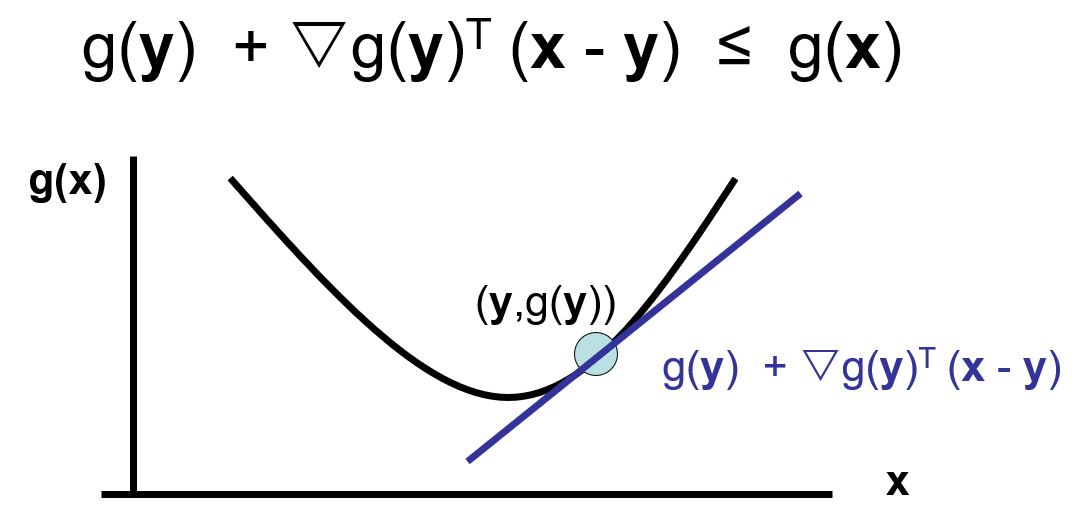
Równoważnie można powiedzieć, że funkcja jednokrotnie różniczkowalna jest wypukła jeżeli zachodzi poniższy warunek:

Zaś dla funkcji podwójnie różniczkowalnej musi zachodzić następujących warunek dla hesjanu:

$H(x) \succeq 0$

Istnieją operacje, które zachowują wypukłość.

Nieujemna suma ważona:

Maksimum funkcji

Optymalizacja wypukła
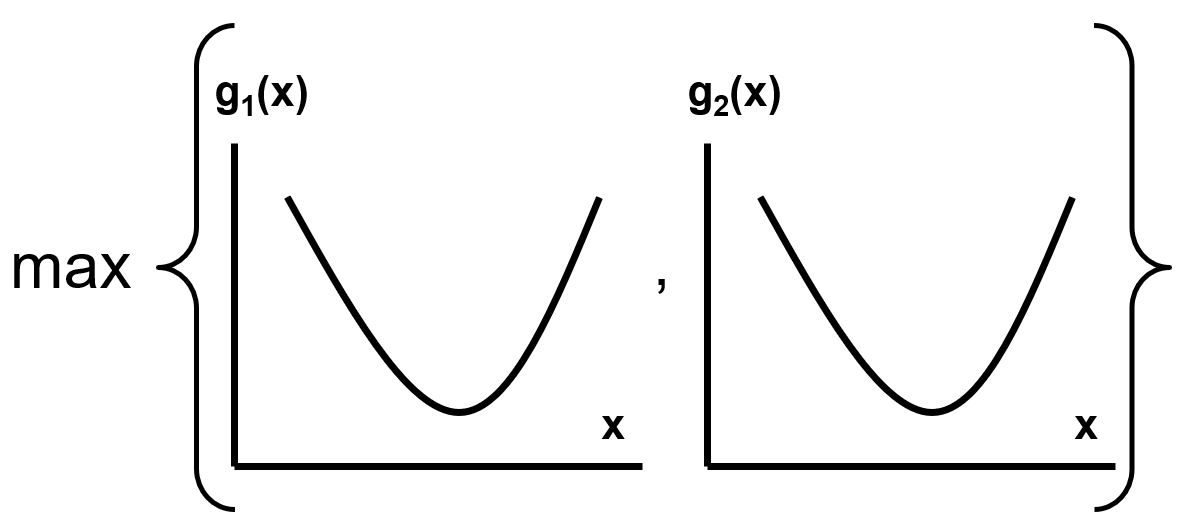
Funkcja celu wypukła i zbiór rozwiązań dopuszczalnych wypukły.

$\min f_0(x)$
p.o.

$f_i(x) \leq 0, \qquad i=1,\ldots,m$

$a^T_ix=b_i, \qquad i=1, \ldots, p$
gdzie

$f_0, f_1, \ldots, f_m$$ są wypukłe, a ograniczenia równościowe afiniczne.

Dla optymalizacji wypukłej lokalne optimum jest również optimum globalnym.

2. Modelowanie zależności

Zadania programowania liniowego.

2.1. Wstęp do programowania liniowego

Programowanie liniowe (PL) to zadanie optymalizacji z ograniczeniami, w którym zależności między zmiennymi należącymi do zbioru liczb rzeczywistych, a parametrami są liniowe. Zadania optymalizacji są opisywane przez dwa rodzaje funkcji: funkcję celu i zbiór ograniczeń, zatem zadania PL są opisywane przez liniową funkcję celu i zbiór ograniczeń liniowych, w których występują zmienne rzeczywiste, ciągłe.

Formułowanie zadań w postaci PL ma bardzo duże znaczenie, ponieważ ciągłość i zależności liniowe gwarantują wypukłość zbiorów rozwiązań, a to z kolei pozwala na zastosowanie efektywnych algorytmów znajdowania optimum. W praktyce jednak mogłoby się wydawać, że rzeczywiste problemy bardzo rzadko są liniowe. Czy programowanie liniowe, poza teoretycznymi pozytywnymi właściwościami ma zatem znaczenie praktyczne? Otóż dwa główne argumenty stoją za tym, aby modelowaniu zależności liniowych poświęcić uwagę:

są liczne klasy zadań, dla których zależności między zmiennymi można ująć w sposób liniowy, również w sytuacjach, w których pozornie zdawałoby się, że nie wystarczą same funkcje liniowe i zmienne ciągłe;
są liczne algorytmy rozwiązywania nieliniowych, lub nieciągłych problemów optymalizacji, które w procesie poszukiwania optimum opierają się na wynikach modeli liniowych.

Celem kolejnych podrozdziałów jest przedstawienie najważniejszych technik modelowania liniowego, interesujących sformułowań przykładowych problemów oraz koncepcji dualności, nierozłącznie wiążącej się z programowaniem liniowym.

Na początek należy w sposób formalny przedstawić zapis zadań PL.

Postać kanoniczna zadania PL jest formułowana dla

$n$ zmiennych ciągłych

$x= (x_1,..., x_n) \in R^n$ jako problem minimalizacji funkcji celu:

$\min_x f(x) = c^T x$ przy ograniczeniach

$Ax \geq b, x\in R^n$ .

Często spotykamy też zapis zadań PL w postaci standardowej, w której dodatkowo wymaga się, aby wszystkie zmienne były nieujemne.

Postać standardowa zadania PL jest formułowana dla nieujemnych zmiennych ciągłych jako problem minimalizacji funkcji celu:

$\min_x f(x) = c^T x$ przy ograniczeniach

$Ax \geq b, x\geq 0$ .

Innym, czasami spotykanym sposobem zapisu zadań PL jest formułowanie problemu w postaci dopełnieniowej, w której do każdego ograniczenia jest wprowadzana jedna pomocnicza zmienna dopełniająca, która niejako reprezentuje zapas ograniczenia dla rozwiązania dopuszczalnego.

Postać dopełnieniowa zadania PL formułuje problem minimalizacji funkcji celu:

$\min_x f(x) = c^T x$ korzystając z nieujemnych zmiennych pomocniczych przy zapisie ograniczeń równościowych

$Ax-x^ \prime=b,\, x^ \prime\geq 0$ .

Czy jednak każdy problem PL można zapisać w równoważnej, np. standardowej postaci? Rozważmy kolejne sytuacje, w których nasze sformułowanie odbiegałoby od postaci standardowej:

problem jest zadaniem maksymalizacji, a nie minimalizacji; wystarczy wtedy zapisanie funkcji celu z przeciwnym znakiem: $\max_x c^Tx \Leftrightarrow -\min_x c^Tx$
ograniczenia są postaci równościowej (przypadek z odwrotnym skierowaniem ograniczeń jest trywialny); wystarczy wtedy zapisanie ograniczeń w postaci pary ograniczeń nierównościowych: $Ax=b \Leftrightarrow Ax \geq 0, Ax\leq 0$
zmienne należą do całej przestrzeni liczb rzeczywistych; wystarczy wtedy zastąpić każdą zmienną rzeczywistą różnicą między zmiennymi nieujemnymi, takimi że pierwsza reprezentuje wartość dodatnią zmiennej, a druga ewentualną wartość ujemną: $x\in R^n \Leftrightarrow x=x^+ - x^-,\; x^+\geq 0, x^-\geq 0$ .

Szczególnie ten trzeci sposób jest wart uwagi, gdyż zastępowanie zmiennej przez parę nieujemnych zmiennych to jedna z dwóch podstawowych technik stosowanych w modelowaniu zadań PL. Zanim jednak przejdziemy do tej części, rozwiążmy przykład ilustracyjny.

Zapisać poniższe zadanie LP w postaci standardowej i przedstawić dane dla tej postaci w formie macierzowej.

$\max x_1 +3x_2-4x_3+x_5$

$\begin{matrix} x_1 &+ x_2&&- x_4&&\geq 10\\ 7x_1 &&+ 3x_3&&+x_5&= 10\\ x_1 &&&&-x_5&\leq 0\\ &x_2&&+x_4&&\leq 15 \end{matrix} \\ x_1, x_2, x_3\geq 0,\; x_4 , x_5 \text{ swobodne}$

Rozwiązanie. Stosujemy techniki podane w punktach 1, 2 i 3 i zapisujemy zadanie w postaci:

$\min -x_1 -3x_2+4x_3-x^+_5+x^-_5$

$\begin{matrix} x_1 &x_2&&- x^+_4&+ x^-_4&&&\geq& 10\\ 7x_1 &&+ 3x_3&&&+x^+_5&-x^-_5&\geq& 10\\ -7x_1 &&- 3x_3&&&-x^+_5&+x^-_5&\geq& -10\\-x_1 &&&&&-x^+_5&+x^-_5&\geq& 0\\ &-x_2&&-x^+_4&+x^-_4&&&\geq& -15 \end{matrix} \\ x_1, x_2, x_3,x^+_4 , x^-_4,x^+_5 , x^-_5\geq 0$

Wtedy odpowiednie wektory i macierze zadania PL mają postać:

$c^T=[-1, -3, 4, 0, 0, -1, 1 ]$

$A= \left| \begin{matrix} 1 & 1&&-1&1\\ 7&&3&&&1&-1\\ -7&&-3&&&-1&1\\-1 &&&&&-1&1\\ &-1&&-1&1&& \end{matrix} \right|\; b= \left| \begin{matrix} 10\\ 10\\ -10\\ 0\\ -15\end{matrix} \right|$

Jak zmieni się zapis powyższego zadania LP w postaci standardowej, gdy przyjmiemy, że to zmienne

$x_1, x_2, x_3$ są zmiennymi swobodnymi, a

$x_4, x_5$ są nieujemne? Jak zmieni się postać odpowiednich wektorów i macierzy zadania PL?

W kolejnym podrozdziale skupimy się na dwóch podstawowych wariantach problemów nie posiadających standardowej liniowej postaci, które jednak można przekształcić w równoważny problem liniowy. Przedstawione metody modelowania zależności liniowych sprowadzają się do:

wprowadzenia do zadania dodatkowych zmiennych,
oraz wprowadzenia dodatkowych ograniczeń odnoszących się do nowych zmiennych.

2.2. Techniki dla prostych zależności nieliniowych

W wielu przypadkach pierwotny problem optymalizacji nie ma standardowej liniowej postaci, ale można go bezpośrednio przekształcić w równoważny problem liniowy. Są to problemy typu:

minmax, czyli minimalizacja największej wartości,
wartość bezwględna, występująca często, gdy koszty są ponoszone, gdy wynik w jakiś sposób powoduje powstanie odchyłki od wartości bazowej, np. wynoszącej zero.

Problem minmax to zadanie optymalizacji z funkcją celu minimalizującą największą z możliwych do osiągnięcia wartości, tj. problem postaci:

$\min \max_i x_i,$

p.o.:

$Ax \geq b, \; x \geq 0.$

Na przykład, w zadaniu harmonogramowania operacji kryterium może być minimalizacja czasu ukończenia całego przedsięwzięcia. Optymalny plan może się różnić od uzyskanego w przypadku przyjęcia innego kryterium, np. dla kryterium minimalizacji średniego czasu ukończenia zadań. Inne typowa sytuacja, w której stosuje się funkcję celu minmax, to dążenie do osiągnięcia jak najbardziej sprawiedliwego rozwiązania, czyli takiego, w którym indywidualne miary zadowolenia są możliwie równe - nie ma między nimi dużych skrajności.

Problem minmax sprowadzamy do postaci PL poprzez:

wprowadzenie dodatkowej zmiennej $y$ reprezentującej minimalizowaną wartość, czyli:
$\min \max_i x_i = \min y$
ograniczenie tej zmiennej od dołu:
$y\geq x_i, \forall i.$

Zauważmy, że w powyższym sposobie korzystamy z tego, że zmienna

$y$ jest minimalizowana, a więc w optimum będzie de facto równa największej z wartości

$x_i$ - mniejsza nie może być, jeśli ma być spełnione ograniczenie, a „nie opłaca się” aby była większa.

Pokazany sposób przeformułowania można zastosować do każdego problemu, który ma funkcję celu typu minmax. Działa on również w przypadku analogicznego celu maxmin, z maksymalizacją zamiast minimalizacji i przy ograniczeniach

$y\leq x_i, \forall i.$

Drugi rodzaj nieliniowej funkcji, którą można przedstawić w postaci zależności liniowych, to funkcja wartości bezwzględnej. Jak zostało wspomniane wcześniej, można się posłużyć takim samym sposobem, jak przy transformowaniu problemu z postaci kanonicznej do standardowej, czyli zastąpieniem zmiennej - czy w tym przypadku, funkcji, różnicą między nieujemnymi składnikami.

Wartość bezwzględną zmiennej

$|x|$ możemy przedstawić w sposób jawny jako sumę nieujemnych odchyłek na plus

$x^+$ i na minus

$x^-$ , czyli:

$\left|x\right| =x^+ + x^-,\;$

gdzie

$x =x^+ - x^-,\;$ oraz

$x^+ \geq 0,\; x^-\geq 0.$

Aby tylko jedna ze zmiennych

$x^+, x^-$ była niezerowa (i de facto równa

$|x|$ ) wystarczy, aby z wystąpieniem odchyłki wiązały się koszty, minimalizowane w funkcji celu.

Problem regresji liniowej. Rozważmy problem wyznaczenia współczynników

$a_j, b$ regresji liniowej, gdy dysponujemy

$m$ obserwacjami zmiennej

$y$ zależnej od

$n$ -wymiarowej zmiennej

$x$ . Szukamy funkcji zależności:

$y^k = \sum_{j=1}^n a_j x_j^k +b +\epsilon_k, \; \forall k = 1..m,$

gdzie

$\epsilon_k$ jest miarą braku dopasowania krzywej regresji od

$k$ -tej obserwacji. Wśród różnych metryk dopasowania krzywej regresji do danych szczególne znaczenie mają:

MAE - Mean Absolute Error (średni bezwględny błąd dopasowania), czyli: $\min\frac{1}{m} \sum_k|\epsilon_k|$
MAXAE - Maximum Absolute Error, czyli: $\min\,\max_k|\epsilon_k|$
RMSE, MSLE jako miary nieliniowe nie mogą być wyznaczane w zadaniach PL.

Zadanie PL wyznaczenia MAE. Stosując wyjaśniony wcześniej sposób otrzymujemy następujące sformułowanie problemu.

\begin{eqnarray} &&\min \frac{1}{m}\sum_k (\epsilon^+_k +\epsilon^-_k)\\ \epsilon^+_k -\epsilon^-_k&\geq&y^k-\sum_{j=1}^n a_jx^k_j-b,\;\;\;\forall k=1,\ldots, m,\\ &&\epsilon^+_k,\epsilon^-_k\geq 0. \end{eqnarray}

Zadanie PL wyznaczenia MAXAE. Dalej, łącząc oba poznane w tym rozdziale sposoby, otrzymujemy następujące sformułowanie problemu, w któym zmienna

$\Delta$ reprezentuje wartość maksymalnego błędu dopasowania.

\begin{eqnarray} &&\min \Delta\\ \epsilon^+_k -\epsilon^-_k&\geq&y^k-\sum_{j=1}^n a_jx^k_j-b,\;\;\;\forall k=1,\ldots, m,\\ \Delta &\geq &\epsilon^+_k +\epsilon^-_k,\;\;\;\forall k=1,\ldots, m,\\ &&\epsilon^+_k,\epsilon^-_k\geq 0. \end{eqnarray}

Zapisz w postaci PL problem minimalizacji czasu trwania całego przedsięwzięcia, składającego się z czterech niezależnych operacji A, B, C i D, gdzie każda

$i$ -ta operacja trwa

$p_i$ dni. Jedynym warunkiem jest ukończenie operacji A oraz B, zanim rozpocznie się wykonywanie operacji D.

2.3. Funkcje kawałkami liniowe

Wiele rzeczywistych problemów wymaga użycia bardziej złożonych funkcji kosztów, niż tylko prostych liniowych współczynników. Funkcje kawałkami liniowe mogą być wtedy interpretowane jako przybliżenia zależności nieliniowych, np. kwadratowych, wykładniczych, logarytmicznych, i in. Ponadto, funkcje tego typu mają zastosowanie jako funkcje kary, umożliwiające pewne naruszanie tzw. miękkich ograniczeń.

W sytuacji, gdy funkcja kawałkami liniowa, którą chcemy użyć w zadaniu spełnia warunek ciągłości i wypukłości, to odpowiedni model optymalizacji może być formułowany jako zadanie PL.

Funkcja kawałkami liniowa

$f(x)$ składa się z

$i\in I$ liniowych odcinków, z których każdy można opisać odpowiednią funkcją liniową:

$f_i(x)=a_ix+b_i$ , gdzie

$a_i$ jest współczynnikiem nachylenia

$i$ -tego odcinka, a

$b_i$ jest współczynnikiem przesunięcia.

Funkcja jest wypukła, gdy współczynniki

$a_i$ dla kolejnych odcinków są niemalejące:

$a_i\leq a_{i+1}$ .

Przykładową funkcję kosztów produkcji, przybliżoną funkcją kawałkami liniową przedstawia poniższy rysunek.

Zauważmy, że wypukłość funkcji powoduje, że prawdziwa jest zależność:

$f(x)= \max_i f_i(x)$ , czyli przy minimalizacji kosztów mamy do czynienia z problemem typu minmax, który wyjaśniliśmy w poprzednim podrozdziale!

Stąd, stosując bezpośrednio technikę zamiany problemu minmax na zapis PL, możemy przedstawić odpowiedni zapis PL dla zadania, w którym występują funkcje kawałkami liniowe.

Minimalizacja funkcji kawałkami liniowej w zadaniu PL wymaga wprowadzenia dodatkowej zmiennej, symbolizującej wartość funkcji w konkretnym odcinku liniowym:

$\min f(x)= \min \max_i\{ a_ix+b_i\} \equiv \min y$

a następnie wprowadzenia tej zmiennej do ograniczeń :

$y \geq a_ix+b_i,\;\forall i.$

Zauważmy przy tym, że rozważana wcześniej funkcja wartości bezwzględnej jest, de facto, funkcją kawałkami liniową. To prowadzi do równoważnego sformułowania problemu z wartością bezwzględną.

Innym sposobem na zapisanie w sposób liniowy

$|x|$ jest spostrzeżenie że:

$f(x) = |x| = \max\{x, -x\}$

czyli możemy zastąpić tą wartość nową zmienną

$y$ , powiązaną z pierwotną zmienną

$x$ ograniczeniami:

$y \geq x,$

$y \geq -x$ .

W zależności od konkretnego problemu, może być bardziej wygodne użycie pierwszego (przedstawionego w poprzednim podrozdziale), lub drugiego sposobu na przedstawienie wartości bezwzględnej, co pokażemy w poniższym przykładzie.

Niepewność współczynników macierzy $A$ . Załóżmy, że w zadaniu

$\{\min_x \mathbf{c}^T x, \mathbf{A}x \geq \mathbf{b}\}$ , współczynniki macierzy

$A$ nie mogą być wyznaczone w sposób dokładny. Oznaczmy je jako

$\tilde{a}_i$ , zatem problem ma postać:

$\min\sum_i c_ix_i,$ p.o.:

$\sum_i\tilde{a}_ix_i\geq b.$

Jeśli można przyjąć, że wartości współczynników mieszczą się w pewnym zakresie

$[L_i, U_i]$ to

$[a_i-\delta_i,a_i+\delta_i]$ , gdzie

$\delta_i=0.5(U_i-L_i)$ oraz

$a_i=0.5(U_i+L_i)$ .
Aby rozwiązanie PL spełniało ograniczenia

$\tilde{a}_ix\geq b$ w każdym przypadku, wystarczy jeśli spełni ograniczenia w najgorszym przypadku:

dla $x_i\geq 0$ to ograniczenie będzie spełnione jeśli $\tilde{a}_ix\geq (a_i-\delta_i)x_i$ ,
dla $x_i\leq 0$ to ograniczenie będzie spełnione jeśli $\tilde{a}_ix\geq (a_i+\delta_i)x_i$ .

Czyli problem można sformułować jako:

$\sum_i\tilde{a}_ix\geq a_ix_i-\sum_i\delta_i|x_i|\geq b$ .

Wtedy stosując metodę przedstawienia wartości bezwzględnej jako f. wypukłej

$|x_i| = y_i$ , używamy teraz nowych zmiennych

$y_i$ w początkowym ograniczeniu, dodając ograniczenia wiążące te zmienne z

$x_i$ dla funkcji celu:

$\min\sum_i c_ix_i,$ p.o.:

\begin{eqnarray} & &\sum_i a_ix_i- \sum_i\delta_i y_i \geq b, \\ &-y_i \leq & x_i\leq y_i,\\ & &y_i\geq 0. \end{eqnarray} Uwaga, często warto uwzględnić dodatkowo współczynnik tolerancji

$\epsilon$ , pozwalający na nieznaczne naruszenie prawej strony ograniczeń: \begin{eqnarray} && \sum_i a_ix_i-\sum_i\delta_i y_i\geq b-\epsilon\max(1,|b|).\end{eqnarray}

Przyjmij, że firma ponosi stały koszt utrzymania magazynu, wynoszący

$C$ , o ile jego pojemność

$P$ jest wykorzystywana w nie więcej niż 80%. W sytuacji, gdy ilość przechowywanych towarów przekracza

$0.8\cdot P$ , ponoszone są dodatkowe koszty, rosnące wraz ze współczynnikiem

$k$ za każdą nadmiarową jednostkę towaru. Przyjmując horyzont planowania

$T$ lat, oraz wielkość zapotrzebowania w wysokości

$d_t$ w każdym roku, zapisz w postaci PL problem wyznaczenia optymalnego planu zakupów towaru w każdym roku. Plan ten, przy znajomości cen zakupu

$c_t$ , powinien minimalizować koszty magazynowania. Wskazówka - zauważ, że koszt magazynowania towaru można przedstawić w postaci funkcji, składającej się z dwóch liniowych kawałków.

2.4. Zależności dualne

Każdy problem PL można przeformułować do symetrycznej postaci, odpowiadającej zadaniu dualnemu:

Problem prymalny ma odpowiadający mu problem dualny, taki że zmienne dualne odpowiadają ograniczenim prymalnym, i vice versa. Np. dla postaci standardowej pary te zapisujemy:

$\min_{x\in \mathcal{R}^n} f(x) = \mathbf{c}^T x \qquad\Leftrightarrow\qquad \max_{\lambda\in \mathcal{R}^m} y(\lambda) = \mathbf{b}^T \lambda\\ \begin{eqnarray} \mathbf{A}x \geq& \mathbf{b}\;\perp\lambda\qquad\qquad\qquad& \qquad\mathbf{A}^T \lambda \leq \mathbf{c}\; \perp x \nonumber\\ x\geq& 0\qquad\qquad\nonumber &\qquad\qquad\lambda\geq 0\end{eqnarray}$
Parę problemów prymalnego i odpowiadającego mu dualnego nazywamy problemami sprzężonymi.

W zapisie zadania PL oznaczamy zmienne dualne dla ograniczenia przy pomocy symbolu

$\mathbf{\perp }$ . Oznaczenie pojawiające się za symbolem

$\perp$ (np.

$\perp\lambda$ powyżej) opisuje zmienną dualną, która jednak w sposób jawny nie jest definiowana w modelu. Wartości zmiennych dualnych (razem z wartościami prymalnych zmiennych decyzyjnych) są zwracane po obliczeniu optimum przez dowolny solwer zadań PL - jako wartość marginalna ograniczenia.

Ogólnie, dla innych postaci niż standardowa, mechanizm konstrukcji sformułowań prymalno-dualnych problemu optymalizacji liniowej można podsumować w następujący sposób:

Kierunek optymalizacji w problemie dualnym jest przeciwny, tj. problem dualny jest zadaniem maksymalizacji, gdy problem prymalny jest zadaniem minimalizacji; w przeciwnym przypadku problem dualny jest zadaniem minimalizacji dla maksymalizacji problemu prymalnego.
Ograniczenia typu równościowego implikują zmienne swobodne odpowiedniego sformułowania sprzężonego, i vice versa.
Ograniczenia typu $\geq$ implikują zmienne nieujemne odpowiedniego sformułowania sprzężonego, i vice versa.
Ograniczenia typu $\leq$ implikują zmienne niedodatnie odpowiedniego sformułowania sprzężonego, i vice versa.

Z powyższego widać, że problem dualny do zadania dualnego jest zadaniem prymalnym.

Z dualnością wiążą się ważne twierdzenia, to jest twierdzenie o słabej i silnej dualności, oraz o warunku komplementarności. Twierdzenia te są aplikacją warunków optymalności Karusha-Kuhna-Tuckera formułowanych dla funkcji nieliniowych, do specjalnego przypadku funkcji liniowych.

Tw. o słabej dualności. Dla dowolnej pary rozwiązań dopuszczalnych $x_0,\lambda_0$ zadań wzajemnie dualnych (przy $\min c^Tx$ ) zachodzi ogólna zależność, nazywana odstępem dualności (duality gap):

$c^Tx \geq b^T \lambda$
Tw. o silnej dualności. Jeśli jedno z zadań sprzężonych ma rozwiązanie optymalne, to ma je również drugie zadanie i zachodzi równość wartości funkcji celu: $c^T\hat{x_0} = b^T\hat{\lambda_0}$ . Jeśli jedno z zadań wzajemnie dualnych jest sprzeczne (zbiór rozwiązań dopuszczalnych jest pusty), to zadanie dualne jest albo sprzeczne, albo nieograniczone.
Warunek komplementarności. Zachodzi własność: $x_s^T\lambda+\lambda_s^Tx=0$ , gdzie $x_s$ i $\lambda_s$ są zmiennymi dopełniającymi dla ograniczeń nieaktywnych. W równoważnej wersji warunek ten ma postać: $\lambda^T(Ax-b)=0$ oraz $(c^T-\lambda^TA)x=0$ .

Dualność ma wiele ważnych zastosowań, w szczególności jest podstawą działania algorytmu simplex dualnego. W kontekście modelowania zależności liniowych niezwykle istotne jest zrozumienie znaczenia zmiennych dualnych, których wartość możemy odczytać rozwiązując dowolny problem optymalizacji liniowej w dowolnym solwerze.

Zmienne dualne, nazywane też: cenami dualnymi, marginalnymi (ang. shadow prices, marginal prices) mają ważną interpretację ekonomiczną - ich wartości mogą być wskazówką, jak alokować ograniczone zasoby (pracownicy, materiały, maszyny, budżet) pomiędzy aktywności. W szczególności:

dla zadań maksymalizacji zysku zmienne dualne można interpretować jako koszty materiałowe (ograniczenie na materiały powoduje, że nie możemy zarobić więcej - ile warto zapłacić za ew. zwiększenie zasobów materiałowych?),
dla zadań minimalizacji kosztu zmienne dualne można intepretować jako zyski jednostkowe (ograniczenie na zapotrzebowanie powoduje, że nie możemy bardziej obniżyć kosztów - które z wymagań ma największy wpływ na ponoszone koszty, czyli powinno być dla nas najbardziej wartościowe?).

Rozważmy problem długoterminowego magazynowania ziaren zbóż w silosie o pojemności

$K$ ton. Ziarno może być kupowane raz w roku, w sierpniu, a sprzedaż może zachodzić raz w roku, w marcu. Jednostkowe ceny ziarna są prognozowane z dużą dokładnością w horyzoncie

$T$ lat, znany jest też jednostkowy koszt magazynowania ziarna w każdym roku. Firma zarządzająca silosem ma nieograniczone środki finansowe na zakup ziarna, przyjmujemy też, że popyt na ziarno jest znacząco większy od pojemności silosa, czyli można kupić i sprzedać dowolną ilość ziarna, a jedynym ograniczeniem jest pojemność silosa.

sformułuj zadanie maksymalizacji zysku, tj. różnicy między przychodem i kosztem;
czy można uzasadnić charakter zależności zysku od pojemności silosa?

W celu sformułowania zadania wprowadźmy następujące oznaczenia. Niech ilość ziarna przechowywanego w roku

$t$ będzie oznaczona jako

$I_t$ . Jest ona równa ilości ziarna, która została w magazynie z poprzedniego roku

$I_{t-1}$ minus ilość ziarna sprzedana w poprzednim roku

$x_{t-1}$ , po powiększeniu o ewentualny zakup w danym roku

$p_t$ :

$I_t = I_{t-1}-x_{t-1}+p_t,\qquad \forall t \in (1,\ldots, T),$

gdzie

$I_0=x_0=0$ (przyjmując, że silos jest pusty, gdy rozpoczynamy planowanie).
W każdym roku nie można sprzedać więcej ziarna, niż mamy w silosie. Ponadto, ilość ziarna w silosie nie może przekroczyć jego pojemności. Stąd ograniczenia:

$x_t \leq I_t ,\qquad \forall t \in (1,\ldots, T),$
$I_t\leq K, \forall t \in (1,\ldots, T).$

Zauważmy, że warunek

$x_t \leq I_t$ jest równoważny stwierdzeniu, że ilość ziarna w silosie nie może być mniejsza od zera, czyli wystarczy równoważny zapis tego ograniczenia

$I_t \geq 0$ . Oznaczając przez

$c^s_t$ cenę ziarna w sierpniu, a przez

$c^m_t$ cenę ziarna w marcu, oraz przez

$h_t$ cenę magazynowania w roku

$t$ , zapisujemy problem PL w postaci:

$\max \sum_{t=1}^T \left( c^m_t x_t - c^s_t p_t - h_t I_t \right)$

p.o.:

$I_t = I_{t-1}-x_{t-1}+p_t,\qquad \forall t \in (1,\ldots, T),$

$\qquad 0\leq I_t\leq K, \qquad \forall t \in (1,\ldots, T). \qquad \perp \lambda_t$

Rozważmy teraz dualne sformułowanie powyższego problemu. Jedynym ograniczeniem, które ma niezerowy współczynnik prawej strony jest ograniczenie na pojemność silosa. Stąd funkcja celu zadania dualnego będzie postaci:

$\min \sum_{t=1}^T K\lambda_t$ . Ponieważ

$K$ jest stałą, nie ma ona wpływu na optymalne wartości zmiennych decyzyjnych dualnego problemu, czyli wystarczy minimalizować

$\sum_{t=1}^T \lambda_t$ . Oznacza to, że optymalny zysk jest liniowo zależny od pojemności silosa.

Zmienne dualne są też ściśle związane z teorią równowagi rynku, gdyż ich wartość w odniesieniu do równania bilansu popytu i podaży odpowiada wartości ceny rynkowej. Cena rynkowa określa rynkową wartość towaru, pozwalając na jednolitą wycenę i porównanie ofert kupna i sprzedaży. Oferty niekonkurencyjne, czyli o zbyt wysokich cenach w przypadku sprzedaży, lub o zbyt niskich cenach w przypadku kupna, nie powinny brać udziału w obrocie. Natomiast oferty konkurencyjne, przyczyniające się do zwiększenia ogólnego dobrobytu rynkowego powinny uczestniczyć w wymianie rynkowej.

Rozważmy problem optymalizacji obrotu pojedynczego towaru, na rynku skupiającym

$S$ sprzedających i

$K$ kupujących. W ramach pojedynczej sesji notowań każdy uczestnik zgłasza ofertę kupna lub sprzedaży, która zawiera maksymalny wolumen towaru, jaki uczestnik jest chętny kupić lub sprzedać, po cenie nie gorszej niż ta, którą oferuje.
Oferty uczestników rynku można opisać następującymi parametrami:

$d^{\max}_k$ maksymalna ilość towaru, którą chce nabyć kupujący $k$ ;
$p^{\max}_s$ maksymalna ilość towaru, którą chce zbyć sprzedający $s$ ;
$e_k$ maksymalna cenę jednostkową, którą jest skłonny zapłacić kupujący $k$ ;
$c_s$ minimalna cenę jednostkową, którą jest skłonny zaakceptować sprzedający $s$ .

Optymalizacja w obrocie giełdowym polega na podjeciu decyzji o wolumenach zawartych transakcji. Przy tym nie ma znaczenia, pomiędzy którą konkretnie parą (lub większą liczbą) uczestników rynku dochodzi do wymiany - ważne jest, aby określić:

$d_k$ ilość zakupionego towaru według

$k$ -tej oferty kupna, oraz

$p_s$ ilość sprzedanego towaru według oferty sprzedazy

$s$ ; tak, aby sumarycznie ilości kupionego i sprzedanego towaru się zgadzały i żeby dobrobyt z przeprowadzonej wymiany był jak największy.
Odpowiednie zadanie optymalizacji ma prostą strukturę:

$\max \sum_{k \in K} e_kd_k - \sum_{s \in S} c_sp_s$

przy ograniczeniach:

$\begin{eqnarray} \sum_{k \in K} d_k &= &\sum_{s \in S} p_s,\\ d_k &\leq &d^{\max}_k,\;\;\forall k\in K\\ p_s &\leq &p^{\max}_s,\;\;\forall s\in S,\\ d_k , p_s &\geq &0.\\ \end{eqnarray}$
Rozwiązaniem optymalnym powyższego zadania jest wielkość wolumenów wybranych do realizacji ofert kupna i sprzedazy, oraz jednolita cena rynkowa, która nie pojawia się jawnie w modelu, ale jest ceną dualną równania bilansu przepływu towarów.

Czy optymalny dobrobyt rynkowy, osiągany w wyniku wymiany towarami między kupującymi a sprzedającymi na rynku jak w poprzednim przykładzie, zależy od wysokości rynkowej ceny towaru? Czy cena rynkowa zależy od wielkości dobrobytu? Odpowiedź uzasadnić.

2.5. Problemy dyskretne

Rozważmy zadanie optymalizacji w ogólnej postaci, składające się z następujących elementów:

Zmienne decyzyjne: $x_j = 1,2,...,n$
Przestrzeń decyzji: $X = R^n$
Zbiór decyzji dopuszczalnych: $Q\subset X$
Wektory (rozwiązania, decyzje) dopuszczalne: $x\in Q$
Miara jakości (wynik) decyzji, funkcja celu, kryterium: $f: R^n\rightarrow R$
Zadanie optymalizacji (programowanie matematyczne):\\
$\max \{ f(x): x\in Q\}$

Wyznaczyć $\bar{x}\in Q$ taki, że
$f(\bar{x}) \geq f(x)\quad \forall x\in Q$

$\bar{x}$ -- rozwiązanie optymalne
$f(\bar{x})$ -- wartość optymalna

W zadaniach liniowych Q jest zbiorem rozwiązań następującego układu ograniczeń:

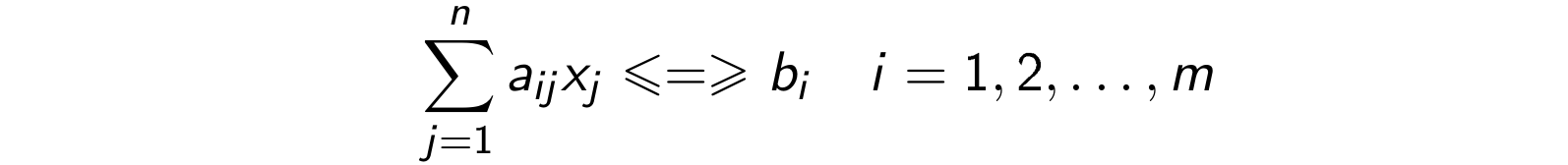
a funkcja celu ma postać:

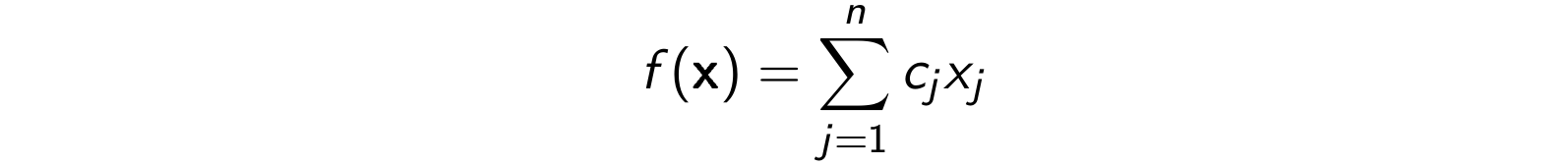
W problemach dyskretnych natomiast zbiór $Q$ jest dyskretny, tzn. jest zbiorem skończonym albo jest skończoną sumą niespójnych składowych. Oznacza to, że zmienne decyzyjne przyjmują wartości całkowitoliczbowe. W takiej sytuacji zadanie optymalizacji, liniowe-całkowitoliczbowe (PLC, ILP), wygląda (w zapisie macierzowym) następująco:

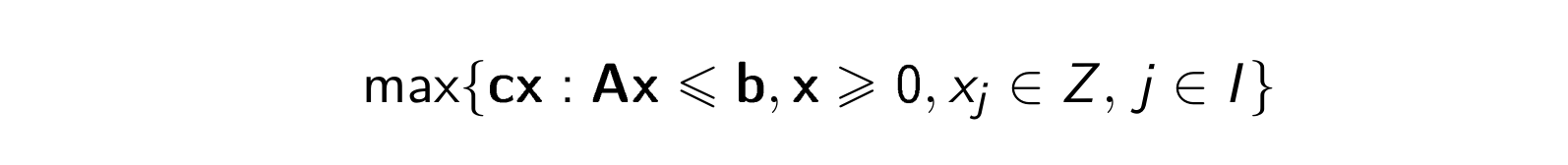
Jeśli w zadaniu mogą występować również zmienne ciągłe, mamy do czynienia z zadaniem mieszanym, liniowym-całkowitoliczbowym (MILP).

Znaczenie problemów MILP wynika z tego, że wiele zagadnień nieliniowych, kombinatorycznych czy logicznych daje się modelować dokładnie bądź w przybliżeniu za pomocą takich modeli. W szczególności modelowanie matematyczne, w tym MILP, możemy traktować jako rodzaj programowania deklaratywnego, analogicznie do języka opisu zapytań SQL. Stąd nazwa programowanie matematyczne.

Przykłady klas problemów, które można rozwiązywać przez optymalizację modeli MILP: zadania harmonogramowania, kombinatoryczne, przydziału zasobów, optymalizacji łańcucha dostaw, optymalizacji sieciowej, etc.

Modele MILP mogą być rozwiązywane za pomocą specjalizowanych algorytmów (branch-and-bound, branch-and-cut, programowanie dynamiczne, itp), często dostępnych w postaci solwerów. Do najbardziej znanych należą: a)komercyjne: CPLEX, GUROBI b) otwarte: CBC, GLPK, ORTOOLS.

2.6. Warunki logiczne

Modele liniowe-całkowitoliczbowe umożliwiają modelowanie różnorodnych warunków logicznych.

Niech zmienna binarna z wartościami $\{0,1\}$ odpowiada zmiennej logicznej z wartościami (fałsz, prawda). Za ich pomocą możemy modelować różnorodne warunki logiczne, przez wprowadzenie odpowiednich ograniczeń oraz ewentualnie dodatkowych zmiennych.

Przykłady prostych warunków logicznych:

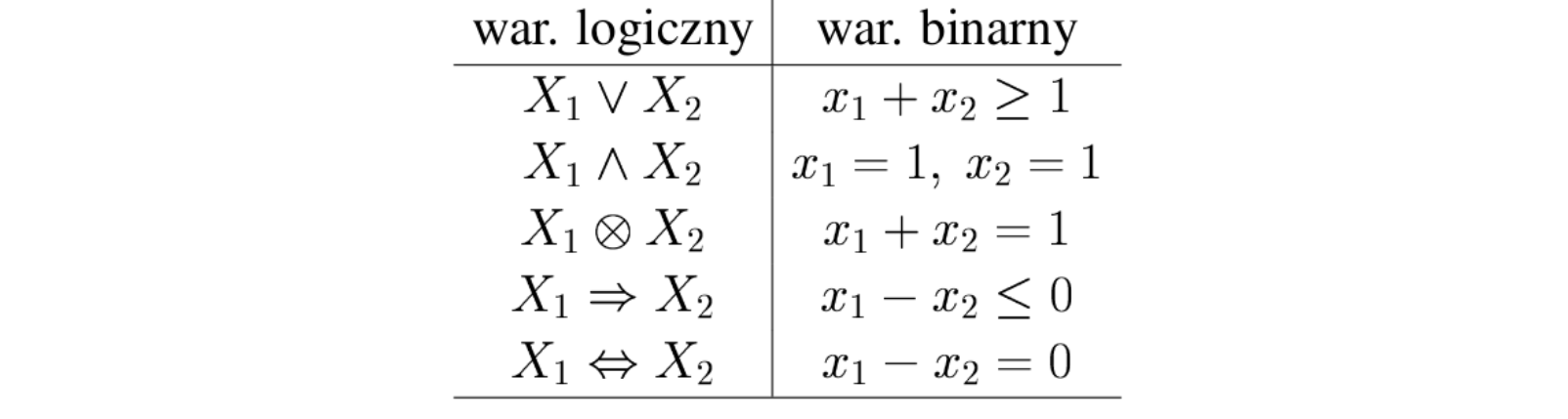
Przykłady złożonych warunków logicznych:

Oraz:

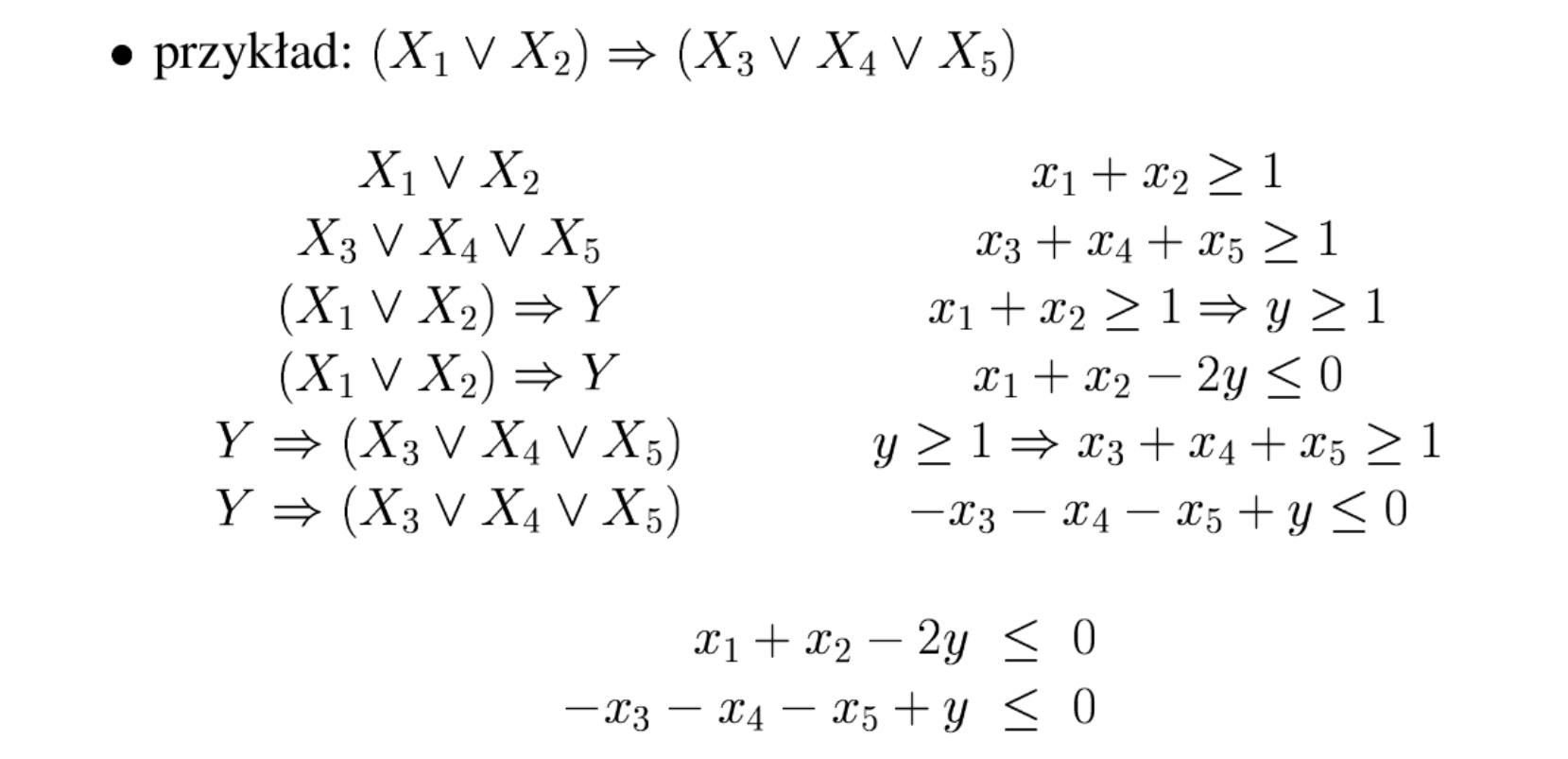
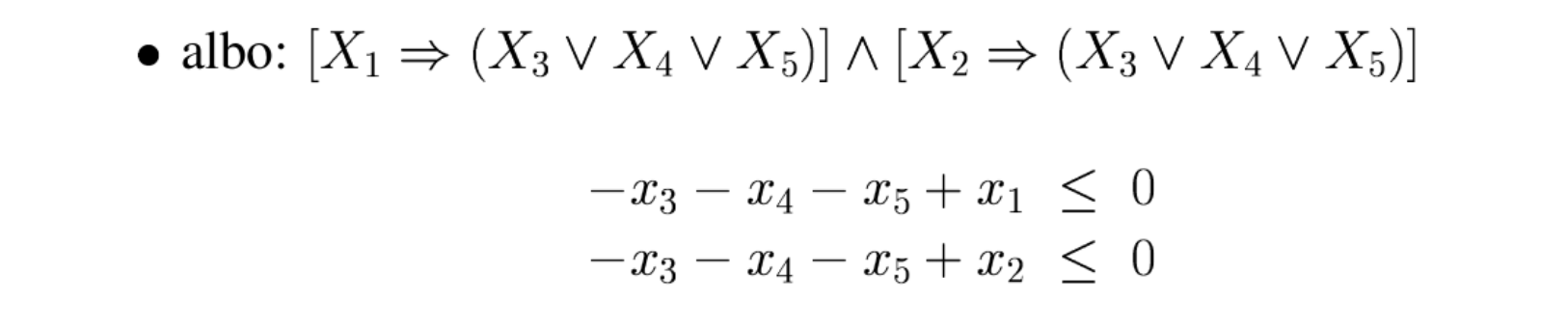
2.7. Flaga dodatniości zmiennej (wyrażenia)

Czasami konieczne jest zamodelowanie zachowania zmiennej binarnej tak, aby przyjmowała ona wartość 1 jeśli pewna inna zmienna lub wyrażenie są dodatnie. Taka zmienna binarna jest nazywana flagą dodatniości.

Niech zmienna ciągła $x$ będzie ograniczona w przedziale wartości: $0\leq x \leq M$ . Niech także dana będzie zmienna binarna $u\in\{0,1\}\). Warunek $u=1$ wtedy gdy $x > 0$ osiągniemy stosując następujące nierówności:

A w przypadku wyrażenia (przykładowo wyrażenia liniowego):

Przykładowo, koszt transportu w zadaniu transportowym, uwzględniający tzw koszt stały, czyli koszt niezależny od ilości przewożonego towaru, naliczany jeśli ilość przewożonego towaru jest niezerowa:

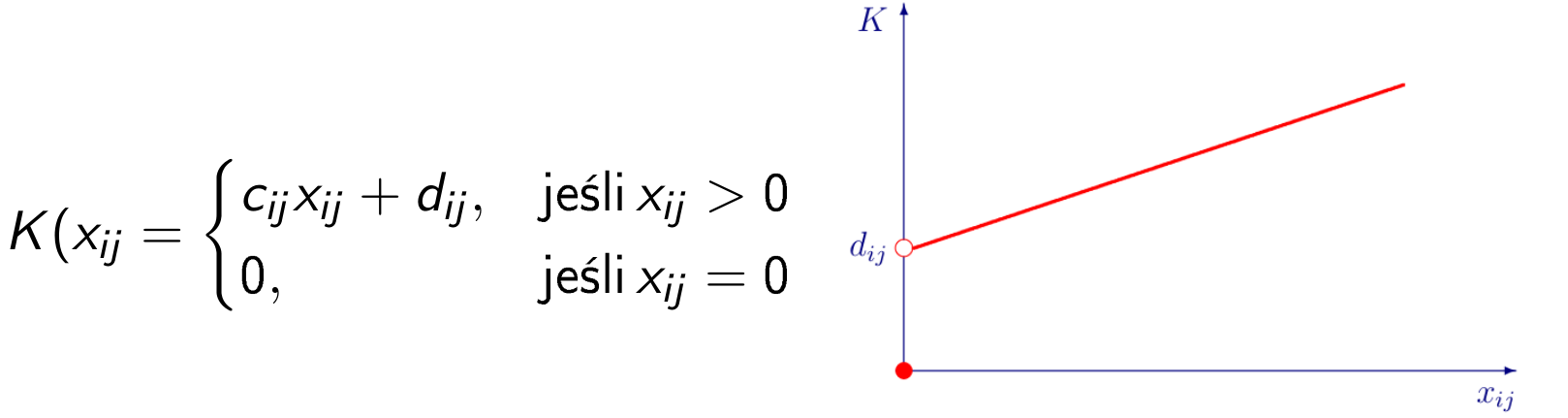
Model mieszany, liniowy-całkowitoliczbowy, zadania transportowego z takim kosztem będzie następujący:

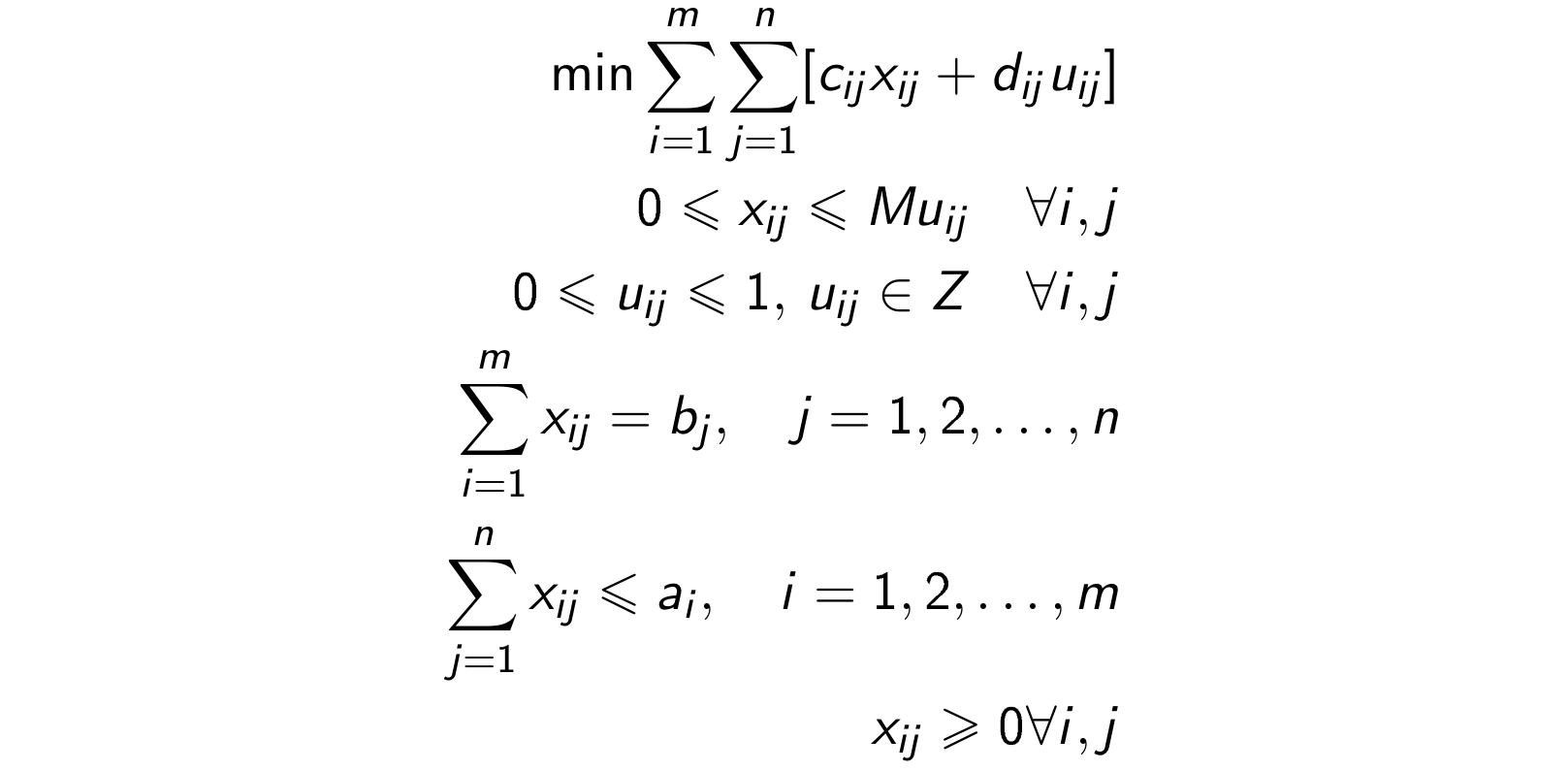
Stosując podobne techniki możemy ograniczyć liczbę zmiennych dodatnich, tzn. co najwyżej $k$ zmiennych $x_j$ przyjmie wartości dodatnie:

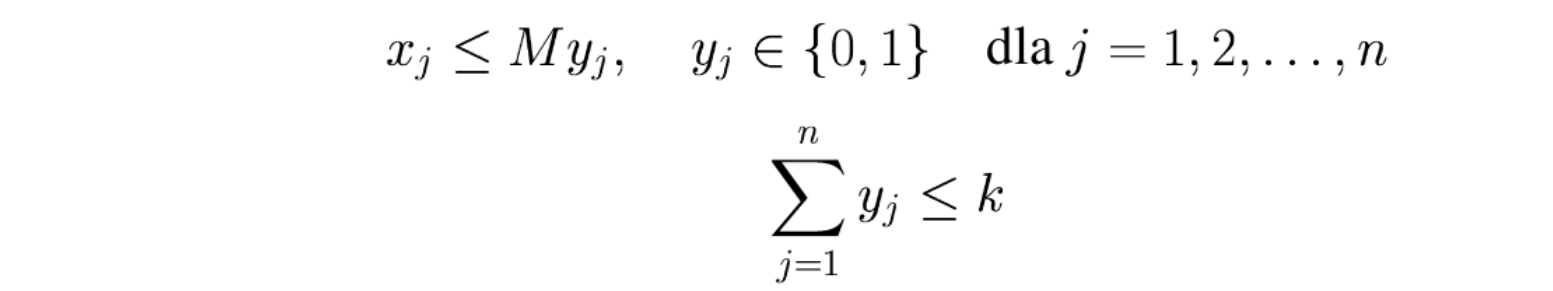
Ponownie przykład zadania transportowego, w którym co najwyżej $k$ dostawców realizuje zapotrzebowanie odbiorcy $j$ :

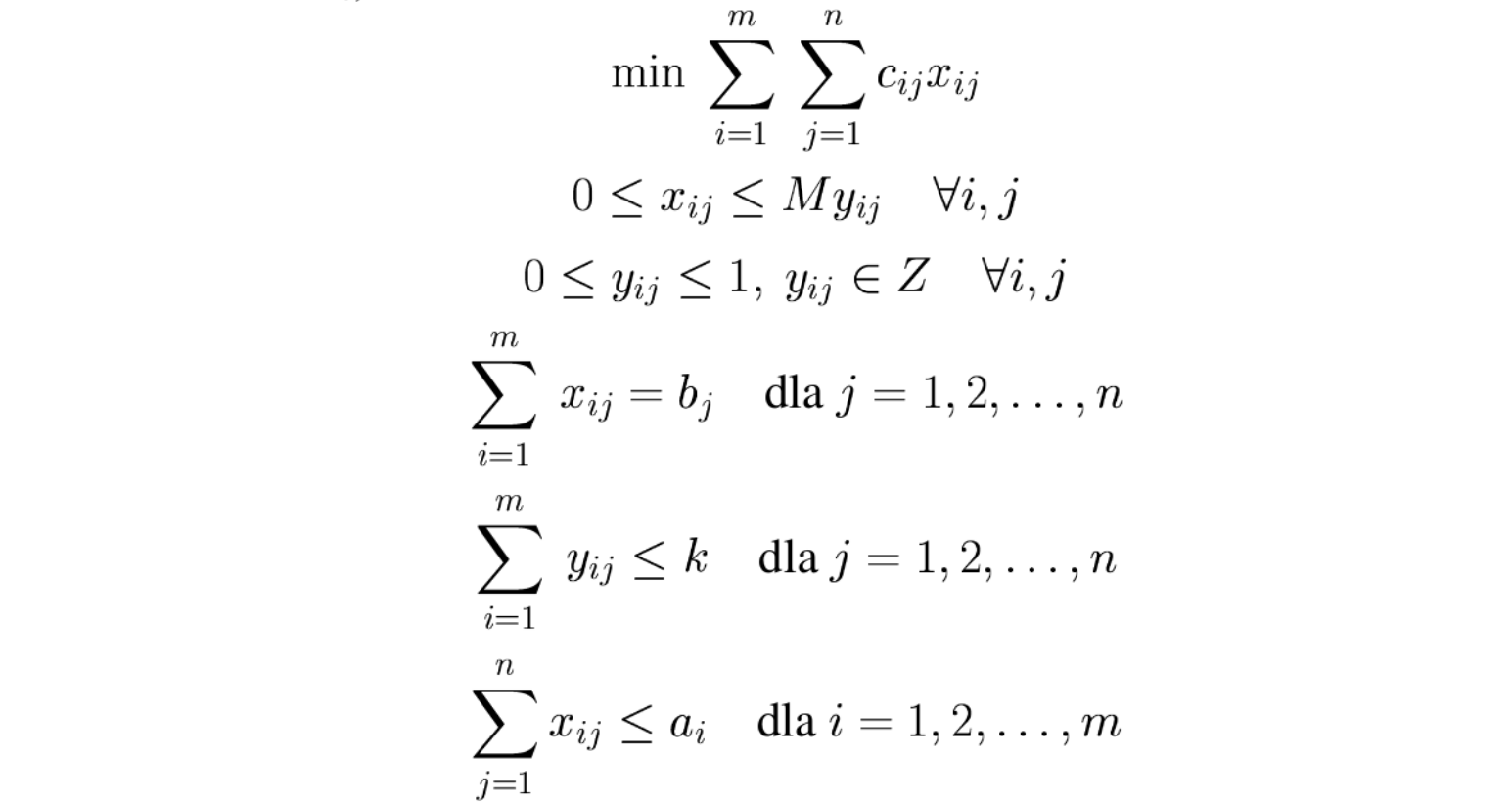
Analogicznie do ograniczenia liczby zmiennych dodatnich możemy wyrazić ograniczoną liczbę naruszonych warunków, czyli niespełnionych ograniczeń. Precyzyjnie, w układzie $m$ nierówności:

co najmniej $k$ warunków musi być spełnionych, a pozostałe $m-k$ nie muszą być spełnione.

Osiągniemy to następującym modelem całkowitoliczbowym:

Rozszerzając ten model możemy maksymalizować liczbę spełnionych warunków:

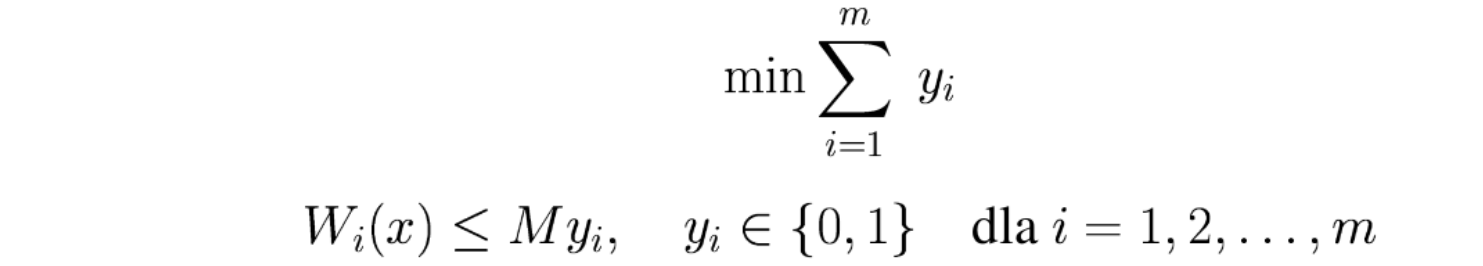
przy czym funkcja celu oznacza liczbę niespełnionych warunków.

2.8. Zbiory niespójne i niewypukłe

Rozważmy zbiór dopuszczalny będący sumą zbiorów:

Chcielibyśmy go zamodelować według szablonu, w którym każdemu podzbiorowi odpowiada pewna zmienna binarna (\y_i\), wg poniższego schematu (schemat te nie jest ostatecznym modelem):

Przykładowo, zbiorowi niespójnemu opisywanemu przez cztery nierówności:

odpowiada następujący model liniowy-całkowitoliczbowy:

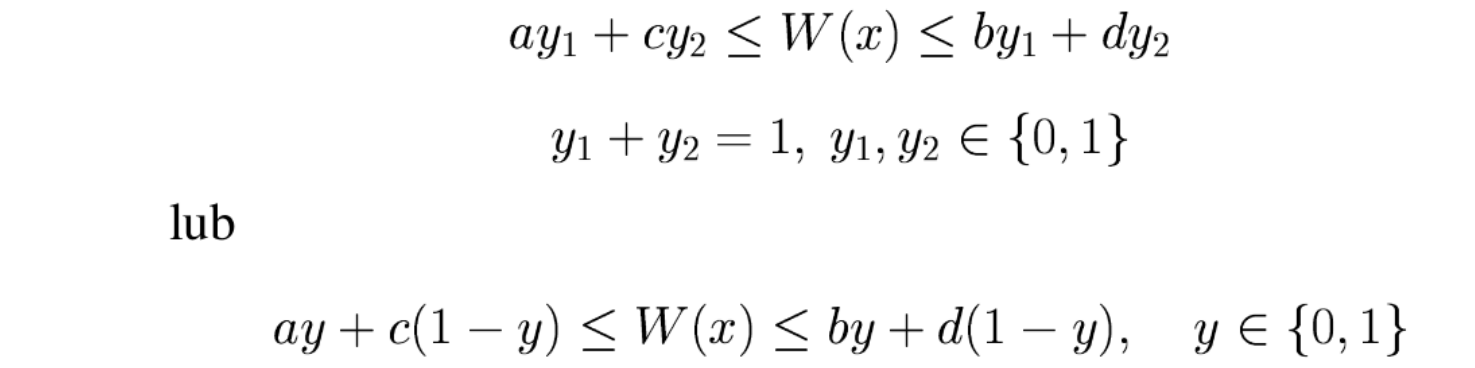
Inny przykład dotyczy modelowania wartości bezwzględnej:

czyli:

Zbiór ten jest opisywany przez następujący model liniowy-całkowitoliczbowy:

Kolejny przykład dotyczy sumy dwóch zbiorów. Poniżej nierówności opisujące te zbiory i ich graficzna reprezentacja:

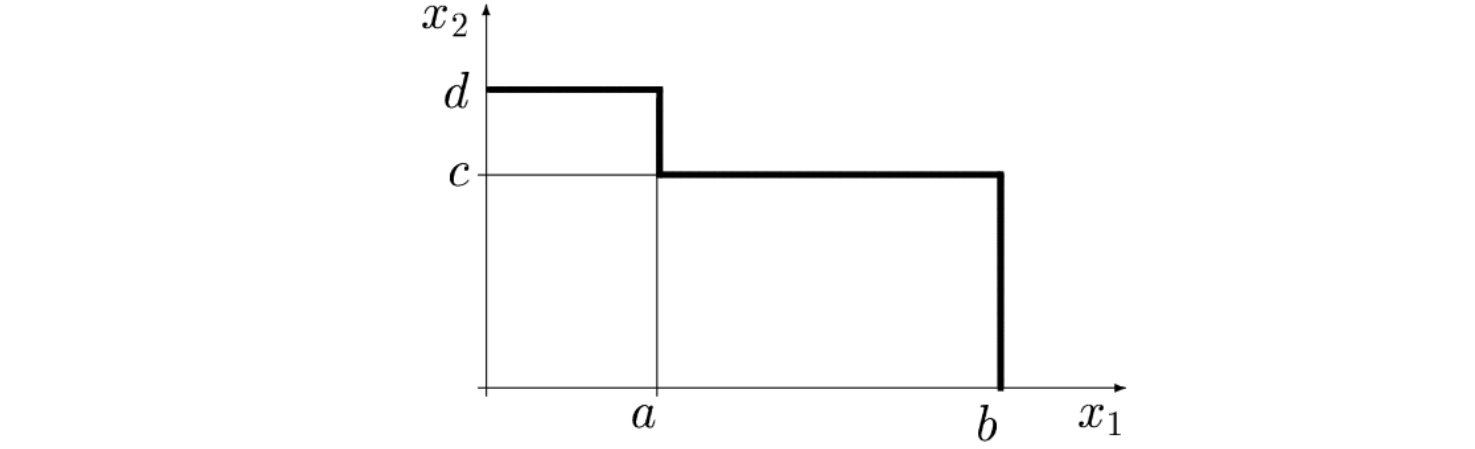
Oraz odpowiadający im model:

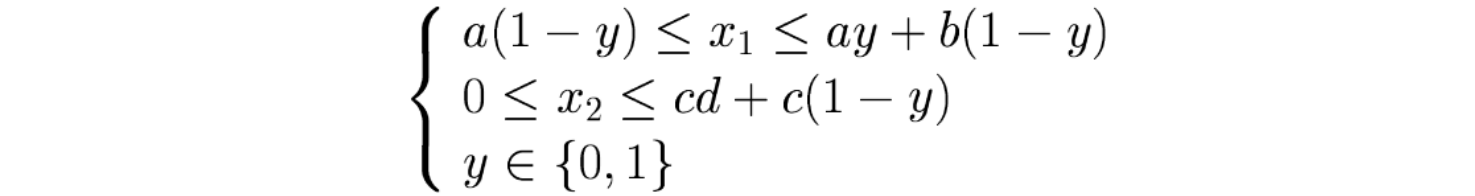
2.9. Przykłady I

Rozważmy następujące zadanie modelowania.

Zadanie 1.

Rozważana jest hodowla ryb. Trzy gatunki ryb mogą być hodowane w dwóch stawach o różnych rozmiarach. Staw 1 mieści maksymalnie 120 ton ryb, a staw 2 – 150 ton ryb. Narybek jest kupowany w cenie, odpowiednio, 2, 2.5, 3 tyś.zł za kilogram. W czasie hodowli ryby pierwszego i drugiego gatunku powiększają swoją masę, odpowiednio, 80 i 100 razy niezależnie tego, w którym stawie się znajdują. Natomiast ryby trzeciego gatunku powiększają swoją masę 130 razy w stawie 1 i 120 razy w stawie 2. Ryby gatunku 2 i 3 nie mogą przebywać razem w jednym stawie. Cena sprzedaży 1 kg ryby wynosi, odpowiednio, 15, 18, 14 zł. Zaplanować hodowlę przynoszącą największy zysk (koszty paszy są pomijane). Sformułować model programowania mieszanego liniowego–całkowitoliczbowego realizujący to zadanie.

Rozwiązanie.

zmienne
$x_{ij}$ - ilość narybku gatunku i w stawie j [kg]
$v_{ij}$ - zmienna binarna = 1 jeśli narybek i jest w stawie j

$M$ - duża stała

ograniczenie zapewniające odpowiednie ustawienie zmiennej v jeśli zmienna x jest dodatnia
$\forall i,j x_{ij} \leq M v_{ij}$

maksymalna pojemność stawów (ilość narybku mnożona przez współczynniki wzrostu)
$80*x_{11}+100*x_{21}+130*x_{31}$
$80*x_{12}+100*x_{22}+120*x_{32}$

gatunek drugi i trzeci nie mogą przebywać w tym samym stawie
$v_{21}+v_{31}$
$v_{22}+v_{32}$

Funkcja celu
max
$15*80*(x_{11}+x_{12}) + 18*100*(x_{21}+x_{22}) + 14*(130*x_{31}+120*x_{32})$ // przychód ze sprzedaży
$-2000*(x_{11}+x_{12})-2500*(x_{21}+x_{22})-3000*(x_{31}+x_{32})$ // koszt zakupu narybku

Zadanie 2.

Dwa węzły sieci internet są połączone z dwoma miastami (każdy z każdym). Aktualne przepustowości łączy wynoszą [Gb]:

W1->M1: 1.5, W1->M2: 0.8, W2->M1: 2.1, W2->M2: 0.9.

Prognozy przewidują, że ruch wzrośnie i miasto pierwsze będzie generowało sumaryczny ruch na poziomie 6.5Gb, a miasto drugie 3.6Gb. Przepustowość danego łącza można powiększyć o wielokrotność 1Gb po ustalonej cenie innej dla każdego łącza [tyś. zł/Gb]:

W1->M1: 180, W1->M2: 120, W2->M1: 160, W2->M2: 150.

Samo rozpoczęcie inwestycji na danym łączu generuje następujący koszt [tyś. zł]:

W1->M1: 250, W1->M2: 250, W2->M1: 320, W2->M2: 200.

Zaplanować inwestycję pokrywającą prognozowany ruch obydwu miast. Sformułować model programowania mieszanego liniowego–całkowitoliczbowego realizujący to zadanie.

Zadanie 3.

Dana jest krzywa ładowania, modelowana za pomocą krzywej schodkowej.

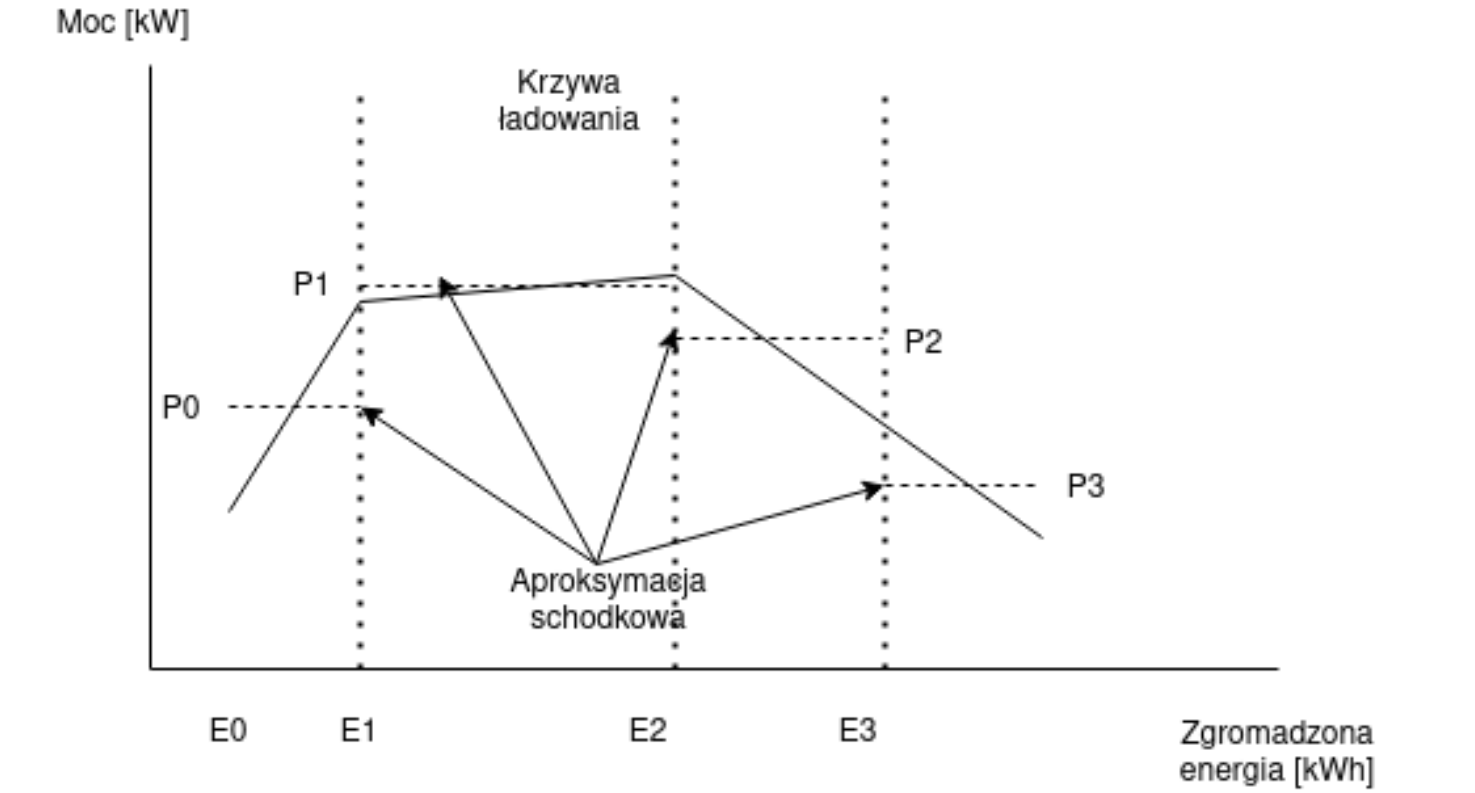
Wartości schodków są parametrami modelu i spełniają zależność:
$p_0 \leq p_1 \geq p_2 \geq p_3$ .

Należy stworzyć model MILP, który prawidłowo wyznaczy wartość zmiennej oznaczającej czas ładowania (ozn. $dt$ , jeśli poziom naładowania akumulatora przed ładowaniem jest dany w postaci zmiennej (ozn. $tank$ ) i a ilość ładowanej na stacji energii również jest dana w postaci zmiennej (ozn. $charge$ ). Zakładamy, że czas ładowania $dt$ jest minimalizowany.

Można przyjąć pewne nieścisłości modelu (sensowne). Generalnie liczba zmiennych binarnych powinna być jak najmniejsza. Model należy przetestować, np w środowisku AMPL.

Należy mieć na względzie, że powyższy model jest częścią większego modelu, np optymalizującego plan ładowania pojazdu na wielu stacjach.

2.10. Wypukłe i niewypukłe funkcje odcinkami liniowe

Rozważamy modelowanie funkcji jednej zmiennej, odcinkami liniowej.

Przykładowo, funkcja odcinkami liniowa może być aproksymacją funkcji nieliniowej, jak na poniższym rysunku: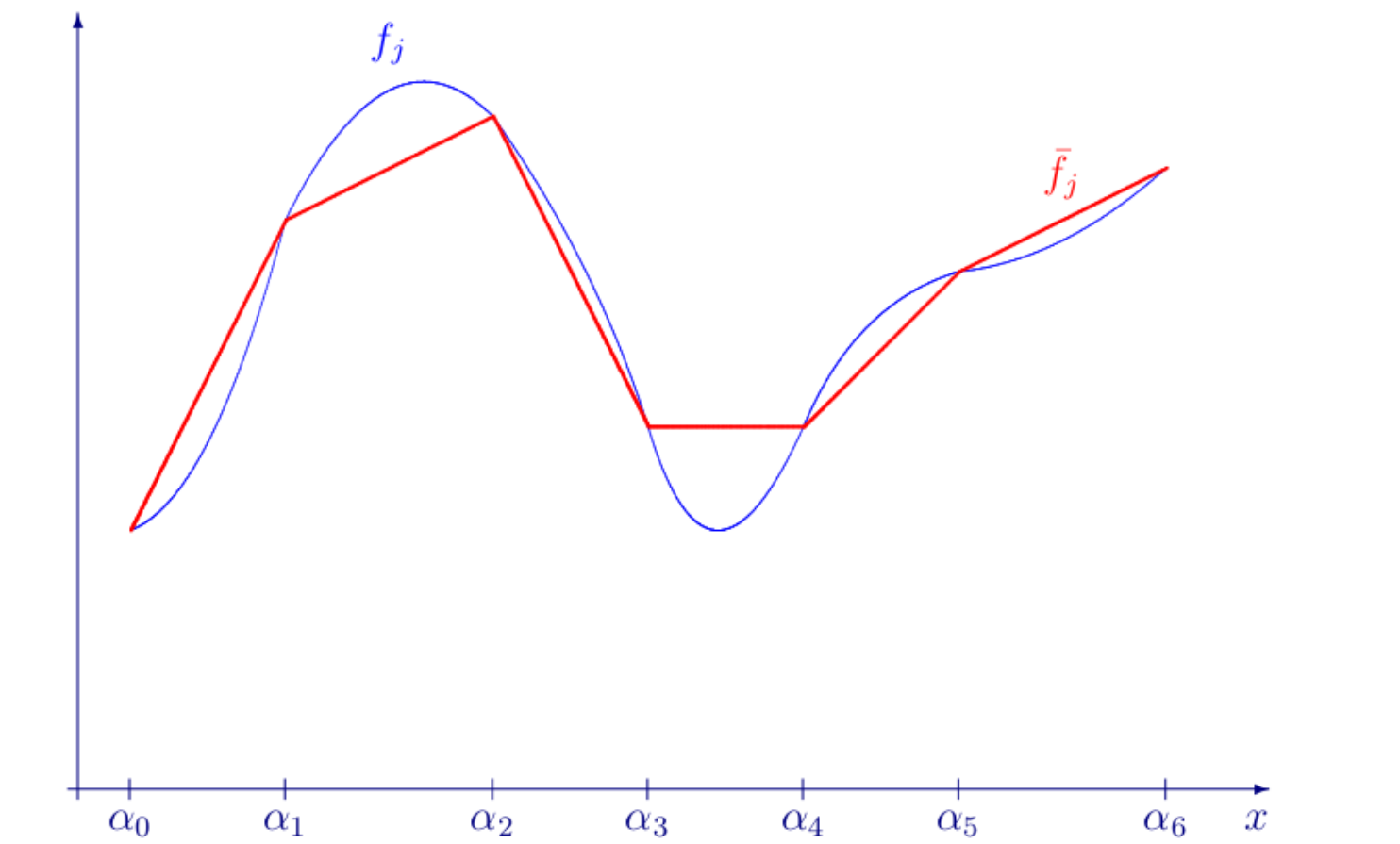

W ogólnym przypadku, model funkcji odcinkami liniowej jest liniowy całkowitoliczbowy. Jednak w niektórych przypadkach modelowanie odbywa się wyłącznie przy pomocy zależności linowych z ciągłymi zmiennymi. Dotyczy to sytuacji gdy maksymalizowana jest funkcja wklęsła lub minimalizowana funkcja wypukła.

Modele liniowe ciągłe

Niech funkcja przedziałami liniowa będzie opisana następującymi równaniami:

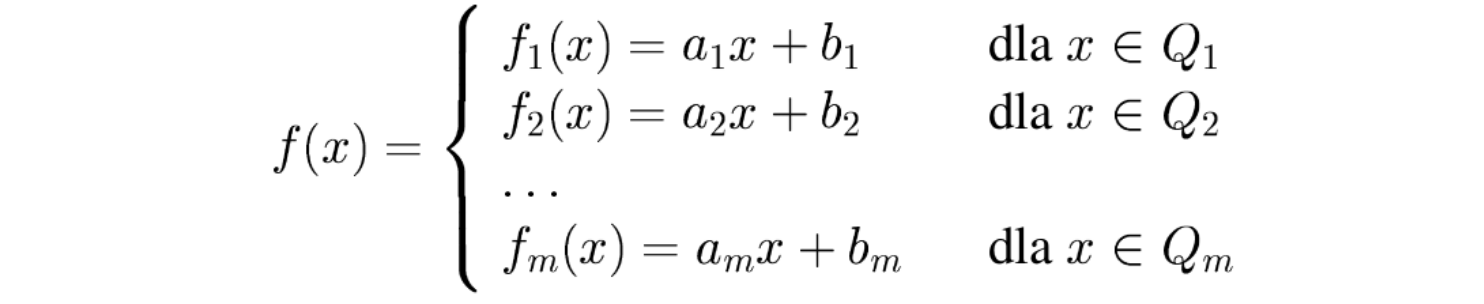
i funkcja

$f(x)$ jest wklęsła czyli:

Wtedy, dla zadania maksymalizacji, może być ona modelowana następująco:

Możliwe jest też wykorzystanie innego podejścia, tzw. przyrostowego, w którym pomocnicze zmienne $x_i$ oznaczają przyrost argumentu w i-tym przedziale. Wtedy funkcja odcinkami liniowe jest wyrażona następującymi zależnościami:

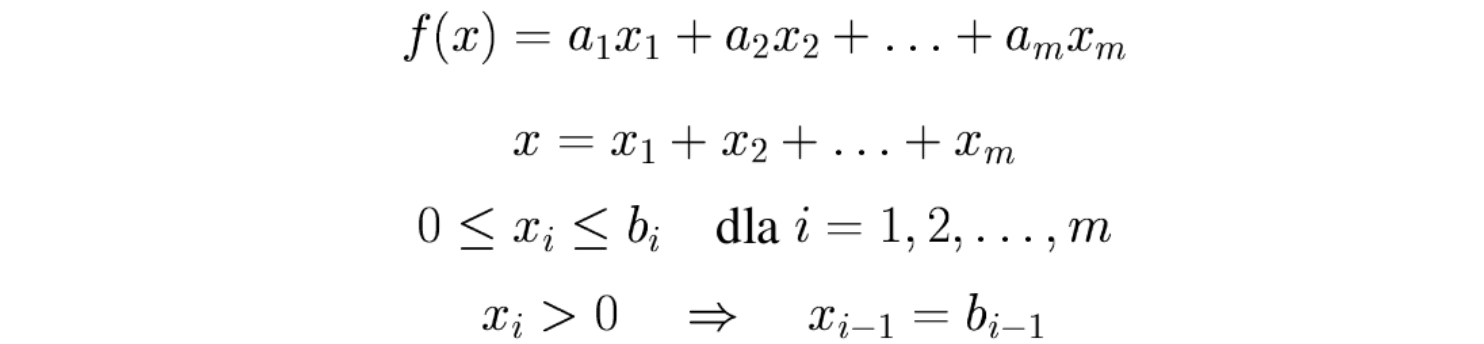
gdzie w przypadku wklęsłej funkcji $f(x)$ zachodzi następująca własność:

jak na poniższym rysunku:

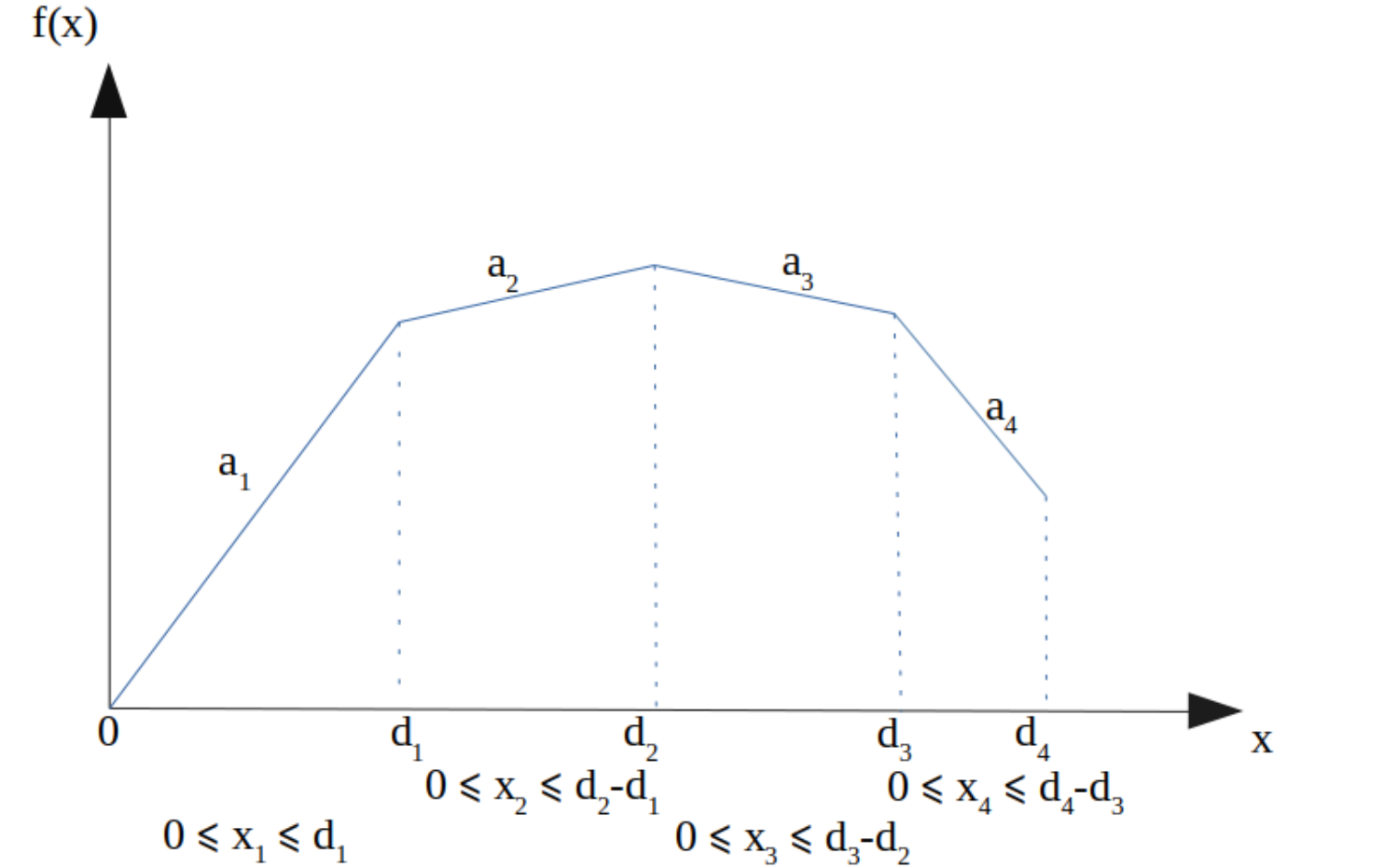
Wtedy funkcja $f(x)$ może być modelowana w następujący sposób:

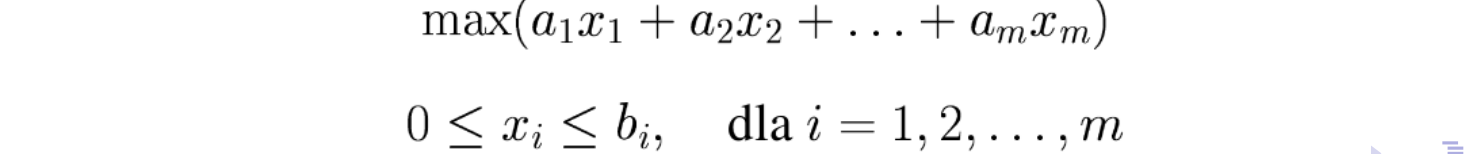
Modele liniowe całkowitoliczbowe

W sytuacji, gdy jest maksymalizowana funkcja wypukła lub minimalizowana funkcja wklęsła, konieczne jest zastosowanie modelu całkowitoliczbowego. Należy pamiętać, że modele całkowitoliczbowe są znacznie trudniejsze jeśli chodzi o ich rozwiązywanie, w związku z tym należy ich używać tylko w sytuacjach niezbędnych.

Rozważmy znowu funkcję przedziałami liniową:

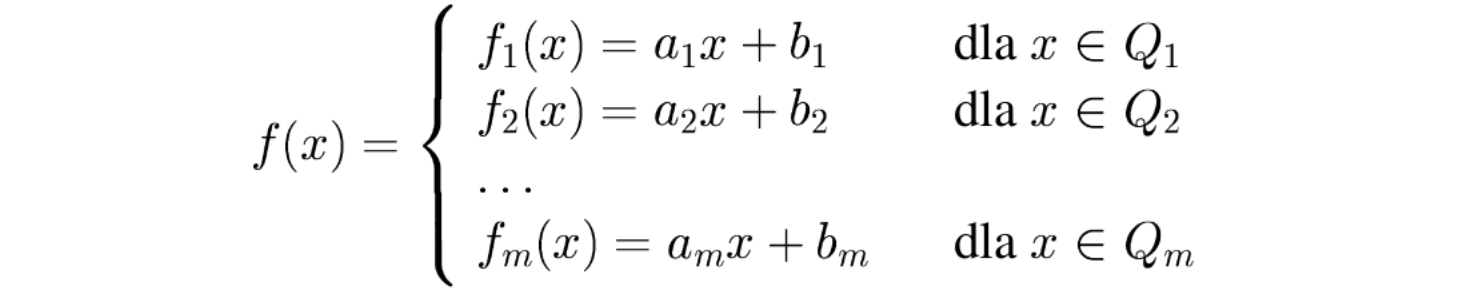
Tym razem jednak, jest ona wypukła, czyli:

Model programowania matematycznego tej funkcji zawiera już zmienne całkowite/binarne ( $y_i$ ) i może być przedstawiony następująco:

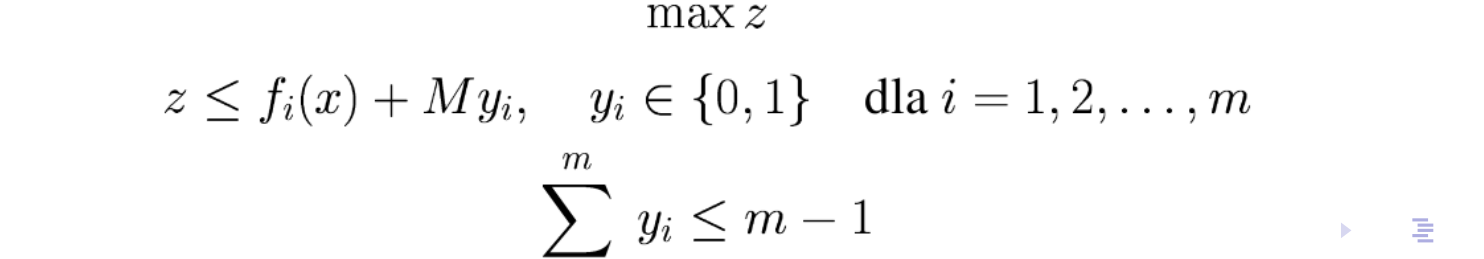
Wersja przyrostowa jest zbliżona do funkcji wklęsłej, ale zawiera dodatkowe zmienne binarne, wymuszające właściwą kolejność ustalania zmiennych reprezentujących przyrosty:

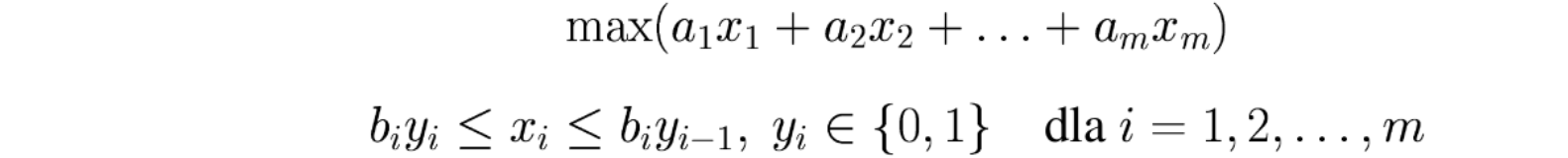
Zaletą modelu przyrostowego jest to, że może być użyty do dowolnej konfiguracji funkcji odcinkami liniowej, która miejscami jest wklęsła a miejscami wypukła. Nie jest to prawdą dla standardowej postaci, która działa prawidłowo tylko dla funkcji wypukłej.

2.11. Przykłady II

Przykład 4.

Zakłady chemiczne mają zamówienie na wyprodukowanie 80kg produktu P. Surowiec potrzebny do jego wytworzenia mogą kupić od dwóch dostawców po różnych cenach, zależnych od wielkości zamówienia. Koszt zakupu surowca od dostawcy pierwszego wynosi 12zł/kg przy zamówieniu poniżej 46kg i 552zł + 14zł/kg przy zamówieniu od 46kg w górę. Koszt zakupu od dostawcy drugiego wynosi 15zł/kg przy zamówieniu poniżej 38kg i 570zł + 10zł/kg przy zamówieniu od 38kg w górę. Zawarte wcześniej umowy z dostawcami przewidują zakup przynajmniej po 30kg surowca od każdego z nich. Surowiec od dostawcy pierwszego jak i surowiec od dostawcy drugiego może być bezpośrednio (bez utraty masy) przerobiony na produkt P. Określić ilości surowców kupowany od dostawców, przy których całkowity koszt wykonania zamówienia jest minimalny. Sformułować zadanie programowania mieszanego całkowitoliczbowego realizujące ten cel. Należy używać zmiennych binarnych i całkowitoliczbowych tylko, jeśli jest to niezbędne.

Przykład 5.

Pewne miasto jest zaopatrywane w wodę przez trzy ujęcia: U1, U2, U3. Ujęcia mogą działać tylko w pewnym zakresie wydajności - U1: 30-60ton/godz,
U2: 25-50ton/godz, lub mogą zostać całkowicie wyłączone. Ujęcie trzecie może pracować w nieograniczonym zakresie. Koszt pracy ujęcia zależy od wydajności z jaką pracuje: dla U1, gdy jego wydajność mieści się w przedziale 30-40ton/godz, koszt pracy wynosi 186zł/tonę. Jeśli natomiast pracuje z większą wydajnością niż 40ton/godz, wtedy koszt ten wynosi 7440zł + 156zł za każdą tonę powyżej 40 ton; dla U2, gdy jego wydajność mieści się w przedziale 25-35ton/godz, koszt pracy wynosi 130zł/tonę. Jeśli natomiast pracuje z większą wydajnością niż 35 ton/godz, wtedy koszt ten wynosi 4550zł + 225zł za każdą tonę powyżej 35 ton. Koszt pracy ujęcia 3 wynosi 200zł/tonę. Ujęcie wyłączone nie generuje żadnego kosztu. Z przyczyn bezpieczeństwa przynajmniej dwa ujęcia muszą być czynne. Zakładając, że miasto musi otrzymywać przynajmniej 65ton/godz, wyznaczyć wydajności z jakimi powinny pracować ujęcia, tak aby zminimalizować godzinny koszt pracy systemu.