Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 2. Modele sieciowe i rozmyte |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | wtorek, 30 grudnia 2025, 08:00 |
Opis
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
Wykłady
W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu
1. Modele sieciowe
W niniejszym module rozważamy modele sieci przepływowych. Niektóre z problemów programowania liniowego można przedstawić w postaci grafu i przepływów w tym grafie. Okazuje się, że takie problemy odznaczają się specjalną strukturą, dzięki której istotnie redukuje się złożoność obliczeniowa względem ogólnych klas problemów do których one należą. Przykładowo, niektóre problemy optymalizacji całkowitoliczbowej, czyli ogólnie problemy trudne do rozwiązywania, można przedstawić w postaci przepływów w sieci. Wiedza, że dany problem można przedstawić w postaci sieci przepływowej niesie ze sobą następujące konsekwencje. Po pierwsze, wiemy, że dany problem ma niższą złożoność obliczeniową. Po drugie możemy zastosować dedykowane algorytm sieciowe. Dodatkowo, dla problemów ze zmiennymi dyskretnymi i przy dodatkowych warunkach, wiemy, że uciąglenie zmiennych dyskretnych prowadzi do problemu, którego rozwiązanie zachowuje warunek całkowitoliczbowości. Dlatego w wielu praktycznych sytuacjach staramy się uzyskać model przepływowy problemu dokonując odpowiednich przeformułowań, odpowiedniego kodowania problemu w zmiennych decyzyjnych.
Modele sieci przepływowych mają szerokie pole zastosowania w praktycznych problemach. Przykładem mogą być sieci transportowo-dystrybucyjne dla towarów, ale również przepływy energii elektrycznej, zarządzanie zasobami telekomunikacyjnymi, czy sieci bardziej abstrakcyjne jak sieci społecznościowe, sieci zależności zadań w projektach, czy zależności w strukturze organizacyjnej przedsiębiorstwa.
1.1. Podstawowe pojęcia
Graf jest spójny jeżeli dla dowolnej pary wierzchołów grafu istnieje ścieżka je łącząca (z pominięciem skierowania łuków).
Graf ważony jest to graf, a którym do łuków zostały przypisane pewne wagi \(w_e, e \in E\).
Powyższe wagi mogą mieć charakter kosztu związanego z przepływem daną krawędzią, przy czym koszt należy rozumieć tu w sposób ogólny: może to być koszt finansowy, ale również czas lub odległość. Wagi mogą przyjmować również znaczenie przepustowości, a więc ograniczenia maksymalnego przepływu daną krawędzią. Generalnie graf może zawierać wiele wag dla pojedynczej krawędzi, ale typowymi parametrami sieci przepływowej są koszty i przepustowości krawędzi.
Przepływem na łuku nazywamy przypisaną do łuku liczbę reprezentującą wielkość przesyłanego towaru.
Wierzchołek \(p\) nazywamy poprzednikiem wierzchołka \(v\) jeżeli w grafie istnieje łuk \(p,v)\). Zbiór wszystkich poprzedników wierzchołka \(v\) oznaczmy przez \(P_v\).
Wierzchołek \(s\) nazywamy następnikiem wierzchołka \(v\) jeżeli w grafie istnieje łuk \(v,s)\). Zbiór wszystkich następników wierzchołka \(v\) oznaczmy przez \(S_v\).
Dywergencją \(b_v\) wierzchołka \(v\) nazywamy \(b_v=\sum_{s \in P_v} f_{sv} - \sum_{p \in P_v} f_{vp}\). Jeżeli \( b_v> 0\) to wierzchołek \(v\) jest źródłem. Jeżeli \( b_v<0\) to wierzchołek \(v\) jest ujściem.
Graf \(H\) jest podgrafem grafu \(G\) jeżeli zbiory wierzchołów i krawędzi \(H\) są podzbiorami odpowiednio zbiorów wierzchołków i krawędzi \(G\).
Drzewem rozpinającym grafu \(G\) nazywamy spójny podgraf, taki, że zawiera wszystkie wierzchołki z grafu \(G\) oraz zawiera \(n-1\) krawędzie, gdzie \(n\) jest liczbą wierzchołów \(G\).
Skojarzeniem nazywamy podzbiór krawędzi grafu \(G\) taki, że krawędzie nie mają wspólnych wierzchołków. Maksymalne skojarzenie, to skojarzenie zawierające maksymalną liczbę krawędzi.
Pokryciem jest podzbiór wierzchołów takich, że wszystkie krawędzie są przylegające do co najmniej jednego wierzchołka z tego zbioru. Z minimalnym pokryciem mamy do czynienia, jeżeli liczba wierzchołków jest najmniejsza.
Graf jest dwudzielnym jeżeli możemy podzielić zbiór wierzchołków na dwa rozłączne podzbiory, takie że w każdym z tych podzbiorów nie ma krawędzi łączących wierzchołki w obrębie zbioru.
Istnieje wiele sposobów reprezentacji sieci przepływowych. Macierz sąsiedztwa jest macierzą kwadratową w której kolumny i wiersze odpowiadają wierzchołkom grafu. Wartość 1 w wierszu \(i\) i kolumnie \(j\) oznacza krawędź skierowaną \((i,j)\). Innym sposobem reprezentacji jest przechowywanie dla każdego wierzchołka listy łuków wychodzących z tego wierzchołka. W programowaniu liniowym najczęściej wykorzystuje się macierz incydencji. Jej wiersze odpowiadają wierzchołkom, a kolumny odpowiadają łukom. Wartość 1 w wierszu \(i\) oraz kolumnie \(j\) oznacza początek łuku \(j\) w wierzchołku \(i\), zaś wartość -1 oznacza, że łuk \(j\) kończy się w wierzchołku \(i\). Jeżeli w sieci przepływowej wyróżnimy wierzchołek źródłowy \(s\) oraz wierzchołek ujściowy \(t\), to ograniczenia modelujące przepływ w sieci mogą przyjąć następującą postać:
\(\sum_{z\in V} f_{v,z} - \sum_{u\in V} f_{u,v} = \left\{\begin{array}{rl}
F& \textit{dla } v=s \\
0&\textit{dla } v\in V\setminus\{s,t\}\\
-F&\textit{dla } v=t
\end{array} \right.\)
gdzie \(F\) jest wielkością przepływu z \(s\) do \(t\), a \(f_{u,v}\leq c_{uv}\) jest przepływem po krawędzi \((u,v)\) ograniczonym przepustowością łuku \(c_{uv}\).
1.2. Zagadnienia modelowane jako problemy w sieciach przepływowych
W sieciach przepływowych formułuje się problemy typowe dla sieci przepływowych, w szczególności problem maksymalnego przepływu i problem przepływu minimalnokosztowego. Cała sztuka modelowania polega na „zakodowaniu” problemu, który chcemy rozwiązać w pojęciach ze świata sieci przepływowych. Najpierw dokonujemy więc pewnego mapowania problemu do problemu w sieci przepływowej. Następnie rozwiązujemy odpowiedni problem w sieci przepływowej. Uzyskany w ten sposób wynik dekodujemy z przestrzeni pojęć sieci przepływowej do domeny wyjściowego problemu. Dlatego istotne jest jednoznaczne i poprawne określenie parametrów sieci przepływowej, zazwyczaj przepustowości i kosztów łuków, oraz wskazanie problemu do rozwiązania na sieci. Przedstawimy teraz dwa kluczowe problemy rozwiązywane w sieciach przepływowych.
Problem maksymalnego przepływu
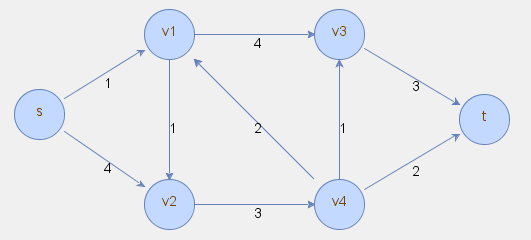
Problem polega na znalezieniu maksymalnego przepływu od wierzchołka źródłowego \(s\) do wierzchołka ujściowego \(t\). W problemie tym muszą zostać zdefiniowane przepustowości krawędzi, natomiast nie są wykorzystywane koszty.
Poniżej znajduje się przykładowa sieć przesyłowa dla problemu maksymalnego przepływu.
Rozwiązanie problemu maksymalnego przepływu zostało zaznaczone poniżej w postaci przepływów podanych w nawiasach kwadratowych.
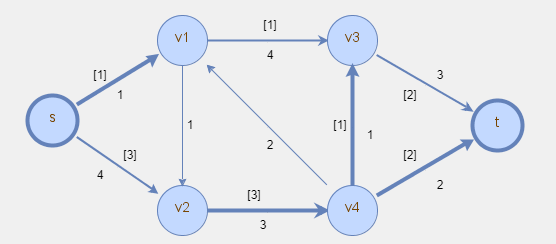
Problem maksymalnego przepływu można rozwiązywać np. algorytmem Forda-Fulkersona. Dla całkowitoliczbowych przepustowości algorytm ten znajduje rozwiązanie całkowitoliczbowe w skończonej liczbie iteracji. Ponieważ w niniejszym materiale skupiamy się na modelowaniu, czytelnika chcącego poznać szczegóły algorytmu odsyłamy do pozycji bibliograficznych.
Model programowania liniowego dla problemu maksymalnego przepływu jest następujący:
\(\max F\)
\(\sum_{v \in V} f_{sv} -F =0\)
\(\sum_{u\in V} f_{vu} - \sum_{u\in V} f_{uv} = 0 \quad v \in V, v \ne s, v \ne t\)
\( 0 \leq f_{uv} \leq c_{uv} \quad (u,v) \in E\)
Z maksymalnym przepływem wiąże się pojęcie minimalnego przekroju.
Przekrojem grafu \(G=(V,E)\) nazywamy podział łuków na dwa rozłączne podzbiory \(S\) oraz \(T= V \setminus S\). Przepustowość przekroju \((S,T)\) to suma przepustowości wszystkich łuków łączących wierzchołki \(s \in S\) z wierzchołkami \(t \in T\).
Wartość dowolnego przepływu w sieci nie może być większa niż przepustowość dowolnego przekroju. W szczególności wartość maksymalnego przepływu w sieci \(G\) jest równa przepustowości minimalnego przekroju w sieci \(G\).
Minimalny przekrój może być wyznaczony np. w ramach ostatniej iteracji algorytmu Forda-Fulkersona, w której finalne znakowanie wierzchołków wyznacza ich podział na podzbiory \(S\) i \(T\).
Problem najtańszego przepływu
Problem najtańszego przepływu wymaga zdefiniowania jednostkowych kosztów przepływ na łukach. Należy znaleźć przepływ o zadanej wielkości z węzła źródłowego \(s\) do ujścia \(t\) przy minimalnym sumarycznym koszcie przepływu.
Poniżej znajduje się przykładowa sieć przesyłowa dla problemu najtańszego przepływu, gdzie pierwsza liczba z pary x/y oznacza przepustowość, a druga koszt.
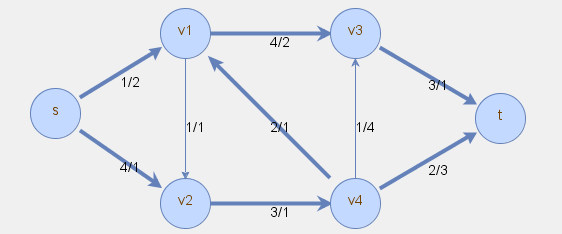
Rozwiązanie problemu najtańszego przepływu zostało zaznaczone poniżej w postaci przepływów podanych w nawiasach kwadratowych.

Problem najtańszego przepływu może być rozwiązywany uproszczoną metodą sympleks lub dedykowanymi algorytmami sieciowymi.
Model programowania liniowego dla problemu minimalnokosztowego przepływu \(F\) jest następujący:
\( \min \sum_{(u,v) \in E} \theta_{uv} f_{uv}\)
\( \sum_{v \in V} f_{sv} = F\)
\(\sum_{u\in V} f_{vu} - \sum_{u\in V} f_{uv} = 0 \quad v \in V, v \ne s, v \ne t\)
\( 0 \leq f_{uv} \leq c_{uv} \quad (u,v) \in E\)
2. Modele rozmyte
Dlaczego potrzebujemy zbiorów rozmytych w modelowaniu matematycznym?
- Teoria prawdopodobieństwa nie jest w stanie uchwycić wszystkich aspektów niepewności. Dotyczy ona niepewności związanej z przypadkowością.
- Zbiory rozmyte pozwalają na określenie nieprezycyjnej i rozmytej informacji (np. temperatura jest wysoka).
- Zbiory rozmyte pozwalają na modelowanie stopniowego przejścia przynależności do zbioru, co było rewolucyjne w pojmowaniu zbiorów i elementów do nich należących.
Przełomowe prace teoretyczne:
Zadeh (1965)
L.A. Zadeh, Fuzzy sets, Information and Control, Volume 8, Issue 3, 1965, Pages 338-353}.
Bellman i Zadeh (1970)
R. E. Bellman and L. A. Zadeh, Decision-Making in a Fuzzy Environment, Management Science , Dec., 1970, Vol. 17, No. 4, pp. B141-B164.
2.1. Pojęcia podstawowe
Funkcja charakterystyczna i funkcja przynależności.
Funkcja charakterystyczna:
\( \varphi_A: \mathbb{X} \mapsto \{0,1\} \)
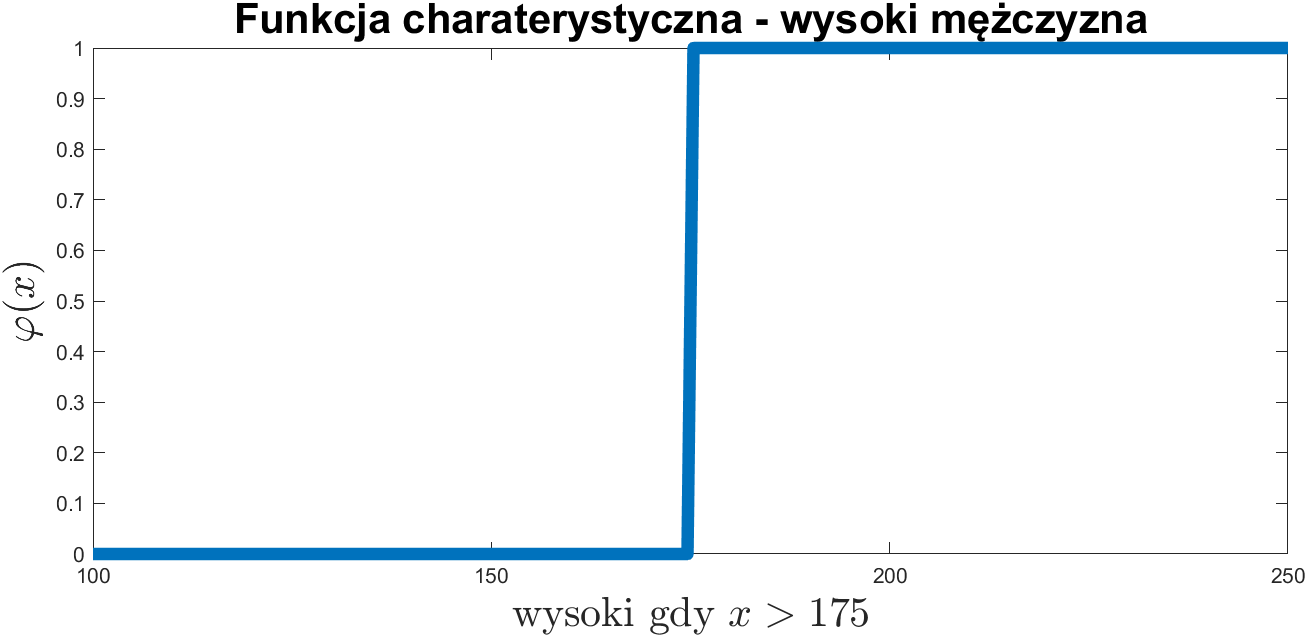
Funkcja przynależności:
\( \mu_A: \mathbb{X} \mapsto [0,1] \)
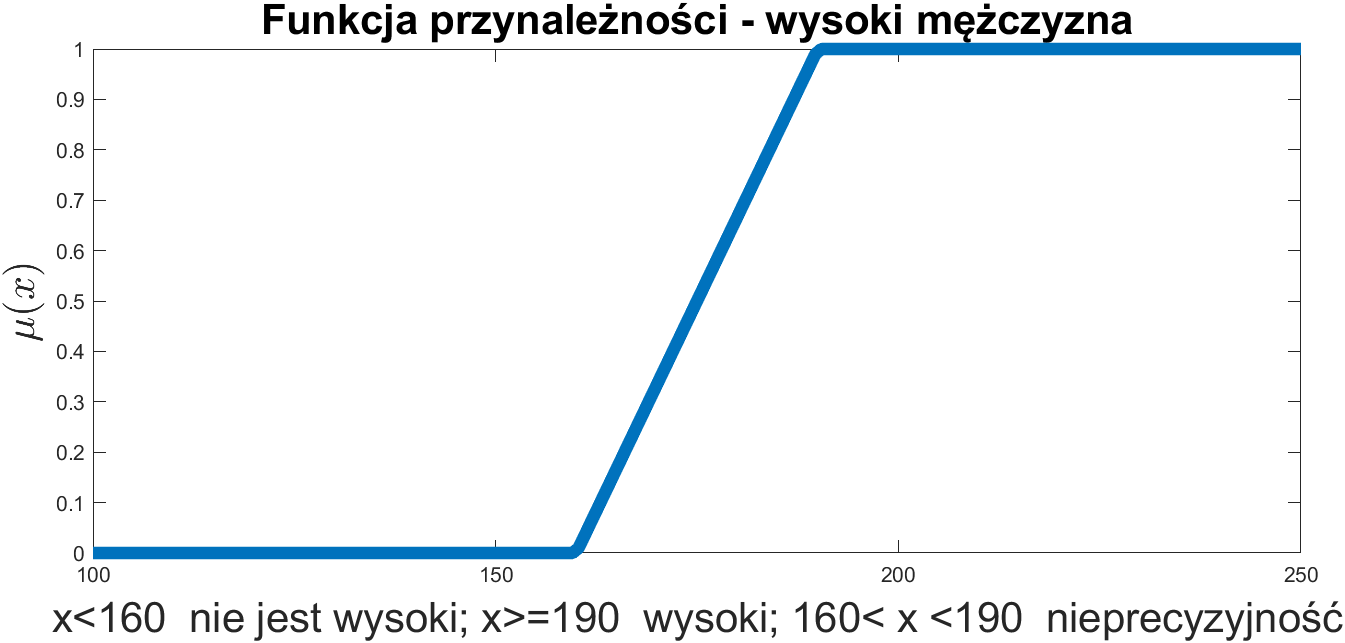
\( \mu _A(x) \) wyraża stopień przynależności \( x \in \mathbb{X} \) do zbioru rozmytego A:
- \( \mu _A(x) = 0\) oznacza, że x nie należy do zbioru A
- \( \mu _A(x) = 1\) oznacza, że x należy do zbioru
- \( \mu _A(x) \in (0,1) \) oznacza stopień przynależności do zbioru A
2.2. Zbiory rozmyte
Zbiór rozmyty
Zbiór rozmyty \(A\) w przestrzeni rozważań \(\mathbb{X}=\{x\}\) (czyli zbiór rozmyty \(A\) w \(\mathbb{X}\)) jest zbiorem par:
$$
A = \{(\mu_A(x),x)\}
$$
Nośnik zbioru rozmytego (ang. support) $A$ w \(\mathbb{X}\) jest zdefiniowany jako zbiór nierozmyty ( \( \emptyset \subseteq supp A \subseteq \mathbb{X}\)):
$$
supp A = \{x \in \mathbb{X}: \mu_A(x) > 0\}
$$
\(\alpha\)- przekrój zbioru rozmytego \(A\) w \(\mathbb{X}\) jest zdefiniowany jako zbiór nierozmyty:
$$
A_{\alpha} = \{x \in \mathbb{X}: \mu_A(x) > \alpha \}, \quad \alpha \in (0,1]
$$
Rodzaje funkcji przynależności:
- Trójkątna funkcja przynależności
- Trapezoidalna funkcja przynależności
- Gausowska funkcja przynależności
- Dzwonowa funkcja przynależności
- Sigmoidalna funkcja przynależności
$$\mu_(x,a,b,c)=\left\{\begin{array}{rcl}
0&& x < a\\
\frac{x-a}{b-a}&& a \leq x \leq b\\
\frac{c-x}{c-b}&& b \leq x \leq c\\
0&& x > c
\end{array} \right.$$
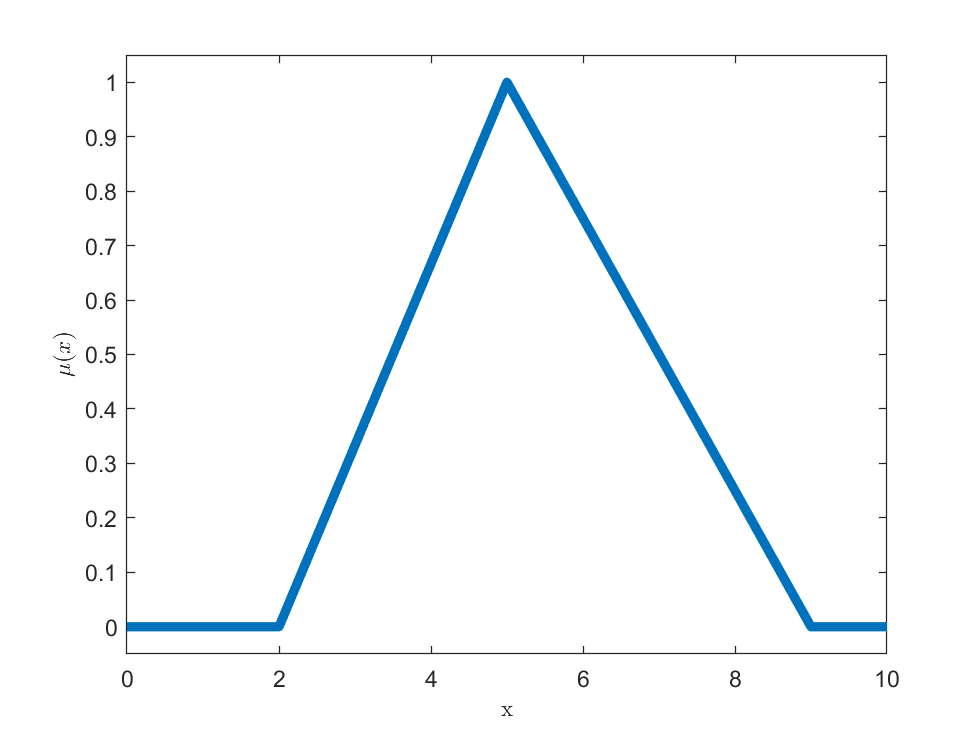
Trapezoidalna funkcja przynależności:
$$\mu_(x,a,b,c,d)=\left\{\begin{array}{rcl}
0&& x < a\\
\frac{x-a}{b-a}&& a \leq x \leq b\\
1&&b \leq x \leq c\\
\frac{d-x}{d-c}&& c \leq x \leq d\\
0&& x > d
\end{array} \right.$$
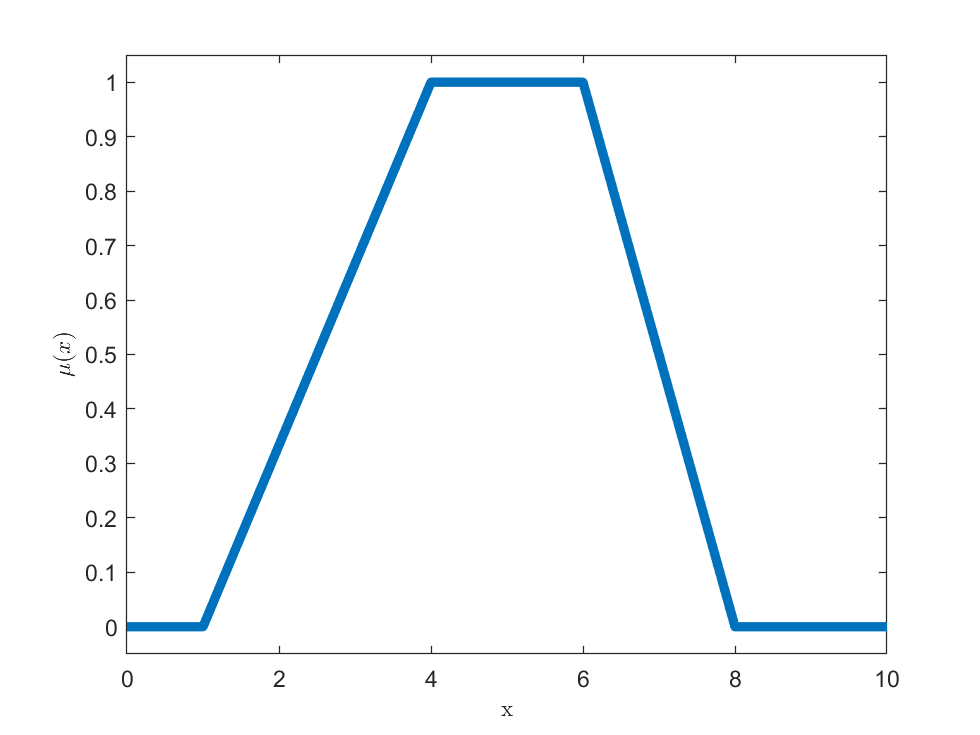
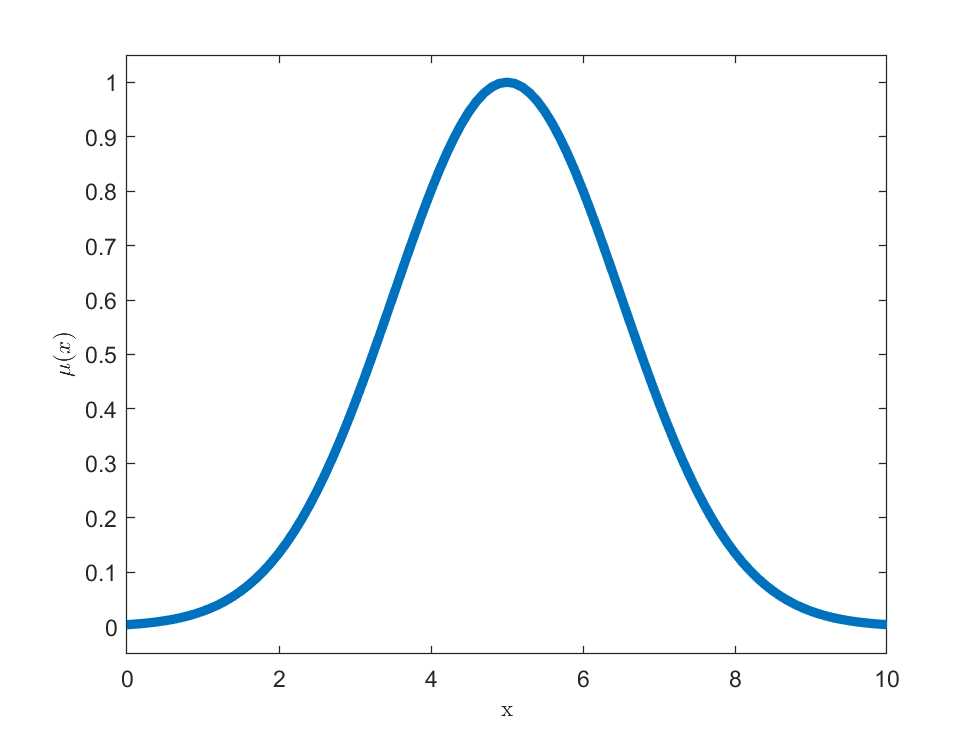
Gausowska funkcja przynależności
$$
\mu_(x,\sigma,c)= \exp(\frac{-(x-c)^2}{2 \sigma^2})
$$
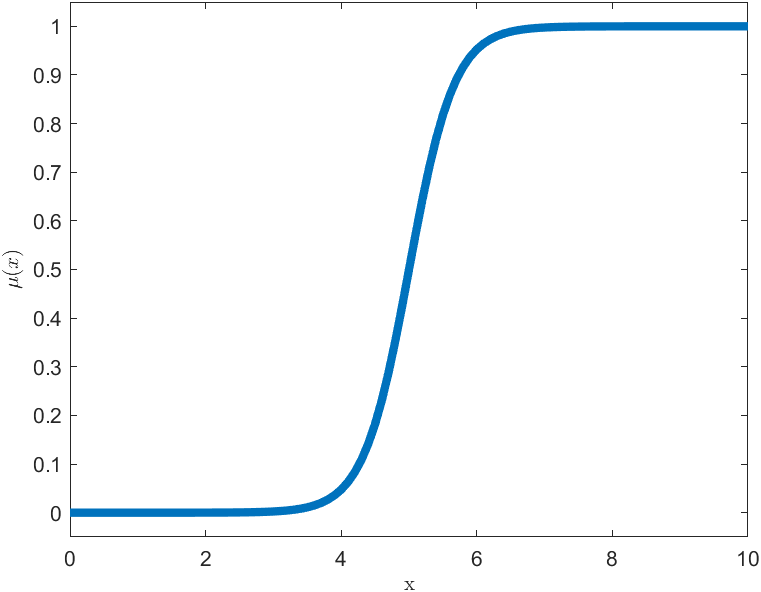
Funkcja sigmoidalna
$$
\mu(x,a,b) = \frac{1}{1+ e^{-a(x-b)}}
$$