Projekt 2
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Integracja Technik Sztucznej Inteligencji |
| Książka: | Projekt 2 |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 6 marca 2026, 02:42 |
Opis
Budowa
i badanie regulatora rozmytego
1. Zadanie
Celem
zadania jest zaprojektowanie, implementacja oraz dostrojenie regulatora
rozmytego, który ma zastąpić podstawowy regulator PID.
2. Realizacja
Należy wykonać następujące kroki:
- Zaprojektować strukturę rozmytego układu regulacji. Układ regulacji powinien uwzględniać niesymetryczne działanie układu oraz ewentualną nieliniowość obiektu.
- Wykonać implementację regulatora rozmytego i uruchomić regulator w trybie symulacji.
- Dostroić parametry regulatora, tak aby uzyskać jakość regulacji porównywalną z jakością regulatora otrzymanego w projekcie 1 (po optymalizacji).
- Ocenić jakość działania układu regulacji.
- Porównać otrzymane rezultaty z tymi z projektu 1 i skomentować wyniki.
3. Założenia
- Optymalizację wykonać dla punkt pracy: \( PV_{PP}=0.2 [m] \). Proszę zwrócić uwagę na niesymetryczne właściwości obiektu - inną dynamikę napełniania i opróżniania.
- Ocenę jakości działania układu regulacji wykonać dla zmian wokół punktu pracy: \( \Delta SP=±0.05 [m] \) oraz dla skrajnie innych punktów pracy (bardzo małych bardzo dużych). W tym celu należy przygotować odpowiedni scenariusz testowy. Zakładamy, że układ regulacji działa z okresem próbkowania \( t_p^{cont}=0.2 [s] \). Z takim okresem zbierane będą dane pomiarowe.
- Do oceny wykorzystywać te same wskaźniki jakości co w projekcie 1>.
4. Uwagi
- Regulator rozmyty musi działać w pętli sprzężenia zwrotnego, w każdym kroku symulacji musi wypracować odpowiednie sterowanie. Przygotowany symulator modeluje działanie obiektu (procesu) jak i układu regulacji.
-
Struktura wewnętrzna symulatora składa się ze ścieżek przetwarzania (
Path), które z kolei zbudowane są z poszczególnych bloków funkcyjnych (pochodne klasyBlock). Uproszona wersja struktury, konieczna do zrozumienia jak zaimplementować i uruchomić nowy blok funkcyjny, została przedstawiona na rysunku poniżej. Szczególnym rodzajem bloku funkcyjnego jest podsystem (Subsystem), który zbudowany jest z określonych składowych bloków funkcyjnych. Poszczególne podsystemy zdefiniowane są w postaci odrębnych klas w bibliotece szablonów (templates.py).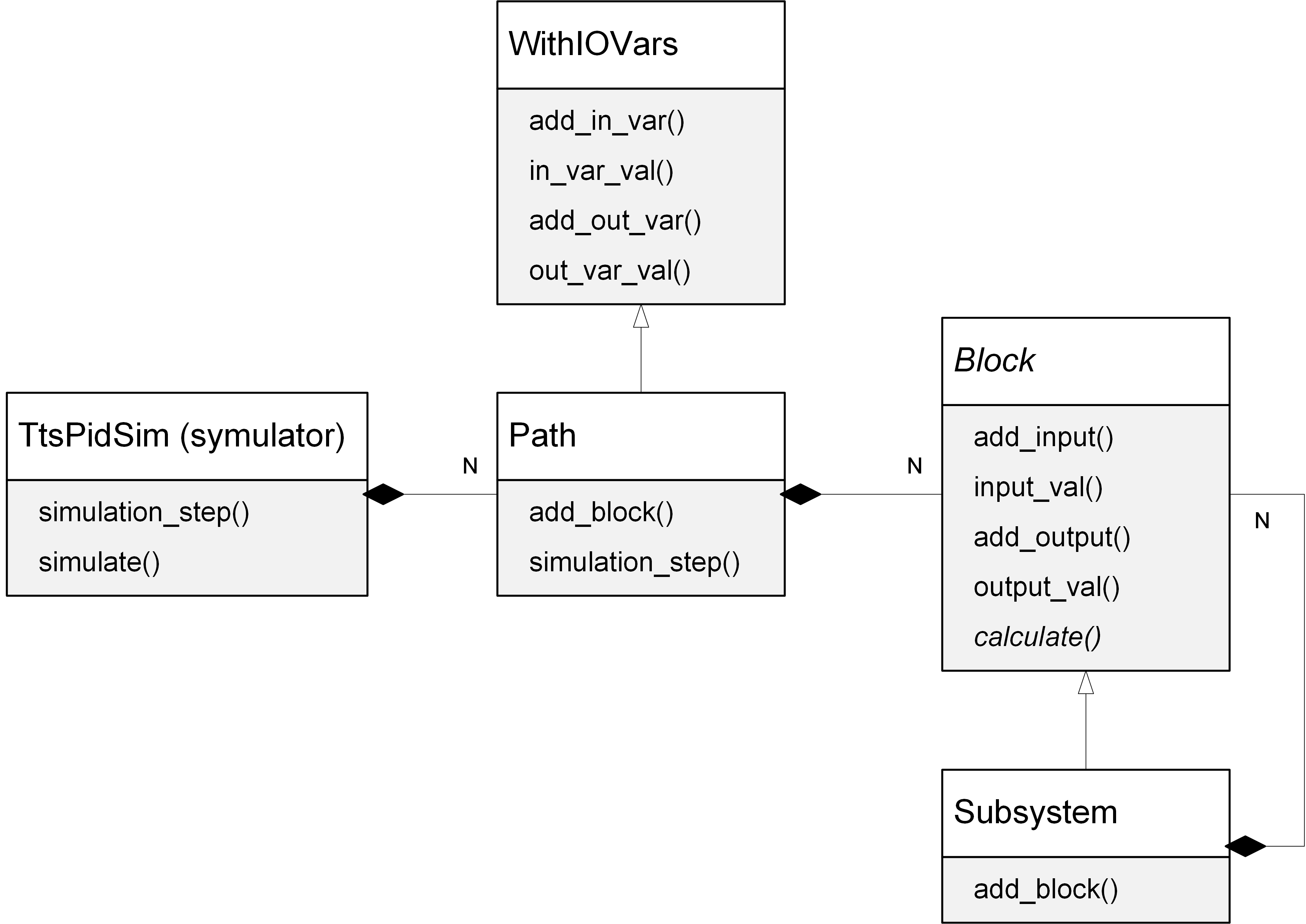
Uproszczony schemat struktury wewnętrznej symulatora -
Przykładem utworzenia podsystemu użytkownika jest szablon regulatora PID – klasa
PID(wtemplates.py). Uproszczony listing klasy pokazano poniżej. Wszystkie elementy składowe regulatora PID i ich konfiguracja zawarte są w konstruktorze__init__().Listing: Definicja klasy PID(skrót)""" Implementation of classical PID controller. """ class PID(Subsystem): """ @param _name unique (in parent object) block name @param _inputs required inputs ([Value, ...]): SP [m], PV [m], mode, cv_man @param _tp sampling time """ def __init__(self, _name, _inputs, _tp): super().__init__(_name, _inputs) # Define processing structure in the form of interconnected subblocks # - add function block sp_filt = self.add_block( FirstOrderInertia('sp_filt', _tp, 1, 0.1) ) # - add block input and connect to subsystem input sp_filt.add_input(self.input(0)) ... # Define subsystem outputs (add and connect to block output): CV [%], e self.add_output(cv.output(0)) self.add_output(e.output(0))Użytkownik odpowiedzialny jest za:
- dodanie poszczególnych bloków składowych,
- podłączenie wejść bloków do wejść podsystemu lub innych bloków,
- zdefiniowanie niezbędnych wyjść podsystemu.
Ważne jest aby nowy regulator rozmyty miał te same wyjścia (i w tej samej kolejności) co regulator klasyczny PID (czyli
CVie, dodatkowo dodano wyjściede) gdyż ma go zastąpić, a inne bloki korzystają z wyjścia regulatora. -
Przykładem zastosowania ścieżki jest ścieżka modułu sterowania (
controller_sim) zdefiniowana w symulatorze. Ze względu na podłączenie kolejnych bloków do wyjścia regulatora zastosowano tą samą nazwę bloku regulatora rozmytego co regulatora PID.Listing: Fragment konstruktora TtsPidSim.__init__()związany z definiowaniem podsystemu sterowania# Controller path # working with tpcont = tpsim * pr.control (default=0.2 [s]) controller_sim = Path('controller_sim', self.pr['control']) self.paths['controller_sim'] = controller_sim # PV measurement. Block also used to make control feedback. pv_noise = controller_sim.add_block( Random('pv_noise', 0, 0.0013333333333) ) pv_measure = controller_sim.add_block( SumDiff('pv_measure', [1, 1]) ) pv_measure.add_input(pv_noise.output(0)) controller = controller_sim.add_block( PID('controller', [sp.output(0), pv_measure.output(0), cvman.output(0)], self.tp*self.pr['control']) ) # add ins/outs: controller parameters self.add_in_var('kp', controller.blocks['kp'].const) self.add_in_var('Ti', controller.blocks['ti'].const) self.add_in_var('Td', controller.blocks['td'].const) self.add_in_var('Bias', controller.blocks['bias'].const) self.add_in_var('Ienable', controller.blocks['i_enable'].const) self.add_in_var('Denable', controller.blocks['d_enable'].const) self.add_in_var('PIDmode', controller.blocks['mode'].const) # - monitoring variables: CV, PV, e self.add_out_var('CV', controller.output(0)) self.add_out_var('PV', pv_measure.output(0)) self.add_out_var('e', controller.output(1)) -
Dodanie nowej struktury przetwarzania, takiej jak regulator rozmyty, można zrealizować poprzez wykorzystanie jednej lub kilku z następujących możliwości:
- dodanie nowego bloku funkcyjnego – wygodne rozwiązanie do realizacji określonych cyklicznych obliczeń na zestawie sygnałów wejściowych i wyznaczających zestaw sygnałów wyjściowych, np. implementacja modelu rozmytego o 2 wejściach i jednym wyjściu,
- dodanie nowej ścieżki – wygodne rozwiązanie do realizacji złożonego przetwarzania składającego się z kilku bloków funkcyjnych (dostępnych w symulatorze lub dodanych przez użytkownika),
- modyfikacja metody
simulation_step()symulatora - nie jest to zalecane podejście, - realizacja przetwarzania poza symulatorem, w tym przypadku symulator działa bez regulatora, a wymiana danych następuje w każdym kroku poprzez zdefiniowane wejścia/wyjścia symulatora - nie jest to zalecane podejście.
5. Przykłady
W przykładzie wykorzystano bibliotekę Fuzzy Logic do realizacji prostego rozmytego systemu wnioskującego. Kod zapisano w notebooku Jupyter-a project_2.ipynb.
Testy prowadzone będą przy założeniu zmian \( \Delta SP=±0.05 [m] \) wokół ustalonego punktu pracy \( SP=0.2 [m] \), okres symulacji \( t_{end}=2700 [s] \).
Załóżmy, że chcemy zaprojektować regulator rozmyty o następującej strukturze:
- wygnały wejściowe: odchyłka \( e \), pochodna odchyłki \( \Delta e \),
-
dla każdego wejścia zdefiniujemy dwa zbiory rozmyte o liniowych funkcjach przynależności typu Z i S położonych symetrycznie względem osi y,
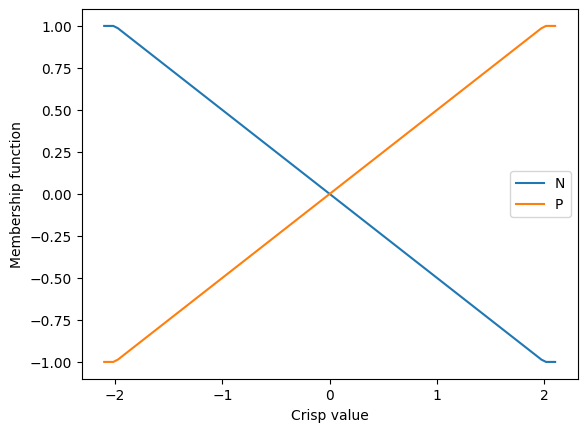
Wykorzystany kształt funkcji przynależności na wejściach modelu rozmytego -
dla wyjścia \( \Delta CV \) zdefiniowano trzy singletony położone symetrycznie względem osi y,
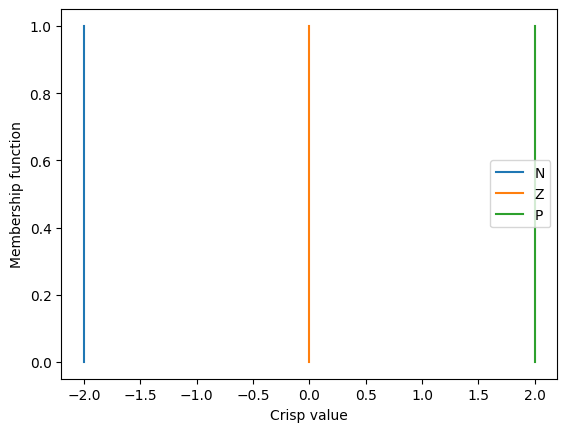
Wykorzystany kształt funkcji przynależności na wejściach modelu rozmytego -
baza wiedzy systemu wnioskującego:
Reguły wnioskowania regulatora rozmytego Reguła R1: \( (e=N \wedge \Delta e=N) \Rightarrow (\Delta CV=N) \) R1: \( (e=N \wedge \Delta e=P) \Rightarrow (\Delta CV=Z) \) R1: \( (e=P \wedge \Delta e=N) \Rightarrow (\Delta CV=Z) \) R1: \( (e=P \wedge \Delta e=P) \Rightarrow (\Delta CV=P) \) - wartość wyjściowa z modelu rozmytego \( |Delta CV \) podawana jest na blok całkujący w celu wyznaczenia wartości \( CV \).
Założono następujące zmienności sygnałów wejściowych i wyjścia:
\( e=<-ke,ke>: ke=0.05 \)
\( \Delta e=<-kde,kde>:kde=0.0005 \)
\( \Delta CV=<-kdCV,kdCV>:kdCV=\frac{10}{t_p^{cont}} \)
Implementację modelu rozmytego w bibliotece Fuzzy Logic pokazano na poniższym listingu. W implementacji wykorzystano skalowanie przedziałów zmienności we/wy do przedziału \( <-1,1> \) przy wykorzystaniu współczynników \( ke \), \( kde \) i \( kdCV \). Ze względu na właściwości biblioteki singletony przybliżono bardzo stromą funkcją trójkątną.
from fuzzylogic.classes import Domain, Set, Rule
from fuzzylogic.functions import R, S, triangular
import matplotlib.pyplot as plt
# Precyzja obliczeń
prec = 0.001
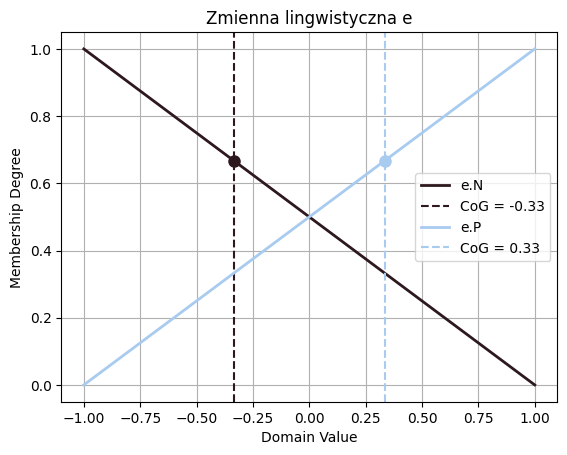
# Definicja zmiennej rozmyte e
e_dom = Domain("e", -1, 1, prec)
e_dom.N = S(-1,1)
e_dom.P = R(-1,1)
plt.figure()
e_dom.N.plot()
e_dom.P.plot()
plt.title('Zmienna lingwistyczna e')
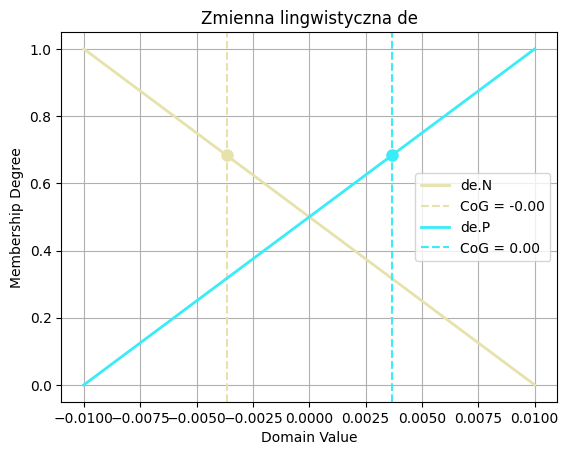
# Definicja zmiennej rozmyte de
de_dom = Domain("de", -1, 1, prec)
de_dom.N = S(-1,1)
de_dom.P = R(-1,1)
plt.figure()
de_dom.N.plot()
de_dom.P.plot()
plt.title('Zmienna lingwistyczna de')
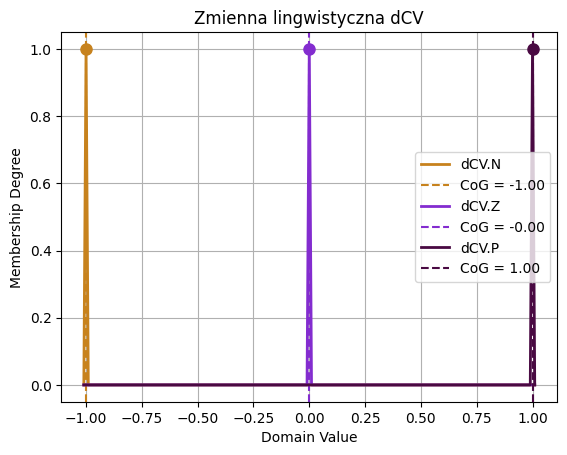
# Definicja zmiennej rozmyte dCV
dcv_dom = Domain("dCV", -1-prec, 1+prec, prec)
dcv_dom.N = triangular(-1-prec, -1+prec)
dcv_dom.Z = triangular(-prec, prec)
dcv_dom.P = triangular(1-prec, 1+prec)
plt.figure()
dcv_dom.N.plot()
dcv_dom.Z.plot()
dcv_dom.P.plot()
plt.title('Zmienna lingwistyczna dCV')
# Definicja reguł wnioskowania
R1 = Rule({(e_dom.N, de_dom.N): dcv_dom.N})
R2 = Rule({(e_dom.N, de_dom.P): dcv_dom.Z})
R3 = Rule({(e_dom.P, de_dom.N): dcv_dom.Z})
R4 = Rule({(e_dom.P, de_dom.P): dcv_dom.P})
# Definicja bazy wiedzy modelu rozmytego
rules = R1 | R2 | R3 | R4
# Przykład wnioskowania
values = {e_dom: -0.25, de_dom: -0.005}
print(R1(values), R2(values), R3(values), R4(values), "=>", rules(values))
Aby osadzić regulator rozmyty w symulatorze przygotowano dedykowany blok funkcyjny SimpleFuzzyController (fuzzy.py). Parametry modelu ke, kde i kdCV zdefiniowano jako sygnały wejściowe bloku, a nie jako parametry wewnętrzne. Wejścia te zostaną wykorzystane w kolejnym projekcie.
"""
Prosty regulator rozmyty z dwoma wejściami: e, de
i jednym wyjściem dCV.
"""
# Simple fuzzy kontroller with 2 inputs: e, de
# and 1 output: dCV
class SimpleFuzzyController(Block):
def __init__(self, _name):
super().__init__(_name)
prec = 0.001
self.e_dom = Domain("e", -1, 1, prec)
self.e_dom.N = S(-1, 1)
self.e_dom.P = R(-1, 1)
self.de_dom = Domain("de", -1, 1, prec)
self.de_dom.N = S(-1, 1)
self.de_dom.P = R(-1, 1)
self.dcv_dom = Domain("dCV", -1-prec, 1+prec, prec)
self.dcv_dom.N = triangular(-1-prec, -1+prec)
self.dcv_dom.Z = triangular(-prec, prec)
self.dcv_dom.P = triangular(1-prec, 1+prec)
R1 = Rule({(self.e_dom.N, self.de_dom.N): self.dcv_dom.N})
R2 = Rule({(self.e_dom.N, self.de_dom.P): self.dcv_dom.Z})
R3 = Rule({(self.e_dom.P, self.de_dom.N): self.dcv_dom.Z})
R4 = Rule({(self.e_dom.P, self.de_dom.P): self.dcv_dom.P})
self.rules = R1 | R2 | R3 | R4
self.add_output()
def calculate(self):
ke = self.input_val(0)
kde = self.input_val(1)
kdcv = self.input_val(2)
e = self.input_val(3)
de = self.input_val(4)
values = {self.e_dom: e/ke, self.de_dom: de/kde}
self.output_val(0, self.rules(values)*kdcv )
W kolejnym kroku przygotowano podsystem sterowania rozmytego FuzzyControl, w którym wykorzystano przygotowany blok funkcyjny. Zabieg ten wykonano w celu uporządkowania kodu symulatora. Krok ten może zostać pominięty, wtedy elementy składowe tego podsystemu trzeba zdefiniować bezpośrednio w jednej ze ścieżek przetwarzania.
class FuzzyControl(Subsystem):
"""
Konstruktor
Należy dodać wejścia: SP [m], PV [m]
@param _tp Czas próbkowania z jakim będzie działać regulator
"""
def __init__(self, _name, _inputs, _tp):
super().__init__(_name, _inputs)
# Obliczenie e=SP-PV oraz de/dt
e = self.add_block( SumDiff('e', [1, -1]) )
e.add_input(self.input(0))
e.add_input(self.input(1))
de = self.add_block( RealDifferentiator('de', _tp, 1, 5) )
de.add_input(e.output(0))
# Bloki do przechowywania parametrów
ke = self.add_block( Const('ke', 1) )
kde = self.add_block( Const('kde', 0.01) )
kdcv = self.add_block( Const('kdCV', 1) )
# Blok regulatora fuzzy
fcontroller = self.add_block( SimpleFuzzyController('fcontroller') )
fcontroller.add_input(ke.output(0))
fcontroller.add_input(kde.output(0))
fcontroller.add_input(kdcv.output(0))
fcontroller.add_input(e.output(0))
fcontroller.add_input(de.output(0))
# Całkowanie sygnału dCV
cv = self.add_block( FirstOrderIntegrator('cv', _tp, 1, 1, [0, 100]) )
cv.add_input(fcontroller.output(0))
# Dodanie wyjść: CV [%], e [m]
self.add_output(cv.output(0))
self.add_output(e.output(0))
self.add_output(de.output(0))
W ostatnim kroku należy podmienić w symulatorze (konstruktor klasy TtsPidSim) zawartość ścieżki przetwarzania controller z poleceń obsługujących regulator PID:
controller = controller_sim.add_block( PID('controller', [sp.output(0), pv_measure.output(0), cvman.output(0)], self.tp*self.pr['control']) )
# add ins/outs: controller parameters
self.add_in_var('kp', controller.blocks['kp'].const)
self.add_in_var('Ti', controller.blocks['ti'].const)
self.add_in_var('Td', controller.blocks['td'].const)
self.add_in_var('Bias', controller.blocks['bias'].const)
self.add_in_var('Ienable', controller.blocks['i_enable'].const)
self.add_in_var('Denable', controller.blocks['d_enable'].const)
self.add_in_var('PIDmode', controller.blocks['mode'].const)
na obsługę regulatora rozmytego:
controller = controller_sim.add_block( FuzzyControl('controller', [sp.output(0), pv_measure.output(0)], self.tp*self.pr['control']) )
# add ins/outs: controller parameters
self.add_in_var('ke', controller.blocks['ke'].const)
self.add_in_var('kde', controller.blocks['kde'].const)
self.add_in_var('kdCV', controller.blocks['kdCV'].const)
# - monitoring variables: de
self.add_out_var('de', controller.output(2))
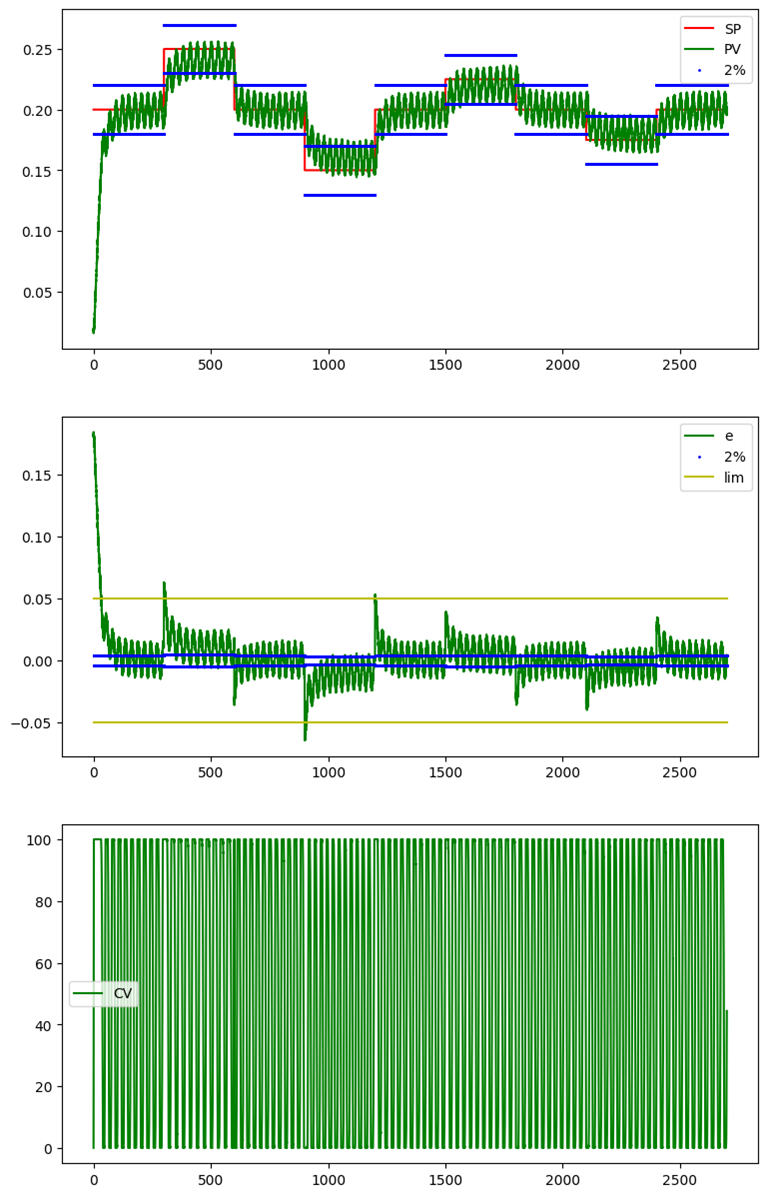
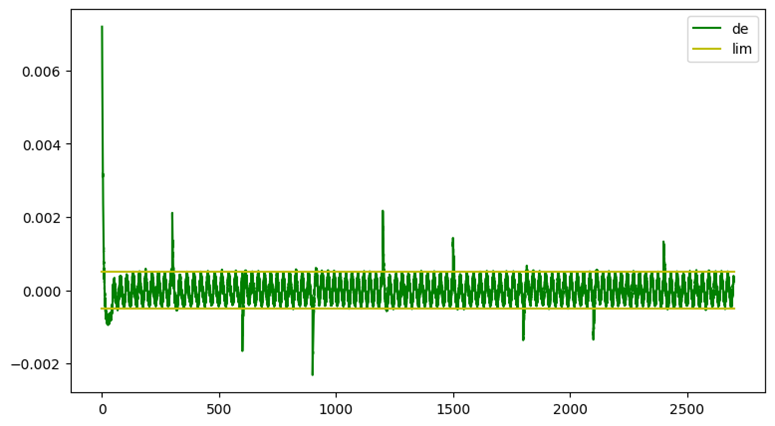
Poniżej pokazano przykładowe wyniki z działania regulatora rozmytego. Jak widać jakość regulacji pozostawia wiele do życzenia – zdecydowanie należy poprawić nastawy tego regulatora, a zapewne także zmienić jego strukturę.