Projekt 3
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Integracja Technik Sztucznej Inteligencji |
| Książka: | Projekt 3 |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 6 marca 2026, 02:42 |
Opis
Rozmyte
przełączanie nastaw regulatora PID
1. Zadanie
Celem
zadania jest uruchomienie regulatora PID, którego parametry będą przełączane płynnie,
np. przy zastosowaniu modelu rozmytego typu TSK, w zależności od aktualnego
punktu pracy.
2. Realizacja
Należy wykonać następujące kroki:
- Dobrać nastawy regulatora PID dla różnych punktów pracy: wartości domyślnej oraz dla skrajnych wartości (małe i duże)
SP. - Zaprojektować mechanizm płynnego przełączania nastaw przy wykorzystaniu logiki rozmytej.
- Ocenić jakość działania układu regulacji we wszystkich rozważanych punktach pracy. Porównać otrzymane rezultaty z tymi z kroku 1, skomentować wyniki.
3. Założenia
- Jako domyślny punkt pracy przyjąć \( PV_{PP}=0.2 [m] \).
4. Uwagi
- Dla domyślnego punktu pracy można zastosować nastawy z projektu 1. Można także wykorzystać przygotowane rozwiązanie z projektu 2 do doboru nastaw dla skrajnych punktów pracy.
- Do płynnego przełączania nastaw można zastosować.
- Do aplikacji wnioskowania rozmytego można zastosować rozwiązania przygotowane w ramach projektu 2, oczywiście po stosownych modyfikacjach.
- W zależności od sposobu realizacji zadania, wygodne może być zastosowanie symulacji wsadowej lub krokowej.
5. Przykłady
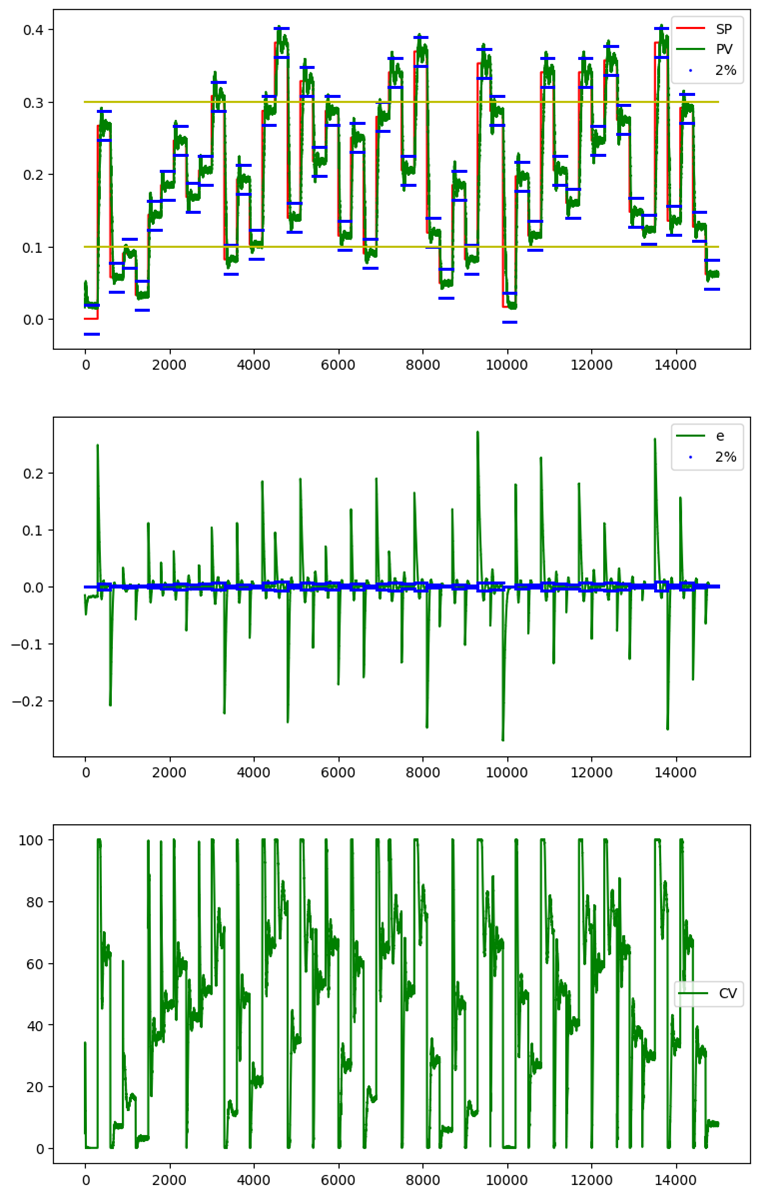
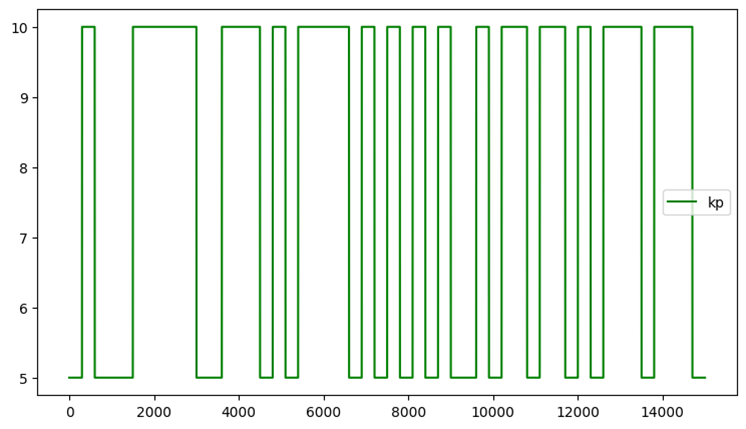
W przykładzie wykorzystano proste przełączanie progowe (nie rozmyte – płynne) nastawy \( k_p \). Założono, że dla skrajnych wartości SP (<0.1 i >0.3) wartość \( k_p=5 \), a dla pozostałego zakresu \( k_p=10 \). Symulację uruchomiono w trybie krokowym. W każdym kroku, w zależności od aktualnej wartości SP ustawiana jest stosowna wartość \( k_p \). Kod zapisano w notebooku Jupyter-a project_3.ipynb.
for i in range(int(tend / tp) + 1):
...
# Ustawienie wartości kp
if sp < 0.1 or sp > 0.3:
k = 5
else:
k = 10
system.in_var_val('kp', k)
kp.append(k)
# Krok symulacji
rval = system.simulation_step(True)
...
Na rysunku poniżej pokazano podsumowanie działania tak zaprojektowanego układu regulacji. Na wykresie linią żółtą symbolicznie oznaczono zakres zmienności \( k_p \). Na dodatkowym przebiegu widać jak zmienia się wartość wzmocnienia \( k_p \). Jak widać, układ działa, chociaż jakość regulacji pozostawia sporo do życzenia.