Projekt 5
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Integracja Technik Sztucznej Inteligencji |
| Książka: | Projekt 5 |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 6 marca 2026, 02:42 |
Opis
Odtwarzanie
charakterystyki statycznej przy wykorzystaniu sieci neuronowych
1. Zadanie
Celem zadania jest odtworzenie zależności \( F_3=f(L_3) \) (charakterystyka wylotu ze zbiornika 3) na podstawie archiwalnych danych procesowych przy wykorzystaniu jednego z modeli sztucznych sieci neuronowych a następnie porównanie otrzymanej charakterystyki ze współczynnikiem przepływu odtworzonym na podstawie modelu analitycznego.
2. Realizacja
Należy wykonać następujące kroki:
- Przeprowadzić stosowny eksperyment i przygotować zbiory danych uczących i testowych. Dane uczące przygotować w dwóch wersjach: dla pełnego zakresu pracy, dla ograniczonego zakresu pracy.
- Wybrać stosowną technikę modelowania (sztuczna sieć neuronowa) i dobrać parametry modelu.
- Przeprowadzić proces uczenia, dla dwóch wersji danych uczących.
- Wyznaczyć współczynnik przepływu na podstawie danych pomiarowych oraz założonego modelu analitycznego zależności wypływu.
- Ocenić i porównać dokładność odtworzenia charakterystyki statycznej dla: modelu neuronowego i dwóch zbiorów danych uczących oraz dla modelowania analitycznego.
3. Założenia
- Biorąc pod uwagę dostępny okres próbkowania oraz wysoką dynamikę tego fragmentu procesu zakładamy, że charakterystyka \( F_3=f(L_3) \) może być przybliżona poprzez zależność statyczną.
- Charakterystyka \( F_3=f(L_3) \) może być opisana następującą zależnością analityczną \( F_2=k_{αS}(L_3) \sqrt{gL_3} \), przy czym współczynnik \( k_{αS} \) może być zależny od wysokości słupa cieczy w zbiorniku 3 (należy sprawdzić).
- Struktura modelu: \( F_3(k)=f(L_3(k)) \), gdzie \( k \) oznacza kolejną chwilę czasową.
4. Przykłady
W przykładzie wykorzystano sieć neuronową typu Sequencial z biblioteki Keras.
Do wygenerowania danych uczących wykorzystano generator CV (przebieg trójkątny) oraz pracę regulatora w trybie sterowania ręcznego. W taki sposób można zebrać możliwie szybko dane to odtworzenia charakterystyki statycznej.
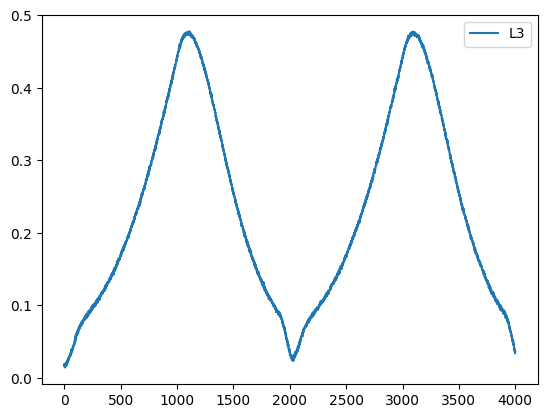
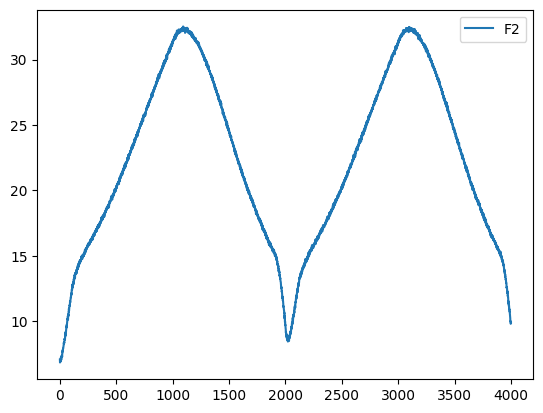
Do testów wykorzystano dane wygenerowane dla przebiegu SP z generatora dla skokowych zmian w całym zakresie pracy. Tryb pracy regulatora ustawiono na automatyczny.
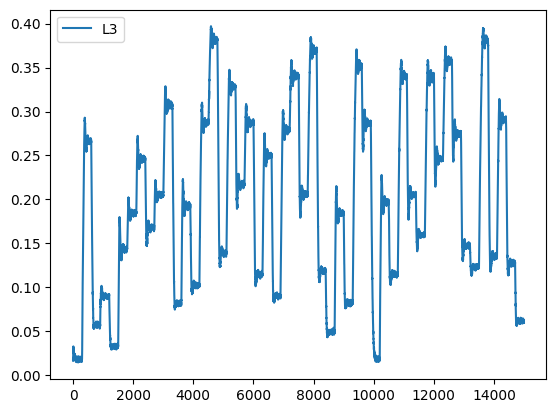
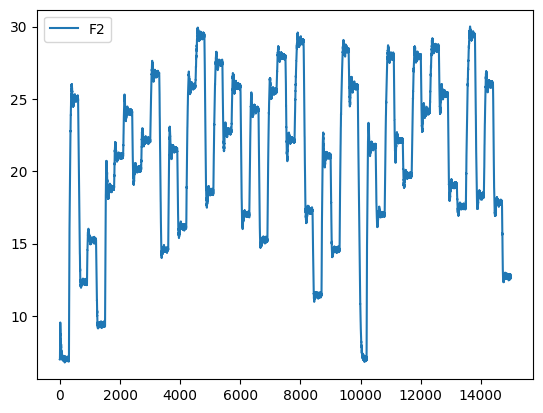
Na rysunku poniżej widać, że zależność \( F_3=f(L_3) \) ma charakter statyczny, nieloniowy.
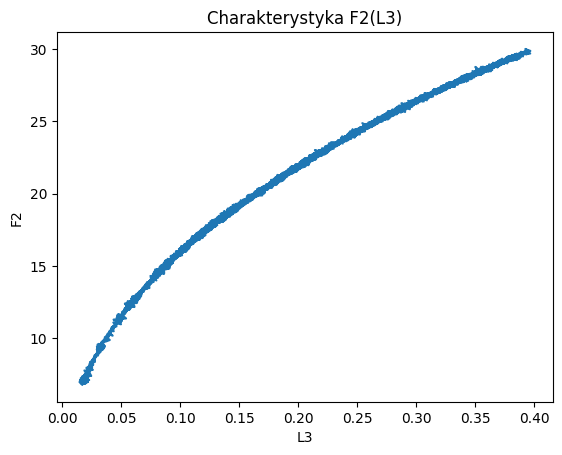
Do modelowania wybrano sieć typu Sequential z biblioteki Keras. Wybrano bardzo prostą strukturę sieci, z jedną warstwą ukrytą i funkcjami aktywacji w postaci tanh oraz optymalizatorem Adam. Wykorzystano normalizację sygnałów wejściowych.
# Narmalizacja
normalizer = tf.keras.layers.Normalization(axis=-1)
normalizer.adapt(np.array(train_features))
# Warstwa wejść i konstrukcja modelu
input_layer = keras.layers.Input(train_features.shape[1:])
model = keras.Sequential([
input_layer,
layers.Dense(2, activation='tanh'),
layers.Dense(1)
])
# Kompilacja modelu
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.02))
# Proce uczenia
history = model.fit(
train_features,
train_labels,
epochs=20,
validation_split = 0.2)
# Predykcja
y = model_saved.predict(test_features)
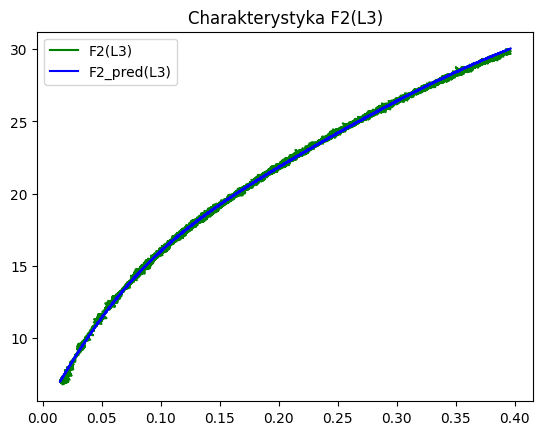
Na rysunku poniżej widać ocenę jakości predykcji wartości L3 dokonywanej przez sieć. Pomimo bardzo prostej struktury i krótkiego procesu uczenia uzyskano dobre wyniki. Charakterystyka statyczna odtwarzana jest w zasadzie bezbłędnie.
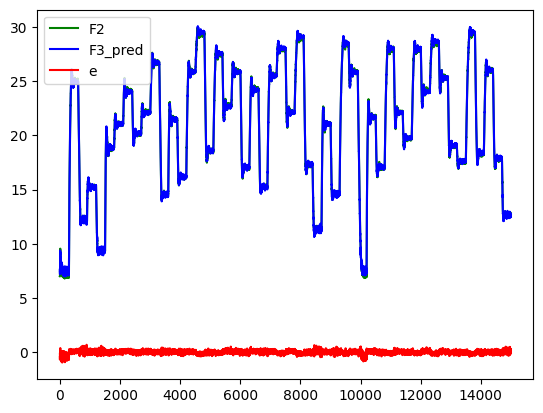
F3 na danych testowych