Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | Wprowadzenie do przetwarzania sygnałów |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | piątek, 13 lutego 2026, 13:32 |
Spis treści
- 1. Wstęp
- 2. Sygnały i ich charakterystyki
- 2.1. Pojęcia podstawowe
- 2.2. Dziedzina i zakres określoności sygnałów
- 2.3. Przekształcenia sygnałów
- 2.4. Operacja splotu i jej zastosowanie do opisu układów liniowych
- 2.5. Parametry energetyczne sygnałów
- 2.6. Korelacja wzajemna i autokorelacja
- 2.7. Sygnały zespolone
- 2.8. Reprezentacja sygnałów w języku Python
- 2.9. Charakterystyki sygnałów w języku Python
- 2.10. Test A - sprawdź swoją wiedzę
- 3. Cyfrowe przetwarzanie sygnałów
- 4. Analiza częstotliwościowa sygnałów
- 5. Analiza częstotliwościowa sygnałów losowych
1. Wstęp
Przetwarzanie sygnałów stanowi jeden z kluczowych obszarów inżynierii biomedycznej, znajdując zastosowanie m.in. w analizie sygnałów fizjologicznych, takich jak EKG, EEG, EMG czy sygnały akustyczne i obrazowe. Zrozumienie podstawowych pojęć związanych z sygnałami oraz metod ich analizy jest niezbędne do prawidłowej interpretacji danych pomiarowych oraz projektowania nowoczesnych systemów diagnostycznych.
Celem niniejszego skryptu jest zapoznanie czytelnika z zagadnieniami związanymi z analizą i cyfrowym przetwarzaniem sygnałów, ze szczególnym uwzględnieniem zastosowań biomedycznych. Materiał został podzielony na kilka tematycznych rozdziałów, które prowadzą od podstawowych definicji do bardziej zaawansowanych metod analizy sygnałów deterministycznych i losowych.
W rozdziale drugim omówione zostały podstawowe pojęcia związane z sygnałami oraz ich parametrami. Rozdział trzeci poświęcony jest cyfrowemu przetwarzaniu sygnałów, w tym operacjom dyskretyzacji, próbkowania oraz podstawowym algorytmom stosowanym w analizie sygnałów w postaci cyfrowej. W rozdziale czwartym przedstawiono analizę częstotliwościową sygnałów deterministycznych, obejmującą m.in. transformatę Fouriera oraz jej zastosowania w analizie widmowej. Rozdział piąty koncentruje się na analizie częstotliwościowej sygnałów losowych. Na końcu każdego rozdziału zamieszczono test sprawdzający, wraz z odpowiedziami, umożliwiający samodzielną ocenę stopnia opanowania omawianego materiału.
W każdym rozdziale zaprezentowane zostały przykłady implementacji omawianych pojęć w języku Python. Pozwala to czytelnikowi nie tylko przyswoić podstawy teoretyczne, lecz także zastosować je w praktycznej analizie i przetwarzaniu sygnałów. Należy zaznaczyć, że ze względu na ograniczenia platformy eSezam oraz brak możliwości wykorzystania dodatkowych wtyczek, zastosowane podświetlanie składni ma charakter uproszczony i może nie w pełni odpowiadać standardowemu wyglądowi kodu Pythona w środowiskach programistycznych (np. PyCharm, VS Code czy Jupyter Notebook).
Dodatkowo, w celu poszerzenia wiedzy, zamieszczono poniżej wybraną literaturę polsko- i anglojęzyczną dotyczącą cyfrowego przetwarzania sygnałów, sygnałów losowych oraz ich zastosowań w analizie sygnałów biomedycznych:
- Rangaraj M. Rangayyan, Sridhar Krishnan, Biomedical Signal Analysis, John Wiley & Sons / Wiley‑IEEE Press, wyd. 3, 2024.
- Richard G. Lyons, Wprowadzenie do cyfrowego przetwarzania sygnałów, Wydawnictwa Komunikacji i Łączności (WKŁ), 2006.
- Zbigniew Gajo, Podstawy cyfrowego przetwarzania sygnałów, Oficyna Wydawnicza Politechniki Warszawskiej, 2019.
- Andrzej Zieliński, Cyfrowe przetwarzanie sygnałów. Od teorii do zastosowań, Wydawnictwa Komunikacji i Łączności (WKŁ), 2014.
- Steven W. Smith, Cyfrowe przetwarzanie sygnałów. Praktyczny poradnik dla inżynierów i naukowców, BTC, Warszawa, 2007.
- Richard G. Lyons, Understanding Digital Signal Processing, Pearson, 3rd ed., 2010.
2. Sygnały i ich charakterystyki
W niniejszym rozdziale przedstawione zostaną podstawowe pojęcia związane z sygnałami oraz ich najważniejsze charakterystyki. Rozpoczniemy od omówienia podstawowych definicji, takich jak sygnał, dziedzina określoności i zakres sygnałów, a także przedstawienia różnic między sygnałami ciągłymi a dyskretnymi. Następnie przyjrzymy się przekształceniom sygnałów - takimi jak przesunięcie, skalowanie i odwrócenie - które pozwalają na elastyczne modelowanie i analizę sygnałów.
W dalszej części rozdziału skoncentrujemy się na operacji splotu, która stanowi fundamentalne pojęcie w analizie i opisie liniowych układów niezmienniczych w czasie. Pokażemy, w jaki sposób splot pozwala określić odpowiedź układu na dowolny sygnał wejściowy, wykorzystując jego odpowiedź impulsową.
Kolejnym omawianym zagadnieniem będą parametry energetyczne sygnałów, takie jak wartość średnia, energia oraz moc średnia, które pozwalają na ilościową ocenę sygnałów, a także operacje korelacji wzajemnej i autokorelacji umożliwiające ocenę podobieństwa sygnałów, wykrywanie opóźnień oraz analizę ich struktury czasowej.
Oprócz sygnałów rzeczywistych, omówione zostaną sygnały zespolone w kontekście ich reprezentacji w dziedzinie amplitudy i fazy, a także przy użyciu części rzeczywistej i urojonej. Pozwoli to na dokładniejszą analizę przebiegów harmonicznych, modulacji oraz filtracji sygnałów, które często występują w praktyce inżynierskiej.
Rozdział zawiera także przykłady implementacji omawianych pojęć w języku Python, obejmujące m.in. generowanie sygnałów, wykonywanie operacji splotu, obliczanie energii i mocy oraz korelację. Umożliwia to czytelnikowi nie tylko przyswojenie podstaw teoretycznych, lecz również ich praktyczne zastosowanie w analizie i przetwarzaniu sygnałów.
2.1. Pojęcia podstawowe
Sygnał jest to funkcja, która opisuje zmianę pewnej wielości fizycznej lub stanu obiektu fizycznego w czasie. Sygnały mogą obejmować m.in. sygnały dźwiękowe, obrazowe, elektryczne i biologiczne.
Przykłady sygnałów:
- mowa człowieka – sygnał akustyczny,
- zdjęcie cyfrowe – sygnał dwuwymiarowy,
- EKG serca – sygnał biomedyczny,
- sygnał radiowy – sygnał elektromagnetyczny,
- napięcie i prąd w układach elektrycznych – sygnał elektryczny.
Pojęcie sygnału będziemy utożsamiać z jego modelem matematycznym. Sygnały mogą być opisane za pomocą funkcji jednej lub wielu zmiennych. W praktyce wykorzystuje się funkcje czasu i/lub położenia w przestrzeni. Funkcje te mogą przyjmować zarówno wartości rzeczywiste, jak i zespolone. W przypadku modeli zespolonych mamy ułatwioną ich analizę formalną, ale kosztem zwiększenia stopnia abstrakcji opisu sygnałów. Jako modele sygnałów wprowadza się również wielkości niefunkcyjne, określane mianem dystrybucji.
Dysponując modelem matematycznym sygnału, możemy dokonać jego przetworzenia, które polega na modyfikowaniu i wydobywaniu użytecznych informacji z sygnału w celu jego poprawy, kompresji, interpretacji, przesyłania czy wizualizacji. Jako główne cele przetwarzania sygnałów można wymienić:
- usuwanie zakłóceń, szumów i artefaktów, np. z nagrań audio i obrazów, pochodzących z aparatury pomiarowej, ruchu pacjenta lub impulsów elektrycznych,
- wzmacnianie użytecznych informacji, np. wyodrębnianie sygnału EKG,
- kompresja danych, np. w formatach MP3 i JPEG, a także zmniejszanie objętości danych biomedycznych w celu ich przesyłania w systemach telemedycyny,
- rozpoznawanie wzorców i zdarzeń, np. mowy lub twarzy, a także wykrywanie napadów epilepsji, migotania przedsionków czy bezdechu sennego,
- analiza sygnału w dziedzinie czasu i częstotliwości, np. w diagnostyce omdleń lub analizy aktywności fal mózgowych w sygnałach EEG.
W teorii przetwarzania sygnałów wyróżnia się podstawowy podział sygnałów na:
- deterministyczne – sygnały w pełni określone poprzez zależności matematyczne, na podstawie których można dokładnie przewidzieć ich wartości w każdym momencie czasu,
- stochastyczne (losowe) – sygnały, których wartości są nieprzewidywalne i zmieniają się w sposób losowy.
W zastosowaniach inżynierskich, elektronicznych, telekomunikacyjnych czy biomedycznych mamy do czynienia zarówno z sygnałami deterministycznymi, jak i losowymi.
Sygnały deterministyczne są powtarzalne i przewidywalne:
- sinusoida – fale nośne w radiu,
- impuls prostokątny – sygnał zegarowy w mikroprocesorach,
- EKG – w warunkach spoczynku i bez zakłóceń (składa się z powtarzalnych cykli pracy serca),
- EMG podczas rytmicznego skurczu – powtarzalny wzorzec aktywności mięśni,
- EEG z wywołanym potencjałem – powtarzalna rekcja mózgu na bodziec (np. błysk światła).
W praktyce sygnały deterministyczne zawierają zakłócenia losowe. Każdy pomiar jest obarczony pewnymi błędami o charakterze losowym, które są zwykle eliminowane przez operację filtracji.
Sygnały losowe zmieniają się w sposób trudny do przewidzenia:
- szum biały – wykorzystywany do testowania odpowiedzi systemu oraz modelowania zakłóceń,
- zakłócenia elektromagnetyczne – występujące w transmisji danych, zasilaczach i czujnikach,
- EEG – aktywność mózgu, zmieniająca się dynamicznie i nieregularnie,
- EMG – aktywność mięśni, silnie losowa podczas dowolnego ruchu,
- zmienne tętno (HRV) – różnice między kolejnymi uderzeniami serca, naturalnie losowe.
Rozdziały 2–4 niniejszego skryptu poświęcone są sygnałom deterministycznym, na podstawie których wyjaśnione zostaną podstawowe sposoby opisu i reprezentacji sygnałów. Pojęcia te zostaną następnie uogólnione na sygnały losowe w rozdziale 5.
2.2. Dziedzina i zakres określoności sygnałów
Sygnały są nośnikami informacji, których wartości można zmierzyć i za ich pomocą przekazywana jest informacja. Może ona mieć charakter ciągły, przyjmując nieskończoną liczbę wartości, lub charakter dyskretny, ograniczony do skończonej liczby wartości. Dziedzina i zakres określoności sygnałów informują o tym, jak zmienia się zmienna niezależna opisująca sygnał, na przykład czas lub przestrzeń, oraz jakie wartości może przyjmować sygnał. Stanowią one podstawowe kryterium podziału sygnałów.
Wyróżnia się trzy podstawowe typy sygnałów:
- analogowe,
- dyskretne,
- cyfrowe.
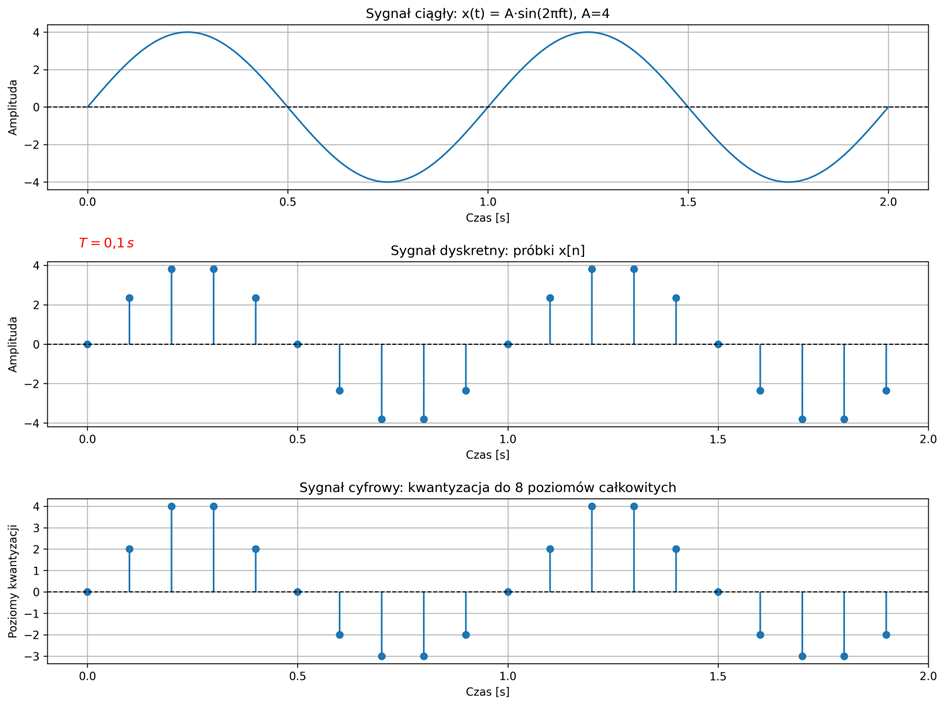
Termin analogowy jest używany przy opisie sygnału, który jest ciągły w czasie i ma ciągły zakres wartości – tzw. ciągły w amplitudzie. W przypadku sygnału dyskretnego, jego wartości określone są tylko w wybranych chwilach czasowych, a amplitudy próbek sygnału należą do zbioru liczb rzeczywistych. Sygnał cyfrowy to sygnał o czasie dyskretnym, którego zbiór wartości również jest dyskretny – tzw. dyskretny w amplitudzie. Sygnały cyfrowe są sygnałami dyskretnymi, dla których przeprowadzono operację kwantowania – przypisywania każdej wartości próbki do najbliższej wartości z ograniczonego zbioru możliwych poziomów. Komputery i systemy cyfrowe nie mogą zapisywać nieskończonej liczby wartości, dlatego dyskretyzacja sygnału w amplitudzie pozwala przetwarzać i przechowywać dane w formie cyfrowej.
W dalszej części rozważań analizowane będą wyłącznie sygnały ciągłe w czasie oraz ich próbkowe wersje dyskretne. Procesy kwantyzacji i kodowania, które są etapami przekształcania sygnału do postaci cyfrowej, nie będą tutaj uwzględniane. Zwykle są one realizowane automatycznie przez przetworniki analogowo-cyfrowe i systemy komputerowe, dlatego nie wpływają na zrozumienie podstawowych problemów związanych z przetwarzaniem sygnałów.
Przyjmijmy formalny zapis jednowymiarowego sygnału jako:
\( x(t) \) lub \( x[n] \)
gdzie:
- \( x(t) \) – sygnał ciągły w czasie \( t \),
- \( x[n] \) – sygnał dyskretny, określony tylko w wybranych chwilach czasowych \( n\in D \).
Zbiór \( D \) wartości zmiennej dyskretnej \( n \) jest zwykle zbiorem wszystkich liczb całkowitych, zbiorem liczb naturalnych lub jego skończonym podzbiorem \( [n_1, n_2] \).
Dziedziną sygnałów ciągłych \( x(t) \) może być:
- zbiór liczb \( \mathbb{R} \) – w modelach matematycznych,
- dodatnia półoś \( [0,\infty) \) – w modelach przyczynowych,
- odcinek \( [t_1, t_2] \) osi czasu – fizycznie istniejące układy.
W przypadku sygnałów dyskretnych \( x[n] \), dziedziną jest zwykle zbiór chwil \( t_n = nT \), \( n\in \mathbf{D} \), odległych od siebie o stały odstęp \( T \), nazywany okresem próbkowania lub przedziałem dyskretyzacji. Istotny dla nas będzie jedynie kolejny numer w ciągu próbek, a nie w jakiej chwili \( t_n \) została pobrana próbka. Dlatego też, argumentem sygnału dyskretnego będzie czas unormowany względem okresu próbkowania, czyli \( n = t_n/T \).
Jeżeli sygnał przyjmuje wartości różne od zera:
- w przedziale nieskończonym, to nazywamy go sygnałem o nieskończonym czasie trwania,
- w przedziale skończonym, to nazywamy go sygnałem o skończonym czasie trwania lub sygnałem impulsowym.
2.3. Przekształcenia sygnałów
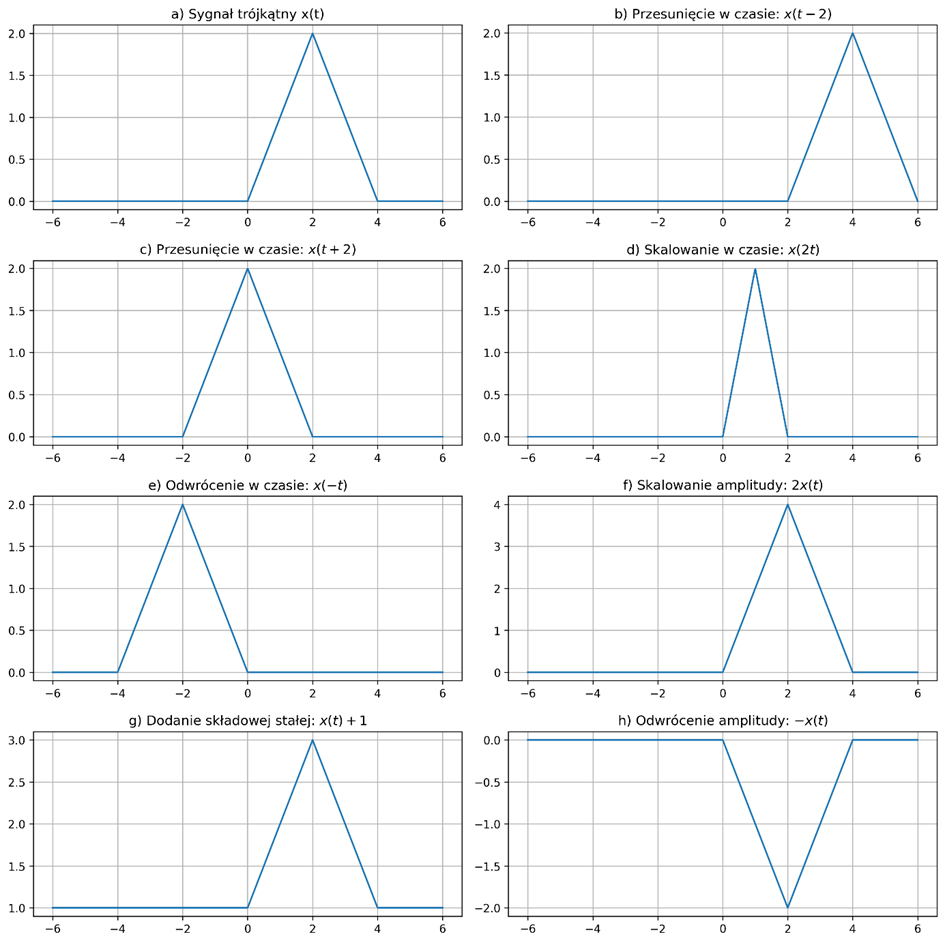
Przekształcenia sygnałów w dziedzinie czasu to operacje, które zmieniają ich kształt, pozycję lub wartości. Do podstawowych operacji można zaliczyć przesunięcie, skalowanie i odwrócenie w czasie, skalowanie amplitudy, dodanie składowej stałej i odwrócenie amplitudy.
- Przesunięcie w czasie – sygnał \( x(t) \) jest przesuwany o \( t_0 \) w lewo lub prawo na osi czasu (rys. 2.3b-c):
\( y(t)=x(t-t_0) \)
- jeśli \( t_0 < 0 \) to mamy do czynienia z przyśpieszeniem sygnału,
- jeśli \( t_0 > 0 \) to mamy do czynienia z jego opóźnieniem.
- Skalowanie w czasie – zmiana szybkości przebiegu sygnału \( x(t) \) poprzez stały współczynnik skalowania czasu \( a \) (rys. 2.3d):
\( y(t)=x(at) \)
- jeśli \( \lvert a \rvert < 1 \) to mamy do czynienia z „rozciąganiem” sygnału w czasie,
- jeśli \( \lvert a \rvert > 1 \) to mamy do czynienia z jego „ściskaniem” w czasie.
- Odwrócenie w czasie – zmiana kierunku przebiegu czasu poprzez odbicie sygnału \( x(t) \) względem osi pionowej (rys. 2.3e):
\( y(t)=x(-t) \)
- Skalowanie amplitudy – zmiana wartości sygnału \( x(t) \) poprzez stały współczynnik skalowania amplitudy \( A \) (rys. 2.3f):
\( y(t)=A\,x(t) \)
- jeśli \( 0 < A < 1 \) to mamy do czynienia z osłabieniem sygnału – amplituda maleje, zachowując kształt w czasie,
- jeśli \( A > 1 \) to mamy do czynienia ze wzmacnianiem sygnału – amplituda rośnie, jednocześnie zachowując jego kształt w czasie,
- jeśli \( A < 0 \) to mamy do czynienia z operacją odwracania w czasie i skalowania amplitudy.
- Dodanie składowej stałej – przesunięcie sygnału \( x(t) \) w górę lub w dół o stałą wartość \( C \) (rys. 2.3g):
\( y(t)=x(t)+C \)
- jeśli \( C < 0 \) to mamy do czynienia z przesunięciem sygnału o \( C \) jednostek w dół, zachowując jego kształt w czasie,
- jeśli \( C > 0 \) to mamy do czynienia z przesunięciem sygnału o \( C \) jednostek w górę, zachowując jego kształt w czasie.
- Odwrócenie amplitudy – zmiana znaku każdej wartości sygnału na przeciwną poprzez odbicie sygnału \( x(t) \) względem osi poziomej (rys. 2.3h):
\( y(t)=-x(t) \)
Przesunięcie z odwróceniem sygnału w czasie posłuży nam do obliczania splotu dwóch sygnałów – operacji opisanej w rozdziale 2.4.
2.4. Operacja splotu i jej zastosowanie do opisu układów liniowych
Istotną klasą systemów w przetwarzaniu sygnałów są systemy liniowe i niezmiennicze w czasie (LTI, ang. Linear Time-Invariant). Systemy LTI to takie, które spełniają dwa podstawowe warunki:
1. liniowość, na którą składa się jednorodność i addytywność:
-
jeżeli sygnał wejściowy \( x(t) \) systemu jest skalowany za pomocą stałego czynnika \( a \), wówczas sygnał wyjściowy \( y(t) \) również jest skalowany przez ten czynnik:
\( H(x(t)) = y(t)\quad\Rightarrow\quad H(a x(t)) = a\cdot y(t) \) -
jeżeli sygnał wejściowy systemu jest sumą sygnałów \( x_1(t) \) i \( x_2(t) \), to aby ten system był addytywny, jego sygnał wyjściowy musi być sumą poszczególnych sygnałów wyjściowych:
\( \begin{cases} H(x_1(t)) = y_1(t) \\ H(x_2(t)) = y_2(t) \end{cases}\quad\Rightarrow\quad H(x_1(t)+x_2(t)) = H(x_1(t)) + H(x_2(t)) = y_1(t) + y_2(t) \)
2. niezmienniczość w czasie:
-
przesunięcie sygnału \( x(t) \) o \( t_0 \) powoduje tylko przesunięcie wyjścia \( y(t) \) o \( t_0 \), bez zmiany kształtu:
\( H(x(t)) = y(t)\quad\Rightarrow\quad H(x(t - t_0)) = y(t - t_0) \)
Powyższe warunki składają się na zasadę superpozycji, którą można analogicznie wyprowadzić dla systemów dyskretnych.
Jeżeli system jest liniowy i niezależny od czasu, to kluczowe staje się pojęcie odpowiedzi impulsowej (ang. Impulse Response). Jest to odpowiedź systemu na pobudzenie w formie impulsu jednostkowego, nazywanego również deltą Diraca (dystrybucja delta) \( \delta(t) \):
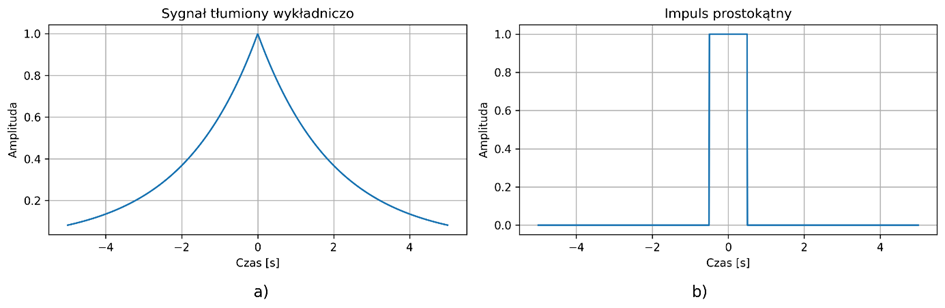
Delta Diraca nie jest funkcją w klasycznym sensie, ale idealizowanym impulsem o nieskończonej amplitudzie i zerowej szerokości – używamy jej przybliżenia. Najczęściej do wizualizacji używa się wąskiego i wysokiego impulsu, np. prostokątnego (rys. 2.4) lub funkcji Gaussa (rys. 2.5).
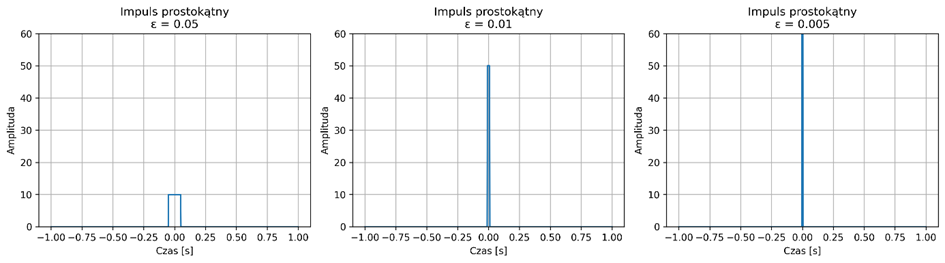
Rys. 2.4. Sekwencja przybliżeń delty Diraca przy użyciu coraz wyższych i węższych impulsów prostokątnych
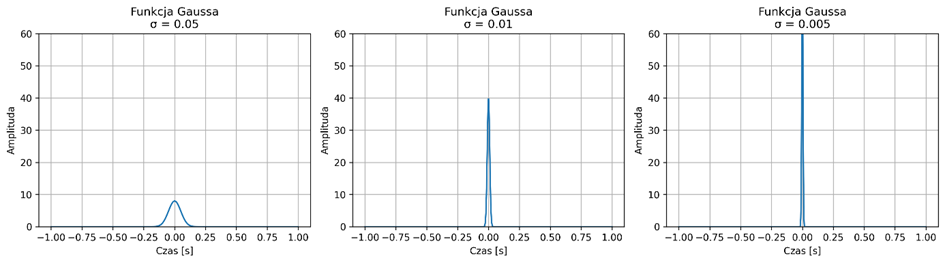
Rys. 2.5. Sekwencja przybliżeń delty Diraca przy użyciu coraz wyższych i węższych krzywych Gaussa
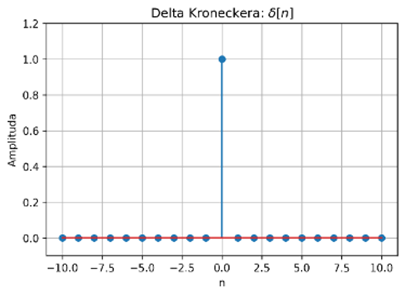
W przypadku sygnałów dyskretnych mamy do czynienia z deltą Kroneckera \( \delta[n] \):
której graficzne przedstawienie zostało pokazane na rys. 2.6. Sygnał ten jest podstawą koncepcji odpowiedzi impulsowej oraz splotu dyskretnego.
Odpowiedź impulsową oznaczamy \( h(t) \) lub \( h[n] \), odpowiednio dla sygnałów ciągłych i dyskretnych. Jeżeli znamy odpowiedź impulsową systemu LTI, to odpowiedź systemu na pobudzenie dowolnym sygnałem możemy obliczyć jako splot tego sygnału z odpowiedzią impulsową.
Splot (ang. Convolution) jest jednym z fundamentalnych pojęć teorii sygnałów. Jest to operacja matematyczna, która oblicza odpowiedź systemu liniowego na dowolny sygnał wejściowy, nakładając odpowiedź impulsową przesuniętą w czasie.
Splot dla:
- sygnałów ciągłych:
- sygnałów dyskretnych:
gdzie \( x \) jest sygnałem wejściowym, \( h \) jest odpowiedzią impulsową systemu oraz \( y \) jest sygnałem wyjściowym, będącym wynikiem splotu. Nakładając odpowiedź impulsową \( h \) na każdą próbkę sygnału \( x \), przesuwając ją w czasie (ciągłym lub dyskretnym) i sumując wpływ wszystkich tych przesunięć, otrzymujemy wynik operacji splotu. Kluczowa jest kolejność wykonywania działań:
1. odwróć w czasie drugi z sygnałów ze względu na \( \tau \) lub \( k \):
2. przesuń go w czasie o czas \( t \) lub o \( n \) próbek:
3. wymnóż pierwszy sygnał ze zmodyfikowanym drugim:
4. scałkuj wynik mnożenia lub zsumuj wszystkie iloczyny próbek.
Znajomość pojęcia splotu pozwala na zrozumienie podstawowych właściwości impulsu Diraca:
-
splot z \( \delta(t) \) – impuls Diraca jest elementem identycznościowym operacji splotu:
\( x(t)\ast \delta(t) = x(t) \) -
splot z przesuniętą deltą \( \delta(t - t_0) \) przesuwa sygnał w czasie o \( t_0 \):
\( x(t)\ast \delta(t - t_0) = x(t - t_0) \)
Zatem, skoro impuls jednostkowy jest sygnałem, który podany na wejście dowolnego liniowego i niezmienniczego w czasie układu powoduje wygenerowanie odpowiedzi równej odpowiedzi impulsowej tego układu:
to odpowiedź takiego systemu na dowolny sygnał wejściowy \( x(t) \) jest jego splotem ze znaną odpowiedzią impulsową \( h(t) \):
W przypadku sygnałów dyskretnych opis systemów LTI za pomocą splotu jest analogiczny:
Oznacza to, że:
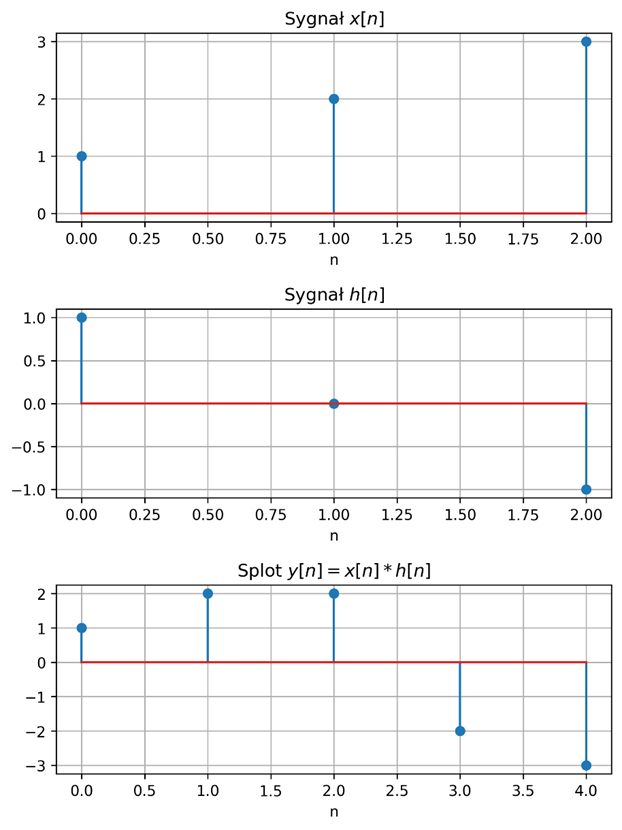
Ponieważ \( x[k] \) i \( h[k] \) mają tylko 3 niezerowe próbki, splot będzie miał długość:
otrzymamy kolejne wartości sygnału \( y[n] \). Kolejne kroki zostały przedstawione w tabeli:

Poniżej przedstawiono wykresy sygnałów i ich splotu:
2.5. Parametry energetyczne sygnałów
Parametry energetyczne sygnałów to miary opisujące ilość energii zawartej w sygnale lub jego moc w czasie, które pozwalają na ilościową ocenę jego właściwości. W analizie i przetwarzaniu sygnałów mają kluczowe znaczenie, ponieważ umożliwiają:
- ocenę amplitudy i intensywności sygnału,
- wykrywanie zmian i anomalii,
- porównywanie i klasyfikowanie sygnałów,
- dobór parametrów filtrów i algorytmów przetwarzania,
- ocenę jakości sygnału.
W kontekście sygnałów biomedycznych analiza parametrów energetycznych jest niezwykle istotna, ponieważ pozwala na ilościową ocenę zarówno aktywności biologicznej, jak i jakości sygnałów rejestrowanych przez aparaturę medyczną. Energia i moc sygnału umożliwiają m.in.:
- ocenę intensywności procesów fizjologicznych – np. amplituda i energia sygnału EKG odzwierciedlają siłę skurczów serca, energia sygnałów EEG koreluje z poziomem aktywności mózgu, a sygnały EMG odzwierciedlają aktywność mięśni,
- wykrywanie nieprawidłowości i patologii – nagłe zmiany energii sygnału mogą wskazywać na arytmie serca, napady epilepsji, migotanie przedsionków lub inne stany chorobowe,
- ocenę jakości sygnału i skuteczności przetwarzania – sygnały o niskiej energii w stosunku do szumu wymagają wzmocnienia lub filtracji, co jest istotne w telemedycynie i zdalnym monitoringu pacjentów,
- dobór parametrów filtrów i algorytmów analizy – energia sygnału pozwala określić, które składowe częstotliwości są istotne, a które stanowią zakłócenia, co ma znaczenie przy projektowaniu algorytmów do analizy EKG, EEG i EMG,
- porównania między pacjentami lub stanami fizjologicznymi – parametry energetyczne umożliwiają obiektywne porównanie sygnałów w różnych warunkach, np. spoczynkowych, wysiłkowych czy patologicznych.
Sygnały deterministyczne przyjmują w dowolnej chwili czasowej wartości rzeczywiste, które są określone przez jawne zależności matematyczne. Z takimi sygnałami wiąże się wiele parametrów, które charakteryzują ich właściwości. Wartość średnia, energia, moc średnia i wartość skuteczna należą do najważniejszych parametrów sygnałów.
- Wartością średnią ciągłego sygnału \( x(t) \), określonego w przedziale \( [t_1, t_2] \), nazywamy wielkość:
- W przypadku sygnału o nieskończonym czasie trwania, wartością średnią nazywamy wielkość graniczną:
- Energią ciągłego sygnału \( x(t) \) nazywamy wielkość:
- Mocą średnią ciągłego sygnału \( x(t) \) nazywamy wielkość graniczną:
- Mocą średnią ciągłego sygnału \( x(t) \) o skończonym czasie trwania, określonego w przedziale \( [t_1, t_2] \), nazywamy wielkość:
- Wartością skuteczną ciągłego sygnału \( x(t) \) jest nazywany pierwiastek z jego mocy:
Wartości energii i mocy sygnału odnoszą się nie bezpośrednio do fizycznych zjawisk, lecz do analizy właściwości sygnału. W teorii sygnałów często nie przypisuje się jednostki sygnału. W takim przypadku wymiarem energii sygnału jest sekunda, natomiast moc jest bezwymiarowa.
Energia i moc charakteryzują właściwości energetyczne sygnału. Na ich podstawie sygnały deterministyczne (ciągłe lub dyskretne) można podzielić na dwie klasy:
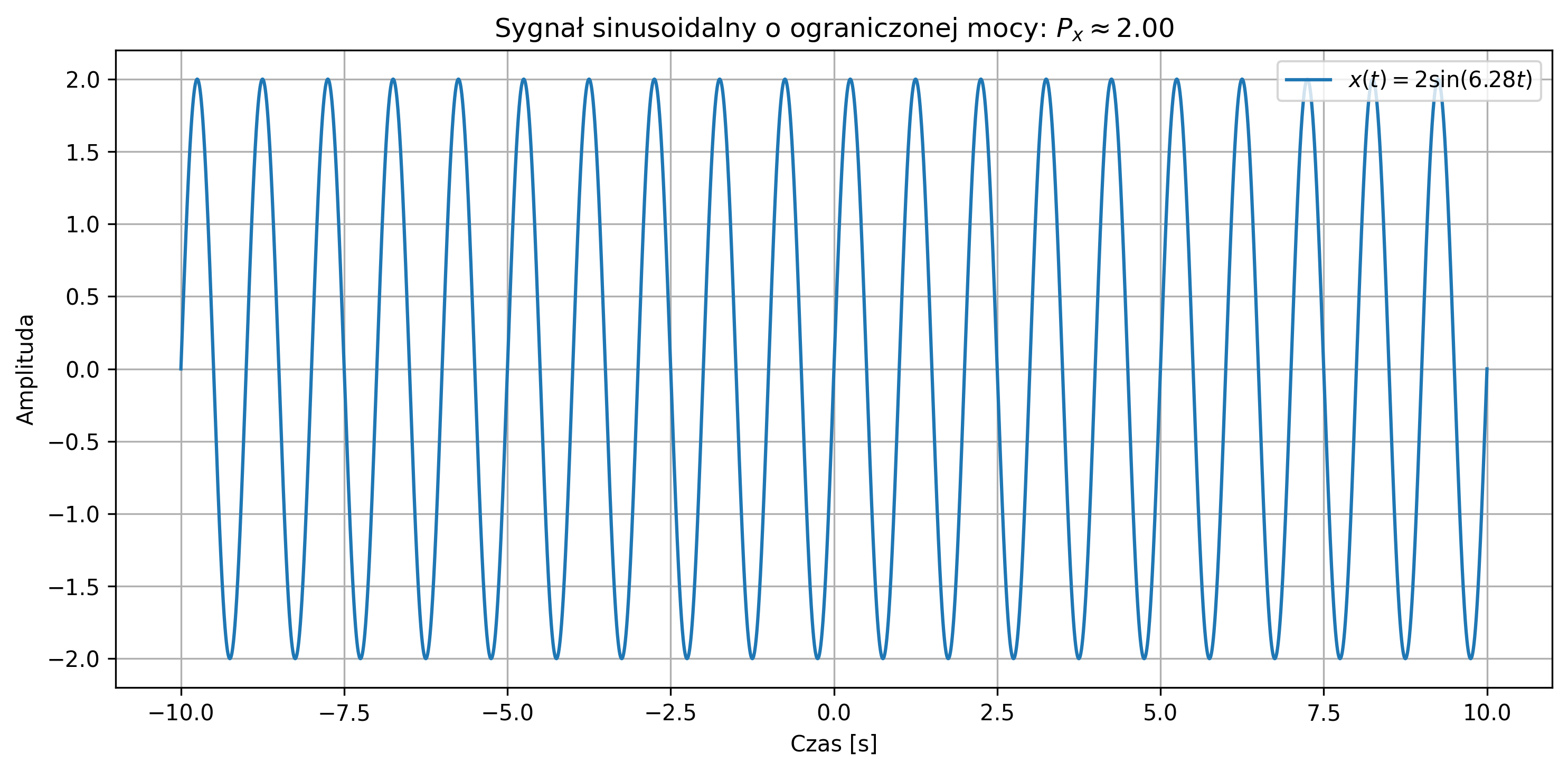
- sygnały o ograniczonej energii, gdy:
- sygnały o ograniczonej mocy, gdy:
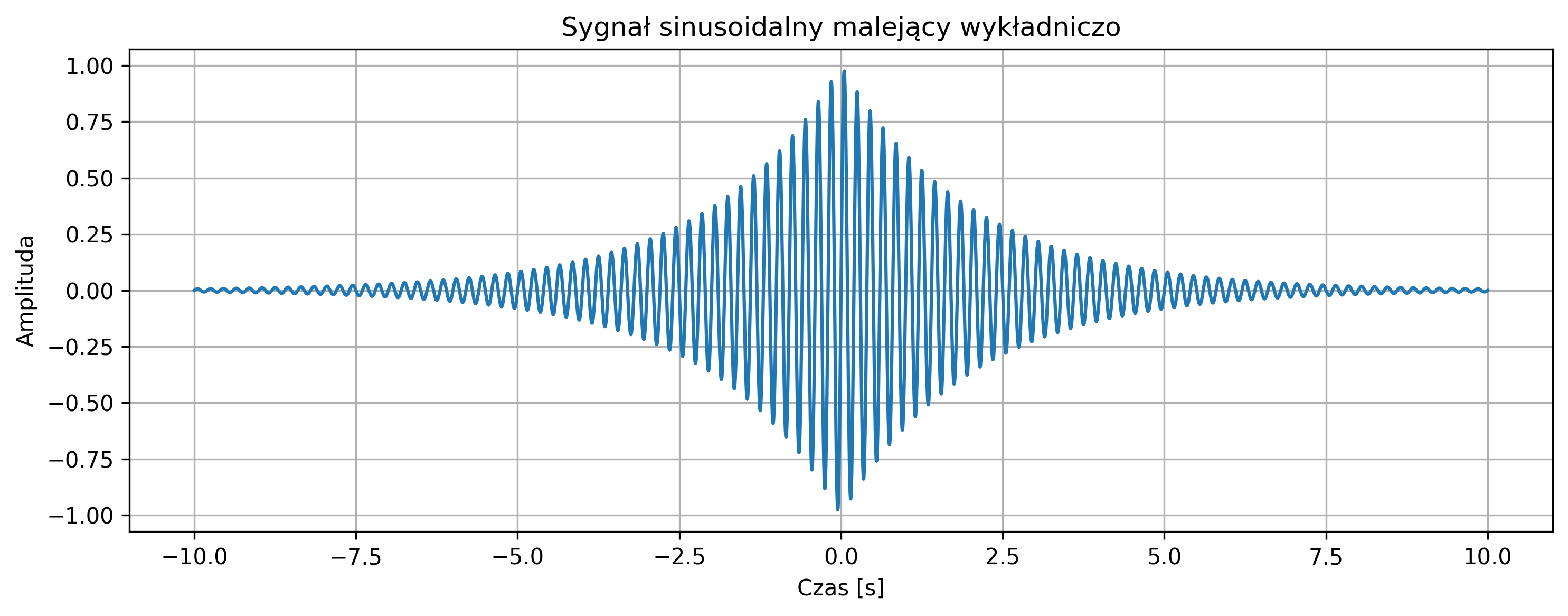
Na rys. 2.8 przedstawiono okresowy sygnał prostokątny o amplitudzie \( A = 2 \), którego moc średnia jest ograniczona i równa \(4\) (\( A^2 \)), zaś jego energia z czasem rośnie do nieskończoności.
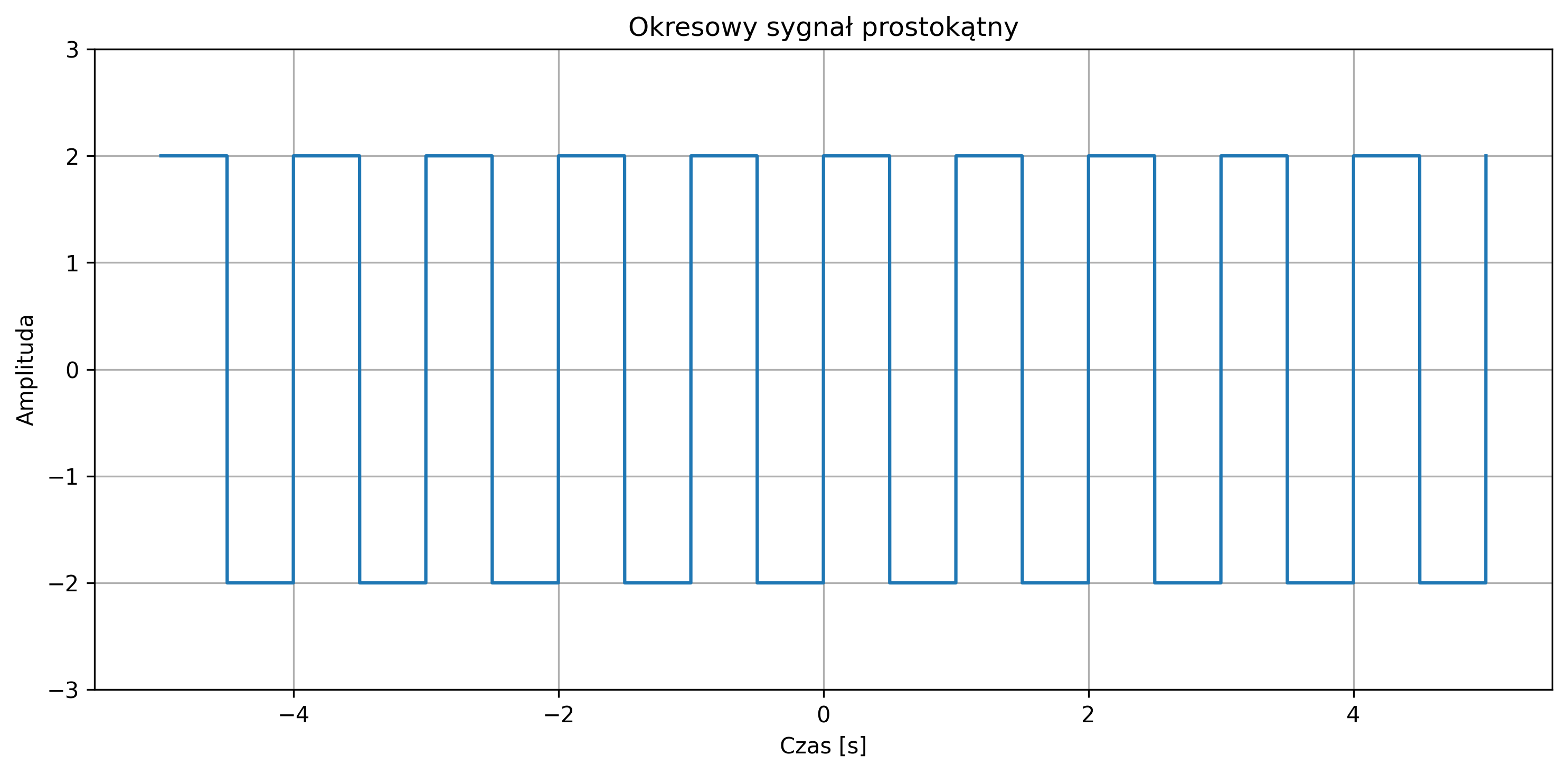
Do sygnałów o ograniczonej energii zaliczamy:
- sygnały impulsowe o ograniczonej amplitudzie, np.:
- impuls prostokątny, trójkątny, radiowy,
- impulsowy skurcz mięśnia w EMG,
- sygnały o nieskończonym czasie trwania, np.:
- sygnał sinusoidalny malejący,
- sygnał Gaussa,
- sygnał wykładniczy malejący – odpowiedź tkanek na krótki impuls stymulacji nerwowej w badaniu przewodnictwa (ENG), podczas którego rejestruje się odpowiedź mięśni lub nerwu,
- sygnały nieustalone, np.:
- drgania tłumione,
- sygnał EEG z napadem padaczkowym – nieregularny i zmienny, po napadzie zwykle wraca do wartości typowych.
Sygnały o ograniczonej mocy i ograniczone w amplitudzie są sygnałami o nieskończonym czasie trwania:
- sygnały nieokresowe, np.:
- długotrwały EMG przy skurczu izometrycznym – stała aktywność mięśnia, np. przy utrzymywaniu pozycji,
- sygnały okresowe, np.:
- sygnał sinusoidalny, fala prostokątna bipolarna,
- długotrwały sygnał EKG – ciągła rejestracja rytmu serca, np. z użyciem Holtera, sygnał okresowy i stabilny, o regularnym rytmie serca.
Szczególną podklasą sygnałów o ograniczonej mocy są sygnały okresowe. Sygnał opisany funkcją okresową czasu nazywamy sygnałem okresowym. Dla sygnału okresowego \( x(t) \) istnieje taka wartość \( T \), dla której spełniony jest warunek:
dla każdego \( t \). Czas \( T \) nazywamy okresem sygnału, \( k \) jest liczbą całkowitą. W każdej chwili czasu \( t \) przesunięcie na osi czasu o okres lub jego wielokrotność nie zmienia wartości sygnału. Odwrotność okresu podstawowego nazywamy częstotliwością sygnału:
Jednostką częstotliwości jest herc (jeden Hz stanowi pojedynczą oscylację, okres lub cykl na sekundę). Częstotliwością kątową (pulsacją) nazywamy szybkość zmiany fazy sygnału okresowego w czasie:
Częstotliwość kątową określa się w radianach na sekundę (rd/s).
Gdy sygnał jest okresowy o okresie \( T \), uśrednianie w czasie nieskończonym jest równoważne uśrednianiu za okres. Wtedy wartością średnią ciągłego sygnału okresowego \( x(t) \) jest:
gdzie \( t_0 \) jest dowolną chwilą. Moc średnia ciągłego sygnału okresowego jest równa mocy średniej w jednym okresie \( T \):
dla dowolnej chwili \( t_0 \). Jeżeli energia sygnału okresowego, przypadająca na pojedynczy okres \( T \), jest różna od zera, to całkowita energia sygnału \( E_x \) jest nieskończona.
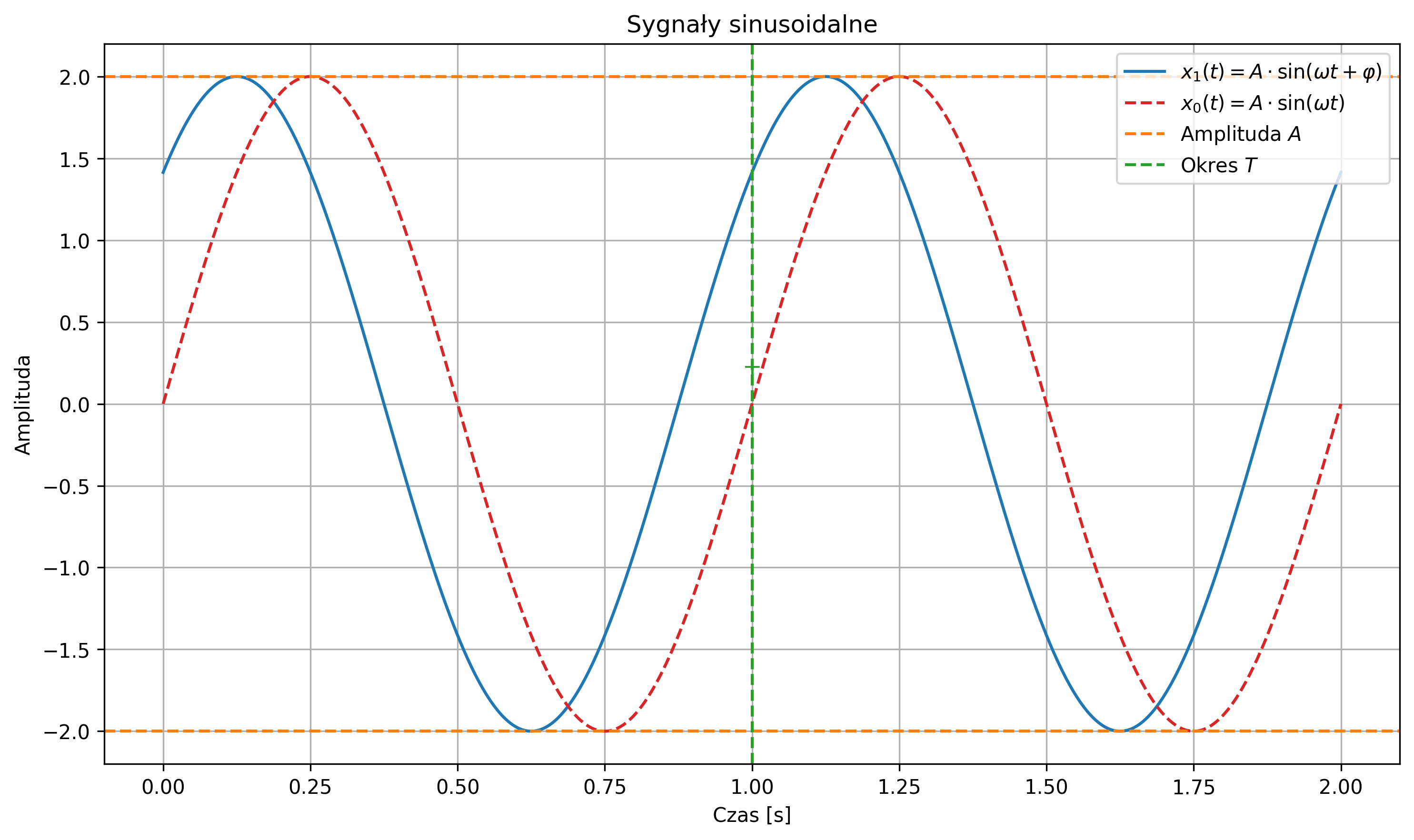
Najbardziej znanym sygnałem okresowym jest sygnał sinusoidalny (rys. 2.9):
gdzie:
- \( A \) to amplituda sygnału,
- \( \omega \) to pulsacja sygnału,
- \( f \) to częstotliwość sygnału,
- \( \varphi \) to faza sygnału.
Wartość średnia sygnału sinusoidalnego wynosi \( 0 \) (w rzeczywistości \( \approx 0 \)), zaś jego moc średnia zależy tylko od amplitudy i jest równa \( A^2 / 2 \). Suma sygnałów sinusoidalnych o różnych częstotliwościach jest także sygnałem okresowym. Stanowi to istotny fakt przy analizie częstotliwościowej sygnałów.
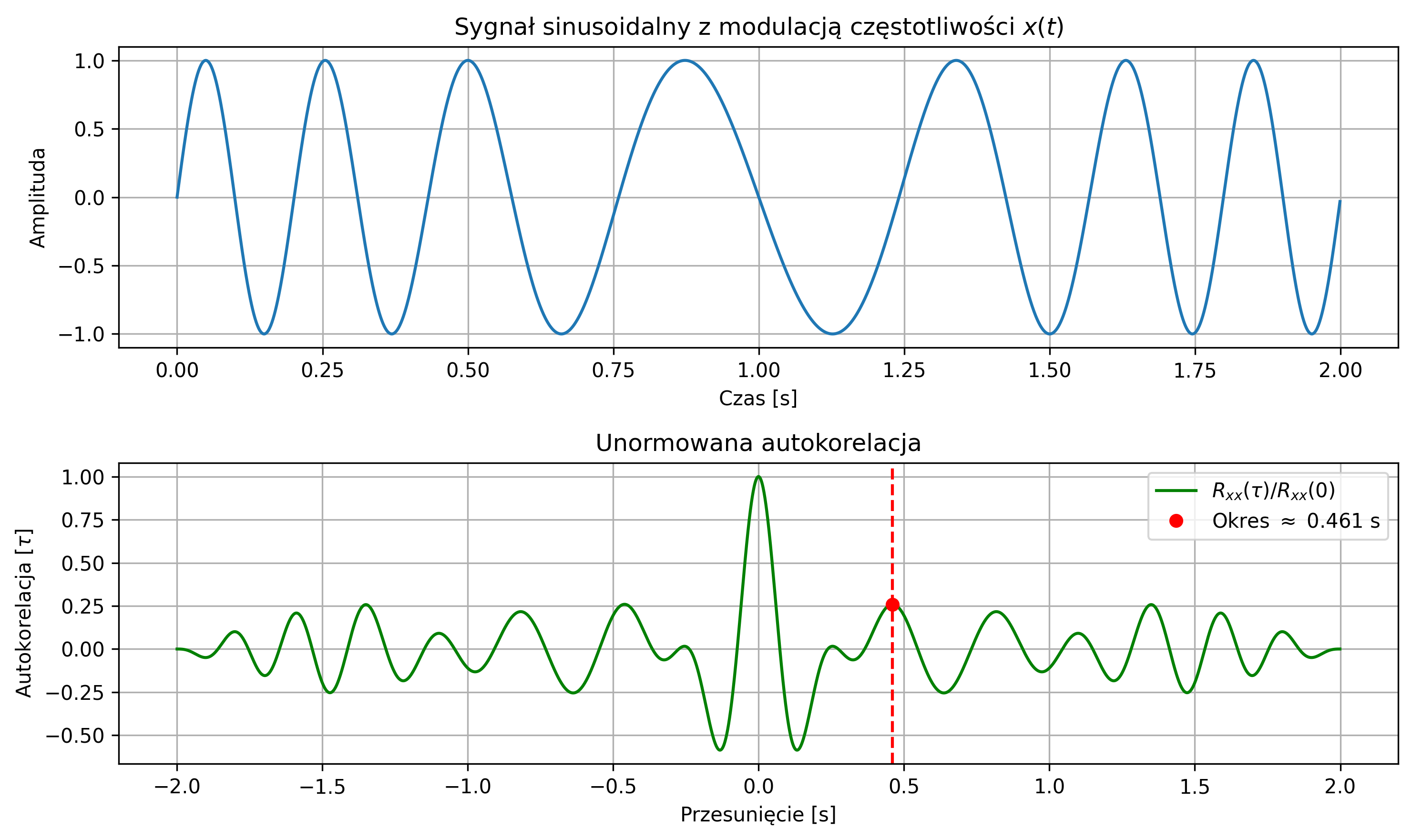
W rzeczywistości możemy mieć do czynienia z sygnałami pseudookresowymi, które nie są idealnie okresowe – kształt przebiegu powtarza się tylko orientacyjnie. Takie pseudookresy występują w sygnałach, np. dźwięku czy EEG i EKG. Przykładem takiego sygnału jest sygnał sinusoidalny z modulacją częstotliwości:
gdzie:
- \( A \) to amplituda sygnału,
- \( f \) to częstotliwość nośna sygnału,
- \( \beta \) to głębokość modulacji,
- \( f_m \) to częstotliwość modulacji.
Ponieważ modulacja takiego sygnału zmienia częstotliwość, ale nie zmienia amplitudy, to moc średnia takiego sygnału nadal wynosi \( A^2 / 2 \).
2.6. Korelacja wzajemna i autokorelacja
Kolejnym, alternatywnym sposobem charakteryzowania sygnałów w dziedzinie czasu jest opis korelacyjny. W przetwarzaniu sygnałów, korelacja wzajemna (ang. Cross-Correlation) jest miarą podobieństwa dwóch sygnałów.
Funkcja korelacji wzajemnej rzeczywistych sygnałów o ograniczonej energii to iloczyn skalarny dwóch sygnałów w funkcji przesunięcia jednego z nich i wyraża się wzorem:
gdzie:
- \( x(t) \) – pierwszy sygnał,
- \( y(t-\tau) \) – drugi sygnał przesunięty, ale nie odwrócony w czasie,
- \( \tau \) – przesunięcie.
Analogicznie definiuje się funkcję korelacji wzajemnej między sygnałem \( y(t) \) a sygnałem \( x(t) \):
W funkcji korelacji, drugi sygnał opóźnia się w stosunku do pierwszego o czas \( \tau \), następnie oba sygnały wymnaża się przez siebie i całkuje ich iloczyn. W ten sposób dla każdego przesunięcia \( \tau \) otrzymuje się wartość, która określa na ile opóźniony drugi sygnał jest podobny do sygnału pierwszego. Jest to operacja bardzo podobna do splotu, gdyż mierzy jak bardzo dwa sygnały są do siebie podobne, gdy jeden z nich jest przesuwany w czasie względem drugiego. Jednakże, w przeciwieństwie do operacji splotu, obliczając korelację nie odwracamy w czasie jednego z sygnałów.
Można pokazać, że
co oznacza, że taką samą wartość iloczynu skalarnego otrzymujemy przy przesunięciu sygnału \( y(t) \) w kierunku opóźnienia o czas \( \tau \), jak i przy przesunięciu sygnału \( x(t) \) o ten sam czas w kierunku przyspieszenia.
Funkcja korelacji wzajemnej dla dyskretnych sygnałów \( x \) i \( y \) przyjmuje postać:
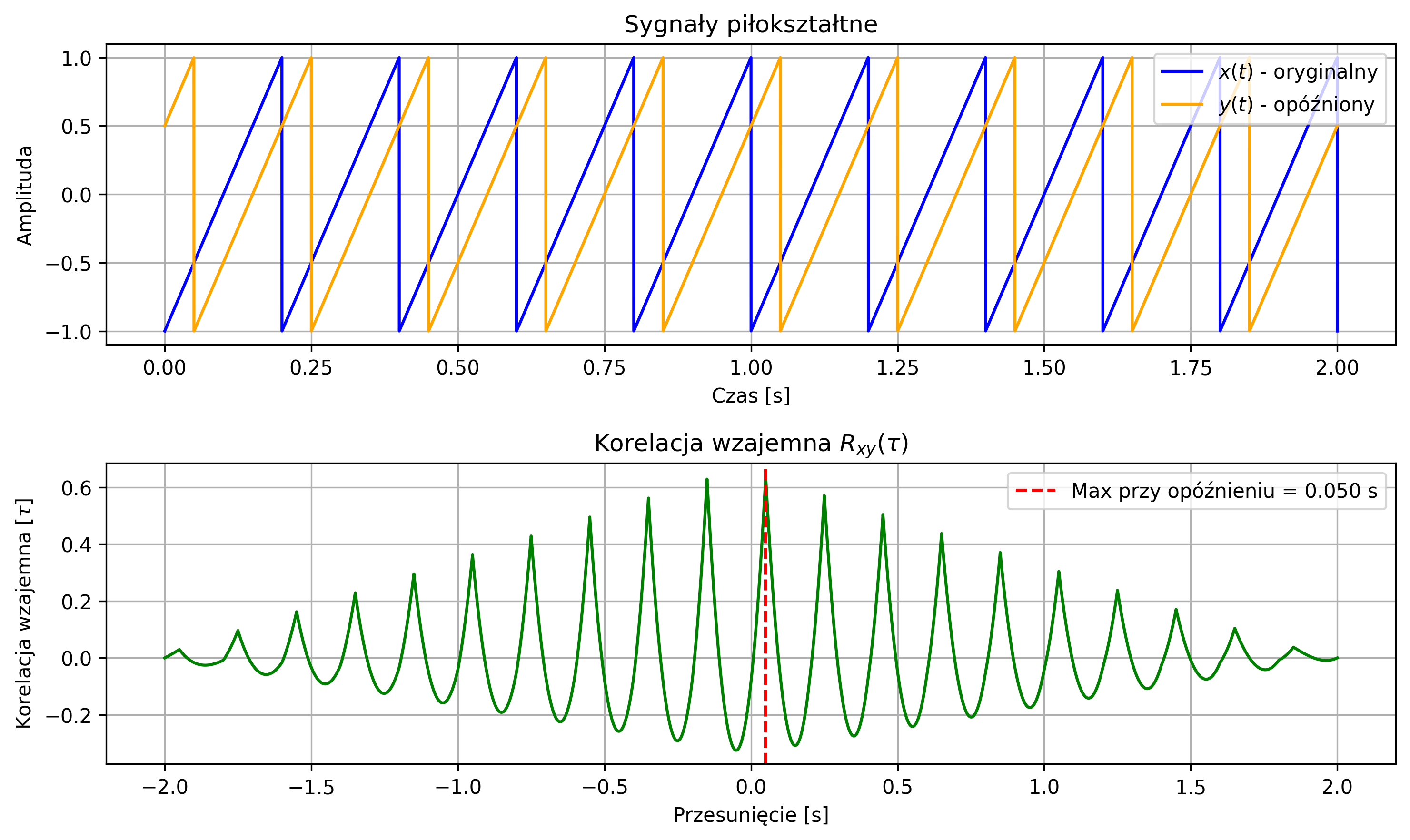
Korelacja wzajemna pozwala wykrywać opóźnienia sygnałów względem siebie – położenie maksimum funkcji korelacji wskazuje na przesunięcie, które daje największe podobieństwo sygnałów.
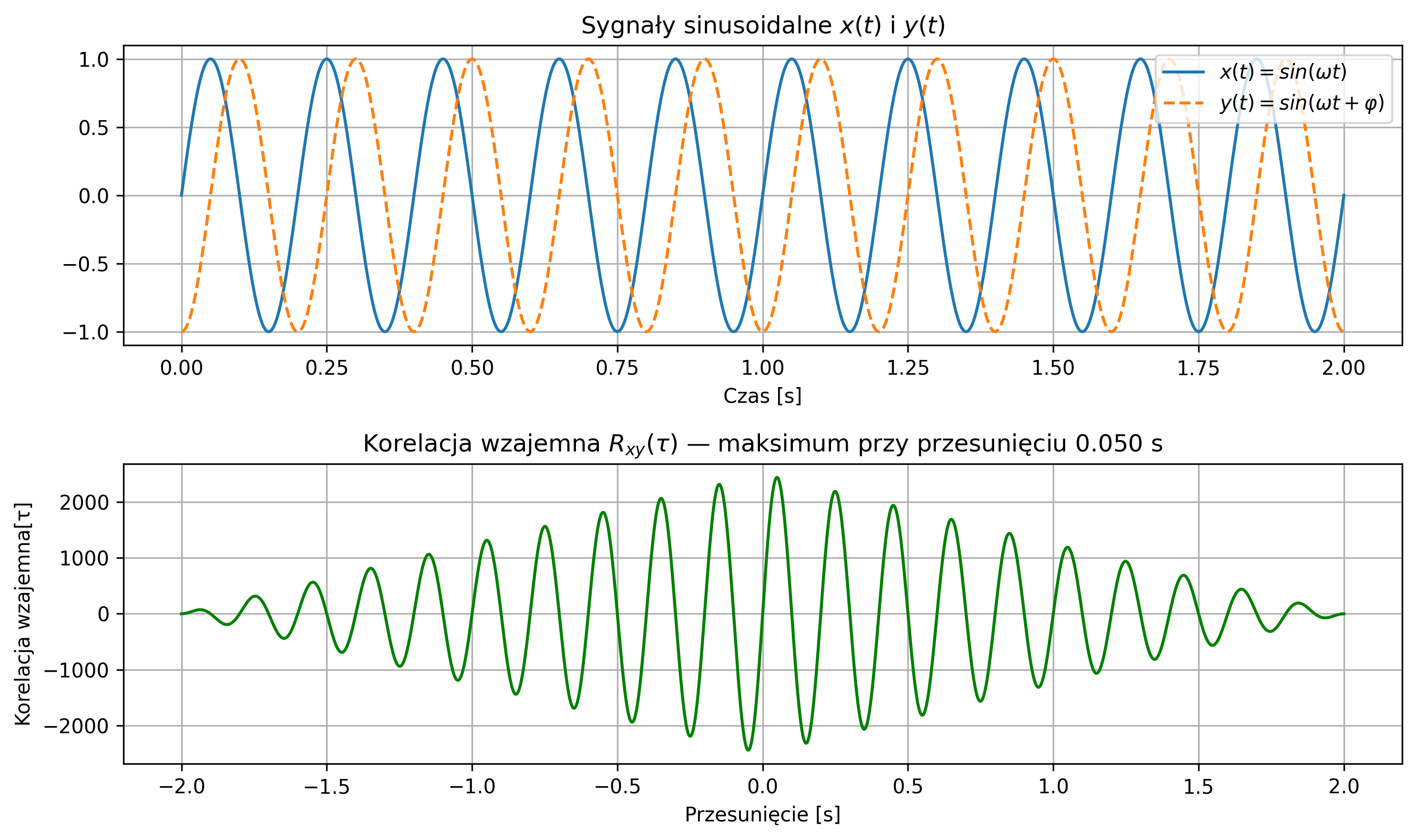
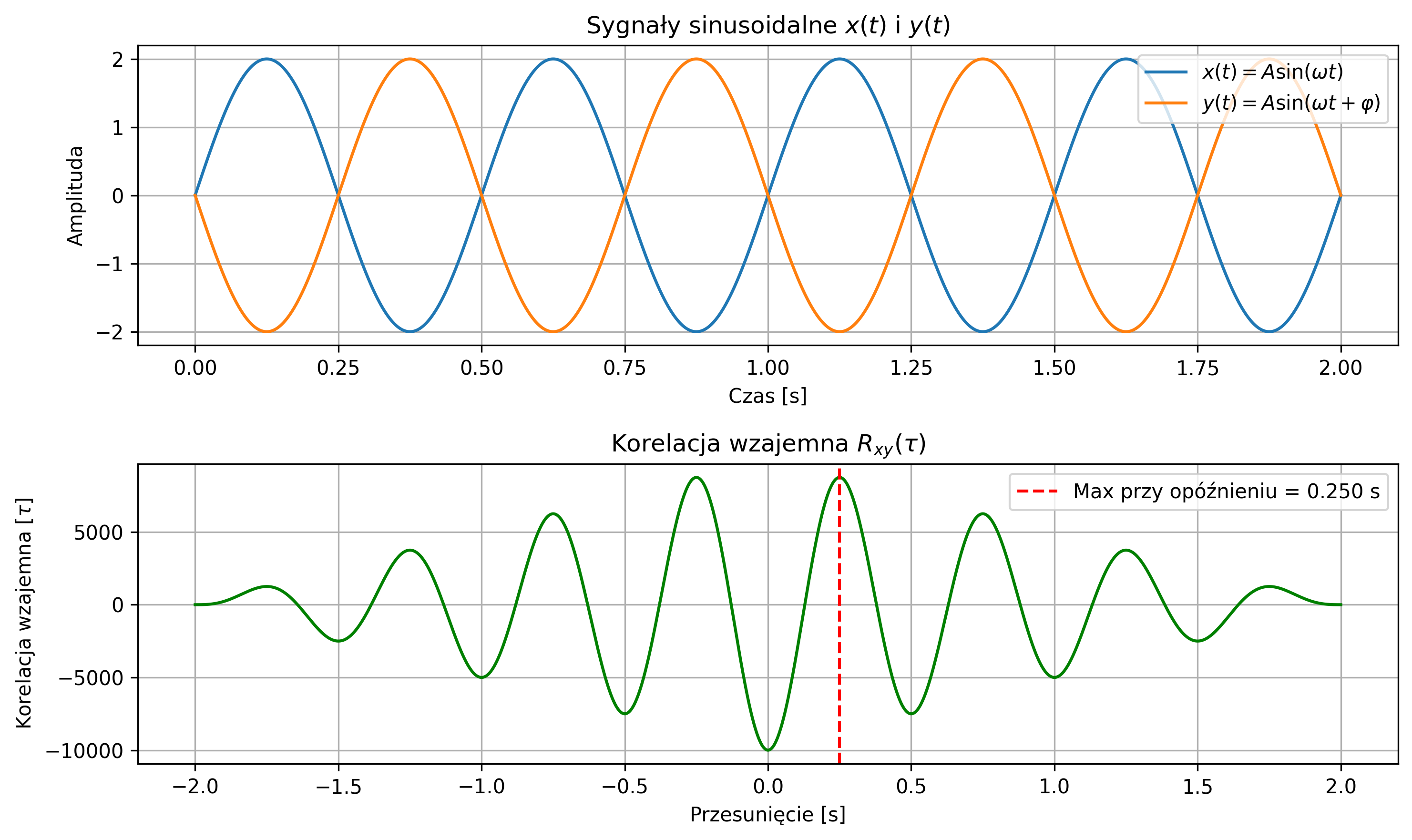
Na rys. 2.10 zostało pokazane wykorzystanie funkcji korelacji wzajemnej do wykrycia przesunięcia jednej sinusoidy:
względem drugiej \( y(t)=\sin(\omega t) \). Wykres korelacji wzajemnej pokazuje maksimum przy opóźnieniu \( \tau \), które wyniosło \( 0.25 \) s (\( \varphi=-7.85 \)).
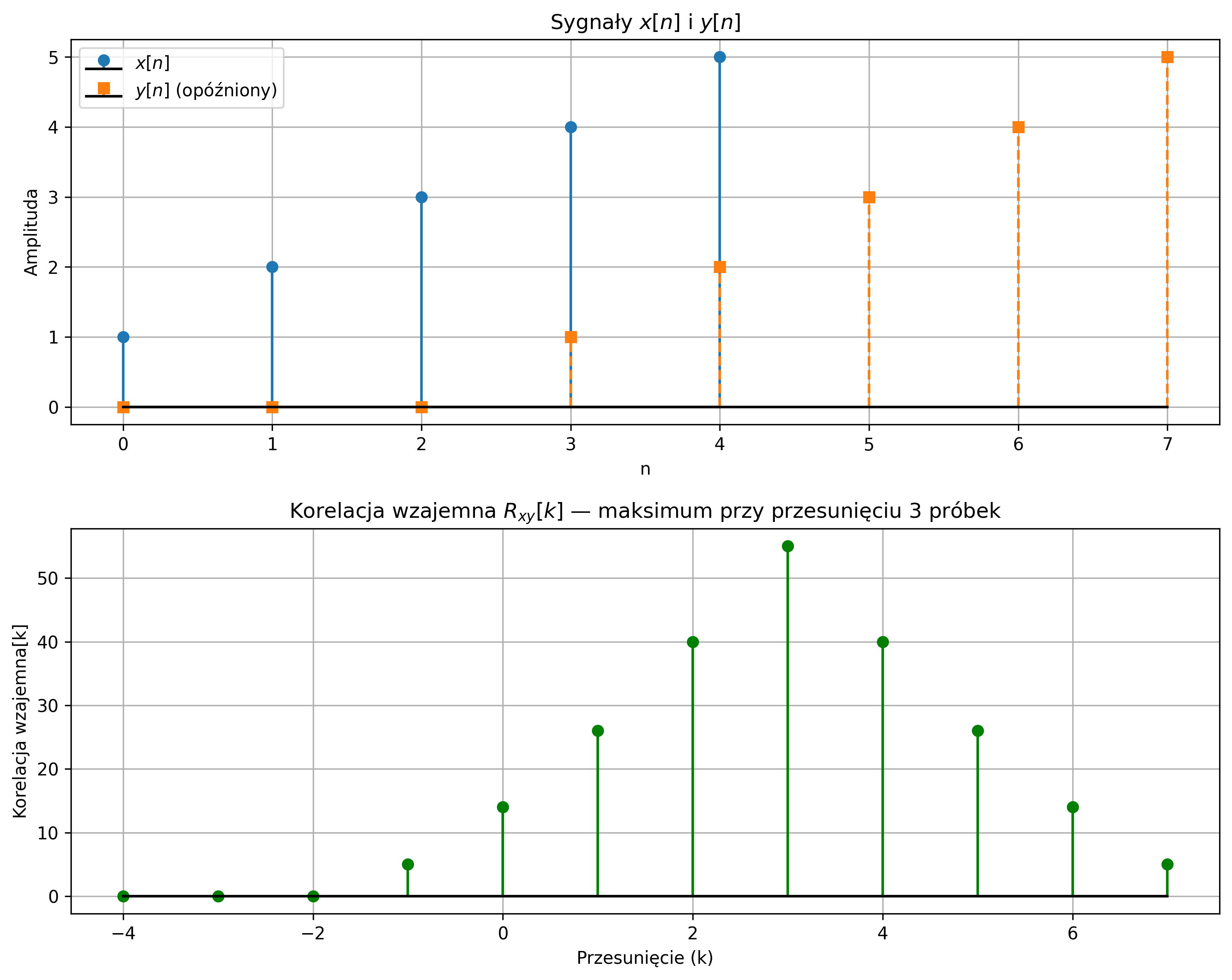
Analogiczny przykład, w wersji dyskretnych sygnałów został przedstawiony na rys. 2.11. Pokazany został przebieg ciągu próbek sygnału \( x = [1,2,3,4,5] \) oraz sygnału \( y \), który jest opóźnionym sygnałem \( x \) o 3 próbki. Korzystając z funkcji korelacji wzajemnej, wykryte zostało opóźnienie jednego sygnału względem drugiego – funkcja korelacji wzajemnej pokazała maksimum przy tym przesunięciu.
Szczególnym przypadkiem korelacji wzajemnej, gdy sygnał jest porównywany sam ze sobą, jest autokorelacja (ang. Autocorrelation). Autokorelacja dla danej wartości przesunięcia opisuje podobieństwo sygnału do jego przesuniętej w czasie kopii. Największe podobieństwo uzyskamy dla zerowego przesunięcia, gdy oba korelowane sygnały są identyczne.
Funkcja autokorelacji dla rzeczywistych sygnałów o ograniczonej energii:
gdzie:
- \( x(t) \) – pierwszy sygnał,
- \( x(t-\tau) \) – ten sam sygnał przesunięty, ale nie odwrócony w czasie,
- \( \tau \) – przesunięcie,
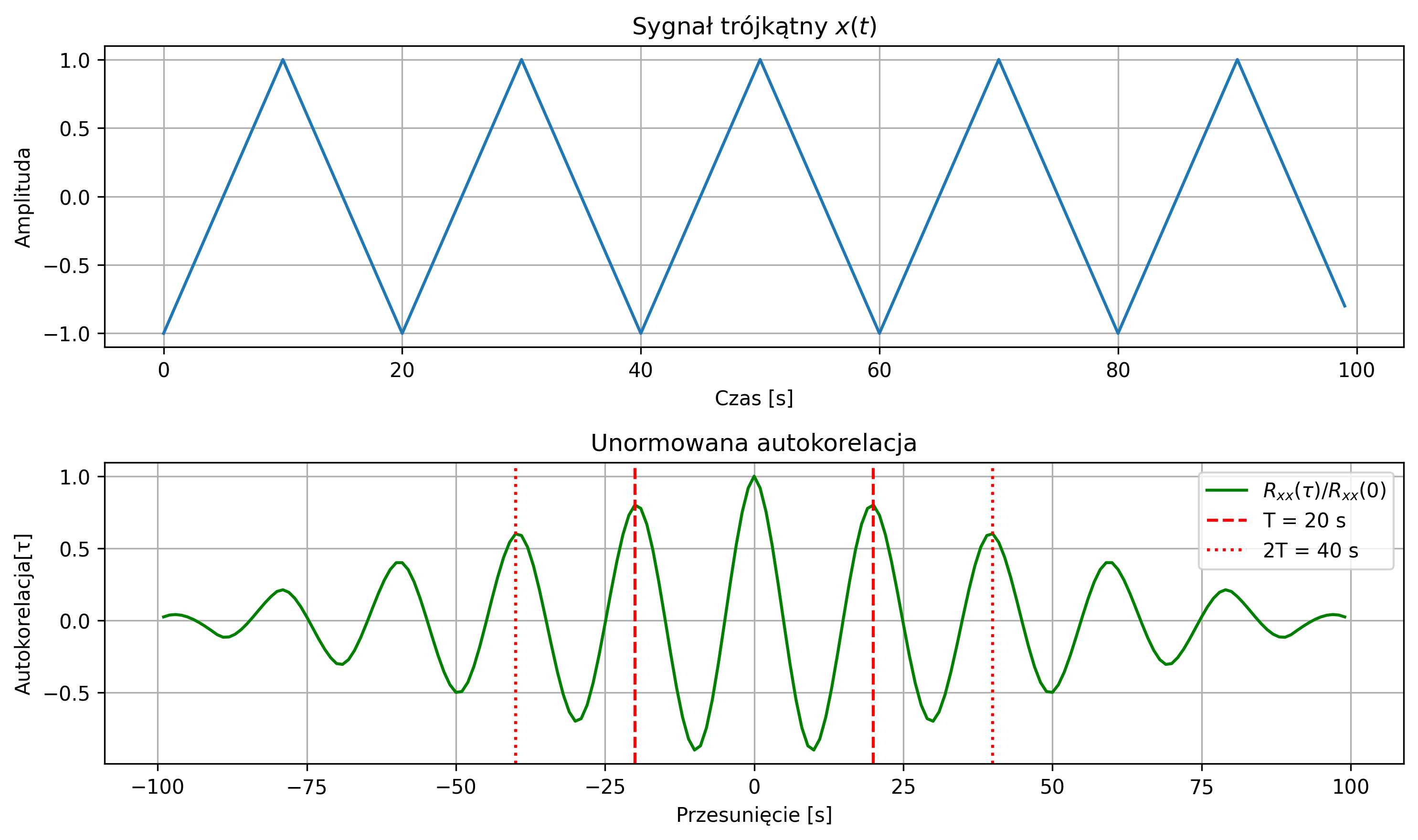
jest rzeczywista i parzysta – nie ma znaczenia, w którą stronę przesuwamy kopię sygnału: \( R_{xx}(\tau)=R_{xx}(-\tau) \).
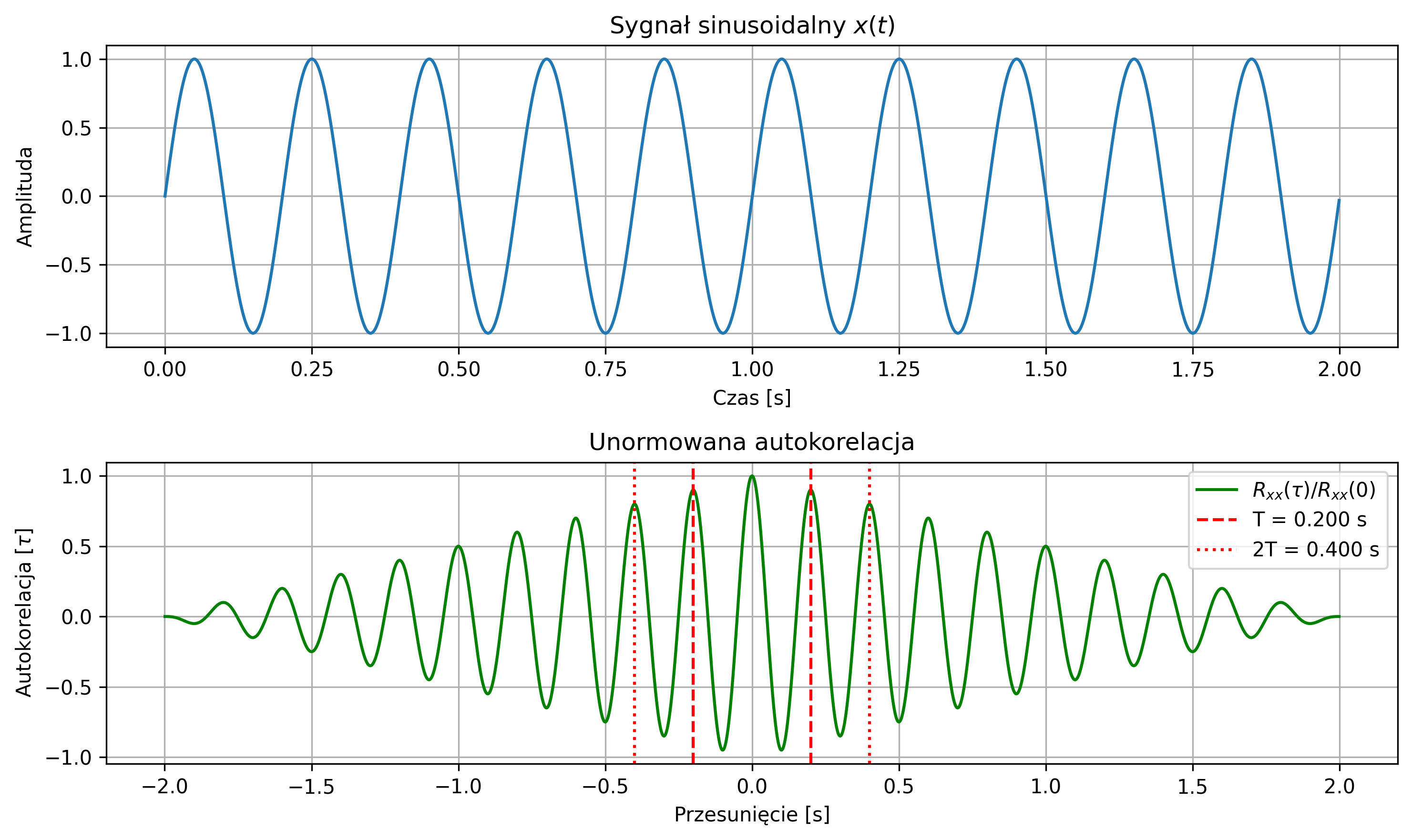
Autokorelacja jest przede wszystkim wykorzystywana do badania okresowości sygnału, ponieważ przyjmuje ona wartości maksymalne dla wartości przesunięcia \( \tau \) równego wielokrotności okresu sygnału. Może również posłużyć do wykrywania pewnych regularności w sygnałach – np. regularnych cykli tętna w przebiegu fal EEG.
Funkcja autokorelacji sygnału o ograniczonej energii jest także funkcją o ograniczonej energii. Zauważmy, że wartość funkcji autokorelacji w punkcie \( \tau = 0 \) jest równa energii sygnału:
Unormowana funkcja autokorelacji powstaje przez podzielenie wartości funkcji autokorelacji przez energię sygnału. Wtedy, dla zerowego przesunięcia, wartość autokorelacji przyjmuje wartość maksymalną, równą \(1\). Dzięki temu można porównywać kształt funkcji autokorelacji różnych sygnałów niezależnie od ich amplitudy i energii.
Na rys. 2.12 przedstawiono wykres sygnału trójkątnego i jego unormowanej funkcji autokorelacji. Ponieważ sygnał jest okresowy, maksima funkcji autokorelacji znajdują się w punktach równych wielokrotności okresu.
2.7. Sygnały zespolone
Oprócz sygnałów rzeczywistych, wykorzystywane są sygnały zespolone, które pomimo abstrakcyjnego charakteru ułatwiają analizę i przetwarzanie – zwłaszcza w dziedzinie częstotliwości. Sygnał zespolony przyjmuje wartości zespolone i ma postać algebraiczną:
gdzie
- \( x(t) = \operatorname{Re}\{z(t)\} \) i \( y(t) = \operatorname{Im}\{z(t)\} \) są sygnałami rzeczywistymi,
- \( j \) jest jednostką urojoną, dla której \( j^2 = -1 \)
Sygnał zespolony można również przedstawić w postaci wykładniczej:
gdzie
- \( |z(t)| = \sqrt{x^2(t)+y^2(t)} \) jest modułem sygnału,
- \( \varphi(t) = \arctan\frac{y(t)}{x(t)} \) jest argumentem sygnału.
Sygnałem sprzężonym z sygnałem \( z(t) \) nazywamy sygnał:
Sygnały zespolone również dzielimy na sygnały o ograniczonej energii i ograniczonej mocy. Wzory na energię i moc sygnałów zespolonych są zdefiniowane identycznie jak w przypadku sygnałów rzeczywistych, z tą różnicą, że w ich sformułowaniach pojawia się moduł \( |x(t)|^2 \) zamiast kwadratu sygnału \( x^2(t) \).
Analogiczne są również wzory na funkcję korelacji wzajemnej i funkcję autokorelacji sygnałów zespolonych o ograniczonej energii, z tą różnicą, że w iloczynie skalarnym pojawia się sprzężone zespolone przesunięcie jednego z sygnałów:
Najbardziej znanymi sygnałami zespolonymi są:
- zespolony sygnał sinusoidalny:
- sygnał analityczny, który powstaje z rzeczywistego sygnału \( x(t) \):
którego częścią rzeczywistą jest sygnał \( x(t) \), a częścią urojoną jest transformata Hilberta sygnału \( x(t) \).
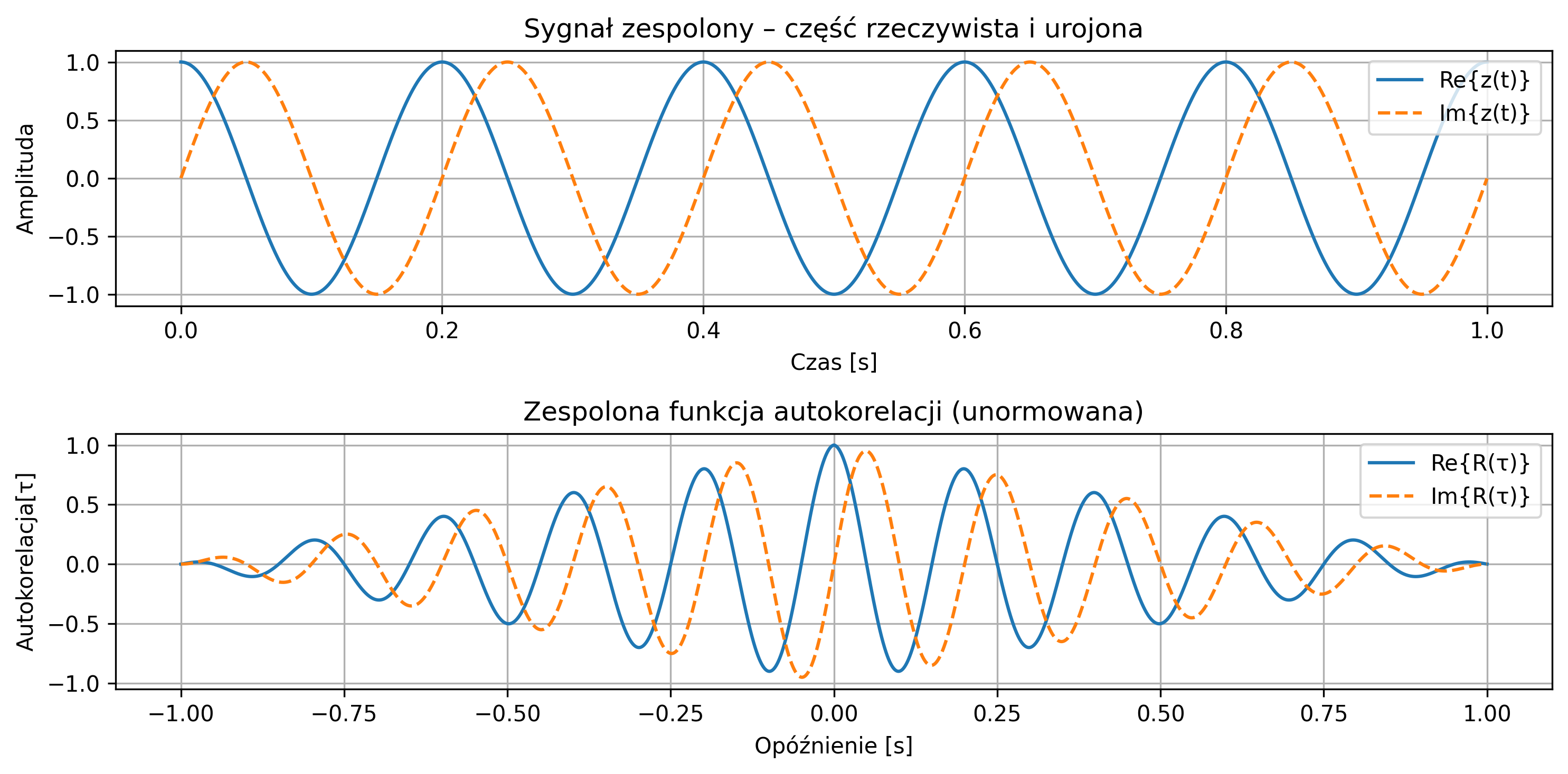
Na rys. 2.14 przedstawiono zespolony sygnał \( z(t) = e^{j2\pi f t} \) – przebieg jego części rzeczywistej i urojonej. Podobnie jak dla sygnałów rzeczywistych, można z wykresów odczytać, jak wyglądają oscylacje w dziedzinie czasu, powtarzalność i strukturę fazową, a także oszacować, jaki jest okres. Energia i moc przykładowego sygnału wynosi \(1\).
- amplituda chwilowa – moduł sygnału,
- faza chwilowa – zmiana kąta argumentu,
- obwiednia sygnału rzeczywistego – sposób, w jaki „kształt” energii sygnału zmienia się w czasie.
Ponadto sygnały zespolone są szeroko stosowane w przetwarzaniu sygnałów biomedycznych, takich jak EKG czy EEG, gdzie analiza fazy i obwiedni jest kluczowa dla diagnozy, na przykład przy wykrywaniu drżeń mięśni, zaburzeń rytmu serca lub analizie związków między regionami mózgu.
2.8. Reprezentacja sygnałów w języku Python
Celem poniższych ćwiczeń jest zapoznanie się z wybranymi typami sygnałów oraz nabycie praktycznych umiejętności w generowaniu i wizualizacji ich przebiegów, a także poznanie podstawowych funkcji i komend w języku Python przydatnych w analizie sygnałów.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów,
# takich jak np. prostokątny, trójkątny, piłokształtny
oraz wymagana jest znajomość między innymi następujących poleceń i funkcji języka Python:
np.arange, np.linspace # tworzenie wektorów czasu
plt.figure, plt.plot, plt.stem # rysowanie wykresów ciągłych i dyskretnych
plt.grid, plt.xlabel, plt.ylabel, plt.title, plt.legend # oznaczanie osi, tytułów, legend i siatki
np.sin, np.exp, np.pi # generowanie sygnałów sinusoidalnych, wykładniczych, stała pi
signal.square, signal.sawtooth, signal.chirp # generowanie sygnałów specjalnych
W zadaniach będziemy łączyć te funkcje w celu generowania, wizualizacji i analizy różnych typów sygnałów. Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do samodzielnego uruchamiania kodów oraz do eksperymentowania z różnymi parametrami sygnałów poprzez ich modyfikację.
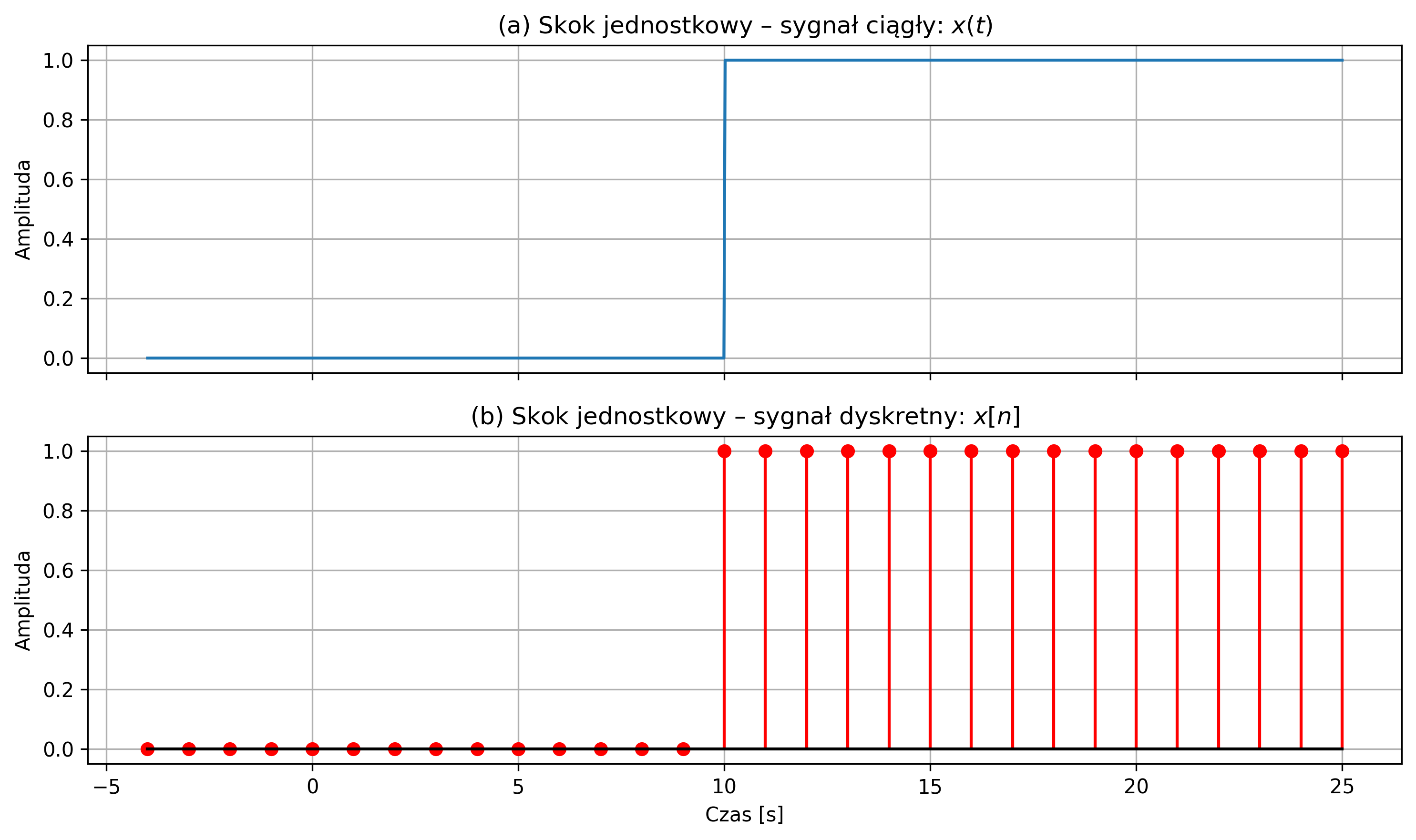
Wygenerować skok jednostkowy określony przez następujące równanie:
Narysować sygnał ciągły \(x(t)\) i jego wersję dyskretną \(x[n]\) dla \(N = 30\) próbek przy częstotliwości próbkowania \(f_s = 1\) Hz.
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
fs = 1 # częstotliwość próbkowania [Hz]
T = 1 / fs # okres próbkowania
n = np.arange(-4, 26) # 30 próbek: od -4 do 25
# Sygnał dyskretny: skok jednostkowy
x_disc = np.where(n >= 10, 1, 0)
# Sygnał ciągły (z większą rozdzielczością)
t_cont = np.linspace(-4, 25, 1000)
x_cont = np.where(t_cont >= 10, 1, 0)
# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=True)
# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont)
axs[0].set_title(r'(a) Skok jednostkowy – sygnał ciągły: $x(t)$')
axs[0].set_ylabel("Amplituda")
axs[0].grid(True)
# Wykres 2: sygnał dyskretny
axs[1].stem(n, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Skok jednostkowy – sygnał dyskretny: $x[n]$')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)
plt.tight_layout()
plt.show()
Wygenerować sygnał sinusoidalny określony przez następujące równanie:
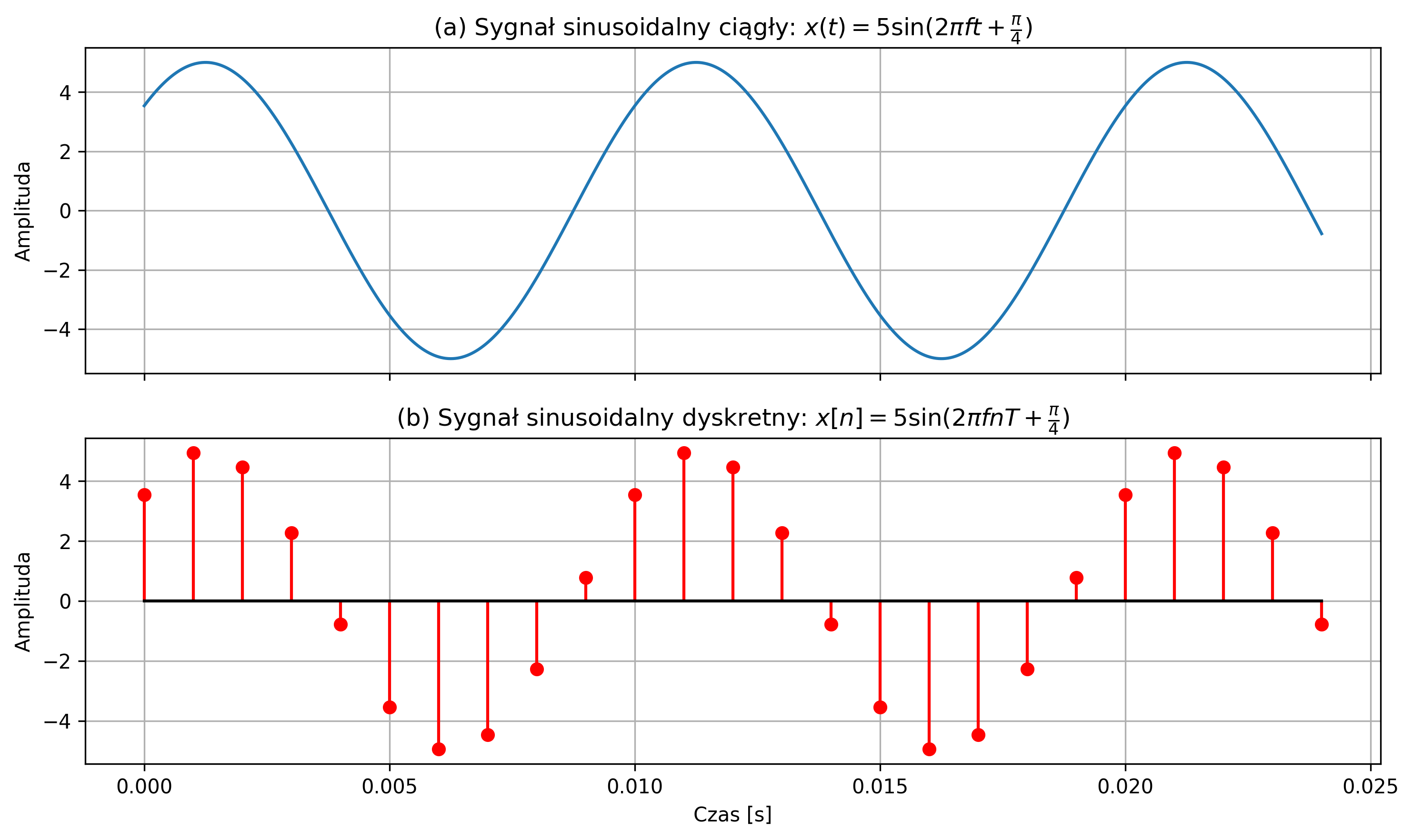
o amplitudzie \( A = 5 \), częstotliwości sygnału \( f = 100 \) Hz i przesunięciu fazowym \( 45^{\circ} \). Narysować sygnał ciągły \(x(t)\) i jego wersję dyskretną \(x[n]\) dla \( N = 25 \) próbek, przyjmując częstotliwość próbkowania \( f_s =1000 \) Hz. Dodatkowo, sporządzić wspólny wykres sygnału ciągłego i dyskretnego na jednym rysunku.
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
fs = 1000 # częstotliwość próbkowania [Hz]
N = 25 # liczba próbek
A = 5 # amplituda
f = 100 # częstotliwość sygnału [Hz]
T = 1 / fs # okres próbkowania
phi = np.pi / 4 # przesunięcie fazowe [rad]
# Oś czasu: ciągła i dyskretna
t_cont = np.linspace(0, (N - 1) / fs, 1000)
n = np.arange(N)
t_disc = n * T
# Sygnały
x_cont = A * np.sin(2 * np.pi * f * t_cont + phi) # sygnał ciągły
x_disc = A * np.sin(2 * np.pi * f * t_disc + phi) # sygnał dyskretny
# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=True)
# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont)
axs[0].set_title(r'(a) Sygnał sinusoidalny ciągły: $x(t) =5\sin(2\pi f t + \frac{\pi}{4})$')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Wykres 2: sygnał dyskretny
axs[1].stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Sygnał sinusoidalny dyskretny: $x[n] = 5\sin(2\pi f nT + \frac{\pi}{4})$')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)
plt.tight_layout()
plt.show()
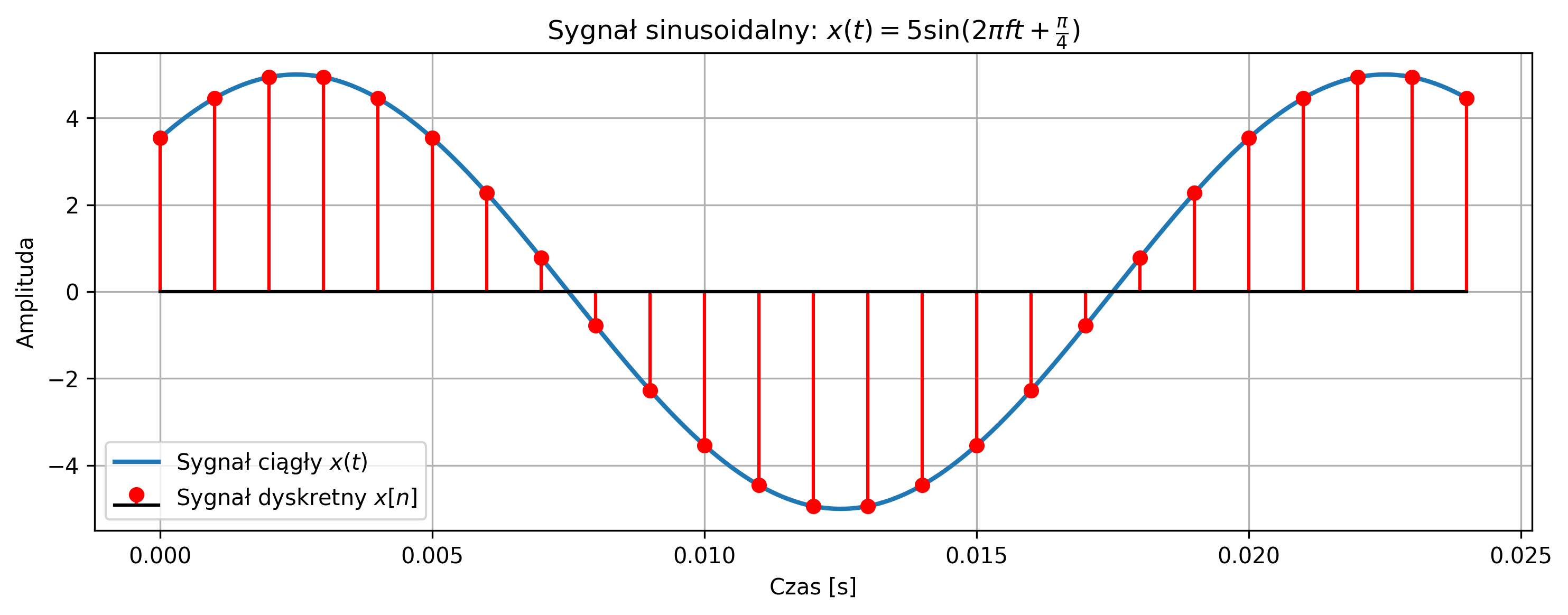
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
fs = 1000 # częstotliwość próbkowania [Hz]
N = 25 # liczba próbek
A = 5 # amplituda
f = 50 # częstotliwość sygnału [Hz]
T = 1 / fs # okres próbkowania
phi = np.pi / 4 # przesunięcie fazowe [rad]
# Oś czasu: ciągła i dyskretna
t_cont = np.linspace(0, (N - 1) / fs, 1000)
n = np.arange(N)
t_disc = n * T
# Sygnały
x_cont = A * np.sin(2 * np.pi * f * t_cont + phi) # sygnał ciągły
x_disc = A * np.sin(2 * np.pi * f * t_disc + phi) # sygnał dyskretny
# Wykres
plt.figure(figsize=(10, 4))
plt.plot(t_cont, x_cont, label=r'Sygnał ciągły $x(t)$', linewidth=2)
plt.stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')
plt.title(r'Sygnał sinusoidalny: $x(t) = 5\sin(2\pi f t + \frac{\pi}{4})$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
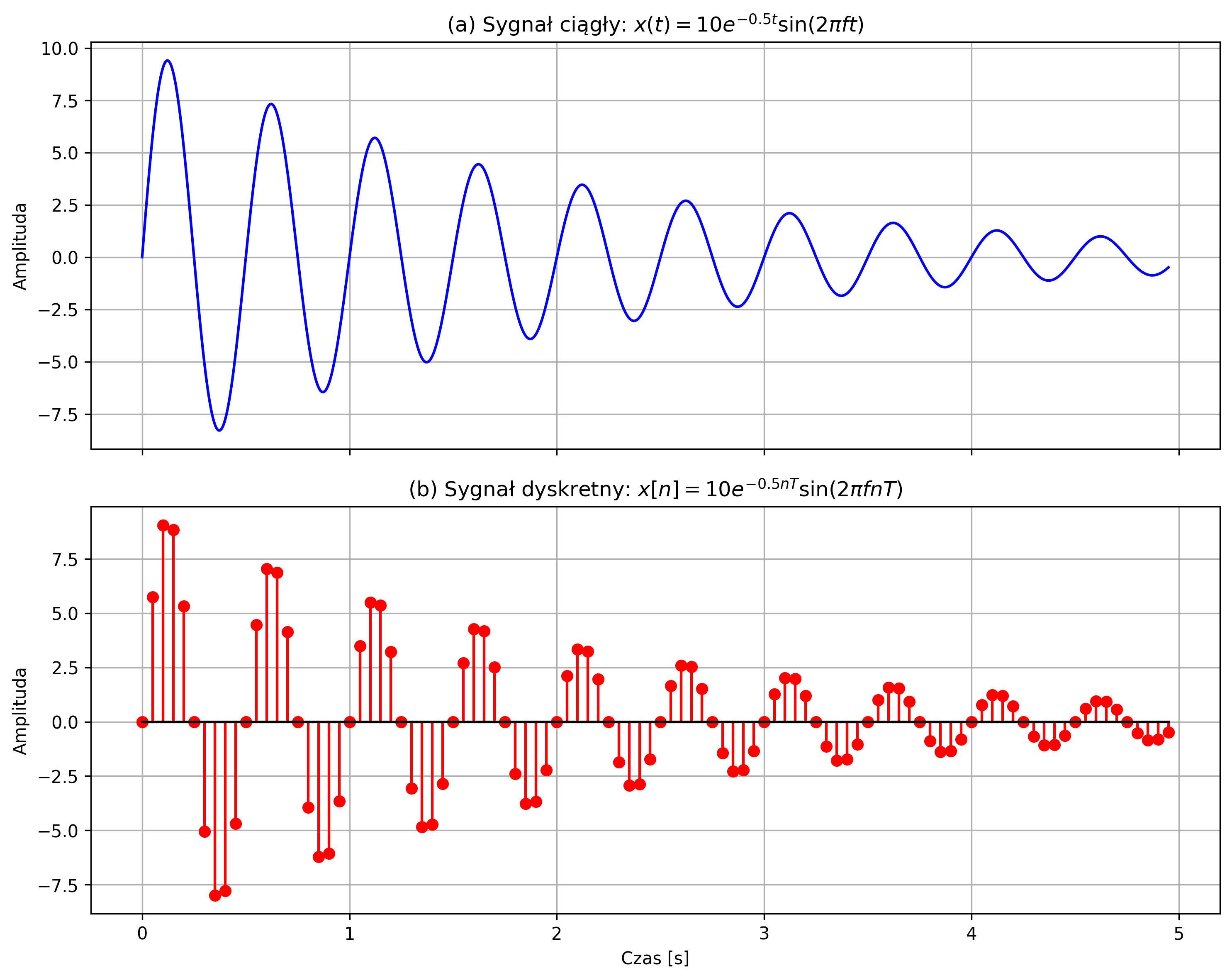
Wygenerować sygnał sinusoidalny tłumiony wykładniczo opisany równaniem:
dla amplitudy \( A = 10 \), częstotliwości sygnału sinusoidalnego \( f = 2 \) Hz i współczynnika tłumienia \(\alpha = 0.5 \). Narysować sygnał ciągły \( x(t) \) i jego wersję dyskretną \( x[n] \) dla \( N = 100 \) próbek, przyjmując częstotliwość próbkowania \( f_s = 20 \) Hz.
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
A = 10 # amplituda
f = 2 # częstotliwość sinusoidy [Hz]
alpha = 0.5 # tłumienie wykładnicze [1/s]
N = 100 # liczba próbek
fs = 20 # częstotliwość próbkowania [Hz]
T = 1 / fs # okres próbkowania
# Sygnał ciągły
t_cont = np.linspace(0, (N - 1) * T, 1000)
x_cont = A * np.exp(-alpha * t_cont) * np.sin(2 * np.pi * f * t_cont)
# Sygnał dyskretny
n = np.arange(N)
t_disc = n * T
x_disc = A * np.exp(-alpha * t_disc) * np.sin(2 * np.pi * f * t_disc)
# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 8), sharex=True)
# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont, color='blue')
axs[0].set_title(r'(a) Sygnał ciągły: $x(t) = 10e^{-0.5t}\sin(2\pi f t)$', fontsize=12)
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Wykres 2: sygnał dyskretny
axs[1].stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Sygnał dyskretny: $x[n] = 10e^{-0.5nT}\sin(2\pi f nT)$', fontsize=12)
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)
plt.tight_layout()
plt.show()
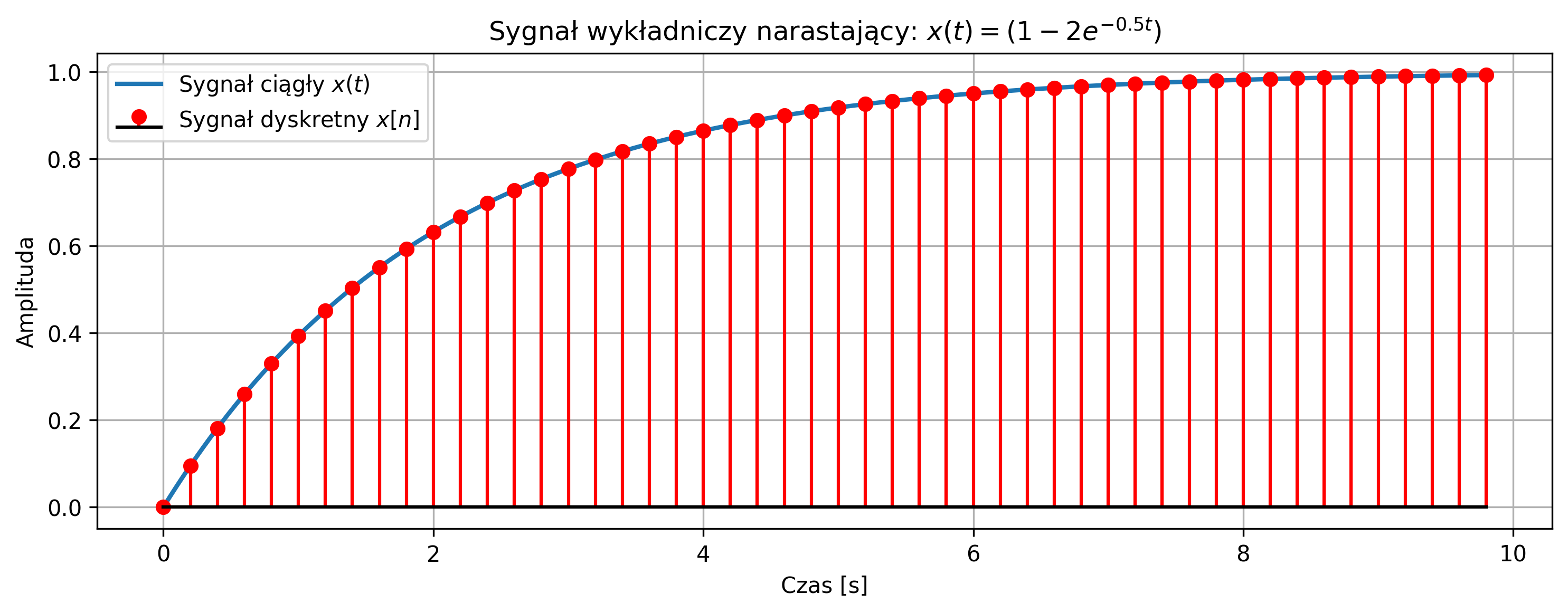
Wygenerować sygnał wykładniczy narastający określony przez następujące równanie:
Narysować na jednym wykresie sygnał ciągły \( x(t) \) oraz jego wersję dyskretną \( x[n] \) dla \( N = 50 \) próbek, przy częstotliwości próbkowania \( f_s = 5\text{ Hz} \).
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
fs = 5 # częstotliwość próbkowania [Hz]
N = 50 # liczba próbek
alpha = -0.5 # wykładnik
T = 1 / fs # okres próbkowania
t_max = (N - 1) / fs
# Czas ciągły i dyskretny
t_cont = np.linspace(0, t_max, 1000)
n = np.arange(N)
t_disc = n * T
x_cont = (1 - np.exp(alpha * t_cont))
x_disc = (1 - np.exp(alpha * t_disc))
# Wspólny wykres
plt.figure(figsize=(10, 4))
plt.plot(t_cont, x_cont, label=r'Sygnał ciągły $x(t)$', linewidth=2)
plt.stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')
plt.title(r'Sygnał wykładniczy narastający: $x(t) = \left(1 - 2e^{-0.5t}\right)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
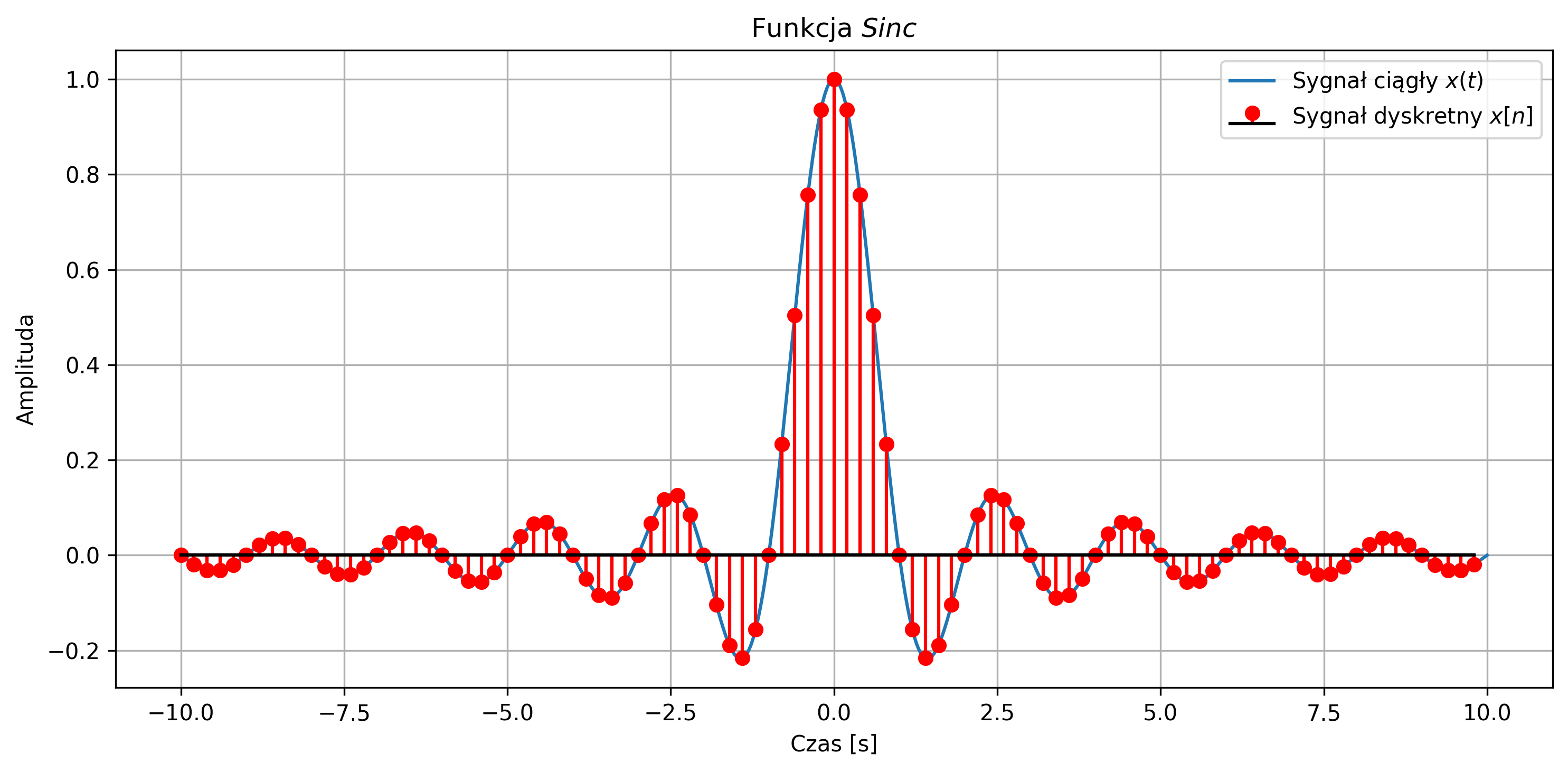
Wygenerować sygnał \(Sinc \) opisany równaniem:
dla częstotliwości sygnału sinusoidalnego \( f = 1 \) Hz. Narysować wspólny wykres sygnału ciągłego \(x(t)\) i dyskretnego \(x[n]\) dla \(N = 100\) próbek, przyjmując częstotliwość próbkowania \(f_s = 5\) Hz.
import numpy as np
import matplotlib.pyplot as plt
# Parametry sygnału
f = 1 # częstotliwość sygnału
fs = 5 # częstotliwość próbkowania
N = 100 # liczba próbek
T = 1 / fs
# Oś czasu - ciągła i dyskretna
t_cont = np.linspace(-10, 10, 1000)
n = np.arange(-N//2, N//2)
t_disc = n * T
# Funkcja Sinc - ciągła i dyskretna
y_cont = np.sinc(f * t_cont)
y_disc = np.sinc(f * t_disc)
# Wspólny wykres
plt.figure(figsize=(10, 5))
# Wersja ciągła i dyskretna
plt.plot(t_cont, y_cont, label=r'Sygnał ciągły $x(t)$')
plt.stem(t_disc, y_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')
plt.title(r'Funkcja $Sinc$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
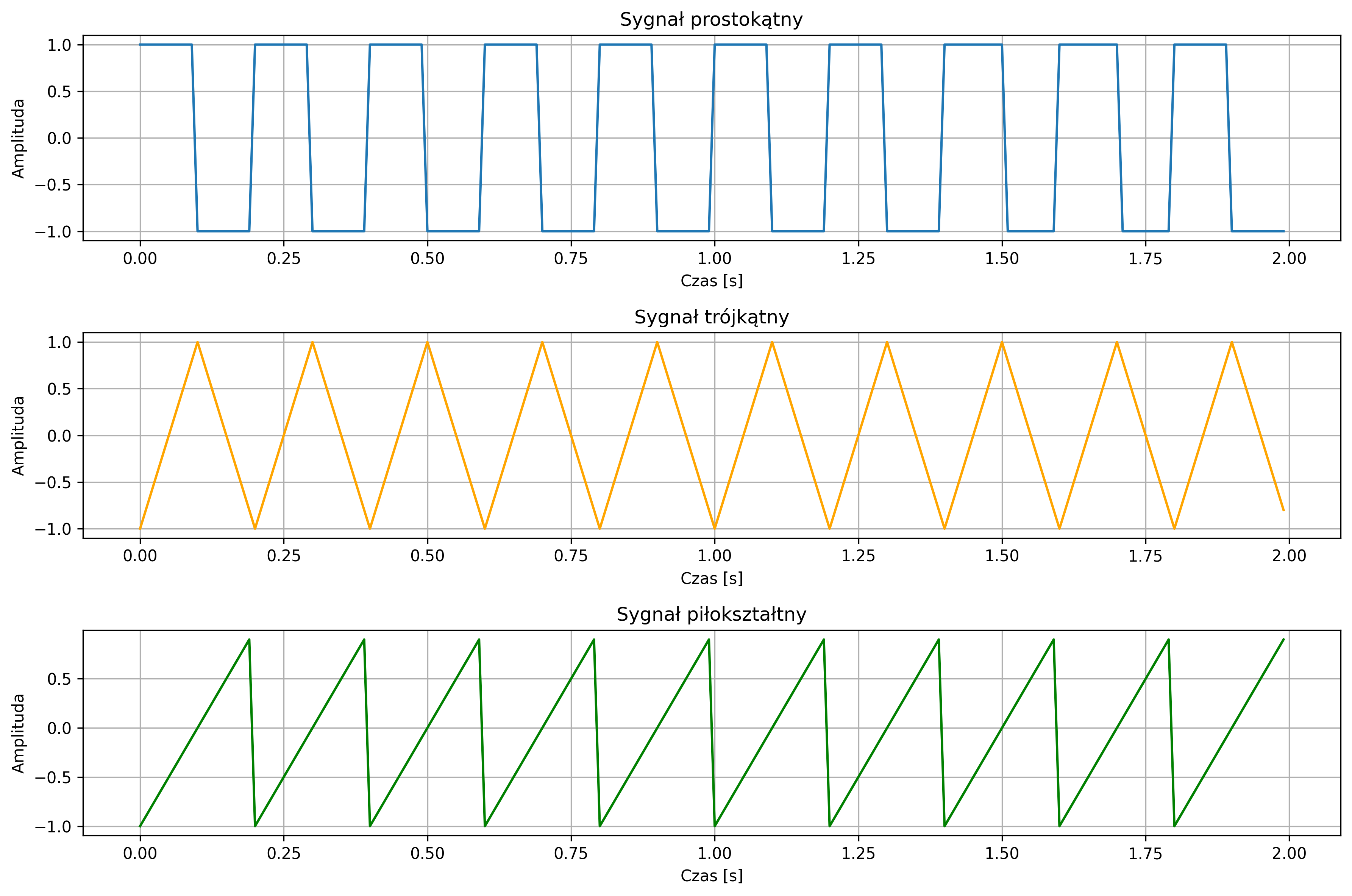
Wygenerować sygnały prostokątny, trójkątny oraz piłokształtny dla częstotliwości \(f = 5\ \text{Hz}\). Dla każdego sygnału narysować wersję ciągłą \(x(t)\) i dyskretną \(x[n]\) dla \(N = 200\) próbek, przyjmując częstotliwość próbkowania \(f_s = 100 \) Hz.
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# Parametry sygnałów
fs = 100 # częstotliwość próbkowania [Hz]
f = 5 # częstotliwość sygnału [Hz]
N = 200 # liczba próbek
T = N / fs # czas trwania sygnału [s]
# Oś czasu
t = np.linspace(0, T, N, endpoint=False)
# Sygnał prostokątny
rect_signal = signal.square(2 * np.pi * f * t, duty=0.5) # duty musi mieścić się w [0,1].
# Sygnał trójkątny
tri_signal = signal.sawtooth(2 * np.pi * f * t, width=0.5) # width=0.5 daje trójkąt
# Sygnał piłokształtny (piłowy)
saw_signal = signal.sawtooth(2 * np.pi * f * t, width=1) # width=1 daje piłę
# Rysowanie wykresów
plt.figure(figsize=(12, 8))
plt.subplot(3,1,1)
plt.plot(t, rect_signal, label='Sygnał prostokątny')
plt.title('Sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.subplot(3,1,2)
plt.plot(t, tri_signal, label='Sygnał trójkątny', color='orange')
plt.title('Sygnał trójkątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.subplot(3,1,3)
plt.plot(t, saw_signal, label='Sygnał piłokształtny', color='green')
plt.title('Sygnał piłokształtny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.tight_layout()
plt.show()
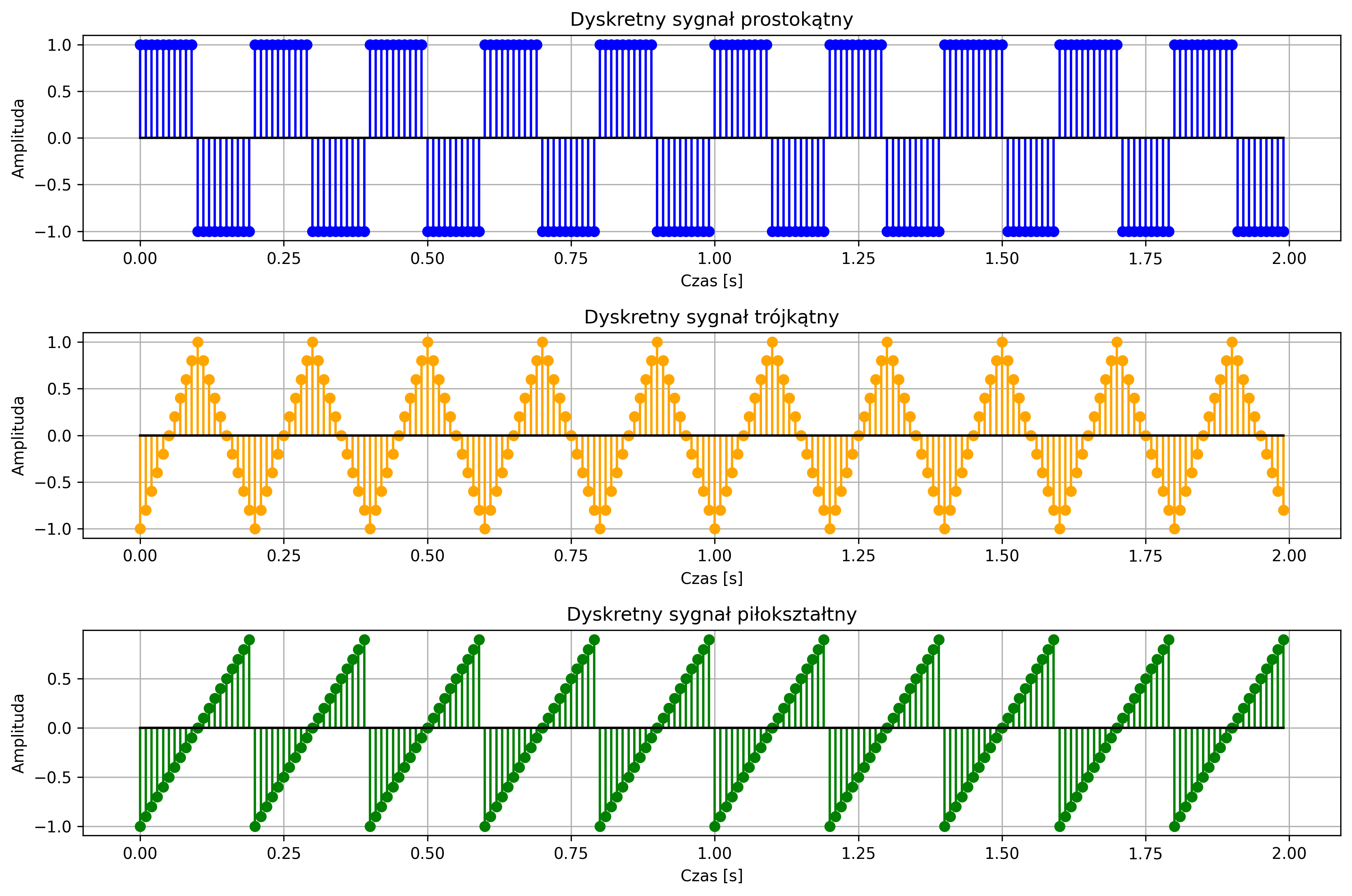
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# Parametry sygnałów
fs = 100 # częstotliwość próbkowania [Hz]
f = 5 # częstotliwość sygnału [Hz]
N = 200 # liczba próbek
T = N / fs # czas trwania sygnału [s]
# Oś czasu dyskretna
n = np.arange(N)
t = n / fs
# Sygnały dyskretne
rect_signal = signal.square(2 * np.pi * f * t, duty=0.5)
tri_signal = signal.sawtooth(2 * np.pi * f * t, width=0.5)
saw_signal = signal.sawtooth(2 * np.pi * f * t, width=1)
# Rysowanie wykresów
plt.figure(figsize=(12, 8))
plt.subplot(3,1,1)
plt.stem(t, rect_signal, linefmt='b-', markerfmt='bo', basefmt='k-')
plt.title('Dyskretny sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.subplot(3,1,2)
plt.stem(t, tri_signal, linefmt='orange', markerfmt='o', basefmt='k-')
plt.title('Dyskretny sygnał trójkątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.subplot(3,1,3)
plt.stem(t, saw_signal, linefmt='green', markerfmt='o', basefmt='k-')
plt.title('Dyskretny sygnał piłokształtny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.tight_layout()
plt.show()
Wygenerować sygnał świergotowy (chirp) o częstotliwości liniowo rosnącej od \(1\) Hz do \(400\) Hz. Przyjąć czas trwania sygnału \(0.1\) sekundy oraz częstotliwość próbkowania \(f_s = 10\ 000\) Hz. Narysować wykres sygnału ciągłego \(x(t)\).
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import chirp
# Parametry
t = np.linspace(0, 0.1, 10000) # czas trwania 0.1 [s]
# Generowanie sygnału świergotowego liniowego od 1 do 400 Hz
x = chirp(t, f0=1, f1=400, t1=0.1, method='linear')
# f0 = 1 częstotliwość początkowa [Hz]
# f1 = 400 częstotliwość końcowa [Hz]
# t1 = 0.1 czas, w którym osiągana jest f1
plt.figure(figsize=(10, 3))
plt.plot(t, x)
plt.title('Sygnał świergotowy liniowy, 1-400 Hz')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.tight_layout()
plt.show()
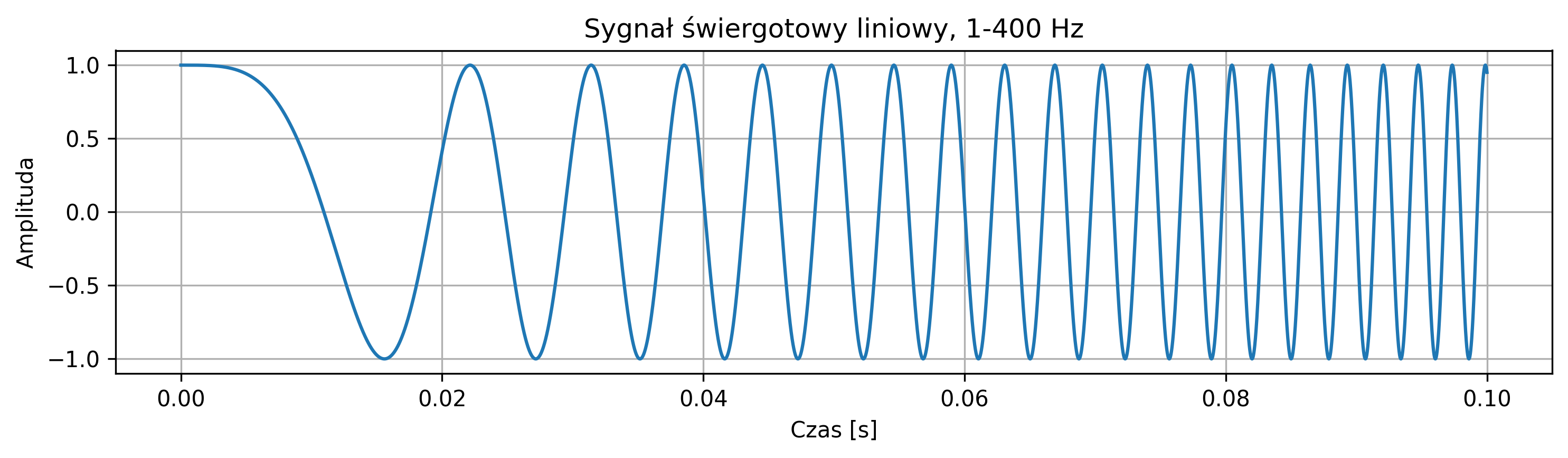
Sygnał świergotowy to sygnał o zmiennej częstotliwości chwilowej. Najprostszym jego przypadkiem jest sygnał sinusoidalny, którego częstotliwość chwilowa jest przestrajana w trakcie generowania. Przestrajanie częstotliwości odbywa się zwykle w sposób liniowy lub logarytmiczny. Sygnały świergotowe stosuje się m.in. do analizy charakterystyk częstotliwościowych urządzeń (np. filtrów, wzmacniaczy, głośników), do wyznaczania odpowiedzi systemu na różne częstotliwości w krótkim czasie, a także do badania reakcji układów biologicznych na bodźce o zmiennej częstotliwości.
Po zapoznaniu się z możliwościami generowania podstawowych sygnałów, możemy prześledzić operację splotu oraz zagadnienia związane z wyznaczaniem odpowiedzi impulsowej systemów LTI.
Wymagana jest znajomość funkcji:
np.convolve # obliczanie splotu dwóch jednowymiarowych sygnałów dyskretnych
# funkcja z biblioteki NumPy, przeznaczona głównie do prostych operacji na wektorach
convolve # obliczanie splotu sygnałów (1D, 2D i wyższych wymiarów)
# funkcja z biblioteki scipy.signal, oferująca większe możliwości
dzięki którym można łatwo wykonać operację splotu, np. w celu wyznaczenia odpowiedzi impulsowej systemów LTI.
Obliczyć splot dwóch ciągów próbek sygnałów: \( X = [2,4,6] \) oraz \( Y = [1,2] \).
Zgodnie z zasadą obliczenia splotu, opisaną w rozdziale 2.4, najpierw odwracamy ciąg próbek \( Y \) w czasie i wyrównujemy go z ciągiem próbek \( X \) tak, aby ostatnia próbka \( Y \) po odwróceniu pokrywała się z pierwszą próbką \( X\). Następnie mnożymy przez siebie pokrywające się próbki i sumujemy wyniki, co daje pierwszą wartość splotu.
X 2 4 6 2 * 1 = 2
Y 2 1 splot = [2]
Odwrócony ciąg próbek \( Y \) przesuwamy w prawo o jedno miejsce i powtarzamy operację:
X 2 4 6 2 * 2 + 4 * 1 = 8
Y 2 1 splot = [2 8]
Następnie przesuwamy ciąg próbek \( Y \) ponownie:
X 2 4 6 4 * 2 + 6 * 1 = 14
Y 2 1 splot = [2 8 14]
Jeżeli żadne próbki sygnałów nie pokrywają się, to kończymy obliczenia:
X 2 4 6 6 * 2 = 12
Y 2 1 splot = [2 8 14 12]
Operacja splotu jest przemienna, co oznacza, że otrzymamy ten sam wynik, jeśli odwrócimy próbki \( X \) i przesuwamy próbki \( Y \). Taki wynik możemy uzyskać w Pythonie:
import numpy as np
X = [2, 4, 6]
Y = [1, 2]
splot = np.convolve(X, Y)
print('Wynik splotu:', splot)
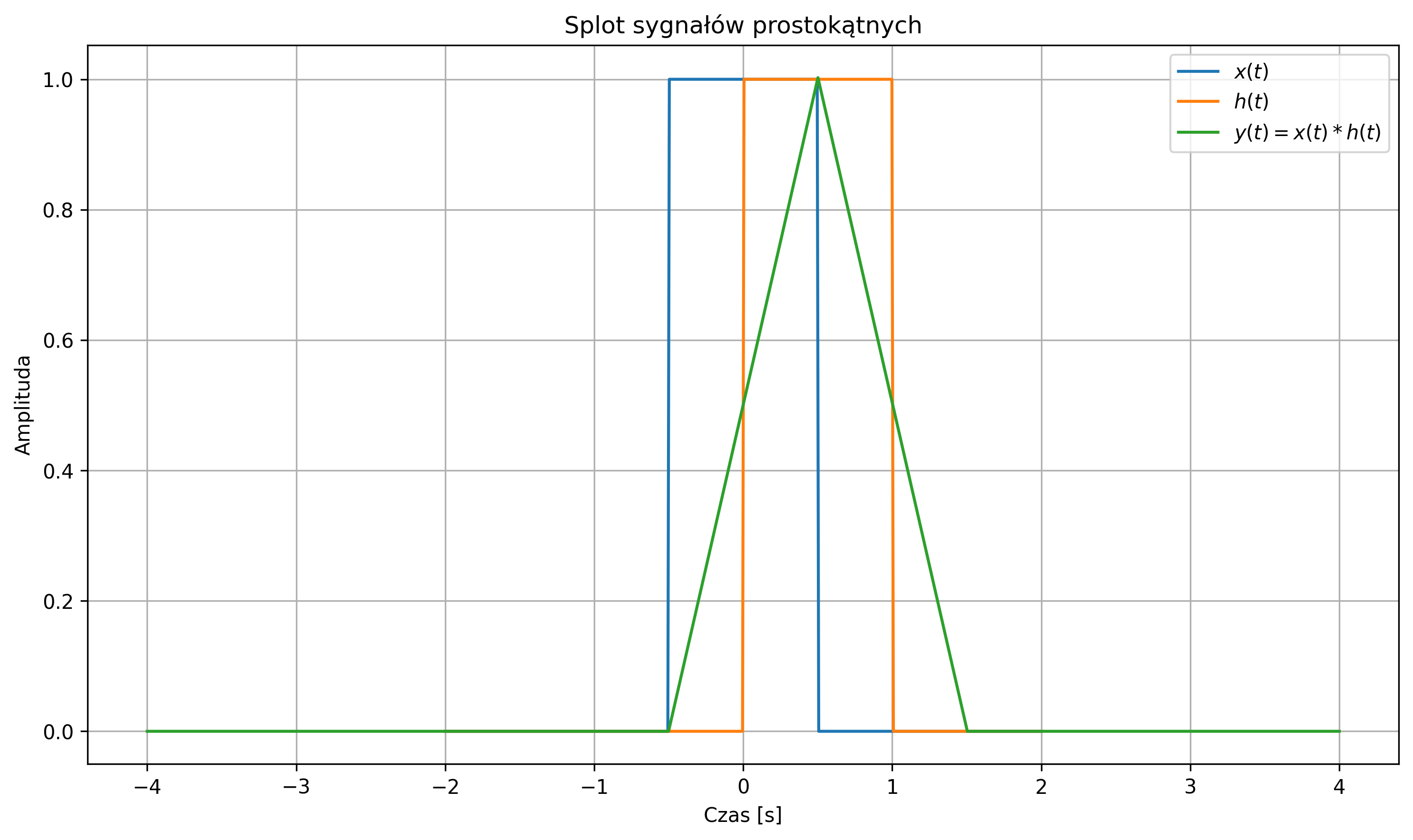
import numpy as np import matplotlib.pyplot as plt from scipy.signal import convolve # obliczanie splotu dwóch sygnałów # Definicja impulsu prostokątnego def rect(t): return np.where(np.abs(t) <= 0.5, 1, 0) # Osie czasu t = np.linspace(-2, 2, 400) dt = t[1] - t[0] # Sygnały x = rect(t) # impuls prostokątny h = rect(t - 0.5) # przesunięty impuls prostokątny # Splot ciągły (jako dyskretny z krokiem dt) y = convolve(x, h, mode='full') * dt t_y = np.linspace(t[0]+t[0], t[-1]+t[-1], len(y)) # Wykresy plt.figure(figsize=(10,6)) plt.plot(t, x, label='$x(t)$') plt.plot(t, h, label='$h(t)$') plt.plot(t_y, y, label='$y(t) = x(t)*h(t)$') plt.title('Splot sygnałów prostokątnych') plt.xlabel('Czas [s]') plt.ylabel('Amplituda') plt.legend() plt.grid(True) plt.tight_layout() plt.show()
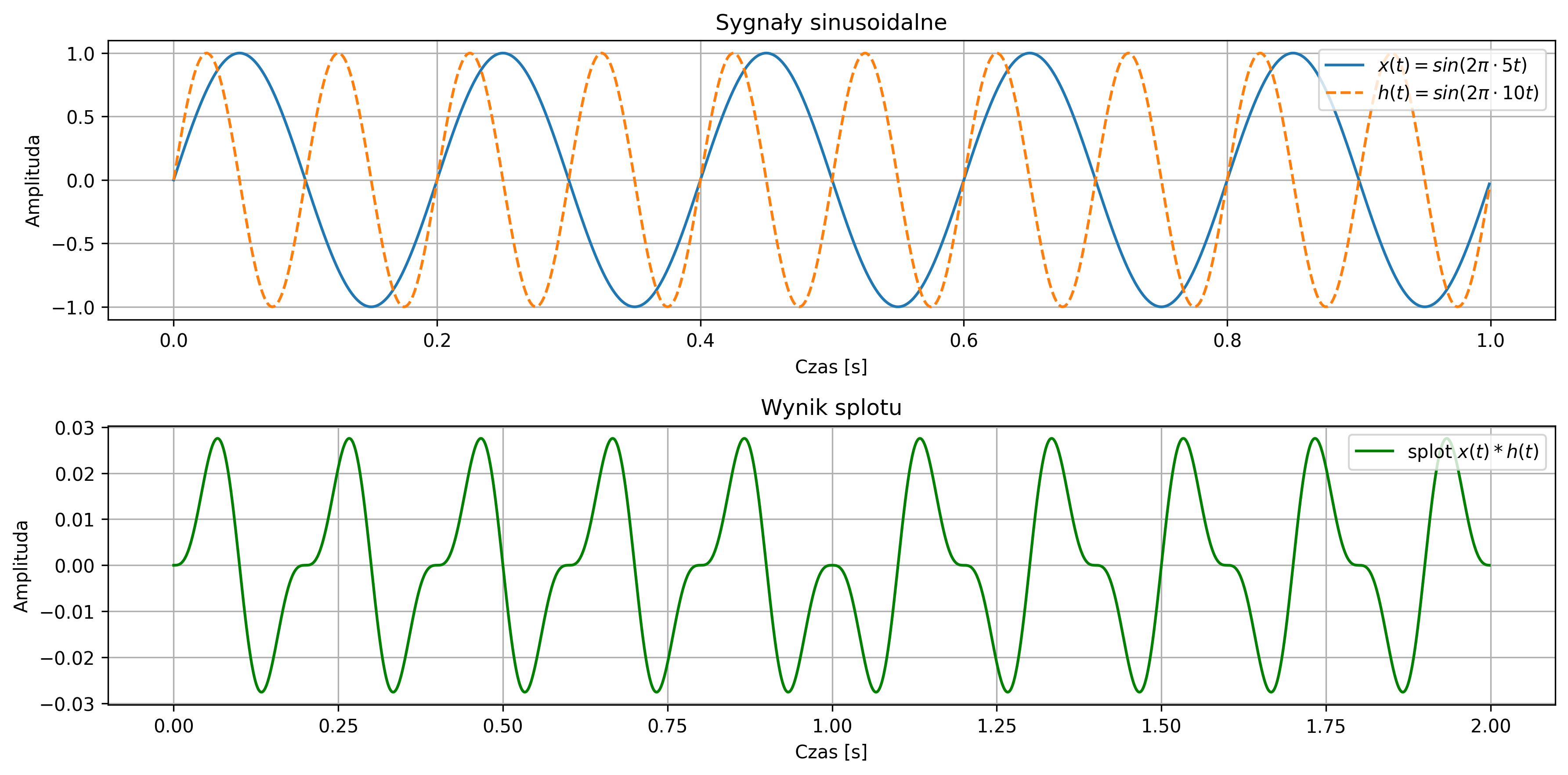
import numpy as np import matplotlib.pyplot as plt from scipy.signal import convolve # Parametry fs = 1000 # częstotliwość próbkowania [Hz] T = 1 / fs # okres próbkowania t = np.arange(0, 1, T) # oś czasu dla 1 sekundy # Częstotliwości sygnałów f1 = 5 # Hz f2 = 10 # Hz x = np.sin(2 * np.pi * f1 * t) h = np.sin(2 * np.pi * f2 * t) # Splot dyskretny y = convolve(x, h, mode='full') * T t_conv = np.arange(0, len(y)) * T # oś czasu dla splotu # Wykresy plt.figure(figsize=(12, 6)) # Wykres 1: oba sygnały wejściowe plt.subplot(2, 1, 1) plt.plot(t, x, label=r'$x(t) = sin(2\pi \cdot 5t)$') plt.plot(t, h, label=r'$h(t) = sin(2\pi \cdot 10t)$', linestyle='--') plt.title('Sygnały sinusoidalne') plt.xlabel('Czas [s]') plt.ylabel('Amplituda') plt.grid(True) plt.legend(loc='upper right') # Wykres 2: wynik splotu plt.subplot(2, 1, 2) plt.plot(t_conv, y, label=r'splot $x(t) * h(t)$', color='green') plt.title('Wynik splotu') plt.xlabel('Czas [s]') plt.ylabel('Amplituda') plt.grid(True) plt.legend(loc='upper right') plt.tight_layout() plt.show()
Wyznaczyć odpowiedź systemu LTI na sygnał wejściowy – impuls prostokątny, trwający \( 1 \) s, jeśli odpowiedź impulsowa systemu jest sygnałem wykładniczym malejącym:
Przypomnijmy, że odpowiedź systemu LTI na dowolny sygnał wejściowy jest splotem sygnału wejściowego z odpowiedzią impulsową.
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve
# Parametry
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t = np.arange(0, 5, T) # od 0 do 5 s
# Sygnał wejściowy: impuls prostokątny trwający 1 [s]
x = np.where(t < 1, 1, 0)
# Odpowiedź impulsowa: sygnał wykładniczy malejąca
h = np.exp(-t)
# Splot
y = convolve(x, h, mode='full') * T
t_conv = np.arange(0, len(y)) * T
# Wykresy
plt.figure(figsize=(12, 7))
plt.subplot(3, 1, 1)
plt.plot(t, x, label=r'$x(t)$: impuls prostokątny')
plt.title(r'Sygnał wejściowy $x(t)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.subplot(3, 1, 2)
plt.plot(t, h, label=r'$h(t) = e^{-t}$', color='orange')
plt.title(r'Odpowiedź impulsowa $h(t)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.subplot(3, 1, 3)
plt.plot(t_conv, y, label=r'$y(t) = x(t) * h(t)$', color='green')
plt.title('Odpowiedź systemu LTI: wynik splotu')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
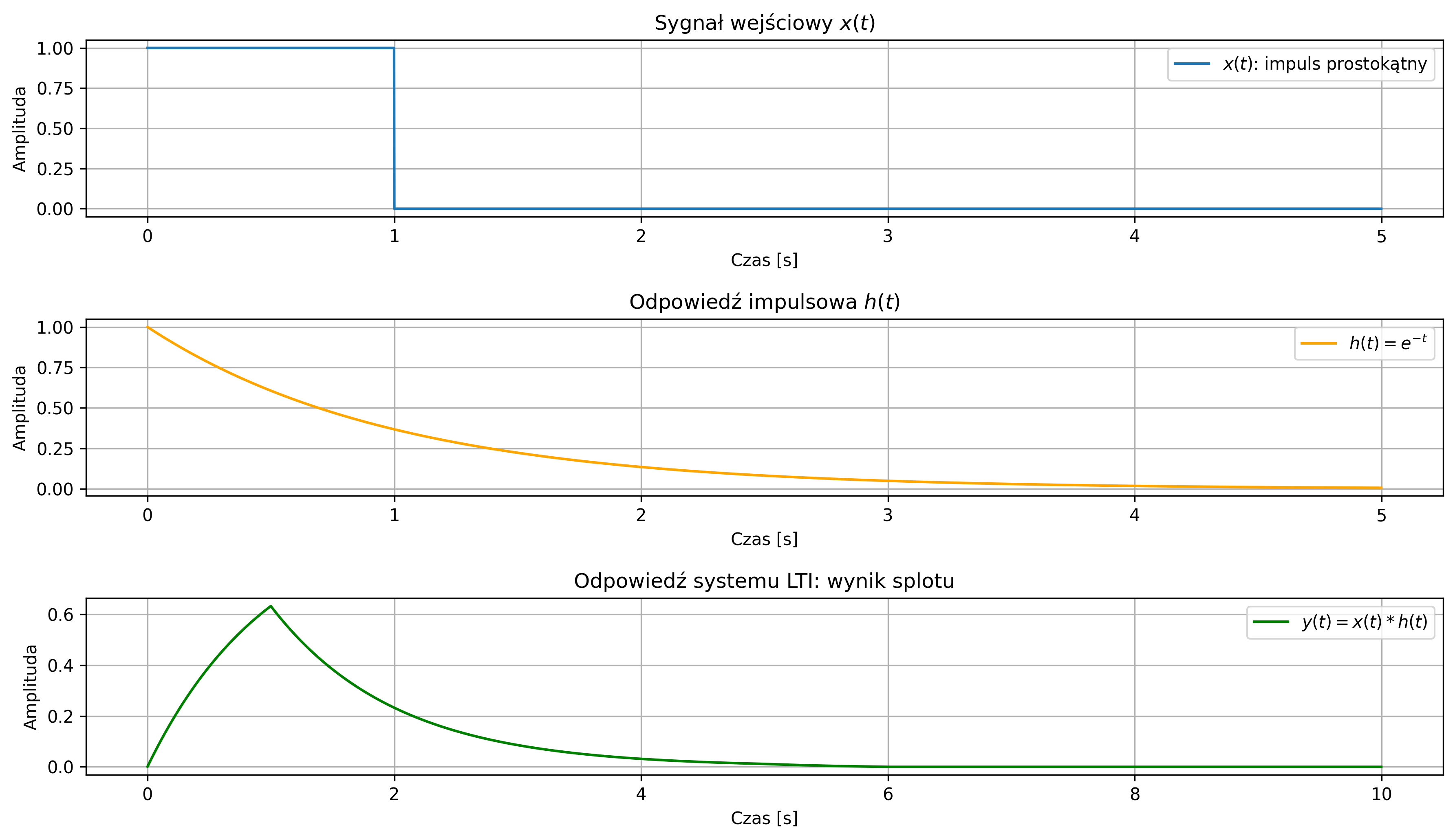
2.9. Charakterystyki sygnałów w języku Python
Celem poniższych ćwiczeń jest zapoznanie się z podstawowymi poleceniami w języku Python do wyznaczania wybranych charakterystyk sygnałów - parametrów energetycznych sygnałów oraz ich korelacji wzajemnej i autokorelacji.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. W trakcie realizacji ćwiczeń wykorzystywane będą następujące biblioteki:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów,
# takich jak np. prostokątny, trójkątny, piłokształtny
import scipy.integrate as integrate # numeryczne obliczanie całek
Rozwiązanie zadań wymaga znajomości podstawowych poleceń oraz funkcji dostępnych w języku Python, w tym m.in.:
np.sum # obliczanie sumy wartości próbek sygnału, np. przy wyznaczaniu energii sygnału
np.mean # wyznaczanie wartości średniej sygnału
np.abs # obliczanie wartości bezwzględnej próbek sygnału
np.max # wyznaczanie maksymalnej wartości sygnału
simpson # numeryczne całkowanie sygnału metodą Simpsona, np. do obliczania energii sygnału ciągłego
signal.correlate # obliczanie korelacji wzajemnej lub autokorelacji sygnałów
signal.correlate_lags # wyznaczanie wektora opóźnień (lagów) odpowiadających wartościom korelacji
Poniżej przedstawiono ćwiczenia zawierające przykładowe implementacje w języku Python. Autor zachęca czytelnika do uruchomienia zaprezentowanych kodów oraz do analizy charakterystyk sygnałów poprzez modyfikację wybranych parametrów sygnałów.
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
# Parametry sygnału
A = 2 # amplituda
f = 1 # częstotliwość [Hz]
omega = 2 * np.pi * f # pulsacja [rad/s]
# Czas obserwacji (symulacja sygnału "nieskończonego")
T_obs = 10
t = np.linspace(-T_obs, T_obs, 10000)
# Sygnał ciągły
x = A * np.sin(omega * t)
# Moc sygnału: numerycznie przybliżona całka
power = (1 / (2 * T_obs)) * simpson(x**2, t)
# Wynik
print(f"Moc sygnału: {power:.2f}")
# Wykres sygnału
plt.figure(figsize=(10, 5))
plt.plot(t, x, label=fr'$x(t) = {A}\sin({omega:.2f} t)$', color='C0')
plt.title(fr'Sygnał sinusoidalny o ograniczonej mocy: $P_x \approx {power:.2f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
na podstawie próbek w przedziale czasu \([-5,5]\).
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
# Zakres czasu
t = np.linspace(-5, 5, 10000)
dt = t[1] - t[0]
# Sygnał Gausso
x = np.exp(-np.pi*t**2)
# Energia
energy = np.sum(np.abs(x)**2) * dt
print(f'Energia sygnału: {energy:.4f}')
# Wartość średnia
mean = np.mean(x)
print(f'Wartość średnia: {mean:.6e}')
# Wykres sygnału
plt.figure(figsize=(9, 4))
plt.plot(t, x, label=r'$x(t) = e^{-\pi t^2}$')
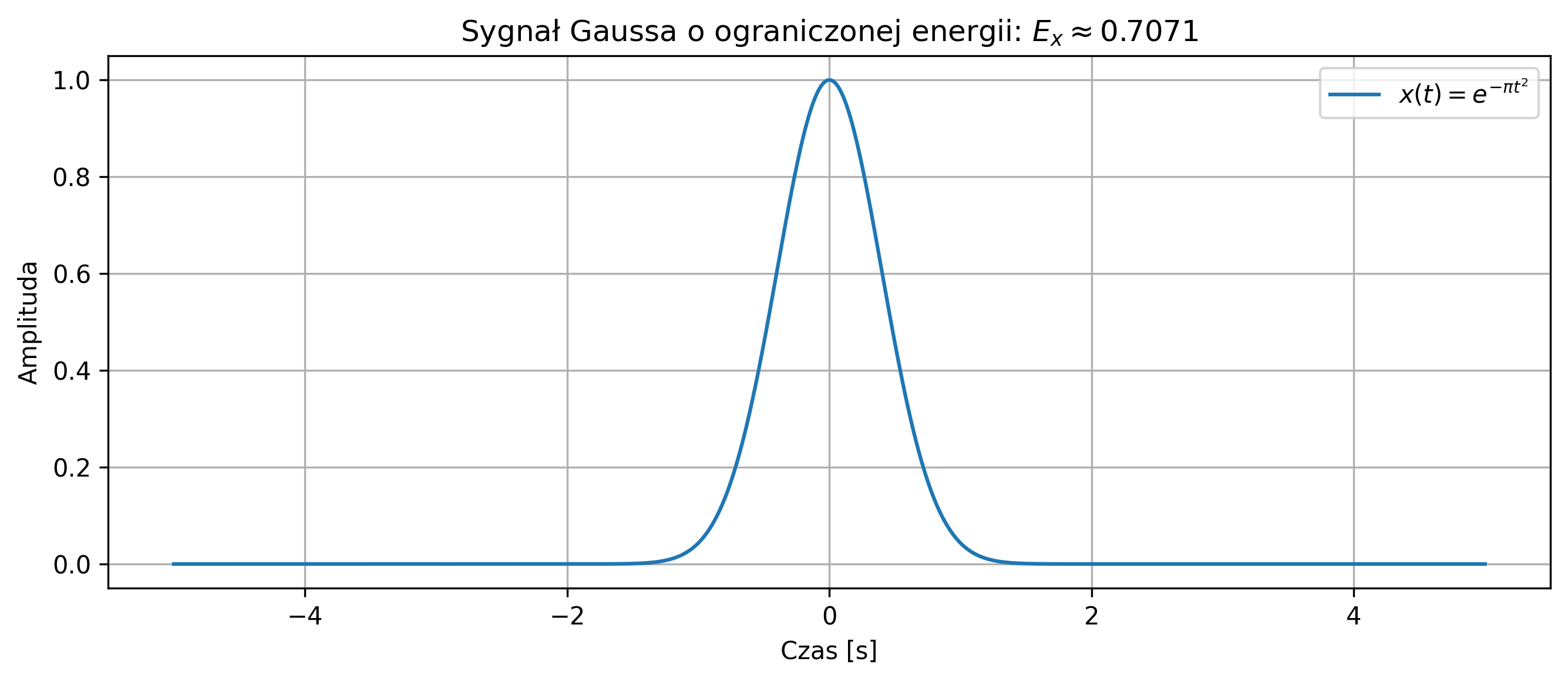
plt.title(fr'Sygnał Gaussa o ograniczonej energii: $E_x \approx {energy:.4f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
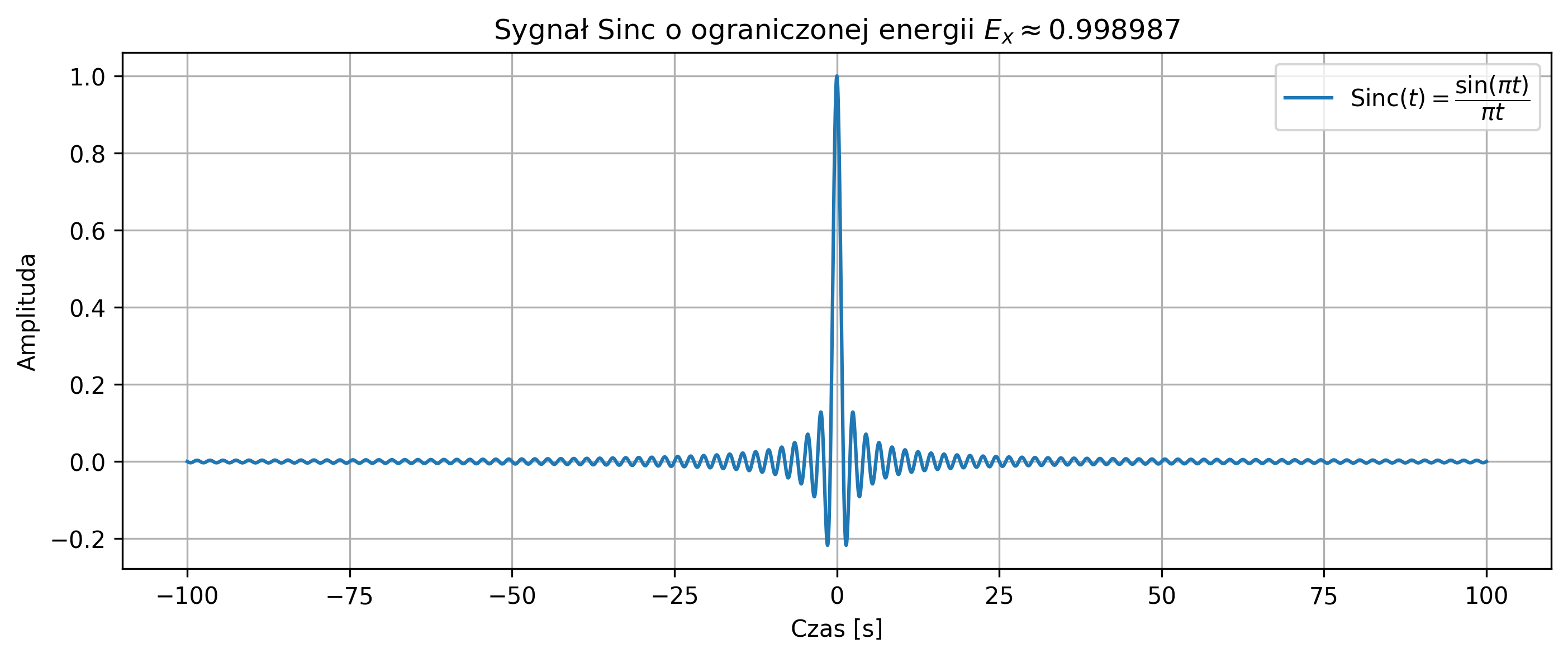
na podstawie próbek w przedziale czasu \([-100,100]\).
import numpy as np
import matplotlib.pyplot as plt
# Zakres czasu
t = np.linspace(-100, 100, 10000)
dt = t[1] - t[0]
# Sygnał Sinc
x = np.sinc(t)
# Obliczenie energii
energy = np.sum(np.abs(x)**2) * dt
print(f'Energia sygnału: {energy:.6f}')
# Wartość średnia
mean = np.mean(x)
print(rf'Wartość średnia sygnału: {mean:.6e}')
# Wykres
plt.figure(figsize=(11, 4))
plt.plot(t, x, label=r'$\mathrm{Sinc}(t) = \dfrac{\sin(\pi t)}{\pi t}$')
plt.title(fr'Sygnał Sinc o ograniczonej energii $E_x \approx {energy:.6f}$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.show()
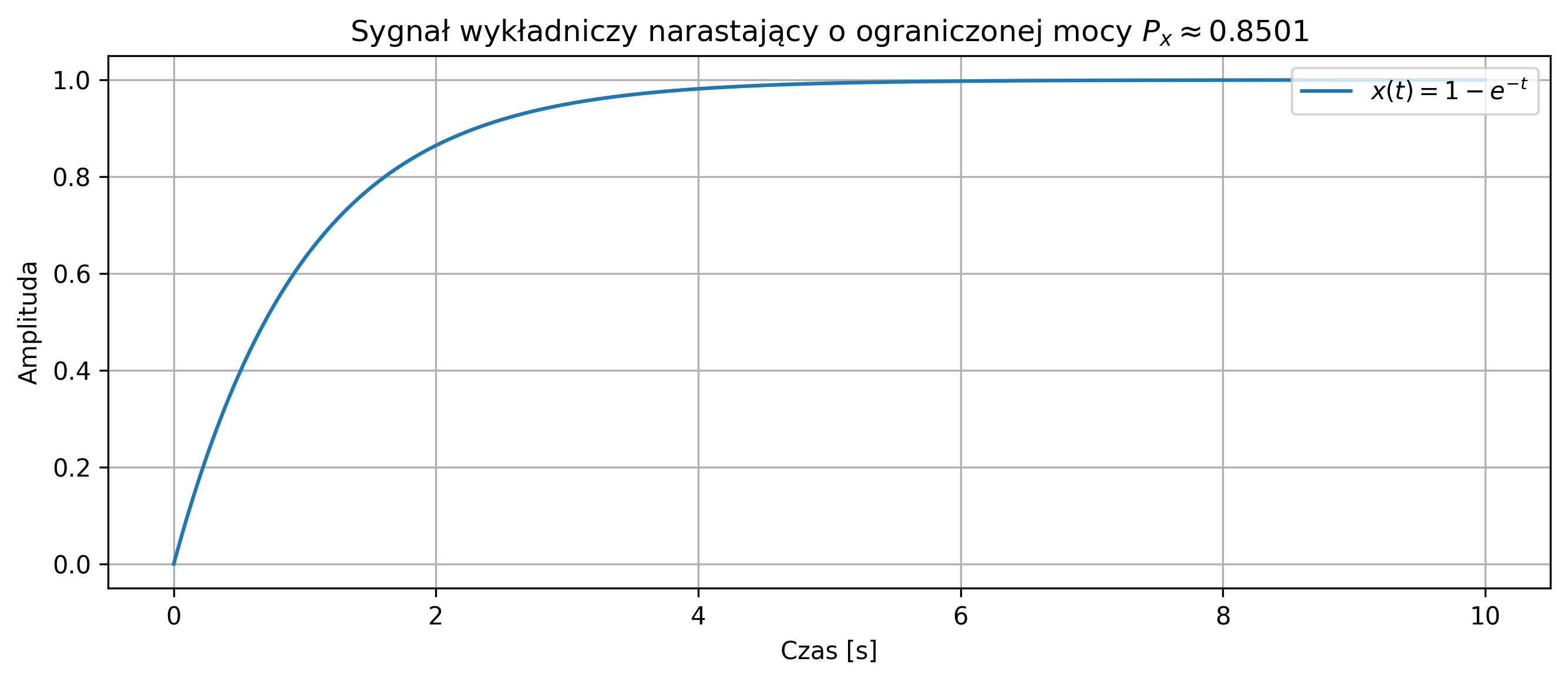
na podstawie jego próbek w przedziale czasu \([0,10]\).
import numpy as np
import matplotlib.pyplot as plt
# Zakres czasu
t = np.linspace(0, 10, 10000)
dt = t[1] - t[0]
# Sygnał wykładniczy narastający
x = 1 - np.exp(-t)
# Moc (energia średnia na przedziale)
power = np.sum(x**2) * dt / 10
print(f'Moc sygnału: {power:.4f}')
# Wartość średnia
mean = np.mean(x)
print(f'Wartość średnia: {mean:.4f}')
# Wykres
plt.figure(figsize=(9, 4))
plt.plot(t, x, label=r'$x(t) = 1 - e^{-t}$')
plt.title('Sygnał wykładniczy narastający')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as signal
# Parametry sygnału
A = 2 # amplituda
f = 2 # częstotliwość [Hz]
omega = 2 * np.pi * f
tau = 0.25 # opóźnienie czasowe w sekundach
varphi = -omega * tau # odpowiadające przesunięcie fazowe
# Czas
t = np.linspace(0, 2, 5000)
# Sygnały
x = A * np.sin(omega * t)
y = A * np.sin(omega * t + varphi) # przesunięcie fazowe odpowiadające opóźnieniu
# Korelacja
r_xy = correlate(y, x, mode='full')
lags = correlation_lags(len(y), len(x), mode='full')
dt = t[1] - t[0]
lags_time = lags * dt
max_lag_time = lags_time[np.argmax(r_xy)]
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
axs[0].plot(t, x, label=r'$x(t) = A \sin(\omega t)$',linestyle='-')
axs[0].plot(t, y, label=r'$y(t) = A \sin(\omega t + \varphi)$',linestyle='-')
axs[0].set_title(fr'Sygnały sinusoidalne $x(t)$ i $y(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
axs[1].plot(lags_time, r_xy, color='green')
axs[1].set_title(f'Korelacja wzajemna $R_{{xy}}(τ)$')
axs[1].axvline(max_lag_time, color='red', linestyle='--',
label = fr'Max przy opóźnieniu = {max_lag_time:.3f} s')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(fr'Korelacja wzajemna $[\tau]$')
axs[1].legend(loc='upper right')
axs[1].grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth, correlate, correlation_lags
# Parametry ciągłego czasu
T_obs = 2 # czas obserwacji [s]
fs = 10000 # częstotliwość próbkowania [Hz]
t = np.linspace(0, T_obs, int(T_obs * fs))
dt = t[1] - t[0]
# Parametry sygnału piłokształtnego
f = 5 # Hz
x = sawtooth(2 * np.pi * f * t)
# Sygnał opóźniony
delay_sec = 0.05 # opóźnienie w sekundach
delay_samples = int(delay_sec * fs) # opóźnienie w próbkach
y = np.roll(x, delay_samples)
# Korelacja wzajemna
r_xy = correlate(y, x, mode='full') * dt
lags = correlation_lags(len(y), len(x), mode='full') * dt
# Znalezienie maksimum korelacji
max_idx = np.argmax(r_xy)
max_lag_time = lags[max_idx]
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
axs[0].plot(t, x, label=rf'$x(t)$ - oryginalny', color='blue')
axs[0].plot(t, y, label=rf'$y(t)$ - opóźniony', color='orange')
axs[0].set_title('Sygnały piłokształtne')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
axs[1].plot(lags, r_xy, color='green')
axs[1].set_title(fr'Korelacja wzajemna $R_{{xy}}(τ)$')
axs[1].axvline(max_lag_time, color='red', linestyle='--',
label=fr'Max przy opóźnieniu = {max_lag_time:.3f} s')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Korelacja wzajemna $[\tau]$')
axs[1].legend(loc='upper right')
axs[1].grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
# Parametry
fs = 1000 # częstotliwość próbkowania [Hz]
A = 1 # amplituda sygnału
f = 5 # częstotliwość sygnału [Hz]
T = 1 / f # okres [s]
t = np.arange(0, 2, 1/fs)
x = A * np.sin(2 * np.pi * f * t)
# Autokorelacja
R_xx = correlate(x, x, mode='full')
lags = correlation_lags(len(x), len(x), mode='full') / fs
# Normalizacja (opcjonalnie)
R_xx = R_xx / np.max(R_xx)
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
# Sygnał
axs[0].plot(t, x)
axs[0].set_title(f'Sygnał sinusoidalny $x(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Autokorelacja
axs[1].plot(lags, R_xx, color='green', label=r"$R_{{xx}}(τ) / R_{{xx}}(0)$")
axs[1].axvline(T, color='r', linestyle='--', label=f'T = {T:.3f} s')
axs[1].axvline(2*T, color='r', linestyle=':', label=f'2T = {2*T:.3f} s')
axs[1].axvline(-T, color='r', linestyle='--')
axs[1].axvline(-2*T, color='r', linestyle=':')
axs[1].set_title('Unormowana autokorelacja')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].grid(True)
axs[1].legend(loc='upper right')
plt.tight_layout()
plt.show()
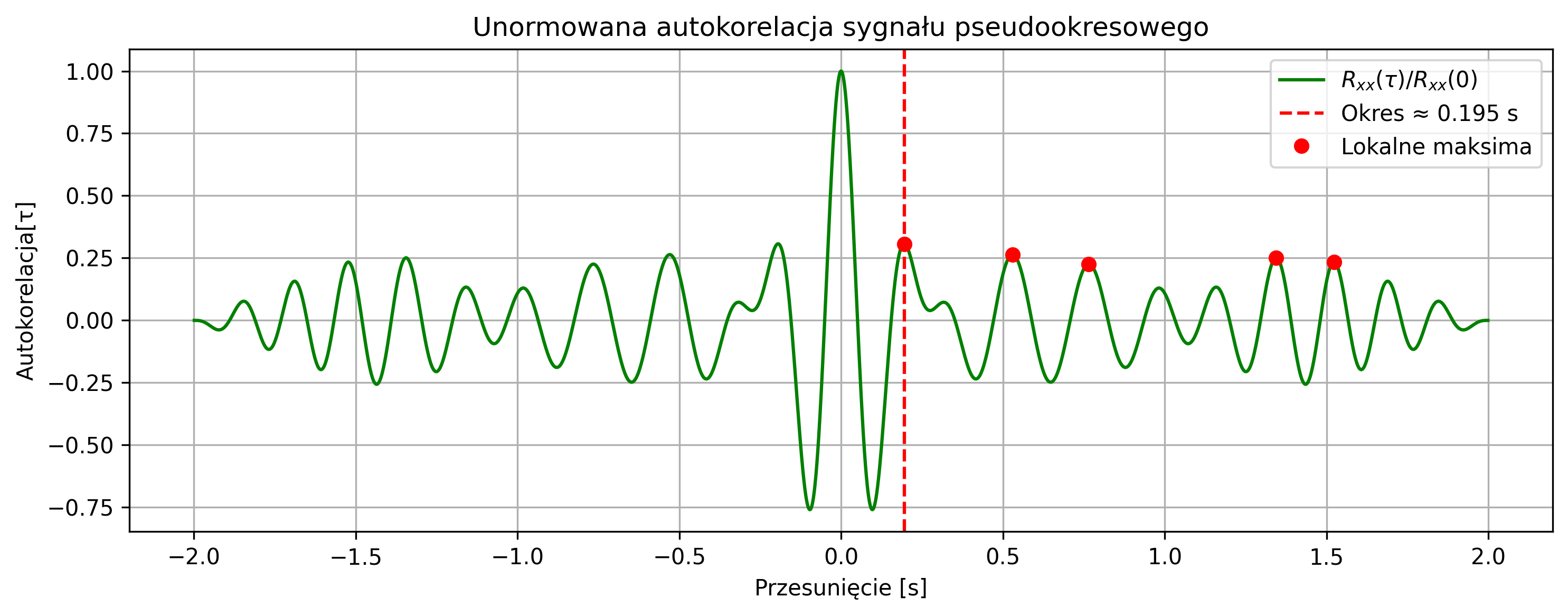
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
from scipy.signal import find_peaks
# Parametry
fs = 1000 # częstotliwość próbkowania [Hz]
A = 1 # amplituda sygnału
f = 3.5 # częstotliwość sygnału [Hz] (częstotliwość nośna sygnału modulowanego)
# czyli spodziewany okres wynosi w przybliżeniu 0.286 s
T = 1 / f # okres [s]
t = np.arange(0, 2, 1/fs) # czas trwania sygnału
# Sygnał pseudookresowy: sinus z modulacją częstotliwości
beta = 0.5 # większa głębokość modulacji
fm = 0.5 # czętotliwość modulacji [Hz]
x = np.sin(2 * np.pi * (f * t + beta * np.sin(2 * np.pi * fm * t)))
# Autokorelacja
R_xx = correlate(x, x, mode='full')
lags = correlation_lags(len(x), len(x), mode='full') / fs
# Normalizacja (opcjonalnie)
R_xx = R_xx / np.max(R_xx)
# Szukamy pików po stronie dodatnich opóźnień
center = len(R_xx) // 2
search_range = R_xx[center+1:] # pomijamy lag=0
lags_range = lags[center+1:]
peaks, properties = find_peaks(search_range, height=0.2, distance=int(0.05 * fs))
# wykryty pik ma mieć wartość co najmniej 0.2 - ignorujemy małe piki wynikające np. z szumu.
# minimalna odległość między pikami (w próbkach) - tu np. 0.05 * 1000 = 50 próbek,
# to chroni przed wykrywaniem zbyt blisko położonych pików.
# Szacowany okres
estimated_period = lags_range[peaks[0]] if len(peaks) > 0 else None
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=False)
# Wykres 1: sygnał
axs[0].plot(t, x)
axs[0].set_title(f'Sygnał sinusoidalny z modulacją częstotliwości $x(t)$')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel("Amplituda")
axs[0].grid(True)
# Wykres 2: autokorelacja
axs[1].plot(lags, R_xx, label=r'$R_{{xx}}(τ) / R_{{xx}}(0)$', color='green')
if estimated_period is not None:
axs[1].plot(estimated_period, R_xx[center + peaks[0]], 'ro',
label=fr'Okres $\approx$ {estimated_period:.3f} s')
axs[1].axvline(estimated_period, color='red', linestyle='--')
axs[1].set_title('Unormowana autokorelacja')
axs[1].set_xlabel('Przesunięcie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
# Informacja tekstowa
if estimated_period is not None:
print(f'Szacowana długość powtarzającego się fragmentu: {estimated_period:.3f} sekundy')
else:
print("Nie wykryto okresu")
- znaczące zmniejszenie głębokości modulacji \( \beta \), by sygnał był mniej „zniekształcony”,
- zwiększenie częstotliwości nośnej,
- zamiast brania całości sygnału z modulacją, wziąć tylko krótki fragment, w którym częstotliwość się nie zmienia zbyt mocno.
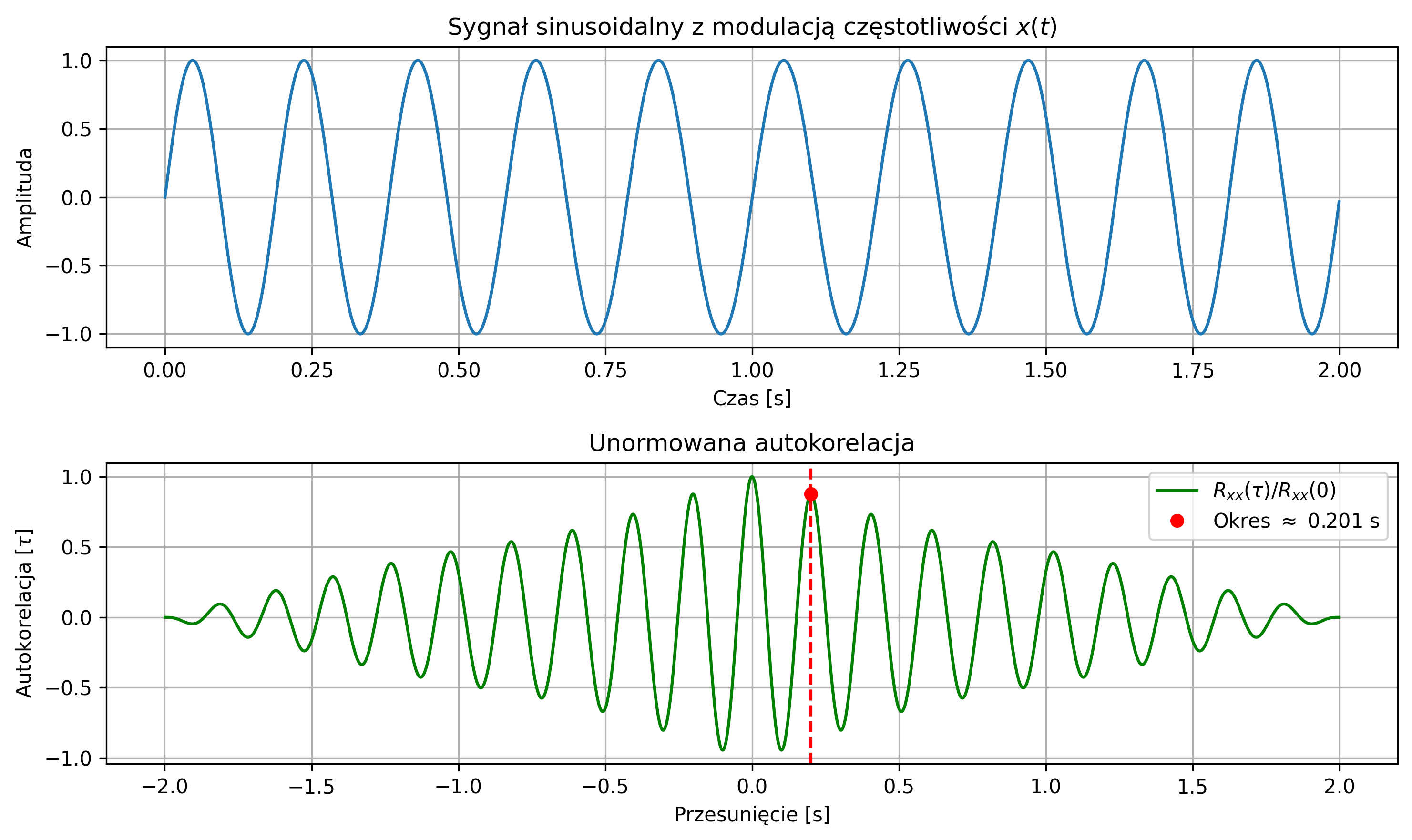
Przyjąć częstotliwość nośną \(50\) Hz i częstotliwość modulacji \(5\) Hz. Obliczyć moc i energię sygnału.
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, correlation_lags
# Parametry czasu
fs = 500
T = 1
t = np.linspace(0, T, int(fs*T), endpoint=False)
# Parametry sygnału
f = 50 # częstotliwość nośna [Hz]
fm = 5 # częstotliwość modulacji [Hz]
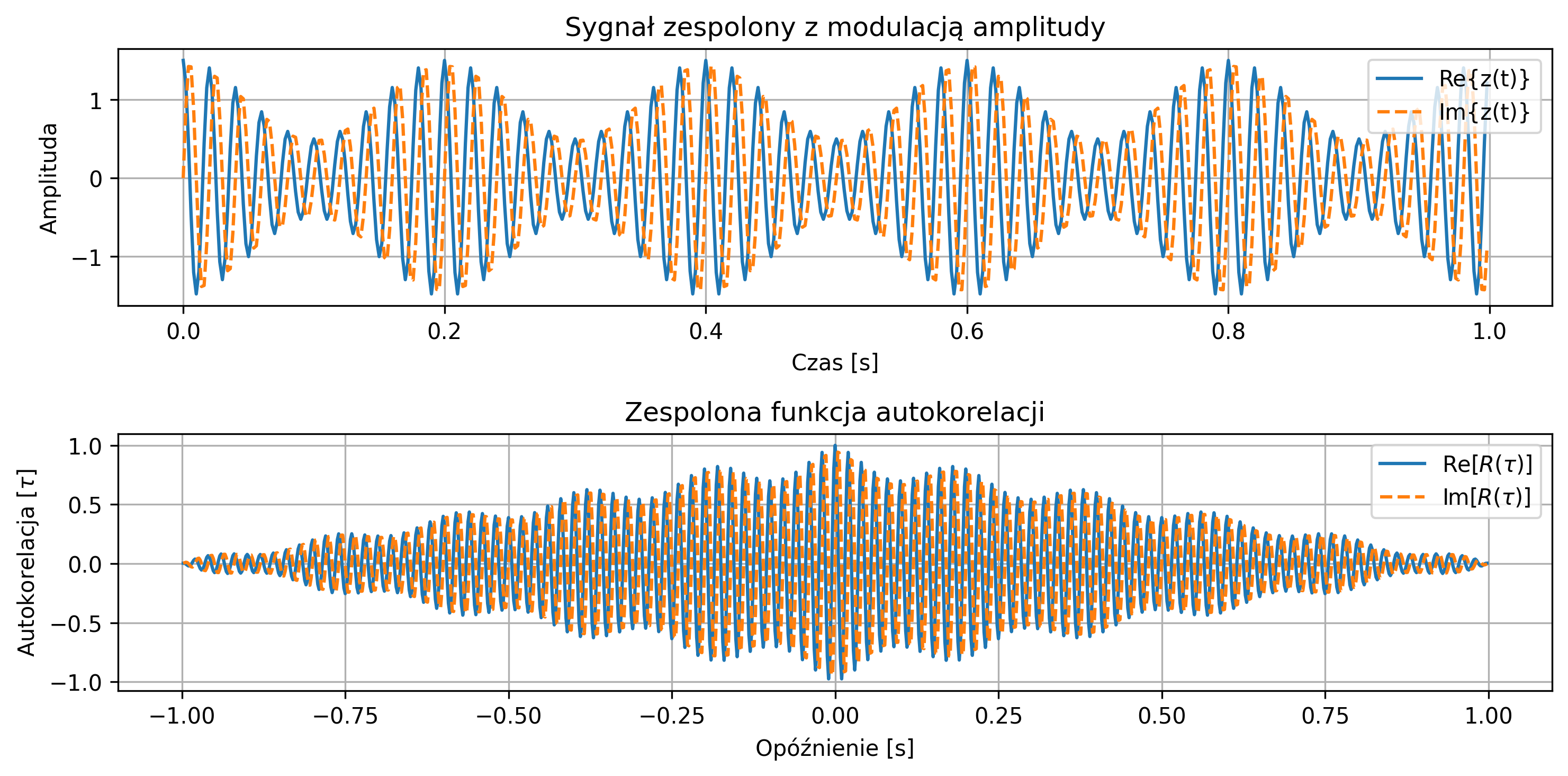
# Sygnał zespolony z modulacją amplitudy
envelope = 1 + 0.5 * np.cos(2 * np.pi * fm * t) # obwiednia
z = envelope * np.exp(1j * 2 * np.pi * f * t)
# Obliczanie mocy i energii
dt = 1 / fs
power = np.mean(np.abs(z)**2)
energy = np.sum(np.abs(z)**2) * dt
# Autokorelacja
corr = correlate(z, z, mode='full') * dt
lags = correlation_lags(len(z), len(z), mode='full') / fs
corr /= np.max(np.abs(corr)) # normalizacja
# Wyniki
print(f'Moc: {power:.4f}')
print(f'Energia: {energy:.4f}')
# Wykres
fig, axs = plt.subplots(2, 1, figsize=(10, 5), sharex=False)
# Sygnał zespolony: Re i Im
axs[0].plot(t, z.real, label='Re{z(t)}')
axs[0].plot(t, z.imag, '--', label='Im{z(t)}')
axs[0].set_title('Sygnał zespolony z modulacją amplitudy')
axs[0].set_xlabel('Czas [s]')
axs[0].set_ylabel('Amplituda')
axs[0].legend(loc='upper right')
axs[0].grid(True)
# Autokorelacja
axs[1].plot(lags, corr.real, label=rf'Re$[R(\tau)]$')
axs[1].plot(lags, corr.imag, '--', label=rf'Im$[R(\tau)]$')
axs[1].set_title('Zespolona funkcja autokorelacji')
axs[1].set_xlabel('Opóźnienie [s]')
axs[1].set_ylabel(rf'Autokorelacja $[\tau]$')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
2.10. Test A - sprawdź swoją wiedzę
Test ma na celu sprawdzenie i utrwalenie wiadomości z zakresu analizy sygnałów, obejmując sygnały analogowe i cyfrowe, systemy LTI, operacje takie jak splot i autokorelacja oraz podstawowe własności sygnałów. Każde pytanie ma trzy odpowiedzi (A, B, C), z których tylko jedna jest poprawna.
Klucz odpowiedzi:
1. B
2. A
3. B
4. C
5. A
6. A
7. B
8. A
9. C
10. A
11. A
12.B
13. B
14. B
15. B
16. C
17. B
18. B
19. C
20. A
21. B
22. A
23. B
24. A
25. C
3. Cyfrowe przetwarzanie sygnałów
Przetwarzanie sygnałów cyfrowych (DSP, ang. Digital Signal Processing) jest dziedziną nauki i techniki zajmującą się analizą, przekształcaniem i interpretacją sygnałów zapisanych w postaci cyfrowej. Obejmuje zarówno teorię, jak i metody numeryczne oraz techniki przetwarzania dźwięku, obrazu i sygnałów biomedycznych. Cyfrowe przetwarzanie sygnałów znalazło szerokie zastosowanie w telekomunikacji, elektronice oraz w nowoczesnej diagnostyce medycznej, na przykład w tomografii komputerowej (CT), rezonansie magnetycznym (MRI), elektroencefalografii (EEG) czy badaniu echa serca (USG).
W systemach cyfrowych, sygnały analogowe (ciągłe w czasie i amplitudzie) muszą zostać zamienione na postać cyfrową – proces ten realizowany jest przez przetwornik analogowo-cyfrowy (A/C), który dokonuje próbkowania i kwantyzacji sygnału. Odpowiednie dobranie parametrów próbkowania ma kluczowe znaczenie dla jakości dalszego przetwarzania sygnału. Jednym z najważniejszych zagadnień w tym kontekście jest twierdzenie Nyquista-Shannona, które określa minimalną częstotliwość próbkowania konieczną do jednoznacznego odtworzenia sygnału. Brak spełnienia tego warunku prowadzi do zjawiska aliasingu – nakładania się widm i utraty informacji o sygnale. Dlatego w praktyce stosuje się filtry antyaliasingowe oraz odpowiednio wysokie częstotliwości próbkowania.
Przetwarzanie sygnałów cyfrowych jest zwykle realizowane przez specjalizowane układy cyfrowe. Dzięki dużej wydajności obliczeniowej możliwa jest obróbka sygnałów w czasie rzeczywistym, co ma kluczowe znaczenie w wielu nowoczesnych systemach technicznych.
W niniejszym rozdziale omówione zostaną zasady poprawnego próbkowania, rola twierdzenia Nyquista-Shannona oraz praktyczne aspekty związane z filtrowaniem antyaliasingowym. Zostaną również przedstawione przykłady w języku Python, ilustrujące skutki nieprawidłowego próbkowania, aliasingu oraz sposoby jego zapobiegania.
3.1. Reprezentacja próbkowania
Próbkowanie to proces przekształcania sygnału ciągłego w sygnał dyskretny poprzez pobieranie jego wartości w równych odstępach czasu. Stanowi ono pierwszy etap konwersji analogowo-cyfrowej (A/C) i jest niezbędne do analizy oraz przetwarzania sygnałów w systemach cyfrowych. W przypadku próbkowania w regularnych odstępach czasu podaje się częstotliwość próbkowania, wyrażaną w liczbie próbek na sekundę, czyli w hercach (Hz). Dla próbkowania wielowymiarowego określa się rozdzielczość w postaci liczby punktów lub pikseli na cal. Obecnie produkowane przetworniki analogowo-cyfrowe oferują maksymalną częstotliwość próbkowania od kilkudziesięciu kiloherców do kilku megaherców.
W wyniku próbkowania równomiernego z okresem \( T \) sygnał analogowy \( x(t) \) jest przetworzony w sygnał dyskretny \( x[n] \), którego argumentem jest czas unormowany względem okresu próbkowania. Proces próbkowania można stosunkowo łatwo modyfikować poprzez zmianę okresu próbkowania. Należy jednak pamiętać, że wpływa to na odwzorowanie sygnału analogowego w zapisie cyfrowym oraz ma istotne znaczenie dla identyfikacji i przetwarzania sygnału.
W rozdziale 2.4 została opisana operacja splotu i jej podstawowa własność – elementem identycznościowym operacji splotu jest impuls Diraca:
\( x(t)\ast \delta(t) = x(t) \) oraz \( x(t)\ast \delta(t-t_0) = x(t-t_0) \)
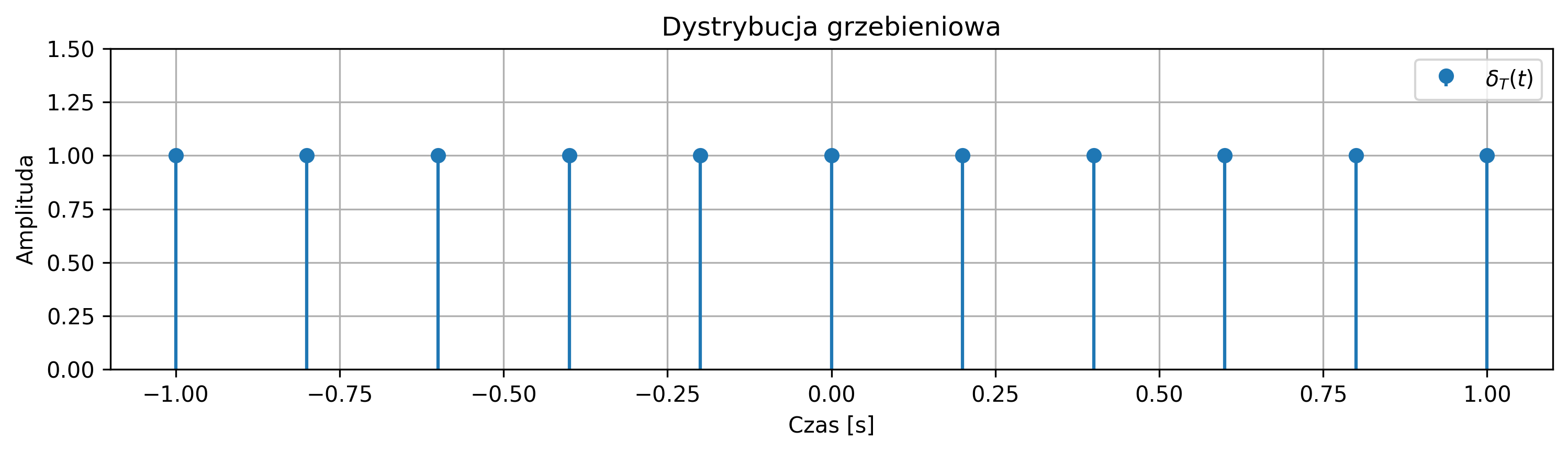
Matematycznie proces próbkowania można opisać jako mnożenie sygnału ciągłego przez funkcję impulsów jednostkowych Diraca rozmieszczonych okresowo – dystrybucję grzebieniową.
Dystrybucja grzebieniowa jest okresowym ciągiem impulsów Diraca, powtarzanych z okresem \( T \). Jej wykres przypomina nieskończony grzebień, którego „zęby” są równoodległe i mają jednakową wysokość:
3.2. Problemy związane z próbkowaniem
Przejście do sygnału cyfrowego pozwala na efektywne przetwarzanie, przechowywanie i transmisję, ale wiąże się z szeregiem potencjalnych problemów technicznych:
- aliasing (zakłócenia aliasowe),
- błąd kwantyzacji,
- opóźnienia,
- ograniczenia sprzętowe,
- artefakty cyfrowe.
Poprawne zaprojektowanie procesu próbkowania i konwersji ma kluczowe znaczenie dla jakości całego systemu cyfrowego.
W procesie próbkowania część informacji o sygnale jest pomijana. Jeżeli zmiany sygnału są bardzo szybkie w porównaniu z częstotliwością próbkowania, dynamika sygnału oryginału nie zostanie uchwycona. Podstawowym zagadnieniem podczas cyfrowego przetwarzania sygnałów jest właściwy dobór częstotliwości próbkowania. Powinna ona być dobrana tak, aby:
- była wystarczająco duża, by dokładnie odwzorowywać zmienność i dynamikę badanego sygnału,
- nie była nadmiernie wysoka, ponieważ zbyt gęste próbkowanie prowadzi do powstania dużej liczby silnie skorelowanych próbek, co zwiększa koszty pamięciowe i obliczeniowe, nie przynosząc istotnych korzyści informacyjnych,
- nie była też zbyt niska, ponieważ zbyt rzadkie próbkowanie może prowadzić do zjawiska, w którym informacje o składowych wysokoczęstotliwościowych zostają zniekształcone lub nieodróżnialne od składowych niskoczęstotliwościowych.
Podczas próbkowania sygnału z częstotliwością \( f_s \) próbek na sekundę, niemożliwe staje się jednoznaczne rozróżnienie między sygnałem sinusoidalnym o częstotliwości \( f \), a sygnałami o częstotliwościach \( f+kf_s \), gdzie \( k \) jest dowolną liczbą całkowitą. Oznacza to, że ten sam zbiór próbek może odpowiadać nieskończonej liczbie sinusoid różniących się całkowitymi wielokrotnościami częstotliwości próbkowania.
Jest to podstawowa właściwość próbkowania i jedna z kluczowych konsekwencji analizy sygnałów w dziedzinie częstotliwości. Niewłaściwie dobrana częstotliwość próbkowania prowadzi często do błędnej interpretacji sygnału analogowego, znanej jako aliasing. Zjawisko to polega na tym, że na podstawie zbyt rzadko pobranych próbek z oryginalnego przebiegu sygnału system cyfrowy interpretuje sygnał jako mający inną częstotliwość, niż w rzeczywistości.
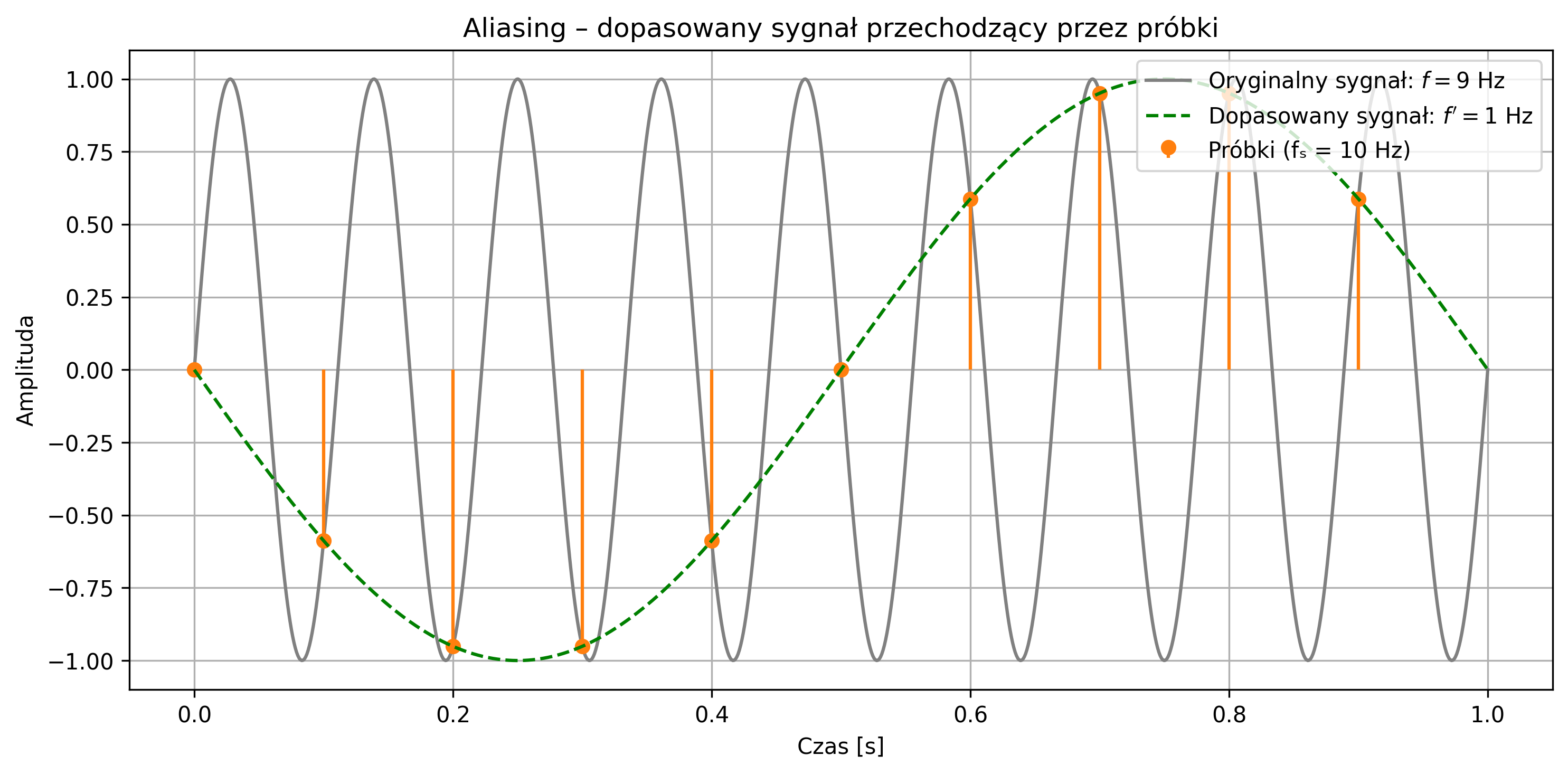
Na rys. 3.3 zostało graficznie przedstawione zjawisko aliasingu. Na pierwszym wykresie próbkowanie sygnału sinusoidalnego (o częstotliwości \(9\) Hz) jest zbyt rzadkie (częstotliwość próbkowania wynosi \(10\) Hz), co skutkuje jego błędnym odwzorowaniem sygnału. System identyfikuje sygnał jako mający niższą częstotliwość, niż w rzeczywistości. Drugi wykres pokazuje poprawne próbkowanie (na poziomie \(30\) Hz) – częstotliwość próbkowania jest wystarczająco wysoka, aby dokładnie odwzorować przebieg oryginalnego sygnału.
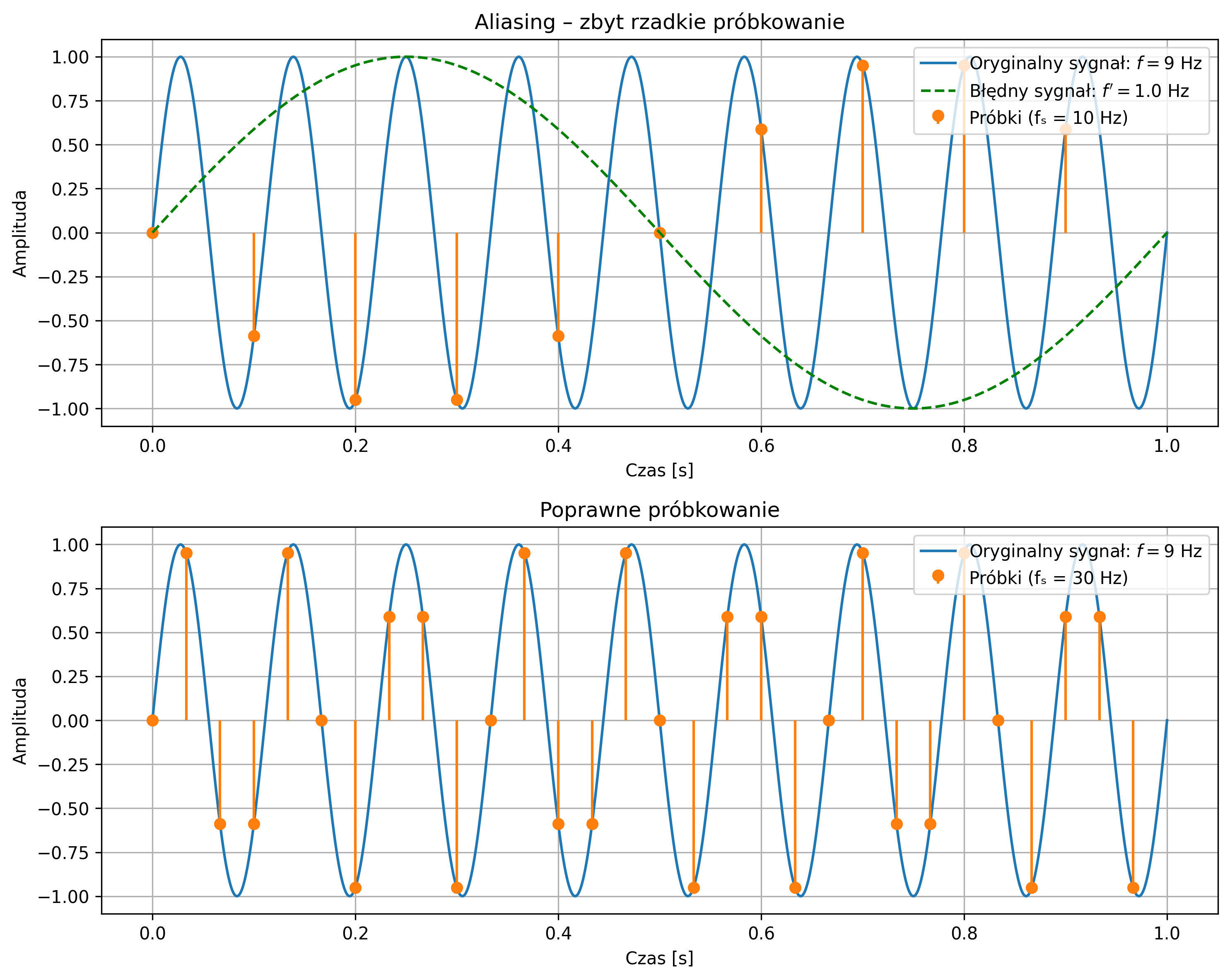
Błędnie odtworzony sygnał (zielona przerywana linia) nie musi przechodzić przez wszystkie próbki, ponieważ on nie jest rekonstrukcją sygnału rzeczywistego, tylko fałszywym sygnałem sinusoidalnym o innej częstotliwości, który mógłby dać te same próbki w tych samych chwilach czasu (rys. 3.4). Jednakże, pomimo tego, że próbkujemy zbyt rzadko, to więcej niż jeden sygnał ciągły może dawać te same próbki – takie same wartości w chwilach próbkowania (np. co \(0.1\) s), mimo że mają zupełnie inne kształty między tymi punktami.
Aby uniknąć aliasingu i móc jednoznacznie odtworzyć sygnał na podstawie jego próbek, konieczne jest spełnienie twierdzenia Nyquista-Shannona, które mówi, że:
gdzie:
- \( x(t) \) – sygnał pasmowo ograniczony do \( f_{max} \),
- \( x[n]=x(nT) \) – próbki sygnału, dla okresu próbkowania \( T=1/f_s \).
Częstotliwość próbkowania musi być co najmniej dwa razy większa od najwyższej częstotliwości zawartej w sygnale. Tę minimalną dopuszczalną częstotliwość próbkowania \( f_s=2f_{max} \) nazywamy częstotliwością Nyquista. Jeśli próbkowanie przebiega zgodnie z tym warunkiem, sygnał może zostać dokładnie zrekonstruowany z próbek.
Gdy częstotliwość sygnału przekracza częstotliwość Nyquista, wysokoczęstotliwościowe składowe sygnału „nakładają się” na niższe, tworząc mylący obraz przebiegu. Zjawisko to stanowi potencjalne źródło błędów, specyficznych dla cyfrowego przetwarzania sygnałów. Dlatego poprawny dobór częstotliwości próbkowania oraz zastosowanie odpowiednich filtrów antyaliasingowych są kluczowe dla wiarygodności cyfrowej analizy sygnałów.
Przypomnijmy, że sygnał spróbkowany to sygnał, który jest dyskretny w czasie, ale w ogólności ciągły w amplitudzie. Oznacza to, że jego wartości występują tylko w wybranych chwilach czasu, lecz same wartości próbek mogą przyjmować dowolne wartości rzeczywiste – należące do zbioru ciągłego. Aby możliwe było jego pełne przetwarzanie w systemach cyfrowych, konieczne jest ograniczenie również zakresu możliwych wartości amplitudy.
Proces ten nazywamy kwantyzacją – polega on na zaokrągleniu wartości próbek do najbliższych poziomów z ustalonego, skończonego zbioru dopuszczalnych wartości. W niniejszym opracowaniu, proces kwantyzacji nie jest uwzględniany, gdyż zwykle jest realizowany automatycznie przez przetworniki analogowo-cyfrowe i systemy komputerowe. Jednakże należy podkreślić, że kwantyzacja wiąże się z powstaniem błędu, tzw. szumu kwantyzacji. Jest to różnica między rzeczywistą wartością próbki, a jej reprezentacją cyfrową. Wartości tego błędu mogą obniżać jakość sygnału.
Kolejnym problemem są opóźnienia. Przetwarzanie cyfrowe zajmuje czas – w systemach czasu rzeczywistego może to prowadzić do opóźnień. Podobnie nieprawidłowe taktowanie może wprowadzić zmienność między odstępami próbkowania. Ponadto, przetworniki mają ograniczony zakres dynamiczny, pasmo przenoszenia i szybkość konwersji. Mogą nie nadążyć za sygnałem, zwłaszcza przy dużych częstotliwościach. Z kolei błędy numeryczne, aliasing, niewłaściwe próbkowanie lub filtrowanie mogą prowadzić do artefaktów w sygnałach – w obrazie, dźwięku lub analizie danych biomedycznych (np. EKG).
3.3. Próbkowanie sygnałów w języku Python
Celem poniższych ćwiczeń jest zapoznanie się z podstawowymi poleceniami języka Python, które umożliwiają poprawne próbkowanie sygnałów ciągłych oraz generowanie ich przebiegów czasowych.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów,
# takich jak np. prostokątny, trójkątny, piłokształtny
oraz wymagana jest znajomość między innymi funkcji:
sawtooth # generowanie sygnału piłokształtnego (scipy.signal)
np.interp # interpolacja liniowa jednowymiarowych danych (NumPy)
Do rekonstrukcji sygnałów wykorzystano metodę interpolacji Sinc, będącą jedną z najdokładniejszych metod rekonstrukcji w teorii cyfrowego przetwarzania sygnałów. W poniższych implementacjach została ona zdefiniowana w postaci funkcji:
sinc_interp()
Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do realizacji poniższych kodów oraz do analizy różnych parametrów próbkowania sygnałów, poprzez ich modyfikację.
Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału piłokształtnego o częstotliwości \(5\) Hz i o czasie trwania \(1\) s. Przyjąć dwie częstotliwości próbkowania: \(40\) Hz i \(6\) Hz.
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth
# Parametry
f = 5 # częstotliwość sygnału [Hz]
T = 1 # czas obserwacji [s]
t_cont = np.linspace(0, T, 2000) # czas ciągły
# Sygnał piłokształtny
x_cont = sawtooth(2 * np.pi * f * t_cont)
# Próbkowanie
fs_good = 40
fs_bad = 6
t_good = np.arange(0, T, 1/fs_good)
x_good = sawtooth(2 * np.pi * f * t_good)
t_bad = np.arange(0, T, 1/fs_bad)
x_bad = sawtooth(2 * np.pi * f * t_bad)
# Rekonstrukcja przez interpolację sinc
def sinc_interp(x, t, t_new):
T = t[1] - t[0]
sinc_matrix = np.sinc((t_new[:, None] - t[None, :]) / T)
return np.dot(sinc_matrix, x)
x_rec_good = sinc_interp(x_good, t_good, t_cont)
x_rec_bad = sinc_interp(x_bad, t_bad, t_cont)
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)
# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label='Sygnał ciągły')
axs[0].plot(t_cont, x_rec_good, 'C0--', label=rf"Rekonstrukcja ($f_s = {fs_good}$ Hz)")
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label='Sygnał ciągły')
axs[1].plot(t_cont, x_rec_bad, 'C1--', label=rf"Rekonstrukcja ($f_s = {fs_bad}$ Hz)")
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
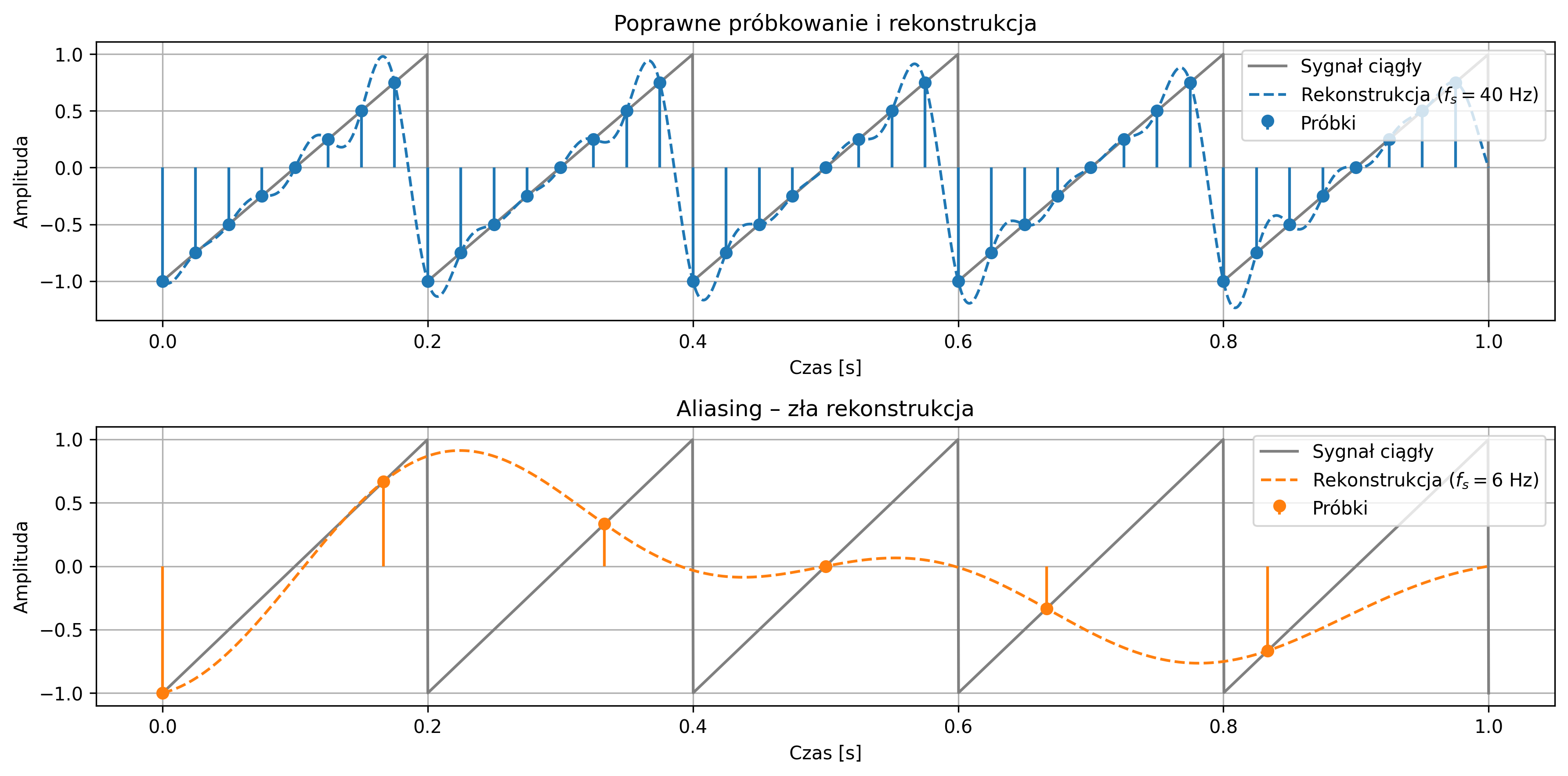
Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału \(\mathrm{Sinc}(30t)\) o czasie trwania \(1\) s. Przyjąć dwie częstotliwości próbkowania: \(60\) Hz i \(10\) Hz.
import numpy as np
import matplotlib.pyplot as plt
# Parametry
T = 1 # czas obserwacji [s]
t_cont = np.linspace(-T/2, T/2, 2000) # czas ciągły
x_cont = np.sinc(30 * t_cont)
# Próbkowanie
fs_good = 60
fs_bad = 10
# Sygnał sinc
t_good = np.arange(-T/2, T/2, 1/fs_good)
x_good = np.sinc(30 * t_good)
t_bad = np.arange(-T/2, T/2, 1/fs_bad)
x_bad = np.sinc(30 * t_bad)
# Interpolacja sinc
def sinc_interp(x, t, t_new):
T = t[1] - t[0]
return np.dot(np.sinc((t_new[:, None] - t[None, :]) / T), x)
x_rec_good = sinc_interp(x_good, t_good, t_cont)
x_rec_bad = sinc_interp(x_bad, t_bad, t_cont)
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)
# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły $sinc(30t)$')
axs[0].plot(t_cont, x_rec_good, 'C0--', label=rf'Rekonstrukcja ($f_s = {fs_good}$ Hz)')
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły $sinc(30t)$')
axs[1].plot(t_cont, x_rec_bad, 'C1--', label=rf'Rekonstrukcja ($f_s = {fs_bad}$ Hz)')
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
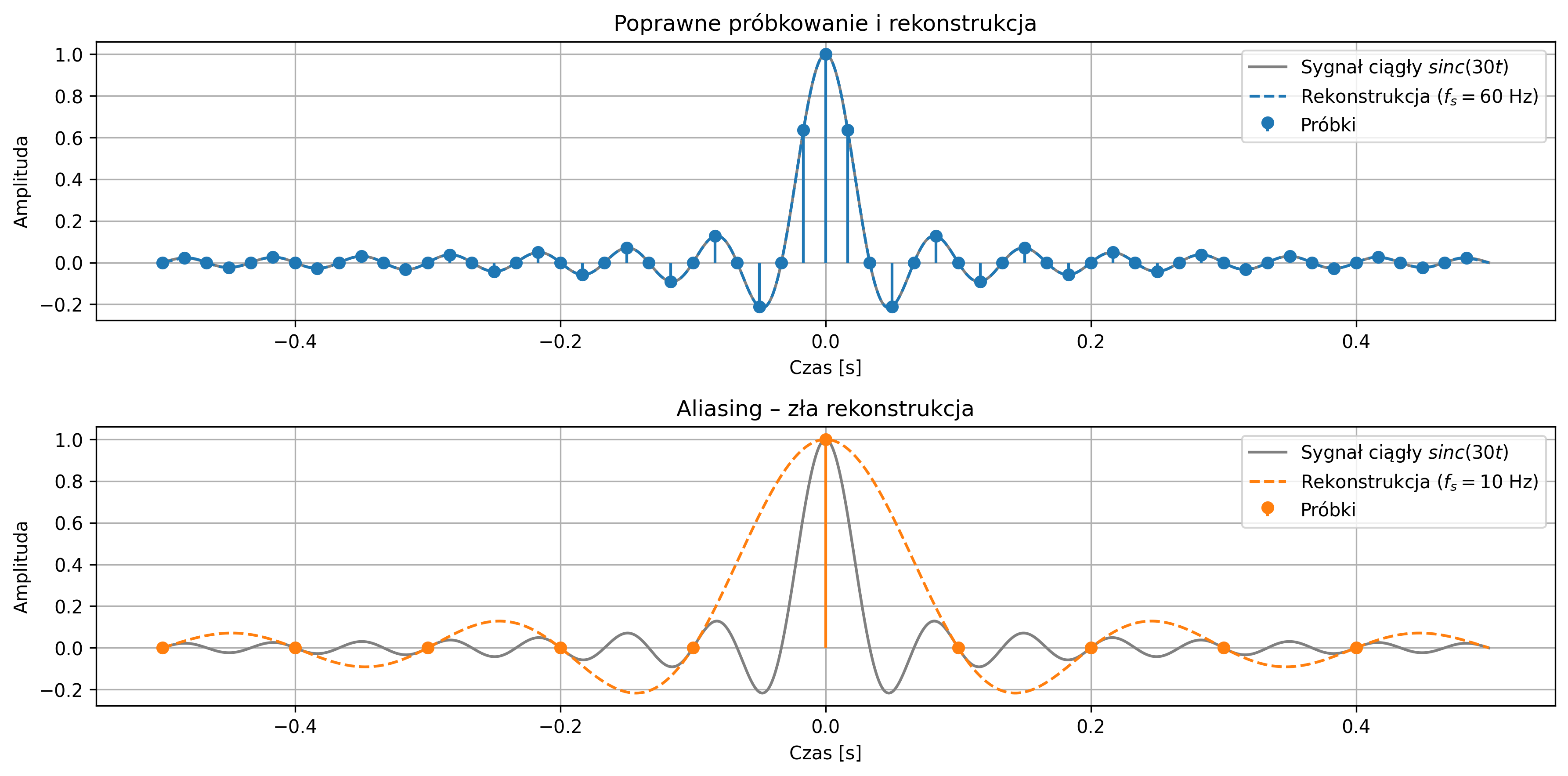
Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału:
Przyjąć dwie częstotliwości próbkowania: \(120\) Hz i \(30\) Hz.
import numpy as np
import matplotlib.pyplot as plt
# Sygnał: suma sinusów (5 Hz + 25 Hz + 40 Hz)
def sum_signal(t):
return (
np.sin(2 * np.pi * 5 * t) + # niska
0.6 * np.sin(2 * np.pi * 25 * t) + # średnia
0.4 * np.sin(2 * np.pi * 40 * t) # wysoka (aliasowana!)
)
# Parametry
T = 2 # czas obserwacji [s]
t_cont = np.linspace(0, T, int(1000 * T), endpoint=False) # czas ciągły
x_cont = sum_signal(t_cont)
# Interpolacja sinc
def sinc_interp(x, t, t_new):
T = t[1] - t[0]
return np.dot(np.sinc((t_new[:, None] - t[None, :]) / T), x)
# Próbkowanie
fs_good = 120
fs_bad = 30
# Sygnały
t_good = np.arange(0, T, 1/fs_good)
x_good = np.interp(t_good, t_cont, x_cont) # do symulacju próbkowania
t_bad = np.arange(0, T, 1/fs_bad)
x_bad = np.interp(t_bad, t_cont, x_cont) # do symulacju próbkowania
t_dense = np.linspace(0, T, 5000)
x_rec_good = sinc_interp(x_good, t_good, t_dense)
x_rec_bad = sinc_interp(x_bad, t_bad, t_dense)
# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)
# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły')
axs[0].plot(t_dense, x_rec_good, 'C0--', label=rf'Rekonstrukcja ($f_s = {fs_good}$ Hz)')
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)
# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły')
axs[1].plot(t_dense, x_rec_bad, 'C1--', label=rf'Rekonstrukcja ($f_s = {fs_bad}$ Hz)')
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
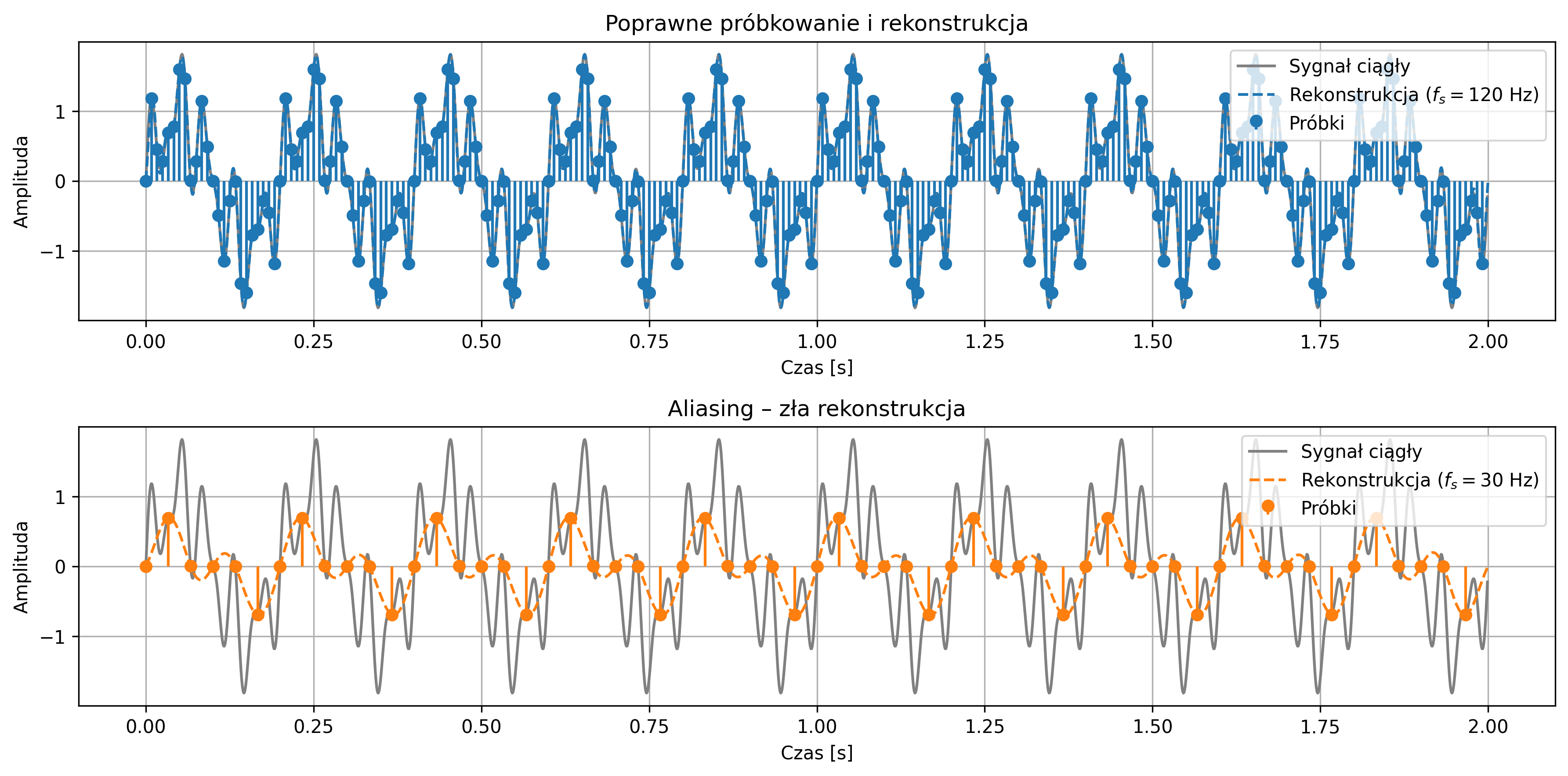
3.4. Test B - sprawdź swoją wiedzę
Test ma na celu sprawdzenie i utrwalenie wiadomości z zakresu próbkowania i konwersji analogowo-cyfrowej sygnałów jednowymiarowych. Każde pytanie zawiera trzy odpowiedzi (A, B, C), z których tylko jedna jest poprawna.
Klucz odpowiedzi:
1. B
2. A
3. C
4. A
5. C
6. A
7. B
8. A
9. C
10. B
11. C
12. B
13. B
14. C
15. A
4. Analiza częstotliwościowa sygnałów
Analiza częstotliwościowa sygnałów polega na przedstawieniu sygnału w dziedzinie częstotliwości zamiast w dziedzinie czasu. Umożliwia to dokładne zbadanie, z jakich składowych częstotliwościowych zbudowany jest dany sygnał, co jest szczególnie istotne w przypadku sygnałów złożonych, takich jak sygnały modulowane, okresowe lub zaszumione. Przekształcenie sygnałów do dziedziny częstotliwości, pozwala ujawniać cechy sygnału, które nie są widocznie w dziedzinie czasu, np. cechy posiadające istotną wartość diagnostyczną.
Podstawowym narzędziem wykorzystywanym w analizie częstotliwościowej jest transformata Fouriera, która pozwala przekształcić sygnał czasowy w jego widmo częstotliwościowe. W przypadku sygnałów dyskretnych stosuje się dyskretną transformatę Fouriera, najczęściej realizowaną za pomocą algorytmu FFT.
Celem analizy częstotliwościowej jest m.in.:
- identyfikacja dominujących częstotliwości w sygnale,
- wykrywanie zakłóceń i szumów,
- projektowanie filtrów dopasowanych do widma sygnału,
- analiza właściwości systemów LTI.
Jeżeli sygnał okresowy można zapisać jako sumę sygnałów sinusoidalnych, to - zgodnie z zasadą superpozycji - gdy taki sygnał przechodzi przez układ liniowy i niezmienniczy w czasie (LTI), można osobno analizować odpowiedź układu na każdą ze składowych harmonicznych. Odpowiedź całkowita będzie sumą tych odpowiedzi. To sprawia, że analiza sygnałów w dziedzinie częstotliwości jest często znacznie prostsza niż analiza w dziedzinie czasu.
W niniejszym rozdziale przedstawione zostaną podstawowe metody analizy częstotliwościowej sygnałów. Omówione zostaną szereg Fouriera i transformata Fouriera, funkcje okna czasowego oraz dyskretna transformata Fouriera (DFT) wraz z jej własnościami. Rozdział obejmuje także opis algorytmów szybkiej transformaty Fouriera (FFT) oraz wskazuje na problemy i ograniczenia związane z wykorzystaniem DFT w praktyce. Dla lepszego zrozumienia materiału przedstawione zostaną liczne przykłady i implementacje w języku Python.
4.1. Szereg Fouriera
Jean-Baptiste Joseph Fourier odkrył, że dowolny sygnał okresowy (spełniający pewne warunki matematyczne) można przedstawić jako szereg Fouriera, czyli sumę funkcji trygonometrycznych – sinusów i cosinusów – o różnych amplitudach, częstotliwościach i fazach. Oznacza to, że szeroka klasa sygnałów może być reprezentowana jako kombinacja liniowa sygnałów harmonicznych.
Sygnałami harmonicznymi nazywamy takie, które można rozłożyć na sumę sygnałów sinusoidalnych o częstotliwościach będących całkowitą wielokrotnością częstotliwości podstawowej – najniższej wspólnej częstotliwości, z którą wszystkie składowe harmoniczne są całkowitymi wielokrotnościami. Pierwsza z tych składowych to składowa podstawowa – jej częstotliwość odpowiada częstotliwości sygnału. Kolejne składowe to tzw. harmoniczne. Suma wszystkich tych składowych tworzy szereg harmoniczny.
Jeśli sygnał \(x(t)\) jest okresowy z okresem \(T_0\), ma skończoną energię, to jego szereg Fouriera ma postać:
gdzie:
- \( f_0 = \dfrac{1}{T_0} \) – częstotliwość podstawowa sygnału,
- \( \omega_0 \) – pulsacja podstawowa,
- \( a_k \) i \( b_k \) – współczynniki Fouriera,
- \( k \) – numer kolejnej harmonicznej.
Istotną rolę odgrywają tzw. warunki Dirichleta, które stanowią zestaw wystarczających, choć nie koniecznych, kryteriów gwarantujących istnienie rozwinięcia Fouriera oraz jego zbieżność. Warunki te wymagają, aby w obrębie jednego okresu funkcja była całkowalna (posiadała skończoną energię), miała skończoną liczbę maksimów i minimów oraz skończoną liczbę punktów nieciągłości. Spełnienie tych warunków zapewnia, że szereg Fouriera będzie zbieżny. W kontekście sygnałów okresowych oznacza to, że większość sygnałów spotykanych w praktyce inżynierskiej, takich jak sygnały prostokątne, piłokształtne czy sygnały sinusoidalne, może być rozwijana w szeregi Fouriera. Jeśli sygnał nie spełnia warunków Dirichleta, nie wyklucza to całkowicie możliwości jego reprezentacji w postaci szeregu Fouriera, jednak analiza wymaga wtedy ujęcia bardziej ogólnego (np. w przestrzeni \(L^2\)).
Rozważmy rozwinięcie w szereg Fouriera sygnału prostokątnego o wartościach z przedziału \([-1,1]\) i okresie \(T = 2\pi\):
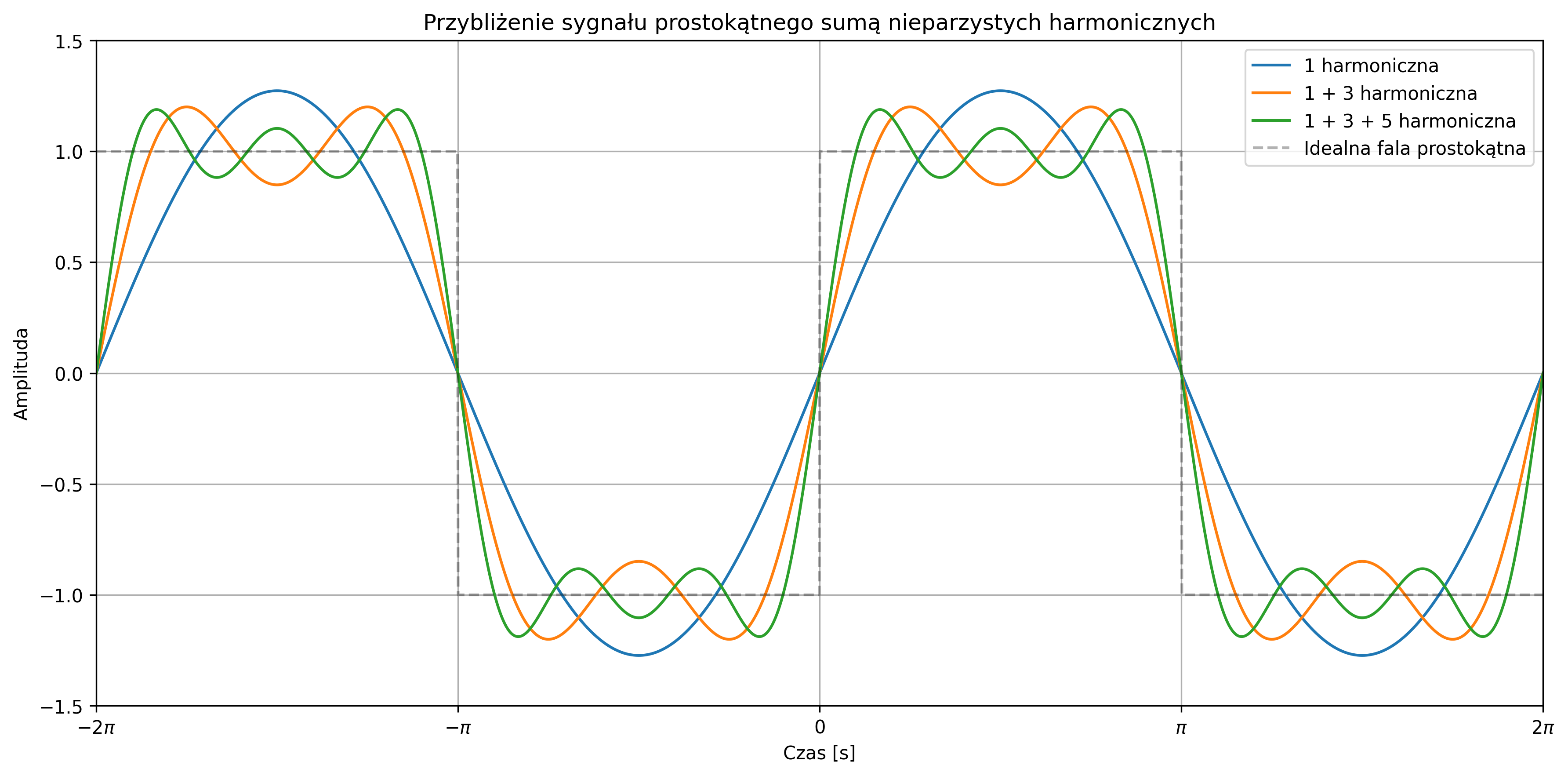
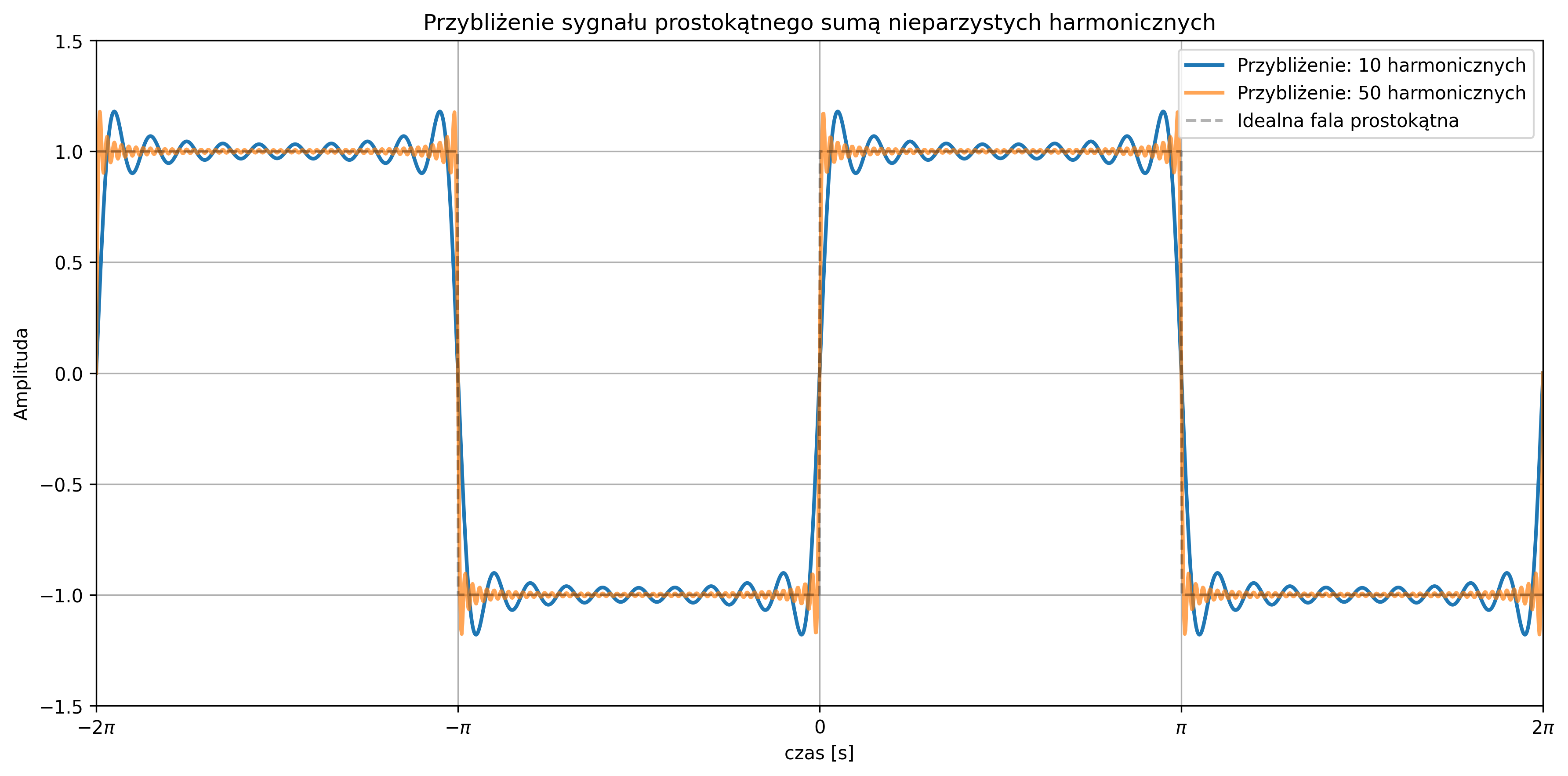
Zamiast używać osobno funkcji \(\sin\) i \(\cos\), można wprowadzić bardziej intuicyjną postać szeregu Fouriera, tzw. postać amplitudowo-fazową, w której każda harmoniczna reprezentowana jest przez jedną funkcję sinusoidalną o określonej amplitudzie \(A_k\) i fazie \(\varphi_k\):
gdzie:
- \( A_k = \sqrt{a_k^2 + b_k^2} \) – amplituda \(k\)-tej harmonicznej,
- \( \varphi_k = \operatorname{arctan}\!\big(-\dfrac{b_k}{a_k}\big) \) – przesunięcie fazowe.
Postać ta pozwala łatwiej wizualizować składniki sygnału w przestrzeni częstotliwości. Zbiór par:
gdzie \( f_k = k f_0 \), tworzy tzw. widmo amplitudowo-fazowe sygnału. Jest to reprezentacja, która pokazuje, jakie częstotliwości wchodzą w skład sygnału i z jakimi amplitudami oraz fazami.
Widmo to może być:
- widmem amplitudowym – przedstawia tylko amplitudy,
- widmem fazowym – pokazuje przesunięcia fazowe,
- pełnym widmem zespolonym.
Reprezentacja widma na wykresie:
- oś pozioma reprezentuje częstotliwość (w Hz) lub pulsację (w rad/s),
- oś pionowa:
- na widmie amplitudowym pokazuje amplitudy składowych harmonicznych – wysokość prążka jest proporcjonalna do wartości amplitudy,
- na widmie fazowym przedstawia przesunięcie fazowe (w rad) dla każdej częstotliwości obecnej w sygnale.
Do charakterystycznych cech widma sygnałów okresowych należą:
- widmo amplitudowe jest prążkowe – zawiera prążki w miejscach odpowiadających harmonicznym sygnału,
- odległość między prążkami wynosi \(\Delta f = \dfrac{1}{T}\) – im dłuższy okres, tym mniejsza odległość między składowymi,
- widmo amplitudowe sygnału rzeczywistego jest parzyste – symetryczne względem osi pionowej (częstotliwości 0),
- widmo fazowe sygnału rzeczywistego jest nieparzyste – symetryczne względem początku układu współrzędnych:
- w przypadku sygnału parzystego faza wynosi 0 lub \(\pi\),
- w przypadku sygnału nieparzystego faza może wynosić \(\pm \dfrac{\pi}{2}\).
Warto zaznaczyć, że:
- zerowe prążki w amplitudzie oznaczają brak danej częstotliwości w sygnale,
- skoki w fazie mogą wynikać z przejść przez 0 w widmie amplitudowym lub z natury sygnału (np. przesunięcia w czasie),
- dla sygnałów nieokresowych widmo staje się ciągłe, a nie prążkowe.
Na rys. 4.3 przedstawiono przykład widma amplitudowo-fazowego sygnału okresowego – sygnału prostokątnego. Prążki odpowiadają tylko nieparzystym harmonicznym, zgodnie z rozwinięciem w szereg Fouriera. Im wyższa harmoniczna, tym mniejsza jest amplituda \(A_k\). Na wykresie fazowym faza stała, równa \(-\dfrac{\pi}{2}\) dla wszystkich harmonicznych.
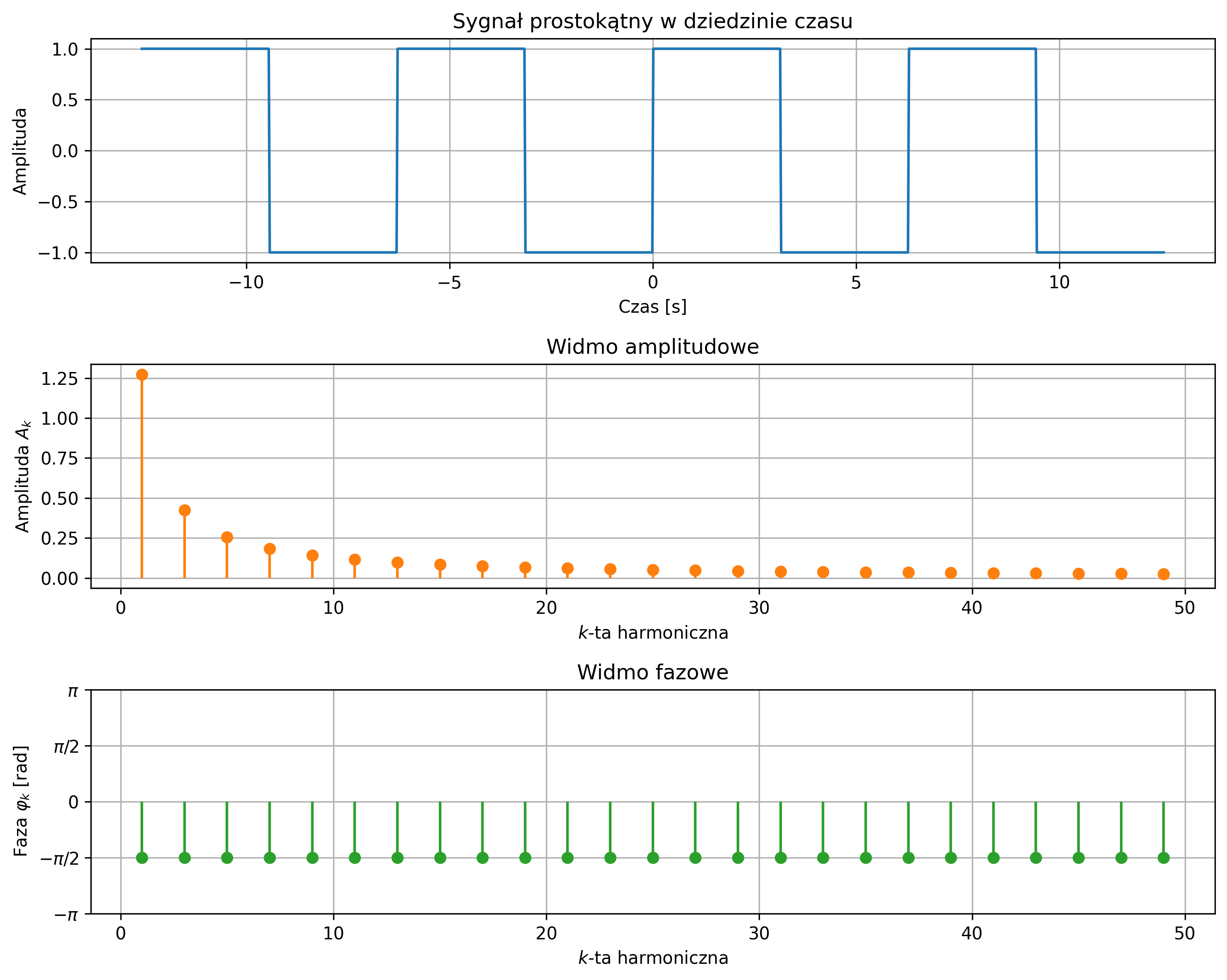
Równoważnie do postaci amplitudowo-fazowej, szereg Fouriera można przedstawić również w postaci tzw. wykładniczej:
gdzie:
- \( \omega_0 = \dfrac{2\pi}{T} \),
- współczynniki \(c_k\) są zespolone oraz opisują amplitudę i fazę poszczególnych harmonicznych.
Wtedy widmo amplitudowe sygnału to wykres wartości \(|c_k|\) w funkcji indeksu \(k\) lub częstotliwości \(f_k = k f_0\), zaś widmo fazowe to wykres argumentu (faz) współczynników. Wersja wykładnicza operuje na współczynnikach zespolonych \(c_k\), natomiast trygonometryczna na rzeczywistych \(a_k\) i \(b_k\).
Na wykresie rys. 4.4 przedstawiony jest przebieg trzech okresów sygnału piłokształtnego w dziedzinie czasu oraz widmo amplitudowe \(|c_k|\). Ponieważ jest to sygnał niesymetryczny, na wykresie amplitudowym znajdują się prążki zarówno dla parzystych, jak i nieparzystych harmonicznych.
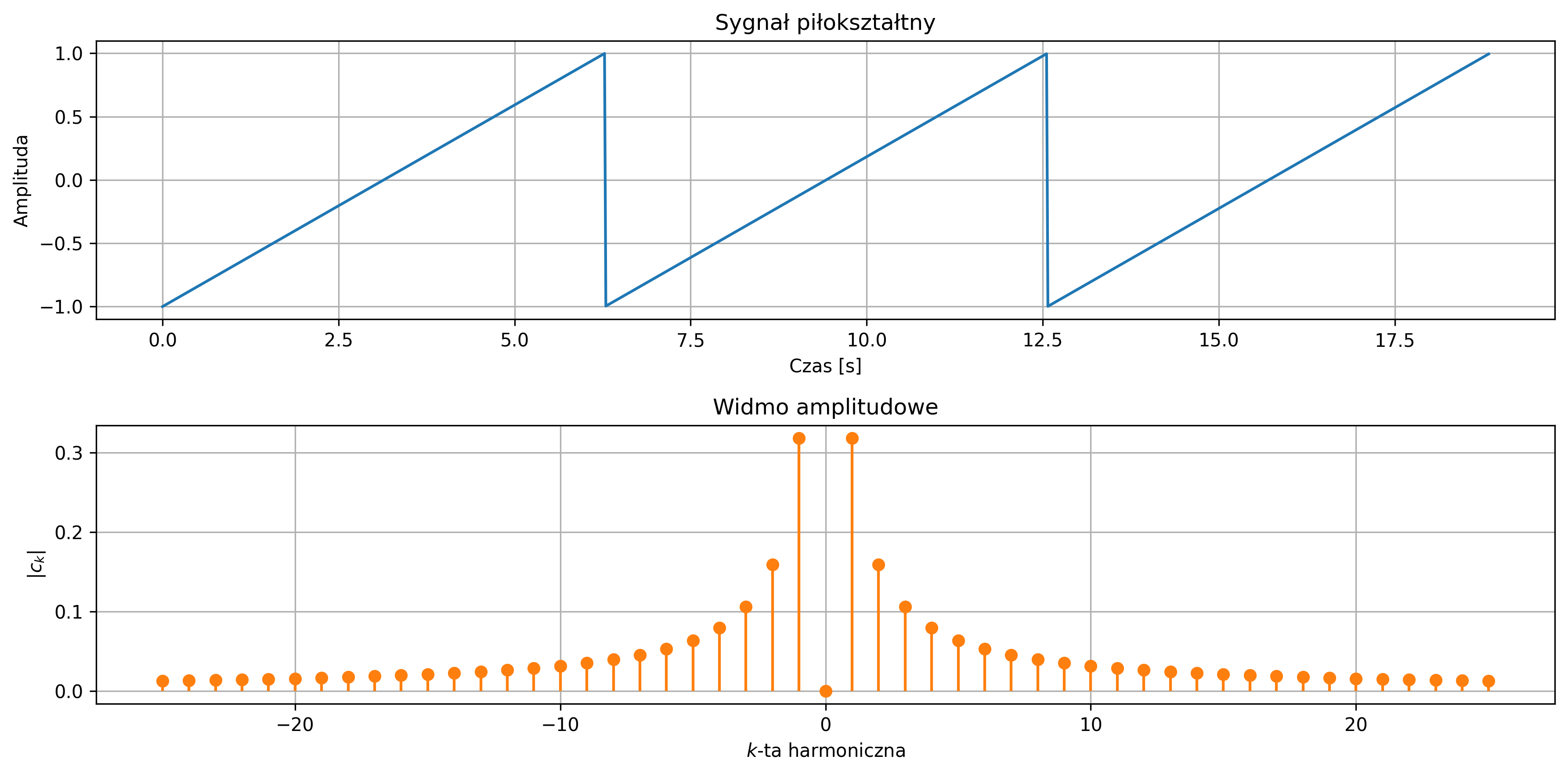
Dla szeregów Fouriera sygnałów okresowych spełnione jest równanie Parsevala:
Oznacza to, że średnia moc sygnału w czasie lub energia w jednym okresie podzielona przez długość okresu jest równa sumie kwadratów modułów współczynników Fouriera, czyli „mocy” poszczególnych harmonicznych.
Teoretyczna wartość energii dla sygnału okresowego piłokształtnego, który został przedstawiony na rys. 4.4, wynosi:
W rzeczywistości suma \(|c_k|^2\) wyniosła \(0.3254\), zaś energia \(0.3323\) – nieznaczne różnice w stosunku do wartości teoretycznej wynikają z przybliżonych obliczeń numerycznych. Należy zaznaczyć, że obliczenia energii są wykonywane tylko na jednym okresie, gdyż współczynniki Fouriera odnoszą się tylko do jednego pełnego okresu. Nie jest to energia całkowita, ponieważ całkowita energia sygnału okresowego wynosi nieskończoność.
W praktyce można obliczyć, jak szybko kumuluje się energia sygnału w kolejnych harmonicznych – ile energii jest zawartej w kilku pierwszych harmonicznych. Na rys. 4.5 przedstawiono wykres udziału energii zgromadzonej w pierwszych \(k\) harmonicznych. Ponieważ widmo amplitudowe jest symetryczne względem składowej stałej, wykresy są sporządzone tylko dla składowej stałej i dodatnich harmonicznych – stanowi to całkowitą reprezentację widmową. Wykres skumulowanej energii pokazuje, że około \(90\%\) energii uzyskujemy przy około \(25\) harmonicznych, zaś \(99\%\) osiągane jest dla około \(50-54\) harmonicznych.
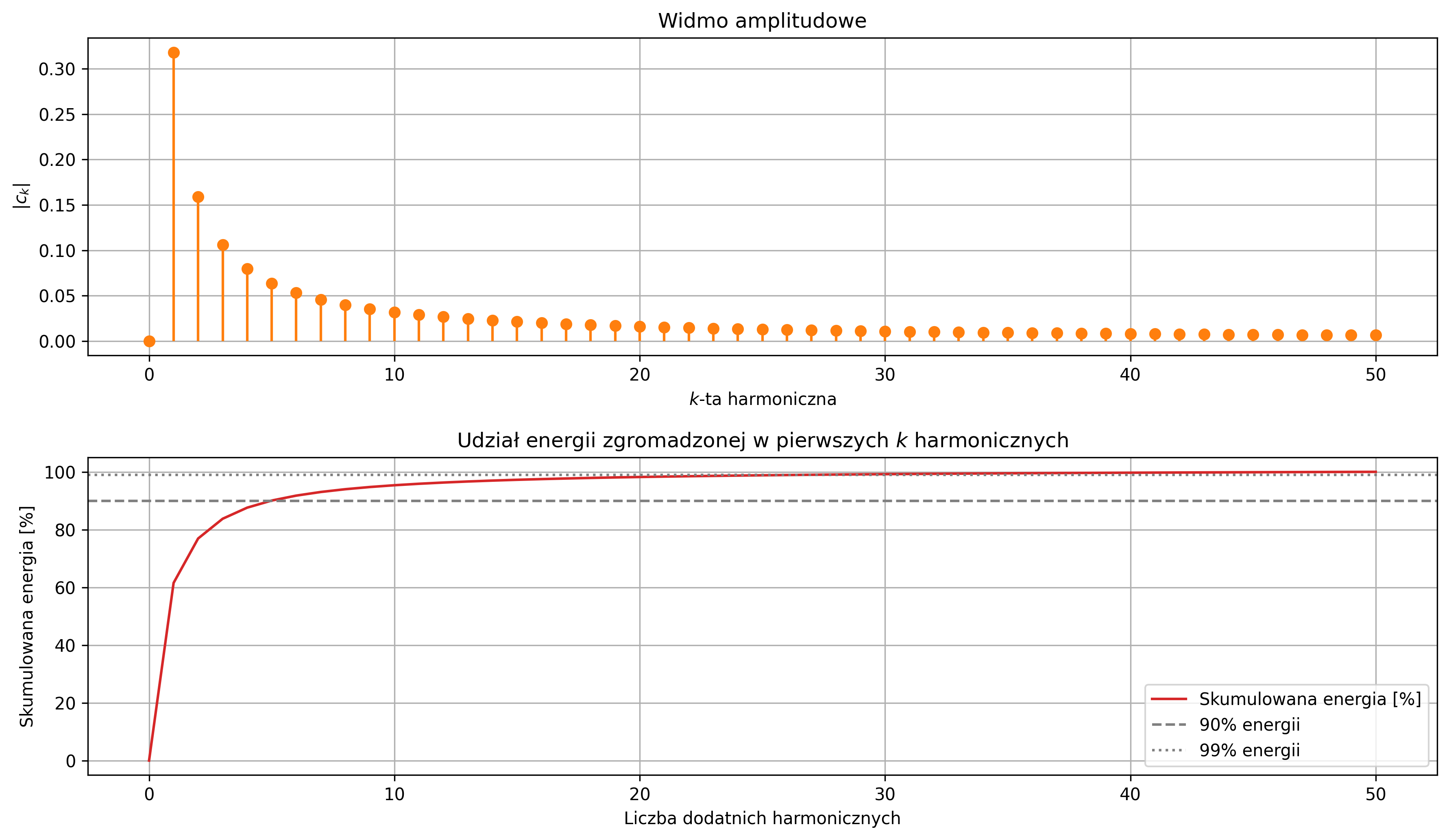
.png)
4.2. Transformata Fouriera
Rozwinięcie sygnału okresowego w szereg Fouriera stanowi fundament dla ogólniejszego narzędzia – transformaty Fouriera, która umożliwia analizę również sygnałów nieokresowych poprzez przejście do dziedziny częstotliwości w sposób ciągły. Gdy sygnał jest nieokresowy, nie da się przedstawić go jako sumy sinusoid o wielokrotnościach jednej częstotliwości. Zamiast tego używa się ciągłego rozkładu po wszystkich pulsacjach \(\omega \in \mathbb{R}\):
To przejście można interpretować jako granicę szeregów Fouriera, gdy okres \(T \rightarrow \infty\) – dyskretne częstotliwości stają się ciągłe, a suma przechodzi w całkę. W ten sposób powstaje ciągła transformata Fouriera, opisująca ciągłe widmo częstotliwościowe.
Zespolona funkcja \(X(\omega)\) jest nazywana prostą transformatą Fouriera sygnału \(x(t)\) lub jego widmem. W celu odtworzenia sygnału z jego widma stosujemy wzór na odwrotną transformatę Fouriera:
Podobnie jak w przypadku szeregów Fouriera, dla danego sygnału \(x(t)\) transformata Fouriera opisuje, jakie składowe częstotliwościowe są obecne w sygnale. Widmo sygnału można przedstawić w postaci biegunowej:
Funkcja:
- \( A(\omega) = |X(\omega)| \) – widmo amplitudowe,
- \( \varphi(\omega) = \operatorname{arg} X(\omega) \) – widmo fazowe.
Widmo amplitudowe pokazuje, ile i z jaką „siłą” dana częstotliwość występuje w sygnale. Widmo fazowe pokazuje przesunięcie fazowe każdej składowej częstotliwościowej w stosunku do odniesienia, co jest kluczowe przy odtwarzaniu sygnału w dziedzinie czasu. Obydwa widma są rzeczywistymi charakterystykami sygnału.
Widma amplitudowe sygnałów często przedstawia się w skali logarytmicznej – w jednostkach decybeli (dB):
Taka prezentacja sygnału ma istotne zalety:
- widmo amplitudowe często obejmuje bardzo szeroki zakres wartości – od bardzo małych do bardzo dużych; skala logarytmiczna umożliwia czytelne przedstawienie tych różnic na jednym wykresie,
- skala dB upraszcza analizę układów – jest wygodna do analizy tłumienia i wzmocnienia (np. \(20\) dB oznacza dziesięciokrotny wzrost amplitudy, zaś \(-6\) dB oznacza około dwukrotne tłumienie).
Przykład pokazujący, że skala logarytmiczna odsłania „ukryte” informacje w sygnale, które są niewidoczne w skali liniowej, został przedstawiony na rys. 4.7. Na górnym wykresie widać tylko dominującą składową \(100\) Hz. Na dolnym wykresie dobrze widoczne są słabe harmoniczne – \(200\) Hz i \(300\) Hz, zauważalne są też ślady szumu w tle.
.png)
Widmo amplitudowo-fazowe dla sygnału nieokresowego – impulsu prostokątnego – zostało przedstawione na rys. 4.8. Widmo amplitudowe ma charakter ciągły i jego największa amplituda osiągana jest przy zerowej częstotliwości. Ponieważ sygnał jest wolno zmienny, na wykresie amplitudowym można zauważyć dużo niskich częstotliwości. Wykres widma fazowego pokazuje, jak są przesunięte składowe sinusoidalne. Ponieważ impuls prostokątny jest parzysty, jego faza przyjmuje wartości tylko \(0\) lub \(\pi\) (zwykłe sinusoidy i ich odbicia względem osi poziomej).
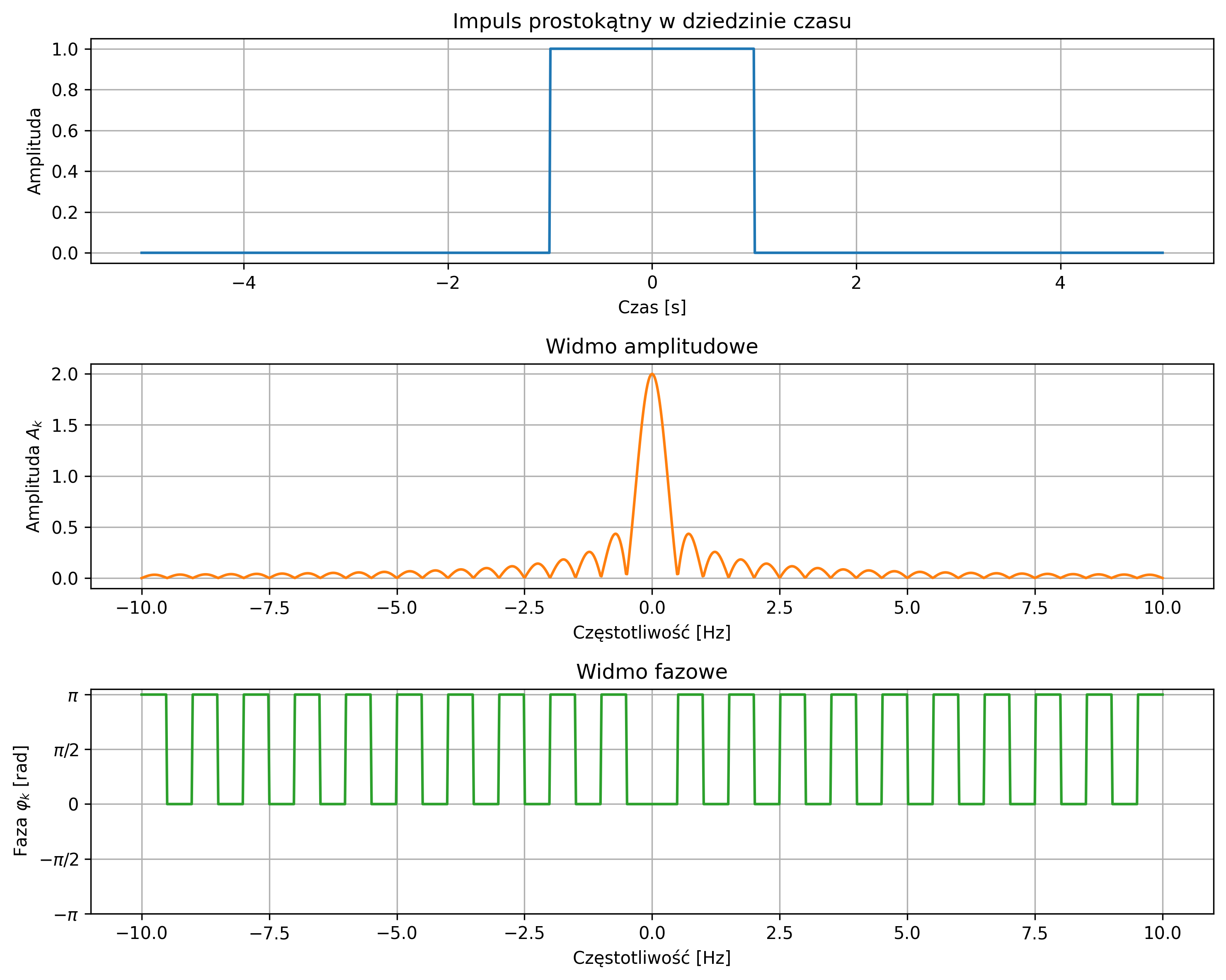
Przyjmijmy następujące oznaczenia:
- \(\mathcal{F}\) – operator prostego przekształcenia Fouriera,
- \(\mathcal{F}^{-1}\) – operator odwrotnego przekształcenia Fouriera.
Podstawowe własności transformaty Fouriera umożliwiają wygodne operowanie na sygnałach oraz analizę i projektowanie systemów LTI.
Na rys. 4.9 przedstawiono wersje sygnału \(\mathrm{Sinc}\) z różnym skalowaniem w czasie: rozciągnięty sygnał, oryginalny i ściśnięty. Odpowiadające im widma amplitudowe są odwrotnie skalowane – im bardziej sygnał rozciągnięty był w czasie, tym jego widmo stawało się węższe i wyższe.
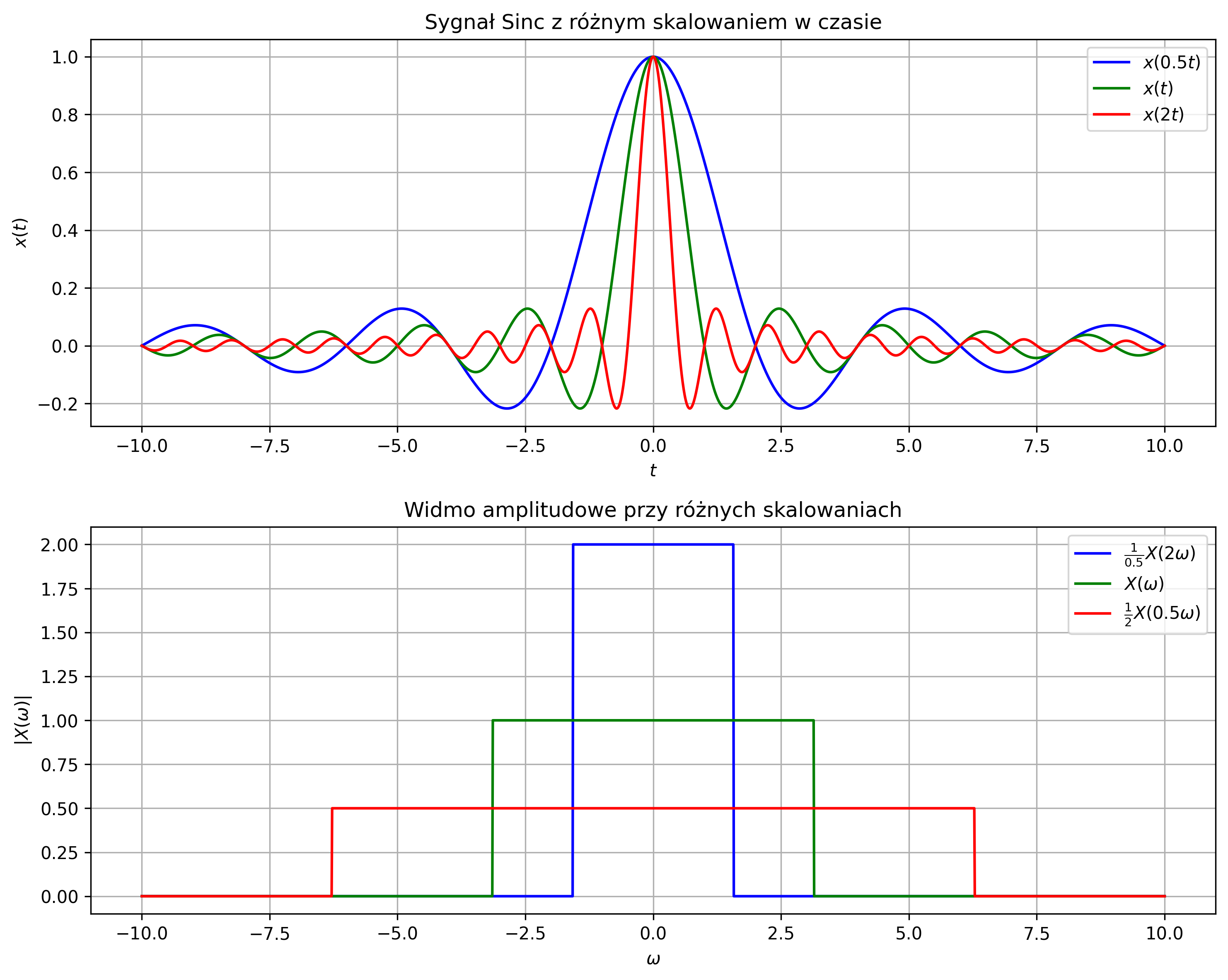
Podobne wnioski można wyciągnąć na podstawie przebiegu impulsu prostokątnego i jego widma amplitudowego, przedstawionego na rys. 4.10. Im węższy impuls w czasie, tym szersze i niższe jest jego widmo.
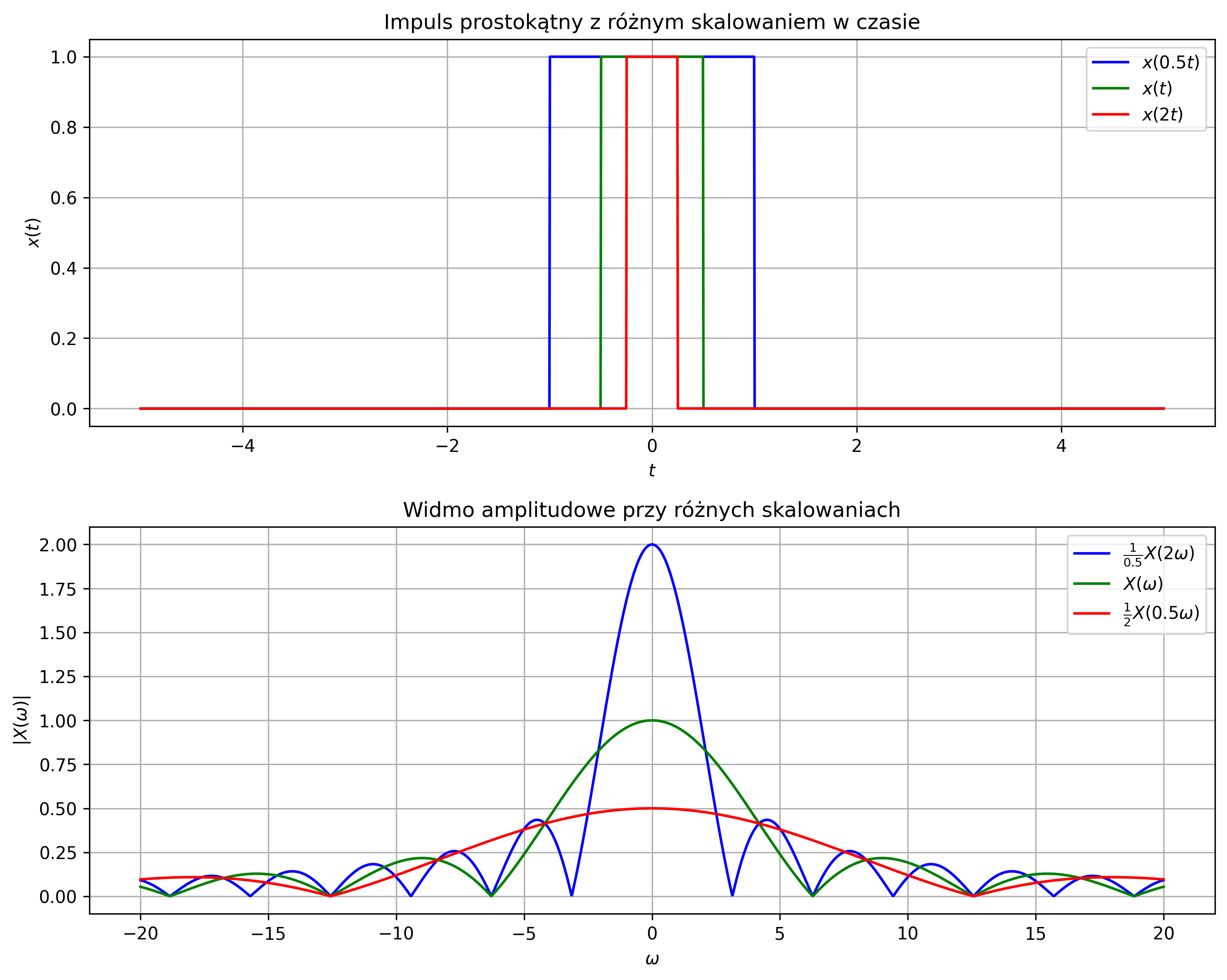
Z własności transformaty Fouriera, a w szczególności z jej zachowania przy zmianie skali, wynika istotna zależność – im krócej trwa sygnał w dziedzinie czasu, tym szersze jest jego widmo w dziedzinie częstotliwości, i odwrotnie. Dlatego sygnały silnie skupione w czasie mają szerokie widmo, a sygnały o wąskim widmie muszą być rozciągnięte w czasie. Zależność tę można wyrazić ilościowo, wprowadzając odpowiednie miary „rozrzutu” sygnału:
- równoważny czas trwania sygnału \(x(t)\):
- równoważna szerokość widma \(X(\omega)\):
Iloczyn równoważnego czasu trwania sygnału i równoważnej szerokości jego widma jest ograniczony od dołu stałą wartością:
Powyższa nierówność określana jest jako zasada nieoznaczoności w teorii sygnałów. Jeśli jedna z tych miar wzrasta, druga proporcjonalnie maleje – nie można tych miar zmniejszać jednocześnie. Równość w powyższej nierówności osiągana jest wyłącznie przez funkcję Gaussa, dlatego jest ona często wykorzystywana jako wzorzec w analizie czasowo-częstotliwościowej.
Własność splotu i mnożenia w transformat Fouriera odgrywa kluczową rolę w przetwarzaniu sygnałów za pomocą układów liniowych. Stanowi ona, że splotowi sygnałów w dziedzinie czasu odpowiada proste mnożenie ich transformat w dziedzinie częstotliwości:
Dzięki temu często skomplikowaną obliczeniowo operację splotu można zastąpić łatwiejszym mnożeniem widm. Analogicznie, mnożeniu sygnałów w dziedzinie czasu odpowiada splot ich widm w dziedzinie częstotliwości:
Jeśli sygnał \(x(t)\) o widmie \(X(\omega)\) po przejściu przez system LTI zamienia się w sygnał \(y(t)\) o widmie \(Y(\omega)\), to stosunek transformaty sygnału wyjściowego do transformaty sygnału wejściowego nazywamy transmitancją widmową:
Wtedy, znając transmitancję widmową układu i widmo sygnału wejściowego, można łatwo wyznaczyć widmo sygnału wyjściowego:
4.3. Funkcje okna czasowego
W praktycznych zastosowaniach, analiza i przetwarzanie sygnałów za pomocą ciągłej transformaty Fouriera napotyka istotne ograniczenie – nie jest możliwe całkowanie od \(-\infty\) do \(+\infty\), jak zakłada definicja transformaty. W rzeczywistości sygnał \(x(t)\) można obserwować lub przetwarzać tylko w ograniczonym przedziale czasu, np. od pewnej chwili \(t_0\) do \(t_0 + T\). Jest to równoznaczne z analizą fragmentu sygnału:
gdzie \( w(t) \) jest funkcją okna czasowego, zwykle prostokątnego, przyjmującą wartość \(1\) w przedziale \([t_0, t_0 + T]\) i \(0\) poza nim. Ma to bezpośredni wpływ na wynikową transformatę Fouriera, ponieważ zgodnie z właściwością iloczynu:
Widmo sygnału zostaje przekształcone przez splot z widmem funkcji okna. Jeśli analizujemy ograniczony w czasie fragment sygnału, to w rzeczywistości widzimy widmo nie oryginalnego sygnału, ale jego wersję przemnożoną przez funkcję okna. Z tego powodu właściwości częstotliwościowe funkcji okna są kluczowe dla jakości analizy widmowej.
Przypomnijmy, że splot z deltą Diraca pozostawia sygnał bez zmian:
Jeśli \( W(\omega) \) byłoby idealną deltą Diraca, to wymnażanie sygnału przez funkcję okna nie wpływałoby na jego widmo – otrzymalibyśmy dokładnie to samo widmo, jak w przypadku sygnału nieskończonego. W praktyce widmo funkcji okna nie może być deltą Diraca, gdyż funkcje o nieskończenie wąskim widmie mają nieskończenie długi przebieg czasowy. Dlatego też dążymy do tego, aby widmo funkcji okna \( W(\omega) \) było jak najbardziej zbliżone do delty Diraca:
- maksymalnie skoncentrowane wokół \(\omega = 0\),
- szybko malejące do zera przy oddalaniu się od tej pulsacji,
- z wąskim listkiem głównym i niskim poziomem listków bocznych (oscylacji po obu stronach).
Zaznaczmy, że ze względu na zasadę nieoznaczoności nie jest możliwe jednoczesne osiągnięcie bardzo wąskiego listka głównego oraz bardzo silnego tłumienia listków bocznych. Każde okno stanowi zatem kompromis między:
- rozdzielczością częstotliwościową – jak dobrze można odróżnić bliskie składowe,
- a tłumieniem zakłóceń widmowych – jak bardzo „przecieka” energia do sąsiednich częstotliwości.
Wpływ szerokości okna prostokątnego na widmo amplitudowe został pokazany na rys. 4.11. W celu pokazania większych szczegółów otrzymanych widm amplitudowych, zamiast skali liniowej zastosowano skalę decybelową. Różnicę można zaobserwować na rys. 4.12, co raz jeszcze potwierdza słuszność wykorzystywania tej skali.
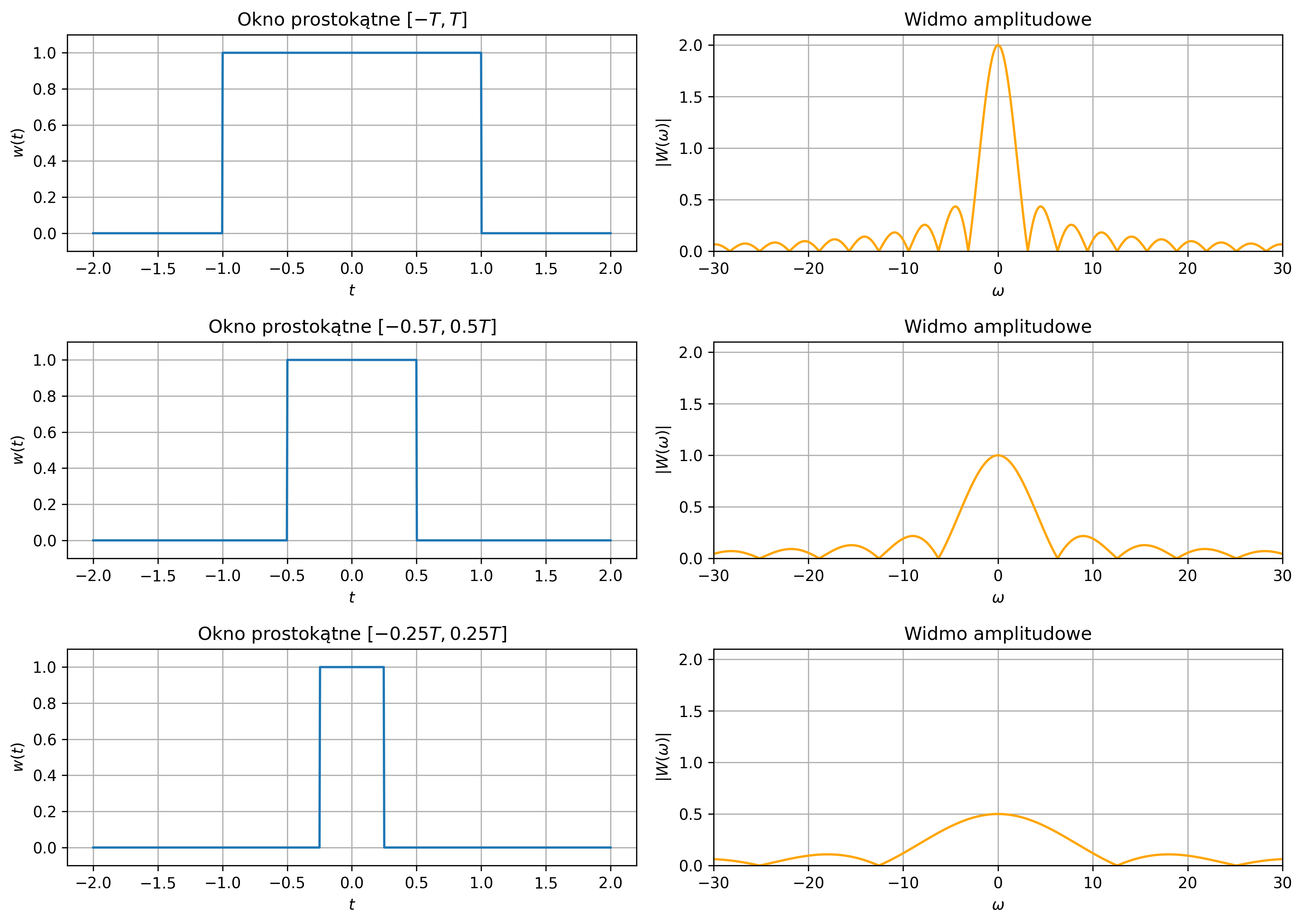
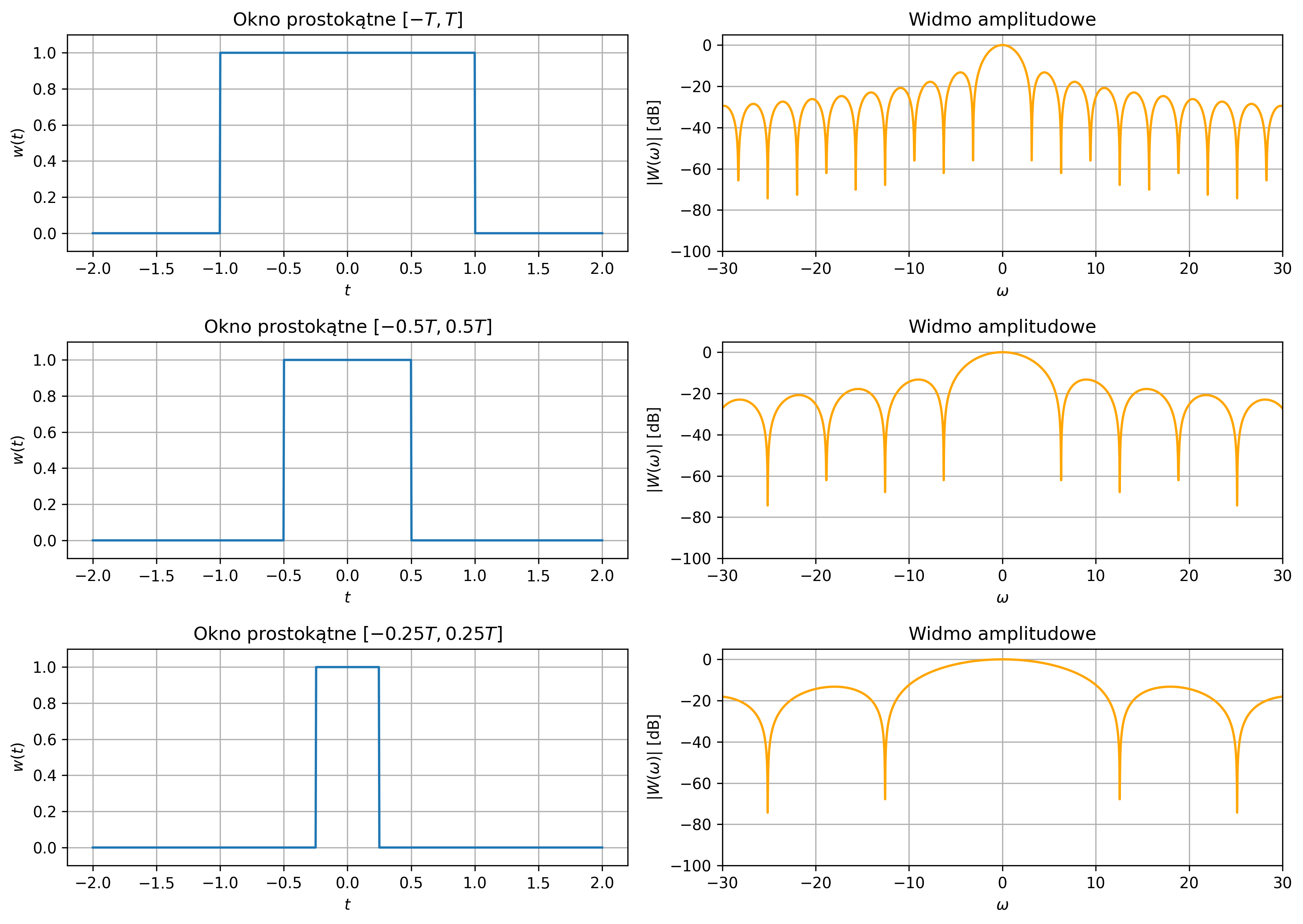
.png)
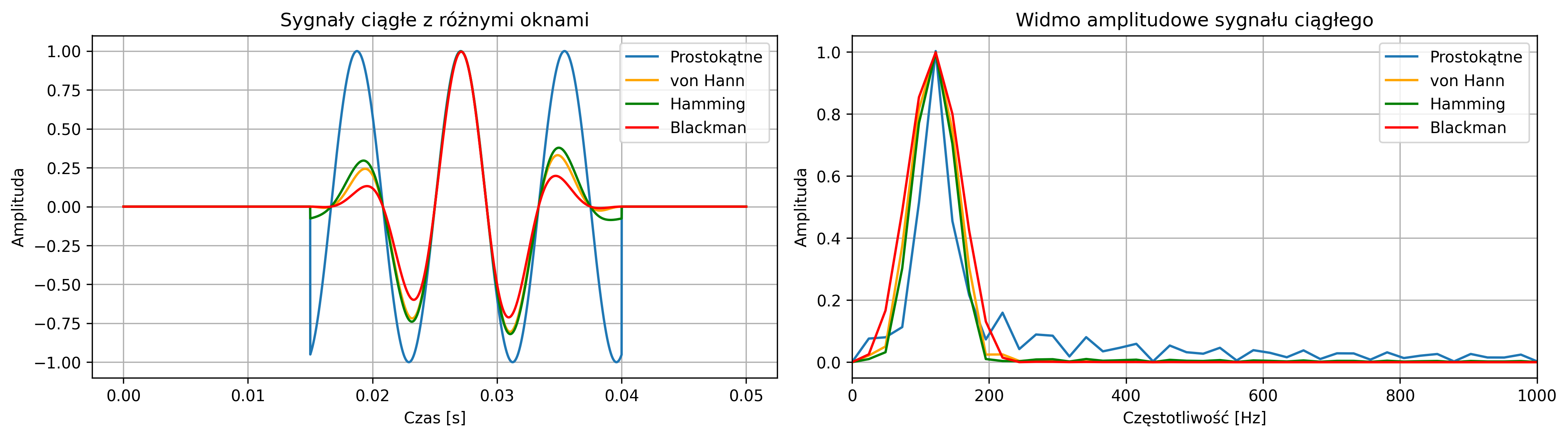
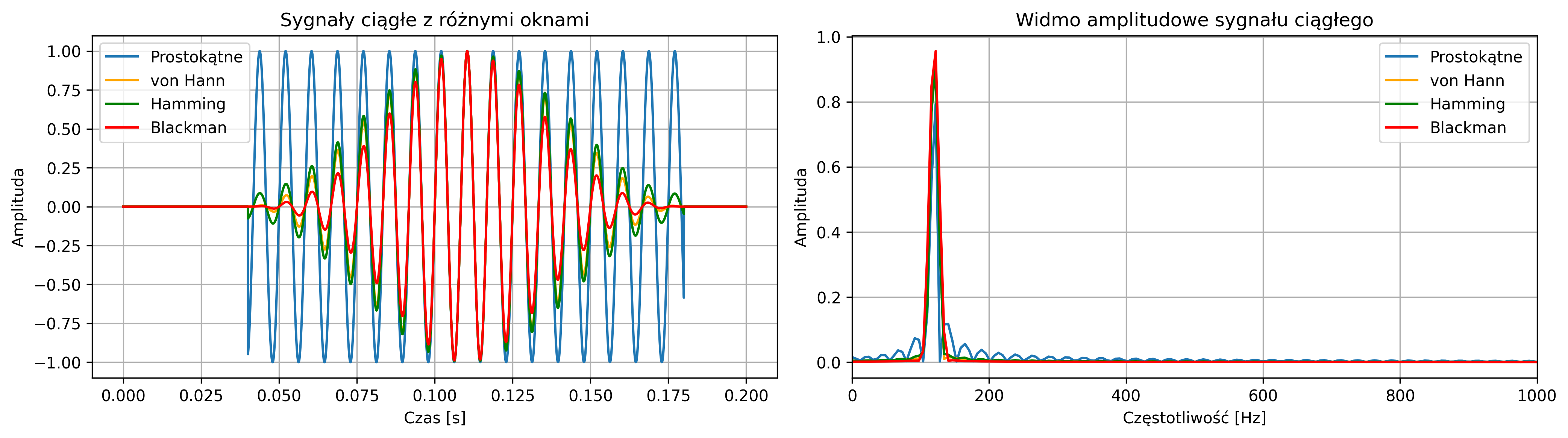
4.4. DFT i jej własności
W praktycznych zastosowaniach analizy częstotliwościowej nie mamy dostępu do sygnału ciągłego \( x(t) \), lecz jedynie do jego wersji dyskretnej – zbioru próbek \( x[n] \), otrzymanych w wyniku próbkowania sygnału analogowego w dziedzinie czasu oraz skwantowania jego amplitudy za pomocą przetwornika analogowo-cyfrowego. Przetwarzanie odbywa się więc na dyskretnym ciągu wartości, a nie na funkcji ciągłej.
Dyskretna transformata Fouriera (DFT) to procedura matematyczna umożliwiająca wyznaczenie składowych częstotliwościowych sygnału dyskretnego o skończonej długości. DFT stanowi wynik kolejnych przekształceń:
1. próbkowania sygnału ciągłego,
2. ograniczenia czasu obserwacji (tzn. przyjęcia skończonego okna czasowego),
3. przyjęcia skończonej liczby próbek \( N \).
W wyniku tych kroków przechodzimy od całkowego przekształcenia ciągłego do postaci dyskretnej, otrzymując wzór na dyskretną transformatę Fouriera:
\( X[k] = \sum_{n=0}^{N-1} x[n] e^{-j k \left(\frac{2\pi}{N}\right) n}, \quad k = 0,1,\ldots, N-1 \)
gdzie:
- \( k \) – numer harmonicznej,
- \( n \) – numer próbki,
- \( N \) – liczba próbek,
- \( T \) – okres próbkowania,
- \( f_s \) – częstotliwość próbkowania.
Zakładamy, że sygnał ciągły i okresowy \( x(t) \), o okresie \( T \), został spróbkowany \( N \) razy w jednym okresie, w chwilach \( t_n = n \cdot T / N \). Próbkowanie odbywa się zgodnie z twierdzeniem Nyquista–Shannona, czyli z częstotliwością próbkowania:
\( f_s = \frac{N}{T} \)
która jest co najmniej dwa razy większa od najwyższej częstotliwości zawartej w sygnale:
\( f_s \geq 2 f_{\max} \)
W przypadku sygnałów okresowych wystarczy spróbkować jeden okres sygnału, aby za pomocą DFT wyznaczyć jego widmo. Jeśli próbkowanie spełnia warunek Nyquista, to DFT dostarcza pełnej informacji o składnikach harmonicznych sygnału.
Odwrotna dyskretna transformata Fouriera (IDFT) wyraża się wzorem:
\( x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j k \left(\frac{2\pi}{N}\right) n} \)
DFT i IDFT tworzą parę odwrotną – jeśli zastosujemy DFT, a następnie IDFT, odzyskamy sygnał \( x[n] \). Niektórzy autorzy przenoszą dzielenie przez \( N \) do równania na \( X[k] \).
Widmo DFT to zbiór \( N \) współczynników \( X[k] \), które reprezentują zawartość częstotliwościową sygnału dyskretnego \( x[n] \). Dlatego każdy współczynnik \( X[k] \) określa:
- amplitudę \( |X[k]| \),
- fazę \( \arg X[k] \),
składowej sinusoidalnej o częstotliwości:
\( f_k = \frac{k}{N} f_s, \quad k = 0,1,\ldots, N-1 \)
Dyskretna transformata Fouriera ma wiele ważnych własności, które są analogiczne do tych znanych z ciągłej transformaty Fouriera, ale z uwagi na dyskretną i skończoną naturę sygnałów DFT, przyjmują one specyficzne formy. Do najważniejszych można zaliczyć:
- symetrię dla sygnałów rzeczywistych – próbki widma położone symetrycznie są parami sprzężone,
- okresowość – widmo DFT jest okresowe z okresem \( N \),
- liniowość – DFT jest przekształceniem liniowym, tzn. przekształcenie kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm.
Z własności symetrii widma wynika, że jeśli sygnał \( N \)-okresowy jest rzeczywisty, a liczba jego próbek jest parzysta, to całe widmo jest w pełni określone przez \( \frac{N}{2} + 1 \) wartości:
- dwie wartości rzeczywiste: \( X[0] \) oraz \( X\left[\frac{N}{2}\right] \),
- oraz \( \frac{N}{2} - 1 \) wartości zespolonych: \( X[1], X[2], \ldots, X\left[\frac{N}{2} - 1\right] \).
Stąd użyteczna informacja jest zawarta tylko w pierwszych \( \frac{N}{2} + 1 \) prążkach.
Na rys. 4.16 pokazane zostały wykresy widma amplitudowego i fazowego dla pewnego sygnału. Ponieważ jest to sygnał rzeczywisty, połowa widma to sprzężone odbicie lewej połowy – dlatego widzimy prążki symetryczne parami. Prążków jest niewiele, ale o wyraźnej amplitudzie (reszta jest zerowa), a także ich fazy mają wartości 0 – możemy przypuszczać, że sygnał jest sumą kilku funkcji harmonicznych.
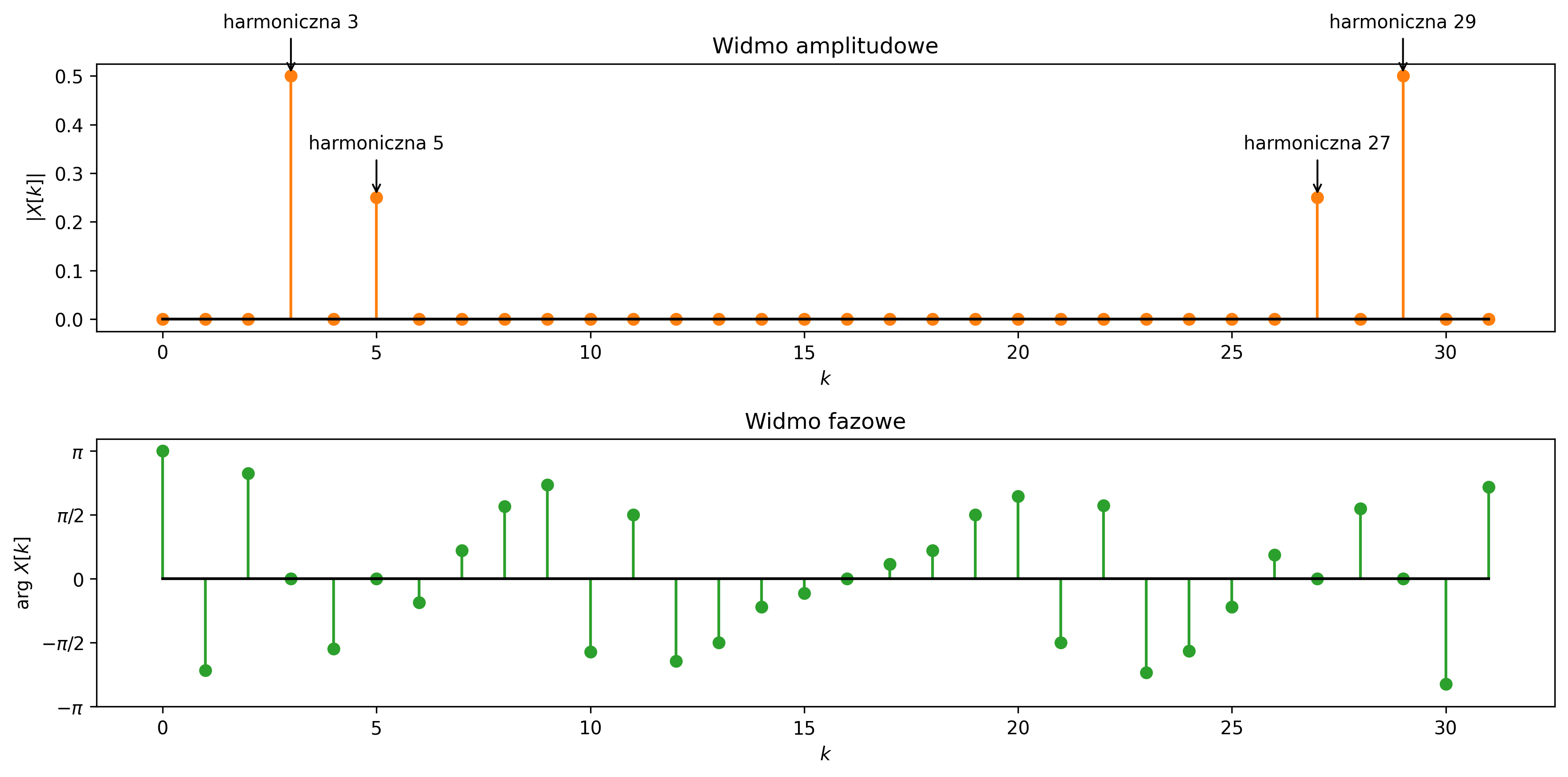
Należy zaznaczyć, że każdy z tych prążków zawiera połowę amplitudy składowej sygnału. Zatem suma amplitud prążków symetrycznych daje rzeczywistą amplitudę składowych sinusoidalnych. Każdy prążek widma wskazuje na obecność składowej o częstotliwości i amplitudzie:
- prążki w \( k = 3 \) i \( k = 29 \) wskazują obecność składowych o \(3\) i \(29\) jednostkach częstotliwości, które mają wysokość \( \approx 0.5 \),
- prążki w \( k = 5 \) i \( k = 27 \) wskazują obecność składowych o \(5\) i \(27\) jednostkach częstotliwości, które mają wysokość \( \approx 0.25 \).
Stąd, aby odtworzyć wzór sygnału z wykresu DFT dla okresu \( N = 32 \), musimy jeszcze obliczyć częstotliwość w zależności od pozycji prążka. Na podstawie wykresu nie możemy tym prążkom przypisać konkretnych częstotliwości, jeśli nie znamy odgórnie częstotliwości próbkowania. Dlatego często przyjmuje się roboczo \( f_s = N \), żeby łatwo przekształcać indeksy prążków na ich częstotliwości:
\( f_k = \frac{k}{N} \cdot f_s = \frac{k}{32} \cdot 32 = k \)
Wtedy indeks \( k \) bezpośrednio odpowiada częstotliwości \( f_k \). Zatem:
\( f_3 = 3 \,\text{Hz} \) oraz \( f_5 = 5 \,\text{Hz} \).
Z wykresu fazowego możemy odczytać, że dla:
- \( k = 3 \) i \( k = 5 \) faza wynosi \(0\),
co sugeruje, że sygnał, który widzimy, jest sumą kosinusów (faza może wynosić \(0\) lub \( \pi \)). W przypadku, gdyby faza wynosiła \( -\frac{\pi}{2} \) lub \( \frac{\pi}{2} \), mielibyśmy do czynienia z sumą sinusów. Stąd wzór sygnału w dziedzinie czasu będzie w postaci:
\( x(n) \approx A_1 \cos\left( 2\pi f_1 t_n \right) + A_2 \cos\left( 2\pi f_2 t_n \right) \)
Po spróbkowaniu sygnału z częstotliwością \( f_s = N \), otrzymamy:
\( t_n = n \cdot \frac{T}{N} = \frac{n}{f_s} = \frac{n}{N} \)
a stąd:
\( x[n] \approx A_1 \cos\left( 2\pi f_1 \frac{n}{f_s} \right) + A_2 \cos\left( 2\pi f_2 \frac{n}{f_s} \right) \)
Skoro zakładamy, że mamy \( N \) próbek DFT, a częstotliwości odpowiadają wartościom indeksów \( k = 1,2,\ldots, N-1 \), wzór, którego szukamy, wygląda następująco:
\( x[n] \approx A_1 \cos\left( 2\pi f_3 \frac{n}{f_s} \right) + A_2 \cos\left( 2\pi f_5 \frac{n}{f_s} \right) \)
Ostatecznie sygnał jest w przybliżeniu postaci:
\( x[n] \approx 1 \cdot \cos\left( 2\pi \cdot 3 \frac{n}{32} \right) + \frac{1}{2} \cos\left( 2\pi \cdot 5 \frac{n}{32} \right) \)
Z rys. 4.16 wynika wniosek, że jeśli sygnał jest sumą kilku funkcji harmonicznych, to DFT pozwala je zidentyfikować – ich amplitudę, częstotliwość i fazę.
W przypadku sygnałów bardziej złożonych, np. sygnału prostokątnego (rys. 4.17), widmo będzie zawierać harmoniczne wyższych rzędów i możemy odtworzyć tylko jego przybliżoną postać przez odwrotną DFT.
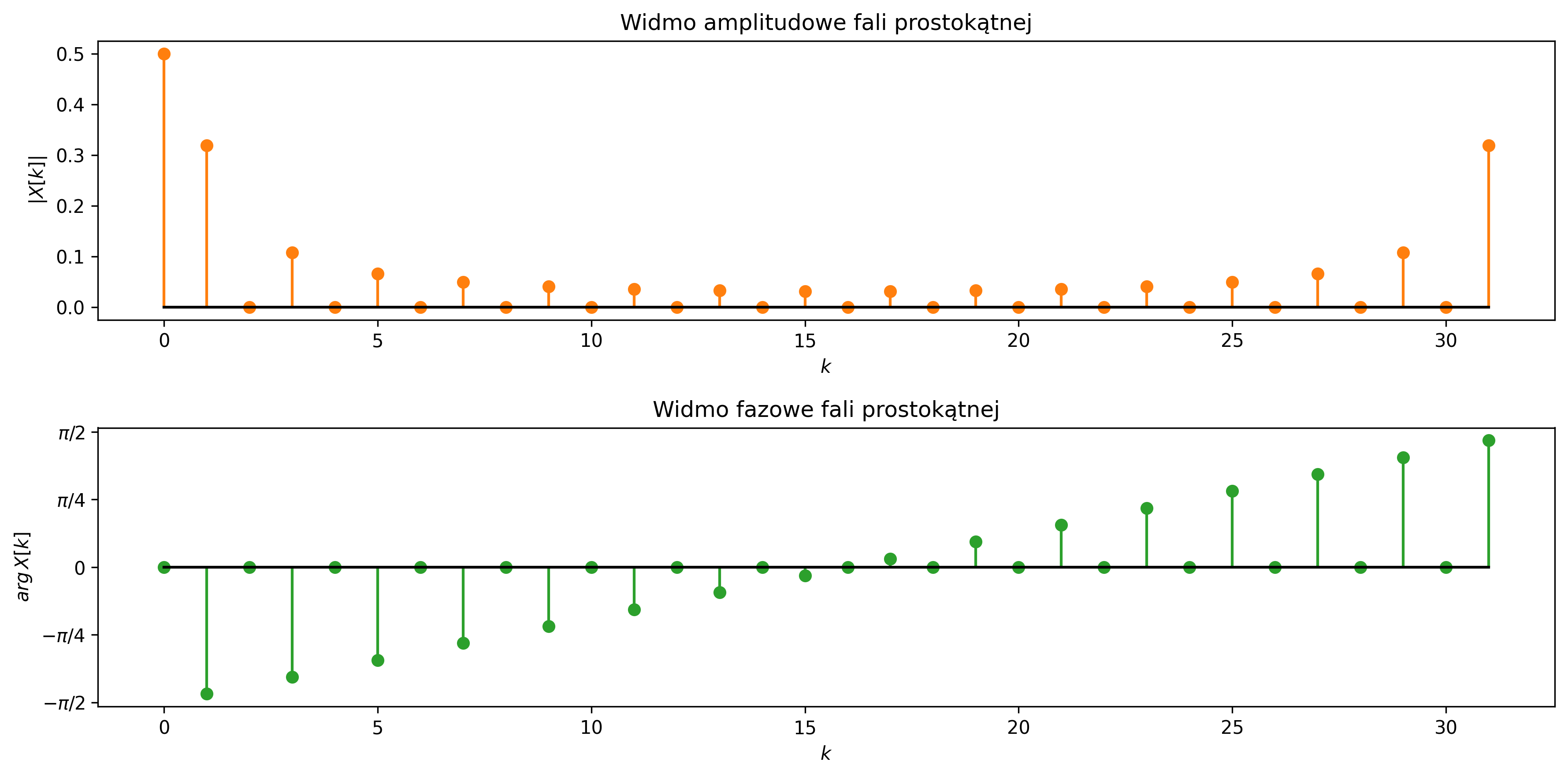
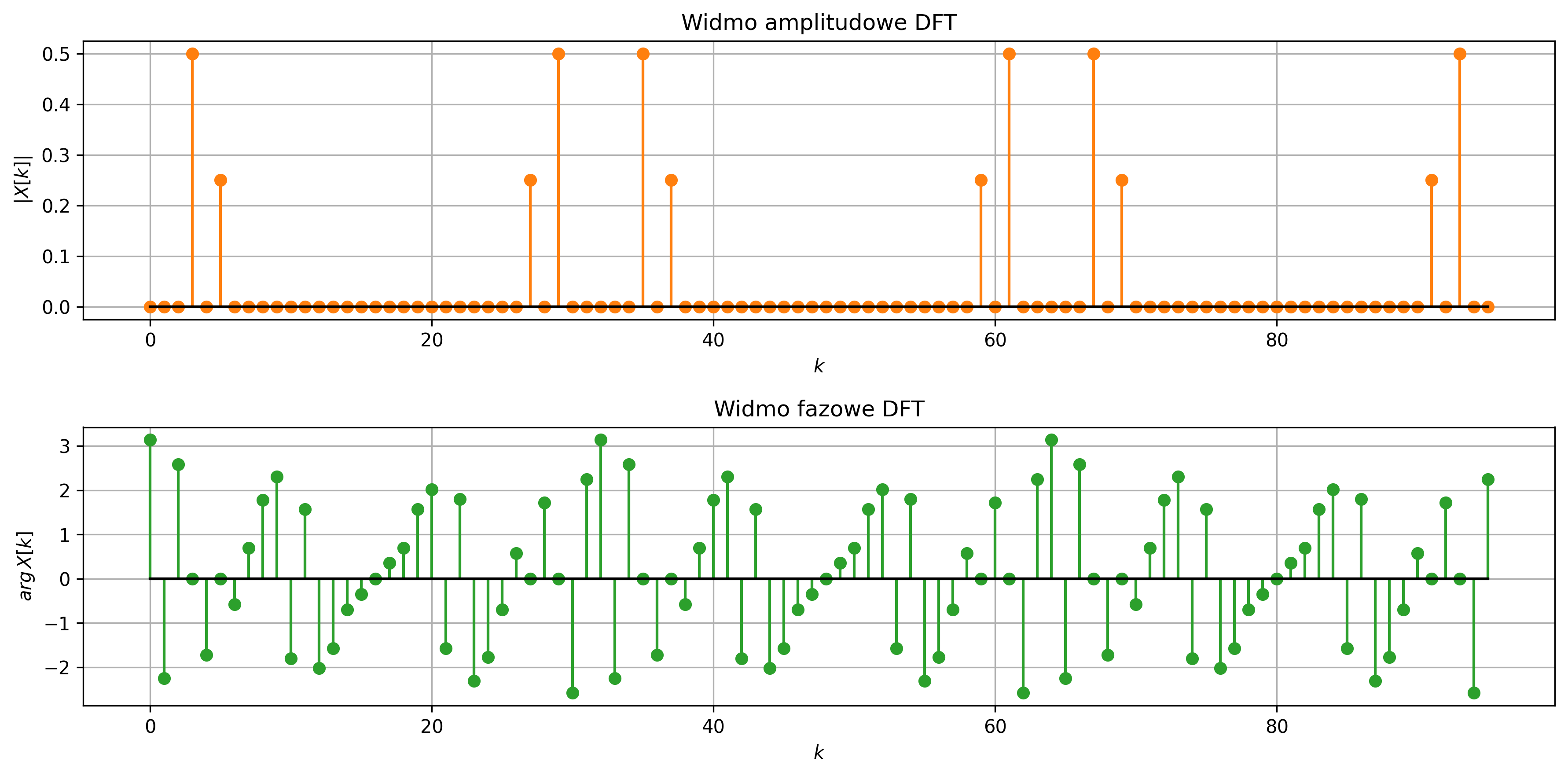
Rozdzielczość częstotliwościowa określa, jak blisko siebie mogą być dwie składowe częstotliwościowe, aby DFT była w stanie je rozróżnić:
\( \Delta f = \frac{f_s}{N} \)
gdzie \( f_s \) jest częstotliwością próbkowania, a \( N \) rozmiarem DFT. Większa wartość \( N \) to lepsza rozdzielczość częstotliwościowa – możemy wykryć subtelne różnice między częstotliwościami w sygnale. Przy zbyt małym \( N \), składowe sygnału położone blisko siebie mogą zlać się w jedno maksimum.
Rozdzielczość czasowa wiąże się z długością analizowanego fragmentu sygnału i jest to minimalny odstęp czasowy pomiędzy dwoma zdarzeniami w sygnale, który umożliwia ich rozróżnienie:
\( \Delta t = \frac{N}{f_s} \)
Dłuższy czas analizy – większe \( N \) – oznacza gorszą rozdzielczość czasową: tracimy informację o tym, kiedy dokładnie w sygnale nastąpiło dane zdarzenie. Jeżeli dwa impulsy w sygnale wystąpią w odstępie mniejszym niż \( \Delta t \), to przy analizie DFT z odcinka zawierającego oba impulsy zostaną one potraktowane jako jedno zdarzenie. W efekcie informacje o ich dokładnym czasie wystąpienia zostaną utracone.
Dlatego w analizie DFT mamy wyraźny kompromis między rozdzielczością czasową i częstotliwościową. Ten kompromis jest szczególnie widoczny w analizie sygnałów zmiennych w czasie, gdzie trzeba balansować między dokładnością czasową a częstotliwościową.
4.5. Algorytmy FFT
Istnieje wiele metod numerycznej optymalizacji obliczeń dyskretnej transformaty Fouriera oraz jej odwrotności (IDFT), których celem jest znaczące ograniczenie liczby wymaganych operacji arytmetycznych. W wyniku tych prac opracowano tzw. algorytmy szybkiej transformaty Fouriera (FFT, ang. Fast Fourier Transform), które stanowią obecnie podstawowe narzędzie w analizie częstotliwościowej sygnałów dyskretnych.
FFT to rodzina algorytmów, które obliczają DFT w sposób znacznie bardziej efektywny niż bezpośrednie podstawienie do wzoru. Zamiast wykonywać \( \mathcal{O}(N^2) \) operacji, jak ma to miejsce w klasycznym podejściu, FFT redukuje złożoność obliczeniową do \( \mathcal{O}(N \log N) \), co ma kluczowe znaczenie przy przetwarzaniu dużych zbiorów danych.
Algorytmy FFT wykorzystują zasadę „dziel i zwyciężaj”, powszechnie stosowaną w informatyce. Polega ona na rekurencyjnym dzieleniu problemu na mniejsze, prostsze podproblemy, aż do momentu, gdy każdy z nich może być rozwiązany szybko i bezpośrednio. Jedną z najbardziej znanych i szeroko stosowanych wersji FFT jest algorytm Cooleya–Tukeya, który wymaga, aby długość sygnału była potęgą dwójki. Podstawową operacją w strukturze FFT jest tzw. „motylek”, który łączy pary próbek wejściowych w sposób umożliwiający ich dalsze przekształcanie w kolejnych etapach algorytmu. Struktura motylkowa pozwala na wykorzystanie symetrii i okresowości zespolonych wykładników w DFT, co umożliwia przyspieszenie obliczeń.
W literaturze często omawia się algorytm FFT typu radix-2, w którym długość analizowanego sygnału (liczba próbek) musi być potęgą liczby dwa. Jest to najprostszy i najbardziej efektywny wariant, pozwalający w pełni wykorzystać strukturę „motylków” i redukcję obliczeń. Jeżeli długość sygnału nie jest potęgą dwójki, a zależy nam na maksymalnym przyspieszeniu obliczeń, można zastosować technikę zero-padding, czyli dopełnienie sygnału zerami do najbliższej długości będącej potęgą dwóch. Nie zmienia to informacji zawartych w sygnale ani rzeczywistej rozdzielczości częstotliwościowej wynikającej z czasu obserwacji, ale zwiększa gęstość próbek w widmie i pozwala wykorzystać szybszy algorytm radix-2.
Implementacja FFT w Pythonie jest jednak znacznie bardziej elastyczna i potrafi obsługiwać sygnały o dowolnej długości. Najszybciej działa w przypadku, gdy liczba próbek jest potęgą dwójki, lecz może również przetwarzać sygnały, których długość jest inną liczbą całkowitą. W takich sytuacjach czas obliczeń może ulec wydłużeniu. Najmniej korzystny przypadek występuje wtedy, gdy liczba próbek jest dużą liczbą pierwszą. Wówczas algorytm nie może zostać zoptymalizowany poprzez podział na mniejsze bloki, co prowadzi do konieczności obliczania DFT bezpośrednio z definicji i wiąże się z największym kosztem obliczeniowym.
Odwrotna szybka transformata Fouriera (IFFT, ang. Inverse Fast Fourier Transform) jest algorytmem służącym do szybkiego wyznaczania odwrotnej dyskretnej transformaty Fouriera (IDFT). Podobnie jak FFT, opiera się na optymalizacji obliczeń, redukując złożoność z \( \mathcal{O}(N^2) \) do \( \mathcal{O}(N \log N) \).
IFFT przekształca sygnał z dziedziny częstotliwości do dziedziny czasu, przy czym dane wejściowe mają postać zespolonych wartości widma (amplitudy i fazy). Matematycznie, IFFT różni się od FFT jedynie znakiem w wykładniku funkcji zespolonej i dodatkowym współczynnikiem skalującym \( 1/N \). W praktycznych implementacjach ten sam algorytm może być użyty zarówno do FFT, jak i IFFT, zmienia się jedynie kierunek obliczeń. Dzięki IFFT możliwe jest np. odtworzenie sygnału w dziedzinie czasu po modyfikacjach widma, takich jak filtracja, zmiana fazy czy wzmocnienie wybranych składowych częstotliwościowych.
4.6. Problemy i ograniczenia DFT
Przykłady, w których transformata DFT dawała poprawne i przejrzyste wyniki, opierały się na starannie dobranych sygnałach wejściowych w postaci przebiegów sinusoidalnych. W takich idealnych przypadkach, częstotliwości składowych sygnału pokrywają się dokładnie z punktami na dyskretnej osi częstotliwościowej DFT, co pozwala na jednoznaczną identyfikację widmową.
W przypadku rzeczywistych sygnałów, które są próbkowane i zwykle mają złożone, nieidealne składowe częstotliwości, wyniki DFT mogą być mylące. Przyczyną tego jest między innymi niedopasowanie częstotliwości sygnału do dyskretnych częstotliwości DFT, efekt przecieku widmowego oraz ograniczona rozdzielczość częstotliwościowa. W efekcie uzyskane widmo może zawierać rozmycia, zniekształcenia i trudności w interpretacji rzeczywistych składników sygnału.
Niepoprawne próbkowanie sygnału
Dyskretną transformatę Fouriera stosuje się do sygnałów dyskretnych, o skończonej długości. Aby uzyskać poprawne wyniki, sygnał musi być odpowiednio próbkowany zgodnie z twierdzeniem Nyquista-Shannona, czyli częstotliwość próbkowania powinna być co najmniej dwukrotnie wyższa niż najwyższa częstotliwość zawarta w sygnale. Nieprzestrzeganie tej zasady prowadzi do aliasingu – zjawiska opisanego w rozdziale 3.2, w którym wyższe składowe częstotliwości „nakładają się” na niższe, co skutkuje błędną interpretacją widma. W praktyce oznacza to, że DFT nie może poprawnie rozróżnić częstotliwości.
Na rys. 4.19 pokazano przykład aliasingu w DFT – jak wyglądają widma sygnału sinusoidalnego o częstotliwości większej i mniejszej niż połowa częstotliwości próbkowania (czyli powyżej częstotliwości Nyquista). Na wykresie przedstawiono przebiegi dwóch ciągłych sygnałów sinusoidalnych o częstotliwościach \(300\) Hz i \(700\) Hz, a także próbki tych sygnałów, próbkowanych z częstotliwością \(1000\) Hz.
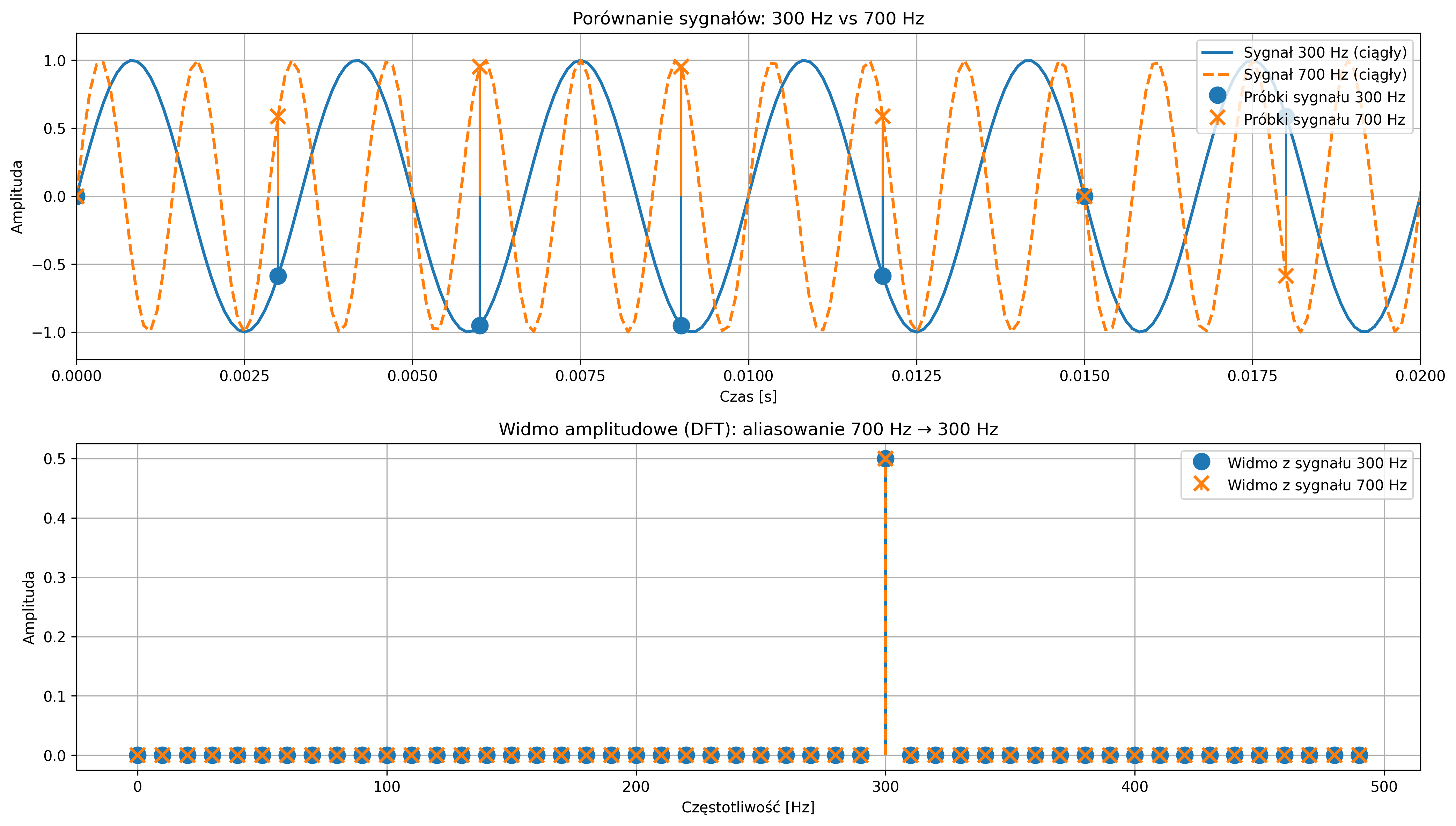
Próbki sygnału sinusoidalnego o częstotliwości \(700\) Hz nie są identyczne z próbkami sygnału \(300\) Hz – różnią się znakiem. DFT nie rozróżnia znaku częstotliwości, a więc sygnały \(300\) Hz i \(700\) Hz dają takie samo widmo amplitudowe, choć różnią się fazą. Wykresy potwierdzają, że sygnał o częstotliwości \(700\) Hz jest spróbkowany zbyt wolno. Jeśli zwiększymy częstotliwość próbkowania z \(1000\) Hz do \(2000\) Hz, to nie zaobserwujemy już aliasingu – obydwie składowe częstotliwościowe będą poprawnie zidentyfikowane (rys. 4.20).
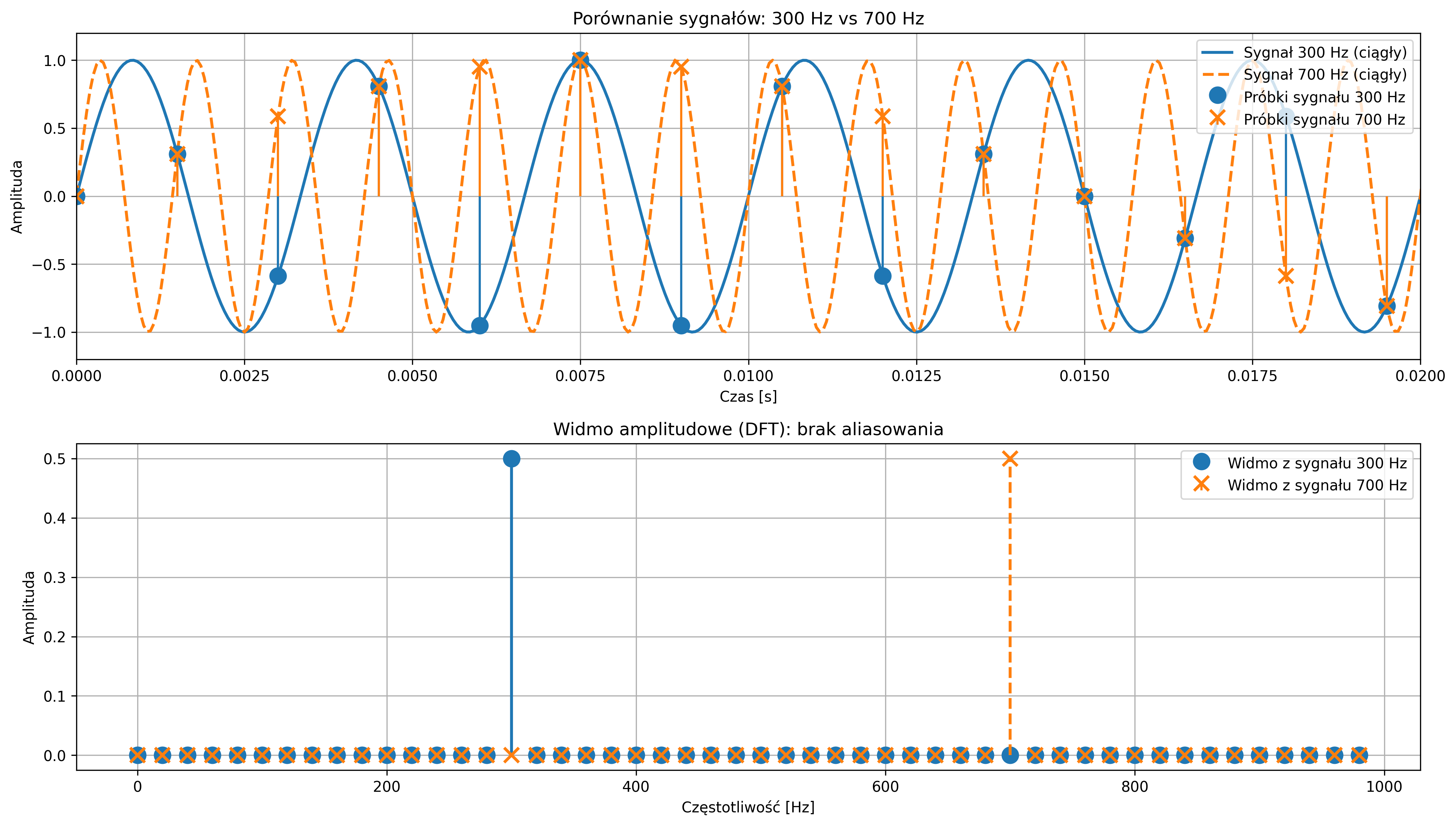
Efekt przecieku widmowego
DFT zakłada, że analizowany fragment sygnału jest okresowy, z okresem równym długości okna czasowego. Jeśli sygnał nie jest idealnie okresowy w tym oknie, w widmie pojawia się tzw. przeciek widmowy (ang. Spectral Leakage). Objawia się to rozmyciem energii sygnału na sąsiednie częstotliwości, co utrudnia dokładną identyfikację składowych widmowych. Przyczyną jest „cięcie” sygnału w czasie (zastosowanie okna prostokątnego), które w dziedzinie częstotliwości odpowiada splotowi z funkcją \(\mathrm{Sinc}\) o szerokim rozproszeniu.
Na rys. 4.21 przedstawiono wykres sygnału sinusoidalnego o częstotliwości \(50\) Hz, który został ucięty poprzez zastosowanie funkcji okna prostokątnego. Wycięty fragment sygnału traktowany jest jako fragment reprezentujący cały, nieskończenie długi sygnał. Porównując nieskończony sygnał okresowy z sygnałem odtworzonym na podstawie wyciętego fragmentu, można zauważyć, że w wyniku zastosowania krótszego (niedopasowanego) okna analizowany sygnał nie może być już traktowany jako „czysta” sinusoida. Przeciek widmowy pojawia się, gdy granice analizowanego fragmentu (okna) „rozrywają” sygnał, czyli sygnał nie łączy się gładko na końcu okna z początkiem następnego okresu (który DFT zakłada jako kontynuację). Wtedy sygnał jest „nieciągły” na granicach okna, a nieciągłości te powodują rozmycie energii widmowej na inne częstotliwości.
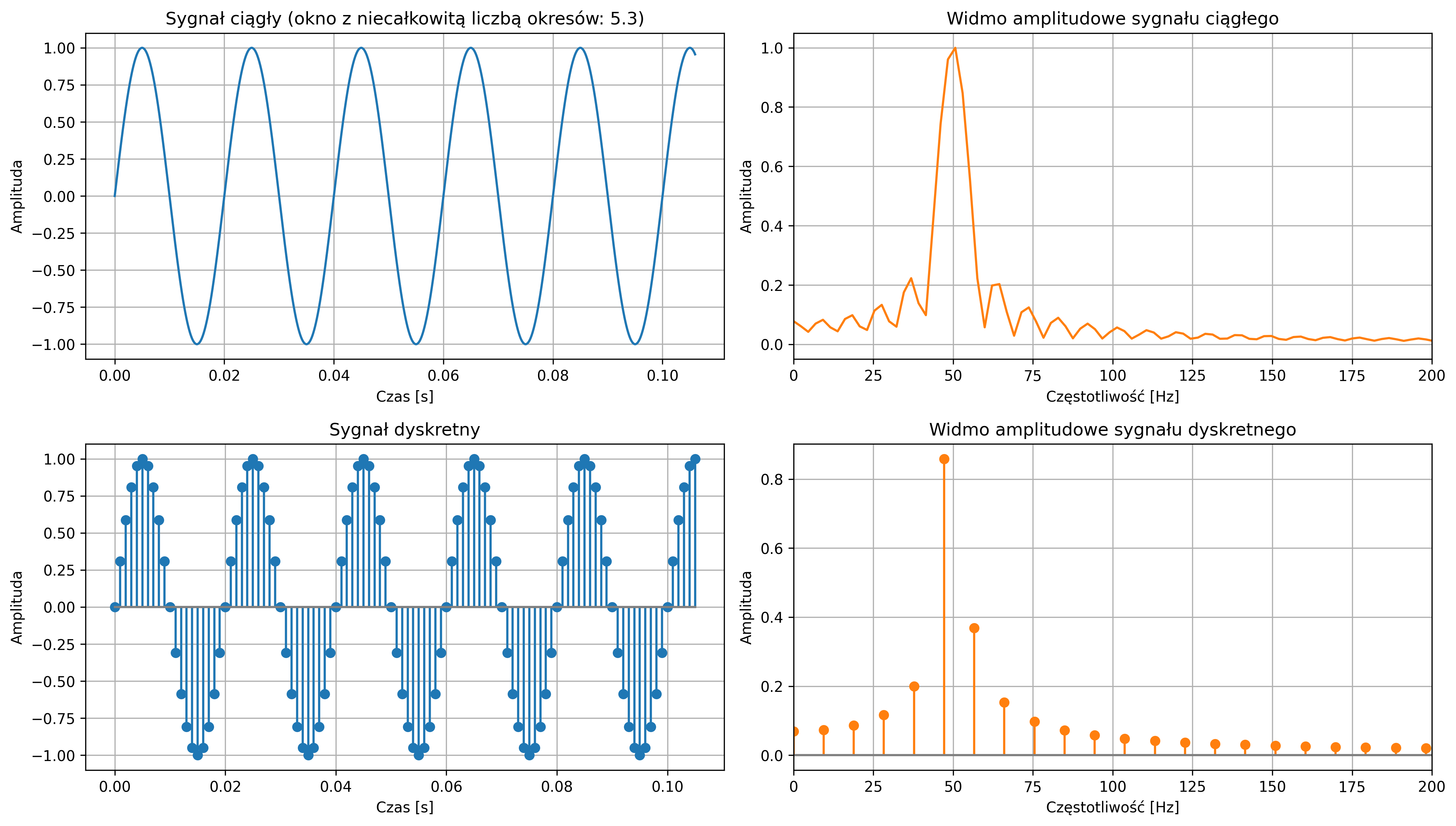
Gdy mamy dokładnie \(5\) okresów sygnału w oknie (rys. 4.22), koniec i początek sygnału idealnie się pokrywają, więc sygnał jest ciągły i okresowy z okresem długości okna – wówczas nie ma przecieku (lub jest on bardzo znikomy, ograniczony jedynie przez numeryczne niedokładności). Na wykresie amplitudowym DFT widzimy jeden prążek, który odpowiada częstotliwości wygenerowanego sygnału.
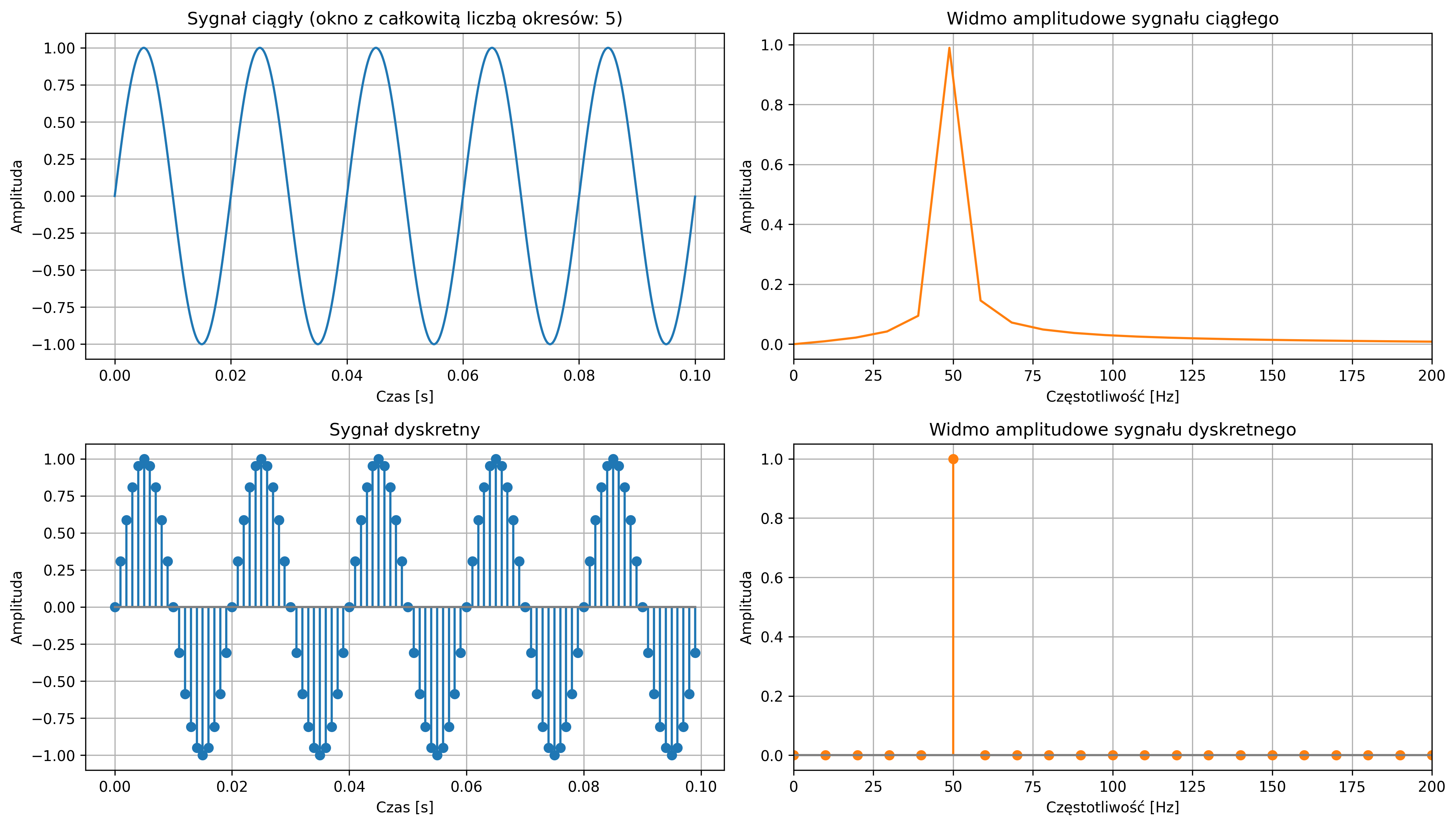
Przypomnijmy, że widmo DFT ma symetrię i zawsze jest okresowe z okresem równym częstotliwości próbkowania \( f_s = N \). Po osiągnięciu końca zakresu \(N\), widmo zaczyna się powtarzać. Dlatego, w przypadku wystąpienia przecieku, zjawisko to również będzie powtarzać się co okres \(N\) – na rys. 4.23 widmo powtarza się co \( N = f_s = 1000 \,\text{Hz} \). Dlatego, w analizie częstotliwościowej sygnału rozważamy tylko próbki w zakresie od 0 do \( \frac{N}{2} - 1 \).
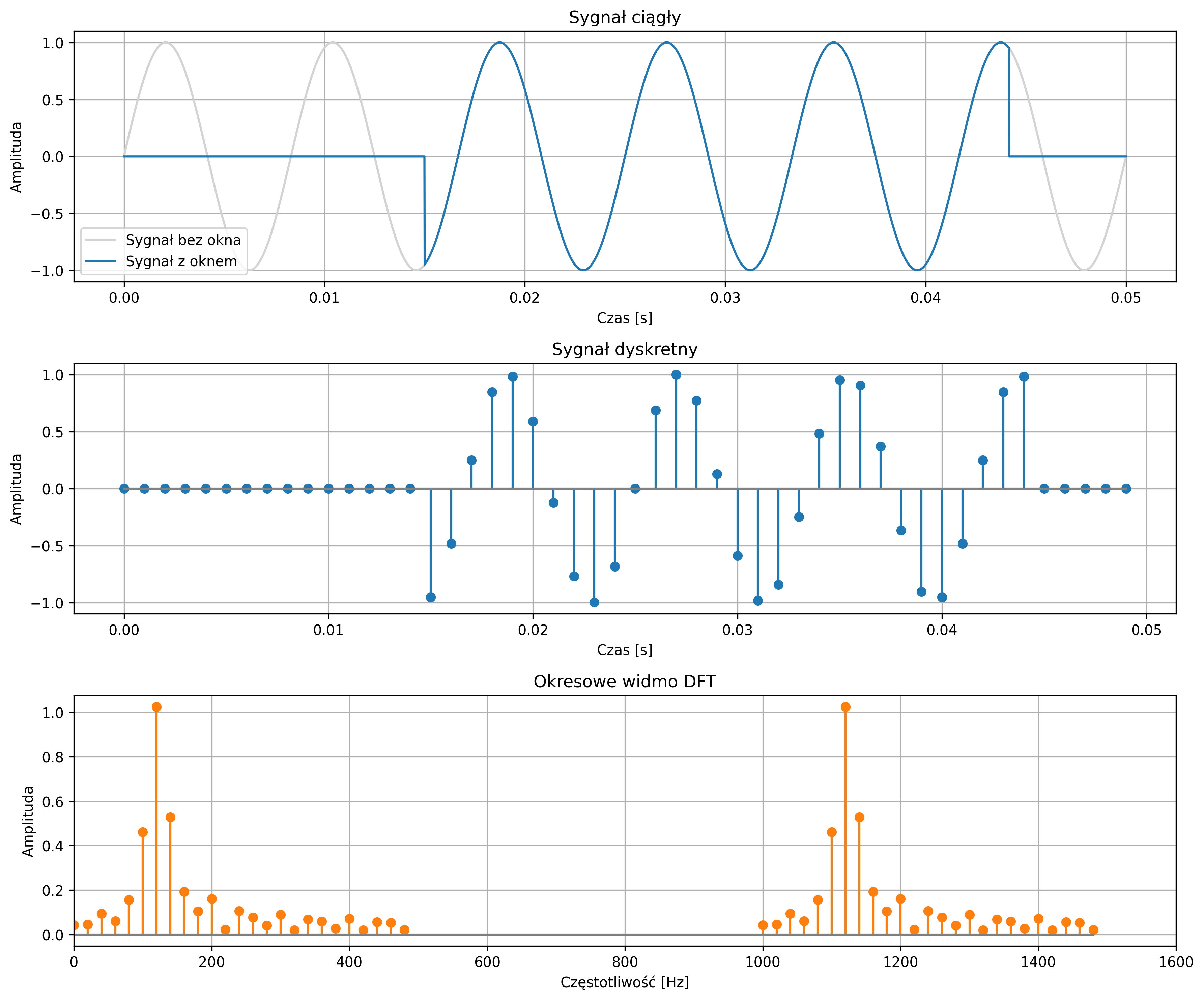
W przypadku prostych sygnałów, takich jak sinusoidy, przeciek widmowy zwykle nie stanowi dużego problemu – jego efekt ogranicza się do obecności niewielkich odstępstw wokół głównego prążka widma. Jednak przy sygnałach o złożonym widmie, przecieki od wielu składowych mogą się nakładać i sumować, powodując znaczne zniekształcenia amplitudowe innych prążków.
Na rys. 4.24 przedstawiono przebiegi sygnału sinusoidalnego, będącego sumą \(4\) składowych sinusoidalnych o częstotliwościach \(50\) Hz, \(120\) Hz, \(200\) Hz i \(300\) Hz. Na wykresie widmowym poprawnie wyciętego, przez okno prostokątne sygnału widać wyraźne prążki widmowe, odpowiadające składowym sygnału. Widmo sygnału uciętego w złym miejscu powoduje rozmycie prążków i zniekształcenia amplitudowe – efekt nakładających się przecieków od wielu składowych.
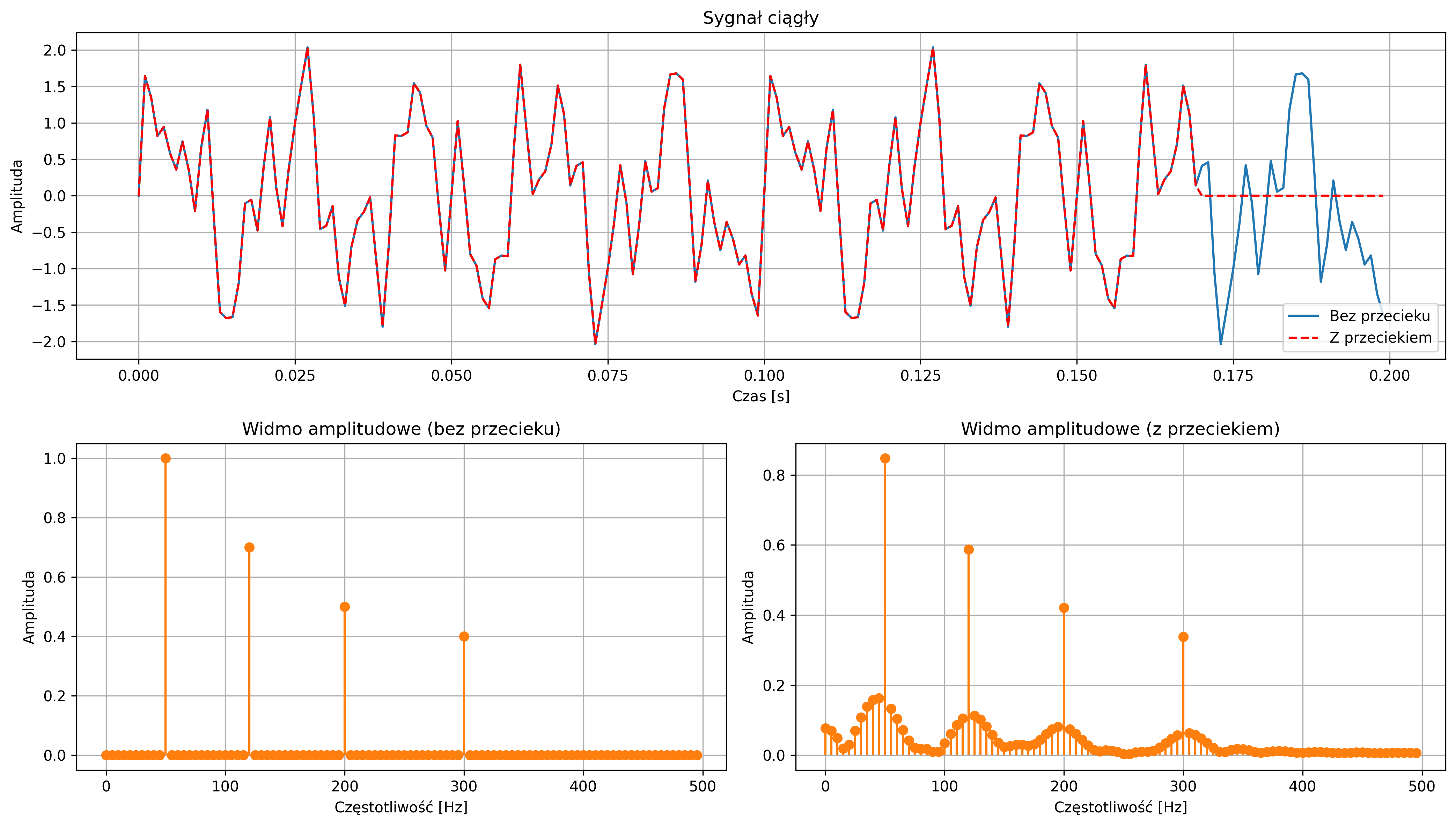
Maksymalny przeciek widmowy w przypadku sygnałów okresowych występuje, gdy częstotliwość analizowanego sygnału leży dokładnie w połowie odstępu pomiędzy dwiema sąsiednimi częstotliwościami widma DFT (np. \(1.5 f_s/N\)). W takiej sytuacji energia sygnału rozkłada się równomiernie na wszystkie prążki widma, a żaden z nich nie odpowiada dokładnie częstotliwości sygnału. W dziedzinie czasu sygnał nie jest wtedy okresowy w obrębie analizowanego okna, co powoduje największą możliwą nieciągłość na jego granicach, a w konsekwencji – najszersze rozmycie energii w widmie amplitudowym.
Zjawiska przecieku nie da się całkowicie uniknąć, ponieważ zawsze analizujemy skończony fragment sygnału. Istnieją jednak techniki, które pozwalają zmniejszyć skutki przecieku. W tym celu stosuje się inne funkcje okna, takie jak okna von Hanna, Hamminga, Blackmana i wiele innych. Ich wspólną cechą jest to, że wartości okna dążą do zera na jego krańcach, co łagodzi gwałtowne skoki na granicach sygnału i znacząco ogranicza przeciek widmowy.
Na rys. 4.25 możemy zaobserwować, że nałożone okno von Hanna i Blackmana silniej tłumią przeciek niż okno prostokątne, ale poszerzają główny listek (prążek).
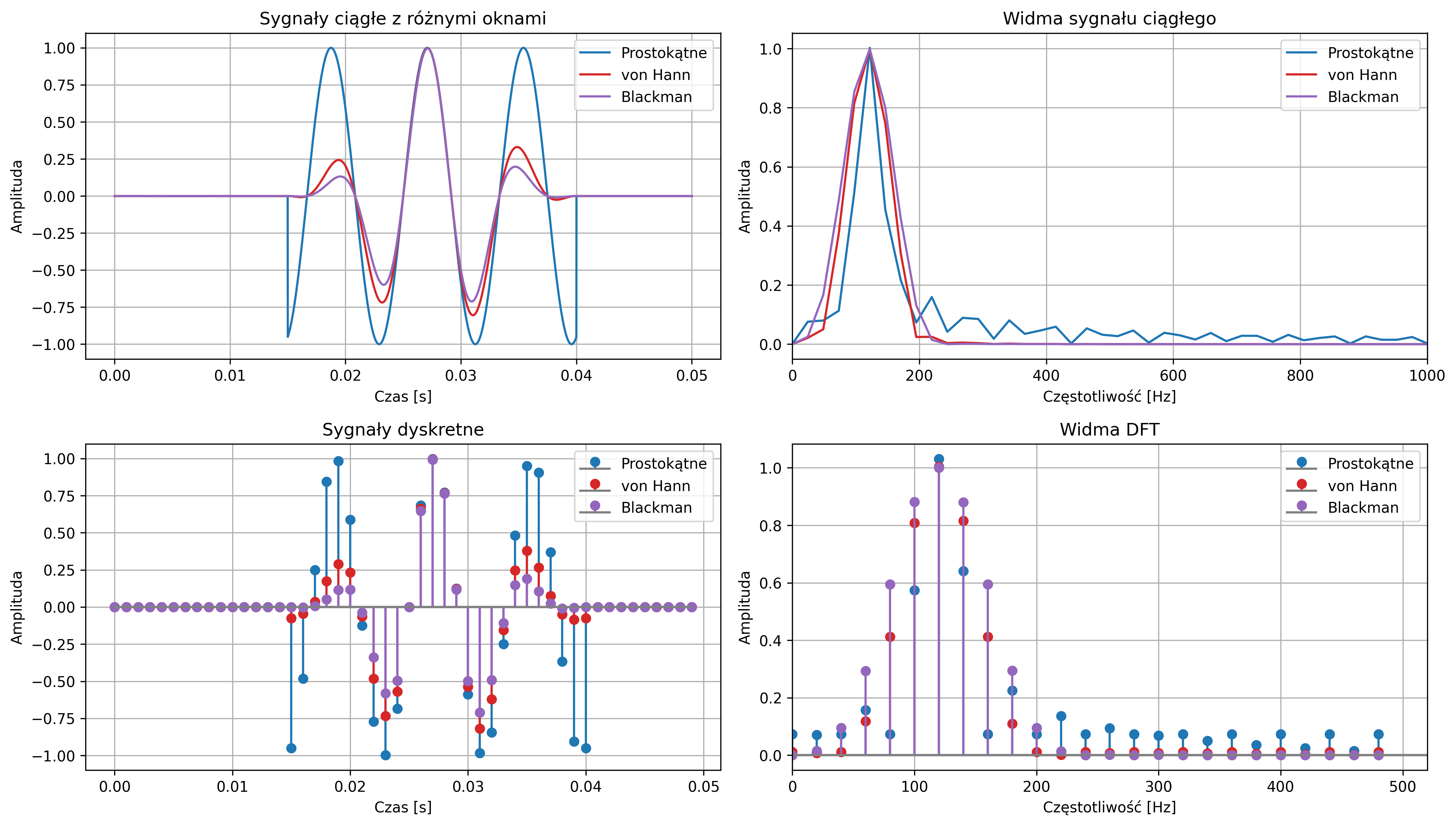
Ograniczona rozdzielczość częstotliwościowa DFT
Przypomnijmy, że w analizie sygnałów przy użyciu DFT istnieje fundamentalny kompromis między rozdzielczością czasową a częstotliwościową. Zwiększając długość analizowanego fragmentu sygnału (większe \(N\)) uzyskujemy lepszą rozdzielczość częstotliwościową, ponieważ prążki w widmie są gęściej rozmieszczone i umożliwiają dokładniejsze rozróżnienie częstotliwości. Jednak jednocześnie pogarsza się rozdzielczość czasowa – analiza dotyczy dłuższego przedziału czasowego, przez co trudniej określić, kiedy dokładnie w sygnale wystąpiły pewne zdarzenia. Odwrotnie, krótsze okna analizy pozwalają lepiej śledzić zmiany w czasie, ale ograniczają precyzję w dziedzinie częstotliwości.
Znaczenie rozdzielczości częstotliwościowej zostało zilustrowane na rys. 4.26. Dla wygenerowanego sygnału sinusoidalnego o częstotliwości \(1000\) Hz, chcemy wykryć częstotliwość prążka widmowego z wykorzystaniem DFT o rozmiarach \(N = 128, 256, 512, 1024, 2048, 4096\).
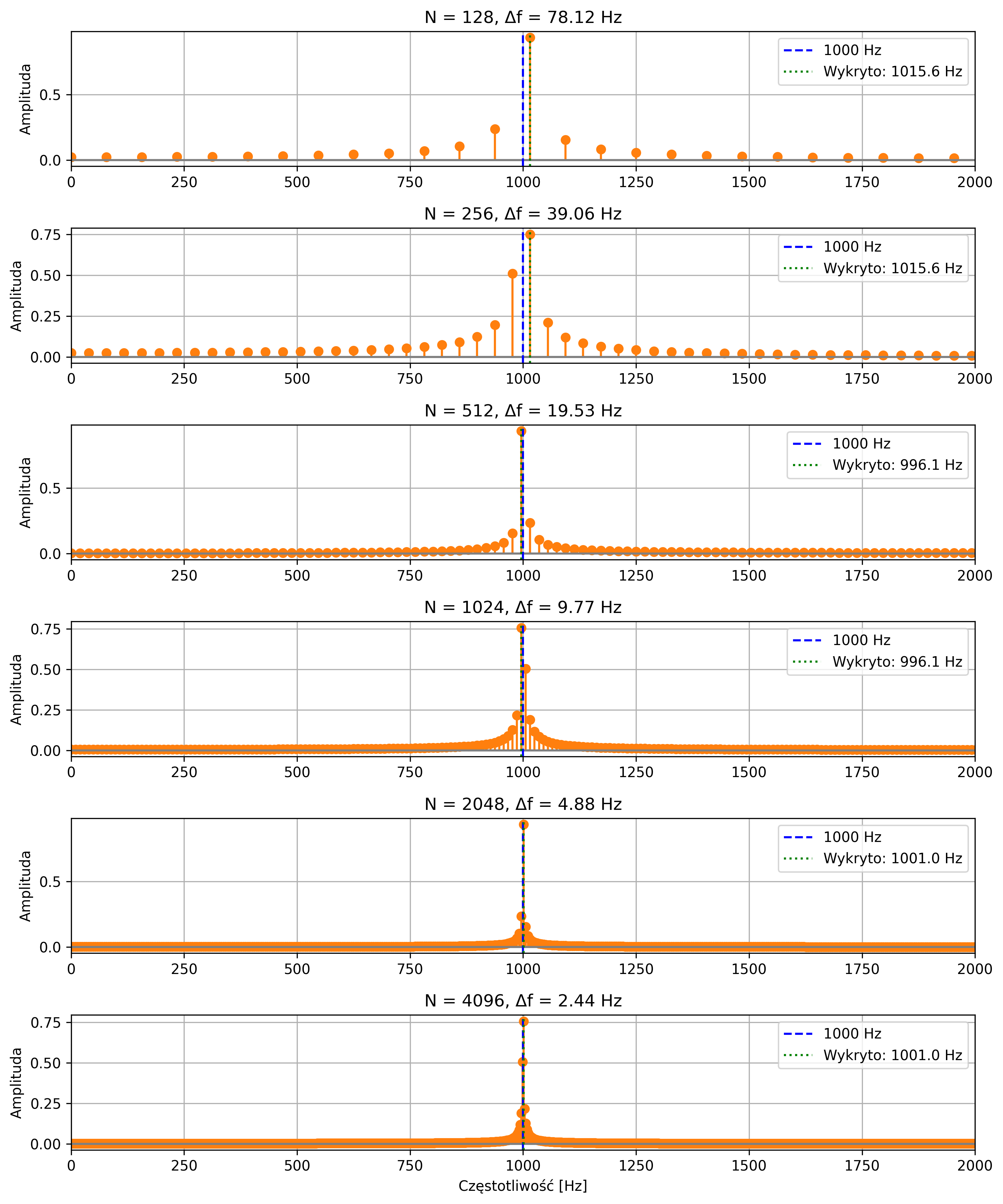
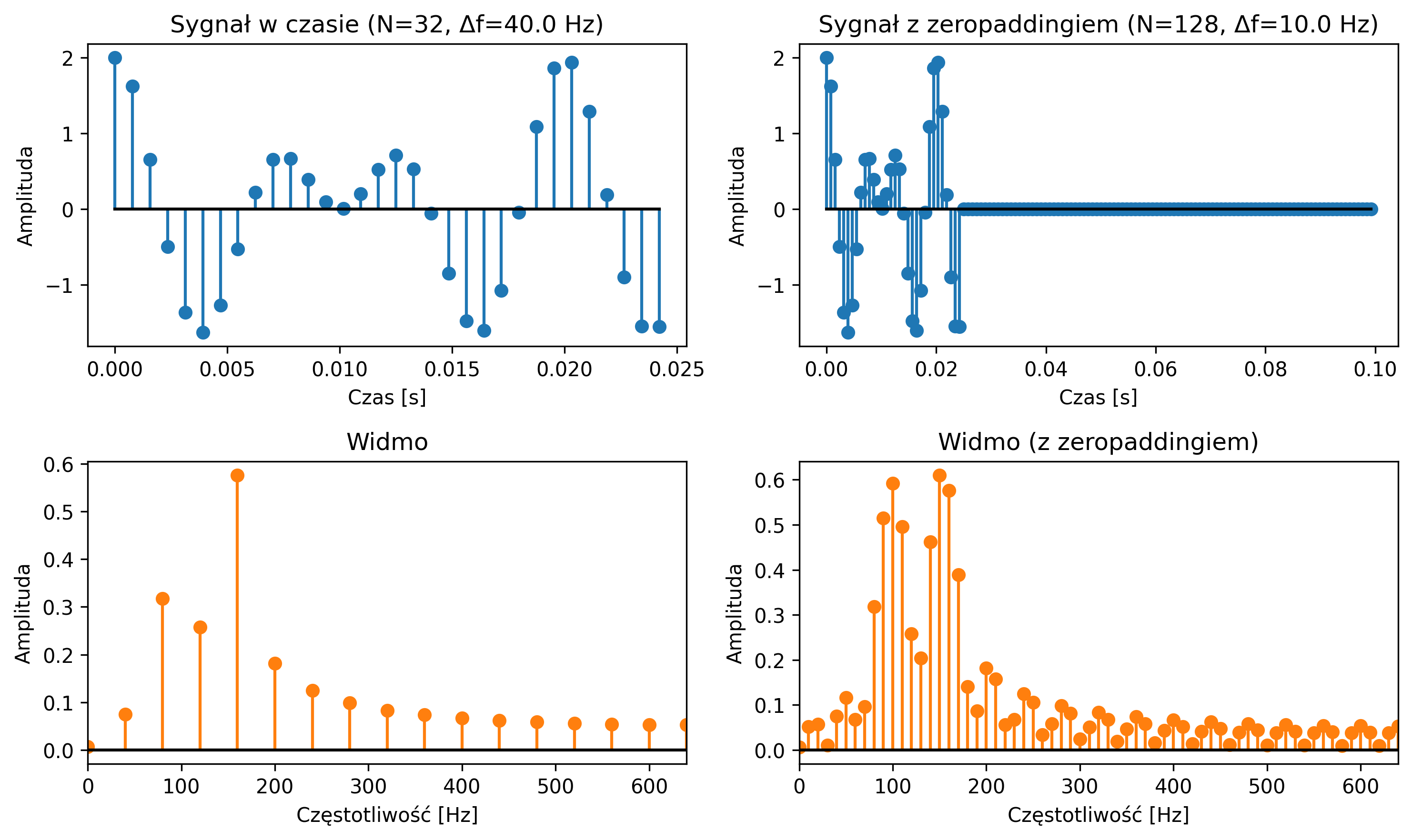
4.7. FFT w języku Python
Zakres ćwiczeń obejmuje generowanie i analizę różnych sygnałów w dziedzinie czasu i częstotliwości. W zadaniach przewidziano m.in.: przybliżanie sygnałów trójkątnych i prostokątnych za pomocą szeregu Fouriera, rysowanie przebiegów w dziedzinie czasu, wyznaczanie widm amplitudowych i fazowych, obliczanie energii sygnałów z użyciem równania Parsevala, stosowanie dyskretnej transformaty Fouriera dla sygnałów złożonych, analizę wpływu parametrów okien czasowych (prostokątne, Hamming, Blackman) na widmo, oraz badanie wpływu liczby punktów DFT na rozdzielczość częstotliwościową sygnałów. Ćwiczenia obejmują sygnały sinusoidalne, piłokształtne, prostokątne i ich kombinacje, z uwzględnieniem różnych częstotliwości próbkowania i długości próbek.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów
from numpy.fft import fft, fftfreq # obliczanie dyskretnej transformaty Fouriera
# i wyznaczanie osi częstotliwości
oraz wymagana jest znajomość między innymi następujących poleceń i funkcji języka Python:
fft # obliczanie dyskretnej transformaty Fouriera (algorytm FFT)
fftfreq # wyznaczanie wektora częstotliwości odpowiadającego FFT
fftshift # przesunięcie widma tak, aby zero częstotliwości było w środku
abs # obliczanie modułu widma (amplituda)
trapezoid # obliczanie całki numeryczną metodą trapezów
hamming # okno Hamminga do ograniczenia przecieku widmowego
blackman # okno Blackmana o silnym tłumieniu listków bocznych
Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do realizacji poniższych kodów oraz do analizy różnych parametrów związanych z wyznaczaniem DFT, poprzez ich modyfikację.
Przybliżyć sygnał trójkątny z wykorzystaniem rozwinięcia w szereg Fouriera o wartościach z przedziału \([-1,1]\) i okresie \( T = 2\pi \):
Wykorzystać \(3\) pierwsze harmoniczne:
import numpy as np
import matplotlib.pyplot as plt
# Czas: 2 okresy
t = np.linspace(-2*np.pi, 2*np.pi, 2000)
# Stała z rozwinięcia Fouriera dla sygnału trójkątnego
A = 8 / (np.pi**2)
# Przybliżenia
f1 = A * ((-1)**0 / (1**2) * np.sin(1*t))
f2 = A * ((-1)**0 / (1**2) * np.sin(1*t) +
(-1)**1 / (3**2) * np.sin(3*t))
f3 = A * ((-1)**0 / (1**2) * np.sin(1*t) +
(-1)**1 / (3**2) * np.sin(3*t) +
(-1)**2 / (5**2) * np.sin(5*t))
# Idealny sygnał trójkątny
triangle_wave = 2/np.pi * np.arcsin(np.sin(t)) # okres 2*pi
# Wykres
plt.figure(figsize=(12, 6))
plt.plot(t, f1, label='1 harmoniczna')
plt.plot(t, f2, label='1 + 3 harmoniczna')
plt.plot(t, f3, label='1 + 3 + 5 harmoniczna')
plt.plot(t, triangle_wave, 'k--', alpha=0.3, label='Sygnał trójkątny')
plt.title('Przybliżenie sygnału trójkątnego sumą nieparzystych harmonicznych')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.ylim(-1.5, 1.5)
plt.xlim(-2*np.pi, 2*np.pi)
plt.xticks(np.arange(-2*np.pi, 2.5*np.pi, np.pi),
[r'$-2\pi$', r'$-\pi$', '0', r'$\pi$', r'$2\pi$'])
plt.tight_layout()
plt.show()
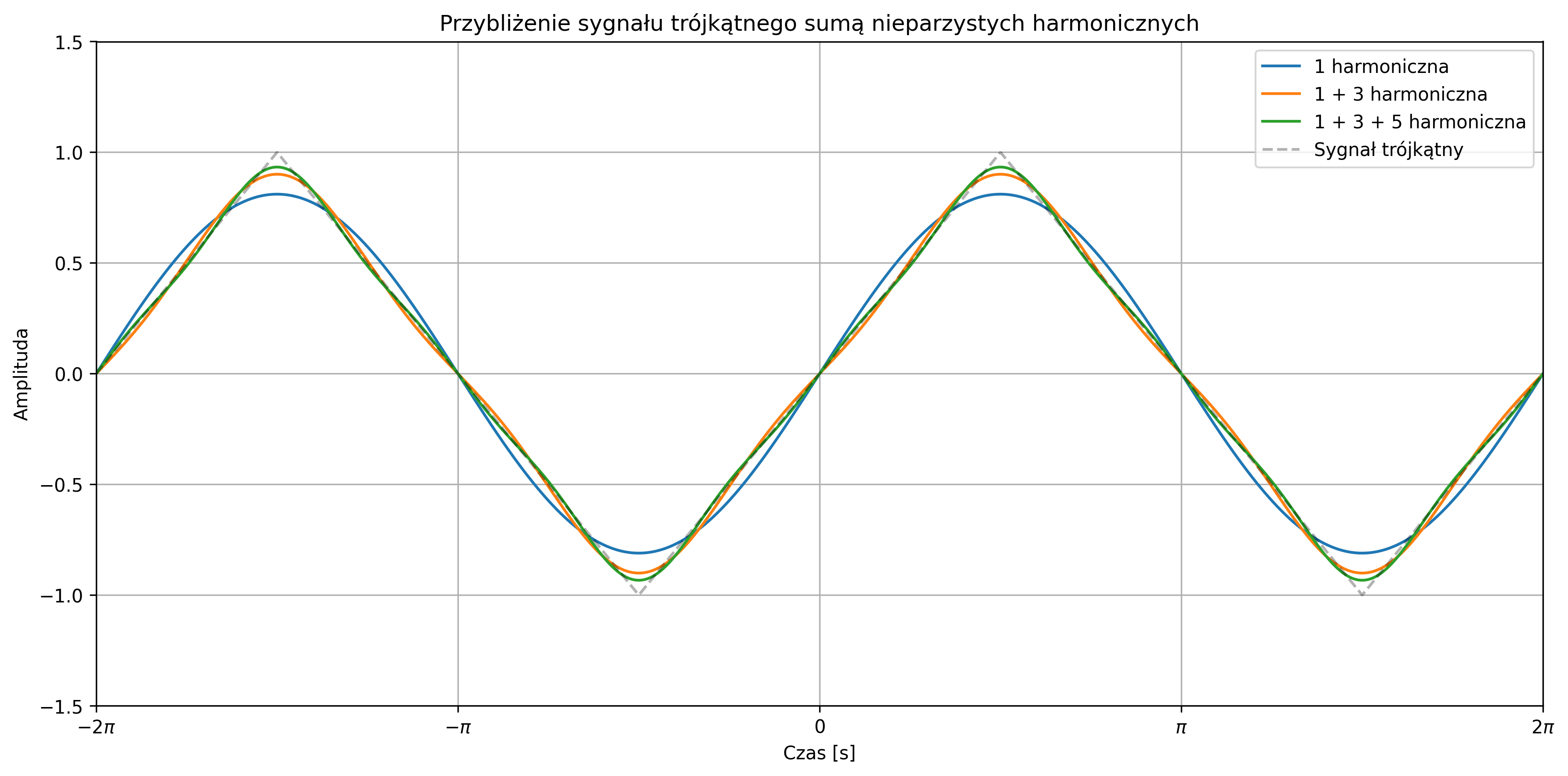
Narysować przebieg czterech okresów sygnału trójkątnego w dziedzinie czasu. Korzystając z wykładniczej postaci szeregu Fouriera narysować widmo amplitudowe \(|c_k|\) i fazowe \(\varphi_k\).
Amplitudy są zgodne z rozwinięciem Fouriera dla sygnału trójkątnego:co można również zapisać w formie:
dla nieparzystego numeru harmonicznej \( k=1,3,5,\ldots \).
Ponieważ jest to sygnał nieparzysty (w wersji sinusowej), fazy są tylko \(0\) lub \(\pi\).
import numpy as np
import matplotlib.pyplot as plt
# Parametry
T = 2 * np.pi # okres sygnału
t = np.linspace(-2*T, 2*T, 1000) # 4 okresy
# Idealny sygnał trójkątny (okres 2*pi, amplituda [-1, 1])
triangle_wave = 2/np.pi * np.arcsin(np.sin(t))
# Liczba harmonicznych
N = 25
k = np.arange(1, 2*N, 2) # nieparzyste harmoniczne: 1, 3, 5, ...
# Współczynnik znaku (-1)^k, gdzie k := (k-1)/2
signs = (-1)**((k - 1) // 2)
# Amplitudy z uwzględnieniem spadku 1/n^2 i znaku
ak = (8 / (np.pi**2)) * signs / (k**2)
# Widmo amplitudowe (moduł ak)
amplitudes = np.abs(ak)
# Widmo fazowe: 0 dla dodatnich współczynników, pi dla ujemnych
phases = np.where(signs > 0, 0, np.pi)
# Wykresy
plt.figure(figsize=(10, 8))
# 1. Sygnał trójkątny
plt.subplot(3, 1, 1)
plt.plot(t, triangle_wave, color='C0')
plt.title('Sygnał trójkątny w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
# 2. Widmo amplitudowe
plt.subplot(3, 1, 2)
plt.stem(k, amplitudes, linefmt='C1-', markerfmt='C1o', basefmt=" ")
plt.title('Widmo amplitudowe')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'Amplituda $A_k$')
plt.grid(True)
# 3. Widmo fazowe
plt.subplot(3, 1, 3)
plt.stem(k, phases, linefmt='C2-', markerfmt='C2o', basefmt=" ")
plt.title('Widmo fazowe')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'Faza $\varphi_k$ [rad]')
plt.yticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"])
plt.grid(True)
plt.tight_layout()
plt.show()
.png)
Narysować przebieg trzech okresów sygnału prostokątnego oraz jego widmo amplitudowe \(|c_k|\). Korzystając z równania Parsevala:
obliczyć energię sygnału (w jednym okresie podzieloną przez długość okresu) jako sumę kwadratów modułów współczynników Fouriera, czyli „mocy” poszczególnych harmonicznych.
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import square
# Parametry sygnału
T = 2 * np.pi # okres sygnału
f = 1 / T # częstotliwość podstawowa
num_periods = 3 # liczba okresów do rysowania
t = np.linspace(0, num_periods * T, 3000, endpoint=False)
# Sygnał prostokątny
x = square(2 * np.pi * f * t, duty=0.5)
# Zespolony szereg Fouriera
N = 25 # liczba harmonicznych
k = np.arange(-N, N + 1) # indeksy harmonicznych
# Współczynniki zespolone szeregu Fouriera dla sygnału prostokątnego
def c_k_fun(ki):
if ki == 0:
return 0
elif ki % 2 == 0:
return 0
else:
return 2 / (1j * ki * np.pi)
# Wektor współczynników
c_k = np.array([c_k_fun(ki) for ki in k])
# Sprawdzenie tożsamości Parsevala (1 okres)
t_single = np.linspace(0, T, 4000, endpoint=False)
x_single = square(2 * np.pi * f * t_single, duty=0.5)
energy_time = (1 / T) * np.trapezoid(np.abs(x_single)**2, t_single)
energy_freq = np.sum(np.abs(c_k)**2)
print(f'Energia w dziedzinie czasu: {energy_time:.6f}')
print(f'Suma |c_k|^2: {energy_freq:.6f}')
# Wykresy
plt.figure(figsize=(12, 7))
# Sygnał w dziedzinie czasu
plt.subplot(2, 1, 1)
plt.plot(t, x, color='C0')
plt.title('Sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
# Widmo amplitudowe współczynników c_k
plt.subplot(2, 1, 2)
plt.stem(k, np.abs(c_k), linefmt='C1-', markerfmt='C1o', basefmt=" ")
plt.title('Widmo amplitudowe zespolonego szeregu Fouriera')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'$|c_k|$')
plt.grid(True)
plt.tight_layout()
plt.show()
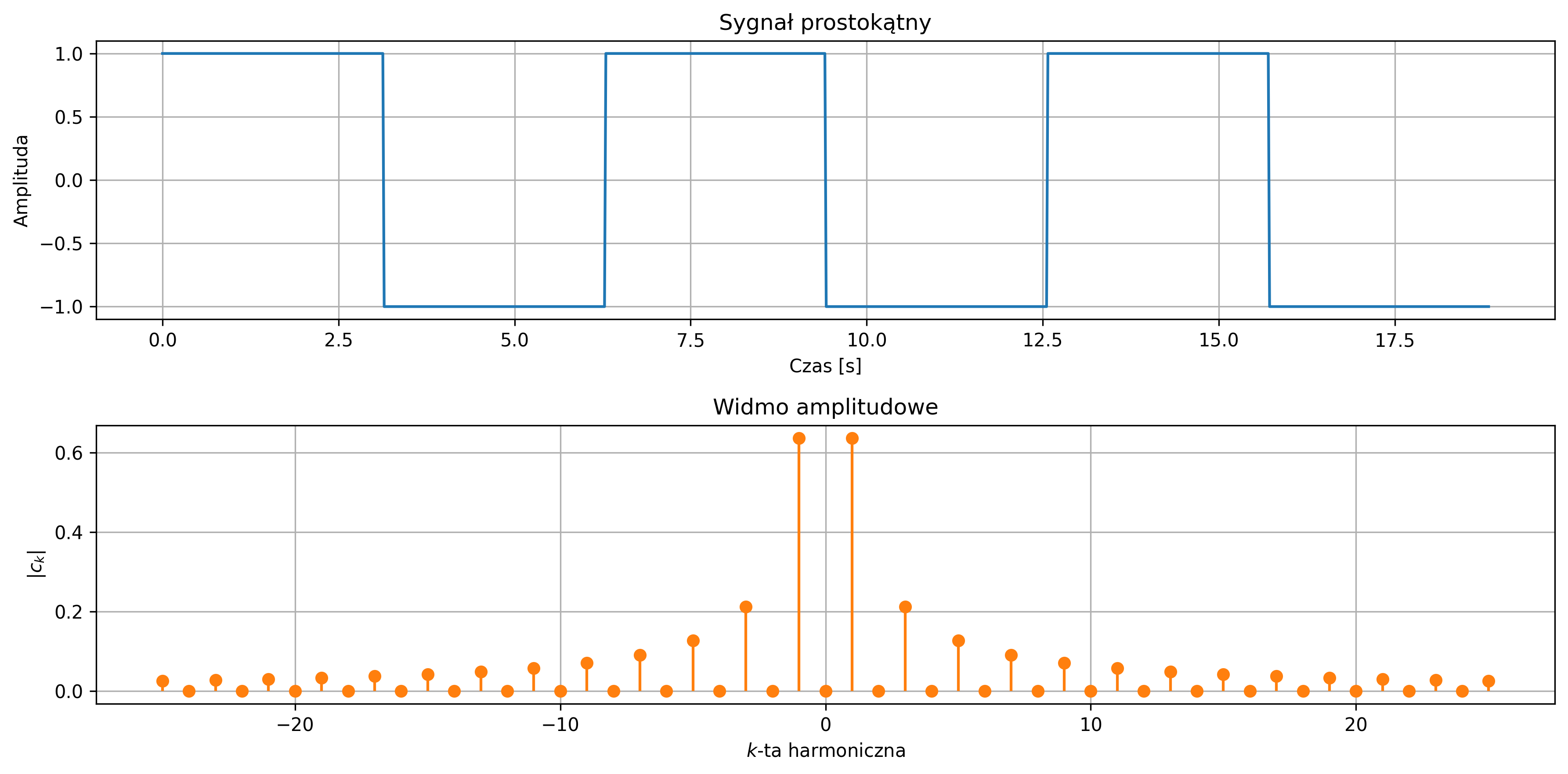
Korzystając z algorytmu FFT narysować widmo amplitudowe i fazowe DFT dla sygnału, będącego sumą dwóch kosinusów i dwóch sinusów:
Przyjąć, że \( f_s = N = 32 \), żeby łatwo przekształcać indeksy prążków na ich częstotliwości:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
# Parametry sygnału
N = 32
n = np.arange(N)
# Mieszana suma: kosinus + sinus
x = (np.cos(2 * np.pi * 3 * n / N) # kosinus 3
- np.cos(2 * np.pi * 5 * n / N) # kosinus 5 z ujemną amplitudą
+ np.sin(2 * np.pi * 7 * n / N) # sinus 7
- 0.5 * np.sin(2 * np.pi * 9 * n / N)) # sinus 9 z ujemną amplitudą
# Znormalizowana DFT
X = fft(x) / N
k = np.arange(N)
# Moduł i faza
amplitude = np.abs(X)
phase = np.angle(X)
# Wykresy
plt.figure(figsize=(12, 6))
# Widmo amplitudowe
plt.subplot(2, 1, 1)
plt.stem(k, amplitude, linefmt='C1-', markerfmt='C1o', basefmt='k-')
plt.title('Widmo amplitudowe')
plt.xlabel(r'$k$')
plt.ylabel(r'$|X[k]|$')
# Oznaczenie harmonicznych
harmonics = [3, 5, 7, 9, N - 3, N - 5, N - 7, N - 9]
for h in harmonics:
plt.annotate(f'harm. {h}',
xy=(h, amplitude[h]),
xytext=(h, amplitude[h] + 0.05),
arrowprops=dict(facecolor='black', arrowstyle='->'),
ha='center')
# Widmo fazowe
plt.subplot(2, 1, 2)
plt.stem(k, phase, linefmt='C2-', markerfmt='C2o', basefmt='k-')
plt.title('Widmo fazowe')
plt.xlabel(r'$k$')
plt.ylabel(r'$\arg\,X[k]$')
# Oś Y w jednostkach pi
ticks = np.pi * np.array([-1, -0.5, 0, 0.5, 1])
labels = [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$\pi/2$', r'$\pi$']
plt.yticks(ticks, labels)
plt.tight_layout()
plt.show()
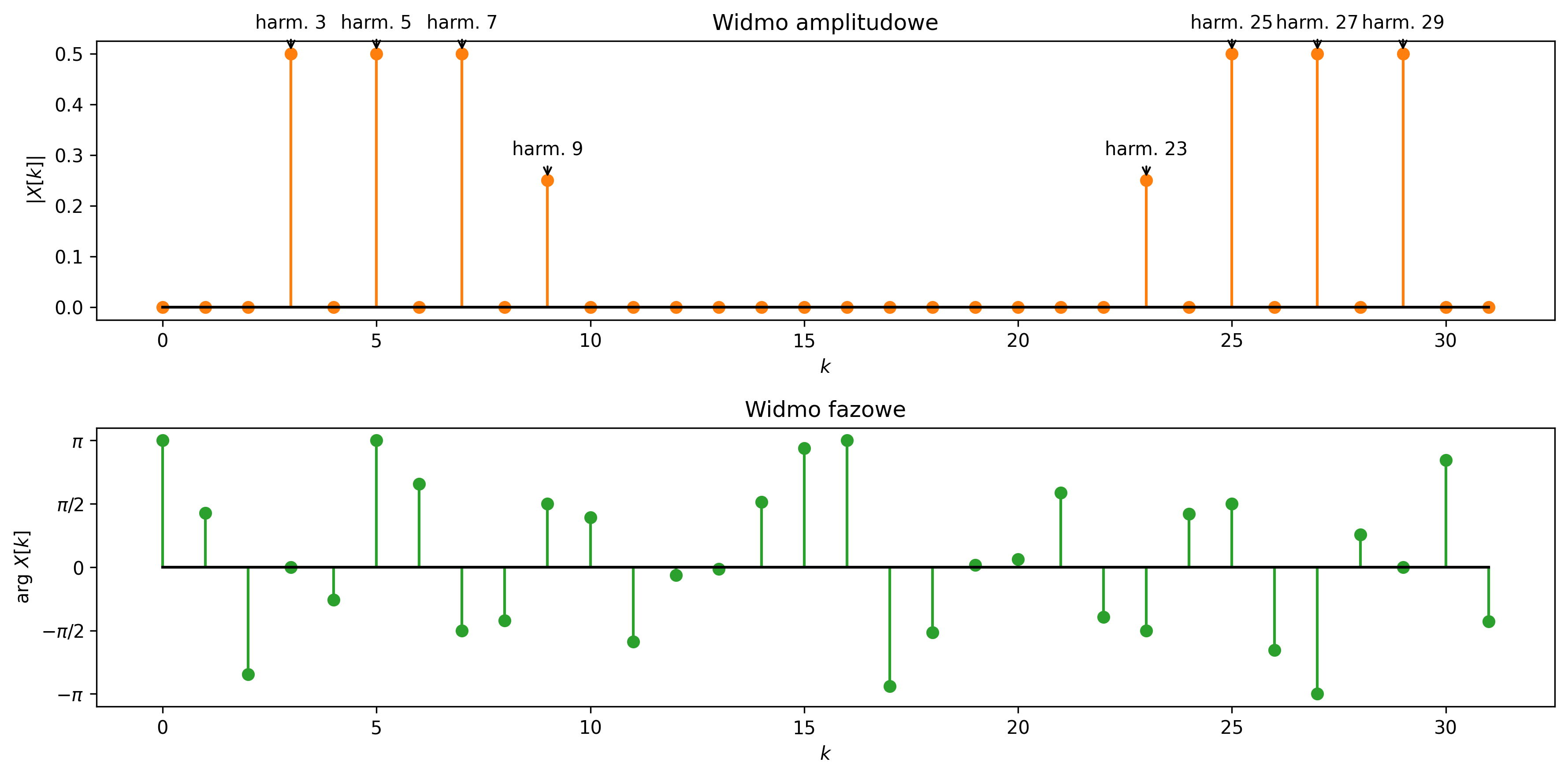
Każdy z symetrycznych prążków (bo sygnał rzeczywisty) zawiera połowę amplitudy składowej sygnału. Zatem suma amplitud prążków symetrycznych daje rzeczywistą amplitudę składowych sinusoidalnych. Każdy prążek widma wskazuje na obecność składowej o częstotliwości i amplitudzie:
- prążki w \( k=3 \) i \( k=29 \) wskazują obecność składowych o \(3\) i \(29\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=5 \) i \( k=27 \) wskazują obecność składowych o \(5\) i \(27\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=7 \) i \( k=25 \) wskazują obecność składowych o \(7\) i \(25\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=9 \) i \( k=23 \) wskazują obecność składowych o \(9\) i \(23\) jednostkach częstotliwości, które mają wysokość \(\approx 0.25\).
Zauważmy, że ujemne wartości amplitudy zmieniają się tylko w niezerowe przesunięcia fazowe, np.:
Z wykresu fazowego możemy odczytać, że dla kosinusów faza wynosi \(0\) lub \(\pi\), a dla sinusów faza wynosi \(\pm\frac{\pi}{2}\) w zależności od znaku amplitudy.
Rozważmy sygnał sinusoidalny o częstotliwości \(120\) Hz. Wyznaczyć widmo amplitudowe sygnału ciągłego trwającego \(0.05\) s z nałożonym oknem prostokątnym o szerokości od \(0.015\) s do \(0.04\) s oraz widmo sygnału dyskretnego, dla częstotliwości próbkowania \(1000\) Hz.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, fftshift
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # krótki odcinek czasu trwania sygnału
t_cont = np.linspace(0, t_max, 5000) # chcemy trakotować jako ciągły
x_cont = np.sin(2 * np.pi * f * t_cont)
# Okno prostokątne (na sygnale ciągłym)
window = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0)
x_cont_win = x_cont * window
# FFT sygnału ciągłego
N_fft = 4096 # rozmiar transformaty
X_fft = fft(x_cont_win, N_fft)
freqs_fft = fftfreq(N_fft, d=t_cont[1] - t_cont[0]) # krok czasowy ok. 1e-5
# odpowiada to próbkowaniu z dużym fs ok. 100 KHz
X_fft_shifted = fftshift(X_fft) # przesunięcie - częstotliwości od 0
freqs_fft_shifted = fftshift(freqs_fft)
X_fft_pos = np.abs(X_fft_shifted[N_fft//2:])
freqs_fft_pos = freqs_fft_shifted[N_fft//2:]
# Próbkowanie
t_disc = np.arange(0, t_max, T)
x_disc = np.sin(2 * np.pi * f * t_disc)
window_disc = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
x_disc_win = x_disc * window_disc
# DFT
N = len(x_disc_win)
X_dft = fft(x_disc_win)
freqs_dft = fftfreq(N, d=T)
X_dft_pos = np.abs(X_dft[:N // 2])
freqs_dft_pos = freqs_dft[:N // 2]
# Powielone widmo DFT – okresowość
repeats = 2 # 2 okresy
rep_freqs = np.concatenate([freqs_dft_pos + i * fs for i in range(repeats)])
rep_mags = np.tile(X_dft_pos, repeats)
rep_indices = np.concatenate([np.arange(N // 2) + i * (N // 2) for i in range(repeats)])
rep_mags = np.tile(X_dft_pos, repeats)
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły + okno
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Sygnał bez okna')
axs[0, 0].plot(t_cont, x_cont_win, color='C0', label='Z oknem prostokątnym')
axs[0, 0].set_title('Sygnał ciągły z oknem prostokątnym')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widmo sygnału ciągłego
axs[0, 1].plot(freqs_fft_pos, X_fft_pos, color='C1')
axs[0, 1].set_xlim(0, 2000) # widmo sięga fs/2, czyli ok. 50 kHz
# ograniczamy do 2000 w celu lepszej wizualizacji
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid()
# Sygnał próbkowany
axs[1, 0].stem(t_disc, x_disc_win, linefmt='C0-', markerfmt='C0o', basefmt='gray')
axs[1, 0].set_title('Sygnał próbkowany (z oknem)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid()
# Widmo DFT (powtarzalność)
axs[1, 1].stem(rep_freqs, rep_mags, linefmt='C1-', markerfmt='C1o', basefmt='gray')
axs[1, 1].set_xlim(0, 1600) # aby pokazać 2 okresy
axs[1, 1].set_title('Widmo DFT – okresowe powtarzanie')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid()
plt.tight_layout()
plt.show()
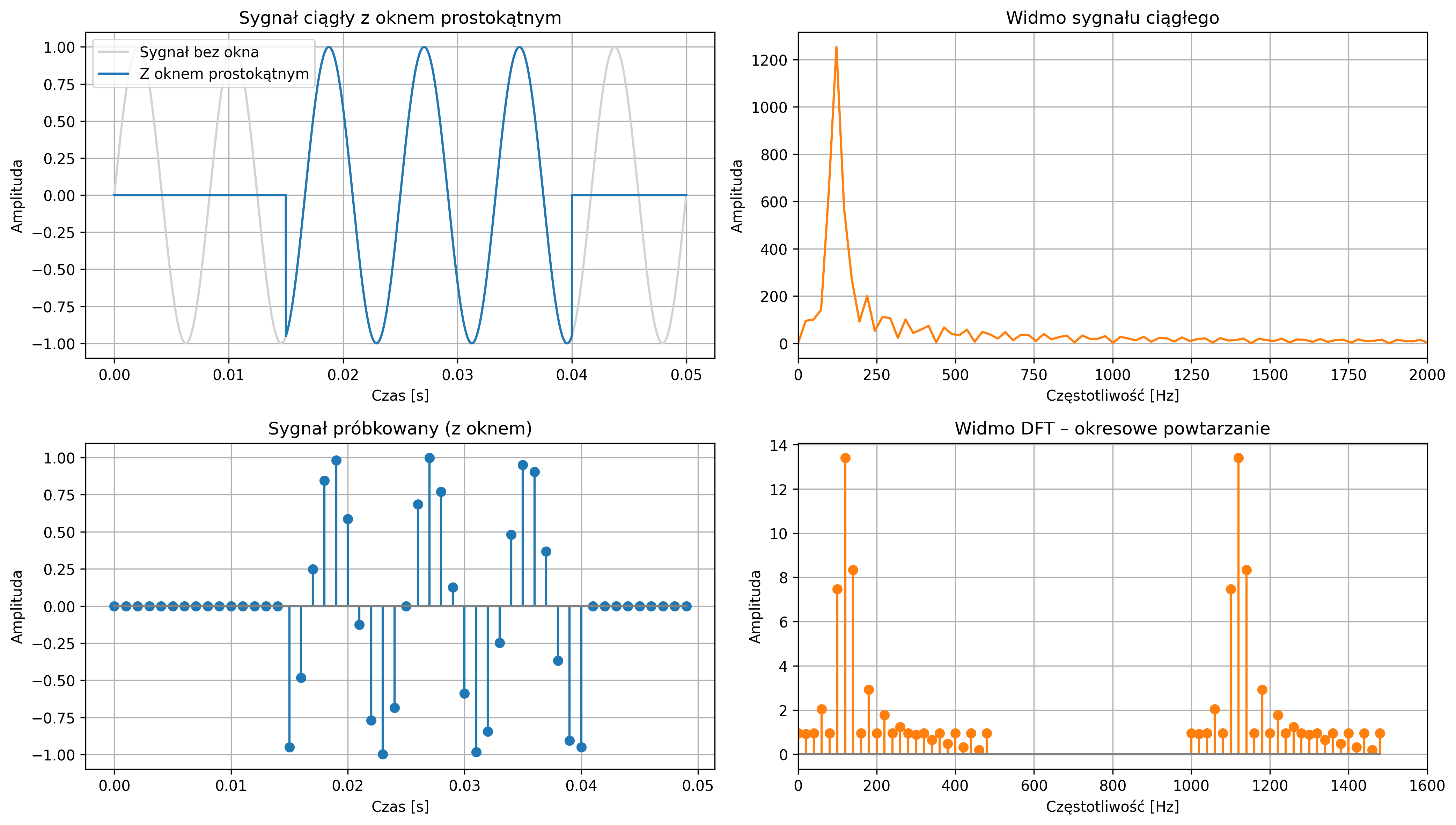
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # krótki odcinek czasu trwania sygnału
# sygnał ciągły (symulowany gęstą siatką, np. 10x gęściej)
oversampling = 10
t_cont = np.linspace(0, t_max, int(fs * oversampling * t_max), endpoint=False)
x_cont = np.sin(2 * np.pi * f * t_cont)
# Okno prostokątne (na sygnale ciągłym)
window = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0)
x_cont_win = x_cont * window
# FFT sygnału ciągłego
N_fft = 4096 # rozmiar transformaty
X_fft = fft(x_cont_win, N_fft)
freqs_fft = fftfreq(N_fft, d=1/(fs*oversampling))
X_fft_pos = np.abs(X_fft[:N_fft//2])
freqs_fft_pos = freqs_fft[:N_fft//2]
# Sygnał próbkowany zgodnie z fs
t_disc = np.arange(0, t_max, T)
x_disc = np.sin(2 * np.pi * f * t_disc)
window_disc = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
x_disc_win = x_disc * window_disc
# DFT
N = len(x_disc_win)
X_dft = fft(x_disc_win)
freqs_dft = fftfreq(N, d=T)
X_dft_pos = np.abs(X_dft[:N // 2])
freqs_dft_pos = freqs_dft[:N // 2]
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły + okno
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Sygnał bez okna')
axs[0, 0].plot(t_cont, x_cont_win, color='C0', label='Z oknem prostokątnym')
axs[0, 0].set_title('Sygnał ciągły z oknem prostokątnym')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widmo sygnału ciągłego
axs[0, 1].plot(freqs_fft_pos, X_fft_pos, color='C1')
axs[0, 1].set_xlim(0, fs/2) # pasmo Nyquista
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid()
# Sygnał próbkowany
axs[1, 0].stem(t_disc, x_disc_win, linefmt='C0-', markerfmt='C0o', basefmt='gray')
axs[1, 0].set_title('Sygnał próbkowany (z oknem)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid()
# Widmo DFT
axs[1, 1].stem(freqs_dft_pos, X_dft_pos, linefmt='C1-', markerfmt='C1o', basefmt='gray')
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title('Widmo DFT (fs=1000 Hz)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid()
plt.tight_layout()
plt.show()
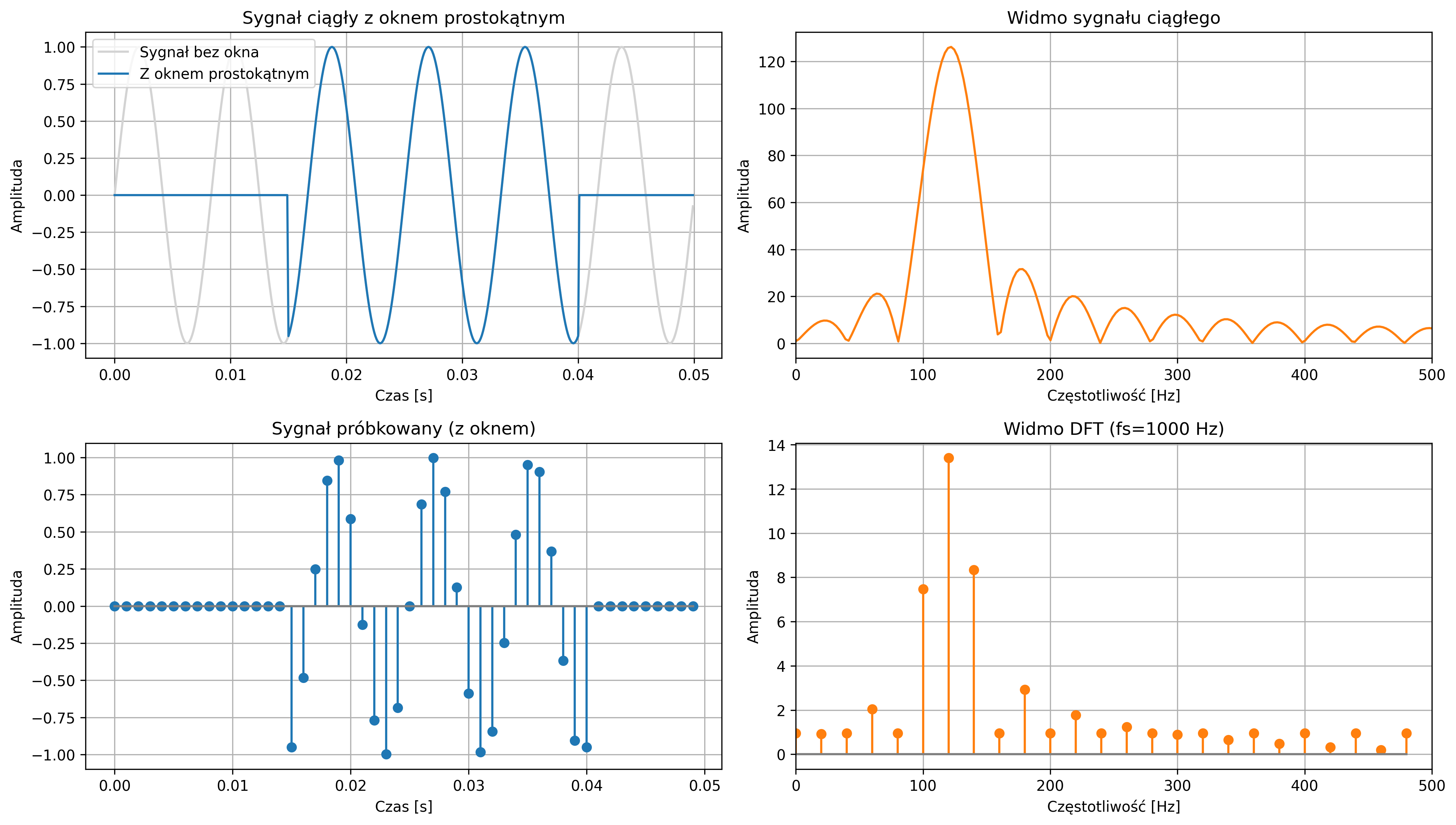
Rozważmy sygnał piłokształtny o częstotliwości \(120\) Hz. Wyznaczyć widmo amplitudowe sygnału ciągłego trwającego \(0.05\) s z nałożonym oknem prostokątnym o szerokości od \(0.015\) s do \(0.04\) s oraz widmo sygnału dyskretnego, dla częstotliwości próbkowania \(1000\) Hz. Zilustrować wpływ użytej funkcji na kształt otrzymanego widma - wykorzystać okno Hamminga i Blackmanna.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy.signal import sawtooth, windows
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # czas trwania sygnału
# sygnał ciągły (symulowany gęstą siatką, np. 10x gęściej)
oversampling = 10
t_cont = np.linspace(0, t_max, int(fs * oversampling * t_max), endpoint=False)
x_cont = sawtooth(2 * np.pi * f * t_cont) # sygnał piłokształtny
# Okna (na sygnale ciągłym)
N_cont = len(t_cont)
win_rect = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0) # prostokątne
win_hamm = windows.hamming(N_cont) * win_rect # Hamming
win_black = windows.blackman(N_cont) * win_rect # Blackmann
# Nałożone sygnały
x_cont_rect = x_cont * win_rect
x_cont_hamm = x_cont * win_hamm
x_cont_black = x_cont * win_black
# FFT sygnału ciągłego z różnymi oknami
N_fft = 4096
freqs_fft = fftfreq(N_fft, d=1/(fs*oversampling))
def fft_mag(x):
X = fft(x, N_fft)
return np.abs(X[:N_fft//2])
freqs_fft_pos = freqs_fft[:N_fft//2]
X_fft_rect = fft_mag(x_cont_rect)
X_fft_hamm = fft_mag(x_cont_hamm)
X_fft_black = fft_mag(x_cont_black)
# Sygnał próbkowany (dla porównania)
t_disc = np.arange(0, t_max, T)
x_disc = sawtooth(2 * np.pi * f * t_disc)
N_disc = len(t_disc)
# Te same okna dyskretne
win_rect_d = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
win_hamm_d = windows.hamming(N_disc) * win_rect_d
win_black_d = windows.blackman(N_disc) * win_rect_d
x_disc_rect = x_disc * win_rect_d
x_disc_hamm = x_disc * win_hamm_d
x_disc_black = x_disc * win_black_d
# FFT dla sygnałów dyskretnych
def dft_mag(x):
X = fft(x)
return np.abs(X[:len(x)//2]), fftfreq(len(x), d=T)[:len(x)//2]
X_dft_rect, freqs_dft_pos = dft_mag(x_disc_rect)
X_dft_hamm, _ = dft_mag(x_disc_hamm)
X_dft_black, _ = dft_mag(x_disc_black)
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły z oknami
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Bez okna')
axs[0, 0].plot(t_cont, x_cont_rect, label='Prostokątne', color='C0')
axs[0, 0].plot(t_cont, x_cont_hamm, label='Hamminga', color='C4')
axs[0, 0].plot(t_cont, x_cont_black, label='Blackmana', color='C2')
axs[0, 0].set_title('Sygnał ciągły z różnymi oknami')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widma ciągłe
axs[0, 1].plot(freqs_fft_pos, X_fft_rect, label='Prostokątne', color='C0')
axs[0, 1].plot(freqs_fft_pos, X_fft_hamm, label='Hamminga', color='C4')
axs[0, 1].plot(freqs_fft_pos, X_fft_black, label='Blackmana', color='C2')
axs[0, 1].set_xlim(0, fs/2)
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].legend()
axs[0, 1].grid()
# Sygnały dyskretne
axs[1, 0].stem(t_disc, x_disc_rect, linefmt='C0-', markerfmt='C0o', basefmt='gray', label='Prostokątne')
axs[1, 0].stem(t_disc, x_disc_hamm, linefmt='C4-', markerfmt='C4o', basefmt='gray', label='Hamminga')
axs[1, 0].stem(t_disc, x_disc_black, linefmt='C2-', markerfmt='C2o', basefmt='gray', label='Blackmana')
axs[1, 0].set_title('Sygnał próbkowany (różne okna)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].legend()
axs[1, 0].grid()
# Widma DFT
axs[1, 1].stem(freqs_dft_pos, X_dft_rect, linefmt='C0-', markerfmt='C0o', basefmt='gray', label='Prostokątne')
axs[1, 1].stem(freqs_dft_pos, X_dft_hamm, linefmt='C4-', markerfmt='C4o', basefmt='gray', label='Hamminga')
axs[1, 1].stem(freqs_dft_pos, X_dft_black, linefmt='C2-', markerfmt='C2o', basefmt='gray', label='Blackmana')
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title('Widmo DFT (różne okna)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].legend()
axs[1, 1].grid()
plt.tight_layout()
plt.show()
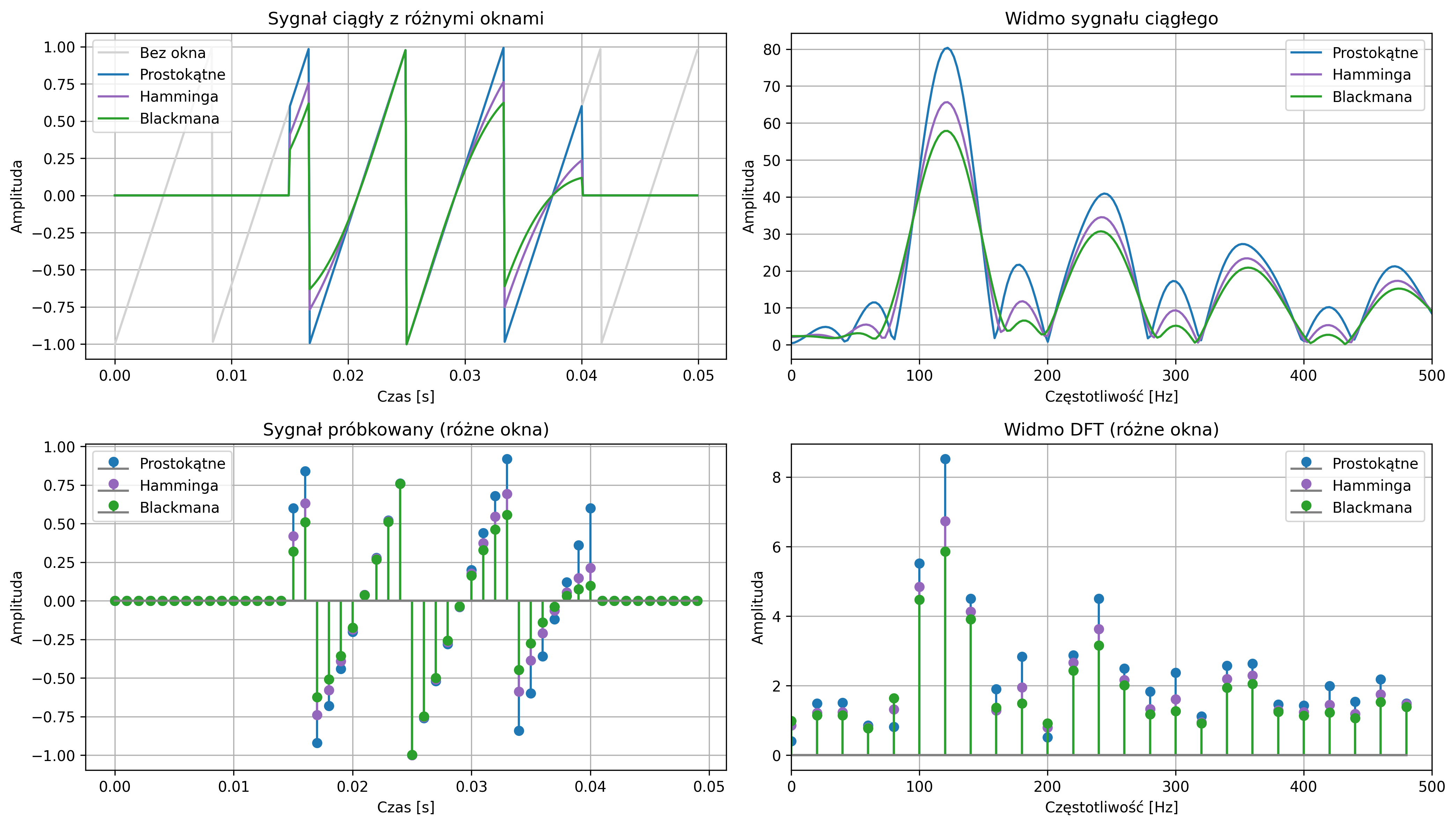
Rozważmy sygnał prostokątny o amplitudzie \(\pm 1\) o częstotliwości \(500\) Hz. Wyznaczyć widmo amplitudowe DFT dla częstotliwości próbkowania \(5000\) Hz. Dokonać analizy wpływu rozmiaru DFT na rozdzielczość częstotliwościową. Przyjąć \( N=128, 256, 1024, 2048, 4096 \).
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy.signal import square
# Parametry
fs = 5000 # częstotliwość próbkowania
f = 500 # Hz
N_list = [128, 256, 512, 1024, 2048, 4096]
# Wykresy
fig, axs = plt.subplots(len(N_list), 1, figsize=(10, 12), sharex=False)
for i, N in enumerate(N_list):
t = np.arange(N) / fs
# Sygnał prostokątny
x = square(2 * np.pi * f * t)
# FFT
X = fft(x)
freqs = fftfreq(N, d=1/fs)
mag = 2 * np.abs(X[:N // 2]) / N
freqs_pos = freqs[:N // 2]
# Szukanie największego prążka
peak_idx = np.argmax(mag)
peak_freq = freqs_pos[peak_idx]
# Widma DFT
axs[i].stem(freqs_pos, mag, basefmt="gray", linefmt="C1-", markerfmt="C1o")
axs[i].axvline(f, color='blue', linestyle='--', label='500 Hz')
axs[i].axvline(peak_freq, color='green', linestyle=':', label=f'Wykryto: {peak_freq:.1f} Hz')
axs[i].set_title(f'N = {N}, Δf = {fs/N:.2f} Hz')
axs[i].set_xlim(0, 1000)
axs[i].set_ylabel('Amplituda')
axs[i].grid(True)
axs[i].legend()
axs[-1].set_xlabel('Częstotliwość [Hz]')
plt.tight_layout()
plt.show()
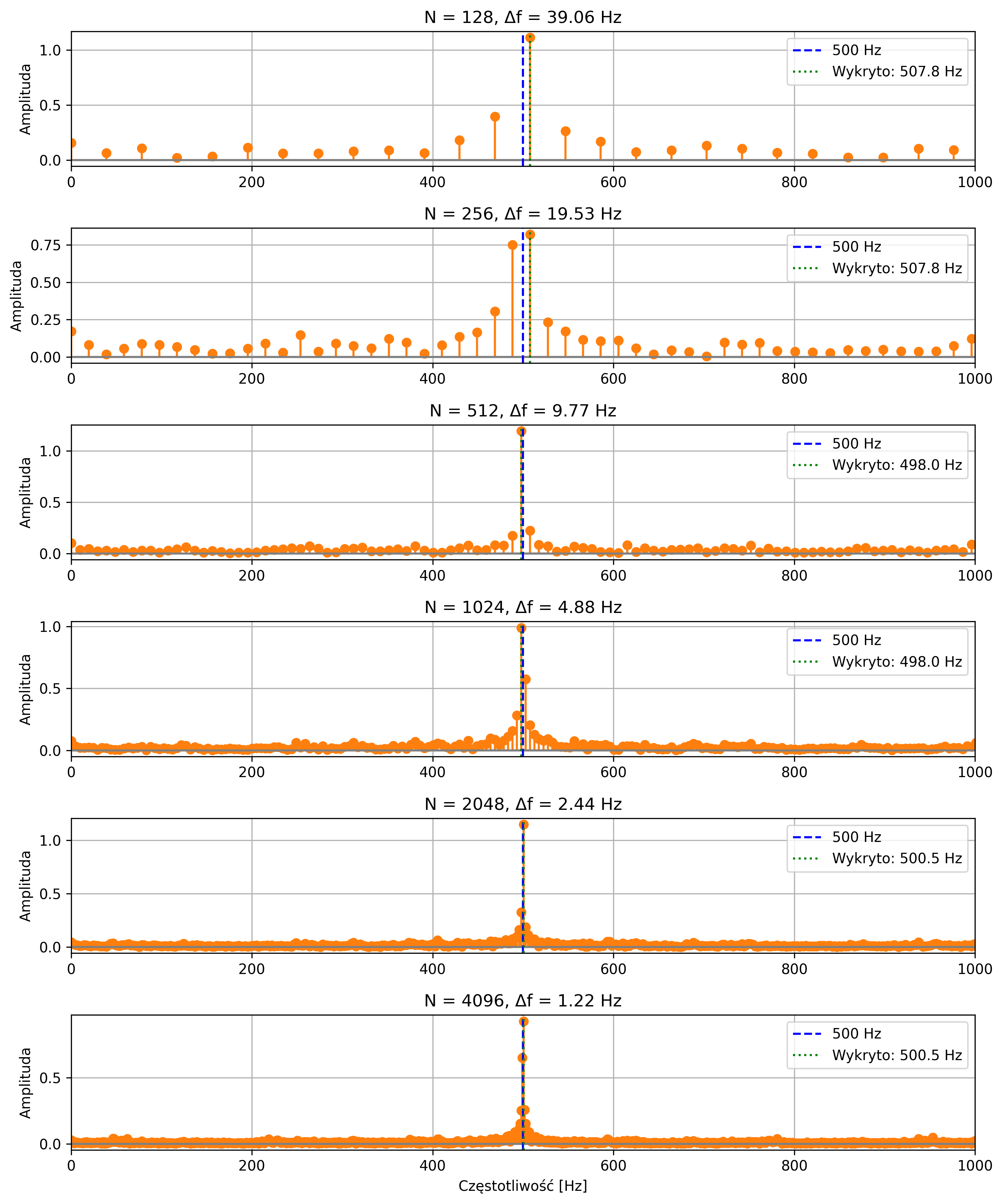
Rozważmy sygnał trójkątny, będący sumą dwóch sygnałów piłokształtnych o współczynniku wypełnienia \(0.5\), amplitudach \(0.5\) i częstotliwościach \(150\) Hz i \(100\) Hz. Przyjmując częstotliwość próbkowania \(1280\) Hz, porównać przebieg \(32\) próbek oryginalnego sygnału i sygnału z dopisanymi 96 zerami na końcu oraz ich widm amplitudowych.
Zauważmy, że rozważać będziemy rozmiary DFT na poziomie: \( N=32 \) oraz \( N=128 \) (po zero-paddingu).
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth
from scipy.fft import fft
# Parametry
fs = 1280 # Hz
f1 = 150 # Hz
f2 = 100 # Hz
def signal_triangle(N):
t = np.arange(N) / fs
# Sygnał trójkątny sumą dwóch piłokształtnych o wypełnieniu 0.5
return t, 0.5*sawtooth(2*np.pi*f1*t, 0.5) + 0.5*sawtooth(2*np.pi*f2*t, 0.5)
def spectrum(x, N):
X = fft(x, N) / len(x)
f = np.arange(N) * fs / N
return f, np.abs(X)
# Dwa przypadki
N1 = 32 # oryginalny
t1, x1 = signal_triangle(N1)
f1_spec, X1 = spectrum(x1, N1)
N2 = 128 # zeropadding
t2, x2 = signal_triangle(N1)
f2_spec, X2 = spectrum(x2, N2)
# Harmoniczne do podświetlenia
harmonics = [f1, f2]
# Wykres
fig, axs = plt.subplots(2, 2, figsize=(12, 6))
# Sygnał oryginalny N=32
axs[0, 0].stem(t1, x1, basefmt="k-", linefmt='C0-', markerfmt='C0o')
axs[0, 0].set_title(rf'Sygnał trójkątny ($N$={N1})')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].grid(True)
# Sygnał z zeropaddingiem N=128
axs[0, 1].stem(np.arange(N2)/fs, np.pad(x2, (0, N2-N1)),
basefmt="k-", linefmt='C0-', markerfmt='C0o')
axs[0, 1].set_title(rf'Sygnał trójkątny z zeropaddingiem ($N$={N2})')
axs[0, 1].set_xlabel('Czas [s]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid(True)
# Widmo dla N=32 z zaznaczeniem harmonicznych
axs[1, 0].stem(f1_spec, X1, basefmt="k-", linefmt='C1-', markerfmt='C1o')
for h in harmonics:
idx = np.argmin(np.abs(f1_spec - h))
axs[1, 0].stem(f1_spec[idx], X1[idx], linefmt='C3-', markerfmt='C3o', basefmt=" ")
axs[1, 0].set_xlim(0, fs/2)
axs[1, 0].set_title(rf'Widmo ($N=32$)')
axs[1, 0].set_xlabel('Częstotliwość [Hz]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid(True)
# Widmo dla N=128 z zaznaczeniem harmonicznych
axs[1, 1].stem(f2_spec, X2, basefmt="k-", linefmt='C1-', markerfmt='C1o')
for h in harmonics:
idx = np.argmin(np.abs(f2_spec - h))
axs[1, 1].stem(f2_spec[idx], X2[idx], linefmt='C3-', markerfmt='C3o', basefmt=" ")
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title(rf'Widmo z zeropaddingiem ($N=128$)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid(True)
plt.tight_layout()
plt.show()
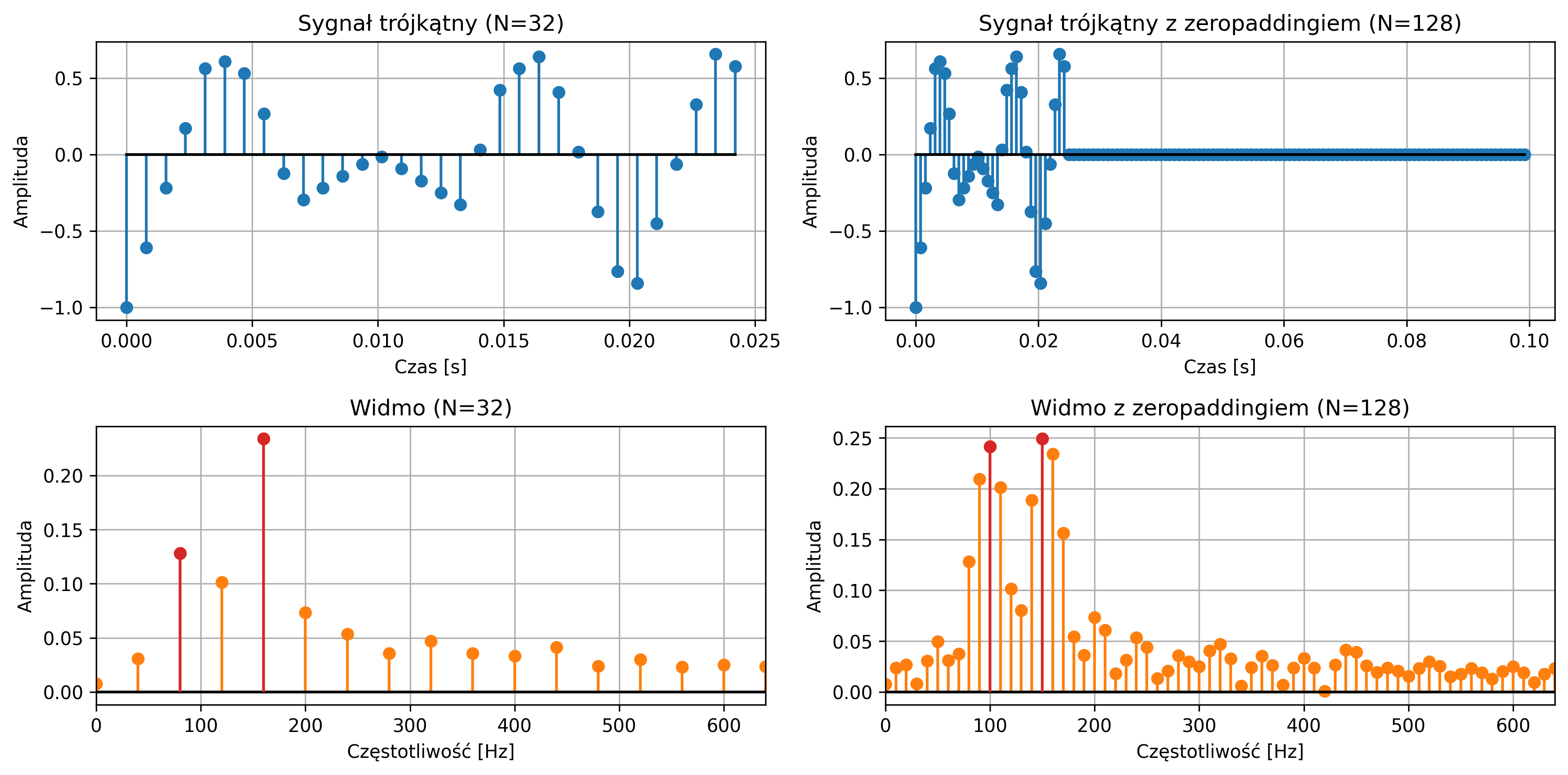
4.8. Test C - sprawdź swoją wiedzę
Test ma na celu sprawdzenie i utrwalenie wiedzy z zakresu analizy częstotliwościowej sygnałów, szeregów i transformaty Fouriera oraz widm sygnałów okresowych i dyskretnych. Każde pytanie zawiera trzy odpowiedzi (A, B, C), z których tylko jedna jest poprawna.
Klucz odpowiedzi:
1.C
2.B
4.A
5.B
6.A
7.B
8.C
9.B
10.C
11.B
12.B
13.C
14.B
15.C
16.B
17.B
18.B
19.B
20.C
21.B
22.B
23.C
24.C
25.B
26.B
27.C
28.B
29.B
30.A
5. Analiza częstotliwościowa sygnałów losowych
W praktyce analizy i przetwarzania sygnałów bardzo często spotykamy się nie tylko z sygnałami deterministycznymi, ale również z sygnałami losowymi. Są to takie sygnały, których wartości chwilowe nie są ściśle przewidywalne, lecz można je opisać w sposób probabilistyczny. Pojęcie sygnału losowego rozszerza się do procesu losowego, który stanowi zbiór wszystkich możliwych realizacji danego sygnału i opisuje jego zachowanie w sensie statystycznym. Ponieważ pojedyncza realizacja może wyglądać zupełnie przypadkowo, analiza procesów losowych opiera się na ich charakterystykach statystycznych, takich jak wartość średnia, wariancja czy funkcja autokorelacji.
Szczególne znaczenie w analizie praktycznej mają procesy stacjonarne w sensie szerokim (WSS). Charakteryzują się one tym, że wartość średnia nie zależy od czasu, a funkcja autokorelacji jest funkcją wyłącznie przesunięcia czasowego, a nie absolutnego czasu. Dzięki temu możliwe jest przejście do opisu w dziedzinie częstotliwości. W przypadku sygnałów losowych zamiast klasycznego widma amplitudowego wprowadza się gęstość widmową mocy (PSD), która określa, jak energia lub moc procesu rozkłada się w funkcji częstotliwości. Zgodnie z twierdzeniem Wienera–Chinczyna, gęstość widmowa mocy jest transformatą Fouriera funkcji autokorelacji.
Taki opis jest szczególnie ważny w zastosowaniach praktycznych, ponieważ wiele rzeczywistych sygnałów – takich jak szumy w układach elektronicznych, sygnały biomedyczne (np. EEG), czy zakłócenia w kanałach telekomunikacyjnych – ma charakter losowy. Analiza w ujęciu statystycznym pozwala wówczas lepiej zrozumieć własności sygnału, szacować stosunek sygnału do szumu, projektować odpowiednie filtry oraz oceniać właściwości układów i kanałów transmisyjnych.
W niniejszym rozdziale przedstawione zostaną podstawowe zagadnienia związane z analizą częstotliwościową sygnałów losowych. Omówione zostaną pojęcia procesów losowych, stacjonarności i ergodyczności, a także metody estymacji podstawowych parametrów procesów losowych. Szczególną uwagę poświęcono gęstości widmowej mocy jako kluczowemu narzędziu opisu własności częstotliwościowych sygnałów losowych. Dla lepszego zrozumienia omawianych zagadnień zaprezentowane zostaną liczne przykłady i implementacje w języku Python.
5.1. Procesy losowe
Sygnał losowy można rozumieć jako proces, w którym wartość chwilowa w danym momencie czasu nie jest z góry określona, lecz opisana w sposób probabilistyczny. Aby to formalnie ująć, każdą próbkę sygnału w chwili \( t \) traktujemy jako zmienną losową.
Zmienna losowa to wielkość, która przyjmuje wartości liczbowe w sposób losowy (stochastyczny), ale z góry określonym prawdopodobieństwem. Jeżeli zamiast jednej zmiennej losowej rozpatrujemy rodzinę zmiennych losowych uporządkowanych w czasie, otrzymujemy proces losowy \( X(t) \). Każda chwila czasu \( t=t_0 \) odpowiada wówczas innej zmiennej losowej \( X(t_0) \), a ich zbiór opisuje cały sygnał losowy. W praktyce proces losowy można traktować jako zbiór wielu możliwych realizacji przebiegu sygnału, z których każda jest jedną realizacją tego procesu. Taki opis umożliwia przejście od analizy chwilowych wartości sygnału do badania jego własności statystycznych, uśrednionych w czasie lub po realizacjach.
Klasycznym przykładem sygnałów o charakterze losowym są sygnały biomedyczne, takie jak EEG (elektroencefalograficzne) oraz EMG (elektromiograficzne). EEG rejestruje bioelektryczną aktywność mózgu przy pomocy elektrod umieszczonych na powierzchni skóry głowy. Charakteryzuje się bardzo niską amplitudą i dużą zmiennością, oraz charakterystycznymi rytmami częstotliwościowymi, związanymi z określonymi stanami pracy mózgu (np. rytmy alfa, beta, theta). Z kolei EMG odzwierciedla aktywność elektryczną mięśni szkieletowych, powstającą w wyniku sumowania potencjałów czynnościowych włókien mięśniowych. Jest to sygnał o wyższych amplitudach niż EEG, a jego przebieg zależy od rodzaju i siły skurczu mięśnia. Oba sygnały traktuje się jako procesy losowe, gdyż ich przebieg chwilowy jest trudny do przewidzenia, natomiast możliwe jest badanie ich statystycznych własności.
Opisem probabilistycznym zmiennej losowej \( X(t_0) \) w chwili \( t=t_0 \) jest m.in. dystrybuanta (CDF, ang. Cumulative Distribution Function), którą definiuje się jako:
czyli prawdopodobieństwo, że w chwili \( t_0 \) amplituda sygnału nie przekroczy wartości \( x \).
Dystrybuanta opisuje, jak rozkładają się wartości amplitud sygnału losowego w danym momencie czasu. Dzięki temu można np. wyznaczać progi detekcji sygnału, badać rozkład amplitud w sygnałach biomedycznych czy porównywać różne stany organizmu (np. sen vs. czuwanie w EEG) w kategoriach zmian rozkładów prawdopodobieństwa.
Dystrybuanta daje pełny opis rozkładu wartości sygnału w wersji skumulowanej – informuje o łącznym prawdopodobieństwie wystąpienia wszystkich wartości mniejszych od wartości \( x \). W praktyce, wygodniej jest analizować nie tyle wartości skumulowane, co dokładne prawdopodobieństwo pojawienia się amplitud w pobliżu danej wartości. Tę rolę spełnia funkcja gęstości prawdopodobieństwa (PDF, ang. Probability Density Function):
czyli pochodna dystrybuanty. Funkcja gęstości prawdopodobieństwa pozwala wskazać, które amplitudy sygnału występują najczęściej, a które są rzadkie, co ma kluczowe znaczenie w analizie różnych procesów losowych.
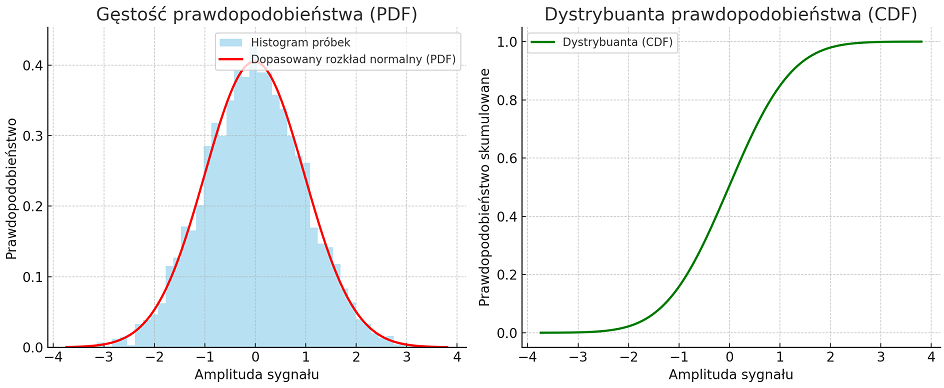
5.2. Stacjonarność i ergodyczność
Procesy losowe są fundamentem teorii sygnałów w przypadkach, gdy analizowane sygnały wykazują charakter stochastyczny. W przetwarzaniu sygnałów szczególnie istotne jest statystyczne opisanie ich właściwości, ponieważ pojedyncza realizacja sygnału może nie dawać pełnego obrazu jego zachowania. Do podstawowych właściwości statystycznych procesu losowego należą wartość oczekiwana oraz wariancja.
Dla ciągłego procesu losowego \( X(t) \) wartość oczekiwana w czasie \( t \) to średnia po wszystkich możliwych realizacjach procesu w tym momencie czasu:
gdzie funkcja gęstości prawdopodobieństwa \( f_{X(t)}(x) \) zależy od wartości zmiennej losowej \( x \) w danym czasie \( t \). W praktyce wartość oczekiwana pozwala określić typowy poziom sygnału w danym punkcie czasowym.
Wariancja opisuje rozrzut wartości sygnału wokół średniej w danym momencie czasu:
Wariancja pozwala określić, jak bardzo realizacje procesu różnią się od wartości oczekiwanej. Wariancja jest istotna przy analizie zmian amplitudy sygnału oraz przy wyznaczaniu pasma dynamiki szumu w systemach przetwarzania sygnałów. W praktyce wygodniej jest korzystać z pojęcia odchylenia standardowego:
Z pojęciem wartości oczekiwanej związana jest funkcja autokorelacji:
gdzie dwuwymiarowa funkcja gęstości prawdopodobieństwa \( f_{X(t_1),X(t_2)}(x_1,x_2) \) zależy od wartości zmiennych losowych \( x_1 \) i \( x_2 \) w czasie, odpowiednio \( t_1 \) i \( t_2 \).
Analogicznie można zdefiniować funkcję kowariancji:
Obydwie charakterystyki opisują liniową zależność między wartościami procesu losowego \( X(t) \) w dwóch różnych momentach czasu. Autokorelacja uwzględnia średnią sygnału, natomiast kowariancja mierzy zależności próbek po usunięciu wpływu wartości średniej, pokazując jedynie zmienną część procesu. Do podstawowych własności funkcji kowariancji należą:
- \( C_{XX}(t_1,t_2)=C_{XX}(t_2,t_1) \) – symetria,
- \( C_{XX}(t,t)=\sigma^2_X(t) \) – kowariancja w tym samym punkcie czasowym to wariancja.
Zauważmy, że kowariancja podaje siłę zależności, ale jej wartość zależy od jednostek i wariancji sygnału. Dokonując normalizacji funkcji kowariancji, otrzymamy unormowaną kowariancję, czyli współczynnik korelacji:
którego wartości mieszczą się w przedziale \( [-1,1] \). Wtedy otrzymujemy relatywną siłę korelacji, niezależnie od jednostek lub amplitudy sygnału.
Analiza zmienności powyższych parametrów sygnałów w czasie prowadzi do rozróżnienia procesów stacjonarnych i niestacjonarnych. Proces stacjonarny w szerokim sensie (WSS, ang. Wide-Sense Stationary) to taki proces losowy, którego średnia i wariancja nie zależą od czasu:
co ułatwia modelowanie i analizę w dziedzinie częstotliwości.
Proces niestacjonarny charakteryzuje się tym, że \( \mu_X(t) \) i/lub wariancja \( \sigma^2_X(t) \) zmieniają się w czasie. W praktyce oznacza to, że właściwości sygnału obserwowane w jednym przedziale czasowym niekoniecznie opisują zachowanie sygnału w innym przedziale. Przykładem może być sygnał EEG, którego amplituda i średnia zmieniają się w zależności od stanu pacjenta.
Na rys. 5.2 pokazano przykładowy przebieg procesu stacjonarnego i niestacjonarnego – ze względu na średnią i wariancję. Pierwszy wykres wskazuje na proces o stałej średniej i wariancji. Na drugim wykresie, proces niestacjonarny ma coraz większe odchylenia od zera, gdyż jego wariancja rośnie. Ostatni wykres ilustruje proces niestacjonarny ze względu na liniowo rosnącą średnią.
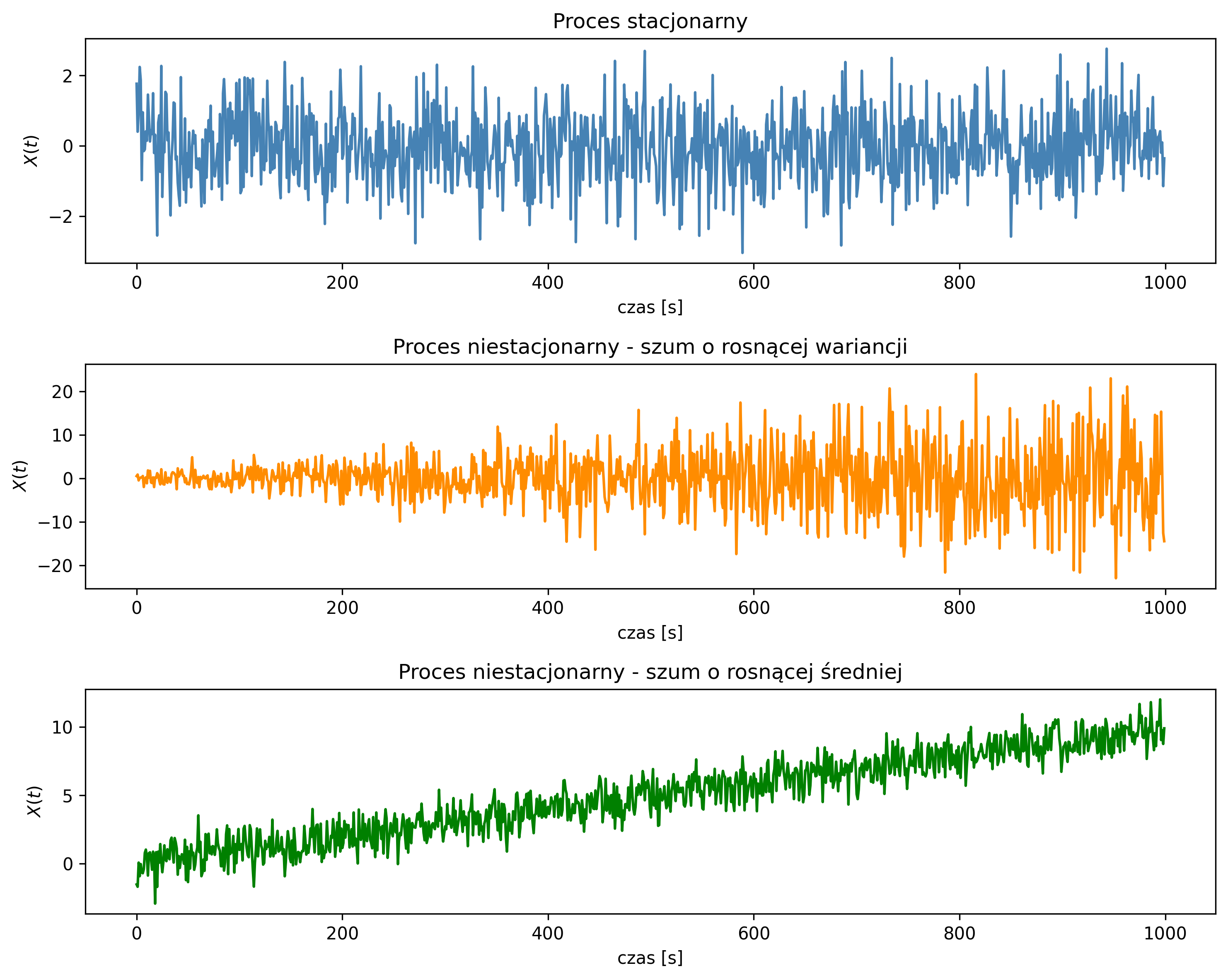
Dla procesu stacjonarnego funkcja autokorelacji i kowariancji oraz współczynnik korelacji zależą tylko od różnicy czasu \( \tau=t_2-t_1 \):
gdzie \( C_{XX}(0)=\sigma^2_X \) jest wariancją sygnału. Zauważmy, że jeśli \( \mu=0 \), to \( R_{XX}(\tau)=C_{XX}(\tau) \). W przypadku \( \tau=0 \):
Funkcja korelacji zawiera w sobie informację o wariancji i średniej realizacji procesu losowego. Z wykresu funkcji korelacji możemy odczytać, jak długo sygnał pamięta swoje przeszłe wartości, czy zależność jest dodatnia czy ujemna, czy proces ma składowe okresowe, a także łatwo porównywać różne sygnały, niezależnie od ich skali:
- siła zależności między próbkami sygnału:
- \( |R_{XX}(\tau)|\approx 1 \) – wartości w momentach \( t \) i \( t+\tau \) są silnie powiązane,
- \( |R_{XX}(\tau)|\approx 0 \) – brak związku,
- kierunek zależności:
- \( R_{XX}(\tau)>0 \) – dodatnia korelacja,
- \( R_{XX}(\tau)<0 \) – ujemna korelacja,
- okresowość:
- jeśli funkcja \( R_{XX}(\tau) \) jest okresowa, to proces ma składowe harmoniczne,
- czas korelacji (czas pamięci procesu):
- im szybciej funkcja \( R_{XX}(\tau) \) opada do zera, tym proces ma krótszą „pamięć” (próbki szybko stają się niezależne).
Przykładem procesu losowego, w którym kolejne próbki są niezależne od pozostałych i mają zerową korelację, jest biały szum. W przetwarzaniu sygnałów biały szum jest często używany jako model zakłóceń losowych lub model sygnału testowego dla systemów liniowych. Do jego charakterystycznych cech należy brak pamięci – autokorelacja jest prawie zerowa dla wszystkich opóźnień poza zerowym, stąd wartość sygnału w dowolnym czasie nie zależy od wartości przeszłych. Biały szum gaussowski to szczególny przypadek białego szumu, którego próbki mają rozkład normalny (Gaussa). Jest szeroko stosowany w analizie sygnałów i systemów liniowych, zwłaszcza w modelowaniu zakłóceń i w teorii filtrów optymalnych. Zarówno biały szum, jak i biały szum gaussowski są procesami losowymi stacjonarnymi w szerokim sensie, czyli mają stałą wartość oczekiwaną (zwykle przyjmuje się \(0\)) i wariancję.
Na rys. 5.3 pokazano, jak funkcja korelacji ujawnia pamięć sygnału i okresowość. Wykresy sygnału sinusoidalnego, sygnału sinusoidalnego z dodanym białym szumem i samego białego szumu oraz odpowiadające im funkcje korelacji uwidaczniają charakterystyczne cechy ich przebiegów. Rozkład korelacji w czasie pokazuje, jak długo sygnały „pamiętają” swoje wartości. Normalizacja pozwala porównywać sygnały niezależnie od amplitudy.
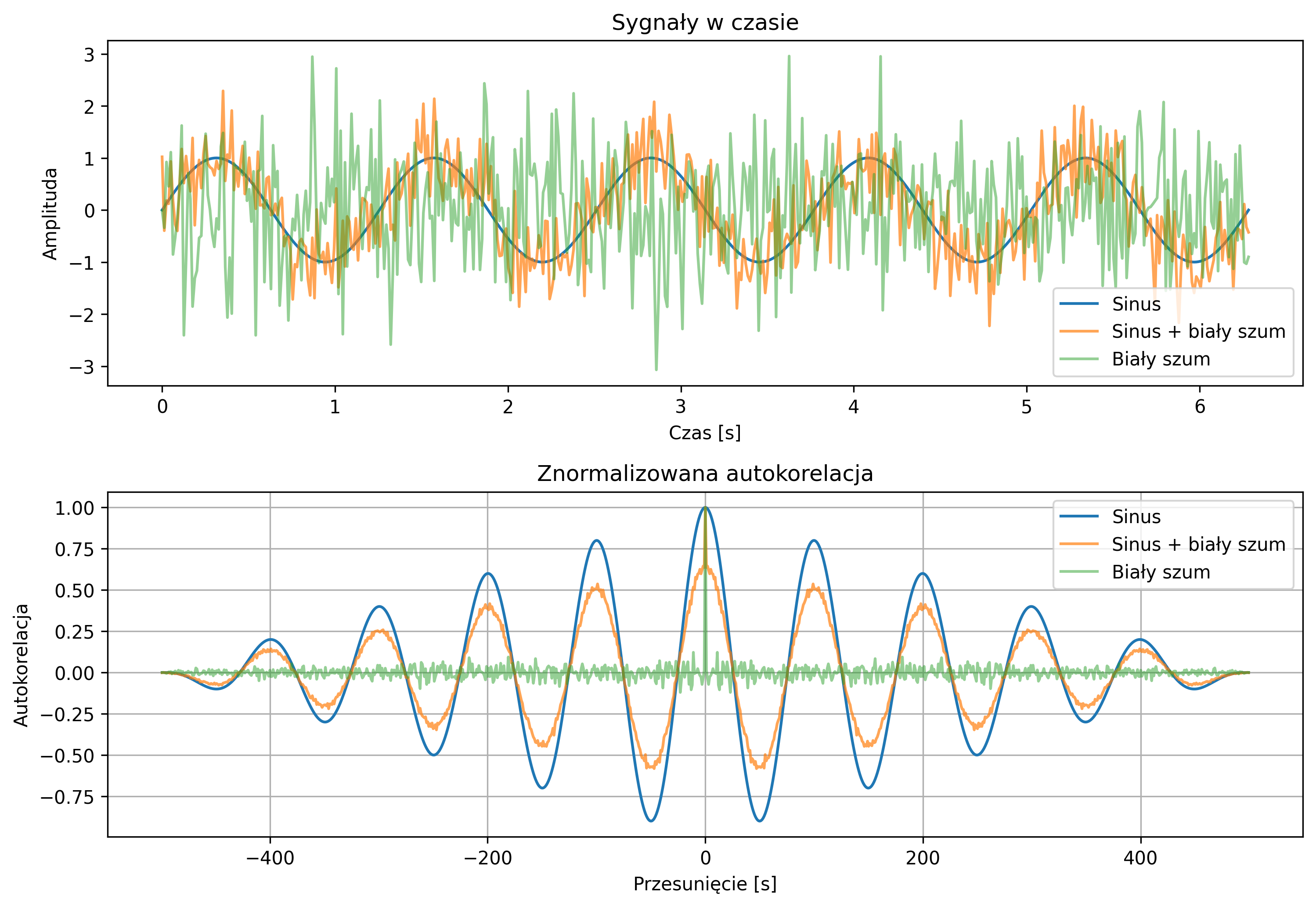
Sygnał sinusoidalny ma wyraźną periodyczną funkcję korelacji – na wykresie pojawiają się maksima i minima lokalne w regularnych odstępach. Oznacza to, że wartości sygnału w określonych przesunięciach są ze sobą silnie powiązane (dodatnio lub ujemnie). Innymi słowy, sygnał „pamięta” swoje przeszłe wartości i ma charakter okresowy. Biały szum ma funkcję korelacji bliską zeru dla wszystkich opóźnień poza zerowym. Wartości próbek są praktycznie niezależne od siebie, a proces nie ma pamięci. Korelacja pokazuje tylko pojedynczy impuls w \( \tau=0 \), czyli sygnał nie zawiera periodyczności. Sygnał sinusoidalny z dodanym białym szumem ma funkcję korelacji, w której nadal widoczne są periodyczne maksima i minima lokalne, jednak są one mniejsze i mniej regularne niż w przypadku czystego sinusa. Oznacza to, że sygnał wciąż zachowuje pewną pamięć swojej struktury okresowej, ale szum częściowo ją „maskuje”, wprowadzając przypadkowe zakłócenia i obniżając poziom korelacji.
Poza stacjonarnością istotnym pojęciem w teorii procesów losowych jest także ergodyczność. Proces losowy jest stacjonarny, gdy jego parametry statystyczne nie zmieniają się w czasie. Jednak w praktyce często dysponujemy tylko jedną długą realizacją procesu i chcielibyśmy z niej oszacować te parametry. Proces losowy \( X(t) \) nazywamy ergodycznym w sensie wartości średniej, jeśli średnia czasowa z jednej realizacji jest równa wartości oczekiwanej:
Proces losowy \( X(t) \) nazywamy ergodycznym w sensie drugiego rzędu, jeżeli jego wartości średnie i korelacje można wyznaczyć na podstawie jednej realizacji w czasie. Oznacza to, że spełnione są zależności:
Oznacza to, że właściwości statystyczne procesu (np. wartość oczekiwana, wariancja, funkcja autokorelacji) można wyznaczyć nie tylko jako średnie po wielu realizacjach procesu (uśrednianie w przestrzeni prawdopodobieństwa), ale także jako średnie wzdłuż jednej, odpowiednio długiej realizacji (uśrednianie w czasie).
W praktyce proces stacjonarny nie zawsze jest ergodyczny. Dla procesów stacjonarnych, które nie spełniają warunku ergodyczności, pojedyncza realizacja procesu nie wystarczy do pełnego odtworzenia charakterystyk – konieczne byłoby dysponowanie wieloma realizacjami. Natomiast w przypadku procesów ergodycznych (np. białego szumu gaussowskiego), analiza jednego długiego przebiegu procesu daje dostęp do wszystkich potrzebnych informacji statystycznych.
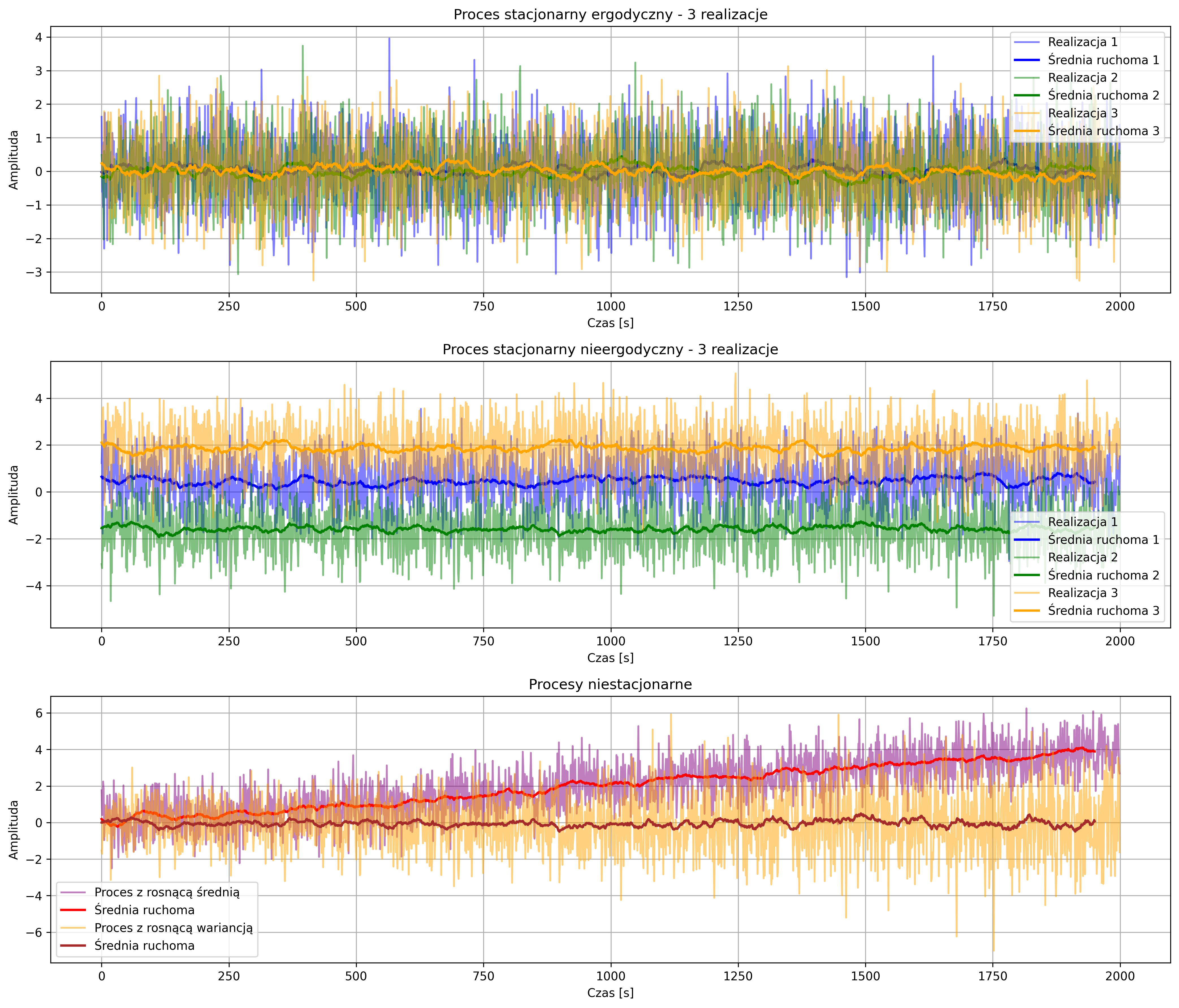
Na pierwszym wykresie rys. 5.4 pokazano trzy niezależne realizacje procesu o stałej średniej i wariancji. Średnie ruchome – wygładzenie sygnału w celu obserwacji lokalnych zmian średniej w czasie (grubsze linie w tych samych kolorach co realizacje) – oscylują wokół tej samej wartości, pokazując, że statystyki jednej realizacji dobrze odzwierciedlają statystyki całego procesu. W przypadku drugiego wykresu, średnie ruchome realizacji pokazują różne poziomy – widać, że statystyki jednej realizacji nie odzwierciedlają statystyk całego procesu, czyli proces nie jest ergodyczny, ale ze względu na stałą wariancję i średnią (każda realizacja procesu z inną, ale stałą średnią) proces jest stacjonarny. Ostatni wykres ilustruje procesy niestacjonarne – ze względu na rosnącą średnią i ze względu na rosnącą wariancję. Średnia ruchoma dla jednego procesu pokazuje wyraźny trend, zaś w przypadku drugiego procesu – pomimo stałości średniej – obserwujemy wzrost zmienności sygnału, co obrazuje brak stacjonarności.
Własność stacjonarności i ergodyczności można również odczytać z wykresu funkcji autokorelacji. W przypadku procesu stacjonarnego funkcja autokorelacji zależy tylko od przesunięcia, a nie od czasu \( t \). Jeśli proces jest stacjonarny i ergodyczny, wszystkie realizacje procesu mają podobną wartość \( R_{XX}(0) \) – średnia i wariancja nie zmieniają się w czasie. Jeśli proces nie jest ergodyczny, realizacje procesu mają różne poziomy przy przesunięciu \( \tau=0 \). Jeśli realizacje mają zarówno różne poziomy, jak i kształty, będziemy mieli do czynienia z procesem niestacjonarnym.
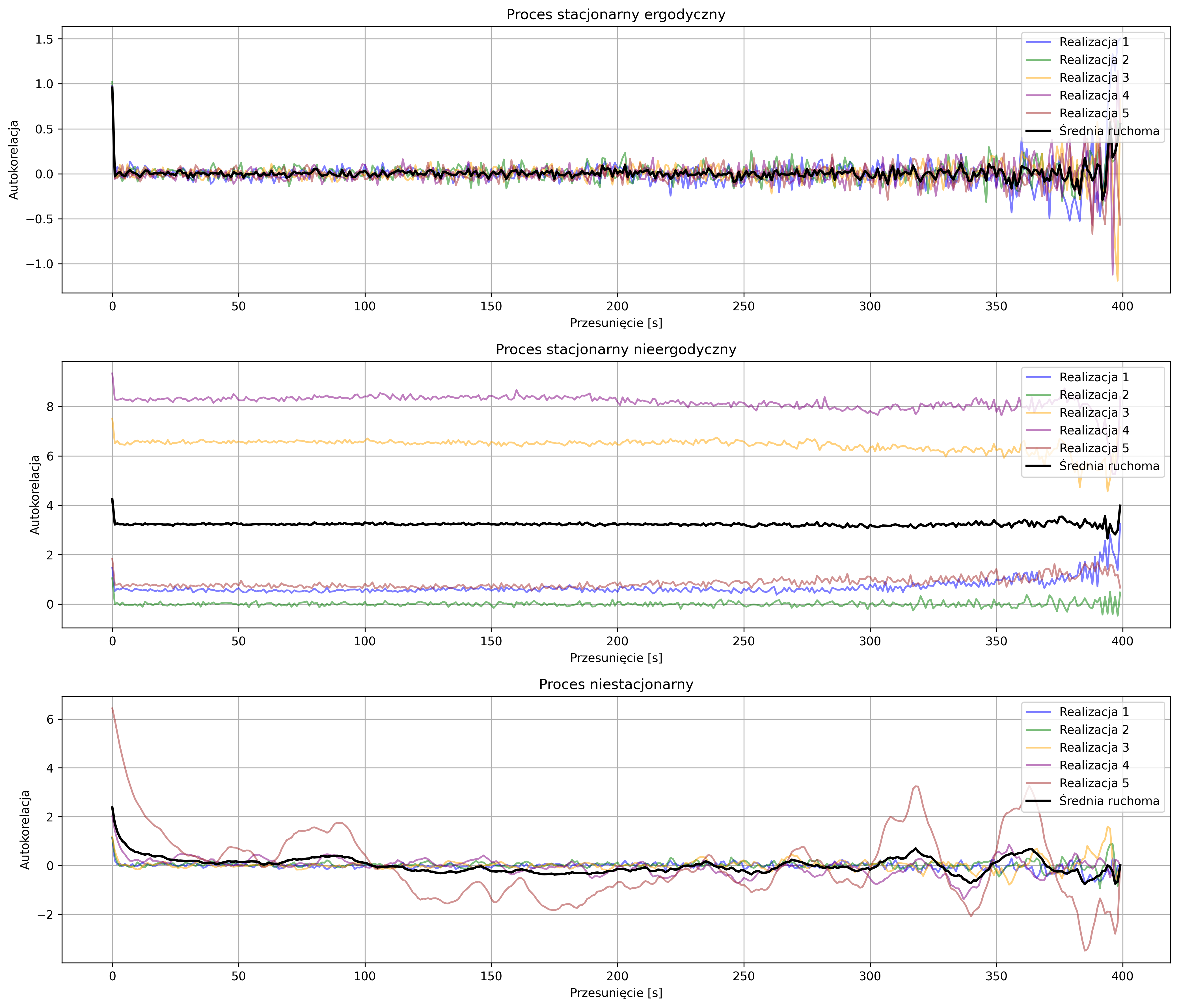
Funkcja autokorelacji stacjonarnego procesu ergodycznego została zilustrowana na górnym wykresie rys. 5.5. Wszystkie realizacje procesu mają podobną wartość \( R_{XX}(0) \) – średnia i wariancja nie zmieniają się w czasie, autokorelacje różnych realizacji procesu nakładają się, a średnia autokorelacja (czarna grubsza linia) dobrze opisuje każdą realizację. W przypadku drugiego wykresu mamy do czynienia z realizacjami, z których każda funkcja autokorelacji ma inną (stałą) średnią – autokorelacje różnych realizacji mają różne poziomy, a średnia autokorelacja nie pokrywa się z żadną realizacją – widać brak ergodyczności. Proces niestacjonarny przedstawiony na ostatnim wykresie charakteryzuje się wyraźnie różnymi kształtami – statystyki zmieniają się w czasie, a średnia autokorelacja nie oddaje właściwości żadnej realizacji.
5.3. Estymacja parametrów procesów losowych
W analizie procesów losowych często nie znamy rozkładu prawdopodobieństwa ani rzeczywistych wartości ich parametrów (np. wartości oczekiwanej, wariancji). Dlatego korzystamy z estymacji, czyli wyznaczania przybliżonych wartości parametrów na podstawie próbek sygnału.
Teoretyczna wartość oczekiwana procesu w czasie ciągłym określona jest jako:
gdzie funkcja gęstości prawdopodobieństwa \( f_{X(t)}(x) \) zależy od wartości zmiennej losowej \( x \) w danym czasie \( t \). Jest to uśrednienie po wielu możliwych realizacjach procesu. W praktyce dysponujemy jedną realizacją sygnału \( X(t) \) obserwowaną w czasie \([0, T]\). Dlatego definiujemy średnią czasową:
Jeżeli proces jest stacjonarny w szerokim sensie i ergodyczny względem wartości średniej, to średnia wyznaczona na podstawie jednej realizacji w czasie jest równa średniej teoretycznej:
Dla procesu losowego w czasie ciągłym, teoretyczna wariancja określona jest jako:
Jeżeli proces jest stacjonarny w szerokim sensie oraz ergodyczny względem wartości średniej i autokorelacji, to wariancja wyznaczona na podstawie jednej realizacji w czasie jest równa wariancji teoretycznej:
W analizie rzeczywistych sygnałów losowych, proces w czasie ciągłym \( X(t) \) jest obserwowany jedynie w dyskretnych chwilach czasu:
gdzie \( T \) oznacza okres próbkowania, a \( f_s = \frac{1}{T} \) to częstotliwość próbkowania. W wyniku próbkowania otrzymujemy proces dyskretny:
Jeżeli proces \( X[n] \) jest stacjonarny w szerokim sensie i ergodyczny względem wartości średniej i autokorelacji, to jego własności statystyczne można oszacować na podstawie jednej realizacji:
Wartości te stanowią estymatory wartości oczekiwanej i wariancji procesu losowego \( X[n] \). W praktyce oznacza to, że do wyznaczenia średniej procesu i rozrzutu procesu wokół średniej nie potrzeba wielu realizacji – wystarczy jedna dostatecznie długa obserwacja w czasie. Jest to warunek umożliwiający analizę widmową procesów losowych.
Na rysunku 5.6 przedstawiono przebieg jednej realizacji stacjonarnego procesu gaussowskiego \( N(2,3^2) \). Dla tej realizacji dokonano estymacji wartości oczekiwanej oraz wariancji procesu. Estymowana wartość oczekiwana \( \hat{\mu}_{X} \approx 2.06 \) odpowiada w przybliżeniu wartości teoretycznej \( \mu = 2 \). W przypadku estymatora wariancji \( \hat{\sigma}^2_{X} \) otrzymano wartość \(8.63\), co również jest zbliżone do wartości teoretycznej \( \sigma^2 = 9 \).
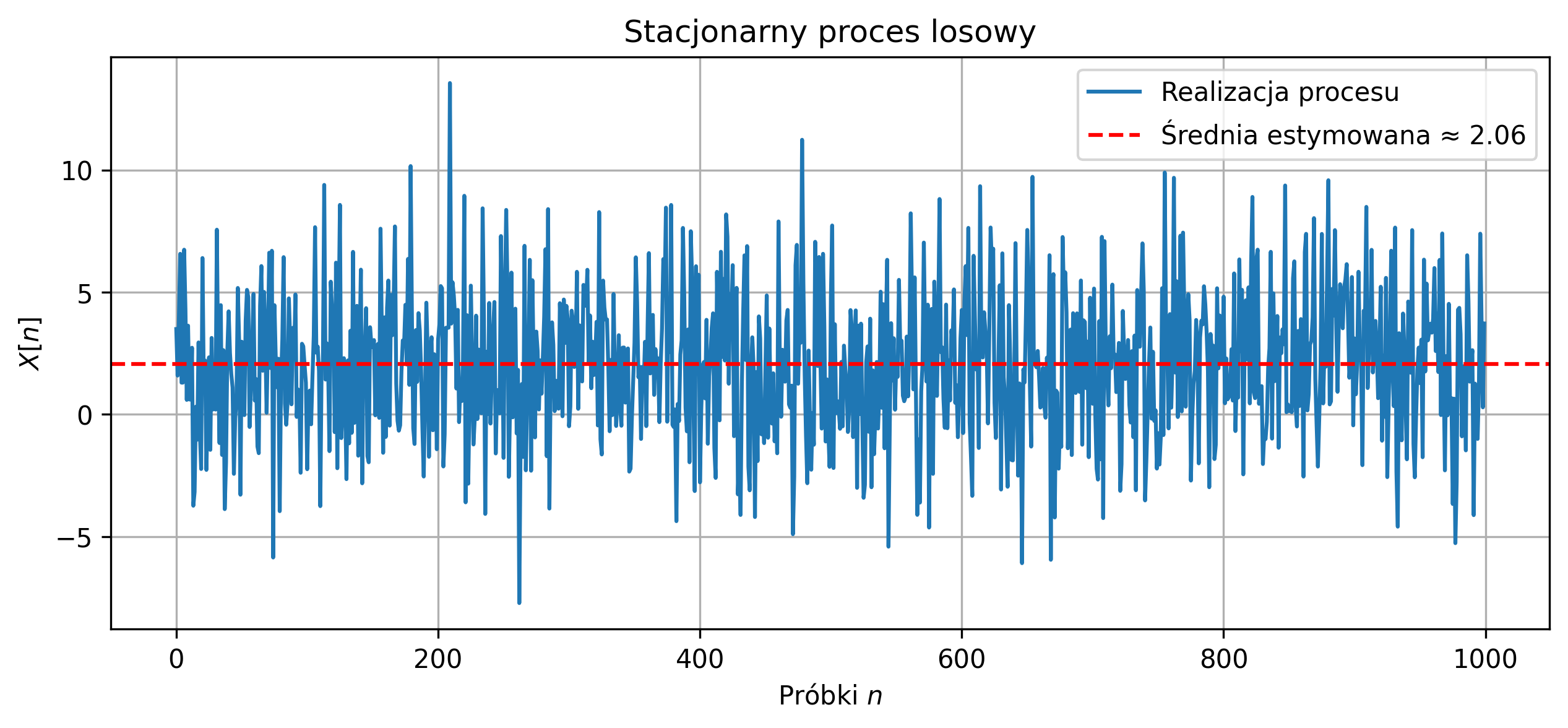
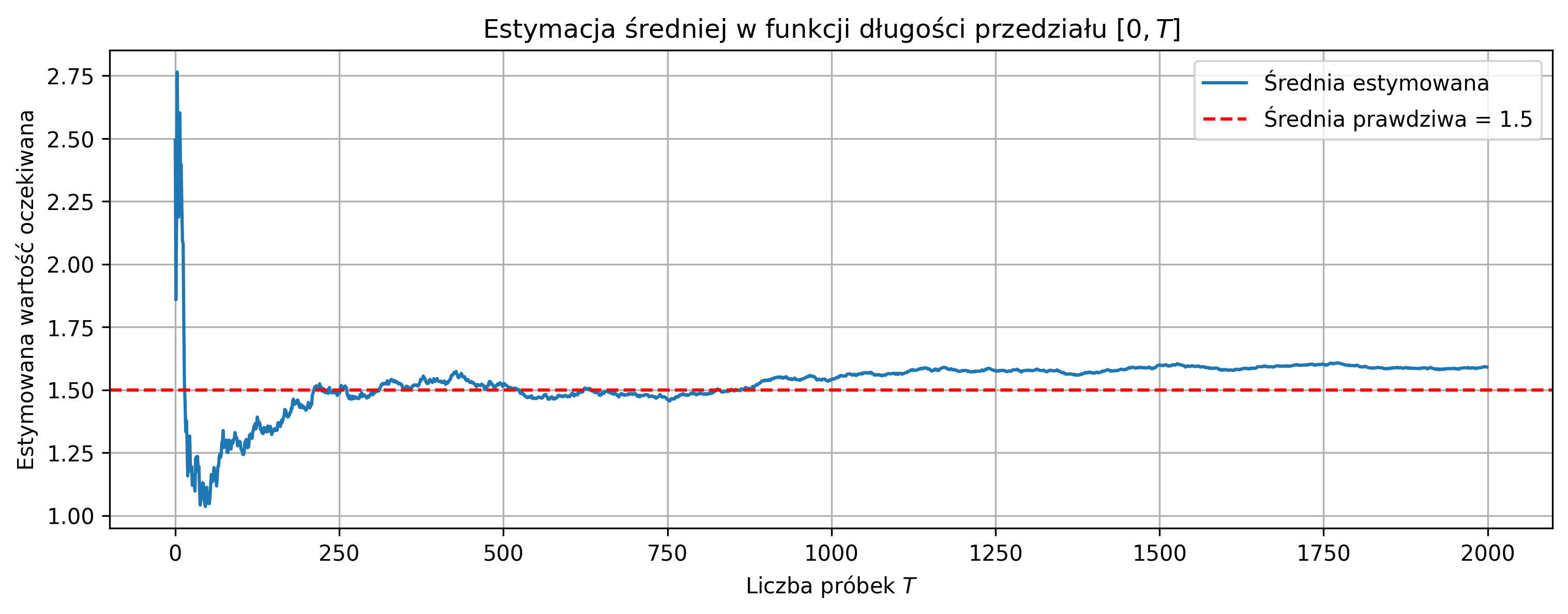
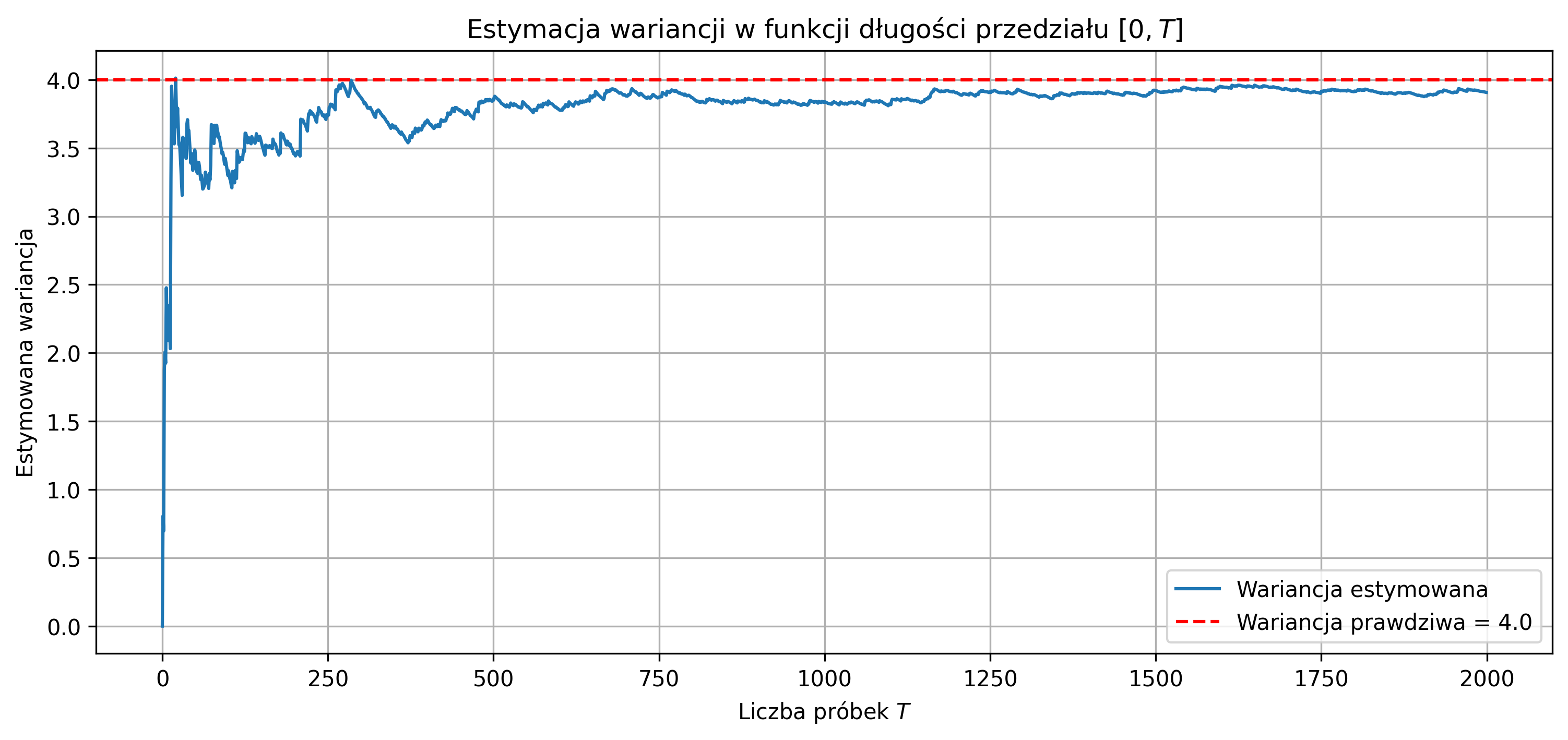
W przypadku, gdy założenia stacjonarności i ergodyczności są złamane, klasyczne estymatory wartości oczekiwanej i wariancji z jednej realizacji nie powinny być stosowane. Na rys. 5.9 i 5.10 zilustrowano proces z trendem średniej – średnia rośnie w czasie, stąd estymator z jednej realizacji nie odzwierciedla wartości typowej procesu, bo proces nie jest stacjonarny. Drugi proces ma zmienną wariancję w czasie (\( \hat{\sigma}^2_X \approx 33.28 \)), więc estymator wariancji z jednej realizacji jest zawodny. Zauważmy, że linia średniej estymowanej nie leży w „środku” sygnału przez cały czas.
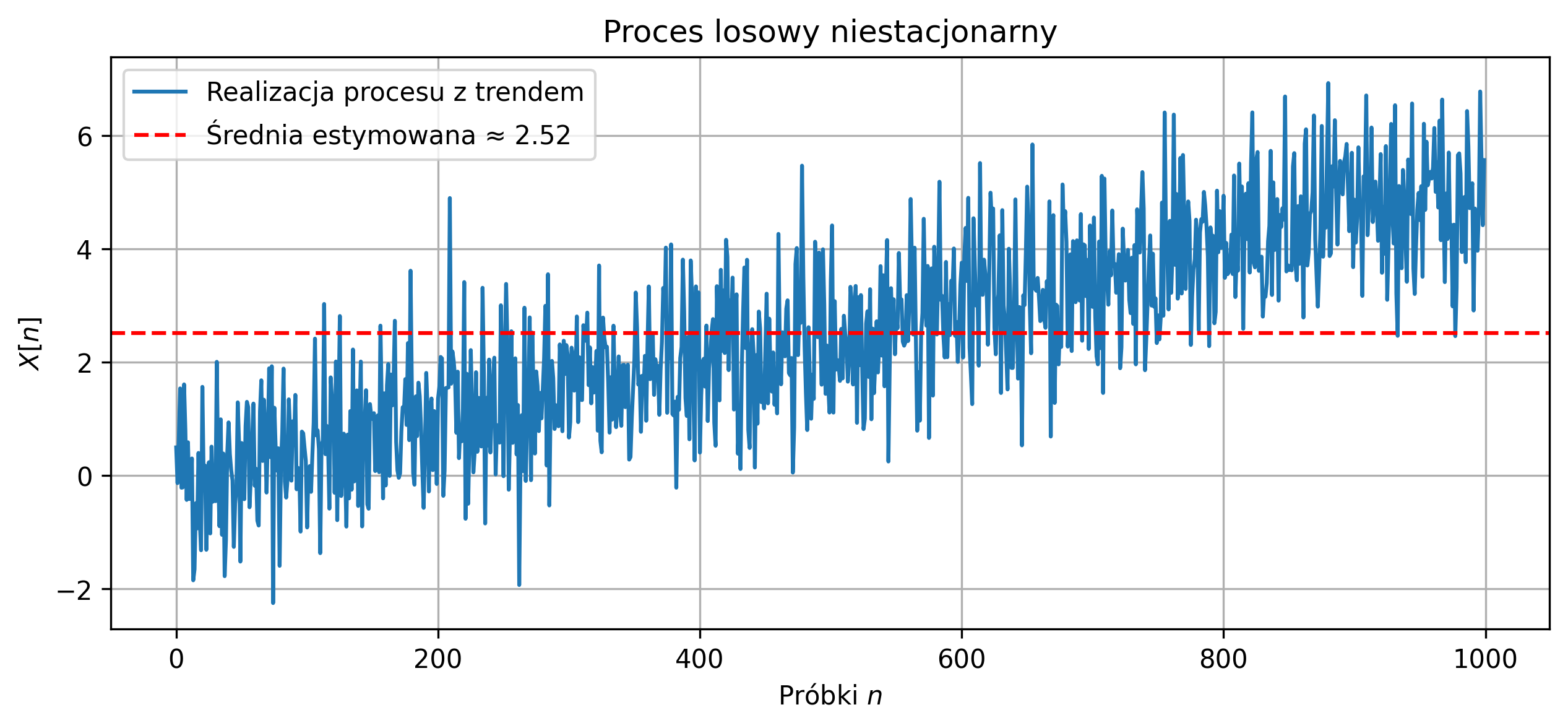
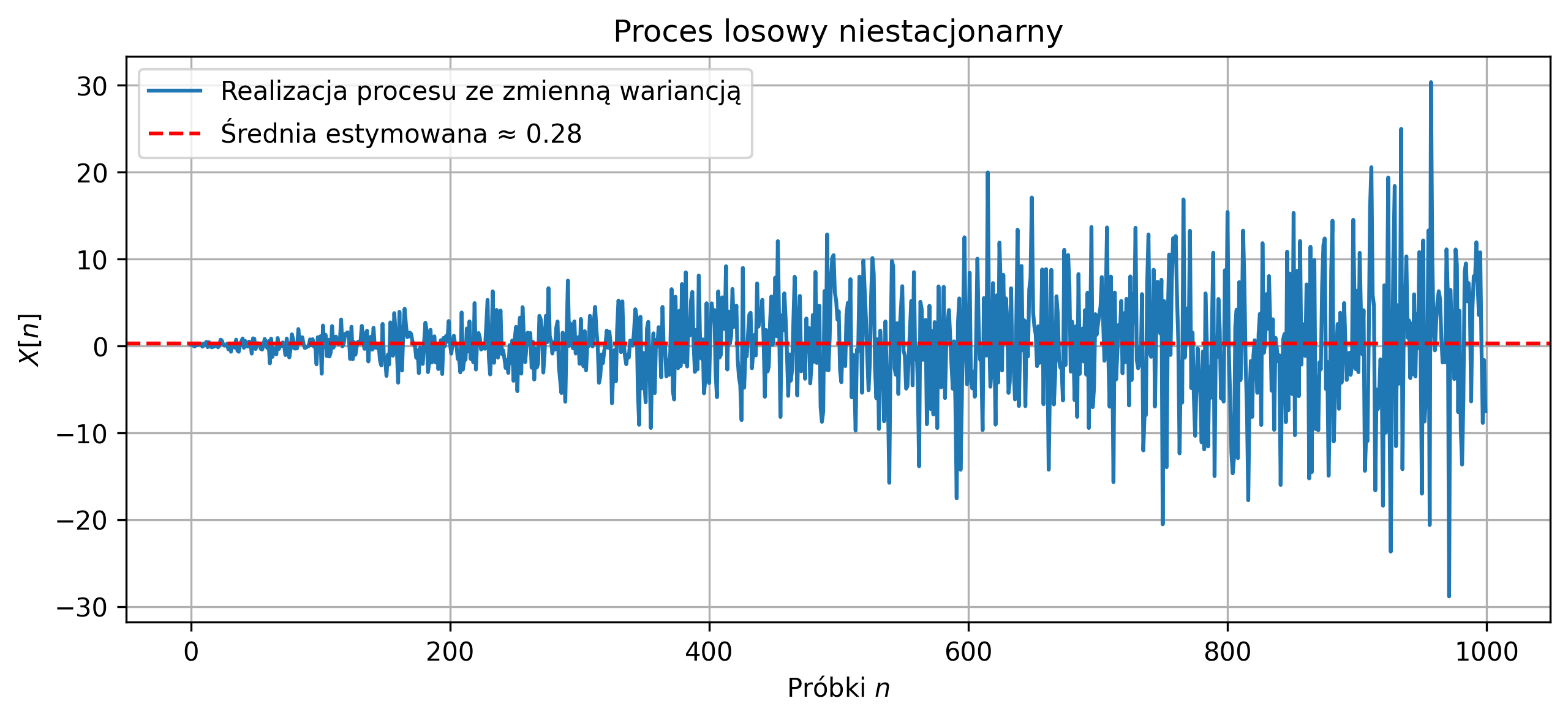
Z pojęciem wartości oczekiwanej związana jest teoretyczna funkcja autokorelacji, która opisuje zależność pomiędzy wartościami procesu losowego \( X(t) \) w dwóch różnych chwilach czasu \( t \) oraz \( t+\tau \). W przypadku procesu w czasie ciągłym definiuje się ją jako wartość oczekiwaną iloczynu:
Dla procesu stacjonarnego w szerokim sensie funkcja ta zależy jedynie od przesunięcia \( \tau \), a nie od konkretnego momentu \( t \):
Jeżeli proces jest dodatkowo ergodyczny względem autokorelacji, to funkcję tę można oszacować z jednej realizacji procesu, uśredniając iloczyny przesuniętych wartości w czasie:
Dla procesu dyskretnego \( X[n] \) funkcja autokorelacji ma postać:
a jej estymator z jednej realizacji (dla \( N \) próbek) zapisuje się jako:
W praktyce, gdy wartość oczekiwana procesu nie jest znana, stosuje się estymator funkcji autokorelacji w postaci:
gdzie \(\hat{\mu}\) jest estymowaną wartością średnią.
Wartość \( \hat{R}_X[0] \) odpowiada wariancji sygnału:
Na rys. 5.11 przedstawiono przebieg jednej realizacji stacjonarnego procesu gaussowskiego \( N(0,1) \). Dla tej realizacji dokonano estymacji funkcji autokorelacji. Dla białego szumu autokorelacja dla \( k = 0 \) jest w przybliżeniu równa wariancji \( \sigma^2 = 1 \), zaś autokorelacja dla \( k > 0 \) jest w przybliżeniu równa \(0\). Widoczny jest efekt ergodyczności – z jednej realizacji można oszacować funkcję autokorelacji procesu stacjonarnego.
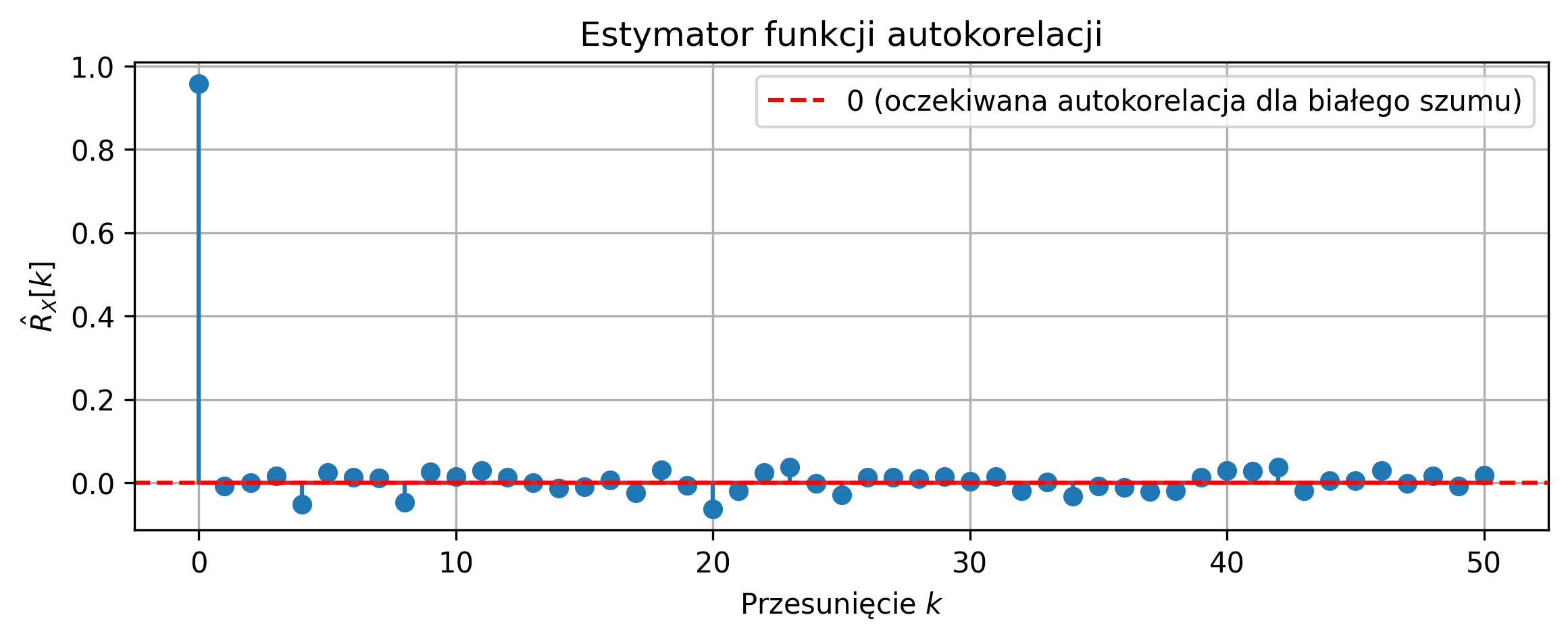
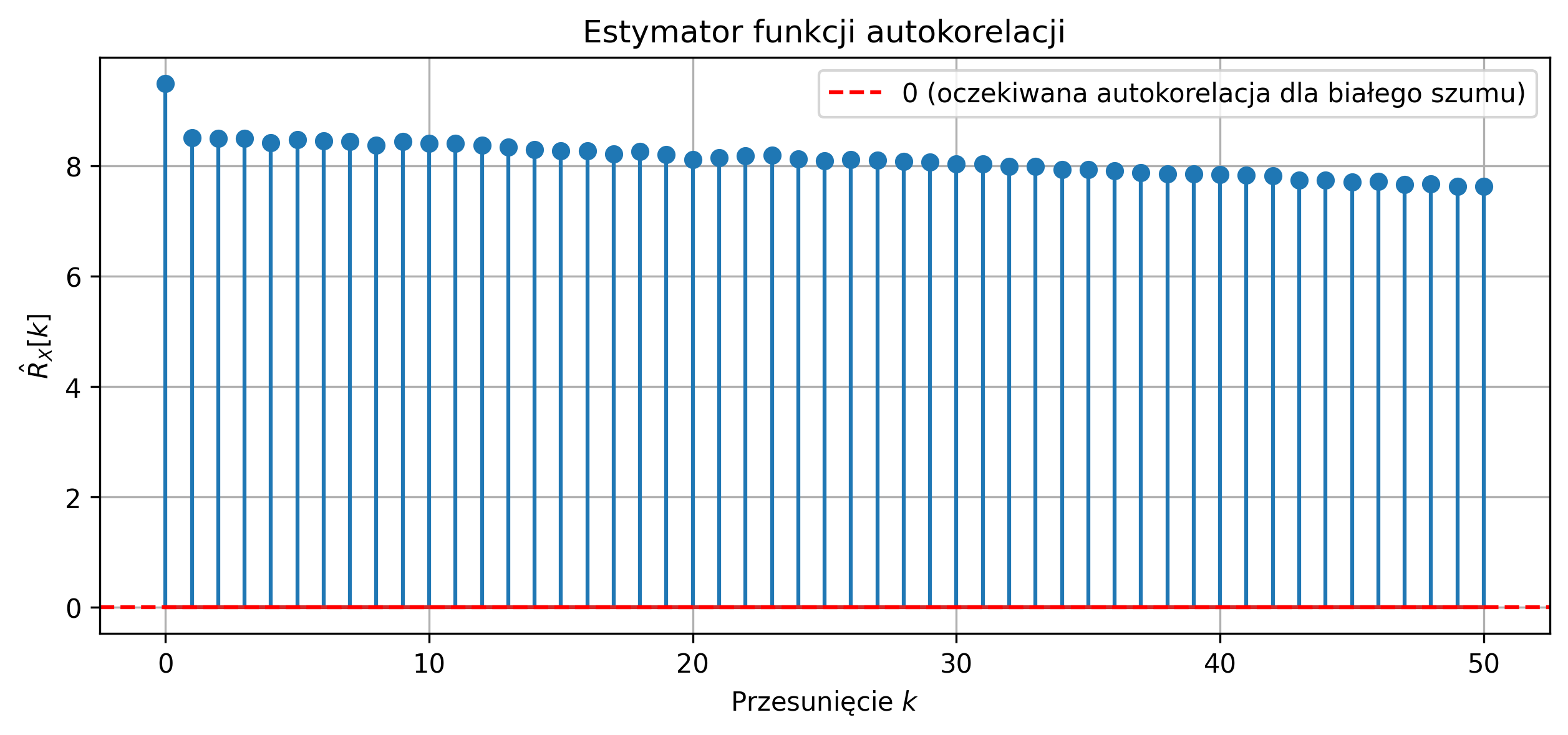
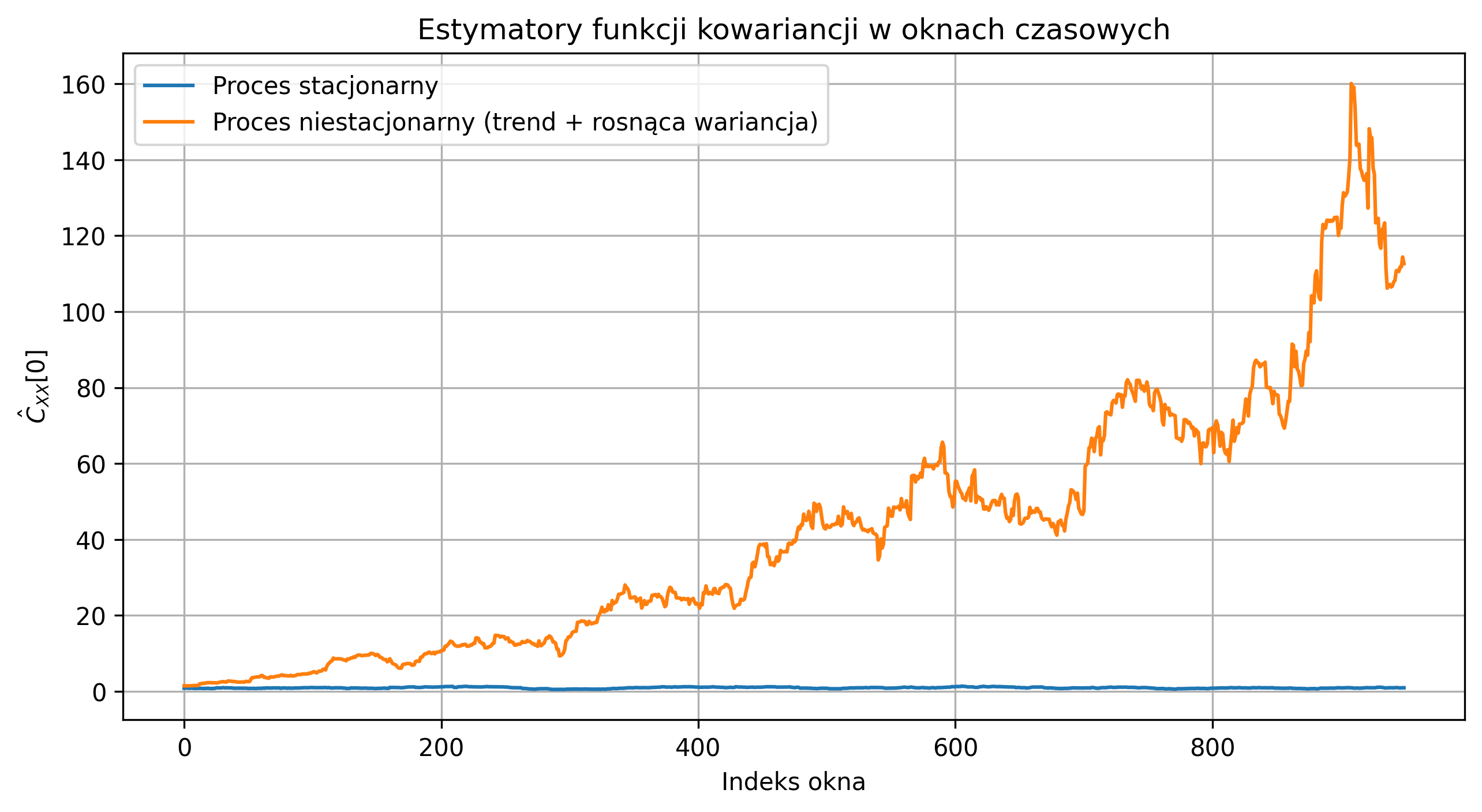
Estymacja kowariancji jest podstawą analizy widmowej sygnałów losowych, ponieważ funkcja autokorelacji jest bezpośrednio związana z gęstością widmową sygnału (poprzez transformację Fouriera), która zostanie omówiona w rozdziale 5.4.
5.4. Gęstość widmowa mocy
W analizie częstotliwościowej, przedstawiamy widmo amplitudowe, czyli moduł transformaty Fouriera sygnału. W analizie sygnałów losowych lub sygnałów z szumem bardziej istotna jest widmowa gęstość mocy (PSD, ang. Power Spectral Density).
Zgodnie z twierdzeniem Wienera-Chinczyna, dla procesu losowego \( X(t) \), który jest stacjonarny w szerokim sensie, gęstość widmowa mocy jest transformatą Fouriera funkcji autokorelacji:
gdzie \( f \) jest częstotliwością wyrażoną w hercach oraz \( R_{XX}(\tau)=E[X(t)X(t+\tau)] \) Odwrotny związek w dziedzinie czasu jest postaci:
Zaznaczmy, że stacjonarność procesu gwarantuje, że gęstość widmowa mocy istnieje i ma jednoznaczny związek z funkcją autokorelacji – funkcja autokorelacji i gęstość widmowej mocy tworzą parę transformat Fouriera. Oznacza to, że znajomość autokorelacji pozwala wyznaczyć gęstość widmową mocy, która opisuje rozkład mocy sygnału w dziedzinie częstotliwości. W ten sposób przechodzimy od charakterystyki procesu w dziedzinie czasu do opisu w dziedzinie częstotliwości.
Dzięki funkcji autokorelacji możemy ocenić, czy proces „pamięta” swoje przeszłe wartości i jak długo utrzymują się zależności między próbkami sygnału. Z kolei gęstość widmowa mocy pokazuje, jak ta „pamięć” i korelacje w czasie przekładają się na obecność określonych częstotliwości w sygnale, czyli jak moc średnia procesu rozkłada się pomiędzy poszczególne składowe częstotliwościowe.
Dla ciągłych, stacjonarnych procesów ergodycznych średnia po wszystkich realizacjach może być zastąpiona średnią po czasie, co prowadzi do praktycznej definicji PSD jako periodogramu:
gdzie \( x(t) \) jest pojedynczą realizacją procesu, \( E[] \) oznacza wartość oczekiwaną, \( X_T(f) \) jest transformatą Fouriera fragmentu sygnału z przedziału czasowego \( [-T, T] \) (o długości \( 2T \)):
oraz \( X_T^{\ast\mathstrut}(f) \) jest sprzężeniem zespolonym tej transformaty. Dla rzeczywistych procesów ergodycznych wartość oczekiwaną można zastąpić średnią po czasie jednej realizacji, co daje oszacowanie PSD w postaci:
Obliczenie periodogramu sprowadza się to do wyznaczenia kwadratu modułu widma i przedstawia zatem rozkład mocy sygnału w funkcji częstotliwości.
PSD wyrażana jest zazwyczaj w jednostkach mocy na jednostkę częstotliwości, np. w \( \textrm{W}/\textrm{Hz} \), \( \textrm{V}^2/\textrm{Hz} \), co oznacza moc przypadającą na jednostkę szerokości pasma częstotliwości. W przypadku reprezentacji logarytmicznej stosuje się jednostkę \( \textrm{dB}/\textrm{Hz} \), określającą moc w decybelach na jednostkę częstotliwości. Umożliwia to porównywanie mocy różnych składowych częstotliwościowych, szczególnie przydatne w przypadku szumów, zakłóceń i analizy statystycznej sygnałów niestacjonarnych.
Dla procesu dyskretnego \( X[n] \), otrzymanego w wyniku próbkowania procesu ciągłego \( X(t) \) z okresem próbkowania \( T \), definicję teoretycznej gęstości widmowej mocy można zapisać jako:
gdzie \( X_N(f) \) jest dyskretną transformatą Fouriera (DTF) fragmentu sygnału \( x[n] \) o długości \( N \) próbek:
W praktyce, dla jednej realizacji procesu ergodycznego, wartość oczekiwaną można zastąpić średnią po czasie, a estymator gęstości widmowej mocy przyjmuje postać periodogramu:
Ponieważ obliczenia w praktyce wykonuje się dla dyskretnych częstotliwości \( f_k=\frac{k}{N T} \) estymator można zapisać w postaci dyskretnej transformaty Fouriera (DFT):
Na rys. 5.14 przedstawiono estymowaną gęstość widmową mocy (PSD) sygnału, obliczoną metodą periodogramu. W analizie wykorzystano sygnał losowy złożony z dwóch składowych sinusoidalnych o częstotliwościach \(50\) Hz oraz \(200\) Hz, na który nałożono szum biały o niewielkiej mocy:
gdzie \( w(t) \) jest szumem białym o rozkładzie \( N(0,\sigma^2) \). Sygnał został spróbkowany z częstotliwością \( f_s=1000 \) Hz, a długość sygnału \( N = 1024 \) próbek. Analiza widma pozwala ocenić, jak energia (lub moc) sygnału rozkłada się w dziedzinie częstotliwości.
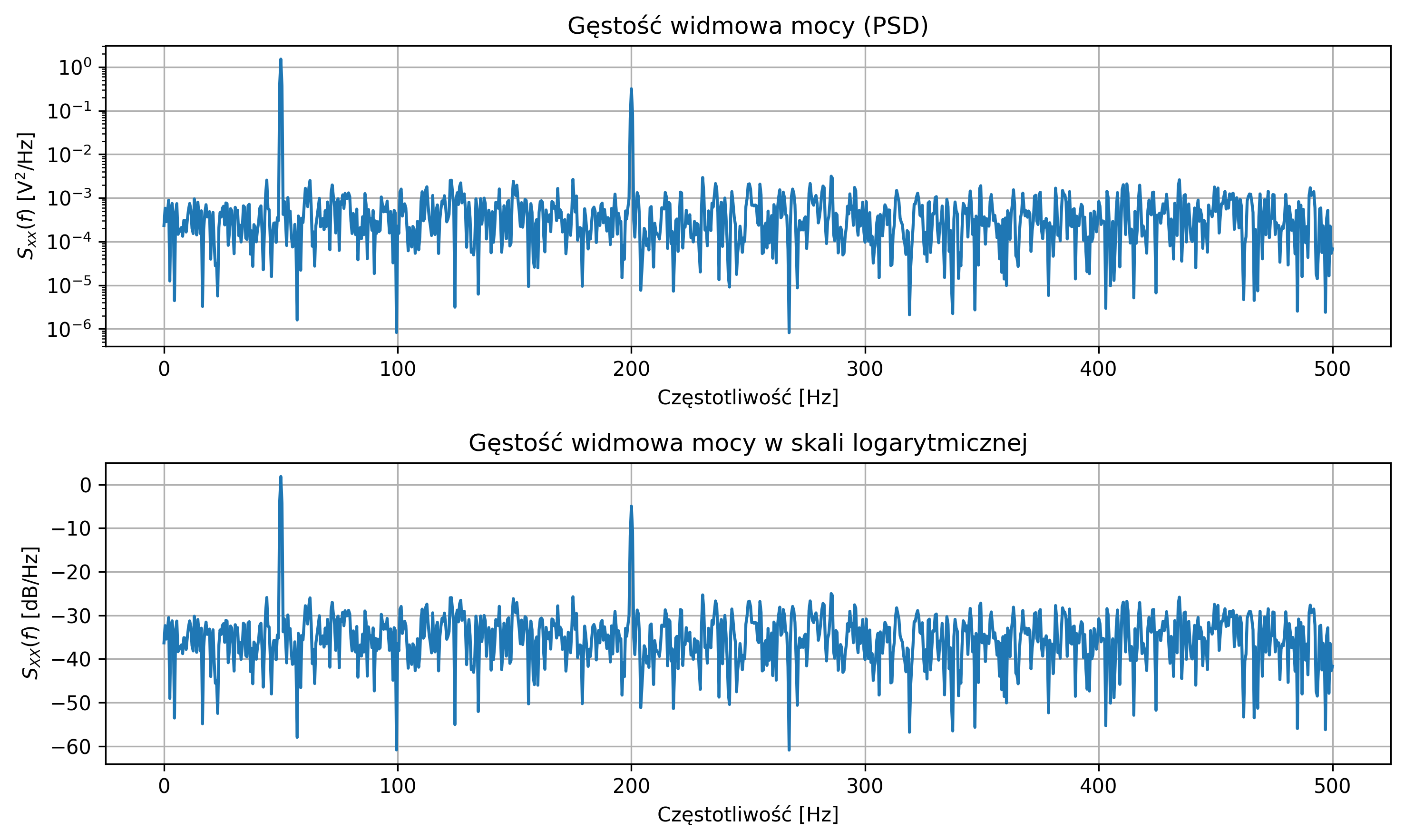
Na górnym wykresie PSD wyrażono w jednostkach liniowych \( \textrm{V}^2/\textrm{Hz} \). Widać wyraźnie dwa lokalne maksima (piki) odpowiadające częstotliwościom \(50\) Hz oraz \(200\) Hz, które odpowiadają składowym sinusoidalnym obecnym w sygnale. Szerokość i wysokość tych pików zależy od długości obserwacji i okna analizy – dłuższy sygnał daje lepszą rozdzielczość częstotliwościową.
Na rysunku 5.15 przedstawiono pięć niezależnych realizacji procesu ergodycznego w czasie. Każda realizacja ma podobny przebieg – sygnał oscyluje wokół zera, a średnia wartość po czasie jest zbliżona do zera. Widoczne jest, że wszystkie realizacje mają podobny charakter losowy, co oznacza, że statystyki procesu (średnia, wariancja) są takie same niezależnie od wybranej realizacji. Oznacza to, że średnia po czasie jest równa średniej po realizacjach, a proces można uznać za ergodyczny.
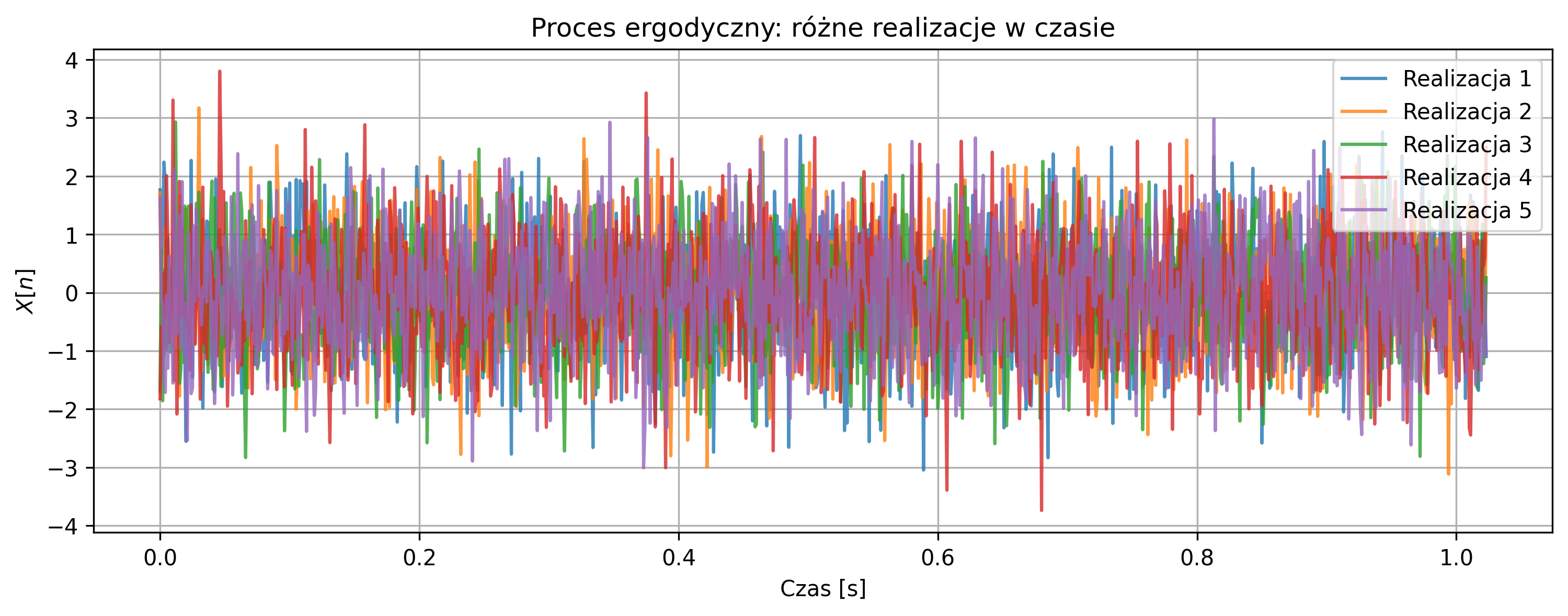
Wykresy periodogramów (oszacowania gęstości widmowej mocy), odpowiadających powyższym realizacjom w czasie, zilustrowano na rysunku 5.16. Widma poszczególnych przebiegów są do siebie podobne i nie zawierają dominującej składowej przy \( f=0 \). Moc jest rozłożona równomiernie w paśmie częstotliwości, co potwierdza stacjonarność i ergodyczność procesu.
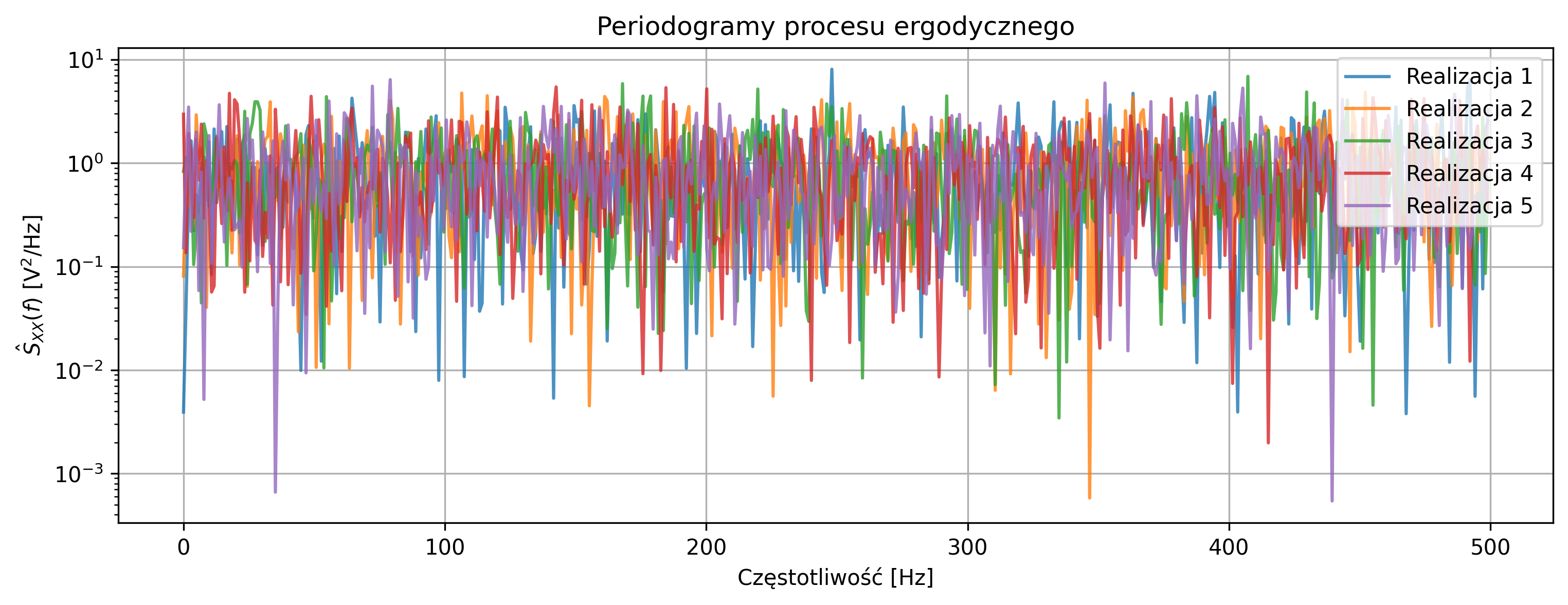
Rozważmy teraz proces losowy zdefiniowany jako
gdzie \( A \) jest losową stałą o rozkładzie \( A \sim N(0,1) \), a \( w[n] \) oznacza biały szum o zerowej wartości oczekiwanej i wariancji \( \sigma_w^2 = 0.01 \). Proces ten jest stacjonarny, gdyż jego własności statystyczne nie zależą od przesunięcia w czasie, jednak nie jest ergodyczny względem wartości średniej, ponieważ każda realizacja ma inne przesunięcie poziomu średniego wynikające z losowej wartości \( A \).
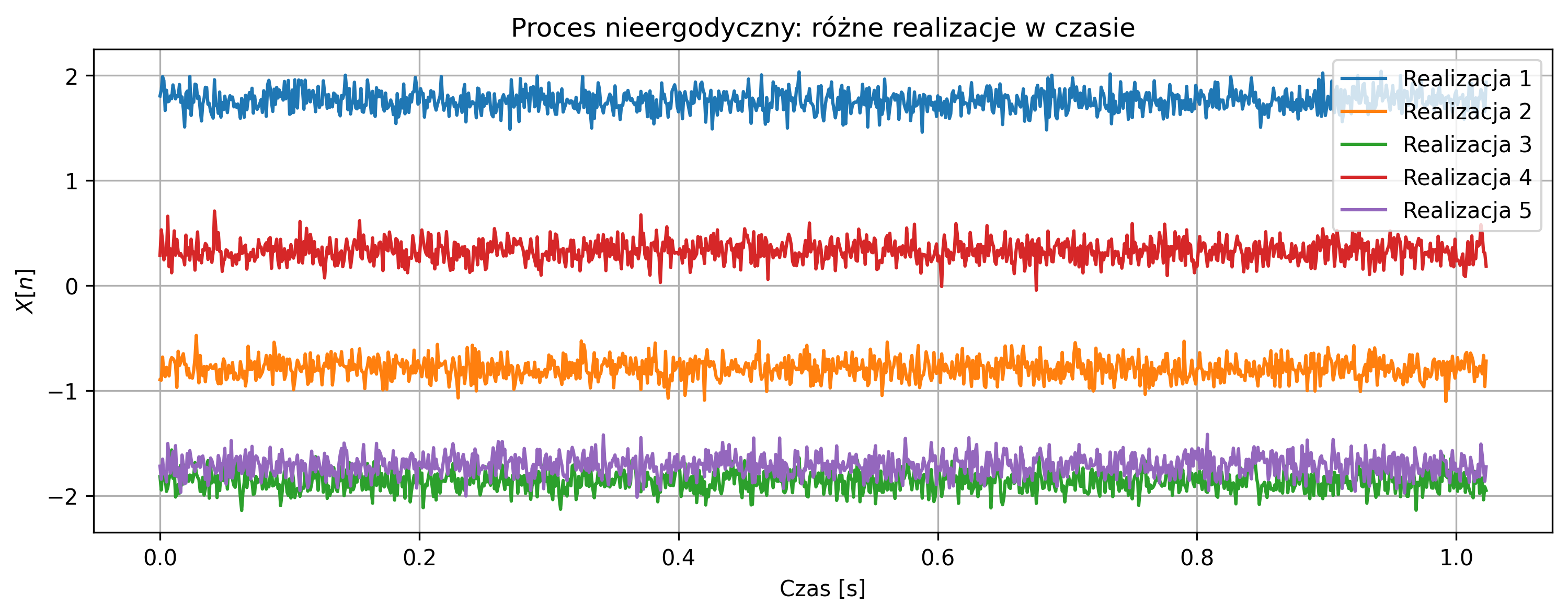
Na rys. 5.17 przedstawiono kilka realizacji tego procesu. Widać, że choć mają podobną strukturę szumową, różnią się poziomem średnim. Oznacza to, że estymacja wartości oczekiwanej na podstawie jednej realizacji nie oddaje rzeczywistej wartości średniej całego procesu. Proces nie jest ergodyczny.
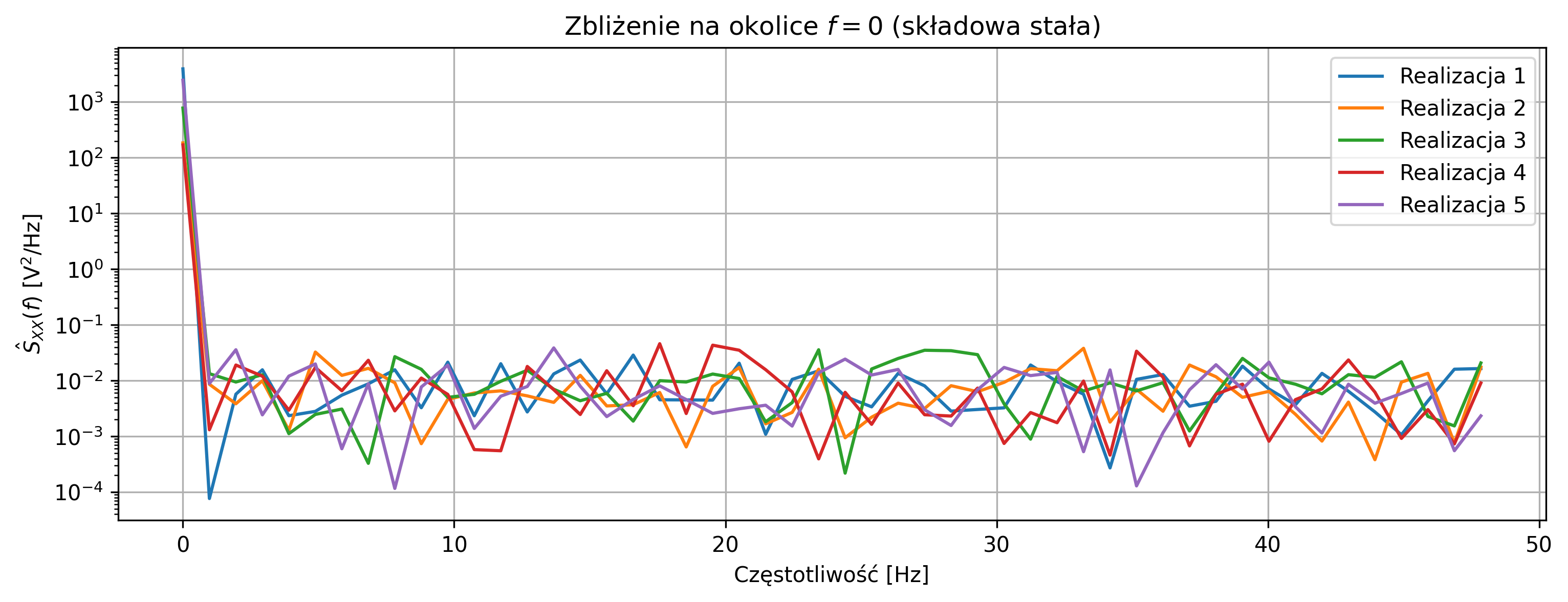
Ponieważ każda realizacja ma inną wartość składowej stałej \( A \), widmo w okolicach częstotliwości \( f=0 \) Hz (składowej stałej) znacząco różni się między realizacjami (rys. 5.18) – powoduje ona bardzo silną koncentrację energii przy częstotliwości \(0\), a wielkość tego piku różni się między realizacjami, bo różna jest wartość \( A^2 \). Widma w pozostałych częstotliwościach są podobne, ponieważ wynikają z białego szumu \( w[n] \). Krzywe periodogramów nie nachodzą na siebie tak regularnie jak w procesie ergodycznym, widmo nie jest stabilne statystycznie – nie da się przewidzieć jednej typowej postaci PSD.
W praktyce obliczeniowej klasyczny periodogram charakteryzuje się dużą wariancją, szczególnie w przypadku procesów losowych, takich jak analizowany proces nieergodyczny. Każda realizacja daje widmo o innej postaci, co utrudnia ocenę rzeczywistej gęstości widmowej mocy sygnału. Aby otrzymać bardziej stabilne i reprezentatywne oszacowanie PSD, stosuje się techniki uśredniania, z których najpopularniejszą jest metoda Welcha (ang. Welch’s Method). Polega ona na podziale sygnału na zachodzące na siebie segmenty, okienkowaniu każdego z nich oraz uśrednieniu uzyskanych periodogramów cząstkowych. Takie podejście znacząco zmniejsza wariancję estymatora PSD kosztem pogorszenia rozdzielczości częstotliwościowej, co w praktyce stanowi korzystny kompromis.
5.5. Procesy losowe i ich parametry w języku Python
Celem poniższych ćwiczeń jest zapoznanie się z podstawowymi narzędziami języka Python, które umożliwiają generowanie, analizę i wizualizację procesów losowych. W szczególności skupimy się na estymacji parametrów statystycznych, takich jak średnia, wariancja, funkcja autokorelacji czy estymatory gęstości widmowej mocy (PSD), a także na analizie ich zachowania dla różnych realizacji procesu – zarówno ergodycznych, jak i nieergodycznych.
Do wykonania ćwiczeń niezbędna jest znajomość podstawowych bibliotek:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
oraz między innymi funkcji:
random.normal # generowanie próbek z rozkładu normalnego (Gaussa) o zadanej średniej i odchyleniu standardowym
correlate # oblicza korelację krzyżową lub autokorelację dwóch sygnałów (wektorów)
mean # obliczanie średniej arytmetycznej elementów tablicy
var # obliczanie wariancji elementów tablicy
std # obliczanie odchylenia standardowego elementów tablicy
convolve # obliczanie splotu (konwolucji) dwóch sygnałów lub wektorów
Wygenerować trzy sygnały dyskretne o długości \( N = 500 \):
- sygnał harmoniczny:
\( x_1[n] = \cos(5 t_n), \)
- sygnał harmoniczny z szumem gaussowskim:
\( x_2[n] = \cos(5 t_n) + 0.5\, w[n] \), gdzie \( w[n] \sim \mathcal{N}(0,1) \),
- biały szum:
\( x_3[n] = v[n],\; v[n] \sim N(0,1). \)
Na wspólnym wykresie czasowym przedstawić przebiegi trzech sygnałów. Na oddzielnym wykresie narysować ich znormalizowane funkcje autokorelacji. Jak zmienia się kształt funkcji autokorelacji po dodaniu szumu do sygnału harmonicznego? Dlaczego autokorelacja białego szumu ma maksimum w punkcie zerowym i szybko wygasa? Jakie cechy autokorelacji pozwalają odróżnić sygnał deterministyczny od stochastycznego?
import numpy as np
import matplotlib.pyplot as plt
# Parametry
N = 500
t = np.linspace(0, 2*np.pi, N)
np.random.seed(0) # dla powtarzalności wyników
# Generacja sygnałów
cos_signal = np.cos(5*t) # czysty kosinus
noisy_signal = cos_signal + 0.5*np.random.randn(N) # kosinus + biały szum
white_noise = np.random.randn(N) # sam biały szum
# Funkcja znormalizowanej autokorelacji
def normalized_correlation(x, y=None):
if y is None:
y = x
corr = np.correlate(x - np.mean(x), y - np.mean(y), mode='full')
corr /= (np.std(x) * np.std(y) * len(x))
return corr
# Obliczamy korelacje
corr_cos = normalized_correlation(cos_signal)
corr_noisy = normalized_correlation(noisy_signal)
corr_noise = normalized_correlation(white_noise)
lags = np.arange(-N+1, N)
# Wykres sygnałów
plt.figure(figsize=(12,8))
plt.subplot(2,1,1)
plt.plot(t, cos_signal, label='Kosinus')
plt.plot(t, noisy_signal, label='Kosinus + biały szum', alpha=0.7)
plt.plot(t, white_noise, label='Biały szum', alpha=0.5)
plt.title('Sygnały w czasie')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.legend()
plt.grid(True)
# Wykres autokorelacji
plt.subplot(2,1,2)
plt.plot(lags, corr_cos, label='Kosinus')
plt.plot(lags, corr_noisy, label='Kosinus + biały szum', alpha=0.7)
plt.plot(lags, corr_noise, label='Biały szum', alpha=0.5)
plt.title('Znormalizowana autokorelacja')
plt.xlabel('Opóźnienie [próbki]')
plt.ylabel('Autokorelacja')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
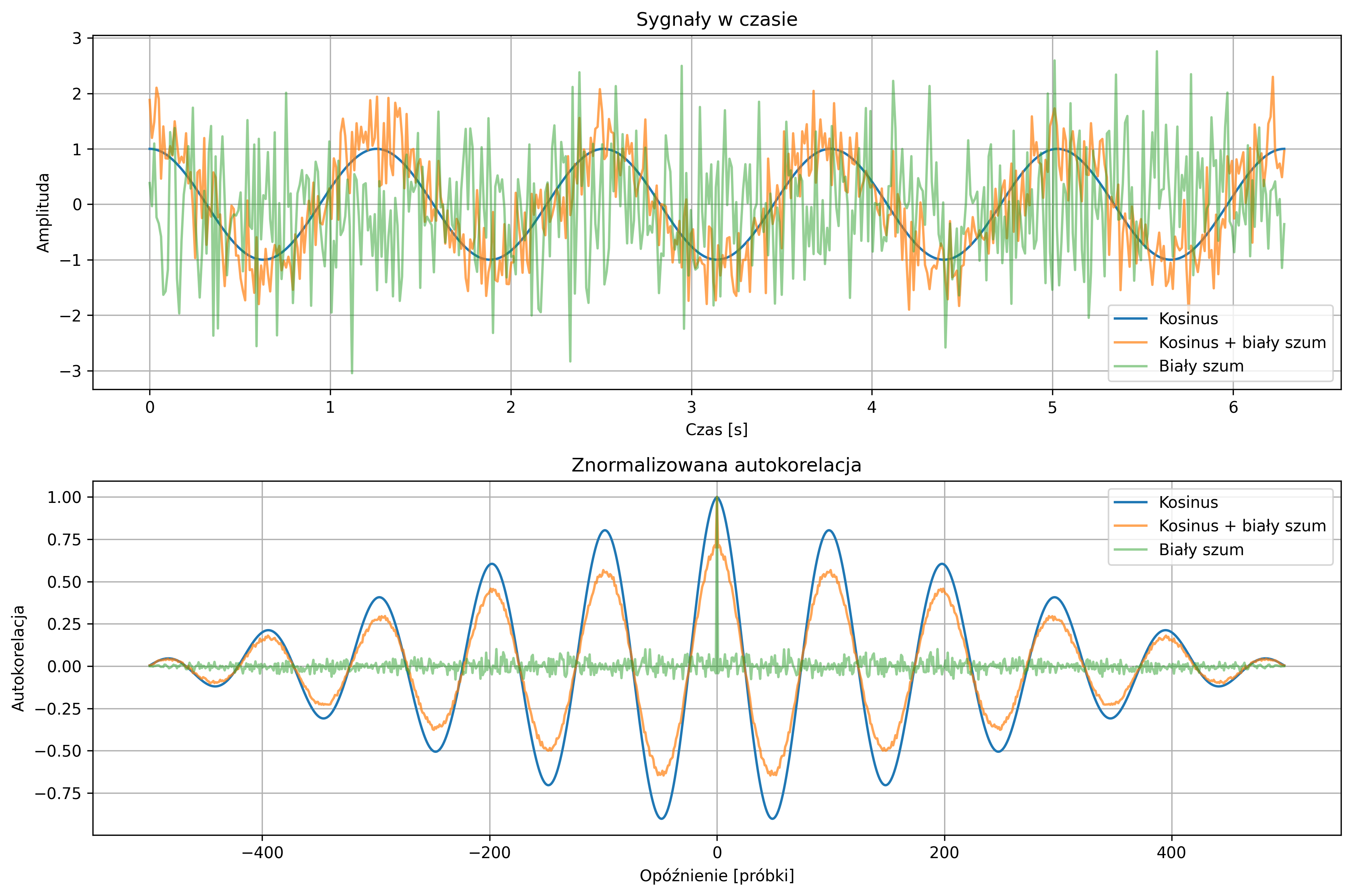
Po dodaniu białego szumu do sygnału kosinusoidalnego obserwujemy, że amplituda funkcji autokorelacji ulega zmniejszeniu, a jej przebieg staje się mniej regularny. Oznacza to, że szum wprowadza losowe zaburzenia, które zakłócają okresową strukturę sygnału deterministycznego.
Autokorelacja białego szumu osiąga maksimum przy zerowym przesunięciu, co wynika z pełnej korelacji sygnału z samym sobą w tym punkcie. Po przesunięciu w lewo lub prawo wartości autokorelacji szybko spadają do zera, ponieważ kolejne próbki szumu są statystycznie niezależne.
Sygnały deterministyczne, takie jak kosinus, mają autokorelacje regularne i często okresowe, co pozwala zauważyć ich powtarzalną strukturę w czasie. Natomiast sygnały stochastyczne, takie jak biały szum, charakteryzują się autokorelacją skoncentrowaną w zerze i bardzo szybko wygasającą poza zerowym przesunięciem, co świadczy o losowym charakterze sygnału.
Analiza autokorelacji jest skuteczną metodą do wykrywania obecności struktury deterministycznej w sygnale, do oceny wpływu zakłóceń losowych oraz pozwala odróżnić sygnały stochastyczne od deterministycznych na podstawie kształtu funkcji autokorelacji.
Wygenerować dwie realizacje sygnałów dyskretnych o długości \( N=2000 \) próbek:
- proces stacjonarny ergodyczny – biały szum gaussowski o średniej \(0\) i wariancji \(1\):
- proces niestacjonarny – biały szum gaussowski z dodanym trendem liniowym (rosnąca średnia w czasie):
Narysować przebiegi czasowe obu procesów na osobnych wykresach, tak aby można było porównać ich charakter. Narysować średnią ruchomą obu realizacji, przy użyciu okna o długości \(50\) próbek. Jakie różnice widać między procesem stacjonarnym a niestacjonarnym? Jak zachowuje się średnia ruchoma dla obu procesów? Jakie cechy procesu ergodycznego pozwalają na jego identyfikację? Dlaczego analiza średniej ruchomej jest pomocna przy wykrywaniu niestacjonarności?
import matplotlib.pyplot as plt
# Parametry
N = 2000 # liczba próbek
t = np.arange(N)
# Proces stacjonarny ergodyczny
np.random.seed(0) # dla powtarzalności wyników
x_stationary = np.random.normal(0, 1, N)
# Proces niestacjonarny
trend = 0.002 * t # trend liniowy (rosnąca średnia)
x_nonstationary = np.random.normal(0, 1, N) + trend
# Wykresy realizacji procesów
plt.figure(figsize=(14,6))
plt.subplot(2,1,1)
plt.plot(t, x_stationary, label='Proces stacjonarny ergodyczny', color='blue')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.title('Proces stacjonarny ergodyczny: biały szum Gaussowski')
plt.grid(True)
plt.subplot(2,1,2)
plt.plot(t, x_nonstationary, label='Proces niestacjonarny', color='darkorange')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.title('Proces niestacjonarny: biały szum z rosnącą średnią')
plt.grid(True)
plt.tight_layout()
plt.show()
# Obliczenie średnich ruchomych
window = 50 # długość okna średniej ruchomej
mean_stationary = np.convolve(x_stationary, np.ones(window)/window, mode='valid')
mean_nonstationary = np.convolve(x_nonstationary, np.ones(window)/window, mode='valid')
# Wykres porównania średnich ruchomych
plt.figure(figsize=(14,4))
plt.plot(mean_stationary, label='Średnia - proces stacjonarny', color='blue')
plt.plot(mean_nonstationary, label='Średnia - proces niestacjonarny', color='darkorange')
plt.xlabel('Czas [s]')
plt.ylabel('Średnia ruchoma')
plt.title('Porównanie średnich ruchomych procesów')
plt.legend()
plt.grid(True)
plt.show()
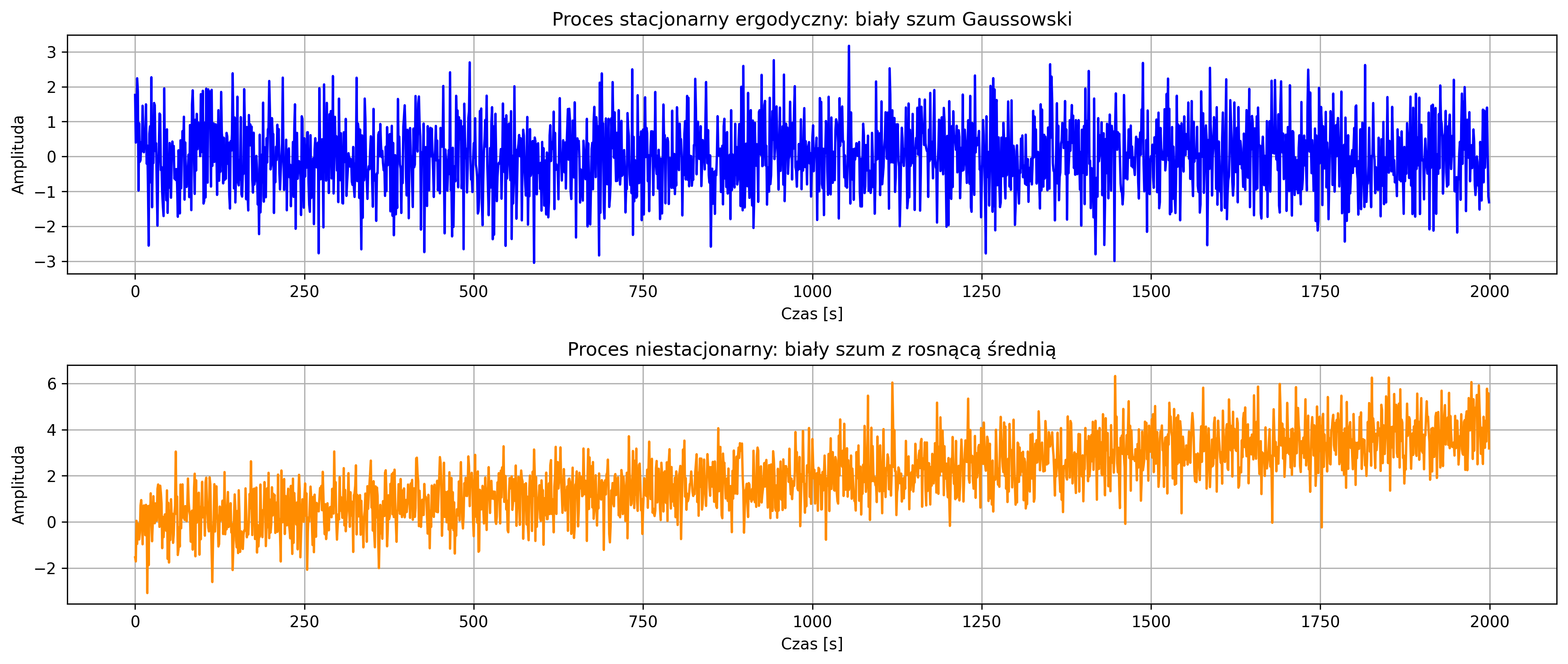
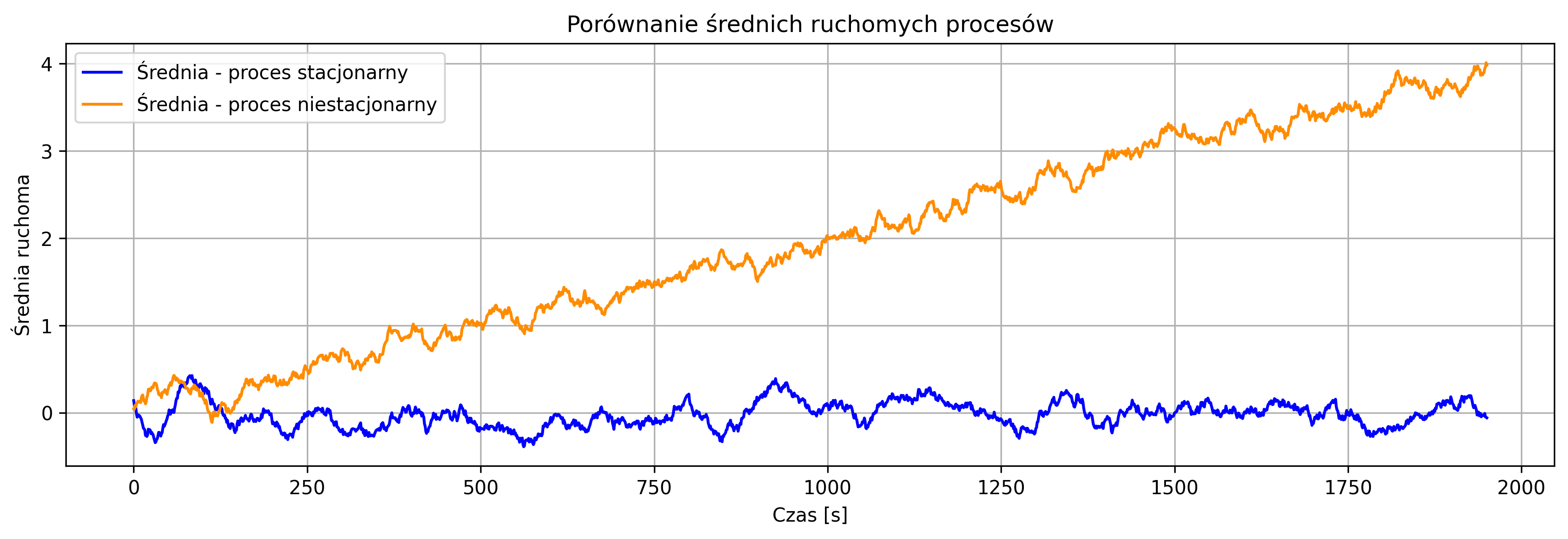
Proces stacjonarny ergodyczny charakteryzuje się losowymi zmianami wokół stałej średniej równej zero. Natomiast proces niestacjonarny wykazuje rosnącą tendencję wartości średniej w czasie, co jest widoczne jako ogólny wzrost przebiegu sygnału.
Średnia ruchoma procesu stacjonarnego oscyluje wokół stałej wartości (blisko zera) i nie wykazuje trendu. W przypadku procesu niestacjonarnego średnia ruchoma systematycznie rośnie, odzwierciedlając narastający trend sygnału.
Proces ergodyczny charakteryzuje się tym, że jego statystyki w czasie (np. średnia i wariancja) są zgodne ze statystykami ensemble, czyli można je oszacować na podstawie pojedynczej realizacji. W szczególności średnia ruchoma nie zmienia się w czasie i przebieg sygnału jest „stabilny” statystycznie.
Analiza średniej ruchomej pozwala zobaczyć zmiany trendu lub odchylenia średniej w czasie. Jeśli średnia ruchoma systematycznie rośnie lub maleje, sygnał jest niestacjonarny, natomiast jeśli oscyluje wokół stałej wartości, sygnał jest stacjonarny. Średnia ruchoma jest więc prostym narzędziem wizualnym do wykrywania niestacjonarności.
Wygeneruj realizację stacjonarnego procesu losowego (biały szum Gaussowski) o zadanej średniej \(\mu_{\text{true}}\) i wariancji \(\sigma_{\text{true}}^2\).
- Oblicz estymatory średniej \(\hat{\mu}\) i wariancji \(\hat{\sigma}^2\) dla całego przebiegu i porównaj je z wartościami prawdziwymi.
- Narysuj przebieg sygnału w dziedzinie czasu i zaznacz linią średnią estymowaną.
- Oblicz estymatory średniej i wariancji w funkcji długości przedziału \([0,n]\) dla \(n=1,2,\dots,N\).
- Narysuj wykresy estymowanej średniej i wariancji w funkcji liczby próbek wraz z liniami wartości prawdziwych \(\mu_{\text{true}}\) i \(\sigma_{\text{true}}^2\).
- Skomentuj, jak estymatory stabilizują się w miarę wzrostu liczby próbek i czy są zgodne z wartościami rzeczywistymi.
import numpy as np
import matplotlib.pyplot as plt
# Parametry procesu losowego
N_total = 2000 # liczba próbek
mu_true = 1.5 # wartość średnia procesu
sigma_true = 2.0 # odchylenie standardowe procesu
np.random.seed(42) # dla powtarzalności
# Generacja realizacji procesu stacjonarnego (biały szum Gaussowski)
X = np.random.normal(loc=mu_true, scale=sigma_true, size=N_total)
# Estymatory dla całego przebiegu
mu_est = np.mean(X)
sigma2_est = np.var(X, ddof=1)
sigma_est = np.sqrt(sigma2_est) # odchylenie standardowe
print(f'Estymowana średnia: {mu_est:.3f} (prawdziwa: {mu_true})')
print(f'Estymowana wariancja: {sigma2_est:.3f} (prawdziwa: {sigma_true**2})')
# Wykres przebiegu sygnału z estymowaną średnią i wariancją
plt.figure(figsize=(12,5))
plt.plot(X, label='Realizacja procesu')
plt.axhline(mu_est, color='r', linestyle='--', label=fr'Średnia estymowana $\approx$ {mu_est:.2f}')
plt.axhline(mu_est + sigma_est, color='g', linestyle=':', label=fr'$\pm$1 odch. std. $\approx$ {sigma_est:.2f}')
plt.axhline(mu_est - sigma_est, color='g', linestyle=':')
plt.title('Stacjonarny proces losowy')
plt.xlabel(rf'Próbki $n$')
plt.ylabel(rf'$X[n]$')
plt.legend()
plt.grid(True)
plt.show()
# Estymatory w funkcji długości podprzedziału [0, n]
mu_est_list = []
sigma2_est_list = []
for n in range(1, N_total+1):
X_sub = X[:n]
mu_est_list.append(np.mean(X_sub))
if n > 1:
sigma2_est_list.append(np.var(X_sub, ddof=1))
else:
sigma2_est_list.append(0.0) # dla n=1 wariancja nie jest zdefiniowana
# Wykres stabilizacji estymowanej średniej
plt.figure(figsize=(12,4))
plt.plot(mu_est_list, label='Średnia estymowana')
plt.axhline(mu_true, color='r', linestyle='--', label=f'Średnia prawdziwa = {mu_true}')
plt.title(rf'Estymacja średniej w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana średnia')
plt.legend()
plt.grid(True)
plt.show()
# Wykres stabilizacji estymowanej wariancji
plt.figure(figsize=(12,4))
plt.plot(sigma2_est_list, label='Wariancja estymowana')
plt.axhline(sigma_true**2, color='r', linestyle='--', label=f'Wariancja prawdziwa = {sigma_true**2}')
plt.title(rf'Estymacja wariancji w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana wariancja')
plt.legend()
plt.grid(True)
plt.show()
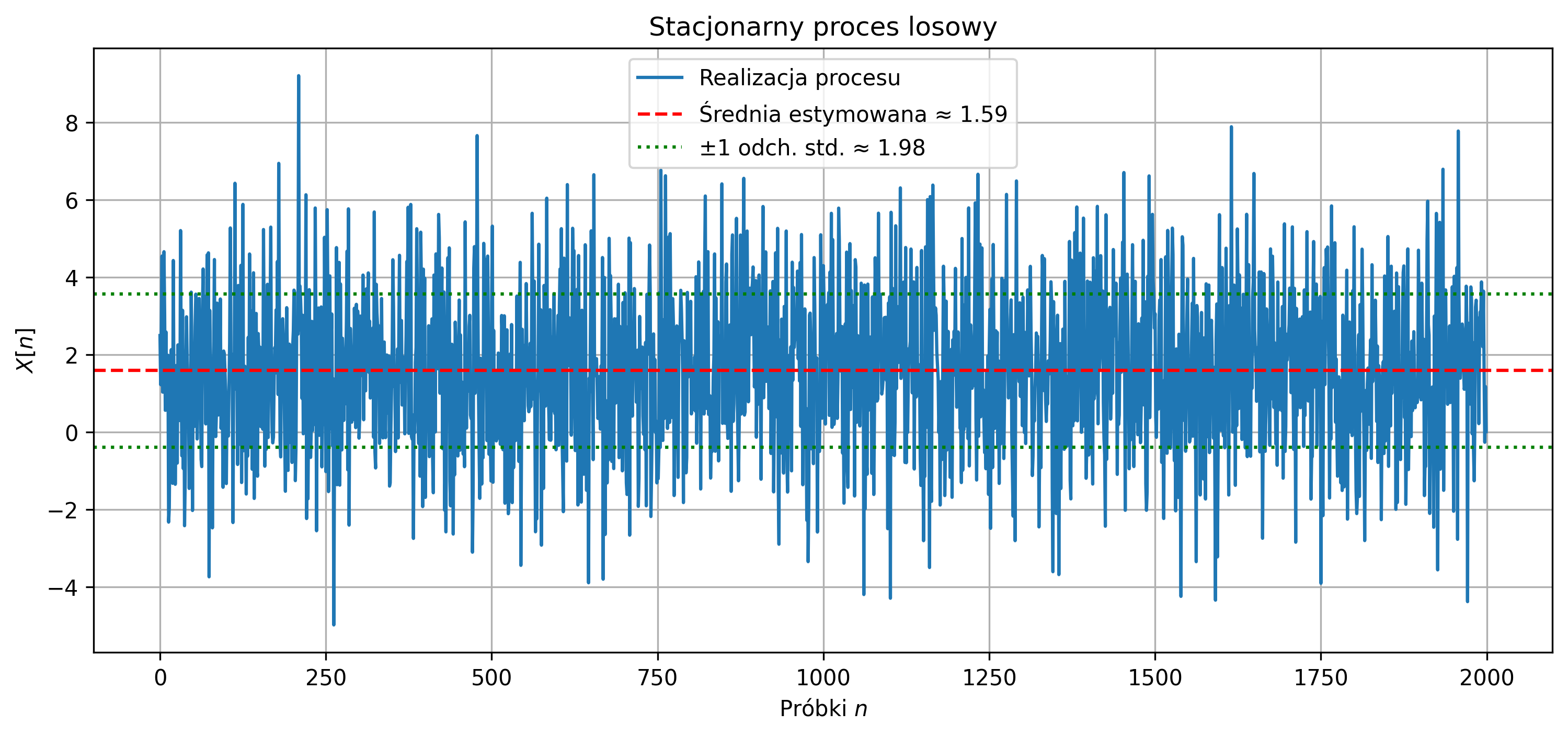
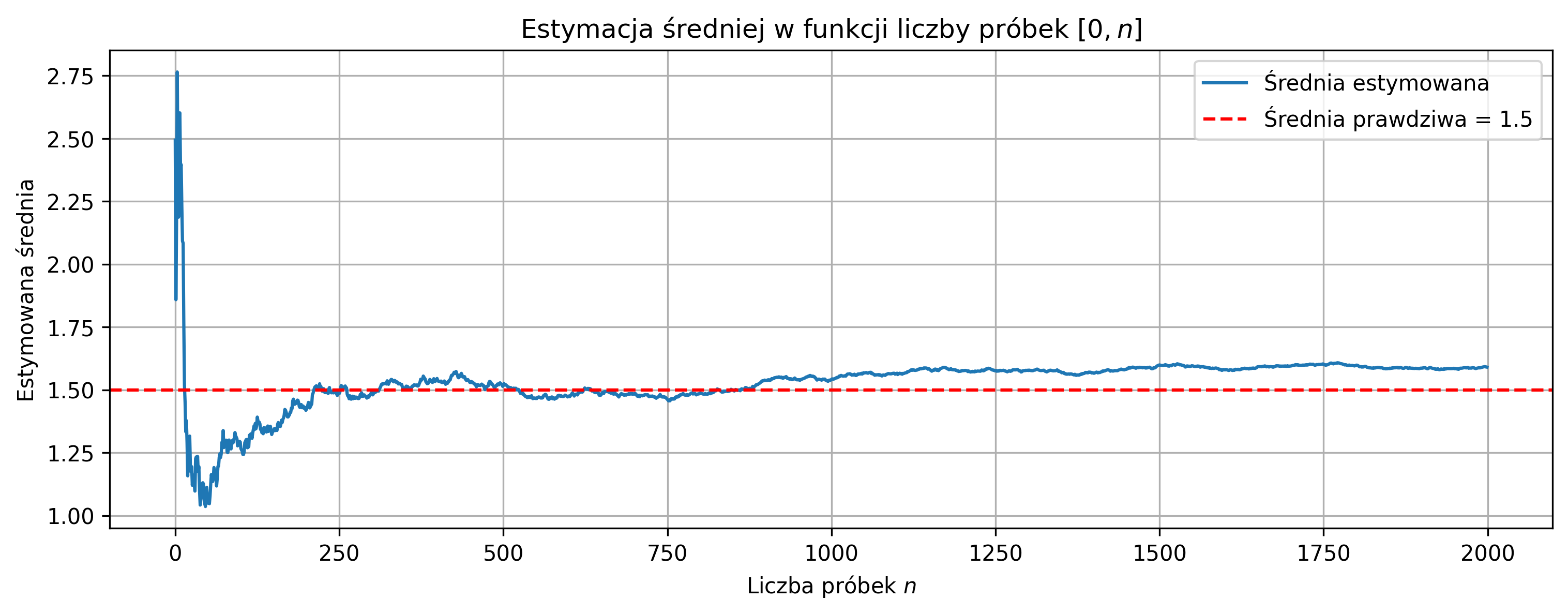
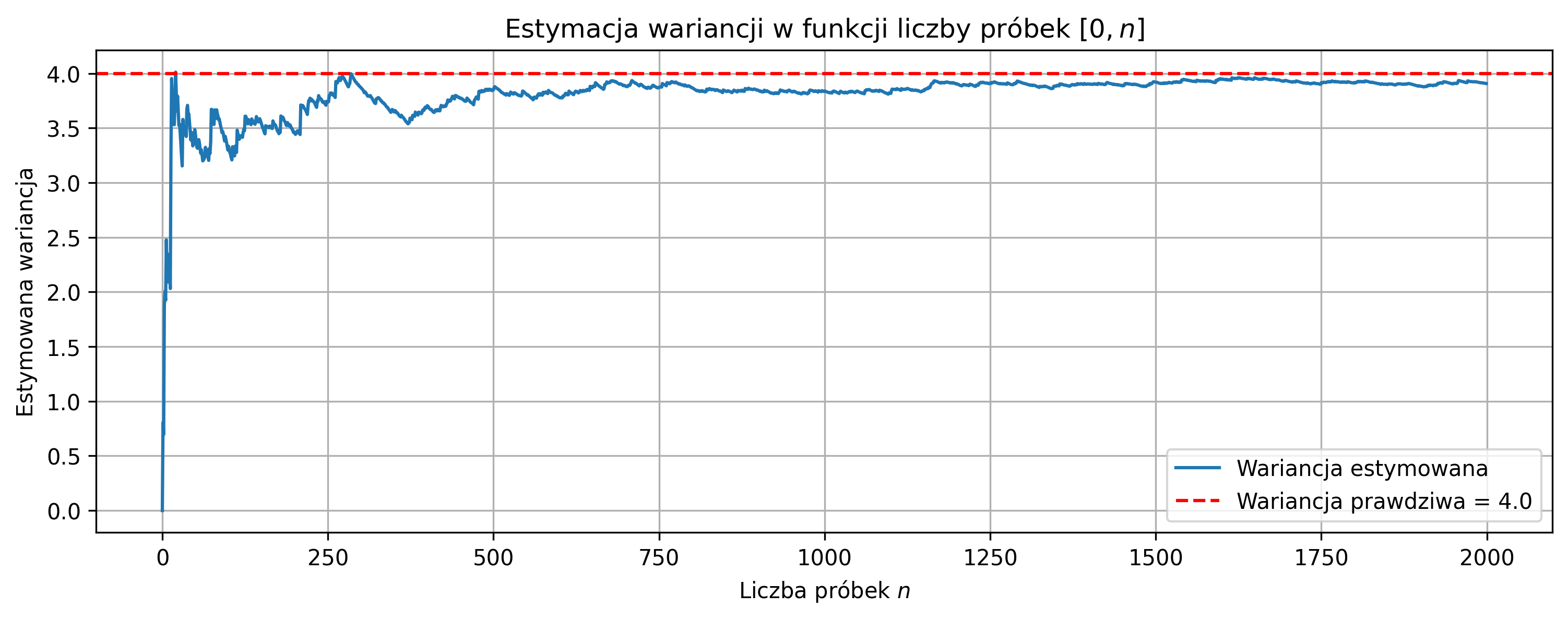
Przy małej liczbie próbek pojedyncze wartości mają duży wpływ na średnią i wariancję, dlatego estymatory są niestabilne. Wraz ze wzrostem liczby próbek średnia i wariancja próbki zbliżają się do wartości oczekiwanej i prawdziwej wariancji. Średnia i wariancja początkowo cechują się dużą zmiennością, a po przekroczeniu pewnej liczby próbek pozostają blisko wartości prawdziwych.
Estymowana średnia: \(\hat{\mu} \approx 1.49\) (prawdziwa: \(1.5\)), estymowana wariancja: \(\hat{\sigma}^2 \approx 3.92\) (prawdziwa: \(4.0\)). Estymatory dobrze przybliżają parametry procesu.
Sygnał oscyluje losowo wokół średniej, większość próbek mieści się w przedziale \(\mu \pm \sigma\), brak trendu - potwierdza to stacjonarność procesu. Większa wariancja powoduje większą zmienność i wolniejszą stabilizację estymatorów, mniejsza wariancja powoduje mniejszą zmienność i szybszą stabilizację estymatorów.
Wygeneruj realizację niestacjonarnego procesu losowego (biały szum Gaussowski) o zadanej średniej \(\mu_{\text{true}}\) i wariancji rosnącej liniowo w czasie: \[ \sigma^2[n] = \sigma_0^2 + k \cdot n, \quad n=0,1,\dots,N-1 \]
- Oblicz estymatory średniej \(\hat{\mu}\) i wariancji \(\hat{\sigma}^2\) dla całego przebiegu oraz porównaj z wartościami średniej i typowej wariancji.
- Narysuj przebieg sygnału w dziedzinie czasu.
- Oblicz estymatory średniej i wariancji w funkcji długości przedziału \([0,n]\) i narysuj wykresy ich zmian w funkcji \(n\).
import numpy as np
import matplotlib.pyplot as plt
# Parametry procesu niestacjonarnego
N_total = 2000 # liczba próbek
mu_true = 1.5 # wartość średnia procesu
sigma0 = 1.0 # początkowe odchylenie standardowe
k = 0.001 # przyrost wariancji na próbkę
np.random.seed(42)
# Generacja procesu niestacjonarnego: biały szum o rosnącej wariancji
time = np.arange(N_total)
sigma_t = sigma0 + k*time # odchylenie standardowe w czasie
X = np.random.normal(loc=mu_true, scale=sigma_t)
# Estymatory dla całego przebiegu
mu_est = np.mean(X)
sigma2_est = np.var(X, ddof=1)
print(f'Estymowana średnia: {mu_est:.3f} (prawdziwa: {mu_true})')
print(f'Estymowana wariancja: {sigma2_est:.3f}')
# Wykres przebiegu sygnału
plt.figure(figsize=(12,4))
plt.plot(time, X, label='Realizacja procesu')
plt.title('Niestacjonarny proces losowy (wariancja rośnie w czasie)')
plt.xlabel(rf'Próbki $n$')
plt.ylabel(rf'$X[n]$')
plt.grid(True)
plt.show()
# Estymatory w funkcji długości podprzedziału [0, n]
mu_est_list = []
sigma2_est_list = []
for n in range(1, N_total+1):
X_sub = X[:n]
mu_est_list.append(np.mean(X_sub))
if n > 1:
sigma2_est_list.append(np.var(X_sub, ddof=1))
else:
sigma2_est_list.append(0.0)
# Wykres estymowanej średniej
plt.figure(figsize=(12,4))
plt.plot(mu_est_list, label='Średnia estymowana')
plt.axhline(mu_true, color='r', linestyle='--', label=f'Średnia prawdziwa = {mu_true}')
plt.title(rf'Estymacja średniej w funkcji liczby próbek $[0,n]$')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana średnia')
plt.legend()
plt.grid(True)
plt.show()
# Wykres estymowanej wariancji
plt.figure(figsize=(12,4))
plt.plot(sigma2_est_list, label='Wariancja estymowana')
plt.title(rf'Estymacja wariancji w funkcji liczby próbek $[0,n]$ (niestacjonarny proces)')
plt.xlabel(rf'Liczba próbek $n$')
plt.ylabel('Estymowana wariancja')
plt.legend()
plt.grid(True)
plt.show()
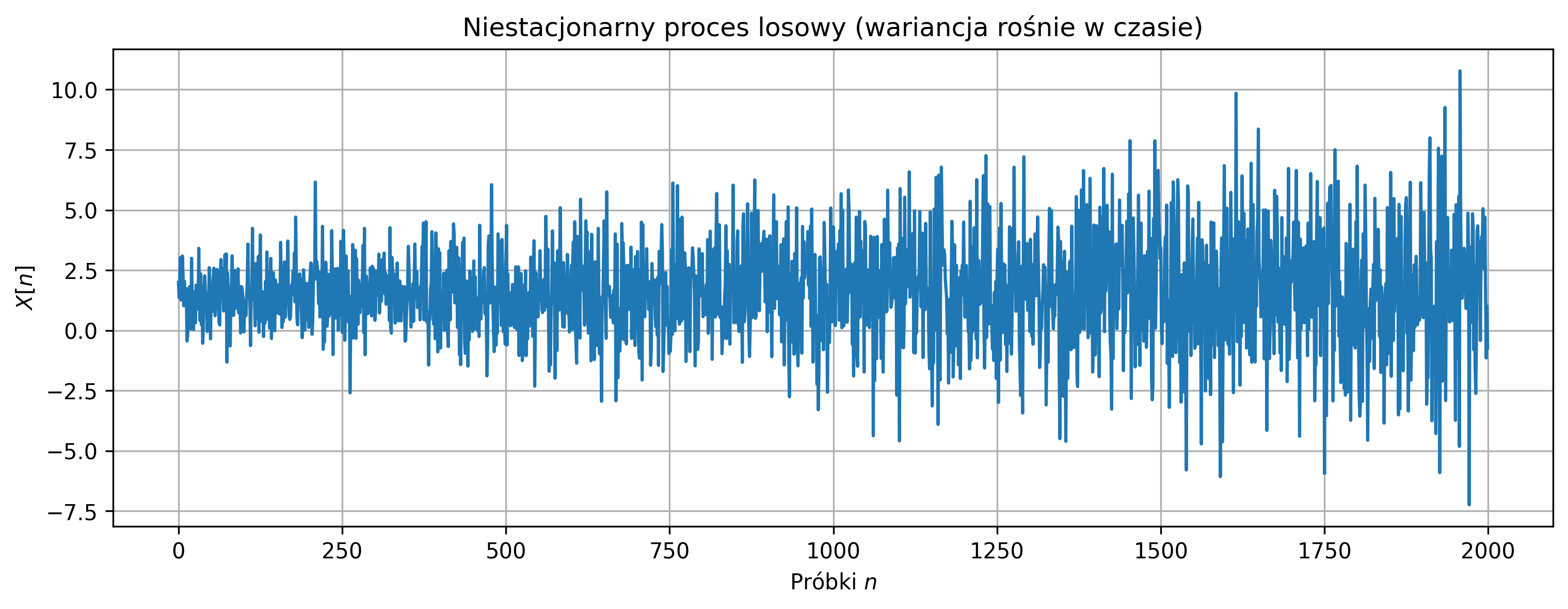
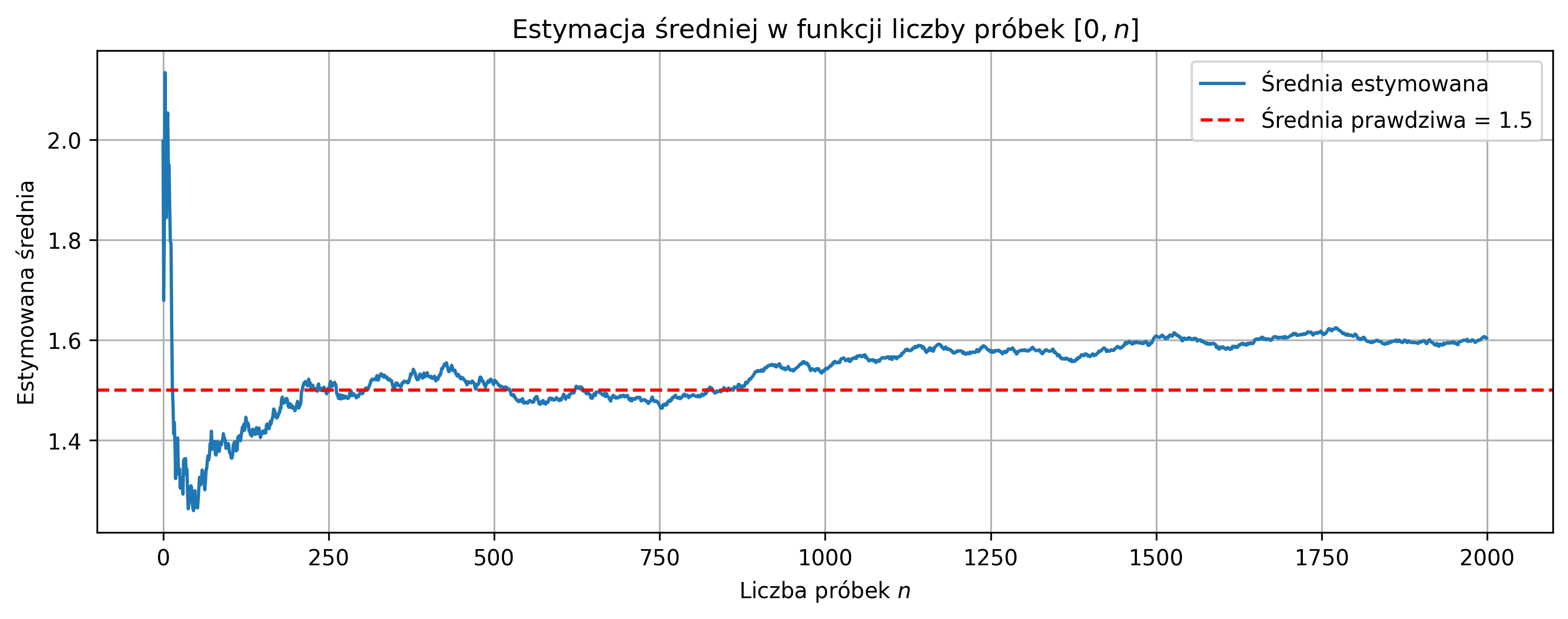
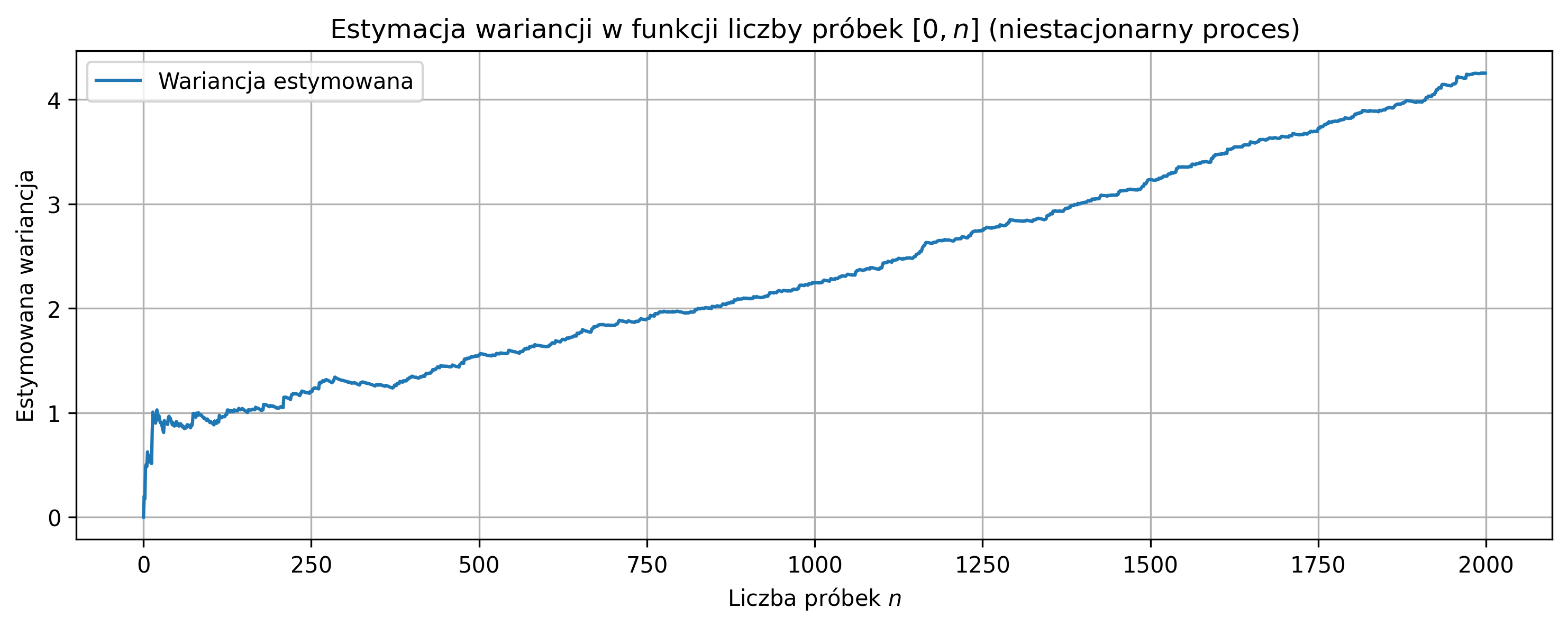
Podobnie jak w procesie stacjonarnym, mała liczba próbek powoduje duży wpływ pojedynczych wartości na średnią i wariancję, dodatkowo lokalna zmiana wariancji zwiększa niestabilność estymatorów. W przypadku niestacjonarnego procesu wariancja rośnie w czasie, więc estymator wariancji nie osiąga jednej stabilnej wartości.
Średnia estymowana stabilizuje się wokół wartości \(\mu_{\text{true}}\), natomiast wariancja rośnie wraz z liczbą próbek, odzwierciedlając niestacjonarność procesu. Estymowana średnia: \(\hat{\mu} \approx 1.50\) (blisko \(\mu_{\text{true}} = 1.5\)), estymowana wariancja: \(\hat{\sigma}^2 \approx\) średnia z całego przebiegu, ale nie odpowiada lokalnym wartościom wariancji, ponieważ proces jest niestacjonarny.
Sygnał oscyluje wokół średniej, ale amplituda próbek rośnie w czasie. Ponieważ wariancja rośnie w czasie, estymator wariancji nigdy nie stabilizuje się na jednej wartości, a średnia stabilizuje się wolniej w porównaniu do procesu stacjonarnego, jeśli początkowa wariancja jest bardzo mała.
Wygeneruj jedną realizację stacjonarnego procesu losowego - białego szumu Gaussowskiego o wartości oczekiwanej \(\mu = 0\) i odchyleniu standardowym \(\sigma = 1\). Na podstawie wygenerowanej realizacji wyznacz estymator funkcji autokorelacji \(\hat{R}_X[k]\) dla przesunięć \(k = 0,1,\dots,K\), korzystając ze wzoru: \[ \hat{R}_X[k] = \frac{1}{N-k} \sum_{n=0}^{N-k-1} \left(X[n] - \hat{\mu}\right)\left(X[n+k] - \hat{\mu}\right), \] gdzie \(\hat{\mu}\) jest estymowaną wartością średnią procesu. Narysuj wykres estymowanej funkcji autokorelacji w funkcji przesunięcia \(k\). Porównaj otrzymaną funkcję autokorelacji z teoretyczną funkcją autokorelacji białego szumu: \[ R_X[k] = \begin{cases} \sigma^2, & k = 0, \\ 0, & k \neq 0. \end{cases} \] Na podstawie wykresu oceń, czy wygenerowany proces można uznać za biały szum oraz skomentuj wpływ skończonej liczby próbek na dokładność estymacji.
import numpy as np
import matplotlib.pyplot as plt
# Parametry procesu
N = 1000 # liczba próbek
mu = 0.0 # wartość oczekiwana
sigma = 1.0 # odchylenie standardowe
max_lag = 50 # maksymalne przesunięcie
np.random.seed(42)
# Generowanie realizacji procesu losowego
# Biały szum Gaussowski N(mu, sigma^2)
X = np.random.normal(loc=mu, scale=sigma, size=N)
# Estymator funkcji autokorelacji
# \hat{R}_X[k] = 1/(N-k) * sum (X[n]-\hat{\mu})(X[n+k]-\hat{\mu})
def autocorr_estimator(x, max_lag):
N = len(x)
mu_hat = np.mean(x)
R_hat = np.zeros(max_lag + 1)
for k in range(max_lag + 1):
R_hat[k] = np.sum(
(x[:N-k] - mu_hat) * (x[k:] - mu_hat)
) / (N - k)
return R_hat
# Estymacja autokorelacji
R_est = autocorr_estimator(X, max_lag)
# Wykres realizacji procesu
plt.figure(figsize=(10,3))
plt.plot(X)
plt.title('Realizacja białego szumu Gaussowskiego')
plt.xlabel(rf'Próbka $n$')
plt.ylabel(rf'$X[n]$')
plt.grid(True)
plt.show()
# Wykres estymowanej autokorelacji
lags = np.arange(max_lag + 1)
plt.figure(figsize=(9,3))
plt.stem(lags, R_est)
plt.axhline(0, color='r', linestyle='--',
label=rf'Teoretyczna autokorelacja dla $k \neq 0$')
plt.title('Estymator funkcji autokorelacji')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{{R}}_{{X[k]}}$')
plt.legend()
plt.grid(True)
plt.show()
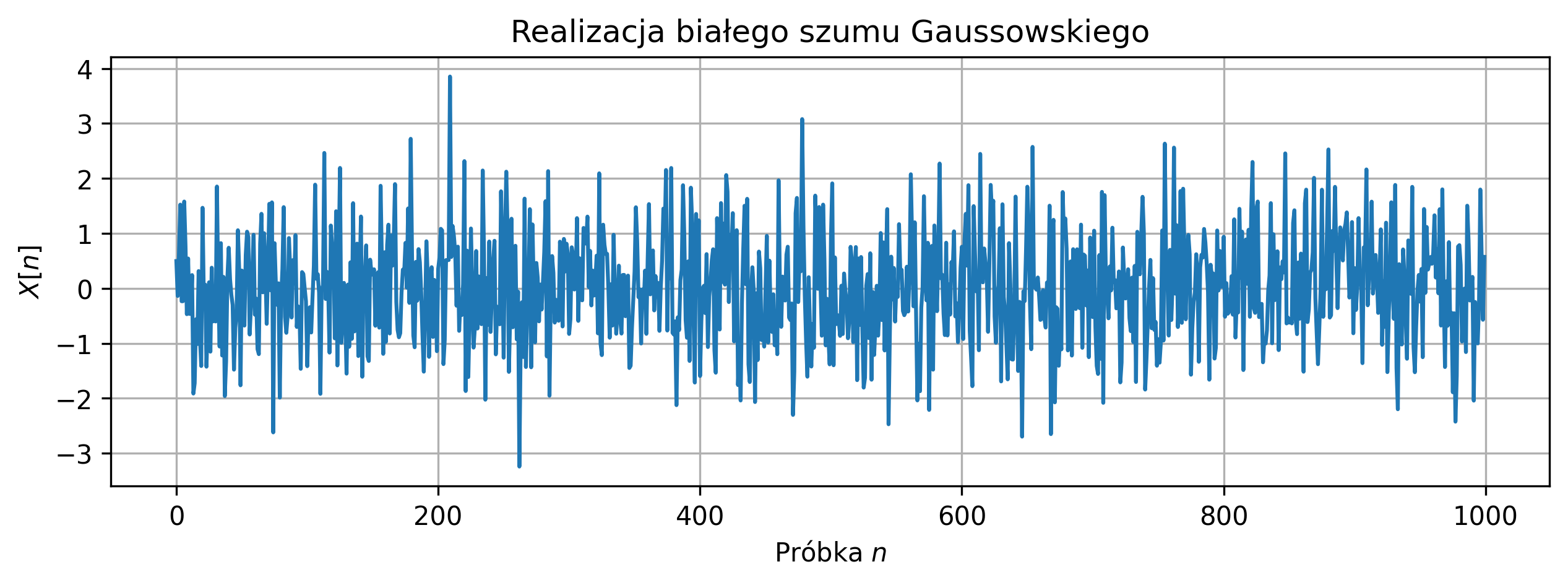
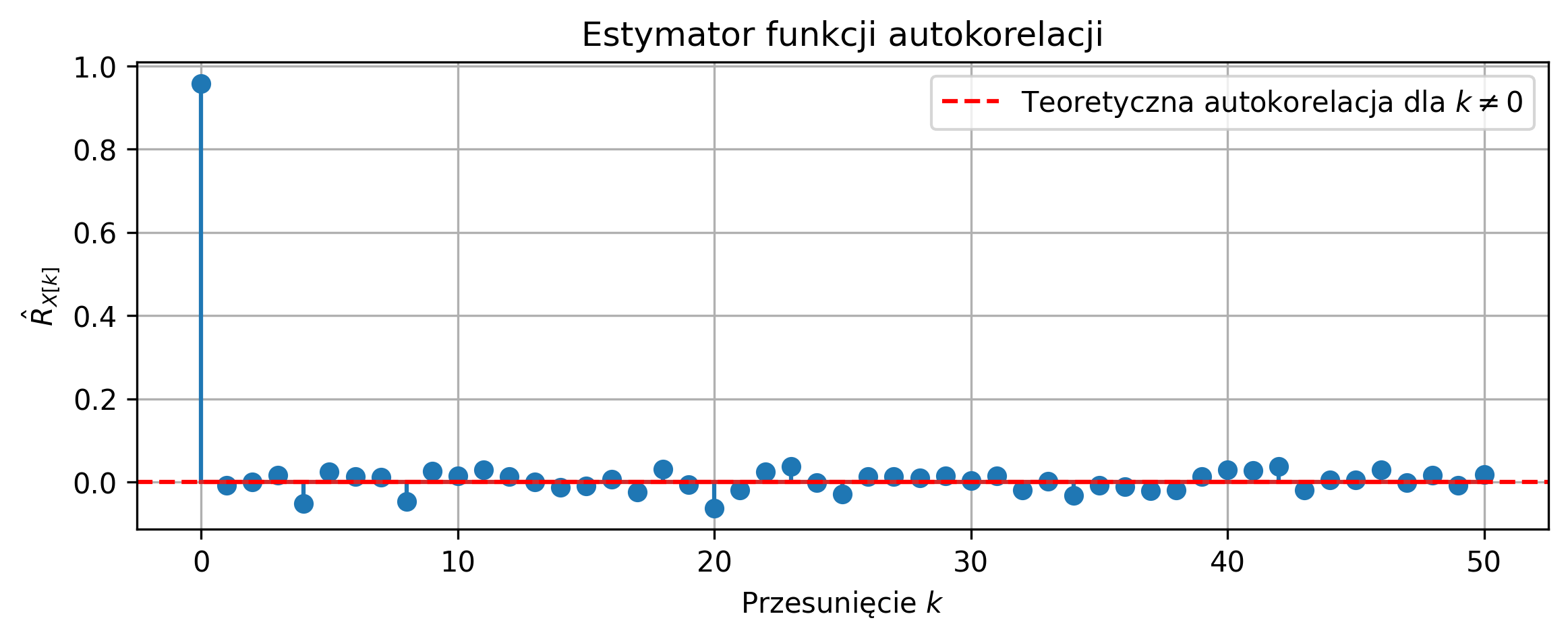
Na podstawie wykresu realizacji procesu losowego można stwierdzić, że sygnał ma charakter losowy i oscyluje wokół zera, co jest zgodne z założeniem zerowej wartości oczekiwanej białego szumu Gaussowskiego.
Estymowana funkcja autokorelacji osiąga największą wartość dla przesunięcia \(k=0\), co odpowiada wariancji procesu losowego. Dla przesunięć \(k>0\) wartości estymowanej autokorelacji są bliskie zeru, co potwierdza brak korelacji pomiędzy próbkami sygnału. Niewielkie odchylenia wartości autokorelacji od zera dla \(k>0\) wynikają ze skończonej liczby próbek i zanikają wraz ze wzrostem liczby próbek \(N\).
Otrzymane wyniki są zgodne z teoretyczną funkcją autokorelacji białego szumu, dla której \(R_X[k]=0\) dla \(k \neq 0\), co potwierdza poprawność zastosowanego estymatora.
Wygeneruj jedną realizację niestacjonarnego procesu losowego w postaci sumy trendu liniowego oraz białego szumu Gaussowskiego: \[ X[n] = a n + W[n], \] gdzie \(a\) jest współczynnikiem trendu, a \(W[n]\) jest białym szumem o zerowej wartości oczekiwanej. Wyznacz estymator funkcji autokorelacji \(\hat{R}_X[k]\) dla przesunięć \(k=0,1,\dots,K\). Narysuj wykres estymowanej funkcji autokorelacji i oceń jej kształt. Usuń trend z sygnału i wyznacz ponownie funkcję autokorelacji. Porównaj oba wykresy i wyciągnij wnioski dotyczące wpływu niestacjonarności na estymację funkcji autokorelacji.
import numpy as np
import matplotlib.pyplot as plt
# Parametry
N = 1000 # liczba próbek
a = 0.01 # współczynnik trendu liniowego
max_lag = 50 # maksymalne przesunięcie autokorelacji
np.random.seed(42)
# Generowanie procesu niestacjonarnego
# X[n] = a*n + W[n]
n = np.arange(N)
trend = a * n
noise = np.random.normal(0, 1, N)
X = trend + noise
# Estymator funkcji autokorelacji
def autocorr_estimator(x, max_lag):
N = len(x)
mu_hat = np.mean(x)
R_hat = np.zeros(max_lag + 1)
for k in range(max_lag + 1):
R_hat[k] = np.sum(
(x[:N-k] - mu_hat) * (x[k:] - mu_hat)
) / (N - k)
return R_hat
# Autokorelacja – proces z trendem
R_trend = autocorr_estimator(X, max_lag)
# Usunięcie trendu
X_detrended = X - trend
# Autokorelacja po usunięciu trendu
R_detrended = autocorr_estimator(X_detrended, max_lag)
# Wykres realizacji procesu
plt.figure(figsize=(12,4))
plt.plot(n, X, label='Proces niestacjonarny')
plt.plot(n, trend, 'r--', label='Trend liniowy')
plt.title('Proces niestacjonarny z trendem liniowym')
plt.xlabel(rf'Próbka $n$')
plt.ylabel(rf'$X[n]$')
plt.legend()
plt.grid(True)
plt.show()
# Autokorelacja – z trendem
lags = np.arange(max_lag + 1)
plt.figure(figsize=(10,4))
plt.stem(lags, R_trend)
plt.axhline(0, color='r', linestyle='--')
plt.title('Estymowana funkcja autokorelacji (z trendem)')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{R}_X[k]$')
plt.grid(True)
plt.show()
# Autokorelacja – po usunięciu trendu
plt.figure(figsize=(10,4))
plt.stem(lags, R_detrended)
plt.axhline(0, color='r', linestyle='--')
plt.title('Estymowana funkcja autokorelacji (po usunięciu trendu)')
plt.xlabel(rf'Przesunięcie $k$')
plt.ylabel(r'$\hat{R}_X[k]$')
plt.grid(True)
plt.show()
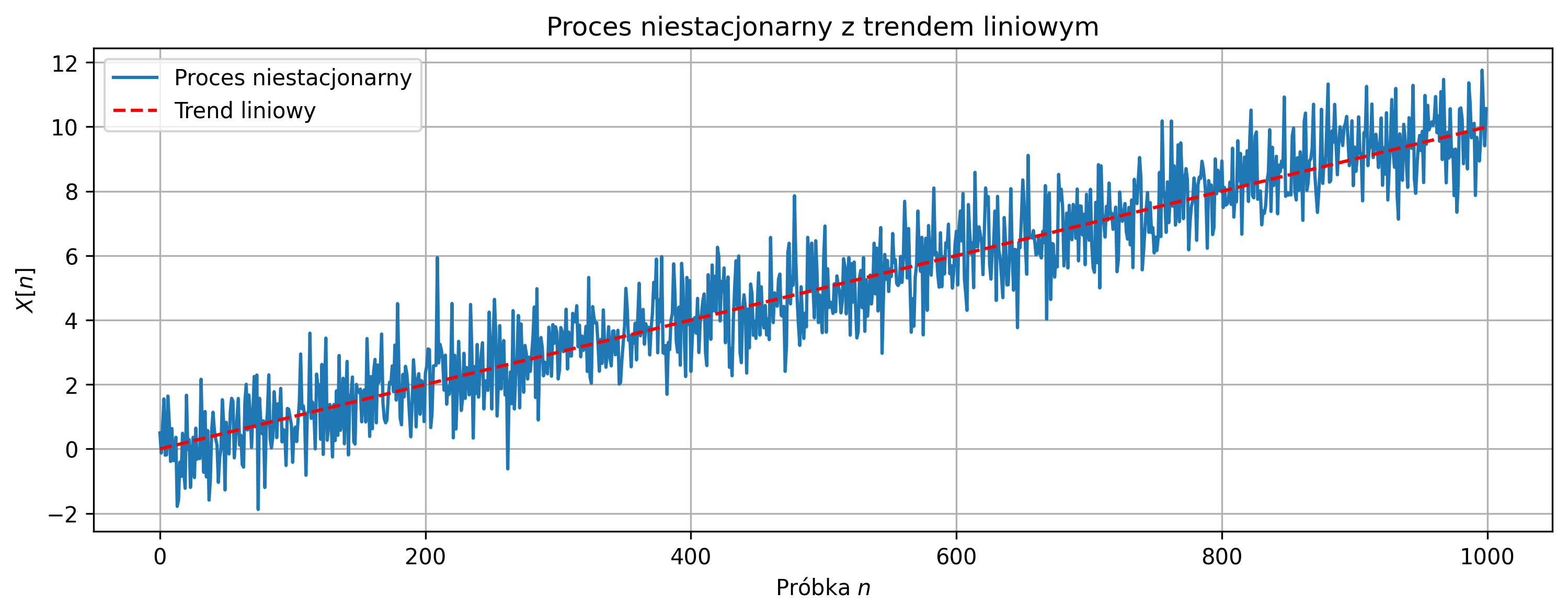
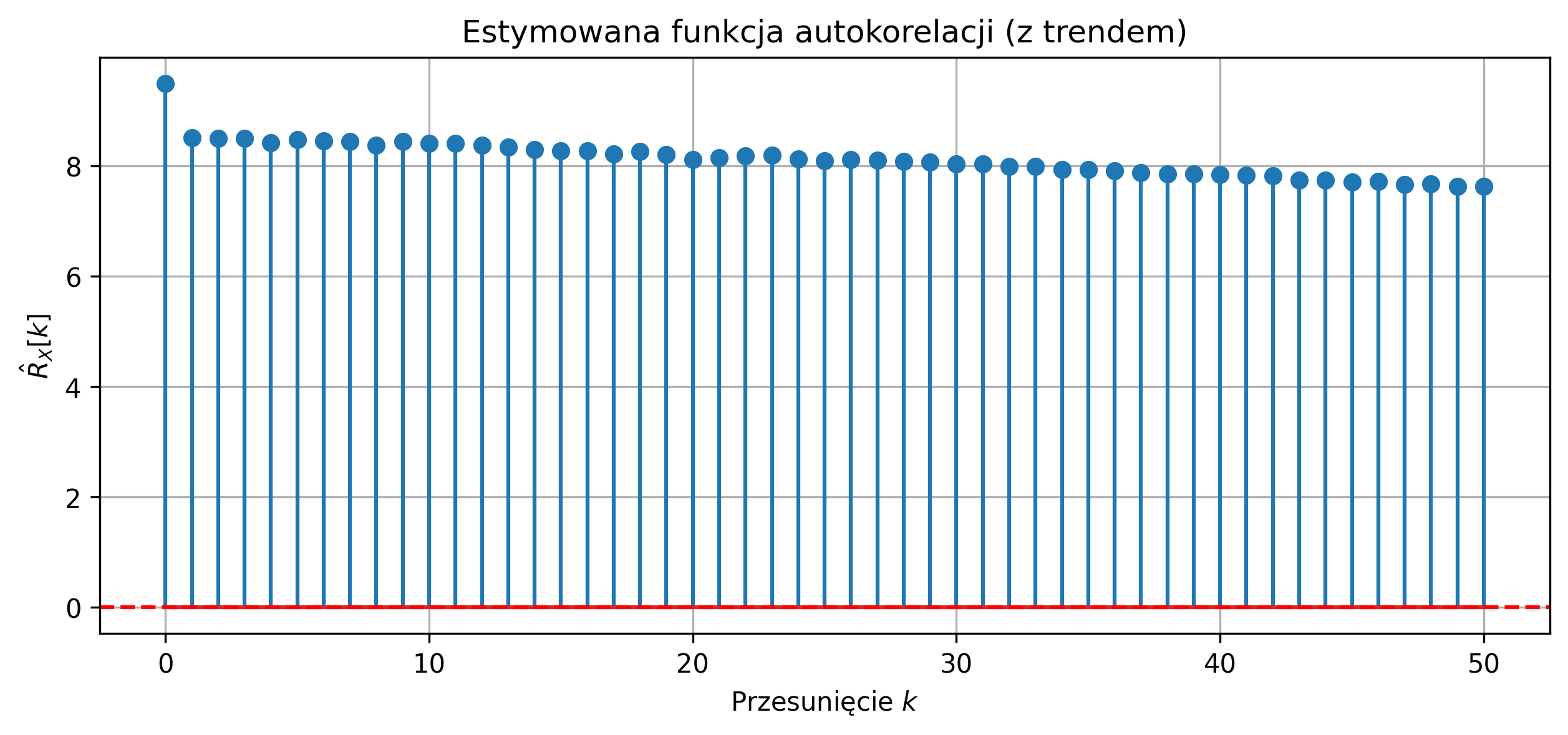
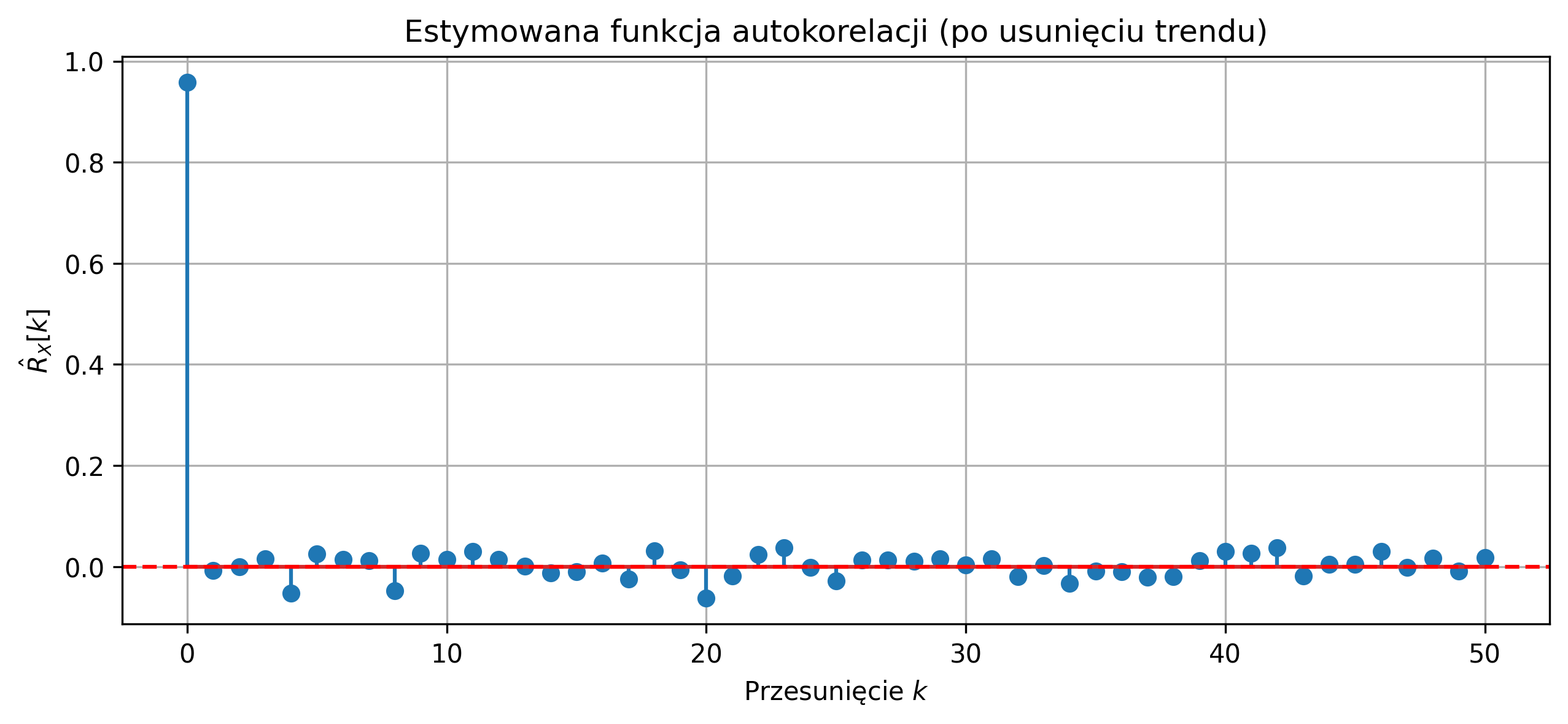
Proces z trendem liniowym jest niestacjonarny, co powoduje, że klasyczna estymacja funkcji autokorelacji nie zanika do zera dla przesunięć \(k>0\). Trend w sygnale wprowadza pozorną korelację pomiędzy próbkami, niezwiązaną z własnościami losowymi procesu. Po usunięciu trendu estymowana funkcja autokorelacji ma maksimum dla \(k=0\) i wartości bliskie zeru dla \(k>0\), co odpowiada własnościom białego szumu.
Wyniki pokazują, że przed estymacją autokorelacji proces niestacjonarny powinien zostać przekształcony do postaci stacjonarnej.
Rozważyć dyskretny proces losowy postaci \[ X[n] = w[n], \] gdzie \(w[n]\) jest białym szumem gaussowskim o zerowej wartości średniej i stałej wariancji \(\sigma_w^2\). Narysuj kilka realizacji procesu w dziedzinie czasu i porównaj ich przebiegi. Dla każdej realizacji wyznacz periodogram jako estymator widmowej gęstości mocy. Zbliżenie na niskie częstotliwości (np. \(f \approx 0\)) pozwoli ocenić, czy w procesie występuje dominująca składowa stała. Na podstawie obserwacji w dziedzinie czasu i częstotliwości oceń, czy proces jest ergodyczny i uzasadnij odpowiedź.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2)
# Parametry
N = 2048
fs = 2000
num_realizations = 6
sigma_w = 1.0
t = np.arange(N) / fs
# Wykres realizacji w czasie
plt.figure(figsize=(12,4))
for i in range(num_realizations):
w = np.random.normal(0, sigma_w, N)
plt.plot(t, w, label=f'Realizacja {i+1}')
plt.title('Proces ergodyczny – realizacje w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel(r'$X[n]$')
plt.grid(True)
plt.legend()
plt.show()
# Periodogramy
freqs = np.fft.fftfreq(N, d=1/fs)
freqs = freqs[:N//2]
plt.figure(figsize=(12,4))
periodograms = []
for i in range(num_realizations):
w = np.random.normal(0, sigma_w, N)
Wf = np.fft.fft(w)
PSD = (1/N) * np.abs(Wf[:N//2])**2
periodograms.append(PSD)
plt.semilogy(freqs, PSD, label=f'Realizacja {i+1}')
plt.title('Periodogramy procesu ergodycznego (biały szum)')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
# Zbliżenie na niskie częstotliwości
plt.figure(figsize=(12,4))
for i, PSD in enumerate(periodograms):
plt.semilogy(freqs[:40], PSD[:40], label=f'Realizacja {i+1}')
plt.title(rf'Zbliżenie na niskie częstotliwości (f $\approx$ 0) – proces ergodyczny')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
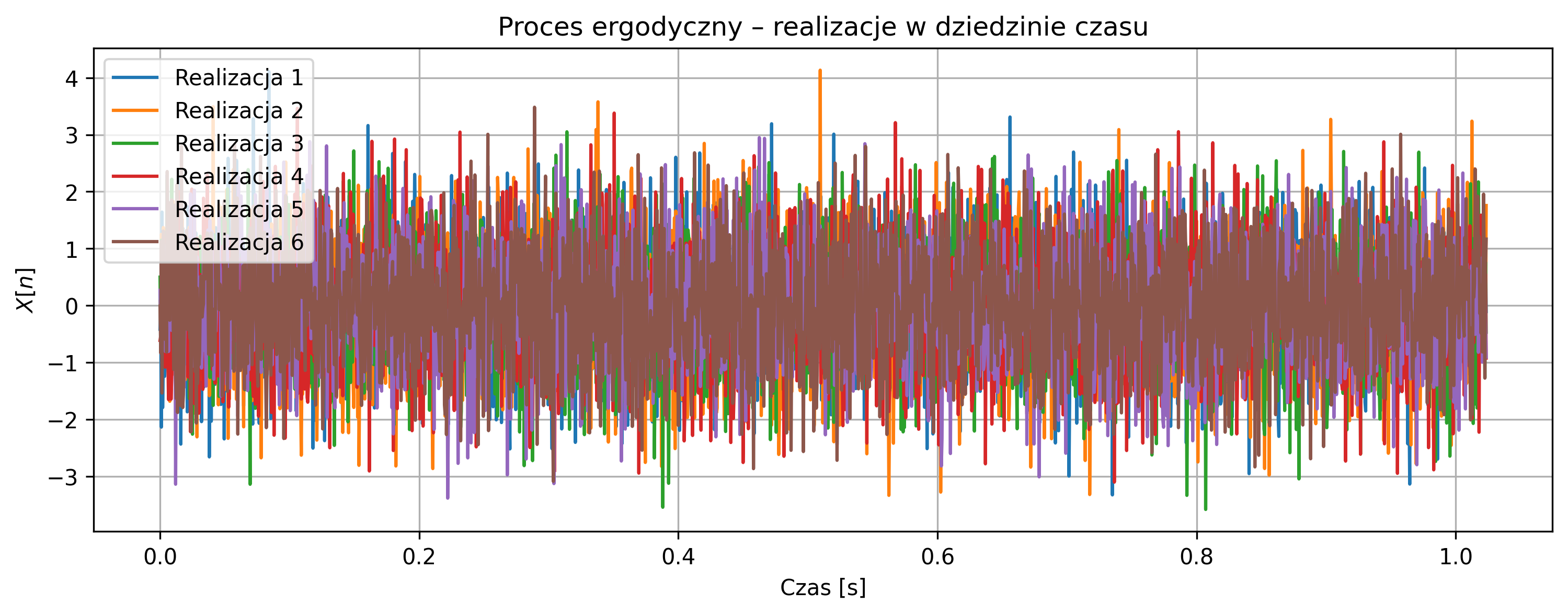
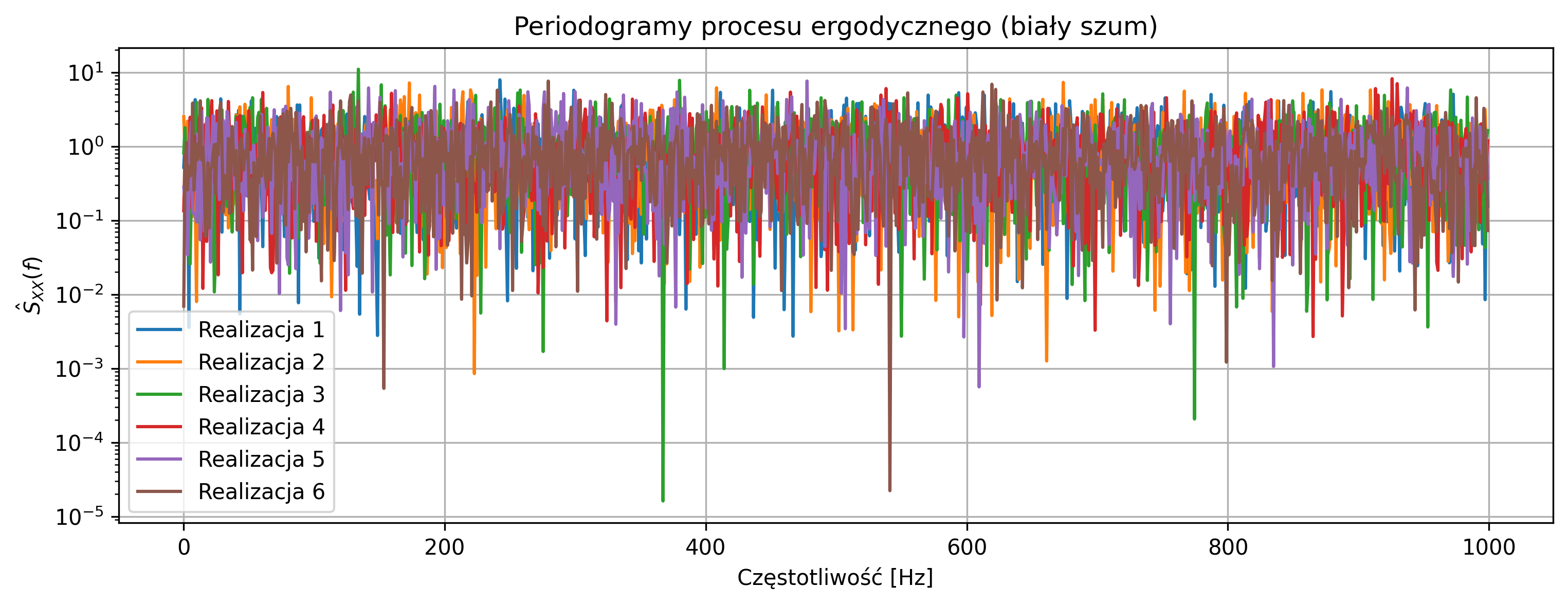
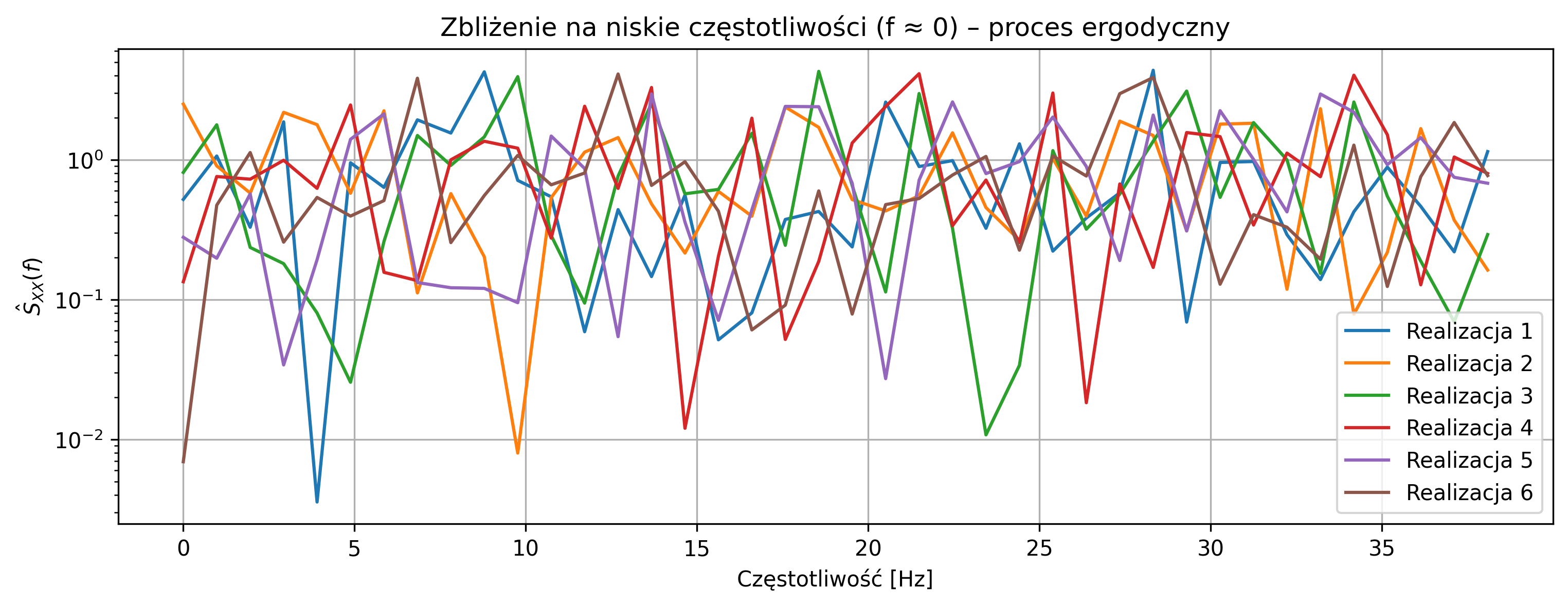
Przebiegi czasowe wszystkich realizacji są podobne i oscylują wokół zera, co wynika z braku losowej składowej stałej.
Periodogramy poszczególnych realizacji są zbliżone, a w pobliżu częstotliwości \(f \approx 0\) nie występują dominujące piki, co różni ten proces od procesu nieergodycznego.
Proces jest ergodyczny - statystyki jednej realizacji (średnia, widmo mocy) odzwierciedlają właściwości całego procesu, co potwierdza zgodność widm między realizacjami.
Wygeneruj kilka niezależnych realizacji procesu losowego w postaci: \[ X[n] = A + W[n], \] gdzie \(A\) jest losową zmienną losową o rozkładzie normalnym, stałą w czasie dla danej realizacji, natomiast \(W[n]\) jest białym szumem Gaussowskim o zerowej wartości oczekiwanej.
Narysuj wykresy kilku realizacji procesu w dziedzinie czasu i porównaj ich przebiegi. Dla każdej realizacji wyznacz periodogram jako estymator widmowej gęstości mocy sygnału. Porównaj otrzymane periodogramy oraz przeanalizuj zachowanie widma w okolicy częstotliwości \(f = 0\). Na podstawie wyników oceń, czy proces jest ergodyczny oraz uzasadnij odpowiedź na podstawie obserwacji w dziedzinie czasu i częstotliwości.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
# Parametry
N = 2048
fs = 2000
num_realizations = 6
sigma_A = 2.0 # wariancja losowej stałej (większa)
sigma_w = 0.05 # wariancja szumu (mniejsza)
t = np.arange(N) / fs
# Wykres realizacji w czasie
plt.figure(figsize=(12,4))
for i in range(num_realizations):
A = np.random.normal(0, sigma_A)
w = np.random.normal(0, sigma_w, N)
X = A + w
plt.plot(t, X, label=f'Realizacja {i+1}')
plt.title('Proces nieergodyczny – realizacje w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel(r'$X[n]$')
plt.grid(True)
plt.legend()
plt.show()
# Periodogramy
freqs = np.fft.fftfreq(N, d=1/fs)
freqs = freqs[:N//2]
plt.figure(figsize=(12,4))
periodograms = []
for i in range(num_realizations):
A = np.random.normal(0, sigma_A)
w = np.random.normal(0, sigma_w, N)
X = A + w
Xf = np.fft.fft(X)
PSD = (1/N) * np.abs(Xf[:N//2])**2
periodograms.append(PSD)
plt.semilogy(freqs, PSD, label=f'Realizacja {i+1}')
plt.title('Periodogramy procesu nieergodycznego')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
# Zbliżenie na okolice f = 0
plt.figure(figsize=(12,4))
for i, PSD in enumerate(periodograms):
plt.semilogy(freqs[:40], PSD[:40], label=f'Realizacja {i+1}')
plt.title(rf'Zbliżenie na okolice $f=0$ (dominacja składowej stałej)')
plt.xlabel('Częstotliwość [Hz]')
plt.ylabel(r'$\hat{S}_{XX}(f)$')
plt.grid(True)
plt.legend()
plt.show()
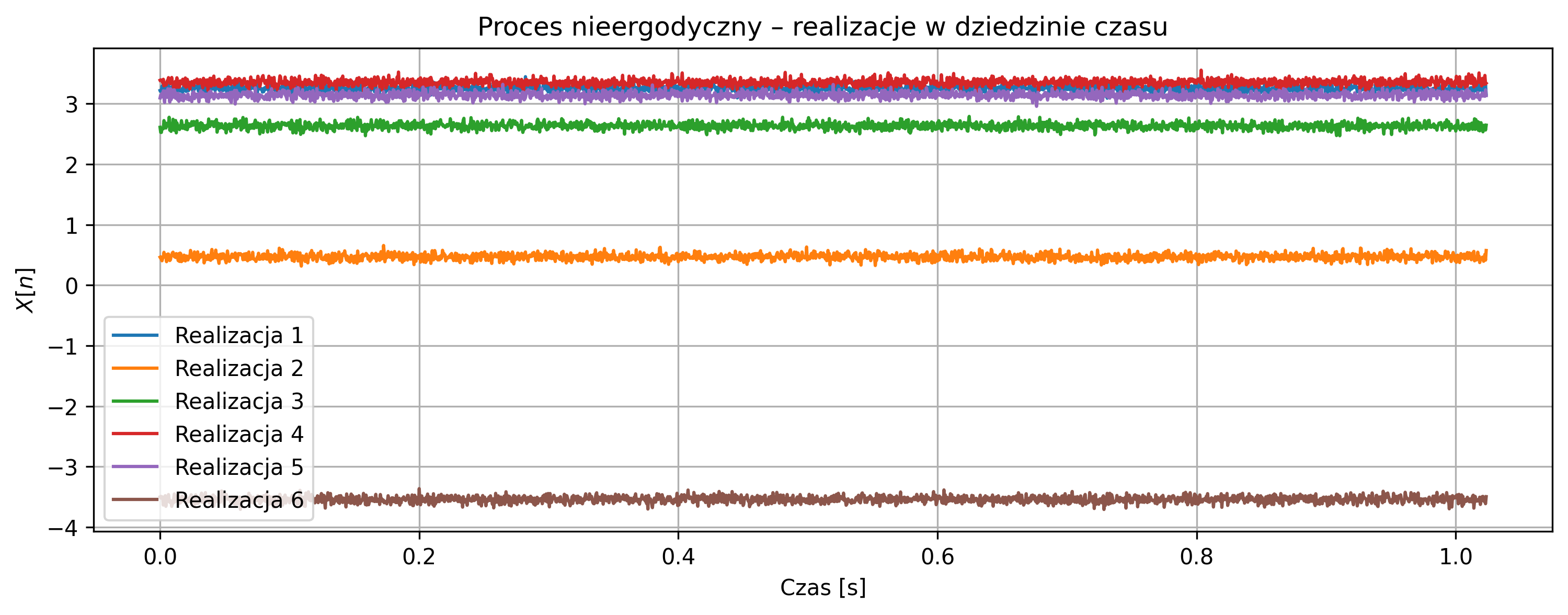
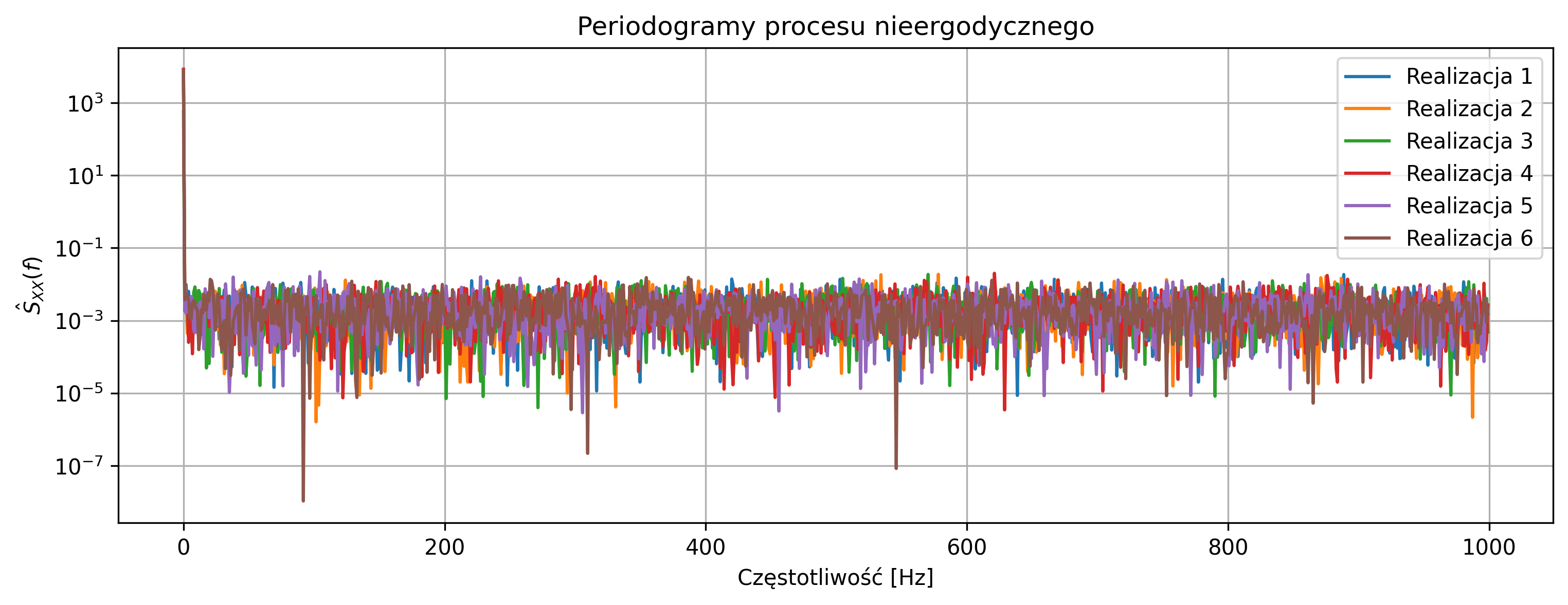
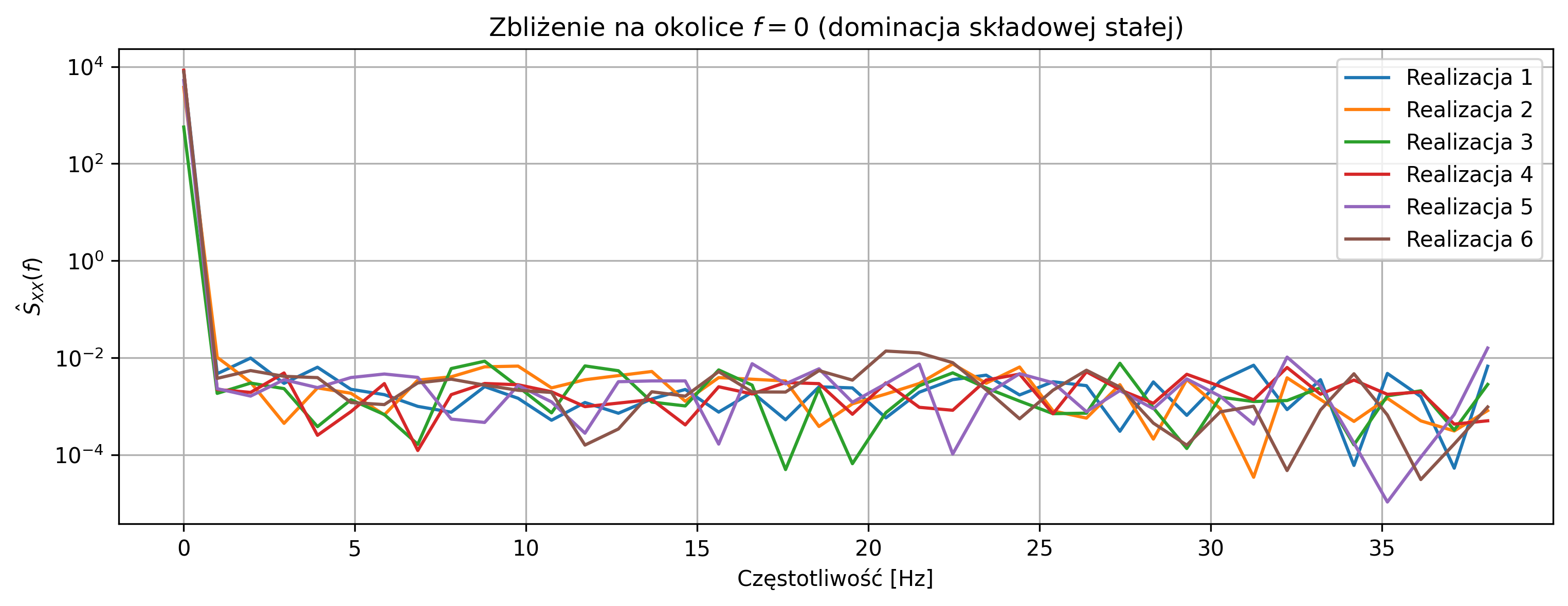
Przebiegi czasowe poszczególnych realizacji różnią się poziomem średniej, co wynika z obecności losowej składowej stałej \(A\), niezmiennej w czasie dla danej realizacji. Zwiększenie wariancji składowej stałej oraz zmniejszenie wariancji szumu powoduje, że różnice między realizacjami są wyraźniejsze zarówno w dziedzinie czasu, jak i częstotliwości.
Periodogramy różnych realizacji znacząco różnią się w okolicy częstotliwości \(f=0\), co wskazuje na losowy charakter składowej stałej i brak wspólnego widma dla wszystkich realizacji. Proces nie jest ergodyczny, ponieważ statystyki wyznaczone z jednej realizacji (np. średnia lub widmo mocy) nie są reprezentatywne dla całego zespołu realizacji.
Otrzymane wyniki potwierdzają, że proces może być stacjonarny w sensie szerokim, ale jednocześnie nie spełnia warunku ergodyczności.
5.6. Test D - sprawdź swoją wiedzę
Test ma na celu sprawdzenie i utrwalenie wiedzy z analizy częstotliwościowej sygnałów losowych, obejmując procesy losowe, autokorelację, kowariancję, stacjonarność, ergodyczność oraz gęstość widmową mocy. Każde pytanie ma trzy odpowiedzi (A, B, C), z których tylko jedna jest poprawna.
Klucz odpowiedzi:
1. C
2. B
3. A
4. A
5. B
6. A
7. A
8. B
9. A
10. B
11. A
12. A
13. C
14. B
15. A
16. A
17. A
18. B
19. C
20. B