Podręcznik
| Strona: | SEZAM - System Edukacyjnych Zasobów Akademickich i Multimedialnych |
| Kurs: | 2. Zaawansowane struktury sieci neuronowych |
| Książka: | Podręcznik |
| Wydrukowane przez użytkownika: | Gość |
| Data: | czwartek, 22 stycznia 2026, 16:39 |
Spis treści
- 1. Sieci radialne RBF
- 1.1. Wprowadzenie
- 1.2. Sieć radialna RBF
- 1.3. Metody uczenia sieci neuronowych radialnych
- 1.4. Metody doboru liczby funkcji bazowych
- 1.5. Program komputerowy uczenia sieci radialnych
- 1.6. Przykład zastosowania sieci radialnej w aproksymacji
- 1.7. Porównanie sieci radialnych z sieciami sigmoidalnymi
- 1.8. Przykład zastosowania sieci RBF w modelu sztucznego nosa elektronicznego
- 1.9. Zadania i problemy
- 1.10. Słownik
- 2. Sieci wektorów nośnych SVM
- 2.1. Pojęcia wstępne
- 2.2. Sieć liniowa SVM w zadaniu klasyfikacji
- 2.3. Sieć nieliniowa SVM w zadaniu klasyfikacji
- 2.4. Sieć SVM do zadań regresji
- 2.5. Przegląd algorytmów rozwiązania zadania dualnego
- 2.6. Program komputerowy uczenia sieci SVM
- 2.7. Przykłady zastosowania sieci SVM
- 2.8. Porównanie sieci SVM z innymi rozwiązaniami neuronowymi
- 2.9. Zadania i problemy
- 2.10. Słownik
- 3. Sieci neuronowe głębokie
- 3.1. Wprowadzenie
- 3.2. Sieć konwolucyjna CNN
- 3.3. Transfer Learning
- 3.4. Przykład użycia sieci ALEXNET w trybie transfer learning
- 3.5. Inne rozwiązania pre-trenowanej architektury sieci CNN
- 3.6. Sieci CNN do detekcji obiektów w obrazie
- 3.7. Sieć U-NET w segmentacji obrazów biomedycznych
- 3.8. Autoenkoder
- 3.9. Autoenkoder wariacyjny
- 3.10. Sieci generatywne GAN
- 3.11. Zadania i problemy
- 3.12. Słownik
- 4. Sieci rekurencyjne
- 5. Literatura
1. Sieci radialne RBF
Wykład ten poświęcony będzie sieciom stosującym neurony o radialnej funkcji aktywacji (zwykle funkcja gaussowska), zwane sieciami RBF [24,46]. W odróżnieniu od sieci perceptonowej stosującej sigmoidalną funkcję aktywacji, niezerową w całym zakresie zmian zmiennej wejściowej, neurony gaussowskie w sieci RBF generują niezerowe wartości sygnałów jedynie w bliskim otoczeniu swojego centrum. Sieć taka stanowi uniwersalny aproksymator o charakterze lokalnym. Przedstawimy strukturę tej sieci oraz algorytmy uczące wykorzystujące lokalny charakter funkcji gaussowskiej. Algorytmy te są wielokrotnie szybsze niż algorytmy uczące sieci MLP. Na zakończenie przedstawimy program uczący sieci RBF oraz wyniki działania tego programu na wybranych problemach testowych.
1.1. Wprowadzenie
Sieci neuronowe wielowarstwowe, pełnią z punktu widzenia matematycznego rolę uniwersalnego aproksymatora funkcji wielu zmiennych, odwzorowując zbiór zmiennych wejściowych \( \mathbf{x} \) w zbiór zmiennych wyjściowych \( \mathbf{y} \). W przypadku sieci MLP jest to aproksymacja typu globalnego, w której ze względu na charakter sigmoidalnej funkcji aktywacji każdy neuron uczestniczy w odwzorowaniu funkcyjnym w całej przestrzeni wartości zmiennej wejściowej. Odwzorowanie wartości funkcji w dowolnym punkcie przestrzeni jest więc dokonywane zbiorowym wysiłkiem wielu neuronów na raz (stąd nazwa aproksymacji globalnej).
Innym komplementarnym sposobem odwzorowania zbioru wejściowego w wyjściowy jest odwzorowanie przy zastosowaniu wielu pojedynczych funkcji o skończonym nośniku, w którym działanie pojedynczego neuronu ogranicza się do wąskiego obszaru przestrzeni wielowymiarowej (w pobliżu centrum tej funkcji). W takim rozwiązaniu odwzorowanie pełnego zbioru danych jest sumą odwzorowań lokalnych, gdzie dla każdego punktu przestrzeni tylko nieliczne neurony charakteryzują się niezerowymi wartościami sygnałów - stąd nazwa aproksymacji lokalnej.
Przykładem są tu sieci o radialnej funkcji bazowej (RBF), w której neuron ukryty realizuje funkcję zmieniającą się radialnie wokół wybranego centrum \( c \) i przyjmującą wartości niezerowe tylko w otoczeniu tego centrum. Typowym przykładem, najczęściej stosowanym w sieciach RBF jest funkcja gaussowska, która w przypadku sieci RBF może być dla argumentu skalarnego zapisana w postaci [24]
| \( \varphi(x)=\exp \left(-\frac{(x-c)^2}{\sigma^2}\right) \) | (4.1) |
Funkcja ta przyjmuje niezerowe wartości jedynie w bliskim otoczeniu centrum \( c \), którego wielkość jest regulowana poprzez parametr szerokości \( \sigma \). W przypadku przestrzeni wielowymiarowej funkcja gaussowska jest opisana wzorem
| \( \varphi(\mathbf{x})=\varphi(\mathbf{x}-\mathbf{c})=\exp \left(-\frac{\|\mathbf{x}-\mathbf{c}\|^2}{\sigma^2}\right) \) | (4.2) |
w którym \( \|\mathbf{x}-\mathbf{c}\| \) oznacza normę euklidesową wektora \( (\mathbf{x}-\mathbf{c}) \). W sieciach RBF (ang. Radial Basis Function) rola neuronu ukrytego sprowadzać się będzie do odwzorowania radialnego przestrzeni wokół jednego punktu zadanego lub grupy takich punktów stanowiących klaster. Superpozycja sygnałów pochodzących od wszystkich neuronów ukrytych (klastrów), dokonywana przez neuron wyjściowy, pozwala uzyskać odwzorowanie całej przestrzeni wielowymiarowej.
Sieci typu radialnego stanowią naturalne uzupełnienie sieci sigmoidalnych. Co więcej, wobec różnej funkcji, jaką pełnią neurony, w sieciach radialnych nie zachodzi potrzeba stosowania wielu warstw ukrytych. Typowa sieć radialna jest strukturą zawierającą warstwę wejściową, do której przykładane są sygnały opisane wektorem wejściowym \( \mathbf{x} \), jedną warstwę ukrytą o neuronach typu radialnego transformującą \( N \) sygnałów wejściowych w przestrzeń \( K\)-wymiarową (\( K \)– liczba neuronów ukrytych) oraz warstwę wyjściową, złożoną z jednego lub większej liczby neuronów liniowych. Rola neuronu wyjściowego sprowadza się jedynie do sumowania wagowego sygnałów pochodzących od neuronów ukrytych tworząc sygnał \( y \). W przypadku zastosowania sieci RBF jako klasyfikatora wystarczy dołączyć na wyjściu blok realizujący funkcję signum o wartości wyjściowej 1 (rozpoznana klasa) lub 0 (brak przynależności do klasy).
1.2. Sieć radialna RBF
Najprostsza sieć neuronowa typu radialnego o jednym wyjściu działa na zasadzie wielowymiarowej aproksymacji, której zadaniem jest odwzorowanie \( p \) różnych wektorów wejściowych \( \mathbf{x}_i \) z przestrzeni wejściowej \( N \)-wymiarowej w zbiór \( p \) liczb rzeczywistych \( y_i \) odpowiadających wartościom zadanym \( d_i \). Interpolacja odpowiada tu przyjęciu \( p \) neuronów ukrytych typu radialnego o centrach w wektorach \( \mathbf{x}_i \) i określeniu takiej funkcji odwzorowania \( F(\mathbf{x}) \), dla której spełnione są warunki
| \( F\left(\mathbf{x}_i\right)=d_i+\varepsilon_i \) | (4.3) |
gdzie \( \varepsilon_i \) reprezentuje akceptowalny błąd dopasowania. Przy ograniczeniu się do \( K \) funkcji bazowych o różnych położeniach centrów \( \mathbf{c}_i \) rozwiązanie aproksymujące można przedstawić w postaci [24, 46]
| \( F(\mathbf{x})=\sum_{i=1}^K w_i \varphi\left(\mathbf{x}-\mathbf{c}_i\right) \) | (4.4) |
gdzie \( K < p \), wektory \( \mathbf{c}_i \) są jest zbiorem centrów, które będą podlegać wyznaczaniu w procesie uczenia.
Rozwiązanie wyrażające funkcję aproksymującą w przestrzeni wielowymiarowej jako sumę wagową lokalnych funkcji bazowych \( \varphi\left(\mathbf{x}-\mathbf{c}_i\right) \) typu radialnego (wzór 4.4) może być zinterpretowany w postaci sieci neuronowej radialnej przedstawionej na rys. 4.1, gdzie przyjęto strukturę o \( M \) wyjściach realizujących odwzorowanie \( y(\mathbf{x}) = F(\mathbf{x}) \). Jest to struktura sieci dwuwarstwowej, w której jedynie warstwa ukryta reprezentuje odwzorowanie nieliniowe realizowane przez neurony o radialnej funkcji bazowej. Neuron wyjściowy jest zwykle liniowy, a jego rolą jest sumowanie wagowe sygnałów pochodzących od neuronów warstwy ukrytej. Waga \(w_0 \), podobnie jak w przypadku funkcji sigmoidalnych, reprezentuje polaryzację, wprowadzającą składnik stałego przesunięcia funkcji.

Uzyskana architektura sieci radialnych ma strukturę analogiczną do struktury wielowarstwowej sieci sigmoidalnej o jednej warstwie ukrytej. Rolę neuronów ukrytych pełnią tu radialne funkcje bazowe, różniące się kształtem od funkcji sigmoidalnych. Mimo podobieństwa istnieją również istotne różnice między obu typami sieci. Sieć radialna ma strukturę ustaloną o jednej warstwie ukrytej podczas gdy sieć sigmoidalna może mieć różną liczbę warstw, a neurony wyjściowe mogą być zarówno liniowe, jak i nieliniowe. Funkcja nieliniowa radialna jest zwykle typu gaussowskiego. Dla każdego neuronu ukrytego w sieci radialnej przyjmuje ona inne wartości parametrów \( \mathbf{c}_i \) oraz \( \mathbf{\sigma}_i \), natomiast w sieci sigmoidalnej stosuje się identyczne funkcje aktywacji. Ponadto zauważmy, że argumentem funkcji radialnej jest euklidesowa odległość danego wektora \( \mathbf{x} \) od wektora centrum \( \mathbf{c}_i \), podczas gdy w sieci sigmoidalnej jest to iloczyn skalarny wektorów \( \mathbf{w} \) oraz \( \mathbf{x} \).
Dalsze rozważania, dla uproszczenia, przedstawione będą dla sieci z jednym wyjściem.
Zadanie aproksymacji polega na dobraniu odpowiedniej liczby oraz parametrów funkcji radialnych \( \varphi\left(\mathbf{x}-\mathbf{c}_i\right) \) i takim doborze wag \( \mathbf{w}_i \) aby rozwiązanie (4.4) najlepiej przybliżało rozwiązanie dokładne. Problem doboru parametrów funkcji radialnych oraz wartości wag \( \mathbf{w}_i \) sieci w problemie regresji można zatem sprowadzić do minimalizacji funkcji celu, którą przy wykorzystaniu normy euklidesowej daje się zapisać w postaci
| \( \min E=\sum_{i=1}^p\left[\sum_{j=0}^K w_j \varphi\left(\mathbf{x}_i-\mathbf{c}_j\right)-d_i\right]^2 \) | (4.5) |
W równaniu tym \( K \) reprezentuje liczbę neuronów radialnych, natomiast \( p \) liczbę par uczących \( \left(\mathbf{x}_i, d_i\right) \), gdzie \( \mathbf{x}_i \) jest wektorem wejściowym, a \( d_i \) - odpowiadającą mu wielkością zadaną na wyjściu. Oznaczmy przez \(\mathbf{d} = [ d_0, d_1, \ldots, d_p]^T \) wektor wielkości zadanych, przez \(\mathbf{w} = [ w_0, w_1, \ldots, w_K]^T \) wektor wag sieci z uwzględnieniem polaryzacji (wartość \( w_0 \)), a przez \( \mathbf{G} \) - macierz radialną, zwaną macierzą Greena
| \( \mathbf{G}=\left[\begin{array}{cccc} \varphi\left(\mathbf{x}_1-\mathbf{c}_1\right) & \varphi\left(\mathbf{x}_1-\mathbf{c}_2\right) & \cdots & \varphi\left(\mathbf{x}_1-\mathbf{c}_K\right) \\ \varphi\left(\mathbf{x}_2-\mathbf{c}_1\right) & \varphi\left(\mathbf{x}_2-\mathbf{c}_2\right) & \cdots & \varphi\left(\mathbf{x}_2-\mathbf{c}_K\right) \\ \cdots & \cdots & \cdots & \cdots \\ \varphi\left(\mathbf{x}_p-\mathbf{c}_1\right) & \varphi\left(\mathbf{x}_p-\mathbf{c}_2\right) & \cdots & \varphi\left(\mathbf{x}_p-\mathbf{c}_K\right) \end{array}\right] \) |
(4.6) |
Przy ograniczeniu liczby funkcji bazowych do \( K \), macierz \( \mathbf{G} \) jest macierzą prostokątną o liczbie wierszy zwykle dużo większej niż liczba kolumn \((p \gg K) \). Przy założeniu znajomości parametrów funkcji radialnych macierz Greena jest ściśle określoną macierzą liczbową, a problem optymalizacyjny (4.6) sprowadza się do rozwiązania układu równań liniowych
| \( [ \mathbf{1} \; \mathbf{G}]{\mathbf{w}}=\mathbf{d} \) | (4.7) |
względem wektora wagowego \(\mathbf{w} \), a \(\mathbf{1} \) jest wektorem jednostkowym związanym z wagą polaryzacji \( w_0 \). Wobec prostokątności macierzy \(\mathbf{G} \) wektor wag \(\mathbf{w} \) wyznacza się, wykorzystując pojęcie pseudoinwersji macierzy \(\mathbf{G} \), to jest
| \( \mathbf{w}=[ \mathbf{1} \; \mathbf{G}]^{+}\mathbf{d} \) | (4.8) |
gdzie znak \( ^{+} \) oznacza pseudoinwersję macierzy prostokątnej. W praktyce numerycznej pseudoinwersja jest obliczana zwykle przy wykorzystaniu dekompozycji SVD [4,16].
1.3. Metody uczenia sieci neuronowych radialnych
Wprowadzone w poprzednim podrozdziale metody doboru wag \( w_i \) warstwy wyjściowej sieci radialnej RBF opierały się na założeniu, że parametry samych funkcji bazowych są znane, w związku z czym macierze Greena są określone w sposób numeryczny i zadanie sprowadza się do rozwiązania nadmiarowego układu równań liniowych o postaci (4.7). W rzeczywistych zastosowaniach liczba neuronów ukrytych \( K < p \) i problem uczenia sieci RBF z uwzględnieniem wybranego typu radialnej funkcji bazowej sprowadza się do:
-
ustalenia liczby neuronów gaussowskich \( K \) oraz doboru centrów \( \mathbf{c}_i \) i parametrów szerokości \( \mathbf{\sigma}_i \) funkcji bazowych Gaussa
-
doboru wag \( w_i \) neuronów warstwy wyjściowej.
4.3.1 Proces samoorganizacji w określeniu parametrów funkcji radialnych
Określenie wartości parametrów funkcji radialnych (centra \( \mathbf{c}_i \) i szerokości \( \mathbf{<span>\sigma}_i \)) można uzyskać przy zastosowaniu algorytmu samoorganizacji poprzez współzawodnictwo. Proces samoorganizacji danych uczących poprzez współzawodnictwo dzieli automatycznie przestrzeń na tak zwane wieloboki Voronoia, przedstawiające obszary dominacji określonych centrów odpowiadających poszczególnym funkcjom radialnym. Przykład takiego podziału przestrzeni dwuwymiarowej pokazano na rys. 4.2.
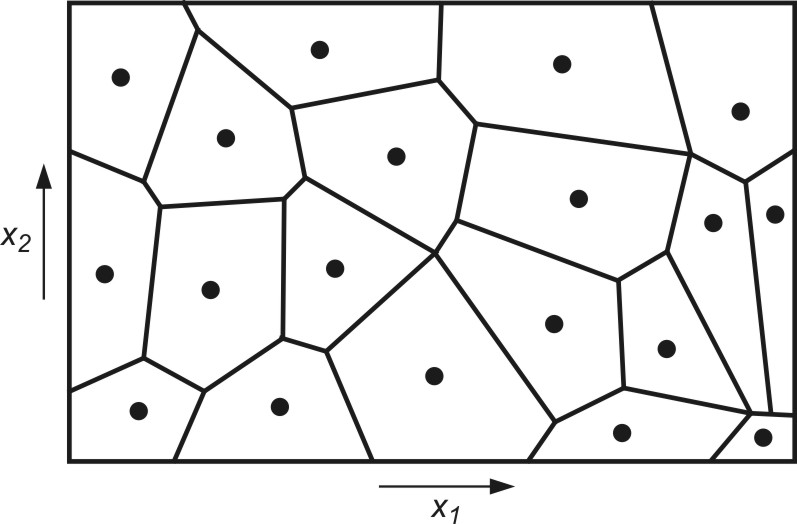
Dane zgrupowane wewnątrz klastra są reprezentowane przez punkt centralny, stanowiący średnią ze wszystkich elementów danego klastra. Centrum klastra utożsamione będzie dalej z centrum c odpowiedniej funkcji radialnej. Liczba tych funkcji jest zatem równa liczbie centrów i może być korygowana przez algorytm samoorganizacji.
Proces podziału danych na klastry można przeprowadzić przy użyciu jednej z wersji algorytmu Linde-Buzo-Graya (LBG) zwanego również algorytmem K-uśrednień (ang. K-means). W wersji bezpośredniej (on-line) tego algorytmu aktualizacja centrów następuje po każdej prezentacji wektora \( \mathbf{x} \) ze zbioru danych uczących. W wersji skumulowanej (off-line) centra są aktualizowane jednocześnie po zaprezentowaniu wszystkich składników zbioru uczącego. W obu przypadkach wstępny wybór centrów odbywa się najczęściej losowo przy wykorzystaniu rozkładu równomiernego w zakresie zmienności poszczególnych składowych wektora \( \mathbf{x} \).
W wersji bezpośredniej (on-line) po zaprezentowaniu \( k \)-tego wektora \( \mathbf{x}_k \) ze zbioru uczącego selekcjonowane jest centrum \( \mathbf{c}_i \) najbliższe w sensie wybranej metryki danemu wektorowi. To centrum podlega aktualizacji zgodnie z algorytmem WTA
| \( \mathbf{c}_i(k+1)=\mathbf{c}_i(k)+\eta\left(\mathbf{x}_k-\mathbf{c}_i(k)\right) \) | (4.9) |
w którym \( \eta \) jest współczynnikiem uczenia o małej wartości (zwykle \( \eta \ll 1 \)), malejącym w czasie do zera. Pozostałe centra nie ulegają zmianie. Każdy wektor uczący \( \mathbf{x} \) jest prezentowany wielokrotnie, zwykle w kolejności losowej aż do ustalenia wartości centrów.
Stosowana jest również odmiana algorytmu, w której centrum zwycięskie adaptowane jest według wzoru (4.9), a jeden lub kilka najbliższych mu centrów odpychane w przeciwnym kierunku, przy czym realizacja procesu odpychania odbywa się zgodnie ze wzorem
| \( \mathbf{c}_i(k+1)=\mathbf{c}_i(k)-\eta_1\left(\mathbf{x}_k-\mathbf{c}_i(k)\right) \) | (4.10) |
Taka modyfikacja algorytmu pozwala na rozsunięcie centrów położonych blisko siebie i lepszą penetrację przestrzeni danych (zwykle \( \eta_1 \) < \(\eta \)).
W wersji skumulowanej uczenia prezentowane są wszystkie wektory uczące \( \mathbf{x} \) i każdy z nich przyporządkowany odpowiedniemu centrum. Zbiór wektorów przypisanych do jednego centrum tworzy klaster, którego nowe centrum jest średnią poszczególnych wektorów składowych
| \( \mathbf{c}_i(k+1)=\frac{1}{N_i} \sum_{j=1}^{N_i} \mathbf{x}_j \) | (4.11) |
gdzie \( N_i \) oznacza liczbę wektorów \( \mathbf{x}_j \) przypisanych w \( k \)-tym cyklu do \( i \)-tego centrum. Uaktualnianie wartości wszystkich centrów odbywa się równolegle. Proces prezentacji zbioru wektorów \( \mathbf{x} \) oraz uaktualniania wartości centrów powtarzany jest wielokrotnie aż do ustalenia się wartości centrów.
W praktyce używa się najczęściej algorytmu bezpośredniego ze względu na jego nieco lepszą zbieżność. Oba algorytmy nie gwarantują jednak bezwzględnej zbieżności do rozwiązania optymalnego w sensie globalnym, a jedynie zapewniają optymalność lokalną, uzależnioną od warunków początkowych i parametrów procesu. Przy niefortunnie dobranych warunkach początkowych pewne centra mogą utknąć w regionie, w którym liczba danych uczących jest znikoma lub żadna i proces modyfikacji ich położeń może zostać zahamowany. Pewnym rozwiązaniem tego problemu jest modyfikacja położeń wielu centrów na raz, ze stopniowaniem wartości stałej uczenia \( \eta \) dla każdego z nich. Centrum najbliższe aktualnemu wektorowi \( \mathbf{x} \) modyfikowane jest najbardziej, pozostałe w zależności od ich odległości względem wektora \( \mathbf{x} \) coraz mniej.
Po ustaleniu położeń centrów dobierane są wartości parametrów \( \sigma \), odpowiadających poszczególnym funkcjom bazowym. Parametr \( \sigma_j \) funkcji radialnej decyduje o kształcie funkcji i wielkości pola recepcyjnego, dla którego wartość tej funkcji jest niezerowa (większa od pewnej ustalonej wartości progowej). Dobór \( \sigma_j \) powinien być taki, aby pola recepcyjne wszystkich funkcji radialnych pokrywały cały obszar danych wejściowych, przy czym sąsiednie pola recepcyjne mogą pokrywać się w stopniu nieznacznym. Przy takim doborze wartości \( \sigma_j \) odwzorowanie funkcji realizowane przez sieci radialne będzie stosunkowo gładkie. W najprostszym rozwiązaniu za wartość \( \sigma_j \) odpowiadającą \( j \)-tej funkcji radialnej przyjmuje się odległość euklidesową \( j \)-tego centrum \( \mathbf{c}_j \) od jego najbliższego sąsiada [24,46]. W innym algorytmie z uwzględnieniem szerszego sąsiedztwa, na wartość \( \sigma_j \) wpływa odległość \( j \)-tego centrum od jego \( q \) najbliższych sąsiadów. Wartość \( \sigma_j \) określa się wtedy ze wzoru
| \( \sigma_j=\sqrt{\frac{1}{q} \sum_{k=1}^q\left\|\mathbf{c}_j-\mathbf{c}_k\right\|^2} \) | (4.12) |
W praktyce wartość \( q \) mieści się zwykle w zakresie od 3 do 6. W przypadku danych o podobnym charakterze zmian stosuje się często stałą wartość \( \sigma_j = \sigma\) dla wszystkich neuronów radialnych (dla danych znormalizowanych typowe wartości jest \( \sigma\) bliskie jedności).
Wstępny dobór liczby funkcji radialnych (neuronów ukrytych) dla każdego problemu jest sprawą kluczową, decydującą o dokładności odwzorowania. Stosuje się ogólną zasadę, że im większy jest wymiar wektora \( \mathbf{x} \) i liczba danych uczących, tym większa wymagana liczba funkcji radialnych. Często przyjmuje się na wstępie liczbę funkcji radialnych jako pewien ułamek (np. 1/3) liczby wszystkich par uczących \( p \).
4.3.2 Dobór wartości wag warstwy wyjściowej
Prosty jest również problem adaptacji wag neuronów warstwy wyjściowej. Zgodnie z zależnością (4.8) wektor wagowy \( \mathbf{x} \) może być wyznaczony w jednym kroku przez pseudoinwersję macierzy \( \mathbf{G} \), czyli \( \mathbf{W}=\left[\begin{array}{ll} \mathbf{1} & \mathbf{G} \end{array}\right]^{+} \cdot \mathbf{d} \). Dla uproszczenia wzorów przyjęto w dalszych rozważaniach oznaczenie rozszerzonej macierzy Greena \( \mathbf{G} \leftarrow [ \mathbf{1} \; \mathbf{G} ] \). W praktyce obliczenie pseudoinwersji macierzy \( \mathbf{G} \) następuje przy zastosowaniu dekompozycji według wartości osobliwych (SVD), według którego
| \( \mathbf{G} = \mathbf{USV}^T \) | (4.13) |
Macierze \( \mathbf{U} \) i \( \mathbf{V} \) są ortogonalne, o wymiarach odpowiednio \( p \times p \) oraz \( K \times K \), podczas gdy \( \mathbf{S} \) jest macierzą pseudodiagonalną o wymiarach \( p \times K \; (p < K) \), zawierającą elementy diagonalne zwane wartościami osobliwymi \( s_1 \geq s_2 \geq \ldots s_K \geq 0 \). Załóżmy, że jedynie \( r \) pierwszych elementów \( s_i \) ma znaczące wartości, a pozostałe są pomijalnie małe. Wtedy można zredukować liczbę kolumn macierzy ortogonalnych \( \mathbf{U} \) i \( \mathbf{V} \) do wartości \( r \), pomijając pozostałe. Utworzone w ten sposób zredukowane macierze \( \mathbf{U}_r \) i \( \mathbf{V}_r \) mają postać
\( \mathbf{U}_r=\left[\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_r\right] \)
\( \mathbf{V}_r=\left[\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_r\right] \)
a macierz \( \mathbf{S}_{r}=\operatorname{diag}\left[{s}_1, {s}_2, \ldots, {s}_{r}\right] \) staje się macierzą w pełni diagonalną (kwadratową). Macierze te aproksymują zależność (4.13) w postaci
| \( \mathbf{G} = \mathbf{U}_r \mathbf{S}_r \mathbf{V}_r^T \) | (4.14) |
Biorąc pod uwagę własności macierzy ortogonalnych (\( \mathbf{Q}^{-1} = \mathbf{Q}^{T} \)) macierz pseudoodwrotna do \( \mathbf{G} \) określona jest teraz prostą zależnością
| \( \mathbf{G}^{+} = \mathbf{V}_r \mathbf{S}_r^{-1} \mathbf{U}_r^T \) | (4.15) |
w której \( \mathbf{S}_r^{-1}=\left[ \frac{1}{s_1}, \frac{1}{s_2}, \ldots, \frac{1}{s_r} \right] \) a wektor wag sieci podlegającej adaptacji określony jest wzorem
| \( \mathbf{w} = \mathbf{V}_r \mathbf{S}_r^{-1} \mathbf{U}_r^T \mathbf{d}\) | (4.16) |
Zaletą takiego podejścia jest dobre uwarunkowanie problemu. Dobór wag wyjściowych sieci odbywa się w jednym kroku przy wykorzystaniu jedynie mnożenia odpowiednich macierzy, przy czym część macierzy (\( \mathbf{U}_r \) i \( \mathbf{V}_r \)) to macierze ortogonalne, z natury dobrze uwarunkowane (współczynnik uwarunkowania równy 1).
Zauważmy, że w uczeniu sieci RBF parametry podlegające adaptacji tworzą dwie niezależnie dobierane grupy: parametry funkcji radialnych adaptowane poprzez grupowanie danych oraz wagi \( \mathbf{w} \) warstwy wyjściowej określane poprzez pseudoinwersję macierzy Greena. Daje to efekt uproszczenia obliczeń i znacznego skrócenia czasu uczenia.
1.4. Metody doboru liczby funkcji bazowych
Dobór liczby funkcji bazowych, utożsamianych z liczbą neuronów ukrytych, jest podstawowym problemem przy właściwym rozwiązaniu problemu aproksymacji. Podobnie jak w sieciach sigmoidalnych, zbyt mała liczba neuronów nie pozwala dostatecznie zredukować błędu dopasowania na zbiorze danych uczących, natomiast zbyt duża ich liczba powoduje wzrost błędu generalizacji na zbiorze testującym. Dobór właściwej liczby neuronów jest uzależniony od wielu czynników, w tym wymiarowości problemu, liczby danych uczących, a przede wszystkim kształtu aproksymowanej funkcji w przestrzeni wielowymiarowej. Zwykle liczba funkcji bazowych \( K \) stanowi jedynie pewien ułamek liczby danych uczących \( p \), przy czym aktualna wartość tego ułamka jest uzależniona od wymiaru wektora \( \mathbf{x} \) oraz od stopnia zróżnicowania wartości zadanych \( d_i \), odpowiadających wektorom wejściowym \( \mathbf{x}_i \) dla \( i = 1,2,\ldots, p \).
4.4.1 Metody heurystyczne
Wobec niemożności określenia a priori dokładnej liczby neuronów ukrytych stosuje się metody adaptacyjne, które pozwalają na ich dodanie lub usunięcie w trakcie procesu uczenia. Powstało wiele metod heurystycznych umożliwiających takie operacje [24]. Zwykle uczenie sieci zaczyna się od pewnej wstępnie założonej liczby neuronów, a następnie kontroluje się zarówno stopień redukcji błędu średniokwadratowego, jak i zmiany wartości adaptowanych parametrów sieci. Najprostszym podejściem jest kolejne zwiększanie liczby neuronów ukrytych, jeśli aktualny błąd uczenia jest zbyt duży. Z kolei jeśli już wstępna wartość błędu jest zadowalająca należy podjąć próbę kolejnego zmniejszania liczby neuronów ukrytych aż do wartości skrajnej przy której dochodzi się do progu akceptowalności błędu.
W bardziej zaawansowanej technice procedura może być bardziej zaawansowana i uzależniona od średniej zmiany wartości wag po określonej liczbie cykli uczących. Jeśli jest zbyt mała \( \sum_i \Delta w_i < \varepsilon \) dodaje się dwie nowe funkcje bazowe (2 neurony) o centrach odpowiadających odpowiednio największej i najmniejszej wartości błędu dopasowania (dwie skrajne wartości błędu dopasowania), kontynuując uczenie tak rozbudowanej struktury. Jednocześnie kontroluje się absolutne wartości wag \( w_i \) poszczególnych neuronów. Jeśli są one mniejsze od założonego na wstępie progu, neurony im odpowiadające podlegają usunięciu. Zarówno dodawanie neuronów, jak i usuwanie odbywa się po określonej liczbie cykli uczących i trwa przez cały czas uczenia, aż do uzyskania odpowiedniej dokładności odwzorowania.
Inne podejście w sterowaniu liczbą neuronów ukrytych zaproponował J. Platt. Jest to metoda łącząca w sobie jednocześnie uczenie samoorganizujące i z nadzorem. Po każdej prezentacji kolejnego wzorca uczącego określana jest odległość euklidesowa między nim a najbliższym centrum istniejącej już funkcji radialnej. Jeśli ta odległość jest większa od założonego progu \( \Delta \), tworzone jest nowe centrum funkcji radialnej (dodawany neuron) w punkcie odpowiadającym prezentowanemu wektorowi \( \mathbf{x} \), po czym sieć podlega standardowemu douczeniu z wykorzystaniem metod gradientowych (uczenie z nadzorem). Proces dodawania neuronów zachodzi aż do uzyskania określonej wartości błędu odwzorowania. Ważnym problemem w tej metodzie jest dobór wartości progu \( \Delta \), decydującej o rozbudowie struktury sieci. Zwykle wartość ta zmienia się wykładniczo z czasem (liczbą iteracji) od wartości maksymalnej na początku procesu do wartości minimalnej na końcu.
4.4.2 Metoda ortogonalizacji Grama-Schmidta
Skuteczną metodą kontroli liczby neuronów ukrytych pozostaje zastosowanie specjalnej techniki uczenia sieci opartej na metodzie ortogonalizacji najmniejszych kwadratów (ang. Orthogonal Least Squares - OLS) i korzystającej z klasycznego algorytmu ortogonalizacji Grama-Schmidta [6,46]. Metoda ta ma wbudowany algorytm określania optymalnej liczby funkcji radialnych w trakcie procesu uczenia.
Punktem wyjścia jest przedstawienie problemu uczenia jako liniowego dopasowania wektora wag sieci \( \mathbf{w} \), minimalizującego wartość wektora błędu \( e \), czyli
| \( \min _{\mathbf{w}} \mathrm{E}=\|e\|^2=|\mathbf{G} \mathbf{w}-\mathbf{d}|^2 \) | (4.17) |
W równaniu tym \( \mathbf{G} \) jest macierzą Greena a \( \mathbf{d} \) wektorem wartości zadanych, \( \mathbf{d} = [d_1, d_2, \ldots, d_n]^T \) o zerowej wartości średniej. Na wstępie przyjmuje się liczbę funkcji radialnych \( K=p\) i centrach \( \mathbf{c}_i = \mathbf{x}_i \). Iloczyn \( \mathbf{Gw} \) podniesiony do kwadratu reprezentuje część pożądaną energii związaną z wartościami sygnałów zadanych wektorem \( \mathbf{d} \). Wartość tej energii podlega optymalizacji w procesie uczenia dążąc do wartości energii zdefiniowanej wektorem \( \mathbf{d} \) (suma kwadratów składników \(d_i\) wektora \( \mathbf{d} \)). Wprowadzając oznaczenia \( \mathbf{g}_i \) dla kolumn macierzy \( \mathbf{G} \) można ją przedstawić w postaci \( \mathbf{G} = [\mathbf{g}_1, \mathbf{g}_2, \ldots, \mathbf{g}_K ] \), w której wektory \(\mathbf{g}_i \) są powiązane z funkcjami bazowymi Gaussa. Metoda ortogonalizacji najmniejszych kwadratów polega na transformacji wektorów \(\mathbf{g}_i \) w zbiór bazowych wektorów ortogonalnych, umożliwiających ocenę indywidualnego wkładu każdego z nich w ogólną wartość energii reprezentowanej przez \(\mathbf{Gw} \) i eliminację pewnej ich liczby (których znaczenie dla procesu jest minimalne) z \( p \) do \( K \), przy czym \(K < p \).
W procesie uczenia macierz \(\mathbf{G} \) o wymiarze \( p \times K \) ulega rozkładowi na iloczyn macierzy \(\mathbf{Q} \) (o wymiarze \( p \times K \) złożonej z ortogonalnych wektorów kolumnowych \(\mathbf{q}_i\), \( \mathbf{Q} = [\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_K ] \) oraz kwadratowej macierzy górnotrójkątnej \(\mathbf{A} \) stopnia \( K \) o jednostkowych wartościach na diagonali
| \( \mathbf{G} =\mathbf{QA} \) | (4.18) |
W równaniu tym
| \( \mathbf{A}=\left[\begin{array}{ccccc} 1 & a_{12} & a_{13} & \cdots & a_{1 K} \\ 0 & 1 & a_{23} & \cdots & a_{2 K} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \cdots & 1 \end{array}\right] \) |
(4.19) |
przy czym macierz ortogonalna \(\mathbf{Q} \) spełnia zależność
| \( \mathbf{Q}^T\mathbf{Q}=\mathbf{H} \) |
(4.20) |
w której \( \mathbf{H} \) jest macierzą diagonalną o elementach diagonalnych \( h_{i i}=\mathbf{q}_i^T \mathbf{q}_i=\sum_{j=1}^K q_{i j}^2 \). Rozwiązanie zadania minimalizacji (4.17) sprowadza się do rozwiązania równania liniowego
| \( \mathbf{Gw} = \mathbf{QAw}=\mathbf{d} \) | (4.21) |
Po wprowadzeniu wektora pomocniczego b
| \( \mathbf{b}=\mathbf{Aw} \) | (4.22) |
równanie (4.21) upraszcza się do postaci
| \( \mathbf{d} = \mathbf{Qb} \) | (4.23) |
Jest to układ \( p \) równań z \( K \) niewiadomymi. Rozwiązanie tego równania (wektor \( \mathbf{\hat{b}} \)) przyjmuje postać
| \( \mathbf{\hat{b}} = [\mathbf{Q}^T\mathbf{Q}]^{-1}\mathbf{Q}^T\mathbf{d}=\mathbf{H}^{-1}\mathbf{Q}^T\mathbf{d} \) |
(4.24) |
Biorąc pod uwagę diagonalny charakter macierzy \( \mathbf{H} \) można podać jawny wzór opisujący poszczególne składniki wektora \( \mathbf{\hat{b}} \)
| \( \hat{b}_i=\frac{\mathbf{q}_i^T \mathbf{d}}{\mathbf{q}_i^T \mathbf{q}_i} \) | (4.25) |
Po określeniu wektora \( \mathbf{\hat{b}} \) można wyznaczyć również wektor poszukiwanych wag \( \mathbf{w} \)
| \( \mathbf{w} = \mathbf{A}^{-1}\mathbf{b} \) | (4.26) |
Przy trójkątnej postaci macierzy \( \mathbf{A} \) rozwiązanie równania (4.26) względem wektora \( \mathbf{w} \) nie sprawia trudności natury obliczeniowej. Ortogonalizacja macierzy \( \mathbf{G} \) opisana zależnością (4.18) może być dokonana różnymi metodami, z których najefektywniejszy jest algorytm ortogonalizacji Grama-Schmidta [6]. W metodzie tej generacja macierzy \( \mathbf{A} \) następuje kolumna po kolumnie z jednoczesnym tworzeniem kolejnych kolumn ortogonalnej macierzy \( \mathbf{Q} \). W kroku k-tym tworzy się kolumnę \( \mathbf{q}_k \) ortogonalną do wszystkich \( k-1 \) kolumn utworzonych wcześniej. Procedurę powtarza się dla kolejnych wartości \( k=2,3,\ldots, K \).
Ważną zaletą metody ortogonalizacji w tym zastosowaniu jest również możliwość selekcji wektorów \( \mathbf{q}_i \) pod względem ich ważności w odwzorowaniu danych uczących. Przy założonej na wstępie liczbie \( K=p \) funkcji radialnych zadanie polega na takim ustawieniu kolejnych wektorów \( \mathbf{q}_i \), aby wyselekcjonować pierwsze \( K_r \) najbardziej znaczące pod względem energetycznym, przy czym zwykle \( K_r \ll p \).
Uwzględnienie w dalszych obliczeniach tylko \( K_r \) funkcji radialnych odpowiada redukcji liczby neuronów ukrytych z wartości wstępnej \( p \) do wartości \( K_r \). Biorąc pod uwagę energię związaną z sygnałami opisanymi wektorem \( \mathbf{d} \) i uwzględniając zależność (4.25) otrzymuje
| \( \mathbf{d}^T \mathbf{d} \cong \sum_{i=1}^p \hat{b}_i^2 \mathbf{q}_i^T \mathbf{q}_i \) |
(4.27) |
Jeśli przyjmie się, że \( \mathbf{d} \) reprezentuje wektor zadany o zerowej wartości średniej, składnik \( \hat{b}_i^2 \mathbf{q}_i^T \mathbf{q}_i \) może być zinterpretowany jako średni wkład \( i \)-tej funkcji bazowej w odwzorowanie funkcji zadanej wektorem \( \mathbf{d} \). Względny udział tego składnika w ogólnym bilansie energii wyraża się zatem wzorem
| \( \varepsilon_i=\frac{\hat{b}_i^2 \mathbf{q}_i^T \mathbf{q}_i}{\mathbf{d}^T \mathbf{d}} \) |
(4.28) |
Wyznaczenie wartości \( \varepsilon_i \) odpowiadających poszczególnym funkcjom bazowym umożliwia określenie ich wkładu w odwzorowanie funkcyjne danych uczących, co ułatwia podjęcie decyzji o redukcji tych, których wpływ jest najmniejszy. Po wyselekcjonowaniu określonej liczby najbardziej znaczących funkcji radialnych proces ortogonalizacji przeprowadza się powtórnie, określając nowe rozwiązanie i selekcjonując następne, najbardziej znaczące funkcje radialne. Przy założeniu wartości startowej \( K=p \) po kilku cyklach ortogonalizacji Grama-Schmidta można wyselekcjonować pożądaną liczbę \(K_r \) najbardziej znaczących funkcji bazowych, eliminując pozostałe. Procedurę określania najbardziej znaczących w odwzorowaniu funkcji radialnych kończy się z chwilą spełnienia warunku
| \( 1-\sum_{j=1}^{K_r} \varepsilon_j < \rho \) |
(4.29) |
gdzie \( 0 < \rho < 1 \) jest przyjętą z góry wartością tolerancji.
W wyniku przeprowadzonej procedury zachowanych zostaje jedynie \(K_r \) najbardziej znaczących funkcji radialnych położonych w centrach określonych poprzez wybrane przez algorytm dane uczące \( \mathbf{x}_i \). Jednocześnie w wyniku działania algorytmu określone są poszczególne składowe \( b_i \) wektora \( \mathbf{b} \), na podstawie których z zależności (4.26) otrzymuje się wartości wag \( \mathbf{w} \) warstwy wyjściowej sieci.
Tolerancja \( \rho \) decydująca o zakończeniu procesu uczenia jest ważnym czynnikiem, od którego zależy z jednej strony dokładność odwzorowania danych uczących, a z drugiej - stopień złożoności sieci neuronowej. W wielu przypadkach jej wartość może być oszacowana na podstawie rozkładu statystycznego danych uczących oraz aktualnych postępów w uczeniu. W praktyce przeprowadza się zwykle wiele procesów uczenia sieci RBF przy różnych wartościach \( \rho \), zachowując jedynie tę, która zapewnia najlepsze działanie sieci na danych weryfikujących (część danych uczących nie biorąca udziału w uczeniu).
1.5. Program komputerowy uczenia sieci radialnych
Algorytm uczenia sieci RBF wykorzystujący zarówno samoorganizację jak i ortogonalizację Grama-Schmidta został zaimplementowany w środowisku Matlab jako pakiet programów RBF. Wywołanie następuje poprzez napisanie nazwy programu głównego RBF_win w oknie komend Matlaba. Pojawia się wówczas menu programu w postaci przedstawionej na rys. 4.3, ułatwiające posługiwanie się programem.
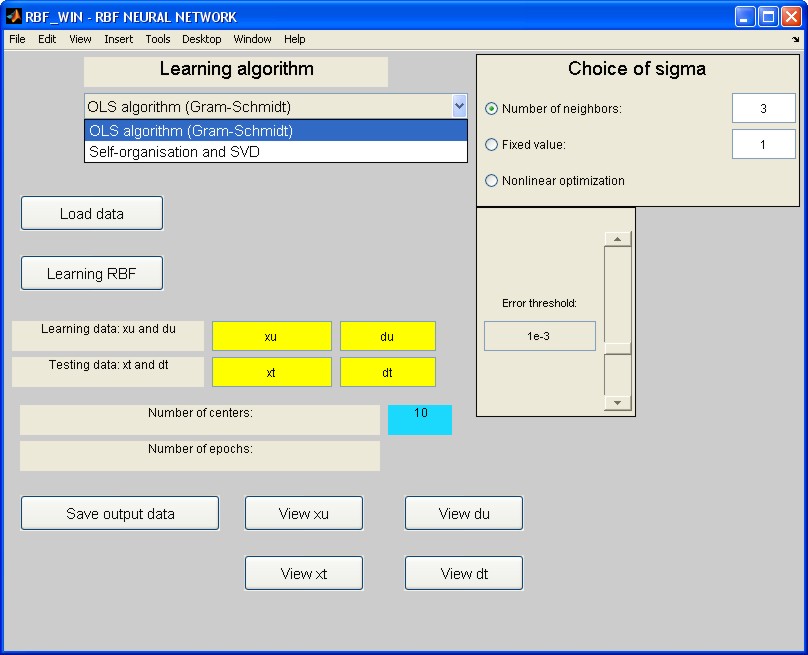
W pierwszej kolejności należy wczytać dane uczące i testujące korzystając z przycisków Learning data oraz Testing data. Zmienne \( xu \) i \( xt \) oznaczają macierze zawierające wektory wierszowe \( \mathbf{x} \) danych wejściowych użytych odpowiednio w uczeniu i testowaniu sieci. Zmienne \( du \) i \( dt \)oznaczają stowarzyszone z nimi wartości sygnałów wartości zadanych na wyjściu sieci (zbiór wektorów \( \mathbf{d} \)). Można również zadać wielkości uczące i testujące zgromadzone w pliku, korzystając z przycisku Load data. Uaktywnienie tego przycisku otwiera okno wczytywania danych (rys. 4.4), które umożliwia wybór odpowiednich zmiennych, zapisanych wcześniej w pliku przez użytkownika ( \( xucz = xu, xtest=xt, ducz=du, dtest=dt \)).
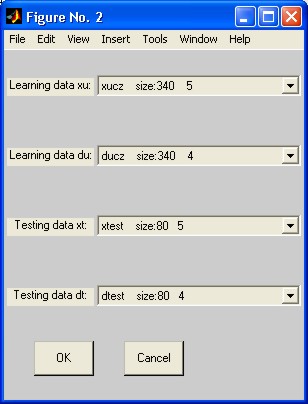
W chwili obecnej w programie zaimplementowany jest algorytm uczący OLS Grama-Schmidta oraz algorytm podstawowy oparty na samoorganizacji i dekompozycji SVD, omówione w punktach poprzednich. Do wyboru konkretnego algorytmu służy pole Learning algorithm, przy czym możliwe jest dołączenie dowolnego innego programu uczącego. Przed uruchomieniem procesu uczenia należy wybrać wartość tolerancji \( \rho \) (przycisk Error threshold) oraz sposób określania szerokości funkcji radialnej \( \sigma \) (pole Choice of sigma). Możliwe jest automatyczne ustalanie wartości \( \sigma \) na podstawie odległości od podanej przez użytkownika liczby najbliższych sąsiadów (opcja Number of neighbors), przyjęcie wartości stałej podanej przez użytkownika (opcja Fixed value) lub wykorzystanie optymalizacji nieliniowej (opcja Nonlinear optimization) dobierającej szerokość funkcji radialnej poprzez jej optymalizację gwarantującą najlepsze dopasowanie do danych uczących (ta opcja działa skutecznie jedynie przy małej liczbie centrów). Wciśnięcie przycisku Learning RBF uruchamia główny proces uczenia sieci. W jego wyniku wyświetlana jest aktualna liczba wygenerowanych centrów (Number of centers). Jednocześnie następuje automatyczne testowanie wytrenowanej sieci na danych uczących, a wynik przekazywany do przestrzeni roboczej Matlaba jako zmienna \( y \). Pojawi się wówczas również dodatkowy przycisk Testing RBF umożliwiający testowanie wytrenowanej sieci na danych testujących nie uczestniczących w uczeniu. Wynik testowania przekazywany jest do przestrzeni roboczej Matlaba również jako zmienna y. Program umożliwia zapamiętanie zarówno sygnałów wyjściowych sieci w pliku (przycisk Save output data) jak i całej struktury oraz parametrów wytrenowanej sieci (przycisk Save network) do jej przyszłego wczytania (przycisk Load network). Rola użytkownika programu sprowadza się do przygotowania danych uczących oraz wyboru parametrów uczenia. Dodatkowo w przypadku danych jednowymiarowych możliwa jest wizualizacja graficzna danych uczących i testujących. Do tego celu służą przyciski View xlearn, View dlearn, View xtest oraz View dtest wyświetlające wykresy odpowiednich sygnałów przy wykorzystaniu funkcji graficznych Matlaba
1.6. Przykład zastosowania sieci radialnej w aproksymacji
Sieci neuronowe o radialnych funkcjach bazowych znajdują zastosowanie zarówno w rozwiązywaniu problemów klasyfikacyjnych (na wyjściu sieci umieszcza się wówczas dodatkowo funkcję typu signum, wskazująca na określona klasę), zadaniach aproksymacji funkcji wielu zmiennych jak i zagadnieniach predykcji, a więc w tym obszarze zastosowań, gdzie sieci sigmoidalne mają od lat ugruntowaną pozycję. Sieci RBF wykonują te same zadania co sieci sigmoidalne choć w rozwiązaniu problemu stosują inny sposób przetwarzania danych, wykorzystujący lokalność odwzorowania. Dzięki tej własności możliwe jest znaczne uproszczenie, a przez to również skrócenie procesu uczenia. Jako przykład zastosowania sieci RBF rozpatrzymy problem aproksymacji funkcji nieliniowej dwu zmiennych opisanej wzorem
| \( f(\mathbf{x})=\frac{\sin \left(\sqrt{x_1^2+x_2^2}\right)}{\sqrt{x_1^2+x_2^2}} \) |
(4.30) |
Dla wytrenowania sieci RBF należy w pierwszej kolejności utworzyć na podstawie tego wzoru zbiór par uczących \( ( \mathbf{x}, d(\mathbf{x})) \). Dane uczące utworzono dla 400 punktów danych, wygenerowanych dla zmiennych \( x_1 \) i \( x_2 \) rozłożonych równomiernie w zakresie (-9, 9). Dane te tworzą kształt funkcji trójwymiarowej przedstawionej na rys. 4.5a. Rys. 4.5b ilustruje położenia centrów funkcji bazowych wyselekcjonowanych przez sieć neuronową a rys. 4.5c i d odpowiednio postać funkcji odtworzonej oraz błąd odwzorowania. Szerokość funkcji radialnych była dobierana automatycznie w uzależnieniu od trzech najbliższych sąsiadów.
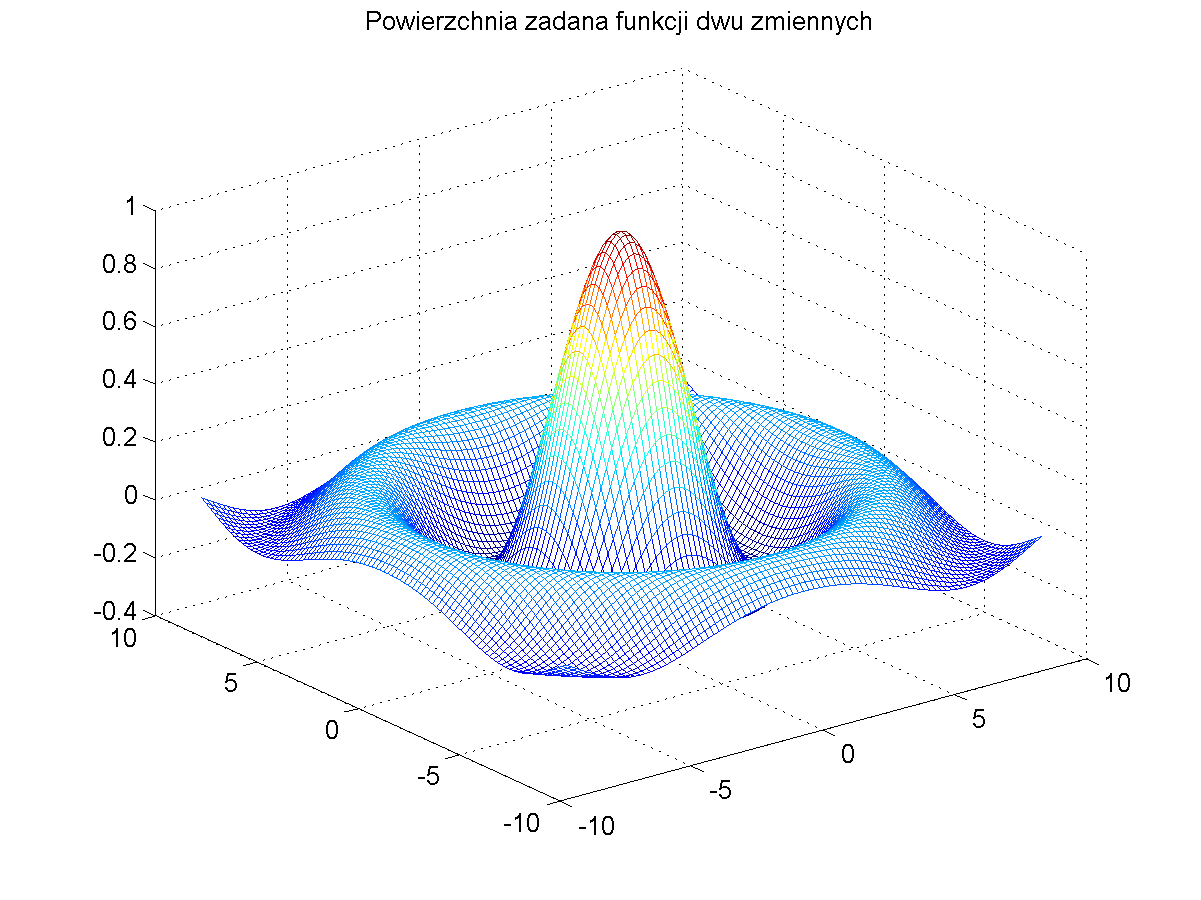
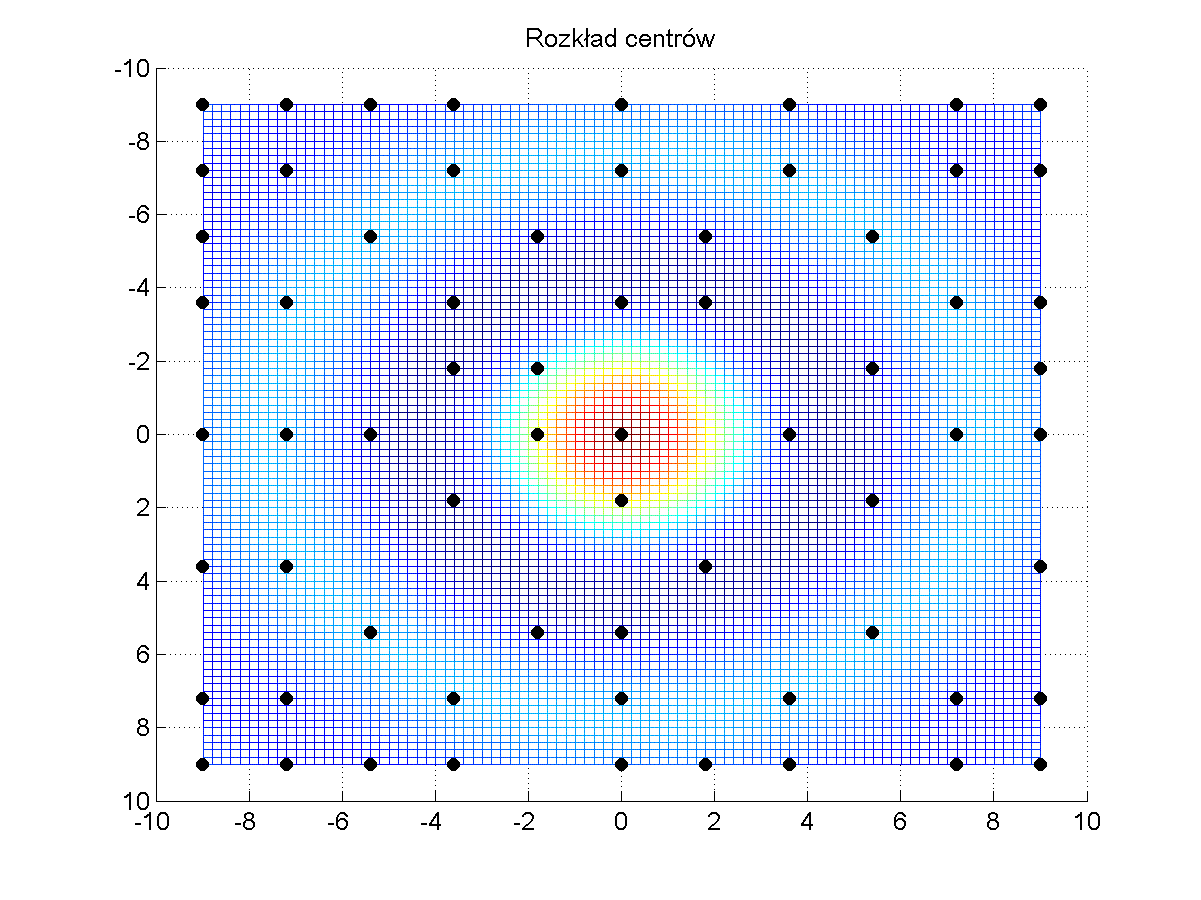
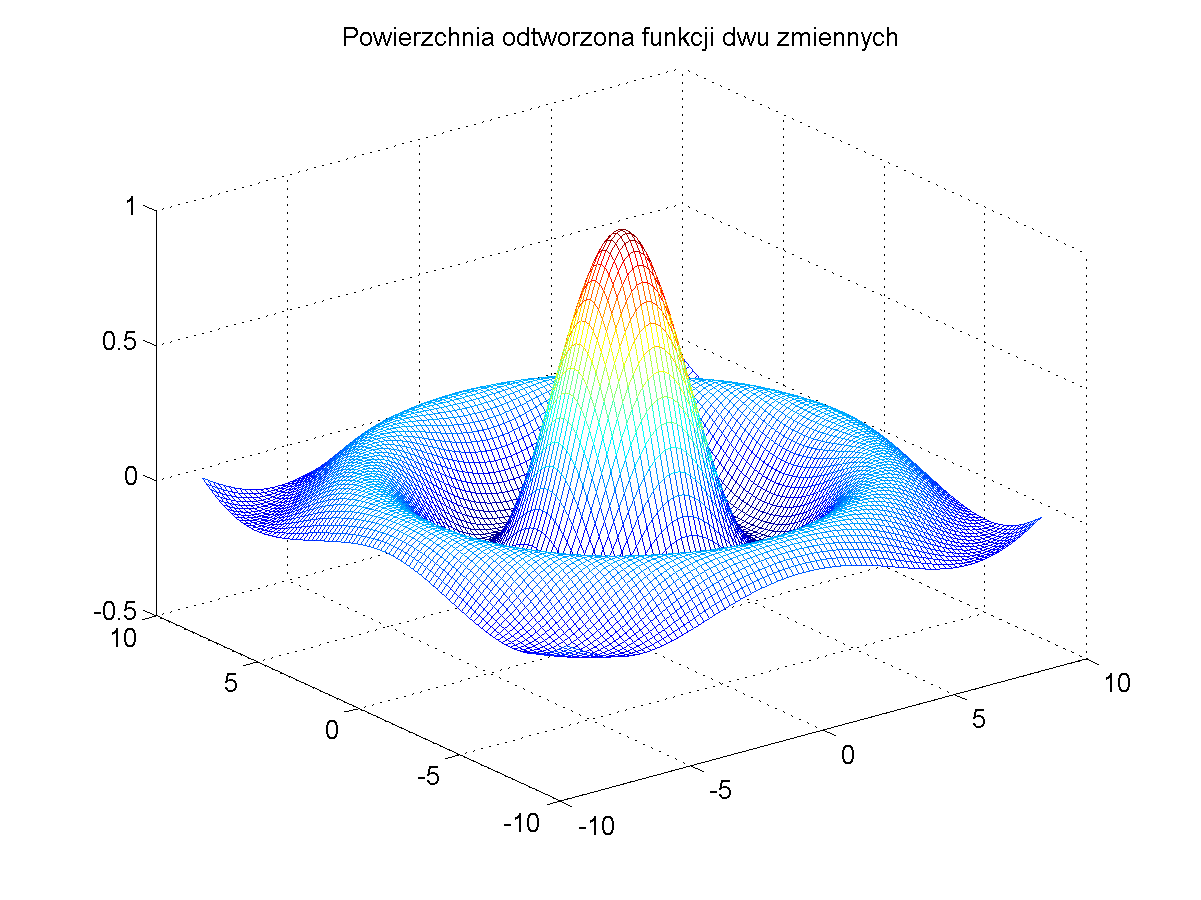
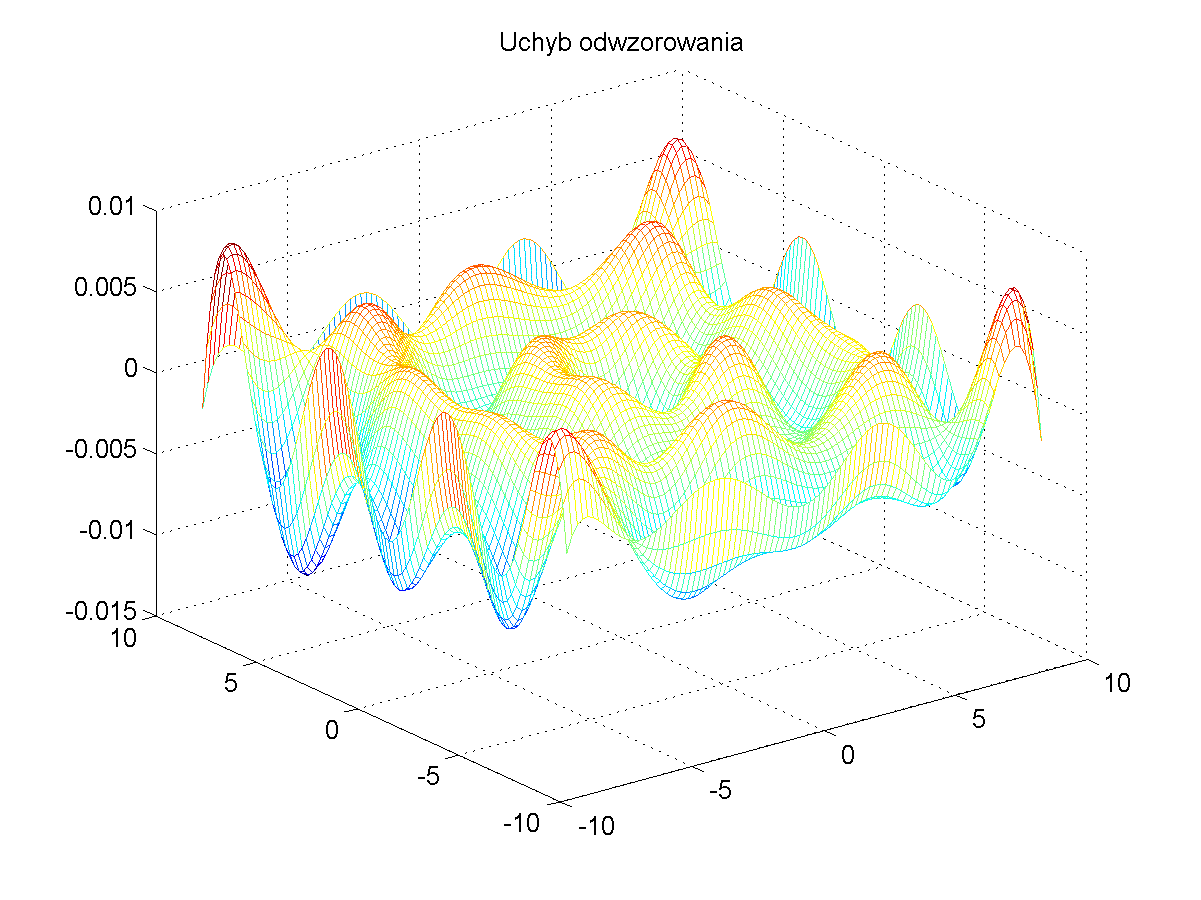
Jak widać odwzorowanie funkcji zadanej przez sieć RBF jest bliskie idealnemu. Błąd odwzorowania nie przekracza w całym zakresie wartości 0.01 i jest akceptowalny z praktycznego punktu widzenia.
1.7. Porównanie sieci radialnych z sieciami sigmoidalnymi
Sieci neuronowe radialne należą do tej samej grupy sieci trenowanych pod nadzorem co sieci sigmoidalne MLP. W stosunku do sieci wielowarstwowych o sigmoidalnych funkcjach aktywacji wyróżniają się pewnymi własnościami szczególnymi, pozwalającymi na łatwiejsze odwzorowanie cech charakterystycznych modelowanego procesu. Sieć sigmoidalna, w której niezerowa wartość funkcji sigmoidalnej rozciąga się od określonego punktu w przestrzeni aż do nieskończoności, reprezentuje aproksymację globalną funkcji zadanej, podczas gdy sieć radialna, opierająca się na funkcjach mających wartość niezerową jedynie w wąskiej przestrzeni wokół centrów, realizuje aproksymację typu lokalnego, której zasięg działania jest zwykle bardziej ograniczony. W efekcie należy się spodziewać, że zdolności generalizacyjne sieci radialnych są gorsze niż sieci sigmoidalnych, zwłaszcza na granicach obszaru danych uczących.
Sieci MLP ze względu na globalny charakter funkcji sigmoidalnej nie mają wbudowanego mechanizmu pozwalającego zidentyfikować region, na który najsilniej odpowiada dany neuron. Wobec niemożliwości fizycznego powiązania obszaru aktywności neuronu z odpowiednim obszarem danych uczących, w sieciach sigmoidalnych trudno jest określić optymalny punkt startowy w procesie uczenia. Biorąc pod uwagę wielomodalność funkcji celu, osiągnięcie minimum globalnego w tych warunkach jest trudne nawet przy wyrafinowanych metodach uczenia.
Sieci radialne radzą sobie z tym problemem znacznie lepiej. Funkcje radialne typu gaussowskiego, najczęściej używane w praktyce, są z natury funkcjami lokalnymi o wartościach niezerowych jedynie wokół określonego centrum. To pozwala łatwo powiązać parametry funkcji bazowych z fizycznym rozmieszczeniem danych uczących w przestrzeni wielowymiarowej. Stąd możliwe jest stosunkowo uzyskanie dobrych wartości startowych w procesie uczenia pod nadzorem. Zastosowanie podobnych algorytmów uczących przy wartościach startowych bliskich optymalnym zwielokrotnia prawdopodobieństwo uzyskania sukcesu dla sieci radialnych.
Uważa się, że sieci radialne lepiej niż sieci sigmoidalne nadają się do takich zadań klasyfikacyjnych, jak wykrywanie uszkodzeń w różnego rodzaju systemach, rozpoznawanie wzorców itp. Zastosowanie sieci radialnych w predykcji tak skomplikowanych szeregów czasowych, jak przewidywanie comiesięcznych zmian zatrudnienia w skali kraju, przewidywanie trendów ekonomicznych itp. pozwala uzyskać dobre rezultaty, porównywalne lub lepsze niż przy zastosowaniu sieci sigmoidalnych.
Ważną zaletą sieci radialnych jest znacznie uproszczony algorytm uczenia. Przy istnieniu tylko jednej warstwy ukrytej i ścisłym powiązaniu aktywności neuronu z odpowiednim obszarem przestrzeni danych uczących, punkt startowy uczenia jest znacznie bliżej rozwiązania optymalnego niż jest to możliwe do uzyskania w sieciach MLP. Dodatkowo możliwe jest oddzielenie etapu doboru parametrów funkcji bazowych od doboru wartości wag sieci (algorytm hybrydowy), co znacznie upraszcza i przyspiesza proces uczenia. Zysk czasowy jest znacznie większy, jeśli uwzględni się procedurę kształtowania optymalnej pod względem zdolności generalizacyjnych struktury sieci. W odniesieniu do sieci MLP jest to zagadnienie bardzo czasochłonne, wymagające zwykle wielokrotnego uczenia lub douczania. W sieciach radialnych przy zastosowaniu zwłaszcza ortogonalizacji, proces optymalnego kształtowania struktury sieci jest stałym fragmentem uczenia, nie wymagającym żadnego dodatkowego wysiłku.
1.8. Przykład zastosowania sieci RBF w modelu sztucznego nosa elektronicznego
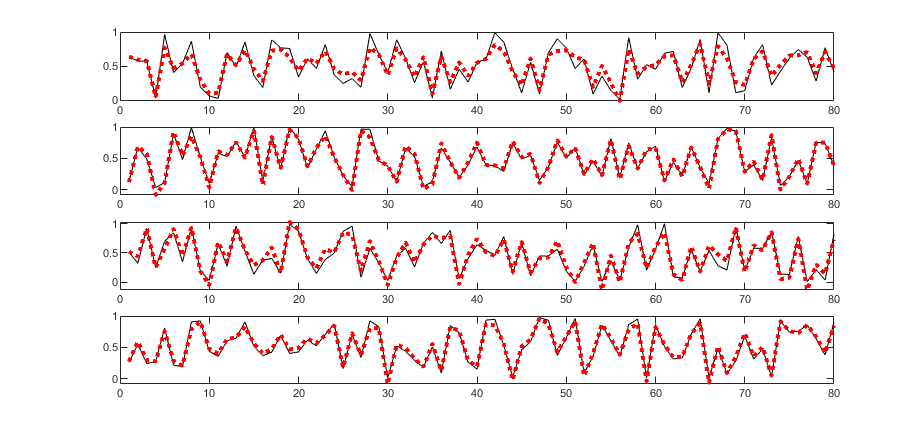
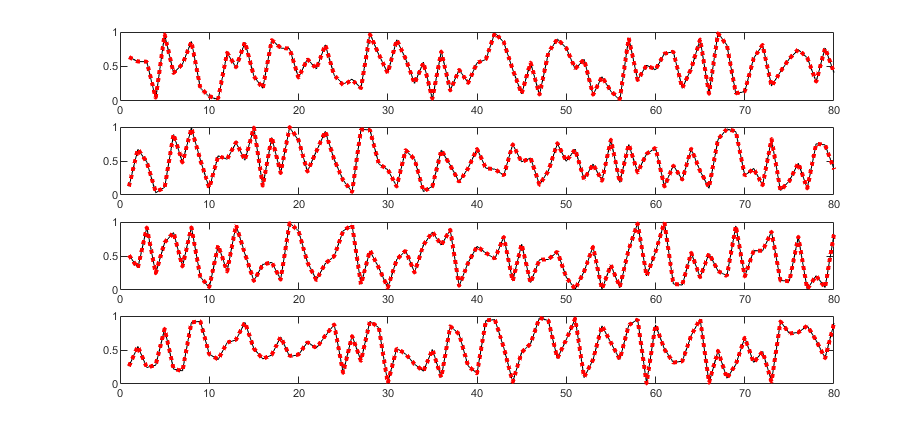
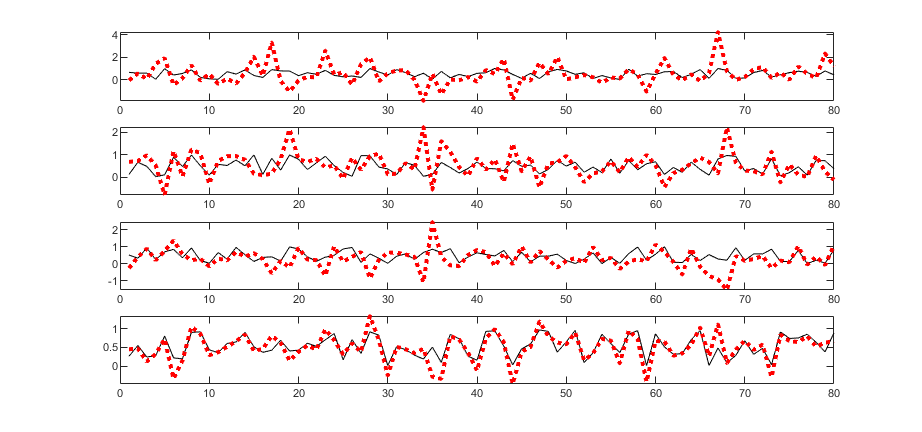
Zadaniem sieci RBF jest określenie stężenia 4 składników gazowych zmieszanych w różnym stosunku przy pomiarze za pomocą 5 czujników półprzewodnikowych firmy FIGARO. W uczeniu zastosowano 340 próbek o różnym stężeniu poszczególnych składników. W testowaniu sieci wytrenowanej użyto 80 próbek. Wynik testowania jest uzależniony od liczby neuronów ukrytych. Zbyt mała ich liczba prowadzi do sieci niedouczonej, zbyt duża liczba do sieci przeuczonej. Rys. 4.6 przedstawia wyniki testowania (wartości zadane względem estymowanych przez sieć) dla liczby neuronów \( K=20 \) (rysunek a), \( K=80 \) (rysunek b) oraz \( K=300\) (rysunek c).
|
a) |
 |
|
b) |
 |
|
c) |
 |
1.9. Zadania i problemy
1. Porównać działanie sieci MLP i RBF pod kątem zalet i wad.
2. Korzystając z funkcji pinv Matlaba wyznaczyć pseudoinwersję macierzy losowej \( \mathbf{A} \) (wygenerowanej przy użyciu funkcji rand) przy założeniu, że macierz ta jest kwadratowa oraz prostokątna o liczbie wierszy większej i mniejszej niż liczba kolumn. Sprawdzić za każdym razem iloczyn macierzy \( \mathbf{A}\mathbf{A}^{-1} \). powiązać wyniki z uwarunkowaniem macierzy (funkcja cond Matlaba). Sprawdzić jak wartość funkcji cond zmienia się z wymiarami macierzy \( \mathbf{A} \).
3. Narysować szczegółową strukturę sieci RBF o dwu wejściach, dwu neuronach ukrytych i jednym wyjściu. Utworzyć sieć dołączoną do niej (sposób tworzenia identyczny jak dla sieci MLP przedstawionej w wykładzie 3). Napisać wyrażenia na gradient funkcji celu względem wag liniowych.
4. Rozważyć problem XOR opisany równaniem
|
x1=[1 1] |
d1=0 |
|
x1=[0 1] |
d1=1 |
|
x1=[1 0] |
d1=1 |
|
x1=[0 0] |
d1=0 |
Sieć RBF modelująca ten problem zawiera 2 neurony ukryte o centrach \( \mathbf{c}_1 = [1 \;1], \mathbf{c}_2 = [0 \; 0], \sigma_1 = \sigma_2 = 1 \). Określić macierz Greena oraz rozwiązanie względem wag \( \mathbf{w} \) przy wykorzystaniu pseudoinwersji. Wykorzystać odpowiednie funkcje macierzowe Matlaba.
5. Dana jest sieć RBF o strukturze przedstawionej na rys. 4.7
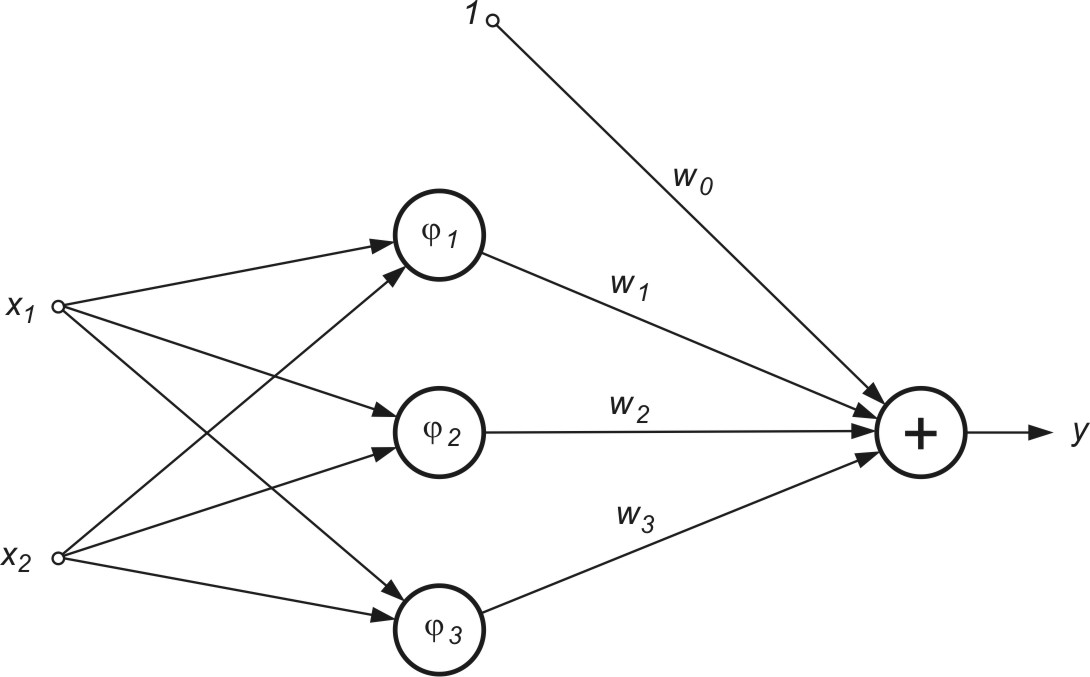
Centra funkcji radialnych dane są w postaci
\( \mathbf{c}_1=\left[\begin{array}{l}
1 \\
1
\end{array}\right], \quad \mathbf{c}_2=\left[\begin{array}{l}
2 \\
2
\end{array}\right], \quad \mathbf{c}_3=\left[\begin{array}{l}
3 \\
0
\end{array}\right] \)
a szerokość wszystkich funkcji równa \( \sigma_1 = 1 \). Wagi sieci są równe: \(w_1 =1, w_2 =0.5, w_3=1.5, w_4=-0.5 \). Sprawdzić przynależność do klasy 1 lub 2 następujących wektorów \( \mathbf{x} \)
\( \mathbf{x}_1=\left[\begin{array}{l} -1 \\ 0 \end{array}\right], \quad \mathbf{x}_2=\left[\begin{array}{l} 2 \\ 1 \end{array}\right], \quad \mathbf{x}_3=\left[\begin{array}{l} 3 \\ 1 \end{array}\right] \)
6. Zaprojektować sieć RBF modelującą funkcję nieliniową dwu zmiennych \( f_1(\mathbf{x})=\sqrt{x_1^2+x_2^2} \) korzystając z programu RBF_win.
7. Wygenerować zbiór danych o rozkładzie losowym typu gaussowskiego o trzech centrach położonych w \( \mathbf{c}_1 = [0.5 \; 1], \mathbf{c}_2 = [0.3 \; 0.8], \mathbf{c}_3 = [0.1 \; 0.5] \) (dla każdego centrum po 50 danych). Przyjąć wspólną wartość \( \sigma = 1 \). Napisać program w Matlabie określający centra 5 neuronów ukrytych przy wykorzystaniu metody off-line uczenia ze współzawodnictwem. Zilustrować graficznie otrzymany wynik na tle danych uczących.
1.10. Słownik
Słownik opanowanych pojęć
Wykład 4
Sieć neuronowa RBF – sieć neuronowa stosująca radialne funkcje aktywacji neuronów.
Aproksymator universalny lokalny – sieć neuronowa wykorzystująca funkcje aktywacji typu lokalnego (np. gaussowskiego)
Funkcja gaussowska – typ funkcji aktywacji bazujący na funkcji Gaussa, definiowany zwykle w postaci \( \varphi(\mathbf{x})=\exp \left(-\frac{\|\mathbf{x}-\mathbf{c}\|^2}{\sigma^2}\right) \), gdzie \( \mathbf{c} \) reprezentuje wektor centrum a \( \sigma \) szerokość funkcji gaussowskiej.
Macierz Greena – macierz zbudowana z funkcji radialnych na bazie danych uczących.
Pseudoinwersja – operacja macierzowa dotycząca procesu odwracania macierzy prostokątnej.
SVD – dekompozycja macierzy według wartości osobliwych.
Wielobok Voronoia – podział przestrzeni danych przedstawiający obszary dominacji określonych centrów odpowiadających poszczególnym funkcjom radialnym.
Grupowanie danych – podział zbioru danych na klastry grupujące dane podobne do siebie.
Algorytm K-uśrednień – metoda podziału zbioru danych na klastry (grupy) reprezentowane przez swoje centra.
Metoda OLS – metoda uczenia sieci RBF wykorzystująca dekompozycję Grama-Schmidta.
Program RBF_win – interfejs graficzny uczenia i testowania sieci RBF w środowisku Matlaba.
Nos elektroniczny – urządzenie do rozpoznawania zapachów przy zastosowaniu sensorów gazowych.
2. Sieci wektorów nośnych SVM
Przedstawione wcześniej sieci neuronowe typu MLP i RBF stosujące w uczeniu minimalizację nieliniowej funkcji celu (błędu), mają wiele wad. Po pierwsze minimalizowana funkcja jest zwykle wielomodalna względem optymalizowanych parametrów, o wielu minimach lokalnych, w których może utknąć proces uczenia w zależności od punktu startowego. Po drugie algorytm uczący nie jest zwykle w stanie kontrolować skutecznie złożoności sieci, stąd przyjęta na wstępie architektura sieci neuronowej i związana z nią wartość VCdim decyduje o przyszłych zdolnościach generalizacyjnych sieci [68]. Nawet sieć RBF stosująca w uczeniu metodę ortogonalizacji ma ograniczenia wynikające z pogarszającego się uwarunkowania macierzy Greena przy dużej liczbie danych uczących i pewnej arbitralności w doborze wartości \( \rho \).
Ten wykład wprowadza nowe podejście do tworzenia struktury i definiowania problemu uczenia sieci neuronowej poprzez modyfikację sposobu uczenia jako takiego doboru wag sieci, aby uzyskać w klasyfikacji najszerszy margines separacji oddzielający skrajne (położone najbliżej siebie) punkty danych uczących obu klas. To zapewni optymalną zdolność generalizacji tak wytrenowanej sieci. Sieć tego typu nosi nazwę SVM (ang. Support Vector Machine). Jej podstawy zostały zdefiniowane przez prof. Vapnika [68] zarówno dla zadania klasyfikacji jak i regresji. Wykład przedstawia podstawy budowy algorytmów uczących obu rodzajów sieci SVM oraz dyskusję uzyskanych wyników.
2.1. Pojęcia wstępne
W ogólności pod pojęciem sieci SVM rozumieć będziemy strukturę neuropodobną o jednej warstwie ukrytej stosującą różne rodzaje funkcji aktywacji i implementującą specjalny sposób uczenia sprowadzający się do programowania kwadratowego. W sieciach SVM rozróżnia się zadanie klasyfikacji i regresji. W przypadku zadania klasyfikacji maksymalizuje się margines separacji między dwoma klasami, przypisanymi danym (\( \mathbf{x}, d_i \)), przy zachowaniu jak najmniejszego błędu klasyfikacji na danych uczących. Zadanie aproksymacji zwane również regresją rozwiązuje się w tych sieciach przez sprowadzenie problemu uczenia do zadania analogicznego do klasyfikacji.
Sieci SVM należą do grupy sieci jednokierunkowych, o jednym neuronie wyjściowym, mają strukturę zwykle dwuwarstwową (warstwa ukryta i wyjściowa) i mogą implementować różne typy funkcji aktywacji, w tym funkcję liniową, wielomianową, radialną oraz sigmoidalną [32,46,68].
2.2. Sieć liniowa SVM w zadaniu klasyfikacji
Załóżmy, że dany jest zbiór par uczących \( (\mathbf{x}_i, d_i) \) dla \(i=1, 2, \ldots, p \) poddany klasyfikacji, w którym \( \mathbf{x}_i \) jest wektorem wejściowym a wartość zadana \( d_i \) jest równa \( 1 \) (klasa 1) bądź \( -1 \) (klasa przeciwstawna). Przy założeniu liniowej separowalności obu klas równanie hiperpłaszczyzny separującej może być zapisane wzorem
\( y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b=0 \)
w której \( \mathbf{w}=[w_1, w_2, \ldots, w_N]^T \) jest \(N\)-wymiarowym wektorem wag a \( \mathbf{x}=[x_1, x_2, \ldots, x_N]^T \), wektorem sygnałów wejściowych \( x_i \). Waga \(b\) stanowi polaryzację. Równania decyzyjne co do przynależności do klas przyjmują postać [68]
| \( \begin{aligned} \mathbf{w}^T \mathbf{x}_i+b > 0 & \rightarrow d_i=1 \\ \mathbf{w}^T \mathbf{x}_i+b < 0 & \rightarrow d_i=-1 \end{aligned} \) | (5.1) |
Za optymalną uważa się taką hiperpłaszczyznę \( y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b=0 \), która maksymalizuje margines separacji między dwoma klasami. Interpretacja marginesu separacji przedstawiona jest na rys. 5.1.
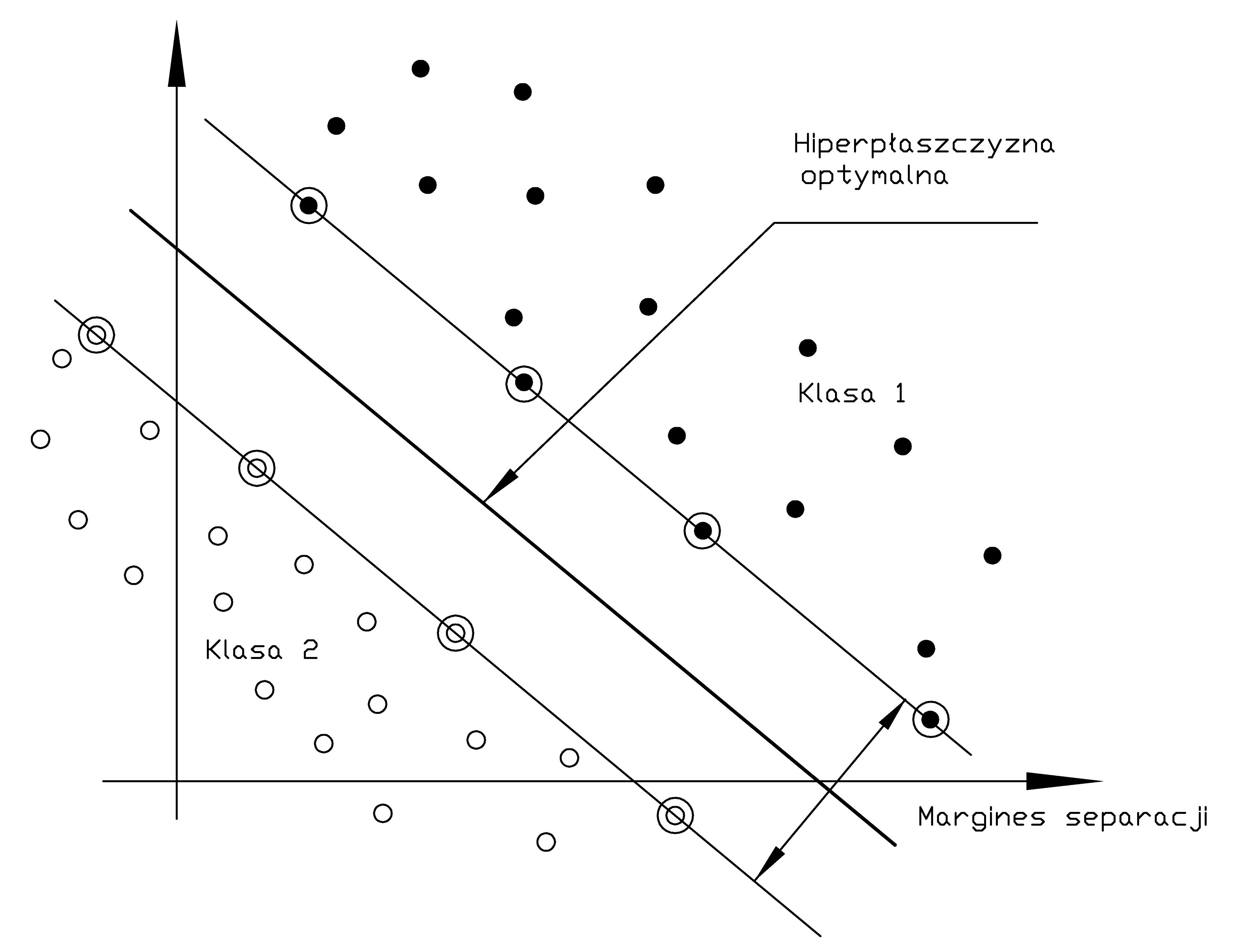
Odległość dowolnego punktu \( \mathbf{x}\) w przestrzeni wielowymiarowej od optymalnej hiperpłaszczyzny określona jest wzorem
| \( r(\mathbf{x})=\frac{y(\mathbf{x})}{\|\mathbf{w}\|} \) | (5.2) |
natomiast odległość początku układu współrzędnych od tej hiperpłaszczyzny jest szczególnym przypadkiem (\( \mathbf{x=0}\) ) i równa się \( r(\mathbf{0}) = b_0/\|\mathbf{w}\| \).
Na etapie uczenia wprowadza się pewien margines tolerancji rozdzielający obie klasy (nazywany marginesem separacji). Duża wartość tego marginesu zwiększa prawdopodobieństwo prawidłowej klasyfikacji dla danych testujących różniących się (z definicji) od danych uczących. Przy uwzględnieniu tolerancji i wprowadzeniu normalizacji warunek prawidłowego przypisania do klas można zapisać wówczas w postaci [68]
| \( \begin{aligned} \mathbf{w}^T \mathbf{x}_i+b \geq 1 & \rightarrow \quad d_i=1 \\ \mathbf{w}^T \mathbf{x}_i+b \leq -1 & \rightarrow \quad d_i=-1 \end{aligned} \) | (5.3) |
Oba równania można zapisać w pojedynczej postaci \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1 \). Jeśli para punktów \( (\mathbf{x}_i, d_i) \) spełnia powyższe równanie ze znakiem równości to wektor \( \mathbf{x}_i \) tworzy tzw. wektor nośny \( \mathbf{x}_{sv} \)(ang. Support Vector - SV). Wektory nośne są tymi punktami danych, które leżą najbliżej optymalnej hiperpłaszczyzny i są najtrudniejsze w klasyfikacji. Co więcej przy założeniu pełnej separowalności liniowej danych należących do obu klas to one decydują o położeniu tej hiperpłaszczyzny i szerokości marginesu separacji, gdyż wszystkie punkty leżące z dala od hiperpłaszczyzny separującej spełniają warunek prawidłowej klasyfikacji z nadmiarem. Dla wektorów podtrzymujących \( \mathbf{x}_{sv} \) z definicji spełniony jest warunek \( \mathbf{w}^T\mathbf{x}_{sv} + b = \pm1 \) dla \( d(\mathbf{x}_{sv})=\pm1 \). Odległość wektorów podtrzymujących \( \mathbf{x}_{sv} \) od hiperpłaszczyzny określona jest zależnością
| \( r\left(\mathbf{x}_{s v}\right)=\frac{y\left(\mathbf{x}_{s v}\right)}{\|\mathbf{w}\|}=\left\{\begin{array}{ccc} \frac{1}{\|\mathbf{w}\|} & \text { dla } & g\left(\mathbf{x}_{sv}\right)=1 \\ -\frac{1}{\|\mathbf{w}\|} & \text { dla } & g\left(\mathbf{x}_{sv}\right)=-1 \end{array}\right. \) | (5.4) |
Margines separacji między obu klasami jest równy podwójnej wartości \( r(\mathbf{x}_{sv}) \), to znaczy
| \( \rho=2 r\left(\mathbf{x}_{sv}\right)=\frac{2}{\|\mathbf{w}\|} \) |
(5.5) |
Dla uzyskania efektu krzepkiej klasyfikacji, mało wrażliwej na szum występujący w danych pomiarowych, pożądana jest jak największa wartość tego marginesu. Z powyższego wzoru widać, że maksymalizacja marginesu separacji między dwoma klasami jest równoważna minimalizacji normy euklidesowej wektora wag \(\mathbf{w}\).
Problem uczenia liniowych sieci SVM, czyli doboru wag sieci dla danych uczących liniowo separowalnych sprowadza się do maksymalizacji marginesu separacji przy spełnieniu warunku (5.3). Nosi on nazwę problemu pierwotnego i zapisuje się go w postaci [68]
| \( \min \limits_w = \frac{1}{2}\mathbf{w}^T\mathbf{w} \) | (5.6) |
przy \( p \) liniowych ograniczeniach funkcyjnych \(i=1, 2, \ldots, p \)
| \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1 \) |
(5.7) |
Jest to problem programowania kwadratowego z liniowymi ograniczeniami względem wag, który rozwiązuje się metodą mnożników Lagrange'a przez minimalizację tak zwanej funkcji Lagrange'a
| \( J(\mathbf{w}, b, \boldsymbol{\alpha})=\frac{1}{2} \mathbf{w}^T \mathbf{w}-\sum_{i=1}^p \alpha_i\left[d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right)-1\right] \) | (5.8) |
w której wektor mnożników Lagrange'a \( \boldsymbol{\alpha} \) składa się z kolejnych mnożników \( \boldsymbol{\alpha}_i \) dla \(i=1, 2, \ldots, p \), o wartościach nieujemnych odpowiadających poszczególnym ograniczeniom, gdzie \( p \) oznacza liczbę par uczących. Mnożniki te rozszerzają liczbę parametrów optymalizowanych w procesie uczenia.
Rozwiązanie problemu minimalizacji funkcji Lagrange'a względem optymalizowanych parametrów \( \mathbf{w}, b, \boldsymbol{\alpha} \) jest określone przez punkt siodłowy funkcji Lagrange’a i odpowiada minimalizacji funkcji \( J(\mathbf{w}, b, \boldsymbol{\alpha}) \) względem wektora \(\mathbf{w},\) i parametru \( b \) oraz maksymalizacji względem wszystkich wartości mnożników tworzących wektor \(\boldsymbol{\alpha} \). Warunki optymalności rozwiązania względem \( \mathbf{w} \) i \( b \), są określone zależnościami
| \( \begin{aligned} & \frac{\partial J(\mathbf{w}, b, \boldsymbol{\alpha})}{\partial \mathbf{w}}=\mathbf{0} \quad \rightarrow \quad \mathbf{w}-\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i=\mathbf{0} \\ & \frac{\partial J(\mathbf{w}, b, \boldsymbol{\alpha})}{\partial b}=0 \quad \rightarrow \quad \sum_{i=1}^p \alpha_i d_i=\mathbf{0} \end{aligned} \) | (5.9) |
Rozwiązanie powyższego układu równań przyjmuje postać
| \( \mathbf{w}=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i \) | (5.10) |
Dla wyznaczenia wartości b można wykorzystać fakt, że w punkcie siodłowym iloczyn mnożnika przez odpowiednie ograniczenie związane z wektorem \(\mathbf{x}_{sv} \) znika. Uwzględniając zależność \( \mathbf{w}^T\mathbf{x}_{sv} + b = \pm1 \) otrzymuje się
| \( b=\pm 1-\mathbf{w}^T\mathbf{x}_{sv} \) | (5.11) |
W przypadku doboru optymalnych wartości mnożników Lagrange’a uczenie sprowadza się do maksymalizacji funkcji Lagrange'a względem tych mnożników. Po wstawieniu zależności (5.10) i (5.11) do wzoru na funkcję Lagrange’a problem pierwotny przekształca się w problem dualny który można sformułować następująco [68]
| \( \max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}} \alpha_{{i}} \alpha_{{j}} d_i d_j \mathbf{x}_i^T \mathbf{x}_j \) |
(5.12) |
przy ograniczeniach
| \( \begin{aligned}
\alpha_i & \geq 0 \\
\sum_{i=1}^p \alpha_i d_i & =0
\end{aligned} \) |
(5.13) |
dla \(i=1, 2, \ldots, p \). Rozwiązanie powyższego problemu optymalizacyjnego względem mnożników Lagrange'a pozwala wyznaczyć wartości optymalne wag w (równanie 5.10) i w następstwie również równanie określające sygnał wyjściowy \( y(\mathbf{x}) \) sieci (równy równaniu hiperpłaszczyzny separującej)
| \( y(\mathbf{x})=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i^T \mathbf{x}+b \) | (5.14) |
Przy rozwiązaniu problemu klasyfikacji wzorców nie w pełni separowalnych liniowo problem sprowadza się do określenia takiej optymalnej hiperpłaszczyzny, która minimalizuje prawdopodobieństwo błędu klasyfikacji na zbiorze uczącym z możliwie najszerszym marginesem separacji. W takim przypadku dane mogą naruszyć strefę marginesu separacji w dwojaki sposób.
-
Punkt danych \( (\mathbf{x}_i, d_i) \) położony jest wewnątrz strefy, ale po właściwej stronie optymalnej hiperpłaszczyzny. Nie występuje wówczas błąd klasyfikacji a jedynie realne zmniejszenie szerokości aktualnego marginesu.
-
Punkt danych \( (\mathbf{x}_i, d_i) \) położony jest wewnątrz lub na zewnątrz strefy, ale po niewłaściwej stronie optymalnej hiperpłaszczyzny. Odpowiada to wystąpieniu błędu klasyfikacji.
W rozwiązaniu problemu klasyfikacji danych nie separowalnych liniowo wprowadza się nieujemnie zdefiniowaną zmienną dopełniającą \( \xi \) zmniejszającą szerokość aktualnego marginesu separacji. Funkcje ograniczeń równościowych można wówczas zapisać w ogólniejszej postaci
| \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \geq 1-\xi_i \) | (5.15) |
gdzie \( \xi_i \) jest nieujemną zmienną dopełniającą dobieraną indywidualnie dla każdej pary danych uczących. Jej wartość większa od zera efektywnie zmniejsza margines separacji, aż do jego przekroczenia, przy czym z definicji \( \xi_i \geq 0 \). Jeśli \( 0 \leq \xi_i \leq 1 \) to punkt danych \( (\mathbf{x}_i, d_i) \) leży wewnątrz strefy separacji po właściwej stronie. Jeśli natomiast \( \xi_i \geq 1 \) to punkt danych leży po niewłaściwej stronie optymalnej hiperpłaszczyzny i wystąpi błąd klasyfikacji. Wektory podtrzymujące spełniają dokładnie równanie \( d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) = 1-\xi_i \) a zatem uwzględnienie ich włącznie z tymi prowadzącymi do błędnej klasyfikacji ma wpływ na położenie optymalnej hiperpłaszczyzny. Uwzględnienie we wprowadzonych wcześniej ograniczeniach wyrażenia \( (1-\xi)_i \) zamiast wartości jednostkowej prowadzi do wzorów optymalizacyjnych o podobnej strukturze jak dla problemu klasyfikacji wzorców separowalnych liniowo. Przy klasyfikacji wzorców nie separowalnych liniowo problem pierwotny może więc być sprowadzony do minimalizacji zmodyfikowanej funkcji celu [59,68]
| \( \min _{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i \) | (5.16) |
przy ograniczeniach liniowych \(i=1, 2, \ldots, p \)
| \( \begin{aligned}
d_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) & \geq 1-\xi_i \\
\xi_{\mathrm{i}} & \geq 0
\end{aligned} \) |
(5.17) |
Czynnik pierwszy we wzorze (5.16)) odpowiada maksymalizacji marginesu separacji, natomiast drugi odpowiada za przyszłe błędy testowania (suma \( \sum_{i=1}^p \xi_i \) jest maksymalnym, górnym oszacowaniem liczby tych błędów). Parametr \( C \) jest wagą z jaką traktowane są błędy testowania w stosunku do marginesu separacji, decydującą o złożoności przyszłej sieci neuronowej. Jest więc parametrem regularyzacyjnym, dobieranym przez użytkownika, na przykład w sposób eksperymentalny, poprzez trening połączony ze sprawdzaniem i oceną na bieżąco wyników. Postępując podobnie jak w przypadku wzorców separowalnych liniowo problem pierwotny jest sprowadzony do problemu dualnego, który można sformułować następująco [68] Dla danego zbioru danych uczących \( (\mathbf{x}_i, d_i) \) należy określić mnożniki Lagrange'a, które maksymalizują wartość funkcji błędu \( Q(\boldsymbol{\alpha}) \)
| \( \max \limits_{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{P}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{P}} \sum_{{j}=1}^{{P}} \alpha_{{i}} \alpha_{{j}} d_i d_j \mathbf{x}_i^T \mathbf{x}_j \) |
(5.18) |
przy ograniczeniach \(i=1, 2, \ldots, p \)
| \( \begin{aligned}
& 0 \leq \alpha_i \leq C \\
& \sum_{i=1}^p \alpha_i d_i=0
\end{aligned} \) |
(5.19) |
przy wartości \( C \) przyjętej z góry przez użytkownika. Ze sformułowania problemu wynika, że ani zmienna dopełniająca ani mnożniki Lagrange'a z nią związane nie pojawiają się w sformułowaniu problemu dualnego. Jedyna różnica w stosunku do problemu separowalności liniowej występuje w ograniczeniu górnym mnożników Lagrange'a. Mnożniki \( \alpha_i \) wynikające z rozwiązania zadania optymalizacyjnego (5.18) z ograniczeniami (5.19) muszą spełniać podstawowy warunek, mówiący że iloczyn mnożnika przez wartość funkcji ograniczenia dla każdej pary danych uczących jest równy zeru. Oznacza to, że wszystkie mnożniki dla których ograniczenie jest nieaktywne (ograniczenia spełnione z nadmiarem) muszą być równe zeru. Niezerowe wartości mnożników występują jedynie dla wektorów nośnych, dla których ograniczenie staje się typu aktywnego, ze znakiem równości (funkcja ograniczenia równa zeru).
Z rozwiązania problemu dualnego określa się wektor wag optymalnej hiperpłaszczyzny w postaci \( \mathbf{w}=\sum_{i=1}^p \alpha_i d_i \mathbf{x}_i \) identycznie jak dla problemu klasyfikacyjnego separowanego liniowo. Zauważmy, że sumowanie w powyższym wzorze dotyczy tylko składników uczących \(\mathbf{x}_i\), dla których mnożniki Lagrange'a są różne od zera. Są to tak zwane wektory nośne (podtrzymujące), których liczbę oznaczymy przez \( N_{sv} \). Jak z powyższego wzoru widać równanie optymalnej hiperpłaszczyzny zależy wyłącznie od wektorów nośnych. Pozostałe wektory ze zbioru danych uczących nie mają żadnego wpływu na wynik rozwiązania.
Równanie określające sygnał wyjściowy \( y(\mathbf{x}) \) sieci liniowej SVM o wagach optymalnych wynika ze wzoru (5.14), które tutaj przepiszemy w postaci
| \( y(\mathbf{x})=\sum_{i=1}^{N_{\text {sv }}} \alpha_i d_i \mathbf{x}_i^T \mathbf{x}+b \) | (5.20) |
Jest to równanie liniowe względem zmiennych wejściowych opisanych wektorem \( \mathbf{x} \) i wagach uzależnionych od niezerowych mnożników Lagrange'a i odpowiadających im wektorów podtrzymujących \( \mathbf{x}_i \) oraz wartości zadanych \( d_i\) stowarzyszonych z nimi.
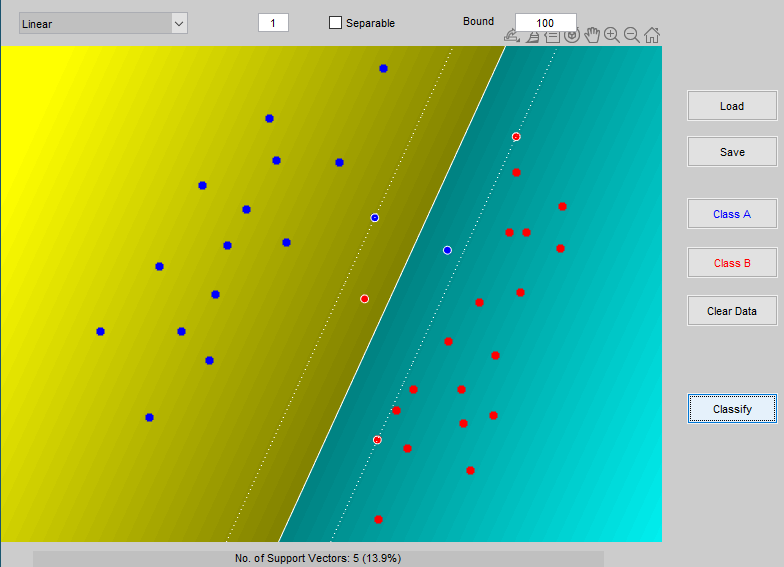
Na rys. 5.2 przedstawiono wynik klasyfikacji danych należących do dwu klas przy zastosowaniu liniowej sieci SVM uzyskany pry użyciu programu Gunna [21]. Wobec niepełnej separowalności danych uczących sieć liniowa dokonała klasyfikacji z 2 błędami (po jednym błędnym przypisaniu do każdej z klas). Margines separacji uwzględnia zmniejszenie odstępu od hiperpłaszczyzny separującej o wartości zmiennych dopełniających. Każdy punkt danych znajdujący się wewnątrz marginesu separacji oraz na obu hiperpłaszczyznach wektorów nośnych tworzy wektor podtrzymujący. W sumie jest ich 5, co stanowi 13.9% ogólnej liczby danych.
2.3. Sieć nieliniowa SVM w zadaniu klasyfikacji
Nieseparowalność liniowa wzorców nie oznacza braku ich separowalności w ogóle. Powszechnym rozwiązaniem, zastosowanym między innymi w poznanych już sieciach RBF jest nieliniowe zrzutowanie danych oryginalnych w inną przestrzeń funkcyjną, w której wzorce te są liniowo separowalne, bądź prawdopodobieństwo ich separowalności jest bliskie jedności. Podstawę matematyczną stanowi tu twierdzenia Covera [59,68], zgodnie z którym wzorce nieseparowalne liniowo w przestrzeni oryginalnej mogą być przetransformowane w inną przestrzeń parametrów, tak zwaną przestrzeń cech, zwykle o wymiarze \( K \ge N \), w której z dużym prawdopodobieństwem stają się separowalne liniowo. Warunkiem jest zastosowanie transformacji nieliniowej o odpowiednio wysokim wymiarze \(K\) przestrzeni cech.
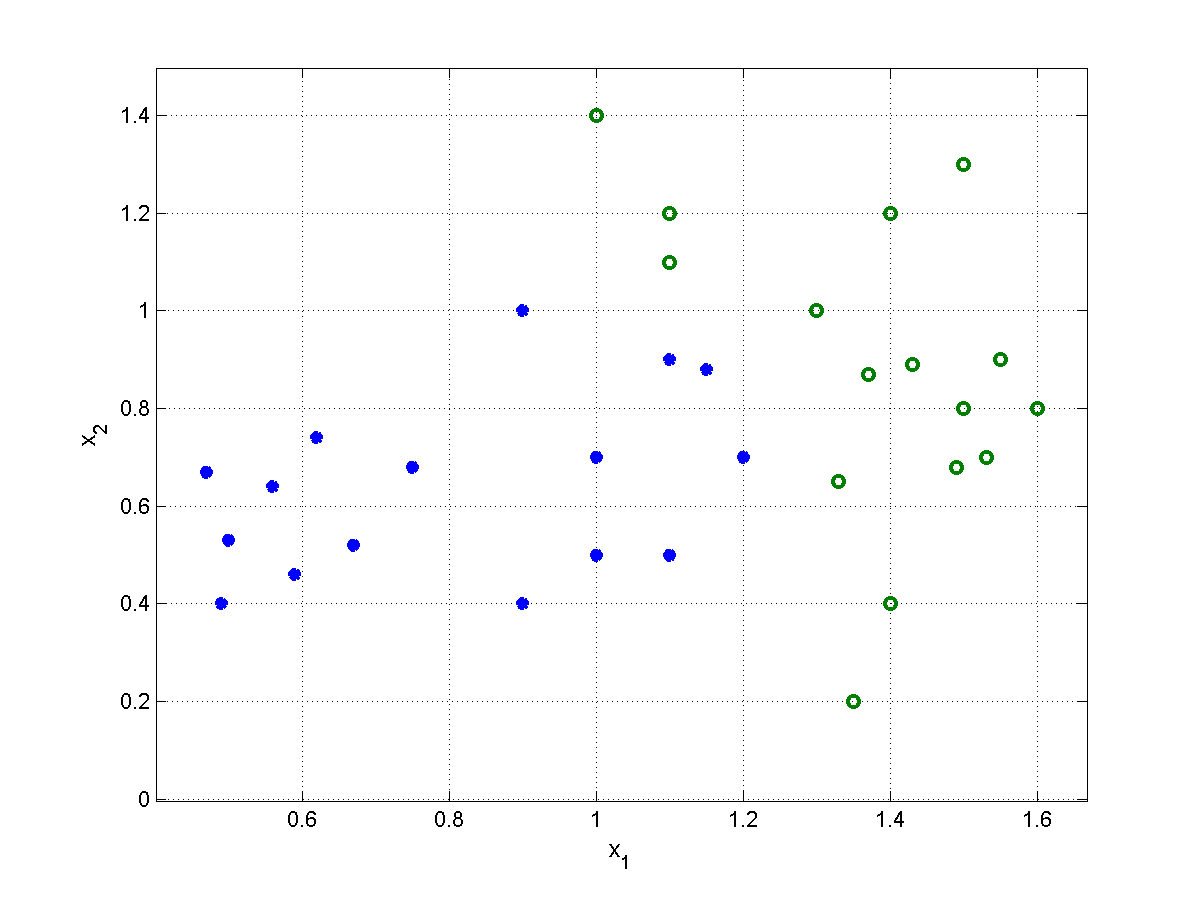
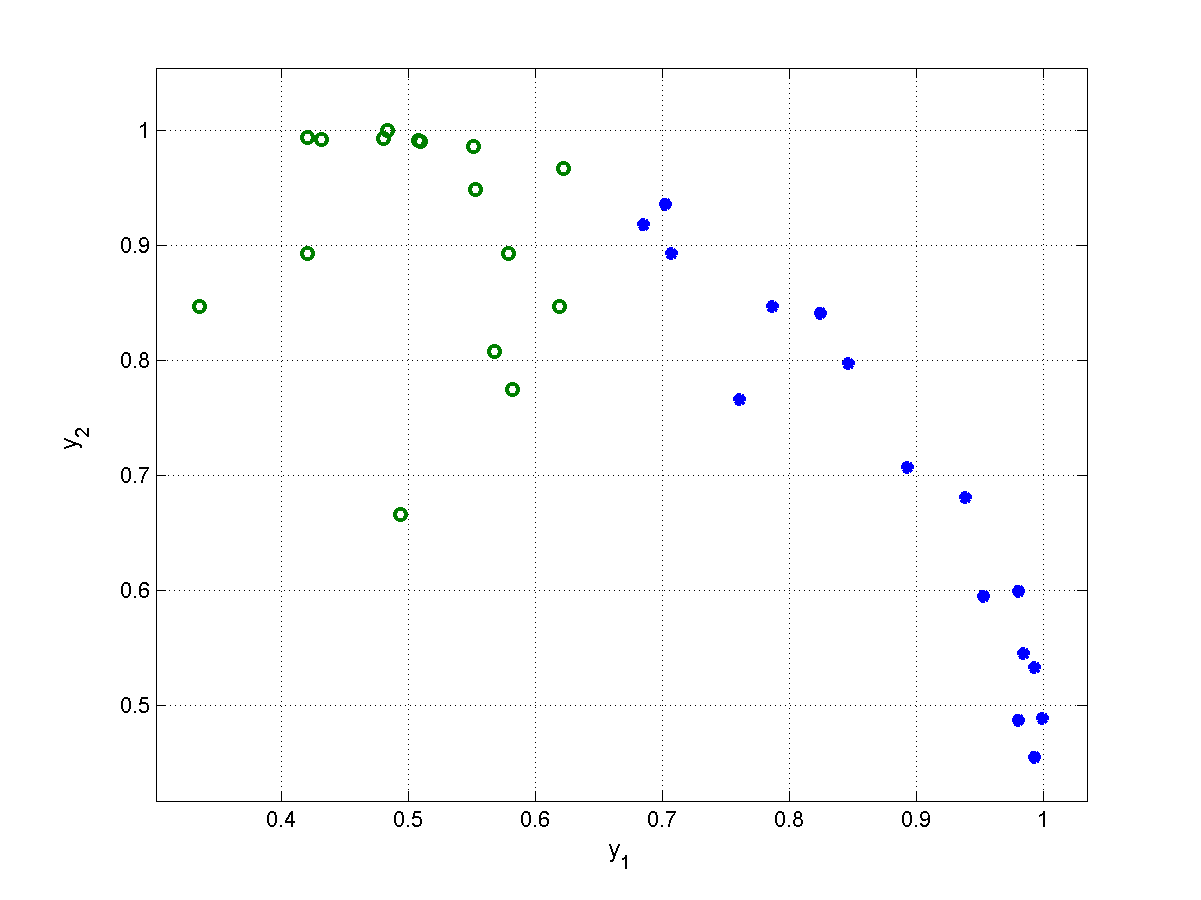
Rys. 5.3 przedstawia szczególny przykład nieliniowej transformacji wzorców należących do dwu klas nieseparowalnych liniowo (klasa \(1\) oznaczona gwiazdką i klasa \(2\) oznaczona symbolem o, obie określone w przestrzeni dwuwymiarowej, \(N=2\)), w przestrzeń funkcyjną zdefiniowaną za pośrednictwem 2 funkcji gaussowskich przy równej dla obu funkcji wartości \(\sigma^2=1,5\) oraz wartościach centrów \(\mathbf{c}_1=[0,5 ;\ 0,5]^T \), \(\mathbf{c}_2=[1,5 ;\ 0,8]^T \). Wzorce oryginalne nieseparowalne w przestrzeni dwuwymiarowej (rys. 5.3a) po transformacji nieliniowej stają się separowalne (rys. 5.3b) i mogą być rozdzielone jedną hiperpłaszczyzną separującą. Zauważmy, że w tym szczególnym przykładzie wystarczyło użycie tylko dwu funkcji nieliniowych, aby przekształcić problem nieseparowalny liniowo w problem całkowicie separowalny.
W ogólności, jeśli \( \mathbf{x} \) oznacza wektor wejściowy opisujący wzorzec, to po zrzutowaniu go w przestrzeń \(K\)-wymiarową jest on reprezentowany przez zbiór \( K\) cech \( \varphi_j(\mathbf{x}) \) dla \( j= 1, 2, \ldots, K \) tworzący wektor \( \boldsymbol{\varphi}(x)=[ \varphi_1(\mathbf{x}), \varphi_2(\mathbf{x}), \ldots, \varphi_K(\mathbf{x})]^T \). W efekcie takiej transformacji równanie hiperpłaszczyzny w przestrzeni liniowej określone wzorem \( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi(\mathbf{x})}+b=0 \) może być zastąpione przez równanie hiperpłaszczyzny w przestrzeni cech, które można zapisać w postaci
| \( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=\sum_{j=1}^K w_j \varphi_j(\mathbf{x})+b=0 \) | (5.21) |
w której \( w_j \) oznaczają wagi prowadzące od \( \varphi_j(\mathbf{x}) \) do neuronu wyjściowego, \( \mathbf{w} = [w_1, w_2, \ldots, w_K]^T\). Wektor wag \( \mathbf{w} \) jest \(K\)-wymiarowy a \(b\) oznacza wagę polaryzacji. Cechy procesu opisane funkcjami \( \varphi_j(\mathbf{x}) \) przejęły rolę poszczególnych zmiennych \( x_j \). Wartość sygnału wyjściowego sieci opisuje teraz równanie
| \( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=0 \) |
(5.22) |
Równaniu (5.22) można przyporządkować strukturę sieci neuronowej analogiczną do sieci RBF, omówioną w rozdziale poprzednim jak to przedstawiono na rys. 5.4.
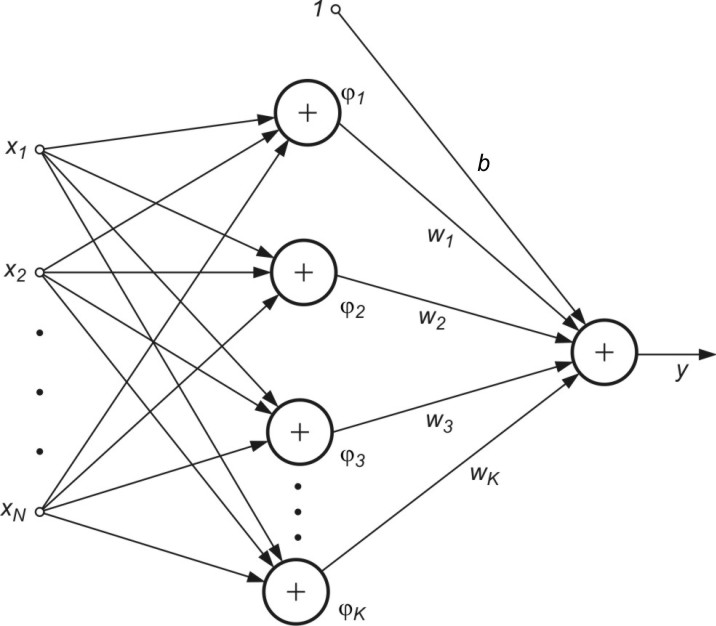
Zasadniczą różnicę w stosunku do sieci RBF stanowi fakt, że funkcje \( \varphi_j(\mathbf{x}) \) mogą przyjmować dowolną postać, w szczególności radialną, sigmoidalną czy wielomianową. Traktując warstwę ukrytą sieci jedynie jako układ rzutujący dane oryginalne w przestrzeń cech, w której są one liniowo separowalne, można traktować sygnały \( \varphi_j(\mathbf{x}) \) jako wymuszenia dla sieci liniowej SVM. Wszystkie zależności wyprowadzone dla sieci liniowej obowiązują zatem również tutaj, przy formalnym zastąpieniu wektora \( \mathbf{x} \) przez wektor \( \boldsymbol{\varphi}(\mathbf{x}) \). W szczególności problem pierwotny uczenia można przepisać w postaci
| \( \min \limits_{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i \) | (5.23) |
przy ograniczeniach liniowych (\(i=1, 2, …, p)\)
| \( \begin{aligned}
d_i\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right) &\geq 1-\xi_i \\
\xi_i &\geq 0
\end{aligned} \) |
(5.24) |
Rozwiązanie problemu pierwotnego odbywa się poprzez jego transformację do problemu dualnego, identycznie jak dla sieci o liniowej separowalności wzorców poprzez minimalizację funkcji Lagrange'a [59,68]
| \( J(\mathbf{w}, b, \boldsymbol{\alpha}, \boldsymbol{\xi}, \boldsymbol{\mu})=\frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i-\sum_{i=1}^p \alpha_i\left[d_i\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right)-1+\xi_i\right]-\sum_{i=1}^p \mu_i \xi_i \) |
(5.25) |
w której mnożniki \( \alpha_i \) odpowiadają ograniczeniom funkcyjnym a \( \mu_i \) ograniczeniom nierównościowym nakładanym na zmienne \( \xi_i \) (wzór 5.24).
Rozwiązanie powyższego problemu optymalizacyjnego zakłada w pierwszym etapie przyrównanie do zera pochodnych funkcji Lagrange'a względem \( \mathbf{w} \), \( b \) oraz \( \xi_i \). Z zależności tych otrzymuje się wyrażenie wektora \( \mathbf{w} \) poprzez mnożniki Lagrange'a oraz dodatkowe zależności funkcyjne, które muszą być spełnione. Po uwzględnieniu tych zależności problem pierwotny przekształca się w problem dualny zdefiniowany wyłącznie względem mnożników Lagrange'a \( \alpha_i \) o następującej postaci (mnożniki \( \mu_i \) zostają wyeliminowane)
| \( \max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}} \alpha_{{i}} \alpha_{{j}} d_i d_j K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) |
(5.26) |
przy ograniczeniach \((i=1, 2,\ldots,p)\)
| \( \begin{aligned} 0 \leq \alpha_i &\leq C \\ \sum_{i=1}^p \alpha_i d_i&=0 \end{aligned} \) | (5.27) |
przy wartości stałej \( C \) przyjętej z góry przez użytkownika. Funkcja \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) występująca w sformułowaniu zadania dualnego jest iloczynem skalarnym funkcji wektorowej \( \boldsymbol{\varphi}(\mathbf{x})=\left[\varphi_1(\mathbf{x}), \varphi_2(\mathbf{x}), \ldots, \varphi_K(\mathbf{x})\right]^T \) określonym dla wektorów \(\mathbf{x}_i \) oraz \(\mathbf{x}_j \)
| \( K\left(\mathbf{x}_i, \mathbf{x}_j\right)=\boldsymbol{\varphi}^T\left(\mathbf{x}_i\right) \boldsymbol{\varphi}\left(\mathbf{x}_j\right) \) | (5.28) |
Iloczyn ten nazywany jest funkcją jądra (ang. kernel function). Z definicji jest to skalarna funkcja symetryczna, to znaczy \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) = K\left(\mathbf{x}_j, \mathbf{x}_i\right) \). Zauważmy, że sformułowanie problemu dualnego nie zawiera ani zmiennych dopełniających ani odpowiadających im mnożników Lagrange'a. Mnożniki \( \mu_i \) muszą spełniać równość \( \mu_i+\alpha_i=C \), ich iloczyn ze zmienną dopełniającą \( \xi_i \) musi być równy zeru, \( \mu_i \xi_i=0 \).
Rozwiązanie problemu dualnego pozwala wyznaczyć optymalne wartości mnożników Lagrange'a, na podstawie których określa się wartości optymalne wag sieci w postaci
| \( \mathbf{w}=\sum_{i=1}^p \alpha_i d_i \boldsymbol{\varphi}\left(\mathbf{x}_i\right) \) |
(5.29) |
Wartość wagi polaryzacyjnej \( b \) wyznacza się podobnie jak w przypadku liniowym wybierając dowolny wektor podtrzymujący \( \mathbf{x}_{sv} \) dla którego \( \xi_i = 0 \) i stosując wzór \( b= \pm 1-\mathbf{w}^T \varphi\left(\mathbf{x}_{s V}\right) \). Po podstawieniu zależności (5.29) do wzoru (5.22) otrzymuje się ostateczne wyrażenie określające sygnał wyjściowy sieci nieliniowej SVM w postaci
| \( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=\sum_{i=1}^{N_{S V}} \alpha_i d_i K\left(\mathbf{x}_i, \mathbf{x}_j\right)+b \) |
(5.30) |
Sygnał wyjściowy sieci zależy od funkcji jądra \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) a nie od funkcji aktywacji \( \varphi(\mathbf{x}) \). W związku z tym wynikową strukturę sieci nieliniowej SVM można przedstawić jak na rys. 5.5.
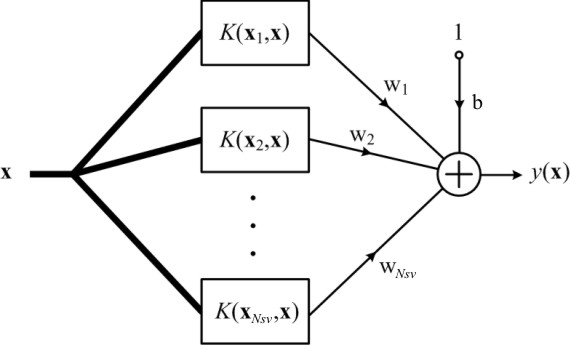
O tym czy funkcja \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) jest kandydatem na jądro spełniającym warunek iloczynu skalarnego dwu bliżej nieokreślonych funkcji wektorowych \( \varphi(\mathbf{x}) \) i \( \varphi(\mathbf{x}_j) \) decyduje spełnienie warunków twierdzenia Mercera [68]. Istnieje wiele funkcji spełniających warunek Mercera, które mogą być użyte do budowy sieci SVM. Do takich funkcji należy między jądro typu gaussowskiego, wielomianowego, funkcje sklejane oraz (przy pewnych ograniczeniach) również jądro sigmoidalne [46,59].
W tabeli 5.1 zestawiono zależności odnoszące się do najczęściej używanych jąder: liniowego, wielomianowego, radialnego oraz sigmoidalnego. Zastosowanie jądra sigmoidalnego prowadzi do powstania sieci perceptronowej o jednej warstwie ukrytej, jądra radialnego - do sieci RBF, natomiast jądra wielomianowego do sieci wielomianowej. Wszystkie te sieci zawierają jedną warstwę ukrytą. W przypadku jądra liniowego sieć jest w pełni liniowa bez warstwy ukrytej.
Tabela 5.1. Przykłady funkcji jąder
|
Funkcja jądra |
Równanie |
Uwagi |
|
Liniowe |
\( K\left(\mathbf{x}_i, \mathbf{x}\right)=\mathbf{x}^T \mathbf{x}_i+\gamma \) |
\( \gamma \) - wartość stała |
|
Wielomianowe |
\( K\left(\mathbf{x}_i, \mathbf{x}\right)=\left(\mathbf{x}^T \mathbf{x}_i+\gamma\right)^q \) |
\(q\) –stopień wielomianu |
|
Gaussowskie |
\( K\left(\mathbf{x}_i, \mathbf{x}\right)=\exp \left(-\gamma\left\|\mathbf{x}-\mathbf{x}_i\right\|^2\right) \) |
\( \gamma \) - wartość stała (odwrotność \( \sigma^2 \)) |
|
Sigmoidalne |
\( K\left(\mathbf{x}_i, \mathbf{x}\right)=\operatorname{tgh}\left(\beta \mathbf{x}^T \mathbf{x}_i+\gamma\right) \) |
\( \beta, \gamma \) - współczynniki liczbowe |
Funkcje jądra dają swój wkład w definicję funkcji celu w zadaniu dualnym dla konkretnych wartości wektorów wejściowych \( \mathbf{x} \). Przy ustalonych przez użytkownika wartościach współczynników tych funkcji składniki związane z jądrem mają charakter liczbowy i rodzaj zastosowanego jądra nie ma żadnego związku z nieliniowością problemu optymalizacyjnego (problem dualny jest zawsze o postaci kwadratowej). Zauważmy, że funkcje jądra \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) są wielkościami skalarnymi i dla wszystkich możliwych kombinacji indeksów \( i, j\) tworząc macierz kwadratową.
Należy podkreślić, że w sieci radialnej liczba funkcji bazowych i ich centra są automatycznie utożsamione z wektorami podtrzymującymi. Sieć SVM o radialnej funkcji jądra może więc być utożsamiona z siecią radialną RBF, choć jej ostateczna struktura jak również sposób uczenia są różne. W sieci sigmoidalnej liczba neuronów ukrytych jest określona również automatycznie przez liczbę wektorów podtrzymujących i położenia tych wektorów.
Istotnym elementem teorii sieci nieliniowej SVM jest fakt, że po zastąpieniu wektora \( \mathbf{x} \) poprzez wektor \( \boldsymbol{\varphi}(\mathbf{x}) \) a iloczynu skalarnego \( \mathbf{x}_i^T \mathbf{x}_j \) przez \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) problem uczenia można sformułować w identyczny sposób jak dla sieci liniowej, jako problem pierwotny i dualny. Rozwiązaniu podlega praktycznie problem dualny, który niezależnie od rodzaju zastosowanej sieci jest sformułowany jako zadanie programowania kwadratowego. W procesie uczenia sieci SVM początkowa liczba wektorów podtrzymujących jest zwykle równa liczbie danych uczących. W zależności od przyjętych wartości ograniczeń (wartość parametru \( C \)) złożoność sieci jest redukowana i tylko część wektorów uczących pozostaje nadal wektorami podtrzymującymi.
Na rys. 5.6 przedstawiono przykład działania klasyfikacyjnego sieci SVM o jądrze radialnym dla rozkładu danych dwuwymiarowych rozmieszczonych jak na rysunku, należących do dwu klas. Jak widać przy odpowiedniej wartości współczynnika \( C \) hiperpłaszczyzna w przestrzeni cech transformuje się w nieliniową krzywą w przestrzeni oryginalnej \( \mathbf{x} \), separującą bezbłędnie obie klasy. Liczba wektorów podtrzymujących zależy od wartości \( C \). Im wyższa jego wartość tym większa kara za przekroczenie ograniczeń i w efekcie węższy margines separacji, a co za tym idzie również mniejsza liczba wektorów podtrzymujących.

Przy małej wartości \( C \) kara za przekroczenie ograniczeń jest niewielka i optymalne wartości wag umożliwiają klasyfikację z wieloma błędami na danych uczących.
5.3.1 Interpretacja mnożników Lagrange'a w rozwiązaniu sieci
Mnożniki Lagrange'a spełniają bardzo ważną rolę w rozwiązaniu problemu uczenia sieci SVM. Każdy mnożnik \( \alpha_i \) jest stowarzyszony z odpowiadającą mu parą uczącą \( (\mathbf{x}_i, d_i) \) stanowiąc współczynnik kary za niespełnienie ograniczenia (w przypadku spełnienia tego ograniczenia wartość mnożnika powinna być zerowa). Z warunków optymalności Kuhna-Tuckera problemu optymalizacyjnego sformułowanego dla sieci SVM wynikają następujące zależności [32,59]
| \( \begin{aligned} & \alpha_i\left[ d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1\right]=0 \\ & 0 \leq \alpha_i \leq C \\ & \mu_i \xi_i=0 \\ & \alpha_i+\mu_i=C \\ & \xi_i \geq 0 \end{aligned} \) | (5.31) |
W przypadku spełnienia ograniczenia mnożnik Lagrange'a z definicji powinien przyjąć wartość zerową eliminując wpływ danego ograniczenia na wartość minimalizowanej funkcji celu. W zależności od obliczonych wartości mnożników \( \alpha_i \) możemy mieć do czynienia z 3 przypadkami.
-
\( \alpha_i = 0 \)
Biorąc pod uwagę warunek Kuhna-Tuckera \( \alpha_i+\mu_i=C \) wartość zmiennej dopełniającej \(\mu_i=C \). Uwzględniając zależność \(\mu_i\xi_i=0\) jest oczywiste, że \(\xi_i=0\), co oznacza, że para ucząca \( (\mathbf{x}_i, d_i) \) spełnia ograniczenie bez zmniejszania szerokości marginesu separacji (klasyfikacja całkowicie poprawna). Co więcej, wobec zerowej wartości \( \alpha_i \) para ta nie wnosi żadnego wkładu do ukształtowanej hiperpłaszczyzny separującej.
-
\( 0 < \alpha_i < C \)
Wartość mnożnika \(\mu_i\) jest równa \(\mu_i=C-\alpha_i\) co oznacza, że dla spełnienia warunki \(\mu_i\xi_i=0\) wartość \(\xi_i=0\) podobnie jak w przypadku poprzednim. Jednakże tym razem wobec niezerowej wartości \(\alpha_i\) zerować się musi czynnik \( d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1 \). Przy zerowej wartości \( \xi_i \) i binarnych wartościach zadanych \( d_i=\pm 1 \) otrzymuje się warunek \( \mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b= \pm 1 \) oznaczający, że wektor \( x_i \) jest wektorem podtrzymującym. Stąd wartość mnożnika z przedziału \( 0 < \alpha_i < C \) oznacza, że para danych uczących położona jest dokładnie na marginesie separacji (klasyfikacja poprawna).
-
\( \alpha_i = C \)
W tym przypadku wobec \( \mu_i = C - \alpha_i = 0 \) mamy \( \xi_i \geq 0 \). Oznacza to, że dana ucząca znalazła się wewnątrz marginesu separacji lub poza tym marginesem (po niewłaściwej stronie), prowadząc bądź do błędu klasyfikacji bądź jedynie do realnego zmniejszenia szerokości marginesu. Wobec \( \alpha_i \neq 0 \) spełniony musi być warunek \( \left[ d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1\right]=0 \), z którego wynika, że \( \mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b=1-\xi_i \). Wartość niezerowa \( \xi_i \) oznacza więc wejście w margines separacji o wartość \( \xi_i \). Jeśli ta wartość jest mniejsza od 1 mamy do czynienia jedynie ze zmniejszeniem marginesu przy poprawnej klasyfikacji. W przeciwnym przypadku, gdy \( \xi_i > 1\) popełniony zostaje błąd (punkt danych po niewłaściwej stronie marginesu separacji).
7.3.2 Problem klasyfikacji przy wielu klasach
Sieci SVM z istoty swego działania dokonują rozdziału danych na dwie klasy. W odróżnieniu od sieci klasycznych, gdzie liczba klas poddanych klasyfikacji może być dowolna, rozpoznanie wielu klas przy pomocy tej techniki wymaga przeprowadzenia wielokrotnej klasyfikacji. Do najbardziej znanych podejść należą tu metody "jeden przeciw pozostałym" i "jeden przeciw jednemu". W metodzie "jeden przeciw pozostałym" przy \( M \) klasach należy skonstruować \( M \) sieci, każda odpowiedzialna za rozpoznanie jednej klasy. Sieć \( i \)-ta jest trenowana na danych uczących, w których przykłady \( i \)-tej klasy są skojarzone z \( d_i=1 \) a pozostałe z \( d_i = -1 \).
Przykładowo przy istnieniu 4 klas problem sprowadza się wytrenowania 4 sieci SVM, każda trenowana na innym zbiorze danych:
-
Sieć 1: (klasa 1: dane klasy 1), (klasa przeciwna: dane klasy 2+3+4)
-
Sieć 2: (klasa 1: dane klasy 2), (klasa przeciwna: dane klasy 1+3+4)
-
Sieć 3: (klasa 1: dane klasy 3), (klasa przeciwna: dane klasy 1+2+4)
-
Sieć 4: (klasa 1: dane klasy 4), (klasa przeciwna: dane klasy 1+2+3)
Po wytrenowaniu wszystkich sieci następuje etap odtwarzania, w którym ten sam wektor \( \mathbf{x} \) jest podawany na każdą sieć SVM. Określane są sygnały wyjściowe \( M \) funkcji decyzyjnych) wszystkich wytrenowanych sieci SVM (w przypadku klasy złożonej zwycięstwa przypisuje się do każdej klasy składowej)
| \( \begin{gathered} y_1(\mathbf{x})=\mathbf{w}_1^T \varphi(\mathbf{x})+b_1 \\ y_2(\mathbf{x})=\mathbf{w}_2^T \varphi(\mathbf{x})+b_2 \\ \ldots \\ y_M(\mathbf{x})=\mathbf{w}_M^T \varphi(\mathbf{x})+b_M \end{gathered} \) | (5.32) |
Wektor \( \mathbf{x} \) jest następnie zaliczany do klasy o największej wartości funkcji decyzyjnej \( y_i(\mathbf{x}) \), poprzez głosowanie większościowe.
Innym równie często stosowanym rozwiązaniem jest metoda "jeden przeciw jednemu" [46]. W metodzie tej konstruuje się \( M(M-1)/2 \) klasyfikatorów typu SVM, rozróżniających za każdym razem 2 klasy danych ze zbioru uczącego, kolejno parowanych ze sobą. Przykładowo przy 4 klasach poszczególne sieci będą trenowane na następujących zbiorach danych (6 sieci SVM)
-
Sieć 1: klasa 1 (dane klasy 1), klasa 2 (dane klasy 2)
-
Sieć 2: klasa 1 (dane klasy 2), klasa 2 (dane klasy 3)
-
Sieć 3: klasa 1 (dane klasy 3), klasa 2 (dane klasy 4)
-
Sieć 4: klasa 1 (dane klasy 2), klasa 2 (dane klasy 3)
-
Sieć 5: klasa 1 (dane klasy 2), klasa 2 (dane klasy 4)
-
Sieć 6: klasa 1 (dane klasy 3), klasa 2 (dane klasy 4)
Po wytrenowaniu wszystkich \( M(M-1)/2 \) sieci można przystąpić do właściwej klasyfikacji przy założeniu konkretnej wartości wektora \( \mathbf{x} \). Oznaczmy równanie decyzyjne sieci SVM rozróżniającej między klasą \( i \)-tą a \( j \)-tą dla danych wejściowych opisanych wektorem \( \mathbf{x} \) w postaci
| \( y_{i j}(\mathbf{x})=\mathbf{w}_{i j}^T \varphi(\mathbf{x})+b_{i j} \) | (5.33) |
Jeśli \( \operatorname{sgn}\left(y_{i j}(\mathbf{x})\right) \) wskazuje na \( i \)-tą klasę, należy zwiększyć o jeden sumę wskazań do tej klasy. W przeciwnym wypadku zwiększyć o jeden sumę wskazań do klasy \( j \)-tej w głosowaniu. Klasa o największej sumie zwycięstw wśród M(M-1)/2 sieci jest uważana za zwycięską (wektor \( \mathbf{x} \) zalicza się ostatecznie do tej klasy).
W ostatnich latach zaproponowano wiele nowych, równie skutecznych podejść do rozpoznawania wielu klas, pozwalających na rozwiązanie problemu w jednej strukturze SVM, przy uwzględnieniu wszystkich danych uczących na raz i z zastosowaniem dekompozycji zbioru uczącego na mniejsze podzbiory dla przyśpieszenia procedury uczenia. Do takich metod należą między innymi metoda Cramera i Singera [9] oraz metoda C. Hsu i C. Lina [28].
2.4. Sieć SVM do zadań regresji
Zadaniem sieci SVM w tym zastosowaniu jest aproksymacja zbioru danych pomiarowych \( (\mathbf{x}_i, d(\mathbf{x})) \) w dziedzinie liczb rzeczywistych. W odróżnieniu od zadania klasyfikacji wielkości zadane \( d_i \) mogą przyjmować dowolne wartości rzeczywiste, a nie tylko binarne \( \pm 1 \), jak to miało miejsce w przypadku klasyfikatorów. Jest to więc zadanie bardziej złożone niż zadanie klasyfikacji. Dla uzyskania największej efektywności działania sieci i uzyskania sformułowania problemu uczenia jako programowania kwadratowego, przyjmuje się funkcję błędu z tolerancją \( \varepsilon \), definiowaną w postaci [68]
| \( L_{\varepsilon}(d, y(\mathbf{x}))=\left\{\begin{array}{ccl} |d-y(\mathbf{x})|-\varepsilon & \text { dla } & |d-y(\mathbf{x})| \geq \varepsilon \\ 0 & \text { dla } & |d-y(\mathbf{x})| < \varepsilon \end{array}\right. \) | (5.34) |
Przyjmiemy podobnie jak w zadaniu klasyfikacji, że dane uczące \( (\mathbf{x}_i, d(\mathbf{x})) \) są aproksymowane przez funkcję
| \( y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b \) |
(5.35) |
Zadaniem uczenia jest taki dobór wektora wagowego \( \mathbf{w} \), liczby neuronów ukrytych (funkcji jąder) oraz parametrów tych funkcji, aby zminimalizować wartość funkcji błędu
| \( \min E=\frac{1}{2} \sum_{i=1}^p L_{\varepsilon}\left(d_i, y\left(\mathbf{x}_i\right)\right) \) |
(5.36) |
przy możliwie największym ograniczeniu wartości wag \( w_i \) sieci. Wprowadzając zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \) o nieujemnych wartościach (każda odpowiedzialna za przekroczenie marginesu tolerancyjnego w górę lub w dół) zadanie pierwotne uczenia można sformułować bardziej ogólnie, analogicznie jak w zadaniu klasyfikacji jako minimalizację wartości wag sieci oraz zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \) i zapisać w postaci [59]
| \( \min \limits_{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C\left[\sum_{i=1}^p (\xi_i+\xi_i^{\prime})\right] \) |
(5.37) |
przy liniowych ograniczeniach funkcyjnych zapisanych dla \( i=1,2,\ldots,p \) w postaci
| \( \begin{aligned} & d_i-\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right) \leq \varepsilon+\xi_i \\ & \left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right)-d_i \leq \varepsilon+\xi_i \\ & \xi_{\mathrm{i}} \geq 0 \\ & \xi_{\mathrm{i}}^{\prime} \geq 0 \end{aligned} \) | (5.38) |
Zauważmy, że dobór wartości zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \) taki, że spełniony jest warunek \( \left| d_i-\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)\right| \leq\left(\varepsilon+\xi_i\right) \) zapewnia wartość \( L_{\varepsilon+\xi_i}\left(d_i, y\left(\mathbf{x}_i\right)\right)=0 \), co automatycznie minimalizuje wartość funkcji błędu \( E \) wyrażonego wzorem (5.36). W sformułowaniu zadania pierwotnego występuje stała \( C \) stanowiąca wielkość regularyzacyjną, ustalającą kompromis między wartością marginesu separacji reprezentowanego przez wagi sieci i wartością funkcji błędu aproksymacji, uzależnionego od przyjętej wartości \( \varepsilon \) oraz uzyskanych w wyniku procesu optymalizacyjnego wartości \( \xi_i \), \(\xi_i^{'} \).
Dla tak postawionego problemu pierwotnego można zdefiniować funkcję Lagrange'a, w której \( \alpha_i \) oraz \( \alpha_i ^{'}\) są mnożnikami o wartościach większych lub równych zeru w zależności od spełnienia ograniczeń funkcyjnych a \( \mu_i \) oraz \( \mu_i ^{'}\) nieujemnymi mnożnikami odpowiadającymi za ograniczenia nakładane na zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \) w zależności (5.38). Zadanie optymalizacji rozwiązuje się minimalizując funkcję Lagrange’a względem wag \( \mathbf{w} \) i zmiennych dopełniających \( \xi_i \), \(\xi_i^{'} \) oraz maksymalizując ją względem mnożników Lagrange'a (punkt siodłowy funkcji Lagrange’a). Z rozwiązania powyższego zadania otrzymuje się sformułowanie problemu dualnego względem mnożników Lagrange'a w postaci [46,68]
| \( \left.\max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} d_i\left(\alpha_{{i}}-\alpha_{{i}}^{\prime}\right)-\varepsilon \sum_{{i}=1}^{{p}} d_i\left(\alpha_{{i}}+\alpha_{{i}}^{\prime}\right)-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}}\left(\alpha_{{i}}-\alpha_{{i}}^{\prime}\right)\left(\alpha_{{j}}-\alpha_{{j}}^{\prime}\right)\right)K\left(\mathbf{x}_i, \mathbf{x}_j\right) \) | (5.39) |
przy ograniczeniach dla \( i=1,2,\ldots,p \)
| \( \begin{aligned} & 0 \leq \alpha_i \leq C \\ & 0 \leq \alpha_i^{\prime} \leq C \\ & \sum_{i=1}^p\left(\alpha_i-\alpha_i^{\prime}\right)=0 \end{aligned} \) | (5.40) |
W zależnościach tych \( C \) jest stałą regularyzacji dobieraną przez użytkownika a \( K\left(\mathbf{x}_i, \mathbf{x}_j\right) =\varphi^T(\mathbf{x}_i)\varphi(\mathbf{x}_j) \). Zmienne dopełniające \( \xi_i \), \(\xi_i^{'} \) oraz towarzyszące im mnożniki Lagrange’a nie występują w sposób jawny w sformułowaniu zadania dualnego, ale są uzależnione od mnożników \( \xi_i \), \(\xi_i^{'} \) spełniając przy tym zależności \( \mu_i=C-\alpha_i \), \( \mu_i^{\prime}=C-\alpha_i^{\prime} \), \( \xi_i \mu_i=0 \) oraz \( \xi_i^{'} \mu_i^{'}=0 \).
Po wyznaczeniu optymalnego rozwiązania problemu dualnego względem mnożników Lagrange'a obliczane są wagi \( \mathbf{w} \) sieci na podstawie zależności
| \( \mathbf{w}=\sum_{i=1}^{N_{sv}}\left(\alpha_i-\alpha_i^{\prime}\right) \boldsymbol{\varphi}\left(\mathbf{x}_i\right) \) |
(5.41) |
w której \( N_{sv} \) oznacza liczbę wektorów nośnych, równą liczbie niezerowych mnożników Lagrange'a. Sygnał wyjściowy \( y(\mathbf{x}) \) sieci opisuje się zatem zależnością
| \( y(\mathbf{x})=\sum_{i=1}^{N_{sv}}\left(\alpha_i-\alpha_i^{\prime}\right) K\left(\mathbf{x}, \mathbf{x}_i\right)+b \) | (5.42) |
Wybór wartości hiperparametrów \( C \) i \( \varepsilon \) wpływa na złożoność sieci SVM. Oba parametry powinny być ustalane przez użytkownika w procesie uczenia. Zadanie aproksymacji jest zatem problemem bardziej złożonym niż klasyfikacja.
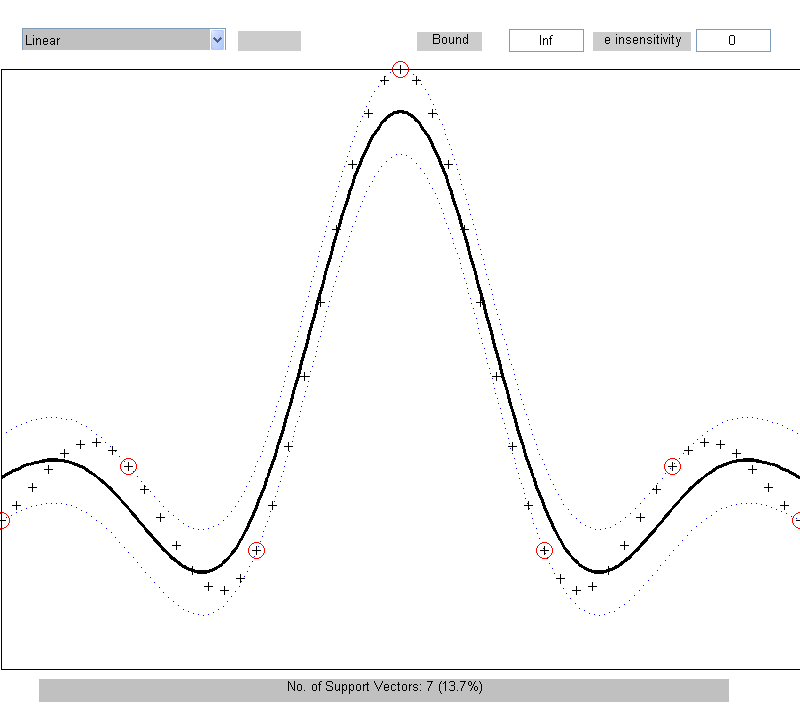
Na rys. 5.7 przedstawiono wyniki działania sieci SVM w trybie regresji uzyskane przy użyciu programu Gunna [21]. Dane pomiarowe (punkty zaznaczone znakiem +) zostały aproksymowane krzywą ciągłą realizowana przez SVM. Spośród danych pomiarowych tylko nieliczne stanowią wektory podtrzymujące (punkty oznaczone znakiem + w kółku), Pozostałe punkty danych mieszczą się wewnątrz strefy zdefiniowanej przez wartość \( \varepsilon \) równą w eksperymencie \( \varepsilon = 0.1 \) i nie wpływają na dobór parametrów sieci.
2.5. Przegląd algorytmów rozwiązania zadania dualnego
Niezależnie od zastosowanego jądra i rodzaju zadania (klasyfikacji czy regresji) główny problem obliczeniowy w sieciach SVM sprowadza się do rozwiązania zadania programowania kwadratowego z ograniczeniami liniowymi. Jakkolwiek jest to temat stosunkowo dobrze opracowany w teorii optymalizacji [14,51] i dostępnych jest wiele profesjonalnych pakietów do rozwiązania tego zadania, pojawiły się trudności związane ze skalą zadania. Liczba danych uczących \( p \) w problemach praktycznych sięga niekiedy setek tysięcy. Koresponduje z nią bezpośrednio liczba zmiennych optymalizowanych (mnożników Lagrange'a). Przy takich wymiarach pojawiają się trudne problemy związane z gospodarowaniem pamięcią i złożonością obliczeniową algorytmów. W efekcie nawet współczesne komputery nie są w stanie efektywnie, w akceptowalnym przez użytkownika czasie rozwiązać problemów o bardzo dużej skali przy zastosowaniu klasycznych metod programowania kwadratowego.
W efekcie prac pojawiło się wiele specjalizowanych procedur sekwencyjnych rozwiązania problemu programowania kwadratowego dostosowanych do sieci SVM i stosujących dekompozycję zbioru uczącego na szereg podzbiorów mniejszych. Większość z nich stosuje strategię ograniczeń aktywnych [43,52]. W strategii tej wszystkie ograniczenia dzieli się na dwa rodzaje: aktywne (ograniczenie ze znakiem równości), biorące udział w rozwiązaniu, i nieaktywne, nie mające w danej chwili wpływu na rozwiązanie (znak nierówności ograniczenia). W kolejnych iteracjach następuje przemieszczanie się poszczególnych ograniczeń z jednego zbioru do drugiego. Powstało wiele suboptymalnych rozwiązań stosujących takie podejście. Do najlepszych należą programy implementujące różne wersje algorytmu programowania sekwencyjnego (BSVM) Platta, program SVMLight Joachimsa czy program LSVM Mangasariana.
Algorytm SVMLight stosuje w rozwiązaniu metodę ograniczeń aktywnych, dobrze znaną i stosowaną w programowaniu kwadratowym [31]. Ze względu na duże rozmiary zbioru danych dzieli się go na mniejsze podzbiory: aktywny, dla którego poszukuje się rozwiązania optymalnego oraz nieaktywny, dla którego wszystkie warunki ograniczeń powinny być z góry spełnione. W każdej iteracji zmienne optymalizowane są zaliczane do 2 kategorii: zmienne wolne (aktywne), poddane aktualizacji i zmienne nieaktywne o wartościach ustalonych przez ograniczenia dolne bądź górne, nie podlegające zmianie. Jeśli wszystkie warunki optymalności są spełnione, rozwiązanie z danej iteracji jest uważane za optymalne. W przeciwnym wypadku algorytm dokonuje przegrupowania zmiennych z obu zbiorów i odpowiednich zmian w macierzy hesjanu przegrupowując jednocześnie podmacierze odpowiadające zmiennym aktywnym i nieaktywnym. Postęp w optymalizacji jest uzależniony od właściwego przypisania zmiennych do obu zbiorów. Stąd istotnym problemem jest wcześniejsze ustalenie, które mnożniki zmierzają do swoich ograniczeń. Pozwala to wyeliminować je ze zbioru zmiennych aktywnych i z góry ograniczyć liczbę zmiennych podlegających aktualizacji. T. Joachims w programie SVMLight skutecznie zaimplementował algorytm heurystyczny estymacji mnożników, pozwalający na szybką redukcję liczebności zmiennych aktualizowanych i znaczne przyśpieszenie procesu uczenia przy bardzo dużej liczbie danych uczących. Szczegóły rozwiązania można znaleźć w pracy [31].
Algorytm SMO (ang. Sequential Minimal Optimization) należy do grupy programowania sekwencyjnego i polega na dekompozycji zadania programowania kwadratowego na mniejsze podzadania, rozwiązywane sekwencyjnie aż do spełnienia wszystkich warunków optymalności Kuhna-Tuckera. W rozwiązaniu zaproponowanym przez Platta [51] i zmodyfikowanym przez Hsu i Lina [28] zwanym dalej algorytmem BSVM, w każdym kroku iteracyjnym rozwiązywane jest podzadanie drugiego rzędu (dwa mnożniki Lagrange'a) przy sekwencyjnej wymianie par mnożników. Optymalizacja dwu mnożników na raz jest najmniejszym możliwym zadaniem posiadającym rozwiązanie analityczne typu jawnego. Dzięki temu algorytm nie wymaga zastosowania dużych pamięci nawet przy ogromnej liczbie danych uczących, a jego zbieżność jest zapewniona przez specjalną metodę wymiany i doboru par mnożników, gwarantującą redukcję wartości funkcji celu w każdym kroku iteracyjnym.
Platt zaproponował dwie pętle przeszukujące dane: zewnętrzną i wewnętrzną. Pętla zewnętrzna dokonuje selekcji pierwszego mnożnika \( \alpha_1 \) a pętla wewnętrzna - mnożnika drugiego \( \alpha_2 \) w taki sposób, że następuje maksymalizacja funkcji celu w problemie dualnym. Pętla zewnętrzna przebiega przez wszystkie pary danych uczących selekcjonując te, dla których \( 0 \leq \alpha_i \leq C \). Następnie sprawdza spełnienie warunków Kuhna-Tuckera dla wyselekcjonowanych przypadków i przyjmuje pierwszą parę danych \( (\mathbf{x}_1, d_1) \), dla której warunki te są naruszone. Mnożnik Lagrange'a odpowiadający tak wyselekcjonowanej parze danych staje się \( \alpha_1 \). Po jego wyselekcjonowaniu pętla wewnętrzna przeszukuje wszystkie przypadki danych dla których \( 0 \leq \alpha_i \leq C \) poszukując takiego \( \mathbf{x}_2 \), dla którego moduł różnicy błędów \( \left|\left(y\left(\mathbf{x}_1\right)-d_1\right)-\left(y\left(\mathbf{x}_2\right)-d_2\right)\right| \) jest największy. Dla tak wyselekcjonowanych przypadków przeprowadzana jest optymalizacja obu mnożników \( \alpha_1 \) i \( \alpha_2 \). Proces powtarzany jest wielokrotnie aż do spełnienia warunków Kuhna-Tuckera [14] dla wszystkich par uczących. Takie rozwiązanie algorytmu programowania sekwencyjnego jest bardzo skuteczne nawet przy liczbie danych dochodzących do setek tysięcy. Algorytm BSVM jest aktualnie uważany obok SVMLight za jedną z najskuteczniejszych metod uczenia sieci SVM. Najważniejszą zaletą przedstawionych tu implementacji znanych wcześniej rozwiązań zadania dualnego jest ograniczenie wymagania pamięci, wzrastające tylko liniowo (proporcjonalnie do liczby danych uczących) i liczby wektorów podtrzymujących. Każdy z tych programów przewyższa zwykle standardowe rozwiązania programowania kwadratowego stosowane dotychczas. Tym nie mniej różnią się one między sobą również w sposób znaczący, zarówno pod względem czasu działania jak i skuteczności (wyznaczenia minimum globalnego funkcji celu).
Należy podkreślić, że choć teoretycznie każdy z algorytmów znajduje minimum globalne funkcji celu, to jakość rozwiązania zależy od tak zwanych "hiperparametrów" ustalanych arbitralnie przez użytkownika, na przykład szerokości funkcji radialnej \( \sigma = 1/\gamma \) i wartości stałej regularyzacji \( C \). Parametry te nie podlegają adaptacji w procesie uczenia i ich niewłaściwe wartości mogą spowodować otrzymanie rozwiązania dalekiego od minimum globalnego, przy czym każda z odmian algorytmu może być w różnym stopniu czuła na założone wartości "hiperparametrów". Aby uniezależnić się od arbitralnego doboru tych parametrów powstało szereg rozwiązań sieci SVM, które pozwalają na dobór tych parametrów w procesie uczenia na podstawie określonych kryteriów przyjętych na wstępie. Do takich rozwiązań należą między innymi nu-SVM, ![]() itp.
itp.
2.6. Program komputerowy uczenia sieci SVM
Wykorzystując możliwości jakie stwarza Matlab opracowany został pakiet programów SVM z interfejsem graficznym pozwalający na symulację sieci SVM, zarówno w trybie uczenia jak i odtwarzania (rys. 5.8) [46].
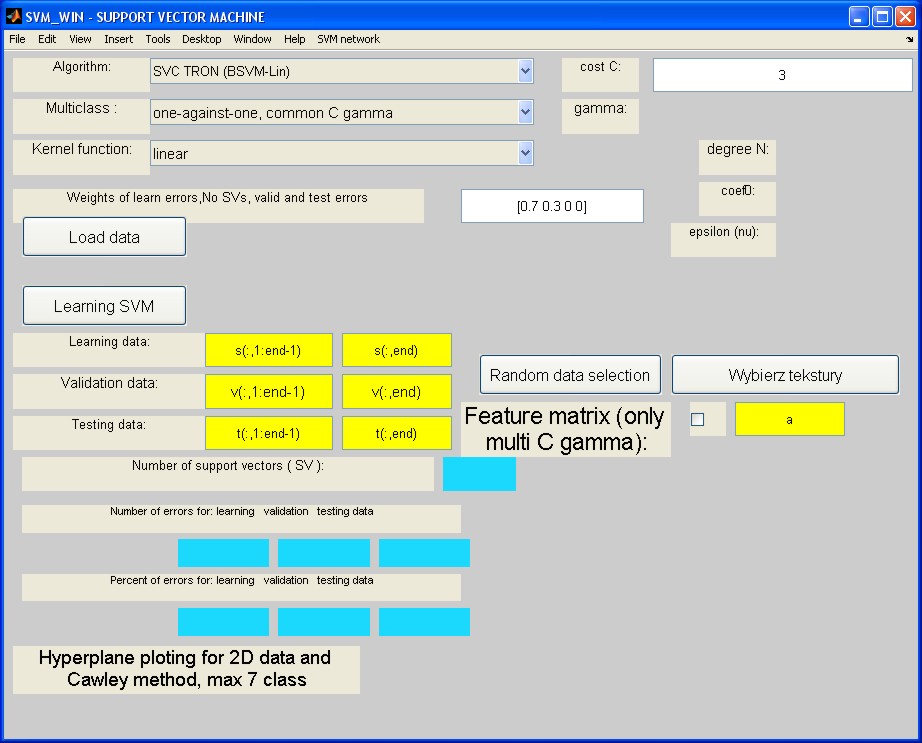
Wywołanie programu odbywa się po napisaniu nazwy pliku głównego SVM_win w oknie komend Matlaba. Przed rozpoczęciem procesu uczenia użytkownik musi wczytać dane uczące learning data i ewentualnie testujące testing data (można wykorzystać przycisk "Load data"). Składają się na nie zbiory wektorów \( \mathbf{x} \) (pola xlearn, xtest) przygotowane w postaci macierzy o tylu wierszach ile jest par danych i kolumnach odpowiadającym poszczególnym zmiennym tworzącym wektor \( \mathbf{x} \) (wektory ułożone poziomo) oraz zbiory wartości zadanych \( d_i \) tworzące wektor kolumnowy, określający wielkości stowarzyszone z wektorami wejściowymi \( \mathbf{x} \) (pola dlearn i dtest). Przy klasyfikacji danych należących do wielu klas: 1, 2, 3, ..., M wektor wartości zadanych \( \mathbf{d} \) jest wektorem kolumnowym, w którym poszczególne pozycje oznaczają numer przypisany klasie (kolejne liczby naturalne). W zadaniu regresji elementami wektora \( \mathbf{d} \) są wartości rzeczywiste (zadane) \( d_i \) stowarzyszone z \( \mathbf{x}_i \). Po zadaniu wartości uczących należy wybrać algorytm uczący sieci klasyfikacyjnej (SVC - Support Vector Classification) bądź regresyjnej (SVR - Support vector Regression). Służy do tego celu przycisk wyboru w polu Algorithm. W przypadku zadania klasyfikacji jest do wyboru osiem algorytmów multi-klasowych. W przypadku regresji dostępne są: algorytm BSVR, nu-SVR, epsilon-SVR oraz MYSVR. W obu przypadkach zalecany jest algorytm BSVM (klasyfikacja) lub BSVR (regresja). W przypadku rozpoznawania wielu klas użytkownik może wybrać między różnymi odmianami podejść do problemu w polu Multiclass. Są to: one-against-one, one-against-all, internal algorithm, (wieloklasowość wbudowana w algorytmie rozwiązania).
Projektując sieć należy zdecydować o typie funkcji jądra (liniowy, wielomianowy, radialny gaussowski oraz sigmoidalny (opcje wyboru w polu Kernel functions). Zalecane jest uniwersalne jądro typu radialnego. W zależności od wybranego typu jądra pojawią się czynne pola wyboru odpowiadających im hiperparametrów (stopień wielomianu \( N \), współczynnik funkcji gaussowskiej \( \gamma \), współczynnik \( \textrm{coef}_0 \) dla funkcji wielomianowej jądra). W przypadku regresji konieczne jest również podanie wartości progu \(\varepsilon \). Niezależnie od rodzaju zadania (klasyfikacja bądź regresja) należy podać wartość współczynnika regularyzacji \( C \) (pole C cost) decydującego o stopniu złożoności wytrenowanej sieci SVM. Zwykle jest to wartość dużo większa od jedności. Naciśnięcie przycisku Learning SVM uruchamia proces uczenia, w wyniku którego program wyznacza wszystkie parametry adaptacyjne sieci (wartości wag, liczbę wektorów podtrzymujących, centra funkcji radialnych lub współczynniki funkcji wielomianowych). Jednocześnie po zakończeniu uczenia sieć automatycznie dokonuje odtworzenia sygnałów wyjściowych dla danych uczących wysyłając wynik do przestrzeni roboczej Matlaba (wektor \( \mathbf{y} \)) oraz wypisując w odpowiednim polu menu głównego liczbę błędów klasyfikacji a także ich procentową wartość dla danych uczących i testujących.
Program SVM jest używany w laboratorium sieci neuronowych Zakładu Elektrotechniki Teoretycznej i Informatyki Stosowanej Politechniki Warszawskiej, między innymi do klasyfikacji tekstur na podstawie wczytanych obrazów tych tekstur. Temu celowi służy przycisk Selection of texture uruchamiający dodatkowe menu wyboru tekstur i generacji ich cech według różnych algorytmów przetwarzania (algorytm Markova, Gabora, GLCM Haralicka, Unsera oraz fraktalny). Obraz tekstury \( 512 \times 512 \) jest dzielony na ramki o wymiarach \( 8\times 8\), przy czym połowa ramek jest używana do uczenia a druga do testowania. Można dokonać losowego przypisania ramek do obu kategorii używając przycisku Random data selection
2.7. Przykłady zastosowania sieci SVM
Działanie programu SVM zademonstrujemy na przykładzie problemu klasyfikacji dwu spiral, uważanego za jedno z trudniejszych zadań klasyfikacyjnych. Zadaniem sieci jest klasyfikacja punktów położonych na dwu wzajemnie przeplatających się spiralach należących do dwu różnych klas. Główny problem właściwego rozpoznania klas polega na tym, że przy niewielkiej zmianie współrzędnych punktu, przynależność do klasy może zmienić się diametralnie. Na rys. 5.9 przedstawiono położenia punktów leżących na dwu spiralach i przynależnych do dwu różnych klas. W rozwiązaniu problemu zastosowano sieć SVM o dwu wejściach, odpowiadających współrzędnym punktów podlegających klasyfikacji oraz jednym neuronie wyjściowym (przynależność do jednej klasy to wartość \( d=1 \), natomiast do drugiej to \( d=2 \)).
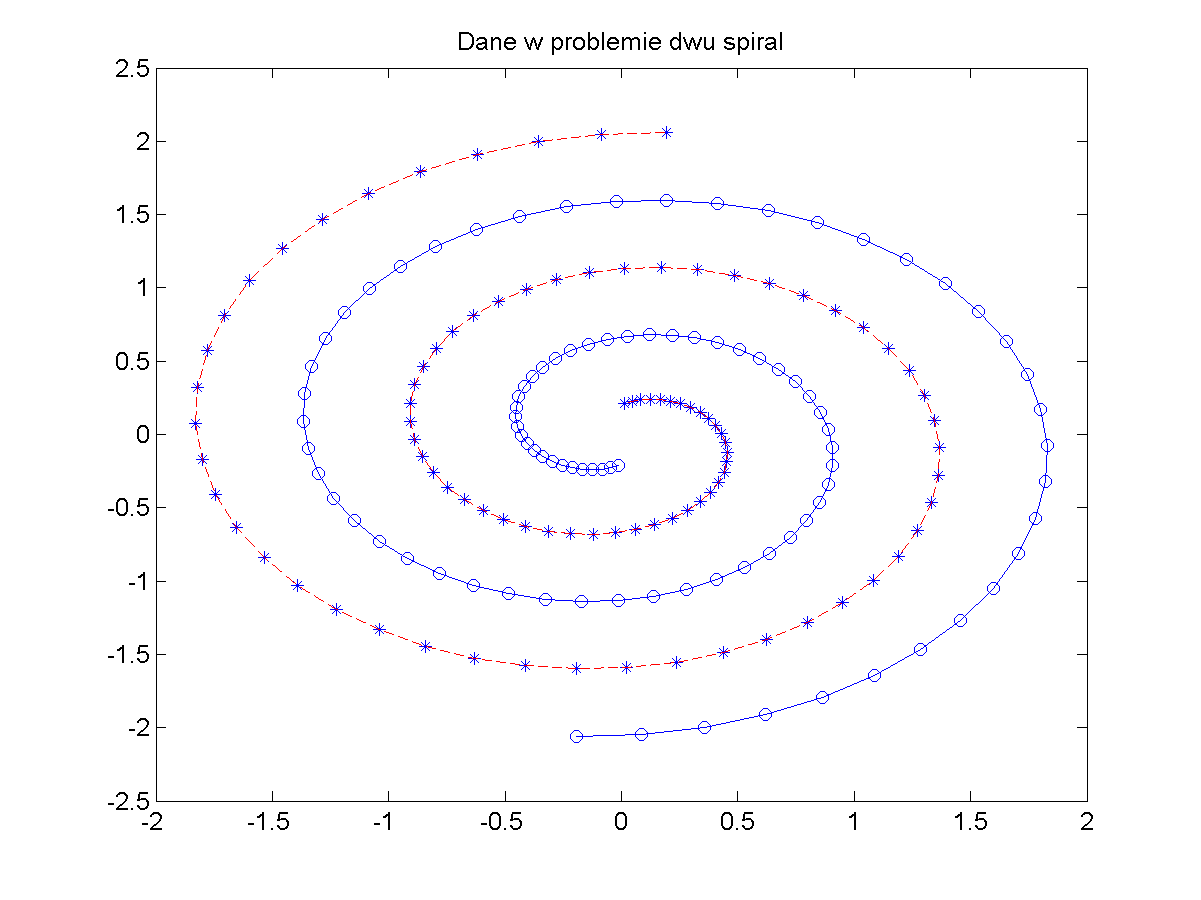
W wyniku zastosowania programu uczącego SVM otrzymano sieć zawierającą 86 wektorów podtrzymujących, która bezbłędnie klasyfikowała wszystkie dane uczące.

Tak zbudowaną sieć poddano testowaniu na danych położonych w przestrzeni kwadratowej wokół danych uczących. W wyniku skanowania tej przestrzeni uzyskano rozkład przynależności punktów do obu klas przedstawiony na rys. 5.10. Jak widać jest to gładki podział strefy wpływów obu spiral, świadczący o doskonałych własnościach generalizacyjnych sieci SVM.
Drugi przykład dotyczy rozpoznania obrazów reprezentujących 9 różnych rodzajów traw na podstawie cech teksturalnych [69]. Typowy wygląd poszczególnych rodzajów traw przedstawiony jest na rys. 5.11. Obraz z rys. 5.11a odpowiada klasie 1, rys. 5.11.b - klasie 2, rys. 5.11c - klasie 3, rys. 5.11d - klasie 4, rys. 5.11e - klasie 5, rys. 5.11f - klasie 6, rys. 5.11g - klasie 7, rys. 5.11h - klasie 8 a rys. 5.11i - klasie 9.
|
a) |
b) |
c) |
|
d) |
e) |
f) |
|
g) |
h) |
i) |
Obrazy tekstur zostały zaczerpnięte z bazy Vistex. Poszczególne klasy różnią się minimalnie pod względem wzrokowym i rozróżnienie między nimi należy do zadań trudnych nawet dla najbardziej skutecznych klasyfikatorów. Obrazy tekstur o wymiarach \( 512 \times 512 \) zostały podzielone na ramki (podobrazy) o wymiarach \( 8 \times 8\). Każda klasa zawierała 32 dane uczące i 32 dane testujące. Tekstury były reprezentowane w eksperymencie przez zbiór 11 cech wynikających z algorytmu Markowa. Połowa ramek uczestniczyła w uczeniu, druga połowa jedynie w testowaniu. Wyniki rozpoznania tekstur użytych w testowaniu, przy zastosowaniu sieci SVM przedstawione są w tabeli 5.2.
Tabela 5.2. Wyniki rozpoznania tekstur traw
|
Nr tekstury |
Liczba błędnych rozpoznań |
Błąd procentowy |
|
1 |
9 |
28,1% |
|
2 |
4 |
12,5% |
|
3 |
6 |
18,8% |
|
4 |
9 |
28,1% |
|
5 |
2 |
6,2% |
|
6 |
7 |
21,9% |
|
7 |
1 |
3,1% |
|
8 |
5 |
15,6% |
|
9 |
1 |
3,1% |
|
Średnio |
4,9 |
15,3% |
Klasyfikacja przy użyciu sieci SVM o \( C=350 \), o radialnej funkcji jądra przy \( \gamma=1 \) oraz 9 klasach wzorców została rozwiązana przy zastosowaniu strategii "jeden-przeciw-jednemu". W konkretnym przypadku przy liczbie klas \( M=9 \) oznaczało to konieczność wytrenowania aż 36 różnych sieci.
2.8. Porównanie sieci SVM z innymi rozwiązaniami neuronowymi
Sieci SVM podobnie jak inne rozwiązania sieci trenowanych pod nadzorem (MLP, RBF) pełnią rolę uniwersalnego aproksymatora danych uczących. Ich główną zaletą jest dobra generalizacja, związana ze stosunkowo małą wrażliwością na liczbę danych uczących, co ma szczególne znaczenie w rozwiązaniu problemów, dla których liczba danych jest ograniczona. Pod tym względem przewyższają zdecydowanie sieci MLP, szczególnie wrażliwe na stosunek liczby danych uczących do liczby wag sieci.
Istotną zaletą sieci SVM jest możliwość płynnej regulacji jej stopnia złożoności wyrażonej miarą \( VCdim \) [59] poprzez sterowanie szerokością marginesu separacji. W klasycznym algorytmie uczenia złożoność sieci (miara \( VCdim \)) rośnie wraz ze zwiększaniem się liczby neuronów ukrytych (z założenia liczba wejść i wyjść sieci nie podlega doborowi, gdyż zależy wyłącznie od problemu podlegającego rozwiązaniu). Jeśli liczbę neuronów ukrytych (reprezentują one cechy procesu) oznaczymy przez \( K \) to w zwykłej sieci zarówno radialnej, wielomianowej jak i sigmoidalnej (w ostatnim przypadku jednowarstwowej) miara \( VCdim=K+1 \). Wartość \(K\) może teoretycznie rosnąć nieograniczenie, zatem dla uzyskania dobrej generalizacji sieci należy odpowiednio zwiększać liczbę danych uczących. W klasycznym sposobie uczenia każdy z tych rodzajów sieci cierpi zatem na problem wielowymiarowości, narastający wraz ze zwiększaniem się wymiarów sieci. Sieci SVM stosujące specjalne sformułowanie zadania uczenia radzą sobie znacznie lepiej z tym problemem. Zostało udowodnione, że oszacowanie miary \( VCdim \) dla sieci SVM spełnia następującą relację matematyczną
| \( V C \operatorname{dim} \leq \min \left\{\left[\text { entier }\left(\frac{D^2}{\rho^2}\right), K\right]+1\right\} \) | (5.44) |
Funkcja entier oznacza najmniejszą liczbę całkowitą większą lub równą najmniejszej wartości zawartej wewnątrz nawiasów, \( \rho \) jest wartością marginesu separacji \( \rho = \frac{2}{\|w\|^2} \), \( K \) - liczbą neuronów ukrytych (liczbą funkcji jądra), a \( D \) - średnicą najmniejszej kuli w przestrzeni \( N \)-wymiarowej, obejmującej wszystkie wektory uczące \( \mathbf{x}_i \) dla \( i = 1, 2, \ldots, p\).
Powyższe oszacowanie potwierdza, że możliwe jest sterowanie wartością miary \( VCdim \), uniezależniające ją od wymiaru \( K \) przestrzeni cech. Uzyskuje się to przez właściwy dobór marginesu separacji \( \rho \). Przy szerokim marginesie możliwe jest bowiem uzyskanie \( \text { entier }\left(\frac{D^2}{\rho^2}\right)< K \) i wówczas oszacowanie jest niezależne od wymiaru wektora cech (liczby neuronów ukrytych). Jest to bardzo ważna zaleta sieci SVM, gdyż umożliwia świadome sterowanie stopniem złożoności sieci i w efekcie jej zdolnością generalizacji.
Dla sieci SVM użytej jako klasyfikator szacuje się często górną granicę prawdopodobieństwa \( P \) wystąpienia błędu klasyfikacji na danych testujących jako stosunek liczby wektorów podtrzymujących do ogólnej liczby danych uczących, pomniejszonej o jeden
| \( P \leq \frac{N_{s v}}{p-1} \) | (5.45) |
Stąd dla zwiększenia zdolności generalizacyjnych sieci dąży się do zmniejszenia liczby wektorów podtrzymujących \( N_{sv} \) nawet kosztem zwiększenia liczby błędnych klasyfikacji na zbiorze danych uczących. Jakkolwiek sieci SVM stanowią rozwiązanie pozwalające kontrolować złożoność sieci i z reguły wykazując lepszą generalizację niż sieci klasyczne, ciągle brakuje dowodu matematycznego, udowadniającego ich lepsze działanie w dowolnym przypadku.
Ważną zaletą sieci SVM jest sprowadzenie problemu uczenia do zadania programowania kwadratowego, charakteryzującego się zwykle występowaniem pojedynczego minimum funkcji celu. Punkt startu w uczeniu nie ma zatem praktycznie żadnego wpływu na wynik końcowy. Zalety tej nie posiada sieć MLP, dla której funkcja celu jest nieliniowa względem optymalizowanych wag. Sieć MLP charakteryzuje się więc wieloma minimami lokalnymi. Jest zatem bardzo wrażliwa na wartości startowe parametrów optymalizowanych. Należy jednak stwierdzić, że jakość rozwiązania sieci SVM zależy w dużej mierze od przyjętych arbitralnie wartości parametrów stałych (tak zwanych "hiperparametrów") do których zaliczamy szerokość funkcji gaussowskiej \( \sigma \), współczynnik \( \gamma \) dla jądra wielomianowego, wartość parametru regularyzacyjnego \( C \) czy tolerancję \( \varepsilon \). Wartości te są dobierane zwykle metodą prób przy użyciu specjalnego zestawu danych weryfikujących, wydzielonych ze zbioru uczącego (metoda "cross validation").
Na podstawie wielu eksperymentów numerycznych przeprowadzonych zarówno na danych syntetycznych typu "benchmark" jak i problemów rzeczywistych można stwierdzić, że sieci SVM są bezkonkurencyjne w stosunku do innych rozwiązań sieci klasycznych w zdecydowanej większości zadań klasyfikacji. W przypadku zadań regresji przewaga sieci SVM nad MLP nie jest już tak oczywista. Zwykle wyniki są tu porównywalne i sieć MLP może stanowić dobrą alternatywę dla SVM.
Interesujące jest porównanie sieci SVM i RBF (obu stosujących funkcje gaussowską neuronów ukrytych) na dobór struktury sieci. Pokażemy to na przykładzie zadania regresji polegającej na kalibracji danych "sztucznego nosa" [5].
Układ pięciu czujników półprzewodnikowych poddano działaniu mieszaniny 4 gazów (tlenku węgla, metanu, propan-butanu i metanolu). Charakterystyki czujników są wysoce nieselektywne i określenie na podstawie ich wskazań stężenia poszczególnych składników wymaga procesu kalibracji, czyli stowarzyszenia poszczególnych stężeń ze wskazaniami czujników. Rolę tę może pełnić dowolna sieć neuronowa trenowana z nauczycielem. W tym eksperymencie pokażemy wyniki dla sieci SVM i RBF. Obie sieci można bez trudu wytrenować w taki sposób, że wskazania sieci będą z błędem mniejszym niż 1% pokrywać się z wartościami idealnymi dla danych testujących. Istotny jest przy tym dobór parametrów uczących stałych: wartości \( \sigma \) dla sieci RBF i \( \gamma \) dla sieci regresyjnej SVM. Te dwa parametry są decydujące o złożoności sieci (liczbie neuronów ukrytych). Zmieniając je można zbadać jak zmienia się zdolność generalizacji sieci przy różnej liczbie neuronów ukrytych. Na rys. 5.12 przedstawiono błędy uczenia i testowania dla obu sieci w funkcji liczby neuronów ukrytych (zależnych od wartości \( \gamma \) w sieci RBF przy użyciu algorytmu Grama-Schmidta i parametru \( \varepsilon \) dla sieci SVM trenowanej przy pomocy algorytmu BSVM).
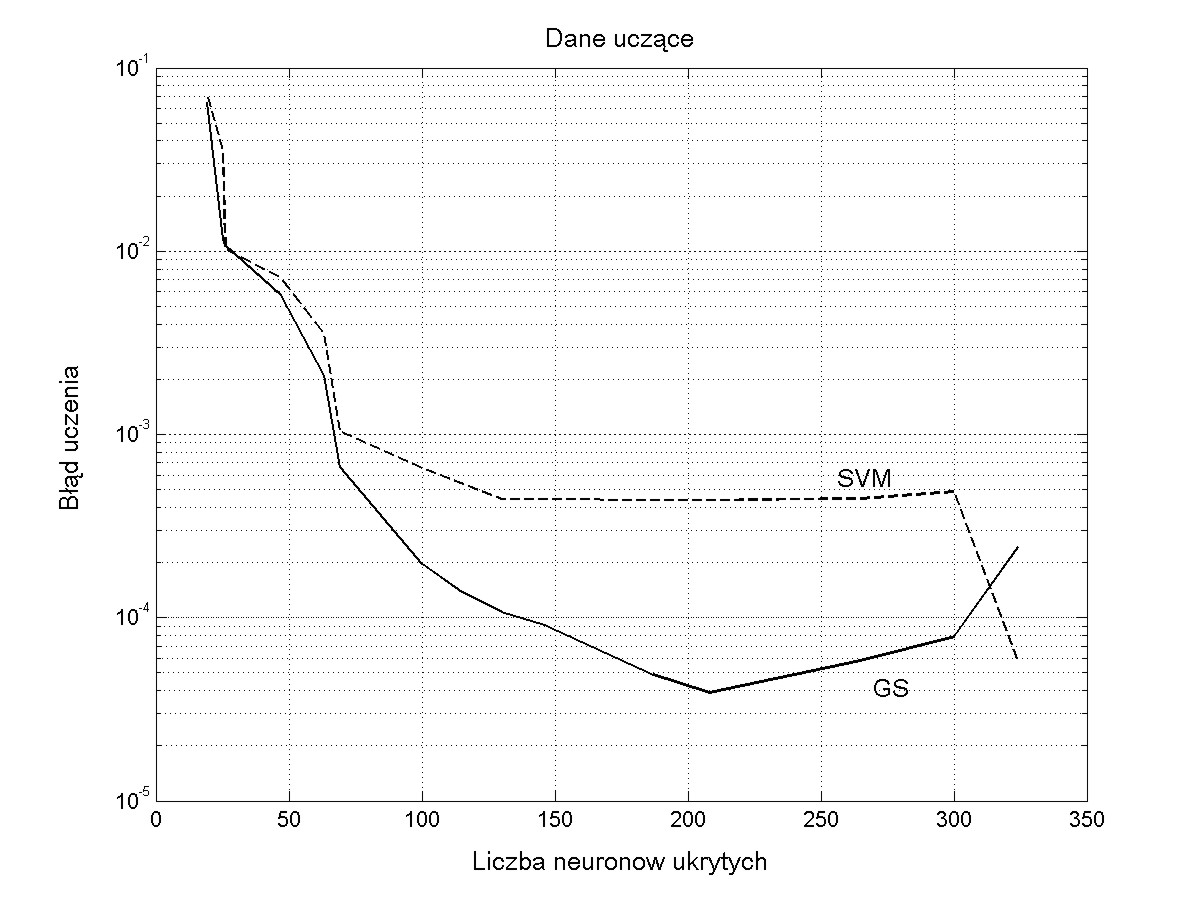
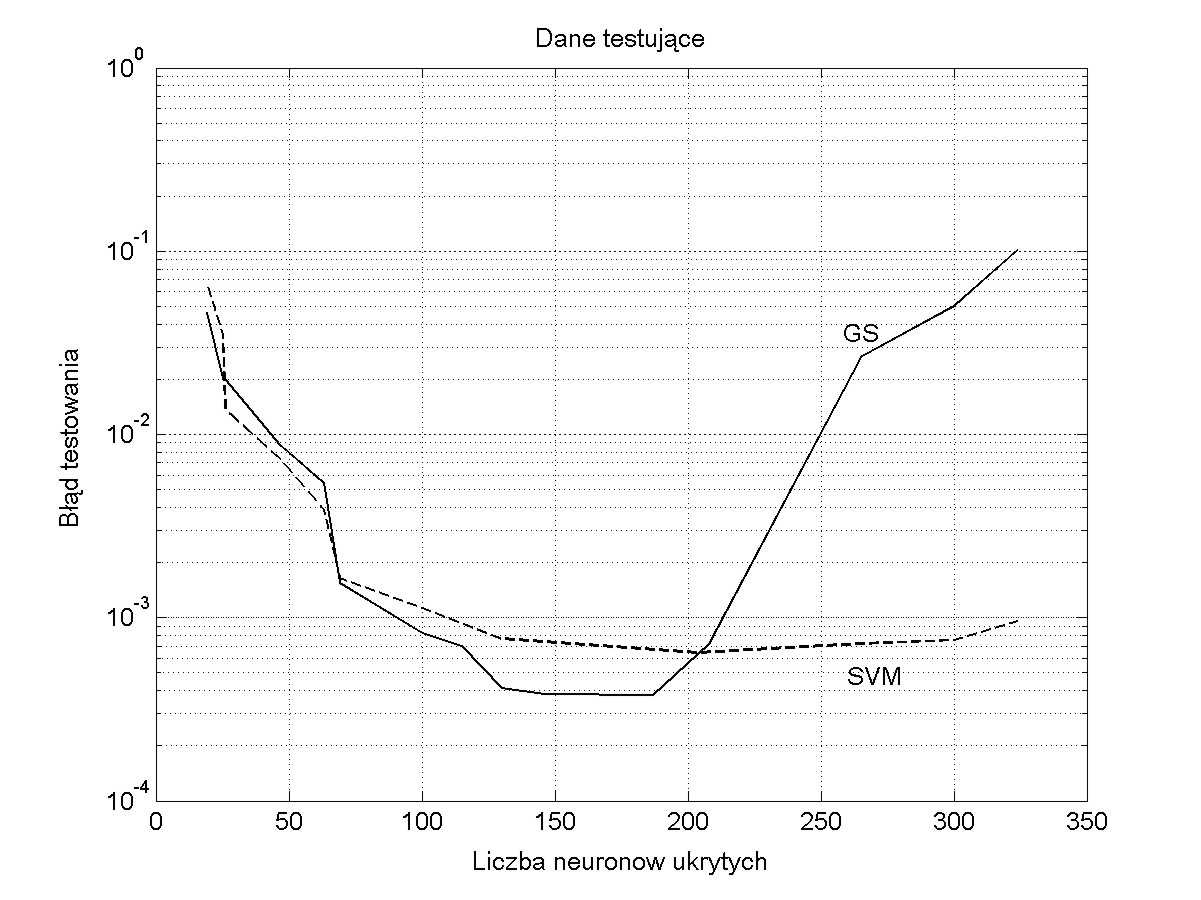
Widoczna jest przewaga sieci SVM pod względem zdolności generalizacyjnych (wyniki na danych testujących z rys. 5.12b) . Sieć ta tylko w niewielkim stopniu jest wrażliwa na dobrane przez użytkownika hiperparametry uczenia i wynikającą stąd liczbę neuronów ukrytych. Tak dobre wyniki otrzymuje się dzięki członowi regularyzacyjnemu związanemu z wartością stałej \( C \). Zalety tej nie ma sieć RBF, dla której po przekroczeniu optymalnej liczby neuronów ukrytych błąd testowania gwałtownie rośnie.
2.9. Zadania i problemy
5.9 Zadania i problemy
1. Równanie hiperpłaszczyzny separującej ma postać: \( y(\mathbf{x})=-2x_1+4x_2+5x_3-2 \). Obliczyć odległość wektora \( \mathbf{x}=[1 \; -3 \; 4] \) od tej hiperpłaszczyzny.
2. Hiperpłaszczyzna separująca sieci SVM opisana jest wzorem \( y(\mathbf{x})=-10x_1+x_2+20 \).
Dane są 2 punkty testowe należące do dwu różnych klas
\( \mathbf{x}_1=\left[\begin{array}{l}
2.5 \\
-3
\end{array}\right] \leftarrow \text { klasa } 1 \)
\( \mathbf{x}_2=\left[\begin{array}{c}
1.6 \\
3
\end{array}\right] \leftarrow \text { klasa } 2 \)
Na skutek tolerancji pomiarów każda ze składowych obu wektorów może zmieniać się w zakresie \( \pm 0,8 \). Sprawdzić w jakich zakresach zmian obu składowych (w granicach tolerancji) wynik klasyfikacji będzie jeszcze prawidłowy.
3. Omówić rolę mnożników Lagrange'a w uczeniu sieci SVM i związek uzyskanych wyników liczbowych z położeniem odpowiednich danych uczących. Rozważyć sieć klasyfikacyjną i regresyjną.
4. Korzystając z programu SVM_win zaprojektować regresyjną sieć SVM modelującą dane odpowiadające funkcji sinusoidalnej, impulsom prostokątnym, funkcji piłokształtnej.
5. Zaprojektować optymalną sieć SVM dla problemu XOR posługując się programem SVM_win.
6. Korzystając z programu SVM_win dokonać klasyfikacji danych należących do 2 rozkładów gaussowskich (2 klasy), częściowo pokrywających się ze sobą. Użyć dwu różnych współczynników regularyzacji \( C=1\) oraz \(C=100\) i dwu różnych funkcji jądra: gaussowskiego i wielomianowego.
7. Napisać program generujący automatycznie dane uczące w problemie symetrii danych dla wektora zero-jedynkowego o 7 składowych. Na przykład wektor wejściowy \( \mathbf{x} =[0 \;0 \;1 \;1 \;1 \;0 \;0] \) jest symetryczny, natomiast wektor \( \mathbf{x} = [ 0 \;1 \;1 \;1 \;1 \;0 \;0] \) jest niesymetryczny. Posługując się tymi danymi wytrenować sieć MLP i SVM tak, aby uzyskać zerowe błędy testowania. Porównać stopień złożoności obu struktur sieciowych.
8. Zbadać liczbę sieci SVM wymaganych do rozwiązania problemu klasyfikacji danych należących do różnych klas przy zastosowaniu strategii "jeden przeciw jednemu" i "jeden przeciw wszystkim". Przedstawić graficznie zależność liczby sieci w obu podejściach od liczby klas.
2.10. Słownik
Słownik opanowanych pojęć
Wykład 5
Sieć SVM – sieć wektorów nośnych Vapnika wykorzystująca oryginalne podejście do problemu uczenia.
Hiperpłaszczyzna separująca – hiperpłaszczyzna rozdzielająca dwie klasy danych w przestrzeni wielowymiarowej.
Hiperpłaszczyzna wektorów nośnych – hiperpłaszczyzna przechodząca przez skrajne punkty danych definiowana dla obu klas podlegających rozpoznaniu.
Wektory nośne – zbiór wektorów danych uczących dla których mnożniki Lagrange’a są różne od zera.
Problem pierwotny uczenia – definicja startowa funkcji celu w sieci SVM.
Problem dualny uczenia – ostateczna postać funkcji celu uzależniona jedynie od mnożników Lagrange’a jako zmiennych podlegających optymalizacji.
Mnożniki Lagrange’a –zmienne optymalizowane w procesie uczenia sieci SVM reprezentujące współczynniki kary za niedotrzymanie ograniczeń.
Margines separacji – minimalna odległość między najbliższymi skrajnymi punktami danych obu klas w sieci SVM.
Parametr regularyzacyjny C – waga z jaką traktowane są błędy testowania w stosunku do marginesu separacji w procesie uczenia sieci SVM.
Twierdzenie Covera – twierdzenie pozwalające przetransformować zbiór danych nieseparowalny liniowo w zbiór separowalny liniowo.
Warunek Mercera – warunek matematyczny aby proponowana funkcja mogła być przyjęta jako jądro przekształcenia gwarantując zbieżność procesu uczenia.
Funkcja jądra – funkcja typu skalarnego (ang. kernel) powstała jako iloczyn skalarny dwu wektorów o identycznej postaci obliczany w dwu różnych punktach przestrzeni.
Metoda „jeden przeciw jednemu” – metoda klasyfikacji wieloklasowej polegająca na tworzeniu równolegle wielu sieci rozpoznających wszystkie kombinacje pojedynczych klas.
Metoda „jeden przeciw pozostałym” – metoda klasyfikacji wieloklasowej polegająca na tworzeniu wielu sieci rozpoznających wszystkie kombinacje pojedynczej klasy względem pozostałych klas uważanych za klasę przeciwstawną.
Funkcja błędu z tolerancją – specjalna definicja błędu przyjmująca wartość zerową, jeśli różnica między wartością zadaną i aktualną mieści się w granicach tolerancji.
Algorytm SMO – algorytm optymalizacji (ang. Sequential Minimal Optimization) bazujący na programowaniu sekwencyjnym i polegający na dekompozycji zadania programowania kwadratowego na mniejsze podzadania, rozwiązywane sekwencyjnie aż do spełnienia wszystkich warunków optymalności Kuhna-Tuckera.
SVM_win – interfejs graficzny w Matlabie do uczenia i testowania sieci SVM.
Problem 2 spiral – problem testowy klasyfikacji punktów położonych na dwu wzajemnie przeplatających się spiralach należących do dwu różnych klas.
3. Sieci neuronowe głębokie
W ostatnich latach ogromny postęp w eksploracji danych dokonał się za pośrednictwem tak zwanego głębokiego uczenia. Głębokie uczenie dotyczy wielowarstwowych sieci neuronowych, które pełnią jednocześnie funkcję generatora cech diagnostycznych dla analizowanego procesu tworząc ostateczny wynik klasyfikacji bądź regresji [1, 2, 18, 26, 37, 50, 70, 78]. Uzyskuje się w ten sposób doskonałe narzędzie zastępujące człowieka przede wszystkim w trudnej dziedzinie opisu procesu za pomocą specjalizowanych deskryptorów, których stworzenie wymaga dużych zdolności eksperckich. Okazuje się przy tym, że takie podejście do bez-interwencyjnej metody generacji cech jest o wiele skuteczniejsze od stosowanych tradycyjnie metod generacji deskryptorów, pozwalając przy tym na poprawę dokładności działania systemu. Z tego powodu technologia sieci głębokich stała się ostatnio bardzo szybko jednym z najbardziej popularnych obszarów w dziedzinie nauk komputerowych.
3.1. Wprowadzenie
Za protoplastę tych sieci można uznać zdefiniowany na początku lat dziewięćdziesiątych wielowarstwowy neocognitron Fukushimy [12]. Prawdziwy rozwój tych sieci zawdzięczamy jednak profesorowi LeCun [37], który zdefiniował podstawową strukturę i algorytm uczący specjalizowanej sieci konwolucyjnej, wielowarstwowej, zwanej „Convolutional Neural Network” (CNN). Aktualnie CNN stanowi podstawową strukturę stosowaną na szeroką skalę w przetwarzaniu obrazów i sygnałów [18]. W międzyczasie powstało wiele odmian sieci będących modyfikacją struktury podstawowej CNN (np. U-net, RCNN) jak również sieci różniących się zasadniczo od CNN, na przykład autoenkoder, jako wielowarstwowe, nieliniowe uogólnienie liniowej sieci PCA [13,33,46,], sieci rekurencyjne typu LSTM (ang. Long Short-Term Memory) [20,58], stanowiące skuteczne rozwiązanie problemu propagacji wstecznej w czasie w systemie ze sprzężeniem zwrotnym, czy ograniczona (wielowarstwowa) maszyna Boltzmanna (ang. Restricted Boltzmann Machine - RBM) używana w sieciach głębokiej wiarygodności (ang. Deep Belief Network – DBN) [18,26].
Cechą wspólną tych rozwiązań, zwłaszcza w przypadku CNN, jest wielowarstwowość ułożenia neuronów i ogromna (idąca w miliony) ilość połączeń wagowych między neuronami. Dla uniknięcia problemu lawinowego narastania liczby adaptowanych wag stosuje się powszechnie połączenia typu lokalnego. W tego typu rozwiązaniach neuron jest zasilany nie przez wszystkie sygnały (na przykład piksele obrazów) warstwy poprzedzającej, jak to jest zorganizowane w sieciach klasycznych, ale przez wybraną małą grupę neuronów (pikseli) tej warstwy, tworzących maskę filtrującą. Analiza całego obrazu następuje poprzez przesuwanie tej maski z ustalonym krokiem (ang. stride) wzdłuż i wszerz obrazu. Charakterystyczną cechą jest przy tym używanie identycznych wartości wag przesuwającej się maski filtracyjnej.
Każdy rodzaj sieci głębokich związany jest z problemem adaptacji ogromnej liczby parametrów sieci w akceptowalnym czasie. Skuteczna implementacja i rozwój koncepcji LeCuna stały się możliwe dzięki olbrzymiemu postępowi w rozwoju technologii informatycznych, pozwalającemu na ogromne przyśpieszenie obliczeń. Połączenie tych najnowszych technologii z proponowanymi rozwiązaniami sieci głębokich stworzyło podstawy zastosowań sztucznej inteligencji w życiu codziennym.
Realne stało się zaprojektowanie pojazdów samosterujących, których podstawą jest rozpoznawanie obrazów i obiektów prezentowanych na tych obrazach w czasie rzeczywistym, sterowanie robotami, skuteczne rozpoznawanie głosu, automatyczna generacja tekstu na podstawie wypowiedzi głosowej, segmentacja złożonych obrazów, zwłaszcza biomedycznych, przewidywanie szeregów czasowych, itp. [2,3]. Ważną sferą zastosowań jest wspomaganie diagnostyki medycznej dzięki skutecznym algorytmom przetwarzania obrazów medycznych, na przykład mikroskopowych, histologicznych itp. W pracy tej najwięcej uwagi poświęcimy najczęściej używanej strukturze sieci CNN.
3.2. Sieć konwolucyjna CNN
Sieci konwolucyjne (ang. Convolutional Neural Networks – CNN) zwane również sieciami splotowymi powstały jako narzędzie analizy i rozpoznawania obrazów wzorowane na sposobie działania naszych zmysłów [18,37]. Wyeliminowały kłopotliwy i trudny dla użytkownika etap manualnego opisu cech charakterystycznych obrazów, stanowiących atrybuty wejściowe dla końcowego etapu klasyfikatora bądź układu regresyjnego. W tym rozwiązaniu sieć sama odpowiada za generację cech. Poszczególne warstwy sieci CNN przetwarzają obrazy z warstwy poprzedzającej (na wstępie jest to zbiór obrazów oryginalnych) poszukując prymitywnych cech (np. grupy pikseli o podobnym stopniu szarości, krawędzie, przecinające się linie itp.). Kolejne warstwy ukryte generują pewne uogólnienia cech z warstwy poprzedzającej organizowane w formie obrazów. Przykład wyników takiego przetworzenia obrazu kolorowego w warstwie ukrytej sieci zawierającej 48 neuronów (każdy wielowejściowy o różnych wartościach wag) pokazano na rys. 6.1. Kolejny kwadrat obrazu wynikowego przedstawia cechy diagnostyczne (w formie podobrazu) utworzone przez każdy z tych neuronów.

Obrazy te w niczym nie przypominają oryginałów, ale reprezentują cechy charakterystyczne dla nich wyrażone w formie szarości pikseli. W efekcie kolejnego wielowarstwowego przetwarzania obrazów z poprzedniej warstwy ostatnia warstwa konwolucyjna generuje obrazy stosunkowo niewielkich wymiarów reprezentujące cechy charakterystyczne dla przetwarzanego zbioru. Obrazy te w poszczególnych warstwach są reprezentowane przez tensory, których elementy są następnie przetwarzane na postać wektorową, będącą początkiem układu w pełni połączonego (ang. fully connected – FC), stanowiącego właściwy klasyfikator bądź układ regresyjny. Przykład takiej struktury CNN przedstawiono na rys. 6.2 [46].
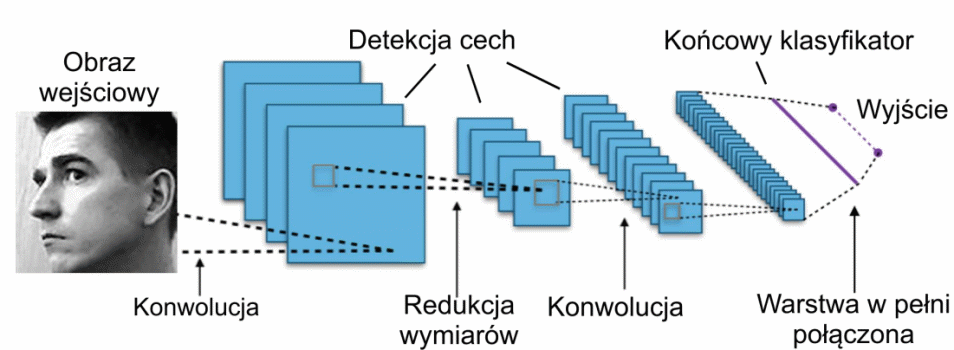
Kolejne warstwy sieci mają zadanie wygenerować w sposób automatyczny (całkowicie poza udziałem człowieka) zbiór cech charakterystycznych dla analizowanych wzorców obrazowych, który następnie podlegają klasycznemu przetworzeniu w decyzję klasyfikacyjną bądź regresyjną.
6.2.2 Podstawowe operacje w sieci CNN
Nazwa sieci CNN pochodzi od operacji splotu (konwolucji) stanowiącej istotny element procesu obliczeniowego. W przypadku obrazów tablica danych jest reprezentowana przez dwuwymiarową macierz \( \mathbf{I} \) o elementach reprezentujących stopnie jasności pikseli \( I(m,n) \) a jądro \( \mathbf{K} \) jest dwuwymiarowe. Operacja splotu dwuwymiarowego jest wówczas zapisana w postaci [18,38]
| \( Y(i, j)=I(i, j) * K(i, j)=\sum_m \sum_n I(m, n) K(i-m, j-n)=\sum_m \sum_n I(i-m, j-n) K(m, n) \) | (6.1) |
W sieciach CNN wejściem dla pierwszej warstwy ukrytej jest zwykle reprezentacja RGB obrazów ustawionych w formie tensora. Operacja konwolucji w pierwszej warstwic konwolucyjnej obejmuje wszystkie trzy kanały RGB obrazu (suma poszczególnych kanałów), każdy z innymi przyjętymi wartościami wag jądra w postaci filtru liniowego stanowiącego neuron analizujący. W dalszych warstwach operacja ta obejmuje wiele (ustalonych przez użytkownika) obrazów z warstwy poprzedzającej (tak zwana konwolucja grupowa).
Przykład operacji konwolucyjnej dla kroku przesunięcia filtru (stride) równego 2 przedstawiono na rys. 6.3 [34]. Dane wejściowe stanowią 3 kanały RGB obrazu. Każdy kanał jest przetwarzany przez odpowiedni dla niego filtr (neuron) a wyniki przetworzenia sumowane z uwzględnieniem polaryzacji tworząc obraz wynikowy. W efekcie, w każdej warstwie konwolucyjnej filtr jest wielowymiarowy, realizujący operacje tensorowe, przy czym wymiar maski filtrującej jest równy \( n_x \times n_y \), a liczba tych masek tworzących jeden filtr jest równa liczbie obrazów wejściowych dla danej warstwy podlegających przetworzeniu (maksymalnie liczba obrazów poprzedniej warstwy). W przypadku pierwszej warstwy konwolucyjnej i obrazowi reprezentowanemu przez 3 kanały RGB każdy filtr składa się z trzech jednostek (patrz filtr \( W0 \) lub \( W1 \)). Liczba obrazów wyjściowych po konwolucji jest równa liczbie zastosowanych filtrów wielokanałowych (w prykładzie są 2 filtry \( W0 \) i \( W1 \)), stąd 2 obrazy wyjściowe reprezentowane na rysunku przez Output Volume.
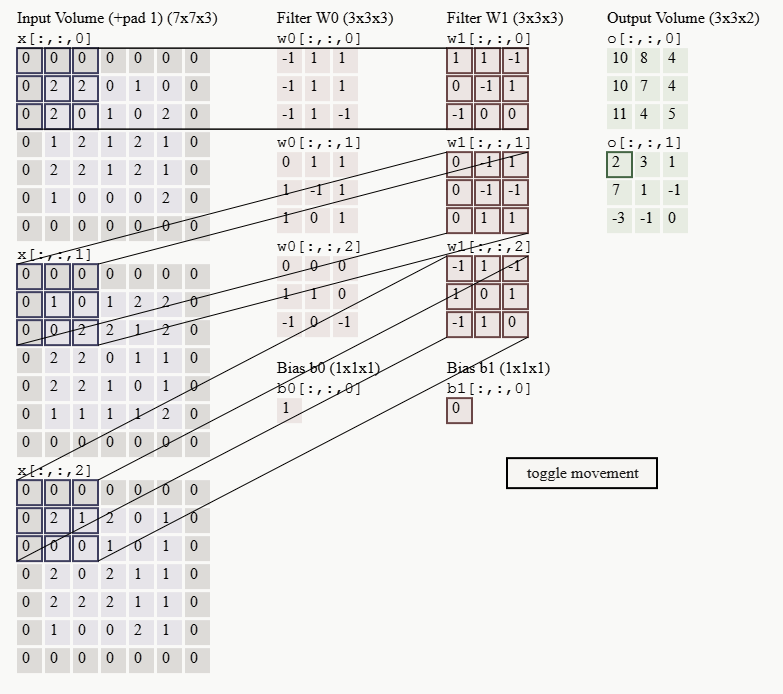
W przetwarzaniu danych operacja konwolucji stosowana w CNN charakteryzuje się ważnymi zaletami w stosunku do zwykłych operacji macierzowych w sieciach klasycznych. Należą do nich: lokalność połączeń, wspólne (powtarzalne) wartości wag połączeń filtru przesuwającego się po obrazie i powstała dzięki temu niezmienniczość (ekwiwariancja) względem przesunięcia.
Każdy sygnał wyjściowy filtru podlega działaniu nieliniowej funkcji aktywacji, która w przypadku CNN przybiera najczęściej postać ReLU (ang. Rectified Linear Unit) opisaną wzorem [18, 78]
| \( y(x)=\left\{\begin{array}{lll} x & \textrm{dla} & x \ge 0 \\ 0 & \textrm{dla} & x \le 0 \end{array}\right. \) | (6.2) |
Funkcja ta charakteryzuje się nieciągłą pochodną. Ten fakt może utrudnić uczenie sieci metodami gradientowymi. Stąd często zastępuje się ją aproksymacją zwaną softplus, zdefiniowaną następująco [18]
| \( y(x) = \ln( 1 + e^x) \) | (6.3a) |
Jej pochodna jest ciągła i reprezentuje sigmoidę unipolarną. W wyniku konwolucji i działania funkcji ReLU uzyskuje się wartości reprezentujące stopień szarości pikseli obrazu wynikowego.
W niektórych implementacjach sieci głębokich, na przykład w GAN stosuje się zmodyfikowaną funkcję aktywacji LReLU (ang. Leaky ReLU), w której w części ujemnej charakterystyki wartości zerowe zastępuje się linią prostą o małym nachyleniu \( a \). Funkcję taką opisuje się wzorem
| \( y(x)=\left\{\begin{array}{lll}
x & \textrm{dla} & x \ge 0 \\
ax & \textrm{dla} & x \le 0
\end{array}\right. \) |
(6.3b) |
przy wartości \(a<1\); typowa wartość to \(a=0.01\).
Stosowana jest również wersja wykładnicza funkcji ReLU, zwana w skrócie ELU (ang. exponential linear unit), która definiowana jest wzorem
| \( y(x)=\left\{\begin{array}{lll} x & \textrm{dla} & x \ge 0 \\ a(e^x -1) & \textrm{dla} & x \le 0 \end{array}\right. \) | (6.3c) |
w którym \( a \) jest hiperparametrem o wartości dodatniej, ułamkowej (typowa wartość \(a=0.01 \)). Badania pokazały, że dzięki zastosowaniu takiej funkcji można uzyskać lepszą dokładność klasyfikatora CNN.
Liczba neuronów konwolucyjnych, filtrujących poszczególne obszary lokalne obrazu ustalana jest przez użytkownika. Każdy neuron (filtr) ma określoną przez użytkownika liczbę wag podlegających doborowi i łączących go z określonym rejonem lokalnym obrazu. Dla typowych wielkości maski 3x3 (małe obrazy) lub 5x5 (obrazy duże) liczba wag neuronu (liczba elementów filtru) staje się więc równa 9 lub 25 (plus waga polaryzacji). Stosuje się również maski punktowe, o wymiarze 1x1. Taka wielkość maski zdecydowanie zmniejsza liczbę adaptowanych parametrów sieci.
Przesuwna maska analizy wędrująca po obrazie wejściowym dostarcza do wyjścia sygnał sumacyjny będący sumą iloczynów jasności pikseli i odpowiednich, połączonych z nimi wag neuronu (wartości elementów filtru) na zasadzie konwolucji. Neuron ze swoimi wagami stanowi więc filtr o stałych parametrach przesuwany po obrazie z określonym krokiem. Przesuwanie maski filtracyjnej neuronu sterowane jest przez wybór wielkości kroku stride. Wielkość stride=1 oznacza, że nowa maska przesuwana jest o jeden piksel obrazu (w kierunku \(x \) lub \( y \)) w stosunku do pozycji poprzedniej maski. Rozmiar obrazu wynikowego zależy od wybranego kroku stride i wielkości maski filtrującej.
W następnym kroku powstały obraz wynikowy poddaje się działaniu operacji łączenia sąsiednich wyników, tzw. operacja „pooling”, redukując w ten sposób wymiar obrazów. Funkcja ta przekształca wynik nieliniowego działania filtracyjnego neuronu w określonym rejonie obrazu poprzez zdefiniowaną statystykę dotyczącą najbliższych mu pikseli pod względem lokalizacji wyników wyjściowych. Typowe funkcje to: max pooling zwracająca wartość maksymalną wyników neuronów znajdujących się w sąsiedztwie prostokątnym aktualnego wyniku oraz average pooling zwracającą wartość średnią wyników w tym obszarze. Przykład takiej operacji uwzględniającej obszar maski 2x2 przedstawiony jest na rys. 6.4.
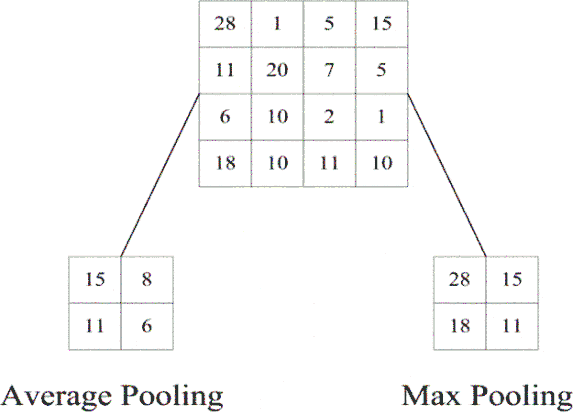
Operacja pooling poza zmniejszeniem wymiaru obrazu pozwala uzyskać reprezentację bardziej inwariantną względem niewielkiego przemieszczenia danych. Stanowi pewne uogólnienie cech reprezentowanych przez sąsiednie grupy pikseli. Często dla zachowania odpowiednich wymiarów obrazu stosuje się operację uzupełnienia brzegów zerami tzw. „zero padding”. Zwykle jest to uzupełnienie symetryczne z obu stron obrazu.
Dodatkowo stosuje się również normalizację stopnia szarości obrazów powstałych w wyniku konwolucji. Najczęściej jest to to operacja stosowana na danych „mini-batch” (małego zestawu danych wybranego losowo aktualnie z pełnego zbioru używanego w operacji konwolucji). Wykonywana jest na bezpośrednich wynikach konwolucji liniowej (po operacji ReLU). Odbywa się poprzez odjęcie wartości średniej i podzieleniu takich wyników przez odchylenie standardowe danych zawartych w „mini-batch” od rzeczywistych wartości obrazu otrzymanych z konwolucji.
Liczba neuronów konwolucyjnych, filtrujących poszczególne obszary lokalne obrazu ustalana jest przez użytkownika i decyduje o liczbie obrazów wynikowych. Wymiar obrazu wynikowego filtracji zależy od wielkości kroku stride, wielkości maski filtrującej i zastosowanego uzupełnienia zerami. Istnieje ścisła relacja wiążąca rozmiar wynikowy O obrazu z rozmiarem obrazu wejściowego W, wielkością filtru F, kroku stride S i wielkością uzupełnienia zerami z obu stron symetrycznie (zero padding P). Wielkości te są powiązane relacją [18]
| \( O=(W−F+2P)/S+1 \) | (6.4) |
określającą wymiar obrazu wyjściowego. Przykładowo, jeśli obraz wejściowy ma wymiar \(7\times 7\) (\(W=7\)), zastosowany filtr \(3\times 3\) (\(F=3\)), stride \(S=1\) oraz \(P=0\) wówczas otrzymuje się obraz wyjściowy o wymiarze \( 5\times 5 \), gdyż \(O=(7-3)/1+1=5 \). Podobnie dla \(S=2\) otrzymuje się wymiar obrazu wyjściowego równy \(3\times 3\).
Przykład graficzny wpływu wielkości kroku stride na wynik operacji w przypadku danych wejściowych jednowymiarowych o 7 elementach (\(W=7\)) przedstawiono na rys. 6.5. W obu przypadkach neuron filtrujący ma trzy połączenia wagowe (\(F=3\)) o wartościach wag równych kolejno: \(1, 0, -1\) oraz brak uzupełnienia zerami (\(P=0\)). Wynik przedstawiony jest dla 2 różnych wartości parametru stride. W pierwszym przypadku jest to wartość stride=1, w drugim stride=2. W zależności od wyboru otrzymuje się różną liczbę elementów wynikowych: w pierwszym przypadku jest to 5 wyników, w drugim tylko trzy.
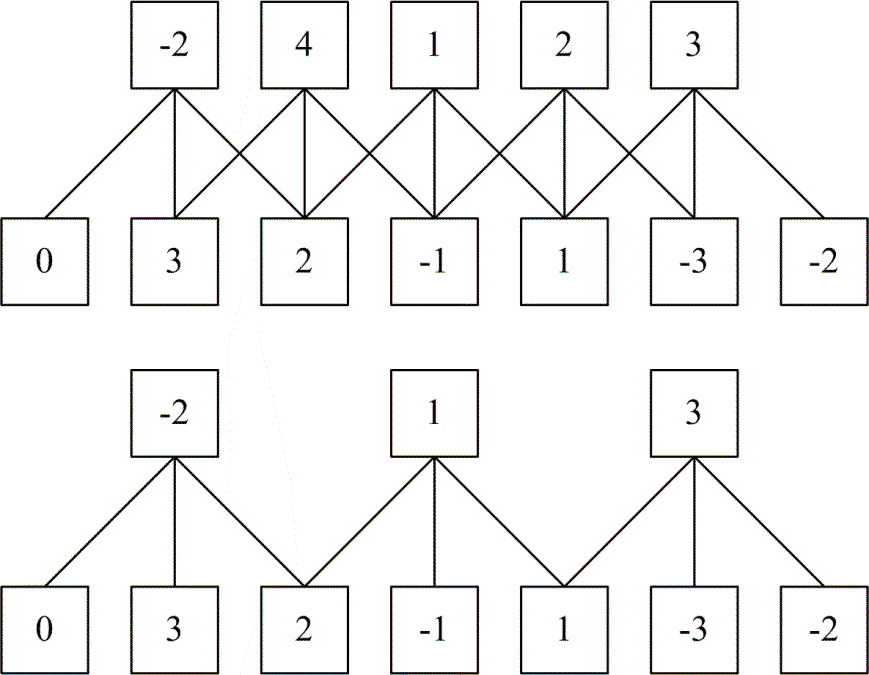
Zdefiniowane wartości parametrów mają ważne znaczenie przy projektowaniu struktur CNN, gdyż niewłaściwie przyjęte liczby mogą prowadzić do niecałkowitych wartości rozmiarów obrazów wejściowych. Przykładowo w architekturze ALEXnet Krizhevskiego [34] wymiar wejściowy obrazów jest równy \(227\times227\times3\) (reprezentacja RGB). Zastosowane przez niego wymiary w pierwszej warstwie ukrytej to \(F=11, S=4, P=0\). Stąd wymiar obrazu wyjściowego po konwolucji jest równy \(O=(227-11)/4+1=55\), czyli obraz \(55\times55\). Gdyby wymiar obrazu wejściowego był równy na przykład \(224\times224\) wówczas wymiar obrazu wyjściowego przy \(S=4\) po konwolucji nie byłby liczbą całkowitą, gdyż wówczas \(O=(224-11)/4+1=54,25\), co blokuje dalszy proces przetwarzania.
W poszczególnych warstwach ukrytych obrazy wynikowe tworzą tensory (strukturę trójwymiarową reprezentowaną przez dwa wymiary obrazu i liczbę przetwarzanych obrazów). Obrazy (macierze) ostatniej warstwy konwolucyjnej są przetwarzane na postać wektorową, stanowiącą początek sieci w pełni połączonej w której każdy neuron jest połączony z każdym sygnałem warstwy poprzedniej – połączenia globalne (ang. Fully Connected layer – FC). Neurony w warstwie o pełnym połączeniu mają unikane wagi, podlegające adaptacji w procesie uczenia.
Przejście z reprezentacji tensorowej (wiele obrazów m-wymiarowych) na postać wektorową (pojedyncze sygnały wektora tworzące wejście dla właściwego klasyfikatora) może odbywać się na wiele sposobów. Jednym z nich jest przyjęcie wszystkich wartości pikselowych poszczególnych obrazów jako cech diagnostycznych i ustawienie ich w formie wektora poprzez operację tzw. reshape. Przy zbyt dużych wymiarach obrazów stosowane może być zmniejszenie rozdzielczości obrazów tensora. Innym rozwiązaniem jest zastosowanie operacji pooling z odpowiednim krokiem stride. W niektórych przypadkach można zaprojektować sieć w taki sposób, że ostatnia warstwa konwolucyjna zawiera tylko pojedynczą wartość dla każdego kanału.
W większości rozwiązań sieci CNN użytej jako klasyfikatora zamiast klasycznej wielowarstwowej sieci neuronowej stosuje się klasyfikator typu softmax, w którym sygnały wejściowe są bezpośrednio przetwarzane na prawdopodobieństwo przynależności do określonej klasy [18]. Liczba neuronów wyjściowych jest równa liczbie klas przy czym każdy neuron podlega adaptacji wag w klasyczny sposób poprzez optymalizację funkcji celu zdefiniowanej w postaci entropii krzyżowej (ang. cross entropy). Wartość sygnału sumacyjnego neuronu \(i\)-tego określona jest wówczas wzorem
| \( u_i(x)=\sum_j w_{i j} x_j+w_0 \) | (6.5a) |
Prawdopodobieństwo przynależności wektora \( \mathbf{x} \) do \(i\)-tej klasy (\(i=1, 2, …, M\)) zależy od wartości funkcji softmax obliczanej dla każdej składowej wektora wyjściowego według wzoru
| \( \operatorname{softmax}\left(u_i\right)=\frac{\exp \left(u_i\right)}{\sum_{j=1}^M \exp \left(u_j\right)} \) | (6.5b) |
Wartość największa funkcji wyznacza przynależność do klasy określonej wskaźnikiem \( i \).
Przystępując do uczenia sieci CNN należy w pierwszej kolejności ustalić liczbę warstw ukrytych (konwolucyjnych), pełniących rolę ekstraktora cech procesu, liczbę neuronów w poszczególnych warstwach (każdy odpowiedzialny za wytworzenie pojedynczego obrazu), wielkość maski filtracyjnej neuronu i związanej z tym liczby połączeń wagowych, rodzaj funkcji aktywacji, wielkość parametru stride w każdej warstwie oraz wybór parametru zero-padding.
Proces uczenia sieci polega na adaptacji parametrów zarówno filtrów w części lokalnie połączonej, jak i wartości wag klasyfikatora końcowego (struktura w pełni połączona). W przypadku warstw ukrytych polega na doborze wag przesuwających się filtrów. Liczba tych wag zależy od przyjętej wielkości maski filtracyjnej. Wielkość maski w przypadku obrazów zależy od ich wielkości. Przy małych obrazach typowy wymiar to \(5\times 5\) (25 wag neuronu), przy dużych - wielkość stosowanej maski może być nawet \(11\times 11\) (121 wag neuronu). Każdy neuron w warstwie powinien wykrywać inne szczegóły obrazu, np. układ pikseli tworzący krawędzie w określonym kierunku, skupienia pikseli tworzące plamki, zmiany jasności w regionie, itp. W procesie uczenia pierwotnego liczba adaptowanych parametrów filtrów w części sieci lokalnie połączonej dominuje w ogólnej populacji zmiennych podlegających optymalizacji.
Uczenie sieci odbywa się to poprzez minimalizację funkcji kosztu. Funkcja kosztu może być definiowana w różny sposób. W sieciach głębokich pełniących rolę klasyfikatora najczęściej stosowana jest definicja kross-entropijna (ang. cross-entropy function), bazująca na prawdopodobieństwie przynależności do określonej klasy, przy czym to prawdopodobieństwo określane jest poprzez znormalizowaną funkcję sigmoidalną zwaną softmax zdefiniowana wzorem (6.5), przy czym największa wartość prawdopodobieństwa wyznacza ostateczną przynależność do jednej spośród M klas. Oznaczmy wartość funkcji softmax w postaci \(f(u_i)\) [18]
| \( f\left(u_i\right)=\frac{\exp \left(u_i\right)}{\sum_{j=1}^n \exp \left(u_j\right)} \) | (6.6) |
Zmienna \(u_i\) w tym wzorze jest sumą wagową sygnałów dopływających do \(i\)-tego neuronu wyjściowego. W zdaniach klasyfikacji wieloklasowej (\(M\) klas) tylko jedna klasa jest prawdziwa (etykieta tej klasy \(d=1\)). Pozostałe klasy mają etykietę \(d=0\). Zatem w procesie uczenia tylko klasa wskazana przez sieć jako prawdziwa bierze udział w obliczaniu funkcji błędu (kosztu) przyjmując \(d=1\). Pozostałe wyjścia mają etykiety \(d=0\) i nie biorą bezpośredniego udziału w definicji funkcji celu. Entropijna (logarytmiczna) definicja funkcji celu zapisana w postaci ogólnej
| \( E=-\sum_{i=1}^{M} d_i \log \left(f\left(u_i\right)\right) \) |
(6.7) |
Wobec tylko jednej wartości \( d_i=d_p\) różnej od zera (równej \(1\)) dla klasy "pozytywnej" może być uproszczona do postaci
| \( E=-\log \left(f(u_i)\right)=-\log \left|\frac{\exp \left(u_i \right)}{\sum_{i=1}^M \exp \left(u_i\right)}\right| \) | (6.8) |
Składniki funkcji celu względem klas “negatywnych” są równe zeru. Tylko klasa wskazana przez sieć bierze bezpośredni udział w tworzeniu funkcji celu. Tym niemniej gradient funkcji celu zależy również od składników klas „negatywnych”, ze względu na postać mianownika w wyrażeniu (6.18). Należy przy tym zauważyć, że składniki gradientu funkcji celu względem sygnału sumacyjnego \(u_n\) dla klas „negatywnych” będą miały identyczną postać, wyrażoną wzorem
| \( \frac{\partial}{\partial u_n}\left(-\log \left(\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}\right)\right)=\frac{\exp \left(u_n\right)}{\sum_{j=1}^M \exp \left(u_j\right)} \) |
(6.9a) |
natomiast dla klasy "pozytywnej", wskazanej przez sieć wyrażenie (sygnał sumacyjny \(u_p\)) będzie miało postać
| \( \frac{\partial}{\partial u_p}\left(-\log \left(\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}\right)\right)=\frac{\exp \left(u_p\right)}{\sum_{j=1}^M \exp \left(u_j\right)}-1 \) | (6.9b) |
Znając wektor gradientu względem poszczególnych sygnałów składniki gradientu względem poszczególnych wag \(w\) występujących w wyrażeniu (6.5) na sygnał sumacyjny są wyznaczane korzystając z własności różniczkowania funkcji złożonej, mianowicie
| \( \frac{\partial E}{\partial w_i}=\frac{\partial E}{\partial u} \frac{\partial u}{\partial w_i}=\frac{\partial E}{\partial u} x_i \) | (6.10) |
Najczęściej stosowanym algorytmem w uczeniu sieci CNN jest stochastyczny algorytm największego spadku z momentem rozpędowym (ang. Stochastic Gradient Descent – SGDM) [18,43]. Adaptacja wag odbywa się iteracyjnie zgodnie ze wzorem
| \( \mathbf{w}(k)=\mathbf{w}(k-1)-\eta \mathbf{g}(k-1)+\alpha[\mathbf{w}(k-1)-\mathbf{w}(k-2)] \) | (6.11) |
w którym \(\alpha\) jest współczynnikiem momentu przyjmowanym z przedziału \([0, 1]\). Dla przyśpieszenia procesu uczenia w poszczególnych iteracjach zamiast pełnego zbioru danych uczących używa się losowo wybranego podzbioru (tzw. minibatch). Powstało wiele modyfikacji tego algorytmu przyśpieszających proces uczenia, z których najczęściej używany (między innymi w Matlabie) jest ADAM (skrót of ang. ADAptive Momenet estimation) [43]. W odróżnieniu od SGD w tej metodzie każdy parametr \(w\) ma adaptacyjnie dobierany współczynnik uczenia uzależniony od momentu statystycznego gradientu pierwszego i drugiego rzędu. Momenty te dla optymalizowanej zmiennej \(w\) definiowane są w postaci średniej kroczącej
-
moment pierwszego rzędu (start z wartości zerowych)
| \( m_w(k)=\beta_1 m_w(k-1)+\left(1-\beta_1\right) g(k) \) | (6.12) |
-
moment drugiego rzędu
| \( v_w(k)=\beta_2 v_w(k-1)+\left(1-\beta_2\right) g^2(k) \) | (6.13) |
gdzie \(\beta_1\) i \(\beta_2\) są hiperparametrami dobieranymi przez użytkownika, zwykle w zakresie \([0.9 – 0.999]\). Na tej podstawie oblicza się estymatę nieobciążoną obu momentów, używaną w adaptacji poszczególnych wag sieci
| \( \hat{m}_w(k)=\frac{m_w(k)}{1-\beta_1^k} \) | (6.14) |
| \( \hat{v}_w(k)=\frac{v_w(k)}{1-\beta_2^k} \) | (6.15) |
Adaptacja wagi \( w\) następuje według wzoru
| \( w(k)=w(k-1)-\eta \frac{\hat{m}_w(k)}{\sqrt{\hat{v}_w(k)}+\varepsilon} \) | (6.16) |
Eksperymenty numeryczne wykazały znaczące przyspieszenie procesu uczenia przy zastosowaniu adaptowanego współczynnika dla każdej wagi. Tym niemniej nie zawsze jakość uzyskanych wyników jest lepsza niż algorytmu SGDM.
Bezpośrednie podejście do adaptacji wszystkich wag przy zastosowaniu globalnej metody propagacji wstecznej uczenia dla całej sieci jest kosztowne obliczeniowo, gdyż wiąże się z ogromną liczbą dobieranych parametrów. Przyśpieszenie procesu uczenia jest możliwe poprzez dobór wstępny wag filtrów warstw konwolucyjnych przy zastosowaniu różnego rodzaju rozwiązań techniki uczenia bez nauczyciela. Stosowane są różne podejścia do tego problemu.
-
Inicjalizacja losowa wag każdego neuronu w każdej warstwie konwolucyjnej. Metoda ta jest znana i przebadana w przypadku klasycznych sieci neuronowych typu ELM (Extreme Learning Machine).
-
Inicjalizacja manualna wykorzystująca doświadczenie użytkownika, ukierunkowana na przykład na wykrywanie krawędzi w określonym kierunku. Można tu zastosować wstępnie klasyczne liniowe filtry cyfrowe obrazu, np. filtry Sobela, Previtta, Canny, Log, itp.
-
Inicjalizacja poprzez grupowanie danych, na przykład przy pomocy algorytmu k-means. W metodzie tej grupowanie przeprowadza się dla losowo wybranych małych fragmentów obrazu i parametry centroidu przyjmuje się jako wartości wag neuronów filtracyjnych.
-
Inicjalizacja poprzez wstępne uczenie zachłanne (greedy learning) z nauczycielem, warstwa po warstwie (najpierw warstwa pierwsza, potem warstwa druga na bazie wyników przetworzenia sygnałów przez warstwę pierwszą itd.). Stosowane są różne warianty tego rozwiązania, pozwalające na znaczne przyśpieszenie procesu uczenia. Po wstępnym doborze wag następuje zwykle douczenie pełnej sieci przy wykorzystaniu metody największego spadku i propagacji wstecznej błędu.
Przy obecnym stanie równoległej techniki obliczeniowej i zastosowaniu procesora graficznego możliwe stało się zastosowanie uczenia z nauczycielem do pełnej (losowo zainicjowanej) sieci w każdej iteracji uczącej (ekstremalne podejście do uczenia). Tym nie mniej przy zastosowaniu takiego podejścia należy się liczyć z długotrwałym procesem uczenia, zwłaszcza jeśli wymiary obrazów wejściowych są duże.
Najczęściej stosowanym podejściem w praktyce inżynierskiej przy tworzeniu sieci CNN jest zastosowanie tzw. metody transfer learning. W tym podejściu korzysta się ze wstępnie nauczonej sieci dostępnej między innymi w Matlabie, o parametrach dobranych przez specjalistów. Użytkownik dokonuje jedynie adaptacji określonej części struktury sieci (zwykle klasyfikatora końcowego) na swoich danych. Parametry warstw odpowiedzialnych za mechanizm generacji cech diagnostycznych pozostają często zamrożone. Uczenie takie odbywa się metodami gradientowymi z zastosowaniem propagacji wstecznej błędu i przebiegają stosunkowo szybko.
W ostatnich implementacjach Matlaba (poczynając od 2016 roku) dostępne są m-pliki do uczenia i testowania sieci CNN. Sposób wykorzystania tych podprogramów można uzyskać przy pomocy komendy help cnn. Użytkownik po wczytaniu danych uczących i testujących definiuje architekturę sieci (liczbę warstw i neuronów warstwie, funkcję aktywacji, rodzaj funkcji pooling, etc.), opcje wyboru parametrów uczenia, następnie dokonuje procesu uczenia (funkcja trainNetwork) i następnie testowania (funkcja classify).
Dane uczące i testujące przygotowane są w postaci tablicy 3-D dla obrazów w skali szarości lub 4-D dla obrazów reprezentowanych w postaci RGB. Pierwsze 2 współrzędne zawierają wartości pikseli w osi x i y obrazu, trzecia współrzędna (przy reprezentacji 4-D) jest równa 1, 2 lub 3 prezentując obraz R, G lub B a ostatnia nr kolejny obrazów w bazie. Dane dotyczące klasy reprezentowanej przez obraz są kodowane numerycznie (klasa 1, 2, 3, itd.) w postaci wektorowej.
3.3. Transfer Learning
Ważnym elementem procesów zachodzących w CNN jest duża niezależność wyniku od rodzaju przetwarzanych obrazów, gdyż niezależnie od typu obrazu system przetwarzania koncentruje się na elementach prymitywnych występujących w każdym obrazie. Stało się to przyczyną powstania specjalnego sposobu wstępnego uczenia sieci CNN, tzw. Transfer Learning na dowolnie dobranym zestawie danych uczących, który podlega jedynie douczeniu na danych użytkownika [30,45]. Dzięki takiemu rozwiązaniu możliwe jest ogromne skrócenie czasu uczenia, a przy tym znaczące polepszenie zdolności generalizacji sieci.
Takim pierwszym prototypem (dostępnym również w Matlabie poczynając od wersji z roku 2017) jest AlexNet [34], zaprojektowany przez grupę naukowców: Alex Krizhevsky, Ilya Sutskever and Geoff Hinton. W implementacji Matlaba struktura sieci AlexNet jest następująca [43]
1 'data' Image Input 227x227x3 images with 'zerocenter' normalization
2 'conv1' Convolution 96 11x11x3 convolutions with stride [4 4] and padding [0 0]
3 'relu1' ReLU
4 'norm1' Cross Channel Normalization with 5 channels per element
5 'pool1' Max Pooling 3x3 max pooling with stride [2 2] and padding [0 0]
6 'conv2' Convolution 256 5x5x48 convolutions with stride [1 1] and padding [2 2]
7 'relu2' ReLU
8 'norm2' Cross Channel Normalization with 5 channels per element
9 'pool2' Max Pooling 3x3 max pooling with stride [2 2] and padding [0 0]
10 'conv3' Convolution 384 3x3x256 convolutions with stride [1 1] and padding [1 1]
11 'relu3' ReLU
12 'conv4' Convolution 384 3x3x192 convolutions with stride [1 1] and padding [1 1]
13 'relu4' ReLU
14 'conv5' Convolution 256 3x3x192 convolutions with stride [1 1] and padding [1 1]
15 'relu5' ReLU
16 'pool5' Max Pooling 3x3 max pooling with stride [2 2] and padding [0 0]
17 'fc6' Fully Connected 4096 fully connected layer
18 'relu6' ReLU
19 'drop6' Dropout 50% dropout
20 'fc7' Fully Connected 4096 fully connected layer
21 'relu7' ReLU
22 'drop7' Dropout 50% dropout
23 'fc8' Fully Connected 1000 fully connected output layer
24 'prob' Softmax softmax
25 'output' Classification 1000 classes
W sumie można wyróżnić w niej 25 podwarstw (włączając w nie konwolucję liniową, operację ReLU, normalizację i pooling). Sieć zawiera 5 warstw konwolucyjnych i 3 warstwy FC. Pierwsza warstwa FC połączona z operacją ReLU jest warstwą zawierającą 4096 cech diagnostycznych. Druga warstwa FC (również połączona z operacją ReLU jest warstwą ukrytą klasyfikatora końcowego zasilająca warstwę wyjściową 1000 neuronów (pozwala na rozpoznanie 1000 klas). Zastosowany w strukturze klasyfikator to softmax. Stosując transfer learning można wyodrębnić sygnały z pierwszej warstwy FC jako cechy diagnostyczne i zasilić nimi dowolnie wybrany inny rodzaj klasyfikatora, np. SVM czy MLP. W wielu współczesnych rozwiązaniach sieci CNN rezygnuje się z warstwy ukrytej w strukturze w pełni połączonej, łącząc bezpośrednio wektor cech (elementy wypłaszczonych tensorów) z neuronami wyjściowymi softmaxu.
3.4. Przykład użycia sieci ALEXNET w trybie transfer learning
Przykład zastosowania dotyczy rozpoznania 20 klas obrazów twarzy. Każda klasa jest reprezentowana przez 25 fotografii w różnym ujęciu i oświetleniu, przy czym klasy umieszczone są w oddzielnych folderach, a liczba tych folderów jest równa liczbie klas. Na tej podstawie program automatycznie przypisuje dane wejściowe do klasy zgodnej z numerem folderu.
% Przykład zastosowania ALEXNET w klasyfikacji obrazów%
wyn=[]; wynVal=[];
Pred_y=[]; Pred_yVal=[];
N_run=1 % liczba powtórzeń procesu
images = imageDatastore( 'C:\chmura\ALEX_obrazy20',... % Baza danych uczących
'IncludeSubfolders',true,...
'ReadFcn', @customreader, ...
'LabelSource','foldernames');
[uczImages,testImages] = splitEachLabel(images,0.8,'randomized');
for i=1:No_run
[trainingImages,validationImages] = splitEachLabel(uczImages,0.70+0.1*randn(1),'randomized');
numTrainImages = numel(trainingImages.Labels);
net = alexnet;
layersTransfer = net.Layers(1:end-6);
inputSize = net.Layers(1).InputSize;
% imageAugmenter = imageDataAugmenter( ...
% 'RandRotation',[-20,20], ...
% 'RandXTranslation',[-3 3], ...
% 'RandYTranslation',[-3 3])
% augimdsTrain = augmentedImageDatastore(inputSize(1:2),trainingImages,'DataAugmentation',imageAugmenter);
augimdsTrain = augmentedImageDatastore(inputSize(1:2),trainingImages);
augimdsTest = augmentedImageDatastore(inputSize(1:2),testImages);
layer = 'fc7';
featuresTrain = activations(net,augimdsTrain,layer,'OutputAs','rows');
featuresTest = activations(net,augimdsTest,layer,'OutputAs','rows');
numClasses = numel(categories(trainingImages.Labels));
layers = [
layersTransfer
fullyConnectedLayer(1000+35*i,'WeightLearnRateFactor',20,'BiasLearnRateFactor',20)
reluLayer()
dropoutLayer(0.5+0.033*randn(1))
fullyConnectedLayer(numClasses,'WeightLearnRateFactor',20,'BiasLearnRateFactor',20)
softmaxLayer
classificationLayer];
miniBatchSize = 10; % bylo 10
numIterationsPerEpoch = floor(numel(trainingImages.Labels)/miniBatchSize);
options = trainingOptions('sgdm',...
'MiniBatchSize',miniBatchSize,...
'MaxEpochs',10,...
'ExecutionEnvironment','gpu',...
'InitialLearnRate',1.3e-4,...
'Verbose',false,...
'ValidationPatience',10,...
'Plots','training-progress',...
'ValidationData',validationImages,...
'ValidationFrequency',numIterationsPerEpoch);
netTransfer = trainNetwork(trainingImages,layers,options);
predictedLabels = classify(netTransfer,testImages);
testLabels = testImages.Labels;
accuracy = (mean(predictedLabels == testLabels))*100
Pred_y=[Pred_y predictedLabels];
wyn=[wyn accuracy] %wyniki poszczególnych powtórzeń procesu uczenia i testowania
end
Program umożliwia wielokrotne uruchomienie uczenia ustawione wartością parametru No_run. W wyniku określona jest względna dokładność rozpoznania klas (wartość accuracy). Przy wielu próbach (No_run > 1) kolejne wyniki umieszczone są w tabeli wyn. Z tej tabeli można obliczyć średnią dokładność klasyfikatora w postaci mean(wyn).
3.5. Inne rozwiązania pre-trenowanej architektury sieci CNN
Sieci CNN ze względu na ich uniwersalność i prostotę użycia w przetwarzaniu obrazów zyskały wiele różnych rozwiązań, poprawiających działanie i ułatwiających uczenie sieci [75]. Istnieje aktualnie wiele dostępnych struktur CNN, wytrenowanych wstępnie i dostosowanych do operacji „transfer learning”. Przykładami takich rozwiązań są między innymi:
-
GoogLeNet – zaprojektowany przez zespół Google, operuje zmniejszoną liczbą parametrów podlegających uczeniu (z 61 milionów w AlexNet do 7 milionów) przez wprowadzenie modułu wstępnego przetwarzania. Poza tym stosuje Average Pooling zamiast Max Pooling, co zmniejsza utratę informacji w kolejnych etapach przetwarzania. Aktualnie programy z tej serii są stale ulepszane pod nazwą inception [63,64]].
-
ResNet ukształtowany przez zespół Kaiming He [25]. Główną nowością jest wprowadzenie dodatkowego połączenia międzywarstwowego co drugą warstwę, jak również zastosowanie tzw. batch normalization, czyli normalizacji zastosowanej do małego zbioru próbek uczących (wartość średnia zerowa i jednostkowa wariancja).
-
EfficientNet – model skalowanej sieci CNN zaproponowany przez M. Tana i Q.V. Le [66]. Cecha charakterystyczną tej architektury jest dobór odpowiednich proporcji parametrów skali dotyczących głębokości (liczba warstw), szerokości (liczba równolegle tworzonych obrazów w warstwie) oraz rozdzielczości obrazów w poszczególnych warstwach.
-
U-NET – struktura sieci CNN opracowana przez zespół Ronnebergera [56] dostosowana specjalnie do zadań segmentacji obrazów, zwłaszcza medycznych. Pozwala na odtworzenie poszczególnych rejonów obrazów w pełnej rozdzielczości.
Matlab ma zaimplementowane wiele gotowych (pre-trenowanych) prototypów takich sieci. Poniżej przedstawione są dostępne aktualnie w Matlabie (Matlab 2021b) modele pre-trenowane oraz ich podstawowe parametry [43].
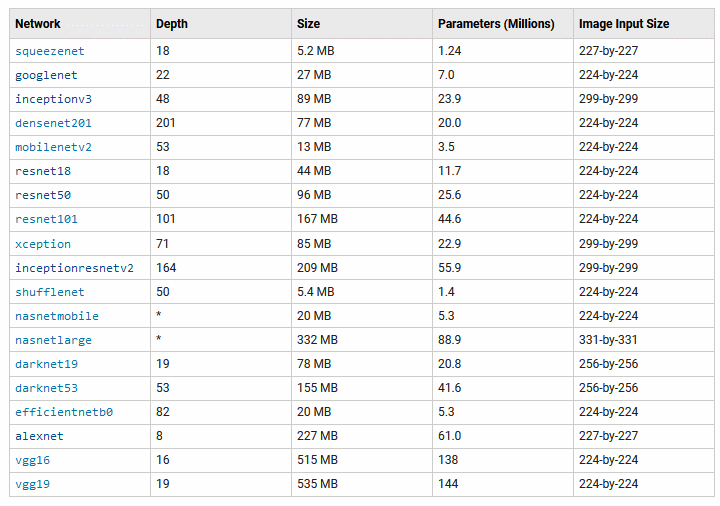
Jednym z problemów w sieciach wielowarstwowych jest zanikanie bądź eksplozja wartości gradientu w procesie uczenia. Przy wzrastającej liczbie warstw ukrytych obserwowany był nawet wzrost błędu dopasowania. Rozwiązanie, zwane Resnet, zaproponowane w [25] polegało na wprowadzeniu dodatkowego połączenia między-warstwowego o tym samym kierunku przepływu sygnałów. Sposób połączenia przedstawiony jest na rys. 6.6, w którym operacje sumowania dotyczą wszystkich elementów poszczególnych warstw.
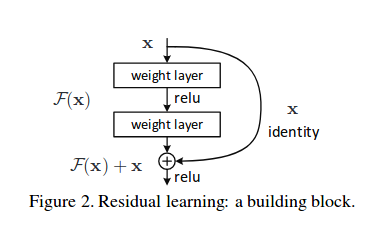
Idea rozwiązania polega a zastąpieniu odwzorowania F(x) reprezentowanego przez 2 warstwy konwolucyjne poprzez odwzorowanie F(x)+x. Oznacza to, że w rzeczywistości wagi sieci adaptowane są w procesie uczenia do odwzorowania resztkowego (residualnego) F(x)-x.
Przykładowy fragment struktury sieci Resnet przedstawiony jest na rys. 6.7. Bloki konwolucji składają się z operacji konwolucji, batch normalization oraz funkcji nieliniowej ReLU.
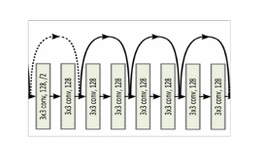
Linie ciągłe dotyczą połączeń międzywarstwowych o tych samych wymiarach macierzy. Połączenie kropkowane dotyczy przypadku, gdy wymiary warstwy startowej i docelowej różnią się (warstwa startowa 256×256, warstwa docelowa 128×128. . Zmniejszanie wymiaru między warstwami uzyskane jest dzięki parametrowi stride (przesunięcia filtra konwolucyjnego) równemu 2. W przypadku odwrotnym, gdy wymiary bloku startowego są mniejsze niż docelowego wymiary x uzupełnia się przez dodanie odpowiedniej liczby zer (tzw. zero padding).
Przykład bardziej złożonej struktury Resnet o 34 warstwach parametrycznych z powiązaniami residualnymi przedstawia rys. 6.8 (Resnet34) [43].

Ważnym problemem występującym w sieciach CNN jest ogromna liczba parametrów adaptowanych w procesie uczenia. Przykładowo, w pierwszym rozwiązaniu sieci AlexNet ich liczba sięga 61 milionów. Oznacza to duże koszty czasowe uczenia takiej sieci jak również jej implementacji scalonej. Stąd wysiłek wielu badaczy jest skierowany na zredukowanie liczby parametrów poprzez odpowiednią modyfikację struktury sieci i sposobu przetwarzania sygnałów. Stosowane są przy tym różne strategie. Jedną z nich jest częściowe zastępowanie większych filtrów, np. 5x5 poprzez filtr 1x1. Oznacza to automatycznie redukcję 25-krotną liczby parametrów w procesie przetwarzania. Innym kierunkiem jest zmniejszenie liczby kanałów (obrazów) wejściowych w poszczególnych warstwach poddanych filtracji 1x1 i 3x3. Tego typu rozwiązanie zastosowano w sieci SqueezeNet [30], wprowadzając specjalne moduły przetwarzania (tzw. Fire module), przedstawione na rys. 6.9.
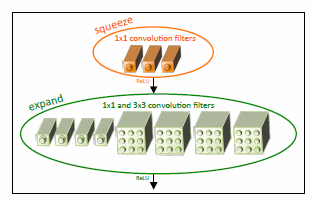
Liczba filtrów 1x1 w warstwie squeeze (a więc i liczba obrazów wyjściowych tej podwarstwy) jest mniejsza niż suma filtrów 1x1 i 3x3 w warstwie expand, co redukuje skutecznie liczbę adaptowanych parametrów. W zaproponowanej strukturze sieci SqueezeNet stosuje się 9 modułów „Fire” zakończonych warstwą conv10 o 1000 obrazów wyjściowych poddanych operacji global average pooling, tworzących 1000 sygnałów wejściowych dla warstwy softmax (brak w sieci warstw ukrytych w pełni połączonych). W sumie sieć Squeezenet zawiera 68 warstw (głębokość równa 18). Dzięki wprowadzonym modułom Fire udało się zredukować liczbę parametrów adaptowanych do 1.24 miliona uzyskując na bazie danych ImageNet tę sama dokładność co AlexNet o 61 milionach parametrów.
Inne rozwiązanie problemu zmniejszenia wymiarów sieci (liczby parametrów poddanych adaptacji) i zmniejszenia liczby operacji zmiennoprzecinkowych w procesie uczenia zostało zastosowane w sieci ShuffleNet [71]. Idea przyśpieszenia obliczeń polega na grupowaniu filtrów 1x1 (tzw. pointwise convolution) w grupy operujące na zredukowanej liczbie kanałów (obrazów) wejściowych, a nie na całym zbiorze obrazów warstwy poprzedniej. Tworzy się równolegle wiele grup operujących na wybranych losowo podgrupach obrazów wejściowych. Niestety część informacji globalnej uzyskanej z takiego grupowego przetworzenia nie wykazuje wzajemnych relacji, ponieważ przetworzeniu podlegały inne zestawy obrazów wejściowych. Stąd autorzy sieci zaproponowali w następnym etapie przetasowanie podgrup (operacja shuffle). Każda grupa wytworzona w etapie poprzednim podlega podziałowi na wiele podgrup. Podgrupy te po przetasowaniu tworzą zestawy obrazów zasilające warstwę następną. Typowy schemat przetwarzania w ramach jednej warstwy przedstawiony jest na rys. 6.10.
|
|
|
Rys. 6.10 Schemat przetwarzania grupowego punktowego (1x1) połączonego z przetasowaniem zastosowane w ShuffleNet: a) ilustracja procesu grupowania i przetasowania, b) schemat komórki podstawowej sieci: GConv oznacza konwolucję typu grupowego, BN – normalizacja danych w zbiorze MiniBatch, Concat – konkatenacja (złączenie) danych z obu kanałów.
W sumie sieć ShuffleNet ma głębokość równą 50 (liczba wszystkich podwarstw równa 203). Udało się zredukować liczbę parametrów adaptowanych do 1.4 miliona przy porównywalnej do AlexNet dokładności działania.
Inne rozwiązanie problemu przyspieszenia obliczeń poprzez zmniejszenie złożoności obliczeniowej zaproponowane zostało w sieci MobileNet [27,61] W sieci tej stosuje się 2 rodzaje konwolucji. Pierwsza z nich tzw. depthwise convolution stosuje pojedynczy filtr do każdego kanału (obrazu). Następuje po niej drugi etap tzw. pointwise convolution, operacja stosująca filtr 1x1 działający na sumie obrazów wytworzonych w etapie poprzednim. Jest to zasadnicza różnica w stosunku do klasycznego rozwiązania konwolucyjnego, w którym filtracja i sumowanie jej wyników w tworzeniu obrazów wyjściowych dotyczyło wielu obrazów wejściowych na raz i występowało dla każdego nowo tworzonego obrazu.

W efekcie organizacja przetwarzania sygnałów w warstwie może być przedstawiona jak na rys. 6.11., na którym 3x3 Depthwise Conv dotyczy działania filtru 3x3 na pojedynczym obrazie, a 1x1 Conv dotyczy konwolucji z filtrem 1x1 działającym na zbiorze wcześniej wygenerowanych obrazach. BN oznacza operację normalizacji na podzbiorze MiniBatch, a ReLU funkcję nieliniową aktywacji. W efekcie uzyskuje się dużą redukcję wymiarów sieci. Zaproponowane rozwiązanie MobileNetv2 w Matlabie zredukowało wymiar sieci do 13MB przy głębokości 53 i 3.5 miliona adaptowanych parametrów.
Ciekawym krokiem w rozwoju sieci głębokich było opracowanie struktury GoogLeNet (traktowana później jako Inception-v1) [63,64]. Idea modyfikacji polega na prowadzeniu równolegle działających filtrów o różnych wymiarach. Każdy z takich filtrów specjalizuje się w rejonach obrazu o różnej skali szczegółowości. Inną modyfikacją było rozszerzanie sieci wszerz, a nie tylko w głąb. Autorzy rozwiązania wprowadzili równolegle działające bloki konwolucyjne stosujące filtry o wymiarach 1×1, 3×3 oraz 5×5. Blok o małych wymiarach 1×1 odpowiedzialny jest za liniową redukcję wymiarowości obrazu wejściowego jednocześnie pozwalając na zmniejszenie czasu obliczeń, w stosunku do większych filtrów konwolucyjnych. Rolę taką pełni komórka zwana Inception. Struktura takiej komórki przedstawiona jest na rys. 6.12.
|
|
|
Rys. 6.12 Struktura komórki Inception [64].
|
Komórka Inception zawiera 4 równolegle połączone gałęzie i w każdej z nich występuje konwolucja 1×1 jako sposób redukcji wymiarowości problemu i złożoności obliczeniowej.
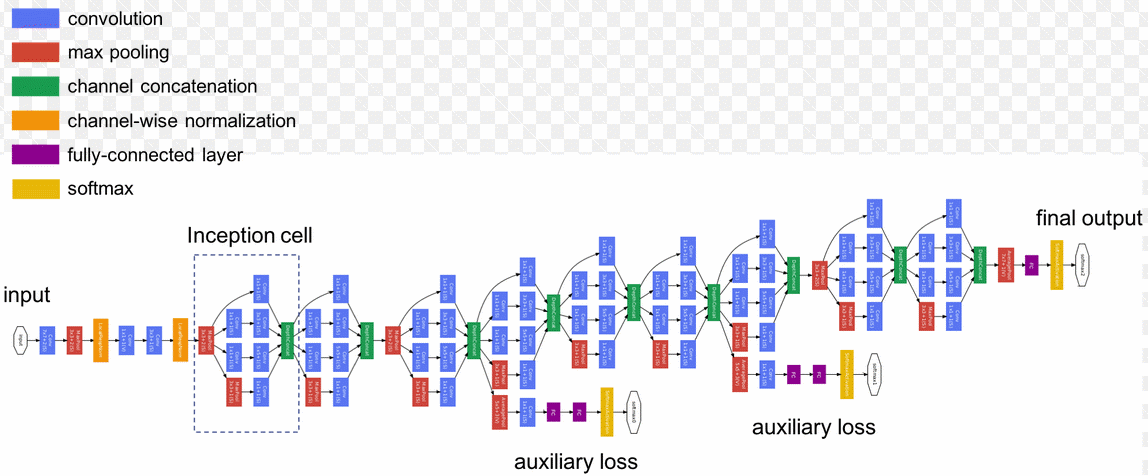 |
|
Rys. 6.13 Architektura sieci GoogLeNet [63].
|
Struktura sieci GoogLeNet składa się z 9 połączonych ze sobą komórek Inception, jak to przedstawiono na rys. 6.13. Zawiera w sumie około 100 niezależnych bloków, przy czym głębokość liczona w liczbie warstw podlegających uczeniu jest równa 22 (nie wliczając warstwy typu pooling). Jak podają autorzy uczenie takiej sieci jest bardzo czasochłonne (około tygodnia przy zastosowaniu kilku GPU pracujących w trybie równoległym).
Dalsze prace zespołu rozwijały powyższy model pod zmienioną nazwą Inception. Powstało kilka kolejno ulepszanych struktur komórki Inception i połączeń warstwowych. Jedną z nich jest hybryda różnych modeli Inception i ResNet, czyli Inception-ResNet-v2, w której dodano połączenie residualne do komórek Inception. Przykład tak zmodyfikowanej struktury komórki przedstawiono na rys. 6. 14.
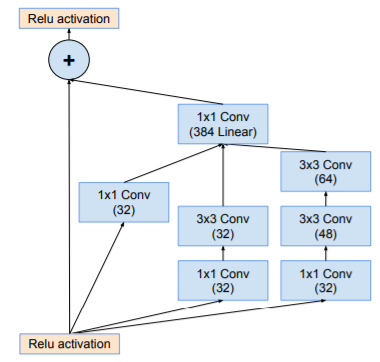
Badania nad skutecznością działania sieci CNN pokazały, że dużą rolę odgrywa dobór odpowiednich proporcji między głębokością (depth) architektury traktowaną jako liczba warstw konwolucyjnych, liczbą równolegle tworzonych obrazów wynikowych w poszczególnych warstwach (width) oraz rozdzielczością obrazów tworzonych w poszczególnych warstwach (resolution). Rys. 6.15 przedstawia ideę skalowania sieci Efficientnet, stworzoną przez M. Tana i Q.V. Le [66].
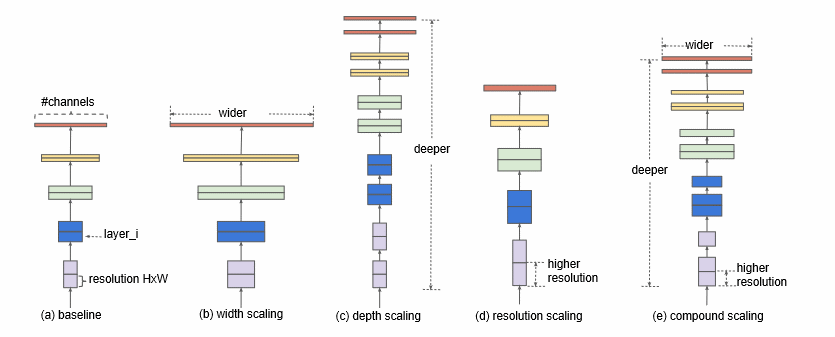
Odpowiednie zwiększenie skali dotyczącej głębokości, szerokości i rozdzielczości w stosunku do struktury konwencjonalnej (baseline) pozwala uzyskać znacznie większą dokładność klasyfikatora przy znakomicie zmniejszonej złożoności obliczeniowej. W pracy tej pokazano porównanie uzyskanej dokładności różnych rozwiązań sieciowych przy odpowiadającej sobie liczbie operacji zmiennoprzecinkowych, wykazując zdecydowaną przewagę sieci EfficientNetB6 w problemie benchmarkowym „ImageNet”.
Oryginalnym rozwiązaniem sieci konwolucyjnych jest sieć DenseNet operująca wieloma połączeniami między-warstwowymi w przód. W klasycznym rozwiązaniu CNN przekazywanie sygnałów następuje kolejno z warstwy na warstwę sąsiadującą (brak połączeń między odległymi warstwami) [17,29]. W efekcie traci się wiele informacji, co prowadzi między innymi do zanikania gradientu (skorygowane w sieci Resnet). Poza tym nie wykorzystuje się bezpośrednio oryginalnych cech wytworzonych w warstwach wcześniejszych osłabiając w efekcie ich działanie. Struktura przetwarzania sygnałów zaproponowana przez autorów [17,29] przedstawiona jest na rys. 6.16.
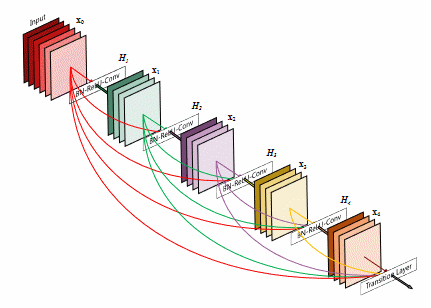
Sygnały wyjściowe poszczególnych warstw przekazywane są bezpośrednio nie tylko na warstwę sąsiednią, ale również na wszystkie warstwy następne. Dzięki temu możliwe stało się ograniczenie głębokości sieci (liczby warstw). Struktura sieci DenseNet przedstawiona jest na rys. 6.17.

Pomiędzy blokami typu Dense stosowane są dodatkowo operacje konwolucji i poolingu. W jej ramach wykonuje się normalizację danych w MiniBatch, konwolucję jednopunktową filtrem 1x1 oraz operacje 2x2 average pooling. Implementacja DenseNet w Matlabie pod nazwą densenet201 zawiera 20 milionów adaptowanych parametrów i głębokość równa 201. Jej skuteczność jest porównywalna z najlepszymi rozwiązaniami sieci.
3.6. Sieci CNN do detekcji obiektów w obrazie
6.6.1 Sieć YOLO
Struktury sieci CNN przedstawione wcześniej stosowane są bezpośrednio w rozwiązywaniu zadań klasyfikacji i regresji, gdzie sieć pracuje w trybie z nauczycielem (na etapie uczenia dane są stowarzyszone ze sobą pary \((\mathbf{</span><span lang="pl-PL"><span>x},\mathbf{d})\)). Oryginalnym obszarem takich zastosowań jest detekcja obiektów, w której poszukuje się konkretnych obiektów występujących w analizowanych obrazach. Jest ona połączona ze wskazaniem współrzędnych tych obszarów (zadanie regresji). W takim rozwiązaniu sieć pracuje więc jednocześnie jako klasyfikator i układ regresyjny. Jest trenowana na zbiorze obrazów w których występują poszukiwane obiekty traktowane jako „destination”. Po zamrożeniu parametrów wytrenowana sieć jest gotowa do wydobycia nauczonych obiektów z serii obrazów nie uczestniczących w uczeniu.
Ważnym rozwiązaniem w tej dziedzinie jest sieć YOLO (skrót od "You Only Look Once"), wykonująca jednocześnie funkcje klasyfikatora i systemu regresyjnego [52,72]. Służy do wykrywania określonych obiektów w obrazie (zadanie klasyfikacji) oraz ich umiejscowienia (zadanie regresji). Obiektami mogą być różne przedmioty występujące na obrazie. Zadanie regresji polega na określeniu współrzędnych wykrytych obiektów. Opracowany system dzieli analizowany obraz na siatkę komórek o wymiarach \(S\times S\). Każda komórka jest odpowiedzialna za wykrycie obiektów, które znajdują się w jej obrębie. Jeśli centrum poszukiwanego obiektu znajdzie się wewnątrz komórki siatki, wówczas ta komórka jest odpowiedzialna za wykryty obiekt. Komórka może być odpowiedzialna za wykrycie jednoczesne \(B\) obiektów, wskazując na współczynnik ufności co do wystąpienia każdego z nich w obrębie danej komórki.
Ważnym elementem rozwiązania jest tu współczynnik ufności IOU (ang. Intersection Over Union), określający w jakim stopniu w danej komórce występuje pokrywanie się rzeczywistego pola obwiedni obiektu z polem prognozowanym obwiedni (tzw. bounding box) dla wszystkich\(B\) badanych obwiedni. Współczynnik ufności \(C\) dla danej komórki reprezentuje prawdopodobieństwo, że określony obiekt znajduje się w obrębie określonej obwiedni (bounding box). Opisuje się go wzorem
| \( C=\operatorname{Pr}(\text { obiekt }) I O U_{\text {pred }}^{\text {truth }} \) | (6.17) |
gdzie \(Pr(obiekt)\) oznacza prawdopodobieństwo wystąpienia obiektu w danej obwiedni a \( I O U_{\text {pred }}^{\text {truth }}\) przyjmuje procentową wartość części wspólnej \( \mathrm{S}_{\text {intersection }} \) powierzchni rzeczywistej i prognozowanej obwiedni do ich całkowitej powierzchni \( \mathrm{S}_{\text {union }} \)
| \( I O U=\frac{\mathrm{S}_{\text {intersection }}}{\mathrm{S}_{\text {union }}} \) | (6.18) |
Rys. 6.18 ilustruje interpretację obu powierzchni. Jeśli określony obiekt nie pojawia się w danej obwiedni współczynnik ufności jest z definicji równy zeru.
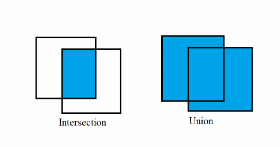
Równolegle z analizą pokrywania się obu obwiedni w komórce obliczane jest warunkowe prawdopodobieństwo klasy obiektu. Jest ono wyrażone wzorem
| \( \operatorname{Pr}\left(\text { klasa }_i \mid \text { obiekt }\right)=\operatorname{Pr}\left(\text { klasa }_i\right) I O U_{\text {pred }}^{\text {truth }} \) | (6.19) |
Każdy „bounding box” skojarzony z komórką jest charakteryzowany w systemie poprzez kilka parametrów: \((x,y)\) – współrzędne centrum obiektu mierzone względem danej komórki, \((w,h)\) – szerokość i wysokość obwiedni (traktowanej jako prostokąt) mierzone względem całego obrazu oraz współczynnik ufności reprezentujący wartość IOU przewidywanej aktualnie obwiedni obiektu względem prawdziwej (tzw. ground truth). Każda komórka jest dodatkowo odpowiedzialna za wykrycie klasy każdego z obiektów i określenia prawdopodobieństwa przynależności klasowej \(Pr(klasa_i|obiekt)\).
Struktura pierwotnie zaproponowanej sieci YOLO [52] przedstawiona jest na rys. 6.19. Zawiera 24 warstwy konwolucyjne lokalnie połączone do generacji cech diagnostycznych i dwie w pełni połączone warstwy odpowiedzialne jednocześnie za zadanie klasyfikacji (rozpoznanie klasy obiektów) oraz zadanie regresji (określenie współrzędnych wystąpienia poszczególnych obiektów). Zastosowany wymiar komórki \(S=7\). Wyjściowa warstwa sieci generuje jednocześnie prawdopodobieństwo przynależności określonej komórki do klasy obiektu (klasyfikacja) oraz współrzędne obwiedni poszczególnych obiektów (regresja). Sieć używa funkcje aktywacji typu Leaky ReLU. Uczenie sprowadza się do odpowiednio zdefiniowanej funkcji celu w postaci błędu średniokwadratowego. Funkcja taka jest złożeniem składników odpowiedzialnych za klasyfikację oraz składników odpowiedzialnych za regresję. W jego procesie przyjmuje się, że każda obwiednia (bounding box) skojarzona jest jedynie z jednym obiektem na podstawie największej wartości IOU.
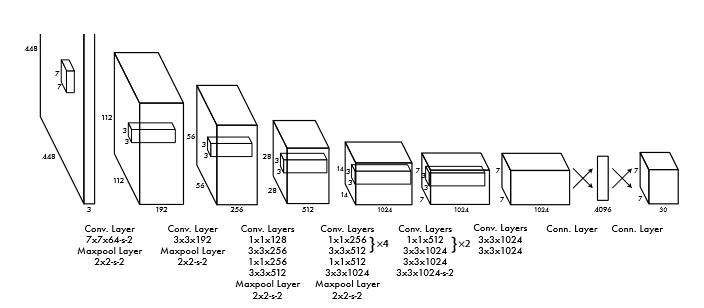
W międzyczasie powstały różne udoskonalone rozwiązania struktury sieci, charakteryzujące się większą szybkością przy mniejszej liczbie parametrów podlegających adaptacji w procesie uczenia. Takim przykładem jest rozwiązanie znane pod nazwą YOLOX [72].
Innym rozwiązaniem segmentacji wykorzystującym sieci CNN jest R-CNN (ang. Region based CNN). Istnieje kilka wersji rozwiązań tego typu. W tym punkcie ograniczymy się do tzw. Faster R-CNN. Ogólna struktura tej sieci przedstawiona jest na rys. 6.20 [53].
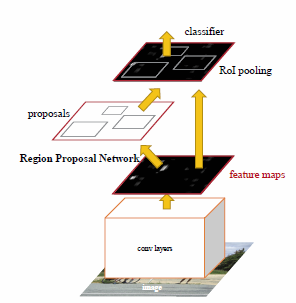
Rozwiązanie bazuje na zastosowaniu dwu podstruktur CNN. Pierwsza z nich, tzw. Region Proposal Network (RPN) jest odpowiedzialna za generację cech diagnostycznych i znajduje rejony obrazu zawierające propozycję ewentualnych obszarów obiektów, które w drugiej części rozwiązania sieciowego zwanej RoI pooling (RoI - region of interest) podlegają weryfikacji, stwierdzającej rzeczywiste istnienie bądź negację określonego obiektu (detekcję). Obie części sieci wykorzystują strukturę wielowarstwową CNN i współpracują ze sobą, zarówno w trybie uczenia jak i testowania.
Ważną rolę odgrywa w rozwiązaniu warstwa RoI pooling. Warstwa ta stosuje max pooling do przetworzenia cech zawartych w każdym istotnym RoI obrazu w niewielkich wymiarów mapę cech (zwykle \(7\times 7\)) na podstawie których definiuje prawdopodobieństwo przynależności badanego RoI obrazu do obiektu i parametry określające jego wymiar.
RPN przyjmuje na wejściu surowe obrazy podlegające analizie i przekazuje na wyjście (do warstwy RoI pooling) propozycje prostokątnych rejonów z estymowanym stopniem przynależności do klas poszukiwanych obiektów. Ma strukturę i zasadę działania sieci CNN. W każdej warstwie używa przesuwającego się filtru (typowy wymiar \(3\times 3\)) działającego na mapie cech ostatniej warstwy konwolucyjnej. Sygnał wyjściowy filtru (po operacji ReLU) odpowiadający każdej pozycji na obrazie jest rzutowany na małowymiarowy wektor cech (typowa wartość 256). Cechy te stanowią wejście dla dwu w pełni połączonych warstw RoI pooling działających równolegle:
-
warstwa regresyjna - generująca na wyjściu współrzędne bloków reprezentujących proponowane rejony odpowiadające pozycji filtru na obrazie,
-
warstwa klasyfikacyjna – estymująca przynależność bloków do określonego obiektu.
Każdej pozycji przesuwającego się okna filtrującego przypisuje się wiele propozycji rejonów, zwanych kotwicami. Ich liczba \(k\) jest ustalana z góry. Stąd warstwa regresyjna generuje \(4k\) wartości (pozycje \(x, y\) lewego górnego piksela rejonu, szerokość \(w\) oraz wysokość \(h\)). Warstwa klasyfikacyjna generuje \(2k\) wartości estymujących prawdopodobieństwo przynależności oraz braku przynależności \(k\)-tego rejonu do poszukiwanego obiektu, reprezentowanego przez ROI. Każdy obraz analizowany jest w 3 skalach i dla 3 wartości współczynników kształtu kotwic (1:1, 1:2 oraz 2:1), co daje 9 kotwic dla każdej pozycji filtru. W przypadku obrazu o wymiarach \(W\times H\) liczba kotwic jest równa \(W ×H×k\).
Uczenie RPN w funkcji klasyfikatora generuje wynik binarny (\(\pm1\)). Znak dodatni (kotwica pozytywna) przypisany jest kotwicy w dwu przypadkach: gdy jej powierzchnia pokrywa się z obiektem poszukiwanym w stopniu powyżej 70% lub w przypadku skrajnym, gdy nie ma żadnego takiego przypadku. Przyjmuje się wówczas kotwice o jak największej wartości współczynnika pokrycia. Wartość negatywna klasyfikatora (kotwica negatywna) jest generowana gdy współczynnik pokrycia kotwicy z obiektem poszukiwanym jest poniżej 30%. Kotwice nie zaliczone ani do pozytywnych ani negatywnych nie biorą udziału w dalszej procedurze uczenia. Uczenie RPN polega na minimalizacji funkcji kosztu definiowanej w postaci [42]
| \( \min L\left(p_i, t_i\right)=\frac{1}{N_{c l}} \sum_i L_{c l}\left(p_i, p_i^*\right)+\lambda \frac{1}{N_{r e g}} \sum_i p_i^* L_{r e g}\left(t_i, t_i^*\right) \) | (6.20) |
W wyrażeniu tym indeksy i reprezentują kotwice, \( p_i \) prawdopodobieństwo, że kotwica należy do obiektu i-tego; \(p_i^{*}\) przyjmuje wartość \(1\) gdy kotwica jest pozytywna lub wartość \(0\) w przypadku gdy kotwica jest negatywna. Parametr \(t_i\) reprezentuje 4 wartości charakteryzujące rejon kotwicy \( (x, y, w, h)\) a \( t_i^{*} \) te same wartości przypisane współrzędnym poszukiwanego obiektu (ground true box) skojarzonego z dodatnią kotwicą. Składnik klasyfikacyjny funkcji kosztu \( L_{c l}(p_i, p_i^*) \) przyjmuje się w postaci logarytmicznej \( L_{c l}(p_i, p_i^*)=-\log p_i \) gdzie \( p_i \) reprezentuje estymowaną wartość prawdopodobieństwa przynależności kotwicy do \(i\)-tego obiektu podlegającego wykryciu. Drugi składnik odpowiada regresji \( L_{r e g}\left(t_i, t_i^*\right)=R\left(t_i-t_i^*\right) \), gdzie funkcja \(R\) reprezentuje przyjętą miarę różnic między wartościami parametrów \((x, y, w, h)\) przypisanych kotwicy i obiektu poszukiwanego [53]. Może ona przyjmować różne postacie. Parametr \( \lambda \) stanowi współczynnik regularyzacji części klasyfikacyjnej i regresyjnej we wzorze (5.6). Przy znormalizowanych wartościach reprezentujących obiekt przyjmuje się zwykle \( \lambda=1\).
W uczeniu gradientowym RPN stosuje się metodę SGDM (przy użyciu tzw. mini-zbiorów generowanych z określonych losowo obszarów obrazów ROI (typowa populacja mini-batches jest równa na przykład 128 a jej skład wynika z losowego wyboru ROI z wielu obrazów). Zakłada się przy tym, że przynajmniej 25% ROI pokrywa się w stopniu 50% z obiektem podlegającym wykryciu. W uczeniu SGD stosuje się zwykle technikę wspomagającą, wykorzystującą metodę momentu rozpędowego.
Sieć RPN generuje propozycje obszarów podlegających dalszej detekcji obiektów reprezentowanych w postaci określonych cech diagnostycznych. Funkcję detektora pełni sieć Fast R-CNN, pełniąca rolę końcowego dostrajania. Dla przyspieszenia uczenia i unifikacji rozwiązania obie części systemu (RPN i Fast R_CNN) współpracują ze sobą w kolejnych cyklach obliczeniowych (tzw. alternative training). Fast R-CNN wykorzystuje jako wejście rejony wskazane przez RPN, inicjalizując z kolei RPN swoimi wynikami w następnych cyklach obliczeniowych. Dzięki temu proces detekcji poszukiwanych obiektów w obrazie jest bardzo szybki [53].
Przykład programu Matlaba wykorzystującego sieć R-CNN do detekcji znaku STOP na obrazach przedstawiony jest poniżej. W uczeniu zastosowano 27 obrazów zawierających znak STOP-u i jeden obraz testowy.
% RCNN do dtekcji znaku STOP
load('rcnnStopSigns.mat', 'stopSigns', 'layers')
imDir = fullfile(matlabroot, 'toolbox', 'vision', 'visiondata',...
'stopSignImages');
addpath(imDir);
options = trainingOptions('sgdm', ...
'MiniBatchSize', 32, ...
'InitialLearnRate', 1e-6, ...
'MaxEpochs', 10);
% Train the R-CNN detector. Training can take a few minutes to complete.
rcnn = trainRCNNObjectDetector(stopSigns, layers, options, 'NegativeOverlapRange', [0 0.3]);
% Test the R-CNN detector on a test image.
img = imread('stopSignTest.jpg');
[bbox, score, label] = detect(rcnn, img, 'MiniBatchSize', 32);
% Display strongest detection result.
[score, idx] = max(score);
bbox = bbox(idx, :);
annotation = sprintf('%s: (Confidence = %f)', label(idx), score);
detectedImg = insertObjectAnnotation(img, 'rectangle', bbox, annotation);
figure
imshow(detectedImg)
Wynik testowania programu na nowym obrazie nie uczestniczącym w uczeniu przedstawiony jest poniżej na rys. 6.21.

3.7. Sieć U-NET w segmentacji obrazów biomedycznych
Segmentacja obrazów biomedycznych ma za zadanie wyłowić w obrazie obszary należące do tej samej klasy (zbiór pikseli o podobnej jasności). Zadanie należy do bardzo trudnych ze względu na dużą różnorodność obszarów, zmienność położenia względnego pikseli względem siebie czy rozmycia granic obszarów jak również barw. Jednym ze skutecznych rozwiązań w tym zakresie jest sieć U-net stworzona przez autorów pracy [56]. Struktura tej sieci przypomina kształt litery U i zawiera podsieć CNN zwężającą oraz drugą podsieć CNN rozszerzającą, obie współpracujące ze sobą. Struktura takiej sieci przedstawiona jest na rys. 6.22. Na każdym poziomie przetwarzania stosowane są 2 warstwy konwolucyjne.
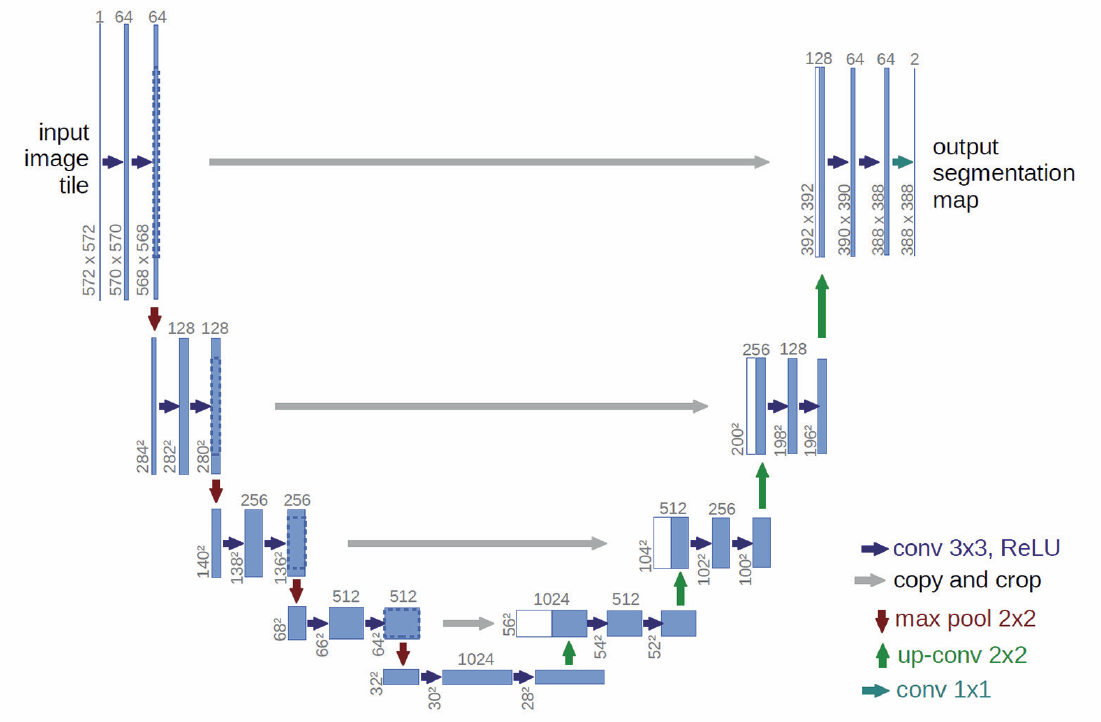
Obrazy występujące w warstwach zwężających (lewa część sieci) o coraz mniejszych wymiarach (operacje pooling) zmniejszają rozdzielczość wyników, co powoduje pogorszenie lokalizacji poszczególnych segmentów. Ta część sieci nazywana jest również enkoderem. W części rozszerzającej struktury (prawa część sieci) operacja pooling w każdej warstwie jest zastąpiona przez operację odwrotną (interpolację) zwaną up-sampling (pooling 2×2 zastępuje 4 piksele przez 1 piksel, natomiast up-sampling 2×2 działa odwrotnie: 1piksel jest replikowany w 4 piksele). Ta część sieci jest również nazywana dekoderem. Sieć U-net nie posiada warstw w pełni połączonych (fully connected layers) typowych w rozwiązaniach CNN.
Część zwężająca U-net stosuje konwolucję przy użyciu maski filtrującej 3×3 z krokiem stride=2, funkcję aktywacji ReLU i max pooling 2×2. W efekcie wymiar mapy cech (obrazu) w każdej kolejnej warstwie jest zmniejszany dwukrotnie, ale jednocześnie generowana jest liczba obrazów wzrastająca 2-krotnie.
Warstwy rozszerzające stosują operację interpolacji (up-sampling) o wymiarze 2×2, w której jeden piksel jest zastępowany 4 pikselami. Stosowane są różne metody, na przykład metoda najbliższych sąsiadów, zastosowanie splinów, itp. Za bardziej optymalną uważa się operację konwolucji transponowanej, zwanej również dekonwolucją, definiowanej jako operacja odwrotna do konwolucji (w praktyce określa się dekonwolucję stosując przekształcenie odwrotne Fouriera). Operacja 2×2 dekonwolucji zwiększa 2-krotnie wymiar mapy cech (obrazu wynikowego) przy dwukrotnie zmniejszonej ich liczbie. Jednocześnie na każdym poziomie warstwowym up-samplingu następuje dołączenie odpowiedniego obrazu niższej rozdzielczości z części zwężającej (część biała obrazów wejściowych na danym poziomie). Podobnie jak w warstwie zwężającej stosowana jest konwolucja z filtrem 3×3 i operacja ReLU. W części końcowej warstwy wyjściowej stosowana jest konwolucja 1×1 tworząca wysegmentowany obraz wyjściowy, w którym każdy piksel jest reprezentowany przez przypisany do niego numer klasy (podział na klastry reprezentujące oddzielne segmenty).
Uczenie sieci odbywa się z udziałem obrazów zawierających segmenty opisane przez eksperta. Proces uczenia ma za zadanie zminimalizować sumę różnic między stopniami szarości pikseli tworzących ROI segmentu zakreślonego przez eksperta i tych wygenerowanych przez warstwę końcową sieci U-net (funkcja celu z użyciem definicji kross-entropijnej). Odbywa się przy zastosowaniu metody stochastycznej największego spadku (SGD) z momentem rozpędowym (SGDM). Szczegóły można znaleźć w publikacji [56].
3.8. Autoenkoder
6.8.1 Struktura autoenkodera
Autoenkoder jest specjalnym rozwiązaniem sztucznej sieci neuronowej, którego zadaniem jest skopiowanie danych wejściowych w wyjściowe z akceptowalnym błędem [18,33] za pośrednictwem warstw ukrytych o zredukowanym wymiarze względem wymiaru danych wejściowych. Jest to wielowarstwowy układ autoasocjacyjny stowarzyszający dane wejściowe ze sobą. Struktura składa się z dwu następujących po sobie części: układu kodującego (enkoder) rzutującego dane wejściowe w postaci wektora x w dane zakodowane reprezentowane przez wektor \( \mathbf{h}=\mathbf{f}(\mathbf{x}) \) i dekodera wykonującego działanie odwrotne rekonstruujące z określoną dokładnością dane wejściowe \( \mathbf{x}^{\prime}=\mathbf{g}(\mathbf{h}) \). Przykład struktury autoenkodera o jednej warstwie sygnałów zakodowanych i części dekodującej przedstawiony jest na rys. 6.23. Dane wejściowe w postaci wektora \( \mathbf{x} \) są kodowane w wektorze \( \mathbf{h} \) jako sygnały ukryte (część tworząca enkoder). Dekodowanie odbywa się w strukturze symetrycznej, odtwarzając za pośrednictwem wektora \( \mathbf{h} \) wektor \( \mathbf{x^{\prime}} \) (część zwana dekoderem).
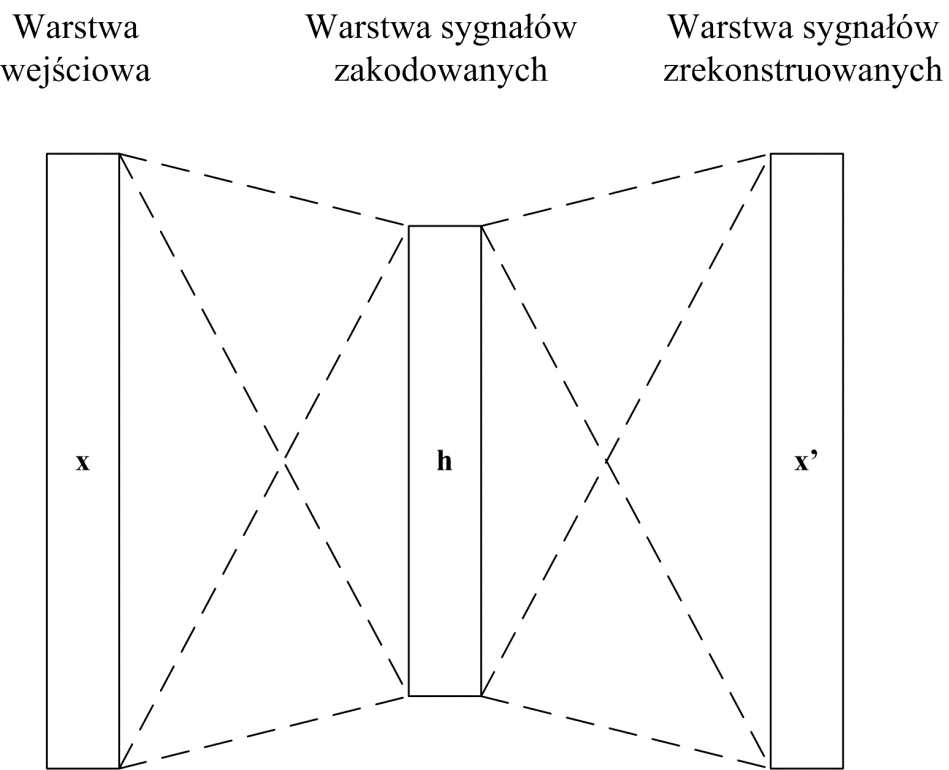
Podstawą działania jest kompresja danych polegająca na wychwyceniu głównych cech procesu reprezentowanego przez zbiór wektorów x. Oznacza to, że dane zrekonstruowane \( \mathbf{x^{\prime}} \) nie reprezentują dokładnych kopii danych wejściowych ale ich aproksymację. Wektor \( \mathbf{h} \) stanowiący podstawę kodowania i następnie rekonstrukcji, reprezentuje zatem cechy główne procesu eliminując elementy nieistotne (traktowane jako szum) zawarte w zbiorze danych wejściowych \( \mathbf{x} \). Autoenkoder jest uogólnieniem dwuwarstwowej sieci liniowej PCA. Różni go od niej liczba warstw, która może być dowolna, jak również nieliniowa funkcja aktywacji neuronów stosowana w przypadku ogólnym.
Bezpośrednie, dokładne kopiowanie danych uczących \( \mathbf{x} \) w siebie nie ma sensu praktycznego, gdyż nie pozwala na wychwycenie najważniejszych cech procesu zawartych w zbiorze danych uczących. Dopiero ograniczenie liczby neuronów warstwy ukrytej definiującej kodowanie danych wejściowych zmusza proces uczenia do wychwycenia cech najważniejszych, i pominięcie cech drugorzędnych, nie mających większego wpływu na wynik rekonstrukcji danych. Proces uczenia sieci może być zdefiniowany jako dobór parametrów (wag neuronowych) prowadzący do minimalizacji funkcji kosztu (celu) \( E(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x})) \) .
Podstawowa definicja funkcji kosztu przyjmowana jest zwykle w postaci wartości błędu średniokwadratowego po wszystkich zmiennych \(n= 1, 2,\ldots, N \) dla danych uczących przy \(k=1, 2, \ldots, p\), przy czym \(N\) jest wymiarem wektora wejściowego a \(p\) liczbą danych uczących (obserwacji).
| \( E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n^{(k)}-x_n^{\prime(k)}\right)^2=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n(k)-g_n\left(\mathbf{h}\left(\mathbf{x}(k)\right)\right)^2\right. \) | (6.21) |
Dla uzyskania lepszej odporności autoenkodera na szum w uczeniu stosuje się również wersję zmodyfikowaną, w której zamiast dopasowywać sygnały wyjściowe \( \mathbf{g}(\mathbf{h}(\mathbf{x})) \) do sygnałów wejściowych \( \mathbf{x} \), porównanie z sygnałami \( \mathbf{x} \) dotyczy odpowiedzi autoenkodera \( \mathbf{g}(\mathbf{h}(\mathbf{x}_s)) \) na sygnały zaszumione \( \mathbf{x}_s \). Układ przetwarza wówczas \( \mathbf{x}_s \) w taki sposób aby uzyskać na wyjściu najlepszą możliwie aproksymację wektorów oryginalnych \( \mathbf{x} \). Oznacza to, że funkcja celu podlegająca minimalizacji przyjmuje zmodyfikowaną formę
| \( E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n(k)-g_n\left(\mathbf{h}\left(\mathbf{x}_s(k)\right)\right)^2\right. \) | (6.22) |
Zastosowanie liniowej funkcji aktywacji neuronów przy jednej warstwie ukrytej prowadzi do znanego rozwiązania PCA. Autoenkoder stosujący nieliniowe funkcje aktywacji i kilka warstw ma wiele zalet w stosunku do rozwiązania liniowego, z których najważniejsze to [18]
-
duża oszczędność (ang. sparsity) w reprezentacji danych,
-
ograniczone wartości pochodnej sygnałów,
-
krzepkość systemu względem szumu oraz brakujących danych.
Oszczędność autoenkodera może być osiągnięta w procesie uczenia poprzez włączenie do funkcji kosztu czynnika kary za nadmiernie rozbudowaną strukturę. Wówczas zmodyfikowana funkcja kosztu \( E \) przyjmie postać
| \( E=E\left(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x}))+\lambda \Omega_1(\mathbf{h})\right. \) | (6.23) |
w której wielkość \( E(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x}))) \) reprezentuje klasyczną definicję funkcji kosztów, a \( \lambda \) stanowi współczynnik regularyzacji. Funkcja \( \Omega_1(\mathbf{h}) \) stanowi karę za zbyt rozbudowaną strukturę układu. Typowa definicja tej funkcji to
| \( \Omega_1(\mathbf{h})=\frac{1}{2} \sum_h \sum_{i, j}\left(w_{i j}^{(h)}\right)^2 \) | (6.24) |
gdzie \( h \) reprezentuje warstwy ukryte zastosowane w rozwiązaniu. W wyniku uczenia wymusza się zmniejszenie wartości wag określonych grup neuronów. W efekcie pewne połączenia synaptyczne o małej wartości wag mają minimalny wpływ na działanie systemu.
Dla dalszego zmniejszenia wpływu zmian danych wejściowych \( \mathbf{x} \) na wynik działania układu wprowadza się regularyzację uwzględniającą pochodne sygnałów warstwy ukrytej względem elementów wektora wejściowego \( \mathbf{x} \). Funkcja regularyzacyjna przyjmuje wówczas następującą formę [18]
| \( \Omega_2(\mathbf{h}, \mathbf{x})=\sum_{h=1}^H\left\|\nabla_x h_i\right\|^2 \) | (6.25) |
w której \( \nabla_x h_i \) oznacza wektor pochodnych sygnałów \( h_i \) warstw ukrytych względem składowych wektora wejściowego \( \mathbf{x} \). Taki rodzaj regularyzacji zmusza algorytm uczący do wytworzenia sygnałów wyjściowych sieci, które zmieniają się niewiele przy niewielkich zmianach wartości sygnałów wejściowych.
Inny rodzaj regularyzacji autoenkodera uwzględnia zgodność średniej statystycznej aktywacji neuronów \( \hat{\rho_i} \) w aktualnym stanie uczenia z jej wartością pożądaną \( \rho_i \). Wartość aktualna jest określona dla pojedynczego neuronu warstwy ukrytej w postaci
| \( \hat{\rho}_i=\frac{1}{p} \sum_{j=1}^p h_i\left(\boldsymbol{x}_j\right) \) | (6.26) |
gdzie \( p \) oznacza liczbę obserwacji (wektorów \( \mathbf{x} \)). Mała wartość średniej aktywacji neuronu oznacza, że neuron ten aktywuje się jedynie dla niewielkiej ilości danych wejściowych, specjalizując się w ich reprezentacji. Dodając taki czynnik do minimalizowanej funkcji kosztu zmusza się neurony do reprezentowania jedynie określonych (specyficznych) cech procesu.
W praktyce czynnik regularyzacyjny definiuje się z wykorzystaniem dywergencji Kullbacka-Leiblera, mierzącego zgodność wartości aktualnej z pożądaną wartością średniej funkcji aktywacji dla określonego zbioru danych. Składnik regularyzacyjny definiuje się w postaci [18]
| \( \Omega_3(\rho)=\sum_i \rho_i \log \left(\frac{\rho_i}{\hat{\rho}_i}\right)+\left(1-\rho_i\right) \log \left(\frac{1-\rho_i}{1-\hat{\rho}_i}\right) \) | (6.27) |
Regularyzacja Kulbacka-Leiblera jest statystyczną miarą zgodności dwu rozkładów stochastycznych. Przyjmuje małą wartość, przy niewielkiej niezgodności i wartość zerową gdy \( \hat{\rho_i} =\rho \). Przy wzrastającej niezgodności miara ta rośnie.
W praktyce definiuje się wartość pożądaną stosunku \( \rho_i /\hat{\rho_i} \) (w Matlabie [38] jest to parametr zwany 'SparsityProportion' przyjmujący wartość dodatnią z przedziału [(0, 1) z wartością wbudowaną 0.05). Dzięki zastosowaniu tego typu regularyzacji poszczególne neurony ukryte „specjalizują” się w wytwarzaniu dużego sygnału jedynie dla małej liczby danych uczących (lokalizacja aktywności) co oznacza w ogólności lepsze, bo wyspecjalizowane działanie sieci.
W efekcie, w procesie uczenia minimalizacji podlega funkcja kosztu zmodyfikowana o poszczególne rodzaje czynników regularyzacyjnych. W ogólności zadanie minimalizacji może przyjąć następującą postać [18,43]
| \( \min E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(\mathbf{x}_n(k)-g_n\left(\mathbf{h}\left(\tilde{\mathbf{x}}(k)\right)\right)^2+\lambda_1 \Omega_1(\mathbf{h})+\lambda_2 \Omega_2(\mathbf{h}, \mathbf{x})+\lambda_3 \Omega_3(\rho)\right. \) | (6.28) |
w której współczynniki \( \lambda_i \) (dobierane przez użytkownika) stanowią wagi, z jakimi poszczególne funkcje regularyzacyjne wpływają na wartość funkcji kosztu. Taka postać wymusza kompromis między zgodnością zrekonstruowanego sygnału wyjściowego układu z wartościami wejściowymi a złożonością tego układu, uwzględniając jednocześnie wrażliwość na niewielkie zmiany mogące nastąpić w rozkładzie wartości sygnałów wejściowym w trybie odtwarzania.
Istnieją różne implementacje algorytmu uczącego. Najbardziej popularne podejście polega na stopniowym uczeniu następujących po sobie warstwach. Proces rozpoczyna się w warstwie pierwszej, dla której sygnałami wejściowymi są sygnały oryginalne opisane wektorem \( \mathbf{x} \)), a sygnały wyjściowe oznaczone są jako \( \hat{\mathbf{x}} \)). Celem uczenia jest dobór liczby neuronów ukrytych i wag tych neuronów, które zapewnią właściwe (zgodnie z regularyzowaną funkcją celu) odtworzenie sygnałów wejściowych w warstwie wyjściowej (rys. 6.24a). W tej sytuacji sygnały warstwy ukrytej stanowią kod sygnałów wejściowych dla następnej warstwy, a warstwa wyjściowa podlega eliminacji.
| a) | 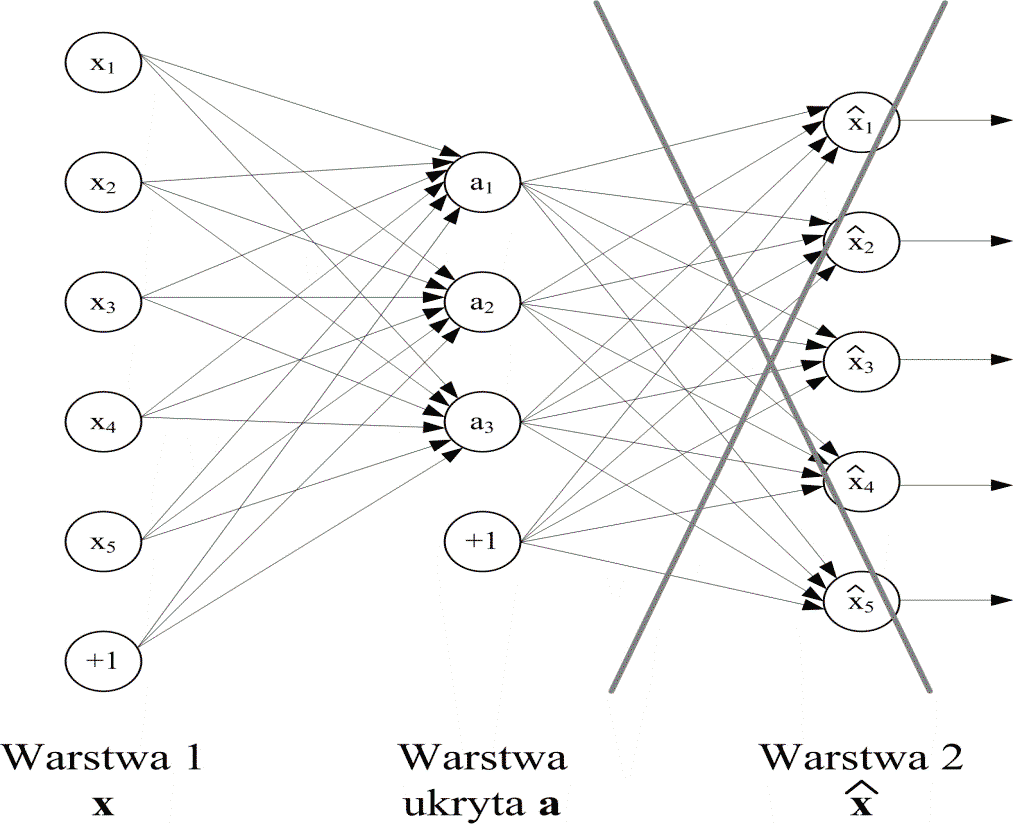 |
|---|---|
| b) | 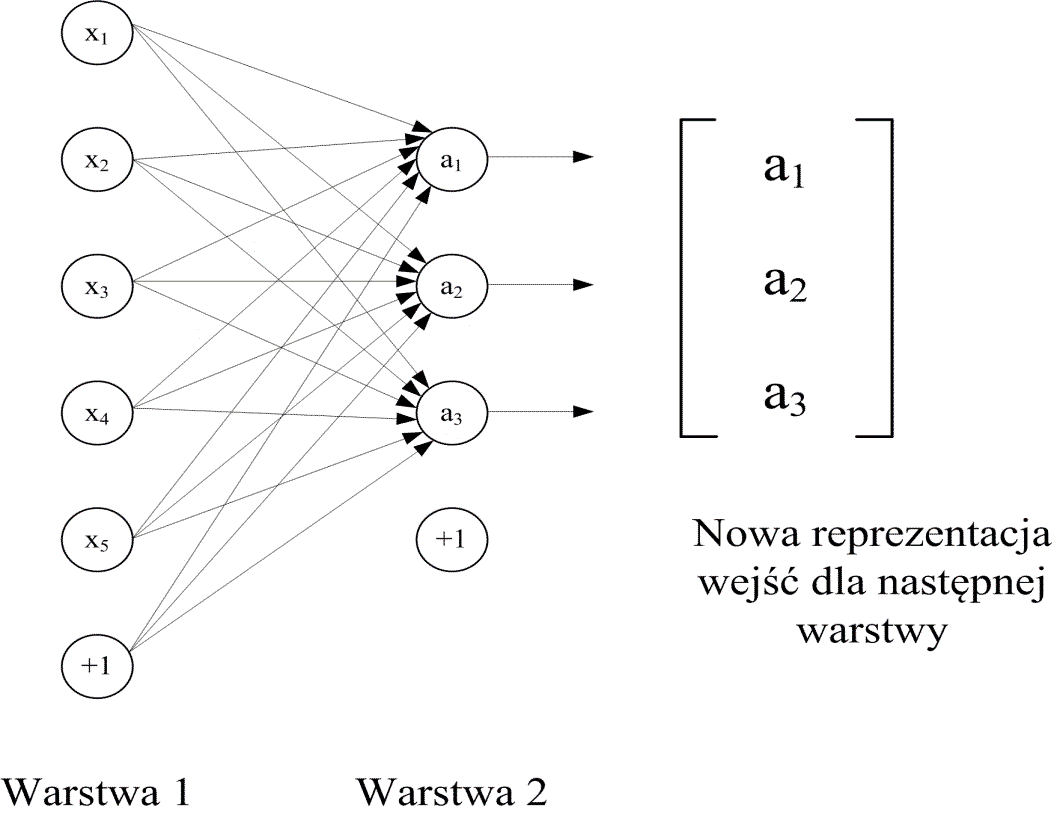 |
Po doborze parametrów warstwy ukrytej odrzuca się warstwę rekonstrukcji i sygnały z warstwy ukrytej stają się wejściowymi dla następnej warstwy (rys. 6.24b). Proces uczenia jest kontynuowany dla następnej warstwy, dobierając jej parametry w taki sposób, aby uzyskać możliwie najlepsze odwzorowanie sygnałów wejściowych \( \mathbf{a} \) w sygnały wyjściowe. W efekcie po odrzuceniu warstwy wyjściowej sieć zawiera dwie warstwy neuronowe \( \mathbf{a} \) i \( \mathbf{b} \) jak to pokazano na rys. 6.25, przy czym liczba neuronów w każdej kolejnej warstwie jest kolejno redukowana, zmuszając sieć do kompresji danych.
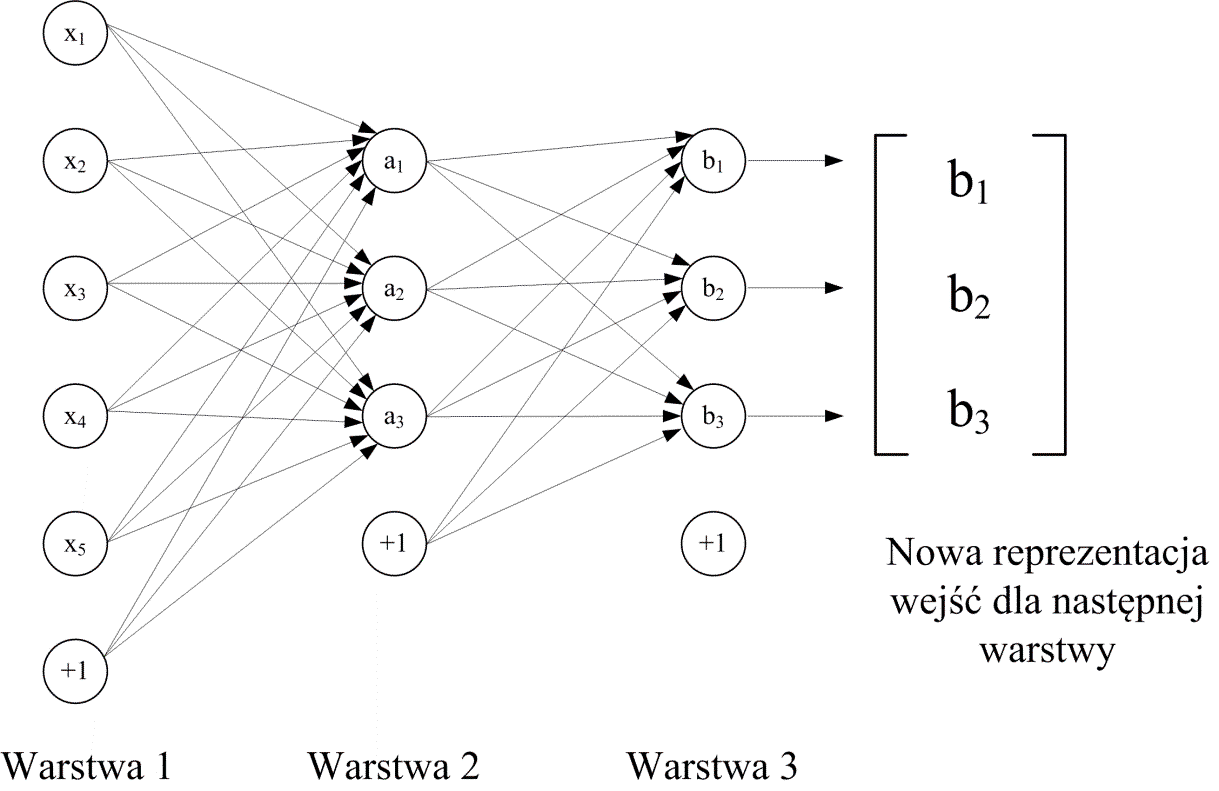
Sygnały warstwy ukrytej \( \mathbf{b} \) stają się ponownie sygnałami wejściowymi dla ukształtowania następnej warstwy o dalej zredukowanej liczbie neuronów Proces jest następnie kontynuowany dla następnych warstw, w sposób identyczny do omówionego. Kształtowanie kolejnych warstw autoenkodera może odbywać się przy użyciu dowolnego algorytmu gradientowego. Jest to stosunkowo prosty proces ze względu na fakt, że w każdym etapie uczenie dotyczy tylko parametrów jednej warstwy.
Ostatnia warstwa ukryta autoenkodera (po wyeliminowaniu warstwy rekonstrukcyjnej) zawiera kodowanie na najwyższym poziomie, zwykle o najbardziej ograniczonej liczbie neuronów. Sygnały wyjściowe tej warstwy stanowią cechy diagnostyczne wyselekcjonowane przez strukturę układu w procesie uczenia z udziałem zbioru danych uczących. Mogą one stanowić atrybuty wejściowe dla końcowego stopnia klasyfikatora bądź układu regresyjnego o dowolnej konstrukcji.
6.8.4 Przykład zastosowania autoenkodera w kodowaniu danych
Poniżej przedstawiony będzie przykład zdolności kodowania autoenkodera dla zbioru 8 obrazów czarno-białych o wymiarach 64x64 reprezentowanych na rys. 6.26 i zawartych w plikach RBx.png. Zbiór ten został użyty najpierw w uczeniu a następnie przetestowane zostało odtwarzanie zakodowanych obrazów (identycznych jak w uczeniu). Zastosowano jedną warstwę ukrytą o 30 neuronach. Współczynnik kompresji równał się więc 4096/30=136.6.

Linie programu Matlaba podane są jak niżej
x1=imread('RB1.png');x2=imread('RB2.png');x3=imread('RB3.png');x4=imread('RB4.png');
x5=imread('RB9.png');x6=imread('RB6.png');x7=imread('RB7.png');x8=imread('RB8.png');
xc{1,1}=x1; xc{1,2}=x2;xc{1,3}=x3; xc{1,4}=x4;
xc{1,5}=x5; xc{1,6}=x6;xc{1,7}=x7; xc{1,8}=x8;
figure(1);
for i = 1:8
subplot(2,4,i);
imshow(xc{i}); title('Original')
end
hiddenSize = 20;
% 'ScaleData',false, ...
autoenc = trainAutoencoder(xc, hiddenSize, ...
'L2WeightRegularization', 0.004, ...
'SparsityRegularization', 4, ...
'SparsityProportion', 0.15, ...
'MaxEpochs', 1000);
xReconstructed = predict(autoenc, xc);
figure(2);
for i = 1:8
subplot(2,4,i);
% imshow((xReconstructed{i})>0.5); title('Reconstructed')
imshow(xReconstructed{i}); title('Reconstructed')
end
figure(3)
for i = 1:8
err=xReconstructed{i}-double(xc{i});
errBW(err<0.5)=0;
errBW(err>=0.5)=1;
nerr(i)=sum(errBW);
subplot(2,4,i);
% imshow(1-err);
imshow(reshape(1-errBW,64,64)); title('Error')
end
liczba_err=nerr
rate_err=nerr/4096*100
Wygląd obrazów w skali szarości odtworzonych po rekonstrukcji przedstawiony jest na rys. 6.27. Szare piksele obrazu (ledwie widoczne) nałożone na inne czarno–białe obrazy odtworzone przez sieć mają niewielkie wartości, które przetworzone na reprezentację czarno-białą nie wnoszą istotnych błędów rekonstrukcji obrazów czarno-białych z rys. 6.27. Błąd rekonstrukcji kolejnych obrazów czarno-białych w postaci liczby błędnych pikseli (po wcześniejszym zaokrągleniu wartości pikseli do 1 lub 0) uzyskany w programie podany jest poniżej
Liczba błędnych pikseli kolejnych obrazów=[ 3 4 7 9 0 8 92 2]
Błąd odtworzenia dotyczył znikomej ilości pikseli w obrazach czarno-białych (oryginalna liczba pikseli każdego obrazu równa 4096). Jeden obraz czarno-biały został odtworzony bezbłędnie (wynik po zaokrągleniu do wartości bitów 1 lub 0). Procentowa zawartość błędów odtworzenia kolejnych obrazów czarno-białych jest równa
Błąd procentowy=[ 0.07% 0.10% 0.17% 0.22% 0 0.19% 2.25% 0.05%]
Należy zauważyć, że jest to wynik rekonstrukcji autoenkodera jedynie w trybie odtwarzania na tych samych danych, które były użyte w uczeniu. Świadczą one o dobrych wynikach uczenia sieci. Na tej podstawie nie można wyciągać daleko idących wniosków co do zdolności generalizacji systemu przy tej wartości współczynnika kompresji.

Sieć autoenkodera znajduje zastosowanie w typowych obszarach przetwarzania danych:
-
Redukcja szumu zakłócającego dane – w tym przypadku zakłada się, że dane wejściowe zniekształcone są szumem; po zakodowaniu i rekonstrukcji szum ten może ulec znacznej redukcji przy właściwym doborze parametrów sieci.
-
Generacja cech diagnostycznych procesu reprezentowanego przez dane uczące. W tym przypadku wyjściem sieci jest warstwa ukryta. W przypadku programu autoencoder Matlaba [43] dostęp do sygnałów h warstwy ukrytej (kodującej) odbywa się komendą
h=encode(autoenc, dane_wej)
gdzie autoenc jest nazwą struktury sieciowej użytej w wywołaniu autoenkodera, a dane_wej jest zbiorem danych które mają podlegać kodowaniu.
Program Matlaba zakłada istnienie jednej warstwy ukrytej. Przy strukturze wielowarstwowej jego wywołanie musi być wielokrotne, przy czym za każdym razem wymuszeniem dla następnej warstwy są sygnały wyjściowe warstwy ukrytej. Ostatnia warstwa ukryta reprezentować będzie najbardziej skompresowane cechy diagnostyczne procesu.
6.8.5 Przykład zastosowania autoenkodera w rozpoznaniu komórek krwiotwórczych
Przykład zastosowania autoenkodera przedstawiony zostanie przy rozpoznaniu 2 rodzajów komórek krwiotwórczych (kodowanie binarne zero-jedynkowe wektora destination \( \mathbf{T} \)) na podstawie 87 cech diagnostycznych typu numerycznego zawartych w macierzy \( \mathbf{X} \). Stosowane są 2 warstwy kodujące (ukryte) i warstwa typu Softmax na wyjściu, działająca w trybie klasyfikacji. Wydruk programu w Matlabie wykonującego zadanie przedstawiony jest poniżej. Dane dotyczące cech diagnostycznych (macierz sygnałów wejściowych \( \mathbf{X} \)) oraz przynależności klasowej kolejnych obserwacji (wektor \( \mathbf{T} \)) zawarte są w pliku Matlaba XT_autoencoder.mat.
load XT_autoencoder.mat
a=randperm(293);Xrand=X(:,a);Trand=T(:,a);
Xucz=Xrand(:,1:193);Tucz=Trand(:,1:193);
Xtest=Xrand(:,194:end); Ttest=Trand(:,194:end);
% Train an autoencoder with a hidden layer of assumed size and a linear transfer function for the% decoder. Set the L2 weight regularizer to 0.001, sparsity regularizer to 4 and sparsity
% proportion to 0.05.
hiddenSize = 60;
autoenc1 = trainAutoencoder(Xucz,hiddenSize,...
'L2WeightRegularization',0.001,...
'SparsityRegularization',4,...
'SparsityProportion',0.05,...
'DecoderTransferFunction','purelin');
% Extract the features in the hidden layer.
features1 = encode(autoenc1,Xucz);
% Train a second autoencoder using the features from the first autoencoder. Do not scale
% the data.
hiddenSize = 29;
autoenc2 = trainAutoencoder(features1,hiddenSize,...
'L2WeightRegularization',0.001,...
'SparsityRegularization',4,...
'SparsityProportion',0.05,...
'DecoderTransferFunction','purelin',...
'ScaleData',false);
% Extract the features in the hidden layer.
features2 = encode(autoenc2,features1);
% Train a softmax layer for classification using the features, features2, from the second
% autoencoder, autoenc2.
softnet = trainSoftmaxLayer(features2,Tucz,'LossFunction','crossentropy');
% Stack the encoders and the softmax layer to form a deep network.
deepnet = stack(autoenc1,autoenc2,softnet);
% Train the deep network on the data.
% Construct Deep Network Using Autoencoders % 2-3
deepnet = train(deepnet,Xucz,Tucz);
% Estimate the cell types using the trained deep network: deepnet.
cell_type = deepnet(Xtest);
% Plot the confusion matrix.
plotconfusion(Ttest,cell_type);
Wynik testowania sieci na danych testujących nie uczestniczących w uczeniu jest zależny od losowego podziału zbioru danych na zbiór uczący i testujący i może przyjmować różne wartości w zależności od ich składu. Przykładowy wynik dla jednej próby w postaci macierzy rozkładu klas (ang. confusion matrix) przedstawiony jest na rys. 6.28.
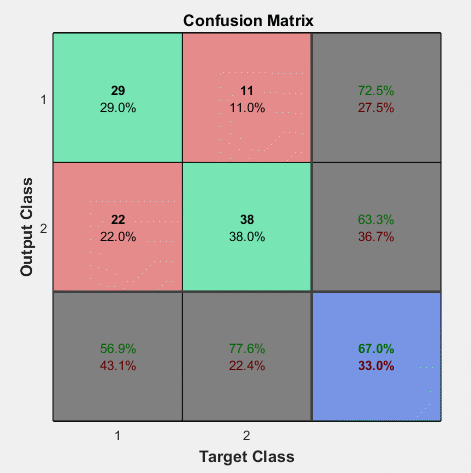
3.9. Autoenkoder wariacyjny
6.9.1 Podstawy działania
Autoencoder wariacyjny (ang. variational autoencoder - VAR) jest innym rozwiązaniem sieci głębokiej umożliwiającym generację obrazów podobnych do oryginału [33,76,77]. Będzie dalej oznaczany skrótem VAR. Sieć taka działa na innych zasadach niż przedstawiona wcześniej sieć klasycznego autoenkodera (AE). Nazwa sieci wywodzi się z bliskiej relacji mechanizmu działania z zasadą regularyzacji sieci i wnioskowania wariacyjnego w statystyce.
Sieć VAR wykorzystuje w swoim działaniu zasadę redukcji wymiarowości danych, tak przeprowadzoną, że możliwe jest odtworzenie danych oryginalnych z określoną dokładnością przy zachowaniu w miarę wiernego odwzorowania rozkładu statystycznego (wartości średniej i wariancji) w poszczególnych rejonach obrazu. Redukcja wymiarowości danych oznacza reprezentację danych poprzez zmniejszoną liczbę cech (deskryptorów) charakteryzujących dostatecznie dokładnie analizowany proces. Redukcja taka może polegać na wyborze ograniczonej liczby zmiennych oryginalnych (bez zmiany ich wartości), bądź na generacji nowego zbioru deskryptorów jako funkcji liniowej (np. PCA) bądź nieliniowej wszystkich zmiennych oryginalnych (AE).
Klasycznym rozwiązaniem tego typu jest autoencoder, poznany wcześniej. Idea uczenia autoenkodera polegała na takim doborze parametrów (wag sieci głębokiej), aby obraz wyjściowy po rekonstrukcji sygnałów skompresowanych przypominał jak najbardziej obraz oryginalny. W procesie uczenia klasycznego autoencodera porównywane były wartości sygnałów bądź piksele obrazów oryginalnego i zrekonstruowanego. Redukcja wymiarowości w takim rozwiązaniu autoencodera może być zinterpretowana jako kompresja danych, w której encoder kompresuje dane z przestrzeni oryginalnej do przestrzeni zredukowanej traktowanej zwykle jako przestrzeń ukryta (ang. latent space), natomiast decoder dokonuje dekompresji czyli rekonstrukcji danych oryginalnych.
Oczywiście, odtworzenie danych oryginalnych poprzez dekompresję charakteryzuje się pewną utratą informacji oryginalnej. Wielkość tej straty uzależniona jest od wymiaru przestrzeni skompresowanej jak również od mechanizmu uczenia sieci. Ilustracja tego typu procesu przetwarzania danych przedstawiona jest na rys. 6.29. Wektor oryginalny \( \mathbf{x} \) kodowany jest w wektor \(\mathbf{e}(\mathbf{x}) \) o zmniejszonym wymiarze, po czym dekodowany w postaci \(\mathbf{d}(\mathbf{e}(\mathbf{x})) \). Istotą klasycznego algorytmu uczenia sieci autoencodera jest taki dobór parametrów sieci, aby utrata informacji oryginalnej, czyli różnica między \(\mathbf{d}(\mathbf{e}(\mathbf{x})) \) a \( \mathbf{x} \) była jak najmniejsza. Minimalizacji podlega funkcja błędu
| \( \min E=\|\mathbf{x}-\mathbf{d}(\mathbf{e}(\mathbf{x}))\|^2 \) | (6.29) |
Zwykle w definicji dodaje się jeszcze czynniki regularyzacyjne, jak to było przedstawione w rozdziale dotyczącym klasycznego autoencodera. Klasyczny autoenkoder ma pewną wadę, wynikającą z nieciągłości danych (na przykład puste przestrzenie między klastrami). Na etapie testowania przy użyciu danych nie uczestniczących w uczeniu dekoder układu wygeneruje nierealistyczny wynik (nieprzystający do danych oryginalnych), gdyż na etapie uczenia nie „widział” danych encodera z obszaru pustego [33].

-
x
e(x)
d(e(x))
Dobrze wytrenowany autoecoder pozwala zwykle odtworzyć dane weryfikacyjne (testujące) pochodzące ze zbioru różnego od zbioru uczącego tylko z określoną dokładnością. Dochodzi przy tym drugi problem: przy niewłaściwym doborze wymiaru przestrzeni zredukowanej (zbyt duży wymiar warstwy ukrytej) może wystąpić efekt utraty zdolności generalizacyjnych (przeuczenie sieci) i odtwarzanie danych oryginalnych ze zbyt dużym błędem.
Remedium na to jest właściwa automatyczna regularyzacja sieci w procesie uczenia. Stąd powstała idea autoencodera wariacyjnego jako rozwiązania w którym proces uczenia podlega automatycznej regularyzacji w specjalny sposób zabezpieczający przed przeuczeniem i zapewniający najlepszą reprezentację danych w przestrzeni ukrytej, umożliwiającą właściwe odtworzenie (generację) procesu oryginalnego. Encoder wariacyjny stosuje kodowanie w warstwie ukrytej nie oryginalnych danych wejściowych, ale dwu wektorów: wektora wartości średnich \( \mu \) oraz wektora odchyleń standardowych \( \sigma \)
W efekcie proces uczenia składa się z następujących etapów [33]:
-
Dane wejściowe są kodowane w przestrzeni ukrytej (zredukowanej) na podstawie rozkładu statystycznego danych (ich dystrybucji). Przyjmując rozkład normalny wystarczy scharakteryzować proces poprzez wartość średnią (oczekiwaną) i macierz kowariancji (zwykle wariancji \( \sigma^2 \)).
-
Punkty z przestrzeni ukrytej (wejście dla dekodera) są próbkowane na podstawie tej dystrybucji.
-
Na podstawie tych próbek dekoder dokonuje rekonstrukcji danych w postaci wektora \( \mathbf{x} \) i oblicza błąd rekonstrukcji.
-
Błąd rekonstrukcji jest kierowany z powrotem do wejścia sieci (propagacja wsteczna) i na tej podstawie metodą gradientową dokonywana jest adaptacja parametrów sieci.
Przykładową generację danych poprzez próbkowanie przy znanym rozkładzie określonym poprzez wektor wartości średnich \( \boldsymbol{\mathbf{\mu}} \) oraz wektor standardowych odchyleń \boldsymbol{\mathbf{\sigma} } dla dekodera przedstawiono poniżej.
|
Wektor \( \boldsymbol{\mathbf{\mu} }\) |
[0.13 1.35 0.27 0.78 ...] |
|
Wektor \( \boldsymbol{\mathbf{\sigma} }\) |
[0.21 0.53 0.88 1.38 ...] |
|
Rozkład statystyczny próbek |
X1~N(0.13, 0.21), X2~N(1.35, 0.53), X3~N(0.27, 0.88), X4~N(0.78, 1.38),... |
|
Wektor po próbkowaniu |
[0.29 1.82 0.87 2.03 ...] |
Zauważmy, że generacja stochastyczna próbek według określonego rozkładu generuje różne wartości nawet przy tych samych wartościach średnich i wariancji. Wektor wartości średnich wskazuje centrum wokół którego z odchyleniem standardowym generowane są próbki. W efekcie decoder uczy się nie pojedynczych (ściśle zdefiniowanych) próbek, ale otoczenia, z którego są one próbkowane. Różnice między klasycznym i wariacyjnym rozwiązaniem autoencodera pokazane są na rys. 28.
|
Autoencoder |
\( \mathbf{x} \) |
\( \mathbf{z}=\mathbf{e}(\mathbf{x}) \) |
\( \mathbf{d}(\mathbf{z}) \) |
|
|
Autoencoder wariacyjny |
\( \mathbf{x} \) |
dystrybucja \( \mathbf{p}(\mathbf{z} | \mathbf{x}) \) |
Próbkowanie \( \mathbf{z} \sim \mathbf{p}(\mathbf{z} | \mathbf{x}) \) |
\( \mathbf{d}(\mathbf{z}) \) |
Rys. 6.28 Ilustracja różnicy między klasycznym i wariacyjnym autoencoderem
Takie rozwiązanie (przy założeniu rozkładu danych jako normalnego) sprowadza się w uczeniu VAR również do reprezentacji danych poprzez wartości średnie i macierz kowariancji, zamiast jedynie reprezentacji poszczególnych danych (pikseli obrazu). Takie rozwiązanie umożliwia regularyzację sieci w prosty sposób: zmusza encoder do zapewnienia normalności rozkładu danych w przestrzeni ukrytej. Proces realizowany przez VAR ten można więc przedstawić jak na rys. 30.
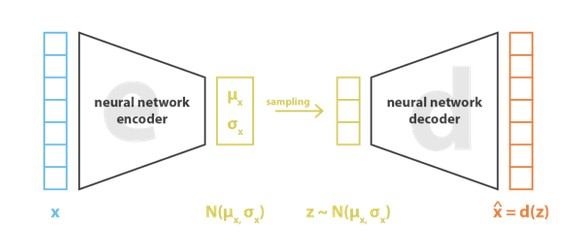
Funkcja celu podlegająca minimalizacji zawiera 2 składniki: składnik rekonstrukcyjny (dopasowanie warstwy wyjściowej do wejściowej) oraz składnik regularyzacyjny, związany z warstwą ukrytą, który dąży do zapewnienia normalności rozkładu danych w warstwie ukrytej. Składnik regularyzacyjny wyrażany jest przy użyciu dywergencji Kulbacka-Leiblera KL() między aktualnie zwracanym rozkładem danych ukrytych a pożądanym rozkładem normalnym. Minimalizowaną funkcję celu można więc zapisać w postaci
| \( \min E=\|\mathbf{x}-\mathbf{d}(\mathbf{z})\|^2+K L\left(N\left(\mu_x, \sigma_x\right), N(0,1)\right) \) | (6.30) |
Aby zapewnić prawidłowy przebieg procesu uczenia należy zapewnić regularyzację zarówno wartości średniej jak i macierzy kowariancji, sprowadzając proces do normalnego o zerowej wartości średniej i jednostkowej macierzy kowariancji. Minimalizacja wartości czynnika regularyzacyjnego odbywa się kosztem składnika rekonstrukcyjnego (składnik pierwszy we wzorze (6.30)). Właściwy balans między składnikami wzoru można uzyskać przez wprowadzenie odpowiedniej wagi w tym zbiorze.
6.9.2. Proces uczenia sieci VAR
Niech \( \mathbf{x} \) oznacza zbiór danych rekonstruowanych, generowany na podstawie ukrytych próbek z warstwy ukrytej \( \mathbf{z} \). W związku z tym wyróżnia się 2 kroki stanowiące metodę probabilistyczną uczenia
-
Próbkowanie zmiennych \( \mathbf{z} \) na podstawie rozkładu \( p(\mathbf{z}) \)
-
Próbkowanie zmiennych \( \mathbf{x} \) na podstawie rozkładu warunkowego \( p(\mathbf{x} | f(\mathbf{z})) \): znajdź rozkład zmiennej dekodowanej \( \mathbf{x} \) przy założeniu znajomości rozkładu zmiennej zakodowanej \( \mathbf{z} \).
Procesy kodowania (operator \( e \)) i dekodowania (operator \( d \)) powiązane są wzorem Bayesa
| \( p(z \mid x)=\frac{p(x \mid z) p(z)}{p(x)}=\frac{p(x \mid z) p(z)}{\sum_{u} p(x \mid u) p(u)} \) | (6.31) |
Przyjmuje się, że \( p(\mathbf{z}) \) ma standardowy rozkład Gaussa \( p(\mathbf{z}) =N(0,\mathbf{1})\), o wartości średniej zerowej i jednostkowej macierzy kowariancji \( \mathbf{1} \). Z kolei \( p(\mathbf{x} \mid \mathbf{z}) \) jest rozkładem gaussowskim, którego wartość średnia jest funkcją deterministyczną \( f(\mathbf{z}) \) zmiennej \( \mathbf{z} \) a macierz kowariancji o postaci jednostkowej pomnożonej przez dodatnią stałą wartość \( c \), co zapisuje się w postaci \( p(\mathbf{x} \mid \mathbf{z})=N(f(\mathbf{z}), c\mathbf{1}) \). Zarówno \( c \) jak i postać funkcji nie są z góry zadane i podlegają estymacji w procesie uczenia. Mianownik w wyrażeniu Bayesa wymaga zastosowania wnioskowania wariacyjnego, techniki stosowanej w złożonych rozkładach statystycznych.
W tym podejściu stosuje się sparametryzowane rodziny rozkładów (zwykle gaussowskich o różnej wartości średniej i macierzy kowariancji). Spośród nich wybiera się tę rodzinę, która minimalizuje błąd aproksymacji na danych pomiarowych (zwykle dywergencję Kulbacka-Leiblera między aproksymacją i wartościami zadanymi). Funkcja \( p(\mathbf{z} \mid \mathbf{x}) \) jest w podejściu wariacyjnym aproksymowana poprzez rozkład gaussowski
| \( q_{x}(\mathbf{z})={N}(\mathrm{g}(\mathbf{x}), \mathrm{h}(\mathbf{x})) \) | (6.32) |
w którym wartość średnia jest aproksymowana przez \( \mathrm{g}(\mathbf{x}) \) a kowariancja przez \( \mathrm{h}(\mathbf{x}) \). Obie funkcje podlegają procesowi minimalizacji z użyciem miary Kulbacka-Leiblera
| \( \left(g^*, h^*\right)=\underset{g, h}{\arg } \min K L\left(q_x(z), p(z \mid x)\right) \) | (6.33) |
Proces ten sprowadza się do rozwiązania problemu optymalizacyjnego o postaci [33]
| \( \left(g^*, h^*\right)=\underset{g, h}{\arg \max }\left(-\frac{\|x-f(z)\|^2}{2 c}-K L\left(q_x(z), p(z)\right)\right ) \) |
(6.34) |
Składnik pierwszy w tym wzorze odpowiada za dopasowanie sygnałów wyjściowych sieci do wartości zadanych \( \mathbf{x} \), natomiast składnik drugi za rozkład statystyczny danych wejściowych i sygnałów w warstwie ukrytej, stanowiąc naturalny składnik regularyzacyjny procesu. Istotnym parametrem jest \( c \). Wartość tej zmiennej pozwala regulować relację między składnikiem pierwszym i drugim. Duża wartość \( c \) oznacza większy wpływ czynnika KL, czyli dopasowania statystycznego obu rozkładów, natomiast mała wartość – większy wpływ dopasowania pikselowego zrekonstruowanego obrazu do oryginalnego.
Funkcje \( f \), \( g \) i \( h \) użyte w modelu matematycznym podlegają w praktyce modelowaniu aproksymacyjnemu przy użyciu sieci neuronowych. Obie funkcje \( g \) i \( h \) wykorzystują wspólny fragment architektury sieci, co można zapisać w postaci
| \( g(\mathbf{x})=g_2\left(g_1(\mathbf{x})\right)=g_2\left({~h}_1(\mathbf{x})\right) \) | (6.35) |
| \( h(\mathbf{x})=h_2\left(h_1(\mathbf{x})\right) \) | (6.36) |
Przyjmuje się w praktyce założenie upraszczające, że \( h(\mathbf{x}) \) jest wektorem złożonym z elementów diagonalnych macierzy kowariancji i jest jednakowych rozmiarów jak \( g(\mathbf{x}) \). Przy rozkładzie gaussowskim zmiennej \( \mathbf{z} \) o wartości średniej \( g(\mathbf{x}) \) i wariancji \( h(\mathbf{x}) \) przyjmuje się, że
| \( z=h(x) \xi+g(x) \) | (6.37) |
gdzie \( \xi \) jest zmienną losową o rozkładzie normalnym \( \xi \sim N(0,1) \). Rys. 6.31 przedstawia ogólną strukturę układową encodera implementującą funkcje \( g(\mathbf{x}) \) oraz \( h(\mathbf{x}) \), przy czym wektor \( g(\mathbf{x}) \) reprezentuje wartości średnie a \( h(\mathbf{x}) \) kowariancje (wartości diagonalne macierzy kowariancji). Rekonstrukcja sygnałów wyjściowych (decoder) realizująca rozkład \( p(\mathbf{x} \mid \mathbf{z}) \) generowany przez encoder zakłada stałą kowariancję i jest implementowana przez strukturę neuronową implementującą funkcję \( f \) o postaci na przykład z rys. 6.31 i 6.32.
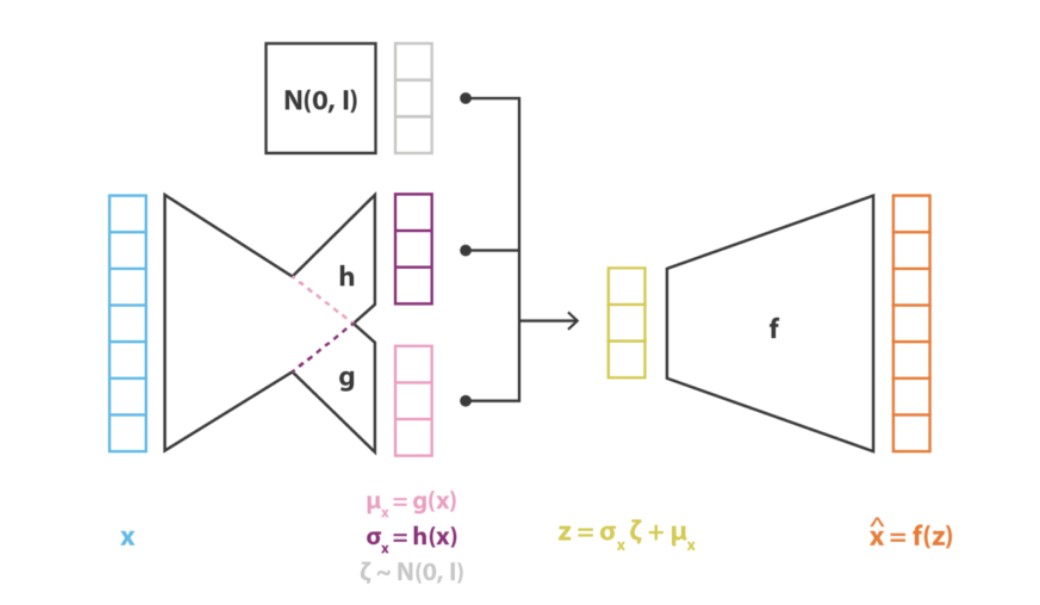
W efekcie proces uczenia sieci z rys. 6.31 sprowadza się do minimalizacji funkcji celu o postaci
| \( \min E=C\|\mathbf{x}-\mathbf{f}(\mathbf{z})\|^2+K L(N(g(x), h(x)), N(0,1)) \) | (6.38) |
Czynnik pierwszy odpowiada za odtworzenie sygnałów wejściowych na wyjściu sieci, natomiast drugi za odwzorowanie rozkładu statystycznego sygnałów wejściowych w sygnałach wyjściowych. Obie struktury (encoder i decoder) są implementowane w postaci głębokiej sieci neuronowej, podlegającej uczeniu typowemu dla sieci głębokich. Przykład takiej sieci pokazany jest na rys. 6.32.
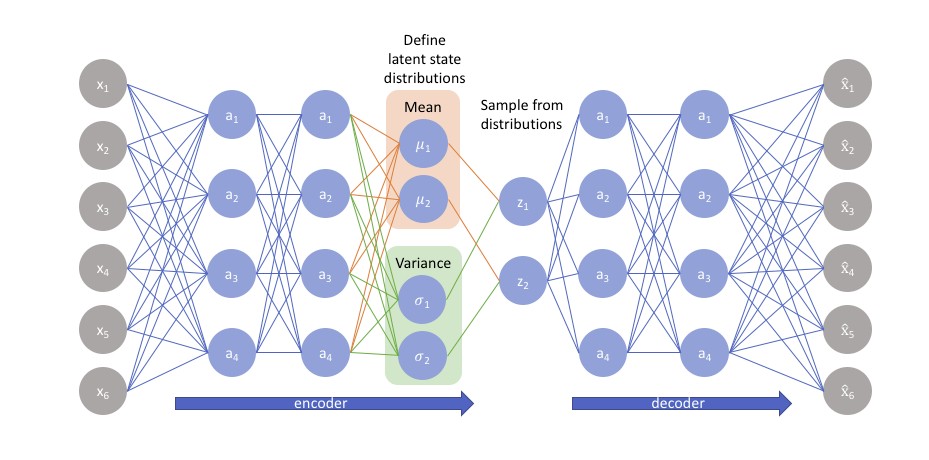
3.10. Sieci generatywne GAN
Sieć generatywna GAN (Generative Adversarial Network- GAN) stworzona przez zespół Iana Goodfellow w 2014 roku, jest implementacją koncepcji przeciwstawienia sobie dwu sieci neuronowych, z których jedna reprezentuje dane rzeczywiste, a druga dane generowane sztucznie, "udając" dane rzeczywiste [19]. Obie sieci rywalizują ze sobą. System jest trenowany w taki sposób aby generator nowych danych był w stanie oszukać rzeczywistość, prezentując dane (sygnały bądź obrazy) które są trudne do odróżnienia od rzeczywistych. Generator sztucznych danych ma za zadanie wygenerować je w taki sposób, aby statystyki danych oryginalnych i danych generowanych przez niego były takie same. Przykładowo w przypadku obrazów, obraz wygenerowany sztucznie powinien przypominać obraz oryginalny.

Idea działania sieci GAN jest przedstawiona na rys. 6.33. Blok \( \mathbf{X} \) reprezentuje dane oryginalne, \( \mathbf{z} \) – wektor losowy zasilający generator \( G \), generujący na tej podstawie dane \( G(\mathbf{z}) \) „udające” dane oryginalne. Dyskryminator \( D \) porównuje dane oryginalne \( \mathbf{X} \) z \( G(\mathbf{z}) \) wygenerowanymi przez generator wskazując na prawdopodobieństwo zgodności obu danych \( \mathbf{X} \) i \( G(\mathbf{z}) \). Proces uczenia sieci polega na takim doborze parametrów, aby oszukać dyskryminator (uznać, że dane wygenerowane sztucznie \( G(\mathbf{z}) \) niczym nie różnią się od danych oryginalnych \( \mathbf{X} \). W efekcie generator \( G \) generuje kolejnych kandydatów do porównania, a dyskryminator \( D \) ocenia ich jakość w stosunku do oryginału.
Proces uczenia polega na maksymalizacji prawdopodobieństwa, że dyskryminator popełni błąd, przyjmując że obie grupy danych (oryginalne i sztucznie wygenerowane) są identyczne pod względem rozkładu statystycznego (maksymalizacja prawdopodobieństwa zaliczenia obu obrazów: oryginalnego i wygenerowanego sztucznie do tej samej klasy). Można go zapisać jako programowanie minimaksowe zdefiniowane w postaci [19]
| \( \min _G \max _D V(G, D)=E_{\mathbf{X} \sim p_{\mathbf{x}}}[\log D(\mathbf{X})]+E_{\mathbf{z} \sim p_{\mathbf{z}}}[\log (1-D(G(\mathbf{z})))] \) | (6.39) |
gdzie symbol \( E \) reprezentuje wartość oczekiwaną, natomiast \( {p}_\mathbf{X} \) i \( {p}_\mathbf{z} \) rozkłady statystyczne odpowiednio danych rzeczywistych (oryginalnych) i wygenerowanych sztucznie. \( D(\mathbf{X}) \) oraz \( G(\mathbf{X}) \) są wartościami generowanymi odpowiednio przez dyskryminator \( D \) i generator \( G \) dla danych \( \mathbf{X} \). W efekcie proces optymalizacyjny ukierunkowany jest na poszukiwanie minimum względem generatora \( G \) i maksimum względem dyskryminatora \( D \).
Generator \( G \) zasilany jest poprzez wektor losowy \( \mathbf{z} \) o określonym wymiarze. Na bazie tego wektora próbuje wygenerować obraz przypominający oryginał \( \mathbf{X} \). Dyskryminator zasilany jest przez obraz oryginalny \( \mathbf{X} \) i obraz wygenerowany przez generator \( G(\mathbf{z}) \). W wyniku ich porównania generuje wartość prawdopodobieństwa, że obraz \( G(\mathbf{z}) \) jest nierozpoznawalny od oryginału \( \mathbf{X} \). Oba modele \( G \) i \( D \) mogą być implementowane przy użyciu różnych struktur sieci neuronowych, aczkolwiek aktualnie najlepsze wyniki uzyskuje się przy użyciu sieci głębokich o strukturze CNN.
Proces uczenia sieci GAN przyjmuje formę iteracyjną. Przy aktualnych parametrach generatora \( G \) wykonuje się \( k \) kroków w optymalizacji dyskryminatora \( D \) a następnie jeden krok optymalizacji generatora. W pętli wewnętrznej adaptacji dyskryminator jest ukierunkowany na rozróżnienie próbek obu obrazów. W kroku drugim dotyczącym adaptacji generatora jego parametry są zmieniane w takim kierunku, aby wynik generatora był bliższy obrazowi oryginalnemu. Po wykonaniu wielu iteracji osiągnięty jest punkt, w którym nie występuje możliwość poprawy wyniku w obu krokach, czyli dyskryminator nie jest w stanie rozróżnić obrazu \( {G}(\mathbf{z}) \) od oryginalnego \( \mathbf{X} \).
Powstało wiele modyfikacji podstawowej struktury GAN polepszających sprawność wykrywania „podróbki” od danych oryginalnych. Przykład takiego rozwiązania zwanego BIGAN (BIdirectional Generative Adversarial Networks) przedstawiony jest na rys. 6.34.
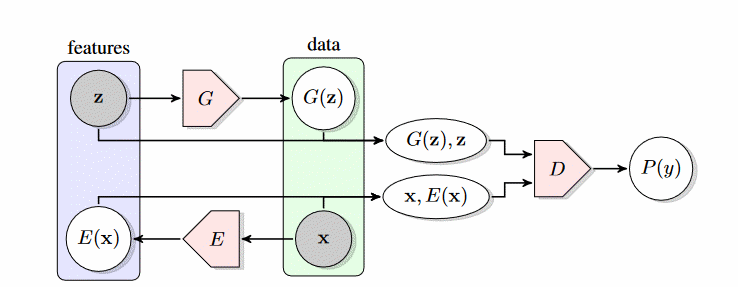
Struktura sieci BIGAN zawiera enkoder \( E \) który transformuje dane oryginalne \( \mathbf{X} \) do przestrzeni wektorowej \( E(\mathbf{X}) \), generując wektor cech o wymiarach identycznych z wektorem losowym \( \mathbf{z} \). Dyskryminator \( D \) sieci BIGAN dokonuje więc rozróżnienia pary danych \( (\mathbf{X}, E(\mathbf{X})) \) oraz \( (G(\mathbf{z}), \mathbf{z}) \) zamiast (\( \mathbf{X} \) versus \( G(\mathbf{z}) \)) w klasycznej implementacji GAN. Jest oczywiste, że enkoder \( E \) próbuje „nauczyć” się inwersji generatora \( G \) (czyli wektora \( \mathbf{z} \)), choć nie występuje tu bezpośrednia komunikacja. Zwiększona informacja (w stosunku do wersji oryginalnej GAN) dostarczona do dyskryminatora umożliwia polepszenie dokładności rozpoznania „podróbki” od oryginału.
Sieci generatywne (GAN i jego różne modyfikacje) znajdują różne zastosowania. Jednym z nich jest wzbogacanie zbioru danych oryginalnych (tak zwana augmentacja zbioru) użytych w uczeniu sieci CNN. Dane wygenerowane przez GAN są podobne statystycznie do danych oryginalnych, ale nie tożsame, co jest warunkiem polepszenia zdolności generalizacyjnych trenowanych sieci. Innym zastosowaniem sieci GAN jest wykrywanie różnic między oryginałami i podróbkami. Dotyczy to zarówno obrazów jak i sygnałów. Sieci te wykazują się zwiększoną czułością w stosunku do innych rozwiązań.
3.11. Zadania i problemy
1.Obraz wejściowy poddany operacjom max i average poolingu ma postać
\( \left[\left.\begin{array}{cccccc}
1 & 12 & 5 & 7 & 23 & 17 \\
4 & 5 & 0 & 9 & 11 & 10 \\
24 & 17 & 2 & 21 & 22 & 12 \\
1 & 5 & 7 & 16 & 8 & 8 \\
15 & 23 & 6 & 4 & 4 & 14 \\
14 & 3 & 11 & 6 & 2 & 0
\end{array} \right]\,\right. \)
Wyznaczyć obrazy wyjściowe po zastosowaniu tych operacji z maską \( 2 \times 2 \). Przyjąć 2 wartości kroku \( stride=1 \) i \( stride=2 \).
2. Wyznaczyć 3 obrazy wyjściowe po operacji konwolucji i ReLU na 2 obrazach wejściowych
\( \begin{aligned} \text { Obr1}=[ & 1 \; 0 \; 3 \\ & 4 \;1\;6 \\ & 0\; 1 \; 1] \end{aligned} \)
\( \begin{aligned} \text { Obr1}=[ & 5 \; 6 \; 1 \\ & 1 \;2\;0 \\ & 4\; 3 \; 1] \end{aligned} \)
przy zastosowaniu 3 par filtrów )każda para generuje jeden obraz wyjściowy)
\( F11=[ 1 \;0; -1\; 1] \), \( F12=[1 \; 4; 0 \; -1] \)
\( F21=[ 2 \; 1; 3\; -1] \), \(F22=[-1 \; 1; 0 \; 2] \)
\( F31=[1 \; -1; -1\; 2]\), \(F32=[4\; 1; 6\; -1] \)
Przyjąć \( stride = 1\).
3. Określić minimalną wartość parametru zero padding w obu wymiarach, aby obraz wejściowy o wymiarach \( 100\times 80 \) poddany operacji pooling z maską \(4 \times 4\) i krokiem \( stride=2 \) dał obraz wynikowy o wymiarach \(50 \times 40\). Wykorzystać wzór
\( O=(W−F+2P)/S+1 \)
4. Wyznaczyć wartość funkcji kross-entropijnej dla sieci CNN o 3 neuronach wyjściowych, jeśli dla pary uczącej \( (x,d) \) należącej do klasy pierwszej \( d=1 \) suma wagowa neuronów wyjściowych była równa \( u1=1.5 \); \(u2=0.9\); \(u3=1.2 \).
3.12. Słownik
Wykład 6
Sieci głębokie – sieci wielowarstwowe, w których kolejne warstwy połączone lokalnie są odpowiedzialne za generację i selekcję cech diagnostycznych procesu. Cechy te są podawane następnie na stopień końcowy realizujący funkcję klasyfikatora bądź regresora.
Sieć CNN – sieć neuronowa konwolucyjna (ang. Convolutional Neural Network) stanowiąca sztandarową postać sieci głębokich.
Autoenkoder – sieć jednokierunkowa wielowarstwowa stanowiąca uogólnienie sieci MLP, stosowana do automatycznej generacji cech diagnostycznych procesu.
Stride – krok przesunięcia maski filtrującej obraz.
Pooling – metoda redukcji wymiaru poprzez łączenie sąsiednich pikseli w postaci wartości średniej lub maksymalnej.
ReLU – dwu-odcinkowo liniowa funkcja aktywacji, przyjmująca jako wyjście wartość argumentu wejściowego, jeśli jest on dodatni lub zero w przeciwnym wypadku.
Zero padding – uzupełnianie obrazu zerami (wierszy i kolumn) dla zwiększenia wymiaru obrazu wejściowego.
Mini batch – mały podzbiór danych wybranych losowo ze zbioru uczącego używany w procesie uczenia sieci głębokiej.
Sofplus – modyfikacja funkcji ReLU zapewniając ciągłość pochodnej.
Softmax – metoda uczenia sieci CNN w zadaniu klasyfikacji.
Struktura sieci w pełni połączona – fragment końcowy struktury sieciowej rozwiązania głębokiego, w którym neurony w sąsiednich warstwach są w pełni połączone wagowo.
Funkcja kross-entropijna – specjalna definicja funkcji celu stosowana w uczeniu sieci głębokich wykorzystująca prawdopodobieństwo przynależności do określonej klasy.
SGDM – stochastyczny algorytm największego spadku z momentem rozpędowym.
ADAM – algorytm uczenia sieci głębokich (ang. ADAptive Momenet estimation) stosujący adaptacyjnie dobierany współczynnik uczenia uzależniony od momentu statystycznego gradientu pierwszego i drugiego rzędu.
Transfer learning – metoda uczenia wstępnie nauczonej sieci głębokiej poprzez adaptację ograniczonej struktury sieci (zwykle klasyfikatora końcowego) na właściwych danych.
ALEXNET – pierwsza sieć CNN wstępnie wytrenowana do użytku publicznego wykorzystywana poprzez transfer learning.
UNET – sieć głęboka CNN stworzona specjalnie do segmentacji obrazów biomedycznych.
YOLO – sieć CNN (ang. You Only Look Once) wykorzystywana do klasyfikacji i regresji.
RCNN – sieć głęboka stworzona specjalnie do segmentacji obrazów (ang. Region based CNN).
Dywergencja Kullbacka-Leiblera – miara odległości między zbiorami w przestrzeni stochastycznej.
Autoencoder wariacyjny – rozwiązanie sieci głębokiej umożliwiające generację obrazów podobnych do oryginału (ang. Variational Autoencoder) .
GAN – sieć stworzona do koncepcji przeciwstawienia sobie dwu sieci neuronowych, z których jedna reprezentuje dane rzeczywiste, a druga dane generowane sztucznie, udając dane rzeczywiste (ang. Generative Adversarial Network).
BIGAN – modyfikacja sieci GAN o polepszonym działaniu.
4. Sieci rekurencyjne
Dotychczas rozważane nieliniowe sieci należały do sieci jednokierunkowych, w których przepływ sygnału odbywał się od wejścia do wyjścia. Ustalanie się wartości sygnałów w takich sieciach odbywało się w tej samej chwili. Odmienny typ stanowią sieci rekurencyjne, w których istnieje sprzężenie zwrotne od wyjścia sieci w kierunku wejścia. Zasadniczą cechą sieci rekurencyjnych jest istnienie sprzężenia zwrotnego między neuronami. Sprzężenie to może wychodzić od neuronów wyjściowych lub neuronów warstwy ukrytej i być przeniesione do wejścia sieci lub do warstwy uprzedniej. Sprzężenie zwrotne powoduje powstanie pewnego stanu nieustalonego w procesie przesyłania sygnałów, stanowiąc istotną różnicę w stosunku do sieci rozważanych dotychczas.
Istnieje duża różnorodność rozwiązań sieci ze sprzężeniem zwrotnym [18,24,46,58]. Sprzężenie zwrotne może być wyprowadzone bądź z warstwy wyjściowej neuronów, bądź z warstwy ukrytej. W każdym torze takiego sprzężenia umieszcza się blok opóźnienia jednostkowego, pozwalający rozpatrywać przepływ sygnałów jako jednokierunkowy (sygnał wyjściowy z poprzedniego cyklu zegarowego stanowi sygnał znany, powiększający jedynie rozmiar wektora wejściowego x sieci). Tak rozumiana sieć rekurencyjna ze względu na sposób tworzenia sygnału wyjściowego działa podobnie jak sieć jednokierunkowa (perceptronowa). Tym niemniej algorytm uczący takiej sieci, adaptujący wartości wag synaptycznych, jest bardziej złożony, Ze względu na zależność wartości sygnałów w chwili t od ich wartości w chwilach poprzedzających i wynikającą z tego bardziej rozbudowaną formułę wektora gradientu. Spośród wielu sieci rekurencyjnych tutaj zostaną przedstawione dwie: sieć Elmana, stanowiąca rozwiązanie płytkie oraz sieć LSTM stanowiąca strukturę głęboką.
Zasadniczą zaletą sieci rekurencyjnych jest uwzględnienie związków między aktualnymi stanami neuronów a ich stanami w chwilach poprzednich. Stąd sieci rekurencyjne są skuteczniejsze w zadaniach predykcji szeregów czasowych, przetwarzaniu mowy czy tekstu.
4.1. Sieć Elmana
10.1.1 Struktura sieci Elmana
Sieć rekurencyjna Elmana charakteryzuje się częściową rekurencją w postaci sprzężenia zwrotnego między warstwą ukrytą a warstwą wejściową [24,46], realizowaną za pośrednictwem jednostkowych opóźnień oznaczanych poprzez blok opisany funkcją \( z^{-1} \). Pełną strukturę tej sieci przedstawiono na rys. 10.1.
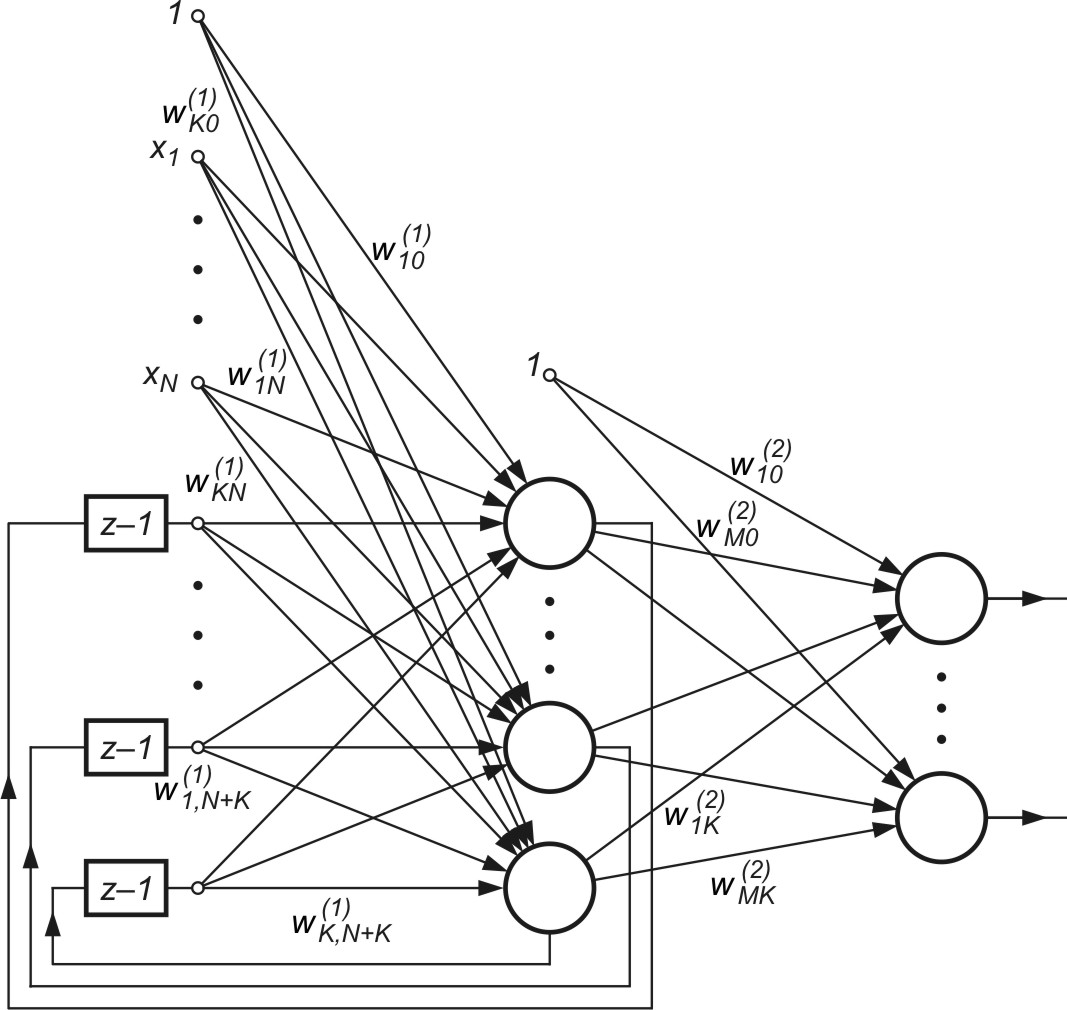
Każdy neuron ukryty ma swój odpowiednik w tak zwanej warstwie kontekstowej, stanowiącej wspólnie z wejściami zewnętrznymi sieci rozszerzoną warstwę wejściową. Warstwę wyjściową tworzą neurony połączone jednokierunkowo tylko z neuronami warstwy ukrytej, tak jak w przypadku sieci MLP. Oznaczmy zewnętrzny wektor wymuszający sieci przez \(\mathbf{x}\) (do jego składu należy także sygnał jednostkowy polaryzacji \(x_0=1\), stany neuronów ukrytych przez \(\mathbf{v}\), a sygnały wyjściowe sieci przez \(\mathbf{y}\). Załóżmy, że wymuszenie \(\mathbf{x}\) w chwili \(k\) podane na sieć generuje w warstwie ukrytej sygnały \(v_i(k) \) a w warstwie wyjściowej sygnały \(y_i(k) \) odpowiadające danej chwili. Biorąc pod uwagę bloki opóźniające w warstwie kontekstowej pełny wektor wejściowy sieci w chwili \(k\) przyjmie postać \( \mathbf{x}(k)=\left[x_0(k), x_1(k), \ldots, x_N(k), v_1(k-1),v_2(k-1), \ldots v_K(k-1) \right] \). Wagi połączeń synaptycznych warstwy pierwszej (ukrytej) oznaczymy przez \(w_{ij}^{(1)} \), warstwy drugiej (wyjściowej) przez \({w}_{ij}^{(2)} \). Przy oznaczeniu sumy wagowej \(i\)-tego neuronu warstwy ukrytej przez \(u_i\), a jego sygnału wyjściowego przez \(v_i\), otrzymuje się
| \(u_i(k)=\sum_{j=0}^{N+K} w_{i j}^{(1)} x_j(k)\) | (10.1) |
| \(v_i(k)=f_1\left(u_i(k)\right)\) | (10.2) |
Wagi \(w_{ij}^{(1)} \) tworzą macierz \(\mathbf{W}^{(1)}\) połączeń synaptycznych w warstwie ukrytej, a \(f_1(u_i)\) jest funkcją aktywacji \(i\)-tego neuronu tej warstwy. Podobnie można oznaczyć przez \(g_i\) sumę wagową \(i\)-tego neuronu warstwy wyjściowej, a przez \(y_i\) odpowiadający mu \(i\)-ty sygnał wyjściowy sieci. Sygnały te są opisane wzorami
| \(g_i(k)=\sum_{j=0}^K w_{i j}^{(2)} v_j(k)\) | (10.3) |
| \(y_i(k)=f_2\left(g_i(k)\right)\) | (10.4) |
Wagi \(w_{ij}^{(2)} \) tworzą z kolei macierz \(\mathbf{W}^{(2)}\) opisującą wagi połączeń synaptycznych neuronów warstwy wyjściowej, a \(f_2(g_i)\) jest funkcją aktywacji \(i\)-tego neuronu tej warstwy.
10.1.2 Algorytmy uczenia sieci Elmana
W uczeniu sieci Elmana, podobnie jak w sieciach MLP, zastosowana będzie metoda gradientowa, wywodzącą się z prac R. Williamsa i D. Zipsera [24,46]. W odróżnieniu od sieci MLP podstawą uczenia jest tu minimalizacja funkcji celu dla każdej chwili czasowej (proces jest rekurencyjny i optymalizacja dotyczyć będzie wielu chwil czasowych aż do ustabilizowania się procesu) Stąd istotnym problemem jest określenie wzorów umożliwiających proste i szybkie obliczenie gradientu funkcji celu. Funkcję celu w chwili \(k\) definiować będziemy jako sumę kwadratów różnic między aktualnymi wartościami sygnałów wyjściowych sieci a ich wielkościami zadanymi dla wszystkich M neuronów wyjściowych. Przy założeniu jednej pary uczącej funkcję celu określa wzór
| \(E(k)=\frac{1}{2} \sum_{i=1}^M\left[y_i(k)-d_i(k)\right]^2=\frac{1}{2} \sum_{i=1}^M e_i(k)^2\) | (10.5) |
gdzie \(e_i(k)=y_i(k)-d_i(k)\) oznacza błąd dopasowania i-tego neuronu do wartości zadanej w chwili k. Przy wielu danych uczących funkcja celu jest sumą tych zależności dla każdej pary danych. Dla określenia gradientu należy zróżniczkować funkcję celu względem wszystkich adaptowanych wag sieci. W przypadku wag ![]() występujących w warstwie wyjściowej, otrzymuje się
występujących w warstwie wyjściowej, otrzymuje się
| \(g_{\alpha \beta}^{(2)}=\frac{\partial E(k)}{\partial w_{\alpha \beta}^{(2)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \frac{d g_i(k)}{d w_{\alpha \beta}^{(2)}}\) | (10.6) |
Po uwzględnieniu wzoru (10.3) i (10.4) zależność (10.6) można przedstawić w postaci
| \(g_{\alpha \beta}^{(2)}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K \frac{d\left(w_{i j}^{(2)} v_j(k)\right)}{d w_{\alpha \beta}^{(2)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K\left(\frac{d v_j}{d w_{\alpha \beta}^{(2)}} w_{i j}^{(2)}+\frac{d w_{i j}^{(2)}}{d w_{\alpha \beta}^{(2)}} v_j(k)\right)\) | (10.7) |
Połączenia między warstwą ukrytą a wyjściową są jednokierunkowe (patrz rys. 10.1), stąd \(\frac{d v_j}{d w_{\alpha \beta}^{(2)}}=0\). Uwzględniając powyższy warunek otrzymuje się ostatecznie dla chwili \(k\)
| \(g_{\alpha \beta}^{(2)}(k)=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=0}^K \frac{d w_{i j}^{(2)}}{d w_{\alpha \beta}^{(2)}} v_j(k)=e_\alpha(k) \frac{d f_2\left(g_\alpha(k)\right)}{d g_\alpha(k)} v_\beta(k)\) | (10.8) |
Po wygenerowaniu gradientu adaptacja wag warstwy wyjściowej może odbywać się podobnie jak w sieci MLP, przy zastosowaniu metody gradientowej. W przypadku wagi \(w_{\alpha \beta}^{(2)}\) zależność ta przyjmuje postać
| \(w_{\alpha \beta}^{(2)}(k+1)=w_{\alpha \beta}^{(2)}(k)+\eta p_{\alpha \beta}^{(2)}(k)\) | (10.9) |
w której \(p_{\alpha \beta}^{(2)}(k)\) oznacza kierunek zmian wartości wag \(w_{\alpha \beta}^{(2)} \) przyjęty w kolejnej iteracji. Wyznaczenie wektora kierunkowego \( \mathbf{p}\) (w szczególności jego składowej \(p_{\alpha \beta}^{(2)}\)) odbywać się może przy użyciu różnych metod, na przykład Levenberga-Marquardta, zmiennej metryki, gradientów sprzężonych czy największego spadku [14].
Przykładowo przy zastosowaniu metody największego spadku kierunek ten wynika bezpośrednio w odpowiedniej składowej gradientu \(p_{\alpha \beta}^{(2)}(k)=-g_{\alpha \beta}^{(2)}(k)\). Proste porównanie z siecią perceptronową wskazuje, że wagi warstwy wyjściowej sieci Elmana poddane są identycznej adaptacji jak wagi neuronów wyjściowych perceptronu wielowarstwowego.
Wzory adaptacji wag warstwy ukrytej w sieci Elmana są bardziej złożone z powodu istnienia sprzężeń zwrotnych między warstwą ukrytą a warstwą wejściową (kontekstową). Obliczenie składowych wektora gradientu funkcji celu względem wag warstwy ukrytej wymaga wykonania znacznie więcej operacji matematycznych i pamiętania ostatnich wartości gradientu. Składowa gradientu funkcji celu względem wagi \(w_{\alpha \beta}^{(1)}\) określona jest wzorem
| \(g_{\alpha \beta}^{(1)}=\frac{\partial E(k)}{\partial w_{\alpha \beta}^{(1)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=1}^K \frac{d\left(v_j(k) w_{i j}^{(2)}\right)}{d w_{\alpha \beta}^{(1)}}=\sum_{i=1}^M e_i(k) \frac{d f_2\left(g_i(k)\right)}{d g_i(k)} \sum_{j=1}^K \frac{d\left(v_j(k)\right)}{d w_{\alpha \beta}^{(1)}} w_{i j}^{(2)}\) | (10.10) |
Po uwzględnieniu zależności (10.2) otrzymuje się
| \(\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j} \sum_{m=0}^{N+K} \frac{d\left(x_m(k) w_{j m}^{(1)}\right)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=0}^{N+K} \frac{d x_m(k)}{d w_{\alpha \beta}^{(1)}} w_{j m}^{(1)}\right]\) | (10.11) |
Gdzie \(\delta_{j \alpha}\) oznacza symbol Kroneckera. Uwzględniając definicję wektora wejściowego \(\mathbf{x}\) dla chwili \(k\) uzyskuje się
| \(\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=N+1}^{N+K} \frac{d v_{m-N}(k-1)}{d w_{\alpha \beta}^{(1)}} w_{j m}^{(1)}\right]=\frac{d f_1\left(u_j\right)}{d u_j}\left[\delta_{j \alpha} x_\beta+\sum_{m=1}^K \frac{d v_m(k-1)}{d w_{\alpha \beta}^{(1)}} w_{j, m+N}^{(1)}\right]\) | (10.12) |
Podstawienie tej zależności do wzoru (10.10) umożliwia obliczenie pochodnych funkcji celu względem wag warstwy ukrytej dla każdej chwili \(k\). Należy zauważyć, że jest to wzór rekurencyjny, określający pochodną w chwili \(k\) w uzależnieniu od jej wartości w chwili poprzedzającej \((k-1)\). Wartości startowe wszystkich pochodnych dla chwili początkowej \(k=0\) przyjmuje się zwykle zerowe. Podsumowując, algorytm uczenia sieci Elmana można przedstawić w następującej postaci:
-
Uczenie rozpocząć od przypisania wszystkim wagom losowych wartości wstępnych. Zwykle przyjmuje się rozkład równomierny, zawierający się w pewnym przedziale wartości, np. \((-1, 1)\).
-
Dla kolejnych chwil czasowych \(k ;\ (k = 0, 1, 2,\ldots)\) określić stan wszystkich neuronów w sieci (sygnały \(v_i\) oraz \(y_i\) w odpowiedzi na pobudzenia wchodzące w skład par uczących. Na tej podstawie wyznaczyć wektor wejściowy \(\mathbf{x}(k)\) dla kolejnej chwili \(k\) (aż do ustabilizowania się odpowiedzi sieci) dla każdej pary danych uczących.
-
Określić wektor błędów dopasowania \(\mathbf{e}(k)\) dla neuronów warstwy wyjściowej w postaci różnic między aktualnymi i zadanymi wartościami sygnałów neuronów wyjściowych.
-
Wyznaczyć wektor gradientu funkcji celu względem wag warstwy wyjściowej i ukrytej, korzystając ze wzorów (10.8) i (10.10).
-
Dokonać uaktualniania wag sieci według zależności (10.9) wynikającej z przyjętej metody wyznaczania kierunku
-
dla neuronów warstwy wyjściowej sieci
-
| \(w_{\alpha \beta}^{(2)}(k+1)=w_{\alpha \beta}^{(2)}(k)+\eta p_{\alpha \beta}^{(2)}(k)\) | (10.13) |
-
dla neuronów warstwy ukrytej sieci
| \(w_{\alpha \beta}^{(1)}(k+1)=w_{\alpha \beta}^{(1)}(k)+\eta p_{\alpha \beta}^{(1)}(k)\) | (10.14) |
Po uaktualnieniu wartości wag następuje powrót do punktu 2 algorytmu dla kolejnej chwili \(k\) aż do ustabilizowania się wartości wag.
W celu uproszczenia oznaczeń przy wyprowadzaniu wzorów adaptacji sieci założono istnienie jednej pary uczącej (wersja algorytmu on-line), w której adaptacja wag następowała po prezentacji każdej pary uczącej \((\mathbf{x}, \mathbf{d})\). Zwykle znacznie skuteczniejszy jest algorytm off-line, w którym adaptacja wag zachodzi dopiero po prezentacji wszystkich par uczących. Realizacja takiej wersji algorytmu jest analogiczna do przedstawionej uprzednio, z tą różnicą, że należy zsumować składowe gradientu od kolejnych par uczących, a proces zmiany wag przeprowadzić każdorazowo dla pełnego zbioru danych uczących.
Omówiony algorytm należy do grupy algorytmów nielokalnych, w których adaptacja jednej wagi wymaga znajomości wartości wszystkich pozostałych wag sieci oraz sygnałów poszczególnych neuronów. Jego wymagania co do pamięci komputera są dodatkowo zwiększone potrzebą przechowywania wszystkich wartości pochodnych \(\frac{d v_j(k)}{d w_{\alpha \beta}^{(1)}}\) odpowiadających poprzednim chwilom czasowym. Pomimo tego sieć rekurencyjna może być konkurencyjna w stosunku do sieci jednokierunkowej MLP, gdyż jej złożona struktura układowa jest w stanie zaadaptować się do wymagań uczących przy znacznie mniejszej liczbie neuronów ukrytych (mniejsza złożoność sieci), pozwalając uzyskać lepsze zdolności generalizacji.
10.1.3 Program uczący sieci Elmana
Przy projektowaniu programu uczącego sieci Elmana wykorzystano toolbox "Neural Network" i inne funkcje wbudowane w programie Matlab [46,43]. Pakiet programów nosi nazwę ELMAN.m (nazwa pliku uruchomieniowego). Uruchomienie programu następuje w oknie komend Matlaba po napisaniu nazwy Elman. Pojawi się wówczas menu główne przedstawione na rys. 10.2.

W lewej części menu znajdują się: pole do zadawania danych uczących (pole Dane uczące), oraz testujących, nie uczestniczących w uczeniu (pole Dane testujące). Wczytywanie danych może odbywać się z jednego pliku z rozszerzeniem .mat grupującego wszystkie 4 grupy danych (macierz zawierająca wektory uczące \(\mathbf{x}_u\), macierz zawierająca uczące wektory zadane \(\mathbf{d}_u\), macierz zawierająca wektory testujące \(\mathbf{x}_t\), macierz zawierająca testujące wektory zadane \(\mathbf{d}_t\). Można również wczytać uprzednio zapamiętaną sieć (przycisk Wczytaj sieć).
Definiowanie struktury sieciowej odbywa się w polu środkowym menu (pole Struktura sieci). Można wybrać liczbę neuronów w warstwie ukrytej (sieć zawiera tylko jedną warstwę ukrytą) jak również rodzaj funkcji aktywacji neuronów. Dostępne są następujące funkcje: liniowa (Lin), sigmoidalna jedno polarna (Sigm) oraz sigmoidalna bipolarna (Bip). Liczba węzłów wejściowych oraz neuronów wyjściowych są automatycznie wyznaczane na podstawie wymiaru wektorów \(\mathbf{x}\) oraz \(\mathbf{d}\) i użytkownik nie może ich zmienić.
W praktycznej implementacji algorytmu uczenia sieci Elmana zastosowano metodę adaptacji wag typu off-line, wykorzystując te same algorytmy uczenia co dla sieci MLP. Różnią je metody określania gradientu (w sieci Elmana istnieje konieczność pamiętania wektora gradientu z poprzednich cykli uczących). Przy zastosowaniu w programie adaptacyjnego współczynnika uczenia ? dopasowującego się do aktualnych zmian wartości funkcji celu w procesie uczenia uzyskuje się sprawne narzędzie, które pozwala na skuteczne przeprowadzenie uczenia sieci odwzorowującej złożone procesy dynamiczne.
10.1.4 Przykładowe zastosowania sieci Elmana w prognozowaniu zapotrzebowania na energię elektryczną
Sieć Elmana jest siecią rekurencyjną o sprzężeniu zwrotnym z warstwy ukrytej do warstwy wejściowej. Ze względu na bezpośredni wpływ sygnałów z chwili (n-1) na stan wymuszenia w n-tej chwili, sieć taka ma naturalną predyspozycję do modelowania ciągów czasowych. Oznacza to, że sieć tego rodzaju może znaleźć zastosowanie w prognozowaniu. Tutaj przedstawimy zastosowanie sieci Elmana do prognozowania profilu 24-godzinnego zapotrzebowania na energię elektryczną w Polskim Systemie Elektroenergetycznym (PSE) z wyprzedzeniem jednodniowym.
Problem predykcji wektora 24-elementowego należy do zadań trudnych ze względu na duże zmiany obciążeń godzinnych nawet w obrębie sąsiednich dni i godzin. Na rys. 10.3 przedstawiono typowy rozkład obciążeń względnych (odniesionych do wartości średniej) w PSE w przeciągu ostatnich 3 lat. Widoczne są znaczne zmiany obciążeń od wartości 0,6 do 1.4 (w wartościach względnych). Przy średnim obciążeniu rzeczywistym na poziomie \(P_m=16019MW\) odchylenie standardowe było równe \( \sigma=2800MW\). Tak duży stosunek odchylenia standardowego do wartości średniej jest miara skali trudności w prognozie.
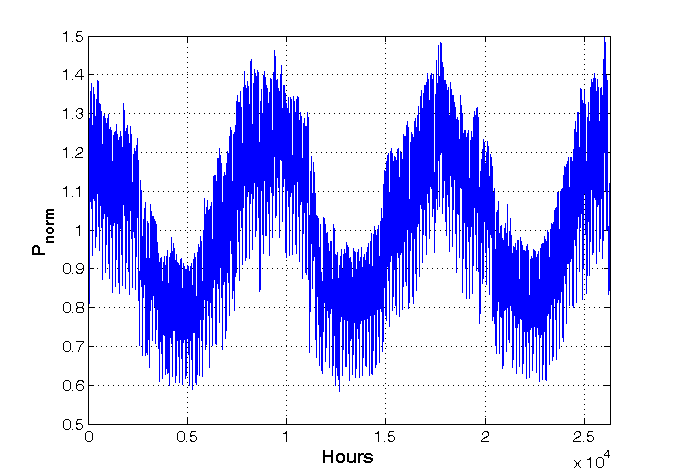
W prognozie wartości względnych obciążeń zastosowano sieć Elmana. Wielkościami wejściowymi (zewnętrznymi) dla sieci prognozującej były
-
Znormalizowane obciążenia ostatnich 4 godzin tego samego dnia oraz 5 godzin z 3 ostatnich dni (4 godziny wstecz i godzina aktualnej prognozy) - w sumie 19 składowych
-
Kod pory roku: 00 – wiosna, 01 - lato, 10 – jesień, 11 – zima – w sumie 2 składowe
-
Kod typu dnia: 11 – dni robocze, 10 – soboty, 01 – piątki, 00 –niedziele i święta - w sumie 2 składowe
Wektor wejściowy zewnętrzny zawierał więc 23 składowe. Neurony w warstwie ukrytej były sigmoidalne, a ich liczba ustalona w wyniku eksperymentów wstępnych równa 8. Liczba neuronów w warstwie wyjściowej była równa liczbie godzin dla których dokonywano prognozy (24). Funkcja aktywacji tych neuronów była liniowa. Strukturę sieci zastosowanej w prognozie można więc zapisać w postaci 23-8-24.
Sieć poddano uczeniu na danych odpowiadających obciążeniom z 2 lat. Po nauczeniu parametry sieci zostały zamrożone i sieć poddano testowaniu na danych z jednego roku (365 dni odpowiadających 8760 godzinom). Wyniki testów zostały porównane ze znanymi wartościami rzeczywistymi dla tych samych godzin. W wyniku porównania określono następujące rodzaje błędów:
-
średni błąd procentowy (MAPE)
| \( M A P E=\frac{1}{n} \sum_{h=1}^n \frac{|P(h)-\widehat{P}(h)|}{|P(h)|} \cdot 100 \% \) | (10.15) |
gdzie \(n\) oznacza liczbę godzin biorących udział w prognozie (u nas 8760 godzin), \(P(h)\) – obciążenie rzeczywiste w godzinie \(h\), a \(\widehat{P}(h)\) obciążenie prognozowane na tę godzinę.
-
błąd średniokwadratowy (MSE)
| \(M S E=\frac{1}{n} \sum_{h=1}^n[P(h)-\widehat{P}(h)]^2\) | (10.16) |
-
znormalizowany błąd średniokwadratowy (NMSE)
| \(NMSE=\frac{MSE}{[\operatorname{mean}(P)]^2}\) | (10.17) |
gdzie \(\operatorname{mean}(P)\) oznacza wartość średnią obciążenia występującą w okresie prognozy.
-
maksymalny błąd procentowy (MAXPE)
| \(MAXPE=\max \left\{\frac{|P(h)-\widehat{P}(h)|}{|P(h)|} \cdot 100 \%\right\}\) | (10.18) |
Tabela 10.1 przedstawia uzyskane wyniki prognozy profilu 24-godzinnego obciążeń w PSE dla jednego roku w postaci błędów średnich. Dane poddane prognozie nie uczestniczyły w uczeniu
Tabela 10.1 Wyniki prognozy profilu 24-godzinnego obciążenia w PSE w postaci różnych rodzajów błędów dla sieci Elmana
|
MAPE [%] |
MAXPE [%] |
MSE [MW2] |
NMSE |
|
2.26 |
24.95 |
3.14e5 |
1.22e-3 |
Dla porównania wzrokowego jakości systemu prognozy na rys. 10.4 przedstawiono nałożone na siebie wartości prognozowane oraz rzeczywiste obciążeń godzinnych dla jednego wybranego tygodnia. Jak widać prognoza dobrze śledzi wartości rzeczywiste.

4.2. Sieć głęboka LSTM
10.2.1 Wprowadzenie
Sieci rekurencyjne LSTM dopuszczają sprzężenia zwrotne między neuronami jedynie w warstwie ukrytej. Typowy przykład takiej struktury zawierającej sprzężenia zwrotne jedynie między neuronami ukrytymi w warstwie przedstawiono na rys. 10.5 [58].
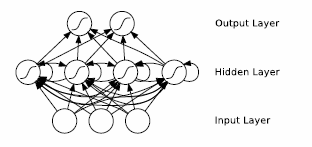
Sygnał wyjściowy neuronu zależy nie tylko od pobudzenia w danej chwili, ale również od stanu neuronów w chwili poprzedniej. Można to przedstawić w postaci rozłożonej w czasie jak na rys. 10.6 [19], w której sprzężenie zostało zamienione na przepływ jednokierunkowy sygnałów z uwzględnieniem kolejnych chwil czasowych. Stan neuronów w kolejnych chwilach: \(t, t+1, t+2\) aż do końca okna pomiarowego \(T\) zależy również od ich stanu w chwilach wcześniejszych. Układ taki można więc traktować jako sieć głęboką.
|
|
\( t \qquad t+1 \qquad t+2 \qquad t \rightarrow T \) |
|
Warstwa wyjściowa Warstwa ukryta Warstwa wejściowa |
|
W uczeniu takiej sieci występuje problem tak zwanego zanikającego gradientu. W kolejnych chwilach czasowych zależność funkcji gradientu od sygnału wejściowego sprzed poprzednich chwil czasowych powoli zanika, co powoduje utratę pewnej ilości informacji pierwotnie dostarczonej do sieci. Ten efekt może być zilustrowany jak na rys. 10.7. Stopień zaczernienia węzłów ilustruje wpływ sygnału wejściowego z chwili \(t=1\) na stan neuronów w chwilach późniejszych (im bardziej ciemny kolor tym większy wpływ). Klasyczne rozwiązanie sieci rekurencyjnej nie gwarantuje więc dobrego zapamiętania wcześniej wytrenowanych wzorców. Oznacza to utratę informacji, która była wprowadzona we wcześniejszych etapach uczenia sieci.
Skuteczne rozwiązanie tego problemu było możliwe dzięki wprowadzeniu specjalizowanej struktury rekurencyjnej, zwanej siecią Long Short-Term Memory (w skrócie LSTM) [58].
| Warstwa wyjściowa |
 |
| Warstwa ukryta | |
| Sygnały wejściowe |
10.2.2 Zasada działania sieci LSTM
Sieć ta należy do sieci rekurencyjnych o strukturze specjalnie dostosowanej do długiego zapamiętywania krótkich wzorców (short term). Składa się z wielu rekurencyjnie połączonych bloków zwanych blokami pamięciowymi [58]. Każdy taki blok zawiera trzy bramki multiplikatywne: wejściową, wyjściową oraz pamięci, pełniące rolę sterowanych zaworów. Typowa struktura komórki bloku pamięciowego używanej w LSTM przedstawiona jest na rys. 10.8.
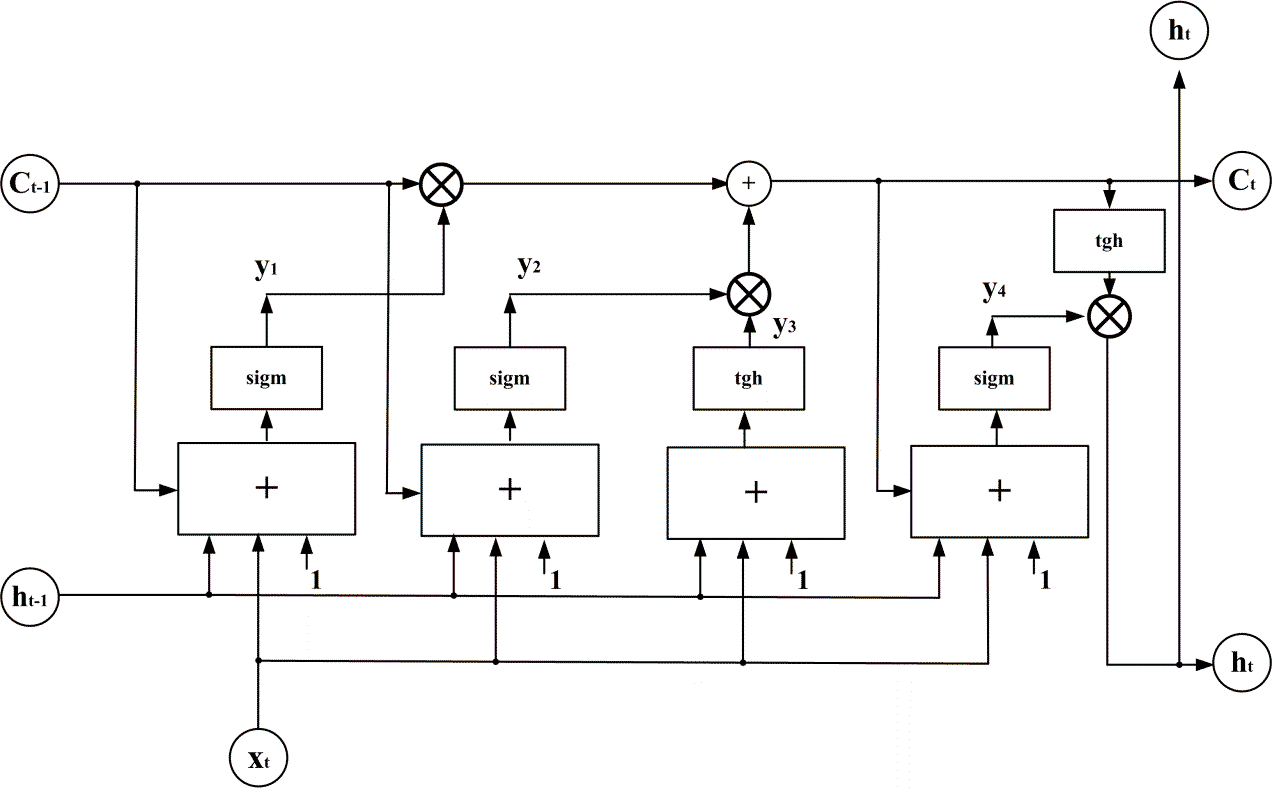
Komórka pamięciowa zawiera trzy wejścia. Są to
Xt – sygnał wejściowy w aktualnej chwili czasowej t
Ct-1 – sygnał pamięci z chwili t-1 poprzedniej komórki pamięci
ht-1 – sygnał wyjściowy z chwili t-1 poprzedniej komórki pamięci
Jednocześnie komórka ta wytwarza dwa rodzaje sygnałów wyjściowych istotnych z punktu widzenia współdziałania komórek ze sobą. Są to
Ct – sygnał pamięci w aktualnej chwili czasowej t danej komórki pamięci
ht – sygnał wyjściowy w aktualnej chwili czasowej t danej komórki pamięci; jest to sygnał wyjściowy neuronu ukrytego podawany na warstwę wyjściową neuronów sieci.
Komórka przetwarza nieliniowo zarówno aktualny sygnał wejściowy podany na jej wejście jak i sygnały wyjściowe oraz pamięci z chwili poprzedniej wszystkich bloków z którymi jest sprzężona. Struktura przepływu sygnałów w dwu kolejnych chwilach czasowych dla sieci LSTM dla jednej komórki może być przedstawiona jak na rys. 10.9.
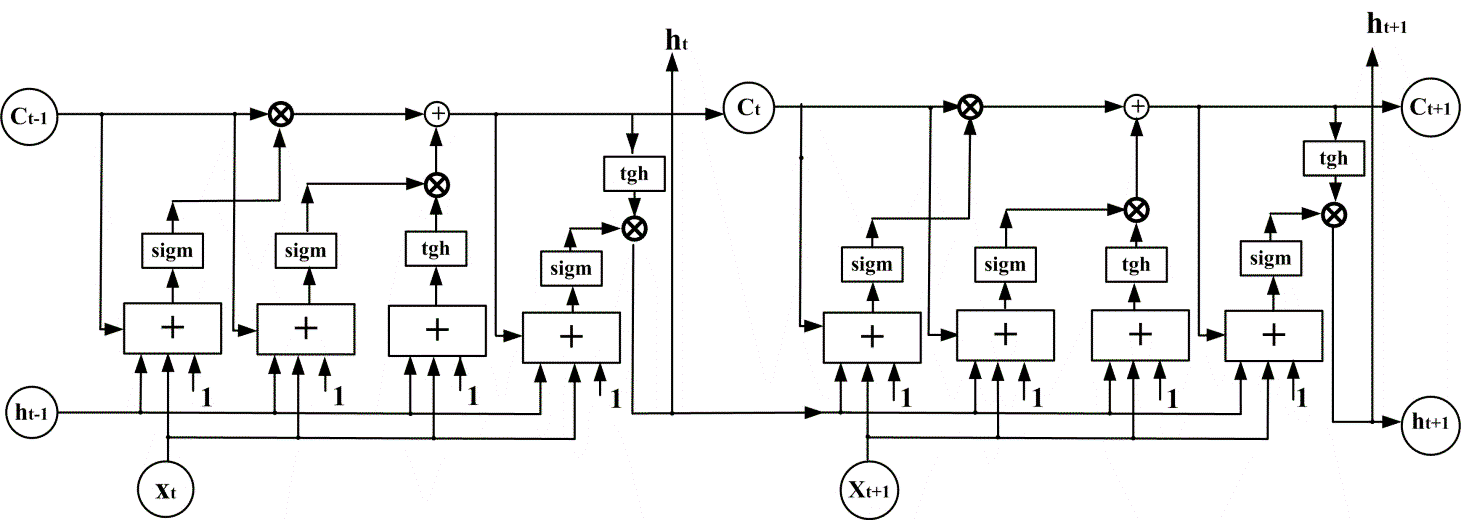
Bardzo istotną rolę w przetwarzaniu sygnałów odgrywają bramki multiplikatywne, oznaczone symbolem ×. Górna bramka z lewej strony komórki jest sterowaną bramką (zaworem) pamięci. Decyduje o tym jaka część pamięci z poprzedniej chwili czasowej przejdzie do chwili następnej. Stanowi zatem regulowany system zaworowy, który przepuszcza w określonym stopniu (od zera do 1) informację zawartą w pamięci z chwili poprzedniej. O poziomie przejścia tej zawartości decyduje sygnał wytworzony przez warstwę neuronową sigmoidalną, widoczną z lewej strony modelu.
Druga bramka (symbol środkowy ×) stanowi następny regulowany zawór nowej pamięci i uczestniczy w wytworzeniu zawartości pamięci Ct dla aktualnej chwili czasowej. Stanowi sterowane połączenie nowo wytworzonego stanu pamięci i pamięci poprzedniej Ct-1, która została przepuszczona przez zawór pierwszy. Połączenie tych informacji następuje w bloku sumatora. W efekcie takiej operacji stara zawartość pamięci Ct-1 zostaje zamieniona na nową Ct.
Poszczególne zawory mają swoje wymuszenia i sygnały wyjściowe. Zawór pamięci jest sterowany poprzez jednowarstwową sieć neuronową o sigmoidalnej (jedno-polarnej) funkcji aktywacji. Sygnały wejściowe dla tej warstwy stanowią: Xt – sygnał wejściowy w aktualnej chwili czasowej t, Ct-1 – sygnał pamięci z chwili t-1 poprzedniej komórki pamięci, ht-1 – sygnał wyjściowy z chwili t-1 poprzedniej komórki pamięci oraz sygnał polaryzacji. Sumacyjny sygnał wyjściowy zaworu pamięci po przetworzeniu sigmoidalnym mnożony jest z sygnałem pamięci z chwili poprzedniej i stanowi dla niej współczynnik z jakim poprzednia pamięć przechodzi do następnej chwili czasowej.
Drugi zawór reprezentowany przez środkowy mnożnik × decyduje o nowym stanie pamięci Ct w chwili t i jest nazywany zaworem nowej pamięci. Składa się z dwu równolegle działających warstw neuronowych. Pierwsza warstwa sigmoidalna jedno-polarna przyjmuje identyczne wymuszenia jak warstwa neuronowa w zaworze pamięci (Xt, Ct-1, ht-1 i polaryzacja) i stanowi przetworzoną zawartość starej pamięci. Druga warstwa operuje jedynie sygnałami Xt, ht-1 oraz polaryzacją, a więc nie zależy od zawartości starej pamięci. Funkcja aktywacji tej warstwy jest sigmoidą bipolarną realizowaną przez funkcję tangensa hiperbolicznego. Mnożnik decyduje o wpływie starej pamięci na stan wyjściowy tego zaworu, który będzie następnie dodany do zawartości starej pamięci wychodzącej z bloku pamięci (symbol sumatora) tworząc aktualny (w chwili t) stan pamięci Ct.
Ostatnią operacją komórki pamięciowej jest wytworzenie sygnału wyjściowego ht w aktualnej chwili czasowej t. Sygnał wyjściowy komórki jest iloczynem dwu sygnałów: aktualnego sygnału pamięci Ct przepuszczonego przez funkcję sigmoidalną bipolarną oraz sygnału wyjściowego z warstwy neuronowej zasilonej poprzez Xt, ht-1 oraz polaryzację. System ten stanowi zawór wyjściowy komórki, decydujący o tym jak duża porcja nowej pamięci zostanie przekazana na wyjście komórki, czyli sygnału komórki, który zasili komórkę w następnej chwili czasowej.
W efekcie wysterowania poszczególnych zaworów możliwe jest przepuszczenie lub zablokowanie określonej porcji informacji z chwil poprzednich. Na rys. 10.10 zilustrowano możliwy wpływ informacji dostarczonej do sieci w chwili t1 na stan komórki w następnych chwilach czasowych. Symbol „o” oznacza pełne otwarcie zaworu a symbol „–„ pełne zamknięcie. Stan wyjścia komórek w poszczególnych chwilach czasowych w zależności od informacji z chwili t1 jest funkcją otwarcia lub zamknięcia odpowiednich zaworów i ilustrowany ciemnym stanem węzła (informacja przechodzi) lub jasnym (przepływ informacji zablokowany).

10.2.3 Uczenie sieci LSTM
W procesie uczenia doborowi podlegają wagi poszczególnych połączeń sieci poprzez minimalizację funkcji błędu na danych uczących w postaci par (wielkość wejściowa x i wielkość zadana na wyjściu d) określonych w kolejnych chwilach czasowych. Minimalizacja odbywa się metodą gradientową przy generacji gradientu poprzez zastosowanie propagacji wstecznej. Sygnały wejściowe przesyłane są najpierw wprzód (w obrębie przyjętego okna czasowego T) a następnie błąd na wyjściu w poszczególnych chwilach czasowych przesyłany jest w kierunku odwrotnym (od wyjścia do wejścia). Na tej podstawie generowane są składniki gradientu względem poszczególnych wag sieci, podobnie jak odbywało się to w klasycznych sieciach neuronowych.
Przyjmijmy oznaczenia wskaźnikowe jak na rys. 10.8. Poszczególne warstwy neuronowe charakteryzowane są poprzez macierze wagowe opisane za pomocą dwu wskaźników: pierwszy pochodzi od numeru przypisanego warstwie, drugi od symbolu wielkości wejściowej dla tej warstwy. Przykładowo w1h oznacza macierz wagową pierwszego zaworu przetwarzającą sygnały wyjściowe komórki ht-1 z poprzedniej chwili wagowej. Funkcja sigmoidalna oznaczona jest symbolem sigm a symbol tgh oznacza funkcję tangensa hiperbolicznego. Wektory sygnałowe w poszczególnych punktach komórki są wyrażone wzorami [58]
| \( \mathbf{y}_1=\operatorname{sigm}\left(\mathbf{W}_{1 c} \mathbf{c}_{\mathbf{t}-1}+\mathbf{W}_{1 h} \mathbf{h}_{t-1}+\mathbf{W}_{1 x} \mathbf{x}_t+\mathbf{w}_{10}\right) \) | (10.19) |
| \(\mathbf{y}_2=\operatorname{sigm}\left(\mathbf{W}_{2 c} \mathbf{c}_{t-1}+\mathbf{W}_{2 h} \mathbf{h}_{t-1}+\mathbf{W}_{2 x} \mathbf{x}_t+\mathbf{w}_{20}\right) \) | (10.20) |
| \(\mathbf{y}_3=\operatorname{tgh}\left(\mathbf{W}_{3 h} \mathbf{h}_{t-1}+\mathbf{W}_{3 x} \mathbf{x}_t+\mathbf{w}_{30}\right) \) | (10.21) |
| \(\mathbf{y}_4=\operatorname{sigm}\left(\mathbf{W}_{4 c} \mathbf{c}_t+\mathbf{W}_{4 h} \mathbf{h}_{t-1}+\mathbf{W}_{4 x} \mathbf{x}_t+\mathbf{w}_{40}\right) \) | (10.22) |
Na tej podstawie tworzone są: stan pamięciowy komórki ct oraz sygnał wyjściowy komórki ht (oba w chwili t). Są one określone wzorami
| \(\mathbf{c}_t=y_2 \cdot y_3+c_{t-1} y_1\) | (10.23) |
| \(\mathbf{h}_t=\boldsymbol{y}_4 \cdot \operatorname{tgh}\left(\mathbf{c}_t\right)\) | (10.24) |
Przetwarzanie wsteczne sygnałów odbywa się w identyczny sposób jak w metodzie klasycznej propagacji wstecznej (odwrócenie kierunku przepływu przy tych samych wartościach wag gałęzi liniowej i zastąpieniu funkcji aktywacji poprzez wartość pochodnej w punkcie pracy sieci o normalnym kierunku przepływu). W przypadku węzła realizującego mnożenie korzysta się z zależności pochodnej iloczynu, zgodnie z którą, jeśli sygnał y jest iloczynem dwu sygnałów v1 i v2, \(y=v_1(w) \cdot v_2(w)\) to
| \(\frac{d y}{d w}=v_1 \frac{d v_2}{d w}+v_2 \frac{d v_2}{d w}\) | (10.25) |
Pełna informacja o gradiencie jest sumą pochodnych po wszystkich krokach czasowych wykonanych wewnątrz okna pomiarowego T. W uczeniu wykorzystuje się z reguły metodę stochastyczną największego spadku z momentem rozpędowym (SGD) lub metodykę ADAM.
10.2.4 Przykład zastosowania sieci LSTM w prognozowaniu zanieczyszczeń atmosferycznych
W tym punkcie pokazane zostanie zastosowanie sieci LSTM do prognozowania godzinnych zmian poziomu 4 zanieczyszczeń atmosferycznych (PM10, SO2, NO2, and ozon) [47]. Prognozowanie poziomu zanieczyszczeń należy do zadań trudnych, ze względu na znaczne różnice występujące między sąsiednimi godzinami tego samego dnia. Widać to wyraźnie na wartościach statystycznych dotyczących tych zanieczyszczeń dla danych zmierzonych w Warszawie (dzielnica Ursynów) pokazanych w tabeli 10.2.
Table 10.2. Parametry statystyczne zanieczyszczeń atmosferycznych poddanych predykcji
|
|
PM10 |
SO2 |
NO2 |
Ozon |
|
Mean \([ \mu g/ m^3 ] \) |
33.56 |
9.89 |
24.82 |
48.43 |
|
Std/mean [%] |
78.20 |
88.82 |
71.92 |
64.20 |
|
Max \([ \mu g/ m^3 ] \) |
414.91 |
57.84 |
203.86 |
189.12 |
|
Min \([ \mu g/ m^3 ] \) |
0.70 |
0.71 |
0.42 |
0.09 |
W rozwiązaniu problemu predykcji zastosowano sieć LSTM o 4 neuronach wyjściowych (każdy odpowiedzialny za predykcję określonego typu zanieczyszczenia). Jako wejście dla sieci (wektor x) zastosowano następujące wielkości: PM10, SO2, NO2, OZON, szybkość wiatru, kierunek wiatru, temperaturę, promieniowanie słoneczne, wilgotność, składowe prędkości wiatru w osi x i y (wszystkie znane wielkości z godziny poprzedzającej predykcję). Liczba neuronów ukrytych zastosowana w strukturze sieci była równa 500. W uczeniu zastosowano metodę ADAM.
Dla zwiększenia dokładności predykcji zastosowano zespół sieci złożony ze struktur LSTM różniących się liczbą neuronów ukrytych (od 300 do 700), wartością „dropout ratio” jak również składem zbioru danych uczących (wybieranych losowo z bazy danych) dla każdej sieci. Procedurę uczenia i testowania na tym samym zbiorze danych testujących powtórzono 5 razy. Wynik zespołu jest średnią arytmetyczną wyników poszczególnych jednostek LSTM.
W tabeli 10.3 przedstawiono wyniki działania systemu przy predykcji pyłów PM10. Wyniki dotyczą takich miar jakości, jak MAPE, MAE, RMSE, MPSE oraz R. MPSE jest zmodyfikowaną wersją MAPE, w której porównuje się normy wektora błędów w stosunku do normy wielkości rzeczywistych – tego typu modyfikacja jest istotna przy bardzo małych (zbliżonych do zera wartości rzeczywistych zanieczyszczenia). Pozytywny wpływ zespołu jest widoczny, choć niezbyt imponujący.
Tabela 10.3. Wyniki predykcji pyłu PM10 (predykcja z wyprzedzeniem godzinnym) [47]
|
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
Średnia członków zespołu |
13.86 |
4.27 |
7.40 |
11.91 |
0.9649 |
|
Zespół |
13.70 |
4.11 |
7.36 |
11.74 |
0.9653 |
Na rys. 10.11 przedstawiono wyniki predykcji porównane z wartościami prawdziwymi (wykres górny) oraz błąd względny predykcji w poszczególnych godzinach.
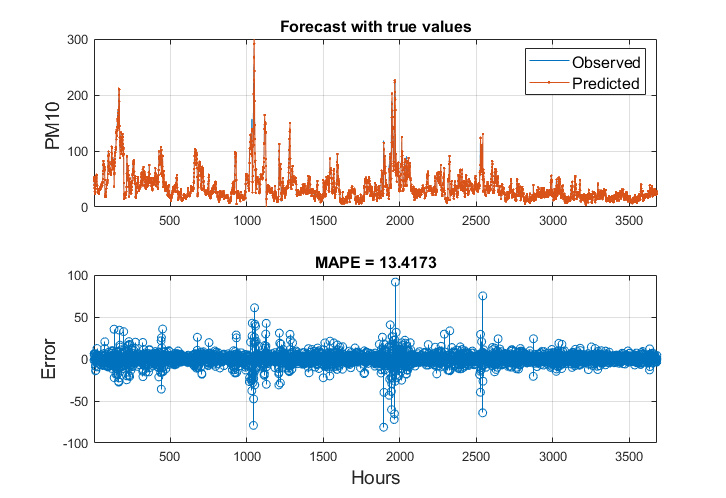
Na rys. 10.12 przedstawiono nałożone na siebie wykresy wielkości rzeczywistych i prognozowanych PM10 dla 120 godzin dla uwypuklenia szczegółów przebiegów podlegających prognozowaniu.
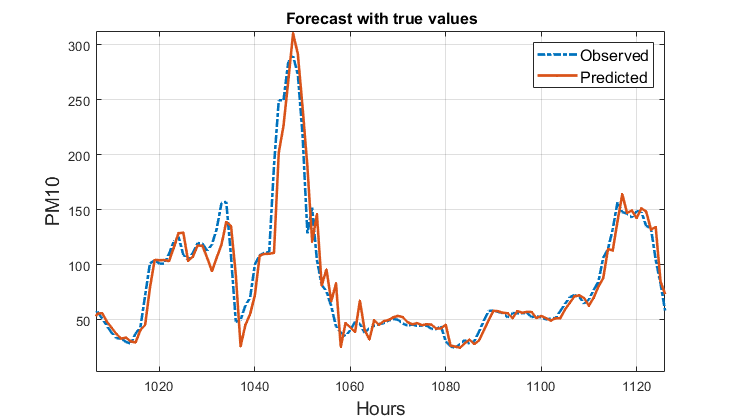
W tabeli 10.4 przedstawiono wyniki predykcji dotyczące pozostałych 3 rodzajów zanieczyszczeń. Podobnie jak w przypadku PM10 wyniki zespołu są na wyższym poziomie niż średnia wyników indywidualnych sieci bez ich fuzji.
Tabela 10.4. Wyniki statystyczne dotyczące predykcji zanieczyszczeń SO2, NO2 ozonu in przy prognozie z wyprzedzeniem 1-godzinnym
|
Zanieczyszczenie |
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
SO2 |
Średnia członków zespołu |
23.48 |
2.22 |
4.40 |
22.20 |
0.8488 |
|
Zespół |
22.82 |
2.15 |
4.30 |
21.52 |
0.8556 |
|
|
NO2 |
Średnia członków zespołu |
19.95 |
4.21 |
6.72 |
17.62 |
0.9157 |
|
Zespół |
19.53 |
4.13 |
6.63 |
17.30 |
0.9180 |
|
|
Ozon |
Średnia członków zespołu |
26.00 |
5.81 |
8.62 |
11.24 |
0.9592 |
|
Zespół |
25.93 |
5.79 |
8.60 |
11.31 |
0.9593 |
Ostatni eksperyment dotyczył predykcji średniodobowych wartości zanieczyszczeniaPM10. Zastosowano zespół 5 sieci LSTM zbudowany na identycznej zasadzie jak w przypadku prognozy godzinnej. Wyniki statystyczne poszczególnych członków zespołu przed integracją i po integracji w zespole przedstawiono w tabeli 10.5. Tym razem widoczna jest znacząca poprawa wyników zespołu w stosunku do średniej jej członków przed fuzją. Przykładowo, wartość błędu MAPE została zredukowana z 8.11% do 7.29% (ponad 10% poprawa względna).
Table 10.5. Wyniki statystyczne predykcji średniodobowej dla pyłu PM10
|
Zanieczyszczenie |
|
MAPE [%] |
MAE \([ \mu g/ m^3 ] \) |
RMSE \([ \mu g/ m^3 ] \) |
MPSE [%] |
R |
|
PM10 |
Średnia członków zespołu |
8.11 |
2.98 |
3.23 |
9.03 |
0.7975 |
|
Zespół |
7.29 |
2.33 |
2.88 |
8.84 |
0.8394 |
4.3. Zadania i problemy
1. Narysować strukturę sieci Elmana zawierającej 3 wejścia zewnętrzne, 5 neuronów ukrytych i 4 neurony wyjściowe. Zdefiniować wektor wejściowy takiej sieci z uwzględnieniem warstwy kontekstowej. Napisać wzór opisujący sygnał wyjściowy dowolnego neuronu i-tego w warstwie wyjściowej.
3. Narysować strukturę sieci rekurencyjnej ze sprzężeniem zwrotnym pochodzącym od neuronów wyjściowych (4 neurony) do warstwy ukrytej zawierającej 3 neurony. Warstwa wejściowa sieci zawiera 2 węzły wejściowe. Napisać wzór określający sygnał dowolnego neuronu wyjściowego.
3. Wykorzystując zbiór danych dotyczących zmian obciążeń 24-godzinnych w PSE (zbiór PSE.mat) wygenerować dane uczące i testujące obejmujące wszystkie pory roku dla predykcji kolejnych wartości 24-godzinnych. Tak przygotowany zbiór wykorzystać w uczeniu i testowaniu sieci Elmana odwzorowującej procesy zmian obciążeń. Dobrać optymalną liczbę neuronów ukrytych.
4. Wykorzystując sieć Elmana dokonać predykcji średnich płac miesięcznych na podstawie jedynie zmian wartości tej zmiennej w przeszłości (biorąc pod uwagę np. kilka ostatnich miesięcy jako zmienne wejściowe dla sieci). Wykorzystać dane statystyczne dla Polski (strona internetowa GUS http://www.stat.gov.pl/). Skomentować wyniki predykcji pod względem dokładności w stosunku do wartości rzeczywistych.
5. Wykorzystując sieć LSTM dokonać predykcji zanieczyszczeń atmosferycznych. Wykorzystać dane rozkładu zanieczyszczeń zgromadzone w pliku pollution.mat
4.4. Słownik
Słownik opanowanych pojęć
Wykład 10
Sieci rekurencyjne – sieci neuronowe ze sprzężeniem zwrotnym.
Sieć Elmana – sieć rekurencyjna ze sprzężeniem zwrotnym od warstwy ukrytej do wejścia.
Program Elman – interfejs graficzny w Matlabie do eksperymentów z siecią Elmana.
LSTM – sieć rekurencyjna ze sprzężeniem zwrotnym między neuronami ukrytymi w warstwie, stosujące specjalny sposób przetwarzania danych pozwalający długo pamiętać krótkie frazy. Stosowana głównie w predykcji szeregów czasowych.
Komórka LSTM – struktura komórki bloku pamięciowego używanej w LSTM.
Bramka multiplikatywna - regulowany zawór pamięci w komórce LSTM.
Zanieczyszczenia atmosferyczne – zanieczyszczenia powietrza cząsteczkami składników zanieczyszczeń, np. PM10, SO2, NO2.
Predykcja szeregów czasowych – przewidywanie następnych wartości szeregu na podstawie wartości z chwil poprzednich.
5. Literatura
1. Bengio Y., LeCun Y., Hinton G., Deep Learning, Nature, 2015, vol. 521, pp. 436–444.
2. Brownlee J., Deep Learning for Natural Language Processing. Develop Deep Learning Models for your Natural Language Problems, Ebook, 2018.
3. Breiman L., Random forests, Machine Learning, 2001, vol. 45, No 11, pp. 5–32.
4. Banerjee S., Linear algebra and matrix analysis for statistics, 2012, London.
5. Brudzewski K., Osowski S., Markiewicz T., Ulaczyk J., Classification of gasoline with supplement of bio-products by means of an electronic nose and SVM neural network, Sensors and Actuators - Chemical, 2006, vol. 113, No 1, pp. 135-141.
6. Chen S., Cowan C.F., Grant P.M., Orthogonal least squares learning algorithm for radial basis function networks, IEEE Trans. Neural Networks, 1991, vol. 2, pp. 302–309.
7. Christensen R., Johnson W. O., Branscum A. J., Hanson T. E., Bayesian ideas and data analysis: an introduction for scientists and statisticians, 2010, Chapman & Hall/CRC Science
8. Cichocki A., Amari S. I., Adaptive blind signal and image processing, 2003, Wiley, New York.
9. Crammer K. , Singer Y., On the learnability and design of output codes for multiclass problems. Computational Learning Theory, 2000, pp. 35-46.
10. Duda, R.O., Hart, P.E., Stork, P., Pattern classification and scene analysis, 2003, Wiley, New York.
11. Fogel, L.J., Intelligence through simulated evolution : forty years of evolutionary programming, 1999, Wiley, New York.
12. Fukushima K.: Neocognitron - a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 1980, vol.. 36, No 4, pp. 193–202, doi:10.1007/bf00344251.
13. Genc H., Cataltepe Z., Pearson T., A new PCA/ICA based feature selection method, IEEE 15th In Signal Processing and Communications Applications, 2007, pp. 1-4.
14. Gill P., Murray W., Wright M., Practical optimization, 1981, Academic Press, London.
15. Goldberg D., Algorytmy genetyczne i ich zastosowania, 2003, WNT Warszawa.
16. Golub G., Van Loan C., Matrix computations, 1996, John Hopkins University Press, Baltimore.
17. Gao H., Liu Z., Van der Maaten L., Weinberger K., Densely connected convolutional networks, CVPR, vol. 1, no. 2, p. 3. 2017.
18. Goodfellow I., Bengio Y., Courville A.: Deep learning 2016, MIT Press, Massachusetts (tłumaczenie polskie: Deep Learning. Współczesne systemy uczące się, Helion, Gliwice, 2018).
19. Goodfellow I., Pouget-Abadie J., Mirza M, Xu M., Warde-Farley B., Ozair D., Courville A. Bengio Y., Generative Adversarial Nets (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680.
20. Greff K., Srivastava R. K., Koutník J., Steunebrink B. R., Schmidhuber J., LSTM: A search space odyssey, IEEE Transactions on Neural Networks and Learning Systems, vol. 28, No 10, pp. 2222-2232, 2017.
21. Gunn S., Support vector machines for classification and regression, ISIS Technical report, 1998, University of Southampton.
22. Guyon I., Elisseeff A., An introduction to variable and feature selection, J. Mach. Learn. Res., 2003, vol. 3, pp. 1157-1182.
23. Guyon, I., Weston, J., Barnhill, S., Vapnik, V., Gene selection for cancer classification using Support Vector Machines, Machine Learning, 2002, vol. 46, pp. 389-422.
24. Haykin S., Neural networks, a comprehensive foundation, Macmillan College Publishing Company, 2000, New York.
25. He K., Zhang X, Ren S, Sun J., Deep Residual Learning for Image Recognition, 2015, http://arxiv.org/abs/1512.03385.
26. Hinton G. E., Salakhutdinov R. R., Reducing the dimensionality of data with neural networks, Science, 313:504-507, 2006.
27. Howard A., Zhu M., Chen B., Kalenichenko D., MobileNets: Efficient convolutional neural networks for mobile vision applications, arXiv: 1704.04861v1 [cs.CV], 2017.
28. Hsu, C.W., Lin, C.J., A comparison methods for multi class support vector machines, IEEE Trans. Neural Networks, 2002, vol. 13, pp. 415-425.
29. Huang G., Liu Z., van der Maaten L., Weinberger K., Densely connected convolutional networks, arXiv: 1606.06993v5 [cs.CV] 2018.
30. Iandola F, Han S., Moskevicz M., Ashraf K., Dally W., Keutzer K, Squeezenet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size, Conference ICLR, 20017. pp. 1-13.
31. Joachims T., Making large scale SVM learning practical, (in ”Advances in kernel methods - support vector learning”, B. Scholkopf, C. Burges, A. Smola eds). MIT Press, Cambridge, 1998, pp. 41-56.
32. Kecman V., Support vector machines, neural networks and fuzzy logic models, 2001, Cambridge, MA: MIT Press.
33. Kingma P, Welling M., An introduction to variational autoencoders, Foundations and Trends in Machine Learning, 12:307-392, 2019.
34. Krizhevsky A., Sutskever I., Hinton G., Image net classification with deep convolutional neural networks, Advances in Neural Information Processing Systems, vol. 25, pp. 1-9, 2012.
35. Kruk M., Świderski B., Osowski S., Kurek J., Słowińska M., Walecka I., Melanoma recognition using extended set of descriptors and classifiers, Eurasip Journal on Image and Video Processing, 2015, vol. 43, pp. 1-10, DOI 10.1186/s13640-015-0099-9
36. Kuncheva L., Combining pattern classifiers: methods and algorithms, 2015, Wiley, New York.
37. LeCun Y., Bengio Y., Convolutional networks for images, speech, and time-series. 1995, in Arbib M. A. (editor), The Handbook of Brain Theory and Neural Networks. MIT Press, Massachusetts.
38. Lecture CS231n: 2017, Stanford Vision Lab, Stanford University.
39. Lee K.C., Han I., Kwon Y., Hybrid Neural Network models for bankruptcy prediction, Decision Support Systems, 18 (1996) 63-72.
40. Leś T., Osowski S., Kruk M., Automatic recognition of industrial tools using artificial intelligence approach, Expert Systems with Applications, 2013, vol. 40, pp. 4777-4784.
41. Lin C. J., Chang, C. C., LIBSVM: a library for support vector machines. http://www. csie. ntu. edu. tw/cjlin/libsvm
42. Markiewicz T., Sieci neuronowe SVM w zastosowaniu do klasyfikacji obrazów komórek szpiku kostnego, rozprawa doktorska Politechniki Warszawskiej, 2006.
43. Matlab user manual MathWorks, 2021, Natick, USA.
44. Michalewicz Z., Algorytmy genetyczne + struktury danych = programy ewolucyjne, WNT, Warszawa 1996.
45. Osowski S., Cichocki A., Siwek K., Matlab w zastosowaniu do obliczeń obwodowych i przetwarzania sygnałów, 2006, Oficyna Wydawnicza PW.
46. Osowski S., Sieci neuronowe do przetwarzania informacji, 2020, Oficyna Wydawnicza PW.
47. Osowski S., Szmurło R., Siwek K., Ciechulski T., Neural approaches to short-time load forecasting in power systems – a comparative study, Energies, 2022, 15, pp. 3265.
48. Osowski S., Siwek K., R. Szupiluk, Ensemble neural network approach for accurate load forecasting in the power system, Applied Mathematics and Computer Science, 2009, vol.19, No.2, pp. 303-315.
49. Osowski S., Metody i narzędzia eksploracji danych , Wydawnictwo BTC, Warszawa, 2013
50. Patterson J., Gibson A., Deep Learning: A Practitioner's Approach (tłumaczenie polskie : Deep learning. Praktyczne wprowadzenie), Helion, Gliwice, 2018.
51. Platt L., Fast training of SVM using sequential optimization (in Scholkopf, B., Burges, B., Smola, A., Eds. Advances in kernel methods – support vector learning. Cambridge: MIT Press), 1998, 185-208.
52. Redmon J., Divval S., Girshick R., Farhafi A., You Only Look Once: unified. Real time object detection, axXiv: 1506.02640v5 [cs.CV], 2016
53. Ren S., He K., Girshick R., Sun J., Faster R-CNN: toward real time object detection with region proposal networks, IEEE trans. PAMI, vol. 39, pp. 1137-1149, 2017
54. Riedmiller M., Braun H.: RPROP – a fast adaptive learning algorithm. Technical Report, University Karlsruhe, Karlsruhe 1992.
55. Ridgeway G., Generalized Boosted Models: A guide to the gbm package. 2007
56. Ronneberger O., Fischer P., Brox T.: U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015, arXiv:1505.04597.
57. Sammon J. W., A nonlinear mapping for data structure analysis, IEEE Trans. on Computers, 1969, vol. 18, pp. 401-409.
58. Schmidhuber J., Deep learning in neural networks: An overview, Neural Networks, vol. 61, pp. 85-117, 2015.
59. Schölkopf B., Smola A., Learning with kernels, 2002, MIT Press, Cambridge MA.
60. Schurmann J., Pattern classification, a unified view of statistical and neural approaches, 1996, Wiley, New York.
61. Sandler, M., Howard, A., Zhu, M., Zhmoginov, A. and Chen, L.C. "MobileNetV2: Inverted Residuals and Linear Bottlenecks." In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 4510-4520). IEEE.
62. Swiderski B., Kurek J., Osowski S., Multistage classification by using logistic regression and neural networks for assessment of financial condition of company, Decision Support Systems, 2012, vol. 52, No 2, pp. 539-547
63. Szegedy C, Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., Going deeper with convolutions, arXiv: 1409.4842v1, 2014.
64. Szegedy C, Ioffe S., Vanhoucke V. Inveption-v4, Inception-ResNet and the impact of residual connections on learning, arXiv:1602.07261v2, 2016.
65. Tan P.N., Steinbach M., Kumar V., Introduction to data mining, 2006, Pearson Education Inc., Boston.
66. Tan M. Le Q., EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, arXiv:1905.11946 [cs.LG], 2020
67. Van der Maaten L., Hinton G., Visualising data using t-SNE, Journal of Machine Learning Research, 2008, vol. 9, pp. 2579-2602.
68. Vapnik V., Statistical learning theory, 1998, Wiley, New York.
69. Wagner T., Texture analysis (w Jahne, B., Haussecker, H., Geisser, P., Eds. Handbook of computer vision and application. Boston: Academic Press), 1999, ss. 275-309.
70. Zeiler M. D., Fergus R.: Visualizing and Understanding Convolutional Networks. 2013, pp. 1-11, https://arxiv.org/abs/1311.2901.
71. Zhang X., Zhou X., Lin M., Sun J., ShuffleNet: an extremely efficient convolutional neural network for mobile devices, arXiv: 1707.01083v2 [cs.CV], 2017.
72. Zheng G., Liu S., Zeming F. W., Sun L. J., YOLOX: Exceeding YOLO Series in 2021, arXiv:2107.08430v2 [cs.CV]
73. https://www.analyticsvidhya.com/blog/2021/09/adaboost-algorithm-a-complete-guide-for-beginners/
74. http://www.bsp.brain.riken.jp/ICALAB, ICALAB Toolboxes. A. Cichocki, S. Amari, K. Siwek, T. Tanaka et al.
75. https://github.com/BVLC/caffe/tree/master/models/bvlc_googlenet.
76. https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
77. https://www.jeremyjordan.me/variational-autoencoders/
78. Osowski S., Szmurło R., Matematyczne modele uczenia maszynowego w językach matlab i Python, OWPW, 2023, Warszawa.