Podręcznik
3. Badanie stabilności - przykłady
Aby zbadać stabilność punktu równowagi \( x_0 \) nieliniowego obiektu autonomicznego stosujemy następujący schemat
- określamy zlinearyzowane równania stanu w punkcie równowagi \( x_0 \)
- obliczamy współczynniki wielomianu charakterystycznego
- stosujemy kryterium Hurwitza, aby sprawdzić czy spełnione są warunki (3.24) oraz (3.25)
Zastosujmy powyższy schemat do badania stabilności punktów równowagi autonomicznych, nieliniowych obiektów i układów regulacji.
Równania stanu dla układu trzech
zbiorników ze stałym sterowaniem \( Q_{we}(t) = Q_{we0} \) (obiekt
autonomiczny) mają postać
\( \begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we0} - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.26)\\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(3.27)\\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.28) \end{eqnarray} \)
Równania punktu równowagi mają postać
\(\begin{eqnarray} H_{20} &=& 2H_{30} \qquad(3.29) \\ H_{10} &=& 3H_{30} \qquad(3.30)\\ Q_{we0} &=& \alpha\sqrt{H_{30}} \qquad(3.31) \end{eqnarray}\)
Sterowanie w obiekcie zlinearyzowanym jest równe zero
\(\begin{equation} \tilde{Q}_{we} = Q_we(t) - Q_{we0} = Q_{we0} - Q_{we0} = 0 \qquad(3.32)\end{equation} \)
Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \qquad(3.33)\end{equation} \)
Z równań punktu równowagi wynika, że
\(\begin{eqnarray}H_{10}-H_{20} &=& 3H_{30}-2H_{30} = H_{30} \qquad(3.34) \\H_{20}-H_{30} &=& 2H_{30}-H_{30} = H_{30} \qquad(3.35)\end{eqnarray}\)
Wprowadźmy te zależności do zlinearyzowanych równań stanu
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{30}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{30}}} & \dfrac{-\alpha}{2A\sqrt{H_{30}}} + \dfrac{-\alpha}{2A\sqrt{H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.36)\)
Wprowadźmy następujące oznaczenie
\(\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} >0\qquad(3.37)\end{equation} \)
Zlinearyzowane równania stanu mogą zostać zapisane jako
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.38)\)
Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego
\(\begin{equation}A = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\end{equation} \qquad(3.39)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 & s & 0 \\0 & 0 & s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \\&=& det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) \nonumber\end{eqnarray}\qquad(3.40)\)
Wyznacznik macierzy rozmiaru \( 3\times 3 \) może być obliczony z następującego wzoru
\(\begin{eqnarray}det \left(\begin{array}{ccc}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right) &=& a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\&& - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{eqnarray}\qquad(3.41)\)
Mamy zatem
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + 0\cdot (-2a)(-a) \\&& - 0 \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a) \\&=& (s^2+6as+8a^2)(s+2a) - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \nonumber \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 \\&=& s^3+8as^2+14a^2s+4a^3\end{eqnarray}\qquad(3.42)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3\end{equation} \qquad(3.43)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar \( 3\times 3 \) i postać
\(\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 & a_1 & a_2 \\0 & 0 & a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 & 14a^2 & 8a \\0 & 0 & 4a^3\end{array}\right)\end{equation} \qquad(3.44)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1 \\4a^3 & 14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 & 14a^2 & 8a \\0 & 0 & 4a^3\end{array}\right|\end{equation} \qquad(3.45)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu równowagi układu trzech zbiorników
- ponieważ \( a>0 \) to wszystkie współczynniki wielomianu charakterystycznego są dodatnie
\(\begin{equation}a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3>0 \end{equation} \qquad(3.46)\)
- minory główne macierzy Hurwitza wynoszą
\(\begin{eqnarray} |8a| &=& 8a >0 \qquad(3.47)\\ \left| \begin{array}{cc} 8a & 1 \\ 4a^3 & 14a^2 \end{array} \right| &=& 8a\cdot 14a^2 - 1\cdot 4a^3 = 112a^3 - 4a^3 = 108a^3 > 0 \qquad(3.48)\\ \left| \begin{array}{ccc} 8a & 1 & 0 \\ 4a^3 & 14a^2 & 8a \\ 0 & 0 & 4a^3 \end{array} \right| &=& 8a \cdot 14a^2 \cdot 4a^3 + 1\cdot 8a \cdot 0 + 0\cdot 4a^3 \cdot 0 \\ && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0 - 1\cdot 4a^3\cdot 4a^3 \nonumber \\ &=& 448a^6 -16a^6 = 432a^6 >0 \nonumber \end{eqnarray}\qquad(3.49)\)
Mamy zatem spełniony warunek dla pierwiastków wielomianu charakterystycznego trzeciego stopnia
\(\begin{equation} Re(s_1) < 0,\ Re(s_2) < 0,\ Re(s_3) < 0 \end{equation} \qquad(3.50)\)
Punkt równowagi obiektu zlinearyzowanego \( \tilde{H}_{10} = 0 \), \( \tilde{H}_{20} = 0 \), \( \tilde{H}_{20} = 0 \) jest stabilny asymptotycznie. Z drugiej metody Lapunowa mamy zatem, że punkt równowagi obiektu nieliniowego \( H_{10} \), \( H_{20} \), \( H_{30} \) ze stałym sterowaniem \( Q_{we0} \) jest stabilny asymptotycznie. Obliczenia były prowadzone dla dowolnego punktu równowagi w układzie trzech zbiorników. Wynika z tego, że wszystkie punkty równowagi tego układu są stabilne asymptotycznie. Ten wynik jest w zgodzie z wynikami symulacji (Rys. 1.3, 1.12).
Zbadajmy teraz stabilność punktu pracy układu regulacji trzech zbiorników z regulatorem P. Równania stanu dla układu regulacji mają postać
\(\begin{eqnarray}\dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}\left(k_p(H_3(t)-H_{30}) + Q_{we0} \right) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.51) \\\dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(3.52) \\\dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.53)\end{eqnarray}\)
Rozważamy punkt pracy określony przez \( H_{10} \), \( H_{20} \), \( H_{30} \) orz \( Q_{we0} \). Zlinearyzowane równania stanu (2.22)-(2.24) dla układu regulacji zapisane w postaci macierzowej mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{k_p}{A} \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 & \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} & \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.54)\)
Podobnie jak to było w przypadku zlinearyzowanych równań stanu dla obiektu korzystamy z (3.34)-(3.35) i wprowadzamy zmienną \( a \) (3.37). Zlinearyzowane równania stanu dla układu regulacji mają teraz postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt} \\ \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\ \tilde{H}_2 \\ \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.55)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}
\right) \right) \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 & s & 0 \\0 & 0 & s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a & -4a & 2a \\0 & a & -2a\end{array}\right) \right) \qquad(3.56) \\&=& det \left(\begin{array}{ccc}s+2a & -2a & -\dfrac{k_p}{A} \\-2a & s+4a & -2a \\0 & -a & s+2a\end{array}\right) r \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + \left(-\dfrac{k_p}{A}\right) (-2a)(-a) \\&& - \left(-\dfrac{k_p}{A}\right) \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a) \\&=& (s^2+6as+8a^2)(s+2a) - 2a^2\dfrac{k_p}{A} - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 - 2a^2\dfrac{k_p}{A} \\&=& s^3+8as^2+14a^2s+4a^3 - 2a^2\dfrac{k_p}{A}\end{eqnarray}\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}\end{equation} \qquad(3.57)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego
\(\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 & a_1 & a_2 \\0 & 0 & a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right)\end{equation} \qquad(3.58)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right|\end{equation}\qquad(3.59) \)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu pracy układu regulacji
- dla uzyskania stabilności asymptotycznej wszystkie współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}>0\end{equation} \qquad(3.60)\)
- dla uzyskania stabilności asymptotycznej wszystkie minory główne macierzy Hurwitza muszą być dodatnie
\( \begin{eqnarray} |8a| &=& 8a >0 \qquad(3.61)\\ \left| \begin{array}{cc} 8a & 1 \\ 4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 \end{array} \right| &=& 8a\cdot 14a^2 - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \\ &=& 112a^3 - 4a^3 + 2a^2\dfrac{k_p}{A} \\ &=& 108a^3 + 2a^2\dfrac{k_p}{A} > 0 \qquad(3.62)\\ \left| \begin{array}{ccc} 8a & 1 & 0 \\ 4a^3 - 2a^2\dfrac{k_p}{A} & 14a^2 & 8a \\ 0 & 0 & 4a^3 - 2a^2\dfrac{k_p}{A} \end{array} \right| &=& 8a \cdot 14a^2 \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \qquad(3.63)\\ && + 1\cdot 8a \cdot 0 + 0\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot 0 \\ && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0 \\ && - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \\ &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left( 8a \cdot 14a^2 - \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \right) \\ &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right) >0 \end{eqnarray}\)
Warunki na stabilność asymptotyczną punktu pracy układu regulacji, zawierające \( k_p \), są następujące
\(\begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A}&>&0 \qquad(3.64) \\108a^3 + 2a^2\dfrac{k_p}{A} &>& 0 \qquad(3.65) \\\left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right) &>& 0 \qquad(3.66)\end{eqnarray}\)
Pozostałe warunki są spełnione ponieważ \( a>0 \). Zauważmy jeszcze, że jeżeli warunki (3.64) i (3.65) są spełnione, to automatycznie warunek (3.66) też jest spełniony. Obliczmy teraz zakres wartości \( k_p \) regulatora, dla których punkt pracy układu regulacji jest stabilny asymptotycznie. Z (3.64) mamy
\( \begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A} &>& 0\qquad\\ 4a^3 >2a^2\dfrac{k_p}{A} /\div 2a^2 \qquad\\2a>\dfrac{k_p}{A} /\cdot A \qquad\\2aA &>& k_p \qquad \\k_p & < & 2aA \qquad(3.67)\end{eqnarray} \)
Z (3.65) mamy
\(\begin{eqnarray}108a^3 + 2a^2\dfrac{k_p}{A} &>& 0\\ 2a^2\dfrac{k_p}{A} &>& -108a^3 \qquad /\div 2a^2 r\\\dfrac{k_p}{A} &>& -54a \qquad /\cdot A r\\k_p &>& -54aA \qquad(3.68)\end{eqnarray} \)
Ostatecznie, punkt pracy zlinearyzowanego, a także nieliniowego układu regulacji jest stabilny asymptotycznie, jeżeli wzmocnienie regulatora proporcjonalnego mieści się w zakresie
\(\begin{equation}-54aA < k_p < 2aA\qquad(3.69)\end{equation} \)
Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy następujące wartości parametrów obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt pracy obiektu \( Q_{we0} = 0.5\), \(H_{10}=0.75 \), \( H_{20}=0.5 \), \( H_{30}=0.25 \). Stała \( a \) wynosi
\(\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} = \dfrac{1}{4\cdot 0.5 \sqrt{0.25}} =1\end{equation} \qquad(3.70)\)
Zakres wzmocnień regulatora P, dla których punkt pracy układu regulacji pozostaje stabilny asymptotycznie (3.69) wynosi
\(\begin{equation}-27 < k_p < 1\end{equation} \qquad(3.71)\)
Przeanalizujmy uzyskany przedział \( k_p \) zapewniający stabilność asymptotyczną punktu pracy. Większa część przedziału zmienności \( k_p \) leży po stronie wartości ujemnych. Jest zgodne z intuicją, ponieważ dla \( k_p < 0 \) korekta sygnału sterującego ma kierunek, który powoduje zmniejszenie odchyłki regulacji. Ten rezultat pozostaje również w zgodzie z wynikami symulacji (Rys. 2.2-2.5). Sprawdźmy jeszcze, czy \( k_p=-27 \) wyznacza granicę stabilności układu. Na podstawie Rys. 2.5 mamy, że dla \( k_p = -24 \) oscylacje sygnału \( H_3 \) są gasnące (stabilność asymptotyczna), natomiast dla dla \( k_p = -32 \) oscylacje są narastające (niestabilność). Dla wartości granicznej \( k_p=-27 \) powinniśmy uzyskać stałe oscylacje. Odpowiedź układu regulacji na niezerowe warunki początkowe \( H_1(t_0) =0.76 \), \( H_2(t_0) =0.51 \), \( H_3(t_0)=0.26 \) dla wzmocnienia regulatora \( k_p=-27 \) została przedstawiona na Rys. 3.1. Zarówno sygnał wyjściowy \( H_{3}(t) \) jak i sygnał sterujący \(Q_{we}(t) \) charakteryzują się przebiegiem oscylacyjnym o stałej amplitudzie oscylacji. Warto zauważyć, że na granicy stabilności oscylacje sygnału sterującego i wyjściowego są przesunięte w fazie o 180 stopni.
Dla obiektu bez regulatora (\( k_p=0 \)) punkt pracy również jest stabilny asymptotycznie i jest to zgodne z wynikami symulacji (Rys. 2.2(a)). Okazuje się jednak, że także dla niewielkich wartości dodatnich \( k_p \) punkt pracy układu regulacji pozostaje stabilny asymptotycznie. Może się to wydawać niezgodne z intuicją, ponieważ dla \( k_p > 0 \) korekta sygnału sterującego ma kierunek, który powoduje zwiększanie odchyłki regulacji. Układ regulacji traci stabilność dopiero dla odpowiednio dużego dodatniego \( k_p \). Zachowanie układu regulacji dla kilku dodatnich wartości \( k_p \) została przedstawiona na Rys. 3.2.
a) Trajektoria \(H_3(t)\)
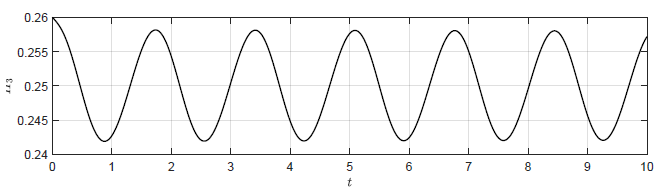
b) Trajektoria \(Q_{we}(t) \)
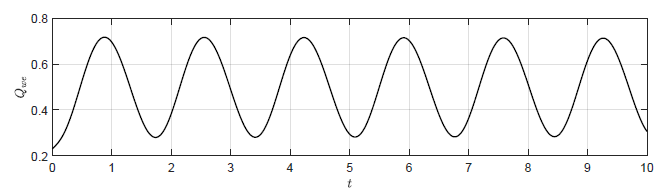
Rysunek 3.1 Trajektorie \( H_3(t) \) orz \( Q_{we} \) w układzie regulacji dla \(
k_p = -27 \).
Dodatnia wartość \( k_p \) powoduje
początkowo wydłużenie czasu regulacji w porównaniu do układu bez regulatora (\(
k_p=0 \)). Dla wartości granicznej \( k_p=1 \) wartość \( H_3(t) \) ustala się
po pewnym czasie, jednak nigdy nie powraca do wartości z punktu pracy \( H_{30}
= 0.25 \). Dla \( k_p>1 \) trajektoria \( h_3(t) \) stopniowo oddala się od
punktu pracy, co świadczy o tym, że punkt pracy układu regulacji jest
niestabilny.
Zajmijmy się teraz badaniem stabilności
punktów równowagi wahadła. Równania stanu dla wahadła ze stałym
sterowaniem \( M(t) = M_{0} \) (obiekt autonomiczny) mają postać
\(\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.72) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M_0 \qquad(3.73)\end{eqnarray}\)
Równania punktu równowagi mają postać
\(\begin{eqnarray}\omega_0 &=& 0 \qquad(3.74)\\M_0 &=& -mglsin\theta_0 \qquad(3.75)\end{eqnarray}\)
Sterowanie w obiekcie zlinearyzowanym jest równe zero
\(\begin{equation}\tilde{M} = M(t) - M_0 = M_0 - M_0 = 0\end{equation} \qquad(3.76)\)
a) \(k_p = 0 \)
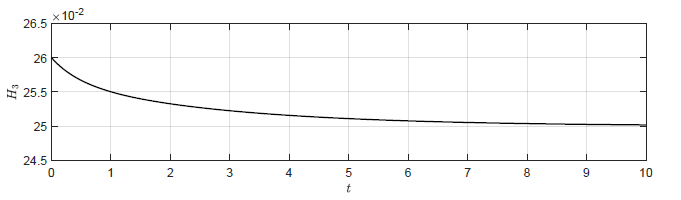
b) \(k_p = 0.5 \)
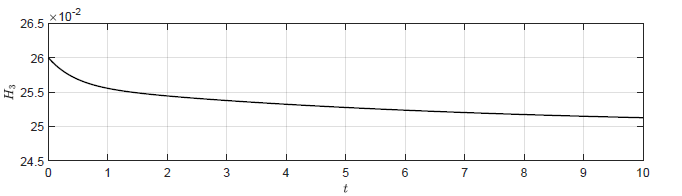
c) \(k_p = 1 \)

d) \(k_p = 1.5 \)
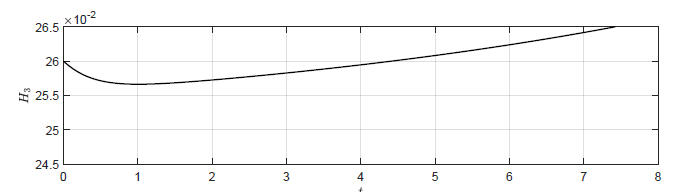
Rysunek 3.2 Trajektorie \( H_3(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) \end{equation} \qquad(3.77)\)
Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego
\(\begin{equation}A = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right)\end{equation}\qquad(3.78) \)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 & 1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 & s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 & -\dfrac{D}{ml^2}\end{array}\right) \right) \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 & s+\dfrac{D}{ml^2}\end{array}\right) \qquad(3.79)\end{eqnarray}\)
Wyznacznik macierzy rozmiaru \( 2\times 2 \) może być obliczony z następującego wzoru
\(\begin{equation}det \left(\begin{array}{ccc}a_{11} & a_{12} \\a_{21} & a_{22} \end{array}\right) = a_{11}a_{22} - a_{12}a_{21} \end{equation} \qquad(3.80)\)
Mamy zatem
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 & s+\dfrac{D}{ml^2}\end{array}\right) \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 \right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0 \nonumber \end{eqnarray}\qquad(3.81)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0\end{equation} \qquad(3.82)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar \( 2\times 2 \) i postać
\(\begin{equation}H = \left(\begin{array}{cc}a_1 & a_2 \\0 & a_0\end{array}\right) = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0\end{array}\right)\end{equation} \qquad(3.83)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0\end{array}\right|\end{equation} \qquad(3.84)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu równowagi wahadła
- współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 >0 \end{equation} \qquad(3.85)\)
- minory główne macierzy Hurwitza muszą być dodatnie
\(\begin{eqnarray} \left|\dfrac{D}{ml^2}\right| &=& \dfrac{D}{ml^2} >0 \qquad(3.86)\\ \left| \begin{array}{cc} \dfrac{D}{ml^2} & 1 \\ 0 & -\dfrac{g}{l}cos\theta_0 \end{array} \right| &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0\right) - 1\cdot 0 = -\dfrac{D}{ml^2}\cdot \dfrac{g}{l}cos\theta_0 > 0 \qquad(3.87)\end{eqnarray}\)
Parametry obiektu \( m,g,l,D \) są dodatnie. O spełnieniu nierówności w kryterium Hurwitza decyduje zatem znak wyrażenia \( cos\theta_0 \). Jeżeli \( cos\theta_0 > 0\) (punkt równowagi powyżej położenia horyzontalnego wahadła), to nie wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest niestabilny. Jeżeli \( cos\theta_0 < 0\) (punkt równowagi poniżej położenia horyzontalnego wahadła), to wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest stabilny asymptotycznie. Te wnioski pozostają w zgodzie z wynikami symulacji. Dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{5\pi}{6} \) obiekt przejawiał zachowanie stabilne (Rys. 1.14), podczas, gdy dla punktu równowagi odpowiadającego \( \theta_0 = \dfrac{\pi}{6} \) obiekt przejawiał zachowanie niestabilne (Rys. 1.15).
Zbadajmy teraz stabilność punktu pracy
układu regulacji wahadła z regulatorem P. Równania stanu dla układu regulacji
mają postać
\(\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.88) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} \left( k_p (\theta(t)-\theta_0) + M_0 \right) \qquad(3.89)\end{eqnarray}\)
Rozważamy punkt pracy określony przez \( \theta_0 \), \( \omega_0 \) orz \( M_0 \). Zlinearyzowane równania stanu (2.61)-(2.62) dla układu regulacji zapisane w postaci macierzowej mają postać
\(\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt} \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) \end{equation} \qquad(3.90)\)
Wielomian charakterystyczny wynosi
\(\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 & 1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right) \right) \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 & s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p & -\dfrac{D}{ml^2}\end{array}\right) \right) \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p & s+\dfrac{D}{ml^2}\end{array}\right) \nonumber \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p \nonumber \end{eqnarray}\qquad(3.91)\)
Współczynniki wielomianu charakterystycznego wynoszą
\(\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{equation} \qquad(3.92)\)
Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego
\(\begin{equation}H = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right)\end{equation} \qquad(3.93)\)
Minory główne macierzy Hurwitza wynoszą
\(\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right|\end{equation} \qquad(3.94)\)
Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu pracy układu regulacji położenia wahadła
- współczynniki wielomianu charakterystycznego muszą być dodatnie
\(\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p >0 \qquad(3.95)\end{equation} \)
- minory główne macierzy Hurwitza muszą być dodatnie
\( \begin{eqnarray} \left|\dfrac{D}{ml^2}\right| &=& \dfrac{D}{ml^2} >0 \qquad(3.96)\\ \left| \begin{array}{cc} \dfrac{D}{ml^2} & 1 \\ 0 & -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p \end{array} \right| &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) - 1\cdot 0 \\ &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) > 0 \qquad(3.97) \end{eqnarray}\)
Nierówności w kryterium Hurwitza będą spełnione jeżeli będzie spełniony warunek
\(\begin{eqnarray}-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p&>&0 \\-\dfrac{g}{l}cos\theta_0 &>&\dfrac{1}{ml^2}k_p \qquad /\cdot ml^2 \\-mglcos\theta_0 &>&k_p \\ k_p & < & -mglcos\theta_0 \end{eqnarray}\)
Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy parametry modelu obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt pracy układu regulacji \( \theta_0=\dfrac{\pi}{6} \), \( \omega_0=0 \), \( M_{0} = -0.5 \). Aby punkt pracy układu regulacji był stabilny \( k_p \) musi spełniać warunek
\(\begin{equation} k_p < -mglcos\theta_0 = -0.1\cdot 10 \cdot 1 \cdot \dfrac{\sqrt{3}}{2} = -\dfrac{\sqrt{3}}{2} \simeq -0.87\end{equation} \qquad(3.98)\)
a) \(k_p = 0.75 \)

b) \(k_p = -0.8 \)
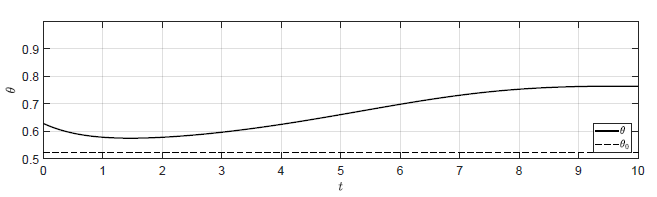
c) \(k_p = -\dfrac{\sqrt{3}}{2} \)
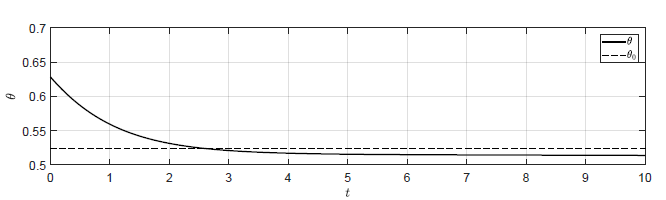
d) \(k_p = -0.9 \)
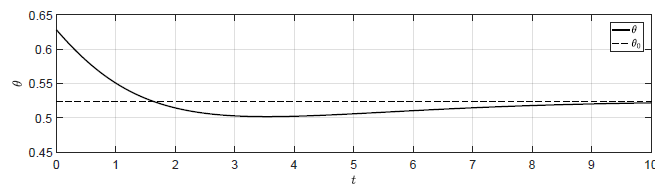
Rysunek 3.3 Trajektorie \( \theta(t) \) w układzie regulacji dla różnych wartości wzmocnienia regulatora \( k_p \).
Ten warunek pozostaje w zgodzie z
wynikami symulacji (Rys. 2.9 i 2.10).
Sprawdźmy jeszcze zachowanie układu dla \( k_p \) bliskich wartości granicznej.
Odpowiedź układu regulacji na warunki początkowe \( \theta(t_0) =
\dfrac{\pi}{5} \), \( \omega(t_0) = -0.1 \) dla różnych wartości \( k_p \)
została przedstawiona na Rys. 3.3. Dla \(k_p
\geq -\dfrac{\sqrt{3}}{2} \) trajektoria \( \theta(t) \) nie powraca do \(
\theta_0 \). Jednak już dla wartości \( k_p \) nieco mniejszej od wartości
granicznej trajektoria \( \theta(t) \) powraca do \( \theta_0 \).
