Podręcznik

Rozważamy n-wymiarową przestrzeń wariantów \(ℝ^n \ni x\). W przestrzeni tej zadana jest funkcja oceniająca (wyboru, celu)

\(f:\mathbb{R}^n\rightarrow\ \mathbb{R},\)

pozwalająca porównywać warianty, przy czym z dwu wariantów ten jest lepszy dla którego funkcja oceniająca przyjmuje mniejszą wartość, oraz zbiór wariantów dopuszczalnych \(D \subseteq ℝ^n,\) gdzie, dla zadania minimalizacji

\(D={x\in\mathbb{R}^n|(\forall j\in\overline{1,m})g_j(x)\le0\land(\forall k\in\overline{1,p})h_k(x)=0\land(\forall i\in\overline{1,r})\ x_i\in[x_i^-,x_i^+]}, \qquad(1.9)\)

a \(g_j:\mathbb{R}^n\rightarrow\ \mathbb{R},j\in\overline{1,m}\) to funkcje  określające  ograniczenia  nierównościowe \(D_\leq\) , natomiast \(h_k:\mathbb{R}^n\rightarrow\mathbb{R},  k\in\overline{1,p}\) to funkcje określające ograniczenia równościowe \(D_= \).  W określeniu zbioru dopuszczalnego wy-różniliśmy jeszcze, często występujące w zdaniach praktycznych, ograniczenia kostkowe \(xi \in [xi–,xi+], i\in\overline{1,r}\), oznaczymy je \(D_K\) ,  chociaż formalnie rzecz biorąc są to ograniczenia nierównościowe. Zauważmy, że w celu uniknięcia niebezpieczeństwa określenia zbioru pustego, ograniczeń  równościowych  nie może być więcej niż \(n \,(p \leq n).\) Z oczywistego powodu, ograniczeń kostkowych też nigdy nie jest więcej niż n. 

Zatem zbiór wariantów dopuszczalnych (1.9) jest iloczynem trzech zbiorów

\(D=D_\le\cap D_=\cap D_K\).

Możemy teraz formalnie określić zadanie optymalizacji.

Wiele zadań praktycznych (nie wszystkie!) można w ten sposób zapisać.

Dlaczego zapisaliśmy zadanie minimalizacji?

Wystarczy więc rozważać tylko jeden z dwu operatorów ekstremalizacji. Do systemu definicji przyjętych w matematyce, lepiej pasuje minimalizacja i w zasadzie wszystkie rozważania teoretyczne prezentowane w literaturze dotyczą minimalizacji.

Zwrócimy teraz krótko uwagę na pewne własności funkcji minimalizowanej i konsekwencje przyjętej definicji zbioru dopuszczalnego.

W zapisanym ogólnym zadaniu optymalizacji ZO trzeba 

znaleźć taki wektor \(x^o\in D\), że \((\forall x \in D) f (x^o) \leq f (x)\) .

Jest to wymaganie porównania wszystkich wariantów (wektorów) x ze zbioru dopuszczalnego D i znalezienia takiego wariantu dopuszczalnego, \(x^o \in D\), którego ocena, \(f (x^o)\), w porównaniu ze ocenami wszystkich wariantów dopuszczalnych jest nie większa, \((\forall x \in D) f (x^o) \leq f (x)\). Tak określony wektor, w opracowaniach dotyczących optymalizacji nazywa się punktem minimum globalnego funkcji f na zbiorze D, bo przy jego ustalaniu porównujemy wszystkie punkty dopuszczalne. 

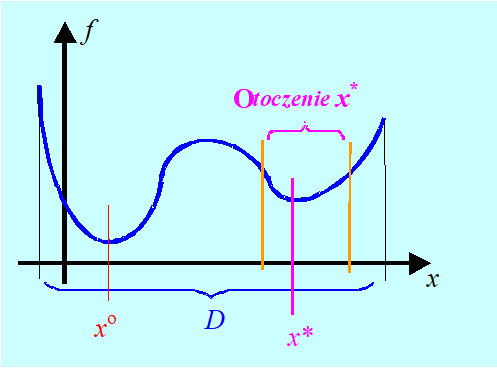
Jaka jest konsekwencja przyjęcia takiej terminologii? Popatrzmy na Rys. 1.6 przedstawiający funkcję jednej zmiennej. Obok minimum globalnego w punkcie \(x^o \)ma ona tzw. minimum lokalne w punkcie \(x^*\). Dokładna definicja jest następująca:

W przedstawionym ogólnym zadaniu optymalizacji szukamy wariantu dopuszczalnego minimalizującego funkcję celu. Takie wymaganie nie występuje w każdym zadaniu optymalizacji. Czasami ważna jest tylko wartość optymalna funkcji oceniającej, natomiast argumenty optymalizujące – nie są interesujące. Rozważa się wtedy zadanie prostsze:

Funkcje minimalizowane mogą być różne, a ich zachowanie zaskakujące. Wygodnym narzędziem pozwalającym zorientować się co nas może czekać w świecie minimalizacji, a także wyrabiającym intuicję są dla funkcji dwu-argumentowych wykresy poziomicowe (mapy).

Takim wykresem posłużymy się do ustalenia ile minimów lokalnych ma funkcja

\(x ↦ f (x) = 2(x_1)^2 + 4x_1(x_2)^3 – 10x_2x_1 + (x_2)^2\)

w zbiorze

\(D = {(x_1,x_2) | x_1 (x_2)^2(2.4 + x_2) \leq 3\wedge {\frac{3}{2}}x_1 + x_2 \geq 0\wedge (–3 \leq x_i \leq 3, i = 1,2)}.\)

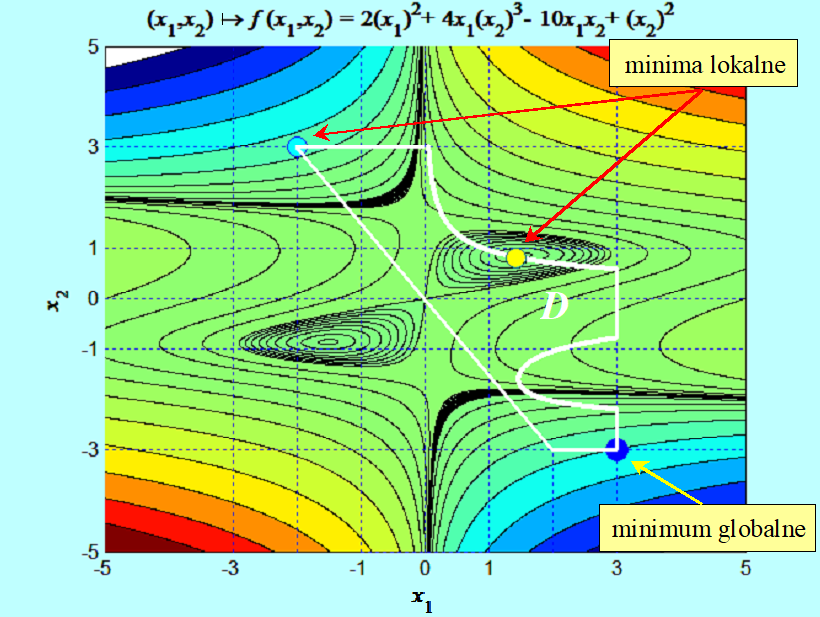
Zauważmy, że funkcja f i funkcje \(g_j \)na pierwszy rzut oka nie sprawiają wrażenia, że geometria zbiorów przez nie wyznaczonych jest tak skomplikowana. Zauważmy, że wszystkie minima lokalne (w tym przykładzie) wynikają z obecności ograniczeń, czasami mówi się, że są indukowane przez ograniczenia.

Zastanówmy się teraz przez chwilę nad strukturą zbioru dopuszczalnego (1.9). Jest on iloczynem trzech zbiorów: \(D=D_\leq \cap\ D_=\cap\ D_K.\) Naszkicujmy te zbiory.

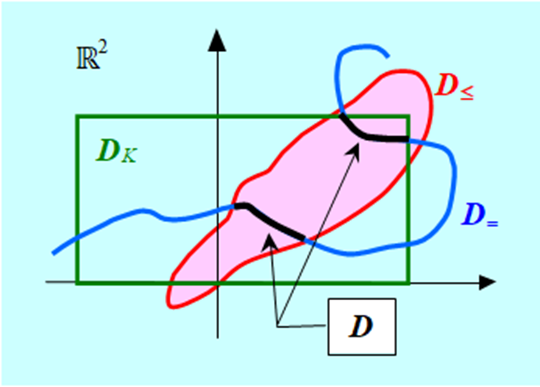
Narysowany zbiór D zaznaczony na czarno jest „mały” i na dodatek składa się z dwu rozłącznych części, które nie mają wnętrza („nie mają punktów w środku”). Widać, że najbardziej restrykcyjne są ograniczenia równościowe. Bez nich, omawiany zbiór dopuszczalny byłby spójny (składałby się z jednej części) i tak jak zbiór z rysunku poprzedniego miał niepuste wnętrze.