Podręcznik
4. Jak tworzyć algorytmy optymalizacji?
Powyżej ustaliliśmy, że zajmować się będziemy różnymi wariantami zadania statycznej minimalizacji ciągłej. Przypomnijmy jego formalne określenie, tj. postać ogólną ZO.
Dana jest n-wymiarowa przestrzeń wariantów \( ℝ^n \ni x \). W przestrzeni tej określone są
- funkcja oceniająca (wyboru, celu) \(f:\mathbb{R}^n\rightarrow\ \mathbb{R},\)
- funkcje określające ograniczenia nierównościowe \ (D \leq g_j:\mathbb{R}^n\rightarrow\mathbb{R},\,j\in\overline{1,m}, \)
- funkcje określające ograniczenia równościowe \( D= h_k:\mathbb{R}^n→\mathbb{R}, k∈¯(1,p) \), które razem z ograniczeniami kostkowymi DK określają
- zbiór wariantów dopuszczalnych
\( D = {x \in \mathbb{R} n |( \forall j \in \overline{1,m}) g_j(x) \leq 0 \wedge( \forall k \in \overline{1,p}) h_k(x) = 0 \wedge ( \forall i \in \overline{1,r}) x_i \in [x_i^–,x_i^+]}. \)
Trzeba znaleźć
\(x^o={\rm argmin}_{\ x\in D}{f}(x).\)
Jak pamiętamy, czasami rozważa się zadanie prostsze:
znaleźć \(f^o=\min_{\ x\in D}{f}(x),\)
w którym szukamy minimalnej wartości funkcji w zbiorze D.
W sformułowaniu zadania minimalizacji jest polecenie „znaleźć”. Ale, w odróżnieniu od wielu innych zadań, matematyka nie dostarcza nam wprost narzędzi pozwalających bezpośrednio to polecenie wypełnić.
Jak znaleźć (o ile istnieje) wartość zmiennej minimalizującej np. funkcję \(x\mapsto x(x-1)\)?
Najprostsza odpowiedź – narysować.
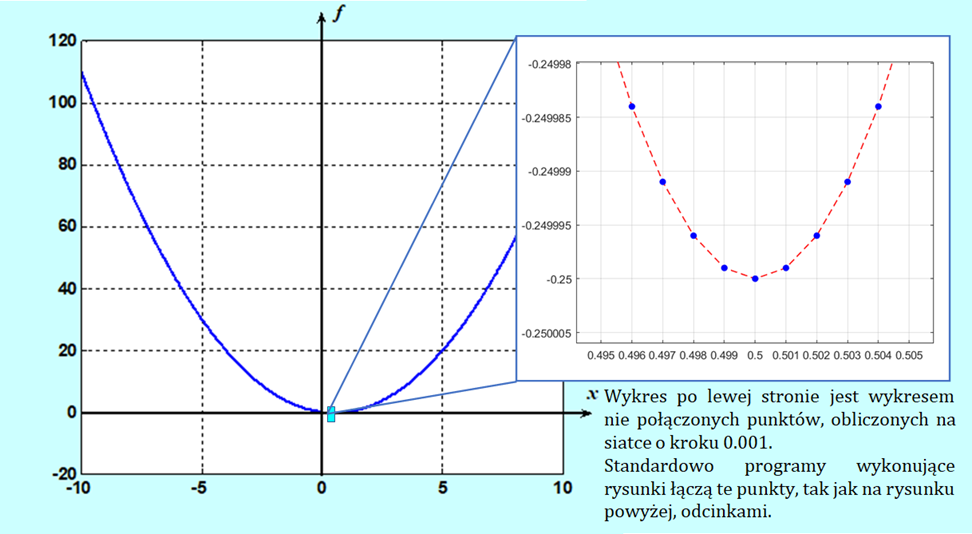
Niestety potrafimy tylko szkicować przebieg funkcji jednej zmiennej (uczyliśmy się tego w ramach badania zmienności funkcji poznając analizę matematyczną). Komputer narysuje funkcję dwu zmiennych. Lecz nawet w tych relatywnie prostych przypadkach analiza rysunku da raczej odpowiedź na pytanie: czy minimum istnieje?, a nie, gdzie dokładnie leży. Posługiwanie się metodami graficznymi (co dla rysunków komputerowych jest de facto przeglądem wartości funkcji w wybranych punktach) niesie też inne niebezpieczeństwa, o których dowiemy się w dalej.
Mamy więc jeszcze dwie drogi realizacji polecenia „znaleźć”
- droga rachunkowa,
- droga właściwie zorganizowanego poszukiwania.
Gdy chcemy pójść drogą pierwszą, tzn. gdy chcemy znaleźć rozwiązanie zadania optymalizacji drogą rachunkową musimy oryginalne sformułowanie przekształcić do postaci pozwalającej na wykonanie stosownych rachunków. Jak się o tym przekonamy (moduł trzeci i piąty) jest to najczęściej odpowiednio określony układ równań i nierówności (obecność nierówności jest kłopotliwa), którego rozwiązanie może być (warunek konieczny!) lub jest (warunek dostateczny) rozwiązaniem analizowanego zadania optymalizacji.
Gdy nie potrafimy, nie możemy, albo nie chcemy skorzystać z metody przekształcenia zadania optymalizacji, do znalezienia jego rozwiązania musimy posłużyć się mniej lub bardziej wymyślną metodą poszukiwania – wybrać algorytm wykonujący ciąg dobrze określonych operacji rachunkowych (kroków), który w momencie zatrzymania wskaże wariant będący rozwiązaniem zadania. Takich algorytmów wymyślono już tysiące. Zauważmy, że wiele z nich podobnych jest do algorytmów rozwiązywania równań i nierówności, bo przecież nie każde równanie potrafimy rozwiązać rachunkowo.
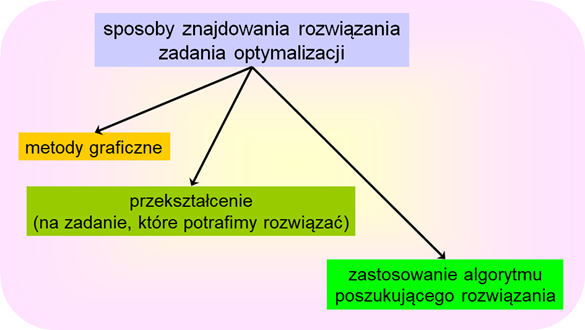
Najczęściej mamy do czynienia z ostatnim przypadkiem wspomnianym powyżej. Po prostu nie można znaleźć rozwiązania zadania optymalizacji drogą rachunkową. Zatem musimy posłużyć się wybranym algorytmem.
Z gruba rzecz biorąc każdy algorytm poszukiwania opiera się na informacji a priori oraz na stosownym przetwarzaniu informacji zdobywanej na bieżąco (w kolejnych krokach poszukiwania). Przy czym, jak się już za chwilę przekonamy, specyfika algorytmów optymalizacji polega na tym, że bieżąca informacja odnosi się tylko do aktualnego punktu (lub jego małego otoczenia), w którym „znajduje” się algorytm – bieżąca informacja jest zawsze lokalna. Informacją a priori może być każda informacja dotycząca własności i kształtu funkcji oceniającej.
Zostawiając na później rozważania teoretyczne prowadzące do określenia stosownych warunków optymalności (wspomnianych układów równań i nierówności, które musi spełniać wariant optymalny) przedstawimy teraz dyskusję prowadzącą do ustalenia podstawowych problemów jakie stoją przed twórcami algorytmów optymalizacji.
Tak się złożyło, że twórcy i badający algorytmy optymalizacji traktują zwykle w swojej codziennej pracy obiekty swoich zainteresowań jak stworzenia, co przy opisie oznacza, że ich funkcjonowanie jest przestawiane jako wynik ich rozmyślnego działania. I ja, jako współtwórca paru algorytmów optymalizacji, też przyjmę dalej taką konwencję.
Wyobraźmy więc sobie, jak może „rozumować” Algorytm (komputerowy), postawiony na schodach o stopniach różnej wysokości, którego zadaniem jest zejście do najniższego poziomu schodów.
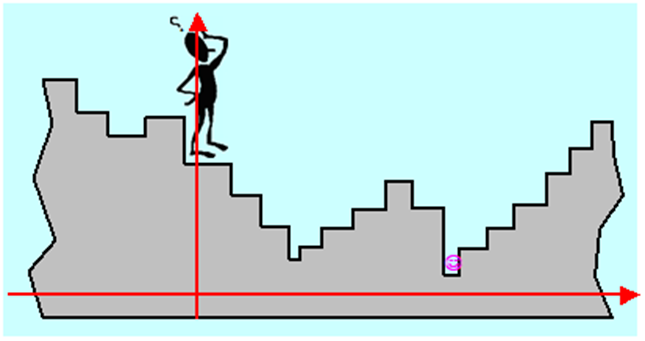
Jest rzeczą oczywistą, że Algorytm całych schodów nie widzi (ograniczenie bieżącej informacji), natomiast potrafi ocenić położenie stopnia w stosunku do ustalonego poziomu odniesienia, nazwiemy je wysokością (dla każdego wariantu potrafi obliczyć wartość funkcji celu). Wie, że stoi na jakimś stopniu i może się ruszać w jedną ze stron, przyjmijmy, że prawą i lewą. Jeżeli założymy, że jest „sprawny fizycznie” to może przeskakiwać kilka stopni na raz. Stopnie na schodach, nawet nieskończonych, można policzyć, każdy stopień to wariant, a więc zbiór wariantów jest przeliczalny.
Jeżeli liczba stopni jest skończona (zbiór dopuszczalny jest skończony, a więc ograniczony) i nie jest zbyt duża w stosunku do szybkości poruszania się po nich Algorytmu, to przy założeniu, że jest on w stanie powiązać w pary stopień i jego wysokość i zapamiętać te pary, postępowanie jest oczywiste: być na wszystkich stopniach, określić ich wysokość i wybrać ten o najniższej (przeszukać wszystkie warianty). Gdy stopni jest bardzo dużo, Algorytm może odwiedzać np. co dziesiąty (przeszukanie wybranych punktów węzłowych), albo wybierać je w sposób przypadkowy zgodnie z rozkładem równomiernym (równomierne przeszukanie przypadkowe). Takie postępowania nie gwarantują jednak znalezienia rozwiązania – Algorytm może przeskoczyć nad stopniem najniższym. Powstaje więc problem dokładności znalezionego rozwiązania, ściśle związany z ilością odwiedzonych stopni (ilością punktów próbnych) ale też i ze sposobem wybierania stopni do odwiedzenia.
Co jednak ma zrobić Algorytm gdy schodów jest nieskończenie dużo (w przypadku schodów – zbiór dopuszczalny nie jest ograniczony, w sytuacji ogólniejszej – nie jest policzalny)?
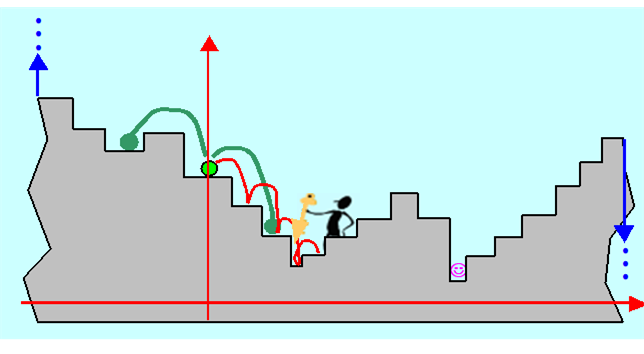
Może, startując ze stopnia, na którym stoi (jasno-zielony) wykonać krok (ustaloną liczbę kroków) w prawo, wrócić i wykonać krok w lewo. W ten sposób ustali, że lokalnie schody opadają w prawo (informacja bieżąca). Wyciągnie stąd wniosek, że należy schodzić w prawo. Gdy ma dużo czasu będzie schodził stopień po stopniu, aż zacznie się wspinać – wycofa się do poprzedniego stopnia i wie (bo przeczytał punkt 2.4), że znalazł lokalne minimum. Gdy jest leniwy to go taki rezultat zadowoli.
A jak Algorytm nie jest leniwy, to co ma robić dalej? Może trzeba zmienić zachowanie od początku, bo przecież w ten sposób znajdzie tylko lokalne minimum?
Inny problem pojawia się, gdy Algorytm nie ma dużo czasu i nie może schodzić stopień po stopniu. Wie że musi się ruszyć w prawo, ale jak długi skok ma wykonać?
Pozostawimy te pytania na razie bez odpowiedzi, a za to skomplikujmy zadanie, które ma rozwiązać nasz Algorytm. Teraz już nie „stoi” na schodach, ale na zboczu pewnego terenu:
Tak jak poprzednio, Algorytm nie widzi rzeźby terenu, natomiast potrafi ocenić wysokość punktu w którym się znajduje lecz wie, że takich punktów składających się na rzeźbę nie da się policzyć.
Jak ma postępować?...
Naukowcy i praktycy pracują nad odpowiedzią na to pytanie od mniej więcej 80 lat, i dalsza część tego podręcznika jest poświęcona zwięzłemu przedstawieniu najistotniejszych, zdaniem autora, dokonań w tej dziedzinie.
Zapiszmy wnioski płynące z naszej analizy zachowania się Algorytmu optymalizacji, nieco je uogólniając.
- Ponieważ nie potrafimy przeanalizować całościowego obrazu zmienności optymalizowanej funkcji (algorytm jest ślepy) możemy się posługiwać tylko wartościami funkcji, lub innych obiektów matematycznych z nią związanych (np. funkcji pochodnej) obliczonymi w wybranych punktach.
- Określenie (wybór) tych punktów ma kluczowe znaczenie dla szybkości działania i skuteczności algorytmu.
- Trzeba określić kryterium, którego spełnienie powinno zagwarantować... I tu następny problem: jeżeli powiemy – zagwarantować znalezienie rozwiązania, to intuicja podpowiada nam, że takiego kryterium nie ma. Możemy tylko powiedzieć – zagwarantować znalezienie lokalnego optimum. Kryterium to nosi nazwę kryterium stopu.
- W sytuacji gdy zbiór dopuszczalny jest ograniczony, najprostszy algorytm, to algorytm przeszukania – deterministyczny na siatce (myślimy o siatce bo oceniane warianty z reguły są opisywane wielu zmiennymi), albo losowy (metoda Monte-Carlo). Ale algorytmy przeszukiwania są czasochłonne.
W 1997 komputer Deep Blue firmy IBM wygrał turniej z ówczesnym szachowym mistrzem świata G. Kasparowem, można zatem pomyśleć – mamy teraz superszybkie komputery dysponujące olbrzymia pamięcią i zdolnością samouczenia się, więc nie warto zajmować się wymyślnymi algorytmami optymalizacji. „Brutalna siła” prostego algorytmu przeszukania pozwoli rozwiązać, każde (nieco ostrożniej, prawie każde) zadanie optymalizacji. Dla dyskretnych zadań z nieskończoną liczbą wariantów i zadań ciągłych (więc z nieprzeliczalną liczbą wariantów) trzeba tylko ustalić dostatecznie gęstą siatkę punktów węzłowych a następnie ją przeszukać.
Stosowanie algorytmu przeszukiwania niesie jednak w sobie niebezpieczeństwo. Najprościej przeszukiwać na równomiernej siatce prostokątnej, takiej jaka posłużyła do otrzymania trójwymiarowego Rysunku 1.21. Stopień zgodności otrzymanego trójwymiarowego wykresu z rzeczywistym przebiegiem funkcji jest więc dobrą miarą trafności wyboru węzłów siatki. Intuicyjnie sądzimy, że im gęstsza siatka, tym lepiej.
Bogactwo zmienności funkcji, które można uzyskać wykonując cztery działania na funkcjach elementarnych jest jednak tak duże, że prosta intuicja nas zawodzi. Pokazuje to Rys. 1.22 przedstawiający trójwymiarowe obrazy tej samej funkcji dwu zmiennych, wykreślone na podstawie wartości obliczonych w węzłach równomiernej siatki prostokątnej o: \( 30 \times 30 = 900 \) węzłach i \(33 \times 33 = 1089\) węzłach.
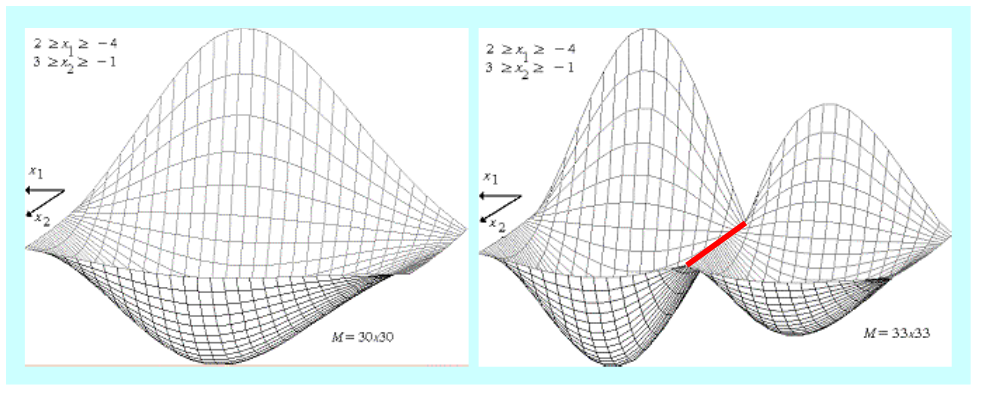
Zwiększenie liczby węzłów o 21% zmieniło całkowicie obraz funkcji:
- z funkcji o jednym minimum globalnym przeistoczyła się w funkcję o dwu minimach lokalnych i nieskończenie wielu maksimach lokalnych (cała prosta zaznaczona na czerwono), z których jedno leży tam, gdzie przedtem leżało minimum globalne!
- z drugiej strony, obliczone wartości minimalne funkcji dla rozważanych siatek nie różnią się znacznie, co intuicyjnie sugeruje, że zadanie znalezienia tylko minimalnej wartości funkcji oceniającej jest łatwiej rozwiązać.
Rysunki przedstawiają funkcję należącą do klasy
\((x_1,x_2)\mapsto-\left|w^m(x_2)\frac{1}{\alpha(x_1)}\sin{(}\beta(x_1))\right|, \qquad(1.19)\)
gdzie \(w^m\) jest wielomianem stopnia \(m\), a funkcje \( \alpha\) i \( \beta\) są funkcjami stałego znaku. Tego typu funkcje oceniające pojawiają się w pewnych zadaniach projektowych, np. związanych z przetwarzaniem sygnałów.
Nasuwa się pytanie: Jaki jest prawdziwy wygląd rozważanej funkcji?
Poniższy rysunek został wykonany na siatce o \(70 \times 70 = 4900\) węzłach i zgodnie z teorią pokazuje właściwe przybliżenie tej funkcji.
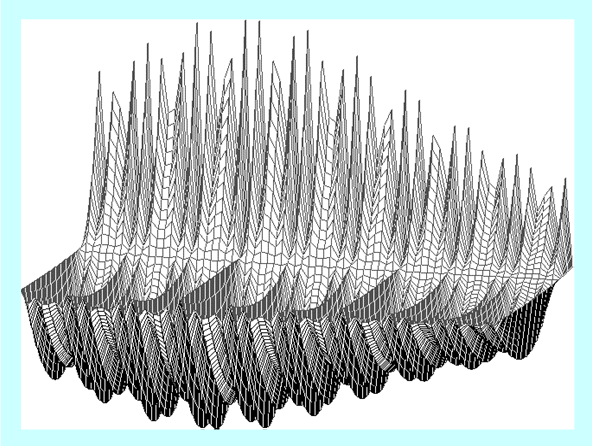
Dokładna analiza pokazała, że minimalna wartość funkcji oceniającej określona na każdej z tych trzech siatek różni się nieznacznie. Oczywiście nie można tego powiedzieć o punktach w których ta wartość jest osiągana. Jednak wyciągniecie stąd wniosku ogólnego, że zadanie w którym szukamy minimalnej wartości funkcji w zbiorze jest na pewno prostsze od „pełnego” zadania optymalizacji w którym szukamy argumentu minimalizującego badaną funkcję, jest pochopne. Tak zdarzyło się dla tej wybranej funkcji i nie wiadomo, czy to jest częsty/typowy przypadek.
Nauka jaka płynie z tego przykładu:
