Podręcznik

Zaczniemy od przypomnienia pojęć rachunku różniczkowego.

Zwracamy uwagę na różnicę między różniczkowalnością funkcji wielu zmiennych w danym punkcie, a istnieniem jej gradientu w tym punkcie.

Określimy teraz ważne dla teorii i algorytmów optymalizacji pojęcie pochodnej kierunkowej.

Następujący lemat pokazując związek pochodnej kierunkowej z gradientem pozwala w prosty sposób policzyć tę pierwszą dla funkcji różniczkowalnych.

Przedstawimy teraz lemat bardzo ważny dla konstruktorów algorytmów optymalizacji.

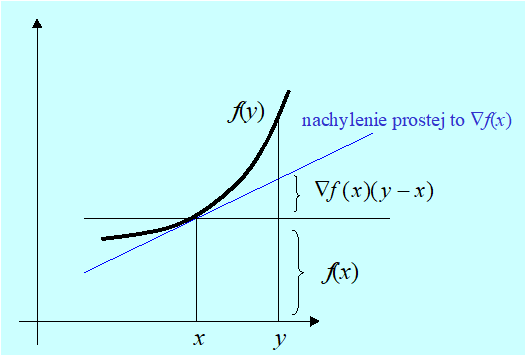
Ilustrację związków wynikających z Lematu 3.3 przedstawiamy na Rys. 3.1.

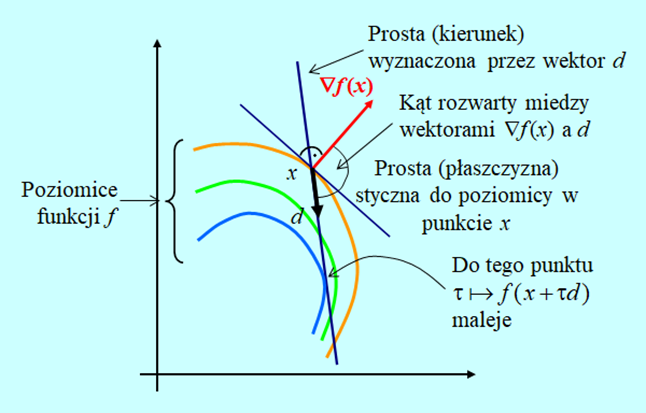
Z rozważań geometrycznych wiadomo, że iloczyn skalarny dwu wektorów jest ujemny (założenie lematu) wtedy gdy kąt miedzy nimi jest rozwarty. Tak też jest na rysunku dla wybranego wektora d. 

Własność przedstawiona w Lemacie 5.3 dała dla zadań minimalizacji następującą definicję.

Z Rys. 3.1 wynika, że w otoczeniu x, (inaczej mówiąc lokalnie) najlepszym kierunkiem poprawy (kierunkiem, w którym lokalnie funkcja najszybciej maleje) jest prosta wyznaczona przez wektor minus gradientu policzonego w tym punkcie, zwanego antygradientem. Pytaniem, które tu się pojawia jest: jak daleko warto poruszać się w tym kierunku? Dyskusję nad tym, wbrew pozorom, niełatwym zagadnieniem przedstawimy później – w punkcie 4.1 modułu czwartego. 

W punkcie 1.3 Modułu pierwszego wspomnieliśmy o funkcjach wypukłych. Odgrywają one istotną rolę w teorii optymalizacji. Przypomnimy teraz definicje oraz podstawowe własności zbiorów i funkcji wypukłych.

Zauważmy, że warunkiem koniecznym wypukłości zbioru \(\mathrm{epi } \) jest wypukłość zbioru X na którym jest określona funkcja f. 

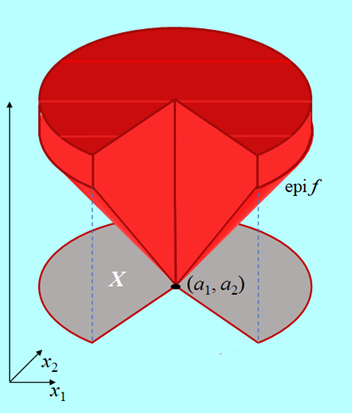
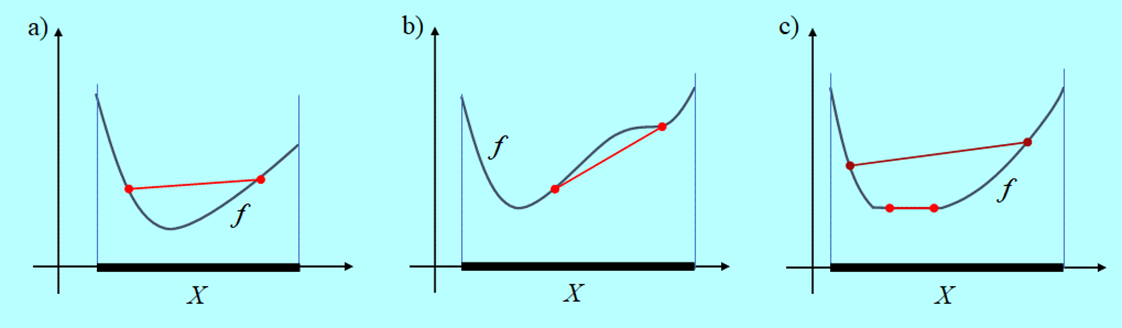
Funkcja przedstawiona na Rys. 3.2 nie jest wypukła dlatego, że zbiór X, na którym jest określona, nie jest wypukły i w konsekwencji jej epigraf nie jest zbiorem wypukłym.

Następny rysunek przedstawia inną przyczynę niewypukłości funkcji określnej na zbiorze wypukłym.

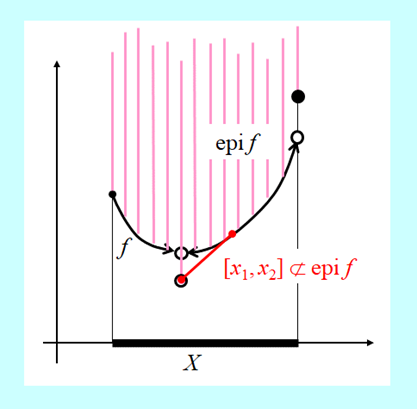
Funkcja na rysunku nie jest ciągła we wnętrzu zbioru swojego określenia X i na jego brzegu. Tylko nieciągłość wewnątrz zbioru X przeszkadza jej wypukłości. 

Można udowodnić lemat następujący.

Posługując się Definicją funkcji wypukłej można udowodnić lemat pozwalający na posługiwanie się alternatywną definicją funkcji wypukłej.

Następny lemat wiąże różniczkowalność i wypukłość funkcji.

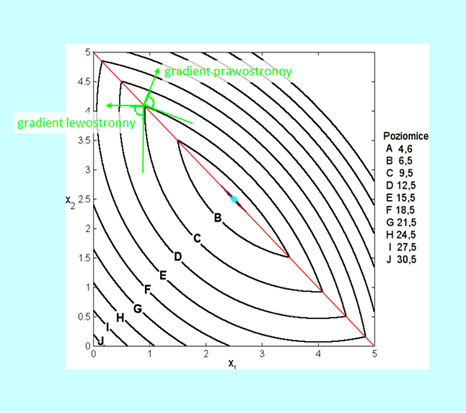
Rys. 3.4 przedstawia funkcję \(x \mapsto f(x)= \left\{\begin{matrix}((x_1-4)^2+(x_2-4)^2\, \mathrm{dla}\, x_1+x_2\leq 5, \\ (x_1-4)^2+(x_2-4)^2+10(x_1+x_2-5) \mathrm{gdy\, jest\, przeciwnie}\end{matrix}\right.  \)

Prosta na płaszczyźnie ma miarę zero (naturalną miarą na płaszczyźnie jest powierzchnia, a prosta ma zerową powierzchnię). Powstaje więc pytanie: Czy zbiór miary zero, a więc mały dla matematyka, jest „duży”, czy „mały” z naszego punktu widzenia? Odpowiedź jest trudna, bo, „idąc do trzech wymiarów”, powierzchnia kuli w naturalnej mierze przestrzeni trójwymiarowej ma miarę zero, ponieważ tu naturalną miarą jest objętość, a powierzchnia ma zerową objętość, itd. Widać więc, że tam gdzie matematyka posługuję się pojęciem miary, np. w rachunku całkowym, rachunku prawdopodobieństwa, własności funkcji na zbiorze miary zero możemy pominąć. W innych sytuacjach, np. takiej z jaką się spotkamy w punkcie 6.1.4 Modułu szóstego (przedstawionej na Rys. 3.4) własności funkcji na takim zbiorze trzeba uwzględnić w analizie problemu.

Podamy teraz definicję uogólnienia funkcji kwadratowej na przypadek wielu zmiennych.

W definicji wymagana jest symetryczność macierzy Q. Jak wiec nazwać funkcję \(x↦x^T Q ̄x\), gdzie macierz \((Q ) ̄\) nie jest symetryczna? 

Podamy teraz warunki wiążące wypukłość danej funkcji z określonymi własnościami jej funkcji pochodnych: gradientu i macierzy Hessego.

Podamy teraz twierdzenie opisujące ważne dla zadań optymalizacji własności funkcji wypukłych.

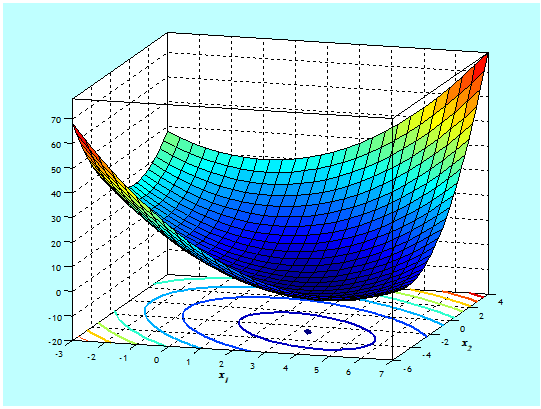
Trójwymiarowy i poziomicowy, wykresy funkcji ściśle wypukłej

\(x↦x^T \begin{bmatrix}1 & \frac{1}{2} \\\frac{1}{2}& 1 \\\end{bmatrix}x+[-4\,⋮\,\,2]x+5,\)

o minimum w \((x_1^o,x_2^o)=(10/3,-8/3)\) przedstawia Rys. 3.8.

Teraz zajmiemy się jeszcze dwiema pożytecznymi właściwościami funkcji wypukłych dotyczącymi ich pochodnej kierunkowej.

W świetle poznanych wcześniej własności, część B. twierdzenia dla wypukłych funkcji różniczkowalnych nie wnosi nowej informacji o ich zachowaniu, bo musi być spełnione: \((∀d)D_+ f(x^o,d)=∇f(x^o)d\) (Lemat 3.2) i jednoczesnie \(∇f  (xo) = 0\) (podane niżej Twierdzenie 3.6). Zostało jednak przytoczone, ponieważ powyższe własności mają też funkcje nieróżniczkowalne a wiele praktycznych zadań optymalizacji nie jest gładkich, ponadto, jak się o tym przekonamy, naturalne pomysły sposobów rozwiązywania zadań optymalizacji z ograniczeniami prowadzą do zadań niegładkich.

Zanim sformułujemy warunek wystarczający istnienia rozwiązania zadania optymalizacji, dla porządku przypomnimy określenie zadania, którym się zajmujemy.

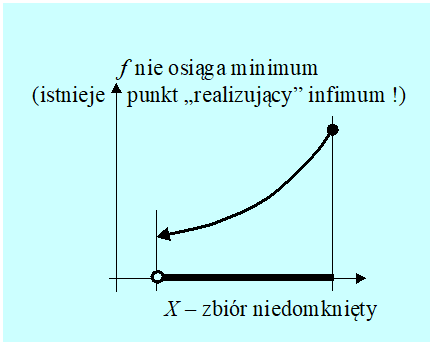
Wymagania przedstawionych wyżej warunków wystarczających można osłabić ale tylko w odniesieniu do rodzaju ciągłości funkcji, założenie o zwartości albo o domkniętości i „uciekaniu” funkcji do nieskończoności musi pozostać, por. rysunek 3.7 na którym zbiór D = X nie jest domknięty.

Dla funkcji jednej zmiennej archetypem funkcji wypukłej jest funkcja kwadratowa z dodatnim współczynnikiem. Funkcja ta oczywiście posiada minimum na dowolnym zbiorze domkniętym, także nieograniczonym. W związku z tym często sądzi się, że wypukłość gwarantuje istnienie minimum funkcji wypukłej na każdym zbiorze domkniętym. Tak jednak nie jest o czym świadczy przykład funkcji wykładniczej \(ℝ \ni x ↦ \mathrm{exp}(x) \in ℝ\), która jest ściśle wypukła i nie ma minimum w swojej, domkniętej przecież dziedzinie. 

Oznacza, to że w przypadku zadań bez ograniczeń, sama wypukłość funkcji wyboru nie rozstrzyga o istnieniu rozwiązania. Inaczej mówiąc, narzędzia pozwalające rozstrzygnąć o istnieniu rozwiązania muszą się odwoływać do innych własności funkcji – muszą być bardziej skomplikowane, np. takie jak Twierdzenie 3.3B.

Przedstawimy teraz podstawowe twierdzenia pozwalające dla funkcji różniczkowalnych zastąpić zadanie optymalizacji bez ograniczeń zadaniem znalezienia rozwiązania stosownego układu równań i sprawdzenia pewnych nierówności. O takiej metodzie rozwiązywania wspominaliśmy w punkcie 1.4 Modułu pierwszego stwierdzając, że gdy chcemy znaleźć rozwiązanie zadania optymalizacji drogą rachunkową, to musimy oryginalne sformułowanie przekształcić do postaci pozwalającej na wykonanie stosownych rachunków. 

Najstarsze twierdzenie pozwalające na stosowne przekształcenie zadania ZOBO, znane w swojej pierwotnej formie już P. Férmatowi około roku 1630, jest następujące.

Nazwaliśmy to twierdzenie warunkiem koniecznym optymalności I rzędu, bo są w nim wykorzystane tylko pochodne cząstkowe rzędu pierwszego funkcji minimalizowanej.

Inna nazwa tego warunku – warunek stacjonarności – nawiązuje do teorii równań różniczkowych, w której, zerowanie się pochodnej rozwiązania w jakimś przedziale, oznacza że jest ono stałe.

Jak możemy wykorzystać warunek konieczny optymalności I rzędu do znajdowania rozwiązania zadania optymalizacji bez ograniczeń? Odpowiedź zapiszemy w postaci następującej procedury.

Procedura redukcji zadania optymalizacji bez ograniczeń do układu równań

1. Stosujemy warunek konieczny optymalności I rzędu do funkcji, które mają gradient w całej przestrzeni (nie możemy „czegoś przegapić”).
2. Zaczynamy od pokazania, że zadanie ma rozwiązanie (możemy posłużyć się twierdzeniem Weierstrassa – twierdzenie (3.2)).
3. Wyliczamy gradient otrzymując wzór określający równanie wektorowe         \(∇f(x ̄ )=0. \qquad (3.1)\)     (warunek stacjonarności, układ n równań skalarnych, tylu ile jest współrzędnych przestrzeni).
4. Rozwiązując to równanie dostajemy zbiór rozwiązań \({x ̄}={x ̄^1,...,x ̄^j,...}.\) Interesują nas oczywiście rozwiązania (wektory) rzeczywiste.
5. Elementy zbioru rozwiązań traktujemy jako „podejrzanych”, których „sprawdzamy na optymalność” tzn. wyliczamy zbiór \({f(x ̄^j)}\) wartości funkcji f, a następnie typujemy jako kandydata na rozwiązanie wektor dla którego wartość funkcji jest najmniejsza (tylko ‘kandydata na’, a nie rozwiązanie, bo twierdzenie jest warunkiem koniecznym!). Oznaczmy go \(x^P \) .
6. Sprawdzamy, czy wektor xP  jest punktem minimum lokalnego i gdy wiemy, że zadanie ma rozwiązanie, to możemy uznać, go za punkt minimum globalnego, \(x^P = x^o\) .

Które z przedstawionych kroków postępowania (które operacje algorytmu) są najtrudniejsze?  Drugi i szósty, bo w przypadkach złożonych wymagają de facto udowodnienia pewnych lematów. Kłopotliwe bywa też szukanie wszystkich rozwiązań równania (3.1), szczególnie gdy szukamy tych rozwiązań numerycznie.

PRZYKŁAD 3.1 strona pierwsza

Poszukajmy punktu minimalizującego funkcję \(x↦f(x)=x^3-12(x-1)^2\).

Jak zwykle się to robi, zbagatelizujmy punkt 2 Procedury redukcji, i przystąpmy do rozwiązywania równania (3.1), które dla tego przypadku jest następujące

\(3x ̄^2-24x ̄+24=0.\)

Z zadaniem punktu 4 nie ma kłopotu. Podejrzanymi punktami są

\(x ̄^1=4-2\sqrt{2 }\)  oraz  \(x ̄^2=4+2\sqrt{2,}\)

a wartości funkcji f w podejrzanych punktach, obliczone przy pomocy kalkulatora, są następujące

\(f(x ̄^1)=1.2548,\, f(x ̄^2)=-89.2548".\)

Jeszcze raz bagatelizujemy konieczność pewnego wysiłku, którego wymaga punkt szósty (jak się o tym przekonamy niekoniecznie związanego z rozważaniami teoretycznymi) i uznajemy za rozwiązanie zadania punkt  \(x^o=x ̄^2=4+2\sqrt{</span></span>2}\).

Na koniec wykonujemy przy pomocy komputera rysunek rozważanej funkcji. 

Rys. 3.10: Uzyskany przy pomocy MATLABa wykres funkcji minimalizowanej

Wykonanie rzetelnego rysunku, a więc posłużenie się oprogramowaniem do którego mamy zaufanie, dla inżyniera bywa namiastką formalnego dowodu. „Uczona” nazwa takiego postępowania to stwierdzenie, że zastosowano metodę symulacyjną. Gdy otrzymane w ten sposób rozwiązanie dobrze sprawdza się w zastosowaniu, inżynier nie musi się kłopotać o wywody teoretyczne. 

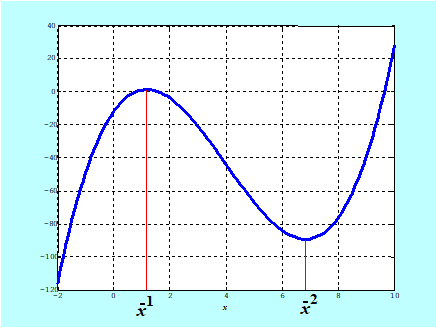
Najlepszym sposobem zwalniającym użytkownika przedstawionego algorytmu od konieczności udowadniania lematów, jest podanie ogólnego twierdzenia formułującego warunek (warunki?) wystarczające optymalności.

Znany przykład funkcji  \(x ↦ x^3\), która w punkcie zerowania się funkcji pochodnej \(x ↦ 3x^2\)  nie ma ani minimum, ani maksimum, wskazuje, że warunki wystarczające optymalności muszą być warunkami wykorzystującymi co najmniej drugie pochodne.

Pierwsze sformułowanie takich warunków pochodzi od G.W. Leibniza (Nova Methodus pro Maximis et Minimis... 1684). Podamy je w sformułowaniu współczesnym.

Twierdzenie formułuje wystarczający warunek optymalności lokalnej (w tezie jest minimum na kuli), i tak jak się spodziewaliśmy, warunek ten jest warunkiem II rzędu.

Przypomnijmy sobie Lemat 3.10 podający warunek wystarczający ścisłej wypukłości funkcji. Porównując ten lemat i twierdzenie Leibniza 3.5 widzimy, że warunek wystarczający optymalności lokalnej do warunku stacjonarności \(∇f(x ̄)=0\) dodaje warunek lokalnej ścisłej wypukłości. Wobec tego jego gwarancje też mogą być lokalne. O zachowaniu funkcji można sądzić po zachowaniu się jej pochodnych, ale informacja ta dotyczy infinitezymalnych  (tak by powiedział Newton) odchyleń od punktu, w którym pochodne są liczone! 

Zatem, dla funkcji dostatecznie gładkich możemy sobie poradzić z zagadnieniem punktu 6. (ostatniego) Procedury redukcji (teraz powinno być jasne, dlaczego jest tam wstawiona uwaga „gdy wiemy, że nasze zadanie ma rozwiązanie”).

Powróćmy do przykładu 3.1

Niestety, z błędami tego typu spotkałem się w poważnych, skądinąd, podręcznikach. Na szczęście tylko próbujących wykorzystać optymalizację a nie poświęconych jej teorii. 

Podkreślmy też, jeszcze raz, że wszelkie rozważania oparte na własnościach funkcji pochodnych, a więc na rachunku różniczkowym mają lokalny charakter. Czy istnieją rezultaty o globalnym charakterze? Wypukłość na pewnym zbiorze ma, że tak powiem, z punktu widzenia tego zbioru, charakter całościowy – globalny. Następujące twierdzenia pokazują, że dla funkcji wypukłych można podać warunki które musi spełniać punkt rozwiązujący nasze zadanie (punkt minimum globalnego) i co więcej są to warunki konieczne i wystarczające.

Dla gładkich funkcji wypukłych konieczny warunek optymalności I rzędu jest jednocześnie warunkiem wystarczającym. 

Jest to piękny rezultat teoretyczny, sprowadzający dla funkcji wypukłych Procedurę redukcji do układu równań wyłącznie do rachunków: liczenia pochodnych i rozwiązywania równań, czyli do takiego postępowania, które zastosowaliśmy w Przykładzie 3.1, niestety jak pokazał Rys. 3.10 do funkcji niewypukłej. Aby było ono poprawne trzeba (tylko) sprawdzić czy funkcja minimalizowana jest klasy \(\mathbf{C}^2\) i na początku realizacji wymagań punktu 6. policzyć macierz Hessego by posługując się Lematem 3.8 stwierdzić jej wypukłość (albo brak wypukłości). Gdy funkcja jest wypukła – istnienie rozwiązania wynika z Twierdzenia 3.5 i jednocześnie wskazany w punkcie 5. punkt (wektor) jest tym szukanym rozwiązaniem. 

I jak tu się nie zgodzić z H. Minkowskim, pierwszym matematykiem, który pod koniec XIX wieku badał własności zbiorów i funkcji wypukłych i podobno stwierdził, że „wszystko co wypukłe jest piękne”. 

Przedstawiona procedura rozwiązywania zadania optymalizacji bez ograniczeń przez redukcję do układu równań ma ograniczone zastosowanie.

• Po pierwsze można ją (w zasadzie) stosować tylko tam, gdzie znamy analityczny wzór określający funkcję wyboru. Jednak w wielu zadaniach praktycznych wartości tej funkcji są wyliczane za pomocą szeregu procedur numerycznych i całościowego wzoru na nią nie znamy. Często jest też tak, że nawet gdy znamy wzory, to posługiwanie się nimi jest żmudne i uciążliwe (tak jest np. w zagadnieniach optymalizacji związanych z pracą robotów) i w zasadzie robimy wszystko, by takiej pracy uniknąć. Powyżej napisaliśmy, w zasadzie, ponieważ opracowano procedury automatycznego różniczkowania (nie mylić z procedurami symbolicznego różniczkowania), które przetwarzają kod wyliczający funkcję wyboru na kod wyliczający jej pochodne. Zatem wymaganie znajomości wzoru nie jest już takie kategoryczne. 
• Po drugie, trzeba równanie (3.1) rozwiązać, a analitycznie potrafimy rozwiązywać tylko równania najprostsze. Musimy więc posłużyć się numerycznymi algorytmami rozwiązywania równań. Powstaje tu pytanie, po co męczyć się nad przekształceniem, czy nie lepiej od razu zastosować numeryczny algorytm znajdowania rozwiązania zadania optymalizacji.
• I na koniec, przyczyna trzecia – wyraźnie sformułowana konieczność udowodnienia, że wyliczony punkt jest rzeczywiście rozwiązaniem, wielu odstręcza.

Zauważmy, że jednym z plusów tej metody jest to, że idealnie nadaje się do, nazwijmy to tak, sprawdzania wiadomości i zdolności rachunkowych studentów.

Jeżeli nie Procedura redukcji do układu równań, to co możemy poradzić naszemu Algorytmowi, którego jakiś czas temu zostawiliśmy samego na zboczu funkcji bananowej:

Odpowiedzi udzielimy w module następnym, a teraz zajmiemy się kwadratowymi przybliżeniami funkcji, które nie koniecznie są wypukłe.