1. Wprowadzenie do matematyki teorii optymalizacji

1.2. Gładkie zadania optymalizacji



W punkcie 1.3 Modułu pierwszego wyróżniliśmy gładkie (różniczkowalne) i niegładkie zadania optymalizacji. Zajmiemy się teraz bliżej własnościami gładkich zadań optymalizacji.

Najpierw trzeba precyzyjnie ustalić jakie zadania optymalizacji uznajemy za gładkie. Rozważania punktu poprzedniego tego rozdziału, w których posługiwaliśmy się co najwyżej drugimi pochodnymi, sugerują że dwukrotna różniczkowalność wystarczy. Mamy więc definicję.

DEFINICJA zadania gładkiego
Zadanie optymalizacji nazywamy gładkim, jeżeli wszystkie funkcje występujące w jego określeniu są klasy \(\mathbf{C}^2\).

Na razie zajmujemy się zadaniami bez ograniczeń, dlatego będziemy się interesować tylko funkcją wyboru f.

Dla funkcji f klasy \(\mathbf{C}^2\) zgodnie z twierdzeniem Taylora mamy

\((∀x ̄,x)f(x)=f(x ̄)+∇f(x ̄)(x-x ̄)+1/2(x-x ̄)^T ∇^2 f(x ̄)(x-x ̄)+ \)

 + nieskończenie mała rzędu 3,gdy \(x-x ̄→0\).

Oznacza, to że dla prawie każdej funkcji f klasy \(\mathbf{C}^2\) i dowolnego punktu \(x ̄\) istnieje takie jego otoczenie \(\mathbf{O}(x ̄)\), w którym funkcja kwadratowa
\(x↦f ̃(x;x ̄)=f(x ̄ )+∇f(x ̄)(x-x ̄)+1/2(x-x ̄)^T ∇^2 f(x ̄)(x-x ̄)=\)
\(=1/2 x^T ∇^2 f(x ̄ )x-x ̄^T ∇^2 f(x ̄ )x+∇f(x ̄ )x+1/2 x ̄^T ∇^2 f(x ̄ ) x ̄-∇f(x ̄ ) x ̄+f(x ̄ )=\)
\(=1/2 x^T ∇^2 f(x ̄)x+c^T (x ̄)x+σ(x ̄)\)
przybliża ją dobrze w tym otoczeniu.
Przykład 3.2
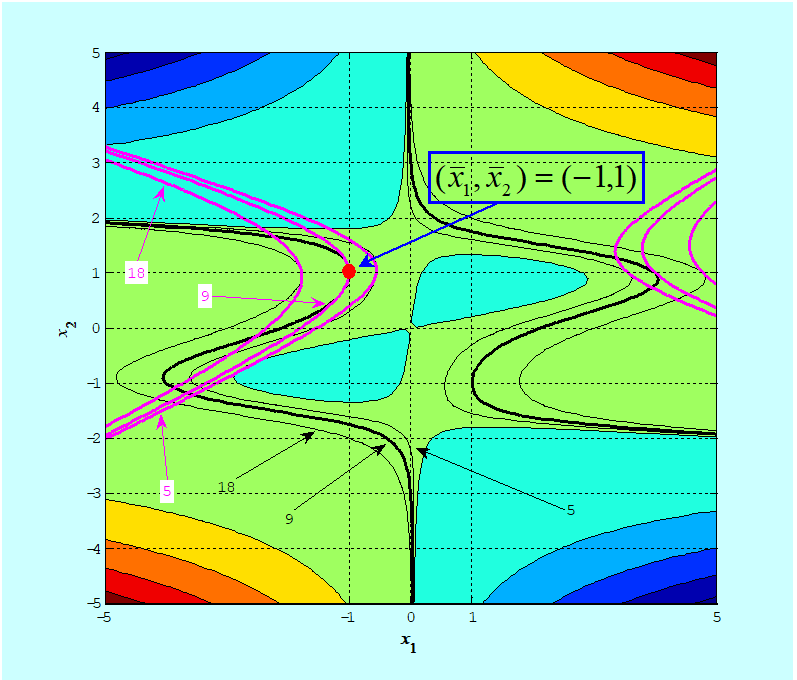
Rozpatrzmy funkcję, której mapę przestawiliśmy w punkcie 1.2.4 Modułu pierwszego, Rys.1.7.
\(x \mapsto f (x) = 2(x1)^2 + 4x1(x2)^3 – 10x2x1 + (x2)^2.\)
Policzmy jej aproksymację w punkcie \((x ̄_1,x ̄_2)=(-1,1)\). Wektor gradientu jest równy
\(∇f(x ̄_1,x ̄_2)=[4x ̄_1+4(x ̄_2 )^3-10x ̄_2⋮12x ̄_1 (x ̄_2 )^2-10x ̄_1+2x ̄_2]_{|_((x ̄_1,x ̄_2)=(-1,1)) }=[-10⋮0],\)
a macierz Hessego
\(∇^2 f(x ̄_1,x ̄_2)=\begin{bmatrix}4 &  12(x ̄_2 )^2-10\\12(x ̄_2 )^2& 24x ̄_1 x ̄_2+2)] \\\end{bmatrix}_{|_((x ̄_1,x ̄_2)=(-1,1)) }=\begin{bmatrix}4 &  2\\2&-22)\\\end{bmatrix}.\)
Zatem funkcja aproksymująca jest równa
\(x↦\tilde{f} (x;(x ̅=(-1,1)))=\frac{1}{2}x^T ∇^2 f(x ̄ )x-x ̄^T ∇^2 f(x ̄ )x+∇f(x ̄ )x+\frac{1}{2}x ̄^T ∇^2 f(x ̄ ) x ̄-∇f(x ̄ ) x ̄+f(x ̄ )=\)
\(=\frac{1}{2}x^T \begin{bmatrix}4 &  2\\2&-22\\\end{bmatrix}x-[-1\,⋮\,1]\begin{bmatrix}4 &  2\\2&-22\\\end{bmatrix}x+[-10\,⋮\,0]x+\)
\(+\frac{1}{2}[-1\,⋮\,1]\begin{bmatrix}4 &  2\\2&-22\\\end{bmatrix}\begin{bmatrix}-1\\1\\\end{bmatrix}-[-10\,⋮\,0]\begin{bmatrix}-1\\1\\\end{bmatrix}+f(1,-1)=  \)
\(=2(x_1 )^2+2x_1 x_2-11(x_2 )^2-8x_1+24x_2-12.\)
Zobaczmy jak aproksymacja wygląda na wykresach: poziomicowych, oraz antygradientów, na których poziomice i antygradienty funkcji f są czarne, a funkcji aproksymującej f ̃ – purpurowe.

Rys. 3.12a): Aproksymacja – poziomice funkcji i funkcji aproksymującej w punkcie (–1.–1)


Rys. 3.12b): Aproksymacja – poziomice i antygradienty funkcji i funkcji aproksymującej oraz otoczenie dobrej aproksymacji


Rys. 3.13: Aproksymacja: a) trójwymiarowy wykres funkcji f , 
b) trójwymiarowy wykres funkcji aproksymującej f ̃
Zauważmy, że otoczenie, w którym aproksymację uznalibyśmy za dobrą nie jest duże i jego kształt jest zbliżony do elipsy o osiach nierównoległych do osi współrzędnych kartezjańskich. Rys. 3.13 pokazuje, że funkcja aproksymowana i funkcja aproksymująca „globalnie” są zupełnie różne, ale, jak wynika z Rys. 3.12b) w otoczeniu punktu aproksymacji (lokalnie) są bardzo podobne.

Podsumujmy nasze dotychczasowe rozważania.

Dla funkcji gładkich (klasy \(\mathbf{C}^2\) ) wzór

\(x↦\tilde{f} (x;x ̄)=1/2 x^T ∇^2 f(x ̄)x+c^T (x ̄)x+σ(x ̄) \qquad (3.2)\)

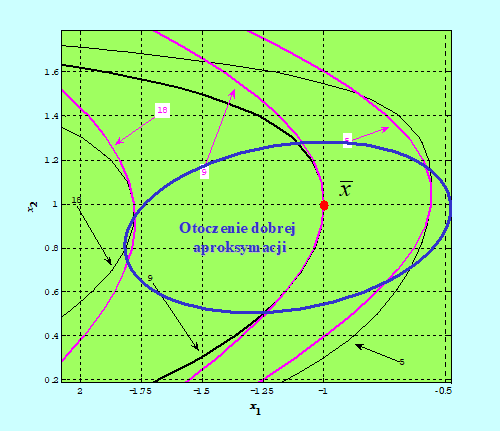
  • nie daje dobrej aproksymacji funkcji f  w całej przestrzeni (nie daje aproksymacji globalnej), natomiast
  • istnieje takie otoczenie (konkretne wskazanie go jest bardzo trudne), w którym wzór ten dobrze przybliża tę funkcję – jest dobrą aproksymacją lokalną.
Ponieważ, w zasadzie nigdy nie znamy otoczenia dobrej aproksymacji mamy dwa wyjścia:
  • pesymisty – nie korzystać ze wzoru (3.2),
  • optymisty – przyjąć, że otoczenie dobrej aproksymacji to jest na tyle duże, że wykorzystanie gradientu i macierzy Hessego obliczonego w danym punkcie przy konstruowaniu algorytmu zmierzającego do punktu optymalnego nie wyprowadzi na manowce.

Tego rodzaju dylemat jest typowy dla sytuacji, w której znajduje się twórca nowych rozwiązań konstrukcyjnych – magister, a więc mistrz, inżynier – a także twórca nowych teorii naukowych. Za podejściem optymisty opowiedział się Albert Einstein, który w 1921 r. stwierdził, że „Raffiniert ist der Herrgott, aber boshaft ist er nicht”.  Co w naszym przypadku przekłada się na przeświadczenie, że nieliniowe zadania optymalizacji związane z rozwiązywaniem zagadnień praktycznych, są takie, że zręczne wykorzystanie możliwości jakie daje posługiwanie się kwadratową aproksymacją (3.2) pozwoli opracować skuteczne algorytmy ich rozwiązywania. Współcześni optymiści mają sławnego poprzednika – Izaaka Newtona, który wymyślił metodę stycznych rozwiązywania równań nieliniowych opartą o jeszcze prostszą aproksymację, bo ograniczoną tylko do składnika afinicznego.