1. Wprowadzenie do matematyki teorii optymalizacji

1.3. Właściwości funkcji kwadratowych

Jako optymiści musimy poznać podstawowe własności funkcji kwadratowych

x\(↦x^T Qx+c^T x+σ, \qquad (3.2)\)

o symetrycznej macierzy Q.

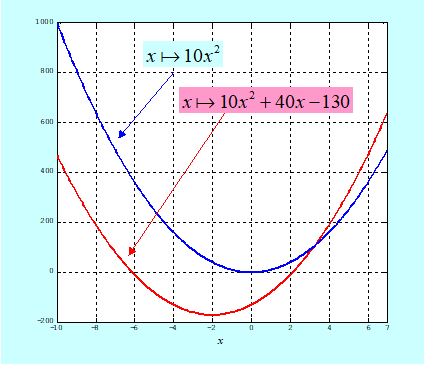
Zauważmy najpierw, że własności tej funkcji są zdeterminowane przez własności formy kwadratowej, czyli macierzy Q. Intuicyjnie – dodanie członu afinicznego „przesuwa” formę kwadratową nie zmieniając jej kształtu, tzn. nie zmienia jej podstawowych własności. Rysunek dla funkcji jednej zmiennej potwierdza tę intuicję.


Rys. 3.14: Funkcja kwadratowa jednej zmiennej i jej pochodna
Przypomnijmy ważną własność symetrycznej macierzy \(Q_{n×n}\) – określoność. 
Macierz Q jest:
dodatnio półokreślona gdy \((∀x)x^T Qx ≥0,\)
dodatnio określona gdy \((∀x≠0)x^T Qx>0,\)
ujemnie półokreślona gdy macierz  – Q jest dodatnio półokreślona,
ujemnie określona, gdy macierz  – Q jest dodatnio określona, 
nieokreślona, gdy nie jest dodatnio półokreślona lub ujemnie półokreślona.
Dodatnią określoność macierzy Q będziemy zapisywać \(Q > 0\),   dodatnią półokreśloność \(Q \geq 0\), itd.
O określoności macierzy \(Q_{n×n}\) można sądzić na podstawie znaków jej elementów.
LEMAT 3.11  
Jeżeli elementy na głównej przekątnej, \(q_{ii}\) , są niedodatnie to macierz Q nie jest dodatnio określona.
Jeżeli elementy na głównej przekątnej, \(q_{ii}\), są ujemne to macierz Q nie jest dodatnio półokreślona (a więc nie jest i dodatnio określona).
Intuicyjnie wydaje się, że tezy lematu powinny być zamienione miejscami! Konieczność użycia sformułowania takiego jak w lemacie wynika z faktu, że dla macierzy zerowej 0 mamy dla każdego \(x: xT\mathbf{0}xT = 0 \geq 0\), zatem macierz ta jest dodatnio (i ujemnie też!) półokreślona.

Zauważmy też, że na podstawie Lematu 3.11 o macierzy \(\begin{bmatrix}1&-2\\-2&1\\\end{bmatrix}\) możemy powiedzieć, że nie jest ujemnie półokreślona (bo macierz \(\begin{bmatrix}-1&2\\2&-1\\\end{bmatrix}\) nie jest dodatnio półokreslona), natomiast ustalenie dodatniej określoności, dodatniej połokreśloności albo nieokreśloności wymaga dalszych rachunków.

Dla macierzy \(2\times 2\) prawdziwy jest lemat

LEMAT 3.12  
Macierz \( Q=\begin{bmatrix}q_{11}&q_{12}\\q_{12}&q_{22}\\\end{bmatrix} \) jest dodatnio określona [dodatnio półokreślona] \(\Leftrightarrow \)
 \(\Leftrightarrow  q_{ii}>0 \,\mathrm{i}\,q_{11} q_{22}-(q_{12} )^2>0 [q_{ii}≥0 \,\mathrm{i} \,q_{11} q_{22}-(q_{12} )^2≥0].\)

Zatem macierz \(\begin{bmatrix}1&-2\\-2&1\\\end{bmatrix}\)  przytoczona powyżej jest nieokreślona (nie jest ujemnie półokreślona i nie jest dodatnio półokreślona).

Wartości własne macierzy
Różne własności kwadratowej macierzy \(Q_{n×n}\) są opisywane przez własności jej wartości własnych tj. n pierwiastków równania charakterystycznego
\(\mathrm{det}⁡( sI-Q)=0\).
Wartości własne (eigenvalues) będziemy dalej oznaczać \(s_1(Q),...,s_i (Q),...,s_n(Q).\)
Zauważmy, że kwadratowa macierz Q jest odwracalna (nieosobliwa) wtedy i tylko wtedy gdy
\((\forall i) s_i (Q) \neq 0\, \mathrm{ bo}\, \mathrm{det}⁡Q \neq 0 \Leftrightarrow (\forall i) si (Q) \neq 0.\)

LEMAT 3.13  
A. Wartości własne macierzy symetrycznej są liczbami rzeczywistymi.
B. \(Q \geq 0 \Leftrightarrow (\forall i) \sigma_i (Q) \geq 0 \).
C. \(Q > 0 \Leftrightarrow (\forall i) \sigma_i (Q) > 0 \).
D. Dla dowolnej macierzy \(A_{n×n}\), macierz \(A^TA\) i macierz \(AA^T\) są dodatnio półokreślone, 
a dodatnio określone gdy macierz A jest odwracalna. 

Prostym wnioskiem z Lematu 3.13 jest, że macierz dodatnio (ujemnie) określona jest odwracalna (nieosobliwa).

Zauważmy też, że w świetle lematu 3.10 [3.8] funkcja kwadratowa oparta na macierzy dodatnio określonej [dodatnio półokreślonej] jest ściśle wypukła [wypukła].

DEFINICJA wektora własnego macierzy
Wektor \(v ^i \neq 0\) będący rozwiązaniem równania
\(Qvi^ = s_i (Q)v^i\)
nazywamy wektorem własnym macierzy Q (związanym z wartością własną \(s_i (Q))\).

Zilustrujemy wprowadzone pojęcia przykładem wyznaczenia wartości własnych i wektorów własnych.

PRZYKŁAD 3.3   
Rozpatrzmy symetryczną macierz \(Q=\begin{bmatrix}2&\frac{2}{3}\\\frac{2}{3}&1\\\end{bmatrix}  \). 
Jej równanie charakterystyczne \(\mathrm{det}⁡( sI-Q)=\mathrm{det}\begin{bmatrix}s-2&-\frac{2}{3}\\-\frac{2}{3}&s-1\\\end{bmatrix}=...=s^2-3s+\frac{14}{9}.\)
Jego pierwiastki (wartości własne) to: \(s_1 (Q)=\dfrac{2}{3},\, s_2 (Q)=\dfrac{7}{3}\), zatem macierz jest określona dodatnio. 
Policzmy teraz wektory własne. Najpierw związany z pierwszą wartością własną\( s_1 (Q)=\dfrac{2}{3}\).
\(\begin{bmatrix}2&\dfrac{2}{3}\\\dfrac{2}{3}&1\\\end{bmatrix} \begin{bmatrix}v_1^1\\v_2^1\\\end{bmatrix}=\dfrac{2}{3} \begin{bmatrix}v_1^1\\v_2^1\\\end{bmatrix}\), czyli   \(\begin{matrix}2v_1^1+\dfrac{2}{3} v_2^1=\dfrac{2}{3} v_1^1\\   \dfrac{2}{3} v_1^1+v_2^1=\dfrac{2}{3} v_2^1 \end{matrix},\) co daje   \(\begin{matrix}4v_1^1+2v_2^1=0\\   2v_1^1+v_2^1=0\end{matrix},\) skąd mamy
równanie dla pierwszego wektora własnego
\(v_2^1=-2v_1^1\).
Analogiczne rachunki dają dla drugiego wektora własnego:
\(v_2^2=1/2 v_1^1.\)

Widać zatem, że wektory własne nie są wyznaczone jednoznacznie, i nie jest to przypadek. W terminologii używanej w teorii metod optymalizacji wektory własne wyznaczają tylko kierunki (proste). Jaki jest z nich pożytek? Narysujmy wykres poziomicowy formy kwadratowej  \(x↦x^T Qx\) dla macierzy Q rozważanej w przykładzie. 


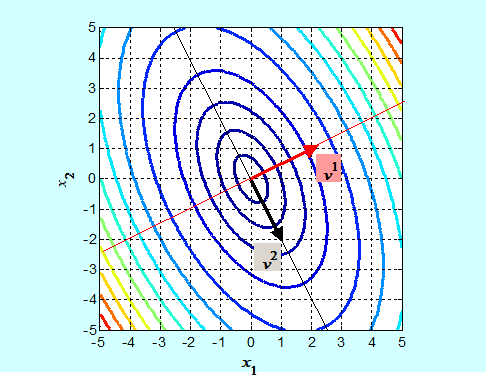
Rys. 3.15: Poziomice funkcji kwadratowej i wektory własne

Jak widać wektory własne leżą na osiach elips, które są poziomicami rozważanej funkcji. Zauważmy, że elipsy są „rozciągnięte” w kierunku \(v^2\), a więc związanym z większą wartością własną \(s_2 (Q)=\frac{7}{3}\). Te zależności są ogólne i odnoszą się do wszystkich sytuacji z jakimi możemy się spotkać analizując funkcje kwadratowe, ale (na szczęście) stosownych wzorów nie będziemy wyprowadzać. 

Przedstawimy teraz z jakimi przypadkami kształtów funkcji kwadratowej

\(x↦x^T Qx+c^T x+σ \)

możemy się spotkać. 

Jest ich pięć:

  • macierz Q jest dodatnio określona,
  • istotnie dodatnio półokreślona (co najmniej jedna wartość własna jest zerowa),
  • nie jest określona,
  • jest określona ujemnie,
  • jest istotnie ujemnie półokreślona.

Niestety, możemy narysować tylko funkcję dwu zmiennych (jak często mówimy, na płaszczyźnie). Przedstawmy zatem wykresy trójwymiarowe i poziomicowe dla pierwszych trzech przypadków, ponieważ funkcje określone ujemnie to „odwrócone w dół” funkcje określone dodatnio. 

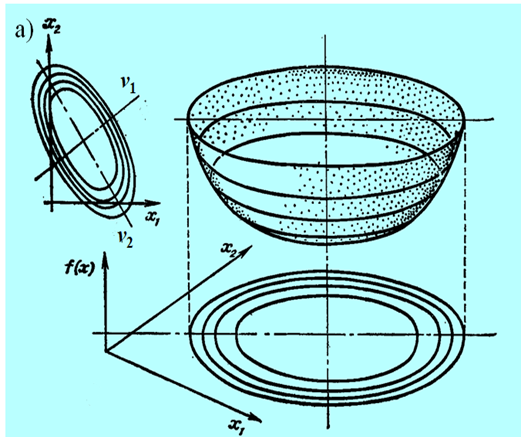
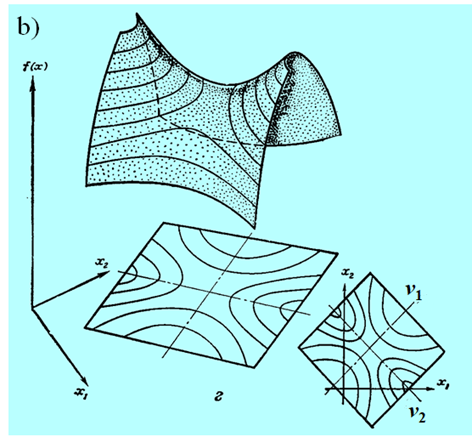
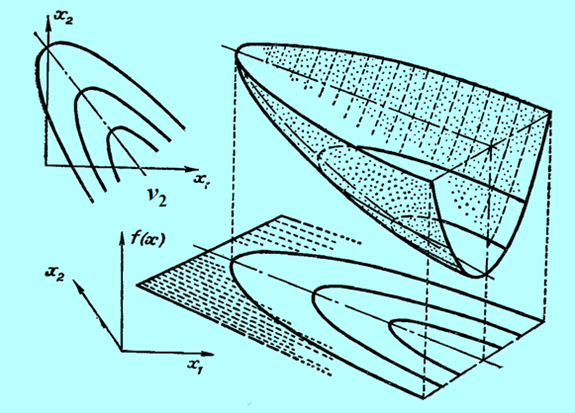
Rys. 3.16: Kształt funkcji kwadratowej dla macierzy Q : a) dodatnio określonej \((s_1 > 0, s_2 > 0)\), archetyp funkcji (ściśle)wypukłej; b) nie określonej \((s_1 > 0, s_2 < 0)\), funkcja ma punkt siodłowy


Rys. 3.17: Kształt funkcji kwadratowej dla dodatnio półokreślona macierzy \(Q (s_1 > 0, s_2 = 0),\)„zgubiony” jeden wektor własny, funkcja nie ma minimum i dąży powoli do -∞  

Następny rysunek nie przedstawia funkcji kwadratowej a formę kwadratową tzn. funkcję \(x↦x^T Qx\) dla tego samego przypadku, tzn. jednej wartości własnej zerowej.


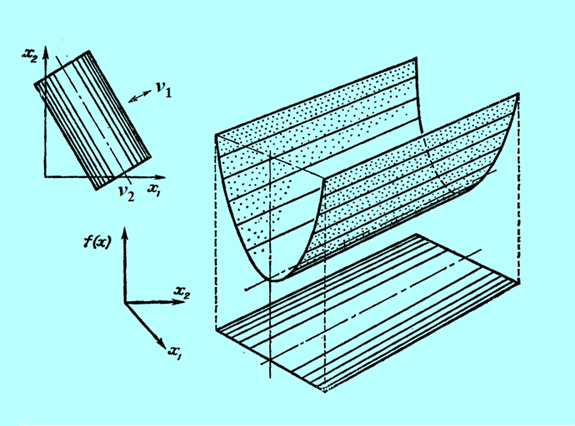
Rys. 3.18: Kształt formy kwadratowej, macierz Q dodatnio półokreślona \((s_1 > 0, s_2 = 0)\)

Widać, że w odróżnieniu od przypadku poprzedniego (Rys. 3.17) funkcja ta ma nieskończenie wiele minimów.

Zauważmy  tu  rzecz  istotną:  Trzeba  być  ostrożnym  z  intuicyjnym  przenoszeniem  wniosków
wyciągniętych w oparciu o własności funkcji jednej zmiennej na własności funkcji wielu zmiennych (nawet dwu!). Posługując się intuicją napisaliśmy parę stron wcześniej, interpretując Rys. 3.14, że „dodanie członu afinicznego ... nie zmienia podstawowych własności formy kwadratowej”. Jak widzimy, nie jest to w ogólności prawdą. Nawet gdy uznamy przypadek o zerowej wartości własnej za nietypowy, to w dokładnej analizie musimy go „wyłapać” i wyeliminować, aby uniknąć przykrych konsekwencji jakie jego wystąpienie wywołuje

Na koniec, wprowadzimy pewną jakościową charakterystykę funkcji kwadratowych. Jest dość oczywiste, że naszemu „ślepemu” Algorytmowi łatwiej jest znaleźć minimum, gdy w każdym kierunku, co najmniej lokalnie, funkcja minimalizowana zachowuje się tak samo – dla dwu zmiennych jej poziomice są zbliżone do okręgu, dla trzech – do kuli, itd. Dobrze byłoby gdyby Algorytm mógł o tym się dowiedzieć. Wiemy, że dla funkcji kwadratowych informacje o kierunkach rozciągnięcia powierzchni stałej wartości (poziomic dla funkcji dwu zmiennych) i jego wielkości niosą wektory własne (por. Rys. 3.15 i następne) ściśle związane z wartościami własnymi macierzy Q. W związku z tym można udowodnić Lemat następujący.

LEMAT 6.1
Jeżeli 
uszeregujmy wartości własne dodatnio określonej macierzy \(Q_{n×n}\) od najmniejszej \(s_1(Q)\) do największej \(s_n(Q)\), 
to 
prawdziwa jest następująca nierówność:  \((∀x)s_1 x^T x≤x^T Qx ≤s_n x^T x.\)
Rezultatem tej nierówności są następujące inkluzje
               \((∀c){x|s_n x^T x≤c}⊆{x|x^T Qx≤c}⊆{x|s_1 x^T x≤c},\)
zwracam uwagę na odwrotną kolejność inkluzji!


Rys. 3.19: Związek wartości własnych i kształtu poziomic dwuwymiarowej funkcji kwadratowej

Wykorzystując oczywistą interpretację powyższych inkluzji nasuwającą się na podstawie Rys. 3.19 zdefiniujemy tzw. uwarunkowanie macierzy w sposób następujący. 

DEFINICJA uwarunkowania macierzy
Dla symetrycznej macierzy Q iloraz 
     \(cr(Q)=\dfrac{max_i⁡| s_i (Q)|}{min_i⁡| s_i (Q)|}≥1\)
nazywamy jej uwarunkowaniem (condition number/ratio).

Uwarunkowanie jest tym jakościowym miernikiem własności funkcji kwadratowej którego szukamy. Powierzchnie stałej wartości funkcji kwadratowej zbudowanej na określonej dodatnio macierzy Q o uwarunkowaniu \(cr(Q)\) bliskim jedności są zbliżone do hiperkul (na płaszczyźnie – okręgów). Funkcja zmienia się w podobny sposób w każdym kierunku. Im większe jest uwarunkowanie, tym gorzej: w jednym kierunku funkcja zmienia się powoli, w prostopadłym bardzo szybko. Gdy \(cr(Q)\) jest duży, praktycznie już od kilku, to taką funkcję kwadratową nazywamy źle uwarunkowaną.

Funkcje celu, które trzeba minimalizować mogą mieć jednak różny kształt, co znakomicie utrudnia ustalenie zasad jakimi ma się kierować Algorytm, którego zadaniem jest minimalizacja. 

Przyjęliśmy jednak postawę optymistyczną zakładającą, że funkcja celu f jest gładka i wzór (3.2)

\(x↦\tilde{f}(x;x ̄)=\frac{1}{2} x^T ∇^2 f(x ̄)x+c^T (x ̄)x+σ(x ̄)\)

gdzie \(x ̄↦c^T (x ̄)=-x ̄^T ∇^2 f(x ̄)+∇f(x ̄),x ̄↦σ(x ̄)=\frac{1}{2} x ̄^T ∇^2 f(x ̄ ) x ̄-∇f(x ̄ ) x ̄+f(x ̄ ) \qquad (3.3)\)

jest jej dobrą aproksymacją. Wiemy, że aproksymacja ta jest lokalna, ale bez formalnego udowadniania tego, przyjmujemy że otoczenie dobrej aproksymacji jest dostatecznie duże (optymizm), por. Rys. 3.12 i 3.13. W takiej sytuacji powyższe rozważania upoważniają do przyjęcia tezy, że jakościowe aspekty zmienności funkcji celu są, tak jak dla funkcji kwadratowych, w całości opisane jej gradientem i macierzą drugich pochodnych (macierzą Hessego). 

Jedną z konsekwencji takiego podejścia jest mówienie o złym uwarunkowaniu funkcji celu traktując uwarunkowanie jej macierzy Hessego jako miarę rozciągnięcia powierzchni stałej wartości (poziomic dla funkcji dwu zmiennych). 

Przedstawmy tak rozumiane uwarunkowanie dla bananowej funkcji Rosenbrocka.


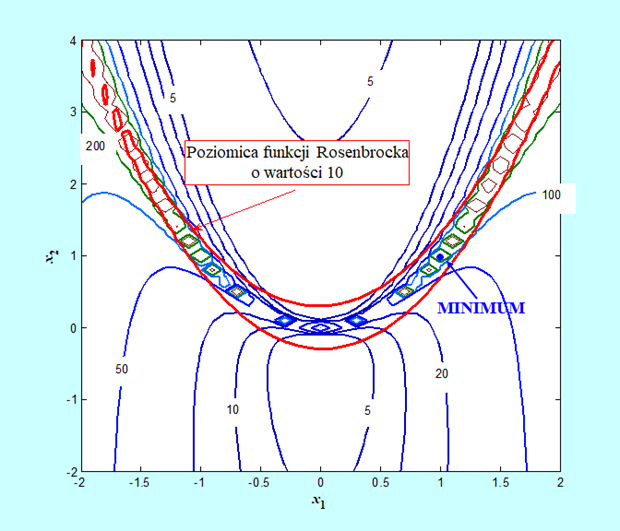
Rys. 3.20: Wykres linii stałego uwarunkowania macierzy Hessego dla funkcji Rosenbrocka, zaznaczono linie w wartościach od 5 do 200

Widać, że funkcja Rosenbrocka jest dobrze dobrana jako „tor badania sprawności” dla różnych algorytmów. Tylko w centralnej części (tam gdzie nie ma minimum) jej uwarunkowanie jest mniejsze od pięciu, natomiast w okolicy minimum jest większe od 100.

Zauważmy też, że wykres (otrzymany przy pomocy MATLABa) trochę oszukuje. Linie stałego uwarunkowania nie tworzą „wysp” jak sugeruje rysunek, taki kształt wynika z przyjętego (świadomie zbyt małego) kroku siatki – 0.1 – na której wykonywany był rysunek.