2. Podstawy metod optymalizacji bez ograniczeń

2.1. Metody rozsiewania punktów próbnych

Przeanalizujmy sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów sąsiedztwa \(\mathbf{S}(x^{(k)})\), zaczepionego w „bieżącym” punkcie \(x^{(k)}\) Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne).

 

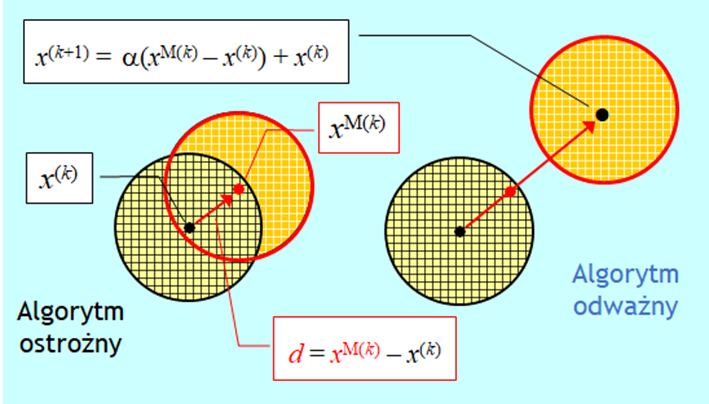
Rys. 3.2: Rozsiewanie punktów próbnych, Algorytm ostrożny i Algorytm odważny

Niech punktem z próby, w którym funkcja wyboru jest najmniejsza jest punkt nazwany \(x^{M(k)}\). Algorytm teraz może być:

  • ostrożny (wiem, że schody opadają w prawo, schodzę w prawo o jeden stopień) – przyjąć \(x^{M(k)}\) za „centrum” nowego sąsiedztwa  \(x^{(k+1)}=x^{M(k)}\)i przeszukiwać je tak jak poprzednio;
  • odważny (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) – przesunąć „centrum” sąsiedztwa poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów \(x^{M(k)} – x^{(k)}\), tzn. ustalić „centrum nowego sąsiedztwa w punkcie 

\(x^{(k+1)} = \alpha (x^{M(k)} – x^{(k)}) +x^{(k)}, \, \alpha > 1 .\)

Dwa podstawowe problemy, które trzeba teraz rozwiązać, to:

  • Jak wybierać \(\alpha\)? Jest to zagadnienie, w którym trzeba odpowiedzieć na trudne pytanie – jak będąc odważnym zachować rozwagę?
  • Jak wybrnąć z sytuacji gdy w kolejnym kroku nie potrafimy poprawić funkcji celu – czy punkt o najmniejszej z dotychczas znalezionych wartości funkcji wyboru uznać za rozwiązanie? Jest to trudne zagadnienie ustalenia kryterium stopu. 

Myślenie o sprawdzaniu sąsiedztwa jako przeszukiwaniu za pomocą równomiernie rozsiewanych punktów doprowadziło do konstrukcji wielu algorytmów probabilistycznych, których nie będziemy w ramach tego wykładu omawiać, oraz różnych algorytmów deterministycznych.

Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm Neldera i Meada zwany też algorytmem pełzającego sympleksu,  w którym sąsiedztwem nie jest kula ale sympleks – zbiór punktów o liczności o jeden większej niż wymiar przestrzeni poszukiwań. Nie będziemy zagłębiali się w szczegóły tego algorytmu (jak ustalić próbę początkową czyli pierwszy sympleks, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do podręcznika A. Stachurski: Wprowadzenie do optymalizacji, Oficyna Wydawnicza PW 2009, podrozdział 3.7. Przedstawimy tylko rysunek pokazujący jak takie pełzanie może wyglądać.

 

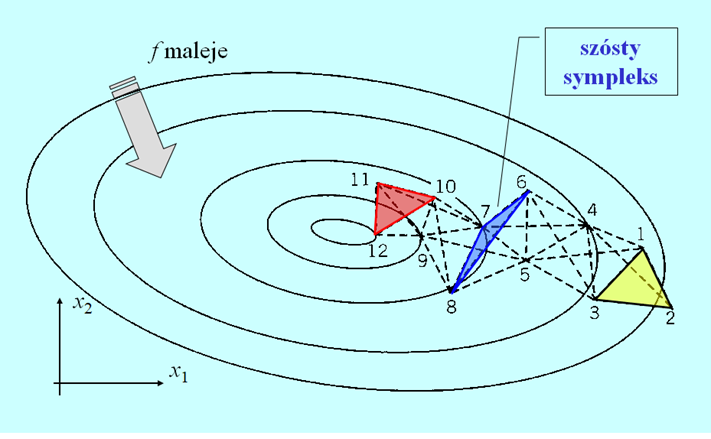
Rys. 3.22: Kolejne kroki algorytmu Neldera i Meada

Widać, że dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo dobrze. W MATLABie jest on zaimplementowany jako funkcja fminsearch i doświadczenia wielu pokoleń studentów pokazały, że jest on narzędziem efektywnym w typowych zastosowaniach laboratoryjnych i projektowych.