2. Podstawy metod optymalizacji bez ograniczeń

2.2. Metody obszaru zaufania

Przejdźmy teraz do omówienia sposobu opartego na założeniu, że Algorytm dysponuje a priori pewną wiedzą o lokalnym zachowaniu funkcji wyboru (wiedza lokalna) i jest na tyle odważny, że chce (i potrafi) tę wiedzę „rozciągnąć” na dużo większe otoczenie. Przyjmujemy zatem, że dookoła punktu bieżącego \(x^{(k)}\) została określona kula \(\mathfrak{K}(x^{(k)}, r)\) i funkcja \(x↦f_M (x;x^{(k)})\), tzw. funkcja modelująca, będąca modelem zachowania się funkcji wyboru \(f\) w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu 3.1.2, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową (3.3) 

\(x↦f_M (x;x^{(k)})=\frac{1}{2} x^T ∇^2 f(x^{(k)})x+c^T (x^{(k)})x+σ(x^{(k)})=x^T Qx+c^T x+σ.\)

W takiej sytuacji przeszukanie otoczenia punktu x(k) może oznaczać tylko jedno – szukanie punktu xM(k), minimalizującego funkcję modelującą na tzw. kuli zaufania \(\mathfrak{K}(x^{(k)}, r)\). 

 

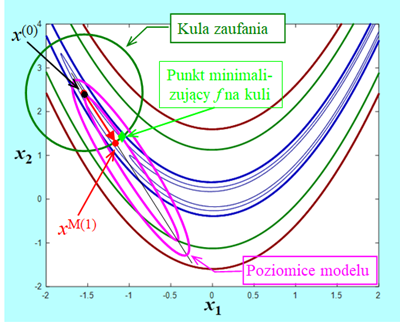
Rys. 3.23: Przeszukanie obszaru zaufania

Do przedstawionego wyżej pomysłu opisującego w jaki sposób Algorytm może otrzymany punkt przetworzyć na środek nowego obszaru eksploracji trzeba dodać istotną uwagę. 

  • Ponieważ punkt \(x^{M(k)}\) został wygenerowany w oparciu o model, to gdy kula jest za duża. może nie być właściwy – wartość rzeczywistej funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Może to pociągnąć za sobą konieczność wielokrotnego rozwiązywania zadania minimalizującego funkcję modelującą na kuli zaczepionej w punkcie bieżącym. 
Przyjmujemy zatem, że punkt minimalizujący funkcję modelującą na kuli zaufania będzie się różnił niewiele< od rzeczywistego minimizatora funkcji celu f na tej kuli, i co ważniejsze, będzie spełniona nierówność

\(f(x^{M(k)} \leq f(x^{(k-1)}), \qquad (3.4)\)

oznaczająca, że funkcja celu z kroku na krok maleje.

W świetle tych rozważań jest oczywiste, że algorytmy wykorzystujące podejście tego typu mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występującego w nich zadania 

 Zadanie poprawy ZKK
 \(\left.\begin{matrix}\mathrm{znalezc\, liczbe\,}\alpha = \mathrm{argmin}_xf_M (x;x^{(k)})=x^T Qx+c^T x+\sigma\\\mathrm{p.o.\,}  x \in \mathfrak{K}(x^{(k)},r)=\left \{((x-x^{(k)} )^T (x-x^{(k)})\leq r^2  \right \} \end{matrix}\right\}\)

co nastąpiło w połowie lat siedemdziesiątych XX w. Wtedy algorytmy tego typu były klasyfikowane jako algorytmy z ograniczonym krokiem. Koniec XX w. przyniósł ponowne zainteresowanie tym podejściem i zmianę nazwy na metody obszaru zaufania (trust region methods).

Podamy teraz podstawową strukturę algorytmu obszaru zaufania.

Podstawowy algorytm metody obszaru zaufania (ideowy)

Inicjalizacja

  • Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}\).
  • Ustal początkowy obszar zaufania \(T0\), np. \(T0= \mathfrak{K}(x^{(0)},r)\), podstaw \(T := T0\).
  • Podstaw \(k := 0\).
Kroki algorytmu

  1.  Dla punktu x wyznacz model \(f_M(\cdot ; x\)) funkcji celu w jego otoczeniu.
  2.  Rozwiązując, np. zadanie ZKK, znajdź przybliżenie xtylda punktu \(xMk=\mathrm{argmin}_{z∈T}⁡f_M  (z;x)\).
  3. Sprawdź czy obszar zaufania należy zmniejszyć do \(TS(x)\) (np. równego= \(\mathfrak{K}(x^,rs)\). Jeżeli tak, podstaw \(T := TS(x)\), idź do 2. W przeciwnym przypadku podstaw \(x :=\) xtylda, idź do 4.
  4. Jeżeli spełnione jest kryterium (test) stopu, to \(x\) przyjmij za rozwiązanie, podstaw ilosc_iteracji := \(k\) i stop. W przeciwnym przypadku idź do 5.
  5.  Sprawdź czy należy powiększyć obszar zaufania do \(TL(x)\) (np. równego \(\mathfrak{K}(x^,rl)\)). Jeżeli tak, podstaw \(T := TL(x)\), idź do 6. W przeciwnym przypadku idź do 6.
  6.  Podstaw \(k := k + 1\), idź do 1.

Wyjaśnień wymaga krok 2., 3., 5. i oczywiście kryterium stopu.

Krok drugi to poszukiwanie przybliżonego rozwiązania zadania minimalizacji funkcji modelującej na obszarze zaufania, np. zadania ZKK, ponieważ wiemy, że zadanie to będzie rozwiązywane stosownie wybranym algorytmem i trzeba się liczyć z możliwością otrzymania niedokładnego rozwiązania.

Krok trzeci i piaty wymagają sprecyzowania, co jest właściwe, a co nie, przy czym ustalenie, kiedy zmniejszać obszar zaufania jest łatwiejsze (wspomnieliśmy o tym wyżej) niż ustalenie kiedy można/należy go powiększać. Wobec tego ich doprecyzowanie wymaga popartej teorią i intuicją głębszej analizy zagadnienia. Nie będziemy tego tematu dalej rozwijać. 

Test stopu jest silnie związany z działaniami kroków 3. i 5., zatem nie można go poprawnie określić dla takiego ogólnego schematu. Jedną rzecz możemy jednak teraz powiedzieć – powinien zawierać warunek określający maksymalną liczbą iteracji.

Kończąc ten krótki opis metody obszaru zaufania zauważmy, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z nowymi – funkcją wyboru i ograniczeniami, ale o niezmiennej, stosunkowo prostej i typowej formie.