Podręcznik

Omawialiśmy podejścia oparte na intuicyjnie oczywistym pomyśle sprawdzania wartości funkcji wyboru w sąsiedztwie punktu bieżącego. Algorytm obszaru zaufania jest odważny, bo zakłada, że kolejne sąsiedztwa będzie mógł wybierać jako „dostatecznie duże” (krok 5.), tak aby różnica \(f(x^{(k-1)})-f(x^{M(k)})\) była większa od zera (warunek (3.4)) i szybko malała (potocznie – „aby szybko zmierzać do celu”). Teraz przedstawimy idee postępowania opartego na silniejszym założeniu, że Algorytm obok umiejętności wykorzystania gradientu i macierzy Hessego do zbudowania lokalnego modelu zachowania funkcji wyboru, jest dodatkowo na tyle zmyślny, że potrafi wykorzystać tę wiedzę do wykonania kroku dającego znaczną poprawę (w naszym przypadku znaczne zmalenie) funkcji wyboru. Podejście to jest oparte na wynikach rozważań teoretycznych pozwalających na wykorzystanie związku kierunku poprawy z gradientem (Lemat 3.3 z punktu 3.1.1). Jak pamiętamy, aby kierunek d był kierunkiem poprawy dla zadania minimalizacji, dla funkcji różniczkowalnej musi zachodzić nierówność

Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający najmniejszą do osiągnięcia w tym kierunku wartość funkcji celu (oczywiście mniejszą niż w punkcie bieżącym), patrz Rys. 3.1. 

Co formalnie znaczy poruszać się wzdłuż kierunku? Dla danego bieżących: punktu x(k) i kierunku d(k) oznacza to pozostawanie w zbiorze

\(P(x^{(k)};d^{(k)})=\left. x \in\mathbb{R}^n |(∃α∈\mathbb{R})x=x^{(k)}+αd^{(k)} \right \}\).

Zgodnie z tym określeniem, znalezienie punktu \(x^{(k+1)}∈P(x^{(k)};d^{(k))}⊂\mathbb{R}^n\) jest równoważne ustaleniu pewnego \(α^{(k)}∈\mathbb{R}\), zatem zmieniając \(\alpha\) od zera do plus nieskończoności ruszamy się wzdłuż prostej \(P(x^{(k)}; d^{(k)})\) w kierunku malenia funkcji celu jeżeli wektor \(d^{(k)}\) spełnia warunek (3.5). Konkretną wartość \(α ̅=α^{(k)}\) – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze \(P(x^{(k)}; d^{(k)})\) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy \(\alpha^{(0)}\), gdy \(f(x^{(k)}+α^{(0)} d^{(k)})<f(x^{(k)})\) to \(\alpha^{(0)}\) uznajemy za długość kroku, gdy przeciwnie – zmniejszamy \(\alpha ^{(0)}\) do \(\alpha ^{(1)}\), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę. Idąc dalej można oprzeć wybór długości kroku na przybliżonej, a gdy się da dokładnej, minimalizacji funkcji celu f na zbiorze \(P(x^{(k)};d^{(k)})\), to znaczy rozwiązując

Formułując to zadanie minimalizacji w kierunku nie wykluczamy sytuacji, w której zadowalamy się jego rozwiązaniem przybliżonym. Ponieważ zbiór dopuszczalny \(P(x^{(k)}; d^{(k)})\) jest określony jednym ograniczeniem równościowym to zadanie ZPK. jest zadaniem minimalizacji funkcji jednej zmiennej \(\alpha (x^{(k)}\) i \(d^{(k)}\) są ustalone!).

Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie jednak istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu istotnie lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. 

Taki sposób rozumowania doprowadził do wniosku, że algorytm znajdowania rozwiązania optymalizacji może być zorganizowany w następujący sposób.

• Najpierw w oparciu na informacji o lokalnym zachowaniu funkcji w danym punkcie np. zawartej w jej pochodnych wyznacza się kierunek poprawy. 
• Na tym kierunku (na, bo kierunek (prostą) traktujemy tu jako zbiór), poszukując poprawy wybiera się, jak na schodach, punkt (stopień) dający akceptowalną poprawę wartości funkcji celu. Może to być wektor dający najniższą wartości funkcji celu – punkt minimalizujący w kierunku. W tym punkcie wyznacza się nowy kierunek poprawy i proces poszukiwania nowego, lepszego punktu powtarza się.

W tym miejscu naszych rozważań warto, podobnie jak w przypadku poprzedniej metody, podkreślić, że podejście wykorzystujące kierunki poprawy zamienia zadanie znalezienia minimum funkcji wielu zmiennych na ciąg naprzemiennego wyznaczania kierunku poprawy i poszukiwaniu punktu dającego poprawę to jest zadania operującego na funkcji jednej zmiennej.

Bardziej formalnie można przedstawioną powyżej procedurę minimalizacji opartą na generowaniu kierunków poprawy opisać następująco.

 Podstawowy algorytm kierunków poprawy (ideowy)

Inicjalizacja

• Wybierz punkt początkowy \(x^{(0)}\), podstaw \(x := x^{(0)}\)
• Podstaw \(k := 0\).

Kroki algorytmu

1.  Dla punktu x wyznacz kierunek poprawy d.
2.  Ustal długość kroku w kierunku poprawy \\alpha\).
3.  Wylicz następny punkt podstawiając \(xnew∶=x+αd.\)
4. Jeżeli spełnione jest kryterium (test) stopu, to xnew przyjmij za rozwiązanie, podstaw \(\mathrm{ilosc\,iteracji} := k\) i stop. W przeciwnym przypadku idź do 5.
5.  Podstaw \(k := k + 1\), podstaw \(x := xnew\), idź do 1.

Powyższy schemat ogólny nie precyzuje jak ustala się kierunek poprawy (krok 1.) i długość kroku (krok 2.), tu najczęściej będzie to zadanie ZPK, oraz nie określa testu stopu. Podobnie jak dla podstawowego algorytmu obszaru zaufania sprecyzowanie działań tych kroków jest związane ze sobą i określa konkretną postać algorytmu. Więcej szczegółów przedstawimy w punkcie 4.2 Modułu czwartego.

Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający „optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. W badaniu wspomnianej wyżej „optymalności” pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o wybraną miarę „małości” gradientu. 

Wspólną cechą przedstawionych metod jest ich iteracyjność – polegają one na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę funkcji celu.

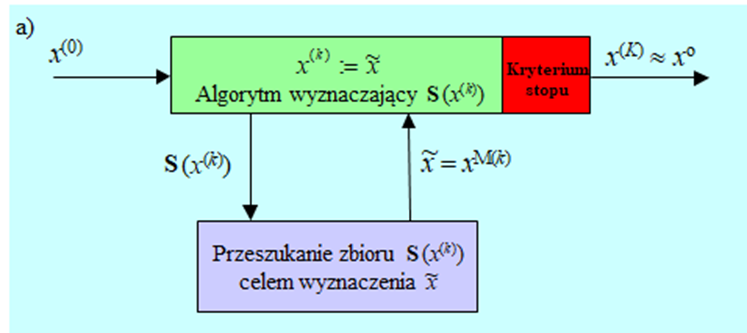
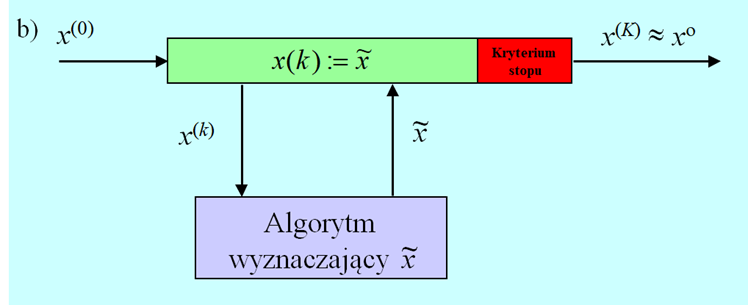
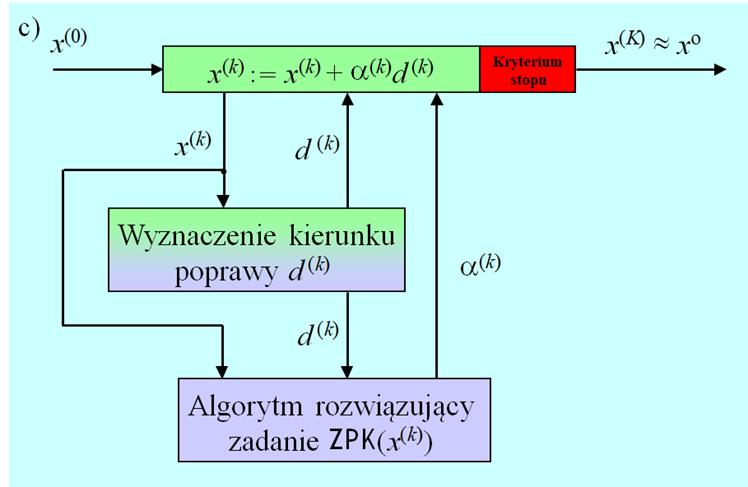
• W metodzie rozsiewania punktów próbnych zbiór do przeszukania może być generowany na różne, w tym losowe, sposoby, a przeszukanie to znalezienie w zbiorze skończonym punktu dającego najmniejszą wartość funkcji celu. 
• W obu kolejnych metodach zbiór podlegającego przeszukaniu jest generowany sposób specyficzny dla metody a znalezienie „następnego” punktu bieżącego polega na:
• Dla metody obszaru zaufania – znalezieniu rozwiązania zadania wielowymiarowej minimalizacji przy ograniczeniach, funkcji modelującej, najczęściej kwadratowej.
• Dla metody kierunków poprawy – poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej.

Na schematach algorytmów przedstawionych na Rys. 2.25 wyraźnie jest zaznaczona pętla główna – zewnętrzna i algorytmy wewnętrzne, które najczęściej też są iteracyjne. Zwróćmy uwagę, że na jedną iterację zewnętrzną może wypadać wiele iteracji wewnętrznych. Tak więc miarą pracochłonności (kosztu, jak się zwykło mówić) algorytmu może być tylko iloczyn liczb tych dwu rodzajów iteracji.

W wyniku działania algorytmów dostajemy ciąg punktów \({x^{(k)} }_{k=0}^∞\), który powinien być zbieżny do rozwiązania. Dla konkretnej realizacji algorytmu tę zbieżność trzeba pokazać, co często jest trudnym zadaniem matematycznym, bo narzędzia, które wypracowała matematyka są słabo przystosowane do badania takich zagadnień.