Podręcznik

Algorytm generuje ciąg punktów, zatem z matematycznego punktu widzenia zbieżność algorytmu to zbieżność ciągu. Z praktycznego punktu widzenia nie jest to dobre utożsamianie, bo zbieżność matematyczna to istnienie skończonej granicy przy dążeniu liczby iteracji k do nieskończoności. Dla wielkich zadań programowania liniowego (paręset tysięcy zmiennych i ograniczeń) na rozwiązania dawane przez metodę Simpleks trzeba „długą chwilę” poczekać.  Wiemy jednak, że algorytm Simplex ma tzw. zbieżność skończoną – stanie gdy znalazł rozwiązanie albo stwierdzi, ze rozwiązanie nie istnieje, możemy więc spokojnie czekać.

Zatem, od końca lat pięćdziesiątych XX w. teorii optymalizacji posługujemy się pojęciem skończonej zbieżności

Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Jednak z biegiem czasu, gdy wzrosło doświadczenie ludzi zajmujących się algorytmami optymalizacji zaczęto zauważać wadę tego pojęcia. I tak jak jego tryumf związany był z metodą Simplex tak samo jego wada została zauważona wtedy, gdy pojawiły się algorytmy skutecznie z nim konkurujące – metody punktu wewnętrznego. Metody te nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej (szybciej wpław niż dookoła po brzegu, patrz Rys. 2.5) a zamawiający wyniki nie lubią za długo czekać. Poza tym zaczęły powstawać systemy wspomagania decyzji (np. w sytuacjach nadzwyczajnych takich jak powódź czy systemy wojskowe), które powinny pracować w czasie rzeczywistym i czekanie godzinę na wynik obliczeń czynie je bezużytecznym. Zmieniło to sposób myślenia o rezultatach algorytmów optymalizacji. Już nie poszukiwanie wariantu najlepszego stało się ich celem ale wariantu ocenianego jako satysfakcjonujący, co w najprostszym przypadku oznacza dostatecznie lepszego, w określonym sensie, od wariantu początkowego.  Dla nas prowadzi to do wniosku ogólnego – z praktycznego punktu widzenia użytkownika/projektanta algorytmu optymalizacji, w sytuacji w której algorytm generuje ciąg o zbieżności nieskończonej szybko zmierzający do niewielkiego otoczenia wariantu (rozwiązania) optymalnego, algorytm o zbieżności skończonej z bardzo dużym K można uznać za gorszy. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod znajdowania rozwiązania zadania programowania liniowego wykorzystujących punkty wewnętrzne.

Tu istotna uwaga. Jak pamiętamy punkt stacjonarny x ̂ może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być rożne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje poniższy rysunek funkcji 

\((x_1,x_2)↦f(x_1,x_2)=x_1^3+x_2^3\).

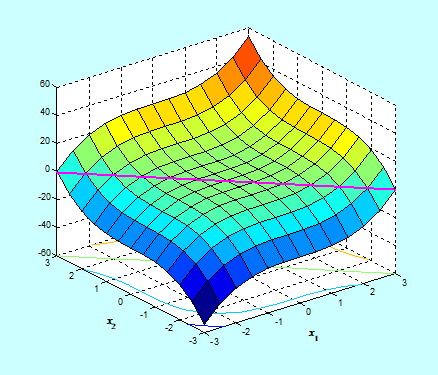
W przypadku tej funkcji punkt stacjonarny to x ̂=(0,0), a ten punkt nie jest, nawet lokalnym, ekstremum. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony na Rys. 2.26, są bardzo rzadkie.

Czasami twórcom algorytmów udaje się udowodnić własność jeszcze słabszą.

W teorii optymalizacji wprowadza się jeszcze dwa rodzaje zbieżności.

Wspomnieliśmy wyżej, że zbieżność może być szybsza lub wolniejsza. Wprowadzono następujące klasy szybkości zbieżności (orders of covergence).

Ciąg \(\left \{ x^{(k)} \right.\left.  \right \}_{k=0}^{\infty }\) otrzymany w kolejnych krokach algorytmu zbieżny do \(x^o\) jest:

• zbieżny liniowo, gdy

\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }v\in ]0,1[\)

(w „głębokim przybliżeniu” ‖x^((k+1))-x^o ‖=ν‖x^((k))-x^o ‖),

• superliniowo tj. szybciej niż liniowo, gdy 

\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }0\),

• kwadratowo, gdy 

\(N(k)=\dfrac{\left \| x^{(k+1)}-x^0 \right \|}{\left \| x^{(k)}-x^0 \right \|}_{\overrightarrow{k\rightarrow \infty} }v\geq 0\),

Nazwy klas zbieżności związane są z szybkością zbiegania do zera typowych ciągów:

• dla zbieżności liniowej – postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. o wzorze

\(h^{(k)}=2^{-k},\,k∈\overline {1,∞}; \,Ν(k)=  \dfrac{2^{-(k+1)}}{2^{-k}} =\dfrac{1}{2}⟶\dfrac{1}{2}>0,\)

• dla zbieżności superliniowej – np. ciągu o wzorze \(h^{(k)}=k^{-k},k∈\overline {1,∞};\, Ν(k)=\dfrac{k^{-(k+1)}}{k^k} =\dfrac{1}{k}→0,\)
• dla zbieżności kwadratowej – np. ciągu o wzorze \(h^{(k)}=2^{-2^k },\,k∈\overline {1,∞};\), \(Ν(k)=(\dfrac{2^{-2^{k+1} }} {((2^{-2^k } )^2 )}=\dfrac{2^{-2}}{2^{-2^k }} →0).\)

Szybkość zbieżności ilustruje poniższy rysunek, na którym przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów.

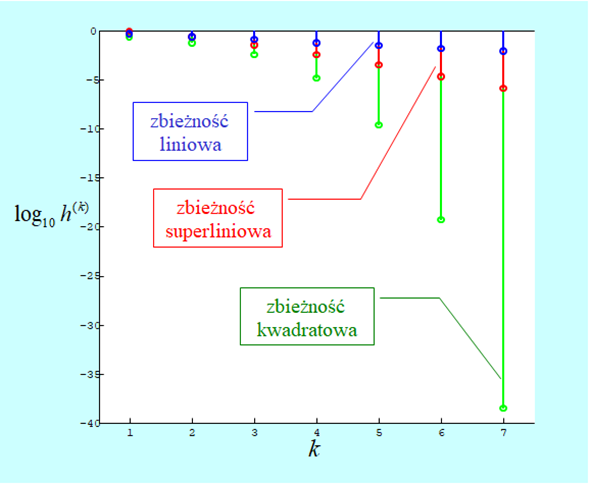
Widać, że zbieżność liniowa jest najwolniejsza, a kwadratowa najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych: szybkość liniowa jest do zaakceptowania, gdy granica  jest dostatecznie mała (praktycznie nie większa niż ¼), zbieżność superliniowa jest w zupełności zadawalająca a kwadratowa jest w zasadzie pojęciem teoretycznym.